i) Να βρεθεί η απόσταση x, ώστε η ράβδος ΑΒ να είναι συνεχώς οριζόντια.
|
|
|
- ÊἙρμῆς Πανταζής
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Στην διάταξη του σχήµατος (1) η ράβδος ΑΒ έχει αµε λητέο βάρος, µήκος L και στο άκρο της Β έχει στερεωθεί σφαίρα µάζας m. Το σηµείο στήριξης Ο της ράβδου απέχει από το άκρο της Β απόσταση x. H ελεύθερη τροχαλία έχει µάζα M και ακτίνα R το δε νήµα που περιβάλλει το αυλάκι της είναι αβαρές και δεν µπορεί να ολισθαίνει πάνω σ αυτό. Αρχικά το σύστηµα κρατείται ακίνητο µε την ράβδο σε οριζόντια θέση και το νήµα ΒΜ τεντωµένο, κάποια δε στιγµή αφήνεται ελεύθερο. i) Να βρεθεί η απόσταση x, ώστε η ράβδος ΑΒ να είναι συνεχώς οριζόντια. ii) Πόση είναι η µετατόπιση του κέντρου της τροχαλίας ύστερα από χρόνο t * αφότου αυτή αφέθηκε ελεύθερη; Δίνεται η ροπή αδράνειας Ι C =mr / της τροχαλίας ως προς άξονα που διέρχεται από το κέντρο της C και είναι κάθε τος στο επίπεδό της και η επιτάχυνση g της βαρύτητας. ΛΥΣΗ: i) Το σύστηµα ράβδος-σφαίρα ισορροπεί υπό την επίδραση του βάρους m g σφαίρας, της δύναµης επαφής Q που δέχεται η ράβδος από το σηµείο στήριξης Ο καθώς και της τάσεως F του νήµατος που είναι δεµένο στο άκρο της Α. Λόγω της ισορροπίας του συστήµατος ισχύει η σχέση: "(O) = 0 Fx + Q 0 - (L - x)=0 F = mg(l - x)/x (1) Σχήµα 1 Eξάλλου η τροχαλία δέχεται το βάρος της M g, και την τάση T από το νήµα ΜΒ, η
2 οποία είναι αντίθετη της δύναµης F. Είναι λογικό να δεχθούµε ότι η τροχαλία εκτελεί υπό την επίδραση των δύο αυτών δυνάµεων επίπεδη κίνηση που θεωρείται ως επαλ ληλία µιας κατακόρυφης µεταφορικής κίνησης και µιας αριστερόστροφης περιστροφι κής κίνησης περί οριζόντιο άξονα που διέρχεται από το κέντρο της C και είναι κάθετος στο επίπεδό της. Εφαρµόζοντας για την µεταφορική κίνηση της τροχαλίας τον δεύτερο νόµο κίνησης του Νεύτωνα παίρνουµε την σχέση: Mg - T = Ma C () όπου a C η επιτάχυνση του κέντρου της τροχαλίας. Eφαρµόζοντας στην συνέχεια για την περιστροφική κίνηση της τροχαλίας τον θεµελιώδη νόµο της στροφικής κίνησης παίρ νουµε την σχέση: TR = I C ' TR = MR '/ T = MR'/ (3) όπου ' η γωνιακή επιτάχυνση της τροχαλίας. Αν αναφερθούµε το σηµείο επαφής Ν του νήµατος µε την τροχαλία, αυτό θεωρούµενο ως σηµείο του νήµατος έχει κάθε στιγµή µηδενική ταχύτητα, διότι το νήµα ΝΒ είναι ακίνητο, θεωρούµενο όµως και ως σηµείο της τροχαλίας έχει ταχύτητα µέτρου v C -ωr, όπου v C η ταχύτητα του κέντρου C της τροχαλίας και η γωνιακή της ταχύτητα. Έτσι κάθε στιγµή ισχύει η σχέση: v C - r = 0 v C = r (4) Έστω ότι µεταξύ των χρονικών στιγµών t και t+dt το µέτρο της ταχύτητας v C µεταβάλλεται κατά dv C και το µέτρο της κατά dω, τοτε από την (4) προκύπτει: dv C = Rd dv C /dt = Rd / dt a C= R' οπότε η (3) γράφεται: T = Ma C / (5) Συνδυάζοντας την (5) µε την () παίρνουµε: Mg - Ma C / = Ma C g = 3a C / a C = g / 3 (6) οπότε η (5) παίρνει την µορφή: T = Mg 3 F = Mg 3 (1) mg Mg (L - x) = x 3 3m(L - x) = xm 3mL= x( M + 3m) x = 3mL M + 3m ii) Από την σχέση (6) προκύπτει ότι η επιτάχυνση του κέντρου C της τροχαλίας είναι σταθερή δηλαδή η κίνησή του είναι οµαλά επιταχυνόµενη και εποµένως η κατακόρυφη προς τα κάτω µετατόπισή του y * σε χρόνο t * δίνεται από την σχέση:
3 (6) y * = a C t * / y * = gt * / 6 P.M. fysikos Δύο ακριβώς όµοιες λεπτές και οµογενείς ράβδοι βάρους αρθρώνονται διά του ενός άκρου τους στο σηµείο Ο, ενώ τα ελευθερα άκρα τους Α και Β εφάπτονται σε τραχύ οριζόντιο δάπεδο το δε επίπεδό τους είναι κατακόρυφο. i) Εάν ασκείται στην άρθρωση Ο οριζόντια δύναµη F, της οποίας ο φορέας είναι παράλληλος προς την ευθεία ΑΒ, να βρεθεί η συνθήκη που εξασφαλίζει την ισορροπία του συστήµατος, όταν η γωνία των δύο ράβδων είναι φ<π. ii) Να εξετάσετε το ίδιο πρόβληµα στην περίπτωση που η δύναµη F είναι κατακόρυφη µε φορά προς τα κάτω. Δίνεται ο συντελεστής οριακής τριβής n µεταξύ των ράβδων και του οριζόντιου δαπέδου. ΛΥΣΗ: i) H δύναµη F είναι οριζόντια και το σύστηµα ισορροπεί. Στο σύστηµα ενεργούν τα βάρη των δύο ράβδων, η οριζόντια δύναµη F και οι δυνά µεις επαφής στις άκρες τους Α και Β από το δάπεδο, που αναλύονται στις στατικές τρι βές T 1, T και στις κάθετες αντιδράσεις N 1, N (σχ. ). Εξετάζοντας την ισορροπία µό νο της ράβδου ΟΑ θα έχουµε την σχέση: "(O) = 0 -T 1 L"#$ + N 1 L%µ$ - L%µ$ / = 0 -T 1 "#$ + N 1 %µ$ - %µ$ = 0 N 1 = T 1 "# + / (1) Σχήµα Με τον ίδιο τρόπο από την ισορροπία της ράβδου ΟΒ καταλήγουµε στην σχέση: N = T "# + / ()
4 Εξάλλου από την ισορροπία του συστήµατος θα έχουµε: και F(y) = 0 N 1 + N - = 0 N 1 + N = (3) F(x) = 0 T 1 + F - T = 0 T - T 1 = F (4) Η (3) λόγω των (1) και () δίνει: T 1 "# + T "# + = (T 1 + T )"# = T 1 + T = "# (5) Προσθέτοντας κατά µέλη τις (4) και (5) παίρνουµε την σχέση: T = F + "# T = F/ + "# / (6) Συνδυάζοντας την (4) µε την (6) παίρνουµε: F/ + "# / - T 1 = F T 1 = "# / - F/ (7) Η (1) λόγω της (7) δίνει: N 1 = ( "# / - F/)$"# + / N 1 = / - F"#/ + / = - F"#/ (8) Η () λόγω της (6) δίνει: N = ( "# / + F/)$"# + / N = / + F"#/ + / = + F"#/ (9) Όµως η ισορροπία του συστήµατος επιβάλλει την σχέση Ν 1 0, η οποία λόγω της (8) δί νει: - F"#/ $ 0 F"#$/ F/ "#$ (10) Εξάλλου επειδή οι τριβές είναι στατικές θα έχουµε τις σχέσεις: T 1 nn 1 " # T nn $ (+ ) T 1 + T n( N 1 + N ) η οποία λόγω των (6), (7), (8) και (9) γράφεται: "# / - F/ + F/ + "# / $ n( - F%"#/ + + F%"#/) "# $ n n "#$ / (10) Oι σχέσεις (10) και (11) αποτελούν τις αναγκαίες συνθήκες για την ισορροπία του συστήµατος.
5 ii) H δύναµη F είναι κατακόρυφη µε φορά προς τα κάτω και το σύστηµα ισορροπεί. Εξετάζοντας πάλι µόνο την ισορροπία της ράβδου ΟΑ θα έχουµε την σχέση: "(O) = 0 - T 1 L"#$ + N 1 L%µ$ - L%µ$ / = 0 -T 1 "#$ + N 1 %µ$ - %µ$ = 0 N 1 = T 1 "# + / (11) Με τον ίδιο τρόπο από την ισορροπία της ράβδου ΟΒ καταλήγουµε στην σχέση: N = T "# + / (1) Σχήµα 3 Εξάλλου από την ισορροπία του σύστήµατος θα έχουµε: και F(y) = 0 N 1 + N - - F N 1 + N = + F (13) F(x) = 0 T 1 - T = 0 T 1 = T (14) Συνδυάζοντας την σχέσεις (11), (1) µε την (14) παίρνουµε Ν 1 =Ν και η (13) δίνει: N 1 = N = + F/ (15) Η (11) λόγω της (15) δίνει: + F/ = T 1 "# + / / + F/ = T 1 "# T 1 = ( + F)"# / (16) Εξάλλου επειδή οι τριβές ειναι στατικές θα έχουµε τις σχέσεις: T 1 nn 1 " # T nn $ (+ ) T 1 + T n( N 1 + N ) T 1 nn 1 η οποία λόγω των (15) και (18) γράφεται:
6 ( + F)"# / $ n( + F/) "# + F"# $ n + nf (n - "#)F $ ("# - n) (17) Aπό την (17) προκύπτει, ότι για n>εφφ θα πρέπει: F "#$ - n n - "#$ ενώ για n<εφφ θα πρέπει: F n - "#$ "#$ - n P.M. fysikos Λεπτή οµογενής ράβδος ΑΒ µήκους L και µάζας m εφάπτεται µε το άκρο της Α σε λείο κατακόρυφο τοίxo και µε το άκρο της Β σε τραχύ οριζόντιο έδαφος, µε το οποίο παρουσιάζει συντελεστή οριακής τριβής n και κλίση φ ως προς αυτό. Επί της ράβδου εφαρµόζεται οριζόντια δύναµη F, της οποίας ο φορέας διέρχεται από το κέντρο µάζας της C, η φορά της είναι όπως στο σχήµα (4) το δε µέτρο της µπορεί να αυξάνεται από πολύ µικρές τιµές. Να δείξετε τα έξης: i) όταν σφφ>n, τότε µε την αύξηση του µέτρου της F θα προηγηθεί ολίσθηση του άκρου Β της ράβδου στο έδαφος και να βρεθεί η τιµή του µέτρου που αντιστοιχεί στην έναρξη της ολίσθησης και ii) όταν σφφ<n, τότε µε την αύξηση του µέτρου της F θα προηγηθεί η ανατ ροπή της ράβδου περί το άκρο της Β και να βρεθεί η αντίστοιχη τιµή του µέτρου της F. iii) Όταν n=1, F=mg και φ=π/3, να δείξετε ότι η ράβδος ανατρέπεται και να βρείτε την γωνιακή της επιτάχυνση κατά την έναρξή της ανατροπής της. Δίνεται η επιτάχυνση g της βαρύτητας και η ροπή αδράνειας Ι Β =ml /3 της ράβδου ως προς άξονα που διέρχεται από το άκρο της Β και είναι κάθετος στην ράβδο. ΛΥΣΗ: Aς δεχθούµε ότι το µέτρο της δύναµης F έχει τιµή που εξασφαλίζει την ισορροπία της ράβδου ΑΒ. Επί της ράβδου εκτός από την δύναµη F ενεργεί το βάρος της = m g, η δυναµη επαφής Q από τον τοίχο της οποίας ο φορέας είναι οριζόντιος, διότι ο τοίχος είναι λείος και τέλος η δύναµη επαφής από το τραχύ οριζόντιο έδαφος, η οποία αναλύεται στην στατική τριβή T και στην κάθετη αντίδραση N (σχ. ). Λόγω της ισορροπίας της ράβδου ισχύουν οι σχέσεις: F(x) = 0 Q + F - T = 0 T = Q + F (1)
7 και F(y) = 0 N - = 0 N = mg () "(B) = 0 F(B ) + Q(B") - (C ) = 0 F L µ" + QLµ" - mg L #$%" = 0 Qµ" = mg#$%" - Fµ" Q = mg"#$ - F%µ$ %µ$ = mg&$ - F (3) Σχήµα 4 Για να µη χάνει την επαφή της η ράβδος µε τον τοίχο, οπότε δεν θα συµβαίνει ανατ ροπή αυτής περί το άκρο της Β, πρέπει Q 0 και λόγω της (3) πρέπει: mg"# - F $ 0 F mg"#$ (4) Για να µη ολισθαίνει το άκρο Β της ράβδου πάνω στο οριζόντιο έδαφος πρέπει Τ nn, η οποία λόγω των (1) και () δίνει: (3) Q + F nmg mg"# - F + F $ nmg F nmg - mg"#$ F nmg - mg"#$ F mg ( n - "#$ ) (5) Οι σχέσεις (4) και (5) αποτελούν τις αναγκαίες συνθήκες για να ισορροπεί η ράβδος ΑΒ µε βάση δε τις σχέσεις αυτές διακρίνουµε τις εξής δύο περιπτώσεις: i) Ισχύει mgσφφ>mg(n-σφφ) ή σφφ>n.
8 Τότε µε την αύξηση του µέτρου της F θα προηγηθεί η ολίσθηση της ράβδου επί του εδάφους, η δε αντίστοιχη οριακή τιµή του µέτρου της θα είναι F 1 =mg(n-σφφ). ii) Ισχύει mgσφφ<mg(n-σφφ) ή σφφ<n. Τότε µε την αύξηση του µέτρου της F θα προηγηθεί η ανατροπή της ράβδου περί το άκρο της Β η δε αντίστοιχη οριακή τιµή του µέτρου της θα είναι F =mgσφφ. Στην περίπτωση που έχουµε φ=π/3, n=1 και F=mg, τότε θα είναι σφφ= 3 /3<1, δηλαδή σφφ<n, που σηµαίνει σύµφωνα µε τα προηγούµενα ότι µε την αύξηση του µέτρου της F η ράβδος θα ανατραπεί περί το άκρο της Β εφ όσον βέβαια το µέτρο της υπερβαίνει την οριακή τιµή mgσφφ, πράγµα που συµβαίνει διότι mg>mgσφ(π/3). Για να υπολογίσουµε την γωνιακή επιτάχυνση ' της ράβδου κατά την έναρξή της ανατροπής της εφαρµόζουµε τον θεµελιώδη νόµο της στροφικής κίνησης, οπότε θα έχουµε την σχέση: "(B) = I B #' F L µ" mg L #$%" = ml &' 3 mg µ" - mg #$%" = ml&' 3 g (µ" - #$%" ) = L&' 3 '= 3g ("µ# - $%&# ) L P.M. fysikos Στην διάταξη του σχήµατος (5) η οµογενής λεπτή ράβδος έχει µήκος L και βάρος P. Το ένα άκρο της ράβδου έχει αρθρωθεί σε σώµα µικρών διαστάσεων, το οποίο εφάπτεται σε τραχύ οριζόντιο έδαφος, µε το οποίο παρουσιάζει συντελεστή οριακής τριβής n. Η ράβδος εφάπτεται σε στα θερό λείο κύλιστρο Ο το οποίο απέχει από το σώµα απόσταση L/3, όταν η κλίση της ράβδου ως προς το έδαφος είναι φ=π/6. Να βρεθεί για ποιές τιµές του βάρους του σώµατος αποφεύγεται η ολίσθησή του επί του εδάφους. ΛΥΣΗ: Aς δεχθούµε ότι το σύστηµα ισορροπεί. Οι δυνάµεις που δέχεται είναι το βάρος P της ράβδου το βάρος του σώµατος, η δύναµη Q που εξασκει το κύλιστρο Ο επί της ράβδου, της οποίας ο φορέας είναι κάθετος στην ράβδο και τέλος η δύναµη επαφής που δέχεται το σώµα από το οριζόντιο έδαφος που αναλύεται στην τριβή T και στην κάθετη αντίδραση. N. Λόγω της ισορροπίας του συστήµατος θα ισχύουν οι σχέσεις: F(x) = 0 T - Q x = 0 T = Qµ" (1) F(y) = 0 N + Q y - P - = 0 N = -Q"#$ + P + () "(A) = 0 PL LQ "#$ - 3 = 0 Q = 3P 4 "#$ (3)
9 Aπό (1) και (3) παίρνουµε: T = 3P"#$%µ$ / 4 (4) Επίσης από () και (3) έχουµε: N = -3P"# $ / 4 + P + (5) Eπειδή η τριβή είναι στατική θα ισχύει και η σχέση: Σχήµα 5 (4),(5) T nn 3P 4 "#$%µ$ & n ' - 3P * ) 4 "# $ + P +, ( + 3P 3Pn "#$%µ$ "# $ - np & n P ( 4n 3"#$%&µ% + 3n"#$ % - 4n) (6) To πρόβληµα έχει λύση εφ όσον ισχύει: 3"#$%µ$ + 3n"# $ - 4n > 0 3"#$%µ$ > -3n"# $ + 4n 3"#$%µ$ > n(4-3"# $) n < 3"#$%µ$ 4-3"# $ P.M. fysikos Λεπτή οµογενής ράβδος µήκους L και µάζας m µπορεί να στρέφεται περί οριζόντιο άξονα που διέρχεται από το ένα άκρο της Ο παραµένουσα σε κατακόρυφο επίπεδο. Αρχικά η ράβδος βρίσκεται στην κατώτερη θέση της όπου και ισορροπεί και κάποια στιγµή ενεργεί στο ελεύθερο άκρο της Α δύναµη σταθερού µέτρου, της οποίας ο φορέας παρα µένει συνεχώς κάθετος στην ράβδο. Όταν η ράβδος έχει στραφεί κατά γωνία φ=π/6 η δύναµη αποσύρεται µε αποτέλεσµα η ράβδος µόλις να φθάνει στην ορίζόντια θέση και στην συνέχεια επανακάµπτει προς την αρχική της θέση.
10 i) Να βρεθεί η γωνιακή επιτάχυνση και η γωνιακή ταχύτητα της ράβδου λίγο πρίν αποσυρθεί η δύναµη. ii) Nα εκφράσετε τον αντίστοιχο ρυθµό µεταβολής της βαρυτικής δυναµικής ενέργειας της ράβδου. Δίνεται η επιτάχυνση g της βαρύτητας και η ροπή αδράνειας Ι Ο =ml /3 της ράβδου ως προς άξονα που διέρχεται από το άκρο της Ο και είναι κάθετος στην ράβδο. ΛΥΣΗ: i) Εφαρµόζοντας για την ράβδο το θεώρηµα κινητικής ενέργειας-έργου κατά τον χρόνο κίνησής της από την κατακόρυφη θέση ΟΑ 1 στην οριζόντια θέση ΟΑ παίρ νουµε την σχέση: K "# - K $%& = W F + W 0-0 = W F + W W F = -W (1) Όµως για το έργο W F έργο W της δύναµης F που ενεργεί στο άκρο Β της ράβδου και για το του βάρους της, ισχύουν οι σχέσεις: W F = FL/6 " # W = -mgl/ $ Σχήµα 6 οπότε η (1) γράφεται: FL/6 = mgl/ F = 3mg/ () όπου F το σταθερό µέτρο της δύναµης F. Εξάλλου εφαρµόζοντας για την ράβδο τον θεµελιώδη νόµο της στροφικής κίνησης λίγο πριν αποσυρθεί η δύναµη F στην θέση φ=π/6, παίρνουµε την σχέση: "(O) = I O #' mg L µ" - FL = ml #' 3 () mg µ (" / 6) - 3mg " = ml#' 3 g 4-3g = L"' 3 '= 3g # L 1-3 & % ( > 0 (3) $ "'
11 όπου ' η γωνιακή επιτάχυνση της ράβδου στην θέση φ=π/6. Εάν είναι η αντίστοιχη γωνιακή ταχύτητα της ράβδου, τότε σύµφωνα µε το θεώρηµα κινητικής ενέργειαςέργου θα έχουµε την σχέση: K ( / 6) - K (0) = W F + W I O - 0 = FL" 6 - mgl 1 - #$% " () & ) ( + ' 6* ml 6 = 3mgL" 6" - mgl # % 1 - $ 3 & ( L = g ' - g " 1-3% $ # ' & L 6 = 3g 4 = 3 3 g L (4) Σχήµα 7 ii) Aς εξετάσουµε την ράβδο σε µια τυχαία θέση φ, όπου η y-συντεταγµένη του κέν τρου µάζας της C είναι y C και η ταχύτητά του v C (σχ. 7). Η βαρυτική δυναµική ενέρ γεια U της ράββου µε επίπεδο αναφοράς το οριζόντιο επίπεδο που διέρχεται από το άκρο της Ο είναι: U = -mgy C (5) Eάν µεταξύ των χρονικών στιγµών t και t+dt η y-συντεταγµένη y C µεταβληθεί κατά dy C, τότε η αντίστοιχη µεταβολή du της βαρυτικής δυναµικής ενέργειας της ράβδου θα είναι: du = -mgdy C du dt = -mg dy C dt = -mgv Cy (6) όπου v Cy η αλγεβρική τιµή της y-συνιστώσας της ταχύτητας v C του κέντρου µάζας, ενώ το διαφορικό πηλίκο du/dt εκφράζει τον ρυθµό µεταβολής της βαρυτικής δυνα µικής ενέργειας της ράβδου στην θέση φ που την εξετάζουµε. Όµως από το σχήµα (7) προκύπτει ότι: v Cy = -v C µ" = -# " Lµ" (7) όπου " η γωνιακή ταχύτητα της ράβδου στην θέση φ. Με βάση την (7) η (6) γράφεται:
12 du dt = mg " L#µ" (8) Η (8) εφαρµοζόµενη στην θέση φ=π/6 δίνει: du$ # & " dt % ' =(/6 = mgl () ' =( / 6 )*µ ( (4) $ # & " 6% du$ # & " dt % ' =(/6 = mgl 3 3 g L = mg 3 3 gl P.M. fysikos Σφαίρα µαζας m και ακτίνας R, τοποθετείται πάνω σε κεκλιµένο επίπεδο γωνίας κλίσεως φ ως προς τον ορίζοντα, η οποία εµποδίζεται να κινηθεί από σταθερό εµπόδιο, όπως φαίνεται στο σχήµα (8). i) Ποιό πρέπει να είναι το οριακό ύψος του εµποδίου, ώστε η σφαίρα να µη ανατρέπεται; ii) Επί της σφαίρας εφαρµόζεται στο ανώτατο σηµείο της οριζόντια σταθερή δύναµη F µέτρου mg/, µε αποτέλεσµα αυτή να περιστρέφεται περί την ακ µή του εµποδίου, χωρίς να ολισθαίνει. Να βρείτε την γωνιακή ταχύτητα και την γωνιακή επιτάχυνση της σφαίρας, την στιγµή που αυτή υπερπηδά το εµπόδιο. Δίνεται η ροπή αδράνειας Ι C =mr /5 της σφαίρας ως προς άξονα διερχόµενο από το κέντρο της C και η επιτάχυνση g της βαρύτητας. ΛYΣH: i) Eάν το ύψος του εµποδίου Σ που τοποθετείται κάτω από την σφαίρα, είναι το ελάχιστο δυνατό, ώστε αυτή να συγκρατείται στο κεκλιµένο επίπεδο, τότε η σφαίρα είναι έτοιµη να εγκαταλείψει το κεκλιµένο επίπεδο, οπότε στην περίπτωση αυτή µπο ρούµε να θεωρήσουµε την σφαίρα σε οριακή ισορροπία υπό την επίδραση του βάρους Σχήµα (8) της και της δύνάµης Q που δέχεται από το εµπόδιο Σ (σχ. 8). Tότε όµως πρέπει οι δύο αυτές δυνάµεις να έχουν τον ίδιο φορέα, αντίθετες φορές και ίσα µέτρα, δηλαδή ο
13 φορέας του βάρους πρέπει να διέρχεται από το σηµείο επαφής ε σφαίρας και εµποδίου. Eάν Ο είναι η προβολή του κέντρου C 0 της σφαίρας πάνω στην προέκταση της άνω επφάνειας του εµποδίου, θα έχουµε από το ορθογώνιο τρίγωνο C 0 εο την σχέση: C 0 O = (C 0 ε)συνφ R h0 = Rσυνφ h0 = R - Rσυνφ h0 = Rηµ (φ/) όπου h 0 το ζητούµενο οριακό ύψος του εµποδίου για το οποίο επίκειται η ανατροπή της σφαίρας. ii) Eάν στο ανώτατο σηµείο Α 0 της σφαίρας επιδράσει οριζόντια σταθερή δύναµη F θα προκαλέσει περιστροφή αυτής περί την ακµή επαφής του εµποδίου µε την σφαίρα και Σχήµα 9 όταν η ευθεία που συνδέει το σηµείο επαφής ε σφαιρας-εµποδίου µε το κέντρο C της σφαίρας γίνει κάθετη στην άνω επιφάνεια του εµποδίου η σφαίρα θα έχει υπερπήδησει το εµπόδιο (σχ. 9). Τότε όµως η σφαίρα θα έχει περιστραφεί από την αρχική θέση κατα γωνία φ και θα έχει αποκτήσει γωνιακή ταχύτητα που θα βρεθεί εάν εφαρµόσουµε για την σφαίρα το θεώρηµα κινητικής ενέργειας-έργου, οπότε θα λάβουµε την σχέση: I " / - 0 = W F + W + W T + W N I " / = W F + W (1) όπου Ι ε η ροπή αδράνειας της σφαίρας περί την ακµή επαφής της ε µε το εµπόδιο, ενώ τα έργα W T, W της τριβής T και της κάθετης αντίδρασης N που δέχεται η σφαίρα N από το εµπόδιο είναι µηδενικά. Εξάλλου σύµφωνα µε το θεώρηµα Steiner ισχύει για την ροπή αδράνειας Ι ε η σχέση: I = I C + mr = mr /5 + mr = 7mR /5 οπότε η (1) γραφεται: 7mR /10 = W F + W () Για τα έργα W F, W της δύναµης F και του βάρους της σφαίρας ισχύουν οι σχέσεις: W F W = F(AA') = mg(rµ")/ ' ( = (C 0 C') = mg(r - R#$%&) ) W = mgrµ" ' F ( W = mgr(1 - #$%&)) (3)
14 H () λόγω των (3) γράφεται: 7mR /10 = mgr"µ# + mgr(1 - $%&') 7R /10 = g"µ# + g( 1 - $%&' ) = 10g( 1 + "µ# - $%&' ) / 7R = 10g( 1 + "µ# - $%&' ) / 7R (4) Tέλος εφαρµόζοντας για την σφαίρα τον θεµελιώδη νόµο της στροφικής κίνησης την στιγµή που αυτή υπερπηδά το εµπόδιο παίρνουµε την σχέση: "(#) = I # $' F(A') + (CC') = 7mR "'/5 mg(r"#$)/ + mg(%µ$) = 7mR &'/5 g"#$ + g%µ$ = 7R&'/5 '= 5g ("#$% + &µ% ) / 7R όπου ' η γωνιακή ταχύτητα της σφαίρας την στιγµή που υπερπηδά το εµπόδιο. P.M. fysikos Οµογενής κύβος ακµής α και µάζας m, µπορεί να στρέφεται περί οριζόντιο άξονα που ταυτίζεται µε µια ακµή του και είναι στερεω µένος σε οριζόντιο έδαφος. Ο κύβος αρχικά εδράζεται επί του εδά φους και κάποια στιγµή ενερ γεί σ αυτόν οριζόντια δύναµη F, της οποίας ο φορέας είναι συνεχώς κάθε τος σε µια ακµή της άνω βάσεώς του και διέρχεται από το µέσον της. i) Εάν το µέτρο της F είναι 3mg/4, θα ανατραπεί ο κύβος και αν αυτό συµβεί ποια θα είναι η γωνιακή του επιτάχυνση και η γωνιακή του ταχύτητα την στιγµή που ολοκληρώνεται η ανατροπή του; ii) Να δείξετε ότι σε κάποια θέση της περιστροφικής κίνησης του κύβου που τον οδηγεί σε ανατροπή, η γωνιακή του ταχύτητα γίνε ται µέγιστη και να βρεθεί ο ρυθµός µεταβολής της κινητικής του ενέργειας στην θέση αυτή. iii) Ποια είναι η γωνιακή επιτάχυνση του κύβου κατά την έναρξη της ανατροπής του; Δίνεται η επιτάχυνση g της βαρύτητας και η ροπή αδράνειας mα /3 του κύβου ως προς µία ακµή του. ΛΥΣΗ: i) Έστω ότι µε την εφαρµογή της οριζόντιας δύναµης F ο κύβος αρχίζει να περιστρέφεται περί την ακµή του Α και τελικά ανατρέπεται, που σηµαίνει ότι την στιγµή της ανατροπής του η διαγώνιος ΑΒ 0 γίνεται κατακό ρυφη (σχ. ). Εφαρµόζοντας για τον κύβο το θεώρηµα κινητικής ενέργειας-έργου απο την στιγµή της έναρξης της ανατροπής του µέχρις ότου αυτή ολοκληρωθεί παίρνουµε την σχέση:
15 I A * / - 0 = W F + W + W Q I A * / = W F + W (1) όπου * η γωνιακή ταχύτητα του κύβου την στιγµή της ανατροπής του, Ι A η ροπή αδράνειας του κύβου περί την ακµή του Α, ενώ το έργο W Q άξονα περιστροφής είναι µηδενικό. Για τα έργα W F, W του κύβου ισχύουν οι σχέσεις: της δύναµης Q από τον της δύναµης F και του βάρους Σχήµα 10 Σχήµα 11 W F = F(B y ) = F(B A)µ" / 4 # $ W = -(C 1 y ) = -mg(ac 1 - Ay )% ( ) W F = F / ( ) W = -mg / 1 - "#$%/4 & ( ' )( W F = F ( ) " $ # $ W = -mg/ - 1 % () Συνδυάζοντας τις σχέσεις (1) και () παίρνουµε: I A * / = F" -mg"/( - 1) (3) Όµως πρέπει ω * 0, η οποία λόγω της (3) κάνει απαιτητή την σχέση: F -mg/( - 1) " 0 F mg ( - 1) (4) Η (4) ικανοποιείται στην περίπτωση που το µέτρο της F είναι ίσο µε 3mg/4 που σηµαί νει ότι η αρχική παραδοχή ότι ο κύβος ανατρέπεται είναι σωστή. Θέτοντας στην σχέση (3) όπου Ι Α =mα /3 και F=3mg/4, παίρνουµε: m 6 " * = 3mg 4 - mg ( - 1)
16 4" * = 9g - 6g ( - 1) * = g ( 15-6 ) / 4" (5) Εξάλλου εάν ' * είναι η γωνιακή επιτάχυνση του κύβου την στιγµή της ανατροπής του, συµφωνα µε τον θεµελιώδη νόµο της στροφικής κίνησης θα έχουµε την σχέση: "(A) = I A #' * F(AB 1 ) Q0 = m" #' * / 3 3mg 4 = m "' * 3 ' * = 9 g " (6) ii) Eάν υπάρχει στην διάρκεια της ανατροπής του κύβου θέση, όπου η γωνιακή ταχύ τητα περιστροφής του γίνεται µέγιστη, πρέπει στην θέση αυτή η γωνιακή του επιτά χυνση να είναι µηδενική και συµφωνα µε τον θεµελιώδη νόµο της στροφικής κίνησης πρέπει η συνισταµένη ροπή όλων των δυνάµεων που δέχεται ο κύβος, περί την ακµή περιστροφής του Α, να είναι µηδενική, δηλαδή στην θέση αυτή θα ισχύει: "(A) = 0 F(AB"#$) - % (AC&µ$)+ Q% 0 = 0 3mg 4 ( "#$%) - mg& 'µ% = "#$ - 1 %µ$ = 0 "# = 3 όπου φ η γωνία της διαγωνίου ΑΒ του κύβου µε την κατακόρυφη διεύθυν ση, η οποία καθορίζει την θέση του κύβου στην οποία η γωνιακή του ταχύ τητα µεγιστοποιείται. Για τον υπολογισµό του ρυθµού µεταβολής της κινητικής ενέργειας του κύβου την οποιαδήποτε χρονική στιγµή t φανταζόµαστε ότι µεταξύ την χρονικών στιγµών t και t+dt η κινητική του ενέργεια µεταβάλλεται κατά dk. Σύµφωνα µε το θεώρηµα κινητι κής ενέργειας-έργου θα έχουµε την σχέση: dk = "(A)d# dk dt = "(A) d# dt dk dt = "(A)# (7) όπου dφ η γωνία στροφής του κύβου στον χρόνο dt. Στην σχέση (7) το διαφορικό πηλί κο dk/dt αναφέρεται στην χρονική στιγµή t και αποτελεί τον ρυθµό µεταβολής της κινητικής ενέργειας του κύβου την στιγµή αυτή, το ω είναι η αλγεβρική τιµή της γωνιακής ταχύτητας του κύβου την στιγµή t και τέλος το άθροισµα "(A) αποτελεί την αντίστοιχη αλγεβρική τιµή της συνισταµένης ροπής των δυνάµεων που ενεργούν στον κύβο, περί τον άξονα περιστροφής του. Όµως στην θέση της µέγιστης γωνιακής ταχύτητας το άθροισµα "(A) είναι µηδενικό, οπότε και ο αντίστοιχος ρυθµός µεταβο λής της κινητικής ενέργειας θα είναι µηδέν. iii) Εφαρµόζοντας για τον κύβο τον θεµελιώδη νόµο της στροφικής κίνησης κατά την έναρξη της ανατροπής του (t=0) παίρνουµε την σχέση: "(A)= I A # ' 0 F - / + Q" 0 = m # ' 0 / 3
17 3mg 4 - mg =m"' 0 3 ' 0 = 3g 8" όπου ' 0 η ζητούµενη γωνιακή επιτάχυνση του κύβου κατά την έναρξη της ανατροπής του. P.M. fysikos Μια οµογενής σφαίρα µαζας Μ και ακτίνας R, ηρεµεί επί οριζοντίου δαπέ δου εφαπτόµενη στην άκρη Α ενός σκαλοπατιού ύψους h, όπως φαίνεται στο σχήµα (1). Βλήµα µάζας m κινούµενο µε οριζόντια ταχύτητα v 0 σφηνώνεται ακαριαία στο κέντρο της σφαίρας. Με την προυπό θεση ότι η σφαίρα δεν αναπηδά ούτε ολισθαίνει πάνω στο εµπόδιο να βρεθεί η ελάχιστη τιµή της v 0, ώστε η σφαίρα να υπερπηδήσει το εµπόδιο. Δίνεται η ροπή αδράνειας Ι C =mr /5 της σφαίρας ως προς άξονα διερχόµενο από το κέντρο της C και η επιτάχυνση g της βαρύτητας. ΛYΣH: Κατά τον πολύ µικρό χρόνο Δt (Δt 0) που διαρκεί η ενσφήνωση του βλήµα τος στην σφαίρα η ροπή του βάρους του συστήµατος βλήµα-σφαίρα περί το άκρο επα φής Α του σκαλοπατιού ελάχιστα µεταβάλλει την στροφορµή του περί το Α, δηλαδή µπορούµε να ισχυριστούµε ότι η εν λόγω στροφορµή του συστήµατος λίγο πριν την εισ χώρηση του βλήµατος είναι ίση µε την στροφορµή του αµέσως µετά την ενφήνωση. Μπορούµε εποµένως να γράψουµε την σχέση: L "#$ %&'( = L )µ*+,- µ./0 L "#$ %&'( = L )µ*+,- µ./0 mv 0 ( R - h) + 0 = I A 0 + mv 0 R mv 0 R - h ( ) = I A 0 + m 0 R (1) Σχήµα 1 Σχήµα 13 όπου Ι Α η ροπή αδράνειας της σφαίρας ως προς άξονα διερχόµενο από το Α και κάθετο στο επίπεδο κίνησής, V 0 η ταχύτητα του κέντρου µάζας της σφαίρας και 0 η γωνιακή της ταχύτητα αµέσως µετά την ενφήνωση του βλήµατος, των οποίων τα µέτρα συνδέον ται µε την σχέση V 0 =Rω 0. Όµως σύµφωνα µε το θεώρηµα Steiner ισχύει: I A = I C + MR = MR /5 + MR = 7MR /5 οπότε η σχέση (1) γράφεται:
18 mv 0 ( R - h) = 7MR 0 /5+ m 0 R 5mv 0 ( R - h) = ( 7M + 5m)R 0 ( ) 0 = 5mv 0 R - h ( 7M + 5m)R () Eφαρµόζοντας το θεώρηµα διατήρησης της µηχανικής ενέργειας για το συσσωµάτωµα βλήµα-σφαίρα κατά τον χρόνο που περιστρέφεται περί το Α, µέχρις ότου υπερπηδήσει το εµπόδιο, παίρνουµε την σχέση: K "# + U "# = K $%& + U $%& I A 0 + mv 0 + ( M + m )g R - h ( ) = = I A + mv + ( M + m )gr 7MR m 0 R - ( M + m)gh = = 7MR 5 + m R ( 7M + 5mR ) 0 R - 10( M + m)gh = = ( 7M + 5mR ) R = 0-10( M + m)gh 7M + 5mR ( ) R (3) όπου V η ταχύτητα του κέντρου της σφαίρας και η γωνιακή της ταχύτητα την στιγµή που υπερπηδά το σκαλοπάτι. Όµως πρέπει η να δεσµεύεται µε την σχέση ω 0, η οποία λόγω της (3) δίνει: 0 " 10( M + m)gh 7M + 5mR ( ) R ( ) ( 7M + 5m) R 4 () 5m v 0 R - h 10( M + m)gh 7M + 5mR ( ) R ( ) 5m v 0 R - h ( ( M + m)gh v 7M + 5m)R 0 ( 7M + 5m) ( M + m)ghr 5m ( R - h) v 0 R ( ) m R - h ( 7M + 5m) ( M + m)gh 5 (v 0 ) min = R ( ) m R - h ( 7M + 5m) ( M + m)gh 5 P.M. fysikos H τροχαλία του σχήµατος (14) έχει µάζα m και ακτίνα R, το επίπεδό της είναι κατακόρυφο παρουσιάζει δε µε το οριζόντιο δάπεδο συντελεστή τριβής ολίσθησης n.
19 i) Nα βρεθεί γωνία φ, ώστε η τροχαλία να περιστρέφεται χωρίς να ολισθαίνει στο οριζόντιο δάπεδο, όταν η δύναµη F που εφαρµόζεται στο άκρο A του νήµατος που περιβάλλει τον λαιµό της τροχαλίας παρουσιάζει το µικρότερο δυνατό µέτρο της. Δίνεται η ροπή αδράνειας I=mR / της τροχαλίας, ως προς τον γεωµετρικό της άξονα, που αποτελεί και τον άξονα περιστροφής της. ΛΥΣΗ: i) Ας δεχθούµε ότι η τροχαλία έχει γνήσια περιστροφή περί τον γεωµετ ρικό της άξονα. Τότε η τριβή T που δέχεται από το δάπεδο είναι τριβή ολισθή σεως και πρέπει να έχει φορά προς τα αριστερά, ώστε να είναι δυνατή η αποφυ γή της µεταφορικής κίνησης της τροχαλίας. Έτσι θα έχουµε τις σχέσεις: F x = T Fµ" = nn (1) Σχήµα 14 όπου F x η οριζόντια συνιστώσα της δύναµης F και N η κάθετη αντίδραση του δαπέ δου. Όµως η τροχαλία κατα τον κατακόρυφη διεύθυνση δεν κινείται, οπότε θα ισχύει: N + F y - = 0 N = mg - F"#$ () όπου F y η κατακόρυφη συνιστώσα της F και το βάρος της τροχαλίας. Συνδυάζον τας τις σχέσεις (1) και () παίρνουµε: Fµ" = n( mg - F#$%" ) F (µ" + n#$%" ) = nmg nmg F= µ" + n#$%" (3) Θέτοντας n=εφθ η (3) γράφεται: nmg F= µ" + #$%&'(" = nmg µ" + µ%&'(" /&'(%
20 nmg"#$ F= %µ&"#$ + %µ$"#& = nmg"#$ %µ(& + $) Aπό την (4) προκύπτει ότι το µέτρο της F γίνεται ελάχιστο όταν ηµ(φ+θ) =1, δηλαδή όταν φ+θ=π/, οπότε θα έχουµε εφφ=σφθ=1/εφθ=1/n και η (1) δίνει: (4) F min = nmg"#$ = nmg 1 + %& $ = nmg (5) 1 + n H () για F=F min δίνει: N = mg - F min "#$ = mg - F min 1 + %& $ (5) N = mg - ( ) nmg n 1 + n = mg 1 - n $ # " 1 + n & = mg % 1 + n 1 + n - n Όµως το τριώνυµο f(n)=n -n+1 έχει ρίζες συζυγείς µιγαδικές και εποµένως είναι για κάθε n οµόσηµο του συντελεστή του όρου n, δηλαδή είναι θετικό που σηµαίνει ότι Ν>0, δηλαδή η τροχαλία δεν χάνει την επαφή της µε το οριζόντιο δάπεδο. Aς δούµε όµως ποια είναι η αντίστοιχη γωνιακή επιτάχυνση ' του καρουλιού. Εφαρµόζοντας για το καρούλι τον θεµελιώδη νόµο της στροφικής κινήσεως παίρνουµε την σχέση: () F min R+TR = I' F min R+nNR = mr '/ F min +n( mg - F min "#$) = mr%'/ " =#/-$ F min ( 1 - n"#$ ) +nmg = mr%'/ F min ( 1 - nµ" ) +nmg = mr#'/ $ F min & 1 - % " # ' (5) ) +nmg = mr*'/ 1 + " # ( nmg # n " n $ & +nmg = mr''/ 1 + n % ng ( 1 + n - n ) +ng = R'/ 1 + n '= ng R " $ # 1 + n - n % 1 + n ' + ng & R
21 '= ng R " $ # 1 + n - n % n ' = ng " $ & R # 1 + n - n n % 1 + n ' & '= ng R " $ # 1 + n + 1% 1 + n ' > 0 (6) & δηλαδή η ελάχιστη τιµή του µέτρου της F είναι συµβατή µε την γνήσια περιστροφή της τροχαλίας. P.M. fysikos Στο καρούλι του σχήµατος (15) ενεργεί η δύναµη F, η οποία εφαρµόζεται στο άκρο A του νήµατος που περιβάλλει το κυλινδρικό σώµα του καρουλιού, του οποίου νήµατος η κλίση φ ως προς την οριζόντια διεύθυνση µπορεί να µεταβάλλεται. i) Nα βρείτε για ποιές τιµές της γωνίας φ το καρούλι κυλίεται στο οριζόντιο έδαφος µετατοπιζόµενο προς τα αριστερά. ii) Tι συµβαίνει µε την κίνηση του καρουλιού, όταν ο φορέας της δύναµης F προεκτεινόµενος τέµνει την ευθεία επαφής του καρουλιού µε το οριζόντιο έδαφος; iii) Κάτω από ποιες συνθήκες το καρούλι µπορεί να έχει γνήσια περιστρο φική κίνηση περί τον γεωµετρικό του άξονα, εφαπτόµενο του οριζόντιου εδάφους. vi) Eάν F=mg και φ=0 για ποιές τιµές του συντελεστή οριακής τριβής µεταξύ του καρουλιού και οριζόντιου επιπέδου είναι δυνατή η κύλισή του στο ορι ζόντιο επίπεδο; Δίνονται οι ακτίνες r και R του κυλινδρικού σώµατος και των κυκλικών βάσεων αντιστοίχως του καρουλιού (R>r) και η ροπή αδρά νειας I αυτού ως προς τον γεωµετρικό του άξονα. ΛΥΣΗ: i) Επειδή θέλουµε το καρούλι να κυλίεται και ο γεωµετρικός του άξονας να µετατοπίζεται προς τα αριστερά, θα πρέπει η περιστροφική του κίνηση περί τον άξονά του να είναι αριστερόστροφη, ώστε να είναι δυνατός ο µηδενισµός της ταχύτητας των σηµείων επαφής Μ του καρουλιού µε το έδαφος. Εφαρµόζοντας για το κέντρο µάζας C του καρουλιού τον δεύτερο νόµο κίνησης του Νεύτωνα παίρνουµε την σχέση: T - F x = ma C T = F"#$ + ma C (1) όπου F x η οριζόντια συνιστώσα της F και T η στατική τριβή από το έδαφος, η οποία πρέπει να έχει την φορά που φαίνεται στο σχήµα (15), ώστε η επιτάχυνση a C του κέν τρου µάζας C να έχει φορά προς τα αριστερά. Εξάλλου για την περιστροφή του καρου λιού περί τον άξονά του ο θεµελιώδης νόµος της στροφικής κίνησης δίνει την σχέση:
22 Fr - TR = I' Fr - TR = Ia C / R () όπου ' η γωνιακή επιτάχυνση του καρουλιού, της οποίας το µέτρο είναι a C /R λόγω της κυλίσεως. Συνδυάζοντας τις σχέσεις (1) και () παίρνουµε: Fr - FR"#$ - mra C = Ia C /R F(r - R"#$) = a C (mr + I/R a C = F(r - R"#$) mr + I/R (3) Σχήµα 15 Οµως πρέπει a C >0, δηλαδή: r - R"#$ > 0 "#$ < r / R Eπειδή η T είναι στατική τριβή πρέπει να ισχύει: T nn T n(mg - F y ) T n(mg - F"µ#) (4) Εξάλλου διαιρώντας κατά µέλη τις (1) και () παίρνουµε: T - F"#$ Fr - TR = mr I TI - FI"#$ = FmRr - TmR T(I + mr ) = F(I + mrr) T = F(I + mrr) I + mr T < F (5) H (4) λόγω της (5) γράφεται: F(I + mrr) # n(mg - F"µ#) F I + mrr I + mr % $ I + mr + nµ" & ( ) nmg ' F nmg (I + mrr)/(i + mr ) + n"µ# (6) H σχέση (6) µαζί και µε την συνφ<r/r εξασφαλίζουν την κύλιση του καρουλιού προς τα αριστερά.
23 ii) Εάν ο φορέας της δύναµης F προεκτεινόµενος διέρχεται από την ευθεία επαφής Μ του καρουλιού µε το έδαφος, τότε συνφ=r/r και η σχέση (3) δίνει a C =0. Tότε για την γωνιακή επιτάχυνση του καρουλιου υπάρχουν δύο ενδεχόνενα. α) Να είναι ω =0, οπότε θα πρέπει να ισχύει: Fr - TR = 0 T = Fr / R T = F"#$ (7) η οποία είναι συµβιβαστή µε την a C =0. β) Να είναι ω 0, οπότε θα πρέπει να ισχύει: Fr - TR 0 T Fr / R T F"#$% η οποία είναι ασυµβίβαστη µε την a C =0 και εποµένως απορρίπτεται. Άρα, όταν συνφ=r/r το καρούλι θα ισορροπεί. Τότε η τριβή T θα είναι στατική και εποµένως θα ισχύει: (7) T nn Fr / R n(mg - F"µ#) Fr / R + nfµ" # nmg F(r / R + nµ") # nmg F nmg r / R + n"µ# F nmg r / R + n 1 - "#$ % F nmg r / R + n 1 - r / R F nrmg r + n R - r (8) Άρα όταν ο φορέας της F διέρχεται από την ευθεία Μ και το µέτρο της ικανοποιεί την σχέση (8) το καρούλι θα ισορροπεί τείνοντας να ολισθήσει προς τα δεξιά. iii) Για να έχει το καρούλι γνήσια περιστροφή περί τον γεωµετρικό του άξονα πρέπει ω >0 και a C =0, ενώ η τριβή θα είναι τριβή ολισθήσεως. Τότε θα έχουµε: F x = T = nn F"#$ = n(mg - F%µ$) και F("#$ + n%µ$) = nmg (9) Fr - TR > 0 F > nnr/r F > nr(mg - Fµ")/r (9) F(1 + nrµ" / r) > nmgr/r nmg(1 + nrµ" / r) #$%" + nµ" > nmgr/r 1 + nrµ" r > R r (#$%" + nµ" ) 1 + nrµ" r > R#$%" r + nrµ" r 1 > R"#$ r "#$ < r R (10)
24 Αν λοιπόν ισχύουν οι σχέσεις (9) και (10) το καρούλι θα έχει γνήσια περιστροφική κί νηση. Παρατήρηση: Θέτοντας n=εφθ η σχέση (9) γράφεται: F = F = nmg "#$ + %&'(µ$ = nmg "#$ + (µ'(µ$ /"#' nmg"#$ "#%"#$ + &µ$&µ% = nmg"#$ "#(% - $) Παρατηρούµε από την (11) ότι για φ=θ το µέτρο της F παίρνει την µικρότερη τιµή του F min, που είναι: (11) F min = nmg"#$ = Aν λοιπόν ισχύει: nmg 1 + %& $ "#$ < r R ή n < r R τότε η γνήσια περιστροφή του καρουλιού µπορεί να εξασφαλιστεί µε την ελάχιστη τιµή του µέτρου της F. iv) Ας δεχθούµε ότι το καρούλι υπό την επίδραση της οριζόντιας δύναµης F κυλίεται. Η κυλισή του ισοδυναµεί µε γνήσια περιστροφή αυτού περί στιγµιαίο άξονα που είναι η ευθεία επαφής Μ µε το έδαφος, η οποία προφανώς είναι δεξιόστροφη και ωφείλεται µό Σχήµα 16 νο στην F, διότι οι ροπές των τριών άλλων δυνάµεων T, N και περί τον άξονα αυτόν είναι µηδενικές. Αυτό σηµαίνει ότι η κίνηση του άξονα του καρουλιού είναι προς δεξιά, ώστε να είναι δυνατός ο µηδενισµός της ταχύτητας των σηµείων επαφής του µε το έδαφος Με βάση τα παραπάνω θα έχουµε τις σχέσεις: F - T = ma C " # TR - Fr = I' $ F - T = ma C " TR - Fr = Ia C /R # (:) F - T TR - Fr = mr I
25 mg - T TR - mgr = mr I mgi - ITR = TmR - m grr mg( I + mrr) = T( I + mr ) T = mg( I + mrr) (1) I + mr Όµως η κύλιση του καρουλιού επιβάλλει την σχέση: (1) mg( I + mrr) T nn T nmg nmg I + mr n I + mrr I + mr P.M. Fysikos
από τον κατακόρυφο τοίχο, της οποίας ο φορέας είναι οριζόντιος και την δύναµη επα φής N!
 Οµογενής συµπαγής κύβος ακµής α και µάζας m, ισορροπεί ακουµπώντας µε µια ακµή του σε κατακόρυφο τοίχο και µε µια του έδρα σε κεκλιµένο επίπεδο γωνίας κλίσεως φ ως προς τον ορίζοντα, όπως φαίνεται στο
Οµογενής συµπαγής κύβος ακµής α και µάζας m, ισορροπεί ακουµπώντας µε µια ακµή του σε κατακόρυφο τοίχο και µε µια του έδρα σε κεκλιµένο επίπεδο γωνίας κλίσεως φ ως προς τον ορίζοντα, όπως φαίνεται στο
Θεωρούµε στερεό σώµα που εκτελεί ως προς ένα αδρανειακό σύστηµα αναφοράς επίπεδη κίνηση.
 Θεωρούµε στερεό σώµα που εκτελεί ως προς ένα αδρανειακό σύστηµα αναφοράς επίπεδη κίνηση. i) Εάν Κ είναι το στιγµιαίο κέντρο περιστροφής του στερεού κάποια στιγµή και C η αντίστοιχη θέση του κέντρου µάζας
Θεωρούµε στερεό σώµα που εκτελεί ως προς ένα αδρανειακό σύστηµα αναφοράς επίπεδη κίνηση. i) Εάν Κ είναι το στιγµιαίο κέντρο περιστροφής του στερεού κάποια στιγµή και C η αντίστοιχη θέση του κέντρου µάζας
i) Nα δείξετε ότι, κάθε στιγµή οι ταχύτητες των δύο πιθήκων ως προς το ακίνητο έδαφος είναι ίσες.
 Δύο πιθηκάκια της ίδιας µάζας αναρριχώνται εκ της ηρεµίας κατά µήκος των τµηµάτων του αβαρούς σχοινιού, που διέρχεται από τον λαιµό µιας σταθερής τροχαλίας (σχ. ). H τροχαλία έχει αµελητέα µάζα και µπορεί
Δύο πιθηκάκια της ίδιας µάζας αναρριχώνται εκ της ηρεµίας κατά µήκος των τµηµάτων του αβαρούς σχοινιού, που διέρχεται από τον λαιµό µιας σταθερής τροχαλίας (σχ. ). H τροχαλία έχει αµελητέα µάζα και µπορεί
, της οποίας το µέτρο ικανοποιεί τη σχέση:
 Στην κορυφή της κεκλιµένης έδρας µιας ορθογώνιας σφήνας µάζας M, η οποία ισορροπεί πάνω σε λείο οριζόντιο έδαφος, αφήνεται µικ ρός κύβος µάζας m. Nα δείξετε ότι η σφήνα κινείται στο σύστη µα αναφοράς του
Στην κορυφή της κεκλιµένης έδρας µιας ορθογώνιας σφήνας µάζας M, η οποία ισορροπεί πάνω σε λείο οριζόντιο έδαφος, αφήνεται µικ ρός κύβος µάζας m. Nα δείξετε ότι η σφήνα κινείται στο σύστη µα αναφοράς του
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ: ΔΥΝΑΜΕΙΣ ΚΑΙ ΡΟΠΕΣ
 ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ: ΔΥΝΑΜΕΙΣ ΚΑΙ ΡΟΠΕΣ Σ ένα στερεό ασκούνται ομοεπίπεδες δυνάμεις. Όταν το στερεό ισορροπεί, δηλαδή ισχύει ότι F 0 και δεν περιστρέφεται τότε το αλγεβρικό άθροισμα των ροπών είναι μηδέν Στ=0,
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ: ΔΥΝΑΜΕΙΣ ΚΑΙ ΡΟΠΕΣ Σ ένα στερεό ασκούνται ομοεπίπεδες δυνάμεις. Όταν το στερεό ισορροπεί, δηλαδή ισχύει ότι F 0 και δεν περιστρέφεται τότε το αλγεβρικό άθροισμα των ροπών είναι μηδέν Στ=0,
Δίνεται η ροπή αδράνειας I=mL 2 /3 της ράβδου ως προς τον άξονα περιστροφής της, η επιτάχυνση! g της βαρύτητας και ότι π 2!10.
 Oµογενής ράβδος σταθερής διατοµής, µάζας m και µήκους L, µπορεί να στρέφεται περί οριζόντιο άξονα που διέρχεται από το ένα άκρο της. Όταν η ράβδος βρίσκεται στην θέση ευσταθούς ισορροπίας της εφαρµόζεται
Oµογενής ράβδος σταθερής διατοµής, µάζας m και µήκους L, µπορεί να στρέφεται περί οριζόντιο άξονα που διέρχεται από το ένα άκρο της. Όταν η ράβδος βρίσκεται στην θέση ευσταθούς ισορροπίας της εφαρµόζεται
Q του νήµατος που το συγκρατεί, συµφωνα δε µε τον δεύτερο νό µο κίνησης του Νεύτωνα θα ισχύει η σχέση: της τάσεως!
 Αβαρής ράβδος αποτελείται από δύο συνεχόµενα τµήµατα ΟΑ και ΑΒ που είναι ορθογώνια µεταξύ τους. Το άκρο Ο της ράβδου είναι αρθρωµένο σε οριζόντιο έδαφος το δε τµήµα της ΟΑ είναι κατακόρυφο και εφάπτεται
Αβαρής ράβδος αποτελείται από δύο συνεχόµενα τµήµατα ΟΑ και ΑΒ που είναι ορθογώνια µεταξύ τους. Το άκρο Ο της ράβδου είναι αρθρωµένο σε οριζόντιο έδαφος το δε τµήµα της ΟΑ είναι κατακόρυφο και εφάπτεται
που εξασκείται στο άκρο της Γ και των αντιδράσεων A! , A 2
 Oµογενής ράβδος BΓ βάρους w, ισορροπεί ώστε τα άκρα της να εφάπτονται σε µια λεία και ακίνητη κοίλη σφαίρα ακτί νας R, όπως φαίνεται στο σχήµα (1). Eάν η κατακόρυφη δύναµη F που εξασκείται στο άκρο Γ της
Oµογενής ράβδος BΓ βάρους w, ισορροπεί ώστε τα άκρα της να εφάπτονται σε µια λεία και ακίνητη κοίλη σφαίρα ακτί νας R, όπως φαίνεται στο σχήµα (1). Eάν η κατακόρυφη δύναµη F που εξασκείται στο άκρο Γ της
(τρίτος νόµος του Νεύτωνα) και την πλάγια αντίδραση του οριζόντιου εδάφους, η οποία αναλύεται στην τριβή ολίσθησης T!
 Επί της κεκλιµένης έδρας µιας ορθογώνιας και ισοσκελούς σφήνας µάζας m, η οποία ισορροπεί πάνω σε οριζόντιο έδαφος, αφήνεται µικρός κύβος µάζας m. Μεταξύ του κύβου και της σφήνας δεν υπάρχει τριβή, ενώ
Επί της κεκλιµένης έδρας µιας ορθογώνιας και ισοσκελούς σφήνας µάζας m, η οποία ισορροπεί πάνω σε οριζόντιο έδαφος, αφήνεται µικρός κύβος µάζας m. Μεταξύ του κύβου και της σφήνας δεν υπάρχει τριβή, ενώ
διέρχεται από το σηµείο τοµής Ο των φορέων του βάρους w! της ράβδου και της οριζόντιας αντίδρασης A!
 Η οµογενής ράβδος ΑΒ του σχήµατος έχει βά ρος w και στηρίζεται διά του άκρου της Α σε τραχύ κεκλιµένο επί πεδο γωνίας κλίσεως φ ως προς τον ορίζοντα, ενώ το άλλο της άκρο Β ακουµπάει σε λείο κατακόρυφο
Η οµογενής ράβδος ΑΒ του σχήµατος έχει βά ρος w και στηρίζεται διά του άκρου της Α σε τραχύ κεκλιµένο επί πεδο γωνίας κλίσεως φ ως προς τον ορίζοντα, ενώ το άλλο της άκρο Β ακουµπάει σε λείο κατακόρυφο
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος ΙΙ Ενδεικτικές Λύσεις Κυριακή 28 Φλεβάρη 2016 Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος ΙΙ Ενδεικτικές Λύσεις Κυριακή 28 Φλεβάρη 2016 Θέµα Α Α.1. Ενα στερεό σώµα περιστρέφεται γύρω από ακλόνητο άξονα. Εάν διπλασιαστεί η στροφορµή
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος ΙΙ Ενδεικτικές Λύσεις Κυριακή 28 Φλεβάρη 2016 Θέµα Α Α.1. Ενα στερεό σώµα περιστρέφεται γύρω από ακλόνητο άξονα. Εάν διπλασιαστεί η στροφορµή
από την άρθρωση και της δύναµης επαφής από τον τοίχο που αναλύεται στην στατική τριβη T!
 Tο ένα άκρο A οµογενούς ράβδου AB αρθρώνεται σε οριζόντιο επίπεδο, ενώ το άλλο της άκρο Β εφάπτεται κατακόρυ φου τοίχου, µε τον οποίο η ράβδος παρουσιάζει συντελεστή οριακής τριβής µ. H άρθρωση της ράβδου
Tο ένα άκρο A οµογενούς ράβδου AB αρθρώνεται σε οριζόντιο επίπεδο, ενώ το άλλο της άκρο Β εφάπτεται κατακόρυ φου τοίχου, µε τον οποίο η ράβδος παρουσιάζει συντελεστή οριακής τριβής µ. H άρθρωση της ράβδου
περί το κέντρο της σφαίρας, ονοµάζεται δε τριβή κυλίσεως. Tο µέτρο της τρι βής κυλίσεως είναι προφανώς ανάλογο του µέτρου της N,!
 Θεωρούµε µια βαρειά σφαίρα, η οποία ισορροπεί επί σχετικά µαλακού εδάφους, ώστε να προκαλεί σ αυτό µια µικρή παραµόρφωση. Λόγω της συµµετρίας που παρουσιάζει η παραµόρφωση αυτή, ως προς την κατακόρυφη
Θεωρούµε µια βαρειά σφαίρα, η οποία ισορροπεί επί σχετικά µαλακού εδάφους, ώστε να προκαλεί σ αυτό µια µικρή παραµόρφωση. Λόγω της συµµετρίας που παρουσιάζει η παραµόρφωση αυτή, ως προς την κατακόρυφη
( ) ( ) 2 1 K = K = m 2. ! = v 2 + v 1 R + r (3) H (1) λόγω της (3) γράφεται: R - v 2. + v 1. v 2. r > 0 (4) ! v K. + v 1 )R - v 2. = v 2. - v.
 Το καρούλι του σχήµατος κυλίεται χωρίς ολίσ θηση πάνω σε οριζόντιο δοκάρι, που ολισθαίνει επί οριζοντίου έδα φους µε ταχύτητα v η οποία έχει την κατεύθυνση του δοκαριού. Η κύλιση του καρουλιού επιτυγχάνεται
Το καρούλι του σχήµατος κυλίεται χωρίς ολίσ θηση πάνω σε οριζόντιο δοκάρι, που ολισθαίνει επί οριζοντίου έδα φους µε ταχύτητα v η οποία έχει την κατεύθυνση του δοκαριού. Η κύλιση του καρουλιού επιτυγχάνεται
Κεφάλαιο 6β. Περιστροφή στερεού σώματος γύρω από σταθερό άξονα
 Κεφάλαιο 6β Περιστροφή στερεού σώματος γύρω από σταθερό άξονα Ροπή Ροπή ( ) είναι η τάση που έχει μια δύναμη να περιστρέψει ένα σώμα γύρω από κάποιον άξονα. d είναι η κάθετη απόσταση του άξονα περιστροφής
Κεφάλαιο 6β Περιστροφή στερεού σώματος γύρω από σταθερό άξονα Ροπή Ροπή ( ) είναι η τάση που έχει μια δύναμη να περιστρέψει ένα σώμα γύρω από κάποιον άξονα. d είναι η κάθετη απόσταση του άξονα περιστροφής
i) Nα βρεθεί η επιτάχυνση του κέντρου Κ της τροχαλίας την στιγµή t=0 αµέσως µετά την θραύση του νήµατος.
 H τροχαλία του σχήµατος () µάζας m και ακτίνας R, ισορροπεί εξαρτηµένη από τα νήµατα ΑΒ και ΓΔ τα οποία είναι ισο κεκλιµένα ως προς την οριζόντια διεύθυνση κατα γωνία φ. Κάποια στιγµή κόβουµε το νήµα ΑΒ
H τροχαλία του σχήµατος () µάζας m και ακτίνας R, ισορροπεί εξαρτηµένη από τα νήµατα ΑΒ και ΓΔ τα οποία είναι ισο κεκλιµένα ως προς την οριζόντια διεύθυνση κατα γωνία φ. Κάποια στιγµή κόβουµε το νήµα ΑΒ
i) Nα βρείτε την επιτάχυνση του κέντρου της τροχαλίας τ 1.
 Στην διάταξη του σχήµατος 1) οι τροχαλίες τ 1 και τ έχουν την ίδια µάζα Μ που θεωρείται συγκεντρωµένη στην περι φέρειά τους και την ίδια ακτίνα R. Στο αυλάκι της σταθερής τροχα λίας τ έχει περιτυλιχθεί
Στην διάταξη του σχήµατος 1) οι τροχαλίες τ 1 και τ έχουν την ίδια µάζα Μ που θεωρείται συγκεντρωµένη στην περι φέρειά τους και την ίδια ακτίνα R. Στο αυλάκι της σταθερής τροχα λίας τ έχει περιτυλιχθεί
i) τον λόγο των µαζών των δύο σφαιριδίων, ώστε αυτά µετά την κρού ση τους να φθάνουν στις αρχικές τους θέσεις και
 Δύο αβαρή και µη εκτατά νήµατα του ίδιου µή κους είναι στερεωµένα στο ίδιο σηµείο Ο, ενώ στις ελεύθερες άκρες των νηµάτων είναι δεµένα δύο σφαιρίδια, µε µάζες 1 και. Eκτρέ πουµε τα σφαιρίδια από την θέση
Δύο αβαρή και µη εκτατά νήµατα του ίδιου µή κους είναι στερεωµένα στο ίδιο σηµείο Ο, ενώ στις ελεύθερες άκρες των νηµάτων είναι δεµένα δύο σφαιρίδια, µε µάζες 1 και. Eκτρέ πουµε τα σφαιρίδια από την θέση
ακτινικής διεύθυνσης και στην οριακή τριβή T!"
 Λεπτή κυκλική στεφάνη ακτίνας R και µάζας m, ισορρο πεί εφαπτόµενη σε δύο υποστηρίγµατα A και Γ, όπως φαίνεται στο σχήµα (1. Eάν ο συντελεστής οριακής τριβής µεταξύ της στεφάνης και των υποστη ριγµάτων
Λεπτή κυκλική στεφάνη ακτίνας R και µάζας m, ισορρο πεί εφαπτόµενη σε δύο υποστηρίγµατα A και Γ, όπως φαίνεται στο σχήµα (1. Eάν ο συντελεστής οριακής τριβής µεταξύ της στεφάνης και των υποστη ριγµάτων
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013
 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013 ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1- Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013 ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1- Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ii) Nα υπολογιστεί η κινητική ενέργεια του συστήµατος σε συνάρτηση µε τον χρόνο. Δίνεται η επιτάχυνση! g της βαρύτητας.
 Στην διάταξη του σχήµατος () η ράβδος ΑΒ είναι οµογενής, έχει µήκος L και µπορεί να στρέφεται περί οριζόντιο άξο να, που διέρχεται από σηµείο Ο ευρισκόµενο σε απόσταση 3L/4 από το άκρο της Α. Η τροχαλία
Στην διάταξη του σχήµατος () η ράβδος ΑΒ είναι οµογενής, έχει µήκος L και µπορεί να στρέφεται περί οριζόντιο άξο να, που διέρχεται από σηµείο Ο ευρισκόµενο σε απόσταση 3L/4 από το άκρο της Α. Η τροχαλία
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ. Α5. α. Λάθος β. Λάθος γ. Σωστό δ. Λάθος ε. Σωστό
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. γ. Α. δ. Α3. γ. Α4. γ. Α5. α. Λάθος β. Λάθος γ. Σωστό δ. Λάθος ε. Σωστό ΘΕΜΑ B B1. Σωστή απάντηση είναι η
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. γ. Α. δ. Α3. γ. Α4. γ. Α5. α. Λάθος β. Λάθος γ. Σωστό δ. Λάθος ε. Σωστό ΘΕΜΑ B B1. Σωστή απάντηση είναι η
ii) ii) Nα καθορίσετε το είδος της ισορροπίας της ράβδου.
 Oµογενής ράβδος Γ, βάρους w και µήκους L, είναι αρθρωµένη στο ένα άκρο της όπως φαίνεται στο σχήµα (), ενώ το άλλο άκρο της είναι δεµένο σε νήµα που διέρχεται από µικρή ακίνητη τροχαλία O, η οποία βρίσκεται
Oµογενής ράβδος Γ, βάρους w και µήκους L, είναι αρθρωµένη στο ένα άκρο της όπως φαίνεται στο σχήµα (), ενώ το άλλο άκρο της είναι δεµένο σε νήµα που διέρχεται από µικρή ακίνητη τροχαλία O, η οποία βρίσκεται
i) Να δείξετε ότι: F max = (m 1 + m 2 όπου! g η επιτάχυνση της βαρύτητας.
 Δύο σώµατα Σ και Σ µε αντίστοιχες µάζες m και m, είναι στερεωµένα στις άκρες ενός κατακόρυφου αβαρούς ελατηρίου, όπως φαίνεται στο σχήµα. Εξασκούµε στο σώµα Σ κατακόρυφη δύναµη µε φορά προς τα κάτω, της
Δύο σώµατα Σ και Σ µε αντίστοιχες µάζες m και m, είναι στερεωµένα στις άκρες ενός κατακόρυφου αβαρούς ελατηρίου, όπως φαίνεται στο σχήµα. Εξασκούµε στο σώµα Σ κατακόρυφη δύναµη µε φορά προς τα κάτω, της
της οποίας ο φορέας σχηµατί ζει γωνία φ=π/6 µε την κατακόρυφη διεύθυνση και ανακλάται µε αντίστοιχη γωνία φ=π/4.
 Οριζόντιος δίσκος µάζας Μ ισορροπεί στηριζόµε νος στο πάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k, του οποίου το άλλο άκρο στηρίζεται στο έδαφος (σχήµα 1). Ένα µικρό σφαιρίδιο µάζας m, προσκρούει
Οριζόντιος δίσκος µάζας Μ ισορροπεί στηριζόµε νος στο πάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k, του οποίου το άλλο άκρο στηρίζεται στο έδαφος (σχήµα 1). Ένα µικρό σφαιρίδιο µάζας m, προσκρούει
ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ ΠΡΟΣΠΑΘΕΙΑ ΣΑΣ ΚΙ 2014
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
θα επιβρα δύνεται. Επειδή η F! /Μ και θα ισχύει η σχέση: /t!
 Ξύλινο κιβώτιο µάζας M κινείται πάνω σε λείο οριζόντιο δάπεδο µε ταχύτητα µέτρου v 0. Ένα βλήµα µάζας m, κινούµενο αντίρροπα προς το κιβώτιο προσπίπτει σ αυτό µε ταχύ τητα µέτρου v 0 και εξέρχεται από
Ξύλινο κιβώτιο µάζας M κινείται πάνω σε λείο οριζόντιο δάπεδο µε ταχύτητα µέτρου v 0. Ένα βλήµα µάζας m, κινούµενο αντίρροπα προς το κιβώτιο προσπίπτει σ αυτό µε ταχύ τητα µέτρου v 0 και εξέρχεται από
[1kgm 2, 5m/s, 3,2cm, 8rad/s][1kgm 2, 5m/s, 3,2cm, 8rad/s]
![[1kgm 2, 5m/s, 3,2cm, 8rad/s][1kgm 2, 5m/s, 3,2cm, 8rad/s] [1kgm 2, 5m/s, 3,2cm, 8rad/s][1kgm 2, 5m/s, 3,2cm, 8rad/s]](/thumbs/61/46095927.jpg) ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 5: ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ ΚΑΙ ΕΡΓΟ ΔΥΝΑΜΗΣ ΣΤΗ ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ 34. Μία κατακόρυφη ράβδος μάζας μήκους, μπορεί να περιστρέφεται στο κατακόρυφο επίπεδο γύρω από
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 5: ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ ΚΑΙ ΕΡΓΟ ΔΥΝΑΜΗΣ ΣΤΗ ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ 34. Μία κατακόρυφη ράβδος μάζας μήκους, μπορεί να περιστρέφεται στο κατακόρυφο επίπεδο γύρω από
i) Nα βρείτε την ταχύτητα του κέντρου της στεφάνης αµέσως µετά την κρού ση, η οποία θεωρείται βραχείας διάρκειας.
 Mια κυκλική στεφάνη ακτίνας R, της οποίας η µάζα θεωρείται συγκεντρωµένη στην περιφέρεια της, κυλίεται ισοταχώς πάνω σε οριζόντιο επίπεδο το δε κέντρο της έχει ταχύτητα v. Kάποια στιγµή η στε φάνη προσκρούει
Mια κυκλική στεφάνη ακτίνας R, της οποίας η µάζα θεωρείται συγκεντρωµένη στην περιφέρεια της, κυλίεται ισοταχώς πάνω σε οριζόντιο επίπεδο το δε κέντρο της έχει ταχύτητα v. Kάποια στιγµή η στε φάνη προσκρούει
ΕΝΟΤΗΤΑ 5: ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ ΚΑΙ ΕΡΓΟ ΔΥΝΑΜΗΣ ΣΤΗ ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β
 ΚΕΦΑΛΑΙΟ 4 Ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 5: ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ ΚΑΙ ΕΡΓΟ ΔΥΝΑΜΗΣ ΣΤΗ ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ ΛΥΜΕΝΑ ΘΕΜΑΤΑ Ερώτηση. ΘΕΜΑ Β Ένα ομογενές σώμα με κανονικό γεωμετρικό σχήμα κυλίεται, χωρίς να
ΚΕΦΑΛΑΙΟ 4 Ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 5: ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ ΚΑΙ ΕΡΓΟ ΔΥΝΑΜΗΣ ΣΤΗ ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ ΛΥΜΕΝΑ ΘΕΜΑΤΑ Ερώτηση. ΘΕΜΑ Β Ένα ομογενές σώμα με κανονικό γεωμετρικό σχήμα κυλίεται, χωρίς να
ii) Nα βρείτε την µέγιστη γωνιακή ταχύτητα της ράβδου.
 Oµογενής ράβδος σταθερής διατοµής, µάζας m και µήκους L, µπορεί να στρέφεται περί οριζόντιο άξονα που διέρχεται από το ένα άκρο της. Όταν η ράβδος βρίσκεται στην θέση ευσταθούς ισορροπίας εφαρµόζεται στο
Oµογενής ράβδος σταθερής διατοµής, µάζας m και µήκους L, µπορεί να στρέφεται περί οριζόντιο άξονα που διέρχεται από το ένα άκρο της. Όταν η ράβδος βρίσκεται στην θέση ευσταθούς ισορροπίας εφαρµόζεται στο
ΛΥΣΗ: Έστω O η θέση ισορροπίας του σφαιριδίου. Στη θέση αυτή το σφαι ρίδιο δέχεται το βάρος του w!, τη δύναµη F
 Ένα ιδανικό ελατήριο σταθεράς k κόβεται σε δύο τµήµατα µε µήκη L και L. Η µία άκρη κάθε τµήµατος συνδέεται στέρεα µε µικρό σφαιρίδιο µάζας m και οι ελέυθερες άκρες τους στερεώνονται σε ακλόνητα σηµεία
Ένα ιδανικό ελατήριο σταθεράς k κόβεται σε δύο τµήµατα µε µήκη L και L. Η µία άκρη κάθε τµήµατος συνδέεται στέρεα µε µικρό σφαιρίδιο µάζας m και οι ελέυθερες άκρες τους στερεώνονται σε ακλόνητα σηµεία
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ. Άσκηση 1. (Κινητική ενέργεια λόγω περιστροφής. Έργο και ισχύς σταθερής ροπής)
 ΕΚΦΩΝΗΣΕΣ ΑΣΚΗΣΕΩΝ Άσκηση 1 (Κινητική ενέργεια λόγω περιστροφής Έργο και ισχύς σταθερής ροπής) Ένας κύβος και ένας δίσκος έχουν ίδια μάζα και αφήνονται από το ίδιο ύψος να κινηθούν κατά μήκος δύο κεκλιμένων
ΕΚΦΩΝΗΣΕΣ ΑΣΚΗΣΕΩΝ Άσκηση 1 (Κινητική ενέργεια λόγω περιστροφής Έργο και ισχύς σταθερής ροπής) Ένας κύβος και ένας δίσκος έχουν ίδια μάζα και αφήνονται από το ίδιο ύψος να κινηθούν κατά μήκος δύο κεκλιμένων
ΟΡΟΣΗΜΟ >Ι 3. δ. Ι Οι τροχοί (1) και (2) του σχήματος είναι ίδιοι. Τότε: και Ι 2
 ΚΕΦΑΛΑΙΟ 4 Ροπή αδράνειας - Θεμελιώδης νόμος της στροφικής κίνησης 4.1 Η ροπή αδράνειας ενός σώματος εξαρτάται: α. μόνο από τη μάζα του σώματος β. μόνο τη θέση του άξονα γύρω από τον οποίο μπορεί να περιστρέφεται
ΚΕΦΑΛΑΙΟ 4 Ροπή αδράνειας - Θεμελιώδης νόμος της στροφικής κίνησης 4.1 Η ροπή αδράνειας ενός σώματος εξαρτάται: α. μόνο από τη μάζα του σώματος β. μόνο τη θέση του άξονα γύρω από τον οποίο μπορεί να περιστρέφεται
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΑΥΕΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/2014
 ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΑΥΕΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/04 ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΑΥΕΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/04 ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα
Συνταγολόγιο Φυσικής Μηχανική Στερεού Σώµατος. Επιµέλεια: Μιχάλης Ε. Καραδηµητρίου, MSc Φυσικός.
 Συνταγολόγιο Φυσικής Μηχανική Στερεού Σώµατος Επιµέλεια: Μιχάλης Ε. Καραδηµητρίου, MSc Φυσικός http://perifysikhs.wordpress.com 1 Κίνηση Ράβδου σε κατακόρυφο επίπεδο Εστω µια οµογενής ϱάβδος ΟΑ µάζας Μ
Συνταγολόγιο Φυσικής Μηχανική Στερεού Σώµατος Επιµέλεια: Μιχάλης Ε. Καραδηµητρίου, MSc Φυσικός http://perifysikhs.wordpress.com 1 Κίνηση Ράβδου σε κατακόρυφο επίπεδο Εστω µια οµογενής ϱάβδος ΟΑ µάζας Μ
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος Ι Ενδεικτικές Λύσεις Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος Ι Ενδεικτικές Λύσεις Θέµα Α Α.1. Η γωνιακή επιτάχυνση ενός οµογενούς δίσκου που στρέφεται γύρω από σταθερό άξονα, που διέρχεται από το κέντρο
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος Ι Ενδεικτικές Λύσεις Θέµα Α Α.1. Η γωνιακή επιτάχυνση ενός οµογενούς δίσκου που στρέφεται γύρω από σταθερό άξονα, που διέρχεται από το κέντρο
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ
 ΠΡΟΒΛΗΜΑ 1 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ Η λεπτή, ομογενής ράβδος ΟΑ του σχήματος έχει μήκος, μάζα και μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο γύρω από οριζόντιο ακλόνητο άξονα (άρθρωση) που διέρχεται
ΠΡΟΒΛΗΜΑ 1 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ Η λεπτή, ομογενής ράβδος ΟΑ του σχήματος έχει μήκος, μάζα και μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο γύρω από οριζόντιο ακλόνητο άξονα (άρθρωση) που διέρχεται
Ένα διαστηµόπλοιο µάζας M, κινείται στο διά στηµα µε σταθερή ταχύτητα V!
 Ένα διαστηµόπλοιο µάζας M, κινείται στο διά στηµα µε σταθερή ταχύτητα V 0. O πιλότος του θέλει ν αλλάξει τη διεύθυνση κίνησης του διαστηµόπλοιου, ώστε η νέα διεύθυνση να γίνει κάθετη προς την αρχική. Για
Ένα διαστηµόπλοιο µάζας M, κινείται στο διά στηµα µε σταθερή ταχύτητα V 0. O πιλότος του θέλει ν αλλάξει τη διεύθυνση κίνησης του διαστηµόπλοιου, ώστε η νέα διεύθυνση να γίνει κάθετη προς την αρχική. Για
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ» 5 o ΔΙΑΓΩΝΙΣΜΑ ΑΠΡΙΛΙΟΣ 2017: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ
 5 o ΔΙΑΓΩΝΙΣΜΑ ΑΠΡΙΛΙΟΣ 017: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. γ. Α. δ. Α3. γ. Α4. γ. Α5. α. Λάθος β. Λάθος γ. Σωστό
5 o ΔΙΑΓΩΝΙΣΜΑ ΑΠΡΙΛΙΟΣ 017: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. γ. Α. δ. Α3. γ. Α4. γ. Α5. α. Λάθος β. Λάθος γ. Σωστό
Όταν υπάρχει ΑΚΙΝΗΤΟ σηµείο
 Όταν υπάρχει ΑΚΙΝΗΤΟ σηµείο ) Οµογενής κύλινδρος µάζας m, ακτίνας R φέρει λεπτή εγκοπή βάθους είναι τυλιγµένο νήµα αµελητέου πάχους. R r=, στην οποία Το άλλο άκρο του νήµατος έχει δεθεί σε οροφή όπως στο
Όταν υπάρχει ΑΚΙΝΗΤΟ σηµείο ) Οµογενής κύλινδρος µάζας m, ακτίνας R φέρει λεπτή εγκοπή βάθους είναι τυλιγµένο νήµα αµελητέου πάχους. R r=, στην οποία Το άλλο άκρο του νήµατος έχει δεθεί σε οροφή όπως στο
i) Το επίπεδο της τροχαλίας είναι οριζόντιο και το έδαφος λείο.
 Πάνω σε οριζόντιο έδαφος ηρεµεί µια τροχαλία µάζας m και ακτίνας R. Στο αυλάκι της τροχαλίας έχει περιτυλιχ θεί αβαρές νήµα στο ελεύθερο άκρο Α του οποίου εξασκείται σταθε ρή οριζόνια δύναµη F. Eάν µέχρις
Πάνω σε οριζόντιο έδαφος ηρεµεί µια τροχαλία µάζας m και ακτίνας R. Στο αυλάκι της τροχαλίας έχει περιτυλιχ θεί αβαρές νήµα στο ελεύθερο άκρο Α του οποίου εξασκείται σταθε ρή οριζόνια δύναµη F. Eάν µέχρις
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 3: ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ - ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ
 ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 3: ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ - ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ 12. Ένας οριζόντιος ομογενής δίσκος ακτίνας μπορεί να περιστρέφεται χωρίς τριβές, γύρω από κατακόρυφο
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 3: ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ - ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ 12. Ένας οριζόντιος ομογενής δίσκος ακτίνας μπορεί να περιστρέφεται χωρίς τριβές, γύρω από κατακόρυφο
Οµογενής σφαίρα µάζας m και ατίνας R, ισορροπεί πάνω σε λείο οριζόντιο επίπεδο. Κάποια στιγµή ενεργεί στην σφαίρα οριζόντια ώθηση!!
 Οµογενής σφαίρα µάζας και ατίνας R, ισορροπεί πάνω σε λείο οριζόντιο επίπεδο. Κάποια στιγµή ενεργεί στην σφαίρα οριζόντια ώθηση βραχείας διάρκειας, της οποίας ο φορέας βρίσκε ται άνωθεν του κέντρου της
Οµογενής σφαίρα µάζας και ατίνας R, ισορροπεί πάνω σε λείο οριζόντιο επίπεδο. Κάποια στιγµή ενεργεί στην σφαίρα οριζόντια ώθηση βραχείας διάρκειας, της οποίας ο φορέας βρίσκε ται άνωθεν του κέντρου της
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013
 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 03 ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α. c Α. d Α3. c Α4. c Α5. Σ, Λ, Σ, Σ, Λ ΘΕΜΑ Β Β. Σωστή απάντηση είναι η (γ). Γνωρίζουμε (σχολικό βιβλίο, σελ. 3) ότι ένα
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 03 ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α. c Α. d Α3. c Α4. c Α5. Σ, Λ, Σ, Σ, Λ ΘΕΜΑ Β Β. Σωστή απάντηση είναι η (γ). Γνωρίζουμε (σχολικό βιβλίο, σελ. 3) ότι ένα
i) την µέγιστη ροπή του ζεύγους δυνάµεων που επιτρέπεται να ενερ γήσει επί του κυλίνδρου, ώστε αυτός να ισορροπεί και
 Oµογενής κύλινδρος µάζας m και ακτίνας R εφάπ τεται στα τοιχώµατα ενός αυλακιού, τα οποία είναι επίπεδες σταθερές επιφάνειες που η τοµή τους είναι οριζόντια. Τα τοιχώµατα είναι ισο κεκλιµένα ως προς τον
Oµογενής κύλινδρος µάζας m και ακτίνας R εφάπ τεται στα τοιχώµατα ενός αυλακιού, τα οποία είναι επίπεδες σταθερές επιφάνειες που η τοµή τους είναι οριζόντια. Τα τοιχώµατα είναι ισο κεκλιµένα ως προς τον
Ένα σώµα µε µεγάλη µάζα Μ, κινείται µε σταθερή
 Ένα σώµα µε µεγάλη µάζα Μ, κινείται µε σταθερή ταχύτητα µέτρου V 0 πάνω σε λείο οριζόντιο έδαφος κατευθυνόµενο προς κατακόρυφο τοίχο. Το σώµα κάποια στιγµή συγκρούεται ελα στικά και µετωπικά µε µια µπάλα
Ένα σώµα µε µεγάλη µάζα Μ, κινείται µε σταθερή ταχύτητα µέτρου V 0 πάνω σε λείο οριζόντιο έδαφος κατευθυνόµενο προς κατακόρυφο τοίχο. Το σώµα κάποια στιγµή συγκρούεται ελα στικά και µετωπικά µε µια µπάλα
ΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 ΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Ο Στις ερωτήσεις -4 να βρείτε τη σωστή πρόταση.. Η ροπή αδράνειας ενός στερεού σώµατος εξαρτάται: α. Από τη ροπή της δύναµης που ασκείται στο στερεό. β. από
ΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Ο Στις ερωτήσεις -4 να βρείτε τη σωστή πρόταση.. Η ροπή αδράνειας ενός στερεού σώµατος εξαρτάται: α. Από τη ροπή της δύναµης που ασκείται στο στερεό. β. από
όπου Α το πλάτος της ταλάντωσης, φ η αρχική της φάση και ω η γωνιακή της συχνότητα. Οι σχέσεις (2) εφαρµοζόµενες τη χρονική στιγµή t=0 δίνουν:
 Tο ένα άκρο κατακόρυφου ιδανικού ελατηρίου είναι στερεωµένο στο οριζόντιο έδαφος, ενώ το άλλο του άκρο είναι ελεύθερο. Mικρό σφαιρίδιο, µάζας m, αφήνεται σε ύψος h από το άκρο Β. Το σφαιρίδιο πέφτοντας
Tο ένα άκρο κατακόρυφου ιδανικού ελατηρίου είναι στερεωµένο στο οριζόντιο έδαφος, ενώ το άλλο του άκρο είναι ελεύθερο. Mικρό σφαιρίδιο, µάζας m, αφήνεται σε ύψος h από το άκρο Β. Το σφαιρίδιο πέφτοντας
i) Nα δείξετε ότι αν το σύστηµα αφεθεί ελεύθερο η τροχαλία τ 1 δεν µπορεί να κυλίεται, άλλά µόνο να ισσρροπεί ή να ολισθαίνει.
 Στην διάταξη του σχήµατος η τροχαλία τ 1 έχει µάζα m 1 και ακτίνα R και στο αυλάκι της έχει περιτυλιχθεί αβαρές νήµα, το οποίο διέρ χεται από τον λαιµό της µικρής τροχαλίας τ στο δε άκρο του έχει δε θεί
Στην διάταξη του σχήµατος η τροχαλία τ 1 έχει µάζα m 1 και ακτίνα R και στο αυλάκι της έχει περιτυλιχθεί αβαρές νήµα, το οποίο διέρ χεται από τον λαιµό της µικρής τροχαλίας τ στο δε άκρο του έχει δε θεί
i) Nα αποδείξετε ότι το σώµα τελικά θα ηρεµήσει ως προς το δοκάρι και να βρείτε την κοινή τους ταχύτητα στο σύστηµα αναφοράς του εδάφους.
 Ένα δοκάρι µεγάλου µήκους και µάζας M, είναι ακίνητο πάνω σε λείο οριζόντιο έδαφος. Στο ένα άκρο του δοκαριού βρίσκεται ξύλινο σώµα µάζας m, το οποίο παρουσιάζει µε την επιφά νεια του δοκαριού συντελεστή
Ένα δοκάρι µεγάλου µήκους και µάζας M, είναι ακίνητο πάνω σε λείο οριζόντιο έδαφος. Στο ένα άκρο του δοκαριού βρίσκεται ξύλινο σώµα µάζας m, το οποίο παρουσιάζει µε την επιφά νεια του δοκαριού συντελεστή
. Αυτό σηµαίνει ότι το κέντρο µάζας κινείται ευθύγραµµα µε σταθερή επιτάχυνση a! = F!
 Οµογενής κυκλικός δίσκος µάζας m και ακτίνας, βρίσκεται πάνω σε λείο οριζόντιο έδαφος µε τον άξονα συµµετρίας του κατα κόρυφο. Εάν σ ένα σηµείο της περιφέρειας του δίσκου εξασκείται συνεχώς µια σταθερή
Οµογενής κυκλικός δίσκος µάζας m και ακτίνας, βρίσκεται πάνω σε λείο οριζόντιο έδαφος µε τον άξονα συµµετρίας του κατα κόρυφο. Εάν σ ένα σηµείο της περιφέρειας του δίσκου εξασκείται συνεχώς µια σταθερή
Ισορροπία στερεού. 3.2.8. Ποιες είναι οι δυνάμεις που ασκούνται; 3.2.9. Ένας Κύλινδρος Πάνω σε μια Σφήνα. Υλικό Φυσικής Χημείας
 3.2.. 3.2.1. Ροπές και ισορροπία. Πάνω σε λείο οριζόντιο επίπεδο βρίσκεται μια ράβδος μήκους l=4m, η οποία μπορεί να στρέφεται γύρω από κατακόρυφο άξονα, ο οποίος διέρχεται από το μέσον της Ο. Ασκούμε
3.2.. 3.2.1. Ροπές και ισορροπία. Πάνω σε λείο οριζόντιο επίπεδο βρίσκεται μια ράβδος μήκους l=4m, η οποία μπορεί να στρέφεται γύρω από κατακόρυφο άξονα, ο οποίος διέρχεται από το μέσον της Ο. Ασκούμε
i) Nα εκφράσετε σε συνάρτηση µε τον χρόνο την γωνιακή ταχύτητα της τροχαλίας.
 Στην διάταξη του σχήµατος ) οι δύο κυκλικοί δίσκοι Δ, Δ έχουν την ιδια ακτίνα R και αντίστοιχες µάζες m, m µπορούν δε να κυλίωνται χωρίς ολίσθηση κατά µήκος δύο κεκλιµέ νων επιπέδων που είναι µεταξύ τους
Στην διάταξη του σχήµατος ) οι δύο κυκλικοί δίσκοι Δ, Δ έχουν την ιδια ακτίνα R και αντίστοιχες µάζες m, m µπορούν δε να κυλίωνται χωρίς ολίσθηση κατά µήκος δύο κεκλιµέ νων επιπέδων που είναι µεταξύ τους
Nα δείξετε τις εξής προτάσεις:
 Nα δείξετε τις εξής προτάσεις: i) Εάν ένα υλικό σηµείο µάζας m κινείται πάνω σ ένα άξονα x x, ώστε κάθε στιγµή η ταχύτητά του v και η αποµάκρυνσή του x ως προς µια αρχή Ο του άξονα, να ικανοποιούν τη σχέση:
Nα δείξετε τις εξής προτάσεις: i) Εάν ένα υλικό σηµείο µάζας m κινείται πάνω σ ένα άξονα x x, ώστε κάθε στιγµή η ταχύτητά του v και η αποµάκρυνσή του x ως προς µια αρχή Ο του άξονα, να ικανοποιούν τη σχέση:
! =A'B=C!! C! = R" (1)
 Οµογενής κύβος ακµής α ισορροπεί επί ακλό νητης σφαιρικής επιφάνειας ακτίνας R, µε το κέντρο µάζας του ακριβώς πάνω από την κορυφή Α της επιφάνειας. Εάν µεταξύ του κύβου και της σφαιρικής επιφάνειας υπάρχει
Οµογενής κύβος ακµής α ισορροπεί επί ακλό νητης σφαιρικής επιφάνειας ακτίνας R, µε το κέντρο µάζας του ακριβώς πάνω από την κορυφή Α της επιφάνειας. Εάν µεταξύ του κύβου και της σφαιρικής επιφάνειας υπάρχει
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ. Άσκηση 1. (Ροπή αδράνειας - Θεμελιώδης νόμος στροφικής κίνησης)
 ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Άσκηση. (Ροπή αδράνειας - Θεμελιώδης νόμος στροφικής κίνησης) Ένας ομογενής οριζόντιος δίσκος, μάζας Μ και ακτίνας R, περιστρέφεται γύρω από κατακόρυφο ακλόνητο άξονα z, ο οποίος διέρχεται
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Άσκηση. (Ροπή αδράνειας - Θεμελιώδης νόμος στροφικής κίνησης) Ένας ομογενής οριζόντιος δίσκος, μάζας Μ και ακτίνας R, περιστρέφεται γύρω από κατακόρυφο ακλόνητο άξονα z, ο οποίος διέρχεται
ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ
 Ονοµατεπώνυµο: Διάρκεια: (3 45)+5=50 min Τµήµα: ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ Ζήτηµα ο Ένα στερεό µπορεί να στρέφεται γύρω από σταθερό άξονα και αρχικά ηρεµεί. Σε µια στιγµή δέχεται (ολική) ροπή
Ονοµατεπώνυµο: Διάρκεια: (3 45)+5=50 min Τµήµα: ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ Ζήτηµα ο Ένα στερεό µπορεί να στρέφεται γύρω από σταθερό άξονα και αρχικά ηρεµεί. Σε µια στιγµή δέχεται (ολική) ροπή
6ο ιαγώνισµα - Μηχανική Στερεού Σώµατος Ι. Θέµα Α
 6ο ιαγώνισµα - Μηχανική Στερεού Σώµατος Ι Ηµεροµηνία : 10 Μάρτη 2013 ιάρκεια : 3 ώρες Ονοµατεπώνυµο: Βαθµολογία % Θέµα Α Στις ερωτήσεις Α.1 Α.4 επιλέξτε την σωστη απάντηση [4 5 = 20 µονάδες] Α.1. Στερεό
6ο ιαγώνισµα - Μηχανική Στερεού Σώµατος Ι Ηµεροµηνία : 10 Μάρτη 2013 ιάρκεια : 3 ώρες Ονοµατεπώνυµο: Βαθµολογία % Θέµα Α Στις ερωτήσεις Α.1 Α.4 επιλέξτε την σωστη απάντηση [4 5 = 20 µονάδες] Α.1. Στερεό
ΛΥΣΗ: Κατά τον πολύ µικρό χρόνο Δt (Δt 0) που ενεργεί επί του σφαιριδίου Γ η ώθηση Ω. =mv. το σφαιρίδιο Β δέχεται τις κρουστικές δυνάµεις F
 Τρία µικρά σφαιρίδια της ίδιας µάζας είναι αρθρωµένα στις άκρες δύο συνεχόµεων ράβδων ΑΒ και ΒΓ αµελητέας µάζας, όπως φαίνεται στο σχήµα (1), το δε σύστηµα ισορροπεί εκτός πεδίου βαρύτητας. Στο σφαιρίδιο
Τρία µικρά σφαιρίδια της ίδιας µάζας είναι αρθρωµένα στις άκρες δύο συνεχόµεων ράβδων ΑΒ και ΒΓ αµελητέας µάζας, όπως φαίνεται στο σχήµα (1), το δε σύστηµα ισορροπεί εκτός πεδίου βαρύτητας. Στο σφαιρίδιο
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 3 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση,
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 3 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση,
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Σάββατο 24 Φλεβάρη 2018 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Σάββατο 24 Φλεβάρη 2018 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4
ΦΥΛΛΟ ΑΞΙΟΛΟΓΗΣΗΣ ΜΗΧΑΝΙΚΟΥ ΣΤΕΡΕΟΥ 1. ΘΕΜΑ Α Στις παρακάτω ερωτήσεις Α1-Α.5 να σημειώσετε την σωστή απάντηση
 ΦΥΛΛΟ ΑΞΙΟΛΟΓΗΣΗΣ ΜΗΧΑΝΙΚΟΥ ΣΤΕΡΕΟΥ 1 ΘΕΜΑ Α Στις παρακάτω ερωτήσεις Α1-Α.5 να σημειώσετε την σωστή απάντηση Α.1 Το στερεό του σχήματος δέχεται αντίρροπες δυνάμεις F 1 kαι F 2 που έχουν ίσα μέτρα. Το μέτρο
ΦΥΛΛΟ ΑΞΙΟΛΟΓΗΣΗΣ ΜΗΧΑΝΙΚΟΥ ΣΤΕΡΕΟΥ 1 ΘΕΜΑ Α Στις παρακάτω ερωτήσεις Α1-Α.5 να σημειώσετε την σωστή απάντηση Α.1 Το στερεό του σχήματος δέχεται αντίρροπες δυνάμεις F 1 kαι F 2 που έχουν ίσα μέτρα. Το μέτρο
διέρχεται από το σηµείο Ο της ράβδου, υπό την επίδραση των βαρών m 1 από τον άξονα περιστροφής, που αναλύεται στην οριζόντια συνιστώσα!
 Θεωρήστε οριζόντια ράβδο αµελητέας µάζας, η οποία µπορεί να περιστρέφεται περί σταθερό οριζόντιο άξονα κάθετο στη ράβδο. Στα άκρα της υπάρχουν δυο διαφορετικές σηµειακές µάζες m, m, που οι αντίστοιχες
Θεωρήστε οριζόντια ράβδο αµελητέας µάζας, η οποία µπορεί να περιστρέφεται περί σταθερό οριζόντιο άξονα κάθετο στη ράβδο. Στα άκρα της υπάρχουν δυο διαφορετικές σηµειακές µάζες m, m, που οι αντίστοιχες
. Εάν η σφαίρα κυλίεται πάνω στο δοκάρι να βρείτε: i) την επιτάχυνση του δοκαριού και του κέντρου της σφαίρας, στο σύστηµα αναφοράς του δαπέδου και
 Οµογενής σφαίρα µάζας m και ακτίνας R είναι ακίνητη πάνω σε οριζόντιο δοκάρι µάζας Μ και µήκους L, που µπορεί να ολισθαίνει χωρίς τριβή επί οριζοντίου δαπέδου. Η σφαίρα εφάπτεται στο δεξιό άκρο Β του δοκαριού
Οµογενής σφαίρα µάζας m και ακτίνας R είναι ακίνητη πάνω σε οριζόντιο δοκάρι µάζας Μ και µήκους L, που µπορεί να ολισθαίνει χωρίς τριβή επί οριζοντίου δαπέδου. Η σφαίρα εφάπτεται στο δεξιό άκρο Β του δοκαριού
Ασκήσεις στροφικής κίνησης στερεού σώµατος
 Ασκήσεις στροφικής κίνησης στερεού σώµατος. Ένας κύλινδρος, βάρους w=0 και διαµέτρου 80 c, περιστρέφεται γύρω από τον γεωµετρικό του άξονα. Ποια σταθερή ροπή (τ) πρέπει να ασκείται, στον κύλινδρο ώστε
Ασκήσεις στροφικής κίνησης στερεού σώµατος. Ένας κύλινδρος, βάρους w=0 και διαµέτρου 80 c, περιστρέφεται γύρω από τον γεωµετρικό του άξονα. Ποια σταθερή ροπή (τ) πρέπει να ασκείται, στον κύλινδρο ώστε
όπου Μ η µάζα της Γης την οποία θεωρούµε σφαίρα οµογενή, G η παγκόσµια σταθερά της βαρύτητας και L!
 Είναι γνωστό ότι, όταν ένα σώµα κινείται µέσα στο βαρυτικό πεδίο της Γης υπό την επίδραση µόνο της Νευτώνειας έλξεως, η τροχιά που διαγράφει το κέντρο µάζας του είναι επίπεδη και µάλιστα το επίπεδό της
Είναι γνωστό ότι, όταν ένα σώµα κινείται µέσα στο βαρυτικό πεδίο της Γης υπό την επίδραση µόνο της Νευτώνειας έλξεως, η τροχιά που διαγράφει το κέντρο µάζας του είναι επίπεδη και µάλιστα το επίπεδό της
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος ΙΙ
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος ΙΙ Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Κυριακή 28 Φλεβάρη 2016 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος ΙΙ Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Κυριακή 28 Φλεβάρη 2016 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1
ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΤΗ ΣΤΡΟΦΟΡΜΗ ΚΑΙ ΣΤΗ ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΣΤΡΟΦΟΡΜΗΣ. Η στροφορμή ενός στερεού σώματος είναι μηδενική, όταν το σώμα δεν περιστρέφεται.
 ο ΓΕΛ ΓΑΛΑΤΣΙΟΥ ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΤΗ ΣΤΡΟΦΟΡΜΗ ΚΑΙ ΣΤΗ ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΣΤΡΟΦΟΡΜΗΣ Διερεύνηση της σχέσης L=ω Η στροφορμή ενός στερεού σώματος είναι μηδενική, όταν το σώμα δεν περιστρέφεται. Η ροπή αδράνειας Ι
ο ΓΕΛ ΓΑΛΑΤΣΙΟΥ ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΤΗ ΣΤΡΟΦΟΡΜΗ ΚΑΙ ΣΤΗ ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΣΤΡΟΦΟΡΜΗΣ Διερεύνηση της σχέσης L=ω Η στροφορμή ενός στερεού σώματος είναι μηδενική, όταν το σώμα δεν περιστρέφεται. Η ροπή αδράνειας Ι
Οµογενής ράβδος µάζας m και µήκους L, κρατεί ται οριζόντια ακουµπώντας σε σταθερή ακίδα που απέχει απόσταση x από το κέντρο µάζας C της ράβδου.
 Οµογενής ράβδος µάζας m και µήκους L, κρατεί ται οριζόντια ακουµπώντας σε σταθερή ακίδα που απέχει απόσταση x από το κέντρο µάζας C της ράβδου. i) Να βρεθεί η απόσταση x, ώστε την στιγµή που η ράβδος αφήνεται
Οµογενής ράβδος µάζας m και µήκους L, κρατεί ται οριζόντια ακουµπώντας σε σταθερή ακίδα που απέχει απόσταση x από το κέντρο µάζας C της ράβδου. i) Να βρεθεί η απόσταση x, ώστε την στιγµή που η ράβδος αφήνεται
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος Ενδεικτικές Λύσεις Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος Ενδεικτικές Λύσεις Θέµα Α Α.1. Ενας δίσκος στρέφεται γύρω από άξονα που διέρχεται από το κέντρο του και είναι κάθετος στο επίπεδό του. Η τιµή
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος Ενδεικτικές Λύσεις Θέµα Α Α.1. Ενας δίσκος στρέφεται γύρω από άξονα που διέρχεται από το κέντρο του και είναι κάθετος στο επίπεδό του. Η τιµή
3.2. Ισορροπία στερεού.
 3.2.. 3.2.1. Ροπές και ισορροπία. Πάνω σε λείο οριζόντιο επίπεδο βρίσκεται μια ράβδος μήκους l=4m, η οποία μπορεί να στρέφεται γύρω από κατακόρυφο άξονα, ο οποίος διέρχεται από το μέσον της Ο. Ασκούμε
3.2.. 3.2.1. Ροπές και ισορροπία. Πάνω σε λείο οριζόντιο επίπεδο βρίσκεται μια ράβδος μήκους l=4m, η οποία μπορεί να στρέφεται γύρω από κατακόρυφο άξονα, ο οποίος διέρχεται από το μέσον της Ο. Ασκούμε
όπου x η οριζόντια µετατόπιση του σώµατος, k θετική σταθερά και! i το µοναδιαίο διάνυσµα του οριζόντιου άξονα x.
 Ένα µικρό σώµα βάλλεται οριζόντια µε ταχύτητα v 0 εντός του πεδίου βαρύτητας της Γης από ένα σηµείο Α που η απόστασή του από το οριζόντιο έδαφος είναι h. Tο σώµα κατά την κίνησή του δέχεται εκτός από το
Ένα µικρό σώµα βάλλεται οριζόντια µε ταχύτητα v 0 εντός του πεδίου βαρύτητας της Γης από ένα σηµείο Α που η απόστασή του από το οριζόντιο έδαφος είναι h. Tο σώµα κατά την κίνησή του δέχεται εκτός από το
Β. Συµπληρώστε τα κενά των παρακάτω προτάσεων
 ΔΙΑΓΩΝΙΣΜΑ ΣΤΟ ΣΤΕΡΕΟ ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΘΕΜΑ Α Α. Στις ερωτήσεις 1 έως 3 επιλέξτε τη σωστή απάντηση 1. Δυο δακτύλιοι µε διαφορετικές ακτίνες αλλά ίδια µάζα κυλάνε χωρίς ολίσθηση σε οριζόντιο έδαφος µε την
ΔΙΑΓΩΝΙΣΜΑ ΣΤΟ ΣΤΕΡΕΟ ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΘΕΜΑ Α Α. Στις ερωτήσεις 1 έως 3 επιλέξτε τη σωστή απάντηση 1. Δυο δακτύλιοι µε διαφορετικές ακτίνες αλλά ίδια µάζα κυλάνε χωρίς ολίσθηση σε οριζόντιο έδαφος µε την
, σταθερής κατεύθυνσης, της οποίας το µέτρο µεταβάλλεται µε τον χρόνο t, σύµφωνα µε την σχέση:
 Σώµα µάζας m σχήµατος ορθογώνιου κιβωτίου, ισορροπεί πάνω σε τραχύ οριζόντιο επίπεδο και στην άνω επιφάνειά του έχει τοποθετηθεί σώµα µάζας m/. Κάποια στιγµή που λαµβάνε ται ως αρχή µέτρησης του χρόνου
Σώµα µάζας m σχήµατος ορθογώνιου κιβωτίου, ισορροπεί πάνω σε τραχύ οριζόντιο επίπεδο και στην άνω επιφάνειά του έχει τοποθετηθεί σώµα µάζας m/. Κάποια στιγµή που λαµβάνε ται ως αρχή µέτρησης του χρόνου
ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΕΡΕΟ. ΘΕΜΑ Α (μοναδες 25)
 ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΕΡΕΟ ΘΕΜΑ Α (μοναδες 25) Α1. Σε στερεό που περιστρέφεται γύρω από σταθερό κατακόρυφο άξονα ενεργεί σταθερή ροπή. Τότε αυξάνεται με σταθερό ρυθμό: α. η ροπή αδράνειας του β. η
ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΕΡΕΟ ΘΕΜΑ Α (μοναδες 25) Α1. Σε στερεό που περιστρέφεται γύρω από σταθερό κατακόρυφο άξονα ενεργεί σταθερή ροπή. Τότε αυξάνεται με σταθερό ρυθμό: α. η ροπή αδράνειας του β. η
Διαγώνισμα Μηχανική Στερεού Σώματος
 Διαγώνισμα Μηχανική Στερεού Σώματος Θέμα Α Στις ημιτελείς προτάσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση η οποία τη συμπληρώνει σωστά
Διαγώνισμα Μηχανική Στερεού Σώματος Θέμα Α Στις ημιτελείς προτάσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση η οποία τη συμπληρώνει σωστά
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/2014
 ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/014 ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α1 Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/014 ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α1 Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
i) Να δείξετε ότι αν για µια τιµή της γωνίας θ η ράβδος ισορροπεί, η ισορροπία αυτή είναι αδιάφορη.
 Η ράβδος του σχήµατος έχει µήκος L, βάρος w και στηρίζεται διά του άκρου της Α επί λείου τοίχου, ενώ το άλλο άκρο της Β ακουµπά ει σε λεία κοίλη επιφάνεια. Η τοµή της επιφάνειας µε κατακόρυφο επίπεδο που
Η ράβδος του σχήµατος έχει µήκος L, βάρος w και στηρίζεται διά του άκρου της Α επί λείου τοίχου, ενώ το άλλο άκρο της Β ακουµπά ει σε λεία κοίλη επιφάνεια. Η τοµή της επιφάνειας µε κατακόρυφο επίπεδο που
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΦΕΒΡΟΥΑΡΙΟΣ 2017 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6
 ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΦΕΒΡΟΥΑΡΙΟΣ 017 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6 Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΦΕΒΡΟΥΑΡΙΟΣ 017 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6 Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό
ii) Να δείξετε ότι το σφαιρίδιο εκτελεί µια µη αρµονική περιοδική ταλάντωση, της οποίας να υπολογίσετε την περίοδο.
 Το σύστηµα του σχήµατος αποτελείται από δύο όµοια ελατήρια στα θεράς και φυσικού µήκους α, των οποίων οι άξονες βρίσκονται πάνω στην ευθεία ΑΒ, όπου Α, Β είναι δύο ακλόνητα σηµεία του επιπέδου. Εκτρέπουµε
Το σύστηµα του σχήµατος αποτελείται από δύο όµοια ελατήρια στα θεράς και φυσικού µήκους α, των οποίων οι άξονες βρίσκονται πάνω στην ευθεία ΑΒ, όπου Α, Β είναι δύο ακλόνητα σηµεία του επιπέδου. Εκτρέπουµε
ii) Nα βρεθεί η κινητική ενέργεια της σφαίρας, όταν το δοκάρι έχει µετατοπιστεί κατά S ως προς το έδαφος.
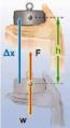 Στην διάταξη του σχήµατος () το δοκάρι Δ έχει µάζα Μ και µπορεί να ολισθαίνει πάνω σε λείο κεκλιµένο επίπεδο γωνίας κλίσεως φ ως προς τον ορίζοντα. Κάποια στιγµή που λαµβά νεται ως αρχή µέτρησης του χρόνου
Στην διάταξη του σχήµατος () το δοκάρι Δ έχει µάζα Μ και µπορεί να ολισθαίνει πάνω σε λείο κεκλιµένο επίπεδο γωνίας κλίσεως φ ως προς τον ορίζοντα. Κάποια στιγµή που λαµβά νεται ως αρχή µέτρησης του χρόνου
ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 1. Ο κύλινδρος και ο δίσκος του σχήματος, έχουν την ίδια μάζα και περιστρέφονται με την ίδια γωνιακή ταχύτητα ω. Ποιό σώμα θα σταματήσει πιο δύσκολα; α) Το Α. β) Το Β. γ) Και τα δύο το ίδιο. 2. Ένας ομογενής
1. Ο κύλινδρος και ο δίσκος του σχήματος, έχουν την ίδια μάζα και περιστρέφονται με την ίδια γωνιακή ταχύτητα ω. Ποιό σώμα θα σταματήσει πιο δύσκολα; α) Το Α. β) Το Β. γ) Και τα δύο το ίδιο. 2. Ένας ομογενής
ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ. Δίνεται ότι η ροπή αδράνειας του δίσκου ως προς τον άξονα Κ είναι Ι= M R
 ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ 1 Η ράβδος ΟΑ του σχήματος μπορεί να στρέφεται γύρω από τον άξονα z z χωρίς τριβές Tη στιγμή t=0 δέχεται την εφαπτομενική δύναμη F σταθερού μέτρου 0 Ν, με φορά όπως φαίνεται στο σχήμα
ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ 1 Η ράβδος ΟΑ του σχήματος μπορεί να στρέφεται γύρω από τον άξονα z z χωρίς τριβές Tη στιγμή t=0 δέχεται την εφαπτομενική δύναμη F σταθερού μέτρου 0 Ν, με φορά όπως φαίνεται στο σχήμα
(σχ. 1). Εφαρ µόζοντας για την µεταφορική συνιστώσα της κύλισης του δίσκου τον
 Oµογενής λεπτός δίσκος ακτίνας R και µάζας m, ακινητεί επί οριζόντιου εδάφους µε το οποίο παρουσιάζει συντελεστή οριακής τριβής µ το δε επιπεδό του είναι κατακόρυφο,. Κάποια στιγµή εφαρµόζεται στο κέντρο
Oµογενής λεπτός δίσκος ακτίνας R και µάζας m, ακινητεί επί οριζόντιου εδάφους µε το οποίο παρουσιάζει συντελεστή οριακής τριβής µ το δε επιπεδό του είναι κατακόρυφο,. Κάποια στιγµή εφαρµόζεται στο κέντρο
3.3. Δυναμική στερεού.
 3.3.. 3.3.1. Ροπή και γωνιακή επιτάχυνση Μια οριζόντια τετράγωνη πλάκα ΑΒΓΔ, πλευράς 1m και μάζας 20kg μπορεί να στρέφεται γύρω από σταθερό άξονα z που περνά από το κέντρο της. Η πλάκα αποκτά γωνιακή ταχύτητα
3.3.. 3.3.1. Ροπή και γωνιακή επιτάχυνση Μια οριζόντια τετράγωνη πλάκα ΑΒΓΔ, πλευράς 1m και μάζας 20kg μπορεί να στρέφεται γύρω από σταθερό άξονα z που περνά από το κέντρο της. Η πλάκα αποκτά γωνιακή ταχύτητα
των Α και Β αντιστοίχως είναι παράλληλες (σχ. 12) που σηµαί Σχήµα 11 Σχήµα 12
 Δύο ακριβώς όµοιες λεπτές ράβδοι OA και AB µήκους L και µάζας m, αρθρώνονται στο σηµείο Α το δε άκρο Ο της ΟΑ αρθρώνεται σε σταθερό υποστήριγµα, ενώ το άκρο Β της ΑΒ µπο ρεί να ολισθαίνει πάνω σε λείο
Δύο ακριβώς όµοιες λεπτές ράβδοι OA και AB µήκους L και µάζας m, αρθρώνονται στο σηµείο Α το δε άκρο Ο της ΟΑ αρθρώνεται σε σταθερό υποστήριγµα, ενώ το άκρο Β της ΑΒ µπο ρεί να ολισθαίνει πάνω σε λείο
6ο Πρόχειρο Τεστ Γ Τάξης Λυκείου Θεµελιώδης Νόµος Στροφικής Κίνησης Σύνολο Σελίδων: πέντε (5) - ιάρκεια Εξέτασης: 90 min Βαθµολογία % Ονοµατεπώνυµο:
 6ο Πρόχειρο Τεστ Γ Τάξης Λυκείου Θεµελιώδης Νόµος Στροφικής Κίνησης Σύνολο Σελίδων: πέντε (5) - ιάρκεια Εξέτασης: 90 min Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4 να γράψετε στο
6ο Πρόχειρο Τεστ Γ Τάξης Λυκείου Θεµελιώδης Νόµος Στροφικής Κίνησης Σύνολο Σελίδων: πέντε (5) - ιάρκεια Εξέτασης: 90 min Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4 να γράψετε στο
ΜΕΡΟΣ Γ! 2η οµάδα λυµένων παραδειγµάτων
 ΜΕΡΟΣ Γ η οµάδα λυµένων παραδειγµάτων Στις άκρες αβαρούς και λεπτής ράβδου µηκούς L, έχουν στερεωθεί δύο όµοιες σφαίρες, µάζας m και ακτίνας R, το δε σύστηµα στρέφεται µε σταθερή γωνιακή ταχύτητα περί
ΜΕΡΟΣ Γ η οµάδα λυµένων παραδειγµάτων Στις άκρες αβαρούς και λεπτής ράβδου µηκούς L, έχουν στερεωθεί δύο όµοιες σφαίρες, µάζας m και ακτίνας R, το δε σύστηµα στρέφεται µε σταθερή γωνιακή ταχύτητα περί
Για τις παραπάνω ροπές αδράνειας ισχύει: α. β. γ. δ. Μονάδες 5
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΘΕΡΙΝΑ Α (ΑΠΑΝΤΗΣΕΙΣ) ΗΜΕΡΟΜΗΝΙΑ: 01-03-2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ M-ΑΓΙΑΝΝΙΩΤΑΚΗ ΑΝ.-ΠΟΥΛΗ Κ. ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΘΕΡΙΝΑ Α (ΑΠΑΝΤΗΣΕΙΣ) ΗΜΕΡΟΜΗΝΙΑ: 01-03-2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ M-ΑΓΙΑΝΝΙΩΤΑΚΗ ΑΝ.-ΠΟΥΛΗ Κ. ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας
i) το πλάτος ταλάντωσης του καροτσιού µετά την ενσωµάτωση του σφαιριδίου σ' αυτό και
 Ένα καροτσάκι που περιέχει άµµο, συνολικής µάζας M, εκτελεί οριζόντια αρµονική ταλάντωση σε λείο επίπεδο, µε τη βοήθεια ιδανικού οριζόντιου ελατηρίου σταθεράς k. Ένα σφαιρίδιο µάζας m
Ένα καροτσάκι που περιέχει άµµο, συνολικής µάζας M, εκτελεί οριζόντια αρµονική ταλάντωση σε λείο επίπεδο, µε τη βοήθεια ιδανικού οριζόντιου ελατηρίου σταθεράς k. Ένα σφαιρίδιο µάζας m
µε φορά προς το κυρτό µέρος του σύρµατος (σχήµα α) η οποία µαζί µε την ακτινική συνιστώσα w!
 Το κυκλικό σύρµα του σχήµατος έχει µάζα m/ και είναι κρεµασµένο από κατακόρυφο σπάγκο αµελητέας µάζας αλλά επαρκούς αντοχής. Δύο όµοιες σηµειακές χάντρες, καθε µιά µε µάζα m, αφήνονται ταυτόχρονα από την
Το κυκλικό σύρµα του σχήµατος έχει µάζα m/ και είναι κρεµασµένο από κατακόρυφο σπάγκο αµελητέας µάζας αλλά επαρκούς αντοχής. Δύο όµοιες σηµειακές χάντρες, καθε µιά µε µάζα m, αφήνονται ταυτόχρονα από την
F r. www.ylikonet.gr 1
 3.5. Έργο Ενέργεια. 3.5.1. Έργο δύναµης- ροπής και Κινητική Ενέργεια. Το οµοαξονικό σύστηµα των δύο κυλίνδρων µε ακτίνες R 1 =0,1m και R =0,5m ηρεµεί σε οριζόντιο επίπεδο. Τυλίγουµε γύρω από τον κύλινδρο
3.5. Έργο Ενέργεια. 3.5.1. Έργο δύναµης- ροπής και Κινητική Ενέργεια. Το οµοαξονικό σύστηµα των δύο κυλίνδρων µε ακτίνες R 1 =0,1m και R =0,5m ηρεµεί σε οριζόντιο επίπεδο. Τυλίγουµε γύρω από τον κύλινδρο
Επαναληπτική άσκηση: Περιστροφή Κρούση - Κύλιση με ολίσθηση
 Επαναληπτική άσκηση: Περιστροφή Κρούση - Κύλιση με ολίσθηση α) Το μέτρο της δύναμης που δέχεται η ράβδος από την άρθρωση λίγο πριν και αμέσως μετά το κόψιμο του νήματος, Η ομογενής και ισοπαχής ράβδος
Επαναληπτική άσκηση: Περιστροφή Κρούση - Κύλιση με ολίσθηση α) Το μέτρο της δύναμης που δέχεται η ράβδος από την άρθρωση λίγο πριν και αμέσως μετά το κόψιμο του νήματος, Η ομογενής και ισοπαχής ράβδος
Μηχανική Στερεού Ασκήσεις Εμπέδωσης
 Μηχανική Στερεού Ασκήσεις Εμπέδωσης Όπου χρειάζεται, θεωρείστε δεδομένο ότι g = 10m/s 2. 1. Μία ράβδος ΟΑ, μήκους L = 0,5m, περιστρέφεται γύρω από σταθερό άξονα που περνάει από το ένα άκρο της Ο, με σταθερή
Μηχανική Στερεού Ασκήσεις Εμπέδωσης Όπου χρειάζεται, θεωρείστε δεδομένο ότι g = 10m/s 2. 1. Μία ράβδος ΟΑ, μήκους L = 0,5m, περιστρέφεται γύρω από σταθερό άξονα που περνάει από το ένα άκρο της Ο, με σταθερή
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β ΛΥΚΕΙΟΥ (ΠΡΟΕΤΟΙΜΑΣΙΑ) ΗΜΕΡΟΜΗΝΙΑ: 19/03/2017 (ΑΠΑΝΤΗΣΕΙΣ) ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 206-207 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β ΛΥΚΕΙΟΥ (ΠΡΟΕΤΟΙΜΑΣΙΑ) ΗΜΕΡΟΜΗΝΙΑ: 9/03/207 (ΑΠΑΝΤΗΣΕΙΣ) ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 206-207 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β ΛΥΚΕΙΟΥ (ΠΡΟΕΤΟΙΜΑΣΙΑ) ΗΜΕΡΟΜΗΝΙΑ: 9/03/207 (ΑΠΑΝΤΗΣΕΙΣ) ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό
Γ ΤΑΞΗ ΤΜΗΜΑ ΟΝΟΜΑ. ΘΕΜΑ 1ο. 7 mr 5. 1 mr. Μονάδες 5. α. 50 W β. 100 W γ. 200 W δ. 400 W
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΟΝΟΜΑ ΤΜΗΜΑ ΕΠΑΝΑΛΗΠΤΙΚΟ ΙΑΓΩΝΙΣΜΑ ΤΕΤΑΡΤΗ 8 ΜΑΡΤΙΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ) ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1ο Στις ερωτήσεις 1-4 να γράψετε
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΟΝΟΜΑ ΤΜΗΜΑ ΕΠΑΝΑΛΗΠΤΙΚΟ ΙΑΓΩΝΙΣΜΑ ΤΕΤΑΡΤΗ 8 ΜΑΡΤΙΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ) ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1ο Στις ερωτήσεις 1-4 να γράψετε
Μηχανικό Στερεό. Μια εργασία για την Επανάληψη
 Μηχανικό Στερεό. Μια εργασία για την Επανάληψη Απλές προτάσεις Για τον έλεγχο της κατανόησης και εφαρμογής των εννοιών Δογραματζάκης Γιάννης 9/5/2013 Απλές προτάσεις για τον έλεγχο της κατανόησης και εφαρμογής
Μηχανικό Στερεό. Μια εργασία για την Επανάληψη Απλές προτάσεις Για τον έλεγχο της κατανόησης και εφαρμογής των εννοιών Δογραματζάκης Γιάννης 9/5/2013 Απλές προτάσεις για τον έλεγχο της κατανόησης και εφαρμογής
Eάν L 1, L 2 είναι τα αντίστοιχα φυσικά µήκη των ελατηρίων ε 1 και ε 2 τότε για την απόσταση ΑΒ των σηµείων στήριξης των ελατηρίων θα έχουµε:
 Tο µικρό σώµα του σχήµατος (1) έχει µάζα m και συγκρατείται στο λείο οριζόντιο έδαφος σε τέτοια θέση, ώστε τα ελατήρια ε 1 και ε να είναι τεντωµένα κατά α απο την φυσική τους κατάσταση. i) Eάν k, k είναι
Tο µικρό σώµα του σχήµατος (1) έχει µάζα m και συγκρατείται στο λείο οριζόντιο έδαφος σε τέτοια θέση, ώστε τα ελατήρια ε 1 και ε να είναι τεντωµένα κατά α απο την φυσική τους κατάσταση. i) Eάν k, k είναι
