Paprastosios DIFERENCIALINĖS LYGTYS
|
|
|
- Μωσῆς Αντωνοπούλου
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Diferencialinių lgčių ir skaičiavimo matematikos katedra Naugarduko g. 24, LT-3225 Vilnius, Lietuva Vilnius universitetas, 23
2 AS, 22
3 TURINYS Lentelių sąrašas Iliustracijų sąrašas Pagrindiniai žmens Pratarmė iv v i i SKYRIUS. Paprastosios diferencialinės lgts ir jų sistemos. Diferencialinė lgtis ir jos sprendiniai Diferencialinė lgtis ir jos apibrėžimo sritis Diferencialinės lgties sprendiniai Kreivių šeimos diferencialinė lgtis Koši uždavins Koši uždavins Sprendinio egzistavimas ir vienatis Ypatingieji sprendiniai Diferencialinių lgčiu sistemos n-osios eilės DL suvedimas į n-osios eilės normaliąją DLS n-osios eilės normaliosios DLS suvedimas į n-osios eilės DL Autonominės ir neautonominės DL SKYRIUS. Tiesinės diferencialinės lgts 23. Tiesinė n-osios eilės diferencialinė lgtis Tiesinis diferencialinis operatorius Funkcijų tiesinis priklausomumas ir nepriklausomumas Tiesinė homogeninė diferencialinė lgtis Tiesinė nehomogeninė diferencialinė lgtis Tiesinė diferencialinė lgtis su pastoviais koeficientais Homogeninės diferencialinės lgties su pastoviais koeficientais sprendiniai Nehomogeninės diferencialinės lgties su pastoviais koeficientais sprendiniai sprendiniai SKYRIUS. Klasikinės DL ir jų integravimas 39. Pirmosios eilės DL integravimas kvadratūromis DL, kai žinoma sprendinio išvestinė
4 .2. Sprendinio tęsins Sprendinio aprėžtumas Apverstosios DL integravimas Sprendinio egzistavimo ir vienaties teorema vienmatei autonominiai lgčiai p-procesas ir projektvinė tiesė Tiesinė homogeninė pirmosios eilės diferencialų lgtis Diferencialinės -formos Lgts su atskirtaisiais ir atsiskiriančiais kintamaisiais Integruojantsis daugiklis σ-procesas ir π-procesas Integruojantsis daugiklis kaip sudėtinė funkcija Pirmosios eilės tiesinės diferencialinės lgts Homogeninė tiesinė diferencialinė lgtis Homogeninė tiesinė diferencialinė lgtis su periodiniu koeficientu Nehomogeninė tiesinė diferencialinė lgtis Bernulio ir Rikačio lgts Bernulio lgtis Rikačio lgtis Aukštesnės eilės lgčių integravimas kvadratūromis Lgtis kurioje ra tik ir (n) Lgtis kurioje ra tik (n ) ir (n) Lgtis kurioje ra tik (n 2) ir (n) Dalkinė rodklė 88 Vardų rodklė 9 Literatūra 92
5 Lentelių sąrašas 3. Integruojančiųjų daugiklių µ(z(, )) egzistavimo sąlgos
6 Paprastosios Diferencialinės Lgts vi
7 Iliustracijų sąrašas. DL = ( 2 ) apibrėžimo srits DL = 2 2 apibrėžimo sritis DL apibrėžimo sritis ir DL sprendinio grafikas Integralinė kreivė ir jos projekcijos: sprendinio grafikas = sin ; sprendinio išvestinės grafikas = cos ; fazinė trajektorija 2 + ( ) 2 = Kreivę apibrėžiančios funkcijos DL = 2 integralinės kreivės DL = integralinės kreivės, kai > DL d + d = integralinės kreivės pvz. DL sprendiniai: (a) išreikštinių sprendinių grafikai; (b) neišreikštiniai sprendiniai DL = cos integralinės kreivės Parabolių ir elipsių šeimos Koši uždavins pirmos eilės lgčiai Koši uždavins antros eilės lgčiai Integralinės kreivės tęsins iki kompakto krašto Neptatęsiamas į dešinę sprendins DL = 3 2/3 integralinės kreivės. DL patingasis taškas ir patingasis sprendins Tiesinės lgties sprendinių erdvė Homogeninės TDL integralinės kreivės Nehomogeninės TDL integralinės kreivės Funkcijų tiesinė priklausombė Lgties = f() sprendinio = ϕ() elgsena intervale (a; b]: (a) lim b b f(ξ) dξ < + ; (c) f(ξ) dξ = +.. b Lgties = g() sprendiniai Lgties = g() stacionarieji sprendiniai Lgties = g() sprendinio = ϕ() elgsena, kai Lgties = 3( ) 2/3 sprendiniai Neišreikštinės ( ) 2 = + 4a 2 DL sprendiniai Projektvinės koordinatės
8 3.8 DL integralinės kreivės įvairiose koordinatėse Laužtės apendiksų ir parazitinių ciklų naikinimas vienajungėje Koncentriniių apskritimų šeima Srities skaidmas atskiriant kintamuosius Spindulių šeima σ-procesas ir Mėbijaus lapas Integralinės kreivės (parabolių šeima = C 2 ) gautos σ-procesu. Tuo pačiu skaičiumi (C) sunumeruotos atitinkamos integralinės kreivės, C = atitinka = tiesę, C = σ koordinačių pradžią Polinės koordinatės, p-procesas ir pusiau begalinis cilindras Hiperbolių šeima ir jų asimptotės Spiralių šeima ir jų vaizdai (eksponentės) gauti π-procesu ant cilindro išklotinės Homogeninės TDL integralinės kreivės Monodromijos operatorius Nulinio sprendinio stabilumas Stabilus periodinis sprendins Bernulio lgties integralinės kreivės
9 Pagrindiniai žmens, įrodmo pradžia ir pabaiga apibrėžimo, pastabos, išvados pabaiga := priskirimo, apibrėžimo žmuo tapatumo žmuo, išdavos sekimo žmuo ( išplaukia ), implikacija ekvivalentiškumo žmuo ( būtina ir pakankama arba tada ir tik tada ) bendrumo kvantorius ( kiekvienas ) egzistavimo kvantorius ( egzistuoja )! egzistavimo ir vienaties kvantorius ( egzistuoja vienintelis ) N {,,2, } natūraliųjų skaičių aibė Z {,-2,-,,,2, } sveikųjų skaičių aibė R realiųjų skaičių aibė R t, R, R realiųjų skaičių t-ašis, -ašis, -ašis C kompleksinių skaičių aibė X ra aibės X elementas, priklauso aibei X X Y aibių sankirta X Y aibių sąjunga X Y aibių Dekarto sąjunga didėjimo žmuo mažėjimo žmuo iškilumas aukštn iškilumas žemn R n erdvės R n elementas v vektorius, A vektorius-stulpelis, matrica C toldžiųjų funkcijų klasė C k toldžiai k-kartų diferencijuojamųjų funkcijų klasė C glodžiųjų funkcijų klasė D( ) (atvaizdžio, lgties) apibrėžimo sritis D( ) (atvaizdžio, lgties) apibrėžimo sritis R( ) (atvaizdžio) reikšmių sritis
10 skrius Paprastosios diferencialinės lgts ir jų sistemos Šiame skriuje susipažinsime su paprastosiomis diferencialinėmis lgtimis ir jų sprendiniais. Suformuluosime pradinį uždavinį. Nagrinėsime diferencialinių lgčių sistemas ir jų ršį su aukštesniosios eilės diferencialine lgtimi.. Diferencialinė lgtis ir jos sprendiniai? Matematikoje funkcija f vadinamas atvaizdis f : R n R, o f(,..., n) žmima funkcijos reikšmė taške (,..., n) R n, tačiau dažnai patogu taip žmėti ir pačią funkciją, kai reikia nurodti jos argumentus. Laiksime, kad visos nagrinėjamos funkcijos ra toldžios savo argumentų atžvilgiu, t.. f C(D), čia D ra sritis. Sritimi vadinama atviroji ir jungioji aibė. Jeigu D ra atviroji aibė, tuomet kiekvienas tos aibės taškas ra vidinis. Realiųjų skaičių tiesėje R jungiosios aibės ra intervalai (a; b), [a; b), (a; b], [a; b], a, b R. Srits ra tik atvirieji intervalai I = (a; b), ( ; b), (a; + ) ir pati tiesė R = ( ; + ). Žmėsime R = [ ; + ], R + = (; + ), R = ( ; ). Sąvoka glodžioji funkcija nėra vienareikšmiškai apibrėžta matematinėje literatūroje. Smooth function (angl.), glatte funktion (vok.) atitinka klasę C, гладкая функция arba непрерывно дифференцируемая функция (rus.) atitinka klasę C. Šiame konspekte glodžąja funkcija vadinsime C klasės funkciją, o toldžiai diferencijuojamas funkcijas atitinka C klasė.? Funkcijos = f() išvestinės gali būti žmimos:,,, (n), f (), f (), f (n) d (), d, d n, ẏ, ÿ. dn Tašku virš kintamojo dažniausiai žmėsime funkcijos = (t) išvestines pagal kintamąjį t, kurio prasmė dažnai ra laikas, žmėsime ẋ := d dt, ẍ := d2 dt 2, (n) = dn dt n... Diferencialinė lgtis ir jos apibrėžimo sritis Tarkime, kad funkcija F (,, p,..., p n ) ra tolžiai diferencijuojama ir būtinai priklauso nuo argumento p n.. apibrėžimas [Paprastoji diferencialinė lgtis]. Paprastąja diferencialine lgtimi (PDL) vadinama lgbė F (,,,..., (n) ) =, (.) kurioje ra nepriklausomas kintamasis, () ieškoma (nežinoma) funkcija.
11 . Diferencialinė lgtis ir jos sprendiniai 2. ppavzds [Paprastosios diferencialinės lgts]. PDL pavzdžiai: = sin, + e =, e + =..2 ppavzds [Diferencialinės dalinių išvestinių lgts]. Lgts u u =, v t = 2 v + 2 v 2 2 nėra PDL, nes į jas įeina ieškomų funkcijų u(, ) ir v(t,, ) dalinės išvestinės. PDL uždaviniuose ieškoma nežinoma vieno kintamojo funkcija, tuo tarpu diferencialinėse dalinių išvestinių lgtse ieškoma kelių kintamųjų funkcija. Kadangi šiame kurse nagrinėsime tik PDL, todėl trumpai jas vadinsime diferencialinėmis lgtimis (DL)..2 apibrėžimas [DL eilė]. Diferencialinės lgties eile vadinama auksčiausios išvestinės eilė diferencialinėje lgtje..3 ppavzds [DL eilė]. DL F (,,,..., (n) ) = ra n-osios eilės, o DL F (,, ) = ra pirmosios eilės.. pavzdje pateiktos pirmosios, trečiosios ir antrosios eilės DL.? Jeigu lgtis (nebūtinai DL) F (,, p,..., p n) = (.2) aprašoma toldžiai diferencijuojama funkcija F ir taške (,, p,..., p n ) išpildta sąlga F ( p,, p n,..., p n ), (.3) tuomet (remdamiesi neišreikštinės funkcijos teorema) (.2) lgtį galima išspręsti p n atžvilgiu taško (,, p,..., p n ) aplinkoje: p n = f(,, p,..., p n ), (.4) čia f ra toldžiai diferencijuojama kintamųjų (,, p,..., p n ) funkcija. DL, užrašta (.) pavidalu, vadinama neišreikštine diferencialine lgtimi.. pavzdje antroji ir trečioji lgts ra neišreikštinės DL. Pastebėsime, kad trečioji lgtis ra iš esmės neišreikštinė, nes negalima išreikšti jokia elementariąja funkcija. Pirmoji lgtis ra pavzds lgties, kurioje išvestinė ra išreikšta kaip kintamųjų ir funkcija. Neišreikštinės (.) DL apibrėžimo sritis ra sritis D F R n+2, kurioje funkcija F (,, p,..., p n ) ra toldi kintamųjų (,, p,..., p n ) atžvilgiu. Jeigu D F nėra jungioji aibė, tuomet nagrinėsime DL kiekvienoje jungumo aibėje atskirai, t.. laiksime, kad ta pati lgbė apibrėžia keletą DL..4 ppavzds [DL apibrėžimo sritis]. DL ( ) = apibrėžimo sritis ra D F = R + R R..5 ppavzds [Kelios DL]. Lgtis + = apibrėžia dvi DL, kurių apibrėžimo srits ra D F = R + R + R ir D 2 F = R R R.
12 3 SKYRIUS. Paprastosios diferencialinės lgts ir jų sistemos [ (:32)] D D 2 f (,( )) = tg D f D f - A a b B. pav. DL = ( 2 ) apibrėžimo srits..2 pav. DL = 2 2 apibrėžimo sritis..3 pav. DL apibrėžimo sritis ir DL sprendinio grafikas..6 ppavzds. DL = ( 2 ) (.5) dešinioji pusė turi prasmę ir ra toldi, kai [ ; ] ir [; + ] (žiūrėk. pav.)..3 apibrėžimas [DL kanoninis pavidalas]. DL ra užrašta kanoniniu pavidalu, jei lgtis išspręsta aukščiausiosios eilės išvestinės atžvilgiu: (n) = f(,,,..., (n ) ). (.6).7 ppavzds [DL kanoninis pavidalas]. DL + e = kanoninis pavidalas ra = + e +. Akivaizdu, kad (.6) DL, užraštos kanoniniu pavidalu, apibrėžimo sritis ra D F = D f R, čia D f ra sritis, kurioje ra apibrėžta ir toldi funkcija f(,,,..., (n ) ). Sritis D f vadinama išreikštinės DL apibrėžimo sritimi.. uždavins. Nustatkite.6 pavzdje apibrėžtų DL apibrėžimo sritis..8 ppavzds [DL apibrėžimo sritis]. DL = 2 2 dešinioji pusė apibrėžta uždarame skritulje {(, ): }, o DL apibrėžimo sritis D f ra vienetinis atvirasis skrituls {(, ): < } su centru koordinačių pradžioje (žiūrėk.2 pav.): D f = {(, ): < }. Pirmosios eilės DL kanoninis pavidalas dar vadinamas normaliuoju. = f(, ) (.7).4 apibrėžimas [pirmosios eilės DL simetrinis pavidalas]. Jeigu v, w C(D), sritis D R 2 ir v(, ) + w(, ), tuomet lgtis v(, ) d + w(, ) d = (.8) vadinama tiesine homogenine pirmosios eilės diferencialų lgtimi.
13 . Diferencialinė lgtis ir jos sprendiniai 4 Jeigu w(, ), tuomet (.8) DL ra ekvivalenti (.7) lgčiai d v(, ) = = f(, ) (.9) d w(, ) taško (, ) aplinkoje D f. Jeigu v(, ), tuomet (.8) DL ra ekvivalenti lgčiai := d d = w(, ) v(, ) = g(, ) (.) taško (, ) aplinkoje D g. Pastaroji DL lgtis dar vadinama apverstąja lgtimi. Lgbė (.8) vadinama DL simetriniu pavidalu..2 uždavins. Užraškite DL = / simetrinį pavidalą ir apverstąją DL.? Jeigu pirmosios eilės DL lgtis užrašta neišreikštiniu pavidalu, tai DL ir ją atitinkanti apverstoji DL užrašomos F (,, ) = ir F (,, ) =, atitinkamai. Kiekvieną antrosios eilės DL galima užrašti pavidalu F (,,, (+( ) 2 ) 3/2 ) =. (.) Paskutinio argumento išraiška (.) lgties kairėje pusėje atitinka kreivės (, ()) kreivį. Šią DL atitinka apverstoji DL F (,,, (+( ) 2 ) 3/2 ) =. (.2) Jeigu duota kreivės parametrizacija ((t), (t)), tuomet jos kreivio formulė ra Aukštesnės eilės DL apverstosios DL pavidalas ra dar sudėtingesnis. ẋÿ ẍẏ (ẋ 2 +ẏ 2 ) 3/2..3 uždavins. Užraškite DL ( ) 2/3 ( ) 2 = apverstąją DL..9 ppavzds. DL e + = (žiūrėk. pavzds, trečioji lgtis) ir jos negalima užrašti kanoniniu pavidalu su elementariąja funkcija f, tačiau ši DL parametrizuojama = ϕ(t) := e t + t, = ψ(t) := t, t.. pastarosios funkcijos ϕ ir ψ paverčia lgtį e + = tapatbe e ψ(t) + ψ(t) ϕ(t) ir rank (ϕ (t), ψ (t)) = rank (e t +, ) =, t R.? Bendruoju atveju n-osios eilės DL parametrizuotasis pavidalas ra: = ϕ(t, t 2,..., t n+ ), = ϕ (t, t 2,..., t n+ ), = ϕ (t, t 2,..., t n+ ),... (n) = ϕ n(t, t 2,..., t n+ ). Laiksime, kad šios parametrizacijos Jakobio matricos rank J = n + ir ϕ, ϕ,..., ϕ n C (D ϕ), D ϕ sritis R n+. Sritį D ϕ vadinsime n-osios eilės DL, užraštos parametrizuotuoju pavidalu, apibrėžimo sritimi. Jeigu parametrizuotojo pavidalo funkcijos ϕ, ϕ,...,ϕ n paverčia (.) DL tapatbe F ( ϕ(t), ϕ (t),..., ϕ n(t) ), tuomet turėsime (.) DL parametrizaciją. Carl Gustav Jacob Jacobi (84-85) vokiečiu matematikas.
14 5 SKYRIUS. Paprastosios diferencialinės lgts ir jų sistemos [ (:32)] ( ( ), ( ))= (sin,cos ) ( )=sin ( )=cos ( ) =.4 pav. Integralinė kreivė ir jos projekcijos: sprendinio grafikas = sin ; sprendinio išvestinės grafikas = cos ; fazinė trajektorija 2 + ( ) 2 =. Nagrinėtame.9 pavzdje = e t + t, = s, = u, = t, D ϕ = R 3 = R t R s R u, tačiau kintamieji s, u lgties e + = parametrizacijoje nenaudojami.. ppavzds [DL parametrizuotasis pavidalas]. DL e = parametrizuojama = s, = e t+u + t + s 2, = u, = t, D ϕ = R 3 = R t R s R u..2. Diferencialinės lgties sprendiniai.5 apibrėžimas [DL sprendins]. Toldžiai diferencijuojama funkcija ϕ C n, vadinama DL sprendiniu, jeigu ją įstatę į DL gauname tapatbę. Apibrėždami sprendinį laiksime, kad intervalas I ra atvirasis, t.. I = (a; b).. ppavzds. DL ( ) 2 = neturi sprendinių, o ( ) = turi vienintelį sprendinį..2 ppavzds. DL = visi sprendiniai užrašomi funkcijų šeima priklausančia nuo vieno parametro C: ϕ() = + C, C R..6 apibrėžimas [DL integralinė kreivė]. Diferencialinės lgties (.6) integraline kreive vadinsime vektorinės funkcijos ((), (),..., (n ) ()), atitinkančios sprendinį (), I, grafiką. Integralinės kreivės projekciją į erdvę (,,..., (n ) ) vadinsime fazine kreive. Fazinė kreivė, kuri turi orentaciją, t.. judėjimo kreive krptį, kai auga, vadinama fazine trajektorija. Fazinė kreivė, atitinkanti sprendinį const, sudarta iš vieno taško. Tokiai fazinei kreivei orentacija neapibrėžta.
15 . Diferencialinė lgtis ir jos sprendiniai 6 I t t t I (, ) =( t t ) = ( ) = ( ), I 2 z z=, C.5 pav. Kreivę apibrėžiančios funkcijos. Integralinė kreivė ra C klasės (vektorinė) funkcija..3 ppavzds. Funkcija = sin ra DL = sprendins. Integralinė kreivė (, sin, cos ), R, priklauso trimatei erdvei D f = R R R (žiūrėk.4 pav.). Integralinės kreivės projekcijos: sprendinio grafikas = sin ; sprendinio išvestinės grafikas = cos ; trajektorija 2 + ( ) 2 =. Funkcija = e ra DL = sprendins. Integralinė kreivė (, e ), R, priklauso dvimatei erdvei D f = R R ir ra funkcijos = e grafikas. Daugumoje vadovėlių integraline kreive vadinamas aukštesnių eilių diferencialinių lgčių sprendinio grafikas. Mes apibrėžėme tokioms lgtims integralinę kreivę kitaip. Pagal apibrėžimą integralinė kreivė priklauso lgties apibrėžimo sričiai D f. Sprendinio grafikas gaunamas kaip integralinės kreivės projekcija į dvimatę plokštumą (, ). Diferencialinė lgtis bus išspręsta, jei rasime visus jos sprendinius. DL sprendinių radimą vadinsime DL integravimu. Kiekviena n-osios eilės DL nusako bendrą geometrinę sprendinius apibrėžiančių kreivių sąvbę. Pirmosios eilės DL F (,, ) = apibrėžia koordinačių, ir sprendinio grafiko liestinės polinkio sąršį. Pirmosios eilės DL sprendinio grafikas ra integralinė kreivė. Pavzdžiui, išreikštinės DL integralinės kreivės liestinės kampo su ašimi tangentas kiekviename taške lgus DL dešiniosios pusės reikšmei tame taške (žiūrėk.3 pav.). Antrosios eilės DL apibrėžia koordinačių, sprendinio grafiko liestinės polinkio ir kreivio sąršį (žiūrėk(.)).? Vienetinis apskritimas plokštumoje R 2 su centru koordinačių pradžioje aprašomas (globaliai) neišreikštine toldžiai diferencijuojama funkcija Ψ(, ) := =. Pusplokštumėje > šio apskritimo dalį galime aprašti toldžiai diferencijuojama funkcija = 2, ( ; ), o pusplokštumėje < funkcija = 2, ( ; ). Tačiau jokia išreikštine funkcija = ψ() negalime aprašti šio apskritimo taškų ( ; ) ir (; ) aplinkoje. Tiesa, šių taškų aplinkoje apskritimas aprašomas funkcijomis
16 7 SKYRIUS. Paprastosios diferencialinės lgts ir jų sistemos [ (:32)] = 2, ( ; ) ir = 2, ( ; ), atitinkamai. Mes pasirinkome atviruosius intervalus, kad nekiltų klausimų dėl funkcijų toldumo ir diferencijamumo apibrėžimų. Beje, funkcija = 2, pvz. taške =, ra tik toldi iš kairės ir šiame taške neegzistuoja net vienpusė išvestinė. Vienetinį apskritimą galima aprašti parametrizuotuoju pavidalu (, ) = (cos t, sin t), t (; 2π) arba t ( π; π). Pastebėsime, kad šio vienetinio apskritimo atveju, galima globalioji parametrizacija t [; 2π], nes abi funkcijos = cos t ir = sin t ra apibrėžtos t R ir ra periodinės su periodu 2π. Bendruoju atveju globaliosios parametrizacijos gali ir nebūti. Jeigu funkcija Ψ C (G), čia sritis G R 2, (, ) G, ir Ψ(, ) (, ) (čia gradientas Ψ = ( Ψ, Ψ )), tuomet egzistuoja taško (, ) aplinka, kurioje funkcija Ψ apibrėžia kreivę, ir ją galima aprašti trimis būdais (žiūrėk.5 pav.): ) neišreikštine toldžiai diferencijuojama funkcija Ψ : R 2 R, tiksliau lgbe Ψ(, ) = Ψ(, ) = C; 2) išreikštine toldžiai diferencijuojama funkcija ψ : I R (arba funkcija = ψ (), ψ C (I ), arba funkcija = ψ (), ψ C (I )); 3) toldžiai diferencijuojama funkcija (ψ, ϕ): I t R 2, t.. parametrizuotuoju pavidalu (, ) = (ψ(t), ϕ(t)), ψ, ϕ C (I t), ψ (t ) + ϕ (t ) =, (, ) = (ψ(t ), ϕ(t )). Įrodmas remiasi neišreikštinės funkcijos teorema. Kita vertus, kreivę, apraštą funkcija = ψ (), galima užrašti neišreištiniu pavidalu Ψ(, ) := ψ () =, ir Ψ =. Parametrizuotąją kreivę taško (, ) aplinkoje galima užrašti išreištiniu pavidalu (jei ψ (t ), tai = ϕ(ψ ()), čia ψ žmime atvirkštinę funkciją, o įrodmas vėl remiasi neišreikštinės funkcijos teorema). Vadinasi, kreivę (lokaliai) irgi galime užrašti tiek neišreikštiniu, tiek išreikštiniu, tie parametrizuotuoju pavidalu. Todėl žemiau pateikti sprendinių apibrėžimai tėra to pačio sprendinio skirtingi užrašmo būdai..7 apibrėžimas [Išreikštinis DL sprendins]. Funkciją = ϕ(), I R, vadinsime (.) DL išreikštiniu sprendiniu, jei ) ϕ C n (I); 2) (, ϕ(), ϕ (),..., ϕ (n) () ) D F, I; 3) F (, ϕ(), ϕ (),..., ϕ (n) () )..4 ppavzds [Pirmosios eilės DL sprendins]. DL = 2 apibrėžta visoje plokštumoje, t.. D f = R 2. Funkcija = ra šios DL sprendins intervaluose ( ; ) ir (; + ), nes kai, tai funkcija = C ir ( ) = ( 2 )2. Taške = sprendins neapibrėžtas, nes jame funkcijos = reikšmė neapibrėžta (žiūrėk.6 pav.). Todėl funkcija = apibrėžia du sprendinius: vieną intervale R, kitą R+. Šių sprendinių integralinės kreivės ra hiperbolės šakos..4 uždavins. Koks DL = 2 sprendins apibrėžtas visoje R?.8 apibrėžimas [Parametrizuotasis DL sprendins]. Dvi funkcijas = ψ(t), = ϕ(t), t I R t (.3) vadinsime (.) DL parametrizuotuoju sprendiniu, jei
17 . Diferencialinė lgtis ir jos sprendiniai pav. DL = 2 integralinės kreivės..7 pav. DL = integralinės kreivės, kai >..8 pav. DL d + d = integralinės kreivės. ) ψ, ϕ C n (I), ψ ; 2) (ψ(t), ϕ(t), dϕ(t) dψ(t),..., 3) F (ψ(t), ϕ(t), dϕ(t) dψ(t),..., d dϕ(t) dψ(t) (... ( dψ(t) ))) D F, t I; d dψ(t) dϕ(t) (... ( dψ(t) )))..5 ppavzds [DL parametrizuotieji sprendiniai]. Sritje > DL = parametrizuotieji sprendiniai ra (žiūrėk.7 pav.) = C cos t, = C sin t, t (; π), C >, nes ψ(t; C) = C cos t C (; π), ψ = C cos t = C sin t, ϕ(t; C) = C sin t C (; π), ir d(c sin t) d(c cos t) = C cos t C sin t C cos t C sin t.? Jeigu = (t), = (t), ir ẋ = d, tuomet dt = d d = ẏ ẋ,.5 uždavins. Raskite išraišką. = d2 d 2 = d d ( ẏ ) = ẋ ẋ d dt ( ẏ ) ÿẋ ẏẍ = ẋ ẋ 3. (.4) Jei sprendins užraštas neišreiktiniu pavidalu Ψ(, ) =, tai ne visada galima iš šio sąršio išreikšti (ir net ) elementariosiomis funkcijomis. Pavzdžiui, e + =..6 uždavins. Ar galima sprendinį, užraštą formule e =, išreikšti elementariąją funkcija..9 apibrėžimas [Neišreikštinis DL sprendins]. Sąršis Φ(, ) =, vadinamas DL neišreikštiniu sprendiniu, jeigu jis apibrėžia DL sprendinį = φ() arba apverstosios DL sprendinį = ψ(). Nagrinėdami DL, visada ieškosime net tik sprendinių = φ(), bet ir apverstosios DL sprendinių = ψ().
18 9 SKYRIUS. Paprastosios diferencialinės lgts ir jų sistemos [ (:32)] Pirmosios eilės DL, užraštai simetriniu pavidalu, funkcija Φ(, ) apibrėžia neišreikštinį sprendinį Φ(, ) =, jei teisinga tapatbė Φ(, ) w(, ) Φ(, ) v(, ). Kanoninio pavidalo (.9) atveju neišreikštinį sprendinį apibrėžia tapatbė dφ Φ(,) := + Φ(,) f(, ), d o kanoninio pavidalo (.) atveju neišreikštinį sprendinį apibrėžia tapatbė dφ d Φ(,) := g(, ) + Φ(,)..7 uždavins. Parodkite, kad lgbė e = apibrėžia DL = neišreikštinį sprendinį..8 uždavins. Užraškite DL, kurios neišreikštinis sprendins ra e + =..6 ppavzds [DL neišreikštinis sprendins]. Funkcija Φ(, ) = C 2, C > apibrėžia DL d = neišreikštinius sprendinius d C 2 = sritje R 2 {(, )}, nes dφ = 2 + 2( dφ ), kai, ir = d d 2( ) + 2, kai (šiuo atveju sprendžiame apverstąją DL d = ). Integralinės kreivės (apskritimai) pavaizduotos.7 pav. d Taške (, ) DL neapibrėžta..7 ppavzds [Antrosios eilės DL sprendiniai]. Nagrinėkime antrosios eilės DL ( ) 2/3 ( ) 2 =, kurios apibrėžimo sritis ra D F = R 4. Funkcija ϕ(; C, C 2) = C 2 + ( C ) 2 ra šios DL sprendins intervale I = (C ; C + ): ϕ(; C, C 2) C 2 (I), ϕ C (; C, C 2) = ( ( C ) 2 ), /2 ϕ (; C, C 2) = ( ( C ) 2 ), 3/2 ir teisinga tapatbė ( ) 2/3 ( ( ( C ) 2 ) 3/2 C ( ( C ) 2 ) /2 ) 2. Kadangi ϕ(; C, C 2) = C 2 + ( C ) 2 ra DL sprendins su bet kokiomis C ir C 2 reikšmėmis, todėl gauname sprendinių šeimą (aibę) priklausančią nuo dviejų parametrų. Pastebėsime, kad funkcija ϕ(; C, C 2) = C 2 ( C ) 2 taip pat ra sprendins su bet kokiomis C ir C 2 reikšmėmis. Tai dar viena sprendinių šeima. DL sprendinių grafikai pavaizduoti.8 pav. Parametrizuotieji sprendiniai ra (, ) = (C + cos t, C 2 + sin t), t I = (; π) arba t I = ( π; )
19 . Diferencialinė lgtis ir jos sprendiniai ( C, C 2 ) (a) (b).9 pav..7 pvz. DL sprendiniai: (a) išreikštiniu sprendiniu grafikai; (b) neišreikštiniai sprendiniai.. pav. DL = cos integralinės kreivės. nes ψ = C + cos t, ϕ = C 2 + sin t C (I), ψ = sin t, kai t π,, π. Pasinaudodami (.4) formulėmis, randame = cos t sin t, = sin 3 t. Istatę šias išraiškas į DL, gauname tapatbę ( ) 2/3 ( cos t ) 2. + sin 3 t sin t Nagrinėjami parametrizuotieji sprendiniai atitinka išreikštinius sprendinius = C 2 + ( C ) 2 ir = C 2 ( C ) 2. Lgbė Φ(, ; C, C 2) ( C ) 2 + ( C 2) 2 = apibrėžia DL ( ) 2/3 ( ) 2 = neišreikštinius sprendinius. Jei C 2, tuomet = 2( C2), ir galime užrašti sprendinių išreikštinius pavidalus Φ = C 2 ± ( C ) 2, (C ; C + ). Perraškime DL pavidalu (.) ( ) 2/3 =. ( + ( ) 2 ) 3/2 Tada neišreikštinis apverstosios DL (žiūrėk (.2)) pavidalas ra ( ) 2/3 =, ( + ( ) 2 ) 3/2 ši DL ekvivalenti duotajai DL. Vadinasi, neišreikštiniai DL sprendiniai ra visi plokštumos vienetiniai apskritimai (žiūrėk.9(b) pav.). Dažniausiai DL lgtis turi begalo daug sprendinių, ir jie sudaro sprendinių šeimas, priklausančias nuo keleto konstantų..8 ppavzds [DL sprendiniai]. Lgties = sprendiniai ra = C ch + C 2sh su C, C 2 R. Šie sprendiniai sudaro kreivių šeimą, priklausančią nuo dviejų konstantų C, C 2.
20 SKYRIUS. Paprastosios diferencialinės lgts ir jų sistemos [ (:32)] Konstantos C,..., C n, įeinančios į DL sprendinio išraišką, vadinamos laisvosiomis. Šios konstantos gali įgti bet kokias reikšmes, o kartais ir begalines reikšmes, t.. ±.. apibrėžimas [Bendrasis DL sprendins]. Bendruoju n-osios eilės DL sprendiniu vadinsime DL sprendinių šeimą = ϕ(; C,..., C n ), priklausančią nuo laisvųjų konstantų C,..., C n, ir pasižminčia savbe, kad sistema = ϕ(; C,..., C n ), = ϕ (; C,..., C n ), (.5)... (n ) = ϕ (n ) (; C,..., C n ) ra vienareikšmiškai išspendžiama laisvųjų konstantų atžvilgiu: C = ψ (,,..., (n ) ),... (.6) C n = ψ n (,,..., (n ) ). Bendrasis sprendins gali būti užraštas parametrizuotu pavidalu arba neišreikštiniu pavidalu = ϕ(t; C,..., C n ), = ψ(t; C,..., C n ), (.7) Ψ(, ; C,..., C n ) =. (.8) Pastaruoju atveju, sprendinių šeima dar vadinama bendruoju integralu. Iš bendrojo sprendinio (bendrojo integralo), imdami konkrečias C,..., C n reikšmes, gauname atskirąjį sprendinį (atskirąjį integralą)..9 ppavzds. Funkcija = sin + C ra DL = cos bendrasis sprendins, o = sin, = sin 2, = sin + atskirieji sprendiniai (žiūrėk. pav.)..2 ppavzds. DL ( ) 2/3 ( ) 2 = sprendiniais ra dvi bendrųjų (išreikštinių) sprendinių šeimos: = C 2+ ( C ) 2 ir = C 2 ( C ) 2. Pavzdžiui, pirmosios šeimos atveju, sistema = C 2 + ( C ) 2, C = ( C) 2 ra vienareikšmiškai išspendžiama laisvųjų konstantų atžvilgiu: C = + + ( ) 2, C2 = + ( ) 2. Abi šias sprendinių šeimas galima apibrėžti vienu bendruoju integralu ( C ) 2 + ( C 2) 2 =, C, C 2 R, kuris taip pat aprašo ir bendruosius sprendinius = C + ( C 2) 2 ir = C ( C 2) 2 apverstajai DL.
21 . Diferencialinė lgtis ir jos sprendiniai 2.9 uždavins. Nustatkite DL eilę ir patikrinkite, ar duotoji funkcija (funkcijos) apibrėžia sprendinį: a) + 9 =, = C cos(3) + C 2 sin(3); b), 5 =, = Ce /2 2; c) = 2, e 2 = C; d) =, = Cch t, = Csh t; e) = + sin, = 3 sin + C; 6 f) = e 2, = e ξ2 dξ + C.. uždavins. Patikrinkite, ar.9 uždavinio sprendiniai apibrėžia bendruosius sprendinius arba integralus..3. Kreivių šeimos diferencialinė lgtis Jeigu spręsdami n-eilės DL radome jos bendrąjį sprendinį (integralą), tuomet turime kreivių šeimą, priklausančią nuo n laisvųjų konstantų. Pabandkime spręsti atvirkštinį uždavinį. Sakkime, duota kreivių šeima, apibrėžta lgtimi Ψ(, ; C,..., C n ) =. Sudarome sistemą Ψ (, ; C,..., C n ) Ψ(, ; C,..., C n ) =, Ψ (,, ; C,..., C n ) Ψ... + Ψ =, Ψ n (,,,..., (n) ; C,..., C n ) Ψn + Ψn + + Ψn (n) =. (n ) Eliminuodami konstantas C,..., C n, gautume šios kreivių šeimos n-osios eilės DL..2 ppavzds [vienetinių apskritimų šeima]. Visų vienetinių apskritimų šeimos plokštumoje lgtis ra ( C ) 2 + ( C 2) 2 =. Diferencijuodami šią lgtį pagal kintamąjį du kartus, gauname Randame 2( C ) + 2( C 2) =, 2 + 2( ) 2 + 2( C 2) =. C = + ( ) 2, C 2 = + ( ) 2. Įstatome šias išraiškas į apskritimų lgtį, gauname kreivių šeimos DL ( + ( ) 2 ) 3 = ( ) 2.
22 3 SKYRIUS. Paprastosios diferencialinės lgts ir jų sistemos [ (:32)] Kreivių šeima priklausanti tik nuo vieno parametro vadinama vienaparametrine kreivių šeima..22 ppavzds [Kreivių šeimos]. Žemiau pateikta keletas vienaparametrinių kreivių šeimų: Sistema. Φ(,, C) := + + C = apibrėžia lgiagrečių (tiesei = ) tiesių šeimą; 2. Φ(,, C) := C 2 = parabolių šeimą (žiūrėk. pav.); 3. Φ(,, C) := 2 /2 + 2 C 2 = koncentrinių elipsių su centru koordinačių pradžioje ir ašimis C 2 ir C šeimą (C > ) (žiūrėk. pav.). Φ(,, C) =, Φ Φ d (,, C) + (,, C) d =. ir ra kreivių šeimos DL, tiesa, užrašta parametriniu pavidalu (parametras C). Vienaparametrinės kreivių šeimos DL sudaroma parametro eliminavimo metodu..23 ppavzds [Kreivių šeimos DL]. Surasime.22 pavzdžio kreivių šeimų DL: { { { + + C =, + = C 2 =, 2C + = 2 /2 + 2 C 2 =, + 2 = = ; { C = / 2, = 2C = 2. = 2 ; Jeigu iš lgties Φ(,, C) = pavksta išreikšti parametrą C = Ψ(, ), tuomet šiai vienaparametrinei šeimai DL ra Ψ Ψ d (, ) + (, ) d =.. uždavins. Suraskite vienaparametrinių kreivių šeimų DL: a) = C; b) e 3 = C; c) = e C2 ; d) = Ce. 2. Koši uždavins Kaip matėme, DL dažniausiai turi be galo daug sprendinių. Norint išskirti kurį nors vieną sprendinį, reikia pareikalauti, kad sprendins tenkintų papildomas sąlgas.
23 2. Koši uždavins 4 2. pav. Paraboliu ir elipsiu šeimos..2 pav. Koši uždavins pirmos eilės lgčiai..3 pav. Koši uždavins antros eilės lgčiai. 2.. Koši uždavins Jeigu sprendžiama n-osios eilės DL F (,,,..., (n) ) =, (2.) tuomet tokiomis sąlgomis laikomos išreikštinio sprendinio ir jo išvestinių iki (n )-os eilės reikšmės, kai = : ( ) =, ( ) =,..., (n ) ( ) = (n ). (2.2) DL su tokiomis sąlgomis vadinama Koši 2 (pradiniu) uždaviniu, o pačios sąlgos pradinėmis. Pradinę sąlgą apibrėžia taškas (,,,..., (n ) ), kuris priklauso D f, jei DL užrašta kanoniniu pavidalu..2 uždavins. Patikrinkite, kad = Ce 2 ra DL = 2 sprendins. Raskite integralinę kreivę, einančią per tašką (, 4)..24 ppavzds. Koši uždavins = /, () = 2 neturi išreikštinio sprendinio, nes taške = DL neapibrėžta. Koši uždavins apverstajai DL = /, (2) = turi sprendinį. Ypač lengva spręsti Koši uždavinį, jeigu žinomas DL bendrasis sprendins ir nėra kitų sprendinių. Šiuo atveju, bendrojo sprendinio sąvoka garantuoja, kad Koši uždavins turi vienintelį sprendinį, nes iš (.5) sistemos galime vienareikšmiškai rasti laisvasias konstantas. Bendrasis sprendins = ϕ(;,,,..., (n ) ) (2.3) ra vadinamas bendrojo sprendinio Koši pavidalu..25 ppavzds. Dl = 2 bendrojo sprendinio Koši pavidalas ra = e 2 2, o DL + = šis pavidalas ra = cos( ) + sin( ). 2 Augustin Louis Cauch ( ) prancūzu matematikas.
24 5 SKYRIUS. Paprastosios diferencialinės lgts ir jų sistemos [ (:32)] 2.2. Sprendinio egzistavimas ir vienatis Kanoninei n-os eilės DL (n) = f(,,,..., (n ) ) (2.4) Koši uždavinio sprendinio egzistavimui pakanka, kad f C(G) sritje G D f R n+ [7].. teorema [Peano 3 ]. Tarkime, funkcija f ra toldi sritje G. Tada egzistuoja (2.4) lgties sprendins = ϕ(), I, tenkinantis (2.2) pradines sąlgas. Tačiau šios teoremos salgų neužtenka Koši uždavinio sprendinio vienačiai [7, 6, 7]..2 teorema [Pikaro 4 ]. Tarkime, funkcija f ir jos dalinės išvestinės f,..., f toldžios sritje G. Tada egzistuoja vienintelis (2.4) lgties sprendins (n ) = ϕ(), I, tenkinantis pradines (2.2) sąlgas..26 ppavzds. Funkcijos = sin ir = cos ra DL + = sprendiniai. Šių dviejų sprendinių grafikai kertasi, tačiau šie sprendiniai nesutampa jokiame intervale (žiūrėk.3 pav.)..3 uždavins. Ar kertasi šio pavzdžio sprendinių integralinės kreivės? Panaši teorema teisinga ir (2.) lgčiai sritje D F [7]. Jos įrodmas išplaukia neišreikštinės funkcijos sąvbių (žiūrėk (.2) (.4) ) ir.2 teoremos..3 teorema. Tarkime, funkcija F C (G) ir taške (,,,..., (n) ) G išpildtos sąlgos F (,,,..., (n) ) =, F (n) (,,,..., (n) ). Tada egzistuoja (2.) lgties vienintelis sprendins = ϕ(), I, tenkinantis (2.2) pradines sąlgas..4 teorema [toldi priklausombė nuo pradinės sąlgos]. Jeigu f C (G), tuomet funkcija ϕ(;,,,..., (n ) ) apibrėžta, toldi ir ϕ C kiekvieno taško ( ;,,,..., (n ) ) aplinkoje. Pikaro teoremą ir toldžią priklausombę nuo pradinės sąlgos įrodsime vėliau, bet jau dabar jomis naudosimės. Šios trs teoremos sprendinio sąvbes formuluoja lokaliai. Jeigu sprendins ra apibrėžtas intervale I (nebūtinai atvirasis), tai jis bus sprendins ir intervale J I. 3 Giuseppe Peano ( ) italu matematikas. 4 Émile Picard (856-94) prancūzu matematikas.
25 2. Koši uždavins 6. apibrėžimas [integralinės kreivės tęsins]. Integralinę kreivę intervale I vadinsime integralinės kreivės intervale J I tęsiniu, o integralinę kreivę intervale J integralinės kreivės intervale I siauriniu. Koši uždavinio su pradinėmis sąlgomis (2.2) integralinė kreivė pratęsiama pirmn (atgal) iki aibės Γ G D f, jeigu egzistuoja sprendins su tomis pačiomis pradinėmis sąlgomis, kurio integralinė kreivė kertasi su Γ taške ( ). Integralinė kreivė pratęsiama pirmn (atgal) neaprėžtai, jeigu egzistuoja sprendins su tomis pačiomis pradinėmis sąlgomis, kuris egzistuoja visiems ( ). Laiksime, kad sprendins turi tęsinį, jeigu jo integralinė kreivė turi tęsinį. Vietoje pirmn (atgal) naudosime taip pat naudosime terminus į dešinę (į kairę). Jeigu sprendins pratęsiamas iš atvirojo intervalo (a; b) į intervalą (a; b] ([a; b)), tuomet tokį tęsinį vadinsime dešiniuoju (kairiuoju) plėtiniu. Sprendins, kurio negalima pratęsti nei į kairę, nei į dešinę, vadinamas pilnuoju sprendiniu, o intervalas J vadinamas sprendinio egzistavimo maksimaliuoju intervalu. Toliau pagal nutlėjimą sprendinį suprasime kaip pilnąjį.? Aibė K R n vadinama kompaktu, jeigu ji ra uždara ir aprėžta. Jeigu kompaktą padengsime atvirųjų aibių denginiu, tuomet galima išrinkti baigtinį podenginį. Ši kompakto sąvbė Hausdorfo 5 topologinėse erdvėse naudojama kaip kompakto apibrėžimas. Didžiausia atviroji aibė, priklausanti aibei A vadinama aibės A vidumi, o mažiausia uždaroji aibė, dengianti aibę A vadinama aibės A uždariniu. Aibės A uždarinio taškai, kurie nepriklauso aibės A vidui, sudaro aibės A kraštą A..5 teorema [apie sprendinio tęsinį]. Tarkime, K G D f ra kompaktas ir pradinė sąlga (,,,..., (n ) ) K ir f C (G). Tada integralinė kreivė pratęsiama iki kompakto krašto ir toks pratęsimas ra vienintelis. Teorema teigia, kad per kievieną vidinį kompakto tašką eina vienintelė integralinė kreivė, kuri pratęsiama iki kompakto krašto (žiūrėk.4 pav.). Tęsinio vienatis suprantama ta prasme, kad dvi integralinės kreivės su tą pačia pradine sąlga sutampa visur kur jos apibrėžtos..27 ppavzds. Koši uždavinio = 2, () =, sprendins užrašomas išreikštine funkcija = /( ). Šį sprendinį galima pratęsti atgal (į kairę) neaprėžtai, tačiau negalima pratęsti pirmn (į dešinę) iki tiesės =, t.. maksimalusis intervalas ra ( ; ). Teorema apie tęsinį lieka teisinga. Jeigu kompaktas ra uždarasis stačiakampis [a; ] [; b], tai sprendins pratęsiamas į kairę iki stačiakampio kraštinės = a su bet kokiu a <, t.. visiems, ir sprendins pratęstas pirmn (į dešinę) pasieks tik viršutinę stačiakampio kraštinę kokį b > bepaimtume (žiūrėk.5) ir niekada nepasieks dešiniosios kraštinės..28 ppavzds. Koši uždavinio =, () =, sprendins užrašomas išreikštine funkcija = e. Šį sprendinį galima pratęsti atgal ir pirmn neaprėžtai, nes su bet kokiu a > sprendins kirs kairiąją ir dešiniąją uždarojo stačiakampio [ a; a] [; e a + ] kraštines. 5 Feli Hausdorff ( ) vokiečiu matematikas.
26 7 SKYRIUS. Paprastosios diferencialinės lgts ir jų sistemos [ (:32)], (),..., (n-) G b K a K.4 pav. Integralinės kreivės tęsins iki kompakto krašto..5 pav. Neptatęsiamas į dešinę sprendins..6 pav. DL = 3 2/3 integralinės kreivės. DL patingasis taškas ir patingasis sprendins. Sritis G, kurios visuose taškuose Koši uždavinio sprendins ra vienintelis, vadinsime DL sprendinio vienaties sritimi. DL du sprendiniai, sutampants viename DL sprendinio vienaties srities G taške, sutampa visoje šioje sritje. Pirmos eilės lgčiai sutampa ir jų integralinės kreivės. Antros eilės DL tokiems sprendiniams integralinės kreivės sutaps, jeigu bendrame taške abu sprendiniai turės tą pačią liestinę..29 ppavzds. Rasime DL = 3 2/3 integralinę kreivę, einančią per tašką (, ). Atitinkamas Koši (pradinis) uždavins ra = 3 2/3, () =. Patikriname, kad funkcija = ( C) 3 ra DL sprendiniai. Įstatome pradines sąlgas: = () = ( C) 3 C = (kitos šakns ra kompleksinės). Vadinasi, šis Koši uždavins turi sprendinį = 3 (žiūrėk.6 pav.). Remiantis.2 teorema daugiau integralinių kreivių, einančių per šį tašką, nėra. Rasime integralinę kreivę, einančią per tašką (, ). Per šį tašką eina jau rasta integralinė kreivė = 3, ir dar viena papildoma integralinė kreivė. Vadinasi, šiuo atveju, Koši uždavinio sprendins nėra vienintelis, ir šis taškas nepriklauso DL sprendinio vienaties sričiai..4 uždavins. Raskite.29 pavzdžio DL sprendinio vienaties sritį (sritis)..2 apibrėžimas. DL sprendins, per kurio kiekvieną tašką eina tik vienas tos DL sprendins, vadinamas atskiruoju sprendiniu..5 uždavins. Raskite Koši uždavinio sprendinius, jei žinomas bendrasis sprendins
27 3. Diferencialinių lgčių sistemos 8 arba bendrasis integralas: a) =, () = ; = C; b) =, () = ; e = C; c) =, () =, () = 3 2 ; = 2 2 d) = + sin, () =, () = ; = 3 3 e) =, (3) = 4; = C. + C + C2; sin + C + C2; 2.3. Ypatingieji sprendiniai DL gali turėti sprendinių, kurių taškuose neišpildta vienaties sąlga. Nagrinėtame.29 pavzdje sprendinio negausime iš bendrojo sprendinio (kubinių parabolių šeimos) = ( C) 3 su jokia konstanta C R (žiūrėk.6 pav.)..6 uždavins. Raskite.29 pavzdžio DL visus sprendinius, kuriems neišpildta vienaties sąlga..3 apibrėžimas [Ypatingasis taškas]. Ypatingaisiais taškais vadinsime tuos integralinės kreivės taškus, kuriose neišpildta sprendinio vienaties sąlga..4 apibrėžimas [Ypatingasis sprendins]. Ypatinguoju sprendiniu vadinsime sprendinį, kurio kiekvienas taškas ra patingasis taškas. Kai kanoninės (2.4) DL dešiniosios pusės funkcija ra toldi ir turi dalines išvestines pagal kintamuosius,,..., (n ), jos patingieji sprendiniai gali būti tik tie, kuriuose tenkinama bent viena sąlga: f =,..., f =. (n ) Neišreikštinės (2.) DL atveju, kai F C (G), patingais gali būti sprendiniai F apibrėžti ir lgbėmis F =, =. (n).7 uždavins. Patikrinkite, kad DL turi duotuosius sprendinius ir suraskite patinguosius sprendinius: a) = 2, = C ( C); b) ( ) =, = sin( C).
28 9 SKYRIUS. Paprastosios diferencialinės lgts ir jų sistemos [ (:32)] 3. Diferencialinių lgčių sistemos Apibendrinsime DL lgties savoką DL sistemoms, t.. nagrinėsime vektorines DL. Nagrinėkime vektorinę DL F (,,,..., (m) ) =, (3.) čia = (,..., n ), F = (F,..., F n ) C (D F ), D F R n(m+)+ ra funkcijos F (kartu ir vektorinės DL apibrėžimo sritis). Tokia vektorinė m-tosios eilės DL dar vadinama m-osios eilės diferencialinių lgčių sistema (DLS). Kintamųjų (, 2,..., n ) erdvė vadinama fazine erdve. Dažniausiai sutinkamos pirmosios eilės DLS: F (,,..., n,,..., n) =, F n (,,..., n,,..., n) =.... (3.2) Kai jakobianas D(F,...,Fn) D(,..., n ), pirmąsias išvestines galima išreikšti per likusius kintamuosius: = f (,,..., n ),... (3.3) n = f n (,,..., n ). Tokią DLS vadiname n-osios eilės normaliąja DLS. Jos vektorinis pavidalas ra = f(, ), f C(D f ), D f R n+. Šiai DLS (vektorinei DL) apibendrinamos visos sąvokos, kurias apibrėžėme skaliarinei DL = f(, ). Pavzdžiui, Koši uždavins užrašomas kaip = f(, ), ( ) =. (3.4).5 apibrėžimas [integralinė kreivė]. Normaliosios DLS (arba vektorinės DL) (3.3) integraline kreive vadinsime vektorinės funkcijos (), I, grafiką. Integralinės kreivės projekciją į fazinę erdvę (, 2,..., n ) vadinsime fazine kreive. Fazinė kreivė, kuri turi orentaciją, t.. judėjimo kreive krptį, kai auga, vadinama fazine trajektorija. Fazinė kreivė, atitinkanti sprendinį () const, sudarta iš vieno taško. Tokiai fazinei kreivei orentacija neapibrėžta. Bendrasis sprendins ir bendrasis integralas apibrėžiami kaip = ϕ(, C), Ψ(,, C) = arba Φ(, ) = C, čia C = (C,..., C n ), o visos funkcijos ra toldžiai diferencijuojamos. Suformuluosime Pikaro, toldžios priklausombės nuo pradinės sąlgos ir sprendinio tęsinio teoremų analogus.
29 3. Diferencialinių lgčių sistemos 2.6 teorema. Tarkime, funkcija f C (G), G R n+. Tada egzistuoja vienintelis (3.4) Koši uždavinio sprendins = ϕ(), I, tenkinantis pradinę sąlgą..7 teorema [toldi priklausombė nuo pradinės sąlgos]. Jeigu f C (G), tuomet funkcija ϕ(;, ) apibrėžta, toldi ir ϕ C kiekvieno taško ( ;, ) aplinkoje..8 teorema [apie sprendinio tęsinį]. Tarkime, K G D f ra kompaktas ir pradinė sąlga (, ) K ir f C (G). Tada integralinė kreivė pratęsiama iki kompakto krašto ir toks pratęsimas ra vienintelis. 3.. n-osios eilės DL suvedimas į n-osios eilės normaliąją DLS Kiekvieną n-osios eilės kanoninę DL galima suvesti į normaliąją DLS. Parodsime tai Koši uždaviniui (n) = f(,,,..., (n ) ), ( ) =,..., (n ) ( ) = (n ). (3.5) Apibrėžkime vektorinę funkciją z = (z, z 2,..., z n ) := (,,..., (n ) ). Tada (3.5) Koši uždavins ekvivalentus nomaliajai DLS z = z 2, z 2 = z 3,... (3.6) z n = z n, z n = f(, z,..., z n ) su pradinėmis sąlgomis z( ) = z := (,,..., (n ) ). Šis suvedimas rodo, kad.2 teorema išplaukia iš.6 teoremos,.4 teorema iš.7 teoremos,.4 teorema iš.8 teoremos..3 ppavzds. Koši uždavins + =, () =, () = suvedamas į antrosios eilės DLS = z, z = su pradinėmis sąlgomis () =, z() =..8 uždavins. Suvesti DL į DLS: a) = sin ; b) ( ) 2 sin + = ; c) = sin ( + ( ) 2 ).
30 2 SKYRIUS. Paprastosios diferencialinės lgts ir jų sistemos [ (:32)] 3.2. n-osios eilės normaliosios DLS suvedimas į n-osios eilės DL Kiekvieną n-osios eilės normaliąją (3.3) DLS galima suvesti į vieną n-osios eilės kanoninę DL. Diferencijuojame vieną DLS lgtį (pvz., pirmąją) n kartą pagal, ir keičiame pirmosios eilės išvestines normaliosios sistemos lgčių dešiniosiomis pusėmis. Taip gaunama n lgčių sistema: = f (,, 2,..., n ) := f (,, 2,..., n ), = f 2 (,, 2,..., n ) := f + n f i= i f i,... (3.7) (n ) = f n (,, 2,..., n ) := f n 2 + n f n 2 i= i f i, (n) = f n (,, 2,..., n ) := f n + n f n i= i f i. Įvedame naują funkciją z() := (). Iš (3.7) sistemos pirmųjų n lgčių išreiškiame 2,..., n (kada tai galima padarti?): 2 = g 2 (, z, z,..., z (n ) ),... n = g n (, z, z,..., z (n ) ), ir įstatome jas į (3.7) sistemos paskutinę lgtį z (n) = f n (, z, g2 (, z, z,..., z (n ) ),..., g n (, z, z,..., z (n ) ) ). Gaunama viena n-osios eilės DL Pradinės sąlgos šiai lgčiai ra z (n) = g(, z, z,..., z (n ) ). z( ) = ( ), z (i) ( ) = f i (, ( ),..., n ( )), i =,..., n..3 ppavzds. Duota DLS dv = w, dw = v. d d Apibrėžiame naują funkciją = v, diferencijuojame pirmąją lgtį pagal, ir gauname = w, = dw w = w =, w = d 2 2 DLS suvesta į antros eilės DL = + arba + + =..9 uždavins. Suveskite DLS į vieną DL: 2. a) u = v, v = u; b) u = v, v = u; c) u = u v, v = u + v.
31 3. Diferencialinių lgčių sistemos Autonominės ir neautonominės DL Jeigu funkcija f DL tiesiogiai nepriklauso nuo kintamojo, tai DL (arba DLS) d d = f (,..., n ), = f()... d n d = f n (,..., n ). vadinama autonomine. Kiekvieną neautominę DLS visada galima suvesti į autonominę d d = f (,,..., n ),... d n d = f m (,,..., n ) d dt = f (,,..., n ), d dt = f (,,..., n ),... d n dt = f n (,,..., n ), čia R n. Ir atvirkščiai, kiekvieną autonominę DLS sritje, kurioje f + f + + f n >, galima suvesti į neautonominę DLS. Pavzdžiui, jeigu f, tai d dt = f (,,..., n ), d dt = f (,,..., n ),... d n dt = f n (,,..., n ) d d d n d = f(,,...,n) f, (,,..., n)... = fn(,,...,n) f, (,,..., n) čia :=..32 ppavzds. Neautonominė DL suvedama į autonominę DLS d dt =, d d = d dt =..2 uždavins. Suveskite neautonomines DL (DLS) į autonomines DL (DLS): a) d d = ; d b) d = z +, dz d = +.
32 2 skrius Tiesinės diferencialinės lgts Šiame skriuje nagrinėsime tiesines n-eilės diferencialines lgtis. Jų išsprendžiamumas susijęs su fundamentaliosios sistemos radimu. Taip pat nagrinėsime atskirąjį atvejį tiesinę DL su pastoviaisiais koeficientais. Kaip kitose matematikos sritse, tiesiniai objektai, ra geriausiai ištirta DL teorijos dalis. Tiesinės DL (ir ne tik DL) ra patingai svarbios PDL teorijoje ir visoje matematinėje analizėje, kadangi pagrindinė analizės idėja teigia, kad kiekviena glodi funkcija kiekvieno taško aplinkoje gerai aproksimuojama tiesine funkcija. Linearizavimo (ištiesinimo) operacija leidžia tiesines lgtis nagrinėti kaip pirmąjį artinį sudėtingoms netiesinėms lgtims.. Tiesinė n-osios eilės diferencialinė lgtis 2. apibrėžimas [Tiesinė DL]. Diferencialinė lgtis z (n) + a ()z (n ) + + a n ()z + a n ()z = f(), (.) vadinama tiesine n-osios eilės diferencialine lgtimi (TDL). Čia f, a i C(I), i =,..., n žinomos toldžiosios (realiosios arba kompleksinės) funkcijos. Sąlgos f, a i C(I), i =,..., n garantuoja, kad egzistuoja vienintelis Koši uždavinio sprendins (sprendinio egzistavimo ir vienaties teorema). Jeigu ieškome sprendinių tarp kompleksinių funkcijų, tuomet vietoje vienos kompleksinės funkcijos z() = Re z() + Im z() ı galime ieškoti dviejų realiųjų funkcijų u = Re z() ir v = Im z(), kurios ra dviejų DL sistemos u (n) + Re a ()u (n ) Im a ()v (n ) + + Re a n()u Im a n()v = Re f(), v (n) + Im a ()u (n ) + Re a ()v (n ) + + Im a n()u + Re a n()v = Im f() sprendins (sprendinių pora). Dar paprastesnis atvejis gaunamas, kai (.) lgties koeficientai ra realiosios funkcijos. Tuomet pastaroji sistema tampa u (n) + a ()u (n ) + + a n()u = Re f(), v (n) + a ()v (n ) + + a n()v = Im f(). (.2) Šioms sistemoms egzistuoja vienintelė sprendinių pora. Toliau šiame skriuje DL ir jos sprendiniai gali būti ir reliosios, ir kompleksinės funkcijos. Atitinkamai skaliarai irgi gali būti iš kūno K = R, arba iš kūno K = C. Jeigu f, tuomet (.) lgtis vadinama homogenine, priešingu atveju nehomogenine. Kiekvienai (nehomogeninei) tiesinei (.) DL galima užrašti atitinkamą homogeninę lgtį.
33 . Tiesinė n-osios eilės diferencialinė lgtis 24.. Tiesinis diferencialinis operatorius? Atvaizdis A: L L 2, L, L 2 tiesinės erdvės, vadinamas tiesiniu operatoriumi, jeigu A(αz + βz 2 ) = αaz + βaz 2, α, β K, z, z 2 L. 2.2 apibrėžimas [Diferencialinis operatorius]. Atvaizdis L n : C n (I) C(I), apibrėžtas formule L n [z] := z (n) + a z (n ) + + a n z + a n z, (.3) vadinamas n-osios eilės diferencialiniu operatoriumi. 2. uždavins. Parodkite, kad C n (I) ra tiesinė erdvė visiems n =,, lema [Tiesinis diferencialinis operatorius]. Diferencialinis operatorius L n ra tiesinis. Įrodmas išplaukia iš išvestinės tiesinių savbių L n [αz + βz 2 ] =(αz + βz 2 ) (n) + a (αz + βz 2 ) (n ) + + a n (αz + βz 2 ) =α ( z (n) + a z (n ) ) + + a n z + β ( z (n) 2 + a z (n ) ) a n z 2 =αl n [z ] + βl n [z 2 ]. Vadinasi, diferencialinis operatorius L n, apibrėžtas (2.2) formule, ra tiesinis operatorius, kuris atvaizduoja tiesinę erdvę C n (I) tiesinėje erdvėje C(I). Tada (.) TDL užsirašo kaip tiesinė lgtis L n [z] = f. (.4)? Tiesinis operatorius A: L L 2 apibrėžia lgtį Az = f. (.5) 2. teigins. Homogeninės lgties Az = sprendiniai sudaro tiesinę daugdarą erdvėje L. Ši tiesinė daugdara sutampa su tiesinio operatoriaus A branduoliu ker A := {z L : Az = } (žiūrėk 2. pav.). Kitais žodžiais, dviejų homogeninės tiesinės lgties sprendinių tiesinis derins ra homogeninės tiesinės lgties sprendins. Atskiru atveju, z = visada ra sprendins. Įrodmas. Iš Az =, Az 2 = A(αz + βz 2 ) = αaz + βaz 2 = α + β =. 2.2 teigins. Tiesinio operatoriaus reikšmių aibė im A := {f L 2 : z L, Az = f} ra tiesinė daugdara erdvėje L 2. Įrodmas. Jeigu Az = f im A ir Az 2 = f 2 im A, tuomet αf + βf 2 = αaz + βaz 2 = A(αz + βz 2 ) im A.
34 25 2 SKYRIUS. Tiesinės diferencialinės lgts [ (:32)] 2. pav. Tiesinės lgties sprendiniu erdvė. 2. išvada. Jeigu f im A, tai nehomogeninės tiesinės lgties Az = f sprendiniai erdvėje L sudaro afininę daugdarą z a + ker A, lgiagrečią ker A (žiūrėk 2. pav.), čia z a ra atskiras nehomogeninės tiesinės lgties sprendins, t.. Az a = f. Kitais žodžiais, dviejų nehomogeninės tiesinės lgties sprendinių skirtumas ra homogeninės tiesinės lgties sprendins. Įrodmas. Iš Az = f, Az a = f A(z z a) = Az Az a = f f =. Kita vertus, jei z ker A, tuomet A(z a + z) = Az a + Az = f + = f. 2.2 išvada [Superpozicijos principas]. Jeigu z ra nehomogeninės TL Az = f sprendins, z 2 ra nehomogeninės tiesinės lgties Az = f 2 sprendins, tuomet z = αz + βz 2 ra tiesinės lgties Az = αf + βf 2 sprendins. Įrodmas. Iš Az = f, Az 2 = f 2 A(αz + βz 2 ) = αaz + βaz 2 = αf + βf uždavins. Suformuluokite 2. ir 2.2 teiginius ir jų išvadas n-osios eilės TDL sprendiniams. 2. ppavzds. Imkime homogeninę tiesinę pirmosios eilės DL z z =. Jos bendrasis sprendins ra z = Ce, C R. Jeigu z = C e ir z 2 = C 2e, tuomet αz + βz 2 = (αc + βc 2)e vėl bus šios TDL sprendins. Sprendinių erdvė ra vienmatė, nes pakanka žinoti vieną nenulinį sprendinį ψ = e, o tada visi kiti sprendiniai z = Cψ (žiūrėk 2.2 pav.). 2.2 ppavzds. Imkime nehomogeninę tiesinę pirmosios eilės DL z z =. Šios lgties atskirasis sprendins ra z a = +. Homogeninės TDL lgties bendrasis sprendins ra z = Ce, todėl bendrasis nehomogeninės TDL bus z = Ce + + (žiūrėk 2.3 pav.). 2.3 ppavzds. Imkime nehomogeninę tiesinę pirmosios eilės DL z z = 2e. Šios lgties atskirasis sprendins ra z a = e. Todėl bendrasis nehomogeninės TDL sprendins ra z = Ce + e. 2.4 ppavzds. Imkime nehomogeninę tiesinę pirmosios eilės DL z z = + e. Kadangi + e = ( ) + ( /2) ( 2e ), todėl iš superpozicijos principo atskirasis nehomogeninės TDL ra z a = (+)+( /2) (e ). Tada bendrasis nehomogeninės TDL sprendins bus z = Ce + + e /2.
35 . Tiesinė n-osios eilės diferencialinė lgtis pav. Homogeninės TDL integralinės kreivės. 2.3 pav. Nehomogeninės TDL integralinės kreivės. 2.4 pav. Funkciju tiesinė priklausombė..2. Funkcijų tiesinis priklausomumas ir nepriklausomumas? Tiesinės erdvės L elementai (vektoriai) v,..., v n ra tiesiškai nepriklausomomi, jeigu lgbė α v + + α nv n = (.6) teisinga tik kai α = = α n =, priešingu atveju turime tiesiškai priklausomus elementus (vektorius). Jeigu elementai ra tiesiškai priklausomi, tuomet i : α i. Tarkime, i = n. Tada funkcija z n tiesiškai išsireiškia per kitas funkcijas z,..., z n. Nagrinėkime tiesines erdves, kurių elementai ra funkcijos. Funkcijos f,..., f n ra tiesiškai nepriklausomos, jeigu tapatbė α f () + + α n f n () (.7) teisinga tik kai α = = α n =, priešingu atveju turime tiesiškai priklausomas funkcijas. 2.5 ppavzds [Funkcijų tiesinė priklausombė]. 2.4 pav. ra pavaizduoti funkcijų F () = ( 2 + )/2, G() = ( 2 )/2, H() = ( 2 )/2 grafikai. Funkcijos F ir G ra tiesiškai nepriklausomos (kodėl?), o funkcijos F ir H ra tiesiškai priklausomos. 2.3 uždavins. Patikrinkite funkcijų f, f 2, f 3 tiesinį priklausomumą: a) f () =, f 2() =, f 3() = 2 ; b) f () =, f 2() = 2, f 3() = apibrėžimas [Vronskio determinantas]. Funkcijų z,..., z n C n (I) Vronskio determinantu vadinama funkcija W [z,..., z n ] C(I): z () z 2 ()... z n () W () = W [z,..., z n ]() := z () z 2()... z n() (.8) z (n ) () z (n ) 2 ()... z n (n ) () Jósef Maria Hoëné Wroński ( ) lenku filosofas, matematikas, fizikas, išradėjas, teisininkas ir ekonomistas.
Paprastosios DIFERENCIALINĖS LYGTYS
 Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Diferencialinių lygčių ir skaičiavimo matematikos katedra Naugarduko g. 24, LT-3225 Vilnius,
Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Diferencialinių lygčių ir skaičiavimo matematikos katedra Naugarduko g. 24, LT-3225 Vilnius,
Paprastosios DIFERENCIALINĖS LYGTYS
 Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Taikomosios matematikos institutas, Diferencialinių lygčių katedra Naugarduko g. 24, LT-3225
Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Taikomosios matematikos institutas, Diferencialinių lygčių katedra Naugarduko g. 24, LT-3225
Dviejų kintamųjų funkcijos dalinės išvestinės
 Dviejų kintamųjų funkcijos dalinės išvestinės Dalinės išvestinės Tarkime, kad dviejų kintamųjų funkcija (, )yra apibrėžta srityje, o taškas 0 ( 0, 0 )yra vidinis srities taškas. Jei fiksuosime argumento
Dviejų kintamųjų funkcijos dalinės išvestinės Dalinės išvestinės Tarkime, kad dviejų kintamųjų funkcija (, )yra apibrėžta srityje, o taškas 0 ( 0, 0 )yra vidinis srities taškas. Jei fiksuosime argumento
Matematika 1 4 dalis
 Matematika 1 4 dalis Analizinės geometrijos elementai. Tiesės plokštumoje lygtis (bendroji, kryptinė,...). Taško atstumas nuo tiesės. Kampas tarp dviejų tiesių. Plokščiosios kreivės lygtis Plokščiosios
Matematika 1 4 dalis Analizinės geometrijos elementai. Tiesės plokštumoje lygtis (bendroji, kryptinė,...). Taško atstumas nuo tiesės. Kampas tarp dviejų tiesių. Plokščiosios kreivės lygtis Plokščiosios
1. Individualios užduotys:
 IV. PAPRASTOSIOS DIFERENCIALINĖS LYGTYS. Individualios užduots: - trumpa teorijos apžvalga, - pavzdžiai, - užduots savarankiškam darbui. Pirmosios eilės diferencialinių lgčių sprendimas.. psl. Antrosios
IV. PAPRASTOSIOS DIFERENCIALINĖS LYGTYS. Individualios užduots: - trumpa teorijos apžvalga, - pavzdžiai, - užduots savarankiškam darbui. Pirmosios eilės diferencialinių lgčių sprendimas.. psl. Antrosios
Vilniaus universitetas. Edmundas Gaigalas A L G E B R O S UŽDUOTYS IR REKOMENDACIJOS
 Vilniaus universitetas Edmundas Gaigalas A L G E B R O S UŽDUOTYS IR REKOMENDACIJOS Vilnius 1992 T U R I N Y S 1. Vektorinė erdvė............................................. 3 2. Matricos rangas.............................................
Vilniaus universitetas Edmundas Gaigalas A L G E B R O S UŽDUOTYS IR REKOMENDACIJOS Vilnius 1992 T U R I N Y S 1. Vektorinė erdvė............................................. 3 2. Matricos rangas.............................................
ANALIZINĖ GEOMETRIJA III skyrius (Medžiaga virtualiajam kursui)
 ngelė aškienė NLIZINĖ GEMETRIJ III skrius (Medžiaga virtualiajam kursui) III skrius. TIESĖS IR PLKŠTUMS... 5. Tiesės lgts... 5.. Tiesės [M, a r ] vektorinė lgtis... 5.. Tiesės [M, a r ] parametrinės lgts...
ngelė aškienė NLIZINĖ GEMETRIJ III skrius (Medžiaga virtualiajam kursui) III skrius. TIESĖS IR PLKŠTUMS... 5. Tiesės lgts... 5.. Tiesės [M, a r ] vektorinė lgtis... 5.. Tiesės [M, a r ] parametrinės lgts...
FDMGEO4: Antros eilės kreivės I
 FDMGEO4: Antros eilės kreivės I Kęstutis Karčiauskas Matematikos ir Informatikos fakultetas 1 Koordinačių sistemos transformacija Antrosios eilės kreivių lgtis prastinsime keisdami (transformuodami) koordinačių
FDMGEO4: Antros eilės kreivės I Kęstutis Karčiauskas Matematikos ir Informatikos fakultetas 1 Koordinačių sistemos transformacija Antrosios eilės kreivių lgtis prastinsime keisdami (transformuodami) koordinačių
X galioja nelygyb f ( x1) f ( x2)
 Monotonin s funkcijos Tegul turime funkciją f : A R, A R. Apibr žimas. Funkcija y = f ( x) vadinama monotoniškai did jančia (maž jančia) aib je X A, jei x1< x2 iš X galioja nelygyb f ( x1) f ( x2) ( f
Monotonin s funkcijos Tegul turime funkciją f : A R, A R. Apibr žimas. Funkcija y = f ( x) vadinama monotoniškai did jančia (maž jančia) aib je X A, jei x1< x2 iš X galioja nelygyb f ( x1) f ( x2) ( f
AIBĖS, FUNKCIJOS, LYGTYS
 AIBĖS, FUNKCIJOS, LYGTYS Aibės sąvoka ir pavyzdžiai Atskirų objektų rinkiniai, grupės, sistemos, kompleksai matematikoje vadinami aibėmis. Šie atskiri objektai vadinami aibės elementais. Kai elementas
AIBĖS, FUNKCIJOS, LYGTYS Aibės sąvoka ir pavyzdžiai Atskirų objektų rinkiniai, grupės, sistemos, kompleksai matematikoje vadinami aibėmis. Šie atskiri objektai vadinami aibės elementais. Kai elementas
Matematinės analizės konspektai
 Matematinės analizės konspektai (be įrodymų) Marius Gedminas pagal V. Mackevičiaus paskaitas 998 m. rudens semestras (I kursas) Realieji skaičiai Apibrėžimas. Uždarųjų intervalų seka [a n, b n ], n =,
Matematinės analizės konspektai (be įrodymų) Marius Gedminas pagal V. Mackevičiaus paskaitas 998 m. rudens semestras (I kursas) Realieji skaičiai Apibrėžimas. Uždarųjų intervalų seka [a n, b n ], n =,
Specialieji analizės skyriai
 Specialieji analizės skyriai. Specialieji analizės skyriai Kompleksinio kinamojo funkcijų teorija Furje eilutės ir Furje integralai Operacinis skaičiavimas Lauko teorijos elementai. 2 Kompleksinio kintamojo
Specialieji analizės skyriai. Specialieji analizės skyriai Kompleksinio kinamojo funkcijų teorija Furje eilutės ir Furje integralai Operacinis skaičiavimas Lauko teorijos elementai. 2 Kompleksinio kintamojo
Matematika 1 3 dalis
 Matematika 1 3 dalis Vektorių algebros elementai. Vektorių veiksmai. Vektorių skaliarinės, vektorinės ir mišriosios sandaugos ir jų savybės. Vektoriai Vektoriumi vadinama kryptinė atkarpa. Jei taškas A
Matematika 1 3 dalis Vektorių algebros elementai. Vektorių veiksmai. Vektorių skaliarinės, vektorinės ir mišriosios sandaugos ir jų savybės. Vektoriai Vektoriumi vadinama kryptinė atkarpa. Jei taškas A
FUNKCIJOS. veiksmu šioje erdvėje apibrėžkime dar viena. a = {a 1,..., a n } ir b = {b 1,... b n } skaliarine sandauga
 VII DAUGELIO KINTAMU JU FUNKCIJOS 71 Bendrosios sa vokos Iki šiol mes nagrinėjome funkcijas, apibrėžtas realiu skaičiu aibėje Nagrinėsime funkcijas, kurios apibrėžtos vektorinėse erdvėse Tarkime, kad R
VII DAUGELIO KINTAMU JU FUNKCIJOS 71 Bendrosios sa vokos Iki šiol mes nagrinėjome funkcijas, apibrėžtas realiu skaičiu aibėje Nagrinėsime funkcijas, kurios apibrėžtos vektorinėse erdvėse Tarkime, kad R
Specialieji analizės skyriai
 Specialieji analizės skyriai. Trigonometrinės Furje eilutės Moksle ir technikoje dažnai susiduriame su periodiniais reiškiniais, apibūdinamais periodinėmis laiko funkcijomis: f(t). 2 Paprasčiausia periodinė
Specialieji analizės skyriai. Trigonometrinės Furje eilutės Moksle ir technikoje dažnai susiduriame su periodiniais reiškiniais, apibūdinamais periodinėmis laiko funkcijomis: f(t). 2 Paprasčiausia periodinė
IV. FUNKCIJOS RIBA. atvira. intervala. Apibrėžimas Sakysime, kad skaičius b yra funkcijos y = f(x) riba taške x 0, jei bet kokiam,
 41 Funkcijos riba IV FUNKCIJOS RIBA Taško x X aplinka vadiname bet koki atvira intervala, kuriam priklauso taškas x Taško x 0, 2t ilgio aplinka žymėsime tokiu būdu: V t (x 0 ) = ([x 0 t, x 0 + t) Sakykime,
41 Funkcijos riba IV FUNKCIJOS RIBA Taško x X aplinka vadiname bet koki atvira intervala, kuriam priklauso taškas x Taško x 0, 2t ilgio aplinka žymėsime tokiu būdu: V t (x 0 ) = ([x 0 t, x 0 + t) Sakykime,
I dalis KLAUSIMŲ SU PASIRENKAMUOJU ATSAKYMU TEISINGI ATSAKYMAI
 008 M. FIZIKOS VALSTYBINIO BRANDOS EGZAMINO VERTINIMO INSTRUKCIJA Pagrindinė sesija Kiekvieno I dalies klausimo teisingas atsakymas vertinamas tašku. I dalis KLAUSIMŲ SU PASIRENKAMUOJU ATSAKYMU TEISINGI
008 M. FIZIKOS VALSTYBINIO BRANDOS EGZAMINO VERTINIMO INSTRUKCIJA Pagrindinė sesija Kiekvieno I dalies klausimo teisingas atsakymas vertinamas tašku. I dalis KLAUSIMŲ SU PASIRENKAMUOJU ATSAKYMU TEISINGI
Įžanginių paskaitų medžiaga iš knygos
 MATEMATINĖ LOGIKA Įžanginių paskaitų medžiaga iš knygos Aleksandras Krylovas. Diskrečioji matematika: vadovėlis aukštųjų mokyklų studentams. Vilnius: Technika, 2009. 320 p. ISBN 978-9955-28-450-5 1 Teiginio
MATEMATINĖ LOGIKA Įžanginių paskaitų medžiaga iš knygos Aleksandras Krylovas. Diskrečioji matematika: vadovėlis aukštųjų mokyklų studentams. Vilnius: Technika, 2009. 320 p. ISBN 978-9955-28-450-5 1 Teiginio
LIETUVOS JAUNŲ J Ų MATEMATIKŲ MOKYKLA
 LIETUVOS JAUNŲ J Ų MATEMATIKŲ MOKYKLA tema. APSKRITIMŲ GEOMETRIJA (00 0) Teorinę medžiagą parengė bei antrąją užduotį sudarė Vilniaus pedagoginio universiteto docentas Edmundas Mazėtis. Apskritimas tai
LIETUVOS JAUNŲ J Ų MATEMATIKŲ MOKYKLA tema. APSKRITIMŲ GEOMETRIJA (00 0) Teorinę medžiagą parengė bei antrąją užduotį sudarė Vilniaus pedagoginio universiteto docentas Edmundas Mazėtis. Apskritimas tai
MATEMATINĖ LOGIKA. Įžanginių paskaitų medžiaga iš knygos
 MATEMATINĖ LOGIKA Įžanginių paskaitų medžiaga iš knygos Aleksandras Krylovas. Diskrečioji matematika: vadovėlis aukštųjų mokyklų studentams. Vilnius: Technika, 2009. 320 p. ISBN 978-9955-28-450-5 Teiginio
MATEMATINĖ LOGIKA Įžanginių paskaitų medžiaga iš knygos Aleksandras Krylovas. Diskrečioji matematika: vadovėlis aukštųjų mokyklų studentams. Vilnius: Technika, 2009. 320 p. ISBN 978-9955-28-450-5 Teiginio
0.1. Bendrosios sąvokos
 .1. BENDROSIOS SĄVOKOS 1.1. Bendrosios sąvokos.1.1. Diferencialinės lygtys su mažuoju parametru F ) x n),x n 1),...,x,x,t;ε =, xt;ε) C n T), T [,+ ), < ε ε ) F x n) t;ε),x n 1) t;ε),...,x t;ε),xt;ε),t;ε,
.1. BENDROSIOS SĄVOKOS 1.1. Bendrosios sąvokos.1.1. Diferencialinės lygtys su mažuoju parametru F ) x n),x n 1),...,x,x,t;ε =, xt;ε) C n T), T [,+ ), < ε ε ) F x n) t;ε),x n 1) t;ε),...,x t;ε),xt;ε),t;ε,
1.4. Rungės ir Kuto metodas
 .4. RUNGĖS IR KUTO METODAS.4. Rungės ir Kuto metodas.4.. Prediktoriaus-korektoriaus metodas Palyginkime išreikštinį ir simetrinį Eulerio metodus. Pirmojo iš jų pagrindinis privalumas tas, kad išreikštinio
.4. RUNGĖS IR KUTO METODAS.4. Rungės ir Kuto metodas.4.. Prediktoriaus-korektoriaus metodas Palyginkime išreikštinį ir simetrinį Eulerio metodus. Pirmojo iš jų pagrindinis privalumas tas, kad išreikštinio
Praeita paskaita. Grafika ir vizualizavimas Atkirtimai dvimatėje erdvėje. Praeita paskaita. 2D Transformacijos. Grafika ir vizualizavimas, VDU, 2010
 Praeita paskaita Grafika ir vizualizavimas Atkirtimai dvimatėje erdvėje Atkarpos Tiesės lgtis = mx+ b kur m krpties koeficientas, o b aukštis, kuriame tiesė kerta ašį Susikirtimo taško apskaičiavimui sulginamos
Praeita paskaita Grafika ir vizualizavimas Atkirtimai dvimatėje erdvėje Atkarpos Tiesės lgtis = mx+ b kur m krpties koeficientas, o b aukštis, kuriame tiesė kerta ašį Susikirtimo taško apskaičiavimui sulginamos
4.1 Skaliarinė sandauga erdvėje R n Tarkime, kad duota vektorinė erdvė R n. Priminsime, kad šios erdvės elementai yra vektoriai vektoriu
 IV DEKARTO KOORDINAČIU SISTEMA VEKTORIAI 41 Skaliarinė sandauga erdvėje R n Tarkime, kad duota vektorinė erdvė R n Priminsime, kad šios erdvės elementai yra vektoriai α = (a 1,, a n ) Be mums jau žinomu
IV DEKARTO KOORDINAČIU SISTEMA VEKTORIAI 41 Skaliarinė sandauga erdvėje R n Tarkime, kad duota vektorinė erdvė R n Priminsime, kad šios erdvės elementai yra vektoriai α = (a 1,, a n ) Be mums jau žinomu
Temos. Intervalinės statistinės eilutės sudarymas. Santykinių dažnių histogramos brėžimas. Imties skaitinių charakteristikų skaičiavimas
 Pirmasis uždavinys Temos. Intervalinės statistinės eilutės sudarymas. Santykinių dažnių histogramos brėžimas. Imties skaitinių charakteristikų skaičiavimas Uždavinio formulavimas a) Žinoma n = 50 tiriamo
Pirmasis uždavinys Temos. Intervalinės statistinės eilutės sudarymas. Santykinių dažnių histogramos brėžimas. Imties skaitinių charakteristikų skaičiavimas Uždavinio formulavimas a) Žinoma n = 50 tiriamo
I.4. Laisvasis kūnų kritimas
 I4 Laisvasis kūnų kitimas Laisvuoju kitimu vadinamas judėjimas, kuiuo judėtų kūnas veikiamas tik sunkio jėos, nepaisant oo pasipiešinimo Kūnui laisvai kintant iš nedidelio aukščio h (dau mažesnio už Žemės
I4 Laisvasis kūnų kitimas Laisvuoju kitimu vadinamas judėjimas, kuiuo judėtų kūnas veikiamas tik sunkio jėos, nepaisant oo pasipiešinimo Kūnui laisvai kintant iš nedidelio aukščio h (dau mažesnio už Žemės
VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS PROGRAMŲ SISTEMŲ KATEDRA. Algoritmų teorija. Paskaitų konspektas
 VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS PROGRAMŲ SISTEMŲ KATEDRA Algoritmų teorija Paskaitų konspektas Dėstytojas: lekt. dr. Adomas Birštunas Vilnius 2015 TURINYS 1. Algoritmo samprata...
VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS PROGRAMŲ SISTEMŲ KATEDRA Algoritmų teorija Paskaitų konspektas Dėstytojas: lekt. dr. Adomas Birštunas Vilnius 2015 TURINYS 1. Algoritmo samprata...
VIII. FRAKTALINĖ DIMENSIJA. 8.1 Fraktalinės dimensijos samprata. Ar baigtinis Norvegijos sienos ilgis?
 VIII FRAKTALINĖ DIMENSIJA 81 Fraktalinės dimensijos samprata Ar baigtinis Norvegijos sienos ilgis? Tarkime, kad duota atkarpa, kurios ilgis lygus 1 Padalykime šia atkarpa n lygiu daliu Akivaizdu, kad kiekvienos
VIII FRAKTALINĖ DIMENSIJA 81 Fraktalinės dimensijos samprata Ar baigtinis Norvegijos sienos ilgis? Tarkime, kad duota atkarpa, kurios ilgis lygus 1 Padalykime šia atkarpa n lygiu daliu Akivaizdu, kad kiekvienos
2008 m. matematikos valstybinio brandos egzamino VERTINIMO INSTRUKCIJA Pagrindinė sesija
 008 M MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA 008 m matematikos valstybinio brandos egzamino VERTINIMO INSTRUKCIJA Pagrindinė sesija 7 uždavinių atsakymai I variantas Užd
008 M MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA 008 m matematikos valstybinio brandos egzamino VERTINIMO INSTRUKCIJA Pagrindinė sesija 7 uždavinių atsakymai I variantas Užd
0.1. Bendrosios sąvokos
 0.1. BENDROSIOS SĄVOKOS 1 0.1. Bendrosios sąvokos 0.1.1. Diferencialinės lygtys su mažuoju parametru F ) x n),x n 1),...,x,x,t;ε = 0, xt;ε) C n T), T [0,+ ), 0 < ε ε 0 ) F x n) t;ε),x n 1) t;ε),...,x t;ε),xt;ε),t;ε
0.1. BENDROSIOS SĄVOKOS 1 0.1. Bendrosios sąvokos 0.1.1. Diferencialinės lygtys su mažuoju parametru F ) x n),x n 1),...,x,x,t;ε = 0, xt;ε) C n T), T [0,+ ), 0 < ε ε 0 ) F x n) t;ε),x n 1) t;ε),...,x t;ε),xt;ε),t;ε
ELEMENTARIOJI TEORIJA
 ELEMENTARIOJI TEORIJA Pirmosios kombinatorikos þinios siekia senàsias Rytø ðalis, kuriose mokëta suskaièiuoti këlinius bei derinius ir sudarinëti magiðkuosius kvadratus, ypaè populiarius viduramþiais.
ELEMENTARIOJI TEORIJA Pirmosios kombinatorikos þinios siekia senàsias Rytø ðalis, kuriose mokëta suskaièiuoti këlinius bei derinius ir sudarinëti magiðkuosius kvadratus, ypaè populiarius viduramþiais.
ATSITIKTINIAI PROCESAI. Alfredas Račkauskas. (paskaitų konspektas 2014[1] )
![ATSITIKTINIAI PROCESAI. Alfredas Račkauskas. (paskaitų konspektas 2014[1] ) ATSITIKTINIAI PROCESAI. Alfredas Račkauskas. (paskaitų konspektas 2014[1] )](/thumbs/72/67447727.jpg) ATSITIKTINIAI PROCESAI (paskaitų konspektas 2014[1] ) Alfredas Račkauskas Vilniaus universitetas Matematikos ir Informatikos fakultetas Ekonometrinės analizės katedra Vilnius, 2014 Iš dalies rėmė Projektas
ATSITIKTINIAI PROCESAI (paskaitų konspektas 2014[1] ) Alfredas Račkauskas Vilniaus universitetas Matematikos ir Informatikos fakultetas Ekonometrinės analizės katedra Vilnius, 2014 Iš dalies rėmė Projektas
Elektronų ir skylučių statistika puslaidininkiuose
 lktroų ir skylučių statistika puslaidiikiuos Laisvų laidumo lktroų gracija, t.y. lktroų prėjimas į laidumo juostą, gali vykti kaip iš dooriių lygmų, taip ir iš valtiės juostos. Gracijos procsas visuomt
lktroų ir skylučių statistika puslaidiikiuos Laisvų laidumo lktroų gracija, t.y. lktroų prėjimas į laidumo juostą, gali vykti kaip iš dooriių lygmų, taip ir iš valtiės juostos. Gracijos procsas visuomt
1 TIES ES IR PLOK TUMOS
 G E O M E T R I J A Gediminas STEPANAUSKAS 1 TIES ES IR PLOK TUMOS 11 Plok²tumos ir ties es plok²tumoje normalin es lygtys 111 Vektorin e forma Plok²tumos α padetis koordina iu sistemos Oxyz atºvilgiu
G E O M E T R I J A Gediminas STEPANAUSKAS 1 TIES ES IR PLOK TUMOS 11 Plok²tumos ir ties es plok²tumoje normalin es lygtys 111 Vektorin e forma Plok²tumos α padetis koordina iu sistemos Oxyz atºvilgiu
2.5. KLASIKINĖS TOLYDŽIŲ FUNKCIJŲ TEOREMOS
 .5. KLASIKINĖS TOLYDŽIŲ FUNKCIJŲ TEOREMOS 5.. Pirmoji Bolcao Koši teorema. Jei fucija f tolydi itervale [a;b], itervalo galuose įgyja priešigų želų reišmes, tai egzistuoja tos tašas cc, ( ab ; ), uriame
.5. KLASIKINĖS TOLYDŽIŲ FUNKCIJŲ TEOREMOS 5.. Pirmoji Bolcao Koši teorema. Jei fucija f tolydi itervale [a;b], itervalo galuose įgyja priešigų želų reišmes, tai egzistuoja tos tašas cc, ( ab ; ), uriame
III. MATRICOS. DETERMINANTAI. 3.1 Matricos A = lentele žymėsime taip:
 III MATRICOS DETERMINANTAI Realiu ju skaičiu lentele 3 Matricos a a 2 a n A = a 2 a 22 a 2n a m a m2 a mn vadinsime m n eilės matrica Trumpai šia lentele žymėsime taip: A = a ij ; i =,, m, j =,, n čia
III MATRICOS DETERMINANTAI Realiu ju skaičiu lentele 3 Matricos a a 2 a n A = a 2 a 22 a 2n a m a m2 a mn vadinsime m n eilės matrica Trumpai šia lentele žymėsime taip: A = a ij ; i =,, m, j =,, n čia
2015 M. MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA Pagrindinė sesija. I dalis
 PATVIRTINTA Ncionlinio egzminų centro direktorius 0 m. birželio d. įskymu Nr. (..)-V-7 0 M. MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA Pgrindinė sesij I dlis Užd. Nr. 4 7
PATVIRTINTA Ncionlinio egzminų centro direktorius 0 m. birželio d. įskymu Nr. (..)-V-7 0 M. MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA Pgrindinė sesij I dlis Užd. Nr. 4 7
Modalumo logikos S4 kai kurios išsprendžiamos klasės
 VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS INFORMATIKOS KATEDRA Magistro baigiamasis darbas Modalumo logikos S4 kai kurios išsprendžiamos klasės Some Decidable Classes of Modal Logic
VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS INFORMATIKOS KATEDRA Magistro baigiamasis darbas Modalumo logikos S4 kai kurios išsprendžiamos klasės Some Decidable Classes of Modal Logic
2009 m. matematikos valstybinio brandos egzamino VERTINIMO INSTRUKCIJA Pagrindinė sesija 1 6 uždavinių atsakymai
 M. MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA PATVIRTINTA Nacionalinio egzaminų centro direktoriaus -6- įsakymu Nr. (..)-V-8 m. matematikos valstybinio brandos egzamino VERTINIMO
M. MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA PATVIRTINTA Nacionalinio egzaminų centro direktoriaus -6- įsakymu Nr. (..)-V-8 m. matematikos valstybinio brandos egzamino VERTINIMO
06 Geometrin e optika 1
 06 Geometrinė optika 1 0.1. EIKONALO LYGTIS 3 Geometrinėje optikoje įvedama šviesos spindulio sąvoka. Tai leidžia Eikonalo lygtis, kuri išvedama iš banginės lygties monochromatinei bangai - Helmholtco
06 Geometrinė optika 1 0.1. EIKONALO LYGTIS 3 Geometrinėje optikoje įvedama šviesos spindulio sąvoka. Tai leidžia Eikonalo lygtis, kuri išvedama iš banginės lygties monochromatinei bangai - Helmholtco
Matematinės analizės egzamino klausimai MIF 1 kursas, Bioinformatika, 1 semestras,
 MIF kurss, Bioinformtik, semestrs, 29 6 Tolydžios tške ir intervle funkciju pibrėžimi Teorem Jei f C[, ], f() = A , ti egzistuoj toks c [, ], kd f(c) = 2 Konverguojnčios ir diverguojnčios eikutės
MIF kurss, Bioinformtik, semestrs, 29 6 Tolydžios tške ir intervle funkciju pibrėžimi Teorem Jei f C[, ], f() = A , ti egzistuoj toks c [, ], kd f(c) = 2 Konverguojnčios ir diverguojnčios eikutės
1 Tada teigini Ne visi šie vaikinai yra studentai galima išreikšti formule. 2 Ta pati teigini galima užrašyti ir taip. 3 Formulė U&B C reiškia, kad
 45 DISKREČIOJI MATEMATIKA. LOGIKA. PAVYZDŽIAI Raidėmis U, B ir C pažymėti teiginiai: U = Vitas yra studentas ; B = Skirmantas yra studentas ; C = Jonas yra studentas. 1 Tada teigini Ne visi šie vaikinai
45 DISKREČIOJI MATEMATIKA. LOGIKA. PAVYZDŽIAI Raidėmis U, B ir C pažymėti teiginiai: U = Vitas yra studentas ; B = Skirmantas yra studentas ; C = Jonas yra studentas. 1 Tada teigini Ne visi šie vaikinai
Matematinė logika. 1 skyrius Propozicinės formulės. žodį, Graikiškas žodis logos (λóγoς) reiškia
 1 skyrius Matematinė logika Graikiškas žodis logos (λóγoς) reiškia mintį, žodį, protą, sąvoką. Logika arba formalioji logika nagrinėja teisingo mąstymo dėsnius ir formas, kai samprotavimų turinys nėra
1 skyrius Matematinė logika Graikiškas žodis logos (λóγoς) reiškia mintį, žodį, protą, sąvoką. Logika arba formalioji logika nagrinėja teisingo mąstymo dėsnius ir formas, kai samprotavimų turinys nėra
Taikomieji optimizavimo metodai
 Taikomieji optimizavimo metodai 1 LITERATŪRA A. Apynis. Optimizavimo metodai. V., 2005 G. Dzemyda, V. Šaltenis, V. Tiešis. Optimizavimo metodai, V., 2007 V. Būda, M. Sapagovas. Skaitiniai metodai : algoritmai,
Taikomieji optimizavimo metodai 1 LITERATŪRA A. Apynis. Optimizavimo metodai. V., 2005 G. Dzemyda, V. Šaltenis, V. Tiešis. Optimizavimo metodai, V., 2007 V. Būda, M. Sapagovas. Skaitiniai metodai : algoritmai,
Algoritmai. Vytautas Kazakevičius
 Algoritmai Vytautas Kazakevičius September 2, 27 2 Turinys Baigtiniai automatai 5. DBA.................................. 5.. Abėcėlė............................ 5..2 Automatai..........................
Algoritmai Vytautas Kazakevičius September 2, 27 2 Turinys Baigtiniai automatai 5. DBA.................................. 5.. Abėcėlė............................ 5..2 Automatai..........................
Diskrečioji matematika
 VILNIAUS UNIVERSITETAS Gintaras Skersys Julius Andrikonis Diskrečioji matematika Pratybų medžiaga Versija: 28 m. sausio 22 d. Vilnius, 27 Turinys Turinys 2 Teiginiai. Loginės operacijos. Loginės formulės
VILNIAUS UNIVERSITETAS Gintaras Skersys Julius Andrikonis Diskrečioji matematika Pratybų medžiaga Versija: 28 m. sausio 22 d. Vilnius, 27 Turinys Turinys 2 Teiginiai. Loginės operacijos. Loginės formulės
Spalvos. Šviesa. Šviesos savybės. Grafika ir vizualizavimas. Spalvos. Grafika ir vizualizavimas, VDU, Spalvos 1
 Spalvos Grafika ir vizualizavimas Spalvos Šviesa Spalvos Spalvų modeliai Gama koregavimas Šviesa Šviesos savybės Vandens bangos Vaizdas iš šono Vaizdas iš viršaus Vaizdas erdvėje Šviesos bangos Šviesa
Spalvos Grafika ir vizualizavimas Spalvos Šviesa Spalvos Spalvų modeliai Gama koregavimas Šviesa Šviesos savybės Vandens bangos Vaizdas iš šono Vaizdas iš viršaus Vaizdas erdvėje Šviesos bangos Šviesa
3 modulis. Funkcijos sąvoka. Laipsninė, rodiklinė ir logaritminė funkcija
 P R O J E K T A S VP--ŠMM-0-V-0-00 MOKYMOSI KRYPTIES PASIRINKIMO GALIMYBIŲ DIDINIMAS -9 METŲ MOKINIAMS, II ETAPAS: GILESNIS MOKYMOSI DIFERENCIJAVIMAS IR INDIVIDUALIZAVIMAS, SIEKIANT UGDYMO KOKYBĖS, REIKALINGOS
P R O J E K T A S VP--ŠMM-0-V-0-00 MOKYMOSI KRYPTIES PASIRINKIMO GALIMYBIŲ DIDINIMAS -9 METŲ MOKINIAMS, II ETAPAS: GILESNIS MOKYMOSI DIFERENCIJAVIMAS IR INDIVIDUALIZAVIMAS, SIEKIANT UGDYMO KOKYBĖS, REIKALINGOS
1 Įvadas Neišspręstos problemos Dalumas Dalyba su liekana Dalumo požymiai... 3
 Skaičių teorija paskaitų konspektas Paulius Šarka, Jonas Šiurys 1 Įvadas 1 1.1 Neišspręstos problemos.............................. 1 2 Dalumas 2 2.1 Dalyba su liekana.................................
Skaičių teorija paskaitų konspektas Paulius Šarka, Jonas Šiurys 1 Įvadas 1 1.1 Neišspręstos problemos.............................. 1 2 Dalumas 2 2.1 Dalyba su liekana.................................
8. LENKIAMŲ PLOKŠTELIŲ ELEMENTAI
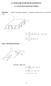 8. LENKIAMŲ PLOKŠELIŲ ELEMENAI 8.1. LENKIAMŲ PLOKŠELIŲ EORIJA Įtempimai: storį: paprastai operuojama įrąžomis įtempimų atstojamosiomis per plokštelės z τ z t τ z M t = zdz, M =...., M =.. t t = τzdz, =
8. LENKIAMŲ PLOKŠELIŲ ELEMENAI 8.1. LENKIAMŲ PLOKŠELIŲ EORIJA Įtempimai: storį: paprastai operuojama įrąžomis įtempimų atstojamosiomis per plokštelės z τ z t τ z M t = zdz, M =...., M =.. t t = τzdz, =
eksponentinės generuojančios funkcijos 9. Grafu
 DISKREČIOJI MATEMATIKA (2 semestras) KOMBINATORIKOS IR GRAFU TEORIJOS PRADMENYS PROGRAMA I KOMBINATORIKA 1 Matematinės indukcijos ir Dirichlė principai 2 Dauginimo taisyklė,,skaičiuok dukart principas
DISKREČIOJI MATEMATIKA (2 semestras) KOMBINATORIKOS IR GRAFU TEORIJOS PRADMENYS PROGRAMA I KOMBINATORIKA 1 Matematinės indukcijos ir Dirichlė principai 2 Dauginimo taisyklė,,skaičiuok dukart principas
ŠVIESOS SKLIDIMAS IZOTROPINĖSE TERPĖSE
 ŠVIESOS SKLIDIMAS IZOTROPIĖSE TERPĖSE 43 2.7. SPIDULIUOTĖS IR KŪO SPALVOS Spinduliuotės ir kūno optiniam apibūdinimui naudojama spalvos sąvoka. Spalvos reiškinys yra nepaprastas. Kad suprasti spalvos esmę,
ŠVIESOS SKLIDIMAS IZOTROPIĖSE TERPĖSE 43 2.7. SPIDULIUOTĖS IR KŪO SPALVOS Spinduliuotės ir kūno optiniam apibūdinimui naudojama spalvos sąvoka. Spalvos reiškinys yra nepaprastas. Kad suprasti spalvos esmę,
Remigijus Leipus. Ekonometrija II. remis
 Remigijus Leipus Ekonometrija II http://uosis.mif.vu.lt/ remis Vilnius, 2013 Turinys 1 Trendo ir sezoniškumo vertinimas bei eliminavimas 4 1.1 Trendo komponentės vertinimas ir eliminavimas........ 4 1.2
Remigijus Leipus Ekonometrija II http://uosis.mif.vu.lt/ remis Vilnius, 2013 Turinys 1 Trendo ir sezoniškumo vertinimas bei eliminavimas 4 1.1 Trendo komponentės vertinimas ir eliminavimas........ 4 1.2
EKONOMETRIJA 1 (Regresinė analizė)
 EKONOMETRIJA 1 Regresinė analizė Kontrolinis Sudarė M.Radavičius 004 05 15 Kai kurių užduočių sprendimai KOMENTARAS. Kai kuriems uždaviniams tik nusakytos sprendimų gairės, kai kurie iš jų suskaidyti į
EKONOMETRIJA 1 Regresinė analizė Kontrolinis Sudarė M.Radavičius 004 05 15 Kai kurių užduočių sprendimai KOMENTARAS. Kai kuriems uždaviniams tik nusakytos sprendimų gairės, kai kurie iš jų suskaidyti į
Ekonometrija. Trendas ir sezoninė laiko eilutės komponentė
 Ekonometrija. Trendas ir sezoninė laiko eilutės komponentė dėst. T. Rekašius, 2012 m. lapkričio 19 d. 1 Duomenys Visi trečiam laboratoriniam darbui reikalingi duomenys yra tekstinio formato failuose http://fmf.vgtu.lt/~trekasius/destymas/2012/ekomet_lab3_xx.dat,
Ekonometrija. Trendas ir sezoninė laiko eilutės komponentė dėst. T. Rekašius, 2012 m. lapkričio 19 d. 1 Duomenys Visi trečiam laboratoriniam darbui reikalingi duomenys yra tekstinio formato failuose http://fmf.vgtu.lt/~trekasius/destymas/2012/ekomet_lab3_xx.dat,
Matematinis modeliavimas
 ALGIRDAS AMBRAZEVIƒIUS Matematinis modeliavimas Vilniaus universitetas 2006 2 TURINYS 1 SKYRIUS PAPRASƒIAUSI MATEMATINIAI MODELIAI 4 11 Pagrindines s vokos 4 12 Fundamentaliu gamtos desniu taikymas 10
ALGIRDAS AMBRAZEVIƒIUS Matematinis modeliavimas Vilniaus universitetas 2006 2 TURINYS 1 SKYRIUS PAPRASƒIAUSI MATEMATINIAI MODELIAI 4 11 Pagrindines s vokos 4 12 Fundamentaliu gamtos desniu taikymas 10
DISPERSINĖ, FAKTORINĖ IR REGRESINĖ ANALIZĖ Laboratorinis darbas Nr. 2
 DISPERSINĖ, FAKTORINĖ IR REGRESINĖ ANALIZĖ Laboratorinis darbas Nr. 2 Marijus Radavičius, Tomas Rekašius 2010 m. vasario 23 d. Santrauka Antras laboratorinis darbas skirtas išmokti sudarinėti daugialypės
DISPERSINĖ, FAKTORINĖ IR REGRESINĖ ANALIZĖ Laboratorinis darbas Nr. 2 Marijus Radavičius, Tomas Rekašius 2010 m. vasario 23 d. Santrauka Antras laboratorinis darbas skirtas išmokti sudarinėti daugialypės
1. Vektoriu veiksmai. Vektoriu skaliarinė, vektorinė ir mišrioji sandaugos
 1. Vektoriu veiksmai. Vektoriu skaliarinė, vektorinė ir mišrioji sandaugos Vektoriu užrašymas MAPLE Vektorius MAPLE galime užrašyti daugeliu būdu. Juos grafiškai vaizduosime paketo Student[LinearAlgebra]
1. Vektoriu veiksmai. Vektoriu skaliarinė, vektorinė ir mišrioji sandaugos Vektoriu užrašymas MAPLE Vektorius MAPLE galime užrašyti daugeliu būdu. Juos grafiškai vaizduosime paketo Student[LinearAlgebra]
4.3. Minimalaus dengiančio medžio radimas
 SKYRIUS. ALGORITMAI GRAFUOSE.. Minimalaus dengiančio medžio radimas Šiame skyriuje susipažinsime su minimaliu dengiančiu medžių radimo algoritmais. Pirmiausia sudarysime dvi taisykles, leidžiančias pasirinkti
SKYRIUS. ALGORITMAI GRAFUOSE.. Minimalaus dengiančio medžio radimas Šiame skyriuje susipažinsime su minimaliu dengiančiu medžių radimo algoritmais. Pirmiausia sudarysime dvi taisykles, leidžiančias pasirinkti
DISPERSINĖ, FAKTORINĖ IR REGRESINĖ ANALIZĖ Laboratorinis darbas Nr. 1
 DISPERSINĖ, FAKTORINĖ IR REGRESINĖ ANALIZĖ Laboratorinis darbas Nr. 1 Marijus Radavičius, Tomas Rekašius 2010 m. vasario 9 d. Santrauka Pirmas laboratorinis darbas skirtas išmokti generuoti nesudėtingus
DISPERSINĖ, FAKTORINĖ IR REGRESINĖ ANALIZĖ Laboratorinis darbas Nr. 1 Marijus Radavičius, Tomas Rekašius 2010 m. vasario 9 d. Santrauka Pirmas laboratorinis darbas skirtas išmokti generuoti nesudėtingus
1 iš 15 RIBOTO NAUDOJIMO
 iš 5 PATVIRTINTA Nacionalinio egzaminų centro direktoriau 00-06-08 įakymu Nr. 6.-S- 00 m. matematiko valtybinio brando egzamino VERTINIMO INSTRUKCIJA Pagrindinė eija 8 uždavinių atakymai Užd. Nr. 5 6 7
iš 5 PATVIRTINTA Nacionalinio egzaminų centro direktoriau 00-06-08 įakymu Nr. 6.-S- 00 m. matematiko valtybinio brando egzamino VERTINIMO INSTRUKCIJA Pagrindinė eija 8 uždavinių atakymai Užd. Nr. 5 6 7
DISKREČIOJI MATEMATIKA
 VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS INFORMATIKOS KATEDRA Valdas Diči ūnas Gintaras Skersys DISKREČIOJI MATEMATIKA Mokymo priemonė Vilnius 2003 Įvadas Išvertus iš lotynu kalbos
VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS INFORMATIKOS KATEDRA Valdas Diči ūnas Gintaras Skersys DISKREČIOJI MATEMATIKA Mokymo priemonė Vilnius 2003 Įvadas Išvertus iš lotynu kalbos
9. KEVALŲ ELEMENTAI. Pavyzdžiai:
 9. KEVALŲ ELEMENTAI Kealai Tai ploni storio krptii kūnai, sudarti iš kreių plokštuų. Geoetrija nusakoa iduriniu pairšiui ir storiu t. Kiekiena pairšiaus taške galia rasti di kreies, atitinkančias inialius
9. KEVALŲ ELEMENTAI Kealai Tai ploni storio krptii kūnai, sudarti iš kreių plokštuų. Geoetrija nusakoa iduriniu pairšiui ir storiu t. Kiekiena pairšiaus taške galia rasti di kreies, atitinkančias inialius
TEORIJA. RINKTINIAI MATEMATIKOS SKYRIAI (Informatikos spec., 2 srautas, magistrantūra, 1 semestras) PROGRAMA. su skaidžia savybe skaičiu
 GRAFU TEORIJA RINKTINIAI MATEMATIKOS SKYRIAI (Informatikos spec, 2 srautas, magistrantūra, 1 semestras) PROGRAMA 1 Pagrindinės sa vokos, pavyzdžiai Grafu veiksmai 2 Grafo parametru sa ryšiai 3 Jungiantysis
GRAFU TEORIJA RINKTINIAI MATEMATIKOS SKYRIAI (Informatikos spec, 2 srautas, magistrantūra, 1 semestras) PROGRAMA 1 Pagrindinės sa vokos, pavyzdžiai Grafu veiksmai 2 Grafo parametru sa ryšiai 3 Jungiantysis
KENGŪRA SENJORAS
 KENGŪROS KONKURSO ORGANIZAVIMO KOMITETAS VU MATEMATIKOS IR INFORMATIKOS FAKULTETAS VU MATEMATIKOS IR INFORMATIKOS INSTITUTAS LIETUVOS MATEMATIKŲ DRAUGIJA KENGŪRA 2016. SENJORAS TARPTAUTINIO MATEMATIKOS
KENGŪROS KONKURSO ORGANIZAVIMO KOMITETAS VU MATEMATIKOS IR INFORMATIKOS FAKULTETAS VU MATEMATIKOS IR INFORMATIKOS INSTITUTAS LIETUVOS MATEMATIKŲ DRAUGIJA KENGŪRA 2016. SENJORAS TARPTAUTINIO MATEMATIKOS
M A T E M A T I K O S P R A K T I K U M A S S U M A T H C A D
 LIETUVOS ŽEMĖS ŪKIO UNIVERSITETAS MATEMATIKOS KATEDRA Antanas Lapinskas M A T E M A T I K O S P R A K T I K U M A S S U M A T H C A D (MOKOMOJI KNYGA) AKADEMIJA 006 UDK 0049 (0754) Sudarė: doc dr Antanas
LIETUVOS ŽEMĖS ŪKIO UNIVERSITETAS MATEMATIKOS KATEDRA Antanas Lapinskas M A T E M A T I K O S P R A K T I K U M A S S U M A T H C A D (MOKOMOJI KNYGA) AKADEMIJA 006 UDK 0049 (0754) Sudarė: doc dr Antanas
Vilniaus universitetas Matematikos ir informatikos fakultetas Informatikos katedra. Gintaras Skersys. Mokymo priemonė
 Vilniaus universitetas Matematikos ir informatikos fakultetas Informatikos katedra Gintaras Skersys Klaidas taisančių kodų teorija Mokymo priemonė Vilnius 2005 I dalis Pagrindinės savokos 1 Įvadas Panagrinėkime
Vilniaus universitetas Matematikos ir informatikos fakultetas Informatikos katedra Gintaras Skersys Klaidas taisančių kodų teorija Mokymo priemonė Vilnius 2005 I dalis Pagrindinės savokos 1 Įvadas Panagrinėkime
Vilius Stakėnas. Kodavimo teorija. Paskaitu. kursas
 Vilius Stakėnas Kodavimo teorija Paskaitu kursas 2002 2 I vadas Informacija perduodama kanalais, kurie kartais iškraipo informacija Tarsime, kad tie iškraipymai yra atsitiktiniai, t y nėra nei sistemingi,
Vilius Stakėnas Kodavimo teorija Paskaitu kursas 2002 2 I vadas Informacija perduodama kanalais, kurie kartais iškraipo informacija Tarsime, kad tie iškraipymai yra atsitiktiniai, t y nėra nei sistemingi,
LIETUVOS RESPUBLIKOS ÐVIETIMO IR MOKSLO MINISTERIJA NACIONALINIS EGZAMINØ CENTRAS 2014 METŲ MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO REZULTATŲ
 LIETUVOS RESPUBLIKOS ÐVIETIMO IR MOKSLO MINISTERIJA NACIONALINIS EGZAMINØ CENTRAS 014 METŲ MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO REZULTATŲ STATISTINĖ ANALIZĖ 014 m. birželio 5 d. matematikos valstybinį
LIETUVOS RESPUBLIKOS ÐVIETIMO IR MOKSLO MINISTERIJA NACIONALINIS EGZAMINØ CENTRAS 014 METŲ MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO REZULTATŲ STATISTINĖ ANALIZĖ 014 m. birželio 5 d. matematikos valstybinį
Įvadas į laboratorinius darbus
 M A T E M A T I N Ė S T A T I S T I K A Įvadas į laboratorinius darbus Marijus Radavičius, Tomas Rekašius 2005 m. rugsėjo 26 d. Reziumė Laboratorinis darbas skirtas susipažinti su MS Excel priemonėmis
M A T E M A T I N Ė S T A T I S T I K A Įvadas į laboratorinius darbus Marijus Radavičius, Tomas Rekašius 2005 m. rugsėjo 26 d. Reziumė Laboratorinis darbas skirtas susipažinti su MS Excel priemonėmis
Ketvirtos eilės Rungės ir Kutos metodo būsenos parametro vektoriaus {X} reikšmės užrašomos taip:
 PRIEDAI 113 A priedas. Rungės ir Kuto metodas Rungės-Kutos metodu sprendiamos diferencialinės lygtys. Norint skaitiniu būdu išspręsti diferencialinę lygtį, reikia žinoti ieškomos funkcijos ir jos išvestinės
PRIEDAI 113 A priedas. Rungės ir Kuto metodas Rungės-Kutos metodu sprendiamos diferencialinės lygtys. Norint skaitiniu būdu išspręsti diferencialinę lygtį, reikia žinoti ieškomos funkcijos ir jos išvestinės
DEFORMUOJAMO KŪNO MECHANIKA 1 dalis
 DEFORMUOJAMO KŪNO MECHANIKA dalis T U R I N Y S. Deformuojamojo kūo mechaikos objektas ir jos ršs su kitais mokslais. Tamprumo teorijos sąvokos ir prielaidos 3. Įtempimų būvio teorija 4. Pusiausvros difereciali
DEFORMUOJAMO KŪNO MECHANIKA dalis T U R I N Y S. Deformuojamojo kūo mechaikos objektas ir jos ršs su kitais mokslais. Tamprumo teorijos sąvokos ir prielaidos 3. Įtempimų būvio teorija 4. Pusiausvros difereciali
2 laboratorinis darbas. TIKIMYBINIAI MODELIAI
 laboratorns darbas laboratorns darbas. TIKIMYBINIAI MODELIAI DARBO TIKSLAS - šstudjuot atstktnų dydžų r vektorų skrstnus, skrstno (passkrstymo) funkcją, tanko funkcją, skatnes charakterstkas r jų savybes.
laboratorns darbas laboratorns darbas. TIKIMYBINIAI MODELIAI DARBO TIKSLAS - šstudjuot atstktnų dydžų r vektorų skrstnus, skrstno (passkrstymo) funkcją, tanko funkcją, skatnes charakterstkas r jų savybes.
TEORIJOS PRADMENYS PROGRAMA
 DISKREČIOJI MATEMATIKA (2 semestras) KOMBINATORIKOS IR GRAFU TEORIJOS PRADMENYS PROGRAMA I KOMBINATORIKA 1 Matematinės inducijos principas 2 Dauginimo taisylė 3 Gretiniai, ėliniai ir deriniai 4 Kartotiniai
DISKREČIOJI MATEMATIKA (2 semestras) KOMBINATORIKOS IR GRAFU TEORIJOS PRADMENYS PROGRAMA I KOMBINATORIKA 1 Matematinės inducijos principas 2 Dauginimo taisylė 3 Gretiniai, ėliniai ir deriniai 4 Kartotiniai
t. y. =. Iš čia seka, kad trikampiai BPQ ir BAC yra panašūs, o jų D 1 pav.
 LIETUVOS JUNŲ J Ų MTEMTIKŲ MOKYKL tema. TRIGONOMETRIJOS TIKYMI GEOMETRIJOJE (008-00) Terinę medžiagą parengė bei šeštąją uždutį sudarė Vilniaus pedaggini universitet dentas Edmundas Mazėtis Šiame darbe
LIETUVOS JUNŲ J Ų MTEMTIKŲ MOKYKL tema. TRIGONOMETRIJOS TIKYMI GEOMETRIJOJE (008-00) Terinę medžiagą parengė bei šeštąją uždutį sudarė Vilniaus pedaggini universitet dentas Edmundas Mazėtis Šiame darbe
5 klasė. - užduotys apie varniuką.
 5 klasė - užduotys apie varniuką. 1. Varniukas iš plastilino lipdė raides ir iš jų sudėliojo užrašą: VARNIUKO OLIMPIADA. Vienodas raides jis lipdė iš tos pačios spalvos plastelino, o skirtingas raides
5 klasė - užduotys apie varniuką. 1. Varniukas iš plastilino lipdė raides ir iš jų sudėliojo užrašą: VARNIUKO OLIMPIADA. Vienodas raides jis lipdė iš tos pačios spalvos plastelino, o skirtingas raides
Statistinė termodinamika. Boltzmann o pasiskirstymas
 Statistinė termodinamika. Boltzmann o pasiskirstymas DNR molekulių vaizdas DNR struktūros pakitimai. Keičiantis DNR molekulės formai keistųsi ir visos sistemos entropija. Mielėse esančio DNR struktūros
Statistinė termodinamika. Boltzmann o pasiskirstymas DNR molekulių vaizdas DNR struktūros pakitimai. Keičiantis DNR molekulės formai keistųsi ir visos sistemos entropija. Mielėse esančio DNR struktūros
Analizės uždavinynas. Vytautas Kazakevičius m. lapkričio 1 d.
 Analizės uždavinynas Vytautas Kazakevičius m. lapkričio d. ii Vienmatė analizė Faktorialai, binominiai koeficientai. Jei a R, n, k N {}, tai k! = 3 k, (k + )!! = 3 5 (k + ), (k)!! = 4 6 (k); a a(a ) (a
Analizės uždavinynas Vytautas Kazakevičius m. lapkričio d. ii Vienmatė analizė Faktorialai, binominiai koeficientai. Jei a R, n, k N {}, tai k! = 3 k, (k + )!! = 3 5 (k + ), (k)!! = 4 6 (k); a a(a ) (a
5 paskaita. 5.1 Kompaktiškosios aibės Sąvokos
 5 pskit 5.1 Kompktiškosios ibės 5.1.1 Sąvokos Iš mtemtinės nlizės kurso žinome dvi svrbis prėžtu reliu ju skičiu ibiu svybes. Pirmoji Bolcno-Vejerštrso teorem: bet kuri beglinė prėžt reliu ju skičiu ibė
5 pskit 5.1 Kompktiškosios ibės 5.1.1 Sąvokos Iš mtemtinės nlizės kurso žinome dvi svrbis prėžtu reliu ju skičiu ibiu svybes. Pirmoji Bolcno-Vejerštrso teorem: bet kuri beglinė prėžt reliu ju skičiu ibė
04 Elektromagnetinės bangos
 04 Elektromagnetinės bangos 1 0.1. BANGINĖ ŠVIESOS PRIGIMTIS 3 Šiame skyriuje išvesime banginę lygtį iš elektromagnetinio lauko Maksvelo lygčių. Šviesa yra elektromagnetinė banga, kurios dažnis yra optiniame
04 Elektromagnetinės bangos 1 0.1. BANGINĖ ŠVIESOS PRIGIMTIS 3 Šiame skyriuje išvesime banginę lygtį iš elektromagnetinio lauko Maksvelo lygčių. Šviesa yra elektromagnetinė banga, kurios dažnis yra optiniame
Teorinė mechanika I. Uždavinių sprendimo vadovas
 VILNIUS GEDIINO TEHNIKOS UNIVERSITETS R. UŠYS, J. KSNUSKS Teorinė mechania I. Uždavinių sprendimo vadovas OKOOJI KNYG Vilnius Technia 00 R. aušs, J. Kasnausas. TEORINĖ EHNIK I. UŽDVINIŲ SPRENDIO VDOVS
VILNIUS GEDIINO TEHNIKOS UNIVERSITETS R. UŠYS, J. KSNUSKS Teorinė mechania I. Uždavinių sprendimo vadovas OKOOJI KNYG Vilnius Technia 00 R. aušs, J. Kasnausas. TEORINĖ EHNIK I. UŽDVINIŲ SPRENDIO VDOVS
Vilijandas Bagdonavi ius. Julius Jonas Kruopis MATEMATIN E STATISTIKA
 VILNIAUS UNIVERSITETO MATEMATIKOS IR INFORMATIKOS FAKULTETAS Vilijandas Bagdonavi ius Julius Jonas Kruopis MATEMATIN E STATISTIKA Vadovelis IV DALIS DAUGIAMAT E STATISTIKA Vilniaus universiteto leidykla
VILNIAUS UNIVERSITETO MATEMATIKOS IR INFORMATIKOS FAKULTETAS Vilijandas Bagdonavi ius Julius Jonas Kruopis MATEMATIN E STATISTIKA Vadovelis IV DALIS DAUGIAMAT E STATISTIKA Vilniaus universiteto leidykla
III.Termodinamikos pagrindai
 III.ermodinamikos pagrindai III.. Dujų plėtimosi darbas egu dujos yra cilindre su nesvariu judančiu stūmokliu, kurio plotas lygus S, ir jas veikia tik išorinis slėgis p. Pradinius dujų parametrus pažymėkime
III.ermodinamikos pagrindai III.. Dujų plėtimosi darbas egu dujos yra cilindre su nesvariu judančiu stūmokliu, kurio plotas lygus S, ir jas veikia tik išorinis slėgis p. Pradinius dujų parametrus pažymėkime
LIETUVOS RESPUBLIKOS ŠVIETIMO IR MOKSLO MINISTERIJA NACIONALINIS EGZAMINŲ CENTRAS 2013 METŲ MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO REZULTATŲ
 LIETUVS RESPUBLIKS ŠVIETIM IR MKSL MINISTERIJ NINLINIS EGZMINŲ ENTRS 03 METŲ MTEMTIKS VLSTYBINI BRNS EGZMIN REZULTTŲ STTISTINĖ NLIZĖ 03 m. birželio 5 d. matematikos valstbinį brandos egzaminą leista laikti
LIETUVS RESPUBLIKS ŠVIETIM IR MKSL MINISTERIJ NINLINIS EGZMINŲ ENTRS 03 METŲ MTEMTIKS VLSTYBINI BRNS EGZMIN REZULTTŲ STTISTINĖ NLIZĖ 03 m. birželio 5 d. matematikos valstbinį brandos egzaminą leista laikti
4 laboratorinis darbas. PARAMETRŲ ĮVERČIAI IR STATISTINĖS HIPOTEZĖS
 PARAMETRŲ ĮVERČIAI IR STATISTINĖS HIPOTEZĖS DARBO TIKSLAS - išstudijuoti parametrų taškiių ir itervaliių įverčių radimo, parametriių ir eparametriių hipotezių tikriimo uždaviius ir jų taikymą Teorijos
PARAMETRŲ ĮVERČIAI IR STATISTINĖS HIPOTEZĖS DARBO TIKSLAS - išstudijuoti parametrų taškiių ir itervaliių įverčių radimo, parametriių ir eparametriių hipotezių tikriimo uždaviius ir jų taikymą Teorijos
Rinktiniai informacijos saugos skyriai. 3. Kriptografija ir kriptografijos protokolai: Klasikinė kriptografija
 Rinktiniai informacijos saugos skyriai 3. Kriptografija ir kriptografijos protokolai: Klasikinė kriptografija Paskaitos tikslai Šioje temoje nagrinėjami klausimai: Perstatų šifrai Keitinių šifrai Vienos
Rinktiniai informacijos saugos skyriai 3. Kriptografija ir kriptografijos protokolai: Klasikinė kriptografija Paskaitos tikslai Šioje temoje nagrinėjami klausimai: Perstatų šifrai Keitinių šifrai Vienos
1. Įvadas. Laisvųjų dalelių kvantinės mechanikos elementai
 1. Įvadas. Laisvųjų dalelių kvantinės mechanikos elementai 1.1. Branduolio nukleonų energijos diskretumo aiškinimas. Dalelė stačiakampėje potencialo duobėje Dalelės banginė funkcija tai koordinačių ir
1. Įvadas. Laisvųjų dalelių kvantinės mechanikos elementai 1.1. Branduolio nukleonų energijos diskretumo aiškinimas. Dalelė stačiakampėje potencialo duobėje Dalelės banginė funkcija tai koordinačių ir
FRANKO IR HERCO BANDYMAS
 VILNIAUS UNIVERSITETAS Kietojo kūno elektronikos katedra Atomo ir branduolio fizikos laboratorija Laboratorinis darbas Nr. FRANKO IR HERCO BANDYMAS Parengė A. Poškus 013-08-31 Turinys Darbo tikslas 1.
VILNIAUS UNIVERSITETAS Kietojo kūno elektronikos katedra Atomo ir branduolio fizikos laboratorija Laboratorinis darbas Nr. FRANKO IR HERCO BANDYMAS Parengė A. Poškus 013-08-31 Turinys Darbo tikslas 1.
1. Įvadas į sistemas ir signalus. 1. Signalas, duomenys, informacija ir žinios
 . Įvadas į sistemas ir signalus. Signalas, duomenys, informacija ir žinios Žodis signalas yra kilęs iš lotyniško žodžio signum ženklas. Signalas tai yra tai kas yra naudojama žiniai perduoti. Signalas
. Įvadas į sistemas ir signalus. Signalas, duomenys, informacija ir žinios Žodis signalas yra kilęs iš lotyniško žodžio signum ženklas. Signalas tai yra tai kas yra naudojama žiniai perduoti. Signalas
Laboratorinis darbas Nr. 2
 M A T E M A T I N Ė S T A T I S T I K A Laboratorinis darbas Nr. 2 Marijus Radavičius, Tomas Rekašius 2005 m. spalio 23 d. Reziumė Antras laboratorinis darbas skirtas išmokti generuoti tikimybinių skirstinių
M A T E M A T I N Ė S T A T I S T I K A Laboratorinis darbas Nr. 2 Marijus Radavičius, Tomas Rekašius 2005 m. spalio 23 d. Reziumė Antras laboratorinis darbas skirtas išmokti generuoti tikimybinių skirstinių
Pav1 Žingsnio perdavimo funkcija gali būti paskaičiuota integruojant VIPF. Paskaičiavus VIPF FFT gaunamo amplitudinė_dažninė ch_ka.
 Įvadas į filtrus Skaitmeniniai filtrai, tai viena iš svarbiausių siganalų apdorojimo dalių. Kadangi skaitmeniniai filtrai turi nepalyginamai daugiau pranašumų nei analoginiai filtrai, tai nulėmė jų populiarumą.
Įvadas į filtrus Skaitmeniniai filtrai, tai viena iš svarbiausių siganalų apdorojimo dalių. Kadangi skaitmeniniai filtrai turi nepalyginamai daugiau pranašumų nei analoginiai filtrai, tai nulėmė jų populiarumą.
EUROPOS CENTRINIS BANKAS
 2005 12 13 C 316/25 EUROPOS CENTRINIS BANKAS EUROPOS CENTRINIO BANKO NUOMONĖ 2005 m. gruodžio 1 d. dėl pasiūlymo dėl Tarybos reglamento, iš dalies keičiančio Reglamentą (EB) Nr. 974/98 dėl euro įvedimo
2005 12 13 C 316/25 EUROPOS CENTRINIS BANKAS EUROPOS CENTRINIO BANKO NUOMONĖ 2005 m. gruodžio 1 d. dėl pasiūlymo dėl Tarybos reglamento, iš dalies keičiančio Reglamentą (EB) Nr. 974/98 dėl euro įvedimo
Atsitiktinių paklaidų įvertinimas
 4.4.4. tsitiktinių paklaidų įvertinimas tsitiktinės paklaidos įvertinamos nurodant du dydžius: pasikliaujamąjį intervalą ir pasikliaujamąją tikimybę. tsitiktinių paklaidų atveju, griežtai tariant, nėra
4.4.4. tsitiktinių paklaidų įvertinimas tsitiktinės paklaidos įvertinamos nurodant du dydžius: pasikliaujamąjį intervalą ir pasikliaujamąją tikimybę. tsitiktinių paklaidų atveju, griežtai tariant, nėra
2018 METŲ MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO REZULTATŲ STATISTINĖ ANALIZĖ
 N A C I O N A L I N I S E G Z A M I N Ų C E N T R A S 018 METŲ MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO REZULTATŲ STATISTINĖ ANALIZĖ 018 m. birželio 9 d. įvyko matematikos valstybinis brandos egzaminas.
N A C I O N A L I N I S E G Z A M I N Ų C E N T R A S 018 METŲ MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO REZULTATŲ STATISTINĖ ANALIZĖ 018 m. birželio 9 d. įvyko matematikos valstybinis brandos egzaminas.
Gabija Maršalkaitė Motiejus Valiūnas. Astronomijos pratybų užduočių komplektas
 Gabija Maršalkaitė Motiejus Valiūnas Astronomijos pratybų užduočių komplektas Vilnius 2014 1 Įvadas 1.1 Astronomijos olimpiados Lietuvoje kylant moksleivių susidomėjimu astronomijos olimpiada buvo pastebėta,
Gabija Maršalkaitė Motiejus Valiūnas Astronomijos pratybų užduočių komplektas Vilnius 2014 1 Įvadas 1.1 Astronomijos olimpiados Lietuvoje kylant moksleivių susidomėjimu astronomijos olimpiada buvo pastebėta,
KLASIKIN E MECHANIKA
 KLASIKIN E MECHANIKA Algirdas MATULIS Puslaidininkiu zikos institutas Vadoveliu serijos papildymas auk²tuju mokyklu tiksliuju mokslu specialybiu studentams Email: amatulis@takas.lt Mob.: +370 654 543 06
KLASIKIN E MECHANIKA Algirdas MATULIS Puslaidininkiu zikos institutas Vadoveliu serijos papildymas auk²tuju mokyklu tiksliuju mokslu specialybiu studentams Email: amatulis@takas.lt Mob.: +370 654 543 06
KADETAS (VII ir VIII klasės)
 ADETAS (VII ir VIII klasės) 1. E 10 000 Galima tikrinti atsakymus. adangi vidutinė kainasumažėjo, tai brangiausia papūga kainavo daugiau kaip 6000 litų. Vadinasi, parduotoji papūga kainavo daugiau kaip
ADETAS (VII ir VIII klasės) 1. E 10 000 Galima tikrinti atsakymus. adangi vidutinė kainasumažėjo, tai brangiausia papūga kainavo daugiau kaip 6000 litų. Vadinasi, parduotoji papūga kainavo daugiau kaip
TIKIMYBIU TEORIJA HAMLETAS MARK AITIS MYKOLO ROMERIO UNIVERSITETAS 2010
 TIKIMYBIU TEORIJA HAMLETAS MARK AITIS MYKOLO ROMERIO UNIVERSITETAS 2010 Tikimybiu teorija nagrin eja atsitiktinius ivykius ir tu ivykiu tikimybes ivykio pasirodymo galimyb es mat, i²reik²t skai iumi p,
TIKIMYBIU TEORIJA HAMLETAS MARK AITIS MYKOLO ROMERIO UNIVERSITETAS 2010 Tikimybiu teorija nagrin eja atsitiktinius ivykius ir tu ivykiu tikimybes ivykio pasirodymo galimyb es mat, i²reik²t skai iumi p,
Vilniaus universitetas Gamtos mokslų fakultetas Kartografijos centras. Giedrė Beconytė. Mokomoji knyga geomokslų specialybių studentams
 Vilniaus universitetas Gamtos mokslų fakultetas Kartografijos centras Giedrė Beconytė DUOMENŲ BAZIŲ PROJEKTAVIMAS Mokomoji knyga geomokslų specialybių studentams Vilnius 2012 Aprobuota VU Gamtos mokslų
Vilniaus universitetas Gamtos mokslų fakultetas Kartografijos centras Giedrė Beconytė DUOMENŲ BAZIŲ PROJEKTAVIMAS Mokomoji knyga geomokslų specialybių studentams Vilnius 2012 Aprobuota VU Gamtos mokslų
MONTE KARLO METODAS. Gediminas Stepanauskas IVADAS Sistemos Modeliai Modeliavimas ir Monte-Karlo metodas...
 MONTE KARLO METODAS Gediminas Stepanauskas 2008 Turinys 1 IVADAS 4 1.1 Sistemos.............................. 4 1.2 Modeliai.............................. 5 1.3 Modeliavimas ir Monte-Karlo metodas.............
MONTE KARLO METODAS Gediminas Stepanauskas 2008 Turinys 1 IVADAS 4 1.1 Sistemos.............................. 4 1.2 Modeliai.............................. 5 1.3 Modeliavimas ir Monte-Karlo metodas.............
