1. Vektoriu veiksmai. Vektoriu skaliarinė, vektorinė ir mišrioji sandaugos
|
|
|
- Δανάη Αποστολίδης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 1. Vektoriu veiksmai. Vektoriu skaliarinė, vektorinė ir mišrioji sandaugos Vektoriu užrašymas MAPLE Vektorius MAPLE galime užrašyti daugeliu būdu. Juos grafiškai vaizduosime paketo Student[LinearAlgebra] pagalba, kurį aktyvuojame komandawith(student[linear Algebra]. Taip pat naudosime paketą linalg: > with(linalg): > with(student[linearalgebra]): 1) Vektoriu užrašymas naudojant baigtiniu aibiu ir baigtiniu seku elementus. Iš pradžiu sudarykime seką. Parašysime sekos Sn=7+*((-1)^n)*n pirmuosius dešimtį nariu. Naudojame komand ą seq: > S:=seq(7+*(-1)^n*n,n=1..10); S := 4, 1,, 19, 8, 5, 14, 1, 0, 7 Šią seką Maple galime traktuoti kaip aibę, susidedančią iš sekos elementų. Norėdami seką S paversti aibe A, sekos narius įterpiame tarp skliaustu {}: > A:={S}; A := { 0, 14, 8,, 4, 1, 19, 5, 1, 7} Komanda A[] aibę A vėl pavaizduoja kaip seką: > S:=A[]; S := 0, 14, 8,, 4, 1, 19, 5, 1, 7 Analogiškai baigtinė seka paverčiama vektoriumi, o vektorius vėl baigtine seka: > V:=[S]; V := [ 0, 14, 8,, 4, 1, 19, 5, 1, 7] > V[]; 0, 14, 8,, 4, 1, 19, 5, 1, 7 ) Vektoriai uzduodami išvardijant visas vektoriaus komponentes: > V:=vector ( [ 1,,,4,5 ] ); V := [1,,, 4, 5] ) Jei vektoriaus komponentes vienodos, patogiausias jo užrašymo būdas toks: > V:=vector( 4, ); V := [,,, ] Čia pirmasis skaičius lygus vektoriaus komponenčiu skaičiui, o antrasis -ju skaitinei vertei. 4) Jei vektoriaus komponentės yra susietos su savo indeksais mums žinoma funkcine priklausomybe (pavyzdžiui, f:= x -> x^), tos funkcijos pagalba galime patogiai uzrasyti vektoriu : > V:=vector ( 7,x->x^);
2 V := [1, 4, 9, 16, 5, 6, 49] Šio vektoriaus komponentės lygios funkcijos reikšmėms taškuose 1,,,4,5,6,7 (pradinė argumento reikšmė visada lygus vienetui). Jei tolesniems skaičiavimams reikalingos kurios nors vektoriaus komponent ės, jos lengvai gaunamos taip: > V[]; 4 Pavyzdžiui, sudėkime -ąją ir 4-ąją vektoriaus komponentes: > Test:=V[]+V[4]; Test := 0 Čia pademonstravome tik kai kuriuos iš galimu vektoriu užrašymo Maple būdu. Pagrindinės vektoriu operacijos MAPLE 1) Vektoriaus komponenčiu kiekį (vektoriaus matavimą) nurodo komanda vectdim: > V:=vector ( 7,x->x^); V := [1, 4, 9, 16, 5, 6, 49] > Kiekis:=vectdim(V); Kiekis := 7 ) Surūšiuoti vektoriaus komponentes galime naudodami komanda sort. Tarkime, kad turime seką S: > S:=seq(7+*(-1)^n*n,n=1..10); S := 4, 1,, 19, 8, 5, 14, 1, 0, 7 Iš jos elementu "pasigaminame" vektoriu : > V:=[S]; V := [4, 1,, 19, 8, 5, 14, 1, 0, 7] Komandos sort pagalba šio vektoriaus komponentes išdėstę didėjančia seka, gausime kitą vektorių, kurį pavadinkime, pavyzdžiui, "Surūšiuotas": > Surusiuotas:=sort(V); Surusiuotas := [ 0, 14, 8,, 4, 1, 19, 5, 1, 7] Norėdami vektoriaus elementus išdėstyti mažėjančia tvarka, naudojame komanda sort(v, > ): > Surusiuotas_mazejanciomis_komponentemis:=sort(V, > ); Surusiuotas_mazejanciomis_komponentemis := [7, 1, 5, 19, 1, 4,, 8, 14, 0] ) Didžiausias ir mažiausias vektoriaus komponentes randame taip: > Maziausia:=min(V[]); Maziausia := 0 > Didziausia:=max(V[]);
3 Didziausia := 7 4) Galime pakeisti vektoriaus komponentę, nurodydami naują jos reikšmę. Pavyzdžiui, vektoriuje V: > V; [4, 1,, 19, 8, 5, 14, 1, 0, 7] keičiame trečiąją komponentę: > V[]:=111; Dabar vektorius V yra šitoks: > V; V := 111 [4, 1, 111, 19, 8, 5, 14, 1, 0, 7] 5) Vektoriaus komponenčiu pertvarkymas komandos map pagalba. Pakeisime komponentes dabartiniu komponenčiu reikšmiu kvadratais: > V =V; V = [4, 1, 111, 19, 8, 5, 14, 1, 0, 7] > W:=map(x->x^,V); W := [16, 169, 11, 61, 64, 65, 196, 961, 400, 169] 6) Kartais praverčia sumos operatorius add.(addition - suma) ir sandaugos operatorius mul (multiplication - sandauga):: Naudojant šiuos operatorius, galima sudėti (add) arba sudauginti (mull) sekos narius, aibės elementus arba vektoriaus komponentes. > Suma:=add(V[i],i=1..vectdim(V)); Suma := 198 > Sandauga:=mul(V[i],i=1..vectdim(V)); Sandauga := ) Vektoriu suma skaičiuojama naudojant įprastą sumos ženklą + (žinoma, sudedami vektoriai turi būti vienmačiai): > Suma:=V+W; Suma := [0, 18, 14, 80, 56, 650, 18, 99, 80, 1406] Vektorius galima pavaizduoti grafiškai Student[LinearAlgebra] subpaketo pagalba. Tik reikia nepamiršti kad vektoriai turi būti tinkamo matavimo (gali turėti tik arba komponentes, kad "tilptu " plokštumoje arba trimatėje erdveje). Taip pat turėkite omenyje, kad Student[LinearAlgebra] vektorius užrašo stulpeliu pavidalu komandos Vector ( o ne vector, kuri yra paketo linalg komanda) pagalba: > V:=Vector([5, -, ]); V := 5 > W:=Vector([4,, 1]);
4 > VectorSumPlot(V,W); W := 4 1 The Sum of Vectors ) Vektoriaus ir skaičiaus sandauga užrašoma taip pat, kaip dvieju skaičių sandauga: > V* =V*; 9) Kampas tarp vektoriu. Tegu turime du vektorius: > V:=vector(,i->i^); V = V := [1, 4, 9] > W:=vector(,i->sqrt(i)); W := [ 1,, ] Apskaičiuosime ju sudaromą kampą komandos angle pagalba: > Kampas:=angle(V,W); Kampas := arccos( ( ) 98 6 ) 588 Jei tokia trigonometrinė išraiška mums netinka, galime apskaičiuoti apytikslę kampo reikšmę komandos evalf pagalba (rezultatą gauname radianais):
5 > Kampas[rad]:=evalf(Kampas); Kampas rad := To paties kampo reikšmę laipsniais gauname šitaip: > Kampas[laips]:=evalf((180/Pi)*angle(V,W)); Kampas laips := ) Vektoriu skaliarinę sandaugą apskaičiuojame naudodami komandą dotprod: > VW:=dotprod(V,W); VW := Žinome, kad statmenu vektorių skaliarinė sandauga lygi nuliui. Jei vektorius U šitoks: > U:=vector(,i->(-1)^i*(-i)^); U := [ 4, 1, 0] tai jis statmenas anksčiau apibrėžtam vektoriui V: > UV:=dotprod(U,V); UV := 0 Skaliarinės sandaugos pagalba randame vektoriaus ilgį (vektoriaus ilgio kvadratas lygus vektoriaus skaliarinei sandaugai iš jo paties) : > Ssandauga:=dotprod(V,V); Ssandauga := 98 > Ilgis:=sqrt(Ssandauga); Ilgis := 7 Apytikslę šio skaičiaus reikšmę gausime su komanda evalf: > Apskaiciuotasilgis:=evalf(Ilgis); Apskaiciuotasilgis := ) Vektorinė sandauga apskaičiuojama naudojant komanda crossprod: > Vsandauga:=crossprod(V,W); Vsandauga := [ 4 9, 9, 4 ] Apytikslėms reikšmėms apskaičiuoti vėlgi naudojama komanda evalf: > Vsandauga_skaiciais:=evalf(crossprod(V,W)); Vsandauga_skaiciais := [ , , ] Pavaizduokime vektorius ir ju vektorinę sandaugą grafiškai. Vektorius reikia užrašome stulpeliu pavidalu naudodami komandą Vector: > V1:=Vector(,i->i^); V1 := > W1:=Vector(,i->(-1)^(i+1)*sqrt(i));
6 W1 := 1 Vektorius V1, W1 ir ju vektorinę sandaugą grafiškai pavaizduosime komandos CrossProductPlot pagalba: > CrossProductPlot(V1, W1, vectorcolors=[green,cyan,yellow]); The Cross Product of Vectors 8 4 z 0 y x 15 0 Čia green, cyan, yellow- vektorių grafiniu vaizdų spalvos. Žinome, kad lygiagretainio, kurio kraštinės yra vektoriai V1 ir W1, plotas lygus ju vektorinės sandaugos ilgiui: > X:=crossprod(V1,W1); X := [ 4 + 9, 9, 4 ] > lygiagretainio_plotas:=sqrt(dotprod(x,x)); lygiagretainio_plotas := (4 + 9 ) + (9 ) + ( 4) > apytikslis_lygiagretainio_plotas:=evalf(%); apytikslis_lygiagretainio_plotas := ) Mišrioji vektoriu sandauga apskaičiuojama naudojant jos apibrėžimą skaliarinės ir vektorinės sandaugu pagalba: > a:=vector( [1,8,] ); > b:=vector( [-1,,-5] ); a := 1 8
7 b := 1 5 > c:=vector( [6,-,-] ); c := 6 > Misrioji_sandauga_abc:=dotprod(crossprod(a,b),c); Misrioji_sandauga_abc := 0 Primename, kad ši mišrioji sandauga lygi gretasienio, kurio briaunos yra vektoriai a,b ir c, tūriui. Vadinasi, ji lygi nuliui, jei vektoriai a,b ir c guli vienoje plokštumoje (yra komplanarūs). Jos šeštoji dalis lygi keturkampės piramidės, kurios trys briaunos sutampa su vektoriais a,b ir c, tūriui. Uždaviniai. 1. Žinomos trikampio ABC viršūnės. Raskite kraštiniu AB, AC ir pusiaukraštinės BE ilgį, kampo BAC dydį (trigonometrine išraiška, laipsniais, radianais), o taip pat vektorinės sandaugos pagalba apskai čiuokite trikampio ABC plotą S. A( 5; -; ), B( -1; 4; ), C( -4; -1; 5).. Duoti keturi vektoriai a( 1, -, 1 ), b( -1, -, -1), c( -, -, 1 ), d( -1, -9, ). Įrodykite, kad vektoriai nėra komplanarūs. Vektorių d išreikškite vektorių a, b, c tiesiniu dariniu: d = la +mb + nc. Pastaba: Tiesinio darinio koeficientams l, m, n rasti sudarykite tiesiniu lygčiu sistemą.. Raskite trikampės piramidės, kurios briaunos yra vektoriai a - b, a* b, bxc tūrį, kur b pažymėtas vektoriaus b ilgis, bxc - vektoriu b ir c vektorinė sandauga. Raskite pasirinkto tos piramidės šono plotą.. Analizinės geometrijos uždaviniai MAPLE Plokštumos geometrijos uždaviniai Naudosime MAPLE paketą geometry. 1. Rasti tiesės, einančios per taškus A(-1,) ir B(1,4), lygtį ir nubrėžti tiesę. > restart;with(geometry): > line(ab,[point(a,-1,),point(b,1,4)]); > Equation(AB,[x,y]); AB 7 x + y = 0 Sutvarkome lygtį operatoriaus \textbf{sort }pagalba:
8 > sort(%,[x,y]); x + y 7 = 0 > draw([a,b,ab],axes=normal,view=[-4..4,1..6],printtext=true); B A Trikampio ABC kraštiniu lygtys yra 4*x-y-4= 0, *x+5*y-4 = 0, *x+*y-10 = 0. Rasti trikampio viršūnes ir plotą. Naudodami geometry paketą, komandos line pagalba apibrėžiame trikampio kraštines: > restart;with(geometry): > line(ab,4*x-y-4=0,[x,y]); AB > line(bc,*x+5*y-4=0,[x,y]); BC > line(ac,*x+*y-10=0,[x,y]); AC Komanda triangle apibrėžia trikampį, kai žinomos jo kraštin ės: > triangle(abc,[ab,bc,ac],[x,y]); ABC Komandos map pagalba randame gautojo trikampio ABC viršūnių koordinates: > vk:=map(coordinates,definedas(abc)); vk := [[ 54, 14 ], [18 11, 8 ], [, 8]] 11
9 Komanda point identifikuoja mūsų trikampio viršūnes kaip ta škus: > point(a,vk[1]);point(b,vk[]);point(c,vk[]); A B C Komanda coordinates nurodo taško koordinates: > coordinates(a); [ 54, 14 ] triangle komandos pagalba galime apibrėžti trikampį žinodami jo viršūnes. > triangle(abc,[a,b,c],[x,y]); ABC Trikampio plotą rasime naudodami area komandą: > area(abc); Nubrėžiame trikampį naudodami draw: > draw(abc,axes=normal,printtext=true); C A B. Duotos trikampio viršūnės A(11; 6), B(-10; 6) ir C(-10,-16). Rasti trikampio pusiaukraštinės AE ir aukštinės BD ilgius, taip pat ju susikirtimo tašką M.
10 > restart:with(geometry): > triangle(abc, [point(a,11,6), point(b,-10,6), point(c,-10,-16)]); ABC Pusiaukraštinės ir aukštinės suradimui naudosime funkcijas median ir altitude. median apskaičiuoja pusiaukraštinę: > median(pusiaukrastine,a,abc,e); pusiaukrastine čia raide E žymėtas antrasis pusiaukraštinės galas. Komanda altitude veikia analogiškai ir randa aukštinę: > altitude(bd,b,abc,d); Warning, a geometry object has been assigned to the protected name D. Use of protected names for geometry objects is not recommended and may break Maple functionality. BD Atstumą tarp tašku išmatuoja funkcija distance: > distance(a,e); 56 Norėdami gauti paprastesnę atsakymo išraišką, galime papildomai naudoti simplify funkciją: > simplify(distance(b,d)); line komanda galime apibrėžti tiesę, jei žinome pora jos tašk u : > line(bd,[b,d],[x,y]); > line(ae,[a,e],[x,y]); bd ae Eguation parašo tiesės lygtį: > Equation(bd); x y = 0 95 Naudodami solve funkciją galime rasti tiesiu susikirtimo tašk ą: > solve({equation(bd),equation(ae)}); {x = , y = }
11 Pažymėkime raide M gautąjį tašką (naudojame point funkciją): > point(m,subs(%,[x,y])); M Nubrėžiame brėžinį su draw: > draw([abc,pusiaukrastine,bd,m],axes=normal,printtext=true,scaling=con > strained); B 5 A M E 5 D 10 C 15 4.Trikampyje su viršūnėmis A(-4; 1), B(6;1), C(6; -4) rasti pusiaukampinės BL ilgį ir įbrėžti apskritimą. > triangle(abc, [point(a,-4,1), point(b,6,1), point(c,6,-4)]): Funkcija bisector randa pusiaukampinę: > bisector(bl,b,abc,l); BL > simplify(distance(b,l)); 10 > draw([abc,bl],printtext=true,axes=normal);
12 A 1 B L C incircle funkcija randa įbrėžtąjį į trikampį apskritimą, kurį pavadiname ibreztasis, o jo centrą pažymėjome raide O: > incircle(ibreztasis,abc, centername =O): Warning, a geometry object has been assigned to the protected name O. Use of protected names for geometry objects is not recommended and may break Maple functionality. > draw([abc,ibreztasis],printtext=true,axes=normal); A 1 B O 4 C
13 5. Rasti elipsės x + 4 y = 8 liestiniu, einančiu per tašką A(1;), lygtis. Parašykime elipsės lygtį ir fiksuokime duotąjį tašką: > with(geometry): > eq:=x^+4*y^=8;x0:=1;y0:=; eq := x + 4 y = 8 x0 := 1 y0 := Dirbdami su kreivėmis, kurios yra kūgio pjūviai, galime naudoti conic funkciją: > conic(c,eq,[x,y]); detail komanda padės mums sužinoti kūgio pjūvio C parametrus: atpažins, kad tai elipsė, duos jos centro ir židiniu koordinates, ašiu ilgius: > detail(c); C name of the object : C \ form of the object : ellipsed\ center : [0, 0 ]\ foci : [[ 6 ˆ(1 / ), 0 ], [6 ˆ(1 / ), 0 ]]\ length of the major axis : 4 ˆ(1 / )\ length of the minor axis : ˆ(1 / )\ equation of the ellipse : xˆ + 4 yˆ 8 = 0 Nusibrėžkime elipsė ir duotąjį tašką: > point(a,x0,y0); > draw([c,a],printtext=true,view=[-4..4,-..4]); A
14 4 A Parašykime tiesės, einančios per duotąjį tašką, lygtį: > eq1:=y=y0+k*(x-x0); eq1 := y = + k (x 1) ir įstatykime gautąjį y į elipsės lygtį naudodami komandą subs: > subs(%,eq); x + 4 ( + k (x 1)) = 8 Išspręskime lygtį kintamojo x atžvilgiu: > solve(%,x); ( k 6 k + 7 k k) k, ( k + 6 k + 7 k k) k Gauname pora x reikšmių kiekvienai k. Jei tiesė lie čia elipsę, tos reikšmės turi sutapti: > solve(%[1]=%[],k); , 7 7 > k1:=%[1];k:=%%[]; k1 := k :=
15 Įstatę šias reikšmes į tiesiu lygtis, gauname du atsakymus: > liestine1:=subs(k=k1,eq1); liestine1 := y = + ( ) (x 1) 7 > liestine:=subs(k=k,eq1); liestine := y = + ( 58 7 ) (x 1) 7 > line(l1,liestine1,[x,y]); L1 > line(l,liestine,[x,y]); > draw([c,a,l1,l],axes=normal,printtext=true); L A > Equation(L1); ( ) x + y = 0 7 > Equation(L); ( ) x + y = 0 7 Erdvės geometrijos uždaviniai
16 Naudosime paketą geomd. 1.Rasti lygtį plokštumos, einančios per tris taškus A(0,, -), B(, -6, 5), C(-4, 0,1). Rasti trikampio ABC plotą ir jo kampu dydžius. > restart:with(geomd): Pasižymime taškus A, B, C, apibrėžiame plok štumą ABC su plane funkcija.ir rašome jos lygtį su Eguation: > point(a,0,, -): > point(b,, -6, 5): > point(c,-4, 0, 1): > plane(pl,[a,b,c]): > Equation(pl,[x,y,z]); 6 16 x 44 y 8 z = 0 Supaprastiname, sutvarkome ir pasižymime: > %/(-); x + y + 19 z = 0 > lygtis:=sort(%,[x,y,z]); lygtis := 8 x + y + 19 z + 1 = 0 triangle komanda apibrėžiame trikampį ABC ir nubr ėžiame jį su draw: > triangle(abc,[a,b,c]); > draw(abc,axes=framed); ABC
17 Plotą randame su area komanda: > plotas:=area(abc); o kampų dydžius su Findangle: > kampasa:=findangle(a,abc); plotas := 101 kampasa := arccos( ) > kampasb:=findangle(b,abc); kampasb := arccos( ) 17 > kampasc:=findangle(c,abc); kampasc := π Atsakymą galime užrašyti išvardindami rastuosius dydžius: > lygtis; plotas =plotas;kampai=ka,kb,kc; 8 x + y + 19 z + 1 = 0 plotas = 101 kampai = ka, kb, kc. Rasti kampą, kurį sudaro tiesė (x-1)/=(y+)/1 = (z-1)/ ir plok štuma 5*x+y-z+4=0. > restart:with(geomd): > plane(pl,5*x+y-z+4 = 0,[x,y,z]): Tiesės lygtį užrašome su line komanda, nurodydami jos tašką ir krypties vektoriaus koordinates: > line(t,[point(a,1,-,1),[,1,]]): > FindAngle(pl,t); arcsin( 4 9 ) Galime rasti apytikslį kampo dydį radianais naudodami komandą evalf, o jo iraišką laipsniais gausime su funkcijos convert pagalba; > evalf(%); > evalf(convert(%,degrees)); degrees. Rasti taško A(1,, ) atstumą iki tiesės x = 7 - t, y = 4-4 t, z = t.
18 > point(a,1,,): line funkcija apibrėžia tiesę pagal jos parametrinę lygtį: > line(t,[7-*t,4-4*t,5+4*t],t): o distance randa atstumą nuo taško iki tiesės: > distance(a,t); 10 4.Duota sukimosi cilindro ašis x = 8 + t, y = 4 - t, z = 7 + t ir taškas A(1,, ) ant jo paviršiaus. Parašyti cilindro lygtį ir nubrėžti cilindrą. > line(t,[8+t,4-*t,7+*t],t): > point(a,1,,): > point(m,x,y,z): Čia M - bet kuris cilindro taškas. Cilindro lygtį galime para šyti sulygindami tašku A ir M atstumus iki jo ašies: > distance(a,t)=distance(m,t); y 18 y + 8 y z z + 5 z = 4 z x 116 x + 8 x + 4 x y > %*; 10 5 = 5 y 18 y + 8 y z z + 5 z 4 z x 116 x + 8 x + 4 x y Dar supaprastiname lygtį pakeldami abi jos puses kvadratu ir sutvarkydami su sort: > map(a->a^,%); 500 = 5 y 18 y + 8 y z z + 5 z 4 z x 116 x + 8 x + 4 x y > L:=sort(rhs(%)-lhs(%),[x,y,z])=0; L := 8 x + 4 x y 4 x z + 5 y + 8 y z + 5 z 116 x 18 y 70 z = 0 Nubrėžiame brėžinį naudodami implicitplotd, plots, displayd: > plots[implicitplotd](l,x=-5..5,y=-5..5,z=-5..5): > draw(t): > plots[displayd]([%%, > %],view=[-5..5,-5..5,-5..5],axes=boxed,orientation=[0,80]);
19 0 10 z y 0 0 x 0 Uždaviniai. 1. Duotos trikampio viršūnės A(,4), B (5,10), C (-1,-1). Nubrėžkite apskritimą, įbrėžtą į šį trikampį, ir apskritimą, apibrėžtą apie trikampį. Rasti šiu apskritimu lygtis ir centrų koordinate.. Duota elipsė 1 x y 4 = 16. Per tašką A(,-1) nubrėžkite stygą, kuri tame taške dalijasi pusiau. Parašykite jos lygtį. Raskite trikampio, kurio viršūn ės yra stygos galuose ir elipsės centre, plotą.. Raskite plokštumos, einančios per taškus A(1,, ), B(4, -5, 6), C(-, 1, ), lygtį. Rasti trikampio ABC plotą, perimetrą ir aukštinę AH.. Antros eilės kreivės ir paviršiai MAPLE 1 Antros eilės kreivės 1. Raskime kreivės 1 x + 1 x y + 8 y 15 = 0 kanoninį pavidalą. > restart; > with(geometry):with(linalg):
20 > eq:=1*x^+1*x*y+8*y^-15 = 0; eq := 1 x + 1 x y + 8 y 15 = 0 > conic( k,eq, [x,y] ): > detail(%); name of the object : k\ form of the object : ellipsed\ center : [0, 0 ]\ foci : [[ /10 10 ˆ(1 / ), 1 /10 10 ˆ(1 / )], [ /10 10 ˆ(1 / ), 1 /10 10 ˆ(1 / )]]\ length of the major axis : 6 ˆ(1 / )\ length of the minor axis : ˆ(1 / )\ equation of the ellipse : 1 xˆ + 1 x y + 8 yˆ 15 = 0 > draw(k,scaling=constrained,axes=normal); Surasime kanoninį šios elipsės lygties pavidalą. Naudosime A.Domarko parašytą programą KFD: > KFD:=proc(q) > option Copyright (c) 1997 A.Domarkas VU ; > local X,N,A,B,k; > indets(q):x:=sort(convert(%,list));n:=nops(x); > A:=hessian(q/,X); > if equal(diag(seq(a[k,k],k=1..n)),a) then > RETURN([seq(X[k]=y k,k=1..n)]) fi; > eigenvects(a);
21 > [seq(op(%[k][]),k=1..nops([%]))]; > map(linalg[normalize], linalg[gramschmidt](%)); > transpose(matrix(n,n,%)); > B:=map(combine,%); > [x1,y1]; #X;#[y.(1..N)]; > evalm(x=b&*(%)); > [seq(x[k]=rhs(%)[k],k=1..n)]; > RETURN(%); > end; KFD := proc(q)... end proc > KFD(lhs(eq)); [x = 10 x1 10 y1 10 x1 +, y = + 10 y1 ] > subs(%,eq); 1 ( 10 x1 10 y1 + ) + 1 ( 10 x1 10 y1 10 x1 + ) ( x1 + 8 ( + 10 y1 ) 15 = > simplify(%); 10 x1 + 0 y1 15 = y1 10 ) Kanoninė lygtis: > (%+(15=15))/15; x1 + y1 = 1 Matome, kad jos pusašiu ilgiai 1 1 6( ) ir 1 1 ( ). Kita kreivė: > sqrt(1/); > eq:=7*x^+144-4*x*y = 0;. eq := 7 x x y = 0 > conic( p,eq, [x,y] ): > detail(%);
22 name of the object : p\ form of the object : hyperbolad\ center : [0, 0 ]\ foci : [[, 4 ], [, 4 ]]\ vertices : [[ 1 /5, 16 /5 ], [1 /5, 16 /5 ]]\ the asymptotes : [ 7 /0 x + 6 /5 y = 0, 5 /4 x = 0 ]\ equation of the hyperbola : 7 xˆ x y = 0 > draw(p,scaling=constrained,axes=normal); > C:=coordinates(center( o,p)); C := [0, 0] > subs(x=x+c[1],y=y+c[],equation(p)); 7 x x y = 0 > expand(%); 7 x x y = 0 > KFD(lhs(%)); [x = 4 5 x1 5 y1 5 x1 +, y = > subs(%,%%); y1 75 ] 7 ( 4 5 x ( 4 5 x y1 + ) y1 5 x1 + ) ( y1 75 ) = 0
23 > expand(%); Kanoninė lygtis: > (%-(144=144))/(-144); 16 x1 9 y = 0. Ištirkite kreivę x1 9 + y1 16 = 1 > eq1:=*x^+*x*y-*x-5*y^-4*y+1 = 0; > conic( p,eq1, [x,y] ): > draw(p,scaling=constrained,axes=normal); eq1 := x + x y x 5 y 4 y + 1 = 0 conic: "degenerate case: two intersecting lines" Tiesiu lygtis galėsime parašyti išskaidę kairiąją lygties pusę: > map(factor,eq); 7 x x y = 0 Tiesių lygtys \mapleinline{inert}{d}{x-y-1 = 0;}{% $x - y - 1=0$% } ir \mapleinline{inert}{d}{*x+5*y-1 = 0;}{% $\,x + 5\,y - 1=0$% }.
24 4. Ištirkite antros eilės kreivę > eq:=61*x+9*y-180*x^-180*x*y-45*y^-5 = 0; eq := 61 x + 9 y 180 x 180 x y 45 y 5 = 0 > p:= p :conic( p,eq, [x,y] ): > detail(%); name of the object : p\ form of the object : parabolad\ vertex : [1511 /1500, 77 /75 ]\ focus : [76 /675, 149 /150 ]\ directrix : 1 /5 5 ˆ(1 / ) x + /5 5 ˆ(1 / ) y 1 /150 5 ˆ(1 / ) = 0 \ equation of the parabola : 61 x + 9 y 180 xˆ 180 x y 45 yˆ 5 = 0 > draw(p,scaling=constrained,axes=normal); Randame viršūnės koordinates > C:=coordinates(vertex( v,p)); C := [ , ] Pastumiame koordinačiu sistemos centrą į viršūnę > subs(x=x+c[1],y=y+c[],equation(p)); 61 x y 180 (x ) 180 (x ) (y + ) 45 (y ) = 0 > expand(%); 5 x 6 5 y 180 x 180 x y 45 y = 0
25 KFD pagalba randame kanonizuojantį keitinį > KFD(lhs(%)); [x = 5 x1 5 y1 5 x1 +, y = Keičiame koordinates > subs(%,%%); 5 y1 5 ] 5 y1 180 ( 5 x1 5 y x1 45 ( 5 y1 ) = > expand(%); ) 180 ( 5 x1 5 5 y1 5 x1 = 0 5 Gauname kanoninę parabolės lygtį > %/5; 5 y1 75 x1 = 0 5 y1 5 x1 + ) ( y1 5 ) Antros eilės paviršiai plots ir plottols paketu pagalba, naudodami funkciją implicitplotd pavaizduokime kai kuriuos antros eilės sukimosi paviršius >. Error,. unexpected > with(plots); [animate, animated, animatecurve, arrow, changecoords, complexplot, complexplotd, conformal, conformald, contourplot, contourplotd, coordplot, coordplotd, densityplot, display, dualaxisplot, fieldplot, fieldplotd, gradplot, gradplotd, implicitplot, implicitplotd, inequal, interactive, interactiveparams, intersectplot, listcontplot, listcontplotd, listdensityplot, listplot, listplotd, loglogplot, logplot, matrixplot, multiple, odeplot, pareto, plotcompare, pointplot, pointplotd, polarplot, polygonplot, polygonplotd, polyhedra_supported, polyhedraplot, rootlocus, semilogplot, setcolors, setoptions, setoptionsd, spacecurve, sparsematrixplot, surfdata, textplot, textplotd, tubeplot] > with(plottools); [arc, arrow, circle, cone, cuboid, curve, cutin, cutout, cylinder, disk, dodecahedron, ellipse, ellipticarc, hemisphere, hexahedron, homothety, hyperbola, icosahedron, line, octahedron, parallelepiped, pieslice, point, polygon, project, rectangle, reflect, rotate, scale, semitorus, sphere, stellate, tetrahedron, torus, transform, translate]
26 1. Sukimosi elipsoidas > implicitplotd(x^/4^+y^/^+z^/^=1,x=-4..4,y=-..,z=-..,scal > ing=constrained, style=patch, axes=boxed); z 0 1 y x 4. Sukimosi paraboloidas > implicitplotd(z=x^/4+y^/4,x=-4..4,y=-4..4,z=0..,scaling=unconstra > ined, style=patch, axes=boxed);.5 z y x 4. Sukimosi hiperboloidas.
27 > implicitplotd(x^/5^+y^/5^-z^/^=-1,x= ,y= ,z=-7..7 >,scaling=unconstrained, style=patch, axes=boxed, > orientation=[10,60]); 6 4 z x y Kūgis. > implicitplotd(*z^=x^+y^,x= ,y= ,z=-7..7,scaling=unco > nstrained, style=patch, axes=boxed, orientation=[0,45]); 4 z y x 10
28 Uždaviniai 1. Raskite kanonines kreiviu 5 x 0 x y + 50 x + 40 y 0 y 11 = 0 ir 41 x + 4 x y 84 x + 9 y 08 y = 0 lygtis.. Nubrėžkite dvišakį sukimosi paraboloidą ir cilindrą.. Nubrėžkite elipsoidą, kurio centras taške (1,,), o ašys atitinkamai lygios,,4. 4. Dvieju ir triju kintamu jų kvadratinės formos n kintamu jų x1,x... xn kvadratine forma vadiname reiškinį: Q( x1, x,..., xn ) = sum(aij*xi*xj, i,j=1..n), (aij = aji),i,j = 1,...,n Akivaizdu, kad kvadratinė forma vienareikšmiškai apibrėžiama simetriška (aij = aji) matrica A=(aij), i,j=1..n. Matricos simetriškumo sąlygą galime užrašyti tokiu pavidalu: aij = (aij + aji)/, Jei x pažymėsime vektorių x=(x1, x,...,xn), o x - jo transponuotąjį vektorių, tai kvadratinę formą galime užrašyti taip: Q( x) = x Ax, čia simbolis &* žymi matricu daugybą. Arba Q(x) = (x,ax), čia skliaustai reiškia juose esančiu dvieju vektoriu : x ir A&*x skaliarinę sandaugą. Simetrišką matricą A diagonalizuoja ortogonalioji matrica P, t.y. tokia kad jos atvirkštinė matrica lygi jos pačios transponuotajai matricai: P P=E, kure - vienetinė matrica. Taigi, jei pažymėsime DA matricos A diagonalizuotąją matricą (t.y. jos Žordano formą), tai DA=P AP,
29 o matricos D=(dij), i=1..n, elementai, kurie nėra pagrindinėje įstrižainėje, lygūs nuliui: dij=o, i=/j. Tiesiškai transformuojant erdvę matricos P pagalba: x=py, kur y=(y1,y,...,yn), kvadratinė forma Q(x) įgyja diagonalinį pavidalą DQ(y): Tada, suprantama, ji lygi: DQ(y):=y DAy=(y,DAy). DQ(y)=sum(dii*yi^); i=1..n, ir dalis dėmenų šioje sumoje gali buti lygūs nuliui. Nenulinių dėmenu diagonaliniame (kanoniniame) kvadratinės formos Q(x) pavidale DQ(y) skaičius vadinamas kvadratinės formos Q(x) rangu. Teigiamų dėmenų skaičius vadinamas formos signatūra. Forma Q(x) vadinama teigiamai (neigiamai) apibrėžta, jei visi matriccos DA elementai teigiami (neigiami). Kitais atvejais sakome, kad Q(x) yra neapibrėžto ženklo kvadratinė forma. Taigi, kadangi (x,ax)=q(x)=dq(y)=(y,day), jeix=py, teigiamas formosq(x) apibrėžtumas reiškia, kad bet kokiam nenuliniam vektoriui x skaliarinė sandauga nelygi 0. > restart; (x,ax) > with(linalg): with(plots): with(plottools): 1. Tarkim, turime dvieju kintamu jų kvadratinę formą Q(x)= *x[1]^ - *x[]^ -1*x[1]*x[]: > Q:=*x[1]^-*x[]^-1*x[1]*x[];X:=[x[1],x[]]; N:=nops(X); Q := x 1 x 1 x 1 x X := [x 1, x ] N :=
30 Sudarome šitos kvadratinės formos matricą: > A:= matrix(,,[[,-6],[-6,-]]); [ ] 6 A := 6 Rasime jos tikrinius vektorius x ir tikrines reikšmes λ (tenkinančius lygtį Ax = λx) > lambda; λ > Tikrinis_vektorius := [eigenvectors(a)]; [ ] [ Tikrinis_vektorius := [[7, 1, {, 1 }], [ 6, 1, { 1, ] }]] Normuojame tikrinius vektorius (pakeičiame juos lygiagrečiais pradiniams vienetinio ilgio vektoriais) normalize komanda : > v1 := normalize(tikrinis_vektorius[1][][1]); > v := normalize(tikrinis_vektorius[][][1]); [ v1 := 1 ] 4 1 4, 6 1 [ 1 4 v :=, 1 ] A: augment komandos pagalba konstruojame matricą P, kuri diagonalizuoja > PA := augment(v1,v); 1 4 PA := Tada P AP=DA: > DA := simplify(evalm(transpose(pa) &* A &* PA)); [ ] 7 0 DA := 0 6 Įsitikiname, kad PA - ortogonali matrica: > evalm(transpose(pa)&*pa):simplify(%); [ ] Randame diagonalizuotąją kvadratinę formą: > Y:=[y[1],y[]]; Y := [y 1, y ] > DQ:=evalm(transpose(Y)&*DA&*Y);
31 DQ := 7 y 1 6 y Akivaizdu, kad kvadratinė forma yra neapibrėžto ženklo, jos rangas, o signatūra lygi 1. Patikrinkime, ar keitinys X=PAY kanonizuoja kvadratinę formą Q: > evalm(x=pa&*y); [ [x 1, x ] = 1 4 y y, 1 4 y1 + ] 1 4 y > K:=[seq(x[k]=rhs(%)[k],k=1..nops(X))]; K := [x 1 = 1 4 y y, x = y y ] > subs(k,q):expand(%); 7 y 1 6 y Naudodami implicitplot nubrėžkime ir palyginkime kreives Q = 1 ir DQ =1: > implicitplot(q=1,x[1]=-..,x[]=-..,scaling=constrained); x[] x[1] 1 > implicitplot(dq=1,y[1]=-..,y[]=-..,scaling=constrained);
32 y[] y[1] 1 Tokiu būdu galime įsivaizduoti kaip tiesinė transformacija X = P&*Y paveikė erdvę.. Tarkime, jog turime triju kintamųju kvadratinę formą: > restart:with(linalg): > Q:=x[1]^+x[]^+5*x[]^-6*x[1]*x[]-*x[1]*x[]+*x[]*x[]; Pažymime kintamuosius Q := x 1 + x + 5 x 6 x 1 x x 1 x + x x > indets(q):x:=sort(convert(%,list));n:=nops(%); X := [x 1, x, x ] N := ir randame kvadratinės formos matricą A: > A := hessian(q/,x); 1 1 A := Kadangi simetrinė matrica A diagonalizuojama, jos diagonalusis pavidalas sutampa su jos Žordano pavidalu. Todėl galime kvadratinės formos matricos A diagonaliojo pavidalo DA ir diagonalizuojančiosios matricos P ieškoti naudodami jordan komandą: > DA := jordan(a,r);
33 DA := Jei mums reikia tik kanoninio kvadratinės formos Q pavidalo, jį galime gauti taip: > Y:=[y (1..nops(X))];evalm(transpose(Y)&*DA&*Y); Y := [y1, y, y ] y1 + y + 6 y Jei mums reikia kvadratinės formos kintamu jų keitinio, kuris kanonizuoja formą, randame diagonalizuojančią matricą R: > print(r); Naudodami col komandą išskiriame matricos R vektorius-stulpelius: > v:=[col(r,1..n)]; [ 1 v := [, 1 ] [ 1, 0,, 1, 1 ] [ 1, 6, 1 6, 1 ] ] GramSchmidt ir normalize komandomis randame ortonormuotąją vektorių erdvės bazę: > GramSchmidt(v,normalized); [ ] [ ] [,, 0,,,, [ 6 6 6, 6, ] 6 ] ir iš bazės vektorių sudarome ortogonaliąją matricą P: > P:=transpose(matrix(N,N,%));orthog(P); 6 6 P := true Apibrėžiame keitinio kintamuosius
34 > Y:=[y (1..nops(X))]; Y := [y1, y, y ] ir apibrėžiame keitinį K=PY: > evalm(x=p&*y); [ ] y1 y 6 y y1 y 6 y y 6 y [x 1, x, x ] = + +,, 6 6 > K:=[seq(x[n]=rhs(%)[n],n=1..N)]; y1 y 6 y y1 y 6 y y 6 y K := [x 1 = + +, x =, x = ] 6 6 Įsitikiname, kad šis keitinys kanonizuoja kvadratinę formą Q: > simplify(subs(k,q)); y1 + y + 6 y Šitaip galime rasti teoriškai bet kokio kintamųjų skaičiaus kvadratin ės formos kanoninį pavidalą.. Raskime kvadratinės formos diagonalinį pavidalą Lagranžo metodu. > restart:with(linalg):with(student): Tarkime, kad mūsų kvadratinė forma tokia: > Q:=*x1^+*x^+*x^-*x1*x-*x1*x+*x*x; Q := x1 + x + x x1 x x1 x + x x completesquare komanda išskiriame kvadratinėje formoje pilną kvadratą kintamojo x1 atžvilgiu: > completesquare(q,x1); (x1 x x ) + 8 x + 4 x x + 8 x Darome tą patį likusioje kvadratinės formos dalyje kintamojo x atžvilgiu: > op(1,%)+completesquare(%-op(1,%),x); (x1 x x 8 (x + x ) + 4 ) + 5 x Naujieji kvadratinės formos kintamieji - pilnu jų kvadratų pagrindai:
35 > indets(%,anything^); > {y1=op(1,%[1]),y=op(1,%[]),y=op(1,%[])}; > K:=solve(%,{x (1..)}); {x, (x + x 4 ), (x1 x x ) } {y1 = x, y = x + x 4, y = x1 x x } K := {x1 = y + y1 4 + y, x = y y1 4, x = y1 } Pakeitę kintamuosius randame kanoninį kvadratinės formos pavidalą: > subs(k,q):simplify(%); y + 5 y1 + 8 y Pavyzdys formos, kurios rangas mažesnis už jos kintamųjų skaičių > A:=matrix(,,[1,,,,0,,,,5]); A := > X:=([x,y,z]); X := [x, y, z] > Q(X):=expand(evalm(transpose(X)&*A&*X)); Q([x, y, z]) := x + 4 x y + 6 x z + 4 y z + 5 z > DQ:=jordan(A,P); > print(p); DQ := Kvadratinės formos kanoninis pavidalas: > X1:=([x1,y1,z1]); X1 := [x1, y1, z1 ] > multiply(transpose(x1),dq,x1); y1 ( 1) + z1 ( + 1)
36 Matome, kad jos rangas lygus. Uždaviniai. 1. Duota kvadratinė forma x y + 15 z 65 xz. Raskite jos kanoninį pavidalą, rangą, signatūrą. Užrašykite diagonalinę matricą ir ortogonalią diagonalizuojančią matricą. Patikrinkite jos ortogonalumą. Nustatykite kvadratinės formos apibr ėžtumą. Įsitikinkite diagonalizuojancios transformacijos pasirinkimo teisingumu. Tą patį padarykite su kvadratine forma Q := 4 x 1 + x 5 x + x 1 x x 1 x + 5 x x.. Sukonstruokite kvadratinę formą, kurios rangas mažesnis už kintamųjų skaičių. Nubrėžkite kreives (paviršius), kuriu taškuose kvadratinė forma įgyja pastovias reikšmes.
Matematika 1 4 dalis
 Matematika 1 4 dalis Analizinės geometrijos elementai. Tiesės plokštumoje lygtis (bendroji, kryptinė,...). Taško atstumas nuo tiesės. Kampas tarp dviejų tiesių. Plokščiosios kreivės lygtis Plokščiosios
Matematika 1 4 dalis Analizinės geometrijos elementai. Tiesės plokštumoje lygtis (bendroji, kryptinė,...). Taško atstumas nuo tiesės. Kampas tarp dviejų tiesių. Plokščiosios kreivės lygtis Plokščiosios
Matematika 1 3 dalis
 Matematika 1 3 dalis Vektorių algebros elementai. Vektorių veiksmai. Vektorių skaliarinės, vektorinės ir mišriosios sandaugos ir jų savybės. Vektoriai Vektoriumi vadinama kryptinė atkarpa. Jei taškas A
Matematika 1 3 dalis Vektorių algebros elementai. Vektorių veiksmai. Vektorių skaliarinės, vektorinės ir mišriosios sandaugos ir jų savybės. Vektoriai Vektoriumi vadinama kryptinė atkarpa. Jei taškas A
Dviejų kintamųjų funkcijos dalinės išvestinės
 Dviejų kintamųjų funkcijos dalinės išvestinės Dalinės išvestinės Tarkime, kad dviejų kintamųjų funkcija (, )yra apibrėžta srityje, o taškas 0 ( 0, 0 )yra vidinis srities taškas. Jei fiksuosime argumento
Dviejų kintamųjų funkcijos dalinės išvestinės Dalinės išvestinės Tarkime, kad dviejų kintamųjų funkcija (, )yra apibrėžta srityje, o taškas 0 ( 0, 0 )yra vidinis srities taškas. Jei fiksuosime argumento
Vilniaus universitetas. Edmundas Gaigalas A L G E B R O S UŽDUOTYS IR REKOMENDACIJOS
 Vilniaus universitetas Edmundas Gaigalas A L G E B R O S UŽDUOTYS IR REKOMENDACIJOS Vilnius 1992 T U R I N Y S 1. Vektorinė erdvė............................................. 3 2. Matricos rangas.............................................
Vilniaus universitetas Edmundas Gaigalas A L G E B R O S UŽDUOTYS IR REKOMENDACIJOS Vilnius 1992 T U R I N Y S 1. Vektorinė erdvė............................................. 3 2. Matricos rangas.............................................
Taylor Polynomials. 2 x2 6 x3 24 x4
 > Taylor Polynomials > Taylor Polynomials about x = 0. A primary use of Taylor polynomials is to find good polynomial approximations to a function near a specified value. As a first example, we use a fourth
> Taylor Polynomials > Taylor Polynomials about x = 0. A primary use of Taylor polynomials is to find good polynomial approximations to a function near a specified value. As a first example, we use a fourth
X galioja nelygyb f ( x1) f ( x2)
 Monotonin s funkcijos Tegul turime funkciją f : A R, A R. Apibr žimas. Funkcija y = f ( x) vadinama monotoniškai did jančia (maž jančia) aib je X A, jei x1< x2 iš X galioja nelygyb f ( x1) f ( x2) ( f
Monotonin s funkcijos Tegul turime funkciją f : A R, A R. Apibr žimas. Funkcija y = f ( x) vadinama monotoniškai did jančia (maž jančia) aib je X A, jei x1< x2 iš X galioja nelygyb f ( x1) f ( x2) ( f
ANALIZINĖ GEOMETRIJA III skyrius (Medžiaga virtualiajam kursui)
 ngelė aškienė NLIZINĖ GEMETRIJ III skrius (Medžiaga virtualiajam kursui) III skrius. TIESĖS IR PLKŠTUMS... 5. Tiesės lgts... 5.. Tiesės [M, a r ] vektorinė lgtis... 5.. Tiesės [M, a r ] parametrinės lgts...
ngelė aškienė NLIZINĖ GEMETRIJ III skrius (Medžiaga virtualiajam kursui) III skrius. TIESĖS IR PLKŠTUMS... 5. Tiesės lgts... 5.. Tiesės [M, a r ] vektorinė lgtis... 5.. Tiesės [M, a r ] parametrinės lgts...
1 TIES ES IR PLOK TUMOS
 G E O M E T R I J A Gediminas STEPANAUSKAS 1 TIES ES IR PLOK TUMOS 11 Plok²tumos ir ties es plok²tumoje normalin es lygtys 111 Vektorin e forma Plok²tumos α padetis koordina iu sistemos Oxyz atºvilgiu
G E O M E T R I J A Gediminas STEPANAUSKAS 1 TIES ES IR PLOK TUMOS 11 Plok²tumos ir ties es plok²tumoje normalin es lygtys 111 Vektorin e forma Plok²tumos α padetis koordina iu sistemos Oxyz atºvilgiu
LIETUVOS JAUNŲ J Ų MATEMATIKŲ MOKYKLA
 LIETUVOS JAUNŲ J Ų MATEMATIKŲ MOKYKLA tema. APSKRITIMŲ GEOMETRIJA (00 0) Teorinę medžiagą parengė bei antrąją užduotį sudarė Vilniaus pedagoginio universiteto docentas Edmundas Mazėtis. Apskritimas tai
LIETUVOS JAUNŲ J Ų MATEMATIKŲ MOKYKLA tema. APSKRITIMŲ GEOMETRIJA (00 0) Teorinę medžiagą parengė bei antrąją užduotį sudarė Vilniaus pedagoginio universiteto docentas Edmundas Mazėtis. Apskritimas tai
4.1 Skaliarinė sandauga erdvėje R n Tarkime, kad duota vektorinė erdvė R n. Priminsime, kad šios erdvės elementai yra vektoriai vektoriu
 IV DEKARTO KOORDINAČIU SISTEMA VEKTORIAI 41 Skaliarinė sandauga erdvėje R n Tarkime, kad duota vektorinė erdvė R n Priminsime, kad šios erdvės elementai yra vektoriai α = (a 1,, a n ) Be mums jau žinomu
IV DEKARTO KOORDINAČIU SISTEMA VEKTORIAI 41 Skaliarinė sandauga erdvėje R n Tarkime, kad duota vektorinė erdvė R n Priminsime, kad šios erdvės elementai yra vektoriai α = (a 1,, a n ) Be mums jau žinomu
FDMGEO4: Antros eilės kreivės I
 FDMGEO4: Antros eilės kreivės I Kęstutis Karčiauskas Matematikos ir Informatikos fakultetas 1 Koordinačių sistemos transformacija Antrosios eilės kreivių lgtis prastinsime keisdami (transformuodami) koordinačių
FDMGEO4: Antros eilės kreivės I Kęstutis Karčiauskas Matematikos ir Informatikos fakultetas 1 Koordinačių sistemos transformacija Antrosios eilės kreivių lgtis prastinsime keisdami (transformuodami) koordinačių
I dalis KLAUSIMŲ SU PASIRENKAMUOJU ATSAKYMU TEISINGI ATSAKYMAI
 008 M. FIZIKOS VALSTYBINIO BRANDOS EGZAMINO VERTINIMO INSTRUKCIJA Pagrindinė sesija Kiekvieno I dalies klausimo teisingas atsakymas vertinamas tašku. I dalis KLAUSIMŲ SU PASIRENKAMUOJU ATSAKYMU TEISINGI
008 M. FIZIKOS VALSTYBINIO BRANDOS EGZAMINO VERTINIMO INSTRUKCIJA Pagrindinė sesija Kiekvieno I dalies klausimo teisingas atsakymas vertinamas tašku. I dalis KLAUSIMŲ SU PASIRENKAMUOJU ATSAKYMU TEISINGI
Specialieji analizės skyriai
 Specialieji analizės skyriai. Trigonometrinės Furje eilutės Moksle ir technikoje dažnai susiduriame su periodiniais reiškiniais, apibūdinamais periodinėmis laiko funkcijomis: f(t). 2 Paprasčiausia periodinė
Specialieji analizės skyriai. Trigonometrinės Furje eilutės Moksle ir technikoje dažnai susiduriame su periodiniais reiškiniais, apibūdinamais periodinėmis laiko funkcijomis: f(t). 2 Paprasčiausia periodinė
Rectangular Polar Parametric
 Harold s Precalculus Rectangular Polar Parametric Cheat Sheet 15 October 2017 Point Line Rectangular Polar Parametric f(x) = y (x, y) (a, b) Slope-Intercept Form: y = mx + b Point-Slope Form: y y 0 = m
Harold s Precalculus Rectangular Polar Parametric Cheat Sheet 15 October 2017 Point Line Rectangular Polar Parametric f(x) = y (x, y) (a, b) Slope-Intercept Form: y = mx + b Point-Slope Form: y y 0 = m
FUNKCIJOS. veiksmu šioje erdvėje apibrėžkime dar viena. a = {a 1,..., a n } ir b = {b 1,... b n } skaliarine sandauga
 VII DAUGELIO KINTAMU JU FUNKCIJOS 71 Bendrosios sa vokos Iki šiol mes nagrinėjome funkcijas, apibrėžtas realiu skaičiu aibėje Nagrinėsime funkcijas, kurios apibrėžtos vektorinėse erdvėse Tarkime, kad R
VII DAUGELIO KINTAMU JU FUNKCIJOS 71 Bendrosios sa vokos Iki šiol mes nagrinėjome funkcijas, apibrėžtas realiu skaičiu aibėje Nagrinėsime funkcijas, kurios apibrėžtos vektorinėse erdvėse Tarkime, kad R
AIBĖS, FUNKCIJOS, LYGTYS
 AIBĖS, FUNKCIJOS, LYGTYS Aibės sąvoka ir pavyzdžiai Atskirų objektų rinkiniai, grupės, sistemos, kompleksai matematikoje vadinami aibėmis. Šie atskiri objektai vadinami aibės elementais. Kai elementas
AIBĖS, FUNKCIJOS, LYGTYS Aibės sąvoka ir pavyzdžiai Atskirų objektų rinkiniai, grupės, sistemos, kompleksai matematikoje vadinami aibėmis. Šie atskiri objektai vadinami aibės elementais. Kai elementas
Temos. Intervalinės statistinės eilutės sudarymas. Santykinių dažnių histogramos brėžimas. Imties skaitinių charakteristikų skaičiavimas
 Pirmasis uždavinys Temos. Intervalinės statistinės eilutės sudarymas. Santykinių dažnių histogramos brėžimas. Imties skaitinių charakteristikų skaičiavimas Uždavinio formulavimas a) Žinoma n = 50 tiriamo
Pirmasis uždavinys Temos. Intervalinės statistinės eilutės sudarymas. Santykinių dažnių histogramos brėžimas. Imties skaitinių charakteristikų skaičiavimas Uždavinio formulavimas a) Žinoma n = 50 tiriamo
1. Individualios užduotys:
 IV. PAPRASTOSIOS DIFERENCIALINĖS LYGTYS. Individualios užduots: - trumpa teorijos apžvalga, - pavzdžiai, - užduots savarankiškam darbui. Pirmosios eilės diferencialinių lgčių sprendimas.. psl. Antrosios
IV. PAPRASTOSIOS DIFERENCIALINĖS LYGTYS. Individualios užduots: - trumpa teorijos apžvalga, - pavzdžiai, - užduots savarankiškam darbui. Pirmosios eilės diferencialinių lgčių sprendimas.. psl. Antrosios
Specialieji analizės skyriai
 Specialieji analizės skyriai. Specialieji analizės skyriai Kompleksinio kinamojo funkcijų teorija Furje eilutės ir Furje integralai Operacinis skaičiavimas Lauko teorijos elementai. 2 Kompleksinio kintamojo
Specialieji analizės skyriai. Specialieji analizės skyriai Kompleksinio kinamojo funkcijų teorija Furje eilutės ir Furje integralai Operacinis skaičiavimas Lauko teorijos elementai. 2 Kompleksinio kintamojo
Elektronų ir skylučių statistika puslaidininkiuose
 lktroų ir skylučių statistika puslaidiikiuos Laisvų laidumo lktroų gracija, t.y. lktroų prėjimas į laidumo juostą, gali vykti kaip iš dooriių lygmų, taip ir iš valtiės juostos. Gracijos procsas visuomt
lktroų ir skylučių statistika puslaidiikiuos Laisvų laidumo lktroų gracija, t.y. lktroų prėjimas į laidumo juostą, gali vykti kaip iš dooriių lygmų, taip ir iš valtiės juostos. Gracijos procsas visuomt
III. MATRICOS. DETERMINANTAI. 3.1 Matricos A = lentele žymėsime taip:
 III MATRICOS DETERMINANTAI Realiu ju skaičiu lentele 3 Matricos a a 2 a n A = a 2 a 22 a 2n a m a m2 a mn vadinsime m n eilės matrica Trumpai šia lentele žymėsime taip: A = a ij ; i =,, m, j =,, n čia
III MATRICOS DETERMINANTAI Realiu ju skaičiu lentele 3 Matricos a a 2 a n A = a 2 a 22 a 2n a m a m2 a mn vadinsime m n eilės matrica Trumpai šia lentele žymėsime taip: A = a ij ; i =,, m, j =,, n čia
t. y. =. Iš čia seka, kad trikampiai BPQ ir BAC yra panašūs, o jų D 1 pav.
 LIETUVOS JUNŲ J Ų MTEMTIKŲ MOKYKL tema. TRIGONOMETRIJOS TIKYMI GEOMETRIJOJE (008-00) Terinę medžiagą parengė bei šeštąją uždutį sudarė Vilniaus pedaggini universitet dentas Edmundas Mazėtis Šiame darbe
LIETUVOS JUNŲ J Ų MTEMTIKŲ MOKYKL tema. TRIGONOMETRIJOS TIKYMI GEOMETRIJOJE (008-00) Terinę medžiagą parengė bei šeštąją uždutį sudarė Vilniaus pedaggini universitet dentas Edmundas Mazėtis Šiame darbe
0.1. Bendrosios sąvokos
 0.1. BENDROSIOS SĄVOKOS 1 0.1. Bendrosios sąvokos 0.1.1. Diferencialinės lygtys su mažuoju parametru F ) x n),x n 1),...,x,x,t;ε = 0, xt;ε) C n T), T [0,+ ), 0 < ε ε 0 ) F x n) t;ε),x n 1) t;ε),...,x t;ε),xt;ε),t;ε
0.1. BENDROSIOS SĄVOKOS 1 0.1. Bendrosios sąvokos 0.1.1. Diferencialinės lygtys su mažuoju parametru F ) x n),x n 1),...,x,x,t;ε = 0, xt;ε) C n T), T [0,+ ), 0 < ε ε 0 ) F x n) t;ε),x n 1) t;ε),...,x t;ε),xt;ε),t;ε
0.1. Bendrosios sąvokos
 .1. BENDROSIOS SĄVOKOS 1.1. Bendrosios sąvokos.1.1. Diferencialinės lygtys su mažuoju parametru F ) x n),x n 1),...,x,x,t;ε =, xt;ε) C n T), T [,+ ), < ε ε ) F x n) t;ε),x n 1) t;ε),...,x t;ε),xt;ε),t;ε,
.1. BENDROSIOS SĄVOKOS 1.1. Bendrosios sąvokos.1.1. Diferencialinės lygtys su mažuoju parametru F ) x n),x n 1),...,x,x,t;ε =, xt;ε) C n T), T [,+ ), < ε ε ) F x n) t;ε),x n 1) t;ε),...,x t;ε),xt;ε),t;ε,
Matematinės analizės konspektai
 Matematinės analizės konspektai (be įrodymų) Marius Gedminas pagal V. Mackevičiaus paskaitas 998 m. rudens semestras (I kursas) Realieji skaičiai Apibrėžimas. Uždarųjų intervalų seka [a n, b n ], n =,
Matematinės analizės konspektai (be įrodymų) Marius Gedminas pagal V. Mackevičiaus paskaitas 998 m. rudens semestras (I kursas) Realieji skaičiai Apibrėžimas. Uždarųjų intervalų seka [a n, b n ], n =,
1.4. Rungės ir Kuto metodas
 .4. RUNGĖS IR KUTO METODAS.4. Rungės ir Kuto metodas.4.. Prediktoriaus-korektoriaus metodas Palyginkime išreikštinį ir simetrinį Eulerio metodus. Pirmojo iš jų pagrindinis privalumas tas, kad išreikštinio
.4. RUNGĖS IR KUTO METODAS.4. Rungės ir Kuto metodas.4.. Prediktoriaus-korektoriaus metodas Palyginkime išreikštinį ir simetrinį Eulerio metodus. Pirmojo iš jų pagrindinis privalumas tas, kad išreikštinio
Įžanginių paskaitų medžiaga iš knygos
 MATEMATINĖ LOGIKA Įžanginių paskaitų medžiaga iš knygos Aleksandras Krylovas. Diskrečioji matematika: vadovėlis aukštųjų mokyklų studentams. Vilnius: Technika, 2009. 320 p. ISBN 978-9955-28-450-5 1 Teiginio
MATEMATINĖ LOGIKA Įžanginių paskaitų medžiaga iš knygos Aleksandras Krylovas. Diskrečioji matematika: vadovėlis aukštųjų mokyklų studentams. Vilnius: Technika, 2009. 320 p. ISBN 978-9955-28-450-5 1 Teiginio
2009 m. matematikos valstybinio brandos egzamino VERTINIMO INSTRUKCIJA Pagrindinė sesija 1 6 uždavinių atsakymai
 M. MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA PATVIRTINTA Nacionalinio egzaminų centro direktoriaus -6- įsakymu Nr. (..)-V-8 m. matematikos valstybinio brandos egzamino VERTINIMO
M. MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA PATVIRTINTA Nacionalinio egzaminų centro direktoriaus -6- įsakymu Nr. (..)-V-8 m. matematikos valstybinio brandos egzamino VERTINIMO
2008 m. matematikos valstybinio brandos egzamino VERTINIMO INSTRUKCIJA Pagrindinė sesija
 008 M MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA 008 m matematikos valstybinio brandos egzamino VERTINIMO INSTRUKCIJA Pagrindinė sesija 7 uždavinių atsakymai I variantas Užd
008 M MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA 008 m matematikos valstybinio brandos egzamino VERTINIMO INSTRUKCIJA Pagrindinė sesija 7 uždavinių atsakymai I variantas Užd
MATEMATINĖ LOGIKA. Įžanginių paskaitų medžiaga iš knygos
 MATEMATINĖ LOGIKA Įžanginių paskaitų medžiaga iš knygos Aleksandras Krylovas. Diskrečioji matematika: vadovėlis aukštųjų mokyklų studentams. Vilnius: Technika, 2009. 320 p. ISBN 978-9955-28-450-5 Teiginio
MATEMATINĖ LOGIKA Įžanginių paskaitų medžiaga iš knygos Aleksandras Krylovas. Diskrečioji matematika: vadovėlis aukštųjų mokyklų studentams. Vilnius: Technika, 2009. 320 p. ISBN 978-9955-28-450-5 Teiginio
VIII. FRAKTALINĖ DIMENSIJA. 8.1 Fraktalinės dimensijos samprata. Ar baigtinis Norvegijos sienos ilgis?
 VIII FRAKTALINĖ DIMENSIJA 81 Fraktalinės dimensijos samprata Ar baigtinis Norvegijos sienos ilgis? Tarkime, kad duota atkarpa, kurios ilgis lygus 1 Padalykime šia atkarpa n lygiu daliu Akivaizdu, kad kiekvienos
VIII FRAKTALINĖ DIMENSIJA 81 Fraktalinės dimensijos samprata Ar baigtinis Norvegijos sienos ilgis? Tarkime, kad duota atkarpa, kurios ilgis lygus 1 Padalykime šia atkarpa n lygiu daliu Akivaizdu, kad kiekvienos
KADETAS (VII ir VIII klasės)
 ADETAS (VII ir VIII klasės) 1. E 10 000 Galima tikrinti atsakymus. adangi vidutinė kainasumažėjo, tai brangiausia papūga kainavo daugiau kaip 6000 litų. Vadinasi, parduotoji papūga kainavo daugiau kaip
ADETAS (VII ir VIII klasės) 1. E 10 000 Galima tikrinti atsakymus. adangi vidutinė kainasumažėjo, tai brangiausia papūga kainavo daugiau kaip 6000 litų. Vadinasi, parduotoji papūga kainavo daugiau kaip
I.4. Laisvasis kūnų kritimas
 I4 Laisvasis kūnų kitimas Laisvuoju kitimu vadinamas judėjimas, kuiuo judėtų kūnas veikiamas tik sunkio jėos, nepaisant oo pasipiešinimo Kūnui laisvai kintant iš nedidelio aukščio h (dau mažesnio už Žemės
I4 Laisvasis kūnų kitimas Laisvuoju kitimu vadinamas judėjimas, kuiuo judėtų kūnas veikiamas tik sunkio jėos, nepaisant oo pasipiešinimo Kūnui laisvai kintant iš nedidelio aukščio h (dau mažesnio už Žemės
IV. FUNKCIJOS RIBA. atvira. intervala. Apibrėžimas Sakysime, kad skaičius b yra funkcijos y = f(x) riba taške x 0, jei bet kokiam,
 41 Funkcijos riba IV FUNKCIJOS RIBA Taško x X aplinka vadiname bet koki atvira intervala, kuriam priklauso taškas x Taško x 0, 2t ilgio aplinka žymėsime tokiu būdu: V t (x 0 ) = ([x 0 t, x 0 + t) Sakykime,
41 Funkcijos riba IV FUNKCIJOS RIBA Taško x X aplinka vadiname bet koki atvira intervala, kuriam priklauso taškas x Taško x 0, 2t ilgio aplinka žymėsime tokiu būdu: V t (x 0 ) = ([x 0 t, x 0 + t) Sakykime,
2.5. KLASIKINĖS TOLYDŽIŲ FUNKCIJŲ TEOREMOS
 .5. KLASIKINĖS TOLYDŽIŲ FUNKCIJŲ TEOREMOS 5.. Pirmoji Bolcao Koši teorema. Jei fucija f tolydi itervale [a;b], itervalo galuose įgyja priešigų želų reišmes, tai egzistuoja tos tašas cc, ( ab ; ), uriame
.5. KLASIKINĖS TOLYDŽIŲ FUNKCIJŲ TEOREMOS 5.. Pirmoji Bolcao Koši teorema. Jei fucija f tolydi itervale [a;b], itervalo galuose įgyja priešigų želų reišmes, tai egzistuoja tos tašas cc, ( ab ; ), uriame
Spalvos. Šviesa. Šviesos savybės. Grafika ir vizualizavimas. Spalvos. Grafika ir vizualizavimas, VDU, Spalvos 1
 Spalvos Grafika ir vizualizavimas Spalvos Šviesa Spalvos Spalvų modeliai Gama koregavimas Šviesa Šviesos savybės Vandens bangos Vaizdas iš šono Vaizdas iš viršaus Vaizdas erdvėje Šviesos bangos Šviesa
Spalvos Grafika ir vizualizavimas Spalvos Šviesa Spalvos Spalvų modeliai Gama koregavimas Šviesa Šviesos savybės Vandens bangos Vaizdas iš šono Vaizdas iš viršaus Vaizdas erdvėje Šviesos bangos Šviesa
Paprastosios DIFERENCIALINĖS LYGTYS
 Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Diferencialinių lygčių ir skaičiavimo matematikos katedra Naugarduko g. 24, LT-3225 Vilnius,
Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Diferencialinių lygčių ir skaičiavimo matematikos katedra Naugarduko g. 24, LT-3225 Vilnius,
06 Geometrin e optika 1
 06 Geometrinė optika 1 0.1. EIKONALO LYGTIS 3 Geometrinėje optikoje įvedama šviesos spindulio sąvoka. Tai leidžia Eikonalo lygtis, kuri išvedama iš banginės lygties monochromatinei bangai - Helmholtco
06 Geometrinė optika 1 0.1. EIKONALO LYGTIS 3 Geometrinėje optikoje įvedama šviesos spindulio sąvoka. Tai leidžia Eikonalo lygtis, kuri išvedama iš banginės lygties monochromatinei bangai - Helmholtco
Paprastosios DIFERENCIALINĖS LYGTYS
 Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Taikomosios matematikos institutas, Diferencialinių lygčių katedra Naugarduko g. 24, LT-3225
Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Taikomosios matematikos institutas, Diferencialinių lygčių katedra Naugarduko g. 24, LT-3225
EKONOMETRIJA 1 (Regresinė analizė)
 EKONOMETRIJA 1 Regresinė analizė Kontrolinis Sudarė M.Radavičius 004 05 15 Kai kurių užduočių sprendimai KOMENTARAS. Kai kuriems uždaviniams tik nusakytos sprendimų gairės, kai kurie iš jų suskaidyti į
EKONOMETRIJA 1 Regresinė analizė Kontrolinis Sudarė M.Radavičius 004 05 15 Kai kurių užduočių sprendimai KOMENTARAS. Kai kuriems uždaviniams tik nusakytos sprendimų gairės, kai kurie iš jų suskaidyti į
VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS PROGRAMŲ SISTEMŲ KATEDRA. Algoritmų teorija. Paskaitų konspektas
 VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS PROGRAMŲ SISTEMŲ KATEDRA Algoritmų teorija Paskaitų konspektas Dėstytojas: lekt. dr. Adomas Birštunas Vilnius 2015 TURINYS 1. Algoritmo samprata...
VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS PROGRAMŲ SISTEMŲ KATEDRA Algoritmų teorija Paskaitų konspektas Dėstytojas: lekt. dr. Adomas Birštunas Vilnius 2015 TURINYS 1. Algoritmo samprata...
Paprastosios DIFERENCIALINĖS LYGTYS
 Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Diferencialinių lgčių ir skaičiavimo matematikos katedra Naugarduko g. 24, LT-3225 Vilnius,
Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Diferencialinių lgčių ir skaičiavimo matematikos katedra Naugarduko g. 24, LT-3225 Vilnius,
Diskrečioji matematika
 VILNIAUS UNIVERSITETAS Gintaras Skersys Julius Andrikonis Diskrečioji matematika Pratybų medžiaga Versija: 28 m. sausio 22 d. Vilnius, 27 Turinys Turinys 2 Teiginiai. Loginės operacijos. Loginės formulės
VILNIAUS UNIVERSITETAS Gintaras Skersys Julius Andrikonis Diskrečioji matematika Pratybų medžiaga Versija: 28 m. sausio 22 d. Vilnius, 27 Turinys Turinys 2 Teiginiai. Loginės operacijos. Loginės formulės
2015 M. MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA Pagrindinė sesija. I dalis
 PATVIRTINTA Ncionlinio egzminų centro direktorius 0 m. birželio d. įskymu Nr. (..)-V-7 0 M. MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA Pgrindinė sesij I dlis Užd. Nr. 4 7
PATVIRTINTA Ncionlinio egzminų centro direktorius 0 m. birželio d. įskymu Nr. (..)-V-7 0 M. MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA Pgrindinė sesij I dlis Užd. Nr. 4 7
Vilniaus universitetas Matematikos ir informatikos fakultetas Informatikos katedra. Gintaras Skersys. Mokymo priemonė
 Vilniaus universitetas Matematikos ir informatikos fakultetas Informatikos katedra Gintaras Skersys Klaidas taisančių kodų teorija Mokymo priemonė Vilnius 2005 I dalis Pagrindinės savokos 1 Įvadas Panagrinėkime
Vilniaus universitetas Matematikos ir informatikos fakultetas Informatikos katedra Gintaras Skersys Klaidas taisančių kodų teorija Mokymo priemonė Vilnius 2005 I dalis Pagrindinės savokos 1 Įvadas Panagrinėkime
1. (a) (5 points) Find the unit tangent and unit normal vectors T and N to the curve. r(t) = 3cost, 4t, 3sint
 1. a) 5 points) Find the unit tangent and unit normal vectors T and N to the curve at the point P, π, rt) cost, t, sint ). b) 5 points) Find curvature of the curve at the point P. Solution: a) r t) sint,,
1. a) 5 points) Find the unit tangent and unit normal vectors T and N to the curve at the point P, π, rt) cost, t, sint ). b) 5 points) Find curvature of the curve at the point P. Solution: a) r t) sint,,
1 Įvadas Neišspręstos problemos Dalumas Dalyba su liekana Dalumo požymiai... 3
 Skaičių teorija paskaitų konspektas Paulius Šarka, Jonas Šiurys 1 Įvadas 1 1.1 Neišspręstos problemos.............................. 1 2 Dalumas 2 2.1 Dalyba su liekana.................................
Skaičių teorija paskaitų konspektas Paulius Šarka, Jonas Šiurys 1 Įvadas 1 1.1 Neišspręstos problemos.............................. 1 2 Dalumas 2 2.1 Dalyba su liekana.................................
Praeita paskaita. Grafika ir vizualizavimas Atkirtimai dvimatėje erdvėje. Praeita paskaita. 2D Transformacijos. Grafika ir vizualizavimas, VDU, 2010
 Praeita paskaita Grafika ir vizualizavimas Atkirtimai dvimatėje erdvėje Atkarpos Tiesės lgtis = mx+ b kur m krpties koeficientas, o b aukštis, kuriame tiesė kerta ašį Susikirtimo taško apskaičiavimui sulginamos
Praeita paskaita Grafika ir vizualizavimas Atkirtimai dvimatėje erdvėje Atkarpos Tiesės lgtis = mx+ b kur m krpties koeficientas, o b aukštis, kuriame tiesė kerta ašį Susikirtimo taško apskaičiavimui sulginamos
LIETUVOS RESPUBLIKOS ŠVIETIMO IR MOKSLO MINISTERIJA NACIONALINIS EGZAMINU CENTRAS MATEMATIKA m. valstybinio brandos egzamino uþduotis
 LIETUVOS RESPUBLIKOS ŠVIETIMO IR MOKSLO MINISTERIJA NACIONALINIS EGZAMINU CENTRAS MATEMATIKA 006 m. valstybinio brandos egzamino uþduotis Pagrindinë sesija 006 m. geguþës 17 d. Trukmë 3 val. Nacionalinis
LIETUVOS RESPUBLIKOS ŠVIETIMO IR MOKSLO MINISTERIJA NACIONALINIS EGZAMINU CENTRAS MATEMATIKA 006 m. valstybinio brandos egzamino uþduotis Pagrindinë sesija 006 m. geguþës 17 d. Trukmë 3 val. Nacionalinis
LIETUVOS RESPUBLIKOS ÐVIETIMO IR MOKSLO MINISTERIJA NACIONALINIS EGZAMINØ CENTRAS 2014 METŲ MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO REZULTATŲ
 LIETUVOS RESPUBLIKOS ÐVIETIMO IR MOKSLO MINISTERIJA NACIONALINIS EGZAMINØ CENTRAS 014 METŲ MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO REZULTATŲ STATISTINĖ ANALIZĖ 014 m. birželio 5 d. matematikos valstybinį
LIETUVOS RESPUBLIKOS ÐVIETIMO IR MOKSLO MINISTERIJA NACIONALINIS EGZAMINØ CENTRAS 014 METŲ MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO REZULTATŲ STATISTINĖ ANALIZĖ 014 m. birželio 5 d. matematikos valstybinį
1 Tada teigini Ne visi šie vaikinai yra studentai galima išreikšti formule. 2 Ta pati teigini galima užrašyti ir taip. 3 Formulė U&B C reiškia, kad
 45 DISKREČIOJI MATEMATIKA. LOGIKA. PAVYZDŽIAI Raidėmis U, B ir C pažymėti teiginiai: U = Vitas yra studentas ; B = Skirmantas yra studentas ; C = Jonas yra studentas. 1 Tada teigini Ne visi šie vaikinai
45 DISKREČIOJI MATEMATIKA. LOGIKA. PAVYZDŽIAI Raidėmis U, B ir C pažymėti teiginiai: U = Vitas yra studentas ; B = Skirmantas yra studentas ; C = Jonas yra studentas. 1 Tada teigini Ne visi šie vaikinai
Trigonometric Formula Sheet
 Trigonometric Formula Sheet Definition of the Trig Functions Right Triangle Definition Assume that: 0 < θ < or 0 < θ < 90 Unit Circle Definition Assume θ can be any angle. y x, y hypotenuse opposite θ
Trigonometric Formula Sheet Definition of the Trig Functions Right Triangle Definition Assume that: 0 < θ < or 0 < θ < 90 Unit Circle Definition Assume θ can be any angle. y x, y hypotenuse opposite θ
DISKREČIOJI MATEMATIKA
 VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS INFORMATIKOS KATEDRA Valdas Diči ūnas Gintaras Skersys DISKREČIOJI MATEMATIKA Mokymo priemonė Vilnius 2003 Įvadas Išvertus iš lotynu kalbos
VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS INFORMATIKOS KATEDRA Valdas Diči ūnas Gintaras Skersys DISKREČIOJI MATEMATIKA Mokymo priemonė Vilnius 2003 Įvadas Išvertus iš lotynu kalbos
ELEMENTARIOJI TEORIJA
 ELEMENTARIOJI TEORIJA Pirmosios kombinatorikos þinios siekia senàsias Rytø ðalis, kuriose mokëta suskaièiuoti këlinius bei derinius ir sudarinëti magiðkuosius kvadratus, ypaè populiarius viduramþiais.
ELEMENTARIOJI TEORIJA Pirmosios kombinatorikos þinios siekia senàsias Rytø ðalis, kuriose mokëta suskaièiuoti këlinius bei derinius ir sudarinëti magiðkuosius kvadratus, ypaè populiarius viduramþiais.
ATSITIKTINIAI PROCESAI. Alfredas Račkauskas. (paskaitų konspektas 2014[1] )
![ATSITIKTINIAI PROCESAI. Alfredas Račkauskas. (paskaitų konspektas 2014[1] ) ATSITIKTINIAI PROCESAI. Alfredas Račkauskas. (paskaitų konspektas 2014[1] )](/thumbs/72/67447727.jpg) ATSITIKTINIAI PROCESAI (paskaitų konspektas 2014[1] ) Alfredas Račkauskas Vilniaus universitetas Matematikos ir Informatikos fakultetas Ekonometrinės analizės katedra Vilnius, 2014 Iš dalies rėmė Projektas
ATSITIKTINIAI PROCESAI (paskaitų konspektas 2014[1] ) Alfredas Račkauskas Vilniaus universitetas Matematikos ir Informatikos fakultetas Ekonometrinės analizės katedra Vilnius, 2014 Iš dalies rėmė Projektas
Analizės uždavinynas. Vytautas Kazakevičius m. lapkričio 1 d.
 Analizės uždavinynas Vytautas Kazakevičius m. lapkričio d. ii Vienmatė analizė Faktorialai, binominiai koeficientai. Jei a R, n, k N {}, tai k! = 3 k, (k + )!! = 3 5 (k + ), (k)!! = 4 6 (k); a a(a ) (a
Analizės uždavinynas Vytautas Kazakevičius m. lapkričio d. ii Vienmatė analizė Faktorialai, binominiai koeficientai. Jei a R, n, k N {}, tai k! = 3 k, (k + )!! = 3 5 (k + ), (k)!! = 4 6 (k); a a(a ) (a
1 iš 15 RIBOTO NAUDOJIMO
 iš 5 PATVIRTINTA Nacionalinio egzaminų centro direktoriau 00-06-08 įakymu Nr. 6.-S- 00 m. matematiko valtybinio brando egzamino VERTINIMO INSTRUKCIJA Pagrindinė eija 8 uždavinių atakymai Užd. Nr. 5 6 7
iš 5 PATVIRTINTA Nacionalinio egzaminų centro direktoriau 00-06-08 įakymu Nr. 6.-S- 00 m. matematiko valtybinio brando egzamino VERTINIMO INSTRUKCIJA Pagrindinė eija 8 uždavinių atakymai Užd. Nr. 5 6 7
Matematinė logika. 1 skyrius Propozicinės formulės. žodį, Graikiškas žodis logos (λóγoς) reiškia
 1 skyrius Matematinė logika Graikiškas žodis logos (λóγoς) reiškia mintį, žodį, protą, sąvoką. Logika arba formalioji logika nagrinėja teisingo mąstymo dėsnius ir formas, kai samprotavimų turinys nėra
1 skyrius Matematinė logika Graikiškas žodis logos (λóγoς) reiškia mintį, žodį, protą, sąvoką. Logika arba formalioji logika nagrinėja teisingo mąstymo dėsnius ir formas, kai samprotavimų turinys nėra
04 Elektromagnetinės bangos
 04 Elektromagnetinės bangos 1 0.1. BANGINĖ ŠVIESOS PRIGIMTIS 3 Šiame skyriuje išvesime banginę lygtį iš elektromagnetinio lauko Maksvelo lygčių. Šviesa yra elektromagnetinė banga, kurios dažnis yra optiniame
04 Elektromagnetinės bangos 1 0.1. BANGINĖ ŠVIESOS PRIGIMTIS 3 Šiame skyriuje išvesime banginę lygtį iš elektromagnetinio lauko Maksvelo lygčių. Šviesa yra elektromagnetinė banga, kurios dažnis yra optiniame
Modalumo logikos S4 kai kurios išsprendžiamos klasės
 VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS INFORMATIKOS KATEDRA Magistro baigiamasis darbas Modalumo logikos S4 kai kurios išsprendžiamos klasės Some Decidable Classes of Modal Logic
VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS INFORMATIKOS KATEDRA Magistro baigiamasis darbas Modalumo logikos S4 kai kurios išsprendžiamos klasės Some Decidable Classes of Modal Logic
Answers - Worksheet A ALGEBRA PMT. 1 a = 7 b = 11 c = 1 3. e = 0.1 f = 0.3 g = 2 h = 10 i = 3 j = d = k = 3 1. = 1 or 0.5 l =
 C ALGEBRA Answers - Worksheet A a 7 b c d e 0. f 0. g h 0 i j k 6 8 or 0. l or 8 a 7 b 0 c 7 d 6 e f g 6 h 8 8 i 6 j k 6 l a 9 b c d 9 7 e 00 0 f 8 9 a b 7 7 c 6 d 9 e 6 6 f 6 8 g 9 h 0 0 i j 6 7 7 k 9
C ALGEBRA Answers - Worksheet A a 7 b c d e 0. f 0. g h 0 i j k 6 8 or 0. l or 8 a 7 b 0 c 7 d 6 e f g 6 h 8 8 i 6 j k 6 l a 9 b c d 9 7 e 00 0 f 8 9 a b 7 7 c 6 d 9 e 6 6 f 6 8 g 9 h 0 0 i j 6 7 7 k 9
Matematinės analizės egzamino klausimai MIF 1 kursas, Bioinformatika, 1 semestras,
 MIF kurss, Bioinformtik, semestrs, 29 6 Tolydžios tške ir intervle funkciju pibrėžimi Teorem Jei f C[, ], f() = A , ti egzistuoj toks c [, ], kd f(c) = 2 Konverguojnčios ir diverguojnčios eikutės
MIF kurss, Bioinformtik, semestrs, 29 6 Tolydžios tške ir intervle funkciju pibrėžimi Teorem Jei f C[, ], f() = A , ti egzistuoj toks c [, ], kd f(c) = 2 Konverguojnčios ir diverguojnčios eikutės
DISPERSINĖ, FAKTORINĖ IR REGRESINĖ ANALIZĖ Laboratorinis darbas Nr. 2
 DISPERSINĖ, FAKTORINĖ IR REGRESINĖ ANALIZĖ Laboratorinis darbas Nr. 2 Marijus Radavičius, Tomas Rekašius 2010 m. vasario 23 d. Santrauka Antras laboratorinis darbas skirtas išmokti sudarinėti daugialypės
DISPERSINĖ, FAKTORINĖ IR REGRESINĖ ANALIZĖ Laboratorinis darbas Nr. 2 Marijus Radavičius, Tomas Rekašius 2010 m. vasario 23 d. Santrauka Antras laboratorinis darbas skirtas išmokti sudarinėti daugialypės
Spherical Coordinates
 Spherical Coordinates MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Spherical Coordinates Another means of locating points in three-dimensional space is known as the spherical
Spherical Coordinates MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Spherical Coordinates Another means of locating points in three-dimensional space is known as the spherical
A := Warning, the protected names norm and trace have been redefined and unprotected
 restart; A:=linalg[matrix](2,2,[1,2,3,4]); 1 2 A := 3 4 with(linalg); Warning, the protected names norm and trace have been redefined and unprotected [BlockDiagonal, GramSchmidt, JordanBlock, LUdecomp,
restart; A:=linalg[matrix](2,2,[1,2,3,4]); 1 2 A := 3 4 with(linalg); Warning, the protected names norm and trace have been redefined and unprotected [BlockDiagonal, GramSchmidt, JordanBlock, LUdecomp,
11 klasei Pirmas skyrius MATEMATIKA. tempus. Bendrasis ir išplėstinis kursas
 11 klasei Pirmas skyrius MATEMATIKA tempus Bendrasis ir išplėstinis kursas MATEMATIKA tempus Bendrasis ir išplėstinis kursas 11 klasei Pirmas skyrius UDK 51(075.3) Ma615 Autoriai: VILIJA DABRIŠIENĖ, MILDA
11 klasei Pirmas skyrius MATEMATIKA tempus Bendrasis ir išplėstinis kursas MATEMATIKA tempus Bendrasis ir išplėstinis kursas 11 klasei Pirmas skyrius UDK 51(075.3) Ma615 Autoriai: VILIJA DABRIŠIENĖ, MILDA
> ##################### FEUILLE N3 237 ###################################### Exercice 1. plot([cos(3*t), sin(2*t), t=-pi..pi]);
![> ##################### FEUILLE N3 237 ###################################### Exercice 1. plot([cos(3*t), sin(2*t), t=-pi..pi]); > ##################### FEUILLE N3 237 ###################################### Exercice 1. plot([cos(3*t), sin(2*t), t=-pi..pi]);](/thumbs/73/69092122.jpg) ##################### FEUILLE N3 37 ###################################### Exercice. plot([cos(3*t), sin(*t), t=-pi..pi]); ###################################### Exercice. restart:plot([*t^4-*t^3,t^-t,
##################### FEUILLE N3 37 ###################################### Exercice. plot([cos(3*t), sin(*t), t=-pi..pi]); ###################################### Exercice. restart:plot([*t^4-*t^3,t^-t,
5 klasė. - užduotys apie varniuką.
 5 klasė - užduotys apie varniuką. 1. Varniukas iš plastilino lipdė raides ir iš jų sudėliojo užrašą: VARNIUKO OLIMPIADA. Vienodas raides jis lipdė iš tos pačios spalvos plastelino, o skirtingas raides
5 klasė - užduotys apie varniuką. 1. Varniukas iš plastilino lipdė raides ir iš jų sudėliojo užrašą: VARNIUKO OLIMPIADA. Vienodas raides jis lipdė iš tos pačios spalvos plastelino, o skirtingas raides
V skyrius ĮVAIRŪS PALŪKANŲ APSKAIČIAVIMO KLAUSIMAI
 V skyrius ĮVAIRŪS PALŪKANŲ APSKAIČIAVIMO KLAUSIMAI Uždirbtų palūkanų suma priklauso ne tik nuo palūkanų normos dydžio, bet ir nuo palūkanų kapitalizavimo dažnio Metinė palūkanų norma nevisada atspindi
V skyrius ĮVAIRŪS PALŪKANŲ APSKAIČIAVIMO KLAUSIMAI Uždirbtų palūkanų suma priklauso ne tik nuo palūkanų normos dydžio, bet ir nuo palūkanų kapitalizavimo dažnio Metinė palūkanų norma nevisada atspindi
Statistinė termodinamika. Boltzmann o pasiskirstymas
 Statistinė termodinamika. Boltzmann o pasiskirstymas DNR molekulių vaizdas DNR struktūros pakitimai. Keičiantis DNR molekulės formai keistųsi ir visos sistemos entropija. Mielėse esančio DNR struktūros
Statistinė termodinamika. Boltzmann o pasiskirstymas DNR molekulių vaizdas DNR struktūros pakitimai. Keičiantis DNR molekulės formai keistųsi ir visos sistemos entropija. Mielėse esančio DNR struktūros
2 laboratorinis darbas. TIKIMYBINIAI MODELIAI
 laboratorns darbas laboratorns darbas. TIKIMYBINIAI MODELIAI DARBO TIKSLAS - šstudjuot atstktnų dydžų r vektorų skrstnus, skrstno (passkrstymo) funkcją, tanko funkcją, skatnes charakterstkas r jų savybes.
laboratorns darbas laboratorns darbas. TIKIMYBINIAI MODELIAI DARBO TIKSLAS - šstudjuot atstktnų dydžų r vektorų skrstnus, skrstno (passkrstymo) funkcją, tanko funkcją, skatnes charakterstkas r jų savybes.
ŠVIESOS SKLIDIMAS IZOTROPINĖSE TERPĖSE
 ŠVIESOS SKLIDIMAS IZOTROPIĖSE TERPĖSE 43 2.7. SPIDULIUOTĖS IR KŪO SPALVOS Spinduliuotės ir kūno optiniam apibūdinimui naudojama spalvos sąvoka. Spalvos reiškinys yra nepaprastas. Kad suprasti spalvos esmę,
ŠVIESOS SKLIDIMAS IZOTROPIĖSE TERPĖSE 43 2.7. SPIDULIUOTĖS IR KŪO SPALVOS Spinduliuotės ir kūno optiniam apibūdinimui naudojama spalvos sąvoka. Spalvos reiškinys yra nepaprastas. Kad suprasti spalvos esmę,
Homework 8 Model Solution Section
 MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
KOMPIUTERINIS PROJEKTAVIMAS
 LIETUVOS ŽEMĖS ŪKIO UNIVERSITETAS Vandens ūkio ir žemėtvarkos fakultetas Statybinių konstrukcijų katedra Tatjana Sankauskienė KOMPIUTERINIS PROJEKTAVIMAS AutoCAD sistemoje Mokomoji knyga inžinerinių specialybių
LIETUVOS ŽEMĖS ŪKIO UNIVERSITETAS Vandens ūkio ir žemėtvarkos fakultetas Statybinių konstrukcijų katedra Tatjana Sankauskienė KOMPIUTERINIS PROJEKTAVIMAS AutoCAD sistemoje Mokomoji knyga inžinerinių specialybių
Algoritmai. Vytautas Kazakevičius
 Algoritmai Vytautas Kazakevičius September 2, 27 2 Turinys Baigtiniai automatai 5. DBA.................................. 5.. Abėcėlė............................ 5..2 Automatai..........................
Algoritmai Vytautas Kazakevičius September 2, 27 2 Turinys Baigtiniai automatai 5. DBA.................................. 5.. Abėcėlė............................ 5..2 Automatai..........................
eksponentinės generuojančios funkcijos 9. Grafu
 DISKREČIOJI MATEMATIKA (2 semestras) KOMBINATORIKOS IR GRAFU TEORIJOS PRADMENYS PROGRAMA I KOMBINATORIKA 1 Matematinės indukcijos ir Dirichlė principai 2 Dauginimo taisyklė,,skaičiuok dukart principas
DISKREČIOJI MATEMATIKA (2 semestras) KOMBINATORIKOS IR GRAFU TEORIJOS PRADMENYS PROGRAMA I KOMBINATORIKA 1 Matematinės indukcijos ir Dirichlė principai 2 Dauginimo taisyklė,,skaičiuok dukart principas
TRANSPORTO PRIEMONIŲ DINAMIKA
 Marijonas Bogdevičius RANSPORO PRIEMONIŲ DINAMIKA Projekto kodas VP-.-ŠMM 7-K--3 Studijų programų atnaujinimas pagal ES reikalavimus, gerinant studijų kokybę ir taikant inovatyvius studijų metodus Vilnius
Marijonas Bogdevičius RANSPORO PRIEMONIŲ DINAMIKA Projekto kodas VP-.-ŠMM 7-K--3 Studijų programų atnaujinimas pagal ES reikalavimus, gerinant studijų kokybę ir taikant inovatyvius studijų metodus Vilnius
Ekonometrija. Trendas ir sezoninė laiko eilutės komponentė
 Ekonometrija. Trendas ir sezoninė laiko eilutės komponentė dėst. T. Rekašius, 2012 m. lapkričio 19 d. 1 Duomenys Visi trečiam laboratoriniam darbui reikalingi duomenys yra tekstinio formato failuose http://fmf.vgtu.lt/~trekasius/destymas/2012/ekomet_lab3_xx.dat,
Ekonometrija. Trendas ir sezoninė laiko eilutės komponentė dėst. T. Rekašius, 2012 m. lapkričio 19 d. 1 Duomenys Visi trečiam laboratoriniam darbui reikalingi duomenys yra tekstinio formato failuose http://fmf.vgtu.lt/~trekasius/destymas/2012/ekomet_lab3_xx.dat,
Ketvirtos eilės Rungės ir Kutos metodo būsenos parametro vektoriaus {X} reikšmės užrašomos taip:
 PRIEDAI 113 A priedas. Rungės ir Kuto metodas Rungės-Kutos metodu sprendiamos diferencialinės lygtys. Norint skaitiniu būdu išspręsti diferencialinę lygtį, reikia žinoti ieškomos funkcijos ir jos išvestinės
PRIEDAI 113 A priedas. Rungės ir Kuto metodas Rungės-Kutos metodu sprendiamos diferencialinės lygtys. Norint skaitiniu būdu išspręsti diferencialinę lygtį, reikia žinoti ieškomos funkcijos ir jos išvestinės
Equations. BSU Math 275 sec 002,003 Fall 2018 (Ultman) Final Exam Notes 1. du dv. FTLI : f (B) f (A) = f dr. F dr = Green s Theorem : y da
 BSU Math 275 sec 002,003 Fall 2018 (Ultman) Final Exam Notes 1 Equations r(t) = x(t) î + y(t) ĵ + z(t) k r = r (t) t s = r = r (t) t r(u, v) = x(u, v) î + y(u, v) ĵ + z(u, v) k S = ( ( ) r r u r v = u
BSU Math 275 sec 002,003 Fall 2018 (Ultman) Final Exam Notes 1 Equations r(t) = x(t) î + y(t) ĵ + z(t) k r = r (t) t s = r = r (t) t r(u, v) = x(u, v) î + y(u, v) ĵ + z(u, v) k S = ( ( ) r r u r v = u
Atsitiktinių paklaidų įvertinimas
 4.4.4. tsitiktinių paklaidų įvertinimas tsitiktinės paklaidos įvertinamos nurodant du dydžius: pasikliaujamąjį intervalą ir pasikliaujamąją tikimybę. tsitiktinių paklaidų atveju, griežtai tariant, nėra
4.4.4. tsitiktinių paklaidų įvertinimas tsitiktinės paklaidos įvertinamos nurodant du dydžius: pasikliaujamąjį intervalą ir pasikliaujamąją tikimybę. tsitiktinių paklaidų atveju, griežtai tariant, nėra
Taikomieji optimizavimo metodai
 Taikomieji optimizavimo metodai 1 LITERATŪRA A. Apynis. Optimizavimo metodai. V., 2005 G. Dzemyda, V. Šaltenis, V. Tiešis. Optimizavimo metodai, V., 2007 V. Būda, M. Sapagovas. Skaitiniai metodai : algoritmai,
Taikomieji optimizavimo metodai 1 LITERATŪRA A. Apynis. Optimizavimo metodai. V., 2005 G. Dzemyda, V. Šaltenis, V. Tiešis. Optimizavimo metodai, V., 2007 V. Būda, M. Sapagovas. Skaitiniai metodai : algoritmai,
Review Exercises for Chapter 7
 8 Chapter 7 Integration Techniques, L Hôpital s Rule, and Improper Integrals 8. For n, I d b For n >, I n n u n, du n n d, dv (a) d b 6 b 6 (b) (c) n d 5 d b n n b n n n d, v d 6 5 5 6 d 5 5 b d 6. b 6
8 Chapter 7 Integration Techniques, L Hôpital s Rule, and Improper Integrals 8. For n, I d b For n >, I n n u n, du n n d, dv (a) d b 6 b 6 (b) (c) n d 5 d b n n b n n n d, v d 6 5 5 6 d 5 5 b d 6. b 6
TEORIJA. RINKTINIAI MATEMATIKOS SKYRIAI (Informatikos spec., 2 srautas, magistrantūra, 1 semestras) PROGRAMA. su skaidžia savybe skaičiu
 GRAFU TEORIJA RINKTINIAI MATEMATIKOS SKYRIAI (Informatikos spec, 2 srautas, magistrantūra, 1 semestras) PROGRAMA 1 Pagrindinės sa vokos, pavyzdžiai Grafu veiksmai 2 Grafo parametru sa ryšiai 3 Jungiantysis
GRAFU TEORIJA RINKTINIAI MATEMATIKOS SKYRIAI (Informatikos spec, 2 srautas, magistrantūra, 1 semestras) PROGRAMA 1 Pagrindinės sa vokos, pavyzdžiai Grafu veiksmai 2 Grafo parametru sa ryšiai 3 Jungiantysis
4.3. Minimalaus dengiančio medžio radimas
 SKYRIUS. ALGORITMAI GRAFUOSE.. Minimalaus dengiančio medžio radimas Šiame skyriuje susipažinsime su minimaliu dengiančiu medžių radimo algoritmais. Pirmiausia sudarysime dvi taisykles, leidžiančias pasirinkti
SKYRIUS. ALGORITMAI GRAFUOSE.. Minimalaus dengiančio medžio radimas Šiame skyriuje susipažinsime su minimaliu dengiančiu medžių radimo algoritmais. Pirmiausia sudarysime dvi taisykles, leidžiančias pasirinkti
TIKIMYBIU TEORIJA HAMLETAS MARK AITIS MYKOLO ROMERIO UNIVERSITETAS 2010
 TIKIMYBIU TEORIJA HAMLETAS MARK AITIS MYKOLO ROMERIO UNIVERSITETAS 2010 Tikimybiu teorija nagrin eja atsitiktinius ivykius ir tu ivykiu tikimybes ivykio pasirodymo galimyb es mat, i²reik²t skai iumi p,
TIKIMYBIU TEORIJA HAMLETAS MARK AITIS MYKOLO ROMERIO UNIVERSITETAS 2010 Tikimybiu teorija nagrin eja atsitiktinius ivykius ir tu ivykiu tikimybes ivykio pasirodymo galimyb es mat, i²reik²t skai iumi p,
43603H. (NOV1243603H01) WMP/Nov12/43603H. General Certificate of Secondary Education Higher Tier November 2012. Unit 3 10 11 H
 Centre Number Surname Candidate Number For Examiner s Use Other Names Candidate Signature Examiner s Initials General Certificate of Secondary Education Higher Tier November 2012 Pages 3 4 5 Mark Mathematics
Centre Number Surname Candidate Number For Examiner s Use Other Names Candidate Signature Examiner s Initials General Certificate of Secondary Education Higher Tier November 2012 Pages 3 4 5 Mark Mathematics
LIETUVOS ŽEMĖS ŪKIO UNIVERSITETAS Vandens ūkio ir žemėtvarkos fakultetas. Algirdas Antanavičius GEODEZIJOS PAGRINDAI
 LIETUVOS ŽEMĖS ŪKIO UNIVERSITETAS Vandens ūkio ir žemėtvarkos fakultetas Algirdas Antanavičius GEODEZIJOS PAGRINDAI metodiniai PATARIMAI kaunas, ARDIVA 2008 UDK 528(076) An-136 Algirdas Antanavičius GEODEZIJOS
LIETUVOS ŽEMĖS ŪKIO UNIVERSITETAS Vandens ūkio ir žemėtvarkos fakultetas Algirdas Antanavičius GEODEZIJOS PAGRINDAI metodiniai PATARIMAI kaunas, ARDIVA 2008 UDK 528(076) An-136 Algirdas Antanavičius GEODEZIJOS
M A T E M A T I K O S P R A K T I K U M A S S U M A T H C A D
 LIETUVOS ŽEMĖS ŪKIO UNIVERSITETAS MATEMATIKOS KATEDRA Antanas Lapinskas M A T E M A T I K O S P R A K T I K U M A S S U M A T H C A D (MOKOMOJI KNYGA) AKADEMIJA 006 UDK 0049 (0754) Sudarė: doc dr Antanas
LIETUVOS ŽEMĖS ŪKIO UNIVERSITETAS MATEMATIKOS KATEDRA Antanas Lapinskas M A T E M A T I K O S P R A K T I K U M A S S U M A T H C A D (MOKOMOJI KNYGA) AKADEMIJA 006 UDK 0049 (0754) Sudarė: doc dr Antanas
New bounds for spherical two-distance sets and equiangular lines
 New bounds for spherical two-distance sets and equiangular lines Michigan State University Oct 8-31, 016 Anhui University Definition If X = {x 1, x,, x N } S n 1 (unit sphere in R n ) and x i, x j = a
New bounds for spherical two-distance sets and equiangular lines Michigan State University Oct 8-31, 016 Anhui University Definition If X = {x 1, x,, x N } S n 1 (unit sphere in R n ) and x i, x j = a
Mock Exam 7. 1 Hong Kong Educational Publishing Company. Section A 1. Reference: HKDSE Math M Q2 (a) (1 + kx) n 1M + 1A = (1) =
 Mock Eam 7 Mock Eam 7 Section A. Reference: HKDSE Math M 0 Q (a) ( + k) n nn ( )( k) + nk ( ) + + nn ( ) k + nk + + + A nk... () nn ( ) k... () From (), k...() n Substituting () into (), nn ( ) n 76n 76n
Mock Eam 7 Mock Eam 7 Section A. Reference: HKDSE Math M 0 Q (a) ( + k) n nn ( )( k) + nk ( ) + + nn ( ) k + nk + + + A nk... () nn ( ) k... () From (), k...() n Substituting () into (), nn ( ) n 76n 76n
AUTOMATINIO VALDYMO TEORIJA
 Saulius LISAUSKAS AUTOMATINIO VALDYMO TEORIJA Projekto kodas VP1-.-ŠMM-7-K-1-47 VGTU Elektronikos fakulteto I pakopos studijų programų esminis atnaujinimas Vilnius Technika 1 VILNIAUS GEDIMINO TECHNIKOS
Saulius LISAUSKAS AUTOMATINIO VALDYMO TEORIJA Projekto kodas VP1-.-ŠMM-7-K-1-47 VGTU Elektronikos fakulteto I pakopos studijų programų esminis atnaujinimas Vilnius Technika 1 VILNIAUS GEDIMINO TECHNIKOS
Lietuvos žemės ūkio universitetas Vandens ūkio ir žemėtvarkos fakultetas. Algirdas Antanavičius. Mokomoji knyga
 Lietuvos žemės ūkio universitetas Vandens ūkio ir žemėtvarkos fakultetas Algirdas Antanavičius GEODEZIJOS PAGRINDAI Mokomoji knyga Akademija, 2007 Redaktorė: M. Židonienė turinys ĮVADAS... 1. Geodezijos
Lietuvos žemės ūkio universitetas Vandens ūkio ir žemėtvarkos fakultetas Algirdas Antanavičius GEODEZIJOS PAGRINDAI Mokomoji knyga Akademija, 2007 Redaktorė: M. Židonienė turinys ĮVADAS... 1. Geodezijos
klasës (grupës) mokinio (-ës) (vardas ir pavardë) 2013 m. pagrindinio ugdymo pasiekimų patikrinimo užduotis
 LIETUVOS RESPUBLIKOS ÐVIETIMO IR MOKSLO MINISTERIJA NACIONALINIS EGZAMINØ CENTRAS (miestas / rajonas, mokykla) klasës (grupës) mokinio (-ës) (vardas ir pavardë) 013 m. pagrindinio ugdymo pasiekimų patikrinimo
LIETUVOS RESPUBLIKOS ÐVIETIMO IR MOKSLO MINISTERIJA NACIONALINIS EGZAMINØ CENTRAS (miestas / rajonas, mokykla) klasës (grupës) mokinio (-ës) (vardas ir pavardë) 013 m. pagrindinio ugdymo pasiekimų patikrinimo
Rectangular Polar Parametric
 Hrold s AP Clculus BC Rectngulr Polr Prmetric Chet Sheet 15 Octoer 2017 Point Line Rectngulr Polr Prmetric f(x) = y (x, y) (, ) Slope-Intercept Form: y = mx + Point-Slope Form: y y 0 = m (x x 0 ) Generl
Hrold s AP Clculus BC Rectngulr Polr Prmetric Chet Sheet 15 Octoer 2017 Point Line Rectngulr Polr Prmetric f(x) = y (x, y) (, ) Slope-Intercept Form: y = mx + Point-Slope Form: y y 0 = m (x x 0 ) Generl
Arenijaus (Arrhenius) teorija
 Rūgštys ir bazės Arenijaus (Arrhenius) teorija Rūgštis: Bazė: H 2 O HCl(d) H + (aq) + Cl - (aq) H 2 O NaOH(k) Na + (aq) + OH - (aq) Tuomet neutralizacijos reakcija: Na + (aq) + OH - (aq) + H + (aq) + Cl
Rūgštys ir bazės Arenijaus (Arrhenius) teorija Rūgštis: Bazė: H 2 O HCl(d) H + (aq) + Cl - (aq) H 2 O NaOH(k) Na + (aq) + OH - (aq) Tuomet neutralizacijos reakcija: Na + (aq) + OH - (aq) + H + (aq) + Cl
8. LENKIAMŲ PLOKŠTELIŲ ELEMENTAI
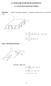 8. LENKIAMŲ PLOKŠELIŲ ELEMENAI 8.1. LENKIAMŲ PLOKŠELIŲ EORIJA Įtempimai: storį: paprastai operuojama įrąžomis įtempimų atstojamosiomis per plokštelės z τ z t τ z M t = zdz, M =...., M =.. t t = τzdz, =
8. LENKIAMŲ PLOKŠELIŲ ELEMENAI 8.1. LENKIAMŲ PLOKŠELIŲ EORIJA Įtempimai: storį: paprastai operuojama įrąžomis įtempimų atstojamosiomis per plokštelės z τ z t τ z M t = zdz, M =...., M =.. t t = τzdz, =
1. Klasifikavimo su mokytoju metodai
 1. Klasifikavimo su mokytoju metodai Klasifikacijos uždavinys yra atpažinimo uždavinys, kurio esmė pagal pateiktus objekto (vaizdo, garso, asmens, proceso) skaitinius duomenis priskirti ji kokiai nors
1. Klasifikavimo su mokytoju metodai Klasifikacijos uždavinys yra atpažinimo uždavinys, kurio esmė pagal pateiktus objekto (vaizdo, garso, asmens, proceso) skaitinius duomenis priskirti ji kokiai nors
1 Adda247 No. 1 APP for Banking & SSC Preparation Website:store.adda247.com
 Adda47 No. APP for Banking & SSC Preparation Website:store.adda47.com Email:ebooks@adda47.com S. Ans.(d) Given, x + x = 5 3x x + 5x = 3x x [(x + x ) 5] 3 (x + ) 5 = 3 0 5 = 3 5 x S. Ans.(c) (a + a ) =
Adda47 No. APP for Banking & SSC Preparation Website:store.adda47.com Email:ebooks@adda47.com S. Ans.(d) Given, x + x = 5 3x x + 5x = 3x x [(x + x ) 5] 3 (x + ) 5 = 3 0 5 = 3 5 x S. Ans.(c) (a + a ) =
2018 METŲ MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO REZULTATŲ STATISTINĖ ANALIZĖ
 N A C I O N A L I N I S E G Z A M I N Ų C E N T R A S 018 METŲ MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO REZULTATŲ STATISTINĖ ANALIZĖ 018 m. birželio 9 d. įvyko matematikos valstybinis brandos egzaminas.
N A C I O N A L I N I S E G Z A M I N Ų C E N T R A S 018 METŲ MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO REZULTATŲ STATISTINĖ ANALIZĖ 018 m. birželio 9 d. įvyko matematikos valstybinis brandos egzaminas.
