ΒΑΣΙΚΕΣ ΕΞEΙΔΙΚΕΥΣΕΙΣ ΣΕ ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΚΑΙ ΔΙΚΤΥΑ ΥΠΟΛΟΓΙΣΤΩΝ
|
|
|
- ÔΠοσειδῶν Ζάνος
- 9 χρόνια πριν
- Προβολές:
Transcript
1 Μεταπτυχιακή Εξειδίκευση στα Πληροφοριακά Συστήματα Θεματική Ενότητα ΠΛΣ-5 ΒΑΣΙΚΕΣ ΕΞEΙΔΙΚΕΥΣΕΙΣ ΣΕ ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΚΑΙ ΔΙΚΤΥΑ ΥΠΟΛΟΓΙΣΤΩΝ - ΣΗΜΕΙΩΣΕΙΣ ΔΙΔΑΣΚΑΛΙΑΣ - Δρ. Λάμπρος Μπισδούνης Σύμβουλος Καθηγητής ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 27
2 Σκοπός της θεματικής ενότητας. Ψηφιακά συστήματα Εξειδίκευση στην ανάλυση και το σχεδιασμό συνδυαστικών και ακολουθιακών ψηφιακών κυκλωμάτων, τα οποία αποτελούν τις βασικές δομικές μονάδες των ψηφιακών συστημάτων και του υλικού (hardware) των υπολογιστών. Εξειδίκευση στην αρχιτεκτονική και οργάνωση των υπολογιστών με έμφαση στη δομή και λειτουργία της κεντρικής μονάδας επεξεργασίας, του συστήματος μνήμης και της διασύνδεσης τους με περιφερειακές μονάδες. Εξειδίκευση σε βασικές έννοιες των δικτύων υπολογιστών, όπως: μοντέλα αναφοράς, δομή-λειτουργία-είδη δικτύων, δίκτυα μεταγωγής, τοπικά δίκτυα, πρωτόκολλο διαδικτύου, πρωτόκολλο μεταφοράς. Κεφάλαιο : υαδικά συστήματα κατάλληλα για την παράσταση πληροφορίας στα ψηφιακά συστήματα και δυαδικοί κώδικες. Κεφάλαιο 2: Βασικά στοιχεία άλγεβρας Boole και λογικές συναρτήσεις. Κεφάλαιο 3: Ελαχιστοποίηση λογικών συναρτήσεων με χρήση χαρτών Καρνώ (Karnaugh) και υλοποίησή τους. Κεφάλαιο 4: Μεθοδολογία ανάλυσης και σχεδιασμού συνδυαστικών κυκλωμάτων και βασικά συνδυαστικά κυκλώματα (αθροιστής, αφαιρέτης, αποκωδικοποιητές, κωδικοποιητές, πολυπλέκτες) που χρησιμοποιούνται για το σχεδιασμό ψηφιακών συστημάτων. Κεφάλαιο 5: Βασικά ακολουθιακά στοιχεία (μανδαλωτές και flip-flop), μεθοδολογία ανάλυσης και σχεδιασμού σύγχρονων ακολουθιακών ψηφιακών κυκλωμάτων. Κεφάλαιο 6: Βασικά ακολουθιακά κυκλώματα (καταχωρητές και μετρητές) που αποτελούν χρήσιμα δομικά στοιχεία για την υλοποίηση ψηφιακών συστημάτων. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 2 2. Οργάνωση και αρχιτεκτονική υπολογιστών Κεφάλαιο : Βασικές μονάδες του υπολογιστή, αρχές λειτουργίας και απόδοση του υπολογιστή, ιστορική αναδρομή. Κεφάλαιο 2: Στοιχεία αριθμητικής υπολογιστών, οργάνωση και λειτουργία της μνήμης, τρόποι διευθυνσιοδότησης, εντολές και εκτέλεση προγραμμάτων συμβολικής γλώσσας (assembly). Κεφάλαιο 3: Σύνολα εντολών επεξεργαστών ARM, Motorola, Intel. Κεφάλαιο 4: Λειτουργίες εισόδου/εξόδου, διακοπές (interrupts), DMA, δίαυλοι, κυκλώματα διασύνδεσης Ε/Ε, τυποποιημένες διασυνδέσεις (πρότυπα) Ε/Ε. Κεφάλαιο 5: Αρχές λειτουργίας μνήμης, τύποι μνημών, απόδοση μνημών, λανθάνουσα μνήμη, ιδεατή μνήμη, διαχείριση μνήμης, συσκευές δευτερεύουσας αποθήκευσης. Κεφάλαιο 6: Ανάλυση αριθμητικών λειτουργιών, λειτουργίες κινητής υποδιαστολής. Κεφάλαιο 7: Λειτουργίες κεντρικής μονάδας επεξεργασίας, προκατασκευασμένος και μικροπρογραμματιζόμενος έλεγχος. Κεφάλαιο 8: ιασωλήνωση για παράλληλη εκτέλεση εντολών, κίνδυνοι δεδομένων και εντολών, επιδράσεις της διασωλήνωσης, υπερβαθμωτοί επεξεργαστές. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 3 3. Επικοινωνίες υπολογιστών και δεδομένων Κεφάλαιο : Βασικές έννοιες επικοινωνιών, μοντέλα και πρότυπα (πρωτόκολλα) επικοινωνιών, αρχιτεκτονική και στρώματα πρωτοκόλλων επικοινωνίας. Κεφάλαιο 2: Ανάλυση λειτουργιών ελέγχου ζεύξης δεδομένων (DLC). Κεφάλαιο 3: ίκτυα μεταγωγής, μεταγωγή κυκλώματος, δρομολόγηση σε δίκτυα μεταγωγής κυκλώματος, σηματοδοσία ελέγχου. Κεφάλαιο 4: Μεταγωγή πακέτου, δρομολόγηση σε δίκτυα μεταγωγής πακέτου, αλγόριθμοι ελάχιστου κόστους. Κεφάλαιο 5: Εφαρμογές και αρχιτεκτονική τοπικών δικτύων (μοντέλο αναφοράς ΙΕΕΕ 82), τοπολογίες τοπικών δικτύων (αρτηρίας, δακτυλίου, αστέρα), ασύρματα τοπικά δίκτυα, γέφυρες διασύνδεσης τοπικών δικτύων. Κεφάλαιο 6: Συστήματα τοπικών δικτύων, Ethernet/IEEE 82.3 (CSMA/CD), Gigabit Ethernet, τοπικά δίκτυα δακτυλίου με κουπόνι (IEEE 82.5, FDDI), τοπικά δίκτυα ATM και διαύλου οπτικής ίνας (FC), IEEE 82.. Κεφάλαιο 7: Βασικές αρχές και αρχιτεκτονικές διαδικτύωσης, πρωτόκολλο διαδικτύου (IP), IPv6, πολλαπλή αποστολή ΙP (multicasting). Κεφάλαιο 8: Πρωτόκολλα μεταφοράς, υπηρεσίες και μηχανισμοί υλοποίησης, TCP, έλεγχος συμφόρησης, UDP. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 4
3 Κεφάλαιο : υαδικά συστήματα και κώδικες Μεταπτυχιακή Εξειδίκευση στα Πληροφοριακά Συστήματα Θ.Ε. ΠΛΣ-5: ΒΑΣΙΚΕΣ ΕΞΙ ΕΙΚΕΥΣΕΙΣ ΣΕ ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΚΑΙ ΙΚΤΥΑ ΥΠΟΛΟΓΙΣΤΩΝ ΣΗΜΕΙΩΣΕΙΣ Ι ΑΣΚΑΛΙΑΣ - ΨΗΦΙΑΚΑ ΣΥΣΤΗΜΑΤΑ - Ψηφιακά συστήματα υαδικοί αριθμοί Μετατροπή αριθμών σε μορφές με άλλη βάση Οκταδικοί και δεκαεξαδικοί αριθμοί Συμπληρώματα αριθμών υαδικοί αριθμοί με πρόσημο και βασικές αριθμητικές πράξεις υαδικοί κώδικες ρ. Λάμπρος Μπισδούνης υαδική λογική και εισαγωγή στις λογικές πύλες Σύμβουλος Καθηγητής ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 5 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 6 Ψηφιακά συστήματα Έχουν σημαντικό ρόλο σε πολλούς τομείς της καθημερινής ζωής (εμπόριο, βιομηχανία, επιστήμη, επικοινωνία, διασκέδαση κλπ.). Χειρίζονται διακριτά στοιχεία πληροφορίας. Οι πρώτοι υπολογιστές χρησιμοποιήθηκαν για αριθμητικούς υπολογισμούς, όπου τα διακριτά στοιχεία πληροφορίας ήταν τα αριθμητικά ψηφία, οπότε προέκυψε και ο όρος ψηφιακός υπολογιστής. Αποτελούνται κυρίως από διασυνδεδεμένα τρανζίστορ. υαδικά αφού χρησιμοποιούν δύο διακριτές τιμές και ένα δυαδικό στοιχείο (bit) μπορεί να λάβει δύο τιμές ( και ). Τα διακριτά στοιχεία πληροφορίας παριστάνονται από ομάδες bit (κώδικες). Πλεονεκτούν επειδή είναι προγραμματιζόμενα, παρουσιάζουν συνεχώς μείωση κόστους, μεγέθους και μπορούν να εκτελέσουν πολύπλοκες λειτουργίες. υαδικοί αριθμοί εκαδικό σύστημα βάση, δέκα ψηφία και οι αριθμητικοί συντελεστές πολλαπλασιάζονται με δυνάμεις του : υαδικό σύστημα βάση 2, δύο ψηφία και οι αριθμητικοί συντελεστές πολλαπλασιάζονται με δυνάμεις του 2: Σύστημα με βάση το r( a i r-): Οι διακριτές ποσότητες που αντιστοιχούν σε διακριτά στοιχεία πληροφορίας προκύπτουν συνήθως από κβαντισμό μιας συνεχούς φυσικής διαδικασίας (μετατροπή αναλογικών πληροφοριών σε ψηφιακές). Σήμερα υπάρχει έντονη τάση χρήσης γλωσσών περιγραφής υλικού (HDL). ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 7 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 8
4 Αριθμοί συστημάτων με διάφορες βάσεις Στην περίπτωση που η βάση είναι μεγαλύτερη του χρησιμοποιούμε τα πρώτα ψηφία του δεκαδικού συστήματος και λατινικά γράμματα γιαταυπόλοιπαψηφία. Αριθμητικές πράξεις στο δυαδικό σύστημα Στις αριθμητικές πράξεις αριθμών με βάση r διαφορετική από το, ισχύουν οι ίδιοι κανόνες με αυτούς των πράξεων των δεκαδικών αριθμών. Πρέπει όμως να προσέχουμε ώστε να χρησιμοποιούμε μόνο τα r επιτρεπτά ψηφία. Κατά την πρόσθεση, εάν προκύπτει κρατούμενο σε κάποια θέση, τότε αυτό προστίθεται στο ψηφίο της αμέσως πιο σημαντικής θέσης. Κατά την αφαίρεση στο δυαδικό σύστημα, το δανεισμένο ψηφίο σε μία θέση προσθέτει 2 στο ψηφίο του μειωτέου (ενώ στο δεκαδικό σύστημα προστίθεται δηλ. ηβάσητουσυστήματος). Για αναπαράσταση δεκαδικών αριθμών μεγαλύτερων του 5, στα υπόλοιπα συστήματα απαιτούνται περισσότερα ψηφία. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 9 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ Αριθμητικές πράξεις στο δυαδικό σύστημα Μετατροπή αριθμού βάσης r σε δεκαδικό αριθμό Απευθείας πρόσθεση περισσότερων από δύο δυαδικών προσθετέων: Πολλαπλασιάζουμε κάθε συντελεστή με την αντίστοιχη δύναμη του r και προσθέτουμε τα γινόμενα που προκύπτουν. Όπως ο πολλαπλασιασμός ανάγεται σε διαδοχικές προσθέσεις, η διαίρεση ανάγεται σε διαδοχικές αφαιρέσεις: Μετατροπή δυαδικού αριθμού σε δεκαδικό: επειδή όταν ένα ψηφίο (bit) του δυαδικού αριθμού είναι ίσο με, δεν αυξάνει το άθροισμα κατά τη διάρκεια της μετατροπής, η μετατροπή δυαδικού αριθμού σε δεκαδικό προκύπτει εάν προσθέσουμε τις δυνάμεις του 2 που αντιστοιχούν στα μη μηδενικά ψηφία. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 2
5 Μετατροπή δεκαδικού αριθμού σε αριθμό βάσης r Εάν ο αριθμός περιέχει υποδιαστολή, είναι αναγκαίο να χωριστεί σε ακέραιο και κλασματικό μέρος, καθώς το καθένα από τα μέρη αυτά θα υποστεί διαφορετική διαδικασία μετατροπής. Η μετατροπή του ακεραίου μέρους του δεκαδικού αριθμού σε αριθμό βάσης r, γίνεται με διαίρεση του αριθμού και όλων των διαδοχικών ακεραίων πηλίκων με τη βάση r και αντίστροφη παράθεση των αντίστοιχων ακεραίων υπολοίπων. Μετατροπή δεκαδικού αριθμού σε αριθμό βάσης r Η μετατροπή του κλασματικού μέρους του δεκαδικού αριθμού σε αριθμό βάσης r γίνεται ως εξής: Αρχικά πολλαπλασιάζουμε το κλασματικό μέρος του δεκαδικού αριθμού με τη βάση r. Εκφράζουμε το αποτέλεσμα του πολλαπλασιασμού ως άθροισμα ενός ακεραίου κι ενός κλασματικού μέρους. Το νέο κλασματικό μέρος πολλαπλασιάζεται με τη βάση r και δίνει ένα νέο ακέραιο και ένα νέο κλασματικό μέρος. Η διαδικασία επαναλαμβάνεται μέχρι το κλασματικό μέρος να γίνει μηδέν ή μέχρι να επιτευχθεί ικανοποιητική ακρίβεια. Οι συντελεστές του δυαδικού αριθμού προκύπτουν με ορθή παράθεση των ακεραίων μερών των γινομένων. Η μετατροπή αριθμών μεταξύ μη δεκαδικών συστημάτων μπορεί να επιτευχθεί εύκολα με τη χρησιμοποίηση του δεκαδικού συστήματος σαν ενδιάμεσο στάδιο. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 3 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 4 Οκταδικοί και δεκαεξαδικοί αριθμοί Η χρήση οκταδικών ή δεκαεξαδικών αριθμών παρέχει εύκολη μετατροπή και συμπίεση των δυαδικών αριθμών που χρησιμοποιούν οι ψηφιακοί υπολογιστές. Κατά τη μετατροπή οκταδικού και δεκαεξαδικού αριθμού σε δυαδικό και αντίστροφα θα πρέπει να λαμβάνεται υπόψη ότι κάθε οκταδικό ή δεκαεξαδικό ψηφίο αντιστοιχεί σε 3 ή 4 δυαδικά ψηφία, αντίστοιχα. Ο χωρισμός του δυαδικού αριθμού σε τριάδες ή τετράδες ψηφίων γίνεται ξεκινώντας από την υποδιαστολή και προχωρώντας προς τα αριστερά και προς τα δεξιά. Μετατροπή βάσης αριθμών: ανακεφαλαίωση Μετατροπή από αριθμητικό σύστημα βάσης r στο δεκαδικό σύστημα: Πολλαπλασιάζουμε τους συντελεστές με τις αντίστοιχες δυνάμεις του r και προσθέτουμε τα γινόμενα. Μετατροπή από δεκαδικό σύστημα σε σύστημα βάσης r: ιακρίνουμε ακέραιο και κλασματικό μέρος. ιαιρούμε το ακέραιο μέρος συνεχώς με τη βάση r και κρατάμε τα υπόλοιπα (με αντίστροφη παράθεση). Πολλαπλασιάζουμε το κλασματικό μέρος συνεχώς με τη βάση r και κρατάμε τα ακέραια μέρη (με ορθή παράθεση). Μετατροπή από οκταδικό ή δεκαεξαδικό σε δυαδικό σύστημα: Αντικαθιστούμε κάθε ψηφίο με τον αντίστοιχο τριψήφιο ή τετραψήφιο δυαδικό αριθμό. Μετατροπή από δυαδικό σε οκταδικό ή δεκαεξαδικό σύστημα: Ομαδοποιούμε τα δυαδικά ψηφία σε τριάδες ή τετράδες και τις αντικαθιστούμε με το αντίστοιχο ψηφίο του οκταδικού ή δεκαεξαδικού συστήματος ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 5 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 6
6 Συμπληρώματα αριθμών Τα συμπληρώματα χρησιμοποιούνται για την απλοποίηση της αφαίρεσης. Χρησιμοποιούνται δύο τύποι συμπληρώματος: Συμπλήρωμα ως προς τη μειωμένη κατά βάση του αριθμητικού συστήματος. Συμπλήρωμα ως προς τη βάση του αριθμητικού συστήματος. Συμπλήρωμα ως προς τη βάση μειωμένη κατά αριθμού Ν με n ψηφία και βάση συστήματος r: (r n ) N. Στο δεκαδικό σύστημα το συμπλήρωμα ως προς 9 του 5467 ισούται με: = (άρα κάθε ψηφίο του συμπληρώματος προκύπτει με την αφαίρεση κάθε ψηφίου του αρχικού αριθμού από το 9). Στο δυαδικό σύστημα (r=2, r-=) το 2 n παριστάνεται από ένα δυαδικό αριθμό, οοποίοςαποτελείταιαπότοψηφίο ακολουθούμενο από n μηδενικά και το συμπλήρωμα ως προς ενός δυαδικού αριθμού προκύπτει εάν αφαιρέσουμε το κάθεψηφίοτουαπότο. Για n=4, 2 4 = () 2,2 4 = () 2 : Συμπλήρωμα ως προς του = Για n=7: Συμπλήρωμα ως προς του = Συμπληρώματα αριθμών Συμπλήρωμα ως προς τη βάση αριθμού Ν με n ψηφία και βάση συστήματος r: (r n N), οπότε το συμπλήρωμα ως προς τη βάση προκύπτει εάν προσθέσουμε στοσυμπλήρωμαωςπροςτηβάσημειωμένηκατά. εκαδικό σύστημα: το συμπλήρωμα ως προς του 5467 ισούται με: = 4533 (άρα κάθε ψηφίο του συμπληρώματος προκύπτει με την αφαίρεση του πρώτου από δεξιά μη μηδενικού ψηφίου από το και των υπολοίπων ψηφίων από το 9). Στο δυαδικό σύστημα το συμπλήρωμα ως προς 2 προκύπτει εάν αφήσουμε τα συνεχόμενα λιγότερο σημαντικά και το πρώτο αναλλοίωτα και αλλάξουμε στη συνέχεια τα με και τα με σταυπόλοιπαπιοσημαντικάψηφία. Συμπλήρωμα ως προς 2 του = Συμπλήρωμα ως προς 2 του = Εάν ο αρχικός αριθμός περιέχει υποδιαστολή, αυτή θα πρέπει να αφαιρεθεί προσωρινά, να υπολογιστεί το συμπλήρωμα και να επαναφερθεί στη συνέχεια στην αρχική της θέση. Επίσης, το συμπλήρωμα του συμπληρώματος μας δίνει τον αρχικό αριθμό. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 7 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 8 Συμπληρώματα αριθμών: ανακεφαλαίωση Συμπλήρωμα ως προς τη βάση μειωμένη κατά (r ): Συμπλήρωμα ως προς τη βάση r: Αφαιρούμε κάθε ψηφίο από το r Υπολογίζουμε το συμπλήρωμα ως προς r και προσθέτουμε ή Αφαιρούμε το πρώτο μη μηδενικό λιγότερο σημαντικό ψηφίο από το r και όλα τα υπόλοιπα περισσότερο σημαντικά ψηφία από το r Αφαίρεση με χρήση συμπληρώματος Κατά τη διενέργεια αφαίρεσης χρησιμοποιούμε την έννοια του δανεικού ψηφίου όταν το ψηφίο του μειωτέου είναι μικρότερο από το ψηφίο του αφαιρετέου, ενώ στα ψηφιακά συστήματα χρησιμοποιούνται τα συμπληρώματα αριθμών. Αφαίρεση δύο αριθμών (Μ Ν) με βάση r και n ψηφία: Προσθέτουμε στο μειωτέο Μ το συμπλήρωμα ως προς r του αφαιρετέου, οπότε: M + (r n N) = M N + r n. Εάν Μ Ν, το άθροισμα θα έχει τελικό κρατούμενο r n το οποίο αγνοούμε και ο υπόλοιπος αριθμός είναι το αποτέλεσμα (Μ Ν). Εάν Μ < Ν, το άθροισμα δεν έχει τελικό κρατούμενο και είναι ίσο με r n (N M) δηλαδή ισούται με το συμπλήρωμα ως προς r του (Ν Μ). Για να λάβουμε το επιθυμητό αποτέλεσμα (Μ Ν), υπολογίζουμε το συμπλήρωμα ως προς r του αθροίσματος (δηλαδή το (Ν Μ)) και του θέτουμε αρνητικό πρόσημο. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 9 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 2
7 Αφαίρεση με χρήση συμπληρώματος 78 = 23 = Συμπλήρωμα ως προς 2 του 23 = = 23 = Συμπλήρωμα ως προς 2 του 78 = ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 2 υαδικοί αριθμοί με πρόσημο Στα ψηφιακά συστήματα όλες οι αριθμητικές πληροφορίες παριστάνονται με δυαδικούς αριθμούς, οπότε και για το πρόσημο των αριθμών μπορεί να χρησιμοποιηθεί ένα ψηφίο (bit) στην τελευταία αριστερά θέση του αριθμού. Η επικρατούσα σύμβαση είναι να θεωρούμε το ψηφίο προσήμου για τους θετικούς και για τους αρνητικούς αριθμούς. Η παράσταση των αριθμών με πρόσημο ονομάζεται παράσταση προσημασμένου μεγέθους (signed-magnitude). Στα ψηφιακά συστήματα είναι πιο βολικό να χρησιμοποιούμε για παράσταση αρνητικών αριθμών το προσημασμένο συμπλήρωμα (signed complement), όπου ένας αρνητικός αριθμός συμβολίζεται με το συμπλήρωμά του. Στην παράσταση οκτώ ψηφίων προσημασμένου μεγέθους, ο δυαδικός αριθμός παριστάνει τον αριθμό 9. Η παράσταση οκτώ ψηφίων προσημασμένου συμπληρώματος ως προς 2 του αριθμού 9 προκύπτει από το συμπλήρωμα ως προς 2 του θετικού αριθμού, συμπεριλαμβανομένου και του ψηφίου (bit) προσήμου (). Με παρόμοιο τρόπο μπορεί να χρησιμοποιηθεί και το συμπλήρωμα ως προς. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 22 υαδικοί αριθμοί με πρόσημο ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 23 Πρόσθεση και αφαίρεση αριθμών με πρόσημο Κατά την αριθμητική πρόσθεση στο σύστημα προσημασμένου μεγέθους απαιτείται σύγκριση προσήμων και μετά πρόσθεση ή αφαίρεση. Εάν τα πρόσημα είναι ίδια, προσθέτουμε τα μεγέθη των αριθμών και θέτουμε στοαποτέλεσματοκοινόπρόσημο. Εάν τα πρόσημα είναι διαφορετικά αφαιρούμεαπότομεγαλύτερομέγεθοςτο μικρότερο με τελικό πρόσημο αυτό του μεγαλυτέρου μεγέθους. Κατά την πρόσθεση στο σύστημα που χρησιμοποιεί προσημασμένο συμπλήρωμα ως προς 2, προσθέτουμε τους δύο αριθμούς, συμπεριλαμβανομένων και των προσήμων και αγνοούμε το κρατούμενο εξόδου. Αφού οι τυχόν αρνητικοί αριθμοί που συμμετέχουν στην πρόσθεση βρίσκονται σε μορφή συμπληρώματος ως προς 2, αν το άθροισμα που προκύπτει είναι αρνητικό, τότε αυτό είναι επίσης σε μορφή συμπληρώματος ως προς 2. Κατά την αφαίρεση στο σύστημα προσημασμένου συμπληρώματος ως προς 2, προσθέτουμε στο μειωτέο το συμπλήρωμα ως προς 2 του αφαιρετέου και αγνοούμε το κρατούμενο. συμπλήρωμα ως προς 2 (-6) - (-3) = = + = = +7 αγνοούμε το κρατούμενο ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 24
8 υαδικοί κώδικες Τα ψηφιακά συστήματα χειρίζονται δυαδικούς αριθμούς, αλλά και διακριτά στοιχεία πληροφορίας που μπορούν να αναπαρασταθούν με δυαδικούς κώδικες. Σε κάθε δυαδικό κώδικα κάθε στοιχείο πρέπει να αντιστοιχεί σε ένα μοναδικό συνδυασμό δυαδικών ψηφίων. Οι συνδυασμοί των ψηφίων (δηλ. τα στοιχεία) που μπορούν να χρησιμοποιηθούν σε έναν κώδικα n ψηφίων είναι από έως 2 n. Κώδικες αναπαράστασης δεκαδικών αριθμών με δυαδικά ψηφία υαδικοί κώδικες Η δυαδική παράσταση 9 ψηφίων του δεκαδικού 395 είναι, ενώ η δυαδική κωδικοποίηση BCD (2 bits) του ιδίου αριθμού είναι. Επομένως, η δυαδική κωδικοποίηση διαφέρει από την παράσταση ενός αριθμού στο δυαδικό σύστημα. Απαιτεί πιο πολλά ψηφία, αλλά πλεονεκτεί στο γεγονός ότι τα δεδομένα παράγονται από ανθρώπους που χρησιμοποιούν το δεκαδικό σύστημα. Ο κώδικας BCD (binary coded decimal) μας δίνει δυαδικά κωδικοποιημένους δεκαδικούς αριθμούς. Οι αριθμητικές πράξεις πρόσθεσης και αφαίρεσης διενεργούνται όπως στους δεκαδικούς αριθμούς ξεκινώντας από τα στοιχεία της λιγότερο σημαντικής θέσης και μεταφέροντας τυχόν κρατούμενο στην αμέσως επόμενη θέση. Ο κώδικας BCD χρησιμοποιεί βάρη 8, 4, 2,, ενώ οι κώδικες 242 και χρησιμοποιούν τα βάρη που δηλώνονται στην ονομασία τους. Κάθε στοιχείο του κώδικα excess-3 προκύπτει από την αντίστοιχη δυαδική τιμή συν 3. Οι κώδικες 242 και excess-3 είναι αυτοσυμπληρωματικοί (δηλ. το συμπλήρωμα ως προς 9 του αντίστοιχου δεκαδικού αριθμού προκύπτει εάν αλλάξουμε τα σε και τα σε ). Στον excess-3, το 395 παριστάνεται ως, ενώ το συμπλήρωμά του ως προς 9 που είναι το 64 παριστάνεται ως. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 25 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 26 Κώδικας Gray Κώδικας χαρακτήρων ASCII Το πλεονέκτημα το κώδικα Gray είναι υπάρχει διαφορά μόνο ενός ψηφίου (bit) μεταξύ δύο γειτονικών αριθμών. Χρησιμοποιείται σε εφαρμογές όπου η κανονική ακολουθία δυαδικών αριθμών μπορεί να παράγει λάθος ή ασαφές αποτέλεσμα κατά τη μετάβαση από έναν αριθμό στον επόμενο. Για παράδειγμα εάν χρησιμοποιηθούν δυαδικοί αριθμοί, μια αλλαγή από το στο μπορεί να προκαλέσει μια λανθασμένη ενδιάμεση τιμή, εάν το τελευταίο δεξιά ψηφίο αλλάξει πιο αργά από τα υπόλοιπα. Τέτοιες εφαρμογές σχετίζονται με την παράσταση ψηφιακών δεδομένων που προκύπτουν από μετατροπή αναλογικών δεδομένων που αποτελούν «συνεχείς» πληροφορίες. Πρότυπος κώδικας αλφαριθμητικών χαρακτήρων για κωδικοποίηση πληροφοριών κειμένου (American standard code for information interchange, ASCII). Χρησιμοποιεί 7 ψηφία (bit) για την κωδικοποίηση 28 χαρακτήρων: δεκαδικών ψηφίων, 26 μικρών και 26 κεφαλαίων γραμμάτων του λατινικού αλφάβητου, 32 ειδικούς χαρακτήρες (π.χ. &,*,+) και 34 (μη εκτυπώσιμων) χαρακτήρων ελέγχου. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 27 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 28
9 Κώδικας χαρακτήρων ASCII Οι μη εκτυπώσιμοι χαρακτήρες ελέγχου επηρεάζουν τη μορφοποίηση του κειμένου (π.χ. BS, HT), διαχωρίζουν την πληροφορία (π.χ. FS) και ελέγχουν την επικοινωνία όταν πρόκειται για μετάδοση κειμένου (π.χ. STX, ETX). ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 29 Κώδικες ανίχνευσης λαθών Για να ανιχνεύσουμε τυχόν λάθη κατά τη μετάδοση δεδομένων, προσθέτουμε ένα 8 ο ψηφίο στους χαρακτήρες ASCII για να υποδηλώσουμε την ισοτιμία (parity) των χαρακτήρων. Το ψηφίο ισοτιμίας περιλαμβάνεται στο σήμα μετάδοσης (στην περισσότερο σημαντική θέση) έτσι ώστε ο αριθμός των να γίνει άρτιος ή περιττός. Τις περισσότερες φορές χρησιμοποιείται η άρτια ισοτιμία (δηλ. περιλαμβάνεται ψηφίο ισοτιμίας έτσι ώστε να προκύπτει άρτιος αριθμός των του χαρακτήρα). Μετά την εισαγωγή του ψηφίου άρτιας ισοτιμίας σε κάθε χαρακτήρα που μεταδίδεται από τον πομπό, οι χαρακτήρες μεταδίδονται και η ισοτιμία κάθε χαρακτήρα ελέγχεται στο δέκτη. Εάν η ισοτιμία του λαμβανόμενου χαρακτήρα δεν είναι άρτια, αυτό σημαίνει ότι τουλάχιστον ένα ψηφίο έχει αλλάξει τιμή κατά τη μετάδοση. Στην περίπτωση όμως που έχουμε άρτιο αριθμό λαθών, δεν μπορούμε με αυτή τη διαδικασία να εξασφαλίσουμε ότι τα λάθη αυτά θα ανιχνευτούν, οπότε απαιτούνται πρόσθετοι κώδικες ανίχνευσης λαθών. Αν ο δέκτης ανιχνεύσει λάθος απαντά με χαρακτήρα ελέγχου NAK ώστε να γίνει αναμετάδοση του χαρακτήρα, ενώ στην περίπτωση που ο δέκτης δεν ανιχνεύσει λάθος απαντά με χαρακτήρα ελέγχου ACK. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 3 υαδική λογική Η δυαδική λογική εξετάζει μεταβλητές που μπορούν να λάβουν δύο διακριτές τιμές (δυαδικές) καθώς και τις λογικές πράξεις των μεταβλητών αυτών. Βασικές λογικές πράξεις: Λογικές πύλες Οι λογικές πύλες αντιστοιχούν σε ηλεκτρονικά κυκλώματα τα οποία δέχονται με σήματα εισόδου και παράγουν ένα σήμα εξόδου. Τα σήματα ισοδυναμούν με λογικό ή. Υπάρχει η δυνατότητα σχεδιασμού και χρησιμοποίησης πυλών πολλαπλών εισόδων. Σχηματικά σύμβολα: Πίνακας αληθείας είναι μια συμπαγής μορφή ορισμού των λογικών πράξεων και περιλαμβάνει όλους τους δυνατούς συνδυασμούς των μεταβλητών και τις τιμές που μπορεί να λάβει το αποτέλεσμα μιας λογικής πράξης για κάθε συνδυασμό. Η δυαδική λογική δεν πρέπει να συγχέεται με τη δυαδική αριθμητική. Για παράδειγμα η λογική πράξη (x + y) διαφέρει από την αντίστοιχη αριθμητική, αφού για παράδειγμα + = (αριθμητική) και + = (λογική). ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 3 ιαγράμματα χρονισμού: δείχνουν την απόκριση των πυλών στους συνδυασμούς σημάτων εισόδου. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 32
10 Κεφάλαιο 2: Άλγεβρα Boole και λογικές συναρτήσεις Ορισμός, αξιώματα, βασικά θεωρήματα και ιδιότητες της άλγεβρας Boole Συναρτήσεις Boole (λογικές συναρτήσεις) Κανονικές μορφές (ελαχιστόροι, μεγιστόροι) και πρότυπες μορφές λογικών συναρτήσεων Λογικές συναρτήσεις δύο μεταβλητών (λογικές πράξεις) Ψηφιακές λογικές πύλες Σχεδιασμός κυκλωμάτων με τη βοήθεια υπολογιστή Βασικοί ορισμοί George Boole, 854: αλγεβρικό σύστημα (άλγεβρα Boole) για συστηματική αντιμετώπιση προβλημάτων λογικής. Edward Huntington, 94: διατύπωση αξιωμάτων άλγεβρας Boole. Claude Elwood Shannon, 938: άλγεβρα Boole δύο τιμών (άλγεβρα διακοπτών) για ανάλυση των ιδιοτήτων των δισταθών ηλεκτρικών κυκλωμάτων διακοπτών. ΗάλγεβραBoole όπως κάθε επαγωγικό μαθηματικό σύστημα ορίζεται από ένα σύνολο στοιχείων, τελεστών και αξιωμάτων. υαδικός τελεστής (binary operator): σε κάθε ζεύγος στοιχείων από ένα σύνολο S αντιστοιχίζει ένα μοναδικό στοιχείο που επίσης ανήκει στο σύνολο S. Παράδειγμα: θεωρώντας τη σχέση (a b = c), το είναι δυαδικός τελεστής εάν καθορίζει έναν κανόνα για να υπολογίζουμε το c απότοζεύγος(a, b) και εφόσον (a, b, c) S. Εάν τα (a, b) S, αλλά ο κανόνας που καθορίζει ο τελεστής καταλήγει σε c S, τότε το δεν είναι δυαδικός τελεστής. ΗάλγεβραBoole είναι μια αλγεβρική δομή που ορίζεται από ένα σύνολο στοιχείων (έστω B) με δύο δυαδικούς συντελεστές + και εφόσον τηρείται μια σειρά αξιωμάτων (αξιώματα του Huntington). ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 33 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 34 Αξιώματα της άλγεβρας Boole Κλειστότητα σε σχέση με τους τελεστές + και (παράδειγμα: το σύνολο των φυσικών αριθμών είναι κλειστό στον τελεστή + αφού για κάθε ζεύγος φυσικών αριθμών προκύπτει μετά από πρόσθεση μοναδικό αποτέλεσμα που ανήκει πάντα στοσύνολοτωνφυσικώναριθμών, ενώ δεν είναι κλειστό στον τελεστή αφού για παράδειγμα 2 3 = που δεν ανήκει στο σύνολο των φυσικών αριθμών. Το είναι ουδέτερο στοιχείο ως προς τον τελεστή +: x + = +x = x. Άλγεβρα Boole δύο τιμών Σύνολο στοιχείων: Β = {, }. υαδικοί τελεστές: + (λογική πράξη Η), (λογική πράξη ΚΑΙ) και τελεστής συμπληρώματος (λογική πράξη ΟΧΙ). x y x + y x y x x Το είναι ουδέτερο στοιχείο ως προς τον τελεστή : x = x = x. Αντιμεταθετική ιδιότητα για πράξεις + και : x + y = y + x και x y = y x. Ηπράξη είναι επιμεριστική ως προς την πράξη + και αντιστρόφως: x (y + z) = (x y) + (x z) και x + (y z) = (x + y) (x + z). Για κάθε στοιχείο x Β υπάρχει στοιχείο x Β που ονομάζεται συμπλήρωμα του x τέτοιο ώστε x + x = και x x =. Υπάρχουν τουλάχιστον δύο στοιχεία (x, y) Β τέτοιαώστεx y(στη άλγεβρα Boole δύο τιμών, το σύνολο περιλαμβάνει μόνο δύο στοιχεία). εν περιλαμβάνεται η προσεταιριστική ιδιότητα της κοινής άλγεβρας, ωστόσο ισχύει και αποδεικνύεται από τα υπόλοιπα αξιώματα. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 35 Ισχύουν όλα τα αξιώματα του Huntington. Αρχή δυϊσμού: κάθε αλγεβρική έκφραση που μπορεί να εξαχθεί από τα αξιώματα εξακολουθεί να ισχύει (παραμένει αληθής) εάν εναλλάξουμε τους τελεστές και τα ουδέτερα στοιχεία (, ). Για να παράγουμε τη δυϊκή μορφή μιας αλγεβρικής έκφρασης, αρκεί απλά να εναλλάξουμε τους τελεστές Η και ΚΑΙ και να αντικαταστήσουμε τα με και τα με. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 36
11 Άλγεβρα Boole δύο τιμών Βασικά θεωρήματα Η κλειστότητα είναι προφανές ότι ισχύει. Τα ουδέτερα στοιχεία είναι για τον τελεστή + και για τον τελεστή : +=, +=+=, =, = =. Η αντιμεταθετική ιδιότητα είναι προφανής από τους πίνακες αληθείας που ορίζουν τους δύο τελεστές. Η ισχύς της επιμεριστικής ιδιότητας φαίνεται από τον παραπάνω πίνακα. Από τον πίνακα συμπληρώματος: x + x = ( + = + =, + = + = ) και x x = ( = =, = = ). Η άλγεβρα έχει τουλάχιστον δύο διαφορετικά στοιχεία αφού. Τα θεωρήματα αποδεικνύονται με χρήση των αξιωμάτων και των θεωρημάτων που έχουν ήδη αποδειχθεί, καθώς και με τη βοήθεια των πινάκων αληθείας. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 37 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 38 Προτεραιότητα τελεστών. Παρένθεση 2. ΟΧΙ 3. ΚΑΙ 4. Η Παραδείγματα (x + y) Υπολογίζουμε το x + y Υπολογίζουμε το συμπλήρωμα του αποτελέσματος x y Υπολογίζουμε τα συμπληρώματα των x και y Υπολογίζουμε το ΚΑΙ των συμπληρωμάτων Λογικές συναρτήσεις Μια λογική συνάρτηση (ή συνάρτηση Boole) εκφράζει μέσω μιας αλγεβρικής έκφρασης τη λογική σχέση μεταξύ δυαδικών μεταβλητών και αποτελείται από δυαδικές μεταβλητές, τις σταθερές τιμές και καιτασύμβολατατριών λογικών πράξεων. Για μια δεδομένη τιμή των δυαδικών μεταβλητών, η συνάρτηση μπορεί να είναι ίση με ή. Οπότε, οι πιθανές τιμές της συνάρτησης προκύπτουν από τον προσδιορισμό της δυαδικής τιμής της αλγεβρικής έκφρασης για όλους τους συνδυασμούς των εμπλεκομένων μεταβλητών. Μια λογική συνάρτηση μπορεί να περιγραφεί μέσω πίνακα αληθείας που περιλαμβάνει στο αριστερό μέρος όλους τους δυνατούς συνδυασμούς των δυαδικών μεταβλητών (2 n για η μεταβλητές) και στο δεξί μέρος μια στήλη που περιέχει την τιμή της συνάρτησης για καθένα από τους συνδυασμούς του αριστερού μέρους. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 39 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 4
12 Λογικές συναρτήσεις Υλοποίηση λογικών συναρτήσεων Κάθε όρος (γινόμενο ή άθροισμα) απαιτεί μια πύλη και κάθε μεταβλητή του όρου (συμπληρωμένη ή μη) ονομάζεται παράγοντας και υποδηλώνει μια είσοδο πύλης. Αφού οι F 3 και F 4 είναι ισότιμες και το κύκλωμα υλοποίησης της F 4 είναι μικρότερο, συμφέρει να εντοπίζουμε απλούστερες εκφράσεις με χρήση αλγεβρικών μετασχηματισμών. Παρατηρούμε ότι η F 3 λαμβάνει τις ίδιες τιμές με την F 4, γεγονός που υποδεικνύει ότι υπάρχουν πολλές αλγεβρικές εκφράσεις για μια λογική συνάρτηση. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 4 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 42 Απλοποίηση με αλγεβρικούς μετασχηματισμούς x (x + y) = x x + x y = + x y = x y x + x y = (x + x ) (x + y) = (x + y) = x + y (x + y) (x + y ) = x + x y + x y + y y = x ( + y + y ) = x Συμπλήρωμα λογικής συνάρτησης Το συμπλήρωμα μιας συνάρτησης F συμβολίζεται ως F και είναι η συνάρτηση που ισούται με όταν F= και με όταν F=. Το συμπλήρωμα μιας λογικής συνάρτησης προκύπτει με εφαρμογή των θεωρημάτων DeMorgan που μπορούν να επεκταθούν για περισσότερες από δύο μεταβλητές: (x + y) (x + y ) = x + y y = x + = x x y + x z + y z = x y + x z + y z (x + x ) = x y + x z + x y z + x y z = x y ( + z) + x z ( + y) = x y + x z Γενικά, χρησιμοποιούμε τα αξιώματα και τα αποδεδειγμένα θεωρήματα της άλγεβρας Boole δύο τιμών. Μερικές φορές, κατάλληλη αύξηση στον αριθμό των παραγόντων μπορεί να οδηγήσει σε απλοποιημένη μορφή της συνάρτησης. Από τη γενικευμένη μορφή των θεωρημάτων DeMorgan προκύπτει ο κανόνας που υποδεικνύει ότι το συμπλήρωμα μιας συνάρτησης προκύπτει από την αλγεβρική μορφή της συνάρτησης με εναλλαγή των τελεστών ΚΑΙ και Η και το συμπλήρωμα όλων των παραγόντων. F = x y z +x y z F = (x + y + z) (x + y + z ) F = x (y z + y z) F = x + (y + z) (y + z ) ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 43 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 44
13 Ελαχιστόροι και μεγιστόροι Ελαχιστόροι και μεγιστόροι Ελαχιστόρος (minterm) ή πρότυπο γινόμενο: η αλγεβρική έκφραση που προκύπτει με την εφαρμογή της λογικής πράξης ΚΑΙ στην κανονική ήσυμπληρωματικήμορφήn μεταβλητών. Παραδείγματα ελαχιστόρων 4 μεταβλητών: x y z w, x y z w, x y z w. Μεγιστόρος (maxterm) ή πρότυπο άθροισμα: η αλγεβρική έκφραση που προκύπτει με την εφαρμογή της λογικής πράξης Η στην κανονική ή συμπληρωματική μορφή n μεταβλητών. Παραδείγματα μεγιστόρων 4 μεταβλητών: x + y + z + w, x + y + z + w, x + y + z + w. Για n μεταβλητές προκύπτουν 2 n ελαχιστόροι και ισάριθμοι μεγιστόροι. Οι μεταβλητές έχουν συμπληρωματικές τιμές στους αντίστοιχους ελαχιστόρους και μεγιστόρους. Κάθε ελαχιστόρος είναι το συμπλήρωμα του αντίστοιχου μεγιστόρου και αντίστροφα. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 45 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 46 Κανονικές μορφές Οι λογικές συναρτήσεις που εκφράζονται σε μορφή αθροίσματος ελαχιστόρων ή γινομένου μεγιστόρων αναφέρονται ως κανονικές μορφές (canonical forms). Οποιαδήποτε λογική συνάρτηση μπορεί να εκφραστεί ως άθροισμα ελαχιστόρων ή γινόμενο μεγιστόρων. F = x y z + x y z + x y z + x y z + x y z = m + m + m 3 + m 4 + m 6 Συμπλήρωμα της F = F = x y z + x y z + x y z = m 2 + m 5 + m 7 Συμπλήρωμα της F = F = (x + y + z) (x + y +z ) (x + y + z ) = M 2 M 5 M 7 Λογική συνάρτηση ως άθροισμα ελαχιστόρων Αναπτύσσουμε τη συνάρτηση σε άθροισμα γινομένων. Συμπληρώνουμε κάθε γινόμενο με τις μεταβλητές που λείπουν πολλαπλασιάζοντας με παράσταση τύπου (x + x ) για κάθε μεταβλητή που λείπει. Εναλλακτικά, κατασκευάζουμε τον πίνακα αληθείας της συνάρτησης απευθείας από την αλγεβρική έκφραση που περιγράφει τη συνάρτηση και στη συνέχεια εντοπίζουμε τους κατάλληλους ελαχιστόρους από τον πίνακα αυτό. x y z F F ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 47 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 48
14 Λογική συνάρτηση ως γινόμενο μεγιστόρων Αναπτύσσουμε τη συνάρτηση σε γινόμενο αθροισμάτων χρησιμοποιώντας την επιμεριστική ιδιότητα: x + y z = (x + y) (x + z). Συμπληρώνουμε κάθε άθροισμα με τις μεταβλητές που λείπουν προσθέτοντας την παράσταση τύπου x x για κάθε μεταβλητή που λείπει. Εναλλακτικά, κατασκευάζουμε τον πίνακα αληθείας της συνάρτησης απευθείας από την αλγεβρική έκφραση που περιγράφει τη συνάρτηση και στη συνέχεια εντοπίζουμε τους κατάλληλους μεγιστόρους από τον πίνακα αυτό. Μετατροπή μεταξύ κανονικών μορφών Έστω F (x, y, z) = x y + x z = Σ (, 3, 6, 7) σε μορφή αθροίσματος ελαχιστόρων με βάση τον πίνακα αληθείας. Υπολογίζουμε τη συμπληρωματική της F: F = Σ (, 2, 4, 5). Υπολογίζουμε τη συμπληρωματική της F που είναι η συνάρτηση Π (, 2, 4, 5), η οποία φυσικά ισούται με την F που έχει μετατραπεί σε κανονική μορφή γινομένου μεγιστόρων. Προκύπτει λοιπόν ο κανόνας μετατροπής που υποδεικνύει ότι εναλλάσσουμε τα σύμβολα Σ και Π και χρησιμοποιούμε εκείνους τους δείκτες ελαχιστόρων ή μεγιστόρων που λείπουν από την αρχική κανονική μορφή. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 49 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 5 Πρότυπες μορφές Οι λογικές συναρτήσεις που εκφράζονται σε μορφή αθροίσματος γινομένων ή γινομένου αθροισμάτων, όπου όμως οι όροι μπορούν να περιέχουν λιγότερους από n παράγοντες (μεταβλητές) αναφέρονται ως πρότυπες μορφές. Γινόμενο είναι η αλγεβρική έκφραση που προκύπτει με την εφαρμογή της λογικής πράξης ΚΑΙ στην κανονική ή συμπληρωματική μορφή μιας ή περισσοτέρων μεταβλητών. Άθροισμα γινομένων είναι η αλγεβρική έκφραση που προκύπτει με την εφαρμογή της λογικής πράξης Η μεταξύ γινομένων. Υλοποίηση πρότυπων μορφών Η υλοποίηση αθροίσματος γινομένων γίνεται με μια ομάδα από πύλες ΚΑΙ για τα γινόμενα (εκτός από τους μονούς παράγοντες) ακολουθούμενη από μια πύλη Η. Η υλοποίηση γινομένου αθροισμάτων γίνεται με μια ομάδα από πύλες Η για τα αθροίσματα (εκτός από τους μονούς παράγοντες) ακολουθούμενη από μια πύλη ΚΑΙ. Και οι δύο υλοποιήσεις γίνονται με χρήση δύο επιπέδων πυλών (που στην ουσία είναι τρία εάν συμπεριλάβουμε και τους αντιστροφείς που απαιτούνται για την εξαγωγή των συμπληρωματικών μορφών των παραγόντων). Άθροισμα είναι η αλγεβρική έκφραση που προκύπτει με την εφαρμογή της λογικής πράξης Η στην κανονική ή συμπληρωματική μορφή μιας ή περισσοτέρων μεταβλητών. Γινόμενο αθροισμάτων είναι η αλγεβρική έκφραση που προκύπτει με την εφαρμογή της λογικής πράξης ΚΑΙ μεταξύ αθροισμάτων. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 5 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 52
15 Υλοποίηση μη πρότυπων μορφών Η υλοποίηση συνάρτησης μη πρότυπης μορφής γίνεται συνήθως σε περισσότερα από δύο επίπεδα πυλών, εκτός και αν μετατραπεί σε πρότυπη μορφή. F = A B + C (D + E) F = A B + C (D + E) = A B + C D + C E Άλλες λογικές πράξεις Για μια συνάρτηση n μεταβλητών υπάρχουν 2 n πιθανοί συνδυασμοί των μεταβλητών αυτών και 2 n πιθανά αποτελέσματα ή έξοδοι. 2 2n Συνεπώς, υπάρχουν πιθανοί συνδυασμοί αποτελεσμάτων (εξόδων) και ισάριθμεςπιθανέςσυναρτήσειςπουμπορούνναδώσουντααποτελέσματα αυτά. Υπάρχουν 2 σταθερές συναρτήσεις που παράγουν σταθερό ή, 4 μοναδιαίες (συμπληρώματος και μεταφοράς) και συναρτήσεις δυαδικών τελεστών. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 53 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 54 Άλλες λογικές πράξεις Ψηφιακές λογικές πύλες Όνομα Σύμβολο Αλγεβρική Πίνακας συνάρτηση αληθείας KAI (AND) H (OR) Αντιστροφέας Απομονωτής ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 55 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 56
16 Ψηφιακές λογικές πύλες Επέκταση σε περισσότερες εισόδους Όνομα Σύμβολο Αλγεβρική Πίνακας συνάρτηση αληθείας ΟΧΙ-ΚΑΙ (NAND) Οι ψηφιακές λογικές πύλες (εκτός του απομονωτή και του αντιστροφέα) μπορούν να επεκταθούν σε περισσότερες από δύο εισόδους. Βασικές προϋποθέσεις είναι να ισχύουν η αντιμεταθετική και η προσεταιριστική ιδιότητα για την αντίστοιχη λογική πράξη. ΟΥΤΕ (NOR) Οι πράξεις ΚΑΙ και Η έχουν τις παραπάνω ιδιότητες, γεγονός που υποδεικνύει ότι οι είσοδοι των αντίστοιχων πυλών είναι ισοδύναμες όσον αφορά τη χρήση τους. Αποκλειστικό-Η (XOR) Αποκλειστικό-ΟΥΤΕ ή ισοδυναμία (XNOR) Επομένως, οι πύλες ΚΑΙ και Η μπορούν να επεκταθούν σε περισσότερες από δύο εισόδους, αρκεί να εισάγουμε τις επιπλέον εισόδους χρησιμοποιώντας τον αντίστοιχο τελεστή. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 57 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 58 Επέκταση σε περισσότερες εισόδους Οι πράξεις ΟΧΙ-ΚΑΙ και ΟΥΤΕ διέπονται από την αντιμεταθετική ιδιότητα, αλλά όχι από την προσεταιριστική: Συνεπώς, για να επεκταθούν σε περισσότερες από μία εισόδους, πρέπει να οριστούν ως εξής: Επέκταση σε περισσότερες εισόδους Οι πράξεις του αποκλειστικού-η και της ισοδυναμίας διέπονται από την αντιμεταθετική και την προσεταιριστική ιδιότητα, οπότε μπορούν να επεκταθούν σε περισσότερες από δύο εισόδους. Η συνάρτηση του αποκλειστικού-η χαρακτηρίζεται ως περιττή, αφού ισούται με εάν στις τιμές των μεταβλητών εισόδου υπάρχει περιττός αριθμός μονάδων. Ησυνάρτησηισοδυναμίας χαρακτηρίζεται ως άρτια, αφού ισούται με εάν στις τιμές των μεταβλητών εισόδου υπάρχει άρτιος αριθμός μονάδων. ΟΧΙ-ΚΑΙ ΟΥΤΕ ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 59 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 6
17 Κεφάλαιο 3: Ελαχιστοποίηση και υλοποίηση Ελαχιστοποίηση (απλοποίηση) λογικών συναρτήσεων με τη μέθοδο του χάρτη Καρνώ (Karnaugh) Ελαχιστοποίηση αθροίσματος γινομένων με χάρτες Καρνώ 2, 3, 4 και 5 μεταβλητών Ελαχιστοποίηση γινομένου αθροισμάτων Συνθήκες αδιαφόρου τιμής λογικών συναρτήσεων Υλοποίηση με πύλες ΟΧΙ-ΚΑΙ (NAND) και ΟΥΤΕ (NOR) Πρόσθετες υλοποιήσεις με δύο επίπεδα πυλών Συνάρτηση αποκλειστικού-η (XOR) Απλοποίηση συναρτήσεων με τη μέθοδο του χάρτη Η πολυπλοκότητα των ψηφιακών πυλών που υλοποιούν μια λογική συνάρτηση είναι άμεσα συνδεδεμένη με την πολυπλοκότητα της αλγεβρικής μορφής των λογικών συναρτήσεων. Η απλοποίηση λογικών συναρτήσεων με χρήση αλγεβρικών μετασχηματισμών είναι δύσχρηστη αφού δεν παρέχει συγκεκριμένους κανόνες και μεθοδολογία. Η παράσταση μιας συνάρτησης με πίνακα αληθείας είναι μοναδική, ενώ η αλγεβρική της παράσταση μπορεί να λάβει αρκετές διαφορετικές μορφές. Η απλοποίηση λογικών συναρτήσεων με τη μέθοδο του χάρτη είναι απλή, άμεση και συστηματική και οδηγεί σε συναρτήσεις με ελάχιστους όρους. Ο χάρτης Καρνώ αποτελεί σχηματική μορφή του πίνακα αληθείας της λογικής συνάρτησης. Μπορεί εύκολα να εφαρμοστεί αν το πλήθος των μεταβλητών είναι μικρότερο των επτά. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 6 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 62 Χάρτης δύο μεταβλητών Χάρτης δύο μεταβλητών Μια λογική συνάρτηση απεικονίζεται σε έναν χάρτη Καρνώ από τα τετράγωνα του χάρτη, οι αντίστοιχοι ελαχιστόροι των οποίων υπάρχουν στην έκφραση της λογικής συνάρτησης σε μορφή αθροίσματος ελαχιστόρων. Αναγνωρίζοντας συγκεκριμένες περιοχές πάνω στο χάρτη, ο χρήστης μπορεί να εξάγει εναλλακτικές αλγεβρικές εκφράσειςτηςίδιαςσυνάρτησηςκαιναεπιλέξει την πιο απλή από αυτές. Οχάρτης2 μεταβλητών περιέχει 4 τετράγωνα (ένα για κάθε ελαχιστόρο). Η μεταβλητή x εμφανίζεται ως συμπλήρωμα στη γραμμή και με την κανονική της μορφή στη γραμμή, ενώ η μεταβλητή y εμφανίζεται ως συμπλήρωμα στη στήλη και με την κανονική της μορφή στη στήλη. x y xy x y xy F = x y F 2 = x y + x y + x y = x + y ύο τετράγωνα του χάρτη με κοινή ακμή δηλ. γειτονικά ή προσκείμενα τετράγωνα διαφέρουν μόνο κατά μία μεταβλητή (η οποία παρουσιάζεται με την κανονική της μορφή στο ένα τετράγωνο και με το συμπλήρωμά της στο άλλο). Συνεπώς, το άθροισμα δύο ελαχιστόρων που ανήκουν σε γειτονικά τετράγωνα μπορεί να απλοποιηθεί με απαλοιφή της μεταβλητής στην οποία διαφέρουν: x y + x y = x (y + y) = x = x και x y + x y = y (x + x ) = y = y. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 63 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 64
18 Χάρτης τριών μεταβλητών Χάρτης τριών μεταβλητών Ο χάρτης τριών μεταβλητών περιέχει 8 τετράγωνα (ένα για κάθε ελαχιστόρο). Οι ελαχιστόροι τοποθετούνται σύμφωνα με τη δυαδική ακολουθία του κώδικα Gray (δηλ. αλλαγή μόνο ενός ψηφίου μεταξύ δύο συνεχόμενων αριθμών). Το άθροισμα δύο ελαχιστόρων που βρίσκονται σε προσκείμενα τετράγωνα μπορεί να απλοποιηθεί σε έναν μόνο όρο (γινόμενο) που περιέχει δύο μεταβλητές (δηλ. απαλείφεταιημεταβλητήπουπαρουσιάζεταιμετηνκανονική της μορφή στο ένα τετράγωνο και με το συμπλήρωμά της στο άλλο). Παράδειγμα: m 5 + m 7 = x y z + x y z = x z (y + y) = x z = x z yz ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 65 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 66 Χάρτης τριών μεταβλητών Η ομαδοποίηση προσκείμενων τετραγώνων μπορεί να γίνει σε ομάδες των 2, 4 ή 8 τετραγώνων ώστε να μπορούν να απαλείφουν μία, δύο ή τρεις μεταβλητές αντίστοιχα, από τους όρους (γινόμενα) που περιέχονται στην αρχική λογική συνάρτηση. Χάρτης τεσσάρων μεταβλητών Ο χάρτης τεσσάρων μεταβλητών περιέχει 6 τετράγωνα ( για κάθε ελαχιστόρο). Οι ελαχιστόροι τοποθετούνται σύμφωνα με την ακολουθία του κώδικα Gray. Η ομαδοποίηση προσκείμενων τετραγώνων μπορεί να γίνει σε ομάδες των 2, 4, 8 ή 6 τετραγώνων ώστε να μπορούν να απαλείφουν, 2, 3 ή 4 μεταβλητές αντίστοιχα, από τους όρους (γινόμενα) της αρχικής λογικής συνάρτησης. Τα γινόμενα 2 μεταβλητών αντιπροσωπεύονται στο χάρτη 3 μεταβλητών από 2 τετράγωνα. Παρουσιάζονται επίσης επικαλύψεις τετραγώνων οι οποίες δεν διαφοροποιούν τη μέθοδο., Η άνω πλευρά του χάρτη θεωρείται προσκείμενη με την κάτω και η δεξιά πλευρά με την αριστερή. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 67 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 68
19 Χάρτης τεσσάρων μεταβλητών Χάρτης τεσσάρων μεταβλητών Τα γινόμενα 3 μεταβλητών αντιπροσωπεύονται στο χάρτη 4 μεταβλητών από 2 τετράγωνα. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 69 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 7 Πρωτεύοντες όροι Πρωτεύοντες όροι Πρωτεύων όρος (prime implicant): γινόμενο παραγόντων που προκύπτει εάν συνδυάσουμε το μέγιστο αριθμό προκείμενων τετραγώνων στο χάρτη Καρνώ. Ο πρωτεύων όρος περιλαμβάνει τον ελάχιστο δυνατό αριθμό μεταβλητών. Κάθε λογική συνάρτηση πρέπει να απλοποιείται χρησιμοποιώντας μόνο πρωτεύοντες όρους έτσι ώστε να ελαχιστοποιείται το κόστος υλοποίησής της, που σημαίνει ότι κάθε μονάδα του χάρτη (ελαχιστόρος) θα πρέπει να καλύπτεται μόνο από πρωτεύοντες όρους. Όσο λιγότεροι πρωτεύοντες όροι χρησιμοποιηθούν για την απλοποίηση μιας λογικής συνάρτησης, τόσο απλούστερο είναι το τελικό αποτέλεσμα. Εάν ένας ελαχιστόρος (τετράγωνο στο χάρτη) εκφράζεται από έναν και μόνο πρωτεύοντα όρο, τότε ο πρωτεύων αυτός όρος ονομάζεται θεμελιώδης πρωτεύον όρος. Για απλούστερο αποτέλεσμα, επιλέγουμε πρώτα όλους τους θεμελιώδεις πρωτεύοντες όρους και στη συνέχεια καλύπτουμε τους υπόλοιπους ελαχιστόρους με τον μικρότερο δυνατό αριθμό από πρωτεύοντες όρους. Οι ελαχιστόροι m και m 5 καλύπτονται μόνο από τους όρους B D και B D, αντίστοιχα, οπότε οι όροι αυτοί είναι θεμελιώδεις. Οι θεμελιώδεις αυτοί όροι καλύπτουν επίσης και τους ελαχιστόρους m 2, m 7, m 8 m, m 3, m 5. Οι εναπομείναντες ελαχιστόροι m 3, m 9 και m μπορούν να καλυφθούν από πρωτεύοντες όρους. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 7 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 72
20 Πρωτεύοντες όροι Για την κάλυψη των m 3, m 9 και m υπάρχουν αρκετοί πιθανοί πρωτεύοντες όροι. Χάρτης πέντε μεταβλητών Ο χάρτης πέντε μεταβλητών είναι δύσχρηστος, αφού περιλαμβάνει μεγάλο αριθμό ελαχιστόρων και η ανίχνευση προσκείμενων τετραγώνων είναι πολύπλοκη. Οπότε, χρησιμοποιούμε δύο χάρτες τεσσάρων μεταβλητών, με μία από τις πέντε μεταβλητές να διαχωρίζει τους δύο χάρτες. Κάθε τετράγωνο στο χάρτη με Α= θεωρείται γειτονικό του αντίστοιχου τετραγώνου του χάρτη με Α=. Συνεπώς θα πρέπει να χρησιμοποιηθούν οι δύο θεμελιώδεις πρωτεύοντες όροι και ένας από τους 4 πιθανούς συνδυασμούς πρωτευόντων όρων που καλύπτουν του ελαχιστόρους m 3 και m 9. ή ή ή ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 73 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 74 Χάρτης πέντε μεταβλητών Ελαχιστοποίηση γινομένου αθροισμάτων Για την ελαχιστοποίηση γινομένου αθροισμάτων βασιζόμαστε σε μια βασική αρχή (θεώρημα DeMorgan): (m + m + + m n ) = M M M n Βήμα ο: Σύνταξη του χάρτη Καρνώ της λογικής συνάρτησης (F). Βήμα 2ο: Ελαχιστοποίηση του συμπληρώματος της λογικής συνάρτησης (F ) με συνδυασμό των προσκείμενων μηδενικών αντί για τις μονάδες, οπότε λαμβάνουμε ένα ελαχιστοποιημένο άθροισμα γινομένων. Βήμα 3ο: Συμπληρώνουμε την ελαχιστοποιημένη συνάρτηση (F ) με χρήση της παραπάνω βασικής αρχής, οπότε προκύπτει η αρχική συνάρτηση (F) ως γινόμενο αθροισμάτων. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 75 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 76
21 Ελαχιστοποίηση γινομένου αθροισμάτων Υλοποίηση ελαχιστοποιημένων συναρτήσεων Η υλοποίηση ελαχιστοποιημένων συναρτήσεων γίνεται με δύο επίπεδα πυλών: ΚΑΙ-Η (όταν η αρχική συνάρτηση ελαχιστοποιείται σε άθροισμα γινομένων) ή Η-ΚΑΙ (όταν η αρχική συνάρτηση ελαχιστοποιείται σε γινόμενο αθροισμάτων). ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 77 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 78 Συνθήκες αδιαφόρου τιμής (αδιάφοροι όροι) Το λογικό άθροισμα ελαχιστόρων μιας λογικής συνάρτησης καθορίζει τις συνθήκες κάτω από τις οποίες μια λογική συνάρτηση έχει τιμή. Ησυνάρτηση έχει τιμή για τους υπόλοιπους ελαχιστόρους. Υπάρχουν εφαρμογές στις οποίες η συνάρτηση δεν ορίζεται για συγκεκριμένους συνδυασμούς μεταβλητών, π.χ. ο τετράμπιτος δυαδικός κώδικας για τα δεκαδικά ψηφία έχει 6 συνδυασμούς που δεν χρησιμοποιούνται. Οι συναρτήσεις που έχουν εξόδους οι οποίες δεν ορίζονται για ορισμένους συνδυασμούς εισόδων ονομάζονται ατελώς ορισμένες συναρτήσεις. Η τιμή που λαμβάνουν αυτές οι συναρτήσεις για ελαχιστόρους που δεν ορίζονται είναι αδιάφορη, οπότε οι ελαχιστόροι που δεν ορίζονται ονομάζονται συνθήκες αδιαφόρου τιμής ή αδιάφοροι όροι. Για να διακρίνουμε τους αδιάφορους όρους από τις τιμές ή, χρησιμοποιούμε το σύμβολο (τιμή) Χ καιοιόροιαυτοίχρησιμοποιούνταιγιαπεραιτέρω απλοποίηση της συνάρτησης. Συνεπώς, η τιμή Χ στο τετράγωνο ενός χάρτη υποδηλώνει ότι είναι αδιάφορο το εάν αποδίδεται στη λογική συνάρτηση η τιμή ή για το συγκεκριμένο ελαχιστόρο. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 79 Συνθήκες αδιαφόρου τιμής (αδιάφοροι όροι) F (w, x, y, z) = Σ (,3,7,,5). Αδιάφοροι όροι: d (w, x, y, z) = Σ (,2,5). Οι ελαχιστόροι της F είναι οι συνδυασμοί των μεταβλητών που κάνουν την τιμή της F ίση με. Οι ελαχιστόροι του d είναι οι αδιάφοροι όροι που μπορούν να έχουν τιμή είτε είτε. Για να καταλήξουμε σε απλοποιημένη έκφραση της F, μπορούμε να συμπεριλάβουμε ή να παραλείψουμε οποιονδήποτε αδιάφορο όρο. Με διαφορετική χρήση των αδιάφορων όρων θα μπορούσε να προκύψει διαφορετική αλλά εξίσου αποδεκτή απλοποιημένη συνάρτηση. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 8
22 Υλοποίηση συναρτήσεων με πύλες ΟΧΙ-ΚΑΙ και ΟΥΤΕ Υλοποίηση συναρτήσεων με πύλες ΟΧΙ-ΚΑΙ (NAND) Οι πύλες ΟΧΙ-ΚΑΙ (NAND) και ΟΥΤΕ (NOR) χρησιμοποιούνται συχνότερα από τις ΚΑΙ (AND) και Η (OR), επειδή είναι πιο εύκολο να κατασκευαστούν με τα βασικά ηλεκτρονικά στοιχεία. Η υλοποίηση λογικών συναρτήσεων με πύλες ΟΧΙ-ΚΑΙ δύο επιπέδων προϋποθέτει ότι η συνάρτηση βρίσκεται σε μορφή αθροίσματος γινομένων. F = AB + CD Εφαρμόζουμε τον κανόνα DeMorgan: F = AB + CD = ((AB) (CD) ) Εάν συνδέσουμε μεταξύ τους τις εισόδους μιας πύλης ΟΧΙ-ΚΑΙ ή ΟΥΤΕ, δημιουργείται ένας αντιστροφέας: (x + x) = (x x) = x. Υλοποιούμε το κύκλωμα με πύλες ΟΧΙ-ΚΑΙ. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 8 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 82 Υλοποίηση συναρτήσεων με πύλες ΟΧΙ-ΚΑΙ (NAND) Υλοποίηση συναρτήσεων με πύλες ΟΧΙ-ΚΑΙ (NAND) Καταλήγουμε στην παρακάτω μεθοδολογία: Βήμα ο: Απλοποίηση λογικής συνάρτησης σε μορφή αθροίσματος γινομένων. Βήμα 2ο: Σχεδιασμός μιας πύλης ΟΧΙ-ΚΑΙ για κάθε όρο του αθροίσματος που περιλαμβάνει περισσότερους από έναν παράγοντες (μεταβλητές). Για τους όρους με ένα παράγοντα χρησιμοποιούμε αντιστροφείς (εκτός κι αν συμπληρώσουμε τον παράγοντα). Βήμα 3ο: Σχεδιασμός μιας πύλης ΟΧΙ-ΚΑΙ δευτέρου επιπέδου με αριθμό εισόδων ίσο με τους όρους του απλοποιημένου αθροίσματος. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 83 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 84
23 Μετατροπή διαγράμματος πυλών ΚΑΙ, Η σεοχι-και Μετατροπή διαγράμματος πυλών ΚΑΙ, Η σεοχι-και Ηδιαδικασίαμετατροπής διαγράμματος πυλών ΚΑΙ και Η σε διάγραμμα πυλών ΟΧΙ-ΚΑΙ περιλαμβάνει τα εξής βήματα: Βήμα ο: Μετατρέπουμε τις πύλες ΚΑΙ σε πύλες ΟΧΙ-ΚΑΙ με σχηματικά σύμβολα ΚΑΙ-αντιστροφής. Βήμα 2ο: Μετατρέπουμε τις πύλες Η σε πύλες ΟΧΙ-ΚΑΙ με σχηματικά σύμβολα αντιστροφής-η. Βήμα 3ο: Ελέγχουμε τους κύκλους αντιστροφής του σχηματικού διαγράμματος. Για κάθε κύκλο που δεν αντισταθμίζεται από άλλον κύκλο στην ίδια γραμμή, εισάγουμε έναν αντιστροφέα ή συμπληρώνουμε την μεταβλητή εισόδου της γραμμής. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 85 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 86 Υλοποίηση συναρτήσεων με πύλες ΟΥΤΕ (NOR) Υλοποίηση συναρτήσεων με πύλες ΟΥΤΕ (NOR) ή Η υλοποίηση λογικών συναρτήσεων με πύλες ΟΥΤΕ δύο επιπέδων προϋποθέτει ότι η συνάρτηση βρίσκεται σε μορφή γινομένου αθροισμάτων. F = (A + B) (C + D) Ε Εφαρμόζουμε τον κανόνα DeMorgan: F = (A + B) (C + D) Ε = ((A+B) + (C+D) + Ε ) Υλοποιούμε το κύκλωμα με πύλες ΟΥΤΕ. Καταλήγουμε στην παρακάτω μεθοδολογία: Βήμα ο: Απλοποίηση λογικής συνάρτησης σε μορφή γινομένου αθροισμάτων. Βήμα ο: Σχεδιασμός μιας πύλης OYTE για κάθε άθροισμα του γινομένου που περιλαμβάνει περισσότερους από έναν παράγοντες (μεταβλητές). Οι όροι με ένα παράγοντα που θα τροφοδοτήσουν απευθείας το δεύτερο επίπεδο πυλών αντικαθίστανται με το συμπλήρωμά τους. Βήμα 3ο: Σχεδιασμός μιας πύλης ΟΥΤΕ δευτέρου επιπέδου με αριθμό εισόδων ίσο με τους όρους του γινομένου αθροισμάτων. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 87 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 88
24 Μετατροπή διαγράμματος πυλών H, KAI σε OYTE Μετατροπή διαγράμματος πυλών H, KAI σε OYTE Η διαδικασία μετατροπής ενός διαγράμματος πυλών Η και ΚΑΙ σε διάγραμμα πυλών ΟΥΤΕ πολλαπλών επιπέδων είναι παρόμοια με εκείνη της μετατροπής σε διάγραμμα πυλών ΟΧΙ-ΚΑΙ: Βήμα ο: Μετατρέπουμε τις πύλες Η σε πύλες ΟΥΤΕ με σχηματικά σύμβολα Η-αντιστροφής Βήμα 2ο: Μετατρέπουμε τις πύλες ΚΑΙ σε πύλες ΟΥΤΕ με σχηματικά σύμβολα αντιστροφής-και. Βήμα 3ο: Κάθε κύκλος αντιστροφής που δεν αντισταθμίζεται από άλλο κύκλο στην ίδια γραμμή χρειάζεται αντιστροφέα ή συμπλήρωση της μεταβλητής εισόδου. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 89 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 9 Πρόσθετες υλοποιήσεις με δύο επίπεδα πυλών Υλοποίηση ΚΑΙ Η αντιστροφή Οι υλοποιήσεις ΚΑΙ ΟΥΤΕ (AND NOR) και ΟΧΙ ΚΑΙ ΚΑΙ (NAND AND) είναι ισοδύναμες και εκτελούν τη λειτουργία ΚΑΙ Η Αντιστροφή (AND OR Invert). Οι υλοποιήσεις Η ΟΧΙ ΚΑΙ (OR NAND) και ΟΥΤΕ Η (NOR OR) είναι επίσης ισοδύναμες και εκτελούν τη λειτουργία Η ΚΑΙ Αντιστροφή (OR AND Invert). Πρόσθετες υλοποιήσεις δύο επιπέδων Υλοποιούν τις συναρτήσεις Υπολογισμός της F σε Συμπλήρωση της F για να πάρουμε έξοδο De Morgan ΚΑΙ - ΟΥΤΕ ΟΧΙ ΚΑΙ - ΚΑΙ ΚΑΙ - Η - ΑΝΤΙΣΤΡΟΦΗ Άθροισμα γινομένων συνδυάζοντας τα στο χάρτη Καρνώ F Η - ΟΧΙ ΚΑΙ ΟΥΤΕ - Η Η - ΚΑΙ - ΑΝΤΙΣΤΡΟΦΗ Γινόμενο αθροισμάτων συνδυάζοντας τις στο χάρτη Καρνώ και συμπληρώνοντας F ΚΑΙ - ΟΥΤΕ ΟΧΙ ΚΑΙ - ΚΑΙ ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 9 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 92
25 Υλοποίηση Η ΚΑΙ αντιστροφή F' = (x+y+z)(x' +y' +z) De Morgan Αποκλειστικό-Η (XOR) Το αποκλειστικό-η είναι μια λογική πράξη που υποδηλώνεται από το σύμβολο και περιγράφεται από τη σχέση: x y = x y + x y Η λογική αυτή πράξη έχει αποτέλεσμα όταν μόνο το x είναι ήμόνοόταντο y είναι, αλλά όχι όταν και τα δύο έχουν την ίδια τιμή. Το αποκλειστικό ΟΥΤΕ που είναι γνωστό και ως ισοδυναμία εκφράζεται από τη σχέση: x y= (x y) = xy+x y (x y) =(xy +x y) =(x +y)(x+y )=xy+x y Η λογική αυτή πράξη έχει αποτέλεσμα εάν τα x και y ισούται με ή εάν ισούνται και τα δύο με μηδέν. Η - ΟΧΙ ΚΑΙ ΟΥΤΕ - Η Ισχύουν οι ταυτότητες: x = x, x = x, x x =, x x =, x y = x y = (x y), που αποδεικνύονται εύκολα με χρήση πίνακα αληθείας ή με αντικατάσταση της πράξης με την λογική της έκφραση. Ισχύουν επίσης η αντιμεταθετική και η επιμεριστική ιδιότητα. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 93 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 94 Υλοποίηση της συνάρτησης Αποκλειστικό-Η (XOR) Με πύλες ΟΧΙ, ΚΑΙ, Η Οι ηλεκτρονικές πύλες αποκλειστικού- Η είναι δύσκολο να κατασκευαστούν σε μία και μόνο βαθμίδα Με πύλες ΟΧΙ-ΚΑΙ x y= xy +x y = (x +y )x + (x +y )y x + y ((x + y ) x) ((x + y ) y) ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 95 Αποκλειστικό-Η (XOR) πολλών μεταβλητών Η συνάρτηση αποκλειστικό-η τριών ή περισσοτέρων μεταβλητών μπορεί εύκολα να μετατραπεί σε λογική έκφραση αθροίσματος ελαχιστόρων: A B C = (A B + A B) C + (A B + A B ) C = = A B C + A B C + A B C + A B C = Σ (, 2, 4, 7) Η συνάρτηση αποκλειστικό-η ισούταιμε όταν μόνο μία μεταβλητή έχει τιμή ή όταν και οι 3 μεταβλητές έχουν τιμή, σε αντίθεση με τη συνάρτηση 2 εισόδων. Αποδεικνύεται ότι στις περιπτώσεις με 3 ή περισσότερες μεταβλητές, ηπροϋπόθεσηνα ισούται η συνάρτηση με είναι ότι πρέπει περιττός αριθμός μεταβλητών να έχει την τιμή (περιττή συνάρτηση). Όλοι οι δυαδικοί αριθμοί που αντιστοιχούν στους 4 ελαχιστόρους της συνάρτησης (,,, ) έχουν περιττό αριθμό μονάδων. Το συμπλήρωμα της (δηλ. η ισοδυναμία που προκύπτει με προσθήκη κύκλου αναστροφής στηπύληεξόδου) είναι άρτια συνάρτηση. ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 96
26 ημιουργία και έλεγχος ισοτιμίας Για να ανιχνεύσουμε τυχόν λάθη κατά τη μετάδοση δεδομένων, προσθέτουμε ένα ψηφίο ισοτιμίας (parity bit) στη δυαδική πληροφορία με σκοπό να ανιχνεύσουμε λάθη κατά τη μετάδοση της. Το ψηφίο ισοτιμίας περιλαμβάνεται στο σήμα μετάδοσης (στην περισσότερο σημαντική θέση) έτσι ώστε ο αριθμός των να γίνει άρτιος ή περιττός. Τις περισσότερες φορές χρησιμοποιείται η άρτια ισοτιμία (δηλ. περιλαμβάνεται ψηφίο ισοτιμίας έτσι ώστε να προκύπτει άρτιος αριθμός των του χαρακτήρα). Μετά την εισαγωγή του ψηφίου άρτιας ισοτιμίας σε κάθε χαρακτήρα που μεταδίδεται από τον πομπό, οι χαρακτήρες μεταδίδονται και η ισοτιμία κάθε χαρακτήρα ελέγχεται στο δέκτη. Εάν η ισοτιμία του λαμβανόμενου χαρακτήρα δεν είναι άρτια, αυτό σημαίνει ότι τουλάχιστον ένα ψηφίο έχει αλλάξει τιμή κατά τη μετάδοση. To κύκλωμα που υλοποιεί το ψηφίο ισοτιμίας στον πομπό λέγεται γεννήτρια ισοτιμίας και το κύκλωμα που ελέγχει το ψηφίο ισοτιμίας στο δέκτη λέγεται ελεγκτής ισοτιμίας. Γεννήτρια ισοτιμίας Για άρτια ισοτιμία το ψηφίο ισοτιμίας (P) πρέπει να δημιουργείται με τέτοιο τρόπο ώστε το συνολικό πλήθος μονάδων (συμπεριλαμβανομένου και του P) να είναι άρτιο. Παρατηρούμε ότι το P ισούται με όταν το πλήθος των μονάδων στις μεταβλητές x, y, z είναι περιττό. Οπότε το P μπορεί να εκφραστεί ως εξής: P = x y z Πίνακας αληθείας γεννήτριας άρτιας ισοτιμίας Μήνυμα τριών ψηφίων Ψηφίο άρτιας ισοτιμίας ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 97 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 98 Ελεγκτής ισοτιμίας Κεφάλαιο 4: Συνδυαστική λογική Τα τρία ψηφία πληροφορίας μαζί με το ψηφίο ισοτιμίας μεταδίδονται στο δέκτη όπου εισέρχονται σε ένα κύκλωμα ελέγχου ισοτιμίας. Τα τέσσερα ψηφία που ελήφθησαν θα πρέπει να έχουν άρτιο πλήθος μονάδων, ενώ εάν προκύψει λάθος κατά τη μετάδοση θα έχουν περιττό πλήθος μονάδων. Η έξοδος του κυκλώματος ελέγχου (C) θα είναι ίση με εάν προκύψει λάθος, δηλ. εάν τα 4 ψηφία έχουν περιττό πλήθος μονάδων: C = x y z P Το ίδιο κύκλωμα μπορεί να χρησιμοποιηθεί και ως γεννήτρια ισοτιμίας εάν θέσουμε στην είσοδο P(αφού z = z). Πίνακας αληθείας ελεγκτή άρτιας ισοτιμίας Ψηφία που ελήφθησαν Ψηφίο ελέγχου ισοτιμίας Λογικά κυκλώματα Συνδυαστικά κυκλώματα ιαδικασία ανάλυσης συνδυαστικών κυκλωμάτων ιαδικασία σχεδιασμού συνδυαστικών κυκλωμάτων υαδικός αθροιστής και αφαιρέτης εκαδικός αθροιστής υαδικός πολλαπλασιαστής Συγκριτής μεγέθους Αποκωδικοποιητές Κωδικοποιητές Πολυπλέκτες ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 99 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
3. Απλοποίηση Συναρτήσεων Boole
 3. Απλοποίηση Συναρτήσεων Boole 3. Μέθοδος του χάρτη Η πολυπλοκότητα ψηφιακών πυλών που υλοποιούν μια συνάρτηση Boole σχετίζεται άμεσα με την πολύπλοκότητα της αλγεβρικής της έκφρασης. Η αλγεβρική αναπαράσταση
3. Απλοποίηση Συναρτήσεων Boole 3. Μέθοδος του χάρτη Η πολυπλοκότητα ψηφιακών πυλών που υλοποιούν μια συνάρτηση Boole σχετίζεται άμεσα με την πολύπλοκότητα της αλγεβρικής της έκφρασης. Η αλγεβρική αναπαράσταση
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Εργαστήριο Ηλεκτρονικής. Ψηφιακά Ηλεκτρονικά. Απλοποίηση Συναρτήσεων Boole. Επιμέλεια Διαφανειών: Δ.
 Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Απλοποίηση Συναρτήσεων Boole Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Απλοποίηση Συναρτήσεων Boole Η πολυπλοκότητα του κυκλώματος
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Απλοποίηση Συναρτήσεων Boole Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Απλοποίηση Συναρτήσεων Boole Η πολυπλοκότητα του κυκλώματος
Περιεχόμενα. Πρώτο Κεφάλαιο. Εισαγωγή στα Ψηφιακά Συστήματα. Δεύτερο Κεφάλαιο. Αριθμητικά Συστήματα Κώδικες
 Πρώτο Κεφάλαιο Εισαγωγή στα Ψηφιακά Συστήματα 1.1 Αναλογικά και Ψηφιακά Σήματα και Συστήματα... 1 1.2 Βασικά Ψηφιακά Κυκλώματα... 3 1.3 Ολοκληρωμένα κυκλώματα... 4 1.4 Τυπωμένα κυκλώματα... 7 1.5 Εργαλεία
Πρώτο Κεφάλαιο Εισαγωγή στα Ψηφιακά Συστήματα 1.1 Αναλογικά και Ψηφιακά Σήματα και Συστήματα... 1 1.2 Βασικά Ψηφιακά Κυκλώματα... 3 1.3 Ολοκληρωμένα κυκλώματα... 4 1.4 Τυπωμένα κυκλώματα... 7 1.5 Εργαλεία
Επανάληψη Βασικών Στοιχείων Ψηφιακής Λογικής
 Επανάληψη Βασικών Στοιχείων Ψηφιακής Λογικής Αριθµοί Διαφόρων Βάσεων Δυαδικά Συστήµατα 2 Υπολογιστική Ακρίβεια Ο αριθµός των δυαδικών ψηφίων αναπαράστασης αριθµών καθορίζει την ακρίβεια των αριθµών σε
Επανάληψη Βασικών Στοιχείων Ψηφιακής Λογικής Αριθµοί Διαφόρων Βάσεων Δυαδικά Συστήµατα 2 Υπολογιστική Ακρίβεια Ο αριθµός των δυαδικών ψηφίων αναπαράστασης αριθµών καθορίζει την ακρίβεια των αριθµών σε
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Εργαστήριο Ηλεκτρονικής. Ψηφιακά Ηλεκτρονικά. Άλγεβρα Boole και Λογικές Πύλες 2. Επιμέλεια Διαφανειών: Δ.
 Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Άλγεβρα Boole και Λογικές Πύλες Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Αξιωματικός Ορισμός Άλγεβρας Boole Άλγεβρα Boole: είναι μία
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Άλγεβρα Boole και Λογικές Πύλες Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Αξιωματικός Ορισμός Άλγεβρας Boole Άλγεβρα Boole: είναι μία
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Εργαστήριο Ηλεκτρονικής. Ψηφιακά Ηλεκτρονικά. Αριθμητικά Συστήματα. Επιμέλεια Διαφανειών: Δ.
 Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Αριθμητικά Συστήματα Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Αριθμητικά Συστήματα Δεκαδικό Σύστημα: Βάση το 10, ψηφία 10 και συντελεστές
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Αριθμητικά Συστήματα Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Αριθμητικά Συστήματα Δεκαδικό Σύστημα: Βάση το 10, ψηφία 10 και συντελεστές
ΠΕΡΙΕΧΟΜΕΝΑ. Πρόλογος...9 ΚΕΦ. 1. ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ - ΚΩΔΙΚΕΣ
 ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος...9 ΚΕΦ. 1. ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ - ΚΩΔΙΚΕΣ 1.1 Εισαγωγή...11 1.2 Τα κύρια αριθμητικά Συστήματα...12 1.3 Μετατροπή αριθμών μεταξύ των αριθμητικών συστημάτων...13 1.3.1 Μετατροπή ακέραιων
ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος...9 ΚΕΦ. 1. ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ - ΚΩΔΙΚΕΣ 1.1 Εισαγωγή...11 1.2 Τα κύρια αριθμητικά Συστήματα...12 1.3 Μετατροπή αριθμών μεταξύ των αριθμητικών συστημάτων...13 1.3.1 Μετατροπή ακέραιων
3 η Θεµατική Ενότητα : Απλοποίηση Συναρτήσεων Boole. Επιµέλεια διαφανειών: Χρ. Καβουσιανός
 3 η Θεµατική Ενότητα : Απλοποίηση Συναρτήσεων oole Επιµέλεια διαφανειών: Χρ. Καβουσιανός Απλοποίηση Συναρτήσεων oole Ø Η πολυπλοκότητα του κυκλώµατος που υλοποιεί µια συνάρτηση oole σχετίζεται άµεσα µε
3 η Θεµατική Ενότητα : Απλοποίηση Συναρτήσεων oole Επιµέλεια διαφανειών: Χρ. Καβουσιανός Απλοποίηση Συναρτήσεων oole Ø Η πολυπλοκότητα του κυκλώµατος που υλοποιεί µια συνάρτηση oole σχετίζεται άµεσα µε
Γ2.1 Στοιχεία Αρχιτεκτονικής. Γ Λυκείου Κατεύθυνσης
 Γ2.1 Στοιχεία Αρχιτεκτονικής Γ Λυκείου Κατεύθυνσης Ορισμός άλγεβρας Boole Η άλγεβρα Boole ορίζεται, ως μία αλγεβρική δομή A, όπου: (α) Το Α είναι ένα σύνολο στοιχείων που περιέχει δύο τουλάχιστον στοιχεία
Γ2.1 Στοιχεία Αρχιτεκτονικής Γ Λυκείου Κατεύθυνσης Ορισμός άλγεβρας Boole Η άλγεβρα Boole ορίζεται, ως μία αλγεβρική δομή A, όπου: (α) Το Α είναι ένα σύνολο στοιχείων που περιέχει δύο τουλάχιστον στοιχεία
Κεφάλαιο 2. Συστήματα Αρίθμησης και Αναπαράσταση Πληροφορίας. Περιεχόμενα. 2.1 Αριθμητικά Συστήματα. Εισαγωγή
 Κεφάλαιο. Συστήματα Αρίθμησης και Αναπαράσταση Πληροφορίας Περιεχόμενα. Αριθμητικά συστήματα. Μετατροπή αριθμών από ένα σύστημα σε άλλο.3 Πράξεις στο δυαδικό σύστημα.4 Πράξεις στο δεκαεξαδικό σύστημα.5
Κεφάλαιο. Συστήματα Αρίθμησης και Αναπαράσταση Πληροφορίας Περιεχόμενα. Αριθμητικά συστήματα. Μετατροπή αριθμών από ένα σύστημα σε άλλο.3 Πράξεις στο δυαδικό σύστημα.4 Πράξεις στο δεκαεξαδικό σύστημα.5
Συνδυαστικά Λογικά Κυκλώματα
 Συνδυαστικά Λογικά Κυκλώματα Ένα συνδυαστικό λογικό κύκλωμα συντίθεται από λογικές πύλες, δέχεται εισόδους και παράγει μία ή περισσότερες εξόδους. Στα συνδυαστικά λογικά κυκλώματα οι έξοδοι σε κάθε χρονική
Συνδυαστικά Λογικά Κυκλώματα Ένα συνδυαστικό λογικό κύκλωμα συντίθεται από λογικές πύλες, δέχεται εισόδους και παράγει μία ή περισσότερες εξόδους. Στα συνδυαστικά λογικά κυκλώματα οι έξοδοι σε κάθε χρονική
Πανεπιστήμιο Δυτικής Μακεδονίας. Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών. Ψηφιακή Σχεδίαση
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ψηφιακή Σχεδίαση Ενότητα 12: Σύνοψη Θεμάτων Δρ. Μηνάς Δασυγένης mdasyg@ieee.org Εργαστήριο Ψηφιακών Συστημάτων και Αρχιτεκτονικής Υπολογιστών http://arch.icte.uowm.gr/mdasyg
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ψηφιακή Σχεδίαση Ενότητα 12: Σύνοψη Θεμάτων Δρ. Μηνάς Δασυγένης mdasyg@ieee.org Εργαστήριο Ψηφιακών Συστημάτων και Αρχιτεκτονικής Υπολογιστών http://arch.icte.uowm.gr/mdasyg
Εισαγωγή στην Πληροφορική & τον Προγραμματισμό
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Εισαγωγή στην Πληροφορική & τον Προγραμματισμό Ενότητα 3 η : Κωδικοποίηση & Παράσταση Δεδομένων Ι. Ψαρομήλιγκος Χ. Κυτάγιας Τμήμα
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Εισαγωγή στην Πληροφορική & τον Προγραμματισμό Ενότητα 3 η : Κωδικοποίηση & Παράσταση Δεδομένων Ι. Ψαρομήλιγκος Χ. Κυτάγιας Τμήμα
Ψηφιακοί Υπολογιστές
 1 η Θεµατική Ενότητα : υαδικά Συστήµατα Ψηφιακοί Υπολογιστές Παλαιότερα οι υπολογιστές χρησιµοποιούνταν για αριθµητικούς υπολογισµούς Ψηφίο (digit) Ψηφιακοί Υπολογιστές Σήµατα (signals) : διακριτά στοιχεία
1 η Θεµατική Ενότητα : υαδικά Συστήµατα Ψηφιακοί Υπολογιστές Παλαιότερα οι υπολογιστές χρησιµοποιούνταν για αριθµητικούς υπολογισµούς Ψηφίο (digit) Ψηφιακοί Υπολογιστές Σήµατα (signals) : διακριτά στοιχεία
1. ΣΥΣΤΗΜΑΤΑ ΑΡΙΘΜΩΝ. α i. (α i β i ) (1.3) όπου: η= το πλήθος ακεραίων ψηφίων του αριθμού Ν. n-1
 1. ΣΥΣΤΗΜΑΤΑ ΑΡΙΘΜΩΝ 1.1 Εισαγωγή Το δεκαδικό σύστημα (Decimal System) αρίθμησης χρησιμοποιείται από τον άνθρωπο και είναι κατάλληλο βέβαια γι αυτόν, είναι όμως εντελώς ακατάλληλο για τις ηλεκτρονικές
1. ΣΥΣΤΗΜΑΤΑ ΑΡΙΘΜΩΝ 1.1 Εισαγωγή Το δεκαδικό σύστημα (Decimal System) αρίθμησης χρησιμοποιείται από τον άνθρωπο και είναι κατάλληλο βέβαια γι αυτόν, είναι όμως εντελώς ακατάλληλο για τις ηλεκτρονικές
ΠΛΗΡΟΦΟΡΙΚΗ I. 4 η ΔΙΑΛΕΞΗ Αριθμητικά Συστήματα
 ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ - ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΕΙΣΑΓΩΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΤΟΥΡΙΣΤΙΚΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ ΚΑΙ ΕΠΙΧΕΙΡΗΣΕΩΝ ΦΙΛΟΞΕΝΙΑΣ ΠΛΗΡΟΦΟΡΙΚΗ I 4 η ΔΙΑΛΕΞΗ Αριθμητικά Συστήματα ΧΑΣΑΝΗΣ ΒΑΣΙΛΕΙΟΣ
ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ - ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΕΙΣΑΓΩΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΤΟΥΡΙΣΤΙΚΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ ΚΑΙ ΕΠΙΧΕΙΡΗΣΕΩΝ ΦΙΛΟΞΕΝΙΑΣ ΠΛΗΡΟΦΟΡΙΚΗ I 4 η ΔΙΑΛΕΞΗ Αριθμητικά Συστήματα ΧΑΣΑΝΗΣ ΒΑΣΙΛΕΙΟΣ
Πρόγραμμα Επικαιροποίησης Γνώσεων Αποφοίτων
 Πρόγραμμα Επικαιροποίησης Γνώσεων Αποφοίτων ΕΝΟΤΗΤΑ Μ1 ΨΗΦΙΑΚΑ ΗΛΕΚΤΡΟΝΙΚΑ Εκπαιδευτής: Γ. Π. ΠΑΤΣΗΣ, Επικ. Καθηγητής, Τμήμα Ηλεκτρονικών Μηχανικών, ΤΕΙ Αθήνας ΚΑΘΟΛΙΚΕΣ ΠΥΛΕΣ NND NOR ΑΛΓΕΒΡΑ OOLE ΘΕΩΡΗΜΑ
Πρόγραμμα Επικαιροποίησης Γνώσεων Αποφοίτων ΕΝΟΤΗΤΑ Μ1 ΨΗΦΙΑΚΑ ΗΛΕΚΤΡΟΝΙΚΑ Εκπαιδευτής: Γ. Π. ΠΑΤΣΗΣ, Επικ. Καθηγητής, Τμήμα Ηλεκτρονικών Μηχανικών, ΤΕΙ Αθήνας ΚΑΘΟΛΙΚΕΣ ΠΥΛΕΣ NND NOR ΑΛΓΕΒΡΑ OOLE ΘΕΩΡΗΜΑ
Σ ή. : υαδικά. Ε ό. ή Ενότητα
 1η Θεµατική Θ ή Ενότητα Ε ό : υαδικά δ ά Συστήµατα Σ ή Μονάδα Ελέγχου Ψηφιακοί Υπολογιστές Αριθµητική Μονάδα Κρυφή Μνήµη Μονάδα Μνήµης ιαχείριση Μονάδων Ι/Ο ίσκοι Οθόνες ικτυακές Μονάδες Πληκτρολόγιο,
1η Θεµατική Θ ή Ενότητα Ε ό : υαδικά δ ά Συστήµατα Σ ή Μονάδα Ελέγχου Ψηφιακοί Υπολογιστές Αριθµητική Μονάδα Κρυφή Μνήµη Μονάδα Μνήµης ιαχείριση Μονάδων Ι/Ο ίσκοι Οθόνες ικτυακές Μονάδες Πληκτρολόγιο,
Αριθµητική υπολογιστών
 Αριθµητική υπολογιστών Μιχάλης ρακόπουλος Υπολογιστική Επιστήµη & Τεχνολογία, #03 1 εκαδικό σύστηµα αρίθµησης Βάση το 10. 10 ψηφία: 0 1 2 3 4 5 6 7 8 9 1 δεκαδικό ψηφίο εκφράζει 1 από 10 πιθανές επιλογές
Αριθµητική υπολογιστών Μιχάλης ρακόπουλος Υπολογιστική Επιστήµη & Τεχνολογία, #03 1 εκαδικό σύστηµα αρίθµησης Βάση το 10. 10 ψηφία: 0 1 2 3 4 5 6 7 8 9 1 δεκαδικό ψηφίο εκφράζει 1 από 10 πιθανές επιλογές
1 η Θεµατική Ενότητα : Δυαδικά Συστήµατα
 1 η Θεµατική Ενότητα : Δυαδικά Συστήµατα Δεκαδικοί Αριθµοί Βάση : 10 Ψηφία : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Αριθµοί: Συντελεστές Χ δυνάµεις του 10 7392.25 = 7x10 3 + 3x10 2 + 9x10 1 + 2x10 0 + 2x10-1 + 5x10-2
1 η Θεµατική Ενότητα : Δυαδικά Συστήµατα Δεκαδικοί Αριθµοί Βάση : 10 Ψηφία : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Αριθµοί: Συντελεστές Χ δυνάµεις του 10 7392.25 = 7x10 3 + 3x10 2 + 9x10 1 + 2x10 0 + 2x10-1 + 5x10-2
ΣΧΕΔΙΑΣΗ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ
 ΣΧΕΔΙΑΣΗ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΑΛΓΕΒΡΑ BOOLE 2017, Δρ. Ηρακλής Σπηλιώτης Γενικοί ορισμοί Αλγεβρική δομή είναι ένα σύνολο στοιχείων και κάποιες συναρτήσεις με πεδίο ορισμού αυτό το σύνολο. Αυτές οι συναρτήσεις
ΣΧΕΔΙΑΣΗ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΑΛΓΕΒΡΑ BOOLE 2017, Δρ. Ηρακλής Σπηλιώτης Γενικοί ορισμοί Αλγεβρική δομή είναι ένα σύνολο στοιχείων και κάποιες συναρτήσεις με πεδίο ορισμού αυτό το σύνολο. Αυτές οι συναρτήσεις
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ
 ΤΕΙ ΙΟΝΙΩΝ ΝΗΣΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΓΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΣΤΗ ΔΙΟΙΚΗΣΗ ΚΑΙ ΣΤΗΝ ΟΙΚΟΝΟΜΙΑ 7 Ο ΜΑΘΗΜΑ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΑΠΟΣΤΟΛΙΑ ΠΑΓΓΕ Περιεχόμενα 2 Δυαδικό Σύστημα Προσημασμένοι δυαδικοί αριθμοί Αφαίρεση
ΤΕΙ ΙΟΝΙΩΝ ΝΗΣΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΓΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΣΤΗ ΔΙΟΙΚΗΣΗ ΚΑΙ ΣΤΗΝ ΟΙΚΟΝΟΜΙΑ 7 Ο ΜΑΘΗΜΑ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΑΠΟΣΤΟΛΙΑ ΠΑΓΓΕ Περιεχόμενα 2 Δυαδικό Σύστημα Προσημασμένοι δυαδικοί αριθμοί Αφαίρεση
Κ15 Ψηφιακή Λογική Σχεδίαση 2: Δυαδικό Σύστημα / Αναπαραστάσεις
 Κ15 Ψηφιακή Λογική Σχεδίαση 2: Δυαδικό Σύστημα / Αναπαραστάσεις Γιάννης Λιαπέρδος TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ Δυαδικό Σύστημα Αρίθμησης Περιεχόμενα 1 Δυαδικό
Κ15 Ψηφιακή Λογική Σχεδίαση 2: Δυαδικό Σύστημα / Αναπαραστάσεις Γιάννης Λιαπέρδος TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ Δυαδικό Σύστημα Αρίθμησης Περιεχόμενα 1 Δυαδικό
ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 3
 ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 3 ΑΠΛΟΠΟΙΗΣΗ και ΥΛΟΠΟΙΗΣΗ ΛΟΓΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Σκοπός: Η κατανόηση της σχέσης µιας λογικής συνάρτησης µε το αντίστοιχο κύκλωµα. Η απλοποίηση λογικών συναρτήσεων
ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 3 ΑΠΛΟΠΟΙΗΣΗ και ΥΛΟΠΟΙΗΣΗ ΛΟΓΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Σκοπός: Η κατανόηση της σχέσης µιας λογικής συνάρτησης µε το αντίστοιχο κύκλωµα. Η απλοποίηση λογικών συναρτήσεων
Δυαδικό Σύστημα Αρίθμησης
 Δυαδικό Σύστημα Αρίθμησης Το δυαδικό σύστημα αρίθμησης χρησιμοποιεί δύο ψηφία. Το 0 και το 1. Τα ψηφία ενός αριθμού στο δυαδικό σύστημα αρίθμησης αντιστοιχίζονται σε δυνάμεις του 2. Μονάδες, δυάδες, τετράδες,
Δυαδικό Σύστημα Αρίθμησης Το δυαδικό σύστημα αρίθμησης χρησιμοποιεί δύο ψηφία. Το 0 και το 1. Τα ψηφία ενός αριθμού στο δυαδικό σύστημα αρίθμησης αντιστοιχίζονται σε δυνάμεις του 2. Μονάδες, δυάδες, τετράδες,
Λογική Σχεδίαση Ψηφιακών Συστημάτων
 Πανεπιστήμιο Θεσσαλίας Τμήμα Πληροφορικής Λογική Σχεδίαση Ψηφιακών Συστημάτων Σταμούλης Γεώργιος georges@uth.gr Δαδαλιάρης Αντώνιος dadaliaris@uth.gr Δυαδική Λογική Η δυαδική λογική ασχολείται με μεταβλητές
Πανεπιστήμιο Θεσσαλίας Τμήμα Πληροφορικής Λογική Σχεδίαση Ψηφιακών Συστημάτων Σταμούλης Γεώργιος georges@uth.gr Δαδαλιάρης Αντώνιος dadaliaris@uth.gr Δυαδική Λογική Η δυαδική λογική ασχολείται με μεταβλητές
ΠΛΗΡΟΦΟΡΙΚΗ I Ενότητα 6
 ΠΛΗΡΟΦΟΡΙΚΗ I Ενότητα 6 ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ Bits & Bytes Bit: η μικρότερη μονάδα πληροφορίας μία από δύο πιθανές καταστάσεις (ναι / όχι, αληθές / ψευδές, n / ff) κωδικοποίηση σε 0 ή 1 δυαδικό σύστημα
ΠΛΗΡΟΦΟΡΙΚΗ I Ενότητα 6 ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ Bits & Bytes Bit: η μικρότερη μονάδα πληροφορίας μία από δύο πιθανές καταστάσεις (ναι / όχι, αληθές / ψευδές, n / ff) κωδικοποίηση σε 0 ή 1 δυαδικό σύστημα
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΠΛΗ-21
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΠΛΗ-2 ΨΗΦΙΑΚΗ ΣΧΕΔΙΑΣΗ ΑΣΚΗΣΕΙΙΣ ΓΡΑΠΤΩΝ ΕΡΓΑΣΙΙΩΝ & ΘΕΜΑΤΩΝ ΕΞΕΤΑΣΕΩΝ ΣΥΝΤΕΛΕΣΤΕΣ
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΠΛΗ-2 ΨΗΦΙΑΚΗ ΣΧΕΔΙΑΣΗ ΑΣΚΗΣΕΙΙΣ ΓΡΑΠΤΩΝ ΕΡΓΑΣΙΙΩΝ & ΘΕΜΑΤΩΝ ΕΞΕΤΑΣΕΩΝ ΣΥΝΤΕΛΕΣΤΕΣ
Πανεπιστήμιο Δυτικής Μακεδονίας. Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών. Ψηφιακή Σχεδίαση
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ψηφιακή Σχεδίαση Ενότητα 3: Ελαχιστοποίηση σε επίπεδο τιμών, Χάρτες Karnaugh, Πρωτεύοντες όροι Δρ. Μηνάς Δασυγένης mdasyg@ieee.org Εργαστήριο Ψηφιακών Συστημάτων
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ψηφιακή Σχεδίαση Ενότητα 3: Ελαχιστοποίηση σε επίπεδο τιμών, Χάρτες Karnaugh, Πρωτεύοντες όροι Δρ. Μηνάς Δασυγένης mdasyg@ieee.org Εργαστήριο Ψηφιακών Συστημάτων
Ψηφιακά Συστήματα. 1. Συστήματα Αριθμών
 Ψηφιακά Συστήματα 1. Συστήματα Αριθμών Βιβλιογραφία 1. Φανουράκης Κ., Πάτσης Γ., Τσακιρίδης Ο., Θεωρία και Ασκήσεις Ψηφιακών Ηλεκτρονικών, ΜΑΡΙΑ ΠΑΡΙΚΟΥ & ΣΙΑ ΕΠΕ, 2016. [59382199] 2. Floyd Thomas L.,
Ψηφιακά Συστήματα 1. Συστήματα Αριθμών Βιβλιογραφία 1. Φανουράκης Κ., Πάτσης Γ., Τσακιρίδης Ο., Θεωρία και Ασκήσεις Ψηφιακών Ηλεκτρονικών, ΜΑΡΙΑ ΠΑΡΙΚΟΥ & ΣΙΑ ΕΠΕ, 2016. [59382199] 2. Floyd Thomas L.,
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία
 ΗΜΥ 100 Εισαγωγή στην Τεχνολογία Στέλιος Τιμοθέου ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ ΜΑΣ ΣΗΜΕΡΑ Συστήματα αρίθμησης Δυαδικό αριθμητικό
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία Στέλιος Τιμοθέου ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ ΜΑΣ ΣΗΜΕΡΑ Συστήματα αρίθμησης Δυαδικό αριθμητικό
Πληροφορική. Ενότητα 4 η : Κωδικοποίηση & Παράσταση Δεδομένων. Ι. Ψαρομήλιγκος Τμήμα Λογιστικής & Χρηματοοικονομικής
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Πληροφορική Ενότητα 4 η : Κωδικοποίηση & Παράσταση Δεδομένων Ι. Ψαρομήλιγκος Τμήμα Λογιστικής & Χρηματοοικονομικής Άδειες Χρήσης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Πληροφορική Ενότητα 4 η : Κωδικοποίηση & Παράσταση Δεδομένων Ι. Ψαρομήλιγκος Τμήμα Λογιστικής & Χρηματοοικονομικής Άδειες Χρήσης
Ελίνα Μακρή
 Ελίνα Μακρή elmak@unipi.gr Μετατροπή Αριθμητικών Συστημάτων Πράξεις στα Αριθμητικά Συστήματα Σχεδίαση Ψηφιακών Κυκλωμάτων με Logism Άλγεβρα Boole Λογικές Πύλες (AND, OR, NOT, NAND, XOR) Flip Flops (D,
Ελίνα Μακρή elmak@unipi.gr Μετατροπή Αριθμητικών Συστημάτων Πράξεις στα Αριθμητικά Συστήματα Σχεδίαση Ψηφιακών Κυκλωμάτων με Logism Άλγεβρα Boole Λογικές Πύλες (AND, OR, NOT, NAND, XOR) Flip Flops (D,
Κεφάλαιο 4. Λογική Σχεδίαση
 Κεφάλαιο 4 Λογική Σχεδίαση 4.1 Εισαγωγή Λογικές συναρτήσεις ονομάζουμε εκείνες για τις οποίες μπορούμε να αποφασίσουμε αν είναι αληθείς ή όχι. Χειριζόμαστε τις λογικές προτάσεις στην συγγραφή λογισμικού
Κεφάλαιο 4 Λογική Σχεδίαση 4.1 Εισαγωγή Λογικές συναρτήσεις ονομάζουμε εκείνες για τις οποίες μπορούμε να αποφασίσουμε αν είναι αληθείς ή όχι. Χειριζόμαστε τις λογικές προτάσεις στην συγγραφή λογισμικού
Τετάρτη 5-12/11/2014. ΣΗΜΕΙΩΣΕΙΣ 3 ου και 4 ου ΜΑΘΗΜΑΤΟΣ ΕΙΔΙΚΟΤΗΤΑ: ΤΕΧΝΙΚΟΣ ΕΦΑΡΜΟΓΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΑΘΗΜΑ: ΑΡΧΙΤΕΚΤΟΝΙΚΗ Η/Υ Α ΕΞΑΜΗΝΟ
 Τετάρτη 5-12/11/2014 ΣΗΜΕΙΩΣΕΙΣ 3 ου και 4 ου ΜΑΘΗΜΑΤΟΣ ΕΙΔΙΚΟΤΗΤΑ: ΤΕΧΝΙΚΟΣ ΕΦΑΡΜΟΓΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΑΘΗΜΑ: ΑΡΧΙΤΕΚΤΟΝΙΚΗ Η/Υ Α ΕΞΑΜΗΝΟ ΕΚΠΑΙΔΕΥΤΗΣ: ΤΡΟΧΙΔΗΣ ΠΑΝΑΓΙΩΤΗΣ 1. Παράσταση και οργάνωση δεδομένων
Τετάρτη 5-12/11/2014 ΣΗΜΕΙΩΣΕΙΣ 3 ου και 4 ου ΜΑΘΗΜΑΤΟΣ ΕΙΔΙΚΟΤΗΤΑ: ΤΕΧΝΙΚΟΣ ΕΦΑΡΜΟΓΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΑΘΗΜΑ: ΑΡΧΙΤΕΚΤΟΝΙΚΗ Η/Υ Α ΕΞΑΜΗΝΟ ΕΚΠΑΙΔΕΥΤΗΣ: ΤΡΟΧΙΔΗΣ ΠΑΝΑΓΙΩΤΗΣ 1. Παράσταση και οργάνωση δεδομένων
Ψηφιακή Σχεδίαση Εργαστήριο Τ.Ε.Ι. ΚΡΗΤΗΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜ. ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ
 Ψηφιακή Σχεδίαση Εργαστήριο Τ.Ε.Ι. ΚΡΗΤΗΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜ. ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ 2015-2016 Άλγεβρα Boole (Boolean Algebra) Βασικοί ορισμοί Η άλγεβρα Boole μπορεί να οριστεί
Ψηφιακή Σχεδίαση Εργαστήριο Τ.Ε.Ι. ΚΡΗΤΗΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜ. ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ 2015-2016 Άλγεβρα Boole (Boolean Algebra) Βασικοί ορισμοί Η άλγεβρα Boole μπορεί να οριστεί
Κεφάλαιο 2 Η έννοια και η παράσταση της πληροφορίας στον ΗΥ. Εφ. Πληροφορικής Κεφ. 2 Καραμαούνας Πολύκαρπος 1
 Κεφάλαιο 2 Η έννοια και η παράσταση της πληροφορίας στον ΗΥ Καραμαούνας Πολύκαρπος 1 2.1Η έννοια της πληροφορίας Δεδομένα Πληροφορία Καραμαούνας Πολύκαρπος 2 2.2 ΗΥ Το βασικό εργαλείο επεξεργασίας και
Κεφάλαιο 2 Η έννοια και η παράσταση της πληροφορίας στον ΗΥ Καραμαούνας Πολύκαρπος 1 2.1Η έννοια της πληροφορίας Δεδομένα Πληροφορία Καραμαούνας Πολύκαρπος 2 2.2 ΗΥ Το βασικό εργαλείο επεξεργασίας και
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ
 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ Κ. Δεμέστιχας Εργαστήριο Πληροφορικής Γεωπονικό Πανεπιστήμιο Αθηνών Επικοινωνία μέσω e-mail: cdemest@aua.gr, cdemest@cn.ntua.gr 1 2. ΑΡΙΘΜΗΤΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ ΜΕΡΟΣ Α 2 Τεχνολογία
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ Κ. Δεμέστιχας Εργαστήριο Πληροφορικής Γεωπονικό Πανεπιστήμιο Αθηνών Επικοινωνία μέσω e-mail: cdemest@aua.gr, cdemest@cn.ntua.gr 1 2. ΑΡΙΘΜΗΤΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ ΜΕΡΟΣ Α 2 Τεχνολογία
Αριθμητικά Συστήματα
 Αριθμητικά Συστήματα Σε οποιοδήποτε αριθμητικό σύστημα, με βάση τον αριθμό Β, ένας ακέραιος αριθμός με πλήθος ψηφίων ν, εκφράζεται ως ακολούθως: α ν-1 α ν-2 α 1 α 0 = α ν-1 Β ν-1 + α ν-2 Β ν-2 + + α 1
Αριθμητικά Συστήματα Σε οποιοδήποτε αριθμητικό σύστημα, με βάση τον αριθμό Β, ένας ακέραιος αριθμός με πλήθος ψηφίων ν, εκφράζεται ως ακολούθως: α ν-1 α ν-2 α 1 α 0 = α ν-1 Β ν-1 + α ν-2 Β ν-2 + + α 1
ΨΗΦΙΑΚΗ ΛΟΓΙΚΗ ΣΧΕ ΙΑΣΗ
 Τµήµα Ηλεκτρολόγων Μηχανικών Εργαστήριο Ενσύρµατης Τηλεπικοινωνίας ΨΗΦΙΑΚΗ ΛΟΓΙΚΗ ΣΧΕ ΙΑΣΗ ιδάσκων: Καθηγητής Ν. Φακωτάκης Τµήµα Ηλεκτρολόγων Μηχανικών Εργαστήριο Ενσύρµατης Τηλεπικοινωνίας ΨΗΦΙΑΚΗ ΛΟΓΙΚΗ
Τµήµα Ηλεκτρολόγων Μηχανικών Εργαστήριο Ενσύρµατης Τηλεπικοινωνίας ΨΗΦΙΑΚΗ ΛΟΓΙΚΗ ΣΧΕ ΙΑΣΗ ιδάσκων: Καθηγητής Ν. Φακωτάκης Τµήµα Ηλεκτρολόγων Μηχανικών Εργαστήριο Ενσύρµατης Τηλεπικοινωνίας ΨΗΦΙΑΚΗ ΛΟΓΙΚΗ
ΕΙΣΑΓΩΓΗ ΣΤΟΥΣ ΥΠΟΛΟΓΙΣΤΕΣ. ΜΑΘΗΜΑ 2 ο. ΑΛΓΕΒΡΑ Boole ΛΟΓΙΚΑ ΚΥΚΛΩΜΑΤΑ
 ΕΙΣΑΓΩΓΗ ΣΤΟΥΣ ΥΠΟΛΟΓΙΣΤΕΣ ΜΑΘΗΜΑ 2 ο ΑΛΓΕΒΡΑ Boole ΛΟΓΙΚΑ ΚΥΚΛΩΜΑΤΑ 2009-10 ΕΙΣΑΓΩΓΗ ΣΤΟΥΣ ΥΠΟΛΟΓΙΣΤΕΣ 1 Άλγεβρα Βοοle η θεωρητική βάση των λογικών κυκλωμάτων Η άλγεβρα Βοοle ορίζεται επάνω στο σύνολο
ΕΙΣΑΓΩΓΗ ΣΤΟΥΣ ΥΠΟΛΟΓΙΣΤΕΣ ΜΑΘΗΜΑ 2 ο ΑΛΓΕΒΡΑ Boole ΛΟΓΙΚΑ ΚΥΚΛΩΜΑΤΑ 2009-10 ΕΙΣΑΓΩΓΗ ΣΤΟΥΣ ΥΠΟΛΟΓΙΣΤΕΣ 1 Άλγεβρα Βοοle η θεωρητική βάση των λογικών κυκλωμάτων Η άλγεβρα Βοοle ορίζεται επάνω στο σύνολο
Κεφάλαιο 1. Συστήματα αρίθμησης και αναπαράστασης
 Κεφάλαιο 1 Συστήματα αρίθμησης και αναπαράστασης 1.1 Εισαγωγή Οι υπολογιστές αναπαριστούν όλα τα είδη πληροφορίας ως δυαδικά δεδομένα. Έτσι, για την ευκολότερη και ταχύτερη επεξεργασία των διαφόρων πληροφοριών,
Κεφάλαιο 1 Συστήματα αρίθμησης και αναπαράστασης 1.1 Εισαγωγή Οι υπολογιστές αναπαριστούν όλα τα είδη πληροφορίας ως δυαδικά δεδομένα. Έτσι, για την ευκολότερη και ταχύτερη επεξεργασία των διαφόρων πληροφοριών,
Αριθμητική Ανάλυση & Εφαρμογές
 Αριθμητική Ανάλυση & Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 2017-2018 Υπολογισμοί και Σφάλματα Παράσταση Πραγματικών Αριθμών Συστήματα Αριθμών Παράσταση Ακέραιου
Αριθμητική Ανάλυση & Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 2017-2018 Υπολογισμοί και Σφάλματα Παράσταση Πραγματικών Αριθμών Συστήματα Αριθμών Παράσταση Ακέραιου
Γενικά Στοιχεία Ηλεκτρονικού Υπολογιστή
 Γενικά Στοιχεία Ηλεκτρονικού Υπολογιστή 1. Ηλεκτρονικός Υπολογιστής Ο Ηλεκτρονικός Υπολογιστής είναι μια συσκευή, μεγάλη ή μικρή, που επεξεργάζεται δεδομένα και εκτελεί την εργασία του σύμφωνα με τα παρακάτω
Γενικά Στοιχεία Ηλεκτρονικού Υπολογιστή 1. Ηλεκτρονικός Υπολογιστής Ο Ηλεκτρονικός Υπολογιστής είναι μια συσκευή, μεγάλη ή μικρή, που επεξεργάζεται δεδομένα και εκτελεί την εργασία του σύμφωνα με τα παρακάτω
Εισαγωγή στους Η/Υ. Γιώργος Δημητρίου. Μάθημα 7 και 8: Αναπαραστάσεις. Πανεπιστήμιο Θεσσαλίας - Τμήμα Πληροφορικής
 Γιώργος Δημητρίου Μάθημα 7 και 8: Αναπαραστάσεις Αναπαράσταση Πληροφορίας Η/Υ Αριθμητικά δεδομένα Σταθερής υποδιαστολής Κινητής υποδιαστολής Μη αριθμητικά δεδομένα Χαρακτήρες Ειδικοί κώδικες Εντολές Γλώσσα
Γιώργος Δημητρίου Μάθημα 7 και 8: Αναπαραστάσεις Αναπαράσταση Πληροφορίας Η/Υ Αριθμητικά δεδομένα Σταθερής υποδιαστολής Κινητής υποδιαστολής Μη αριθμητικά δεδομένα Χαρακτήρες Ειδικοί κώδικες Εντολές Γλώσσα
Εισαγωγή στην Πληροφορική ΓΕΝΙΚΟ ΤΜΗΜΑ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ TEI ΧΑΛΚΙ ΑΣ
 Εισαγωγή στην Πληροφορική 1 Περιεχόµενα - Κωδικοποιήσεις - Αριθµητικά Συστήµατα 2 Ηλεκτρονικός Υπολογιστής Είπαµε ότι είναι, µία Ηλεκτρονική Μηχανή, που δουλεύει κάτω από τον έλεγχο εντολών αποθηκευµένων
Εισαγωγή στην Πληροφορική 1 Περιεχόµενα - Κωδικοποιήσεις - Αριθµητικά Συστήµατα 2 Ηλεκτρονικός Υπολογιστής Είπαµε ότι είναι, µία Ηλεκτρονική Μηχανή, που δουλεύει κάτω από τον έλεγχο εντολών αποθηκευµένων
Υπολογιστές και Πληροφορία 1
 ΗΜΥ-20: Σχεδιασμός Ψηφιακών Συστημάτων Σκοπός του μαθήματος Λογικός Σχεδιασμός και Σχεδιασμός Η/Υ Εισαγωγή, Υπολογιστές και Πληροφορία Διδάσκουσα: Μαρία Κ. Μιχαήλ Βασικές έννοιες & εργαλεία που χρησιμοποιούνται
ΗΜΥ-20: Σχεδιασμός Ψηφιακών Συστημάτων Σκοπός του μαθήματος Λογικός Σχεδιασμός και Σχεδιασμός Η/Υ Εισαγωγή, Υπολογιστές και Πληροφορία Διδάσκουσα: Μαρία Κ. Μιχαήλ Βασικές έννοιες & εργαλεία που χρησιμοποιούνται
Πανεπιστήμιο Δυτικής Μακεδονίας. Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών. Ψηφιακή Σχεδίαση
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ψηφιακή Σχεδίαση Ενότητα 1: Εισαγωγή σε βασικές έννοιες δυαδικού συστήματος Δρ. Μηνάς Δασυγένης mdasyg@ieee.org Εργαστήριο Ψηφιακών Συστημάτων και Αρχιτεκτονικής
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ψηφιακή Σχεδίαση Ενότητα 1: Εισαγωγή σε βασικές έννοιες δυαδικού συστήματος Δρ. Μηνάς Δασυγένης mdasyg@ieee.org Εργαστήριο Ψηφιακών Συστημάτων και Αρχιτεκτονικής
2 η Θεµατική Ενότητα : Άλγεβρα Boole και Λογικές Πύλες. Βασικοί Ορισµοί
 2 η Θεµατική Ενότητα : Άλγεβρα Boole και Λογικές Πύλες Βασικοί Ορισµοί υαδικός Τελεστής (Binary Operator): σε κάθε ζεύγος από το S αντιστοιχίζει ένα στοιχείο του S = set, σύνολο Συνηθισµένα Αξιώµατα (α,
2 η Θεµατική Ενότητα : Άλγεβρα Boole και Λογικές Πύλες Βασικοί Ορισµοί υαδικός Τελεστής (Binary Operator): σε κάθε ζεύγος από το S αντιστοιχίζει ένα στοιχείο του S = set, σύνολο Συνηθισµένα Αξιώµατα (α,
Ενότητα 4 ΛΟΓΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ ΛΟΓΙΚΑ ΚΥΚΛΩΜΑΤΑ ΔΥΟ ΕΠΙΠΕΔΩΝ
 Ενότητα 4 ΛΟΓΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ ΛΟΓΙΚΑ ΚΥΚΛΩΜΑΤΑ ΔΥΟ ΕΠΙΠΕΔΩΝ Γενικές Γραμμές Λογικές Συναρτήσεις 2 Επιπέδων Συμπλήρωμα Λογικής Συνάρτησης Πίνακας Αλήθειας Κανονική Μορφή Αθροίσματος Γινομένων Λίστα Ελαχιστόρων
Ενότητα 4 ΛΟΓΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ ΛΟΓΙΚΑ ΚΥΚΛΩΜΑΤΑ ΔΥΟ ΕΠΙΠΕΔΩΝ Γενικές Γραμμές Λογικές Συναρτήσεις 2 Επιπέδων Συμπλήρωμα Λογικής Συνάρτησης Πίνακας Αλήθειας Κανονική Μορφή Αθροίσματος Γινομένων Λίστα Ελαχιστόρων
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Εργαστήριο Ηλεκτρονικής. Ψηφιακά Ηλεκτρονικά. Συνδυαστική Λογική. Επιμέλεια Διαφανειών: Δ.
 Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Συνδυαστική Λογική Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Ψηφιακά Κυκλώματα Τα ψηφιακά κυκλώματα διακρίνονται σε συνδυαστικά (combinational)
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Συνδυαστική Λογική Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Ψηφιακά Κυκλώματα Τα ψηφιακά κυκλώματα διακρίνονται σε συνδυαστικά (combinational)
Αριθμητικά Συστήματα
 Αριθμητικά Συστήματα Οργάνωση Δεδομένων (1/2) Bits: Η μικρότερη αριθμητική μονάδα ενός υπολογιστικού συστήματος, η οποία δείχνει δύο καταστάσεις, 0 ή 1 (αληθές η ψευδές). Nibbles: Μονάδα 4 bit που παριστά
Αριθμητικά Συστήματα Οργάνωση Δεδομένων (1/2) Bits: Η μικρότερη αριθμητική μονάδα ενός υπολογιστικού συστήματος, η οποία δείχνει δύο καταστάσεις, 0 ή 1 (αληθές η ψευδές). Nibbles: Μονάδα 4 bit που παριστά
Πανεπιστήμιο Δυτικής Μακεδονίας. Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών. Ψηφιακή Σχεδίαση
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ψηφιακή Σχεδίαση Ενότητα 2: Αλγεβρα Boole, Δυαδική Λογική, Ελαχιστόροι, Μεγιστόροι Δρ. Μηνάς Δασυγένης mdasyg@ieee.org Εργαστήριο Ψηφιακών Συστημάτων και
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ψηφιακή Σχεδίαση Ενότητα 2: Αλγεβρα Boole, Δυαδική Λογική, Ελαχιστόροι, Μεγιστόροι Δρ. Μηνάς Δασυγένης mdasyg@ieee.org Εργαστήριο Ψηφιακών Συστημάτων και
5.1 Θεωρητική εισαγωγή
 ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 5 ΚΩ ΙΚΟΠΟΙΗΣΗ BCD Σκοπός: Η κατανόηση της µετατροπής ενός τύπου δυαδικής πληροφορίας σε άλλον (κωδικοποίηση/αποκωδικοποίηση) µε τη µελέτη της κωδικοποίησης BCD
ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 5 ΚΩ ΙΚΟΠΟΙΗΣΗ BCD Σκοπός: Η κατανόηση της µετατροπής ενός τύπου δυαδικής πληροφορίας σε άλλον (κωδικοποίηση/αποκωδικοποίηση) µε τη µελέτη της κωδικοποίησης BCD
ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ. Κεφάλαιο 3
 ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ Κεφάλαιο 3 Κεντρική Μονάδα Επεξεργασίας Κεντρική Μονάδα Επεξεργασίας Μονάδα επεξεργασίας δεδομένων Μονάδα ελέγχου Μονάδα επεξεργασίας δεδομένων Δομή Αριθμητικής Λογικής Μονάδας
ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ Κεφάλαιο 3 Κεντρική Μονάδα Επεξεργασίας Κεντρική Μονάδα Επεξεργασίας Μονάδα επεξεργασίας δεδομένων Μονάδα ελέγχου Μονάδα επεξεργασίας δεδομένων Δομή Αριθμητικής Λογικής Μονάδας
a -j a 5 a 4 a 3 a 2 a 1 a 0, a -1 a -2 a -3
 ΑΣΚΗΣΗ 5 ΑΘΡΟΙΣΤΕΣ - ΑΦΑΙΡΕΤΕΣ 5.1. ΣΚΟΠΟΣ Η πραγματοποίηση της αριθμητικής πρόσθεσης και αφαίρεσης με λογικά κυκλώματα. 5.2. ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ ΣΥΣΤΗΜΑΤΑ ΑΡΙΘΜΗΣΗΣ: Κάθε σύστημα αρίθμησης χαρακτηρίζεται
ΑΣΚΗΣΗ 5 ΑΘΡΟΙΣΤΕΣ - ΑΦΑΙΡΕΤΕΣ 5.1. ΣΚΟΠΟΣ Η πραγματοποίηση της αριθμητικής πρόσθεσης και αφαίρεσης με λογικά κυκλώματα. 5.2. ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ ΣΥΣΤΗΜΑΤΑ ΑΡΙΘΜΗΣΗΣ: Κάθε σύστημα αρίθμησης χαρακτηρίζεται
Ψηφιακά Κυκλώματα Ι. Μάθημα 1: Δυαδικά συστήματα - Κώδικες. Λευτέρης Καπετανάκης
 ΤΛ2002 Ψηφιακά Κυκλώματα Ι Μάθημα 1: Δυαδικά συστήματα - Κώδικες Λευτέρης Καπετανάκης ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΡΗΤΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΗΣ Άνοιξη 2011 ΤΛ-2002: L1 Slide 1 Ψηφιακά Συστήματα ΤΛ-2002:
ΤΛ2002 Ψηφιακά Κυκλώματα Ι Μάθημα 1: Δυαδικά συστήματα - Κώδικες Λευτέρης Καπετανάκης ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΡΗΤΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΗΣ Άνοιξη 2011 ΤΛ-2002: L1 Slide 1 Ψηφιακά Συστήματα ΤΛ-2002:
ΑΣΠΑΙΤΕ Εργαστήριο Ψηφιακών Συστημάτων & Μικροϋπολογιστών Εργαστηριακές Ασκήσεις για το μάθημα «Λογική Σχεδίαση» ΑΣΚΗΣΗ 3 ΠΙΝΑΚΕΣ KARNAUGH
 ΑΣΚΗΣΗ 3 ΠΙΝΑΚΕΣ KARNAUGH 3.1 ΣΚΟΠΟΣ Η κατανόηση της απλοποίησης λογικών συναρτήσεων με χρήση της Άλγεβρας Boole και με χρήση των Πινάκων Karnaugh (Karnaugh maps). 3.2 ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ 3.2.1 ΑΠΛΟΠΟΙΗΣΗ
ΑΣΚΗΣΗ 3 ΠΙΝΑΚΕΣ KARNAUGH 3.1 ΣΚΟΠΟΣ Η κατανόηση της απλοποίησης λογικών συναρτήσεων με χρήση της Άλγεβρας Boole και με χρήση των Πινάκων Karnaugh (Karnaugh maps). 3.2 ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ 3.2.1 ΑΠΛΟΠΟΙΗΣΗ
Ύλη Λογικού Σχεδιασµού Ι
 4 η Θεµατική Ενότητα : Συνδυαστική Λογική Ύλη Λογικού Σχεδιασµού Ι Κεφ 2 Κεφ 3 Κεφ 4 Κεφ 6 Συνδυαστική Λογική 2 Εισαγωγή Λογικά Κυκλώµατα Συνδυαστικά: Οι έξοδοι είναι συνάρτηση των εισόδων Ακολουθιακά:
4 η Θεµατική Ενότητα : Συνδυαστική Λογική Ύλη Λογικού Σχεδιασµού Ι Κεφ 2 Κεφ 3 Κεφ 4 Κεφ 6 Συνδυαστική Λογική 2 Εισαγωγή Λογικά Κυκλώµατα Συνδυαστικά: Οι έξοδοι είναι συνάρτηση των εισόδων Ακολουθιακά:
Λογική Σχεδίαση Ι - Εξεταστική Φεβρουαρίου 2013 Διάρκεια εξέτασης : 160 Ονοματεπώνυμο : Α. Μ. Έτος σπουδών:
 Λογική Σχεδίαση Ι - Εξεταστική Φεβρουαρίου 23 Διάρκεια εξέτασης : 6 Ονοματεπώνυμο : Α. Μ. Έτος σπουδών: Θέμα (,5 μονάδες) Στις εισόδους του ακόλουθου κυκλώματος c b a εφαρμόζονται οι κάτωθι κυματομορφές.
Λογική Σχεδίαση Ι - Εξεταστική Φεβρουαρίου 23 Διάρκεια εξέτασης : 6 Ονοματεπώνυμο : Α. Μ. Έτος σπουδών: Θέμα (,5 μονάδες) Στις εισόδους του ακόλουθου κυκλώματος c b a εφαρμόζονται οι κάτωθι κυματομορφές.
Ενότητα 8 Η ΠΥΛΗ XOR ΚΑΙ ΟΙ ΕΦΑΡΜΟΓΕΣ ΤΗΣ ΚΩΔΙΚΟΠΟΙΗΣΗ
 Ενότητα 8 Η ΠΛΗ XOR ΚΑΙ ΟΙ ΕΦΑΡΜΟΓΕΣ ΤΗΣ ΚΩΔΙΚΟΠΟΙΗΣΗ Γενικές Γραμμές Πύλες XOR και XNOR λοποιήσεις με AND-OR-INV Κώδικας Ισοτιμίας (Parity) Άρτια και Περιττή Συνάρτηση Κυκλώματα ανίχνευσης λαθών Συγκριτές
Ενότητα 8 Η ΠΛΗ XOR ΚΑΙ ΟΙ ΕΦΑΡΜΟΓΕΣ ΤΗΣ ΚΩΔΙΚΟΠΟΙΗΣΗ Γενικές Γραμμές Πύλες XOR και XNOR λοποιήσεις με AND-OR-INV Κώδικας Ισοτιμίας (Parity) Άρτια και Περιττή Συνάρτηση Κυκλώματα ανίχνευσης λαθών Συγκριτές
ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ. ΑΝΔΡΕΑΣ Δ. ΤΣΙΓΚΟΠΟΥΛΟΣ Δρ. ΗΛΕΚΤΡΟΛΟΓΟΣ ΜΗΧΑΝΙΚΟΣ EΠΙΚΟΥΡΟΣ ΚΑΘΗΓΗΤΗΣ ΣΝΔ
 ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ ΑΝΔΡΕΑΣ Δ. ΤΣΙΓΚΟΠΟΥΛΟΣ Δρ. ΗΛΕΚΤΡΟΛΟΓΟΣ ΜΗΧΑΝΙΚΟΣ EΠΙΚΟΥΡΟΣ ΚΑΘΗΓΗΤΗΣ ΣΝΔ ΣΧΟΛΗ ΝΑΥΤΙΚΩΝ ΔΟΚΙΜΩΝ ΠΕΙΡΑΙΑΣ 2014 - 2 - - 3 - ΠΕΡΙΕΧΟΜΕΝΑ ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ...5 ΠΡΟΛΟΓΟΣ...5 1. ΕΙΣΑΓΩΓΗ...7
ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ ΑΝΔΡΕΑΣ Δ. ΤΣΙΓΚΟΠΟΥΛΟΣ Δρ. ΗΛΕΚΤΡΟΛΟΓΟΣ ΜΗΧΑΝΙΚΟΣ EΠΙΚΟΥΡΟΣ ΚΑΘΗΓΗΤΗΣ ΣΝΔ ΣΧΟΛΗ ΝΑΥΤΙΚΩΝ ΔΟΚΙΜΩΝ ΠΕΙΡΑΙΑΣ 2014 - 2 - - 3 - ΠΕΡΙΕΧΟΜΕΝΑ ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ...5 ΠΡΟΛΟΓΟΣ...5 1. ΕΙΣΑΓΩΓΗ...7
Αθροιστές. Ημιαθροιστής
 Αθροιστές Η πιο βασική αριθμητική πράξη είναι η πρόσθεση. Για την πρόσθεση δύο δυαδικών ψηφίων υπάρχουν τέσσερις δυνατές περιπτώσεις: +=, +=, +=, +=. Οι τρεις πρώτες πράξεις δημιουργούν ένα άθροισμα που
Αθροιστές Η πιο βασική αριθμητική πράξη είναι η πρόσθεση. Για την πρόσθεση δύο δυαδικών ψηφίων υπάρχουν τέσσερις δυνατές περιπτώσεις: +=, +=, +=, +=. Οι τρεις πρώτες πράξεις δημιουργούν ένα άθροισμα που
Παράσταση αριθμών «κινητής υποδιαστολής» floating point
 Παράσταση αριθμών «κινητής υποδιαστολής» floating point Με n bits μπορούμε να παραστήσουμε 2 n διαφορετικούς αριθμούς π.χ. με n=32 μπορούμε να παραστήσουμε τους αριθμούς από έως 2 32 -= 4,294,967,295 4
Παράσταση αριθμών «κινητής υποδιαστολής» floating point Με n bits μπορούμε να παραστήσουμε 2 n διαφορετικούς αριθμούς π.χ. με n=32 μπορούμε να παραστήσουμε τους αριθμούς από έως 2 32 -= 4,294,967,295 4
2. ΑΡΙΘΜΗΤΙΚΗ ΤΟΥ ΥΠΟΛΟΓΙΣΤΗ. 2.1 Αριθμητικά συστήματα
 2. ΑΡΙΘΜΗΤΙΚΗ ΤΟΥ ΥΠΟΛΟΓΙΣΤΗ 2.1 Αριθμητικά συστήματα Κάθε πραγματικός αριθμός χ μπορεί να παρασταθεί σε ένα αριθμητικό σύστημα με βάση β>1 με μια δυναμοσειρά της μορφής, -οο * = ± Σ ψ β " (2 1) η - ν
2. ΑΡΙΘΜΗΤΙΚΗ ΤΟΥ ΥΠΟΛΟΓΙΣΤΗ 2.1 Αριθμητικά συστήματα Κάθε πραγματικός αριθμός χ μπορεί να παρασταθεί σε ένα αριθμητικό σύστημα με βάση β>1 με μια δυναμοσειρά της μορφής, -οο * = ± Σ ψ β " (2 1) η - ν
9. OIΚΟΥΜΕΝΙΚΕΣ ΠΥΛΕΣ ΠΟΛΛΑΠΛΩΝ ΕΙΣΟ ΩΝ
 ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ 61 9. OIΚΟΥΜΕΝΙΚΕΣ ΠΥΛΕΣ ΠΟΛΛΑΠΛΩΝ ΕΙΣΟ ΩΝ I. Βασική Θεωρία Οι πύλες NAND και NOR ονομάζονται οικουμενικές πύλες (universal gates) γιατί κάθε συνδυαστικό κύκλωμα μπορεί να υλοποιηθεί
ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ 61 9. OIΚΟΥΜΕΝΙΚΕΣ ΠΥΛΕΣ ΠΟΛΛΑΠΛΩΝ ΕΙΣΟ ΩΝ I. Βασική Θεωρία Οι πύλες NAND και NOR ονομάζονται οικουμενικές πύλες (universal gates) γιατί κάθε συνδυαστικό κύκλωμα μπορεί να υλοποιηθεί
2 η Θεµατική Ενότητα : Άλγεβρα Boole και Λογικές Πύλες. Επιµέλεια διαφανειών: Χρ. Καβουσιανός
 2 η Θεµατική Ενότητα : Άλγεβρα Boole και Λογικές Πύλες Επιµέλεια διαφανειών: Χρ. Καβουσιανός Βασικοί Ορισµοί Δυαδικός Τελεστής (Binary Operator): σε κάθε ζεύγος από το Σ αντιστοιχίζει ένα στοιχείο του
2 η Θεµατική Ενότητα : Άλγεβρα Boole και Λογικές Πύλες Επιµέλεια διαφανειών: Χρ. Καβουσιανός Βασικοί Ορισµοί Δυαδικός Τελεστής (Binary Operator): σε κάθε ζεύγος από το Σ αντιστοιχίζει ένα στοιχείο του
2 η Θεµατική Ενότητα : Άλγεβρα Boole και Λογικές Πύλες
 2 η Θεµατική Ενότητα : Άλγεβρα Boole και Λογικές Πύλες Βασικοί Ορισµοί υαδικός Τελεστής (Binary Operator): σε κάθε ζεύγος από το S αντιστοιχίζει ένα στοιχείο του S. Συνηθισµένα Αξιώµατα (α, β, γ, 0) Σ,,
2 η Θεµατική Ενότητα : Άλγεβρα Boole και Λογικές Πύλες Βασικοί Ορισµοί υαδικός Τελεστής (Binary Operator): σε κάθε ζεύγος από το S αντιστοιχίζει ένα στοιχείο του S. Συνηθισµένα Αξιώµατα (α, β, γ, 0) Σ,,
Εισαγωγή στην επιστήμη των υπολογιστών
 Εισαγωγή στην επιστήμη των υπολογιστών Υπολογιστές και Δεδομένα Κεφάλαιο 3ο Αναπαράσταση Αριθμών www.di.uoa.gr/~organosi 1 Δεκαδικό και Δυαδικό Δεκαδικό σύστημα 2 3 Δεκαδικό και Δυαδικό Δυαδικό Σύστημα
Εισαγωγή στην επιστήμη των υπολογιστών Υπολογιστές και Δεδομένα Κεφάλαιο 3ο Αναπαράσταση Αριθμών www.di.uoa.gr/~organosi 1 Δεκαδικό και Δυαδικό Δεκαδικό σύστημα 2 3 Δεκαδικό και Δυαδικό Δυαδικό Σύστημα
! Εάν ο αριθμός διαθέτει περισσότερα bits, χρησιμοποιούμε μεγαλύτερες δυνάμεις του 2. ! Προσοχή στη θέση του περισσότερο σημαντικού bit!
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 25-6 Πράξεις με δυαδικούς αριθμούς (αριθμητικές ) http://di.ionio.gr/~mistral/tp/csintro/ Αριθμοί Πράξεις με δυαδικούς αριθμούς
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 25-6 Πράξεις με δυαδικούς αριθμούς (αριθμητικές ) http://di.ionio.gr/~mistral/tp/csintro/ Αριθμοί Πράξεις με δυαδικούς αριθμούς
Λογική Σχεδίαση Ψηφιακών Συστημάτων
 Πανεπιστήμιο Θεσσαλίας Τμήμα Πληροφορικής Λογική Σχεδίαση Ψηφιακών Συστημάτων Σταμούλης Γεώργιος georges@uth.gr Δαδαλιάρης Αντώνιος dadaliaris@uth.gr Δυαδικοί Αριθμοί Η γενική αναπαράσταση ενός οποιουδήποτε
Πανεπιστήμιο Θεσσαλίας Τμήμα Πληροφορικής Λογική Σχεδίαση Ψηφιακών Συστημάτων Σταμούλης Γεώργιος georges@uth.gr Δαδαλιάρης Αντώνιος dadaliaris@uth.gr Δυαδικοί Αριθμοί Η γενική αναπαράσταση ενός οποιουδήποτε
Πράξεις με δυαδικούς αριθμούς
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 25-6 Πράξεις με δυαδικούς αριθμούς (αριθμητικές πράξεις) http://di.ionio.gr/~mistral/tp/csintro/ Μ.Στεφανιδάκης Πράξεις με δυαδικούς
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 25-6 Πράξεις με δυαδικούς αριθμούς (αριθμητικές πράξεις) http://di.ionio.gr/~mistral/tp/csintro/ Μ.Στεφανιδάκης Πράξεις με δυαδικούς
Δυαδικές συναρτήσεις Άλγεβρα Boole Λογικά διαγράμματα
 Δυαδικές συναρτήσεις Άλγεβρα Boole Λογικά διαγράμματα 1. Για a=1, b=1 και c=0, υπολογίστε τις τιμές των λογικών παραστάσεων ab c, a+b +c, a+b c και ab +c Δώστε τα σύνολα τιμών των δυαδικών μεταβλητών a,
Δυαδικές συναρτήσεις Άλγεβρα Boole Λογικά διαγράμματα 1. Για a=1, b=1 και c=0, υπολογίστε τις τιμές των λογικών παραστάσεων ab c, a+b +c, a+b c και ab +c Δώστε τα σύνολα τιμών των δυαδικών μεταβλητών a,
Εισαγωγή. Συνδυαστικά: Οι έξοδοι είναι συνάρτηση των εισόδων
 4 η Θεµατική Ενότητα : Συνδυαστική Λογική Εισαγωγή Λογικά Κυκλώµατα Συνδυαστικά: Οι έξοδοι είναι συνάρτηση των εισόδων Ακολουθιακά: Οι έξοδοι είναι συνάρτηση των εισόδων και της κατάστασης των στοιχείων
4 η Θεµατική Ενότητα : Συνδυαστική Λογική Εισαγωγή Λογικά Κυκλώµατα Συνδυαστικά: Οι έξοδοι είναι συνάρτηση των εισόδων Ακολουθιακά: Οι έξοδοι είναι συνάρτηση των εισόδων και της κατάστασης των στοιχείων
1. Βάσεις αριθμητικών συστημάτων 2. Μετατροπές μεταξύ ξύβάσεων 3. Αρνητικοί δυαδικοί αριθμοί 4. Αριθμητικές πράξεις δυαδικών αριθμών
 ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ MHXANIKOI Η/Υ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΥΑ ΙΚΟΙ ΑΡΙΘΜΟΙ (ΑΚΕΡΑΙΟΙ ΑΡΙΘΜΟΙ) Γ. Τσιατούχας Παράρτηµα A ιάρθρωση 1. Βάσεις αριθμητικών συστημάτων 2. Μετατροπές μεταξύ ξύβάσεων 3. Αρνητικοί
ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ MHXANIKOI Η/Υ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΥΑ ΙΚΟΙ ΑΡΙΘΜΟΙ (ΑΚΕΡΑΙΟΙ ΑΡΙΘΜΟΙ) Γ. Τσιατούχας Παράρτηµα A ιάρθρωση 1. Βάσεις αριθμητικών συστημάτων 2. Μετατροπές μεταξύ ξύβάσεων 3. Αρνητικοί
Ελίνα Μακρή
 Ελίνα Μακρή elmak@unipi.gr Μετατροπή Αριθμητικών Συστημάτων Πράξεις στα Αριθμητικά Συστήματα Σχεδίαση Ψηφιακών Κυκλωμάτων με Logism Άλγεβρα Boole Λογικές Πύλες (AND, OR, NOT, NAND, XOR) Flip Flops (D,
Ελίνα Μακρή elmak@unipi.gr Μετατροπή Αριθμητικών Συστημάτων Πράξεις στα Αριθμητικά Συστήματα Σχεδίαση Ψηφιακών Κυκλωμάτων με Logism Άλγεβρα Boole Λογικές Πύλες (AND, OR, NOT, NAND, XOR) Flip Flops (D,
4.1 Θεωρητική εισαγωγή
 ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 4 ΥΑ ΙΚΟΣ ΑΘΡΟΙΣΤΗΣ-ΑΦΑΙΡΕΤΗΣ Σκοπός: Να µελετηθούν αριθµητικά κυκλώµατα δυαδικής πρόσθεσης και αφαίρεσης. Να σχεδιαστούν τα κυκλώµατα από τους πίνακες αληθείας
ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 4 ΥΑ ΙΚΟΣ ΑΘΡΟΙΣΤΗΣ-ΑΦΑΙΡΕΤΗΣ Σκοπός: Να µελετηθούν αριθµητικά κυκλώµατα δυαδικής πρόσθεσης και αφαίρεσης. Να σχεδιαστούν τα κυκλώµατα από τους πίνακες αληθείας
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα. Αρχιτεκτονική-Ι. Ενότητα 1: Εισαγωγή στην Αρχιτεκτονική -Ι
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Αρχιτεκτονική-Ι Ενότητα 1: Εισαγωγή στην Αρχιτεκτονική -Ι Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Αρχιτεκτονική-Ι Ενότητα 1: Εισαγωγή στην Αρχιτεκτονική -Ι Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Εργαστήριο ΨΗΦΙΑΚΗ ΛΟΓΙΚΗ. Εισαγωγή
 Εισαγωγή Εργαστήριο ΨΗΦΙΑΚΗ ΛΟΓΙΚΗ Ξεκινάµε την εργαστηριακή µελέτη της Ψηφιακής Λογικής των Η/Υ εξετάζοντας αρχικά τη µορφή των δεδοµένων που αποθηκεύουν και επεξεργάζονται οι υπολογιστές και προχωρώντας
Εισαγωγή Εργαστήριο ΨΗΦΙΑΚΗ ΛΟΓΙΚΗ Ξεκινάµε την εργαστηριακή µελέτη της Ψηφιακής Λογικής των Η/Υ εξετάζοντας αρχικά τη µορφή των δεδοµένων που αποθηκεύουν και επεξεργάζονται οι υπολογιστές και προχωρώντας
Ενότητα 5 ΑΠΛΟΠΟΙΗΣΗ ΛΟΓΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΔΥΟ ΕΠΙΠΕΔΩΝ
 Ενότητα 5 ΑΠΛΟΠΟΙΗΣΗ ΛΟΓΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΔΥΟ ΕΠΙΠΕΔΩΝ Γενικές Γραμμές Χάρτης Karnaugh (K-map) Prime Implicants (πρωταρχικοί όροι) Διαδικασία Απλοποίησης με K-map ΑδιάφοροιΣυνδυασμοίΕισόδων Διεπίπεδες Υλοποιήσεις
Ενότητα 5 ΑΠΛΟΠΟΙΗΣΗ ΛΟΓΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΔΥΟ ΕΠΙΠΕΔΩΝ Γενικές Γραμμές Χάρτης Karnaugh (K-map) Prime Implicants (πρωταρχικοί όροι) Διαδικασία Απλοποίησης με K-map ΑδιάφοροιΣυνδυασμοίΕισόδων Διεπίπεδες Υλοποιήσεις
ΨΗΦΙΑΚΗ ΛΟΓΙΚΗ ΣΧΕ ΙΑΣΗ
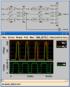 Τµήµα Ηλεκτρολόγων Μηχανικών Εργαστήριο Ενσύρµατης Τηλεπικοινωνίας ΨΗΦΙΑΚΗ ΛΟΓΙΚΗ ΣΧΕ ΙΑΣΗ ιδάσκων: Καθηγητής Ν. Φακωτάκης Τµήµα Ηλεκτρολόγων Μηχανικών Εργαστήριο Ενσύρµατης Τηλεπικοινωνίας ΨΗΦΙΑΚΗ ΛΟΓΙΚΗ
Τµήµα Ηλεκτρολόγων Μηχανικών Εργαστήριο Ενσύρµατης Τηλεπικοινωνίας ΨΗΦΙΑΚΗ ΛΟΓΙΚΗ ΣΧΕ ΙΑΣΗ ιδάσκων: Καθηγητής Ν. Φακωτάκης Τµήµα Ηλεκτρολόγων Μηχανικών Εργαστήριο Ενσύρµατης Τηλεπικοινωνίας ΨΗΦΙΑΚΗ ΛΟΓΙΚΗ
K24 Ψηφιακά Ηλεκτρονικά 6: Πολυπλέκτες/Αποπολυπλέκτες
 K24 Ψηφιακά Ηλεκτρονικά 6: Πολυπλέκτες/Αποπολυπλέκτες TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ ΤΕΧΝΟΛΟΓΙΚΟ Περιεχόμενα 1 2 3 4 Λειτουργία Πολυπλέκτης (Mul plexer) Ο
K24 Ψηφιακά Ηλεκτρονικά 6: Πολυπλέκτες/Αποπολυπλέκτες TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ ΤΕΧΝΟΛΟΓΙΚΟ Περιεχόμενα 1 2 3 4 Λειτουργία Πολυπλέκτης (Mul plexer) Ο
ΠΕΡΙΕΧΟΜΕΝΑ 1 ΚΕΦΑΛΑΙΟ ΟΙ ΥΠΟΛΟΓΙΣΤΕΣ ΑΠΟ ΤΗΝ ΑΡΧΑΙΟΤΗΤΑ ΜΕΧΡΙ ΣΗΜΕΡΑ Ιστορική αναδρομή Υπολογιστικές μηχανές
 ΠΕΡΙΕΧΟΜΕΝΑ 1 ΚΕΦΑΛΑΙΟ 1... 11 ΟΙ ΥΠΟΛΟΓΙΣΤΕΣ ΑΠΟ ΤΗΝ ΑΡΧΑΙΟΤΗΤΑ ΜΕΧΡΙ... 11 ΣΗΜΕΡΑ... 11 1.1 Ιστορική αναδρομή... 13 1.1.1 Υπολογιστικές μηχανές στην αρχαιότητα... 13 1.1.2 17ο έως τον 19ο... 14 1.1.3
ΠΕΡΙΕΧΟΜΕΝΑ 1 ΚΕΦΑΛΑΙΟ 1... 11 ΟΙ ΥΠΟΛΟΓΙΣΤΕΣ ΑΠΟ ΤΗΝ ΑΡΧΑΙΟΤΗΤΑ ΜΕΧΡΙ... 11 ΣΗΜΕΡΑ... 11 1.1 Ιστορική αναδρομή... 13 1.1.1 Υπολογιστικές μηχανές στην αρχαιότητα... 13 1.1.2 17ο έως τον 19ο... 14 1.1.3
Ελίνα Μακρή
 Ελίνα Μακρή elmak@unipi.gr Μετατροπή Αριθμητικών Συστημάτων Πράξεις στα Αριθμητικά Συστήματα Σχεδίαση Ψηφιακών Κυκλωμάτων με Logism Άλγεβρα Boole Λογικές Πύλες (AND, OR, NOT, NAND, XOR) Flip Flops (D,
Ελίνα Μακρή elmak@unipi.gr Μετατροπή Αριθμητικών Συστημάτων Πράξεις στα Αριθμητικά Συστήματα Σχεδίαση Ψηφιακών Κυκλωμάτων με Logism Άλγεβρα Boole Λογικές Πύλες (AND, OR, NOT, NAND, XOR) Flip Flops (D,
ΜΕΡΟΣ 1 ο : Δυαδικές συναρτήσεις Άλγεβρα Boole Λογικά διαγράμματα
 ΜΕΡΟΣ 1 ο : Δυαδικές συναρτήσεις Άλγεβρα Boole Λογικά διαγράμματα 1. Για a=1, b=1 και c=0, υπολογίστε τις τιμές των λογικών παραστάσεων ab c, a+b +c, a+b c και ab +c Δώστε τα σύνολα τιμών των δυαδικών
ΜΕΡΟΣ 1 ο : Δυαδικές συναρτήσεις Άλγεβρα Boole Λογικά διαγράμματα 1. Για a=1, b=1 και c=0, υπολογίστε τις τιμές των λογικών παραστάσεων ab c, a+b +c, a+b c και ab +c Δώστε τα σύνολα τιμών των δυαδικών
Ενότητα 2 ΑΛΓΕΒΡΑ BOOLE ΛΟΓΙΚΕΣ ΠΥΛΕΣ
 Ενότητα 2 ΛΓΕΡ BOOLE ΛΟΓΙΚΕΣ ΠΥΛΕΣ Άλγεβρα Boole Γενικές Γραμμές ξιώματα Huntington και Θεωρήματα ρχή του Δυϊσμού Λογικές πύλες NAND και NOR Υλοποιήσεις με πύλες NAND ή πύλεςnor πομονωτές τριών καταστάσεων
Ενότητα 2 ΛΓΕΡ BOOLE ΛΟΓΙΚΕΣ ΠΥΛΕΣ Άλγεβρα Boole Γενικές Γραμμές ξιώματα Huntington και Θεωρήματα ρχή του Δυϊσμού Λογικές πύλες NAND και NOR Υλοποιήσεις με πύλες NAND ή πύλεςnor πομονωτές τριών καταστάσεων
Πρόγραμμα Επικαιροποίησης Γνώσεων Αποφοίτων
 Πρόγραμμα Επικαιροποίησης Γνώσεων Αποφοίτων ΕΝΟΤΗΤΑ Μ ΨΗΦΙΑΚΑ ΗΛΕΚΤΡΟΝΙΚΑ Εκπαιδευτής: Γ. Π. ΠΑΤΣΗΣ, Επικ. Καθηγητής, Τμήμα Ηλεκτρονικών Μηχανικών, ΤΕΙ Αθήνας ΜΕΘΟΔΟΣ ΑΠΛΟΠΟΙΗΣΗΣ ΛΟΓΙΚΗΣ ΣΥΝΑΡΤΗΣΗΣ ΜΕ
Πρόγραμμα Επικαιροποίησης Γνώσεων Αποφοίτων ΕΝΟΤΗΤΑ Μ ΨΗΦΙΑΚΑ ΗΛΕΚΤΡΟΝΙΚΑ Εκπαιδευτής: Γ. Π. ΠΑΤΣΗΣ, Επικ. Καθηγητής, Τμήμα Ηλεκτρονικών Μηχανικών, ΤΕΙ Αθήνας ΜΕΘΟΔΟΣ ΑΠΛΟΠΟΙΗΣΗΣ ΛΟΓΙΚΗΣ ΣΥΝΑΡΤΗΣΗΣ ΜΕ
Βοηθητικές Σημειώσεις στη ΛΟΓΙΚΗ ΣΧΕΔΙΑΣΗ
 Βοηθητικές Σημειώσεις στη ΛΟΓΙΚΗ ΣΧΕΔΙΑΣΗ ΠΜΣ στις Τεχνολογίες και Συστήματα Ευρυζωνικών Εφαρμογών και Υπηρεσιών Διδάσκων : Παρασκευάς Κίτσος Επίκουρος Καθηγητής pkitsos@teimes.gr 1 Τμήμα των διαλέξεων
Βοηθητικές Σημειώσεις στη ΛΟΓΙΚΗ ΣΧΕΔΙΑΣΗ ΠΜΣ στις Τεχνολογίες και Συστήματα Ευρυζωνικών Εφαρμογών και Υπηρεσιών Διδάσκων : Παρασκευάς Κίτσος Επίκουρος Καθηγητής pkitsos@teimes.gr 1 Τμήμα των διαλέξεων
1 η Θεµατική Ενότητα : Αριθµητικά Κυκλώµατα. Επιµέλεια διαφανειών: Χρ. Καβουσιανός
 η Θεµατική Ενότητα : Αριθµητικά Κυκλώµατα Επιµέλεια διαφανειών: Χρ. Καβουσιανός Άθροιση + + + + a +b 2c+s + Κρατούµενο προηγούµενης βαθµίδας κρατούµενο άθροισµα Μεταφέρεται στην επόµενη βαθµίδα σηµαντικότητας
η Θεµατική Ενότητα : Αριθµητικά Κυκλώµατα Επιµέλεια διαφανειών: Χρ. Καβουσιανός Άθροιση + + + + a +b 2c+s + Κρατούµενο προηγούµενης βαθµίδας κρατούµενο άθροισµα Μεταφέρεται στην επόµενη βαθµίδα σηµαντικότητας
Εισαγωγή στους Ηλεκτρονικούς Υπολογιστές. 5 ο Μάθημα. Λεωνίδας Αλεξόπουλος Λέκτορας ΕΜΠ. url:
 στους Ηλεκτρονικούς Υπολογιστές 5 ο Μάθημα Λεωνίδας Αλεξόπουλος Λέκτορας ΕΜΠ email: leo@mail.ntua.gr url: http://users.ntua.gr/leo Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
στους Ηλεκτρονικούς Υπολογιστές 5 ο Μάθημα Λεωνίδας Αλεξόπουλος Λέκτορας ΕΜΠ email: leo@mail.ntua.gr url: http://users.ntua.gr/leo Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Αριθμητικά Συστήματα Η ανάγκη του ανθρώπου για μετρήσεις οδήγησε αρχικά στην επινόηση των αριθμών Κατόπιν, στην επινόηση συμβόλων για τη παράσταση
 Αριθμητικά Συστήματα Η ανάγκη του ανθρώπου για μετρήσεις οδήγησε αρχικά στην επινόηση των αριθμών Κατόπιν, στην επινόηση συμβόλων για τη παράσταση τους Κατόπιν, στην επινόηση συμβόλων για τη παράσταση
Αριθμητικά Συστήματα Η ανάγκη του ανθρώπου για μετρήσεις οδήγησε αρχικά στην επινόηση των αριθμών Κατόπιν, στην επινόηση συμβόλων για τη παράσταση τους Κατόπιν, στην επινόηση συμβόλων για τη παράσταση
ΣΧΕΔΙΑΣΗ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ
 ΣΧΕΔΙΑΣΗ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΣΥΝΔΥΑΣΤΙΚΗ ΛΟΓΙΚΗ 2017, Δρ. Ηρακλής Σπηλιώτης Συνδυαστικά και ακολουθιακά κυκλώματα Τα λογικά κυκλώματα χωρίζονται σε συνδυαστικά (combinatorial) και ακολουθιακά (sequential).
ΣΧΕΔΙΑΣΗ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΣΥΝΔΥΑΣΤΙΚΗ ΛΟΓΙΚΗ 2017, Δρ. Ηρακλής Σπηλιώτης Συνδυαστικά και ακολουθιακά κυκλώματα Τα λογικά κυκλώματα χωρίζονται σε συνδυαστικά (combinatorial) και ακολουθιακά (sequential).
Ψηφιακά Συστήματα. 6. Σχεδίαση Συνδυαστικών Κυκλωμάτων
 Ψηφιακά Συστήματα 6. Σχεδίαση Συνδυαστικών Κυκλωμάτων Βιβλιογραφία 1. Φανουράκης Κ., Πάτσης Γ., Τσακιρίδης Ο., Θεωρία και Ασκήσεις Ψηφιακών Ηλεκτρονικών, ΜΑΡΙΑ ΠΑΡΙΚΟΥ & ΣΙΑ ΕΠΕ, 2016. [59382199] 2. Floyd
Ψηφιακά Συστήματα 6. Σχεδίαση Συνδυαστικών Κυκλωμάτων Βιβλιογραφία 1. Φανουράκης Κ., Πάτσης Γ., Τσακιρίδης Ο., Θεωρία και Ασκήσεις Ψηφιακών Ηλεκτρονικών, ΜΑΡΙΑ ΠΑΡΙΚΟΥ & ΣΙΑ ΕΠΕ, 2016. [59382199] 2. Floyd
Εισαγωγή στους Υπολογιστές
 Εισαγωγή στους Υπολογιστές Ενότητα 9: Ψηφιακή Αριθμητική Βασίλης Παλιουράς Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Ψηφιακή Αριθμητική Σκοποί ενότητας 2 Περιεχόμενα ενότητας
Εισαγωγή στους Υπολογιστές Ενότητα 9: Ψηφιακή Αριθμητική Βασίλης Παλιουράς Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Ψηφιακή Αριθμητική Σκοποί ενότητας 2 Περιεχόμενα ενότητας
Πρόγραμμα Επικαιροποίησης Γνώσεων Αποφοίτων ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ
 Πρόγραμμα Επικαιροποίησης Γνώσεων Αποφοίτων ΕΝΟΤΗΤΑ Μ1 ΨΗΦΙΑΚΑ ΗΛΕΚΤΡΟΝΙΚΑ Εκπαιδευτής: Γ. Π. ΠΑΤΣΗΣ, Επικ. Καθηγητής, Τμήμα Ηλεκτρονικών Μηχανικών, ΤΕΙ Αθήνας ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ 1. Ποια είναι η βάση
Πρόγραμμα Επικαιροποίησης Γνώσεων Αποφοίτων ΕΝΟΤΗΤΑ Μ1 ΨΗΦΙΑΚΑ ΗΛΕΚΤΡΟΝΙΚΑ Εκπαιδευτής: Γ. Π. ΠΑΤΣΗΣ, Επικ. Καθηγητής, Τμήμα Ηλεκτρονικών Μηχανικών, ΤΕΙ Αθήνας ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ 1. Ποια είναι η βάση
Συστήματα Αρίθμησης. Συστήματα Αρίθμησης 1. PDF created with FinePrint pdffactory Pro trial version
 Συστήματα Αρίθμησης Στην καθημερινή μας ζωή χρησιμοποιούμε το δεκαδικό σύστημα αρίθμησης. Στο σύστημα αυτό χρησιμοποιούμε δέκα διαφορετικά σύμβολα τα :,, 2, 3, 4, 5, 6,7 8, 9. Για τον αριθμό 32 θα χρειαστούμε
Συστήματα Αρίθμησης Στην καθημερινή μας ζωή χρησιμοποιούμε το δεκαδικό σύστημα αρίθμησης. Στο σύστημα αυτό χρησιμοποιούμε δέκα διαφορετικά σύμβολα τα :,, 2, 3, 4, 5, 6,7 8, 9. Για τον αριθμό 32 θα χρειαστούμε
σύνθεση και απλοποίησή τους θεωρήµατα της άλγεβρας Boole, αξιώµατα του Huntington, κλπ.
 Εισαγωγή Εργαστήριο 2 ΛΟΓΙΚΑ ΚΥΚΛΩΜΑΤΑ Σκοπός του εργαστηρίου είναι να κατανοήσουµε τον τρόπο µε τον οποίο εκφράζεται η ψηφιακή λογική υλοποιώντας ασκήσεις απλά και σύνθετα λογικά κυκλώµατα (χρήση του
Εισαγωγή Εργαστήριο 2 ΛΟΓΙΚΑ ΚΥΚΛΩΜΑΤΑ Σκοπός του εργαστηρίου είναι να κατανοήσουµε τον τρόπο µε τον οποίο εκφράζεται η ψηφιακή λογική υλοποιώντας ασκήσεις απλά και σύνθετα λογικά κυκλώµατα (χρήση του
Εισαγωγή στην πληροφορική
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Εισαγωγή στην πληροφορική Ενότητα 3: Δυαδικά Συστήματα Αγγελίδης Παντελής Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Άδειες Χρήσης Το παρόν εκπαιδευτικό
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Εισαγωγή στην πληροφορική Ενότητα 3: Δυαδικά Συστήματα Αγγελίδης Παντελής Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Άδειες Χρήσης Το παρόν εκπαιδευτικό
Υπάρχουν δύο τύποι μνήμης, η μνήμη τυχαίας προσπέλασης (Random Access Memory RAM) και η μνήμη ανάγνωσης-μόνο (Read-Only Memory ROM).
 Μνήμες Ένα από τα βασικά πλεονεκτήματα των ψηφιακών συστημάτων σε σχέση με τα αναλογικά, είναι η ευκολία αποθήκευσης μεγάλων ποσοτήτων πληροφοριών, είτε προσωρινά είτε μόνιμα Οι πληροφορίες αποθηκεύονται
Μνήμες Ένα από τα βασικά πλεονεκτήματα των ψηφιακών συστημάτων σε σχέση με τα αναλογικά, είναι η ευκολία αποθήκευσης μεγάλων ποσοτήτων πληροφοριών, είτε προσωρινά είτε μόνιμα Οι πληροφορίες αποθηκεύονται
Ηλεκτρονική Μάθημα VIΙ Ψηφιακά Κυκλώματα Ψηφιακή Λογική. Καθηγητής Αντώνιος Γαστεράτος Τμήμα Μηχανικών Παραγωγής και Διοίκησης, Δ.Π.Θ.
 Ηλεκτρονική Μάθημα VIΙ Ψηφιακά Κυκλώματα Ψηφιακή Λογική Καθηγητής Αντώνιος Γαστεράτος Τμήμα Ε.ΔΙ.Π. Μηχανικών Δρ. Αθανάσιος Παραγωγής Ψωμούλης και Διοίκησης, Δ.Π.Θ. Τμήμα Μηχανικών Παραγωγής και Διοίκησης,
Ηλεκτρονική Μάθημα VIΙ Ψηφιακά Κυκλώματα Ψηφιακή Λογική Καθηγητής Αντώνιος Γαστεράτος Τμήμα Ε.ΔΙ.Π. Μηχανικών Δρ. Αθανάσιος Παραγωγής Ψωμούλης και Διοίκησης, Δ.Π.Θ. Τμήμα Μηχανικών Παραγωγής και Διοίκησης,
