OLIMPIADA DE CHIMIE etapa judeţeană
|
|
|
- Ἡρόδοτος Βασιλείου
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Clasa a VIII-a OLIMPIADA DE CHIMIE etapa judeţeană
2
3 Str. General Berthelot nr , Sector 1, Cod , Bucureşti Tel: +40 (0) Fax: +40 (0) DIRECȚIA GENERALĂ EDUCAȚIE ȘI ÎNVĂȚARE PE TOT PARCURSUL VIEȚII OLIMPIADA DE CHIMIE etapa judeţeană Clasa a IX-a 16 ianuarie 2011 Subiectul I puncte 2 Se consideră elementul X, al cărui ion X are configuraţia electronică: s 2s 2p 3s 3p 3d. Elementul X participă la următoarele transformări: X + Cl 2 A + NaOH - C B + NaOH D X + NaOH + E D + HCl A + C + E - F Se cer: a) identifică substanţele notate cu literele X, A, B, C, D, E, F şi scrie ecuaţiile chimice ale reacţiilor; b) calculează masa unui atom al elementului X, exprimată în kg, ştiind că 13,08 g X conţin 24 3, e ; c) precizează caracterul acido-bazic al substanţei B şi justifică răspunsul prin scrierea ecuaţiilor reacţiilor chimice corespunzătoare; d) precizează tipurile de legături din compuşii B şi D; e) precizează tipurile de reţele cristaline ale compuşilor B, D, E, F; f) indică natura forţelor ce asigură coeziunea particulelor în cristal pentru compuşii E şi F. Subiectul II puncte Un amestec solid, format din hidrogenocarbonaţii X şi Y, în raport molar 1 : 3, conţine 60,3% O. Hidrogenocarbonatul Y conţine 57,14 % O. Prin încălzirea amestecului la temperatură ridicată rezultă un nou amestec binar solid de substanţe compuse care conţine 3,6 g C. Se cer: a) identifică hidrogenocarbonaţii X şi Y; b) determină masa amestecului iniţial de hidrogenocarbonaţi; c) calculează compoziţia amestecului solid rezultat în urma descompunerii termice (în procente de masă). Subiectul III puncte Celula elementară a clorurii de sodiu, reprezentată în figura 1, este un cub. Un cristal de clorură de sodiu este reprezentat printr-un ansamblu de astfel de celule elementare. În cristal, raza ionului Na este 1,16, iar raza ionului Cl este 1,66. Densitatea clorurii de sodiu se poate calcula făcând raportul dintre masa celulei elementare şi volumul acesteia. Se cer: a) numărul de ioni de sodiu, Na, care se găsesc în celula elementară; b) densitatea,, a cristalului de clorură de sodiu, exprimată în 3 g/cm. Figura 1 Cl Na
4 Str. General Berthelot nr , Sector 1, Cod , Bucureşti Tel: +40 (0) Fax: +40 (0) DIRECȚIA GENERALĂ EDUCAȚIE ȘI ÎNVĂȚARE PE TOT PARCURSUL VIEȚII Subiectul IV puncte A. Se dizolvă piatră vânătă, CuSO4 5H2O, în 25 g de apă distilată şi, la 20 0 C, se obţine o soluţie saturată. Ştiind că, la 20 0 C, 100 g de apă dizolvă maxim 20,9 g de CuSO 4, iar la 10 0 C, 100 g de apă dizolvă maxim 18 g de CuSO 4, se cer: a) masa de piatră vânătă care s-a dizolvat pentru a se obţine soluţia saturată la 20 0 C; b) masa cristalohidratului, CuSO4 5H2O, depus prin răcirea soluţiei de la 20 0 C la 10 0 C. (10 puncte) B. O probă de cupru, impurificat cu magneziu, reacţionează în totalitate cu 77 g de soluţie de acid sulfuric, de concentraţie 70%. După reacţie, soluţia obţinută se diluează, se răceşte (se consideră că sărurile din soluţie cristalizează integral) şi apoi se filtrează. Se separă astfel 74,8 g de amestec de cristalohidraţi ( CuSO4 5H2O şi MgSO4 nh2o ) în care la 1 mol de apă corespund 28,75 g de amestec de săruri anhidre. Se cer: a) determină puritatea probei de cupru; b) stabileşte formula cristalohidratului MgSO4 nh2o ; c) calculează compoziţia amestecului de cristalohidraţi (în procente de masă); (15 puncte) Se dau : numere atomice: Na 11; Mg 12; Ca 20; Fe 26; Cu 29; Zn 30; Br 35; mase atomice: H 1; C 12; N 14; O 16; S 32; Na 23; Cl 35,5 ; Mg 24; Ca 40; Cu 64; numărul lui Avogadro: N A = 6, particule/mol constanta generală a gazului ideal: R = 0,082 atm L/(mol K) 10 1 = 10 m NOTĂ: Timp de lucru 3 ore. Se acordă 10 puncte din oficiu. S U C C E S! Subiecte selecţionate şi prelucrate de Vasile Sorohan, profesor la Colegiul Costache Negruzzi Iaşi
5 DIRECȚIA GENERALĂ EDUCAȚIE ȘI ÎNVĂȚARE PE TOT PARCURSUL VIEȚII. Clasa a X-a OLIMPIADA DE CHIMIE etapa judeţeană 16 ianuarie 2011 Subiectul I...20 puncte A. Efectuează următoarele transfomări: Etenă acetilenă Metan 1,3- dicloropropan B. a. Reprezintă formulele structurale ce corespund izomerilor de constituţie cu formula moleculară C 6 H 12. b. Care dintre structurile de la punctul a prezintă izomerie geometrică? C. Se dă schema: 2A B+3H 2 NaNH 2 +CH 3 Cl B C D WO 3 /Al 2 O 3 2D E + B +H 2 (Pd/Pb 2+ ) 2NBS +H 2 /Ni 2KOH/etanol +J +2NBS +O 3 E F G H I K L M -2HBr Ştiind că J are d aer =0,9688; iar substanţa K este un compus ciclic nesaturat; identificaţi şi denumiţi substanţele notate cu litere. Scrieţi ecuaţiile reacţilor chimice şi precizaţi condiţiile de reacţie. Subiectul II...20 puncte A. In scopul obţinerii policlorurii de vinil, se pleacă de la 67,2 m 3 C 2 H 2. Dacă puritatea acetilenei este 80%, randamentul adiţiei este 75%, iar al polimerizării 90%, ce cantitate de polimer 98% puritate se poate obţine? B. Identifică monomerii A şi B din următoarea schemă de reacţii, dacă x = y: Str. General Berthelot nr , Sector 1, , Bucureşti Tel: +40 (0) Fax: +40 (0)
6 Subiectul III puncte Terpinenii sunt hidrocarburi ce apar în uleiurile eterice de măghiran şi coriandru. Se cunosc trei izomeri α,β,γ. Formula moleculară şi formulele structurale ale celor trei izomeri se pot determina pe baza următoarelor informaţii: 1)La arderea a 0,2 moli terpinen rezultă o cantitate de apă care reţinută în 100 g oleum cu 10% SO 3 duce la formarea unei soluţii cu c=79,38%; 2)Volumul de CO 2 rezultat la arderea a 0,2 moli este reţinut total în 2 L soluţie NaOH cu c=2m, cu formare de sare neutră; 3)Aceeaşi cantitate de 0,2 moli hidrocarbură reacţionează cu 1000 g soluţie Br 2 cu c=16% şi după îndepărtarea produsului organic rezultat concentraţia soluţiei devine 10,25%; Formulele structurale ale celor trei izomeri se determină pe baza reacţiilor de oxidare: Izomerul α formează la reacţia cu O 3 şi H 2 O 6-metil-2,5 heptandionă + X(compus dicarbonilic saturat cu 55,17% O); Izomerul β formează la oxidare cu KMnO 4 /H + CO 2 +H 2 O + acid 7-metil-3,6- dicetooctanoic; Izomerul γ - formează la oxidare cu K 2 Cr 2 O 7 /H + acid 4-metil-3-cetopentanoic +Y(cetoacid identic cu cel obţinut la oxidarea hidrocarburii ciclice C 4 H 6 ce are C cuaternar; Se cere: a)formula moleculară pentru terpinen; b) formulele structurale ale celor trei izomeri; c) volumul de soluţie KMnO 4 /H + cu c=5n consumat la oxidarea a 0,2 moli de α- terpinen; d) raportul molar β terpinen :K 2 Cr 2 O 7 : H 2 SO 4 la oxidare; e) dacă cei trei terpineni adiţionează fiecare câte 2 moli de HCl, câţi produşi diferiţi rezultă şi câţi izomeri geometrici prezintă; f) dintre cei trei terpineni care ar putea participa la sinteza dien- argumentaţi. Subiectul IV puncte Se dă echilibrul: AlCl 3 A B 0 60 C Kp = 0,25 Despre A se ştie : prin combustia a 0,05 moli de A în 50,4 L aer, stoechiometric s-au obţinut 53,76 L amestec de gaze (H 2 O-gaz). O parte din gaze se reţin pe 54 g soluţie H 2 SO 4 59,4%, concentraţia scăzând la 54%. Despre B se ştie că admite 4 radicali monovalenţi, pe când A admite un singur radical monovalent şi prezintă 2 conformeri. Reprezintă formulele structurale ale compuşilor ciclici A şi B precum şi gradul de conversie a compusului A în B. Se dau : mase atomice: H 1; C 12; N 14; O 16; K 39; Mn 55; Br 80; S- 32. volumul molar = 22,4 L constanta generală a gazului ideal=0,082 atm L/(mol K) NOTĂ: Timp de lucru 3 ore. Se acordă 10 puncte din oficiu. Subiecte propuse de Carmen-Gina Ciobîcă, profesor la Colegiul Tehnic de Industrie Alimentară Suceava
7
8 DIRECȚIA GENERALĂ EDUCAȚIE ȘI ÎNVĂȚARE PE TOT PARCURSUL VIEȚII Clasa a XI-a OLIMPIADA DE CHIMIE etapa judeţeană 16 ianuarie 2011 Subiectul I...20 puncte Pentru obţinerea etilaminei se alchilează total 108 moli amoniac cu 70 moli bromură de etil, rezultând un amestec organic care conţine cei patru produşi de alchilare. În scopul stabilirii compoziţiei amestecului de reacţie, acesta se împarte în două jumătăţi: - o jumătate din amestec se dizolvă în metanol şi se tratează cu o soluţie metanolică, saturată de azotat de argint, obţinându-se 374 g precipitat; - cealaltă jumătate din amestec se tratează cu o soluţie acidifiată de azotit de sodiu, rezultând un volum de 280 L N 2 (c.n.). Se cere: 1. Să se scrie ecuaţiile reacţiilor chimice de alchilare a amoniacului şi ecuaţiile reacţiilor chimice pe baza cărora s-a determinat compoziţia amestecului de reacţie; 2. Să se determine compoziţia procentuală molară a amestecului organic obţinut; 3. Să se calculeze randamentul de obţinere a etilaminei din bromură de etil; 4. Să se calculeze masa produsului obţinut prin reducerea produsului de condensare a etilaminei separate din amestec cu un compus carbonilic alifatic saturat, ştiind că produsul de condensare conţine 24,56 % N iar randamentul reacţiei de reducere este 70%. 5. Să se scrie ecuaţiile reacţiilor descrise la punctul 4. Subiectul II puncte Scrieţi ecuaţiile reacţiilor chimice prin care au loc următoarele transformări: 1. metan etanolamina 2. benzen 2,6-dicloroanilină 3. toluen 2-cloro-4-nitrobenzoat de benzil 4. naftalină β-fluoronaftalină 5. glicerină, benzen H 2 C=CH-CH-C 6 H 5 O-CO-CH 3 6. fenol acid 2-oxo-hexandioic 7. benzen benzidină ( p,p -diaminodifenil) Subiectul III...25 puncte 1. Despre compusul T se cunosc următoarele date: - prin ardere formează dioxid de carbon şi apă; - conţine 53,33 % C în procente de masă; - are densitatea vaporilor faţă de un amestec de CO 2 şi N 2, în raport molar de 1:3, egală cu 2,8125; Str. General Berthelot nr , Sector 1, , Bucureşti Tel: +40 (0) Fax: +40 (0)
9 - prin tratarea a 1,8 g compus T cu iodură de metilmagneziu se formează 896 ml metan (c.n.). Să se precizeze formulele structurale posibile pentru compusul T ştiind că dintr-o probă de compus T se separă prin cristalizare două fracţiuni. 2. Despre alchinele izomere A,B,C,D,E,F şi G se cunosc următoarele date: - prin tratarea unui amestec de alchine izomere cu soluţie de brom dizolvat în CCl 4, acesta îşi măreşte masa cu 390,24%; - alchinele izomere A, B, C, D, E, F şi G se hidrogenează total, astfel: A, B şi C se transformă în acelaşi alcan H; D se transformă în alcanul I; E şi F se transformă în alcanul J; G se transformă în alcanul K; - alchinele care reacţionează cu reactivul Tollens sunt A, D, E şi G; - prin hidrogenarea alchinelor cu catalizator de Pd, în prezenţa PbCO 3, şi apoi adiţia bromului dizolvat în CCl 4, au loc următoarele transformări: din A se obţine amestecul racemic R 1 ; din B se obţine o mezoformă M şi amestecul racemic R 2 ; din C se obţin două amestecuri racemice R 3 şi R 4 ; din D se obţin două amestecuri racemice R 5 şi R 6 ; din E se obţine amestecul racemic R 7 ; din F se obţin două amestecuri racemice R 8 şi R 9. Să se determine formulele de structură ale substanţelor şi amestecurile racemice notate cu litere. Subiectul IV puncte Se sulfonează 920 kg toluen cu un oleum ce conţine 34,1224% S, conversia totală fiind de 80%. Din produsul principal al monosulfonării se obţin 648 kg p-crezol, iar produsul secundar se transformă în acid salicilic. Se cere: 1. Să se scrie ecuaţiile reacţiilor chimice prin care se obţine p-crezol din toluen; 2. Să se calculeze conversia utilă şi randamentul monosulfonării; 3. Să se calculeze masa de oleum cu 34,1224% S folosită, dacă acidul rezidual conţine 72,5% H 2 SO 4 ; 4. Să se calculeze masa de oleum cu 30% SO 3 liber, necesară refacerii acidului rezidual la concentraţia iniţială; 5. Să se calculeze masa de acid salicilic care se obţine, dacă randamentul global al transformării produsului secundar în acid salicilic este de 85%; 6. Să se determine formulele de structură ale substanţelor notate cu litere care se obţin din acid salicilic, conform schemei următoare: Se dau : masele atomice: H 1; C 12; N 14; O 16; S 32; Br 80; Ag 108. volumul molar = 22,4 L NOTĂ: Timp de lucru 3 ore. Se acordă 10 puncte din oficiu. Subiecte selectate de Maiereanu Alina, profesor la Colegiul Naţional Al.I.Cuza, Focşani, judeţul Vrancea
10 DIRECȚIA GENERALĂ EDUCAȚIE ȘI ÎNVĂȚARE PE TOT PARCURSUL VIEȚII Clasa a XII-a OLIMPIADA DE CHIMIE etapa judeţeană 16 ianuarie 2011 Subiectul I puncte A. Un amestec binar conține 32,078% CO (procente de masă) și 84 grame hidrocarbură. Amestecul este supus arderii într-un calorimetru de Cu. Masa calorimetrului este de 1,75 kg, iar acesta conține 20 l apă (ρ=1kg/l). În urma arderii amestecului temperatura apei crește cu 53,26 C. Folosind următoarele date termochimice, determinați formula hidrocarburii: CO 2 (g) CO(g) H 2 O(l) C x H y (g) Căldura de formare (kcal/mol) 94,05 26,41 68,32-29,8 Căldura de combustie hidrocarbură (kcal/mol) Căldura specifică a cuprului (cal/g ) 0,09 Căldura specifică a apei (cal/g ) 1 649,76 B. Pentru a evapora complet un mol de apă la temperatura de 40 C și presiune constantă este necesară o cantitate de căldură (căldură latentă de evaporare) de 4, J/mol. Calculați variația energiei interne a unui mol de apă la trecerea din stare lichidă în stare gazoasă. Subiectul al II-lea puncte Un volum de 19,0896 litri gaz A se descompune după o cinetică de ordinul I într-un vas închis, la o temperatură constantă de 600 C, conform reacției A(g) B(g) + C(g). După o oră de reacție conversia lui A ajunge la 0,4, iar la timpul de înjumătățire al concentrației inițiale, presiunea în recipient ajunge la 1,125 atm. Să se determine: a) Viteza de reacție inițială b) Viteza de reacție după 90 de minute Subiectul al III-lea puncte A. Aerul conține aerosoli de proveniți din dezintegrarea radonului. Radioizotopul este adus la sol prin precipitații atmosferice. Dacă, în momentul căderii, zăpada căzută conține o anumită activitate specifică datorată izotopului ; în decursul anilor această activitate va scădea după legea de dezintegrare a Presupunând că activitatea specifică inițială a zăpezii, într-un loc dat, nu variază în decursul timpului, prin compararea activității specifice a zăpezii, recoltată la diferite adâncimi, se poate determina vârsta acesteia. Str. General Berthelot nr , Sector 1, , Bucureşti Tel: +40 (0) Fax: +40 (0) Pagină 1 din 2
11 Determinările făcute la Polul Sud într-o stațiune de cercetare în anul 2010 au condus la următoarele rezultate: viteza de numărare corespunzătoare activității specifice a zăpezii de la suprafață era de 0= 48 impulsuri/min kg, iar cea corespunzătoare zăpezii recoltate la o adâncime de 10 metri era = 3 impulsuri/min kg. Să se determine anul în care a căzut zăpada recoltată la adâncimea respectivă. B. Într-un recipient se găsește un amestec format din substanțele A și B. Concentrațiile inițiale ale substanțelor din amestec sunt și În anumite condiții de reacție are loc transformarea, la volum constant, după o cinetică de ordinul I. La timpul t concentrațiile substanțelor vor fi și. Stabiliți condiția pentru care este valabilă următoarea relație: Subiectul al IV-lea puncte Reacția de descompunere a calcarului se realizează la temperatura de 1200K. Căldura necesară reacției de descompunere se obține prin arderea stoechiometrică a metanului în aer (20% O 2 ). Se consideră că metanul și calcarul pătrund în cuptor în condiții standard, pierderile de căldură sunt nule și căldura cedată la arderea metanului este utilizată atât pentru descompunerea calcarului, cât și pentru încălzirea reactanților la temperatura de 1200K. Se folosesc următoarele date: Căldura de formare standard (kj/mol) Capacitatea calorică molară medie (J/mol K) CaCO 3 (s) CaO(s) CO 2 (g) CH 4 (g) H 2 O(g) N 2 (g) O 2 (g) ,1 393,51 74,85 241, ,8 51,09 48,53 59,31 38,12 31,05 32,97 a) Să se calculeze volumul de metan necesar descompunerii unei tone de calcar b) Să se determine procentul de CO 2 din amestecul gazos final. Se dau : mase atomice: H 1; C 12; O 16; Ca 40 constanta generală a gazului ideal R = 8,31 J/mol K = 0,082 atm L/(mol K) NOTĂ: Timp de lucru 3 ore. Se acordă 10 puncte din oficiu. Subiecte propuse de profesor Mădălina Neacșu, inspector școlar de specialitate, I.S.J. Dolj Pagină 2 din 2
Capitolul 2 - HIDROCARBURI 2.3.ALCHINE
 Capitolul 2 - HIDROCARBURI 2.3.ALCHINE TEST 2.3.3 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. 1. Acetilena poate participa la reacţii de
Capitolul 2 - HIDROCARBURI 2.3.ALCHINE TEST 2.3.3 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. 1. Acetilena poate participa la reacţii de
Capitolul 2-HIDROCARBURI-2.3.-ALCHINE Exerciţii şi probleme
 Capitolul 2 - HIDROCARBURI 2.3.ALCHINE Exerciţii şi probleme E.P.2.3. 1. Denumeşte conform IUPAC următoarele alchine: Se numerotează catena cea mai lungă ce conţine şi legătura triplă începând de la capătul
Capitolul 2 - HIDROCARBURI 2.3.ALCHINE Exerciţii şi probleme E.P.2.3. 1. Denumeşte conform IUPAC următoarele alchine: Se numerotează catena cea mai lungă ce conţine şi legătura triplă începând de la capătul
Capitolul 2 - HIDROCARBURI 2.5.ARENE
 Capitolul 2 - HIDROCARBURI 2.5.ARENE TEST 2.5.2 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. 1. Radicalul C 6 H 5 - se numeşte fenil. ( fenil/
Capitolul 2 - HIDROCARBURI 2.5.ARENE TEST 2.5.2 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. 1. Radicalul C 6 H 5 - se numeşte fenil. ( fenil/
Capitolul 2 - HIDROCARBURI 2.4.ALCADIENE
 Capitolul 2 - HIDROCARBURI 2.4.ALCADIENE Exerciţii şi probleme E.P.2.4. 1. Scrie formulele de structură ale următoarele hidrocarburi şi precizează care dintre ele sunt izomeri: Rezolvare: a) 1,2-butadiena;
Capitolul 2 - HIDROCARBURI 2.4.ALCADIENE Exerciţii şi probleme E.P.2.4. 1. Scrie formulele de structură ale următoarele hidrocarburi şi precizează care dintre ele sunt izomeri: Rezolvare: a) 1,2-butadiena;
Capitolul 2 - HIDROCARBURI 2.4.ALCADIENE
 Capitolul 2 - HIDROCARBURI 2.4.ALCADIENE TEST 2.4.1 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. Rezolvare: 1. Alcadienele sunt hidrocarburi
Capitolul 2 - HIDROCARBURI 2.4.ALCADIENE TEST 2.4.1 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. Rezolvare: 1. Alcadienele sunt hidrocarburi
a. 11 % b. 12 % c. 13 % d. 14 %
 1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
Aplicaţii ale principiului I al termodinamicii la gazul ideal
 Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Capitolul 2 - HIDROCARBURI 2.5.ARENE
 Capitolul 2 - HIDROCARBURI 2.5.ARENE TEST 2.5.3 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. 1. Sulfonarea benzenului este o reacţie ireversibilă.
Capitolul 2 - HIDROCARBURI 2.5.ARENE TEST 2.5.3 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. 1. Sulfonarea benzenului este o reacţie ireversibilă.
Capitolul 2-HIDROCARBURI-2.2.-ALCHENE Exerciţii şi probleme
 Capitolul 2 - HIDROCARBURI 2.2.ALCHENE Exerciţii şi probleme E.P.2.2.1. Denumeşte conform IUPAC următoarele alchene: A CH 3 CH 3 CH 2 C 3 C 4 H C 5 CH 3 C 2 H CH 3 C 6 H 2 C 1 H 3 C 7 H 3 3-etil-4,5,5-trimetil-2-heptenă
Capitolul 2 - HIDROCARBURI 2.2.ALCHENE Exerciţii şi probleme E.P.2.2.1. Denumeşte conform IUPAC următoarele alchene: A CH 3 CH 3 CH 2 C 3 C 4 H C 5 CH 3 C 2 H CH 3 C 6 H 2 C 1 H 3 C 7 H 3 3-etil-4,5,5-trimetil-2-heptenă
Capitolul 2-HIDROCARBURI-2.5.-ARENE Exerciţii şi probleme
 Capitolul 2 - HIDROCARBURI 2.5.ARENE Exerciţii şi probleme E.P.2.5. 1. Denumeşte conform IUPAC următoarele hidrocarburi aromatice mononucleare: Determină formula generală a hidrocarburilor aromatice mononucleare
Capitolul 2 - HIDROCARBURI 2.5.ARENE Exerciţii şi probleme E.P.2.5. 1. Denumeşte conform IUPAC următoarele hidrocarburi aromatice mononucleare: Determină formula generală a hidrocarburilor aromatice mononucleare
Liceul de Ştiinţe ale Naturii Grigore Antipa Botoşani
 Fişă de lucru RANDAMENT. CONVERSIE UTILĂ. CONVERSIE TOTALĂ 1. Randament A. Hidrocarburile alifatice pot fi utilizate drept combustibili, sau pot fi transformate în compuşi cu aplicaţii practice. 1. Scrieţi
Fişă de lucru RANDAMENT. CONVERSIE UTILĂ. CONVERSIE TOTALĂ 1. Randament A. Hidrocarburile alifatice pot fi utilizate drept combustibili, sau pot fi transformate în compuşi cu aplicaţii practice. 1. Scrieţi
Capitolul 1-INTRODUCERE ÎN STUDIUL CHIMIEI ORGANICE Exerciţii şi probleme
 Capitolul 1- INTRODUCERE ÎN STUDIUL CHIMIEI ORGANICE Exerciţii şi probleme ***************************************************************************** 1.1. Care este prima substanţă organică obţinută
Capitolul 1- INTRODUCERE ÎN STUDIUL CHIMIEI ORGANICE Exerciţii şi probleme ***************************************************************************** 1.1. Care este prima substanţă organică obţinută
II. 5. Probleme. 20 c 100 c = 10,52 % Câte grame sodă caustică se găsesc în 300 g soluţie de concentraţie 10%? Rezolvare m g.
 II. 5. Problee. Care ete concentraţia procentuală a unei oluţii obţinute prin izolvarea a: a) 0 g zahăr în 70 g apă; b) 0 g oă cautică în 70 g apă; c) 50 g are e bucătărie în 50 g apă; ) 5 g aci citric
II. 5. Problee. Care ete concentraţia procentuală a unei oluţii obţinute prin izolvarea a: a) 0 g zahăr în 70 g apă; b) 0 g oă cautică în 70 g apă; c) 50 g are e bucătărie în 50 g apă; ) 5 g aci citric
Capitolul 4-COMPUŞI ORGANICI CU ACŢIUNE BIOLOGICĂ-
 Capitolul 4 COMPUŞI ORGANICI CU ACŢIUNE BIOLOGICĂ 4.1.ZAHARIDE.PROTEINE. Exerciţii şi probleme E.P.4.1. 1. Glucoza se oxidează cu reactivul Tollens [Ag(NH 3 ) 2 ]OH conform ecuaţiei reacţiei chimice. Această
Capitolul 4 COMPUŞI ORGANICI CU ACŢIUNE BIOLOGICĂ 4.1.ZAHARIDE.PROTEINE. Exerciţii şi probleme E.P.4.1. 1. Glucoza se oxidează cu reactivul Tollens [Ag(NH 3 ) 2 ]OH conform ecuaţiei reacţiei chimice. Această
CLASA a X a PROBA TEORETICĂ Filiera tehnologică toate profilurile/specializările/calificările
 CLASA a X a PROBA TEORETICĂ Filiera tehnologică toate profilurile/specializările/calificările Subiectul I 20 Fiecare item are un singur răspuns corect. Notaţi în tabel cu X numai răspunsul corect. Pentru
CLASA a X a PROBA TEORETICĂ Filiera tehnologică toate profilurile/specializările/calificările Subiectul I 20 Fiecare item are un singur răspuns corect. Notaţi în tabel cu X numai răspunsul corect. Pentru
I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare.
 Capitolul 3 COMPUŞI ORGANICI MONOFUNCŢIONALI 3.2.ACIZI CARBOXILICI TEST 3.2.3. I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. 1. Reacţia dintre
Capitolul 3 COMPUŞI ORGANICI MONOFUNCŢIONALI 3.2.ACIZI CARBOXILICI TEST 3.2.3. I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. 1. Reacţia dintre
a. 0,1; 0,1; 0,1; b. 1, ; 5, ; 8, ; c. 4,87; 6,15; 8,04; d. 7; 7; 7; e. 9,74; 12,30;1 6,08.
 1. În argentometrie, metoda Mohr: a. foloseşte ca indicator cromatul de potasiu, care formeazǎ la punctul de echivalenţă un precipitat colorat roşu-cărămiziu; b. foloseşte ca indicator fluoresceina, care
1. În argentometrie, metoda Mohr: a. foloseşte ca indicator cromatul de potasiu, care formeazǎ la punctul de echivalenţă un precipitat colorat roşu-cărămiziu; b. foloseşte ca indicator fluoresceina, care
1. PROPRIETĂȚILE FLUIDELOR
 1. PROPRIETĂȚILE FLUIDELOR a) Să se exprime densitatea apei ρ = 1000 kg/m 3 în g/cm 3. g/cm 3. b) tiind că densitatea glicerinei la 20 C este 1258 kg/m 3 să se exprime în c) Să se exprime în kg/m 3 densitatea
1. PROPRIETĂȚILE FLUIDELOR a) Să se exprime densitatea apei ρ = 1000 kg/m 3 în g/cm 3. g/cm 3. b) tiind că densitatea glicerinei la 20 C este 1258 kg/m 3 să se exprime în c) Să se exprime în kg/m 3 densitatea
5.1. Noţiuni introductive
 ursul 13 aitolul 5. Soluţii 5.1. oţiuni introductive Soluţiile = aestecuri oogene de două sau ai ulte substanţe / coonente, ale căror articule nu se ot seara rin filtrare sau centrifugare. oonente: - Mediul
ursul 13 aitolul 5. Soluţii 5.1. oţiuni introductive Soluţiile = aestecuri oogene de două sau ai ulte substanţe / coonente, ale căror articule nu se ot seara rin filtrare sau centrifugare. oonente: - Mediul
Subiectul III (30 puncte) Varianta 001
 Subiectul III (30 puncte) Varianta 001 Proteinele şi zaharidele sunt compuşi organici cu acţiune biologică. 1. Scrieţi formula de structură pentru o tripeptidă P care conţine glicină, valină şi serină
Subiectul III (30 puncte) Varianta 001 Proteinele şi zaharidele sunt compuşi organici cu acţiune biologică. 1. Scrieţi formula de structură pentru o tripeptidă P care conţine glicină, valină şi serină
Reactia de amfoterizare a aluminiului
 Problema 1 Reactia de amfoterizare a aluminiului Se da reactia: Al (s) + AlF 3(g) --> AlF (g), precum si presiunile partiale ale componentelor gazoase in functie de temperatura: a) considerand presiunea
Problema 1 Reactia de amfoterizare a aluminiului Se da reactia: Al (s) + AlF 3(g) --> AlF (g), precum si presiunile partiale ale componentelor gazoase in functie de temperatura: a) considerand presiunea
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE
 DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
Modele de subiecte propuse pentru concursul Acad. Cristofor Simionescu
 Modele de subiecte propuse pentru concursul Acad. Cristofor Simionescu Ediția a-5-a, 18 noiembrie 2017, Iași Clasa a XII-a, secțiunea a-2-a: Chimie Aplicată în Protecția Mediului Alegeţi răspunsul corect
Modele de subiecte propuse pentru concursul Acad. Cristofor Simionescu Ediția a-5-a, 18 noiembrie 2017, Iași Clasa a XII-a, secțiunea a-2-a: Chimie Aplicată în Protecția Mediului Alegeţi răspunsul corect
Subiectul II (30 puncte) Varianta 001
 Subiectul II (30 puncte) Varianta 001 Compuşii cloruraţi obţinuţi din hidrocarburile alifatice au importante aplicaţii practice. 1. Scrieţi ecuaţiile reacţiilor chimice, prin care se obţin din metan: monoclorometan,
Subiectul II (30 puncte) Varianta 001 Compuşii cloruraţi obţinuţi din hidrocarburile alifatice au importante aplicaţii practice. 1. Scrieţi ecuaţiile reacţiilor chimice, prin care se obţin din metan: monoclorometan,
Examenul de bacalaureat naţional 2015 Proba E. d) Chimie organică (nivel I/ nivel II)
 Examenul de bacalaureat naţional 2015 Proba E. d) Chimie organică (nivel I/ nivel II) Varianta 9 Toate subiectele sunt obligatorii. Se acordă din oficiu. Timpul de lucru efectiv este de 3 ore. SUBIECTUL
Examenul de bacalaureat naţional 2015 Proba E. d) Chimie organică (nivel I/ nivel II) Varianta 9 Toate subiectele sunt obligatorii. Se acordă din oficiu. Timpul de lucru efectiv este de 3 ore. SUBIECTUL
Planul determinat de normală şi un punct Ecuaţia generală Plane paralele Unghi diedru Planul determinat de 3 puncte necoliniare
 1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM 1 electronica.geniu.ro
 Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
OLIMPIADA NAȚIONALĂ DE CHIMIE
 MINISTERUL EDUCAȚIEI ȘI CERCETĂRII ȘTIINȚIFICE INSPECTORATUL ȘCOLAR JUDEȚEAN GALAȚI OLIMPIADA NAȚIONALĂ DE CHIMIE EDIȚIA a XLIX-a GALAȚI 5-10 APRILIE 2015 Proba teoretică Clasa a VIII-a Subiectul I (20
MINISTERUL EDUCAȚIEI ȘI CERCETĂRII ȘTIINȚIFICE INSPECTORATUL ȘCOLAR JUDEȚEAN GALAȚI OLIMPIADA NAȚIONALĂ DE CHIMIE EDIȚIA a XLIX-a GALAȚI 5-10 APRILIE 2015 Proba teoretică Clasa a VIII-a Subiectul I (20
REACŢII DE ADIŢIE NUCLEOFILĂ (AN-REACŢII) (ALDEHIDE ŞI CETONE)
 EAŢII DE ADIŢIE NULEFILĂ (AN-EAŢII) (ALDEIDE ŞI ETNE) ompușii organici care conțin grupa carbonil se numesc compuși carbonilici și se clasifică în: Aldehide etone ALDEIDE: Formula generală: 3 Metanal(formaldehida
EAŢII DE ADIŢIE NULEFILĂ (AN-EAŢII) (ALDEIDE ŞI ETNE) ompușii organici care conțin grupa carbonil se numesc compuși carbonilici și se clasifică în: Aldehide etone ALDEIDE: Formula generală: 3 Metanal(formaldehida
Subiecte Clasa a VII-a
 lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
COLEGIUL NATIONAL CONSTANTIN CARABELLA TARGOVISTE. CONCURSUL JUDETEAN DE MATEMATICA CEZAR IVANESCU Editia a VI-a 26 februarie 2005.
 SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
5.5. REZOLVAREA CIRCUITELOR CU TRANZISTOARE BIPOLARE
 5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
ITEMI MODEL PENTRU UNITATEA DE ÎNVĂŢARE: Alcooli
 LIEUL TEORETI GRIGORE ANTIPA BOTOŞANI - ITEMI MODEL PENTRU UNITATEA DE ÎNVĂŢARE: Alcooli Subiectul A: Indicaţi care dintre afirmaţiile de mai jos sunt adevărate şi care sunt false, completând cu litera
LIEUL TEORETI GRIGORE ANTIPA BOTOŞANI - ITEMI MODEL PENTRU UNITATEA DE ÎNVĂŢARE: Alcooli Subiectul A: Indicaţi care dintre afirmaţiile de mai jos sunt adevărate şi care sunt false, completând cu litera
Unitatea atomică de masă (u.a.m.) = a 12-a parte din masa izotopului de carbon
 ursul.3. Mării şi unităţi de ăsură Unitatea atoică de asă (u.a..) = a -a parte din asa izotopului de carbon u. a.., 0 7 kg Masa atoică () = o ărie adiensională (un nuăr) care ne arată de câte ori este
ursul.3. Mării şi unităţi de ăsură Unitatea atoică de asă (u.a..) = a -a parte din asa izotopului de carbon u. a.., 0 7 kg Masa atoică () = o ărie adiensională (un nuăr) care ne arată de câte ori este
CONCURSUL DE CHIMIE CORIOLAN DRĂGULESCU 2017
 Universitatea Politehnica Timişoara Facultatea de Chimie Industrială şi Ingineria Mediului Clasa a IX-a Chimie anorganică CONCURSUL DE CHIMIE CORIOLAN DRĂGULESCU 2017 1. (2 p) Precizaţi poziţia în sistemul
Universitatea Politehnica Timişoara Facultatea de Chimie Industrială şi Ingineria Mediului Clasa a IX-a Chimie anorganică CONCURSUL DE CHIMIE CORIOLAN DRĂGULESCU 2017 1. (2 p) Precizaţi poziţia în sistemul
Subiecte Clasa a VIII-a
 Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Rezolvarea problemelor la chimie prin metoda algebrică
 Ministerul Educaţiei şi Tineretului al Republicii Moldova Colegiul Pedagogic Ion Creangă, Bălţi Liceul Teoretic Ion Creangă Rezolvarea problemelor la chimie prin metoda algebrică Autor: Postolache Ion,
Ministerul Educaţiei şi Tineretului al Republicii Moldova Colegiul Pedagogic Ion Creangă, Bălţi Liceul Teoretic Ion Creangă Rezolvarea problemelor la chimie prin metoda algebrică Autor: Postolache Ion,
Sisteme diferenţiale liniare de ordinul 1
 1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
14. Se dă următorul compus:
 CLASA a XI-a 1. Care din următorii compuşi este un derivat halogenat vicinal: a) 1,2-dicloropropanul; b) 1,1-dicloropropanul; c) 1-bromopropanul; d) 2-bromo-2-metilpropanul; e) 1,3,5-tricloropropanul.
CLASA a XI-a 1. Care din următorii compuşi este un derivat halogenat vicinal: a) 1,2-dicloropropanul; b) 1,1-dicloropropanul; c) 1-bromopropanul; d) 2-bromo-2-metilpropanul; e) 1,3,5-tricloropropanul.
Metode iterative pentru probleme neliniare - contractii
 Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Universitatea Dunărea de Jos din Galaţi CULEGERE DE TESTE PENTRU ADMITEREA 2015 DISCIPLINA: CHIMIE ORGANICĂ
 Universitatea Dunărea de Jos din Galaţi CULEGERE DE TESTE PENTRU ADMITEREA 2015 DISCIPLINA: CHIMIE ORGANICĂ CULEGEREA DE TESTE ESTE RECOMANDATĂ PENTRU CANDIDAȚII CARE VOR SUSȚINE CONCURS DE ADMITERE LA
Universitatea Dunărea de Jos din Galaţi CULEGERE DE TESTE PENTRU ADMITEREA 2015 DISCIPLINA: CHIMIE ORGANICĂ CULEGEREA DE TESTE ESTE RECOMANDATĂ PENTRU CANDIDAȚII CARE VOR SUSȚINE CONCURS DE ADMITERE LA
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate.
 Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
(a) se numeşte derivata parţială a funcţiei f în raport cu variabila x i în punctul a.
 Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Problema a II - a (10 puncte) Diferite circuite electrice
 Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
Algebra si Geometrie Seminar 9
 Algebra si Geometrie Seminar 9 Decembrie 017 ii Equations are just the boring part of mathematics. I attempt to see things in terms of geometry. Stephen Hawking 9 Dreapta si planul in spatiu 1 Notiuni
Algebra si Geometrie Seminar 9 Decembrie 017 ii Equations are just the boring part of mathematics. I attempt to see things in terms of geometry. Stephen Hawking 9 Dreapta si planul in spatiu 1 Notiuni
Toate subiectele sunt obligatorii. Timpul de lucru efectiv este de 3 ore. Se acordă din oficiu 10 puncte. SUBIECTUL I.
 Modelul 4 Se acordă din oficiu puncte.. Fie numărul complex z = i. Calculaţi (z ) 25. 2. Dacă x şi x 2 sunt rădăcinile ecuaţiei x 2 9x+8 =, atunci să se calculeze x2 +x2 2 x x 2. 3. Rezolvaţi în mulţimea
Modelul 4 Se acordă din oficiu puncte.. Fie numărul complex z = i. Calculaţi (z ) 25. 2. Dacă x şi x 2 sunt rădăcinile ecuaţiei x 2 9x+8 =, atunci să se calculeze x2 +x2 2 x x 2. 3. Rezolvaţi în mulţimea
Curs 14 Funcţii implicite. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi"
 Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
R R, f ( x) = x 7x+ 6. Determinați distanța dintre punctele de. B=, unde x și y sunt numere reale.
 5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
5. FUNCŢII IMPLICITE. EXTREME CONDIŢIONATE.
 5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
Seminariile Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reziduurilor
 Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile
 Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Acizi carboxilici heterofuncționali.
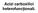 Acizi carboxilici heterofuncționali. 1. Acizi carboxilici halogenați. R R 2 l l R 2 R l Acizi α-halogenați Acizi β-halogenați l R 2 2 l Acizi γ-halogenați Metode de obținere. 1. alogenarea directă a acizilor
Acizi carboxilici heterofuncționali. 1. Acizi carboxilici halogenați. R R 2 l l R 2 R l Acizi α-halogenați Acizi β-halogenați l R 2 2 l Acizi γ-halogenați Metode de obținere. 1. alogenarea directă a acizilor
Esalonul Redus pe Linii (ERL). Subspatii.
 Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
Laborator 11. Mulţimi Julia. Temă
 Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii transversale, scrisă faţă de una dintre axele de inerţie principale:,
 REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor X) functia f 1
 Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Capitolul 1. Avansarea reacţiei
 Capitolul. vansarea reacţiei. Definiţii preliminarii Cinetica chimică studiază transformarea chimică a sistemelor în timp. Reacţia chimică transformă reactanţii în produşi. Intermediarii sunt substanţele
Capitolul. vansarea reacţiei. Definiţii preliminarii Cinetica chimică studiază transformarea chimică a sistemelor în timp. Reacţia chimică transformă reactanţii în produşi. Intermediarii sunt substanţele
Metoda rezolvării problemelor de determinare a formulelor chimice
 inisterul Educaţiei şi Tineretului al Republicii oldova Colegiul Pedagogic Ion Creangă, Bălţi Liceul Teoretic Ion Creangă etoda rezolvării problemelor de determinare a formulelor chimice Autor Postolache
inisterul Educaţiei şi Tineretului al Republicii oldova Colegiul Pedagogic Ion Creangă, Bălţi Liceul Teoretic Ion Creangă etoda rezolvării problemelor de determinare a formulelor chimice Autor Postolache
Universitatea Dunărea de Jos din Galaţi CULEGERE DE TESTE PENTRU ADMITEREA 2014 DISCIPLINA: CHIMIE ORGANICĂ. Capitolul Hidrocarburi
 Universitatea Dunărea de Jos din Galaţi CULEGERE DE TESTE PENTRU ADMITEREA 2014 DISCIPLINA: CHIMIE ORGANICĂ Capitolul Hidrocarburi CULEGEREA DE TESTE ESTE RECOMANDATĂ PENTRU CANDIDAȚII CARE VOR SUSȚINE
Universitatea Dunărea de Jos din Galaţi CULEGERE DE TESTE PENTRU ADMITEREA 2014 DISCIPLINA: CHIMIE ORGANICĂ Capitolul Hidrocarburi CULEGEREA DE TESTE ESTE RECOMANDATĂ PENTRU CANDIDAȚII CARE VOR SUSȚINE
In cazul sistemelor G-L pentru care nu se aplica legile amintite ale echilibrului de faza, relatia y e = f(x) se determina numai experimental.
 ECHILIBRUL FAZELOR Este descris de: Legea repartitiei masice Legea fazelor Legea distributiei masice La echilibru, la temperatura constanta, raportul concentratiilor substantei dizolvate in doua faze aflate
ECHILIBRUL FAZELOR Este descris de: Legea repartitiei masice Legea fazelor Legea distributiei masice La echilibru, la temperatura constanta, raportul concentratiilor substantei dizolvate in doua faze aflate
Lectia 4 proiect-17.10.2010 Clasa a VIII-a Grupa de performanta. Mulaje, chituri pentru geamuri FeSO 4.7H 2 0 Calaican Mordant in vopsitorie
 Lectia 4 proiect-17.10.2010 Clasa a VIII-a Grupa de performanta COMPOZITIA PROCENTUALA A UNUI AMESTEC.SOLUTII.CRISTALOHIDRATI. REGULA DREPTUNGIULUI O serie de substante retin un numar de molecule de apa,
Lectia 4 proiect-17.10.2010 Clasa a VIII-a Grupa de performanta COMPOZITIA PROCENTUALA A UNUI AMESTEC.SOLUTII.CRISTALOHIDRATI. REGULA DREPTUNGIULUI O serie de substante retin un numar de molecule de apa,
2. STATICA FLUIDELOR. 2.A. Presa hidraulică. Legea lui Arhimede
 2. STATICA FLUIDELOR 2.A. Presa hidraulică. Legea lui Arhimede Aplicația 2.1 Să se determine ce masă M poate fi ridicată cu o presă hidraulică având raportul razelor pistoanelor r 1 /r 2 = 1/20, ştiind
2. STATICA FLUIDELOR 2.A. Presa hidraulică. Legea lui Arhimede Aplicația 2.1 Să se determine ce masă M poate fi ridicată cu o presă hidraulică având raportul razelor pistoanelor r 1 /r 2 = 1/20, ştiind
MARCAREA REZISTOARELOR
 1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
III. Serii absolut convergente. Serii semiconvergente. ii) semiconvergentă dacă este convergentă iar seria modulelor divergentă.
 III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
MODEL DE SUBIECT Chimie organică (nivel I / nivel II)
 Bun venit dragi elevi! Am speranţa, că ciclul de emisiuni destinate pregătirii examenului de Bacalaureat-proba de Chimie organică sau Chimie anorganică şi generală, va fi util pentru alegerea voastră.
Bun venit dragi elevi! Am speranţa, că ciclul de emisiuni destinate pregătirii examenului de Bacalaureat-proba de Chimie organică sau Chimie anorganică şi generală, va fi util pentru alegerea voastră.
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor
 Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Probleme clasa a VII-a
 Probleme clasa a VII-a 1.Un cui de fier este supus unor transformări chimice prin; a) îndoire b) magnetizare c) rupere d) ruginire 2.Substanţele obţinute în urma vaporizăriii: a) îşi modifică compoziţia
Probleme clasa a VII-a 1.Un cui de fier este supus unor transformări chimice prin; a) îndoire b) magnetizare c) rupere d) ruginire 2.Substanţele obţinute în urma vaporizăriii: a) îşi modifică compoziţia
Integrala nedefinită (primitive)
 nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
ENUNŢURI ŞI REZOLVĂRI 2013
 ENUNŢURI ŞI REZOLVĂRI 8. Un conductor de cupru ( ρ =,7 Ω m) are lungimea de m şi aria secţiunii transversale de mm. Rezistenţa conductorului este: a), Ω; b), Ω; c), 5Ω; d) 5, Ω; e) 7, 5 Ω; f) 4, 7 Ω. l
ENUNŢURI ŞI REZOLVĂRI 8. Un conductor de cupru ( ρ =,7 Ω m) are lungimea de m şi aria secţiunii transversale de mm. Rezistenţa conductorului este: a), Ω; b), Ω; c), 5Ω; d) 5, Ω; e) 7, 5 Ω; f) 4, 7 Ω. l
Componente şi Circuite Electronice Pasive. Laborator 3. Divizorul de tensiune. Divizorul de curent
 Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
Numele și prenumele elevului: Unitatea de învățământ:
 clasa 9 Numele și prenumele elevului: Unitatea de învățământ: Concurs "Academician Cristofor Simionescu" - Ediția a IV-a - 2016 Formular de concurs Clasa a IX-a Toate subiectele sunt obligatorii, un singur
clasa 9 Numele și prenumele elevului: Unitatea de învățământ: Concurs "Academician Cristofor Simionescu" - Ediția a IV-a - 2016 Formular de concurs Clasa a IX-a Toate subiectele sunt obligatorii, un singur
Definiţia generală Cazul 1. Elipsa şi hiperbola Cercul Cazul 2. Parabola Reprezentari parametrice ale conicelor Tangente la conice
 1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
EXAMENUL DE BACALAUREAT Proba E/F
 EXAMENUL DE BACALAUREAT - 2009 Proba E/F Toate subiectele A-F sunt obligatorii. Subiectul G1 este obligatoriu numai pentru NIVELUL I. Subiectul G2 este obligatoriu numai pentru NIVELUL II. Timpul efectiv
EXAMENUL DE BACALAUREAT - 2009 Proba E/F Toate subiectele A-F sunt obligatorii. Subiectul G1 este obligatoriu numai pentru NIVELUL I. Subiectul G2 este obligatoriu numai pentru NIVELUL II. Timpul efectiv
Examen AG. Student:... Grupa: ianuarie 2016
 16-17 ianuarie 2016 Problema 1. Se consideră graful G = pk n (p, n N, p 2, n 3). Unul din vârfurile lui G se uneşte cu câte un vârf din fiecare graf complet care nu-l conţine, obţinându-se un graf conex
16-17 ianuarie 2016 Problema 1. Se consideră graful G = pk n (p, n N, p 2, n 3). Unul din vârfurile lui G se uneşte cu câte un vârf din fiecare graf complet care nu-l conţine, obţinându-se un graf conex
Studiu privind soluţii de climatizare eficiente energetic
 Studiu privind soluţii de climatizare eficiente energetic Varianta iniţială O schemă constructivă posibilă, a unei centrale de tratare a aerului, este prezentată în figura alăturată. Baterie încălzire/răcire
Studiu privind soluţii de climatizare eficiente energetic Varianta iniţială O schemă constructivă posibilă, a unei centrale de tratare a aerului, este prezentată în figura alăturată. Baterie încălzire/răcire
Asupra unei inegalităţi date la barajul OBMJ 2006
 Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
1 C L A S A a I X - a
 9 Clasa Numele și prenumele elevului: Unitatea de învățământ: Concurs "Academician Cristofor Simionescu" - Ediția a V-a, 2017 Formular de concurs Clasa a IX-a, CHIMIE APLICATĂ ÎN PROTECȚIA MEDIULUI Toate
9 Clasa Numele și prenumele elevului: Unitatea de învățământ: Concurs "Academician Cristofor Simionescu" - Ediția a V-a, 2017 Formular de concurs Clasa a IX-a, CHIMIE APLICATĂ ÎN PROTECȚIA MEDIULUI Toate
Curs 1 Şiruri de numere reale
 Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
a n (ζ z 0 ) n. n=1 se numeste partea principala iar seria a n (z z 0 ) n se numeste partea
 Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Olimpiada Naţională de Matematică Etapa locală Clasa a IX-a M 1
 Calea 13 Septembrie, r 09, Sector 5, 0507, București Tel: +40 (0)1 317 36 50 Fax: +40 (0)1 317 36 54 Olimpiada Naţioală de Matematică Etapa locală -00016 Clasa a IX-a M 1 Fie 1 abc,,, 6 şi ab c 1 Să se
Calea 13 Septembrie, r 09, Sector 5, 0507, București Tel: +40 (0)1 317 36 50 Fax: +40 (0)1 317 36 54 Olimpiada Naţioală de Matematică Etapa locală -00016 Clasa a IX-a M 1 Fie 1 abc,,, 6 şi ab c 1 Să se
ANALIZE FIZICO-CHIMICE MATRICE APA. Tip analiza Tip proba Metoda de analiza/document de referinta/acreditare
 ph Conductivitate Turbiditate Cloruri Determinarea clorului liber si total Indice permanganat Suma Ca+Mg, apa de suprafata, apa, apa grea, apa de suprafata, apa grea, apa de suprafata, apa grea, apa de
ph Conductivitate Turbiditate Cloruri Determinarea clorului liber si total Indice permanganat Suma Ca+Mg, apa de suprafata, apa, apa grea, apa de suprafata, apa grea, apa de suprafata, apa grea, apa de
Testare la disciplina CHIMIE. Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu. Timpul de lucru efectiv este de 90 minute.
 Colegiul Naţional Al.I.Cuza Focşani Testare la disciplina CHIMIE Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu. Timpul de lucru efectiv este de 90 minute. Clasa a IX-a Subiectul I.
Colegiul Naţional Al.I.Cuza Focşani Testare la disciplina CHIMIE Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu. Timpul de lucru efectiv este de 90 minute. Clasa a IX-a Subiectul I.
CURS XI XII SINTEZĂ. 1 Algebra vectorială a vectorilor liberi
 Lect. dr. Facultatea de Electronică, Telecomunicaţii şi Tehnologia Informaţiei Algebră, Semestrul I, Lector dr. Lucian MATICIUC http://math.etti.tuiasi.ro/maticiuc/ CURS XI XII SINTEZĂ 1 Algebra vectorială
Lect. dr. Facultatea de Electronică, Telecomunicaţii şi Tehnologia Informaţiei Algebră, Semestrul I, Lector dr. Lucian MATICIUC http://math.etti.tuiasi.ro/maticiuc/ CURS XI XII SINTEZĂ 1 Algebra vectorială
CHIMIE ORGANICĂ CLASA a XII-a
 CHIMIE ORGANICĂ CLASA a XII-a 1. Puritatea unei substanţe organice se verifică prin: a) efectuarea analizei elementare calitative; b) invariabilitatea constantelor fizice la repetarea purificării; c) testarea
CHIMIE ORGANICĂ CLASA a XII-a 1. Puritatea unei substanţe organice se verifică prin: a) efectuarea analizei elementare calitative; b) invariabilitatea constantelor fizice la repetarea purificării; c) testarea
Curs 4 Serii de numere reale
 Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Modele de teste grilă pentru examenul de admitere la Facultatea de Medicină şi Farmacie, specializarea Farmacie*
 Universitatea UNIVERSITATEA DUNĂREA DE JOS din GALAŢI Facultatea de Medicină şi Farmacie, Specializarea Farmacie Modele de teste grilă pentru examenul de admitere la Facultatea de Medicină şi Farmacie,
Universitatea UNIVERSITATEA DUNĂREA DE JOS din GALAŢI Facultatea de Medicină şi Farmacie, Specializarea Farmacie Modele de teste grilă pentru examenul de admitere la Facultatea de Medicină şi Farmacie,
Examenul de bacalaureat național 2014 Proba E. d) Chimie organică (nivel I/ nivel II)
 Ministerul Educației Naționale Centrul Național de Evaluare şi Examinare Examenul de bacalaureat național 2014 Proba E. d) Chimie organică (nivel I/ nivel II) Filiera teoretică profil real, specializarea
Ministerul Educației Naționale Centrul Național de Evaluare şi Examinare Examenul de bacalaureat național 2014 Proba E. d) Chimie organică (nivel I/ nivel II) Filiera teoretică profil real, specializarea
riptografie şi Securitate
 riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
CONCURSUL DE CHIMIE ORGANICĂ MARGARETA AVRAM
 LICEUL TEORETIC TRAIAN CONSTANŢA CLAS a X-a VARIANTA II CONCURSUL DE CHIMIE ORGANICĂ MARGARETA AVRAM - 2017 La întrebările de la 1-20, alege un singur răspuns: 1. Sunt adevarate urmatoarele afirmații cu
LICEUL TEORETIC TRAIAN CONSTANŢA CLAS a X-a VARIANTA II CONCURSUL DE CHIMIE ORGANICĂ MARGARETA AVRAM - 2017 La întrebările de la 1-20, alege un singur răspuns: 1. Sunt adevarate urmatoarele afirmații cu
Valori limită privind SO2, NOx şi emisiile de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili
 Anexa 2.6.2-1 SO2, NOx şi de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili de bioxid de sulf combustibil solid (mg/nm 3 ), conţinut de O 2 de 6% în gazele de ardere, pentru
Anexa 2.6.2-1 SO2, NOx şi de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili de bioxid de sulf combustibil solid (mg/nm 3 ), conţinut de O 2 de 6% în gazele de ardere, pentru
2. Sisteme de forţe concurente...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...3
 SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
5.4. MULTIPLEXOARE A 0 A 1 A 2
 5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
GEOMETRIE PLANĂ TEOREME IMPORTANTE ARII. bh lh 2. abc. abc. formula înălţimii
 GEOMETRIE PLNĂ TEOREME IMPORTNTE suma unghiurilor unui triunghi este 8º suma unghiurilor unui patrulater este 6º unghiurile de la baza unui triunghi isoscel sunt congruente într-un triunghi isoscel liniile
GEOMETRIE PLNĂ TEOREME IMPORTNTE suma unghiurilor unui triunghi este 8º suma unghiurilor unui patrulater este 6º unghiurile de la baza unui triunghi isoscel sunt congruente într-un triunghi isoscel liniile
PROBLEME DE CHIMIE ORGANICĂ
 FNDUL SCIAL EURPEAN Programul peraţional Sectorial pentru Dezvoltarea Resurselor Umane 2007 2013 Axa prioritară: 1 Educaţia şi formarea profesională în sprijinul creşterii economice şi dezvoltării societăţii
FNDUL SCIAL EURPEAN Programul peraţional Sectorial pentru Dezvoltarea Resurselor Umane 2007 2013 Axa prioritară: 1 Educaţia şi formarea profesională în sprijinul creşterii economice şi dezvoltării societăţii
Tranzistoare bipolare şi cu efect de câmp
 apitolul 3 apitolul 3 26. Pentru circuitul de polarizare din fig. 26 se cunosc: = 5, = 5, = 2KΩ, = 5KΩ, iar pentru tranzistor se cunosc următorii parametrii: β = 200, 0 = 0, μa, = 0,6. a) ă se determine
apitolul 3 apitolul 3 26. Pentru circuitul de polarizare din fig. 26 se cunosc: = 5, = 5, = 2KΩ, = 5KΩ, iar pentru tranzistor se cunosc următorii parametrii: β = 200, 0 = 0, μa, = 0,6. a) ă se determine
Subiectul C. Acidul tartric (A) este folosit ca substanńă acidulantă în industria alimentară şi are formula de structură:
 Ministerul EducaŃiei, Cercetării, Tineretului şi Sportului Centrul NaŃional de Evaluare şi Examinare Examenul de bacalaureat 2012 Proba E. d) Proba scrisă la CHIMIE ORGANICĂ (Nivel I/Nivel II) Model Filiera
Ministerul EducaŃiei, Cercetării, Tineretului şi Sportului Centrul NaŃional de Evaluare şi Examinare Examenul de bacalaureat 2012 Proba E. d) Proba scrisă la CHIMIE ORGANICĂ (Nivel I/Nivel II) Model Filiera
SEMINAR 14. Funcţii de mai multe variabile (continuare) ( = 1 z(x,y) x = 0. x = f. x + f. y = f. = x. = 1 y. y = x ( y = = 0
 Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
OLIMPIADA DE CHIMIE etapa județeană/a municipiului Bucureşti 17 martie 2018 Clasa a X-a
 LIMPIADA DE IMIE etapa județeană/a municipiului Bucureşti 17 martie 2018 lasa a X-a Varianta 1 Indicații: Pentru rezolvarea problemelor utilizați masele atomice rotunjite din TABELUL PEIDI AL ELEMENTEL
LIMPIADA DE IMIE etapa județeană/a municipiului Bucureşti 17 martie 2018 lasa a X-a Varianta 1 Indicații: Pentru rezolvarea problemelor utilizați masele atomice rotunjite din TABELUL PEIDI AL ELEMENTEL
Conice. Lect. dr. Constantin-Cosmin Todea. U.T. Cluj-Napoca
 Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
CONCURSUL DE MATEMATICĂ APLICATĂ ADOLF HAIMOVICI, 2017 ETAPA LOCALĂ, HUNEDOARA Clasa a IX-a profil științe ale naturii, tehnologic, servicii
 Clasa a IX-a 1 x 1 a) Demonstrați inegalitatea 1, x (0, 1) x x b) Demonstrați că, dacă a 1, a,, a n (0, 1) astfel încât a 1 +a + +a n = 1, atunci: a +a 3 + +a n a1 +a 3 + +a n a1 +a + +a n 1 + + + < 1
Clasa a IX-a 1 x 1 a) Demonstrați inegalitatea 1, x (0, 1) x x b) Demonstrați că, dacă a 1, a,, a n (0, 1) astfel încât a 1 +a + +a n = 1, atunci: a +a 3 + +a n a1 +a 3 + +a n a1 +a + +a n 1 + + + < 1
