Probability theory. Distributions. Inequalities. Convergence. E, Var, E k k. f[ ] (2 ) k ~ [, ] E[ [ ]( )] E[ [ ]]

Chapter 15 Identifying Failure & Repair Distributions

Chape 5 Idefyg Falue & Repa Dsbuos Paamee Esmao maxmum lkelhood esmao C. Ebelg, Io o Relably & Maaably Chape 5 Egeeg, d ed. Wavelad Pess, Ic. Copygh 00 Maxmum Lkelhood Esmao (MLE) Fd esmaes fo he dsbuo

George S. A. Shaker ECE477 Understanding Reflections in Media. Reflection in Media

Geoge S. A. Shake C477 Udesadg Reflecos Meda Refleco Meda Ths hadou ages a smplfed appoach o udesad eflecos meda. As a sude C477, you ae o equed o kow hese seps by hea. I s jus o make you udesad how some

FORMULAE SHEET for STATISTICS II

Síscs II Degrees Ecoomcs d Mgeme FOMULAE SHEET for STATISTICS II EPECTED VALUE MOMENTS AND PAAMETES - Vr ( E( E( - Cov( E{ ( ( } E( E( E( µ ρ Cov( - E ( b E( be( Vr( b Vr( b Vr( bcov( THEOETICAL DISTIBUTIONS

Chapter 1 Fundamentals in Elasticity

D. of o. NU Fs s ν ss L. Pof. H L ://s.s.. D. of o. NU. Po Dfo ν Ps s - Do o - M os - o oos : o o w Uows o: - ss - - Ds W ows s o qos o so s os. w ows o fo s o oos s os of o os. W w o s s ss: - ss - -

Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α

Α Ρ Χ Α Ι Α Ι Σ Τ Ο Ρ Ι Α Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α Σ η µ ε ί ω σ η : σ υ ν ά δ ε λ φ ο ι, ν α µ ο υ σ υ γ χ ω ρ ή σ ε τ ε τ ο γ ρ ή γ ο ρ ο κ α ι α τ η µ έ λ η τ ο ύ

MATH 38061/MATH48061/MATH68061: MULTIVARIATE STATISTICS Solutions to Problems on Matrix Algebra

MATH 38061/MATH48061/MATH68061: MULTIVARIATE STATISTICS Solutios to Poblems o Matix Algeba 1 Let A be a squae diagoal matix takig the fom a 11 0 0 0 a 22 0 A 0 0 a pp The ad So, log det A t log A t log

Vidyalankar. Vidyalankar S.E. Sem. III [BIOM] Applied Mathematics - III Prelim Question Paper Solution. 1 e = 1 1. f(t) =

. (a). (b). (c) f() L L e i e Vidyalakar S.E. Sem. III [BIOM] Applied Mahemaic - III Prelim Queio Paper Soluio L el e () i ( ) H( ) u e co y + 3 3y u e co y + 6 uy e i y 6y uyy e co y 6 u + u yy e co y

Errata (Includes critical corrections only for the 1 st & 2 nd reprint)

Wedesday, May 5, 3 Erraa (Icludes criical correcios oly for he s & d repri) Advaced Egieerig Mahemaics, 7e Peer V O eil ISB: 978474 Page # Descripio 38 ie 4: chage "w v a v " "w v a v " 46 ie : chage "y

Exam Statistics 6 th September 2017 Solution

Exam Statstcs 6 th September 17 Soluto Maura Mezzett Exercse 1 Let (X 1,..., X be a raom sample of... raom varables. Let f θ (x be the esty fucto. Let ˆθ be the MLE of θ, θ be the true parameter, L(θ be

LAPLACE TRANSFORM TABLE

LAPLACE TRANSFORM TABLE Th Laplac afom of am mpl fuco a gv h Tabl. Fuco U mpul U Sp U Ramp Expoal Rpad Roo S Co Polyomal Dampd Dampd co f δ u -a -a co,,... -a -a co F / / /a /a / /!/ /a a/a Thom : Shf

On Quasi - f -Power Increasing Sequences

Ieaioal Maheaical Fou Vol 8 203 o 8 377-386 Quasi - f -owe Iceasig Sequeces Maheda Misa G Deae of Maheaics NC College (Auooous) Jaju disha Mahedaisa2007@gailco B adhy Rolad Isiue of echoy Golahaa-76008

RG Tutorial xlc3.doc 1/10. To apply the R-G method, the differential equation must be represented in the form:

G Tuorial xlc3.oc / iear roblem i e C i e C ( ie ( Differeial equaio for C (3 Thi fir orer iffereial equaio ca eaily be ole bu he uroe of hi uorial i o how how o ue he iz-galerki meho o fi ou he oluio.

!"!# ""$ %%"" %$" &" %" "!'! " #$!

" "" %%"" %" &" %" " " " % ((((( ((( ((((( " %%%% & ) * ((( "* ( + ) (((( (, (() (((((* ( - )((((( )((((((& + )(((((((((( +. ) ) /(((( +( ),(, ((((((( +, 0 )/ (((((+ ++, ((((() & "( %%%%%%%%%%%%%%%%%%%(

i i (3) Derive the fixed-point iteration algorithm and apply it to the data of Example 1.

Howor#3 urvval Aalyss Na: Huag Xw 黃昕蔚 Quso: uppos ha daa ( follow h odl ( ( > ad <

) 2. δ δ. β β. β β β β. r k k. tll. m n Λ + +

Techical Appedix o Hamig eposis ad Helpig Bowes: The ispaae Impac of Ba Cosolidaio (o o be published bu o be made available upo eques. eails of Poofs of Poposiios 1 ad To deive Poposiio 1 s exac ad sufficie

Finite Integrals Pertaining To a Product of Special Functions By V.B.L. Chaurasia, Yudhveer Singh University of Rajasthan, Jaipur

Global Joal of Scece oe eeac Vole Ie 4 Veo Jl Te: Doble Bld Pee eewed Ieaoal eeac Joal Pble: Global Joal Ic SA ISSN: 975-5896 e Iegal Peag To a Podc of Secal co B VBL Caaa Ydee Sg e of aaa Ja Abac - A

Latent variable models Variational approximations.

CS 3750 Mache Learg Lectre 9 Latet varable moel Varatoal appromato. Mlo arecht mlo@c.ptt.e 539 Seott Sqare CS 750 Mache Learg Cooperatve vector qatzer Latet varable : meoalty bary var Oberve varable :

The one-dimensional periodic Schrödinger equation

The one-dmensonal perodc Schrödnger equaon Jordan Bell jordan.bell@gmal.com Deparmen of Mahemacs, Unversy of Torono Aprl 23, 26 Translaons and convoluon For y, le τ y f(x f(x y. To say ha f : C s unformly

Derivation of the Filter Coefficients for the Ramp Invariant Method as Applied to Base Excitation of a Single-degree-of-Freedom System Revision B

Dervao of he Fler Coeffce for he Ramp Ivara Meho a Apple o Bae Excao of a Sgle-egree-of-Freeom Sem Revo B B om Irve Emal: om@vbraoaa.com Aprl, 0 Irouco Coer he gle-egree-of-freeom em Fgure. m &&x k c &&

On Zero-Sum Stochastic Differential Games

O Zeo-Sum Sochac Dffeeal Game Eha Bayaka, Sog Yao Abac We geealze he eul of Flemg ad Sougad 13 o zeo-um ochac dffeeal game o he cae whe he cool ae ubouded. We do h by povg a dyamc pogammg pcple ug a coveg

Probabilistic Image Processing by Extended Gauss-Markov Random Fields

Pobablsc mage Pocessng b Eended Gauss-Makov Random Felds Kauuk anaka Munek asuda Ncolas Mon Gaduae School of nfomaon Scences ohoku Unves Japan and D. M. engon Depamen of Sascs Unves of Glasgow UK 3 Sepembe

Perturbation Series in Light-Cone Diagrams of Green Function of String Field

Petuto Sees ht-coe Dms of ee Fucto of St Fel Am-l Te-So Km Chol-M So- m Detmet of Eey Scece Km l Su Uvesty Pyoy DPR Koe E-y Km l Su Uvesty Pyoy DPR Koe Detmet of Physcs Km l Su Uvesty Pyoy DPR Koe Astct

S 5 S 1 S 2 S 6 S 9 S 7 S 3 S 4 S 8

4.9.. HM-..,,.... :, HM-,,,,.... " " - ",.. " ".,,,,,,.,,.,,..,.,. Byfy, Zaa..,,.. W-F-,, (W-F -. :,,, -,,,,,.,, :, (, W-F, (Byfy, Zaa, GSM,..,.,, (...,,,. HM(Howad-Maays- [5, 6, 9, ],. S S 5 S 9 S S 6

Déformation et quantification par groupoïde des variétés toriques

Défomation et uantification pa goupoïde de vaiété toiue Fédéic Cadet To cite thi veion: Fédéic Cadet. Défomation et uantification pa goupoïde de vaiété toiue. Mathématiue [math]. Univeité d Oléan, 200.

.. ntsets ofa.. d ffeom.. orp ism.. na s.. m ooth.. man iod period I n open square. n t s e t s ofa \quad d ffeom \quad orp ism \quad na s \quad m o

G G - - -- - W - - - R S - q k RS ˆ W q q k M G W R S L [ RS - q k M S 4 R q k S [ RS [ M L ˆ L [M O S 4] L ˆ ˆ L ˆ [ M ˆ S 4 ] ˆ - O - ˆ q k ˆ RS q k q k M - j [ RS ] [ M - j - L ˆ ˆ ˆ O ˆ [ RS ] [ M

Solve the difference equation

Solve the differece equatio Solutio: y + 3 3y + + y 0 give tat y 0 4, y 0 ad y 8. Let Z{y()} F() Taig Z-trasform o both sides i (), we get y + 3 3y + + y 0 () Z y + 3 3y + + y Z 0 Z y + 3 3Z y + + Z y

Α Ρ Ι Θ Μ Ο Σ : 6.913

Α Ρ Ι Θ Μ Ο Σ : 6.913 ΠΡΑΞΗ ΚΑΤΑΘΕΣΗΣ ΟΡΩΝ ΔΙΑΓΩΝΙΣΜΟΥ Σ τ η ν Π ά τ ρ α σ ή μ ε ρ α σ τ ι ς δ ε κ α τ έ σ σ ε ρ ι ς ( 1 4 ) τ ο υ μ ή ν α Ο κ τ ω β ρ ί ο υ, η μ έ ρ α Τ ε τ ά ρ τ η, τ ο υ έ τ ο υ ς δ

Latent variable models Variational approximations.

CS 3750 Mache Learg Lectre 9 Latet varable moel Varatoal appromato. Mlo arecht mlo@c.ptt.e 539 Seott Sqare CS 750 Mache Learg Cooperatve vector qatzer Latet varable : meoalty bary var Oberve varable :

Edexcel FP3. Hyperbolic Functions. PhysicsAndMathsTutor.com

Eeel FP Hpeoli Futios PhsisAMthsTuto.om . Solve the equtio Leve lk 7seh th 5 Give ou swes i the fom l whee is tiol ume. 5 7 Sih 5 Cosh osh 7 Sih 5osh's 7 Ee e I E e e 4 e te 5e 55 O 5e 55 te e 4 O Ge 45

Edexcel FP3. Hyperbolic Functions. PhysicsAndMathsTutor.com

Eecel FP Hpeolic Fuctios PhsicsAMthsTuto.com . Solve the equtio Leve lk 7sech th 5 Give ou swes i the fom l whee is tiol ume. 5 7 Sih 5 Cosh cosh c 7 Sih 5cosh's 7 Ece e I E e e 4 e te 5e 55 O 5e 55 te

CS 1675 Introduction to Machine Learning Lecture 7. Density estimation. Milos Hauskrecht 5329 Sennott Square

CS 675 Itroducto to Mache Learg Lecture 7 esty estmato Mlos Hausrecht mlos@cs.tt.edu 539 Seott Square ata: esty estmato {.. } a vector of attrbute values Objectve: estmate the model of the uderlyg robablty

Note: Please use the actual date you accessed this material in your citation.

MIT OpeCueWae hp://cw.m.eu 6.13/ESD.13J Elecmagec a pplca, Fall 5 Pleae ue he llwg ca ma: Maku Zah, Ech Ippe, a Dav Sael, 6.13/ESD.13J Elecmagec a pplca, Fall 5. (Maachue Iue Techlgy: MIT OpeCueWae). hp://cw.m.eu

2. Α ν ά λ υ σ η Π ε ρ ι ο χ ή ς. 3. Α π α ι τ ή σ ε ι ς Ε ρ γ ο δ ό τ η. 4. Τ υ π ο λ ο γ ί α κ τ ι ρ ί ω ν. 5. Π ρ ό τ α σ η. 6.

Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α 1. Ε ι σ α γ ω γ ή 2. Α ν ά λ υ σ η Π ε ρ ι ο χ ή ς 3. Α π α ι τ ή σ ε ι ς Ε ρ γ ο δ ό τ η 4. Τ υ π ο λ ο γ ί α κ τ ι ρ ί ω ν 5. Π ρ ό τ α σ η 6. Τ ο γ ρ α φ ε ί ο 1. Ε ι σ α γ ω

L.K.Gupta (Mathematic Classes) www.pioeermathematics.com MOBILE: 985577, 4677 + {JEE Mai 04} Sept 0 Name: Batch (Day) Phoe No. IT IS NOT ENOUGH TO HAVE A GOOD MIND, THE MAIN THING IS TO USE IT WELL Marks:

arxiv: v1 [math.pr] 13 Jul 2010

L Soluo of Bacward Sochac Dffereal quao wh Jum Sog Yao arv:17.6v1 mah.pr 13 Jul 1 Abrac I h aer, we udy a mul-dmeoal bacward ochac dffereal equao wh jum BSDJ ha ha o-lchz geeraor ad ubouded radom me horzo.

1. For each of the following power series, find the interval of convergence and the radius of convergence:

Math 6 Practice Problems Solutios Power Series ad Taylor Series 1. For each of the followig power series, fid the iterval of covergece ad the radius of covergece: (a ( 1 x Notice that = ( 1 +1 ( x +1.

( ) ( ) ( ) ( ) ( ) λ = 1 + t t. θ = t ε t. Continuum Mechanics. Chapter 1. Description of Motion dt t. Chapter 2. Deformation and Strain

Continm Mechanics. Official Fom Chapte. Desciption of Motion χ (,) t χ (,) t (,) t χ (,) t t Chapte. Defomation an Stain s S X E X e i ij j i ij j F X X U F J T T T U U i j Uk U k E ( F F ) ( J J J J)

(a,b) Let s review the general definitions of trig functions first. (See back cover of your book) sin θ = b/r cos θ = a/r tan θ = b/a, a 0

TRIGONOMETRIC IDENTITIES (a,b) Let s eview the geneal definitions of tig functions fist. (See back cove of you book) θ b/ θ a/ tan θ b/a, a 0 θ csc θ /b, b 0 sec θ /a, a 0 cot θ a/b, b 0 By doing some

Estimators when the Correlation Coefficient. is Negative

It J Cotemp Math Sceces, Vol 5, 00, o 3, 45-50 Estmators whe the Correlato Coeffcet s Negatve Sad Al Al-Hadhram College of Appled Sceces, Nzwa, Oma abur97@ahoocouk Abstract Rato estmators for the mea of

( ) ρ ρ + + = + d dt. ME 309 Formula Sheet. dp g dz = ρ. = f +ΣΚ and HS. +α + z = +α + z. δ =δ = δ =θ= τ =ρ =ρ. Page 1 of 7. Basic Equations.

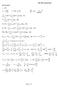Basic Eqaions ME 9 Fomla Shee R µ F F A A ηv V el η η A Vssem ( ) V el A F F V A ( ) S B XYZ XYZ el g F F a V V A S B / XYZ el M M A V ( ) S B el ( ) Q W ev e A hee V e g ino on el V consan (o invisci

Reflection Models. Reflection Models

Reflecon Models Today Types of eflecon models The BRDF and eflecance The eflecon equaon Ideal eflecon and efacon Fesnel effec Ideal dffuse Thusday Glossy and specula eflecon models Rough sufaces and mcofaces

Other Test Constructions: Likelihood Ratio & Bayes Tests

Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :

x E[x] x xµº λx. E[x] λx. x 2 3x +2

¾ λ¹ ÐÓÒ Ó ÙÖ ½ ¼ º õ ¹ ¹ ÙÖ ¾ ÙÖ º ÃÐ ¹ ½ ¼º ¹ Ð Ñ ÐÙÐÙ µ λ¹ λ¹ ÐÙÐÙ µº λ¹ º ý ½ ¼ ø λ¹ ÃÐ º λ¹ ÌÙÖ Ò ÌÙÖ º ÌÙÖ Ò ÚÓÒ Æ ÙÑ ÒÒ ¹ ÇÊÌÊ Æ Ä Çĺ ý λ¹ ¹ º Ö ÙØ ÓÒ Ñ Ò µ Ø ¹ ÓÛ ÓÑÔÙØ Ö µ ¹ λ¹ º λ¹ ÙÒØ ÓÒ Ð

ΘΕΩΡΙΑ ΚΑΙ ΕΦΑΡΜΟΓΕΣ ΣΤΗΝ ΑΝΑΛΥΣΗ ΠΑΛΙΝΔΡΟΜΗΣΗΣ. Αρτέμιος Αποστόλου Στρογγύλης

ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΘΕΩΡΙΑ ΚΑΙ ΕΦΑΡΜΟΓΕΣ ΣΤΗΝ ΑΝΑΛΥΣΗ ΠΑΛΙΝΔΡΟΜΗΣΗΣ Αρτέμιος Αποστόλου Στρογγύλης ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΣΑΜΟΣ 3 Στους γονείς μου Ελένη και Αποστόλη

C 1 D 1. AB = a, AD = b, AA1 = c. a, b, c : (1) AC 1 ; : (1) AB + BC + CC1, AC 1 = BC = AD, CC1 = AA 1, AC 1 = a + b + c. (2) BD 1 = BD + DD 1,

1 1., BD 1 B 1 1 D 1, E F B 1 D 1. B = a, D = b, 1 = c. a, b, c : (1) 1 ; () BD 1 ; () F; D 1 F 1 (4) EF. : (1) B = D, D c b 1 E a B 1 1 = 1, B1 1 = B + B + 1, 1 = a + b + c. () BD 1 = BD + DD 1, BD =

Appendix. The solution begins with Eq. (2.15) from the text, which we repeat here for 1, (A.1)

Aenix Aenix A: The equaion o he sock rice. The soluion egins wih Eq..5 rom he ex, which we reea here or convenience as Eq.A.: [ [ E E X, A. c α where X u ε, α γ, an c α y AR. Take execaions o Eq. A. as

3607 Ν. 7.28/88. E.E., Παρ. I, Αρ. 2371,

E.E., Παρ. I, Αρ. 271, 16.12. 607 Ν. 7.2/ περί Συμπληρματικύ Πρϋπλγισμύ Νόμς (Αρ. 5) τυ 19 εκδίδεται με δημσίευση στην επίσημη εφημερίδα της Κυπριακής Δημκρατίας σύμφνα με τ Άρθρ 52 τυ Συντάγματς- - Αριθμός

Vidyamandir Classes. Solutions to Revision Test Series - 2/ ACEG / IITJEE (Mathematics) = 2 centre = r. a

Per -.(D).() Vdymndr lsses Solutons to evson est Seres - / EG / JEE - (Mthemtcs) Let nd re dmetrcl ends of crcle Let nd D re dmetrcl ends of crcle Hence mnmum dstnce s. y + 4 + 4 6 Let verte (h, k) then

9.1 Introduction 9.2 Lags in the Error Term: Autocorrelation 9.3 Estimating an AR(1) Error Model 9.4 Testing for Autocorrelation 9.

9.1 Inroducion 9.2 Lags in he Error Term: Auocorrelaion 9.3 Esimaing an AR(1) Error Model 9.4 Tesing for Auocorrelaion 9.5 An Inroducion o Forecasing: Auoregressive Models 9.6 Finie Disribued Lags 9.7

Homework 8 Model Solution Section

MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx

Parts Manual. Trio Mobile Surgery Platform. Model 1033

Trio Mobile Surgery Platform Model 1033 Parts Manual For parts or technical assistance: Pour pièces de service ou assistance technique : Für Teile oder technische Unterstützung Anruf: Voor delen of technische

SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM

SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max

Αλληλεπίδραση ακτίνων-χ με την ύλη

Άσκηση 8 Αλληλεπίδραση ακτίνων-χ με την ύλη Δ. Φ. Αναγνωστόπουλος Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων Ιωάννινα 2013 Άσκηση 8 ii Αλληλεπίδραση ακτίνων-χ με την ύλη Πίνακας περιεχομένων

Lecture 6. Goals: Determine the optimal threshold, filter, signals for a binary communications problem VI-1

Lecue 6 Goals: Deemine e opimal esold, file, signals fo a binay communicaions poblem VI- Minimum Aveage Eo Pobabiliy Poblem: Find e opimum file, esold and signals o minimize e aveage eo pobabiliy. s s

6.642, Continuum Electromechanics, Fall 2004 Prof. Markus Zahn Lecture 8: Electrohydrodynamic and Ferrohydrodynamic Instabilities

6.64, Continuum Electromechnics, Fll 4 Prof. Mrus Zhn Lecture 8: Electrohydrodynmic nd Ferrohydrodynmic Instilities I. Mgnetic Field Norml Instility Courtesy of MIT Press. Used with permission. A. Equilirium

( ) ( t) ( 0) ( ) dw w. = = β. Then the solution of (1.1) is easily found to. wt = t+ t. We generalize this to the following nonlinear differential

Periodic oluion of van der Pol differenial equaion. by A. Arimoo Deparmen of Mahemaic Muahi Iniue of Technology Tokyo Japan in Seminar a Kiami Iniue of Technology January 8 9. Inroducion Le u conider a

5 Ι ^ο 3 X X X. go > 'α. ο. o f Ο > = S 3. > 3 w»a. *= < ^> ^ o,2 l g f ^ 2-3 ο. χ χ. > ω. m > ο ο ο - * * ^r 2 =>^ 3^ =5 b Ο? UJ. > ο ο.

728!. -θ-cr " -;. '. UW -,2 =*- Os Os rsi Tf co co Os r4 Ι. C Ι m. Ι? U Ι. Ι os ν ) ϋ. Q- o,2 l g f 2-2 CT= ν**? 1? «δ - * * 5 Ι -ΐ j s a* " 'g cn" w *" " 1 cog 'S=o " 1= 2 5 ν s/ O / 0Q Ε!θ Ρ h o."o.

A A O B C C A A. A0 = A 45 A 1 = B Q Ak 2. Ak 1

! " " #$%&'(&) *+,-. /01 34 564784 37964 :4 ; ?@ 34 E156F57E1 GHE H567JF4 H5F:7H4 K06 LF37:4 M4N45F415 30 6PG34 0F EK0 F17JF4415 R465071 K6ES3P4 :4 E156F57E1 3M07:4 :4 4 4F3 7156F415 4 E15 6H9H3H 7KE7S34

PDF hosted at the Radboud Repository of the Radboud University Nijmegen

PDF hosted at the Radboud Repository of the Radboud University Nijmegen The following full text is a publisher's version. For additional information about this publication click this link. http://hdl.handle.net/2066/52779

Chap. 6 Pushdown Automata

Chap. 6 Pushdown Automata 6.1 Definition of Pushdown Automata Example 6.1 L = {wcw R w (0+1) * } P c 0P0 1P1 1. Start at state q 0, push input symbol onto stack, and stay in q 0. 2. If input symbol is

APPENDIX A DERIVATION OF JOINT FAILURE DENSITIES

APPENDIX A DERIVAION OF JOIN FAILRE DENSIIES I his Appedi we prese he derivaio o he eample ailre models as show i Chaper 3. Assme ha he ime ad se o ailre are relaed by he cio g ad he sochasic are o his

ο ο 3 α. 3"* > ω > d καΐ 'Ενορία όλις ή Χώρί ^ 3 < KN < ^ < 13 > ο_ Μ ^~~ > > > > > Ο to X Η > ο_ ο Ο,2 Σχέδι Γλεγμα Ο Σ Ο Ζ < o w *< Χ χ Χ Χ < < < Ο

18 ρ * -sf. NO 1 D... 1: - ( ΰ ΐ - ι- *- 2 - UN _ ί=. r t ' \0 y «. _,2. "* co Ι». =; F S " 5 D 0 g H ', ( co* 5. «ΰ ' δ". o θ * * "ΰ 2 Ι o * "- 1 W co o -o1= to»g ι. *ΰ * Ε fc ΰ Ι.. L j to. Ι Q_ " 'T

LAD Estimation for Time Series Models With Finite and Infinite Variance

LAD Estimatio for Time Series Moels With Fiite a Ifiite Variace Richar A. Davis Colorao State Uiversity William Dusmuir Uiversity of New South Wales 1 LAD Estimatio for ARMA Moels fiite variace ifiite

SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM

SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max

21. Stresses Around a Hole (I) 21. Stresses Around a Hole (I) I Main Topics

I Main Topics A Intoducon to stess fields and stess concentaons B An axisymmetic poblem B Stesses in a pola (cylindical) efeence fame C quaons of equilibium D Soluon of bounday value poblem fo a pessuized

! "#" "" $ "%& ' %$(%& % &'(!!")!*!&+ ,! %$( - .$'!"

! "#" "" $ "%& ' %$(%&!"#$ % &'(!!")!*!&+,! %$( -.$'!" /01&$23& &4+ $$ /$ & & / ( #(&4&4!"#$ %40 &'(!"!!&+ 5,! %$( - &$ $$$".$'!" 4(02&$ 4 067 4 $$*&(089 - (0:;

tel , version 1-7 Feb 2013

!"## $ %&' (") *+ '#),! )%)%' *, -#)&,-'" &. % /%%"&.0. )%# "#",1 2" "'' % /%%"&30 "'' "#", /%%%" 4"," % /%%5" 4"," "#",%" 67 &#89% !"!"# $ %& & # &$ ' '#( ''# ))'%&##& *'#$ ##''' "#$ %% +, %'# %+)% $

ΠΑΡΑΡΤΗΜΑ ΤΡΙΤΟ ΤΗΣ ΕΠΙΣΗΜΗΣ ΕΦΗΜΕΡΙΔΑΣ ΤΗΣ ΔΗΜΟΚΡΑΤΙΑΣ Αρ της 30ής ΣΕΠΤΕΜΒΡΙΟΥ 2004 ΑΙΟΙΚΗΤΪΚΕΣ ΠΡΑΞΕΙΣ

K.AJI. 75/2004 ΠΑΡΑΡΤΗΜΑ ΤΡΙΤ ΤΗΣ ΕΠΙΣΗΜΗΣ ΕΦΗΜΕΡΙΔΑΣ ΤΗΣ ΔΗΜΚΡΑΤΙΑΣ Αρ. 906 της 0ής ΣΕΠΤΕΜΒΡΙΥ 2004 ΑΙΙΚΗΤΪΚΕΣ ΠΡΑΞΕΙΣ ΜΕΡΣ Ι Κννιστικές Διικητικές Πράξεις Αριθμός 75 Ι ΠΕΡΙ ΦΑΡΜΑΚΩ ΑΘΡΩΠΙΗΣ ΡΗΣΗΣ (ΕΛΕΓΣ

Analysis of optimal harvesting of a prey-predator fishery model with the limited sources of prey and presence of toxicity

ES Web of Confeences 7, 68 (8) hps://doiog/5/esconf/8768 ICEIS 8 nalsis of opimal havesing of a pe-pedao fishe model wih he limied souces of pe and pesence of oici Suimin,, Sii Khabibah, and Dia nies Munawwaoh

The Neutrix Product of the Distributions r. x λ

ULLETIN u. Maaysia Math. Soc. Secod Seies 22 999 - of the MALAYSIAN MATHEMATICAL SOCIETY The Neuti Poduct of the Distibutios ad RIAN FISHER AND 2 FATMA AL-SIREHY Depatet of Matheatics ad Copute Sciece

UNIVERSITÀ DEGLI STUDI DI BOLOGNA. DIPARTIMENTO DI INGEGNERIA ELETTRICA Viale Risorgimento n BOLOGNA (ITALIA) FOR THE CURRENT DISTRIBUTION

UVERSÀ DEG SUD D BOOGA DPAREO D GEGERA EERCA Vl Rogo - 36 BOOGA (AA AAYCA SOUOS FOR HE CURRE DSRBUO A RUHERFORD CABE WH SRADS. F. Bch Ac h gocl o of h ol co coffc og h of Rhfo cl vg. h olo fo h gl l c

Homework for 1/27 Due 2/5

Name: ID: Homework for /7 Due /5. [ 8-3] I Example D of Sectio 8.4, the pdf of the populatio distributio is + αx x f(x α) =, α, otherwise ad the method of momets estimate was foud to be ˆα = 3X (where

Analytical Expression for Hessian

Analytical Expession fo Hessian We deive the expession of Hessian fo a binay potential the coesponding expessions wee deived in [] fo a multibody potential. In what follows, we use the convention that

Το άτομο του Υδρογόνου

Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες

SWOT 1. Analysis and Planning for Cross-border Co-operation in Central European Countries. ISIGInstitute of. International Sociology Gorizia

SWOT 1 Analysis and Planning for Cross-border Co-operation in Central European Countries ISIGInstitute of International Sociology Gorizia ! " # $ % ' ( )!$*! " "! "+ +, $,,-,,.-./,, -.0",#,, 12$,,- %

Veliine u mehanici. Rad, snaga i energija. Dinamika. Meunarodni sustav mjere (SI) 1. Skalari. 2. Vektori - poetak. 12. dio. 1. Skalari. 2.

Vele u ehc Rd, g eegj D. do. Sl. Veo 3. Tezo II. ed 4. Tezo IV. ed. Sl: 3 0 pod je jedc (ezo ulog ed). Veo: 3 3 pod je jedc (ezo pog ed) 3. Tezo dugog ed 3 9 pod je jedc 4. Tezoeog ed 3 4 8 pod je jedc

CONSULTING Engineering Calculation Sheet

E N G I N E E R S Consulting Engineers jxxx 1 Structure Design - EQ Load Definition and EQ Effects v20 EQ Response Spectra in Direction X, Y, Z X-Dir Y-Dir Z-Dir Fundamental period of building, T 1 5.00

Łs t r t rs tø r P r s tø PrØ rø rs tø P r s r t t r s t Ø t q s P r s tr. 2stŁ s q t q s t rt r s t s t ss s Ø r s t r t. Łs t r t t Ø t q s

Łs t r t rs tø r P r s tø PrØ rø rs tø P r s r t t r s t Ø t q s P r s tr st t t t Ø t q s ss P r s P 2stŁ s q t q s t rt r s t s t ss s Ø r s t r t P r røs r Łs t r t t Ø t q s r Ø r t t r t q t rs tø

ITU-R P (2009/10)

ITU-R.45-4 (9/) % # GHz,!"# $$ # ITU-R.45-4.. (IR) (ITU-T/ITU-R/ISO/IEC).ITU-R http://www.tu.t/itu-r/go/patets/e. (http://www.tu.t/publ/r-rec/e ) () ( ) BO BR BS BT F M RA S RS SA SF SM SNG TF V.ITU-R

! " #$% & '()()*+.,/0.

! " #$% & '()()*+,),--+.,/0. 1!!" "!! 21 # " $%!%!! &'($ ) "! % " % *! 3 %,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,0 %%4,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,5

Gapso t e q u t e n t a g ebra P open parenthesis N closing parenthesis fin i s a.. pheno mno nd iscovere \ centerline

G q v v G q v H 4 q 4 q v v ˆ ˆ H 4 ] 4 ˆ ] W q K j q G q K v v W v v H 4 z ] q 4 K ˆ 8 q ˆ j ˆ O C W K j ˆ [ K v ˆ [ [; 8 ] q ˆ K O C v ˆ ˆ z q [ R ; ˆ 8 ] R [ q v O C ˆ ˆ v - - ˆ - ˆ - v - q - - v -

E.E. Παρ. Ill (I) 429 Κ.Δ.Π. 150/83 Αρ. 1871,

E.E. Πρ. ll () 429 Κ.Δ.Π. 50/ Αρ. 7, 24.6. Αρθμός 50 ΠΕΡ ΤΑΧΥΔΡΜΕΩΝ ΝΜΣ (ΚΕΦ. 0 ΚΑ ΝΜ 42 ΤΥ 96 ΚΑ 7 ΤΥ 977) Δάτγμ δνάμ τ άρθρ 7() Τ Υπργκό Σμβύλ, σκώντς τς ξσίς π πρέχντ Κ»>. 0. σ' τό δνάμ τ δφί τ άρθρ

17 Monotonicity Formula And Basic Consequences

Lectues o Vaifols Leo Sio Zhag Zui 7 Mootoicity Foula A Basic Cosequeces I this sectio we assue that U is oe i R, V v( M,θ) has the geealize ea cuvatue H i U ( see 6.5), a we wite µ fo µ V ( H θ as i 5.).

ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 2012

ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Γ ΛΥΚΕΙΟΥ ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ ο : Έστω z, z C με (z ) και (z ) Αν f() ( z )( z )( z )( z

Refined Hyers-Ulam approximation for Jensen and Euler-Lagrange Mappings

Reed Hyes-Ul oo o Jese d Eule-Lgge Mgs Joh Mchel Rsss d M (Sk Joh Rsss Pedgogcl Dee E E Seco o Mhecs d Iocs Nol d Cods Uvesy o Ahes 0 Hocous S. Ahes GREECE e-l: jsss@edu.uo.g URL:h://www.edu.uo.g/~jsss/

ο3 3 gs ftffg «5.s LS ό b a. L Μ κ5 =5 5 to w *! .., TJ ο C5 κ .2 '! "c? to C φ io -Ρ (Μ 3 Β Φ Ι <^ ϊ bcp Γί~ eg «to ιο pq ΛΛ g Ό & > I " CD β U3

I co f - bu. EH T ft Wj. ta -p -Ρ - a &.So f I P ω s Q. ( *! C5 κ u > u.., TJ C φ Γί~ eg «62 gs ftffg «5.s LS ό b a. L κ5 =5 5 W.2 '! "c? io -Ρ ( Β Φ Ι < ϊ bcp «δ ι pq ΛΛ g Ό & > I " CD β U (Ν φ ra., r

Nonlinear Motion. x M x. x x. cos. 2sin. tan. x x. Sextupoles cause nonlinear dynamics, which can be chaotic and unstable. CHESS & LEPP CHESS & LEPP

Georg.otaetter@Corell.eu USPAS Avace Accelerator Phic - ue 6 CESS & EPP CESS & EPP 56 Setupole caue oliear aic which ca be chaotic a utable. l M co i i co l i i co co i i co l l l l ta ta α l ta co i i

Example 1: THE ELECTRIC DIPOLE

Example 1: THE ELECTRIC DIPOLE 1 The Electic Dipole: z + P + θ d _ Φ = Q 4πε + Q = Q 4πε 4πε 1 + 1 2 The Electic Dipole: d + _ z + Law of Cosines: θ A B α C A 2 = B 2 + C 2 2ABcosα P ± = 2 ( + d ) 2 2

6. MAXIMUM LIKELIHOOD ESTIMATION

6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ

[ ] ( l) ( ) Option 2. Option 3. Option 4. Correct Answer 1. Explanation n. Q. No to n terms = ( 10-1 ) 3

Q. No. The fist d lst tem of A. P. e d l espetively. If s be the sum of ll tems of the A. P., the ommo diffeee is Optio l - s- l+ Optio Optio Optio 4 Coet Aswe ( ) l - s- - ( l ) l + s+ + ( l ) l + s-

Ρομποτικός Έλεγχος Δύναμης / Μηχανικής Αντίστασης

Σχολή Ηλεκτρολόγων Μηχ/κών και Μηχ/κών Υπολογιστών, Ε.Μ.Π., Ακαδημαϊκό Έτος 7-8, 7ο Εξάμηνο Μάθημα: Ρομποτική Ι Αυτόματος Έλεγχος Ρομπότ 3 (Έλεγχος Δύναμης) Κων/νος Τζαφέστας Τομέας Σημάτων, Ελέγχου &

(ii) x[y (x)] 4 + 2y(x) = 2x. (vi) y (x) = x 2 sin x

ΕΥΓΕΝΙΑ Ν. ΠΕΤΡΟΠΟΥΛΟΥ ΕΠΙΚ. ΚΑΘΗΓΗΤΡΙΑ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΑΣΚΗΣΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ «ΕΦΑΡΜΟΣΜΕΝΑ ΜΑΘΗΜΑΤΙΚΑ ΙΙΙ» ΠΑΤΡΑ 2015 1 Ασκήσεις 1η ομάδα ασκήσεων 1. Να χαρακτηρισθούν πλήρως

SUPERPOSITION, MEASUREMENT, NORMALIZATION, EXPECTATION VALUES. Reading: QM course packet Ch 5 up to 5.6

SUPERPOSITION, MEASUREMENT, NORMALIZATION, EXPECTATION VALUES Readig: QM course packet Ch 5 up to 5. 1 ϕ (x) = E = π m( a) =1,,3,4,5 for xa (x) = πx si L L * = πx L si L.5 ϕ' -.5 z 1 (x) = L si

Στοχαστικές διαδικασίες. Γραµµικά συστήµατα. Αλυσίδες Markov. Θεωρία πληροφοριών. Γιάννης Α. Φίλης

ΣΤΟΧΑΣΤΙΚΕΣ ΙΑ ΙΚΑΣΙΕΣ Στοχαστικές διαδικασίες Γραµµικά συστήµατα Αλυσίδες Markov Θεωρία πληροφοριών Γιάννης Α Φίλης Πολυτεχνείο Κρήτης - Σεπτέµβριος 6 ΠΕΡΙΕΧΟΜΕΝΑ I ΟΡΙΣΜΟΣ ΚΑΙ ΣΥΝΑΡΤΗΣΕΙΣ ΣΤΟΧΑΣΤΙΚΩΝ

Ó³ Ÿ , º 1(130).. 7Ä ±μ. Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê

Ó³ Ÿ. 006.. 3, º 1(130).. 7Ä16 Š 530.145 ˆ ƒ ˆ ˆŒ ˆŸ Š ƒ.. ±μ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê É μ ² Ö Ó μ μ Ö μ μ²õ μ É μ ÌÉ ±ÊÎ É ² ³ É μ - Î ±μ μ ÊÌ ±μ Ëμ ³ μ- ±² μ ÒÌ ³μ ²ÖÌ Ê ±. ³ É ÔÉμ μ μ μ Ö, Ö ²ÖÖ Ó ±μ³

!"#!"!"# $ "# '()!* '+!*, -"*!" $ "#. /01 023 43 56789:3 4 ;8< = 7 >/? 44= 7 @ 90A 98BB8: ;4B0C BD :0 E D:84F3 B8: ;4BG H ;8

Fourier Series. Fourier Series

ECE 37 Z. Aliyazicioglu Elecrical & Compuer Egieerig Dep. Cal Poly Pomoa Periodic sigal is a fucio ha repeas iself every secods. x() x( ± ) : period of a fucio, : ieger,,3, x() 3 x() x() Periodic sigal

Ορισμός : Η συνάρτηση X : Ω είναι μετρήσιμη εάν 1. της τυχαίας μεταβλητής X : Ω, είναι το πεδίο τιμών της X. Δηλαδή είναι το υποσύνολο του { }

Ορισμός : Η συνάρτηση : Ω είναι μετρήσιμη εάν B B B B = ω Ω : ω B = B { όπου { { Μία μετρήσιμη συνάρτηση : Ω ονομάζεται τυχαία μεταβλητή Ορισμός: Ο χώρος καταστάσεων της τυχαίας μεταβλητής : Ω είναι το

Appendix B Table of Radionuclides Γ Container 1 Posting Level cm per (mci) mci

3 H 12.35 Y β Low 80 1 - - Betas: 19 (100%) 11 C 20.38 M β+, EC Low 400 1 5.97 13.7 13 N 9.97 M β+ Low 1 5.97 13.7 Positrons: 960 (99.7%) Gaas: 511 (199.5%) Positrons: 1,199 (99.8%) Gaas: 511 (199.6%)

A NOTE ON ENNOLA RELATION. Jae Moon Kim and Jado Ryu* 1. INTRODUCTION

TAIWANESE JOURNAL OF MATHEMATICS Vol 8, No 5, pp 65-66, Ocober 04 DOI: 0650/m804665 Th paper avalable ole a hp://ouralawamahocorw A NOTE ON ENNOLA RELATION Jae Moo Km ad Jado Ryu* Abrac Eola ve a example