ψ(x) ψ (x) =exp[iγ a Θ a ] ψ(x) =1+iΓ a Θ a ψ ±

Homework #6. A circular cylinder of radius R rotates about the long axis with angular velocity

Homwork #6 1. (Kittl 5.1) Cntrifug. A circular cylindr of radius R rotats about th long axis with angular vlocity ω. Th cylindr contains an idal gas of atoms of mass m at tmpratur. Find an xprssion for

Convection Derivatives February 17, E+01 1.E-01 1.E-02 1.E-03 1.E-04 1.E-05 1.E-06 1.E-07 1.E-08 1.E-09 1.E-10. Error

onvcton rvtvs brry 7, nt Volm Mtho or onvcton rvtvs Lrry rtto Mchncl ngnrng 69 omttonl l ynmcs brry 7, Otln Rv nmrcl nlyss bscs oncl rslts or son th sorc nlyss Introc nt-volm mtho or convcton Not n or

Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α

Α Ρ Χ Α Ι Α Ι Σ Τ Ο Ρ Ι Α Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α Σ η µ ε ί ω σ η : σ υ ν ά δ ε λ φ ο ι, ν α µ ο υ σ υ γ χ ω ρ ή σ ε τ ε τ ο γ ρ ή γ ο ρ ο κ α ι α τ η µ έ λ η τ ο ύ

.. ntsets ofa.. d ffeom.. orp ism.. na s.. m ooth.. man iod period I n open square. n t s e t s ofa \quad d ffeom \quad orp ism \quad na s \quad m o

G G - - -- - W - - - R S - q k RS ˆ W q q k M G W R S L [ RS - q k M S 4 R q k S [ RS [ M L ˆ L [M O S 4] L ˆ ˆ L ˆ [ M ˆ S 4 ] ˆ - O - ˆ q k ˆ RS q k q k M - j [ RS ] [ M - j - L ˆ ˆ ˆ O ˆ [ RS ] [ M

r r t r r t t r t P s r t r P s r s r r rs tr t r r t s ss r P s s t r t t tr r r t t r t r r t t s r t rr t Ü rs t 3 r r r 3 rträ 3 röÿ r t

r t t r t ts r3 s r r t r r t t r t P s r t r P s r s r P s r 1 s r rs tr t r r t s ss r P s s t r t t tr r 2s s r t t r t r r t t s r t rr t Ü rs t 3 r t r 3 s3 Ü rs t 3 r r r 3 rträ 3 röÿ r t r r r rs

Assessment of otoacoustic emission probe fit at the workfloor

Assessment of otoacoustic emission probe fit at the workfloor t s st tt r st s s r r t rs t2 t P t rs str t t r 1 t s ér r tr st tr r2 t r r t s t t t r t s r ss r rr t 2 s r r 1 s r r t s s s r t s t

HONDA. Έτος κατασκευής

Accord + Coupe IV 2.0 16V (CB3) F20A2-A3 81 110 01/90-09/93 0800-0175 11,00 2.0 16V (CB3) F20A6 66 90 01/90-09/93 0800-0175 11,00 2.0i 16V (CB3-CC9) F20A8 98 133 01/90-09/93 0802-9205M 237,40 2.0i 16V

ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s

P P P P ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s r t r 3 2 r r r 3 t r ér t r s s r t s r s r s ér t r r t t q s t s sã s s s ér t

Α Ρ Ι Θ Μ Ο Σ : 6.913

Α Ρ Ι Θ Μ Ο Σ : 6.913 ΠΡΑΞΗ ΚΑΤΑΘΕΣΗΣ ΟΡΩΝ ΔΙΑΓΩΝΙΣΜΟΥ Σ τ η ν Π ά τ ρ α σ ή μ ε ρ α σ τ ι ς δ ε κ α τ έ σ σ ε ρ ι ς ( 1 4 ) τ ο υ μ ή ν α Ο κ τ ω β ρ ί ο υ, η μ έ ρ α Τ ε τ ά ρ τ η, τ ο υ έ τ ο υ ς δ

rs r r â t át r st tíst Ó P ã t r r r â

rs r r â t át r st tíst P Ó P ã t r r r â ã t r r P Ó P r sã rs r s t à r çã rs r st tíst r q s t r r t çã r r st tíst r t r ú r s r ú r â rs r r â t át r çã rs r st tíst 1 r r 1 ss rt q çã st tr sã

Παρασκευή 1 Νοεμβρίου 2013 Ασκηση 1. Λύση. Παρατήρηση. Ασκηση 2. Λύση.

(, ) =,, = : = = ( ) = = = ( ) = = = ( ) ( ) = = ( ) = = = = (, ) =, = = =,,...,, N, (... ) ( + ) =,, ( + ) (... ) =,. ( ) = ( ) = (, ) = = { } = { } = ( ) = \ = { = } = { = }. \ = \ \ \ \ \ = = = = R

General theorems of Optical Imaging systems

Gnral thorms of Optcal Imagng sstms Tratonal Optcal Imagng Topcs Imagng qualt harp: mags a pont sourc to a pont Dstorton fr: mags a shap to a smlar shap tgmatc Imagng Imags a pont sourc to a nfntl sharp

Alterazioni del sistema cardiovascolare nel volo spaziale

POLITECNICO DI TORINO Corso di Laurea in Ingegneria Aerospaziale Alterazioni del sistema cardiovascolare nel volo spaziale Relatore Ing. Stefania Scarsoglio Studente Marco Enea Anno accademico 2015 2016

ασθενείς αλληλεπιδράσεις

Parity Χαρακτηρίζει τη συμμετρία ενός φυσικού μεέθους ως προς ορισμένους διακριτούς χωρικούς μετασχηματισμούς. H arity είναι μία παρατηρούμενη ποσότητα στη φύση. Pˆ Hrmitian Αν η χαμιλτονιανή της αλληλεπίδρασης

Wb/ Μ. /Α Ua-, / / Βζ * / 3.3. Ηλεκτρομαγνητισμός Ι Μ. 1. Β = k. 3. α) Β = Κ μ Π 2. B-r, 2 10~ ~ 2 α => I = ~ } Α k M I = 20Α

ΛΥΣΗ ΠΡΟΒΛΗΜΑΤΩΝ 3.3 39 3.3. Ηλεκτρομαγνητισμός 1. Β = k 21 9 1Π 2 β = 10 " ίιτκ τ^β = 2 10 " τ 3. α) Β = Κ μ 21 B-r, 2 10~ 5 20 10~ 2 α => I = ~ } Α k M -2 2-10 I = 20Α ϊ)β 2 2Ι = Κ ψ- _ 10' 10^40 7 2

ο ο 3 α. 3"* > ω > d καΐ 'Ενορία όλις ή Χώρί ^ 3 < KN < ^ < 13 > ο_ Μ ^~~ > > > > > Ο to X Η > ο_ ο Ο,2 Σχέδι Γλεγμα Ο Σ Ο Ζ < o w *< Χ χ Χ Χ < < < Ο

18 ρ * -sf. NO 1 D... 1: - ( ΰ ΐ - ι- *- 2 - UN _ ί=. r t ' \0 y «. _,2. "* co Ι». =; F S " 5 D 0 g H ', ( co* 5. «ΰ ' δ". o θ * * "ΰ 2 Ι o * "- 1 W co o -o1= to»g ι. *ΰ * Ε fc ΰ Ι.. L j to. Ι Q_ " 'T

5 Ι ^ο 3 X X X. go > 'α. ο. o f Ο > = S 3. > 3 w»a. *= < ^> ^ o,2 l g f ^ 2-3 ο. χ χ. > ω. m > ο ο ο - * * ^r 2 =>^ 3^ =5 b Ο? UJ. > ο ο.

728!. -θ-cr " -;. '. UW -,2 =*- Os Os rsi Tf co co Os r4 Ι. C Ι m. Ι? U Ι. Ι os ν ) ϋ. Q- o,2 l g f 2-2 CT= ν**? 1? «δ - * * 5 Ι -ΐ j s a* " 'g cn" w *" " 1 cog 'S=o " 1= 2 5 ν s/ O / 0Q Ε!θ Ρ h o."o.

2. Α ν ά λ υ σ η Π ε ρ ι ο χ ή ς. 3. Α π α ι τ ή σ ε ι ς Ε ρ γ ο δ ό τ η. 4. Τ υ π ο λ ο γ ί α κ τ ι ρ ί ω ν. 5. Π ρ ό τ α σ η. 6.

Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α 1. Ε ι σ α γ ω γ ή 2. Α ν ά λ υ σ η Π ε ρ ι ο χ ή ς 3. Α π α ι τ ή σ ε ι ς Ε ρ γ ο δ ό τ η 4. Τ υ π ο λ ο γ ί α κ τ ι ρ ί ω ν 5. Π ρ ό τ α σ η 6. Τ ο γ ρ α φ ε ί ο 1. Ε ι σ α γ ω

Chapter 1 Fundamentals in Elasticity

D. of o. NU Fs s ν ss L. Pof. H L ://s.s.. D. of o. NU. Po Dfo ν Ps s - Do o - M os - o oos : o o w Uows o: - ss - - Ds W ows s o qos o so s os. w ows o fo s o oos s os of o os. W w o s s ss: - ss - -

ON THE MEASUREMENT OF

ON THE MEASUREMENT OF INVESTMENT TYPES: HETEROGENEITY IN CORPORATE TAX ELASTICITIES HENDRIK JUNGMANN, SIMON LORETZ WORKING PAPER NO. 2016-01 t s r t st t t2 s t r t2 r r t t 1 st t s r r t3 str t s r ts

Self and Mutual Inductances for Fundamental Harmonic in Synchronous Machine with Round Rotor (Cont.) Double Layer Lap Winding on Stator

Sel nd Mutul Inductnces or Fundmentl Hrmonc n Synchronous Mchne wth Round Rotor (Cont.) Double yer p Wndng on Sttor Round Rotor Feld Wndng (1) d xs s r n even r Dene S r s the number o rotor slots. Dene

Some Geometric Properties of a Class of Univalent. Functions with Negative Coefficients Defined by. Hadamard Product with Fractional Calculus I

Itrtol Mthtcl Foru Vol 6 0 o 64 379-388 So otrc Proprts o Clss o Uvlt Fuctos wth Ntv Cocts Dd y Hdrd Product wth Frctol Clculus I Huss Jr Adul Huss Dprtt o Mthtcs d Coputr pplctos Coll o Sccs Uvrsty o

Estimation of grain boundary segregation enthalpy and its role in stable nanocrystalline alloy design

Supplemental Material for Estimation of grain boundary segregation enthalpy and its role in stable nanocrystalline alloy design By H. A. Murdoch and C.A. Schuh Miedema model RKM model ΔH mix ΔH seg ΔH

i i (3) Derive the fixed-point iteration algorithm and apply it to the data of Example 1.

Howor#3 urvval Aalyss Na: Huag Xw 黃昕蔚 Quso: uppos ha daa ( follow h odl ( ( > ad <

r t t r t t à ré ér t é r t st é é t r s s2stè s t rs ts t s

r t r r é té tr q tr t q t t q t r t t rrêté stér ût Prés té r ré ér ès r é r r st P t ré r t érô t 2r ré ré s r t r tr q t s s r t t s t r tr q tr t q t t q t r t t r t t r t t à ré ér t é r t st é é

Physique des réacteurs à eau lourde ou légère en cycle thorium : étude par simulation des performances de conversion et de sûreté

Physique des réacteurs à eau lourde ou légère en cycle thorium : étude par simulation des performances de conversion et de sûreté Alexis Nuttin To cite this version: Alexis Nuttin. Physique des réacteurs

ITU-R P (2009/10)

ITU-R.45-4 (9/) % # GHz,!"# $$ # ITU-R.45-4.. (IR) (ITU-T/ITU-R/ISO/IEC).ITU-R http://www.tu.t/itu-r/go/patets/e. (http://www.tu.t/publ/r-rec/e ) () ( ) BO BR BS BT F M RA S RS SA SF SM SNG TF V.ITU-R

What is SUSY? Supersymmetry is a boson-fermion symmetry that is aimed to unify all forces in Nature including gravity within a singe framework

What s SUSY? Supersymmetry s a boson-fermon symmetry that s amed to unfy all forces n Nature ncludng gravty wthn a snge framework Q boson >= fermon > Q fermon >= boson > j = = { Q, Q } = δ ( σ ) [,] bb

Lifting Entry (continued)

ifting Entry (continued) Basic planar dynamics of motion, again Yet another equilibrium glide Hypersonic phugoid motion Planar state equations MARYAN 1 01 avid. Akin - All rights reserved http://spacecraft.ssl.umd.edu

ITU-R BT ITU-R BT ( ) ITU-T J.61 (

ITU-R BT.439- ITU-R BT.439- (26-2). ( ( ( ITU-T J.6 ( ITU-T J.6 ( ( 2 2 2 3 ITU-R BT.439-2 4 3 4 K : 5. ITU-R BT.24 :. ITU-T J.6. : T u ( ) () (S + L = M) :A :B :C : D :E :F :G :H :J :K :L :M :S :Tsy :Tlb

Το άτομο του Υδρογόνου

Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες

A N A L I S I S K U A L I T A S A I R D I K A L I M A N T A N S E L A T A N S E B A G A I B A H A N C A M P U R A N B E T O N

I N F O T E K N I K V o l u m e 1 5 N o. 1 J u l i 2 0 1 4 ( 61-70) A N A L I S I S K U A L I T A S A I R D I K A L I M A N T A N S E L A T A N S E B A G A I B A H A N C A M P U R A N B E T O N N o v i

Solar Neutrinos: Fluxes

Solar Neutrinos: Fluxes pp chain Sun shines by : 4 p 4 He + e + + ν e + γ Solar Standard Model Fluxes CNO cycle e + N 13 =0.707MeV He 4 C 1 C 13 p p p p N 15 N 14 He 4 O 15 O 16 e + =0.997MeV O17

P P Ó P. r r t r r r s 1. r r ó t t ó rr r rr r rí st s t s. Pr s t P r s rr. r t r s s s é 3 ñ

P P Ó P r r t r r r s 1 r r ó t t ó rr r rr r rí st s t s Pr s t P r s rr r t r s s s é 3 ñ í sé 3 ñ 3 é1 r P P Ó P str r r r t é t r r r s 1 t r P r s rr 1 1 s t r r ó s r s st rr t s r t s rr s r q s

Radio détection des rayons cosmiques d ultra-haute énergie : mise en oeuvre et analyse des données d un réseau de stations autonomes.

Radio détection des rayons cosmiques d ultra-haute énergie : mise en oeuvre et analyse des données d un réseau de stations autonomes. Diego Torres Machado To cite this version: Diego Torres Machado. Radio

A NEW FORM OF MULTIVARIATE GENERALIZED DOUBLE EXPONENTIAL FAMILY OF DISTRIBUTIONS OF KIND-2

Journal of Rlablty and Statstcal Studs; ISSN (Prnt: 0974-804, (Onln: 9-5666 Vol. 0, Issu (07: 79-0 A NEW FORM OF MULTIVARIATE GENERALIZED DOUBLE EXPONENTIAL FAMILY OF DISTRIBUTIONS OF KIND- G.S. Davd Sam

Representing Relations Using Digraph

M R n = M R, Κλειστότητες, Ισοδυναµίες, Μερικές ιατάξεις Ορέστης Τελέλης tllis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Σύνοψη Προηγούµενου EXAMPLE 6 from th finition of Booln powrs. Exris

Appendix B Table of Radionuclides Γ Container 1 Posting Level cm per (mci) mci

3 H 12.35 Y β Low 80 1 - - Betas: 19 (100%) 11 C 20.38 M β+, EC Low 400 1 5.97 13.7 13 N 9.97 M β+ Low 1 5.97 13.7 Positrons: 960 (99.7%) Gaas: 511 (199.5%) Positrons: 1,199 (99.8%) Gaas: 511 (199.6%)

ΖΕΡΔΑΛΗΣ ΣΩΤΗΡΙΟΣ ΤΟ ΟΥΤΙ ΣΤΗ ΒΕΡΟΙΑ (1922-ΣΗΜΕΡΑ) ΘΕΣΣΑΛΟΝΙΚΗ 2005 1

(1922- ) 2005 1 2 .1.2 1.1.2-3 1.2.3-4 1.3.4-5 1.4.5-6 1.5.6-10.11 2.1 2.2 2.3 2.4.11-12.12-13.13.14 2.5 (CD).15-20.21.22 3 4 20.,,.,,.,.,,.,.. 1922., (= )., (25/10/2004), (16/5/2005), (26/1/2005) (7/2/2005),,,,.,..

E.E. Παρ. Ill (I) 429 Κ.Δ.Π. 150/83 Αρ. 1871,

E.E. Πρ. ll () 429 Κ.Δ.Π. 50/ Αρ. 7, 24.6. Αρθμός 50 ΠΕΡ ΤΑΧΥΔΡΜΕΩΝ ΝΜΣ (ΚΕΦ. 0 ΚΑ ΝΜ 42 ΤΥ 96 ΚΑ 7 ΤΥ 977) Δάτγμ δνάμ τ άρθρ 7() Τ Υπργκό Σμβύλ, σκώντς τς ξσίς π πρέχντ Κ»>. 0. σ' τό δνάμ τ δφί τ άρθρ

!#$%!& '($) *#+,),# - '($) # -.!, '$%!%#$($) # - '& %#$/0#!#%! % '$%!%#$/0#!#%! % '#%3$-0 4 '$%3#-!#, '5&)!,#$-, '65!.#%

" #$%& '($) *#+,),# - '($) # -, '$% %#$($) # - '& %#$0##% % '$% %#$0##% % '1*2)$ '#%3$-0 4 '$%3#-#, '1*2)$ '#%3$-0 4 @ @ @

ELE 3310 Tutorial 11. Reflection of plane waves Wave impedance of the total field

L 0 Tuto Rfcton of pn wvs Wv mpdnc of th tot fd Rfcton of M wvs Rfcton tks pc whn n M wv hts on bound. Pt of th wv gts fctd, nd pt of t gts tnsmttd. Popgton dctons nd mptuds of th fctd nd tnsmttd wvs dpnd

Appendix A. Stability of the logistic semi-discrete model.

Ecological Archiv E89-7-A Elizava Pachpky, Rogr M. Nib, and William W. Murdoch. 8. Bwn dicr and coninuou: conumr-rourc dynamic wih ynchronizd rproducion. Ecology 89:8-88. Appndix A. Sabiliy of h logiic

Solutions - Chapter 4

Solutions - Chapter Kevin S. Huang Problem.1 Unitary: Ût = 1 ī hĥt Û tût = 1 Neglect t term: 1 + hĥ ī t 1 īhĥt = 1 + hĥ ī t ī hĥt = 1 Ĥ = Ĥ Problem. Ût = lim 1 ī ] n hĥ1t 1 ī ] hĥt... 1 ī ] hĥnt 1 ī ]

16 Electromagnetic induction

Chatr : Elctromagntic Induction Elctromagntic induction Hint to Problm for Practic., 0 d φ or dφ 0 0.0 Wb. A cm cm 7 0 m, A 0 cm 0 cm 00 0 m B 0.8 Wb/m, B. Wb/m,, dφ d BA (B.A) BA 0.8 7 0. 00 0 80 0 8

DISPLAY SUPPLY: FILTER STANDBY

ircuit iagrams and PW Layouts. ircuit iagrams and PW Layouts J.0 P. 0 isplay Supply P: ilter Standby MNS NPUT -Vac 00 P-V- V_OT 0 0 0 0 0 0 0 0 SPLY SUPPLY: LT STNY 0 M0 V 0 T,/0V MSU -VOLTS NOML... STNY

Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού.

Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού. Περιοδικός πίνακας: α. Είναι µια ταξινόµηση των στοιχείων κατά αύξοντα

A hybrid PSTD/DG method to solve the linearized Euler equations

A hybrid PSTD/ method to solve the linearized Euler equations ú P á ñ 3 rt r 1 rt t t t r t rs t2 2 t r s r2 r r Ps s tr r r P t s s t t 2 r t r r P s s r r 2s s s2 t s s t t t s t r t s t r q t r r t

Matrices and Determinants

Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z

AcO. O OAc OCH 3. Compound Number. (chloroform) Notes: M. Mozuch #36/46/Ac 21 mg. Acetone DMSO. CDCl 3. Atom

Copoun Nuber 3 C DMS.7.7 74 7..8 7 4.. 88 87 c c.0. 3. 7.99 0. 0.4 98 97 84 98 9.. 3.4 74.4.0. 98 9 9 9 9..77.0 73. 0..03 9 7 8 78 84. 98.8 98.0 88 C 3 C 3 3 4.4.3 4. 4. 0.3..7.7 3.7 77 7 3 c C= c C= 70.

Inductive Component Index. Inductance ( nh /μh / mh )

Wound Chip Inductor ( nh /μh / mh ) CM2520-3 2.50 x 2.00 x 1.80 0.010μH~100μH 0.53A~60mA Microtelevisions, liquid crystal television, CM3225-L 3.20 x 2.50 x 2.20 0.12μH~150μH 0.45A~65mA video cameras,

P r s r r t. tr t. r P

P r s r r t tr t r P r t s rés t t rs s r s r r t é ér s r q s t r r r r t str t q q s r s P rs t s r st r q r P P r s r r t t s rés t t r t s rés t t é ér s r q s t r r r r t r st r q rs s r s r r t str

ACI sécurité informatique KAA (Key Authentification Ambient)

ACI sécurité informatique KAA (Key Authentification Ambient) Samuel Galice, Veronique Legrand, Frédéric Le Mouël, Marine Minier, Stéphane Ubéda, Michel Morvan, Sylvain Sené, Laurent Guihéry, Agnès Rabagny,

Multi-GPU numerical simulation of electromagnetic waves

Multi-GPU numerical simulation of electromagnetic waves Philippe Helluy, Thomas Strub To cite this version: Philippe Helluy, Thomas Strub. Multi-GPU numerical simulation of electromagnetic waves. ESAIM:

LEM. Non-linear externalities in firm localization. Giulio Bottazzi Ugo Gragnolati * Fabio Vanni

LEM WORKING PAPER SERIES Non-linear externalities in firm localization Giulio Bottazzi Ugo Gragnolati * Fabio Vanni Institute of Economics, Scuola Superiore Sant'Anna, Pisa, Italy * University of Paris

ibemo Kazakhstan Republic of Kazakhstan, West Kazakhstan Oblast, Aksai, Pramzone, BKKS office complex Phone: ; Fax:

Spare Parts. Cartridges. Chipbreakers Wrenches / Spanners Springs / Washers / Plugs / Nuts / Punches

1~20 Screws ins Shims artridges lamps lamp Sets hipbreakers Wrenches / Spanners Springs / Washers / lugs / Nuts / unches 2~6 7 8~11 12 13 14~15 16 17~18 19 1 Screws escription imension (mm) ngle ( ) H

Łs t r t rs tø r P r s tø PrØ rø rs tø P r s r t t r s t Ø t q s P r s tr. 2stŁ s q t q s t rt r s t s t ss s Ø r s t r t. Łs t r t t Ø t q s

Łs t r t rs tø r P r s tø PrØ rø rs tø P r s r t t r s t Ø t q s P r s tr st t t t Ø t q s ss P r s P 2stŁ s q t q s t rt r s t s t ss s Ø r s t r t P r røs r Łs t r t t Ø t q s r Ø r t t r t q t rs tø

Solving an Air Conditioning System Problem in an Embodiment Design Context Using Constraint Satisfaction Techniques

Solving an Air Conditioning System Problem in an Embodiment Design Context Using Constraint Satisfaction Techniques Raphael Chenouard, Patrick Sébastian, Laurent Granvilliers To cite this version: Raphael

(... )..!, ".. (! ) # - $ % % $ & % 2007

(! ), "! ( ) # $ % & % $ % 007 500 ' 67905:5394!33 : (! ) $, -, * +,'; ), -, *! ' - " #!, $ & % $ ( % %): /!, " ; - : - +', 007 5 ISBN 978-5-7596-0766-3 % % - $, $ &- % $ % %, * $ % - % % # $ $,, % % #-

! " #$% & '()()*+.,/0.

! " #$% & '()()*+,),--+.,/0. 1!!" "!! 21 # " $%!%!! &'($ ) "! % " % *! 3 %,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,0 %%4,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,5

Q π (/) ^ ^ ^ Η φ. <f) c>o. ^ ο. ö ê ω Q. Ο. o 'c. _o _) o U 03. ,,, ω ^ ^ -g'^ ο 0) f ο. Ε. ιη ο Φ. ο 0) κ. ο 03.,Ο. g 2< οο"" ο φ.

II 4»» «i p û»7'' s V -Ζ G -7 y 1 X s? ' (/) Ζ L. - =! i- Ζ ) Η f) " i L. Û - 1 1 Ι û ( - " - ' t - ' t/î " ι-8. Ι -. : wî ' j 1 Τ J en " il-' - - ö ê., t= ' -; '9 ',,, ) Τ '.,/,. - ϊζ L - (- - s.1 ai

Αλληλεπίδραση ακτίνων-χ με την ύλη

Άσκηση 8 Αλληλεπίδραση ακτίνων-χ με την ύλη Δ. Φ. Αναγνωστόπουλος Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων Ιωάννινα 2013 Άσκηση 8 ii Αλληλεπίδραση ακτίνων-χ με την ύλη Πίνακας περιεχομένων

Jeux d inondation dans les graphes

Jeux d inondation dans les graphes Aurélie Lagoutte To cite this version: Aurélie Lagoutte. Jeux d inondation dans les graphes. 2010. HAL Id: hal-00509488 https://hal.archives-ouvertes.fr/hal-00509488

Modèles de représentation multi-résolution pour le rendu photo-réaliste de matériaux complexes

Modèles de représentation multi-résolution pour le rendu photo-réaliste de matériaux complexes Jérôme Baril To cite this version: Jérôme Baril. Modèles de représentation multi-résolution pour le rendu

Relativsitic Quantum Mechanics. 3.1 Dirac Equation Summary and notation 3.1. DIRAC EQUATION SUMMARY AND NOTATION. April 22, 2015 Lecture XXXIII

3.1. DIRAC EQUATION SUMMARY AND NOTATION April, 015 Lctur XXXIII Rlativsitic Quantum Mchanics 3.1 Dirac Equation Summary and notation W found that th two componnt spinors transform according to A = ± σ

?=!! #! % &! & % (! )!! + &! %.! / ( + 0. 1 3 4 5 % 5 = : = ;Γ / Η 6 78 9 / : 7 ; < 5 = >97 :? : ΑΒ = Χ : ΔΕ Φ8Α 8 / Ι/ Α 5/ ; /?4 ϑκ : = # : 8/ 7 Φ 8Λ Γ = : 8Φ / Η = 7 Α 85 Φ = :

One and two particle density matrices for single determinant HF wavefunctions. (1) = φ 2. )β(1) ( ) ) + β(1)β * β. (1)ρ RHF

One and two partcle densty matrces for sngle determnant HF wavefunctons One partcle densty matrx Gven the Hartree-Fock wavefuncton ψ (,,3,!, = Âϕ (ϕ (ϕ (3!ϕ ( 3 The electronc energy s ψ H ψ = ϕ ( f ( ϕ

Spare Parts P2~P6. Screws. Cartridges Clamp Sets Clamps Chipbreakers Wrenches Wrenches / Springs / Nuts / Punches / Others P13~P14 P15 P17~P18

1~18 Screws ins Shims artridges lamp Sets lamps hipbreakers Wrenches Wrenches / Springs / Nuts / unches / Others 2~6 7 8~12 12 13~14 15 16 17~18 18 1 Screws imension (mm) ngle ( ) Torque escription (N

Consommation marchande et contraintes non monétaires au Canada ( )

Consommation marchande et contraintes non monétaires au Canada (1969-2008) Julien Boelaert, François Gardes To cite this version: Julien Boelaert, François Gardes. Consommation marchande et contraintes

ΠΕΡΙΟΔΙΚΟ ΣΥΣΤΗΜΑ ΤΩΝ ΣΤΟΙΧΕΙΩΝ (1) Ηλία Σκαλτσά ΠΕ ο Γυμνάσιο Αγ. Παρασκευής

ΠΕΡΙΟΔΙΚΟ ΣΥΣΤΗΜΑ ΤΩΝ ΣΤΟΙΧΕΙΩΝ (1) Ηλία Σκαλτσά ΠΕ04.01 5 ο Γυμνάσιο Αγ. Παρασκευής Όπως συμβαίνει στη φύση έτσι και ο άνθρωπος θέλει να πετυχαίνει σπουδαία αποτελέσματα καταναλώνοντας το λιγότερο δυνατό

ΓΗ ΚΑΙ ΣΥΜΠΑΝ. Εικόνα 1. Φωτογραφία του γαλαξία μας (από αρχείο της NASA)

ΓΗ ΚΑΙ ΣΥΜΠΑΝ Φύση του σύμπαντος Η γη είναι μία μονάδα μέσα στο ηλιακό μας σύστημα, το οποίο αποτελείται από τον ήλιο, τους πλανήτες μαζί με τους δορυφόρους τους, τους κομήτες, τα αστεροειδή και τους μετεωρίτες.

Ν Κ Π 6Μ Θ 5 ϑ Μ % # =8 Α Α Φ ; ; 7 9 ; ; Ρ5 > ; Σ 1Τ Ιϑ. Υ Ι ς Ω Ι ϑτ 5 ϑ :Β > 0 1Φ ς1 : : Ξ Ρ ; 5 1 ΤΙ ϑ ΒΦΓ 0 1Φ ς1 : ΒΓ Υ Ι : Δ Φ Θ 5 ϑ Μ & Δ 6 6

# % & ( ) +, %. / % 0 1 / 1 4 5 6 7 8 # 9 # : ; < # = >? 1 :; < 8 > Α Β Χ 1 ; Δ 7 = 8 1 ( 9 Ε 1 # 1 ; > Ε. # ( Ε 8 8 > ; Ε 1 ; # 8 Φ? : ;? 8 # 1? 1? Α Β Γ > Η Ι Φ 1 ϑ Β#Γ Κ Λ Μ Μ Η Ι 5 ϑ Φ ΒΦΓ Ν Ε Ο Ν

Gapso t e q u t e n t a g ebra P open parenthesis N closing parenthesis fin i s a.. pheno mno nd iscovere \ centerline

G q v v G q v H 4 q 4 q v v ˆ ˆ H 4 ] 4 ˆ ] W q K j q G q K v v W v v H 4 z ] q 4 K ˆ 8 q ˆ j ˆ O C W K j ˆ [ K v ˆ [ [; 8 ] q ˆ K O C v ˆ ˆ z q [ R ; ˆ 8 ] R [ q v O C ˆ ˆ v - - ˆ - ˆ - v - q - - v -

Ι ΙΟΤΗΤΕΣ ΤΩΝ ΑΤΟΜΩΝ. Παππάς Χρήστος Επίκουρος Καθηγητής

ΗΛΕΚΤΡΟΝΙΚΗ ΟΜΗ ΚΑΙ Ι ΙΟΤΗΤΕΣ ΤΩΝ ΑΤΟΜΩΝ Παππάς Χρήστος Επίκουρος Καθηγητής ΤΟ ΜΕΓΕΘΟΣ ΤΩΝ ΑΤΟΜΩΝ Ατομική ακτίνα (r) : ½ της απόστασης μεταξύ δύο ομοιοπυρηνικών ατόμων, ενωμένων με απλό ομοιοπολικό δεσμό.

Robust Segmentation of Focal Lesions on Multi-Sequence MRI in Multiple Sclerosis

Robust Segmentation of Focal Lesions on Multi-Sequence MRI in Multiple Sclerosis Daniel García-Lorenzo To cite this version: Daniel García-Lorenzo. Robust Segmentation of Focal Lesions on Multi-Sequence

ΕΠΙΤΟΙΧΙΟΙ ΛΕΒΗΤΕΣ ΑΕΡΙΟΥ ΖΕΝΑ ΑΝΕΣΗ ΚΑΙ ΕΥΚΟΛΙΑ!

Zena E ASYLIFE ΕΠΙΤΟΙΧΙΟΙ ΛΕΒΗΤΕΣ ΑΕΡΙΟΥ ΖΕΝΑ ΑΝΕΣΗ ΚΑΙ ΕΥΚΟΛΙΑ! Θέλετε να αποκτήσετε την άνεση ενός λέβητα αερίου χωρίς να υπερβείτε τον οικονομικό σας προϋπολογισμό; Ο Zena είναι η ιδανική επιλογή για

%78 (!*+$&%,+$&*+$&%,-. /0$12*343556

! %78 ( 9 :: "#$% $&'"(" )!*$&%,$&*$&%,-. /$*343556 $ $& %$&.;$& $(# $"*("$# $ "$?, !* $&,#$"&::> $&( &$#, #$&# $"#&"& @($&%%>A!" #$ % µ & ' (#$ )! ) * ' "!)!,-./.' ) " $ &

ΝΟΜΟΣ ΤΗΣ ΠΕΡΙΟ ΙΚΟΤΗΤΑΣ : Οι ιδιότητες των χηµικών στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού.

1. Ο ΠΕΡΙΟ ΙΚΟΣ ΠΙΝΑΚΑΣ Οι άνθρωποι από την φύση τους θέλουν να πετυχαίνουν σπουδαία αποτελέσµατα καταναλώνοντας το λιγότερο δυνατό κόπο και χρόνο. Για το σκοπό αυτό προσπαθούν να οµαδοποιούν τα πράγµατα

P P Ô. ss rt çã r s t à rs r ç s rt s 1 ê s Pr r Pós r çã ís r t çã tít st r t

P P Ô P ss rt çã r s t à rs r ç s rt s 1 ê s Pr r Pós r çã ís r t çã tít st r t FELIPE ANDRADE APOLÔNIO UM MODELO PARA DEFEITOS ESTRUTURAIS EM NANOMAGNETOS Dissertação apresentada à Universidade Federal

Annulations de la dette extérieure et croissance. Une application au cas des pays pauvres très endettés (PPTE)

Annulations de la dette extérieure et croissance. Une application au cas des pays pauvres très endettés (PPTE) Khadija Idlemouden To cite this version: Khadija Idlemouden. Annulations de la dette extérieure

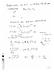Prblma dl smipian Cas i cs ω µ Cas sin cs i cs Cas fas [ ] [ ] ] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ttal S S J L J J L A d I I A d I d I V d d V V d d V n J n J ˆ 0 ˆ ˆ ˆ 0 ˆ 0 ˆ ˆ ˆ 0 S S S S i i

Points de torsion des courbes elliptiques et équations diophantiennes

Points de torsion des courbes elliptiques et équations diophantiennes Nicolas Billerey To cite this version: Nicolas Billerey. Points de torsion des courbes elliptiques et équations diophantiennes. Mathématiques

Hydraulic network simulator model

Hyrauc ntwor smuator mo!" #$!% & #!' ( ) * /@ ' ", ; -!% $!( - 67 &..!, /!#. 1 ; 3 : 4*

ΠΕΡΙΟΔΙΚΟΣ ΠΙΝΑΚΑΣ ΣΤΟΙΧΕΙΩΝ

ΠΕΡΙΟΔΙΚΟΣ ΠΙΝΑΚΑΣ ΣΤΟΙΧΕΙΩΝ Περίοδοι περιοδικού πίνακα Ο περιοδικός πίνακας αποτελείται από 7 περιόδους. Ο αριθμός των στοιχείων που περιλαμβάνει κάθε περίοδος δεν είναι σταθερός, δηλ. η περιοδικότητα

ΜΕΤΑΠΤΥΧΙΑΚΗ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ. Ελευθερίου Β. Χρυσούλα. Επιβλέπων: Νικόλαος Καραμπετάκης Καθηγητής Α.Π.Θ.

ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΘΕΩΡΗΤΙΚΗ ΠΛΗΡΟΦΟΡΙΚΗ ΚΑΙ ΘΕΩΡΙΑ ΣΥΣΤΗΜΑΤΩΝ ΚΑΙ ΕΛΕΓΧΟΥ Αναγνώριση συστημάτων με δεδομένη συνεχή και κρουστική συμπεριφορά

n n 1 n+1 2 2 Farmers in Random Insurance Group Farmers in Random Insurance Group Insured Plots Control Plots 1st Choice Plots Insured plot Adverse Selection Moral Hazard Control plot 1st Choice Plots

➆t r r 3 r st 40 Ω r t st 20 V t s. 3 t st U = U = U t s s t I = I + I

tr 3 P s tr r t t 0,5A s r t r r t s r r r r t st 220 V 3r 3 t r 3r r t r r t r r s e = I t = 0,5A 86400 s e = 43200As t r r r A = U e A = 220V 43200 As A = 9504000J r 1 kwh = 3,6MJ s 3,6MJ t 3r A = (9504000

1. Επειδή η κίνηση του αυτοκινήτου είναι ομαλή, ισχύει:

Κεφάλαιο 1.1 1. Επειδή η κίνηση του αυτοκινήτου είναι ομαλή, ισχύει: s 120 υ = - ή - υ = t 4 m / s ή - v=30m/s.?n / Για τα αντίστοιχα διαγράμματα έχουμε: u(m/s)>. ψ.. s(m)> ι ί>:;.. 2. Το τρένο βρίσκεται

Forêts aléatoires : aspects théoriques, sélection de variables et applications

Forêts aléatoires : aspects théoriques, sélection de variables et applications Robin Genuer To cite this version: Robin Genuer. Forêts aléatoires : aspects théoriques, sélection de variables et applications.

ss rt çã r s t à rs r ç s rt s 1 ê s Pr r Pós r çã ís r t çã tít st r t

ss rt çã r s t à rs r ç s rt s 1 ê s Pr r Pós r çã ís r t çã tít st r t FichaCatalografica :: Fichacatalografica https://www3.dti.ufv.br/bbt/ficha/cadastrarficha/visua... Ficha catalográfica preparada

Multi-dimensional Central Limit Theorem

Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t tme

Network Neutrality Debate and ISP Inter-Relations: Traffi c Exchange, Revenue Sharing, and Disconnection Threat

Network Neutrality Debate and ISP Inter-Relations: Traffi c Exchange, Revenue Sharing, and Disconnection Threat Pierre Coucheney, Patrick Maillé, runo Tuffin To cite this version: Pierre Coucheney, Patrick

Πρότυπο Αδρονίων µε Στατικά κουάρκ Ι

Πρότυπο Αδρονίων µε Στατικά κουάρκ Ι I,S: SU() group I : SU() group ΠΡΟΤΥΠΟ ΤΩΝ ΑΔΡΟΝΙΩΝ ΜΕ ΣΤΑΤΙΚΑ QUARKS QUARK ATOMS Πλήθος Βαρυονίων & Μεσονίων ~ 96 - αρχικά οι κανονικότητες (patterns) των αδρονικών

Ε Π Ι Μ Ε Λ Η Τ Η Ρ Ι Ο Κ Υ Κ Λ Α Δ Ω Ν

Ε ρ μ ο ύ π ο λ η, 0 9 Μ α ρ τ ί ο υ 2 0 1 2 Π ρ ο ς : Π ε ρ ιφ ε ρ ε ι ά ρ χ η Ν ο τ ίο υ Α ιγ α ί ο υ Α ρ ι θ. Π ρ ω τ. 3 4 2 2 κ. Ι ω ά ν ν η Μ α χ α ι ρ ί δ η F a x : 2 1 0 4 1 0 4 4 4 3 2, 2 2 8 1

ITU-R F.1891 (2011/05) ! "# . /) 0 1 ",MHz ,

(0/05)! "# &' () * $ + # $ %. /) 0 ",MHz 7 075-5 850, F ii.. (IPR) (ITU-T/ITU-R/ISO/IEC).ITU-R http://www.itu.int/itu-r/go/patents/en. (http://www.itu.int/publ/r-rec/en ) () ( ) BO BR BS BT F M P RA RS

ΦΑΚΕΛΟΣ ΠΙΣΤΟΠΟΙΗΣΗΣ ΠΙΝΑΚΑ ΑΝΕΛΚΥΣΤΗΡΑ ISL_V4

ΦΑΚΕΛΟΣ ΠΙΣΤΟΠΟΙΗΣΗΣ ΠΙΝΑΚΑ ΑΝΕΛΚΥΣΤΗΡΑ ISL_V VERSION V (REV.8) ΕΡΓΟΣΤΑΣΙΟ: ΠΕΡΡΑΙΒΟΥ, ΘΕΣΣΑΛΟΝΙΚΗ, ΕΛΛΑΔΑ Τηλ. 0 99 email: info@istechnology.gr FAX. 0 99 URL: www.istechnology.gr Copyright IS technology

5 Haar, R. Haar,. Antonads 994, Dogaru & Carn Kerkyacharan & Pcard 996. : Haar. Haar, y r x f rt xβ r + ε r x β r + mr k β r k ψ kx + ε r x, r,.. x [,

4 Chnese Journal of Appled Probablty and Statstcs Vol.6 No. Apr. Haar,, 6,, 34 E-,,, 34 Haar.., D-, A- Q-,. :, Haar,. : O.6..,..,.. Herzberg & Traves 994, Oyet & Wens, Oyet Tan & Herzberg 6, 7. Haar Haar.,

Formulas of Agrawal s Fiber-Optic Communication Systems NA n 2 ; n n. NA( )=n1 a

Formula o grawal Fiber-Oti Communiation Sytem Chater (ntroution) 8 / max m M / E nh N h M m 4 6.66. J e 9.6 / m log /mw SN / / /, NZ SN log / Z max N E Chater (Otial Fiber) Setion - (Geometrial Oti erition)

PARTS LIST. 1. EXPLODED VIEW 1.1 FINAL ASSEMBLY <M1> The instruction manual to be provided with this product will differ according to the destination.

ARTS IST SATY RCAUTIO arts identified by the symbol are critical for safety. Replace only with specified part numbers. BWAR O BOUS ARTS arts that do not meet specifications may cause trouble in regard