➆t r r 3 r st 40 Ω r t st 20 V t s. 3 t st U = U = U t s s t I = I + I
|
|
|
- Ἰάκωβος Γαλάνης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 tr 3 P s tr r t t 0,5A s r t r r t s r r r r t st 220 V 3r 3 t r 3r r t r r t r r s e = I t = 0,5A s e = 43200As t r r r A = U e A = 220V As A = J r 1 kwh = 3,6MJ s 3,6MJ t 3r A = ( J)/( J) = 2,64 kwh r s st 3 r 3 3 tr r 100 kω 50 kω 40 kω r t 3 ➆t r r 3 r st 20 Ω r t st 12 V t s t t s 3 s 3 3 s 3 r r tr 3 t 3 3 t t st r r r 3 t st U = U = U t s s t I = I + I 3 r 3 r r t 1/(RX) = 1/(R2) + 1/(R3) = 1/(20 Ω) + 1/(20 Ω) = 2/(20 Ω) => RX = 10Ω s r => R = R1 + RX + R4 = = 20Ω + 10Ω + 20Ω = 50 Ω s t => I = U/R = (12 V)/(50 Ω) = 0,24 A r I = I1 = I4 = I2 + I3 s 0,24 A = I2 + I3 I2 = 0,12 A = I3 ➆t r r 3 r st 40 Ω r t st 20 V t s t t s 3 s 3 3 s tr t s r st t t s 3 s 3 s t s r r r r t t 3 r I = I 1 + I 3 + I 4 r s 3 t st I 1 I 2 r r 3 r 3 1/R = 1/(R 1 + R 2 ) + 1/(R 3 ) + 1/(R 4 ) 1/R = 1/(40 Ω + 40 Ω) + 1/(40 Ω) + 1/(40 Ω)
2 3 r R = 16Ω Pr r t t r 3 3 r t t I = U/R I = (20 V)/(16 Ω) I = 1,25 A r tr t r t I 3 = I 4 I 3 = U/R I 3 = 20V/(40 Ω) I 3 = 0,5A r t I 1 = I 2 I = 2I 1 + I 3 + I 4 I 1 = (I I 3 I 4 )/2 I 1 = (1,25 A 1 A)/2 I 1 = 0,125 A 3 s I = I 1 + I 3 + I 4 I 1 = I I 3 I 4 I 1 = 1,25 A 1 A I 1 = 0,25 A = I 2 t t 3 t I = I 1 + I 3 + I 4 = 0,5A + 0,5A + 0,25 A = 1,25 A t P t st 12 V t st t s r 3 r st 1 A s t s r 3 r st
3 ➆t r r t t s r s 3 r s R 1 = 16 Ω R 2 = 22 Ω R 3 = 10 Ω R 4 = 8 Ω t st t r t st r r t t s 3 trt r s r 3 U 2 = 5.79 V I 4 = A R = 12.2 Ω t r r r 3 0,5Ω Pr t r r 2,63 W r 3 3 r 3 1 Ω s t tr st tr r st t st t r ➎ r r V 250 W r r t st 220 V r r tr tr t Pr r t st t r s r t s t t st r r r 220 V s r R = (U 2 )/P 3r r r r R = (U 2 )/P R = ((110 V) 2 )/(250 W) = 48,4Ω r r r => 250 W P tr 500 W r 0,3mm s r 3 t 3 t r r 3 t st 220 V ζ = 1,4(Ωmm 2 )/m 3 r 3 3 r r t st 2 V t st s ζ Cu = 0,017 (Ωmm 2 )/m ζ Al = 1,4Ωmm 2 )/m r r r 3 r s 1 mm 2 2 mm 2 3 mm r r t st 12 V s t st s 3 s 3 r 3 3 r s t 2 A t t t s ζ C u = 0,017 Ωmm 2 )/m ζ A l = 1,4Ωmm 2 /m r r r t t r 3 3 r r t st 200 V r t r r t 50 ma r r t st r 3 r t tr 100 Ω r r r r t r 3 3 r r t 100 ma t t r 3 3 r t st 250 V r r t t s 3 3 r r tr 5 Ω 10 A t 1 m s r s 0,1mm 2 t t s s r st s 1 s Pr 3 s s r 3 t t 3 r = 8,9g/cm 3 c p = 378J/(kgK) ζ = 0,017 (Ωmm 2 )/m
4 3 t t 3 r t s t 1 dm 3 /s st r r 3 r st 1 Ω s s r r r t st 220 V t s 70% tr tr 3 s r P r s r s 1 mm 2 3 t 3 t 10 A 3 1 s s s r = 8,9g/cm 3 c p = 378J/(kgK) ζ = 0,017 (Ωmm 2 )/m r 3 3 t st 110 V tr 40 W r r tr r r t t st 220 V r r s r s 0,05 mm 2 Pr t s r r r t r r r r 3 2 Ω r r 3 5 Ω r r r t t 0,70 A r 0,35 A st t st t r r r st 3 r r t st 30 V Pr r r 3 30 W r t st 30 V r 3 60 W r t st 220 V t t s 3 r t st s r tr t r 3 s r t st 220 V tr s 40 m s t r t s 3 tr t r t s t r str 3 s r t st 220 V t str r 3 r st t t t str t r t r st r tr st t r tr t sr r s r r 0,8mm t 10 A t t r s r r 0,8mm s r tr r s r tr st 0, 75 mm/s st t r tr r 3 st t 8,93 kg/dm 3 tr st s t s r 0,5mm t 5 A tr st r t r r t r t r 0 C st t r tr 3 st t 7,15 kg/dm 3 tr st s t s r 1 mm t 2 A tr st r t r r t r t r 10 C ➎ r r t r t st 220 V tr 100 W r t r t t s 3 s r r 1 kwh s t 3 r st r st 3 1 kwh r r t t r r 3 r 1 KWh s t 1 kwh = 1000 Wh = 1000 W 3600 s = J r 3 st t Q = q i m m = Q/(q t ) m = J 336k J/kg m = 11kg r 3 3 s 3 1 kwh s 3 r r s r m r Pr 100 W r 220 V r 40 W r t st 220 V ➎ r 3 3 r r t st 220 V r s r t t s 3 r t st s r tr t r s s 3 s
5 1 l t tr r W r t st 220 V r r t t s 3 s s s r 3 80 C 3 1 m r s 1 mm 2 r t st 1,5V r r st t t s 3 3 r r 3 r t st st 3 3 r tr r s 3 t r r t r t r s s 3 3 s 3 r t t 3 s t r ➎ 1 ➎ 2 ➎ 3 ➎ 4 t Pr r s 3 r s r r r 3 r t r ➎ r 3 s r ➎ 1 ➎ 2 ➎ 3 ➎ 4 s r r t r t r t s 3 t 3 s s t r 3 r 3 3 t t r 3 s s r 625 mah t s st s 3 r ➎ 3 t r r s t r r r ➎ 2 tr 3 s r t t 3 t s t s r r 3 ➎ 2 r r tr r s 3 t r r t r t r s s 3 3 s 3 r t t 3 s t r ➎ 1 ➎ 2 ➎ 3 ➎ 4 t Pr r s 3 r s r r r 3 r t r ➎ r 3 s r ➎ 1 ➎ 2 ➎ 3 ➎ 4 s r r t r t r t s 3 t 3 s s t r 3 r 3 3 t t r 3 s s r 725 mah t s st s 3 r ➎ 1 t r r s t r r r ➎ 3 tr 3 s r t t 3 t s t s r r 3 ➎ 3 r r
6 tr tr e 1 = 3mAs e 2 = 3 mas st r 3 10 cm 3 st t r 3 cm r 7 cm st tr t e = 0,5mAs tr s F = F 1 + F 2 = 1, N tr e 1 = 5 mas e 2 = 5 mas st r 3 10 cm 3 st t r 7 cm r 3 cm st tr t e = 0,3mAs tr s F = F 1 F 2 = 1, N e 2 = 1µC e 1 = 1µC st r 3 50 cm t r st st tr 1 C = 1 As st tr t 1 m r st tr t 1 m r e 2 = 2 µc 3 t r s t t 8 mf r t st 500 V t 3 r 3 s 3 3 cm 3 s t s r 3 t r 3 r 3 4 dm r 400 cm 2 r t st 2000 V t t s r st 3 t r r 3 t t 3 s 0,2mg As s 3 3 t r s r t r t s str 10 cm s t e 1 = e 2 = As s e 3 = As s tr t st tr sr e 1 e 2 r 3 1, As 2, As st 3 4 cm st tr t r r 5 cm r 3 cm s r r r 2 cm 3 s 50 g tr 3 0,5µC 60 cm r s tr 3 st 100 V/m r r tr t 3 t r st 4 cm r 3 s r r 1 µm r t t st r t t st s st 3e o st t 0,9g/cm 3 r 3 s r 5,6mm s 2 g s t 0,5m t r st r 3 20 cm tr st r r 3 t 3 st t 0,8g/cm 3 st t r t t 3r r s t e 1 = e 2 = As s t 15 cm r st r tr st t s t t 15 3r s r r r m 1 = m 2 = 0,1g s t 15 cm r st r tr st t r t s r r t t 30 st r
7 3 t r s t t 1 nf s r 0,008 µas t st t r s 3 t r r r tr 3 t r t st 3 t r s t t 10 pf 3 r s st t t tr t t 2 pf t st 3 t r r 560 V P t 3 t r t r t r 20 dm 2 st 3 mm r 3 3 t st 2 kv s r st st tr r tr 3 t r tr t 3 t r r t 100 cm 2 st 2 mm s s 3r 3 t r r t st 500 V t tr 3 r r 3 r 3 6 mm t t st s r r r 3 t 1 km 3 s r t 3 10 As t st s str s r 0,5km 2 3 r 3 3 s r Pr st tr s s st tr 3 t r tr Pr t 3 st 3 t tr s s s 3 t 1,4cm st tr 3 t r r tr r r t s r r t t r P s s s r s s t s r s r 3 Pr s s s s r r r t s 3 r t r F r r s s st r 3 s s r r t t 3 r r s s r 3 t r s st t st r t s 3 r t U e µ s r r s st t st t t 3 t r r t t 3 r t t r s t st 3 t r s st r 3 r t s 3 r t d U r r t st s st r 3 st tr 3 t r t r r r t t 3 r st tr s r s r t s r 3 s 3,0g r tr 0,74 m r s tr tr s s r st r t r r t s 3 r t E ϕ[ ] r r t s st st tr s r r t t 3 r e 5 µas
8 s r s r t s r 3 s 4,5g r tr 1,24 m r s tr tr s s r st r t r r t s 3 r t E ϕ[ ] r r t s st st tr s r r t t 3 r e 7 µas t st t t r 3 1 m T st t t r 3 10 m t t P 1 m 3 r 3 r 3 tr t r s st t s 3 r s s 10 N 3 t t 2 A 3 3 r st r r 1 m st t t sr t r t 50 A r 20 A s r t s r t st r s r B t t B t = B 1 + B 2 = B 1 + B 2 = µ0i1 + µ0i2 = µ0 2π d 2 2π d 2πd (I 1 + I 2 ) =... T 2 r d = 1m t I 1 = 50A I 2 = 20A 3 3 r st r r 1 m st t t sr t r t 50 A r 20 A st s r t st st s r B t t B t = B 1 + B 2 = B 1 B 2 = µ0i1 µ0i2 = µ0 2π d 2 2π d 2πd (I 1 I 2 ) =... T 2 r d = 1m t I 1 = 50A I 2 = 20A st st 3 r st 10 cm P r t t 2 A r t 3 A s r t s r 3r st t t t r 3 4 cm r 6 cm r s t 14 cm r 4 cm r r s s r s 1,2cm 2 r t t r s s r r t s r t st t t st t = 2,7g/cm 3 t t I = 2,7A S = 1,2cm 2 al = 2,7 g cm t r I = 2,7A 3 s F m = I l B r s s r t 3 F m = IlB t s t r t s s F g = mg = al V g = al Slg s 3 B = alsg I =... T st t t s t 0,3A st r t 3 20 cm s r r 4 cm t r t s 3 s 3 t s 3 s t t st t
9 I = 0,3A N = 2000 l = 0,2m r = 2cm t r B = µ0ni l =... T Φ 1 = BS = Bπr 2 =... Vs Φ t = NBS = NBπr 2 =... Vs t r s t st L = µ0n2 πr 2 l =... H r t t st t cm r r 5 cm t 3 st t 50 gaussov t tr s 3 t t r t Vs r tr rt t r t 2 cm 2 cm s t 3 st t 0,4T r t r t 1 ma t s t s r t r r t P a = 2cm N = 100 B = 0,4T I = 1mA s r M max = NIBS = NIBa 2 =... Nm t r sin ϕ = M polovica M max = Mmax 2M max = 1 2 ϕ = 30 t r t s 3 t 40 cm r s 6 cm 2 s 3 t t 5 A t st t t sr t 50 cm r r 8 cm t s r r 2 cm 4 cm s t st t r t r r r t r t t 10 A 0,2A N 1 = 100 l 1 = 0,5m r 1 = 4cm t r N 2 = 1000 l 2 = 4cm r 2 = 1cm t 3 I 1 = 10A I 2 = 0,2A r M 1 = N 2 B 1 πr2i 2 µ 2 = N 0N 1I 1 2 l 1 πr2i 2 2 =... Nm P t 80 cm r r 10 cm t t 2 A t s r r 6 cm t r s 3 s t t 60 r t s st t 1 A tr s t t t r t s 3 t N 1 = 200 l 1 = 0,8m r 1 = 5cm t r N 2 = 1000 r 2 = 3cm t r ϕ = 60 t 3 I 1 = 2A µ M = N 0N 1I 1 2 l 1 πr2i 2 2 sin ϕ =... Nm A = L1I2 1 2 = µ0n2 1 πr2 1 I2 1 2l 1 Φ m = L 1 I 1 = µ0n2 1 πr2 1 I1 l 1 =... J =... Vs r t t 40 cm r r 20 cm s 3 t t t 8 A t r t s 3 t r t t 50 cm r r 20 cm s 3 t t t 10 A st t t r t
10 P t s r r 5 cm 40 cm t t 0,5A st t t t s r s t s t s 3 t t r t s 3 t t st t 3 t 2, 5 A 3r t r t 0, 2 mvs r r 10 cm 60 cm t r t s s r s r s t t r t 64 ma t t st r t r s r t s st t 3 s t 3 40 cm st s r 3 3 s t s r 3 3 st s r t s r s 3 t t t t s s 3 rt 3 60 r t 3 t t s 3 t st t 3 s t 3, Vs/m 2 ➎ 3 d = 1000m r r 2r = 1mm st s t r t l = 2 m t r st ζ = 0,017 Ωmm 2 /m r st t st t tr st r t st 17V t l = N2r r N t t t r t t N = l/(2r) = (2 m)/(1 mm) = 2000 d t N r t s 2πR t r d = N2πR r R r t t r r t R t = d N2π = d2r 2πl = r R = ζ l S = t s 3 I = U R = 3 t st t t B = µoni l = t t t s tr st 1080 km/h r s r t st s r r 3 r 3 15 m t st t t T r t st t t T U i = v ( l B) t r B = (B x,0,b z ) l = (0,l,0) v = (v,0,0) s 3r t rs s r r t U i = vlb z =... V t 3 r 3 r 17 m t s tr st 980 km/h r t r t t 3, 4 ma t s t t t t s r s r s r 3 P t 3 st t 0,7T s 10 cm s s tr st 50 cm/s t t s r r s r r t st t t st
11 t 3 st t 0,6T r 1 m r s tr st 1 m/s s r s r r t s s 3 t t 5 A s s 3 t s r r t s s r t s 200 g F = F m = I i lb =... N s ma = I i lb a = IilB m =... m s 2 t 3 st t B s r r s tr st v ➎ s s t α s r r t s s r t δ r t st 3 t 3 t r t s 3 s 3 3 r U i = v ( l B) t r 3 t t st U i = v cos(δ)lb sin(α) t s 3 r 3 s t 10 m st s r 3 3 t r t t 10 A B z = 3, Vs/m 2 s r r 2 cm t t r t 3 st t 1 T t st s s r t t r U i t = Φ m = NBS = NBπr 2 =... Vs P r 3 t 1 m r r 20 cm t 10 A t st s s r r r t t U i t = L I = µ 0N 2 SI l =... Vs P t 80 cm r r 10 cm t t 2 A t s r r 6 cm t r s 3 s t t 30 s r s t t t r t s 3 t t st s s r t t s 3 t 3 st N 1 = 100 l 1 = 0,8m r 1 = 5cm I 1 = 2A t r N 2 = 1000 r 2 = 3cm ϕ = 30 A = L1I2 1 2 = µ0n2 1 SI2 1 2l 1 Φ m = L 1 I 1 =... Vs =... J U i t = N 2 B 1 S 2 cos ϕ = µ0n1n2πr2 2I1 cos ϕ l 1 =... Vs 0,7m t s s s s 3 3 A t t t 3 r 2 cm r t st t t r r t tr s s t s r t l 1 = 0,7m N 1 = 100 I t = 3 A s N 2 = 200 r 2 = 2cm U i = µ0n1n2πr2 2 l 1 I t =... V t 50 cm r r 20 cm 3 10 cm r r t t st s r r r t t t 10 A
12 N t = 1000 r t = 10cm l t = 50cm l p = 10cm I t = 10A t st s r U i = v p ( l p B t ) = ω p lpb 2 t t 3 r M = J p α p F g r sin α F m r = J p α p sin α α a p = xωp 2 x r t m p gr αx I i l p B t r 2 = J p a p 3 r r 3 t r t ω 2 = g 6l p UiBt 6l p pζ 2 Ui 2 = ω2 plpb 4 t 2 r t r t U i1 = B2 t l2 p 12 pζ + Btlp (B 3 U i1 = B2 t l2 p 12 pζ Btlp (B 3 t l2+24glp 2 p p ζ2 ) 12 pζ t l2+24glp 2 p p ζ2 ) 12 pζ r t r 3 s t 3 r r str t 3 st t 1 Vs/m 2 r t s s str 3 r s st s st t tr st t tr st = 2,7g/cm 3 s r ζ = 0,026 Ωmm 2 /m t r F g = F m t r I i ab = 4 Sag U i R B = 4Sg t Bav = 16 ζag B v = 16 ζg B 2 s 1000 r s 1 dm 2 rt r s r s 3 sr t r t tr s s 3tr st t t r t s 0,5kgm 2 s r tr st 3 t s t 50 Nm r s tr s s t 3 r 3 t 3 st t 0,5T 3 s 3 t 5 3 r s s st s t r t st r t t t st
Answers to practice exercises
Answers to practice exercises Chapter Exercise (Page 5). 9 kg 2. 479 mm. 66 4. 565 5. 225 6. 26 7. 07,70 8. 4 9. 487 0. 70872. $5, Exercise 2 (Page 6). (a) 468 (b) 868 2. (a) 827 (b) 458. (a) 86 kg (b)
r t t r t t à ré ér t é r t st é é t r s s2stè s t rs ts t s
r t r r é té tr q tr t q t t q t r t t rrêté stér ût Prés té r ré ér ès r é r r st P t ré r t érô t 2r ré ré s r t r tr q t s s r t t s t r tr q tr t q t t q t r t t r t t r t t à ré ér t é r t st é é
Assessment of otoacoustic emission probe fit at the workfloor
Assessment of otoacoustic emission probe fit at the workfloor t s st tt r st s s r r t rs t2 t P t rs str t t r 1 t s ér r tr st tr r2 t r r t s t t t r t s r ss r rr t 2 s r r 1 s r r t s s s r t s t
A 1 A 2 A 3 B 1 B 2 B 3
16 0 17 0 17 0 18 0 18 0 19 0 20 A A = A 1 î + A 2 ĵ + A 3ˆk A (x, y, z) r = xî + yĵ + zˆk A B A B B A = A 1 B 1 + A 2 B 2 + A 3 B 3 = A B θ θ A B = ˆn A B θ A B î ĵ ˆk = A 1 A 2 A 3 B 1 B 2 B 3 W = F
m 1, m 2 F 12, F 21 F12 = F 21
m 1, m 2 F 12, F 21 F12 = F 21 r 1, r 2 r = r 1 r 2 = r 1 r 2 ê r = rê r F 12 = f(r)ê r F 21 = f(r)ê r f(r) f(r) < 0 f(r) > 0 m 1 r1 = f(r)ê r m 2 r2 = f(r)ê r r = r 1 r 2 r 1 = 1 m 1 f(r)ê r r 2 = 1 m
m i N 1 F i = j i F ij + F x
N m i i = 1,..., N m i Fi x N 1 F ij, j = 1, 2,... i 1, i + 1,..., N m i F i = j i F ij + F x i mi Fi j Fj i mj O P i = F i = j i F ij + F x i, i = 1,..., N P = i F i = N F ij + i j i N i F x i, i = 1,...,
ITU-R P (2012/02)
ITU-R P.56- (0/0 P ITU-R P.56- ii.. (IPR (ITU-T/ITU-R/ISO/IEC.ITU-R ttp://www.itu.int/itu-r/go/patents/en. (ttp://www.itu.int/publ/r-rec/en ( ( BO BR BS BT F M P RA RS S SA SF SM SNG TF V 0.ITU-R ITU 0..(ITU
γ 1 6 M = 0.05 F M = 0.05 F M = 0.2 F M = 0.2 F M = 0.05 F M = 0.05 F M = 0.05 F M = 0.2 F M = 0.05 F 2 2 λ τ M = 6000 M = 10000 M = 15000 M = 6000 M = 10000 M = 15000 1 6 τ = 36 1 6 τ = 102 1 6 M = 5000
m r = F m r = F ( r) m r = F ( v) F = F (x) m dv dt = F (x) vdv = F (x)dx d dt = dx dv dt dx = v dv dx
m r = F m r = F ( r) m r = F ( v) x F = F (x) m dv dt = F (x) d dt = dx dv dt dx = v dv dx vdv = F (x)dx 2 mv2 x 2 mv2 0 = F (x )dx x 0 K = 2 mv2 W x0 x = x x 0 F (x)dx K K 0 = W x0 x x, x 2 x K 2 K =
(... )..!, ".. (! ) # - $ % % $ & % 2007
(! ), "! ( ) # $ % & % $ % 007 500 ' 67905:5394!33 : (! ) $, -, * +,'; ), -, *! ' - " #!, $ & % $ ( % %): /!, " ; - : - +', 007 5 ISBN 978-5-7596-0766-3 % % - $, $ &- % $ % %, * $ % - % % # $ $,, % % #-
r r t r r t t r t P s r t r P s r s r r rs tr t r r t s ss r P s s t r t t tr r r t t r t r r t t s r t rr t Ü rs t 3 r r r 3 rträ 3 röÿ r t
r t t r t ts r3 s r r t r r t t r t P s r t r P s r s r P s r 1 s r rs tr t r r t s ss r P s s t r t t tr r 2s s r t t r t r r t t s r t rr t Ü rs t 3 r t r 3 s3 Ü rs t 3 r r r 3 rträ 3 röÿ r t r r r rs
ITU-R SF ITU-R SF ( ) GHz 14,5-14,0 1,2.902 (WRC-03) 4.4. MHz GHz 14,5-14 ITU-R SF.1585 ( " " .ITU-R SF.
1 (008-003) * (ITU-R 54/4 ITU-R 6/9 ). 1. 4. 3. GHz 14,5-14,0 1,.90 (WRC-03) ( 4.4 ( - ) MHz 6 45-5 95 GHz 14,5-14 ( 4.4 " " ( ( ( ( ITU-R SF.1585 ( ( (ATPC) ( (.ITU-R SF.1650-1 " " * ITU-R SM.1448 / (
Ασκήσεις Προβλήματα. Μετρήσεις Μονάδες Γνωρίσματα της Ύλης
Ασκήσεις Προβλήματα Μετρήσεις Μονάδες Γνωρίσματα της Ύλης 19. Ποιες μονάδες χρησιμοποιούν συνήθως οι χημικοί για την πυκνότητα των: α) στερεού, β) υγρού και γ) αερίου σώματος; Να εξηγήσετε τη διαφορά.
P P Ó P. r r t r r r s 1. r r ó t t ó rr r rr r rí st s t s. Pr s t P r s rr. r t r s s s é 3 ñ
P P Ó P r r t r r r s 1 r r ó t t ó rr r rr r rí st s t s Pr s t P r s rr r t r s s s é 3 ñ í sé 3 ñ 3 é1 r P P Ó P str r r r t é t r r r s 1 t r P r s rr 1 1 s t r r ó s r s st rr t s r t s rr s r q s
Leaving Certificate Applied Maths Higher Level Answers
0 Leavin Certificate Applied Maths Hiher Level Answers ) (a) (b) (i) r (ii) d (iii) m ) (a) 0 m s - 9 N of E ) (b) (i) km h - 0 S of E (ii) (iii) 90 km ) (a) (i) 0 6 (ii) h 0h s s ) (a) (i) 8 m N (ii)
Φυσική για Μηχανικούς
Φυσική για Μηχανικούς Απλή Αρμονική Ταλάντωση Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά
Alterazioni del sistema cardiovascolare nel volo spaziale
POLITECNICO DI TORINO Corso di Laurea in Ingegneria Aerospaziale Alterazioni del sistema cardiovascolare nel volo spaziale Relatore Ing. Stefania Scarsoglio Studente Marco Enea Anno accademico 2015 2016
2 μ Gauss 1. Equation Chapter 1 Section 1 GAUSS GAUSS
2 μ Gauss 1 Equation Chapter 1 Section 1 2 GAUSS GAUSS 2 2 μ Gauss μ μ μ μ μ μ μ. μ μ μ μ. μ μ μ μ Coulomb μ. μ 1: μ μ μ μ μ, μ. μ μ. μ μ. μ μ μ μ μμ. μμ μ μ μ. μ μ μμ μ. μ μ μ. μ μ μ μ μ. μ μ μ μ μ μ
Introductory Circuit Analysis
Instructor s Resource Manual to accompany Introductory Circuit Analysis Eleventh Edition Robert L. Boylestad Upper Saddle River, New Jersey Columbus, Ohio Contents CHAPTER CHAPTER 9 CHAPTER 3 3 CHAPTER
ΑΝΩΤΑΤΟ ΣΥΜΒΟΥΛΙΟ ΕΠΙΛΟΓΗΣ ΠΡΟΣΩΠΙΚΟΥ ΕΡΩΤΗΜΑΤΟΛΟΓΙΟ
ΑΝΩΤΑΤΟ ΣΥΜΒΟΥΛΙΟ ΕΠΙΛΟΓΗΣ ΠΡΟΣΩΠΙΚΟΥ ΔΙΑΓΩΝΙΣΜΟΣ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΕΤΟΥΣ 008 ( ΠΡΟΚΗΡΥΞΗ 5Π /008) ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΔΙΑΓΩΝΙΣΜΟΥ Κλάδος-Ειδικότητες: ΠΕ 17.03 ΗΛΕΚΤΡΟΛΟΓΩΝ, ΤΕΧΝΟΛΟΓΩΝ ΕΝΕΡΓΕΙΑΚΗΣ ΤΕΧΝΙΚΗΣ (κατεύθυνσης:
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΛΥΣΕΙΣ
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΕΤΑΡΗ 1 ΙΟΥΝΙΟΥ 019 ΛΥΣΕΙΣ ΘΕΜΑ Α A1. β Α. γ Α3. α Α. γ Α5. α) Λάθος β) Σωστό γ) Λάθος δ) Σωστό ε) Σωστό ΘΕΜΑ Β Β1. Σωστή απάντηση η ii. Μονάδες Εφαρμόζουμε ΑΔΟ για την κρούση των
ΔΙΑΣΤΑΣΕΙΣ ΚΑΙ ΜΟΝΑΔΕΣ
Σχολή Χημικών Μηχανικών, 2 ο εξάμηνο ΑΝΑΛΥΣΗ ΣΥΣΤΗΜΑΤΩΝ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ ΔΙΑΣΤΑΣΕΙΣ ΚΑΙ ΜΟΝΑΔΕΣ Γιώργος Μαυρωτάς, Επ. Καθηγητής Εργαστήριο Βιομηχανικής & Ενεργειακής Οικονομίας, Σχολή ΧΜ, ΕΜΠ Εισαγωγή
= 0.927rad, t = 1.16ms
P 9. [a] ω = 2πf = 800rad/s, f = ω 2π = 27.32Hz [b] T = /f = 7.85ms [c] I m = 25mA [d] i(0) = 25cos(36.87 ) = 00mA [e] φ = 36.87 ; φ = 36.87 (2π) = 0.6435 rad 360 [f] i = 0 when 800t + 36.87 = 90. Now
Εισαγωγική Άσκηση. Γνωριμία με το εργαστήριο
ΤΙ ΘΑ ΠΡΕΠΕΙ ΝΑ ΙΑΒΑΣΕΙΣ: Εισαγωγική Άσκηση Γνωριμία με το εργαστήριο Τη «Θεωρητική εισαγωγή» από την άσκηση 0 στις σελίδες 18-19 του βιβλίου σου. Ακόμη τις παραγράφους που έχουν τίτλο «Λειτουργία του
Φυσικές και χημικές ιδιότητες
Φυσικές και χημικές ιδιότητες Φυσικές ιδιότητες Οι ιδιότητες που προσδιορίζονται χωρίς αλλοίωση της χημικής σύστασης της ουσίας (π.χ. σ. τήξεως, σ. ζέσεως, πυκνότητα, χρώμα, γεύση, σκληρότητα). Χημικές
8η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ1 Ασκήσεις 8 ου Κεφαλαίου
8η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ1 Ασκήσεις 8 ου Κεφαλαίου 1. Ένα σύρμα μεγάλου μήκους φέρει ρεύμα 30 Α, με φορά προς τα αριστερά κατά μήκος του άξονα x. Ένα άλλο σύρμα μεγάλου μήκους φέρει
Φυσική για Μηχανικούς
Φυσική για Μηχανικούς Απλή Αρμονική Ταλάντωση Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά
ΕΠΑΝΑΛΗΠΤΙΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ
Επαναληπτικά μαθήματα φυσικής 1 ΕΠΑΝΑΛΗΠΤΙΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ ΕΠΙΜΕΛΕΙΑ: ΑΤΡΕΙΔΗΣ ΓΙΩΡΓΟΣ ΘΕΣΣΑΛΟΝΙΚΗ 2015 16 2 Φροντιστήρια δυαδικό Επαναληπτικά μαθήματα φυσικής 3 ΜΑΘΗΜΑ 1 Μεγέθη Μονάδες Γραφικές παραστάσεις
Σχολική Χρονιά Πανελλήνιες Πανελλήνιες Εξετάσεις - 23 Μάη Φυσική Θετικού Προσανατολισµού Ενδεικτικές Λύσεις.
Πανελλήνιες Εξετάσεις - 23 Μάη 2016 Α.1 (ϐ) Α.2 (γ) Α.3 (ϐ) Α.4 (δ) Α.5 Σ,Λ, Σ, Λ, Λ Φυσική Θετικού Προσανατολισµού Ενδεικτικές Λύσεις Θέµα Α Θέµα Β Β.1. (iii). ο Παρατηρητής αντιλαµβάνεται απευθείας από
ΗΛΙΑΣΚΟΣ ΦΡΟΝΤΙΣΤΗΡΙΑ. Θετικής - Τεχνολογικής Κατεύθυνσης Φυσική Γ Λυκείου ΥΠΗΡΕΣΙΕΣ ΠΑΙΔΕΙΑΣ ΥΨΗΛΟΥ ΕΠΙΠΕΔΟΥ. Επιμέλεια: ΘΕΟΛΟΓΟΣ ΤΣΙΑΡΔΑΚΛΗΣ
ΗΛΙΑΣΚΟΣ ΦΡΟΝΤΙΣΤΗΡΙΑ ΥΠΗΡΕΣΙΕΣ ΠΑΙΔΕΙΑΣ ΥΨΗΛΟΥ ΕΠΙΠΕΔΟΥ Θετικής - Τεχνολογικής Κατεύθυνσης Φυσική Γ Λυκείου Επιμέλεια: ΘΕΟΛΟΓΟΣ ΤΣΙΑΡΔΑΚΛΗΣ e-mail: info@iliaskos.gr www.iliaskos.gr - f= f= f t+ 0 ) max
ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s
P P P P ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s r t r 3 2 r r r 3 t r ér t r s s r t s r s r s ér t r r t t q s t s sã s s s ér t
13SYMV
«..», 5.7.2013, : 1 ι ιω,!ιι &!ι "ι, "# # 16 ι ωι #ι # $,. ω ι!ι,!,. ι%" &ι, ' ι, "# (! 40,! «%"» ι!) #* : 1. + (+/,--/77443/2012/10.08.2010 # ι! ι.//',-+/,--/77444/4667/2062/03.08.2012 # ι ω!ωι!. 2. +.
η η η η GAR = 1 F RR η F RR F AR F AR F RR η F RR F AR µ µ µ µ µ µ Γ R N=mxn W T X x mean X W T x g W P x = W T (x g x mean ) X = X x mean P x = W T X d P x P i, i = 1, 2..., G M s t t
1 2 3 4 5 6 7 8 9 10 2 12,999,976 km 9,136,765 km 1,276,765 km 499,892 km 245,066 km 112,907 km 36,765 km 24,159 km 7899 km 2408 km 76 km 12 14 16 3 6 11 1 12 7 1 2 5 4 3 9 10 8 18 20 21 22 23 24 25 26
2 3 4 5 6 7 8 9 10 12,999,976 km 9,136,765 km 1,276,765 km 499,892 km 245,066 km 112,907 km 36,765 km 24,159 km 7899 km 2408 km 76 km 12 14 16 9 10 1 8 12 7 3 1 6 2 5 4 3 11 18 20 21 22 23 24 26 28 30
Li % % % % % % % % % % 3d 4s V V V V d V V V n O V V V O V n O V n O % % X X % % % 10 10 cm Li Li Li LiMO 2 Li 1 x MO 2 + xl + 1 + xe C + xl + 1 + xe Li x C LiMO 2 +C Li x C + Li 1 x MO 2
Εισαγωγή στις Φυσικές Επιστήμες ( ) Ονοματεπώνυμο Τμήμα
Εισαγωγή στις Φυσικές Επιστήμες (9-7-5) Ονοματεπώνυμο Τμήμα Θέμα ο Ερώτημα Ένα σώμα μάζας kg τοποθετείται σε ένα κεκλιμένο επίπεδο και συνδέεται μέσω του νήματος αβαρούς τροχαλίας με ένα ελατήριο αμελητέας
Για τον ορισμό της ισχύος θα χρησιμοποιηθεί η παρακάτω διάταξη αποτελούμενη από ένα κύκλωμα Κ και μία πηγή Π:
1. Ηλεκτρικό ρεύμα Το ηλεκτρικό ρεύμα ορίζεται ως ο ρυθμός μιας συνισταμένης κίνησης φορτίων. Δηλαδή εάν στα άκρα ενός μεταλλικού αγωγού εφαρμοστεί μια διαφορά δυναμικού, τότε το παραγόμενο ηλεκτρικό πεδίο
Ασκήσεις Κεφ. 1, Κινηματική υλικού σημείου Κλασική Μηχανική, Τμήμα Μαθηματικών Διδάσκων: Μιχάλης Ξένος, email : mxenos@cc.uoi.gr 10 Απριλίου 2012 1. Αν το διάνυσμα θέσης υλικού σημείου είναι: r(t) = [ln(t
rs r r â t át r st tíst Ó P ã t r r r â
rs r r â t át r st tíst P Ó P ã t r r r â ã t r r P Ó P r sã rs r s t à r çã rs r st tíst r q s t r r t çã r r st tíst r t r ú r s r ú r â rs r r â t át r çã rs r st tíst 1 r r 1 ss rt q çã st tr sã
Physique des réacteurs à eau lourde ou légère en cycle thorium : étude par simulation des performances de conversion et de sûreté
Physique des réacteurs à eau lourde ou légère en cycle thorium : étude par simulation des performances de conversion et de sûreté Alexis Nuttin To cite this version: Alexis Nuttin. Physique des réacteurs
ITU-R P (2012/02) &' (
ITU-R P.530-4 (0/0) $ % " "#! &' ( P ITU-R P. 530-4 ii.. (IPR) (ITU-T/ITU-R/ISO/IEC).ITU-R http://www.itu.int/itu-r/go/patents/en. ITU-T/ITU-R/ISO/IEC (http://www.itu.int/publ/r-rec/en ) () ( ) BO BR BS
Αλληλεπίδραση ακτίνων-χ με την ύλη
Άσκηση 8 Αλληλεπίδραση ακτίνων-χ με την ύλη Δ. Φ. Αναγνωστόπουλος Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων Ιωάννινα 2013 Άσκηση 8 ii Αλληλεπίδραση ακτίνων-χ με την ύλη Πίνακας περιεχομένων
Κεφάλαιο 1 ο : Οι Φυσικοί αριθμοί
2 ΕΡΩΤΗΣΕΙΙΣ ΘΕΩΡΙΙΑΣ ΑΠΟ ΤΗΝ ΥΛΗ ΤΗΣ ΑΡΙΙΘΜΗΤΙΙΚΗΣ -- ΑΛΓΕΒΡΑΣ Κεφάλαιο 1 ο : Οι Φυσικοί αριθμοί Α. 1. 1 1. Ποιοι αριθμοί ονομάζονται φυσικοί και ποια είναι η χαρακτηριστική τους ιδιότητα; Οι αριθμοί
Κεφάλαιο 9. Περιστροφική κίνηση. Ροπή Αδράνειας-Ροπή-Στροφορμή
Κεφάλαιο 9 Περιστροφική κίνηση Ροπή Αδράνειας-Ροπή-Στροφορμή 1rad = 360o 2π Γωνιακή ταχύτητα (μέτρο). ω μεση = θ 1 θ 2 = θ t 2 t 1 t θ ω = lim t 0 t = dθ dt Μονάδες: περιστροφές/λεπτό (rev/min)=(rpm)=
Exercises in Electromagnetic Field
DR. GYURCSEK ISTVÁN Exercises in Electromagnetic Field Sources and additional materials (recommended) Gyurcsek I. Elmer Gy.: Theories in Electric Circuits, Globe Edit 206, ISBN:97833307343 Simonyi K.:
ibemo Kazakhstan Republic of Kazakhstan, West Kazakhstan Oblast, Aksai, Pramzone, BKKS office complex Phone: ; Fax:
Ασκήσεις Εμπέδωσης Μηχανικ ές ταλαντώέ σέις
Ασκήσεις Εμπέδωσης Μηχανικ ές ταλαντώέ σέις Όπου χρειάζεται, θεωρείστε ότι g = 10m/s 2 1. Σε μία απλή αρμονική ταλάντωση η μέγιστη απομάκρυνση από την θέση ισορροπίας είναι Α = 30cm. Ο χρόνος που χρειάζεται
d dx x 2 = 2x d dx x 3 = 3x 2 d dx x n = nx n 1
d dx x 2 = 2x d dx x 3 = 3x 2 d dx x n = nx n1 x dx = 1 2 b2 1 2 a2 a b b x 2 dx = 1 a 3 b3 1 3 a3 b x n dx = 1 a n +1 bn +1 1 n +1 an +1 d dx d dx f (x) = 0 f (ax) = a f (ax) lim d dx f (ax) = lim 0 =
Network Neutrality Debate and ISP Inter-Relations: Traffi c Exchange, Revenue Sharing, and Disconnection Threat
Network Neutrality Debate and ISP Inter-Relations: Traffi c Exchange, Revenue Sharing, and Disconnection Threat Pierre Coucheney, Patrick Maillé, runo Tuffin To cite this version: Pierre Coucheney, Patrick
.. ntsets ofa.. d ffeom.. orp ism.. na s.. m ooth.. man iod period I n open square. n t s e t s ofa \quad d ffeom \quad orp ism \quad na s \quad m o
G G - - -- - W - - - R S - q k RS ˆ W q q k M G W R S L [ RS - q k M S 4 R q k S [ RS [ M L ˆ L [M O S 4] L ˆ ˆ L ˆ [ M ˆ S 4 ] ˆ - O - ˆ q k ˆ RS q k q k M - j [ RS ] [ M - j - L ˆ ˆ ˆ O ˆ [ RS ] [ M
Το άτομο του Υδρογόνου
Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες
GEEPLUS VM1614. Force (N) vs Displacement (mm) Peak. Max 'ON' time. Force. Model No. VM
VM1614 2 VM1614 18 VM1614 125 VM1614 1 GEEPLUS VM1614 P 1 is the continuous (1% ED) excitation power at mounted to a massive heatsink at 2 C P 1 5 W Total Mass 15 g T max 13 C Coil Mass 3 g R 2 2.8.2 mh.7
Α/Α Ερώτησης Ερώτηση Α/Α Απάντησης Επιλογές Απάντησης 1 Το σύστηµα µονάδων που χρησιµοποιείται σήµερα περιλαµβάνει ως θεµελιώδη µεγέθη: 1 1 Μήκος,
Α/Α Ερώτησης Ερώτηση Α/Α Απάντησης Επιλογές Απάντησης 1 Το σύστηµα µονάδων που χρησιµοποιείται σήµερα περιλαµβάνει ως θεµελιώδη µεγέθη: 1 1 Μήκος, Μάζα, Χρόνος, Ένταση Μαγνητικού Πεδίου, Θερµοκρασία 1
Μεγέθη και Μονάδες. Ειδικά Θέµατα Φυσικής
Μεγέθη και Μονάδες Ειδικά Θέµατα Φυσικής 1 Γενικές Πληροφορίες Βιβλίο: Ειδικά Θέµατα Φυσικής, Ι.Ε. Φραγκιαδάκης, Εκδόσεις ΖΗΤΗ Ώρες Μαθήµατος: Πέµπτη 17:00 19:00 / Αίθουσα Γ (Ισόγειο Κτηρίου Γεωπονίας)
Westfalia Bedienungsanleitung. Nr
Westfalia Bedienungsanleitung Nr. 108230 Erich Schäfer KG Tel. 02737/5010 Seite 1/8 RATED VALUES STARTING VALUES EFF 2 MOTOR OUTPUT SPEED CURRENT MOMENT CURRENT TORQUE TYPE I A / I N M A / M N Mk/ Mn %
5 Ι ^ο 3 X X X. go > 'α. ο. o f Ο > = S 3. > 3 w»a. *= < ^> ^ o,2 l g f ^ 2-3 ο. χ χ. > ω. m > ο ο ο - * * ^r 2 =>^ 3^ =5 b Ο? UJ. > ο ο.
728!. -θ-cr " -;. '. UW -,2 =*- Os Os rsi Tf co co Os r4 Ι. C Ι m. Ι? U Ι. Ι os ν ) ϋ. Q- o,2 l g f 2-2 CT= ν**? 1? «δ - * * 5 Ι -ΐ j s a* " 'g cn" w *" " 1 cog 'S=o " 1= 2 5 ν s/ O / 0Q Ε!θ Ρ h o."o.
Points de torsion des courbes elliptiques et équations diophantiennes
Points de torsion des courbes elliptiques et équations diophantiennes Nicolas Billerey To cite this version: Nicolas Billerey. Points de torsion des courbes elliptiques et équations diophantiennes. Mathématiques
* _0916* Συστήματα κίνησης \ Αυτόματα συστήματα κίνησης \ Ενσωμάτωση συστήματος \ Υπηρεσίες. Διόρθωση. Σύγχρονοι γραμμικοί κινητήρες SL2
Συστήματα κίνησης \ Αυτόματα συστήματα κίνησης \ Ενσωμάτωση συστήματος \ Υπηρεσίες *23059508_0916* Διόρθωση Σύγχρονοι γραμμικοί κινητήρες SL2 Έκδοση 09/2016 23059508/EL SEW-EURODRIVE Driving the world
Α Ρ Ι Θ Μ Ο Σ : 6.913
Α Ρ Ι Θ Μ Ο Σ : 6.913 ΠΡΑΞΗ ΚΑΤΑΘΕΣΗΣ ΟΡΩΝ ΔΙΑΓΩΝΙΣΜΟΥ Σ τ η ν Π ά τ ρ α σ ή μ ε ρ α σ τ ι ς δ ε κ α τ έ σ σ ε ρ ι ς ( 1 4 ) τ ο υ μ ή ν α Ο κ τ ω β ρ ί ο υ, η μ έ ρ α Τ ε τ ά ρ τ η, τ ο υ έ τ ο υ ς δ
Εξέταση Προσοµοίωσης Γ τάξης Ενιαίου Λυκείου Απρίλης 2013 Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης Συνοπτικές Λύσεις. Θέµα Β
Φσική Γ Λκείο Α.1. Α.2. Α.3. Α.. Α.1. Εξέταση Προσοµοίωσης Γ τάξης Ενιαίο Λκείο Απρίλης 2013 Φσική Θετικής και Τεχνολογικής Κατεύθνσης Σνοπτικές Λύσεις (δ) (ϐ) (δ) (γ) Λ, Σ, Σ, Σ, Σ Θέµα Α Θέµα Β Β.1.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ- ΤΜΗΜΑ ΦΥΣΙΚΗΣ- ΤΟΜΕΑΣ ΘΕΩΡΗΤΙΚΗΣ ΦΥΣΙΚΗΣ ΜΑΘΗΜΑ: ΚΛΑΣΙΚΗ ΜΗΧΑΝΙΚΗ Ι(ΤΜΗΜΑ ΑΡΤΙΩΝ) ΔΙΔΑΣΚΩΝ: Αν. Καθηγητής Ι.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ- ΤΜΗΜΑ ΦΥΣΙΚΗΣ- ΤΟΜΕΑΣ ΘΕΩΡΗΤΙΚΗΣ ΦΥΣΙΚΗΣ ΜΑΘΗΜΑ: ΚΛΑΣΙΚΗ ΜΗΧΑΝΙΚΗ ΙΤΜΗΜΑ ΑΡΤΙΩΝ) ΔΙΔΑΣΚΩΝ: Αν. Καθηγητής Ι. ΡΙΖΟΣ ΛΥΣΕΙΣ ΘΕΜΑΤΩΝ ΕΞΕΤΑΣΕΩΝ ΠΕΡΙΟΔΟΥ ΦΕΒΡΟΥΑΡΙΟΥ 9 ΘΕΜΑ.4 μονάδες)
Επειδή η χορδή ταλαντώνεται µε την θεµελιώδη συχνότητα θα ισχύει. Όπου L είναι το µήκος της χορδής. Εποµένως, =2 0,635 m 245 Hz =311 m/s
1. Μία χορδή κιθάρας µήκους 636 cm ρυθµίζεται ώστε να παράγει νότα συχνότητας 245 Hz, όταν ταλαντώνεται µε την θεµελιώδη συχνότητα. (a) Βρείτε την ταχύτητα των εγκαρσίων κυµάτων στην χορδή. (b) Αν η τάση
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 19 Ταλαντώσεις Απλή αρμονική κίνηση ΦΥΣ102 1 Ταλαντώσεις Ελατηρίου Όταν ένα αντικείμενο
1.1 Δύο σφαίρες με φορτίο 2Cb έχουν τα κέντρα τους σε απόσταση 2m. Πόση είναι η δύναμη που αναπτύσσεται μεταξύ τους; Λύση
Περιεχόμενα Πρόλογος... 9 Κεφάλαιο : Συνεχή ρεύματα... Κεφάλαιο : Λυμένες ασκήσεις... 59 Κεφάλαιο : Παραδείγματα και ασκήσεις προς λύση... 8 Κεφάλαιο 4: Συνδέσεις πηγών... 99 Κεφάλαιο 5: Ενέργεια-ισχύς-έργο-
' ( )* * +,,, ) - ". &!: &/#&$&0& &!& $#/&! 1 2!#&, #/&2!#&3 &"&!3, #&- &2!#&, "#4 $!&$3% 2!% #!.1 & &!" //! &-!!
..!! "#$% #&" 535.34 ' ( )* *,,, ) - ". &!: 1.4.7 &/#&$&& &!&11 5.7.1 $#/&! 1!#&, #/&!#&3 &"&!3, #&- &!#&, "#4 $!&$3%!% #!.1 & &!" //! &-!!% 3 #&$&/!: /&!&# &-!!%, "#&&# 56$.., //! &-!!% ).. &$ 13 .
3. Υπολογίστε το μήκος κύματος de Broglie (σε μέτρα) ενός αντικειμένου μάζας 1,00kg που κινείται με ταχύτητα1 km/h.
1 Ο ΚΕΦΑΛΑΙΟ ΑΣΚΗΣΕΙΣ 1. Ποια είναι η συχνότητα και το μήκος κύματος του φωτός που εκπέμπεται όταν ένα e του ατόμου του υδρογόνου μεταπίπτει από το επίπεδο ενέργειας με: α) n=4 σε n=2 b) n=3 σε n=1 c)
Ασκήσεις Κλασικής Μηχανικής, Τμήμα Μαθηματικών Διδάσκων: Μιχάλης Ξένος, email : mxenos@cc.uoi.gr 30 Μαρτίου 2014 Κεφάλαιο Ι: Κινηματική του Υλικού Σημείου 1. Αν το διάνυσμα θέσης υλικού σημείου είναι:
ΜΕΤΡΗΣΕΙΣ ΜΗΚΟΥΣ Η ΜΕΣΗ ΤΙΜH
ΜΕΤΡΗΣΕΙΣ ΜΗΚΟΥΣ Η ΜΕΣΗ ΤΙΜH ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ Τι πρέπει να γνωρίζεις Θεωρία. Τι ονομάζουμε μέγεθος;.2 Τι είναι τα φυσικά φαινόμενα; Με τη μελέτη των φυσικών φαινομένων ασχολούνται οι φυσικές επιστήμες, όπως
ΗΛΙΑΣΚΟΣ ΦΡΟΝΤΙΣΤΗΡΙΑ. Γενικής Παιδείας Βιολογία Γ Λυκείου ΥΠΗΡΕΣΙΕΣ ΠΑΙΔΕΙΑΣ ΥΨΗΛΟΥ ΕΠΙΠΕΔΟΥ. Επιμέλεια: ΚΩΣΤΑΣ ΓΚΑΤΖΕΛΑΚΗΣ
ΗΛΙΑΣΚΟΣ ΦΡΟΝΤΙΣΤΗΡΙΑ ΥΠΗΡΕΣΙΕΣ ΠΑΙΔΕΙΑΣ ΥΨΗΛΟΥ ΕΠΙΠΕΔΟΥ Γενικής Παιδείας Βιολογία Γ Λυκείου Επιμέλεια: ΚΩΣΤΑΣ ΓΚΑΤΖΕΛΑΚΗΣ e-mail: info@iliaskos.gr www.iliaskos.gr 1 2010 2011 µ..., µ..,... 2011. 1:, 19-21
Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού.
Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού. Περιοδικός πίνακας: α. Είναι µια ταξινόµηση των στοιχείων κατά αύξοντα
ITU-R P (2009/10)
ITU-R.45-4 (9/) % # GHz,!"# $$ # ITU-R.45-4.. (IR) (ITU-T/ITU-R/ISO/IEC).ITU-R http://www.tu.t/itu-r/go/patets/e. (http://www.tu.t/publ/r-rec/e ) () ( ) BO BR BS BT F M RA S RS SA SF SM SNG TF V.ITU-R
ΠΡΟΤΥΠΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Α ΛΥΚΕΙΟΥ
ΠΡΟΤΥΠΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Α ΛΥΚΕΙΟΥ Μ. ΔΙΑΚΟΝΟΥ, Β. ΟΡΦΑΝΟΠΟΥΛΟΣ, Χ. Δ. ΦΑΝΙΔΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 2014-2015 1. α. Από τις παρακάτω έννοιες
με ίσες μάζες ισορροπούν κρεμασμένα από κατακόρυφα ιδανικά ελατήρια με σταθερές k 1 και k 2 /2. Απομακρύνουμε τα σώματα Σ 1
ΑΣΚΗΣΕΙΣ ( Σε όλα τα προβλήματα - εκτός από το 9 - στα οποία υπεισέρχεται βαρύτητα να θεωρήσετε την τιμή της βαρυτικής επιτάχυνσης ίση με και 10 m/s 2, Να θεωρήσετε επίσης για την τιμή του π ότι π 2 =
ΚΑΤΑΝΟΜΗ BOLTZMANN ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΚΑΤΑΝΟΜΗ BOLTZMA ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ Περιεχόμενα 1. Κατανομή Bltzmann. Ασκήσεις 1 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 1. Κατανομή Bltzmann
Sheet H d-2 3D Pythagoras - Answers
1. 1.4cm 1.6cm 5cm 1cm. 5cm 1cm IGCSE Higher Sheet H7-1 4-08d-1 D Pythagoras - Answers. (i) 10.8cm (ii) 9.85cm 11.5cm 4. 7.81m 19.6m 19.0m 1. 90m 40m. 10cm 11.cm. 70.7m 4. 8.6km 5. 1600m 6. 85m 7. 6cm
1. Ένα σώμα m=1 kg εκτελεί γ.α.τ. και η μεταβολή της επιτάχυνσής του σε συνάρτηση με το χρόνο φαίνεται στο σχήμα.
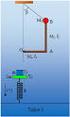. Ένα σώμα m= kg εκτελεί γ.α.τ. και η μεταβολή της επιτάχυνσής του σε συνάρτηση με το χρόνο φαίνεται στο σχήμα. α. Να βρείτε τη σταθερά D και την ολική ενέργεια του ταλαντωτή. β. Να γράψετε τις εξισώσεις
Hygromécanique des panneaux en bois et conservation du patrimoine culturel. Des pathologies... aux outils pour la conservation
Hygromécanique des panneaux en bois et conservation du patrimoine culturel. Des pathologies... aux outils pour la conservation Bertrand Marcon To cite this version: Bertrand Marcon. Hygromécanique des
Jeux d inondation dans les graphes
Jeux d inondation dans les graphes Aurélie Lagoutte To cite this version: Aurélie Lagoutte. Jeux d inondation dans les graphes. 2010. HAL Id: hal-00509488 https://hal.archives-ouvertes.fr/hal-00509488
ΔΙΑΜΟΡΦΩΣΕΙΣ ΧΩΡΙΣ ΑΦΑΙΡΕΣΗ ΥΛΙΚΟΥ - ΤΡΙΒΟΛΟΓΙΑ
ΑΛΕΞΑΝΔΡΕΙΟ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΟΧΗΜΑΤΩΝ ΔΙΑΜΟΡΦΩΣΕΙΣ ΧΩΡΙΣ ΑΦΑΙΡΕΣΗ ΥΛΙΚΟΥ - ΤΡΙΒΟΛΟΓΙΑ Ασκήσεις Δρ Γ. Παραδεισιάδης Αναπληρωτής Καθηγητής ΘΕΣΣΑΛΟΝΙΚΗ
2013/2012. m' Z (C) : V= (E): (C) :3,24 m/s. (A) : T= (1-z).g. (D) :4,54 m/s
( ) 03/0 - o l P z o M l =.P S. ( ) m' Z l=m m=kg m =,5Kg g=0/kg : : : : Q. (A) : V= (B) : V= () : V= (D) : V= (): : V :Q. (A) :4m/s (B) :0,4 m/s () :5m/s (D) :0,5m/s (): : M T : Q.3 (A) : T=(-z).g (B)
Φυσική για Μηχανικούς
Φυσική για Μηχανικούς Απλή Αρμονική Ταλάντωση Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά
Υπολογισμός Εξατμισοδιαπνοής της καλλιέργειας αναφοράς Μέθοδος Penman-Monteith FAO 56 (τροποποιημένη)
Υπολογισμός Εξατμισοδιαπνοής της καλλιέργειας αναφοράς Μέθοδος Penman-Monteith FAO 56 (τροποποιημένη) Ο υπολογισμός της εξατμισοδιαπνοής μπορεί να γίνει από μια εξίσωση της ακόλουθης μορφής: ETa ks kc
Προϊοντικό φυλλάδιο. Ηλεκτρονικοί μετρητές ενέργειας σειράς C Οικονομικοί και εύκολοι στη χρήση
Προϊοντικό φυλλάδιο Ηλεκτρονικοί μετρητές ενέργειας σειράς C Οικονομικοί και εύκολοι στη χρήση Ηλεκτρονικοί μετρητές ενέργειας σειράς C Με μια ματιά Κύριες εφαρμογές Μέτρηση κατανάλωσης ενέργειας σε οικιακές
ΤΥΠΟΛΟΓΙΟ ΙΜΑΝΤΟΚΙΝΗΣΕΩΝ
ΤΥΠΟΛΟΓΙΟ ΙΜΑΝΤΟΚΙΝΗΣΕΩΝ β ελκόμενος κλάδος β n 2 n 1 α 1 d d 2 α 1 2 (α) κινητήρια τροχαλία έλκων κλάδος a β κινούμενη τροχαλία F 2 n 1 α 1 F 2 FA κινητήρια τροχαλία F 1 (β) F 1 Σχήμα 1 (α) Γεωμετρικά
ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ B ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
Θέμα Α ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ B ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Στις παρακάτω ερωτήσεις πολλαπλής επιλογής Α-Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
Στοιχεία εισαγωγής για τη Φυσική Α Λυκείου
Στοιχεία εισαγωγής για τη Φυσική Α Λυκείου 1 ΑΛΓΕΒΡΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΚΑΙ ΠΡΟΤΕΡΑΙΟΤΗΤΑ ΠΡΑΞΕΩΝ 1.1 Προτεραιότητα Πράξεων Η προτεραιότητα των πράξεων είναι: (Από τις πράξεις που πρέπει να γίνονται πρώτες,
5 η Εβδομάδα Έργο και κινητική ενέργεια. Ομαλή κυκλική κίνηση Έργο δύναμης Κινητική ενέργεια Θεώρημα έργου ενέργειας
5 η Εβδομάδα Έργο και κινητική ενέργεια Ομαλή κυκλική κίνηση Έργο δύναμης Κινητική ενέργεια Θεώρημα έργου ενέργειας Ομαλή κυκλική κίνηση Κίνηση σωματίου σε κύκλο με ταχύτητα σταθερού μέτρου. Επιτάχυνση
UNIVERSITE DE PERPIGNAN VIA DOMITIA
Délivré par UNIVERSITE DE PERPIGNAN VIA DOMITIA Préparée au sein de l école doctorale Energie et Environnement Et de l unité de recherche Procédés, Matériaux et Énergie Solaire (PROMES-CNRS, UPR 8521)
Νόμος Faraday Κανόνας Lenz Αυτεπαγωγή - Ιωάννης Γκιάλας 27 Μαίου 2014
Νόμος Faraday Κανόνας Lenz Αυτεπαγωγή - Ιωάννης Γκιάλας 7 Μαίου 014 Στόχοι διάλεξης Πώς να: υπολογίζει την μεταβολή της μαγνητικής ροής. εφαρμόζει το νόμο του Faraday για τον υπολογισμό της επαγόμενης
Σετ τροχών σύσφιξης B
01/2011 Πρωτότυπο οδηγιών χειρισμού 999285509 gr Πρέπει να φυλάσσονται για μελλοντική χρήση Σετ τροχών σύσφιξης B Αρ. προϊόντος 586168000 από έτος κατασκευής 2008 Περιγραφή προϊόντος Περιγραφή προϊόντος
! : ;, - "9 <5 =*<
ITU-R M.473- (00/0)! (TDMA/FDMA) ""# $ %!& ' " ( ) 34 --./ 0, (MSS) * * )! +, 56 78 89 : ;, - "9
LEM. Non-linear externalities in firm localization. Giulio Bottazzi Ugo Gragnolati * Fabio Vanni
LEM WORKING PAPER SERIES Non-linear externalities in firm localization Giulio Bottazzi Ugo Gragnolati * Fabio Vanni Institute of Economics, Scuola Superiore Sant'Anna, Pisa, Italy * University of Paris
Πυκνωτές και διηλεκτρικά. Ιωάννης Γκιάλας 21 Μαρτίου 2014
Πυκνωτές και διηλεκτρικά Ιωάννης Γκιάλας 1 Μαρτίου 014 Μεταλλικά σώματα (τυχαίου σχήματος) που συνδέονται με τους πόλους μίας μπαταρίας Φορτίο πυκνωτή = φορτίο ενός οπλισμού Δυναμικό πυκνωτή η διαφορά
11 η Εβδομάδα Δυναμική Περιστροφικής κίνησης. Έργο Ισχύς στην περιστροφική κίνηση Στροφορμή
11 η Εβδομάδα Δυναμική Περιστροφικής κίνησης Έργο Ισχύς στην περιστροφική κίνηση Στροφορμή Έργο και ισχύς στην περιστροφική κίνηση Εφαπτομενική δύναμη που περιστρέφει τον τροχό κατά dθ dw F ds = F R dθ
ΦΥΕ 14 6η ΕΡΓΑΣΙΑ Παράδοση ( Οι ασκήσεις είναι ϐαθµολογικά ισοδύναµες)
ΑΣΚΗΣΗ 1 ΦΥΕ 14 6η ΕΡΓΑΣΙΑ Παράδοση 30-06-08 ( Οι ασκήσεις είναι ϐαθµολογικά ισοδύναµες) Α) Τρία σηµειακά ϕορτία τοποθετούνται στις κορυφές ενός τετραγώνου πλευράς α, όπως ϕαίνεται στο σχήµα 1. Υπολογίστε
1 2 k(x 0 x e ) 2 = 1 2 mv2 1x = K 1 K 1 = 1 2 (100 N/m)(0.20 m 0 m)2 = 2.0J
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-112: Φυσική Ι Χειµερινό Εξάµηνο 2016 ιδάσκων : Γ. Καφεντζής Τρίτο Φροντιστήριο Ασκηση 1. Ενα οριζόντιο ελατήριο µε σταθερά 100 N/m συµπιέζεται κατά 20
sin(30 o ) 4 cos(60o ) = 3200 Nm 2 /C (7)
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-112: Φυσική Ι Χειµερινό Εξάµηνο 2016 ιδάσκων : Γ. Καφεντζής Πέµπτη Σειρά Ασκήσεων - Λύσεις Ασκηση 1. (αʹ Η ηλεκτρική ϱοή διαµέσου µιας επιφάνειας A είναι
!"#$ % &# &%#'()(! $ * +
,!"#$ % &# &%#'()(! $ * + ,!"#$ % &# &%#'()(! $ * + 6 7 57 : - - / :!", # $ % & :'!(), 5 ( -, * + :! ",, # $ %, ) #, '(#,!# $$,',#-, 4 "- /,#-," -$ '# &",,#- "-&)'#45)')6 5! 6 5 4 "- /,#-7 ",',8##! -#9,!"))
ΕΡΓΟΣΤΑΣΙΟ ΠΑΡΑΓΩΓΗΣ ΠΥΡΗΝΕΛΑΙΟΥ ΜΗΧΑΝΟΛΟΓΙΚΗ ΜΕΛΕΤΗ
ΕΡΓΟΔΟΤΗΣ: ΕΡΓΟ: ΕΡΓΟΣΤΑΣΙΟ ΠΑΡΑΓΩΓΗΣ ΠΥΡΗΝΕΛΑΙΟΥ ΤΟΠΟΘΕΣΙΑ: ΜΗΧΑΝΟΛΟΓΙΚΗ ΜΕΛΕΤΗ ΚΑΡΥΩΤΑΚΗ 5 Α 166 73 ΒΟΥΛΑ ΤΗΛ. 210 8995934, ΦΑΞ 210 8951760 e-mail info@inik.gr 1 1. ΤΕΧΝΙΚΟ ΥΠΟΜΝΗΜΑ α. Ονοματεπώνυμο