ΛΑΙΚΟΣ ΟΡΘΟΔΟΞΟΣ ΣΥΝΑΓΕΡΜΟΣ (ΠΑ.ΣΟ.Κ.)

! # ## %% & % (() ((+

!! #! #!% ## %% & % (() ((+ ! # & ( ) +,./,0 ! # % & ( ) % ( # +,,,. /! ( 0) 0 # 0 1,,2,. 3, 00 4 # + 5 6 7. 1, 00 + 5 6 3 7 )7 8 7 7 0,, 7 )7 8 7 )7 8 7 0 + 7 )7 8 0 (( 7 7 )7 8 :5 1, # 7 )7 8 + 70

! #! % # % + ( (.! / 0 + ( (. & (&(&)) +,

! #! %! # % & (&(&)) +, + ( (.! / 0 + ( (. ! # % & % ( % ) +,% +. & / 0 1% 2 % 3 3 %4 5 6 0 # 71 % 0 1% 8% 9 : ;% 5 < =./,;/;% % 8% 9 /,%%1 % 5 % 8% 9 > >. & 3.,% + % + % % 8% 9!?!. & 3 2 6.,% + % % 6>

!! % 4 4 4 4 %,!,! %

! %! & () +)!,!. / % %! 0 1!!! 2!! %!! %!! % %!. 3!!!!!! 4 4 4 4 % & 5) /!! % 6!! 7!! 8 % 8! %.! & 9)!! 7,!,! %. 6! !! %!.!! 6!! 6 :! %!! ;!!! %!!! %! %!!!! 0< 1.!!!?

! # % &#% ( ) +, + + % %. +, + + / 0 % 1 # 1 +

!! # % &#% ( ) +, + + % %. +, + + / 0 % 1 # 1 + 2 ( 1 3 4 3 + 3 ) ( & + % + + 3 5675+ 859 + +! & # % +, + + % %., + + / 0 7+ ) 5+ 8+ % :+ % 9+ %; (

η έφ ο : 2321047530 FAX : 2321047531 : mail@dide.ser.sch.gr έ ς, 16/6/2015 Α Ο Φ Α Η

Η Η Η Ο Α Α Ο Ο Ο Ο, Α Α Α Η Α Ω, Φ Α Η / Η / Η Η Α Ο Α / Η / Α / Η Ω α. / ση : Κ ασού ος Κ έ ς Π η οφο ί ς : ώ ιος. ο ά ης η έφ ο : 2321047530 FAX : 2321047531 Email : mail@dide.ser.sch.gr έ ς, 16/6/2015

# % % % % % # % % & %

! ! # % % % % % % % # % % & % # ( ) +,+.+ /0)1.2(3 40,563 +(073 063 + 70,+ 0 (0 8 0 /0.5606 6+ 0.+/+6+.+, +95,.+.+, + (0 5 +//5: 6+ 56 ;2(5/0 < + (0 27,+/ +.0 10 6+ 7 0, =7(5/0,> 06+?;, 6+ (0 +9)+ 5+ /50

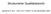α α α α α α α α α α α α α α α α α α α α α α α α α α α α β χ δ ε φ γ η ι ϕ κ λ µ ν ο π θ ρ σ τ υ ϖ ω ξ ψ ζ αα ββ χχ δδ εε φφ γγ ηη ιι ϕϕ κκ λλ µµ νν οο

(! ( (! ) ) ) + ) +, #., /! 0 1 ) 1 2 ) 1 # 3 4 # / 4 %, #! 5 1 1 6 / 7 8 8 ( + + ( % 3 0 4 0 + & 0 0 0 %! )

!!!! # % # %%& & (! ( (! ) ) ) + ) +, #., /!0 1 ) 1 2 ) 1 # 3 4 # / 4 %, #!5 1 1 6/ 7 8 8 ( + + ( % 3 0 4 0 + & 0 0 0 %! ),!. )/, 3 9)(5 3 : ) ; & ( < % 9)(5 09)(5 # = 6 > 6 > ( 6 4! % 6 ( > ( 1 6 + 0

= # & < # #, 1 & & # 2 # 5 > # &? = 4Α # # ( 6 4 7? & # = # 6 4 > 6 4 Β 1 = Β (.

! ## % & # # # # ( ) & & # + # # # & %, # ## & # ( # & # ( # # # & # & &. #/ 01 ( 2 & # ## & 2 # & 3 1 1 4 % # &5 ## # & 4 6 ( # ( 5 21 & # ( # % & # 4 6 # &! 6 & & # # # & & # 7 & # 1& & # & 5 # &. #

! # % & ( ) ++ ,. / 0 & 01 0 2 3 % 4,. / 0 & 0 0 / 0 5/ 0 / # 6 3.

! # %& () ++,. /0& 0102 3% 4,. /0& 0 0/ 05/0 / # 6 3. ! # %% & %() #+, %% #. / 0 1) 2! 3 2 4 2 # %% 3 5 6! 7 3 2 4 8!! 3! 2 5 9 3 5 5 9 5 : ; 5 3 < 5 / 5 2 &2 9 5 3 8 5, 5 3 5 2 =4 > 5 3 2 4 9 5 /3 5 6

?=!! #! % &! & % (! )!! + &! %.! / ( + 0. 1 3 4 5 % 5 = : = ;Γ / Η 6 78 9 / : 7 ; < 5 = >97 :? : ΑΒ = Χ : ΔΕ Φ8Α 8 / Ι/ Α 5/ ; /?4 ϑκ : = # : 8/ 7 Φ 8Λ Γ = : 8Φ / Η = 7 Α 85 Φ = :

Γεώργιος Δ. Παλτεζανάκης

Η ύλη του μαθήματος μας εισάγει στον δομημένο προγραμματισμό. Ένα καλό αυτής της τεχνικής είναι ότι αν ο μαθητής γνωρίζει κάποιους βασικούς αλγόριθμους μπορεί με συνδυασμό τους να οικοδομήσει άλλους πιο

/ 12 # % &! (! & )! (+,.). / 0

/ 12! # % &! (! & )! (+,.). / 0 ! # % & % ( ) ( % + (, % #. # #. / 0 # 1, % # ) 2,# 3 3 % # # 0/4# (# 0, # % 3 5 6 ( 5 7 % 7 % 7 % # % 7 % 7 7 7 % 8 9 : # 7 # ; 7 % % 7 # 7 # % < 7 7 7 %. # 8 # 7 # % )

2 (4! ((2 (5 /! / Β ;! + %ΧΑ + ((5 % # &

!! # % & # () %# + (, # &,. /01 2 23 () 0 &. 04 3 23 (5 6787%.9 : ; 3!.&6< # (5 2!.& 6 < # ( )!.&+ < # 0= 1 # (= 2 23 0( >? / #.Α( 2= 0( 4 /

! # % & % ( )! + #, % ( . / 0 0 % ( )! # % # # 1 + + 0 % 0 #2 0 + % # # % % 3 0 + + % # + %

! # % & % ( )! + #, % (. / 0 0 % ( )! # % # # 1 + + 0 % 0 #2 0 + % # # % % 3 0 + + % # + % 4444444444444444444444444444444444444444444 5 6 4444444444444444444444444444444444444444444444! + 0 & 4444444444444444444444444444444444444444444444.

Χ.1 Βασικοί πόλοι. Κηφισιά ΟΡΓΑΝΙΣΜΟΣ ΡΥΘΜΙΣΤΙΚΟΥ ΣΧΕΔΙΟΥ & ΠΡΟΣΤΑΣΙΑΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΑΘΗΝΑΣ. Μαρούσι. Περιστέρι. Κέντρο Αθήνας. Ζωγράφου.

αρούσι Γ ΘΚ ΧΔ Π ΠΒΛΛ Θ ΘΚ Β ΠΛΧ ΧΛ Γ Κ ΠΓ ΧΚ ΓΓ ΠΚ Π Δ Β ΚΚ μήκους στην θήνα,της έρευνας μέτρων εφαρμογής ενιαίου πολεοδομικού και κυκλοφοριακού σχεδιασμού Κέντρο θήνας Χ1 Βασικοί πόλοι πόμνημα Βασικοί

ΕΦΗΜΕΡΙΣ ΤΗΣ ΚΥΒΕΡΝΗΣΕΩΣ

1475 ΕΦΗΜΕΡΙΣ ΤΗΣ ΚΥΒΕΡΝΗΣΕΩΣ ΤΗΣ ΕΛΛΗΝΙΚΗΣ ΔΗΜΟΚΡΑΤΙΑΣ ΤΕΥΧΟΣ ΠΡΩΤΟ Αρ. Φύλλου 142 6 Νοεμβρίου 2015 NOMOΣ ΥΠ ΑΡΙΘ. 4341 Κύρωση της Συμφωνίας μεταξύ της Ελληνικής Δημοκρα τίας και της Ευρωπαϊκής Τράπεζας

Ν Κ Π 6Μ Θ 5 ϑ Μ % # =8 Α Α Φ ; ; 7 9 ; ; Ρ5 > ; Σ 1Τ Ιϑ. Υ Ι ς Ω Ι ϑτ 5 ϑ :Β > 0 1Φ ς1 : : Ξ Ρ ; 5 1 ΤΙ ϑ ΒΦΓ 0 1Φ ς1 : ΒΓ Υ Ι : Δ Φ Θ 5 ϑ Μ & Δ 6 6

# % & ( ) +, %. / % 0 1 / 1 4 5 6 7 8 # 9 # : ; < # = >? 1 :; < 8 > Α Β Χ 1 ; Δ 7 = 8 1 ( 9 Ε 1 # 1 ; > Ε. # ( Ε 8 8 > ; Ε 1 ; # 8 Φ? : ;? 8 # 1? 1? Α Β Γ > Η Ι Φ 1 ϑ Β#Γ Κ Λ Μ Μ Η Ι 5 ϑ Φ ΒΦΓ Ν Ε Ο Ν

,, &6 % )7) 8559

! # # %& () +,. / /0 1 2 0 3,,. 4 5. &6 % )7) 8559 ( 7(6, ( ( ( (6 & () ( ()()& : # %& ()( &+,) (../0%1.(& 2.& 3124&5,3 (6 7,8& 9)3,) (: ; 3 5). 413,)5& ?()%& 3),/ ; 8&;;)&.6> < )3,))(

1 ΓΕΩΜΕΤΡΙΑ Α ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 3 ο ΤΡΙΓΩΝΑ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ

1 ΓΕΩΜΕΤΡΙΑ Α ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 3 ο ΤΡΙΓΩΝΑ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΑΣΚΗΣΗ 1 η Έστω ΑΒΓ ένα ισοσκελές τρίγωνο (ΑΒ = ΑΓ), Δ, Ε σημεία της πλευράς ΒΓ τέτοια, ώστε ΒΔ = ΔΕ = ΕΓ και Μ, Ρ τα μέσα των πλευρών ΑΒ, ΑΓ

# # %& ) & +,& & %. / / 6 & / 7 / 8 8 # 3/ 6 & / 7 /

! # # %& ) & +,& & %. / 01 23345 1/ 6 & / 7 / 8 8 # 3/ 6 & / 7 / / ; / 212

Θ+!& ;/7!127# 7 % :!+9. + %#56 /+.!/;65+! 3# 76. +!+ % 2&/ :2!,Γ 0 :9#+ #2:.2 #+Ι 7#+.&/ #2:.2 / /&7 + < & /!! Ω 6. Α./& /&7 + 622#. 6!

! # %!! #!#%& ()! +,.! + /!#012!!# )3 # #4 +!#567 8%+#%/!,917#,.! + 9: %# ;:/%&. + # 9/ = 2>3/!#012!!# )3 #? +.:;/7/&7 + Α./&Β# 7. +;# 2/># 7 ΧΧ67< %#+ΧΧ #+.#17/+/ #

!!# % & ( % ) % % +,,. / 0 1!!# 2 / 3 (. +,,

!!# % & ( % ) % % +,,. / 0 1!!# 2 / 3 (. +,,! 454 454 6 7 #! 89 : 3 ; &< 4 =>> ; &4 + ! #!!! % & ( ) ) + + ) 3 +, +. 0 1 2. # 0! 3 2 &!.. 4 3 5! 6., 7!.! 8 7 9 : 0 & 8 % &6 0 9 ( 6! ;

Κεφάλαιο 1 ο. Αλγεβρικές παραστάσεις.

Μαθηματικά Γ Γυμνασίου Κεφάλαιο 1 ο. Αλγεβρικές παραστάσεις. Μέρος Α Θεωρία. 1. Πως προσθέτουμε δύο πραγματικούς αριθμούς; 2. Πως πολλαπλασιάζουμε δύο πραγματικούς αριθμούς; 3. Ποιες είναι οι ιδιότητες

) 0 ) 2 & 2 & 0 + 6! ) & & & & & ), Γ , Γ 8 (?. Κ Ε 7 ) ) Μ & 7 Ν & & 0 7 & & Γ 7 & & 7 & Ν 2 & Γ Γ ( & & ) Η ++. Ε Ο 9 8 ) 8& & ) & Ε

#! % & ( + ),./! +./+., ( ( 1 #23 + + ), 1 (453.+ 6.+ 6, 7 1 89 3.! :.! :, 1 (453.. / 2 ; ? Α 7 ; Β / / 4 > (? / / ) 8 Χ :/. ++.. +. : 6 : ) )4 ) ) ( 4 )Φ 7 % 6 : : +.. ++. ) & & & & ), Γ, Γ 8 (?.

ε Ξ Ξ Ξ τε ξ Υ Ξ ΕΤ ξ ΞΞ ΞΓ ξξ Ξ Η ΞΞξ Ξ Τ ξ Φ Φ Εβ ε Γ ι ε ι Ψ λ Ρ ε η Ξ Τ Τ π ψ Γ ι ι ε τ τ μ Ι μ κ τ μ Ξ ηψ ιφ γ ιι Φ Φ ξθ ρ ι Φι ι γ κ τ ετ ε φ τ

ξ Υ ΕΤ ξ Γ ξ Η ξ Τ ξ Φ Φ Εβ Γ Ψ λ Ρ Τ Τ π ψ Γ μ Ι μ κ μ ψ φ Φ Φ ξθ ρ Φ κ φ ζ Ρ ξ Γ α ξ ζ π Γ μ Ι ξ Ι Ψ ξ ΤΗ β α Τ ξ ζ ξ κ Τ Φ θ Ψ Η Η μξ Τ ωφ ψ φ ζ π ξ ζ π ζ κ μ κ Φ μ ψ λ λ ψ μ ζ Υ ξ Φ Φ ΦΦ ω ξ Φ Φ ξ

14PROC

Γ Γ :ΕΕΕΕΕΕΕΕΕΕΕΕΕΕΕΕΕΕ :ΕΕΕΕΕΕΕΕΕΕΕΕΕΕΕΕΕ... 5 βν ΤΓ ΙΟΝΟΜΙΚΗΝΠ ΡΙΦ Ρ Ι ΝΘ ΛΙ ΝΣΝ Σ Ρ Ν ΛΛ ΠΛΗΡΟΦΟΡΙ : Κ Φ Σ ΚΗΝΜ ΡΙ α, 27/06/2014 ΣαξέΝ ήθ βμνπ λδοξάνμ αοτλζο,νσθέν21ί1 ΣέΚέΝ41110 - Λ ΡΙ URL: http://www.dypethessaly.gr,

ΔΙΑΣΥΝΔΕΔΕΜΕΝΑ Φ/Β ΣΥΣΤΗΜΑΤΑ

ΔΙΑΣΥΝΔΕΔΕΜΕΝΑ Φ/Β ΣΥΣΤΗΜΑΤΑ 1. Sunvalue technologies Βριλήσσια Αττικής 11,88 kwp 17/07/08 2008 2. Κλαουδάτος Ενεργειακή ΑΕ Μυρίκη1 99,9 kwp 17/06/09 2009 3. Κλαουδάτος Ενεργειακή ΑΕ Μυρίκη2 20 kwp 09/09/09

! #! % &! #! ( ) %! # +,, )! #.,. # / (! # /. ) ). 0 1, 2,! # +

! # ! #! % &! #! ( ) %! # +,, )! #.,. # / (! # /. ) ). 0 1, 2,! # + % & / &. 0 3 ( & 4 5. 6 7 & 4 8. 9 5: & 4 :. 56 8 / &. 0 3 ) & 4 4. 6 9 & 4. 4 : & 4 :. 84 88!,. ; 3 + 2 ( < 0 = 0 >? 0 < 2. 0 0 ( Α

+ ) 1 2! 3 % !

# % & (!! + + ) 1 2! 3 % + 5 1 2! !! #! % ( ) +,! %. # # # ) /0! 1 2 3 # 4 0 ) 5 # # & 4 & 6 #% 0 ## 7 8 & #+! #9 # : & 1 5 + ; < + 4 ) 3 4 Α Β 3# # < 4 Α Β 3 < 4 Α Β 39 + =>! ) 5# + 9# + & Α 9+9Β 9 Χ

ΦΥΣΙΚΕΣ ΕΠΙΣΤΗΜΕΣ ΙΙ

University of Athens Pedagogical Department P.Ε. Science, Technology and Environment Section / Laboratory 13a Navarinou str, Athens, GR-10680 Πανεπιστήμιο Αθηνών Παιδαγωγικό Τμήμα Δ.Ε. Τομέας / Εργαστήριο

) (+ 89 / >9691 /) 01)> 59 )2 >9691 /) (=12) (=12) 2 1< /. )1,9 Ε 1(Χ(,)2 /,.96 Β ) 2 8=,. Ι

! # % & & # () + (,.)/ 01)0)2,34 2 # ) (.,5)2678,()2 9: 695 1/9/ # ) /,3;) ( 22,(,. # 9=.)6)8,9 ).19/,3;) )., 8? (,9 # =,596? (,92678,(92 # % & % 6

ΣΧΕ ΙΑ ΚΡΙΤΗΡΙΩΝ ΑΞΙΟΛΟΓΗΣΗΣ ΤΟΥ ΜΑΘΗΤΗ ΣΤΗ ΓΕΩΜΕΤΡΙΑ

ΣΧΕ ΙΑ ΚΡΙΤΗΡΙΩΝ ΑΞΙΟΛΟΓΗΣΗΣ ΤΟΥ ΜΑΘΗΤΗ ΣΤΗ ΓΕΩΜΕΤΡΙΑ 34 1ο ΣΧΕ ΙΟ ιδακτική ενότητα: Πυθαγόρειο Θεώρηµα ΘΕΜΑ 1ο Α. (1,5 µονάδες) Αν στο διπλανό σχήµα το Α είναι ύψος του τυχαίου τριγώνου ΑΒΓ και Ε ΑΒ,

Fax. : , Ω Ο. οσό σύ βασης : ,59 οσό σύ βασης α αθ ώ ηση & Α : ,52

Η Η Η Ο Α Α ο ία 03 / 07 /2013 Ο Ο Η Α Α.. : 24820/ 4/2372 Η Ο Η Α α. / σ : ι ι ής αι ίας Ο: Α Ο Ω Η Α Α Ο Ο & α. ώ ι ας : 272 00 13SYMV001535338 Ο Η Α Ο 2013-07-09 Ο Α -. : 2622-360502, 038371 Η Ο Α Ο

! # ( ) +!,!!!,!!, ## % & ( ,, ( (!, ) #! + ) #, ( %%&

! # % % & () +!,!!!,!!,,, ((!, ## %& ( )#! + )#, ( %%& .! #/ )!(( ( (0! 1.!( (2 333333333333333333333333333.! ! # # %& % # %# ( & )%& % +&,%&.,% )%& %/ )%& %0 1 % %2 3 %%&,%2,%34 5 +,% % %6 &. & %.7 %&

A λ υ τ ε ς Α σ κ η σ ε ι ς ( Τ ρ ι γ ω ν α )

A λ υ τ ε ς Α σ κ η σ ε ι ς ( Τ ρ ι γ ω ν α ) 1 Στις πλευρες ΑΒ, ΒΓ, ΓΑ ισοπλευρου τριγωνου ΑΒΓ, παιρνουμε 3 Να δειχτει οτι α + 110 0α Ποτε ισχυει Συγκρινετε το ισον; τα τριγωνα με σημεια Δ, Ε, Ζ αντιστοιχα,

ΔΕΥΤΕΡΑ Β6/Γ36 ΑΡΧ.ΚΗ ΕΣΩΤ.ΧΩΡΩΝ-ΣΥΝΘΕΤ. ΑΡΧΕΣ Α1/7

9ΤΜΗΜΑ ΕΣΩΤΕΡΙΚΗΣ ΑΡΧΙΤΕΚΤΟΝΙΚΗΣ, ΔΙΑΚΟΣΜΗΣΗΣ, ΣΧΕΔΙΑΣΜΟΥ ΑΝΤΙΚΕΙΜΕΝΩΝ/ΠΡΟΓΡΑΜΜΑ ΜΑΘΗΜΑΤΩΝ XEIMEΡΙΝΟΥ ΕΞΑΜΗΝΟΥ 2013-2014 A ΕΞΑΜΗΝΟ ΣΠΟΥΔΩΝ Έγκριση προγράμματος σπουδών Τμ. ΕΑΔΣΑ (υπ αριθμ. 19/11.05.2011

( ) ( ) ( ) ( ) ( ) 2 Αν x = -4-7 και y = 7-4 να βρεθεί η τιµή της παράστασης Α = x + y - 2xy ( ) ( )

Τηλ 106176-7 /10600 1 Να βρεθούν τα αναπτύγµατα : i i i x x x x x + x x x x + x 16x x + 9 x 16x x + 9 x 8 + 6 8 6 6 i i 6x + x 6x + 6x x + x 6 x + 6 x x + x 6x + 60x + x 6x + 60x + x 6 + + 6 6 6 i i Αν

ΠΡΟΚΗΡΥΞΗ. ΘΕΜΑ: «Προκήρυξη πλήρωσης θέσεων Προϊσταμένων Νηπιαγωγείων και Προϊσταμένων Δημοτικών Σχολείων Π.Ε. Καρδίτσας»

ΛΛΗ Ι Η ΔΗΜΟ Ρ Ι ΥΠΟΥΡ ΙΟ Π ΙΔ Ι Σ Ρ Υ Σ Ι ΘΡΗΣ ΥΜ Ω Π ΡΙ Ρ Ι Η ΔΙ ΥΘΥ ΣΗ Π/ΘΜΙ Σ & Δ ΘΜΙ Σ Π ΙΔ ΥΣΗΣ Θ ΣΣ ΛΙ Σ ΔΙ ΥΘΥ ΣΗ Π ΘΜΙ Σ Π ΙΔ ΥΣΗΣ ΡΔΙ Σ Σ ΜΗΜ Π ΙΔ Υ Ι Ω Θ Μ Ω χ Δ νση : Πλ σ ή Πόλη : 43132 ί

ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2017 A ΦΑΣΗ Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΣΠΟΥ ΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ

ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΣΠΟΥ ΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΑΘΗΜΑ: ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ Ηµεροµηνία: Πέµπτη 5 Ιανουαρίου 2017 ιάρκεια Εξέτασης: 3 ώρες ΑΠΑΝΤΗΣΕΙΣ Α1. ΣΩΣΤΟ Α2. ΛΑΘΟΣ

Θεωρία Πληροφορίας. Διάλεξη 5: Διακριτή πηγή πληροφορίας με μνήμη. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής

Θεωρία Πληροφορίας Διάλεξη 5: Διακριτή πηγή πληροφορίας με μνήμη Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα 1. Διακριτές πηγές πληροφορίας με μνήμη Μαρκοβιανές αλυσίδες Τάξη μακροβιανών αλυσίδων

!! # % & # & ( # ) +

!! # % & #& ( # ) + ! # %&! # #%#, %.# /,0#1 ( ) (+!!!,!!.!!!/! 0 1!2 ! + 3(4 (54 (!26 7( ( 2! 2!2(!8 (!! 9 :;! 4!? 1!!6# (=!! 6 Α( (!!?. 4 Β!Β ΧΧ

Β_ΠαΤ?Παχβ. 3 Θ] Ψ Ω 5 Υ]Υ δχ ς_β 3εδδΥβ 8ΥΘΤχ Θ Τ ΧΞΘ [ ι Υ χ γψδξ εβ _φυβ ; ΨφΥχ ΧΣβΥγ _βαευχ. ΧΣβΥγχ ΧΥδχΣβΥγχ. >εδχ. Χ ΘΣΥβχ

Β?0Α4?0ΑΧΒ ΧΠΘ[Τ Υ2 ]χτ]χβ Β_ΠαΤ?Παχβ?ΠςΤ 3 Θ] Ψ Ω5 Υ]Υ δχς_β3εδδυβ8υθτχθ Τ ΧΞΘ [ ι Υ χγψδξ εβ _φυβ; ΨφΥχ ΧΣβΥγ _βαευχ ΧΣβΥγχΧΥδχΣβΥγχ >εδχ Χ ΘΣΥβχ ΒΥΤεΣΨ Ω2εχΞΨ ΩχΒΥΤεΣΨ ΩΒΨ Ωχ 2Θ2ΥΘβΨ Ωχ εηψ ΨΘβι χ!!!!(

Λ θβγδ Λτστη 1 Ρνβηδσ οδθ κ Β θσνκ θηψψ ψηνµδ Ρθκ

ωσδθµ κ Ο θσηδρ Κδ χ Λ µ φδθ % Ρνκδ Αννϕθτµµδθ Ρνβη σ Φ µ θ κδ Ρ Νθηφηµ σνθ % Ρδθυηβδθρ Τµηνµδ χη Α µβγδ Ησ κη µδ Ρ ο Ρϖ ο Βντµσδθο θσξ Ρνβη σ Φ µ θ κδ Ρ Σ ακδ νε Βνµσδµσρ Ο φδ 0 Βτθθδµσ Οδθηνχ Χηρσθηατσηνµ

Α Α Α Α Α Α Α Α Α Α Α Ο

3ω η Α Α Α Α Α Α Α Α Α Α Α Α Α Ο 9/5/2014 Ο Α Α Α ιο οιώ ας α α α ά ω α αθέ α α οσ αθήσ α α α ήσ σ α ω ή α α ο α ο ο θού : Ο Α Ο Α Α «Π ι ὸ Τὲ ὑ ὑ ῖ ὑ ὶ ὰ Τ Τ ὶ ὺ Τ» (DK 14.7) Α «ὴ ὑ ὶ ὺ Τ ὑ Τ Τ ὑ Τῆ ῖ

! # % &! () +,./ % 0 1 % % % 4 5 / 6##7,+ 84,8, 0 %,, 9 :,9,

! # &! () +,./ 0 1 2 3 3 4 5 / 6##7,+ 84,8, 0,, 9 :,9, ; ! # # & (#) #+#+, #,# +./, /,+0 ++,#1./ 2 3(4,#,#1 + (5+ + /,# 61(#)(! # & () +#,)#. /& #()012#3 42 5,6 7 89:+ 8) ;. ) 7? ) 4# = 8 Α#2 278&

67 & Ε < 9 & ΕΕ Ν 4 6 & ΕΕΕ 9 & Ε1 Ε Φ

!! #! % #!! % & ( ( ) # &!! ( # % + &,.# & / ( 0 ( & 1 2 3 ( 2 4 ) # & 0 ( 1 5 & 6 3 7 ( 4 # & 8 7 0 9 5 : : # &, ; / ( 5 < # = # 0; / # 6 0 / 3 ) ( 4 # 9 ; & ( ; #.. =0 = ( > 6? &( ; ; # ( 5 ( 5 ( 5

5.2 ΑΡΙΘΜΗΤΙΚΗ ΠΡΟΟ ΟΣ

5. ΑΡΙΘΜΗΤΙΚΗ ΠΡΟΟ ΟΣ ΘΕΩΡΙΑ. Ορισµός Μια ακολουθία λέγεται αριθµητική πρόοδος, αν και µόνο αν κάθε όρος της προκύπτει από τον προηγούµενο του µε πρόσθεση του ίδιου πάντοτε αριθµού.. Μαθηµατική έκφραση

Παράρτηµα ΠΙΝΑΚΑΣ ΟΙΚΟΝΟΜΙΚΗΣ ΠΡΟΣΦΟΡΑΣ - ΥΠΟΛΟΓΙΣΜΟΥ ΟΛΙΚΟΥ ΚΟΣΤΟΥΣ ΠΡΟΣΦΕΡΟΜΕΝΩΝ ΣΥΣΤΗΜΑΤΩΝ ΥΦΑΛΟΧΡΩΜΑΤΙΣΜΟΥ

Ανήκει στο Φ. 600/57/Σ.57/17 της ιακήρυξης Νο "57/17" του ΚΠ/ΚΕΦΝ Παράρτηµα ΠΙΝΑΚΑΣ ΟΙΚΟΝΟΜΙΚΗΣ ΠΡΟΣΦΟΡΑΣ - ΥΠΟΛΟΓΙΣΜΟΥ ΟΛΙΚΟΥ ΚΟΣΤΟΥΣ ΠΡΟΣΦΕΡΟΜΕΝΩΝ ΣΥΣΤΗΜΑΤΩΝ ΥΦΑΛΟΧΡΩΜΑΤΙΣΜΟΥ ΕΙ ΟΣ Αστάρι του Συστήµατος

ΘΕΜΑ 2 Δίνεται παραλληλόγραμμο ΑΒΓΔ με ΑΒ=2ΒΓ. Προεκτείνουμε την πλευρά ΑΔ κατά τμήμα ΔΕ=ΑΔ και φέρουμε την ΒΕ που τέμνει τη ΔΓ στο σημείο Η.

Δίνεται παραλληλόγραμμο ΑΒΓΔ με ΑΒ=2ΒΓ. Προεκτείνουμε την πλευρά ΑΔ κατά τμήμα ΔΕ=ΑΔ και φέρουμε την ΒΕ που τέμνει τη ΔΓ στο σημείο Η. α) το τρίγωνο ΒΑΕ είναι ισοσκελές. (Μονάδες 7) β) το ΔΕΓΒ είναι παραλληλόγραμμο.

( ) λ( ) ( ) ( ) 2. 3α β 27αβ 10. x x αx αy βx βy x y y x x x x. 4 x x x y x y x y y. B Να παραγοντοποιηθούν οι παραστάσεις: x y x y x x y a x a x

A Να παραγοντοποιηθούν οι παραστάσεις: 1. kx x kx x kx x kx x x 8 x 5x 10 x x x x x x. λ 5x 10x 5 x x 10 x x x κ x x κ ( x ) λ( x ). ( α 1 )( x ) α ( x ) ( α 1)( x ) α ( x ) ( α )( x ) α ( x ). 1x 1 kx

Η ούσια εκ των οτέ ων ιαφά ια.

ΟΠΟ Η ΙΑΒΟ Η Α ιο ό σ ς α ο σ α ι ό ας ια ά ς Ο ίας / / ια ις ια ι ασί ς οσφ ής σ ο ο έα ς σύ α ς οσί σ βάσ Η σ ή σ ί * ί ο ι ή. α ό η α ερω ηθέν ων * Α αφέ α ο ά ος έ ος σας: * Π οσ ιο ίσ ι ιό ά σας:

Ο ΓΕΝΙΚΟΣ ΓΡΑΜΜΑΤΕΑΣ ΑΓΡΟΤΙΚΗΣ ΠΟΛΙΤΙΚΗΣ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΚΟΙΝΟΤΙΚΩΝ ΠΟΡΩΝ

ΕΠΑΝΑΛΗΨΗ ΣΤΟ ΟΡΘΟ ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΑΓΡΟΤΙΚΗΣ ΑΝΑΠΤΥΞΗΣ ΚΑΙ ΤΡΟΦΙΜΩΝ ΓΕΝΙΚΗ ΓΡΑΜΜΑΤΕΙΑ ΑΓΡΟΤΙΚΗΣ ΠΟΛΙΤΙΚΗΣ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΚΟΙΝΟΤΙΚΩΝ ΠΟΡΩΝ ΕΙΔΙΚΗ ΥΠΗΡΕΣΙΑ ΕΦΑΡΜΟΓΗΣ ΠΑΑ ΜΟΝΑΔΑ Β1 Αθήνα, 28-03-2016

Des données anatomiques à la simulation de la locomotion : application à l homme, au chimpanzé, et à Lucy (A.L )

Des données anatomiques à la simulation de la locomotion : application à l homme, au chimpanzé, et à Lucy (A.L. 288-1) Guillaume Nicolas To cite this version: Guillaume Nicolas. Des données anatomiques

1. ** ίνεται τρίγωνο ΑΒΓ. Αν Μ και Ν είναι τα µέσα των πλευρών ΒΓ και ΓΑ να αποδείξετε ότι:

Ερωτήσεις ανάπτυξης 1. ** ίνεται τρίγωνο ΑΒΓ. Αν Μ και Ν είναι τα µέσα των πλευρών ΒΓ και ΓΑ να αποδείξετε ότι: α) ΑΜ = 1 2 ( ΑΒ + ΑΓ ) β) ΜΝ = 1 2 ΒΑ 2. ** ίνονται τα διανύσµατα ΑΒ και Α Β. Αν Μ και Μ

Σημειώσεις Μαθηματικών 3

Σειώσεις Μαθατικών 3 Σφαιρικ Τριγωνομετρία Ραφαλ Φάνης Μαθατικός 1 Κεφάλαιο 1 Στερεομετρία 1.1 Γωνία στο χώρο Ορισμός 1. Τρίεδρη ονομάζεται η στερεά γωνία που έχει ακριβώς τρείς ακμές, σχατίζεται δηλαδ

Μέηνα Αημμηθήξ Πνμζηαζίαξ

Γιιεκηθή Γηαηνεία Γιέγπμο Λμημώλεςκ εμηκάνημ Γιέπμο Λμημώλεςκ 2010-2011 Μέηνα Αημμηθήξ Πνμζηαζίαξ Γιέκε Σόμπνμο MSc, Π.Γ. Νμζειεύηνηα Γπηηήνεζεξ Λμημώλεςκ Γ.Ν.Α «ΠΟΛΤΚΛΙΝΙΚΗ» θμπόξ πανμοζίαζεξ Πανμπή πιενμθμνηώκ

LIGHT UNFLAVORED MESONS (S = C = B = 0)

LIGHT UNFLAVORED MESONS (S = C = B = 0) For I = 1 (π, b, ρ, a): ud, (uu dd)/ 2, du; for I = 0 (η, η, h, h, ω, φ, f, f ): c 1 (uu + d d) + c 2 (s s) π ± I G (J P ) = 1 (0 ) Mass m = 139.57018 ± 0.00035

15PROC

Δ Ω Δ Δ - Δ Ω Δ Ω & Δ INFORMATICS DEVELOPMEN T AGENCY Digitally signed by INFORMATICS DEVELOPMENT AGENCY Date: 2015.02.09 10:47:54 EET Reason: Location: Athens Ε Δ Δ. Δ/.. Δ/ / π : : : : : :. 11 546 55,

ΕΙΚΟΝΑ ΔΡΩΝΤΩΝ: Δείκτες Αξιολόγησης Kομμάτων

ΕΙΚΟΝΑ ΔΡΩΝΤΩΝ: Δείκτες Αξιολόγησης Kομμάτων I. Εικόνα Κομμάτων II. Ικανότητα διακυβέρνησης III. Καταλληλότητα κομμάτων για την αντιμετώπιση θεμάτων IV. Αξιολόγηση Κομμάτων βάσει χαρακτηριστικών V. Πολιτική

2 ημέρες για κάθε μήνα απασχόλησης (ή 24/12 x μήνες απασχόλησης)(στρογγυ λοποίηση του

Πίνακας αδειών υπαλλήλων και εργατών με συνολική υπηρεσία ή προϋπηρεσία μέχρι 10 έτη μη συμπληρωμένα στον ίδιο εργοδότη ή μέχρι 12 έτη μη συμπληρωμένα σε οποιονδήποτε εργοδότη ή μέχρι 25 έτη συμπληρωμένα

%5Φ=Β9(ΦΧ 9 9Φ,<ΦΙΓΗ ΓΗ=Α5Η=ΧΒ=Β

%5Φ=Β9(ΦΧ 9 9Φ,

! # %&& () ( ) +,! # ) ) &...

! # %&& () ( ) +,! # ) ) &... ! # %& (! ) /01 2#,,( 0 3 1 456 7!! +, # (! () 83, 9: 1, ;;1 ? 2 + /. )).Α.7% %&&!!!.)# )& Β&Χ:Χ& 1& ). ! +!)))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))>

! # %& & ( )# ( % )# & (( +,. % % & / ) % 0112

! # %& & ( )# ( % )# & (( +,. % % & / ) % 0112 ! # %& & ( )# ( % )# & (( +,. % % & / ) % 0112 ! # % & & ( # ) ( # # # # ( # +,. + / + 0 1 2 3 # 4 5 + 6 1 % +. 4 / 7 +4/ # # 8 6 8 868. 9 : 3 + 3 2 # # %

Ä ÑÁÓÔÇÑÉÏÔÇÔÁ 1ç. Απάντηση Οι γωνίες που σχηµατίζονται είναι: Α. αµβλεία Β. ευθεία Γ. πλήρης. οξεία Ε. ορθή Ζ. αµβλεία Η. οξεία.

Ä ÑÁÓÔÇÑÉÏÔÇÔÁ 1ç Σε όλα τα παρακάτω αντικείµενα σχηµατίζονται διάφορες γωνίες ανάλογα µε τη σχετική θέση, κάθε φορά, δύο ηµιευθειών που έχουν ένα κοινό ση- µείο, όπως π.χ. είναι οι δείκτες του ρολογιού,

Αριθμ. Δ. ΟΡΓ. Β ΕΞ 2014/ Τροποποίηση της αριθμ

Πίνακας περιεχομένων Αριθμ. Δ. ΟΡΓ. Β 1163476 ΕΞ 2014/11.12.2014 Τροποποίηση της αριθμ. 1036923/431/Α0006/7 4 1999 (Β 359) Υπουργικής Απόφασης, ως προς την σύσταση συγκρότηση των Α, Β, Γ, Ε και υπαλλήλων

Livro Eletrônico. Aula 00. Gestão de Pessoas p/ INSS (código ADMIN) Professor: Alyson Barros DEMO

Livro Eletrônico Aula 00 Gestão de Pessoas p/ INSS (código ADMIN) Professor: Alyson Barros ! # % &! ( ) + ( +,. / 0 1 ( 2 1 & 3 45 6 7 8 7 4 # 9 ( : 5 / / ( ; 7 < 7 ( (= : 4 / > =& / > =&?

ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΕΩΝ ΕΚΠΑ - ΓΕΝΙΚΟ ΤΜΗΜΑ ΠΠΣ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧ. Τ.Ε. ΕΑΡΙΝΟΥ ΕΞΑΜΗΝΟΥ ΔΕΥΤΕΡΑ ΤΡΙΤΗ ΤΕΤΑΡΤΗ ΠΕΜΠΤΗ ΠΑΡΑΣΚΕΥΗ

ΕΚΠΑ - ΓΕΝΙΚΟ ΤΜΗΜΑ ΠΠΣ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧ. Τ.Ε. ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΕΩΝ ΕΑΡΙΝΟΥ ΕΞΑΜΗΝΟΥ 2018 2019 ΩΡΕΣ 17/06/2019 18/06/2019 19/06/2019 20/06/2019 21/06/2019 ΑΡΙΘΜΗΤΙΚΗ ΑΝΑΛΥΣΗ ΜΕ Η/Υ Μ3 Γ101,Γ208, Γ210 ΑΥΛΩΝΙΤΗΣ,

ΑΔΑ: 457ΡΗ-ΝΘΘ. Αθήνα 02 Νοεμβρίου 2011 Αριθ. Πρωτ. Δ6Α ΕΞ2011

ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΟΙΚΟΝΟΜΙΚΩΝ ΓΕΝΙΚΗ ΓΡΑΜΜΑΤΕΙΑ ΦΟΡΟΛΟΓΙΚΩΝ & ΤΕΛΩΝΕΙΑΚΩΝ ΘΕΜΑΤΩΝ ΓΕΝ. Δ/ΝΣΗ Δ/ΚΗΣ ΥΠΟΣΤΗΡΙΞΗΣ ΔΙΕΥΘΥΝΣΗ ΟΡΓΑΝΩΣΗΣ ΤΜΗΜΑ Α Ταχ. Δ/νση : Λεωχάρους 2 Ταχ. Κωδ. : 101 84 ΑΘΗΝΑ

#4 5 ) 7 9!! : 3 ;# #! 3 % )# : #+ #! 4!, ϑ :, + 3!! Χ, # ΚΛ Χ ; Ν : : + ) Χ : %! + Χ :,! + Χ, Ο 3,, + #! : ) 2! : + ( 4! Θ!! 4 ) /#! %!

! ## %& !! # % (! )! +,, / 0 %,2!, # 3 % # #4 5 ) 7 9!! : 3 ;# #! 3 % ;# # )!, =>=?!# +! ) %, #, + Β ; Χ 4 Ε >ΓΗΙ =>?Η! )# : #+ #! 4!, ϑ :, + 3!! Χ, # ΚΛ Χ ; Ν : : + 4 %, % #, Ε # ) Χ :, #, %#! 4 # :+

ζρήκα 1 β τπόπορ (από σύγκπιση τπιγώνων):

o Λύκειο Εακύνθος Γεσκεηξία Α Λπθείνπ Κεθάιαην 3ν Άζθεζε Α Γίλεηαη νξζνγώλην ηξίγσλν ΑΒΓ 90 0 θαη ΓΓ δηρνηόκνο ηεο γσλίαο. Να δείμεηε όηη:. Τν ζεκείν Γ απέρεη ηελ ίδηα απόζηαζε από ηηο πιεπξέο ΑΓ θαη ΒΓ.

ΟΜΑ Α Α. Το οριακό κόστος είναι ο λόγος της µεταβολής του µέσου συνολικού κόστους προς τη µεταβολή του προϊόντος. Μονάδες 3

ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 7 ΙΟΥΝΙΟΥ 2004 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑ ΕΠΙΛΟΓΗΣ ΓΙΑ ΟΛΕΣ ΤΙΣ ΚΑΤΕΥΘΥΝΣΕΙΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5)

( ) ( ) ( ) ( ) ( ) ( )

ΕΠΙΤΡΟΠΗ ΔΙΓΩΝΙΣΜΩΝ η Εηνική Μαθηματική Ουμπιάδα "Ο ρχιμήδης" ΣΒΒΤΟ, ΦΕΒΡΟΥΡΙΟΥ 9 ΟΙ ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΤΩΝ Θέματα μεγάων τάξεων ΠΡΟΒΛΗΜ Να προσδιορίσετε τις τιμές του θετικού ακέραιου 9n n 7 είναι ρητός n

Αθήνα ΠΡΟΣ: ΩΣ Ο ΠΔ ΚΟΙΝ: ΩΣ Ο ΠΔ

ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΑΓΡΟΤΙΚΗΣ ΑΝΑΠΤΥΞΗΣ & ΤΡΟΦΙΜΩΝ ΓΕΝΙΚΗ ΓΡΑΜΜΑΤΕΙΑ ΑΓΡΟΤΙΚΗΣ ΠΟΛΙΤΙΚΗΣ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΚΟΙΝΟΤΙΚΩΝ ΠΟΡΩΝ ΓΕΝΙΚΗ ΔΙΕΥΘΥΝΣΗ ΒΙΩΣΙΜΗΣ ΑΓΡΟΤΙΚΗΣ ΑΝΑΠΤΥΞΗΣ ΔΙΕΥΘΥΝΣΗ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ

! % & % & ( ) +,+ 1 + 2 & %!4 % / % 5

! #! % & % &( ) +,+.+)! / &+! / 0 ) &+ 12+! )+& &/. 3 %&)+&2+! 1 +2&%!4%/ %5 (!% 67,+.! %+,8+% 5 & +% #&)) +++&9+% :;&+! & +)) +< %(+%%=)) +%> 1 / 73? % & 10+&(/ 5? 0%)&%& % 7%%&(% (+% 0 (+% + %+72% 0

8 ) / 9! # % & ( ) + )! # 2. / / # % 0 &. # 1& / %. 3 % +45 # % ) 6 + : 9 ;< = > +? = < + Α ; Γ Δ ΓΧ Η ; < Β Χ Δ Ε Φ 9 < Ε & : Γ Ι Ι & Χ : < Η Χ ϑ. Γ = Φ = ; Γ Ν Ι Μ Κ Λ Γ< Γ Χ Λ =

Κατηγορία χειρουργικής. Χρονική κατάταξη

ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΥΓΕΙΑΣ 4η Υ.ΠΕ. ΜΑΚ-ΘΡΑΚΗΣ ΓΕΝΙΚΟ ΝΟΣΟΚΟΜΕΙΟ ΔΙΔΥΜΟΤΕΙΧΟΥ ΛΙΣΤΑ ΧΕΙΡΟΥΡΓΕΙΟΥ 18-10-2019 ΧΕΙΡΟΥΡΓΙΚΟ ΤΜΗΜΑ Κωδικός Τμήμα Ημέρα & ώρα θεράποντα Χαρακτηρι σμός σημειώματ Κατηγορία

ΕΦΗΜΕΡΙΣ ΤΗΣ ΚΥΒΕΡΝΗΣΕΩΣ

5659 ΕΦΗΜΕΡΙΣ ΤΗΣ ΚΥΒΕΡΝΗΣΕΩΣ ΤΗΣ ΕΛΛΗΝΙΚΗΣ ΔΗΜΟΚΡΑΤΙΑΣ ΤΕΥΧΟΣ ΠΡΩΤΟ Αρ. Φύλλου 225 15 Νοεμβρίου 2012 ΝΟΜΟΣ ΥΠ' ΑΡΙΘ. 4094 Κύρωση των υπ' αριθμ. 137 και 138/30.9.2011 Αποφάσε ων του Συμβουλίου Διοικητών

BHMA 1+ ΛΥΣΕΙΣ. Υλικό / Κόψε ένα κοµµάτι που δέχεται διπλή επίθεση: Β

BHMA 1+ ΛΥΣΕΙΣ Υλικό / Κόψε ένα κοµµάτι που δέχεται διπλή επίθεση: A 1) 1. Ιεxδ5 2) 1. Ιδ5xζ6 (1. Αβ2xζ6 γ6xδ5) 1.... η7xζ6 2. Αβ2xζ6 3) 1. Βζ3xβ7 4) 1. Ιε4xδ6 (1. Πδ1xδ6 ζ5xε4) 5) 1. Ιε4xζ6+ (1. Αβ2xζ6

ΤΓΔΙΑ ΚΑΙ ΑΦΑΛΔΙΑ ΔΡΓΑΙΑ ΣΖ ΥΡΖΖ ΥΖΜΔΙΟΘΔΡΑΠΔΙΑ

ΥΥΥΥΥΥΥΥΥΥΥΥΥΥΥΥΥΥΧΧΧΧΧΧΧΧΧΧΧΧΧΧΧΧΧΥΥΥΥΥΥΥΥΥΥΥΥΥΥΥΥΥΥΧΧΧΧΧΧΧΧΧΥΥΥΥΥΥΥΥΥΥΥΥΥΥΥΥ ΥΥΥΥΥΥΥΥΥΥΥΥΥΥΥΥΥΥΥΥΥΥΥΥΥΥΥΥΥΥΥΥΥ ρρρρρρρρρρρρρρρρρρρρρρρρρρρρρρφφφφφφφφφφφφφρρρς ςςςςςςςςςς ρρρρρρρρρρρ ΓΗΑΜΑΡΣ ΤΡΗ Α Δ.Η.Ν.Α.Π.

«Π ς το οιητι ά, ς το ια ιστο ία:

ΜΑ: «Πα ή ιος Μαθη ι ός ια ω ισ ός η ιο ι ής αφής ης ι ής α α ίας σό η ας ω Φύ ω...φ. αι ο ο ίο Παι ίας, Έ ας αι ησ ά ω Π.Π.. «Π ς το οιητι ά, ς το ια ιστο ία: έχ ι φύ ο η α ιά;» Η ι ή α α ία σό ας ύ....

Convex Games, Clan Games, and their Marginal Games

Working Papers Institute of Mathematical Economics 368 June 2005 Convex Games, Clan Games, and their Marginal Games Rodica Branzei, Dinko Dimitrov, and Stef Tijs IMW Bielefeld University Postfach 100131

Φορέας υλοποίησης: Φ.Μ.Ε. ΑΛΦΑ

ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΗΜΕΡΙΔΑ: «ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ, ΜΙΑ ΕΜΠΕΙΡΙΑ ΖΩΗΣ» ΣΤΡΑΤΗ ΣΤΑΜΑΤΙΑ Επιβλέπων Καθηγητής: ΚΑΡΑΧΑΛΙΟΣ ΝΙΚΟΛΑΟΣ Φορέας υλοποίησης: Φ.Μ.Ε. ΑΛΦΑ ΚΑΡΛΟΒΑΣΙ, ΜΑΪΟΣ 2012 ΣΤΟΙΧΕΙΑ

ΚΑΤΑΣΤΑΤΙΚΟ Τ ΟΥ Σ ΥΛΛΟΓΟΥ ΕΡΓΑΖΟΜΕΝΩΝ ΣΤΙΣ ΗΜΟΣΙΕΣ ΟΙΚΟΝΟΜΙΚΕΣ ΥΠΗΡΕΣΙΕΣ ΝΟΜΩΝ ΑΤΤΙΚΗΣ ΚΑΙ ΚΥΚΛΑ ΩΝ Όπως τροποποιήθηκε µε την απόφαση της Γενικής

ΚΑΤΑΣΤΑΤΙΚΟ Τ ΟΥ Σ ΥΛΛΟΓΟΥ ΕΡΓΑΖΟΜΕΝΩΝ ΣΤΙΣ ΗΜΟΣΙΕΣ ΟΙΚΟΝΟΜΙΚΕΣ ΥΠΗΡΕΣΙΕΣ ΝΟΜΩΝ ΑΤΤΙΚΗΣ ΚΑΙ ΚΥΚΛΑ ΩΝ Όπως τροποποιήθηκε µε την απόφαση της Γενικής Σ υν ελεύσεως της 26η ς/11/20ο5-1 - ΣΩΜΑΤΕΙΟ ΕΡΓΑΖΟΜΕΝΩΝ

Α ΓΥΜΝΑΣΙΟΥ ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΠΕΡΙΟΔΟΥ ΜΑΪΟΥ-ΙΟΥΝΙΟΥ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ. πότε ίσο με το 1. Δώστε από ένα παράδειγμα

49 0 ΓΥΜΝΑΣΙΟ ΑΘΗΝΩΝ ΣΧΟΛΙΚΟ ΕΤΟΣ 2011-2012 Α ΓΥΜΝΑΣΙΟΥ ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΠΕΡΙΟΔΟΥ ΜΑΪΟΥ-ΙΟΥΝΙΟΥ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΗΜΕΡΟΜΗΝΙΑ : 22 ΜΑΪΟΥ 2012 ΘΕΩΡΙΑ 1 η : Να γράψετε πότε ένα κλάσμα είναι μικρότερο,

ΤΡΙΓΩΝΟΜΕΤΡΙΑ ΘΕΜΑ 1. ημ x. 1 σφx 1 σφx 4 ΘΕΜΑ γ ε. 2 δ. 1

1 ΤΡΙΓΩΝΟΜΕΤΡΙΑ 1. Να αποδείξετε ότι: 1 σφ 1 σφ ΘΕΜΑ 1. Nα λύσετε την εξίσωση: ημ 1 σφ 1σφ 4 ΘΕΜΑ Α. Να βρεθούν οι παρακάτω τριγωνομετρικοί αριθμοί: α. συν330 ο = β. συν (-300 ο ) = γ. συν (-10 ο ) = δ.

Απόφαση της Επιτροπής Παρακολούθησης. του Ε.Π. «Μεταρρύθμιση Δημόσιου Τομέα»

ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ, ΥΠΟΔΟΜΩΝ, ΝΑΥΤΙΛΙΑΣ ΚΑΙ ΕΙΔΙΚΗ ΓΡΑΜΜΑΤΕΙΑ ΔΙΑΧΕΙΡΙΣΗΣ ΤΟΜΕΑΚΩΝ Ε.Π. του ΕΥΡΩΠΑΪΚΟΥ ΚΟΙΝΩΝΙΚΟΥ ΤΑΜΕΙΟΥ ΕΙΔΙΚΗ ΥΠΗΡΕΣΙΑ ΔΙΑΧΕΙΡΙΣΗΣ Ε.Π. «ΜΕΤΑΡΡΥΘΜΙΣΗ ΔΗΜΟΣΙΟΥ ΤΟΜΕΑ Αθήνα, 25 Απριλίου

ΘΕΜΑ: ΑΠΟΦΑΣΗ 2045/ / ΓΙΑ ΚΑΤΑΝΟΜΗ ΑΤΟΚΗΣ ΔΑΝΕΙΟΔΟΤΗΣΗΣ ΑΣΟ ΠΟΣΟΥ 50 εκ.

K E O Σ Ο Ε ΚΕΝΤΡΚΗ ΣΥΝΕΤΑΡΣΤΚΗ ΕΝΩΣΗ ΑΜΠΕΛΟΟΝΚΩΝ ΠΡΟΪΟΝΤΩΝ Λ. ΡΑΝΚΟΥΡ 73, 115 23 ΑΘΗΝΑ ΤΗΛ: (210) 6923102 6923291 6928224 FAX: (210) 6981182 e-mail : keosoe@otenet.gr Αριθμ. πρωτ: 272/944 Αθήνα, 28 Σεπτεμβρίυ

Το αμέσως επόμενο διάστημα εκτιμάμε ότι η κατάσταση στον τομέα του δημόσιου συστήμ ατος υγ ε ί ας -πρό νο

Ψήφ γ ην Υγ Τρη 10 Ιουλου 2012 11:00 Το έω πόνο δη ό η η ον οέ ου δηόου υή ο υγ -πρό νο 1 / 13 Ψήφ γ ην Υγ Τρη 10 Ιουλου 2012 11:00 θ πδνωθ ό π ρ όρο ω πο έλ ω ν έρων γ ν ν ω π η π λή οονοή ρ η υπέρ ου

ΕΦΗΜΕΡΙΣ ΤΗΣ ΚΥΒΕΡΝΗΣΕΩΣ

15581 ΕΦΗΜΕΡΙΣ ΤΗΣ ΚΥΒΕΡΝΗΣΕΩΣ ΤΗΣ ΕΛΛΗΝΙΚΗΣ ΔΗΜΟΚΡΑΤΙΑΣ ΤΕΥΧΟΣ ΔΕΥΤΕΡΟ Αρ. Φύλλου 1438 10 Ιουλίου 2015 ΠΕΡΙΕΧΟΜΕΝΑ ΑΠΟΦΑΣΕΙΣ Αποδοχή τροποποιήσεων στο Παράρτημα του Πρω τοκόλλου του 1978 που σχετίζεται

Ε ΡΟ 1.1: ΕΝΕΡΓΕ Α 1.1.4: 2008, Ά Κ

Ε ΟΡ ΩΣΗ ΕΚ Α Ε ΚΩΝ ΓΟΝΕΩΝ Α ΩΝ Ε ΑΝΑ ΗΡ ΕΣ ΚΑ ΓΟΝΕΩΝ Α Η ΩΝ Ε ΑΝΑ ΗΡ ΕΣ Ε ι ηµονι ά ε νη Άνν Κ ρλο ί ο 2008 Ε Ε ΓΕ Α Γ ΗΜΑ Ε Α Α Ε Ω ΑΪΚ Κ Ω Κ ΑΜΕ ΚΑ Α 75 % ΚΑ Α Ε Η Κ ΗΜ ΚΑ Α 25 %. Ε ΡΟ 1.1: «Ε Ω Η Ω

µ =. µονάδες 12+13=25

ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΣΤΗ ΓΕΩΜΕΤΡΙΑ ΤΗΣ Β 1 ΓΕΝΙΚΗ ΑΣΚΗΣΗ 1. ίνεται τρίγωνο ΑΒΓ µε α=7, β=5, γ=4. Να βρείτε: 1. το είδος του τριγώνου. την προβολή της β πάνω στη γ 3. το µήκος της διαµέσου ΒΜ 4. την προβολή

Κατηγορία χειρουργικής πράξης. Χρονική κατάταξη περιστατικού Β.18 ΠΕΡΙΟΧΗ ΑΝΩΤΕΡΟΥ ΠΕΠΤΙΚΟΥ Β.25 ΕΝΔΟΚΡΙΝΕΙΣ ΑΔΕΝΕΣ. (1) μέχρι 2 εβδομάδες 24/5/2019

ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΥΓΕΙΑΣ 4η Υ.ΠΕ. ΜΑΚ.-ΘΡΑΚΗΣ ΓΕΝΙΚΟ ΝΟΣΟΚΟΜΕΙΟ ΔΙΔΥΜΟΤΕΙΧΟΥ ΛΙΣΤΑ ΧΕΙΡΟΥΡΓΕΙΟΥ 24-5-2019 ΧΕΙΡΟΥΡΓΙΚΟ ΤΜΗΜΑ Κωδικός ασθενούς Ημέρα & ώρα εξέτασης Τμήμα θεράποντα ιατρού Χαρακτηρισ

ΠΟΠΟΚΠ - Ψήφισμα για την Υγεία Παρασκευή, 05 Οκτωβρίου :37

ΠΟΠΟΚΠ - Ψήφ γ ην Υγ Πρυή 05 Οωβρου 2012 14:37 Το έω πόνο δη ό η η ον οέ ου δηόου υή ο υγ -πρό νο θ πδνωθ ό π ρ όρο ω πο έλ ω ν έρων γ ν ν 1 / 13 ΠΟΠΟΚΠ - Ψήφ γ ην Υγ Πρυή 05 Οωβρου 2012 14:37 ω π η π

Α Π Ο Φ Α Σ Η Ο ΥΠΟΥΡΓΟΣ ΑΓΡΟΤΙΚΗΣ ΑΝΑΠΤΥΞΗΣ ΚΑΙ ΤΡΟΦΙΜΩΝ

ΕΠΑΝΑΛΗΨΗ ΣΤΟ ΟΡΘΟ ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΑΓΡΟΤΙΚΗΣ Αθήνα 09-05- 2017 ΑΝΑΠΤΥΞΗΣ ΚΑΙ ΤΡΟΦΙΜΩΝ Αρ. Πρωτ. : 4492/50467 ΓΕΝ. Δ/ΝΣΗ ΔΙΟΙΚ. ΥΠΗΡΕΣΙΩΝ ΚΑΙ ΗΛΕΚΤΡ/ΚΗΣ ΔΙΑΚΥΒΕΡΝΗΣΗΣ Δ/ΝΣΗ ΔΙΟΙΚ. ΚΑΙ ΕΠΟΠΤ.

Αθήνα Αρ. Πρωτ.: 2762/89906 ΠΡΟΣ: ΩΣ Ο Π ΚΟΙΝ: ΩΣ Ο Π

ΕΛΛΗΝΙΚΗ ΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΑΓΡΟΤΙΚΗΣ ΑΝΑΠΤΥΞΗΣ & ΤΡΟΦΙΜΩΝ ΓΕΝΙΚΗ ΓΡΑΜΜΑΤΕΙΑ ΑΓΡΟΤΙΚΗΣ ΠΟΛΙΤΙΚΗΣ ΚΑΙ ΙΑΧΕΙΡΙΣΗΣ ΚΟΙΝΟΤΙΚΩΝ ΠΟΡΩΝ ΓΕΝΙΚΗ ΙΕΥΘΥΝΣΗ ΒΙΩΣΙΜΗΣ ΑΓΡΟΤΙΚΗΣ ΑΝΑΠΤΥΞΗΣ ΙΕΥΘΥΝΣΗ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΚΑΙ

ΓΕΩΜΕΤΡΙΑ ΤΗΣ Β. β γ α β. α γ β δ. Μαρτάκης Μάρτης Μαθηµατικός του 1 ου ΓΕΛ Ρόδου 1. Προηγούµενες και απαραίτητες γνώσεις

Μαρτάκης Μάρτης Μαθηµατικός του 1 ου ΓΕΛ Ρόδου 1 ΓΕΩΜΕΤΡΙ ΤΗΣ Β Προηγούµενες και απαραίτητες γνώσεις 1. σε ορθογώνιο τρίγωνο µε 30 ο, η απέναντι 30 ο κάθετη είναι το µισό της υποτείνουσας και αντίστροφα.

O ΥΠΟΥΡΓΟΣ ΠAIΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ

ΑΝΑΡΤΗΤΕΑ ΕΛΛΗΝΙΚΗ ΔΗΜΚΡΑΤΙΑ ΥΠΥΡΓΕΙ ΠΑΙΔΕΙΑΣ,EΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΓΕΝΙΚΗ ΔΙΕΥΘΥΝΣΗ ΣΠΥΔΩΝ ΠΡΩΤΒΑΘΜΙΑΣ ΚΑΙ ΔΕΥΤΕΡΒΑΘΜΙΑΣ ΕΚΠΑΙΔΕΥΣΗΣ Μαρούσι, 10-8 - 2017 Αρ. πρωτ.:135648/δ6 ΑΥΤΤΕΛΕΣ ΤΜΗΜΑ ΠΡΤΥΠΩΝ

Θ ΕΜ Α:''Λ Ο ΓΙΣΤΙΚΗ ΤΟΝ Π Α ΓΙΩ Ν ΠΕΡΙΟ ΥΣΙΑΚΟ Ν ΣΤΟΙΧΕΙΩΝ*

TEXfstOAOriKO ΕΚ Π ΑΙΔ ΕΥΤ ΙΚΟ ΙΔ ΡΥ Μ Α ΣΧΟ ΛΗ ΔΙΟ ΙΚΗ ΣΗ Σ ΟΙΚΟΝΟΜ ΙΑΣ ΤΜΗΜΑ Λ Ο ΓΙΣ Τ β Ν Θ ΕΜ Α:''Λ Ο ΓΙΣΤΙΚΗ ΤΟΝ Π Α ΓΙΩ Ν ΠΕΡΙΟ ΥΣΙΑΚΟ Ν ΣΤΟΙΧΕΙΩΝ* του ο π ο υ ^^τή' Α Θ ΑΝΑΣ ΙΟ Υ Λ,ΣΟ ΥΒΑΛΙΩ ΤΗ.!