r 2 P + C. + sin(4θ ) 8 sin(2θ ) ( ) V (r, θ) = 1 (r ) l P P 1 (x) = x, P 2 (x) = 1 2 (3x2 1), P 3 (x) = 1 2 (5x3 3x) V=0 V=0
|
|
|
- Ἰωακείμ Δουμπιώτης
- 6 χρόνια πριν
- Προβολές:
Transcript
1 : α Πρόβημα 36 από Griffiths: Μια σφαίρα ακτίνας με κέντρο στην αρχή των αξόνων φέρει πυκνότητα φορτίου ρr θ k r sin θ όπου k είναι μία σταθερά και r r θ είναι οι γνωστές σφαιρικές συντεταγμένες Βρείτε το προσεγγιστικό δυναμικό για σημεία του άξονα μακριά από τη σφαίρα β Επαναάβατε για σημεία πάνω στον άξονα Δίνεται ο τετραποικός όρος του πουποικού αναπτύγματος V τετρ r P 4πε r 3 ˆr ˆr ρ r dτ με P ˆr ˆr 3 ˆr ˆr και το οοκήρωμα sin 4 θ dθ 3θ 8 sinθ + sin4θ + C 4 3 : Σε Καρτεσιανό σύστημα έχουμε τρία φορτία +q στις θέσεις και δύο φορτία q στις θέσεις α Ποιος ο προσεγγιστικός τύπος για το δυναμικό V V r σε αποστάσεις r από το ; β Κρατώντας και την επόμενη διόρθωση δείξτε ότι η έκφραση του δυναμικού σε σφαιρικές συντεταγμένες είναι V V r r sin θ sin φ cos φ 3 : Σφαιρικός φοιός απειροστού πάχους και ακτίνας είναι φορτισμένος με φορτίο επιφανειακής πυκνότητας σθ όπου θ η σφαιρική συντεταγμένη συστήματος με αρχή το κέντρο του φοιού α Αν η ακτινική συνιστώσα του ηεκτρικού πεδίου πάνω στο επίπεδο του ισημερινού θ π/ είναι μηδέν δηαδή E r r θ π/ ποιο είναι το συνοικό φορτίο του φοιού; β Αν έξω από το φοιό η ακτινική συνιστώσα του ηεκτρικού πεδίου πάνω στον ημιάξονα συμμετρίας θ είναι E r r > θ E 5 r ποια η διποική ροπή του φοιού; γ Ποια η επιφανειακή πυκνότητα σθ αν ξέρουμε ότι E r r < θ 3E r ; 4 Υπόδειξη: Η ύση της εξίσωσης Lplce V r θ r b lp l+ l cos θ έξω από κάποια αξισυμμετρική κατανομή φορτίου είναι ισοδύναμη με το πουποικό ανάπτυγμα V r θ r l P 4πɛ r l+ l ˆr ˆr dq Δίνονται τα πουώνυμα Legendre P P P 3 P και η τιμή τους P l 4 : Δύο γειωμένα αγώγιμα ημιεπίπεδα βρίσκονται στις θέσεις φ και φ σε κυινδρικές συντεταγμένες ϖ φ δη σχηματίζουν γωνία μεταξύ τους Στη θέση ϖ δη σε απόσταση από τον κοινό άξονα των επιπέδων τον άξονα βρίσκεται ηεκτρόδιο σε δυναμικό V Μονωτικά στρώματα εμποδίζουν το ηεκτρόδιο να έρθει σε επαφή με τα γειωμένα επίπεδα α V V α Δείξτε ότι το δυναμικό στην περιοχή που περικείεται από το ηεκτρόδιο και τα επίπεδα είναι V 4V ϖ nπ/ nπφ sin π n35 n Υπόδειξη: Χωρίστε τις μεταβητές στη συνάρτηση του δυναμικού V Πϖ Φφ δείτε τι δίνει η εξίσωση Lplce αά μην απαιτήσετε η συνάρτηση Φφ να έχει περίοδο π Αντ αυτού απαιτήσετε Φφ και Φφ β Δείξτε ότι το αποτέεσμα γράφεται σε κειστή μορφή V V π rctn ϖ/π/ sin πφ/ ϖ/ π/ Παρατήρηση: Το πρόβημα είναι όμοιο με το παράδειγμα 33 του Griffiths σχέση 336 με y φ και ln/ϖ Γενικότερα τα προβήματα επίυσης της εξίσωσης Lplce με κυινδρική συμμετρία σε χωρίο {φ < φ < φ ϖ < ϖ < ϖ } των κυινδρικών συντεταγμένων είναι όμοια με αυτά των διδιάστατων καρτεσιανών σε χωρίο {y < y < y < < } διότι η εξίσωση Lplce γράφεται όπως στις καρτεσιανές με ln ϖ y φ 5 : Θέμα o από εξέταση της //5: Ημικύινδρος απείρου μήκους έχει ως συντεταγμένες < ϖ < b < φ < π < < + και δυναμικά στην επιφάνειά του όπως στο σχήμα με V σταθ V O Να βρεθεί το δυναμικό στο εσωτερικό του Υπόδειξη: Δείξτε ότι η εξίσωση Lplce b V Νεκτάριος Βαχάκης //5
2 ϖ + V με τον μετασχηματισμό ϖ be ln b ϖ γίνεται V ϖ ϖ ϖ ϖ φ + V φ και άρα προκύπτει το γνωστό πρόβημα του επόμενου σχήματος στις συντεταγμένες και φ φ V π O πρόβημα αυτό είναι της μορφής V V µ Προσδιορίστε τη σταθερά οοκήρωσης στην έκφραση της dv dµ από την συνθήκη πού μακρυά από τον αγωγό το πεδίο να είναι E 4πε r ˆr Επιέγοντας κατάηα τις σταθερές b και c βρείτε: β τη συνοική και από τις δυο πευρές επιφανειακή πυκνότητα σϖ σε αγώγιμο κυκικό δίσκο ακτίνας γ τη συνοική γραμμική πυκνότητα φορτίου σε ένα ραβδόμορφο αγωγό 6 : Θέμα o από εξέταση της //: α Δείξτε ότι η συνάρτηση V θ A ln cot θ/]+ B σε σφαιρικές συντεταγμένες όπου A και B σταθερές είναι αρμονική δη ικανοποιεί την εξίσωση Lplce V θ VV β Βρείτε το ηεκτροστατικό δυναμικό στο χώρο μεταξύ της επιφάνειας κώνου και άπειρης γειωμένης πάκας Ο κώνος έχει τον άξονά του κάθετο στην πάκα την κορυφή του σε μονωμένη επαφή με την πάκα και έχει φορτιστεί σε σταθερό δυναμικό V Υπόδειξη: Χρησιμοποιήστε σαν γενική ύση την συνάρτηση του ερωτήματος α 7 : Αγωγός με εειψοειδές σχήμα + y + b c είναι φορτισμένος με φορτίο α Ποια η κατανομή φορτίου στην επιφάνειά του και ποιο το ηεκτρικό πεδίο που δημιουργεί; Υπόδειξη: Ανάογα με το αν b > c ή b < c μπορούν να χρησιμοποιηθούν γεωειδείς ή ωοειδείς σφαιροειδείς συντεταγμένες δες παρακάτω Από τη μορφή που έχει η Lplcin φαίνεται ότι η ύση για το 8 : Σημειακό φορτίο q βρίσκεται σε θέση r από ένα ιδανικό δίποο ροπής p Το δίποο δημιουργεί πεδίο E d 3 p r r r p στη θέση του q οπότε ασκεί 4πε r 5 δύναμη F q qe d και ροπή N q r F q στο φορτίο α Δείξτε ότι η δύναμη και η ροπή που ασκεί το φορτίο στο δίποο είναι F d F q N d N q β Εστω το p είναι στερεωμένο στην αρχή συστήματος συντεταγμένων Oy του οποίου ο άξονας είναι ομόρροπος με την p Σε ποιες θέσεις του φορτίου η δύναμη F q είναι κάθετη στον άξονα και έχει φορά προς σημείο του άξονα αυτού; 9 : Ηεκτρικό δίποο p p ŷ είναι στερεωμένο στο κέντρο συστήματος συντεταγμένων Oy Ενα δεύτερο δίποο p p ˆ είναι εεύθερο να κινείται στην ευθεία y b με b σταθερό χωρίς να αάζει η διποική του ροπή α Ποια η δύναμη που ασκείται στο p στη διεύθυνση της ευθείας πάνω στην οποία κινείται; β Ποια η ενέργεια αηεπίδρασης των διπόων; γ Ποιο σημείο της ευθείας αποτεεί σημείο ευσταθούς ισορροπίας του p ; : Θέμα o από εξέταση της 6//: Ενα ηεκτρικό δίποο με διποική ροπή p p ẑ βρίσκεται στην αρχή των αξόνων Ενα δεύτερο δίποο διποικής ροπής p p ẑ βρίσκεται πάνω στον άξονα και d σε απόσταση d από την αρχή Βρείτε την δύναμη μεταξύ τους Είναι εκτική ή απωστική; p p y Μια άη μέθοδος επίυσης μπορεί να βρεθεί στο βιβίο του Willim lph Smythe Sttic nd Dynmic Electricity 3rd edition McGrw-Hill Book Compny σε -4 Νεκτάριος Βαχάκης //5
3 ΤΥΠΟΛΟΓΙΟ Καρτεσιανές y Κυινδρικές ϖ φ Σφαιρικές r θ φ ϖ cos φ r sin θ cos φ y ϖ sin φ y r sin θ sin φ r cos θ v v ˆ + v y ŷ + v ẑ v ϖ ˆϖ + v φ ˆφ + v ẑ v rˆr + v θ ˆθ + vφ ˆφ f f f ˆ + y ŷ + f ẑ f ϖ ˆϖ + f ϖ φ ˆφ + f ẑ f r ˆr + f r θ ˆθ + f r sin θ φ ˆφ v v + v y y + v ϖv ϖ ϖ ϖ + v φ ϖ φ + v r v r r + v θ sin θ + r r sin θ θ r sin θ v y v y v ˆ+ v v v ϖ φ v φ vφ sin θ ˆϖ+ v ] θ ˆr+ vϖ ŷ+ vy v v r sin θ θ φ v r ˆφ+ ϖ ϖvφ ẑ y ϖ ϖ v ] r sin θ φ rv ] φ ˆθ+ r ϖ rvθ ẑ v ] r ˆφ φ r r θ f f + f y + f ϖ f + f ϖ ϖ ϖ ϖ φ + f r r f + r r r sin θ f + sin θ θ θ d l dˆ + dyŷ + dẑ dϖ ˆϖ + ϖdφ ˆφ + dẑ drˆr + rdθˆθ + r sin θdφ ˆφ d dydˆ + ddŷ + ddyẑ ϖdφd ˆϖ + dϖd ˆφ + ϖdϖdφẑ r sin θdθdφˆr + r sin θdrdφˆθ + rdrdθ ˆφ dτ ddyd ϖdϖdφd r sin θdrdθdφ v φ φ f r sin θ φ Γεωειδείς σφαιροειδείς συντεταγμένες µ φ ν Είναι ορθογώνιες καμπυόγραμμες συντεταγμένες που ορίζονται από τις παρακάτω σχέσεις με θετική σταθερά και µ φ < π π/ ν π/ cosh µ cos ν cos φ y cosh µ cos ν sin φ sinh µ sin ν + y cosh µ + sinh µ εειψοειδές y cos φ sin φ επίπεδο + y cos ν sin μονόχωνο υπερβοοειδές ν µ rcsinh + y y + { } + y sin φ y + y φ κοινή ύση των cos φ ν rcsin + y y + Τα στοιχεία μήκους και τα μοναδιαία γράφονται h µ sinh µ + sin ν ˆµ h φ cosh µ cos ν ˆφ sin φ ˆ + cos φ ŷ h ν sinh µ + sin ν ˆν ˆµ ˆφ sinh µ cos ν cos φ ˆ + sin φ ŷ + cosh µ sin νẑ sinh µ + sin ν το στοιχειώδες μήκος είναι d r h µ dµˆµ + h φ dφ ˆφ + h ν dνˆν ενώ η Lplcin hφ h ν V + hµ h ν h µ h φ h ν µ h µ µ φ h φ sinh µ + sin ν cosh µ + cosh µ µ µ cos ν και η κίση V h µ µ ˆµ + h φ φ ˆφ + h ν ν ˆν + φ ν cos ν ] + ν ν Νεκτάριος Βαχάκης //5 hµ h φ h ν ] ν V cosh µ cos ν φ
4 Ωοειδείς σφαιροειδείς συντεταγμένες µ ν φ Είναι ορθογώνιες καμπυόγραμμες συντεταγμένες που ορίζονται από τις παρακάτω σχέσεις με θετική σταθερά και µ ν π φ < π + y sinh µ sin ν cos φ y sinh µ sin ν sin φ sinh µ + cosh µ εειψοειδές cosh µ cos ν cos ν + y sin δίχωνο υπερβοοειδές ν y cos φ sin φ επίπεδο µ rcsinh + y y y ν rccos + y y y { } φ κοινή ύση των cos φ + y sin φ y + y Τα στοιχεία μήκους και τα μοναδιαία γράφονται h µ sinh µ + sin ν h ν sinh µ + sin ν h φ sinh µ sin ν ˆµ ˆν cosh µ sin ν cos φ ˆ + sin φ ŷ + sinh µ cos νẑ sinh µ + sin ν sinh µ cos ν cos φ ˆ + sin φ ŷ cosh µ sin νẑ sinh µ + sin ν ˆφ sin φ ˆ + cos φ ŷ ˆµ ˆν το στοιχειώδες μήκος είναι d r h µ dµˆµ + h ν dνˆν + h φ dφ ˆφ ενώ η Lplcin hν h φ V + hµ h φ h µ h ν h φ µ h µ µ ν h ν sinh µ + sin ν sinh µ µ sinh µ µ και η κίση V h µ µ ˆµ + h ν ν ˆν + h φ φ ˆφ + sin ν + ] hµ h ν ν φ h φ φ sin ν ] + ν ν V sinh µ sin ν φ Νεκτάριος Βαχάκης //5
5 ΛΥΣΕΙΣ: : α β Για σημεία πάνω στον άξονα είναι r ˆ και ˆr ˆ ±ˆ Άρα ˆr ˆr ± sin θ cos φ διότι το μοναδιαίο προς τυχαίο σημείο της κατανομής με σφαιρικές συντεταγμένες r θ φ είναι ˆr sin θ cos φ ˆ + sin θ sin φ ŷ + cos θ ẑ Μονοποικός όρος δεν υπάρχει αφού V μον P ˆr ˆr ρ r dτ και με τις αντικατα- 4πε r στάσεις P ˆr ˆr ρ r k r r sin θ kπ5 384ε 3 Θα μπορούσαμε να βρούμε τους όρους του πουποικού αναπτύγματος του δυναμικού αφού πρώτα βρούμε το φορτίο την διποική ροπή και την τετραποική ροπή της κατανομής Το φορτίο της κατανομής είναι q ρ r dτ π π k r dr sin θ dθ dφ άρα δεν υπάρχει μονοποικός όρος V μον q 4πε r Η διποική ροπή της κατανομής είναι p r dq όγω συμμετρίας αφού η πυκνότητα σε οποιαδήποτε ζεύγη θέσεων ± r είναι ίδια αν η θέση r αντιστοιχεί σε σφαιρικές συντεταγμένες r θ φ δη r r sin θ cos φ ˆ + r sin θ sin φ ŷ + r cos θ ẑ τότε το αντίθετο διάνυσμα θέσης r αντιστοιχεί σε σφαιρικές συντεταγμένες r π θ φ + π οπότε για κάθε r η συνεισφορά r ρ r dτ στην διποική ροπή αναιρείται από τη συνεισφορά από το αντίθετο διάνυσμα θέσης Το ίδιο προκύπτει από p r ρ r dτ αν αντικαταστήσουμε r r sin θ cos φ ˆ + r sin θ sin φ ŷ + r cos θ ẑ οπότε βρίσκουμε τις συνιστώσες p π π k r r dr sin 3 θ dθ cos φ dφ p y k k π π r r dr sin 3 θ dθ sin φ dφ p π π r r dr sin θ cos θ dθ dφ και όες προκύπτουν μηδέν Ο τετραποικός όρος του δυναμικού μπορεί να γραφεί μέσω της τετραποικής ροπής της κατανομής dτ r sin θ dr dθ dφ και οοκηρώνοντας στα διαστήματα r ] θ π] φ π] βρίσκουμε 3 V μον k π π ij i r dr sin θ dθ dφ j r δ ij ρ r dτ όπου 4πε r Διποικός όρος δεν υπάρχει γιατί V διπ y 3 σαν V τετρ 3 4πε r 5 ij ij i j r P 4πε r ˆr ˆr ρ r dτ και αντικαθιστώντας ή ισοδύναμα V τετρ ˆr ˆr με τον τανυστή P ˆr ˆr ˆr ˆr ± sin θ cos φ βρίσκουμε V διπ 4πε 3 r r 3 ± k π π δεύτερης τάξης r r I ρ rdτ r r dr sin 3 θ dθ cos φ dφ 4πε 3 Αντικαθιστώντας στην έκφραση του V τετρ το πουώνυμο P ˆr ˆr 3 sin θ cos φ i Αυτό γιατί 3 ˆr r r i 3 j 3 r i j r j βρίσκουμε 3 r j /6 V τετρ k {}}{ j r i j r δ i j ij ij r r το r r 3 οποίο γράφεται και σαν γινόμενο πινάκων dr 8πε 3 ] 3 π π π y r 3y 3 r π 3 sin 4 θ dθ cos φ dφ sin θ dθ dφ 3y 3y r y 3y r r r 3 3y 3 r r }{{}}{{}}{{}}{{} 3π/8 π π/ π r οπότε V τετρ 3 ˆr r r ρ r dτ 4πε r 3 3 4πε r 3 i j ij r r Για τη δεδομένη κατανομή ij είναι με στοιχεία: 3 r 3y 3 3y 3y r 3y 3 3y 3 r dq 3 sin θ cos φ ρ rr 4 sin θdrdθdφ π k sin 3 θ cos φ sin φρ rr 4 drdθdφ 3 3 sin θ cos φ cos θρ rr 4 drdθdφ 3 3 sin θ sin φ cos θρ rr 4 drdθdφ 3 33 cos θ ρ rr 4 sin θdrdθdφ π k 5 ενώ τα υπόοιπα στοιχεία προκύπτουν από 4 το γεγονός ότι ο είναι συμμετρικός και με μηδενικό ίχνος 33 π k 5 48 Νεκτάριος Βαχάκης //5
6 δη π k 5 48 Σε σημεία του άξονα είναι i δ i r οπότε V τετρ 4πε 5 kπ5 384ε 3 Ομοια για σημεία του άξονα ερώτημα α είναι i δ i3 r οπότε V τετρ 4πε 5 33 kπ 5 9ε 3 Σε οποιοδήποτε σημείο y έξω από τη σφαίρα r r ο τετραποικός όρος είναι V τετρ 8πε r 5 πk 5 ] y 384ε r 5 y πk 5 y πk 5 3 cos θ 384ε + y + 5/ 384ε r 3 Οπως αναμενόταν μιας και η κατανομή φορτίου είναι αξισυμμετρική το αποτέεσμα είναι ανάογο της αξισυμμετρικής ύσης της εξίσωσης Lplce r P lcos θ με l l+ : Εστω q q q 3 +q q 4 q 5 q και οι θέσεις r r ˆ + ŷ r 3 ˆ ŷ r 4 ˆ+ŷ r 5 ˆ ŷ με r 3 r r 5 r 4 α Το συνοικό φορτίο δεν είναι μηδέν επομένως σε μεγάες αποστάσεις κυριαρχεί ο μονοποικός όρος V V μον 5 q i q 4πε r i 4πε r 5 β Η διποική ροπή είναι p q i r i επομένως i ο διποικός όρος V διπ p ˆr μηδενίζεται 4πε r 5 Αιώς: V διπ 4πε r 5 4πε r ˆr q i r i i i q i r i P ˆr ˆr i }{{} } ˆr ˆr i {{ } ˆr r i Ο τετραποικός όρος V τετρ 4πε r 3 με ri P ˆr ˆr i ri 3 ˆr ˆr i ˆr sin θ cos φ ˆ + sin θ sin φ ŷ + cos θ ẑ r r r 3 r 4 r 5 ˆr r ˆr r sin θ cos φ + sin θ sin φ ˆr r 3 ˆr r ˆr r 4 sin θ cos φ+ sin θ sin φ ˆr r 5 ˆr r 4 γράφεται V τετρ q 4πε r 3 sin θ sin φ cos φ q 4πε r r sin θ sin φ cos φ οπότε η προσεγγιστική έκφραση του δυναμικού είναι το άθροισμα του μονοποικού και του τετραποικού όρου δη V q 4πε r r sin θ sin φ cos φ Το ίδιο μπορεί να βρεθεί κατευθείαν από το ανάπτυγμα Tylor της έκφρασης του δυναμικού V 5 q i 5 q i i 4πε r r i i 4πε r r r i + ri 5 q i 4πε r i ˆr r ως προς i r + r r i r 3 : Απαιτώντας το δυναμικό να μην απειρίζεται στα r και r να μηδενίζεται για r και να είναι συνεχές στην ακτίνα r έχουμε b l V l+ rl P l cos θ αν r b l r P lcos θ αν r l+ Η άη οριακή συνθήκη στην ακτίνα r σχετίζεται με την ασυνέχεια της E r συνιστώσας του πεδίου lb l l+ rl P l cos θ αν r < l + b l P r l+ l cos θ αν r > Η ασυνέχεια της E r δίνει την ακόουθη έκφραση της E r r επιφανειακής πυκνότητας φορτίου του φοιού l + b l σθ ε P l+ l cos θ lb l α Πρέπει l+ rl P l για κάθε r < l + b l και P r l+ l για κάθε r > οπότε πρέπει να είναι b l P l για κάθε l Για l είναι αφού P Αυτό σημαίνει ότι δεν υπάρχει ο μονοποικός όρος στο πουποικό που αντιστοιχεί 4πε r ανάπτυγμα του δυναμικού 5 q i ri ] P ˆr ˆr i bl i στον όρο 3 ˆr r i ri r P lcos θ της ύσης για r > l+ με b και άρα το συνοικό φορτίο της κατα- 4πε νομής του φοιού είναι μηδέν Αιώς: Το συνοικό φορτίο του φοιού είναι π π σd σθ sin θdθ dφ Γενικότερα η σχέση b l P l συνεπάγεται ότι όα τα b l με άρτια l πρέπει να μηδενίζονται Αυτό γιατί η τιμή των πουωνύμων Legendre P l είναι μηδέν για περιττό l τα P l είναι περιττά αν l περιττό και μη μηδενική για άρτιο l Νεκτάριος Βαχάκης //5
7 πε l + b l l π P l cos θ sin θdθ }{{} P lp d Από τη σχέση ορθογωνιότητας των πουωνύμων Legendre το τεευταίο οοκήρωμα είναι μη μηδενικό μόνο για l οπότε το συνοικό φορτίο προκύπτει 4πε b l + b l 5 β P r l+ l E r b l 5 E δ l3 4 ανάπτυγμα του δυναμικού p cos θ ] 4πε r bl Ο διποικός όρος στο πουποικό αντιστοιχεί στον όρο r P lcos θ της ύσης για r > με l+ l b p Αφού b η διποική ροπή του φοιού 4πε είναι μηδέν Αιώς: Η διποική ροπή του φοιού είναι p rσd Αντικαθιστώντας r sin θ cos φˆ+ sin θ sin φŷ+ cos θ βρίσκουμε p p ˆ 3 π σθ sin θdθ π cos φdφ p y p ŷ 3 π σθ sin θdθ π sin φdφ p p ẑ 3 π σθ sin θ cos θdθ π dφ l + b π l πε P l l cos θ sin θ cos θdθ }{{} P lp d Από τη σχέση ορθογωνιότητας των πουωνύμων Legendre το τεευταίο οοκήρωμα είναι μη μηδενικό μόνο για l οπότε η διποική ροπή προκύπτει p 4πε b ẑ lb l γ l+ rl P l cos θ 3 r 4 E b l 5 E δ l3 Άρα σ ε E P 3 cos θ 7 8 ε E 5 cos 3 θ 3 cos θ 4 : α Η εξίσωση Lplce σε κυινδρικές συντεταγμένες και για κυινδρικά συμμετρικό δυναμικό V V ϖ φ γράφεται ϖ + V ϖ ϖ ϖ ϖ φ Με χωρισμό μεταβητών V Πϖ Φφ καταήγουμε στην ϖ d ϖ dπ + d Φ Η εξίσωση ως προς Φ είναι Π dϖ dϖ Φ dφ }{{}}{{} C C d Φ Φ dφ C d Φ dφ + CΦ Για C έχει ύσεις και φ για C < έχει ύσεις e Cφ και e Cφ και για C > έχει ύσεις sin Cφ και cos Cφ Η απαίτηση να μηδενίζεται η ύση για φ αά και για φ μας οδηγεί να επιέξουμε τη σταθερά C θετική και σαν ύση μόνο το ημίτονο Η ύση αυτή sin Cφ μηδενίζεται ταυτοτικά στο φ Απαιτούμε να μηδενίζεται και στη γωνία φ δη sin C C nπ με n N οπότε nπ nπφ C και η ύση είναι η sin Θα μπορούσαμε αμέσως να γράψουμε τη ύση σαν επαηία των sin nπφ αφού από τη θεωρία Fourier ξέρουμε ότι κάθε συνάρτηση ορισμένη στο διάστημα φ μπορεί να επεκταθεί σαν περιττή στο φ και στη συνέχεια περιοδική με περίοδο οπότε αναπτύσσεται στα παραπάνω ημίτονα Για κάθε C η ύση της ϖ d ϖ dπ nπ Π dϖ dϖ είναι επαηία των δυνάμεων ϖ ±nπ/ Αυτό μπορεί να δειχθεί είτε δοκιμάζοντας ύσεις της μορφής ϖ ξ οπότε καταήγουμε στο ότι η σταθερά ξ ικανοποιεί το πουώνυμο ξ n π / ξ ±nπ/ είτε αφού κάνουμε πρώτα το μετασχηματισμό ln ϖ οπότε ϖ d dϖ ϖ d d dϖ d d και η διαφορική αποποιείται σε d Π nπ d d Π η οποία είναι γραμμική ομογενής και έχει ύσεις e ξ με ξ n π / Αφού e ξ ϖ ξ και οι δύο μέθοδοι δίνουν ύση Π A n ϖ nπ/ + B n ϖ nπ/ και για το δυναμικό V An ϖ nπ/ + B n ϖ nπ/ sin nπφ n Αιώς: Μπορούμε να θέσουμε ln ϖ και ϖ d dϖ στην εξίσωση Lplce ϖ ϖ ϖ ϖ ϖ + V οπότε αυτή αποκτά ϖ φ μορφή V + V ίδια με την αντίστοιχη φ εξίσωση σε Καρτεσιανές και ύνεται με χωρισμό μεταβητών κατά τα γνωστά Οι συντεεστές A n και B n θα βρεθούν από τις υπόοιπες οριακές συνθήκες για το δυναμικό Για να μην απειρίζεται το δυναμικό στον άξονα ϖ πρέπει B n Η συνθήκη V ϖ V δίνει A n nπ/ sin nπφ n V η οποία με τέχνασμα Fourier δίνει A n nπ/ sin nπφ mπφ sin n dφ V sin mπφ }{{} dφ }{{} δnm mπ m ] A m mπ/ V mπ m ] οπότε μόνο οι συντεεστές με περιττό m επιζούν και έχουν τιμή A m 4V mπ mπ/ Νεκτάριος Βαχάκης //5 Αντικαθιστώντας στη γενική
8 n }{{} ύση βρίσκουμε τη ζητούμενη μορφή V 4V ϖ mπ/ mπφ sin π m35 m β Γράφοντας sin mπφ Im e imπφ/ και τους περιττούς φυσικούς αριθμούς m n + έχουμε V 4V π Im ϖ n+π/ e in+πφ/] n n + 4V π Im n+ ϖ π/ όπου e iπφ/ n n + n+ Το άθροισμα n d n n + n n d διότι προέκυψε άθορισμα όρων γεωμετρικής προόδου με όγο μέτρου < για ϖ < Άρα V 4V π Im d V π Im d + d V + π Im ln + + Γράφοντας τον μιγαδικό re iϑ το αποτέεσμα είναι V V Im ln r + iϑ π V π ϑ Αρκεί οιπόν να βρούμε τη φάση του ϖ π/ + Είναι + + e iπφ/ ϖ π/ e iπφ/ ϖ π/ + e iπφ/] ϖ π/ e iπφ/] ϖ π/ e iπφ/] ϖ π/ e iπφ/] ϖ π/ ϖ π/ πφ + i sin ϖ π/ ϖ π/ επομένως ϑ πφ + cos ϖ π/ πφ sin rctn ϖ π/ και η κειστή μορφή του ϖ π/ πφ δυναμικού είναι V V sin π rctn ϖ π/ 5 : Με ϖ d dϖ dϖ ϖ ϖ ϖ d dϖ d be be V βρίσκουμε την ζητούμενη V + V που είναι η φ εξίσωση Lplce στις «καρτεσιανές» συντεταγμένες και φ Ο ημικύινδρος μετασχηματίζεται στο χώρο < < + < φ < π < < + με δυναμικά στα όρια όπως στο δεύτερο σχήμα Ο χωρισμός μεταβητών οδηγεί σε ύση της μορ- φής V C n e n sinnφ η οποία ικανοποιεί τις n σωστές οριακές συνθήκες στις πευρές φ φ π και + Οι σταθερές C n προκύπτουν από την οριακή V V C n sinnφ V Με n τέχνασμα Fourier βρίσκουμε C n V πn n ] 4V ;ρα η ύση είναι V n35 πn e n lnb/ϖ sinnφ 4V ϖ n ή V sinnφ n35 πn b Το πρόβημα θα μπορούσε να υθεί όπως την άσκηση 4 είναι υποπερίπτωσή της για π Η ύση μπορεί να γραφεί σε κειστή μορφή V V bϖ sin φ rctn για r < b φ π π b ϖ Ενας άος τρόπος ύσης βασίζεται στο θεώρημα μοναδικότητας Εστω πρόβημα Ι είναι αυτό της παρούσας άσκησης και πρόβημα ΙΙ η εύρεση του δυναμικού στο εσωτερικό δύο ημικυίνδρων < φ < π και π < φ < π φορτισμένων σε δυναμικά ±V αντίστοιχα που φτιάχνουν ένα κενό κυινδρικό φοιό όπως στο θέμα της εξέτασης 8// Λόγω συμμετρίας το δυναμικό στο πρόβημα ΙΙ μηδενίζεται στο επίπεδο που χωρίζει τους ημικυίνδρους φ π Επομένως στα όρια του χώρου r < b φ π τα προβήματα Ι και ΙΙ έχουν ίδια δυναμικά και το θεώρημα μοναδικότητας μας εξασφαίζει ότι και στο εσωτερικό του χώρου αυτού η ύση θα είναι κοινή Το πρόβημα ΙΙ μπορεί να υθεί χρησιμοποιώντας την γενική ύση της εξίσωσης Lplce σε κυινδρικές συντεταγμένες Κρατώντας τους όρους που είναι περιττοί και πεπερασμένοι στον άξονα ϖ γράφουμε V n ϖ n sinnφ n Η οριακή V ϖb n b n sinnφ { n +V < φ < π με τέχνασμα Fourier δίνει V π < φ < π τους συντεεστές n V n ] οπότε πnb n 4V ϖ n V sinnφ πn b n35 Νεκτάριος Βαχάκης //5
9 6 : α Αντικαθιστώντας την δοσμένη V V θ στην d dv V sin θ βέπουμε ότι δίνει μηδέν είναι sin θ dv dθ A sin θ d cot θ/ r sin θ dθ dθ cot θ/ dθ sin θ A sinθ/ cosθ/ A Ισχύει και το αντίστροφο δη αν θέουμε d dv V με V V θ τότε sin θ r sin θ dθ dθ sin θ dv dθ A V A dθ sin θ A ln cot θ/] + B β Ψάχνουμε ύση της μορφής V θ A ln cot θ/] + B που ικανοποιεί τις οριακές συνθήκες V θπ/ και V θθ V Θέουμε ύση της Lplce στο χώρο θ θ π/ με σταθερά δυναμικά στα όρια θ θ και θ π/ οπότε είναι ογικό να περιμένουμε η ύση να είναι συνάρτηση μόνο του θ Η πρώτη οριακή δίνει A ln cot π/4] + B B ενώ η δεύτερη δίνει A ln cot θ /] V ln cot θ/] Άρα η ύση είναι V V ln cot θ /] 7 : α Εστω b > c οπότε ο αγωγός έχει σχήμα γεωειδούς εειψοειδούς Θέτοντας b c b cosh µ c sinh µ η εξίσωση του εειψοειδούς γράφεται + y cosh + µ sinh µ δη µ µ σε γεωειδείς σφαιροειδείς συντεταγμένες Στις συντεταγμένες αυτές η ύση της Lplcin η οποία πρέπει να ικανοποιεί οριακές συνθήκες V µ σταθερό το δυναμικό του αγωγού και V µ θεωρώντας το δυναμικό στο άπειρο μηδέν γενικότερα μπορεί να είναι μια σταθερά είναι της μορφής V V µ Από το τυποόγιο προκύπτει ότι V µ dv dµ C cosh µ όπου C σταθερά οοκήρωσης Το ηεκτρικό πεδίο είναι E V C ˆµ Πού μακρυά από τον h µ cosh µ αγωγό είναι ˆµ ˆr r cosh µ eµ h µ r οπότε μια άη έκφραση του πεδίου είναι E ˆµ 4πε 3 cosh + y µ sinh µ 4 cosh 4 µ + 4 sinh 4 µ Μια τρίτη έκφραση του πεδίου προκύπτει χρησιμοποιώντας τις ακόουθες εκφράσεις που προκύπτουν από αυτές του τυποόγιου ϖ ϖ + cosh µ ϖ + + ϖ + cos ν h µ ϖ + ] /4 ϖ + + ] /4 όπου βέβαια ϖ + y Η επιφανειακή πυκνότητα φορτίου στον αγωγό είναι µµ + 4π cosh µ sinh µ + sin ν Θέτοντας cosh µ b/ sinh µ c/ b c και sin ν /c βρίσκουμε σ σ ε E ˆµ Μια ισοδύναμη έκφραση όπως άμεσα μπορεί να επαηθευτεί αφού 4πbc + b c /c4 + y + είναι η σ b c + y 4πb c + Αν b < c οπότε ο αγωγός έχει σχήμα ωοειδούς εειψοειδούς θέτουμε c b c cosh µ b sinh µ και χρησιμοποιούμε ωοειδείς σφαιροειδείς συντεταγμένες Ακοουθώντας τα ίδια βήματα με πριν καταήγουμε στην έκφραση του πεδίου E 4πε h µ sinh µ ˆµ ˆµ 4πε sinh µ sinh µ + sin ν Οπως και πριν μπορούμε να δείξουμε ότι h µ + y sinh µ cosh µ 4 sinh 4 µ + 4 cosh 4 οπότε μια µ έκφραση του πεδίου είναι E ˆµ 4πε 3 cosh µ sinh + y µ οπότε E C 4 sinh 4 µ + 4 cosh 4 µ r ˆr Για να ισούται αυτό το πεδίο με Η επιφανειακή πυκνότητα του αγωγού προκύπτει σ το πεδίο φορτίου όπως «φαίνεται» ο αγωγός από μεγάες αποστάσεις πρέπει C 4πh µ sinh µ µµ 4πb + c b + y /b 4 4πε ή σ Σε κάθε σημείο έξω από τον αγωγό είναι E + y 4πε h µ cosh µ ˆµ 4πb c + ˆµ b 4 c 4 4πε cosh µ sinh µ + sin ν Μια δεύτερη ύση του προβήματος στην περίπτωση Μετά από πράξεις μπορούμε να δείξουμε ότι b < c βασίζεται στο ότι μια γραμμική κατανομή φορτίου σταθερής πυκνότητας και πεπερασμένου μή- h µ + y sinh µ cosh µ 4 cosh 4 µ + 4 sinh 4 µ κους δημιουργεί πεδίο του οποίου οι ισοδυναμικές Νεκτάριος Βαχάκης //5 b 4 c 4
10 επιφάνειες είναι ωοειδή εειψοειδή οπότε μπορεί να χρησιμοποιηθεί η μέθοδος των ειδώων Για το πεδίο της γραμμικής κατανομής φορτίου την οποία τοποθετούμε στον άξονα στο τμήμα < < είναι V ϖ dq r 4πε }{{} r }{{} 4πε ϖ ˆϖ+ẑ ẑ Θέτοντας ϖ tn θ με π/ < θ < π/ υποογίζουμε το οοκήρωμα d ϖ + d ϖ + dθ d sin θ + sin θ cos θ sin ln θ sin θ ln + sin θ ln + tn θ + tn θ cos θ ln + + ϖ ϖ Επομένως το δυναμικό σε σημείο ϖ φ προκύπτει V ϖ ϖ + + ln 4πε ϖ + + Με l ϖ + + και l ϖ + τις αποστάσεις του σημείου ϖ φ από τα άκρα της γραμμικής κατανομής φορτίου το δυναμικό γράφεται V ϖ ln l + 4πε l Είναι l l l + l l + και 4 l l + l + l l + l l l + l 4 l + l l l l l l + l 4 l + l + l l 4 l + l l l 4 l + l + l + l Άρα το δυναμικό γράφεται V ϖ ln l + l + και οι ισοδυναμικές επιφάνειες είναι πράγματι εειψοειδή l + l στα- 4πε l + l θερό coth πε V ή ισοδύναμα αφού αντικαταστήσουμε τα l ϖ + ± και ϖ μετά από κάποιες πράξεις sinh πε V + tnh πε V Αν θεωρήσουμε τώρα τον αγωγό με εειψοειδές σχήμα ϖ b + c αν αυτός αποτεεί μια ισοδυναμική επιφάνεια V V του προηγούμενου προβήματος το δυναμικό έξω από τον αγωγό είναι ίδιο στα δυο προβήματα σύμφωνα με το θεώρημα μοναδικότητας ϖ sinh πε V + ϖ b + c Αρκεί οιπόν οι επιφάνειες tnh πε V και να ταυτίζονται κάτι που συμβαίνει αν sinh πε b και V tnh πε c Πρέπει επίσης το φορτίο που περικείει η επιφάνεια του V εειψοειδούς να είναι ίδιο στις δύο κατανομές από νόμο Guss δη Οι τρεις τεευταίες σχέσεις δίνουν τα στοιχεία του φορτισμένου τμήματος ειδώου που τοποθετούμε στο εσωτερικό του αγωγού c b και το δυναμικό του αγωγού V 8πε ln c + c Η ύση οιπόν στο εξωτερικό του αγωγού είναι V 8πε ln ϖ + + ϖ ˆϖ ϖẑ ˆϖ ϖẑ E 8πε ϖ + + ϖ + ϖ όπου c b στο εσωτερικό του αγωγού είναι V 8πε ln c + c και E Το αποτέεσμα αυτό είναι ίδιο με αυτό που προέκυψε χρησιμοποιώντας ωοειδείς σφαιροειδείς συντεταγμένες δη το E ˆµ κάτι που φαίνεται 4πε h µ sinh µ χρησιμοποιώντας τις ακόουθες σχέσεις που προκύπτουν από το τυποόγιο + + ϖ + + ϖ cosh µ + + ϖ + ϖ cos ν h µ + ϖ ] /4 + + ϖ ] /4 cos ν h µ + ϖ + + ϖ ϖ sin ν h µ tnh µ ϖ + ϖ β Είναι b και c b δη υποπερίπτωση του γεωειδούς εειψοειδούς για το οποίο βρήκαμε ότι η επιφανειακή πυκνότητα είναι σ Είναι c 4πbc + b c /c4 αά ο όγος /c είναι πεπερασμένος και προκύπτει από την εξίσωση του εειψοειδούς ϖ b + c c ϖ Επομένως η συνοική και από τις δύο πευρές επιφανειακή πυκνότητα του δίσκου είναι Νεκτάριος Βαχάκης //5
11 σϖ 4πb }{{} c + b c /c }{{}}{{} σϖ π ϖ ϖ γ Είναι b < c και c το μήκος του ραβδόμορφου αγωγού Ο αγωγός είναι ωοειδές εειψοειδές με επιφάνεια b sin ν cos φ y b sin ν sin φ c cos ν Το στοιχείο επιφάνειας πάνω στο εειψοειδές το οποίο έχει σταθερό µ είναι d h ν dνh φ dφ ή οοκηρώνοντας ως προς την γωνία φ αφού πρόκειται για αξισυμμετρική επιφάνεια η οοκήρωση π δίνει απά π d πh ν dνh φ Επομένως το φορτίο σε ένα τμήμα της επιφάνειας από c cos ν ως +d με d c sin ν dν > είναι dq σπh ν h φ dν Το φορτίο ανά μήκος είναι dq d σπh dν νh φ d και αφού d c sin ν dν και σ 4πh µ sinh µ προκύπτει σταθερή γραμμική πυκνότητα c 3 Αιώς: dq d σd και η στοιχειώδης επιφάνεια μπορεί να γραφτεί d πϖ ds όπου d ds dϖ + d d dϖ + d Η κίση της επιφάνειας μπορεί να βρεθεί από την εξίσωσή της ϖ b + c ϖ dϖ + d b c dϖ d b c ϖ ενώ σ Αντικαθι- ϖ 4πb c + στώντας βρίσκουμε πϖσ b 4 c 4 dϖ dφ + c d Παρατηρήστε ότι στη δεύτερη απόδειξη δεν χρησιμοποιήσαμε κάπου ότι b < c Πράγματι το αποτέεσμα ισχύει και για αγωγό με σχήμα γεωειδές εειψοειδές με b > c κάτι που μπορεί εύκοα να αποδειχθεί και με τον πρώτο τρόπο χρησιμοποιώντας όμως γεωειδείς και όχι ωοειδείς σφαιροειδείς συντεταγμένες 8 : α Η δύναμη που ασκεί το φορτίο στο δίποο είναι Fd p Eq όπου E q q r d r q 4πε r d r q 3 q το πεδίο που δημιουργεί το φορτίο στη θέση 4πε 3 του διπόου Παρότι το διάνυσμα από το φορτίο στο δίποο ισούται με r δεν είναι βοικό να κάνουμε την αντικατάσταση πριν την παραγώγιση γιατί ο διαφορικός τεεστής p δρα στο και όχι στο r Στο σύστημα συντεταγμένων με αρχή το φορτίο έχουμε οιπόν F d q p με 4πε 3 p p 3 p 3 3 }{{} 4 }{{} p / 3 p 3 p Αντικαθιστώντας τώρα r 5 προκύπτει πράγματι Fd qe d όπως αναμενόταν από τον τρίτο νόμο Newton Οι παραγωγίσεις μπορούν να γίνουν και σε συγκεκριμένο σύστημα αναφοράς αποφεύγοντας διανυσματική ανάυση Θεωρώντας σύστημα qxy Z με κέντρο το φορτίο και φορά του άξονα Z ίδια με τη φορά της διποικής ροπής του διπόου p pẑ είναι E q q X ˆX + Y Ŷ + Z Ẑ 4πε X + Y + Z και Fd p E 3/ Z q qp Ẑ 4πε X + Y + Z 3Z X ˆX + Y Ŷ + Z Ẑ ] 3/ X + Y + Z 5/ q r qe 4πε 5 d Ενας άος τρόπος να βρεθεί η δύναμη είναι μέσω της δυναμικής ενέργειας αηεπίδρασης μεταξύ διπόου και φορτίου Αυτή είναι U p E q q p r d r q Η U προκύπτει και από τη 4πε r d r q 3 σχέση U qv d με το δυναμικό του διπόου στη p ˆr θέση του φορτίου V d 4πε r p r q r d 4πε r q r d 3 p 3 3 p Είναι Fq q U q p r q r d q όπου ο 4πε r q r d 3 δείκτης q δείχνει ότι ο τεεστής δρα στο r q Ομοια F d d U q p r d r q d 4πε r d r q 3 Οι παραγωγίσεις δίνουν q p r q r d r q r d 3 3 p r q r d q r r q r d 4 q r d q p r q r q r d 3 r q r d 3 p r q r d r q r d 4 r q r d p r q r d 3 και όμοια αντι- 3 Ισοδύναμος τρόπος: Το φορτίο στο μήκος του αγωγού από σε ή στις ωοειδείς σφαιροειδείς συντεταγμένες από π/ π ν π/ σε ν είναι q σ d dν ν 4πh µ sinh µ h νh φ dφ π/ dν sin ν ν cos ν Άρα το c φορτίο ανά μήκος είναι dq d c Νεκτάριος Βαχάκης //5
12 μεταθέτοντας τα q και d p r d r q d r d r q 3 3 p r d r q r d r q r d r q 4 r d r q p r d r q 3 Άρα προκύπτει F q qe d και F d F q Το γεγονός ότι οι δυνάμεις είναι αντίθετες μπορεί να ειδωθεί σαν συνέπεια του ότι U U r d r q οπότε q U d U Η ροπή που ασκεί το φορτίο στο δίποο ως προς το κέντρο του διπόου είναι Nd p E q Αφού E q q r είναι Nd q r p Αυτή είναι αντίθετη της N q r F d αφού η τεευταία 4πε r 3 4πε r 3 είναι Nq r qe d q r 3 p r r r p 4πε r 5 q r p Οπως αναμενόταν οιπόν από τον 4πε r 3 τρίτο νόμο Newton οι ροπές ως προς το ίδιο σημείο είναι αντίθετες β Πρέπει Fq ẑ και Fq ˆϖ < Αφού F q q 3 p r r r p 4πε r 5 ppẑ qp 3 r r ẑ 4πε r 5 η πρώτη συνθήκη δίνει 3 r cos θ ± 3 όπου θ η σφαιρική συντεταγμένη Δη Fq ẑ στους δύο κώνους θ rccos και θ π rccos Σε κυινδρικές r ϖ + και άρα F q ẑ ϖ ± ϖ οι εξισώσεις των δύο κώνων Στους δύο αυτούς κώνους είναι F 3 r ˆϖ d ˆϖ qp 4πε r 5 3 cos θ sin θ qp Το πρόσημο καθορίζεται από το πρόσημο του φορτίου q και από τη γωνία θ Αν το 4πε r 3 φορτίο είναι θετικό είναι Fq ˆϖ < στον κώνο θ ενώ αν το φορτίο είναι αρνητικό είναι F q ˆϖ < στον κώνο θ Το σχήμα δείχνει τις δυναμικές γραμμές του διποικού πεδίου και τους κώνους όπου το πεδίο είναι κάθετο στον άξονα δη παράηο στο ˆϖ Στον πάνω κώνο το E d είναι ομόρροπο στο ˆϖ οπότε η δύναμη είναι αντίρροπη του ˆϖ αν q < ενώ στον κάτω κώνο το E d είναι αντίρροπο στο ˆϖ οπότε η δύναμη είναι αντίρροπη του ˆϖ αν q > Οι συνθήκες F q ẑ και Fq ˆϖ < σημαίνουν ότι η δύναμη από το δίποο μπορεί να παίξει το ρόο κεντρομόου δύναμης αν δώσουμε στο φορτίο κατάηη αρχική ταχύτητα οπότε αυτό θα εκτεεί ομαή κυκική κίνηση με κέντρο σημείο του άξονα Συγκεκριμένα η διεύθυνση της ταχύτητας πρέπει να είναι η ˆφ και από την απαίτηση mv ϖ F cos θ sin θ q ˆϖ qp3 4πε r 3 όπου m η μάζα του φορτίου με r ϖ/ sin θ cos θ / 3 και sin θ /3 προκύπτει ότι η στροφορμή του φορτίου πρέπει να είναι mϖv m q p 3 3 πε 9 : α F F ˆ p E ] ˆ ] yb E yb p Η παραγώγιση γίνεται ως προς οπότε μπορούμε να θέσουμε τις τεικές τιμές των y και πριν την κάνουμε Στη θέση r ˆ + bŷ που βρίσκεται το p το p δημιουργεί πεδίο 3 p r r r E ] p yb 4πε r 5 p 3bˆ + b ŷ 4πε ] p p 4πε d d yb Άρα F + b 5/ 3b 3bp p b 4 + b 5/ 4πε + b 7/ β U p E 3 p r p r r p p 4πε r 5 p p 3b 4πε + b Παρατηρούμε ότι F 5/ du d όπως περιμέναμε F U ϖ -b/ b/ Νεκτάριος Βαχάκης //5
13 γ Σημεία ισορροπίας το ±b/ στο οποίο F Ισοδύναμα σημεία ισορροπίας είναι τα ακρότατα της δυναμικής ενέργειας αφού F du d Για b/ + είναι F < και για b/ είναι F > δη η F προσπαθεί και στις δύο περιπτώσεις να επαναφέρει το δίποο στη θέση ισορροπίας δύναμη επαναφοράς Επομένως το b/ είναι ευσταθές σημείο ισορροπίας Το ότι η F είναι δύναμη επαναφοράς δη df < είναι ισοδύναμο με το ότι η δυναμική ενέργεια είναι εάχιστη αφού df d b/ d U d d du και άρα στο σημείο b/ είναι και d b/ d U d > b/ Για b/ + είναι F > και για b/ είναι F < δη η F προσπαθεί και στις δύο περιπτώσεις να απομακρύνει το δίποο από τη θέση ισορροπίας δύναμη απωστική Επομένως το b/ είναι ασταθές σημείο ισορροπίας Το ότι η F είναι απωστική δύναμη δη df > είναι ισοδύναμο με το ότι η δυνα- d b/ μική ενέργεια είναι μέγιστη αφού df d U d d και du άρα στο σημείο b/ είναι και d b/ d U d < b/ : Η δύναμη που ασκεί το p p ẑ στο p p ẑ είναι F p ] E ] y d p E y όπου E y d 3 p r r r ] p p ẑ άρα προκύπτει 4πε r 5 4πε 3 rẑ εκτική δύναμη F 3p p πε d ẑ 4 Το p ασκεί στο p αντίθετη δύναμη F F Μπορούμε να βρούμε τη δύναμη και μέσω της δυναμικής ενέργειας αηεπίδρασης δη σαν F U όπου U p E Λόγω συμμετρίας η δύναμη έχει μόνο ẑ συνιστώσα οπότε αρκεί να βρούμε την U U σε θέσεις r ẑ του p γύρω από την d Είναι E y p 4πε ẑ U p ẑ E 3 p p 4πε και F 3 du ẑ 3p p d d πε d ẑ 4 Νεκτάριος Βαχάκης //5
R 1. e 2r V = Gauss E + 1 R 2
 : Γραμμική πυκνότητα φορτίου βρίσκεται στον άξονα αγώγιμου κυινδρικού φοιού εσωτερικής ακτίνας και εξωτερικής α) Να υποογιστεί η επαγόμενη πυκνότητα φορτίου στις δύο όψεις του φοιού, αν το συνοικό του
: Γραμμική πυκνότητα φορτίου βρίσκεται στον άξονα αγώγιμου κυινδρικού φοιού εσωτερικής ακτίνας και εξωτερικής α) Να υποογιστεί η επαγόμενη πυκνότητα φορτίου στις δύο όψεις του φοιού, αν το συνοικό του
z a R 3 (με R 3 > R 3 ); 2R P O a
 : Θέμα o από εξέταση της 9/9/: Κύβος από διηεκτρικό υικό κατααμβάνει τον όγκο x, y, z και φέρει μόνιμη πόωση P k r kxˆx + yŷ + zẑ). α) Βρείτε τα χωρικά και επιφανειακά δέσμια φορτία. β) Ποια η συνοική
: Θέμα o από εξέταση της 9/9/: Κύβος από διηεκτρικό υικό κατααμβάνει τον όγκο x, y, z και φέρει μόνιμη πόωση P k r kxˆx + yŷ + zẑ). α) Βρείτε τα χωρικά και επιφανειακά δέσμια φορτία. β) Ποια η συνοική
m 1 m 2 2 (z 2 + R 2 ). 3/2
 1 : Θέμα o από εξέταση της 2/2/2: α) Ποια η γενική μορή δηλ ανεξαρτήτως συστήματος συντεταγμένων) του μαγνητικού πεδίου B που δημιουργεί μαγνητικό δίπολο ροπής m σε σημείο P τέτοιο ώστε το διάνυσμα από
1 : Θέμα o από εξέταση της 2/2/2: α) Ποια η γενική μορή δηλ ανεξαρτήτως συστήματος συντεταγμένων) του μαγνητικού πεδίου B που δημιουργεί μαγνητικό δίπολο ροπής m σε σημείο P τέτοιο ώστε το διάνυσμα από
( 1) ,, r > R H = 2 arctan s c. s c. I ρn z 2. P 0 (u) = 1, P 1 (u) = u. M =M M = M. c k. s ln ( u 2 + c 2) du = s ln ( s 2 + c 2) 2s + n=0
 : Θέμα 4 o από εξέταση της 4/9/7: α Σχετικά με τις οριακές συνθήκες των πεδίων B και H, αποδείξτε τα ακόλουθα α Η συνιστώσα του B κάθετα στην επιφάνεια διαχωρισμού δύο μέσων είναι συνεχής α Η εφαπτομενική
: Θέμα 4 o από εξέταση της 4/9/7: α Σχετικά με τις οριακές συνθήκες των πεδίων B και H, αποδείξτε τα ακόλουθα α Η συνιστώσα του B κάθετα στην επιφάνεια διαχωρισμού δύο μέσων είναι συνεχής α Η εφαπτομενική
3 + O. 1 + r r 0. 0r 3 cos 2 θ 1. r r0 M 0 R 4
 Μηχανική Ι Εργασία #7 Χειμερινό εξάμηνο 8-9 Ν. Βλαχάκης. (α) Ποια είναι η ένταση και το δυναμικό του βαρυτικού πεδίου που δημιουργεί μια ομογενής σφαίρα πυκνότητας ρ και ακτίνας σε όλο το χώρο; Σχεδιάστε
Μηχανική Ι Εργασία #7 Χειμερινό εξάμηνο 8-9 Ν. Βλαχάκης. (α) Ποια είναι η ένταση και το δυναμικό του βαρυτικού πεδίου που δημιουργεί μια ομογενής σφαίρα πυκνότητας ρ και ακτίνας σε όλο το χώρο; Σχεδιάστε
P n ( x) = ( 1) n P n (x), P n (x)p l (x)dx = 2. P n (x)dx =
 ο σετ ασκήσεων Ηλεκτρομαγνητισμού Ι : Δύο αγώγιμα συμπαγή ημισφαίρια ακτίνας τοποθετούνται όπως στο σχήμα και χωρίζονται από ένα λεπτό μονωτικό στρώμα. Φορτίζουμε τα ημισφαίρια ώστε να αποκτήσουν δυναμικό
ο σετ ασκήσεων Ηλεκτρομαγνητισμού Ι : Δύο αγώγιμα συμπαγή ημισφαίρια ακτίνας τοποθετούνται όπως στο σχήμα και χωρίζονται από ένα λεπτό μονωτικό στρώμα. Φορτίζουμε τα ημισφαίρια ώστε να αποκτήσουν δυναμικό
= 0, dp 1 (cos θ) = sin θ, dp 2(cos θ) = 3 sin θ cos θ. B = , r R
 1 : Θέμα 4 o από εξέταση της 7//6: Σφαιρικός φλοιός εσωτερικής ακτίνας a και εξωτερικής b είναι ομογενώς μαγνητισμένος με μαγνήτιση M. α Ποιο το μαγνητικό πεδίο B και το πεδίο H που δημιουργεί σε κάθε
1 : Θέμα 4 o από εξέταση της 7//6: Σφαιρικός φλοιός εσωτερικής ακτίνας a και εξωτερικής b είναι ομογενώς μαγνητισμένος με μαγνήτιση M. α Ποιο το μαγνητικό πεδίο B και το πεδίο H που δημιουργεί σε κάθε
A = a 2 r 2 sin θ cos θ, r < R. C 1 ln ϖ + C 2. ( ) r = R. 2 A 2 = 0.
 : Θέμα 3 o από εξέταση της 7/5/8: Τα επίπεδα +a, a σε σύστημα Oxy) διαρρέονται από +a K επιφανειακά ρεύματα K ˆx, y K ˆx, αντίστοιχα, όπως στο σχήμα. Να βρεθεί a διανυσματικό δυναμικό A K σε όλο το χώρο.
: Θέμα 3 o από εξέταση της 7/5/8: Τα επίπεδα +a, a σε σύστημα Oxy) διαρρέονται από +a K επιφανειακά ρεύματα K ˆx, y K ˆx, αντίστοιχα, όπως στο σχήμα. Να βρεθεί a διανυσματικό δυναμικό A K σε όλο το χώρο.
Το πρόβλημα των μηδενικών ιδιοτιμών.
 Το πρόβημα των μηδενικών ιδιοτιμών. Από την προηγούμενη συζήτηση έχει γίνει φανερό ότι αν η ομογενής διαφορική εξίσωση L ϕ ( = 0έχει μη μηδενική ύση (ή ύσεις που να ικανοποιεί τις (ομογενείς συνοριακές
Το πρόβημα των μηδενικών ιδιοτιμών. Από την προηγούμενη συζήτηση έχει γίνει φανερό ότι αν η ομογενής διαφορική εξίσωση L ϕ ( = 0έχει μη μηδενική ύση (ή ύσεις που να ικανοποιεί τις (ομογενείς συνοριακές
Λύση Εξίσωσης Laplace: Χωρισμός Μεταβλητών
 Λύση Εξίσωσης Laplace: Χωρισμός Μεταβλητών Δομή Διάλεξης Μέθοδος χωριζόμενων μεταβλητών σε καρτεσιανές συν/νες (οριακές συνθήκες σε επίπεδο). Μέθοδος χωριζόμενων μεταβλητών σε σφαιρικές συν/νες (οριακές
Λύση Εξίσωσης Laplace: Χωρισμός Μεταβλητών Δομή Διάλεξης Μέθοδος χωριζόμενων μεταβλητών σε καρτεσιανές συν/νες (οριακές συνθήκες σε επίπεδο). Μέθοδος χωριζόμενων μεταβλητών σε σφαιρικές συν/νες (οριακές
Εφαρμοσμένα Μαθηματικά ΙΙ 10ο Σετ Ασκήσεων (Λύσεις) Ιδιοτιμές - Ιδιοδιανύσματα
 Εφαρμοσμένα Μαθηματικά ΙΙ ο Σετ Ασκήσεων (Λύσεις) Ιδιοτιμές - Ιδιοδιανύσματα Επιμέεια: Ι. Λυχναρόπουος. Έστω ο πίνακας 3. Δείξτε ότι το διάνυσμα v (,3) είναι ένα ιδιοδιάνυσμα που αντιστοιχεί στην ιδιοτιμή
Εφαρμοσμένα Μαθηματικά ΙΙ ο Σετ Ασκήσεων (Λύσεις) Ιδιοτιμές - Ιδιοδιανύσματα Επιμέεια: Ι. Λυχναρόπουος. Έστω ο πίνακας 3. Δείξτε ότι το διάνυσμα v (,3) είναι ένα ιδιοδιάνυσμα που αντιστοιχεί στην ιδιοτιμή
πάχος 0 πλάτος 2a μήκος
 B1) Δεδομένου του τύπου E = 2kλ/ρ που έχει αποδειχθεί στο μάθημα και περιγράφει το ηλεκτρικό πεδίο Ε μιας άπειρης γραμμής φορτίου με γραμμική πυκνότητα φορτίου λ σε σημείο Α που βρίσκεται σε απόσταση ρ
B1) Δεδομένου του τύπου E = 2kλ/ρ που έχει αποδειχθεί στο μάθημα και περιγράφει το ηλεκτρικό πεδίο Ε μιας άπειρης γραμμής φορτίου με γραμμική πυκνότητα φορτίου λ σε σημείο Α που βρίσκεται σε απόσταση ρ
ΦΥΕ 14 6η ΕΡΓΑΣΙΑ Παράδοση ( Οι ασκήσεις είναι ϐαθµολογικά ισοδύναµες)
 ΑΣΚΗΣΗ 1 ΦΥΕ 14 6η ΕΡΓΑΣΙΑ Παράδοση 30-06-08 ( Οι ασκήσεις είναι ϐαθµολογικά ισοδύναµες) Α) Τρία σηµειακά ϕορτία τοποθετούνται στις κορυφές ενός τετραγώνου πλευράς α, όπως ϕαίνεται στο σχήµα 1. Υπολογίστε
ΑΣΚΗΣΗ 1 ΦΥΕ 14 6η ΕΡΓΑΣΙΑ Παράδοση 30-06-08 ( Οι ασκήσεις είναι ϐαθµολογικά ισοδύναµες) Α) Τρία σηµειακά ϕορτία τοποθετούνται στις κορυφές ενός τετραγώνου πλευράς α, όπως ϕαίνεται στο σχήµα 1. Υπολογίστε
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
ds ds ds = τ b k t (3)
 Γενικά Μαθηματικά ΙΙΙ Πρώτο σετ ασκήσεων, Λύσεις Άσκηση 1 Γνωρίζουμε ότι το εφαπτόμενο διάνυσμα ( t), ορίζεται ως: t = r = d r ds (1) και επιπλέον το διάνυσμα της καμπυλότητας ( k), ορίζεται ως: d t k
Γενικά Μαθηματικά ΙΙΙ Πρώτο σετ ασκήσεων, Λύσεις Άσκηση 1 Γνωρίζουμε ότι το εφαπτόμενο διάνυσμα ( t), ορίζεται ως: t = r = d r ds (1) και επιπλέον το διάνυσμα της καμπυλότητας ( k), ορίζεται ως: d t k
Πρόβλημα 4.9.
 Πρόβλημα 4.9. Να βρεθεί το δυναμικό V() παντού στο χώρο ενός θετικά φορτισμένου φύλλου απείρων διαστάσεων με επιφανειακή πυκνότητα φορτίου σ. Πάρτε τον άξονα κάθετα στο φύλλο και θεωρήστε ότι το φύλλο
Πρόβλημα 4.9. Να βρεθεί το δυναμικό V() παντού στο χώρο ενός θετικά φορτισμένου φύλλου απείρων διαστάσεων με επιφανειακή πυκνότητα φορτίου σ. Πάρτε τον άξονα κάθετα στο φύλλο και θεωρήστε ότι το φύλλο
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα αυτής της
Φυσική για Μηχανικούς Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα αυτής της
Κλασική Ηλεκτροδυναμική Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΤΕΧΝΙΚΕΣ ΥΠΟΛΟΓΙΣΜΟΥ ΗΛΕΚΤΡΙΚΟΥ ΔΥΝΑΜΙΚΟΥ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΤΕΧΝΙΚΕΣ ΥΠΟΛΟΓΙΣΜΟΥ ΗΛΕΚΤΡΙΚΟΥ ΔΥΝΑΜΙΚΟΥ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
Κύμα ονομάζουμε τη διάδοση μιας διαταραχής από σημείο σε σημείο του χώρου με ορισμένη ταχύτητα.
 ΕΙΣΑΓΩΓΗ ΕΝΝΟΙΑ ΤΟΥ ΚΥΜΑΤΟΣ Τι ονομάζουμε κύμα; Κύμα ονομάζουμε τη διάδοση μιας διαταραχής από σημείο σε σημείο του χώρου με ορισμένη ταχύτητα. Η διαταραχή μπορεί να είναι α. Η ταάντωση των μορίων του
ΕΙΣΑΓΩΓΗ ΕΝΝΟΙΑ ΤΟΥ ΚΥΜΑΤΟΣ Τι ονομάζουμε κύμα; Κύμα ονομάζουμε τη διάδοση μιας διαταραχής από σημείο σε σημείο του χώρου με ορισμένη ταχύτητα. Η διαταραχή μπορεί να είναι α. Η ταάντωση των μορίων του
dv 2 dx v2 m z Β Ο Γ
 Μηχανική Ι Εργασία #2 Χειμερινό εξάμηνο 218-219 Ν Βλαχάκης 1 Στην άσκηση 4 της εργασίας #1 αρχικά για t = είναι φ = και η ταχύτητα του σώματος είναι v με φορά κάθετη στο νήμα ώστε αυτό να τυλίγεται στον
Μηχανική Ι Εργασία #2 Χειμερινό εξάμηνο 218-219 Ν Βλαχάκης 1 Στην άσκηση 4 της εργασίας #1 αρχικά για t = είναι φ = και η ταχύτητα του σώματος είναι v με φορά κάθετη στο νήμα ώστε αυτό να τυλίγεται στον
) z ) r 3. sin cos θ,
 Μηχανική Ι Εργασία #5 Χειμερινό εξάμηνο 4-5 Ν. Βλαχάκης. Σώμα μάζας m κινείται στο πεδίο δύναμης της πρώτης άσκησης της τέταρτης εργασίας με λ, αλλά επιπλέον είναι υποχρεωμένο να κινείται μόνο στην ευθεία
Μηχανική Ι Εργασία #5 Χειμερινό εξάμηνο 4-5 Ν. Βλαχάκης. Σώμα μάζας m κινείται στο πεδίο δύναμης της πρώτης άσκησης της τέταρτης εργασίας με λ, αλλά επιπλέον είναι υποχρεωμένο να κινείται μόνο στην ευθεία
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ. Ν. Τράκας, Ι. Ράπτης 2/4/2018
 ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) 7-8 η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ Ν. Τράκας Ι. Ράπτης /4/8 Παράδοση των 3 4 5 μέχρι /4/8 [Σε χειρόγραφη μορφή στο μάθημα ή σε μορφή ενιαίου αρχείου PDF στις
ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) 7-8 η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ Ν. Τράκας Ι. Ράπτης /4/8 Παράδοση των 3 4 5 μέχρι /4/8 [Σε χειρόγραφη μορφή στο μάθημα ή σε μορφή ενιαίου αρχείου PDF στις
Παραδείγματα Ιδιοτιμές Ιδιοδιανύσματα Ι. Λυχναρόπουλος
 Παραδείγματα Ιδιοτιμές Ιδιοδιανύσματα Ι. Λυχναρόπουος Παράδειγμα Να βρείτε τις ιδιοτιμές και τα αντίστοιχα ιδιοδιανύσματα του πίνακα 3. Επίσης να προσδιοριστούν οι ιδιοχώροι και οι γεωμετρικές ποαπότητες
Παραδείγματα Ιδιοτιμές Ιδιοδιανύσματα Ι. Λυχναρόπουος Παράδειγμα Να βρείτε τις ιδιοτιμές και τα αντίστοιχα ιδιοδιανύσματα του πίνακα 3. Επίσης να προσδιοριστούν οι ιδιοχώροι και οι γεωμετρικές ποαπότητες
Ορίζοντας την δυναμική ενέργεια σαν: Για μετακίνηση του φορτίου ανάμεσα στις πλάκες: Ηλεκτρικό Δυναμικό 1
 Ηλεκτρική Δυναμική Ενέργεια Ένα ζεύγος παράλληλων φορτισμένων μεταλλικών πλακών παράγει ομογενές ηλεκτρικό πεδίο Ε. Το έργο που παράγεται πάνω σε θετικό δοκιμαστικό φορτίο είναι: W W Fl q y q l q y Ορίζοντας
Ηλεκτρική Δυναμική Ενέργεια Ένα ζεύγος παράλληλων φορτισμένων μεταλλικών πλακών παράγει ομογενές ηλεκτρικό πεδίο Ε. Το έργο που παράγεται πάνω σε θετικό δοκιμαστικό φορτίο είναι: W W Fl q y q l q y Ορίζοντας
ΝΟΜΟΣ ΤΟΥ GAUSS ΚΕΦ.. 23
 ΝΟΜΟΣ ΤΟΥ GAUSS ΚΕΦ.. 23 Ροή (γενικά): Ηλεκτρική Ροή Η ποσότητα ενός μεγέθους που διέρχεται από μία επιφάνεια. Ε Ε dα dα θ Ε Ε θ Ηλεκτρική ροή dφ Ε μέσω στοιχειώδους επιφάνειας da (αφού da στοιχειώδης
ΝΟΜΟΣ ΤΟΥ GAUSS ΚΕΦ.. 23 Ροή (γενικά): Ηλεκτρική Ροή Η ποσότητα ενός μεγέθους που διέρχεται από μία επιφάνεια. Ε Ε dα dα θ Ε Ε θ Ηλεκτρική ροή dφ Ε μέσω στοιχειώδους επιφάνειας da (αφού da στοιχειώδης
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
GMm. 1 2GM ) 2 + L2 2 + R L=4.5 L=4 L=3.7 L= 1 2 =3.46 L= V (r) = L 2 /2r 2 - L 2 /r 3-1/r
 Ονοματεπώνυμο: Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών, Τμήμα Φυσικής Εξετάσεις στη Μηχανική Ι, Τμήμα Κ Τσίγκανου & Ν Βλαχάκη, Σεπτεμβρίου 05 Διάρκεια εξέτασης 3 ώρες, Καλή επιτυχία = bonus ερωτήματα),
Ονοματεπώνυμο: Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών, Τμήμα Φυσικής Εξετάσεις στη Μηχανική Ι, Τμήμα Κ Τσίγκανου & Ν Βλαχάκη, Σεπτεμβρίου 05 Διάρκεια εξέτασης 3 ώρες, Καλή επιτυχία = bonus ερωτήματα),
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΠΕΔΙΑ Ι 10. Η μέθοδος των ειδώλων
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΠΕΔΙΑ Ι. Η μέθοδος των ειδώλων Περιγραφή της μεθόδου Σημειακό φορτίο και αγώγιμο επίπεδο Φορτίο μεταξύ δύο αγωγίμων ημιεπιπέδων Σημειακό φορτίο έξω από γειωμένη σφαίρα Σημειακό φορτίο
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΠΕΔΙΑ Ι. Η μέθοδος των ειδώλων Περιγραφή της μεθόδου Σημειακό φορτίο και αγώγιμο επίπεδο Φορτίο μεταξύ δύο αγωγίμων ημιεπιπέδων Σημειακό φορτίο έξω από γειωμένη σφαίρα Σημειακό φορτίο
ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ, Αγωγοί Διηλεκτρικά. Ν. Τράκας, Ι. Ράπτης Ζωγράφου 27.3.
 ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) 8-9 η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ Αγωγοί Διηλεκτρικά Ν. Τράκας Ι. Ράπτης Ζωγράφου 7.3.9 Να επιστραφούν λυμένες μέχρι.4.9 οι ασκήσεις 3 4 5 [ΠΡΟΣΟΧΗ: Οι λύσεις
ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) 8-9 η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ Αγωγοί Διηλεκτρικά Ν. Τράκας Ι. Ράπτης Ζωγράφου 7.3.9 Να επιστραφούν λυμένες μέχρι.4.9 οι ασκήσεις 3 4 5 [ΠΡΟΣΟΧΗ: Οι λύσεις
Δυναμική Ενέργεια σε Ηλεκτρικό πεδίο, Διαφορά ηλεκτρικού δυναμικού. Ιωάννης Γκιάλας 14 Μαρτίου 2014
 Δυναμική Ενέργεια σε Ηλεκτρικό πεδίο, Διαφορά ηλεκτρικού δυναμικού Ιωάννης Γκιάλας 14 Μαρτίου 2014 Έργο ηλεκτροστατικής δύναμης W F Δl W N i i1 F Δl i Η μετατόπιση Δl περιγράφεται από ένα διάνυσμα που
Δυναμική Ενέργεια σε Ηλεκτρικό πεδίο, Διαφορά ηλεκτρικού δυναμικού Ιωάννης Γκιάλας 14 Μαρτίου 2014 Έργο ηλεκτροστατικής δύναμης W F Δl W N i i1 F Δl i Η μετατόπιση Δl περιγράφεται από ένα διάνυσμα που
Ασκήσεις 2 ου Κεφαλαίου, Νόμος του Gauss
 Ασκήσεις 2 ου Κεφαλαίου, Νόμος του Guss 22.36.Μία αγώγιμη σφαίρα με φορτίο q έχει ακτίνα α. Η σφαίρα βρίσκεται στο εσωτερικό μίας κοίλης ομόκεντρης αγώγιμης σφαίρας με εσωτερική ακτίνα και εξωτερική ακτίνα.
Ασκήσεις 2 ου Κεφαλαίου, Νόμος του Guss 22.36.Μία αγώγιμη σφαίρα με φορτίο q έχει ακτίνα α. Η σφαίρα βρίσκεται στο εσωτερικό μίας κοίλης ομόκεντρης αγώγιμης σφαίρας με εσωτερική ακτίνα και εξωτερική ακτίνα.
γ /ω=0.2 γ /ω=1 γ /ω= (ω /g) v. (ω 2 /g)(x-l 0 ) ωt. 2m.
 Μηχανική Ι Εργασία #7 Χειμερινό εξάμηνο 015-016 Ν. Βλαχάκης 1. Σώμα μάζας m και φορτίου q κινείται σε κατακόρυφο άξονα x, δεμένο σε ελατήριο σταθεράς k = mω του οποίου το άλλο άκρο είναι σταθερό. Το σύστημα
Μηχανική Ι Εργασία #7 Χειμερινό εξάμηνο 015-016 Ν. Βλαχάκης 1. Σώμα μάζας m και φορτίου q κινείται σε κατακόρυφο άξονα x, δεμένο σε ελατήριο σταθεράς k = mω του οποίου το άλλο άκρο είναι σταθερό. Το σύστημα
lim Δt Δt 0 da da da dt dt dt dt Αν ο χρόνος αυξηθεί κατά Δt το διάνυσμα θα γίνει Εξετάζουμε την παράσταση
 Έστω διάνυσμα a( t a ( t i a ( t j a ( t k Αν ο χρόνος αυξηθεί κατά Δt το διάνυσμα θα γίνει a( t Δt a ( t Δt i a ( t Δt j a ( t Δt k Εξετάζουμε την παράσταση z z a( t Δt - a( t Δa a ( t Δt - a ( t lim
Έστω διάνυσμα a( t a ( t i a ( t j a ( t k Αν ο χρόνος αυξηθεί κατά Δt το διάνυσμα θα γίνει a( t Δt a ( t Δt i a ( t Δt j a ( t Δt k Εξετάζουμε την παράσταση z z a( t Δt - a( t Δa a ( t Δt - a ( t lim
Εξίσωση Laplace Θεωρήματα Μοναδικότητας
 Εξίσωση Laplace Θεωρήματα Μοναδικότητας Δομή Διάλεξης Εξίσωση Laplace πλεονεκτήματα μεθόδου επίλυσης της για εύρεση ηλεκτρικού δυναμικού Ιδιότητες λύσεων εξίσωσης Laplace σε 1, 2 και 3 διαστάσεις Θεώρημα
Εξίσωση Laplace Θεωρήματα Μοναδικότητας Δομή Διάλεξης Εξίσωση Laplace πλεονεκτήματα μεθόδου επίλυσης της για εύρεση ηλεκτρικού δυναμικού Ιδιότητες λύσεων εξίσωσης Laplace σε 1, 2 και 3 διαστάσεις Θεώρημα
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
ΠΑΓΚΟΣΜΙΑ ΕΛΞΗ ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 69 946778 ΠΑΚΟΣΜΙΑ ΕΛΞΗ ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 69 946778 www.poias.weebly.co ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 69 946778 ΠΑΚΟΣΜΙΑ ΕΛΞΗ ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 69 946778 www.poias.weebly.co ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ
Ηλεκτρομαγνητισμός. Ηλεκτρικό πεδίο νόμος Gauss. Νίκος Ν. Αρπατζάνης
 Ηλεκτρομαγνητισμός Ηλεκτρικό πεδίο νόμος Gauss Νίκος Ν. Αρπατζάνης Νόμος Gauss Ο νόµος του Gauss εκφράζει τη σχέση μεταξύ της συνολικής ηλεκτρικής ροής που διέρχεται από μια κλειστή επιφάνεια και του φορτίου
Ηλεκτρομαγνητισμός Ηλεκτρικό πεδίο νόμος Gauss Νίκος Ν. Αρπατζάνης Νόμος Gauss Ο νόµος του Gauss εκφράζει τη σχέση μεταξύ της συνολικής ηλεκτρικής ροής που διέρχεται από μια κλειστή επιφάνεια και του φορτίου
Ενότητα 4: Κεντρικές διατηρητικές δυνάμεις
 Ενότητα 4: Κεντρικές διατηρητικές δυνάμεις Έστω F=f κεντρικό πεδίο δυνάμεων. Είναι εύκολο να δείξουμε ότι F=0, δηλ. είναι διατηρητικό: F= V. Σε σφαιρικές συντεταγμένες, γενικά: V ma = F =, V maθ = Fθ =,
Ενότητα 4: Κεντρικές διατηρητικές δυνάμεις Έστω F=f κεντρικό πεδίο δυνάμεων. Είναι εύκολο να δείξουμε ότι F=0, δηλ. είναι διατηρητικό: F= V. Σε σφαιρικές συντεταγμένες, γενικά: V ma = F =, V maθ = Fθ =,
g = 1, b = 1, c = 7. V eff (r) = L2 V eff (r).
 Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Τμήμα Φυσικής Εξετάσεις στη Μηχανική Ι Τμήμα Κ Τσίγκανου & Ν Βαχάκη 5 Σεπτεμβρίου Διάρκεια εξέτασης ώρες Καή επιτυχία ( bonus ερωτήματα) Ονοματεπώνυμο: ΑΜ:
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Τμήμα Φυσικής Εξετάσεις στη Μηχανική Ι Τμήμα Κ Τσίγκανου & Ν Βαχάκη 5 Σεπτεμβρίου Διάρκεια εξέτασης ώρες Καή επιτυχία ( bonus ερωτήματα) Ονοματεπώνυμο: ΑΜ:
TO ΠΡΟΒΛΗΜΑ ΤΗΣ ΤΟΠΟΘΕΤΗΣΗΣ ΠΟΛΩΝ ΜE ΑΝΑΤΡΟΦΟΔΟΤΗΣΗ ΤΩΝ ΜΕΤΑΒΛΗΤΩΝ ΚΑΤΑΣΤΑΣΗΣ
 TO ΠΡΟΒΛΗΜΑ ΤΗΣ ΤΟΠΟΘΕΤΗΣΗΣ ΠΟΛΩΝ ΜE ΑΝΑΤΡΟΦΟΔΟΤΗΣΗ ΤΩΝ ΜΕΤΑΒΛΗΤΩΝ ΚΑΤΑΣΤΑΣΗΣ. ΕΙΣΑΓΩΓΗ Ας θεωρήσουμε το σύστημα ανοικτού βρόχου που περιγράφεται από τις εξισώσεις κατάστασης (.) και (.2): x Ax+ Bu (.)
TO ΠΡΟΒΛΗΜΑ ΤΗΣ ΤΟΠΟΘΕΤΗΣΗΣ ΠΟΛΩΝ ΜE ΑΝΑΤΡΟΦΟΔΟΤΗΣΗ ΤΩΝ ΜΕΤΑΒΛΗΤΩΝ ΚΑΤΑΣΤΑΣΗΣ. ΕΙΣΑΓΩΓΗ Ας θεωρήσουμε το σύστημα ανοικτού βρόχου που περιγράφεται από τις εξισώσεις κατάστασης (.) και (.2): x Ax+ Bu (.)
Εφαρμογές Νόμος Gauss, Ηλεκτρικά πεδία. Ιωάννης Γκιάλας 7 Μαρτίου 2014
 Εφαρμογές Νόμος Gauss, Ηλεκτρικά πεδία Ιωάννης Γκιάλας 7 Μαρτίου 14 Άσκηση: Ηλεκτρικό πεδίο διακριτών φορτίων Δύο ίσα θετικά φορτία q βρίσκονται σε απόσταση α μεταξύ τους. Να βρεθεί η ακτίνα του κύκλου,
Εφαρμογές Νόμος Gauss, Ηλεκτρικά πεδία Ιωάννης Γκιάλας 7 Μαρτίου 14 Άσκηση: Ηλεκτρικό πεδίο διακριτών φορτίων Δύο ίσα θετικά φορτία q βρίσκονται σε απόσταση α μεταξύ τους. Να βρεθεί η ακτίνα του κύκλου,
ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ., 1 i n, με σταθερό όρο b F και συντελεστές a i
 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Γραμμικά συστήματα Μία εξίσωση της μορφής K () καείται γραμμική εξίσωση μεταητών i i με σταθερό όρο F και συντεεστές i F όπου το F θα είναι το σώμα των πραγματικών ή μιγαδικών αριθμών
ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Γραμμικά συστήματα Μία εξίσωση της μορφής K () καείται γραμμική εξίσωση μεταητών i i με σταθερό όρο F και συντεεστές i F όπου το F θα είναι το σώμα των πραγματικών ή μιγαδικών αριθμών
Ολοκληρώματα. Κώστας Γλυκός ΜΑΘΗΜΑΤΙΚΟΣ. Ασκήσεις για ΑΕΙ και ΤΕΙ. Kglykos.gr. σε Ολοκληρώματα. τεχνικές. 108 ασκήσεις. εκδόσεις.
 Ολοκληρώματα Κώστας Γλυκός Ασκήσεις για ΑΕΙ και ΤΕΙ σε Ολοκληρώματα τεχνικές 08 ασκήσεις Ι δ ι α ί τ ε ρ α μ α θ ή μ α τ α 6 9 7. 0 0. 8 8. 8 8 Kglkos.gr / / 0 9 εκδόσεις Καλό πήξιμο Τα πάντα για τα Ολοκληρώματα
Ολοκληρώματα Κώστας Γλυκός Ασκήσεις για ΑΕΙ και ΤΕΙ σε Ολοκληρώματα τεχνικές 08 ασκήσεις Ι δ ι α ί τ ε ρ α μ α θ ή μ α τ α 6 9 7. 0 0. 8 8. 8 8 Kglkos.gr / / 0 9 εκδόσεις Καλό πήξιμο Τα πάντα για τα Ολοκληρώματα
website:
 Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 31 Μαρτίου 2019 1 Δυνάμεις μάζας και επαφής Δυνάμεις μάζας ή δυνάμεις όγκου ονομάζονται οι δυνάμεις που είναι
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 31 Μαρτίου 2019 1 Δυνάμεις μάζας και επαφής Δυνάμεις μάζας ή δυνάμεις όγκου ονομάζονται οι δυνάμεις που είναι
(i) f(x, y) = xy + iy (iii) f(x, y) = e y e ix. f(z) = U(r, θ) + iv (r, θ) ; z = re iθ
 ΜΑΘΗΜΑΤΙΚΗ ΦΥΣΙΚΗ (ΜΕΤΑΠΤΥΧΙΑΚΟ) 6 Νοεμβρίου 07 Αναλυτικές συναρτήσεις Άσκηση (i) Δείξτε ότι η συνάρτηση f(z) είναι αναλυτική σε χωρίο D του μιγαδικού επιπέδου εάν και μόνο εάν η if(z) είναι αναλυτική
ΜΑΘΗΜΑΤΙΚΗ ΦΥΣΙΚΗ (ΜΕΤΑΠΤΥΧΙΑΚΟ) 6 Νοεμβρίου 07 Αναλυτικές συναρτήσεις Άσκηση (i) Δείξτε ότι η συνάρτηση f(z) είναι αναλυτική σε χωρίο D του μιγαδικού επιπέδου εάν και μόνο εάν η if(z) είναι αναλυτική
Το ελαστικο κωνικο εκκρεμε ς
 Το ελαστικο κωνικο εκκρεμε ς 1. Εξισώσεις Euler -Lagrange x 0 φ θ z F l 0 y r m B Το ελαστικό κωνικό εκκρεμές αποτελείται από ένα ελατήριο με σταθερά επαναφοράς k, το οποίο αναρτάται από ένα σταθερό σημείο,
Το ελαστικο κωνικο εκκρεμε ς 1. Εξισώσεις Euler -Lagrange x 0 φ θ z F l 0 y r m B Το ελαστικό κωνικό εκκρεμές αποτελείται από ένα ελατήριο με σταθερά επαναφοράς k, το οποίο αναρτάται από ένα σταθερό σημείο,
(α) 1. (β) Το σύστημα βρίσκεται υπό διαφορά δυναμικού 12 V: U ολ = 1 2 C ολ(δv) 2 = J.
 4 η Ομάδα Ασκήσεων Δύο πυκνωτές C=5 μf και C=40 μf συνδέονται παράλληλα στους ακροδέκτες πηγών τάσης VS=50 V και VS=75 V αντίστοιχα και φορτίζονται Στην συνέχεια αποσυνδέονται και συνδέονται μεταξύ τους,
4 η Ομάδα Ασκήσεων Δύο πυκνωτές C=5 μf και C=40 μf συνδέονται παράλληλα στους ακροδέκτες πηγών τάσης VS=50 V και VS=75 V αντίστοιχα και φορτίζονται Στην συνέχεια αποσυνδέονται και συνδέονται μεταξύ τους,
Ηλεκτρική δυναμική ενέργεια
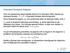 Ηλεκτρική δυναμική ενέργεια Όταν ένα δοκιμαστικό φορτίο βρεθεί μέσα σε ένα ηλεκτρικό πεδίο, δέχεται μια ηλεκτρική δύναμη: F e =q o E. Η ηλεκτρική δύναμη είναι συντηρητική. Έστω δοκιμαστικό φορτίο, q 0,
Ηλεκτρική δυναμική ενέργεια Όταν ένα δοκιμαστικό φορτίο βρεθεί μέσα σε ένα ηλεκτρικό πεδίο, δέχεται μια ηλεκτρική δύναμη: F e =q o E. Η ηλεκτρική δύναμη είναι συντηρητική. Έστω δοκιμαστικό φορτίο, q 0,
ΚΕΦΑΛΑΙΑ 3,4. Συστήµατα ενός Βαθµού ελευθερίας. k Για E 0, η (1) ισχύει για κάθε x. Άρα επιτρεπτή περιοχή είναι όλος ο άξονας
 ΚΕΦΑΛΑΙΑ,4. Συστήµατα ενός Βαθµού ελευθερίας. Να βρεθούν οι επιτρεπτές περιοχές της κίνησης στον άξονα ' O για την απωστική δύναµη F, > και για ενέργεια Ε. (α) Είναι V και οι επιτρεπτές περιοχές της κίνησης
ΚΕΦΑΛΑΙΑ,4. Συστήµατα ενός Βαθµού ελευθερίας. Να βρεθούν οι επιτρεπτές περιοχές της κίνησης στον άξονα ' O για την απωστική δύναµη F, > και για ενέργεια Ε. (α) Είναι V και οι επιτρεπτές περιοχές της κίνησης
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Ολοκληρώματα. Κώστας Γλυκός ΜΑΘΗΜΑΤΙΚΟΣ. Ασκήσεις για ΑΕΙ και ΤΕΙ. Kglykos.gr. σε Ολοκληρώματα. τεχνικές. 108 ασκήσεις. εκδόσεις.
 Ολοκληρώματα Κώστας Γλυκός Ασκήσεις για ΑΕΙ και ΤΕΙ σε Ολοκληρώματα τεχνικές 08 ασκήσεις Ι δ ι α ί τ ε ρ α μ α θ ή μ α τ α 6 9 7. 0 0. 8 8. 8 8 Kglkos.gr / / 0 7 εκδόσεις Καλό πήξιμο τηλ. Οικίας : 0-60.78
Ολοκληρώματα Κώστας Γλυκός Ασκήσεις για ΑΕΙ και ΤΕΙ σε Ολοκληρώματα τεχνικές 08 ασκήσεις Ι δ ι α ί τ ε ρ α μ α θ ή μ α τ α 6 9 7. 0 0. 8 8. 8 8 Kglkos.gr / / 0 7 εκδόσεις Καλό πήξιμο τηλ. Οικίας : 0-60.78
ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΜΑΘΗΜΑ : ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ I (Βασικό 3 ου Εξαμήνου) Διδάσκων : Δ.Σκαρλάτος ΜΑΘΗΜΑΤΙΚΟ ΤΥΠΟΛΟΓΙΟ. Α. Τριγωνομετρικές Ταυτότητες
 ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΜΑΘΗΜΑ : ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ I (Βασικό 3 ου Εξαμήνου) Διδάσκων : Δ.Σκαρλάτος ΜΑΘΗΜΑΤΙΚΟ ΤΥΠΟΛΟΓΙΟ Α. Τριγωνομετρικές Ταυτότητες Β. Αναπτύγματα σε σειρές Για
ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΜΑΘΗΜΑ : ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ I (Βασικό 3 ου Εξαμήνου) Διδάσκων : Δ.Σκαρλάτος ΜΑΘΗΜΑΤΙΚΟ ΤΥΠΟΛΟΓΙΟ Α. Τριγωνομετρικές Ταυτότητες Β. Αναπτύγματα σε σειρές Για
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ - ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΜΑΘΗΜΑ : HΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ - ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΜΑΘΗΜΑ : HΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι (Υποχρεωτικό ου Εξαμήνου) Διδάσκων : Δ.Σκαρλάτος, Επίκουρος Καθηγητής ΣΗΜΕΙΩΣΕΙΣ # 5 : ΤΟ ΗΛΕΚΤΡΙΚΟ ΔΙΠΟΛΟ Ορισμός : Με τον όρο «ηλεκτρικό
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ - ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΜΑΘΗΜΑ : HΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι (Υποχρεωτικό ου Εξαμήνου) Διδάσκων : Δ.Σκαρλάτος, Επίκουρος Καθηγητής ΣΗΜΕΙΩΣΕΙΣ # 5 : ΤΟ ΗΛΕΚΤΡΙΚΟ ΔΙΠΟΛΟ Ορισμός : Με τον όρο «ηλεκτρικό
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 2005
 ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 5 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ A στω µια συν ρτηση f, η οποία είναι ορισµ νη σε ένα κειστό δι στηµα [α, β] Αν: η f είναι συνεχής στο [α, β] και fα fβ δείξτε ότι για κάθε
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 5 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ A στω µια συν ρτηση f, η οποία είναι ορισµ νη σε ένα κειστό δι στηµα [α, β] Αν: η f είναι συνεχής στο [α, β] και fα fβ δείξτε ότι για κάθε
GMR L = m. dx a + bx + cx. arcsin 2cx b b2 4ac. r 3. cos φ = eg. 2 = 1 c
 Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών, Τμήμα Φυσικής Εξετάσεις στη Μηχανική Ι, Τμήμα Κ. Τσίγκανου & Ν. Βλαχάκη, 9 Μαΐου 01 Διάρκεια εξέτασης 3 ώρες, Καλή επιτυχία bonus ερωτήματα Ονοματεπώνυμο:,
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών, Τμήμα Φυσικής Εξετάσεις στη Μηχανική Ι, Τμήμα Κ. Τσίγκανου & Ν. Βλαχάκη, 9 Μαΐου 01 Διάρκεια εξέτασης 3 ώρες, Καλή επιτυχία bonus ερωτήματα Ονοματεπώνυμο:,
ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ
 ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν μια
ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν μια
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ Ι Φεβρουάριος 2004
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ Ι Φεβρουάριος 4 Τµήµα Π. Ιωάννου & Θ. Αποστολάτου Απαντήστε µε σαφήνεια και συντοµία. Η ορθή πλήρης απάντηση θέµατος εκτιµάται περισσότερο από τη
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ Ι Φεβρουάριος 4 Τµήµα Π. Ιωάννου & Θ. Αποστολάτου Απαντήστε µε σαφήνεια και συντοµία. Η ορθή πλήρης απάντηση θέµατος εκτιµάται περισσότερο από τη
ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ
 ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ ΒΙΒΛΙΟΓΡΑΦΙΑ H.D. H.D. Young Πανεπιστημιακή Φυσική Εκδόσεις Παπαζήση Alonso Alonso / Finn Θεμελιώδης Πανεπιστημιακή Φυσική Α. Φίλιππας, Λ. Ρεσβάνης (Μετ.) R. A. Seway Φυσική
ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ ΒΙΒΛΙΟΓΡΑΦΙΑ H.D. H.D. Young Πανεπιστημιακή Φυσική Εκδόσεις Παπαζήση Alonso Alonso / Finn Θεμελιώδης Πανεπιστημιακή Φυσική Α. Φίλιππας, Λ. Ρεσβάνης (Μετ.) R. A. Seway Φυσική
ΕΙΔΙΚΗ ΘΕΩΡΙΑ ΤΗΣ ΣΧΕΤΙΚΟΤΗΤΑΣ
 ΕΙΔΙΚΗ ΘΕΩΡΙΑ ΤΗΣ ΣΧΕΤΙΚΟΤΗΤΑΣ Διδάσκων: Θεόδωρος Ν. Τομαράς 1. Μετασχηματισμοί συντεταγμένων και συμμετρίες. 1α. Στροφές στο επίπεδο. Θεωρείστε δύο καρτεσιανά συστήματα συντεταγμένων στο επίπεδο, στραμμένα
ΕΙΔΙΚΗ ΘΕΩΡΙΑ ΤΗΣ ΣΧΕΤΙΚΟΤΗΤΑΣ Διδάσκων: Θεόδωρος Ν. Τομαράς 1. Μετασχηματισμοί συντεταγμένων και συμμετρίες. 1α. Στροφές στο επίπεδο. Θεωρείστε δύο καρτεσιανά συστήματα συντεταγμένων στο επίπεδο, στραμμένα
I. ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. math-gr
 I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
ΚΕΦΑΛΑΙΟ 4: ΙΔΙΟΤΙΜΕΣ ΚΑΙ ΙΔΙΟΔΙΑΝΥΣΜΑΤΑ
 ΚΕΦΑΛΑΙΟ ΚΕΦΑΛΑΙΟ :. ΟΡΙΣΜΟΙ Δίνεται ο πίνακας Παρατηρήστε τι γίνεται όταν ποαπασιάζουμε τον Α με το διάνυσμα u u u παίρνουμε δηαδή ένα διάνυσμα ποαπάσιο του u. Η αναζήτηση διανυσμάτων που έχουν παρόμοια
ΚΕΦΑΛΑΙΟ ΚΕΦΑΛΑΙΟ :. ΟΡΙΣΜΟΙ Δίνεται ο πίνακας Παρατηρήστε τι γίνεται όταν ποαπασιάζουμε τον Α με το διάνυσμα u u u παίρνουμε δηαδή ένα διάνυσμα ποαπάσιο του u. Η αναζήτηση διανυσμάτων που έχουν παρόμοια
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Εξέταση στη Μηχανική ΙI 11 Ιουνίου 2012
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Εξέταση στη Μηχανική ΙI Ιουνίου 202 Απαντήστε και στα 4 Θέματα με σαφήνεια και απλότητα. Οι ολοκληρωμένες απαντήσεις στα ερωτήματα εκτιμώνται ιδιαιτέρως. Καλή σας επιτυχία.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Εξέταση στη Μηχανική ΙI Ιουνίου 202 Απαντήστε και στα 4 Θέματα με σαφήνεια και απλότητα. Οι ολοκληρωμένες απαντήσεις στα ερωτήματα εκτιμώνται ιδιαιτέρως. Καλή σας επιτυχία.
ΘΕΩΡΗΤΙΚΗ ΜΗΧΑΝΙΚΗ Ι Σεπτέμβριος 2012
 ΘΕΩΡΗΤΙΚΗ ΜΗΧΑΝΙΚΗ Ι Σεπτέμβριος ΘΕΜΑ α) Υλικό σημείο μάζας κινείται στον άξονα Ο υπό την επίδραση του δυναμικού V=V() Αν για t=t βρίσκεται στη θέση = με ενέργεια Ε δείξτε ότι η κίνησή του δίνεται από
ΘΕΩΡΗΤΙΚΗ ΜΗΧΑΝΙΚΗ Ι Σεπτέμβριος ΘΕΜΑ α) Υλικό σημείο μάζας κινείται στον άξονα Ο υπό την επίδραση του δυναμικού V=V() Αν για t=t βρίσκεται στη θέση = με ενέργεια Ε δείξτε ότι η κίνησή του δίνεται από
Εξαιτίας της συμβολής δύο κυμάτων του ίδιου πλάτους και της ίδιας συχνότητας. που διαδίδονται ταυτόχρονα στο ίδιο γραμμικό ελαστικό μέσο
 ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ Τι ονομάζουμε στάσιμο κύμα f()=0.5sin() Εξαιτίας της συμβοής δύο κυμάτων του ίδιου πάτους και της ίδιας συχνότητας που διαδίδονται ταυτόχρονα στο ίδιο γραμμικό εαστικό μέσο με αντίθετη φορά,
ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ Τι ονομάζουμε στάσιμο κύμα f()=0.5sin() Εξαιτίας της συμβοής δύο κυμάτων του ίδιου πάτους και της ίδιας συχνότητας που διαδίδονται ταυτόχρονα στο ίδιο γραμμικό εαστικό μέσο με αντίθετη φορά,
Διάνυσμα: έχει μέτρο, διεύθυνση και φορά
 Διάνυσμα: έχει μέτρο, διεύθυνση και φορά Πολλά φυσικά μεγέθη είναι διανυσματικά (π.χ. δύναμη, ταχύτητα, επιτάχυνση, γωνιακή ταχύτητα, ροπή, στροφορμή ) Συμβολισμός του διανύσματος: Συμβολισμός του μέτρου
Διάνυσμα: έχει μέτρο, διεύθυνση και φορά Πολλά φυσικά μεγέθη είναι διανυσματικά (π.χ. δύναμη, ταχύτητα, επιτάχυνση, γωνιακή ταχύτητα, ροπή, στροφορμή ) Συμβολισμός του διανύσματος: Συμβολισμός του μέτρου
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΙΚΟ ΠΕΔΙΟ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΙΚΟ ΠΕΔΙΟ 1 1. ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ Οι αρχαίοι Έλληνες ανακάλυψαν από το 600 π.χ. ότι, το κεχριμπάρι μπορεί να έλκει άλλα αντικείμενα όταν το τρίψουμε με μαλλί.
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΙΚΟ ΠΕΔΙΟ 1 1. ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ Οι αρχαίοι Έλληνες ανακάλυψαν από το 600 π.χ. ότι, το κεχριμπάρι μπορεί να έλκει άλλα αντικείμενα όταν το τρίψουμε με μαλλί.
11. Η έννοια του διανύσµατος 22. Πρόσθεση & αφαίρεση διανυσµάτων 33. Βαθµωτός πολλαπλασιασµός 44. Συντεταγµένες 55. Εσωτερικό γινόµενο
 Παραουσίαση βιβίου Μαθηµατικών Προσαναταισµού Β Λυκείου. Η έννοια του διανύσµατος. Πρόσθεση & αφαίρεση διανυσµάτων 33. Βαθµωτός ποαπασιασµός 44. Συντεταγµένες 55. Εσωτερικό γινόµενο Παραουσίαση βιβίου
Παραουσίαση βιβίου Μαθηµατικών Προσαναταισµού Β Λυκείου. Η έννοια του διανύσµατος. Πρόσθεση & αφαίρεση διανυσµάτων 33. Βαθµωτός ποαπασιασµός 44. Συντεταγµένες 55. Εσωτερικό γινόµενο Παραουσίαση βιβίου
ΕΡΓΑΣΙΑ 6. Ημερομηνία Παράδοσης: 29/6/09
 ΕΡΓΑΣΙΑ 6 Ημερομηνία Παράδοσης: 9/6/9 1. Ένας ομογενώς φορτισμένος μονωτικός κυκλικός δίσκος ακτίνας με συνολικό φορτίο τοποθετείται στο επίπεδο xy. Να βρείτε το ηλεκτρικό πεδίο σε σημείο P που βρίσκεται
ΕΡΓΑΣΙΑ 6 Ημερομηνία Παράδοσης: 9/6/9 1. Ένας ομογενώς φορτισμένος μονωτικός κυκλικός δίσκος ακτίνας με συνολικό φορτίο τοποθετείται στο επίπεδο xy. Να βρείτε το ηλεκτρικό πεδίο σε σημείο P που βρίσκεται
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Μηχανική Ι 17 Φεβρουαρίου 2015
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Μηχανική Ι 17 Φεβρουαρίου 2015 Τμήμα Θ. Αποστολάτου & Π. Ιωάννου Απαντήστε και στα 4 προβλήματα με σαφήνεια και απλότητα. Οι ολοκληρωμένες απαντήσεις στα ερωτήματα εκτιμώνται
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Μηχανική Ι 17 Φεβρουαρίου 2015 Τμήμα Θ. Αποστολάτου & Π. Ιωάννου Απαντήστε και στα 4 προβλήματα με σαφήνεια και απλότητα. Οι ολοκληρωμένες απαντήσεις στα ερωτήματα εκτιμώνται
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Κβαντομηχανική Ι 6o Σετ Ασκήσεων. Άσκηση 1
 Χειμερινό εξάμηνο 6-7 Κβαντομηχανική Ι 6o Σετ Ασκήσεων Άσκηση a) Τρόπος α : Λύνουμε όλους (ή έστω μερικούς από) τους συνδυασμούς [l i, r j ]: [l x, x] = [l y, y] = [l z, x] = i ħ y Κ.ο.κ., και συμπεραίνουμε
Χειμερινό εξάμηνο 6-7 Κβαντομηχανική Ι 6o Σετ Ασκήσεων Άσκηση a) Τρόπος α : Λύνουμε όλους (ή έστω μερικούς από) τους συνδυασμούς [l i, r j ]: [l x, x] = [l y, y] = [l z, x] = i ħ y Κ.ο.κ., και συμπεραίνουμε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Πτυχιακή εξέταση στη Μηχανική ΙI 20 Σεπτεμβρίου 2007
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Πτυχιακή εξέταση στη Μηχανική ΙI 0 Σεπτεμβρίου 007 Τμήμα Π. Ιωάννου & Θ. Αποστολάτου Απαντήστε στα ερωτήματα που ακολουθούν με σαφήνεια, ακρίβεια και απλότητα. Όλα τα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Πτυχιακή εξέταση στη Μηχανική ΙI 0 Σεπτεμβρίου 007 Τμήμα Π. Ιωάννου & Θ. Αποστολάτου Απαντήστε στα ερωτήματα που ακολουθούν με σαφήνεια, ακρίβεια και απλότητα. Όλα τα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Εξετάσεις στη ΜΗΧΑΝΙΚΗ Ι 26 Ιανουαρίου 2016
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Εξετάσεις στη ΜΗΧΑΝΙΚΗ Ι 26 Ιανουαρίου 2016 Τμήμα Π. Ιωάννου & Θ. Αποστολάτου Στις παρενθέσεις δίνονται τα μόρια του κάθε ερωτήματος. Σε ένα σωματίδιο που κινείται στον
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Εξετάσεις στη ΜΗΧΑΝΙΚΗ Ι 26 Ιανουαρίου 2016 Τμήμα Π. Ιωάννου & Θ. Αποστολάτου Στις παρενθέσεις δίνονται τα μόρια του κάθε ερωτήματος. Σε ένα σωματίδιο που κινείται στον
Δομή Διάλεξης. Ορισμός Ηλεκτρικού Δυναμικού και συσχέτιση με το Ηλεκτρικό Πεδίο
 Ηλεκτρικό Δυναμικό Δομή Διάλεξης Ορισμός Ηλεκτρικού Δυναμικού και συσχέτιση με το Ηλεκτρικό Πεδίο Ιδιότητες ηλεκτρικού δυναμικού (χρησιμότητα σε υπολογισμούς, σημείο αναφοράς, αρχή υπέρθεσης) Διαφορικές
Ηλεκτρικό Δυναμικό Δομή Διάλεξης Ορισμός Ηλεκτρικού Δυναμικού και συσχέτιση με το Ηλεκτρικό Πεδίο Ιδιότητες ηλεκτρικού δυναμικού (χρησιμότητα σε υπολογισμούς, σημείο αναφοράς, αρχή υπέρθεσης) Διαφορικές
E = P t = IAt = Iπr 2 t = J (1)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-112: Φυσική Ι Χειµερινό Εξάµηνο 2016 ιδάσκων : Γ. Καφεντζής Τέταρτη Σειρά Ασκήσεων - Λύσεις Ασκηση 1. Η ενέργεια που παραδίδεται στο αυτί µας σε χρόνο
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-112: Φυσική Ι Χειµερινό Εξάµηνο 2016 ιδάσκων : Γ. Καφεντζής Τέταρτη Σειρά Ασκήσεων - Λύσεις Ασκηση 1. Η ενέργεια που παραδίδεται στο αυτί µας σε χρόνο
Λύσεις Προαιρετικής Eργασίας Τεχνικές Εκτίμησης
 Λύσεις Προαιρετικής Eργασίας Τεχνικές Εκτίμησης 2010-2011 kolako@ced.upatras.gr 10 Μαρτίου 2011 Πρόβημα 1 Ερώτημα ) Έστω W S και W B ο μέσος χρόνος αναμονής στην ουρά του σταθμού S και B αντίστοιχα. Λαμβάνοντας
Λύσεις Προαιρετικής Eργασίας Τεχνικές Εκτίμησης 2010-2011 kolako@ced.upatras.gr 10 Μαρτίου 2011 Πρόβημα 1 Ερώτημα ) Έστω W S και W B ο μέσος χρόνος αναμονής στην ουρά του σταθμού S και B αντίστοιχα. Λαμβάνοντας
Τρίτη, 31 Μαΐου 2005 Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΜΑΘΗΜΑΤΙΚΑ
 ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 5 Τρίτη, Μαΐου 5 Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΜΑΘΗΜΑΤΙΚΑ ΘΕΜΑ o A.. Έστω µια συνάρτηση f, η οποία είναι ορισµένη σε ένα κειστό διάστηµα [α, β]. Αν η f είναι συνεχής στο [α, β] και f(α) f(β)
ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 5 Τρίτη, Μαΐου 5 Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΜΑΘΗΜΑΤΙΚΑ ΘΕΜΑ o A.. Έστω µια συνάρτηση f, η οποία είναι ορισµένη σε ένα κειστό διάστηµα [α, β]. Αν η f είναι συνεχής στο [α, β] και f(α) f(β)
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
L2 {mk. K Z 1Z 2 e 2. v 8 ě 4 ˆ 10 7 m/s. Z 2 79, e 1.6ˆ10 19 C, 9ˆ10 9 Nm 2 /C 2
 Ονοματεπώνυμο: Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών, Τμήμα Φυσικής Εξετάσεις στη Μηχανική Ι, Τμήμα Κ. Τσίγκανου & Ν. Βαχάκη, Ιανουαρίου Διάρκεια εξέτασης 3 ώρες, Καή επιτυχία ( = bonus ερωτήματα),
Ονοματεπώνυμο: Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών, Τμήμα Φυσικής Εξετάσεις στη Μηχανική Ι, Τμήμα Κ. Τσίγκανου & Ν. Βαχάκη, Ιανουαρίου Διάρκεια εξέτασης 3 ώρες, Καή επιτυχία ( = bonus ερωτήματα),
( ) ( ) ( ) ( ) ( ) ( )
 ΕΠΙΤΡΟΠΗ ΔΙΑΓΩΝΙΣΜΩΝ η Εηνική Μαθηματική Ουμπιάδα "Ο Αρχιμήδης" ΣΑΒΒΑΤΟ, ΦΕΒΡΟΥΑΡΙΟΥ 009 ΟΙ ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ Θέματα μεγάων τάξεων ΠΡΟΒΛΗΜΑ Να προσδιορίσετε τις τιμές του θετικού ακέραιου 9n Α n 7 είναι
ΕΠΙΤΡΟΠΗ ΔΙΑΓΩΝΙΣΜΩΝ η Εηνική Μαθηματική Ουμπιάδα "Ο Αρχιμήδης" ΣΑΒΒΑΤΟ, ΦΕΒΡΟΥΑΡΙΟΥ 009 ΟΙ ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ Θέματα μεγάων τάξεων ΠΡΟΒΛΗΜΑ Να προσδιορίσετε τις τιμές του θετικού ακέραιου 9n Α n 7 είναι
14. ΜΕΘΟ ΟΙ ΓΙΑ ΤΗΝ ΕΠΙΛΥΣΗ ΜΗ-ΓΡΑΜΜΙΚΩΝ ΠΡΟΒΛΗΜΑΤΩΝ
 4. ΜΕΘΟ ΟΙ ΓΙΑ ΤΗΝ ΕΠΙΛΥΣΗ ΜΗ-ΓΡΑΜΜΙΚΩΝ ΠΡΟΒΛΗΜΑΤΩΝ 4. Η µέθοδος Newn-Raphsn για µη γραµµική ανάυση Η γενική εξίσωση ισορροπίας ενός µη γραµµικού συστήµατος γράφεται: F ( ) = F q () όπου είναι οι εσωτερικές
4. ΜΕΘΟ ΟΙ ΓΙΑ ΤΗΝ ΕΠΙΛΥΣΗ ΜΗ-ΓΡΑΜΜΙΚΩΝ ΠΡΟΒΛΗΜΑΤΩΝ 4. Η µέθοδος Newn-Raphsn για µη γραµµική ανάυση Η γενική εξίσωση ισορροπίας ενός µη γραµµικού συστήµατος γράφεται: F ( ) = F q () όπου είναι οι εσωτερικές
14 ΚΑΜΠΥΛΟΓΡΑΜΜΕΣ ΣΥΝΤΕΤΑΓΜΕΝΕΣ
 SECTION 4 ΚΑΜΠΥΛΟΓΡΑΜΜΕΣ ΣΥΝΤΕΤΑΓΜΕΝΕΣ 4. Γενικοί Ορισµοί Η θέση ενός σηµείου P στον τρισδιάστατο Ευκλείδειο χώρο µπορεί να καθορισθεί µε ορθογώνιες καρτεσιανές συντεταγµένες (x y οι οποίες µετριώνται
SECTION 4 ΚΑΜΠΥΛΟΓΡΑΜΜΕΣ ΣΥΝΤΕΤΑΓΜΕΝΕΣ 4. Γενικοί Ορισµοί Η θέση ενός σηµείου P στον τρισδιάστατο Ευκλείδειο χώρο µπορεί να καθορισθεί µε ορθογώνιες καρτεσιανές συντεταγµένες (x y οι οποίες µετριώνται
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Μαθηματικά για μηχανικούς ΙΙ ΑΣΚΗΣΕΙΣ
 Μαθηματικά για μηχανικούς ΙΙ ΑΣΚΗΣΕΙΣ Κεφάλαιο 1 1 Να βρείτε (και να σχεδιάσετε) το πεδίο ορισμού των πιο κάτω συναρτήσεων f (, ) 9 4 (γ) f (, ) f (, ) 16 4 1 Να υπολογίσετε το κάθε όριο αν υπάρχει ή να
Μαθηματικά για μηχανικούς ΙΙ ΑΣΚΗΣΕΙΣ Κεφάλαιο 1 1 Να βρείτε (και να σχεδιάσετε) το πεδίο ορισμού των πιο κάτω συναρτήσεων f (, ) 9 4 (γ) f (, ) f (, ) 16 4 1 Να υπολογίσετε το κάθε όριο αν υπάρχει ή να
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Μηχανική Ι 24 Σεπτεμβρίου 2018
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Μηχανική Ι 24 Σεπτεμβρίου 2018 Καλή σας επιτυχία. Σύνολο πόντων 130. Τμήμα Π. Ιωάννου & Θ. Αποστολάτου Πρόβλημα Α 1. Να γραφεί το διάνυσμα της έντασης του βαρυτικού πεδίου
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Μηχανική Ι 24 Σεπτεμβρίου 2018 Καλή σας επιτυχία. Σύνολο πόντων 130. Τμήμα Π. Ιωάννου & Θ. Αποστολάτου Πρόβλημα Α 1. Να γραφεί το διάνυσμα της έντασης του βαρυτικού πεδίου
Δομή Διάλεξης. Εύρεση επαγόμενων επιφανειακών φορτίων. Εύρεση δύναμης που ασκείται στο πραγματικό φορτίο και αποθηκευμένης ηλεκτροστατικής ενέργειας.
 Μέθοδος Ειδώλων Δομή Διάλεξης 1 ο παράδειγμα εφαρμογής μεθόδου ειδώλων για εύρεση δυναμικού με δεδομένες οριακές συνθήκες και ύπαρξη συμμετρίας: Φορτίο πάνω από άπειρο επίπεδο αγωγό. Εύρεση επαγόμενων
Μέθοδος Ειδώλων Δομή Διάλεξης 1 ο παράδειγμα εφαρμογής μεθόδου ειδώλων για εύρεση δυναμικού με δεδομένες οριακές συνθήκες και ύπαρξη συμμετρίας: Φορτίο πάνω από άπειρο επίπεδο αγωγό. Εύρεση επαγόμενων
ΠΡΟΣΑΡΜΟΓΗ ( )( ) αν R 0 και G 0 τότε θεωρούμε ότι η γραμμή μεταφοράς δεν έχει απώλειες και ο παράγοντας διάδοσης γίνεται: L C
 ΠΡΟΣΑΡΜΟΓΗ. ΓΡΑΜΜΗ ΜΕΤΑΦΟΡΑΣ ΧΩΡΙΣ ΑΠΩΛΕΙΕΣ Ο παράγοντας διάδοσης μιας γραμμής μεταφοράς είναι: γ zy + jω G + jωc α+ jβ αν και G τότε θεωρούμε ότι η γραμμή μεταφοράς δεν έχει απώειες και ο παράγοντας διάδοσης
ΠΡΟΣΑΡΜΟΓΗ. ΓΡΑΜΜΗ ΜΕΤΑΦΟΡΑΣ ΧΩΡΙΣ ΑΠΩΛΕΙΕΣ Ο παράγοντας διάδοσης μιας γραμμής μεταφοράς είναι: γ zy + jω G + jωc α+ jβ αν και G τότε θεωρούμε ότι η γραμμή μεταφοράς δεν έχει απώειες και ο παράγοντας διάδοσης
ΣΗΜΕΙΩΣΕΙΣ ΣΤΟΙΧΕΙΑ ΔΙΑΝΥΣΜΑΤΙΚΗΣ ΑΝΑΛΥΣΗΣ
 ΣΗΜΕΙΩΣΕΙΣ ΣΤΟΙΧΕΙΑ ΙΑΝΥΣΜΑΤΙΚΗΣ ΑΝΑΛΥΣΗΣ Σκοπός Σκοπός του κεφαλαίου είναι η ανασκόπηση βασικών μαθηματικών εργαλείων που αφορούν τη μελέτη διανυσματικών συναρτήσεων [π.χ. E(, t) ]. Τα εργαλεία αυτά είναι
ΣΗΜΕΙΩΣΕΙΣ ΣΤΟΙΧΕΙΑ ΙΑΝΥΣΜΑΤΙΚΗΣ ΑΝΑΛΥΣΗΣ Σκοπός Σκοπός του κεφαλαίου είναι η ανασκόπηση βασικών μαθηματικών εργαλείων που αφορούν τη μελέτη διανυσματικών συναρτήσεων [π.χ. E(, t) ]. Τα εργαλεία αυτά είναι
Πυκνότητα φορτίου. dq dv. Μικρή Περιοχή. φορτίου. Χωρική ρ Q V. Επιφανειακή σ. dq da Γραµµική λ Q A. σ = dq dl. Q l. Γ.
 Πυκνότητα φορτίου Πυκνότητα φορτίου Οµοιόµορφη Μικρή Περιοχή Χωρική ρ Q V ρ= dq dv Επιφανειακή σ Q A σ = dq da Γραµµική λ Q l λ= dq dl Γ. Βούλγαρης 1 Παράσταση της έντασης Ηλεκτρικού Πεδίου. Η Εφαπτόµενη
Πυκνότητα φορτίου Πυκνότητα φορτίου Οµοιόµορφη Μικρή Περιοχή Χωρική ρ Q V ρ= dq dv Επιφανειακή σ Q A σ = dq da Γραµµική λ Q l λ= dq dl Γ. Βούλγαρης 1 Παράσταση της έντασης Ηλεκτρικού Πεδίου. Η Εφαπτόµενη
ΗΛΕΚΤΡΙΚΟ ΥΝΑΜΙΚΟ (ΚΕΦΑΛΑΙΟ 23)
 ΗΛΕΚΤΡΙΚΟ ΥΝΑΜΙΚΟ (ΚΕΦΑΛΑΙΟ 23) Υπενθύμιση/Εισαγωγή: Λέμε ότι ένα πεδίο δυνάμεων είναι συντηρητικό (ή διατηρητικό) όταν το έργο που παράγεται από το πεδίο δυνάμεων κατά τη μετατόπιση ενός σώματος από μία
ΗΛΕΚΤΡΙΚΟ ΥΝΑΜΙΚΟ (ΚΕΦΑΛΑΙΟ 23) Υπενθύμιση/Εισαγωγή: Λέμε ότι ένα πεδίο δυνάμεων είναι συντηρητικό (ή διατηρητικό) όταν το έργο που παράγεται από το πεδίο δυνάμεων κατά τη μετατόπιση ενός σώματος από μία
(x(x 2 + y 2 + z 2 ) 1/2,y(x 2 + y 2 + z 2 ) 1/2,z(x 2 + y 2 + z 2 ) 1/2) =0 x y z. div A =0
 1 Pìblhma 1 α) gad = (x 2 + y 2 + z 2 ) 1/2 = (x(x 2 + y 2 + z 2 ) 1/2,y(x 2 + y 2 + z 2 ) 1/2,z(x 2 + y 2 + z 2 ) 1/2) β) = div = x x + y y + z z =3 cul = x y z γ) Εχουμε A = ω x ω y ω z x y z =(ω yz
1 Pìblhma 1 α) gad = (x 2 + y 2 + z 2 ) 1/2 = (x(x 2 + y 2 + z 2 ) 1/2,y(x 2 + y 2 + z 2 ) 1/2,z(x 2 + y 2 + z 2 ) 1/2) β) = div = x x + y y + z z =3 cul = x y z γ) Εχουμε A = ω x ω y ω z x y z =(ω yz
Μαθηματικά για μηχανικούς ΙΙ ΛΥΣΕΙΣ/ΑΠΑΝΤΗΣΕΙΣ ΑΣΚΗΣΕΩΝ
 Μαθηματικά για μηχανικούς ΙΙ ΛΥΣΕΙΣ/ΑΠΑΝΤΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Κεφάλαιο 1 1 Να βρείτε (και να σχεδιάσετε) το πεδίο ορισμού των πιο κάτω συναρτήσεων f (, ) 9 4 (γ) f (, ) f (, ) 16 4 1 D (, ) :9 0, 4 0 (, ) :
Μαθηματικά για μηχανικούς ΙΙ ΛΥΣΕΙΣ/ΑΠΑΝΤΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Κεφάλαιο 1 1 Να βρείτε (και να σχεδιάσετε) το πεδίο ορισμού των πιο κάτω συναρτήσεων f (, ) 9 4 (γ) f (, ) f (, ) 16 4 1 D (, ) :9 0, 4 0 (, ) :
ΑΣΚΗΣΗ-1: ΗΛΕΚΤΡΙΚΑ ΠΕΔΙΑ
 ΑΣΚΗΣΗ-1: ΗΛΕΚΤΡΙΚΑ ΠΕΔΙΑ Ημερομηνία:. ΤΜΗΜΑ:.. ΟΜΑΔΑ:. Ονομ/νυμο: Α.Μ. Συνεργάτες Ονομ/νυμο: Α.Μ. Ονομ/νυμο: Α.Μ. ΠΕΡΙΛΗΨΗ ΤΗΣ ΑΣΚΗΣΗΣ (καθένας με δικά του λόγια, σε όλες τις γραμμές) ΒΑΘΜΟΣ#1: ΥΠΟΓΡΑΦΗ:
ΑΣΚΗΣΗ-1: ΗΛΕΚΤΡΙΚΑ ΠΕΔΙΑ Ημερομηνία:. ΤΜΗΜΑ:.. ΟΜΑΔΑ:. Ονομ/νυμο: Α.Μ. Συνεργάτες Ονομ/νυμο: Α.Μ. Ονομ/νυμο: Α.Μ. ΠΕΡΙΛΗΨΗ ΤΗΣ ΑΣΚΗΣΗΣ (καθένας με δικά του λόγια, σε όλες τις γραμμές) ΒΑΘΜΟΣ#1: ΥΠΟΓΡΑΦΗ:
Ασκήσεις 6 ου Κεφαλαίου
 Ασκήσεις 6 ου Κεφαλαίου 1. Μία ράβδος ΟΑ έχει μήκος l και περιστρέφεται γύρω από τον κατακόρυφο άξονα Οz, που είναι κάθετος στο άκρο της Ο με σταθερή γωνιακή ταχύτητα ω. Να βρεθεί r η επαγώμενη ΗΕΔ στη
Ασκήσεις 6 ου Κεφαλαίου 1. Μία ράβδος ΟΑ έχει μήκος l και περιστρέφεται γύρω από τον κατακόρυφο άξονα Οz, που είναι κάθετος στο άκρο της Ο με σταθερή γωνιακή ταχύτητα ω. Να βρεθεί r η επαγώμενη ΗΕΔ στη
L 2 z. 2mR 2 sin 2 mgr cos θ. 0 π/3 π/2 π L z =0.1 L z = L z =3/ 8 L z = 3-1. V eff (θ) =L z. 2 θ)-cosθ. 2 /(2sin.
 Μηχανική Ι Εργασία #5 Χειμερινό εξάμηνο 15-16 Ν. Βλαχάκης 1. Σημειακό σώμα μάζας m είναι δεμένο σε αβαρές και μη εκτατό νήμα ακτίνας R και κινείται κάτω από την επίδραση του βάρους του mgẑ και της τάσης
Μηχανική Ι Εργασία #5 Χειμερινό εξάμηνο 15-16 Ν. Βλαχάκης 1. Σημειακό σώμα μάζας m είναι δεμένο σε αβαρές και μη εκτατό νήμα ακτίνας R και κινείται κάτω από την επίδραση του βάρους του mgẑ και της τάσης
ΚΕΦΑΛΑΙΟ 2. Τρισδιάστατες κινήσεις
 ΚΕΦΑΛΑΙΟ Τρισδιάστατες κινήσεις Οι µονοδιάστατες κινήσεις είναι εύκολες αλλά ζούµε σε τρισδιάστατο χώρο Θα δούµε λοιπόν τώρα πως θα αντιµετωπίζοµε την κίνηση υλικού σηµείου στις τρεις διαστάσεις Ας θεωρήσοµε
ΚΕΦΑΛΑΙΟ Τρισδιάστατες κινήσεις Οι µονοδιάστατες κινήσεις είναι εύκολες αλλά ζούµε σε τρισδιάστατο χώρο Θα δούµε λοιπόν τώρα πως θα αντιµετωπίζοµε την κίνηση υλικού σηµείου στις τρεις διαστάσεις Ας θεωρήσοµε
