Ορμή - Κρούσεις, ΦΥΣ Διαλ.19 1
|
|
|
- Ἰεφθάε Μαρκόπουλος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Ορμή - Κρούσεις, ΦΥΣ Διαλ.19 1
2 ΦΥΣ Διαλ.19 2 Κρούσεις σε 2 διαστάσεις q Για ελαστικές κρούσεις! p 1 + p! 2 = p! 1! + p! 2! όπου p = (p x,p y ) Δηλαδή είναι 2 εξισώσεις, µια για κάθε διεύθυνση (x,y) και υπάρχει και µια τρίτη εξίσωση λόγω διατήρησης της µηχανικής ενέργειας Αν m 1, m 2, v 1, v 2 είναι γνωστά τότε έχουµε 3 εξισώσεις µε 4 αγνώστους p' 1x, p' 1y, p' 2x, p' 2y Ø Εποµένως χρειαζόµαστε κάτι ακόµα για τη τελική κατάσταση
3 ΦΥΣ Διαλ.19 3 Κρούσεις σε 2 διαστάσεις - Παράδειγµα Ø Το σώμα 1 πριν την κρούση κινείται με ταχύτητα v 1i ενώ το σώμα 2 είναι σε ηρεμία v 2i =0 Πριν τη κρούση Ø Στη x-διεύθυνση η αρχική ορμή είναι m 1 v 1i Ø Στη y-διεύθυνση η αρχική ορμή είναι μηδέν q Μετά την κρούση τα σώματα κινούνται με κάποιες γωνίες θ και φ ως προς την x-διεύθυνση Μετά την κρούση Το σώμα 1 έχει ταχύτητα:! 1x! 2x =! 1 cos" =! 2 cos" q Μετά την κρούση τα σώματα έχουν συνιστώσες ταχύτητας στη y-διεύθυνση. Το σώμα 1 έχει ταχύτητα: ενώ το σώμα 2 έχει ταχύτητα:! 1y! 2y =! 1 sin" =! 2 sin" Η ορµή στην x-διεύθυνση είναι m 1! 1 cos" + m 2! 2 cos# ( ) Η ορµή στην y-διεύθυνση είναι m 1! 2 sin" + m 2! 2 sin #$! m 1 " 2 sin# $ m 2 " 2 sin%! 2y =! 2 sin ("#) (κανονικά )
4 Μεθοδολογία λύσης ασκήσεων q Προσδιορίστε ένα σύστηµα συντεταγµένων και ορίστε τις ταχύτητες των σωµάτων του συστήµατος ως προς τους άξονες αυτού του συστήµατος q Σχεδιάστε και προσδιορίστε όλα τα διανύσµατα των ταχυτήτων και ότι άλλη πληροφορία σας δίνεται στο πρόβληµα q Γράψτε τις εξισώσεις για την x- και y- συνιστώσα της ορµής κάθε σώµατος πριν και µετά την κρούση. Μην ξεχνάτε τα απαραίτητα πρόσηµα ανάλογα µε τη διεύθυνση q Γράψτε τις εξισώσεις για την ολική ορµή του συστήµατος στην x-διεύθυνση πριν και µετά την κρούση και εξισώστε Επαναλάβετε και για την ολική ορµή στην y-διεύθυνση q Εξετάστε το είδος της κρούσης: Ø Για µη ελαστική κρούση, η µηχανική ενέργεια δεν διατηρείται και θα χρειάζεστε και άλλες πληροφορίες από το πρόβληµα. Ø Για πλαστική κρούση, τα σώµατα έχουν την ίδια ταχύτητα µετά την κρούση. Λύστε τις εξισώσεις των ορµών ως προς τους αγνώστους. Ø Για ελαστική κρούση, η µηχανική ενέργεια διατηρείται. Εξισώστε την µηχανική ενέργεια πριν και µετά την κρούση για να βρείτε επιπλέον σχέσεις µεταξύ των ταχυτήτων ΦΥΣ Διαλ.19 4
5 Κρούσεις - Παραδείγματα ΦΥΣ Διαλ.19 5 q Θα αποδείξουμε ότι σε ελαστική μη κεντρική κρούση δύο σωμάτων ίδιας μάζας, ένα εκ των οποίων αρχικά είναι ακίνητο, η γωνία μεταξύ των διανυσμάτων των τελικών ταχυτήτων είναι πάντοτε 90 ο m 1 v 1 Πριν ŷ m 2 q Από διατήρηση της ορμής έχουμε: (1) ˆ x mv = m! v 1 cos" 1 + m! v 2 cos" 2 (2) ˆ y = m! v 1 sin" 1 # m! v 2 sin" 2 q Από διατήρηση της ενέργειας έχουμε: 1 2 mv = 1 2 m v 12! m v! 2 2 (3)! v 2 1 = v 1 " 2 + v "! v 2 1 # v 1 " 2 # v " = 0 Έχουμε 3 εξισώσεις και θέλουμε να ξέρουμε θ 1 +θ 2 xˆ θ 1 θ 2! v 1 = v 1 " cos# 1 + v " 2 cos# 2! 0 = " v 1 sin# 1 $ " v 2 sin# 2 Μετά
6 ΦΥΣ Διαλ.19 6 Παράδειγμα (συνέχεια) Υψώνουμε στο τετράγωνο τις σχέσεις (1) και (2) οπότε και παίρνουμε (1) v 1 = v 1! cos" 1 + v! 2 cos" 2! v 2 1 = v 1 " 2 cos 2 # 1 + " v cos 2 # v 1 " v " 2 cos# 1 cos# 2 (2) 0 = v 1! sin" 1 #! v 2 sin" 2! 0 = v 1 " 2 sin 2 # 1 + v " sin 2 # 2 $ 2 v 1 " v " 2 sin# 1 sin# 2 Προσθέτοντας τις δύο παραπάνω σχέσεις παίρνουμε: v 2 1 = v 1! 2 + v! + 2 v 1! v! 2 (cos" 1 cos" 2 # sin" 1 sin" 2 ) cos(! 1 +! 2 ) = cos! 1 cos! 2 " sin! 1 sin! 2 Άρα καταλήγουμε με την σχέση: (3) v 2 1 = v 1! 2 + v! + 2 v 1! v! 2 cos(" 1 + " 2 ) # v 2 1! v 1 " 2! v " = 2 v 1 " v " 2 cos(# 1 + # 2 ) Το αριστερό μέλος όμως είναι η (3) και επομένως 2 v 1! v! 2 cos(" 1 + " 2 ) = 0 # cos(" 1 + " 2 ) = 0 # " 1 + " 2 = 90 0 Σε 2-D τα σώματα είναι 90 ο μακριά. Για 1-D η θ 1 δεν ορίζεται
7 ΦΥΣ Διαλ.19 7 Παράδειγμα Ελαστική κρούση που περιέχει μάζες και ελατήρια. v 1 v 2 m 1 m 2 Tη χρονική στιγμή t', η μάζα m 1 έχει ταχύτητα v' 1 και το ελατήριο συσπειρώνεται. Ποια είναι η ταχύτητα v' 2 τη στιγμή t'? Ø Από διατήρηση της ορμής:!!!! m 1 v 1 + m 2 v 2 = m 1 v 1! + m 2 v! 2 Mόνο η v' 2 είναι άγνωστη Ø Από διατήρηση της ενέργειας: 1 2 m 1v m 2v = 1 2 m v 12! m v! Αυτή η σχέση δίνει την συσπείρωση του ελατηρίου την χρονική στιγμή t' kx 2
8 ΦΥΣ Διαλ.19 8 Παράδειγμα - Πλαστική κρούση 1-D m v Πριν M M+m Μετά Από διατήρηση της ορμής: m v! + 0 = (m + M) v!!! v! " =! m v M + m!! v Αν οι μάζες ήταν ίδιες τότε Μ=m και η παραπάνω σχέση δίνει: v! = 2 Παρατηρούμε ότι η κινητική ενέργεια πριν και μετά την κρούση είναι: K i = 1 2 mv2 K = 1 2 (2m) v! 2 = m v2 4 = K i 2 "!K = K " K i = "m v2 4 Ένα μέρος της ενέργειας έχει χαθεί σε μορφή θερμότητας.
9 ΦΥΣ Διαλ.19 9 Παράδειγμα Πλαστική κρούση 2-D m v 30 ο 45 ο u=? 2m θ=? v m Πριν την κρούση p x = mvcos mvcos45 0 p y =!mvsin mvsin45 0 Σύμφωνα με τη διατήρηση της ορμής: p x =! p x p y =! p y (1) (2) Ποια είναι η τελική ταχύτητα u και η γωνία θ? Η ορμή p είναι ένα διάνυσμα. Επομένως όπως έχουμε δει αυτό σημαίνει διατήρηση ως προς κάθε κατεύθυνση (αν ήμασταν στο χώρο 3-d) Μετά την κρούση! p x = 2m" cos#! p y = 2m" sin# Δηλαδή 2 εξισώσεις με 2 αγνώστους (υ και θ) Διαιρώντας την (1) με την (2) έχουμε: 1 2! 1 2 = tan" # " = 7.5 Aπό την εξίσωση: p x = p" x! mv( + ) = 2m# cos 7.5! # = 0.79v
10 ΦΥΣ Διαλ Προβλήματα ορμής/ώθησης με μεταβαλλόμενη μάζα Τρένο κινείται με σταθερή ταχύτητα, v=1m/sec, κάτω από ένα σιλό το οποίο αποθέτει σιτάρι με ρυθμό 1kgr/sec. Τι δύναμη χρειάζεται για να συνεχίσει να κινείται το τρένο? Λύση Ποιο είναι το σύστημά μας? Το τρένο και το σιτάρι στο τρένο dm =1kgr /sec ρυθμός αύξησης του σιταριού dt v Σιτάρι που πέφτει: p x = 0 αλλά υπάρχει p y. Χτυπά στο τρένο, οπότε p y= 0, ενώ αναπτύσσει p x To τρένο πρέπει να προσφέρει τη δύναμη για την αλλαγή αυτή της ορμής Το τρένο έχει σαν «εργαλεία» την κάθετη δύναμη και την τριβή Το σιτάρι ασκεί στο τρένο ίση και αντίθετη δύναμη και το τρένο επιβραδύνεται Η μηχανή είναι αυτή που πρέπει να δώσει την ώθηση που χρειάζεται
11 ΦΥΣ Διαλ Τρένο (συνέχεια) Θεωρείστε ένα μικρό χρονικό διάστημα Δt M = M i + dm dt!t p x i = M i v p x αφού θέλουμε v τρένου =σταθ. I x =!p x = F x!t = p x " = M i + dm # $ dt!t % & ' v " p x i F x = dm dt v =1 m sec!1kgr sec =1N = v dm dt!t # Αλλαγή της μάζας του τρένου Αυτή είναι η δύναμη που πρέπει να αναπτυχθεί από την μηχανή του τρένου ώστε το τρένο να εξακολουθεί να κινείται με σταθερή ταχύτητα
12 ΦΥΣ Διαλ ο Παράδειγμα - Πύραυλοι, αεροπλάνα κλπ q Κίνηση πυραύλων Κλασσικό πρόβλημα Πύραυλος με αρχική μάζα M Π Εκτοξεύει μάζα με ταχύτητα V εκτ (σχετικά με τον πύραυλο). Ποια είναι η ταχύτητα όταν η μάζα του είναι m Λύση Για ένα απομονωμένο σύστημα (πύραυλος-εξάτμιση) ξέρουμε ότι dp dt = 0! p = "#$%. Ας υποθέσουμε ότι η μάζα του πυραύλου αλλάζει από Μ+dm σε Μ και η ταχύτητά του από v σε v+dv dm dm Μ Μ i =M+dm v v-v εκτ Μ v+dv
13 Πύραυλος ΦΥΣ Διαλ Εφαρμόζοντας διατήρηση της ορμής έχουμε: p i = p! ( M + "m)v = M v + "v ( ) + "m( v # v $%& ) ( )! Mv + v"m = Mv + M "v + v"m # v $%& "m! M "v = v #$% "m Έστω τώρα ότι Δt 0 τότε Δm dm και ΔΜ dm ενώ dm = -dm. Δt 0 dm! Mdv = "v #$% dm! dv = "v #$% M v M dm! " dv = #v $%& v i "! v # v i = #v $%& ln M M i M ( )! v = v i " v #$% ln M " ln M i M M ( ) Mi %! v = v i + v "#$ ln M ( i ' * Απειρίζεται καθώς το M & ) 0 Αν η αρχική µάζα του πυραύλου είναι M = 10 x m è v = 2.3v εκτ Αν η µάζα είναι Μ = 100 x m è v = 4.6v εκτ Το κέρδος σε ταχύτητα πολύ μικρό μεγαλώνοντας την μάζα του πυραύλου
Ορμή - Κρούσεις. ΦΥΣ Διαλ.23 1
 Ορμή - Κρούσεις ΦΥΣ 111 - Διαλ.3 1 Χτύπημα καράτε ΦΥΣ 111 - Διαλ.3 q Σπάσιμο μιας σανίδας ξύλου με την ώθηση I = FΔt = Δp = mδυ Δt πολύ μικρό και Δp = σταθ. è F μεγάλη Ø Σώματα: ü Χέρι: M xεριού =3Kg,
Ορμή - Κρούσεις ΦΥΣ 111 - Διαλ.3 1 Χτύπημα καράτε ΦΥΣ 111 - Διαλ.3 q Σπάσιμο μιας σανίδας ξύλου με την ώθηση I = FΔt = Δp = mδυ Δt πολύ μικρό και Δp = σταθ. è F μεγάλη Ø Σώματα: ü Χέρι: M xεριού =3Kg,
Κεφάλαιο 8. Ορμή, ώθηση, κρούσεις
 Κεφάλαιο 8 Ορμή, ώθηση, κρούσεις Στόχοι 8 ου Κεφαλαίου Ορμή και ώθηση. Διατήρηση της ορμής. Μη ελαστικές κρούσεις. Ελαστικές κρούσεις. Κέντρο μάζας. Η μεταβολή της ορμής ενός σωματίου κατά τη διάρκεια
Κεφάλαιο 8 Ορμή, ώθηση, κρούσεις Στόχοι 8 ου Κεφαλαίου Ορμή και ώθηση. Διατήρηση της ορμής. Μη ελαστικές κρούσεις. Ελαστικές κρούσεις. Κέντρο μάζας. Η μεταβολή της ορμής ενός σωματίου κατά τη διάρκεια
Ποια η ταχύτητά του τη στιγµή που έχει περάσει πλήρως από την τρύπα? Λύση µε διατήρηση της ενέργειας. + K f. ! 0 + 0 = mg " L & $ !
 Παράδειγµα Ενέργειες Το ακόλουθο πρόβληµα µπορεί να λυθεί είτε µε χρήση των νόµων του Newton ( F=mα ) ή Διατήρηση ενέργειας. Ένα µικρό τµήµα σχοινιού κρέµεται προς τα κάτω µέσα από µια τρύπα σε λείο τραπέζι.
Παράδειγµα Ενέργειες Το ακόλουθο πρόβληµα µπορεί να λυθεί είτε µε χρήση των νόµων του Newton ( F=mα ) ή Διατήρηση ενέργειας. Ένα µικρό τµήµα σχοινιού κρέµεται προς τα κάτω µέσα από µια τρύπα σε λείο τραπέζι.
Σύστηµα αναφοράς κέντρου µάζας
 ΦΥΣ - Διαλ.6 Σύστηµα αναφοράς κέντρου µάζας Έστω σώµατα µάζας m και m κινούµενα µε ταχύτητες υ και υ Η ταχύτητα του ΚΜ δίνεται από τη σχέση: υ cm = m υ + m υ m + m Σε ένα σύστηµα το οποίο συνδέεται µε
ΦΥΣ - Διαλ.6 Σύστηµα αναφοράς κέντρου µάζας Έστω σώµατα µάζας m και m κινούµενα µε ταχύτητες υ και υ Η ταχύτητα του ΚΜ δίνεται από τη σχέση: υ cm = m υ + m υ m + m Σε ένα σύστηµα το οποίο συνδέεται µε
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα. ΔΙΑΛΕΞΗ 07 Ορμή Κρούσεις ΦΥΣ102 1
 Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 07 Ορμή Κρούσεις ΦΥΣ102 1 Ορμή και Δύναμη Η ορμή p είναι διάνυσμα που ορίζεται από
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 07 Ορμή Κρούσεις ΦΥΣ102 1 Ορμή και Δύναμη Η ορμή p είναι διάνυσμα που ορίζεται από
Έργο Ενέργεια Παραδείγµατα
 ΦΥΣ 131 - Διαλ.17 1 Έργο Ενέργεια Παραδείγµατα Mn Επανάληψη Έργο δύναμης W = Έργο συνισταμένης δυνάμεων W = E "#$ Βαρυτική δυναμική ενέργεια U g " 1 2 F d r Ελαστική δυναμική ενέργεια U " = 1 2 kx 2 ΦΥΣ
ΦΥΣ 131 - Διαλ.17 1 Έργο Ενέργεια Παραδείγµατα Mn Επανάληψη Έργο δύναμης W = Έργο συνισταμένης δυνάμεων W = E "#$ Βαρυτική δυναμική ενέργεια U g " 1 2 F d r Ελαστική δυναμική ενέργεια U " = 1 2 kx 2 ΦΥΣ
ΦΥΣ Πριν αρχίσετε συµπληρώστε τα στοιχεία σας (ονοµατεπώνυµο και αριθµό ταυτότητας).
 ΦΥΣ. 111 2 η Πρόοδος: 24-Νοεµβρίου-2018 Πριν αρχίσετε συµπληρώστε τα στοιχεία σας (ονοµατεπώνυµο και αριθµό ταυτότητας). Ονοµατεπώνυµο Αριθµός Ταυτότητας Απενεργοποιήστε τα κινητά σας. Σας δίνονται 9 προβλήµατα
ΦΥΣ. 111 2 η Πρόοδος: 24-Νοεµβρίου-2018 Πριν αρχίσετε συµπληρώστε τα στοιχεία σας (ονοµατεπώνυµο και αριθµό ταυτότητας). Ονοµατεπώνυµο Αριθµός Ταυτότητας Απενεργοποιήστε τα κινητά σας. Σας δίνονται 9 προβλήµατα
ΦΥΣ 111 Γενική Φυσική Ι 8 η Εργασία Επιστροφή:
 ΦΥΣ 111 Γενική Φυσική Ι 8 η Εργασία Επιστροφή: 09.11.18 1. Μία µάζα 3m που κινείται ανατολικά µε ταχύτητα υ, συγκρούεται πλαστικά µε µια µάζα 2m που κινείται βορειοανατολικά µε ταχύτητα 2υ. Ποιά είναι
ΦΥΣ 111 Γενική Φυσική Ι 8 η Εργασία Επιστροφή: 09.11.18 1. Μία µάζα 3m που κινείται ανατολικά µε ταχύτητα υ, συγκρούεται πλαστικά µε µια µάζα 2m που κινείται βορειοανατολικά µε ταχύτητα 2υ. Ποιά είναι
ΛΥΣΕΙΣ ΔΙΑΓΩΝΙΣΜΑΤΟΣ ΦΕΒΡΟΥΑΡΙΟΥ 2001. + mu 1 2m. + u2. = u 1 + u 2. = mu 1. u 2, u 2. = u2 u 1 + V2 = V1
 ΛΥΣΕΙΣ ΔΙΑΓΩΝΙΣΜΑΤΟΣ ΦΕΒΡΟΥΑΡΙΟΥ 00 ΘΕΜΑ : (α) Ταχύτητα ΚΜ: u KM = mu + mu m = u + u Εποµένως u = u u + u = u u, u = u u + u = u u (β) Διατήρηση ορµής στο ΚΜ: mu + mu = mv + mv u + u = V + V = 0 V = V
ΛΥΣΕΙΣ ΔΙΑΓΩΝΙΣΜΑΤΟΣ ΦΕΒΡΟΥΑΡΙΟΥ 00 ΘΕΜΑ : (α) Ταχύτητα ΚΜ: u KM = mu + mu m = u + u Εποµένως u = u u + u = u u, u = u u + u = u u (β) Διατήρηση ορµής στο ΚΜ: mu + mu = mv + mv u + u = V + V = 0 V = V
ΦΥΣ Πριν αρχίσετε συµπληρώστε τα στοιχεία σας (ονοµατεπώνυµο και αριθµό ταυτότητας).
 ΦΥΣ. 111 2 η Πρόοδος: 24-Νοεµβρίου-2018 Πριν αρχίσετε συµπληρώστε τα στοιχεία σας (ονοµατεπώνυµο και αριθµό ταυτότητας). Ονοµατεπώνυµο Αριθµός Ταυτότητας Απενεργοποιήστε τα κινητά σας. Σας δίνονται 9 προβλήµατα
ΦΥΣ. 111 2 η Πρόοδος: 24-Νοεµβρίου-2018 Πριν αρχίσετε συµπληρώστε τα στοιχεία σας (ονοµατεπώνυµο και αριθµό ταυτότητας). Ονοµατεπώνυµο Αριθµός Ταυτότητας Απενεργοποιήστε τα κινητά σας. Σας δίνονται 9 προβλήµατα
Έργο Ενέργεια. ΦΥΣ 131 - Διαλ.15 1
 Έργο Ενέργεια ΦΥΣ 131 - Διαλ.15 1 ΦΥΣ 131 - Διαλ.15 2 Έργο, Κινητική Ενέργεια και Δυναμική Ενέργεια q Βέλος εκτοξεύεται από ένα τόξο: Ø Η δύναμη μεταβάλλεται καθώς το τόξο επανέρχεται στην αρχική του θέση
Έργο Ενέργεια ΦΥΣ 131 - Διαλ.15 1 ΦΥΣ 131 - Διαλ.15 2 Έργο, Κινητική Ενέργεια και Δυναμική Ενέργεια q Βέλος εκτοξεύεται από ένα τόξο: Ø Η δύναμη μεταβάλλεται καθώς το τόξο επανέρχεται στην αρχική του θέση
Ενδεικτικές Λύσεις. Θέµα Α. (α) υ 2 = 0
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κρούσεις Ενδεικτικές Λύσεις Θέµα Α Α.. Σε κάθε κρούση ανάµεσα σε δύο σώµατα µικρών διαστάσεων : (ϐ) η µεταβολή της ορµής του ενός είναι αντίθετη της µεταβολής της ορµής
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κρούσεις Ενδεικτικές Λύσεις Θέµα Α Α.. Σε κάθε κρούση ανάµεσα σε δύο σώµατα µικρών διαστάσεων : (ϐ) η µεταβολή της ορµής του ενός είναι αντίθετη της µεταβολής της ορµής
ΕΡΓΑΣΙΑ 3 ΟΡΜΗ-ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΟΡΜΗΣ
 ΕΡΓΑΣΙΑ 3 ΟΡΜΗ-ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΟΡΜΗΣ Παρατηρήσεις-Υποδείξεις Μετωπική λέγεται η κρούση κατά την οποία τα διανύσματα των ταχυτήτων πριν την κρούση των σωμάτων που συγκρούονται βρίσκονται στην ίδια ευθεία.
ΕΡΓΑΣΙΑ 3 ΟΡΜΗ-ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΟΡΜΗΣ Παρατηρήσεις-Υποδείξεις Μετωπική λέγεται η κρούση κατά την οποία τα διανύσματα των ταχυτήτων πριν την κρούση των σωμάτων που συγκρούονται βρίσκονται στην ίδια ευθεία.
ΕΛΑΤΗΡΙΟ ΚΑΙ ΕΛΑΣΤΙΚΗ ΚΡΟΥΣΗ
 ΕΛΑΤΗΡΙΟ ΚΑΙ ΕΛΑΣΤΙΚΗ ΚΡΟΥΣΗ Δύο ελαστικές σφαίρες Σ1 και Σ ίδιας µάζας είναι συνδεδεµένες µεταξύ τους µε ιδανικό ελατήριο σταθεράς k το οποίο βρίσκεται στο φυσικό του µήκος lo. Οι σφαίρες αρχικά ηρεµούν
ΕΛΑΤΗΡΙΟ ΚΑΙ ΕΛΑΣΤΙΚΗ ΚΡΟΥΣΗ Δύο ελαστικές σφαίρες Σ1 και Σ ίδιας µάζας είναι συνδεδεµένες µεταξύ τους µε ιδανικό ελατήριο σταθεράς k το οποίο βρίσκεται στο φυσικό του µήκος lo. Οι σφαίρες αρχικά ηρεµούν
( ) Παράδειγµα. Τροχαλία. + ΔE δυν. = E κιν. + E δυν
 ΦΥΣ 111 - Διαλ.33 1 Παράδειγµα Θεωρήστε δυο σώµατα τα οποία συνδέονται µέσω µιας αβαρούς τροχαλίας όπως στο σχήµα. Από διατήρηση ενέργειας υπολογίστε την ταχύτητα των δυο σωµάτων όταν η µάζα m 2 έχει κατέβει
ΦΥΣ 111 - Διαλ.33 1 Παράδειγµα Θεωρήστε δυο σώµατα τα οποία συνδέονται µέσω µιας αβαρούς τροχαλίας όπως στο σχήµα. Από διατήρηση ενέργειας υπολογίστε την ταχύτητα των δυο σωµάτων όταν η µάζα m 2 έχει κατέβει
ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ
 1 ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ 1. Σε κάθε κρούση ισχύει α. η αρχή διατήρησης της μηχανικής ενέργειας. β. η αρχή διατήρησης της ορμής. γ. η αρχή διατήρησης του ηλεκτρικού φορτίου. δ. όλες οι παραπάνω αρχές.
1 ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ 1. Σε κάθε κρούση ισχύει α. η αρχή διατήρησης της μηχανικής ενέργειας. β. η αρχή διατήρησης της ορμής. γ. η αρχή διατήρησης του ηλεκτρικού φορτίου. δ. όλες οι παραπάνω αρχές.
ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 3//7/2013 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΑΠΑΝΤΗΣΕΙΣ ΓΡΑΠΤΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ
 ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 3//7/013 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΑΠΑΝΤΗΣΕΙΣ ΓΡΑΠΤΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ ΩΡΕΣ ΑΣΚΗΣΗ 1 Σώμα μάζας m=0.1 Kg κινείται σε οριζόντιο δάπεδο ευθύγραμμα με την
ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 3//7/013 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΑΠΑΝΤΗΣΕΙΣ ΓΡΑΠΤΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ ΩΡΕΣ ΑΣΚΗΣΗ 1 Σώμα μάζας m=0.1 Kg κινείται σε οριζόντιο δάπεδο ευθύγραμμα με την
ΕΡΓΑΣΙΑ 3 ΟΡΜΗ-ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΟΡΜΗΣ
 ΕΡΓΑΣΙΑ 3 ΟΡΜΗ-ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΟΡΜΗΣ Παρατηρήσεις-Υποδείξεις Μετωπική λέγεται η κρούση κατά την οποία τα διανύσματα των ταχυτήτων πριν την κρούση των σωμάτων που συγκρούονται βρίσκονται στην ίδια ευθεία.
ΕΡΓΑΣΙΑ 3 ΟΡΜΗ-ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΟΡΜΗΣ Παρατηρήσεις-Υποδείξεις Μετωπική λέγεται η κρούση κατά την οποία τα διανύσματα των ταχυτήτων πριν την κρούση των σωμάτων που συγκρούονται βρίσκονται στην ίδια ευθεία.
Κίνηση σε δύο διαστάσεις
 ΦΥΣ 131 - Διαλ.07 1 Κίνηση σε δύο διαστάσεις Διαδρομή του σώματος Τελική θέση Αρχική θέση Η κίνηση που κάνει το αυτοκίνητο καθώς στρίβει περιορίζεται σε ένα οριζόντιο επίπεδο - Η αλλαγή στο διάνυσμα θέσης
ΦΥΣ 131 - Διαλ.07 1 Κίνηση σε δύο διαστάσεις Διαδρομή του σώματος Τελική θέση Αρχική θέση Η κίνηση που κάνει το αυτοκίνητο καθώς στρίβει περιορίζεται σε ένα οριζόντιο επίπεδο - Η αλλαγή στο διάνυσμα θέσης
Κέντρο Μάζας - Παράδειγμα
 Κέντρο Μάζας - Παράδειγμα ΦΥΣ 131 - Διαλ.1 1 Ο Ρωμαίο (m R =77kg) διασκεδάζει την Ιουλιέτα (m I =55kg) παίζοντας την κιθάρα του καθισμένος στην πρύμνη της βάρκας τους (μήκους.7 m) που είναι ακίνητη στα
Κέντρο Μάζας - Παράδειγμα ΦΥΣ 131 - Διαλ.1 1 Ο Ρωμαίο (m R =77kg) διασκεδάζει την Ιουλιέτα (m I =55kg) παίζοντας την κιθάρα του καθισμένος στην πρύμνη της βάρκας τους (μήκους.7 m) που είναι ακίνητη στα
Κεφάλαιο Μ9. Ορµή και κρούση
 Κεφάλαιο Μ9 Ορµή και κρούση Μοντέλα ανάλυσης µε βάση την ορµή Η δύναµη και η επιτάχυνση συνδέονται µέσω του δεύτερου νόµου του Νεύτωνα. Όταν η δύναµη και η επιτάχυνση µεταβάλλονται ως προς τον χρόνο, η
Κεφάλαιο Μ9 Ορµή και κρούση Μοντέλα ανάλυσης µε βάση την ορµή Η δύναµη και η επιτάχυνση συνδέονται µέσω του δεύτερου νόµου του Νεύτωνα. Όταν η δύναµη και η επιτάχυνση µεταβάλλονται ως προς τον χρόνο, η
1. Κινηµατική. x dt (1.1) η ταχύτητα είναι. και η επιτάχυνση ax = lim = =. (1.2) Ο δεύτερος νόµος του Νεύτωνα παίρνει τη µορφή: (1.
 1. Κινηµατική Βιβλιογραφία C. Kittel W. D. Knight M. A. Rueman A. C. Helmholz και B. J. Moe Μηχανική. Πανεπιστηµιακές Εκδόσεις Ε.Μ.Π. 1998. Κεφ.. {Μαθηµατικό Συµπλήρωµα Μ1 Παράγωγος} {Μαθηµατικό Συµπλήρωµα
1. Κινηµατική Βιβλιογραφία C. Kittel W. D. Knight M. A. Rueman A. C. Helmholz και B. J. Moe Μηχανική. Πανεπιστηµιακές Εκδόσεις Ε.Μ.Π. 1998. Κεφ.. {Μαθηµατικό Συµπλήρωµα Μ1 Παράγωγος} {Μαθηµατικό Συµπλήρωµα
2. Οι νόµοι της κίνησης, οι δυνάµεις και οι εξισώσεις κίνησης
 Οι νόµοι της κίνησης, οι δυνάµεις και οι εξισώσεις κίνησης Βιβλιογραφία C Kittel, W D Knight, A Rudeman, A C Helmholz και B J oye, Μηχανική (Πανεπιστηµιακές Εκδόσεις ΕΜΠ, 1998) Κεφ, 3 R Spiegel, Θεωρητική
Οι νόµοι της κίνησης, οι δυνάµεις και οι εξισώσεις κίνησης Βιβλιογραφία C Kittel, W D Knight, A Rudeman, A C Helmholz και B J oye, Μηχανική (Πανεπιστηµιακές Εκδόσεις ΕΜΠ, 1998) Κεφ, 3 R Spiegel, Θεωρητική
ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ ΠΛΑΓΙΑ ΠΛΑΣΤΙΚΗ ΚΡΟΥΣΗ ΚΑΙ ΤΑΛΑΝΤΩΣΗ
 ΤΑΛΑΝΤΩΣΗ ΜΕΤΑ ΑΠΟ ΠΛΑΓΙΑ ΚΡΟΥΣΗ.. Σώμα που κινείται με κάποια ταχύτητα που σχηματίζει γωνία ως προς το κεκλιμένο επίπεδο συγκρούεται πλαστικά με άλλο σώμα δεμένο στο άκρο οριζοντίου ελατηρίου. Ξύλινο
ΤΑΛΑΝΤΩΣΗ ΜΕΤΑ ΑΠΟ ΠΛΑΓΙΑ ΚΡΟΥΣΗ.. Σώμα που κινείται με κάποια ταχύτητα που σχηματίζει γωνία ως προς το κεκλιμένο επίπεδο συγκρούεται πλαστικά με άλλο σώμα δεμένο στο άκρο οριζοντίου ελατηρίου. Ξύλινο
1. Για το σύστηµα που παριστάνεται στο σχήµα θεωρώντας ότι τα νήµατα είναι αβαρή και µη εκτατά, τις τροχαλίες αµελητέας µάζας και. = (x σε μέτρα).
 Θέμα ο. ια το σύστηµα που παριστάνεται στο σχήµα θεωρώντας ότι τα νήµατα είναι αβαρή και µη εκτατά, τις τροχαλίες αµελητέας µάζας και M= M = M, υπολογίστε την επιτάχυνση της µάζας. ίνεται το g. (0) Λύση.
Θέμα ο. ια το σύστηµα που παριστάνεται στο σχήµα θεωρώντας ότι τα νήµατα είναι αβαρή και µη εκτατά, τις τροχαλίες αµελητέας µάζας και M= M = M, υπολογίστε την επιτάχυνση της µάζας. ίνεται το g. (0) Λύση.
ΦΥΣ η Πρόοδος: 18-Νοεµβρίου-2017
 ΦΥΣ. 111 2 η Πρόοδος: 18-Νοεµβρίου-2017 Πριν αρχίσετε συµπληρώστε τα στοιχεία σας (ονοµατεπώνυµο και αριθµό ταυτότητας). Ονοµατεπώνυµο Αριθµός Ταυτότητας Απενεργοποιήστε τα κινητά σας. Η εξέταση αποτελείται
ΦΥΣ. 111 2 η Πρόοδος: 18-Νοεµβρίου-2017 Πριν αρχίσετε συµπληρώστε τα στοιχεία σας (ονοµατεπώνυµο και αριθµό ταυτότητας). Ονοµατεπώνυµο Αριθµός Ταυτότητας Απενεργοποιήστε τα κινητά σας. Η εξέταση αποτελείται
ΦΥΣ η Πρόοδος: 18-Νοεµβρίου-2017
 ΦΥΣ. 111 2 η Πρόοδος: 18-Νοεµβρίου-2017 Πριν αρχίσετε συµπληρώστε τα στοιχεία σας (ονοµατεπώνυµο και αριθµό ταυτότητας). Ονοµατεπώνυµο Αριθµός Ταυτότητας Απενεργοποιήστε τα κινητά σας. Η εξέταση αποτελείται
ΦΥΣ. 111 2 η Πρόοδος: 18-Νοεµβρίου-2017 Πριν αρχίσετε συµπληρώστε τα στοιχεία σας (ονοµατεπώνυµο και αριθµό ταυτότητας). Ονοµατεπώνυµο Αριθµός Ταυτότητας Απενεργοποιήστε τα κινητά σας. Η εξέταση αποτελείται
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ
 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ Διατήρηση Ορμής Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός htt://hyiccore.wordre.co/ Βασικές Έννοιες Μέχρι τώρα έχουμε ασχοληθεί με την μελέτη ενός σώματος και μόνο. Πλέον
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ Διατήρηση Ορμής Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός htt://hyiccore.wordre.co/ Βασικές Έννοιες Μέχρι τώρα έχουμε ασχοληθεί με την μελέτη ενός σώματος και μόνο. Πλέον
Κίνηση σε μία διάσταση
 Κίνηση σε μία διάσταση ΦΥΣ 131 - Διαλ.5 1 q Ανακεφαλαιώνοντας θέσης τροχιάς μετατόπισης Δx = x f - x i, χρονικού διαστήματος Δ = f i, μέση ταχύτητα v = x x στιγμιαία ταχύτητα x v = lim " = d x d παράγωγος
Κίνηση σε μία διάσταση ΦΥΣ 131 - Διαλ.5 1 q Ανακεφαλαιώνοντας θέσης τροχιάς μετατόπισης Δx = x f - x i, χρονικού διαστήματος Δ = f i, μέση ταχύτητα v = x x στιγμιαία ταχύτητα x v = lim " = d x d παράγωγος
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ Ι Φεβρουάριος 2004
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ Ι Φεβρουάριος 4 Τµήµα Π. Ιωάννου & Θ. Αποστολάτου Απαντήστε µε σαφήνεια και συντοµία. Η ορθή πλήρης απάντηση θέµατος εκτιµάται περισσότερο από τη
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ Ι Φεβρουάριος 4 Τµήµα Π. Ιωάννου & Θ. Αποστολάτου Απαντήστε µε σαφήνεια και συντοµία. Η ορθή πλήρης απάντηση θέµατος εκτιµάται περισσότερο από τη
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ
 7 η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Α ΦΑΣΗ) ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 7 η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Πρώτη Φάση) Κυριακή, 16 Δεκεμβρίου, 01 Προτεινόμενες Λύσεις Πρόβλημα-1 (15 μονάδες) Μια
7 η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Α ΦΑΣΗ) ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 7 η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Πρώτη Φάση) Κυριακή, 16 Δεκεμβρίου, 01 Προτεινόμενες Λύσεις Πρόβλημα-1 (15 μονάδες) Μια
Mηχανή Atwood µε κινούµενη τροχαλία
 ΦΥΣ 131 - Διαλ.11 1 Mηχανή Atwood µε κινούµενη τροχαλία Θεωρείστε τη µηχανή Atwood του σχήµατος. (α) Να γραφούν οι τρεις εξισώσεις Fmα. Θεωρείστε θετική τη φορά προς τα πάνω. (β) Να βρεθεί η επιτάχυνση
ΦΥΣ 131 - Διαλ.11 1 Mηχανή Atwood µε κινούµενη τροχαλία Θεωρείστε τη µηχανή Atwood του σχήµατος. (α) Να γραφούν οι τρεις εξισώσεις Fmα. Θεωρείστε θετική τη φορά προς τα πάνω. (β) Να βρεθεί η επιτάχυνση
Α. Η επιτάχυνση ενός σωματιδίου ως συνάρτηση της θέσης x δίνεται από τη σχέση ax ( ) = bx, όπου b σταθερά ( b= 1 s ). Αν η ταχύτητα στη θέση x
 Εισαγωγή στις Φυσικές Επιστήμες (4 7 09) Μηχανική ΘΕΜΑ Α. Η επιτάχυνση ενός σωματιδίου ως συνάρτηση της θέσης x δίνεται από τη σχέση ax ( ) = bx, όπου b σταθερά ( b= s ). Αν η ταχύτητα στη θέση x 0 = 0
Εισαγωγή στις Φυσικές Επιστήμες (4 7 09) Μηχανική ΘΕΜΑ Α. Η επιτάχυνση ενός σωματιδίου ως συνάρτηση της θέσης x δίνεται από τη σχέση ax ( ) = bx, όπου b σταθερά ( b= s ). Αν η ταχύτητα στη θέση x 0 = 0
4 η Εργασία (Ηµεροµηνία Παράδοσης: 10-5-2004)
 Άσκηση (Μονάδες ) 4 η Εργασία (Ηµεροµηνία Παράδοσης: -5-4) Α) Αστροναύτης µάζας 6 Κg βρίσκεται µέσα σε διαστηµόπλοιο που κινείται µε σταθερή ταχύτητα προς τον Άρη. Σε κάποιο σηµείο του ταξιδιού βρίσκεται
Άσκηση (Μονάδες ) 4 η Εργασία (Ηµεροµηνία Παράδοσης: -5-4) Α) Αστροναύτης µάζας 6 Κg βρίσκεται µέσα σε διαστηµόπλοιο που κινείται µε σταθερή ταχύτητα προς τον Άρη. Σε κάποιο σηµείο του ταξιδιού βρίσκεται
Παράδειγµα διατήρησης στροφορµής
 Παράδειγµα διατήρησης στροφορµής ΦΥΣ 3 - Διαλ.6 Κολόνα πέφτει σε γίγαντα. Δίνονται η µάζα του γίγαντα Μ, της κολόνας m, το µήκος της κολόνας l, η ταχύτητα της κολόνας v. H κίνηση γίνεται σε λεία επιφάνεια.
Παράδειγµα διατήρησης στροφορµής ΦΥΣ 3 - Διαλ.6 Κολόνα πέφτει σε γίγαντα. Δίνονται η µάζα του γίγαντα Μ, της κολόνας m, το µήκος της κολόνας l, η ταχύτητα της κολόνας v. H κίνηση γίνεται σε λεία επιφάνεια.
ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 16/2/2012 ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ A ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ Ι
 ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 6//0 ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ A ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ Ι ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ ΩΡΕΣ ΑΣΚΗΣΗ Σωματίδιο μάζας m = Kg κινείται ευθύγραμμα και ομαλά στον
ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 6//0 ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ A ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ Ι ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ ΩΡΕΣ ΑΣΚΗΣΗ Σωματίδιο μάζας m = Kg κινείται ευθύγραμμα και ομαλά στον
Φυσική Γ Λυκείου. Ορμή. Ορμή συστήματος σωμάτων Τ Υ Π Ο Λ Ο Γ Ι Ο Κ Ρ Ο Υ Σ Ε Ω Ν. Θετικού προσανατολισμού
 Τ Υ Π Ο Λ Ο Γ Ι Ο Κ Ρ Ο Υ Σ Ε Ω Ν Φυσική Γ Λυκείου Θετικού προσανατολισμού Ορμή Ορμή Ρ ενός σώματος ονομάζουμε το διανυσματικό μέγεθος που έχει μέτρο το γινόμενο της μάζας m του σώματος επί την ταχύτητά
Τ Υ Π Ο Λ Ο Γ Ι Ο Κ Ρ Ο Υ Σ Ε Ω Ν Φυσική Γ Λυκείου Θετικού προσανατολισμού Ορμή Ορμή Ρ ενός σώματος ονομάζουμε το διανυσματικό μέγεθος που έχει μέτρο το γινόμενο της μάζας m του σώματος επί την ταχύτητά
Κεφάλαιο 1 : Μετασχηματισμοί Γαλιλαίου.
 Κεφάλαιο : Μετασχηματισμοί Γαλιλαίου.. Γεγονότα, συστήματα αναφοράς και η αρχή της Νευτώνειας Σχετικότητας. Ως φυσικό γεγονός ορίζεται ένα συμβάν το οποίο λαμβάνει χώρα σε ένα σημείο του χώρου μια συγκεκριμένη
Κεφάλαιο : Μετασχηματισμοί Γαλιλαίου.. Γεγονότα, συστήματα αναφοράς και η αρχή της Νευτώνειας Σχετικότητας. Ως φυσικό γεγονός ορίζεται ένα συμβάν το οποίο λαμβάνει χώρα σε ένα σημείο του χώρου μια συγκεκριμένη
1. Σώμα που συγκρούεται ανελαστικά με άλλο σώμα δεμένο στο άκρο οριζοντίου ελατηρίου.
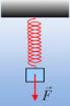 ΤΑΛΑΝΤΩΣΗ ΜΕΤΑ ΑΠΟ ΚΡΟΥΣΗ.. Σώμα που συγκρούεται ανελαστικά με άλλο σώμα δεμένο στο άκρο οριζοντίου ελατηρίου. Σώμα μάζας = g κινείται σε λείο οριζόντιο επίπεδο με ταχύτητα υ μέτρου υ = 5 /s συγκρούεται
ΤΑΛΑΝΤΩΣΗ ΜΕΤΑ ΑΠΟ ΚΡΟΥΣΗ.. Σώμα που συγκρούεται ανελαστικά με άλλο σώμα δεμένο στο άκρο οριζοντίου ελατηρίου. Σώμα μάζας = g κινείται σε λείο οριζόντιο επίπεδο με ταχύτητα υ μέτρου υ = 5 /s συγκρούεται
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις Θέµα Α Α.. Κατά την πλαστική κρούση δύο σωµάτων ισχύει ότι : (δ) η ορµή του συστήµατος των δύο σωµάτων παραµένει
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις Θέµα Α Α.. Κατά την πλαστική κρούση δύο σωµάτων ισχύει ότι : (δ) η ορµή του συστήµατος των δύο σωµάτων παραµένει
Ορμή. Απλούστερη περίπτωση: σύστημα δυο σωματίων, μάζας m 1 και m 2 σε αποστάσεις x 1 και x 2, αντίστοιχα, από την αρχή ενός συστήματος συντεταγμένων
 Y Ορμή ΚΕΝΤΡΟ ΜΑΖΑΣ Όταν ένα σώμα περιστρέφεται ή ταλαντεύεται κατά την κίνησή του, υπάρχει ένα σημείο του σώματος που λέγεται Κέντρο Μάζας, το οποίο κινείται με τον ίδιο τρόπο με τον οποίο θα κινιόταν
Y Ορμή ΚΕΝΤΡΟ ΜΑΖΑΣ Όταν ένα σώμα περιστρέφεται ή ταλαντεύεται κατά την κίνησή του, υπάρχει ένα σημείο του σώματος που λέγεται Κέντρο Μάζας, το οποίο κινείται με τον ίδιο τρόπο με τον οποίο θα κινιόταν
ΦΥΣ. 131 ΕΡΓΑΣΙΑ # 6
 ΦΥΣ. 131 ΕΡΓΑΣΙΑ # 6 1. Ένα αυγό µάζας 0.250kgr πέφτει από ένα ύψος 2.0 στο έδαφος. (α) Υπολογίστε την ώθηση που εξασκεί η δύναµη της βαρύτητας στο αυγό κατά τη διάρκεια της πτώσης του στο έδαφος. (β)
ΦΥΣ. 131 ΕΡΓΑΣΙΑ # 6 1. Ένα αυγό µάζας 0.250kgr πέφτει από ένα ύψος 2.0 στο έδαφος. (α) Υπολογίστε την ώθηση που εξασκεί η δύναµη της βαρύτητας στο αυγό κατά τη διάρκεια της πτώσης του στο έδαφος. (β)
Διαγώνισμα Φυσικής Γ Λυκείου Απλή αρμονική ταλάντωση Κρούσεις
 Διαγώνισμα Φυσικής Γ Λυκείου Απλή αρμονική ταλάντωση Κρούσεις ~ Διάρκεια: 3 ώρες ~ Θέμα Α Α1. Η ορμή συστήματος δύο σωμάτων που συγκρούονται διατηρείται: α. Μόνο στην πλάγια κρούση. β. Μόνο στην έκκεντρη
Διαγώνισμα Φυσικής Γ Λυκείου Απλή αρμονική ταλάντωση Κρούσεις ~ Διάρκεια: 3 ώρες ~ Θέμα Α Α1. Η ορμή συστήματος δύο σωμάτων που συγκρούονται διατηρείται: α. Μόνο στην πλάγια κρούση. β. Μόνο στην έκκεντρη
Στροφορµή. ΦΥΣ 131 - Διαλ.25 1
 Στροφορµή ΦΥΣ 131 - Διαλ.25 1 ΦΥΣ 131 - Διαλ.25 2 Στροφορµή q Ένα από τα βασικά µεγέθη που σχετίζονται µε την περιστροφική κίνηση είναι η στροφορµή q Θυµηθείτε ότι για µάζα m που κινείται µε ταχύτητα v
Στροφορµή ΦΥΣ 131 - Διαλ.25 1 ΦΥΣ 131 - Διαλ.25 2 Στροφορµή q Ένα από τα βασικά µεγέθη που σχετίζονται µε την περιστροφική κίνηση είναι η στροφορµή q Θυµηθείτε ότι για µάζα m που κινείται µε ταχύτητα v
ΦΥΣ Διαλ Σύνοψη εννοιών. Κινηµατική: Περιγραφή της κίνησης ενός σώµατος. Θέση και µετατόπιση Ταχύτητα Μέση Στιγµιαία Επιτάχυνση Μέση
 Κινηµατική ΦΥΣ 111 - Διαλ.04 2 Σύνοψη εννοιών Κινηµατική: Περιγραφή της κίνησης ενός σώµατος Θέση και µετατόπιση Ταχύτητα Μέση Στιγµιαία Επιτάχυνση Μέση Στιγµιαία Κίνηση - Τροχιές ΦΥΣ 111 - Διαλ.04 3!
Κινηµατική ΦΥΣ 111 - Διαλ.04 2 Σύνοψη εννοιών Κινηµατική: Περιγραφή της κίνησης ενός σώµατος Θέση και µετατόπιση Ταχύτητα Μέση Στιγµιαία Επιτάχυνση Μέση Στιγµιαία Κίνηση - Τροχιές ΦΥΣ 111 - Διαλ.04 3!
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 5) - ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α. δ.. β. 3. δ. 4. γ. 5. α.λ, β.λ, γ.σ, δ.λ, ε.σ. ΘΕΜΑ B B. Σωστ απάντηση είναι η (γ). Τα παιδιά πριν
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 5) - ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α. δ.. β. 3. δ. 4. γ. 5. α.λ, β.λ, γ.σ, δ.λ, ε.σ. ΘΕΜΑ B B. Σωστ απάντηση είναι η (γ). Τα παιδιά πριν
4.1. Κρούσεις. Κρούσεις. 4.1.Ταχύτητες κατά την ελαστική κρούση Η Ορμή είναι διάνυσμα. 4.3.Κρούση και Ενέργεια.
 4.1.. 4.1.Ταχύτητες κατά την ελαστική κρούση. Σε λείο οριζόντιο επίπεδο κινείται ένα σώμα Α μάζας m 1 =0,2kg με ταχύτητα υ 1 =6m/s και συγκρούεται κεντρικά και ελαστικά με δεύτερο σώμα Β μάζας m 2 =0,4kg.
4.1.. 4.1.Ταχύτητες κατά την ελαστική κρούση. Σε λείο οριζόντιο επίπεδο κινείται ένα σώμα Α μάζας m 1 =0,2kg με ταχύτητα υ 1 =6m/s και συγκρούεται κεντρικά και ελαστικά με δεύτερο σώμα Β μάζας m 2 =0,4kg.
ΦΥΣ Διάλ Άλγεβρα. 1 a. Άσκηση για το σπίτι: Διαβάστε το παράρτημα Β του βιβλίου
 ΦΥΣ 131 - Διάλ. 4 1 Άλγεβρα a 1 a a ( ± y) a a ± y log a a 10 log a ± logb log( ab ± 1 ) log( a n ) n log( a) ln a a e ln a ± ln b ln( ab ± 1 ) ln( a n ) nln( a) Άσκηση για το σπίτι: Διαβάστε το παράρτημα
ΦΥΣ 131 - Διάλ. 4 1 Άλγεβρα a 1 a a ( ± y) a a ± y log a a 10 log a ± logb log( ab ± 1 ) log( a n ) n log( a) ln a a e ln a ± ln b ln( ab ± 1 ) ln( a n ) nln( a) Άσκηση για το σπίτι: Διαβάστε το παράρτημα
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα. ΔΙΑΛΕΞΗ 03 Νόμοι κίνησης του Νεύτωνα
 Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 03 Νόμοι κίνησης του Νεύτωνα ΦΥΣ102 1 Δύναμη είναι: Η αιτία που προκαλεί μεταβολή
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 03 Νόμοι κίνησης του Νεύτωνα ΦΥΣ102 1 Δύναμη είναι: Η αιτία που προκαλεί μεταβολή
5. Το διάγραμμα του σχήματος παριστάνει την ταχύτητα ενός σώματος που εκτελεί απλή αρμονική ταλάντωση σε συνάρτηση με τον χρόνο.
 ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 9/0/06 ΘΕΜΑ Α Στις ερωτήσεις 7 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Mια μικρή σφαίρα προσκρούει
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 9/0/06 ΘΕΜΑ Α Στις ερωτήσεις 7 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Mια μικρή σφαίρα προσκρούει
 Ασκήσεις Κλασικής Μηχανικής, Τμήμα Μαθηματικών Διδάσκων: Μιχάλης Ξένος, email : mxenos@cc.uoi.gr 19 Απριλίου 2013 Κεφάλαιο Ι 1. Να γραφεί το διάνυσμα της ταχύτητας και της επιτάχυνσης υλικού σημείου σε
Ασκήσεις Κλασικής Μηχανικής, Τμήμα Μαθηματικών Διδάσκων: Μιχάλης Ξένος, email : mxenos@cc.uoi.gr 19 Απριλίου 2013 Κεφάλαιο Ι 1. Να γραφεί το διάνυσμα της ταχύτητας και της επιτάχυνσης υλικού σημείου σε
Α. ο σώμα αρχίζει να κινείται όταν η προωστική δύναμη γίνει ίση με τη δύναμη της τριβής. Έχουμε δηλαδή
 Εισαγωγή στις Φυσικές Επιστήμες (8-7-007) Μηχανική Ονοματεπώνυμο Τμήμα ΘΕΜΑ A. Υλικό σώμα μάζας βρίσκεται σε οριζόντιο επίπεδο με μέγιστο συντελεστή στατικής τριβής η και συντελεστή τριβής ολίσθησης μ.
Εισαγωγή στις Φυσικές Επιστήμες (8-7-007) Μηχανική Ονοματεπώνυμο Τμήμα ΘΕΜΑ A. Υλικό σώμα μάζας βρίσκεται σε οριζόντιο επίπεδο με μέγιστο συντελεστή στατικής τριβής η και συντελεστή τριβής ολίσθησης μ.
Διαγώνισμα Φυσικής Β Λυκείου. ~ Ορμή Διατήρηση ορμής ~
 Διαγώνισμα Φυσικής Β Λυκείου ~ Ορμή Διατήρηση ορμής ~ Θέμα Α Στις παρακάτω ερωτήσεις να επιλέξετε τη σωστή απάντηση. 1) Σε μία πλαστική κρούση δύο σωμάτων: i) Κάθε σώμα υφίσταται μόνιμη παραμόρφωση και
Διαγώνισμα Φυσικής Β Λυκείου ~ Ορμή Διατήρηση ορμής ~ Θέμα Α Στις παρακάτω ερωτήσεις να επιλέξετε τη σωστή απάντηση. 1) Σε μία πλαστική κρούση δύο σωμάτων: i) Κάθε σώμα υφίσταται μόνιμη παραμόρφωση και
Ευθύγραμμη ομαλή κίνηση
 Διάγραμμα s - Ευθύγραμμη Κίνηση (m) Μέση αριθμητική ταχύτητα (μονόμετρο) Μέση διανυσματική ταχύτητα Μέση επιτάχυνση 1 4 Διάγραμμα u - (sec) Απόσταση (x) ονομάζουμε την ευθεία που ενώνει την αρχική και
Διάγραμμα s - Ευθύγραμμη Κίνηση (m) Μέση αριθμητική ταχύτητα (μονόμετρο) Μέση διανυσματική ταχύτητα Μέση επιτάχυνση 1 4 Διάγραμμα u - (sec) Απόσταση (x) ονομάζουμε την ευθεία που ενώνει την αρχική και
p1 p1 p1 p1 p1 p1 p1 mv m p1 m m p1
 ΚΕΦΑΛΑΙΟ 5 Ο, ΕΝΟΤΗΤΑ : ΚΡΟΥΣΕΙΣ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β Ερώτηση. Σώμα Σ μάζας που κινείται προς τα δεξιά στη θετική κατεύθυνση με ταχύτητα μέτρου υ συγκρούεται κεντρικά και πλαστικά με ακίνητο σώμα Σ διπλάσιας
ΚΕΦΑΛΑΙΟ 5 Ο, ΕΝΟΤΗΤΑ : ΚΡΟΥΣΕΙΣ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β Ερώτηση. Σώμα Σ μάζας που κινείται προς τα δεξιά στη θετική κατεύθυνση με ταχύτητα μέτρου υ συγκρούεται κεντρικά και πλαστικά με ακίνητο σώμα Σ διπλάσιας
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/6 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/6 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις - Γ έκδοση
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις - Γ έκδοση Α.1. Κατά την πλαστική κρούση δύο σωµάτων ισχύει ότι : (δ) η ορµή του συστήµατος των δύο σωµάτων παραµένει
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις - Γ έκδοση Α.1. Κατά την πλαστική κρούση δύο σωµάτων ισχύει ότι : (δ) η ορµή του συστήµατος των δύο σωµάτων παραµένει
Τα είδη της κρούσης, ανάλογα µε την διεύθυνση κίνησης των σωµάτων πριν συγκρουστούν. (α ) Κεντρική (ϐ ) Εκκεντρη (γ ) Πλάγια
 8 Κρούσεις Στην µηχανική µε τον όρο κρούση εννοούµε τη σύγκρουση δύο σωµάτων που κινούνται το ένα σχετικά µε το άλλο.το ϕαινόµενο της κρούσης έχει δύο χαρακτηριστικά : ˆ Εχει πολύ µικρή χρονική διάρκεια.
8 Κρούσεις Στην µηχανική µε τον όρο κρούση εννοούµε τη σύγκρουση δύο σωµάτων που κινούνται το ένα σχετικά µε το άλλο.το ϕαινόµενο της κρούσης έχει δύο χαρακτηριστικά : ˆ Εχει πολύ µικρή χρονική διάρκεια.
Περι-Φυσικής. Θέµα Α. ιαγώνισµα - Ενεργειακά εργαλεία στην Μηχανική. Ονοµατεπώνυµο: Βαθµολογία % (α) µόνο από το µέτρο της δύναµης.
 ιαγώνισµα - Ενεργειακά εργαλεία στην Μηχανική Ηµεροµηνία : 31 Μάρτη 2013 ιάρκεια : 3 ώρες Ονοµατεπώνυµο: Βαθµολογία % Θέµα Α Στις ερωτήσεις Α.1 Α.4 επιλέξτε την σωστή απάντηση (4 5 = 20 µονάδες ) Α.1.
ιαγώνισµα - Ενεργειακά εργαλεία στην Μηχανική Ηµεροµηνία : 31 Μάρτη 2013 ιάρκεια : 3 ώρες Ονοµατεπώνυµο: Βαθµολογία % Θέµα Α Στις ερωτήσεις Α.1 Α.4 επιλέξτε την σωστή απάντηση (4 5 = 20 µονάδες ) Α.1.
1. Κίνηση Υλικού Σημείου
 1. Κίνηση Υλικού Σημείου Εισαγωγή στην Φυσική της Γ λυκείου Τροχιά: Ονομάζεται η γραμμή που συνδέει τις διαδοχικές θέσεις του κινητού. Οι κινήσεις ανάλογα με το είδος της τροχιάς διακρίνονται σε: 1. Ευθύγραμμες
1. Κίνηση Υλικού Σημείου Εισαγωγή στην Φυσική της Γ λυκείου Τροχιά: Ονομάζεται η γραμμή που συνδέει τις διαδοχικές θέσεις του κινητού. Οι κινήσεις ανάλογα με το είδος της τροχιάς διακρίνονται σε: 1. Ευθύγραμμες
ΦΥΣ. 131 ΕΡΓΑΣΙΑ # 6
 ΦΥΣ. 131 ΕΡΓΑΣΙΑ # 6 1. Ένα αυγό µάζας 0.250kg πέφτει από ένα ύψος 2.0 m στο έδαφος. (α) Υπολογίστε την ώθηση που εξασκεί η δύναµη της βαρύτητας στο αυγό κατά τη διάρκεια της πτώσης του στο έδαφος. (β)
ΦΥΣ. 131 ΕΡΓΑΣΙΑ # 6 1. Ένα αυγό µάζας 0.250kg πέφτει από ένα ύψος 2.0 m στο έδαφος. (α) Υπολογίστε την ώθηση που εξασκεί η δύναµη της βαρύτητας στο αυγό κατά τη διάρκεια της πτώσης του στο έδαφος. (β)
Κίνηση με σταθερή επιτάχυνση, α(t) =σταθ.
 ΦΥΣ 111 - Διαλ.6 1 Κίνηση με σταθερή επιτάχυνση, α() =σταθ. Από την εξίσωση κίνησης = a( )d + Αντικαθιστώντας στην x = x + ( )d x = x + ( a + )d = x + ( a)d + d = a + (1) x = x + 1 a + () Λύνοντας ως προς
ΦΥΣ 111 - Διαλ.6 1 Κίνηση με σταθερή επιτάχυνση, α() =σταθ. Από την εξίσωση κίνησης = a( )d + Αντικαθιστώντας στην x = x + ( )d x = x + ( a + )d = x + ( a)d + d = a + (1) x = x + 1 a + () Λύνοντας ως προς
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ» 1 o ΔΙΑΓΩΝΙΣΜΑ ΝΟΕΜΒΡΙΟΣ 2018: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ο ΔΙΑΓΩΝΙΣΜΑ ΚΡΟΥΣΕΙΣ - ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Αα. γ Αα. β Α3α. β Α4α. α Αβ. γ Αβ. δ Α3β. δ Α4β. δ Α5. Σ, Λ, Σ, Λ, Σ ΘΕΜΑ Β Β. Σωστή απάντηση η γ. Ισχύει:
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ο ΔΙΑΓΩΝΙΣΜΑ ΚΡΟΥΣΕΙΣ - ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Αα. γ Αα. β Α3α. β Α4α. α Αβ. γ Αβ. δ Α3β. δ Α4β. δ Α5. Σ, Λ, Σ, Λ, Σ ΘΕΜΑ Β Β. Σωστή απάντηση η γ. Ισχύει:
ΚΡΟΥΣΕΙΣ. the flipped class project. Διαφάνειες μαθήματος
 ΚΡΟΥΣΕΙΣ Διαφάνειες μαθήματος Ορμή Κάθε κινούμενο σώμα έχει ορμή και κινητική ενέργεια Η ορμή είναι διανυσματικό μέγεθος Σχέση Κινητικής ενέργειας Ορμής : K K K Kg Σχέση Δύναμης- Ορμής : Η δύναμη (αίτιο)
ΚΡΟΥΣΕΙΣ Διαφάνειες μαθήματος Ορμή Κάθε κινούμενο σώμα έχει ορμή και κινητική ενέργεια Η ορμή είναι διανυσματικό μέγεθος Σχέση Κινητικής ενέργειας Ορμής : K K K Kg Σχέση Δύναμης- Ορμής : Η δύναμη (αίτιο)
0 Φυσική Β Λυκείου Διατήρηση της ορμής. Διατήρηση της ορμής. Κώστας Παρασύρης Φυσικός
 0 Φυσική Β Λυκείου Διατήρηση της ορμής Διατήρηση της ορμής Φυσική Β Λυκείου Διατήρηση της ορμής Σύστημα σωμάτων Εσωτερικές, εξωτερικές δυνάμεις Ως σύστημα στη φυσική θεωρούμε ένα σύνο δύο ή περισσοτέρων
0 Φυσική Β Λυκείου Διατήρηση της ορμής Διατήρηση της ορμής Φυσική Β Λυκείου Διατήρηση της ορμής Σύστημα σωμάτων Εσωτερικές, εξωτερικές δυνάμεις Ως σύστημα στη φυσική θεωρούμε ένα σύνο δύο ή περισσοτέρων
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ
 7 η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Α ΦΑΣΗ) ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 7 η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Πρώτη Φάση) Κυριακή, 16 Δεκεμβρίου, 01 Απενεργοποιήστε τα κινητά σας τηλέφωνα!!! Παρακαλώ
7 η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Α ΦΑΣΗ) ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 7 η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Πρώτη Φάση) Κυριακή, 16 Δεκεμβρίου, 01 Απενεργοποιήστε τα κινητά σας τηλέφωνα!!! Παρακαλώ
ΕΙΣΑΓΩΓΙΚΑ ΣΧΟΛΙΑ Η δύναμη που ασκείται σε ένα σώμα προκαλεί μεταβολή της ταχύτητάς του δηλαδή επιτάχυνση.
 ΕΙΣΑΓΩΓΙΚΑ ΣΧΟΛΙΑ Η δύναμη που ασκείται σε ένα σώμα προκαλεί μεταβολή της ταχύτητάς του δηλαδή επιτάχυνση. Η δύναμη είναι ένα διανυσματικό μέγεθος. Όταν κατά την κίνηση ενός σώματος η δύναμη είναι μηδενική
ΕΙΣΑΓΩΓΙΚΑ ΣΧΟΛΙΑ Η δύναμη που ασκείται σε ένα σώμα προκαλεί μεταβολή της ταχύτητάς του δηλαδή επιτάχυνση. Η δύναμη είναι ένα διανυσματικό μέγεθος. Όταν κατά την κίνηση ενός σώματος η δύναμη είναι μηδενική
ΘΕΜΑ Α: ΔΙΑΡΚΕΙΑ: 180min ΤΜΗΜΑ:. ONOMA/ΕΠΩΝΥΜΟ: ΗΜΕΡΟΜΗΝΙΑ: ΘΕΜΑ 1 ο ΘΕΜΑ 2 ο ΘΕΜΑ 3 ο ΘΕΜΑ 4 ο ΣΥΝΟΛΟ ΜΟΝΑΔΕΣ
 Γ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΔΙΑΡΚΕΙΑ: 8min ONOM/ΕΠΩΝΥΜΟ: ΗΜΕΡΟΜΗΝΙΑ: ΤΜΗΜΑ:. ΘΕΜΑ ο ΘΕΜΑ ο ΘΕΜΑ 3 ο ΘΕΜΑ 4 ο ΣΥΝΟΛΟ ΜΟΝΑΔΕΣ ΘΕΜΑ Α:. Σφαίρα μάζας m = m κινείται με ταχύτητα αλγεβρικής τιμής +υ και συγκρούεται
Γ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΔΙΑΡΚΕΙΑ: 8min ONOM/ΕΠΩΝΥΜΟ: ΗΜΕΡΟΜΗΝΙΑ: ΤΜΗΜΑ:. ΘΕΜΑ ο ΘΕΜΑ ο ΘΕΜΑ 3 ο ΘΕΜΑ 4 ο ΣΥΝΟΛΟ ΜΟΝΑΔΕΣ ΘΕΜΑ Α:. Σφαίρα μάζας m = m κινείται με ταχύτητα αλγεβρικής τιμής +υ και συγκρούεται
1 Η ΠΡΟΟΔΟΣ. Ενδεικτικές λύσεις κάποιων προβλημάτων. Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέτασης
 1 Η ΠΡΟΟΔΟΣ Ενδεικτικές λύσεις κάποιων προβλημάτων Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέτασης Ο Ένα υλικό σημείο κινείται επάνω σε μια ευθεία έτσι ώστε η απομάκρυνση του να δίνεται
1 Η ΠΡΟΟΔΟΣ Ενδεικτικές λύσεις κάποιων προβλημάτων Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέτασης Ο Ένα υλικό σημείο κινείται επάνω σε μια ευθεία έτσι ώστε η απομάκρυνση του να δίνεται
dx cos x = ln 1 + sin x 1 sin x.
 Μηχανική Ι Εργασία #5 Χειμερινό εξάμηνο 17-18 Ν. Βλαχάκης 1. Εστω πεδίο δύναμης F = g () cos y ˆ + λ g() sin y ŷ, όπου λ = σταθερά και g() = 1 e π/ B C (σε κατάλληλες μονάδες). (α) Υπολογίστε πόση ενέργεια
Μηχανική Ι Εργασία #5 Χειμερινό εξάμηνο 17-18 Ν. Βλαχάκης 1. Εστω πεδίο δύναμης F = g () cos y ˆ + λ g() sin y ŷ, όπου λ = σταθερά και g() = 1 e π/ B C (σε κατάλληλες μονάδες). (α) Υπολογίστε πόση ενέργεια
1 η ΟΜΑΔΑ. ΦΥΣ η Πρόοδος: 15-Νοεµβρίου-2008
 η ΟΜΑΔΑ Σειρά Θέση ΦΥΣ. 3 η Πρόοδος: 5-Νοεµβρίου-008 Πριν αρχίσετε συµπληρώστε τα στοιχεία σας (ονοµατεπώνυµο και αριθµό ταυτότητας). Ονοµατεπώνυµο Αριθµός ταυτότητας Η εξέταση αποτελείται από µέρη. Το
η ΟΜΑΔΑ Σειρά Θέση ΦΥΣ. 3 η Πρόοδος: 5-Νοεµβρίου-008 Πριν αρχίσετε συµπληρώστε τα στοιχεία σας (ονοµατεπώνυµο και αριθµό ταυτότητας). Ονοµατεπώνυµο Αριθµός ταυτότητας Η εξέταση αποτελείται από µέρη. Το
ΦΥΣ Διαλ Δυναµική
 ΦΥΣ 131 - Διαλ.08 1 Δυναµική Ø F(δύναµη), m(µάζα), E(ενέργεια), p(ορµή), Ø Πως ένα σώµα αλληλεπιδρά µε το περιβάλλον του Ø Γιατί σώµατα κινούνται µε το τρόπο που κινούνται q Θεµελιώδεις νόµοι της µηχανικής:
ΦΥΣ 131 - Διαλ.08 1 Δυναµική Ø F(δύναµη), m(µάζα), E(ενέργεια), p(ορµή), Ø Πως ένα σώµα αλληλεπιδρά µε το περιβάλλον του Ø Γιατί σώµατα κινούνται µε το τρόπο που κινούνται q Θεµελιώδεις νόµοι της µηχανικής:
ΘΕΩΡΗΤΙΚΗ ΜΗΧΑΝΙΚΗ Ι Φεβρουάριος 2013
 ΘΕΩΡΗΤΙΚΗ ΜΗΧΑΝΙΚΗ Ι Φεβρουάριος 0 ΘΕΜΑ α) Να βρεθούν οι επιτρεπτές περιοχές της κίνησης στον άξονα x Ox για την απωστική δύναµη F x, > 0 και για ενέργεια Ε. β) Υλικό σηµείο µάζας m µπορεί να κινείται
ΘΕΩΡΗΤΙΚΗ ΜΗΧΑΝΙΚΗ Ι Φεβρουάριος 0 ΘΕΜΑ α) Να βρεθούν οι επιτρεπτές περιοχές της κίνησης στον άξονα x Ox για την απωστική δύναµη F x, > 0 και για ενέργεια Ε. β) Υλικό σηµείο µάζας m µπορεί να κινείται
Physics by Chris Simopoulos
 ΟΙ ΝΟΜΟΙ ΤΟΥ ΝΕΥΤΩΝΑ - ΤΡΙΒΗ 1ος νόμος του Νεύτωνα ή νόμος της αδράνειας της ύλης. «Σε κάθε σώμα στο οποίο δεν ενεργούν δυνάμεις ή αν ενεργούν έχουν συνισταμένη μηδέν δεν μεταβάλλεται η κινητική του κατάσταση.
ΟΙ ΝΟΜΟΙ ΤΟΥ ΝΕΥΤΩΝΑ - ΤΡΙΒΗ 1ος νόμος του Νεύτωνα ή νόμος της αδράνειας της ύλης. «Σε κάθε σώμα στο οποίο δεν ενεργούν δυνάμεις ή αν ενεργούν έχουν συνισταμένη μηδέν δεν μεταβάλλεται η κινητική του κατάσταση.
ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β
 ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ : ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β Ερώτηση Ένα σώμα εκτελεί απλή
ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ : ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β Ερώτηση Ένα σώμα εκτελεί απλή
Λυμένες ασκήσεις. Έργο σταθερής δύναμης
 Λυμένες ασκήσεις Έργο σταθερής δύναμης 1. Στο σώμα που απεικονίζεται δίπλα τα μέτρα των δυνάμεων είναι F = 20 N, F 1 = 20 N, T = 5 N, B = 40 N. Το σώμα μετατοπίζεται οριζόντια κατά S = 10 m. Να βρεθούν
Λυμένες ασκήσεις Έργο σταθερής δύναμης 1. Στο σώμα που απεικονίζεται δίπλα τα μέτρα των δυνάμεων είναι F = 20 N, F 1 = 20 N, T = 5 N, B = 40 N. Το σώμα μετατοπίζεται οριζόντια κατά S = 10 m. Να βρεθούν
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ» 1 o ΔΙΑΓΩΝΙΣΜΑ ΝΟΕΜΒΡΙΟΣ 2016: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ
 o ΔΙΑΓΩΝΙΣΜΑ ΝΟΕΜΒΡΙΟΣ 06: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 5) - ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α. δ.. β. 3. δ. 4. γ. 5. α.λ, β.λ, γ.σ, δ.λ, ε.σ.
o ΔΙΑΓΩΝΙΣΜΑ ΝΟΕΜΒΡΙΟΣ 06: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 5) - ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α. δ.. β. 3. δ. 4. γ. 5. α.λ, β.λ, γ.σ, δ.λ, ε.σ.
ΦΥΣ Διαλ.12. Παράδειγμα Τάσεων
 ΦΥΣ 111 - Διαλ.1 1 Παράδειγμα Τάσεων Το παιδί της διπλανής εικόνας θέλει να φθάσει ένα µήλο στο δέντρο χωρίς να σκαρφαλώσει. Χρησιµοποιεί ένα σχοινί αµελητέας µάζας και µια αβαρή τροχαλία. Τραβάει το σχοινί
ΦΥΣ 111 - Διαλ.1 1 Παράδειγμα Τάσεων Το παιδί της διπλανής εικόνας θέλει να φθάσει ένα µήλο στο δέντρο χωρίς να σκαρφαλώσει. Χρησιµοποιεί ένα σχοινί αµελητέας µάζας και µια αβαρή τροχαλία. Τραβάει το σχοινί
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις Β έκδοση Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις Β έκδοση Θέµα Α Α.1. Κατά την πλαστική κρούση δύο σωµάτων ισχύει ότι : (δ) η ορµή του συστήµατος των δύο σωµάτων
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις Β έκδοση Θέµα Α Α.1. Κατά την πλαστική κρούση δύο σωµάτων ισχύει ότι : (δ) η ορµή του συστήµατος των δύο σωµάτων
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Β ΛΥΚΕΙΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΕΦΑΛΑΙΟ 1.1 (ΟΡΙΖΟΝΤΙΑ ΒΟΛΗ - ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ - ΟΡΜΗ) ΚΥΡΙΑΚΗ 20 ΝΟΕΜΒΡΙΟΥ 2016
 ΑΡΧΗ ΗΣ ΣΕΛΙΔΑΣ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Β ΛΥΚΕΙΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΕΦΑΛΑΙΟ. (ΟΡΙΖΟΝΤΙΑ ΒΟΛΗ - ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ - ΟΡΜΗ) ΚΥΡΙΑΚΗ 0 ΝΟΕΜΒΡΙΟΥ 06 ΘΕΜΑ Α Α δ Α γ Α3 β Α δ Α5. α Σωστό β Λάθος γ Σωστό δ Σωστό ε Λάθος
ΑΡΧΗ ΗΣ ΣΕΛΙΔΑΣ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Β ΛΥΚΕΙΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΕΦΑΛΑΙΟ. (ΟΡΙΖΟΝΤΙΑ ΒΟΛΗ - ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ - ΟΡΜΗ) ΚΥΡΙΑΚΗ 0 ΝΟΕΜΒΡΙΟΥ 06 ΘΕΜΑ Α Α δ Α γ Α3 β Α δ Α5. α Σωστό β Λάθος γ Σωστό δ Σωστό ε Λάθος
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 1 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 5) ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1α έως Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 1 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 5) ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1α έως Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί
Γ ΛΥΚΕΙΟΥ ΜΗΧΑΝΙΚΗ ΣΥΣΤΗΜΑΤΟΣ ΣΩΜΑΤΩΝ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ
 ΜΗΧΑΝΙΚΗ ΣΥΣΤΗΜΑΤΟΣ ΣΩΜΑΤΩΝ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ ΟΡΜΗ ΥΛΙΚΟΥ ΣΗΜΕΙΟΥ ΣΩΜΑΤΟΣ ΚΑΙ ΣΥΣΤΗΜΑΤΟΣ ΣΩΜΑΤΩΝ Το αποτέλεσμα μιας σύγκρουσης δύο σωμάτων εξαρτάται από τις ορμές τους. Όταν δύο κριάρια συγκρούονται και
ΜΗΧΑΝΙΚΗ ΣΥΣΤΗΜΑΤΟΣ ΣΩΜΑΤΩΝ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ ΟΡΜΗ ΥΛΙΚΟΥ ΣΗΜΕΙΟΥ ΣΩΜΑΤΟΣ ΚΑΙ ΣΥΣΤΗΜΑΤΟΣ ΣΩΜΑΤΩΝ Το αποτέλεσμα μιας σύγκρουσης δύο σωμάτων εξαρτάται από τις ορμές τους. Όταν δύο κριάρια συγκρούονται και
11 η Εβδομάδα Δυναμική Περιστροφικής κίνησης. Έργο Ισχύς στην περιστροφική κίνηση Στροφορμή
 11 η Εβδομάδα Δυναμική Περιστροφικής κίνησης Έργο Ισχύς στην περιστροφική κίνηση Στροφορμή Έργο και ισχύς στην περιστροφική κίνηση Εφαπτομενική δύναμη που περιστρέφει τον τροχό κατά dθ dw F ds = F R dθ
11 η Εβδομάδα Δυναμική Περιστροφικής κίνησης Έργο Ισχύς στην περιστροφική κίνηση Στροφορμή Έργο και ισχύς στην περιστροφική κίνηση Εφαπτομενική δύναμη που περιστρέφει τον τροχό κατά dθ dw F ds = F R dθ
ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) 2ο set - μέρος Α - Απαντήσεις ΘΕΜΑ Β
 ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ.: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ο set - μέρος Α - Απαντήσεις ΘΕΜΑ Β Ερώτηση. Ένα σώμα εκτελεί
ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ.: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ο set - μέρος Α - Απαντήσεις ΘΕΜΑ Β Ερώτηση. Ένα σώμα εκτελεί
ΜΑΘΗΜΑ 2.2 ΑΡΧΗ ΔΙΑΤΗΡΗΣΗΣ ΤΗΣ ΟΡΜΗΣ
 Έννοια Φαινόμενα ΜΑΘΗΜΑ 2.2 ΑΡΧΗ ΔΙΑΤΗΡΗΣΗΣ ΤΗΣ ΟΡΜΗΣ Όταν ένας άνθρωπος περπατά κατά μήκος μιας βάρκας αυτή κινείται σε αντίθετη κατεύθυνση με αυτόν. Όταν ένας ακίνητος παγοδρόμος σπρώξει έναν άλλο επίσης
Έννοια Φαινόμενα ΜΑΘΗΜΑ 2.2 ΑΡΧΗ ΔΙΑΤΗΡΗΣΗΣ ΤΗΣ ΟΡΜΗΣ Όταν ένας άνθρωπος περπατά κατά μήκος μιας βάρκας αυτή κινείται σε αντίθετη κατεύθυνση με αυτόν. Όταν ένας ακίνητος παγοδρόμος σπρώξει έναν άλλο επίσης
Ασκήσεις (διάφορες, στροφορμής και δυναμικής συστήματος σωματιδίων)
 Προσπαθείστε να λύσετε τις: Ασκήσεις (διάφορες, στροφορμής και δυναμικής συστήματος σωματιδίων Διάφορες: l. inn: : 7.6, 7.76, 7.78 Serwy: Κεφ.. 9:, 55, 65, 8, 85 Στροφορμή: : : 7.5, 7.8, 7., 7.6 Δυν. Συστ.
Προσπαθείστε να λύσετε τις: Ασκήσεις (διάφορες, στροφορμής και δυναμικής συστήματος σωματιδίων Διάφορες: l. inn: : 7.6, 7.76, 7.78 Serwy: Κεφ.. 9:, 55, 65, 8, 85 Στροφορμή: : : 7.5, 7.8, 7., 7.6 Δυν. Συστ.
Κρούσεις. A. Ανάλογα με τη διεύθυνση των ταχυτήτων πριν την κρούση.
 Κρούσεις Κρούση στη μηχανική είναι η αλληλεπίδραση δυο ή περισσότερων σωμάτων λόγω επαφής η οποία διαρκεί πολύ μικρό χρονικό διάστημα και αναπτύσσονται πολύ μεγάλες δυνάμεις, με αποτέλεσμα την απότομη
Κρούσεις Κρούση στη μηχανική είναι η αλληλεπίδραση δυο ή περισσότερων σωμάτων λόγω επαφής η οποία διαρκεί πολύ μικρό χρονικό διάστημα και αναπτύσσονται πολύ μεγάλες δυνάμεις, με αποτέλεσμα την απότομη
( ) ) V(x, y, z) Παραδείγματα. dt + "z ˆk + z d ˆk. v 2 =!x 2 +!y 2 +!z 2. F =! "p. T = 1 2 m (!x2 +!y 2 +!z 2
 ΦΥΣ 211 - Διαλ.04 1 Παραδείγματα Κίνηση ενός και μόνο σωματιδίου, χρησιμοποιώντας Καρτεσιανές συντεταγμένες και συντηρητικές δυνάμεις. Οι εξισώσεις Lagrange θα πρέπει να επιστρέφουν τα ίδια αποτελέσματα
ΦΥΣ 211 - Διαλ.04 1 Παραδείγματα Κίνηση ενός και μόνο σωματιδίου, χρησιμοποιώντας Καρτεσιανές συντεταγμένες και συντηρητικές δυνάμεις. Οι εξισώσεις Lagrange θα πρέπει να επιστρέφουν τα ίδια αποτελέσματα
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ 2019
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ 019 Κινηματική ΑΣΚΗΣΗ Κ.1 Η επιτάχυνση ενός σώματος που κινείται ευθύγραμμα δίνεται από τη σχέση a = (4 t ) m s. Υπολογίστε την ταχύτητα και το διάστημα που διανύει το σώμα
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ 019 Κινηματική ΑΣΚΗΣΗ Κ.1 Η επιτάχυνση ενός σώματος που κινείται ευθύγραμμα δίνεται από τη σχέση a = (4 t ) m s. Υπολογίστε την ταχύτητα και το διάστημα που διανύει το σώμα
ΕΝΟΤΗΤΑ 1.2 ΔΥΝΑΜΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ
 ΕΝΟΤΗΤΑ 1.2 ΔΥΝΑΜΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ 1. Τι λέμε δύναμη, πως συμβολίζεται και ποια η μονάδα μέτρησής της. Δύναμη είναι η αιτία που προκαλεί τη μεταβολή της κινητικής κατάστασης των σωμάτων ή την παραμόρφωσή
ΕΝΟΤΗΤΑ 1.2 ΔΥΝΑΜΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ 1. Τι λέμε δύναμη, πως συμβολίζεται και ποια η μονάδα μέτρησής της. Δύναμη είναι η αιτία που προκαλεί τη μεταβολή της κινητικής κατάστασης των σωμάτων ή την παραμόρφωσή
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΑ 5 ΚΑΙ 1 (ΚΡΟΥΣΕΙΣ - ΤΑΛΑΝΤΩΣΕΙΣ) ΚΥΡΙΑΚΗ 15 ΝΟΕΜΒΡΙΟΥ 2015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ 3
 ΑΡΧΗ 1 ΗΣ ΣΕΛΙΔΑΣ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΑ 5 ΚΑΙ 1 (ΚΡΟΥΣΕΙΣ - ΤΑΛΑΝΤΩΣΕΙΣ) ΚΥΡΙΑΚΗ 15 ΝΟΕΜΒΡΙΟΥ 015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ 3 ΘΕΜΑ A Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς
ΑΡΧΗ 1 ΗΣ ΣΕΛΙΔΑΣ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΑ 5 ΚΑΙ 1 (ΚΡΟΥΣΕΙΣ - ΤΑΛΑΝΤΩΣΕΙΣ) ΚΥΡΙΑΚΗ 15 ΝΟΕΜΒΡΙΟΥ 015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ 3 ΘΕΜΑ A Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΣΕΠΤΕΜΒΡΙΟΣ 2015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7
 ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΣΕΠΤΕΜΒΡΙΟΣ 2015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7 ΘΕΜΑ 1 Ο : Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό σας
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΣΕΠΤΕΜΒΡΙΟΣ 2015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7 ΘΕΜΑ 1 Ο : Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό σας
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 25/09/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 25/09/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 25/09/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4
E = 1 2 k. V (x) = Kx e αx, dv dx = K (1 αx) e αx, dv dx = 0 (1 αx) = 0 x = 1 α,
 Μαθηματική Μοντελοποίηση Ι 1. Φυλλάδιο ασκήσεων Ι - Λύσεις ορισμένων ασκήσεων 1.1. Άσκηση. Ενα σωμάτιο μάζας m βρίσκεται σε παραβολικό δυναμικό V (x) = 1/2x 2. Γράψτε την θέση του σαν συνάρτηση του χρόνου,
Μαθηματική Μοντελοποίηση Ι 1. Φυλλάδιο ασκήσεων Ι - Λύσεις ορισμένων ασκήσεων 1.1. Άσκηση. Ενα σωμάτιο μάζας m βρίσκεται σε παραβολικό δυναμικό V (x) = 1/2x 2. Γράψτε την θέση του σαν συνάρτηση του χρόνου,
2) Ορμή και ρυθμός μεταβολής της στην κυκλική κίνηση. 3) Ένα σύστημα σωμάτων σε πτώση. 4) Ένα σύστημα επιταχύνεται. Γ) Ορμή και διατήρηση ορμής
 Γ) Ορμή και διατήρηση ορμής 1) Στο ταβάνι, στον τοίχο ή στο πάτωμα; Βρισκόμαστε σε ένα δωμάτιο όπου ταβάνι τοίχος και δάπεδο έχουν φτιαχτεί από το ίδιο υλικό και κάνουμε το εξής πείραμα. Εκτοξεύουμε μπαλάκι
Γ) Ορμή και διατήρηση ορμής 1) Στο ταβάνι, στον τοίχο ή στο πάτωμα; Βρισκόμαστε σε ένα δωμάτιο όπου ταβάνι τοίχος και δάπεδο έχουν φτιαχτεί από το ίδιο υλικό και κάνουμε το εξής πείραμα. Εκτοξεύουμε μπαλάκι
Κεφάλαιο 8 Ορμή, Ώθηση και Κρούσεις
 Κεφάλαιο 8 Ορμή, Ώθηση και Κρούσεις Η ορμή είναι από τα πλέον βασικά φυσικά μεγέθη. Επεκτείνει την κατανόηση των νόμων του Νεύτωνα. Και όπως η ενέργεια είναι μια ποσότητα που διατηρείται στο σύμπαν. d
Κεφάλαιο 8 Ορμή, Ώθηση και Κρούσεις Η ορμή είναι από τα πλέον βασικά φυσικά μεγέθη. Επεκτείνει την κατανόηση των νόμων του Νεύτωνα. Και όπως η ενέργεια είναι μια ποσότητα που διατηρείται στο σύμπαν. d
των δύο σφαιρών είναι. γ.
 ΘΕΜΑ B Σφαίρα µάζας κινούµενη µε ταχύτητα µέτρου υ συγκρούεται κεντρικά και ελαστικά µε ακίνητη σφαίρα ίσης µάζας Να βρείτε τις σχέσεις που δίνουν τις ταχύτητες των δύο σφαιρών, µετά την κρούση, µε εφαρµογή
ΘΕΜΑ B Σφαίρα µάζας κινούµενη µε ταχύτητα µέτρου υ συγκρούεται κεντρικά και ελαστικά µε ακίνητη σφαίρα ίσης µάζας Να βρείτε τις σχέσεις που δίνουν τις ταχύτητες των δύο σφαιρών, µετά την κρούση, µε εφαρµογή
ΕΡΓΟ - ΕΝΕΡΓΕΙΑ F 2 F 3 F 1 F 4
 1. F 2 F 3 F 1 F 4 Στο σώμα του παραπάνω σχήματος βάρους Β = 20Ν ασκούνται οι δυνάμεις F 1 = 5Ν, F 2 = 10Ν, F 3 = 15Ν και F 4 = 10Ν. Αν το σώμα μετακινηθεί οριζόντια προς τα δεξιά κατά 2m να υπολογισθεί
1. F 2 F 3 F 1 F 4 Στο σώμα του παραπάνω σχήματος βάρους Β = 20Ν ασκούνται οι δυνάμεις F 1 = 5Ν, F 2 = 10Ν, F 3 = 15Ν και F 4 = 10Ν. Αν το σώμα μετακινηθεί οριζόντια προς τα δεξιά κατά 2m να υπολογισθεί
11 η Εβδομάδα Δυναμική Περιστροφικής κίνησης. Έργο Ισχύς στην περιστροφική κίνηση Στροφορμή Αρχή διατήρησης στροφορμής
 11 η Εβδομάδα Δυναμική Περιστροφικής κίνησης Έργο Ισχύς στην περιστροφική κίνηση Στροφορμή Αρχή διατήρησης στροφορμής Έργο και ισχύς στην περιστροφική κίνηση Εφαπτομενική δύναμη που περιστρέφει τον τροχό
11 η Εβδομάδα Δυναμική Περιστροφικής κίνησης Έργο Ισχύς στην περιστροφική κίνηση Στροφορμή Αρχή διατήρησης στροφορμής Έργο και ισχύς στην περιστροφική κίνηση Εφαπτομενική δύναμη που περιστρέφει τον τροχό
