Energetski transformatori
|
|
|
- Μέλισσα Παχής
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Eergetski trasformatori Osovi podaci: prijeosi omjer aziva saga spoj trasformatora relativi apo kratkog spoja mogućost promjee prijeosog omjera (regulacija) ači hlađeja
2 Prijeosi omjer: Trasformatori sage omjer broja zavoja primare i sekudare strae trasformatora približo je jedak omjeru primaog i sekudarog apoa za trasformator u prazom hodu često se prijeosi omjer avodi kao omjer azivih apoa primare i sekudare strae trasformatora (za trofazi trasformator to su liijske vrijedosti) realo, da bi se kompezirao pad apoa u trasformatoru (a djelomičo i u mreži), trasformatori se grade tako da a sekudaroj strai imaju određei broj zavoja više (pr. 5%) pri tome se pod sekudarom straom podrazumijeva o straa a koju se trasformira eergija silazi trasformatori: sekudara straa je iskoaposka (pr. /.5 kv) uzlazi trasformatori: sekudara straa je višeaposka (pr. 5.5/ kv) ako se trasformator u mreži koristi i kao uzlazi i kao silazi, oda prijeosi omjer ovisi o prilikama u mrežama koje povezuje
3 Naziva saga: Trasformatori sage za dvoamoti trasformator to je privida saga za koju je dimezioira trasformator, a dobiva se iz izraza: S = 3 U prethoda defiicija, iako se koristi u većii propisa, ije u skladu s defiicijom koja se uobičajeo koristi kao defiicija azive sage strojeva aziva saga stroja je izlaza saga, pa bi izlazu sagu dvoamotog trasformatora trebalo određivati preko sekudarog apoa pri azivoj sekudaroj struji (a e preko U sekudarog apoa u prazom hodu) o u tom bi slučaju sekudari apo opterećeog trasformatora ovisio o faktoru sage opterećeja, zbog čega bi azivu sagu bilo potrebo defiirati s obzirom a faktor sage opterećeja trasformatora
4 Naziva saga: Trasformatori sage trasformatori se stadardiziraju prema azivim sagama: za /x kv:, 4, 63 MVA za 3(35)/ kv:.6, 4, 8, 6 MVA za /.4 kv: 5,, 4, 5, 4, 63,, kva za troamote trasformatore potrebo je pozavati azivu sagu svakog amota posebo pr. 6/4/ MVA pri tome je aziva saga trasformacije među pojediim amotima ograičea azivom sagom oog amota koji ima maju azivu sagu (pr. S =4 MVA, S 3 = MVA, S 3 = MVA)
5 Trasformatori sage Spoj trasformatora: grupa spoja trasformatora ovisi o zahtjevima mreže (pr. da li se u mreži uzemljuje ultočka) za povezivaje VN mreža ajčešće korištee grupe spoja su: Yy Yd5 Dy5 Yy upotrebljava se za trasformatore majih saga, pogotovo kada su obje ultočke uzemljee bilo eposredo, bilo preko prigušice Dy5 ili Yd5 se koriste kada je potrebo u uzemljiti ultočku samo a jedoj strai Yd5 je povoljo koristiti za spoj elektrae s mrežom (tada se geerator spaja a amot spoje u trokut čime se postiže da treći harmoik koji se pojavljuje pri magetiziraju trasformatora e prelazi u mrežu)
6 Trasformatori sage Spoj trasformatora: daas se sve više koriste troamoti trasformatori, pogotovo ako se radi o vrlo visokim apoima Yyd5 amoti ajvišeg i sredjeg apoa su spojei a zvijezdu koju je moguće uzemljiti (ormalo se uzemljuju mreže višeg apoa) Yyd5 koristi se i kada je uzmeljea samo jeda ultočka, odoso ako se predviđa priključak sikroog kompezatora (spaja se a amot spoje u trokut) Yd5y koristi se u elektraama za priključak vlastitog potroška (geerator je priključe a amot spoje u trokut) Yd5d5 trasformacija eergije dvaju geeratora preko jedog trasformatora (geeratori su priključei a amot spoje u trokut)
7 Trasformatori sage Relativi apo kratkog spoja (u k ): priroda karakteristika svakog trasformatora koja proizlazi iz jegove izvedbe (geometrije) što se tiče ormalog pogoa povoljiji je maji u k, dok u uvjetima kratkog spoja veći ormalo se kreće između 3 i % iže vrijedosti se odose a trasformatore majih saga Promjea prijeosog omjera (regulacija): radi mogućosti regulacije apoa trasformatori se izvode s određeim brojem zavoja koji se mogu isključiti ili uključiti iz prijeosog omjera razlikujemo : trasformatore s otcjepima regulacijske trasformatore
8 Trasformatori sage Promjea prijeosog omjera (regulacija): trasformatori s otcjepima: prijeosi omjer je moguće mijejati samo u bezaposkom staju običo se izvode s: 3 položaja preklopke: pr. 3kV ± 5%/,5 kv => 3.5/.5 kv; 3/.5 kv; 8.5/.5 kv 5 položaja preklopke: pr. 3 kv ± x5%/.5 kv uobičajei otcjepi su ±4% ili ±5% (ali može i ±.5% ili ±7.5%) s obzirom a kostrukciju trasformatora izvedba otcjepa je epovolja (aksijale sile među amotima zbog esimetrije amota, refleksija vala preapoa a otvoreim otcjepima i sl.) pa je otcjepe potrebo izbjegavati ako je moguće
9 Trasformatori sage Promjea prijeosog omjera (regulacija): regulacijski trasformator: moguće je mijejati prijeosi omjer za vrijeme pogoa izvode s većim brojem otcjepa ego tzv. trasformatori s otcjepima uobičajeo se maksimala regulacija kreće u graicama ± % ili ± % pri tome je apo jedog stupja regulacije.5 % pr. za kv ± x.5% /.5 kv moguć je položaj regulacijske sklopke (od 6.5/.5 kv do 93.5/.5 kv) regulacijska sklopka može se smjestiti i a VN i a NN strau, ali običo se smješta a VN strau jer su tamo struje maje pa je regulacijska sklopka jeftiija i lakša
10 Trasformatori sage Promjea prijeosog omjera (regulacija): regulacijski trasformator: izvedbe: kao jeda jediica u koju je smješte trasformator i regulacijska sklopka dvije jediice u jedoj se alazi trasformator fiksog prijeosog omjera, a u drugoj autotrasformator s regulacijskom sklopkom druga kombiacija je povoljija glede sigurosti pogoa jer u slučaju kvara a ekoj od kompoeti druge jediice, prva jediica (trasformator) ostaje u pogou primjea: HE ije potrebo predvidjeti regulacijske trasformatore jer se promjea apoa može postići regulacijom apoa a geeratoru TE ekoomičije je ostvariti veliki opseg regulacije apoa regulacijskim trasformatorom ego izgradjom geeratora s mogućošću takve regulacije
11 Trasformatori sage Nači hlađeja: hlađeje prirodim strujajem zraka pored stjeki kotla trasformatora ili prigrađeih hladioika hlađeje prisilom cirkulacijom ulja kroz hladioik koji se hladi prirodim strujajem zraka, prisilom vetilacijom, ili vodom
12 Trasformatori sage Paralela rad trasformatora: da bi bio moguć paralela rad trasformatora i omogućilo se puo iskorišteje jihove azive sage, potrebo je ispuiti sljedeće uvjete: jedaki prijeosi omjeri približo jedaki azivi apoi ista grupa spoja približo jedaki relativi apoi kratkog spoja omjer azivih prividih saga e veći od 3:
13 Trasformatori sage Paralela rad trasformatora: jedaki prijeosi omjeri: ako su ejedaki prijeosi omjeri: pr. 3/ i 3/.5 kv prazi hod: trasformator s većim sekudarim apoom (3/.5 kv) protjerati će struju izjedačeja kroz oba trasformatora ΔV ΔV ΔV S a = = Z X u k U a ΔV = (%) V uk ΔV = V u k prazi hod opterećei trasformatori pr. uk = 5%, a = 5% ΔV V = 5%
14 Trasformatori sage Paralela rad trasformatora: jedaki prijeosi omjeri: ako su ejedaki prijeosi omjeri: pr. 3/ i 3/.5 kv opterećei trasformatori: opterećivajem a sekudaroj strai povećati će se opterećeja jedog, a smajivati opterećeje drugog trasformatora prije ego što sekudaro priključeo opterećeje dosege vrijedost zbroja jihovih azivih saga doći do azivog opterećeja prvog trasformatora zači, mogućost opterećivaja paralelo spojeih trasformatora ejedakih prijeosih omjera zato je maja od zbroja jihovih azivih saga (tim više što je ΔV razlika prijeosih omjera veća, a u k maji) prazi hod opterećei trasformatori
15 Trasformatori sage Paralela rad trasformatora: približo jedaki azivi apoi: azivi apoi paralelo spojeih trasformatora e moraju biti u potpuosti jedaki pr. mogu se paralelo spojiti dva trasformatora jedakih prijeosih omjera, ali različitih azivih apoa: 3/ kv i 3.5/.5 kv ako je pogoski apo višeaposke strae jedak višem azivom apou (3.5 kv), teći će ešto povećaa struje magetiziraja kroz prvi trasformator treba voditi račua da je trasformator građe tako da može izdržati pogo s apoom koji je do 5% viši od azivog
16 Trasformatori sage Paralela rad trasformatora: ista grupa spoja: paralelim spajajem trasformatora različitih grupa spoja potekla bi velika struja izjedačeja pr. za ajmaji fazi pomak sekudarih apoa (3 ), razlika sekudarih apoa (ΔV/V)%=5%, pa bi struja izjedačeja (pr. za u k =%) bila bi veća od.5 =>ije moguć paralela rad trasformatora različitih grupa spoja zamjeom stezaljki kod priključka a sabirice moguće je postići da se trasformator poaša prema mreži kao da je druge grupa spoja (pr. a slici su prikazai razi priključci Yd trasformatora tako da se o poaša prema mreži kao da je u spoju Yd5)
17 Trasformatori sage Paralela rad trasformatora: približo jedaki relativi apoi kratkog spoja: opterećeje među trasformatorima s jedakim relativim apoom kratkog spoja (u k = =u k ) dijeli se proporcioalo azivim sagama trasformatora, zbog čega je trasformatore moguće opteretiti sagom koja odgovara zbroj azivih saga pojediih trasformatora ako relativi apoi kratkog spoja isu jedaki: Z = Z =... = Z u U Z ki i = i =,.. Si S i i = i =,.. 3U uk u S = k S S S =... = uk S S
18 Trasformatori sage Paralela rad trasformatora: približo jedaki relativi apoi kratkog spoja: ako relativi apoi kratkog spoja isu jedaki: maksimalo dopušteo opterećeja grupe: Smax = uk mi S i i= uki Si Si = Smax uki Sj j= ukj tada je trasformator s ajmajim relativim apoom kratkog spoja azivo optereće gorji izraz vrijedi i sasvim općeito za eko opterećeje S S max a sekudaroj strai
19 Trasformatori sage Paralela rad trasformatora: približo jedaki relativi apoi kratkog spoja: paralelo spajaje trasformatora za koje je ajveća pojediača razlika relativih apoa kratkog spoja veća od % aritmetičke sredie svih relativih apoa kratkog spoja, kao trajo rješeje ije opravdao iz ekoomskih razloga zbog emogućosti iskorišteja jihove pue sage (zbroj azivih saga pojediih trasformatora u paralelom radu) omjer azivih prividih saga e veći od 3:: jedakost padova apoa u svim paralelo spojeim trasformatorima i po izosu i po fazi biti će postiguta samo ako je omjer R/X svih trasformatora jedak taj je uvjet ormalo ispuje u trasformatorima približo jedakih azivih saga
20 Trasformatori sage Paralela rad trasformatora: omjer azivih prividih saga e veći od 3:: ako je omjer azivih saga veći od :3, postojati će velika razlika između omjera R/X u trasformatorima i pored toga što su im relativi apoi kratkog spoja jedaki, pa će se pojaviti struja izjedačeja već u prazom hodu slika prikazuje padove apoa u dva trasformatora: iste azive sage istih relativih apoa kratkog spoja različitih omjer R/X uz pretpostavku da kroz oba trasformatora teku jedake struje, što bi bilo poželjo s obzirom a mogućost iskorišteja trasformatora a sekudaru se javljaju različiti apoi V i V, pa će u paralelom spoju razlika apoa δv protjerati struju izjedačeja kroz trasformatore
21 Prigušice amjea: smajeje struja kratkog spoja, a poekad da omoguće paralela rad trasformatora sa zato različitim relativim apoima kratkog spoja izvedba: svitak bez željeza (tri faze su međusobo električki odvojee) spajaje: u seriju s potrošačima i izvorima podaci: azivi apo (U ) azivi apo dijela mreže gdje se prigušica ugrađuje i prema kojem je dimezioiraa jezia izolacija prolaza saga (S ) saga koja se trajo može preositi prigušicom a da se pri tome jezii amoti e zagriju preko dopuštee vrijedosti pri tome je aziva struja prigušice: = S 3 U
22 Prigušice podaci: relativi apo kratkog spoja (U k ) defiira se a aaloga ači kao i kod trasformatora pokus: a stezaljke amota jede faze prigušice arie se takav apo V k da prigušicom proteke struja uk = Xd = 3Vk U Vk = % 3Vk U S u = k U S (Ω) prigušice se grade za azive apoe do 35 kv i u k =5,6, i %
23 izbor prigušice: azivi apo prolaza saga Prigušice uz kotrolu s obzirom a (prema VDE): diamičku graiču struju prigušice pri kratkom spoju mora vrijediti da je udara struja pri ajepovoljijem kratkom spoju u dijelu mreže gdje se prigušica ugrađuje maja od 5 termička graiča struja pri kratkom spoju mora vrijediti da je termička struja pri ajepovoljijem kratkom spoju u dijelu mreže gdje se prigušica ugrađuje maja od
24 Kabeli elemet koji služi za međusobo povezivaje dijelova postrojeja ili postrojeja i trošila kabeli se razlikuju prema: ačiu izolacije: ulji, pliski, impregirai papir, termoplastiči polietile, poliviilklorid, umrežei polietile, etilepropile zaštiti od mehaičkih oštećeja: olovo, čeliča traka, čeliča žica i sl. vrsta vodiča: bakar,alumiij izbor kabela: azivi apo maksimala struja u ormalom pogou (aziva struja) pr. za bakree trožile kabele s papirom izolacijom
25 izbor kabela: Kabeli maksimala struja u ormalom pogou (aziva struja) prema maksimaloj struji u ormalom pogou u ekom dijelu mreže ( max ) odabire se iz kataloga proizvođača odgovarajući kabel takvog presjeka q da vrijedi: tabl k k k 3 k 4 max gdje su k, k, k3, k4 korekcioi faktori defiirai uvjetima polagaja: k < za kabel polože s pokrovom (.8-.9), k = za kabel polože bez pokrova k ako se u istom rovu alazi više kabela (ili jedožilih kabelskih sistema) H. Požar, Visokoaposka rasklopa postrojeja, str. 37 k 3 ako je kabel polože u zemlju ili zrak, ali se temperatura tla ili zraka razlikuje od C - H. Požar, Visokoaposka rasklopa postrojeja, str. 373 k 4 ako je kabel polože u zrak - H. Požar, Visokoaposka rasklopa postrojeja, str. 37
26 izbor kabela: Kabeli struja kratkog spoja mjerodava za ugrijavaje presjek odabra prema maksimaloj struji u ormalom pogou potrebo je kotrolirati s obzirom a dozvoljeo zagrijavaje za vrijeme trajaja kratkog spoja može se izvesti (za karakterističe vrijedosti ovise o materijalu kabela), da je potreba presjek kabela s obzirom a zagrijavaje za vrijeme trajaja kratkog spoja: q ks α t gdje je: α veličia koja ovisi o materijalu vodiča i dozvoljeom adzagrijavaju u vrijeme trajaja kratkog spoja pr. kabeli s bakreim vodičima α [7,9] kabeli s alumiijskim vodičima α [,4] t struja kratkog spoja mjerodava za ugrijavaje pri ajepovoljijoj vrsti kratkog spoja kroz kabel (ka) t trajaje kratkog spoja (s) t (mm )
27 izbor kabela: ukoliko ije ispujeo Kabeli qks q mora se iz kataloga proizvođača uzeti kabel prvog većeg presjeka koji zadovoljava taj uvjet
28 Mjeri trasformatori uređaji za mjereje i zaštitu, bez obzira a aposku raziu, se e priključuju direkto a vodove jer bi to zato poskupilo jihovu izvedbu visoki apoi: izolacija, dimezije istrumeata i releja velike struje: presjeci vodiča, sile među vodičima stoga se upotrebljavaju mjeri trasformatori koji pogoske apoe (aposki mjeri trasformatori) i struje (struji mjeri trasformatori) trasformiraju a stadarde vrijedosti: struje do 5A (A) apoi do V a taj ači se istrumeti i releji mogu stadardizirati što zato pojedostavljuje jihovo projektiraje i proizvodju
29 Struji mjeri trasformatori Nači rada: kao i trasformatori sage imaju primari i sekudari amot s željezom jezgrom od limova (slika a) primari se amot spaja u seriju s potrošačima pa je a taj ači struja kroz taj amot gotovo eovisa o teretu a sekudaroj strai a slici b prikazaa je ekvivaleta shema strujog mjerog trasformatora, a a slici c prikazaa je shema istog trasformatora uz pretpostavku prijeosog omjera : E E ( = = ( Z + Z) Z ) = = ( )
30 Struji mjeri trasformatori Nači rada: struja magetiziraja uz kostatu primaru struju ovisi o impedaciji priključeoj a sekudaroj strai: ( ) ( ) ( ) ( ) ( ) ( ) f (Z) U f (Z) Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z E E = = + + = = + = + = + = + = = raste raste Z
31 Nači rada: Struji mjeri trasformatori usporedba SMT s trasformatorom sage za trasformator sage U i su eovisi o impedaciji tereta priključeog a sekudaru strau iz tih razlika slijedi i različito poašaje ovih trasformatora u prazom hodu i kratkom spoju a stezaljkama sekudare strae PRAZN HOD SMT-a: kroz primari amot teče struja koju trebaju potrošači, pa kako u sekudarom amotu ema struje, iti protjecaja koje bi se suprostavilo protjecaju primare struje, ukupa struja = služi za magetiziraje jezgre tolika struja magetiziraja, kad primara struja ostae u graicama azive vrijedosti, dovesti će do zatog povećaja idukcije u željezoj jezgri posljedičo dolazi do:. povećaje gubitaka u željezu dolazi do zagrijavaja jezgre, pa može doći i do izgaraja izolacije, te da željezi limovi promijee magetska svojstva
32 Nači rada: Struji mjeri trasformatori PRAZN HOD SMT-a: φ. povišeje apoa a stezaljkama SMT-a povišeje apoa a sekudarim stezaljkama SMT-a može ugroziti izolaciju SMT-a i dovesti u opasost osoblje e kod trasformatora sage su tok φ i i elektromotora sila e siuse veličie, φ dok struja magetiziraja sadrži osim φ osovog vala i valove trostruke i viših frekvecija i e kod SMT-a u prazom hodu je struja = siusa zato tok tok φ i elektromotora t sila e e mogu biti siusi radi oblika krivulje magetiziraja (petlje histereze) radi agle promjee toka u području u kojem je tok blizu vrijedosti ula, dolazi do zatih apoa (e=-dφ/dt) stoga se e smije ostavljati otvore sekudari amot SMT-a
33 Struji mjeri trasformatori Nači rada: KRATK SPOJ SMT-a: ema ikakve opasosti po SMT ako se jegove sekudare stezaljke kratko spoje sekudara struja ovisi samo o primaroj struji (što je S privida aziva saga SMT-a veća ovaj je izraz točiji) zaključak: SMT je moguće ostaviti trajo u pogou s kratko spojeim sekudarim stezaljkama jer će pri tome struja a sekudaroj strai biti tek ezato veća od struje u ormalom pogou uz priključeu impedaciju Z Z uz Z Z Z Z E ) ( Z = = = = =
34 Struji mjeri trasformatori Osove karakteristike: prijeosi omjer struja pogreška kuta pogreška klasa točosti struji višekratik azivi teret ili aziva saga trasformatora
35 Struji mjeri trasformatori Prijeosi omjer: omjer primare i sekudare azive struje (e odgovara omjeru broja zavoja zbog struje magetiziraja ) prema primaroj azivoj struji SMT-a se odabire tako da oa bude eposredo veća od maksimale pogoske struje u dijelu mreže gdje se SMT priključuje (treba izbjegavati velike razlike između i max_pog ) jer su time veće struje pogreške SMT-a stadarde vrijedosti primarih struja: m*, m*5, m*, m*3, m*5, m*75 (A) m=,, stadarde vrijedosti sekudarih struja: 5 () A A se koristi samo kada je duljia vodova između SMT-a i uređaja (mjerih ili zaštitih) velika a taj je ači za iste R gubitke potreba maji presjek vodova u sekudarom krugu
36 Struji mjeri trasformatori Prijeosi omjer: A ije preporučljivo koristiti kada je saga i struji višekratik SMT-a velik (što zači da sekudara struja vrlo vjero prati porast primare struje za vrijedosti struja puo veće od azivih vrijedosti) jer će u slučaju kratkog spoja u primarom strujom krugu doći do začajog povećaja sekudarog apoa, pa time i mogućosti proboja izolacije u sekudarom krugu pr. eka je SMT azive sage 4 kva, struji višekratik =, U =4 V, pri kratkom spoju u primarom krugu sekudara struje može postići i = A, zbog čega je i U =x4=4 V zači, A je preporuka koristiti u postrojejima gdje struje kratkog spoja isu velike i gdje je moguće koristiti SMT maje sage, što je gotovo redovit slučaj u rasklopim postrojejima s U 6 kv ako su u postrojejima primare azive struje velike, može se koristiti i A kako bi se smajio sekudari apo ( => => => E ~ )
37 Struji mjeri trasformatori Struja pogreška: defiicija: Δi = K % K je prijeosi omjer (omjer primare i sekudare azive struje) i su apsolute vrijedosti primare i sekudare struje Kuta pogreška: defiiraa je kutom između primare i sekudare struje (pozitiva je ako sekudara struja prethodi primaroj)
38 Struji mjeri trasformatori Klasa točosti (kl): kada bi SMT bio izvede s prijeosim omjerom K jedakim omjeru broj zavoja sekudare i primare strae ( / ), struja pogreška bi stalo bila egativa ( ) ( ) i K K i < = = Δ = = = Δ ako SMT ima maji broj zavoja a sekudaroj strai (K> / ), oda vrijedost od Δi može biti i pozitiva, ali i ula za eku vrijedost od K K i > < = = = Δ >
39 Struji mjeri trasformatori Klasa točosti: odgovara maksimalo dopušteoj strujoj pogrešci SMTa pri azivoj struji i azivom teretu pr. SMT klase točosti kl=. ima dozvoljeu struju pogrešku Δi±.% pri i Z razlikujemo slijedeće klase točosti: osim pri azivoj struji defiirau su i maksimalo dozvoljee struje pogreške i pri primarim strujama <
40 Struji mjeri trasformatori Struji višekratik (): jime je opisao poašaje SMT-a pri primarim strujama puo većim od azive vrijedosti, adstruja karakteristika SMT-a povećajem primare struje, uz kostatu impedaciju a sekudaroj strai, raste pogreška SMT-a ako primara struja toliko araste da idukcija zato prijeđe koljeo a krivulji magetiziraja, porast sekudare biti će proporcioala s porastom primare struje, jer će se tad trasformator poašati kao da željeza ema a slici je prikazaa ovisost relative sekudare struje ( / ) o relativoj primaroj struji ( / ) crtkai pravac prikazivao bi ovisost relativih struja kada e bi bilo struje pogreške (Δi=)
41 Struji mjeri trasformatori Struji višekratik (): struji višekratik () je višekratik primare azive struje pri kojem je struja pogreška, uz sekudaro priključeu azivu impedaciju, % struji višekratik je defiira apscisom točke u kojoj se adstruja karakteristika siječe s pravcem Δi=% (pr. a slici su prikazae adstruje karakteristike dva SMT sa =4 i =)
42 Struji mjeri trasformatori Struji višekratik (): struji višekratik ovisi o impedaciji priključeoj a sekudaru strau ukoliko a sekudaru strau ije priključea aziva impedacija Z, već Z, ovi struji višekratik, izosi: Z Z a slici je prikaza utjecaj sekudaro priključeog tereta a struji višekratik SMT-a izborom SMT-a s malim strujim višekratikom štite se priključei uređaji od prevelikih struja što je iteresato ukoliko je riječ o mjerim istrumetima (<5) ta je zaštita samo privida ukoliko je impedacija priključeih istrumeata maja od azive impedacije SMT-a
43 Struji mjeri trasformatori Struji višekratik (): radi toga je potrebo ukoliko priključei istrumeti emaju dovoljo veliku impedaciju, u seriju s jima priključiti dodatu impedaciju ukoliko se a sekudaru strau SMT-a priključuju zaštiti uređaji, radi jihova ispravog djelovaja potreba je vjera prijeos i velikih primarih struja a sekudaru strau (pr. struje kvara u primarom krugu) stoga se za zaštite uređaje koriste SMT-ovi s strujim višekratikom: 5<< adstruji i termički releji > diferecijali releji <<< distati releji
44 Struji mjeri trasformatori Nazivi teret, Z ili aziva saga, S : s obzirom da o sekudaro priključeoj impedaciji (teretu) ovisi struja magetiziraja (pa time i pogreška SMT-a), potrebo je prilikom odabira SMT-a pozavati kakvi će istrumeti ili releji biti priključei a sekudaru strau SMT-a, jer o tome ovisi jegova kostrukcija P = ( Z + Z) = 4.44 B f q što je veći teret a sekudaroj strai (uređaji se uvijek spajaju u seriju kako bi jima tekla ista struja ), potreba je veća saga P SMT-a => ako želimo zbog struje magetiziraja (struje pogreške) magetsku idukciju održati malom to oda zači da je potrebo povećati presjek jezgre SMT-a
45 Struji mjeri trasformatori Nazivi teret, Z ili aziva saga, S : azivu sekudaru sagu, odoso maksimalu sagu kojom je moguće opteretiti SMT ako se žali ostati u graicama struje pogreške, moguće je defiirati a dva ačia: stariji: pomoću azive impedacije, Z oviji: pomoću azive sage, P pri čemu vrijedi: Termička graiča struja: P = Z (VA) maksimala efektiva vrijedost primare struje koju SMT uz kratko spojee sekudare stezaljke može izdržati s, a da se pri tome prekomjero e zagrije ( ter =(6-) )
46 Struji mjeri trasformatori Termička graiča struja: ako kratki spoj traje t sekudi oda je termička graiča struja, ter: ' ter = ter Diamička graiča struja: tjemea vrijedost struje kratkog spoja koju SMT može izdržati uz kratko spojee sekudare stezaljke, a da ga e oštete sile koje se pri tome javljaju ( di =(- 5) ) za mjesto priključka SMT-a mora vrijediti: u di t
47 Struji mjeri trasformatori zvedbe: suhi: porculaski izolator sekudari amot sa željezom jezgrom u poprečoj rupi malih dimezija može se motirati u bilo kojem položaju izrađuje se za azive apoe do 35 kv samo za uutrašju motažu Kočar, suhi SMT, kv
48 Struji mjeri trasformatori zvedbe: maloulji: oba izvoda prolaze paralelo kroz zajedički izolator za apoe do 35 kv izvedba sa metalim kotlom Kočar, maloulji SMT, kv za apoe 6 kv i više, amoti i jezgra alaze se u izolatoru ovije izvedbe - amoti i jezgra alaze se u kotlu a du izolatora Kočar, maloulji SMT, kv
49 Struji mjeri trasformatori zvedbe: zamkasti: primari amot se amata kroz dva provoda izolatora zbog velikih mehaičkih aprezaja uutar zamke pri kratkom spoju, provodi se izolatori pojačavaju metalom kostrukcijom a glavama i sredii ugrađuju se tamo gdje je epovolja štapa izvedba radi malih primarih struja ili gdje je potreba mogućost prespajaja a primaroj strai (moguće je izvesti, ali je složeo zbog ulaza a jedoj a izlaza amota a drugoj strai) može se motirati u bilo kojem položaju izvodi se za azive apoe do 35 kv Kočar, zamkasti SMT, kv
50 zvedbe: štapi: Struji mjeri trasformatori primari amot ima jeda vodič koriste se gdje god je to moguće s obzirom a veličiu primare struje jer imaju gotovo beskoačo veliku diamičku graiču struju za male primare struje štapi SMT ima i malo amperzavoja ( =), pa su epovolji ako je potreba veća aziva saga P = 4.44 B f q Kočar, štapi SMT, 35 (3) kv ormalo se izvode za primare azive struje od A i više mogu se prespajati samo sekudaro mogu se ugraditi u bilo kojem položaju ormalo se izvode za apoe do 35 kv
51 Struji mjeri trasformatori Shema spoja: spojevi SMT-a za mjereje: a) u jedoj fazi b) u dvije faze c) u tri faze u svim slučajevima, jeda od sekudarih stezaljki, kao i metalo kućište, spojea je a stezaljku za uzemljeje da bi se poslužo osoblje zaštitilo u slučaju spoja između primarog i sekudarog amota
52 Naposki mjeri trasformatori Nači rada: izvedba kao i ormala trasformator sage priključe paralelo potrošačima a gotovo kostata apo (eovisa o impedaciji priključeoj a sekudari amot NMT-a) osova razlika spram trasformatora sage relativo je slabo optereće kako bi pogreška mjereja bila što maja struja magetiziraja je ovisa samo o primarom apou Osove karakteristike: prijeosi omjer aposka pogreška klasa točosti kuta pogreška azivi teret ili saga NMT-a
53 Naposki mjeri trasformatori Prijeosi omjer: omjer azivog primarog i azivog sekudarog apoa azivi primari apo je jedak liijskom azivom apou mreže (pr. kv) ako se radi o dvopolo izoliraom NMT-u azivi primari apo je jedak fazom azivom apou mreže (pr. / 3 kv) ako se radi o jedopolo izoliraom NMT-u u prvom slučaju je sekudari azivi apo V, a u drugom slučaju / 3 V Naposka pogreška: defiicija: Δu = k U U U % k = prijeosi omjer NMT-a=U /U
54 Naposki mjeri trasformatori Kuta pogreška: defiira se aalogo kutoj pogrešci SMT-a razlika kuta sekudarog i primarog apoa Klasa točosti: jedaka je maksimalo dozvoljeoj aposkoj pogrešci kada je primari apo u graicama.8-. U prema VDE razlikujemo slijedeće klase točosti NMT-a: dopuštee kute pogreške za te klase točosti su: pogreška) 5 4 (za klasu točosti 3 ije defiiraa dozvoljea kuta
55 Naposki mjeri trasformatori Naziva saga: maksimala saga istrumeata a sekudaroj strai kojom je moguće opteretiti NMT a da aposka i kuta pogreška ostau u graicama vrijedosti defiiraih klasom točosti pri veći opterećejima raste aposka pogreška NMT-a (pr. za opterećeje koje je dva puta veće od azivog, aposka pogreška može biti tri puta veća od oe dopuštee klasom točosti) realo je graiča termička saga, kojom je moguće trajo opteretiti NMT a da se pri tome e zagrije izad dopuštee vrijedosti, ekoliko puta veća od jegove azive sage
56 Naposki mjeri trasformatori zvedbe: dva tipa NMT-a: dvopolo izolirai ima dva visokoaposka priključka jedopolo izolirai ima samo jeda visokoaposki priključak (drugi je kraj visokoaposkog amota spoje s metalim kućištem i uzemlje Kočar, maloulji dvopolo izolirai NMT, 35 (3) kv Kočar, maloulji jedopolo izolirai NMT, 35 (3) kv
57 Naposki mjeri trasformatori zvedbe: oba tipa mogu se upotrijebiti za mjereje u trofazom sustavu i to spajajem u slog aposkih trasformatora da bi se ostvario slog aposkih trasformatora, potreba su dva dvopolo izoliraa NMT-a ili tri jedopolo izoliraa NMT-a u prvom slučaju mogu se mjeriti samo liijski apoi u drugom slučaju mogu se mjeriti i liijski i fazi apoi
58 Naposki mjeri trasformatori zvedbe: suhi NMT-ovi se izvode za apoe do 3 kv Kočar, maloulji jedopolo izolirai NMT, kv svi aktivi dijelovi smještei su u izolator apuje uljem, dok metala glava izolatora služi kao ulji kozervator a glavi izolatora alaze se dvije stezaljke između kojih je spoj s primarim amotom za apoe do 35 kv NMT-ovi se izvode kao ulji ili maloulji (predost ima uporaba malouljih radi maje opasosti od zapaljeja ili eksplozije za uutarju motažu i apoe do 35 kv izvode se i NMT-ovi s izolacijom od umjetih smola za apoe do 35 kv upotrebljavaju se i jedopolo i dvopolo izolirai NMT-ovi za apoe izad 35 kv ekoomičija je uporaba sloga od tri jedopolo izoliraa NMT-a jer ajveći dio troškova otpada a izolatore
Riješeni zadaci: Nizovi realnih brojeva
 Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Dvanaesti praktikum iz Analize 1
 Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
odvodi u okoliš? Rješenje 1. zadatka Zadano: q m =0,5 kg/s p 1 =1 bar =10 5 Pa zrak w 1 = 15 m/s z = z 2 -z 1 =100 m p 2 =7 bar = Pa
 .vježba iz Terodiaike rješeja zadataka 1. Zadatak Kopresor usisava 0,5 kg/s zraka tlaka 1 bar i 0 o C, tlači ga i istiskuje u eizolirai tlači cjevovod. Na ulazo presjeku usise cijevi brzia je 15 /s. Izlazi
.vježba iz Terodiaike rješeja zadataka 1. Zadatak Kopresor usisava 0,5 kg/s zraka tlaka 1 bar i 0 o C, tlači ga i istiskuje u eizolirai tlači cjevovod. Na ulazo presjeku usise cijevi brzia je 15 /s. Izlazi
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
( x) ( ) dy df dg. =, ( x) e = e, ( ) ' x. Zadatak 001 (Marinela, gimnazija) Nađite derivaciju funkcije f(x) = a + b x. ( ) ( )
 Zadatak (Mariela, gimazija) Nađite derivaciju fukcije f() a + b c + d Rješeje Neka su f(), g(), h() fukcije ezavise varijable, a f (), g (), h () derivacije tih fukcija po Osova pravila deriviraja Derivacija
Zadatak (Mariela, gimazija) Nađite derivaciju fukcije f() a + b c + d Rješeje Neka su f(), g(), h() fukcije ezavise varijable, a f (), g (), h () derivacije tih fukcija po Osova pravila deriviraja Derivacija
Polarizacija. Procesi nastajanja polarizirane svjetlosti: a) refleksija b) raspršenje c) dvolom d) dikroizam
 Polarzacja Proces asajaja polarzrae svjelos: a refleksja b raspršeje c dvolom d dkrozam Freselove jedadžbe Svjelos prelaz z opčkog sredsva deksa loma 1 u sredsvo deksa loma, dolaz do: refleksje (prema
Polarzacja Proces asajaja polarzrae svjelos: a refleksja b raspršeje c dvolom d dkrozam Freselove jedadžbe Svjelos prelaz z opčkog sredsva deksa loma 1 u sredsvo deksa loma, dolaz do: refleksje (prema
1.4 Tangenta i normala
 28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
3n an = 4n3/2 +2n+ n 5n 3/2 +5n+2 n a 2 n = n 2. ( 2) n Dodatak. = 0, lim n! 2n 6n + 1
 Nizovi 5 a = 5 +3+ + 6 a = 3 00 + 00 3 +5 7 a = +)+) ) 3 3 8 a = 3 +3+ + +3 9 a = 3 5 0 a = 43/ ++ 5 3/ +5+ a = + + a = + ) 3 a = + + + 4 a = 3 3 + 3 ) 5 a = +++ 6 a = + ++ 3 a = +)!++)! +3)! a = ) +3
Nizovi 5 a = 5 +3+ + 6 a = 3 00 + 00 3 +5 7 a = +)+) ) 3 3 8 a = 3 +3+ + +3 9 a = 3 5 0 a = 43/ ++ 5 3/ +5+ a = + + a = + ) 3 a = + + + 4 a = 3 3 + 3 ) 5 a = +++ 6 a = + ++ 3 a = +)!++)! +3)! a = ) +3
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
Općenito, iznos normalne deformacije u smjeru normale n dan je izrazom:
 Otporost mterijl. Zdtk ZDTK: U točki čeliče kostrukije postvlje su tri osjetil z mjereje deformij prem slii. ri opterećeju kostrukije izmjeree su reltive ormle (dužiske deformije: b ( - b 3 - -6 - ( b
Otporost mterijl. Zdtk ZDTK: U točki čeliče kostrukije postvlje su tri osjetil z mjereje deformij prem slii. ri opterećeju kostrukije izmjeree su reltive ormle (dužiske deformije: b ( - b 3 - -6 - ( b
KONDENZATOR. (Q, Q O i q imaju algebarsko značenje prema istom referentnom smeru u grani sa kondenzatorom).
 KONDENZATOR Sistem od dva provodika, razdvojea dielektrikom, koji može imati zate vredosti kapaciteta zove se kodezator. Kapacitet kodezatora srazmera je dielektričoj kostati sredie i površii provodika
KONDENZATOR Sistem od dva provodika, razdvojea dielektrikom, koji može imati zate vredosti kapaciteta zove se kodezator. Kapacitet kodezatora srazmera je dielektričoj kostati sredie i površii provodika
KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI. NEUTRALNI ELEMENT GRUPOIDA.
 KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI NEUTRALNI ELEMENT GRUPOIDA 1 Grupoid (G, ) je asocijativa akko važi ( x, y, z G) x (y z) = (x y) z Grupoid (G, ) je komutativa akko važi ( x, y G) x y = y x Asocijativa
KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI NEUTRALNI ELEMENT GRUPOIDA 1 Grupoid (G, ) je asocijativa akko važi ( x, y, z G) x (y z) = (x y) z Grupoid (G, ) je komutativa akko važi ( x, y G) x y = y x Asocijativa
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
Granične vrednosti realnih nizova
 Graiče vredosti realih izova Fukcija f : N R, gde je N skup prirodih brojeva a R skup realih brojeva, zove se iz realih brojeva ili reala iz. Opšti čla iza f je f(), N, i običo se obeležava sa f, dok se
Graiče vredosti realih izova Fukcija f : N R, gde je N skup prirodih brojeva a R skup realih brojeva, zove se iz realih brojeva ili reala iz. Opšti čla iza f je f(), N, i običo se obeležava sa f, dok se
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
II. ANALITIČKA GEOMETRIJA PROSTORA
 II. NLITIČK GEMETRIJ RSTR I. I (Točka. Ravia.) d. sc. Mia Rodić Lipaović 9./. Točka u postou ( ; i, j, k ) Kateijev pavokuti koodiati sustav k i j T T (,, ) oložaj točke u postou je jedoačo odeñe jeim
II. NLITIČK GEMETRIJ RSTR I. I (Točka. Ravia.) d. sc. Mia Rodić Lipaović 9./. Točka u postou ( ; i, j, k ) Kateijev pavokuti koodiati sustav k i j T T (,, ) oložaj točke u postou je jedoačo odeñe jeim
Metoda najmanjih kvadrata
 Metoda ajmajh kvadrata Moday, May 30, 011 Metoda ajmajh kvadrata (MNK) MNK smo već uvel u proučavaju leare korelacje; gdje smo tražl da suma kvadrata odstupaja ekspermetalh točaka od pravca koj h a ajbolj
Metoda ajmajh kvadrata Moday, May 30, 011 Metoda ajmajh kvadrata (MNK) MNK smo već uvel u proučavaju leare korelacje; gdje smo tražl da suma kvadrata odstupaja ekspermetalh točaka od pravca koj h a ajbolj
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
 Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
PRIMJER 3. MATLAB filtdemo
 PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
BIPOLARNI TRANZISTOR Auditorne vježbe
 BPOLARN TRANZSTOR Auditorne vježbe Struje normalno polariziranog bipolarnog pnp tranzistora: p n p p - p n B0 struja emitera + n B + - + - U B B U B struja kolektora p + B0 struja baze B n + R - B0 gdje
BPOLARN TRANZSTOR Auditorne vježbe Struje normalno polariziranog bipolarnog pnp tranzistora: p n p p - p n B0 struja emitera + n B + - + - U B B U B struja kolektora p + B0 struja baze B n + R - B0 gdje
( , 2. kolokvij)
 A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika. Monotonost i ekstremi. Katica Jurasić. Rijeka, 2011.
 Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
NOMENKLATURA ORGANSKIH SPOJEVA. Imenovanje aromatskih ugljikovodika
 NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
Funkcije dviju varjabli (zadaci za vježbu)
 Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
VJEŽBE 3 BIPOLARNI TRANZISTORI. Slika 1. Postoje npn i pnp bipolarni tranziostori i njihovi simboli su dati na slici 2 i to npn lijevo i pnp desno.
 JŽ 3 POLAN TANZSTO ipolarni tranzistor se sastoji od dva pn spoja kod kojih je jedna oblast zajednička za oba i naziva se baza, slika 1 Slika 1 ipolarni tranzistor ima 3 izvoda: emitor (), kolektor (K)
JŽ 3 POLAN TANZSTO ipolarni tranzistor se sastoji od dva pn spoja kod kojih je jedna oblast zajednička za oba i naziva se baza, slika 1 Slika 1 ipolarni tranzistor ima 3 izvoda: emitor (), kolektor (K)
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
PRILOG. Tab. 1.a. Dozvoljena trajna opterećenja bakarnih pravougaonih profila u(a) za θ at =35 C i θ=30 C, (θ tdt =65 C)
 PRILOG Tab. 1.a. Dozvoljena trajna opterećenja bakarnih pravougaonih profila u(a) za θ at =35 C i θ=30 C, (θ tdt =65 C) Tab 3. Vrednosti sačinilaca α i β za tipične konstrukcije SN-sabirnica Tab 4. Minimalni
PRILOG Tab. 1.a. Dozvoljena trajna opterećenja bakarnih pravougaonih profila u(a) za θ at =35 C i θ=30 C, (θ tdt =65 C) Tab 3. Vrednosti sačinilaca α i β za tipične konstrukcije SN-sabirnica Tab 4. Minimalni
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
7 Algebarske jednadžbe
 7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
FAKULTET PROMETNIH ZNANOSTI
 SVUČILIŠT U ZAGU FAKULTT POMTNIH ZNANOSTI predmet: Nastavnik: Prof. dr. sc. Zvonko Kavran zvonko.kavran@fpz.hr * Autorizirana predavanja 2016. 1 Pojačala - Pojačavaju ulazni signal - Zahtjev linearnost
SVUČILIŠT U ZAGU FAKULTT POMTNIH ZNANOSTI predmet: Nastavnik: Prof. dr. sc. Zvonko Kavran zvonko.kavran@fpz.hr * Autorizirana predavanja 2016. 1 Pojačala - Pojačavaju ulazni signal - Zahtjev linearnost
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE GODINE 8. RAZRED TOČNI ODGOVORI
 21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
Matematika 1 - vježbe. 11. prosinca 2015.
 Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
RIJEŠENI ZADACI I TEORIJA IZ
 RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
Niz i podniz. Definicija Svaku funkciju a : N S zovemo niz u S. Za n N pišemo a(n) = a n i nazivamo n-tim članom niza.
 2. NIZOVI 1 / 78 Niz i podiz 2 / 78 Niz i podiz Defiicija Svaku fukciju a : N S zovemo iz u S. Za N pišemo a() = a i azivamo -tim člaom iza. Ozaka za iz je (a ) N ili (a ) ili samo (a ). Kodomea iza može
2. NIZOVI 1 / 78 Niz i podiz 2 / 78 Niz i podiz Defiicija Svaku fukciju a : N S zovemo iz u S. Za N pišemo a() = a i azivamo -tim člaom iza. Ozaka za iz je (a ) N ili (a ) ili samo (a ). Kodomea iza može
DESETA VEŽBA 1. zadatak:
 DEETA VEŽBA zadata: Trasformator čiji su podaci: VA cu 4 W W u 5 % radi pri eom opterećeju uz fator sage φ 8 (id) ritom su omiali gubici u baru cu određei pri temperaturi od C Za radu temperaturu trasformatora
DEETA VEŽBA zadata: Trasformator čiji su podaci: VA cu 4 W W u 5 % radi pri eom opterećeju uz fator sage φ 8 (id) ritom su omiali gubici u baru cu određei pri temperaturi od C Za radu temperaturu trasformatora
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
PRIJENOS i DISTRIBUCIJA ELEKTRIČNE ENERGIJE
 TEHNČK FAKULTET SVEUČLŠTA U RJEC Sveučilišni diplomski studij elektrotehnike PRJENOS i DSTRBUCJA ELEKTRČNE ENERGJE 1. KONSTRUKCJSK RAD - ZBOR PRESJEKA ELEKTROENERGETSKOG KABELA Kabelskim elektroenergetskim
TEHNČK FAKULTET SVEUČLŠTA U RJEC Sveučilišni diplomski studij elektrotehnike PRJENOS i DSTRBUCJA ELEKTRČNE ENERGJE 1. KONSTRUKCJSK RAD - ZBOR PRESJEKA ELEKTROENERGETSKOG KABELA Kabelskim elektroenergetskim
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
SEKUNDARNE VEZE međumolekulske veze
 PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
Centralni granični teorem i zakoni velikih brojeva
 Poglavlje 8 Cetrali graiči teorem i zakoi velikih brojeva 8.1 Cetrali graiči teorem Lema 8.1 Za 1/ x 1 vrijedi Dokaz: Stavimo log1 + x x x. fx := log1 + x x, x [ 1/, 1]. Očito f0 = 0. Nadalje, po teoremu
Poglavlje 8 Cetrali graiči teorem i zakoi velikih brojeva 8.1 Cetrali graiči teorem Lema 8.1 Za 1/ x 1 vrijedi Dokaz: Stavimo log1 + x x x. fx := log1 + x x, x [ 1/, 1]. Očito f0 = 0. Nadalje, po teoremu
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
MATEMATIKA 1 8. domaća zadaća: RADIJVEKTORI. ALGEBARSKE OPERACIJE S RADIJVEKTORIMA. LINEARNA (NE)ZAVISNOST SKUPA RADIJVEKTORA.
 Napomena: U svim zadatcima O označava ishodište pravokutnoga koordinatnoga sustava u ravnini/prostoru (tj. točke (0,0) ili (0, 0, 0), ovisno o zadatku), označava skalarni umnožak, a vektorski umnožak.
Napomena: U svim zadatcima O označava ishodište pravokutnoga koordinatnoga sustava u ravnini/prostoru (tj. točke (0,0) ili (0, 0, 0), ovisno o zadatku), označava skalarni umnožak, a vektorski umnožak.
Riješeni zadaci: Limes funkcije. Neprekidnost
 Riješeni zadaci: Limes funkcije. Neprekidnost Limes funkcije Neka je 0 [a, b] i f : D R, gdje je D = [a, b] ili D = [a, b] \ { 0 }. Kažemo da je es funkcije f u točki 0 jednak L i pišemo f ) = L, ako za
Riješeni zadaci: Limes funkcije. Neprekidnost Limes funkcije Neka je 0 [a, b] i f : D R, gdje je D = [a, b] ili D = [a, b] \ { 0 }. Kažemo da je es funkcije f u točki 0 jednak L i pišemo f ) = L, ako za
Definicija: Beskonačni niz realnih brojeva je funkcija a : N R. Umjesto zapisa a(1), a(2),,a(n), može se koristiti zapis a 1,
 Defiicija: Beskoači iz realih brojeva je fukcija a : N R i Umjesto zapisa a(), a(),,a(), može se koristiti zapis a, a,,a, Broj a zove se opći čla iza, a cijeli iz se kratko ozačuje (a ). Niz je : -rastući
Defiicija: Beskoači iz realih brojeva je fukcija a : N R i Umjesto zapisa a(), a(),,a(), može se koristiti zapis a, a,,a, Broj a zove se opći čla iza, a cijeli iz se kratko ozačuje (a ). Niz je : -rastući
OSNOVI ELEKTRONIKE VEŽBA BROJ 1 OSNOVNA KOLA SA DIODAMA
 ELEKTROTEHNIČKI FAKULTET U BEOGRADU KATEDRA ZA ELEKTRONIKU OSNOVI ELEKTRONIKE SVI ODSECI OSIM ODSEKA ZA ELEKTRONIKU LABORATORIJSKE VEŽBE VEŽBA BROJ 1 OSNOVNA KOLA SA DIODAMA Autori: Goran Savić i Milan
ELEKTROTEHNIČKI FAKULTET U BEOGRADU KATEDRA ZA ELEKTRONIKU OSNOVI ELEKTRONIKE SVI ODSECI OSIM ODSEKA ZA ELEKTRONIKU LABORATORIJSKE VEŽBE VEŽBA BROJ 1 OSNOVNA KOLA SA DIODAMA Autori: Goran Savić i Milan
Geodetski fakultet, dr. sc. J. Beban-Brkić Predavanja iz Matematike OSNOVNI TEOREMI DIFERENCIJALNOG RAČUNA
 Geodetski akultet dr s J Beba-Brkić Predavaja iz Matematike OSNOVNI TEOREMI DIFERENCIJALNOG RAČUNA Teoremi koje ćemo avesti u ovom poglavlju su osovi teoremi koji osiguravaju ispravost primjea diereijalog
Geodetski akultet dr s J Beba-Brkić Predavaja iz Matematike OSNOVNI TEOREMI DIFERENCIJALNOG RAČUNA Teoremi koje ćemo avesti u ovom poglavlju su osovi teoremi koji osiguravaju ispravost primjea diereijalog
konst. Električni otpor
 Sveučilište J. J. Strossmayera u sijeku Elektrotehnički fakultet sijek Stručni studij Električni otpor hmov zakon Pri protjecanju struje kroz vodič pojavljuje se otpor. Georg Simon hm je ustanovio ovisnost
Sveučilište J. J. Strossmayera u sijeku Elektrotehnički fakultet sijek Stručni studij Električni otpor hmov zakon Pri protjecanju struje kroz vodič pojavljuje se otpor. Georg Simon hm je ustanovio ovisnost
Otpornost R u kolu naizmjenične struje
 Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Linearna algebra 2 prvi kolokvij,
 1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
Pismeni ispit iz matematike GRUPA A 1. Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj, zatim naći 4 z.
 Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
nvt 1) ukoliko su poznate struje dioda. Struja diode D 1 je I 1 = I I 2 = 8mA. Sada je = 1,2mA.
 IOAE Dioda 8/9 I U kolu sa slike, diode D su identične Poznato je I=mA, I =ma, I S =fa na 7 o C i parametar n= a) Odrediti napon V I Kolika treba da bude struja I da bi izlazni napon V I iznosio 5mV? b)
IOAE Dioda 8/9 I U kolu sa slike, diode D su identične Poznato je I=mA, I =ma, I S =fa na 7 o C i parametar n= a) Odrediti napon V I Kolika treba da bude struja I da bi izlazni napon V I iznosio 5mV? b)
T r. T n. Naponi na bokovima zubaca
 Napoi a bokovima zubaca U treutoj tački dodira spregutih profila zubaca dejstvuje ormala sila i to u pravcu dodirice profila. Na mestima dodira spregutih zubaca astaju lokale elastiče deformacije, tako
Napoi a bokovima zubaca U treutoj tački dodira spregutih profila zubaca dejstvuje ormala sila i to u pravcu dodirice profila. Na mestima dodira spregutih zubaca astaju lokale elastiče deformacije, tako
POVRŠINA TANGENCIJALNO-TETIVNOG ČETVEROKUTA
 POVRŠIN TNGENIJLNO-TETIVNOG ČETVEROKUT MLEN HLP, JELOVR U mnoštvu mnogokuta zanimljiva je formula za površinu četverokuta kojemu se istoobno može upisati i opisati kružnica: gje su a, b, c, uljine stranica
POVRŠIN TNGENIJLNO-TETIVNOG ČETVEROKUT MLEN HLP, JELOVR U mnoštvu mnogokuta zanimljiva je formula za površinu četverokuta kojemu se istoobno može upisati i opisati kružnica: gje su a, b, c, uljine stranica
5. Karakteristične funkcije
 5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
Strukture podataka i algoritmi 1. kolokvij 16. studenog Zadatak 1
 Strukture podataka i algoritmi 1. kolokvij Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i službeni šalabahter. Predajete samo papire koje ste dobili. Rezultati i uvid u kolokvije: ponedjeljak,
Strukture podataka i algoritmi 1. kolokvij Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i službeni šalabahter. Predajete samo papire koje ste dobili. Rezultati i uvid u kolokvije: ponedjeljak,
Linearna algebra 2 prvi kolokvij,
 Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Iz zadatka se uočava da je doslo do tropolnog kratkog spoja na sabirnicama B, pa je zamjenska šema,
 . Na slici je jednopolno prikazan trofazni EES sa svim potrebnim parametrima. U režimu rada neposredno prije nastanka KS kroz prekidač protiče struja (168-j140)A u naznačenom smjeru. Fazni stav struje
. Na slici je jednopolno prikazan trofazni EES sa svim potrebnim parametrima. U režimu rada neposredno prije nastanka KS kroz prekidač protiče struja (168-j140)A u naznačenom smjeru. Fazni stav struje
3. razred gimnazije- opšti i prirodno-matematički smer ALKENI. Aciklični nezasićeni ugljovodonici koji imaju jednu dvostruku vezu.
 ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI)
 IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
TRIGONOMETRIJA TROKUTA
 TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
Dimenzioniranje SN/NN kabela i transformatora
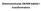 Dmezoraje SN/NN kabela trasformatora Za NN mrežu prkazau slkom potrebo je odredt presjek glavh adzemh trofazh zvoda te moofazh podzvoda obzrom a dozvolje pad apoa kod krajjeg potrošača od 6% dozvoljeu
Dmezoraje SN/NN kabela trasformatora Za NN mrežu prkazau slkom potrebo je odredt presjek glavh adzemh trofazh zvoda te moofazh podzvoda obzrom a dozvolje pad apoa kod krajjeg potrošača od 6% dozvoljeu
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
S t r a n a 1. 1.Povezati jonsku jačinu rastvora: a) MgCl 2 b) Al 2 (SO 4 ) 3 sa njihovim molalitetima, m. za so tipa: M p X q. pa je jonska jačina:
 S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
Novi Sad god Broj 1 / 06 Veljko Milković Bulevar cara Lazara 56 Novi Sad. Izveštaj o merenju
 Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
π π ELEKTROTEHNIČKI ODJEL i) f (x) = x 3 x 2 x + 1, a = 1, b = 1;
 1. Provjerite da funkcija f definirana na segmentu [a, b] zadovoljava uvjete Rolleova poučka, pa odredite barem jedan c a, b takav da je f '(c) = 0 ako je: a) f () = 1, a = 1, b = 1; b) f () = 4, a =,
1. Provjerite da funkcija f definirana na segmentu [a, b] zadovoljava uvjete Rolleova poučka, pa odredite barem jedan c a, b takav da je f '(c) = 0 ako je: a) f () = 1, a = 1, b = 1; b) f () = 4, a =,
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
 TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
Matematička analiza 1 dodatni zadaci
 Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo Najpre da se podsetimo tablice i osnovnih pravila:. C0.. (. ( n n n-. (a a lna 6. (e e 7. (log a 8. (ln ln a (>0 9. ( 0 0. (>0 (ovde je >0 i a >0. (cos. (cos - π. (tg kπ cos. (ctg
IZVODI ZADACI (I deo Najpre da se podsetimo tablice i osnovnih pravila:. C0.. (. ( n n n-. (a a lna 6. (e e 7. (log a 8. (ln ln a (>0 9. ( 0 0. (>0 (ovde je >0 i a >0. (cos. (cos - π. (tg kπ cos. (ctg
MATEMATIKA 2. Grupa 1 Rexea zadataka. Prvi pismeni kolokvijum, Dragan ori
 MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
METODA SEČICE I REGULA FALSI
 METODA SEČICE I REGULA FALSI Zadatak: Naći ulu fukcije f a itervalu (a,b), odoso aći za koje je f()=0. Rešeje: Prvo, tražimo iterval (a,b) a kome je fukcija eprekida, mootoa i važi: f(a)f(b)
METODA SEČICE I REGULA FALSI Zadatak: Naći ulu fukcije f a itervalu (a,b), odoso aći za koje je f()=0. Rešeje: Prvo, tražimo iterval (a,b) a kome je fukcija eprekida, mootoa i važi: f(a)f(b)
Društvo matematičara Srbije. Pripreme za Juniorske olimpijade školske 2007/2008. Matematička indukcija
 Društvo matematičara Srbije Pripreme za Juiorske olimpijade školske 007/008 -Dord e Baralić Tel:063/706-706-6 e-mail:djolebar@ptt.yu Matematička idukcija Primer 1. Dokazati da je > za sve N. Ituitivo zamo
Društvo matematičara Srbije Pripreme za Juiorske olimpijade školske 007/008 -Dord e Baralić Tel:063/706-706-6 e-mail:djolebar@ptt.yu Matematička idukcija Primer 1. Dokazati da je > za sve N. Ituitivo zamo
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
(P.I.) PRETPOSTAVKA INDUKCIJE - pretpostavimo da tvrdnja vrijedi za n = k.
 1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
radni nerecenzirani materijal za predavanja R(f) = {f(x) x D}
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Trigonometrijske funkcije
 9 1. Trigoometrijske fukcije 1.1. Ako je α + β π,izračuaj 1 + tg α)1 + tg β). 4 1.. Izračuaj zbroj log a tg 1 + log a tg +...+ log a tg 89. 1.3. Izračuaj 40 0 si 0 bez uporabe tablica ili račuala. 1.4.
9 1. Trigoometrijske fukcije 1.1. Ako je α + β π,izračuaj 1 + tg α)1 + tg β). 4 1.. Izračuaj zbroj log a tg 1 + log a tg +...+ log a tg 89. 1.3. Izračuaj 40 0 si 0 bez uporabe tablica ili račuala. 1.4.
Nizovi. Definicija. Niz je funkcija. a: R. Oznake: (a n ) ili a n } Zadatak 2.1 Napišite prvih nekoliko članova nizova zadanih općim članom:
 Nizovi Defiicija Niz je fukcija Ozake: (a ) ili a } a: R Zadatak Napišite prvih ekoliko člaova izova zadaih općim člaom: a = a = ( ) (c) a = Zadatak Odredite opće člaove izova: 3 5 7 9 ; 3 7 5 3 ; (c)
Nizovi Defiicija Niz je fukcija Ozake: (a ) ili a } a: R Zadatak Napišite prvih ekoliko člaova izova zadaih općim člaom: a = a = ( ) (c) a = Zadatak Odredite opće člaove izova: 3 5 7 9 ; 3 7 5 3 ; (c)
Elektronički Elementi i Sklopovi
 Sadržaj predavanja: 1. Strujna zrcala pomoću BJT tranzistora 2. Strujni izvori sa BJT tranzistorima 3. Tranzistor kao sklopka 4. Stabilizacija radne točke 5. Praktični sklopovi s tranzistorima Strujno
Sadržaj predavanja: 1. Strujna zrcala pomoću BJT tranzistora 2. Strujni izvori sa BJT tranzistorima 3. Tranzistor kao sklopka 4. Stabilizacija radne točke 5. Praktični sklopovi s tranzistorima Strujno
TRANSFORMATORI. opća mreža (400 kv - izbacivanje 220kV) razdjelna mreža (110, 35, 20 kv) (izbacivanje 10 kv) na 400 kv.
 ANSFOMAOI opća mreža (400 kv - izbacivanje 0kV) na 400 kv razdjelna mreža (0, 35, 0 kv) (izbacivanje 0 kv) potrošna mreža ransformator u praznom hodu N - primarni N - sekundarni GN - gornjeg napona DN
ANSFOMAOI opća mreža (400 kv - izbacivanje 0kV) na 400 kv razdjelna mreža (0, 35, 0 kv) (izbacivanje 0 kv) potrošna mreža ransformator u praznom hodu N - primarni N - sekundarni GN - gornjeg napona DN
INTELIGENTNO UPRAVLJANJE
 INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
XI dvoqas veжbi dr Vladimir Balti. 4. Stabla
 XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
SISTEMI NELINEARNIH JEDNAČINA
 SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
MJERA I INTEGRAL završni ispit 4. srpnja (Knjige, bilježnice, dodatni papiri i kalkulatori nisu dozvoljeni!)
 1. (ukupo 8 bodova) MJERA I INTEGRAL završi ispit 4. srpja 216. (Kjige, bilježice, dodati papiri i kalkulatori isu dozvoljei!) (a) (2 boda) Defiirajte p za ekspoete p [1, +. (b) (6 bodova) Dokažite da
1. (ukupo 8 bodova) MJERA I INTEGRAL završi ispit 4. srpja 216. (Kjige, bilježice, dodati papiri i kalkulatori isu dozvoljei!) (a) (2 boda) Defiirajte p za ekspoete p [1, +. (b) (6 bodova) Dokažite da
