Υπολογισιμότητα και Πολυπλοκότητα Computability and Complexity
|
|
|
- Δαμοκλής Κοτζιάς
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Υπολογισιμότητα και Πολυπλοκότητα Computability and Complexity Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - ΕΜΠ Μάιος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
2 Πολυπλοκότητα Περιεχόμενα 1 Υπολογισιμότητα 2 Αυτόματα και Τυπικές Γλώσσες 3 Πολυπλοκότητα Αλληλεπίδραση, PCP Μέτρηση Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
3 I Χρησιμοποιώντας το μοντέλο δένδρων υπολογισμού, θα ορίσουμε κλάσεις πολυπλοκότητας που βασίζονται στις πιθανότητες, με βάση τυχαίες επιλογές Αυτή η προσέγγιση είναι πολύ χρήσιμη από πρακτική άποψη, αφού σε πολλές εφαρμογές, είναι ικανοποιητικός ένας αλγόριθμος ο οποίος κάνοντας κάποιες τυχαίες επιλογές, δίνει στις περισσότερες των περιπτώσεων το σωστό αποτέλεσμα Ένας πιθανοκρατικός αλγόριθμος είναι συνήθως πιο απλός στην διατύπωσή του και στην πράξη πιο αποδοτικός από έναν αντίστοιχο ντετερμινιστικό που επιλύει το ίδιο πρόβλημα Για παράδειγμα, απλοί πιθανοκρατικοί αλγόριθμοι για τον έλεγχο αν ένας αριθμός είναι πρώτος υπάρχουν από την δεκαετία του 1970 και χρησιμοποιούνται στην πράξη έναντι πιο περίπλοκων ντετερμινιστικών τύπου AKS Στα πλαίσια του μοντέλου δένδρων υπολογισμού, θα θεωρήσουμε ότι η επιλογή σε κάθε κόμβο του δένδρου γίνεται τυχαία με πιθανότητα 1/2 για κάθε παιδί του κόμβου Για να δείξουμε ότι η «συντριπτική» πλειοψηφία των υπολογισμών δίνει το σωστό αποτέλεσμα, εισαγάγουμε έναν νέο ποσοδείκτη, τον D + Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
4 Πολυπλοκότητα II Με την βοήθεια του D +, ορίζουμε την κλάση BPP, από το Bounded Probabilistic Polynomial: Ορισμός (BPP = (D +, D + )) L P BPP ðñ DR P P: # x P L ùñ D + yr(x, y) x R L ùñ D + y R(x, y) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
5 III Με άλλα λόγια, σε ένα δέντρο για την κλάση BPP έχουμε την «συντριπτική» πλειοψηφία των φύλλων να δίνει το σωστό αποτέλεσμα Στον παραπάνω ορισμό, δεν έχει μεγάλη σημασία ο ακριβής ορισμός της «συντριπτικής» πλειοψηφίας, αλλά πρέπει να είναι οπωσδήποτε φραγμένος (εξ ου και το bounded του BPP) πάνω από το 1/2 Το ποσοστό της πλειοψηφίας μπορεί να είναι, ενδεικτικά, μεγαλύτερο από 1/2 + ε, 1/2 + 1/p( x ), 2/3, 99%, 1 2 p( x ) (όπου p( x ) ą 1) Αυτή η δυνατότητα επιλογής υπάρχει, επειδή με πολυωνυμικές επαναλήψεις του αντίστοιχου αλγορίθμου, είναι δυνατόν να αυξήσουμε την πιθανότητα επιτυχίας, όσο θέλουμε Αλγόριθμοι BPP ονομάζονται Monte Carlo ή αλλιώς two-sided error, επειδή ανεξάρτητα από το αποτέλεσμα (ναι ή όχι), υπάρχει κάποια πιθανότητα λάθους Είναι προφανές ότι η κλάση BPP είναι κλειστή ως προς συμπλήρωμα Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
6 IV Ας θεωρήσουμε τώρα αλγορίθμους οι οποίοι κάνουν λάθος μόνον για την μία απάντηση (one sided error) Έτσι, προκύπτει η κλάση RP (Randomized Polynomial): Ορισμός (RP = (D L P RP ðñ DR P P: # x P L ùñ D + yr(x, y) x R L R(x, y) Σε αυτήν την κλάση, αν ο αντίστοιχος RP αλγόριθμος δώσει απάντηση «ναι» (δηλαδή το κατηγόρημα R υπολογιστεί αληθές), είμαστε σίγουροι ότι x P L Αντίθετα, η απάντηση «όχι» του RP αλγορίθμου δεν είναι «σίγουρη» Προφανώς, ισχύουν: RP Ď BPP, corp Ď BPP, αλλά δεν γνωρίζουμε αν RP = corp Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
7 V Μία άλλη πολύ χρήσιμη κλάση, είναι αυτή που ορίζεται με τομή των RP και corp, η ZPP = RP X corp Η ονομασία προέρχεται από το Zero error Probabilistic Polynomial, γιατί μπορεί εύκολα να δειχτεί ότι ένα πρόβλημα είναι στο ZPP αν υπάρχει πιθανοκρατικός αλγόριθμος ο οποίος τρέχει σε αναμενόμενο πολυωνυμικό χρόνο και δίνει πάντοτε σωστή απάντηση Πράγματι, αν ένα πρόβλημα είναι στο ZPP, σημαίνει ότι έχουμε ένα RP και έναν corp αλγόριθμο για αυτό, οπότε αρκεί να τρέχουμε εναλλακτικά τους δύο αλγορίθμους, μέχρι ο ένας να δώσει την «σίγουρή» του απάντηση Βέβαια, μπορεί να χρειαστεί να τρέχουμε εναλλακτικά τους δύο αλγορίθμους για πάντα, αλλά με μεγάλη πιθανότητα θα έχουμε μία «σίγουρη» απάντηση, μετά από μερικές επαναλήψεις Εναλλακτικά, μπορούμε να πούμε ότι ένας ZPP αλγόριθμος έχει τρεις εξόδους: «ναι», «όχι» (για τις «σίγουρες» απαντήσεις), και «δεν ξέρω» (για τις όχι «σίγουρες») Οι αλγόριθμοι στο ZPP ονομάζονται Las Vegas Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
8 VI Δεδομένου ότι υπάρχουν αρκετοί πιθανοκρατικοί αλγόριθμοι ευρείας χρήσης για πρακτικά προβλήματα, πολλοί τοποθετούν τους εφικτούς (feasible) υπολογισμούς πάνω από το P, στις πιθανοτικές κλάσεις BPP, RP, ZPP Πάντως, δεν γνωρίζουμε αν υπάρχουν πλήρη προβλήματα για τις κλάσεις που ορίστηκαν παραπάνω (BPP, RP, ZPP) Αν τώρα το ποσοστό λάθους ενός πιθανοκρατικού αλγορίθμου δεν φραχθεί μακριά από το 1/2, τότε έχουμε απλώς την βεβαιότητα ότι στο μοντέλο δένδρων υπολογισμού παραπάνω από τα μισά υπολογιστικά μονοπάτια δίνουν την σωστή απάντηση Για να δηλώσουμε το παραπάνω χρησιμοποιούμε τον ποσοδείκτη D 1/2 Για unbounded two-sided error, έχουμε την κλάση PP (Probabilistic Polynomial): Ορισμός (PP = (D 1/2, D 1/2 )) L P PP ðñ DR P P: # x P L ùñ D 1/2 yr(x, y) x R L ùñ D 1/2 y R(x, y) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
9 VII Λόγω της έλλειψης φράγματος για την πιθανότητα λάθους, δεν μπορούμε να χρησιμοποιήσουμε την τεχνική της επανάληψης για να βελτιώσουμε την πιθανότητα σωστού αποτελέσματος από έναν PP αλγόριθμο Μία άλλη ένδειξη για το ανέφικτο της κλάσης PP σε σχέση με τις BPP, RP, ZPP, προκύπτει από το παρακάτω αποτέλεσμα: Πρόταση NP Ď PP Πρέπει επίσης να σημειώσουμε ότι δεν λάβαμε καθόλου υπ όψιν μας, ως υπολογιστικό πόρο, των αριθμό των τυχαίων bits που χρησιμοποιεί ένας πιθανοκρατικός αλγόριθμος Στην πράξη, κάθε «τυχαίο» bit που χρειαζόμαστε δεν είναι χωρίς τίμημα, αφού το λαμβάνουμε από κάποια γεννήτρια ψευδοτυχαίων bits Τέλος, αναφέρουμε και την κλάση RL (Randomized Logspace) που περιέχει τα προβλήματα που έχουν one-sided error αλγόριθμο που χρησιμοποιεί λογαριθμικό χώρο και πολυωνυμικό ως προς το μήκος της εισόδου αριθμό τυχαίων bits Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
10 Πολυωνυμική Ιεραρχία I Αντίστοιχα με προηγούμενο κεφάλαιο, όπου ορίσαμε μαντεία και την αριθμητική ιεραρχία, θα ορίσουμε την πολυωνυμική ιεραρχία, η οποία έχει παρόμοια δομή, αλλά βρίσκεται πολύ χαμηλότερα από άποψη υπολογιστικής πολυπλοκότητας Υπενθυμίζουμε την έννοια του υπολογισμού με μαντείο: Ένας αλγόριθμος χρησιμοποιεί ένα μαντείο για το πρόβλημα Π, αν έχει την δυνατότητα κατά την διάρκεια του υπολογισμού, να ρωτάει το μαντείο για κάποιο στιγμιότυπο x του προβλήματος Π, αν x P Π, και το μαντείο να του απαντά άμεσα με ένα «ναι» ή με ένα «όχι» Όσο δύσκολο και να είναι το πρόβλημα P, ο αλγόριθμος δεν σπαταλά επιπλέον υπολογιστικούς πόρους Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
11 Πολυωνυμική Ιεραρχία II Ορισμός (Κλάσεις με μαντεία) C Π : η κλάση των προβλημάτων τα οποία λύνονται με αλγόριθμο στην κλάση C ο οποίος χρησιμοποιεί μαντείο για το πρόβλημα Π C Co = ď ΠPC o C Π Για παράδειγμα, η κλάση P SAT αποτελείται από τα προβλήματα που λύνονται με ντετερμινιστικό πολυωνυμικό αλγόριθμο ο οποίος χρησιμοποιεί μαντείο για το πρόβλημα SAT Άλλη περιγραφή της ίδιας κλάσης είναι: P NP (αφού το SAT είναι NP-πλήρες) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
12 Πολυωνυμική Ιεραρχία III Ορισμός (k ě 0) Σ p 0 = Πp 0 = p 0 = P Σ p k+1 = NPΣp k, Π p k+1 = coσp k+1, p k+1 = PΣp k, Σ p k = Σp k X Πp k Πολυωνυμική ιεραρχία: PH = Ť kpn Σp k Ισχύουν τα παρακάτω: Σ p 1 = NP, Πp 1 = conp και για κάθε k ě 0: Σp k Ď Σp k+1 και Π p k Ď Σp k+1 Αν και δεν έχει αποδειχθεί το αυστηρό των παραπάνω εγκλεισμών (όπως στην αριθμητική ιεραρχία), εν τούτοις πιστεύουμε ότι η ιεραρχία είναι αυστηρή (strict) Αν η PH δεν είναι αυστηρή, τότε θα υπάρχει κάποιο k για το οποίο PH = Σ p k, οπότε λέμε ότι η πολυωνυμική ιεραρχία καταρρέει στο k-οστό επίπεδο (collapses at the k-th level) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
13 Πολυωνυμική Ιεραρχία IV PSPACE Π p 3 Σ p 3 Σ p 3 p 3 Π p 2 Σ p 2 Σ p 2 = Σp 2 X Πp 2 PH p 2 = PNP Π p 1 = conp Σp 1 = NP Σ p 1 p 1 = P Σχήμα: Η πολυωνυμική ιεραρχία PH Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
14 Πολυωνυμική Ιεραρχία Εναλλαγή Ποσοδεικτών I Ένας εναλλακτικός τρόπος ορισμού της πολυωνυμικής ιεραρχίας είναι με την βοήθεια εναλλαγής ποσοδεικτών (D Επισημαίνουμε ότι, σε κάθε περίπτωση, οι ποσοδείκτες αναφέρονται σε αντικείμενα το μέγεθος των οποίων είναι φραγμένο από κάποιο πολυώνυμο p ως προς το μήκος της εισόδου Πρόταση L P Σ p k ανν υπάρχει κατηγόρημα R υπολογιζόμενο σε πολυωνυμικό χρόνο και πολυώνυμο p που φράσσει το μέγεθος των αντικειμένων των ποσοδεικτών, τέτοια ώστε: x P L ðñ Dy 1@y 2 Qy k R(x, y 1, y 2,, y k), # D, k περιττό όπου Q k άρτιο Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
15 Πολυωνυμική Ιεραρχία Εναλλαγή Ποσοδεικτών II Παρομοίως, για την κλάση Π p k μόνο που τώρα η ακολουθία των ποσοδεικτών αρχίζει Πρόταση L P Π p k ανν υπάρχει κατηγόρημα R υπολογιζόμενο σε πολυωνυμικό χρόνο και πολυώνυμο p που φράσσει το μέγεθος των αντικειμένων των ποσοδεικτών, τέτοια ώστε: όπου Q = x P L 1Dy 2 Qy k R(x, y 1, y 2,, y k), k περιττό D, k άρτιο Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
16 Πολυωνυμική Ιεραρχία Alternating TM I Η εναλλαγή των ποσοδεικτών στην πολυωνυμική ιεραρχία δίνει το έναυσμα για τον ορισμό της μηχανής Turing με εναλλασσόμενη λειτουργία Αν θεωρήσουμε την δενδρική αναπαράσταση των υπολογισμών μίας NP μηχανής Turing, η μηχανή απαντά ναι, αν υπάρχει ένα τουλάχιστον φύλλο που λέει «ναι» Μπορούμε να θεωρήσουμε ότι κάθε κόμβος στο δένδρο υπολογίζει την διάζευξη (_) των αποτελεσμάτων από τα παιδιά του και την προωθεί στον γονέα του (τα φύλλα απλώς προωθούν προς τα πάνω), μέχρι το αποτέλεσμα να φτάσει στην ρίζα Αντίστοιχα, μία conp μηχανή Turing αποδέχεται όταν στην δενδρική αναπαράσταση όλα τα φύλλα λένε «ναι», οπότε μπορούμε να θεωρήσουμε ότι ο κάθε κόμβος συλλέγει τα αποτέλεσμα των παιδιών του και προωθεί στον γονέα του την σύζευξη (^) των αποτελεσμάτων από τα παιδιά του, πάλι μέχρι το σωστό αποτέλεσμα να φτάσει στην ρίζα Λέμε ότι όλοι οι κόμβοι στο δένδρο μίας NP μηχανής είναι τύπου _, ή D, ή υπαρξιακού Λέμε ότι όλοι οι κόμβοι στο δένδρο μίας conp μηχανής είναι τύπου ^, ή καθολικού Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
17 Πολυπλοκότητα Πολυωνυμική Ιεραρχία Alternating TM II Μία εναλλασσόμενη μηχανή Turing είναι μία μηχανή Turing στην οποία το αντίστοιχο υπολογιστικό δένδρο έχει εσωτερικούς κόμβους τύπου _ ή ^ Σημασία έχει το πλήθος εναλλαγών τύπου Το μέγιστο πλήθος εναλλαγών (σε ένα μονοπάτι), που πιθανώς να είναι φραγμένο, αποτελεί μέτρο των δυνατοτήτων μίας τέτοιας μηχανής Για παράδειγμα, το υπολογιστικό δένδρο του παρακάτω σχήματος έχει πλήθος εναλλαγών τύπου ίσο με 2 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
18 Πολυπλοκότητα Πολυωνυμική Ιεραρχία Alternating TM III ^ yes yes yes yes ^ ^ ^ _ no no no no Σχήμα: Υπολογιστικό δένδρο με εναλλαγές Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
19 Πολυωνυμική Ιεραρχία Alternating TM IV Μπορεί να δειχθεί ότι η πολυωνυμική ιεραρχία είναι ακριβώς η κλάση των γλωσσών που γίνεται αποδεκτή από μηχανές Turing που έχουν φραγμένο πλήθος εναλλαγών Πιο συγκεκριμένα: L P Σ p k ανν η L γίνεται αποδεκτή από μηχανή Turing που έχει το πολύ k εναλλαγές τύπου και αρχίζει με τύπο _ L P Π p k ανν η L γίνεται αποδεκτή από μηχανή Turing που έχει το πολύ k εναλλαγές τύπου και αρχίζει με τύπο ^ Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
20 Παραλληλοποιήσιμα προβλήματα I Για να μελετήσουμε παράλληλους υπολογισμούς θα εισάγουμε ένα νέο μοντέλο υπολογισμού, το κύκλωμα Ένα κύκλωμα είναι ένας κατευθυνόμενος ακυκλικός γράφος, στον οποίο έχουμε ένα σύνολο κόμβων εισόδου και έναν κόμβο που είναι η έξοδος Θεωρούμε ότι οι είσοδοι στο κύκλωμα είναι αληθοτιμές (ή αλλιώς οι τιμές 0 και 1) και κάθε εσωτερικός κόμβος αντιστοιχεί σε μία λογική συνάρτηση (ή αλλιώς πύλη gate) με πλήθος εισόδων, όσες οι ακμές που καταλήγουν σε αυτόν Αν ένα κύκλωμα C έχει n εισόδους του ενός bit: x 1, x 2,, x n, τότε για κάθε x P t0, 1u n, υπολογίζει μία μοναδική τιμή στην έξοδο, την C(x) Αν C(x) = 1, λέμε ότι το κύκλωμα C αποδέχεται την είσοδο των n bit: x Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
21 Παραλληλοποιήσιμα προβλήματα II Η αναντιστοιχία του παραπάνω ορισμού αποδοχής, σε σχέση με την αποδοχή, ας πούμε, σε μία μηχανή Turing, είναι ότι ένα κύκλωμα, λόγω της αμετάβλητης φύσης του, μπορεί να απαντά για εισόδους μήκους ακριβώς n, ενώ μία μηχανή Turing (ή ένας αλγόριθμος γενικότερα) δέχεται εισόδους οποιουδήποτε μεγέθους Για τον λόγο αυτό θα θεωρούμε μία οικογένεια κυκλωμάτων tc 1, C 2, u, όπου κάθε C n έχει n κόμβους εισόδου Η γλώσσα που αποδέχεται μία οικογένεια κυκλωμάτων είναι η L(C) = tx C x (x) = 1u Το πρόβλημα είναι ότι οι οικογένειες κυκλωμάτων (σε αντίθεση με τις μηχανές Turing) δεν είναι αριθμήσιμες Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
22 Παραλληλοποιήσιμα προβλήματα III Για να ξεπεράσουμε την παραπάνω δυσκολία, θα περιοριστούμε σε ομοιόμορφες οικογένειες κυκλωμάτων (uniform circuit families) Για αυτές υπάρχει αλγόριθμος και μάλιστα αποδοτικός ο οποίος δεδομένου n κατασκευάζει την αναπαράσταση του κυκλώματος C n της οικογένειας Μία επιλογή είναι οι P-ομοιόμορφες οικογένειες, που χρησιμοποιούν πολυωνυμικό αλγόριθμο κατασκευής Επειδή όμως τα κυκλώματα χρησιμοποιούνται συνήθως για ορισμό κλάσεων χαμηλότερα από το P, θα χρησιμοποιήσουμε μία άλλη πιο περιορισμένη έννοια ομοιομορφίας: Ορισμός Μία οικογένεια κυκλωμάτων είναι DLOGTIME-ομοιόμορφη αν υπάρχει μηχανή Turing (με δυνατότητα τυχαίας προσπέλασης στην ταινία εισόδου) που απαντά τις παρακάτω ερωτήσεις σε χρόνο O(log n): Υπάρχει σύνδεση από τον κόμβο u στον κόμβο v στο C n ; Τι είδους πύλη έχει ο κόμβος u; Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
23 Παραλληλοποιήσιμα προβλήματα IV Το μέγεθος (size) ενός κυκλώματος είναι το πλήθος των κόμβων που περιέχει ο αντίστοιχος γράφος Το μέγεθος αποτελεί μέτρο του κόστους κατασκευής του κυκλώματος και συνήθως δεν θεωρείται περισσότερο από πολυωνυμικό ως προς το μήκος της εισόδου Το μέγεθος, όμως, δεν αποτελεί και πολύ καλό μέτρο του χρόνου υπολογισμού σε ένα κύκλωμα, επειδή εν γένει πολλές λογικές πύλες λειτουργούν παράλληλα Οι πύλες που πρέπει να περιμένουν διαδοχικά ενδιάμεσα αποτελέσματα είναι αυτές που βρίσκονται σε κάθε μονοπάτι από μία είσοδο στην έξοδο Για τον λόγο αυτό, πιο σημαντικό είναι το βάθος (depth) ενός κυκλώματος, που ορίζεται ως το μήκος του μακρύτερου μονοπατιού από είσοδο στην έξοδο Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
24 Παραλληλοποιήσιμα προβλήματα V Επίσης, σημαντικό είναι το είδος των λογικών πυλών που χρησιμοποιούνται σε κάθε κύκλωμα Πιο συγκεκριμένα, θεωρούμε τα παρακάτω είδη λογικών πυλών: 1 Λογικές πύλες με περιορισμένο αριθμό εισόδων (bounded fan-in), καθώς και εναδικές πύλες Αρκεί να θεωρήσουμε δυαδικές πύλες ^ και _ (μαζί με τις εναδικές πύλες ) 2 Λογικές πύλες ^ και _ με απεριόριστο αριθμό εισόδων (unbounded fan-in), καθώς και εναδικές πύλες 3 Πύλες κατωφλίου (threshold) με απεριόριστο αριθμό εισόδων, καθώς και εναδικές πύλες Αρκεί, αντί για γενικές πύλες κατωφλίου, να χρησιμοποιήσουμε την πύλη πλειοψηφίας (majority gate), που δίνει στην έξοδο 1 αν και μόνον αν τουλάχιστον r/2 από τις r εισόδους της είναι 1 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
25 Παραλληλοποιήσιμα προβλήματα VI Με βάση τα παραπάνω μπορούμε να ορίσουμε τις παρακάτω κλάσεις: Ορισμός (k ě 0): 1 NC k : η κλάση των γλωσσών που γίνονται αποδεκτές από DLOGTIME-ομοιόμορφες οικογένειες κυκλωμάτων πολυωνυμικού μεγέθους και βάθους O(log k n), με χρήση πυλών του 1ου είδους (bounded fan-in) 2 AC k : η κλάση των γλωσσών που γίνονται αποδεκτές από DLOGTIME-ομοιόμορφες οικογένειες κυκλωμάτων πολυωνυμικού μεγέθους και βάθους O(log k n), με χρήση πυλών του 2ου είδους (unbounded fan-in) 3 TC k : η κλάση των γλωσσών που γίνονται αποδεκτές από DLOGTIME-ομοιόμορφες οικογένειες κυκλωμάτων πολυωνυμικού μεγέθους και βάθους O(log k n), με χρήση πυλών του 3ου είδους (threshold gates) 4 SC k : η κλάση των γλωσσών που γίνονται αποδεκτές από DTM σε πολυωνυμικό χρόνο και σε O(log k n) χώρο Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
26 Παραλληλοποιήσιμα προβλήματα VII Επίσης, ορίζεται NC = Ť kpn NCk Η τελευταία κλάση λέγεται και Nick s Class, από τον Nicholas Pippenger, που ήταν από τους πρώτους που μελέτησε τέτοια κυκλώματα Στην πραγματικότητα, πολλά άλλα μοντέλα παράλληλου υπολογισμού (πχ CRAM), εκτός από τα κυκλώματα, μπορούν να χρησιμοποιηθούν για τον ορισμό της κλάσης NC, κάτι που αποτελεί ένδειξη για την ευρωστία της κλάσης και την στενή σχέση της με τα παραλληλοποιήσιμα προβλήματα Το «A» στην AC k οφείλεται στην εναλλαγή (alternation), αφού αποδεικνύεται ότι η κλάση AC k, για k ě 1, είναι ακριβώς οι γλώσσες που γίνονται αποδεκτές από εναλλασσόμενη μηχανή Turing που χρησιμοποιεί O(log n) χώρο και κάνει το πολύ O(log k n) εναλλαγές Το «T» στην TC k προέρχεται από το threshold Η ονομασία SC, Steve s Class, προέρχεται από τον Steve Cook Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
27 Παραλληλοποιήσιμα προβλήματα VIII Πιο συγκεκριμένα οι κλάσεις σχετίζονται μεταξύ τους ως εξής: Θεώρημα Για κάθε k ě 0, NC k Ď AC k Ď TC k Ď NC k+1 Σε σχέση με άλλες γνωστές κλάσεις, ισχύει: Θεώρημα Regular Ď NC 1 Ď L = SC 1 Ď NL Ď AC 1 Regular Ă CF Ă AC 1 Δηλαδή το πρόβλημα του ελέγχου αν μία συμβολοσειρά παράγεται από δεδομένη γλώσσα χωρίς συμφραζόμενα (context free) ανήκει στην κλάση NC 2 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
28 Αλληλεπίδραση, PCP Διαλογική αλληλεπίδραση (interactivity) I Διαλογικά συστήματα αποδείξεων (IP) Ας θεωρήσουμε έναν αποδείκτη (prover) που προσπαθεί να αποδείξει την αλήθεια μίας πρότασης του τύπου «x P L» σε κάποιον άλλο, που τον ονομάζουμε επαληθευτή (verifier) Ο αποδείκτης είναι παντοδύναμος, με την έννοια ότι είναι ένας αλγόριθμος χωρίς περιορισμούς στο μέγεθος των αγαθών που χρησιμοποιεί (χρόνος, χώρος) Αντίθετα, ο επαληθευτής είναι απλώς ένας πιθανοτικός αλγόριθμος πολυωνυμικού χρόνου Ο επαληθευτής και ο αποδείκτης συμμετέχουν σε ένα πρωτόκολλο επικοινωνίας στέλνοντας μηνύματα Ανάλογα με τα μηνύματα που λαμβάνει ο V από τον P, ο V αποδέχεται την απόδειξη, αλλιώς την απορρίπτει Ο αποδείκτης μπορεί να μην είναι έντιμος, και να θέλει να πείσει τον επαληθευτή ότι «x P L», ακόμη και για x για τα οποία «x R L» Ο επαληθευτής, απέναντι στον παντοδύναμο αποδείκτη, μπορεί να χρησιμοποιήσει εκτός του πολυωνυμικού χρόνου, κυρίως την τυχαιότητα που διαθέτει Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
29 Αλληλεπίδραση, PCP Διαλογική αλληλεπίδραση (interactivity) II Διαλογικά συστήματα αποδείξεων (IP) Η κλάση IP ορίστηκε από τους Goldwasser, Micali, Rackoff: Ορισμός L P IP: x P L ùñ υπάρχει αποδείκτης (prover) P, ώστε ο επαληθευτής (verifier) V πάντοτε αποδέχεται (δηλαδή έχουμε πιθανότητα αποδοχής ίση με 1) x R L ùñ για κάθε αποδείκτη (prover) P, ο επαληθευτής V δεν αποδέχεται με συντριπτική πιθανότητα Ας θεωρήσουμε το πρόβλημα μη ισομορφισμού γράφων: «Δίνονται δύο γράφοι Είναι μη ισομορφικοί;» Αυτό το πρόβλημα ανήκει στο conp Θα δώσουμε ένα πρωτόκολλο για το πρόβλημα μη ισομορφισμού γράφων, που θα δείχνει ότι το πρόβλημα είναι στο IP Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
30 Αλληλεπίδραση, PCP Διαλογική αλληλεπίδραση (interactivity) III Διαλογικά συστήματα αποδείξεων (IP) Αρχικά, ο επαληθευτής έχει τους δύο γράφους G 1 και G 2 Επιλέγει τυχαία έναν από τους δύο, έστω των G i, και υπολογίζει έναν τυχαίο ισομορφικό γράφο του G i, έστω τον H (αυτό γίνεται διαλέγοντας τυχαία μία μετάθεση των n κορυφών του γράφου G i) Στέλνει τον γράφο H στον αποδείκτη, ζητώντας ένα j τέτοιο ώστε ο G j να είναι ισομορφικός του H Ο αποδείκτης απαντά με ένα j P t1, 2u Ο επαληθευτής αποδέχεται αν όντως i = j, αλλιώς απορρίπτει Στην περίπτωση που όντως οι G 1, G 2 είναι μη ισομορφικοί, ο P, αφού είναι παντοδύναμος, βρίσκει με ποιον (μοναδικό) γράφο είναι ισομορφικός ο H που του έστειλε ο V και δίνει την σωστή τιμή για να αποδεχθεί ο V Αν τώρα οι G 1, G 2 είναι ισομορφικοί, ο P αδυνατεί να συμπεράνει από ποιον γράφο προήλθε ο ισομορφικός H, άρα δεν μπορεί να κάνει κάτι καλύτερο από το να στείλει τυχαία ένα από τα t1, 2u στον V Έτσι, αν οι δύο γράφοι είναι μη ισομορφικοί ο V δεν αποδέχεται με πιθανότητα 1/2 Τα παραπάνω σκιαγραφούν μία απόδειξη ότι το πρόβλημα μη ισομορφισμού γράφων ανήκει στην IP Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
31 Αλληλεπίδραση, PCP Διαλογική αλληλεπίδραση (interactivity) IV Διαλογικά συστήματα αποδείξεων (IP) Στην πραγματικότητα, κάθε γλώσσα στην πολυωνυμική ιεραρχία έχει πρωτόκολλο IP Μάλιστα, έχει αποδειχθεί το ακόμη ισχυρότερο αποτέλεσμα: Θεώρημα (Shamir) IP = PSPACE Τι γίνεται όμως στην περίπτωση που ο επαληθευτής μπορεί να διαλέγεται με δύο ή περισσότερους αποδείκτες; Αν οι αποδείκτες επικοινωνούν μεταξύ τους, τότε παραμένουμε στην κλάση IP (πρακτικά, ένας αποδείκτης, ως παντοδύναμος αλγόριθμος, μπορεί να εξομοιώνει οσουσδήποτε άλλους) Αν όμως, οι αποδείκτες δεν έχουν επικοινωνία μεταξύ τους, τότε προκύπτει η ισχυρότερη κλάση MIP (Multi IP) Μάλιστα ισχύει: MIP = NEXP Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
32 Αλληλεπίδραση, PCP Διαλογική αλληλεπίδραση (interactivity) I Κλάσεις Arthur-Merlin Στην κλάση IP ο επαληθευτής κρατά «κρυφά» τα τυχαία bits που χρησιμοποιεί Μάλιστα, στην απόδειξη ότι το πρόβλημα μη ισομορφισμού γράφων είναι στην IP, αυτό αποτελεί βασικό συστατικό της απόδειξης Φαίνεται ότι αν ο επαληθευτής είναι υποχρεωμένος να αποκαλύπτει τα bits του, προκύπτει μία μικρότερη κλάση γλωσσών από την IP Σε αυτήν την κλάση γλωσσών ο αποδείκτης ονομάζεται Merlin και ο επαληθευτής Arthur (αυτή η περιγραφή οφείλεται στον Babai) Μάλιστα, μπορούμε να θεωρήσουμε ότι τα μηνύματα του Arthur είναι ακόμα πιο περιορισμένα: απλώς στέλνει τα τυχαία bits στον Merlin Ανάλογα με τις απαντήσεις του Merlin, ο Arthur αποφασίζει αν θα αποδεχθεί Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
33 Αλληλεπίδραση, PCP Διαλογική αλληλεπίδραση (interactivity) II Κλάσεις Arthur-Merlin Λέμε ότι οι Arthur και Merlin παίζουν ένα παιχνίδι k κινήσεων μεταξύ τους (κάθε κίνηση αντιστοιχεί σε ένα μήνυμα): αν ο Arthur κινείται πρώτος το παιχνίδι συμβολίζεται με AM(k), ενώ αν κινείται πρώτος ο Merlin με MA(k) Για παράδειγμα, AM(1) = A, AM(2) = AM, AM(3) = AMA, MA(1) = M, MA(2) = MA, MA(3) = MAM Μία άλλη διαφορά σε σχέση με την κλάση IP είναι ότι χρειάζεται να φράξουμε τις πιθανότητες μακριά από το 1/2 (πάλι δεν έχει μεγάλη σημασία η ακριβής τιμή) Τυπικά, για την κλάση AM(k), έχουμε: Ορισμός L P AM(k) ανν υπάρχει παιχνίδι k κινήσεων όπου παίζει πρώτος ο Arthur και στο οποίο αν: x P L ùñ ο Arthur πείθεται με πιθανότητα μεγαλύτερη από 2/3 ότι x P L x R L ùñ ο Arthur πείθεται με πιθανότητα μικρότερη από 1/3 ότι x P L Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
34 Αλληλεπίδραση, PCP Διαλογική αλληλεπίδραση (interactivity) III Κλάσεις Arthur-Merlin Με την βοήθεια των γενικευμένων ποσοδεικτών οι κλάσεις μπορούν να γραφτούν ως εξής (Zachos): AM = AM(2) = (D + D, D MA = MA(2) = (DD + ), και για άρτιο k, αν AM(k) = (Q 1, Q 2 ), όπου Q 1, Q 2 ακολουθίες ποσοδεικτών: AM(k + 1) = (Q 1D +, Q 2D + ), AM(k + 2) = (Q 1D + D, Q 2D Η παραπάνω περιγραφή, μπορεί να απλοποιηθεί ως εξής (Zachos): AM = AM(2) = (@D, D MA = MA(2) = + ), και για άρτιο k, αν AM(k) = (Q 1, Q 2), όπου Q 1, Q 2 ακολουθίες ποσοδεικτών: AM(k + 1) = (Q Q 2 D + ), AM(k + 2) = (Q Q 2 D Χρησιμοποιώντας ιδιότητες των ποσοδεικτών προκύπτουν τα παρακάτω αποτελέσματα: Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
35 Αλληλεπίδραση, PCP Διαλογική αλληλεπίδραση (interactivity) IV Κλάσεις Arthur-Merlin Πρόταση MA Ď AM Πρόταση Η ιεραρχία των παιχνιδιών Arthur-Merlin καταρρέει, δηλαδή: AM = AM(k) = MA(k + 1), για κάθε k ě 2 Αν και όπως είπαμε, η κλάση Arthur-Merlin με πολυωνυμικό πλήθος μηνυμάτων αλληλεπίδρασης φαίνεται ασθενέστερη (λόγω δημοσιοποίησης των τυχαίων bits) σε σχέση με την IP, εν τούτοις οι Goldwasser, Sipser απέδειξαν ότι είναι ισοδύναμες Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
36 Αλληλεπίδραση, PCP Διαλογική αλληλεπίδραση (interactivity) I Probabilistic Checable Proofs PCP Αν αντικαταστήσουμε στις διαλογικές αποδείξεις, τον αποδείκτη με μία απλή απόδειξη, έχουμε την κλάση PCP Ας πούμε ότι στην PCP, ο αποδείκτης δεν έχει καμμία άλλη επικοινωνία, εκτός από το να γράψει στην αρχή της αλληλεπίδρασης με τον επαληθευτή V μίαν απόδειξη και να την στείλει στον V Πρέπει να σημειώσουμε ότι οι αποδείξεις αυτές ελέγχονται πιθανοτικά από τον V Τυπικά: Ορισμός L P PCP: x P L ùñ υπάρχει απόδειξη Π τέτοια ώστε ο επαληθευτής (verifier) V πάντοτε αποδέχεται (δηλαδή έχουμε πιθανότητα αποδοχής ίση με 1) x R L ùñ για κάθε «απόδειξη» Π, ο επαληθευτής V δεν αποδέχεται με συντριπτική πιθανότητα Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
37 Αλληλεπίδραση, PCP Διαλογική αλληλεπίδραση (interactivity) II Probabilistic Checable Proofs PCP Αυτή η κλάση φαίνεται πολύ ισχυρότερη από την IP γιατί πλέον ο επαληθευτής έχει να «αντιμετωπίσει» ένα στατικό αντικείμενο (την απόδειξη) και όχι ένα προσαρμοζόμενο στις ερωτήσεις του (τον αποδείκτη) Και πράγματι αποδεικνύεται ότι PCP = MIP(= NEXP) Για τον λόγο αυτό, θα θεωρήσουμε περιορισμούς της κλάσης PCP Θα θεωρήσουμε δύο είδη αγαθών που δεν μπορεί να χρησιμοποιεί αφειδώς ο επαληθευτής: τυχαιότητα (με την μορφή τυχαίων bits) bits της απόδειξης που εξετάζονται (ερωτήσεις, ή αλλιώς queries, στην απόδειξη) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
38 Αλληλεπίδραση, PCP Διαλογική αλληλεπίδραση (interactivity) III Probabilistic Checable Proofs PCP Ορισμός Η κλάση PCP(r(n), q(n)) αποτελείται από τις γλώσσες L P PCP για τις οποίες ο πιθανοτικός πολυωνυμικού χρόνου επαληθευτής V χρησιμοποιεί O(r(n)) τυχαία bits και ελέγχει O(q(n)) bits στην απόδειξη Για παράδειγμα, ήδη γνωστές κλάσεις πολυπλοκότητας μπορούν να οριστούν με την βοήθεια των παραπάνω: PCP = PCP(poly(n), poly(n)), P = PCP(0, 0), NP = PCP(0, poly(n)), corp = PCP(poly(n), 0) Ένα πολύ σημαντικό αποτέλεσμα (Arora, Lund, Motwani, Sudan, Szegedy) είναι το εξής: Θεώρημα (PCP) NP = PCP(log n, 1) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
39 Αλληλεπίδραση, PCP Διαλογική αλληλεπίδραση (interactivity) IV Probabilistic Checable Proofs PCP Μία εφαρμογή του θεωρήματος PCP είναι σε αποδείξεις μη προσεγγισιμότητας Το βασικό εργαλείο στην απόδειξη του προηγουμένου θεωρήματος είναι μία μέθοδος (PCP encoding) που διαχέει ένα πιθανό λάθος μίας απόδειξης σε όλα τα κομμάτια της απόδειξης, έτσι ώστε ο επαληθευτής να έχει συντριπτική πιθανότητα να διαγνώσει το λάθος Η μέθοδος αυτή βασίζεται σε τεχνικές κωδίκων διόρθωσης λαθών (error correcting codes) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
40 Μέτρηση Μέτρητικές Κλάσεις I Μετρητικές κλάσεις ορίζονται με βάση το πλήθος των λύσεων που έχει κάποιο πρόβλημα Πρόκειται δηλαδή για κλάσεις συναρτήσεων (όπως η FP) Ενδιαφέρον έχουν οι παρακάτω δύο κλάσεις: Ορισμός #P είναι η κλάση των συναρτήσεων f για τις οποίες υπάρχει μη ντετερμινιστική μηχανή Turing πολυωνυμικού χρόνου, το υπολογιστικό δέντρο της οποίας έχει ακριβώς f(x) υπολογιστικά μονοπάτια που αποδέχονται (για είσοδο x) Ορισμός #L είναι η κλάση των συναρτήσεων f για τις οποίες υπάρχει μη ντετερμινιστική μηχανή Turing λογαριθμικού χώρου, το υπολογιστικό δέντρο της οποίας έχει ακριβώς f(x) υπολογιστικά μονοπάτια που αποδέχονται (για είσοδο x) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
41 Μέτρηση Μέτρητικές Κλάσεις II Σε μετρητικές κλάσεις χρήσιμες είναι αναγωγές που διατηρούν το πλήθος των λύσεων Ένα χαρακτηριστικό παράδειγμα πλήρους προβλήματος για την #P είναι το πρόβλημα #SAT: «Δίνεται τύπος σε συζευκτική κανονική μορφή Πόσες διαφορετικές αναθέσεις υπάρχουν που ικανοποιούν τον τύπο;» Είναι προφανές ότι φ P SAT ανν #SAT(φ) 0 Ο Valiant έδειξε ότι υπάρχουν προβλήματα απόφασης στο P (πχ ύπαρξη τέλειου ταιριάσματος σε γραφήματα) των οποίων το αντίστοιχο μετρητικό πρόβλημα (πχ #PERFECT MATCHINGS) είναι #P-πλήρες Μερικά αποτελέσματα για αυτές τις κλάσεις: FP Ď #P Ď FPSPACE, P PP = P #P, FL Ď #L Ď FNC 2 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
42 Μέτρηση Μέτρητικές Κλάσεις III Θεώρημα (Toda) PH Ď P #P Η απόδειξη αποτελείται από δύο βασικούς εγκλεισμούς, όπως φαίνεται στα παρακάτω λήμματα: Lemma PH Ď BPP P Απόδειξη: 1 P P = P (Papadimitriou-Zachos) 2 NP Ď BPP ñ PH Ď BPP (Zachos) 3 NP Ď RP P (Valiant-Vazirani) Ď BPP P Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
43 Μέτρηση Μέτρητικές Κλάσεις IV 4 NP P Ď BPP P P (3 με μαντείο P) 1 ñ NP P Ď BPP P 5 NP P Ď BPP P ñ PH P Ď BPP P (2 με μαντείο P) 6 PH P = PH Ď BPP P l Lemma BPP P Ď P #P Χωρίς απόδειξη l Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Μάιος / 43
Τυχαιότητα (Randomness) I
 I Χρησιμοποιώντας το μοντέλο δένδρων υπολογισμού, θα ορίσουμε κλάσεις πολυπλοκότητας που βασίζονται στις πιθανότητες, με βάση τυχαίες επιλογές. Αυτή η προσέγγιση είναι πολύ χρήσιμη από πρακτική άποψη,
I Χρησιμοποιώντας το μοντέλο δένδρων υπολογισμού, θα ορίσουμε κλάσεις πολυπλοκότητας που βασίζονται στις πιθανότητες, με βάση τυχαίες επιλογές. Αυτή η προσέγγιση είναι πολύ χρήσιμη από πρακτική άποψη,
Στοιχεία Θεωρίας Υπολογισμού
 Κεφάλαιο 3 Στοιχεία Θεωρίας Υπολογισμού Στο κεφάλαιο αυτό παρουσιάζεται μια εισαγωγή σε βασικές έννοιες της θεωρίας υπολογισμού, με έμφαση στην υπολογιστική πολυπλοκότητα. Η εξοικείωση με τις έννοιες αυτές
Κεφάλαιο 3 Στοιχεία Θεωρίας Υπολογισμού Στο κεφάλαιο αυτό παρουσιάζεται μια εισαγωγή σε βασικές έννοιες της θεωρίας υπολογισμού, με έμφαση στην υπολογιστική πολυπλοκότητα. Η εξοικείωση με τις έννοιες αυτές
Διαλογικά Συσ τήματα Αποδείξεων Διαλογικά Συστήματα Αποδείξεων Αντώνης Αντωνόπουλος Κρυπτογραφία & Πολυπλοκότητα 17/2/2012
 Αντώνης Αντωνόπουλος Κρυπτογραφία & Πολυπλοκότητα 17/2/2012 Εισαγωγή Ορισμός Επέκταση του NP συστήματος αποδείξεων εισάγωντας αλληλεπίδραση! Ενα άτομο προσπαθεί να πείσει ένα άλλο για το ότι μία συμβολοσειρά
Αντώνης Αντωνόπουλος Κρυπτογραφία & Πολυπλοκότητα 17/2/2012 Εισαγωγή Ορισμός Επέκταση του NP συστήματος αποδείξεων εισάγωντας αλληλεπίδραση! Ενα άτομο προσπαθεί να πείσει ένα άλλο για το ότι μία συμβολοσειρά
Recursive and Recursively Enumerable sets I
 Recursive and Recursively Enumerable sets I Ορισμός Το σύνολο A είναι αναδρομικό ανν η χαρακτηριστική του συνάρτηση X A είναι αναδρομική. Το σύνολο A είναι αναδρομικά αριθμήσιμο (recursively enumerable)
Recursive and Recursively Enumerable sets I Ορισμός Το σύνολο A είναι αναδρομικό ανν η χαρακτηριστική του συνάρτηση X A είναι αναδρομική. Το σύνολο A είναι αναδρομικά αριθμήσιμο (recursively enumerable)
Υπολογισιμότητα και Πολυπλοκότητα Computability and Complexity
 Υπολογισιμότητα και Πολυπλοκότητα Computability and Complexity Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - ΕΜΠ Απρίλιος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ
Υπολογισιμότητα και Πολυπλοκότητα Computability and Complexity Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - ΕΜΠ Απρίλιος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ
Τεχνικές Αποδείξεις Κάτω Φραγμάτων
 Τεχνικές Αποδείξεις Κάτω Φραγμάτων Θέλουμε να δείξουμε κυκλωματικά κάτω φράγματα για ομοιόμορφες κλάσεις επειδή: Δίνουν μεγάλη πληροφορία για τις κλάσεις αυτές: π.χ. αν EXP P /poly σημαίνει Ότι παρότι
Τεχνικές Αποδείξεις Κάτω Φραγμάτων Θέλουμε να δείξουμε κυκλωματικά κάτω φράγματα για ομοιόμορφες κλάσεις επειδή: Δίνουν μεγάλη πληροφορία για τις κλάσεις αυτές: π.χ. αν EXP P /poly σημαίνει Ότι παρότι
Κυκλώματα και βασικές Ιδιότητες
 Κυκλώματα και βασικές Ιδιότητες Κύκλωμα C Κατευθυνόμενος ακυκλικός γράφος με n πηγές (κάθε μία αντιστοιχεί σε ένα bit εισόδου) και μία καταβόθρα (το bit εξόδου). Οι ενδιάμεσοι κόμβοι αντιστοιχούν σε κάποια
Κυκλώματα και βασικές Ιδιότητες Κύκλωμα C Κατευθυνόμενος ακυκλικός γράφος με n πηγές (κάθε μία αντιστοιχεί σε ένα bit εισόδου) και μία καταβόθρα (το bit εξόδου). Οι ενδιάμεσοι κόμβοι αντιστοιχούν σε κάποια
Αυτόματα και Υπολογιστικά Μοντέλα Automata and Models of Computation
 Αυτόματα και Υπολογιστικά Μοντέλα Automata and Models of Computation Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - Ε.Μ.Π. Φεβρουάριος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab
Αυτόματα και Υπολογιστικά Μοντέλα Automata and Models of Computation Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - Ε.Μ.Π. Φεβρουάριος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab
Το 10ο πρόβλημα του Hilbert I
 Το 10ο πρόβλημα του Hilbert I Το 1900 στο Παρίσι, ο David Hilbert έκανε μια ομιλία για τα 23 πιο σπουδαία μαθηματικά προβλήματα που κληρονομούσε ο 20ος αιώνας από τον 19ο. Το 10ο ήταν: Απόφανση περί επιλυσιμότητας
Το 10ο πρόβλημα του Hilbert I Το 1900 στο Παρίσι, ο David Hilbert έκανε μια ομιλία για τα 23 πιο σπουδαία μαθηματικά προβλήματα που κληρονομούσε ο 20ος αιώνας από τον 19ο. Το 10ο ήταν: Απόφανση περί επιλυσιμότητας
ΔΥΣΚΟΛΙΑ ΣΤΗΝ ΠΡΟΣΕΓΓΙΣΙΜΟΤΗΤΑ
 ΔΥΣΚΟΛΙΑ ΣΤΗΝ ΠΡΟΣΕΓΓΙΣΙΜΟΤΗΤΑ Επιμέλεια : Γεωργίου Κωστής Παρουσίαση στα πλαίσια του μαθήματος: Δίκτυα και πολυπλοκότητα Φεβρουάριος 004 μπλ Κίνητρα για τη μελέτη της μη προσεγγισιμότητας Ο πληρέστερος
ΔΥΣΚΟΛΙΑ ΣΤΗΝ ΠΡΟΣΕΓΓΙΣΙΜΟΤΗΤΑ Επιμέλεια : Γεωργίου Κωστής Παρουσίαση στα πλαίσια του μαθήματος: Δίκτυα και πολυπλοκότητα Φεβρουάριος 004 μπλ Κίνητρα για τη μελέτη της μη προσεγγισιμότητας Ο πληρέστερος
Chapter 7, 8 : Time, Space Complexity
 CSC 314: Switching Theory Chapter 7, 8 : Time, Space Complexity 19 December 2008 1 1 Κλάση NP 2 Μη-Ντετερμινιστικές Μηχανές Turing: Eίναι δυνατόν σε μια συνολική κατάσταση να υπάρχουν πολλές δυνατές επόμενες
CSC 314: Switching Theory Chapter 7, 8 : Time, Space Complexity 19 December 2008 1 1 Κλάση NP 2 Μη-Ντετερμινιστικές Μηχανές Turing: Eίναι δυνατόν σε μια συνολική κατάσταση να υπάρχουν πολλές δυνατές επόμενες
Επίπεδα Γραφήματα : Προβλήματα και Υπολογιστική Πολυπλοκότητα
 Αλγόριθμοι πολυωνυμικού χρόνου Ένας αλγόριθμος πολυωνυμικού χρόνου έχει χρόνο εκτέλεσης όπου είναι μία (θετική) σταθερά Κλάση πολυπλοκότητας : περιλαμβάνει τα προβλήματα που επιδέχονται λύση σε πολυωνυμικό
Αλγόριθμοι πολυωνυμικού χρόνου Ένας αλγόριθμος πολυωνυμικού χρόνου έχει χρόνο εκτέλεσης όπου είναι μία (θετική) σταθερά Κλάση πολυπλοκότητας : περιλαμβάνει τα προβλήματα που επιδέχονται λύση σε πολυωνυμικό
CSC 314: Switching Theory
 CSC 314: Switching Theory Course Summary 9 th January 2009 1 1 Θέματα Μαθήματος Ερωτήσεις Τι είναι αλγόριθμος? Τι μπορεί να υπολογιστεί? Απαντήσεις Μοντέλα Υπολογισμού Δυνατότητες και μη-δυνατότητες 2
CSC 314: Switching Theory Course Summary 9 th January 2009 1 1 Θέματα Μαθήματος Ερωτήσεις Τι είναι αλγόριθμος? Τι μπορεί να υπολογιστεί? Απαντήσεις Μοντέλα Υπολογισμού Δυνατότητες και μη-δυνατότητες 2
Θεωρία Υπολογισμού και Πολυπλοκότητα
 Θεωρία Υπολογισμού και Πολυπλοκότητα Κλάσεις P, NP NP-πληρότητα 15 Απριλίου 2008 Δρ. Παπαδοπούλου Βίκη 1 Υπολογίσιμα και Εφικτά Υπολογίσιμα Προβλήματα Είδαμε ότι 1. Οτιδήποτε μπορούμε να περιγράψουμε με
Θεωρία Υπολογισμού και Πολυπλοκότητα Κλάσεις P, NP NP-πληρότητα 15 Απριλίου 2008 Δρ. Παπαδοπούλου Βίκη 1 Υπολογίσιμα και Εφικτά Υπολογίσιμα Προβλήματα Είδαμε ότι 1. Οτιδήποτε μπορούμε να περιγράψουμε με
Θεώρημα Υπάρχουν υπολογίσιμες συναρτήσεις που δεν είναι πρωταρχικές αναδρομικές.
 Υπολογισιμότητα Θεώρημα Υπάρχουν υπολογίσιμες συναρτήσεις που δεν είναι πρωταρχικές αναδρομικές. Απόδειξη: Διαγωνιοποίηση. Μηχανιστική απαρίθμηση πρωταρχικών αναδρομικών συναρτήσεων: φ 0, φ 1, φ 2, Ορίζουμε:
Υπολογισιμότητα Θεώρημα Υπάρχουν υπολογίσιμες συναρτήσεις που δεν είναι πρωταρχικές αναδρομικές. Απόδειξη: Διαγωνιοποίηση. Μηχανιστική απαρίθμηση πρωταρχικών αναδρομικών συναρτήσεων: φ 0, φ 1, φ 2, Ορίζουμε:
Κεφάλαιο 8. NP και Υπολογιστική Δυσεπιλυσιμότητα. Παύλος Εφραιμίδης V1.1,
 Κεφάλαιο 8 NP και Υπολογιστική Δυσεπιλυσιμότητα Παύλος Εφραιμίδης V1.1, 2015-01-19 Χρησιμοποιήθηκε υλικό από τις αγγλικές διαφάνειες του Kevin Wayne. 1 πρόβλημα αναζήτησης (search problem) Ένα πρόβλημα
Κεφάλαιο 8 NP και Υπολογιστική Δυσεπιλυσιμότητα Παύλος Εφραιμίδης V1.1, 2015-01-19 Χρησιμοποιήθηκε υλικό από τις αγγλικές διαφάνειες του Kevin Wayne. 1 πρόβλημα αναζήτησης (search problem) Ένα πρόβλημα
Κεφάλαιο 8. NP και Υπολογιστική Δυσεπιλυσιμότητα. Χρησιμοποιήθηκε υλικό από τις αγγλικές διαφάνειες του Kevin Wayne.
 Κεφάλαιο 8 NP και Υπολογιστική Δυσεπιλυσιμότητα Χρησιμοποιήθηκε υλικό από τις αγγλικές διαφάνειες του Kevin Wayne. 1 πρόβλημα αναζήτησης (search problem) Ένα πρόβλημα αναζήτησης είναι ένα πρόβλημα στο
Κεφάλαιο 8 NP και Υπολογιστική Δυσεπιλυσιμότητα Χρησιμοποιήθηκε υλικό από τις αγγλικές διαφάνειες του Kevin Wayne. 1 πρόβλημα αναζήτησης (search problem) Ένα πρόβλημα αναζήτησης είναι ένα πρόβλημα στο
Πιθανοτικοί Αλγόριθμοι
 Πιθανοτικοί Αλγόριθμοι ιδάσκοντες: Σ. Ζάχος,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Πιθανοτικοί Αλγόριθμοι Πιθανοτικός
Πιθανοτικοί Αλγόριθμοι ιδάσκοντες: Σ. Ζάχος,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Πιθανοτικοί Αλγόριθμοι Πιθανοτικός
Σχήματα McCarthy I. Το σχήμα McCarthy είναι ένα γενικότερο προγραμματιστικό σχήμα:
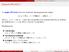 Σχήματα McCarthy I Το σχήμα McCarthy είναι ένα γενικότερο προγραμματιστικό σχήμα: f(x, y) = if g(...) = 0 then h(...) else k(...) όπου g(...), h(...) και k(...) είναι όροι-συναρτήσεις που κατασκευάζονται
Σχήματα McCarthy I Το σχήμα McCarthy είναι ένα γενικότερο προγραμματιστικό σχήμα: f(x, y) = if g(...) = 0 then h(...) else k(...) όπου g(...), h(...) και k(...) είναι όροι-συναρτήσεις που κατασκευάζονται
Πολυπλοκότητα. Παράμετροι της αποδοτικότητας ενός αλγόριθμου: Χρόνος εκτέλεσης. Απαιτούμενοι πόροι, π.χ. μνήμη, εύρος ζώνης. Προσπάθεια υλοποίησης
 Παράμετροι της αποδοτικότητας ενός αλγόριθμου: Χρόνος εκτέλεσης Απαιτούμενοι πόροι, π.χ. μνήμη, εύρος ζώνης Προσπάθεια υλοποίησης Παράμετροι της αποδοτικότητας ενός αλγόριθμου: Χρόνος εκτέλεσης Απαιτούμενοι
Παράμετροι της αποδοτικότητας ενός αλγόριθμου: Χρόνος εκτέλεσης Απαιτούμενοι πόροι, π.χ. μνήμη, εύρος ζώνης Προσπάθεια υλοποίησης Παράμετροι της αποδοτικότητας ενός αλγόριθμου: Χρόνος εκτέλεσης Απαιτούμενοι
Θεωρία Υπολογισμού Άρτιοι ΑΜ. Διδάσκων: Σταύρος Κολλιόπουλος. eclass.di.uoa.gr. Περιγραφή μαθήματος
 Περιγραφή μαθήματος Θεωρία Υπολογισμού Άρτιοι ΑΜ Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας (Θεωρία Αλγορίθμων). Διδάσκων: Σταύρος Κολλιόπουλος
Περιγραφή μαθήματος Θεωρία Υπολογισμού Άρτιοι ΑΜ Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας (Θεωρία Αλγορίθμων). Διδάσκων: Σταύρος Κολλιόπουλος
Θεωρία Υπολογισμού Αρτιοι ΑΜ Διδάσκων: Σταύρος Κολλιόπουλος eclass.di.uoa.gr
 Θεωρία Υπολογισμού Άρτιοι ΑΜ Διδάσκων: Σταύρος Κολλιόπουλος eclass.di.uoa.gr Περιγραφή μαθήματος Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας
Θεωρία Υπολογισμού Άρτιοι ΑΜ Διδάσκων: Σταύρος Κολλιόπουλος eclass.di.uoa.gr Περιγραφή μαθήματος Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας
Πολλοί τρόποι περιγραφής αλγορίθμων. Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις.
 Θέση Church-Turing I Πολλοί τρόποι περιγραφής αλγορίθμων. Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις Θέση Church-Turing: Όλες οι υπολογίσιμες συναρτήσεις
Θέση Church-Turing I Πολλοί τρόποι περιγραφής αλγορίθμων. Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις Θέση Church-Turing: Όλες οι υπολογίσιμες συναρτήσεις
Σειρά Προβλημάτων 5 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) { Μ η Μ είναι μια ΤΜ η οποία διαγιγνώσκει το πρόβλημα ΙΣΟΔΥΝΑΜΙΑ ΤΜ (διαφάνεια 9 25)} (α) Γνωρίζουμε ότι το
Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) { Μ η Μ είναι μια ΤΜ η οποία διαγιγνώσκει το πρόβλημα ΙΣΟΔΥΝΑΜΙΑ ΤΜ (διαφάνεια 9 25)} (α) Γνωρίζουμε ότι το
Υποθέσεις - - Θεωρήματα Υποθέσεις - Θεωρήματα Στα μαθηματικά και στις άλλες επιστήμες κάνουμε συχνά υποθέσεις. Οταν δείξουμε ότι μια υπόθεση είναι αλη
 Υποθέσεις - - Θεωρήματα Μαθηματικά Πληροφορικής 1ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Υποθέσεις - - Θεωρήματα Υποθέσεις - Θεωρήματα Στα μαθηματικά και στις άλλες επιστήμες
Υποθέσεις - - Θεωρήματα Μαθηματικά Πληροφορικής 1ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Υποθέσεις - - Θεωρήματα Υποθέσεις - Θεωρήματα Στα μαθηματικά και στις άλλες επιστήμες
Υπολογισιμότητα και Πολυπλοκότητα Computability and Complexity
 Υπολογισιμότητα και Πολυπλοκότητα Computability and Complexity Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - ΕΜΠ Ιούνιος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ
Υπολογισιμότητα και Πολυπλοκότητα Computability and Complexity Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - ΕΜΠ Ιούνιος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ
Σειρά Προβλημάτων 5 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) ({ G η G είναι μια ασυμφραστική γραμματική που δεν παράγει καμιά λέξη με μήκος μικρότερο του 2 } (β) { Μ,w
Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) ({ G η G είναι μια ασυμφραστική γραμματική που δεν παράγει καμιά λέξη με μήκος μικρότερο του 2 } (β) { Μ,w
Μηχανές Turing (T.M) I
 Μηχανές Turing (T.M) I Οι βασικές λειτουργίες μιας TM είναι: Διάβασε το περιεχόμενο του τρέχοντος κυττάρου Γράψε 1 ή 0 στο τρέχον κύτταρο Κάνε τρέχον το αμέσως αριστερότερο ή το αμέσως δεξιότερο κύτταρο
Μηχανές Turing (T.M) I Οι βασικές λειτουργίες μιας TM είναι: Διάβασε το περιεχόμενο του τρέχοντος κυττάρου Γράψε 1 ή 0 στο τρέχον κύτταρο Κάνε τρέχον το αμέσως αριστερότερο ή το αμέσως δεξιότερο κύτταρο
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας. Διάλεξη 13: Παραλλαγές Μηχανών Turing και Περιγραφή Αλγορίθμων
 ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 13: Παραλλαγές Μηχανών Turing και Περιγραφή Αλγορίθμων Τι θα κάνουμε σήμερα Εισαγωγή Πολυταινιακές Μηχανές Turing (3.2.1) Μη Ντετερμινιστικές Μηχανές
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 13: Παραλλαγές Μηχανών Turing και Περιγραφή Αλγορίθμων Τι θα κάνουμε σήμερα Εισαγωγή Πολυταινιακές Μηχανές Turing (3.2.1) Μη Ντετερμινιστικές Μηχανές
Θεωρία Υπολογισμού και Πολυπλοκότητα
 Θεωρία Υπολογισμού και Πολυπλοκότητα Κεφάλαιο 14. Χρονική Πολυπλοκότητα 17, 20, 24 Απριλίου 2007 Δρ. Παπαδοπούλου Βίκη 1 Υπολογίσιμα και Εφικτά Υπολογίσιμα Προβλήματα Είδαμε ότι 1. Οτιδήποτε μπορούμε να
Θεωρία Υπολογισμού και Πολυπλοκότητα Κεφάλαιο 14. Χρονική Πολυπλοκότητα 17, 20, 24 Απριλίου 2007 Δρ. Παπαδοπούλου Βίκη 1 Υπολογίσιμα και Εφικτά Υπολογίσιμα Προβλήματα Είδαμε ότι 1. Οτιδήποτε μπορούμε να
Κλάση NP, NP-Complete Προβλήματα
 Κλάση NP, NP-Complete Προβλήματα Βαγγέλης ούρος douros@aueb.gr 1 11/6/2012 Αλγόριθμοι, Εαρινό Εξάμηνο 2012, Φροντιστήριο #14 Προβλήματα Απόφασης & Βελτιστοποίησης 2 Πρόβλημα Απόφασης: Κάθε πρόβλημα που
Κλάση NP, NP-Complete Προβλήματα Βαγγέλης ούρος douros@aueb.gr 1 11/6/2012 Αλγόριθμοι, Εαρινό Εξάμηνο 2012, Φροντιστήριο #14 Προβλήματα Απόφασης & Βελτιστοποίησης 2 Πρόβλημα Απόφασης: Κάθε πρόβλημα που
Λύσεις 4ης Σειράς Ασκήσεων
 Λύσεις 4ης Σειράς Ασκήσεων Άσκηση 1 Αναγάγουμε τν Κ 0 που γνωρίζουμε ότι είναι μη-αναδρομική (μη-επιλύσιμη) στην γλώσσα: L = {p() η μηχανή Turing Μ τερματίζει με είσοδο κενή ταινία;} Δοσμένης της περιγραφής
Λύσεις 4ης Σειράς Ασκήσεων Άσκηση 1 Αναγάγουμε τν Κ 0 που γνωρίζουμε ότι είναι μη-αναδρομική (μη-επιλύσιμη) στην γλώσσα: L = {p() η μηχανή Turing Μ τερματίζει με είσοδο κενή ταινία;} Δοσμένης της περιγραφής
Υπολογιστική Πολυπλοκότητα Εξέταση Ιουνίου 2017 Σελ. 1 από 5
 Υπολογιστική Πολυπλοκότητα Εξέταση Ιουνίου 2017 Σελ. 1 από 5 Στη σελίδα αυτή γράψτε μόνο τα στοιχεία σας. Γράψτε τις απαντήσεις σας στις επόμενες σελίδες, κάτω από τις αντίστοιχες ερωτήσεις. Στις απαντήσεις
Υπολογιστική Πολυπλοκότητα Εξέταση Ιουνίου 2017 Σελ. 1 από 5 Στη σελίδα αυτή γράψτε μόνο τα στοιχεία σας. Γράψτε τις απαντήσεις σας στις επόμενες σελίδες, κάτω από τις αντίστοιχες ερωτήσεις. Στις απαντήσεις
Σειρά Προβλημάτων 5 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) { G 1, G 2 οι G 1 και G 2 είναι δύο CFG που παράγουν μια κοινή λέξη μήκους 144 } (β) { D,k το D είναι ένα DFA
Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) { G 1, G 2 οι G 1 και G 2 είναι δύο CFG που παράγουν μια κοινή λέξη μήκους 144 } (β) { D,k το D είναι ένα DFA
Σειρά Προβλημάτων 5 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) { R η R είναι μια κανονική έκφραση η οποία παράγει μια μη πεπερασμένη γλώσσα} (β) { G η G είναι μια CFG η οποία
Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) { R η R είναι μια κανονική έκφραση η οποία παράγει μια μη πεπερασμένη γλώσσα} (β) { G η G είναι μια CFG η οποία
Chapter 7, 8 : Completeness
 CSC 314: Switching Theory Chapter 7, 8 : Completeness 19 December 2008 1 1 Αναγωγές Πολυωνυμικού Χρόνου Ορισμός. f: Σ * Σ * ονομάζεται υπολογίσιμη σε πολυνωνυμικό χρόνο αν υπάρχει μια πολυωνυμικά φραγμένη
CSC 314: Switching Theory Chapter 7, 8 : Completeness 19 December 2008 1 1 Αναγωγές Πολυωνυμικού Χρόνου Ορισμός. f: Σ * Σ * ονομάζεται υπολογίσιμη σε πολυνωνυμικό χρόνο αν υπάρχει μια πολυωνυμικά φραγμένη
PSEUDORANDOM GENERATORS- PREDICATES & ZK PROOFS
 PSEUDORANDOM GENERATORS- PREDICATES & ZK PROOFS ΑΛΓΟΡΙΘΜΟΙ ΚΑΙ ΠΟΛΥΠΛΟΚΟΤΗΤΑ 2 Επιμέλεια: Νικόλαος Λάμπρου μπλ 2014 Γεννήτρια ψευδοτυχαίων αριθμών Άτυπος ορισμός: Έστω μια συνάρτηση G από strings σε strings.λέμε
PSEUDORANDOM GENERATORS- PREDICATES & ZK PROOFS ΑΛΓΟΡΙΘΜΟΙ ΚΑΙ ΠΟΛΥΠΛΟΚΟΤΗΤΑ 2 Επιμέλεια: Νικόλαος Λάμπρου μπλ 2014 Γεννήτρια ψευδοτυχαίων αριθμών Άτυπος ορισμός: Έστω μια συνάρτηση G από strings σε strings.λέμε
Κεφάλαιο 8. NP και Υπολογιστική Δυσεπιλυσιµότητα. Χρησιµοποιήθηκε υλικό από τις αγγλικές διαφάνειες του Kevin Wayne.
 Κεφάλαιο 8 NP και Υπολογιστική Δυσεπιλυσιµότητα Χρησιµοποιήθηκε υλικό από τις αγγλικές διαφάνειες του Kevin Wayne. 1 πρόβληµα αναζήτησης (search problem) Ένα πρόβληµα αναζήτησης είναι ένα πρόβληµα στο
Κεφάλαιο 8 NP και Υπολογιστική Δυσεπιλυσιµότητα Χρησιµοποιήθηκε υλικό από τις αγγλικές διαφάνειες του Kevin Wayne. 1 πρόβληµα αναζήτησης (search problem) Ένα πρόβληµα αναζήτησης είναι ένα πρόβληµα στο
Φροντιστήριο 11 Λύσεις
 Άσκηση 1 Φροντιστήριο 11 Λύσεις Να αποδείξετε ότι η κλάση Ρ είναι κλειστή ως προς τις πράξεις της ένωσης, της συναρμογής και του συμπληρώματος. Θα πρέπει να δείξουμε ότι: (α) Ένωση: Αν οι Λ 1 και Λ 2 είναι
Άσκηση 1 Φροντιστήριο 11 Λύσεις Να αποδείξετε ότι η κλάση Ρ είναι κλειστή ως προς τις πράξεις της ένωσης, της συναρμογής και του συμπληρώματος. Θα πρέπει να δείξουμε ότι: (α) Ένωση: Αν οι Λ 1 και Λ 2 είναι
UP class. & DES και AES
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Σημειώσεις Διαλέξεων UP class & DES και AES Επιμέλεια σημειώσεων: Ιωάννης Νέμπαρης Μάριος Κουβαράς Διδάσκοντες: Στάθης Ζάχος
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Σημειώσεις Διαλέξεων UP class & DES και AES Επιμέλεια σημειώσεων: Ιωάννης Νέμπαρης Μάριος Κουβαράς Διδάσκοντες: Στάθης Ζάχος
Κλάσεις Πολυπλοκότητας
 Κλάσεις Πολυπλοκότητας Παύλος Εφραιμίδης pefraimi ee.duth.gr Κλάσεις Πολυπλοκότητας 1 Οι κλάσεις πολυπλοκότητας P και NP P: Polynomial ΗκλάσηP περιλαμβάνει όλα τα υπολογιστικά προβλήματα που μπορούν
Κλάσεις Πολυπλοκότητας Παύλος Εφραιμίδης pefraimi ee.duth.gr Κλάσεις Πολυπλοκότητας 1 Οι κλάσεις πολυπλοκότητας P και NP P: Polynomial ΗκλάσηP περιλαμβάνει όλα τα υπολογιστικά προβλήματα που μπορούν
Chapter 7, 8 : Time, Space Complexity
 CSC 314: Switching Theory Chapter 7, 8 : Time, Space Complexity 12 December 2008 1 1 Υπολογίσιμα και Εφικτά Υπολογίσιμα Προβλήματα Είδαμε ότι 1. Οτιδήποτεμπορούμεναπεριγράψουμεμεένααλγόριθμο μπορεί να
CSC 314: Switching Theory Chapter 7, 8 : Time, Space Complexity 12 December 2008 1 1 Υπολογίσιμα και Εφικτά Υπολογίσιμα Προβλήματα Είδαμε ότι 1. Οτιδήποτεμπορούμεναπεριγράψουμεμεένααλγόριθμο μπορεί να
Υπολογιστική Πολυπλοκότητα
 Υπολογιστική Πολυπλοκότητα ιδάσκοντες: Σ. Ζάχος,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Άδεια Χρήσης Το παρόν εκπαιδευτικό
Υπολογιστική Πολυπλοκότητα ιδάσκοντες: Σ. Ζάχος,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Άδεια Χρήσης Το παρόν εκπαιδευτικό
Θεωρία Υπολογισμού και Πολυπλοκότητα Κανονικές Γλώσσες (1)
 Θεωρία Υπολογισμού και Πολυπλοκότητα Κανονικές Γλώσσες () Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Πεπερασμένα Αυτόματα (Κεφάλαιο., Sipser) Ορισμός πεπερασμένων αυτομάτων και ορισμός του
Θεωρία Υπολογισμού και Πολυπλοκότητα Κανονικές Γλώσσες () Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Πεπερασμένα Αυτόματα (Κεφάλαιο., Sipser) Ορισμός πεπερασμένων αυτομάτων και ορισμός του
για NP-Δύσκολα Προβλήματα
 Προσεγγιστικοί Αλγόριθμοι για NP-Δύσκολα Προβλήματα Διδάσκοντες: Σ. Ζάχος, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο
Προσεγγιστικοί Αλγόριθμοι για NP-Δύσκολα Προβλήματα Διδάσκοντες: Σ. Ζάχος, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο
Περιεχόμενα 1 Πρωτοβάθμια Λογική Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων ) / 60
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Σειρά Προβλημάτων 5 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Πιο κάτω υπάρχει ένα σχεδιάγραμμα που τοποθετεί τις κλάσεις των κανονικών, ασυμφραστικών, διαγνώσιμων και αναγνωρίσιμων γλωσσών μέσα στο σύνολο όλων των γλωσσών. Ακολουθούν
Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Πιο κάτω υπάρχει ένα σχεδιάγραμμα που τοποθετεί τις κλάσεις των κανονικών, ασυμφραστικών, διαγνώσιμων και αναγνωρίσιμων γλωσσών μέσα στο σύνολο όλων των γλωσσών. Ακολουθούν
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Λογική Δημήτρης Πλεξουσάκης 3ο μέρος σημειώσεων: Μέθοδος της Επίλυσης Τμήμα Επιστήμης Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται στην άδεια
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Λογική Δημήτρης Πλεξουσάκης 3ο μέρος σημειώσεων: Μέθοδος της Επίλυσης Τμήμα Επιστήμης Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται στην άδεια
Προσεγγιστικοί Αλγόριθμοι για NP- ύσκολα Προβλήματα
 Προσεγγιστικοί Αλγόριθμοι για NP- ύσκολα Προβλήματα ιδάσκοντες: Σ. Ζάχος,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Άδεια
Προσεγγιστικοί Αλγόριθμοι για NP- ύσκολα Προβλήματα ιδάσκοντες: Σ. Ζάχος,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Άδεια
Υποθέσεις - Θεωρήματα. Μαθηματικά Πληροφορικής 1ο Μάθημα. Η χρυσή τομή. Υποθέσεις - Εικασίες
 Υποθέσεις - - Θεωρήματα Υποθέσεις - - Θεωρήματα Υποθέσεις - Θεωρήματα Μαθηματικά Πληροορικής ο Μάθημα Στα μαθηματικά και στις άλλες επιστήμες κάνουμε συχνά υποθέσεις. Οταν δείξουμε ότι μια υπόθεση είναι
Υποθέσεις - - Θεωρήματα Υποθέσεις - - Θεωρήματα Υποθέσεις - Θεωρήματα Μαθηματικά Πληροορικής ο Μάθημα Στα μαθηματικά και στις άλλες επιστήμες κάνουμε συχνά υποθέσεις. Οταν δείξουμε ότι μια υπόθεση είναι
Αλγόριθμοι και πολυπλοκότητα: 4 η σειρά ασκήσεων ΣΗΜΜΥ - Ε.Μ.Π.
 Αλγόριθμοι και πολυπλοκότητα: 4 η σειρά ασκήσεων CO.RE.LAB. ΣΗΜΜΥ - Ε.Μ.Π. Άσκηση 1 η : Παιχνίδι επιλογής ακμών Έχουμε ένα ακυκλικό κατευθυνόμενο γράφο, μια αρχική κορυφή και δυο παίκτες. Οι παίκτες διαδοχικά
Αλγόριθμοι και πολυπλοκότητα: 4 η σειρά ασκήσεων CO.RE.LAB. ΣΗΜΜΥ - Ε.Μ.Π. Άσκηση 1 η : Παιχνίδι επιλογής ακμών Έχουμε ένα ακυκλικό κατευθυνόμενο γράφο, μια αρχική κορυφή και δυο παίκτες. Οι παίκτες διαδοχικά
Σειρά Προβλημάτων 5 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) { D το D είναι ένα DFA το οποίο αποδέχεται όλες τις λέξεις στο Σ * } (α) Για να διαγνώσουμε το πρόβλημα μπορούμε
Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) { D το D είναι ένα DFA το οποίο αποδέχεται όλες τις λέξεις στο Σ * } (α) Για να διαγνώσουμε το πρόβλημα μπορούμε
Αλγόριθµοι και Πολυπλοκότητα
 Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 15 Ιουνίου 2009 1 / 26 Εισαγωγή Η ϑεωρία
Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 15 Ιουνίου 2009 1 / 26 Εισαγωγή Η ϑεωρία
6. Kerenidis I., de Wolf R., Exponential lower bound for 2-query locally decodable codes via a quantum argument, 2004.
 Κεφάλαιο 35 Κβαντική Πολυπλοκότητα Η προβολή της [κλασσικής] Θεωρίας Υπολογιστικής Πολυπλοκότητας, στον χώρο της Κβαντικής Μηχανικής, ορίζει την Θεωρία Κβαντικής Υπολογιστικής Πολυπλοκότητας: μίας νέας
Κεφάλαιο 35 Κβαντική Πολυπλοκότητα Η προβολή της [κλασσικής] Θεωρίας Υπολογιστικής Πολυπλοκότητας, στον χώρο της Κβαντικής Μηχανικής, ορίζει την Θεωρία Κβαντικής Υπολογιστικής Πολυπλοκότητας: μίας νέας
Κατώτερα φράγματα Κατώτερο φράγμα: εκτίμηση της ελάχιστης εργασίας που απαιτείται για την επίλυση ενός προβλήματος. Παραδείγματα: Αριθμός συγκρίσεων π
 Περιορισμοί Αλγοριθμικής Ισχύος Κατηγοριοποίηση πολυπλοκοτήτων Κατώτερα φράγματα Κατώτερο φράγμα: εκτίμηση της ελάχιστης εργασίας που απαιτείται για την επίλυση ενός προβλήματος. Παραδείγματα: Αριθμός
Περιορισμοί Αλγοριθμικής Ισχύος Κατηγοριοποίηση πολυπλοκοτήτων Κατώτερα φράγματα Κατώτερο φράγμα: εκτίμηση της ελάχιστης εργασίας που απαιτείται για την επίλυση ενός προβλήματος. Παραδείγματα: Αριθμός
4η Γραπτή Ασκηση Αλγόριθμοι και Πολυπλοκότητα CoReLab ΣΗΜΜΥ 7 Φεβρουαρίου 2017 CoReLab (ΣΗΜΜΥ) 4η Γραπτή Ασκηση 7 Φεβρουαρίου / 38
 4η Γραπτή Άσκηση Αλγόριθμοι και Πολυπλοκότητα CoReLab ΣΗΜΜΥ 7 Φεβρουαρίου 2017 CoReLab (ΣΗΜΜΥ) 4η Γραπτή Άσκηση 7 Φεβρουαρίου 2017 1 / 38 Άσκηση 1 Πρέπει να βρούμε όλες τις καλές προτάσεις φίλων για τον
4η Γραπτή Άσκηση Αλγόριθμοι και Πολυπλοκότητα CoReLab ΣΗΜΜΥ 7 Φεβρουαρίου 2017 CoReLab (ΣΗΜΜΥ) 4η Γραπτή Άσκηση 7 Φεβρουαρίου 2017 1 / 38 Άσκηση 1 Πρέπει να βρούμε όλες τις καλές προτάσεις φίλων για τον
ILP-Feasibility conp
 Διάλεξη 19: 23.12.2014 Θεωρία Γραμμικού Προγραμματισμού Γραφέας: Χαρίλαος Τζόβας Διδάσκων: Σταύρος Κολλιόπουλος 19.1 Θεωρία Πολυπλοκότητας και προβλήματα απόφασης Για να μιλήσουμε για προβλήματα και τον
Διάλεξη 19: 23.12.2014 Θεωρία Γραμμικού Προγραμματισμού Γραφέας: Χαρίλαος Τζόβας Διδάσκων: Σταύρος Κολλιόπουλος 19.1 Θεωρία Πολυπλοκότητας και προβλήματα απόφασης Για να μιλήσουμε για προβλήματα και τον
Υπολογιστική Πολυπλοκότητα
 Υπολογιστική Πολυπλοκότητα ημήτρης Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Υπολογιστική Πολυπλοκότητα Γιατί κάποια (επιλύσιμα) προβλήματα είναι δύσκολο
Υπολογιστική Πολυπλοκότητα ημήτρης Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Υπολογιστική Πολυπλοκότητα Γιατί κάποια (επιλύσιμα) προβλήματα είναι δύσκολο
f(t) = (1 t)a + tb. f(n) =
 Παράρτημα Αʹ Αριθμήσιμα και υπεραριθμήσιμα σύνολα Αʹ1 Ισοπληθικά σύνολα Ορισμός Αʹ11 (ισοπληθικότητα) Εστω A, B δύο μη κενά σύνολα Τα A, B λέγονται ισοπληθικά αν υπάρχει μια συνάρτηση f : A B, η οποία
Παράρτημα Αʹ Αριθμήσιμα και υπεραριθμήσιμα σύνολα Αʹ1 Ισοπληθικά σύνολα Ορισμός Αʹ11 (ισοπληθικότητα) Εστω A, B δύο μη κενά σύνολα Τα A, B λέγονται ισοπληθικά αν υπάρχει μια συνάρτηση f : A B, η οποία
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Μη Ντετερμινισμός και NP-Πληρότητα
 Μη Ντετερμινισμός και NP-Πληρότητα Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Μη Ντετερμινιστικές Μηχανές Turing Μη ντετερμινιστική
Μη Ντετερμινισμός και NP-Πληρότητα Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Μη Ντετερμινιστικές Μηχανές Turing Μη ντετερμινιστική
ΠΕΡΙΕΧΟΜΕΝΑ. Πρόλογος στη δεύτερη έκδοση
 Πρόλογος του επιµελητή xiii Πρόλογος στην πρώτη έκδοση xv Προς τους ϕοιτητές.......................... xv Προς τους διδάσκοντες........................ xvii Ηπρώτηέκδοση........................... xviii
Πρόλογος του επιµελητή xiii Πρόλογος στην πρώτη έκδοση xv Προς τους ϕοιτητές.......................... xv Προς τους διδάσκοντες........................ xvii Ηπρώτηέκδοση........................... xviii
Αλγόριθμοι και Πολυπλοκότητα
 Αλγόριθμοι και Πολυπλοκότητα Ροή Δικτύου Δημήτρης Μιχαήλ Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Μοντελοποίηση Δικτύων Μεταφοράς Τα γραφήματα χρησιμοποιούνται συχνά για την μοντελοποίηση
Αλγόριθμοι και Πολυπλοκότητα Ροή Δικτύου Δημήτρης Μιχαήλ Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Μοντελοποίηση Δικτύων Μεταφοράς Τα γραφήματα χρησιμοποιούνται συχνά για την μοντελοποίηση
Σειρά Προβλημάτων 4 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing (αυθεντικός ορισμός) η οποία να διαγιγνώσκει τη γλώσσα { ww w {a,b}* }. (β) Να διατυπώσετε την τυπική περιγραφή
Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing (αυθεντικός ορισμός) η οποία να διαγιγνώσκει τη γλώσσα { ww w {a,b}* }. (β) Να διατυπώσετε την τυπική περιγραφή
4η Γραπτή Ασκηση Αλγόριθμοι και Πολυπλοκότητα CoReLab ΣΗΜΜΥ 3/2/2019 CoReLab (ΣΗΜΜΥ) 4η Γραπτή Ασκηση 3/2/ / 37
 4η Γραπτή Άσκηση Αλγόριθμοι και Πολυπλοκότητα CoReLab ΣΗΜΜΥ 3/2/2019 CoReLab (ΣΗΜΜΥ) 4η Γραπτή Άσκηση 3/2/2019 1 / 37 Άσκηση 1 Πρέπει να βρούμε όλες τις καλές προτάσεις φίλων για τον i ανάμεσα σε όλους
4η Γραπτή Άσκηση Αλγόριθμοι και Πολυπλοκότητα CoReLab ΣΗΜΜΥ 3/2/2019 CoReLab (ΣΗΜΜΥ) 4η Γραπτή Άσκηση 3/2/2019 1 / 37 Άσκηση 1 Πρέπει να βρούμε όλες τις καλές προτάσεις φίλων για τον i ανάμεσα σε όλους
Μη Ντετερμινισμός και NP-Πληρότητα
 Μη Ντετερμινισμός και NP-Πληρότητα Διδάσκοντες: Σ Ζάχος, Δ Φωτάκης Επιμέλεια διαφανειών: Δ Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Μη Ντετερμινιστικές
Μη Ντετερμινισμός και NP-Πληρότητα Διδάσκοντες: Σ Ζάχος, Δ Φωτάκης Επιμέλεια διαφανειών: Δ Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Μη Ντετερμινιστικές
Αλγόριθμοι Προσέγγισης για NP-Δύσκολα Προβλήματα
 Αλγόριθμοι Προσέγγισης για NP-Δύσκολα Προβλήματα Διδάσκοντες: E. Ζάχος, Α. Παγουρτζής Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο
Αλγόριθμοι Προσέγγισης για NP-Δύσκολα Προβλήματα Διδάσκοντες: E. Ζάχος, Α. Παγουρτζής Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο
d(v) = 3 S. q(g \ S) S
 Διάλεξη 9: 9.11.2016 Θεωρία Γραφημάτων Διδάσκων: Σταύρος Κολλιόπουλος Γραφέας: Παναγιωτίδης Αλέξανδρος Θεώρημα 9.1 Εστω γράφημα G = (V, E), υπάρχει τέλειο ταίριασμα στο G αν και μόνο αν για κάθε S υποσύνολο
Διάλεξη 9: 9.11.2016 Θεωρία Γραφημάτων Διδάσκων: Σταύρος Κολλιόπουλος Γραφέας: Παναγιωτίδης Αλέξανδρος Θεώρημα 9.1 Εστω γράφημα G = (V, E), υπάρχει τέλειο ταίριασμα στο G αν και μόνο αν για κάθε S υποσύνολο
HY118-Διακριτά Μαθηματικά. Τι είδαμε την προηγούμενη φορά. Θεωρία γράφων / γραφήματα. 25 -Γράφοι. ΗΥ118, Διακριτά Μαθηματικά Άνοιξη 2017
 HY118-Διακριτά Μαθηματικά Τι είδαμε την προηγούμενη φορά Παρασκευή, 12/05/2017 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Υπογράφημα Συμπληρωματικά γραφήματα Ισομορφισμός γράφων Υπολογιστική πολυπλοκότητα
HY118-Διακριτά Μαθηματικά Τι είδαμε την προηγούμενη φορά Παρασκευή, 12/05/2017 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Υπογράφημα Συμπληρωματικά γραφήματα Ισομορφισμός γράφων Υπολογιστική πολυπλοκότητα
ΘΕΩΡΙΑ ΥΠΟΛΟΓΙΣΜΩΝ ΚΑΙ ΑΥΤΟΜΑΤΩΝ
 ΘΕΩΡΙΑ ΥΠΟΛΟΓΙΣΜΩΝ ΚΑΙ ΑΥΤΟΜΑΤΩΝ Ενότητα 12: Μη ντετερμινιστικές μηχανές Turing Ρεφανίδης Ιωάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
ΘΕΩΡΙΑ ΥΠΟΛΟΓΙΣΜΩΝ ΚΑΙ ΑΥΤΟΜΑΤΩΝ Ενότητα 12: Μη ντετερμινιστικές μηχανές Turing Ρεφανίδης Ιωάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
4.3 Ορθότητα και Πληρότητα
 4.3 Ορθότητα και Πληρότητα Συστήματα αποδείξεων όπως η μορφολογική παραγωγή και η κατασκευή μοντέλων χρησιμοποιούνται για να δείξουμε την εγκυρότητα εξαγωγών συμπερασμάτων. Ένα σύστημα αποδείξεων μπορεί
4.3 Ορθότητα και Πληρότητα Συστήματα αποδείξεων όπως η μορφολογική παραγωγή και η κατασκευή μοντέλων χρησιμοποιούνται για να δείξουμε την εγκυρότητα εξαγωγών συμπερασμάτων. Ένα σύστημα αποδείξεων μπορεί
Φροντιστήριο 10 Λύσεις
 Άσκηση 1 Φροντιστήριο 10 Λύσεις Να κατασκευάσετε μια μηχανή Turing με δύο ταινίες η οποία να αποδέχεται στην πρώτη της ταινία μια οποιαδήποτε λέξη w {0,1} * και να γράφει τη λέξη w R στη δεύτερη της ταινία.
Άσκηση 1 Φροντιστήριο 10 Λύσεις Να κατασκευάσετε μια μηχανή Turing με δύο ταινίες η οποία να αποδέχεται στην πρώτη της ταινία μια οποιαδήποτε λέξη w {0,1} * και να γράφει τη λέξη w R στη δεύτερη της ταινία.
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Μη επιλυσιμότητα I. Απόδειξη. Ορίζουμε # # =
 Μη επιλυσιμότητα I Θεώρημα Το TOT (πρόβλημα ολικής συνάρτησης) είναι μη επιλύσιμο, δηλαδή η f δεν είναι αναδρομική όπου: 1, αν φ x είναι ολική f(x) = 0, αλλιώς Απόδειξη. Ορίζουμε h(x) = φ x (x) + 1, αν
Μη επιλυσιμότητα I Θεώρημα Το TOT (πρόβλημα ολικής συνάρτησης) είναι μη επιλύσιμο, δηλαδή η f δεν είναι αναδρομική όπου: 1, αν φ x είναι ολική f(x) = 0, αλλιώς Απόδειξη. Ορίζουμε h(x) = φ x (x) + 1, αν
Θεωρία Υπολογισμού και Πολυπλοκότητα Κανονικές Γλώσσες (2)
 Θεωρία Υπολογισμού και Πολυπλοκότητα Κανονικές Γλώσσες (2) Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Κανονικές Εκφράσεις (1.3) Τυπικός Ορισμός Ισοδυναμία με κανονικές γλώσσες Μη Κανονικές
Θεωρία Υπολογισμού και Πολυπλοκότητα Κανονικές Γλώσσες (2) Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Κανονικές Εκφράσεις (1.3) Τυπικός Ορισμός Ισοδυναμία με κανονικές γλώσσες Μη Κανονικές
L A P. w L A f(w) L B (10.1) u := f(w)
 Κεφάλαιο 10 NP -πληρότητα Σύνοψη Οι γλώσσες στην κλάση πολυπλοκότητας P μπορούν να αποφασίζονται σε πολωνυμικό χρόνο. Οι επιστήμονες πιστεύουν, αν και δε μπορούν να το αποδείξουν ότι η P είναι ένα γνήσιο
Κεφάλαιο 10 NP -πληρότητα Σύνοψη Οι γλώσσες στην κλάση πολυπλοκότητας P μπορούν να αποφασίζονται σε πολωνυμικό χρόνο. Οι επιστήμονες πιστεύουν, αν και δε μπορούν να το αποδείξουν ότι η P είναι ένα γνήσιο
HY118-Διακριτά Μαθηματικά. Θεωρία γράφων/ γραφήματα. Τι έχουμε δει μέχρι τώρα. Ισομορφισμός γράφων: Μία σχέση ισοδυναμίας μεταξύ γράφων.
 HY118-Διακριτά Μαθηματικά Θεωρία γράφων/ γραφήματα Τρίτη, 15/05/2018 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr 16-May-18 1 1 16-May-18 2 2 Τι έχουμε δει μέχρι τώρα Κατευθυνόμενοι μη κατευθυνόμενοι
HY118-Διακριτά Μαθηματικά Θεωρία γράφων/ γραφήματα Τρίτη, 15/05/2018 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr 16-May-18 1 1 16-May-18 2 2 Τι έχουμε δει μέχρι τώρα Κατευθυνόμενοι μη κατευθυνόμενοι
Εθνικό Μετσόβιο Πολυτεχνείο
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Στοιχεία Θεωρίας Αριθμών & Εφαρμογές στην Κρυπτογραφία PROJECT Συνοπτική Παρουσίαση του Κβαντικού Αλγόριθμου Παραγοντοποίησης
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Στοιχεία Θεωρίας Αριθμών & Εφαρμογές στην Κρυπτογραφία PROJECT Συνοπτική Παρουσίαση του Κβαντικού Αλγόριθμου Παραγοντοποίησης
Θεωρία Γραφημάτων 6η Διάλεξη
 Θεωρία Γραφημάτων 6η Διάλεξη Α. Συμβώνης Εθνικο Μετσοβειο Πολυτεχνειο Σχολη Εφαρμοσμενων Μαθηματικων και Φυσικων Επιστημων Τομεασ Μαθηματικων Φεβρουάριος 2016 Α. Συμβώνης (ΕΜΠ) Θεωρία Γραφημάτων 6η Διάλεξη
Θεωρία Γραφημάτων 6η Διάλεξη Α. Συμβώνης Εθνικο Μετσοβειο Πολυτεχνειο Σχολη Εφαρμοσμενων Μαθηματικων και Φυσικων Επιστημων Τομεασ Μαθηματικων Φεβρουάριος 2016 Α. Συμβώνης (ΕΜΠ) Θεωρία Γραφημάτων 6η Διάλεξη
Κρυπτοσύστημα RSA (Rivest, Shamir, Adlemann, 1977) Υπολογιστική Θεωρία Αριθμών και Κρυπτογραφία
 Υπολογιστική Θεωρία Αριθμών και Κρυπτογραφία Κρυπτογραφία Δημοσίου Κλειδιού Άρης Παγουρτζής Στάθης Ζάχος Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Κρυπτοσύστημα
Υπολογιστική Θεωρία Αριθμών και Κρυπτογραφία Κρυπτογραφία Δημοσίου Κλειδιού Άρης Παγουρτζής Στάθης Ζάχος Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Κρυπτοσύστημα
2 ) d i = 2e 28, i=1. a b c
 ΑΣΚΗΣΕΙΣ ΘΕΩΡΙΑΣ ΓΡΑΦΩΝ (1) Εστω G απλός γράφος, που έχει 9 κορυφές και άθροισμα βαθμών κορυφών μεγαλύτερο του 7. Αποδείξτε ότι υπάρχει μια κορυφή του G με βαθμό μεγαλύτερο ή ίσο του 4. () Αποδείξτε ότι
ΑΣΚΗΣΕΙΣ ΘΕΩΡΙΑΣ ΓΡΑΦΩΝ (1) Εστω G απλός γράφος, που έχει 9 κορυφές και άθροισμα βαθμών κορυφών μεγαλύτερο του 7. Αποδείξτε ότι υπάρχει μια κορυφή του G με βαθμό μεγαλύτερο ή ίσο του 4. () Αποδείξτε ότι
Κατανεμημένα Συστήματα Ι
 Κατανεμημένα Συστήματα Ι Εκλογή αρχηγού και κατασκευή BFS δένδρου σε σύγχρονο γενικό δίκτυο Παναγιώτα Παναγοπούλου Περίληψη Εκλογή αρχηγού σε γενικά δίκτυα Ορισμός του προβλήματος Ο αλγόριθμος FloodMax
Κατανεμημένα Συστήματα Ι Εκλογή αρχηγού και κατασκευή BFS δένδρου σε σύγχρονο γενικό δίκτυο Παναγιώτα Παναγοπούλου Περίληψη Εκλογή αρχηγού σε γενικά δίκτυα Ορισμός του προβλήματος Ο αλγόριθμος FloodMax
u v 4 w G 2 G 1 u v w x y z 4
 Διάλεξη :.0.06 Θεωρία Γραφημάτων Γραφέας: Σ. Κ. Διδάσκων: Σταύρος Κολλιόπουλος. Εισαγωγικοί ορισμοί Ορισμός. Γράφημα G καλείται ένα ζεύγος G = (V, E) όπου V είναι το σύνολο των κορυφών (ή κόμβων) και E
Διάλεξη :.0.06 Θεωρία Γραφημάτων Γραφέας: Σ. Κ. Διδάσκων: Σταύρος Κολλιόπουλος. Εισαγωγικοί ορισμοί Ορισμός. Γράφημα G καλείται ένα ζεύγος G = (V, E) όπου V είναι το σύνολο των κορυφών (ή κόμβων) και E
Αυτόματα. Παράδειγμα: πωλητής καφέ (iii) Παράδειγμα: πωλητής καφέ (iv) Εισαγωγή στην Επιστήμη των Υπολογιστών 6
 Εισαγωγή στην Επιστήμη των Υπολογιστών 3η ενότητα: Αυτόματα και Τυπικές Γραμματικές http://www.corelab.ece.ntua.gr/courses/ Αυτόματα Τρόπος κωδικοποίησης αλγορίθμων. Τρόπος περιγραφής συστημάτων πεπερασμένων
Εισαγωγή στην Επιστήμη των Υπολογιστών 3η ενότητα: Αυτόματα και Τυπικές Γραμματικές http://www.corelab.ece.ntua.gr/courses/ Αυτόματα Τρόπος κωδικοποίησης αλγορίθμων. Τρόπος περιγραφής συστημάτων πεπερασμένων
HY118-Διακριτά Μαθηματικά. Θεωρία γράφων/ γραφήματα. Τι είδαμε την προηγούμενη φορά. Συνεκτικότητα. 25 -Γράφοι
 HY118-Διακριτά Μαθηματικά Θεωρία γράφων/ γραφήματα Πέμπτη, 17/05/2018 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr 17-May-18 1 1 17-May-18 2 2 Τι είδαμε την προηγούμενη φορά Ισομορφισμός γράφων Υπολογιστική
HY118-Διακριτά Μαθηματικά Θεωρία γράφων/ γραφήματα Πέμπτη, 17/05/2018 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr 17-May-18 1 1 17-May-18 2 2 Τι είδαμε την προηγούμενη φορά Ισομορφισμός γράφων Υπολογιστική
Διάλεξη 18: Πρόβλημα Βυζαντινών Στρατηγών. ΕΠΛ 432: Κατανεμημένοι Αλγόριθμοι
 Διάλεξη 8: Πρόβλημα Βυζαντινών Στρατηγών ΕΠΛ 432: Κατανεμημένοι Αλγόριθμοι Ορισμός Προβλήματος Τι θα δούμε σήμερα Συνθήκες Συμφωνίας κάτω από Βυζαντινό Στρατηγό Πιθανοτικοί αλγόριθμοι επίλυσης Βυζαντινής
Διάλεξη 8: Πρόβλημα Βυζαντινών Στρατηγών ΕΠΛ 432: Κατανεμημένοι Αλγόριθμοι Ορισμός Προβλήματος Τι θα δούμε σήμερα Συνθήκες Συμφωνίας κάτω από Βυζαντινό Στρατηγό Πιθανοτικοί αλγόριθμοι επίλυσης Βυζαντινής
Διάλεξη 17: Συμφωνία με Βυζαντινά Σφάλματα. ΕΠΛ 432: Κατανεμημένοι Αλγόριθμοι
 Διάλεξη 17: Συμφωνία με Βυζαντινά Σφάλματα ΕΠΛ 432: Κατανεμημένοι Αλγόριθμοι Βυζαντινά Σφάλματα Τι θα δούμε σήμερα Κάτω Φράγμα για Αλγόριθμους Συμφωνίας με Βυζαντινά Σφάλματα: n > 3f Αλγόριθμος Συμφωνίας
Διάλεξη 17: Συμφωνία με Βυζαντινά Σφάλματα ΕΠΛ 432: Κατανεμημένοι Αλγόριθμοι Βυζαντινά Σφάλματα Τι θα δούμε σήμερα Κάτω Φράγμα για Αλγόριθμους Συμφωνίας με Βυζαντινά Σφάλματα: n > 3f Αλγόριθμος Συμφωνίας
ΑΛΓΟΡΙΘΜΟΙ ΚΑΙ ΠΟΛΥΠΛΟΚΟΤΗΤΑ 2 ΕΠΙΜΕΛΕΙΑ :ΣΤΟΥΚΑ ΑΙΚΑΤΕΡΙΝΗ-ΠΑΝΑΓΙΩΤΑ ΜΕΤΑΠΤΥΧΙΑΚΟ:ΜΠΛΑ
 ΑΛΓΟΡΙΘΜΟΙ ΚΑΙ ΠΟΛΥΠΛΟΚΟΤΗΤΑ 2 ΕΠΙΜΕΛΕΙΑ :ΣΤΟΥΚΑ ΑΙΚΑΤΕΡΙΝΗ-ΠΑΝΑΓΙΩΤΑ ΜΕΤΑΠΤΥΧΙΑΚΟ:ΜΠΛΑ Η Alice θέλει να στείλει ένα μήνυμα m(plaintext) στον Bob μέσα από ένα μη έμπιστο κανάλι και να μην μπορεί να το
ΑΛΓΟΡΙΘΜΟΙ ΚΑΙ ΠΟΛΥΠΛΟΚΟΤΗΤΑ 2 ΕΠΙΜΕΛΕΙΑ :ΣΤΟΥΚΑ ΑΙΚΑΤΕΡΙΝΗ-ΠΑΝΑΓΙΩΤΑ ΜΕΤΑΠΤΥΧΙΑΚΟ:ΜΠΛΑ Η Alice θέλει να στείλει ένα μήνυμα m(plaintext) στον Bob μέσα από ένα μη έμπιστο κανάλι και να μην μπορεί να το
Σημειώσεις Λογικής I. Εαρινό Εξάμηνο Καθηγητής: Λ. Κυρούσης
 Σημειώσεις Λογικής I Εαρινό Εξάμηνο 2011-2012 Καθηγητής: Λ. Κυρούσης 2 Τελευταία ενημέρωση 28/3/2012, στις 01:37. Περιεχόμενα 1 Εισαγωγή 5 2 Προτασιακή Λογική 7 2.1 Αναδρομικοί Ορισμοί - Επαγωγικές Αποδείξεις...................
Σημειώσεις Λογικής I Εαρινό Εξάμηνο 2011-2012 Καθηγητής: Λ. Κυρούσης 2 Τελευταία ενημέρωση 28/3/2012, στις 01:37. Περιεχόμενα 1 Εισαγωγή 5 2 Προτασιακή Λογική 7 2.1 Αναδρομικοί Ορισμοί - Επαγωγικές Αποδείξεις...................
t M (w) T ( w ) O( n) = O(n 2 )
 Κεφάλαιο 9 Υπολογιστική Πολυπλοκότητα Σύνοψη Πέρα από το ερώτημα του αν για ένα πρόβλημα υπάρχει Μηχανή Turing, που το επιλύει, μας απασχολεί επίσης και το ερώτημα του αν ένα πρόβλημα είναι «πρακτικά»
Κεφάλαιο 9 Υπολογιστική Πολυπλοκότητα Σύνοψη Πέρα από το ερώτημα του αν για ένα πρόβλημα υπάρχει Μηχανή Turing, που το επιλύει, μας απασχολεί επίσης και το ερώτημα του αν ένα πρόβλημα είναι «πρακτικά»
Ασκήσεις Επανάληψης. Επανάληψη Εαρινό Εξάμηνο 2019 Σελίδα 1
 Ασκήσεις Επανάληψης Άσκηση 1 (Τελική Εξέταση 5/015) Να δείξετε ότι η πιο κάτω γλώσσα δεν είναι διαγνώσιμη. { Μ L(M) {ΘΕΩΡΙΑ, ΥΠΟΛΟΓΙΣΜΟΥ} και L(M) 3} (Για την αναγωγή μπορείτε να χρησιμοποιήσετε τη γνωστή
Ασκήσεις Επανάληψης Άσκηση 1 (Τελική Εξέταση 5/015) Να δείξετε ότι η πιο κάτω γλώσσα δεν είναι διαγνώσιμη. { Μ L(M) {ΘΕΩΡΙΑ, ΥΠΟΛΟΓΙΣΜΟΥ} και L(M) 3} (Για την αναγωγή μπορείτε να χρησιμοποιήσετε τη γνωστή
Κρυπτογραφία. Κεφάλαιο 4 Αλγόριθμοι Δημοσίου Κλειδιού (ή ασύμμετροι αλγόριθμοι)
 Κρυπτογραφία Κεφάλαιο 4 Αλγόριθμοι Δημοσίου Κλειδιού (ή ασύμμετροι αλγόριθμοι) Κρυπτοσυστήματα Δημοσίου κλειδιού Αποστολέας P Encryption C Decryption P Παραλήπτης Προτάθηκαν το 1976 Κάθε συμμετέχων στο
Κρυπτογραφία Κεφάλαιο 4 Αλγόριθμοι Δημοσίου Κλειδιού (ή ασύμμετροι αλγόριθμοι) Κρυπτοσυστήματα Δημοσίου κλειδιού Αποστολέας P Encryption C Decryption P Παραλήπτης Προτάθηκαν το 1976 Κάθε συμμετέχων στο
Αλγόριθμοι για ανάθεση συχνοτήτων και έλεγχο αποδοχής κλήσεων σε κυψελικά ασύρματα δίκτυα
 Αλγόριθμοι για ανάθεση συχνοτήτων και έλεγχο αποδοχής κλήσεων σε κυψελικά ασύρματα δίκτυα (μέρος ΙIΙ) Έλεγχος αποδοχής κλήσεων Οάπληστος(Greedy) αλγόριθμος ελέγχου αποδοχής κλήσεων Ο αλγόριθμος ταξινόμησης
Αλγόριθμοι για ανάθεση συχνοτήτων και έλεγχο αποδοχής κλήσεων σε κυψελικά ασύρματα δίκτυα (μέρος ΙIΙ) Έλεγχος αποδοχής κλήσεων Οάπληστος(Greedy) αλγόριθμος ελέγχου αποδοχής κλήσεων Ο αλγόριθμος ταξινόμησης
ΑΛΓΟΡΙΘΜΟΙ ΚΑΙ ΠΟΛΥΠΛΟΚΟΤΗΤΑ Φεβρουάριος 2005 Σύνολο μονάδων: 91
 Ε.Μ.Πoλυτεχνείο ΣΗΜΜΥ, ΣΕΜΦΕ Τομέας Τεχνολογίας Πληροφορικής & Υπολογιστών Διδάσκων: Ε.Ζαχος Ονοματεπώνυμο:... Αριθμός Μητρώου:... Σχολή:... εξάμηνο:... ΑΛΓΟΡΙΘΜΟΙ ΚΑΙ ΠΟΛΥΠΛΟΚΟΤΗΤΑ Φεβρουάριος 005 Σύνολο
Ε.Μ.Πoλυτεχνείο ΣΗΜΜΥ, ΣΕΜΦΕ Τομέας Τεχνολογίας Πληροφορικής & Υπολογιστών Διδάσκων: Ε.Ζαχος Ονοματεπώνυμο:... Αριθμός Μητρώου:... Σχολή:... εξάμηνο:... ΑΛΓΟΡΙΘΜΟΙ ΚΑΙ ΠΟΛΥΠΛΟΚΟΤΗΤΑ Φεβρουάριος 005 Σύνολο
q(g \ S ) = q(g \ S) S + d = S.
 Διάλεξη 9: 9.11.2016 Θεωρία Γραφημάτων Διδάσκων: Σταύρος Κολλιόπουλος Γραφέας: Παναγιωτίδης Αλέξανδρος & Σ. Κ. Θεώρημα 9.1 Εστω γράφημα G = (V, E), υπάρχει τέλειο ταίριασμα στο G αν και μόνο αν για κάθε
Διάλεξη 9: 9.11.2016 Θεωρία Γραφημάτων Διδάσκων: Σταύρος Κολλιόπουλος Γραφέας: Παναγιωτίδης Αλέξανδρος & Σ. Κ. Θεώρημα 9.1 Εστω γράφημα G = (V, E), υπάρχει τέλειο ταίριασμα στο G αν και μόνο αν για κάθε
ΑΝΑΛΥΣΗ 1 ΠΕΜΠΤΟ ΜΑΘΗΜΑ, Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ 1 ΠΕΜΠΤΟ ΜΑΘΗΜΑ, 17-10-13 Μ. Παπαδημητράκης. 1 Την προηγούμενη φορά αναφέραμε (και αποδείξαμε στην περίπτωση n = 2) το θεώρημα που λέει ότι, αν n N, n 2, τότε για κάθε y 0 υπάρχει μοναδική μηαρνητική
ΑΝΑΛΥΣΗ 1 ΠΕΜΠΤΟ ΜΑΘΗΜΑ, 17-10-13 Μ. Παπαδημητράκης. 1 Την προηγούμενη φορά αναφέραμε (και αποδείξαμε στην περίπτωση n = 2) το θεώρημα που λέει ότι, αν n N, n 2, τότε για κάθε y 0 υπάρχει μοναδική μηαρνητική
12. ΑΝΙΣΩΣΕΙΣ Α ΒΑΘΜΟΥ. είναι δύο παραστάσεις μιας μεταβλητής x πού παίρνει τιμές στο
 ΓΕΝΙΚΑ ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Έστω f σύνολο Α, g Α ΒΑΘΜΟΥ είναι δύο παραστάσεις μιας μεταβλητής πού παίρνει τιμές στο Ανίσωση με έναν άγνωστο λέγεται κάθε σχέση της μορφής f f g g ή, η οποία αληθεύει για ορισμένες
ΓΕΝΙΚΑ ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Έστω f σύνολο Α, g Α ΒΑΘΜΟΥ είναι δύο παραστάσεις μιας μεταβλητής πού παίρνει τιμές στο Ανίσωση με έναν άγνωστο λέγεται κάθε σχέση της μορφής f f g g ή, η οποία αληθεύει για ορισμένες
Πολλοί τρόποι περιγραφής αλγορίθμων. Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις
 Θέση Church-Turing Κανονική μορφή Kleene Θέση Church-Turing I Πολλοί τρόποι περιγραφής αλγορίθμων Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις Θέση Church-Turing:
Θέση Church-Turing Κανονική μορφή Kleene Θέση Church-Turing I Πολλοί τρόποι περιγραφής αλγορίθμων Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις Θέση Church-Turing:
Στοιχεία Θεωρίας Αριθμών & Εφαρμογές στην Κρυπτογραφία
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Σημειώσεις Διαλέξεων Στοιχεία Θεωρίας Αριθμών & Εφαρμογές στην Κρυπτογραφία Επιμέλεια σημειώσεων: Ζωή Παρασκευοπούλου Νίκος
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Σημειώσεις Διαλέξεων Στοιχεία Θεωρίας Αριθμών & Εφαρμογές στην Κρυπτογραφία Επιμέλεια σημειώσεων: Ζωή Παρασκευοπούλου Νίκος
ΑΛΓΟΡΙΘΜΟΙ. Ενότητα 11: Περιορισμοί της Αλγοριθμικής Ισχύος
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΑΛΓΟΡΙΘΜΟΙ Ενότητα 11: Περιορισμοί της Αλγοριθμικής Ισχύος Ιωάννης Μανωλόπουλος, Καθηγητής Αναστάσιος Γούναρης, Επίκουρος Καθηγητής Άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΑΛΓΟΡΙΘΜΟΙ Ενότητα 11: Περιορισμοί της Αλγοριθμικής Ισχύος Ιωάννης Μανωλόπουλος, Καθηγητής Αναστάσιος Γούναρης, Επίκουρος Καθηγητής Άδειες
