Κεφάλαιο 7. Εκτίµησης παραµέτρων στην πράξη

Transcript

1 Κεφάλαιο 7 Εκτίµησης παραµέτρων στην πράξη

2 7. Επιλογή της µεόδου εκτίµησης Στο Κεφάλαιο 6 συζητήσαµε µεόδους εκτίµησης παραµέτρων. Εν γένει διαφορετικές µέοδοι οδηγούν σε διαφορετικούς εκτιµητές. Προκειµένου να επιλέξουµε την πλέον ενδεδειγµένη µέοδο, ιδιαίτερα εάν πρόκειται να αναλύσουµε µεγάλο όγκο πειραµατικών δεδοµένων, α πρέπει να συνυπολογίσουµε πλήος παραγόντων που αφορούν τις ιδιότητες των εκτιµητών αλλά και την δυνατότητα πρακτικής εφαρµογής της µεόδου αλλά και των αποτελεσµάτων της εκτίµησης. Τα ακόλουα πέντε κριτήρια επιλογής µεόδου εκτίµησης δεν είναι τα µοναδικά αλλά συµπυκνώνουν τις σηµαντικότερες «αρετές» τις οποίες επιζητούµε συνήως από έναν εκτιµητή.. Συνέπεια και προκατάληψη: Ο εκτιµητής α πρέπει να είναι συνεπής ώστε η εκτίµηση να τείνει προς την αληή τιµή των παραµέτρων καώς το πλήος των πειραµατικών δεδοµένων αυξάνει. Ο εκτιµητής α πρέπει να είναι απαλλαγµένος από προκατάληψη. Στην περίπτωση όπου η εκτίµηση είναι προκατεληµένη, η προκατάληψη α πρέπει να εκτιµάται και η εκτίµηση να διορώνεται, όπως α δείξουµε στην επόµενη υποενότητα.. Περιεχόµενο σε Πληροφορία: Συνήως µε την µέοδο της εκτίµησης παραµέτρων επιδιώκουµε την συµπύκνωση της πληροφορίας, η οποία εµπεριέχεται στα διαέσιµα πειραµατικά δεδοµένα αναφορικά µε την τιµή κάποιων φυσικών µεγεών, σε ένα ή µερικά νούµερα. Συνεπώς το αποτέλεσµα της εκτίµησης α πρέπει α πρέπει να περιέχει όλη την δυνατή πληροφορία. 3. Αποδοτικότητα: Επιδιώκουµε την επιλογή εκτιµητών µε την ελάχιστη δυνατή διασπορά. Όσο µικρότερη είναι η διασπορά της εκτίµησης τόσο ακριβέστερη είναι η προσέγγιση της αληούς τιµής. 4. Εξάρτηση από παραδοχές. Στις περισσότερες των περιπτώσεων, είµαστε αναγκασµένοι να προβούµε σε υποέσεις, π.χ. όσον αφορά την συναρτησιακή µορφή της πυκνότητας πιανότητας ή το πρότυπο προσαρµογής. Επιδιώκουµε να επιλέγουµε τέτοιες συναρτησιακές µορφές ή να επιβάλουµε περιορισµούς (π.χ. πεδίο τιµών των µεταβλητών) µε τρόπο που δεν α «καταστρέψει» εντελώς την διαδικασία εκτίµησης 3. Τα κριτήρια αυτά προτείνοντα από τους ade et all, Secton 8., page 43 Επί παραδείγµατι, ας υποέσουµε ότι έλουµε να εκτιµήσουµε το σφάλµα µέτρησης µίας πειραµατικής συσκευής, η οποία µετράει τις τιµές του φυσικού µεγέους Χ, διαέτοντας Ν µετρήσεις x (=,,3, ) και τις αντίστοιχες αληείς τιµές του φυσικού µεγέους. Είναι προφανές ότι α πρέπει να εξετάσουµε την περίπτωση όπου το µετρητικό σφάλµα της συσκευής εξαρτάται από την αληή τιµή του φυσικού µεγέους. Η πληροφορία αυτή εµπεριέχεται στα πειραµατικά δεδοµένα και η επιλεγείσα µέοδος εκτίµησης α πρέπει να έχει την δυνατότητα να προσδιορίσει το µετρητικό σφάλµα ως συνάρτηση της αληούς τιµής. 3 Ας υποέσουµε ότι οι τιµές του φυσικού µεγέους Υ εξαρτάται από το µέγεος Χ µε σχέση εκετικής µορφής: ax e. Εάν επιλέξουµε ως πρότυπο προσαρµογής µε την µέοδο των ελαχίστων τετραγώνων της µορφής:sn(b x + c) και επιδιώξουµε να εκτιµήσουµε τις παραµέτρους b και c, κατά πάσα πιανότητα, α αποτύχουµε. Αντίετα, εάν επιλέξουµε ως πρότυπο προσαρµογής την πολυονυµική συνάρτηση : µπορούµε να εκτιµήσουµε τις παραµέτρους w και να περιγράψουµε µε ικανοποιητική ακρίβεια την εξάρτηση των µεγεών Υ και Χ. Παρατηρήσετε ότι η ανάλυση σε σειρά Teylor του αληούς προτύπου έχει πολυονυµική µορφή. Αρκεί το πλήος των πειραµατικών σηµείων να είναι αρκετά µεγάλο ώστε να µπορέσουµε να χρησιµοποιήσουµε ικανοποιητικό αριµό όρων,. = 0 w x

3 εβαίως, η γενικότητα στην επιλογή συναρτήσεων και περιορισµών α αποβεί εις βάρος της ακρίβειας (σφάλµα) της εκτίµησης. 5. Ελάχιστο κόστος σε χρόνο και απλότητα: Επιδιώκουµε την χρήση µεόδων που η εφαρµογή τους δεν απαιτεί µεγάλο χρόνο επεξεργασίας ή ιδιαίτερη δυσκολία στην εκτέλεση της επεξεργασίας. Επίσης, το αποτέλεσµα της εκτίµησης α πρέπει να συνοδεύεται από τις ελάχιστες παραδοχές (π.χ. για την ισχύ φυσικών εωριών και µοντέλων) και πάντοτε α πρέπει να συνοδεύεται από τις απαραίτητες επεξηγήσεις ώστε να είναι εύκολο από κάε άλλο ενδιαφερόµενο να το χρησιµοποιήσει. Επισηµαίνεται, ότι δεν υπάρχουν γενικές οδηγίες για την επιλογή µεόδου εκτίµησης σε κάε πρόβληµα ανάλυσης πειραµατικών δεδοµένων. Εν τέλει, η επιλογή και η χρήση µεόδων εκτίµησης επαφίονται στην εµπειρία και δηµιουργικότητα του επιστήµονα. 7. Άρση της προκατάληψης. Έστω ότι διαέτουµε Ν µετρήσεις της ποσότητας Χ, x (=,,3, ), µε συνάρτηση πυκνότητας πιανότητας f(x; ). Έστω επίσης η συνεπής εκτίµηση της παραµέτρου, µε αληή τιµή 0, η οποία όµως πάσχει από προκατάληψη: b =Ε 0 Εάν η συνάρτηση πυκνότητας πιανότητας είναι γνωστή, µπορούµε να υπολογίσουµε την ποσότητα b και στην συνέχεια να ορίσουµε τον µη προκαταληµένο εκτιµητή: = b 7.. Στην περίπτωση αυτή η διασπορά της εκτίµησης α παραµένει η ίδια: V = V V[ b] = V αρκεί να γνωρίζουµε την αληή τιµή της παραµέτρου ώστε να υπολογίσουµε την προκατάληψη χωρίς σφάλµα. Ωστόσο, σε κάε πρακτική εφαρµογή, η αληής τιµή 0 δεν είναι γνωστή. Το µόνο που µπορούµε να κάνουµε είναι να εκτιµήσουµε την προκατάληψη, οπότε το σφάλµα της εκτίµησης της προκατάληψης συµµετέχει στην αύξηση του σφάλµατος της εκτίµησης της παραµέτρου. Παράδειγµα 7..: Έχουµε δείξει ότι η σύγχρονη εκτίµηση, µε την µέοδο της µεγίστης πιανοφάνειας, των παραµέτρων µ και σ της κανονικής συνάρτησης πιανότητας των µετρήσεων x,x, K,x, οδηγεί σε εκτιµήσεις µκαισεκ των οποίων η δεύτερη: { } Ν σ σ = ( < x> x ), σ =σ Ν = πάσχει από προκατάληψη. Προκειµένου να ορίσουµε νέο εκτιµητή χωρίς προκατάληψη εφαρµόζουµε την σχέση 7..: Ν σ s = ( < x> x ) =σ Ν = Στην περίπτωση της κανονικής συνάρτησης πυκνότητας πιανότητας βρίσκεται ότι: 4 Ν V σ = σ 7..3 Ν

4 Συνδυάζοντας τις σχέσεις 7.. και 7..3 καταλήγουµε ότι: V s = σ 7..4 Ν Η σχέση 7..4 αντιστοιχεί σε αύξηση του σφάλµατος στην εκτίµηση κατά: σ V s V σ = 7..5 Ν Ν 4 Ερώτηση: Δείξετε ότι για Ν>3 η αύξηση 7..5 του σφάλµατος είναι µικρότερη από την προκατάληψη. Στην περίπτωση όπου η συνάρτηση πυκνότητας πιανότητας των δεδοµένων δεν είναι γνωστοί υπάρχουν διάφοροι τρόποι για την µείωση της προκατάληψης. Στο επόµενα αναφέρεται η πλέον εύχρηστη από αυτές τις µεόδους. Αναλύοντας 4 την αναµενόµενη τιµή της εκτίµησης σε σειρά, ως προς /Ν, εκφράζουµε ως: Ε Ν = 0 + β+ d 7..6 Ν Ν όπου χρησιµοποιήσαµε το σύµβολο Ν για να δηλώσουµε ότι η εκτίµηση επετεύχη µε Ν µετρήσεις. Παρατηρήστε ότι η κύρια συνεισφορά στην απόκλιση από την αληή τιµή, προέρχεται από τον όρο που είναι ανάλογος το /Ν. Ας χωρίσουµε τα δεδοµένα σε δύο οµάδες και ας επαναλάβουµε την εκτίµηση της ιδίας παραµέτρου, µε τα δύο ήµισυ. Ε / / 0 Ν =Ε = + β+ Ν d 7..7 Ν Ν Συνεπώς: ( Ε + ) = / / 0 + Ν Ν Ν d 7.8 Ν Δηλαδή ο εκτιµητής ( + ) έχει µικρότερη προκατάληψη (τάξης Ν Ν/ Ν/ Ν ) από τον εκτιµητή Ν. Ν < ' >, όπου ' < > Ένας άλλος εκτιµητής, γενικής χρήσης, είναι ο Ν Ν είναι ο µέσος όρος των εκτιµήσεων που επιτυγχάνονται από όλους τους συνδυασµούς Ν- γεγονότων. Ν 7.3 Εκτίµηση παραµέτρων µε την µέοδο των ορογωνίων συναρτήσεων. Μία ειδική περίπτωση της µεόδου των ροπών προκύπτει όταν η συνάρτηση πυκνότητας πιανότητας των παρατηρήσεων, f(x;), µπορεί να εκφρασεί ως ανάπτυγµα ορογωνίων συναρτήσεων g (x). Σ αυτή την περίπτωση η συνάρτηση πυκνότητας πιανότητας α έχει την µορφή: 4 λέπε ade et al, Secton 7.3. page 6

5 r f(x;) = a + g (x) = g (x) g (x)dx = δ j j g (x)dx = Η αναµενόµενη τιµή των ορογωνίων συναρτήσεων, g (x), είναι: r [ g (x) ] = g (x) a + λ g (x) dx λ= f(x; ) r =a g (x)dx + g (x) g (x)dx = λ λ λ= 7.3. Οι αναµενόµενες τιµές, g(x), [ ] µπορούν να υπολογισούν προσεγγιστικά πειραµατικές παρατηρήσεις και τον νόµο των µεγάλων αριµών ως: Ε[ g (x) ] = = lm g (x ) = από τις Επειδή η εκτίµηση της παραµέτρου ανάγεται, σε άροισµα Ν τυχαίων µεταβλητών, g (x ) =,,.., η εκτίµηση,,α κατανέµεται σύµφωνα µε κανονική συνάρτηση πιανότητας, µε µέση τιµή ίση µε την αναµενόµενη τιµή της ορογώνιας συνάρτησης: g (x ) [ g (x) ] = = = όπως υπαγορεύει το εώρηµα του κεντρικού ορίου.. Η σχέση δηλώνει επίσης ότι η εκτίµηση, µε την µέοδο των ορογωνίων συναρτήσεων, είναι συνεπής. Η διασπορά των εκτιµήσεων (δηλαδή η ακρίβεια) άροισµα : V( ) = V[ g(x) ] όπου V [ g (x ) ] = g (x j) = j α εκφράζεται ως το ακόλουο Τελικά η διασπορά της εκτίµησης α είναι : V g (x ) = ( ) =

6 Παράδειγµα 7.3.: Η έκφραση f (x ) = α + Σ g (x), µε τις g (x) να είναι ορογώνιες συναρτήσεις, προκύπτει πολύ συχνά στην µελέτη γωνιακών κατανοµών, λόγω διατήρησης της στροφορµής. Επί παραδείγµατι, κατά την διάσπαση του βαρυονίου Λ 0, σε ένα πρωτόνιο (p) και ένα πιόνιο (π), το συνηµίτονο της γωνίας (cosφ) που σχηµατίζει η διεύυνση κίνησης του πιονίου στο σύστηµα κέντρου µάζας του Λ 0 µε την διεύυνση κίνησης του Λ 0 στο σύστηµα εργαστηρίου, χαρακτηρίζεται από συνάρτηση πυκνότητας πιανότητας της µορφής: f(cos φ ;P) = [ + a P cosφ ] όπου P είναι η παράµετρος πόλωσης και a είναι η παράµετρος ασυµµετρίας, την οποία α εωρήσουµε ότι είναι γνωστή. Ας µελετήσουµε την συνάρτηση g: g(cos φ ) = R cosφ αναζητώντας την τιµή της παραµέτρου ώστε να πληρούνται οι απαιτήσεις της σχέσεις ( R cosφdcosφ ) = 0 3cosφ g( cosφ) = R ( R cosφ) ( R cosφ) d(cosφ) = = 3 Επιλέγοντας R=(3/) /, η συνάρτηση, g(cosφ) =R cosφ, είναι ορογώνια και η συνάρτηση πυκνότητας πιανότητας γράφεται ως: 3 a P f(cosφ;p) = + a P cosφ = g( cosφ) Κατά συνέπεια ο πολλαπλασιαστικός όρος πόλωσης P, µπορεί να εκτιµηεί ως: a P 3 3 cosφ = cos 3 φ = 3 P = cosφ a α P και κατ επέκταση ο συντελεστής Για απλούστευση ας γράψουµε την συνάρτηση πυκνότητας πιανότητας του προηγουµένου παραδείγµατος ως f (x;) = ½ ( + x), όπου - x και x = cosφ. Η παράµετρος έχει απορροφήσει τους σταερούς όρους και τις παραµέτρους πόλωσης και ασυµµετρίας. Εφαρµόζοντας τις σχέσεις και 7.3.6, η διασπορά της εκτίµησης της

7 παραµέτρου, µε την µέοδο των ορογωνίων συναρτήσεων, βρίσκεται ότι α είναι ίση µε (3- )/Ν. Ας επαναλάβουµε την εκτίµηση της ιδίας παραµέτρου µε την µέοδο της µέγιστης πιανοφάνειας. Χρησιµοποιώντας τις ασυµπτωτικές ιδιότητες της µεόδου βρίσκουµε ότι: V lnl = = d = ln (+ x ) d d = ln(+ x ) d + ln < 5 = 3 K (3 ) = Δηλαδή, η διασπορά της εκτίµησης µε την µέοδο της µεγίστης πιανοφάνειας είναι µικρότερη της διασποράς που αντιστοιχεί στην µέοδο των ορογωνίων συναρτήσεων.

8 7.3 Εκτεταµένη µέοδος µεγίστης πιανοφάνειας Η συνάρτηση της πιανοφάνειας εξαρτάται αποκλειστικά από την συναρτησιακή µορφή της συνάρτησης πυκνότητας πιανότητας των τυχαίων µεταβλητών που χαρακτηρίζουν το πρόβληµα. Δεν µεταφέρει καµία πληροφορία αναφορικά µε τον αριµό των γεγονότων που αναµένει να συλλέξει κανείς στο συγκεκριµένο πείραµα, έστω και εάν το αναµενόµενο πλήος γεγονότων εξαρτάται από τις υπό εκτίµηση παραµέτρους Παράδειγµα 7.3. Ας υποέσουµε ότι σε ένα πείραµα ανιχνεύονται ακτίνες Χ και µετρείται η ενέργεια, Ε, κάε,. Οι ακτίνες Χ ενός από τα φωτόνια που ανιχνεύονται στην ενεργειακή περιοχή [ ] παράγοντα από δύο διαφορετικούς φυσικούς µηχανισµούς, Α και. Η ενεργειακή κατανοµή των φωτονίων τύπου Α χαρακτηρίζεται από την συνάρτηση πυκνότητας πιανότητας f () A και τα φωτόνια από τον µηχανισµό έχουν ενέργειες σύµφωνα µε την συνάρτηση πυκνότητας πιανότητας f B(). Προφανώς: A B f d = f d = 7.3. Επιπλέον, ο αναµενόµενος αριµός των φωτονίων τύπου που αντιστοιχεί στο χρόνο διάρκειας του πειράµατος είναι µ ενώ ο αντίστοιχος αριµός φωτονίων τύπου Α δίνεται από την ακόλουη σχέση: µ Α = R 7.3. όπου R είναι γνωστή σταερά και η παράµετρος α εκτιµηεί από τα πειραµατικά δεδοµένα. Τα πειραµατικά δεδοµένα συνίστανται από µετρήσεις της ενέργειας Ν φωτονίων: Ε=,, K,. { } Η πιανότητα ώστε ένα από τα φωτόνια που ανιχνεύηκαν, ανεξαρτήτως της ενέργειάς του, να προέρχεται από τον µηχανισµό Α, είναι: µ Α R w A = = µ Α +µ R +µ Η αντίστοιχη πιανότητα για τα φωτόνια τύπου δίνεται από την σχέση: µ B µ B w B = = µ +µ R +µ Α Οι πιανότητες ώστε ένα από τα φωτόνια που ανιχνεύηκαν, στην ενεργειακή περιοχή [Ε, Ε +d], να προέρχεται από τον µηχανισµό A ή, α εκφράζεται ώς:

9 R P w f d f d = = A A A A R +µ µ PB( ) = w B fb( ) d = f ( ) d R +µ Συνεπώς, η συνάρτηση πυκνότητας πιανότητας, F(), που περιγράφει τα πειραµατικά δεδοµένα είναι: R µ F() = fa ( ) + f ( ) R+µ R+µ F()d = H συνάρτηση πιανοφάνειας των πειραµατικών δεδοµένων εκφράζεται ως: R µ L(; ) = fa( ) + f ( ) = R+µ R+µ Παρατηρήστε ότι η πιανοφάνεια (7.3.7) εξαρτάται από την παράµετρο µόνο όταν οι δύο φυσικοί µηχανισµοί παράγουν ακτίνες Χ µε διαφορετικές ενεργειακές κατανοµές. f = f η σχέση και η συνάρτηση πιανοφάνειας (7.3.7) Επί παραδείγµατι, εάν A δεν µεταφέρουν καµία πληροφορία για την παράµετρο ( F() f ( ) f ( ) = = ). Ωστόσο, µπορούµε να αντλήσουµε πληροφορία για την παράµετρο από το πλήος των φωτονίων που ανιχνεύηκαν. Η πιανότητα ώστε τα Ν φωτόνια που ανιχνεύηκαν να εµπεριέχουν φωτόνια από τον µηχανισµό Α, µε τιµή της παραµέτρου ίση µε, α δίνεται από την ακόλουη συνάρτηση πιανότητας: ( R ) ( R ) Ν +µ e +µ P = Ν! Όπου R +µ είναι ο αναµενόµενος αριµός φωτονίων στον ανιχνευτή και από τους δύο µηχανισµούς.. Η µεγιστοποίηση της πιανότητας 7.3.8, κατά αντίστοιχο τρόπο της µεόδου µεγίστης πιανοφάνειας, καταλήγει στην εκτίµηση της αληούς τιµής της παραµέτρου. Προφανώς, η σχέση εκφράζει την πιανότητα ανίχνευσης Ν φωτονίων ανεξάρτητα της f και f. Κατά συνέπεια, ο συνδυασµός των µορφής των ενεργειακών κατανοµών, A συναρτήσεων πιανοφάνειας, και 7.3.8, αναµένεται να ενισχύσει την ακρίβεια της εκτίµησης. Προκειµένου να συµπεριλάβουµε στη εκτίµηση των παραµέτρων και την πληροφορία που εµπεριέχει ο συνολικός αριµός των δεδοµένων, πολλαπλασιάζουµε τη συνάρτηση πιανοφάνειας µε την πιανότητα ανίχνευσης Ν γεγονότων, η οποία εκφράζεται από Possonan συνάρτηση πιανότητας,. A

10 Ν ν( ) ( ν( ) ) e L(x; ) = f (x, ) L (x; ) = f (x, ) Ε = Ν! = L(x; )dx dx L dx = L (x; )dx dx L dx = = 0 όπου, x { x,x,,x } = K είναι οι Ν µετρήσεις και ν() είναι η αναµενόµενη τιµή του πλήους των µετρήσεων, η οποία εν γένει είναι συνάρτηση της παραµέτρου. Η στατιστική συνάρτηση L(x;) Ε, που ορίσηκε στην σχέση 7.3.9, καλείται εκτεταµένη (extended) συνάρτηση πιανοφάνειας. ( x;) lnl Κατ αντιστοιχία της σχέσης 6.6.6, η αναµενόµενη τιµή της ποσότητας, ισούται µε µηδέν. lnl( x;) lnl( x;) = L( x;dxdx ) dx K = = L( x;dxdx ) dx = 0 K = lnl ( x;) Ως συνέπεια του εωρήµατος του κεντρικού ορίου, η ποσότητα, ως άροισµα lnl ( x;) ν( ) τυχαίων µεταβλητών: = ln( f ( x ; )) ν, α κατανέµεται = σύµφωνα µε κανονική συνάρτηση πυκνότητας πιανότητας καώς το πλήος των µετρήσεων lnl ( x;) α τείνει προς το άπειρο. Η διασπορά της µεταβλητής ευρίσκεται κατ αντιστοιχία της σχέσης ως: lnl Ε(x;) lnl Ε(x;) lnl Ε(x;) V = 0 = L Ε(x;)dxdx dx Ν K Ν= lnl Ε(x;) lnl Ε(x;) = L Ε(x;)dxdx K dx Ν = Ε = Ν= 0 ΙΕ, lnl Αναπτύσσοντας την συνήκη µεγιστοποίησης, = 0, σε σειρά Taylor, σε µία = περιοχή τιµών της παραµέτρου γύρω από την αληή της τιµή, αγνοώντας όρους ανώτερης της πρώτης τάξεως ως προς, καταλήγουµε ότι: lnlε( x; ) lnlε( x; ) lnlε( x; ) = + ( 0) 0 + LLLLL = 443 = όροι µεγαλύτερης τάξης = 0 = 0 ( )

11 ( x;) lnlε = 0 0 = 7.3. lnlε ( x;) = 0 Εάν ο παρανοµαστής στην σχέση 7.3. είναι σταερά ή µεταβάλλεται πολύ λίγο για τιµές της παραµέτρου πλησίον της τιµής 0, η απόκλιση της εκτίµησης από την πραγµατική τιµή, ( ), α είναι ανάλογη της πρώτης παραγώγου του λογαρίµου της πιανοφάνειας. Κατά 0 ( x;) lnl συνέπεια, α κατανέµεται όπως και η µεταβλητή, δηλαδή σύµφωνα µε κανονική συνάρτηση πιανότητας µε µέση τιµή ίση µε το µηδέν και διασπορά ίση µε: ln L ( x; ) ln L ( x; ) V -Ε =0 = 0 V = = ln L( x; ) ln L( x; ) = 0 =0 Επαναλαµβάνοντας τους συλλογισµούς της σχέσης συµπεραίνουµε ότι για µεγάλο πλήος µετρήσεων ισχύει ότι: ( x;) lnl ν ν = ln ( ν( ) f( x ; ) ) = ln ( ν( ) f( x ; ) ) = ν lnl ( x;) ώστε µπορούµε να γράψουµε την σχέση ως: = lm ln ( ν ( ) f ( x ; )) = M M j = ln L ( x; ) - V =0 = = ln L x; ln L x; =0 = Παράδειγµα 7.3. Στο Παράδειγµα 7.3. παρουσιάστηκε ένα υποετικό πείραµα ανίχνευσης φωτονίων, τα οποία παράγονται από δύο διαφορετικούς φυσικούς µηχανισµούς. Στόχος του πειράµατος είναι η εκτίµηση της παραµέτρου, η οποία καορίζει το ποσοστό φωτονίων τύπου Α. Η εκτίµηση της παραµέτρου µε την µέοδο µεγιστοποίησης της πιανοφάνειας καταλήγει ότι:

12 R f +µ f L(; ) A = ln = = R + µ = A R f R = = = R fa f +µ R+µ Έναν συνήη τρόπο για να επιλυούν εξισώσεις όπως η προσφέρει η µέοδος των διαδοχικών προσεγγίσεων. Παρατηρήσετε ότι στην περίπτωση όπου f A() ; f B() η εξίσωση καταλήγει σε ταυτότητα και δεν προσφέρει καµία πληροφορία για την παράµετρο. Αντίετα, εάν οι ενεργειακές κατανοµές των φωτονίων από τους δύο µηχανισµούς διαφέρουν µεταξύ τους, µεταφέρεται πληροφορία για την αληή τιµή της παραµέτρου. Παραδείγµατος χάριν, εάν οι ενεργειακές κατατοµές είναι της µορφής: =φ A( ) ; Ε [ ε, ε] fa ( ) = 0; Ε [ ε, ε ] =φ A( ) ; Ε [ ε3, ε4] f ( ) = 0; Ε [ ε 3, ε 4] ε, ε και ε, ε είναι διαφορετικές και µη αλληλοκαλυπτόµενες υπο-περιοχές του όπου [ ] [ 3 4] ενεργειακού διαστήµατος [ Ε, Ε ] προέλευσης κάε φωτονίου. Έστω ότι ανιχνεύηκαν n φωτόνια στην περιοχή [ ε, ε ] φωτόνια που προέρχονται από τον µηχανισµό Α) και Ν-n φωτόνια στην περιοχή [ ε, ε ] περίπτωση αυτή η σχέση γράφεται:, είναι εύκολο να πιστοποιήσουµε τον µηχανισµό 3 4 (δηλαδή. Στην Αναλύσετε το δεξιό µέλος της εξίσωσης σε σειρά του, γύρω από την τιµή =h0. Επιλέξετε την τιµή h 0 πλησίον της αληούς τιµής της παραµέτρου, επιστρατεύοντας όλη την πρότερη γνώση που διαέτετε. R fa( ) R + = h0 R fa( ) f( ) +µ = h0 R+µ ( A ) + = ( h ) 0 R fa +µ f = ( h0 R+µ ) > (( 0 ) ) + d h = 0 R f R h ( 0 ) Κρατήστε όρους µέχρι πρώτης τάξης και επιλύσετε την γραµµική εξίσωση που προκύπτει ως προς. Θέσετε h =, αναλύσετε σε σειρά στην γειτονία του h και επιλύσετε την γραµµική εξίσωση. Επαναλάβατε την διαδικασία µέχρι η διαφορά δ=h j+ - h j να είναι αρκετά µικρότερη από το στατιστικό σφάλµα που αναµένετε.

13 R φ R 0 n R R +µ = 0 n A = = R φa R+µ και = n µ R ( Ν n) Επειδή, για µεγάλο πλήος παρατηρήσεων, Ν, ισχύει µε καλή προσέγγιση ότι µ ( n) σχέση καταλήγει στην αναµενόµενη εκτίµηση: n =. R ;,η Για σχετικά µεγάλο Ν, όπως υπαγορεύουν οι ασυµπτωτικές ιδιότητες της µεόδου µεγίστης πιανοφάνειας, η εκτίµηση κατανέµεται σύµφωνα µε κανονική συνάρτηση πυκνότητας πιανότητας, µε αναµενόµενη τιµή ίση µε την αληή τιµή και διασπορά ίση µε: V = ( ) ln L x; =0 ( A ) R f R = = ( 0 R fa +µ f ) ( 0 R +µ ) εβαίως, επειδή η αληής τιµή δεν είναι γνωστή, χρησιµοποιούµε αντ αυτής την εκτίµηση : ( R f A( ) ) R V = = ( R fa( ) f ( ) ) ( +µ R+µ ) Ας αντιµετωπίσουµε το ίδιο πρόβληµα χρησιµοποιώντας την µέοδο της εκτεταµένης συνάρτησης πιανοφάνειας: L (; ) = ( R ) Ν +µ R e R fa f +µ +µ Ν! R+µ = Η συνήκη µεγιστοποίησης και εκτίµησης της αληούς τιµής της παραµέτρου, γράφεται ως:

14 L (; ) = = ( ) = ln R f +µ f R +µ A = = R fa( ) = R = 0 = R f A +µ f 7.3. Η εξίσωση 7.3. λύνεται µε την µέοδο των διαδοχικών προσεγγίσεων, αλλά εύκολα παρατηρεί κανείς ότι, στην περίπτωση όπου f A() ; f B(), η εκτίµηση της αληούς τιµής είναι εφικτή και βρίσκεται να είναι: Ν µ =. R Παρατηρήστε ακόµα ότι, για µεγάλο πλήος παρατηρήσεων, όταν µε καλή προσέγγιση ισχύει ότι R +µ ;, η σχέση είναι ισοδύναµη της σχέσης Πράγµατι η µέοδος της εκτεταµένης συνάρτησης πιανοφάνειας προσφέρει σηµαντική επιπλέον πληροφορία όταν το πλήος των παρατηρήσεων είναι µικρό. Εάν οι ενεργειακές κατανοµές των φωτονίων εκφράζονται από τις συναρτήσεις πυκνότητας πιανότητας που ορίσηκαν µε την σχέση και κατά την διάρκεια εκτέλεσης του ε, ε, τότε η σχέση 7.3. καταλήγει πειράµατος ανιχνεύηκαν n φωτόνια στην περιοχή, [ ] ότι: n n R 0 = = = R 7.3. και ευρίσκεται σε πλήρη συµφωνία µε τα αποτελέσµατα της κλασικής µεόδου µεγίστης πιανοφάνειας. Επισηµαίνεται όµως ότι, ενώ η σχέση 7.3. ισχύει για κάε Ν, καταλήξαµε στα αποτελέσµατα της κλασικής µεόδου υποέτοντας ότι το πλήος των µετρήσεων είναι µ ; n αρκετά µεγάλο ώστε να ισχύει µε καλή προσέγγιση: Όπως εδείχη σ αυτή την υποενότητα, οι εκτιµήσεις µε την µέοδο της εκτεταµένης συνάρτησης πιανοφάνειας έχουν ανάλογες ασυµπτωτικές ιδιότητες µε τις εκτιµήσεις της κλασσικής µεόδου µέγιστης πιανοφάνειας. Δηλαδή, οι εκτιµήσεις δεν πάσχουν από προκατάληψη και κατανέµονται σύµφωνα µε κανονική συνάρτηση πιανότητας. Η διασπορά της εκτίµησης, σ αυτό το παράδειγµα, βρίσκεται να είναι: V = ln L ( x; ) = ( R fa( ) ) = = ( 0 R fa +µ f ) και για κάε πρακτική χρήση, προσεγγίζεται ως:

15 ( R fa( ) ) V = = ( R fa( ) +µ f( )) Απλή σύγκριση των σχέσεων και αρκεί να πείσει τον αναγνώστη ότι στο συγκεκριµένο παράδειγµα η µέοδος της εκτεταµένης συνάρτησης πιανοφάνειας καταλήγει σε ακριβέστερη εκτίµηση. Ερώτηση: Υπολογίσετε την ακρίβεια της εκτίµησης κάε µεόδου, όταν οι ενεργειακές κατανοµές είναι της µορφής n n Υπόδειξη: Θέσετε Ε = και στις σχέσεις και για να καταλήξετε ότι: R R V n n,v = R = R n Ερώτηση: Από τους Ν µαητές µίας τάξης οι Ε προήχησαν ενώ οι Α (=Ν-Ε) απέτυχαν στις εξετάσεις. Εκτιµήσετε πλήος των επιτυχόντων, των πλήος αποτυχόντων και τα στοιχεία του πίνακα συνδιασποράς των εκτιµήσεων. Υπόδειξη: Η πιανοφάνεια εκφράζεται από την δυονυµική συνάρτηση πιανότητας:! L(,A;p) = p ( p) A, όπου p συµβολίζει την πιανότητα επιτυχίας. Η πιανότητα p!a! ln L(,A;p) εκτιµάται ως: = 0 p = = p A+ p= p Η διασπορά της εκτίµησης της πιανότητας είναι: ln L(,A;p) A Vp [ ] = p = + p p= p ( p) 0, όπου p 0 είναι η αληής τιµή. A ( ) Η διασπορά εκτιµάται ως: p p Vp [ ] = + = p ( p ) Οι εκτιµήσεις του αριµού επιτυχόντων και αποτυχόντων είναι: p,a ( p) τα στοιχεία του πίνακα συνδιασποράς είναι: ( ) cov,a = V V A. = = και Ε Α V [ = V p] = Ν V V Ε Α [ p Α = ] = Ν και

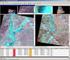
16 Ερώτηση: Στην προηγούµενη ερώτηση χρησιµοποιήσετε την εκτεταµένη συνάρτηση πιανοφάνειας, εωρώντας ότι ο συνολικός αριµός των µαητών µίας τάξης δεν είναι σταερός αλλά παίρνει τιµές σύµφωνα µε Possonan συνάρτηση πιανότητας. Υπόδειξη: Η εκτεταµένη συνάρτηση πιανοφάνειας εκφράζεται ως: m m e! A L(, A;p) = p ( p)!!a! m ma m e ma e =! A! όπου m είναι η αναµενόµενη τιµή του αριµού των µαητών της τάξης και m = p m,m = p m είναι οι αναµενόµενοι αριµοί επιτυχόντων και αποτυχόντων A αντίστοιχα. Από την συνήκη µεγιστοποίησης κανείς καταλήγει ότι: ln L( m, m A;p) = 0 m m= m ma= m A m = ln L( m, m A;p) ma = A = 0 m A m= m ma= m A Τα στοιχεία του πίνακα συνδιασποράς εύκολα ευρίσκονται ίσα µε: V,V A A,cov,A = = = 0 Στο παράδειγµα αυτό, η διασπορά των εκτιµήσεων βρίσκεται µεγαλύτερη από την διασπορά των αντίστοιχων εκτιµήσεων µε την κλασική µέοδο µεγίστης πιανοφάνειας, διότι ουσιαστικά εκτιµούνται δύο µεταβλητές έναντι µίας που εκτιµάται µε την κλασική πιανοφάνεια. Επισηµαίνεται όµως, ότι οι εκτιµήσεις των παραµέτρων Ε και Α είναι στατιστικά ανεξάρτητες όταν χρησιµοποιείται η εκτεταµένη πιανοφάνεια ενώ στην άλλη περίπτωση οι εκτιµήσεις είχαν 00 αντι-συσχέτιση (συντελεστής συσχέτισης ίσος µε -). 7.4 Εκτίµηση παραµέτρων από ιστογράµµατα. Έστω ότι σ ένα πείραµα έλουµε να προσδιορίσουµε την φυσική παράµετρο, η οποία καορίζει το ενεργειακό φάσµα εκποµπής φωτονίων από ένα φυσικό σύστηµα. Έστω ότι η συνάρτηση πυκνότητας πιανότητας του µήκους κύµατος περιγράφεται από την συνάρτηση: f(λ,) και τα πειραµατικά δεδοµένα συνίστανται στις µετρήσεις του µήκους κύµατος Ν φωτονίων: λ= { λ, λ, λ3, K λν}, στην ενεργό περιοχή του οργάνου µέτρησης. Είναι προφανές ότι η ανάλυση δεδοµένων αυτού του πειράµατος ανάγεται σε κλασική εκτίµηση παραµέτρων µε την µέοδο της µέγιστης πιανοφάνειας. Δυστυχώς, οι πραγµατικές πειραµατικές συνήκες δυσκολεύουν την εφαρµογή αυτής της µεόδου και σε πολλές περιπτώσεις την καιστούν αδύνατη. Επί παραδείγµατι, η ανιχνευτική διάταξη πάσχει από Επί παραδείγµατι, να προσδιορίσουµε την ερµοκρασία ενός ουρανίου σώµατος από το φάσµα εκποµπής του, εωρώντας ότι η εκποµπή περιγράφεται από το εωρητικό πρότυπο του µέλανος σώµατος.

17 µετρητικά σφάλµατα και περιορισµένη απόδοση η οποία είναι συνάρτηση του φυσικού µεγέους που µετράµε. Θα αντιµετωπίσουµε το γενικό πρόβληµα στην υποπαράγραφο 7.7. Εν προκειµένω, ας υποέσουµε ότι η ανιχνευτική συσκευή µπορεί µόνο να κατατάσσει το υπό µέτρηση µήκος κύµατος σε µία από τις περιοχές, εύρους Δλ, στις οποίες υποδιαιρείται η ενεργός περιοχή του οργάνου µέτρησης. Τα πειραµατικά δεδοµένα συνίστανται από το πληος n= n,n,n, K n που συλλέχηκαν στις αντίστοιχες υποπεριοχές (ιστούς) των φωτονίων { } 3 µε όρια ( λ, λ + ], =0,,,3, και παρίστανται γραφικά στο Σχήµα λ (αυαίρετες µονάδες) Σχήµα 7.4.: Η ανιχνευτική διάταξη κατατάσσει κάε φωτόνιο σε µία από τις =00 υποπεριοχές µήκους κύµατος, ιδίου εύρους Δλ=9, που καλύπτουν την ενεργό περιοχή του οργάνου µέτρησης [00,3000]. Τα πειραµατικά δεδοµένα παρίστανται ως ιστόγραµµα Εκτίµηση µε την µέοδο µέγιστης πιανοφάνειας Η συνολική πληροφορία εµπεριέχεται στην συνάρτηση πιανοφάνειας, που στην περίπτωση αυτής της οµαδοποίησης των δεδοµένων ανάγεται στην πολυωνυµική συνάρτηση πυκνότητας πιανότητας: Ν! n L( n; ) = ( p ( ) ) n!n! L n! = 7.4. λ p = f λ; dλ λ Ερώτηση: Δώσετε την γενική έκφραση της διασποράς της εκτίµησης της παραµέτρου, µε την µέοδο της µεγίστης πιανοφάνειας 7.4., για µεγάλο αριµό ιστών,. Υπόδειξη: Η εκτίµηση της παραµέτρου προκύπτει από την µεγιστοποίηση της πιανοφάνειας: ln L( n; ) n p ( ) = = 0 = p 7.4. = =

18 Για αρκετά µεγάλο αριµό ιστών, ώστε να ισχύουν οι ασυµπτωτικές ιδιότητες της µεόδου µέγιστης πιανοφάνειας, η διασπορά της εκτίµησης της τιµής της παραµέτρου α είναι: n p( ) n p ( ) V = = ln L( n; ) α = ( p ) p( 0) 0 = = 0 0 = 0 όπου 0 είναι η πραγµατική τιµή της παραµέτρου. Η σχέση α προσεγγίζεται µε την ακόλουη έκφραση: V = = n p n p ln L( n; ) = ( ( )) p ( p ) = = = β Εάν επιπλέον του φάσµατος και το πλήος των φωτονίων που ανιχνεύονται εξαρτάται από την παράµετρο, τότε ενδείκνυται να χρησιµοποιήσουµε την εκετεταµένη συνάρτηση πιανοφάνειας: Ν M( ) ( ) M e Ν! L( n; ) = p! n!n! L n! = µ = n µ ( ) ( µ ( ) ) e n! e = M p n!n! L n! = µ ( ) = = όπου λ λ n ( ) n µ =Μ p =Μ f λ; dλ είναι το αναµενόµενο πλήος παρατηρήσεων στην υποπεριοχή ( λ, λ + ]. Ερώτηση: Δείξετε ότι, στην περίπτωση όπου το πλήος των γεγονότων σε κάε ιστό είναι µεγάλο, η συνάρτηση εκτεταµένης πιανοφάνειας µπορεί να γραφεί ώς γινόµενο κανονικών συναρτήσεων. Υπόδειξη: Σύµφωνα µε το εώρηµα του κεντρικού ορίου, για n, η Posonan συνάρτηση n µ µ e πιανότητας : τείνει προς κανονική συνάρτηση, µε την ίδια αναµενόµενη τιµή και n! ( n) µ µ ίδια διασπορά, e π µ Συνεπώς, η συνάρτηση εκτεταµένης πιανοφάνειας λαµβάνει την µορφή:

19 lm L ( n; ) = e = π µ n n KKK n ( n) µ ( ) µ Ερώτηση: Δώσετε την γενική έκφραση της διασποράς της εκτίµησης της παραµέτρου, που προκείπτει από την εκτεταµένη συνάρτηση πιανοφάνειας 7.4.3, για µεγάλο αριµό ιστών,. Υπόδειξη: Η εκτίµηση της παραµέτρου προκύπτει από την µεγιστοποίηση της εκτεταµένης πιανοφάνειας: ln L( n; ) = n ln µ ( ) µ ( ) = = = n µ µ µ ( ) = = = M n µ = 0 = = µ = = Η διασπορά της εκτίµησης της παραµέτρου υπολογίζεται, όταν, ως: V = ln L ( n; ) = = + ( ( )) ( µ ) n µ n µ Μ = = µ = = Εύκολα µπορείτε να δείξετε ότι η χρήση της εκτεταµένης συνάρτησης πιανοφάνειας καταλήγει σε εκτίµηση µε µικρότερη διασπορά από εκείνη της κλασικής µεόδου µεγίστης πιανοφάνειας. Οι δύο µέοδοι είναι εντελώς ισοδύναµες όταν το αναµενόµενο πλήος συνολικών γεγονότων, Μ(), δεν εξαρτάται από την παράµετρο. Ερώτηση: Δείξετε ότι η εκτίµηση µε την µέοδο της εκτεταµένης συνάρτησης πιανοφάνειας καταλήγει σε εκτίµηση µε µικρότερη διασπορά από εκείνη της κλασικής µεόδου µεγίστης πιανοφάνειας. µ =Μ p και αντί του την Υπόδειξη: Αντικαιστώντας στην σχέση 7.4.6: πραγµατική τιµή της παραµέτρου, µετά από πράξεις, καταλήγουµε στην ακόλουη σχέση:

20 n p( ) n p ( ) V = = ( p ) p( 0) 0 = 0 =0 Ο όρος n n = Μ ( ) = Μ ( ) + + ( Μ( )) Μ ( 0 ) 0 = 0 =0 n στην σχέση µπορεί να γραφεί ως: = ( n ) n = µ + µ = = = x 4 43 M( 0 ) = M = x x = n µ = 0 x είναι: Κάε τυχαία µεταβλητή x( 0) έχει αναµενόµενη τιµή: ( 0) ( 0) ενώ η διασπορά της τυχαίας µεταβλητής ( 0) V x ( ) = V n µ ( ) = V[ n ] =µ ( ) 0 0. Εύκολα διαπιστώνεται ότι ισχύουν οι 0 προϋποέσεις για την εφαρµογή του νόµου των µεγάλων αριµών για να γραφεί η σχέση ως: n x( 0) + M( 0) = M( 0) = Συνεπώς, για µεγάλο αριµό ιστών, η σχέση παίρνει την µορφή. n p( ) n p ( ) V = = ( p ) p( 0) 0 = 0 =0 0 Μ + Μ( ) = Συγκρίνοντας µε την σχέση α εύκολα καταλήγει κανείς ότι η εκτεταµένη συνάρτηση πιανοφάνειας µεταφέρει περισσότερη πληροφορία αναφορικά µε την παράµετρο από ότι η κλασική συνάρτηση πιανοφάνειας και συνεπώς η διασπορά είναι µικρότερη από την αντίστοιχη διασπορά της κλασικής µεόδου. Ερώτηση: Δείξετε ότι η κλασική µέοδος µεγίστης πιανοφάνειας και η µέοδος της εκτεταµένης συνάρτησης πιανοφάνειας καταλήγουν στα ίδια αποτελέσµατα, όταν το αναµενόµενο πλήος συνολικών γεγονότων δεν εξαρτάται από την παράµετρο,. µ =Μ p και προβείτε σε Υπόδειξη: Θέσετε στις σχέσεις και απλοποιήσεις.

21 7.4. Εκτίµηση µε την µέοδο ελαχίστων τετραγώνων Ας υποέσουµε ότι το πλήος των ιστών,, είναι αρκετά µεγάλο ώστε οι πιανότητες p ( 0 ), να ανιχνευεί ένα γεγονός στην υποπεριοχή, είναι πολύ µικρές. Η υπόεση αυτή εγγυάται ότι p p ) µεταξύ κάε ζεύγους τυχαίων µεταβλητών, n και n j, είναι η συσχέτιση ( 0 j 0 αµελητέα. Επιπλέον, εάν το πλήος των δεδοµένων, Ν, είναι αρκετά µεγάλο ώστε κάε τυχαία µεταβλητή n να κατανέµεται σύµφωνα µε κανονική συνάρτηση πιανότητας µε µέση τιµή m p Vn = p( ), ορίζουµε 3 την στατιστική ( ) = ( ) και διασπορά ισούται µε [ ] 0 0 συνάρτηση ελαχίστων τετραγώνων ως: Q = ( µ ( ) n) µ ( ) = Η ποσότητα Q δεν α πρέπει να έχει κατ ανάγκη τις ιδιότητες του χ, διότι η διασπορά στον παρανοµαστή εξαρτάται από την παράµετρο. Εύκολα µπορείτε επίσης να διαπιστώσετε ότι δεν είναι ισοδύναµη της συνάρτησης πιανοφάνειας. Παρ όλα αυτά, αποδεικνύεται ότι η εκτίµηση παραµέτρων µε την ελαχιστοποίηση της 7.4.0, ασυµτωτικά, έχει ιδανικές ιδιότητες 4 : είναι συνεπής, η εκτίµηση συµπεριφέρεται σύµφωνα µε κανονική συνάρτηση πυκνότητας πιανότητας και είναι αποδοτική έχοντας την ελάχιστη διασπορά. Συνήως, αντί της σχέσης ελαχιστοποιείται η ποσότητα: Q = ( µ ) n = 7.4. n όπου η άγνωστη ποσότητα µ προσεγγίζεται µε την «µέτρηση» n. Για µεγάλο πλήος ιστών, οι εκτιµητές και 7.4. συµπίπτουν µε την µέοδο της µεγίστης πιανοφάνειας. Επισηµαίνεται, ότι η µέοδος της µεγίστης πιανοφάνειας έχει ευρύτερο φάσµα εφαρµογών, µε πολύ λιγότερες παραδοχές όσον αφορά στον αριµό των υποπεριοχών και τον πληυσµό γεγονότων σε κάε υποπεριοχή. 3 Όταν το πλήος Ν τείνει στο άπειρο, η πολυονυµική συνάρτηση πιανότητας τείνει προς κανονική κατανοµή διαστάσεων. Επιπλέον, λόγω της αµοιβαίας ανεξαρτησίας των n, η συνάρτηση πυκνότητας πιανότητας ( m( ) n) m ανάγεται σε γινόµενο κανονικών συναρτήσεων: e. = π m ( ) Εν άλλοις λόγοις, κάε µία από τις αµοιβαία ανεξάρτητες τυχαίες µεταβλητές n= { n,n, K n} χαρακτηρίζεται από κανονική συνάρτηση πιανότητας, µε µέση τιµή m( 0) = p( 0) και διασπορά Vn [ ] = p( ). 0 4 Kendal Vol. II

22 7.5 Μέοδοι εκτίµησης παραµέτρων υπό συνήκες δέσµευσης. Συνήως, οι παράµετροι αντιστοιχούν σε φυσικές ποσότητες που ικανοποιούν φυσικούς νόµους. Παραδείγµατος χάριν, στην περίπτωση που αποσκοπούµε στην σύγχρονη εκτίµηση της αληούς τιµής του µέτρου της ορµής (P 0 ) και της ενέργειας ( 0 ) ενός σωµατίου, από µετρήσεις της ενέργειας (Ε) και της ορµής (P), α πρέπει να επιβάλουµε την συνήκη ότι η αληής τιµή της ενέργειας και η αληής τιµή της ορµής συνδέονται µε την σχέση: 4 = P c + m c, όπου m είναι η µάζα του σωµατίου και c είναι η ταχύτητα του φωτός. 0 0 Σ αυτή την υποενότητα α συζητηούν µέοδοι εκτίµησης παραµέτρων, = {,, } οι οποίοι υπόκεινται σε m συνήκες δέσµευσης, της µορφής g( ) = 0: ( K ) ( K ) g = g,, = 0 g = g,, = 0 KKKK ( K ) g = g,, = 0 m m 7.5. K, Η πλέον εύκολη και αποδοτική µέοδος να συµπεριληφούν οι συνήκες δέσµεύσης 7.5. στην µέοδο εκτίµησης συνίσταται σε κατάλληλη επιλογή νέων παραµέτρων. Επί παραδείγµατι, εάν οι παράµετροι και υφίστανται τον περιορισµό: g, = + = α µπορούσαµε να αντικαταστήσουµε, στην συνάρτηση πυκνότητας πιανότητας ή στην και στη έκφραση των ελαχίστων τετραγώνων, την τιµή της παραµέτρου µε συνέχεια να εφαρµόσουµε την µέοδο εκτίµησης µόνο για την εναποµένουσα παράµετρο,. Μία άλλη περίπτωση αφορά περιορισµούς στο πεδίο τιµών των παραµέτρων. Συχνά αντιµετωπίζονται προβλήµατα όπου η παράµετρος α πρέπει να παίρνει τιµές µόνο στο διάστηµα [a,b]. Στις περιπτώσεις αυτές ενδείκνυται η έκφραση της τιµής της παραµέτρου συναρτήσει µίας άλλης µεταβλητής, ψ, ως: = a + ( sn ψ+ ) ( b a) και η εφαρµογή της µεόδου εκτίµησης για τον προσδιορισµό της τιµής της παραµέτρου ψ,,. στο διάστηµα Άλλες φορές, το πρόβληµα συνίσταται στην εκτίµηση των ποσοστών συµµετοχής, β, επί µέρους κατηγοριών στο συνολικό αποτέλεσµα. Σ αυτές τις περιπτώσεις, οι παράµετροι υπόκεινται στους ακόλουους περιορισµούς: = 0 β =,,3... και β = Ενδείκνυται η ακόλουη σειρά µετασχηµατισµού των παραµέτρων:

23 β = r ( r ) r β = β = r r r 3 3 M= M M M M M M M ( r ) ( r ) L ( r ) r ( r ) ( r ) L ( r )( r ) β = β = όπου: r ( sn ) = ψ ψ= ψ, ψ, K, ψ και εκτιµώνται οι τιµές των παραµέτρων { } Ερώτηση: Δείξετε ότι οι παράµετροι β, όπως ορίζονται από τις σχέσεις και 7.4.7, ικανοποιούν τις συνήκες Στις περισσότερες περιπτώσεις εκτίµησης παραµέτρων υπό συνήκες δέσµευσης, δεν είναι εύκολο να εφαρµοσούν οι απλές µέοδοι ορισµού νέων µεταβλητών. Μία γενική µέοδος για να συµπεριλάβει κανείς τις συνήκες δέσµευσης στους εκτιµητές αναφέρεται στην χρήση πολλαπλασιαστών Lagrange Mέοδος της µεγίστης πιανοφάνειας µε Lagrangan πολλαπλασιαστές. Έστω x, (,,3, ) = K τα πειραµατικά δεδοµένα και πιανοφάνειας που εξαρτάται από παραµέτρους ικανοποιούν τις συνήκες Ορίζουµε την στατιστική συνάρτηση: m F(x; α, ) = ln L(x; ) + α g ( ) = Ν L(x; ) = f (x; ) η συνάρτηση =,,,3, = K οι οποίες πρέπει όπου οι παράγοντες α (=,,3,,m) ονοµάζονται πολλαπλασιαστές Lagrange και αναζητούµε =,,3, K καια j=,,3, K m για τις οποίες η έκφραση τις τιµές των παραµέτρων έχει ακρότατο. Δηλαδή: j 5 Εύκολα µπορεί να δει κανείς ότι στην περίπτωση όπου η συνάρτηση πυκνότητας πιανότητας είναι συµµετρική ως προς τις παραµέτρους β, δεν α είναι κατ ανάγκη συµµετρική και ως προς τις παραµέτρους ψ. Εξετάσετε ως παράδειγµα την περίπτωση όπου η συνάρτηση πυκνότητας πιανότητας είναι γραµµική συνάρτηση των παραµέτρων β, ή την περίπτωση όπου το πρότυπο προσαρµογής µε την µέοδο των ελαχίστων τετραγώνων είναι γραµµική συνάρτηση των παραµέτρων β. Με τους µετασχηµατισµούς και επιβάλλονται οι δεσµεύσεις στις παραµέτρους αλλά χάνεται η συµµετρία του προβλήµατος.

24 F(x;, α) ln L(x; ) g( ) m j = + α j = 0, =,,3,, = = j = = α=α = α=α ( K ) F(x;, α) g() = n = 0 n=,,3,,m αn ( K ) Οι εκτιµήσεις των παραµέτρων, που βρίσκονται ως λύσεις του συστήµατος των εξισώσεων 7.4.9, ικανοποιούν τις συνήκες δέσµευσης και έχουν τις συνήεις ασυµπτωτικές ιδιότητες των εκτιµήσεων της µεόδου µεγίστης πιανοφάνειας. Επισηµαίνεται ότι οι πολλαπλασιαστές Lagrange αποτελούν και αυτοί παραµέτρους µε τιµές που εκτιµώνται από την Ο πίνακας συνδιασποράς των εκτιµήσεων των παραµέτρων: ( bb,b b b b ) T (, ) K + + K + m K ααk αm δίνονται από τον αντίστροφο του πίνακα πληροφορίας ως: Α V= ( Iα, ) = Ε Τ ο = α=α F(x;, α) L(x; ) Α λµ = =, λ=,,, και µ=,,, λ µ = λ µ α=α F(x;, α) g m( ) λ µ = λ α=α = T ( K ) ( K ) B λµ = =, λ=,, K, και µ =,, K, m α = F(x;, α) Oλµ = = 0, λ=,,,m και µ=,,,m α α λ µ = α=α ( K ) ( K ) 7.4. Α Όταν ο πίνακας Ε Τ αντιστρέφεται µπορεί κανείς, µε επίπονες αλλά απλές ο = α=α πράξεις, να καταλήξει 6 στις ακόλουες απλές εκφράσεις: Τ V = A A B V[ α ] B A 7.4. V Τ [ α ] = ( B A B) καώς και στη διαπίστωση ότι οι παράµετροι έχουν µηδενική συσχέτιση µε τους πολλαπλασιαστές α. Παρατηρήστε ότι ο πρώτος όρος στην έκφραση των στοιχείων του πίνακα συνδιασποράς των παραµέτρων αντιστοιχεί στα στοιχεία του αντίστοιχου πίνακα στην περίπτωση που δεν 6 Αναπτύσσοντας τις µερικές παραγώγους, τιµές των παραµέτρων. λέπε ade, Sect F(x;, α) F(x;, α) και α σε σειρά Taylor, γύρω από τις πραγµατικές

25 επιβάλλεται καµία συνήκη δέσµευσης. Ο αρνητικός δεύτερος όρος εκφράζει την µείωση της διασποράς που επιφέρει η επιπλέον πληροφορία την οποία µεταφέρουν οι συνήκες δέσµευσης. Α Στην περίπτωση όπου ο πίνακας Ε Τ ο τροποποιηεί η σχέση ως: = α=α m m = = F (x; α, ) = ln L(x; ) + α g ( ) g ( ) και να επαναληφεί η µέοδος που περιγράφηκε προηγουµένως. δεν είναι αντιστρέψιµος ενδείκνυται να 7.5. Mέοδος των ελαχίστων τετραγώνων µε Lagrangan πολλαπλασιαστές. Ας εξετάσουµε την περίπτωση όπου τα δεδοµένα συνίστανται από ζεύγη µετρήσεων, y,x,(=,,3 K,) όπου οι µετρήσεις x δεν πάσχουν από µετρητικά σφάλµατα. { } Επιδιώκουµε την προσαρµογή του γραµµικού προτύπου: y(x) = H = h λ(x) λ λ= όπου ο µονοδιάστατος πίνακας (διάνυσµα) = ( K ) παριστά τις παραµέτρους που α εκτιµηούν. Οι τυχαίες µεταβλητές, ε, που παριστούν τις αποκλίσεις των µετρήσεων από τις προβλέψεις του προτύπου προσαρµογής: y = h λ(x ) λ +ει λ= έχουν συνδιασπορές που εκφράζονται από τα στοιχεία του πίνακα V. Επιπλέον, α υποέσουµε ότι δέσµευσης: j = j j l = R, =,,3,...,m L = R όπου ο πίνακας L έχει ως στοιχεία τους συντελεστές l j. οι παράµετροι υπόκεινται στις ακόλουες, m συνήκες Θα χρησιµοποιήσουµε m Langrangan πολλαπλασιαστές, τους οποίους παριστούν στα α = α α K α στατιστική συνάρτηση : Τ QL = Q + α ( L R) Τ Τ = ( y H ) V ( y H ) + α ( L R) T στοιχεία του µονοδιάστατου πίνακα T m και α ορίσουµε την ακόλουη 7.4.7

26 όπου το διάνυσµα y παριστά τις µετρήσεις y( =,,3 K,). Οι συνήκες ακρότατου της ποσότητας 7.4.7: QL QL = 0και = 0( για =,,... και λ =,,...,m) αλ κανονικές εξισώσεις: Τ Τ Τ H V H + L α= H V y L = R Οι εξισώσεις 7.4.8, µετά την αντικατάσταση: Τ C= H V H Τ S= H V y γράφονται ως: C L T S = L 0 α R, καταλήγουν στις ακόλουες T Εάν οι πίνακες C και LC L µπορούν να αντιστραφούν, η λύση της δίνεται 7 ως: T F G S = 7.4. α G R όπου T W = L C L F= C L W L C G = W L C = W T 7.4. Οι συνδιασπορές µεταξύ των παραµέτρων εκφράζονται 8 από τα στοιχεία των ακολούων πινάκων: V = F V [ α ] = W cov α, = 0 Αποδεικνύεται 9, ότι οι εκτιµήσεις των παραµέτρων δεν πάσχουν από προκατάληψη, όπως ακριβώς και οι εκτιµήσεις µε την µέοδο ελαχίστων τετραγώνων µε γραµµικό πρότυπο 7 λέπε ade et al, Sect λέπε ade et al, Sect λέπε ade et al, Sect. 8.4.

27 προσαρµογής, και ότι η αναµενόµενη τιµή των Lagrangan πολλαπλασιαστών είναι ίση µε µηδέν.