Tehnike molekularne biologije Industrijska primena Klinička enzimologija
|
|
|
- Ὅμηρ Σερπετζόγλου
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Primena enzima
2 Tehnike molekularne biologije Industrijska primena Klinička enzimologija
3
4
5 Kloniranje gena podrazumeva: Isecanje i otvaranje prečišćene ene plazmidne DNA Ubacivanje i spajanje target DNA sa plazmidnom DNA u reakciji katalizovanoj ligazom Isecanje i spajanje DNA se mora pratiti, npr. elektroforezom Transformacija vešta tačkog rekombinantnog DNA molekula u E. coli ćeliju ili nekog drugog domaćina
6
7
8 DNK moze biti umnožena: DNK polimeraza 1. Potrebna je DNK matrica 2. Potrebni su DNK & RNK prajmeri koji asosuju sa matricom i poseduju 3 hidroksilnu grupu na (dezoksi)ribozi 3. Replikacija teče isključivo u 5 3 pravcu, pri čemu četiri 5 - deoksinukleozid trifosfata služe kao izvor monomera 4. Replikaciju diktira matrica u skladu sa Watson-Crick-ovim pravilima sparivanja baza
9 DNK fragmenti mogu biti spojeni korišćenjem enzima
10 Praznine u DNK mogu biti popunjene: DNK ligaze
11 Mehanizam dejstva DNK ligaze 1. Adenil grupa NAD + se prebacuje na ε-amino grupu Lys i formira neobičan fosfoamidni adukt koji se lako izoluje. 2. Adenil grupa aktiviranog enzima se prebacuje na 5 terminus prekida da bi oformio adeniliranu DNK. AMP se vezuje za 5 nukleotid preko pirofosfatne veze (a ne fosfodiestarske). 3. DNK ligaza katalizuje formiranje fosfodiestarske veze napadom 3 hidroksila na 5 fosforil grupu, zatvarajući tako prekid i oslobañajući AMP.
12 Dvostruki DNK lanac moze biti isečen en na specifičnim sekvencama: Restrikciona endonukleaza
13
14 Spajanje DNK komplementarno homopolimetrickim repovima: Terminalna transferaza
15 TdT Aminokiselinska sekvenca i raspored sekundarnih struktura kataliticnog centra TdT
16 Procesivna nasuprot distributivne polimerizacije Enzimi koji disosuju nakon svake adicije i koji mogu da deluju na više lanaca se označavaju kao DISTRIBUTIVNI Oni koji procesuju duž istog lanca bez disocijacije se označavaju kao PROCESIVNI
17 Industrijska primena enzima
18 Imobilizacija enzima Prednosti imobilizovanih enzima: Višekratna upotreba Reakcija se može lako kontrolisati i zaustaviti jednostavnim izdvajanjem biokatalizatora Povećana stabilnost biokatalizatora Povećana produktivnost Mogućnost automatizacije Model sistemi za proučavanje enzima vezanih za membrane ćelija
19 Postupci imobilizacije Adsorpcija enzima na čvrstim nosačima Kovalentno vezivanje za čvrste nosače Smeštanje enzima u polupropustljivu membranu Obuhvatanje enzima nosačem Imobilizacija enzima na granici faza tečno no-tečno
20 Adsorpcija enzima načvrstim nosačima Adsorpcija se zasniva na slabim privlačnim silama Pristupačnost adsorbensa Blagi reakcioni uslovi Aktivnost imobilizovanog enzima velika Jednostavnost Široka primenljivost Mogućnost regeneracije Nespecifičnost Desorpcija sa nosača usled slabih veza Često potrebno i dodatno umrežavanje Kontaminacija proizvoda Odsustvo opštih protokola Načini izvodjenja adsorpcije: Statička metoda Dinamička metoda Metoda elektrotaloženja enja Adsorpcija u koloni
21 Mehanizam adsorpcije Difuzija molekula enzima do površine nosača Difuzija molekula enzima unutar pora nosača Formiranje monomolekulskog sloja enzima
22 Adsorpcija enzima načvrstim nosačima Uticaj različitih itih činilaca na adsorpciju enzima: ph i jonska jačina Specifična površina nosača Osobine enzima i nosača Temperatura Koncentracija enzima Specifična površina nosača Neporozan nosač Porozan nosač Mikroporozan Mezoporozan Makroporozan (dijametar veći od 50 nm)
23 Adsorpcija enzima na prethodno modifikovanim nosačima ima: Prethodna modifikacija nosača često može doprineti jačem vezivanju enzima na nosač.. Pored povećanja jačine vzivanja, modifikacija nosača često omogućuje uje bolje katalitičke ke osobine imbilisanog enzima usled stvaranja povoljne mikrookoline Obrada nosača puferima Obrada nosača rastvorima koji sadrže jone metala Obrada nosača albuminom Komercijalno dostupni nosači za imobilizaciju Ne postoji univerzalan nosač, ali on bi trebalo da poseduje osobine kao što su: velika površina ina, mehanička i termička stabilnost, odgovarajući oblik i veličina ina čestica, rezistentnost na mikrobiološku ku kontaminaciju, mogućnost da se lako regeneriše. Nosači se dele prema hemijskom sastavu na neorganske i organske,, a prema morfološkim osobinama na neporozne i porozne.
24 Nosači koji se koriste za adsorpciju Neorganski nosači Silicijum Aluminijum Zeoliti Porozno staklo Oksidi metala Keramika Aktivni ugalj Organski nosači Celuloza Skrob Dekstran Polisaharidi algi: : agar, agaroza, alginat, karagenan Hitin, hitozan-polisaharidi sa amino grupama
25 Kovalentno vezivanje enzima na čvrste nosače Stabilni imobilisani preparati Nema kontaminacije proizvoda Velika raznovrsnost postupaka Moguće reakcije sa svim supstratima Nema difuzionih limitacija Skupa i složena metoda Teška optimizacija uslova (inhibitori, modifikatori) Gubitak aktivnosti enzim Teška regeneracija nosača
26 Osobine kovalentne imobilizacije enzima Enzimi se obično imobilišu preko amino grupe, karboksilne grupe, sulfidrilne grupe, imidazolne grupe, hidroksilne grupe ili fenolnog jezgra tirozina. Mali je broj grupa koje su toliko aktivne da se odmah može pristupiti njihovom povezivanju. Usled toga, veoma retko se nosači koriste direktno za vezivanje enzima i u većini slučajeva ajeva, treba prethodno aktivirati bilo nosač, bilo enzim. Metde kovalentnog vezivanja su obično složene ene, skupe i sastoje se iz najmanje dve faze: aktivacije ili modifikacije nosača i vezivanje enzima za nosač. Pod aktivacijom nosača podrazumeva se izvoñenje hemijske reakcije izmeñu nosača i aktivatora, pri čemu se na njegovoj površini stvaraju nove elektrofilne grupe koje pokazuju veliku reaktivnost prema nukleofilnim grupama u molekulu enzima. I neorganski i organski nosači se aktiviraju uvoñenjem hemijski reaktivnijih grupa.
27 Osobine kovalentne imobilizacije Kovalentno imibilisani enzimi su stabilni u širokom opsegu spoljnih uslova i nalaze veliku primenu u medicini i prehrambenoj industriji gde ne sme doći do kontaminacije proizvoda proteinima Prema broju postupaka i specifičnih agenase koji se koriste ovaj metod imobilizacije raznovrsniji je od ostalih metoda. Odabiranjem odgovarajućih nosača i modifikacijom odreñenih funkcionalnih grupa nosača i enzima mogu se nameski menjati karakteristike imobilisanog enzima. Veoma je važno pri hemijskom vezivanju enzima za nosač da učestvuju samo one funkcionalne grupe u molekulu enzima koje nisu bitne za njegovu aktivnost. Bitno je i da te grupe budu reaktivne, kako bi imobilizacija bila selektivna I dabi se odvijala u blagim uslovima pri kojima neće doći do denaturacije enzima. Nosač ne sme da ima nikakve reaktivne grupe koje bi bile u stanju da vežu supstrat, ili neka druga jedinjenja.. Pored toga, na nosaču ne sme da bude fizičke adsorpcije enzima kao ni adsorpcije neke druge supstance iz rastvora.
28 Ciljevi kovalentne imobilizacije Imobilisani enzim treba da zadrži što više od početne aktivnosti, što se može postići na različite ite načine ine: Izborom nosača i metoda koji omogućavaju blage uslove imobilizacije Da se smanji količina ina enzima vezanog u nekatalitičkoj koj konformaciji (imobilizacija u prisustvu supstrata, proizvoda, inhibitora ili nekog drugog liganda) Da se smanje sterne smetnje Primena meñuagenasa čime se omogućava da se enzim udalji sa površine nosača.
29 Obuhvatanje enzima nosačem Metode imobilizacije koje se zasnivaju na obuhvatanju enzima nosačem se grubo mogu podeliti na zarobljavanje enzima u polimerne matrice i umrežavanje enzima funkcionalnim agensima. Smeštanje enzima u trodimenzionalnu mrežu gusto isprepletenih polimernih lanaca, koji stvaraju gel, pri čemu matrica gela treba da bude dovoljno porozna da kroz nju mogu neometano da prolaze molekuli supstrata i proizvoda reakcije,, a da enzim ne može da napusti matricu i preñe u okolni rastvor. Enzim bi trebalo da bude ravnomerno distribuiran unutar polimera. Izmeñu molekula enzima I polimernih lanaca mogu da se formiraju jonske i vodonične ne veze koje doprinose da enzim ostane unutar gela. Za imobilizaciju se najviše koriste gelovi na bazi poliakrilamida.
30 Umrežavanje enzima Umrežavanje enzima se zasniva na intra- i intermolekulskom vezivanju molekula enzima i bifunkcionalnog agensa. Molekuli enzima se vezuju meñu sobom, ili sa drugim proteinima preko bifunkcionalnog agensa I grade trodimenzionalne agregate koji su nerastvorni u vodi. Agensi koji se najčešće koriste su glutaraldehid, bis- diazobenzidin, dialdehid skroba, alifatični amini. Mala primena ove metode je zbog velikog utroška enzima, a imobilizovani preparat ima loše mehaničke osobine. Motoda se može kombinovati sa adsorpcijom enzima na čvrste nosače I naknadnom umrežavanju imobilizovanog enzima bifunkcionalnih agensima.
31 Smeštanje enzima iza polupropustljive barijere Enzim se smešta iza čvrste polupropustljive barijere, koja najčešće propušta supstrat i proizvode reakcije,, a zadržava ava enzim u ograničenom prostoru (inkapsulacija enzima). Alternativno, enzim se nalazi mehanički zarobljen, adsorbovan, ili kovalentno vezan u samoj poroznoj barijeri (imobilizacija enzima u membranama).
32 Primena enzima u industriji hrane
33 Osnovne komponente hrane Biopolimeri Proteini Ugljeni hidrati Lipidi Jedinjenja malih molekulskih masa estri mono- i disaharidi Terpeni Fenoli glikozidi
34 Enzimi kao aditivi u industriji hrane Izvori Biljke Životinje Mikroorganizmi Rekombinantna tehnologija Prednosti Mild technology Visoka specifičnost Širok izbor enzimskih specifičnosti u prirodi Prirodni (organski) Ne-toksi toksični Egzogeni enzimi screening novih enzima klasičnim tehnikama iz prirodnih izvora Protein inžinjeringom injeringom (in vitro evolucija) Endogeni enzimi Endogeni inhibitori
35 Osnovne grupe enzima koje su našle primenu u industriji hrane Hidrolaze Proteaze Lipaze Glikohidrolaze (pektinaze i celulaze) Oksidaze i transferaze Tirozinaze Lakaze Peroksidaze Transaminaze Glukozo-oksidaze oksidaze
36 Lakaza (p-difenol( oksidaza, EC ) Polifenol oksidaza koja sadrži i bakar Fiziološka uloga je u sintezi lignina Izvori Bakterije Gljive Biljke Supstrati Polifenoli Metoksi supstituisani fenoli Diamini (ali ne i Tyr!)
37 Mehanizam dejstva lakaze
38 Primena lakaze u industriji Razgradnja opasnih materija u industrijskim vodama Proizvodnja vina, piva, sokova i hleba Odredjivanje koncentracije askorbinske kiseline Geliranje pektina iz šećerne erne repe Biosenzori
39 Upotreba lakaze u proizvodnji vina Sastav vina Etanol Organske kiseline Soli Fenolna jedinjenja (boja i ukus) Madeirizacija Derivati cinaminske kiseline Derivati katehina Antocijanidini Malvidin (monoglukozid antocijanidina, glavni izvor boje u grožñu ñu) Oksidacija aldehida, amino kiselina i proteina u vinu katalizovana gvožñem ñem,, bakrom, ili enzimima Polifenoli se mogu ukloniti polivinilpolipirolidonom (selektivno?) Madeirizacija se može e sprečiti dodavanjem sumpor-dioksida Enzimski aditivi u proizvodnji vina Lakaze (ph optimum 2.5-4, stabilnost u kiseloj sredini, reverzibilna inhibicija sulfitima) Tanaze Fenolaze Antocijanaze Imobilizovani enzimi
40 Stabilizacija piva Uklanjanje fenola i viška kiseonika Odreñivanje askorbinske kiseline Na bazi inhibicije oksidacije 2,3-diaminofenazina Uklanjanje kiseonika iz proizvoda na bazi ulja (majonez i sl.) Poboljšanje ukusa čokolade Proizvodnja hleba Poboljšava mehanička svojstva glutenskih struktura (povećava se volumen i mekoća)
41 Upotreba oksidaza u proizvodnji hleba i peciva: molekularne osnove Tokom mešanja testa nastaje kompleska kvaternarna struktura (gluten) koja se sastoji od kovalentno povezanih gluteninskih podjedinica. Veze koje učestvuju u u gradjenju ovih struktura su disulfidne i ditirozin veze. HMW gluteninska podjedinica je mase kd i veoma kompleksne strukture.
42
43 Peroksidazom indukovano ukršteno povezivanje tirozina i ferulinske kiseline In vivo, peroxidaza ukršteno povezuje komponente ćelijskih zidova biljaka preko ferulinske kiseline esterifikovane polisaharidima. Ovaj enzim deluje i na tirozin. U smeši i proteina i saharida, moguće e su homo- i heteroveze izmedju tirozina i ferulinske kiseline.
44 Brzina konverzije različitih itih supstata peroksidazom
45
46
47
48 Transglutaminazom indukovano ukršteno povezivanje proteina brašna
49
50
51
52
53 Uticaj transglutaminaze na fiziko- hemijske osobine proteina mleka Transglutaminaza (TGaza) je enzim koji katalizuje acil transfer sa glutamina na slobodnu amino grupu (α( ili ε- amino grupu lizina). Na taj način se formira izopeptidna veza ε-(γ-glutamil) lizin, koja može e da bude inter, ili intramolekulska. Intermolekulska veza koja tako nastaje je odgovorna za fenomen ukrštenog povezivanja proteina tokom tretmana ovim enzimom, proteina mleka, brašna, ili mesa. Ukršteno teno-povezani proteini tih namirnica imaju bolje mehaničke osobine i lakše e se dalje obradjuju.
54
55
56
57
58
59 Dejstvo lakaze i transglutaminaze na proteine mesa
60
61 Protein-polisaharid heteroadukti
62
63
64 Klinički aspekti enzimologije
65 Odredjivanje enzimskih aktivnosti za kliničku ku dijagnozu Enzim bi trebalo da bude prisutan u krvi, urinu ili nekom lako dostupnom tkivnom fluidu. Enzimski test bi trebalo da bude jednostavan Razlike u enzimskoj aktivnosti izmedju normalnog i patološkog stanja bi trebalo da budu dijagnostički značajne ajne uz dobru korelaciju izmedju enzimske e aktivnosti i patološkog stanja Poželjno je i da je enzim dovoljno stabilan. Enzimi su prisutni u serumu kao: plazma-specifi specifični enzimi; plazma-nespecifi nespecifični ni enzimi.
66 inicijalna dijagnostika; praćenje toka bolesti; praćenje odgovora pacijenta na tretman. Idealno je pratiti aktivnost u serumu enzima koji je visoko tkivno-specifi specifičan (kisela-fosfataza u prostati ili acetil-holinesteraza u eritrocitima)... Neki enzimi imaju tkivno-specifi specifične izoenzimske forme (laktat-dehidrogenaza) koje je moguće razlikovati elektroforezom.
67 Odreñivanje enzimske aktivnosti pri postavljanju kliničke ke dijagnoze
68
69 Klinička enzimologija bolesti jetre Aspartat aminotransferaza (SGOT), alanin aminotransferaza (SGPT), alkalna fosfataza i γ- glutamiltransferaza. Laktat dehidrogenaza i izocitrat dehidrogenaza. Ornitin karbamoiltransferaza. Oboljenja jetre: hepatitis (viralni ili toksični), ciroza, primarni i sekundarni tumori jetre, obstrukcija žučne kese, tumori... Akutna, intermitenta ili hronična na stanja. Aktivnost aminotransferaza tj. odnos SGOT i SGPT Alkalne fosfataze su prisutne u jetri i kostima, izoenzimske forme...
70 Klinička enzimologija bolesti jetre Aktivnost alkalne fosfataze je praćena merenjem hidrolize p-nitrofenil fosfata. Aktivnost γ-glutamiltransferaze je praćena merenjem intenziteta otpuštanja p- nitroanilina kad se γ-glutamil-p-nitroanilid upotrebljava kao jedan od supstrata. p-nitroanilin apsorbuje na 400 nm
71 AP/SGPT odnos... γ-glutamiltransferaza hronični alkoholizam (ciroza jetre), metastaze...
72 Klinička enzimologija bolesti srca Kreatin kinaza (izoforme, osim CK-3 (MM tip) iz skeletnih mišića, ima i oko 15 % CK-2 (MB tip) izoforme), SGOT i laktat dehidrogenaza (takodje se prati izoenzimski profil). SGOT/SGPT u miokardu je 20-25, a u jetri Medjutim, CK i GT su precizniji pokazatelji.
73 α-amilaza - Pankreas i pljuvačne žlezde - Akutni pankreatitis (20-30 puta) - Hronični pankreatitis ili karcinom pankreaza malo povišen nivo. - Zbog niske Mm (49 kd) može e se detektovati i u urinu (kao i uropepsinogen). Kreatin-kinaza i fruktozo-bisfosfat aldolaza - Oboljenja skeletnih mišića a (distrofije), izoenzimkski profil CK Alkalna fosfataza - Veliki broj izoformi. Nalazi se u velikom broju tkiva: intestinalni epitelijum, bubrezi, kosti, leukociti, jetra i placenta. - Tri tipa: placentalni (termostabilan), intestinalni i iz drugih tkiva Kisela fosfataza - Nalazi se u velikom broju tkiva: jetra, slezina, eritrociti i prostata. p - Važan an za dijagnostiku kancera prostate. - Veoma je labilan, kontaminacija usled lize eritrocita (inhibicija tartaratom i formaldehidom). - Prostatični enzim je veoma specifičan za timoftalein fosfat.
74 Otkrivanje & značaj aj enzimske deficijencije (nedostatka) Za detekciju oboljenja se redje koriste enzimski testovi detektuju se metaboliti (fenilketourija se detektuje merenjem fenilpiruvata u urinu ili krvi). Neke urodjene greške u metabolizmu su relativno neškodljive (albinizam, alkaptonurija), ali druge se moraju detektovati rano da bi se štetni efekti defekta sprečili na vreme. Fenilketourija i galaktozemija npr.
75 Otkrivanje & značaj aj enzimske deficijencije (nedostatka)
76 Otkrivanje & značaj aj enzimske deficijencije (nedostatka) Kod fenilketourije nedostaje enzim fenilalanin-4-monooksigenaza koji katalizuje reakciju:
77 Zbog toga se Phe razgradjuje putem minornog mehanizma preko gradjenja fenilpiruvata
78 Kod galaktozemije deficijentni enzim je galaktozo-1- fosfat uridiltransferaza. Ovaj enzim je prisutan u brojnim tkivima, uključujući eritrocite. Detektuje se testom na liziranim eritrocitima.
79 Najčešća urodjena bolest koja deluje na eritrocite je deficijencija glukozo-6-fosfat dehidrogenaze. Manifestuje se kao hemolitička anemija indukovana snižavanjem nivoa glutationa (nakon tretmana lekovima koji inhibiraju ovaj enzim koji je prisutan u veoma malim koncentracijama). Snižava se intracelularna koncentracija NADPH koji je neophodan za redukciju oksidovanog glutationa.
80 Drugi primer osetljivosti na lekove koja je povezana sa urodjenom deficijencijom je u slučaju serum holinesteraze (pseudoholinesteraza). Sukcinil holin (mišićni relaksant) u slučaju deficijencije pseudoholinesteraze se ne razgradjuje normalno i daleko duže e deluje nego kod normalnih subjekata. Ovaj enzim kod deficijentnih osoba ima daleko višu u Km za sve testirane supstrate nego normalna forma ovog enzima.
81 Upotreba enzima radi odreñivanja koncentracije metabolita od kliničkog kog značaja aja Metablit se enzimski transformiše u proizvod čija koncentracija se odredjuje spektrofotometrijski. Visoka specifičnost enzima omogućava odredjivanje metabolita u prisustvu brojnih drugih supstanci u urinu ili serumu. Kuplovane reakcije omogućavaju pomeranje ravnoteže na desno tj. u povoljnom smeru. Takodje, moguće je i hemijski ukloniti proizvod enzimske reakcije.
82 Upotreba enzima radi odreñivanja koncentracije metabolita od kliničkog kog značaja aja 2-oksoglutarat reaguje sa hidrazinom...
83 Odredjivanje glukozg lukoze u krvi
84 Mokraćna kiselina
85 Urea
86 Holesterol, holesterolski estri & trigliceridi Merenje nivoa serumskih triglicerida u plazmi i serumu je korisno pri praćenju toka dijabetesa, nefroza i obstrukcije žuči. Merenje se može vršiti I enzimski, obično nakon alkalne hidrolize triglicerida. Glicerol koji se tako dobija se može odredjivati u testu koji koristi sledeći kuplovani sistem:
87 Ostali metaboliti
88
Primenjen. jena enzimologija. 1a. Istraživačke laboratorije 1b. Industrija. 2. Kliničke laboratorije
 Primenjen jena enzimologija 1a. Istraživačke laboratorije 1b. Industrija 2. Kliničke laboratorije Klinički aspekti enzimologije Odredjivanje enzimskih aktivnosti za kliničku ku dijagnostiku Enzim bi trebalo
Primenjen jena enzimologija 1a. Istraživačke laboratorije 1b. Industrija 2. Kliničke laboratorije Klinički aspekti enzimologije Odredjivanje enzimskih aktivnosti za kliničku ku dijagnostiku Enzim bi trebalo
SEKUNDARNE VEZE međumolekulske veze
 PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
S t r a n a 1. 1.Povezati jonsku jačinu rastvora: a) MgCl 2 b) Al 2 (SO 4 ) 3 sa njihovim molalitetima, m. za so tipa: M p X q. pa je jonska jačina:
 S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Aminokiseline. Anabolizam azotnihjedinjenja: Biosinteza aminokiselina, glutationa i biološki aktivnih amina 22.12.2014
 Anabolizam azotnihjedinjenja: Biosinteza aminokiselina, glutationa i biološki aktivnih amina Predavanja iz opšte biohemije Školska 2014/2015. godina Aminokiseline 1 Metabolizam aminokiselina Proteini iz
Anabolizam azotnihjedinjenja: Biosinteza aminokiselina, glutationa i biološki aktivnih amina Predavanja iz opšte biohemije Školska 2014/2015. godina Aminokiseline 1 Metabolizam aminokiselina Proteini iz
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
3. razred gimnazije- opšti i prirodno-matematički smer ALKENI. Aciklični nezasićeni ugljovodonici koji imaju jednu dvostruku vezu.
 ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
Teorijske osnove informatike 1
 Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
INTELIGENTNO UPRAVLJANJE
 INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
SISTEMI NELINEARNIH JEDNAČINA
 SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
CILJNA MESTA DEJSTVA LEKOVA
 FARMACEUTSKA HEMIJA 1 CILJNA MESTA DEJSTVA LEKVA Predavač: Prof. dr Slavica Erić Ciljna mesta dejstva leka CILJNA MESTA NA MLEKULARNM NIVU: lipidi (lipidi ćelijske membrane) ugljeni hidrati (obeleživači
FARMACEUTSKA HEMIJA 1 CILJNA MESTA DEJSTVA LEKVA Predavač: Prof. dr Slavica Erić Ciljna mesta dejstva leka CILJNA MESTA NA MLEKULARNM NIVU: lipidi (lipidi ćelijske membrane) ugljeni hidrati (obeleživači
Novi Sad god Broj 1 / 06 Veljko Milković Bulevar cara Lazara 56 Novi Sad. Izveštaj o merenju
 Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI)
 IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
HEMIJSKA VEZA TEORIJA VALENTNE VEZE
 TEORIJA VALENTNE VEZE Kovalentna veza nastaje preklapanjem atomskih orbitala valentnih elektrona, pri čemu je region preklapanja između dva jezgra okupiran parom elektrona. - Nastalu kovalentnu vezu opisuje
TEORIJA VALENTNE VEZE Kovalentna veza nastaje preklapanjem atomskih orbitala valentnih elektrona, pri čemu je region preklapanja između dva jezgra okupiran parom elektrona. - Nastalu kovalentnu vezu opisuje
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE GODINE 8. RAZRED TOČNI ODGOVORI
 21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
IMOBILIZACIJA AKTIVNIH TVARI ZA BIOLOŠKO PREPOZNAVANJE
 IMBILIZACIJA AKTIVI TVARI ZA BILŠK PREPZAVAJE EZIMI ATITIJELA RECEPTRI MIKRRGAIZMI ŽIVTIJSKE ILI BILJE STAICE ŽIVTIJSKA I BILJA VLAKA KLJUČI PRCES PRI IZRADI BISEZRA IMBILIZACIJA BILŠKE TVARI - AJČEŠĆE
IMBILIZACIJA AKTIVI TVARI ZA BILŠK PREPZAVAJE EZIMI ATITIJELA RECEPTRI MIKRRGAIZMI ŽIVTIJSKE ILI BILJE STAICE ŽIVTIJSKA I BILJA VLAKA KLJUČI PRCES PRI IZRADI BISEZRA IMBILIZACIJA BILŠKE TVARI - AJČEŠĆE
100g maslaca: 751kcal = 20g : E maslac E maslac = (751 x 20)/100 E maslac = 150,2kcal 100g med: 320kcal = 30g : E med E med = (320 x 30)/100 E med =
 100g maslaca: 751kcal = 20g : E maslac E maslac = (751 x 20)/100 E maslac = 150,2kcal 100g med: 320kcal = 30g : E med E med = (320 x 30)/100 E med = 96kcal 100g mleko: 49kcal = 250g : E mleko E mleko =
100g maslaca: 751kcal = 20g : E maslac E maslac = (751 x 20)/100 E maslac = 150,2kcal 100g med: 320kcal = 30g : E med E med = (320 x 30)/100 E med = 96kcal 100g mleko: 49kcal = 250g : E mleko E mleko =
III VEŽBA: FURIJEOVI REDOVI
 III VEŽBA: URIJEOVI REDOVI 3.1. eorijska osnova Posmatrajmo neki vremenski kontinualan signal x(t) na intervalu definisati: t + t t. ada se može X [ k ] = 1 t + t x ( t ) e j 2 π kf t dt, gde je f = 1/.
III VEŽBA: URIJEOVI REDOVI 3.1. eorijska osnova Posmatrajmo neki vremenski kontinualan signal x(t) na intervalu definisati: t + t t. ada se može X [ k ] = 1 t + t x ( t ) e j 2 π kf t dt, gde je f = 1/.
Mehanizmidejstvaenzima. Himotripsin
 Mehanizmidejstvaenzima Himotripsin Principi katalize Specifična kiselo-bazna kataliza Elektrostatska kataliza Elektrofilna kataliza Nukleofilna kataliza (kovalentna kataliza) Nukleofilna kataliza Opšta
Mehanizmidejstvaenzima Himotripsin Principi katalize Specifična kiselo-bazna kataliza Elektrostatska kataliza Elektrofilna kataliza Nukleofilna kataliza (kovalentna kataliza) Nukleofilna kataliza Opšta
Sekundarne struktura proteina Fibrilni proteini
 Sekundarne struktura proteina Fibrilni proteini Nivoi strukture proteina (strukturna hijerarhija) proteina Nivoi strukture proteina Primarna struktura Sekundarna struktura Super-sekundarna struktura Tercijarnastruktura
Sekundarne struktura proteina Fibrilni proteini Nivoi strukture proteina (strukturna hijerarhija) proteina Nivoi strukture proteina Primarna struktura Sekundarna struktura Super-sekundarna struktura Tercijarnastruktura
REAKCIJE ELIMINACIJE
 REAKIJE ELIMINAIJE 1 . DEIDROALOGENAIJA (-X) i DEIDRATAIJA (- 2 O) su najčešći tipovi eliminacionih reakcija X Y + X Y 2 Dehidrohalogenacija (-X) X strong base + " X " X = l, Br, I 3 E 2 Mehanizam Ova
REAKIJE ELIMINAIJE 1 . DEIDROALOGENAIJA (-X) i DEIDRATAIJA (- 2 O) su najčešći tipovi eliminacionih reakcija X Y + X Y 2 Dehidrohalogenacija (-X) X strong base + " X " X = l, Br, I 3 E 2 Mehanizam Ova
Zavrxni ispit iz Matematiqke analize 1
 Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
10. STABILNOST KOSINA
 MEHANIKA TLA: Stabilnot koina 101 10. STABILNOST KOSINA 10.1 Metode proračuna koina Problem analize tabilnoti zemljanih maa vodi e na određivanje odnoa između rapoložive mičuće čvrtoće i proečnog mičućeg
MEHANIKA TLA: Stabilnot koina 101 10. STABILNOST KOSINA 10.1 Metode proračuna koina Problem analize tabilnoti zemljanih maa vodi e na određivanje odnoa između rapoložive mičuće čvrtoće i proečnog mičućeg
DOLOČANJE)ENCIMSKE)AKTIVNOSTI)V)KLINIČNE)NAMENE)
 DLČANJEENCIMSKEAKTIVNSTIVKLINIČNENAMENE 20encimovseru=nskopregledujevkliniki 1954sougotovilipovezanostsrčnegainfarktainpovišanekonc. aspartataminotransferazevserumu danesnarapolagovelikoabzapreciznodoločanjekoncproteinov
DLČANJEENCIMSKEAKTIVNSTIVKLINIČNENAMENE 20encimovseru=nskopregledujevkliniki 1954sougotovilipovezanostsrčnegainfarktainpovišanekonc. aspartataminotransferazevserumu danesnarapolagovelikoabzapreciznodoločanjekoncproteinov
MERNA NESIGURNOST BEO-LAB
 MERNA NESIGURNOST BEO-LAB Ispitivani parametar Jedinica mere 1. Urea 2. Kreatinin µmol/l Merna nesigurnost L1: ± 0.20 7,05 L2: ±0,69 21,78 L1: ± 4,0 L2: ± 26,5 Za Koncentraciju analita do- 108 387 L1:
MERNA NESIGURNOST BEO-LAB Ispitivani parametar Jedinica mere 1. Urea 2. Kreatinin µmol/l Merna nesigurnost L1: ± 0.20 7,05 L2: ±0,69 21,78 L1: ± 4,0 L2: ± 26,5 Za Koncentraciju analita do- 108 387 L1:
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
NOMENKLATURA ORGANSKIH SPOJEVA. Imenovanje aromatskih ugljikovodika
 NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
MEĐUMOLEKULSKE SILE JON-DIPOL DIPOL VODONIČNE NE VEZE DIPOL DIPOL-DIPOL DIPOL-INDUKOVANI INDUKOVANI JON-INDUKOVANI DISPERZNE SILE
 MEĐUMLEKULSKE SILE JN-DIPL VDNIČNE NE VEZE DIPL-DIPL JN-INDUKVANI DIPL DIPL-INDUKVANI INDUKVANI DIPL DISPERZNE SILE MEĐUMLEKULSKE SILE jake JNSKA VEZA (metal-nemetal) KVALENTNA VEZA (nemetal-nemetal) METALNA
MEĐUMLEKULSKE SILE JN-DIPL VDNIČNE NE VEZE DIPL-DIPL JN-INDUKVANI DIPL DIPL-INDUKVANI INDUKVANI DIPL DISPERZNE SILE MEĐUMLEKULSKE SILE jake JNSKA VEZA (metal-nemetal) KVALENTNA VEZA (nemetal-nemetal) METALNA
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI. NEUTRALNI ELEMENT GRUPOIDA.
 KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI NEUTRALNI ELEMENT GRUPOIDA 1 Grupoid (G, ) je asocijativa akko važi ( x, y, z G) x (y z) = (x y) z Grupoid (G, ) je komutativa akko važi ( x, y G) x y = y x Asocijativa
KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI NEUTRALNI ELEMENT GRUPOIDA 1 Grupoid (G, ) je asocijativa akko važi ( x, y, z G) x (y z) = (x y) z Grupoid (G, ) je komutativa akko važi ( x, y G) x y = y x Asocijativa
Kiselo bazni indikatori
 Kiselo bazni indikatori Slabe kiseline ili baze koje imaju različite boje nejonizovanog i jonizovanog oblika u rastvoru Primer: slaba kiselina HIn(aq) H + (aq) + In (aq) nejonizovani oblik jonizovani oblik
Kiselo bazni indikatori Slabe kiseline ili baze koje imaju različite boje nejonizovanog i jonizovanog oblika u rastvoru Primer: slaba kiselina HIn(aq) H + (aq) + In (aq) nejonizovani oblik jonizovani oblik
Obrada signala
 Obrada signala 1 18.1.17. Greška kvantizacije Pretpostavka je da greška kvantizacije ima uniformnu raspodelu 7 6 5 4 -X m p x 1,, za x druge vrednosti x 3 x X m 1 X m = 3 x Greška kvantizacije x x x p
Obrada signala 1 18.1.17. Greška kvantizacije Pretpostavka je da greška kvantizacije ima uniformnu raspodelu 7 6 5 4 -X m p x 1,, za x druge vrednosti x 3 x X m 1 X m = 3 x Greška kvantizacije x x x p
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f
 IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
Dijagonalizacija operatora
 Dijagonalizacija operatora Problem: Može li se odrediti baza u kojoj zadani operator ima dijagonalnu matricu? Ova problem je povezan sa sljedećim pojmovima: 1 Karakteristični polinom operatora f 2 Vlastite
Dijagonalizacija operatora Problem: Može li se odrediti baza u kojoj zadani operator ima dijagonalnu matricu? Ova problem je povezan sa sljedećim pojmovima: 1 Karakteristični polinom operatora f 2 Vlastite
Riješeni zadaci: Nizovi realnih brojeva
 Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Antene. Srednja snaga EM zračenja se dobija na osnovu intenziteta fluksa Pointingovog vektora kroz sferu. Gustina snage EM zračenja:
 Anene Transformacija EM alasa u elekrični signal i obrnuo Osnovne karakerisike anena su: dijagram zračenja, dobiak (Gain), radna učesanos, ulazna impedansa,, polarizacija, efikasnos, masa i veličina, opornos
Anene Transformacija EM alasa u elekrični signal i obrnuo Osnovne karakerisike anena su: dijagram zračenja, dobiak (Gain), radna učesanos, ulazna impedansa,, polarizacija, efikasnos, masa i veličina, opornos
Linearna algebra 2 prvi kolokvij,
 1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
PRERADA GROŽðA. Sveučilište u Splitu Kemijsko-tehnološki fakultet. Zavod za prehrambenu tehnologiju i biotehnologiju. Referati za vježbe iz kolegija
 Sveučilište u Splitu Kemijsko-tehnološki fakultet Zavod za prehrambenu tehnologiju i biotehnologiju Referati za vježbe iz kolegija PRERADA GROŽðA Stručni studij kemijske tehnologije Smjer: Prehrambena
Sveučilište u Splitu Kemijsko-tehnološki fakultet Zavod za prehrambenu tehnologiju i biotehnologiju Referati za vježbe iz kolegija PRERADA GROŽðA Stručni studij kemijske tehnologije Smjer: Prehrambena
Izbor statističkih testova Ana-Maria Šimundić
 Izbor statističkih testova Ana-Maria Šimundić Klinički zavod za kemiju Klinička jedinica za medicinsku biokemiju s analitičkom toksikologijom KBC Sestre milosrdnice Izbor statističkog testa Tajna dobrog
Izbor statističkih testova Ana-Maria Šimundić Klinički zavod za kemiju Klinička jedinica za medicinsku biokemiju s analitičkom toksikologijom KBC Sestre milosrdnice Izbor statističkog testa Tajna dobrog
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
Grafičko prikazivanje atributivnih i geografskih nizova
 Grafičko prikazivanje atributivnih i geografskih nizova Biserka Draščić Ban Pomorski fakultet u Rijeci 17. veljače 2011. Grafičko prikazivanje atributivnih nizova Atributivni nizovi prikazuju se grafički
Grafičko prikazivanje atributivnih i geografskih nizova Biserka Draščić Ban Pomorski fakultet u Rijeci 17. veljače 2011. Grafičko prikazivanje atributivnih nizova Atributivni nizovi prikazuju se grafički
OBRTNA TELA. Vladimir Marinkov OBRTNA TELA VALJAK
 OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
LANCI & ELEMENTI ZA KAČENJE
 LANCI & ELEMENTI ZA KAČENJE 0 4 0 1 Lanci za vešanje tereta prema standardu MSZ EN 818-2 Lanci su izuzetno pogodni za obavljanje zahtevnih operacija prenošenja tereta. Opseg radne temperature se kreće
LANCI & ELEMENTI ZA KAČENJE 0 4 0 1 Lanci za vešanje tereta prema standardu MSZ EN 818-2 Lanci su izuzetno pogodni za obavljanje zahtevnih operacija prenošenja tereta. Opseg radne temperature se kreće
Numerička matematika 2. kolokvij (1. srpnja 2009.)
 Numerička matematika 2. kolokvij (1. srpnja 29.) Zadatak 1 (1 bodova.) Teorijsko pitanje. (A) Neka je G R m n, uz m n, pravokutna matrica koja ima puni rang po stupcima, tj. rang(g) = n. (a) Napišite puni
Numerička matematika 2. kolokvij (1. srpnja 29.) Zadatak 1 (1 bodova.) Teorijsko pitanje. (A) Neka je G R m n, uz m n, pravokutna matrica koja ima puni rang po stupcima, tj. rang(g) = n. (a) Napišite puni
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Osnovne veličine, jedinice i izračunavanja u hemiji
 Osnovne veličine, jedinice i izračunavanja u hemiji Pregled pojmova veličina i njihovih jedinica koje se koriste pri osnovnim izračunavanjima u hemiji dat je u Tabeli 1. Tabela 1. Veličine i njihove jedinice
Osnovne veličine, jedinice i izračunavanja u hemiji Pregled pojmova veličina i njihovih jedinica koje se koriste pri osnovnim izračunavanjima u hemiji dat je u Tabeli 1. Tabela 1. Veličine i njihove jedinice
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
PROSTA GREDA (PROSTO OSLONJENA GREDA)
 ROS GRED (ROSO OSONJEN GRED) oprečna sila i moment savijanja u gredi y a b c d e a) Zadana greda s opterećenjem l b) Sile opterećenja na gredu c) Određivanje sila presjeka grede u presjeku a) Unutrašnje
ROS GRED (ROSO OSONJEN GRED) oprečna sila i moment savijanja u gredi y a b c d e a) Zadana greda s opterećenjem l b) Sile opterećenja na gredu c) Određivanje sila presjeka grede u presjeku a) Unutrašnje
Usluge koje se rade na lični zahtev
 Usluge koje se rade na lični zahtev Redni broj Naziv usluge 1 Uzorkovanje krvi (venepunkcija) 2 Uzorkovanje krvi (mikrouzorkovanje) 3 Specijalistički pregled prvi 4 Specijalistički pregled kontrolni 5
Usluge koje se rade na lični zahtev Redni broj Naziv usluge 1 Uzorkovanje krvi (venepunkcija) 2 Uzorkovanje krvi (mikrouzorkovanje) 3 Specijalistički pregled prvi 4 Specijalistički pregled kontrolni 5
Dvanaesti praktikum iz Analize 1
 Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
(P.I.) PRETPOSTAVKA INDUKCIJE - pretpostavimo da tvrdnja vrijedi za n = k.
 1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
ТЕМПЕРАТУРА СВЕЖЕГ БЕТОНА
 ТЕМПЕРАТУРА СВЕЖЕГ БЕТОНА empertur sežeg beton menj se tokom remen i zisi od ećeg broj utijnih prmetr: Početne temperture mešine (n izsku iz mešie), emperture sredine, opote hidrtije ement, Rzmene topote
ТЕМПЕРАТУРА СВЕЖЕГ БЕТОНА empertur sežeg beton menj se tokom remen i zisi od ećeg broj utijnih prmetr: Početne temperture mešine (n izsku iz mešie), emperture sredine, opote hidrtije ement, Rzmene topote
Strukture podataka i algoritmi 1. kolokvij 16. studenog Zadatak 1
 Strukture podataka i algoritmi 1. kolokvij Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i službeni šalabahter. Predajete samo papire koje ste dobili. Rezultati i uvid u kolokvije: ponedjeljak,
Strukture podataka i algoritmi 1. kolokvij Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i službeni šalabahter. Predajete samo papire koje ste dobili. Rezultati i uvid u kolokvije: ponedjeljak,
Cenovnik zdravstvenih usluga na lični zahtev
 Institut za transfuziju krvi Srbije Br.1/9/1.5 Beograd, 24.12.2015. Cenovnik zdravstvenih usluga na lični zahtev Redni 1 1-000026 Uzorkovanje krvi (venepunkcija) 120,00 2 1-000018 Uzorkovanje krvi (mikrouzorkovanje)
Institut za transfuziju krvi Srbije Br.1/9/1.5 Beograd, 24.12.2015. Cenovnik zdravstvenih usluga na lični zahtev Redni 1 1-000026 Uzorkovanje krvi (venepunkcija) 120,00 2 1-000018 Uzorkovanje krvi (mikrouzorkovanje)
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
 Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE
 **** MLADEN SRAGA **** 011. UNIVERZALNA ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE SKUP REALNIH BROJEVA α Autor: MLADEN SRAGA Grafički urednik: BESPLATNA - WEB-VARIJANTA Tisak: M.I.M.-SRAGA
**** MLADEN SRAGA **** 011. UNIVERZALNA ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE SKUP REALNIH BROJEVA α Autor: MLADEN SRAGA Grafički urednik: BESPLATNA - WEB-VARIJANTA Tisak: M.I.M.-SRAGA
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
 TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
PT ISPITIVANJE PENETRANTIMA
 FSB Sveučilišta u Zagrebu Zavod za kvalitetu Katedra za nerazorna ispitivanja PT ISPITIVANJE PENETRANTIMA Josip Stepanić SADRŽAJ kapilarni učinak metoda ispitivanja penetrantima uvjeti promatranja SADRŽAJ
FSB Sveučilišta u Zagrebu Zavod za kvalitetu Katedra za nerazorna ispitivanja PT ISPITIVANJE PENETRANTIMA Josip Stepanić SADRŽAJ kapilarni učinak metoda ispitivanja penetrantima uvjeti promatranja SADRŽAJ
ISPITNA PITANJA OSNOVI BIOHEMIJE
 UNIVERZITET PRIVREDNA AKADEMIJA, NOVI SAD STOMATOLOŠKI FAKULTET PANČEVO ISPITNA PITANJA OSNOVI BIOHEMIJE Prof. dr Esma R. Isenović 1. Biohemija kao nauka, zadaci izučavanja i discipline 1. Koja je definicija
UNIVERZITET PRIVREDNA AKADEMIJA, NOVI SAD STOMATOLOŠKI FAKULTET PANČEVO ISPITNA PITANJA OSNOVI BIOHEMIJE Prof. dr Esma R. Isenović 1. Biohemija kao nauka, zadaci izučavanja i discipline 1. Koja je definicija
RIJEŠENI ZADACI I TEORIJA IZ
 RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
XI dvoqas veжbi dr Vladimir Balti. 4. Stabla
 XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
UPOTREBA ENZIMA U OBRADI HRANE
 UPTREBA ENZIMA U BRADI HRANE PDRUČJA PREHRAMBENE INDUSTRIJE U KJIMA SE KRISTE ENZIMSKI PRCESI BRADA PEKARSKIH PRIZVDA BRADA VĆA I VĆNIH SKVA UPTREBA ENZIMA U PIVARSTVU BRADA MLIJEČNIH PRIZVDA BRADA MESA
UPTREBA ENZIMA U BRADI HRANE PDRUČJA PREHRAMBENE INDUSTRIJE U KJIMA SE KRISTE ENZIMSKI PRCESI BRADA PEKARSKIH PRIZVDA BRADA VĆA I VĆNIH SKVA UPTREBA ENZIMA U PIVARSTVU BRADA MLIJEČNIH PRIZVDA BRADA MESA
PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE)
 (Enegane) List: PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE) Na mjestima gdje se istovremeno troši električna i toplinska energija, ekonomičan način opskrbe energijom
(Enegane) List: PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE) Na mjestima gdje se istovremeno troši električna i toplinska energija, ekonomičan način opskrbe energijom
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
Sortiranje prebrajanjem (Counting sort) i Radix Sort
 Sortiranje prebrajanjem (Counting sort) i Radix Sort 15. siječnja 2016. Ante Mijoč Uvod Teorem Ako je f(n) broj usporedbi u algoritmu za sortiranje temeljenom na usporedbama (eng. comparison-based sorting
Sortiranje prebrajanjem (Counting sort) i Radix Sort 15. siječnja 2016. Ante Mijoč Uvod Teorem Ako je f(n) broj usporedbi u algoritmu za sortiranje temeljenom na usporedbama (eng. comparison-based sorting
Linearna algebra 2 prvi kolokvij,
 Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
Reverzibilni procesi
 Reverzbln proces Reverzbln proces: proces pr koja sste nkada nje vše od beskonačno ale vrednost udaljen od ravnoteže, beskonačno ala proena spoljašnjh uslova ože vratt sste u blo koju tačku, proena ože
Reverzbln proces Reverzbln proces: proces pr koja sste nkada nje vše od beskonačno ale vrednost udaljen od ravnoteže, beskonačno ala proena spoljašnjh uslova ože vratt sste u blo koju tačku, proena ože
C kao nukleofil (Organometalni spojevi)
 C kao nukleofil (Organometalni spojevi) 1 Nastajanje nukleofilnih C atoma i njihova adicija na karbonilnu grupu Ukupan proces je jedan od najkorisnijih sintetskih postupaka za stvaranje C-C veze 2 Priroda
C kao nukleofil (Organometalni spojevi) 1 Nastajanje nukleofilnih C atoma i njihova adicija na karbonilnu grupu Ukupan proces je jedan od najkorisnijih sintetskih postupaka za stvaranje C-C veze 2 Priroda
Seminar 13.b. Glikogen GLIKOGEN. B. Mildner
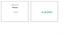 Seminar 13.b Glikogen B. Mildner GLIKOGEN 1 Glikogen Nereducirani kraj Glikogen je jako dostupni skladišni oblik glukoze; kao i jako velik, razgranat polimer; Glukozne jedinice su povezane α-1,4-glikozidnim
Seminar 13.b Glikogen B. Mildner GLIKOGEN 1 Glikogen Nereducirani kraj Glikogen je jako dostupni skladišni oblik glukoze; kao i jako velik, razgranat polimer; Glukozne jedinice su povezane α-1,4-glikozidnim
Pravilo 1. Svaki tip entiteta ER modela postaje relaciona šema sa istim imenom.
 1 Pravilo 1. Svaki tip entiteta ER modela postaje relaciona šema sa istim imenom. Pravilo 2. Svaki atribut entiteta postaje atribut relacione šeme pod istim imenom. Pravilo 3. Primarni ključ entiteta postaje
1 Pravilo 1. Svaki tip entiteta ER modela postaje relaciona šema sa istim imenom. Pravilo 2. Svaki atribut entiteta postaje atribut relacione šeme pod istim imenom. Pravilo 3. Primarni ključ entiteta postaje
3/25/2016. Hemijske komponente ćelije
 Hemijske komponente ćelije Molekuli u ćeliji Najbitniji molekuli u ćeliji su poznati. Putevi sinteze i razgradnje su poznati za većinu ćelijskih konstituenata. Hemijska energija pokreće biosintezu. Organizacija
Hemijske komponente ćelije Molekuli u ćeliji Najbitniji molekuli u ćeliji su poznati. Putevi sinteze i razgradnje su poznati za većinu ćelijskih konstituenata. Hemijska energija pokreće biosintezu. Organizacija
OSNOVI ELEKTRONIKE VEŽBA BROJ 1 OSNOVNA KOLA SA DIODAMA
 ELEKTROTEHNIČKI FAKULTET U BEOGRADU KATEDRA ZA ELEKTRONIKU OSNOVI ELEKTRONIKE SVI ODSECI OSIM ODSEKA ZA ELEKTRONIKU LABORATORIJSKE VEŽBE VEŽBA BROJ 1 OSNOVNA KOLA SA DIODAMA Autori: Goran Savić i Milan
ELEKTROTEHNIČKI FAKULTET U BEOGRADU KATEDRA ZA ELEKTRONIKU OSNOVI ELEKTRONIKE SVI ODSECI OSIM ODSEKA ZA ELEKTRONIKU LABORATORIJSKE VEŽBE VEŽBA BROJ 1 OSNOVNA KOLA SA DIODAMA Autori: Goran Savić i Milan
APROKSIMACIJA FUNKCIJA
 APROKSIMACIJA FUNKCIJA Osnovni koncepti Gradimir V. Milovanović MF, Beograd, 14. mart 2011. APROKSIMACIJA FUNKCIJA p.1/46 Osnovni problem u TA Kako za datu funkciju f iz velikog prostora X naći jednostavnu
APROKSIMACIJA FUNKCIJA Osnovni koncepti Gradimir V. Milovanović MF, Beograd, 14. mart 2011. APROKSIMACIJA FUNKCIJA p.1/46 Osnovni problem u TA Kako za datu funkciju f iz velikog prostora X naći jednostavnu
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
MATEMATIKA 2. Grupa 1 Rexea zadataka. Prvi pismeni kolokvijum, Dragan ori
 MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri
 Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Inženjerska grafika geometrijskih oblika (5. predavanje, tema1)
 Inženjerska grafika geometrijskih oblika (5. predavanje, tema1) Prva godina studija Mašinskog fakulteta u Nišu Predavač: Dr Predrag Rajković Mart 19, 2013 5. predavanje, tema 1 Simetrija (Symmetry) Simetrija
Inženjerska grafika geometrijskih oblika (5. predavanje, tema1) Prva godina studija Mašinskog fakulteta u Nišu Predavač: Dr Predrag Rajković Mart 19, 2013 5. predavanje, tema 1 Simetrija (Symmetry) Simetrija
Cauchyjev teorem. Postoji više dokaza ovog teorema, a najjednostvniji je uz pomoć Greenove formule: dxdy. int C i Cauchy Riemannovih uvjeta.
 auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
