NERASTAVLJIVE VEZE I SPOJEVI. Zakovični spojevi
|
|
|
- Θήρα Τρικούπη
- 7 χρόνια πριν
- Προβολές:
Transcript
1 NERASTAVLJIVE VEZE I SPOJEVI Zakovični spojevi Zakovice s poluokruglom glavom - za čelične konstrukcije (HRN M.B ), (lijevi dio slike) - za kotlove pod tlakom (desni dio slike) Nazivni promjer (sirove) zakovice d Promjer zakovane zakovice d Presjek zakovane zakovice A = d π 4 Dimenzije zakovica se vide u donjoj tablici. Duljina sirove zakovice l ovisi o ukupnoj debljini limova l. Proračun zakovičnih spojeva Zakovice računamo s obzirom na presjek A u zakovanom stanju, tj. prema promjeru rupe d, što je zakovica pri zakivanju gotovo sasvim ispuni. Sila F, koju može prenositi limena traka debljine s i širine, jednake razmaku t me u zakovicama u redu, je ( ) F = t d s δ = A τ, = d s p dop s dop dop gdje su: δ dop - dopušteno vlačno naprezanje zakovice τ s, dop - dopušteno smično naprezanje zakovice p dop - dopušteni bočni pritisak (između zakovice i lima). Zavari Oblici zavarenih spojeva (HRN C.T )
2 Vrste šavova i njihovi znakovi (HRN C.T ) Dopunske oznake za oblik površine šava: ravna: - ispupčena: udubljena:
3 Označavanje zavara na crtežima - strelicom Proračun zavarenih spojeva Naprezanja na vlak (tlak) δ zbog djelovanja sile F i naprezanje na savijanje δ f zbog djelovanja momenta M iznose u osnovnim slučajevima zavarenih spojeva debljine zavara a i duljine l: Naprezanja u dvostranim zavarima: δ = F a l δ f 6 M = a l
4 F δ = a l+ a l a = a + a δ f M = W ' '' a = a ' + a '' Dopuštena naprezanja u zavaru δ dop zav znatno su manja od normalnih dopuštenih naprezanja δ δ = α δ. dop : dop zav dop Koeficijent zavarivanja α veoma ovisi o statičkom i dinamičkom opterećenju, vrsti zavarenog spoja i izvedbi zavara. Njegove su vrijednosti približno u slijedećim granicama: Pri običnoj izvedbi zavarenog spoja te se vrijednosti mogu smanjiti i do 50%. Stezni spojevi Stezne spojeve dobivamo navlačenjem obruča unutarnjeg promjera d na rukavac većeg vanjskog promjera D, i to - obično - hlađenjem rukavca i zagrijavanjem obruča. Relativna deformacija ε rukavca i obruča (s obzirom na prvobitni promjer rukavca) iznosi: D d d ε = = D D Pritisak p na plohi između rukavca i obruča u stegnutom stanju ovisi o dopuštenim naprezanjima u rukavcu δ dop i obruču δ dop : p d δ dop D Po Hookeovu zakonu vrijedi za rukavac i obruč ε p d + D = E d D p d δ dop D d + D m + E d D m gdje su: E i E - moduli elastičnosti za rukavac i obruč, m i m - Poissonovi koeficijenti za rukavac i obruč. Stezna deformacija
5 d = D p ε p Temperaturne razlike, potrebne pri navlačenju: Hlađenje rukavca za temperaturnu razliku T 0 -T uzrokuje suženje rukavca za d dok zagrijavanje obruča za temperaturnu razliku T -T 0 uzrokuje proširenje obruča za d : α ( ) d = α d ( T T ) d = D T T 0 0 gdje su: T 0 - temperatura okoline, T - temperatura ohlađenog rukavca, T - temperatura zagrijanog obruča, α i α - koeficijenti temperaturnog rastezanja rukavca i obruča (v. str. 58). Ukipna promjena promjera treba biti veća od tražene stezne deformacije d + d > d Prijenosna sila F steznog spoja je F = µ D π l p gdje je l duljina korisne prijenosne površine rukavca. Koeficijent trenja µ na plohi između rukavca i obruča u stegnutom stanju iznosi 0,05...0,9 (za srednje tvrdi čelik oko 0,6). Prijenosni moment M t steznog spoja je M d t = F Razlikujemo klinove (s nagobim :00) i pera. Klinovi prema HRN: Rastavljivi spojevi Spojevi klinovima Pera d - promjer osovine b - širina klina, pera h - visina klina, pera dubina utora: t - na osovini t - na glavini za klinove t - na glavini za pera Osnovni standardizirani klinovi i pera Klinovi (HRN M.C ). - Plosnati klinovi (HRN.M.C.0-957). - Pera, visoka (HRN M.C ). - Pera, niska (HRN M.C ).
6 Utorni spojevi Utorni spojevi s ravnim bokovima (HRN M.C ) Unutarnji promjer d Vanjski promjer D - za laku izvedbu D - za srednju izvedbu D Širina utora b Broj utora n Spojevi svornjacima i zaticima Svornjaci Standardizirani promjeri d Obrađeni svornjaci bez glave (HRN M.C ) d = mm Obrađeni svornjaci s malom glavom (HRN M.C ) d = mm Poluobrađeni svornjaci s velikom glavom (HRN M.C ) d = mm Poluobrađeni svornjaci s malom glavom (HRN M.C ) d = mm Zatici Standardizirani promjeri d 0,6 0,8,5, Cilindrični zatici - u tolerancijskom polju h 8 (HRN M.C.0-95) d = 0, mm - u tolerancijskom polju h (HRN M.C.0-95) d = 0, mm - u tolerancijskom polju m 6 (HRN M.C.03-95) d =... 50mm Zakaljeni cilindrični zatici (60 HRC) - u tolerancijkom polju m 6 (HRN M.C.04-95) d = 0,8... 0mm Konični zatici (:50),(promjer d mjeri se na užem kraju) (HRN M.C.05-95) d = 0, mm
NOSIVI DIJELOVI MEHATRONIČKIH KONSTRUKCIJA
 NOSIVI DIJELOVI MEHATRONIČKIH KONSTRUKCIJA Zavareni spojevi - I. dio 1 ZAVARENI SPOJEVI Nerastavljivi spojevi Upotrebljavaju se prije svega za spajanje nosivih mehatroničkih dijelova i konstrukcija 2 ŠTO
NOSIVI DIJELOVI MEHATRONIČKIH KONSTRUKCIJA Zavareni spojevi - I. dio 1 ZAVARENI SPOJEVI Nerastavljivi spojevi Upotrebljavaju se prije svega za spajanje nosivih mehatroničkih dijelova i konstrukcija 2 ŠTO
SPOJEVI S GLAVINOM. Pomoćni nastavni materijali uz kolegij "Konstrukcijski elementi I" Ak. godina 2010./11.
 SPOJEVI S GLAVINOM Pomoćni nastavni materijali uz kolegij "Konstrukcijski elementi I" Ak. godina 010./11. Nositelji kolegija: Prof. dr. sc. Božidar Križan Prof. dr. sc. Saša Zelenika - 1 - SPOJEVI S GLAVINOM
SPOJEVI S GLAVINOM Pomoćni nastavni materijali uz kolegij "Konstrukcijski elementi I" Ak. godina 010./11. Nositelji kolegija: Prof. dr. sc. Božidar Križan Prof. dr. sc. Saša Zelenika - 1 - SPOJEVI S GLAVINOM
Dimenzioniranje nosaa. 1. Uvjeti vrstoe
 Dimenzioniranje nosaa 1. Uvjeti vrstoe 1 Otpornost materijala prouava probleme 1. vrstoe,. krutosti i 3. elastine stabilnosti konstrukcija i dijelova konstrukcija od vrstog deformabilnog materijala. Moraju
Dimenzioniranje nosaa 1. Uvjeti vrstoe 1 Otpornost materijala prouava probleme 1. vrstoe,. krutosti i 3. elastine stabilnosti konstrukcija i dijelova konstrukcija od vrstog deformabilnog materijala. Moraju
SPOJEVI S GLAVINOM. Pomoćni nastavni materijali uz kolegij "Konstrukcijski elementi I" Ak. godina 2006./07.
 SPOJEVI S GLAVINOM Pomoćni nastavni materijali uz kolegij "Konstrukcijski elementi I" Ak. godina 2006./07. Nositelji kolegija: Prof. dr. sc. Božidar Križan Doc. dr. sc. Saša Zelenika - 1 - SPOJEVI S GLAVINOM
SPOJEVI S GLAVINOM Pomoćni nastavni materijali uz kolegij "Konstrukcijski elementi I" Ak. godina 2006./07. Nositelji kolegija: Prof. dr. sc. Božidar Križan Doc. dr. sc. Saša Zelenika - 1 - SPOJEVI S GLAVINOM
Ĉetverokut - DOMAĆA ZADAĆA. Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke.
 Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
3525$&8158&1(',=$/,&(6$1$92-1,095(7(120
 Srednja masinska skola OSOVE KOSTRUISAJA List1/8 355$&8158&1(',=$/,&(6$1$9-1,095(7(10 3ROD]QLSRGDFL maksimalno opterecenje Fa := 36000 visina dizanja h := 440 mm Rucna sila Fr := 350 1DYRMQRYUHWHQR optereceno
Srednja masinska skola OSOVE KOSTRUISAJA List1/8 355$&8158&1(',=$/,&(6$1$9-1,095(7(10 3ROD]QLSRGDFL maksimalno opterecenje Fa := 36000 visina dizanja h := 440 mm Rucna sila Fr := 350 1DYRMQRYUHWHQR optereceno
PREDNAPETI BETON Primjer nadvožnjaka preko autoceste
 PREDNAPETI BETON Primjer nadvožnjaka preko autoceste 7. VJEŽBE PLAN ARMATURE PREDNAPETOG Dominik Skokandić, mag.ing.aedif. PLAN ARMATURE PREDNAPETOG 1. Rekapitulacija odabrane armature 2. Određivanje duljina
PREDNAPETI BETON Primjer nadvožnjaka preko autoceste 7. VJEŽBE PLAN ARMATURE PREDNAPETOG Dominik Skokandić, mag.ing.aedif. PLAN ARMATURE PREDNAPETOG 1. Rekapitulacija odabrane armature 2. Određivanje duljina
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
PRORAČUN GLAVNOG KROVNOG NOSAČA
 PRORAČUN GLAVNOG KROVNOG NOSAČA STATIČKI SUSTAV, GEOMETRIJSKE KARAKTERISTIKE I MATERIJAL Statički sustav glavnog krovnog nosača je slobodno oslonjena greda raspona l11,0 m. 45 0 65 ZAŠTITNI SLOJ BETONA
PRORAČUN GLAVNOG KROVNOG NOSAČA STATIČKI SUSTAV, GEOMETRIJSKE KARAKTERISTIKE I MATERIJAL Statički sustav glavnog krovnog nosača je slobodno oslonjena greda raspona l11,0 m. 45 0 65 ZAŠTITNI SLOJ BETONA
SRĐAN PODRUG ELEMENTI STROJEVA
 S V E U Č I L I Š T E U S P L I T U FAKULTET ELEKTROTEHNIKE, STROJARSTVA I BRODOGRADNJE U SPLITU SRĐAN PODRUG ELEMENTI STROJEVA Predavanja za stručni i preddiplomski studij BRODOGRADNJE za školsku godinu
S V E U Č I L I Š T E U S P L I T U FAKULTET ELEKTROTEHNIKE, STROJARSTVA I BRODOGRADNJE U SPLITU SRĐAN PODRUG ELEMENTI STROJEVA Predavanja za stručni i preddiplomski studij BRODOGRADNJE za školsku godinu
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Novi Sad god Broj 1 / 06 Veljko Milković Bulevar cara Lazara 56 Novi Sad. Izveštaj o merenju
 Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
Opšte KROVNI POKRIVAČI I
 1 KROVNI POKRIVAČI I FASADNE OBLOGE 2 Opšte Podela prema zaštitnim svojstvima: Hladne obloge - zaštita hale od atmosferskih padavina, Tople obloge - zaštita hale od atmosferskih padavina i prodora hladnoće
1 KROVNI POKRIVAČI I FASADNE OBLOGE 2 Opšte Podela prema zaštitnim svojstvima: Hladne obloge - zaštita hale od atmosferskih padavina, Tople obloge - zaštita hale od atmosferskih padavina i prodora hladnoće
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
p d R r E 1, ν 1 Slika 15. Stezni spoj glavčina-osovina (vratilo); puna osovina (slika a), šuplja osovina (slika b)
 BLOSTJN POSU JV - STZN SPOJ STZN SPOJ zazi za naezanja i omake ko sastavljenih cijevi mogu se abiti ko oačuna steznog soja gje elementi soja mogu biti o istog ili o azličitih mateijala.. SPOJ OSOVN GLAVČN
BLOSTJN POSU JV - STZN SPOJ STZN SPOJ zazi za naezanja i omake ko sastavljenih cijevi mogu se abiti ko oačuna steznog soja gje elementi soja mogu biti o istog ili o azličitih mateijala.. SPOJ OSOVN GLAVČN
TRIGONOMETRIJA TROKUTA
 TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
ZAKOVIČNI SPOJEVI su nerastavljivi spojevi dvaju ili više strojnih dijelova ostvareni pomoću zakovica. Zakovice su normirani elementi.
 ZAKOVIČNI SPOJEVI su nerastavljivi spojevi dvaju ili više strojnih dijelova ostvareni pomoću zakovica. Zakovice su normirani elementi. Zakovične spojeve su u strojogradnji, brodogradnji i drugim čeličnim
ZAKOVIČNI SPOJEVI su nerastavljivi spojevi dvaju ili više strojnih dijelova ostvareni pomoću zakovica. Zakovice su normirani elementi. Zakovične spojeve su u strojogradnji, brodogradnji i drugim čeličnim
Zadatak 4b- Dimenzionisanje rožnjače
 Zadatak 4b- Dimenzionisanje rožnjače Rožnjača je statičkog sistema kontinualnog nosača raspona L= 5x6,0m. Usvaja se hladnooblikovani šuplji profil pravougaonog poprečnog preseka. Raster rožnjača: λ r 2.5m
Zadatak 4b- Dimenzionisanje rožnjače Rožnjača je statičkog sistema kontinualnog nosača raspona L= 5x6,0m. Usvaja se hladnooblikovani šuplji profil pravougaonog poprečnog preseka. Raster rožnjača: λ r 2.5m
LOGO ISPITIVANJE MATERIJALA ZATEZANJEM
 LOGO ISPITIVANJE MATERIJALA ZATEZANJEM Vrste opterećenja Ispitivanje zatezanjem Svojstva otpornosti materijala Zatezna čvrstoća Granica tečenja Granica proporcionalnosti Granica elastičnosti Modul
LOGO ISPITIVANJE MATERIJALA ZATEZANJEM Vrste opterećenja Ispitivanje zatezanjem Svojstva otpornosti materijala Zatezna čvrstoća Granica tečenja Granica proporcionalnosti Granica elastičnosti Modul
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
Konstruisanje. Dobro došli na... SREDNJA MAŠINSKA ŠKOLA NOVI SAD DEPARTMAN ZA PROJEKTOVANJE I KONSTRUISANJE
 Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
VIJČANI SPOJ VIJCI HRN M.E2.257 PRIRUBNICA HRN M.E2.258 BRTVA
 VIJČANI SPOJ PRIRUBNICA HRN M.E2.258 VIJCI HRN M.E2.257 BRTVA http://de.wikipedia.org http://de.wikipedia.org Prirubnički spoj cjevovoda na parnom stroju Prirubnički spoj cjevovoda http://de.wikipedia.org
VIJČANI SPOJ PRIRUBNICA HRN M.E2.258 VIJCI HRN M.E2.257 BRTVA http://de.wikipedia.org http://de.wikipedia.org Prirubnički spoj cjevovoda na parnom stroju Prirubnički spoj cjevovoda http://de.wikipedia.org
ZAVARENI SPOJEVI. Definicija (DIN 1910 HRN C.T3001): zavarenih dijelova: zavareni sklop.
 Nastavna jedinica: ZAVARENI SPOJEVI (elementi za spajanje nerastavljivi spojevi) Definicija (DIN 1910 HRN C.T001): Zavareni spoj: spoj komponenata pomoću zavara. Više elemenata međusobno povezanih zavarivanjem:
Nastavna jedinica: ZAVARENI SPOJEVI (elementi za spajanje nerastavljivi spojevi) Definicija (DIN 1910 HRN C.T001): Zavareni spoj: spoj komponenata pomoću zavara. Više elemenata međusobno povezanih zavarivanjem:
Kolegij: Konstrukcije Rješenje zadatka 2. Okno Građevinski fakultet u Zagrebu. Efektivna. Jedinična težina. 1. Glina 18,5 21,
 Kolegij: Konstrukcije 017. Rješenje zadatka. Okno Građevinski fakultet u Zagrebu 1. ULAZNI PARAETRI. RAČUNSKE VRIJEDNOSTI PARAETARA ATERIJALA.1. Karakteristične vrijednosti parametara tla Efektivna Sloj
Kolegij: Konstrukcije 017. Rješenje zadatka. Okno Građevinski fakultet u Zagrebu 1. ULAZNI PARAETRI. RAČUNSKE VRIJEDNOSTI PARAETARA ATERIJALA.1. Karakteristične vrijednosti parametara tla Efektivna Sloj
konst. Električni otpor
 Sveučilište J. J. Strossmayera u sijeku Elektrotehnički fakultet sijek Stručni studij Električni otpor hmov zakon Pri protjecanju struje kroz vodič pojavljuje se otpor. Georg Simon hm je ustanovio ovisnost
Sveučilište J. J. Strossmayera u sijeku Elektrotehnički fakultet sijek Stručni studij Električni otpor hmov zakon Pri protjecanju struje kroz vodič pojavljuje se otpor. Georg Simon hm je ustanovio ovisnost
PRETHODNI PRORACUN VRATILA (dimenzionisanje vratila)
 Predet: Mašinski eleenti Proračun vratila strana Dienzionisati vratilo elektrootora sledecih karakteristika: oinalna snaga P = 3kW roj obrtaja n = 400 in Shea opterecenja: Faktor neravnoernosti K =. F
Predet: Mašinski eleenti Proračun vratila strana Dienzionisati vratilo elektrootora sledecih karakteristika: oinalna snaga P = 3kW roj obrtaja n = 400 in Shea opterecenja: Faktor neravnoernosti K =. F
DIMENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE
 TEORIJA ETONSKIH KONSTRUKCIJA T- DIENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE 3.5 f "2" η y 2 D G N z d y A "" 0 Z a a G - tačka presek koja određje položaj sistemne
TEORIJA ETONSKIH KONSTRUKCIJA T- DIENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE 3.5 f "2" η y 2 D G N z d y A "" 0 Z a a G - tačka presek koja određje položaj sistemne
TABLICE I DIJAGRAMI iz predmeta BETONSKE KONSTRUKCIJE II
 TABLICE I DIJAGRAMI iz predmeta BETONSKE KONSTRUKCIJE II TABLICA 1: PARCIJALNI KOEFICIJENTI SIGURNOSTI ZA DJELOVANJA Parcijalni koeficijenti sigurnosti γf Vrsta djelovanja Djelovanje Stalno Promjenjivo
TABLICE I DIJAGRAMI iz predmeta BETONSKE KONSTRUKCIJE II TABLICA 1: PARCIJALNI KOEFICIJENTI SIGURNOSTI ZA DJELOVANJA Parcijalni koeficijenti sigurnosti γf Vrsta djelovanja Djelovanje Stalno Promjenjivo
35(7+2'1,3525$&8195$7,/$GLPHQ]LRQLVDQMHYUDWLOD
![35(7+2'1,3525$&8195$7,/$GLPHQ]LRQLVDQMHYUDWLOD 35(7+2'1,3525$&8195$7,/$GLPHQ]LRQLVDQMHYUDWLOD](/thumbs/60/45174330.jpg) Predmet: Mašinski elementi Proraþun vratila strana 1 Dimenzionisati vratilo elektromotora sledecih karakteristika: ominalna snaga P 3kW Broj obrtaja n 14 min 1 Shema opterecenja: Faktor neravnomernosti
Predmet: Mašinski elementi Proraþun vratila strana 1 Dimenzionisati vratilo elektromotora sledecih karakteristika: ominalna snaga P 3kW Broj obrtaja n 14 min 1 Shema opterecenja: Faktor neravnomernosti
4. STATIČKI PRORAČUN STUBIŠTA
 JBG 4. STTIČKI PRORČUN STUBIŠT PROGR IZ KOLEGIJ BETONSKE I ZIDNE KONSTRUKCIJE 9 6 5 5 SVEUČILIŠTE U ZGREBU JBG 4. Statiči proračun stubišta 4.. Stubišni ra 4... naliza opterećenja 5 5 4 6 8 0 Slia 4..
JBG 4. STTIČKI PRORČUN STUBIŠT PROGR IZ KOLEGIJ BETONSKE I ZIDNE KONSTRUKCIJE 9 6 5 5 SVEUČILIŠTE U ZGREBU JBG 4. Statiči proračun stubišta 4.. Stubišni ra 4... naliza opterećenja 5 5 4 6 8 0 Slia 4..
Vrijedi: OD 20. LIPNJA Lindab CJENiK Cijene su izražene u KN exw Lučko Zagreb, bez PDV-a; Cjenik vrijedi od
 Vrijedi: OD 20 LIPNJA 2012 Lindab CJENiK 2012 Sustav za odvodnju oborinskih voda i dodaci Lindab Elite sustav zaštite proizvoda >>> 3 Lindab Rainline Lindab Elite R Žlijeb Duljina: 4 m i 6 m 190 Elite
Vrijedi: OD 20 LIPNJA 2012 Lindab CJENiK 2012 Sustav za odvodnju oborinskih voda i dodaci Lindab Elite sustav zaštite proizvoda >>> 3 Lindab Rainline Lindab Elite R Žlijeb Duljina: 4 m i 6 m 190 Elite
Numerička matematika 2. kolokvij (1. srpnja 2009.)
 Numerička matematika 2. kolokvij (1. srpnja 29.) Zadatak 1 (1 bodova.) Teorijsko pitanje. (A) Neka je G R m n, uz m n, pravokutna matrica koja ima puni rang po stupcima, tj. rang(g) = n. (a) Napišite puni
Numerička matematika 2. kolokvij (1. srpnja 29.) Zadatak 1 (1 bodova.) Teorijsko pitanje. (A) Neka je G R m n, uz m n, pravokutna matrica koja ima puni rang po stupcima, tj. rang(g) = n. (a) Napišite puni
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
ANALIZA DJELOVANJA (OPTEREĆENJA) - EUROKOD
 GRAĐEVINSKO - ARHITEKTONSKI FAKULTET Katedra za metalne i drvene konstrukcije Kolegij: METALNE KONSTRUKCIJE ANALIZA DJELOVANJA (OPTEREĆENJA) - EUROKOD TLOCRTNI PRIKAZ NOSIVOG SUSTAVA OBJEKTA 2 PRORAČUN
GRAĐEVINSKO - ARHITEKTONSKI FAKULTET Katedra za metalne i drvene konstrukcije Kolegij: METALNE KONSTRUKCIJE ANALIZA DJELOVANJA (OPTEREĆENJA) - EUROKOD TLOCRTNI PRIKAZ NOSIVOG SUSTAVA OBJEKTA 2 PRORAČUN
Proračun potrebne glavne snage rezanja i glavnog strojnog vremena obrade
 Zaod a tehnologiju Katedra a alatne strojee Proračun potrebne glane snage reanja i glanog strojnog remena obrade Sadržaj aj ježbe be: Proračun snage kod udužnog anjskog tokarenja Glano strojno rijeme kod
Zaod a tehnologiju Katedra a alatne strojee Proračun potrebne glane snage reanja i glanog strojnog remena obrade Sadržaj aj ježbe be: Proračun snage kod udužnog anjskog tokarenja Glano strojno rijeme kod
BIPOLARNI TRANZISTOR Auditorne vježbe
 BPOLARN TRANZSTOR Auditorne vježbe Struje normalno polariziranog bipolarnog pnp tranzistora: p n p p - p n B0 struja emitera + n B + - + - U B B U B struja kolektora p + B0 struja baze B n + R - B0 gdje
BPOLARN TRANZSTOR Auditorne vježbe Struje normalno polariziranog bipolarnog pnp tranzistora: p n p p - p n B0 struja emitera + n B + - + - U B B U B struja kolektora p + B0 struja baze B n + R - B0 gdje
BETONSKE KONSTRUKCIJE 2
 BETONSE ONSTRUCIJE 2 vježbe, 31.10.2017. 31.10.2017. DATUM SATI TEMATSA CJELINA 10.- 11.10.2017. 2 17.-18.10.2017. 2 24.-25.10.2017. 2 31.10.- 1.11.2017. uvod ponljanje poznatih postupaka dimenzioniranja
BETONSE ONSTRUCIJE 2 vježbe, 31.10.2017. 31.10.2017. DATUM SATI TEMATSA CJELINA 10.- 11.10.2017. 2 17.-18.10.2017. 2 24.-25.10.2017. 2 31.10.- 1.11.2017. uvod ponljanje poznatih postupaka dimenzioniranja
Geometrijske karakteristike poprenih presjeka nosaa. 9. dio
 Geometrijske karakteristike poprenih presjeka nosaa 9. dio 1 Sile presjeka (unutarnje sile): Udužna sila N Poprena sila T Moment uvijanja M t Moment savijanja M Napreanja 1. Normalno napreanje σ. Posmino
Geometrijske karakteristike poprenih presjeka nosaa 9. dio 1 Sile presjeka (unutarnje sile): Udužna sila N Poprena sila T Moment uvijanja M t Moment savijanja M Napreanja 1. Normalno napreanje σ. Posmino
Riješeni zadaci: Limes funkcije. Neprekidnost
 Riješeni zadaci: Limes funkcije. Neprekidnost Limes funkcije Neka je 0 [a, b] i f : D R, gdje je D = [a, b] ili D = [a, b] \ { 0 }. Kažemo da je es funkcije f u točki 0 jednak L i pišemo f ) = L, ako za
Riješeni zadaci: Limes funkcije. Neprekidnost Limes funkcije Neka je 0 [a, b] i f : D R, gdje je D = [a, b] ili D = [a, b] \ { 0 }. Kažemo da je es funkcije f u točki 0 jednak L i pišemo f ) = L, ako za
METALNE KONSTRUKCIJE ZGRADA
 METALNE KONSTRUKCIJE ZGRADA 1 Skr. predmeta i red. br. teme Dodatne napomene objašnjenja uputstva RASPORED SADRŽAJA NA SLAJDOVIMA NASLOV TEME PODNASLOVI Osnovni sadržaj. Važniji pojmovi i sadržaji su štampani
METALNE KONSTRUKCIJE ZGRADA 1 Skr. predmeta i red. br. teme Dodatne napomene objašnjenja uputstva RASPORED SADRŽAJA NA SLAJDOVIMA NASLOV TEME PODNASLOVI Osnovni sadržaj. Važniji pojmovi i sadržaji su štampani
Izravni posmik. Posmična čvrstoća tla. Laboratorijske metode određivanja kriterija čvratoće ( c i φ )
 Posmična čvrstoća tla Posmična se čvrstoća se često prikazuje Mohr-Coulombovim kriterijem čvrstoće u - σ dijagramu c + σ n tanφ Kriterij čvrstoće C-kohezija φ -kut trenja c + σ n tan φ φ c σ n Posmična
Posmična čvrstoća tla Posmična se čvrstoća se često prikazuje Mohr-Coulombovim kriterijem čvrstoće u - σ dijagramu c + σ n tanφ Kriterij čvrstoće C-kohezija φ -kut trenja c + σ n tan φ φ c σ n Posmična
6. Plan armature prednapetog nosača
 6. Plan armature prednapetog nosača 6.1. Rekapitulacija odabrane armature Prednapeta armatura odabrano:3 natege 6812 Uzdužna nenapeta armatura. u polju donji rub nosača (mjerodavna je provjera nosivosti
6. Plan armature prednapetog nosača 6.1. Rekapitulacija odabrane armature Prednapeta armatura odabrano:3 natege 6812 Uzdužna nenapeta armatura. u polju donji rub nosača (mjerodavna je provjera nosivosti
( ) p a. poklopac. Rješenje:
 5 VJEŽB - RIJEŠENI ZDI IZ MENIKE LUID 1 1 Treb odrediti silu koj drži u rvnoteži poklopc B jedinične širine, zlobno vezn u točki, u položju prem slici Zdno je : =0,84 m; =0,65 m; =5,5 cm; =999 k/m B p
5 VJEŽB - RIJEŠENI ZDI IZ MENIKE LUID 1 1 Treb odrediti silu koj drži u rvnoteži poklopc B jedinične širine, zlobno vezn u točki, u položju prem slici Zdno je : =0,84 m; =0,65 m; =5,5 cm; =999 k/m B p
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
PT ISPITIVANJE PENETRANTIMA
 FSB Sveučilišta u Zagrebu Zavod za kvalitetu Katedra za nerazorna ispitivanja PT ISPITIVANJE PENETRANTIMA Josip Stepanić SADRŽAJ kapilarni učinak metoda ispitivanja penetrantima uvjeti promatranja SADRŽAJ
FSB Sveučilišta u Zagrebu Zavod za kvalitetu Katedra za nerazorna ispitivanja PT ISPITIVANJE PENETRANTIMA Josip Stepanić SADRŽAJ kapilarni učinak metoda ispitivanja penetrantima uvjeti promatranja SADRŽAJ
SVEUČILIŠTE U MOSTARU GRAĐEVINSKI FAKULTET
 SVEUČILIŠTE U MOSTRU GRĐEVINSKI FKULTET Kolegij: Osnove betonskih konstrukcija k. 013/014 god. 8. pismeni (dodatni) ispit - 10.10.014. god. Zadatak 1 Dimenzionirati i prikazati raspored usvojene armature
SVEUČILIŠTE U MOSTRU GRĐEVINSKI FKULTET Kolegij: Osnove betonskih konstrukcija k. 013/014 god. 8. pismeni (dodatni) ispit - 10.10.014. god. Zadatak 1 Dimenzionirati i prikazati raspored usvojene armature
Akvizicija tereta. 5660t. Y= masa drva, X=masa cementa. Na brod će se ukrcati 1733 tona drva i 3927 tona cementa.
 Akvizicija tereta. Korisna nosivost broda je 6 t, a na brodu ia 8 cu. ft. prostora raspoloživog za sještaj tereta pod palubu. Navedeni brod treba krcati drvo i ceent, a na palubu ože aksialno ukrcati 34
Akvizicija tereta. Korisna nosivost broda je 6 t, a na brodu ia 8 cu. ft. prostora raspoloživog za sještaj tereta pod palubu. Navedeni brod treba krcati drvo i ceent, a na palubu ože aksialno ukrcati 34
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri
 Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Zdaci iz trigonometrije trokuta Izračunaj ostale elemente trokuta pomoću zadanih:
 Zdaci iz trigonometrije trokuta... 1. Izračunaj ostale elemente trokuta pomoću zadanih: a) a = 1 cm, α = 66, β = 5 ; b) a = 7.3 cm, β =86, γ = 51 ; c) b = 13. cm, α =1 48`, β =13 4`; d) b = 44.5 cm, α
Zdaci iz trigonometrije trokuta... 1. Izračunaj ostale elemente trokuta pomoću zadanih: a) a = 1 cm, α = 66, β = 5 ; b) a = 7.3 cm, β =86, γ = 51 ; c) b = 13. cm, α =1 48`, β =13 4`; d) b = 44.5 cm, α
ZASTORI SUNSET CURTAIN Kućište od željeza zaštićeno epoksidnim prahom, opruge od željeza. Lako i brzo se montiraju.
 ZSTORI ZSTORI SUNSET URTIN Kućište od željeza zaštićeno epoksidnim prahom, opruge od željeza. Lako i brzo se montiraju. ŠIRIN (mm) VISIN (mm) Z PROZOR IM. (mm) TV25 40360 360 400 330x330 TV25 50450 450
ZSTORI ZSTORI SUNSET URTIN Kućište od željeza zaštićeno epoksidnim prahom, opruge od željeza. Lako i brzo se montiraju. ŠIRIN (mm) VISIN (mm) Z PROZOR IM. (mm) TV25 40360 360 400 330x330 TV25 50450 450
PRIJENOS i DISTRIBUCIJA ELEKTRIČNE ENERGIJE
 TEHNČK FAKULTET SVEUČLŠTA U RJEC Sveučilišni diplomski studij elektrotehnike PRJENOS i DSTRBUCJA ELEKTRČNE ENERGJE 1. KONSTRUKCJSK RAD - ZBOR PRESJEKA ELEKTROENERGETSKOG KABELA Kabelskim elektroenergetskim
TEHNČK FAKULTET SVEUČLŠTA U RJEC Sveučilišni diplomski studij elektrotehnike PRJENOS i DSTRBUCJA ELEKTRČNE ENERGJE 1. KONSTRUKCJSK RAD - ZBOR PRESJEKA ELEKTROENERGETSKOG KABELA Kabelskim elektroenergetskim
GEOTEHNIČKO INŽENJERSTVO
 GEOTEHNIČKO INŽENJERSTVO POMOĆNI DIJAGRAMI, TABLICE I FORMULE ZA ISPIT dopunjeno za ak.god. 016/017 Slika 1. Parcijalni koeficijenti za GEO/STR za djelovanja, parametre materijala i otpore prema EC-7 Slika.
GEOTEHNIČKO INŽENJERSTVO POMOĆNI DIJAGRAMI, TABLICE I FORMULE ZA ISPIT dopunjeno za ak.god. 016/017 Slika 1. Parcijalni koeficijenti za GEO/STR za djelovanja, parametre materijala i otpore prema EC-7 Slika.
7. Proračun nosača naprezanih poprečnim silama
 5. ožujka 2018. 7. Proračun nosača naprezanih poprečnim silama Primjer sloma zbog djelovanja poprečne sile SLIKA 1. T- nosač slomljen djelovanjem poprečne sile Do sloma armirano-betonske grede uslijed
5. ožujka 2018. 7. Proračun nosača naprezanih poprečnim silama Primjer sloma zbog djelovanja poprečne sile SLIKA 1. T- nosač slomljen djelovanjem poprečne sile Do sloma armirano-betonske grede uslijed
MEHANIČKE KARAKTERISTIKE ČELIKA
 Pitanja iz Metalnih konstrukcija za usmeni deo ispita Prvi i drugi deo Osnovne osobine čelika koje se moraju znati bez obzira na pitanja MEHANIČKE KARAKTERISTIKE ČELIKA Najvažnije karakteristike za proračun
Pitanja iz Metalnih konstrukcija za usmeni deo ispita Prvi i drugi deo Osnovne osobine čelika koje se moraju znati bez obzira na pitanja MEHANIČKE KARAKTERISTIKE ČELIKA Najvažnije karakteristike za proračun
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
UZDUŽNA DINAMIKA VOZILA
 UZDUŽNA DINAMIKA VOZILA MODEL VOZILA U UZDUŽNOJ DINAMICI Zanemaruju se sva pomeranja u pravcima normalnim na pravac kretanja (ΣZ i = 0, ΣY i = 0) Zanemaruju se svi vidovi pobuda na oscilovanje i vibracije,
UZDUŽNA DINAMIKA VOZILA MODEL VOZILA U UZDUŽNOJ DINAMICI Zanemaruju se sva pomeranja u pravcima normalnim na pravac kretanja (ΣZ i = 0, ΣY i = 0) Zanemaruju se svi vidovi pobuda na oscilovanje i vibracije,
TOLERANCIJE I DOSJEDI
 11.2012. VELEUČILIŠTE U RIJECI Prometni odjel OSNOVE STROJARSTVA TOLERANCIJE I DOSJEDI 1 Tolerancije dimenzija Nijednu dimenziju nije moguće izraditi savršeno točno, bez ikakvih odstupanja. Stoga, kada
11.2012. VELEUČILIŠTE U RIJECI Prometni odjel OSNOVE STROJARSTVA TOLERANCIJE I DOSJEDI 1 Tolerancije dimenzija Nijednu dimenziju nije moguće izraditi savršeno točno, bez ikakvih odstupanja. Stoga, kada
MATERIJALI I MEHANIČKA SVOJSTVA MATERIJALA. Prof. dr. sc. Ivica Kladarić
 MATERIJALI I MEHANIČKA SVOJSTVA MATERIJALA Statički vlačni pokus Prof. dr. sc. Ivica Kladarić 1 UVOD Metalni materijali najviše se upotrebljavaju u tehničkoj praksi zbog povoljnih mehaničkih, tehnoloških,
MATERIJALI I MEHANIČKA SVOJSTVA MATERIJALA Statički vlačni pokus Prof. dr. sc. Ivica Kladarić 1 UVOD Metalni materijali najviše se upotrebljavaju u tehničkoj praksi zbog povoljnih mehaničkih, tehnoloških,
4. STATIČKI PRORAČUN STUBIŠTA
 JBAG 4. STATIČKI PRORAČUN STUBIŠTA PROGRA IZ KOLEGIJA BETONSKE I ZIDANE KONSTRUKCIJE 9 5 SVEUČILIŠTE U ZAGREBU JBAG 4. Statiči proračun stubišta 4.. Stubišni ra 4... Analiza opterećenja 5 5 4 6 8 5 6 0
JBAG 4. STATIČKI PRORAČUN STUBIŠTA PROGRA IZ KOLEGIJA BETONSKE I ZIDANE KONSTRUKCIJE 9 5 SVEUČILIŠTE U ZAGREBU JBAG 4. Statiči proračun stubišta 4.. Stubišni ra 4... Analiza opterećenja 5 5 4 6 8 5 6 0
zastori sunset curtain Kućište od željeza zaštićeno epoksidnim prahom, opruge od željeza. Lako i brzo se montiraju.
 zastori zastori sunset curtain Kućište od željeza zaštićeno epoksidnim prahom, opruge od željeza. Lako i brzo se montiraju. (mm) (mm) za PROZOR im (mm) tv25 40360 360 400 330x330 tv25 50450 450 500 410x410
zastori zastori sunset curtain Kućište od željeza zaštićeno epoksidnim prahom, opruge od željeza. Lako i brzo se montiraju. (mm) (mm) za PROZOR im (mm) tv25 40360 360 400 330x330 tv25 50450 450 500 410x410
Funkcije dviju varjabli (zadaci za vježbu)
 Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
Priveznice W re r R e o R p o e p S e l S ing n s
 Priveznice Wire Rope Slings PRIVEZNICE OD ČEIČNO UŽEA (RAE) jenosruke SINE WIRE ROPE SINS Sanar EN P P P P P P P P P P P P ozvoljeno operećenje kg elemeni priveznice prekina jenokrako vešanje ) ouvaanje
Priveznice Wire Rope Slings PRIVEZNICE OD ČEIČNO UŽEA (RAE) jenosruke SINE WIRE ROPE SINS Sanar EN P P P P P P P P P P P P ozvoljeno operećenje kg elemeni priveznice prekina jenokrako vešanje ) ouvaanje
Srednjenaponski izolatori
 Srednjenaponski izolatori Linijski potporni izolatori tip R-ET Komercijalni naziv LPI 24 N ET 1) LPI 24 L ET/5 1)2) LPI 24 L ET/6 1)2) LPI 38 L ET 1) Oznaka prema IEC 720 R 12,5 ET 125 N R 12,5 ET 125
Srednjenaponski izolatori Linijski potporni izolatori tip R-ET Komercijalni naziv LPI 24 N ET 1) LPI 24 L ET/5 1)2) LPI 24 L ET/6 1)2) LPI 38 L ET 1) Oznaka prema IEC 720 R 12,5 ET 125 N R 12,5 ET 125
ČELIČNA UŽAD 6 X 7 + T.J. = 42 6 X 7 + J.J. = 49. Ø 1,5-20 mm 6 X 19 + T.J. = X 19 + J.J. = 133. Ø 3-30 mm
 ČELIČNA UŽAD STANDARD - OPIS Broj žica dimenzije DIN 3053 19 Ø 1-10 mm DIN 3054 37 Ø 3-10 mm DIN 3055 6 X 7 + T.J. = 42 6 X 7 + J.J. = 49 Ø 1,5-20 mm DIN 3060 6 X 19 + T.J. = 114 6 X 19 + J.J. = 133 Ø
ČELIČNA UŽAD STANDARD - OPIS Broj žica dimenzije DIN 3053 19 Ø 1-10 mm DIN 3054 37 Ø 3-10 mm DIN 3055 6 X 7 + T.J. = 42 6 X 7 + J.J. = 49 Ø 1,5-20 mm DIN 3060 6 X 19 + T.J. = 114 6 X 19 + J.J. = 133 Ø
PRILOG. Tab. 1.a. Dozvoljena trajna opterećenja bakarnih pravougaonih profila u(a) za θ at =35 C i θ=30 C, (θ tdt =65 C)
 PRILOG Tab. 1.a. Dozvoljena trajna opterećenja bakarnih pravougaonih profila u(a) za θ at =35 C i θ=30 C, (θ tdt =65 C) Tab 3. Vrednosti sačinilaca α i β za tipične konstrukcije SN-sabirnica Tab 4. Minimalni
PRILOG Tab. 1.a. Dozvoljena trajna opterećenja bakarnih pravougaonih profila u(a) za θ at =35 C i θ=30 C, (θ tdt =65 C) Tab 3. Vrednosti sačinilaca α i β za tipične konstrukcije SN-sabirnica Tab 4. Minimalni
Glavni elementi postrojenja Sabirnice
 su okosnica svakog rasklopnog postrojenja. One povezuju vodove koji dovode i odvode električnu energiju te transformatore koji povezuju mreže različitih naponskih razina. Sabirnički vodiči su najčešće
su okosnica svakog rasklopnog postrojenja. One povezuju vodove koji dovode i odvode električnu energiju te transformatore koji povezuju mreže različitih naponskih razina. Sabirnički vodiči su najčešće
Proizvoljno opterećenje tijela može zahtijevati složenu analizu naprezanja i deformacija,
 1. Osnove čvrstoće 1.1. Pojam i vrste opterećenja Nauka o čvrstoći proučava utjecaj vanjskih sila i momenata na ponašanje čvrstih (realnih) tijela. Djelovanje vanjskih sila i momenata na tijelo naziva
1. Osnove čvrstoće 1.1. Pojam i vrste opterećenja Nauka o čvrstoći proučava utjecaj vanjskih sila i momenata na ponašanje čvrstih (realnih) tijela. Djelovanje vanjskih sila i momenata na tijelo naziva
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
STATIČKI PRORAČUN KROVIŠTA SA DVOSTRUKOM STOLICOM
 STATIČKI PRORAČUN KROVIŠTA SA DVOSTRUKOM STOLICOM Autor: Ivan Volarić, struč. spec. ing. aedif. Zagreb, Siječanj 2017. TEHNIČKI OPIS KONSTRUKCIJE OPIS PROJEKTNOG ZADATKA Projektni zadatak prema kojem je
STATIČKI PRORAČUN KROVIŠTA SA DVOSTRUKOM STOLICOM Autor: Ivan Volarić, struč. spec. ing. aedif. Zagreb, Siječanj 2017. TEHNIČKI OPIS KONSTRUKCIJE OPIS PROJEKTNOG ZADATKA Projektni zadatak prema kojem je
Zadatak 003 (Vesna, osnovna škola) Kolika je težina tijela koje savladava silu trenja 30 N, ako je koeficijent trenja 0.5?
 Zadata 00 (Jasna, osnovna šola) Kolia je težina tijela ase 400 g? Rješenje 00 Masa tijela izražava se u ilograia pa najprije orao 400 g pretvoriti u ilograe. Budući da g = 000 g, orao 400 g podijeliti
Zadata 00 (Jasna, osnovna šola) Kolia je težina tijela ase 400 g? Rješenje 00 Masa tijela izražava se u ilograia pa najprije orao 400 g pretvoriti u ilograe. Budući da g = 000 g, orao 400 g podijeliti
SEKUNDARNE VEZE međumolekulske veze
 PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
PRORAČUN ČVRSTOĆE POSUDE POD TLAKOM. Marina MALINOVEC PUČEK
 PRORAČUN ČVRSTOĆE POSUDE POD TLAKOM Marina MALINOVEC PUČEK PRORAČUN ČVRSTOĆE roisan za POSUDE POD TLAKOM definiranje oterećenja NORME rezultat roračuna AD Merkblatt HRN DIN EN 13445-3 1) DIN EN 12952-3
PRORAČUN ČVRSTOĆE POSUDE POD TLAKOM Marina MALINOVEC PUČEK PRORAČUN ČVRSTOĆE roisan za POSUDE POD TLAKOM definiranje oterećenja NORME rezultat roračuna AD Merkblatt HRN DIN EN 13445-3 1) DIN EN 12952-3
UVOD U TEORIJU ELASTIČNOSTI
 1. UVOD U TEORIJU EASTIČNOSTI 1 1.1 Uvod... 1-1 1.2 Naprezanje i deformacija. Modul elastičnosti... 1-2 Mikroskopski opis elastičnosti... 1-2 Elastičnost - makroskopski prikaz... 1-3 1.3 Istezanje - naprezanje
1. UVOD U TEORIJU EASTIČNOSTI 1 1.1 Uvod... 1-1 1.2 Naprezanje i deformacija. Modul elastičnosti... 1-2 Mikroskopski opis elastičnosti... 1-2 Elastičnost - makroskopski prikaz... 1-3 1.3 Istezanje - naprezanje
BETONSKE KONSTRUKCIJE 3 M 1/r dijagrami
 BETONSKE KONSTRUKCIJE 3 M 1/r dijagrami Izv. prof. dr.. Tomilav Kišiček dipl. ing. građ. 0.10.014. Betonke kontrukije III 1 NBK1.147 Slika 5.4 Proračunki dijagrami betona razreda od C1/15 do C90/105, lijevo:
BETONSKE KONSTRUKCIJE 3 M 1/r dijagrami Izv. prof. dr.. Tomilav Kišiček dipl. ing. građ. 0.10.014. Betonke kontrukije III 1 NBK1.147 Slika 5.4 Proračunki dijagrami betona razreda od C1/15 do C90/105, lijevo:
ZAVARENI SPOJEVI (elementi za spajanje nerastavljivi spojevi)
 ZAVARENI SPOJEVI (elementi za spajanje nerastavljivi spojevi) Zavarivanje = spajanje dijelova koji su na mjestu spoja dovođenjem topline omekšani ili rastopljeni, uz dodavanje dodatnog materijala ili bez
ZAVARENI SPOJEVI (elementi za spajanje nerastavljivi spojevi) Zavarivanje = spajanje dijelova koji su na mjestu spoja dovođenjem topline omekšani ili rastopljeni, uz dodavanje dodatnog materijala ili bez
Vrijedi relacija: Suma kvadrata cosinusa priklonih kutova sile prema koordinatnim osima jednaka je jedinici.
 Za adani sustav prostornih sila i j k () oktant i j k () oktant koje djeluju na materijalnu toku odredite: a) reultantu silu? b) ravnotežnu silu? a) eultanta sila? i j k 8 Vektor reultante: () i 8 j k
Za adani sustav prostornih sila i j k () oktant i j k () oktant koje djeluju na materijalnu toku odredite: a) reultantu silu? b) ravnotežnu silu? a) eultanta sila? i j k 8 Vektor reultante: () i 8 j k
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
 Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
RIJEŠENI ZADACI I TEORIJA IZ
 RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
Cenovnik spiro kanala i opreme - FON Inžinjering D.O.O.
 Cenovnik spiro kanala i opreme - *Cenovnik ažuriran 09.02.2018. Spiro kolena: Prečnik - Φ (mm) Spiro kanal ( /m) 90 45 30 Muf/nipli: Cevna obujmica: Brza diht spojnica: Elastična konekcija: /kom: Ø100
Cenovnik spiro kanala i opreme - *Cenovnik ažuriran 09.02.2018. Spiro kolena: Prečnik - Φ (mm) Spiro kanal ( /m) 90 45 30 Muf/nipli: Cevna obujmica: Brza diht spojnica: Elastična konekcija: /kom: Ø100
PRORAČUN REMENSKIH PRIJENOSA
 FAKULTET ELEKTROTEHNIKE, STROJARSTVA I BRODOGRADNJE SPLIT Damir Jelaska Srđan Podrug PRORAČUN REMENSKIH PRIJENOSA (Uputstvo) Split, siječanj 00. . UPUTSVO ZA PRORAČUN PRIJENOSA SA PLOSNATIM REMENOM Zadatak:
FAKULTET ELEKTROTEHNIKE, STROJARSTVA I BRODOGRADNJE SPLIT Damir Jelaska Srđan Podrug PRORAČUN REMENSKIH PRIJENOSA (Uputstvo) Split, siječanj 00. . UPUTSVO ZA PRORAČUN PRIJENOSA SA PLOSNATIM REMENOM Zadatak:
VAŽNO. Posmino naprezanje τ
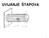 UVIJANJE ŠTAPOVA 1 VAŽNO Posmino naprezanje τ τ ρ I o 2 aksimalno posmino naprezanja τ za: ρ r d 2 τ maks W 0 3 Polarni momen romosi: I o 4 d π 32 [ ] 4 cm Polarni momen opora: W o 3 d π 16 cm [ ] 3 4
UVIJANJE ŠTAPOVA 1 VAŽNO Posmino naprezanje τ τ ρ I o 2 aksimalno posmino naprezanja τ za: ρ r d 2 τ maks W 0 3 Polarni momen romosi: I o 4 d π 32 [ ] 4 cm Polarni momen opora: W o 3 d π 16 cm [ ] 3 4
ISPITNA PITANJA IZ PREDMETA METALNE I DRVENE KONSTRUKCIJE deo 1 Opšti deo i spojna sredstva
 ISPITNA PITANJA IZ PREDMETA METALNE I DRVENE KONSTRUKCIJE deo 1 Opšti deo i spojna sredstva 1. KARAKTERISTIKE METALNIH KONSTRUKCIJA (istorijat, prednosti i nedostaci, primena) Metalne konstrukcije u građevinarstvu
ISPITNA PITANJA IZ PREDMETA METALNE I DRVENE KONSTRUKCIJE deo 1 Opšti deo i spojna sredstva 1. KARAKTERISTIKE METALNIH KONSTRUKCIJA (istorijat, prednosti i nedostaci, primena) Metalne konstrukcije u građevinarstvu
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
Zavod za tehnologiju, Katedra za alatne strojeve: GLODANJE
 Glodanje je postupak obrade odvajanjem čestica (rezanjem) obradnih površina proizvoljnih oblika. Izvodi se na alatnim strojevima, glodalicama, pri čemu je glavno (rezno) gibanje kružno kontinuirano i pridruženo
Glodanje je postupak obrade odvajanjem čestica (rezanjem) obradnih površina proizvoljnih oblika. Izvodi se na alatnim strojevima, glodalicama, pri čemu je glavno (rezno) gibanje kružno kontinuirano i pridruženo
( ) π. I slučaj-štap sa zglobovima na krajevima F. Opšte rešenje diferencijalne jednačine (1): min
 Kritična sia izvijanja Kritična sia je ona najmanja vrednost sie pritisa pri ojoj nastupa gubita stabinosti, odnosno, pri ojoj štap iz stabine pravoinijse forme ravnoteže preazi u nestabinu rivoinijsu
Kritična sia izvijanja Kritična sia je ona najmanja vrednost sie pritisa pri ojoj nastupa gubita stabinosti, odnosno, pri ojoj štap iz stabine pravoinijse forme ravnoteže preazi u nestabinu rivoinijsu
Q (promjenjivo) P (stalno) c uk=50 (kn/m ) =17 (kn/m ) =20 (kn/m ) 2k=0 (kn/m ) N 60=21 d=0.9 (m)
 L = L 14.1. ZADATAK Zadan je pilot kružnog poprečnog presjeka, postavljen kroz dva sloja tla. Svojstva tla i dimenzije pilota su zadane na skici. a) Odrediti graničnu nosivost pilota u vertikalnom smjeru.
L = L 14.1. ZADATAK Zadan je pilot kružnog poprečnog presjeka, postavljen kroz dva sloja tla. Svojstva tla i dimenzije pilota su zadane na skici. a) Odrediti graničnu nosivost pilota u vertikalnom smjeru.
ČVRSTOĆA 13. GEOMETRIJSKE KARAKTERISTIKE RAVNIH PRESJEKA ŠTAPA
 ČVRSTOĆA 13. GEOMETRIJSKE KARAKTERISTIKE RAVNIH PRESJEKA ŠTAPA STATIČKI MOMENTI I MOMENTI INERCIJE RAVNIH PLOHA Kao što pri aksijalnom opterećenju štapa apsolutna vrijednost naprezanja zavisi, između ostalog,
ČVRSTOĆA 13. GEOMETRIJSKE KARAKTERISTIKE RAVNIH PRESJEKA ŠTAPA STATIČKI MOMENTI I MOMENTI INERCIJE RAVNIH PLOHA Kao što pri aksijalnom opterećenju štapa apsolutna vrijednost naprezanja zavisi, između ostalog,
DINAMIČKA MEHANIČKA ANALIZA (DMA)
 Karakterizacija materijala DINAMIČKA MEHANIČKA ANALIZA (DMA) Dr.sc.Emi Govorčin Bajsić,izv.prof. Zavod za polimerno inženjerstvo i organsku kemijsku tehnologiju Da li je DMA toplinska analiza ili reologija?
Karakterizacija materijala DINAMIČKA MEHANIČKA ANALIZA (DMA) Dr.sc.Emi Govorčin Bajsić,izv.prof. Zavod za polimerno inženjerstvo i organsku kemijsku tehnologiju Da li je DMA toplinska analiza ili reologija?
1 - KROVNA KONSTRUKCIJA : * krovni pokrivač, daska, letva: = 0,60 kn/m 2 * sneg, vetar : = 1,00 kn/m 2
 OPTEREĆENJE KROVNE KONSTRUKCIJE : * krovni pokrivač, daska, letva: = 0,60 kn/m 2 * sneg, vetar : = 1,00 kn/m 2 1.1. ROGOVI : * nagib krovne ravni : α = 35 º * razmak rogova : λ = 80 cm 1.1.1. STATIČKI
OPTEREĆENJE KROVNE KONSTRUKCIJE : * krovni pokrivač, daska, letva: = 0,60 kn/m 2 * sneg, vetar : = 1,00 kn/m 2 1.1. ROGOVI : * nagib krovne ravni : α = 35 º * razmak rogova : λ = 80 cm 1.1.1. STATIČKI
Elektrodinamika ( ) ELEKTRODINAMIKA Q t l R = ρ R R R R = W = U I t P = U I
 Elektrodinamika ELEKTRODINAMIKA Jakost električnog struje I definiramo kao količinu naboja Q koja u vremenu t prođe kroz presjek vodiča: Q I = t Gustoća struje J je omjer jakosti struje I i površine presjeka
Elektrodinamika ELEKTRODINAMIKA Jakost električnog struje I definiramo kao količinu naboja Q koja u vremenu t prođe kroz presjek vodiča: Q I = t Gustoća struje J je omjer jakosti struje I i površine presjeka
Tip ureappleaja: ecovit Jedinice VKK 226 VKK 286 VKK 366 VKK 476 VKK 656
 TehniËki podaci Tip ureappeaja: ecovit Jedinice VKK 226 VKK 286 VKK 366 VKK 476 VKK 66 Nazivna topotna snaga (na /),122,,28, 7,436,,47,6 1,16,7 Nazivna topotna snaga (na 60/) 4,21,,621, 7,23,,246,4 14,663,2
TehniËki podaci Tip ureappeaja: ecovit Jedinice VKK 226 VKK 286 VKK 366 VKK 476 VKK 66 Nazivna topotna snaga (na /),122,,28, 7,436,,47,6 1,16,7 Nazivna topotna snaga (na 60/) 4,21,,621, 7,23,,246,4 14,663,2
Rijeseni neki zadaci iz poglavlja 4.5
 Rijeseni neki zdci iz poglvlj 4.5 Prije rijesvnj zdtk prisjetimo se itnih stvri koje ce ns prtiti tijekom njihovog promtrnj. Definicij: (Trigonometrij prvokutnog trokut) ktet nsuprot kut ϕ sin ϕ hipotenuz
Rijeseni neki zdci iz poglvlj 4.5 Prije rijesvnj zdtk prisjetimo se itnih stvri koje ce ns prtiti tijekom njihovog promtrnj. Definicij: (Trigonometrij prvokutnog trokut) ktet nsuprot kut ϕ sin ϕ hipotenuz
SVEUČILIŠTE U ZAGREBU FAKULTET STROJARSTVA I BRODOGRADNJE ZAVRŠNI RAD. Marko Džoić. Zagreb, 2012.
 SVEUČILIŠTE U ZAGREBU FAKULTET STROJARSTVA I BRODOGRADNJE ZAVRŠNI RAD Marko Džoić Zagreb, 01. SVEUČILIŠTE U ZAGREBU FAKULTET STROJARSTVA I BRODOGRADNJE ZAVRŠNI RAD Mentor: Doc. dr. sc. Dragan Žeželj Student:
SVEUČILIŠTE U ZAGREBU FAKULTET STROJARSTVA I BRODOGRADNJE ZAVRŠNI RAD Marko Džoić Zagreb, 01. SVEUČILIŠTE U ZAGREBU FAKULTET STROJARSTVA I BRODOGRADNJE ZAVRŠNI RAD Mentor: Doc. dr. sc. Dragan Žeželj Student:
ISPIT GRUPA A - RJEŠENJA
 Pismeni ispit iz OTPORNOSTI MATERIJALA I - grupa A 1. Kruta poluga AB oslonjena je na dva čelična štapa u A i B i opterećena trouglastim opterećenjem, kao na slici desno. Ako su oba štapa iste dužine L,
Pismeni ispit iz OTPORNOSTI MATERIJALA I - grupa A 1. Kruta poluga AB oslonjena je na dva čelična štapa u A i B i opterećena trouglastim opterećenjem, kao na slici desno. Ako su oba štapa iste dužine L,
OTPORNOST MATERIJALA 1
 OTPORNOST MATERIJALA 1 10. PREDAVANJE: ČISTO SMICANJE. PRORAČUN VAROVA, VIJAKA I ZAKOVICA. 2. svibnja 2017. Prošli tjedan smo naučili... da osim ANALITIČKE METODE za proračun progiba i zaokreta na grednim
OTPORNOST MATERIJALA 1 10. PREDAVANJE: ČISTO SMICANJE. PRORAČUN VAROVA, VIJAKA I ZAKOVICA. 2. svibnja 2017. Prošli tjedan smo naučili... da osim ANALITIČKE METODE za proračun progiba i zaokreta na grednim
TEORIJA BETONSKIH KONSTRUKCIJA 79
 TEORIJA BETOSKIH KOSTRUKCIJA 79 Primer 1. Odrediti potrebn površin armatre za stb poznatih dimenzija, pravogaonog poprečnog preseka, opterećen momentima savijanja sled stalnog ( g ) i povremenog ( w )
TEORIJA BETOSKIH KOSTRUKCIJA 79 Primer 1. Odrediti potrebn površin armatre za stb poznatih dimenzija, pravogaonog poprečnog preseka, opterećen momentima savijanja sled stalnog ( g ) i povremenog ( w )
Krute veze sa čeonom pločom
 Krute veze sa čeonom pločom Metalne konstrukcije 2 P6-1 Polje primene krutih veza sa čeonom pločom Najčešće se koriste za : Veze greda sa stubovima kod okvirnih nosača; Montažne nastavke nosača; Kontinuiranje
Krute veze sa čeonom pločom Metalne konstrukcije 2 P6-1 Polje primene krutih veza sa čeonom pločom Najčešće se koriste za : Veze greda sa stubovima kod okvirnih nosača; Montažne nastavke nosača; Kontinuiranje
PRIMJER 3. MATLAB filtdemo
 PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Linearna algebra 2 prvi kolokvij,
 1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
