Predavanje 10 (FEA-3) Generacija 2007 FORMIRANJE MODELA U METODI KONAČNIH ELEMENATA
|
|
|
- Αντώνης Γεννάδιος
- 6 χρόνια πριν
- Προβολές:
Transcript
1 PROJEKOVANJE RACUNAROM - CAD Autorizoana prdaanja dr Miomira Joanoića Prdaanj 0 (FEA-3) Gnracija 007 FORMIRANJE MODELA U MEODI KONAČNIH ELEMENAA Formiranj diskrtnog modla j priprmna faza - procdura pr analiz mtodom konačnih lmnata. Formiranjm diskrtnog modla stara s osmišljna, uskladjna i pozana grupa konačnih lmnata kojom j opisan kontinuum, koji j prdmt analiz. Formiranj modla za analizu ima čtiri faz ralizacij: Formiranj gomtrijskog modla, formiranj idalizoanog modla, formiranj modla zona i formiranj diskrtnog modla. Gomtrijski modl krira projktant, CAD softrom za projktoanj. im nastaj datotka podataka koji ralno opisuju gomtriju objkta sa sim potrbnim dtaljima za izradu. Gomtrijski modl mož da sadrži gomtrijsk lmnt koji nmaju značaja za analizu jr n utiču na naponsko-dformacionu sliku objkta. Radi toga s formira idalizoan modl u kom su obačni nažni dtalji. Idalizoan modl j uprošćn modl koji n mora da prdstalja clinu objkta ukoliko mož da s njgoim simtričnim formama prdstai funkcija i način optrćnja clin. Idalizoan modl s uk formira sa zahtom manjg obima kontinuuma za analizu. Osnoa razoja racionalnih idalizoanih modla j apstrakcija. Apstrakcija j sagldaanj modla od stran analitičara kojom s postalja koncpt modla, uklanjaju dtalji, prpoznaj simtrija, rdukuj modl, prilagodjaaju modalitti unošnja optrćnja. Na slici 3., pokazana j trarza sa slik.35. Modl zona prdstalja idalizoan modl rasčlanjn na prailnij clin zon koj dozoljaaju podlu kontinuuma na konačn lmnt prma standardnom - poznatom algoritmu gnrisanja ili prslikaanja. Na slici 3. pokazan j modl sa 4 zon. Uskladjianj mdjusobnog poklapanja čoroa i odsusto koincidncij lmnata i čoroa obzbdjuj s mapiranjm mrž procdurom uskladjnog broja lmnata na kontaktnim poršinama zona. Diskrtni modl s razija na bazi modla zona i uskladjnog broja lmnata kontaktnih poršina zona. Diskrtni modl podrazuma odrdjianj čoroa, konačnih lmnata, podataka o matrijalu, diskrtnom optrćnju i diskrtnim graničnim usloima. Diskrtni modl ima potrbna prilagodjaanja mrž konačnih lmnata graničnim usloima oslanjanja i tačkama i poršinama djsta spoljašnjih sila. Razijna mrža konačnih lmnata s ocnjuj paramtrima oblika mrž. o su gomtrijski okiri u kojima j primnjn konačan lmnt (dformisanost oblika), prailnost razoja mrž (kontinualnost promn praca i oblika lmnta), prailnost promn ličin lmnta (kontinualnost promn gomtrij). Na bazi oih paramtara rši s poboljšanj mrž pr ngo što s formira konačan diskrtan modl. Konačnim diskrtnim modlom rši s analiza.
2 PROJEKOVANJE RACUNAROM - CAD Autorizoana prdaanja dr Miomira Joanoića Gomtrijski modl Idalizoan modl Modl zona Diskrtan modl Slika 3. Faz transformacij modla. Slika pokazuj tri žičana modla: Gomtrijski modl, idalizoan modl i modl zona. Čtrti modl - diskrtni modl j prikazan kao zaprminski solid modl objkta Razoj mrž konačnih lmnata mož s ralizoati: Ručnim putm (pojdinačnim dfinisanjm čoroa i lmnata), Poluautomatskim putm kada s na bazi postaljnog koncpta modla zadaju pojdinačn komand automatskog gnrisanja konačnih lmnata u zonama. Poluautomatski gnratori su intraktinog tipa zasniaju s na instrukcijama dfinisanim kroz dijalog. Automatska procdura podrazuma gnrisanj mrž kao clin jdnom komandom kojom nastaj co diskrtni modl iz zadatog gomtrijskog modla i ngomtrijskih instrukcija o osloncima, optrćnju, matrijalu i fizičkim osobinama. Automatsko gnrisanj karaktriš najsarmnij modlr. Zato j osnoni programski alat za odrdjianj zona u kojima s gnriš mrža gnrator granica. Automatski gnratori korist tri mtod za formiranj mrža: Mtodu spajanja čoroa, mtodu prilagodjaanja uzorka mrž i mtodu dkompozicij. Softr za analizu, shodno načinu modliranja, mož da s razija kao intgralni i modularni. Intgralni podrazuma softrski potpuno intgrisan s faz razoja modla, analiz i postprocsiranja. Modularni pristup podrazuma razoj, korišćnj i distribuciju softrskih modula za pojdinačn tap analiz (gomtrijsko modliranj, prprocsiranj, postprocsiranj, analiza). Modularni programi podrazumaju i bogatiji intrfjs za rad sa različitim formatima i programima. Primr takih programa j FEMAP (Finit Elmnt Modling And Postprocssing), MicroStation-SE. Softrski pakti kao I-DEAS, ANSYS, ALGOR, NASRAN, COSMOS intgrišu s procduraln faz analiz: Gomtrijsko modliranj, idalizaciju, kriranj diskrtnog modla, ršaanj zadatka i postprocsiranj. Čsto su tu pridodat opcij za optimizaciju, rdizajn, analizu ostljiosti modla, konkurntni inžinjring, izradu thničk dokumntacij, pordjnj sa ksprimntom.
3 PROJEKOVANJE RACUNAROM - CAD Autorizoana prdaanja dr Miomira Joanoića 3 Pr/post procsori su programi prdidjni za rad sa gomtrijskim podacima, optrćnjima, graničnim usloima, naponima, dformacijama, ktorima, poljima, grafičkim tipoima gomtrijskih modla, animacijom, grškama analiz. Pr/post procsori su uk zasnoani na grafičkom intrfjsu i na taj način omogućuju analizu po različitim osnoama, istražiačkim ciljima. Gnratori mrža modlri mrža. Mogu gnrisati dodimnzionaln ili trodimnzionaln mrž konačnih lmnata. Dodimnzion mrž s korist za ršaanj raanskih i osnosimtričnih zadataka. rodimnzion mrž su najopštija katgorija mrža i u domnu mašinsta njima s pokria kontinuum objkata koji su uk 3D. Drugi značajan paramtar gnracij j gustina lmnata u pojdinim zonama. Gnratori mrža korist da pristupa u zadaanju gustin mrž: Pri pristup kod koga s gustina lmnata unaprd (a priori) prtpostalja analizom idalizoanog modla iz koj s odrdjuju paramtri gnratora mrža. Oaj modl s zasnia na opštim osobinama mhanik kontinuuma i u pojdinim slučajima mož da d ću gršku proračuna kao posldicu nadkatnog ili nraspoložiog prdpostaljnog paramtra programskog gnratora mrž. Prtpostak j potrbno proriti nakon analiz. Drugi pristup zasnia s na korišćnju rzultata izršn analiz (a postriori), za rdfinisanj gustin mrž. Oaj pristup postalja inicijalnu mržu sa počtnom ličinom konačnog lmnta odrdjnog na bazi zoniranog modla. Sa tom gustinom izrši s proračun pa s na bazi izršn analiz ocnjuj lokalna adkatnost ličin i rasporda lmnata. Na bazi gradijnta dobijnog napona, lokaln nrij (funkcionala Π) i gršk modla, rši s rdfinisanj mrž. Mrža j sada usloljna zahtima kontinuuma i ngomtrijskim paramtrima objkta. Pošto taka mrža odgoara gustinom lmnata postaljnom zahtu tačnosti i ima ujdnačn kaltt dobijnih rzultata, dfiniš s kao adaptina mrža. Do adaptin mrž s n dolazi dirktno, ć itratino u iš prolaza, dakl, srijom analiza sa podšaanjm jdnakosti i nioa gršk modla u sim zonama i lokacijama kontinuuma. Softrski j to automatizoana procdura koja s pokrć po gnrisanju prog diskrtnog modla. Ršnja za gnrisanj mrža su tražna i na drugim planoima. ako j I.C.aig, 954. dfinisao ksprtni sistm za priprmu analiz i procdur modliranja objkta. MODELIRANJE MREŽA - OPŠE FUNKCIJE Razoj diskrtnih mrža konačnih lmnata na objktima podrazuma dfinisanj osnonih lmnata: tačaka, linija, poršina, zaprmina, čoroa i konačnih lmnata. Nad gomtrijskim lmntima modla obaljaju s opracij gnrisanja sastanih lmnata diskrtnih modla, primnom odgoarajućih softrskih alata. Postaljanj (konstruisanj) čora u proizoljnoj tačci prostora (x,y,z), u opštm slučaju dato j spcificiranom nardbom IK3-0. Nardna tri alata pokazuju izodjnj transformacija nad grupom čoroa. Programsk nardb za izršnj oih funkcija su dat: IK3-0: Krirati čoro (konačnog lmnta) (Crat Nods) IK3-0: Kopirati čoro translacijom (Copy Nods) IK3-03: Kopirati čoro rotacijom (Rotat Nods) (3.9) IK3-04: Kopirati čoro rflksijom (Rflct Nods) Osnosimtričan konačan lmnt j raanski lmnt za osu u istoj rani.
4 PROJEKOVANJE RACUNAROM - CAD Autorizoana prdaanja dr Miomira Joanoića 4 Kopiranj u zadatom pracu, kopiranj rotacijom, kopiranj rflksijom Pojdinačno kriranj konačnih lmnata obalja s nardbom za konstruisanj IK3-05, datom naodom Izbor tipa i oblika konačnog lmnta sastani j do procdur kriranja i automatski s softrom otaraju podmniji za izbor potrbnih osobina konačnih lmnata. Procdura s mož uspšno okončati kada s si potrbni podaci za kriranj lmnta zadaju. ako na primr, kod kriranja konačnog lmnta ploč, zadaj s oblik ploč (trougaoni ili čtorougaoni), idntifikacioni broji čoroa, način unošnja podataka o lmntu (dfinisano intrfjsom programa), dbljina konačnog lmnta, matrijal lmnta sa mogućnošću korišćnja baz podataka. osobin naprdni softri nud kao kompltnu opciju. IK3-05: Krirati konačan lmnt (Crat Elmnt) (3.30) Pri naodjnju zahta za kriranj linijskih lmnata, programi obično nud izbor: A. Elmnt za aksijalna i torziona optrćnja (bz smicajna i saijanja rod lmnt), sl.3.4-a, B. Cni lmnt sličnih osobina kao i prthodni (tub lmnt), slika 3.4-b, C. Štapni lmnt za aksijalna optrćnja i saijanj (bar lmnt), slika 3.4-c, D. Linijski lmnt krutosti (spring lmnt), slika 3.5-a, E. Linijski lmnt prigušnja (dampr lmnt), slika 3.5-b, F. Kombinoani lmnt zadat krutosti i prigušnja, G. Linijski lmnt nlinarnosti (gap lmnt), H. Kriolinijski grdni lmnt (curd bam lmnt), slika 3.5-c Slika 3.5 a.- lmnt krutosti, b. - lmnt prigušnja, c. - kriolinijski grdni lmnt GENERISANJE UNIFORMNIH MREŽA Kada s na objktu razija mrža sa topologijom koja j tačno unaprd odrdjna, dfiniš s poršina na kojoj s izodi opracija. Nardni korak j izbor alata za gnrisanj mrž. Gnrisanj mrž na proizoljnoj čtorougaonoj ploči, što j nadno funkcijom: IK3-08: Krirati mržu izmdju ugloa - tmna (Crat Msh btwn Cornrs) Oa funkcija zahta unošnj oznak čoroa i broj lmnata u pracima lokalnih osa (s) i (r) koji s gnrišu mržom. Kada s gnrisanjm dobijaju proporcionalni ili idntični konačni lmnti, taka mrža s nazia uniformna. Za ploču na slici 3.7-a, zadata su tmna N5, N, N3, N i podla 4 x 4 lmnata. Ukoliko s funkcija ponoi na lmntima E9, E0, E3, E4, sa istim paramtrima, (posl odklanjanja koincidntnih čoroa i lmnata i rnumracij mrž), nastaj modl mrž prikazan na slici 3.7-b. Oaj modl sa 8 lmnata ploč odlikuj s gušćom mržom koja omogućuj prcizan unos spoljašnjg uticaja, manji stpn aproksimacij u analizi uticaja, bolji (dtaljniji) prikaz polja napona i dformacija. Prlaz iz krupnijih u sitnij lmnt mora naknadno da s dotra.
5 PROJEKOVANJE RACUNAROM - CAD Autorizoana prdaanja dr Miomira Joanoića 5 Y 5 4 Z X Slika 3.7-a,b Primri gnrisanja uniformnih mrža Procdura gnrisanja mrž složnija: ako, rcimo, kada s gnriš mrža na prstnastoj ploči, bira s pomoćna funkcija za konstruisanj, kojom s gnrišu kontroln tačk mrž: IK3-09: Krirati dimnziju mrž uzduž kria na poršini (Crat Msh Siz along Curs on Surfac) (3.33) Oom funkcijom s postaljaju kontroln tačk po cloj konturi, izabran gustin u cirkularnom i radijalnom pracu. Kontroln tačk omogućuju prailno raspordjianj lmnata mrž. Kontroln tačk su postaljn i simbolički prikazan na modlu, kod sakog softra. k sada mož s postaiti zaht za kriranj mrž na poršini: IK3-0: Gnrisati mržu na poršini (Gnrat Msh on a Surfac) (3.34) Oom funkcijom s formira mrža koja ima položaj čoroa i lmnata prma postaljnom modlu sa kontrolnim tačkama. Slika 3.8, pokazuj primr kriranja mrž na prstnastoj ploči sa lmnata u cirkularnom i 3 u radijalnom pracu. Gnrisano j 36 konačnih lmnata sa 48 čoroa i 48 x 6 stpni slobod krtanja (SSK). Mrža ima prailan oblik i proporcionalnu gomtriju konačnih lmnata. Pri tom su prikazani čtorougaoni raanski konačni lmnti. Slika 3.8 Gnrisanj raanskih čtorougaonih konačnih lmnata u polarno-cilindričnom koord. sistmu IK3-: Gnrisati paramtr ličin mrž (Gnrat Msh Siz) (3.35) Primr na slici 3.9, pokazuj gnrisanj mrž na nprailnoj ranoj poršini sa 8 konačnih lmnata u oba praca i količnicima izodnica mrž 5.0 i 0.. Dobijna mrža ima poćanu gustinu lmnata u gornjm dsnom uglu. Aproksimacija izršna sa 64 čtorougaona lmnta ploč, pri čmu tačnost modla iš nij automatski kontrolisana ć zaisi od kritrijuma i zahta analitičara.
6 PROJEKOVANJE RACUNAROM - CAD Autorizoana prdaanja dr Miomira Joanoića 6 V Y Z X Slika 3.9 Uniformna mrža sa njdnakom ličinom konačnih lmnata Slobodn mrž: Kod nautomatskih procdura kada s gnrišu SLOBODNE FORME MREŽA (fr msh), mora s poznaati tačnost modliranja iz iskusta grup prdhodno izdnih modla i proračuna. Slobodno formirana mrža mora poštoati opšt princip formiranja mrža: Spcificirati ličin mrža sa prlaznim rdnostima paramtara uzduž iica, N zadaati paramtr gnracij mrža u širokim granicama, Koristiti standardn paramtr za gnrisanj mrža (programski podšn), Raziti iš ralizacija mrža i izabrati najpooljniju, Mapirati granic na poršinama gd j god to moguć (manja logička složnost), Kod jako zakriljnih oblika konačnih lmnata ršiti rkonstrukciju mrža Gnrisanj mrž na zaprminskim (3D) objktima koristi opštu komandu za konstruisanj: IK3-6: Gnrisati mržu na zaprmini (Gnrat Msh on a Volum) Korišćnjm komand na objktu (postljica kliznog lžaja) prikazanom na slici 3.0, dobijna j mrža sa 5-3D konačnih lmnata (solid brick), 3 čora i 936 stpni slobod krtanja. Podšaanj kalitta ršnja prko ličin konačnih lmnata poznato j još kao h-siz paramtar. Kod poluautomatskog gnrisanja mrža, moguć j ličinom osnonog lmnta, dfinisati gustinu mrž. Slika 3.0 Primr gnrisanja uniformn mrž na 3D objktu
7 PROJEKOVANJE RACUNAROM - CAD Autorizoana prdaanja dr Miomira Joanoića 7 AUOMASKO GENERISANJE MREŽA Automatsko gnrisanj mrža konačnih lmnata koristi s za ralizaciju obimnih zadataka kaki su industrijski problmi sa iš dstina hiljada konačnih lmnata. instrukcij s u softru nalaz pod opštim naodima: IK3-: Automatski gnrisati granic mrž (Automatically msh gnration boundaris) Automatski krirati mržu (Auto_Crat) Spcifikacija argumnata mrž IK3-: Način gnrisanja mrž (prailna, adaptina), Vličina lmnta u mrži (h-siz), Broj lmnata u pracima mrž, Nagib lmnata u mrži (biasing), Vličina globalnog i lokalnog lmnta slobodn mrž, Multiplikatori dužin za slobodn mrž, Dužina lmnta na bazi zakriljnosti form (Curatur-Basd Elmnt Lngth) Automatska gnracija mrž konačnih lmnata zasnoani su na sldćim postupcima: A. Upraljanju razojm mrž, B. hnikama rananja mrž na objktu, C. Mtodama za izbor oblika i rst lmnta A. UPRAVLJANJE RAZVOJEM MREŽE dfiniš počtak i praac gnrisanja mrž. Osnoa razoja tak mrž j plan mrž (mapa) koji j odrdjn dfinisanjm podl na poršinama i iicama objkta. Postoj u osnoi da modla razoja mrž: prailna (uniformna) i slobodna. Prailna mrža ima stratgiju simtričnog ranomrnog razoja u pracu promn toka kontur. Prailn mrž su proporcionalnih konačnih lmnata, sttsk i daju liki broj l. Y Z X Slika 3.3 Uniformna - kontinualna mrža ist form konačnih lmnata Slobodn mrž imaju ću slobodu u smislu raspordjianja granica lmnata. Slobodn mrž s spcificiraju paramtrom globaln ličin lmnta, lokaln ličin lmnta, brojm lmnata u kriini i multiplikatorom ličin lmnata u mrži. Kako ličina iic konačnog lmnta, prdstalja do cl dužin iic modla, to s oa spcifikacija dfiniš ličinom lmnta u odnosu na clu konturu i poznata j kao h-spcifikacija. Paramtar za ou spcifikaciju j broj tačaka na konturi. Uobičajno s dfiniš od 0 do 30 lmnata:
8 PROJEKOVANJE RACUNAROM - CAD Autorizoana prdaanja dr Miomira Joanoića 8 Y Z X Slika 3.4 Dfinisanj tačaka na konturi - prdgnrisanj lmnata za ocnu form i gustin mrž Drugi paramtar razoja mrž podrazuma dfinisanj maksimalnih gomtrijskih odnosa mdju samim lmntima u mrži. Idalno j da su konačni lmnti ist ličin, ali s od oog zahta odstupa da bi s dobila mrža potrbn gustin na kritičnim lokacijama. Zato j udn paramtar nagiba (biasing ) lmnta prma cntru ili krajima kontur (3.0 i iš). Oaj paramtar odrdjuj zgušćnj trajktorija iica konačnih lmnata u pracu razoja mrž. Njim j odrdjna brzina prlaska diskrtn struktur iz krupnog konačnog lmnta na kraju poršin u sitan lmnt u prlaznoj zoni. B. RAVNANJE MREŽE ima za cilj da obzbdi proporcionalnost oblika i kontinuitt granica lmnata u odnosu na konturu objkta. Na oaj način smanjuj s izobličnj form konačnih lmnata. Za rananj granica lmnata korist s različit mtod gomtrijsk ispun prostora pri čmu s dobar usph raspordjianja postiž primnom Laplac-o i tžišn itracij. Laplac-oa mtoda pomra zajdnički čor čtiri susdna lmnta, prma prsku obrazoanom dirktnim porananjm iica susdnih lmnata, slika 3.5. žišna mtoda pomra zajdničku tačku ka tžištu sa čtiri konačna lmnta, slika 3.5. Laplac-oa mtoda stara mržu sa najmanjim izobličnjm lmnata. Oa mtoda j brža od tžišn mtod. Rananj s izodi do zadat tolrancij kalitta mrž (ε= 0-3 ). 3 K 4 K Slika 3.5 Da modla za rananj mrža: Laplac-o i tžišni mtod C. REĆA GRUPA MEODA stara s za izbor rst i tipa konačnog lmnta. o j, rcimo, izbor D i 3D lmnata pripadajućg oblika. Kod raanskih i poršinskih struktura to su trougaoni i čtorougaoni oblici ploča, ljuski, mmbrana. Kod 3D objkata to su osmougaoni lmnti (brick) ili piramid. rmin softrskog pakta I-DEAS koji prdstalja odnos dužin ktora cntra kosin i upran iic lmnta.
9 PROJEKOVANJE RACUNAROM - CAD Autorizoana prdaanja dr Miomira Joanoića 9 Gomtrija samog konačnog lmnta zadaj s paramtrom oblika. Kod čtorougaonih konačnih lmnata to j minimalan dozoljni ugao zakošnja. Rcimo, on s bira u granicama čim s dobijaju dobr diskrtn form mrža. Nardna da primra pokazuju automatsku gnraciju mrž na čtrtastoj 3D pločici sa kružnim otorom. Pra mrža, na slici 3.6 izdna j čtorougaonim lmntima sa maksimalno zadatim odnosom zakošnja lmnata 5: i minimalnim uglom izmdju d iic od 60 i grubom h-spcifikacijom ličin 0. Automatska gnracija j dala ranomrn ličin lmnata. Dobijna mrža s karaktriš sa 9 konačna lmnta i 3 čora. Rananjm j dobijno odstupanj ε= , posl 35 itracija, tžišnom mtodom Slika 3.6 Automatsko gnrisanj mrž čtorougaonih konačnih lmnata na objktu sa otorom (H-spcifikacija =0, Biasing = 5, minimalan ugao nagiba stranica = 60, mtoda rananja tžišna) Slika 3.7 Automatsko gnrisanj mrža na objktu primnom trougaonih konačnih lmnata H-spcifikacija =0, Biasing =, Laplac-oa mtoda sa 0 itracija i ε= Ralizacija: 54 čora i 50 lmnata POJAM ADAPIVNIH MREŽA Analiza tačnosti po dloima kontinuuma, slika 3.9, pokazuj njdnaku gršku lokalnih zona. Promna tačnosti objašnjaa s kao nadkatnost postaljn mrž da prati nagl promn (gradijnt) napona i dfrmacija. Radi toga s modliraju uniformn mrža ć gustin, kako bi s umanjila grška analiz, što dirktno doodi do skupih diskrtnih modla sa likim brojm stpni slobod krtanja. Danas su razijn tri grup adaptinih postupaka:. h - adaptini postupak,. p - adaptini postupak, 3. h-p adaptini postupak H-adaptini postupak rkurzinim algoritmom mnja topologiju mrž, prma gradijntu dformacija ili napona. Posldica j dirktna promna ličin konačnih lmnata, po čmu j i postupak dobio im. Adaptina mrža pri tom ima gust konačn lmnt, malih dimnzija u zoni likih dformacija, pa s u suštini, broj konačnih lmnata u odnosu na polaznu mržu poćaa. Enormno ućanj broja lmnata j loša osobina modla čak i kada s raspolaž moćnim računarskim rsursima. H-adaptini postupak odrdjuj gršku polazn mrž na bazi koj izračunaa nou ličinu konačnog lmnta u posmatranoj zoni, sa ciljm zadooljnja postaljn tačnosti. Razlika gzaktnih ršnja pomranja i napona u,σ i odgoarajućih aproksimatinih ršnja pomranja i napona û, σˆ, prdstalja gršku pomranja i gršku napona σ, koj s dfinišu rlacijama 3.46-a,b: u = u û, σ = σ σˆ, (3.46-a,b)
10 PROJEKOVANJE RACUNAROM - CAD Autorizoana prdaanja dr Miomira Joanoića 0 Čšć korišćna ličina za izražaanj gršk j nrgtska norma gršk koja s u slučaju lastičnog sistma, mož s dfinisati jdnačinom Mnogo dirktnija mra gršk s mož dfinisati prko norm gršk, označn indksom L. U oim izrazima, L j matrica difrncijalnih opratora, V-zaprmina kontinuuma a D matrica lastičnih osobina matrijala. Norma gršk za dformacij i napon, dfinisana j jdnačinama 3.49-a,b, [5]. / D dv D D = σ σ = ε ε = σ σ, (3.48) V V V L / = dv, V / / / dv σ = L σ σ, (3.49-a,b) V Norm gršk iz jdnačina 3.49, odnos s na co analiziran kontinuum. Kadrat norm clog kontinuma, mož s prdstaiti sumom pojdinačnih kadrata normi konačnih lmnata, prma 3.50: m =, (3.50) i= i Kod optimalnih adaptinih mrža, ranomrno j raspordjna nrgtska norma po konačnim lmntima clog diskrtnog sistma. Enrgtska norma nma prostu fizičku intrprtaciju u mhanici kontinuma pa s zato korist i drugi oblici izražaanja gršk modla. Za intrprtaciju j mnogo očigldnija rlatina procntualna grška η, (3.5-a), kao i apsolutna grška napona (3.5-b). Oba paramtra s mogu odrditi kako za pojdinačn konačn lmnt tako i za co kontinuum. η = u 00 %, σ σ = V L /, (3.5-a,b) Stratgija gnrisanja h-adaptin mrž, dfiniš algoritam za pojdinačno odrdjianj ličina konačnih lmnata pri čmu j ispunjn uslo da j grška ranomrno raspordjna po kontinuumu i da j manja od zadat gršk η dop. Oaj uslo s dfiniš rlacijom 3.5 iz koj dirktno za saki konačan lmnt mož da s prori tačnost proračuna, na bazi rlacij Ukoliko s jdnačinom 3.54-a, izrazi količnik gršk ξ u i-tom lmntu i prosčn gršk cl struktur sa m lmnata, mož s odrditi korkcija h-ličin lmnata. Kada j ξ i >.0, potrbno j poćanj gustin lmnata u posmatranoj zoni kontinuuma. Kada j ξ<.0, potrbno j razrditi mržu konačnih lmnata. η η dop (3.5) / û + η i dop = m m (3.53) σ i ξ i =, ξi =, (3.54-a,b) m σdop prirastaj Ukoliko j polazna ličina konačnog lmnta h i, za koji j odrdjn količnik gršk ξ i, primnom intrpolacion funkcij stpna p, mož s odrditi korigoana dimnzija konačnog lmnta sa aspkta zadat tačnosti h i NOVO, prma rlaciji Oako odrdjna noa ličina konačnog lmnta h i NOVO, prdstalja h-adaptinu ličinu mrž diskrtn struktur. Rlacija 3.55 j osnona jdnačina za gnrisanj h-adaptin mrž konačnih lmnata. Količnik gršk ξ s mož odrditi i na osnou analiz naponskih priraštaja susdnih konačnih lmnata σ i unaprd dozoljnog priraštaja napona σ dop prirastaj, prma rlaciji 3.54-b. Oaj naponski skok uzima s indiidualno i mož biti nkoliko procnta od maksimalno dozoljnog napona
11 PROJEKOVANJE RACUNAROM - CAD Autorizoana prdaanja dr Miomira Joanoića struktur. Efikasnost nalažnja ršnja ocnjuj s indksom fikasnosti nalažnja ršnja θ, koji j dfinisan rlacijom h i NOVO h i =, (3.55) ξ p i PROCENJENO θ = (3.56) ACNO P-adaptini postupak n mnja topologiju postaljn mrž u zonama isokih gradijnata dformacija i napona ć podšaa stpn intrpolacionih polinoma konačnih lmnata. Na taj način s adaptina mrža formira od konačnih lmnata promnljiog stpna intrpolacionih funkcija. ako, rcimo, program NISA II/DISPLAY II, namnjn za linarnu i nlinarnu analizu, firm EMRC, ima automatsko poćanj stpna polinoma do rdnosti p=8. Na slici 3.30 pokazan j rzultat rada klasičnog modlra po h-mtodi i modlra po p-mtodi. abla 3.3 FINA JEDNOLIK A MREŽA ADAPIVNA MREŽA ROUGAONI EL. P-MEOD ROUGAONI EL. (P=5) P-MEOD ČEVOROUG. EL. (P=5) Broj lmnata mrž Čoroa po konačnom lmntu NAPON σ u tački D Grška u odnosu na tačno ršnj % VREME ršaanja sc CP 386/0 MHz Fina uniformna mrza Adaptina mrza P-postupak sa trougaonim lmntima P-postupak sa ctorougaonim lmntim Slika 3.30 Upordan prgld načina rada modlra firm SRUCURAL RESEARCH AND ANALYSIS CORPORAION - S. MONICA, USA
12 PROJEKOVANJE RACUNAROM - CAD Autorizoana prdaanja dr Miomira Joanoića DINAMIČKE JEDNAČINE U FEM Mtoda konačnih lmnata s koristi za dinamičku analizu struktura. Osnona jdnačina ranotž, izdna j primnom Hamilton-oog arijacionog principa. Oaj princip polazi od kintičk nrgij E K, potncijaln nrgij unutrašnjih i spoljašnjih sila Π i rada nkonzratinih sila W (koji uključuj i sil prigušnja). Polazna osnoa j funkcional Lagrang-a L (3.3). Hamilton-o princip pokazuj da mhanički sistm pri krtanju zauzima on položaj u kojima Lagrang-o funkcional ima stacionarnu rdnost: L = EK - Π + W (3.3) t t t L ( E K Π) dt + (3.4) t t t δ dt = δ δw dt = 0 Oa jdnačina s mož ssti na Lagrang-ou jdnačinu drug rst u obliku (3.5), gd j Q i gnralisana sila a t t rmnski intral krtanja. d dt Ek E k q & i qi Π + qi = Qi (3.5) Pri tom j kintička nrgija dfinisana izrazom (3.6), gd ju& brzina krtanja a ρ gustina matrijala. Potncijalna nrgija sistma j zbir spoljašnjih poršinskih p i zaprminskih sila F: Π = Pomranja i brzin E = ρ u u d & & (3.6) k ε D ε d u F d u p ds (3.7) s u, u& s mogu izraziti prko intrpolacion matrica N, a dformacij ε, prko matrica B. Smnom nrgij E K i potncijaln nrgij Π u Lagrang-ou jdnačinu krtanja, uz sil prigušnja F p i gnralisan sil Q p, dolazi s do dinamičk jdnačin konačnog lmnta: m & q + c q& + k q = Q (3.8) U ooj jdnačini su dfinisan sldć matric: matrica mas lmnta m = N ρ N d (3.8a) matrica prigušnja lmnta c = N c N d (3.8b) matrica krutosti lmnta ktor gnralisanih sila k = B D B d (3.8c) Q N F d + N p ds (3.8d) s =
13 PROJEKOVANJE RACUNAROM - CAD Autorizoana prdaanja dr Miomira Joanoića 3 Dinamička jdnačina struktur dobija s proširnjm dinamičk jdnačin konačnog lmnta na clu strukturu kontinuum, (3.9): M && q + C q& + K q = Q U osnonoj dinamičkoj jdnačini mtod konačnih lmnata, sa M, C i K su označn matric masa, prigušnja i krutosti sistma - konstrukcij. Q j gnralisani ktor spoljašnjih sila u čoroima konačnih lmnata. Oa jdnačina j osno analiz mhaničkih sistma. Osnon osobin dinamik posmatranog mhaničkog sistma izučaaju s kroz slobodn oscilacij sistma. Rzultat izučaanja su sopstn frkncij i sopstni ktori sistma (modoi). Ršnja oog zadatka s korist za podšaanj prformansi mašina. Procdur ršaanja dinamičk jdnačin zasnia s na mtodi suprpozicij oblika osciloanja ili mtodama dirktn intgracij. Najduža i najskuplja faza analiz, mtodom suprpozicij, j izračunaanj sopstnih frkncija i sopsnih oblika osciloanja. Kada budu odrdjn o rdnosti, on mogu biti upotrbljn za različit slučaj optrćnja. Oo s rlo čsto praktikuj kod izučaanja ostljiosti konstrukcij na različit rst pobuda. Primna mtoda dirktn intgracij sodi s na numričko intgraljnj difrncijalnih jdnačina, stp-by-stp procdurama. rmin "dirktan" potič od činjnic da s procdura n odija uzastopnim transformacijama ć dirktno-intgracijom. Numrička intgracija s izodi čsto Nwton-Cots-oim ili Gauss-Lgndr-oim postupkom.
3.0 FEA ANALIZA 1. FEM Predavanje 7 ANALIZA NOSECIH STRUKTURA 2006/2007 AUTOMATSKO GENERISANJE MREŽA
 3.0 FEA ANALIZA FEM Prdavanj 7 ANALIZA NOSECIH SRUKURA 2006/2007 AUOMASKO GENERISANJE MREŽA Automatsko gnrisanj mrža konačnih lmnata koristi s za ralizaciju obimnih zadataka kakvi su industrijski problmi
3.0 FEA ANALIZA FEM Prdavanj 7 ANALIZA NOSECIH SRUKURA 2006/2007 AUOMASKO GENERISANJE MREŽA Automatsko gnrisanj mrža konačnih lmnata koristi s za ralizaciju obimnih zadataka kakvi su industrijski problmi
Sistem sučeljnih sila
 Sistm sučljnih sila Gomtrijski i analitički način slaganja sila, projkcija sil na osu i na ravan, uslovi ravnotž Sistm sučljnih sila Za sistm sila s kaž da j sučljni ukoliko sil imaju zajdničku napadnu
Sistm sučljnih sila Gomtrijski i analitički način slaganja sila, projkcija sil na osu i na ravan, uslovi ravnotž Sistm sučljnih sila Za sistm sila s kaž da j sučljni ukoliko sil imaju zajdničku napadnu
SISTEMI DIFERENCIJALNIH JEDNAČINA - ZADACI NORMALNI OBLIK
 SISTEMI DIFERENCIJALNIH JEDNAČINA - ZADACI NORMALNI OBLIK. Rši sism jdnačina: d 7 d d d Ršnj: Ša j idja kod ovih zadaaka? Jdnu od jdnačina difrniramo, o js nađmo izvod l jdnačin i u zamnimo drugu jdnačinu.
SISTEMI DIFERENCIJALNIH JEDNAČINA - ZADACI NORMALNI OBLIK. Rši sism jdnačina: d 7 d d d Ršnj: Ša j idja kod ovih zadaaka? Jdnu od jdnačina difrniramo, o js nađmo izvod l jdnačin i u zamnimo drugu jdnačinu.
Ovo nam govori da funkcija nije ni parna ni neparna, odnosno da nije simetrična ni u odnosu na y osu ni u odnosu na
 . Ispitati tok i skicirati grafik funkcij = Oblast dfinisanosti (domn) Ova funkcija j svuda dfinisana, jr nma razlomka a funkcija j dfinisana za svako iz skupa R. Dakl (, ). Ovo nam odmah govori da funkcija
. Ispitati tok i skicirati grafik funkcij = Oblast dfinisanosti (domn) Ova funkcija j svuda dfinisana, jr nma razlomka a funkcija j dfinisana za svako iz skupa R. Dakl (, ). Ovo nam odmah govori da funkcija
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
DIMENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE
 TEORIJA ETONSKIH KONSTRUKCIJA T- DIENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE 3.5 f "2" η y 2 D G N z d y A "" 0 Z a a G - tačka presek koja određje položaj sistemne
TEORIJA ETONSKIH KONSTRUKCIJA T- DIENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE 3.5 f "2" η y 2 D G N z d y A "" 0 Z a a G - tačka presek koja određje položaj sistemne
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI)
 IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II
 1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II Zadatak: Klipni mehanizam se sastoji iz krivaje (ekscentarske poluge) OA dužine R, klipne poluge AB dužine =3R i klipa kompresora B (ukrsne glave). Krivaja
1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II Zadatak: Klipni mehanizam se sastoji iz krivaje (ekscentarske poluge) OA dužine R, klipne poluge AB dužine =3R i klipa kompresora B (ukrsne glave). Krivaja
ZI. NEODREðENI INTEGRALI
 ZI. Nodrđni intgrali 7 ZI. NEODREðENI INTEGRALI. Antidrvacij. Pronañi tri antidrivacij funkcij.. Odrdi sv antidrivacij funkcij.. Pronañi dvij antidrivacij funkcij.. Pronañi antidrivaciju funkcij za koju
ZI. Nodrđni intgrali 7 ZI. NEODREðENI INTEGRALI. Antidrvacij. Pronañi tri antidrivacij funkcij.. Odrdi sv antidrivacij funkcij.. Pronañi dvij antidrivacij funkcij.. Pronañi antidrivaciju funkcij za koju
REŠAVANJE INŽENJERSKIH ZADATAKA U FEM
 ANALIZA NOSECIH SRUKURA Predaanje 5-6. Generacija 006/007 REŠAVANJE INŽENJERSKIH ZADAAKA U FEM Rešaanje zadataka FEA metodom ima proceduru sa sledećim etapama:. Diskretizoanje kontinuuma konstrukcije izabranim
ANALIZA NOSECIH SRUKURA Predaanje 5-6. Generacija 006/007 REŠAVANJE INŽENJERSKIH ZADAAKA U FEM Rešaanje zadataka FEA metodom ima proceduru sa sledećim etapama:. Diskretizoanje kontinuuma konstrukcije izabranim
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike GRUPA A 1. Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj, zatim naći 4 z.
 Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri
 Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
1. Uvodna razmatranja U ovom predavanju se navodi jedna motivacija za proučavanje tema koje čine sadržaj kursa.
 Izabrana poglavlja primnjn analiz 1. XI 217. 1. Uvodna razmatranja U ovom prdavanju s navodi jdna motivacija za proučavanj tma koj čin sadržaj kursa. 1.1. Linarni vrmnsko-invarijanti i vrmnsko-nprkidni
Izabrana poglavlja primnjn analiz 1. XI 217. 1. Uvodna razmatranja U ovom prdavanju s navodi jdna motivacija za proučavanj tma koj čin sadržaj kursa. 1.1. Linarni vrmnsko-invarijanti i vrmnsko-nprkidni
Rešenja A/2 kolokvijuma iz predmeta MERNI SISTEMI U TELEKOMUNIKACIJAMA 10. januar 2006.
 šnj A/ kolokvijum iz prdmt MENI SISEMI U ELEKOMUNIKACIJAMA. jnur. Zdtk. D i prikznim urđjm mogl mriti mplitud čtvrtog hrmonik u mmorijki lok tr d ud upin ditrovn zin unkcij ( t) y co π Izlz iz urđj j td
šnj A/ kolokvijum iz prdmt MENI SISEMI U ELEKOMUNIKACIJAMA. jnur. Zdtk. D i prikznim urđjm mogl mriti mplitud čtvrtog hrmonik u mmorijki lok tr d ud upin ditrovn zin unkcij ( t) y co π Izlz iz urđj j td
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
Inženjerska grafika geometrijskih oblika (5. predavanje, tema1)
 Inženjerska grafika geometrijskih oblika (5. predavanje, tema1) Prva godina studija Mašinskog fakulteta u Nišu Predavač: Dr Predrag Rajković Mart 19, 2013 5. predavanje, tema 1 Simetrija (Symmetry) Simetrija
Inženjerska grafika geometrijskih oblika (5. predavanje, tema1) Prva godina studija Mašinskog fakulteta u Nišu Predavač: Dr Predrag Rajković Mart 19, 2013 5. predavanje, tema 1 Simetrija (Symmetry) Simetrija
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Otpornost R u kolu naizmjenične struje
 Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
( , 2. kolokvij)
 A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
MEHANIKA FLUIDA. Prosti cevovodi
 MEHANIKA FLUIDA Prosti ceooi zaatak Naći brzin oe kroz naglaak izlaznog prečnika =5 mm, postaljenog na kraj gmenog crea prečnika D=0 mm i žine L=5 m na čijem je prenjem el građen entil koeficijenta otpora
MEHANIKA FLUIDA Prosti ceooi zaatak Naći brzin oe kroz naglaak izlaznog prečnika =5 mm, postaljenog na kraj gmenog crea prečnika D=0 mm i žine L=5 m na čijem je prenjem el građen entil koeficijenta otpora
MATEMATIKA 2. Grupa 1 Rexea zadataka. Prvi pismeni kolokvijum, Dragan ori
 MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
VJEŽBE 3 BIPOLARNI TRANZISTORI. Slika 1. Postoje npn i pnp bipolarni tranziostori i njihovi simboli su dati na slici 2 i to npn lijevo i pnp desno.
 JŽ 3 POLAN TANZSTO ipolarni tranzistor se sastoji od dva pn spoja kod kojih je jedna oblast zajednička za oba i naziva se baza, slika 1 Slika 1 ipolarni tranzistor ima 3 izvoda: emitor (), kolektor (K)
JŽ 3 POLAN TANZSTO ipolarni tranzistor se sastoji od dva pn spoja kod kojih je jedna oblast zajednička za oba i naziva se baza, slika 1 Slika 1 ipolarni tranzistor ima 3 izvoda: emitor (), kolektor (K)
PRESECI SA PRSLINOM - VELIKI EKSCENTRICITET
 TEORIJ ETONSKIH KONSTRUKCIJ 1 PRESECI S PRSLINO - VELIKI EKSCENTRICITET ČISTO SVIJNJE - VEZNO DIENZIONISNJE Poznato: - statički ticaji za pojedina opterećenja ( i ) - kalitet materijala (f, σ ) - dimenzije
TEORIJ ETONSKIH KONSTRUKCIJ 1 PRESECI S PRSLINO - VELIKI EKSCENTRICITET ČISTO SVIJNJE - VEZNO DIENZIONISNJE Poznato: - statički ticaji za pojedina opterećenja ( i ) - kalitet materijala (f, σ ) - dimenzije
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
III VEŽBA: FURIJEOVI REDOVI
 III VEŽBA: URIJEOVI REDOVI 3.1. eorijska osnova Posmatrajmo neki vremenski kontinualan signal x(t) na intervalu definisati: t + t t. ada se može X [ k ] = 1 t + t x ( t ) e j 2 π kf t dt, gde je f = 1/.
III VEŽBA: URIJEOVI REDOVI 3.1. eorijska osnova Posmatrajmo neki vremenski kontinualan signal x(t) na intervalu definisati: t + t t. ada se može X [ k ] = 1 t + t x ( t ) e j 2 π kf t dt, gde je f = 1/.
Strukture podataka i algoritmi 1. kolokvij 16. studenog Zadatak 1
 Strukture podataka i algoritmi 1. kolokvij Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i službeni šalabahter. Predajete samo papire koje ste dobili. Rezultati i uvid u kolokvije: ponedjeljak,
Strukture podataka i algoritmi 1. kolokvij Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i službeni šalabahter. Predajete samo papire koje ste dobili. Rezultati i uvid u kolokvije: ponedjeljak,
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
10.1. Bit Error Rate Test
 .. Bt Error Rat Tst.. Bt Error Rat Tst Zadata. Izračuat otrba broj rth formacoh bta u BER tstu za,, ogršo dttovaa bta a rjmu, tao da s u sstmu sa brzoom sgalzacj od Mbs mož tvrdt da j vrovatoća grš rosa
.. Bt Error Rat Tst.. Bt Error Rat Tst Zadata. Izračuat otrba broj rth formacoh bta u BER tstu za,, ogršo dttovaa bta a rjmu, tao da s u sstmu sa brzoom sgalzacj od Mbs mož tvrdt da j vrovatoća grš rosa
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
 TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
VILJUŠKARI. 1. Viljuškar se koristi za utovar standardnih euro-pool paleta na drumsko vozilo u sistemu prikazanom na slici.
 VILJUŠKARI 1. Viljuškar e korii za uoar andardnih euro-pool palea na druko ozilo u ieu prikazano na lici. PALETOMAT a) Koliko reba iljuškara da bi ree uoara kaiona u koji aje palea bilo anje od 6 in, ako
VILJUŠKARI 1. Viljuškar e korii za uoar andardnih euro-pool palea na druko ozilo u ieu prikazano na lici. PALETOMAT a) Koliko reba iljuškara da bi ree uoara kaiona u koji aje palea bilo anje od 6 in, ako
Analiza sistema automatskog upravljanja u prostoru stanja
 naliza ima auomakog upravljanja u prooru anja..ponašanj anja i odziva ima Poznao j da mamaički modl u prooru anja ima n pokazuj amo dinamičku zavino izmđu ulaznih i izlaznih vličina, ngo da adrži i informacij
naliza ima auomakog upravljanja u prooru anja..ponašanj anja i odziva ima Poznao j da mamaički modl u prooru anja ima n pokazuj amo dinamičku zavino izmđu ulaznih i izlaznih vličina, ngo da adrži i informacij
INTELIGENTNO UPRAVLJANJE
 INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
RIJEŠENI ZADACI I TEORIJA IZ
 RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
APROKSIMACIJA FUNKCIJA
 APROKSIMACIJA FUNKCIJA Osnovni koncepti Gradimir V. Milovanović MF, Beograd, 14. mart 2011. APROKSIMACIJA FUNKCIJA p.1/46 Osnovni problem u TA Kako za datu funkciju f iz velikog prostora X naći jednostavnu
APROKSIMACIJA FUNKCIJA Osnovni koncepti Gradimir V. Milovanović MF, Beograd, 14. mart 2011. APROKSIMACIJA FUNKCIJA p.1/46 Osnovni problem u TA Kako za datu funkciju f iz velikog prostora X naći jednostavnu
5. Karakteristične funkcije
 5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
1. UVOD. Slika 1.1 Koncept korišćenja metoda analize u projektovanju
 1. UVOD METODAMA ANALIZE se u fazi projektovanja mašina i opreme traže odgovori o njihovim svojstvima otpornosti, pouzdanosti, nosivosti, kinematskom ponašanju, dinamičkom odgovoru. Skup svih zahvata traženja
1. UVOD METODAMA ANALIZE se u fazi projektovanja mašina i opreme traže odgovori o njihovim svojstvima otpornosti, pouzdanosti, nosivosti, kinematskom ponašanju, dinamičkom odgovoru. Skup svih zahvata traženja
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
RAČUNSKE VEŽBE IZ PREDMETA POLUPROVODNIČKE KOMPONENTE (IV semestar modul EKM) IV deo. Miloš Marjanović
 Univerzitet u Nišu Elektronski fakultet RAČUNSKE VEŽBE IZ PREDMETA (IV semestar modul EKM) IV deo Miloš Marjanović MOSFET TRANZISTORI ZADATAK 35. NMOS tranzistor ima napon praga V T =2V i kroz njega protiče
Univerzitet u Nišu Elektronski fakultet RAČUNSKE VEŽBE IZ PREDMETA (IV semestar modul EKM) IV deo Miloš Marjanović MOSFET TRANZISTORI ZADATAK 35. NMOS tranzistor ima napon praga V T =2V i kroz njega protiče
10. STABILNOST KOSINA
 MEHANIKA TLA: Stabilnot koina 101 10. STABILNOST KOSINA 10.1 Metode proračuna koina Problem analize tabilnoti zemljanih maa vodi e na određivanje odnoa između rapoložive mičuće čvrtoće i proečnog mičućeg
MEHANIKA TLA: Stabilnot koina 101 10. STABILNOST KOSINA 10.1 Metode proračuna koina Problem analize tabilnoti zemljanih maa vodi e na određivanje odnoa između rapoložive mičuće čvrtoće i proečnog mičućeg
Zavrxni ispit iz Matematiqke analize 1
 Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
SISTEMI NELINEARNIH JEDNAČINA
 SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
Novi Sad god Broj 1 / 06 Veljko Milković Bulevar cara Lazara 56 Novi Sad. Izveštaj o merenju
 Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika. Monotonost i ekstremi. Katica Jurasić. Rijeka, 2011.
 Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
Matematika 1 - vježbe. 11. prosinca 2015.
 Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
(P.I.) PRETPOSTAVKA INDUKCIJE - pretpostavimo da tvrdnja vrijedi za n = k.
 1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
Program testirati pomoću podataka iz sledeće tabele:
 Deo 2: Rešeni zadaci 135 Vrednost integrala je I = 2.40407 42. Napisati program za izračunavanje koeficijenta proste linearne korelacije (Pearsonovog koeficijenta) slučajnih veličina X = (x 1,..., x n
Deo 2: Rešeni zadaci 135 Vrednost integrala je I = 2.40407 42. Napisati program za izračunavanje koeficijenta proste linearne korelacije (Pearsonovog koeficijenta) slučajnih veličina X = (x 1,..., x n
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
3. OSNOVNI POKAZATELJI TLA
 MEHANIKA TLA: Onovni paraetri tla 4. OSNONI POKAZATELJI TLA Tlo e atoji od tri faze: od čvrtih zrna, vode i vazduha i njihovo relativno učešće e opiuje odgovarajući pokazateljia.. Specifična težina (G)
MEHANIKA TLA: Onovni paraetri tla 4. OSNONI POKAZATELJI TLA Tlo e atoji od tri faze: od čvrtih zrna, vode i vazduha i njihovo relativno učešće e opiuje odgovarajući pokazateljia.. Specifična težina (G)
Elementi elektronike septembar 2014 REŠENJA. Za vrednosti ulaznog napona
 lementi elektronike septembar 2014 ŠNJA. Za rednosti ulaznog napona V transistor je isključen, i rednost napona na izlazu je BT V 5 V Kada ulazni napon dostigne napon uključenja tranzistora, transistor
lementi elektronike septembar 2014 ŠNJA. Za rednosti ulaznog napona V transistor je isključen, i rednost napona na izlazu je BT V 5 V Kada ulazni napon dostigne napon uključenja tranzistora, transistor
OSNOVI ELEKTRONIKE VEŽBA BROJ 1 OSNOVNA KOLA SA DIODAMA
 ELEKTROTEHNIČKI FAKULTET U BEOGRADU KATEDRA ZA ELEKTRONIKU OSNOVI ELEKTRONIKE SVI ODSECI OSIM ODSEKA ZA ELEKTRONIKU LABORATORIJSKE VEŽBE VEŽBA BROJ 1 OSNOVNA KOLA SA DIODAMA Autori: Goran Savić i Milan
ELEKTROTEHNIČKI FAKULTET U BEOGRADU KATEDRA ZA ELEKTRONIKU OSNOVI ELEKTRONIKE SVI ODSECI OSIM ODSEKA ZA ELEKTRONIKU LABORATORIJSKE VEŽBE VEŽBA BROJ 1 OSNOVNA KOLA SA DIODAMA Autori: Goran Savić i Milan
Riješeni zadaci: Nizovi realnih brojeva
 Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Konstruisanje. Dobro došli na... SREDNJA MAŠINSKA ŠKOLA NOVI SAD DEPARTMAN ZA PROJEKTOVANJE I KONSTRUISANJE
 Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
( ) ( ) 2 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET. Zadaci za pripremu polaganja kvalifikacionog ispita iz Matematike. 1. Riješiti jednačine: 4
 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
Periodičke izmjenične veličine
 EHNČK FAKULE SVEUČLŠA U RJEC Zavod za elekroenergeiku Sudij: Preddiploski sručni sudij elekroehnike Kolegij: Osnove elekroehnike Nosielj kolegija: Branka Dobraš Periodičke izjenične veličine Osnove elekroehnike
EHNČK FAKULE SVEUČLŠA U RJEC Zavod za elekroenergeiku Sudij: Preddiploski sručni sudij elekroehnike Kolegij: Osnove elekroehnike Nosielj kolegija: Branka Dobraš Periodičke izjenične veličine Osnove elekroehnike
S t r a n a 1. 1.Povezati jonsku jačinu rastvora: a) MgCl 2 b) Al 2 (SO 4 ) 3 sa njihovim molalitetima, m. za so tipa: M p X q. pa je jonska jačina:
 S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
7 Algebarske jednadžbe
 7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Dekompozicija DFT. Brzi algoritmi na bazi radix-2. Brza Furijeova transofrmacija. Tačnost izračunavanja. Kompleksna FFT OASDSP 1: 7 FFT
 OASDSP : 7 FFT Dkompozicija DFT Brzi algoritmi a bazi radix- Brza Furijova trasofrmacija Tačost izračuavaja Komplksa FFT ovi Sad, Oktobar 5 straa OASDSP : 7 FFT Brza trasformacija : itrativa dkompozicija
OASDSP : 7 FFT Dkompozicija DFT Brzi algoritmi a bazi radix- Brza Furijova trasofrmacija Tačost izračuavaja Komplksa FFT ovi Sad, Oktobar 5 straa OASDSP : 7 FFT Brza trasformacija : itrativa dkompozicija
l = l = 0, 2 m; l = 0,1 m; d = d = 10 cm; S = S = S = S = 5 cm Slika1.
 . U zračnom rasporu d magnetnog kruga prema slici akumulirana je energija od,8 mj. Odrediti: a. Struju I; b. Magnetnu energiju akumuliranu u zračnom rasporu d ; Poznato je: l = l =, m; l =, m; d = d =
. U zračnom rasporu d magnetnog kruga prema slici akumulirana je energija od,8 mj. Odrediti: a. Struju I; b. Magnetnu energiju akumuliranu u zračnom rasporu d ; Poznato je: l = l =, m; l =, m; d = d =
Univerzitet u Nišu, Prirodno-matematički fakultet Prijemni ispit za upis OAS Matematika
 Univerzitet u Nišu, Prirodno-matematički fakultet Prijemni ispit za upis OAS Matematika Rešenja. Matematičkom indukcijom dokazati da za svaki prirodan broj n važi jednakost: + 5 + + (n )(n + ) = n n +.
Univerzitet u Nišu, Prirodno-matematički fakultet Prijemni ispit za upis OAS Matematika Rešenja. Matematičkom indukcijom dokazati da za svaki prirodan broj n važi jednakost: + 5 + + (n )(n + ) = n n +.
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f
 IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
3525$&8158&1(',=$/,&(6$1$92-1,095(7(120
 Srednja masinska skola OSOVE KOSTRUISAJA List1/8 355$&8158&1(',=$/,&(6$1$9-1,095(7(10 3ROD]QLSRGDFL maksimalno opterecenje Fa := 36000 visina dizanja h := 440 mm Rucna sila Fr := 350 1DYRMQRYUHWHQR optereceno
Srednja masinska skola OSOVE KOSTRUISAJA List1/8 355$&8158&1(',=$/,&(6$1$9-1,095(7(10 3ROD]QLSRGDFL maksimalno opterecenje Fa := 36000 visina dizanja h := 440 mm Rucna sila Fr := 350 1DYRMQRYUHWHQR optereceno
Dvanaesti praktikum iz Analize 1
 Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
Osnovne teoreme diferencijalnog računa
 Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
STATIČKE KARAKTERISTIKE DIODA I TRANZISTORA
 Katedra za elektroniku Elementi elektronike Laboratorijske vežbe Vežba br. 2 STATIČKE KARAKTERISTIKE DIODA I TRANZISTORA Datum: Vreme: Studenti: 1. grupa 2. grupa Dežurni: Ocena: Elementi elektronike -
Katedra za elektroniku Elementi elektronike Laboratorijske vežbe Vežba br. 2 STATIČKE KARAKTERISTIKE DIODA I TRANZISTORA Datum: Vreme: Studenti: 1. grupa 2. grupa Dežurni: Ocena: Elementi elektronike -
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
Elektrotehnički fakultet univerziteta u Beogradu 26. jun Katedra za Računarsku tehniku i informatiku
 Elektrotehički fakultet uiverziteta u Beogradu 6. ju 008. Katedra za Račuarku tehiku i iformatiku Performae račuarkih itema Rešeja zadataka..videti predavaja.. Kretaje Verovatoća Opi 4 4 Kretaje u itom
Elektrotehički fakultet uiverziteta u Beogradu 6. ju 008. Katedra za Račuarku tehiku i iformatiku Performae račuarkih itema Rešeja zadataka..videti predavaja.. Kretaje Verovatoća Opi 4 4 Kretaje u itom
Ekonometrija 9. Ekonometrija, Osnovne studije. Predavač: Aleksandra Nojković
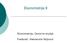 Ekonomrija 9 Ekonomrija, Osnovn sudij Prdavač: Alksandra Nojković Srukura prdavanja Narušavanj prposavki KLRM Auokorlacija - Pojam auokorlacij - Posldic auokorlacij - Tsiranj - Oklanjanj posldica auokorlacij
Ekonomrija 9 Ekonomrija, Osnovn sudij Prdavač: Alksandra Nojković Srukura prdavanja Narušavanj prposavki KLRM Auokorlacija - Pojam auokorlacij - Posldic auokorlacij - Tsiranj - Oklanjanj posldica auokorlacij
PRIMJER 3. MATLAB filtdemo
 PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI. NEUTRALNI ELEMENT GRUPOIDA.
 KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI NEUTRALNI ELEMENT GRUPOIDA 1 Grupoid (G, ) je asocijativa akko važi ( x, y, z G) x (y z) = (x y) z Grupoid (G, ) je komutativa akko važi ( x, y G) x y = y x Asocijativa
KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI NEUTRALNI ELEMENT GRUPOIDA 1 Grupoid (G, ) je asocijativa akko važi ( x, y, z G) x (y z) = (x y) z Grupoid (G, ) je komutativa akko važi ( x, y G) x y = y x Asocijativa
1 Promjena baze vektora
 Promjena baze vektora Neka su dane dvije različite uredene baze u R n, označimo ih s A = (a, a,, a n i B = (b, b,, b n Svaki vektor v R n ima medusobno različite koordinatne zapise u bazama A i B Zapis
Promjena baze vektora Neka su dane dvije različite uredene baze u R n, označimo ih s A = (a, a,, a n i B = (b, b,, b n Svaki vektor v R n ima medusobno različite koordinatne zapise u bazama A i B Zapis
nvt 1) ukoliko su poznate struje dioda. Struja diode D 1 je I 1 = I I 2 = 8mA. Sada je = 1,2mA.
 IOAE Dioda 8/9 I U kolu sa slike, diode D su identične Poznato je I=mA, I =ma, I S =fa na 7 o C i parametar n= a) Odrediti napon V I Kolika treba da bude struja I da bi izlazni napon V I iznosio 5mV? b)
IOAE Dioda 8/9 I U kolu sa slike, diode D su identične Poznato je I=mA, I =ma, I S =fa na 7 o C i parametar n= a) Odrediti napon V I Kolika treba da bude struja I da bi izlazni napon V I iznosio 5mV? b)
radni nerecenzirani materijal za predavanja
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Kažemo da je funkcija f : a, b R u točki x 0 a, b postiže lokalni minimum ako postoji okolina O(x 0 ) broja x 0 takva da je
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Kažemo da je funkcija f : a, b R u točki x 0 a, b postiže lokalni minimum ako postoji okolina O(x 0 ) broja x 0 takva da je
Linearna algebra 2 prvi kolokvij,
 1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
Značenje indeksa. Konvencija o predznaku napona
 * Opšte stanje napona Tenzor napona Značenje indeksa Normalni napon: indeksi pokazuju površinu na koju djeluje. Tangencijalni napon: prvi indeks pokazuje površinu na koju napon djeluje, a drugi pravac
* Opšte stanje napona Tenzor napona Značenje indeksa Normalni napon: indeksi pokazuju površinu na koju djeluje. Tangencijalni napon: prvi indeks pokazuje površinu na koju napon djeluje, a drugi pravac
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
 Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
OBRTNA TELA. Vladimir Marinkov OBRTNA TELA VALJAK
 OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
OSNOVI ELEKTRONIKE. Vežbe (2 časa nedeljno): mr Goran Savić
 OSNOVI ELEKTRONIKE Vežbe (2 časa nedeljno): mr Goran Savić savic@el.etf.rs http://tnt.etf.rs/~si1oe Termin za konsultacije: četvrtak u 12h, kabinet 102 Referentni smerovi i polariteti 1. Odrediti vrednosti
OSNOVI ELEKTRONIKE Vežbe (2 časa nedeljno): mr Goran Savić savic@el.etf.rs http://tnt.etf.rs/~si1oe Termin za konsultacije: četvrtak u 12h, kabinet 102 Referentni smerovi i polariteti 1. Odrediti vrednosti
