Μέθοδοι ανάλυσης οικονοµικής σκοπιµότητας έργων. Κοινωνικο- οικονοµικές. Ο ορισµός του έργου. Τεχνική αξιολόγησης έργων
|
|
|
- Ἀράχνη Μεσσηνέζης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Το ανικείµενο ων µεθόδων αξιολόγησης έργων: 7 Μέθοδοι ανάλυσης κοινωνικο-οικονοµικής οικονοµικής σκοπιµόηας έργων Να αναλύσει και εκιµήσει ποσοικά ις ωφέλειες και ις δαπάνες που δηµιουργούναι από ην υλοποίηση ου εξεαζόµενου έργου να υπολογίσει εάν συµφέρει ή όχι η υλοποίηση ου να προσδιορίσει ην πλέον συµφέρουσα Οι ωφέλειες και οι δαπάνες και ο εάν ένα έργο είναι συµφέρον ή όχι, εξαράαι από ους σόχους που έχουν εθεί και υπό ους οποίους αναλύουµε ο έργο Η πολιεία έχει σόχο να αυξήσει ην κοινωνική ευηµερία, και εποµένως α κοινωνικά και χρηµαικά οφέλη που συνεπάγεαι ο έργο θα πρέπει να αιιολογούν ο ύψος ης επένδυσης. Ο ιδιώης επενδυής έχει σόχο να µεγισοποιήσει ο κέρδος ου. Τα κοινωνικά οφέλη δεν επηρεάζουν ο κέρδος ου και εποµένως δεν α λαµβάνει υπόψη. Συγκρίνει ο κόσος καασκευής και λειουργίας µε α χρηµαικά έσοδα για να κρίνει εάν ο έργο σκόπιµο ή όχι Ο ορισµός ου έργου Ένα σύνολο αλληλοσχειζόµενων δαπανών, ενεργειών / δρασηριοήων και πολιικών που σχεδιάζοναι για ην επίευξη ων σόχων που έχει µια χώρα για ην οικονοµική και κοινωνική ανάπυξη µέσα σε µια συγκεκριµένη χρονική περίοδο. (Nash) Ο όρος έργο µπορεί να αναφέρεαι : σην καασκευή νέας ή αναβάθµιση υπάρχουσας υποδοµής µεαφορών σην εφαρµογή µέρων διαχείρισης ενός µεαφορικού συσήµαος, πχ. η ιµολογιακή πολιική ή ένα νέο έργο διαχείρισης ης κυκλοφορίας (κυκλοφοριακές ρυθµίσεις) σε µια ολοκληρωµένη σραηγική µεαφορών. Το ανικείµενο ων µεθόδων αξιολόγησης έργων: Κράος Κοινωνικο- οικονοµικές µελέες σκοπιµόηας Κοινωνικά οφέλη εξοικονόµηση χρόνου Μείωση αυχηµάων βελίωση περιβαλλονικών συνθηκών Κόση καασκευής λειουργίας συνήρησης όκοι Χρηµαικά οφέλη Έσοδα διοδίων Έσοδα από άλλες εγκαασάσεις Επιδόηση ηµοσίου Ιδιώης επενδυής Χρηµαοοικονοµικές µελέες σκοπιµόηας Κόση καασκευής λειουργίας συνήρησης όκοι + ή - + ή - Τεχνική αξιολόγησης έργων Οι εχνικές αξιολόγησης βασίζοναι σην έννοια ης αποδοικόηας. Η έννοια ης αποδοικόηας καά Pareto: Ένα σύσηµα είναι αποδοικό καά Pareto εάν οποιαδήποε µεαβολή σο σύσηµα θα έχει σαν αποέλεσµα, έσω και µια συνισώσα ου συσήµαος να εθεί σε δυσµενέσερη θέση. Ο ορισµός ης αποδοικόηας καά Pareto είναι πολύ περιορισικός, δεδοµένου όι οποιαδήποε αλλαγή σε ένα σύσηµα θα έχει θεικές συνέπειες για κάποιους και αρνηικές για κάποιους άλλους Μια πιο ελασική αξιολόγηση ης αποδοικόηας είναι µέσω ης υνηικής Βελισοποίησης καά Pareto (Potential Pareto Iproveent). Σύµφωνα µε αυή ην αρχή µέρος από α οφέλη ενός έργου µπορούν να χρησιµοποιηθούν για να αποζηµιώσουν εκείνους που εέθησαν σε δυσµενέσερη καάσαση. Εάν α οφέλη επαρκούν για ην πληρωµή ων αποζηµιώσεων, ο έργο θεωρείαι αποδοικό (αποδοικό καά Kaldor-Hicks). Η αρχή υνηικής Βελισοποίησης καά Pareto αποελεί ην βάση ων µεθόδων αξιολόγησης ων έργων. Εάν α συνολικά οφέλη από ένα έργο είναι µεγαλύερα από α συνολικά κόση, όε η υλοποίηση ου έργου συνεπάγεαι ένα καθαρό όφελος για η κοινωνία σο σύνολο ης σύνολο και εποµένως ο έργο είναι σκόπιµο. ένα απλό παράδειγµα «χρηµαο«χρηµαο-οικονοµικής» οικονοµικής» αξιολόγησης και η έννοια ης διαχρονικής αξίας ου χρήµαος Επένδυση Α: Αγορά ακινήου Α Επένδυση Β: Αγορά ακινήου Β Ηµεροµηνία αγοράς :--6 Ηµεροµηνία αγοράς :--6 Συνολικό κόσος:. Συνολικό κόσος: 5. Έσοδα 6 : 54 καθαρά φόρων Έσοδα 6 : 6 καθαρά φόρων Εήσια έσοδα αποδίδοναι σο έλος Εήσια έσοδα αποδίδοναι σο έλος κάθε έους κάθε έους Κάθε έος α έσοδα αυξάνοναι καά Κάθε έος α έσοδα αυξάνοναι καά 3% 3% Ποια επένδυση είναι πιο συµφέρουσα?
2 Η διαχρονική µεαβολή ης αξίας: µέθοδος ης µελλονικής αξίας Κανόνας επιλογής Επιλέγουµε εκείνη ην που µεγισοποιεί α καθαρά κέρδη Χρησιµοποιούµε αυόν ον κανόνα, µε ιµές που έχουν προσαρµοσθεί σον χρόνο Εξακολουθούµε να επιλέγουµε ην µε ην µεγαλύερη αξία Επιλέγουµε ην αγορά µε βάση ην µελλονική αξία ων δύο εναλλακικών λύσεων. Υπολειµµαική αξία Η διαχρονική µεαβολή ης αξίας: µέθοδος ης παρούσας αξίας Το ίδιο πρόβληµα αλλά ο εξεάζουµε ανίσροφα Η επένδυση Β είναι προιµόερη (?) Πόσα χρήµαα θα πρέπει να οποθεήσεις σε ραπεζικό λογαριασµό µε επιόκιο i = 3% για ένα χρόνο, έσι ώσε να πάρεις 5. µεά από ένα χρόνο? Μελλονική αξία FV : FV= PV x (+i), όπου PV η παρούσα αξία Y PV=FV/(+i); PV=5./(+3%)=.94 Εφόσον απαιείαι µεγαλύερο ποσό να κααεθεί σην ράπεζα, θα αγοράζαµε ο οικόπεδο που έχει ο χαµηλόερο αρχικό κόσος επένδυσης,. Η διαχρονική µεαβολή ης αξίας: µέθοδος ης µελλονικής αξίας Εξεάζουµε ένα απλό παράδειγµα: Αγορά ενός οικοπέδου ώρα:. Θα αξίζει 5. σε ένα χρόνο (σίγουρα) Θα πρέπει να λάβουµε υπόψη και ο ευκαιριακό κόσος Εναλλακική Τοποθέηση ων. σε ράπεζα που προσφέρει επιόκιο 3% : εποµένως. x (+3%) = 3. Η διαχρονική µεαβολή ης αξίας: µέθοδος ης παρούσας αξίας Ας ανάγουµε όλα σε παρούσες αξίες Η παρούσα επένδυση. για αγορά οικοπέδου αναπαρίσααι σαν. Η παρούσα αξία ου ποσού ων 5. που λαµβάνουµε µεά από ένα χρόνο είναι +5./(,3) =.94 Εποµένως η καθαρή παρούσα αξία (Net Present Value) ου οφέλους NPV= = $.94 Αφού NPV είναι θεική, θα πρέπει να αγοράσουµε ο οικόπεδο έχει θεικά καθαρά κέρδη. Θα αγοράζαε ο οικόπεδο? χρησιµοποιούµε αρνηικό πρόσηµο διόι ο ποσό αυό ο δίδουµε, δηλ. αποελεί έξοδο.
3 Η διαχρονική µεαβολή ης αξίας: Γιαί ένας επενδυής προιµάει να εισπράξει ένα χρηµαικό πόσο σήµερα από όι µεά από ένα χρόνο? να πληρώσει ένα χρηµαικό ποσό µεά από ένα χρόνο από όι σήµερα? Η επένδυση Α είναι προιµόερη Το ποσό µπορεί να επενδυθεί για ένα χρόνο και να αποφέρει κέρδη Η αγορασική δύναµη ου χρήµαος θα είναι χαµηλόερη µεά από ένα χρόνο, λόγω πληθωρισµού. Τιµές ου επιοκίου αναγωγής Υπάρχουν διαφορεικές απόψεις για ο ποιες ιµές είναι οι πλέον καάλληλες για ην αξιολόγηση ων επενδύσεων Επιόκιο αγοράς και ο διεθνές επιόκιο Σύµφωνα µε ην αρχή ης ίσης ανιµεώπισης δηµοσίων και ιδιωικών επενδύσεων θα πρέπει να χρησιµοποιείαι ο ίδιο επιόκιο σε δηµόσιες και ιδιωικές επενδύσεις Y θεωρείαι Νεοφιλελεύθερη πολιική Για ις δηµόσιες επενδύσεις, Κοινωνικό επιόκιο διαχρονικής προίµησης, όπου η κοινωνική προσφορά έχει ιδιαίερη βαρύηα Κοινωνική πολιική ύσκολο να εκιµηθεί Επηρεάζεαι από εσωερικό πληθωρισµό και σκοπιµόηες εσωερικής οικονοµικής πολιικής. Επιόκιο που αναπαρισά ο ευκαιριακό κόσος κεφαλαίου Θεωρηικά βέλιση οικονοµική αποδοικόηα Προϋποθέει συνθήκες έλειου αναγωνισµού και άρισης οικονοµικής ανάπυξης Εποµένως αν δεν λάβουµε υπόψη ην µεαβολή ης διαχρονικής αξίας ου κόσους και ων ωφελειών µπορεί να οδηγηθούµε σε λάθος αποφάσεις. Σο παράδειγµα που παρουσιάσθηκε, η βέλιση επένδυση είναι η Α. Όµως αν δεν λάβουµε υπόψη ην διαχρονική µεαβολή ης αξίας ου χρήµαος, θα είχαµε επιλέξει ην επένδυση Β. Εποµένως καά ην αξιολόγηση ων έργων θα πρέπει να ορίσουµε: ην διάρκεια ης εκµεάλλευσης ου έργου αλλά και ην διάρκεια υλοποίησης ην υπολειµµαική αξία ου έργου, δηλ. ην αξία ου σο έλος ης περιόδου εκµεάλλευσης ο επιόκιο που θα χρησιµοποιήσουµε για να ανάγουµε σε παρούσες ή µελλονικές αξίες Έσω όι ο επιόκιο αναγωγής είναι 3% Y Τεχνική αξιολόγησης έργων: η ανάλυση κόσους - ωφελειών Για ον έλεγχο ης οικονοµικής αποδοικόηας ενός έργου απαιείαι να αποιµηθούν α κόση και α οφέλη από ο έργο εκφρασµένα σε µονάδες χρήµαος. Όλες οι επενδύσεις απαιούν πόρους (αµειακές εκροές) σην φάση υλοποίησης ου έργου. Σην φάση ης παραγωγικής λειουργίας, δηλ. σο µέλλον, οι επενδύσεις αποκοµίζουν έσοδα (αµειακές εισροές). Το έργο είναι οικονοµικά αποδοικό εάν α οφέλη µερούµενα σε χρήµα είναι µεγαλύερα από α κόση. Το πιο αποδοικό έργο είναι εκείνο για ο οποίο η διαφορά είναι η µεγαλύερη ή ο λόγος ων ωφελειών προς α κόση είναι µεγαλύερος.
4 Ανάλυση κόσους οφέλους Τα κόση και α οφέλη καανέµοναι σε πολλά χρόνια, και εποµένως απαιείαι µια µέθοδος που να λαµβάνει υπόψη ις επιπώσεις ης χρονικής καανοµής ων διαφόρων συνισωσών ου κόσους και ων ωφελειών. Οι εκροές και εισροές είναι διαχρονικές, δηλ. συµβαίνουν σε διαφορεικές χρονικές σιγµές, και εποµένως δεν µπορούν να αθροισούν λόγω ης διαφορεικής αξίας ου χρήµαος Πραγµαικό και ονοµασικό επιόκιο Ονοµασικό επιόκιο : η ρέχουσα ιµή ου επιοκίου χρησιµοποιείαι όαν επεξεργαζόµασε ρέχονα σοιχεία και ισορικά σοιχεία (σε ρέχουσες ιµές). Πραγµαικό επιόκιο: σαθερό επιόκιο, χρησιµοποιείαι όαν α σοιχεία που επεξεργαζόµασε προσαρµόζοναι σε σαθερές ιµές για ένα έος βάση Το πραγµαικό επιόκιο υπολογίζεαι από ο ονοµασικό λαµβάνονας υπόψη ον πληθωρισµό πχ. Χρησιµοποιώνας ον δείκη ιµών κααναλωή. Σην αξιολόγηση επενδύσεων : Εάν α σοιχεία κόσους και οφέλους δίδοναι σε πραγµαικές ιµές, χρησιµοποίησε ο πραγµαικό επιόκιο. Εάν σε ονοµασικές/ρέχουσες ιµές, χρησιµοποίησε ο ονοµασικό επιόκιο. Και οι δύο µέθοδοι θα δώσουν α ίδια αποελέσµαα. Ανάλυση κόσους οφέλους Το συνολικό κόσος είναι : ο διαχρονικό άθροισµα ων δαπανών Τα συνολικά οφέλη είναι : ο διαχρονικό άθροισµα ων ωφελειών για να είναι συγκρίσιµα α µεγέθη θα πρέπει να πρέπει αναφέροναι σε κάποια κοινή χρονική σιγµή, δηλ. ο έος βάσης Ως έος βάσης συνήθως επιλέγεαι η / ου έους έναρξης καασκευής Πραγµαικό επιόκιο Τα επιόκια ης αγοράς είναι ονοµασικά, και ανανακλούν (περιλαµβάνουν) ον πληθωρισµό. Πως υπολογίζουµε ο πραγµαικό από ο ονοµασικό επιόκιο? έσω: r = Πραγµαικό επιόκιο i = ο ονοµασικό επιόκιο = ο πληθωρισµός Απλή µέθοδος: r ~ i- <-> r+~i Μεγαλύερη ακρίβεια : r=(i-)/(+) γιαί? Προεξόφληση και αναοκισµός Για να αθροισούν οι διαχρονικές εισροές και εκροές ενός έργου, µπορούν να χρησιµοποιηθούν δύο εναλλακικές µέθοδοι Μέθοδος ης προεξόφλησης Μεαροπή ων µελλονικών αξιών, FV, σε σηµερινές (παρούσες, PV) µε βάση κάποιο επιόκιο, i. PV = FV / ( + i) t Προεξοφληικό επιόκιο Μέθοδος ου αναοκισµού Αναγωγή ων σηµερινών αξιών, PV, σε µελλονικές, FV, µε βάση κάποιο επιόκιο, i FV = PV. ( + i) t Επιόκιο αναοκισµού t είναι η χρονική περίοδος προεξόφλησης ή αναοκισµού σε έη, όαν ο επιόκιο είναι ο εήσιο επιόκιο. Οόρος επιόκιο αναγωγής µπορεί να χρησιµοποιηθεί γενικά. Για αναγωγή σε παρούσες ιµές ο επιόκιο αναγωγής είναι ο προεξοφληκό επιόκιο Για αναγωγή σε µελλονικές ιµές, ο επιόκιο αναγωγής είναι ο επιόκιο αναοκισµού. Πραγµαικό επιόκιο αναγωγής Έσω C ο κεφάλαιο σε (ρέχουσες) ιµές ου έους Ν Με µε ονοµασικό επιόκιο i% µεά από ένα χρόνο, η αξία σε ρέχουσες ιµές, δηλ. ου έους Ν+, FVn θα είναι FVn = C.(+i) Όµως λόγω ου πληθωρισµού %, η αγορασική αξία ου FVn (σε ιµές ου έους Ν), δηλ. η πραγµαική ιµή, FVr, θα είναι FVr = FVn / ( + ) Έσω r ο πραγµαικό επιόκιο. Τόε µπορούµε να υπολογίσουµε ο πραγµαική ιµή FVr: FVr = C.(+r) Εποµένως FVr = C.(+i)/(+) = C.(+r) Y + r = (+i)/(+) Y r = (i-) / (+) Παράδειγµα: εάν i=%, =4% Απλή προσέγγιση : r=6%, Ακριβής: r=5.77%
5 κριήρια αξιολόγησης: Η Καθαρή Παρούσα Αξία κριήρια αξιολόγησης: Εσωερικός Συνελεσής Αναπόδοικόηας,, ΕΣΑ, (internal( rate of return, IRR) Η Καθαρή Παρούσα Αξία, ΚΠΑ, (Net Present Value, NPV) είναι ένα από α πιο συνηθισµένα κριήρια αξιολόγησης επενδύσεων. Βασίζεαι σον κανόνα σύµφωνα µε ον οποίο επιλέγεαι εκείνη η που αποφέρει α περισσόερα καθαρά οφέλη, λαµβάνονας υπόψη και ην διαχρονική µεαβολή ης αξίας ου χρήµαος. Προκύπει εάν προεξοφλήσουµε σήµερα (παρούσα αξία) για κάθε έος ξεχωρισά ην διαφορά µεαξύ ων µελλονικών εσόδων (εισροών) και εξόδων (εκροών) για ολόκληρο ον υπολογιζόµενο χρονικό ορίζονα (ή διάρκεια ζωής ου έργου) µε βάση ένα συνελεσή προεξόφλησης (δηλ. ο επιόκιο αναγωγής). ε : O εσωερικός συνελεσής απόδοσης ή αναποδοικόηας, ΕΣΑ, είναι ο υπολογιζόµενο επιόκιο µε ο οποίο η παρούσα αξία ων αµειακών εισροών ισούαι µε ην παρούσα αξία ων αµειακών εκροών. Ο ΕΣΑ είναι ο επιόκιο που εξισώνει ην συνολική παρούσα αξία ων εσόδων και εξόδων, δηλ. εξισώνει ην ΚΠΑ µε µηδέν. Ν = [ Ταµειακ ές εισρο ές ( ) Ταµειακ ές εκρο ές ( )] ( + ε ) = Εάν ο ε είναι υψηλόερο από ο επιόκιο προεξόφλησης, i που ισχύει σην αγορά (ε > i ) ο σχέδιο επένδυσης που αξιολογείαι κρίνεαι αποδεκό. Εάν ο ε είναι χαµηλόερο από ο επιόκιο προεξόφλησης, i που ισχύει σην αγορά (ε < i ) ο σχέδιο επένδυσης που αξιολογείαι απορρίπεαι. κριήρια αξιολόγησης: Η Καθαρή Παρούσα Αξία Υπολογισµός ων εισροών και εκροών για κάθε έος Επιλογή καάλληλου επιοκίου προεξόφλησης Υπολογισµός ης παρούσας αξίας ης καθαρής αµειακής ροής (διαφοράς µεαξύ εισροών και εκροών) Η καθαρή παρούσα αξία υπολογίζεαι από ην σχέση [ Ταµειακ ές εισρο ές ( ) Ταµειακ ές εκρο ές ( )] Ν ΚΠΑ = = ( + i) κριήρια αξιολόγησης: Εσωερικός Συνελεσής Απόδοσης, ΕΣΑ, (internal( rate of return, IRR) Εάν υπάρχουν εναλλακικά σενάρια επενδύσεων, επιλέγεαι εκείνο που έχει ο υψηλόερο ε, υπό ον όρο όι ε > i. Εάν ο ε είναι χαµηλόερο από ο επιόκιο προεξόφλησης, i που ισχύει σην αγορά (ε < i ) ο σχέδιο επένδυσης που αξιολογείαι απορρίπεαι. Όπου : i = ο προεξοφληικό επιόκιο (επιόκιο αναγωγής) = ο χρόνος ή περίοδος προεξόφλησης Ν = o χρονικός ορίζονας ανάλυσης. κριήρια αξιολόγησης: Η Καθαρή Παρούσα Αξία [ Ταµειακ ές εισρο ές ( ) Ταµειακ ές εκρο ές ( )] = ΚΠΑ = Ν = ( + i) ΚΠΑ = Ν Ταµειακ ές εισρο ές ( ) = ( + i) = ( + i) α) αν ΚΠΑ είναι θεική δηλ. η αποδοικόηα είναι µεγαλύερη από ο επιόκιο προεξόφλησης, η επένδυση είναι αποδεκή β) αν ΚΠΑ είναι αρνηική δηλ. η αποδοικόηα είναι µικρόερη από ο επιόκιο προεξόφλησης, η επένδυση απορρίπεαι γ) αν ΚΠΑ είναι µηδέν δηλ. η αποδοικόηα είναι ίση µε ο επιόκιο προεξόφλησης, η επένδυση γίνεαι αποδεκή αν δεν υπάρχει καλύερη εναλλακική. Ν Ταµειακ ές εκρο ές ( ) κριήρια αξιολόγησης: Λόγος Συνολικού Οφέλους / συνολικού Κόσους Ένα άλλο κριήριο αξιολόγησης είναι ο λόγος ου οφέλους προς ο κόσος B C = Ν Ν Ταµειακ ές εισρο ές ( ) /( + i) Ταµειακ ές εκρο ές ( ) /( + i) Ανίσοιχα, για ιµές ου λόγου >, η επένδυση θεωρείαι αποδοική, ενώ για ιµές < απορρίπεαι
6 Η συνάρηση ης καθαρής παρούσας αξίας σο Excel Excel NPV & IRR Αξιολόγηση έργου παράκαµψης οικισµού Εναλλακικές λύσεις: ΕΛ : η µηδενική, δηλ, να µην καασκευασθεί η παράκαµψη. Η κυκλοφορία θα εξακολουθεί να γίνεαι Γ µέσω ου οικισµού, ακολουθώνας ην διαδροµή Β Ο : η εναλλακική, σύµφωνα A Κ µε ην οποία θα καασκευασθεί η παράκαµψη Ακ. Η κυκλοφορία από και προς ον οικισµό θα χρησιµοποιεί ον υφισάµενο δρόµο. Η διαµπερής κυκλοφορία θα γίνεαι µέσω ης παράκαµψης εφόσον ο γενικευµένο κόσος µεακίνησης µέσω ης παράκαµψης είναι χαµηλόερο από όι µέσω ου υφισάµενου δρόµου. Για ον υπολογισµό ων ωφελειών και ου κόσους ο οδικό δίκυο χωρίζεαι σε µήµαα µε οµοιόµορφα χαρακηρισικά, π.χ. ΑΒ,,, Η συνάρηση ου εσωερικού δείκη απόδοσης σο Excel Υπολογισµός Ωφελειών :. Μεαβολές σους χρόνους µεακίνησης Εναλλακική Οδικό µήµα Φόροι Οδικό µήµα ΙΧ Β.Ο Εναλλακική ΑΒ Q ΙΧ ΑΒ Q ΒΟ ΑΒ ΑΒ ΕΛ Q ΙΧ Q ΒΟ ΕΛ Q ΙΧ Q ΒΟ q ΙΧ A q BO A ΑΒ q ΙΧ AB q BO AΒ q ΙΧ q BO q ΙΧ q BO Χρόνοι ΙΧ Τ ΑΒ ΙΧ Τ ΙΧ Τ ΙΧ t A ΙΧ t AB ΙΧ t ΙΧ t ΙΧ διαδροµής Β.Ο Τ ΑΒ ΒΟ Τ ΒΟ Τ ΒΟ t A BO t AΒ BO t BO t BO Οι χρόνοι διαδροµής θα πρέπει να υπολογίζοναι σαν συνάρηση ων χαρακηρισικών ης διαδροµής και ου φόρου Q i Ο φόρος οχηµάων καηγορίας i σο µήµα για ην εναλ. ΕΛ qi Ο φόρος οχηµάων καηγορίας i σο µήµα για ην εναλ. T i Ο χρόνος διαδροµής ενός οχήµαος καηγορίας i σο µήµα για ην ΕΛ t i Ο χρόνος διαδροµής ενός οχήµαος καηγορίας i σο µήµα για ην ΑΒ Αξιολόγηση έργου : Γενικές καευθύνσεις µέσα από µια απλουσευική προσέγγιση σο παράδειγµα ης µελέης σκοπιµόηας ης παράκαµψης ενός οικισµού ανάλυση κοινωνικοοικονοµικής σκοπιµόηας Θεωρούµε: Ωφέλειες : Μείωσηαυχηµάων Εξοικονόµηση χρόνου Λειουργικό κόσος οχηµάων Κόση : Κόσος µελεών, απαλλοριώσεων Κόσος καασκευής Κόσος συνήρησης Κόσος λειουργίας A Β Ο Γ Κ Ανίσοιχα από ην κυκλοφοριακή µελέη δίδοναι α ακόλουθα µεγέθη P i,k p i,k Ο i,k ο i,k = ο ποσοσό ων οχηµάων καηγορίας i, που κινούναι σο µήµα µε σκοπό µεακίνησης k (σκοποί: προς/από, σα πλαίσια ης ς, αγορές, αναψυχή, κλπ), για ην περίπωση ης ΕΛ = ο ανίσοιχο ποσοσό για ην περίπωση ης = Η µέση πληρόηα ων οχηµάων καηγορίας i, που κινούναι σο µήµα µε σκοπό µεακίνησης k (σκοποί: προς/από, σα πλαίσια ης ς, αγορές, αναψυχή, κλπ), για ην περίπωση ης ΕΛ = Η ανίσοιχη µέση πληρόηα για ην περίπωση ης Με βάση α παραπάνω µεγέθη υπολογίζεαι ο συνολικό κόσος ου χρόνου διαδροµής για ΕΛ και. = ΕΛ Qi Pi, k Oi, k Ti k i TC VOT, = qi pi, k oi, k ti k i TC VOT, i k i k Όπου VOT i, k ηαξία ου χρόνου ενός µεακινούµενου µε όχηµα καηγορίας i και µε σκοπό µεακίνησης k.
7 Υπολογισµός Ωφελειών :. Μεαβολές λειουργικού κόσους οχηµάων Το λειουργικό κόσος ανά χλµ εξαράαι από ην αχύηα κίνησης. Από ις προβλέψεις ων κυκλοφοριακών φόρων και ις διαοµές ων οδικών µηµάων είναι δυναόν να υπολογίσουµε ην αχύηα κίνησης ων οχηµάων και συνεπώς ο λειουργικό κόσος. Εσι µπορούµε να ορίσουµε ις ακόλουθες µεαβληές : C i vc i L = ο λειουργικό κόσος/χλµ ενός οχήµαος καηγορίας i που κινείαι σο µήµα για ην εναλ. ΕΛ = ο λειουργικό κόσος/χλµ ενός οχήµαος καηγορίας i που κινείαι σο µήµα για ην εναλ. = ο µήκος ου µήµαος εναλ. ΕΛ Υπολογισµός Κόσους ο έος : C C Συνολικό κόσος Κόσος µελεών, απαλλοριώσεων Κόσος καασκευής ( ) = ( SC( ) + CC( ) OMC( )) ΕΛ + ( ) = + OMCΕΛ( )) ΕΛ + Κόσος λειουργίας κ& συνήρησης Τα συνολικά λειουργικά κόση για ις λύσεις ΕΛ και υπολογίζοναι : i i VOC Q L VC ΕΛ = i i i VOC q L vc = i Κόση : C() = C ΕΛ ) C ( ) ( ΕΛ Υπολογισµός Ωφελειών : 3. Μεαβολές σον αριθµό ων αυχηµάων Υπολογισµός Καθαρής Παρούσας Αξίας: Η πιθανόηα να συµβεί ένα αύχηµα καθορίζεαι από α γεωµερικά και λειουργικά χαρακηρισικά ης οδού, και ο ισορικό αυχηµάων. Τα αυχήµαα µπορούν να χωρισθούν σε καηγορίες ανάλογα µε ην σοβαρόηα ους. Κάθε καηγορία αυχήµαος έχει και διαφορεικό κόσος Από ανάλυση σοιχείων αυχηµάων µπορούµε να ορίσουµε α ακόλουθα µεγέθη: AR ar = η πιθανόηα να συµβεί αύχηµα καηγορίας σο µήµα για ην εναλ. ΕΛ. (εκφράζεαι συνήθως σε αυχήµαα / οχ.χλµ) = η πιθανόηα να συµβεί αύχηµα καηγορίας σο µήµα για ην εναλ.. AC = ο κόσος ενός αυχήµαος καηγορίας Τα συνολικά κόση αυχηµάων για ις λύσεις ΕΛ και υπολογίζοναι : i i TAC Q L AR AC ΕΛ = i i TAC q L ar AC = ΚΠΑ = ΚΠΑ( ) = ΚΠΑ( ΕΛ) = ν ν ( B( ) C( )) = ( + i) = ( B ( ) C ( )) ( + i) ν ( BΕΛ( ) CΕΛ( )) = ( + i) ΚΠΑ = ΚΠΑ( ) ΚΠΑ( ΕΛ) Υπολογισµός Ωφελειών ο έος : = - (όφελος από ΕΛ) = - (όφελος από ) εναλ. Συνολικό όφελος Κόσος χρόνου διαδροµής Λειουργικό κόσος Κόσος Αυχηµάων B ( ) = ( TC( ) + VOC( ) TAC( )) ΕΛ + ΕΛ B ( ) = ( TCΕΛ( ) + VOCΕΛ( ) TACΕΛ( )) ΕΛ + Οφέλη: Β() = B ΕΛ ) B ( ) ( ΕΛ Όαν εξεάζουµε ην κάθε µεµονωµένα, α οφέλη (µε ην καθιερωµένη έννοια) είναι αρνηικά και ισούναι µε : (κόσος χρόνου + λειουργικό κόσος + κόσος αυχηµ.) Συγκρίνονας όµως ις δύο εναλλακικές λύσεις έχουµε θεικά οφέλη εφόσον, α κόση ων οχηµάων σην είναι χαµηλόερα από α ανίσοιχα σην ΕΛ.
8 Παράδειγµα σύγκριση έργων µε διαφορεική διάρκεια ζωής Θεωρείσε έργα υποδοµών Ίσης ικανόηας εξυπηρέησης αλλά µε διαφορεική διάρκεια ζωής () 7 χρόνια και () 35 χρόνια Κόσος Επένδυσης () = εκ., Κόσος Επένδυσης () = 5 εκ. Καθαρά εήσια οφέλη () = 6.5 εκ., Καθαρά εήσια οφέλη () = 4. εκ. Το επιόκιο αναγωγής είναι 5% Πως µπορούµε να συγκρίνουµε? Μπορούµε να υπολογίσουµε ην ΚΠΑ για ο καθένα? Περιγραφή ων έργων κάθε εναλλακικής ς:. Για ον προϋπολογισµό ων επιµέρους έργων θα δίδοναι: Κόσος χρήσης µηχανηµάων και µεαφορικών µέσων σε ιµές χωρίς φόρους (π.χ. καυσίµου) και ΦΠΑ Κόσος αγοράς ή καασκευής υλικών σε ιµές αγοράς χωρίς φόρους Κόσος εργαικών και προσωπικού διεύθυνσης Κόσος εργασιών που αφορούν ανακαασκευές/ροποποιήσεις υφισάµενων δικύων, ΟΚΩ κλπ Κόσος επίβλεψης ιεύθυνσης έργων Κόσος πρόσκησης ή ενοικίασης δανειοθαλάµων, αποθεσιοθαλάµων κλπ Εκάσεις που α) θα απαλλοριωθούν για καασκευή ου έργου (ανά καηγορία χρήσης β) θα απαλλοριωθούν ή ενοικιασθούν σαν δανειοθάλαµοι, αποθεσιοθάλαµοι, και γ) που θα απαιηθούν σαν εργοαξιακοί χώροι Ποσοικά σοιχεία εγκαασάσεων που θα καεδαφισούν καά καηγορία και αριθµό θιγοµένων Παράδειγµα σύγκριση έργων µε διαφορεική διάρκεια ζωής Υποθέουµε όι µεά από α πρώα 35 χρόνια µπορούµε να καασκευάσουµε πάλι ο έργο (). ΚΠΑ()=-+(6.5/.5) /.5 7 =5.73 ΚΠΑ(α)=-5+(4./.5)+..+4./.5 35 =8.77 ΚΠΑ(α + β)=8.77+(8.77/.5 35 )=.7 Τα δύο έργα γίνοναι συγκρίσιµα Το έργο είναι καλύερο Περιγραφή ων έργων κάθε εναλλακικής ς:. Κόσος ων ενεργειών που απαιούναι πριν από ην καασκευή Κόσος µελεών και ερευνών (κυκλοφοριακών, γεωλογικών, εδαφοεχνικών) συνήθως λαµβάνεαι σαν ένα ποσοσό ου κόσους καασκευής απάνες διοίκησης συµβούλων Κόσος απαλλοριώσεων µπορεί να διαφέρει ανάλογα µε ην 3. Από α εύχη ης µελέης, ο κόσος καασκευής, µε ην ακόλουθη ανάλυση: Χωµαουργικά υποδιαιρούµενα σις επιµέρους εργασίες: α) Εκσκαφές, β) δάνεια, αποθέσεις, γ) επιχώµαα, δ) λοιπές εργασίες. Τεχνικά έργα υποδιαιρούµενα σις επιµέρους εργασίες: α) άνω διαβάσεις, β) κάω διαβάσεις, γ) γέφυρες, κοιλαδογέφυρες, δ) σήραγγες και σκεπασά µήµαα Cut&Cover ε) έργα ελέγχου οµβρίων, σ) έργα ελέγχου υπογείων υδάων. Οδοσρωσία Ασφαλικά Σήµανση εξοπλισµός οδού Έργα πρασίνου Λοιπά έργα αποκαάσασης οπικού δικύου ή άλλων δικύων Παρουσίαση εναλλακικών λύσεων : Η παρουσίαση κάθε εναλλακικής ς περιλαµβάνει α ακόλουθα σοιχεία:. Τίλος και κωδικός αριθµός. Σχέδιο όπου παρουσιάζοναι οι εναλλακικές λύσεις 3. Κααγραφή ων κύριων χαρακηρισικών ης εναλλακικής ς Τεχνικά χαρακηρισικά: κλίσεις, ακίνες, διαοµή κλπ Τεχνικά έργα (γέφυρες, σήραγγες κλπ) Λειουργικά χαρακηρισικά: αχύηα µελέης, V85 Χρονική περίοδος εκέλεσης ης καασκευής: χρόνος είναι η αρχή εκέλεσης όλης ης καασκευής Ο εήσιος µέσος ηµερήσιος κυκλοφοριακός φόρος () για ις καηγορίες α) κανονικής (καά ις άσεις) κυκλοφορίας β) Προσελκυόµενης κυκλοφορίας (από άλλους δρόµους ή/και µεαφορικά µέσα) και γ) παραγώγου κυκλοφορίας (δηµιουργούµενης, δηλ. νέες µεακινήσεις που προκύπουν από ην µείωση ου γενικευµένου κόσους κάω από ο όριο που έκανε αυές ις µεακινήσεις απαγορευικές) 4. Κόσος καασκευής, απαλλοριώσεων, κλπ 5. Σύνοψη ων εκιµώµενων περιβαλλονικών επιπώσεων 6. Η εκιµώµενη σκοπιµόηα ης επένδυσης (από προδιαγραφές Μελεών Σκοπιµόηας ΥΠΕΧΩ Ε) Περιγραφή ων έργων κάθε εναλλακικής ς: 4. Για ην εκίµηση ων δαπανών συνήρησης και λειουργίας, να λαµβάνοναι υπόψη οι ακόλουθες καηγορίες δαπανών: Επισκόπηση έλεγχος και ιοικηικές δαπάνες Περιοδική συνήρηση, ελαφρά και βαριά Έκακη συνήρηση απάνες ηλεκροφωισµού Ειδικές δαπάνες Ασυνόµευση Απαραίηα σοιχεία για εκίµηση κόσους καασκευής και συνήρησης Εκίµηση ποσοήων καασκευής και συνήρησης
9 µεθοδολογία ης οικονοµικής ανάλυσης. Επιλογή βασικών οικονοµικών δεδοµένων. Χρηµαικό και οικονοµικό κόσος 3. Εκίµηση κόσους ων έργων 4. Υπολογισµός λειουργικού κόσους οχηµάων 5. Υπολογισµός κόσους αυχηµάων 6. Αξία εξοικονόµησης χρόνου 7. Εκίµηση ωφελειών κάθε εναλλακικής ς 8. Υπολογισµός αποελεσµαικόηας κάθε εναλλακικής ς (από προδιαγραφές Μελεών Σκοπιµόηας ΥΠΕΧΩ Ε) 9. Ανάλυση κινδύνων Ανάλυση ευαισθησίας. Επιλογή βασικών οικονοµικών δεδοµένων.3 Επιόκιο αναγωγής Η οικονοµική ισοδυναµία ενός µεγέθους Α n που εκδηλώνεαι ην χρονική σιγµή t=n µε ένα µέγεθος Α που εκδηλώνεαι ην χρονική σιγµή t=, εκφράζεαι µε ην σχέση: A = An. n ( + e) e είναι ο επιόκιο αναγωγής. Σις χρηµαοοικονοµικές αναλύσεις, ο e έχει ην έννοια ου προεξοφληικού επιοκίου. Σις οικονοµικές αναλύσεις ο e εκφράζει ον ρυθµό αποµείωσης ης οικονοµικής αξίας ου θεωρούµενου µεγέθους συναρήσει ου χρόνου. Η επιλογή ου θα πρέπει να αιιολογείαι από ον µελεηή (αν και συνήθως η ιµή ου προσδιορίζεαι σην σύµβαση ανάθεσης). Θα ελέγχεαι η ευαισθησία ων αποελεσµάων ης οικονοµικής αξιολόγησης για ρεις ιµές ου επιοκίου: ην πιθανή µέγιση, ην πλέον πιθανή, και ην πιθανή ελάχιση.. Επιλογή βασικών οικονοµικών δεδοµένων. Χρονικός ορίζονας οικονοµικής ανάλυσης οικονοµικής ζωής ου έργου Οι χρονικές περίοδοι οµαδοποιούναι σις καηγορίες α) περίοδος µελέης απαλλοριώσεων β) περίοδος καασκευής γ) περίοδος λειουργίας Η συνολική χρονική περίοδος υποδιαιρείαι σε ισόχρονα χρονικά διασήµαα (έη ή εξάµηνα) που χρησιµοποιούναι ως χρονικές µονάδες Η χρονική µονάδα να περιγράφεαι µε σαφήνεια Απαιείαι για ο διάγραµµα εισροών - εκροών Θα πρέπει να ορισθεί αν οι εισροές εκροές λαµβάνοναι σην αρχή ή έλος ης χρονικής µονάδας. Χρηµαικό και οικονοµικό κόσος Κόση και οφέλη θα πρέπει να αποιµώναι σε οικονοµικές ιµές και όχι σε ιµές αγοράς (λογισικές/χρηµαικές). Οι οικονοµικές ιµές δεν περιλαµβάνουν ιµολογιακές παραµορφώσεις π.χ. φόροι, δασµοί, ΦΠΑ κλπ, και υπολογίζοναι από ις ιµές ης αγοράς αφού αφαιρεθούν οι µεαβιβασικές πληρωµές, φόροι κλπ. ιευκρινίζοναι οι ακόλουθες έννοιες για ον προσδιορισµό ων οικονοµικών ιµών από ις χρηµαικές ιµές Μεαβιβασικές πληρωµές: ανιπροσωπεύουν απλή µεαβίβαση χρηµαικών πόρων και όχι χρήση-ανάλωση-απώλεια πόρων, π.χ. φόροι, δασµοί, επιδοήσεις, επιχορηγήσεις. Οι απαλλοριώσεις θεωρηικά είναι µεαβιβασικές πληρωµές, συνήθως όµως θεωρούναι ως οικονοµικά µεγέθη που ανιπροσωπεύουν ην ανάλωση πόρου που είναι η σέρηση δυναόηας άλλων χρήσεων ης περιοχής που θα κααλάβει ο έργο.. Επιλογή βασικών οικονοµικών δεδοµένων. Τρέχουσες και σαθερές ιµές Θα πρέπει να γίνει επιλογή µεαξύ ρεχουσών ή σαθερών ιµών, για να ορισθεί αν οι αναλύσεις γίνοναι µε συνεκίµηση ου πληθωρισµού ή όχι. Χρηµαικό και οικονοµικό κόσος Εργοδοικές εισφορές: είναι οι κραήσεις για ην ασφάλιση ων εργαζοµένων, που θεωρούναι ως µελλονική αποζηµίωση σε περιόδους όπου παρουσιάζεαι έλλειψη προσφοράς ς. Εποµένως υπολογίζοναι ως µέρος ου κόσους ς και περιλαµβάνοναι ως κόσος σην οικονοµική ανα. Φόροι, δασµοί : είναι καθαρά µεαβιβασικές πληρωµές και γι αυό θα πρέπει να αφαιρούναι από ις ιµές αγοράς. Οι Φόροι αφαιρούναι από όλες ις δαπάνες χρήσης (λειουργικό κόσος) ου έργου Από ις δαπάνες καασκευής αφαιρούναι όλοι οι φόροι εισοδήµαος ου καασκευασή Ο ΦΠΑ δεν µεέχει σις ιµές Φόροι εισοδήµαος εργαζοµένων δεν αφαιρούναι, γιαί θεωρούναι όι ανισαθµίζουν ις δαπάνες για ην διασφάλιση αποδεκού περιβάλλονος εκέλεσης και λειουργίας ου έργου από ην Κραική Αρχή
10 . Χρηµαικό και οικονοµικό κόσος απάνες επισκευής και συνήρησης : υπολογίζοναι σο οικονοµικό κόσος σύµφωνα µε α προηγούµενα. Ισορικές απάνες: είναι δαπάνες που έγιναν σο παρελθόν, όπως γενικές µελέες και διοικηικές δαπάνες, που δεν συµπεριλαµβάνοναι συνήθως γιαί αφορούν δαπάνες ενοπισµού επενδύσεων και εποµένως θεωρούναι γενικές δρασηριόηες. Όµως εξειδικευµένες δαπάνες για ο συγκεκριµένο έργο, όπως µελέες, έρευνες θα πρέπει να συµπεριλαµβάνοναι. 4. Υπολογισµός λειουργικού κόσους οχηµάων Το λειουργικό κόσος οχηµάων εκφράζεαι σαν κόσος ανά χλµ. Είναι γενικά υψηλόερο για χαµηλές και για υψηλές αχύηες. Το κόσος διαφέρει ανά καηγορία οχήµαος Ο µελεηής θα πρέπει να ορίσει ις υπικές καηγορίες οχηµάων, και ην σύνθεση ης κυκλοφορίας, δηλ. α ποσοσά κάθε καηγορίας Με χρήση καάλληλου συγκοινωνιακού µονέλου, γίνοναι προβλέψεις ων µελλονικών φόρων ανά καηγορία οχήµαος και για κάθε διαδροµή που ενώνει κάθε ζεύγος Προέλευσης Προορισµού ων µεακινήσεων. Υπολογίζοναι έσι α οχηµαοχιλιόµερα που διανύοναι από κάθε καηγορία οχήµαος Πολλαπλασιάζονας µε ο ανίσοιχο λειουργικό κόσος, υπολογίζεαι ο συνολικό λειουργικό κόσος οχηµάων 3. Εκίµηση κόσους ων έργων Βασικές δαπάνες για ην καασκευή, συνήρηση και λειουργία Για κάθε εναλλακική θα εκιµώναι οι ποσόηες καασκευής και συνήρησης Τα κόση υπολογίζοναι από ις ποσόηες και ιµές µονάδας Θα πρέπει να διακρίνοναι: ο κόσος εργασιών και ερευνών που αφορούν µελεηικές δρασηριόηες Το κόσος διεύθυνσης-διοίκησης και επίβλεψης Το κόσος συνήρησης Το κόσος λειουργίας, π.χ. ηλεκροφωισµός, - δεν περιλαµβάνει ο οικονοµικό κόσος χρήσης ου έργου (από ους χρήσες, δηλ. ο λειουργικό κόσος οχηµάων) 4. Υπολογισµός λειουργικού κόσους οχηµάων εδοµένου όι α γεωµερικά χαρακηρισικά δεν είναι οµοιόµορφα για όλο ο µήκος ου δρόµου (διαφορεικές αχύηες λειουργίας, διαφορεικές κλίσεις, κλπ, που επηρεάζουν ην καανάλωση καυσίµου) ο έργο διαιρείαι σε υποµήµαα µε οµοιόµορφα χαρακηρισικά και συγκεκριµένο λειουργικό κόσος οχήµαος Με βάση α ανωέρω υπολογίζεαι ο αριθµός ων οχηµαοχιλιοµέρων ανά µήµα και καηγορία οχήµαος Πολλαπλασιάζονας µε ο ανίσοιχο λειουργικό κόσος, και αθροίζονας για όλα α υποµήµαα και καηγορίες οχηµάων υπολογίζουµε ο συνολικό λειουργικό κόσος Οι ιµές ου λειουργικού κόσους ανά καηγορία οχήµαος αποελούν ανικείµενο εξειδικευµένης µελέης 3. Εκίµηση κόσους ων έργων Άλλες δαπάνες Αφορούν πρόσθεα κόση που προκαλούναι από ις καασκευασικές δρασηριόηες, και από ην ύπαρξη και λειουργία ου οδικού έργου. Ενδεικικά αναφέροναι: υσλειουργία (π.χ. καθυσερήσεις) ου υφισάµενου οδικού, σιδηροδροµικού δικύου Τυχόν αναγκαία επιβολή περιορισικών µέρων χρήσεων γης. 5. Υπολογισµός κόσους αυχηµάων Υπολογίζεαι από ον προβλεπόµενο αριθµό αυχηµάων και ο κόσος ου αυχήµαος Με βάση ισορικά σοιχεία εκιµώναι οι δείκες αυχηµάων, δηλ. ο αριθµός ων αυχηµάων ανά οχηµαοχιλιόµερο. Το κόσος ων αυχηµάων αποελεί ένα ιδιαίερα δύσκολο πρόβληµα, και αποελεί ανικείµενο εξειδικευµένης κοινωνικοοικονοµικής ανάλυσης. Είναι δυναόν να προβλέποναι διαφορεικές καηγορίες αυχηµάων, ανάλογα µε ην σφοδρόηα ους, και ανίσοιχα θα υπολογίζεαι ο κόσος για κάθε καηγορία αυχήµαος.
11 6. Αξία εξοικονόµησης χρόνου Η αξία ου χρόνου µπορεί να αναπαρισά ην αξία ου χρόνου ς ου µεακινούµενου ή ην επιθυµία που έχει ένας µεακινούµενος να πληρώσει για να εξοικονοµήσει χρόνο διαδροµής. Η αξία ου χρόνου εκφράζεαι για κάθε µεακινούµενο σε ΕΥΡΩ/ωρα Εξεάζεαι σο µάθηµα Σχεδιασµός Μεαφορών (8ο εξ.) Συνήθως χρησιµοποιούναι διαφορεικές ιµές ης αξίας ου χρόνου ανάλογα µε ον σκοπό ης µεακίνησης. Ιδιαίερη σηµασία θα πρέπει να δίνεαι σην αξία ου χρόνου ων εµπορευµαικών µεακινήσεων. Η αξία ου χρόνου µεαβάλλεαι ανάλογα µε ο εµπόρευµα. Ο υπολογισµός ης αξίας ου χρόνου αποελεί ανικείµενο εξειδικευµένης µελέης. 7. Εκίµηση ωφελειών κάθε εναλλακικής ς 7. Ωφέλειες από µείωση ου χρόνου µεακίνησης Η ωφέλεια από ην µείωση ου χρόνου διαδροµής υπολογίζεαι για κάθε χρόνο λειουργίας από ην σχέση: ΩΤ = Όπου Τ,Α [( T T, ). + ( T T, )(. QI,5. )]. V,, + είναι ο χρόνος διαδροµής για ο σύνολο ης διανυόµενης απόσασης, για ένα µεακινούµενο ή αγαθό που ανήκει σην καηγορία, και Α είναι η εναλλακική. V είναι η αξία ου χρόνου για ένα µεακινούµενο ης καηγορίας (η καηγορία αφορά συνήθως ον σκοπό ης µεακίνησης, ή ην καηγορία ου εµπορεύµαος) 7. Εκίµηση ωφελειών κάθε εναλλακικής ς Κάθε εναλλακική συγκρίνεαι µε ην βασική µηδενική (υφισάµενη καάσαση) Ιδιαίερη προσοχή απαιείαι σον υπολογισµό ων ωφελειών για ην παράγωγη κυκλοφορία. Η παράγωγη κυκλοφορία συνεισφέρει σο πλεόνασµα ου κααναλωή όπως φαίνεαι σο σχήµα. Η ωφέλεια (πλεόνασµα κααναλωή) όαν ο κόσος αξιδιού µειώνεαι από C σε C είναι η C EFC. H συνεισφορά ης παράγωγής κυκλοφορίας (D -D ) είναι EFG που ισούαι µε :,5 x (D -D ) x (C -C ) Ενώ η ωφέλεια από ην µείωση ου κόσους για ην κανονική κυκλοφορία D είναι: D x (C -C ) Κόσος αξιδιού από ο Α σο Β C C G E F D D Αριθµός µεακινήσεων από ο Α σο Β. 7. Εκίµηση ωφελειών κάθε εναλλακικής ς 7.3 Ωφέλειες από ην µείωση ων αυχηµάων Η ωφέλεια από ην µείωση ων αυχηµάων υπολογίζοναι για κάθε χρόνο λειουργίας από ην σχέση: ΩΑ = ( RT RT, ). C A, Όπου RT, είναι ο αριθµός ων αυχηµάων σο υφισάµενο οδικό δίκυο ανά καηγορία αυχήµαος. RT, είναι ο αριθµός ων αυχηµάων σο οδικό δίκυο όπως θα διαµορφωθεί βάσει ης εναλλακικής ς που εξεάζεαι, ανά καηγορία αυχήµαος. C A ο µέσο κόσος για αυχήµαα καηγορίας. 7. Εκίµηση ωφελειών κάθε εναλλακικής ς 7. Ωφέλειες από µείωση ου λειουργικού κόσους Η κυκλοφοριακή µελέη διαχωρίζει ην προβλεπόµενη κυκλοφορία σε α) κανονική (σύµφωνα µε άσεις) β) προσελκυόµενη QI, που εκρέπεαι από άλλες οδούς η µεαφορικά µέσα γ) παράγωγη κυκλοφορία, που αφορά νέα κίνηση που δεν υπήρχε προηγουµένως Η ωφέλεια σε λειουργικό κόσος υπολογίζεαι για κάθε έος λειουργίας από ην σχέση: Λ [( O O ) + ( O O ).( QI,5. )] = i, i,. i i, i, i + i Όπου O i,α είναι ο λειουργικό κόσος για ο σύνολο ης διανυόµενης απόσασης, για ένα όχηµα καηγορίας i, και Α είναι η εναλλακική. Α= για ην µηδενική. i 8. Υπολογισµός αποελεσµαικόηας κάθε εναλλακικής ς Η αποελεσµαικόηας ης επένδυσης για κάθε εναλλακική εκιµάαι µε σύγκριση ων ωφελειών και ου κόσους ου έργου όπως εξελίσσοναι καά ην διάρκεια ης χρονικής περιόδου αξιολόγησης. Υπολογίζοναι οι διάφοροι δείκες αποελεσµαικόηας όπως «Καθαρή Παρούσα Αξία» και «είκης Εσωερικής Απόδοσης» Οι συγκρίσεις γίνοναι ως προς ην µηδενική Ως χρονική µονάδα χρησιµοποιείαι συνήθως ο έος
12 8. Υπολογισµός αποελεσµαικόηας κάθε εναλλακικής ς Χρησιµοποιώνας α ακόλουθα µεγέθη: Κ n οικονοµικό κόσος ης επένδυσης σο έος n Σ n οικονοµικό κόσος συνήρησης και λειουργίας σο έος n Y υπολειµµαική αξία ων έργων Ω n ωφέλειες σο έος n συνολικός αριθµός εών χρονικής αξιολόγησης ΚΠΑ καθαρή παρούσα αξία υπολογιζόµενη σο έος βάση η περίοδος αποπληρωµής ης επένδυσης B/C ο λόγος ωφελειών προς κόσος 8. Υπολογισµός αποελεσµαικόηας κάθε εναλλακικής ς Θα προείνεαι η που συγκενρώνει α περισσόερα πλεονεκήµαα βάσει ων ιµών που προκύπουν για ους δείκες/κριήρια. α αποελέσµαα ης αξιολόγησης θα πρέπει να συγκρίνοναι µε ους δείκες που έχουν προκύψει από ανίσοιχες αναλύσεις για παρόµοια έργα. Ο εσωερικός δείκης αναποδοικόηας (irr) θα πρέπει να συγκρίνεαι µε ις ιµές ου επιοκίου αναγωγής και υχόν ιµές ου irr που θεωρούναι ως οι καώερες αποδεκές. υπολογίζοναι οι διάφοροι δείκες αποδοικόηας ης επένδυσης 8. Υπολογισµός αποελεσµαικόηας κάθε εναλλακικής ς Α) η περίοδος αποπληρωµής ης επένδυσης,, είναι ο έος για ο οποίο ισχύει: K n ( Ω n Σn ) = n n n= ( + e) n= ( + e) Β) η Καθαρή Παρούσα Αξία: : ΚΠΑ = K n Y ( Ω n Σn + + n n n= ( + e) ( + e) n= ( + e) ) 9. Ανάλυση κινδύνων Ανάλυση ευαισθησίας Θα πρέπει να εκιµώναι οι κίνδυνοι ου έργου και ης επένδυσης Καηγορίες κινδύνων Κίνδυνοι που αφορούν ην φυσική υπόσαση ου έργου και µπορεί να εµφανισθούν καά ην καασκευή ή/και καά ην λειουργία. Συνεπάγοναι πρόσθεο κόσος ή/και ανασολή ης λειουργίας και εποµένως απώλεια ωφελειών Κίνδυνοι που αφορούν ους χρήσες (πχ. Αυχήµαα) Κίνδυνοι ροµοκραικών ενεργειών Κίνδυνοι που αφορούν ην απόδοση ης επένδυσης και µπορεί να εκδηλώνοναι µε: a) Απόοµη και σαθεροποιούµενη µείωση ης ζήησης (π.χ. από ανάπυξη αναγωνισικού µεαφορικού συσήµαος) b) Μη υλοποίηση προβλεπόµενων σχεδίων ανάπυξης πόλων έλξης και παραγωγής µεαφορικού έργου c) Μείωση δυναόηας χρήσης ου έργου λόγω νεωερων και αυσηρόερων κανόνων περιβαλλονικής προσασίας d) Αναροπή ης δυναόηας χρηµαοδόησης e) Γενικόερες οικονοµικές διααραχές, πχ. Πολιική ασαθεια, εµπόλεµη καάσαση, οικονοµική ύφεση 8. Υπολογισµός αποελεσµαικόηας κάθε εναλλακικής ς Γ) η ο λόγος ωφελειών κόσους : B / C = n= ) ο είκης Εσωερικής Αναποδοικόηας : ( Ω n Σn ) n n= ( + e) K n Y n ( + e) ( + e) Είναι ο επιόκιο αναγωγής e για ο οποίο B/C= ή ΚΠΑ= 9. Ανάλυση κινδύνων Ανάλυση ευαισθησίας Ορισµένοι κίνδυνοι µπορούν να εισάγοναι σην οικονοµική ανάλυση σαν πρόσθεο κόσος Θα πρέπει να γίνοναι προάσεις µείωσης ων κινδύνων Ανάλυση ευαισθησίας Η µελέη θα πρέπει να περιλαµβάνει κααγραφή ων παραδοχών και εκίµηση ης διακύµανσης ους Θα πρέπει να κααρίζοναι διάφορα σενάρια µε συνδυασµούς ιµών ων διαφόρων µεγεθών που παρουσιάζουν διακύµανση και κρισίµων µεγεθών που προσδιορίσθηκαν σην ανάλυση κινδύνων Τα αποελέσµαα θα πρέπει να υπολογίζοναι για διαφορεικούς συνδυασµούς υποθέσεων και να περιλαµβάνουν : α) ην πλέον αισιόδοξη εξέλιξη ης κυκλοφορίας β) ην πλέον πιθανή εξέλιξη ης κυκλοφορίας γ) ην πλέον απαισιόδοξη εξέλιξη ης κυκλοφορίας
13 Παράδειγµα: Αξιολόγηση έργου παράκαµψης οικισµού Ανικείµενο : Μελέη σκοπιµόηας ης καασκευής ης παράκαµψης ου οικισµού εδοµένα : Μήκος υπάρχονος δρόµου = 4χλµ Γ Μήκος εξεαζόµενης παράκαµψης = 3,4 χλµ Ο Β ιαοµή υπάρχουσας οδού Ενός οικισµού = 6,5 µ Εκός οικισµού 7µ/8µ Κ ιαοµή παράκαµψης µ/µ A Από αναγνωρισική µελέη η συγκεκριµένη χάραξη αποελεί ην µοναδική εφική Θα απαιηθεί : χρόνος για ολοκλήρωση µελεών (π.χ. 6), 3 χρόνια για καασκευή (7, 8, 9), θα δοθεί σην κυκλοφορία ο. εδοµένα Χαρακηρισικά µεακινήσεων ΚΑΤΑΝΟΜΗ ΑΝΑ ΣΚΟΠΟ ΜΕΤΑΚΙΝΗΣΗΣ Καηγορία οχήµαος Ι.Χ. Λεωφορεία Σκοπός µεακίνησης ΠΛΗΡΟΤΗΤΑ ΟΧΗΜΑΤΩΝ Καηγορία Πληρόηα οχήµαος Ι.Χ. Φορηγά Λεωφορεία 3% : από και προς 3% : σα πλαίσια ης ς 4% : άλλοι σκοποί 4% : από και προς 6% : άλλοι σκοποί,,3,8 8, Σκοπός µεακίνησης Από & προς, σα πλαίσια ς Άλλοι σκοποί γενικά : Το έργο δεν θα επηρεάσει ην καανοµή ης κυκλοφορίας γιαί δεν υπάρχει εναλλακική σύνδεση εν υπάρχει σιδηροδροµική σύνδεση Οι προβλέψεις έγιναν µε ανάλυση ης διαχρονικής εξέλιξης ων φόρων Προβλέπεαι όι η κυκλοφορία επιβαικών ΙΧ και ων βαρέων οχηµάων (λεωφορεία και φορηγά) αυξάνεαι µε ρυθµό,5% εησίως. Η διάρκεια ζωής ου έργου είναι έη, µεά ην οποία η υπολειµµαική αξία ου έργου θεωρείαι µηδενική κόσος µελεών, ερευνών, απαλλοριώσεων είναι 5. ο συνολικό κόσος καασκευής είναι 3.6. και καανέµεαι ισόποσα σα ρία έη καασκευής. ο κόσος λειουργίας και συνήρησης είναι 5. κάθε έος. Σο 7ο και 5ο έος ο κόσος λειουργίας και συνήρησης είναι. Το επιόκιο αναγωγής είναι 8% εδοµένα Χαρακηρισικά µεακινήσεων (συνέχεια) ΑΞΙΑ ΤΟΥ ΧΡΟΝΟΥ Σκοπός µεακίνησης ΙΧ σα πλαίσια ς Προς και από Άλλοι σκοποί µεακίνησης Φορηγά οχήµαα ΚΟΣΤΟΣ ΑΤΥΧΗΜΑΤΩΝ Συµβάν Θαναηφόρο αύχηµα Αύχηµα µε ραυµαισµό Αύχηµα µε υλικές ζηµιές µόνο Κόσος Αξία ( /hr) 8, 5, 3,5 4, εδοµένα Kυκλοφοριακά χαρακηρισικά εδοµένα Λειουργικά Χαρακηρισικά οχηµάων ΤΑΧΥΤΗΤΕΣ ΚΥΚΛΟΦΟΡΙΑΣ ΚΑΙ ΧΡΟΝΟΙ ΙΑΝΥΣΗΣ Εναλλακική ΕΛ Οδικό µήµα ΑΒ/ ΑΒ/ Ταχύηα (χλµ/ώρα) Ι.Χ. Β.Ο Χρόνος διάνυσης (sec) Ι.Χ. Β.Ο. 96, , ,9 4 4 ΚΑΤΑΝΑΛΩΣΗ ΚΑΥΣΙΜΟΥ ΑΝΑ ΕΙ ΟΣ ΟΧΗΜΑΤΟΣ Οδικό µήµα Είδος οχήµαος ΙΧ ΒΟ Καανάλωση καυσίµου (lt/k),95,75 ΙΧ,75 ΑΒ, ΒΟ,5 ΙΧ, ΒΟ,3 Το κόσος ης βενζίνης προ φόρων θεωρείαι όι θα είναι,65 /lt και ου περελαίου κίνησης,6 /lt
14 Προβλέψεις κυκλοφοριακών φόρων για ο ο έος λειουργίας Οδικό δίκυο Χ A Β A Ο Γ B Ισοδύναµος χάρης κόµβων-συνδέσµων ου µονέλου συγκοινωνιακού σχεδιασµού Γ Ψ Προβλέψεις κυκλοφοριακών φόρων για ο ο έος λειουργίας (κανονική κυκλοφορία) Ι.Χ. (φορηγά/λεωφ) Προβλεπόµενοι κυκλοφοριακοί 5 B Γ φόροι για ην µηδενική (9/6 (δηλ. εάν δεν καασκευασθεί η παράκαµψη) ΕΛ A Προβλεπόµενοι κυκλοφοριακοί φόροι κανονική κυκλοφορία () για ην εναλλακική (δηλ. εάν καασκευασθεί η παράκαµψη) A 6 8 (5/4) (6/) B 3 (9/4 (9/) Γ 6 8 (5/4) (6/) ιαφορεικές συνισώσες ου φόρου Ι.Χ. για ην ΕΛ Χ =+5+55 =8 Β = = 5 A Γ 55 Ψ Προβλέψεις κυκλοφοριακών φόρων για ο ο έος λειουργίας (παράγωγη κυκλοφορία) Ι.Χ. (φορηγά/λεωφ) Προβλεπόµενη παράγωγη κυκλοφορία () για ην εναλλακική (δηλ. εάν καασκευασθεί η παράκαµψη) A 6 (4/) B (6/ (/) Γ (4/) 6 ιαφορεικές συνισώσες ου φόρου Ι.Χ. για ην Χ = 5+55 = 6 5 Β A 55 5 Χ A Γ = = 3 55 Ψ Ψ Προβλέψεις κυκλοφοριακού φόρων για ο ο έος λειουργίας Εναλλα κική ΕΛ AB, ΑΒ, Φόρος (ΙΧ) (Φορη γά) (Λεωφ) : η συνολική κυκλοφορία (σην ΕΛ είναι κανονική (δεν υπάρχει παράγωγη) : η κανονική κυκλοφορία : η παράγωγη κυκλοφορία 3 4
15 Ανάλυση Ωφελειών Υπολογισµός φόρων () ανά σκοπό µεακίνησης (Α) ΙΧ (Β) (Γ) ( ) Λεωφορεία Φορηγά (Α.) Εξοικονόµηση χρόνου αξιδιού Κανονική κυκλοφ. Παράγωγη κυκλοφ. ΩΤ ΙΧ,Ν ΩΤ ΙΧ,G (Β.) Εξοικονόµηση χρόνου αξιδιού Κανονική Παράγωγη ΩΤ Λ,Ν ΩΤ Λ,G (Γ.) Εξοικονόµηση χρόνου αξιδιού Κανονική Παράγωγη ΩΤ Φ,Ν ΩΤ Φ,G Μείωση αυχηµάων ΩΑ (Α.) Λειουργικό κόσος οχηµάων Κανονική ΩΛ ΙΧ,Ν Παράγωγη ΩΛ ΙΧ,G (Β.) Λειουργικό κόσος οχηµάων Κανονική Παράγωγη ΩΛ Λ,Ν ΩΛ Λ,G (Γ.) Λειουργικό κόσος οχηµάων Κανονική Παράγωγη ΩΛ Φ,Ν ΩΛ Φ,G Εναλ. () ΕΛ () AB, ΑΒ, Φόρος (3) Συνολικό (ΙΧ) (4) % ΙΧ ανά σκοπό µεακίνησης προς/από (5) 3% 3% 3% 3% 3% 3% 3% 3% σα πλαισια ς (6) 3% 3% 3% 3% 3% 3% 3% 3% άλλοι σκοποί (7) 4% 4% 4% 4% 4% 4% 4% 4% προς/ από (8) = (4)*(5) (ΙΧ) σα πλαισια ς (9)= (4)*(6) άλλοι σκοποί () = (4)*(7) Υπολογισµός αριθµού µεακινούµενων µε ΙΧ ανά σκοπό µεακίνησης Ανάλυση Κόσους (Ε) (ΣΤ) (Ζ) Κόσος µελεών, ερευνών, απαλλοριώσεων Κόσος καασκευής Κόσος λειουργίας και συνήρησης Εναλ. () ΕΛ () AB, ΑΒ, Φόρ ος (3) Συνολικό (ΙΧ) (4) προς/α πό (5) (ΙΧ) σα πλαισια ς (6) άλλοι σκοπο ί προς/ από εργασί α (8) = (7) (5)*, , ,6 Αριθµός µεακινούµενων µε ΙΧ (εήσιος µέσος ηµερήσιος) σα πλαισια ς (9) = (6)*, , ,9 Πληρόηα ΙΧ µε σκοπό από/προς =, µεακινούµενοι / όχηµα Πληρόηα ΙΧ µε σκοπό σα πλαίσια ης ς =,3 µεακιν/όχηµα Πληρόηα ΙΧ µε άλλο σκοπό µεακίνησης =,8 µεακιν/όχηµα άλλοι σκοποί () = (7)*, Ανάλυση ωφελειών Α.) Εξοικονόµηση χρόνου - Επιβαικά Ι.Χ. οχήµαα Η ωφέλεια από ην εξοικονόµηση ου χρόνου αξιδιού εκφράζεαι σε χρήµα, πολλαπλασιάζονας ον χρόνο επί ην χρηµαική αξία ου χρόνου Η ιµή ης αξίας ου χρόνου εξαράαι από ον σκοπό ης µεακίνησης (ΙΧ) (Εήσια Μέση Ηµερήσια Κυκλοφορία σύνολο ΙΧ οχηµάων) Κυκλοφορία οχηµάων προς/από Κυκλοφορία οχηµάων σα πλαίσια ς Κυκλοφορία οχηµάων άλλοι σκοποί x πληρόηα οχηµάων x x Πληρόηα οχηµάων Πληρόηα οχηµάων προς/από άλλοι σκοποί σα πλαίσια ς x x x Χρόνος µεακίνησης Χρόνος µεακίνησης Χρόνος µεακίνησης x x x Αξία ου χρόνου Αξία ου χρόνου Αξία ου χρόνου προς/από σα πλαίσια ς άλλοι σκοποί = συνολικό κόσος = συνολικό κόσος = συνολικό κόσος χρόνου µεακινούµενων από/προς χρόνου µεακινούµενων σα πλαίσια ς χρόνου µεακινούµενων για άλλους σκοπούς Υπολογισµός συνολικού χρόνου αξιδιού για ους µεακινούµενους µε ΙΧ, ανά σκοπό µεακίνησης. Εναλ. () ΕΛ () AB, ΑΒ, Φόρος (3) Αριθµός µεακινούµενων µε ΙΧ (εήσιος µέσος ηµερήσιος) προς/ από (4) , ,6 σα πλαισια ς (5) , ,9 άλλοι σκοποί (6) Χρόνοι διάνυσης µηµάων (sec) (7) ,4,4 Συνολικός χρόνος µεακινούµενων µε ΙΧ (Συνολικός εήσιος σε hr) προς/ από (8) = =(4)*(7)* 365/ σα πλαίσια ς (9) = = (5)*(7)* 365/ άλλοι σκοποί () = =(6)*(7)* 365/
16 Υπολογισµός ωφέλειας λόγω µείωσης ου χρόνου µεακίνησης. Α..α) κανονική κυκλοφορία Άλλοι σκοποί 3,5 Εναλ. () ΕΛ Τµή- µα () AB, ΑΒ, Συνολικός χρόνος µεακινούµενων µε ΙΧ (εήσιος σε hr) σα προς/ από πλαισια ς (3) (4) άλλοι σκοποί (5) Σκοπός µεακίνησης Προς / από Σα πλαίσια ς Αξία συνολικού χρόνου µεακινήσεων µε ΙΧ προς/ από (6)=(3)* (εήσιο σύνολο σε ) σα πλαισια ς (7)=(4)*8 (8)=(5)*3, άλλοι σκοποί Αξία χρόνου Αξία συνολικού χρόνου µεακινήσεων µε ΙΧ (εήσιο σύνολο σε ) (9) ΑΒ+ ΑΒ+ 5, 8, όλοι οι σκοποί µεακίνησης () Συνολική ωφέλεια εξοικονόµησης χρόνου ης κανονικής κυκλοφορίας για ο ο έος λειουργίας : ΩΤ ΙΧ,Ν = = ΩΤ ΙΧ,Ν = () Υπολογισµός µεακινούµενων µε λεωφορεία ανά σκοπό µεακίνησης Ενλ. λύσ η Τµή µα Συνολικός Εήσιος Αριθµός Μεακινούµενων µε Λεωφορεία () () (3) (4) (5)=365*(4)*8 (6) ΑΒ, ΕΛ % % ΑΒ, % 4% 3.4 4% 4% 3.4 4% 3.4 % Πληρόηα λεωφορείου 8 επιβάες/όχηµα % µεακινούµενων µε Λεωφορείων ανά σκοπό µεακίνησης προς / από άλλοι σκοποί (7) 6% 6% 6% 6% 6% 6% 6% % Συνολικός Εήσιος Αριθµός Μεακινούµενων µε Λεωφορεία προς/ από (8)=(5)*(6) άλλοι σκοποί (9)=(5)*(7) Υπολογισµός ωφέλειας λόγω µείωσης ου χρόνου µεακίνησης. Α..β) Παράγωγη κυκλοφορία Εναλ. ΕΛ AB, ΑΒ, Φόρος προς/ από,6 36 Αριθµός µεακινούµενων µε ΙΧ (εήσιος µέσος ηµερήσιος) σα πλαισια ς 3,4 39,6 4,9 79,4 Συνολική ωφέλεια εξοικονόµησης χρόνου ης παράγωγης κυκλοφορίας Σκοπός Προς/από Σα πλαίσια ς Άλλοι σκοποί Συνολική ωφέλεια χρόνου 39,5 *{ [,6*(96-96) + 36*(36-4) + 39,6*( ,4) ] * (365/36) },5 *{ [ 3,4*(96-96) + 39*(36-4) + 4,9*( ,4) ] * (365/36) },5 *{ [ 43*(96-96) + 7*(36-4) + 79*( ,4) ] * (365/36) } άλλοι σκοποί 43 7 Αξία χρόνου 5 8 3,5 Χρόνοι διάνυσης µηµάων (sec) , 9.373, ,9 ΩΤ ΙΧ,G =.349,4 Υπολογισµός ωφέλειας λόγω µείωσης Σκοπός µεακίνησης ου χρόνου µεακίνησης. Προς / από Β..α) κανονική κυκλοφορία Άλλοι σκοποί 3,5 Εναλ. () ΕΛ () AB, ΑΒ, Συνολικό (Λεωφορεία) Φόρος Φόρος (3) Συνολικός Εήσιος Αριθµός µεακινούµενων µε Λεωφορεία προς/από (4) άλλοι σκοποί (5) Χρόνοι διάνυσης µηµάων (sec) (6),9 36, Συνολικός χρόνος µεακινούµενων µε Λεωφορρεία (εήσιος σε hr) Προς /από (7)=(4)*(6) / Αξία χρόνου 5, άλλοι σκοποί (8) = (5) *(6) / Συνολική ωφέλεια εξοικονόµησης χρόνου ης κανονικής κυκλοφορίας για ο έος λειουργίας ΩT Λ,Ν : = [ ( ) ( ) ] * 5, + [ ( ) ( ) ] * 3,5 => ΩΤ Λ,Ν = ,5 Ανάλυση ωφελειών Β.) Εξοικονόµηση χρόνου - Λεωφορεία Υπολογισµός ωφέλειας λόγω µείωσης ου χρόνου µεακίνησης. Β..β) Παράγωγη κυκλοφορία (Λεωφορεία) (Εήσια Μέση Ηµερήσια Κυκλοφορία σύνολο Λεωφορείων) x Κυκλοφοριακός φόρος Λεωφορείων Πληρόηα Λεωφορείων = συνολικό αριθµός µεακινούµενων µε λεωφορείο % από/προς % για άλλους σκοπούς Εναλ. ΕΛ AB, Φόρος Συνολικός Εήσιος Αριθµός µεακινούµενων µε Λεωφορεία προς/από άλλοι σκοποί Χρόνοι διάνυσης µηµάων (sec), x x Μεακινούµενοι από/προς Χρόνος µεακίνησης Αξία ου χρόνου από/προς x Μεακινούµενοι για άλλους σκοπούς Χρόνος µεακίνησης x Αξία ου χρόνου άλλοι σκοποί Σκοπός Άλλοι σκοποί Συνολική ωφέλεια χρόνου,5 *{ [ 3.4*(,9+, ) ] /36} Αξία χρόνου 3,5 συνολική αξία.636,8 = συνολικό κόσος χρόνου = µεακινούµενων από/προς συνολικό κόσος χρόνου µεακινούµενων για άλλους σκοπούς ΩΤ Λ,G =,636,8
17 Ανάλυση ωφελειών Γ.) Εξοικονόµηση χρόνου αξιδιού - Φορηγά Εναλ. Φόρος Λύση (Φορηγά) () () (3) (4) ΕΛ AB, 3 4 ΑΒ, Αξία εξοικονόµησης χρόνου Χρόνος διάνυσης (5),9 36,9, Συνολικός χρόνος αξιδιού Φορηγών (εήσιος σε hr) (6) =(4)*(5)*365/ αξία χρόνου για φορηγά οχήµαα = 4 Γ..α) Κανονική κυκλοφορία: [ ( ) ( ) ]*4 => ΩT Φ,Ν = 5.5,6 Γ..β) Παράγωγη κυκλοφορία:,5 * { *[(,9+,9+36) 53] }*(365/36)*4 => ΩT Φ,G = 585,9 Ανάλυση ωφελειών Γ.) Μεαβολή Λειουργικού κόσους Φορηγών Εναλ ΕΛ AB, ΑΒ, Φόρος (Φορηγά) Γ..α) Κανονική κυκλοφορία:,6 * [ ( ) - ( ) ] => 5 8 Γ..β) Παράγωγη κυκλοφορία:,5 * {,6 * 365 * [ 4* *(,5-5)* + 6**(,3-,3) + *(*,5+*,5+*,3 3,4*,75) ] } => µήκος µήµαος 3,4 3,4 Μέση καανάλωση,5,3,5,5,3,3,75,75 συνολική κααναλωση (lt/εος) Ω Φ,Ν = 6.865,7 Ω Φ,G = 87,7 Α.) Μεαβολή Λειουργικού κόσους ΙΧ επιβαικών οχηµάων Εναλλακικ ή ΕΛ Ανάλυση ωφελειών AB, ΑΒ, Φόρος (ΙΧ) µήκος µήµαος 3,4 3,4 µεση κααναλωση,75,,75,75,,,95,95 συνολική κααναλωση (lt/εος) Α..α) Κανονική κυκλοφορία:,65 * [ ( ) - ( ) ] => Ω IX,N = 7.686,9 Α..β) Παράγωγη κυκλοφορία:,5 * {,65 * 365 / 36 * [ *6**(,75-,75) + **(,-,) + *(*,+(+)*,75 3,4*,95) ] } => Ω IX,G = 35,3 ) ) Υπολογισµός Ωφελειών από ην µείωση ων αυχηµάων ΕΙΚΤΕΣ ΑΤΥΧΗΜΑΤΩΝ Εναλλακι κή ΕΛ ΑΤΥΧΗΜΑΤΩΝ (συµβάνα ανά 8 οχηµαοχιλιόµερα) Οδικό συµβάν µήµα Θάναος Τραυµαισµός ΑΒ/ ΑΒ/ 4,5 3 4,5 3, Υλικές Ζηµιές Ανάλυση ωφελειών Β.) Μεαβολή Λειουργικού κόσους Λεωφορείων Εναλ ΕΛ AB, ΑΒ, Φόρος (Λεωφορεία) Β..α)_ Κανονική κυκλοφορία:,6 * [ ( ) - ( ) ] => 3 4 µήκος µήµαος 3,4 3,4 µέση καανάλωση,5,3,5,5,3,3,75,75 συνολική καανάλωση (lt/εος) Ω Λ,Ν =7,7 ΠΡΟΒΛΕΨΕΙΣ ΚΥΚΛΟΦΟΡΙΑΚΩΝ ΦΟΡΤΩΝ ΓΙΑ ΤΟ ο έος λειουργίας Εναλ. ΕΛ AB, ΑΒ, Φόρος (ΙΧ) (Φορηγά) (Λεωφ) 3 4 Συνολική Β..β) Παράγωγη κυκλοφορία:,5 * {,6 * 365 / 36 * [ *[ (+)*,5 + *,3] *3,4*,75 ] } => Ω Λ,G =36,
18 ΠΡΟΒΛΕΨΕΙΣ ΑΤΥΧΗΜΑΤΩΝ για ο ο έος λειουργίας Υπολογισµός ΚΟΣΤΟΥΣ Εναλ. ΕΛ AB+ Συνολ 8 8 µήκος µήµαος οχηµχλµ / έος Θάναοι / έος,68,6 Τραυµαισµοί / έος,683,544 Υλικές Ζηµιές / έος,58 5,47 Από α δεδοµένα ου προβλήµαος: Ε) κόσος µελεών, ερευνών, απαλλοριώσεων (ΚΜ) : = 5. ο έος ΑΒ , ,4,33,,4,83,9,536,767,475 ΣΤ) κόσος καασκευής: ο συνολικό κόσος καασκευής είναι 3.6. και καανέµεαι σα ρία έη καασκευής Ζ) κόσος λειουργίας και συνήρησης (ΚΛ): 5. κάθε έος, σο έος 7ο και 5ο έος ο κόσος λειουργίας και συνήρησης είναι. Υπολογισµός κόσους Αυχηµάων για ο ο έος λειουργίας Εναλ ΕΛ Θαναηφόρα αύχηµαα / έος Κόσος Θαναηφόρων αυχηµάων Τραυµαισµοί / έος Συµβάν Θαναηφόρο αύχηµα Αύχηµα µε ραυµαισµό Αύχηµα µε υλικές ζηµιές µόνο Υλικές Ζηµιές / έος Κόσος Τραυµαισµών Κόσος Κόσος Υλικών Ζηµιών Συνολικό κόσος AB+,68,683, ,6,544 5, ΑΒ+,4,4, ,33,83, ,,9, ) Η ωφέλεια από ην µείωση ων αυχηµάων υπολογίζεαι σαν η διαφορά => ΩΑ = 97.5 έ ο ς Μελέες / Έρευνες / Απαλλοριώσει ς 5. ΚΟΣΤΗ Συνήρηση / Λειουργία Καασκευή =79.4/(+8%) εξοικονοµ ηση χρόνου ΩΦΕΛΕΙΕΣ µειωση λειουργικού κόσου ς µειωση αυχη- µάων ΚΑΘΑΡΗ ΩΦΕΛΕΙΑ ΠΑΡΟΥΣΑ ΑΞΙΑ ΚΑΘΑΡΩΝ ΩΦΕΛΕΙΩΝ Υπολογισµός Συνολικών Ωφελειών Τα συνολικά οφέλη ο ο έος λειουργίας υπολογίζοναι αθροίζονας α επιµέρους οφέλη: Μείωσης Λειουργικού Εξοικονόµησης χρόνου κόσους οχηµάων ΩΤ ΙΧ,Ν 56.55, Ω IX,N 7.686,9 ΩΤ ΙΧ,G.349,4 Ω IX,G 35,3 ΩΤ Λ,Ν ,5 Ω Λ,Ν 7,7 ΩΤ Λ,G.636,8 Ω Λ,G 36, ΩT Φ,Ν 5.5,6 Ω Φ,Ν 6.865,7 ΩT Φ,G 585,9 Ω Φ,G 87,7 ΣΥΝΟΛΟ ΣΥΝΟΛΟ Μείωσης Αυχηµάων ΩΑ = 97.5 έ ο ς Μελέες / Έρευνες / Απαλλοριώσε ις ΚΟΣΤΗ Καασκε υή Συνήρησ η / Λειουργί α εξοικονο µηση χρόνου ΩΦΕΛΕΙΕΣ µειωση λειουρ -γικού κόσου ς µειωσ η αυχη- µάων ΚΑΘΑΡΗ ΩΦΕΛΕΙ Α ΚΑΘΑΡΗ ΠΑΡΟΥΣΑ ΑΞΙΑ ΤΗΣ ΕΠΕΝ ΥΣΗΣ ΠΑΡΟΥΣΑ ΑΞΙΑ ΚΑΘΑΡΩΝ ΩΦΕΛΕΙΩΝ
19 Παράδειγµα: απόσβεση εξοπλισµού και επιπώσεις φορολόγησης Για ην εκέλεση έργου διάρκειας 3 εών, απαιείαι να χρησιµοποιηθούν εξειδικευµένα όργανα µερήσεων. Τα χαρακηρισικά ων διαφορεικών ύπων που µπορούν να χρησιµοποιηθούν δίδοναι σον πίνακα: Τιµή αγοράς Χρόνος ρύθµισης οργάνου Χρόνος µέρησης Εήσιο κόσος συνήρησης/επισκευών Τύπος Α Τύπος Β Τύπος Γ Πριν από µια µέρηση ο όργανο θα πρέπει να έχει ρυθµισθεί. Το όργανο δεν χρειάζεαι να ρυθµισθεί πάλι πριν ην επόµενη µέρηση εκός εάν µεακινηθεί. Για ον χειρισµό ου οργάνου/µερήσεις απαιείαι ένας µηχανικός µε αµοιβή 35 /ώρα και ένας βοηθός µε αµοιβή /ώρα Παράδειγµα: απόσβεση εξοπλισµού και επιπώσεις φορολόγησης H απόσβεση ανιπροσωπεύει ην µείωση ης αξίας ου εξοπλισµού. Η απόσβεση θεωρείαι έξοδο ης εαιρείας (δεδοµένου όι ο εξοπλισµός αποελεί περιουσιακό σοιχείο ης εαιρείας και η αξία ου µειώνεαι) και εποµένως θα πρέπει να λαµβάνεαι υπόψη καά ον υπολογισµό ου φόρου. Όπως ήδη αναφέραµε, δεν δίνεαι πληροφορία για α οφέλη αλλά µόνο για α κόση. Όµως ο υπολογισµός ου φόρου γίνεαι σα κέρδη ης εαιρείας. Από α σοιχεία που έχουµε α οφέλη είναι αρνηικά (= - κόσος) και εποµένως και ο φόρος που υπολογίζεαι έχει αρνηικό πρόσηµο. Αυό σηµαίνει όι ο υπολογιζόµενος αρνηικός φόρος ανιπροσωπεύει ην µείωση ου πραγµαικού φόρου (επί ων κερδών) που θα έχει η εαιρεία λόγω ων εξόδων (δηλ. κόσος ς και απόσβεση εξοπλισµού). Παράδειγµα: απόσβεση εξοπλισµού και επιπώσεις φορολόγησης Τύπος Α Παράδειγµα: απόσβεση εξοπλισµού και επιπώσεις φορολόγησης Το επιόκιο αναγωγής είναι 5%, η υπολειµµαική αξία µεά α 3 χρόνια είναι, και η απόσβεση ου κόσους αγοράς θεωρείαι οµοιόµορφα καανεµηµένη καά ην διάρκεια αυής ης περιόδου. ο συνελεσής φορολόγησης είναι 4% Ζηούµενα: Ποιος ύπος οργάνου είναι ο πιο οικονοµικά συµφέρον για ένα έργο διάρκειας 3 εών όπου απαιούναι 5 µερήσεις κάθε έος, θεωρώνας όι καά µέσο όρο, ο όργανο θα πρέπει να µεακινείαι κάθε 5 µερήσεις? Έ ο ς () 3 Αγορά () - 8. Χρόνος ρύθµισης (ins) (3) Χρόνος µέρησης (ins) (4) Κόσος Εργασίας (5) = (4)* (35+)/ Κόσος Συνήρησης (6) Εισόδηµα (7) = (5) + (6) Απόσβεση αρχικής απάνης (8) = 8/ Φορολογηέο Εισόδηµα (9) = (7) + (8) Φόρος () = (9)*4% Εισόδηµα µεά Φόρο () = (9)+ () Καθαρή Παρούσα Αξία ()=/ (+i) n (3) : Χρόνος ρύθµισης = x (5/5) (4) : Χρόνος µέρησης = 6 x 5 (8) : η αρχική δαπάνη 8. καανέµεαι οµοιόµορφα καά ην διάρκεια ων ριών χρόνων. Για κάθε έος η απόσβεση ισούαι µε ο κόσος αγοράς/3 Παράδειγµα: απόσβεση εξοπλισµού και επιπώσεις φορολόγησης εν δίδοναι εκιµήσεις ων εήσιων ωφελειών που προκύπουν από ην χρήση ων διαφορεικών ύπων οργάνων. Όµως προφανώς υπάρχουν οφέλη (π.χ. εξοικονόµηση χρόνου σχέση µε άλλα όργανα), αλλά η ανάλυση θα πρέπει να βασίζεαι σα σοιχεία που δίδοναι και που όλα αφορούν κόση. Κάθε όργανο θα έχει αρνηική Καθαρή Παρούσα Αξία (δεδοµένου όι µόνο α κόση λαµβάνοναι υπόψη) και θα πρέπει να επιλέξεε εκείνο ον ύπο που έχει ην υψηλόερη ΚΠΑ. Εάν εφαρµόζουµε ους κανόνες κόσους οφέλους καά γράµµα, όε σις περιπώσεις που δεν ορίζοναι σαφώς α οφέλη από ην αγορά, δεν θα µπορούσαµε να προείνουµε οποιαδήποε αγορά/ επένδυση. Προφανώς α οφέλη από ις µερήσεις που είναι απαραίηες για ο έργο είναι θεικά και µεγαλύερα από ο κόσος ου εξοπλισµού Τύπος Β Έ ο ς 3 Αγορά -3. Τύπος Γ Έ ο ς 3 Αγορά -4. Χρόνος ρύθµισης (ins) Χρόνος ρύθµισης (ins) Χρόνος µέρησης (ins) Χρόνος µέρησης (ins) Κόσος Εργασίας Κόσος Εργασίας Κόσος Συνήρησης... Κόσος Συνήρησης Εισόδηµα Εισόδηµα Απόσβεση αρχικής απάνης Απόσβεση αρχικής απάνης Φορολογηέο Εισόδηµα Φορολογηέο Εισόδηµα Φόρος Φόρος Εισόδηµα µεά Φόρο Εισόδηµα µεά Φόρο Καθαρή Παρούσα Αξία Καθαρή Παρούσα Αξία
Σχεδιασμός συγκοινωνιακών έργωνοικονομικά
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Σχολή Αγρονό ων Το ογράφων Μηχανικών ΕΜΠ Εργαστήριο Συγκοινωνιακής Τεχνικής Σχεδιασμός συγκοινωνιακών έργωνοικονομικά στοιχεία Κωνσταντίνος Αντωνίου Ανα ληρωτής Καθηγητής ΕΜΠ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Σχολή Αγρονό ων Το ογράφων Μηχανικών ΕΜΠ Εργαστήριο Συγκοινωνιακής Τεχνικής Σχεδιασμός συγκοινωνιακών έργωνοικονομικά στοιχεία Κωνσταντίνος Αντωνίου Ανα ληρωτής Καθηγητής ΕΜΠ
Πως λύνεται ένα πρόβληµα.
 Πως λύνεαι ένα πρόβληµα. Όπως έχουµε ήδη αναφέρει, α βήµαα για ην παραγωγή λογισµικού είναι: 1. Καανόηση προβλήµαος 2. Επίλυση ου προβλήµαος 3. Λογικός έλεγχος ης λύσης (αν υπάρχουν λάθη πήγαινε σο 1.)
Πως λύνεαι ένα πρόβληµα. Όπως έχουµε ήδη αναφέρει, α βήµαα για ην παραγωγή λογισµικού είναι: 1. Καανόηση προβλήµαος 2. Επίλυση ου προβλήµαος 3. Λογικός έλεγχος ης λύσης (αν υπάρχουν λάθη πήγαινε σο 1.)
ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ
 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Οι κινηήρες αυής ης καηγορίας ροφοδοούναι από κάποια πηγή συνεχούς άσης. Από καασκευασικής απόψεως, δεν παρουσιάζουν καμία διαφορά σε σχέση με ις γεννήριες ΣΡ. Βασικό πλεονέκημά
ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Οι κινηήρες αυής ης καηγορίας ροφοδοούναι από κάποια πηγή συνεχούς άσης. Από καασκευασικής απόψεως, δεν παρουσιάζουν καμία διαφορά σε σχέση με ις γεννήριες ΣΡ. Βασικό πλεονέκημά
ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ
 ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ 4.1 Η ΥΙΟΘΕΤΗΣΗ ΝΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ: ΣΤΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Όαν η εχνολογία εξελίσσεαι η πρώη ερώηση µας είναι καά πόσο θα υιοθεηθεί δεδοµένου ης µεγάλης εγκαεσηµένης
ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ 4.1 Η ΥΙΟΘΕΤΗΣΗ ΝΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ: ΣΤΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Όαν η εχνολογία εξελίσσεαι η πρώη ερώηση µας είναι καά πόσο θα υιοθεηθεί δεδοµένου ης µεγάλης εγκαεσηµένης
Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ
 Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ Θεωρούµε όι Έσω X µία διακριή χρονοσειρά 0 ± ±. µ x Ε{X } και γ { X X } E { [ X µ ][ X µ ] } ( 0 ± cov + + x x Το φάσµα ισχύος ης X ορίζεαι
Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ Θεωρούµε όι Έσω X µία διακριή χρονοσειρά 0 ± ±. µ x Ε{X } και γ { X X } E { [ X µ ][ X µ ] } ( 0 ± cov + + x x Το φάσµα ισχύος ης X ορίζεαι
ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ. LT και μονάδες στο SI, kgm/s 2 ή N. υνισταμένη. υνισταμένη. d dt. d dt.
 ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ Έσω ένα υδραυλικό σύσημα ο οποίο περιέχεαι σε έναν όγκο ελέγχου C συνολικού όγκου και ο οποίο αναλλάσει μάζα με ο περιβάλλον με ρυθμούς (παροχές
ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ Έσω ένα υδραυλικό σύσημα ο οποίο περιέχεαι σε έναν όγκο ελέγχου C συνολικού όγκου και ο οποίο αναλλάσει μάζα με ο περιβάλλον με ρυθμούς (παροχές
Εργαστηριακή Άσκηση Το σύστημα αναμονής M/G/1
 Εργασηριακή Άσκηση 4 5 Το σύσημα αναμονής M/G/ Γιάννης Γαροφαλάκης, Καθηγηής Αθανάσιος Ν.Νικολακόπουλος, Phd(c) Σκοπός ης παρούσας εργασίας είναι η εξερεύνηση ων βασικών ιδιοήων ενός από α κλασικόερα μονέλα
Εργασηριακή Άσκηση 4 5 Το σύσημα αναμονής M/G/ Γιάννης Γαροφαλάκης, Καθηγηής Αθανάσιος Ν.Νικολακόπουλος, Phd(c) Σκοπός ης παρούσας εργασίας είναι η εξερεύνηση ων βασικών ιδιοήων ενός από α κλασικόερα μονέλα
ΕΛΕΓΧΟΣ ΒΙΟΜΗΧΑΝΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΚΕΦΑΛΑΙΟ 2 ΚΕΦΑΛΑΙΟ 2. Πλεονεκτήματα ψηφιακού ελέγχου
 ΚΕΦΑΛΑΙΟ Πλεονεκήμαα ψηφιακού ελέγχου Ικανόηα για επεξεργασία αλγορίθμων με λογισμικό ανί για harwar. Αλλαγή ου σχεδιασμού χωρίς αλλαγές σο harwar. Μείωση μεγέθους, βάρους, ισχύος καθώς και χαμηλό κόσος.
ΚΕΦΑΛΑΙΟ Πλεονεκήμαα ψηφιακού ελέγχου Ικανόηα για επεξεργασία αλγορίθμων με λογισμικό ανί για harwar. Αλλαγή ου σχεδιασμού χωρίς αλλαγές σο harwar. Μείωση μεγέθους, βάρους, ισχύος καθώς και χαμηλό κόσος.
ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ
 Ε. Μ. ΠΟΛΥΤΕΧΝΕΙΟ Τµήµα Αγρονόµων-Τοπογράφων Μηχανικών Εργασήριο Συγκοινωνιακής Τεχνικής ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ 1. Τόξο
Ε. Μ. ΠΟΛΥΤΕΧΝΕΙΟ Τµήµα Αγρονόµων-Τοπογράφων Μηχανικών Εργασήριο Συγκοινωνιακής Τεχνικής ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ 1. Τόξο
Γιάννη Σ. Μπούταλη Αναπληρωτή Καθηγητή Δ.Π.Θ. ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθητικές σημειώσεις στο μάθημα ΣΑΕ ΙΙ
 Γιάννη Σ Μπούαλη Αναπληρωή Καθηγηή ΔΠΘ ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθηικές σημειώσεις σο μάθημα ΣΑΕ ΙΙ Ξάνθη, Μάιος 7 Ι Μπούαλη Λύση ων εξισώσεων καάσασης ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ Σε αυό ο κεφάλαιο
Γιάννη Σ Μπούαλη Αναπληρωή Καθηγηή ΔΠΘ ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθηικές σημειώσεις σο μάθημα ΣΑΕ ΙΙ Ξάνθη, Μάιος 7 Ι Μπούαλη Λύση ων εξισώσεων καάσασης ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ Σε αυό ο κεφάλαιο
13. Συνήθεις διαφορικές εξισώσεις
 Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής 67 3 Σνήθεις διαφορικές εξισώσεις 3 Ορισµοί Μια εξίσση πο περιέχει παραγώγος κάποιας σνάρησης, ονοµάζεαι διαφορική εξίσση ( Ε) Αν η σνάρηση
Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής 67 3 Σνήθεις διαφορικές εξισώσεις 3 Ορισµοί Μια εξίσση πο περιέχει παραγώγος κάποιας σνάρησης, ονοµάζεαι διαφορική εξίσση ( Ε) Αν η σνάρηση
Ανάπτυξη και Αξιολόγηση Στρατηγικής Κεντρικού Ελέγχου Ροών σε Αποχετευτικά ίκτυα µε Έµφαση στην Εφαρµογή της στον Ελλαδικό Χώρο
 ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ: Μηχανικών Παραγωγής & ιοίκησης Ανάπυξη και Αξιολόγηση Σραηγικής Κενρικού Ελέγχου Ροών σε Αποχεευικά ίκυα µε Έµφαση σην Εφαρµογή ης σον Ελλαδικό Χώρο ιαριβή που υπεβλήθη για ην
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ: Μηχανικών Παραγωγής & ιοίκησης Ανάπυξη και Αξιολόγηση Σραηγικής Κενρικού Ελέγχου Ροών σε Αποχεευικά ίκυα µε Έµφαση σην Εφαρµογή ης σον Ελλαδικό Χώρο ιαριβή που υπεβλήθη για ην
ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ
 ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ Για κάθε γραµµικό και χρονικά αναλλοίωο σύσηµα συνεχούς χρόνου ισχύει όι η απόκριση y() ου όαν αυό διεγείρεαι από είσοδο x() δίνεαι από η σχέση: y () = x( ) h ( ) d = x ()
ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ Για κάθε γραµµικό και χρονικά αναλλοίωο σύσηµα συνεχούς χρόνου ισχύει όι η απόκριση y() ου όαν αυό διεγείρεαι από είσοδο x() δίνεαι από η σχέση: y () = x( ) h ( ) d = x ()
Κεφάλαιο 4 Ιδανικοί χημικοί αντιδραστήρες
 Κεφάλαιο 4 Ιδανικοί χημικοί ανιδρασήρες Με βάση α σοιχεία για ην κινηική και η σοιχειομερία ων ανιδράσεων, μπορούμε ώρα να προχωρήσουμε σην ανάλυση ορισμένων βασικών ύπων χημικών ανιδρασήρων. Η ανάλυση
Κεφάλαιο 4 Ιδανικοί χημικοί ανιδρασήρες Με βάση α σοιχεία για ην κινηική και η σοιχειομερία ων ανιδράσεων, μπορούμε ώρα να προχωρήσουμε σην ανάλυση ορισμένων βασικών ύπων χημικών ανιδρασήρων. Η ανάλυση
Κεφάλαιο 3 ο. Κυκλώματα με στοιχεία αποθήκευσης ενέργειας
 Κεφάλαιο 3 ο Κυκλώμαα με σοιχεία αποθήκευσης ενέργειας Η διαφορά μεαξύ ης ανάλυσης ων ωμικών κυκλωμάων, που μελεήσαμε ως ώρα, και ων κυκλωμάων που ακολουθούν είναι όι οι εξισώσεις που προκύπουν από ην
Κεφάλαιο 3 ο Κυκλώμαα με σοιχεία αποθήκευσης ενέργειας Η διαφορά μεαξύ ης ανάλυσης ων ωμικών κυκλωμάων, που μελεήσαμε ως ώρα, και ων κυκλωμάων που ακολουθούν είναι όι οι εξισώσεις που προκύπουν από ην
ΦΥΣΙΚΗ Ι. ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ ΣΩΜΑΤΟΣ Ισορροπία Σωματιδίου Στατική Ισορροπία Στερεού Σώματος
 ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης Δύναμης Σύνθεση Δυνάμεων ΡΟΠΗ Η Έννοια ης Ροπής Ροπή Πολλών Δυνάμεων Ζεύγος Δυνάμεων ΦΥΣΙΚΗ Ι ΤΜΗΜΑ Α Α. Καραμπαρμπούνης, Ε. Συλιάρης ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ,, 4 5 ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ
ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης Δύναμης Σύνθεση Δυνάμεων ΡΟΠΗ Η Έννοια ης Ροπής Ροπή Πολλών Δυνάμεων Ζεύγος Δυνάμεων ΦΥΣΙΚΗ Ι ΤΜΗΜΑ Α Α. Καραμπαρμπούνης, Ε. Συλιάρης ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ,, 4 5 ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ
ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ
 ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ V. ΜΙΚΡΟΠΛΑΣΤΙΚΟΤΗΤΑ ΤΩΝ ΚΡΥΣΤΑΛΛΩΝ 1. Εισαγωγή Ση µέχρι ώρα συζήησή µας για ην µηχανική συµπεριφορά ων µεαλλικών υλικών, όπου εξεάσαµε ην ελασική και ην πλασική ους συµπεριφορά
ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ V. ΜΙΚΡΟΠΛΑΣΤΙΚΟΤΗΤΑ ΤΩΝ ΚΡΥΣΤΑΛΛΩΝ 1. Εισαγωγή Ση µέχρι ώρα συζήησή µας για ην µηχανική συµπεριφορά ων µεαλλικών υλικών, όπου εξεάσαµε ην ελασική και ην πλασική ους συµπεριφορά
Κεφάλαιο 5 Πολλαπλοί χημικοί αντιδραστήρες
 Κεφάλαιο 5 Πολλαπλοί χημικοί ανιδρασήρες Σε ορισμένες περιπώσεις, σε μια χημική βιομηχανία, η χρήση ενός μόνο χημικού ανιδρασήρα δεν είναι όσο αποελεσμαική όσο θα ήαν επιθυμηό. Συνεπώς, είναι απαραίηο
Κεφάλαιο 5 Πολλαπλοί χημικοί ανιδρασήρες Σε ορισμένες περιπώσεις, σε μια χημική βιομηχανία, η χρήση ενός μόνο χημικού ανιδρασήρα δεν είναι όσο αποελεσμαική όσο θα ήαν επιθυμηό. Συνεπώς, είναι απαραίηο
Ολοκλήρωση διεργασίας χρησιμοποιώντας την τεχνολογία σύγκλισης (Pinch Technology)
 Θέμα: Ολοκλήρωση διεργασίας χρησιμοποιώνας ην εχνολογία σύγκλισης (Pinch Technology) Εισηγηές: Εμμανουήλ Κοζαμπασάκης, Πανεπισήμιο ου Maπchester, Ινσιούο Ε πισήμης και Τεχνολογίας, UMST, U.K. καθηγ. Bodo
Θέμα: Ολοκλήρωση διεργασίας χρησιμοποιώνας ην εχνολογία σύγκλισης (Pinch Technology) Εισηγηές: Εμμανουήλ Κοζαμπασάκης, Πανεπισήμιο ου Maπchester, Ινσιούο Ε πισήμης και Τεχνολογίας, UMST, U.K. καθηγ. Bodo
ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ 90º. 180º ω. Οι απαντήσεις και τα σχετικά σχόλια
 Φυσική καεύθυνσης Γ Σερεό σώµα ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ άξονας 9º 18º Ο ροχός ου σχήµαος έχει ροπή αδράνειας Ι και σρέφεαι γύρ από ον άξονά ου µε γνιακή αχύηα µέρου.
Φυσική καεύθυνσης Γ Σερεό σώµα ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ άξονας 9º 18º Ο ροχός ου σχήµαος έχει ροπή αδράνειας Ι και σρέφεαι γύρ από ον άξονά ου µε γνιακή αχύηα µέρου.
_Σχήµα 2_. Σελίδα 1 από 5. τον οποίο γίνεται η µεταπτωτική κίνηση. Άξονας περιστροφής τροχού. Άξονας γύρω από. τον οποίο γίνεται η µεταπτωτική κίνηση
 ιονύσης Μηρόπουλος Κίνηση σερεού Παραηρήσεις ση µεαπωική κίνηση ενός σρεφόµενου ροχού Η ανάρηση αυή έγινε µε αφορµή: 1) Την πολύ καλή και ενδιαφέρουσα ανάρηση ου συναδέλφου Νίκου αµαόπουλου µε ίλο «Μεαπωική
ιονύσης Μηρόπουλος Κίνηση σερεού Παραηρήσεις ση µεαπωική κίνηση ενός σρεφόµενου ροχού Η ανάρηση αυή έγινε µε αφορµή: 1) Την πολύ καλή και ενδιαφέρουσα ανάρηση ου συναδέλφου Νίκου αµαόπουλου µε ίλο «Μεαπωική
Θεματική ενότητα : Βασικά εργαλεία και Μέθοδοι για τον έλεγχο της ποιότητας.
 Εργασία 5 Θεμαική ενόηα : Βασικά εργαλεία και Μέθοδοι για ον έλεγχο ης ποιόηας. Άσκηση 1 (η άσκηση έχει λυθεί βάσει ων διευκρινίσεων που δόθηκαν από ον καθηγηή ) α) Το καάλληλο σαισικό εργαλείο που θα
Εργασία 5 Θεμαική ενόηα : Βασικά εργαλεία και Μέθοδοι για ον έλεγχο ης ποιόηας. Άσκηση 1 (η άσκηση έχει λυθεί βάσει ων διευκρινίσεων που δόθηκαν από ον καθηγηή ) α) Το καάλληλο σαισικό εργαλείο που θα
Η Έννοια της τυχαίας ιαδικασίας
 Η Έννοια ης υχαίας ιαδικασίας Η έννοια ης υχαίας διαδικασίας, βασίζεαι σην επέκαση ης έννοιας ης υχαίας µεαβληής, ώσε να συµπεριλάβει ο χρόνο. Σεκάθεαποέλεσµα s k ενόςπειράµαοςύχης ανισοιχούµε, σύµφωναµεκάποιοκανόνα,
Η Έννοια ης υχαίας ιαδικασίας Η έννοια ης υχαίας διαδικασίας, βασίζεαι σην επέκαση ης έννοιας ης υχαίας µεαβληής, ώσε να συµπεριλάβει ο χρόνο. Σεκάθεαποέλεσµα s k ενόςπειράµαοςύχης ανισοιχούµε, σύµφωναµεκάποιοκανόνα,
ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ
 Σ. Η. ΔΡΙΤΣΟΣ, 07 ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ οκός Οπλισµένου Σκυροέµαος Ενισχυµένη µε Σρώση Οπλισµένου Σκυροέµαος Φ0 Φ0 η ΑΡΙΘΜΗΤΙΚΗΕΦΑΡΜΟΓΗ Yλικά : C5/30, Φ0 S Άνοιγµαοκού:
Σ. Η. ΔΡΙΤΣΟΣ, 07 ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ οκός Οπλισµένου Σκυροέµαος Ενισχυµένη µε Σρώση Οπλισµένου Σκυροέµαος Φ0 Φ0 η ΑΡΙΘΜΗΤΙΚΗΕΦΑΡΜΟΓΗ Yλικά : C5/30, Φ0 S Άνοιγµαοκού:
3 Συσχετίσεις σε χρονοσειρές
 3 Συσχείσεις σε χρονοσειρές Η χρονοσειρά ενός χρημαισηριακού δείκη { y, y,, yn } ως πραγμαοποίηση μιας σοχασικής διαδικασίας { t } t= ης μεαβολής ων ιμών ου δείκη { x, x,, xn} πραγμαοποίηση μιας άλλης
3 Συσχείσεις σε χρονοσειρές Η χρονοσειρά ενός χρημαισηριακού δείκη { y, y,, yn } ως πραγμαοποίηση μιας σοχασικής διαδικασίας { t } t= ης μεαβολής ων ιμών ου δείκη { x, x,, xn} πραγμαοποίηση μιας άλλης
Μεγαλύτερες περιπέτειες
 Μεγαλύερες εριέειες Μεά ην ανάρηση «Ένα σύσημα σωμάων σε εριέειες» ας άμε ένα βήμα αρακάω, ση μελέη ου συσήμαος σωμάων και ης εφαρμογής ου γενικευμένου νόμου ου Νεύωνα. --------------------------------------
Μεγαλύερες εριέειες Μεά ην ανάρηση «Ένα σύσημα σωμάων σε εριέειες» ας άμε ένα βήμα αρακάω, ση μελέη ου συσήμαος σωμάων και ης εφαρμογής ου γενικευμένου νόμου ου Νεύωνα. --------------------------------------
Εργαστήριο Ηλεκτρικών κυκλωμάτων
 Εργασήριο Ηλεκρικών κυκλωμάων Αυό έργο χορηγείαι με άδεια Creaive Commons Aribuion-NonCommercial-ShareAlike Greece 3.. Σκοπός ων πειραμάων Ονομ/νυμο: Μηρόπουλος Σπύρος Τμήμα: Ε6 Το εργασήριο πραγμαοποιήθηκε
Εργασήριο Ηλεκρικών κυκλωμάων Αυό έργο χορηγείαι με άδεια Creaive Commons Aribuion-NonCommercial-ShareAlike Greece 3.. Σκοπός ων πειραμάων Ονομ/νυμο: Μηρόπουλος Σπύρος Τμήμα: Ε6 Το εργασήριο πραγμαοποιήθηκε
Α Σ Κ Η Σ Η 1 ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΣΦΑΛΜΑΤΟΣ ΚΑΛΩΔΙΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ MURRAY
 Α Σ Κ Η Σ Η ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΣΦΑΛΜΑΤΟΣ ΚΑΛΩΔΙΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ MURRAY Γενικά Με η μέθοδο Murray, όπου χρησιμοποιούναι οι ιδιόηες ης γέφυρας Wheatstone, μπορούν να προσδιορισούν σφάλμαα διαρροής προς η γη και
Α Σ Κ Η Σ Η ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΣΦΑΛΜΑΤΟΣ ΚΑΛΩΔΙΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ MURRAY Γενικά Με η μέθοδο Murray, όπου χρησιμοποιούναι οι ιδιόηες ης γέφυρας Wheatstone, μπορούν να προσδιορισούν σφάλμαα διαρροής προς η γη και
ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ
 ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ. Ιξώδες Έσω ροή µεαξύ δύο παράλληλων πλακών εµβαδού Α και ανοίγµαος Η (Σχ. ). Σχ. du ιαµηική άση: =η =η γ dy () όπου: γ ο ρυθµός διάµησης, η ο ιξώδες. Παραηρήσεις για
ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ. Ιξώδες Έσω ροή µεαξύ δύο παράλληλων πλακών εµβαδού Α και ανοίγµαος Η (Σχ. ). Σχ. du ιαµηική άση: =η =η γ dy () όπου: γ ο ρυθµός διάµησης, η ο ιξώδες. Παραηρήσεις για
ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ
 1 Κεφάλαιο 1 ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ 1.1 Εισαγωγή Ένα από α βασικόερα ανικείμενα σο επάγγελμα ου μηχανικού είναι η λεγόμενη διασασιολόγηση ή σχεδιασμός δομικών σοιχείων
1 Κεφάλαιο 1 ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ 1.1 Εισαγωγή Ένα από α βασικόερα ανικείμενα σο επάγγελμα ου μηχανικού είναι η λεγόμενη διασασιολόγηση ή σχεδιασμός δομικών σοιχείων
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΛΟΓΙΣΤΙΚΗΣ ΚΑΙ ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗΣ Προσδιορισμός ης αξίας που δημιουργείαι για ους μεόχους με βάση ο οικονομικό και λογισικό κέρδος σα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΛΟΓΙΣΤΙΚΗΣ ΚΑΙ ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗΣ Προσδιορισμός ης αξίας που δημιουργείαι για ους μεόχους με βάση ο οικονομικό και λογισικό κέρδος σα
Δυναμική συμπεριφορά των λογικών κυκλωμάτων MOS. Διάλεξη 10
 Δυναμική συμπεριφορά ων λογικών κυκλωμάων MOS Διάλεξη 10 Δομή ης διάλεξης Εισαγωγή Ανισροφέας NMOS με φορίο ύπου αραίωσης Ανισροφέας CMOS Διάφορα ζηήμαα Ασκήσεις Δυναμική συμπεριφορά ων λογικών κυκλωμάων
Δυναμική συμπεριφορά ων λογικών κυκλωμάων MOS Διάλεξη 10 Δομή ης διάλεξης Εισαγωγή Ανισροφέας NMOS με φορίο ύπου αραίωσης Ανισροφέας CMOS Διάφορα ζηήμαα Ασκήσεις Δυναμική συμπεριφορά ων λογικών κυκλωμάων
ΦΥΣΙΚΗ Ι. ΤΜΗΜΑ Α Ε. Στυλιάρης
 (Με ιδέες και υλικό από ΔΙΑΝΥΣΜΑΤΑ ΣΤΟΝ ΤΡΙΣΔΙΑΣΤΑΤΟ ΧΩΡΟ Καρεσιανές Συνεαγμένες Εσωερικό Γινόμενο Διανυσμάων Εξωερικό Γινόμενο Διανυσμάων Βαθμωό Γινόμενο Τριών Διανυσμάων ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης
(Με ιδέες και υλικό από ΔΙΑΝΥΣΜΑΤΑ ΣΤΟΝ ΤΡΙΣΔΙΑΣΤΑΤΟ ΧΩΡΟ Καρεσιανές Συνεαγμένες Εσωερικό Γινόμενο Διανυσμάων Εξωερικό Γινόμενο Διανυσμάων Βαθμωό Γινόμενο Τριών Διανυσμάων ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης
, e + Σε ένα δείγμα ίδιων ραδιενεργών πυρήνων η πιθανότητα διάσπασης για κάποιο συγκεκριμένο πυρήνα είναι τυχαία.
 ΚΕΦΑΛΑΙΟ 6 : ΠΥΡΗΝΙΚΕΣ ΔΙΑΣΠΑΣΕΙΣ Πυρηνικοί Μεασχημαισμοί Οι δυναοί πυρηνικοί μεσχημαισμοί είναι : Εκπομπή σωμαιδίων-α : 4 2 H Εκπομπή σωμαιδίων-β : - ν, + Εκπομπή ακίνων-γ : φωόνιο Σχάση : διάσπαση πυρήνα
ΚΕΦΑΛΑΙΟ 6 : ΠΥΡΗΝΙΚΕΣ ΔΙΑΣΠΑΣΕΙΣ Πυρηνικοί Μεασχημαισμοί Οι δυναοί πυρηνικοί μεσχημαισμοί είναι : Εκπομπή σωμαιδίων-α : 4 2 H Εκπομπή σωμαιδίων-β : - ν, + Εκπομπή ακίνων-γ : φωόνιο Σχάση : διάσπαση πυρήνα
ΑΘΡΟΙΣΤΙΚΗ ΑΜΟΙΒΑΙΑ ΠΛΗΡΟΦΟΡΙΑ ΩΣ ΣΤΑΤΙΣΤΙΚΟ ΕΛΕΓΧΟΥ ΜΗ-ΓΡΑΜΜΙΚΟΤΗΤΑΣ ΧΡΟΝΟΣΕΙΡΩΝ
 Ελληνικό Σαισικό Ινσιούο Πρακικά 8 ου Πανελληνίου Συνεδρίου Σαισικής (5) σελ.35-34 ΑΘΡΟΙΣΤΙΚΗ ΑΜΟΙΒΑΙΑ ΠΛΗΡΟΦΟΡΙΑ ΩΣ ΣΤΑΤΙΣΤΙΚΟ ΕΛΕΓΧΟΥ ΜΗ-ΓΡΑΜΜΙΚΟΤΗΤΑΣ ΧΡΟΝΟΣΕΙΡΩΝ Παπάνα Αγγελική και Κουγιουμζής Δημήρης
Ελληνικό Σαισικό Ινσιούο Πρακικά 8 ου Πανελληνίου Συνεδρίου Σαισικής (5) σελ.35-34 ΑΘΡΟΙΣΤΙΚΗ ΑΜΟΙΒΑΙΑ ΠΛΗΡΟΦΟΡΙΑ ΩΣ ΣΤΑΤΙΣΤΙΚΟ ΕΛΕΓΧΟΥ ΜΗ-ΓΡΑΜΜΙΚΟΤΗΤΑΣ ΧΡΟΝΟΣΕΙΡΩΝ Παπάνα Αγγελική και Κουγιουμζής Δημήρης
Κανονισμός Πυροπροστασίας Κτιρίων (π.δ. 41/2018)
 Κανονισμός Πυροπροσασίας Κιρίων (π.δ. 41/2018) Πεδίο Εφαρμογής Πεδίο Εφαρμογής Α. Σα κίρια ή μήμαα κιρίων, που ανεγείροναι μεά ην έναρξη ισχύος ου και ων οποίων οι χρήσεις εμπίπουν σε μία από ις περιπώσεις
Κανονισμός Πυροπροσασίας Κιρίων (π.δ. 41/2018) Πεδίο Εφαρμογής Πεδίο Εφαρμογής Α. Σα κίρια ή μήμαα κιρίων, που ανεγείροναι μεά ην έναρξη ισχύος ου και ων οποίων οι χρήσεις εμπίπουν σε μία από ις περιπώσεις
ΦΥΣ 145 Υπολογιστικές Μέθοδοι στη Φυσική. Τελική εξέταση 5 Μάη 2007 Ομάδα 2 η
 ΦΥΣ 145 Υπολογισικές Μέθοδοι ση Φυσική Τελική εξέαση 5 Μάη 2007 Ομάδα 2 η Γράψε ο ονομαεπώνυμο, αριθμό αυόηας και ο password σας σο πάνω μέρος ης αυής ης σελίδας. Πρέπει να απανήσεε και σα 5 προβλήμαα
ΦΥΣ 145 Υπολογισικές Μέθοδοι ση Φυσική Τελική εξέαση 5 Μάη 2007 Ομάδα 2 η Γράψε ο ονομαεπώνυμο, αριθμό αυόηας και ο password σας σο πάνω μέρος ης αυής ης σελίδας. Πρέπει να απανήσεε και σα 5 προβλήμαα
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I ΕΙΣΑΓΩΓΗ ΒΑΣΙΚΑ ΣΗΜΑΤΑ Μοναδιαία βηµαική συνάρηση (Ui Sep Fucio) U () =, U () =, .5 - -
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I ΕΙΣΑΓΩΓΗ ΒΑΣΙΚΑ ΣΗΜΑΤΑ Μοναδιαία βηµαική συνάρηση (Ui Sep Fucio) U () =, U () =, .5 - -
ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ. 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διατμητικής Αντοχής Εδάφους. Διδάσκοντες: Β. Χρηστάρας Καθηγητής Β. Μαρίνος, Αν.
 ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διαμηικής Ανοχής Εδάφους Συνοχή (c) Γωνία ριβής (φ ο ) Διδάσκονες: Β. Χρησάρας Καθηγηής Β. Μαρίνος, Αν. Καθηγηής Εργασήριο Τεχνικής Γεωλογίας και
ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διαμηικής Ανοχής Εδάφους Συνοχή (c) Γωνία ριβής (φ ο ) Διδάσκονες: Β. Χρησάρας Καθηγηής Β. Μαρίνος, Αν. Καθηγηής Εργασήριο Τεχνικής Γεωλογίας και
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΜΒΑ «Νέες Αρχές ιοίκησης Επιχειρήσεων» ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ υναµικά Μονέλα Χωροθέησης σο Σχειασµό Εφοιασικής Αλυσίας ΕΠΙΜΕΛΕΙΑ: ΛΑΜΠΡΟΠΟΥΛΟΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΜΒΑ «Νέες Αρχές ιοίκησης Επιχειρήσεων» ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ υναµικά Μονέλα Χωροθέησης σο Σχειασµό Εφοιασικής Αλυσίας ΕΠΙΜΕΛΕΙΑ: ΛΑΜΠΡΟΠΟΥΛΟΣ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΗΜΑΤΩΝ ΕΛΕΓΧΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΗΜΑΤΩΝ ΕΛΕΓΧΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ ΝΙΚΟΛΑΟΣ Κ. ΜΠΕΚΙΑΡΗΣ ΛΥΜΠΕΡΗΣ ΤΕΧΝΙΚΕΣ ΓΡΑΜΜΙΚΩΝ ΚΑΙ ΜΗ ΓΡΑΜΜΙΚΩΝ ΕΛΕΓΚΤΩΝ ΣΥΣΤΗΜΑΤΩΝ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΗΜΑΤΩΝ ΕΛΕΓΧΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ ΝΙΚΟΛΑΟΣ Κ. ΜΠΕΚΙΑΡΗΣ ΛΥΜΠΕΡΗΣ ΤΕΧΝΙΚΕΣ ΓΡΑΜΜΙΚΩΝ ΚΑΙ ΜΗ ΓΡΑΜΜΙΚΩΝ ΕΛΕΓΚΤΩΝ ΣΥΣΤΗΜΑΤΩΝ
ΑΞΙΟΛΟΓΗΣΗ ΕΚΤΙΜΗΤΩΝ ΑΜΟΙΒΑΙΑΣ ΠΛΗΡΟΦΟΡΙΑΣ ΑΠΟ ΙΣΤΟΓΡΑΜΜΑ ΣΕ ΧΡΟΝΟΣΕΙΡΕΣ
 Ελληνικό Σαισικό Ινσιούο Πρακικά ου Πανελληνίου Συνεδρίου Σαισικής (7), σελ 39-336 ΑΞΙΟΛΟΓΗΣΗ ΕΚΤΙΜΗΤΩΝ ΑΜΟΙΒΑΙΑΣ ΠΛΗΡΟΦΟΡΙΑΣ ΑΠΟ ΙΣΤΟΓΡΑΜΜΑ ΣΕ ΧΡΟΝΟΣΕΙΡΕΣ Παπάνα Αγγελική, Κουγιουμζής Δημήρης Γενικό Τμήμα
Ελληνικό Σαισικό Ινσιούο Πρακικά ου Πανελληνίου Συνεδρίου Σαισικής (7), σελ 39-336 ΑΞΙΟΛΟΓΗΣΗ ΕΚΤΙΜΗΤΩΝ ΑΜΟΙΒΑΙΑΣ ΠΛΗΡΟΦΟΡΙΑΣ ΑΠΟ ΙΣΤΟΓΡΑΜΜΑ ΣΕ ΧΡΟΝΟΣΕΙΡΕΣ Παπάνα Αγγελική, Κουγιουμζής Δημήρης Γενικό Τμήμα
d k dt k a ky(t) = dt k b kx(t) (3.1)
 Κεφάλαιο 3 Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 3. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Είδαμε σο προηγούμενο κεφάλαιο κάποια εισαγωγικά
Κεφάλαιο 3 Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 3. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Είδαμε σο προηγούμενο κεφάλαιο κάποια εισαγωγικά
ΠΑΙΓΝΙΟΘΕΩΡΗΤΙΚΗ ΜΕΛΕΤΗ ΠΟΛΥΕΠΙΠΕ ΩΝ ΑΡΧΙΤΕΚΤΟΝΙΚΩΝ WEB CACHING
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΜΕΤΑΠΤΥΧΙΑΚΗ ΕΞΕΙ ΙΚΕΥΣΗ ΣΤΑ ΠΛΗΡΟΦΟΡΙΑΚΑ ΣΥΣΤΗΜΑΤΑ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΠΑΙΓΝΙΟΘΕΩΡΗΤΙΚΗ ΜΕΛΕΤΗ ΠΟΛΥΕΠΙΠΕ ΩΝ ΑΡΧΙΤΕΚΤΟΝΙΚΩΝ
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΜΕΤΑΠΤΥΧΙΑΚΗ ΕΞΕΙ ΙΚΕΥΣΗ ΣΤΑ ΠΛΗΡΟΦΟΡΙΑΚΑ ΣΥΣΤΗΜΑΤΑ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΠΑΙΓΝΙΟΘΕΩΡΗΤΙΚΗ ΜΕΛΕΤΗ ΠΟΛΥΕΠΙΠΕ ΩΝ ΑΡΧΙΤΕΚΤΟΝΙΚΩΝ
Παραγωγή Κυµατοµορφών FM:
 Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής και ση συνέχεια χρησιµοοιείαι ολλαλασιασµός
Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής και ση συνέχεια χρησιµοοιείαι ολλαλασιασµός
Παραγωγή Κυµατοµορφών FM:
 Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής ζώνης και ση συνέχεια χρησιµοοιείαι
Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής ζώνης και ση συνέχεια χρησιµοοιείαι
ΑΞΙΟΛΟΓΗΣΗ ΣΤΟ ΣΧΕΔΙΑΣΜΟ ΤΟΥ ΧΩΡΟΥ ΠΑΡΑΔΕΙΓΜΑ ΕΦΑΡΜΟΓΗΣ ΑΝΑΛΥΣΗΣ ΚΟΣΤΟΥΣ ΟΦΕΛΟΥΣ. Υπεύθυνη μαθήματος Αναστασία Στρατηγέα Αναπλ. Καθηγ. Ε.Μ.Π.
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΑΓΡΟΝΟΜΩΝ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΓΕΩΓΡΑΦΙΑΣ ΚΑΙ ΠΕΡΙΦΕΡΕΙΑΚΟΥ ΣΧΕΔΙΑΣΜΟΥ ΑΞΙΟΛΟΓΗΣΗ ΣΤΟ ΣΧΕΔΙΑΣΜΟ ΤΟΥ ΧΩΡΟΥ ΠΑΡΑΔΕΙΓΜΑ ΕΦΑΡΜΟΓΗΣ ΑΝΑΛΥΣΗΣ ΚΟΣΤΟΥΣ ΟΦΕΛΟΥΣ Υπεύθυνη
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΑΓΡΟΝΟΜΩΝ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΓΕΩΓΡΑΦΙΑΣ ΚΑΙ ΠΕΡΙΦΕΡΕΙΑΚΟΥ ΣΧΕΔΙΑΣΜΟΥ ΑΞΙΟΛΟΓΗΣΗ ΣΤΟ ΣΧΕΔΙΑΣΜΟ ΤΟΥ ΧΩΡΟΥ ΠΑΡΑΔΕΙΓΜΑ ΕΦΑΡΜΟΓΗΣ ΑΝΑΛΥΣΗΣ ΚΟΣΤΟΥΣ ΟΦΕΛΟΥΣ Υπεύθυνη
Πανεπιστήµιο Θεσσαλίας
 Πανεπισήιο Θεσσαλίας Τήα Ηλεκρολόγων Μηχανικών & Μηχανικών Υπολογισών Άσκηση : Λυένες Ασκήσεις Έσω ένα σύσηα νήης, σο οποίο έχουε προσθέσει ια κρυφή νήη θυάων 6 θέσεων εαξύ ης κρυφής νήης δεδοένων L και
Πανεπισήιο Θεσσαλίας Τήα Ηλεκρολόγων Μηχανικών & Μηχανικών Υπολογισών Άσκηση : Λυένες Ασκήσεις Έσω ένα σύσηα νήης, σο οποίο έχουε προσθέσει ια κρυφή νήη θυάων 6 θέσεων εαξύ ης κρυφής νήης δεδοένων L και
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΑΞΙΟΛΟΓΗΣΗ ΕΠΕΝ ΥΣΕΩΝ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΜΑΘΗΜΑ: ΛΕΙΤΟΥΡΓΙΕΣ ΕΠΙΧΕΙΡΗΣΕΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΑΚΩΝ ΚΑΙ ΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΙΟΙΚΗΣΗ ΠΛΗΡΟΦΟΡΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΜΑΘΗΜΑ: ΛΕΙΤΟΥΡΓΙΕΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΑΞΙΟΛΟΓΗΣΗ ΕΠΕΝ ΥΣΕΩΝ ιδάσκων:
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΑΚΩΝ ΚΑΙ ΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΙΟΙΚΗΣΗ ΠΛΗΡΟΦΟΡΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΜΑΘΗΜΑ: ΛΕΙΤΟΥΡΓΙΕΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΑΞΙΟΛΟΓΗΣΗ ΕΠΕΝ ΥΣΕΩΝ ιδάσκων:
Θέματα Περασμένων Εξετάσεων και Απαντήσεις
 Θέμαα Περασμένων Εξεάσεων και Απανήσεις Εξεάσεις Ιουνίου. ΘΕΜΑ.,5 μονάδα Δίνεαι ο ΓΧΑ σύσημα με κρουσική απόκριση iπ h co8 π π Να βρεθεί η έξοδός ου αν η είσοδός είναι co π co 6π co 8π i W, < Εφαρμόζονας
Θέμαα Περασμένων Εξεάσεων και Απανήσεις Εξεάσεις Ιουνίου. ΘΕΜΑ.,5 μονάδα Δίνεαι ο ΓΧΑ σύσημα με κρουσική απόκριση iπ h co8 π π Να βρεθεί η έξοδός ου αν η είσοδός είναι co π co 6π co 8π i W, < Εφαρμόζονας
Εισαγωγή στη Θεωρία Σημάτων και Συστημάτων
 Εισαγωγή ση Θεωρία Σημάων και Συσημάων Ιωάννης Χαρ. Κασαβουνίδης Τμήμα Μηχ. Η/Υ Τηλεπ. & Δικύων Πανεπισήμιο Θεσσαλίας ΦΘινοπωρινό Εξάμηνο 9/ Άσκηση Να υπολογίσεε ο παρακάω άθροισμα: Θυμίζουμε ην ανάπυξη
Εισαγωγή ση Θεωρία Σημάων και Συσημάων Ιωάννης Χαρ. Κασαβουνίδης Τμήμα Μηχ. Η/Υ Τηλεπ. & Δικύων Πανεπισήμιο Θεσσαλίας ΦΘινοπωρινό Εξάμηνο 9/ Άσκηση Να υπολογίσεε ο παρακάω άθροισμα: Θυμίζουμε ην ανάπυξη
Σχολή Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών ιαχείριση Ενέργειας και Περιβαλλοντική Πολιτική
 ιαχείριση Ενέργειας και Περιβαλλοντική Πολιτική 5. Οικονομική Αξιολόγηση Ενεργειακών Επενδύσεων Καθηγητής Ιωάννης Ψαρράς Εργαστήριο Συστημάτων Αποφάσεων & ιοίκησης Γρ. 0.2.7. Ισόγειο Σχολής Ηλεκτρολόγων
ιαχείριση Ενέργειας και Περιβαλλοντική Πολιτική 5. Οικονομική Αξιολόγηση Ενεργειακών Επενδύσεων Καθηγητής Ιωάννης Ψαρράς Εργαστήριο Συστημάτων Αποφάσεων & ιοίκησης Γρ. 0.2.7. Ισόγειο Σχολής Ηλεκτρολόγων
y(t) = T [x(t)] (7.1)
![y(t) = T [x(t)] (7.1) y(t) = T [x(t)] (7.1)](/thumbs/93/114087149.jpg) Κεφάλαιο 7 Ανάλυση Συσημάων σο Πεδίο ου Χρόνου 7. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Τι είναι όμως α συσήμαα και γιαί α χρησιμοποιούμε;
Κεφάλαιο 7 Ανάλυση Συσημάων σο Πεδίο ου Χρόνου 7. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Τι είναι όμως α συσήμαα και γιαί α χρησιμοποιούμε;
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΤΕΥΘΥΝΣΗ ΜΑΘΗΜΑΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ Βέλισες σραηγικές διακοπής μιας Μαρκοβιανής αλυσίδας ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΒΑΣΙΛΕΙΟΣ ΖΑΧΑΡΙΑΔΗΣ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΤΕΥΘΥΝΣΗ ΜΑΘΗΜΑΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ Βέλισες σραηγικές διακοπής μιας Μαρκοβιανής αλυσίδας ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΒΑΣΙΛΕΙΟΣ ΖΑΧΑΡΙΑΔΗΣ
ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ 1 ΣΕΙΡΑΣ FOURIER. Ανάπτυξη σειράς Dirac σε σειρά Fourier (Εκθετική Fourier):
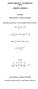 ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ 7-5-7 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ ΣΕΙΡΑΣ FOURIER Ανάπυξη σειράς Dirac σε σειρά Fourier (Εκθεική Fourier): s () = δ ( k) k = c s e d e inω inω () n = = = ιόι f () δ (
ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ 7-5-7 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ ΣΕΙΡΑΣ FOURIER Ανάπυξη σειράς Dirac σε σειρά Fourier (Εκθεική Fourier): s () = δ ( k) k = c s e d e inω inω () n = = = ιόι f () δ (
Ενότητα Ζ Η ΕΝΝΟΙΑ, ΟΙ ΤΥΠΟΙ ΚΑΙ ΤΑ ΚΡΙΤΗΡΙΑ ΑΣΤΟΧΙΑΣ
 Ενόηα Ζ ΚΑΜΠΤΟΔΙΑΤΜΗΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΦΟΡΕΩΝ Η ΕΝΝΟΙΑ, ΟΙ ΤΥΠΟΙ ΚΑΙ ΤΑ ΚΡΙΤΗΡΙΑ ΑΣΤΟΧΙΑΣ 1. ΚΑΜΠΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΦΟΡΕΩΝ 1.1.1 Παραμορφώσεις Καθύψος ης Διαομής 1.1 MΗΧΑΝΙΣΜΟΣ ΑΝΑΛΗΨΗΣ ΔΡΩΣΑΣ ΡΟΠΗΣ Όπως φαίνεαι
Ενόηα Ζ ΚΑΜΠΤΟΔΙΑΤΜΗΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΦΟΡΕΩΝ Η ΕΝΝΟΙΑ, ΟΙ ΤΥΠΟΙ ΚΑΙ ΤΑ ΚΡΙΤΗΡΙΑ ΑΣΤΟΧΙΑΣ 1. ΚΑΜΠΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΦΟΡΕΩΝ 1.1.1 Παραμορφώσεις Καθύψος ης Διαομής 1.1 MΗΧΑΝΙΣΜΟΣ ΑΝΑΛΗΨΗΣ ΔΡΩΣΑΣ ΡΟΠΗΣ Όπως φαίνεαι
ΑΞΙΟΛΟΓΗΣΗ ΣΤΟ ΣΧΕΔΙΑΣΜΟ ΤΟΥ ΧΩΡΟΥ. ΑΣΚΗΣΗ 1 η Μέθοδος Κόστους-Οφέλους Κοινωνικο-Οικονομική Αξιολόγηση Έργου Γέφυρας Ρίου Αντιρρίου
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΑΓΡΟΝΟΜΩΝ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΓΕΩΓΡΑΦΙΑΣ ΚΑΙ ΠΕΡΙΦΕΡΕΙΑΚΟΥ ΣΧΕΔΙΑΣΜΟΥ ΑΞΙΟΛΟΓΗΣΗ ΣΤΟ ΣΧΕΔΙΑΣΜΟ ΤΟΥ ΧΩΡΟΥ ΑΣΚΗΣΗ 1 η Μέθοδος Κόστους-Οφέλους Κοινωνικο-Οικονομική
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΑΓΡΟΝΟΜΩΝ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΓΕΩΓΡΑΦΙΑΣ ΚΑΙ ΠΕΡΙΦΕΡΕΙΑΚΟΥ ΣΧΕΔΙΑΣΜΟΥ ΑΞΙΟΛΟΓΗΣΗ ΣΤΟ ΣΧΕΔΙΑΣΜΟ ΤΟΥ ΧΩΡΟΥ ΑΣΚΗΣΗ 1 η Μέθοδος Κόστους-Οφέλους Κοινωνικο-Οικονομική
Τι ενδιαφέρει τον ιδιώτη
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΠΜΣ «Επιστήµη και Τεχνολογία Υδατικών Πόρων» Οικονοµικά του Περιβάλλοντος και των Υδατικών Πόρων Αξιολόγηση επενδύσεων Τι ενδιαφέρει τον ιδιώτη Πόσα χρήµατα θα επενδύσω; Πότε
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΠΜΣ «Επιστήµη και Τεχνολογία Υδατικών Πόρων» Οικονοµικά του Περιβάλλοντος και των Υδατικών Πόρων Αξιολόγηση επενδύσεων Τι ενδιαφέρει τον ιδιώτη Πόσα χρήµατα θα επενδύσω; Πότε
Νόμος Αmpere. i r. Β dl = Β(dl ακτ +dl τοξ ) = Β rdθ = 2π. Β dl = μ ο i
 Νόος Αmpee = o Τυχαία κλεισή διαδροή προσεγγιζεαι από ακινικά ευθ. ήαα και κυκλικά όξα dθ dθ dl ακινικά = 0 dl όξα = dθ dl = (dl ακ +dl οξ ) = dθ = o dθ = o dθ Ρευαοφόρο ς αγωγός dl = ο Νόος Αmpee Το ολοκλήρωα
Νόος Αmpee = o Τυχαία κλεισή διαδροή προσεγγιζεαι από ακινικά ευθ. ήαα και κυκλικά όξα dθ dθ dl ακινικά = 0 dl όξα = dθ dl = (dl ακ +dl οξ ) = dθ = o dθ = o dθ Ρευαοφόρο ς αγωγός dl = ο Νόος Αmpee Το ολοκλήρωα
Ανάλυση της µηχανικής συµπεριφοράς της συνάφειας ράβδων οπλισµού FRP µε σκυρόδεµα
 Ανάλυση ης µηχανικής συµπεριφοράς ης συνάφειας ράβδων οπλισµού FRP µε σκυρόδεµα Β. Καραζαφέρης MΕ, Υποψήφιος διδάκωρ ΕΜΠ Μ. Καής Επίκουρος Καθηγηής ΕΜΠ Λέξεις κλειδιά: FRP, συνάφεια, πεπερασµένα σοιχεία
Ανάλυση ης µηχανικής συµπεριφοράς ης συνάφειας ράβδων οπλισµού FRP µε σκυρόδεµα Β. Καραζαφέρης MΕ, Υποψήφιος διδάκωρ ΕΜΠ Μ. Καής Επίκουρος Καθηγηής ΕΜΠ Λέξεις κλειδιά: FRP, συνάφεια, πεπερασµένα σοιχεία
Οδηγός Οικονοµικής Ανάλυσης: Οικονοµική Αξιολόγηση των Επιλογών Καθαρότερης Παραγωγής
 Οδηγός Οικονοµικής Ανάλυσης: Οικονοµική Αξιολόγηση των Επιλογών Καθαρότερης Παραγωγής. Τι Προσφέρει ο Οδηγός; Καθοδήγηση σχετικά µε την οικονοµική ανάλυση των επιλογών καθαρότερης παραγωγής o Εισαγωγή:
Οδηγός Οικονοµικής Ανάλυσης: Οικονοµική Αξιολόγηση των Επιλογών Καθαρότερης Παραγωγής. Τι Προσφέρει ο Οδηγός; Καθοδήγηση σχετικά µε την οικονοµική ανάλυση των επιλογών καθαρότερης παραγωγής o Εισαγωγή:
Η τεχνική της Καθαρής Παρούσας Αξίας ( Net Present Value)
 Η τεχνική της Καθαρής Παρούσας Αξίας ( Net Present Value) Σύμφωνα με αυτή την τεχνική θα πρέπει να επιλέγουμε επενδυτικά σχέδια τα οποία έχουν Καθαρή Παρούσα Αξία μεγαλύτερη του μηδενός. Συγκεκριμένα δίνεται
Η τεχνική της Καθαρής Παρούσας Αξίας ( Net Present Value) Σύμφωνα με αυτή την τεχνική θα πρέπει να επιλέγουμε επενδυτικά σχέδια τα οποία έχουν Καθαρή Παρούσα Αξία μεγαλύτερη του μηδενός. Συγκεκριμένα δίνεται
Ορισμός: u(t) = 0 (t < 0) και u(t) = 1 (t 0) (4.1) Από τις (4.3) και (4.4), προκύπτει ότι το βηματικό σήμα u(t) είναι σήμα ισχύος.
 4. ΑΝΑΛΥΣΗ ΒΑΣΙΚΩΝ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΗΜΑΤΩΝ 4.. To βημαικό σήμα (step signal) u(t) Ορισμός: u(t) = 0 (t < 0) και u(t) = (t 0) (4.) Μέση ιμή: = (4.) Ενέργεια: Ε = lim [T ] [-, ] u (t).dt (4.3) Μέση
4. ΑΝΑΛΥΣΗ ΒΑΣΙΚΩΝ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΗΜΑΤΩΝ 4.. To βημαικό σήμα (step signal) u(t) Ορισμός: u(t) = 0 (t < 0) και u(t) = (t 0) (4.) Μέση ιμή: = (4.) Ενέργεια: Ε = lim [T ] [-, ] u (t).dt (4.3) Μέση
η αποδοτική κατανοµή των πόρων αποδοτική κατανοµή των πόρων Οικονοµική αποδοτικότητα Οικονοµία των µεταφορών Η ανεπάρκεια των πόρων &
 5 η αποδοτική κατανοµή των πόρων Οικονοµική αποδοτικότητα: Η αποτελεί θεµελιώδες πρόβληµα σε κάθε σύγχρονη οικονοµία. Το πρόβληµα της αποδοτικής κατανοµής των πόρων µπορεί να εκφρασθεί µε 4 βασικά ερωτήµατα
5 η αποδοτική κατανοµή των πόρων Οικονοµική αποδοτικότητα: Η αποτελεί θεµελιώδες πρόβληµα σε κάθε σύγχρονη οικονοµία. Το πρόβληµα της αποδοτικής κατανοµής των πόρων µπορεί να εκφρασθεί µε 4 βασικά ερωτήµατα
Οργάνωση & Διαχείριση Υπόγειων Εργων ΔΠΜΣ Σχεδιασμός & Κατασκευή Υπόγειων Εργων Κατερίνα Αδάμ, Μ. Sc., Ph.D Aναπληρώτρια Καθηγήτρια, Σχολή ΜΜΜ
 Οργάνωση & Διαχείριση Υπόγειων Εργων ΔΠΜΣ Σχεδιασμός & Κατασκευή Υπόγειων Εργων Κατερίνα Αδάμ, Μ. Sc., Ph.D Aναπληρώτρια Καθηγήτρια, Σχολή ΜΜΜ 27/10/2017 Χειμερινό Εξάμηνο, 2017-2018 1 Ανάλυση Κόστους
Οργάνωση & Διαχείριση Υπόγειων Εργων ΔΠΜΣ Σχεδιασμός & Κατασκευή Υπόγειων Εργων Κατερίνα Αδάμ, Μ. Sc., Ph.D Aναπληρώτρια Καθηγήτρια, Σχολή ΜΜΜ 27/10/2017 Χειμερινό Εξάμηνο, 2017-2018 1 Ανάλυση Κόστους
Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ
 Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ ΕΙΣΑΓΩΓΗ Όπως είαι γωσό, η Μουσική είαι Μαθημαικά και (σο βάθος) υπάρχει, μία «αδιόραη αρμοία» μεαξύ αυώ ω δύο. Έα μουσικό έργο, διέπεαι από μαθημαικούς όμους, σε ό,ι αφορά ις σχέσεις
Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ ΕΙΣΑΓΩΓΗ Όπως είαι γωσό, η Μουσική είαι Μαθημαικά και (σο βάθος) υπάρχει, μία «αδιόραη αρμοία» μεαξύ αυώ ω δύο. Έα μουσικό έργο, διέπεαι από μαθημαικούς όμους, σε ό,ι αφορά ις σχέσεις
Ροπή δύναμης. Τι προκαλεί την επιτάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω του. Τι προκαλεί την γωνιακή επιτάχυνση ενός στερεού σώματος;
 Τι προκαλεί ην επιάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω ου Τι προκαλεί ην γωνιακή επιάχυνση ενός σερεού σώμαος; Η ροπή δύναμης F Για να αλλάξουμε ην περισροφική καάσαση ενός σώμαος παίζουν
Τι προκαλεί ην επιάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω ου Τι προκαλεί ην γωνιακή επιάχυνση ενός σερεού σώμαος; Η ροπή δύναμης F Για να αλλάξουμε ην περισροφική καάσαση ενός σώμαος παίζουν
ΟΙΚΟΝΟΜΙΚΗ ΓΕΩΓΡΑΦΙΑ 4 η ΑΣΚΗΣΗ ΟΙΚΟΝΟΜΟΤΕΧΝΙΚΗ ΜΕΛΕΤΗ ΣΚΟΠΙΜΟΤΗΤΑΣ Εισαγωγή Άσκησης
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΑΓΡΟΝΟΜΩΝ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΓΕΩΓΡΑΦΙΑΣ ΚΑΙ ΠΕΡΙΦΕΡΕΙΑΚΟΥ ΣΧΕΔΙΑΣΜΟΥ ΟΙΚΟΝΟΜΙΚΗ ΓΕΩΓΡΑΦΙΑ 4 η ΑΣΚΗΣΗ ΟΙΚΟΝΟΜΟΤΕΧΝΙΚΗ ΜΕΛΕΤΗ ΣΚΟΠΙΜΟΤΗΤΑΣ Εισαγωγή Άσκησης ΥΠΕΥΘΥΝΗ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΑΓΡΟΝΟΜΩΝ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΓΕΩΓΡΑΦΙΑΣ ΚΑΙ ΠΕΡΙΦΕΡΕΙΑΚΟΥ ΣΧΕΔΙΑΣΜΟΥ ΟΙΚΟΝΟΜΙΚΗ ΓΕΩΓΡΑΦΙΑ 4 η ΑΣΚΗΣΗ ΟΙΚΟΝΟΜΟΤΕΧΝΙΚΗ ΜΕΛΕΤΗ ΣΚΟΠΙΜΟΤΗΤΑΣ Εισαγωγή Άσκησης ΥΠΕΥΘΥΝΗ
Προσφορά και κόστος. Κατηγορίες κόστους. Οριακό κόστος και µεγιστοποίηση του κέρδους. Μέσο κόστος. TC MC = q TC AC ) AC
 Μέσο κόστος µέσο συνολικό κόστος (AC) 3 Προσφορά και κόστος µέσο µεταβλητό κόστος (AVC) µέσο σταθερό κόστος (AFC) Το µέσο σταθερό κόστος µειώνεται, διότι το συνολικό σταθερό κόστος κατανέµεται σε περισσότερη
Μέσο κόστος µέσο συνολικό κόστος (AC) 3 Προσφορά και κόστος µέσο µεταβλητό κόστος (AVC) µέσο σταθερό κόστος (AFC) Το µέσο σταθερό κόστος µειώνεται, διότι το συνολικό σταθερό κόστος κατανέµεται σε περισσότερη
ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗ ΑΝΑΛΥΣΗ & ΔΙΟΙΚΗΤΙΚΗ Ε.ΜΙΧΑΗΛΙΔΟΥ - 1 ΤΟΜΟΣ Β ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗ ΑΝΑΛΥΣΗ & ΔΙΟΙΚΗΤΙΚΗ
 ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗ ΑΝΑΛΥΣΗ & ΔΙΟΙΚΗΤΙΚΗ Ε.ΜΙΧΑΗΛΙΔΟΥ - 1 ΤΟΜΟΣ Β ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗ ΑΝΑΛΥΣΗ & ΔΙΟΙΚΗΤΙΚΗ Κεφάλαιο 1 Η ΔΙΑΧΡΟΝΙΚΗ ΑΞΙΑ ΤΟΥ ΧΡΗΜΑΤΟΣ Επιτόκιο: είναι η αμοιβή του κεφαλαίου για κάθε μονάδα χρόνου
ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗ ΑΝΑΛΥΣΗ & ΔΙΟΙΚΗΤΙΚΗ Ε.ΜΙΧΑΗΛΙΔΟΥ - 1 ΤΟΜΟΣ Β ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗ ΑΝΑΛΥΣΗ & ΔΙΟΙΚΗΤΙΚΗ Κεφάλαιο 1 Η ΔΙΑΧΡΟΝΙΚΗ ΑΞΙΑ ΤΟΥ ΧΡΗΜΑΤΟΣ Επιτόκιο: είναι η αμοιβή του κεφαλαίου για κάθε μονάδα χρόνου
ΥΠΟΛΟΓΙΣΤΙΚΑ ΜΟΝΤΕΛΑ ΚΥΚΛΟΦΟΡΙΑΣ ΚΑΙ ΔΙΑΔΟΣΗΣ ΠΕΤΡΕΛΑΪΚΗΣ ΡΥΠΑΝΣΗΣ ΣΤΗΝ ΠΕΡΙΟΧΗ ΤΟΥ ΛΙΜΕΝΑ ΘΕΣΣΑΛΟΝΙΚΗΣ
 8ο Πανελλήνιο Συμποσιο Ωκεανογαφίας & Αλιείας ΥΠΟΛΟΓΙΣΤΙΚΑ ΜΟΝΤΕΛΑ ΚΥΚΛΟΦΟΡΙΑΣ ΚΑΙ ΔΙΑΔΟΣΗΣ ΠΕΤΡΕΛΑΪΚΗΣ ΡΥΠΑΝΣΗΣ ΣΤΗΝ ΠΕΡΙΟΧΗ ΤΟΥ ΛΙΜΕΝΑ ΘΕΣΣΑΛΟΝΙΚΗΣ Χισόφοος Γ. Κουίας*, Αχιλλέας Γ. Σαμαάς** *Ο.Λ.Θ. Α.Ε.,
8ο Πανελλήνιο Συμποσιο Ωκεανογαφίας & Αλιείας ΥΠΟΛΟΓΙΣΤΙΚΑ ΜΟΝΤΕΛΑ ΚΥΚΛΟΦΟΡΙΑΣ ΚΑΙ ΔΙΑΔΟΣΗΣ ΠΕΤΡΕΛΑΪΚΗΣ ΡΥΠΑΝΣΗΣ ΣΤΗΝ ΠΕΡΙΟΧΗ ΤΟΥ ΛΙΜΕΝΑ ΘΕΣΣΑΛΟΝΙΚΗΣ Χισόφοος Γ. Κουίας*, Αχιλλέας Γ. Σαμαάς** *Ο.Λ.Θ. Α.Ε.,
6. Οικονοµική Αξιολόγηση Ενεργειακών Επενδύσεων
 ιαχείριση Ενέργειας και Περιβαλλοντική Πολιτική 6. Οικονοµική Αξιολόγηση Ενεργειακών Επενδύσεων Καθηγητής Ιωάννης Ψαρράς Εργαστήριο Συστηµάτων Αποφάσεων & ιοίκησης Γρ. 0.2.7. Ισόγειο Σχολής Ηλεκτρολόγων
ιαχείριση Ενέργειας και Περιβαλλοντική Πολιτική 6. Οικονοµική Αξιολόγηση Ενεργειακών Επενδύσεων Καθηγητής Ιωάννης Ψαρράς Εργαστήριο Συστηµάτων Αποφάσεων & ιοίκησης Γρ. 0.2.7. Ισόγειο Σχολής Ηλεκτρολόγων
Διαχείριση Εφοδιαστικής Αλυσίδας Μέρος 5 Αξιολόγηση Εναλλακτικών Σεναρίων ΔΡ. ΙΩΑΝΝΗΣ ΡΟΜΠΟΓΙΑΝΝΑΚΗΣ
 2018 Διαχείριση Εφοδιαστικής Αλυσίδας Μέρος 5 Αξιολόγηση Εναλλακτικών Σεναρίων ΔΡ. ΙΩΑΝΝΗΣ ΡΟΜΠΟΓΙΑΝΝΑΚΗΣ Για την ανάλυση και αξιολόγησης των εναλλακτικών σχεδίων εξέλιξης της ζήτησης σε μια ΕΑ, που θα
2018 Διαχείριση Εφοδιαστικής Αλυσίδας Μέρος 5 Αξιολόγηση Εναλλακτικών Σεναρίων ΔΡ. ΙΩΑΝΝΗΣ ΡΟΜΠΟΓΙΑΝΝΑΚΗΣ Για την ανάλυση και αξιολόγησης των εναλλακτικών σχεδίων εξέλιξης της ζήτησης σε μια ΕΑ, που θα
Αξιολόγηση Επενδυτικών Σχεδίων
 Αξιολόγηση Επενδυτικών Σχεδίων Ενότητα 3: Κριτήρια Αξιολόγησης Επενδύσεων Δ. Δαμίγος Μ. Μενεγάκη Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό,
Αξιολόγηση Επενδυτικών Σχεδίων Ενότητα 3: Κριτήρια Αξιολόγησης Επενδύσεων Δ. Δαμίγος Μ. Μενεγάκη Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό,
Συστήματα Χρηματοοικονομικής Διοίκησης
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Συστήματα Χρηματοοικονομικής Διοίκησης Ακαδημαϊκό Έτος 2007 2008 Εξάμηνο 8 ο 7η Διάλεξη: Αξιολόγηση Επενδύσεων Ιωάννης Ψαρράς
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Συστήματα Χρηματοοικονομικής Διοίκησης Ακαδημαϊκό Έτος 2007 2008 Εξάμηνο 8 ο 7η Διάλεξη: Αξιολόγηση Επενδύσεων Ιωάννης Ψαρράς
11.1.2 Κριτήρια αξιολόγησης επενδύσεων
 Επιχειρησιακό Πρόγραμμα Εκπαίδευση και ια Βίου Μάθηση Πρόγραμμα ια Βίου Μάθησης ΑΕΙ για την Επικαιροποίηση Γνώσεων Αποφοίτων ΑΕΙ: Σύγχρονες Εξελίξεις στις Θαλάσσιες Κατασκευές Α.Π.Θ. Πολυτεχνείο Κρήτης
Επιχειρησιακό Πρόγραμμα Εκπαίδευση και ια Βίου Μάθηση Πρόγραμμα ια Βίου Μάθησης ΑΕΙ για την Επικαιροποίηση Γνώσεων Αποφοίτων ΑΕΙ: Σύγχρονες Εξελίξεις στις Θαλάσσιες Κατασκευές Α.Π.Θ. Πολυτεχνείο Κρήτης
ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗ ΔΙΟΙΚΗΣΗ. ΑΣΚΗΣΕΙΣ-ΠΡΑΞΕΙΣ Εισαγωγική εισήγηση Νο1
 ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗ ΔΙΟΙΚΗΣΗ ΑΣΚΗΣΕΙΣ-ΠΡΑΞΕΙΣ Εισαγωγική εισήγηση Νο1 ΒΑΣΙΚΑ ΒΗΜΑΤΑ ΕΡΩΤΗΜΑΤΑ Είναι η επένδυση συμφέρουσα; Ποιός είναι ο πραγματικός χρόνος αποπληρωμής της επένδυσης; Κατά πόσο επηρεάζεται
ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗ ΔΙΟΙΚΗΣΗ ΑΣΚΗΣΕΙΣ-ΠΡΑΞΕΙΣ Εισαγωγική εισήγηση Νο1 ΒΑΣΙΚΑ ΒΗΜΑΤΑ ΕΡΩΤΗΜΑΤΑ Είναι η επένδυση συμφέρουσα; Ποιός είναι ο πραγματικός χρόνος αποπληρωμής της επένδυσης; Κατά πόσο επηρεάζεται
( p) (1) (2) ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΟΡΓΑΝΩΣΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ. Α.Α.Δράκος
 ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΟΡΓΑΝΩΣΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΣΗΜΕΙΩΣΕΙΣ ΔΙΔΑΣΚΟΝΤΑ ΣΤΗ ΧΡΗΜΑΤΟΔΟΤΙΚΗ ΔΙΟΙΚΗΣΗ Δράκος 4-5 4.) ΠΛΗΘΩΡΙΣΜΟΣ ΚΑΙ ΚΙΝΔΥΝΟΣ ΣΤΗΝ ΑΞΙΟΛΟΓΗΣΗ ΕΠΕΝΔΥΣΕΩΝ 4.. ΑΞΙΟΛΟΓΗΣΗ
ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΟΡΓΑΝΩΣΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΣΗΜΕΙΩΣΕΙΣ ΔΙΔΑΣΚΟΝΤΑ ΣΤΗ ΧΡΗΜΑΤΟΔΟΤΙΚΗ ΔΙΟΙΚΗΣΗ Δράκος 4-5 4.) ΠΛΗΘΩΡΙΣΜΟΣ ΚΑΙ ΚΙΝΔΥΝΟΣ ΣΤΗΝ ΑΞΙΟΛΟΓΗΣΗ ΕΠΕΝΔΥΣΕΩΝ 4.. ΑΞΙΟΛΟΓΗΣΗ
Μέθοδοι Αξιολόγησης Επενδύσεων:
 TΕΙ ΚΡΗΤΗΣ ΣΧΟΛΗ ΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ ΠΑΡΑ ΟΣΕΙΣ V. Βασικές Μέθοδοι Αξιολόγησης Επενδύσεων. ιδάσκων, Μακρυγιωργάκης Μάριος BSc, ΜΒΑ, MSc, PhD-c. Μέθοδοι Αξιολόγησης Επενδύσεων: Οι επενδυτικές αποφάσεις
TΕΙ ΚΡΗΤΗΣ ΣΧΟΛΗ ΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ ΠΑΡΑ ΟΣΕΙΣ V. Βασικές Μέθοδοι Αξιολόγησης Επενδύσεων. ιδάσκων, Μακρυγιωργάκης Μάριος BSc, ΜΒΑ, MSc, PhD-c. Μέθοδοι Αξιολόγησης Επενδύσεων: Οι επενδυτικές αποφάσεις
ΚΙΝΗΤΙΚΗ ΑΛΥΣΩΤΩΝ ΑΝΤΙΔΡΑΣΕΩΝ ΠΟΛΥΜΕΡΙΣΜΟΥ ΚΑΙ ΜΟΡΙΑΚΗ ΚΑΤΑΝΟΜΗ ΤΩΝ ΛΑΜΒΑΝΟΜΕΝΩΝ ΠΡΟΪΟΝΤΩΝ
 ΚΙΝΗΤΙΚΗ ΑΛΥΣΩΤΩΝ ΑΝΤΙΔΡΑΣΕΩΝ ΠΟΛΥΜΕΡΙΣΜΟΥ ΚΑΙ ΜΟΡΙΑΚΗ ΚΑΤΑΝΟΜΗ ΤΩΝ ΛΑΜΒΑΝΟΜΕΝΩΝ ΠΡΟΪΟΝΤΩΝ Η ρόοδος ης ανίδρασης μορί να υολογισί: Τιλοδόηση διλών δσμών Μαβολή ου όγκου ου μέσου ης ανίδρασης Μέρηση ης
ΚΙΝΗΤΙΚΗ ΑΛΥΣΩΤΩΝ ΑΝΤΙΔΡΑΣΕΩΝ ΠΟΛΥΜΕΡΙΣΜΟΥ ΚΑΙ ΜΟΡΙΑΚΗ ΚΑΤΑΝΟΜΗ ΤΩΝ ΛΑΜΒΑΝΟΜΕΝΩΝ ΠΡΟΪΟΝΤΩΝ Η ρόοδος ης ανίδρασης μορί να υολογισί: Τιλοδόηση διλών δσμών Μαβολή ου όγκου ου μέσου ης ανίδρασης Μέρηση ης
ΕΠΙΧΕΙΡΗΜΑΤΙΚΟΤΗΤΑ ΚΑΙ ΚΑΙΝΟΤΟΜΙΑ. ΚΥΡΙΑΚΗ ΚΟΣΜΙΔΟΥ ΑΝΑΠΛΗΡΩΤΡΙΑ ΚΑΘΗΓΗΤΡΙΑ
 ΕΠΙΧΕΙΡΗΜΑΤΙΚΟΤΗΤΑ ΚΑΙ ΚΑΙΝΟΤΟΜΙΑ ΑΞΙΟΛΟΓΗΣΗ ΕΠΕΝΔΥΤΙΚΩΝ ΠΡΟΓΡΑΜΜΑΤΩΝ ΚΥΡΙΑΚΗ ΚΟΣΜΙΔΟΥ ΑΝΑΠΛΗΡΩΤΡΙΑ ΚΑΘΗΓΗΤΡΙΑ kosmid@econ.auth.gr ΣΗΜΕΙΩςΕΙς ΑΠΟ ΤΟ ΒΙΒΛΙΟ: ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗ ΔΙΟΙΚΗςΗ ΘΕΩΡΙΑ ΚΑΙ ΠΡΑΚΤΙΚΗ,
ΕΠΙΧΕΙΡΗΜΑΤΙΚΟΤΗΤΑ ΚΑΙ ΚΑΙΝΟΤΟΜΙΑ ΑΞΙΟΛΟΓΗΣΗ ΕΠΕΝΔΥΤΙΚΩΝ ΠΡΟΓΡΑΜΜΑΤΩΝ ΚΥΡΙΑΚΗ ΚΟΣΜΙΔΟΥ ΑΝΑΠΛΗΡΩΤΡΙΑ ΚΑΘΗΓΗΤΡΙΑ kosmid@econ.auth.gr ΣΗΜΕΙΩςΕΙς ΑΠΟ ΤΟ ΒΙΒΛΙΟ: ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗ ΔΙΟΙΚΗςΗ ΘΕΩΡΙΑ ΚΑΙ ΠΡΑΚΤΙΚΗ,
3. ΦΑΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ ΣΗΜΑΤΩΝ (ΑΝΑΛΥΣΗ FOURIER)
 3. ΦΑΣΜΑΙΚΗ ΑΝΑΛΥΣΗ ΣΗΜΑΩΝ (ΑΝΑΛΥΣΗ FOURIER) 3.. Γενικά Ένα σήμα μπορεί να αναπαρασαθεί με έναν από ους παρακάω ισοδύναμους ρόπους: Ως χρονικά μεαβαλλόμενη άση (κυμαομορφή) x(t) (αναπαράσαση σο πεδίο ου
3. ΦΑΣΜΑΙΚΗ ΑΝΑΛΥΣΗ ΣΗΜΑΩΝ (ΑΝΑΛΥΣΗ FOURIER) 3.. Γενικά Ένα σήμα μπορεί να αναπαρασαθεί με έναν από ους παρακάω ισοδύναμους ρόπους: Ως χρονικά μεαβαλλόμενη άση (κυμαομορφή) x(t) (αναπαράσαση σο πεδίο ου
Slide 8.1. ΤΕΙ Πειραιά Μεταπτυχιακό Πρόγραμμα Λογιστική και Χρηματοοικονομική. Δευτέρα 27 Ιανουαρίου & Τετάρτη 29 Ιανουαρίου
 Slide 8.1 ΤΕΙ Πειραιά Μεταπτυχιακό Πρόγραμμα Λογιστική και Χρηματοοικονομική Δευτέρα 27 Ιανουαρίου & Τετάρτη 29 Ιανουαρίου Slide 8.2 Η μέθοδος λήψης αποφάσεων για αξιολόγηση επενδυτικών πλάνων Μετά το
Slide 8.1 ΤΕΙ Πειραιά Μεταπτυχιακό Πρόγραμμα Λογιστική και Χρηματοοικονομική Δευτέρα 27 Ιανουαρίου & Τετάρτη 29 Ιανουαρίου Slide 8.2 Η μέθοδος λήψης αποφάσεων για αξιολόγηση επενδυτικών πλάνων Μετά το
Μεταλλική συμπεριφορά
 Μεαλλική συμπεριφορά Χαρακηρισικά μεαλλικής συμπεριφοράς Μεγάλη θερμική και ηλεκρονιακή αγωγιμόηα Μεγάλο μέρο ελασικόηας όγκου (Β=10 11 Pa) Μεαλλική λάμψη Ι. Μονέλο Drude (Jelliu) Σύμβαση προσήμου: e:
Μεαλλική συμπεριφορά Χαρακηρισικά μεαλλικής συμπεριφοράς Μεγάλη θερμική και ηλεκρονιακή αγωγιμόηα Μεγάλο μέρο ελασικόηας όγκου (Β=10 11 Pa) Μεαλλική λάμψη Ι. Μονέλο Drude (Jelliu) Σύμβαση προσήμου: e:
? Συμπεριφορά ψαθυρών υλικών 11/6/2018. Δρ. Σωτήρης Δέμης. Σημειώσεις Εργαστηριακής Άσκησης Κριτήρια Αστοχίας Διάτμηση Τοιχοποιίας
 11/6/018 Σημειώεις Εργαηριακής Άκηης Κριήρια Αοχίας Διάμηη Τοιχοποιίας Δρ. Σωήρης Δέμης Πολιικός Μηχανικός (Πανεπιημιακός Υπόροφος) Έως ώρα Καααικός νόμος όλκιμων υλικών (αξονική κααπόνιη ε μία διεύθυνη)
11/6/018 Σημειώεις Εργαηριακής Άκηης Κριήρια Αοχίας Διάμηη Τοιχοποιίας Δρ. Σωήρης Δέμης Πολιικός Μηχανικός (Πανεπιημιακός Υπόροφος) Έως ώρα Καααικός νόμος όλκιμων υλικών (αξονική κααπόνιη ε μία διεύθυνη)
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΠΕΡΙΛΗΨΗ ΣΥΜΒΟΛΙΣΜΩΝ NOTATION ΓΙΑ ΙΑΝΥΣΜΑΤΑ ΚΑΙ ΤΑΝΥΣΤΕΣ -Bd, Steat and Lghtfoot "Tanpot Phenomena" -Bd, Amtong and Haage
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΠΕΡΙΛΗΨΗ ΣΥΜΒΟΛΙΣΜΩΝ NOTATION ΓΙΑ ΙΑΝΥΣΜΑΤΑ ΚΑΙ ΤΑΝΥΣΤΕΣ -Bd, Steat and Lghtfoot "Tanpot Phenomena" -Bd, Amtong and Haage
Πανεπιστήμιο Πειραιώς Τμήμα Πληροφορικής Πρόγραμμα Μεταπτυχιακών Σπουδών «Πληροφορική»
 Πανεπισήμιο Πειραιώς Τμήμα Πληροφορικής Πρόγραμμα Μεαπυχιακών Σπουδών «Πληροφορική» Μεαπυχιακή Διαριβή Τίλος Διαριβής Αλγόριθμοι Αποικίας Μυρμηγκιών Ονομαεπώνυμο Φοιηή Φρανζέσκος Νομικός Παρώνυμο Γεώργιος
Πανεπισήμιο Πειραιώς Τμήμα Πληροφορικής Πρόγραμμα Μεαπυχιακών Σπουδών «Πληροφορική» Μεαπυχιακή Διαριβή Τίλος Διαριβής Αλγόριθμοι Αποικίας Μυρμηγκιών Ονομαεπώνυμο Φοιηή Φρανζέσκος Νομικός Παρώνυμο Γεώργιος
Αξιολόγηση Επενδύσεων. Διάλεξη 3 Μέθοδοι Αξιολόγησης Επενδύσεων Δράκος και Καραθανάσης, Κεφ 3 και Κεφ 4
 Αξιολόγηση Επενδύσεων Διάλεξη 3 Μέθοδοι Αξιολόγησης Επενδύσεων Δράκος και Καραθανάσης, Κεφ 3 και Κεφ 4 1 Περίγραμμα Διάλεξης Η Καθαρή Παρούσα Αξία (ΚΠΑ) Ο Εσωτερικός Βαθμός Απόδοσης (ΕΒΑ) Ο Χρόνος Επανείσπραξης
Αξιολόγηση Επενδύσεων Διάλεξη 3 Μέθοδοι Αξιολόγησης Επενδύσεων Δράκος και Καραθανάσης, Κεφ 3 και Κεφ 4 1 Περίγραμμα Διάλεξης Η Καθαρή Παρούσα Αξία (ΚΠΑ) Ο Εσωτερικός Βαθμός Απόδοσης (ΕΒΑ) Ο Χρόνος Επανείσπραξης
TO MONTEΛΟ ΤΗΕ ΕΡΠΙΣΗΣ (Reptation Model)
 TO MOTEΛΟ ΤΗΕ ΕΡΠΙΣΗΣ (epttion Moel) Η έννοια ου σωλήνα (tube) σις περιελίξεις (entglements). Αλληλεπιδράσεις-interpenetrtion Τοπολογικοί περιορισμοί (σην lterl/κάθεη κίνηση) Tube moel [e Gennes ; Ewrs
TO MOTEΛΟ ΤΗΕ ΕΡΠΙΣΗΣ (epttion Moel) Η έννοια ου σωλήνα (tube) σις περιελίξεις (entglements). Αλληλεπιδράσεις-interpenetrtion Τοπολογικοί περιορισμοί (σην lterl/κάθεη κίνηση) Tube moel [e Gennes ; Ewrs
ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΟΡΓΑΝΩΣΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ. Α.Α.Δράκος 2014-2015
 ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΟΡΓΑΝΩΣΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΣΗΜΕΙΩΣΕΙΣ ΔΙΔΑΣΚΟΝΤΑ ΣΤΗ ΧΡΗΜΑΤΟΔΟΤΙΚΗ ΔΙΟΙΚΗΣΗ 1 3.) ΑΝΑΛΥΣΗ ΚΑΘΑΡΩΝ ΤΑΜΕΙΑΚΩΝ ΡΟΩΝ Α.Α.Δράκος 2014-2015 Α. Εισαγωγικά Oι Καθαρές
ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΟΡΓΑΝΩΣΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΣΗΜΕΙΩΣΕΙΣ ΔΙΔΑΣΚΟΝΤΑ ΣΤΗ ΧΡΗΜΑΤΟΔΟΤΙΚΗ ΔΙΟΙΚΗΣΗ 1 3.) ΑΝΑΛΥΣΗ ΚΑΘΑΡΩΝ ΤΑΜΕΙΑΚΩΝ ΡΟΩΝ Α.Α.Δράκος 2014-2015 Α. Εισαγωγικά Oι Καθαρές
Αριθμητικά Μοντέλα Επιλογής Έργων
 Αριθμητικά Μοντέλα Επιλογής Έργων Διακρίνονται σε χρηματοοικονομικά μοντέλα και σε μοντέλα βαθμολόγησης. Τα χρηματοοικονομικά μοντέλα είναι: Περίοδος αποπληρωμής επενδεδυμένων κεφαλαίων (Payback Period)
Αριθμητικά Μοντέλα Επιλογής Έργων Διακρίνονται σε χρηματοοικονομικά μοντέλα και σε μοντέλα βαθμολόγησης. Τα χρηματοοικονομικά μοντέλα είναι: Περίοδος αποπληρωμής επενδεδυμένων κεφαλαίων (Payback Period)
ΕΙΣΑΓΩΓΗ Γενικότερος σκοπός του Προγράμματος NETCASTLE
 Τ οδι ασυν ορι ακ όπρογ ραμμαi P A ηςε υρωπαϊ κ ήςέν σωης-ε λ λ άδας Αλ βαν ί ας-20072013 γ ι α ην Αλ βαν ί α Τ Ε ΛΙ ΚΗΕ ΚΘΕ ΣΗ Προόδουκ αι Αξ ι ολ όγ ησης ουπρογ ράμμα ος NET CAS T L E γ ι α ην Αλ βαν
Τ οδι ασυν ορι ακ όπρογ ραμμαi P A ηςε υρωπαϊ κ ήςέν σωης-ε λ λ άδας Αλ βαν ί ας-20072013 γ ι α ην Αλ βαν ί α Τ Ε ΛΙ ΚΗΕ ΚΘΕ ΣΗ Προόδουκ αι Αξ ι ολ όγ ησης ουπρογ ράμμα ος NET CAS T L E γ ι α ην Αλ βαν
Ο Ι ΚΟ Ν Ο Μ Ι Κ Α / Σ ΤΑΤ Ι Σ Τ Ι Κ Η
 Ο Ι ΚΟ Ν Ο Μ Ι Κ Α / Σ ΤΑΤ Ι Σ Τ Ι Κ Η Σ χ ε τ ι κ ά μ ε τ ι ς ε κ τ ι μ ή σ ε ι ς - σ υ ν ο π τ ι κ ά Σεμινάριο Εκτιμήσεων Ακίνητης Περιουσίας, ΣΠΜΕ, 2018 ΣΤΑΤΙΣΤΙΚΗ Σ Χ Ε Τ Ι Κ Α Μ Ε Τ Ι Σ Ε Κ Τ Ι Μ
Ο Ι ΚΟ Ν Ο Μ Ι Κ Α / Σ ΤΑΤ Ι Σ Τ Ι Κ Η Σ χ ε τ ι κ ά μ ε τ ι ς ε κ τ ι μ ή σ ε ι ς - σ υ ν ο π τ ι κ ά Σεμινάριο Εκτιμήσεων Ακίνητης Περιουσίας, ΣΠΜΕ, 2018 ΣΤΑΤΙΣΤΙΚΗ Σ Χ Ε Τ Ι Κ Α Μ Ε Τ Ι Σ Ε Κ Τ Ι Μ
Βασικές έννοιες για αξία χρήματος και επενδύσεις. Δρ. Αθανάσιος Δαγούμας, Λέκτορας Οικονομικής της Ενέργειας & των Φυσικών Πόρων, Παν.
 Βασικές έννοιες για αξία χρήματος και επενδύσεις Δρ. Αθανάσιος Δαγούμας, Λέκτορας Οικονομικής της Ενέργειας & των Φυσικών Πόρων, Παν. Πειραιώς Βασικοί Ορισμοί Διαχρονική Αξία Χρήματος Το χρήµα έχει δύο
Βασικές έννοιες για αξία χρήματος και επενδύσεις Δρ. Αθανάσιος Δαγούμας, Λέκτορας Οικονομικής της Ενέργειας & των Φυσικών Πόρων, Παν. Πειραιώς Βασικοί Ορισμοί Διαχρονική Αξία Χρήματος Το χρήµα έχει δύο
ΟΙΚΟΝΟΜΙΚΗ ΑΞΙΟΛΟΓΗΣΗ ΟΔΙΚΩΝ ΕΡΓΩΝ
 ΟΙΚΟΝΟΜΙΚΗ ΑΞΙΟΛΟΓΗΣΗ ΟΔΙΚΩΝ ΕΡΓΩΝ ΠΑΡΑΔΕΙΓΜΑΤΑ ΠΑΡΑΔΕΙΓΜΑ 1 Η υπάρχουσα οδική σύνδεση μεταξύ δύο πόλεων έχει κατασκευαστεί πριν πολλά χρόνια και παρουσιάζει σήμερα αυξημένο κόστος συντήρησης καθώς και
ΟΙΚΟΝΟΜΙΚΗ ΑΞΙΟΛΟΓΗΣΗ ΟΔΙΚΩΝ ΕΡΓΩΝ ΠΑΡΑΔΕΙΓΜΑΤΑ ΠΑΡΑΔΕΙΓΜΑ 1 Η υπάρχουσα οδική σύνδεση μεταξύ δύο πόλεων έχει κατασκευαστεί πριν πολλά χρόνια και παρουσιάζει σήμερα αυξημένο κόστος συντήρησης καθώς και
ΚΕΦΑΛΑΙΟ IΙΙ: TAΣΕΙΣ ΣΤΟ Ε ΑΦΟΣ. 1. Τάσεις σε συνεχή μέσα (ε πανάληψη) 2. Τάσεις σε α-συνεχή. μέσα. 3. Ενεργός και Ολική τάση
 ΚΕΦΑΛΑΙΟ IΙΙ: 3. Ενεργός και Ολική άη TAΣΕΙΣ ΣΤΟ Ε ΑΦΟΣ. Τάεις ε υνεχή μέα (ε πανάληψη). Τάεις ε α-υνεχή μέα 4. Γεωαικές άεις (λόγω ιδίου βάρους) 5. Τάεις λόγω εξωερικών φορίων Θεωρία Ελαικόηας Καανομή
ΚΕΦΑΛΑΙΟ IΙΙ: 3. Ενεργός και Ολική άη TAΣΕΙΣ ΣΤΟ Ε ΑΦΟΣ. Τάεις ε υνεχή μέα (ε πανάληψη). Τάεις ε α-υνεχή μέα 4. Γεωαικές άεις (λόγω ιδίου βάρους) 5. Τάεις λόγω εξωερικών φορίων Θεωρία Ελαικόηας Καανομή
Αξιολόγηση Επενδυτικών Σχεδίων
 Αξιολόγηση Επενδυτικών Σχεδίων Ενότητα 2: Πίνακας Ταμειακών Ροών Δ. Δαμίγος Μ. Μενεγάκη Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως
Αξιολόγηση Επενδυτικών Σχεδίων Ενότητα 2: Πίνακας Ταμειακών Ροών Δ. Δαμίγος Μ. Μενεγάκη Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως
Μεταπτυχιακό Πρόγραμμα Σπουδών του Παν. Πειραιώς ΕΝΕΡΓΕΙΑ: Στρατηγική, Δίκαιο & Οικονομία
 Μεταπτυχιακό Πρόγραμμα Σπουδών του Παν. Πειραιώς ΕΝΕΡΓΕΙΑ: Στρατηγική, Δίκαιο & Οικονομία Μεταπτυχιακό Μάθημα: Χρηματοδότηση Ενεργειακών Επενδύσεων & Διαχείριση Κινδύνου Δρ. Αθανάσιος Δαγούμας, Λέκτορας
Μεταπτυχιακό Πρόγραμμα Σπουδών του Παν. Πειραιώς ΕΝΕΡΓΕΙΑ: Στρατηγική, Δίκαιο & Οικονομία Μεταπτυχιακό Μάθημα: Χρηματοδότηση Ενεργειακών Επενδύσεων & Διαχείριση Κινδύνου Δρ. Αθανάσιος Δαγούμας, Λέκτορας
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΑΞΙΟΛΟΓΗΣΗΣ ΕΠΕΝ ΥΣΕΩΝ. Περιεχόµενα
 ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΑΞΙΟΛΟΓΗΣΗΣ ΕΠΕΝ ΥΣΕΩΝ Περιεχόµενα Επενδύσεις Η έννοια της επένδυσης Φάσεις ολοκλήρωσης µίας επένδυσης Επιπτώσεις από την προώθηση µίας επένδυσης Αξιολόγηση επενδύσεων υσκολίες ιδιωτικο-οικονοµικής
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΑΞΙΟΛΟΓΗΣΗΣ ΕΠΕΝ ΥΣΕΩΝ Περιεχόµενα Επενδύσεις Η έννοια της επένδυσης Φάσεις ολοκλήρωσης µίας επένδυσης Επιπτώσεις από την προώθηση µίας επένδυσης Αξιολόγηση επενδύσεων υσκολίες ιδιωτικο-οικονοµικής
