Συνδυαστική Βελτιστοποίηση
|
|
|
- Θεοφάνης Γούσιος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 1 Άγγελος Σιφαλέρας sifalera@uom.gr 3 η Διάλεξη
2 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 2 Εφαρμογή Ακεραίου Προγραμματισμού (1/4) Project Selection Έστω ότι αξιολογούνται 5 προτάσεις επενδυτικών έργων σε ένα πλάνο 3-ετούς προγραμματισμού. Ο παρακάτω πίνακας δίνει τα αναμενόμενα έσοδα, καθώς και τα αντίστοιχα ετήσια έξοδα που προκύπτουν από κάθε έργο: Έξοδα (εκ. ) έτος Έργο 1 ο έτος 2 ο έτος 3 ο έτος Αναμενόμενα έσοδα Διαθέσιμο κεφάλαιο (εκ. )
3 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 3 Εφαρμογή Ακεραίου Προγραμματισμού (2/4) Project Selection a) Να διαμορφώσετε ένα μαθηματικό μοντέλο ακεραίου προγραμματισμού για να σας βοηθήσει να επιλέξετε ποιά προγράμματα θα έπρεπε να επιλεχθούν προς υλοποίηση αυτήν την 3-ετία. b) Τι αλλάζει στο μοντέλο, εάν πρέπει το 5 ο έργο να επιλέγεται οπωσδήποτε όταν επιλέγεται είτε το 1 ο έργο είτε το 3 ο έργο? c) Τι αλλάζει στο μοντέλο, εάν τα έργα 2 και 3 δεν μπορούν ταυτόχρονα να επιλεχθούν?
4 Εφαρμογή Ακεραίου Προγραμματισμού (3/4) Project Selection a) ma z = st (περιορισμοί διαθέσιμου κεφαλαίου 1ου έτους) j (περιορισμοί διαθέσιμου κεφαλαίου 2ου έτους) (περιορισμοί διαθέσιμου κεφαλαίου 3ου έτους) 1, εάν το έργο j επιλεχθεί = j = , αλλιώς b) c) Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 4
5 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 5 Εφαρμογή Ακεραίου Προγραμματισμού (4/4) Project Selection # # Project Selection Problem # # variables var 1 binary; # 1st type of project var 2 binary; # 2nd type of project var 3 binary; # 3rd type of project var 4 binary; # 4th type of project var 5 binary; # 5th type of project # objective function maimize profit: 20*1 + 40*2 + 20*3 + 15*4 + 30*5; # constraints s.t. Year_1: 5*1 + 4*2 + 3*3 + 7*4 + 8*5 <= 25; s.t. Year_2: 1 + 7*2 + 9*3 + 4*4 + 6*5 <= 25; s.t. Year_3: 8*1 + 10*2 + 2* *5 <= 25;
6 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 6 Set Covering Problem, (1/6) Σε αυτήν την κατηγορία προβλημάτων, αντιμετωπίζουμε την ενδεχόμενη επικάλυψη υπηρεσιών οι οποίες είναι δυνατόν να προσφέρονται από έναν αριθμό εγκαταστάσεων σε έναν αριθμό περιοχών. Ο σκοπός είναι να προσδιορίσουμε τον ελάχιστο αριθμό εγκαταστάσεων οι οποίες θα καλύπτουν (δηλαδή θα ικανοποιούν τις ανάγκες) σε κάθε περιοχή. Για παράδειγμα υδραγωγεία μπορούν να κατασκευαστούν σε διάφορες τοποθεσίες, όπου το κάθε υδραγωγείο εξυπηρετεί διαφορετικό σύνολο περιοχών. Επικάλυψη προκύπτει όταν μια περιοχή μπορεί να εξυπηρετηθεί από περισσότερα του ενός υδραγωγεία.
7 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 7 Set Covering Problem: παράδειγμα (2/6) Έστω ότι το Α.Π.Θ. στην προσπάθεια του να αυξήσει το επίπεδο ασφάλειας μέσα στους χώρους του, προτίθεται να εγκαταστήσει έναν ελάχιστο αριθμό τηλεφωνικών συσκευών έτσι ώστε κάθε ένας από τους κύριους δρόμους των χώρων του Α.Π.Θ. να εξυπηρετείται από τουλάχιστον μια τηλεφωνική συσκευή. Έστω ότι ο χάρτης με τους κύριους δρόμους του Α.Π.Θ. είναι ο εξής: Οδός Α Οδός Β Οδός G Οδός F Οδός E Οδός H Οδός I Οδός C Οδός D Οδός J Οδός K
8 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 8 Set Covering Problem: παράδειγμα (3/6) Μας συμφέρει να τοποθετήσουμε τις τηλεφωνικές συσκευές στις γωνίες των δρόμων, ούτως ώστε η κάθε τηλεφωνική συσκευή να εξυπηρετεί τουλάχιστον δύο δρόμους. Επομένως, η διάταξη των δρόμων απαιτεί το πολύ 8 τηλεφωνικές συσκευές. 1 Οδός Α 2 Οδός Β 3 Οδός G Οδός F Οδός E Οδός H Οδός I 4 Οδός C Οδός D Οδός J Οδός K
9 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 9 Set Covering Problem: παράδειγμα (4/6) Μαθηματική μοντελοποίηση προβλήματος: Μεταβλητές απόφασης: j 1, εάν το τηλέφωνο τοποθετηθεί στην περιοχή = 0, αλλιώς j
10 Set Covering Problem: παράδειγμα (5/6) min z = (Οδός Α) + 1 (Οδός B) (Οδός C) j (Οδός D) (Οδός E) + 1 (Οδός F) + 1 (Οδός G) + 1 (Οδός H) + 1 (Οδός I) (Οδός J) + 1 (Οδός K) = (0,1), j = Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 10
11 Set Covering Problem: παράδειγμα (6/6) param n; #maimum number of corners set street; set corner{street}; var {1..n}binary; minimize z: sum {j in 1..n} [j]; subject to limit {i in street}: sum {j in corner[i]} [j]>=1; data; param n:=8; set street:=a B C D E F G H I J K; set corner[a]:=; set corner[b]:=2 3; set corner[c]:=4 5; set corner[d]:=7 8; set corner[e]:=6 7; set corner[f]:=2 6; set corner[g]:=1 6; set corner[h]:=4 7; set corner[i]:=2 4; set corner[j]:=5 8; set corner[k]:=3 5; option solver cple; solve; display z,; ampl: model Set_Covering.mod; CPLEX : optimal integer solution; objective 4 8 MIP simple iterations 0 branch-and-bound nodes z = 4 [*] := ; ampl: Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 11
12 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 12 Ακέραιος Προγραμματισμός & δυϊκές τιμές Σε μαθηματικά μοντέλα α.π. δεν μπορούμε εύκολα να ερμηνεύσουμε τις δυϊκές τιμές του προβλήματος. Εξαιτίας της διακριτής φύσης των π.α.π. οι δυϊκές τιμές που προκύπτουν στη βέλτιστη λύση ενός π.α.π., δεν μπορούν να χρησιμοποιηθούν εύκολα στην πράξη. Οπότε, όταν συναντούμε δυϊκές τιμές στην αναφορά επίλυσης ενός λογισμικού (π.χ. Lingo), οι οποίες αντιστοιχούν σε ακέραιες μεταβλητές, τότε πρέπει να τις αγνοήσουμε.
13 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 13 Αλγόριθμοι ακεραίου προγραμματισμού Μέθοδοι κλάδου και φραγής Στις μεθόδους αυτές η λύση στο πρόβλημα του ακεραίου ή μικτού ακεραίου προγραμματισμού έρχεται μετά από τη λύση μιας σειράς προβλημάτων γραμμικού προγραμματισμού που σχηματίζουν ένα δένδρο με κλαδιά. Τεχνικές περιορισμού του εφικτού χώρου Οι αλγόριθμοι περιορισμού του εφικτού χώρου στοχεύουν στη δημιουργία συμπληρωματικών ανισοτήτων, οι οποίες θα περιορίσουν το χώρο των εφικτών λύσεων, έτσι ώστε το γραμμικό πρόβλημα να έχει λύση με ακέραιες τις μεταβλητές εκείνες που απαιτεί το μικτό πρόβλημα ακεραίου προγραμματισμού ή απλώς το ακέραιο. Μέθοδοι απαρίθμησης Διαμεριστικοί αλγόριθμοι Αλγόριθμοι βασισμένοι στη θεωρία ομάδων
14 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 14 Αλγόριθμος κλάδου και φραγής, (1/10) Branch & Bound Algorithm (BBΑ) Μια ιστορική αναδρομή A.H. Land & A.G. Doig (1960). An automatic method of solving discrete programming problems, Econometrica, 28(3), G.J Li & B.W Wah (1984). Computational efficiency of parallel approimate branch-and-bound algorithms, in Proceedings of the International Conference on Parallel Processing, pp E.L Lawler & D.W Wood (1986). Branch-and-bound methods: A survey, Operations Research, 14,
15 Αλγόριθμος κλάδου και φραγής, (2/10) Branch & Bound Algorithm (BBΑ) Εφαρμογή στο π.α.π.: ma z = st , ακέραιοι CPLEX : optimal integer solution; objective 50 2 MIP simple iterations 0 branch-and-bound nodes ampl: display 1,2; 1 = 3 2 = 4 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 15
16 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 16 Αλγόριθμος κλάδου και φραγής, (3/10) Branch & Bound Algorithm (BBΑ) Γραφική επίλυση α.π.
17 Αλγόριθμος κλάδου και φραγής, (4/10) Branch & Bound Algorithm (BBΑ) Αντίστοιχο γραμμικό πρόβλημα χαλάρωσης: ma z = st , 0 CPLEX : optimal solution; objective dual simple iterations (1 in phase I) ampl: display 1,2; 1 = = 2.5 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 17
18 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 18 Αλγόριθμος κλάδου και φραγής, (5/10) Branch & Bound Algorithm (BBΑ) Γραφική επίλυση γ.π. χαλάρωσης
19 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 19 ma z = st , 0 Αλγόριθμος κλάδου και φραγής, (6/10) Branch & Bound Algorithm (BBΑ) ma z = st , 0 ma z = st , 0
20 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 20 Αλγόριθμος κλάδου και φραγής, (7/10) Branch & Bound Algorithm (BBΑ) Γραφική επίλυση 3 ου υπό-προβλήματος Γραφική επίλυση 2 ου υπό-προβλήματος
21 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 21 ma z = st , 0 ma z = st , 0 Αλγόριθμος κλάδου και φραγής, (8/10) Branch & Bound Algorithm (BBΑ) ma z = st , 0 ma z = st , 2 0 ma z = st , 0
22 ma z = st , 0 ma z = st , 0 ma z = st , 0 Αλγόριθμος κλάδου και φραγής, (9/10) Branch & Bound Algorithm (BBΑ) ma z = st , 0 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 22 ma z = st , 2 0 ma z = st , 0 ma z = st , 0
23 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 23 Αλγόριθμος κλάδου και φραγής, (10/10) Branch & Bound Algorithm (BBΑ) Αρχικά λύνουμε το αντίστοιχο γ.π. χαλάρωσης του α.π. ή μικτού γ.α.π. Αν το πρόβλημα χαλάρωσης, μας δίνει ακέραιες λύσεις, τότε αυτή είναι και η λύση του α.π. Σε κάθε περίπτωση, η τιμή της αντικειμενικής συνάρτησης στη λύση του γ.π. χαλάρωσης, αποτελεί ένα άνω φράγμα για την τιμή της αντικειμενικής συνάρτησης για το α.π. ή μικτό γ.α.π., όταν έχουμε πρόβλημα μεγιστοποίησης. Κατά ανάλογο τρόπο, αποτελεί ένα κάτω φράγμα, όταν έχουμε πρόβλημα ελαχιστοποίησης. Εξετάζουμε τις λύσεις του γ.π. χαλάρωσης για τις μεταβλητές εκείνες οι οποίες δεν είναι ακέραιες ενώ αυτό απαιτείται. Επιλέγουμε εκείνη που έχει το μεγαλύτερο δεκαδικό μέρος. Αν υπάρχουν δύο ή περισσότερες τέτοιες επιλέγουμε αυθαίρετα μια από όλες. Σχηματίζουμε δύο κλαδιά (υπό-προβλήματα) με βάση αυτή τη μεταβλητή.
24 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 24 Μέθοδοι περιορισμού του εφικτού χώρου: cutting-plane method Κυρτό περίβλημα (conve hull) ενός συνόλου S από n σημεία είναι το ελάχιστο κυρτό πολύγωνο P τέτοιο ώστε κάθε ένα από τα n σημεία στο S βρίσκεται πάνω στο σύνορο του S ή στο εσωτερικό του S. Ralph E. Gomory, Outline of an Algorithm for Integer Solutions to Linear Programs, Bulletin of the American Mathematical Society, 64, , Cornuejols, Gerard, Revival of the Gomory Cuts in the 1990s, Annals of Operations Research, 149(1), 63-66, Cornuejols, Gerard, Valid inequalities for mied integer linear programs. Mathematical Programming, 112(1), 3-44, 2008.
25 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 25 Ιδέα: Εξέτασε όλες τις πιθανές τιμές των ακεραίων μεταβλητών (έστω π.χ., { 1,..., z }, όπου z n) και λύσε τα προβλήματα γραμμικής βελτιστοποίησης στις εναπομείναντες (συνεχείς) μεταβλητές: for 1 { 1, 1 + 1,..., 1 } do for 2 { 2, 2 + 1,..., 2 } do... for z { z, z + 1,..., z } do Solve LP in k +1,..., n with 1,..., k fied. Update tentative optimal solution if necessary. end for... end for end for Print (final) optimal solution or report infeasibility. Πολυπλοκότητα? Επίλυση MIP s: Πλήρη απαρίθμηση
26 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 26 Συλλογές μετρό-προβλημάτων (Benchmarks), (1/3) Η συλλογή MIPLIB 2010 διατίθεται δωρεάν από την ιστοσελίδα: Koch T., Achterberg T., Andersen E., Bastert O., Berthold T., Biby R., Danna E., Gamrath G., Gleiner A., Heinz S., Lodi A., Mittelmann H., Ralphs T., Salvagnin D., Steffy D., & Wolter K. (2011). MIPLIB 2010 Mied Integer Programming Library version 5. Mathematical Programming Computation, 3(2), (URL: Achterberg T., Koch T., & Martin A. (2006). MIPLIB 2003, Operations Research Letters, 34(4), (URL: Biby R., Ceria S., McZeal C., & Savelsbergh M. (1998). An updated mied integer programming library: MIPLIB 3.0. Optima, 58, Biby R., Boyd E., & Indovina R. (1992). MIPLIB: a test set of mied integer programming problems, SIAM News, 25(2), 16.
27 Συλλογές μετρό-προβλημάτων (Benchmarks), (2/3) Η νέα έκδοση αποτελείται από 361 στιγμιότυπα προβλημάτων ταξινομημένα σε διάφορες κατηγορίες. Η συλλογή περιέχει το κυρίως σύνολο προβλημάτων benchmark το οποίο περιλαμβάνει 87 στιγμιότυπα προβλημάτων, τα οποία είναι όλα επιλύσιμα από τους σημερινές υλοποιήσεις των αλγορίθμων, καθώς και ένα (challenge) σύνολο από 164 στιγμιότυπα προβλημάτων, πολλά από τα οποία ακόμη και στη σημερινή εποχή παραμένουν άλυτα. Πλήθος λυμένων προβλημάτων της συλλογής MIPLIB 2010 τα οποία είναι κατηγοριοποιημένα ως εύκολα, δύσκολα, ή άλυτα. «Εύκολο» σημαίνει ότι, το συγκεκριμένο πρόβλημα μπορεί να επιλυθεί μέσα σε μια ώρα χρησιμοποιώντας έναν εμπορικό λύτη προβλημάτων μ.π.α.π., «δύσκολο» σημαίνει ότι το πρόβλημα λύνεται μεν, αλλά απαιτείται περισσότερος υπολογιστικός χρόνος. Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 27
28 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 28 Συλλογές μετρό-προβλημάτων (Benchmarks), (3/3) Η συλλογή MIPLIB 2003 διατίθεται δωρεάν από την ιστοσελίδα: Σύγκριση του πλήθους των λυμένων προβλημάτων της συλλογής MIPLIB 2003 στην αρχή κάθε έτους.
29 Συλλογές μετρό-προβλημάτων για προβλήματα μικτούακεραίου μη γραμμικού προγραμματισμού Η συλλογή MINLPLib διατίθεται δωρεάν από την ιστοσελίδα: Bussieck, M.R., Drud, A.S. & Meeraus, A. (2003). MINLPLib - A collection of test models for mied-integer nonlinear programming, INFORMS Journal on Computing, 15(1), (URL: MINLPLib Model Statistics: Η συλλογή MINLPLib περιέχει και τη συλλογή MacMINLP: Leyffer, S. (2000). MacMINLP AMPL collection of mied integer nonlinear programs. Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 29
30 Συλλογές μετρό-προβλημάτων για προβλήματα ολικής βελτιστοποίησης (global optimization) Bussieck, M. (2004). Globallib a collection of nonlinear programming problems. Η βιβλιοθήκη Globallib αποτελεί μια συλλογή μοντέλων μη γραμμικού προγραμματισμού, σε γλώσσα GAMS. Μπορεί εύκολα να γίνει μετατροπή των προβλημάτων της Globallib από μορφή.gms σε.lp,.mps,.mod, κ.α. μέσω του παρακάτω εργαλείου: PAVER GAMS Model Translation Web Submission Tool (GMS2XX) Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 30
31 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 31 Συλλογές μετρό-προβλημάτων για σχεδίαση δικτύων τηλεπικοινωνιών SNDlib 1.0 Survivable Network Design Library SNDlib is a library of test instances for Survivable fied telecommunication Network Design Orlowski S., Wessäly R., Pióro M., and Tomaszewski A. (2010). SNDlib 1.0 Survivable Network Design Library, Networks, 55(3), (URL: FAP web FAP web is a web-site devoted to Frequency Assignment Problems (FAPs) in wireless communication networks
32 Open Source λογισμικά πακέτα βελτιστοποίησης για Μικτό Ακέραιο Γραμμικό Προγραμματισμό GLPK (GNU Linear Programming Kit). Το πακέτο GLPK υποστηρίζει τη γλώσσα μοντελοποίησης GNU MathProg, η οποία αποτελεί υποσύνολο της γλώσσας μοντελοποίησης AMPL. Διατίθεται δωρεάν από την ιστοσελίδα: GLPK Lab for Windows. Σύνολο εργαλείων και βιβλιοθηκών, βασισμένο στο πακέτο GLPK. Επίσης, παρέχει και ένα γραφικό περιβάλλον επεξεργασίας κώδικα GNU MathProg. Διατίθεται δωρεάν από την ιστοσελίδα: GUSEK (GLPK Under Scite Etended Kit). Άλλο ένα σύνολο εργαλείων και βιβλιοθηκών, βασισμένο στο πακέτο GLPK. Επίσης, παρέχει και ένα γραφικό περιβάλλον επεξεργασίας κώδικα GNU MathProg. Διατίθεται δωρεάν από την ιστοσελίδα: lp_solve. Το πακέτο lp_solve (free με άδεια GNU lesser general public license) αποτελεί έναν λύτη προβλημάτων μικτού ακέραιου γραμμικού προγραμματισμού. Το πακέτο περιέχει και το γραφικό περιβάλλον επεξεργασίας κώδικα GNU MathProg με όνομα LPSolve IDE. Διατίθεται δωρεάν από την ιστοσελίδα: Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 32
33 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 33 Gurobi Optimizer State-of-the-Art Mathematical Programming Solver Παρουσίαση επίλυσης μετρό-προβλημάτων από τη συλλογή MIPLIB 2010, με τον λύτη Gurobi: 1 «εύκολο πρόβλημα»: 30_70_4.5_0.95_100 (12,526 γραμμές 10,976 στήλες, 46,640 μη μηδενικές τιμές παραμέτρων 10,975 δυαδικές μεταβλητές, και 1 συνεχή μεταβλητή). m = read("d:/lab_files/mps_eamples/30_70_4.5_0.95_100.mps") m.optimize()
34 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 34 30_70_4.5_0.95_100.mps
35 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 35 Χαρακτηριστικό παράδειγμα υπολογιστικής δυσκολίας Ακεραίου Προγραμματισμού (1/3) Αν και υπάρχουν εξαιρετικά αποτελεσματικοί λύτες προβλημάτων γραμμικής βελτιστοποίησης, η επίλυση προβλημάτων ακέραιης βελτιστοποίησης μπορεί να είναι ιδιαίτερα δύσκολη πρόκληση, ακόμη και για ορισμένα προβλήματα μικρής διάστασης. Για παράδειγμα, το παρακάτω πρόβλημα (unbounded knapsack problem), δεν είναι δυνατόν να λυθεί ούτε και μετά από ώρες υπολογισμού, χρησιμοποιώντας ακόμη και την πρόσφατη έκδοση του state-of-the-art λύτη Gurobi: min z = = i Ν, i = 1..5 Karen Aardal and Arjen K. Lenstra (2004) Hard equality constrained integer knapsacks, Mathematics of Operations Research, 29(3), (URL:
36 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 36 Χαρακτηριστικό παράδειγμα υπολογιστικής δυσκολίας Ακεραίου Προγραμματισμού (2/3) #--- Variables --- var 1 integer >= 0; var 2 integer >= 0; var 3 integer >= 0; var 4 integer >= 0; var 5 integer >= 0; #--- Objective function --- minimize cost: 213*1-1928* *3-2345*4-9123*5; #--- Constraints --- s.t. C1: 12223* * * * *5 = ; model Hard_IP_1.mod; option solver gurobi_ampl; solve; display 1, 2, 3, 4, 5;
37 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 37 Χαρακτηριστικό παράδειγμα υπολογιστικής δυσκολίας Ακεραίου Προγραμματισμού (3/3)
ΣΥΝΔΥΑΣΤΙΚΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ
 Ενότητα 3 Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύπου άδειας
Ενότητα 3 Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύπου άδειας
Ευρετικές Μέθοδοι. Ενότητα 2: Βασικές έννοιες των σύγχρονων ευρετικών μεθόδων. Άγγελος Σιφαλέρας. Μεταπτυχιακό Εφαρμοσμένης Πληροφορικής
 Ευρετικές Μέθοδοι Ενότητα 2: Βασικές έννοιες των σύγχρονων ευρετικών μεθόδων Μεταπτυχιακό Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Ευρετικές Μέθοδοι Ενότητα 2: Βασικές έννοιες των σύγχρονων ευρετικών μεθόδων Μεταπτυχιακό Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Συνδυαστική Βελτιστοποίηση
 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 1 Συνδυαστική Βελτιστοποίηση Άγγελος Σιφαλέρας sifalera@uom.gr 1 η Διάλεξη Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 2 Ανακοινώσεις Μετά από κάθε
Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 1 Συνδυαστική Βελτιστοποίηση Άγγελος Σιφαλέρας sifalera@uom.gr 1 η Διάλεξη Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 2 Ανακοινώσεις Μετά από κάθε
Συνδυαστική Βελτιστοποίηση
 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 1 Συνδυαστική Βελτιστοποίηση Άγγελος Σιφαλέρας sifalera@uom.gr 2 η Διάλεξη Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 2 Το πρόβλημα του Γραμμικού
Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 1 Συνδυαστική Βελτιστοποίηση Άγγελος Σιφαλέρας sifalera@uom.gr 2 η Διάλεξη Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 2 Το πρόβλημα του Γραμμικού
ΓΡΑΜΜΙΚΟΣ & ΔΙΚΤΥΑΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ
 ΓΡΑΜΜΙΚΟΣ & ΔΙΚΤΥΑΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Ενότητα 6: Κατηγοριοποίηση Λογισμικού Βελτιστοποίησης, Χρήση Standard Excel Solver Σαμαράς Νικόλαος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΓΡΑΜΜΙΚΟΣ & ΔΙΚΤΥΑΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Ενότητα 6: Κατηγοριοποίηση Λογισμικού Βελτιστοποίησης, Χρήση Standard Excel Solver Σαμαράς Νικόλαος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
SÔntomec plhroforðec gia to glpsol (glpk)
 SÔntomec plhroforðec gia to glpsol (glpk) gpol@di.uoa.gr Genikˆ gia to GLPK kai to glpsol Το GLPK (GNU Linear Programming Kit) είναι μια βιβλιοθήκη συναρτήσεων για τη γλώσσα C/C++ η οποία χρησιμοποιείται
SÔntomec plhroforðec gia to glpsol (glpk) gpol@di.uoa.gr Genikˆ gia to GLPK kai to glpsol Το GLPK (GNU Linear Programming Kit) είναι μια βιβλιοθήκη συναρτήσεων για τη γλώσσα C/C++ η οποία χρησιμοποιείται
Γραµµικός Προγραµµατισµός (ΓΠ)
 Γραµµικός Προγραµµατισµός (ΓΠ) Περίληψη Επίλυση δυσδιάστατων προβληµάτων Η µέθοδος simplex Τυπική µορφή Ακέραιος Προγραµµατισµός Προγραµµατισµός Παραγωγής Προϊόν Προϊόν 2 Παραγωγική Δυνατότητα Μηχ. 4 Μηχ.
Γραµµικός Προγραµµατισµός (ΓΠ) Περίληψη Επίλυση δυσδιάστατων προβληµάτων Η µέθοδος simplex Τυπική µορφή Ακέραιος Προγραµµατισµός Προγραµµατισµός Παραγωγής Προϊόν Προϊόν 2 Παραγωγική Δυνατότητα Μηχ. 4 Μηχ.
ΣΥΝΔΥΑΣΤΙΚΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ
 Ενότητα Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύπου άδειας
Ενότητα Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύπου άδειας
ΑΚΕΡΑΙΟΣ ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ
 ΑΚΕΡΑΙΟΣ ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Ολοκληρωμένη μαθηματική τεχνική βελτιστοποίησης Ευρύτατο φάσμα εφαρμογών Εισαγωγή ακέραιων/λογικών/βοηθητικών μεταβλητών Δυνατότητα γραμμικοποίησης με 0-1 μεταβλητές
ΑΚΕΡΑΙΟΣ ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Ολοκληρωμένη μαθηματική τεχνική βελτιστοποίησης Ευρύτατο φάσμα εφαρμογών Εισαγωγή ακέραιων/λογικών/βοηθητικών μεταβλητών Δυνατότητα γραμμικοποίησης με 0-1 μεταβλητές
Ακέραιος Γραμμικός Προγραμματισμός
 Τμήμα Μηχανικών Πληροφορικής ΤΕ 2016-2017 Ακέραιος Γραμμικός Προγραμματισμός Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα τελευταία ενημέρωση: 12/01/2017 1 Ακέραιος Γραμμικός Προγραμματισμός Όταν για
Τμήμα Μηχανικών Πληροφορικής ΤΕ 2016-2017 Ακέραιος Γραμμικός Προγραμματισμός Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα τελευταία ενημέρωση: 12/01/2017 1 Ακέραιος Γραμμικός Προγραμματισμός Όταν για
Ακέραιος Γραμμικός Προγραμματισμός
 Τμήμα Πληροφορικής & Τηλεπικοινωνιών Πανεπιστήμιο Ιωαννίνων 2018-2019 Ακέραιος Γραμμικός Προγραμματισμός Γκόγκος Χρήστος- Γεωργία Φουτσιτζή Επιχειρησιακή Έρευνα τελευταία ενημέρωση: 12/01/2017 1 Ακέραιος
Τμήμα Πληροφορικής & Τηλεπικοινωνιών Πανεπιστήμιο Ιωαννίνων 2018-2019 Ακέραιος Γραμμικός Προγραμματισμός Γκόγκος Χρήστος- Γεωργία Φουτσιτζή Επιχειρησιακή Έρευνα τελευταία ενημέρωση: 12/01/2017 1 Ακέραιος
Ακέραιος Γραμμικός Προγραμματισμός
 Τμήμα Μηχανικών Πληροφορικής ΤΕ 2017-2018 Ακέραιος Γραμμικός Προγραμματισμός Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα τελευταία ενημέρωση: 12/01/2017 1 Ακέραιος Γραμμικός Προγραμματισμός Όταν για
Τμήμα Μηχανικών Πληροφορικής ΤΕ 2017-2018 Ακέραιος Γραμμικός Προγραμματισμός Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα τελευταία ενημέρωση: 12/01/2017 1 Ακέραιος Γραμμικός Προγραμματισμός Όταν για
Μοντελοποίηση προβληµάτων
 Σχεδιασµός Αλγορίθµων Ακέραιος προγραµµατισµός Αποδοτικοί Αλγόριθµοι Μη Αποδοτικοί Αλγόριθµοι Σχεδιασµός Αλγορίθµων Ακέραιος προγραµµατισµός Αποδοτικοί Αλγόριθµοι Μη Αποδοτικοί Αλγόριθµοι Θεωρία γράφων
Σχεδιασµός Αλγορίθµων Ακέραιος προγραµµατισµός Αποδοτικοί Αλγόριθµοι Μη Αποδοτικοί Αλγόριθµοι Σχεδιασµός Αλγορίθµων Ακέραιος προγραµµατισµός Αποδοτικοί Αλγόριθµοι Μη Αποδοτικοί Αλγόριθµοι Θεωρία γράφων
Εφαρμογές Επιχειρησιακής Έρευνας. Δρ. Γεώργιος Κ.Δ. Σαχαρίδης
 Εφαρμογές Επιχειρησιακής Έρευνας Δρ. Γεώργιος Κ.Δ. Σαχαρίδης 1 Outline Introduction to mathematical programming Introduction to scheduling Flow shop optimization Scheduling of crude oil Decomposition techniques
Εφαρμογές Επιχειρησιακής Έρευνας Δρ. Γεώργιος Κ.Δ. Σαχαρίδης 1 Outline Introduction to mathematical programming Introduction to scheduling Flow shop optimization Scheduling of crude oil Decomposition techniques
Εισαγωγή στο Γραμμικό Προγραμματισμό
 Τμήμα Μηχανικών Πληροφορικής ΤΕ 2016-2017 Εισαγωγή στο Γραμμικό Προγραμματισμό Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα τελευταία ενημέρωση: 15/10/2016 1 Παραδείγματα Που στοχεύει ο Γραμμικός Προγραμματισμός;
Τμήμα Μηχανικών Πληροφορικής ΤΕ 2016-2017 Εισαγωγή στο Γραμμικό Προγραμματισμό Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα τελευταία ενημέρωση: 15/10/2016 1 Παραδείγματα Που στοχεύει ο Γραμμικός Προγραμματισμός;
Γραμμικός Προγραμματισμός και Βελτιστοποίηση (Εργαστήριο 2)
 Τμήμα Μηχανικών Πληροφορικής Γραμμικός Προγραμματισμός και Βελτιστοποίηση (Εργαστήριο 2) Δρ. Δημήτρης Βαρσάμης Επίκουρος Καθηγητής Μάρτιος 2015 Δρ. Δημήτρης Βαρσάμης Γραμμικός Προγραμματισμός (E 1) Μάρτιος
Τμήμα Μηχανικών Πληροφορικής Γραμμικός Προγραμματισμός και Βελτιστοποίηση (Εργαστήριο 2) Δρ. Δημήτρης Βαρσάμης Επίκουρος Καθηγητής Μάρτιος 2015 Δρ. Δημήτρης Βαρσάμης Γραμμικός Προγραμματισμός (E 1) Μάρτιος
Επιχειρησιακή Έρευνα
 Επιχειρησιακή Έρευνα Ενότητα 9: Δυϊκή Θεωρία Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
Επιχειρησιακή Έρευνα Ενότητα 9: Δυϊκή Θεωρία Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ & ΣΥΝΔΥΑΣΤΙΚΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΚΕΦΑΛΑΙΟ 1
 ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ & ΣΥΝΔΥΑΣΤΙΚΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΚΕΦΑΛΑΙΟ 1 1 Βελτιστοποίηση Στην προσπάθεια αντιμετώπισης και επίλυσης των προβλημάτων που προκύπτουν στην πράξη, αναπτύσσουμε μαθηματικά μοντέλα,
ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ & ΣΥΝΔΥΑΣΤΙΚΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΚΕΦΑΛΑΙΟ 1 1 Βελτιστοποίηση Στην προσπάθεια αντιμετώπισης και επίλυσης των προβλημάτων που προκύπτουν στην πράξη, αναπτύσσουμε μαθηματικά μοντέλα,
Επιχειρησιακή Έρευνα
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Επιχειρησιακή Έρευνα Ενότητα #3: Ακέραιος Προγραμματισμός Αθανάσιος Σπυριδάκος Καθηγητής Τμήμα Διοίκησης Επιχειρήσεων Άδειες Χρήσης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Επιχειρησιακή Έρευνα Ενότητα #3: Ακέραιος Προγραμματισμός Αθανάσιος Σπυριδάκος Καθηγητής Τμήμα Διοίκησης Επιχειρήσεων Άδειες Χρήσης
Διαχείριση Εφοδιαστικής Αλυσίδας ΙΙ
 Διαχείριση Εφοδιαστικής Αλυσίδας ΙΙ 1 η Διάλεξη: Αναδρομή στον Μαθηματικό Προγραμματισμό 2019, Πολυτεχνική Σχολή Εργαστήριο Συστημάτων Σχεδιασμού, Παραγωγής και Λειτουργιών Περιεχόμενα 1. Γραμμικός Προγραμματισμός
Διαχείριση Εφοδιαστικής Αλυσίδας ΙΙ 1 η Διάλεξη: Αναδρομή στον Μαθηματικό Προγραμματισμό 2019, Πολυτεχνική Σχολή Εργαστήριο Συστημάτων Σχεδιασμού, Παραγωγής και Λειτουργιών Περιεχόμενα 1. Γραμμικός Προγραμματισμός
Κεφάλαιο 5ο: Ακέραιος προγραμματισμός
 Κεφάλαιο 5ο: Ακέραιος προγραμματισμός 5.1 Εισαγωγή Ο ακέραιος προγραμματισμός ασχολείται με προβλήματα γραμμικού προγραμματισμού στα οποία μερικές ή όλες οι μεταβλητές είναι ακέραιες. Ένα γενικό πρόβλημα
Κεφάλαιο 5ο: Ακέραιος προγραμματισμός 5.1 Εισαγωγή Ο ακέραιος προγραμματισμός ασχολείται με προβλήματα γραμμικού προγραμματισμού στα οποία μερικές ή όλες οι μεταβλητές είναι ακέραιες. Ένα γενικό πρόβλημα
Επιχειρησιακή Έρευνα
 Επιχειρησιακή Έρευνα Ενότητα 10: Το πρόβλημα μεταφοράς: μαθηματικό μοντέλο και μεθοδολογία επίλυσης Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Επιχειρησιακή Έρευνα Ενότητα 10: Το πρόβλημα μεταφοράς: μαθηματικό μοντέλο και μεθοδολογία επίλυσης Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Βασίλειος Μαχαιράς Πολιτικός Μηχανικός Ph.D.
 Βασίλειος Μαχαιράς Πολιτικός Μηχανικός Ph.D. Ακέραιος προγραμματισμός πολύ-κριτηριακές αντικειμενικές συναρτήσεις Πανεπιστήμιο Θεσσαλίας Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής Διάλεξη 12-13 η /2017
Βασίλειος Μαχαιράς Πολιτικός Μηχανικός Ph.D. Ακέραιος προγραμματισμός πολύ-κριτηριακές αντικειμενικές συναρτήσεις Πανεπιστήμιο Θεσσαλίας Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής Διάλεξη 12-13 η /2017
Μάθημα Επιλογής 8 ου εξαμήνου
 EΘNIKO ΜEΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Ανάλυσης, Σχεδιασμού & Ανάπτυξης Διεργασιών & Συστημάτων Υπολογιστικές Μέθοδοι Ανάλυσης και Σχεδιασμού Μάθημα Επιλογής 8 ου εξαμήνου Διδάσκων:
EΘNIKO ΜEΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Ανάλυσης, Σχεδιασμού & Ανάπτυξης Διεργασιών & Συστημάτων Υπολογιστικές Μέθοδοι Ανάλυσης και Σχεδιασμού Μάθημα Επιλογής 8 ου εξαμήνου Διδάσκων:
Πληροφοριακά Συστήματα Διοίκησης. Επισκόπηση μοντέλων λήψης αποφάσεων Τεχνικές Μαθηματικού Προγραμματισμού
 Πληροφοριακά Συστήματα Διοίκησης Επισκόπηση μοντέλων λήψης αποφάσεων Τεχνικές Μαθηματικού Προγραμματισμού Σημασία μοντέλου Το μοντέλο δημιουργεί μια λογική δομή μέσω της οποίας αποκτούμε μια χρήσιμη άποψη
Πληροφοριακά Συστήματα Διοίκησης Επισκόπηση μοντέλων λήψης αποφάσεων Τεχνικές Μαθηματικού Προγραμματισμού Σημασία μοντέλου Το μοντέλο δημιουργεί μια λογική δομή μέσω της οποίας αποκτούμε μια χρήσιμη άποψη
ΣΥΝΔΥΑΣΤΙΚΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ
 Ενότητα 4 Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύπου άδειας
Ενότητα 4 Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύπου άδειας
Ευρετικές Μέθοδοι. Ενότητα 3: Ευρετικές μέθοδοι αρχικοποίησης και βελτίωσης για το TSP. Άγγελος Σιφαλέρας. Μεταπτυχιακό Εφαρμοσμένης Πληροφορικής
 Ευρετικές Μέθοδοι Ενότητα 3: Ευρετικές μέθοδοι αρχικοποίησης και βελτίωσης για το TSP Μεταπτυχιακό Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Ευρετικές Μέθοδοι Ενότητα 3: Ευρετικές μέθοδοι αρχικοποίησης και βελτίωσης για το TSP Μεταπτυχιακό Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Παράλληλος προγραμματισμός περιστροφικών αλγορίθμων εξωτερικών σημείων τύπου simplex ΠΛΟΣΚΑΣ ΝΙΚΟΛΑΟΣ
 Παράλληλος προγραμματισμός περιστροφικών αλγορίθμων εξωτερικών σημείων τύπου simplex ΠΛΟΣΚΑΣ ΝΙΚΟΛΑΟΣ Διπλωματική Εργασία Μεταπτυχιακού Προγράμματος στην Εφαρμοσμένη Πληροφορική Κατεύθυνση: Συστήματα Υπολογιστών
Παράλληλος προγραμματισμός περιστροφικών αλγορίθμων εξωτερικών σημείων τύπου simplex ΠΛΟΣΚΑΣ ΝΙΚΟΛΑΟΣ Διπλωματική Εργασία Μεταπτυχιακού Προγράμματος στην Εφαρμοσμένη Πληροφορική Κατεύθυνση: Συστήματα Υπολογιστών
ΠΙΝΑΚΑΣ 3-1 Προσομοιωση και Βελτιστοποιηση Συστηματος (Haimes, 1977) ΠΡΑΓΜΑΤΙΚΗ ΑΠΟΚΡΙΣΗ ΦΥΣΙΚΟΥ ΣΥΣΤΗΜΑΤΟΣ ΜΑΘΗΜΑΤΙΚΗ ΑΠΟΚΡΙΣΗ ΣΥΣΤΗΜΑΤΟΣ
 3 ΤΕΧΝΙΚΕΣ ΑΝΑΛΥΣΗΣ 3.1 Εισαγωγη ΣΥΣΤΗΜΑΤΩΝ Τα συστηματα εφαρμοζονται σε αναπτυξιακα προγραμματα, σε μελετες σχεδιασμου εργων, σε προγραμματα διατηρησης ή προστασιας περιβαλλοντος και υδατικων πορων και
3 ΤΕΧΝΙΚΕΣ ΑΝΑΛΥΣΗΣ 3.1 Εισαγωγη ΣΥΣΤΗΜΑΤΩΝ Τα συστηματα εφαρμοζονται σε αναπτυξιακα προγραμματα, σε μελετες σχεδιασμου εργων, σε προγραμματα διατηρησης ή προστασιας περιβαλλοντος και υδατικων πορων και
Συστήματα Επιχειρηματικής Ευφυίας. CPLEX και OPL: ένα λογισμικό επίλυσης προβλημάτων Γραμμικού Προγραμματισμού
 Συστήματα Επιχειρηματικής Ευφυίας CPLEX και OPL: ένα λογισμικό επίλυσης προβλημάτων Γραμμικού Προγραμματισμού Προβλήματα Γραμμικού Προγραμματισμού Πρόβλημα Γραμμικού Προγραμματισμού - ΓΠ (Linear Programming
Συστήματα Επιχειρηματικής Ευφυίας CPLEX και OPL: ένα λογισμικό επίλυσης προβλημάτων Γραμμικού Προγραμματισμού Προβλήματα Γραμμικού Προγραμματισμού Πρόβλημα Γραμμικού Προγραμματισμού - ΓΠ (Linear Programming
max 17x x 2 υπό 10x 1 + 7x 2 40 x 1 + x 2 5 x 1, x 2 0.
 Υπολογιστικές Μέθοδοι στη Θεωρία Αποφάσεων Ενότητα 11 Επίλυση στον Ακέραιο Προγραμματισμό Αντώνης Οικονόμου Τμήμα Μαθηματικών Πανεπιστήμιο Αθηνών Προπτυχιακό πρόγραμμα σπουδών 6 Μαΐου 2016 Η μέθοδος κλάδος-φράγμα
Υπολογιστικές Μέθοδοι στη Θεωρία Αποφάσεων Ενότητα 11 Επίλυση στον Ακέραιο Προγραμματισμό Αντώνης Οικονόμου Τμήμα Μαθηματικών Πανεπιστήμιο Αθηνών Προπτυχιακό πρόγραμμα σπουδών 6 Μαΐου 2016 Η μέθοδος κλάδος-φράγμα
ΓΡΑΜΜΙΚΟΣ & ΔΙΚΤΥΑΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ
 ΓΡΑΜΜΙΚΟΣ & ΔΙΚΤΥΑΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Ενότητα 3: Μαθηματικό Πρότυπο, Κανονική Μορφή, Τυποποιημένη Μορφή Σαμαράς Νικόλαος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΓΡΑΜΜΙΚΟΣ & ΔΙΚΤΥΑΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Ενότητα 3: Μαθηματικό Πρότυπο, Κανονική Μορφή, Τυποποιημένη Μορφή Σαμαράς Νικόλαος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Βελτιστοποίηση κατανομής πόρων συντήρησης οδοστρωμάτων Πανεπιστήμιο Πατρών - Πολυτεχνική Σχολή Τμήμα Πολιτικών Μηχανικών
 Βελτιστοποίηση κατανομής πόρων συντήρησης οδοστρωμάτων Πανεπιστήμιο Πατρών - Πολυτεχνική Σχολή Τμήμα Πολιτικών Μηχανικών Πάτρα 17 - Μαΐου - 2017 Παναγιώτης Τσίκας Σκοπός του προβλήματος Σκοπός του προβλήματος,
Βελτιστοποίηση κατανομής πόρων συντήρησης οδοστρωμάτων Πανεπιστήμιο Πατρών - Πολυτεχνική Σχολή Τμήμα Πολιτικών Μηχανικών Πάτρα 17 - Μαΐου - 2017 Παναγιώτης Τσίκας Σκοπός του προβλήματος Σκοπός του προβλήματος,
ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ & ΣΥΝΔΥΑΣΤΙΚΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ. Κεφάλαιο 3 Μορφοποίηση Προβλημάτων Ακέραιου Προγραμματισμού
 ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ & ΣΥΝΔΥΑΣΤΙΚΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ Κεφάλαιο 3 Μορφοποίηση Προβλημάτων Ακέραιου Προγραμματισμού 1 Σχέση γραμμικού και ακέραιου προγραμματισμού Ενα πρόβλημα ακέραιου προγραμματισμού είναι
ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ & ΣΥΝΔΥΑΣΤΙΚΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ Κεφάλαιο 3 Μορφοποίηση Προβλημάτων Ακέραιου Προγραμματισμού 1 Σχέση γραμμικού και ακέραιου προγραμματισμού Ενα πρόβλημα ακέραιου προγραμματισμού είναι
Ο ΗΓΙΕΣ ΓΙΑ ΤΟ ΠΡΟΓΡΑΜΜΑ LINDO ΚΑΙ ΤΗΝ ΕΠΙΛΥΣΗ ΠΡΟΒΛΗΜΑΤΩΝ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ
 Ο ΗΓΙΕΣ ΓΙΑ ΤΟ ΠΡΟΓΡΑΜΜΑ LINDO ΚΑΙ ΤΗΝ ΕΠΙΛΥΣΗ ΠΡΟΒΛΗΜΑΤΩΝ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Το LINDO (Linear Interactive and Discrete Optimizer) είναι ένα πολύ γνωστό λογισµικό για την επίλυση προβληµάτων γραµµικού,
Ο ΗΓΙΕΣ ΓΙΑ ΤΟ ΠΡΟΓΡΑΜΜΑ LINDO ΚΑΙ ΤΗΝ ΕΠΙΛΥΣΗ ΠΡΟΒΛΗΜΑΤΩΝ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Το LINDO (Linear Interactive and Discrete Optimizer) είναι ένα πολύ γνωστό λογισµικό για την επίλυση προβληµάτων γραµµικού,
Σχεδιασμός επέκτασης του συστήματος ηλεκτροπαραγωγής με τη χρήση Πολυκριτηριακού Γραμμικού Προγραμματισμού
 3ο Πανελλήνιο Επιστημονικό Συνέδριο Χημικής Μηχανικής Αθήνα,, IούνιοςI 200 Σχεδιασμός επέκτασης του συστήματος ηλεκτροπαραγωγής με τη χρήση Πολυκριτηριακού Γραμμικού Προγραμματισμού Γιώργος Μαυρωτάς Δανάη
3ο Πανελλήνιο Επιστημονικό Συνέδριο Χημικής Μηχανικής Αθήνα,, IούνιοςI 200 Σχεδιασμός επέκτασης του συστήματος ηλεκτροπαραγωγής με τη χρήση Πολυκριτηριακού Γραμμικού Προγραμματισμού Γιώργος Μαυρωτάς Δανάη
2 η ΕΝΟΤΗΤΑ ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ
 ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΜΠ ΕΙΣΑΓΩΓΗ ΣΤΗN ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΣΥΣΤΗΜΑΤΩΝ 2 η ΕΝΟΤΗΤΑ ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Μ. Καρλαύτης Ν. Λαγαρός Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες Χρήσης Creative
ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΜΠ ΕΙΣΑΓΩΓΗ ΣΤΗN ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΣΥΣΤΗΜΑΤΩΝ 2 η ΕΝΟΤΗΤΑ ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Μ. Καρλαύτης Ν. Λαγαρός Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες Χρήσης Creative
Ευρετικές Μέθοδοι. Ενότητα 1: Εισαγωγή στις ευρετικές μεθόδους. Άγγελος Σιφαλέρας. Μεταπτυχιακό Εφαρμοσμένης Πληροφορικής ΕΥΡΕΤΙΚΕΣ ΜΕΘΟΔΟΙ
 Ευρετικές Μέθοδοι Ενότητα 1: Εισαγωγή στις ευρετικές μεθόδους Μεταπτυχιακό Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Ευρετικές Μέθοδοι Ενότητα 1: Εισαγωγή στις ευρετικές μεθόδους Μεταπτυχιακό Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Εισαγωγή στο Γραμμικό Προγραμματισμό
 Τμήμα Μηχανικών Πληροφορικής ΤΕ 2017-2018 Εισαγωγή στο Γραμμικό Προγραμματισμό Φουτσιτζή Γεωργία-Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα τελευταία ενημέρωση: 15/10/2016 1 Περιεχόμενα Γραμμικός
Τμήμα Μηχανικών Πληροφορικής ΤΕ 2017-2018 Εισαγωγή στο Γραμμικό Προγραμματισμό Φουτσιτζή Γεωργία-Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα τελευταία ενημέρωση: 15/10/2016 1 Περιεχόμενα Γραμμικός
ΣΥΝΔΥΑΣΤΙΚΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ
 Ενότητα 10 Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύπου άδειας
Ενότητα 10 Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύπου άδειας
ΠΑΡΑΔΕΙΓΜΑΤΑ ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ ΜΕ ΤΗ ΧΡΗΣΗ Η/Υ (2 ο Φυλλάδιο)
 ΠΕΡΙΕΧΟΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ ΜΕ ΤΗ ΧΡΗΣΗ Η/Υ (2 ο Φυλλάδιο) ΙΩΑΝΝΗΣ ΝΤΖΟΥΦΡΑΣ Παραδείγματα 3 5 : Προβλήματα μεταφοράς (transportation problems)... 3 Παράδειγματα 3-5: Linear Programming
ΠΕΡΙΕΧΟΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ ΜΕ ΤΗ ΧΡΗΣΗ Η/Υ (2 ο Φυλλάδιο) ΙΩΑΝΝΗΣ ΝΤΖΟΥΦΡΑΣ Παραδείγματα 3 5 : Προβλήματα μεταφοράς (transportation problems)... 3 Παράδειγματα 3-5: Linear Programming
ΚΕΦΑΛΑΙΟ ΟΓΔΟΟ: Εισαγωγή στον Ακέραιο Προγραμματισμό. Εφαρμογές χρησιμοποιώντας το R
 ΚΕΦΑΛΑΙΟ ΟΓΔΟΟ: Εισαγωγή στον Ακέραιο Προγραμματισμό. Εφαρμογές χρησιμοποιώντας το R Σύνοψη Τα προβλήματα ακεραίου γραμμικού προγραμματισμού αποτελούν μια ειδική κατηγορία προβλημάτων. Ωστόσο, η ιδιαίτερη
ΚΕΦΑΛΑΙΟ ΟΓΔΟΟ: Εισαγωγή στον Ακέραιο Προγραμματισμό. Εφαρμογές χρησιμοποιώντας το R Σύνοψη Τα προβλήματα ακεραίου γραμμικού προγραμματισμού αποτελούν μια ειδική κατηγορία προβλημάτων. Ωστόσο, η ιδιαίτερη
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ
 ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΠΛΗΡΟΦΟΡΙΑΚΑ ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΟΥ ΚΑΙ ΑΚΕΡΑΙΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Νοέμβριος 2006 Αθήνα Κεφάλαιο 3 ο Πληροφοριακά συστήματα
ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΠΛΗΡΟΦΟΡΙΑΚΑ ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΟΥ ΚΑΙ ΑΚΕΡΑΙΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Νοέμβριος 2006 Αθήνα Κεφάλαιο 3 ο Πληροφοριακά συστήματα
Βασίλειος Μαχαιράς Πολιτικός Μηχανικός Ph.D.
 Βασίλειος Μαχαιράς Πολιτικός Μηχανικός Ph.D. Κλασικές Τεχνικές Βελτιστοποίησης Πανεπιστήμιο Θεσσαλίας Σχολή Θετικών Επιστημών ΤμήμαΠληροφορικής Διάλεξη 2 η /2017 Μαθηματική Βελτιστοποίηση Η «Μαθηματική
Βασίλειος Μαχαιράς Πολιτικός Μηχανικός Ph.D. Κλασικές Τεχνικές Βελτιστοποίησης Πανεπιστήμιο Θεσσαλίας Σχολή Θετικών Επιστημών ΤμήμαΠληροφορικής Διάλεξη 2 η /2017 Μαθηματική Βελτιστοποίηση Η «Μαθηματική
ΠΑΡΑΔΕΙΓΜΑΤΑ ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ ΜΕ ΤΗ ΧΡΗΣΗ Η/Υ (3 ο Φυλλάδιο)
 ΠΕΡΙΕΧΟΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ ΜΕ ΤΗ ΧΡΗΣΗ Η/Υ (3 ο Φυλλάδιο) ΙΩΑΝΝΗΣ ΝΤΖΟΥΦΡΑΣ (C) 2002 ΧΙΟΣ Παράδειγμα 8: Πρόβλημα ελαχίστης Διαδρομής (Shortest path problem)... 4 LINDO: Integer Linear
ΠΕΡΙΕΧΟΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ ΜΕ ΤΗ ΧΡΗΣΗ Η/Υ (3 ο Φυλλάδιο) ΙΩΑΝΝΗΣ ΝΤΖΟΥΦΡΑΣ (C) 2002 ΧΙΟΣ Παράδειγμα 8: Πρόβλημα ελαχίστης Διαδρομής (Shortest path problem)... 4 LINDO: Integer Linear
Κεφάλαιο 6. Μέθοδοι επίλυσης προβλημάτων ακέραιου προγραμματισμού
 Κεφάλαιο 6 Μέθοδοι επίλυσης προβλημάτων ακέραιου προγραμματισμού 1 Γραφική επίλυση Η γραφική μέθοδος επίλυσης μπορεί να χρησιμοποιηθεί μόνο για πολύ μικρά προβλήματα με δύο ή το πολύ τρεις μεταβλητές απόφασης.
Κεφάλαιο 6 Μέθοδοι επίλυσης προβλημάτων ακέραιου προγραμματισμού 1 Γραφική επίλυση Η γραφική μέθοδος επίλυσης μπορεί να χρησιμοποιηθεί μόνο για πολύ μικρά προβλήματα με δύο ή το πολύ τρεις μεταβλητές απόφασης.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΠΡΟΣΘΗΚΗ ΕΠΙΠΕΔΩΝ ΤΟΜΩΝ ΓΙΑ ΤΗΝ ΕΠΙΛΥΣΗ ΜΙΑΣ ΕΙΔΙΚΗΣ ΟΜΑΔΑΣ ΠΡΟΒΛΗΜΑΤΩΝ ΜΕΙΚΤΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Μεταπτυχιακή Εργασία ΠΡΟΣΘΗΚΗ ΕΠΙΠΕΔΩΝ ΤΟΜΩΝ ΓΙΑ ΤΗΝ ΕΠΙΛΥΣΗ ΜΙΑΣ ΕΙΔΙΚΗΣ ΟΜΑΔΑΣ ΠΡΟΒΛΗΜΑΤΩΝ ΜΕΙΚΤΗΣ ΑΚΕΡΑΙΑΣ ΔΙΕΠΙΠΕΔΗΣ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Μεταπτυχιακή Εργασία ΠΡΟΣΘΗΚΗ ΕΠΙΠΕΔΩΝ ΤΟΜΩΝ ΓΙΑ ΤΗΝ ΕΠΙΛΥΣΗ ΜΙΑΣ ΕΙΔΙΚΗΣ ΟΜΑΔΑΣ ΠΡΟΒΛΗΜΑΤΩΝ ΜΕΙΚΤΗΣ ΑΚΕΡΑΙΑΣ ΔΙΕΠΙΠΕΔΗΣ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗΣ
Επιχειρησιακή έρευνα (ασκήσεις)
 Επιχειρησιακή έρευνα (ασκήσεις) ΤΕΙ Ηπείρου (Τμήμα Λογιστικής και Χρηματοοικονομικής) Γκόγκος Χρήστος (06-01-2015) 1. Γραφική επίλυση προβλημάτων Γραμμικού Προγραμματισμού A) Με τη βοήθεια της γραφικής
Επιχειρησιακή έρευνα (ασκήσεις) ΤΕΙ Ηπείρου (Τμήμα Λογιστικής και Χρηματοοικονομικής) Γκόγκος Χρήστος (06-01-2015) 1. Γραφική επίλυση προβλημάτων Γραμμικού Προγραμματισμού A) Με τη βοήθεια της γραφικής
Επιχειρησιακή Έρευνα I
 Επιχειρησιακή Έρευνα I Operations/Operational Research (OR) Κωστής Μαμάσης Παρασκευή 09:00 12:00 Σημειώσεις των Α. Platis, K. Mamasis Περιεχόμενα EE 1&2 Εισαγωγή Μαθηματικός Προγραμματισμός - Γραμμικός
Επιχειρησιακή Έρευνα I Operations/Operational Research (OR) Κωστής Μαμάσης Παρασκευή 09:00 12:00 Σημειώσεις των Α. Platis, K. Mamasis Περιεχόμενα EE 1&2 Εισαγωγή Μαθηματικός Προγραμματισμός - Γραμμικός
Περιεχόμενα Πρόλογος 5ης αναθεωρημένης έκδοσης ΚΕΦΆΛΆΙΟ 1 Ο ρόλος της επιχειρησιακής έρευνας στη λήψη αποφάσεων ΚΕΦΆΛΆΙΟ 2.
 Περιεχόμενα Πρόλογος 5ης αναθεωρημένης έκδοσης... 11 Λίγα λόγια για βιβλίο... 11 Σε ποιους απευθύνεται... 12 Τι αλλάζει στην 5η αναθεωρημένη έκδοση... 12 Το βιβλίο ως διδακτικό εγχειρίδιο... 14 Ευχαριστίες...
Περιεχόμενα Πρόλογος 5ης αναθεωρημένης έκδοσης... 11 Λίγα λόγια για βιβλίο... 11 Σε ποιους απευθύνεται... 12 Τι αλλάζει στην 5η αναθεωρημένη έκδοση... 12 Το βιβλίο ως διδακτικό εγχειρίδιο... 14 Ευχαριστίες...
Προσεγγιστικοί Αλγόριθμοι
 Πολλά NP-πλήρη προβλήματα έχουν μεγάλο πρακτικό ενδιαφέρον. http://xkcd.com/287/ Πολλά NP-πλήρη προβλήματα έχουν μεγάλο πρακτικό ενδιαφέρον. Πως μπορούμε να αντιμετωπίσουμε το γεγονός ότι είναι απίθανη(;)
Πολλά NP-πλήρη προβλήματα έχουν μεγάλο πρακτικό ενδιαφέρον. http://xkcd.com/287/ Πολλά NP-πλήρη προβλήματα έχουν μεγάλο πρακτικό ενδιαφέρον. Πως μπορούμε να αντιμετωπίσουμε το γεγονός ότι είναι απίθανη(;)
ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΜΑΘΗΜΑΤΙΚΗ ΔΙΑΤΥΠΩΣΗ, Διαλ. 2. Ανωτάτη Σχολή Παιδαγωγικής και Τεχνολογικής Εκπαίδευσης 8/4/2017
 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΜΑΘΗΜΑΤΙΚΗ ΔΙΑΤΥΠΩΣΗ, Διαλ. 2 Ανωτάτη Σχολή Παιδαγωγικής και Τεχνολογικής Εκπαίδευσης 8/4/2017 Αντικειμενικοί στόχοι Η μελέτη των βασικών στοιχείων που συνθέτουν ένα πρόβλημα βελτιστοποίησης
ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΜΑΘΗΜΑΤΙΚΗ ΔΙΑΤΥΠΩΣΗ, Διαλ. 2 Ανωτάτη Σχολή Παιδαγωγικής και Τεχνολογικής Εκπαίδευσης 8/4/2017 Αντικειμενικοί στόχοι Η μελέτη των βασικών στοιχείων που συνθέτουν ένα πρόβλημα βελτιστοποίησης
Οπτικοποίηση: ένας αποτελεσματικός τρόπος για την βελτίωση της κατανόησης του αλγορίθμου simplex
 17 ο Συνέδριο της Ε.Ε.Ε.Ε. «Διαχείριση Κινδύνων» 1 Οπτικοποίηση: ένας αποτελεσματικός τρόπος για την βελτίωση της κατανόησης του αλγορίθμου simplex Visualization: an effective way for understanding the
17 ο Συνέδριο της Ε.Ε.Ε.Ε. «Διαχείριση Κινδύνων» 1 Οπτικοποίηση: ένας αποτελεσματικός τρόπος για την βελτίωση της κατανόησης του αλγορίθμου simplex Visualization: an effective way for understanding the
Θεωρία Παιγνίων και Αποφάσεων. Ενότητα 5: Εύρεση σημείων ισορροπίας σε παίγνια μηδενικού αθροίσματος. Ε. Μαρκάκης. Επικ. Καθηγητής
 Θεωρία Παιγνίων και Αποφάσεων Ενότητα 5: Εύρεση σημείων ισορροπίας σε παίγνια μηδενικού αθροίσματος Ε. Μαρκάκης Επικ. Καθηγητής Περίληψη Παίγνια μηδενικού αθροίσματος PessimisIc play Αμιγείς max-min και
Θεωρία Παιγνίων και Αποφάσεων Ενότητα 5: Εύρεση σημείων ισορροπίας σε παίγνια μηδενικού αθροίσματος Ε. Μαρκάκης Επικ. Καθηγητής Περίληψη Παίγνια μηδενικού αθροίσματος PessimisIc play Αμιγείς max-min και
ΜΕΘΟΔΟΙ ΑΕΡΟΔΥΝΑΜΙΚΗΣ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Εργαστήριο Θερμικών Στροβιλομηχανών Μονάδα Παράλληλης ης Υπολογιστικής Ρευστοδυναμικής & Βελτιστοποίησης ΜΕΘΟΔΟΙ ΑΕΡΟΔΥΝΑΜΙΚΗΣ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗΣ (7 ο Εξάμηνο Σχολής Μηχ.Μηχ. ΕΜΠ)
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Εργαστήριο Θερμικών Στροβιλομηχανών Μονάδα Παράλληλης ης Υπολογιστικής Ρευστοδυναμικής & Βελτιστοποίησης ΜΕΘΟΔΟΙ ΑΕΡΟΔΥΝΑΜΙΚΗΣ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗΣ (7 ο Εξάμηνο Σχολής Μηχ.Μηχ. ΕΜΠ)
ΤΜΗΜΑΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟΠΑΤΡΩΝ ΑΚ. ΕΤΟΣ ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ
 ΤΜΗΜΑΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟΠΑΤΡΩΝ ΑΚ. ΕΤΟΣ2013-2014 ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Τα προβλήματα τους Ακεραίου γραμμικού Προγραμματισμού (Integer Linear Programming) είναι
ΤΜΗΜΑΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟΠΑΤΡΩΝ ΑΚ. ΕΤΟΣ2013-2014 ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Τα προβλήματα τους Ακεραίου γραμμικού Προγραμματισμού (Integer Linear Programming) είναι
ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ & ΣΥΝΔΥΑΣΤΙΚΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ. Κεφάλαιο 2 Μορφοποίηση Προβλημάτων Ακέραιου Προγραμματισμού
 ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ & ΣΥΝΔΥΑΣΤΙΚΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ Κεφάλαιο 2 Μορφοποίηση Προβλημάτων Ακέραιου Προγραμματισμού 1 Μεταξύ δύο περιορισμών, ο ένας πρέπει να ισχύει Έστω ότι για την κατασκευή ενός προϊόντος
ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ & ΣΥΝΔΥΑΣΤΙΚΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ Κεφάλαιο 2 Μορφοποίηση Προβλημάτων Ακέραιου Προγραμματισμού 1 Μεταξύ δύο περιορισμών, ο ένας πρέπει να ισχύει Έστω ότι για την κατασκευή ενός προϊόντος
Ποσοτικές Μέθοδοι στη Διοίκηση Έργων (Y100)
 Μεταπτυχιακό Πρόγραμμα Σπουδών Διοίκηση και Διαχείριση Έργων και Προγραμμάτων Ποσοτικές Μέθοδοι στη Διοίκηση Έργων (Y100) Μέρος ΙΙ Τεχνικές Μαθηματικού Προγραμματισμού Μαθηματικά Μοντέλα Εισαγωγή Μεθοδολογία
Μεταπτυχιακό Πρόγραμμα Σπουδών Διοίκηση και Διαχείριση Έργων και Προγραμμάτων Ποσοτικές Μέθοδοι στη Διοίκηση Έργων (Y100) Μέρος ΙΙ Τεχνικές Μαθηματικού Προγραμματισμού Μαθηματικά Μοντέλα Εισαγωγή Μεθοδολογία
ΠΩΣ ΝΑ ΟΡΙΣΕΤΕ ΚΑΙ ΝΑ ΕΠΙΛΥΣΕΤΕ ΕΝΑ ΠΡΟΓΡΑΜΜΑ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΜΕ ΤΟΝ SOLVER ΤΟΥ EXCEL
 ΠΩΣ ΝΑ ΟΡΙΣΕΤΕ ΚΑΙ ΝΑ ΕΠΙΛΥΣΕΤΕ ΕΝΑ ΠΡΟΓΡΑΜΜΑ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΜΕ ΤΟΝ SOLVER ΤΟΥ EXCEL 1. Στο Tools menu, click Solver. 2. Εάν η επιλογή Solver δεν είναι διαθέσιµη στο Tools menu, πρέπει να το
ΠΩΣ ΝΑ ΟΡΙΣΕΤΕ ΚΑΙ ΝΑ ΕΠΙΛΥΣΕΤΕ ΕΝΑ ΠΡΟΓΡΑΜΜΑ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΜΕ ΤΟΝ SOLVER ΤΟΥ EXCEL 1. Στο Tools menu, click Solver. 2. Εάν η επιλογή Solver δεν είναι διαθέσιµη στο Tools menu, πρέπει να το
On line αλγόριθμοι δρομολόγησης για στοχαστικά δίκτυα σε πραγματικό χρόνο
 On line αλγόριθμοι δρομολόγησης για στοχαστικά δίκτυα σε πραγματικό χρόνο Υπ. Διδάκτωρ : Ευαγγελία Χρυσοχόου Επιβλέπων Καθηγητής: Αθανάσιος Ζηλιασκόπουλος Τμήμα Μηχανολόγων Μηχανικών Περιεχόμενα Εισαγωγή
On line αλγόριθμοι δρομολόγησης για στοχαστικά δίκτυα σε πραγματικό χρόνο Υπ. Διδάκτωρ : Ευαγγελία Χρυσοχόου Επιβλέπων Καθηγητής: Αθανάσιος Ζηλιασκόπουλος Τμήμα Μηχανολόγων Μηχανικών Περιεχόμενα Εισαγωγή
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ
 ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Νοέμβριος 006 Αθήνα Κεφάλαιο ο Ακέραιος και μικτός προγραμματισμός. Εισαγωγή Μια από τις
ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Νοέμβριος 006 Αθήνα Κεφάλαιο ο Ακέραιος και μικτός προγραμματισμός. Εισαγωγή Μια από τις
Probabilistic Approach to Robust Optimization
 Probabilistic Approach to Robust Optimization Akiko Takeda Department of Mathematical & Computing Sciences Graduate School of Information Science and Engineering Tokyo Institute of Technology Tokyo 52-8552,
Probabilistic Approach to Robust Optimization Akiko Takeda Department of Mathematical & Computing Sciences Graduate School of Information Science and Engineering Tokyo Institute of Technology Tokyo 52-8552,
Fermat, 1638, Newton Euler, Lagrange, 1807
 Εισαγωγή Μαθ Προγρ Κλασικά Προβλ Επεκτάσεις Υπολογιστικές Μέθοδοι στη Θεωρία Αποφάσεων Ενότητα 1 Εισαγωγή Αντώνης Οικονόμου Τμήμα Μαθηματικών Πανεπιστήμιο Αθηνών Προπτυχιακό πρόγραμμα σπουδών 3 Μαρτίου
Εισαγωγή Μαθ Προγρ Κλασικά Προβλ Επεκτάσεις Υπολογιστικές Μέθοδοι στη Θεωρία Αποφάσεων Ενότητα 1 Εισαγωγή Αντώνης Οικονόμου Τμήμα Μαθηματικών Πανεπιστήμιο Αθηνών Προπτυχιακό πρόγραμμα σπουδών 3 Μαρτίου
ΕΝΑΣ ΝΕΟΣ ΤΡΟΠΟΣ ΔΗΜΙΟΥΡΓΙΑΣ ΤΥΧΑΙΩΝ ΒΕΛΤΙΣΤΩΝ ΓΡΑΜΜΙΚΩΝ ΠΡΟΒΛΗΜΑΤΩΝ ΚΑΙ ΜΙΑ ΣΥΓΚΡΙΤΙΚΗ ΥΠΟΛΟΓΙΣΤΙΚΗ ΜΕΛΕΤΗ
 ΕΝΑΣ ΝΕΟΣ ΤΡΟΠΟΣ ΔΗΜΙΟΥΡΓΙΑΣ ΤΥΧΑΙΩΝ ΒΕΛΤΙΣΤΩΝ ΓΡΑΜΜΙΚΩΝ ΠΡΟΒΛΗΜΑΤΩΝ ΚΑΙ ΜΙΑ ΣΥΓΚΡΙΤΙΚΗ ΥΠΟΛΟΓΙΣΤΙΚΗ ΜΕΛΕΤΗ Παπαρρίζος Κωνσταντίνος, Σαμαράς Νικόλαος, Στεφανίδης Γεώργιος Τμ. Εφαρμοσμένης Πληροφορικής
ΕΝΑΣ ΝΕΟΣ ΤΡΟΠΟΣ ΔΗΜΙΟΥΡΓΙΑΣ ΤΥΧΑΙΩΝ ΒΕΛΤΙΣΤΩΝ ΓΡΑΜΜΙΚΩΝ ΠΡΟΒΛΗΜΑΤΩΝ ΚΑΙ ΜΙΑ ΣΥΓΚΡΙΤΙΚΗ ΥΠΟΛΟΓΙΣΤΙΚΗ ΜΕΛΕΤΗ Παπαρρίζος Κωνσταντίνος, Σαμαράς Νικόλαος, Στεφανίδης Γεώργιος Τμ. Εφαρμοσμένης Πληροφορικής
Διαχείριση Εφοδιαστικής Αλυσίδας
 Διαχείριση Εφοδιαστικής Αλυσίδας 4 η Διάλεξη: Βελτιστοποίηση πολλαπλών στόχων (Μulti-objective optimization) 2019 Εργαστήριο Συστημάτων Σχεδιασμού, Παραγωγής και Λειτουργιών Ατζέντα Εισαγωγή στην βελτιστοποίηση
Διαχείριση Εφοδιαστικής Αλυσίδας 4 η Διάλεξη: Βελτιστοποίηση πολλαπλών στόχων (Μulti-objective optimization) 2019 Εργαστήριο Συστημάτων Σχεδιασμού, Παραγωγής και Λειτουργιών Ατζέντα Εισαγωγή στην βελτιστοποίηση
Συνδυαστική Βελτιστοποίηση
 Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 1 Άγγελος Σιφαλέρας sifalera@uom.gr 4 η Διάλεξη Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 2 Knapsack Problem, (1/9) Ένας επενδυτής διαθέτει ένα χρηματικό
Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 1 Άγγελος Σιφαλέρας sifalera@uom.gr 4 η Διάλεξη Τμήμα Εφαρμοσμένης Πληροφορικής, Παν. Μακεδονίας 2 Knapsack Problem, (1/9) Ένας επενδυτής διαθέτει ένα χρηματικό
Συστήματα Παραγωγής ΠΑΡΑΔΕΙΓΜΑ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ
 Συστήματα Παραγωγής ΠΑΡΑΔΕΙΓΜΑ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Περιεχόμενα 1 Γενικά στοιχεία γραμμικού προγραμματισμού 2 Παράδειγμα γραμμικού προγραμματισμού και γραφικής επίλυσης του 3 Γραμμικός προγραμματισμός
Συστήματα Παραγωγής ΠΑΡΑΔΕΙΓΜΑ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Περιεχόμενα 1 Γενικά στοιχεία γραμμικού προγραμματισμού 2 Παράδειγμα γραμμικού προγραμματισμού και γραφικής επίλυσης του 3 Γραμμικός προγραμματισμός
Παρουσίαση: Γραμμικός Προγραμματισμός (Αλγόριθμος Simplex). Λύση δυο προβλημάτων με χρήση της μεθόδου simplex και το excel.
 Παρουσίαση: Γραμμικός Προγραμματισμός (Αλγόριθμος Simplex). Λύση δυο προβλημάτων με χρήση της μεθόδου simplex και το excel. Γκούμας Στράτος. Πτυχιούχος Οικονομολόγος. MSc Εφαρμοσμένη Οικονομική και Χρηματοοικονομική
Παρουσίαση: Γραμμικός Προγραμματισμός (Αλγόριθμος Simplex). Λύση δυο προβλημάτων με χρήση της μεθόδου simplex και το excel. Γκούμας Στράτος. Πτυχιούχος Οικονομολόγος. MSc Εφαρμοσμένη Οικονομική και Χρηματοοικονομική
Ποσοτικές Μέθοδοι στη Διοίκηση Έργων (Y100)
 Μεταπτυχιακό Πρόγραμμα Σπουδών Διοίκηση και Διαχείριση Έργων και Προγραμμάτων Ποσοτικές Μέθοδοι στη Διοίκηση Έργων (Y100) Μέρος ΙΙ Τεχνικές Μαθηματικού Προγραμματισμού Μαθηματικά Μοντέλα Εισαγωγή Μεθοδολογία
Μεταπτυχιακό Πρόγραμμα Σπουδών Διοίκηση και Διαχείριση Έργων και Προγραμμάτων Ποσοτικές Μέθοδοι στη Διοίκηση Έργων (Y100) Μέρος ΙΙ Τεχνικές Μαθηματικού Προγραμματισμού Μαθηματικά Μοντέλα Εισαγωγή Μεθοδολογία
Τμήμα Μηχανικών Πληροφορικής ΤΕ Δυϊκότητα. Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα. τελευταία ενημέρωση: 1/12/2016
 Τμήμα Μηχανικών Πληροφορικής ΤΕ 2016-2017 Δυϊκότητα Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα τελευταία ενημέρωση: 1/12/2016 1 Το δυϊκό πρόβλημα Για κάθε πρόβλημα Γραμμικού Προγραμματισμού υπάρχει
Τμήμα Μηχανικών Πληροφορικής ΤΕ 2016-2017 Δυϊκότητα Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα τελευταία ενημέρωση: 1/12/2016 1 Το δυϊκό πρόβλημα Για κάθε πρόβλημα Γραμμικού Προγραμματισμού υπάρχει
Βασίλειος Μαχαιράς Πολιτικός Μηχανικός Ph.D.
 Βασίλειος Μαχαιράς Πολιτικός Μηχανικός Ph.D. Μη γραμμικός προγραμματισμός: βελτιστοποίηση με περιορισμούς Πανεπιστήμιο Θεσσαλίας Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής Διάλεξη 9-10 η /2017 Τι παρουσιάστηκε
Βασίλειος Μαχαιράς Πολιτικός Μηχανικός Ph.D. Μη γραμμικός προγραμματισμός: βελτιστοποίηση με περιορισμούς Πανεπιστήμιο Θεσσαλίας Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής Διάλεξη 9-10 η /2017 Τι παρουσιάστηκε
4.γ. μερική επανάληψη, εισαγωγή στη βελτιστοποίηση υδατικών συστημάτων. Δρ Μ.Σπηλιώτης
 4.γ. μερική επανάληψη, εισαγωγή στη βελτιστοποίηση υδατικών συστημάτων Δρ Μ.Σπηλιώτης Ολοκληρωμένη διαχείριση υδατικών πόρων (integrated water resources management), έμφαση στην εξέταση όλων των πτυχών
4.γ. μερική επανάληψη, εισαγωγή στη βελτιστοποίηση υδατικών συστημάτων Δρ Μ.Σπηλιώτης Ολοκληρωμένη διαχείριση υδατικών πόρων (integrated water resources management), έμφαση στην εξέταση όλων των πτυχών
Πληροφοριακά Συστήματα Διοίκησης. Εισαγωγή στον Γραμμικό Προγραμματισμό
 Πληροφοριακά Συστήματα Διοίκησης Εισαγωγή στον Γραμμικό Προγραμματισμό Τι είναι ο Γραμμικός Προγραμματισμός; Είναι το σημαντικότερο μοντέλο στη Λήψη Αποφάσεων Αντικείμενό του η «άριστη» κατανομή περιορισμένων
Πληροφοριακά Συστήματα Διοίκησης Εισαγωγή στον Γραμμικό Προγραμματισμό Τι είναι ο Γραμμικός Προγραμματισμός; Είναι το σημαντικότερο μοντέλο στη Λήψη Αποφάσεων Αντικείμενό του η «άριστη» κατανομή περιορισμένων
Optimization, PSO) DE [1, 2, 3, 4] PSO [5, 6, 7, 8, 9, 10, 11] (P)
![Optimization, PSO) DE [1, 2, 3, 4] PSO [5, 6, 7, 8, 9, 10, 11] (P) Optimization, PSO) DE [1, 2, 3, 4] PSO [5, 6, 7, 8, 9, 10, 11] (P)](/thumbs/85/92153760.jpg) ( ) 1 ( ) : : (Differential Evolution, DE) (Particle Swarm Optimization, PSO) DE [1, 2, 3, 4] PSO [5, 6, 7, 8, 9, 10, 11] 2 2.1 (P) (P ) minimize f(x) subject to g j (x) 0, j = 1,..., q h j (x) = 0, j
( ) 1 ( ) : : (Differential Evolution, DE) (Particle Swarm Optimization, PSO) DE [1, 2, 3, 4] PSO [5, 6, 7, 8, 9, 10, 11] 2 2.1 (P) (P ) minimize f(x) subject to g j (x) 0, j = 1,..., q h j (x) = 0, j
ΗΜΥ 325: Επαναληπτικές Μέθοδοι. Διδάσκων: Χρίστος Παναγιώτου
 ΗΜΥ 325: Επαναληπτικές Μέθοδοι Διδάσκων: Χρίστος Παναγιώτου ΗΜΥ 325: Επαναληπτικές Μέθοδοι. A. Levitin, Introduction to the Design and Analysis of Algorithms, 2 nd Ed. Περίληψη µαθήµατος Επιπρόσθετες Πληροφορίες
ΗΜΥ 325: Επαναληπτικές Μέθοδοι Διδάσκων: Χρίστος Παναγιώτου ΗΜΥ 325: Επαναληπτικές Μέθοδοι. A. Levitin, Introduction to the Design and Analysis of Algorithms, 2 nd Ed. Περίληψη µαθήµατος Επιπρόσθετες Πληροφορίες
Επιχειρησιακή Έρευνα
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Επιχειρησιακή Έρευνα Ενότητα #3: Ασκήσεις Αθανάσιος Σπυριδάκος Καθηγητής Τμήμα Διοίκησης Επιχειρήσεων Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Επιχειρησιακή Έρευνα Ενότητα #3: Ασκήσεις Αθανάσιος Σπυριδάκος Καθηγητής Τμήμα Διοίκησης Επιχειρήσεων Άδειες Χρήσης Το παρόν εκπαιδευτικό
Διαχείριση Ταμιευτήρα
 Διαχείριση Ταμιευτήρα Μονοκριτηριακή βελτιστοποίηση Διαχείριση υδατικών πόρων Ανάγκη σύνθεσης επιστημών Σημερινό μάθημα: έμφαση στη χρήση εννοιών και μεθόδων από την επιχειρησιακή έρευνα Κουτσογιάννης,
Διαχείριση Ταμιευτήρα Μονοκριτηριακή βελτιστοποίηση Διαχείριση υδατικών πόρων Ανάγκη σύνθεσης επιστημών Σημερινό μάθημα: έμφαση στη χρήση εννοιών και μεθόδων από την επιχειρησιακή έρευνα Κουτσογιάννης,
Η γραφική μέθοδος επίλυσης προβλημάτων Γραμμικού Προγραμματισμού
 Η γραφική μέθοδος επίλυσης προβλημάτων Γραμμικού Προγραμματισμού Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα Τμήμα Μηχανικών Πληροφορικής ΤΕ 2016-2017 τελευταία ενημέρωση: 21/10/2016 1 Γραφική μέθοδος
Η γραφική μέθοδος επίλυσης προβλημάτων Γραμμικού Προγραμματισμού Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα Τμήμα Μηχανικών Πληροφορικής ΤΕ 2016-2017 τελευταία ενημέρωση: 21/10/2016 1 Γραφική μέθοδος
ΕΥΧΑΡΙΣΤΙΕΣ. Θεσσαλονίκη, Δεκέμβριος 2005. Κώστας Δόσιος
 ΕΥΧΑΡΙΣΤΙΕΣ Μου δίνεται η ευκαιρία με την περάτωση της παρούσης διδακτορικής διατριβής να σημειώσω ότι, είναι ιδιαίτερα δύσκολο και κοπιαστικό να ολοκληρώσεις το έργο που ξεκινάς κάποια στιγμή έχοντας
ΕΥΧΑΡΙΣΤΙΕΣ Μου δίνεται η ευκαιρία με την περάτωση της παρούσης διδακτορικής διατριβής να σημειώσω ότι, είναι ιδιαίτερα δύσκολο και κοπιαστικό να ολοκληρώσεις το έργο που ξεκινάς κάποια στιγμή έχοντας
Αλγοριθμικές Τεχνικές. Brute Force. Διαίρει και Βασίλευε. Παράδειγμα MergeSort. Παράδειγμα. Τεχνικές Σχεδιασμού Αλγορίθμων
 Τεχνικές Σχεδιασμού Αλγορίθμων Αλγοριθμικές Τεχνικές Παύλος Εφραιμίδης, Λέκτορας http://pericles.ee.duth.gr Ορισμένες γενικές αρχές για τον σχεδιασμό αλγορίθμων είναι: Διαίρει και Βασίλευε (Divide and
Τεχνικές Σχεδιασμού Αλγορίθμων Αλγοριθμικές Τεχνικές Παύλος Εφραιμίδης, Λέκτορας http://pericles.ee.duth.gr Ορισμένες γενικές αρχές για τον σχεδιασμό αλγορίθμων είναι: Διαίρει και Βασίλευε (Divide and
I student. Μεθοδολογική προσέγγιση και απαιτήσεις για την ανάπτυξη των αλγορίθμων δρομολόγησης Χρυσοχόου Ευαγγελία Επιστημονικός Συνεργάτης ΙΜΕΤ
 I student Μεθοδολογική προσέγγιση και απαιτήσεις για την ανάπτυξη των αλγορίθμων δρομολόγησης Χρυσοχόου Ευαγγελία Επιστημονικός Συνεργάτης ΙΜΕΤ Ινστιτούτο Bιώσιμης Κινητικότητας και Δικτύων Μεταφορών (ΙΜΕΤ)
I student Μεθοδολογική προσέγγιση και απαιτήσεις για την ανάπτυξη των αλγορίθμων δρομολόγησης Χρυσοχόου Ευαγγελία Επιστημονικός Συνεργάτης ΙΜΕΤ Ινστιτούτο Bιώσιμης Κινητικότητας και Δικτύων Μεταφορών (ΙΜΕΤ)
Τ.Ε.Ι. ΑΝΑΤΟΛΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΚΑΙ ΘΡΑΚΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ
 Τ.Ε.Ι. ΑΝΑΤΟΛΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΚΑΙ ΘΡΑΚΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΕΙΣΗΓΗΤΗΣ: Δρ. Ιωάννης Σ. Τουρτούρας Μηχανικός Παραγωγής & Διοίκησης Δ.Π.Θ. Χρηματοδότηση Το παρόν εκπαιδευτικό
Τ.Ε.Ι. ΑΝΑΤΟΛΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΚΑΙ ΘΡΑΚΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΕΙΣΗΓΗΤΗΣ: Δρ. Ιωάννης Σ. Τουρτούρας Μηχανικός Παραγωγής & Διοίκησης Δ.Π.Θ. Χρηματοδότηση Το παρόν εκπαιδευτικό
Δομές Δεδομένων και Αλγόριθμοι
 Δομές Δεδομένων και Αλγόριθμοι Χρήστος Γκόγκος ΤΕΙ Ηπείρου Χειμερινό Εξάμηνο 2014-2015 Παρουσίαση 1 Εισαγωγή 1 / 14 Δομές Δεδομένων και Αλγόριθμοι Δομή Δεδομένων Δομή δεδομένων είναι ένα σύνολο αποθηκευμένων
Δομές Δεδομένων και Αλγόριθμοι Χρήστος Γκόγκος ΤΕΙ Ηπείρου Χειμερινό Εξάμηνο 2014-2015 Παρουσίαση 1 Εισαγωγή 1 / 14 Δομές Δεδομένων και Αλγόριθμοι Δομή Δεδομένων Δομή δεδομένων είναι ένα σύνολο αποθηκευμένων
Διαδικασία μετατροπής σε τυπική μορφή
 ΤΕΙ Δυτικής Μακεδονίας -Τμήμα Διοίκησης επιχειρήσεων- Μάθημα: Ποσοτικές μέθοδοι στη διοίκηση επιχειρήσεων- ΣΤ Εξάμηνο Ημερομηνία: Τρίτη 25 ΑΠΡ 2017, 1 η γραπτή Πρόοδος Εκπαιδευτής: Βασίλειος Ισμυρλής,
ΤΕΙ Δυτικής Μακεδονίας -Τμήμα Διοίκησης επιχειρήσεων- Μάθημα: Ποσοτικές μέθοδοι στη διοίκηση επιχειρήσεων- ΣΤ Εξάμηνο Ημερομηνία: Τρίτη 25 ΑΠΡ 2017, 1 η γραπτή Πρόοδος Εκπαιδευτής: Βασίλειος Ισμυρλής,
ΜΑΘΗΜΑ: Εισαγωγή στις Αρχές της Επιστήμης των Η/Υ. 1 η ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ
 ΜΑΘΗΜΑ: Εισαγωγή στις Αρχές της Επιστήμης των Η/Υ 1 η ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Στόχος Θεματικής Ενότητας Οι μαθητές να περιγράφουν τους βασικούς τομείς της Επιστήμης των Υπολογιστών και να μπορούν
ΜΑΘΗΜΑ: Εισαγωγή στις Αρχές της Επιστήμης των Η/Υ 1 η ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Στόχος Θεματικής Ενότητας Οι μαθητές να περιγράφουν τους βασικούς τομείς της Επιστήμης των Υπολογιστών και να μπορούν
ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ (Γ.Π.).) (LINEAR PROGRAMMING)
 ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ (Γ.Π.).) (LINEAR PROGRAMMING) Δρ. Βασιλική Καζάνα Αναπλ. Καθηγήτρια ΤΕΙ Καβάλας, Τμήμα Δασοπονίας & Διαχείρισης Φυσικού Περιβάλλοντος Δράμας Εργαστήριο Δασικής Διαχειριστικής
ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ (Γ.Π.).) (LINEAR PROGRAMMING) Δρ. Βασιλική Καζάνα Αναπλ. Καθηγήτρια ΤΕΙ Καβάλας, Τμήμα Δασοπονίας & Διαχείρισης Φυσικού Περιβάλλοντος Δράμας Εργαστήριο Δασικής Διαχειριστικής
Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος
 Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος Χιωτίδης Γεώργιος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος Χιωτίδης Γεώργιος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΒΕΛΤΙΣΤΟΣ ΣΧΕΔΙΑΣΜΟΣ ΤΩΝ ΚΑΤΑΣΚΕΥΩΝ. Δρ. Πολ. Μηχ. Κόκκινος Οδυσσέας
 ΒΕΛΤΙΣΤΟΣ ΣΧΕΔΙΑΣΜΟΣ ΤΩΝ ΚΑΤΑΣΚΕΥΩΝ Δρ. Πολ. Μηχ. Κόκκινος Οδυσσέας Σχεδιασμός αντικειμένων, διεργασιών, δραστηριοτήτων (π.χ. τεχνικά έργα, έπιπλα, σκεύη κτλ) ΠΡΟΚΑΤΑΡΚΤΙΚΗ ΜΕΛΕΤΗ (conceptual design) ΠΡΟΜΕΛΕΤΗ
ΒΕΛΤΙΣΤΟΣ ΣΧΕΔΙΑΣΜΟΣ ΤΩΝ ΚΑΤΑΣΚΕΥΩΝ Δρ. Πολ. Μηχ. Κόκκινος Οδυσσέας Σχεδιασμός αντικειμένων, διεργασιών, δραστηριοτήτων (π.χ. τεχνικά έργα, έπιπλα, σκεύη κτλ) ΠΡΟΚΑΤΑΡΚΤΙΚΗ ΜΕΛΕΤΗ (conceptual design) ΠΡΟΜΕΛΕΤΗ
Γραμμικός Προγραμματισμός
 Γραμμικός Προγραμματισμός Άλλες μορφές ΓΠ Αναθεωρημένη SIMPLEX Interior Point Approach Sensitivity Analysis (Παράδειγμα) Η Μέθοδος Simple Η μέθοδος υποθέτει ότι το πρόβλημα είναι διατυπωμένο στην τυπική
Γραμμικός Προγραμματισμός Άλλες μορφές ΓΠ Αναθεωρημένη SIMPLEX Interior Point Approach Sensitivity Analysis (Παράδειγμα) Η Μέθοδος Simple Η μέθοδος υποθέτει ότι το πρόβλημα είναι διατυπωμένο στην τυπική
max c 1 x 1 + c 2 x c n x n υπό a 11 x 1 + a 12 x a 1n x n b 1 a 21 x 1 + a 22 x a 2n x n b 2 a m1 x 1 + a m2 x a mn x n b m
 Υπολογιστικές Μέθοδοι στη Θεωρία Αποφάσεων Ενότητα 10 Εισαγωγή στον Ακέραιο Προγραμματισμό Αντώνης Οικονόμου Τμήμα Μαθηματικών Πανεπιστήμιο Αθηνών Προπτυχιακό πρόγραμμα σπουδών 29 Φεβρουαρίου 2016 Προβλήματα
Υπολογιστικές Μέθοδοι στη Θεωρία Αποφάσεων Ενότητα 10 Εισαγωγή στον Ακέραιο Προγραμματισμό Αντώνης Οικονόμου Τμήμα Μαθηματικών Πανεπιστήμιο Αθηνών Προπτυχιακό πρόγραμμα σπουδών 29 Φεβρουαρίου 2016 Προβλήματα
Τ.Ε.Ι. ΑΝΑΤΟΛΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΚΑΙ ΘΡΑΚΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΜΑΘΗΜΑΤΙΚΗ ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΠΡΟΒΛΗΜΑΤΩΝ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ
 Τ.Ε.Ι. ΑΝΑΤΟΛΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΚΑΙ ΘΡΑΚΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΜΑΘΗΜΑΤΙΚΗ ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΠΡΟΒΛΗΜΑΤΩΝ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΕΙΣΗΓΗΤΗΣ: Δρ. Ιωάννης Σ. Τουρτούρας Μηχανικός Παραγωγής & Διοίκησης
Τ.Ε.Ι. ΑΝΑΤΟΛΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΚΑΙ ΘΡΑΚΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΜΑΘΗΜΑΤΙΚΗ ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΠΡΟΒΛΗΜΑΤΩΝ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΕΙΣΗΓΗΤΗΣ: Δρ. Ιωάννης Σ. Τουρτούρας Μηχανικός Παραγωγής & Διοίκησης
Αλγοριθμικές Τεχνικές
 Αλγοριθμικές Τεχνικές Παύλος Εφραιμίδης, Λέκτορας http://pericles.ee.duth.gr Αλγοριθμικές Τεχνικές 1 Τεχνικές Σχεδιασμού Αλγορίθμων Ορισμένες γενικές αρχές για τον σχεδιασμό αλγορίθμων είναι: Διαίρει και
Αλγοριθμικές Τεχνικές Παύλος Εφραιμίδης, Λέκτορας http://pericles.ee.duth.gr Αλγοριθμικές Τεχνικές 1 Τεχνικές Σχεδιασμού Αλγορίθμων Ορισμένες γενικές αρχές για τον σχεδιασμό αλγορίθμων είναι: Διαίρει και
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ. Πτυχιακή εργασία
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ Πτυχιακή εργασία ΕΠΙΛΥΣΗ ΤΟΥ ΠΡΟΒΛΗΜΑΤΟΣ ΧΡΟΝΟΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΜΕΤΑΔΟΣΗΣ ΣΕ ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ ΜΕ ΣΥΣΚΕΥΕΣ ΔΙΑΚΡΙΤΩΝ ΤΙΜΩΝ ΙΣΧΥΟΣ ΜΕ ΤΗ ΧΡΗΣΗ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ Πτυχιακή εργασία ΕΠΙΛΥΣΗ ΤΟΥ ΠΡΟΒΛΗΜΑΤΟΣ ΧΡΟΝΟΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΜΕΤΑΔΟΣΗΣ ΣΕ ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ ΜΕ ΣΥΣΚΕΥΕΣ ΔΙΑΚΡΙΤΩΝ ΤΙΜΩΝ ΙΣΧΥΟΣ ΜΕ ΤΗ ΧΡΗΣΗ
Scheduling on Unrelated Parallel Machines
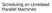 Scheduling on Unrelated Parallel Machines Problem Formulation Given a set J of jobs, a set M of machines, and for each j J and i M, pij Z+, is the time taken to process job j on machine i, the problem
Scheduling on Unrelated Parallel Machines Problem Formulation Given a set J of jobs, a set M of machines, and for each j J and i M, pij Z+, is the time taken to process job j on machine i, the problem
Η γραφική μέθοδος επίλυσης προβλημάτων Γραμμικού Προγραμματισμού
 Η γραφική μέθοδος επίλυσης προβλημάτων Γραμμικού Προγραμματισμού Γεωργία Φουτσιτζή-Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα Τμήμα Μηχανικών Πληροφορικής ΤΕ 2017-2018 τελευταία ενημέρωση: 21/10/2016
Η γραφική μέθοδος επίλυσης προβλημάτων Γραμμικού Προγραμματισμού Γεωργία Φουτσιτζή-Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα Τμήμα Μηχανικών Πληροφορικής ΤΕ 2017-2018 τελευταία ενημέρωση: 21/10/2016
Asset & Liability Management Διάλεξη 3
 Πανεπιστήμιο Πειραιώς ΠΜΣ στην «Αναλογιστική Επιστήμη και Διοικητική Κινδύνου» Asset & Liability Management Διάλεξη 3 Cash-flow matching Μιχάλης Ανθρωπέλος anthropel@unipi.gr http://web.xrh.unipi.gr/faculty/anthropelos
Πανεπιστήμιο Πειραιώς ΠΜΣ στην «Αναλογιστική Επιστήμη και Διοικητική Κινδύνου» Asset & Liability Management Διάλεξη 3 Cash-flow matching Μιχάλης Ανθρωπέλος anthropel@unipi.gr http://web.xrh.unipi.gr/faculty/anthropelos
Προβλήματα Μεταφορών (Transportation)
 Προβλήματα Μεταφορών (Transportation) Παραδείγματα Διατύπωση Γραμμικού Προγραμματισμού Δικτυακή Διατύπωση Λύση Γενική Μέθοδος Simplex Μέθοδος Simplex για Προβλήματα Μεταφοράς Παράδειγμα: P&T Co ΗεταιρείαP&T
Προβλήματα Μεταφορών (Transportation) Παραδείγματα Διατύπωση Γραμμικού Προγραμματισμού Δικτυακή Διατύπωση Λύση Γενική Μέθοδος Simplex Μέθοδος Simplex για Προβλήματα Μεταφοράς Παράδειγμα: P&T Co ΗεταιρείαP&T
Ένα πρόβλημα κατάρτισης προγράμματος εργασίας.
 Ένα πρόβλημα κατάρτισης προγράμματος εργασίας. Έστω ένα πλήθος πληρωμάτων I, σε καθένα από τα οποία ανατίθεται καθημερινά κάποιο καθήκον (εργασία, βάρδια), από ένα συνολικό πλήθος Κ εργασιών. Ο στόχος
Ένα πρόβλημα κατάρτισης προγράμματος εργασίας. Έστω ένα πλήθος πληρωμάτων I, σε καθένα από τα οποία ανατίθεται καθημερινά κάποιο καθήκον (εργασία, βάρδια), από ένα συνολικό πλήθος Κ εργασιών. Ο στόχος
Θεωρία Αποφάσεων και Βελτιστοποίηση
 Θεωρία Αποφάσεων και Βελτιστοποίηση http://www.di.uoa.gr/ telelis/opt.html Ορέστης Τελέλης telelis@di.uoa.gr Τµήµα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήµιο Αθηνών Θεωρία Αποφάσεων και Βελτιστοποίηση
Θεωρία Αποφάσεων και Βελτιστοποίηση http://www.di.uoa.gr/ telelis/opt.html Ορέστης Τελέλης telelis@di.uoa.gr Τµήµα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήµιο Αθηνών Θεωρία Αποφάσεων και Βελτιστοποίηση
Εργαστηριακές Ασκήσεις
 EΘNIKO ΜEΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Ανάλυσης, Σχεδιασμού & Ανάπτυξης Διεργασιών & Συστημάτων Υπολογιστικές Μέθοδοι Ανάλυσης και Σχεδιασμού Εργαστηριακές Ασκήσεις Διδάσκων: Α.
EΘNIKO ΜEΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Ανάλυσης, Σχεδιασμού & Ανάπτυξης Διεργασιών & Συστημάτων Υπολογιστικές Μέθοδοι Ανάλυσης και Σχεδιασμού Εργαστηριακές Ασκήσεις Διδάσκων: Α.
