Biokemija I, 25. predavanje 1. del, , A. Videtič Paska. Proteini - splošno
|
|
|
- Μέλισσα Παπαντωνίου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Biokemija I, 25. predavanje 1. del, , A. Videtič Paska Proteini - splošno Razdelitev po strukturi in funkciji. Ravni proteinske strukture: - primarna in - sekundarna struktura
2 Sinteza proteinov prevajanje (translacija) DNA primarni transkript (mrna) mrna se procesira mrna se prevede v proteine nekatere AK se modificirajo
3 gr. proteios glavni oz. prvi v vrsti Proteini - splošno So polimeri aminokislin (AK) Večinoma sestavljeni iz 20 L-AK ki se med seboj povezujejo s peptidno vezjo So najpogostejša makromolekula v celici ali delih celice Preko proteinov se izraža genetska informacija So zelo raznoliki (po velikosti, strukturi,...) zato lahko opravljajo številne različne vloge Boyer: Temelji biokemije / Študentska založba, Ljubljana, 2005 a) luciferin b) hemoglobin c) keratin Lehninger: Priciples of Biochemistry / W. H. Freeman and Company, New York, 2008 Vsi proteini, ki so kodirani v DNA določenega organizma proteom Poznavanje vloge vseh proteinov kodiranih v genomu proteomika
4 Boyer: Temelji biokemije / Študentska založba, Ljubljana, 2005
5 AK se med seboj povezujejo s peptidno vezjo peptidna vez Boyer: Temelji biokemije / Študentska založba, Ljubljana, 2005 Nastanek peptidne vezi
6 Peptidi in proteini Peptidi so krajše molekule, navadno od 2 do približno 100 AK. Tudi najmanjši peptidi imajo pomembno biološko vlogo: Peptidna hormona umetno sladilo Polipeptidi so sestavljeni z 10 do 100 AK (M r < Da ali 10 kda). Proteini so velike molekule, ki imajo od 100 do nekaj 1000 AK (večina ~ 2000 AK; M r > Da ali 10 kda). Proteini so lahko sestavljeni iz več polipeptidnih verig (podenot). Glede na kemijsko sestavo so proteini lahko enostavni ali sestavljeni (= konjugirani vsebujejo neproteinske elemente, ki jih imenujemo prostetične skupine). Glede na obliko molekule ločimo globulane in fibrilarne proteine. Boyer: Temelji biokemije / Študentska založba, Ljubljana, 2005
7 Latnosti peptidov in proteinov: molekulska masa Enota za molekulsko maso proteinov je dalton (Da), ki ustreza masi enega vodikovega atoma Iz števila AK lahko določimo M r proteina in obratno: Povprečna M r vseh 20 AK je 138 Povprečna M r AK v proteinih je 128 Ob formaciji peptidne vezi se odcepi voda (M r H 2 O = 18) = 110 M r proteina = št. AK ostankov * 110 in Št. AK ostankov = M r proteina / 110
8 Lastnosti proteinov: kemijska sestava Glede na kemijsko sestavo so proteini lahko enostavni ali sestavljeni (= konjugirani vsebujejo molekule, ki niso AK in jih imenujemo prostetične skupine). Vrsta proteina Prosteična skupina Primer Lipoproteini Lipidi β 1 -lipoprotein v krvi Glikoproteini Ogljikovi hidrati Imunoglobulin G Fosfoproteini Fosfatna skupina Kazein v mleku Hemoproteini Hem (železo in protoporfirin) Hemoglobin Flavoproteini Flavinski nukleotidi Sukcinatna dehidrogenaza Metaloproteini Lehninger: Priciples of Biochemistry / W. H. Freeman and Company, New York, 2008 Železo Cink Kalcij Feritin Alkoholna dehidrogenaza Kalmodulin
9 Lastnosti proteinov: oblika in topnost Globularni proteini Topni v H 2 O Urejeni ter dinamični in fleksibilni Dinamična vloga Vrsta proteina Hemoglobin Mioglobin Ribonukleaza Lizocim Citokrom c Imunoglobulin Aktin Vloga Transport kisika Skladiščenje kisika Hidroliza RNA Hidroliza bakterijske stene Transport elektronov Obramba (protitelesa) Gibanje (mišični proteini) Fibrilarni proteini Netopni v H 2 O Urejena in toga konformacija Velika natezna čvrstost Vrsta proteina Kolagen Keratin Miozin Elastin Vloga Strukturni protein Strukturni protein Gibanje (mišični protein) Prožnost Boyer: Temelji biokemije / Študentska založba, Ljubljana, 2005
10 Primerjava nekaterih lastnosti proteinov Protein Citokrom C (človeški) Hemoglobin (človeški) Serumski albumin (človeški) Imunoglobulin G (človeški) Molekulska masa (Da) Št. AK ostankov Feritrin RNA polimeraza (E. coli) Apolipoprotein B (človeški) Glutamin sintetaza (E. coli) Titin (človeški) Št. polipeptidnih verig
11 Proteini se med seboj razlikujejo po aminokislinski sestavi Lehninger: Priciples of Biochemistry / W. H. Freeman and Company, New York, 2008 Aminokislina Goveji citokrom c Ala 6 22 Arg 2 4 Asn 5 14 Asp 3 9 Cys 2 10 Gln 3 10 Glu 9 5 Gly His 3 2 Ile 6 10 Leu 6 19 Lys Met 2 2 Phe 4 6 Pro 4 9 Ser 1 28 Thr 8 23 Trp 1 8 Tyr 4 4 Val 3 23 Skupaj Goveji kimotripsinogen
12 Razvrstitev proteinov glede na njihove biološke vloge Katalitska (encimi) Oporna (strukturni proteini; npr. lasje, nohti, vezivno tkivo, perje,...) Obrambna (protitelesa, antibiotiki) Prenašalna (transportni proteini) Skladiščna (proteini v mleku, v jajčnem beljaku) Signalna (peptidni hormoni) Gibalna (krčenje mišic) Druge vloge (lučka pri kresnički)
13 Ravni proteinske strukture Primarna struktura AK zaporedje Sekundarna stuktura α-vijačnica, β-struktura, β-zavoj Terciarna struktura trodimenzionalna (3D) struktura predstavlja zvitje proteina v prostoru Kvartarna struktura združevanje več podenot proteina Boyer: Temelji biokemije / Študentska založba, Ljubljana, 2005
14 Primarna struktura proteinov Primarna struktura proteinov = zaporedje AK ostankov v polipeptidu. Določene AK in njihova zaporedja favorizirajo nastanek spefičnih sekundarnih struktur. Primarna struktura (značilna sestava in zaporedje AK ostankov) določa tridimenzionalno strukturo. Primarna struktura proteina določa njegovo funkcijo.
15 Primarna struktura proteinov Določanje AK sestave: a) 6 M HCl, 12h, 110 C b) Barvanje z ninhidrinom c) 1-fluoro-2,4-dinitrobenzen (FDNB; določanje AK na N-koncu) ločevanje AK z ionsko izmenjevalno kormatografijo ali s HPLC Boyer: Temelji biokemije / Študentska založba, Ljubljana, 2005
16 Primarna struktura proteinov Določanje AK zaporedja: Direktni (a, b) in indirektni (c) način določanja a) Edmanova degradacija b) Masna spektrometrija c) Sekvenciranje gena Odcepljanje z N-konca peptida Boyer: Temelji biokemije / Študentska založba, Ljubljana, 2005 Lehninger: Priciples of Biochemistry / W. H. Freeman and Company, New York, 2008
17 Pomen poznavanja aminokislinskih zaporedij Ugotavljanje razmerij med proteini in njihovo razvrščanje po podobnosti v družine (vsaj 25% podobnost v zaporedju AK ostankov in/ali v strukturnih in funkcijskih lasnostih; npr. globinska družina) in naddružine (dve ali več družin z malo podobnosti v AK zaporedju in/ali s podobnim strukturnim motivom in/ali funkcijskimi podobnostmi) Sledenje molekularni evoluciji in ugotavljanje sorodnosti dveh organizmov Proučevanje z vidika sprememb (zamenjav AK), ki vodijo do nepravilnega delovanja proteinov bolezni Sklepanje o morebitni trodimenzionalni strukturi in s tem funkciji proteina Informacije o vseh znanih proteinih v podatkovnih zbirkah Lehninger: Priciples of Biochemistry / W. H. Freeman and Company, New York, 2008 Evolucijsko drevo bakterij na osnovi sekvence GroEL
18 Elementi (urejene) sekundarne strukture: desnosučna α-vijačnica Med N-H in C=O oddaljenima štiri AK ostanke v verigi se tvori maksimalno število vodikovih vezi, ki strukturo stabilizirajo Na vsak obrat vijačnice je 3,6 AK-ostankov Stranske verige štrlijo iz vijačnice Koti: φ med -120 in -60 ; ψ = -60 Pogled v smeri osi vijačnice Pogled s strani vijačnice Vodikove vezi v vijačnici Lehninger: Priciples of Biochemistry / W. H. Freeman and Company, New York, 2008 Boyer: Temelji biokemije / Študentska založba, Ljubljana, 2005
19 Dejavniki, ki vplivajo na stabilnost α-vijačnice Nagnjenje AK ostanka k tvorbi α-vijačnice AK ostanki z nabojem/aromatski pogosto 3-4 AK narazen vzpostavitev elektrostatskih ali hidrofobnih interakcij Sterično oviranje med velikimi stranskimi skupinami AK ostankov v polipeptidu Pro in Gly redko v α-vijačnici Dipolni moment na koncih α-vijačnice: N-konec več negativno nabitih AK ostankov C-konec več pozitivno nabitih AK ostankov N-konec Lehninger: Priciples of Biochemistry / W. H. Freeman and Company, New York, 2008 C-konec
20 Elementi (urejene) sekundarne strukture: β-struktura - Je lahko a) paralelna (koti φ = -119 in ψ = 113 ) ali b) antiparalelna (koti φ = -139 in ψ = 135 ) C N C N -Stabilizirana je s H-vezmi - Stranske skupine izmenično štrlijo nad oz. pod strukturo -V β-strukturi keratinov sta pogosti AK Gly in Ala C N N C Lehninger: Priciples of Biochemistry / W. H. Freeman and Company, New York, 2008
21 Elementi (neurejene) sekundarne strukture: β-zavoj Spremenijo smer polipetidni verigi Povezujejo predele urejenih sekundarnih struktur (α-vijačnice in β-strukture) Sestavljajo ga 4 AK; med 1. in 4. AK ostankom je vodikova vez Pogosti AK Gly in Pro ~ 6 % peptidnih vezi s Pro je v cis konfiguraciji (najpogosteje v β-zavoju) Boyer: Temelji biokemije / Študentska založba, Ljubljana, 2005 Lehninger: Priciples of Biochemistry / W. H. Freeman and Company, New York, 2008
22 Relativna verjetnost za pojavljanje določenega AK ostanka v katerem izmed treh elementov sekundarne strukture Lehninger: Priciples of Biochemistry / W. H. Freeman and Company, New York, 2005
23 Sekundarne strukture v proteinu Zastopanost elementov sekundarne stukture v prionih je povezana z nastankom bolezni.
24 Proteine razdelimo po strukturi na: Globularni in fibrilarni Povzetek Proteine razdelimo po kemijski sestavi na: Enostavni in sestavljeni Funkcije proteinov: katalitska, transportna, gibalna, oporna, obrambna, skladiščna, signalna Ravni proteinske strukture: - primarna: - določa 3D strukturo proteina - ugotavljanje evolucijske podonosti organizmov - razvrščanje proteinov v družine in naddružine - povezovanje boleznimi - sekundarna: - elementi: α-vijačnica, β-struktura, β-zavoj - določene AK imajo preferenco za določen element - določimo jo lahko z definiranjem kotov φ in ψ
25 Ravni strukture proteinov Primarna struktura: zaporedje aminokislinskih (ak) ostankov v polipeptidni verigi Sekundarna struktura nanaša se na lokalno konformacijo (bližnji ak ostanki) nekaterih delov polipeptida; primeri: - α-desnosučna vijačnica - β-struktura (paralelna, antiparalelna, mešana) - β-zavoj Terciarna struktura trodimenzionalna (3D) struktura polipeptidne verige v prostoru Kvartarna struktura 3D struktura več polipeptidnih verig (podenot), ki sestavljajo molekulo proteina (oligomerni proteini)
26 Terciarna (tridimenzionalna; 3D) struktura proteinov Protein zavzame določeno konformacijo - razporeditev vseh atomov v prostoru. Prehod iz ene konformacije v drugo poteka BREZ prekinitve kovalentnih vezi (rotacije okoli vezi, itd.) 3D struktura je določena z ak zaporedjem polipeptida Izolirani protein običajno obstaja v eni ali le nekaj stabilnih oblikah (nativna konformacija, ki odraža funkcijo proteina; je na najnižjem energijskem nivoju, G min.) Za stabilizacijo strukture so najpomembnejše šibke interakcije in v nekaterih primerih kovalentne disulfidne vezi (-S-S- mostički, npr inzulin) Le nekaj različnih osnovnih strukturnih vzorcev najdemo v tisočih naravnih proteinih Funkcija proteina je odvisna od njegove strukture
27 Stabilnost proteina definiramo kot težnjo po vzdrževanju nativne 3D konformacije Proteini so v nativni konformaciji delno stabilni, G za prehod iz zvitega v nezvito stanje je le kj/mol. Nezvit protein ima veliko konformacijsko entropijo (lahko zavzame veliko število različnih konformacij). Ta entropija, skupaj vodikovimi vezmi nekaterih aminokislinskih radikalov z vodo, vzdržuje nezvito stanje. Kemijske interakcije, ki delujejo proti nezvitemu stanju in stabilizirajo nativno, pravilno zvito konformacijo, so disulfidne vezi in šibke interakcije (vodikove vezi, hidrofobne in elektrostatske interakcije). Največ prispevajo hidrofobne interakcije.
28 Nativna konformacija hipotetičnga proteina, kjer je prikazan pomen nekovalentnih interakcij v 3D strukturi proteina Boyer R: Temelji biokemije, Študentska založba Scripta, Ljubljana 2005
29 Interakcije, ki vzdržujejo konformacijo proteinov Elektrostatske interakcije Vodikove vezi Disulfidni mostiček
30 Določanje tridimenzionalne strukture proteinov z X-žarkovno kristalografijo Prikaz elektronske gostote dela mioglobina Vzorec difrakcije na filmu
31 Določanje tridimenzionalne strukture proteinov z NMR Jedrska magnetna resonanca (NMR), protein v raztopini metoda omogoča identifikacijo različnih konformacij proteina (merjenje jedrnega spinskega kotnega momenta kvantnomehanska funkcija, ki jo vsebujejo nekatera jedra: 1H, 13C, 15N, 10F, 31P)
32 JEDRSKA MAGNETNA RESONANCA (NMR) NMR uporablja lastnost atomskih jeder, da imajo magnetni moment, zaradi česar se v magnetnem polju obnašajo podobno kot magnetna igla. Magnetna igla se v zemeljskem magnetnem polju obrne vedno proti severu, jedrski magnetni moment s spinom 1/2 ( 1 H, 13 C, 15 N, 31 p, 19 F...) pa se v močnem magnetnem polju lahko postavijo samo v smeri magnetnega polja ali pa v nasprotni smeri. Ti dve stanji imata različno energijo. ''Od zunaj'' lahko povzročimo prehajanje jeder iz enega stanja v drugo z uporabo šibkega radiofrekvenčnega magnetnega polja (10 MHz MHz). Kvanti energije, ki jih radiofrekvenčno polje dovaja vzorcu, morajo biti točno enaki energijski razliki med obema jedrskima stanjema. Kadar je ta pogoj izpolnjen - pravimo, da smo v resonanci - jedra absorbirajo energijo radiofrekvenčnega polja, kar zaznamo kot signal (kemijski premik). Pojav sta leta 1946 neodvisno odkrila Felix Bloch in Edward Mill Purcell in za njegovo okritje leta 1952 skupaj prejela Nobelovo nagrado za fiziko.
33 Kako deluje jedrska magnetna resonanca? Resonančna frekvenca je za vsako vrsto jeder drugačna (npr. za 1 H je 90 MHz, za 13 C pa 22.5 MHz). Resonančne frekvence enakih jeder, ki čutijo različna lokalna magnetna polja, so različne. Prav zato se jedrska magnetna resonanca uspešno uporablja v področjih kemije, biologije in farmakologije, kot nedestruktivna metoda pri rutinskih analizah in za študij strukture in dinamike molekul. Protonski NMR spekter aminokislin. (Povzeto po Aldrich knjižnici NMR spektrov.)
34 Zvijanje polipeptidne verige je omejeno z naslednjimi zahtevami: dolžine vezi med atomi in koti med vezmi naj bodo čim manj deformirani atomi se ne morejo približati bolj, kot je vsota njihovih van der Waals-ovih radijev zvitje proteinov je stabilizirano s šibkimi interakcijami (vodikove, hidrofobne, van der Waalsove, ionske interakcije) zaradi omejitev, ki jo predstavlja toga peptidna vez (ni možna rotacija okrog CO-NH vezi!!!), je dovoljena samo rotacija okrog enojnih vezi N-C α in C α -CO Konformacijo peptida definirajo trije torzijski koti: Φ, Ψ kjer vsak kot definira rotacijo okoli ene od treh ponavljajočih vezi. Torzijski kot (dihedral angle) je kot na stiku dveh ravnin. V primeru peptidov so ravnine definirane z dvema zaporednima vektorjema vezi. Trije vektorji vezi lahko definirajo dve ravnini, kjer je centralni vektor skupen obema ravninama.
35 Peptidna vez ima delni značaj dvojne vezi. V polipeptidni verigi rotacija okoli peptidne vezi ni možna. Možne so le nekatere rotacije okoli Φ in Ψ. Ravnotežje med resonančnimi oblikami Φ : (C) - N - C -C Ψ : (N) - C C - N Φ Ψ Φ Ψ Del polipeptidne verige s poudarjenimi ravninami (modro), v katerih ležijo atomi peptidnih vezi
36 Prostorska orientacija atomov peptidne vezi in relativna orientacija ravnin, v katerih ležijo peptidne vezi Cis-trans izomerija peptidne vezi Rotacija okrog enojnih vezi (99,95%) (a) Možne rotacije kotov in za in (b) prepovedana vrednost kotov in zaradi prostorskih (steričnih) ovir
37 Ramachandranov diagram soodvisnost vrednosti kotov Φ in Ψ Dovoljene konformacije L-alanina nedovoljene konformacije 3D
38 Ramachandranov diagram dovoljenih sekundarnih struktur Encim piruvat kinaza Teoretično dovoljene konformacije Realno stanje vsaka točke predstavlja aminokislino. Zajete so vse aminokisline, razen glicina.
39 Terciarna struktura - zvitje proteinov je osnova za strukturno klasifikacijo globularnih proteinov Do danes znanih ~1000 različnih zvitij. Terciarna struktura je bolj ohranjena kot primarna struktura (znana 3D struktura več kot proteinov) Primerjava terciarne strukture proteinov podatki o evolucijski oddaljenosti organizmov Strukturni motivi (zvitja supersekundarna struktura) v različnih proteinih opravljajo podobno funkcijo, npr. vezava ligandov, vezava drugih proteinov... Primeri zvitja proteinov supersekundarna struktura: - - zanka - kot povezava struktur križna povezava struktur -sodček
40 Kvartarna struktura Poliovirus -rotacijska simetrija Oligomerni proteini (več polipeptidnih verig podenot/protomerov, povezanih s šibkimi interakcijami) - dimer - 2 podenoti - oligomer 4-8 podenot (npr. tetramer) -multimer večje št. podenot -različne podenote, asimetrična struktura - enake podenote ali skupki podenot, simetrična struktura; Virus tobačnega mozaika - vijačna simetrija: podenote se dodajajo na način vijačnice
41 Vloga kvartarne strukture Regulatorna vloga: vezava liganda sproži interakcije med podenotami velika sprememba v aktivnosti proteina kot odraz na majhne spremembe konc. regulatornih molekul. (Primer: hemoglobin) Strukturna vloga: asociacija fibrilarnih proteinov v višjo strukturo. (Primer: kolagen) Kataliza večstopenjskih reakcij. (Primer: ribosom) hemoglobin
42 POVZETEK
IZBIRNI PREDMET, APRIL/MAJ 2013 STRUKTURA IN FUNKCIJA PROTEINOV. 2. predavanje: Od 1D do 3D strukture proteinov 1. del.
 IZBIRNI PREDMET, APRIL/MAJ 2013 STRUKTURA IN FUNKCIJA PROTEINOV 2. predavanje: Od 1D do 3D strukture proteinov 1. del Matjaž Zorko E-mail: zorko@mf.uni-lj.si DOSEGLJIVO: http://ibk.mf.uni-lj.si/teaching/objave/izbir1mz.htm
IZBIRNI PREDMET, APRIL/MAJ 2013 STRUKTURA IN FUNKCIJA PROTEINOV 2. predavanje: Od 1D do 3D strukture proteinov 1. del Matjaž Zorko E-mail: zorko@mf.uni-lj.si DOSEGLJIVO: http://ibk.mf.uni-lj.si/teaching/objave/izbir1mz.htm
ZGRADBA PROTEINOV SILE, KI STABILIZIRAJO 3D ZGRADBO PROTEINOV PEPTIDNA VEZ
 ZGRADBA PROTEINOV SILE, KI STABILIZIRAJO 3D ZGRADBO PROTEINOV PEPTIDNA VEZ α-heliks β-nagubana RAVNINA β-obrat STRUKTURNI MOTIVI STABILNOST PROTEINOV KVARTARNA ZGRADBA PROTEINOV ENA ALI VEČ KONFORMACIJ
ZGRADBA PROTEINOV SILE, KI STABILIZIRAJO 3D ZGRADBO PROTEINOV PEPTIDNA VEZ α-heliks β-nagubana RAVNINA β-obrat STRUKTURNI MOTIVI STABILNOST PROTEINOV KVARTARNA ZGRADBA PROTEINOV ENA ALI VEČ KONFORMACIJ
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 5. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 14. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 22. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Funkcijske vrste. Matematika 2. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 2. april Gregor Dolinar Matematika 2
 Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 21. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Tretja vaja iz matematike 1
 Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK
 1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
STRUKTURNE LASTNOSTI AMINOKISLIN
 AMINOKISLINE Amino-karboksilne kisline (izjema: prolin, iminokarboksilna kislina) Vloga aminokislin: 1. Gradniki proteinov 2. Vir energije 3. Izhodišče za sintezo drugih pomembnih biomolekul (nukleinske
AMINOKISLINE Amino-karboksilne kisline (izjema: prolin, iminokarboksilna kislina) Vloga aminokislin: 1. Gradniki proteinov 2. Vir energije 3. Izhodišče za sintezo drugih pomembnih biomolekul (nukleinske
IZPIT IZ ANALIZE II Maribor,
 Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
Pripravili: Ana Bernard in Eva Srečnik Dopolnil: Matic Dolinar
 Pripravili: Ana Bernard in Eva Srečnik Dopolnil: Matic Dolinar Študijsko leto 2011/2012 KAZALO: 1. UVOD V BIOKEMIJO 2. PRENOS BIOLOŠKIH INFORMACIJ: CELIČNA KOMUNIKACIJA 3. BIOLOŠKE MOLEKULE V VODI 4. AMINOKISLINE,
Pripravili: Ana Bernard in Eva Srečnik Dopolnil: Matic Dolinar Študijsko leto 2011/2012 KAZALO: 1. UVOD V BIOKEMIJO 2. PRENOS BIOLOŠKIH INFORMACIJ: CELIČNA KOMUNIKACIJA 3. BIOLOŠKE MOLEKULE V VODI 4. AMINOKISLINE,
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 10. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Funkcije proteinov (pogojene s strukturo)
 Funkcije proteinov (pogojene s strukturo) Oporna funkcija (strukturni proteini, npr keratini, kolagen...) Transport/skladiščenje določenih molekul (ligandov, npr. Hb, Mb) Uravnavanje procesov (DNA-vezavni
Funkcije proteinov (pogojene s strukturo) Oporna funkcija (strukturni proteini, npr keratini, kolagen...) Transport/skladiščenje določenih molekul (ligandov, npr. Hb, Mb) Uravnavanje procesov (DNA-vezavni
Diferencialna enačba, v kateri nastopata neznana funkcija in njen odvod v prvi potenci
 Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
1 Uvod v biokemijo. Slika. Nekakj spoznanj s področja biokemije.
 Univerza na Primorskem, Fakulteta za vede o zdravju Prehransko svetovanje - dietetika, 1. stopenjski študij Predmet: Biokemija, 1. letnik Avtorica: Doc. dr. Zala Jenko Pražnikar 1 Uvod v biokemijo Biokemijo
Univerza na Primorskem, Fakulteta za vede o zdravju Prehransko svetovanje - dietetika, 1. stopenjski študij Predmet: Biokemija, 1. letnik Avtorica: Doc. dr. Zala Jenko Pražnikar 1 Uvod v biokemijo Biokemijo
IZPIT IZ BIOKEMIJE ZA BIOLOGE (1. ROK)
 IZPIT IZ BIOKEMIJE ZA BIOLOGE (1. ROK) 25. 01. 2006. Vpisna številka: Št. točk: Procenti: Ocena: Na vprašanja 1-19 odgovoriš tako, da obkrožiš črko pred odgovorom, za katerega meniš, da je pravilen. Možnih
IZPIT IZ BIOKEMIJE ZA BIOLOGE (1. ROK) 25. 01. 2006. Vpisna številka: Št. točk: Procenti: Ocena: Na vprašanja 1-19 odgovoriš tako, da obkrožiš črko pred odgovorom, za katerega meniš, da je pravilen. Možnih
Sekundarne struktura proteina Fibrilni proteini
 Sekundarne struktura proteina Fibrilni proteini Nivoi strukture proteina (strukturna hijerarhija) proteina Nivoi strukture proteina Primarna struktura Sekundarna struktura Super-sekundarna struktura Tercijarnastruktura
Sekundarne struktura proteina Fibrilni proteini Nivoi strukture proteina (strukturna hijerarhija) proteina Nivoi strukture proteina Primarna struktura Sekundarna struktura Super-sekundarna struktura Tercijarnastruktura
Celični'stiki' Vrsta&povezave:'' celica.celica' celica.matriks'
 Celični'stiki' Vrsta&povezave:'' celica.celica' celica.matriks' Povezava&in&adhezija&omogoča:'' zvezo'med'celico'in'skupnostjo'' kompartmentizacijo' prepoznavanje'in'signalizacijo' proliferacija,'diferenciacija,'migracija'
Celični'stiki' Vrsta&povezave:'' celica.celica' celica.matriks' Povezava&in&adhezija&omogoča:'' zvezo'med'celico'in'skupnostjo'' kompartmentizacijo' prepoznavanje'in'signalizacijo' proliferacija,'diferenciacija,'migracija'
Analiza'3D'struktur'makromolekul'in' modeliranje'
 Univerza'v'Ljubljani,'Fakulteta'za'kemijo'in'kemijsko'tehnologijo' Univerzitetni%študijski%program%Biokemija,%2.%letnik,%študijsko%leto%2013/2014% Analiza'3D'struktur'makromolekul'in' modeliranje' Miha%Pavšič%
Univerza'v'Ljubljani,'Fakulteta'za'kemijo'in'kemijsko'tehnologijo' Univerzitetni%študijski%program%Biokemija,%2.%letnik,%študijsko%leto%2013/2014% Analiza'3D'struktur'makromolekul'in' modeliranje' Miha%Pavšič%
1. Definicijsko območje, zaloga vrednosti. 2. Naraščanje in padanje, ekstremi. 3. Ukrivljenost. 4. Trend na robu definicijskega območja
 ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 15. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
Booleova algebra. Izjave in Booleove spremenljivke
 Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 12. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
Frekvenčna analiza neperiodičnih signalov. Analiza signalov prof. France Mihelič
 Frekvenčna analiza neperiodičnih signalov Analiza signalov prof. France Mihelič Vpliv postopka daljšanja periode na spekter periodičnega signala Opazujmo družino sodih periodičnih pravokotnih impulzov
Frekvenčna analiza neperiodičnih signalov Analiza signalov prof. France Mihelič Vpliv postopka daljšanja periode na spekter periodičnega signala Opazujmo družino sodih periodičnih pravokotnih impulzov
Funkcije proteinov, pogojene s strukturo
 Funkcije proteinov, pogojene s strukturo Transport/skladiščenje določenih molekul (ligandov, npr. Hb, Mb) Uravnavanje procesov (DNA-vezavni proteini) Oporna funkcija (strukturni proteini: keratini, kolagen)
Funkcije proteinov, pogojene s strukturo Transport/skladiščenje določenih molekul (ligandov, npr. Hb, Mb) Uravnavanje procesov (DNA-vezavni proteini) Oporna funkcija (strukturni proteini: keratini, kolagen)
Kontrolne karte uporabljamo za sprotno spremljanje kakovosti izdelka, ki ga izdelujemo v proizvodnem procesu.
 Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
Tabele termodinamskih lastnosti vode in vodne pare
 Univerza v Ljubljani Fakulteta za strojništvo Laboratorij za termoenergetiko Tabele termodinamskih lastnosti vode in vodne pare po modelu IAPWS IF-97 izračunano z XSteam Excel v2.6 Magnus Holmgren, xsteam.sourceforge.net
Univerza v Ljubljani Fakulteta za strojništvo Laboratorij za termoenergetiko Tabele termodinamskih lastnosti vode in vodne pare po modelu IAPWS IF-97 izračunano z XSteam Excel v2.6 Magnus Holmgren, xsteam.sourceforge.net
*M * Osnovna in višja raven MATEMATIKA NAVODILA ZA OCENJEVANJE. Sobota, 4. junij 2011 SPOMLADANSKI IZPITNI ROK. Državni izpitni center
 Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Definicija. definiramo skalarni produkt. x i y i. in razdaljo. d(x, y) = x y = < x y, x y > = n (x i y i ) 2. i=1. i=1
 Funkcije več realnih spremenljivk Osnovne definicije Limita in zveznost funkcije več spremenljivk Parcialni odvodi funkcije več spremenljivk Gradient in odvod funkcije več spremenljivk v dani smeri Parcialni
Funkcije več realnih spremenljivk Osnovne definicije Limita in zveznost funkcije več spremenljivk Parcialni odvodi funkcije več spremenljivk Gradient in odvod funkcije več spremenljivk v dani smeri Parcialni
Delovna točka in napajalna vezja bipolarnih tranzistorjev
 KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
NEPARAMETRIČNI TESTI. pregledovanje tabel hi-kvadrat test. as. dr. Nino RODE
 NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
ZVIJANJE PROTEINOV, RAZGRADNJA IN USMERJANJE
 ZVIJANJE PROTEINOV, RAZGRADNJA IN USMERJANJE ZVIJANJE PROTEINOV Spontano Stanje odtajane kroglice Molekularni šaperoni POST-TRANSLACIJSKE MODIFIKACIJE PROTEINOV RAZGRADNJA Ubikvitin Proteasom USMERJANJE
ZVIJANJE PROTEINOV, RAZGRADNJA IN USMERJANJE ZVIJANJE PROTEINOV Spontano Stanje odtajane kroglice Molekularni šaperoni POST-TRANSLACIJSKE MODIFIKACIJE PROTEINOV RAZGRADNJA Ubikvitin Proteasom USMERJANJE
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * NAVODILA ZA OCENJEVANJE. Sreda, 3. junij 2015 SPLOŠNA MATURA
 Državni izpitni center *M15143113* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sreda, 3. junij 2015 SPLOŠNA MATURA RIC 2015 M151-431-1-3 2 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor Naloga Odgovor
Državni izpitni center *M15143113* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sreda, 3. junij 2015 SPLOŠNA MATURA RIC 2015 M151-431-1-3 2 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor Naloga Odgovor
Jure Stojan in Marko Goličnik Medicinska fakulteta
 Univerza v Ljubljani, Fakulteta za farmacijo, 2015/16 Program: Laboratorijska biomedicina Predmet: MOLEKULARNA ENCIMOLOGIJA Jure Stojan in Marko Goličnik Medicinska fakulteta Prof. dr. Matjaž Zorko do
Univerza v Ljubljani, Fakulteta za farmacijo, 2015/16 Program: Laboratorijska biomedicina Predmet: MOLEKULARNA ENCIMOLOGIJA Jure Stojan in Marko Goličnik Medicinska fakulteta Prof. dr. Matjaž Zorko do
13. Jacobijeva metoda za računanje singularnega razcepa
 13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
Kotne in krožne funkcije
 Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
Družina globinov pri človeku in bolezni.
 Družina globinov pri človeku in bolezni www.muhlenberg.edu/ Mioglobin in hemoglobin spadata v družino globinov Globinsko zvitje Mb β podenota Hb Podobnost aminokislinskega zaporedja Podobnost 3D strukture
Družina globinov pri človeku in bolezni www.muhlenberg.edu/ Mioglobin in hemoglobin spadata v družino globinov Globinsko zvitje Mb β podenota Hb Podobnost aminokislinskega zaporedja Podobnost 3D strukture
SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK
 SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
I. OSNOVNI STRUKTURNI PRINCIPI
 I. OSNOVNI STRUKTURNI PRINCIPI 1. Gradnja Vsi proteini so polimeri 20 različnih amino, kislin, povezanih s peptidnimi vezmi Funkcija proteina je odvisna od 3D strukture, ki je povezana z AK sekvenco ta
I. OSNOVNI STRUKTURNI PRINCIPI 1. Gradnja Vsi proteini so polimeri 20 različnih amino, kislin, povezanih s peptidnimi vezmi Funkcija proteina je odvisna od 3D strukture, ki je povezana z AK sekvenco ta
Osnove matematične analize 2016/17
 Osnove matematične analize 216/17 Neža Mramor Kosta Fakulteta za računalništvo in informatiko Univerza v Ljubljani Kaj je funkcija? Funkcija je predpis, ki vsakemu elementu x iz definicijskega območja
Osnove matematične analize 216/17 Neža Mramor Kosta Fakulteta za računalništvo in informatiko Univerza v Ljubljani Kaj je funkcija? Funkcija je predpis, ki vsakemu elementu x iz definicijskega območja
1. TVORBA ŠIBKEGA (SIGMATNEGA) AORISTA: Največ grških glagolov ima tako imenovani šibki (sigmatni) aorist. Osnova se tvori s. γραψ
 TVORBA AORISTA: Grški aorist (dovršnik) izraža dovršno dejanje; v indikativu izraža poleg dovršnosti tudi preteklost. Za razliko od prezenta ima aorist posebne aktivne, medialne in pasivne oblike. Pri
TVORBA AORISTA: Grški aorist (dovršnik) izraža dovršno dejanje; v indikativu izraža poleg dovršnosti tudi preteklost. Za razliko od prezenta ima aorist posebne aktivne, medialne in pasivne oblike. Pri
6 ogljikovih atomov: HEKSOZE (npr. glukoza, fruktoza, galaktoza) Ločimo dve vrsti glukoze: α glukoza in. β glukoza, ki se
 OGLJIKOVI HIDRATI Monosaharidi enostavni sladkorji Spojine C, H, O v razmerju 1:2:1 3 ogljikovi atomi: TRIOZE 5 ogljikovih atomov: PENTOZE (npr. riboza, deoksiriboza) 6 ogljikovih atomov: HEKSOZE (npr.
OGLJIKOVI HIDRATI Monosaharidi enostavni sladkorji Spojine C, H, O v razmerju 1:2:1 3 ogljikovi atomi: TRIOZE 5 ogljikovih atomov: PENTOZE (npr. riboza, deoksiriboza) 6 ogljikovih atomov: HEKSOZE (npr.
Funkcije več spremenljivk
 DODATEK C Funkcije več spremenljivk C.1. Osnovni pojmi Funkcija n spremenljivk je predpis: f : D f R, (x 1, x 2,..., x n ) u = f (x 1, x 2,..., x n ) kjer D f R n imenujemo definicijsko območje funkcije
DODATEK C Funkcije več spremenljivk C.1. Osnovni pojmi Funkcija n spremenljivk je predpis: f : D f R, (x 1, x 2,..., x n ) u = f (x 1, x 2,..., x n ) kjer D f R n imenujemo definicijsko območje funkcije
ΑΝΤΙΓΡΑΦΗ ΚΑΙ ΕΚΦΡΑΣΗ ΤΗΣ ΓΕΝΕΤΙΚΗΣ ΠΛΗΡΟΦΟΡΙΑΣ
 ΜΙΝΟΠΕΤΡΟΣ ΚΩΝΣΤΑΝΤΙΝΟΣ ΦΥΣΙΚΟΣ - Ρ/Η ΚΑΘΗΓΗΤΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΥΠΕΥΘΥΝΟΣ ΣΕΦΕ 2 ου ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΡΑΜΑΤΟΣ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΒΙΟΛΟΓΙΑΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΑΝΤΙΓΡΑΦΗ ΚΑΙ ΕΚΦΡΑΣΗ ΤΗΣ ΓΕΝΕΤΙΚΗΣ ΠΛΗΡΟΦΟΡΙΑΣ
ΜΙΝΟΠΕΤΡΟΣ ΚΩΝΣΤΑΝΤΙΝΟΣ ΦΥΣΙΚΟΣ - Ρ/Η ΚΑΘΗΓΗΤΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΥΠΕΥΘΥΝΟΣ ΣΕΦΕ 2 ου ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΡΑΜΑΤΟΣ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΒΙΟΛΟΓΙΑΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΑΝΤΙΓΡΑΦΗ ΚΑΙ ΕΚΦΡΑΣΗ ΤΗΣ ΓΕΝΕΤΙΚΗΣ ΠΛΗΡΟΦΟΡΙΑΣ
Malgorzata Korycka-Machala, Marcin Nowosielski, Aneta Kuron, Sebastian Rykowski, Agnieszka Olejniczak, Marcin Hoffmann and Jaroslaw Dziadek
 Molecules 2017, 21, 154; doi:10.3390/molecules22010154 Supplementary Materials: Naphthalimides Selectively Inhibit the Activity of Bacterial, Replicative DNA Ligases and Display Bactericidal Effect against
Molecules 2017, 21, 154; doi:10.3390/molecules22010154 Supplementary Materials: Naphthalimides Selectively Inhibit the Activity of Bacterial, Replicative DNA Ligases and Display Bactericidal Effect against
matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):
![matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij): matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):](/thumbs/87/96579490.jpg) 4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
- Geodetske točke in geodetske mreže
 - Geodetske točke in geodetske mreže 15 Geodetske točke in geodetske mreže Materializacija koordinatnih sistemov 2 Geodetske točke Geodetska točka je točka, označena na fizični površini Zemlje z izbrano
- Geodetske točke in geodetske mreže 15 Geodetske točke in geodetske mreže Materializacija koordinatnih sistemov 2 Geodetske točke Geodetska točka je točka, označena na fizični površini Zemlje z izbrano
Integralni račun. Nedoločeni integral in integracijske metrode. 1. Izračunaj naslednje nedoločene integrale: (a) dx. (b) x 3 +3+x 2 dx, (c) (d)
 Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
vaja Izolacija kromosomske DNA iz vranice in hiperkromni efekt. DNA RNA Protein. ime deoksirbonukleinska kislina ribonukleinska kislina
 transkripcija translacija Protein 12. vaja Izolacija kromosomske iz vranice in hiperkromni efekt sladkorji deoksiriboza riboza glavna funkcija dolgoročno shranjevanje genetskih informacij prenos informacij
transkripcija translacija Protein 12. vaja Izolacija kromosomske iz vranice in hiperkromni efekt sladkorji deoksiriboza riboza glavna funkcija dolgoročno shranjevanje genetskih informacij prenos informacij
Tercijarna struktura globuralnih proteina. Rendgenska strukturna analiza proteina Konformaciona stabilnost proteina Supersekundarne strukture/domeni
 Tercijarna struktura globuralnih proteina Rendgenska strukturna analiza proteina Konformaciona stabilnost proteina Supersekundarne strukture/domeni Nivoi strukture proteina (strukturna hijerarhija) Tercijarna
Tercijarna struktura globuralnih proteina Rendgenska strukturna analiza proteina Konformaciona stabilnost proteina Supersekundarne strukture/domeni Nivoi strukture proteina (strukturna hijerarhija) Tercijarna
Nukleinske kisline. Nukleotidi. DNA je nosilka dednih genetskih informacij.
 Nukleinske kisline DNA je nosilka dednih genetskih informacij. RNA je posrednik, ki omogoča sintezo proteinov na osnovi zapisa na DNA. Nukleotidi Nukleinske kisline so polimeri nukleotidov. OH... RNA ribonukleinska
Nukleinske kisline DNA je nosilka dednih genetskih informacij. RNA je posrednik, ki omogoča sintezo proteinov na osnovi zapisa na DNA. Nukleotidi Nukleinske kisline so polimeri nukleotidov. OH... RNA ribonukleinska
ÂÓÈÎ ÁÈ ÙÔ K ÙÙ ÚÔ 1 Ô KÂÊ Ï ÈÔ 1.1 E Ë Î ÙÙ ÚˆÓ 1.1.1 ÚÔÎ Ú ˆÙÈÎ Î ÙÙ Ú
 11 1 Ô KÂÊ Ï ÈÔ ÂÓÈÎ ÁÈ ÙÔ K ÙÙ ÚÔ 1.1 E Ë Î ÙÙ ÚˆÓ Στο κεφάλαιο αυτό θα αναφερθούμε σύντομα στο κύτταρο, τα είδη (ευκαρυωτικά και προκαρυωτικά) και γενικά στα διάφορα στοιχεία του, όπως πυρήνα, κυτταρόπλασμα
11 1 Ô KÂÊ Ï ÈÔ ÂÓÈÎ ÁÈ ÙÔ K ÙÙ ÚÔ 1.1 E Ë Î ÙÙ ÚˆÓ Στο κεφάλαιο αυτό θα αναφερθούμε σύντομα στο κύτταρο, τα είδη (ευκαρυωτικά και προκαρυωτικά) και γενικά στα διάφορα στοιχεία του, όπως πυρήνα, κυτταρόπλασμα
vaja Kvan*ta*vno določanje proteinov. 6. vaja Kvan*ta*vno določanje proteinov. 6. vaja Kvan*ta*vno določanje proteinov
 28. 3. 11 UV- spektrofotometrija Biuretska metoda Absorbanca pri λ=28 nm (A28) UV- spektrofotometrija Biuretska metoda vstopni žarek intenziteta I Lowrijeva metoda Bradfordova metoda Bradfordova metoda
28. 3. 11 UV- spektrofotometrija Biuretska metoda Absorbanca pri λ=28 nm (A28) UV- spektrofotometrija Biuretska metoda vstopni žarek intenziteta I Lowrijeva metoda Bradfordova metoda Bradfordova metoda
Encimi. Splošne lastnosti - osnove delovanja, specifičnost, energijski vidik nekatalizirane in encimsko katalizirane reakcije
 Encimi Splošne lastnosti - osnove delovanja, specifičnost, energijski vidik nekatalizirane in encimsko katalizirane reakcije Kofaktorji, koencimi in prostetične skupine Mehanizmi encimske katalize Klasifikacija
Encimi Splošne lastnosti - osnove delovanja, specifičnost, energijski vidik nekatalizirane in encimsko katalizirane reakcije Kofaktorji, koencimi in prostetične skupine Mehanizmi encimske katalize Klasifikacija
Statistična analiza. doc. dr. Mitja Kos, mag. farm. Katedra za socialno farmacijo Univerza v Ljubljani- Fakulteta za farmacijo
 Statistična analiza opisnih spremenljivk doc. dr. Mitja Kos, mag. arm. Katedra za socialno armacijo Univerza v Ljubljani- Fakulteta za armacijo Statistični znaki Proučevane spremenljivke: statistični znaki
Statistična analiza opisnih spremenljivk doc. dr. Mitja Kos, mag. arm. Katedra za socialno armacijo Univerza v Ljubljani- Fakulteta za armacijo Statistični znaki Proučevane spremenljivke: statistični znaki
Ζεύγη βάσεων ΓΕΝΕΤΙΚΗ. Γουανίνη Κυτοσίνη. 4α. Λειτουργία γενετικού υλικού. Φωσφοδιεστερικός δεσμός
 εύγη βάσεων Αδενίνη Θυμίνη Γουανίνη Κυτοσίνη ΓΕΝΕΤΙΚΗ Φωσφοδιεστερικός δεσμός 4α. Λειτουργία γενετικού υλικού 1 ΛΕΙΤΟΥΡΓΙΑ ΓΕΝΕΤΙΚΟΥ ΥΛΙΚΟΥ Αντιγραφή (διπλασιασμός) DNA: DNA DNA Έκφραση γενετικής πληροφορίας:
εύγη βάσεων Αδενίνη Θυμίνη Γουανίνη Κυτοσίνη ΓΕΝΕΤΙΚΗ Φωσφοδιεστερικός δεσμός 4α. Λειτουργία γενετικού υλικού 1 ΛΕΙΤΟΥΡΓΙΑ ΓΕΝΕΤΙΚΟΥ ΥΛΙΚΟΥ Αντιγραφή (διπλασιασμός) DNA: DNA DNA Έκφραση γενετικής πληροφορίας:
CILJNA MESTA DEJSTVA LEKOVA
 FARMACEUTSKA HEMIJA 1 CILJNA MESTA DEJSTVA LEKVA Predavač: Prof. dr Slavica Erić Ciljna mesta dejstva leka CILJNA MESTA NA MLEKULARNM NIVU: lipidi (lipidi ćelijske membrane) ugljeni hidrati (obeleživači
FARMACEUTSKA HEMIJA 1 CILJNA MESTA DEJSTVA LEKVA Predavač: Prof. dr Slavica Erić Ciljna mesta dejstva leka CILJNA MESTA NA MLEKULARNM NIVU: lipidi (lipidi ćelijske membrane) ugljeni hidrati (obeleživači
Splošno o interpolaciji
 Splošno o interpolaciji J.Kozak Numerične metode II (FM) 2011-2012 1 / 18 O funkciji f poznamo ali hočemo uporabiti le posamezne podatke, na primer vrednosti r i = f (x i ) v danih točkah x i Izberemo
Splošno o interpolaciji J.Kozak Numerične metode II (FM) 2011-2012 1 / 18 O funkciji f poznamo ali hočemo uporabiti le posamezne podatke, na primer vrednosti r i = f (x i ) v danih točkah x i Izberemo
Fazni diagram binarne tekočine
 Fazni diagram binarne tekočine Žiga Kos 5. junij 203 Binarno tekočino predstavljajo delci A in B. Ti se med seboj lahko mešajo v različnih razmerjih. V nalogi želimo izračunati fazni diagram take tekočine,
Fazni diagram binarne tekočine Žiga Kos 5. junij 203 Binarno tekočino predstavljajo delci A in B. Ti se med seboj lahko mešajo v različnih razmerjih. V nalogi želimo izračunati fazni diagram take tekočine,
Kotni funkciji sinus in kosinus
 Kotni funkciji sinus in kosinus Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z oznako cos x, DEFINICIJA V PRAVOKOTNEM TRIKOTNIKU: Kotna funkcija sinus je definirana kot razmerje
Kotni funkciji sinus in kosinus Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z oznako cos x, DEFINICIJA V PRAVOKOTNEM TRIKOTNIKU: Kotna funkcija sinus je definirana kot razmerje
Na pregledni skici napišite/označite ustrezne točke in paraboli. A) 12 B) 8 C) 4 D) 4 E) 8 F) 12
 Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
Gimnazija Krˇsko. vektorji - naloge
 Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
DNA in RNA: zgradba in vloga. Velika predavalnica IJS,
 DNA in RNA: zgradba in vloga Velika predavalnica IJS, 10. 4. 2014 Nukleinske kisline Shranjevanje, prenašanje in izražanje genetske informacije. Dve vrsti nukleinskih kislin: deoksiribonukleinska kislina
DNA in RNA: zgradba in vloga Velika predavalnica IJS, 10. 4. 2014 Nukleinske kisline Shranjevanje, prenašanje in izražanje genetske informacije. Dve vrsti nukleinskih kislin: deoksiribonukleinska kislina
Poglavje 10. Molekule Kovalentna vez
 Poglavje 10 Molekule Atomi se vežejo v molekule. Vezavo med atomi v molkuli posredujejo zunanji - valenčni elektroni. Pri vseh molekularnih vezeh negativni naboj elektronov posreduje med pozitinvimi ioni
Poglavje 10 Molekule Atomi se vežejo v molekule. Vezavo med atomi v molkuli posredujejo zunanji - valenčni elektroni. Pri vseh molekularnih vezeh negativni naboj elektronov posreduje med pozitinvimi ioni
1. Trikotniki hitrosti
 . Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
. Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
3/25/2016. Hemijske komponente ćelije
 Hemijske komponente ćelije Molekuli u ćeliji Najbitniji molekuli u ćeliji su poznati. Putevi sinteze i razgradnje su poznati za većinu ćelijskih konstituenata. Hemijska energija pokreće biosintezu. Organizacija
Hemijske komponente ćelije Molekuli u ćeliji Najbitniji molekuli u ćeliji su poznati. Putevi sinteze i razgradnje su poznati za većinu ćelijskih konstituenata. Hemijska energija pokreće biosintezu. Organizacija
Najpomembnejši človeški Hb
 Najpomembnejši človeški Hb Vrsta Struktura podenot Razširjenost HbA (odrasli) α 2 β 2 97% Hb odraslih HbA 2 (odrasli) α 2 δ 2 2-3% Hb odraslih HbF (fetalni) *α 2 γ 2 Najpomembnejši Hb v 3. trimestru nosečnosti
Najpomembnejši človeški Hb Vrsta Struktura podenot Razširjenost HbA (odrasli) α 2 β 2 97% Hb odraslih HbA 2 (odrasli) α 2 δ 2 2-3% Hb odraslih HbF (fetalni) *α 2 γ 2 Najpomembnejši Hb v 3. trimestru nosečnosti
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
Multivariatna analiza variance
 (MANOVA) MANOVA je multivariatna metoda za proučevanje odvisnosti med več odvisnimi (številskimi) in več neodvisnimi (opisnimi) spremenljivkami. (MANOVA) MANOVA je multivariatna metoda za proučevanje odvisnosti
(MANOVA) MANOVA je multivariatna metoda za proučevanje odvisnosti med več odvisnimi (številskimi) in več neodvisnimi (opisnimi) spremenljivkami. (MANOVA) MANOVA je multivariatna metoda za proučevanje odvisnosti
SEMINAR IZ MOLEKULSKEGA MODELIRANJA PRI FARMACEVTSKI KEMIJI III
 SEMINAR IZ MOLEKULSKEGA MODELIRANJA PRI FARMACEVTSKI KEMIJI III 1. DEL TEORETIČNE OSNOVE MOLEKULSKEGA MODELIRANJA doc. Andrej Perdih e-mail: andrej.perdih@ki.si 1. DEL: TEORETIČNE OSNOVE MOLEKULSKEGA MODELIRANJA
SEMINAR IZ MOLEKULSKEGA MODELIRANJA PRI FARMACEVTSKI KEMIJI III 1. DEL TEORETIČNE OSNOVE MOLEKULSKEGA MODELIRANJA doc. Andrej Perdih e-mail: andrej.perdih@ki.si 1. DEL: TEORETIČNE OSNOVE MOLEKULSKEGA MODELIRANJA
Transformator. Delovanje transformatorja I. Delovanje transformatorja II
 Transformator Transformator je naprava, ki v osnovi pretvarja napetost iz enega nivoja v drugega. Poznamo vrsto različnih izvedb transformatorjev, glede na njihovo specifičnost uporabe:. Energetski transformator.
Transformator Transformator je naprava, ki v osnovi pretvarja napetost iz enega nivoja v drugega. Poznamo vrsto različnih izvedb transformatorjev, glede na njihovo specifičnost uporabe:. Energetski transformator.
SPLOŠNO O BELJAKOVINAH STRUKTURA BELJAKOVIN
 SPLOŠNO O BELJAKOVINAH Beljakovine so najvažnejša sestavina vsake celice, kajti vsi življenski procesi so odvisni od njih. So makromolekularnespojine, sestavljeneiz ogljika, vodika, kisika in dušika ter
SPLOŠNO O BELJAKOVINAH Beljakovine so najvažnejša sestavina vsake celice, kajti vsi življenski procesi so odvisni od njih. So makromolekularnespojine, sestavljeneiz ogljika, vodika, kisika in dušika ter
Poglavje 7. Poglavje 7. Poglavje 7. Regulacijski sistemi. Regulacijski sistemi. Slika 7. 1: Normirana blokovna shema regulacije EM
 Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
Neavtorizirani povzetki izbranih predavanj iz biokemije. UN študij Okolje Politehnika Nova Gorica. doc. dr. Marko Dolinar
 Neavtorizirani povzetki izbranih predavanj iz biokemije UN študij Okolje Politehnika Nova Gorica doc. dr. Marko Dolinar obravnavane teme v študijskem letu 2003/2004: Pretok genetskih informacij (5. poglavje)
Neavtorizirani povzetki izbranih predavanj iz biokemije UN študij Okolje Politehnika Nova Gorica doc. dr. Marko Dolinar obravnavane teme v študijskem letu 2003/2004: Pretok genetskih informacij (5. poglavje)
4 ο ΚΕΦΑΛΑΙΟ. Γ ε ν ε τ ι κ ή
 4 ο ΚΕΦΑΛΑΙΟ Γ ε ν ε τ ι κ ή 1. Κύκλος της ζωής του κυττάρου 3ο Γελ. Ηλιούπολης επιμέλεια: Αργύρης Γιάννης 2 2. Μοριακή Γενετική i). Ροή της γενετικής πληροφορίας DNA RNA πρωτεΐνες νουκλεΐκά οξέα ή πρωτεΐνες
4 ο ΚΕΦΑΛΑΙΟ Γ ε ν ε τ ι κ ή 1. Κύκλος της ζωής του κυττάρου 3ο Γελ. Ηλιούπολης επιμέλεια: Αργύρης Γιάννης 2 2. Μοριακή Γενετική i). Ροή της γενετικής πληροφορίας DNA RNA πρωτεΐνες νουκλεΐκά οξέα ή πρωτεΐνες
PONOVITEV SNOVI ZA 4. TEST
 PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
Osnove elektrotehnike uvod
 Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
Numerično reševanje. diferencialnih enačb II
 Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
II. LIMITA IN ZVEZNOST FUNKCIJ
 II. LIMITA IN ZVEZNOST FUNKCIJ. Preslikave med množicami Funkcija ali preslikava med dvema množicama A in B je predpis f, ki vsakemu elementu x množice A priredi natanko določen element y množice B. Važno
II. LIMITA IN ZVEZNOST FUNKCIJ. Preslikave med množicami Funkcija ali preslikava med dvema množicama A in B je predpis f, ki vsakemu elementu x množice A priredi natanko določen element y množice B. Važno
8. Diskretni LTI sistemi
 8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
GEL ELEKTROFOREZA. Seminar pri predmetu Molekularna Biofizika. Avtorica: Tjaša Parkelj
 GEL ELEKTROFOREZA Seminar pri predmetu Molekularna Biofizika Avtorica: Tjaša Parkelj Povzetek: V tem seminarju bom predstavila fizikalno ozadje elektroforeze. Začela bom z opisom gibanja nabitega delca
GEL ELEKTROFOREZA Seminar pri predmetu Molekularna Biofizika Avtorica: Tjaša Parkelj Povzetek: V tem seminarju bom predstavila fizikalno ozadje elektroforeze. Začela bom z opisom gibanja nabitega delca
Nukleinske kisline. ribosomska informacijska prenašalna
 Nukleinske kisline Nukleinske kisline vloga pri shranjevanju, prenašanju in izražanju genetske informacije: DNA RNA proteini zgradba in delovanje celice 2 osnovni vrsti nukleinskih kislin: deoksiribonukleinska
Nukleinske kisline Nukleinske kisline vloga pri shranjevanju, prenašanju in izražanju genetske informacije: DNA RNA proteini zgradba in delovanje celice 2 osnovni vrsti nukleinskih kislin: deoksiribonukleinska
VEKTORJI. Operacije z vektorji
 VEKTORJI Vektorji so matematični objekti, s katerimi opisujemo določene fizikalne količine. V tisku jih označujemo s krepko natisnjenimi črkami (npr. a), pri pisanju pa s puščico ( a). Fizikalne količine,
VEKTORJI Vektorji so matematični objekti, s katerimi opisujemo določene fizikalne količine. V tisku jih označujemo s krepko natisnjenimi črkami (npr. a), pri pisanju pa s puščico ( a). Fizikalne količine,
Matematika 1. Gabrijel Tomšič Bojan Orel Neža Mramor Kosta
 Matematika Gabrijel Tomšič Bojan Orel Neža Mramor Kosta 6. november 200 Poglavje 2 Zaporedja in številske vrste 2. Zaporedja 2.. Uvod Definicija 2... Zaporedje (a n ) = a, a 2,..., a n,... je predpis,
Matematika Gabrijel Tomšič Bojan Orel Neža Mramor Kosta 6. november 200 Poglavje 2 Zaporedja in številske vrste 2. Zaporedja 2.. Uvod Definicija 2... Zaporedje (a n ) = a, a 2,..., a n,... je predpis,
Domače naloge za 2. kolokvij iz ANALIZE 2b VEKTORSKA ANALIZA
 Domače naloge za 2. kolokvij iz ANALIZE 2b VEKTORSKA ANALIZA. Naj bo vektorsko polje R : R 3 R 3 dano s predpisom R(x, y, z) = (2x 2 + z 2, xy + 2yz, z). Izračunaj pretok polja R skozi površino torusa
Domače naloge za 2. kolokvij iz ANALIZE 2b VEKTORSKA ANALIZA. Naj bo vektorsko polje R : R 3 R 3 dano s predpisom R(x, y, z) = (2x 2 + z 2, xy + 2yz, z). Izračunaj pretok polja R skozi površino torusa
FUNKCIJA PROTEINOV, PRIMERI FIBRILARNI PROTEINI. α KERATIN
 FUNKCIJA PROTEINOV, PRIMERI FIBRILARNI PROTEINI keratin, kolagen, fibroin, spidroin GLOBULARNI PROTEINI domenska zgradba proteinov MIOGLOBIN, HEMOGLOBIN vezava kisika zgradba konformacijske spremembe ob
FUNKCIJA PROTEINOV, PRIMERI FIBRILARNI PROTEINI keratin, kolagen, fibroin, spidroin GLOBULARNI PROTEINI domenska zgradba proteinov MIOGLOBIN, HEMOGLOBIN vezava kisika zgradba konformacijske spremembe ob
Funkcije proteinov (pogojene s strukturo)
 Funkcije proteinov (pogojene s strukturo) Oporna funkcija (strukturni proteini, npr keratini, kolagen...) Transport/skladiščenje molekul (ligandov, npr. O2 v Hb, Mb) Uravnavanje - DNA-vezavni proteini
Funkcije proteinov (pogojene s strukturo) Oporna funkcija (strukturni proteini, npr keratini, kolagen...) Transport/skladiščenje molekul (ligandov, npr. O2 v Hb, Mb) Uravnavanje - DNA-vezavni proteini
Simbolni zapis in množina snovi
 Simbolni zapis in množina snovi RELATIVNA MOLEKULSKA MASA ON MOLSKA MASA Relativna molekulska masa Ker so atomi premajhni, da bi jih merili z običajnimi tehtnicami, so ugotovili, kako jih izračunati. Izražamo
Simbolni zapis in množina snovi RELATIVNA MOLEKULSKA MASA ON MOLSKA MASA Relativna molekulska masa Ker so atomi premajhni, da bi jih merili z običajnimi tehtnicami, so ugotovili, kako jih izračunati. Izražamo
p 1 ENTROPIJSKI ZAKON
 ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
GENETIKA od dvojne vijaënice do kloniranja
 RADOVAN KOMEL GENETIKA od dvojne vijaënice do kloniranja PriroËnik za uëitelje GENETIKA od dvojne vijačnice do kloniranja Priročnik za učitelje Avtor: dr. Radovan Komel Recenzentka: Marjeta Dobravc, prof.biol.
RADOVAN KOMEL GENETIKA od dvojne vijaënice do kloniranja PriroËnik za uëitelje GENETIKA od dvojne vijačnice do kloniranja Priročnik za učitelje Avtor: dr. Radovan Komel Recenzentka: Marjeta Dobravc, prof.biol.
CM707. GR Οδηγός χρήσης... 2-7. SLO Uporabniški priročnik... 8-13. CR Korisnički priručnik... 14-19. TR Kullanım Kılavuzu... 20-25
 1 2 3 4 5 6 7 OFFMANAUTO CM707 GR Οδηγός χρήσης... 2-7 SLO Uporabniški priročnik... 8-13 CR Korisnički priručnik... 14-19 TR Kullanım Kılavuzu... 20-25 ENG User Guide... 26-31 GR CM707 ΟΔΗΓΟΣ ΧΡΗΣΗΣ Περιγραφή
1 2 3 4 5 6 7 OFFMANAUTO CM707 GR Οδηγός χρήσης... 2-7 SLO Uporabniški priročnik... 8-13 CR Korisnički priručnik... 14-19 TR Kullanım Kılavuzu... 20-25 ENG User Guide... 26-31 GR CM707 ΟΔΗΓΟΣ ΧΡΗΣΗΣ Περιγραφή
1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου...
 ΑΠΟΖΗΜΙΩΣΗ ΘΥΜΑΤΩΝ ΕΓΚΛΗΜΑΤΙΚΩΝ ΠΡΑΞΕΩΝ ΣΛΟΒΕΝΙΑ 1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου... 3 1 1. Έντυπα αιτήσεων
ΑΠΟΖΗΜΙΩΣΗ ΘΥΜΑΤΩΝ ΕΓΚΛΗΜΑΤΙΚΩΝ ΠΡΑΞΕΩΝ ΣΛΟΒΕΝΙΑ 1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου... 3 1 1. Έντυπα αιτήσεων
pretvarja v nestrupeno obliko, ki lahko vstopa v biosintezo nukleotidov *i) NH 4
 1. Piruvat karboksilaza a) je aktivirana z acetil koencimom A b) je regulatorni encim glukoneogeneze c) se nahaja v citosolu d) vsebuje prostetično skupino biotin e) potrebuje za svojo aktivnost NADH *f)
1. Piruvat karboksilaza a) je aktivirana z acetil koencimom A b) je regulatorni encim glukoneogeneze c) se nahaja v citosolu d) vsebuje prostetično skupino biotin e) potrebuje za svojo aktivnost NADH *f)
MAGNETNI MATERIALI. 1. Mehkomagnetni materiali 2. Trdomagnetni materiali
 MAGNETNI MATERIALI 1. Mehkomagnetni materiali 2. Trdomagnetni materiali Magnetni materiali in njihove lastnosti Slika 5.1 Magnetenje različnih vrst snovi Magnetne lastnosti snovi v B = µ v H Permeabilnost
MAGNETNI MATERIALI 1. Mehkomagnetni materiali 2. Trdomagnetni materiali Magnetni materiali in njihove lastnosti Slika 5.1 Magnetenje različnih vrst snovi Magnetne lastnosti snovi v B = µ v H Permeabilnost
Funkcije proteinov (pogojene s strukturo)
 Funkcije proteinov (pogojene s strukturo) Oporna funkcija (strukturni proteini, npr keratini, kolagen...) Transport/skladiščenje določenih molekul (ligandov, npr. Hb, Mb) Uravnavanje procesov (DNA-vezavni
Funkcije proteinov (pogojene s strukturo) Oporna funkcija (strukturni proteini, npr keratini, kolagen...) Transport/skladiščenje določenih molekul (ligandov, npr. Hb, Mb) Uravnavanje procesov (DNA-vezavni
Αµινοξέα και πεπτίδια Φύλλο εργασίας - αξιολόγησης
 Αµινοξέα και πεπτίδια Φύλλο εργασίας - αξιολόγησης Τάξη. Ονοµατεπώνυµο Μάθηµα Γνωστικό αντικείµενο: Χηµεία,Βιοχηµεία......................... ιδακτική ενότητα Αµινοξέα και πεπτίδια Τµήµα........... Απαιτούµενος
Αµινοξέα και πεπτίδια Φύλλο εργασίας - αξιολόγησης Τάξη. Ονοµατεπώνυµο Μάθηµα Γνωστικό αντικείµενο: Χηµεία,Βιοχηµεία......................... ιδακτική ενότητα Αµινοξέα και πεπτίδια Τµήµα........... Απαιτούµενος
Οι πρωτεΐνες δομούνται από ένα σύνολο αμινοξέων. 1/10/2015 Δ.Δ. Λεωνίδας
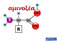 αμινοξέα Οι πρωτεΐνες δομούνται από ένα σύνολο αμινοξέων Λυσίνη CORN Ισομερές L Ισομερές D R = πλευρική αλυσίδα (side chain) Τα περισσότερα αμινοξέα είναι ασύμμετρα Όλα τα αμινοξέα που βρίσκονται στις
αμινοξέα Οι πρωτεΐνες δομούνται από ένα σύνολο αμινοξέων Λυσίνη CORN Ισομερές L Ισομερές D R = πλευρική αλυσίδα (side chain) Τα περισσότερα αμινοξέα είναι ασύμμετρα Όλα τα αμινοξέα που βρίσκονται στις
Univerza v Ljubljani Fakulteta za računalništvo in informatiko MATEMATIKA. Polona Oblak
 Univerza v Ljubljani Fakulteta za računalništvo in informatiko MATEMATIKA Polona Oblak Ljubljana, 04 CIP - Kataložni zapis o publikaciji Narodna in univerzitetna knjižnica, Ljubljana 5(075.8)(0.034.) OBLAK,
Univerza v Ljubljani Fakulteta za računalništvo in informatiko MATEMATIKA Polona Oblak Ljubljana, 04 CIP - Kataložni zapis o publikaciji Narodna in univerzitetna knjižnica, Ljubljana 5(075.8)(0.034.) OBLAK,
BIOXHMEIA, TOMOΣ I ΠANEΠIΣTHMIAKEΣ EKΔOΣEIΣ KPHTHΣ ΑΠΕΙΚΟΝΙΣΗ ΜΟΡΙΑΚΩΝ ΔΟΜΩΝ
 BIOXHMEIA, TOMOΣ I ΠANEΠIΣTHMIAKEΣ EKΔOΣEIΣ KPHTHΣ ΑΠΕΙΚΟΝΙΣΗ ΜΟΡΙΑΚΩΝ ΔΟΜΩΝ ΑΠΕΙΚΟΝΙΣΗ ΜΟΡΙΑΚΩΝ ΔΟΜΩΝ ΜΟΡΙΑΚΑ ΜΟΝΤΕΛΑ 1: ΧΩΡΟΠΛΗΡΩΤΙΚΟ ΜΟΝΤΕΛΟ (SPACE-FILLING) 1: ΧΩΡΟΠΛΗΡΩΤΙΚΟ ΜΟΝΤΕΛΟ (SPACE-FILLING)
BIOXHMEIA, TOMOΣ I ΠANEΠIΣTHMIAKEΣ EKΔOΣEIΣ KPHTHΣ ΑΠΕΙΚΟΝΙΣΗ ΜΟΡΙΑΚΩΝ ΔΟΜΩΝ ΑΠΕΙΚΟΝΙΣΗ ΜΟΡΙΑΚΩΝ ΔΟΜΩΝ ΜΟΡΙΑΚΑ ΜΟΝΤΕΛΑ 1: ΧΩΡΟΠΛΗΡΩΤΙΚΟ ΜΟΝΤΕΛΟ (SPACE-FILLING) 1: ΧΩΡΟΠΛΗΡΩΤΙΚΟ ΜΟΝΤΕΛΟ (SPACE-FILLING)
