FUNCŢII OPENGL PENTRU REDARE ANTI-ALIASING
|
|
|
- Κυβηλη Τρικούπης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 FUNCŢII OPENGL PENTRU REDARE ANTI-ALIASING Biblioteca OpenGL pune la dispoziţie două modalităţi de redare anti-aliasing: prin combinarea culorilor (blending) şi prin buffer de acumulare (A-buffer) ANTI-ALIASING PRIN COMBINAREA CULORILOR Această metodă dă rezultate de netezire numai dacă se renunţă la mecanismul Z-buffer (buffer-ul de adâncime) şi se desenează suprafeţele în ordinea în care sunt transmise bibliotecii. În această situaţie, culoarea unui pixel acoperit parţial de un poligon se obţine prin combinarea culorii poligonului cu culoarea pixelului, aflată în buffer-ul de culoare. În modul RGBA, OpenGL multiplică componenta A (alpha) a culorii poligoului cu ponderea de acoperire (raportul dintre aria acoperită de fragmentul pligonului şi aria pixelului). Această valoare poate fi folosită pentru ponderarea culorii în fiecare pixel prin combinare cu factorul GL_SRC_ALPHA pentru sursă şi factorul GL_ONE_MINUS_SRC_ALPHA pentru destinaţie. Pentru efectuarea acestor calcule mai este necesară validarea anti-aliasing-ului prin apelul funcţiei glenable() cu unul din argumentele GL_POINT_SMOOTH, GL_LINE_SMOOTH, GL_POLYGON_SMOOTH pentru puncte, linii şi, respectiv, poligoane. Exemplul 1. Programul din acest exemplu este folosit pentru generarea imaginilor din figura 1 în care se desenează două triunghiuri cu şi fără anti-aliasing. Funcţiile Init() şi Display() ale programului dezvoltat sub GLUT sunt următoarele: void Init() glclearcolor(1.0, 1.0, 1.0, 1.0); gllinewidth(1.5); glblendfunc(gl_src_alpha, GL_ONE_MINUS_SRC_ALPHA); void Display() int i; glclear(gl_color_buffer_bit GL_DEPTH_BUFFER_BIT); glcolor3f(0.0, 0.0, 0.0); gltranslated(0.0, 0.0, -25.0); //triunghiuri cu aliasing gldisable(gl_blend); gldisable(gl_line_smooth); gldisable(gl_polygon_smooth); gltranslated(-8.0, 0.0, 0.0); glbegin(gl_line_loop); glvertex3d(-3, -3, 0); glvertex3d(3, -2, 0); glvertex3d(2, 3, 0); glend(); 1
2 gltranslated(-2.0, 0.0, 0.0); glbegin(gl_polygon); glvertex3d(-3, -3, 0); glvertex3d(3, -2, 0); glvertex3d(2, 3, 0); glend(); //triunghiuri cu anti-aliasing glenable(gl_blend); glenable(gl_line_smooth); glenable(gl_polygon_smooth); gltranslated(4.0, 0.0, 0.0); glbegin(gl_line_loop); glvertex3d(-3, -3, 0); glvertex3d(3, -2, 0); glvertex3d(2, 3, 0); glend(); gltranslated(10.0, 0.0, 0.0); glbegin(gl_polygon); glvertex3d(-3, -3, 0); glvertex3d(3, -2, 0); glvertex3d(2, 3, 0); glend(); glutswapbuffers(); Deoarece anti-aliasing-ul se realizează prin combinarea culorilor, este necesară şi validarea combinării culorilor (glenable(gl_blend)) pentru poligoanele cu anti-aliasing. (a) (b) Fig. 1. (a) Două poligoane cu aliasing. (b) Aceleaşi poligoane cu anti-aliasing Acest mod de filtrare anti-aliasing este foarte simplist şi nu poate fi folosit decât pentru suprafeţe sau linii care nu se suprapun şi pot fi redate fără eliminarea suprafeţelor ascunse, aşa cum a fost situaţia în acest exemplu. Dacă se redau obiecte tridimensionale complexe sau mai multe obiecte în scenă, este necesar să fie asigurată eliminarea suprafeţelor ascunse. Combinarea 2
3 culorilor nu funcţionează corect împreună cu mecanismul Z-buffer, iar generarea imaginilor fără eliminarea suprafeţelor ascunse este lipsită de realism. Dacă se invalidează buffer-ul de adâncime, eliminarea suprafeţelor ascunse trebuie asigurată printr-un alt mecanism, de exemplu prin ordonarea suprafeţelor după adâncime. Dar eliminarea suprafeţelor ascunse prin ordonarea suprafeţelor după adâncime este un procedeu costisitor şi care nu poate fi implementat pentru scene complexe, cu un număr mare de obiecte. Soluţia acceptabilă ca performanţe şi rezultate pentru redarea anti-aliasing a scenelor complexe este folosirea unui buffer de acumulare (A-buffer). ANTI-ALIASING PRIN EŞANTIONARE STOCASTICĂ Principiul de bază al acestei metode este de a perturba în mod aleator poziţia punctelor de eşantionare. În acest fel, frecvenţele înalte ale imaginii, peste limita Nyquist, sunt transformate în zgomot, care apare în spectrul eşantioanelor în locul zgomotului de spectru transpus, şi poate fi eliminat prin filtrare. În figura 2, o undă sinusoidală este eşantionată cu o frecvenţă mai mare decât limita Nyquist. Perturbaţia punctului de eşantionare introduce o eroare în amplitudinea eşantioanelor, care apare ca zgomot în spectrul imaginii eşantionate. În cazul unei imagini, aceasta este eşantionată de mai multe ori în poziţii de eşantionare care sunt obţinute prin perturbare aleatoare faţă de centrul pixelului, pe o distanţă egală cu dimensiunea pixelului. Imaginile succesive obţinute pentru toate poziţiile de eşantionare sunt mediate pentru fiecare pixel (pe componente de culoare) rezultând imaginea finală, din care a fost eliminat zgomotul aleator datorat perturbării poziţiilor eşantionate. Fiecare imagine se creează într-un buffer de culoare şi apoi se adaugă ponderat la un buffer, care iniţial este şters. Acest buffer este numit buffer de acumulare sau eşantionare. În final, imaginea obţinută în buffer-ul de acumulare este transferată în buffer-ul de imagine. intervalul erorii de eșantionare interval de eșantionare interval de perturbare Fig. 2. Eșantionarea unei unde sinusoidale cu o frecvență peste limita Nyquist Implementarea tehnicilor de anti-aliasing diferă foarte mult de la un sistem grafic la altul. O imagine de calitate (fără zgomot de spectru transpus - aliasing) necesită atât rezoluţii mari ale imaginii, care permit creşterea frecvenţei de eşantionare, cât şi filtrarea imaginii, prin care se limitează spectrul imaginii la o 3
4 valoare care asigură eşantionarea şi reconstrucţia fără zgomot (sau cu zgomot redus) a imaginii. În sistemele grafice folosite în diferite aplicaţii de realitate virtuală, asigurarea unei filtrări anti-aliasing de calitate este o condiţie foarte importantă, mai ales în simulatoarele de antrenament. În cursul antrenamentelor de zbor, mişcarea dezordonată (crowl) a obiectelor, ca şi apariţia sau dispariţia obiectelor mici, datorată anti-aliasing-ului, au un efect negativ puternic asupra deprinderilor pe care trebuie să le însuşească piloţii. De aceea, s-au făcut eforturi deosebite pentru implementarea hardware a Z-buffer-ului, sau a texturării. Calitatea implementării procedeelor de antialiasing este un criteriu important de selecţie a unui sistem grafic, şi, bineînţeles, reprezintă un procent important din costul acestuia. Biblioteca OpenGL implementează un buffer de acumulare care este folosit atât pentru redarea anti-aliasing a scenelor, cât şi pentru crearea altor efecte vizuale, ca iluminarea cu surse multiple de lumină sau estomparea imaginii unui obiect datorită mişcării acestuia (motion blur). Buffer-ul de acumulare se defineşte cu aceeaşi dimensiune ca şi buffer-ul de culoare şi buffer-ul de adâncime. În fiecare locaţie (x, y) a buffer-ului de acumulare se memorează culoarea unui pixel, corespunzător pixelului cu aceeaşi adresă (x, y) în buffer-ul de culoare. Asupra buffer-ului de acumulare se pot efectua operaţii prin apelul funcţiei: void glaccum( GLenum op, GLfloat value); Parametrul op selectează operaţia, iar parametrul value este un număr care este folosit în unele operaţii. Operaţiile posibile sunt GL_ACCUM, GL_LOAD, GL_RETURN, GL_ADD şi GL_MULT. GL_ACCUM citeşte fiecare pixel din buffer-ul curent de citire, selectat anterior cu funţia glreadbuffer(), multiplică valorile R,G,B,A ale pixelului cu valoarea value şi rezultatul îl adună la valoarea corespunzătoare (cu aceeași adresă de pixel) din buffer-ul de acumulare. GL_LOAD se execută asemănător cu operaţia GL_ACCUM, cu deosebirea că valorile rezultate înlocuiesc valorile existente în buffer-ul de acumulare. GL_RETURN preia valorile fiecărui pixel din buffer-ul de acumulare, le multiplică cu valoarea value, iar rezultatul îl înscrie în buffer-ul de scriere selectat anterior printr-o funcţie gldrawbuffer(). GL_ADD şi GL_MULT adună sau înmulţeşte valoarea componentelor R,G,B,A a fiecărui pixel din buffer-ul de acumulare cu valoarea value, rezultatul fiind depus înapoi în buffer-ul de acumulare. Pentru operaţia GL_MULT, value se limitează în intervalul [-1.0, 1.0]. Înainte de începerea fiecărei operaţii de acumulare buffer-ul de acumulare se şterge prin apelul funcţiei glclear(gl_accum_buffer_bit). Culoarea de ştergere a buffer-ului de acumulare trebuie să fie (0,0,0,0), şi se setează la iniţializare prin apelul funcţiei glclearaccum(0.0, 0.0, 0.0, 0.0). Buffer-ul de acumulare se foloseşte pentru implementarea anti-aliasing-ului prin eşantionare stocastică. Imaginea este eşantionată în poziţii de eşantionare care sunt perturbate aleator faţă de centrul pixelului, pe o distanţă egală cu dimensiunea pixelului. Imaginile succesive obţinute pentru toate poziţiile de eşantionare sunt 4
5 mediate pentru fiecare componentă de culoare a fiecărui pixel, rezultând imaginea finală, din care a fost eliminat zgomotul aleator datorat perturbării poziţiilor de eşantionare. Fiecare imagine se creează într-un buffer de culoare şi apoi se adaugă ponderat la buffer-ul de acumulare (iniţial şters) prin funcţia glaccum(gl_accum, 1/n), unde n este numărul de poziţii succesive de eşantionare. Imaginea rezultată în buffer-ul de eşantionare este transferată în buffer-ul de culoare prin funcţia glaccum(gl_return, 1.0). La generarea fiecărei imagini corespunzătoare unei poziţii de eşantionare se execută testul de adâncime (Z-buffer), deci imaginea finală elimină suprafeţele ascunse. Aşa cum se vede în figura 3, efectele de aliasing sunt mult diminuate prin acest procedeu, dar, dacă este implementat soft, timpul de calcul este foarte mare, cel puţin de n ori mai mare decât timpul necesar pentru aceeaşi imagine redată fără antialiasing. Implementarea hardware a tehnicii de anti-aliasing este absolut necesară în grafica interactivă. Programul prin care s-a realizat această imagine este dat în exemplul următor. Figura 3. Obiecte cu iluminare şi umbrire. La stânga, obiectul este desenat cu aliasing. La dreapta, obiectul este desenat cu anti-aliasng folosind un buffer de acumulare. Exemplul 2. Redarea anti-aliasing a obiectelor cu umbrire şi eliminarea suprafeţelor ascunse se poate implementa folosind buffer-ul de acumulare astfel: #include <GL/freeglut.h> #define ACCSIZE 16 static float W = 6; static float WX, WY; static float N = -10; static float F = 10; //numarul de esantionari //dimensiunea maxima a ferestrei //dimensiuni fereastra //distanta de vizualizare near //distanta de vizualizare far void Init() GLfloat ambient[] = 0.4, 0.4, 0.4, 1.0; GLfloat diffuse[] = 1.0, 1.0, 1.0, 1.0; GLfloat specular[] = 1.0, 1.0, 1.0, 1.0; GLfloat position[] = 1.0, 0.2, 1.0, 0.0; GLfloat mat_ambient[] = 0.2, 0.2, 0.2, 1.0; GLfloat mat_diffuse[] = 0.9, 0.2, 0.1, 1.0; 5
6 GLfloat mat_specular[] = 0.9, 0.6, 0.6, 1.0; GLfloat mat_shininess[] = 50.0; gllightfv(gl_light0, GL_AMBIENT, ambient); gllightfv(gl_light0, GL_DIFFUSE, diffuse); gllightfv(gl_light0, GL_SPECULAR, specular); gllightfv(gl_light0, GL_POSITION, position); glmaterialfv(gl_front, GL_AMBIENT, mat_ambient); glmaterialfv(gl_front, GL_DIFFUSE, mat_diffuse); glmaterialfv(gl_front, GL_SPECULAR, mat_specular); glmaterialfv(gl_front, GL_SHININESS, mat_shininess); glenable(gl_lighting); glenable(gl_light0); glenable(gl_depth_test); glclearaccum(0.0, 0.0, 0.0, 0.0); glclearcolor(0.8, 0.8, 0.8, 1.0); GLfloat jitter16[][2] = 0.375, , 0.625, , 0.875, , 0.125, , 0.375, , 0.875, , 0.625, , 0.375, , 0.625, , 0.125, , 0.125, , 0.375, , 0.875, , 0.875, , 0.125, , 0.625, ; void Display() int i; glclear(gl_accum_buffer_bit); GLint viewport[4]; glgetintegerv(gl_viewport, viewport); //Redarea cu anti-aliasing a obiectului for(i = 0; i < ACCSIZE; i++) gltranslatef(jitter16[i][0]*2*wx/viewport[2], jitter16[i][1]*2*wy/viewport[3], 0.0); gltranslated(1.5, -1, -8); glrotatef(15.0, 1.0, 0.0, 0.0); glrotatef(20.0, 0.0, 1.0, 0.0); glclear(gl_depth_buffer_bit GL_COLOR_BUFFER_BIT); glutsolidteapot(1.0); glaccum(gl_accum, 1.0/ACCSIZE); glaccum(gl_return, 1.0); //Obiectul redat fara anti-aliasing gltranslated(-1.5, -1.0, -8.0); glrotatef(15.0, 1.0, 0.0, 0.0); glrotatef(20.0, 0.0, 1.0, 0.0); glutsolidteapot(1.0); 6
7 glflush(); void Reshape(int w, int h) h = (h == 0)? 1 : h; glviewport(0, 0, w, h); glmatrixmode(gl_projection); glloadidentity(); if(w <= h) WX = W / 2; WY = W * (GLfloat)h / (GLfloat)(w * 2); else WX = W * (GLfloat)w / (GLfloat)(h * 2); WY = W / 2; glortho(-wx, WX, -WY, WY, N, F); glmatrixmode(gl_modelview); glloadidentity(); void main(int argc, char* argv[]) glutinit(&argc, argv); glutinitdisplaymode(glut_single GLUT_RGB GLUT_DEPTH GLUT_ALPHA GLUT_ACCUM); glutinitwindowsize(500, 500); glutinitwindowposition(100, 100); glutcreatewindow("acumulare"); Init(); glutdisplayfunc(display); glutreshapefunc(reshape); glutmainloop(); În funcţia de iniţializare Init() se defineşte sistemul de iluminare (surse de lumină şi materiale), se stabilesc culorile de ştergere ale buffer-ului de culoare şi de acumulare şi se validează buffer-ul de adâncime. Unele din comenzile din iniţializare nu au mai fost introduse dacă s-au folosit valorile implicite ale bibliotecii OpenGL. De exemplu, în execuţia cu un singur buffer de culoare (stabilită la iniţializare), buffer-ul de citire şi de scriere curent este implicit buffer-ul de culoare GL_FRONT, şi nu s-au mai apelat funcţiile glreadbuffer() şi gldrawbuffer(). Perturbarea poziţiei de eşantionare se obţine prin perturbarea poziţiei centrului porţii de afişare. În acest exemplu s-a folosit o proiecţie ortografică în care transformările inverse de la poarta de afişare în sistemul universal se execută mai simplu. Fereastra este definită ca o fereastră simetrică, de dimensiuni 2*WX, 2*WY, calculate în funcţia Reshape(). Perturbaţia grilei de eşantionare se obţine prin modificarea centrului porţii cu valorile aleatoare ( ε x, ε y) care se citesc din tabelul 7
8 jitter. Acest tabel conţine perechi de valori în număr egal cu numărul de acumulări dorite (ACCSIZE), care sunt poziţii aleatoare pe suprafaţa unui pixel. Perturbaţiile în poarta de afişare se transformă în perturbare a poziţiei centrului ferestrei de vizualizare prin scalare cu factorii de scalare 2*WX/viewport[2], 2*WY/viewport[3]. Aceste deplasări ale poziţiei centrului ferestrei de vizualizare sunt echivalente cu deplasări în sens invers ale obiectelor scenei. În proiecţia ortografică, deplasarea obiectelor care conduce la deplasarea centrului porţii de afişare şi, deci, la perturbarea poziţiei grilei de eşantionare se obţine prin instrucţiunea: gltranslatef(jitter16[i][0]*2*wx/viewport[2], jitter16[i][1]*2*wy/viewport[3], 0.0); În proiecţia perspectivă, deplasarea obiectelor trebuie să fie calculată în funcţie de matricea de proiecţie perspectivă. 8
Metode iterative pentru probleme neliniare - contractii
 Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
III. Serii absolut convergente. Serii semiconvergente. ii) semiconvergentă dacă este convergentă iar seria modulelor divergentă.
 III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate.
 Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM 1 electronica.geniu.ro
 Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
MARCAREA REZISTOARELOR
 1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor X) functia f 1
 Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
5. FUNCŢII IMPLICITE. EXTREME CONDIŢIONATE.
 5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
(a) se numeşte derivata parţială a funcţiei f în raport cu variabila x i în punctul a.
 Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor
 Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
 4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
Curs 14 Funcţii implicite. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi"
 Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE
 DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
Planul determinat de normală şi un punct Ecuaţia generală Plane paralele Unghi diedru Planul determinat de 3 puncte necoliniare
 1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
Metode de interpolare bazate pe diferenţe divizate
 Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
5.5. REZOLVAREA CIRCUITELOR CU TRANZISTOARE BIPOLARE
 5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
Aplicaţii ale principiului I al termodinamicii la gazul ideal
 Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Laborator 11. Mulţimi Julia. Temă
 Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Sisteme diferenţiale liniare de ordinul 1
 1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
R R, f ( x) = x 7x+ 6. Determinați distanța dintre punctele de. B=, unde x și y sunt numere reale.
 5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
Subiecte Clasa a VIII-a
 Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Modele de iluminare şi reflexie în OpenGL
 EGC -Lucrarea 9 Modele de iluminare şi reflexie în OpenGL 4. Modele de umbrire a suprafeńelor 4.1 Tipuri de modele de umbrire utilizate în OpenGL Prin model de umbrire (shading) înńelegem un model prin
EGC -Lucrarea 9 Modele de iluminare şi reflexie în OpenGL 4. Modele de umbrire a suprafeńelor 4.1 Tipuri de modele de umbrire utilizate în OpenGL Prin model de umbrire (shading) înńelegem un model prin
2.1 Sfera. (EGS) ecuaţie care poartă denumirea de ecuaţia generală asferei. (EGS) reprezintă osferă cu centrul în punctul. 2 + p 2
 .1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
.1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
riptografie şi Securitate
 riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
Luminarea obiectelor. {glenable gldisable} (GL_LIGHTING)
 Luminarea obiectelor Pentru vizualizarea unei scene este necesar să se determine culoarea pentru fiecare pixel din zona de desenare. Culoarea pixelului depinde de: 1. proprietăţile zonei din scena care
Luminarea obiectelor Pentru vizualizarea unei scene este necesar să se determine culoarea pentru fiecare pixel din zona de desenare. Culoarea pixelului depinde de: 1. proprietăţile zonei din scena care
Definiţia generală Cazul 1. Elipsa şi hiperbola Cercul Cazul 2. Parabola Reprezentari parametrice ale conicelor Tangente la conice
 1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
Integrala nedefinită (primitive)
 nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
Problema a II - a (10 puncte) Diferite circuite electrice
 Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
 10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
Curs 1 Şiruri de numere reale
 Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
a n (ζ z 0 ) n. n=1 se numeste partea principala iar seria a n (z z 0 ) n se numeste partea
 Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Componente şi Circuite Electronice Pasive. Laborator 3. Divizorul de tensiune. Divizorul de curent
 Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
prin egalizarea histogramei
 Lucrarea 4 Îmbunătăţirea imaginilor prin egalizarea histogramei BREVIAR TEORETIC Tehnicile de îmbunătăţire a imaginilor bazate pe calculul histogramei modifică histograma astfel încât aceasta să aibă o
Lucrarea 4 Îmbunătăţirea imaginilor prin egalizarea histogramei BREVIAR TEORETIC Tehnicile de îmbunătăţire a imaginilor bazate pe calculul histogramei modifică histograma astfel încât aceasta să aibă o
a. 11 % b. 12 % c. 13 % d. 14 %
 1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
5.4. MULTIPLEXOARE A 0 A 1 A 2
 5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
Esalonul Redus pe Linii (ERL). Subspatii.
 Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii transversale, scrisă faţă de una dintre axele de inerţie principale:,
 REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
Zgomotul se poate suprapune informaţiei utile în două moduri: g(x, y) = f(x, y) n(x, y) (6.2)
 Lucrarea 6 Zgomotul în imagini BREVIAR TEORETIC Zgomotul este un semnal aleator, care afectează informaţia utilă conţinută într-o imagine. El poate apare de-alungul unui lanţ de transmisiune, sau prin
Lucrarea 6 Zgomotul în imagini BREVIAR TEORETIC Zgomotul este un semnal aleator, care afectează informaţia utilă conţinută într-o imagine. El poate apare de-alungul unui lanţ de transmisiune, sau prin
V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile
 Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Curs 4 Serii de numere reale
 Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Conice. Lect. dr. Constantin-Cosmin Todea. U.T. Cluj-Napoca
 Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
III. Reprezentarea informaţiei în sistemele de calcul
 Metode Numerice Curs 3 III. Reprezentarea informaţiei în sistemele de calcul III.1. Reprezentarea internă a numerelor întregi III. 1.1. Reprezentarea internă a numerelor întregi fără semn (pozitive) Reprezentarea
Metode Numerice Curs 3 III. Reprezentarea informaţiei în sistemele de calcul III.1. Reprezentarea internă a numerelor întregi III. 1.1. Reprezentarea internă a numerelor întregi fără semn (pozitive) Reprezentarea
Componente şi Circuite Electronice Pasive. Laborator 4. Măsurarea parametrilor mărimilor electrice
 Laborator 4 Măsurarea parametrilor mărimilor electrice Obiective: o Semnalul sinusoidal, o Semnalul dreptunghiular, o Semnalul triunghiular, o Generarea diferitelor semnale folosind placa multifuncţională
Laborator 4 Măsurarea parametrilor mărimilor electrice Obiective: o Semnalul sinusoidal, o Semnalul dreptunghiular, o Semnalul triunghiular, o Generarea diferitelor semnale folosind placa multifuncţională
Lab06: Extragerea trăsăturilor şi selecţia trăsăturilor. Aplicaţie pentru recunoaşterea obiectelor bazată pe formă.
 Lab06: Extragerea trăsăturilor şi selecţia trăsăturilor Aplicaţie pentru recunoaşterea obiectelor bazată pe formă. Aplicație practică a extragerii şi selecţiei trăsăturilor Recunoaşterea celor 4 forme
Lab06: Extragerea trăsăturilor şi selecţia trăsăturilor Aplicaţie pentru recunoaşterea obiectelor bazată pe formă. Aplicație practică a extragerii şi selecţiei trăsăturilor Recunoaşterea celor 4 forme
1.7. AMPLIFICATOARE DE PUTERE ÎN CLASA A ŞI AB
 1.7. AMLFCATOARE DE UTERE ÎN CLASA A Ş AB 1.7.1 Amplificatoare în clasa A La amplificatoarele din clasa A, forma de undă a tensiunii de ieşire este aceeaşi ca a tensiunii de intrare, deci întreg semnalul
1.7. AMLFCATOARE DE UTERE ÎN CLASA A Ş AB 1.7.1 Amplificatoare în clasa A La amplificatoarele din clasa A, forma de undă a tensiunii de ieşire este aceeaşi ca a tensiunii de intrare, deci întreg semnalul
Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].
![Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].](/thumbs/72/67648751.jpg) Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
Seminariile Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reziduurilor
 Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
LUCRAREA NR. 1 STUDIUL SURSELOR DE CURENT
 LUCAEA N STUDUL SUSELO DE CUENT Scopul lucrării În această lucrare se studiază prin simulare o serie de surse de curent utilizate în cadrul circuitelor integrate analogice: sursa de curent standard, sursa
LUCAEA N STUDUL SUSELO DE CUENT Scopul lucrării În această lucrare se studiază prin simulare o serie de surse de curent utilizate în cadrul circuitelor integrate analogice: sursa de curent standard, sursa
Modele de iluminare şi reflexie în OpenGL
 Modele de iluminare şi reflexie în OpenGL În lumea reală, atunci când lumina provenită de la diferite surse de lumină cade asupra obiectelor opace, o parte este absorbită de obiecte, iar o parte este reflectată.
Modele de iluminare şi reflexie în OpenGL În lumea reală, atunci când lumina provenită de la diferite surse de lumină cade asupra obiectelor opace, o parte este absorbită de obiecte, iar o parte este reflectată.
Profesor Blaga Mirela-Gabriela DREAPTA
 DREAPTA Fie punctele A ( xa, ya ), B ( xb, yb ), C ( xc, yc ) şi D ( xd, yd ) în planul xoy. 1)Distanţa AB = (x x ) + (y y ) Ex. Fie punctele A( 1, -3) şi B( -2, 5). Calculaţi distanţa AB. AB = ( 2 1)
DREAPTA Fie punctele A ( xa, ya ), B ( xb, yb ), C ( xc, yc ) şi D ( xd, yd ) în planul xoy. 1)Distanţa AB = (x x ) + (y y ) Ex. Fie punctele A( 1, -3) şi B( -2, 5). Calculaţi distanţa AB. AB = ( 2 1)
Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25
 Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25 LAGĂRELE CU ALUNECARE!" 25.1.Caracteristici.Părţi componente.materiale.!" 25.2.Funcţionarea lagărelor cu alunecare.! 25.1.Caracteristici.Părţi componente.materiale.
Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25 LAGĂRELE CU ALUNECARE!" 25.1.Caracteristici.Părţi componente.materiale.!" 25.2.Funcţionarea lagărelor cu alunecare.! 25.1.Caracteristici.Părţi componente.materiale.
Εισαγωγή στην OpenGL
 Εισαγωγή στην OpenGL Περιεχόµενα εισαγωγικής ενότητας: Γενικά χαρακτηριστικά της OpenGL Βιβλιοθήκες που της OpenGL Ένα τυπικό πρόγραµµα Τι είναι η OpenGL; Η OpenGL δεν είναι µια συγκεκριµένη βιβλιοθήκη
Εισαγωγή στην OpenGL Περιεχόµενα εισαγωγικής ενότητας: Γενικά χαρακτηριστικά της OpenGL Βιβλιοθήκες που της OpenGL Ένα τυπικό πρόγραµµα Τι είναι η OpenGL; Η OpenGL δεν είναι µια συγκεκριµένη βιβλιοθήκη
Subiecte Clasa a VII-a
 lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
2. Sisteme de forţe concurente...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...3
 SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
Geometrie computationala 2. Preliminarii geometrice
 Platformă de e-learning și curriculă e-content pentru învățământul superior tehnic Geometrie computationala 2. Preliminarii geometrice Preliminarii geometrice Spatiu Euclidean: E d Spatiu de d-tupluri,
Platformă de e-learning și curriculă e-content pentru învățământul superior tehnic Geometrie computationala 2. Preliminarii geometrice Preliminarii geometrice Spatiu Euclidean: E d Spatiu de d-tupluri,
Algoritmica grafurilor XI. Cuplaje in grafuri. Masuri de calitate. Numere Ramsey
 Algoritmica grafurilor XI. Cuplaje in grafuri. Masuri de calitate. Numere Ramsey Mihai Suciu Facultatea de Matematică și Informatică (UBB) Departamentul de Informatică Mai, 16, 2018 Mihai Suciu (UBB) Algoritmica
Algoritmica grafurilor XI. Cuplaje in grafuri. Masuri de calitate. Numere Ramsey Mihai Suciu Facultatea de Matematică și Informatică (UBB) Departamentul de Informatică Mai, 16, 2018 Mihai Suciu (UBB) Algoritmica
Asupra unei inegalităţi date la barajul OBMJ 2006
 Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
Reflexia şi refracţia luminii.
 Reflexia şi refracţia luminii. 1. Cu cat se deplaseaza o raza care cade sub unghiul i =30 pe o placa plan-paralela de grosime e = 8,0 mm si indicele de refractie n = 1,50, pe care o traverseaza? Caz particular
Reflexia şi refracţia luminii. 1. Cu cat se deplaseaza o raza care cade sub unghiul i =30 pe o placa plan-paralela de grosime e = 8,0 mm si indicele de refractie n = 1,50, pe care o traverseaza? Caz particular
Capitolul 4. Integrale improprii Integrale cu limite de integrare infinite
 Capitolul 4 Integrale improprii 7-8 În cadrul studiului integrabilităţii iemann a unei funcţii s-au evidenţiat douăcondiţii esenţiale:. funcţia :[ ] este definită peintervalînchis şi mărginit (interval
Capitolul 4 Integrale improprii 7-8 În cadrul studiului integrabilităţii iemann a unei funcţii s-au evidenţiat douăcondiţii esenţiale:. funcţia :[ ] este definită peintervalînchis şi mărginit (interval
prin operaţii punctuale
 Lucrarea 3 Îmbunătăţirea imaginilor prin operaţii punctuale BREVIAR TEORETIC Termenul general de îmbunătăţire a imaginilor se referă la o clasă largă de operaţii, ce au ca scop mărirea detectabilităţii
Lucrarea 3 Îmbunătăţirea imaginilor prin operaţii punctuale BREVIAR TEORETIC Termenul general de îmbunătăţire a imaginilor se referă la o clasă largă de operaţii, ce au ca scop mărirea detectabilităţii
Realizat de: Ing. mast. Pintilie Lucian Nicolae Pentru disciplina: Sisteme de calcul în timp real Adresă de
 Teorema lui Nyquist Shannon - Demonstrație Evidențierea conceptului de timp de eșantionare sau frecvență de eșantionare (eng. sample time or sample frequency) IPOTEZĂ: DE CE TIMPUL DE EȘANTIONARE (SAU
Teorema lui Nyquist Shannon - Demonstrație Evidențierea conceptului de timp de eșantionare sau frecvență de eșantionare (eng. sample time or sample frequency) IPOTEZĂ: DE CE TIMPUL DE EȘANTIONARE (SAU
Ecuaţia generală Probleme de tangenţă Sfera prin 4 puncte necoplanare. Elipsoidul Hiperboloizi Paraboloizi Conul Cilindrul. 1 Sfera.
 pe ecuaţii generale 1 Sfera Ecuaţia generală Probleme de tangenţă 2 pe ecuaţii generale Sfera pe ecuaţii generale Ecuaţia generală Probleme de tangenţă Numim sferă locul geometric al punctelor din spaţiu
pe ecuaţii generale 1 Sfera Ecuaţia generală Probleme de tangenţă 2 pe ecuaţii generale Sfera pe ecuaţii generale Ecuaţia generală Probleme de tangenţă Numim sferă locul geometric al punctelor din spaţiu
Proiectarea filtrelor prin metoda pierderilor de inserţie
 FITRE DE MIROUNDE Proiectarea filtrelor prin metoda pierderilor de inserţie P R Puterea disponibila de la sursa Puterea livrata sarcinii P inc P Γ ( ) Γ I lo P R ( ) ( ) M ( ) ( ) M N P R M N ( ) ( ) Tipuri
FITRE DE MIROUNDE Proiectarea filtrelor prin metoda pierderilor de inserţie P R Puterea disponibila de la sursa Puterea livrata sarcinii P inc P Γ ( ) Γ I lo P R ( ) ( ) M ( ) ( ) M N P R M N ( ) ( ) Tipuri
8 Intervale de încredere
 8 Intervale de încredere În cursul anterior am determinat diverse estimări ˆ ale parametrului necunoscut al densităţii unei populaţii, folosind o selecţie 1 a acestei populaţii. În practică, valoarea calculată
8 Intervale de încredere În cursul anterior am determinat diverse estimări ˆ ale parametrului necunoscut al densităţii unei populaţii, folosind o selecţie 1 a acestei populaţii. În practică, valoarea calculată
Conice - Câteva proprietǎţi elementare
 Conice - Câteva proprietǎţi elementare lect.dr. Mihai Chiş Facultatea de Matematicǎ şi Informaticǎ Universitatea de Vest din Timişoara Viitori Olimpici ediţia a 5-a, etapa I, clasa a XII-a 1 Definiţii
Conice - Câteva proprietǎţi elementare lect.dr. Mihai Chiş Facultatea de Matematicǎ şi Informaticǎ Universitatea de Vest din Timişoara Viitori Olimpici ediţia a 5-a, etapa I, clasa a XII-a 1 Definiţii
Valori limită privind SO2, NOx şi emisiile de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili
 Anexa 2.6.2-1 SO2, NOx şi de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili de bioxid de sulf combustibil solid (mg/nm 3 ), conţinut de O 2 de 6% în gazele de ardere, pentru
Anexa 2.6.2-1 SO2, NOx şi de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili de bioxid de sulf combustibil solid (mg/nm 3 ), conţinut de O 2 de 6% în gazele de ardere, pentru
Functii Breviar teoretic 8 ianuarie ianuarie 2011
 Functii Breviar teoretic 8 ianuarie 011 15 ianuarie 011 I Fie I, interval si f : I 1) a) functia f este (strict) crescatoare pe I daca x, y I, x< y ( f( x) < f( y)), f( x) f( y) b) functia f este (strict)
Functii Breviar teoretic 8 ianuarie 011 15 ianuarie 011 I Fie I, interval si f : I 1) a) functia f este (strict) crescatoare pe I daca x, y I, x< y ( f( x) < f( y)), f( x) f( y) b) functia f este (strict)
SERII NUMERICE. Definiţia 3.1. Fie (a n ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0
 SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
Captura imaginilor. este necesară o sursă de lumină (λ: lungimea de undă a sursei)
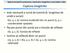 Captura imaginilor este necesară o sursă de lumină (λ: lungimea de undă a sursei) E(x, y, z, λ): lumina incidentă într-un punct (x, y, z coordonatele spațiale) fiecare punct din scenă are o funcție de
Captura imaginilor este necesară o sursă de lumină (λ: lungimea de undă a sursei) E(x, y, z, λ): lumina incidentă într-un punct (x, y, z coordonatele spațiale) fiecare punct din scenă are o funcție de
2. Circuite logice 2.5. Sumatoare şi multiplicatoare. Copyright Paul GASNER
 2. Circuite logice 2.5. Sumatoare şi multiplicatoare Copyright Paul GASNER Adunarea în sistemul binar Adunarea se poate efectua în mod identic ca la adunarea obişnuită cu cifre arabe în sistemul zecimal
2. Circuite logice 2.5. Sumatoare şi multiplicatoare Copyright Paul GASNER Adunarea în sistemul binar Adunarea se poate efectua în mod identic ca la adunarea obişnuită cu cifre arabe în sistemul zecimal
Examen AG. Student:... Grupa:... ianuarie 2011
 Problema 1. Pentru ce valori ale lui n,m N (n,m 1) graful K n,m este eulerian? Problema 2. Să se construiască o funcţie care să recunoască un graf P 3 -free. La intrare aceasta va primi un graf G = ({1,...,n},E)
Problema 1. Pentru ce valori ale lui n,m N (n,m 1) graful K n,m este eulerian? Problema 2. Să se construiască o funcţie care să recunoască un graf P 3 -free. La intrare aceasta va primi un graf G = ({1,...,n},E)
SEMINAR 14. Funcţii de mai multe variabile (continuare) ( = 1 z(x,y) x = 0. x = f. x + f. y = f. = x. = 1 y. y = x ( y = = 0
 Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
2. Circuite logice 2.4. Decodoare. Multiplexoare. Copyright Paul GASNER
 2. Circuite logice 2.4. Decodoare. Multiplexoare Copyright Paul GASNER Definiţii Un decodor pe n bits are n intrări şi 2 n ieşiri; cele n intrări reprezintă un număr binar care determină în mod unic care
2. Circuite logice 2.4. Decodoare. Multiplexoare Copyright Paul GASNER Definiţii Un decodor pe n bits are n intrări şi 2 n ieşiri; cele n intrări reprezintă un număr binar care determină în mod unic care
Exemple de probleme rezolvate pentru cursurile DEEA Tranzistoare bipolare cu joncţiuni
 Problema 1. Se dă circuitul de mai jos pentru care se cunosc: VCC10[V], 470[kΩ], RC2,7[kΩ]. Tranzistorul bipolar cu joncţiuni (TBJ) este de tipul BC170 şi are parametrii β100 şi VBE0,6[V]. 1. să se determine
Problema 1. Se dă circuitul de mai jos pentru care se cunosc: VCC10[V], 470[kΩ], RC2,7[kΩ]. Tranzistorul bipolar cu joncţiuni (TBJ) este de tipul BC170 şi are parametrii β100 şi VBE0,6[V]. 1. să se determine
Principiul Inductiei Matematice.
 Principiul Inductiei Matematice. Principiul inductiei matematice constituie un mijloc important de demonstratie in matematica a propozitiilor (afirmatiilor) ce depind de argument natural. Metoda inductiei
Principiul Inductiei Matematice. Principiul inductiei matematice constituie un mijloc important de demonstratie in matematica a propozitiilor (afirmatiilor) ce depind de argument natural. Metoda inductiei
V O. = v I v stabilizator
 Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
CONCURSUL DE MATEMATICĂ APLICATĂ ADOLF HAIMOVICI, 2017 ETAPA LOCALĂ, HUNEDOARA Clasa a IX-a profil științe ale naturii, tehnologic, servicii
 Clasa a IX-a 1 x 1 a) Demonstrați inegalitatea 1, x (0, 1) x x b) Demonstrați că, dacă a 1, a,, a n (0, 1) astfel încât a 1 +a + +a n = 1, atunci: a +a 3 + +a n a1 +a 3 + +a n a1 +a + +a n 1 + + + < 1
Clasa a IX-a 1 x 1 a) Demonstrați inegalitatea 1, x (0, 1) x x b) Demonstrați că, dacă a 1, a,, a n (0, 1) astfel încât a 1 +a + +a n = 1, atunci: a +a 3 + +a n a1 +a 3 + +a n a1 +a + +a n 1 + + + < 1
Stabilizator cu diodă Zener
 LABAT 3 Stabilizator cu diodă Zener Se studiază stabilizatorul parametric cu diodă Zener si apoi cel cu diodă Zener şi tranzistor. Se determină întâi tensiunea Zener a diodei şi se calculează apoi un stabilizator
LABAT 3 Stabilizator cu diodă Zener Se studiază stabilizatorul parametric cu diodă Zener si apoi cel cu diodă Zener şi tranzistor. Se determină întâi tensiunea Zener a diodei şi se calculează apoi un stabilizator
CIRCUITE INTEGRATE MONOLITICE DE MICROUNDE. MMIC Monolithic Microwave Integrated Circuit
 CIRCUITE INTEGRATE MONOLITICE DE MICROUNDE MMIC Monolithic Microwave Integrated Circuit CUPRINS 1. Avantajele si limitarile MMIC 2. Modelarea dispozitivelor active 3. Calculul timpului de viata al MMIC
CIRCUITE INTEGRATE MONOLITICE DE MICROUNDE MMIC Monolithic Microwave Integrated Circuit CUPRINS 1. Avantajele si limitarile MMIC 2. Modelarea dispozitivelor active 3. Calculul timpului de viata al MMIC
Aparate de măsurat. Măsurări electronice Rezumatul cursului 2. MEE - prof. dr. ing. Ioan D. Oltean 1
 Aparate de măsurat Măsurări electronice Rezumatul cursului 2 MEE - prof. dr. ing. Ioan D. Oltean 1 1. Aparate cu instrument magnetoelectric 2. Ampermetre şi voltmetre 3. Ohmetre cu instrument magnetoelectric
Aparate de măsurat Măsurări electronice Rezumatul cursului 2 MEE - prof. dr. ing. Ioan D. Oltean 1 1. Aparate cu instrument magnetoelectric 2. Ampermetre şi voltmetre 3. Ohmetre cu instrument magnetoelectric
a. 0,1; 0,1; 0,1; b. 1, ; 5, ; 8, ; c. 4,87; 6,15; 8,04; d. 7; 7; 7; e. 9,74; 12,30;1 6,08.
 1. În argentometrie, metoda Mohr: a. foloseşte ca indicator cromatul de potasiu, care formeazǎ la punctul de echivalenţă un precipitat colorat roşu-cărămiziu; b. foloseşte ca indicator fluoresceina, care
1. În argentometrie, metoda Mohr: a. foloseşte ca indicator cromatul de potasiu, care formeazǎ la punctul de echivalenţă un precipitat colorat roşu-cărămiziu; b. foloseşte ca indicator fluoresceina, care
Κεφάλαιο 6 ο Φωτορεαλισµός
 Κεφάλαιο 6 ο Φωτορεαλισµός Εισαγωγή Στο Κεφάλαιο αναλύσαµε τις µεθόδους απόδοσης χρωµάτων σε επιφάνειες κατά τη σχεδίασή τους στη σκηνή. Ωστόσο, εάν ενδιαφερόµαστε για την απόδοση σκηνών που προσοµοιώνουν
Κεφάλαιο 6 ο Φωτορεαλισµός Εισαγωγή Στο Κεφάλαιο αναλύσαµε τις µεθόδους απόδοσης χρωµάτων σε επιφάνειες κατά τη σχεδίασή τους στη σκηνή. Ωστόσο, εάν ενδιαφερόµαστε για την απόδοση σκηνών που προσοµοιώνουν
COLEGIUL NATIONAL CONSTANTIN CARABELLA TARGOVISTE. CONCURSUL JUDETEAN DE MATEMATICA CEZAR IVANESCU Editia a VI-a 26 februarie 2005.
 SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
Să se arate că n este număr par. Dan Nedeianu
 Primul test de selecție pentru juniori I. Să se determine numerele prime p, q, r cu proprietatea că 1 p + 1 q + 1 r 1. Fie ABCD un patrulater convex cu m( BCD) = 10, m( CBA) = 45, m( CBD) = 15 și m( CAB)
Primul test de selecție pentru juniori I. Să se determine numerele prime p, q, r cu proprietatea că 1 p + 1 q + 1 r 1. Fie ABCD un patrulater convex cu m( BCD) = 10, m( CBA) = 45, m( CBD) = 15 și m( CAB)
Seminar 5 Analiza stabilității sistemelor liniare
 Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Analiza funcționării și proiectarea unui stabilizator de tensiune continuă realizat cu o diodă Zener
 Analiza funcționării și proiectarea unui stabilizator de tensiune continuă realizat cu o diodă Zener 1 Caracteristica statică a unei diode Zener În cadranul, dioda Zener (DZ) se comportă ca o diodă redresoare
Analiza funcționării și proiectarea unui stabilizator de tensiune continuă realizat cu o diodă Zener 1 Caracteristica statică a unei diode Zener În cadranul, dioda Zener (DZ) se comportă ca o diodă redresoare
* K. toate K. circuitului. portile. Considerând această sumă pentru toate rezistoarele 2. = sl I K I K. toate rez. Pentru o bobină: U * toate I K K 1
 FNCȚ DE ENERGE Fie un n-port care conține numai elemente paive de circuit: rezitoare dipolare, condenatoare dipolare și bobine cuplate. Conform teoremei lui Tellegen n * = * toate toate laturile portile
FNCȚ DE ENERGE Fie un n-port care conține numai elemente paive de circuit: rezitoare dipolare, condenatoare dipolare și bobine cuplate. Conform teoremei lui Tellegen n * = * toate toate laturile portile
Examen AG. Student:... Grupa: ianuarie 2016
 16-17 ianuarie 2016 Problema 1. Se consideră graful G = pk n (p, n N, p 2, n 3). Unul din vârfurile lui G se uneşte cu câte un vârf din fiecare graf complet care nu-l conţine, obţinându-se un graf conex
16-17 ianuarie 2016 Problema 1. Se consideră graful G = pk n (p, n N, p 2, n 3). Unul din vârfurile lui G se uneşte cu câte un vârf din fiecare graf complet care nu-l conţine, obţinându-se un graf conex
Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R. 4.1 Proprietăţi topologice ale lui R Puncte de acumulare
 Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R În cele ce urmează, vom studia unele proprietăţi ale mulţimilor din R. Astfel, vom caracteriza locul" unui punct în cadrul unei mulţimi (în limba
Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R În cele ce urmează, vom studia unele proprietăţi ale mulţimilor din R. Astfel, vom caracteriza locul" unui punct în cadrul unei mulţimi (în limba
Metode Runge-Kutta. 18 ianuarie Probleme scalare, pas constant. Dorim să aproximăm soluţia problemei Cauchy
 Metode Runge-Kutta Radu T. Trîmbiţaş 8 ianuarie 7 Probleme scalare, pas constant Dorim să aproximăm soluţia problemei Cauchy y (t) = f(t, y), a t b, y(a) = α. pe o grilă uniformă de (N + )-puncte din [a,
Metode Runge-Kutta Radu T. Trîmbiţaş 8 ianuarie 7 Probleme scalare, pas constant Dorim să aproximăm soluţia problemei Cauchy y (t) = f(t, y), a t b, y(a) = α. pe o grilă uniformă de (N + )-puncte din [a,
Algoritmi genetici. 1.1 Generalităţi
 1.1 Generalităţi Algoritmii genetici fac parte din categoria algoritmilor de calcul evoluţionist şi sunt inspiraţi de teoria lui Darwin asupra evoluţiei. Idea calculului evoluţionist a fost introdusă în
1.1 Generalităţi Algoritmii genetici fac parte din categoria algoritmilor de calcul evoluţionist şi sunt inspiraţi de teoria lui Darwin asupra evoluţiei. Idea calculului evoluţionist a fost introdusă în
GENERATOR DE SECVENŢE BINARE PSEUDOALEATOARE
 GENERATOR DE SECVENŢE BINARE PSEUDOALEATOARE 1. Consideraţii teoretice Zgomotul alb este un proces aleator cu densitate spectrală de putere constantă într-o bandă infinită de frecvenţe. Zgomotul cvasialb
GENERATOR DE SECVENŢE BINARE PSEUDOALEATOARE 1. Consideraţii teoretice Zgomotul alb este un proces aleator cu densitate spectrală de putere constantă într-o bandă infinită de frecvenţe. Zgomotul cvasialb
Orice izometrie f : (X, d 1 ) (Y, d 2 ) este un homeomorfism. (Y = f(x)).
 Teoremă. (Y = f(x)). Orice izometrie f : (X, d 1 ) (Y, d 2 ) este un homeomorfism Demonstraţie. f este continuă pe X: x 0 X, S Y (f(x 0 ), ε), S X (x 0, ε) aşa ca f(s X (x 0, ε)) = S Y (f(x 0 ), ε) : y
Teoremă. (Y = f(x)). Orice izometrie f : (X, d 1 ) (Y, d 2 ) este un homeomorfism Demonstraţie. f este continuă pe X: x 0 X, S Y (f(x 0 ), ε), S X (x 0, ε) aşa ca f(s X (x 0, ε)) = S Y (f(x 0 ), ε) : y
Titlul: Modulaţia în amplitudine
 LABORATOR S.C.S. LUCRAREA NR. 1-II Titlul: Modulaţia în aplitudine Scopul lucrării: Generarea senalelor MA cu diferiţi indici de odulaţie în aplitudine, ăsurarea indicelui de odulaţie în aplitudine, ăsurarea
LABORATOR S.C.S. LUCRAREA NR. 1-II Titlul: Modulaţia în aplitudine Scopul lucrării: Generarea senalelor MA cu diferiţi indici de odulaţie în aplitudine, ăsurarea indicelui de odulaţie în aplitudine, ăsurarea
CIRCUITE LOGICE CU TB
 CIRCUITE LOGICE CU T I. OIECTIVE a) Determinarea experimentală a unor funcţii logice pentru circuite din familiile RTL, DTL. b) Determinarea dependenţei caracteristicilor statice de transfer în tensiune
CIRCUITE LOGICE CU T I. OIECTIVE a) Determinarea experimentală a unor funcţii logice pentru circuite din familiile RTL, DTL. b) Determinarea dependenţei caracteristicilor statice de transfer în tensiune
Curs 2 DIODE. CIRCUITE DR
 Curs 2 OE. CRCUTE R E CUPRN tructură. imbol Relația curent-tensiune Regimuri de funcționare Punct static de funcționare Parametrii diodei Modelul cu cădere de tensiune constantă Analiza circuitelor cu
Curs 2 OE. CRCUTE R E CUPRN tructură. imbol Relația curent-tensiune Regimuri de funcționare Punct static de funcționare Parametrii diodei Modelul cu cădere de tensiune constantă Analiza circuitelor cu
Electronică anul II PROBLEME
 Electronică anul II PROBLEME 1. Găsiți expresiile analitice ale funcției de transfer şi defazajului dintre tensiunea de ieşire şi tensiunea de intrare pentru cuadrupolii din figurile de mai jos și reprezentați-le
Electronică anul II PROBLEME 1. Găsiți expresiile analitice ale funcției de transfer şi defazajului dintre tensiunea de ieşire şi tensiunea de intrare pentru cuadrupolii din figurile de mai jos și reprezentați-le
3.4. Minimizarea funcţiilor booleene
 56 3.4. Minimizarea funcţiilor booleene Minimizarea constă în obţinerea formei celei mai simple de exprimare a funcţiilor booleene în scopul reducerii numărului de circuite şi a numărului de intrări ale
56 3.4. Minimizarea funcţiilor booleene Minimizarea constă în obţinerea formei celei mai simple de exprimare a funcţiilor booleene în scopul reducerii numărului de circuite şi a numărului de intrări ale
II. 5. Probleme. 20 c 100 c = 10,52 % Câte grame sodă caustică se găsesc în 300 g soluţie de concentraţie 10%? Rezolvare m g.
 II. 5. Problee. Care ete concentraţia procentuală a unei oluţii obţinute prin izolvarea a: a) 0 g zahăr în 70 g apă; b) 0 g oă cautică în 70 g apă; c) 50 g are e bucătărie în 50 g apă; ) 5 g aci citric
II. 5. Problee. Care ete concentraţia procentuală a unei oluţii obţinute prin izolvarea a: a) 0 g zahăr în 70 g apă; b) 0 g oă cautică în 70 g apă; c) 50 g are e bucătărie în 50 g apă; ) 5 g aci citric
2 Transformări liniare între spaţii finit dimensionale
 Transformări 1 Noţiunea de transformare liniară Proprietăţi. Operaţii Nucleul şi imagine Rangul şi defectul unei transformări 2 Matricea unei transformări Relaţia dintre rang şi defect Schimbarea matricei
Transformări 1 Noţiunea de transformare liniară Proprietăţi. Operaţii Nucleul şi imagine Rangul şi defectul unei transformări 2 Matricea unei transformări Relaţia dintre rang şi defect Schimbarea matricei
REDRESOARE MONOFAZATE CU FILTRU CAPACITIV
 REDRESOARE MONOFAZATE CU FILTRU CAPACITIV I. OBIECTIVE a) Stabilirea dependenţei dintre tipul redresorului (monoalternanţă, bialternanţă) şi forma tensiunii redresate. b) Determinarea efectelor modificării
REDRESOARE MONOFAZATE CU FILTRU CAPACITIV I. OBIECTIVE a) Stabilirea dependenţei dintre tipul redresorului (monoalternanţă, bialternanţă) şi forma tensiunii redresate. b) Determinarea efectelor modificării
