Modele de iluminare şi reflexie în OpenGL
|
|
|
- Θεοφιλά Πολίτης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Modele de iluminare şi reflexie în OpenGL În lumea reală, atunci când lumina provenită de la diferite surse de lumină cade asupra obiectelor opace, o parte este absorbită de obiecte, iar o parte este reflectată. Ochiul percepe lumina reflectată de obiect, pentru a interpreta forma, culoarea şi alte detalii ale obiectului. Pentru calculul iluminării în grafica pe calculator trebuie să fie definite sursele de lumină şi interacńiunea dintre lumină şi suprafeńe. Un model de iluminare defineşte natura luminii emise de o sursă de lumină, adică distribuńia intensităńii luminii. Un model de reflexie descrie interacńiunea dintre lumină şi o suprafańă, în funcńie de proprietăńile suprafeńei şi natura sursei de lumină. Implementarea unui model de reflexie în procesul de calculare a intensităńii culorii fiecărui pixel este cunoscută sub numele de tehnică de umbrire. Biblioteca OpenGL implementează modelul de reflexie Phong şi modelele de umbrire poligonală şi umbrire Gouraud. În mod implicit, sistemul de iluminare este inactivat şi pentru desenarea primitivelor geometrice se foloseşte culoarea curentă. Pentru validarea iluminării obiectelor, se activează sistemul de iluminare OpenGL prin apelul funcńiei glenable(gl_lighting). Pentru calculul iluminării obiectelor trebuie să fie definite: sursele de lumină, materialul suprafeńelor, modelul de umbrire a suprafeńelor. 1. Specificarea culorii OpenGL permite utilizarea a două moduri de reprezentare a culorilor de afişare: - modul RGBA: pentru fiecare pixel se memorează valorile R (Red), G (Green), B (Blue) şi A (Alpha); - modul indexat: pentru fiecare pixel se memorează un număr, reprezentând un index într-o tabelă de culori. Modul RGBA este cel mai utilizat. În modul RGBA, pentru selectarea culorii curente se folosesc funcńiile glcolor#(). void glcolor3b s i f d ub us ui (TYPE r, TYPE g, TYPE b); void glcolor4b s i f d ub us ui (TYPE r, TYPE g, TYPE b, TYPE a); void glcolor3b s i f d ub us uiv (const TYPE *v); void glcolor4b s i f d ub us uiv (const TYPE *v); FuncŃiile glcolor3() specifică un triplet (R, G, B). FuncŃiile glcolor4() adaugă la tripletul (R, G, B) o valoare de opacitate, numită valoare alfa (A). Valorile R, G, B şi A variază în domeniul [ 0,1]. Valoarea implicită a opacităńii este 1.0. Când sunt specificate valori din afara domeniului [ 0,1], acestea se mapează liniar în acest interval. 1
2 2. Definirea surselor de lumină Lucrarea 8 În OpenGL se pot defini mai multe surse de lumină punctiforme. Numărul de surse de lumină admise variază în funcńie de implementare, dar cel puńin opt surse sunt disponibile în orice bibliotecă OpenGL. Fiecare sursă de lumină poate fi validată prin apelul funcńiei glenable(gl_lighti), unde i este indexul sursei de lumină. O sursă de lumină se caracterizează prin intensitate şi pozińia în scenă. Intensitatea unei surse de lumină se specifică pentru fiecare componentă de iluminare (ambientală, de difuzie şi speculară) printr-un vector în spańiul culorilor în modelul RGBA. PoziŃia unei surse se specifică printr-un vector în coordonate omogene corespunzătoare sistemului de referinńă universal. FuncŃia de definire a unui parametru al sursei de lumină este funcńia gllight#() care are mai multe variante în funcńie de tipul argumentelor. void gllightf(glenum light, GLenum pname, const GLfloat params); void gllighti(glenum light, GLenum pname, const GLint params); void gllightfv(glenum light, GLenum pname, const GLfloat *params); void gllightiv(glenum light, GLenum pname, const GLint *params); Argumentul light reprezintă indexul sursei de lumină şi poate lua un nume simbolic de forma GL_LIGHT0, GL_LIGHT1,..., GL_LIGHTi,unde 0 i GL_MAX_LIGHTS -1. Numărul maxim de surse de lumină depinde de implementarea bibliotecii. Argumentul pname specifică un parametru al sursei de lumină. Sunt acceptate mai multe valori, dinte care unele se referă la intensitatea culorii, iar altele la pozińia sursei (tabelul 1). pname Valoare implicită SemnificaŃie GL_AMBIENT (0.0, 0.0, 0.0, 1.0) intensitatea ambiantă a luminii (RGBA) GL_DIFFUSE (1.0, 1.0, 1.0, 1.0) intensitatea luminii difuze (RGBA) GL_SPECULAR (1.0, 1.0, 1.0, 1.0) intensitatea luminii speculare (RGBA) GL_POSITION (0.0, 0.0, 1.0, 0.0) pozińia (x, y,z, w) GL_SPOT_DIRECTION (0.0, 0.0, -1.0) direcńia (x, y, z) a spotului de lumină GL_SPOT_EXPONENT 0.0 exponentul spotului de lumină GL_SPOT_CUTOFF unghiul spotului de lumină GL_CONSTANT_ATTENUATION 1.0 factor de atenuare constant GL_LINEAR_ATTENUATION 0.0 factor de atenuare liniar GL_QUADRATIC_ATTENUATION 0.0 factor de atenuare cuadratic Tabelul 1. Valorile GL_AMBIENT, GL_DIFFUSE şi GL_SPECULAR ale argumentului pname permit definirea componentelor intensităńii culorii sursei de lumină. În primele două funcńii argumentul params reprezintă valoarea care se va atribui parametrului indicat de pname. În celelalte două funcńii, argumentul params reprezintă un pointer la un vector de patru valori (de tip întreg sau virgulă flotantă), care specifică intensităńile RGBA ale componentei de iluminare ambientală, difuză şi speculară. Valorile implicite ale intensităńilor sunt (0.0, 0.0, 0.0, 1.0) pentru componenta ambientală şi pentru componenta difuză şi speculară a oricărei lumini cu excepńia luminii cu index 0, care are intensitatea difuză şi speculară implicită (1.0, 1.0, 1.0, 1.0). 2
3 În acest model de definire a sursei de lumină, componenta ambientală (GL_AMBIENT) se referă la intensitatea RGBA pe care o sursă de lumină o adaugă iluminării globale a scenei. Componenta de iluminare difuză (GL_DIFFUZE) este cel mai apropiat mod de reprezentare a ceea ce se consideră culoarea sursei de lumină. Componenta de iluminare (GL_SPECULAR) afectează culoarea zonei strălucitoare (hightlight) a obiectelor luminate de sursa respectivă. Valoarea transparenńei surselor de lumină (alpha) este ignorată dacă nu se validează calculul transparenńei (color blending). Valoarea GL_POSITION a argumentului pname permite definirea pozińiei sursei de lumină. În această situańie, argumentul params este un pointer la un vector de patru numere (întregi sau virgulă flotantă) care reprezintă pozińia în coordonate omogene în sistemul de referinńă universal al sursei de lumină. Această pozińie este transformată prin aplicarea valorii matricei de modelare-vizualizare din momentul apelului funcńiei gllight#(), astfel încât sursa de lumină va avea coordonatele transformate în sistemul de referinńă de observare, unde se calculează intensitatea în vârfurile primitivelor geometrice. Dacă componenta w a pozińiei este 0, atunci lumina este tratată ca o lumină direcńională plasată la infinit, în direcńia definită de componentele x, y, z şi se utilizează această direcńie pentru calculul componentelor de reflexie difuză şi speculară. Dacă w 0, atunci sursa este o sursă pozińională şi se foloseşte localizarea acesteia pentru calculul direcńiei de iluminare a suprafeńelor. PoziŃia implicită a unei surse este (0, 0, 1, 0), deci sursa este plasată la infinit pe axa z şi ea luminează obiectele în direcńia z. SecvenŃa de instrucńiuni pentru definirea intensităńii şi pozińiei sursei de lumină de indice 0 arată astfel: GLfloat light_ambient[] = 1.0, 0.0, 0.0, 0.0 ; GLfloat light_diffuse[] = 1.0, 0.0, 0.0, 0.0 ; GLfloat light_specular[] = 1.0, 1.0, 1.0, 0.0 ; GLfloat light_position[] = 1.0, 1.0, 1.0, 0.0 ; gllightfv(gl_light0, GL_AMBIENT, light_ambient); gllightfv(gl_light0, GL_DIFFUSE, light_diffuse); gllightfv(gl_light0, GL_SPECULAR, light_specular); gllightfv(gl_light0, GL_POSITION, light_position); În iluminarea reală, intensitatea luminii primite de un obiect scade odată cu creşterea distanńei acestuia fańă de sursa de lumină. Dat fiind că sursele de lumină direcńionale (care au w = 0 ) se consideră plasate la infinit, nu are sens calculul atenuării cu distanńa, astfel încât atenuarea este invalidată pentru astfel de surse. Pentru sursele pozińionale, se foloseşte un factor de atenuare cu valoarea: f 1 = (1) 2 k + k r k r c l + q unde: r = distanńa dintre sursa de lumină şi vârful în care se calculează iluminarea k = GL_CONSTANT_ATTENUATION; c k = GL_LINEAR_ATTENUATION; l k = GL_QUADRATIC_ ATTENUATION; q 3
4 Lucrarea 8 Implicit aceşti parametri au valorile k = 1, k = 0, k = 0, dar ei pot fi setańi prin apelul uneia din funcńiile gllightf() sau gllighti() astfel: c gllightf(gl_light0, GL_CONSTANT_ATTENUATION, 2.0); gllightf(gl_light0, GL_LINEAR_ ATTENUATION, 1.0); gllightf(gl_light0, GL_QUADRATIC_ ATTENUATION, 0.5); l Dacă se folosesc mai multe surse de lumină, pentru fiecare din ele se definesc componentele intensităńii, pozińia şi caracteristicile de atenuare. q 3. Definirea proprietăńilor materialelor În modele simple de reflexie (ca de exemplu cazul modelului Phong) se consideră că lumina reflectată de o suprafańă este constituită din trei componente: reflexia difuză; reflexia speculară; reflexia ambientală. Reflexia difuză joacă cel mai important rol în culoarea pe care o prezintă o suprafańă. Ea reprezintă culoarea pe care o are suprafańa luminată direct şi depinde de componenta de difuzie a luminii incidente, provenită de la una sau mai multe surse de lumină, de coeficientul de reflexie de difuzie (reflectanńa de difuzie) a materialului şi de unghiul dintre direcńia luminii şi normala la suprafańă. PoziŃia de observare nu influenńează componenta de difuzie a luminii reflectate. În cazul unei surse punctiforme intensitatea luminii difuzate este: I d = k d k c I r 0 r l n, (2) 2 + k r+ k r l q unde k d - coeficientul de reflexie de difuzie, l r - vectorul unitate îndreptat spre sursa de lumină, n r normala la suprafańă, r - distanńa la sursa respectivă, I0 - intensitatea sursei de lumină. Reflexia ambientală afectează culoarea de ansamblu pe care o prezintă o suprafańă şi ea devine sesizabilă atunci când suprafańa nu este luminată direct. Ca şi reflexia difuză, această componentă nu depinde de pozińia de observare. În modelul de reflexie Phong intensitatea dată de componenta ambientală este: I = k I, (3) g a a k a fiind coeficientul de reflexie pentru lumina ambientală. Reflexia speculară produce iluminarea mai puternică (hightlight) a unei zone a obiectului, în funcńie de pozińia de observare (fig.1). În cazul unei singure surse punctiforme, intensitatea luminii reflectate specular este: I Is ks 0 r = ( v r ) n 2, (4) k + k r+ k r c l q 4
5 unde k s - coeficient de reflexie speculară, r - versorul direcńiei de oglindire, v r - versorul direcńiei de observare şi n - coeficient care simulează rugozitatea materialului. l r n r r r Ω v r Fig. 1. Reflexia speculară Phong Prin combinarea relańiilor (2)-(4) se obńine relańia de calcul a culorii unei suprafeńe: c r r r [ k l n+ k ( v) ] n I 0 r 2 d s lr+ kqr I = Iaka +. (5) k + k Din cele prezentate anterior rezultă că pentru calculul intensităńii culorii unei suprafeńe, trebuie definińi coeficienńii de reflexie ambientală, difuză şi speculară. Aceste proprietăńi sunt considerate proprietăńi de material ale suprafeńei şi se specifică prin apelul uneia sau mai multora din cele patru variante ale funcńiei glmaterial#(): void glmateriali(glenum face, GLenum pname, GLint param); void glmaterialf(glenum face, GLenum pname, GLfloat param); void glmaterialiv(glenum face, GLenum pname, GLint *param); void glmaterialfv(glenum face, GLenum pname, GLfloat *param); În aceste funcńii, argumentul face este numele feńei şi depinde de orientarea acesteia; poate lua ca valori constantele simbolice GL_FRONT, GL_BACK, GL_FRONT_AND_BACK. Argumentul pname specifică proprietatea materialului, care se defineşte prin apelul funcńiei glmaterial#(). Acest argument poate lua una din următoarele valorile date în tabelul 2. Nume parametru Valoare implicită SemnificaŃie GL_AMBIENT (0.2, 0.2, 0.2, 1.0) reflectanńa (coeficient de reflexie) ambientală GL_DIFFUSE (0.8, 0.8, 0.8, 1.0) reflectanńa de difuzie GL_AMBIENT_AND_DIFFUSE reflectanńa ambientală şi de difuzie GL_SPECULAR (0.0, 0.0, 0.0, 1.0) reflectanńa speculară GL_SHININESS 0.0 exponentul de reflexie speculară GL_EMISSION (0.0, 0.0, 0.0, 1.0) intensitatea luminii emise GL_COLOR_INDEXES (0,1,1) indicii culorilor ambientală, difuză şi speculară Tabelul 2 5
6 Lucrarea 8 FuncŃiile glmateriali() şi glmaterialf() se folosesc numai pentru setarea strălucirii (GL_SHININESS) la valoarea dată prin argumentul param. FuncŃiile glmaterialiv() şi glmaterialfv() se folosesc pentru specificarea celorlalte proprietăńi. Dacă argumentul pname este GL_COLOR_INDEX atunci param este un pointer la un vector de trei valori de tip întreg, care conńine indicii culorilor ambientală, de difuzie şi speculară ale materialului. În celelalte situańii, param este un pointer la un vector de patru valori de tip întreg sau cu virgulă flotantă, care sunt componentele roşu, verde, albastru şi alpha (transparenńă) ale componentei de reflexie specificate prin parametrul pname (ambientală, difuză, speculară, emisie). Reflexia difuză şi ambientală se specifică de cele mai multe ori cu aceeaşi culoare (aşa cum sunt suprafeńele reale) folosind parametrul GL_AMBIENT_AND_DIFFUSE în apelul funcńiei glmaterial#(). Specificarea culorii produse de reflexia speculară se face prin parametrul GL_SPECULAR, iar dimensiunea şi strălucirea zonei prin parametrul GL_SHININESS. Se poate observa că modelul OpenGL de reflexie permite adăugarea unei componente emisive a luminii reflectate de o suprafańă. Componenta de emisie a unei suprafeńe se specifică prin parametrul GL_EMISSION. Acest efect este folosit pentru simularea lămpilor sau a altor surse de lumină din scenă. FuncŃia glmaterial#() defineşte proprietăńile materialului curent, care se aplică tuturor vârfurilor introduse după acesta prin funcńiile glvertex#()sau prin diferite funcńii de modelare din biblioteca GLUT (de exemplu glutsolidsphere()). ProprietăŃile materialului curent se menńin până la următorul apel al funcńiei glmaterial#(). Calculele de iluminare se pot executa diferit pentru feńele orientate direct (GL_FRONT) şi cele orientate invers (GL_BACK). Un exemplu de definire a unui material este dat prin următoarele instrucńiuni: GLfloat mat_ambient[] = 1.0, 0.0, 0.0, 1.0 ; GLfloat mat_diffuse[] = 1.0, 0.0, 0.0, 1.0 ; GLfloat mat_specular[] = 1.0, 1.0, 1.0, 1.0 ; GLfloat mat_shininess = 50.0; glmaterialfv(gl_front, GL_AMBIENT, mat_ambient); glmaterialfv(gl_front, GL_DIFFUSE, mat_diffuse); glmaterialfv(gl_front, GL_SPECULAR, mat_specular); glmaterialf(gl_front, GL_SHININESS, mat_shininess); 4. Modele de umbrire a suprafeńelor 4.1 Tipuri de modele de umbrire utilizate în OpenGL Prin model de umbrire (shadding) înńelegem un model prin care de determină culoarea de afişare a unui obiect. Modele de umbrire mai sunt numite şi modele de colorare. În OpenGL sunt implementate două modele de umbrire (de colorare): umbrire constantă sau poligonală; umbrire Gouraud. Modelul de umbrire se defineşte prin apelul funcńiei: 6
7 glshademodel(glenum mode); unde argumentul mode poate lua una din valorile GL_FLAT, pentru modelul de umbrire poligonală, sau GL_SMOOTH, pentru modelul de umbrire Gouraud. Valoarea implicită este GL_SMOOTH. În cazul în care nu este validat sistemul de iluminare (prin apelul funcńiei glenable(gl_lighting)) culoarea care se atribuie vârfurilor primitivelor geometrice este culoarea curentă, setată prin apelul unei funcńii glcolor#(). Dacă se defineşte modelul de umbrire poligonală (GL_FLAT), primitivele geometrice se generează de culoare constantă (culoarea curentă întâlnită la primul vârf introdus prin funcńia glvertex#()). În cazul modelul de umbrire Gouraud (GL_SMOOTH) culorile definite în vârfuri se folosesc pentru calculul intensităńii culorilor pixelilor primitivei geometrice prin interpolare liniară. Culoarea fiecărui vârf este tratată individual. Pentru un segment de dreaptă, culoarea se obńine prin interpolarea culorilor vârfului. Pentru un poligon, culorile punctelor interioare se obńin prin interpolare pe baza culorilor vârfurilor (fig.1). De exemplu, intensitatea punctelor de pe linia y = y se calculează astfel: I P I Q I M s I1 I2 I1 ( y y), y1 y2 I1 I4 I1 ( y y), (1) y1 y4 I P IQ = I P ( xp xm ). x x = 1 = 1 P Q y s 1 2 P M Q y = 4 y s O 3 Fig. 1 Interpolarea liniară a intensităńilor vârfurilor în modelul Gouraud x s 7
8 Lucrarea 8 5. AplicaŃii Exemplul 1 Să se afişeze un triunghi folosind modelul de colorare (umbrire) Gouraud. Vârfurile triunghiului au culorile roşu, verde şi, respectiv, albastru (fig. 2). Fig. 2 Afişarea unui triunghi folosind modelul Gouraud SoluŃie. Programul care realizează imaginea din fig. 2 este următorul: #include <gl/glut.h> GOURAUD.CPP void init() //selecteaza culoarea de fond glclearcolor(...); glshademodel(...); // void triangle() // se va folosi glbegin() cu parametrul corespunzator pentru //desenarea triunghiului void display() glclear(...); triangle(); glflush(); 8
9 void reshape (int w, int h) glviewport(0, 0, (GLsizei)w, (GLsizei)h); glmatrixmode(gl_projection); if(w <= h) gluortho2d(0, 30, 0, 30*(GLfloat)h/(GLfloat)w); else gluortho2d(0, 30*(GLfloat)w/(GLfloat)h, 0, 30); glmatrixmode(gl_modelview); int main(int argc, char** argv)... Exemplul 2 Să se evidenńieze diferenńa dintre umbrirea poligonală şi umbrirea Gouraud în cazul unei sfere reprezentate prin reńea de poligoane şi iluminată cu o sursă de lumină. Sursa de lumină se r r r r plasează la infinit, pe direcńia dată de vectorul l = i + j+ k. La apăsarea butonului stâng al mouse-ului sfera se afişează folosind umbrirea poligonală, iar la apăsarea butonului drept sfera se afişează folosind umbrirea Gouraud (fig. 3). Se utilizează proiecńia perspectivă şi apoi proiecńia ortografică. SoluŃie. Programul care generează imaginile din figura 3 este următorul: O parte din funcńii sunt date mai jos. a) b) Fig. 3 a) umbrire poligonală; b) umbrire Gouraud void init() GLfloat mat_specular[] = 1, 1, 1, 1; GLfloat mat_shininess= 50; 9
10 Lucrarea 8 GLfloat light_position[] = 1, 1, 1, 0; glclearcolor(0.0, 0.0, 0.0, 0.0); glshademodel(gl_smooth); //GL_FLAT pentru culoare uniforma glmaterialfv(gl_front, GL_SPECULAR, mat_specular); glmaterialf(gl_front, GL_SHININESS, mat_shininess); gllightfv(gl_light0, GL_POSITION, light_position); glenable(gl_lighting); glenable(gl_light0); glenable(gl_depth_test); void reshape (int w, int h) glviewport(0, 0, (GLsizei)w, (GLsizei)h); glmatrixmode(gl_projection); gluperspective(60.0, (GLfloat)w/(GLfloat)h, 1, 20.0); /* proiectie ortografica if(w <= h) glortho(-1.5, 1.5, -1.5*(GLfloat)h/(GLfloat)w, 1.5*(GLfloat)h/(GLfloat)w, -10, 10); else glortho(-1.5*(glfloat)w/(glfloat)h, 1.5*(GLfloat)w/(GLfloat)h, -1.5, 1.5, -10, 10); */ glmatrixmode(gl_modelview); gltranslatef(0,0,-6); //pentru proiectie perspectiva void mouse(int button, int state, int x, int y)... Exemplul 3 Să se afişeze sfera din exemplul 2, folosind modelul Gouraud. La apăsarea unuia din cele trei butoane ale mouse-ului se vor schimba coeficienńii de difuzie ai materialului: butonul din stânga schimbă componenta roşie, cel din mijloc componenta verde şi cel din dreapta componenta albastră. Pentru modificare parametrilor de material se poate folosi funcńia: void glcolormaterial(glenum face, GLenum mode); Această funcńie actualizează proprietăńile de material specificate de parametrul mode pentru feńele specificate de parametrul face. Astfel, o modificare asupra culorii curente, folosind funcńia glcolor#() actualizează imediat proprietăńile de material specificate. SoluŃie. Principalele funcńii din program sunt prezentate mai jos. 10
11 GLfloat mat_diffuse[4] = 0.5, 0.5, 0.5, 1.0 ; void init(void) GLfloat mat_specular[] = 1.0, 1.0, 1.0, 1.0 ; GLfloat light_position[] = 1.0, 1.0, 1.0, 0.0 ; glmaterialfv(gl_front, GL_DIFFUSE, mat_diffuse); glmaterialfv(gl_front, GL_SPECULAR, mat_specular); glmaterialf(gl_front, GL_SHININESS, 25.0); gllightfv(gl_light0, GL_POSITION, light_position); glenable(gl_lighting); glenable(gl_light0); glcolormaterial(gl_front, GL_DIFFUSE); glenable(gl_color_material); glenable(gl_depth_test); glshademodel (GL_SMOOTH); glclearcolor (0.0, 0.0, 0.0, 0.0); //implicit void reshape (int w, int h) glviewport (0, 0, (GLsizei) w, (GLsizei) h); glmatrixmode (GL_PROJECTION); gluperspective(60.0, (GLfloat)w/(GLfloat)h, 1, 20.0); /* if (w <= h) glortho (-1.5, 1.5, -1.5*(GLfloat)h/(GLfloat)w, 1.5*(GLfloat)h/(GLfloat)w, -10.0, 10.0); else glortho (-1.5*(GLfloat)w/(GLfloat)h, 1.5*(GLfloat)w/(GLfloat)h, -1.5, 1.5, -10.0, 10.0); */ glmatrixmode(gl_modelview); gltranslatef(0,0,-6); //pentru proiectie perspectiva void mouse(int button, int state, int x, int y) switch (button) case GLUT_LEFT_BUTTON: if (state == GLUT_DOWN) // schimba rosu mat_diffuse[0] += 0.1; if (mat_diffuse[0] > 1.0) mat_diffuse[0] = 0.0; glcolor4fv(mat_diffuse); glutpostredisplay(); break;... 11
12 Lucrarea 8 Exemplul 4 Să se realizeze o aplicańie în care o sursă de lumină este rotită în jurul unui tor. Când este apăsat un buton al mouse-ului, sursa de lumină îşi schimbă pozińia cu 30 grade. Sursa de lumină se va reprezenta printr-un mic cub wireframe. SoluŃie. Programul care realizează cerinńele problemei este prezentat mai jos. #include <gl/glut.h> MISCARE_SURSA.CPP static int spin = 0; void init(void) glclearcolor (0.0, 0.0, 0.0, 0.0); glshademodel (GL_SMOOTH); glenable(gl_lighting); glenable(gl_light0); glenable(gl_depth_test); /* - dupa efectuarea transformarii de modelare (glrotated) trebuie resetata pozitia sursei, deoarce este plasata într-o noua pozitie in sistemul universal. - cubul reprezinta pozitia sursei de lumina */ void display(void) GLfloat position[] = 0.0, 0.0, 1.5, 1.0 ; glclear (GL_COLOR_BUFFER_BIT GL_DEPTH_BUFFER_BIT); glpushmatrix (); gltranslatef (0.0, 0.0, -5.0); //transformare de observare glpushmatrix (); glrotated ((GLdouble) spin, 1.0, 0.0, 0.0); gllightfv (GL_LIGHT0, GL_POSITION, position); gltranslated (0.0, 0.0, 1.5); gldisable (GL_LIGHTING); glcolor3f (0.0, 1.0, 1.0); glutwirecube (0.1); glenable (GL_LIGHTING); glpopmatrix (); glutsolidtorus (0.275, 0.85, 8, 15); glpopmatrix (); glutswapbuffers(); glflush (); void reshape (int w, int h) glviewport (0, 0, (GLsizei) w, (GLsizei) h); glmatrixmode (GL_PROJECTION); gluperspective(40.0, (GLfloat) w/(glfloat) h, 1.0, 20.0); 12
13 glmatrixmode(gl_modelview); void mouse(int button, int state, int x, int y) switch (button) case GLUT_LEFT_BUTTON: if (state == GLUT_DOWN) spin = (spin + 30) % 360; glutpostredisplay(); break; default: break; int main(int argc, char** argv) glutinit(&argc, argv); glutinitdisplaymode (GLUT_DOUBLE GLUT_RGB GLUT_DEPTH); glutinitwindowsize (500, 500); glutinitwindowposition (100, 100); glutcreatewindow (argv[0]); init (); glutdisplayfunc(display); glutreshapefunc(reshape); glutmousefunc(mouse); glutmainloop(); return 0; 13
Modele de iluminare şi reflexie în OpenGL
 EGC -Lucrarea 9 Modele de iluminare şi reflexie în OpenGL 4. Modele de umbrire a suprafeńelor 4.1 Tipuri de modele de umbrire utilizate în OpenGL Prin model de umbrire (shading) înńelegem un model prin
EGC -Lucrarea 9 Modele de iluminare şi reflexie în OpenGL 4. Modele de umbrire a suprafeńelor 4.1 Tipuri de modele de umbrire utilizate în OpenGL Prin model de umbrire (shading) înńelegem un model prin
Luminarea obiectelor. {glenable gldisable} (GL_LIGHTING)
 Luminarea obiectelor Pentru vizualizarea unei scene este necesar să se determine culoarea pentru fiecare pixel din zona de desenare. Culoarea pixelului depinde de: 1. proprietăţile zonei din scena care
Luminarea obiectelor Pentru vizualizarea unei scene este necesar să se determine culoarea pentru fiecare pixel din zona de desenare. Culoarea pixelului depinde de: 1. proprietăţile zonei din scena care
MARCAREA REZISTOARELOR
 1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate.
 Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
(a) se numeşte derivata parţială a funcţiei f în raport cu variabila x i în punctul a.
 Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Planul determinat de normală şi un punct Ecuaţia generală Plane paralele Unghi diedru Planul determinat de 3 puncte necoliniare
 1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE
 DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
Laborator 11. Mulţimi Julia. Temă
 Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Κεφάλαιο 6 ο Φωτορεαλισµός
 Κεφάλαιο 6 ο Φωτορεαλισµός Εισαγωγή Στο Κεφάλαιο αναλύσαµε τις µεθόδους απόδοσης χρωµάτων σε επιφάνειες κατά τη σχεδίασή τους στη σκηνή. Ωστόσο, εάν ενδιαφερόµαστε για την απόδοση σκηνών που προσοµοιώνουν
Κεφάλαιο 6 ο Φωτορεαλισµός Εισαγωγή Στο Κεφάλαιο αναλύσαµε τις µεθόδους απόδοσης χρωµάτων σε επιφάνειες κατά τη σχεδίασή τους στη σκηνή. Ωστόσο, εάν ενδιαφερόµαστε για την απόδοση σκηνών που προσοµοιώνουν
5. FUNCŢII IMPLICITE. EXTREME CONDIŢIONATE.
 5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
a. 11 % b. 12 % c. 13 % d. 14 %
 1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
FUNCŢII OPENGL PENTRU REDARE ANTI-ALIASING
 FUNCŢII OPENGL PENTRU REDARE ANTI-ALIASING Biblioteca OpenGL pune la dispoziţie două modalităţi de redare anti-aliasing: prin combinarea culorilor (blending) şi prin buffer de acumulare (A-buffer) ANTI-ALIASING
FUNCŢII OPENGL PENTRU REDARE ANTI-ALIASING Biblioteca OpenGL pune la dispoziţie două modalităţi de redare anti-aliasing: prin combinarea culorilor (blending) şi prin buffer de acumulare (A-buffer) ANTI-ALIASING
Metode iterative pentru probleme neliniare - contractii
 Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
5.5. REZOLVAREA CIRCUITELOR CU TRANZISTOARE BIPOLARE
 5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM 1 electronica.geniu.ro
 Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Aplicaţii ale principiului I al termodinamicii la gazul ideal
 Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Metode de interpolare bazate pe diferenţe divizate
 Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
a n (ζ z 0 ) n. n=1 se numeste partea principala iar seria a n (z z 0 ) n se numeste partea
 Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
5.4. MULTIPLEXOARE A 0 A 1 A 2
 5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
Esalonul Redus pe Linii (ERL). Subspatii.
 Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
Curs 4 Serii de numere reale
 Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Curs 14 Funcţii implicite. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi"
 Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor X) functia f 1
 Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
 4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor
 Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Curs 1 Şiruri de numere reale
 Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Subiecte Clasa a VII-a
 lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
Problema a II - a (10 puncte) Diferite circuite electrice
 Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
R R, f ( x) = x 7x+ 6. Determinați distanța dintre punctele de. B=, unde x și y sunt numere reale.
 5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
Subiecte Clasa a VIII-a
 Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile
 Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Curs 2 DIODE. CIRCUITE DR
 Curs 2 OE. CRCUTE R E CUPRN tructură. imbol Relația curent-tensiune Regimuri de funcționare Punct static de funcționare Parametrii diodei Modelul cu cădere de tensiune constantă Analiza circuitelor cu
Curs 2 OE. CRCUTE R E CUPRN tructură. imbol Relația curent-tensiune Regimuri de funcționare Punct static de funcționare Parametrii diodei Modelul cu cădere de tensiune constantă Analiza circuitelor cu
Εισαγωγή στην OpenGL
 Εισαγωγή στην OpenGL Περιεχόµενα εισαγωγικής ενότητας: Γενικά χαρακτηριστικά της OpenGL Βιβλιοθήκες που της OpenGL Ένα τυπικό πρόγραµµα Τι είναι η OpenGL; Η OpenGL δεν είναι µια συγκεκριµένη βιβλιοθήκη
Εισαγωγή στην OpenGL Περιεχόµενα εισαγωγικής ενότητας: Γενικά χαρακτηριστικά της OpenGL Βιβλιοθήκες που της OpenGL Ένα τυπικό πρόγραµµα Τι είναι η OpenGL; Η OpenGL δεν είναι µια συγκεκριµένη βιβλιοθήκη
Sisteme diferenţiale liniare de ordinul 1
 1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
Conice. Lect. dr. Constantin-Cosmin Todea. U.T. Cluj-Napoca
 Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
Asupra unei inegalităţi date la barajul OBMJ 2006
 Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
Integrala nedefinită (primitive)
 nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
REPREZENTĂRI GRAFICE ÎN SPAłIUL TRIDIMENSIONAL (3D)
 LUCRAREA Nr. REPREZENTĂRI GRAFICE ÎN SPAłIUL TRIDIMENSIONAL (3D). Obiective Utilizarea mediului de programare Matlab pentru crearea şi controlul reprezentărilor grafice în spańiul tridimensional. 2. NoŃiuni
LUCRAREA Nr. REPREZENTĂRI GRAFICE ÎN SPAłIUL TRIDIMENSIONAL (3D). Obiective Utilizarea mediului de programare Matlab pentru crearea şi controlul reprezentărilor grafice în spańiul tridimensional. 2. NoŃiuni
 10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
III. Serii absolut convergente. Serii semiconvergente. ii) semiconvergentă dacă este convergentă iar seria modulelor divergentă.
 III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].
![Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].](/thumbs/72/67648751.jpg) Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
Exemple de probleme rezolvate pentru cursurile DEEA Tranzistoare bipolare cu joncţiuni
 Problema 1. Se dă circuitul de mai jos pentru care se cunosc: VCC10[V], 470[kΩ], RC2,7[kΩ]. Tranzistorul bipolar cu joncţiuni (TBJ) este de tipul BC170 şi are parametrii β100 şi VBE0,6[V]. 1. să se determine
Problema 1. Se dă circuitul de mai jos pentru care se cunosc: VCC10[V], 470[kΩ], RC2,7[kΩ]. Tranzistorul bipolar cu joncţiuni (TBJ) este de tipul BC170 şi are parametrii β100 şi VBE0,6[V]. 1. să se determine
Reflexia şi refracţia luminii.
 Reflexia şi refracţia luminii. 1. Cu cat se deplaseaza o raza care cade sub unghiul i =30 pe o placa plan-paralela de grosime e = 8,0 mm si indicele de refractie n = 1,50, pe care o traverseaza? Caz particular
Reflexia şi refracţia luminii. 1. Cu cat se deplaseaza o raza care cade sub unghiul i =30 pe o placa plan-paralela de grosime e = 8,0 mm si indicele de refractie n = 1,50, pe care o traverseaza? Caz particular
Definiţia generală Cazul 1. Elipsa şi hiperbola Cercul Cazul 2. Parabola Reprezentari parametrice ale conicelor Tangente la conice
 1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
Seminariile Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reziduurilor
 Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
2.1 Sfera. (EGS) ecuaţie care poartă denumirea de ecuaţia generală asferei. (EGS) reprezintă osferă cu centrul în punctul. 2 + p 2
 .1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
.1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii transversale, scrisă faţă de una dintre axele de inerţie principale:,
 REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
riptografie şi Securitate
 riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
Criptosisteme cu cheie publică III
 Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
SERII NUMERICE. Definiţia 3.1. Fie (a n ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0
 SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...4
 SEMINAR 3 MMENTUL FRŢEI ÎN RAPRT CU UN PUNCT CUPRINS 3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere...1 3.1. Aspecte teoretice...2 3.2. Aplicaţii rezolvate...4 3. Momentul forţei
SEMINAR 3 MMENTUL FRŢEI ÎN RAPRT CU UN PUNCT CUPRINS 3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere...1 3.1. Aspecte teoretice...2 3.2. Aplicaţii rezolvate...4 3. Momentul forţei
Sistemul de vizualizare OpenGL. 1. Definirea proiecńiei perspectivă şi a volumului de vizualizare
 Grafică pe calculator în C şi OpenGL Sistemul de izualizare OpenGL 1. Definirea proiecńiei perspectiă şi a olumului de izualizare În OpenGL un punct este reprezentat printr-un ector coloană. Pentru matricele
Grafică pe calculator în C şi OpenGL Sistemul de izualizare OpenGL 1. Definirea proiecńiei perspectiă şi a olumului de izualizare În OpenGL un punct este reprezentat printr-un ector coloană. Pentru matricele
Componente şi Circuite Electronice Pasive. Laborator 3. Divizorul de tensiune. Divizorul de curent
 Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
Ecuaţia generală Probleme de tangenţă Sfera prin 4 puncte necoplanare. Elipsoidul Hiperboloizi Paraboloizi Conul Cilindrul. 1 Sfera.
 pe ecuaţii generale 1 Sfera Ecuaţia generală Probleme de tangenţă 2 pe ecuaţii generale Sfera pe ecuaţii generale Ecuaţia generală Probleme de tangenţă Numim sferă locul geometric al punctelor din spaţiu
pe ecuaţii generale 1 Sfera Ecuaţia generală Probleme de tangenţă 2 pe ecuaţii generale Sfera pe ecuaţii generale Ecuaţia generală Probleme de tangenţă Numim sferă locul geometric al punctelor din spaţiu
8. ProprietăŃi statistice ale imaginilor de intensitate
 Procesarea Imailor - aborator 8: ProprietăŃi statistice ale imailor de tensitate 8. ProprietăŃi statistice ale imailor de tensitate 8.. Introducere În această lucrare se vor prezenta prcipalele trăsături
Procesarea Imailor - aborator 8: ProprietăŃi statistice ale imailor de tensitate 8. ProprietăŃi statistice ale imailor de tensitate 8.. Introducere În această lucrare se vor prezenta prcipalele trăsături
1.7. AMPLIFICATOARE DE PUTERE ÎN CLASA A ŞI AB
 1.7. AMLFCATOARE DE UTERE ÎN CLASA A Ş AB 1.7.1 Amplificatoare în clasa A La amplificatoarele din clasa A, forma de undă a tensiunii de ieşire este aceeaşi ca a tensiunii de intrare, deci întreg semnalul
1.7. AMLFCATOARE DE UTERE ÎN CLASA A Ş AB 1.7.1 Amplificatoare în clasa A La amplificatoarele din clasa A, forma de undă a tensiunii de ieşire este aceeaşi ca a tensiunii de intrare, deci întreg semnalul
2. Sisteme de forţe concurente...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...3
 SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
Captura imaginilor. este necesară o sursă de lumină (λ: lungimea de undă a sursei)
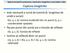 Captura imaginilor este necesară o sursă de lumină (λ: lungimea de undă a sursei) E(x, y, z, λ): lumina incidentă într-un punct (x, y, z coordonatele spațiale) fiecare punct din scenă are o funcție de
Captura imaginilor este necesară o sursă de lumină (λ: lungimea de undă a sursei) E(x, y, z, λ): lumina incidentă într-un punct (x, y, z coordonatele spațiale) fiecare punct din scenă are o funcție de
prin egalizarea histogramei
 Lucrarea 4 Îmbunătăţirea imaginilor prin egalizarea histogramei BREVIAR TEORETIC Tehnicile de îmbunătăţire a imaginilor bazate pe calculul histogramei modifică histograma astfel încât aceasta să aibă o
Lucrarea 4 Îmbunătăţirea imaginilor prin egalizarea histogramei BREVIAR TEORETIC Tehnicile de îmbunătăţire a imaginilor bazate pe calculul histogramei modifică histograma astfel încât aceasta să aibă o
III. Reprezentarea informaţiei în sistemele de calcul
 Metode Numerice Curs 3 III. Reprezentarea informaţiei în sistemele de calcul III.1. Reprezentarea internă a numerelor întregi III. 1.1. Reprezentarea internă a numerelor întregi fără semn (pozitive) Reprezentarea
Metode Numerice Curs 3 III. Reprezentarea informaţiei în sistemele de calcul III.1. Reprezentarea internă a numerelor întregi III. 1.1. Reprezentarea internă a numerelor întregi fără semn (pozitive) Reprezentarea
Seminar 5 Analiza stabilității sistemelor liniare
 Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Profesor Blaga Mirela-Gabriela DREAPTA
 DREAPTA Fie punctele A ( xa, ya ), B ( xb, yb ), C ( xc, yc ) şi D ( xd, yd ) în planul xoy. 1)Distanţa AB = (x x ) + (y y ) Ex. Fie punctele A( 1, -3) şi B( -2, 5). Calculaţi distanţa AB. AB = ( 2 1)
DREAPTA Fie punctele A ( xa, ya ), B ( xb, yb ), C ( xc, yc ) şi D ( xd, yd ) în planul xoy. 1)Distanţa AB = (x x ) + (y y ) Ex. Fie punctele A( 1, -3) şi B( -2, 5). Calculaţi distanţa AB. AB = ( 2 1)
OpenGL. Εισαγωγή στην OpenGL Βασικά Γεωμετρικά Σχήματα Παράλληλη (ορθογραφική) προβολή. Μάθημα: Γραφικά Υπολογιστών και Εικονική Πραγματικότητα
 OpenGL Εισαγωγή στην OpenGL Βασικά Γεωμετρικά Σχήματα Παράλληλη (ορθογραφική) προβολή Κατερίνα Παπαδοπούλου / pakate@unipi.gr Μάθημα: Γραφικά Υπολογιστών και Εικονική Πραγματικότητα OpenGL Εισαγωγή Είναι
OpenGL Εισαγωγή στην OpenGL Βασικά Γεωμετρικά Σχήματα Παράλληλη (ορθογραφική) προβολή Κατερίνα Παπαδοπούλου / pakate@unipi.gr Μάθημα: Γραφικά Υπολογιστών και Εικονική Πραγματικότητα OpenGL Εισαγωγή Είναι
TEMA 9: FUNCȚII DE MAI MULTE VARIABILE. Obiective:
 TEMA 9: FUNCȚII DE MAI MULTE VARIABILE 77 TEMA 9: FUNCȚII DE MAI MULTE VARIABILE Obiective: Deiirea pricipalelor proprietăţi matematice ale ucţiilor de mai multe variabile Aalia ucţiilor de utilitate şi
TEMA 9: FUNCȚII DE MAI MULTE VARIABILE 77 TEMA 9: FUNCȚII DE MAI MULTE VARIABILE Obiective: Deiirea pricipalelor proprietăţi matematice ale ucţiilor de mai multe variabile Aalia ucţiilor de utilitate şi
V O. = v I v stabilizator
 Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
LUCRAREA NR. 1 STUDIUL SURSELOR DE CURENT
 LUCAEA N STUDUL SUSELO DE CUENT Scopul lucrării În această lucrare se studiază prin simulare o serie de surse de curent utilizate în cadrul circuitelor integrate analogice: sursa de curent standard, sursa
LUCAEA N STUDUL SUSELO DE CUENT Scopul lucrării În această lucrare se studiază prin simulare o serie de surse de curent utilizate în cadrul circuitelor integrate analogice: sursa de curent standard, sursa
y y x x 1 y1 Elemente de geometrie analiticã 1. Segmente 1. DistanŃa dintre douã puncte A(x 1,y 1 ), B(x 2,y 2 ): AB = 2. Panta dreptei AB: m AB =
 Elemente de geometrie analiticã. Segmente. DistanŃa dintre douã puncte A(, ), B(, ): AB = ) + ( ) (. Panta dreptei AB: m AB = +. Coordonatele (,) ale mijlocului segmentului AB: =, =. Coordonatele punctului
Elemente de geometrie analiticã. Segmente. DistanŃa dintre douã puncte A(, ), B(, ): AB = ) + ( ) (. Panta dreptei AB: m AB = +. Coordonatele (,) ale mijlocului segmentului AB: =, =. Coordonatele punctului
Laborator 1: INTRODUCERE ÎN ALGORITMI. Întocmit de: Claudia Pârloagă. Îndrumător: Asist. Drd. Gabriel Danciu
 INTRODUCERE Laborator 1: ÎN ALGORITMI Întocmit de: Claudia Pârloagă Îndrumător: Asist. Drd. Gabriel Danciu I. NOŢIUNI TEORETICE A. Sortarea prin selecţie Date de intrare: un şir A, de date Date de ieşire:
INTRODUCERE Laborator 1: ÎN ALGORITMI Întocmit de: Claudia Pârloagă Îndrumător: Asist. Drd. Gabriel Danciu I. NOŢIUNI TEORETICE A. Sortarea prin selecţie Date de intrare: un şir A, de date Date de ieşire:
Componente şi Circuite Electronice Pasive. Laborator 4. Măsurarea parametrilor mărimilor electrice
 Laborator 4 Măsurarea parametrilor mărimilor electrice Obiective: o Semnalul sinusoidal, o Semnalul dreptunghiular, o Semnalul triunghiular, o Generarea diferitelor semnale folosind placa multifuncţională
Laborator 4 Măsurarea parametrilor mărimilor electrice Obiective: o Semnalul sinusoidal, o Semnalul dreptunghiular, o Semnalul triunghiular, o Generarea diferitelor semnale folosind placa multifuncţională
COLEGIUL NATIONAL CONSTANTIN CARABELLA TARGOVISTE. CONCURSUL JUDETEAN DE MATEMATICA CEZAR IVANESCU Editia a VI-a 26 februarie 2005.
 SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
VII.2. PROBLEME REZOLVATE
 Teoria Circuitelor Electrice Aplicaţii V PROBEME REOVATE R7 În circuitul din fiura 7R se cunosc: R e t 0 sint [V] C C t 0 sint [A] Se cer: a rezolvarea circuitului cu metoda teoremelor Kirchhoff; rezolvarea
Teoria Circuitelor Electrice Aplicaţii V PROBEME REOVATE R7 În circuitul din fiura 7R se cunosc: R e t 0 sint [V] C C t 0 sint [A] Se cer: a rezolvarea circuitului cu metoda teoremelor Kirchhoff; rezolvarea
Examen AG. Student:... Grupa: ianuarie 2016
 16-17 ianuarie 2016 Problema 1. Se consideră graful G = pk n (p, n N, p 2, n 3). Unul din vârfurile lui G se uneşte cu câte un vârf din fiecare graf complet care nu-l conţine, obţinându-se un graf conex
16-17 ianuarie 2016 Problema 1. Se consideră graful G = pk n (p, n N, p 2, n 3). Unul din vârfurile lui G se uneşte cu câte un vârf din fiecare graf complet care nu-l conţine, obţinându-se un graf conex
SEMINAR 14. Funcţii de mai multe variabile (continuare) ( = 1 z(x,y) x = 0. x = f. x + f. y = f. = x. = 1 y. y = x ( y = = 0
 Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
Codificatorul SN74148 este un codificator zecimal-bcd de trei biţi (fig ). Figura Codificatorul integrat SN74148
 5.2. CODIFICATOAE Codificatoarele (CD) sunt circuite logice combinaţionale cu n intrări şi m ieşiri care furnizează la ieşire un cod de m biţi atunci când numai una din cele n intrări este activă. De regulă
5.2. CODIFICATOAE Codificatoarele (CD) sunt circuite logice combinaţionale cu n intrări şi m ieşiri care furnizează la ieşire un cod de m biţi atunci când numai una din cele n intrări este activă. De regulă
Toate subiectele sunt obligatorii. Timpul de lucru efectiv este de 3 ore. Se acordă din oficiu 10 puncte. SUBIECTUL I.
 Modelul 4 Se acordă din oficiu puncte.. Fie numărul complex z = i. Calculaţi (z ) 25. 2. Dacă x şi x 2 sunt rădăcinile ecuaţiei x 2 9x+8 =, atunci să se calculeze x2 +x2 2 x x 2. 3. Rezolvaţi în mulţimea
Modelul 4 Se acordă din oficiu puncte.. Fie numărul complex z = i. Calculaţi (z ) 25. 2. Dacă x şi x 2 sunt rădăcinile ecuaţiei x 2 9x+8 =, atunci să se calculeze x2 +x2 2 x x 2. 3. Rezolvaţi în mulţimea
2. Circuite logice 2.4. Decodoare. Multiplexoare. Copyright Paul GASNER
 2. Circuite logice 2.4. Decodoare. Multiplexoare Copyright Paul GASNER Definiţii Un decodor pe n bits are n intrări şi 2 n ieşiri; cele n intrări reprezintă un număr binar care determină în mod unic care
2. Circuite logice 2.4. Decodoare. Multiplexoare Copyright Paul GASNER Definiţii Un decodor pe n bits are n intrări şi 2 n ieşiri; cele n intrări reprezintă un număr binar care determină în mod unic care
5.1. Noţiuni introductive
 ursul 13 aitolul 5. Soluţii 5.1. oţiuni introductive Soluţiile = aestecuri oogene de două sau ai ulte substanţe / coonente, ale căror articule nu se ot seara rin filtrare sau centrifugare. oonente: - Mediul
ursul 13 aitolul 5. Soluţii 5.1. oţiuni introductive Soluţiile = aestecuri oogene de două sau ai ulte substanţe / coonente, ale căror articule nu se ot seara rin filtrare sau centrifugare. oonente: - Mediul
Să se arate că n este număr par. Dan Nedeianu
 Primul test de selecție pentru juniori I. Să se determine numerele prime p, q, r cu proprietatea că 1 p + 1 q + 1 r 1. Fie ABCD un patrulater convex cu m( BCD) = 10, m( CBA) = 45, m( CBD) = 15 și m( CAB)
Primul test de selecție pentru juniori I. Să se determine numerele prime p, q, r cu proprietatea că 1 p + 1 q + 1 r 1. Fie ABCD un patrulater convex cu m( BCD) = 10, m( CBA) = 45, m( CBD) = 15 și m( CAB)
4. Măsurarea tensiunilor şi a curenţilor electrici. Voltmetre electronice analogice
 4. Măsurarea tensiunilor şi a curenţilor electrici oltmetre electronice analogice oltmetre de curent continuu Ampl.c.c. x FTJ Protectie Atenuator calibrat Atenuatorul calibrat divizor rezistiv R in const.
4. Măsurarea tensiunilor şi a curenţilor electrici oltmetre electronice analogice oltmetre de curent continuu Ampl.c.c. x FTJ Protectie Atenuator calibrat Atenuatorul calibrat divizor rezistiv R in const.
SEMINARUL 3. Cap. II Serii de numere reale. asociat seriei. (3n 5)(3n 2) + 1. (3n 2)(3n+1) (3n 2) (3n + 1) = a
 Capitolul II: Serii de umere reale. Lect. dr. Lucia Maticiuc Facultatea de Hidrotehică, Geodezie şi Igieria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucia MATICIUC SEMINARUL 3. Cap. II Serii
Capitolul II: Serii de umere reale. Lect. dr. Lucia Maticiuc Facultatea de Hidrotehică, Geodezie şi Igieria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucia MATICIUC SEMINARUL 3. Cap. II Serii
Capitolul 4. Integrale improprii Integrale cu limite de integrare infinite
 Capitolul 4 Integrale improprii 7-8 În cadrul studiului integrabilităţii iemann a unei funcţii s-au evidenţiat douăcondiţii esenţiale:. funcţia :[ ] este definită peintervalînchis şi mărginit (interval
Capitolul 4 Integrale improprii 7-8 În cadrul studiului integrabilităţii iemann a unei funcţii s-au evidenţiat douăcondiţii esenţiale:. funcţia :[ ] este definită peintervalînchis şi mărginit (interval
Zgomotul se poate suprapune informaţiei utile în două moduri: g(x, y) = f(x, y) n(x, y) (6.2)
 Lucrarea 6 Zgomotul în imagini BREVIAR TEORETIC Zgomotul este un semnal aleator, care afectează informaţia utilă conţinută într-o imagine. El poate apare de-alungul unui lanţ de transmisiune, sau prin
Lucrarea 6 Zgomotul în imagini BREVIAR TEORETIC Zgomotul este un semnal aleator, care afectează informaţia utilă conţinută într-o imagine. El poate apare de-alungul unui lanţ de transmisiune, sau prin
Examen AG. Student:... Grupa:... ianuarie 2011
 Problema 1. Pentru ce valori ale lui n,m N (n,m 1) graful K n,m este eulerian? Problema 2. Să se construiască o funcţie care să recunoască un graf P 3 -free. La intrare aceasta va primi un graf G = ({1,...,n},E)
Problema 1. Pentru ce valori ale lui n,m N (n,m 1) graful K n,m este eulerian? Problema 2. Să se construiască o funcţie care să recunoască un graf P 3 -free. La intrare aceasta va primi un graf G = ({1,...,n},E)
* K. toate K. circuitului. portile. Considerând această sumă pentru toate rezistoarele 2. = sl I K I K. toate rez. Pentru o bobină: U * toate I K K 1
 FNCȚ DE ENERGE Fie un n-port care conține numai elemente paive de circuit: rezitoare dipolare, condenatoare dipolare și bobine cuplate. Conform teoremei lui Tellegen n * = * toate toate laturile portile
FNCȚ DE ENERGE Fie un n-port care conține numai elemente paive de circuit: rezitoare dipolare, condenatoare dipolare și bobine cuplate. Conform teoremei lui Tellegen n * = * toate toate laturile portile
Capitolul 4 Amplificatoare elementare
 Capitolul 4 mplificatoare elementare 4.. Etaje de amplificare cu un tranzistor 4... Etajul emitor comun V CC C B B C C L L o ( // ) V gm C i rπ // B // o L // C // L B ro i B E C E 4... Etajul colector
Capitolul 4 mplificatoare elementare 4.. Etaje de amplificare cu un tranzistor 4... Etajul emitor comun V CC C B B C C L L o ( // ) V gm C i rπ // B // o L // C // L B ro i B E C E 4... Etajul colector
Cum folosim cazuri particulare în rezolvarea unor probleme
 Cum folosim cazuri particulare în rezolvarea unor probleme GHEORGHE ECKSTEIN 1 Atunci când întâlnim o problemă pe care nu ştim s-o abordăm, adesea este bine să considerăm cazuri particulare ale acesteia.
Cum folosim cazuri particulare în rezolvarea unor probleme GHEORGHE ECKSTEIN 1 Atunci când întâlnim o problemă pe care nu ştim s-o abordăm, adesea este bine să considerăm cazuri particulare ale acesteia.
Subiecte Clasa a V-a
 (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul numarului intrebarii
(40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul numarului intrebarii
GEOMETRIE PLANĂ TEOREME IMPORTANTE ARII. bh lh 2. abc. abc. formula înălţimii
 GEOMETRIE PLNĂ TEOREME IMPORTNTE suma unghiurilor unui triunghi este 8º suma unghiurilor unui patrulater este 6º unghiurile de la baza unui triunghi isoscel sunt congruente într-un triunghi isoscel liniile
GEOMETRIE PLNĂ TEOREME IMPORTNTE suma unghiurilor unui triunghi este 8º suma unghiurilor unui patrulater este 6º unghiurile de la baza unui triunghi isoscel sunt congruente într-un triunghi isoscel liniile
Ecuatii exponentiale. Ecuatia ce contine variabila necunoscuta la exponentul puterii se numeste ecuatie exponentiala. a x = b, (1)
 Ecuatii exponentiale Ecuatia ce contine variabila necunoscuta la exponentul puterii se numeste ecuatie exponentiala. Cea mai simpla ecuatie exponentiala este de forma a x = b, () unde a >, a. Afirmatia.
Ecuatii exponentiale Ecuatia ce contine variabila necunoscuta la exponentul puterii se numeste ecuatie exponentiala. Cea mai simpla ecuatie exponentiala este de forma a x = b, () unde a >, a. Afirmatia.
Lab06: Extragerea trăsăturilor şi selecţia trăsăturilor. Aplicaţie pentru recunoaşterea obiectelor bazată pe formă.
 Lab06: Extragerea trăsăturilor şi selecţia trăsăturilor Aplicaţie pentru recunoaşterea obiectelor bazată pe formă. Aplicație practică a extragerii şi selecţiei trăsăturilor Recunoaşterea celor 4 forme
Lab06: Extragerea trăsăturilor şi selecţia trăsăturilor Aplicaţie pentru recunoaşterea obiectelor bazată pe formă. Aplicație practică a extragerii şi selecţiei trăsăturilor Recunoaşterea celor 4 forme
Geometrie computationala 2. Preliminarii geometrice
 Platformă de e-learning și curriculă e-content pentru învățământul superior tehnic Geometrie computationala 2. Preliminarii geometrice Preliminarii geometrice Spatiu Euclidean: E d Spatiu de d-tupluri,
Platformă de e-learning și curriculă e-content pentru învățământul superior tehnic Geometrie computationala 2. Preliminarii geometrice Preliminarii geometrice Spatiu Euclidean: E d Spatiu de d-tupluri,
Ovidiu Gabriel Avădănei, Florin Mihai Tufescu,
 vidiu Gabriel Avădănei, Florin Mihai Tufescu, Capitolul 6 Amplificatoare operaţionale 58. Să se calculeze coeficientul de amplificare în tensiune pentru amplficatorul inversor din fig.58, pentru care se
vidiu Gabriel Avădănei, Florin Mihai Tufescu, Capitolul 6 Amplificatoare operaţionale 58. Să se calculeze coeficientul de amplificare în tensiune pentru amplficatorul inversor din fig.58, pentru care se
Universitatea din Bucureşti Facultatea de Matematică şi Informatică. Algebră (1)
 Universitatea din ucureşti.7.4 Facultatea de Matematică şi Informatică oncursul de admitere iulie 4 omeniul de licenţă alculatoare şi Tehnologia Informaţiei lgebră (). Fie x,y astfel încât x+y = şi x +
Universitatea din ucureşti.7.4 Facultatea de Matematică şi Informatică oncursul de admitere iulie 4 omeniul de licenţă alculatoare şi Tehnologia Informaţiei lgebră (). Fie x,y astfel încât x+y = şi x +
Γραφικά µε Υπολογιστές
 Ιόνιο Πανεπιστήµιο, Τµήµα Πληροφορικής Γραφικά µε Υπολογιστές Εργαστήριο 3 Υλικά, φωτισµός και χρωµατισµός Στο εργαστήριο αυτό θα δούµε το µοντέλο φωτισµού που υποστηρίζει η OpenGL, και πώς να αλλάζουµε
Ιόνιο Πανεπιστήµιο, Τµήµα Πληροφορικής Γραφικά µε Υπολογιστές Εργαστήριο 3 Υλικά, φωτισµός και χρωµατισµός Στο εργαστήριο αυτό θα δούµε το µοντέλο φωτισµού που υποστηρίζει η OpenGL, και πώς να αλλάζουµε
Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25
 Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25 LAGĂRELE CU ALUNECARE!" 25.1.Caracteristici.Părţi componente.materiale.!" 25.2.Funcţionarea lagărelor cu alunecare.! 25.1.Caracteristici.Părţi componente.materiale.
Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25 LAGĂRELE CU ALUNECARE!" 25.1.Caracteristici.Părţi componente.materiale.!" 25.2.Funcţionarea lagărelor cu alunecare.! 25.1.Caracteristici.Părţi componente.materiale.
Analiza funcționării și proiectarea unui stabilizator de tensiune continuă realizat cu o diodă Zener
 Analiza funcționării și proiectarea unui stabilizator de tensiune continuă realizat cu o diodă Zener 1 Caracteristica statică a unei diode Zener În cadranul, dioda Zener (DZ) se comportă ca o diodă redresoare
Analiza funcționării și proiectarea unui stabilizator de tensiune continuă realizat cu o diodă Zener 1 Caracteristica statică a unei diode Zener În cadranul, dioda Zener (DZ) se comportă ca o diodă redresoare
, m ecuańii, n necunoscute;
 Sisteme liniare NotaŃii: a ij coeficienńi, i necunoscute, b i termeni liberi, i0{1,,..., n}, j0{1,,..., m}; a11 1 + a1 +... + a1 nn = b1 a11 + a +... + an n = b (S), m ecuańii, n necunoscute;... am11 +
Sisteme liniare NotaŃii: a ij coeficienńi, i necunoscute, b i termeni liberi, i0{1,,..., n}, j0{1,,..., m}; a11 1 + a1 +... + a1 nn = b1 a11 + a +... + an n = b (S), m ecuańii, n necunoscute;... am11 +
3. REPREZENTAREA PLANULUI
 3.1. GENERALITĂŢI 3. REPREZENTAREA PLANULUI Un plan este definit, în general, prin trei puncte necoliniare sau prin o dreaptă şi un punct exterior, două drepte concurente sau două drepte paralele (fig.3.1).
3.1. GENERALITĂŢI 3. REPREZENTAREA PLANULUI Un plan este definit, în general, prin trei puncte necoliniare sau prin o dreaptă şi un punct exterior, două drepte concurente sau două drepte paralele (fig.3.1).
Grafică pe calculator. Mihai-Sorin Stupariu
 Grafică pe calculator Mihai-Sorin Stupariu Sem. I, 2015-2016 Cuprins 1 Generalităţi 3 1.1 Exemplu de program OpenGL................... 3 1.2 Despre OpenGL........................... 4 1.3 Biblioteci utilizate
Grafică pe calculator Mihai-Sorin Stupariu Sem. I, 2015-2016 Cuprins 1 Generalităţi 3 1.1 Exemplu de program OpenGL................... 3 1.2 Despre OpenGL........................... 4 1.3 Biblioteci utilizate
8 Intervale de încredere
 8 Intervale de încredere În cursul anterior am determinat diverse estimări ˆ ale parametrului necunoscut al densităţii unei populaţii, folosind o selecţie 1 a acestei populaţii. În practică, valoarea calculată
8 Intervale de încredere În cursul anterior am determinat diverse estimări ˆ ale parametrului necunoscut al densităţii unei populaţii, folosind o selecţie 1 a acestei populaţii. În practică, valoarea calculată
