HY422 Ειςαγωγή ςτα υςτήματα VLSI. 5/9/ ΗΤ422 - Διάλεξθ 10θ Χρονιςμόσ. Γενικό Μοντζλο φγχρονου Κυκλώματοσ
|
|
|
- Ἔρεβος Λούλης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 HY422 Ειςαγωγή ςτα υςτήματα VLSI Διδάςκων: Χ. ωτηρίου, Βοηθόσ: Π. Ματθαιάκησ 1 ΗΤ422 - Διάλεξθ 10θ Χρονιςμόσ Περιεχόμενα Γενικό Μοντζλο φγχρονου Κυκλώματοσ Είδθ Μονοπατιών τατικι Χρονικι Ανάλυςθ Βάςθ Περιοριςμών Χρόνοσ Αναχώρθςθσ, Χρόνοσ Άφιξθσ, Ενεργζσ Ακμζσ Παράδειγμα τατικισ Χρονικισ Ανάλυςθσ Χρονικοί Περιοριςμοί ςτο Ρολόι Απόκλιςθ (Skew), Σρίκλιςμα (Jitter) χεδίαςθ Δζντρων Φραγι Ρολογιοφ (Clock Gating) 2 ΗΤ422 - Διάλεξθ 10θ Χρονιςμόσ 1
2 Περιεχόμενα Γενικό Μοντζλο φγχρονου Κυκλώματοσ Είδθ Μονοπατιών τατικι Χρονικι Ανάλυςθ Βάςθ Περιοριςμών Χρόνοσ Αναχώρθςθσ, Χρόνοσ Άφιξθσ, Ενεργζσ Ακμζσ Παράδειγμα τατικισ Χρονικισ Ανάλυςθσ Χρονικοί Περιοριςμοί ςτο Ρολόι Απόκλιςθ (Skew), Σρίκλιςμα (Jitter) χεδίαςθ Δζντρων Φραγι Ρολογιοφ (Clock Gating) 3 ΗΤ422 - Διάλεξθ 10θ Χρονιςμόσ Γενικό Μοντέλο ύγχρονου Κυκλώματοσ Πιθανή Ανάδπαζη Ππυηεύοςζερ Είζοδοι (Primary Inputs) Πιθανή Ανάδπαζη υνδυαςτικι Λογικι (.Λ.) Καηασυπηηέρ Πιθανή Ανάδπαζη υνδυαςτικι Λογικι (.Λ.) Καηασυπηηέρ Ππυηεύοςζερ Έξοδοι (Primary Outputs) Ρολόι υνδζςεισ, Καταχωρθτζσ αποτελοφνται από πολλαπλά bit Καταχωρητζσ φνολο Flip-flop υνοριακά τοιχεία Ππυηεύοςζερ Είζοδοι (Primary Inputs) υνδυαςτική Λογική (ςφννεφο) Σοπικζσ Ζξοδοι = f(σοπικών Ειςόδων) Είναι πικανό να υπάρχει ανάδραςθ μεταξφ των τμθμάτων 4 2
3 Περιεχόμενα Γενικό Μοντζλο φγχρονου Κυκλώματοσ Είδθ Μονοπατιών τατικι Χρονικι Ανάλυςθ Βάςθ Περιοριςμών Χρόνοσ Αναχώρθςθσ, Χρόνοσ Άφιξθσ, Ενεργζσ Ακμζσ Παράδειγμα τατικισ Χρονικισ Ανάλυςθσ Χρονικοί Περιοριςμοί ςτο Ρολόι Απόκλιςθ (Skew), Σρίκλιςμα (Jitter) χεδίαςθ Δζντρων Φραγι Ρολογιοφ (Clock Gating) 5 ΗΤ422 - Διάλεξθ 10θ Χρονιςμόσ τατική Χρονική Ανάλυςη D Q D Q υνδυαςτικι Λογικι (.Λ.) D Q D Q Ρολόι Χρονικζσ Παράμετροι Καταχωρητών T clk : Περίοδοσ Ρολογιοφ T su : Setup time T hd : Hold time T c2q : Clock to Q (worst-case) T c2qm : Clock to Q (min) Χρονικζσ Παράμετροι.Λ. T cl : Μζγιςτθ Κακυςτζρθςθ.Λ. Κπίζιμο μονοπάηι T clm : Ελάχιςτθ Κακυςτζρθςθ.Λ. Ελάχιστο μονοπάτι 6 3
4 ΧΑ Ελάχιςτη Περίοδοσ D Q υνδυαςτικι 1 Λογικι (.Λ.) D Q 2 D Q CL out Clk Clk In T su T hd a b Q T 1 c2q a b T c2qm CL out A B T clogm T cl T su2 T clk T c2q + T cl + T su 7 ΧΑ Περιοριςμόσ Διατήρηςησ (Hold) D Q υνδυαςτικι 1 Λογικι (.Λ.) D Q 2 D Q Clk Clk In T su T hd a b Q T 1 c2q a b T c2qm CL out A B T clm T cl T hd2 T hd T c2qm + T clm 8 4
5 Περιεχόμενα Γενικό Μοντζλο φγχρονου Κυκλώματοσ Είδθ Μονοπατιών τατικι Χρονικι Ανάλυςθ Βάςθ Περιοριςμών Χρόνοσ Αναχώρθςθσ, Χρόνοσ Άφιξθσ, Ενεργζσ Ακμζσ Παράδειγμα τατικισ Χρονικισ Ανάλυςθσ Χρονικοί Περιοριςμοί ςτο Ρολόι Απόκλιςθ (Skew), Σρίκλιςμα (Jitter) χεδίαςθ Δζντρων Φραγι Ρολογιοφ (Clock Gating) 9 ΗΤ422 - Διάλεξθ 10θ Χρονιςμόσ Παράδειγμα (1/6) T and = 2ns, T or = 1ns, T mux = 3ns, T c2q = 0.5ns, T c2qm = 0.2ns, T su =0.4ns, T hd = 0.3ns Ποιό είναι το κρίσιμο μονοπάτι; Πόςθ είναι θ ελάχιςτθ περίοδοσ ρολογιοφ; Καλφπτονται όλεσ οι ςυνκικεσ χρονιςμοφ; 10 5
6 Παράδειγμα (2/6) T and = 2ns, T or = 1ns, T mux = 3ns, T c2q = 0.5ns, T c2qm = 0.2ns, T su =0.4ns, T hd = 0.3ns Ποιό είναι το κρίςιμο μονοπάτι; 11 Παράδειγμα (3/6) T and = 2ns, T or = 1ns, T mux = 3ns, T c2q = 0.5ns, T c2qm = 0.2ns, T su =0.4ns, T hd = 0.3ns Πόςθ είναι θ ελάχιςτθ περίοδοσ ρολογιοφ; T min = T c2q + T and + T mux + T and + T su = 7.9 ns 12 6
7 Παράδειγμα (4/6) T and = 2ns, T or = 1ns, T mux = 3ns, T c2q = 0.5ns, T c2qm = 0.2ns, T su =0.4ns, T hd = 0.3ns Καλφπτονται όλεσ οι ςυνκικεσ χρονιςμοφ; OXI!!! Ζχουμε T clm = 0 ns και T c2qm = 0.2ns Πρζπει T hd T c2qm + T clm 13 Παράδειγμα (5/6) 0 T and = 2ns, T or = 1ns, T mux = 3ns, T c2q = 0.5ns, T c2qm = 0.2ns, T su =0.4ns, T hd = 0.3ns Καλφπτονται όλεσ οι ςυνκικεσ χρονιςμοφ; Πρζπει T hd T c2qm + T clm Προςκζτουμε μια πφλθ με Σ or = 1ns (αρκεί;) Ζςτω T orm = T or και γενικά για όλεσ τισ πφλεσ, Σώρα ΝAI!!! Ζχουμε T clm = 1ns και T c2qm = 0.2ns 14 7
8 Παράδειγμα (6/6) T and = 2ns, T or = 1ns, T mux = 3ns, T c2q = 0.5ns, T c2qm = 0.2ns, T su =0.4ns, T hd = 0.3ns Καλφπτονται όλεσ οι ςυνκικεσ χρονιςμοφ; Πρζπει T hd T c2qm + T clogm υνικωσ βάηουμε 2 αντιςτροφείσ (ζςτω T invm = 0.3ns) ΟΚ!!! Ζχουμε T clm = 0.6 ns και T c2qm = 0.2ns 15 Περιεχόμενα Γενικό Μοντζλο φγχρονου Κυκλώματοσ Είδθ Μονοπατιών τατικι Χρονικι Ανάλυςθ Βάςθ Περιοριςμών Χρόνοσ Αναχώρθςθσ, Χρόνοσ Άφιξθσ, Ενεργζσ Ακμζσ Παράδειγμα τατικισ Χρονικισ Ανάλυςθσ Χρονικοί Περιοριςμοί ςτο Ρολόι Απόκλιςθ (Skew), Σρίκλιςμα (Jitter) χεδίαςθ Δζντρων Φραγι Ρολογιοφ (Clock Gating) 16 ΗΤ422 - Διάλεξθ 10θ Χρονιςμόσ 8
9 Περιοριςμοί ςτο Ρολόι Απόκλιςη (Skew) D AQ B Clk Δ Αν Δ = 0, το ςφςτθμα εναλλάςςει τιμζσ ΑΒ, ΒΑ, το παραπάνω παράδειγμα απόκλιςθσ άφιξθσ μπορεί να εμπεριζχεται και ςυνδυαςτικι λογικι μεταξφ Α, Β. Σι κα ςυμβεί κακώσ το Δ 0, και το Δ μεγαλώνει; Ο διακζςιμοσ χρόνοσ ΒΑ μικραίνει Αν Δ Σc2q, τότε θ είςοδοσ του Β κα ζχει γίνει Β, μια και κα ζχει επαναγραφεί το Α, άρα κα μείνουμε με ΒΒ, ΒΒ, 17 Απόκλιςη (Skew) και Σρίκλιςμα (Jitter) Απόκλιςη (Skew) τακερι από κφκλο ςε κφκλο Απόκλιςθ ςτουσ χρόνουσ άφιξθσ ςτο ςιμα ρολογιοφ ςτα διαφορετικά ςθμεία του κυκλώματοσ Σρίκλιςμα (Jitter) Μεταβλθτι απόκλιςθ από μεταβατικά, περιοδικά θ μθ φαινόμενα ςε ςυγκεκριμζνο ςθμείο του κυκλώματοσ Τ jitter Τ skew 18 9
10 Θετική και Αρνητική Απόκλιςη (α) Θεηική Απόκλιζη Ρολόι και Δεδομένα ππορ ηην ίδια καηεύθςνζη (β) Απνηηική Απόκλιζη Ρολόι και Δεδομένα ππορ ανηίθεηη καηεύθςνζη 19 Θετική Απόκλιςη Η ακμή αποζηολήρ καηαθηάνει ππιν ηην ακμή λήτηρ 20 10
11 Αρνητική Απόκλιςη Η ακμή λήτηρ καηαθηάνει ππιν ηην ακμή αποζηολήρ 21 Σρίκλιςμα (Jitter) Σο τρίκλιςμα προκαλεί δυναμικι μεταβολι τθσ περιόδου Σ από κφκλο ςε κφκλο 22 11
12 ΧΑ με Απόκλιςη και Σρίκλιςμα Απόκλιση: T sk = δ Τρίκλισμα : T jt t clk1 t clk2 T clk T c2q + T cl + T su + T sk + 2T jt (σείπιζηη πεπίπηυζη μέγιζηηρ καθςζηέπηζηρ) T hd T c2qm + T clm -T sk - 2T jt (σείπιζηη πεπίπηυζη ελάσιζηηρ καθςζηέπηζηρ 23 Πηγέσ Απόκλιςησ, Σρικλίςματοσ (1): Γεννιτρια ρολογιοφ (PLL) Σρίκλιςμα (3): Μεταβλθτότθτα ςτισ υνδζςεισ Απόκλιςθ (2): Μεταβλθτότθτα ςτουσ οδθγοφσ Απόκλιςθ (4, 5): Μεταβλθτότθτα ςτθν τάςθ πθγισ, κερμοκραςία Σρίκλιςμα και Απόκλιςθ (6, 7): Αλλθλοεπίδραςθ μζςω Χωρθτικότθτασ (Παραςιτικζσ υνδζςεισ Πυκνωτών) Σρίκλιςμα 25 12
13 Δέντρα/Δίκτυα Ρολογιού και ΧΑ Καταχωρθτισ Χπόνοι Άθιξηρ Ενιςχυτισ Buffer Καταχωρθτισ Ρίηα - CLK Ενιςχυτισ Buffer Απόκλιζη Καταχωρθτισ Καταχωρθτισ Σφποι Δικτφων Ρολογιοφ Δζντρο (όπωσ δεξιά) Πλζγμα (Mesh) Ενιςχυτισ Buffer Καταχωρθτισ Καταχωρθτισ 26 Διάταξη Η-Δένδρου Με ηέλεια ιζοζκέλιζη ηυν μονοπαηιών η απόκλιζη μποπεί να γίνει μηδέν Μποπεί να ςποζηηπίξει θπαγή ηος πολογιού ζε διάθοπα επίπεδα ηος δένδπος 27 13
14 Πραγματικό Η-Δέντρο 28 Περιεχόμενα Γενικό Μοντζλο φγχρονου Κυκλώματοσ Είδθ Μονοπατιών τατικι Χρονικι Ανάλυςθ Βάςθ Περιοριςμών Χρόνοσ Αναχώρθςθσ, Χρόνοσ Άφιξθσ, Ενεργζσ Ακμζσ Παράδειγμα τατικισ Χρονικισ Ανάλυςθσ Χρονικοί Περιοριςμοί ςτο Ρολόι Απόκλιςθ (Skew), Σρίκλιςμα (Jitter) χεδίαςθ Δζντρων Φραγι Ρολογιοφ (Clock Gating) 29 ΗΤ422 - Διάλεξθ 10θ Χρονιςμόσ 14
15 Φραγή Ρολογιού (Clock Gating) Κατά ζνα μεγάλο ποςοςτό, οι καταχωρθτζσ διατθροφν τθν τιμι τουσ από κφκλο ςε κφκλο Ιδζα τόχοσ να εμποδίςουμε την ςχετική μετάβαςη του ρολογιοφ Μείωςη δυναμικήσ κατανάλωςησ ενζργειασ clk clk en en_1 en_2 en_3 en_4 30 Φραγή Ρολογιού με χρήςη Μανταλωτή Σο ςιμα ενεργοποίθςθσ (Enable) είναι ςτακερό μόνο πριν την ςχετική ακμή Χρησιμοποιούμε μανταλωτή πολικότητας αντίθετης των flip-flop Enable Clock D G Latch Q Gated_clock Clock Stability region Enable Q Gated_clock 31 15
16 Παράδειγμα Alpha MHz, 0.35μm CMOS t cycle = 1.67ns t rise = 0.35ns t skew = 50ps Πολλαπλά τοπικά ρολόγια με δυνατότθτα φραγισ 2.8 nf φορτίο ςτο ρολόι 40 cm απόςταςθ ςτουσ τελευταίουσ οδθγοφσ PLL 32 ΗΤ422 - Διάλεξθ 10θ Χρονιςμόσ Παράδειγμα Alpha MHz, 0.35μm CMOS 33 ΗΤ422 - Διάλεξθ 10θ Χρονιςμόσ 16
17 Παράδειγμα Alpha MHz, 0.35μm CMOS ps ps GCLK Skew (at Vdd/2 Crossings) GCLK Rise Times (20% to 80% Extrapolated to 0% to 100%) 34 ΗΤ422 - Διάλεξθ 10θ Χρονιςμόσ 17
HY220 Εργαςτήριο Ψηφιακών Κυκλωμάτων. Διδάςκων: Χ. ωτηρίου, Βοηθοί: Ε. Κουναλάκησ, Π. Ματτθαιάκησ, Δ. Σςαλιαγκόσ.
 HY220 Εργαςτήριο Ψηφιακών Κυκλωμάτων Διδάςκων: Χ. ωτηρίου, Βοηθοί: Ε. Κουναλάκησ, Π. Ματτθαιάκησ, Δ. Σςαλιαγκόσ http://www.csd.uoc.gr/~hy220 1 Περιεχόμενα Κακυςτζρθςθ και παράγοντεσ που τθν επθρεάηουν
HY220 Εργαςτήριο Ψηφιακών Κυκλωμάτων Διδάςκων: Χ. ωτηρίου, Βοηθοί: Ε. Κουναλάκησ, Π. Ματτθαιάκησ, Δ. Σςαλιαγκόσ http://www.csd.uoc.gr/~hy220 1 Περιεχόμενα Κακυςτζρθςθ και παράγοντεσ που τθν επθρεάηουν
HY333 Εργαστηριακή Σχεδίαση Ψηφιακών Κυκλωμάτων με εργαλεία Ηλεκτρονικού Σχεδιαστικού Αυτοματισμού.
 HY333 Εργαστηριακή Σχεδίαση Ψηφιακών Κυκλωμάτων με εργαλεία Ηλεκτρονικού Σχεδιαστικού Αυτοματισμού Διδάσκων: Χ. Σωτηρίου http://inf-server.inf.uth.gr/courses/ce333/ 1 Περιεχόμενα Καθυστέρηση και παράγοντες
HY333 Εργαστηριακή Σχεδίαση Ψηφιακών Κυκλωμάτων με εργαλεία Ηλεκτρονικού Σχεδιαστικού Αυτοματισμού Διδάσκων: Χ. Σωτηρίου http://inf-server.inf.uth.gr/courses/ce333/ 1 Περιεχόμενα Καθυστέρηση και παράγοντες
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων
 ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Χειμερινό Εξάμηνο 2015-2016 ΗΥ220 -Γιώργος Καιλοκαιρινός & Βασίλης Παπαευσταθίου 1 Λογικές Πύλες, Στοιχεία Μνήμης, Συνδυαστική Λογική και Κυματομορφές ΗΥ220 -Γιώργος
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Χειμερινό Εξάμηνο 2015-2016 ΗΥ220 -Γιώργος Καιλοκαιρινός & Βασίλης Παπαευσταθίου 1 Λογικές Πύλες, Στοιχεία Μνήμης, Συνδυαστική Λογική και Κυματομορφές ΗΥ220 -Γιώργος
Χρονισμός Σύγχρονων Κυκλωμάτων, Καταχωρητές και Μανταλωτές. Χειμερινό Εξάμηνο
 HY220 Χρονισμός Σύγχρονων Κυκλωμάτων, Καταχωρητές και Μανταλωτές Χειμερινό Εξάμηνο 2009 20102010 Γενικό Μοντέλο Σύγχρονων Κυκλωμάτων clock input input CL reg CL reg output option feedback Τα καλώδια, εκτός
HY220 Χρονισμός Σύγχρονων Κυκλωμάτων, Καταχωρητές και Μανταλωτές Χειμερινό Εξάμηνο 2009 20102010 Γενικό Μοντέλο Σύγχρονων Κυκλωμάτων clock input input CL reg CL reg output option feedback Τα καλώδια, εκτός
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων
 ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Χειμερινό Εξάμηνο 2017-2018 Λογικές Πύλες, Στοιχεία Μνήμης, Συνδυαστική Λογική και Κυματομορφές ΗΥ220 - Βασίλης Παπαευσταθίου & Γιώργος Καλοκαιρινός 1 Τα βασικά της
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Χειμερινό Εξάμηνο 2017-2018 Λογικές Πύλες, Στοιχεία Μνήμης, Συνδυαστική Λογική και Κυματομορφές ΗΥ220 - Βασίλης Παπαευσταθίου & Γιώργος Καλοκαιρινός 1 Τα βασικά της
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωµάτων
 ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωµάτων Χειµερινό Εξάµηνο 2017-2018 Χρονισµός Σύγχρονων Κυκλώµατων, Καταχωρητές και Μανταλωτές ΗΥ220 - Γιώργος Καλοκαιρινός & Βασίλης Παπαευσταθίου 1 Γενικό Μοντέλο Σύγχρονων
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωµάτων Χειµερινό Εξάµηνο 2017-2018 Χρονισµός Σύγχρονων Κυκλώµατων, Καταχωρητές και Μανταλωτές ΗΥ220 - Γιώργος Καλοκαιρινός & Βασίλης Παπαευσταθίου 1 Γενικό Μοντέλο Σύγχρονων
HY330 Ψηφιακά Κυκλώματα - Εισαγωγή στα Συστήματα VLSI. 1 ΗΥ330 - Διάλεξη 7η - Ακολουθιακά Κυκλώματα
 HY330 Ψηφιακά - Εισαγωγή στα Συστήματα VLSI Διδάσκων: Χ. Σωτηρίου, Βοηθοί: θα ανακοινωθούν http://inf-server.inf.uth.gr/courses/ce330 1 Μανταλωτές θετικής, αρνητικής πολικότητας Σχεδίαση με Μανταλωτές
HY330 Ψηφιακά - Εισαγωγή στα Συστήματα VLSI Διδάσκων: Χ. Σωτηρίου, Βοηθοί: θα ανακοινωθούν http://inf-server.inf.uth.gr/courses/ce330 1 Μανταλωτές θετικής, αρνητικής πολικότητας Σχεδίαση με Μανταλωτές
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωµάτων
 ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωµάτων Χειµερινό Εξάµηνο 2006-2007 Χρονισµός Σύγχρονων Κυκλώµατων, Καταχωρητές και Μανταλωτές ΗΥ220 - Βασίλης Παπαευσταθίου 1 Γενικό Μοντέλο Σύγχρονων Κυκλωµάτων clock input
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωµάτων Χειµερινό Εξάµηνο 2006-2007 Χρονισµός Σύγχρονων Κυκλώµατων, Καταχωρητές και Μανταλωτές ΗΥ220 - Βασίλης Παπαευσταθίου 1 Γενικό Μοντέλο Σύγχρονων Κυκλωµάτων clock input
Κεφάλαιο 7 ο. Γ. Τσιατούχας. VLSI Technology and Computer Architecture Lab. Ακολουθιακή Λογική 2
 ΚΥΚΛΩΜΑΤΑ VLSI Ακολουθιακή Λογική Κεφάλαιο 7 ο Γ. Τσιατούχας ΚΥΚΛΩΜΑΤΑ VLSI Διάρθρωση 1. Δισταθή κυκλώματα Μεταστάθεια 2. Μανδαλωτές 3. Flip Flops Flops 4. Δομές διοχέτευσης 5. Διανομή ρολογιού 6. Συγχρονισμός
ΚΥΚΛΩΜΑΤΑ VLSI Ακολουθιακή Λογική Κεφάλαιο 7 ο Γ. Τσιατούχας ΚΥΚΛΩΜΑΤΑ VLSI Διάρθρωση 1. Δισταθή κυκλώματα Μεταστάθεια 2. Μανδαλωτές 3. Flip Flops Flops 4. Δομές διοχέτευσης 5. Διανομή ρολογιού 6. Συγχρονισμός
 HY422 Ειςαγωγό ςτα Συςτόματα VLSI Διδϊςκων: Χ. Σωτηρύου, Βοηθόσ: Π. Ματθαιϊκησ http://www.csd.uoc.gr/~hy422 1 Μανταλωτζσ κετικισ, αρνθτικισ πολικότθτασ χεδίαςθ με Μανταλωτζσ Κακυςτζρθςθ FF τφπου HLFF (AM
HY422 Ειςαγωγό ςτα Συςτόματα VLSI Διδϊςκων: Χ. Σωτηρύου, Βοηθόσ: Π. Ματθαιϊκησ http://www.csd.uoc.gr/~hy422 1 Μανταλωτζσ κετικισ, αρνθτικισ πολικότθτασ χεδίαςθ με Μανταλωτζσ Κακυςτζρθςθ FF τφπου HLFF (AM
HY523 Εργαςτηριακή Σχεδίαςη Ψηφιακών Κυκλωμάτων με εργαλεία Ηλεκτρονικού Σχεδιαςτικού Αυτοματιςμού. http://www.csd.uoc.gr/~hy523. 2 ΗΥ523 - Χωροκζτθςθ
 HY523 Εργαςτηριακή Σχεδίαςη Ψηφιακών Κυκλωμάτων με εργαλεία Ηλεκτρονικού Σχεδιαςτικού Αυτοματιςμού Διδάςκων: Χ. Σωτηρίου http://www.csd.uoc.gr/~hy523 1 ΗΥ523 - Χωροκζτθςθ Περιεχόμενα Δομζσ Ειςόδου/Εξόδου
HY523 Εργαςτηριακή Σχεδίαςη Ψηφιακών Κυκλωμάτων με εργαλεία Ηλεκτρονικού Σχεδιαςτικού Αυτοματιςμού Διδάςκων: Χ. Σωτηρίου http://www.csd.uoc.gr/~hy523 1 ΗΥ523 - Χωροκζτθςθ Περιεχόμενα Δομζσ Ειςόδου/Εξόδου
7 η διάλεξη Ακολουθιακά Κυκλώματα
 7 η διάλεξη Ακολουθιακά Κυκλώματα 1 2 3 4 5 6 7 Παραπάνω βλέπουμε ακολουθιακό κύκλωμα σχεδιασμένο με μανταλωτές διαφορετικής φάσης. Παρατηρούμε ότι συνδυαστική λογική μπορεί να προστεθεί μεταξύ και των
7 η διάλεξη Ακολουθιακά Κυκλώματα 1 2 3 4 5 6 7 Παραπάνω βλέπουμε ακολουθιακό κύκλωμα σχεδιασμένο με μανταλωτές διαφορετικής φάσης. Παρατηρούμε ότι συνδυαστική λογική μπορεί να προστεθεί μεταξύ και των
Κεφάλαιο 10 ο. Γ. Τσιατούχας. VLSI Systems and Computer Architecture Lab. Ακολουθιακή Λογική 2
 ΚΥΚΛΩΜΑΤΑ VLSI Πανεπιστήμιο Ιωαννίνων Ακολουθιακή Λογική Κεφάλαιο 10 ο Τμήμα Μηχανικών Η/Υ και Πληροφορικής Γ. Τσιατούχας ΚΥΚΛΩΜΑΤΑ VLSI Διάρθρωση 1. Δισταθή κυκλώματα Μεταευστάθεια 2. Μανδαλωτές 3. Flip
ΚΥΚΛΩΜΑΤΑ VLSI Πανεπιστήμιο Ιωαννίνων Ακολουθιακή Λογική Κεφάλαιο 10 ο Τμήμα Μηχανικών Η/Υ και Πληροφορικής Γ. Τσιατούχας ΚΥΚΛΩΜΑΤΑ VLSI Διάρθρωση 1. Δισταθή κυκλώματα Μεταευστάθεια 2. Μανδαλωτές 3. Flip
3 θ διάλεξθ Επανάλθψθ, Επιςκόπθςθ των βαςικϊν γνϊςεων τθσ Ψθφιακισ Σχεδίαςθσ
 3 θ διάλεξθ Επανάλθψθ, Επιςκόπθςθ των βαςικϊν γνϊςεων τθσ Ψθφιακισ Σχεδίαςθσ 1 2 3 4 5 6 7 Παραπάνω φαίνεται θ χαρακτθριςτικι καμπφλθ μετάβαςθσ δυναμικοφ (voltage transfer characteristic) για ζναν αντιςτροφζα,
3 θ διάλεξθ Επανάλθψθ, Επιςκόπθςθ των βαςικϊν γνϊςεων τθσ Ψθφιακισ Σχεδίαςθσ 1 2 3 4 5 6 7 Παραπάνω φαίνεται θ χαρακτθριςτικι καμπφλθ μετάβαςθσ δυναμικοφ (voltage transfer characteristic) για ζναν αντιςτροφζα,
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων. Χειμερινό Εξάμηνο
 ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Ρολόι και Χρονισμός Χειμερινό Εξάμηνο 2009 2010 Synchronous Timing Όλα τα στοιχεία στο σύστημα ενημερώνονται ταυτόχρονα με ένα κεντρικό ρολόι Στην πραγματικότητα Clock
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Ρολόι και Χρονισμός Χειμερινό Εξάμηνο 2009 2010 Synchronous Timing Όλα τα στοιχεία στο σύστημα ενημερώνονται ταυτόχρονα με ένα κεντρικό ρολόι Στην πραγματικότητα Clock
HY523 Εργαςτηριακό χεδύαςη Ψηφιακών Κυκλωμϊτων με εργαλεύα Ηλεκτρονικού χεδιαςτικού Αυτοματιςμού.
 HY523 Εργαςτηριακό χεδύαςη Ψηφιακών Κυκλωμϊτων με εργαλεύα Ηλεκτρονικού χεδιαςτικού Αυτοματιςμού Διδϊςκων: Χ. ωτηρύου http://www.csd.uoc.gr/~hy523 1 Περιεχόμενα Ροι Φυςικισ χεδίαςθσ χεδίαςθ με Κακιερωμζνα
HY523 Εργαςτηριακό χεδύαςη Ψηφιακών Κυκλωμϊτων με εργαλεύα Ηλεκτρονικού χεδιαςτικού Αυτοματιςμού Διδϊςκων: Χ. ωτηρύου http://www.csd.uoc.gr/~hy523 1 Περιεχόμενα Ροι Φυςικισ χεδίαςθσ χεδίαςθ με Κακιερωμζνα
Σχεδίαση CMOS Ψηφιακών Ολοκληρωμένων Κυκλωμάτων
 Σχεδίαση CMOS Ψηφιακών Ολοκληρωμένων Κυκλωμάτων Αγγελική Αραπογιάννη Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Η λειτουργία RESET R IN OUT Εάν το σήμα R είναι λογικό «1» στην έξοδο
Σχεδίαση CMOS Ψηφιακών Ολοκληρωμένων Κυκλωμάτων Αγγελική Αραπογιάννη Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Η λειτουργία RESET R IN OUT Εάν το σήμα R είναι λογικό «1» στην έξοδο
HY422 Ειςαγωγή ςτα Συςτήματα VLSI. HY422 - Διάλεξθ 4θ - Διαςυνδζςεισ
 HY422 Ειςαγωγή ςτα Συςτήματα VLSI Διδάςκων: Χ. Σωτηρίου, Βοηθόσ: Π. Ματτθαιάκησ http://www.csd.uoc.gr/~hy422 Περιεχόμενα Διαςυνδζςεισ Μοντελοποίθςθ των Παραςιτικών Διαςυνδζςεισ ςε ζνα Πραγματικό Κφκλωμα
HY422 Ειςαγωγή ςτα Συςτήματα VLSI Διδάςκων: Χ. Σωτηρίου, Βοηθόσ: Π. Ματτθαιάκησ http://www.csd.uoc.gr/~hy422 Περιεχόμενα Διαςυνδζςεισ Μοντελοποίθςθ των Παραςιτικών Διαςυνδζςεισ ςε ζνα Πραγματικό Κφκλωμα
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ. Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 15: Καταχωρητές (Registers)
 ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 15: Καταχωρητές (Registers) ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Περίληψη q Καταχωρητές Παράλληλης
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 15: Καταχωρητές (Registers) ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Περίληψη q Καταχωρητές Παράλληλης
ΤΙΤΛΟΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΚΑΤΑΧΩΡΗΤΕΣ ΟΛΙΣΘΗΤΕΣ
 ΣΧΟΛΗ ΑΣΠΑΙΤΕ ΤΜΗΜΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ ΤΙΤΛΟΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΚΑΤΑΧΩΡΗΤΕΣ ΟΛΙΣΘΗΤΕΣ 1) Το παρακάτω κύκλωμα του σχήματος 1 είναι ένας καταχωρητής-ολισθητής
ΣΧΟΛΗ ΑΣΠΑΙΤΕ ΤΜΗΜΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ ΤΙΤΛΟΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΚΑΤΑΧΩΡΗΤΕΣ ΟΛΙΣΘΗΤΕΣ 1) Το παρακάτω κύκλωμα του σχήματος 1 είναι ένας καταχωρητής-ολισθητής
«Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο Διάλεξη 8 η : Μηχανές Πεπερασμένων Κaταστάσεων σε FPGAs
 ΤΕΙ Δυτικής Ελλάδας Τμήμα Μηχανικών Πληροφορικής ΤΕ Εργαστήριο Σχεδίασης Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων «Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο 2016-2017 Διάλεξη 8 η :
ΤΕΙ Δυτικής Ελλάδας Τμήμα Μηχανικών Πληροφορικής ΤΕ Εργαστήριο Σχεδίασης Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων «Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο 2016-2017 Διάλεξη 8 η :
HY437 Αλγόριθμοι CAD
 HY437 Αλγόριθμοι CAD Διδάςκων: Χ. Σωτηρίου http://inf-server.inf.uth.gr/courses/ce437/ 1 Περιεχόμενα Ζλεγχοσ Σφαλμάτων μετά τθν Καταςκευι Μοντζλο Κολλθμζνο-ςτο-0, -1 Παραδείγματα Διαδικαςίασ Ελζγχου Λογικι
HY437 Αλγόριθμοι CAD Διδάςκων: Χ. Σωτηρίου http://inf-server.inf.uth.gr/courses/ce437/ 1 Περιεχόμενα Ζλεγχοσ Σφαλμάτων μετά τθν Καταςκευι Μοντζλο Κολλθμζνο-ςτο-0, -1 Παραδείγματα Διαδικαςίασ Ελζγχου Λογικι
ΗΜΥ 210: Σχεδιασμός Ψηφιακών Συστημάτων. Καταχωρητές 1
 ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Καταχωρητές Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Περίληψη Καταχωρητές Παράλληλης Φόρτωσης Καταχωρητές
ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Καταχωρητές Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Περίληψη Καταχωρητές Παράλληλης Φόρτωσης Καταχωρητές
Συπικζσ Γλϊςςεσ Περιγραφισ Τλικοφ Διάλεξθ 5
 Τμήμα Μησανικών Πληποφοπικήρ, Τ.Ε.Ι. Ηπείπος Ακαδημαϊκό Έτορ 2016-2017, 6 ο Εξάμηνο Συπικζσ Γλϊςςεσ Περιγραφισ Τλικοφ Διάλεξθ 5 Διδάςκων Σςιακμάκθσ Κυριάκοσ, Phd MSc in Electronic Physics (Radioelectrology)
Τμήμα Μησανικών Πληποφοπικήρ, Τ.Ε.Ι. Ηπείπος Ακαδημαϊκό Έτορ 2016-2017, 6 ο Εξάμηνο Συπικζσ Γλϊςςεσ Περιγραφισ Τλικοφ Διάλεξθ 5 Διδάςκων Σςιακμάκθσ Κυριάκοσ, Phd MSc in Electronic Physics (Radioelectrology)
Σχεδίαςη Σφγχρονων Ακολουθιακών Κυκλωμάτων
 Σχεδίαςη Σφγχρονων Ακολουθιακών Κυκλωμάτων Πίνακεσ Διζγερςησ των FF Όπωσ είδαμε κατά τθ μελζτθ των FF, οι χαρακτθριςτικοί πίνακεσ δίνουν τθν τιμι τθσ επόμενθσ κατάςταςθσ κάκε FF ωσ ςυνάρτθςθ τθσ παροφςασ
Σχεδίαςη Σφγχρονων Ακολουθιακών Κυκλωμάτων Πίνακεσ Διζγερςησ των FF Όπωσ είδαμε κατά τθ μελζτθ των FF, οι χαρακτθριςτικοί πίνακεσ δίνουν τθν τιμι τθσ επόμενθσ κατάςταςθσ κάκε FF ωσ ςυνάρτθςθ τθσ παροφςασ
Xρονισμός ψηφιακών κυκλωμάτων
 Xρονισμός ψηφιακών κυκλωμάτων Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Φθινόπωρο 2008 ΗΥ220 1 Περιεχόμενα μαθήματος Καθυστέρηση λογικών πυλών και των συνδυαστικών κυκλωμάτων
Xρονισμός ψηφιακών κυκλωμάτων Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Φθινόπωρο 2008 ΗΥ220 1 Περιεχόμενα μαθήματος Καθυστέρηση λογικών πυλών και των συνδυαστικών κυκλωμάτων
Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου. Ψθφιακά Ηλεκτρονικά. Ενότθτα 9 : Διαδικαςία φνκεςθσ Φϊτιοσ Βαρτηιϊτθσ
 Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακά Ηλεκτρονικά Ενότθτα 9 : Διαδικαςία φνκεςθσ Φϊτιοσ Βαρτηιϊτθσ 1 Ανοιχτά Σμιμα Ψθφιακά Ηλεκτρονικά Ενότητα 9: Διαδικαςία φνκεςθσ Φϊτιοσ
Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακά Ηλεκτρονικά Ενότθτα 9 : Διαδικαςία φνκεςθσ Φϊτιοσ Βαρτηιϊτθσ 1 Ανοιχτά Σμιμα Ψθφιακά Ηλεκτρονικά Ενότητα 9: Διαδικαςία φνκεςθσ Φϊτιοσ
HY121 Ηλεκτρικϊ Κυκλώματα
 HY121 Ηλεκτρικϊ Κυκλώματα Διδϊςκων: Χ. Σωτηρύου, Βοηθού: Ε. Βαςιλϊκησ, Δ. Πούλιοσ http://www.csd.uoc.gr/~hy121 1 Περιεχόμενα Συςκευζσ ςτο Πυρίτιο Πυρίτιο n και p Δίοδοσ Θετικι, αρνθτικι πόλωςθ Εξίςωςθ
HY121 Ηλεκτρικϊ Κυκλώματα Διδϊςκων: Χ. Σωτηρύου, Βοηθού: Ε. Βαςιλϊκησ, Δ. Πούλιοσ http://www.csd.uoc.gr/~hy121 1 Περιεχόμενα Συςκευζσ ςτο Πυρίτιο Πυρίτιο n και p Δίοδοσ Θετικι, αρνθτικι πόλωςθ Εξίςωςθ
Περίληψη. ΗΜΥ-210: Λογικός Σχεδιασµός Εαρινό Εξάµηνο Παράδειγµα: Καταχωρητής 2-bit. Καταχωρητής 4-bit. Μνήµη Καταχωρητών
 ΗΜΥ-210: Λογικός Σχεδιασµός Εαρινό Κεφάλαιο 7 i: Καταχωρητές Περίληψη Καταχωρητές Παράλληλης Φόρτωσης Καταχωρητές Ολίσθησης Σειριακή Φόρτωση Σειριακή Ολίσθηση Καταχωρητές Ολίσθησης Παράλληλης Φόρτωσης
ΗΜΥ-210: Λογικός Σχεδιασµός Εαρινό Κεφάλαιο 7 i: Καταχωρητές Περίληψη Καταχωρητές Παράλληλης Φόρτωσης Καταχωρητές Ολίσθησης Σειριακή Φόρτωση Σειριακή Ολίσθηση Καταχωρητές Ολίσθησης Παράλληλης Φόρτωσης
HY437 Αλγόριθμοι CAD
 HY437 Αλγόριθμοι CAD Διδάςκων: Χ. Σωτηρίου http://inf-server.inf.uth.gr/courses/ce437/ 1 ΗΥ437 - Πολυεπίπεδθ Λογικι Απλοποίθςθ με Περιεχόμενα Είδθ Αδιάφορων Τιμϊν ςε Πολφ-επίπεδα Δυαδικά Δίκτυα Αδιάφορεσ
HY437 Αλγόριθμοι CAD Διδάςκων: Χ. Σωτηρίου http://inf-server.inf.uth.gr/courses/ce437/ 1 ΗΥ437 - Πολυεπίπεδθ Λογικι Απλοποίθςθ με Περιεχόμενα Είδθ Αδιάφορων Τιμϊν ςε Πολφ-επίπεδα Δυαδικά Δίκτυα Αδιάφορεσ
26-Nov-09. ΗΜΥ 210: Λογικός Σχεδιασμός, Χειμερινό Εξάμηνο Καταχωρητές 1. Διδάσκουσα: Μαρία Κ. Μιχαήλ
 ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 2009 Καταχωρητές Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Περίληψη Καταχωρητές Παράλληλης
ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 2009 Καταχωρητές Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Περίληψη Καταχωρητές Παράλληλης
HY225 Οργϊνωςη Υπολογιςτών
 HY225 Οργϊνωςη Υπολογιςτών Διδϊςκοντεσ: Δ. Νικολόπουλοσ, Χ. ωτηρύου. http://www.csd.uoc.gr/~hy225 1 Πωσ μετρϊμε την Απόδοςη; Ορίηουμε Απόδοςθ = 1/(Χρόνοσ Εκτζλεςθσ) «Χ είναι ν φορζσ γρθγορότερο από το
HY225 Οργϊνωςη Υπολογιςτών Διδϊςκοντεσ: Δ. Νικολόπουλοσ, Χ. ωτηρύου. http://www.csd.uoc.gr/~hy225 1 Πωσ μετρϊμε την Απόδοςη; Ορίηουμε Απόδοςθ = 1/(Χρόνοσ Εκτζλεςθσ) «Χ είναι ν φορζσ γρθγορότερο από το
Σχεδιασμός Ψηφιακών Συστημάτων
 ΗΜΥ 2: Σχεδιασμό Ψηφιακών Συστημάτων, Χειμερινό Εξάμηνο 27 Νοε-7 ΗΜΥ-2: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 27 Ακολουθιακά Κυκλώματα: Μανδαλωτές (Latches) και Flip-Flops Flops Διδάσκουσα:
ΗΜΥ 2: Σχεδιασμό Ψηφιακών Συστημάτων, Χειμερινό Εξάμηνο 27 Νοε-7 ΗΜΥ-2: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 27 Ακολουθιακά Κυκλώματα: Μανδαλωτές (Latches) και Flip-Flops Flops Διδάσκουσα:
Περιεχόμενα. Πρόλογος... XI. Κεφάλαιο 1. Συστήματα Βασισμένα σε FPGA Κεφάλαιο 2. Τεχνολογία VLSI Εισαγωγή Βασικές Αρχές...
 Περιεχόμενα Πρόλογος... XI Κεφάλαιο 1. Συστήματα Βασισμένα σε FPGA... 1 1.1 Εισαγωγή... 1 1.2 Βασικές Αρχές... 1 1.2.1 Boolean Άλγεβρα... 1 1.2.2 Σχηματικά και Λογικά Σύμβολα... 6 1.3 Ψηφιακή Σχεδίαση
Περιεχόμενα Πρόλογος... XI Κεφάλαιο 1. Συστήματα Βασισμένα σε FPGA... 1 1.1 Εισαγωγή... 1 1.2 Βασικές Αρχές... 1 1.2.1 Boolean Άλγεβρα... 1 1.2.2 Σχηματικά και Λογικά Σύμβολα... 6 1.3 Ψηφιακή Σχεδίαση
Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου. Ψθφιακά Ηλεκτρονικά. Ενότθτα 10 : Καταχωρθτζσ Φϊτιοσ Βαρτηιϊτθσ
 Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακά Ηλεκτρονικά Ενότθτα 10 : Καταχωρθτζσ Φϊτιοσ Βαρτηιϊτθσ 1 Ανοιχτά Ακαδημαϊκά Σμιμα Ψθφιακά Ηλεκτρονικά Ενότητα 10: Καταχωρθτζσ Φϊτιοσ
Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακά Ηλεκτρονικά Ενότθτα 10 : Καταχωρθτζσ Φϊτιοσ Βαρτηιϊτθσ 1 Ανοιχτά Ακαδημαϊκά Σμιμα Ψθφιακά Ηλεκτρονικά Ενότητα 10: Καταχωρθτζσ Φϊτιοσ
HY437 Αλγόριθμοι CAD
 HY437 Αλγόριθμοι CAD Διδϊςκων: Χ. Σωτηρύου http://inf-server.inf.uth.gr/courses/ce437/ 1 Περιεχόμενα Στόχοι τθσ Τεχνολογικισ Απεικόνιςθσ Περιγραφι σ ωσ Βαςικοί Γράφοι Μεταςχθματιςμόσ Δυαδικοφ Κυκλϊματοσ
HY437 Αλγόριθμοι CAD Διδϊςκων: Χ. Σωτηρύου http://inf-server.inf.uth.gr/courses/ce437/ 1 Περιεχόμενα Στόχοι τθσ Τεχνολογικισ Απεικόνιςθσ Περιγραφι σ ωσ Βαςικοί Γράφοι Μεταςχθματιςμόσ Δυαδικοφ Κυκλϊματοσ
Κ. ΕΥΣΤΑΘΙΟΥ, Γ. ΠΑΠΑΔΟΠΟΥΛΟΣ ΠΑΤΡΑ
 ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΝΙΚΗΣ & ΥΠΟΛΟΓΙΣΤΩΝ ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ ΣΗΜΕΙΩΣΕΙΣ ΑΠΑΡΙΘΜΗΤΕΣ Κ. ΕΥΣΤΑΘΙΟΥ, Γ. ΠΑΠΑΔΟΠΟΥΛΟΣ
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΝΙΚΗΣ & ΥΠΟΛΟΓΙΣΤΩΝ ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ ΣΗΜΕΙΩΣΕΙΣ ΑΠΑΡΙΘΜΗΤΕΣ Κ. ΕΥΣΤΑΘΙΟΥ, Γ. ΠΑΠΑΔΟΠΟΥΛΟΣ
Ψηφιακή Λογική και Σχεδίαση
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Αρχιτεκτονική Υπολογιστών 25-6 Ψηφιακή Λογική και Σχεδίαση (στοιχεία και μέθοδοι χρονισμού) http://di.ionio.gr/~mistral/tp/comparch/ Μ.Στεφανιδάκης Πέρα από τη συνδυαστική
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Αρχιτεκτονική Υπολογιστών 25-6 Ψηφιακή Λογική και Σχεδίαση (στοιχεία και μέθοδοι χρονισμού) http://di.ionio.gr/~mistral/tp/comparch/ Μ.Στεφανιδάκης Πέρα από τη συνδυαστική
Ακολουκιακά Λογικά Κυκλώματα
 Ακολουκιακά Λογικά Κυκλώματα Τα ψθφιακά λογικά κυκλϊματα που μελετιςαμε μζχρι τϊρα ιταν ςυνδυαςτικά κυκλϊματα. Στα ςυνδυαςτικά κυκλϊματα οι ζξοδοι ςε κάκε χρονικι ςτιγμι εξαρτϊνται αποκλειςτικά και μόνο
Ακολουκιακά Λογικά Κυκλώματα Τα ψθφιακά λογικά κυκλϊματα που μελετιςαμε μζχρι τϊρα ιταν ςυνδυαςτικά κυκλϊματα. Στα ςυνδυαςτικά κυκλϊματα οι ζξοδοι ςε κάκε χρονικι ςτιγμι εξαρτϊνται αποκλειςτικά και μόνο
Χρονική ανάλυση και χρονισμός ψηφιακών κυκλωμάτων
 Χρονική ανάλυση και χρονισμός ψηφιακών κυκλωμάτων Γιώργος Δημητρακόπουλος Δημοκρίτειο Πανεπιστήμιο Θράκης Φθινόπωρο 2013 Συστήματα VLSI 1 What we should learn Συστήματα VLSI 2 Delay Definitions t pdr :
Χρονική ανάλυση και χρονισμός ψηφιακών κυκλωμάτων Γιώργος Δημητρακόπουλος Δημοκρίτειο Πανεπιστήμιο Θράκης Φθινόπωρο 2013 Συστήματα VLSI 1 What we should learn Συστήματα VLSI 2 Delay Definitions t pdr :
Ψθφιακά Ηλεκτρονικά. Ενότθτα 5 : Ανάλυςθ κυκλώματοσ με D και JK FLIP- FLOP Φώτιοσ Βαρτηιώτθσ
 Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακά Ηλεκτρονικά Ενότθτα 5 : Ανάλυςθ κυκλώματοσ με D και JK FLIP- FLOP Φώτιοσ Βαρτηιώτθσ 1 Ανοιχτά Ακαδημαϊκά Μαθήματα ςτο ΤΕΙ Ηπείρου Σμιμα
Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακά Ηλεκτρονικά Ενότθτα 5 : Ανάλυςθ κυκλώματοσ με D και JK FLIP- FLOP Φώτιοσ Βαρτηιώτθσ 1 Ανοιχτά Ακαδημαϊκά Μαθήματα ςτο ΤΕΙ Ηπείρου Σμιμα
Ελίνα Μακρή
 Ελίνα Μακρή elmak@unipi.gr Μετατροπή Αριθμητικών Συστημάτων Πράξεις στα Αριθμητικά Συστήματα Σχεδίαση Ψηφιακών Κυκλωμάτων με Logism Άλγεβρα Boole Λογικές Πύλες (AND, OR, NOT, NAND, XOR) Flip Flops (D,
Ελίνα Μακρή elmak@unipi.gr Μετατροπή Αριθμητικών Συστημάτων Πράξεις στα Αριθμητικά Συστήματα Σχεδίαση Ψηφιακών Κυκλωμάτων με Logism Άλγεβρα Boole Λογικές Πύλες (AND, OR, NOT, NAND, XOR) Flip Flops (D,
«Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων» Χειμερινό εξάμηνο Ακολουθιακός Κώδικας
 «Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων» Χειμερινό εξάμηνο 2016-2017 Ακολουθιακός Κώδικας Παρασκευάς Κίτσος http://diceslab.cied.teiwest.gr Επίκουρος Καθηγητής Tμήμα Μηχανικών Πληροφορικής ΤΕ E-mail: pkitsos@teimes.gr
«Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων» Χειμερινό εξάμηνο 2016-2017 Ακολουθιακός Κώδικας Παρασκευάς Κίτσος http://diceslab.cied.teiwest.gr Επίκουρος Καθηγητής Tμήμα Μηχανικών Πληροφορικής ΤΕ E-mail: pkitsos@teimes.gr
K24 Ψηφιακά Ηλεκτρονικά 9: Flip-Flops
 K24 Ψηφιακά Ηλεκτρονικά 9: TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ ΤΕΧΝΟΛΟΓΙΚΟ Περιεχόμενα 1 2 3 Γενικά Ύστερα από τη μελέτη συνδυαστικών ψηφιακών κυκλωμάτων, θα μελετήσουμε
K24 Ψηφιακά Ηλεκτρονικά 9: TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ ΤΕΧΝΟΛΟΓΙΚΟ Περιεχόμενα 1 2 3 Γενικά Ύστερα από τη μελέτη συνδυαστικών ψηφιακών κυκλωμάτων, θα μελετήσουμε
Δημοκρίτειο Πανεπιστήμιο Θράκης Τμήμα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών. Συστήματα VLSI. Πρόοδος Άνοιξη 2018
 Δημοκρίτειο Πανεπιστήμιο Θράκης Τμήμα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Γ. Δημητρακόπουλος Συστήματα VLSI Πρόοδος Άνοιξη 2018 Άσκηση 1 Όλο το κύκλωμα τροφοδοτείται με το ίδιο ρολόι και το
Δημοκρίτειο Πανεπιστήμιο Θράκης Τμήμα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Γ. Δημητρακόπουλος Συστήματα VLSI Πρόοδος Άνοιξη 2018 Άσκηση 1 Όλο το κύκλωμα τροφοδοτείται με το ίδιο ρολόι και το
ΠΕΡΙΕΧΟΜΕΝΑ ΠΕΡΙΕΧΟΜΕΝΑ.3 ΑΣΥΓΧΡΟΝΟΣ ΔYΑΔΙΚΟΣ ΑΠΑΡΙΘΜΗΤΗΣ.5 ΑΣΥΓΧΡΟΝΟΣ ΔΕΚΑΔΙΚΟΣ ΑΠΑΡΙΘΜΗΤΗΣ.7 ΑΣΥΓΧΡΟΝΟΣ ΔΕΚΑΔΙΚΟΣ ΑΠΑΡΙΘΜΗΤΗΣ ΜΕ LATCH.
 ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΝΙΚΗΣ & ΥΠΟΛΟΓΙΣΤΩΝ ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ ΣΗΜΕΙΩΣΕΙΣ ΑΠΑΡΙΘΜΗΤΕΣ Κ. ΕΥΣΤΑΘΙΟΥ, Γ. ΠΑΠΑΔΟΠΟΥΛΟΣ
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΝΙΚΗΣ & ΥΠΟΛΟΓΙΣΤΩΝ ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ ΣΗΜΕΙΩΣΕΙΣ ΑΠΑΡΙΘΜΗΤΕΣ Κ. ΕΥΣΤΑΘΙΟΥ, Γ. ΠΑΠΑΔΟΠΟΥΛΟΣ
What we should learn. Συστήματα VLSI 2
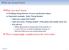 What we should learn Συστήματα VLSI 2 Delay Definitions t pdr : rising propagation delay From input to rising output crossing V DD /2 t pdf : falling propagation delay From input to falling output crossing
What we should learn Συστήματα VLSI 2 Delay Definitions t pdr : rising propagation delay From input to rising output crossing V DD /2 t pdf : falling propagation delay From input to falling output crossing
Ελλθνικι Δθμοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου. Ψθφιακά Ηλεκτρονικά. Ενότθτα 13 : Άλλοι Μετρθτζσ Φϊτιοσ Βαρτηιϊτθσ
 Ελλθνικι Δθμοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακά Ηλεκτρονικά Ενότθτα 13 : Άλλοι Μετρθτζσ Φϊτιοσ Βαρτηιϊτθσ 1 Ανοιχτά Τμιμα Ψθφιακά Ηλεκτρονικά Ενότητα 13: Άλλοι Μετρθτζσ Φϊτιοσ Βαρτηιϊτθσ
Ελλθνικι Δθμοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακά Ηλεκτρονικά Ενότθτα 13 : Άλλοι Μετρθτζσ Φϊτιοσ Βαρτηιϊτθσ 1 Ανοιχτά Τμιμα Ψθφιακά Ηλεκτρονικά Ενότητα 13: Άλλοι Μετρθτζσ Φϊτιοσ Βαρτηιϊτθσ
Ψηφιακή Σχεδίαση Ενότητα 10:
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ψηφιακή Σχεδίαση Ενότητα 10: Καταχωρητές & Μετρητές Δρ. Μηνάς Δασυγένης mdasyg@ieee.org Εργαστήριο Ψηφιακών Συστημάτων και Αρχιτεκτονικής Υπολογιστών http://arch.icte.uowm.gr/mdasyg
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ψηφιακή Σχεδίαση Ενότητα 10: Καταχωρητές & Μετρητές Δρ. Μηνάς Δασυγένης mdasyg@ieee.org Εργαστήριο Ψηφιακών Συστημάτων και Αρχιτεκτονικής Υπολογιστών http://arch.icte.uowm.gr/mdasyg
Ακολουθιακό κύκλωμα Η έξοδος του κυκλώματος εξαρτάται από τις τιμές εισόδου ΚΑΙ από την προηγούμενη κατάσταση του κυκλώματος
 1 Συνδυαστικό κύκλωμα Η έξοδος του κυκλώματος εξαρτάται ΜΟΝΟ από τις εισόδους του Εάν γνωρίζουμε τις τιμές των εισόδων του κυκλώματος, τότε μπορούμε να προβλέψουμε ακριβώς τις εξόδους του Ακολουθιακό κύκλωμα
1 Συνδυαστικό κύκλωμα Η έξοδος του κυκλώματος εξαρτάται ΜΟΝΟ από τις εισόδους του Εάν γνωρίζουμε τις τιμές των εισόδων του κυκλώματος, τότε μπορούμε να προβλέψουμε ακριβώς τις εξόδους του Ακολουθιακό κύκλωμα
HY121 Ηλεκτρικϊ Κυκλώματα
 HY Ηλεκτρικϊ Κυκλώματα Διδϊςκων: Χ. Σωτηρύου, Βοηθού: Ε. Βαςιλϊκησ, Δ. Πούλιοσ http://www.csd.uoc.gr/~hy Περιεχόμενα Στατικζσ Πφλεσ CMOS και Μεγζκθ Τρανηίςτορ Λογικι Λόγου Αντίςταςθσ/Μεγεκών (NMOS) Διαφορικι
HY Ηλεκτρικϊ Κυκλώματα Διδϊςκων: Χ. Σωτηρύου, Βοηθού: Ε. Βαςιλϊκησ, Δ. Πούλιοσ http://www.csd.uoc.gr/~hy Περιεχόμενα Στατικζσ Πφλεσ CMOS και Μεγζκθ Τρανηίςτορ Λογικι Λόγου Αντίςταςθσ/Μεγεκών (NMOS) Διαφορικι
Σχεδιασμός Ψηφιακών Συστημάτων
 ΗΜΥ 2: Σχεδιασμό Ψηφιακών Συστημάτων, Χειμερινό Εξάμηνο 28 Νοε-8 ΗΜΥ-2: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 28 Ανάλυση Ακολουθιακών Κυκλωμάτων Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου
ΗΜΥ 2: Σχεδιασμό Ψηφιακών Συστημάτων, Χειμερινό Εξάμηνο 28 Νοε-8 ΗΜΥ-2: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 28 Ανάλυση Ακολουθιακών Κυκλωμάτων Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου
Χρονισμός ψηφιακών κυκλωμάτων
 Χρονισμός ψηφιακών κυκλωμάτων Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Γ. Δημητρακόπουλος HY422 1 Tρόποι χρονισμού Πως μπορούμε να συνδέσουμε τα στοιχεία αποθήκευσης με τη
Χρονισμός ψηφιακών κυκλωμάτων Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Γ. Δημητρακόπουλος HY422 1 Tρόποι χρονισμού Πως μπορούμε να συνδέσουμε τα στοιχεία αποθήκευσης με τη
Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου. Ψθφιακά Ηλεκτρονικά. Ενότθτα 11 : Μετρθτζσ Ριπισ Φϊτιοσ Βαρτηιϊτθσ
 Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακά Ηλεκτρονικά Ενότθτα 11 : Μετρθτζσ Ριπισ Φϊτιοσ Βαρτηιϊτθσ 1 Ανοιχτά Σμιμα Ψθφιακά Ηλεκτρονικά Ενότητα 11: Μετρθτζσ Ριπισ Φϊτιοσ Βαρτηιϊτθσ
Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακά Ηλεκτρονικά Ενότθτα 11 : Μετρθτζσ Ριπισ Φϊτιοσ Βαρτηιϊτθσ 1 Ανοιχτά Σμιμα Ψθφιακά Ηλεκτρονικά Ενότητα 11: Μετρθτζσ Ριπισ Φϊτιοσ Βαρτηιϊτθσ
Σχεδίαση υψηλών επιδόσεων pipelining παράλληλη επεξεργασία
 Σχεδίαση υψηλών επιδόσεων pipelining παράλληλη επεξεργασία Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Φθινόπωρο 2008 ΗΥ220 1 Περιεχόμενα μαθήματος Ρυθμός εκτέλεσης εργασιών
Σχεδίαση υψηλών επιδόσεων pipelining παράλληλη επεξεργασία Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Φθινόπωρο 2008 ΗΥ220 1 Περιεχόμενα μαθήματος Ρυθμός εκτέλεσης εργασιών
Ελλθνικι Δθμοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου. Ψθφιακά Ηλεκτρονικά. Ενότθτα 1 : Ειςαγωγι. Φϊτιοσ Βαρτηιϊτθσ
 Ελλθνικι Δθμοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακά Ηλεκτρονικά Ενότθτα 1 : Ειςαγωγι Φϊτιοσ Βαρτηιϊτθσ 1 Ανοιχτά Ακαδημαϊκά Μαθήματα Τμιμα Ψθφιακά Ηλεκτρονικά Ενότητα 1: Ειςαγωγι Φϊτιοσ
Ελλθνικι Δθμοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακά Ηλεκτρονικά Ενότθτα 1 : Ειςαγωγι Φϊτιοσ Βαρτηιϊτθσ 1 Ανοιχτά Ακαδημαϊκά Μαθήματα Τμιμα Ψθφιακά Ηλεκτρονικά Ενότητα 1: Ειςαγωγι Φϊτιοσ
Ακολουθιακό κύκλωμα Η έξοδος του κυκλώματος εξαρτάται από τις τιμές εισόδου ΚΑΙ από την προηγούμενη κατάσταση του κυκλώματος
 1 Συνδυαστικό κύκλωμα Η έξοδος του κυκλώματος εξαρτάται ΜΟΝΟ από τις εισόδους του Εάν γνωρίζουμε τις τιμές των εισόδων του κυκλώματος, τότε μπορούμε να προβλέψουμε ακριβώς τις εξόδους του Ακολουθιακό κύκλωμα
1 Συνδυαστικό κύκλωμα Η έξοδος του κυκλώματος εξαρτάται ΜΟΝΟ από τις εισόδους του Εάν γνωρίζουμε τις τιμές των εισόδων του κυκλώματος, τότε μπορούμε να προβλέψουμε ακριβώς τις εξόδους του Ακολουθιακό κύκλωμα
Τεχνικζσ Ανάλυςησ Διοικητικών Αποφάςεων
 Τεχνικζσ Ανάλυςησ Διοικητικών Αποφάςεων Ενότητα 3: υςτιματα ουρϊν αναμονισ Κακθγθτισ Γιάννθσ Γιαννίκοσ χολι Οργάνωςθσ και Διοίκθςθσ Επιχειριςεων Σμιμα Διοίκθςθσ Επιχειριςεων Σκοποί ενότητασ Μελζτθ ςυςτθμάτων
Τεχνικζσ Ανάλυςησ Διοικητικών Αποφάςεων Ενότητα 3: υςτιματα ουρϊν αναμονισ Κακθγθτισ Γιάννθσ Γιαννίκοσ χολι Οργάνωςθσ και Διοίκθςθσ Επιχειριςεων Σμιμα Διοίκθςθσ Επιχειριςεων Σκοποί ενότητασ Μελζτθ ςυςτθμάτων
Κεφάλαιο 7: Μοντελοποίθςθ ςυμπεριφοράσ
 Κεφάλαιο 7: Μοντελοποίθςθ ςυμπεριφοράσ τόχοι Κατανόθςθ των κανόνων και των γενικϊν κατευκφνςεων για τα διαγράμματα ακολουκίασ και επικοινωνίασ, κακϊσ και για τισ ςυμπεριφορικζσ μθχανζσ καταςτάςεων. Κατανόθςθ
Κεφάλαιο 7: Μοντελοποίθςθ ςυμπεριφοράσ τόχοι Κατανόθςθ των κανόνων και των γενικϊν κατευκφνςεων για τα διαγράμματα ακολουκίασ και επικοινωνίασ, κακϊσ και για τισ ςυμπεριφορικζσ μθχανζσ καταςτάςεων. Κατανόθςθ
ΑΣΚΗΣΗ 2: Μελζτη πυκνωτών. Στόχοσ. Θεωρητικό υπόβαθρο. Εκτζλεςη τησ άςκηςησ. Θα μελετιςουμε επίπεδουσ πυκνωτζσ με και χωρίσ διθλεκτρικό.
 ΑΣΚΗΣΗ 2: Μελζτη πυκνωτών Στόχοσ Θα μελετιςουμε επίπεδουσ πυκνωτζσ με και χωρίσ διθλεκτρικό. Οι πυκνωτζσ αποκθκεφουν ενζργεια με τθν μορφι θλεκτρικοφ πεδίου. Το θλεκτρικό πεδίο δθμιουργείται ανάμεςα ςε
ΑΣΚΗΣΗ 2: Μελζτη πυκνωτών Στόχοσ Θα μελετιςουμε επίπεδουσ πυκνωτζσ με και χωρίσ διθλεκτρικό. Οι πυκνωτζσ αποκθκεφουν ενζργεια με τθν μορφι θλεκτρικοφ πεδίου. Το θλεκτρικό πεδίο δθμιουργείται ανάμεςα ςε
Εργαστηριακή άσκηση στο μάθημα του Αυτομάτου Ελέγχου (ΜΜ803)
 Εργαστηριακή άσκηση στο μάθημα του Αυτομάτου Ελέγχου (ΜΜ803) Το ςφςτθμα τθσ φωτογραφίασ αποτελείται από ζνα κινθτιρα ςτον άξονα του οποίου ζχουμε προςαρμόςει ζνα φορτίο. Στον κινθτιρα υπάρχει ςυνδεδεμζνοσ
Εργαστηριακή άσκηση στο μάθημα του Αυτομάτου Ελέγχου (ΜΜ803) Το ςφςτθμα τθσ φωτογραφίασ αποτελείται από ζνα κινθτιρα ςτον άξονα του οποίου ζχουμε προςαρμόςει ζνα φορτίο. Στον κινθτιρα υπάρχει ςυνδεδεμζνοσ
ΘΕΡΜΟΔΤΝΑΜΙΚΗ IΙ. Ενότθτα 4: Χθμικζσ αντιδράςεισ αερίων τακερά Χθμικισ Ιςορροπίασ Πρότυπθ Ελεφκερθ Ενζργεια
 ΘΕΡΜΟΔΤΝΑΜΙΚΗ IΙ Ενότθτα 4: Χθμικζσ αντιδράςεισ αερίων τακερά Χθμικισ Ιςορροπίασ Πρότυπθ Ελεφκερθ Ενζργεια ογομών Μπογοςιάν Πολυτεχνικι χολι Σμιμα Χθμικών Μθχανικών κοποί ενότθτασ κοπόσ τθσ ενότθτασ αυτισ
ΘΕΡΜΟΔΤΝΑΜΙΚΗ IΙ Ενότθτα 4: Χθμικζσ αντιδράςεισ αερίων τακερά Χθμικισ Ιςορροπίασ Πρότυπθ Ελεφκερθ Ενζργεια ογομών Μπογοςιάν Πολυτεχνικι χολι Σμιμα Χθμικών Μθχανικών κοποί ενότθτασ κοπόσ τθσ ενότθτασ αυτισ
«Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων» Χειμερινό εξάμηνο Μηχανές Πεπερασμένων Καταστάσεων
 «Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων» Χειμερινό εξάμηνο 2016-2017 Μηχανές Πεπερασμένων Καταστάσεων Παρασκευάς Κίτσος http://diceslab.cied.teiwest.gr Επίκουρος Καθηγητής Tμήμα Μηχανικών Πληροφορικής ΤΕ
«Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων» Χειμερινό εξάμηνο 2016-2017 Μηχανές Πεπερασμένων Καταστάσεων Παρασκευάς Κίτσος http://diceslab.cied.teiwest.gr Επίκουρος Καθηγητής Tμήμα Μηχανικών Πληροφορικής ΤΕ
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI II
 Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI II Επιμέλεια: Γεώργιος Θεοδωρίδης, Επίκουρος Καθηγητής Ανδρέας Εμερετλής, Υποψήιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI II Επιμέλεια: Γεώργιος Θεοδωρίδης, Επίκουρος Καθηγητής Ανδρέας Εμερετλής, Υποψήιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα
ΑΝΩΣΑΣΟ ΕΚΠΑΙΔΕΤΣΙΚΟ ΙΔΡΤΜΑ ΠΕΙΡΑΙΑ ΣΕΧΝΟΛΟΓΙΚΟΤ ΣΟΜΕΑ ΧΟΛΗ ΣΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΣΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΑΤΣΟΜΑΣΙΜΟΤ Σ.Ε.
 ΑΝΩΣΑΣΟ ΕΚΠΑΙΔΕΤΣΙΚΟ ΙΔΡΤΜΑ ΠΕΙΡΑΙΑ ΣΕΧΝΟΛΟΓΙΚΟΤ ΣΟΜΕΑ ΧΟΛΗ ΣΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΣΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΑΤΣΟΜΑΣΙΜΟΤ Σ.Ε. ΤΣΗΜΑΣΑ ΑΤΣΟΜΑΣΟΤ ΕΛΕΓΧΟΤ Ι ΑΚΗΕΙ ΠΡΑΞΗ Καθηγητήσ: Δ. ΔΗΜΟΓΙΑΝΝΟΠΟΤΛΟ Καθ. Εφαρμ:. ΒΑΙΛΕΙΑΔΟΤ
ΑΝΩΣΑΣΟ ΕΚΠΑΙΔΕΤΣΙΚΟ ΙΔΡΤΜΑ ΠΕΙΡΑΙΑ ΣΕΧΝΟΛΟΓΙΚΟΤ ΣΟΜΕΑ ΧΟΛΗ ΣΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΣΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΑΤΣΟΜΑΣΙΜΟΤ Σ.Ε. ΤΣΗΜΑΣΑ ΑΤΣΟΜΑΣΟΤ ΕΛΕΓΧΟΤ Ι ΑΚΗΕΙ ΠΡΑΞΗ Καθηγητήσ: Δ. ΔΗΜΟΓΙΑΝΝΟΠΟΤΛΟ Καθ. Εφαρμ:. ΒΑΙΛΕΙΑΔΟΤ
Σχεδιασμός Ψηφιακών Συστημάτων
 ΗΜΥ 2: Σχεδιασμό Ψηφιακών Συστημάτων, Χειμερινό Εξάμηνο 28 ΗΜΥ-2: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 28 Ακολουθιακά Κυκλώματα: Μανδαλωτές (Latches) και Flip-Flops Flops Διδάσκουσα: Μαρία
ΗΜΥ 2: Σχεδιασμό Ψηφιακών Συστημάτων, Χειμερινό Εξάμηνο 28 ΗΜΥ-2: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 28 Ακολουθιακά Κυκλώματα: Μανδαλωτές (Latches) και Flip-Flops Flops Διδάσκουσα: Μαρία
Ενότητα ΑΡΧΕΣ ΑΚΟΛΟΥΘΙΑΚΗΣ ΛΟΓΙΚΗΣ LATCHES & FLIP-FLOPS
 Ενότητα ΑΡΧΕΣ ΑΚΟΛΟΥΘΙΑΚΗΣ ΛΟΓΙΚΗΣ LATCHES & FLIP-FLOPS Γενικές Γραμμές Ακολουθιακή Λογική Μεταστάθεια S-R RLatch h( (active high h&l low) S-R Latch with Enable Latch Flip-Flop Ασύγχρονοι είσοδοι PRESET
Ενότητα ΑΡΧΕΣ ΑΚΟΛΟΥΘΙΑΚΗΣ ΛΟΓΙΚΗΣ LATCHES & FLIP-FLOPS Γενικές Γραμμές Ακολουθιακή Λογική Μεταστάθεια S-R RLatch h( (active high h&l low) S-R Latch with Enable Latch Flip-Flop Ασύγχρονοι είσοδοι PRESET
Μικροηλεκτρονική - VLSI
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μικροηλεκτρονική - VLSI Ενότητα 7: Ακολουθιακή Λογική Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε. Άδειες
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μικροηλεκτρονική - VLSI Ενότητα 7: Ακολουθιακή Λογική Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε. Άδειες
ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΥΛΙΚΟ ΚΑΙ ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ. Ενότητα 1. Λογικής Σχεδίασης. Καθηγητής Αντώνης Πασχάλης
 ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΣΧΕΔΙΑΣΗ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ - VHL ΥΛΙΚΟ ΚΑΙ ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ Ενότητα 1 Αρχές και Πρακτικές Ακολουθιακής Λογικής Σχεδίασης Καθηγητής Αντώνης Πασχάλης 217 Γενικές
ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΣΧΕΔΙΑΣΗ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ - VHL ΥΛΙΚΟ ΚΑΙ ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ Ενότητα 1 Αρχές και Πρακτικές Ακολουθιακής Λογικής Σχεδίασης Καθηγητής Αντώνης Πασχάλης 217 Γενικές
Θέματα χρονισμού σε φλιπ-φλοπ και κυκλώματα VLSI
 Εθνικό Μετσόβιο Πολυτεχνείο Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Τομέας Επικοινωνιών, Ηλεκτρονικής και Συστημάτων Πληροφορικής Εισαγωγή στην Σχεδίαση Συστημάτων VLSI Θέματα χρονισμού
Εθνικό Μετσόβιο Πολυτεχνείο Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Τομέας Επικοινωνιών, Ηλεκτρονικής και Συστημάτων Πληροφορικής Εισαγωγή στην Σχεδίαση Συστημάτων VLSI Θέματα χρονισμού
ΤΙΤΛΟΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΣΥΓΧΡΟΝΟΙ ΜΕΤΡΗΤΕΣ
 ΣΧΟΛΗ ΑΣΠΑΙΤΕ ΤΜΗΜΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ ΤΙΤΛΟΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΣΥΓΧΡΟΝΟΙ ΜΕΤΡΗΤΕΣ 1) Οι σύγχρονοι μετρητές υλοποιούνται με Flip-Flop τύπου T
ΣΧΟΛΗ ΑΣΠΑΙΤΕ ΤΜΗΜΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ ΤΙΤΛΟΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΣΥΓΧΡΟΝΟΙ ΜΕΤΡΗΤΕΣ 1) Οι σύγχρονοι μετρητές υλοποιούνται με Flip-Flop τύπου T
ΗΥ220: Εργαστήριο σχεδίασης ψηφιακών κυκλωμάτων Χριστόφορος Κάχρης
 Πανεπιστήμιο Κρήτης Τμήμα Επιστήμης Υπολογιστών ΗΥ220: Εργαστήριο σχεδίασης ψηφιακών κυκλωμάτων Χριστόφορος Κάχρης 4-11-2009 Πρόοδος Θέμα 1 ο (25%): 1. Βρείτε την μεγίστη συχνότητα λειτουργίας του παρακάτω
Πανεπιστήμιο Κρήτης Τμήμα Επιστήμης Υπολογιστών ΗΥ220: Εργαστήριο σχεδίασης ψηφιακών κυκλωμάτων Χριστόφορος Κάχρης 4-11-2009 Πρόοδος Θέμα 1 ο (25%): 1. Βρείτε την μεγίστη συχνότητα λειτουργίας του παρακάτω
Δυναμικι Μθχανϊν I. Διάλεξθ 16. Χειμερινό Εξάμθνο 2013 Τμιμα Μθχανολόγων Μθχ., ΕΜΠ
 Δυναμικι Μθχανϊν I Διάλεξθ 16 Χειμερινό Εξάμθνο 2013 Τμιμα Μθχανολόγων Μθχ., ΕΜΠ 1 Ανακοινϊςεισ Office Hours: Δευτζρα 1-3 μμ, Εργαςτιριο Εμβιομθχανικισ, Ιςόγειο Κτθρίου Μ (210 772-1516) DMmeche2013@gmail.com
Δυναμικι Μθχανϊν I Διάλεξθ 16 Χειμερινό Εξάμθνο 2013 Τμιμα Μθχανολόγων Μθχ., ΕΜΠ 1 Ανακοινϊςεισ Office Hours: Δευτζρα 1-3 μμ, Εργαςτιριο Εμβιομθχανικισ, Ιςόγειο Κτθρίου Μ (210 772-1516) DMmeche2013@gmail.com
HY220 Εργαςτήριο Ψηφιακών Κυκλωμάτων. 9/28/ ΗΥ220 - Διάλεξθ 3θ, Επανάλθψθ
 HY220 Εργαςτήριο Ψηφιακών Κυκλωμάτων Διδάςκων: Χ. Σωτηρίου, Βοηθοί: Ε. Κουναλάκησ, Π. Ματτθαιάκησ http://www.csd.uoc.gr/~hy220 1 Περιεχόμενα Συςτιματα Αρικμϊν και Δυαδικοί Αρικμοί Ψθφιακι Λογικι Ηλεκτρικά
HY220 Εργαςτήριο Ψηφιακών Κυκλωμάτων Διδάςκων: Χ. Σωτηρίου, Βοηθοί: Ε. Κουναλάκησ, Π. Ματτθαιάκησ http://www.csd.uoc.gr/~hy220 1 Περιεχόμενα Συςτιματα Αρικμϊν και Δυαδικοί Αρικμοί Ψθφιακι Λογικι Ηλεκτρικά
Seventron Limited. Οδηγίες χρήσης EnglishOnlineTests.com
 Seventron Limited Οδηγίες χρήσης EnglishOnlineTests.com EnglishOnlineTests.com Seventron.com March 2013 Περιεχόμενα Πίνακασ ελζγχου/control Panel... 2 Προςκικθ μακθτι... 3 Ανάκεςθ μακθτι ςε ενότθτα...
Seventron Limited Οδηγίες χρήσης EnglishOnlineTests.com EnglishOnlineTests.com Seventron.com March 2013 Περιεχόμενα Πίνακασ ελζγχου/control Panel... 2 Προςκικθ μακθτι... 3 Ανάκεςθ μακθτι ςε ενότθτα...
Ιςοηυγιςμζνα δζντρα και Β- δζντρα. Δομζσ Δεδομζνων
 Ιςοηυγιςμζνα δζντρα και Β- δζντρα Δομζσ Δεδομζνων Περιεχόμενα Ιςοηυγιςμζνα δζντρα Μζκοδοι ιςοηφγιςθσ δζντρων Μονι Περιςτροφι Διπλι Περιςτροφι Β - δζντρα Ιςοηυγιςμζνα δζντρα Η μορφι ενόσ δυαδικοφ δζντρου
Ιςοηυγιςμζνα δζντρα και Β- δζντρα Δομζσ Δεδομζνων Περιεχόμενα Ιςοηυγιςμζνα δζντρα Μζκοδοι ιςοηφγιςθσ δζντρων Μονι Περιςτροφι Διπλι Περιςτροφι Β - δζντρα Ιςοηυγιςμζνα δζντρα Η μορφι ενόσ δυαδικοφ δζντρου
ΗΜΥ 210: Σχεδιασμό Ψηφιακών Συστημάτων, Χειμερινό Εξάμηνο 2008
 ΗΜΥ-211: Εργαστήριο Σχεδιασμού Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 2009 Ακολουθιακά Κυκλώματα: Μανδαλωτές (Latches), Flip-FlopsFlops και Μετρητές Ριπής Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων
ΗΜΥ-211: Εργαστήριο Σχεδιασμού Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 2009 Ακολουθιακά Κυκλώματα: Μανδαλωτές (Latches), Flip-FlopsFlops και Μετρητές Ριπής Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ
 ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 12: Ανάλυση Ακολουθιακών Κυκλωµάτων (Κεφάλαιο 6.2) Μηχανές Καταστάσεων ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy)
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 12: Ανάλυση Ακολουθιακών Κυκλωµάτων (Κεφάλαιο 6.2) Μηχανές Καταστάσεων ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy)
ΑΣΚΗΣΗ 9. Tα Flip-Flop
 ΑΣΚΗΣΗ 9 Tα Flip-Flop 9.1. ΣΚΟΠΟΣ Η κατανόηση της λειτουργίας των στοιχείων μνήμης των ψηφιακών κυκλωμάτων. Τα δομικά στοιχεία μνήμης είναι οι μανδαλωτές (latches) και τα Flip-Flop. 9.2. ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ
ΑΣΚΗΣΗ 9 Tα Flip-Flop 9.1. ΣΚΟΠΟΣ Η κατανόηση της λειτουργίας των στοιχείων μνήμης των ψηφιακών κυκλωμάτων. Τα δομικά στοιχεία μνήμης είναι οι μανδαλωτές (latches) και τα Flip-Flop. 9.2. ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ
Ενδεικτικζσ Λφςεισ Θεμάτων
 c AM (t) x(t) ΤΕΙ Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σειρά Β Ειςηγητήσ: Δρ Απόςτολοσ Γεωργιάδησ ΕΠΙΚΟΙΝΩΝΙΕΣ Ι Ενδεικτικζσ Λφςεισ Θεμάτων Θζμα 1 ο (1 μον.) Ζςτω περιοδικό ςιμα πλθροφορίασ με περίοδο.
c AM (t) x(t) ΤΕΙ Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σειρά Β Ειςηγητήσ: Δρ Απόςτολοσ Γεωργιάδησ ΕΠΙΚΟΙΝΩΝΙΕΣ Ι Ενδεικτικζσ Λφςεισ Θεμάτων Θζμα 1 ο (1 μον.) Ζςτω περιοδικό ςιμα πλθροφορίασ με περίοδο.
ΛΕΙΣΟΤΡΓΙΚΆ ΤΣΉΜΑΣΑ. 7 θ Διάλεξθ Διαχείριςθ Μνιμθσ Μζροσ Γ
 ΛΕΙΣΟΤΡΓΙΚΆ ΤΣΉΜΑΣΑ 7 θ Διάλεξθ Διαχείριςθ Μνιμθσ Μζροσ Γ ελιδοποίθςθ (1/10) Σόςο θ κατάτμθςθ διαμεριςμάτων ςτακεροφ μεγζκουσ όςο και θ κατάτμθςθ διαμεριςμάτων μεταβλθτοφ και άνιςου μεγζκουσ δεν κάνουν
ΛΕΙΣΟΤΡΓΙΚΆ ΤΣΉΜΑΣΑ 7 θ Διάλεξθ Διαχείριςθ Μνιμθσ Μζροσ Γ ελιδοποίθςθ (1/10) Σόςο θ κατάτμθςθ διαμεριςμάτων ςτακεροφ μεγζκουσ όςο και θ κατάτμθςθ διαμεριςμάτων μεταβλθτοφ και άνιςου μεγζκουσ δεν κάνουν
Μετατροπι Αναλογικοφ Σιματοσ ςε Ψθφιακό. Διάλεξθ 10
 Μετατροπι Αναλογικοφ Σιματοσ ςε Ψθφιακό Διάλεξθ 10 Γενικό Σχιμα Μετατροπζασ Αναλογικοφ ςε Ψθφιακό Ψθφιακό Τθλεπικοινωνιακό Κανάλι Μετατροπζασ Ψθφιακοφ ςε Αναλογικό Τα αναλογικά ςιματα μετατρζπονται ςε
Μετατροπι Αναλογικοφ Σιματοσ ςε Ψθφιακό Διάλεξθ 10 Γενικό Σχιμα Μετατροπζασ Αναλογικοφ ςε Ψθφιακό Ψθφιακό Τθλεπικοινωνιακό Κανάλι Μετατροπζασ Ψθφιακοφ ςε Αναλογικό Τα αναλογικά ςιματα μετατρζπονται ςε
Slide 1. Εισαγωγή στη ψυχρομετρία
 Slide 1 Εισαγωγή στη ψυχρομετρία 1 Slide 2 Σφντομη ειςαγωγή ςτη ψυχρομετρία. Διάγραμμα Mollier (πίεςησ-ενθαλπίασ P-H) Σο διάγραμμα Mollier είναι μία γραφικι παράςταςθ ςε ζναν άξονα ςυντεταγμζνων γραμμϊν
Slide 1 Εισαγωγή στη ψυχρομετρία 1 Slide 2 Σφντομη ειςαγωγή ςτη ψυχρομετρία. Διάγραμμα Mollier (πίεςησ-ενθαλπίασ P-H) Σο διάγραμμα Mollier είναι μία γραφικι παράςταςθ ςε ζναν άξονα ςυντεταγμζνων γραμμϊν
CLK CLK D Q D Q. Όταν η είσοδος αλλάζει μέσα D στο παράθυρο δειγματοληψίας Q η έξοδος μπορεί να γίνει
 Βασικές αρχές συγχρονισμού Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Φθινόπωρο 2008 ΗΥ220 1 Περιεχόμενα μαθήματος Δειγματοληψία ασύγχρονων σημάτων ή επικοινωνία μεταξύ διαφορετικών
Βασικές αρχές συγχρονισμού Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Φθινόπωρο 2008 ΗΥ220 1 Περιεχόμενα μαθήματος Δειγματοληψία ασύγχρονων σημάτων ή επικοινωνία μεταξύ διαφορετικών
Ψηφιακή Σχεδίαση. Δρ. Μηνάς Δασυγένης Εργαστήριο Ψηφιακών Συστημάτων και Αρχιτεκτονικής Υπολογιστών
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ψηφιακή Σχεδίαση Ενότητα 8: Μανδαλωτές SR, S R D Flip-Flops Αφέντη Σκλάβου, Σχεδιασμός Ακολουθιακών κυκλωμάτων, Πίνακας Καταστάσεων, Διάγραμμα Καταστάσεων
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ψηφιακή Σχεδίαση Ενότητα 8: Μανδαλωτές SR, S R D Flip-Flops Αφέντη Σκλάβου, Σχεδιασμός Ακολουθιακών κυκλωμάτων, Πίνακας Καταστάσεων, Διάγραμμα Καταστάσεων
Εςωτερικό υδραγωγείο
 Εςωτερικό υδραγωγείο Εςωτερικό υδραγωγείο ι εςωτερικό δίκτυο φδρευςθσ είναι το ςφςτθμα που αποτελείται από τον κεντρικό τροφοδοτικό αγωγό και το δίκτυο των αγωγϊν για τθ διανομι του νεροφ ςτουσ καταναλωτζσ
Εςωτερικό υδραγωγείο Εςωτερικό υδραγωγείο ι εςωτερικό δίκτυο φδρευςθσ είναι το ςφςτθμα που αποτελείται από τον κεντρικό τροφοδοτικό αγωγό και το δίκτυο των αγωγϊν για τθ διανομι του νεροφ ςτουσ καταναλωτζσ
Παράςταςη ακεραίων ςτο ςυςτημα ςυμπλήρωμα ωσ προσ 2
 Παράςταςη ακεραίων ςτο ςυςτημα ςυμπλήρωμα ωσ προσ 2 Δρ. Χρήζηος Ηλιούδης Μθ Προςθμαςμζνοι Ακζραιοι Εφαρμογζσ (ςε οποιαδιποτε περίπτωςθ δεν χρειάηονται αρνθτικοί αρικμοί) Καταμζτρθςθ. Διευκυνςιοδότθςθ.
Παράςταςη ακεραίων ςτο ςυςτημα ςυμπλήρωμα ωσ προσ 2 Δρ. Χρήζηος Ηλιούδης Μθ Προςθμαςμζνοι Ακζραιοι Εφαρμογζσ (ςε οποιαδιποτε περίπτωςθ δεν χρειάηονται αρνθτικοί αρικμοί) Καταμζτρθςθ. Διευκυνςιοδότθςθ.
HY220 Εργαςτόριο Ψηφιακών Κυκλωμϊτων
 HY220 Εργαςτόριο Ψηφιακών Κυκλωμϊτων Διδϊςκων: Χ. Σωτηρύου, Βοηθού: Ε. Κουναλϊκησ, Π. Ματτθαιϊκησ 1 υγχρονιςμόσ Οριςμόσ και Περιπτϊςεισ Καμπφλθ Μεταβίβαςθσ και Μθχανικό Ανάλογο υγχρονιςμόσ με FF Μεταςτάκεια
HY220 Εργαςτόριο Ψηφιακών Κυκλωμϊτων Διδϊςκων: Χ. Σωτηρύου, Βοηθού: Ε. Κουναλϊκησ, Π. Ματτθαιϊκησ 1 υγχρονιςμόσ Οριςμόσ και Περιπτϊςεισ Καμπφλθ Μεταβίβαςθσ και Μθχανικό Ανάλογο υγχρονιςμόσ με FF Μεταςτάκεια
HY437 Αλγόριθμοι CAD
 HY437 Αλγόριθμοι CAD Διδάςκων: Χ. Σωτηρίου http://inf-server.inf.uth.gr/courses/ce437/ 1 Περιεχόμενα Κανονικζσ Μορφζσ Οριςμόσ των Δυαδικών Διαγραμμάτων Αποφάςεων (Binary Decision Diagrams BDDs) Αναπαράςταςθ
HY437 Αλγόριθμοι CAD Διδάςκων: Χ. Σωτηρίου http://inf-server.inf.uth.gr/courses/ce437/ 1 Περιεχόμενα Κανονικζσ Μορφζσ Οριςμόσ των Δυαδικών Διαγραμμάτων Αποφάςεων (Binary Decision Diagrams BDDs) Αναπαράςταςθ
ΝΟΜΟΙ ΚΙΝΗΗ ΠΛΑΝΗΣΩΝ ΣΟΤ ΚΕΠΛΕΡ
 ΝΟΜΟΙ ΚΙΝΗΗ ΠΛΑΝΗΣΩΝ ΣΟΤ ΚΕΠΛΕΡ 1. Νόμοσ των ελλειπτικών τροχιών Η τροχιζσ των πλανθτϊν είναι ελλείψεισ, των οποίων τθ μία εςτία κατζχει ο Ήλιοσ. Προφανϊσ όλοι οι πλανιτεσ του ίδιου πλανθτικοφ ςυςτιματοσ
ΝΟΜΟΙ ΚΙΝΗΗ ΠΛΑΝΗΣΩΝ ΣΟΤ ΚΕΠΛΕΡ 1. Νόμοσ των ελλειπτικών τροχιών Η τροχιζσ των πλανθτϊν είναι ελλείψεισ, των οποίων τθ μία εςτία κατζχει ο Ήλιοσ. Προφανϊσ όλοι οι πλανιτεσ του ίδιου πλανθτικοφ ςυςτιματοσ
ΣΕΙ ΔΤΣ. ΜΑRΚΕΔΟΝΙΑ ΧΟΛΗ ΣΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΣΜΗΜΑ ΗΛΕΚΣΡΟΛΟΓΙΑ ΜΑΘΗΜΑ: ΗΛΕΚΣΡΟΣΕΧΝΙΑ Ι
 ΣΕΙ ΔΤΣ. ΜΑRΚΕΔΟΝΙΑ ΧΟΛΗ ΣΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΣΜΗΜΑ ΗΛΕΚΣΡΟΛΟΓΙΑ ΜΑΘΗΜΑ: ΗΛΕΚΣΡΟΣΕΧΝΙΑ Ι Λφσεις Θεμάτων Εξετάσεων Χειμερινοφ Εξαμήνου Περιόδου 200-20 4 Φεβρουαρίου 20 (Ν. Πουλάκθσ, e-mail: Poulakis@kozani.teikoz.gr
ΣΕΙ ΔΤΣ. ΜΑRΚΕΔΟΝΙΑ ΧΟΛΗ ΣΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΣΜΗΜΑ ΗΛΕΚΣΡΟΛΟΓΙΑ ΜΑΘΗΜΑ: ΗΛΕΚΣΡΟΣΕΧΝΙΑ Ι Λφσεις Θεμάτων Εξετάσεων Χειμερινοφ Εξαμήνου Περιόδου 200-20 4 Φεβρουαρίου 20 (Ν. Πουλάκθσ, e-mail: Poulakis@kozani.teikoz.gr
Ακολουθιακές εντολές. (Peter Ashenden, The Students Guide to VHDL)
 Ακολουθιακές εντολές (Peter Ashenden, The Students Guide to VHDL) Εντολή If Τα βασικά χαρακτηριστικά της είναι τα εξής: Μπορεί να χρησιµοποιηθεί για τον έλεγχο µίας ή περισσοτέρων συνθηκών. Η πρώτη συνθήκη
Ακολουθιακές εντολές (Peter Ashenden, The Students Guide to VHDL) Εντολή If Τα βασικά χαρακτηριστικά της είναι τα εξής: Μπορεί να χρησιµοποιηθεί για τον έλεγχο µίας ή περισσοτέρων συνθηκών. Η πρώτη συνθήκη
Πρόγραμμα Μεταπτυχιακών Σπουδών «Πληροφορική και Εφαρμογές»
 Πρόγραμμα Μεταπτυχιακών Σπουδών «Πληροφορική και Εφαρμογές» Αρχές Ψηφιακής Τεχνολογίας Σχεδιασμός σύνθετων συστημάτων Γιάννης Βογιατζής 28-29 Βασικές λογικές πύλες = Driver = AND = + OR = XOR = Inverter
Πρόγραμμα Μεταπτυχιακών Σπουδών «Πληροφορική και Εφαρμογές» Αρχές Ψηφιακής Τεχνολογίας Σχεδιασμός σύνθετων συστημάτων Γιάννης Βογιατζής 28-29 Βασικές λογικές πύλες = Driver = AND = + OR = XOR = Inverter
Σο θλεκτρικό κφκλωμα
 Σο θλεκτρικό κφκλωμα Για να είναι δυνατι θ ροι των ελεφκερων θλεκτρονίων, για να ζχουμε θλεκτρικό ρεφμα, απαραίτθτθ προχπόκεςθ είναι θ φπαρξθ ενόσ κλειςτοφ θλεκτρικοφ κυκλϊματοσ. Είδθ κυκλωμάτων Σα κυκλϊματα
Σο θλεκτρικό κφκλωμα Για να είναι δυνατι θ ροι των ελεφκερων θλεκτρονίων, για να ζχουμε θλεκτρικό ρεφμα, απαραίτθτθ προχπόκεςθ είναι θ φπαρξθ ενόσ κλειςτοφ θλεκτρικοφ κυκλϊματοσ. Είδθ κυκλωμάτων Σα κυκλϊματα
Προςζξτε ότι για τα A, B ςε ςειρά, θ πθγι του πάνω, όταν είναι ανοικτό φτάνει μόνο τα (Vdd Vtn)V.
 1 2 Όπωσ και ςτον αντιςτροφζα, ζτςι και ςτισ βαςικζσ ι πολφπλοκεσ ςτατικζσ διατάξεισ τρανηίςτορ μποροφμε να χρθςιμοποιιςουμε το μοντζλο τθσ ιςοδφναμθσ αντίςταςθσ. Με αυτό τον τρόπο προκφπτουν πιο πολφπλοκα
1 2 Όπωσ και ςτον αντιςτροφζα, ζτςι και ςτισ βαςικζσ ι πολφπλοκεσ ςτατικζσ διατάξεισ τρανηίςτορ μποροφμε να χρθςιμοποιιςουμε το μοντζλο τθσ ιςοδφναμθσ αντίςταςθσ. Με αυτό τον τρόπο προκφπτουν πιο πολφπλοκα
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Εργαστήριο Ηλεκτρονικής. Ψηφιακά Ηλεκτρονικά. Ακολουθιακή Λογική. Επιμέλεια Διαφανειών: Δ.
 Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Ακολουθιακή Λογική Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Εισαγωγή Είσοδοι Συνδυαστικό Κύκλωμα Έξοδοι Στοιχεία Μνήμης Κατάσταση
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Ακολουθιακή Λογική Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Εισαγωγή Είσοδοι Συνδυαστικό Κύκλωμα Έξοδοι Στοιχεία Μνήμης Κατάσταση
Πανεπιςτιμιο Κφπρου ΟΙΚ 223: Μακθματικά για οικονομολόγουσ ΙΙ Διδάςκων:
 Πανεπιςτιμιο Κφπρου ΟΙΚ 3: Μακθματικά για οικονομολόγουσ ΙΙ Διδάςκων: Φάμπιο Αντωνίου τοιχεία Επικοινωνίασ: email: fantoniou@aueb.gr ; fabio@ucy.ac.cy Σθλ:893683 Προςωπικι Ιςτοςελίδα: fantoniou.wordpress.com
Πανεπιςτιμιο Κφπρου ΟΙΚ 3: Μακθματικά για οικονομολόγουσ ΙΙ Διδάςκων: Φάμπιο Αντωνίου τοιχεία Επικοινωνίασ: email: fantoniou@aueb.gr ; fabio@ucy.ac.cy Σθλ:893683 Προςωπικι Ιςτοςελίδα: fantoniou.wordpress.com
2
 1 2 3 Η βαςικι λειτουργία του τρανηίςτορ είναι να διακόπτει ι να επιτρζπει τθν παροχι ρεφματοσ μεταξφ των δυο του άκρων, βάςθ του δυναμικοφ ςτθν πφλθ του, είναι δθλαδι ζνασ θλεκτρικόσ διακόπτθσ ελεγχόμενοσ
1 2 3 Η βαςικι λειτουργία του τρανηίςτορ είναι να διακόπτει ι να επιτρζπει τθν παροχι ρεφματοσ μεταξφ των δυο του άκρων, βάςθ του δυναμικοφ ςτθν πφλθ του, είναι δθλαδι ζνασ θλεκτρικόσ διακόπτθσ ελεγχόμενοσ
Ψηφιακή Λογική Σχεδίαση
 Ψηφιακή Λογική Σχεδίαση Επιμέλεια: Νίκος Φακωτάκης, Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα Αδειοδότησης Το παρόν υλικό διατίθεται
Ψηφιακή Λογική Σχεδίαση Επιμέλεια: Νίκος Φακωτάκης, Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα Αδειοδότησης Το παρόν υλικό διατίθεται
ΑΤΡΜΑΣΕ ΕΠΙΚΟΙΝΩΝΙΕ ΑΚΗΕΙ
 ΑΤΡΜΑΣΕ ΕΠΙΚΟΙΝΩΝΙΕ ΑΚΗΕΙ Άςκθςθ 1 Η μζγιςτθ τιμι του ρεφματοσ που διαρρζει μία κεραία είναι 0.5 Α, θ αντίςταςθ ακτινοβολίασ τθσ είναι 200 Ω, θ πυκνότθτα ιςχφοσ ςε απόςταςθ 10 km από τθν κεραία είναι 1
ΑΤΡΜΑΣΕ ΕΠΙΚΟΙΝΩΝΙΕ ΑΚΗΕΙ Άςκθςθ 1 Η μζγιςτθ τιμι του ρεφματοσ που διαρρζει μία κεραία είναι 0.5 Α, θ αντίςταςθ ακτινοβολίασ τθσ είναι 200 Ω, θ πυκνότθτα ιςχφοσ ςε απόςταςθ 10 km από τθν κεραία είναι 1
