Senzori si traductoare. Prof. dr. ing. Valer DOLGA,
|
|
|
- Μνημοσύνη Τομαραίοι
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Senzori si traductoare Prof. dr. ing. Valer DOLGA,
2 Cuprins_ Introducere Senzor video - robot Principii de realizare a senzorului video Prelucrarea informatiei optice Segmentarea imaginii Imagine si contur Extragerea conturului Topologia zonelor Codificarea imaginii Modelarea imaginii Exemplu Iluminarea scenei de lucru Concluzii Prof. dr. ing. Valer DOLGA 2
3 Introducere control şi inspecţie: stări de suprafeţe, culori, aspect, forme, contur, dimensiuni (liniare, plane sau spaţiale); verificarea: prezenţei sau absenţei unui subiect, simboluri, caracter, semnătură; identificărişi localizări de obiecte: în plan (2D) sau spaţiu (3D); lectură (cu sau fără recunoaştere): caractere alfanumerice, valori numerice; urmărirea unui contur: cordon de sudură etc. în fabricaţia flexibilă - 3 clase mari de utilizare a senzorilor vizuali (această impărţire nu este unică: a) inspecţia b) identificarea obiectelor c) controlulşi comanda RI. Prof. dr. ing. Valer DOLGA 3
4 a) Inspecţia : 7 % din aplicatii măsurări tridimensionale; verificarea prezenţei sau absenţei componentelor în scena observată; controlul de calitate. Un exemplu edificator: inspecţia măştilor fotografice pentru circuitele integrate: O inspecţie clasică (de ex. manuală) necesită - 5 ore de muncă / mască; varianta automatizată necesită - 5 minute. b) Identificarea : Într-o serie de aplicaţii industriale este necesară identificarea pieselor pentru a se lua o decizie şi a se realiza un clasament c) Controlul şi comanda RI: pe baza informaţiei obţinute de la senzorul vizual se pot estima poziţiile de situare a unor piese, coordonatele de prehensare, se pot determina distanţe, prezenţa unor obstacole etc. Prof. dr. ing. Valer DOLGA 4
5 Identificarea unor piese Recunoaşterea unei caroserii Prof. dr. ing. Valer DOLGA 5
6 Senzor video - robot Legatura senzor vizual-robot industrial A (i - ) i R3*3 = T *3 A x3 = s p = A s Ap [ ] T M x y z p T [ x y z ] = A [ x y z ] T p p p p p p p p p Prof. dr. ing. Valer DOLGA 6
7 Principii de realizare a senzorilor video Tubul orticon Tubul vidicon Prof. dr. ing. Valer DOLGA 7
8 Performanţele caracteristice cerute unui tub : a) sensibiltatea şi caracteristica de transfer. Tuburile vidicon posedă o fotosensibilitate ridicată. Orice precizare privind sensibilitatea trebuie să includă o referinţă la nivelul de iluminare şi la tensiunea şi curentul de obscuritate la care au fost măsurate. b) răspunsul în timp sau remanenţa. Remanenţa este consecinţa a doua cauze: remanenţa inerentă în procesul de descărcare al fasciculului electronic şi inerţia procesului fotoconductiv. Remanenţa descreşte cu creşterea iluminării. c) rezoluţia imaginii. Tubul vidicon posedă o rezoluţie liniară înaltă (până la 7 linii de explorare). Rezoluţia este limitată în principal de dimensiunea finită a fasciculului de baleiaj focalizat. d) geometria imaginii. Distorsiunea imaginii este stabilită de optica electronică a tubului ca şi de acţiunea câmpurilor de baleiaj şi de focalizare ale fasciculului electronic. O îmbunătăţire considerabilă a geometriei se poate obţine prin creşterea diametrului bobinelor de deflexie. e) răspusul spectral (dependenţa sensibilităţii de lungimea de undă) Prof. dr. ing. Valer DOLGA 8
9 Matrice de fotodiode pe corp solid (sidiconul). Senzor vizual cu matrice de diode pe suport solid Senzor vizual Prof. dr. ing. Valer DOLGA 9
10 Conceptul transferului de sarcină a fost descris de Boyle şi Smith de la Bell Telephone în 97; Tehnologia dispozitivelor cu transfer de sarcină (CTD - Charge transfer device); Alte variante: dispozitive cu acumulare de sarcină BBD (bucket brigade devices); Principiul dispozitivelor cuplate prin sarcină (CCD) dispozitive cu injectare de sarcini CID (charge injection devices). senzorul CCD = matrice de elemente fotosensibile executate pe cristal semiconductor prin metoda microfotolitografierii dacă pe suprafaţa acestui sistem se proiectează un relief luminos în fiecare element se formează o sarcină localizată de purtători da sarcină minoritară şi de mărime proporţională cu mărimea fluxului luminos pe elementul dat şi cu timpul de acumulare; Distribuţia mărimilor sarcinilor acumulate repetă relieful luminos vizualizat. Prof. dr. ing. Valer DOLGA
11 După experirarea timpului de acumulare (de obicei este fix) sarcinile sunt deplasate succesiv pe linii şi cadre şi îndepărtate din structura senzorului prin dispozitivul de ieşire (registru); Semnalul astfel obţinut formează semnalul video Dintre parametrii principali ai acestor senzori: domeniul spectral.2(.4)..., nm; fotosensibilitate integrală 5 µa/lx ; rezoluţie liniară linii/mm; neomogenitate a fotosensibilităţii până la % Prof. dr. ing. Valer DOLGA
12 Prof. dr. ing. Valer DOLGA 2
13 Prof. dr. ing. Valer DOLGA 3
14 Senzori vizuali liniari punct sensibil = imagine elementară = pixel numărul maxim de pixeli - determinat de lungimea dispozitivului şi dimensiunea fiecărui punct sensibil Senzori vizuali bidimensionali Organizarea citirii unui senzor vizual liniar Prof. dr. ing. Valer DOLGA 4
15 Prelucrarea informatiei senzorului vizual A. tratarea imaginii. Metoda imaginii binare Sistemul de coordonate ataşat matricii H Cresterea contrastelor Tehnica siluetei Prof. dr. ing. Valer DOLGA 5
16 Histograma imaginii Principiul obţinerii imaginii binare fie o imagine definită prin: "L" nivele de gri; "N" numărul total de pixeli "n(i)" numărul de pixeli de semnal "i" S = N L [ i n( i) ] i= u j j = i n N i= j v( j) = n i N i= ( ) [ ( i) ] σ 2 = Prof. dr. ing. Valer DOLGA 6 ( ) [ S v( j) u( j) ] v [ - v ] (j) (j) 2 max
17 2. Metoda nivelului de gri Alterarea imaginii (a) şi soluţionarea problemei (b) Intensitatea ataşată unui pixel este "netezită" la valoarea: Histograma în gri: a) imagine întunecată; b) imagine luminoasă y+ q x+ p i, S ( x, y) = i( n m) n= y q m= x p - "S" este o suprafaţă centrată pe pixelul vizat având coordonatele xşi y; -S = (2p + )(2q + ) ; -2p + este numărul de pixeli după axa x ataşaţi suprafeţe; -2q + este numărul de pixeli după axa y ataşaţi suprafeţei Prof. dr. ing. Valer DOLGA 7
18 Metoda gradientului = inlocuirea intensităţii fiecărui pixel printr-o valoare dependentă de punctele vecine Suma gradienţilor ponderaţi pe linie ("G x ") sau pe coloană ("G y ") este descrisă de operatorul matricial: Matricea 3 x 3 G = 3 i = 3 j = p ij c ij "p ij " - elementele matricii nivelelor de gri din jurul punctului analizat "c ij " sunt elementele matricii de pondere C x = a a a 2 3 a a a 2 3 C y = b b b 2 b 2 b 3 b 3 Prof. dr. ing. Valer DOLGA 8
19 C x = Matricea Sobel C y = Matricea Prewitt = C x C y = Prof. dr. ing. Valer DOLGA 9 C x C y = +G G = G 2 y 2 x Amplitudinea nivelului de gri: Orientarea nivelului de gri: = x y G G arctg θ Metoda transformatei Fourier
20 Segmentarea imaginii Segmentarea imaginii = operaţia de extragere teoretică (separare) a unor zone particulare din imaginea tratată anterior. Pixelii aparţinători acestor zone au o proprietate comună (de ex. aparţin la obiectul vizualizat). În mod curent se aplică două metode: a) extragerea conturului - se separă toţi pixelii cuprinşi în interiorul unor linii cu contrast puternic; b) topologia zonelor - se separă toţi pixelii dintr-o zonă care respectă o aceeaşi stare logică. pixel Prof. dr. ing. Valer DOLGA 2
21 Imagine si contur Linie contur Parametrul Simbol Valori tipice Linii N 256, 52, 525, 625, 24, 35 Coloane M , 768, 24, 32 Nivele de gri L 2, 64, 256, 24, 496, 6384 Pixel de contur Prof. dr. ing. Valer DOLGA 2
22 Extragerea conturului Extragerea conturului = Extragerea conturului: a - scanarea imaginii; b - semnal video; c - informaţie memorată definirea limitelor imaginii unui obiect vizualizat în scopul stocării acestei informaţii în memoria sistemului de comandă. - două "zone" de control care se deplasează pe limita internă şi externă a conturului teoretic; Extragerea conturului la piese complexe - limita reală a conturului este descrisă de locul geometric al distanţei minime dintre centrele celor două "zone". Prof. dr. ing. Valer DOLGA 22
23 Topologia zonelor Imagine vizualizata si matricea de analiza k 4 ( x, y ) = [ I ( x, y ) K ( x, y ) ] U n= n U n Funcţiile logice I n, K n Matrice de analiza a a a a a2 a3 a4 = a2 = a2 =(a + a4 ) a3 a urmeaza o noua zona a si a 2 apartin la aceeasi zona a o apartine la zona a sau a 4 a2 =( a a4 ) a3 a apartine cu a 3 Prof. dr. ing. Valer DOLGA 23
24 origine Codificarea imaginii Exemplu de codificare: a) codul Freeman; b) - contururi tratate Sens de parcurgere Cod : Cod contur: contur exterior: contur interior: Prof. dr. ing. Valer DOLGA 24
25 Modelarea imaginii h ij = {,, daca (i, daca (i, j) obiect j) obiect Determinarea parametrilor geometrici ai imaginii Aria imaginii vizualizate: A= n- i= ( n- j= h ij ) Perimetrul conturului ( Γ ) al imaginii: P = ( Γ ) m unde m = {,daca m este numar impar 2, daca m este numar par m = cifra din codul Freeman Prof. dr. ing. Valer DOLGA 25
26 origine Exemplu A = 99 pixeli h ij = ij P = pixeli h ij = h 2, = h = Codul Freeman: Prof. dr. ing. Valer DOLGA 26
27 Coordonatele centrului de greutate (Xs, Ys) al suprafeţei delimitate de contur : n- n- X s = A j= ( i= i h ij ) Y s = A n- i= ( n- j= j h ij ) Momentele de inerţie axiale ale suprafeţei (faţă de axele Ox, Oy) şi momentul de inerţie centrifugal: J J x y = = n- i= n- j= i j 2 2 n- ( h j= n- ( h i= ij ij ) ) J xy J,2= ( J x + J y ) ± ( 2 4 = J n- i= x - i( J y n- j= ) 2 j h + J ij 2 xy ) 2 α = 2 J xy arctg ( 2 J y - J Prof. dr. ing. Valer DOLGA 27 y O α x x )
28 Opţional se mai pot calcula: Parametrii caracteristici (poligon circumscris, raze) raportul Y max / X max dintre dimensiunile de gabarit pe direcţie verticalăşi orizontală; complexitatea conturului X max /P ; compactitatea figurii: A/(X max Y max ) ; simetria X S /X max, Y S /Y max. Prof. dr. ing. Valer DOLGA 28
29 Operatia de determinare a unor parametri a) măsurări independente de piesa vizualizată (aria, perimetrul etc); cercuri echidistante; parametri: numărul segmentelor de intersecţie ale conturului cu cercurile de explorare, Măsurări independente de piesă unghiul α min maximă. pentru raza Prof. dr. ing. Valer DOLGA 29
30 b) Masurari dependente de piesa vizualizata functii inregistrate pe cercul de raza R, R2-3 * "" corelaţia dintre unghiulφşi raza R. Controlul câmpului vizual Măsurări dependente de piesă piese Controlul câmpului vizual Prof. dr. ing. Valer DOLGA 3
31 Iluminarea scenei de lucru - suprafeţe difuze (a) (lămpi fluorescente - b, reflectoare difuze); - condensoare (c), - proiectoare (d); - colimatoare (e). Corpuri de iluminat Iluminare frontală Prof. dr. ing. Valer DOLGA 3
32 Imagine in cimp intunecat Imagine în câmp luminos Prof. dr. ing. Valer DOLGA 32
33 Iluminare cu ajutorul oglinzii reflectoare Iluminare prin prisma divizoare Iluminare paralelă Metoda de iluminare din spate Prof. dr. ing. Valer DOLGA 33
34 Utilizarea unei suprafeţe reflectorizante Iluminare monocromatică Utilizarea condensorului Utilizarea colimatorului Prof. dr. ing. Valer DOLGA 34
35 Poziţionarea senzorului vizual Prof. dr. ing. Valer DOLGA 35
36 - sursa lumina; 2, 3, 4, 5 oglinzi; 6 filtru optic 7 senzor video CCD 8 piesa pentru sudat Sursa de lumină şi senzorul vizual în structură compactă Prof. dr. ing. Valer DOLGA 36
37 Concluzii Cerinţe principale pentru un senzor vizual: simplitate în deservire; viteză mare de prelucrare a informaţiei; flexibilitate, posibilitate de adaptare la diferite sarcini (de ex. regim de bandă rulantă, descărcarea paletelor, controlul pieselor etc.); sensibilitate geometrică cât mai mare; cost redus; posibilităţi simple de conectare în cadrul sistemului; siguranţă ridicată în funcţionare; sensibilitate redusă la factori perturbatori. Prof. dr. ing. Valer DOLGA 37
Planul determinat de normală şi un punct Ecuaţia generală Plane paralele Unghi diedru Planul determinat de 3 puncte necoliniare
1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
Metode iterative pentru probleme neliniare - contractii
Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
5.5. REZOLVAREA CIRCUITELOR CU TRANZISTOARE BIPOLARE
5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate.
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Definiţia generală Cazul 1. Elipsa şi hiperbola Cercul Cazul 2. Parabola Reprezentari parametrice ale conicelor Tangente la conice
1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
Profesor Blaga Mirela-Gabriela DREAPTA
DREAPTA Fie punctele A ( xa, ya ), B ( xb, yb ), C ( xc, yc ) şi D ( xd, yd ) în planul xoy. 1)Distanţa AB = (x x ) + (y y ) Ex. Fie punctele A( 1, -3) şi B( -2, 5). Calculaţi distanţa AB. AB = ( 2 1)
R R, f ( x) = x 7x+ 6. Determinați distanța dintre punctele de. B=, unde x și y sunt numere reale.
5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
Ecuaţia generală Probleme de tangenţă Sfera prin 4 puncte necoplanare. Elipsoidul Hiperboloizi Paraboloizi Conul Cilindrul. 1 Sfera.
pe ecuaţii generale 1 Sfera Ecuaţia generală Probleme de tangenţă 2 pe ecuaţii generale Sfera pe ecuaţii generale Ecuaţia generală Probleme de tangenţă Numim sferă locul geometric al punctelor din spaţiu
Captura imaginilor. este necesară o sursă de lumină (λ: lungimea de undă a sursei)
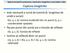Captura imaginilor este necesară o sursă de lumină (λ: lungimea de undă a sursei) E(x, y, z, λ): lumina incidentă într-un punct (x, y, z coordonatele spațiale) fiecare punct din scenă are o funcție de
1.7. AMPLIFICATOARE DE PUTERE ÎN CLASA A ŞI AB
1.7. AMLFCATOARE DE UTERE ÎN CLASA A Ş AB 1.7.1 Amplificatoare în clasa A La amplificatoarele din clasa A, forma de undă a tensiunii de ieşire este aceeaşi ca a tensiunii de intrare, deci întreg semnalul
Sisteme diferenţiale liniare de ordinul 1
1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
Curs 2 DIODE. CIRCUITE DR
Curs 2 OE. CRCUTE R E CUPRN tructură. imbol Relația curent-tensiune Regimuri de funcționare Punct static de funcționare Parametrii diodei Modelul cu cădere de tensiune constantă Analiza circuitelor cu
V O. = v I v stabilizator
Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Erori si incertitudini de măsurare. Modele matematice Instrument: proiectare, fabricaţie, Interacţiune măsurand instrument:
Erori i incertitudini de măurare Sure: Modele matematice Intrument: proiectare, fabricaţie, Interacţiune măurandintrument: (tranfer informaţie tranfer energie) Influente externe: temperatura, preiune,
Esalonul Redus pe Linii (ERL). Subspatii.
Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
Toate subiectele sunt obligatorii. Timpul de lucru efectiv este de 3 ore. Se acordă din oficiu 10 puncte. SUBIECTUL I.
Modelul 4 Se acordă din oficiu puncte.. Fie numărul complex z = i. Calculaţi (z ) 25. 2. Dacă x şi x 2 sunt rădăcinile ecuaţiei x 2 9x+8 =, atunci să se calculeze x2 +x2 2 x x 2. 3. Rezolvaţi în mulţimea
(a) se numeşte derivata parţială a funcţiei f în raport cu variabila x i în punctul a.
Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Curs 14 Funcţii implicite. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi"
Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Seminar 5 Analiza stabilității sistemelor liniare
Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii transversale, scrisă faţă de una dintre axele de inerţie principale:,
REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
Componente şi Circuite Electronice Pasive. Laborator 3. Divizorul de tensiune. Divizorul de curent
Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM 1 electronica.geniu.ro
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
CIRCUITE INTEGRATE MONOLITICE DE MICROUNDE. MMIC Monolithic Microwave Integrated Circuit
CIRCUITE INTEGRATE MONOLITICE DE MICROUNDE MMIC Monolithic Microwave Integrated Circuit CUPRINS 1. Avantajele si limitarile MMIC 2. Modelarea dispozitivelor active 3. Calculul timpului de viata al MMIC
Aplicaţii ale principiului I al termodinamicii la gazul ideal
Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
III. Serii absolut convergente. Serii semiconvergente. ii) semiconvergentă dacă este convergentă iar seria modulelor divergentă.
III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
5.4. MULTIPLEXOARE A 0 A 1 A 2
5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
5. FUNCŢII IMPLICITE. EXTREME CONDIŢIONATE.
5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
Curs 1 Şiruri de numere reale
Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Integrala nedefinită (primitive)
nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
MARCAREA REZISTOARELOR
1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
Seminariile Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reziduurilor
Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Algebra si Geometrie Seminar 9
Algebra si Geometrie Seminar 9 Decembrie 017 ii Equations are just the boring part of mathematics. I attempt to see things in terms of geometry. Stephen Hawking 9 Dreapta si planul in spatiu 1 Notiuni
Examen AG. Student:... Grupa: ianuarie 2016
16-17 ianuarie 2016 Problema 1. Se consideră graful G = pk n (p, n N, p 2, n 3). Unul din vârfurile lui G se uneşte cu câte un vârf din fiecare graf complet care nu-l conţine, obţinându-se un graf conex
Conice. Lect. dr. Constantin-Cosmin Todea. U.T. Cluj-Napoca
Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
COLEGIUL NATIONAL CONSTANTIN CARABELLA TARGOVISTE. CONCURSUL JUDETEAN DE MATEMATICA CEZAR IVANESCU Editia a VI-a 26 februarie 2005.
SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
Curs 4 Serii de numere reale
Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Examen AG. Student:... Grupa:... ianuarie 2011
Problema 1. Pentru ce valori ale lui n,m N (n,m 1) graful K n,m este eulerian? Problema 2. Să se construiască o funcţie care să recunoască un graf P 3 -free. La intrare aceasta va primi un graf G = ({1,...,n},E)
Control confort. Variator de tensiune cu impuls Reglarea sarcinilor prin ap sare, W/VA
Control confort Variatoare rotative electronice Variator rotativ / cap scar 40-400 W/VA Variatoare rotative 60-400W/VA MGU3.511.18 MGU3.559.18 Culoare 2 module 1 modul alb MGU3.511.18 MGU3.559.18 fi ldeş
2. Sisteme de forţe concurente...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...3
SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
Reflexia şi refracţia luminii.
Reflexia şi refracţia luminii. 1. Cu cat se deplaseaza o raza care cade sub unghiul i =30 pe o placa plan-paralela de grosime e = 8,0 mm si indicele de refractie n = 1,50, pe care o traverseaza? Caz particular
a. 11 % b. 12 % c. 13 % d. 14 %
1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
Capitolul 4 Amplificatoare elementare
Capitolul 4 mplificatoare elementare 4.. Etaje de amplificare cu un tranzistor 4... Etajul emitor comun V CC C B B C C L L o ( // ) V gm C i rπ // B // o L // C // L B ro i B E C E 4... Etajul colector
Subiecte Clasa a VII-a
lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...4
SEMINAR 3 MMENTUL FRŢEI ÎN RAPRT CU UN PUNCT CUPRINS 3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere...1 3.1. Aspecte teoretice...2 3.2. Aplicaţii rezolvate...4 3. Momentul forţei
2. STATICA FLUIDELOR. 2.A. Presa hidraulică. Legea lui Arhimede
2. STATICA FLUIDELOR 2.A. Presa hidraulică. Legea lui Arhimede Aplicația 2.1 Să se determine ce masă M poate fi ridicată cu o presă hidraulică având raportul razelor pistoanelor r 1 /r 2 = 1/20, ştiind
4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
Lab06: Extragerea trăsăturilor şi selecţia trăsăturilor. Aplicaţie pentru recunoaşterea obiectelor bazată pe formă.
Lab06: Extragerea trăsăturilor şi selecţia trăsăturilor Aplicaţie pentru recunoaşterea obiectelor bazată pe formă. Aplicație practică a extragerii şi selecţiei trăsăturilor Recunoaşterea celor 4 forme
Aparate de măsurat. Măsurări electronice Rezumatul cursului 2. MEE - prof. dr. ing. Ioan D. Oltean 1
Aparate de măsurat Măsurări electronice Rezumatul cursului 2 MEE - prof. dr. ing. Ioan D. Oltean 1 1. Aparate cu instrument magnetoelectric 2. Ampermetre şi voltmetre 3. Ohmetre cu instrument magnetoelectric
Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25
Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25 LAGĂRELE CU ALUNECARE!" 25.1.Caracteristici.Părţi componente.materiale.!" 25.2.Funcţionarea lagărelor cu alunecare.! 25.1.Caracteristici.Părţi componente.materiale.
Capitolul 14. Asamblari prin pene
Capitolul 14 Asamblari prin pene T.14.1. Momentul de torsiune este transmis de la arbore la butuc prin intermediul unei pene paralele (figura 14.1). De care din cotele indicate depinde tensiunea superficiala
Segmentarea imaginilor
Lucrarea 0 Segmentarea imaginilor BREVIAR TEORETIC Segmentarea reprezintă împărţirea imaginii în zone de interes, după anumite criterii. Fiecărui pixel i se va atribui o valoare, 0 sau, reprezentând apartenenţa
prin egalizarea histogramei
Lucrarea 4 Îmbunătăţirea imaginilor prin egalizarea histogramei BREVIAR TEORETIC Tehnicile de îmbunătăţire a imaginilor bazate pe calculul histogramei modifică histograma astfel încât aceasta să aibă o
Capitolul COTAREA DESENELOR TEHNICE LECŢIA 21
Capitolul COTAREA DESENELOR TEHNICE LECŢIA 21! 21.1. Generalităţi.! 21.2. Elementele cotării.! 21.3. Aplicaţii.! 21.1. Generalităţi! Dimensiunea este o caracteristică geometrică liniară sau unghiulară,care
a n (ζ z 0 ) n. n=1 se numeste partea principala iar seria a n (z z 0 ) n se numeste partea
Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Subiecte Clasa a VIII-a
Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Geometrie computationala 2. Preliminarii geometrice
Platformă de e-learning și curriculă e-content pentru învățământul superior tehnic Geometrie computationala 2. Preliminarii geometrice Preliminarii geometrice Spatiu Euclidean: E d Spatiu de d-tupluri,
Componente şi Circuite Electronice Pasive. Laborator 4. Măsurarea parametrilor mărimilor electrice
Laborator 4 Măsurarea parametrilor mărimilor electrice Obiective: o Semnalul sinusoidal, o Semnalul dreptunghiular, o Semnalul triunghiular, o Generarea diferitelor semnale folosind placa multifuncţională
Procesarea Imaginilor
Procesarea Imaginilor SEGMENTAREA IMAGINILOR Mihai Ivanovici Universitatea Transilvania din Braşov Page 1 of 29 1 Segmentarea reprezintă împărţirea imaginii în zone de interes, după anumite criterii Fiecărui
Spatii liniare. Exemple Subspaţiu liniar Acoperire (înfăşurătoare) liniară. Mulţime infinită liniar independentă
Noţiunea de spaţiu liniar 1 Noţiunea de spaţiu liniar Exemple Subspaţiu liniar Acoperire (înfăşurătoare) liniară 2 Mulţime infinită liniar independentă 3 Schimbarea coordonatelor unui vector la o schimbare
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
Proiectarea filtrelor prin metoda pierderilor de inserţie
FITRE DE MIROUNDE Proiectarea filtrelor prin metoda pierderilor de inserţie P R Puterea disponibila de la sursa Puterea livrata sarcinii P inc P Γ ( ) Γ I lo P R ( ) ( ) M ( ) ( ) M N P R M N ( ) ( ) Tipuri
Senzori si traductoare. Prof. dr. ing. Valer DOLGA,
Senzori si traductoare Prof. dr. ing. Valer DOLGA, Cuprins 11 Senzori tactili Prof. dr. ing. Valer DOLGA 2 Senzori tactili - Senzorii tactili imită posibilităţile senzitive ale mâinii umane; - pulpa degetului
Capitolul 30. Transmisii prin lant
Capitolul 30 Transmisii prin lant T.30.1. Sa se precizeze domeniile de utilizare a transmisiilor prin lant. T.30.2. Sa se precizeze avantajele si dezavantajele transmisiilor prin lant. T.30.3. Realizati
Metode de caracterizare structurala in stiinta nanomaterialelor: aplicatii practice
Metode de caracterizare structurala in stiinta nanomaterialelor: aplicatii practice Utilizare de metode complementare de investigare structurala Proba investigata: SrTiO 3 sub forma de pulbere nanostructurata
10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
Conice - Câteva proprietǎţi elementare
Conice - Câteva proprietǎţi elementare lect.dr. Mihai Chiş Facultatea de Matematicǎ şi Informaticǎ Universitatea de Vest din Timişoara Viitori Olimpici ediţia a 5-a, etapa I, clasa a XII-a 1 Definiţii
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor X) functia f 1
Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Lectia VII Dreapta si planul
Planul. Ecuatii, pozitii relative Dreapta. Ecuatii, pozitii relative Aplicatii Lectia VII Dreapta si planul Oana Constantinescu Oana Constantinescu Lectia VII Planul. Ecuatii, pozitii relative Dreapta.
Metode de interpolare bazate pe diferenţe divizate
Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].
![Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].](/thumbs/72/67648751.jpg "Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].")
Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
Matrice. Determinanti. Sisteme liniare
Matrice 1 Matrice Adunarea matricelor Înmulţirea cu scalar. Produsul 2 Proprietăţi ale determinanţilor Rangul unei matrice 3 neomogene omogene Metoda lui Gauss (Metoda eliminării) Notiunea de matrice Matrice
Lucrarea Nr. 5 Circuite simple cu diode (Aplicaţii)
ucrarea Nr. 5 Circuite simple cu diode (Aplicaţii) A.Scopul lucrării - Verificarea experimentală a rezultatelor obţinute prin analiza circuitelor cu diode modelate liniar pe porţiuni ;.Scurt breviar teoretic
2 Transformări liniare între spaţii finit dimensionale
Transformări 1 Noţiunea de transformare liniară Proprietăţi. Operaţii Nucleul şi imagine Rangul şi defectul unei transformări 2 Matricea unei transformări Relaţia dintre rang şi defect Schimbarea matricei
1. PROPRIETĂȚILE FLUIDELOR
1. PROPRIETĂȚILE FLUIDELOR a) Să se exprime densitatea apei ρ = 1000 kg/m 3 în g/cm 3. g/cm 3. b) tiind că densitatea glicerinei la 20 C este 1258 kg/m 3 să se exprime în c) Să se exprime în kg/m 3 densitatea
2.1 Sfera. (EGS) ecuaţie care poartă denumirea de ecuaţia generală asferei. (EGS) reprezintă osferă cu centrul în punctul. 2 + p 2
.1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
Aplicaţii ale principiului I al termodinamicii în tehnică
Aplicaţii ale principiului I al termodinamicii în tehnică Sisteme de încălzire a locuinţelor Scopul tuturor acestor sisteme, este de a compensa pierderile de căldură prin pereţii locuinţelor şi prin sistemul
* K. toate K. circuitului. portile. Considerând această sumă pentru toate rezistoarele 2. = sl I K I K. toate rez. Pentru o bobină: U * toate I K K 1
FNCȚ DE ENERGE Fie un n-port care conține numai elemente paive de circuit: rezitoare dipolare, condenatoare dipolare și bobine cuplate. Conform teoremei lui Tellegen n * = * toate toate laturile portile
4. Măsurarea tensiunilor şi a curenţilor electrici. Voltmetre electronice analogice
4. Măsurarea tensiunilor şi a curenţilor electrici oltmetre electronice analogice oltmetre de curent continuu Ampl.c.c. x FTJ Protectie Atenuator calibrat Atenuatorul calibrat divizor rezistiv R in const.
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
2CP Electropompe centrifugale cu turbina dubla
2CP Electropompe centrifugale cu turbina dubla DOMENIUL DE UTILIZARE Capacitate de până la 450 l/min (27 m³/h) Inaltimea de pompare până la 112 m LIMITELE DE UTILIZARE Inaltimea de aspiratie manometrică
III. Reprezentarea informaţiei în sistemele de calcul
Metode Numerice Curs 3 III. Reprezentarea informaţiei în sistemele de calcul III.1. Reprezentarea internă a numerelor întregi III. 1.1. Reprezentarea internă a numerelor întregi fără semn (pozitive) Reprezentarea
V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile
Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
DEFINITIVAT 1993 PROFESORI I. sinx. 0, dacă x = 0
DEFINITIVAT 1993 TIMIŞOARA PROFESORI I 1. a) Metodica predării noţiunii de derivată a unei funcţii. b) Să se reprezinte grafic funci a sinx, dacă x (0,2π] f : [0,2π] R, f(x) = x. 0, dacă x = 0 2. Fie G
Orice izometrie f : (X, d 1 ) (Y, d 2 ) este un homeomorfism. (Y = f(x)).
Teoremă. (Y = f(x)). Orice izometrie f : (X, d 1 ) (Y, d 2 ) este un homeomorfism Demonstraţie. f este continuă pe X: x 0 X, S Y (f(x 0 ), ε), S X (x 0, ε) aşa ca f(s X (x 0, ε)) = S Y (f(x 0 ), ε) : y
Valori limită privind SO2, NOx şi emisiile de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili
Anexa 2.6.2-1 SO2, NOx şi de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili de bioxid de sulf combustibil solid (mg/nm 3 ), conţinut de O 2 de 6% în gazele de ardere, pentru
CURS MECANICA CONSTRUCŢIILOR
CURS 10+11 MECANICA CONSTRUCŢIILOR Conf. Dr. Ing. Viorel Ungureanu CINEMATICA SOLIDULUI RIGID In cadrul cinematicii punctului material s-a arătat ca a studia mişcarea unui punct înseamnă a determina la
CIRCUITE CU DZ ȘI LED-URI
CICUITE CU DZ ȘI LED-UI I. OBIECTIVE a) Determinarea caracteristicii curent-tensiune pentru diode Zener. b) Determinarea funcționării diodelor Zener în circuite de limitare. c) Determinarea modului de
Vectori liberi Produs scalar Produs vectorial Produsul mixt. 1 Vectori liberi. 2 Produs scalar. 3 Produs vectorial. 4 Produsul mixt.
liberi 1 liberi 2 3 4 Segment orientat liberi Fie S spaţiul geometric tridimensional cu axiomele lui Euclid. Orice pereche de puncte din S, notată (A, B) se numeşte segment orientat. Dacă A B, atunci direcţia
2. Circuite logice 2.4. Decodoare. Multiplexoare. Copyright Paul GASNER
2. Circuite logice 2.4. Decodoare. Multiplexoare Copyright Paul GASNER Definiţii Un decodor pe n bits are n intrări şi 2 n ieşiri; cele n intrări reprezintă un număr binar care determină în mod unic care
Exemple de probleme rezolvate pentru cursurile DEEA Tranzistoare bipolare cu joncţiuni
Problema 1. Se dă circuitul de mai jos pentru care se cunosc: VCC10[V], 470[kΩ], RC2,7[kΩ]. Tranzistorul bipolar cu joncţiuni (TBJ) este de tipul BC170 şi are parametrii β100 şi VBE0,6[V]. 1. să se determine
CURS XI XII SINTEZĂ. 1 Algebra vectorială a vectorilor liberi
Lect. dr. Facultatea de Electronică, Telecomunicaţii şi Tehnologia Informaţiei Algebră, Semestrul I, Lector dr. Lucian MATICIUC http://math.etti.tuiasi.ro/maticiuc/ CURS XI XII SINTEZĂ 1 Algebra vectorială
Câmp de probabilitate II
1 Sistem complet de evenimente 2 Schema lui Poisson Schema lui Bernoulli (a bilei revenite) Schema hipergeometrică (a bilei neîntoarsă) 3 4 Sistem complet de evenimente Definiţia 1.1 O familie de evenimente
BARAJ DE JUNIORI,,Euclid Cipru, 28 mai 2012 (barajul 3)
BARAJ DE JUNIORI,,Euclid Cipru, 8 mi 0 (brjul ) Problem Arătţi că dcă, b, c sunt numere rele cre verifică + b + c =, tunci re loc ineglitte xy + yz + zx Problem Fie şi b numere nturle nenule Dcă numărul
Laborator 11. Mulţimi Julia. Temă
Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Problema a II - a (10 puncte) Diferite circuite electrice
Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
Sisteme de Recunoastere a Formelor Laborator 3-4 Histograma Orientarilor Gradientilor
Sisteme de Recunoastere a Formelor Laborator 3-4 Histograma Orientarilor Gradientilor 1. Obiectie Descriptorii de tip histograma a orientarii gratientilor, sau descriptori HOG, sunt descriptori de trasatori
CARACTERISTICI GENERALE ALE TRADUCTOARELOR. Caracteristicile statice şi indicatori de calitate deduşi din caracteristicile statice
ENZORI ŞI TRADUCTOARE note de curs - Eugenie Posdărăscu CARACTERITICI GENERALE ALE TRADUCTOARELOR tudiul traductoarelor prin prisma sistemelor automate impune un studiu al comportamentelor acestora atât
Conice şi cercuri tangente
Conice şi cercuri tangente Ioan POP 1 Abstract It proves how to obtain the non-degenerate conics, ellipse, hyperbola and parabola, of some basic tangent problems Keywords: circle, ellipse, hyperbola, parabola
Criptosisteme cu cheie publică III
Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
GEOMETRIE PLANĂ TEOREME IMPORTANTE ARII. bh lh 2. abc. abc. formula înălţimii
GEOMETRIE PLNĂ TEOREME IMPORTNTE suma unghiurilor unui triunghi este 8º suma unghiurilor unui patrulater este 6º unghiurile de la baza unui triunghi isoscel sunt congruente într-un triunghi isoscel liniile