Compresia de imagini. Standardul JPEG
|
|
|
- ĒΓαβριήλ Παυλόπουλος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Tehnici de Compresie a Semnalelor Multimedia Lucrare de laborator Compresia de imagini. Standardul JPEG I. Obiectivul lucrării Lucrarea îşi propune familiarizarea cu metodele şi algoritmii utilizaţi în compresia de imagini, în particular cele folosite în standardul JPEG. Pentru aceasta se foloseşte o implementare în Matlab a unui codor şi decodor JPEG. II. Compresia de imagini II.1 Definiţia imaginii. Reprezentarea în format necomprimat O imagine este o suprafaţă de obicei dreptunghiulară caracterizată, la nivelul oricărui punct al ei, de o anumită culoare. Ideal, culoarea variază continuu în oricare direcţie. Din păcate, în sistemele numerice, nu se pot utiliza mărimi care variază continuu, ci doar forma discretizată a acestora. Astfel, o imagine trebuie să fie discretizată înainte de a se pune problema reprezentării numerice. Discretizarea constă în împărţirea imaginii într-un caroiaj asemănător unei table de şah. Fiecare porţiune de imagine delimitată de acest caroiaj va fi considerată ca având o culoare uniformă - o medie a culorii existente pe această secţiune. Aceste porţiuni poartă denumirea de pixeli ; ca atare, vorbim de reprezentarea unei imagini printr-o matrice de pixeli (noţiune arhi-cunoscută astăzi, când unul din criteriile de alegere a unei camere foto este numărul de megapixeli câte milioane de pixeli are senzorul de imagine). II.2 Spaţii de culoare. RGB şi YUV. Comparaţie Pasul următor îl constituie găsirea unei reprezentări pentru culoare. Orice culoare poate fi descompusă în trei culori primare (de exemplu roşu-r, verde-g şi albastru-b), cu alte cuvinte orice imagine poate fi obţinută prin suprapunerea aditivă a trei radiaţii luminoase având aceste trei culori şi intensităţi diferite. Deci, pentru a reprezenta numeric o culoare, este suficient să se reprezinte intensităţile luminoase ale celor trei culori primare. Dacă se alocă, de exemplu, câte 8 biţi pentru fiecare componentă, se pot coda 256 nivele de intensitate, astfel: absenţa culorii (intensitate zero) se codifică prin valoarea în binar sau 00 în hexazecimal, iar intensitatea maximă, prin cea mai mare valoare ce poate fi reprezentată pe 8 biţi, şi anume, în binar sau FF în hexazecimal. Reprezentarea în format RGB ţine însă mai mult de modalităţile tehnice de captare şi reproducere a imaginii şi mai puţin de mecanismul fiziologic de percepere a culorii. 1
2 Prin diferite experimente s-a constatat că din punct de vedere al capacităţii de percepere a detaliilor, ochiul este mai sensibil la intensitatea luminoasă a culorii decât la nuanţă. Din acest motiv prezintă interes o altă modalitate de reprezentare a culorii care să ţină cont de această observaţie, un exemplu fiind reprezentarea YUV utilizată în televiziunea în culori. În acest caz, în locul celor trei componente primare R,G,B se utilizează alte trei mărimi derivate din acestea, şi anume: Y = 0,3R + 0,59G + 0,11B U = R Y = 0, 7R 0,59G 0,11B V = B Y = 0,3R 0, ,89B (10.1) În cazul acestei reprezentări, componenta Y corespunde intensităţii luminoase percepute pentru respectiva culoare (coeficienţii 0,30, 0,59 şi 0,11 reprezintă strălucirile relative la alb ale celor trei culori primare roşu, verde şi, respectiv, albastru). Această componentă mai este întâlnită şi sub numele de luminanţă. Componentele U şi V sunt cele care definesc nuanţa culorii, din acest motiv, sunt denumite componente de crominanţă. Acestea se calculează ca diferenţa dintre componenta roşie, respectiv albastră, şi cea de luminanţă. Avantajul reprezentării YUV este acela că separă componenta de luminanţă, pentru care ochiul este foarte sensibil la detalii, de componentele de nuanţă pentru care sensibilitatea este mai redusă. Acest lucru face posibilă reducerea informaţiei asociate unei imagini prin utilizarea unei rezoluţii mai reduse pentru componentele de crominanţă. În cazul televiziunii în culori se realizează o "compresie" prin limitarea benzii de frecvenţă alocate semnalelor de crominanţă (de exemplu în sistemul PAL semnalele U şi V au o bandă de 1,3MHz faţă de semnalul Y care are o bandă de 6MHz). În cazul standardului JPEG, componentele de crominanţă sunt subeşantionate cu un factor de 2 pe linii şi pe coloane (se reţine câte un singur pixel din doi, atât pe linii cât şi coloane). În concluzie, fiecare pixel este caracterizat de un triplet de trei valori numerice, fie ele componentele (R,G,B) sau (Y,U,V). Ca atare, imaginea întreagă este determinată de cele trei matrici corespunzătoare. Componenta R Componenta G 2
3 Componenta B Componenta Y Componenta U Componenta V Fig. 1. Componentele R, G, B, Y, U, V ale imaginii 1.a II.3 Abordări folosite în compresia de imagini În continuare se reiau câteva metode folosite în compresie, evidenţiind aplicabilitatea lor în compresia de imagini. Metodele generale de compresie de date: 1. Cuantizarea scalară poate fi folosită pentru a compresa imagini, dar performanţele ei sunt mediocre. De exemplu, o imagine cu 8 biţi/pixel poate fi compresată prin cuantizare scalară eliminând cei mai nesemnificativi patru biţi ai fiecărui pixel. Aceasta conduce la o rată de compresie de 0,5, care pe lângă faptul că nu este semnificativă, determină în acelaşi timp şi reducerea numărul de culori (sau nuanţe de gri) de la 256 la doar 16. O astfel de reducere nu numai ca descreşte pe ansamblu calitatea imaginii reconstruite, dar poate chiar crea benzi de diferite culori, un efect observabil şi deranjant. 2. Cuantizarea vectorială poate fi folosită cu mai mult succes pentru a compresa imagini. 3. Metodele statistice funcţionează mai bine când simbolurile ce trebuie compresate au probabilităţi diferite. O secvenţă de intrare în care mesajele au aceeaşi probabilitate nu se va compresa eficient. În acest sens, într-o imagine alb-negru sau color în tonuri continue, diferitele culori sau nuanţe de gri se dovedesc de multe ori a avea aproximativ aceleaşi probabilităţi. De aceea metodele statistice nu sunt o alegere bună pentru compresia unor astfel de imagini, şi sunt necesare noi abordări. Imaginile cu discontinuităţi de culoare, în care pixeli adiacenţi au culori foarte diferite, se compresează mai bine cu metodele statistice, dar în acest caz nu este uşoară predicţia pixelilor. 3
4 4. Metodele de compresie bazate pe dicţionar tind, de asemenea, să nu aibă succes în cazul imaginilor cu tonuri continue. O astfel de imagine conţine de obicei pixeli adiacenţi în culori similare, dar nu conţine modele repetitive. Chiar şi o imagine care conţine modele repetitive, cum sunt liniile verticale, le poate pierde când este digitizată. O linie verticală în imaginea originală poate deveni uşor oblică atunci când imaginea este digitizată. O linie verticală ideală este prezentată în Fig. 2a. În Fig. 2.b linia este presupusă a fi perfect digitizată în zece pixeli, aşezaţi vertical. Totuşi, dacă imaginea este plasată în digitizor uşor oblic, procesul de digitizare poate fi imperfect, şi pixelii rezultaţi pot arăta ca în Fig. 2.c. a) b) c) Fig. 2. Digitizare perfectă şi imperfectă. O altă problemă a compresiei imaginilor bazate pe dicţionar este aceea că astfel de metode scanează imaginea rând cu rând, şi pot pierde astfel corelaţii verticale între pixeli. Metodele tradiţionale sunt nesatisfăcătoare pentru compresia de imagini, astfel încât au fost necesare abordări noi, care, deşi diferite, se bazează pe eliminarea redundanţei din imagine, folosind următorul principiu: Principiul compresiei de imagine. Dacă se selectează aleator un pixel dintr-o imagine, există o probabilitate mare ca vecinii săi să aibă aceeaşi culoare sau culori foarte apropiate. Compresia de imagine este, deci, bazată pe faptul că pixelii învecinaţi sunt puternic corelaţi. Această corelare se numeşte şi redundanţă spaţială. II.4 Transformări folosite în compresia de imagini. DCT şi DST, Walsh- Hadamard, Haar, wavelet, KLT. Comparaţie. Transformări separabile O imagine poate fi compresată prin transformarea pixelilor săi (care sunt corelaţi) într-o reprezentare unde aceştia sunt decorelaţi. Compresia este obţinută dacă valorile noi sunt mai mici, în medie, decât cele originale. Compresia cu pierdere de informaţie poate fi obţinută prin cuantizarea valorilor transformate. Decodorul primeşte valorile transformate din secvenţa compresată şi reconstruieşte datele originale (exacte sau aproximate), prin aplicarea transformării inverse. Transformările discutate în această secţiune sunt ortogonale. Termenul de decorelare se referă la faptul că valorile transformate sunt independente unele de altele. Ca urmare, ele pot fi codate independent, ceea ce face mai simplă construirea unui model statistic. O imagine poate fi compresată, dacă reprezentarea sa are redundanţă. Redundanţa în imagini derivă din corelarea pixelilor. Dacă se transformă imaginea într-o reprezentare în care pixelii sunt decorelaţi, se elimină redundanţa şi imaginea a devenit în totalitate compresată. 4
5 Fig. 3. Rotirea unui grup de puncte (decorelare): noile coordonate au valori mai mici O transformare unidimensională discretă poate fi reprezentată printr-o matrice A. Coloanele acestei matrici sunt elementele bazei în care este reprezentat semnalul, iar aplicarea transformatei A înseamnă a găsi coeficienţii semnalului dacă îl descompunem în baza formată din coloanele matricii A. O transformare este ortogonală dacă şi numai dacă inversa matricii este totuna cu transpusa sa. Aplicarea unei transformate ortogonale unui semnal echivalează cu calcularea produsului între matricea transpusă A T şi semnal (vector coloană). Invers, matricea transformatei inverse este inversa matricii transformării iniţiale = Fig.4. Exemplu de transformare discretă O transformare ortogonală este echivalentă cu o rotire a sistemului de coordonate (a vectorilor bazei) în care este reprezentat semnalul. Transformări bidimensionale În cazul unei transformate unidimensionale, un semnal este reprezentat ca o sumă ponderată a unor semnale dintr-o bază (de ex. în spaţiu x = a i + b j + c k, baza fiind sistemul de coordonate (i,j,k), sau la Fourier semnalul este reprezentat ca o sumă de sinusoide). În cazul discret, elementele bazei sunt coloanele matricii transformării, A. Aplicarea transformării înseamnă găsirea coeficienţilor necesari elementelor bazei pentru ca suma lor ponderată să fie egală cu semnalul. În cazul unor transformări bidimensionale, o imagine 2D este descompusă ca o sumă ponderată de imagini 2D ce formează baza. Coeficienţii elementelor bazei sunt spectrul semnalului. O transformare este separabilă dacă transformarea bidimensională (pe imagini) este echivalentă cu aplicarea de două ori a unei transformate unidimensionale, întâi pe fiecare coloană, apoi pe fiecare linie a rezultatului (sau invers, întâi pe linii, apoi pe 5
6 coloane). Această proprietate (dacă există) reduce mult complexitatea calculului. În general, transformările prezentate în continuare sunt separabile. Utilitatea unei transformări În general, pixelii unei imagini au valori semnificative, situate în jurul unei valori medii. Cuantizarea acestor valori ar produce erori vizibile. Pentru ca erorile de cuantizare să fie cât mai neobservabile, ar fi de preferat ca majoritatea coeficienţilor obţinuţi după transformare să aibă valori apropiate de zero, altfel spus majoritatea informaţiei să fie concentrată doar în câţiva coeficienţi nenuli, restul fiind neglijabili. Această proprietate poartă numele de compactarea energiei. Exemple de transformări bidimensionale: 1. Transformarea Karhunen-Loève (KLT): elementele bazei sunt vectorii proprii ai setului de blocuri 8x8 în care este împărţită imaginea. KLT este transformarea cea mai bună din punct de vedere al compresiei (cel mai redus număr de coeficienţi nenuli). Din păcate, fiind compusă din vectorii proprii ai imaginii, este dependentă de imaginea în sine la decodare, când nu se cunoaşte imaginea, ci vrem să o aflăm, nu cunoaştem nici transformata. Ca atare, nu poate fi folosită în practică. 2. Transformarea Walsh-Hadamard (WHT): descompune o imagine într-o sumă ponderată a următoarelor elemente din bază (în exemplu, pentru imagini 4x4) Fig.5. Elementele bazei transformării Walsh-Hadamard Transformarea cosinus discretă (DCT) DCT unidimensională În practică se foloseşte DCT bi-dimensională, dar pentru uşurinţa înţelegerii se consideră mai întâi DCT uni-dimensională. Se consideră formele de undă w(f)=cos(fθ), pentru 0 θ π, cu frecvenţele f=0, 1,...,7, şi θ = π, π, π, π, π, π, π, π (10.26)
7 Fiecare formă de undă w(f) este eşantionată în opt puncte, pentru a forma un vector al bazei v f. Cei opt vectori rezultaţi v f, f=0, 1,...,7 (un total de 64 de numere) sunt prezentaţi în Tabelul 1. Aceştia reprezintă baza pentru DCT uni-dimensională. Tabelul 1. Vectorii rezultaţi prin eşantionarea formei de undă w(f) în punctele date de (10.26) θ 0,196 0,589 0,982 1,374 1,767 2,160 2,553 2,945 cos 0θ cos 1θ 0,981 0,831 0,556 0,195-0,195-0,556-0,831-0,981 cos 2θ 0,924 0,383-0,383-0,924-0,924-0,383 0,383 0,924 cos 3θ 0,831-0,195-0,981-0,556 0,556 0,981 0,195-0,831 cos 4θ 0,707-0,707-0,707 0,707 0,707-0,707-0,707 0,707 cos 5θ 0,556-0,981 0,195 0,831-0,831-0,195 0,981-0,556 cos 6θ 0,383-0,924 0,924 0,383-0,383 0,924-0,924 0,383 cos 7θ 0,195 0,556 0,831 0,981 0,981-0,831 0,556-0,195 Aceşti opt vectori v i sunt ortonormali (datorită alegerii particulare a celor opt puncte de eşantionare) şi pot fi organizaţi într-o matrice de transformare 8 8. Pentru că această matrice este ortonormală, ea este o matrice de rotaţie, deci, DCT unidimensională poate fi interpretă ca o rotaţie în opt dimensiuni. Cel mai simplu mod de a calcula DCT uni-dimensională, în practică, este cu relaţia 7 1 (2t + 1) f π G f = C f pt cos 2 t= 0 16 (10.27) unde 1, f = 0, C f = 2 1, f > 0, pentru f = 0,1,...,7. (10.28) Se începe cu un set de opt valori de date p t (pixeli, eşantioane de sunet, sau alte date) şi se obţine un set de opt coeficienţi DCT, G. Decodorul primeşte coeficienţii DCT în seturi de opt, şi aplică transformarea inversă DCT (IDCT) pentru a reconstrui valorile de date originale (tot în grupuri de câte opt). IDCT se calculează cu relaţia 7 1 (2t + 1) jπ pt = C jg j cos 2 j= 0 16, pentru t=0, 1,..., 7 (10.29) DCT bi-dimensională Din experienţă se ştie că pixelii unei imagini sunt corelaţi pe două dimensiuni, nu doar pe una (un pixel este corelat cu vecinii săi de la stânga şi de la dreapta, deasupra şi dedesubt). De aceea metodele de compresie a imaginii folosesc DCT bi-dimensională, dată de relaţia f 7
8 n 1 n 1 1 (2y + 1) jπ (2x + 1) iπ Gij = CiC j pxy cos cos, (10.30) 2n x= 0 y= 0 2n 2n pentru 0 i, j n-1. Imaginea este împărţită în blocuri de n n pixeli p xy (de obicei se foloseşte n=8), şi ecuaţia (10.30) este folosită pentru a obţine un bloc de 8 8 coeficienţi DCT, G, pentru fiecare bloc de pixeli. Dacă compresia este cu pierdere de informaţie, ij coeficienţii sunt cuantizaţi. Decodorul reconstruieşte un bloc de (aproximate sau precise) prin calculul IDCT. n 1 n 1 1 (2y + 1) jπ (2x + 1) iπ pxy = CiC jgij cos cos (10.31) 2n i= 0 j= 0 2n 2n unde 1, f = 0, C f = 2 pentru f = 0,1,...,7 1, f > 0, valori de date DCT bi-dimensională poate fi interpretată în două moduri diferite, ca o rotaţie (de fapt, două rotaţii separate), şi ca bază a unui spaţiu vectorial n-dimensional. În prima interpretare se consideră un bloc de n n pixeli. Mai întâi se consideră fiecare rând al acestui bloc ca un punct ( px,0 ; px,1 ;...; px, n 1) în spaţiul n-dimensional, şi se roteşte punctul cu ajutorul transformării date de suma din interior n 1 (2y + 1) jπ G1x, j = C j pxy cos y= 0 2n (10.32) a ecuaţiei (10.30). Aceasta transformare are ca rezultat un bloc G1 x,j de n n coeficienţi, unde primul element al fiecărui rând este dominant şi restul elementelor sunt mici. Suma exterioară a ecuaţiei (10.30) este n 1 1 (2x + 1) iπ Gij = C i G1x, j cos 2n x= 0 2n (10.33) Aici, coloanele lui G1 x,j sunt considerate puncte în spaţiul n-dimensional, şi sunt rotite. Rezultatul este un coeficient mare în colţul stânga-sus al blocului şi n 2-1 coeficienţi mici în rest. Această interpretare consideră DCT bi-dimensional ca două rotaţii separate, fiecare în n dimensiuni. Este interesant de observat că două rotaţii în n dimensiuni sunt mai rapide decât una în n 2 dimensiuni, deoarece în al doilea caz este necesară o matrice de rotaţie de dimensiune n 2 n 2. A două interpretare (presupunând n = 8) foloseşte ecuaţia (10.30) pentru a crea 64 blocuri de 8 8 valori fiecare. Cele 64 de blocuri sunt apoi folosite ca bază a unui spaţiu de vectori 64-dimensionali (sunt imagini de bază). Imaginile de bază folosite în DCT bidimensională sunt date în Fig.6. Orice bloc B de 8 8 pixeli poate fi exprimat ca o combinaţie liniară a imaginilor de bază, şi cele 64 de ponderi ale acestei combinaţii liniare sunt coeficienţii DCT ai blocului B. 8
9 Fig. 6. Imaginile de bază pentru transformata discretă cosinus bi-dimensinală Transformarea Discretă Sinus Transformarea discretă sinus, DST, este complementara DCT. DCT asigură performanţe apropiate transformatei K-L optime, în ceea ce priveşte compactarea, când corelaţia coeficienţilor ρ este mare, iar DST asigură performanţe apropiate transformatei K-L optime, când ρ este mic. Datorită acestei proprietăţi, este adesea folosită ca transformată complementară a DCT în codarea de imagini şi audio. Elementele matricei transformate pentru o DST de dimensiune n n sunt date de 2 π ( i + 1)( j + 1) [ S] = i, j sin ; i, j = 0,1,..., n 1 (10.34) n 2n Dezavantajul acestei transformări poate fi observat când se consideră exemplul a opt valori de date identice ce trebuie transformate. Astfel de valori sunt, desigur, perfect corelate. Când sunt reprezentate grafic ele devin o linie orizontală. Aplicând DCT acestor valori, se produce doar un coeficient DC; toţi coeficienţii AC fiind nuli. DCT compactează toată energia datelor într-un unic coeficient DC, a cărui valoare este identică cu a datelor. IDCT poate reconstrui exact cele opt valori (cu excepţia unor modificări minore date de precizia limitată de calcul). Aplicarea DST asupra aceloraşi opt valori, pe de altă parte, conduce la şapte coeficienţi AC a căror sumă este o formă de undă care trece prin cele opt puncte corespunzătoare datelor, dar oscilează între aceste puncte. Acest comportament, are trei dezavantaje, în principal: 1. Energia datelor originale nu este compactată; 2. Cei şapte coeficienţi nu sunt decorelaţi (pe când datele sunt perfect corelate); 3. Cuantizând cei şapte coeficienţi se poate ajunge la o puternică scădere a calităţii reconstrucţiei realizate de DST inversă Din aceste cauze, în practică se foloseşte transformarea DCT. 9
10 III. Standardul JPEG Formatul JPEG este recomandat pentru afişarea de imagini redate cu o foarte mare varietate de culori sau pentru imagini de precizie fotografică. JPEG foloseşte o tehnică de compresie variabilă, care are drept rezultat obţinerea de fişiere foarte mici în comparaţie cu alte formate. Există patru moduri principale de operare specificate de standardul JPEG : - modul de bază, în care fiecare componentă a imaginii este codată printr-o singură scanare stânga-dreapta, respectiv sus-jos; - codarea expandată DCT cu pierderi, în care se realizează o codare progresivă a spectrelor imaginii de intrare; - codarea fără pierderi, în care imaginea este codată astfel încât se garantează reproducerea exactă la decodare; - codarea ierarhică, în care imaginea este codată la rezoluţii multiple. În continuare, se va prezenta detaliat numai primul dintre acestea, celelalte numai principial III.1 Schema de principiu Fig. 7. Algoritmul de codare JPEG III.2 Codarea: etape 1. RGB YUV În procedurile de compresie a imaginii se preferă o reprezentare a culorii diferită de cea normală (R,G,B), şi anume, reprezentarea (Y,U,V), obţinută cu relaţiile (10.1). Valorile componentelor Y, U şi V sunt cuprinse între -128 şi 127. Datorită absenţei detaliilor şi contrastului scăzut al componentelor U şi V, acestora li se aplică o subeşantionare cu factorul 2 pe ambele direcţii, verticală şi orizontală, ţinându-se cont de faptul că percepţia ochiului este mai mică la semnalele de crominanţă, faţă de cele de luminanţă. Modul de realizare a subeşantionării constă în 10
11 înlocuirea blocurilor de 2x2 puncte cu un singur punct care are intensitatea egală cu media celor Blocuri 8x8 Procedura de compresie se aplică unor blocuri de imagine de 8x8 puncte. Dacă nici una din dimensiunile imaginii nu este multiplu de 8, codorul copie ultima coloană sau linie până când lungimea finală este multiplu de 8. Aceste linii sau coloane suplimentare sunt îndepărtate în timpul procesului de decodare. Cele trei componente Y, U' şi V' sunt descompuse în blocuri de dimensiune 8x8. Datorită rezoluţiei reduse, în urma subeşantionării, rezultă că la 4 (2x2) blocuri ale componentei Y corespunde câte un singur bloc al componentelor U', respectiv V'. În cazul formatului JPEG cele trei componente ale blocurilor de imagine sunt prelucrate întreţesut. Pentru o numerotare a blocurilor, conform Fig. 8, ordinea prelucrării acestora va fi Y1, Y2, Y3, Y4, U1, V1, Y5, Y6, Y7, Y8, U2, V2,... Fiecare bloc este prelucrat utilizând aceeaşi procedură. Fig. 8. Ordinea prelucrării blocurilor 3. Aplicare DCT Valorile originale ale componentelor Y, U, V sunt cuprinse în domeniul [0, 2 b-1 ], unde b reprezintă numărul de biţi/eşantion. Aceste valori sunt deplasate în domeniul [-2 b- 1,2 b-1-1], centrate faţă de zero, pentru a putea realiza o precizie de calcul mai mare la aplicarea DCT (Discrete Cosine Transform Transformata Cosinus Discretă). Pentru primul nivel de codare JPEG, b=8, astfel încât valorile originale cuprinse în intervalul [0, 255] sunt deplasate în intervalul [-128, 127]. Fiecare componentă este apoi divizată în blocuri de 8x8 pixeli, aşa cum se poate observa şi în Fig. 7. Fiecărui bloc astfel obţinut i se aplică transformata cosinus discretă bi-dimensională, folosind ecuaţiile: (2y + 1) jπ (2x + 1) iπ DCT: Gij = CiC j pxy cos cos (10.35) 4 x= 0 y= (2y + 1) jπ (2x + 1) iπ IDCT: pxy = CiC jgij cos cos (10.36) 4 i= 0 j= unde 1 Ci = C j =, dacă i = j = 0 2 C = C = 1, în rest i j 11
12 Tabelul 2. Exemplu de matrice 8x8 căreia i se aplică transformata DCT Tabelul 3. Transformata DCT a matricei 8x8 din Tabelul Se poate observa că elementele acestei matrice au valorile mari concentrate în colţul din stânga sus, restul fiind valori mici, aproape nule. Explicaţia acestui fenomen este dată de faptul că transformata cosinus discretă realizează o descompunere "în frecvenţă". Astfel, coeficienţii din colţul din stânga sus corespund frecvenţelor joase - variaţii lente de intensitate între pixeli, iar pe măsură ce se avansează către colţul din dreapta-jos coeficienţii corespund frecvenţelor înalte - variaţii rapide de intensitate, date de detaliile fine din imagine. În general, într-o imagine reală frecvenţele înalte au o pondere mai redusă decât cele joase, ceea ce explică valorile obţinute în urma transformării. 4. Cuantizare coeficienţi Operaţia de cuantizare este singura în care se pierde informaţie. Algoritmul JPEG utilizează coeficienţi de cuantizare pentru a cuantiza diferiţii coeficienţi de intrare. Mărimea pasului de cuantizare este organizată într-un tabel, numit tabel de cuantizare. Un exemplu de tabel de cuantizare din recomandările JPEG este prezentat în Tabelul 4. Fiecare valoare cuantizată este reprezentată de o etichetă. Prin cuantizare se întelege împărţirea element cu element a matricii G cu o matrice de cuantizare Q, cu reţinerea doar a părţii întregi, rezultând o matrice I. (a) Tabelul 4. Coeficienţii de cuantizare pentru luminanţă (a) şi pentru crominanţă (b)
13 (b) Eticheta corespunzătoare valorii cuantizate a coeficienţilor G ij ai transformatei este G ij Ii, j = + 0,5 t (10.36) Qij t unde Qij este elementul (i,j) din tabelul de cuantizare şi x este cel mai mare întreg mai mic decât x. Se consideră coeficientul G 00 din Tabelul 3, care este 39, 88. Din tabelul 4a, t Q 00 este 16, deci, 39,88 I00 = + 0,5 = 2,9925 = 2 16 (10.37) Valoarea reconstruită este obţinută din etichetă, prin multiplicarea acesteia cu intrarea corespunzătoare în tabelul de cuantizare. Deci, valoarea reconstruită a θ 00 va fi I Q adică 2*16=32. Eroarea de cuantizare în acest caz este 39, 88-32=7, 88. t Similar, din Tabelele 3 şi 4a, G 01 este 6, 56 şi t Q 01 este 11, deci 6,56 I01 = + 0,5 = 1,096 = 1 11 (10.38) Valoarea reconstruită este 11 şi eroarea de cuantizare este 11-6,56 = 4, Codarea coeficienţilor o DC Coeficienţii DC ai fiecărui bloc se codează diferenţial, adică se codează numai diferenţa faţă de coeficientul DC al blocului precedent. Codarea se face utilizând tabelul prezentat mai jos, în felul următor: 1. Se caută clasa din care face parte numărul (ex.: 9 clasa 4) 2. Se numără al câtâlea număr din clasă este, începând cu poziţia 0, nu 1! (ex.: 9 este al 9-lea număr din clasă, considerând -7, primul număr, ca fiind pe poziţia 0) 3. Codul = codul clasei urmat de poziţia numărului în clasă, în baza 2. (ex: codul lui 9 este ) 13
14 Tabelul 5. Codarea diferenţelor etichetelor DC Clasa Codul Huffman corespunzător clasei o AC Ordinea în care este parcursă matricea în vederea codificării coeficienţilor de tip AC se alege în aşa fel încât să se profite cât mai bine de distribuţia valorilor coeficienţilor. Se urmăreşte gruparea valorilor nule în şiruri cât mai lungi, deoarece acest fapt permite o codare mai eficientă (compresie maximă). Fig. 9. Parcurgerea în zig zag a matricei coeficienţilor cuantizaţi 14
15 Deoarece valorile diferite de zero sunt concentrate într-un colţ al matricei, o parcurgere de tipul linie cu linie nu este eficientă. De aceea se preferă o parcurgere în zigzag, ordinea de extragere a elementelor din matrice fiind prezentată în Fig. 9. Rezultă o înşiruire liniară coeficienţilor. În continuare, se asociază un cod combinaţiei dintre numărul de valori nule (dacă există) care precede un element diferit de zero şi valoarea acestuia din urmă. Practic se codifică perechi (Număr de zerouri, Z Valoare, x) în locul fiecărui coeficient în parte. În realitate, din considerente de reducere a numărului de combinaţii posibile, numărul de zerouri se limitează la 16. În cazul în care există mai mult de 16 elemente nule se emit coduri speciale (ZRL) care semnifică 16 zerouri care nu sunt urmate de un element diferit de zero. De exemplu, 18 zerouri urmate de un element cu valoarea -21 se vor coda printrun ZRL urmat de codul corespunzător perechii (2,-21). De asemenea, în cazul în care dintr-un anumit punct al şirului până la sfârşitul acestuia nu mai există nici un element diferit de zero, se emite un alt cod special (EOB) în locul tuturor valorilor nule rămase. În concluzie, pentru fiecare număr x, precedat de Z zerouri, care formează perechea (Z,x), codorul trebuie: - să găsească numărul de zerouri consecutive Z, care îl preced; - să determine linia i şi coloana C din Tabelul 5 corespunzătoare numărului; - să identifice din Tabelul 6, după numărul Z şi clasa i, codul Huffman corespunzător perechii; - la cuvântul de cod Huffman găsit se concatenează reprezentarea pe i biţi a coloanei C III.3 Decodarea Lanţul de decodare JPEG este parcurs în ordine inversă codării. Astfel, imaginea compresată JPEG este supusă în primul pas unui decodor entropic. După decodarea entropică, se aplică decuantizarea, folosind aceiaşi coeficienţi care au fost folosiţi şi la cuantizare, prezentaţi în Tabelele 4 a,b. În urma decuantizării se obţin coeficienţii transformatei cosinus discrete din Tabelul 7. Aceşti coeficienţi sunt trimişi blocului de transformare cosinus discretă inversă, IDCT, care aplică transformarea dată de relaţia Acestora li se adună 128 şi se obţine blocul reconstruit prezentat în Tabelul 8. Calitatea acestei imagini depinde de numărul de coeficienţi păstraţi la codare. Dacă se vor păstra toţi coeficienţii nenuli, atunci imaginea reconstruită va fi foarte asemănătoare cu originalul 15
16 Tabelul 6. Codarea coeficienţilor AC pentru luminanţă 16
17 IV. Desfăşurarea lucrării 1. Studiaţi programul Matlab ataşat lucrării 2. Studiaţi imaginile RGB şi YUV de la pag. 2 şi 3. În care imagine observaţi cele mai multe detalii? În care imagini nu se observă detaliile? Care dintre cele două reprezentări credeţi că este mai potrivită în vederea compresiei? 3. Utilizând programul Matlab Transformate.m, studiaţi diverse transformări bidimensionale pentru imaginile de test. Care dintre acestea conduce la cel mai mic număr de coeficienţi semnificativi? Care ar fi cea mai utilă pentru compresie? Unde se situează, cu precădere, coeficienţii dominanţi în transformata DCT? De ce se înşiruiesc în zig-zag coeficienţii DCT? 4. Utilizând programul Matlab ataşat, modificaţi valorile din tabela de cuantizare şi observaţi efectele asupra raportului de compresie. Când este compresia mai puternică? Ce se întâmplă cu calitatea imaginii în acest caz? 17
18 5. Cum arată imaginea în cazul în care cuantizarea este foarte puternică? Acest fenomen poartă numele de blocking, iar algoritmii care urmăresc reducerea vizibilităţii acestuia sunt algoritmi de de-blocking, Seminar: rezolvarea de exerciţii de codare a coeficienţilor DC şi AC cuantizaţi conform cu standardul JPEG. 18
Esalonul Redus pe Linii (ERL). Subspatii.
 Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
MARCAREA REZISTOARELOR
 1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
prin egalizarea histogramei
 Lucrarea 4 Îmbunătăţirea imaginilor prin egalizarea histogramei BREVIAR TEORETIC Tehnicile de îmbunătăţire a imaginilor bazate pe calculul histogramei modifică histograma astfel încât aceasta să aibă o
Lucrarea 4 Îmbunătăţirea imaginilor prin egalizarea histogramei BREVIAR TEORETIC Tehnicile de îmbunătăţire a imaginilor bazate pe calculul histogramei modifică histograma astfel încât aceasta să aibă o
Planul determinat de normală şi un punct Ecuaţia generală Plane paralele Unghi diedru Planul determinat de 3 puncte necoliniare
 1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
Metode iterative pentru probleme neliniare - contractii
 Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate.
 Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Metode de interpolare bazate pe diferenţe divizate
 Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM 1 electronica.geniu.ro
 Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Curs 14 Funcţii implicite. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi"
 Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Seminar 5 Analiza stabilității sistemelor liniare
 Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
(a) se numeşte derivata parţială a funcţiei f în raport cu variabila x i în punctul a.
 Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
5. FUNCŢII IMPLICITE. EXTREME CONDIŢIONATE.
 5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
Sisteme diferenţiale liniare de ordinul 1
 1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE
 DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
Curs 4 Serii de numere reale
 Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Subiecte Clasa a VIII-a
 Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor X) functia f 1
 Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Integrala nedefinită (primitive)
 nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor
 Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Definiţia generală Cazul 1. Elipsa şi hiperbola Cercul Cazul 2. Parabola Reprezentari parametrice ale conicelor Tangente la conice
 1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
R R, f ( x) = x 7x+ 6. Determinați distanța dintre punctele de. B=, unde x și y sunt numere reale.
 5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
III. Serii absolut convergente. Serii semiconvergente. ii) semiconvergentă dacă este convergentă iar seria modulelor divergentă.
 III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
Transformate pentru semnale multidimensionale
 Transformate pentru semnale multidimensionale Semnale 1D: s(t) Unele caracteristici ale semnalului pot fi ușor descrise în domeniul frecvență Transformata Fourier: s(t) S(ω) (sau s(t) S(f t )) unde t este
Transformate pentru semnale multidimensionale Semnale 1D: s(t) Unele caracteristici ale semnalului pot fi ușor descrise în domeniul frecvență Transformata Fourier: s(t) S(ω) (sau s(t) S(f t )) unde t este
Zgomotul se poate suprapune informaţiei utile în două moduri: g(x, y) = f(x, y) n(x, y) (6.2)
 Lucrarea 6 Zgomotul în imagini BREVIAR TEORETIC Zgomotul este un semnal aleator, care afectează informaţia utilă conţinută într-o imagine. El poate apare de-alungul unui lanţ de transmisiune, sau prin
Lucrarea 6 Zgomotul în imagini BREVIAR TEORETIC Zgomotul este un semnal aleator, care afectează informaţia utilă conţinută într-o imagine. El poate apare de-alungul unui lanţ de transmisiune, sau prin
Criptosisteme cu cheie publică III
 Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
1.7. AMPLIFICATOARE DE PUTERE ÎN CLASA A ŞI AB
 1.7. AMLFCATOARE DE UTERE ÎN CLASA A Ş AB 1.7.1 Amplificatoare în clasa A La amplificatoarele din clasa A, forma de undă a tensiunii de ieşire este aceeaşi ca a tensiunii de intrare, deci întreg semnalul
1.7. AMLFCATOARE DE UTERE ÎN CLASA A Ş AB 1.7.1 Amplificatoare în clasa A La amplificatoarele din clasa A, forma de undă a tensiunii de ieşire este aceeaşi ca a tensiunii de intrare, deci întreg semnalul
Curs 1 Şiruri de numere reale
 Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
a. 11 % b. 12 % c. 13 % d. 14 %
 1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
5.5. REZOLVAREA CIRCUITELOR CU TRANZISTOARE BIPOLARE
 5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
5.4. MULTIPLEXOARE A 0 A 1 A 2
 5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
III. Reprezentarea informaţiei în sistemele de calcul
 Metode Numerice Curs 3 III. Reprezentarea informaţiei în sistemele de calcul III.1. Reprezentarea internă a numerelor întregi III. 1.1. Reprezentarea internă a numerelor întregi fără semn (pozitive) Reprezentarea
Metode Numerice Curs 3 III. Reprezentarea informaţiei în sistemele de calcul III.1. Reprezentarea internă a numerelor întregi III. 1.1. Reprezentarea internă a numerelor întregi fără semn (pozitive) Reprezentarea
Seminariile Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reziduurilor
 Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Laborator 11. Mulţimi Julia. Temă
 Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Problema a II - a (10 puncte) Diferite circuite electrice
 Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
Aplicaţii ale principiului I al termodinamicii la gazul ideal
 Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
 4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].
![Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].](/thumbs/72/67648751.jpg) Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile
 Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Laborator 1: INTRODUCERE ÎN ALGORITMI. Întocmit de: Claudia Pârloagă. Îndrumător: Asist. Drd. Gabriel Danciu
 INTRODUCERE Laborator 1: ÎN ALGORITMI Întocmit de: Claudia Pârloagă Îndrumător: Asist. Drd. Gabriel Danciu I. NOŢIUNI TEORETICE A. Sortarea prin selecţie Date de intrare: un şir A, de date Date de ieşire:
INTRODUCERE Laborator 1: ÎN ALGORITMI Întocmit de: Claudia Pârloagă Îndrumător: Asist. Drd. Gabriel Danciu I. NOŢIUNI TEORETICE A. Sortarea prin selecţie Date de intrare: un şir A, de date Date de ieşire:
2.1 Sfera. (EGS) ecuaţie care poartă denumirea de ecuaţia generală asferei. (EGS) reprezintă osferă cu centrul în punctul. 2 + p 2
 .1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
.1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
a n (ζ z 0 ) n. n=1 se numeste partea principala iar seria a n (z z 0 ) n se numeste partea
 Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
4. CODAREA SEMNALELOR VIDEO
 4. CODAREA SEMNALELOR VIDEO 4.1. Semnale video - concepte de bază Proprietăţile sistemelor video se bazează pe proprietăţile de percepţie ale ochiului. Cel mai mic detaliu ce poate fi reprodus într-o imagine
4. CODAREA SEMNALELOR VIDEO 4.1. Semnale video - concepte de bază Proprietăţile sistemelor video se bazează pe proprietăţile de percepţie ale ochiului. Cel mai mic detaliu ce poate fi reprodus într-o imagine
2 Transformări liniare între spaţii finit dimensionale
 Transformări 1 Noţiunea de transformare liniară Proprietăţi. Operaţii Nucleul şi imagine Rangul şi defectul unei transformări 2 Matricea unei transformări Relaţia dintre rang şi defect Schimbarea matricei
Transformări 1 Noţiunea de transformare liniară Proprietăţi. Operaţii Nucleul şi imagine Rangul şi defectul unei transformări 2 Matricea unei transformări Relaţia dintre rang şi defect Schimbarea matricei
SERII NUMERICE. Definiţia 3.1. Fie (a n ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0
 SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
Asupra unei inegalităţi date la barajul OBMJ 2006
 Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
Spatii liniare. Exemple Subspaţiu liniar Acoperire (înfăşurătoare) liniară. Mulţime infinită liniar independentă
 Noţiunea de spaţiu liniar 1 Noţiunea de spaţiu liniar Exemple Subspaţiu liniar Acoperire (înfăşurătoare) liniară 2 Mulţime infinită liniar independentă 3 Schimbarea coordonatelor unui vector la o schimbare
Noţiunea de spaţiu liniar 1 Noţiunea de spaţiu liniar Exemple Subspaţiu liniar Acoperire (înfăşurătoare) liniară 2 Mulţime infinită liniar independentă 3 Schimbarea coordonatelor unui vector la o schimbare
4. CODAREA SEMNALELOR VIDEO
 4. CODAREA SEMNALELOR VIDEO 4.1. Semnale video - concepte de bază Proprietăţile sistemelor video se bazează pe proprietăţile de percepţie ale ochiului. Cel mai mic detaliu ce poate fi reprodus într-o imagine
4. CODAREA SEMNALELOR VIDEO 4.1. Semnale video - concepte de bază Proprietăţile sistemelor video se bazează pe proprietăţile de percepţie ale ochiului. Cel mai mic detaliu ce poate fi reprodus într-o imagine
COLEGIUL NATIONAL CONSTANTIN CARABELLA TARGOVISTE. CONCURSUL JUDETEAN DE MATEMATICA CEZAR IVANESCU Editia a VI-a 26 februarie 2005.
 SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
riptografie şi Securitate
 riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
1.3 Baza a unui spaţiu vectorial. Dimensiune
 .3 Baza a unui spaţiu vectorial. Dimensiune Definiţia.3. Se numeşte bază a spaţiului vectorial V o familie de vectori B care îndeplineşte condiţiile de mai jos: a) B este liniar independentă; b) B este
.3 Baza a unui spaţiu vectorial. Dimensiune Definiţia.3. Se numeşte bază a spaţiului vectorial V o familie de vectori B care îndeplineşte condiţiile de mai jos: a) B este liniar independentă; b) B este
2. Sisteme de forţe concurente...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...3
 SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
Analiza și Prelucrarea Digitală a Semnalelor Video
 Analiza și Prelucrarea Digitală a Semnalelor Video Conf. dr. ing. Radu Ovidiu Preda radu@comm.pub.ro Ș.l. dr. ing. Ionuţ Pirnog ionut@comm.pub.ro Site disciplină: www.comm.pub.ro/preda/apdsv Analiza și
Analiza și Prelucrarea Digitală a Semnalelor Video Conf. dr. ing. Radu Ovidiu Preda radu@comm.pub.ro Ș.l. dr. ing. Ionuţ Pirnog ionut@comm.pub.ro Site disciplină: www.comm.pub.ro/preda/apdsv Analiza și
Conice. Lect. dr. Constantin-Cosmin Todea. U.T. Cluj-Napoca
 Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
Componente şi Circuite Electronice Pasive. Laborator 4. Măsurarea parametrilor mărimilor electrice
 Laborator 4 Măsurarea parametrilor mărimilor electrice Obiective: o Semnalul sinusoidal, o Semnalul dreptunghiular, o Semnalul triunghiular, o Generarea diferitelor semnale folosind placa multifuncţională
Laborator 4 Măsurarea parametrilor mărimilor electrice Obiective: o Semnalul sinusoidal, o Semnalul dreptunghiular, o Semnalul triunghiular, o Generarea diferitelor semnale folosind placa multifuncţională
SEMINAR 14. Funcţii de mai multe variabile (continuare) ( = 1 z(x,y) x = 0. x = f. x + f. y = f. = x. = 1 y. y = x ( y = = 0
 Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
IV. CUADRIPOLI SI FILTRE ELECTRICE CAP. 13. CUADRIPOLI ELECTRICI
 V. POL S FLTE ELETE P. 3. POL ELET reviar a) Forma fundamentala a ecuatiilor cuadripolilor si parametrii fundamentali: Prima forma fundamentala: doua forma fundamentala: b) Parametrii fundamentali au urmatoarele
V. POL S FLTE ELETE P. 3. POL ELET reviar a) Forma fundamentala a ecuatiilor cuadripolilor si parametrii fundamentali: Prima forma fundamentala: doua forma fundamentala: b) Parametrii fundamentali au urmatoarele
Teme de implementare in Matlab pentru Laboratorul de Metode Numerice
 Teme de implementare in Matlab pentru Laboratorul de Metode Numerice As. Ruxandra Barbulescu Septembrie 2017 Orice nelamurire asupra enunturilor/implementarilor se rezolva in cadrul laboratorului de MN,
Teme de implementare in Matlab pentru Laboratorul de Metode Numerice As. Ruxandra Barbulescu Septembrie 2017 Orice nelamurire asupra enunturilor/implementarilor se rezolva in cadrul laboratorului de MN,
 10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
Examen AG. Student:... Grupa: ianuarie 2016
 16-17 ianuarie 2016 Problema 1. Se consideră graful G = pk n (p, n N, p 2, n 3). Unul din vârfurile lui G se uneşte cu câte un vârf din fiecare graf complet care nu-l conţine, obţinându-se un graf conex
16-17 ianuarie 2016 Problema 1. Se consideră graful G = pk n (p, n N, p 2, n 3). Unul din vârfurile lui G se uneşte cu câte un vârf din fiecare graf complet care nu-l conţine, obţinându-se un graf conex
prin operaţii punctuale
 Lucrarea 3 Îmbunătăţirea imaginilor prin operaţii punctuale BREVIAR TEORETIC Termenul general de îmbunătăţire a imaginilor se referă la o clasă largă de operaţii, ce au ca scop mărirea detectabilităţii
Lucrarea 3 Îmbunătăţirea imaginilor prin operaţii punctuale BREVIAR TEORETIC Termenul general de îmbunătăţire a imaginilor se referă la o clasă largă de operaţii, ce au ca scop mărirea detectabilităţii
Algebra si Geometrie Seminar 9
 Algebra si Geometrie Seminar 9 Decembrie 017 ii Equations are just the boring part of mathematics. I attempt to see things in terms of geometry. Stephen Hawking 9 Dreapta si planul in spatiu 1 Notiuni
Algebra si Geometrie Seminar 9 Decembrie 017 ii Equations are just the boring part of mathematics. I attempt to see things in terms of geometry. Stephen Hawking 9 Dreapta si planul in spatiu 1 Notiuni
2. Circuite logice 2.4. Decodoare. Multiplexoare. Copyright Paul GASNER
 2. Circuite logice 2.4. Decodoare. Multiplexoare Copyright Paul GASNER Definiţii Un decodor pe n bits are n intrări şi 2 n ieşiri; cele n intrări reprezintă un număr binar care determină în mod unic care
2. Circuite logice 2.4. Decodoare. Multiplexoare Copyright Paul GASNER Definiţii Un decodor pe n bits are n intrări şi 2 n ieşiri; cele n intrări reprezintă un număr binar care determină în mod unic care
Subiecte Clasa a VII-a
 lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
4. Măsurarea tensiunilor şi a curenţilor electrici. Voltmetre electronice analogice
 4. Măsurarea tensiunilor şi a curenţilor electrici oltmetre electronice analogice oltmetre de curent continuu Ampl.c.c. x FTJ Protectie Atenuator calibrat Atenuatorul calibrat divizor rezistiv R in const.
4. Măsurarea tensiunilor şi a curenţilor electrici oltmetre electronice analogice oltmetre de curent continuu Ampl.c.c. x FTJ Protectie Atenuator calibrat Atenuatorul calibrat divizor rezistiv R in const.
RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii transversale, scrisă faţă de una dintre axele de inerţie principale:,
 REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
Să se arate că n este număr par. Dan Nedeianu
 Primul test de selecție pentru juniori I. Să se determine numerele prime p, q, r cu proprietatea că 1 p + 1 q + 1 r 1. Fie ABCD un patrulater convex cu m( BCD) = 10, m( CBA) = 45, m( CBD) = 15 și m( CAB)
Primul test de selecție pentru juniori I. Să se determine numerele prime p, q, r cu proprietatea că 1 p + 1 q + 1 r 1. Fie ABCD un patrulater convex cu m( BCD) = 10, m( CBA) = 45, m( CBD) = 15 și m( CAB)
1.4 Schimbarea bazei unui spaţiu vectorial
 Algebră liniară, geometrie analitică şi diferenţială. Schimbarea bazei unui spaţiu vectorial După cum s-a văzut deja, într-un spaţiu vectorial V avem mai multe baze, iar un vector x V va avea câte un sistem
Algebră liniară, geometrie analitică şi diferenţială. Schimbarea bazei unui spaţiu vectorial După cum s-a văzut deja, într-un spaţiu vectorial V avem mai multe baze, iar un vector x V va avea câte un sistem
3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...4
 SEMINAR 3 MMENTUL FRŢEI ÎN RAPRT CU UN PUNCT CUPRINS 3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere...1 3.1. Aspecte teoretice...2 3.2. Aplicaţii rezolvate...4 3. Momentul forţei
SEMINAR 3 MMENTUL FRŢEI ÎN RAPRT CU UN PUNCT CUPRINS 3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere...1 3.1. Aspecte teoretice...2 3.2. Aplicaţii rezolvate...4 3. Momentul forţei
Metode Runge-Kutta. 18 ianuarie Probleme scalare, pas constant. Dorim să aproximăm soluţia problemei Cauchy
 Metode Runge-Kutta Radu T. Trîmbiţaş 8 ianuarie 7 Probleme scalare, pas constant Dorim să aproximăm soluţia problemei Cauchy y (t) = f(t, y), a t b, y(a) = α. pe o grilă uniformă de (N + )-puncte din [a,
Metode Runge-Kutta Radu T. Trîmbiţaş 8 ianuarie 7 Probleme scalare, pas constant Dorim să aproximăm soluţia problemei Cauchy y (t) = f(t, y), a t b, y(a) = α. pe o grilă uniformă de (N + )-puncte din [a,
Subiecte Clasa a V-a
 (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul numarului intrebarii
(40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul numarului intrebarii
2. Circuite logice 2.5. Sumatoare şi multiplicatoare. Copyright Paul GASNER
 2. Circuite logice 2.5. Sumatoare şi multiplicatoare Copyright Paul GASNER Adunarea în sistemul binar Adunarea se poate efectua în mod identic ca la adunarea obişnuită cu cifre arabe în sistemul zecimal
2. Circuite logice 2.5. Sumatoare şi multiplicatoare Copyright Paul GASNER Adunarea în sistemul binar Adunarea se poate efectua în mod identic ca la adunarea obişnuită cu cifre arabe în sistemul zecimal
Captura imaginilor. este necesară o sursă de lumină (λ: lungimea de undă a sursei)
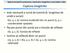 Captura imaginilor este necesară o sursă de lumină (λ: lungimea de undă a sursei) E(x, y, z, λ): lumina incidentă într-un punct (x, y, z coordonatele spațiale) fiecare punct din scenă are o funcție de
Captura imaginilor este necesară o sursă de lumină (λ: lungimea de undă a sursei) E(x, y, z, λ): lumina incidentă într-un punct (x, y, z coordonatele spațiale) fiecare punct din scenă are o funcție de
2. CONDENSATOARE 2.1. GENERALITĂŢI PRIVIND CONDENSATOARELE DEFINIŢIE UNITĂŢI DE MĂSURĂ PARAMETRII ELECTRICI SPECIFICI CONDENSATOARELOR SIMBOLURILE
 2. CONDENSATOARE 2.1. GENERALITĂŢI PRIVIND CONDENSATOARELE DEFINIŢIE UNITĂŢI DE MĂSURĂ PARAMETRII ELECTRICI SPECIFICI CONDENSATOARELOR SIMBOLURILE CONDENSATOARELOR 2.2. MARCAREA CONDENSATOARELOR MARCARE
2. CONDENSATOARE 2.1. GENERALITĂŢI PRIVIND CONDENSATOARELE DEFINIŢIE UNITĂŢI DE MĂSURĂ PARAMETRII ELECTRICI SPECIFICI CONDENSATOARELOR SIMBOLURILE CONDENSATOARELOR 2.2. MARCAREA CONDENSATOARELOR MARCARE
CURS XI XII SINTEZĂ. 1 Algebra vectorială a vectorilor liberi
 Lect. dr. Facultatea de Electronică, Telecomunicaţii şi Tehnologia Informaţiei Algebră, Semestrul I, Lector dr. Lucian MATICIUC http://math.etti.tuiasi.ro/maticiuc/ CURS XI XII SINTEZĂ 1 Algebra vectorială
Lect. dr. Facultatea de Electronică, Telecomunicaţii şi Tehnologia Informaţiei Algebră, Semestrul I, Lector dr. Lucian MATICIUC http://math.etti.tuiasi.ro/maticiuc/ CURS XI XII SINTEZĂ 1 Algebra vectorială
Ovidiu Gabriel Avădănei, Florin Mihai Tufescu,
 vidiu Gabriel Avădănei, Florin Mihai Tufescu, Capitolul 6 Amplificatoare operaţionale 58. Să se calculeze coeficientul de amplificare în tensiune pentru amplficatorul inversor din fig.58, pentru care se
vidiu Gabriel Avădănei, Florin Mihai Tufescu, Capitolul 6 Amplificatoare operaţionale 58. Să se calculeze coeficientul de amplificare în tensiune pentru amplficatorul inversor din fig.58, pentru care se
Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R. 4.1 Proprietăţi topologice ale lui R Puncte de acumulare
 Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R În cele ce urmează, vom studia unele proprietăţi ale mulţimilor din R. Astfel, vom caracteriza locul" unui punct în cadrul unei mulţimi (în limba
Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R În cele ce urmează, vom studia unele proprietăţi ale mulţimilor din R. Astfel, vom caracteriza locul" unui punct în cadrul unei mulţimi (în limba
Lectia VI Structura de spatiu an E 3. Dreapta si planul ca subspatii ane
 Subspatii ane Lectia VI Structura de spatiu an E 3. Dreapta si planul ca subspatii ane Oana Constantinescu Oana Constantinescu Lectia VI Subspatii ane Table of Contents 1 Structura de spatiu an E 3 2 Subspatii
Subspatii ane Lectia VI Structura de spatiu an E 3. Dreapta si planul ca subspatii ane Oana Constantinescu Oana Constantinescu Lectia VI Subspatii ane Table of Contents 1 Structura de spatiu an E 3 2 Subspatii
Curs 2 DIODE. CIRCUITE DR
 Curs 2 OE. CRCUTE R E CUPRN tructură. imbol Relația curent-tensiune Regimuri de funcționare Punct static de funcționare Parametrii diodei Modelul cu cădere de tensiune constantă Analiza circuitelor cu
Curs 2 OE. CRCUTE R E CUPRN tructură. imbol Relația curent-tensiune Regimuri de funcționare Punct static de funcționare Parametrii diodei Modelul cu cădere de tensiune constantă Analiza circuitelor cu
Toate subiectele sunt obligatorii. Timpul de lucru efectiv este de 3 ore. Se acordă din oficiu 10 puncte. SUBIECTUL I.
 Modelul 4 Se acordă din oficiu puncte.. Fie numărul complex z = i. Calculaţi (z ) 25. 2. Dacă x şi x 2 sunt rădăcinile ecuaţiei x 2 9x+8 =, atunci să se calculeze x2 +x2 2 x x 2. 3. Rezolvaţi în mulţimea
Modelul 4 Se acordă din oficiu puncte.. Fie numărul complex z = i. Calculaţi (z ) 25. 2. Dacă x şi x 2 sunt rădăcinile ecuaţiei x 2 9x+8 =, atunci să se calculeze x2 +x2 2 x x 2. 3. Rezolvaţi în mulţimea
Tratarea numerică a semnalelor
 LUCRAREA 5 Tratarea numerică a semnalelor Filtre numerice cu răspuns finit la impuls (filtre RFI) Filtrele numerice sunt sisteme discrete liniare invariante în timp care au rolul de a modifica spectrul
LUCRAREA 5 Tratarea numerică a semnalelor Filtre numerice cu răspuns finit la impuls (filtre RFI) Filtrele numerice sunt sisteme discrete liniare invariante în timp care au rolul de a modifica spectrul
Matrice. Determinanti. Sisteme liniare
 Matrice 1 Matrice Adunarea matricelor Înmulţirea cu scalar. Produsul 2 Proprietăţi ale determinanţilor Rangul unei matrice 3 neomogene omogene Metoda lui Gauss (Metoda eliminării) Notiunea de matrice Matrice
Matrice 1 Matrice Adunarea matricelor Înmulţirea cu scalar. Produsul 2 Proprietăţi ale determinanţilor Rangul unei matrice 3 neomogene omogene Metoda lui Gauss (Metoda eliminării) Notiunea de matrice Matrice
Capitolul 11 COMPRESIA DE IMAGINI 11.1 INTRODUCERE
 Capitolul COMPRESIA DE IMAGINI. INTRODUCERE Domeniul compresiei (codării) de imagini este legat de minimizarea numărului de biţi necesari pentru a reface o imagine, cu aplicaţii în special în transmisia
Capitolul COMPRESIA DE IMAGINI. INTRODUCERE Domeniul compresiei (codării) de imagini este legat de minimizarea numărului de biţi necesari pentru a reface o imagine, cu aplicaţii în special în transmisia
Erori si incertitudini de măsurare. Modele matematice Instrument: proiectare, fabricaţie, Interacţiune măsurand instrument:
 Erori i incertitudini de măurare Sure: Modele matematice Intrument: proiectare, fabricaţie, Interacţiune măurandintrument: (tranfer informaţie tranfer energie) Influente externe: temperatura, preiune,
Erori i incertitudini de măurare Sure: Modele matematice Intrument: proiectare, fabricaţie, Interacţiune măurandintrument: (tranfer informaţie tranfer energie) Influente externe: temperatura, preiune,
Seminar Algebra. det(a λi 3 ) = 0
 Rezolvari ale unor probleme propuse "Matematica const în a dovedi ceea ce este evident în cel mai puµin evident mod." George Polya P/Seminar Valori si vectori proprii : Solutie: ( ) a) A = Valorile proprii:
Rezolvari ale unor probleme propuse "Matematica const în a dovedi ceea ce este evident în cel mai puµin evident mod." George Polya P/Seminar Valori si vectori proprii : Solutie: ( ) a) A = Valorile proprii:
Transformări de frecvenţă
 Lucrarea 22 Tranformări de frecvenţă Scopul lucrării: prezentarea metodei de inteză bazate pe utilizarea tranformărilor de frecvenţă şi exemplificarea aceteia cu ajutorul unui filtru trece-jo de tip Sallen-Key.
Lucrarea 22 Tranformări de frecvenţă Scopul lucrării: prezentarea metodei de inteză bazate pe utilizarea tranformărilor de frecvenţă şi exemplificarea aceteia cu ajutorul unui filtru trece-jo de tip Sallen-Key.
Ecuatii trigonometrice
 Ecuatii trigonometrice Ecuatiile ce contin necunoscute sub semnul functiilor trigonometrice se numesc ecuatii trigonometrice. Cele mai simple ecuatii trigonometrice sunt ecuatiile de tipul sin x = a, cos
Ecuatii trigonometrice Ecuatiile ce contin necunoscute sub semnul functiilor trigonometrice se numesc ecuatii trigonometrice. Cele mai simple ecuatii trigonometrice sunt ecuatiile de tipul sin x = a, cos
Seminar 3. Problema 1. a) Reprezentaţi spectrul de amplitudini şi faze pentru semnalul din figură.
 Seminar 3 Problema 1. a) Reprezentaţi spectrul de amplitudini şi faze pentru semnalul din figură. b) Folosind X ( ω ), determinaţi coeficienţii dezvoltării SFE pentru semnalul () = ( ) xt t x t kt şi reprezentaţi
Seminar 3 Problema 1. a) Reprezentaţi spectrul de amplitudini şi faze pentru semnalul din figură. b) Folosind X ( ω ), determinaţi coeficienţii dezvoltării SFE pentru semnalul () = ( ) xt t x t kt şi reprezentaţi
10 REPREZENTAREA DIGITALĂ
 10 REPREZENTAREA DIGITALĂ 10.1 Niveluri logice În reprezentarea digitală pentru exprimarea cantitativă a informaţiei se folosesc semnale electrice care pot avea doar două niveluri de tensiune: un nivel
10 REPREZENTAREA DIGITALĂ 10.1 Niveluri logice În reprezentarea digitală pentru exprimarea cantitativă a informaţiei se folosesc semnale electrice care pot avea doar două niveluri de tensiune: un nivel
Sisteme liniare - metode directe
 Sisteme liniare - metode directe Radu T. Trîmbiţaş 27 martie 2016 1 Eliminare gaussiană Să considerăm sistemul liniar cu n ecuaţii şi n necunoscute Ax = b, (1) unde A K n n, b K n 1 sunt date, iar x K
Sisteme liniare - metode directe Radu T. Trîmbiţaş 27 martie 2016 1 Eliminare gaussiană Să considerăm sistemul liniar cu n ecuaţii şi n necunoscute Ax = b, (1) unde A K n n, b K n 1 sunt date, iar x K
Lab06: Extragerea trăsăturilor şi selecţia trăsăturilor. Aplicaţie pentru recunoaşterea obiectelor bazată pe formă.
 Lab06: Extragerea trăsăturilor şi selecţia trăsăturilor Aplicaţie pentru recunoaşterea obiectelor bazată pe formă. Aplicație practică a extragerii şi selecţiei trăsăturilor Recunoaşterea celor 4 forme
Lab06: Extragerea trăsăturilor şi selecţia trăsăturilor Aplicaţie pentru recunoaşterea obiectelor bazată pe formă. Aplicație practică a extragerii şi selecţiei trăsăturilor Recunoaşterea celor 4 forme
Vectori liberi Produs scalar Produs vectorial Produsul mixt. 1 Vectori liberi. 2 Produs scalar. 3 Produs vectorial. 4 Produsul mixt.
 liberi 1 liberi 2 3 4 Segment orientat liberi Fie S spaţiul geometric tridimensional cu axiomele lui Euclid. Orice pereche de puncte din S, notată (A, B) se numeşte segment orientat. Dacă A B, atunci direcţia
liberi 1 liberi 2 3 4 Segment orientat liberi Fie S spaţiul geometric tridimensional cu axiomele lui Euclid. Orice pereche de puncte din S, notată (A, B) se numeşte segment orientat. Dacă A B, atunci direcţia
V O. = v I v stabilizator
 Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Seria Balmer. Determinarea constantei lui Rydberg
 Seria Balmer. Determinarea constantei lui Rydberg Obiectivele lucrarii analiza spectrului in vizibil emis de atomii de hidrogen si determinarea lungimii de unda a liniilor serie Balmer; determinarea constantei
Seria Balmer. Determinarea constantei lui Rydberg Obiectivele lucrarii analiza spectrului in vizibil emis de atomii de hidrogen si determinarea lungimii de unda a liniilor serie Balmer; determinarea constantei
Componente şi Circuite Electronice Pasive. Laborator 3. Divizorul de tensiune. Divizorul de curent
 Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
Tranzistoare bipolare şi cu efect de câmp
 apitolul 3 apitolul 3 26. Pentru circuitul de polarizare din fig. 26 se cunosc: = 5, = 5, = 2KΩ, = 5KΩ, iar pentru tranzistor se cunosc următorii parametrii: β = 200, 0 = 0, μa, = 0,6. a) ă se determine
apitolul 3 apitolul 3 26. Pentru circuitul de polarizare din fig. 26 se cunosc: = 5, = 5, = 2KΩ, = 5KΩ, iar pentru tranzistor se cunosc următorii parametrii: β = 200, 0 = 0, μa, = 0,6. a) ă se determine
Lucrare. Varianta aprilie I 1 Definiţi noţiunile de număr prim şi număr ireductibil. Soluţie. Vezi Curs 6 Definiţiile 1 şi 2. sau p b.
 Lucrare Soluţii 28 aprilie 2015 Varianta 1 I 1 Definiţi noţiunile de număr prim şi număr ireductibil. Soluţie. Vezi Curs 6 Definiţiile 1 şi 2 Definiţie. Numărul întreg p se numeşte număr prim dacă p 0,
Lucrare Soluţii 28 aprilie 2015 Varianta 1 I 1 Definiţi noţiunile de număr prim şi număr ireductibil. Soluţie. Vezi Curs 6 Definiţiile 1 şi 2 Definiţie. Numărul întreg p se numeşte număr prim dacă p 0,
Profesor Blaga Mirela-Gabriela DREAPTA
 DREAPTA Fie punctele A ( xa, ya ), B ( xb, yb ), C ( xc, yc ) şi D ( xd, yd ) în planul xoy. 1)Distanţa AB = (x x ) + (y y ) Ex. Fie punctele A( 1, -3) şi B( -2, 5). Calculaţi distanţa AB. AB = ( 2 1)
DREAPTA Fie punctele A ( xa, ya ), B ( xb, yb ), C ( xc, yc ) şi D ( xd, yd ) în planul xoy. 1)Distanţa AB = (x x ) + (y y ) Ex. Fie punctele A( 1, -3) şi B( -2, 5). Calculaţi distanţa AB. AB = ( 2 1)
Cum folosim cazuri particulare în rezolvarea unor probleme
 Cum folosim cazuri particulare în rezolvarea unor probleme GHEORGHE ECKSTEIN 1 Atunci când întâlnim o problemă pe care nu ştim s-o abordăm, adesea este bine să considerăm cazuri particulare ale acesteia.
Cum folosim cazuri particulare în rezolvarea unor probleme GHEORGHE ECKSTEIN 1 Atunci când întâlnim o problemă pe care nu ştim s-o abordăm, adesea este bine să considerăm cazuri particulare ale acesteia.
Exemple de probleme rezolvate pentru cursurile DEEA Tranzistoare bipolare cu joncţiuni
 Problema 1. Se dă circuitul de mai jos pentru care se cunosc: VCC10[V], 470[kΩ], RC2,7[kΩ]. Tranzistorul bipolar cu joncţiuni (TBJ) este de tipul BC170 şi are parametrii β100 şi VBE0,6[V]. 1. să se determine
Problema 1. Se dă circuitul de mai jos pentru care se cunosc: VCC10[V], 470[kΩ], RC2,7[kΩ]. Tranzistorul bipolar cu joncţiuni (TBJ) este de tipul BC170 şi are parametrii β100 şi VBE0,6[V]. 1. să se determine
Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25
 Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25 LAGĂRELE CU ALUNECARE!" 25.1.Caracteristici.Părţi componente.materiale.!" 25.2.Funcţionarea lagărelor cu alunecare.! 25.1.Caracteristici.Părţi componente.materiale.
Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25 LAGĂRELE CU ALUNECARE!" 25.1.Caracteristici.Părţi componente.materiale.!" 25.2.Funcţionarea lagărelor cu alunecare.! 25.1.Caracteristici.Părţi componente.materiale.
