και των πλευρών του,,, 1 αντίστοιχα τέτοια, ώστε. 3 Να αποδείξετε ότι: α) / / / /. (Μονάδες 10)
|
|
|
- Ερμόλαος Κομνηνός
- 9 χρόνια πριν
- Προβολές:
Transcript
1 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ 04 ΓΕΩΜΕΤΡΙΑ Β ΛΥΚΕΙΟΥ ΤΑΞΙΝΟΜΗΣΗ ΘΕΜΑΤΩΝ ΑΝΑ ΕΝΟΤΗΤΑ ΘΕΩΡΗΜΑ ΘΑΛΗ ΘΕΜΑ ο ΘΕΜΑ Δίνεται τρίγωνο ABΓ με AB=9, AΓ=5. Από το βαρύκεντρο φέρνουμε ευθεία παράλληλη στην πλευρά BΓ που τέμνει τις AB,AΓ στα Δ,E αντίστοιχα. α) Να αποδείξετε ότι AΔ = AB και AE =. (Μονάδες 5) EΓ β) Να υπολογίσετε τα μήκη των τμημάτων AΔ, ΓE. (Μονάδες 0) ΘΕΜΑ -904 Στο τρίγωνο του παρακάτω σχήματος, το τμήμα είναι παράλληλο στην πλευρά του τριγώνου. Από το σημείο φέρουμε την παράλληλη προς τη η οποία τέμνει την στο σημείο. Να αποδείξετε ότι: α) Α (Μονάδες 0) β) (Μονάδες 0) γ) Ζ (Μονάδες 5) Δ Ε Β Γ ΘΕΜΑ -906 Δίνεται τρίγωνο και τυχαίο σημείο στην πλευρά. Φέρνουμε από το σημείο παράλληλες στις πλευρές και που τέμνουν αντίστοιχα τις πλευρές και στα σημεία και. Να αποδείξετε ότι: E B α) (Μονάδες 0) A B β) (Μονάδες 0) γ) (Μονάδες 5) ΘΕΜΑ -90 Δίνεται κυρτό τετράπλευρο και τα σημεία,, και των πλευρών του,,, αντίστοιχα τέτοια, ώστε. Να αποδείξετε ότι: α) / / / /. (Μονάδες 0) β) (Μονάδες 0) γ) το παραλληλόγραμμο. (Μονάδες 5) Επιμέλεια: xr.tsif@gmail.com Σελίδα
2 ΘΕΜΑ -905 Δίνεται τρίγωνο και τα σημεία και των πλευρών και αντίστοιχα ώστε. Από το σημείο φέρνουμε παράλληλη προς την, η οποία τέμνει την στο σημείο. Να αποδείξετε ότι : α) Τα τρίγωνα και είναι όμοια. (Μονάδες 0) β). (Μονάδες 5) ΘΕΜΑ -906 Οι διαγώνιοι του τραπεζίου ( // ) με τέμνονται στο. Η παράλληλη από το προς την τέμνει την στο. Αν, 9 και 6, να αποδείξετε ότι: α) 7. (Μονάδες ) β) 4. (Μονάδες ) Α Β Ο Μ Δ Γ ΘΕΜΑ 4-4 ΘΕΜΑ 4ο Δύο οχήματα κινούμενα με σταθερές ταχύτητες υ και υ, περνούν ταυτόχρονα τη χρονική στιγμή t 0 = 0 από τα σημεία Α και Β αντίστοιχα και συναντιούνται στο σημείο Γ όπως φαίνεται στο σχήμα. (Δίνεται ότι η ταχύτητα ενός σώματος που κινείται με σταθερή ταχύτητα είναι ίση με το διάστημα που κινήθηκε προς τον αντίστοιχο χρόνο.) Επιμέλεια: xr.tsif@gmail.com Σελίδα
3 α) Μετά από χρόνο t το όχημα που περνά από το σημείο Α βρίσκεται στο σημείο Δ της διαδρομής ΑΓ ενώ το όχημα που περνά από το σημείο Β βρίσκεται στο σημείο Ε της διαδρομής ΒΓ. Να αποδείξετε ότι ΔΕ//ΑΒ. (Μονάδες ) β) Έστω Ζ σημείο της διαδρομής ΑΓ και Η σημείο της διαδρομής ΒΓ. Αν ΖΗ//ΑΒ, να αποδείξετε ότι τα οχήματα περνούν ταυτόχρονα από τις θέσεις Ζ και Η. (Μονάδες ) ΘΕΜΑ -90 ΘΕΩΡΗΜΑ ΔΙΧΟΤΟΜΩΝ ΘΕΜΑ ο Στο κυρτό τετράπλευρο του παρακάτω σχήματος, η διχοτόμος της γωνίας είναι παράλληλη στην πλευρά και τέμνει τη στο και τη στο. Αν, 8, 9 και 6, να αποδείξετε ότι: α) 6 (Μονάδες ) β) 9 (Μονάδες ) ΘΕΜΑ Δίνεται τρίγωνο ( ) και, η εσωτερική και η εξωτερική διχοτόμος του αντίστοιχα. Αν είναι 6,, 5 και 5, να αποδείξετε ότι: α) 4 (Μονάδες ) β) Α (Μονάδες ) Β Δ Γ Ε Επιμέλεια: xr.tsif@gmail.com Σελίδα
4 ΘΕΜΑ -8 Δίνεται τρίγωνο ΑΒΓ με ΑΔ διχοτόμο της. Φέρουμε τις διχοτόμους ΔΕ και ΔΖ των γωνιών και αντίστοιχα. α) Να συμπληρώσετε τα κενά στις παρακάτω ισότητες: i.. ii.. (Μονάδες 0) β) Να αποδείξετε ότι:. (Μονάδες 5) ΘΕΜΑ -90 ΟΜΟΙΑ ΠΟΛΥΓΩΝΑ ΘΕΜΑ ο Στο παρακάτω σχήμα, τα πολύγωνα και είναι όμοια και έχουν και. α) Να προσδιορίσετε το λόγο ομοιότητάς τους. Να αιτιολογήσετε την απάντησή σας. (Μονάδες 8) β) Να υπολογίσετε το μήκος x της πλευράς. (Μονάδες 8) γ) Να βρείτε την περίμετρο του πολυγώνου. (Μονάδες 9) Επιμέλεια: xr.tsif@gmail.com Σελίδα 4
5 ΘΕΜΑ ΟΜΟΙΑ ΤΡΙΓΩΝΑ ΘΕΜΑ ο Θεωρούμε δύο τρίγωνα ABΓ και. α) Να εξετάσετε σε ποιές από τις παρακάτω περιπτώσεις τα τρίγωνα ABΓ και είναι όμοια και να δικαιολογήσετε την απάντησή σας. 0 5, AB=8, AΓ=, 47, 8, 47, 95, 0, 0 5. AB=ΑΓ,,. (Μονάδες 5) β) Στις περιπτώσεις που το τρίγωνο ABΓ είναι όμοιο με το, να γράψετε τους ίσους λόγους των ομόλογων πλευρών τους. (Μονάδες 0) ΘΕΜΑ Στο παρακάτω σχήμα τα τμήματα AΕ και BΔ τέμνονται στο Γ. Να αποδείξετε ότι τα τρίγωνα ABΓ και ΕΔΓ είναι όμοια σε κάθε μια από τις παρακάτω περιπτώσεις: α) AB//ΔΕ. (Μονάδες ) β) BΓ= ΔΓ και ΕΓ=. (Μονάδες ) ΘΕΜΑ -899 α) Να εξετάσετε αν δύο τρίγωνα ABΓ και είναι όμοια σε κάθε μία από τις παρακάτω περιπτώσεις: i) AΓ=4, BΓ=6, BΑ=8, 0, 40, 48. ii) , 8, 6, 4. (Μονάδες 5) β) Έστω τρίγωνο ABΓ με πλευρές AΒ=6, AΓ=7 και BΓ=8. Ποιο θα είναι το μήκος των πλευρών ενός τριγώνου το οποίο είναι όμοιο με το τρίγωνο ABΓ, με λόγο ομοιότητας ; (Μονάδες 0) ΘΕΜΑ -90 Από ένα σημείο Σ που βρίσκεται έξω από έναν δοσμένο κύκλο φέρουμε τα εφαπτόμενα τμήματα ΣΑ και ΣΒ και μία τέμνουσα ΣΓΔ. Να αποδείξετε ότι: α) i. Τα τρίγωνα ΣΒΓ και ΣΔΒ είναι όμοια. ii. Τα τρίγωνα ΣΑΓ και ΣΔΑ είναι όμοια. (Μονάδες 6) β) ΑΓ ΒΔ=ΑΔ ΒΓ (Μονάδες 9) ΘΕΜΑ -904 Τα παρακάτω τρίγωνα και έχουν, και 5,, 8 και 5. Επιμέλεια: xr.tsif@gmail.com Σελίδα 5
6 α) Να αποδείξετε ότι τα τρίγωνα και είναι όμοια. (Μονάδες 8) β) Να συμπληρώσετε την ισότητα των λόγων με τις κατάλληλες πλευρές του τριγώνου ΔΕΖ: (Μονάδες 9) γ) Να υπολογίσετε τα x και y. (Μονάδες 8) ΘΕΜΑ -905 Στο σχήμα που ακολουθεί, το τμήμα είναι παράλληλο στην πλευρά του τριγώνου και επιπλέον ισχύουν 4, 5 και 6. α) Να αποδείξετε ότι τα τρίγωνα και είναι όμοια. (Μονάδες 9) β) Με τη βοήθεια του ερωτήματος α) να συμπληρώσετε τα κενά στην ισότητα: (Μονάδες 9) γ) Ένας μαθητής χρησιμοποιεί την αναλογία 4 5 για να υπολογίσει το x. 6 x Να εξηγήσετε γιατί αυτή η αναλογία είναι λάθος, να γράψετε τη σωστή και να υπολογίσετε την τιμή του x. (Μονάδες 7) ΘΕΜΑ -907 Τα παρακάτω τρίγωνα και είναι ορθογώνια με ορθές τις γωνίες και αντίστοιχα. Επιπλέον, για τις πλευρές των τριγώνων και αντίστοιχα ισχύουν 8, 4 και, 8. α) Να αποδείξετε ότι τα τρίγωνα και είναι όμοια. (Μονάδες 0) β) Με τη βοήθεια του ερωτήματος α) να συμπληρώσετε κατάλληλα τα κενά: Επιμέλεια: xr.tsif@gmail.com Σελίδα 6
7 (Μονάδες 9) γ) Από τις παρακάτω ισότητες να επιλέξετε τη σωστή i. ii. iii. iv.. (Μονάδες 6) 8 4 ΘΕΜΑ -909 Στο σχήμα που ακολουθεί ισχύουν //, 6, 8, 5 και 0. Α 8 Β 6 Ε 0 5 Δ Γ α) Να βρείτε δυο ζεύγη ίσων γωνιών των τριγώνων και. Να αιτιολογήσετε την απάντησή σας. (Μονάδες 8) β) Να αποδείξετε ότι τα τρίγωνα και είναι όμοια και να γράψετε την ισότητα των λόγων των ομόλογων πλευρών τους. (Μονάδες 9) γ) Να υπολογίσετε τα τμήματα και. (Μονάδες 8) ΘΕΜΑ -90 Να χρησιμοποιήσετε τις πληροφορίες που σας δίνονται για το κάθε ζεύγος τριγώνων των παρακάτω σχημάτων, προκειμένου να απαντήσετε στα ακόλουθα: α) Ποιο από τα παρακάτω ζεύγη τριγώνων είναι όμοια και ποιο δεν είναι; Να αιτιολογήσετε την απάντησή σας. (Μονάδες 4) β) Για το ζεύγος των όμοιων τριγώνων του προηγούμενου ερωτήματος, i. να γράψετε την ισότητα των λόγων των ομόλογων πλευρών. (Μονάδες 6) ii. να βρείτε το λόγο ομοιότητάς τους. (Μονάδες 5) ο ζεύγος: τρίγωνα και ο ζεύγος: τρίγωνα και Λ Α Κ Κ 0 Ε 40 0 Λ 6 Μ Η 5 Β Γ Ζ 9 Δ Επιμέλεια: xr.tsif@gmail.com Σελίδα 7
8 ΘΕΜΑ -900 Στη διχοτόμο της γωνίας x O y θεωρούμε τα σημεία, τέτοια ώστε. Η κάθετος στην στο σημείο τέμνει την πλευρά x στο σημείο και έστω η προβολή του στην y. Να αποδείξετε ότι: α) Τα τρίγωνα και είναι όμοια. (Μονάδες 0) β). (Μονάδες 5) x Ε Ο Α Β δ Δ y ΘΕΜΑ -08 Στο ακόλουθο σχήμα είναι και ΒΓ=6. α) Να δικαιολογήσετε γιατί τα τρίγωνα ΑΒΓ και ΑΔE είναι όμοια και να συμπληρώσετε τα κενά στην ισότητα (Μονάδες 5) β) Αν ο λόγος ομοιότητας των τριγώνων ΑΒΓ και ΑΔE είναι ίσος με, να βρείτε το μήκος του τμήματος ΔE. (Μονάδες 0) ΘΕΜΑ -0 Θεωρούμε τρίγωνο ΑΒΓ με ΑΔ εσωτερική διχοτόμο της γωνίας και Ε σημείο της ΑΔ τέτοιο ώστε. Από το Ε φέρνουμε παράλληλες προς τις πλευρές ΑΒ και ΑΓ που τέμνουν τη ΒΓ στα Ζ και Η αντίστοιχα. Να αποδείξετε ότι: α) β). (Μονάδες ). (Μονάδες ) Επιμέλεια: xr.tsif@gmail.com Σελίδα 8
9 ΘΕΜΑ 4ο ΘΕΜΑ Σε οξυγώνιο τρίγωνο φέρουμε τα ύψη του και. α) Αν το τρίγωνο είναι και σκαληνό, τότε: i. Να αποδείξετε ότι τα τρίγωνα και είναι όμοια. (Μονάδες 0) ii. Να δικαιολογήσετε γιατί τα τρίγωνα και δεν μπορεί να είναι όμοια. (Μονάδες 0) β) Αν το τρίγωνο είναι και ισοσκελές με κορυφή το, τότε μπορούμε να ισχυριστούμε ότι τα τρίγωνα και είναι όμοια; Να αιτιολογήσετε την απάντησή σας. (Μονάδες 5) ΘΕΜΑ Στην πλευρά παραλληλογράμμου θεωρούμε σημείο τέτοιο, ώστε και στην πλευρά θεωρούμε σημείο τέτοιο, ώστε. Αν η διαγώνιος τέμνει τις και στα σημεία και αντίστοιχα, να αποδείξετε ότι: α). (Μονάδες ) β). (Μονάδες ) 5 ΘΕΜΑ Δίνεται τρίγωνο. Θεωρούμε τη διάμεσο του και τυχαίο σημείο του τμήματος. Από το φέρουμε ευθεία παράλληλη στην που τέμνει την πλευρά στο και την προέκτασή της στο. α) Να συμπληρώσετε τις αναλογίες και να αιτιολογήσετε την επιλογή σας: i) ii) (Μονάδες ) β) Να αποδείξετε ότι το άθροισμα είναι σταθερό, για οποιαδήποτε θέση του στο. (Μονάδες ) ΘΕΜΑ Στο παρακάτω σκαληνό τρίγωνο θεωρούμε τα σημεία και στις πλευρές και αντίστοιχα, έτσι ώστε να AE A A AB ισχύουν: και. α) Να αποδείξετε ότι (Μονάδες 9) β) Να εξετάσετε αν ισχύει AE E A B. (Μονάδες 8) γ) Να εξετάσετε αν το τμήμα ΒΓ είναι παράλληλο στο τμήμα ΔΕ. Να αιτιολογήσετε πλήρως τις απαντήσεις σας. (Μονάδες 8) Επιμέλεια: xr.tsif@gmail.com Σελίδα 9
10 ΘΕΜΑ Δίνεται τραπέζιο ΑΒΓΔ (ΑΒ//ΓΔ) και σημείο Μ της πλευράς του ΑΔ ώστε. Από το Μ φέρνουμε παράλληλη προς τις βάσεις του τραπεζίου, η οποία τέμνει τις ΑΓ και ΒΓ στα σημεία Κ και N αντίστοιχα. Να αποδείξετε ότι: α) β) (Μονάδες 8) (Μονάδες 8) γ) (Μονάδες 9) ΘΕΜΑ Δίνεται ισοσκελές τρίγωνο ΑΒΓ με ΑΒ = ΑΓ, 6 και η διχοτόμος του ΒΔ. α) Να αποδείξετε ότι: Α i) Τα τρίγωνα ΒΔΓ και ΑΒΓ είναι όμοια. (Μονάδες 6) ii) ΑΔ ΑΓ ΔΓ (Μονάδες 9) 6 0 β) Αν ΑΓ =, να υπολογίσετε το μήκος του τμήματος ΑΔ. (Μονάδες 0) Δ Β Γ Επιμέλεια: xr.tsif@gmail.com Σελίδα 0
11 ΚΕΦΑΛΑΙΟ 9ο ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΣΕ ΟΡΘΟΓΩΝΙΟ ΘΕΜΑ ο ΘΕΜΑ Ένας άνθρωπος σπρώχνει ένα κουτί προς τα πάνω στη ράμπα του παρακάτω σχήματος. α) Να αποδείξετε ότι για το ύψος y, που απέχει το κουτί από το έδαφος κάθε χρονική στιγμή, ισχύει ότι s y, όπου s το μήκος που έχει διανύσει το κουτί πάνω στη ράμπα. (Μονάδες 5) 4 β) Όταν το κουτί απέχει από το έδαφος m, να βρείτε: i. Το μήκος s που έχει διανύσει το κουτί στη ράμπα. (Μονάδες ) ii. Την απόσταση του σημείου Δ από την άκρη της ράμπας Α. (Μονάδες 7) ΘΕΜΑ Σε τρίγωνο ABΓ η διχοτόμος της γωνίας τέμνει την πλευρά BΓ σε σημείο Δ, τέτοιο ώστε. 4 α) Να αποδείξετε ότι. (Μονάδες ) 4 β) Αν επιπλέον ισχύει ότι 5, να εξετάσετε αν το τρίγωνο ΑΒΓ είναι ορθογώνιο. 4 Να δικαιολογήσετε την απάντησή σας. (Μονάδες ) ΘΕΜΑ α) Ποιες από τις παρακάτω τριάδες θετικών αριθμών μπορούν να θεωρηθούν μήκη πλευρών ορθογωνίου τριγώνου; Να δικαιολογήσετε την απάντησή σας. i.,4,5. ii. λ, 4λ, 5λ ( λ > 0). iii. 4, 5, 6. (Μονάδες8) β) Στο παρακάτω ορθογώνιο τρίγωνο να αποδείξετε ότι, το μήκος x είναι ακέραιο Επιμέλεια: xr.tsif@gmail.com Σελίδα
12 πολλαπλάσιο του 4. (Μονάδες 7) ΘΕΜΑ Δίνεται ορθογώνιο τρίγωνο ( 90 ) με ύψος και 8, μήκη των παρακάτω τμημάτων: α). β). γ). 5. Να υπολογίσετε τα (Μονάδες 9) (Μονάδες 8) (Μονάδες 8) ΘΕΜΑ Δίνεται ορθογώνιο τρίγωνο ( 90 ) με 4 και ύψος. 5 α) Να υπολογίσετε το μήκος του τμήματος. (Μονάδες 0) β) Να αποδείξετε ότι 9. (Μονάδες 0) 5 γ) Να βρείτε το εμβαδόν του τριγώνου. (Μονάδες 5) ΘΕΜΑ -6 Δίνεται τρίγωνο ΑΒΓ με ΑΒ = 8 cm και ΒΓ = 0 cm. Η διχοτόμος της γωνίας Β τέμνει την πλευρά ΑΓ στο σημείο Δ. Αν ΑΔ = 9 cm τότε: α) Να βρείτε το μήκος της πλευράς ΑΓ. (Μονάδες ) β) Να αποδείξετε ότι το τρίγωνο ΑΒΓ είναι ορθογώνιο. (Μονάδες ) ΘΕΜΑ -7 Δίνεται τετράγωνο ΑΒΓΔ πλευράς α. Στην πλευρά ΑΒ παίρνουμε ένα τμήμα και στην ΑΔ 5 4 ένα τμήμα. Αν το εμβαδόν του πενταγώνου ΕΒΓΔΖ είναι 76, να υπολογίσετε: 5 α) Το μήκος α της πλευράς του τετραγώνου ΑΒΓΔ. (Μονάδες ) β) Την περίμετρο του πενταγώνου ΕΒΓΔΖ. (Μονάδες ) Επιμέλεια: xr.tsif@gmail.com Σελίδα
13 ΘΕΜΑ 4ο ΘΕΜΑ Σε κύκλο κέντρου θεωρούμε δύο χορδές του και που τέμνονται σε ένα σημείο. α) Αν το σημείο είναι το μέσο του τόξου, να αποδείξετε ότι: i. Όταν η χορδή είναι κάθετη στη χορδή, τότε ii. Όταν η χορδή δεν είναι κάθετη στη χορδή, ισχύει η σχέση AM AB=AΓ. (Μονάδες 8) AM AB=AΓ ; Να αιτιολογήσετε την απάντησή σας. (Μονάδες 9) β) Αν για τις χορδές και που τέμνονται σε σημείο ισχύει ότι AM AB=AΓ, να αποδείξετε ότι το σημείο είναι το μέσο του τόξου. (Μονάδες 8) ΘΕΜΑ Δίνεται κύκλος (O,R) και μία διάμετρός του ΑΒ. Με διαμέτρους τα τμήματα ΟΑ και ΟΒ γράφουμε τους κύκλους κέντρων Κ και Λ αντίστοιχα. Ένας τέταρτος κύκλος κέντρου Μ και ακτίνας ρ εφάπτεται εξωτερικά των κύκλων κέντρων Κ και Λ και εσωτερικά του κύκλου κέντρου Ο. α) Να εκφράσετε τις διακέντρους ΚΜ, ΛΜ και ΟΜ των αντιστοίχων κύκλων ως συνάρτηση των ακτίνων τους, δικαιολογώντας την απάντησή σας. (Μονάδες ) R β) Να αποδείξετε ότι. (Μονάδες ) ΘΕΜΑ Ένα κινητό ξεκινάει από ένα σημείο Α και κινείται βόρεια χιλιόμετρα, κατόπιν συνεχίζει 0 χιλιόμετρα ανατολικά, στη συνέχεια προχωράει 4 χιλιόμετρα βόρεια και τέλος 4 χιλιόμετρα ανατολικά καταλήγοντας στο σημείο Ε. α) Αν από το σημείο Ε επιστρέψει στο σημείο Α από το οποίο ξεκίνησε,κινούμενο ευθύγραμμα, να βρείτε την απόσταση ΑΕ που θα διανύσει. (Μονάδες ) β) Τα σημεία Α, Γ και Ε είναι συνευθειακά; Να αιτιολογήσετε πλήρως την απάντησή σας (Μονάδες ) Επιμέλεια: xr.tsif@gmail.com Σελίδα
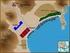
14 ΘΕΜΑ 4-5 Ιδιοκτήτης μεγάλης ακίνητης περιουσίας διαθέτει προς πώληση μια ιδιοκτησία του, η οποία περιλαμβάνει τρία διαδοχικά οικόπεδα με συνολική πρόσοψη 95 m σε ακτή θάλασσας, τα οποία αποτυπώνονται στο σχέδιο που ακολουθεί. Οι επιφάνειες της ιδιοκτησίας και των οικοπέδων είναι σχήματος ορθογωνίου τραπεζίου. Σημειώνεται ότι, ως πρόσοψη οικοπέδου θεωρείται το μήκος της πλευράς του οικοπέδου που συνορεύει με την ακτή της θάλασσας. (σημειώνεται ότι το σχέδιο δεν έχει γίνει υπό κλίμακα) α) Να υπολογίσετε το μήκος της πρόσοψης του κάθε οικοπέδου. (Μονάδες ) β) Αν τα μήκη των δυο άλλων πλευρών της ιδιοκτησίας είναι ανάλογα των αριθμών και, να υπολογίσετε την περίμετρο της ιδιοκτησίας. (Δίνεται ότι 689 = 7 ). (Μονάδες ) ΓΕΝΙΚΕΥΣΗ ΠΥΘΑΓΟΡΕΙΟΥ ΘΕΜΑ ο ΘΕΜΑ -900 Τα μήκη των πλευρών τριγώνου ABΓ είναι 8, 6 και 5. α) Να αποδείξετε ότι το τρίγωνο είναι αμβλυγώνιο. (Μονάδες ) β) Να υπολογίσετε τις προβολές της πλευράς AB στις πλευρές AΓ και BΓ. (Μονάδες 4) ΘΕΜΑ Δίνεται τρίγωνο με πλευρές 6, 9 και α) Να αποδείξετε ότι 7. (Μονάδες 8) β) Να βρείτε το είδος του τριγώνου ως προς τις γωνίες του. (Μονάδες 8) γ) Να υπολογίσετε την προβολή της πάνω στη. (Μονάδες 9) Επιμέλεια: xr.tsif@gmail.com Σελίδα 4
15 ΘΕΜΑ -9 Δίνεται τρίγωνο ΑΒΓ με μήκη πλευρών α=5, β=7 και γ=. α) Να αποδείξετε ότι 0 0. (Μονάδες ) β) Να υπολογίσετε την προβολή της πλευράς α πάνω στην ευθεία ΑΒ. (Μονάδες ) ΘΕΜΑ -9 Δίνεται τρίγωνο ΑΒΓ με ΑΒ=, ΑΓ=6, ΒΓ=8. α) Να βρείτε το είδος του τριγώνου ΑΒΓ ως προς τις γωνίες του. (Μονάδες 0) β) Να υπολογίσετε την προβολή της πλευράς ΑΓ πάνω στην ευθεία ΒΓ. (Μονάδες 5) ΘΕΜΑ - 0 Σε αμβλυγώνιο τρίγωνο ΑΒΓ ( 90 ) φέρουμε τα ύψη του ΑΔ, ΒΕ και ΓΖ. α) Ποια από τις παρακάτω ισότητες είναι λανθασμένη; Στη συνέχεια να την γράψετε σωστά. Α. β = α +γ αβδ Β. γ = β +α βαε Γ. α = β +γ + βαε (Μονάδες ) β) Αν α=7, β=4 και γ=5, να υπολογίσετε την προβολή της ΒΓ πάνω στην ΑΓ. (Μονάδες ) ΘΕΜΑ - Σε οξυγώνιο τρίγωνο ΑΒΓ φέρουμε το ύψος του ΒΔ. Αν ΑΒ=7, ΑΓ=0 και 0 0, να υπολογίσετε: α) το τμήμα ΑΔ. (Μονάδες 8) β) την πλευρά ΒΓ. (Μονάδες 7) Επιμέλεια: xr.tsif@gmail.com Σελίδα 5
16 ΘΕΜΑ -904 ΘΕΩΡΗΜΑΤΑ ΔΙΑΜΕΣΩΝ ΘΕΜΑ ο Δίνεται τρίγωνο με πλευρές 7, 4 και μβ. α) Να αποδείξετε ότι 5. (Μονάδες ) β) Να βρείτε το είδος του τριγώνου ως προς τις γωνίες του. (Μονάδες ) ΘΕΜΑ -9 Δίνεται κύκλος (Κ,R) και δύο διάμετροί του ΑΒ και ΓΔ. Έστω Μ εξωτερικό σημείο του κύκλου τέτοιο, ώστε ΑΜ=0, ΒΜ= και ΓΜ=4. α) Να αποδείξετε ότι : ΜΑ + ΜΒ = (ΜΚ + R ) (Μονάδες 9) β) Να αποδείξετε ότι : ΜΓ + ΜΔ = (ΜΚ + R ) (Μονάδες 7) γ) Να υπολογίσετε το μήκος του ΔΜ. (Μονάδες 9) ΘΕΜΑ -04 Σε τρίγωνο ΑΒΓ είναι ΑΒ = 6, ΑΓ = 8. Φέρουμε το ύψος του ΑΔ και τη διάμεσο ΑΜ και ισχύει ότι: ΔΜ =. α) Να αποδείξετε ότι ΒΓ = 7. (Μονάδες ) β) Να βρείτε το μήκος του ύψους ΑΔ. (Μονάδες ) Επιμέλεια: xr.tsif@gmail.com Σελίδα 6
17 ΘΕΜΑ -06 Δίνεται τρίγωνο ΑΒΓ με μήκη πλευρών ΒΓ = α, ΑΓ = α και AB = α, όπου α > 0. Να αποδείξετε ότι: α) Το τρίγωνο ΑΒΓ είναι ορθογώνιο και να βρείτε ποια είναι η ορθή γωνία. (Μονάδες ) β), όπου γ μ η διάμεσος του ΑΒΓ που αντιστοιχεί στην πλευρά ΑΒ. (Μονάδες ) ΘΕΜΑ -09 Δίνεται τρίγωνο ΑΒΓ για το οποίο έχουμε β=7, γ=6 και η διάμεσος του 89 α. α) Να αποδείξετε ότι α = 9. (Μονάδες ) β) Να υπολογίσετε την προβολή ΜΔ της διαμέσου ΑΜ πάνω στην πλευρά α. (Μονάδες ) ΘΕΜΑ -4 0 Σε ορθογώνιο τρίγωνο ΑΒΓ ( 90 ) με ΑΒ > ΑΓ, φέρουμε τη διάμεσό του ΑΜ και το ύψος του ΑΔ. α) Να εξετάσετε αν οι παρακάτω σχέσεις είναι σωστές ή λανθασμένες. Αν κάποια είναι ΘΕΜΑ 4- λανθασμένη να την ξαναγράψετε διορθωμένη. Α. β + γ = 4μ α Β. β γ = α ΜΔ (Μονάδες 0) β) Αν ΑΒ=8 και ΑΓ=6, να υπολογίσετε την προβολή ΜΔ της διαμέσου ΑΜ στην πλευρά ΒΓ. ΘΕΜΑ 4ο (Μονάδες 5) Δίνεται τρίγωνο ΑΒΓ με πλευρές α, β, γ για το οποίο ισχύει ότι: β + γ = α. Φέρουμε τα ύψη ΒΔ, ΓΕ και τη διάμεσο ΑΜ το μέσο της οποίας είναι το σημείο Ζ. Να αποδείξετε ότι: α) 90. (Μονάδες 6) Επιμέλεια: xr.tsif@gmail.com Σελίδα 7
18 β) γ).. (Μονάδες 0) (Μονάδες 9) ΤΕΜΝΟΥΣΕΣ ΚΥΚΛΟΥ ΘΕΜΑ ο ΘΕΜΑ - Δίνεται ορθογώνιο τρίγωνο ΑΒΓ με τη γωνία Α ορθή και το ύψος του ΑΔ. Ένας κύκλος διέρχεται από τα σημεία Δ, Γ και τέμνει την ΒΑ στο Ε και την προέκτασή της στο Ζ έτσι ώστε: ΒΕ=6, ΒΖ=8 και ΒΔ=4. Να υπολογίσετε τα μήκη των τμημάτων: α) ΒΓ. (Μονάδες ) β) ΑΒ. (Μονάδες ) ΘΕΜΑ 4ο ΘΕΜΑ Κυρτό τετράπλευρο ABΓΔ είναι εγγεγραμμένο σε κύκλο. Οι διαγώνιοί του AΓ και BΔ τέμνονται στο σημείο M, το οποίο είναι το μέσο της διαγωνίου BΔ. Να αποδείξετε ότι: α) B 4MA M (Μονάδες 7 ) β) γ) AB A AM A (Μονάδες 9 ) AB B A A (Μονάδες 9 ) ΘΕΜΑ Θεωρούμε τρίγωνο ΑΒΓ με διάμεσο 5 AM. Αν τα ύψη του ΑΔ και ΒΕ τέμνονται στο σημείο Η, να αποδείξετε ότι: α) Η γωνία Α του τριγώνου ΑΒΓ είναι οξεία. (Μονάδες ) β) AH AΔ=AΓ AE (Μονάδες ) ΘΕΜΑ 4-4 Δίνεται κύκλος κέντρου Ο και μία διάμετρός του ΑΒ. Από σημείο Ε στην προέκταση της διαμέτρου ΑΒ προς το Α, φέρουμε την εφαπτομένη ΕΓ του κύκλου. Η κάθετη στην ΑΒ στο Επιμέλεια: xr.tsif@gmail.com Σελίδα 8
19 σημείο Ε, τέμνει την προέκταση της ΒΓ (προς το Γ) σε σημείο Δ. α) Να επιλέξετε τη σωστή ισότητα: i. ΕΓ = ΕΑ ΑΒ ii. ΕΓ = ΕΑ ΕΒ iii. ΕΓ = ΕΟ ΕΒ iv. ΕΓ = ΕΟ ΟΒ (Μονάδες 6) β) Να αποδείξετε ότι: i. ΒΓ ΒΔ = ΒΑ ΒΕ. (Μονάδες 9) ii. ΕΒ = ΕΓ + ΒΓ ΒΔ. (Μονάδες 9) ΚΕΦΑΛΑΙΟ 0ο ΙΣΟΔΥΝΑΜΑ ΣΧΗΜΑΤΑ ΘΕΜΑ Δίνεται τρίγωνο ΑΒΓ και τα σημεία Δ και Ε των πλευρών του ΑΒ και ΑΓ αντίστοιχα, ώστε AE. Από το σημείο Α φέρνουμε ΑB A ευθεία (ε) παράλληλη στη ΒΓ. Η ευθεία (ε) τέμνει τις προεκτάσεις των ΒΕ και ΓΔ στα σημεία Ζ, Η αντίστοιχα. Να αποδείξετε ότι: α) // (Μονάδες 8) β) γ).. (Μονάδες 8) (Μονάδες 9) Επιμέλεια: xr.tsif@gmail.com Σελίδα 9
20 ΕΜΒΑΔΑ ΒΑΣΙΚΩΝ ΣΧΗΜΑΤΩΝ ΘΕΜΑ -908 Δίνεται ισοσκελές τραπέζιο ( // ) και BE το ύψος του. Αν είναι AB=, ΓΔ=7 και BΓ=4, τότε, α) να αποδείξετε ότι. (Μονάδες ) β) να υπολογίσετε το εμβαδόν του τριγώνου. (Μονάδες ) ΘΕΜΑ -89 Δίνεται τρίγωνο ΑΒΓ και Δ εσωτερικό σημείο του ΒΓ. Φέρουμε από το Δ παράλληλες στις πλευρές ΑΒ και ΑΓ. Η παράλληλη στην ΑΒ τέμνει την ΑΓ στο σημείο Ζ και η παράλληλη στην ΑΓ τέμνει την ΑΒ στο σημείο Ε. Θεωρούμε Κ και Λ τα μέσα των ΒΔ και ΔΓ αντίστοιχα. Να αποδείξετε ότι:. Μονάδες 7 α). Μονάδες 7 β) γ). Μονάδες ΘΕΜΑ -94 Στο τρίγωνο ΑΒΓ θεωρούμε Δ εσωτερικό σημείο της ΒΓ και έστω Μ στο μέσον της ΑΔ. ΘΕΜΑ -97 Να αποδείξετε ότι:. (Μονάδες ) α). (Μονάδες ) β) Σε τετράγωνο ΑΒΓΔ πλευράς α, θεωρούμε σημείο Ε της πλευράς ΔΓ έτσι ώστε ΔΕ= cm. Αν ισχύει ότι 8, τότε: α) Να αποδείξετε ότι η πλευρά του τετραγώνου α είναι 8 cm. (Μονάδες ) β) Να υπολογίσετε το μήκος του τμήματος ΒΕ. (Μονάδες ) Επιμέλεια: xr.tsif@gmail.com Σελίδα 0
21 ΘΕΜΑ -98 Σε παραλληλόγραμμο ΑΒΓΔ θεωρούμε Μ το μέσο της ΑΔ. Προεκτείνουμε τη ΔΓ προς το Γ κατά ΓΕ = ΔΓ. Να αποδείξετε ότι:. (Μονάδες ) α) β). (Μονάδες ) ΕΜΒΑΔΑ ΟΜΟΙΩΝ ΣΧΗΜΑΤΩΝ ΘΕΜΑ -908 Σε ημικύκλιο διαμέτρου κέντρου θεωρούμε σημείο του. Η χορδή τέμνει το ημικύκλιο διαμέτρου στο. Να αποδείξετε ότι: ΘΕΜΑ 4-90 α) Τα τρίγωνα και είναι όμοια. (Μονάδες ) β) ( ) 4 ( ) (Μονάδες ) Δίνεται τρίγωνο ΑΒΓ εγγεγραμμένο σε κύκλο (Ο,R) τέτοιο ώστε να ισχύει. Αν η προέκτασή της διαμέσου του ΑΜ τέμνει τον κύκλο στο σημείο Ρ, να αποδείξετε ότι : α) (Μονάδες 8) β) MP= 6 (Μονάδες 8) γ) ( ) 6 ( ) (Μονάδες 9) Επιμέλεια: xr.tsif@gmail.com Σελίδα
22 ΘΕΜΑ 4-90 Δίνονται δύο κύκλοι (O,α) και (K,β) με, οι οποίοι εφάπτονται εξωτερικά στο. Φέρνουμε το κοινό εφαπτόμενο τμήμα AB, με A, B σημεία των κύκλων (O,α) και (K,β) αντίστοιχα. Από το θεωρούμε την κάθετη στο AB, η οποία τέμνει τα ευθύγραμμα τμήματα AK και AB στα σημεία και αντίστοιχα. Να αποδείξετε ότι : α) αβ MΛ= α+β (Μονάδες 8) β) αβ ΛN= α+β (Μονάδες 8) γ) Αν E,E είναι τα εμβαδά των κύκλων (O, ) και (K, ) αντίστοιχα, τότε: E E (AΛN) = (KMΛ) (Μονάδες 9) ΘΕΜΑ Δίνεται τρίγωνο ΑΒΓ και σημεία Μ, Λ και Ζ πάνω στις πλευρές ΑΒ, ΑΓ και ΒΓ αντίστοιχα τέτοια, ώστε AM AB, AΛ AΓ και BZ BΓ. α) Να αποδείξετε ότι (AMΛ) (ABΓ). (Μονάδες 7) β) Να αποδείξετε ότι (MZΛ) 5. (Μονάδες ) (ABΓ) 8 γ) Να υπολογίσετε το λόγο των εμβαδών (AMZΛ). (Μονάδες 6) (ABΓ) ΘΕΜΑ 4-0 Ένα οικόπεδο ΑΒΓΔ σχήματος ορθογωνίου τραπεζίου ( 90 ) έχει πλευρές ΓΔ = 40 m, ΑΒ = 60 m και ΑΔ = 0 m. Ένας δρόμος αποκόπτει από το οικόπεδο το κομμάτι ΖΕΚΓ σχήματος παραλληλογράμμου. Αν ΔΖ = 0 m και ΑΕ = 0 m τότε: α) Να υπολογίσετε το εμβαδόν (ΚΓΒ). (Μονάδες 5) β) Να υπολογίσετε το εμβαδόν του οικοπέδου που αποκόπτει ο δρόμος. (Μονάδες 5) γ) Να υπολογίσετε το πλάτος (υ) του δρόμου. (Μονάδες 9) δ) Να υπολογίσετε την ΒΓ. (Μονάδες 6) Επιμέλεια: xr.tsif@gmail.com Σελίδα
23 ΘΕΜΑ 4-9 Δίνεται ημικύκλιο κέντρου Ο και διαμέτρου ΑΒ = R. Στην προέκταση του ΑΒ προς το Β, θεωρούμε ένα σημείο Μ, τέτοιο ώστε ΒΜ = R. Από το Μ φέρουμε το εφαπτόμενο τμήμα ΜΓ στο ημικύκλιο. Φέρουμε εφαπτόμενη στο ημικύκλιο στο σημείο Α η οποία τέμνει την αποδείξετε ότι: α) ΜΓ = R. προέκταση του τμήματος ΜΓ στο σημείο Δ. Να (Μονάδες 8) β) ΜΟ ΜΑ =ΜΓ ΜΔ. (Μονάδες 8) γ) (ΑΟΓΔ) = (ΜΟΓ). (Μονάδες 9) ΘΕΜΑ 4-8 Δίνεται κύκλος (Κ,R) και διάμετρός του ΑΒ. Από σημείο Ε στην προέκταση της ΑΒ προς το μέρος του Β φέρουμε εφαπτόμενο τμήμα στον κύκλου και έστω Γ το σημείο επαφής. Στο σημείο Ε φέρουμε κάθετη στην ΑΒ η οποία τέμνει την προέκταση της ΑΓ στο σημείο Δ. Να αποδείξετε ότι: α) Το τετράπλευρο ΒΕΔΓ είναι εγγράψιμο. (Μονάδες 8) β) ΑΓ ΑΔ = ΑΕ ΒΕ ΑΕ. (Μονάδες 0) γ) ( ) ( ). (Μονάδες 7) Επιμέλεια: xr.tsif@gmail.com Σελίδα
24 ΑΛΛΟΙ ΤΥΠΟΙ ΓΙΑ ΤΟ ΕΜΒΑΔΟΝ ΤΡΙΓΩΝΟΥ ΘΕΜΑ ο ΘΕΜΑ -0 Δίνεται τρίγωνο ΑΒΓ με ΑΓ = cm ΒΓ = cm και γωνία 0 0. α) Να αποδείξετε ότι ΑΒ = cm. (Μονάδες 0) β) Να υπολογίσετε το εμβαδόν του τριγώνου ΑΒΓ. (Μονάδες 8) γ) Να υπολογίσετε την ακτίνα του περιγεγραμμένου κύκλου του τριγώνου ΑΒΓ. (Μονάδες 7) ΘΕΜΑ 4-7 ΘΕΜΑ 4ο Δίνεται τρίγωνο ΑΒΓ και σημεία Μ, Λ και Ζ πάνω στις πλευρές ΑΒ, ΑΓ και ΒΓ αντίστοιχα τέτοια ώστε, και. α) Να αποδείξετε ότι ( ) ( ). (Μονάδες 7) β) Να αποδείξετε ότι ( ) 5. (Μονάδες ) ( ) 8 γ) Να υπολογίσετε το λόγο των εμβαδών ( ). (Μονάδες 6) ( ) ΘΕΜΑ 4- Δίνονται δύο κύκλοι (Ο,8), (K,) με διάκεντρο ΟΚ = η οποία τους τέμνει στα σημεία Γ και Δ αντίστοιχα. Αν ΑΒ είναι κοινό εξωτερικό εφαπτόμενο τμήμα των δυο κύκλων και ΚΜ κάθετο τμήμα στην ΟΑ τότε να αποδείξετε ότι: α) ΜΚ = 6. (Μονάδες 6) β) (ΑΟΚΒ) = 0. (Μονάδες 5) γ) Να υπολογίσετε τη γωνία ΜΟΚ. (Μονάδες 7) δ) (ΟΑΓ) = 6(ΔΒΚ). (Μονάδες 7) Επιμέλεια: xr.tsif@gmail.com Σελίδα 4
25 ΘΕΜΑ 4-6 Σε ισοσκελές τρίγωνο ΑΒΓ (ΑΒ=ΑΓ) προεκτείνουμε την πλευρά ΑΓ κατά τμήμα προέκταση του ύψους ΑΜ, τέμνει την ΒΔ στο Ε, να αποδείξετε ότι: α). (Μονάδες 8) β) ( ). (Μονάδες 9) ( ) γ) ( ) 5. (Μονάδες 8) ( ). Αν η ΚΕΦΑΛΑΙΟ ΚΑΝΟΝΙΚΑ ΠΟΛΥΓΩΝΑ ΘΕΜΑ -95 Με ένα σύρμα μήκους c κατασκευάζουμε ένα κανονικό εξάγωνο. α) Να εκφράσετε την πλευρά του εξαγώνου ως συνάρτηση του c. (Μονάδες 0) β) Να αποδείξετε ότι, το εμβαδόν του εξαγώνου ισούται με c. (Μονάδες 5) 4 ΘΕΜΑ 4- Δίνεται κύκλος (Ο,R) και μία διάμετρός του ΒΓ. Η κάθετος στο μέσο Ε της ακτίνας ΟΒ τέμνει το ένα ημικύκλιο στο σημείο Α και η εφαπτομένη του κύκλου στο σημείο Β τέμνει την προέκταση της χορδής ΑΓ στο σημείο Δ. α) Να αποδείξετε ότι: i. ΑΓ = λ = R. (Μονάδες 8) ii. A. (Μονάδες 8) β) Να υπολογίσετε το λόγο των εμβαδών: ( A ) ( ). (Μονάδες 9) Επιμέλεια: xr.tsif@gmail.com Σελίδα 5
26 ΜΗΚΟΣ ΚΥΚΛΟΥ ΘΕΜΑ 4- Με διάμετρο την ακτίνα ΟΑ ενός κύκλου (Ο, R) γράφουμε κύκλο (Κ) και από το Ο φέρουμε ημιευθεία που σχηματίζει με την ακτίνα ΟΑ γωνία 0 και τέμνει τον κύκλο (Ο) στο Γ και τον κύκλο (Κ) στο Δ. α) Να αποδείξετε ότι τα τόξα ΑΓ και ΑΔ έχουν ίσα μήκη. (Μονάδες 0) β) Να υπολογίσετε ως συνάρτηση της ακτίνας R του κύκλου (Ο, R) την περίμετρο του μικτόγραμμου (σκιασμένου) τριγώνου ΑΔΓ. (Μονάδες 5) ΕΜΒΑΔΟΝ ΚΥΚΛΟΥ ΘΕΜΑ -96 Σε τετράγωνο ΑΒΓΔ με πλευρά 0, θεωρούμε τον εγγεγραμμένο κύκλο του κέντρου Ο και εντός του κύκλου το εγγεγραμμένο τετράγωνο ΚΛΜΝ. α) Να αποδείξετε ότι (ΚΛΜΝ)=50. (Μονάδες ) β) Να αποδείξετε ότι το εμβαδόν του γραμμοσκιασμένου χωρίου του κύκλου που βρίσκεται στο εξωτερικό του τετραγώνου ΚΛΜΝ και εσωτερικά του κύκλου, είναι 5(π ). (Μονάδες ) ΘΕΜΑ -00 Στο παρακάτω σχήμα οι κύκλοι (Ο, R) και (Κ, ρ) εφάπτονται εσωτερικά στο σημείο Α. Από το άκρο Β της διαμέτρου ΑΒ του κύκλου (Ο, R) φέρουμε το εφαπτόμενο τμήμα ΒΓ του κύκλου (Κ, ρ) και είναι ΒΓ=. Αν η διάμετρος ΒΑ τέμνει τον κύκλο (Κ, ρ) στο Δ και ισχύει ότι ΒΔ=8, τότε: α) Να αποδείξετε ότι για τις ακτίνες R και ρ των κύκλων (Ο, R) και (Κ, ρ) ισχύουν R=9 και ρ=5. (Μονάδες 5) β) Να υπολογίσετε το εμβαδόν του χωρίου (σκιασμένο) που περικλείεται μεταξύ των κύκλων. (Μονάδες 0) Επιμέλεια: xr.tsif@gmail.com Σελίδα 6
27 ΘΕΜΑ -0 Στο παρακάτω σχήμα, τα καμπυλόγραμμα τμήματα ΒΑ, ΑΓ, ΖΔ και ΔΕ είναι ίσα ημικύκλια. Αν ΒΕ//AΔ//ΓΖ, ΒΕ=ΑΔ=ΓΖ=0 και το ύψος του σχήματος είναι 4, να υπολογίσετε: α) Την περίμετρο του σχήματος. (Μονάδες ) β) Το εμβαδόν του. (Μονάδες ) ΘΕΜΑ -05 Από σημείο Α εκτός κύκλου (Ο, R) φέρουμε τέμνουσα ΑΒΓ έτσι ώστε ΑΒ=ΒΓ. Αν ΟΑ = R 7 τότε: α) Να αποδείξετε ότι ΒΓ = λ = R. (Μονάδες ) β) Να υπολογίσετε το εμβαδόν του κυκλικού τμήματος ΓΔΒ. (Μονάδες ) ΘΕΜΑ 4-5 Δίνεται κύκλος (Ο,R) διαμέτρου ΑΒ και ημιευθεία Αx τέτοια, ώστε η γωνία ΒΑx να είναι 0 o. Η Αx τέμνει τον κύκλο στο σημείο Γ. Φέρουμε την εφαπτομένη του κύκλου στο σημείο Β, η οποία τέμνει την Αx στο σημείο Ρ. Να αποδείξετε ότι: α) ΒΓ = R. (Μονάδες 5) β) ( ). (Μονάδες 8) ( ) 4 γ) ΡΒ = R. (Μονάδες 6) δ) Το εμβαδόν του κυκλικού τμήματος που περιέχεται στην κυρτή γωνία ΒΟΓ είναι: Ε = R ( ) (Μονάδες 6). Επιμέλεια: xr.tsif@gmail.com Σελίδα 7
28 ΘΕΜΑ 4-5 περιέχεται στην επίκεντρη γωνία Σε τετράγωνο ΑΒΓΔ με πλευρά 0, κατασκευάζουμε ημικύκλια με διαμέτρους τις πλευρές του τετραγώνου που βρίσκονται στο εσωτερικό του και έχουν κοινό σημείο το κέντρο Ο του τετραγώνου. α) Να υπολογίσετε το εμβαδόν του κυκλικού τομέα που περιέχεται στην επίκεντρη γωνία, όπου Θ το μέσο της πλευράς ΑΔ. (Μονάδες 5) β) Να αποδείξετε ότι το εμβαδόν του κυκλικού τμήματος που είναι 5 ( ). (Μονάδες 0) 4 γ) Να αποδείξετε ότι το εμβαδόν του γραμμοσκιασμένου μέρους του τετραγώνου, είναι 50 (4 π). (Μονάδες 0) ΘΕΜΑ 4-6 Σε τετράγωνο ΑΒΓΔ πλευράς α, γράφουμε τεταρτοκύκλιο εσωτερικά του τετραγώνου με κέντρο Α και ακτίνα α. α) Αν Χ είναι το χωρίο του τετραγώνου που βρίσκεται εξωτερικά του τεταρτοκύκλιου, να αποδείξετε ότι το εμβαδόν του είναι: (Χ ) = (4 ). (Μονάδες 5) 4 β) Με διάμετρο ΑB κατασκευάζουμε ημικύκλιο εσωτερικά του τετραγώνου. Αν Χ είναι το χωρίο του ημικυκλίου και Χ το χωρίο του τεταρτοκυκλίου που βρίσκεται εξωτερικά του ημικυκλίου, να υπολογίσετε τα εμβαδά των δύο χωρίων X και Χ. (Μονάδες ) γ) Ποιο από τα χωρία Χ και Χ έχει το μεγαλύτερο εμβαδόν; Να δικαιολογήσετε την απάντησή σας. (Μονάδες 9) ΘΕΜΑ 4-9 Δύο ίσοι κύκλοι (Κ,R) και (Λ,R) τέμνονται στα σημεία Α και Β έτσι ώστε το μήκος της διακέντρου τους να είναι ΚΛ = R. α) Να δείξετε ότι το τετράπλευρο ΚΑΛΒ είναι τετράγωνο. (Μονάδες 0) β) Να υπολογίσετε το εμβαδόν του κοινού χωρίου των δύο κύκλων. (Μονάδες 5) Επιμέλεια: xr.tsif@gmail.com Σελίδα 8
29 ΘΕΜΑ 4-0 Σε κύκλο (Ο,R) θεωρούμε τα σημεία Γ και Δ που διαιρούν τη διάμετρό του ΑΒ = δ σε τρία ίσα τμήματα. Στο ένα από τα δύο ημιεπίπεδα της ΑΒ γράφουμε τα ημικύκλια με διαμέτρους τις ΑΓ και ΑΔ και στο αντικείμενο ημιεπίπεδο γράφουμε τα ημικύκλια με διαμέτρους ΒΔ και ΒΓ. Να αποδείξετε: α) Το εμβαδόν Ε του κυκλικού δίσκου διαμέτρου ΑΒ = δ ισούται με. (Μονάδες 5) 4 β) Το μήκος του καμπυλόγραμμου σχήματος ΑΓΒΔΑ (το γραμμοσκιασμένο) ισούται με το μήκους του κύκλου (Ο,R). (Μονάδες 0) γ) Οι καμπύλες γραμμές ΑΓΒ και ΑΔΒ διαιρούν τον κυκλικό δίσκο διαμέτρου ΑΒ = δ σε τρία ισεμβαδικά χωρία τα Ε, Ε, Ε. (Μονάδες 0) ΘΕΜΑ 4- ΘΕΜΑ 4- Στα άκρα της χορδής ΑΒ = R ενός κύκλου (Ο, R), φέρουμε τα εφαπτόμενα τμήματα ΣΑ και ΣΒ. Αν η ΣΟ τέμνει το τόξο ΑΒ στο σημείο Μ, τότε: α) Να αποδείξτε ότι: i) το τρίγωνο ΑΟΒ είναι ορθογώνιο, (Μονάδες 0) ii) R( ). (Μονάδες 5) β) Να υπολογίσετε το γραμμοσκιασμένο εμβαδόν (ΣΑΒ) ως συνάρτηση της ακτίνας R του κύκλου. (Μονάδες 0) Σε κύκλο κέντρου Ο και ακτίνας R = 6 cm εγγράφουμε τετράγωνο ΑΒΓΔ και στο τετράγωνο εγγράφουμε νέο κύκλο. α) Να υπολογίσετε: i. Το εμβαδόν του τετραγώνου. (Μονάδες 7) ii. Το εμβαδόν E του γραμμοσκιασμένου χωρίου, δηλαδή του χωρίου του τετραγώνου ΑΒΓΔ που βρίσκεται έξω από τον εγγεγραμμένο κύκλο του. (Μονάδες 9) β) Να συγκρίνετε το εμβαδόν E του γραμμοσκιασμένου χωρίου με το εμβαδόν του τμήματος του κύκλου ακτίνας R που βρίσκεται έξω από το τετράγωνο ΑΒΓΔ. (Μονάδες 9) Επιμέλεια: xr.tsif@gmail.com Σελίδα 9
30 ΘΕΜΑ 4-90 Δίνεται κύκλος (Ο,R), η διάμετρος του ΒΓ και η χορδή του ΑΒ = R. Η εφαπτομένη του κύκλου στο σημείο Γ τέμνει την προέκταση της χορδής ΒΑ στο σημείο Δ. Να βρείτε ως συνάρτηση της ακτίνας R: α) Το εμβαδόν του τριγώνου ΑΒΓ. (Μονάδες 8) β) Το μήκος του ευθυγράμμου τμήματος ΓΔ. (Μονάδες 8) γ) Το εμβαδόν του (σκιασμένου) μικτόγραμμου τριγώνου ΑΔΓ (Μονάδες 9) ΘΕΜΑ 4-99 Δίνεται κύκλος (Ο,R) και σημείο Μ τέτοιο, ώστε η δύναμή του ως προς τον κύκλο (Ο,R) να γ) Να αποδείξετε ότι (ΟΑΓΒ) = είναι R. Αν ΜΑ, ΜΒ είναι τα εφαπτόμενα τμήματα από το σημείο Μ προς τον κύκλο, τότε : α) Να αποδείξετε ότι ΜΑ= R (Μονάδες 6) β) Να βρείτε ως συνάρτηση της ακτίνας R το εμβαδόν i) του τετραπλεύρου ΟΑΜΒ (Μονάδες 6) ii) του (σκιασμένου) μικτόγραμμου τριγώνου ΑΜΒ R, όπου Γ είναι το σημείο τομής του κύκλου με το (Μονάδες 8) ευθύγραμμο τμήμα ΟΜ. (Μονάδες 5) ΘΕΜΑ 4-0 Δύο ίσοι κύκλοι (Κ,R), (Λ,R) τέμνονται στα σημεία Α, Β, όπως φαίνεται στο παρακάτω σχήμα και έχουν διάκεντρο ΚΛ = R. α) Να βρείτε τη γωνία (Μονάδες 7) β) Να βρείτε ως συνάρτηση της ακτίνας R το εμβαδόν: Επιμέλεια: xr.tsif@gmail.com Σελίδα 0
31 i) Του τετραπλεύρου ΑΚΒΛ. (Μονάδες 0) ii) Του σκιασμένου μηνίσκου. (Μονάδες 8) ΘΕΜΑ 4-07 Δίνεται κανονικό εξάγωνο ΑΒΓΔΕΖ εγγεγραμμένο σε κύκλο (Ο,R). Φέρουμε τα τμήματα ΑΓ, ΑΔ και ΑΜ, όπου Μ το μέσο του ΓΔ. Να αποδείξετε ότι: R α) (ΑΒΓΔΕΖ) =. (Μονάδες 5) β) (ΑΜΔ) = R. (Μονάδες 7) 4 γ) (ΑΜΔΕΖ) = (ΑΒΓΜ) (Μονάδες 5) R (4 ). δ) Το εμβαδόν του (σκιασμένου) κυκλικού τμήματος που περικλείεται από τη χορδή ΑΓ και το τόξο ΑΒΓ είναι ίσο με: (Μονάδες 8) Επιμέλεια: xr.tsif@gmail.com Σελίδα
2ηέκδοση 20Ιανουαρίου2015
 ηέκδοση 0Ιανουαρίου015 ΦΡΟΝΤΙΣΤΗΡΙΟ Μ.Ε. ΣΥΓΧΡΟΝΗ ΜΑΘΗΣΗ (β-πακέτο ασκήσεων) 1 89 Δίνεται τρίγωνο ΑΒΓ και Δ εσωτερικό σημείο του ΒΓ. Φέρουμε από το Δ παράλληλες στις πλευρές ΑΒ και ΑΓ. Η παράλληλη στην
ηέκδοση 0Ιανουαρίου015 ΦΡΟΝΤΙΣΤΗΡΙΟ Μ.Ε. ΣΥΓΧΡΟΝΗ ΜΑΘΗΣΗ (β-πακέτο ασκήσεων) 1 89 Δίνεται τρίγωνο ΑΒΓ και Δ εσωτερικό σημείο του ΒΓ. Φέρουμε από το Δ παράλληλες στις πλευρές ΑΒ και ΑΓ. Η παράλληλη στην
ΘΕΜΑΤΑ ΑΠΟ ΤΗΝ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ
 ΑΝΑΛΟΓΙΕΣ Α. ΘΕΩΡΗΜΑ ΘΑΛΗ ΘΕΜΑ Ο 1. Δίνεται τρίγωνο ABΓ με AB=9, AΓ=15. Από το βαρύκεντρο φέρνουμε ευθεία παράλληλη στην πλευρά BΓ που τέμνει τις AB,AΓ στα Δ,E αντίστοιχα. α) Να αποδείξετε ότι AΔ = AB
ΑΝΑΛΟΓΙΕΣ Α. ΘΕΩΡΗΜΑ ΘΑΛΗ ΘΕΜΑ Ο 1. Δίνεται τρίγωνο ABΓ με AB=9, AΓ=15. Από το βαρύκεντρο φέρνουμε ευθεία παράλληλη στην πλευρά BΓ που τέμνει τις AB,AΓ στα Δ,E αντίστοιχα. α) Να αποδείξετε ότι AΔ = AB
ΡΑΛΛΕΙΟ ΓΕΛ ΘΗΛΕΩΝ ΠΕΙΡΑΙΑ ΣΧ. ΕΤΟΣ ΕΠΑΝΑΛΗΨΗ Γεωμετρίας Β Λυκείου. // ) και BE
 ΡΑΛΛΕΙΟ ΓΕΛ ΘΗΛΕΩΝ ΠΕΙΡΑΙΑ ΣΧ. ΕΤΟΣ 06-7 Επειδή το ζητήσατε κορίτσια μου: Α. ΘΕΩΡΙΑ Τα κεφάλαια: ΕΠΑΝΑΛΗΨΗ Γεωμετρίας Β Λυκείου 9 ο Μετρικές σχέσεις, 0 ο Εμβαδά, ο Μέτρηση Κύκλου, την διδαχθείσα ύλη Β.
ΡΑΛΛΕΙΟ ΓΕΛ ΘΗΛΕΩΝ ΠΕΙΡΑΙΑ ΣΧ. ΕΤΟΣ 06-7 Επειδή το ζητήσατε κορίτσια μου: Α. ΘΕΩΡΙΑ Τα κεφάλαια: ΕΠΑΝΑΛΗΨΗ Γεωμετρίας Β Λυκείου 9 ο Μετρικές σχέσεις, 0 ο Εμβαδά, ο Μέτρηση Κύκλου, την διδαχθείσα ύλη Β.
Γεωμετρία Β Λυκείου Τράπεζα θεμάτων
 Γεωμετρία Β Λυκείου Τράπεζα θεμάτων www.askisopolis.gr η έκδοση - - 0 Μεταβολές από την προηγούμενη έκδοση Αφαιρέθηκαν οι ασκήσεις _90, _900 και _907 Αλλαγές: Στην άσκηση _909 άλλαξε το β ερώτημα, στην
Γεωμετρία Β Λυκείου Τράπεζα θεμάτων www.askisopolis.gr η έκδοση - - 0 Μεταβολές από την προηγούμενη έκδοση Αφαιρέθηκαν οι ασκήσεις _90, _900 και _907 Αλλαγές: Στην άσκηση _909 άλλαξε το β ερώτημα, στην
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ - 2 ο ΘΕΜΑ
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ - ο ΘΕΜΑ ΚΕΦΑΛΑΙΟ 7 : ΑΝΑΛΟΓΙΕΣ. Δίνεται τρίγωνο ΑΒΓ (ΑΒ>ΑΓ) και ΑΔ, ΑΕ η εσωτερική και η εξωτερική διχοτόμος του αντίστοιχα. Αν είναι ΑΒ=6, ΔΒ=, ΒΓ=5 και ΒΕ=5, να αποδείξετε ότι: α) ΑΓ
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ - ο ΘΕΜΑ ΚΕΦΑΛΑΙΟ 7 : ΑΝΑΛΟΓΙΕΣ. Δίνεται τρίγωνο ΑΒΓ (ΑΒ>ΑΓ) και ΑΔ, ΑΕ η εσωτερική και η εξωτερική διχοτόμος του αντίστοιχα. Αν είναι ΑΒ=6, ΔΒ=, ΒΓ=5 και ΒΕ=5, να αποδείξετε ότι: α) ΑΓ
Φεργαδιώτης Αθανάσιος ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΣΤΗΝ ΓΕΩΜΕΤΡΙΑ Β ΛΥΚΕΙΟΥ. Θέμα 2 ο (29)
 Φεργαδιώτης Αθανάσιος ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΣΤΗΝ ΓΕΩΜΕΤΡΙΑ Β ΛΥΚΕΙΟΥ Θέμα 2 ο (29) -2- Τράπεζα θεμάτων Γεωμετρίας Β Λυκείου Φεργαδιώτης Αθανάσιος -3- Τράπεζα θεμάτων Γεωμετρίας Β Λυκείου Φεργαδιώτης Αθανάσιος
Φεργαδιώτης Αθανάσιος ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΣΤΗΝ ΓΕΩΜΕΤΡΙΑ Β ΛΥΚΕΙΟΥ Θέμα 2 ο (29) -2- Τράπεζα θεμάτων Γεωμετρίας Β Λυκείου Φεργαδιώτης Αθανάσιος -3- Τράπεζα θεμάτων Γεωμετρίας Β Λυκείου Φεργαδιώτης Αθανάσιος
Γεωμετρία Β Λυκείου. Τράπεζα Θεμάτων 18-22/1/2015
 Τράπεζα Θεμάτων 8 -//0 ο Θέμα Δικαιοσυνόπουλος Νίκος Κολλινιάτη Γιωργία Μιχαήλογλου Στέλιος Πατσιμάς Δημήτρης Θεωρήματα διχοτόμων..8.δίνεται τρίγωνο ΑΒΓ με ΑΔ διχοτόμο της γωνίας και Φέρουμε τις διχοτόμους
Τράπεζα Θεμάτων 8 -//0 ο Θέμα Δικαιοσυνόπουλος Νίκος Κολλινιάτη Γιωργία Μιχαήλογλου Στέλιος Πατσιμάς Δημήτρης Θεωρήματα διχοτόμων..8.δίνεται τρίγωνο ΑΒΓ με ΑΔ διχοτόμο της γωνίας και Φέρουμε τις διχοτόμους
Θεώρημα Θαλή. μ10. μ 10 γ) Δίνεται κυρτό τετράπλευρο ΑΒΓΔ και τα σημεία Ε,Ζ,Η και Θ των πλευρών του ΑΔ, ΑΒ, ΒΓ, ΓΔ αντίστοιχα τέτοια, ώστε
 Θεώρημα Θαλή.8975. Θεωρούμε τρίγωνο ΑΒΓ με AB 9 και 5. Από το βαρύκεντρο Θ του τριγώνου, φέρουμε ευθεία ε παράλληλη στην πλευρά ΒΓ, που τέμνει τις ΑΒ και ΑΓ στα σημεία Δ και Ε αντίστοιχα. α) Να αποδείξετε
Θεώρημα Θαλή.8975. Θεωρούμε τρίγωνο ΑΒΓ με AB 9 και 5. Από το βαρύκεντρο Θ του τριγώνου, φέρουμε ευθεία ε παράλληλη στην πλευρά ΒΓ, που τέμνει τις ΑΒ και ΑΓ στα σημεία Δ και Ε αντίστοιχα. α) Να αποδείξετε
ΘΕΜΑ 4 Ο ΑΒ 3 ΕΓ Α ΑΒ,
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΚΕΦΑΛΑΙΟ 7 Ο - ΑΝΑΛΟΓΙΕΣ ΘΕΜΑ Ο Άσκηση (_8975) Θεωρούμε τρίγωνο ΑΒΓ ΑΒ=9 και ΑΓ=5. Από το βαρύκεντρο Θ του τριγώνου, φέρουμε ευθεία ε παράλληλη στην πλευρά ΒΓ, που τέμνει τις ΑΒ και ΑΓ
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΚΕΦΑΛΑΙΟ 7 Ο - ΑΝΑΛΟΓΙΕΣ ΘΕΜΑ Ο Άσκηση (_8975) Θεωρούμε τρίγωνο ΑΒΓ ΑΒ=9 και ΑΓ=5. Από το βαρύκεντρο Θ του τριγώνου, φέρουμε ευθεία ε παράλληλη στην πλευρά ΒΓ, που τέμνει τις ΑΒ και ΑΓ
Σε κύκλο κέντρου Ο θεωρούμε δύο χορδές του ΑΒ και ΓΔ που τέμνονται σε ένα σημείο Μ. α) Αν το σημείο Α είναι το μέσο του τόξου ΓΔ, να αποδείξετε ότι:
 GI_V_GEO_4_8976 Σε οξυγώνιο τρίγωνο ΑΒΓ φέρουμε τα ύψη του ΑΔ και ΒΕ. α) Αν το τρίγωνο ΑΒΓ είναι και σκαληνό, τότε: i. Να αποδείξετε ότι τα τρίγωνα ΑΔΓ και ΒΕΓ είναι όμοια. (Μονάδες 0) ii. Να δικαιολογήσετε
GI_V_GEO_4_8976 Σε οξυγώνιο τρίγωνο ΑΒΓ φέρουμε τα ύψη του ΑΔ και ΒΕ. α) Αν το τρίγωνο ΑΒΓ είναι και σκαληνό, τότε: i. Να αποδείξετε ότι τα τρίγωνα ΑΔΓ και ΒΕΓ είναι όμοια. (Μονάδες 0) ii. Να δικαιολογήσετε
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ. ΓΕΩΜΕΤΡΙΑ Β τάξης Γενικού Λυκείου 2 ο Θέμα. Εκφωνήσεις - Λύσεις των θεμάτων. Έκδοση 1 η (14/11/2014)
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΓΕΩΜΕΤΡΙΑ Β τάξης Γενικού Λυκείου ο Θέμα Εκφωνήσεις - Λύσεις των θεμάτων Έκδοση 1 η (14/11/014) Θέματα ης Ομάδας GI_V_GEO 18975 Δίνεται τρίγωνο ABΓμε AB=9, AΓ=15. Από το βαρύκεντρο φέρνουμε
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΓΕΩΜΕΤΡΙΑ Β τάξης Γενικού Λυκείου ο Θέμα Εκφωνήσεις - Λύσεις των θεμάτων Έκδοση 1 η (14/11/014) Θέματα ης Ομάδας GI_V_GEO 18975 Δίνεται τρίγωνο ABΓμε AB=9, AΓ=15. Από το βαρύκεντρο φέρνουμε
Γεωμετρία Β Λυκείου Τράπεζα θεμάτων
 Γεωμετρία Β Λυκείου Τράπεζα θεμάτων www.askisopolis.gr 9--0 Θεώρημα Θαλή.897. Θεωρούμε τρίγωνο ΑΒΓ με AB 9 και. Από το βαρύκεντρο Θ του τριγώνου, φέρουμε ευθεία ε παράλληλη στην πλευρά ΒΓ, που τέμνει τις
Γεωμετρία Β Λυκείου Τράπεζα θεμάτων www.askisopolis.gr 9--0 Θεώρημα Θαλή.897. Θεωρούμε τρίγωνο ΑΒΓ με AB 9 και. Από το βαρύκεντρο Θ του τριγώνου, φέρουμε ευθεία ε παράλληλη στην πλευρά ΒΓ, που τέμνει τις
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ
 Φεργαδιώτης Αθανάσιος ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΣΤA ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ Θέμα 4 ο (14) -- Τράπεζα θεμάτων Μαθηματικών προσανατολισμού Β Λυκείου Φεργαδιώτης Αθανάσιος -- Τράπεζα θεμάτων Μαθηματικών
Φεργαδιώτης Αθανάσιος ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΣΤA ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ Θέμα 4 ο (14) -- Τράπεζα θεμάτων Μαθηματικών προσανατολισμού Β Λυκείου Φεργαδιώτης Αθανάσιος -- Τράπεζα θεμάτων Μαθηματικών
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΚΕΦΑΛΑΙΟ 8 Ο - ΟΜΟΙΟΤΗΤΑ ΘΕΜΑ 2 Ο
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΚΕΦΑΛΑΙΟ 8 Ο - ΟΜΟΙΟΤΗΤΑ ΘΕΜΑ 2 Ο Άσκηση 1 (2_18984) Θεωρούμε δύο τρίγωνα ΑΒΓ και ΔΕΖ. (α) Να εξετάσετε σε ποιες από τις παρακάτω περιπτώσεις τα τρίγωνα ΑΒΓ και ΔΕΖ είναι όμοια και να δικαιολογήσετε
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΚΕΦΑΛΑΙΟ 8 Ο - ΟΜΟΙΟΤΗΤΑ ΘΕΜΑ 2 Ο Άσκηση 1 (2_18984) Θεωρούμε δύο τρίγωνα ΑΒΓ και ΔΕΖ. (α) Να εξετάσετε σε ποιες από τις παρακάτω περιπτώσεις τα τρίγωνα ΑΒΓ και ΔΕΖ είναι όμοια και να δικαιολογήσετε
ΚΕΦΑΛΑΙΟ 9 ο ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΣΕ ΟΡΘΟΓΩΝΙΟ ΤΡΙΓΩΝΟ
 ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΣΕ ΟΡΘΟΓΩΝΙΟ ΤΡΙΓΩΝΟ ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ Βασικά θεωρήματα Σε κάθε ορθογώνιο τρίγωνο, το τετράγωνο μιας κάθετης πλευράς του είναι ίσο με το γινόμενο της υποτείνουσας επί την προβολή της
ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΣΕ ΟΡΘΟΓΩΝΙΟ ΤΡΙΓΩΝΟ ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ Βασικά θεωρήματα Σε κάθε ορθογώνιο τρίγωνο, το τετράγωνο μιας κάθετης πλευράς του είναι ίσο με το γινόμενο της υποτείνουσας επί την προβολή της
ΕΠΑΝΑΛΗΨΗ ΓΕΩΜΕΤΡΙΑΣ Β ΛΥΚΕΙΟΥ ( α μέρος )
 ΕΠΑΝΑΛΗΨΗ ΓΕΩΜΕΤΡΙΑΣ Β ΛΥΚΕΙΟΥ ( α μέρος ) Ερωτήσεις Θεωρίας Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε στο τετράδιό
ΕΠΑΝΑΛΗΨΗ ΓΕΩΜΕΤΡΙΑΣ Β ΛΥΚΕΙΟΥ ( α μέρος ) Ερωτήσεις Θεωρίας Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε στο τετράδιό
Τάξη A Μάθημα: Γεωμετρία
 Τάξη A Μάθημα: Γεωμετρία Η Θεωρία σε Ερωτήσεις Ερωτήσεις Κατανόησης Επαναληπτικά Θέματα Επαναληπτικά Διαγωνίσματα Περιεχόμενα Τρίγωνα Α. Θεωρία-Αποδείξεις Σελ.2 Β. Θεωρία-Ορισμοί..Σελ.9 Γ. Ερωτήσεις Σωστού
Τάξη A Μάθημα: Γεωμετρία Η Θεωρία σε Ερωτήσεις Ερωτήσεις Κατανόησης Επαναληπτικά Θέματα Επαναληπτικά Διαγωνίσματα Περιεχόμενα Τρίγωνα Α. Θεωρία-Αποδείξεις Σελ.2 Β. Θεωρία-Ορισμοί..Σελ.9 Γ. Ερωτήσεις Σωστού
Γεωμετρία Β Λυκείου Τράπεζα θεμάτων
 Γεωμετρία Β Λυκείου Τράπεζα θεμάτων www.askisopolis.gr η έκδοση 7 - - 05 Μεταβολές από την προηγούμενη έκδοση Προστέθηκαν 50 ασκήσεις Θεώρημα Θαλή.8975. Θεωρούμε τρίγωνο ΑΒΓ με AB 9 και 5. Από το βαρύκεντρο
Γεωμετρία Β Λυκείου Τράπεζα θεμάτων www.askisopolis.gr η έκδοση 7 - - 05 Μεταβολές από την προηγούμενη έκδοση Προστέθηκαν 50 ασκήσεις Θεώρημα Θαλή.8975. Θεωρούμε τρίγωνο ΑΒΓ με AB 9 και 5. Από το βαρύκεντρο
ΓΕΩΜΕΤΡΙΑ Β ΛΥΚΕΙΟΥ (ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ)
 ΩΜΤΡΙ ΛΥΚΙΟΥ (ΤΡΠΖ ΘΜΤΩΝ) GI_V_GEO_2_18975 ίνεται τρίγωνο AB με AB=9, A=15. πό το βαρύκεντρο φέρνουμε ευθεία παράλληλη στην πλευρά B που τέμνει τις AB,A στα,e αντίστοιχα. α) Να αποδείξετε ότι A = 2 AB
ΩΜΤΡΙ ΛΥΚΙΟΥ (ΤΡΠΖ ΘΜΤΩΝ) GI_V_GEO_2_18975 ίνεται τρίγωνο AB με AB=9, A=15. πό το βαρύκεντρο φέρνουμε ευθεία παράλληλη στην πλευρά B που τέμνει τις AB,A στα,e αντίστοιχα. α) Να αποδείξετε ότι A = 2 AB
Ασκήσεις για τις εξετάσεις Μάη Ιούνη στη Γεωμετρία Β Λυκείου του ΜΑΝΩΛΗ ΨΑΡΡΑ
 Ασκήσεις για τις εξετάσεις Μάη Ιούνη 014 στη Γεωμετρία Β Λυκείου του ΜΑΝΩΛΗ ΨΑΡΡΑ Άσκηση 1 η Δίνεται παραλληλόγραμμο ΑΒΓΔ και. Με διάμετρο τη διαγώνιο ΑΓ γράφουμε κύκλο με κέντρο Ο που τέμνει τη ΓΔ στο
Ασκήσεις για τις εξετάσεις Μάη Ιούνη 014 στη Γεωμετρία Β Λυκείου του ΜΑΝΩΛΗ ΨΑΡΡΑ Άσκηση 1 η Δίνεται παραλληλόγραμμο ΑΒΓΔ και. Με διάμετρο τη διαγώνιο ΑΓ γράφουμε κύκλο με κέντρο Ο που τέμνει τη ΓΔ στο
ΤΕΤΡΑΚΤΥΣ ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Αμυραδάκη 20, Νίκαια (210-4903576) ΝΟΕΜΒΡΙΟΣ 2013 ΤΑΞΗ... Β ΛΥΚΕΙΟΥ... ΜΑΘΗΜΑ...ΓΕΩΜΕΤΡΙΑΣ...
 Αμυραδάκη 0, Νίκαια (10-4903576) ΤΑΞΗ... Β ΛΥΚΕΙΟΥ... ΘΕΜΑ 1 ΝΟΕΜΒΡΙΟΣ 013 Α. Να αποδείξετε ότι σε κάθε ορθογώνιο τρίγωνο, το τετράγωνο του ύψους που αντιστοιχεί στην υποτείνουσα του ισούται με το γινόμενο
Αμυραδάκη 0, Νίκαια (10-4903576) ΤΑΞΗ... Β ΛΥΚΕΙΟΥ... ΘΕΜΑ 1 ΝΟΕΜΒΡΙΟΣ 013 Α. Να αποδείξετε ότι σε κάθε ορθογώνιο τρίγωνο, το τετράγωνο του ύψους που αντιστοιχεί στην υποτείνουσα του ισούται με το γινόμενο
ΓΕΩΜΕΤΡΙΑ - ΚΕΦΑΛΑΙΟ 4ο Το Θεώρημα του Θαλή και οι Συνέπειές του
 ΓΕΩΜΕΤΡΙΑ - ΚΕΦΑΛΑΙΟ 4ο Το Θεώρημα του Θαλή και οι Συνέπειές του 198 ΕΡΩΤΗΣΕΙΣ ΑΝΑΠΤΥΞΗΣ ΚΑΙ ΑΝΤΙΚΕΙΜΕΝΙΚΟΥ ΤΥΠΟΥ 1. Στο παρακάτω σχήμα το τρίγωνο ΑΒΓ είναι ορθογώνιο στο Α. Αν ΑΔ ΒΓ, ΕΔ ΑΒ τότε το τρίγωνο
ΓΕΩΜΕΤΡΙΑ - ΚΕΦΑΛΑΙΟ 4ο Το Θεώρημα του Θαλή και οι Συνέπειές του 198 ΕΡΩΤΗΣΕΙΣ ΑΝΑΠΤΥΞΗΣ ΚΑΙ ΑΝΤΙΚΕΙΜΕΝΙΚΟΥ ΤΥΠΟΥ 1. Στο παρακάτω σχήμα το τρίγωνο ΑΒΓ είναι ορθογώνιο στο Α. Αν ΑΔ ΒΓ, ΕΔ ΑΒ τότε το τρίγωνο
ΓΕΩΜΕΤΡΙΑ Β ΛΥΚΕΙΟΥ ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ
 Ο ΓΕΛ ΣΤΑΥΡΟΥΠΟΛΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 015-016 ΓΕΩΜΕΤΡΙΑ Β ΛΥΚΕΙΟΥ ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΕΠΙΜΕΛΕΙΑ ΧΑΛΑΤΖΙΑΝ ΠΑΥΛΟΣ ΚΕΦΑΛΑΙΟ 9 Ο : ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΟΡΘΕΣ ΠΡΟΒΟΛΕΣ Το τμήμα ΒΔ λέγεται προβολή του.. πάνω στην Το τμήμα
Ο ΓΕΛ ΣΤΑΥΡΟΥΠΟΛΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 015-016 ΓΕΩΜΕΤΡΙΑ Β ΛΥΚΕΙΟΥ ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΕΠΙΜΕΛΕΙΑ ΧΑΛΑΤΖΙΑΝ ΠΑΥΛΟΣ ΚΕΦΑΛΑΙΟ 9 Ο : ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΟΡΘΕΣ ΠΡΟΒΟΛΕΣ Το τμήμα ΒΔ λέγεται προβολή του.. πάνω στην Το τμήμα
ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ. ΓΕΩΜΕΤΡΙΑ Β ΛΥΚΕΙΟΥ Κεφάλαιο 9ο: Ερωτήσεις του τύπου «Σωστό-Λάθος»
 ΕΩΜΕΤΡΙΑ Β ΥΚΕΙΟΥ Κεφάλαιο 9ο: ΜΕΤΡΙΚΕ ΧΕΕΙ Ερωτήσεις του τύπου «ωστό-άθος» Να χαρακτηρίσετε με (σωστό) ή (λάθος) τις παρακάτω προτάσεις. 1. * Αν σε τρίγωνο ΑΒ ισχύει ΑΒ = Α + Β, τότε το τρίγωνο είναι:
ΕΩΜΕΤΡΙΑ Β ΥΚΕΙΟΥ Κεφάλαιο 9ο: ΜΕΤΡΙΚΕ ΧΕΕΙ Ερωτήσεις του τύπου «ωστό-άθος» Να χαρακτηρίσετε με (σωστό) ή (λάθος) τις παρακάτω προτάσεις. 1. * Αν σε τρίγωνο ΑΒ ισχύει ΑΒ = Α + Β, τότε το τρίγωνο είναι:
4 ΔΙΑΜΕΣΟΣ ΟΡΘΟΓΩΝΙΟΥ ΤΡΙΓΩΝΟΥ
 4 ΔΙΑΜΕΣΟΣ ΟΡΘΟΓΩΝΙΟΥ ΤΡΙΓΩΝΟΥ 1. Δίνεται ορθογώνιο και ισοσκελές τρίγωνο ΑΒΓ( ˆ =90 ο ) και ΑΔ η διχοτόμος της γωνίας A. Από το σημείο Δ φέρουμε παράλληλη προς την ΑΒ που τέμνει την πλευρά ΑΓ στο σημείο
4 ΔΙΑΜΕΣΟΣ ΟΡΘΟΓΩΝΙΟΥ ΤΡΙΓΩΝΟΥ 1. Δίνεται ορθογώνιο και ισοσκελές τρίγωνο ΑΒΓ( ˆ =90 ο ) και ΑΔ η διχοτόμος της γωνίας A. Από το σημείο Δ φέρουμε παράλληλη προς την ΑΒ που τέμνει την πλευρά ΑΓ στο σημείο
ΙΣΟΤΗΤΑ ΤΡΙΓΩΝΩΝ. 1. Καθεμιά από τις παρακάτω προτάσεις μπορεί να είναι σωστή ή λάθος Να γράψετε Σ στο
 ΙΣΟΤΗΤΑ ΤΡΙΓΩΝΩΝ. 1. Καθεμιά από τις παρακάτω προτάσεις μπορεί να είναι σωστή ή λάθος Να γράψετε Σ στο τέλος της πρότασης αν αυτή είναι Σωστή και Λ αν αυτή είναι Λάθος: ύο τρίγωνα είναι ίσα αν έχουν ίσες
ΙΣΟΤΗΤΑ ΤΡΙΓΩΝΩΝ. 1. Καθεμιά από τις παρακάτω προτάσεις μπορεί να είναι σωστή ή λάθος Να γράψετε Σ στο τέλος της πρότασης αν αυτή είναι Σωστή και Λ αν αυτή είναι Λάθος: ύο τρίγωνα είναι ίσα αν έχουν ίσες
ΚΕΦΑΛΑΙΟ 8 ο ΟΜΟΙΟΤΗΤΑ
 ΟΜΟΙΟΤΗΤΑ Ορισμός: Δύο ευθύγραμμα σχήματα ονομάζονται όμοια, αν έχουν τις πλευρές τους ανάλογες και τις γωνίες που σχηματίζονται από ομόλογες πλευρές τους ίσες μία προς μία. ΚΡΙΤΗΡΙΑ ΟΜΟΙΟΤΗΤΑΣ ΤΡΙΓΩΝΩΝ
ΟΜΟΙΟΤΗΤΑ Ορισμός: Δύο ευθύγραμμα σχήματα ονομάζονται όμοια, αν έχουν τις πλευρές τους ανάλογες και τις γωνίες που σχηματίζονται από ομόλογες πλευρές τους ίσες μία προς μία. ΚΡΙΤΗΡΙΑ ΟΜΟΙΟΤΗΤΑΣ ΤΡΙΓΩΝΩΝ
ΠΑΝΑΓΟΠΟΥΛΟΣ ΑΝΤΩΝΗΣ ΜΑΘΗΜΑΤΙΚΟΣ Β ΛΥΚΕΙΟΥ ΓΕΩΜΕΤΡΙΑ Σελίδα 1
 ΚΕΦΑΛΑΙΟ 11 Ο ΜΕΤΡΗΣΗ ΚΥΚΛΟΥ 11.6 ΠΡΟΣΕΓΓΙΣΗ ΤΟΥ ΕΜΒΑΔΟΥ ΚΥΚΛΟΥ ΜΕ ΚΑΝΟΝΙΚΑ ΠΟΛΥΓΩΝΑ 11.7 ΕΜΒΑΔΟΝ ΚΥΚΛΙΚΟΥ ΤΟΜΕΑ ΚΑΙ ΚΥΚΛΙΚΟΥ ΤΜΗΜΑΤΟΣ 11.8 ΤΕΤΡΑΓΩΝΙΣΜΟΣ ΚΥΚΛΟΥ ΘΕΩΡΙΑ 1 (Εμβαδόν κυκλικού δίσκου) Θεωρούμε
ΚΕΦΑΛΑΙΟ 11 Ο ΜΕΤΡΗΣΗ ΚΥΚΛΟΥ 11.6 ΠΡΟΣΕΓΓΙΣΗ ΤΟΥ ΕΜΒΑΔΟΥ ΚΥΚΛΟΥ ΜΕ ΚΑΝΟΝΙΚΑ ΠΟΛΥΓΩΝΑ 11.7 ΕΜΒΑΔΟΝ ΚΥΚΛΙΚΟΥ ΤΟΜΕΑ ΚΑΙ ΚΥΚΛΙΚΟΥ ΤΜΗΜΑΤΟΣ 11.8 ΤΕΤΡΑΓΩΝΙΣΜΟΣ ΚΥΚΛΟΥ ΘΕΩΡΙΑ 1 (Εμβαδόν κυκλικού δίσκου) Θεωρούμε
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΜΗΚΟΣ ΚΥΚΛΟΥ ΕΜΒΑΔΟΝ ΚΥΚΛΟΥ
 ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΜΗΚΟΣ ΚΥΚΛΟΥ ΕΜΒΑΔΟΝ ΚΥΚΛΟΥ ΘΕΩΡΙΑ : Μήκος κύκλου: L = Εμβαδόν κύκλου: Ε = ( όπου π = 3,14) Γνωρίζοντας ότι σε γωνία 360 0 αντιστοιχεί κύκλος με μήκος L και εμβαδόν Ε έχουμε : α) ημικύκλιο
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΜΗΚΟΣ ΚΥΚΛΟΥ ΕΜΒΑΔΟΝ ΚΥΚΛΟΥ ΘΕΩΡΙΑ : Μήκος κύκλου: L = Εμβαδόν κύκλου: Ε = ( όπου π = 3,14) Γνωρίζοντας ότι σε γωνία 360 0 αντιστοιχεί κύκλος με μήκος L και εμβαδόν Ε έχουμε : α) ημικύκλιο
Γεωμετρία Βˊ Λυκείου. Κεφάλαιο 9 ο. Μετρικές Σχέσεις
 Γεωμετρία Β Λυκείου Κεφάλαιο 9 Γεωμετρία Βˊ Λυκείου Κεφάλαιο 9 ο Μετρικές Σχέσεις ΚΕΦΑΛΑΙΟ 9 ο ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΣΕ ΟΡΘΟΓΩΝΙΑ ΤΡΙΓΩΝΑ Μετρικές σχέσεις ονομάζουμε τις σχέσεις μεταξύ των μέτρων των στοιχείων
Γεωμετρία Β Λυκείου Κεφάλαιο 9 Γεωμετρία Βˊ Λυκείου Κεφάλαιο 9 ο Μετρικές Σχέσεις ΚΕΦΑΛΑΙΟ 9 ο ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΣΕ ΟΡΘΟΓΩΝΙΑ ΤΡΙΓΩΝΑ Μετρικές σχέσεις ονομάζουμε τις σχέσεις μεταξύ των μέτρων των στοιχείων
Θέματα ενδοσχολικών εξετάσεων Γεωμετρίας Β Λυκείου Σχ. έτος , Ν. Δωδεκανήσου ΘΕΜΑΤΑ ΕΝΔΟΣΧΟΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ
 ΘΕΜΑΤΑ ΕΝΔΟΣΧΟΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΓΕΩΜΕΤΡΙΑ ΣΧΟΛΙΚΟ ΕΤΟΣ: 013-014 Επιμέλεια: Καραγιάννης Ιωάννης Σχολικός Σύμβουλος Μαθηματικών Μαθηματικός Περιηγητής 1 ΠΡΟΛΟΓΟΣ Η συλλογή των θεμάτων
ΘΕΜΑΤΑ ΕΝΔΟΣΧΟΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΓΕΩΜΕΤΡΙΑ ΣΧΟΛΙΚΟ ΕΤΟΣ: 013-014 Επιμέλεια: Καραγιάννης Ιωάννης Σχολικός Σύμβουλος Μαθηματικών Μαθηματικός Περιηγητής 1 ΠΡΟΛΟΓΟΣ Η συλλογή των θεμάτων
ΚΕΦΑΛΑΙΟ 9 ο ΓΕΝΙΚΕΥΣΗ ΠΥΘΑΓΟΡΕΙΟΥ ΘΕΩΡΗΜΑΤΟΣ
 ΓΕΝΙΚΕΥΣΗ ΠΥΘΑΓΟΡΕΙΟΥ ΘΕΩΡΗΜΑΤΟΣ Θεώρημα οξείας γωνίας Το τετράγωνο πλευράς τριγώνου, που βρίσκεται απέναντι από οξεία γωνία, είναι ίσο με το άθροισμα των τετραγώνων των δύο άλλων πλευρών του, ελαττωμένο
ΓΕΝΙΚΕΥΣΗ ΠΥΘΑΓΟΡΕΙΟΥ ΘΕΩΡΗΜΑΤΟΣ Θεώρημα οξείας γωνίας Το τετράγωνο πλευράς τριγώνου, που βρίσκεται απέναντι από οξεία γωνία, είναι ίσο με το άθροισμα των τετραγώνων των δύο άλλων πλευρών του, ελαττωμένο
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΘΕΩΡΗΤΙΚΗ ΓΕΩΜΕΤΡΙΑ
 ΓΕΩΜΕΤΡΙΑ Α ΛΥΚΕΙΟΥ ΘΕΩΡΙΑ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΘΕΩΡΗΤΙΚΗ ΓΕΩΜΕΤΡΙΑ ΟΡΙΣΜΟΙ Ευθύγραμμο τμήμα είναι το κομμάτι της ευθείας που έχει αρχή και τέλος. Ημιευθεια Είναι το κομμάτι της ευθείας που έχει αρχή αλλά όχι
ΓΕΩΜΕΤΡΙΑ Α ΛΥΚΕΙΟΥ ΘΕΩΡΙΑ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΘΕΩΡΗΤΙΚΗ ΓΕΩΜΕΤΡΙΑ ΟΡΙΣΜΟΙ Ευθύγραμμο τμήμα είναι το κομμάτι της ευθείας που έχει αρχή και τέλος. Ημιευθεια Είναι το κομμάτι της ευθείας που έχει αρχή αλλά όχι
ΑΒ ίνεται τραπέζιο ΑΒΓ (ΑΒ//Γ ) και σηµείο Μ της πλευράς του Α ώστε =. Από το
 1. ίνεται ισοσκελές τρίγωνο ΑΒΓ µε ΑΒ=ΑΓ, Â =36o και η διχοτόµος του Β. α) Να αποδείξετε ότι: i) Τα τρίγωνα Β Γ και ΑΒΓ είναι όµοια. ii) A 2 =ΑΓ Γ β) Αν θεωρήσουµε το ΑΓ ως µοναδιαίο τµήµα (ΑΓ=1), να υπολογίσετε
1. ίνεται ισοσκελές τρίγωνο ΑΒΓ µε ΑΒ=ΑΓ, Â =36o και η διχοτόµος του Β. α) Να αποδείξετε ότι: i) Τα τρίγωνα Β Γ και ΑΒΓ είναι όµοια. ii) A 2 =ΑΓ Γ β) Αν θεωρήσουµε το ΑΓ ως µοναδιαίο τµήµα (ΑΓ=1), να υπολογίσετε
1 ο Αχαρνών 197 Αγ. Νικόλαος 210.8651962. 2 ο Αγγ. Σικελιανού 43 Περισσός 210.2718688
 1 ο Αχαρνών 197 Αγ. Νικόλαος 10.865196 ο Αγγ. Σικελιανού 4 Περισσός 10.718688 AΣΚΗΣΕΙΣ ΓΕΩΜΕΤΡΙΑΣ Β ΛΥΚΕΙΟΥ 1. Θεωρούμε ορθογώνιο τρίγωνο ΑΒΓ (Α =90Ο ) και Α το ύψος του. Αν Ε και Ζ είναι οι προβολές του
1 ο Αχαρνών 197 Αγ. Νικόλαος 10.865196 ο Αγγ. Σικελιανού 4 Περισσός 10.718688 AΣΚΗΣΕΙΣ ΓΕΩΜΕΤΡΙΑΣ Β ΛΥΚΕΙΟΥ 1. Θεωρούμε ορθογώνιο τρίγωνο ΑΒΓ (Α =90Ο ) και Α το ύψος του. Αν Ε και Ζ είναι οι προβολές του
ΑΣΚΗΣΕΙΣ ΓΕΩΜΕΤΡΙΑΣ Β ΛΥΚΕΙΟΥ
 ΑΣΚΗΣΕΙΣ ΓΕΩΜΕΤΡΙΑΣ Β ΛΥΚΕΙΟΥ 1. Να επιλέξετε μια απάντηση για κάθε ερώτηση και να δικαιολογήσετε σύντομα την απάντησή σας. i. Αν η εξωτερική γωνία ενός κανονικού ν-γώνου ισούται με 0 ο, τότε το ν ισούται
ΑΣΚΗΣΕΙΣ ΓΕΩΜΕΤΡΙΑΣ Β ΛΥΚΕΙΟΥ 1. Να επιλέξετε μια απάντηση για κάθε ερώτηση και να δικαιολογήσετε σύντομα την απάντησή σας. i. Αν η εξωτερική γωνία ενός κανονικού ν-γώνου ισούται με 0 ο, τότε το ν ισούται
ΜΕΤΡΗΣΗ ΚΥΚΛΟΥ ΘΕΜΑΤΑ ΓΙΑ ΕΡΓΑΣΙΑ
 ΜΕΤΡΗΣΗ ΚΥΚΛΟΥ ΘΕΜΑΤΑ ΓΙΑ ΕΡΓΑΣΙΑ 1) Ο λόγος των μηκών δύο κύκλων ( Ο, ρ ) και ( Ο, ρ ) είναι 1 3. Αν ρ = 1,15 cm να βρείτε : Την ακτίνα ρ. Το μήκος του ( Ο, ρ ) Το λόγο των διαμέτρων τους. 2) Οι περίμετροι
ΜΕΤΡΗΣΗ ΚΥΚΛΟΥ ΘΕΜΑΤΑ ΓΙΑ ΕΡΓΑΣΙΑ 1) Ο λόγος των μηκών δύο κύκλων ( Ο, ρ ) και ( Ο, ρ ) είναι 1 3. Αν ρ = 1,15 cm να βρείτε : Την ακτίνα ρ. Το μήκος του ( Ο, ρ ) Το λόγο των διαμέτρων τους. 2) Οι περίμετροι
Ερωτήσεις τύπου «Σωστό - Λάθος» Σωστό Λάθος
 Εγγράψιμα και περιγράψιμα τετράπλευρα Ερωτήσεις τύπου «Σωστό - Λάθος» Σωστό Λάθος 1. Ένα τετράπλευρο είναι εγγράψιμο σε κύκλο αν είναι παραλληλόγραμμο.. Ένα τετράπλευρο είναι εγγράψιμο σε κύκλο αν είναι
Εγγράψιμα και περιγράψιμα τετράπλευρα Ερωτήσεις τύπου «Σωστό - Λάθος» Σωστό Λάθος 1. Ένα τετράπλευρο είναι εγγράψιμο σε κύκλο αν είναι παραλληλόγραμμο.. Ένα τετράπλευρο είναι εγγράψιμο σε κύκλο αν είναι
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ - ΓΕΩΜΕΤΡΙΑΣ Α ΛΥΚΕΙΟΥ
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ - ΓΕΩΜΕΤΡΙΑΣ Α ΛΥΚΕΙΟΥ ΘΕΜΑ 1 Ο - Α ( απόδειξη θεωρήματος) 1 ) Να αποδειχθεί ότι : «Οι διαγώνιοι ορθογωνίου είναι ίσες». ( 5.3 σελ 100 ) 2 ) Να αποδειχθεί ότι τα εφαπτόμενα τμήματα κύκλου
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ - ΓΕΩΜΕΤΡΙΑΣ Α ΛΥΚΕΙΟΥ ΘΕΜΑ 1 Ο - Α ( απόδειξη θεωρήματος) 1 ) Να αποδειχθεί ότι : «Οι διαγώνιοι ορθογωνίου είναι ίσες». ( 5.3 σελ 100 ) 2 ) Να αποδειχθεί ότι τα εφαπτόμενα τμήματα κύκλου
1 ΘΕΜΑΤΑ ΓΡΑΠΤΩΝ ΠΡΟΑΓΩΓΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΓΕΩΜΕΤΡΙΑ Β ΛΥΚΕΙΟΥ
 1 ΘΕΜΑΤΑ ΓΡΑΠΤΩΝ ΠΡΟΑΓΩΓΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΓΕΩΜΕΤΡΙΑ Β ΛΥΚΕΙΟΥ α). Να αποδείξετε ότι : Σε κάθε ορθογώνιο τρίγωνο το τετράγωνο του ύψους που αντιστοιχεί στην υποτείνουσα ισούται με το γινόμενο των προβολών
1 ΘΕΜΑΤΑ ΓΡΑΠΤΩΝ ΠΡΟΑΓΩΓΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΓΕΩΜΕΤΡΙΑ Β ΛΥΚΕΙΟΥ α). Να αποδείξετε ότι : Σε κάθε ορθογώνιο τρίγωνο το τετράγωνο του ύψους που αντιστοιχεί στην υποτείνουσα ισούται με το γινόμενο των προβολών
5o ΚΕΦΑΛΑΙΟ : Παραλληλόγραμμα - Τραπέζια
 5o ΚΕΦΑΛΑΙΟ : Παραλληλόγραμμα - Τραπέζια 7 η διδακτική ενότητα : Παραλληλόγραμμα-Είδη παραλληλογράμμων 1. Να εξετάσετε αν είναι σωστή ή λανθασμένη καθεμιά από τις επόμενες προτάσεις: α) Οι διαγώνιοι κάθε
5o ΚΕΦΑΛΑΙΟ : Παραλληλόγραμμα - Τραπέζια 7 η διδακτική ενότητα : Παραλληλόγραμμα-Είδη παραλληλογράμμων 1. Να εξετάσετε αν είναι σωστή ή λανθασμένη καθεμιά από τις επόμενες προτάσεις: α) Οι διαγώνιοι κάθε
A λ υ τ ε ς Α σ κ η σ ε ι ς ( Τ ρ ι γ ω ν α )
 A λ υ τ ε ς Α σ κ η σ ε ι ς ( Τ ρ ι γ ω ν α ) 1 Στις πλευρες ΑΒ, ΒΓ, ΓΑ ισοπλευρου τριγωνου ΑΒΓ, παιρνουμε 3 Να δειχτει οτι α + 110 0α Ποτε ισχυει Συγκρινετε το ισον; τα τριγωνα με σημεια Δ, Ε, Ζ αντιστοιχα,
A λ υ τ ε ς Α σ κ η σ ε ι ς ( Τ ρ ι γ ω ν α ) 1 Στις πλευρες ΑΒ, ΒΓ, ΓΑ ισοπλευρου τριγωνου ΑΒΓ, παιρνουμε 3 Να δειχτει οτι α + 110 0α Ποτε ισχυει Συγκρινετε το ισον; τα τριγωνα με σημεια Δ, Ε, Ζ αντιστοιχα,
ΚΕΦΑΛΑΙΟ 9 ο ΘΕΩΡΗΜΑΤΑ ΔΙΑΜΕΣΩΝ
 1 ο Θεώρημα διαμέσου ΘΕΩΡΗΜΑΤΑ ΔΙΑΜΕΣΩΝ Σε κάθε τρίγωνο, το άθροισμα των τετραγώνων δύο πλευρών τριγώνου ισούται με το διπλάσιο του τετραγώνου της περιεχόμενης διαμέσου, αυξημένο κατά το μισό του τετραγώνου
1 ο Θεώρημα διαμέσου ΘΕΩΡΗΜΑΤΑ ΔΙΑΜΕΣΩΝ Σε κάθε τρίγωνο, το άθροισμα των τετραγώνων δύο πλευρών τριγώνου ισούται με το διπλάσιο του τετραγώνου της περιεχόμενης διαμέσου, αυξημένο κατά το μισό του τετραγώνου
Επαναληπτικό Διαγώνισµα Γεωµετρίας Β Λυκείου
 Επαναληπτικό Διαγώνισµα Γεωµετρίας Β Λυκείου Θέµα 1 Α. Να υπολογίσετε την πλευρά λ και το απόστηµα α τετραγώνου εγγεγραµµένου σε κύκλο (Ο, R) συναρτήσει της ακτίνας R (10 Μονάδες) Β. Να χαρακτηρίσετε τις
Επαναληπτικό Διαγώνισµα Γεωµετρίας Β Λυκείου Θέµα 1 Α. Να υπολογίσετε την πλευρά λ και το απόστηµα α τετραγώνου εγγεγραµµένου σε κύκλο (Ο, R) συναρτήσει της ακτίνας R (10 Μονάδες) Β. Να χαρακτηρίσετε τις
 ΚΕΦΑΛΑΙΟ 1 ο ΠΡΩΤΑΡΧΙΚΕΣ ΓΕΩΜΕΤΡΙΚΕΣ ΕΝΝΟΙΕΣ Τα αξιώματα είναι προτάσεις που δεχόμαστε ως αληθείς, χωρίς απόδειξη: Από δύο σημεία διέρχεται μοναδική ευθεία. Για κάθε ευθεία υπάρχει τουλάχιστον ένα σημείο
ΚΕΦΑΛΑΙΟ 1 ο ΠΡΩΤΑΡΧΙΚΕΣ ΓΕΩΜΕΤΡΙΚΕΣ ΕΝΝΟΙΕΣ Τα αξιώματα είναι προτάσεις που δεχόμαστε ως αληθείς, χωρίς απόδειξη: Από δύο σημεία διέρχεται μοναδική ευθεία. Για κάθε ευθεία υπάρχει τουλάχιστον ένα σημείο
ΚΕΦΑΛΑΙΟ 7 ο ΑΝΑΛΟΓΙΕΣ
 ΑΝΑΛΟΓΙΕΣ ΘΕΩΡΗΜΑ ΤΟΥ ΘΑΛΗ Βασικά θεωρήματα Αν τρεις τουλάχιστον παράλληλες ευθείες τέμνουν δύο άλλες ευθείες, ορίζουν σε αυτές τμήματα ανάλογα. (αντίστροφο Θεωρήματος Θαλή) Θεωρούμε δύο ευθείες δ και
ΑΝΑΛΟΓΙΕΣ ΘΕΩΡΗΜΑ ΤΟΥ ΘΑΛΗ Βασικά θεωρήματα Αν τρεις τουλάχιστον παράλληλες ευθείες τέμνουν δύο άλλες ευθείες, ορίζουν σε αυτές τμήματα ανάλογα. (αντίστροφο Θεωρήματος Θαλή) Θεωρούμε δύο ευθείες δ και
ΚΕΦΑΛΑΙΟ 11 Ο ΜΕΤΡΗΣΗ ΚΥΚΛΟΥ 11.3 ΕΓΓΡΑΦΗ ΒΑΣΙΚΩΝ ΚΑΝΟΝΙΚΩΝ ΠΟΛΥΓΩΝΩΝ ΣΕ ΚΥΚΛΟ ΚΑΙ ΤΑ ΣΤΟΙΧΕΙΑ ΤΟΥΣ
 ΚΕΦΑΛΑΙΟ 11 Ο ΜΕΤΡΗΣΗ ΚΥΚΛΟΥ 113 ΕΓΓΡΑΦΗ ΒΑΣΙΚΩΝ ΚΑΝΟΝΙΚΩΝ ΠΟΛΥΓΩΝΩΝ ΣΕ ΚΥΚΛΟ ΚΑΙ ΤΑ ΣΤΟΙΧΕΙΑ ΤΟΥΣ ΘΕΩΡΙΑ Θα ασχοληθούμε με την εγγραφή μερικών βασικών κανονικών πολυγώνων σε κύκλο και θα υπολογίσουμε
ΚΕΦΑΛΑΙΟ 11 Ο ΜΕΤΡΗΣΗ ΚΥΚΛΟΥ 113 ΕΓΓΡΑΦΗ ΒΑΣΙΚΩΝ ΚΑΝΟΝΙΚΩΝ ΠΟΛΥΓΩΝΩΝ ΣΕ ΚΥΚΛΟ ΚΑΙ ΤΑ ΣΤΟΙΧΕΙΑ ΤΟΥΣ ΘΕΩΡΙΑ Θα ασχοληθούμε με την εγγραφή μερικών βασικών κανονικών πολυγώνων σε κύκλο και θα υπολογίσουμε
Απαντήσεις Λύσεις σε Θέματα από την Τράπεζα Θεμάτων. Μάθημα: Γεωμετρία Α Λυκείου
 Απαντήσεις Λύσεις σε Θέματα από την Τράπεζα Θεμάτων Μάθημα: Γεωμετρία Α Λυκείου Παρουσιάζουμε συνοπτικές λύσεις σε επιλεγμένα Θέματα («Θέμα 4 ο») από την Τράπεζα θεμάτων. Το αρχείο αυτό τις επόμενες ημέρες
Απαντήσεις Λύσεις σε Θέματα από την Τράπεζα Θεμάτων Μάθημα: Γεωμετρία Α Λυκείου Παρουσιάζουμε συνοπτικές λύσεις σε επιλεγμένα Θέματα («Θέμα 4 ο») από την Τράπεζα θεμάτων. Το αρχείο αυτό τις επόμενες ημέρες
Ασκήσεις - Πυθαγόρειο Θεώρηµα
 Ασκήσεις - Πυθαγόρειο Θεώρηµα. Έστω ορθογώνιο τρίγωνο ΑΒΓ ( Â = 90 ο ) µε ΒΓ = 0 και ΑΓ =. Αν το µέσο της ΒΓ και Ε ΒΓ (Ε σηµείο της ΑΒ) τότε το µήκος της ΑΕ είναι: i) 3 3,5 i 4 iv) 4,5 v) 5. Έστω ορθογώνιο
Ασκήσεις - Πυθαγόρειο Θεώρηµα. Έστω ορθογώνιο τρίγωνο ΑΒΓ ( Â = 90 ο ) µε ΒΓ = 0 και ΑΓ =. Αν το µέσο της ΒΓ και Ε ΒΓ (Ε σηµείο της ΑΒ) τότε το µήκος της ΑΕ είναι: i) 3 3,5 i 4 iv) 4,5 v) 5. Έστω ορθογώνιο
1. ** Σε ισοσκελές τρίγωνο ΑΒΓ µε κορυφή το Α, έχουµε ΒΓ = 4 cm και ΑΒ = 7 cm. Να υπολογίσετε: ii. Το ύψος ΒΚ
 Ερωτήσεις ανάπτυξης 1. ** Σε ισοσκελές τρίγωνο ΑΒΓ µε κορυφή το Α, έχουµε ΒΓ = 4 cm και ΑΒ = 7 cm. Να υπολογίσετε: i. Το ύψος ΑΗ ii. Το ύψος ΒΚ. ** Σε ένα τετράγωνο ΑΒΓ ισχύει ΑΒ + ΑΓ = +. Να υπολογίσετε:
Ερωτήσεις ανάπτυξης 1. ** Σε ισοσκελές τρίγωνο ΑΒΓ µε κορυφή το Α, έχουµε ΒΓ = 4 cm και ΑΒ = 7 cm. Να υπολογίσετε: i. Το ύψος ΑΗ ii. Το ύψος ΒΚ. ** Σε ένα τετράγωνο ΑΒΓ ισχύει ΑΒ + ΑΓ = +. Να υπολογίσετε:
ΕΠΑΝΑΛΗΨΗ ΓΕΩΜΕΤΡΙΑΣ Β ΛΥΚΕΙΟΥ
 ΕΠΝΛΗΨΗ ΕΩΜΕΤΡΙΣ ΛΥΚΕΙΟΥ 1 Σε τρίγωνο με > και ορθόκεντρο Η να δείξετε ότι: Δίνεται τρίγωνο στο οποίο ισχύει: α β γ βγ Να δείξετε ότι: A 10 Δίνεται τρίγωνο με πλευρές α, β, γ και διάμεσο μα ν ισχύει η
ΕΠΝΛΗΨΗ ΕΩΜΕΤΡΙΣ ΛΥΚΕΙΟΥ 1 Σε τρίγωνο με > και ορθόκεντρο Η να δείξετε ότι: Δίνεται τρίγωνο στο οποίο ισχύει: α β γ βγ Να δείξετε ότι: A 10 Δίνεται τρίγωνο με πλευρές α, β, γ και διάμεσο μα ν ισχύει η
Θέματα ενδοσχολικών εξετάσεων Άλγεβρας Α Λυκείου Σχ. έτος , Ν. Δωδεκανήσου ΘΕΜΑΤΑ ΕΝΔΟΣΧΟΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΤΑΞΗ: Α ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ
 ΘΕΜΑΤΑ ΕΝΔΟΣΧΟΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΤΑΞΗ: Α ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΓΕΩΜΕΤΡΙΑ ΣΧΟΛΙΚΟ ΕΤΟΣ: 2013-2014 Επιμέλεια: Καραγιάννης Ιωάννης Σχολικός Σύμβουλος Μαθηματικών Μαθηματικός Περιηγητής 1 ΠΡΟΛΟΓΟΣ Η συλλογή των θεμάτων
ΘΕΜΑΤΑ ΕΝΔΟΣΧΟΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΤΑΞΗ: Α ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΓΕΩΜΕΤΡΙΑ ΣΧΟΛΙΚΟ ΕΤΟΣ: 2013-2014 Επιμέλεια: Καραγιάννης Ιωάννης Σχολικός Σύμβουλος Μαθηματικών Μαθηματικός Περιηγητής 1 ΠΡΟΛΟΓΟΣ Η συλλογή των θεμάτων
Οι γωνίες και που ονομάζονται «εντός εναλλάξ γωνίες» και είναι ίσες. «εντός-εκτός και επί τα αυτά μέρη γωνίες» και είναι ίσες.
 ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΑΝΑΒΡΥΤΩΝ ΜΑΘΗΜΑΤΑ ΓΙΑ ΤΟΝ ΔΙΑΓΩΝΙΣΜΟ «ΘΑΛΗΣ» ΤΑΞΗ Α ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΓΕΩΜΕΤΡΙΑ ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ 1. Μεσοκάθετος ενός ευθύγραμμου τμήματος ΑΒ ονομάζεται η ευθεία που είναι κάθετη
ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΑΝΑΒΡΥΤΩΝ ΜΑΘΗΜΑΤΑ ΓΙΑ ΤΟΝ ΔΙΑΓΩΝΙΣΜΟ «ΘΑΛΗΣ» ΤΑΞΗ Α ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΓΕΩΜΕΤΡΙΑ ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ 1. Μεσοκάθετος ενός ευθύγραμμου τμήματος ΑΒ ονομάζεται η ευθεία που είναι κάθετη
Γεωμετρία Β Λυκείου ΚΕΦΑΛΑΙΟ 8: ΟΜΟΙΟΤΗΤΑ
 ΚΕΦΑΛΑΙΟ 8: ΟΜΟΙΟΤΗΤΑ 36 ΚΕΦΑΛΑΙΟ 9: ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ 37 ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΣΕ ΤΥΧΑΙΟ ΤΡΙΓΩΝΟ 38 39 40 41 ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΣΕ ΚΥΚΛΟ 4 43 44 ΚΕΦΑΛΑΙΟ 10:ΕΜΒΑΔΑ ΕΠΙΠΕΔΩΝ ΣΧΗΜΑΤΩΝ 45 46 47 48 49 50 51 5 53
ΚΕΦΑΛΑΙΟ 8: ΟΜΟΙΟΤΗΤΑ 36 ΚΕΦΑΛΑΙΟ 9: ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ 37 ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΣΕ ΤΥΧΑΙΟ ΤΡΙΓΩΝΟ 38 39 40 41 ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΣΕ ΚΥΚΛΟ 4 43 44 ΚΕΦΑΛΑΙΟ 10:ΕΜΒΑΔΑ ΕΠΙΠΕΔΩΝ ΣΧΗΜΑΤΩΝ 45 46 47 48 49 50 51 5 53
ΘΕΜΑΤΑ. β. ΜΗΔ = 45 Μονάδες 5. Θέμα 4 ο Δίνεται ορθογώνιο τρίγωνο ΑΒΓ ( Α = 90 ) με ΑΓ > ΑΒ, η διάμεσός του ΑΖ και έστω Δ και
 Α. Να χαρακτηρίσετε Σωστές (Σ) ή Λάθος (Λ) τις παρακάτω προτάσεις: α. Οι διχοτόμοι δύο διαδοχικών και παραπληρωματικών γωνιών σχηματίζουν ορθή γωνία. β. Οι διαγώνιες κάθε παραλληλογράμμου είναι ίσες μεταξύ
Α. Να χαρακτηρίσετε Σωστές (Σ) ή Λάθος (Λ) τις παρακάτω προτάσεις: α. Οι διχοτόμοι δύο διαδοχικών και παραπληρωματικών γωνιών σχηματίζουν ορθή γωνία. β. Οι διαγώνιες κάθε παραλληλογράμμου είναι ίσες μεταξύ
 Κεφάλαιο 6 Παράλληλες Ευθείες και Τετράπλευρα Ορισμός. Δύο ευθείες ονομάζονται παράλληλες όταν ανήκουν στο ίδιο επίπεδο και δεν τέμνονται. Δύο παράλληλες ευθείες ε και ζ συμβολίζονται ε ζ. Γωνίες δύο ευθειών
Κεφάλαιο 6 Παράλληλες Ευθείες και Τετράπλευρα Ορισμός. Δύο ευθείες ονομάζονται παράλληλες όταν ανήκουν στο ίδιο επίπεδο και δεν τέμνονται. Δύο παράλληλες ευθείες ε και ζ συμβολίζονται ε ζ. Γωνίες δύο ευθειών
µ =. µονάδες 12+13=25
 ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΣΤΗ ΓΕΩΜΕΤΡΙΑ ΤΗΣ Β 1 ΓΕΝΙΚΗ ΑΣΚΗΣΗ 1. ίνεται τρίγωνο ΑΒΓ µε α=7, β=5, γ=4. Να βρείτε: 1. το είδος του τριγώνου. την προβολή της β πάνω στη γ 3. το µήκος της διαµέσου ΒΜ 4. την προβολή
ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΣΤΗ ΓΕΩΜΕΤΡΙΑ ΤΗΣ Β 1 ΓΕΝΙΚΗ ΑΣΚΗΣΗ 1. ίνεται τρίγωνο ΑΒΓ µε α=7, β=5, γ=4. Να βρείτε: 1. το είδος του τριγώνου. την προβολή της β πάνω στη γ 3. το µήκος της διαµέσου ΒΜ 4. την προβολή
ΚΕΦΑΛΑΙΟ 10 Ο ΕΜΒΑΔΑ 10.5 ΛΟΓΟΣ ΕΜΒΑΔΩΝ ΟΜΟΙΩΝ ΤΡΙΓΩΝΩΝ - ΠΟΛΥΓΩΝΩΝ 10.6 ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ ΠΟΛΥΓΩΝΟΥ ΣΕ ΙΣΟΔΥΝΑΜΟ ΤΟΥ
 ΚΕΦΑΛΑΙΟ 0 Ο ΕΜΒΑΔΑ 0.5 ΛΟΓΟΣ ΕΜΒΑΔΩΝ ΟΜΟΙΩΝ ΤΡΙΓΩΝΩΝ - ΠΟΛΥΓΩΝΩΝ 0.6 ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ ΠΟΛΥΓΩΝΟΥ ΣΕ ΙΣΟΔΥΝΑΜΟ ΤΟΥ ΘΕΩΡΙΑ Αν θεωρήσουμε δύο τρίγωνα ΑΒΓ και Α Β Γ με εμβαδά Ε και Ε αντίστοιχα. Τότε είναι:
ΚΕΦΑΛΑΙΟ 0 Ο ΕΜΒΑΔΑ 0.5 ΛΟΓΟΣ ΕΜΒΑΔΩΝ ΟΜΟΙΩΝ ΤΡΙΓΩΝΩΝ - ΠΟΛΥΓΩΝΩΝ 0.6 ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ ΠΟΛΥΓΩΝΟΥ ΣΕ ΙΣΟΔΥΝΑΜΟ ΤΟΥ ΘΕΩΡΙΑ Αν θεωρήσουμε δύο τρίγωνα ΑΒΓ και Α Β Γ με εμβαδά Ε και Ε αντίστοιχα. Τότε είναι:
Γεωμετρία Β Λυκείου Θεωρήματα διχοτόμων Αρμονικά συζυγή Ομοιότητα τριγώνων.
 Γεωμετρία Β Λυκείου Θεωρήματα διχοτόμων Αρμονικά συζυγή Ομοιότητα τριγώνων. Καρδαμίτσης Σπύρος «Τὰ ὅμοια πολύγωνα εἴς τε ὅμοια τρίγωνα διαιρεῖται καὶ εἰς ἴσα τὸ πλῆθος καὶ ὁμόλογα τοῖς ὅλοις, καὶ τὸ πολύγωνον
Γεωμετρία Β Λυκείου Θεωρήματα διχοτόμων Αρμονικά συζυγή Ομοιότητα τριγώνων. Καρδαμίτσης Σπύρος «Τὰ ὅμοια πολύγωνα εἴς τε ὅμοια τρίγωνα διαιρεῖται καὶ εἰς ἴσα τὸ πλῆθος καὶ ὁμόλογα τοῖς ὅλοις, καὶ τὸ πολύγωνον
ΕΠΑΝΑΛΗΨΗ ΓΕΩΜΕΤΡΙΑΣ Α ΛΥΚΕΙΟΥ ( α μέρος )
 Πυθαγόρειο ενικό Λύκειο Σάμου ΕΠΝΛΗΨΗ ΕΩΜΕΤΡΙΣ ΛΥΚΕΙΟΥ ( α μέρος ) Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε στο τετράδιό
Πυθαγόρειο ενικό Λύκειο Σάμου ΕΠΝΛΗΨΗ ΕΩΜΕΤΡΙΣ ΛΥΚΕΙΟΥ ( α μέρος ) Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε στο τετράδιό
ΘΕΜΑΤΑ ΠΡΟΑΓΩΓΙΚΩΝ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ ΜΑΪΟΣ ΙΟΥΝΙΟΣ
 ΘΕΜΑΤΑ ΠΡΟΑΓΩΓΙΚΩΝ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ ΜΑΪΟΣ ΙΟΥΝΙΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: A ΓΕΩΜΕΤΡΙΑ ΘΕΜΑ Α Α1. Να αποδείξετε ότι σε κάθε ορθογώνιο τρίγωνο η διάμεσος που αντιστοιχεί στην υποτείνουσα ισούται με το μισό της.
ΘΕΜΑΤΑ ΠΡΟΑΓΩΓΙΚΩΝ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ ΜΑΪΟΣ ΙΟΥΝΙΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: A ΓΕΩΜΕΤΡΙΑ ΘΕΜΑ Α Α1. Να αποδείξετε ότι σε κάθε ορθογώνιο τρίγωνο η διάμεσος που αντιστοιχεί στην υποτείνουσα ισούται με το μισό της.
ΚΕΦΑΛΑΙΟ 10 Ο ΕΜΒΑΔΑ 10.1 ΠΟΛΥΓΩΝΙΚΑ ΧΩΡΙΑ 10.2 ΕΜΒΑΔΟΝ ΕΥΘΥΓΡΑΜ. ΣΧΗΜ. ΙΣΟΔΥΝΑΜΑ ΕΥΘΥΓΡΑΜ. ΣΧΗΜ. 10.3 ΕΜΒΑΔΟΝ ΒΑΣΙΚΩΝ ΕΥΘΥΓΡΑΜΜΩΝ ΣΧΗΜΑΤΩΝ
 ΚΕΦΑΛΑΙΟ 0 Ο ΕΜΒΑΔΑ 0. ΠΟΛΥΓΩΝΙΚΑ ΧΩΡΙΑ 0. ΕΜΒΑΔΟΝ ΕΥΘΥΓΡΑΜ. ΣΧΗΜ. ΙΣΟΔΥΝΑΜΑ ΕΥΘΥΓΡΑΜ. ΣΧΗΜ. 0.3 ΕΜΒΑΔΟΝ ΒΑΣΙΚΩΝ ΕΥΘΥΓΡΑΜΜΩΝ ΣΧΗΜΑΤΩΝ ΘΕΩΡΙΑ (Πολυγωνικά χωρία) Ας θεωρήσουμε ένα πολύγωνο, για παράδειγμα
ΚΕΦΑΛΑΙΟ 0 Ο ΕΜΒΑΔΑ 0. ΠΟΛΥΓΩΝΙΚΑ ΧΩΡΙΑ 0. ΕΜΒΑΔΟΝ ΕΥΘΥΓΡΑΜ. ΣΧΗΜ. ΙΣΟΔΥΝΑΜΑ ΕΥΘΥΓΡΑΜ. ΣΧΗΜ. 0.3 ΕΜΒΑΔΟΝ ΒΑΣΙΚΩΝ ΕΥΘΥΓΡΑΜΜΩΝ ΣΧΗΜΑΤΩΝ ΘΕΩΡΙΑ (Πολυγωνικά χωρία) Ας θεωρήσουμε ένα πολύγωνο, για παράδειγμα
Βασικές Γεωμετρικές έννοιες
 Βασικές Γεωμετρικές έννοιες Σημείο Με την άκρη του μολυβιού μου ακουμπώντας την σε ένα κομμάτι χαρτί αφήνω ένα σημάδι το οποίο το λέω σημείο. Το σημείο το δίνω όνομα γράφοντας πάνω απ αυτό ένα κεφαλαίο
Βασικές Γεωμετρικές έννοιες Σημείο Με την άκρη του μολυβιού μου ακουμπώντας την σε ένα κομμάτι χαρτί αφήνω ένα σημάδι το οποίο το λέω σημείο. Το σημείο το δίνω όνομα γράφοντας πάνω απ αυτό ένα κεφαλαίο
Επαναληπτικό Διαγώνισμα Γεωμετρίας Α Λυκείου
 Επαναληπτικό Διαγώνισμα Γεωμετρίας Α Λυκείου Θέμα Α. Να αποδείξετε ότι το ευθύγραμμο τμήμα που ενώνει τα μέσα των δύο πλευρών τριγώνου, είναι παράλληλο προς την τρίτη πλευρά και ίσο με το μισό της (7 μονάδες)
Επαναληπτικό Διαγώνισμα Γεωμετρίας Α Λυκείου Θέμα Α. Να αποδείξετε ότι το ευθύγραμμο τμήμα που ενώνει τα μέσα των δύο πλευρών τριγώνου, είναι παράλληλο προς την τρίτη πλευρά και ίσο με το μισό της (7 μονάδες)
Αναλογίες. ΘΕΜΑ 2ο. (Μονάδες 5) β) Να υπολογίσετε το ΓΒ συναρτήσει του κ. (Μονάδες 5) ΑΒ από το σημείο Γ ; (Μονάδες 15)
 Αναλογίες 2_20863. Στο παρακάτω σχήμα είναι 12 και 8. α) Να υπολογίσετε τους λόγους και. (Μονάδες 6) β) Να υπολογίσετε το ΑΓ συναρτήσει του κ. (Μονάδες 5) γ) Να υπολογίσετε τον λόγο. Σε τι λόγο λ διαιρείται
Αναλογίες 2_20863. Στο παρακάτω σχήμα είναι 12 και 8. α) Να υπολογίσετε τους λόγους και. (Μονάδες 6) β) Να υπολογίσετε το ΑΓ συναρτήσει του κ. (Μονάδες 5) γ) Να υπολογίσετε τον λόγο. Σε τι λόγο λ διαιρείται
ΑΣΚΗΣΕΙΣ 3 Ο ΚΕΦΑΛΑΙΟ
 ΑΣΚΗΣΕΙΣ 3 Ο ΚΕΦΑΛΑΙΟ 1) Από εξωτερικό σημείο Ρ ενός κύκλου (Ο,ρ) φέρνουμε τα εφαπτόμενα τμήματα ΡΑ και ΡΒ. Αν Μ είναι ένα τυχαίο εσωτερικό σημείο του ευθύγραμμου τμήματος ΟΡ, να αποδείξετε ότι: α) τα
ΑΣΚΗΣΕΙΣ 3 Ο ΚΕΦΑΛΑΙΟ 1) Από εξωτερικό σημείο Ρ ενός κύκλου (Ο,ρ) φέρνουμε τα εφαπτόμενα τμήματα ΡΑ και ΡΒ. Αν Μ είναι ένα τυχαίο εσωτερικό σημείο του ευθύγραμμου τμήματος ΟΡ, να αποδείξετε ότι: α) τα
ΚΕΦΑΛΑΙΟ 10 Ο ΕΜΒΑΔΑ 10.1 ΠΟΛΥΓΩΝΙΚΑ ΧΩΡΙΑ 10.2 ΕΜΒΑΔΟΝ ΕΥΘΥΓΡΑΜ. ΣΧΗΜ. ΙΣΟΔΥΝΑΜΑ ΕΥΘΥΓΡΑΜ. ΣΧΗΜ ΕΜΒΑΔΟΝ ΒΑΣΙΚΩΝ ΕΥΘΥΓΡΑΜΜΩΝ ΣΧΗΜΑΤΩΝ
 ΚΕΦΑΛΑΙΟ 10 Ο ΕΜΒΑΔΑ 10.1 ΠΟΛΥΓΩΝΙΚΑ ΧΩΡΙΑ 10. ΕΜΒΑΔΟΝ ΕΥΘΥΓΡΑΜ. ΣΧΗΜ. ΙΣΟΔΥΝΑΜΑ ΕΥΘΥΓΡΑΜ. ΣΧΗΜ. 10.3 ΕΜΒΑΔΟΝ ΒΑΣΙΚΩΝ ΕΥΘΥΓΡΑΜΜΩΝ ΣΧΗΜΑΤΩΝ ΘΕΩΡΙΑ 1 (Πολυγωνικά χωρία) Ας θεωρήσουμε ένα πολύγωνο, για παράδειγμα
ΚΕΦΑΛΑΙΟ 10 Ο ΕΜΒΑΔΑ 10.1 ΠΟΛΥΓΩΝΙΚΑ ΧΩΡΙΑ 10. ΕΜΒΑΔΟΝ ΕΥΘΥΓΡΑΜ. ΣΧΗΜ. ΙΣΟΔΥΝΑΜΑ ΕΥΘΥΓΡΑΜ. ΣΧΗΜ. 10.3 ΕΜΒΑΔΟΝ ΒΑΣΙΚΩΝ ΕΥΘΥΓΡΑΜΜΩΝ ΣΧΗΜΑΤΩΝ ΘΕΩΡΙΑ 1 (Πολυγωνικά χωρία) Ας θεωρήσουμε ένα πολύγωνο, για παράδειγμα
1=45. β) Να υπολογίσετε τη γωνία φ.
 1. Στο σχήµα που ακολουθεί, η Αx είναι εφαπτοµένη του κύκλου (Ο, ρ) σε σηµείο του Α και επιπλέον ισχύουν ΓΑ x =85 0 και BA =40 0. α) Να αποδείξετε ότι ˆΒ 1=45. β) Να υπολογίσετε τη γωνία φ. 2. Στο ακόλουθο
1. Στο σχήµα που ακολουθεί, η Αx είναι εφαπτοµένη του κύκλου (Ο, ρ) σε σηµείο του Α και επιπλέον ισχύουν ΓΑ x =85 0 και BA =40 0. α) Να αποδείξετε ότι ˆΒ 1=45. β) Να υπολογίσετε τη γωνία φ. 2. Στο ακόλουθο
ΠΩΣ ΕΙΧΝΩ ΟΤΙ ΥΟ ΕΥΘΕΙΕΣ ΕΙΝΑΙ ΠΑΡΑΛΛΗΛΕΣ 1. είχνω ότι τέµνονται από τρίτη ευθεία και σχηµατίζονται γωνίες
 ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΧΟΛΙΑ στη γεωµετρία της Α τάξης ΠΩΣ ΕΙΧΝΩ ΟΤΙ ΥΟ ΕΥΘΕΙΕΣ ΕΙΝΑΙ ΚΑΘΕΤΕΣ 1. είχνω ότι η γωνία τους είναι 90 ο 2. είχνω ότι είναι διχοτόµοι δύο εφεξής και παραπληρωµατικών γωνιών. 3. είχνω ότι
ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΧΟΛΙΑ στη γεωµετρία της Α τάξης ΠΩΣ ΕΙΧΝΩ ΟΤΙ ΥΟ ΕΥΘΕΙΕΣ ΕΙΝΑΙ ΚΑΘΕΤΕΣ 1. είχνω ότι η γωνία τους είναι 90 ο 2. είχνω ότι είναι διχοτόµοι δύο εφεξής και παραπληρωµατικών γωνιών. 3. είχνω ότι
Σε τρίγωνο ΑΒΓ το τετράγωνο πλευράς απέναντι από οξεία γωνία ισούται με το άθροισμα των τετραγώνων των άλλων δύο πλευρών ελαττωμένο κατά το διπλάσιο τ
 ΚΥΠΡΙΑΝΟΣ ΕΥΑΓΓΕΛΟΣ ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΣΤΑ ΟΡΘΟΓΩΝΙΑ ΤΡΙΓΩΝΑ Το τετράγωνο μιας κάθετης πλευράς είναι ίσο με την υποτείνουσα επί την προβολή της πλευράς στην υποτείνουσα. ΑΒ 2 = ΒΓ ΑΔ ή ΑΓ 2 = ΒΓ ΓΔ Σε κάθε
ΚΥΠΡΙΑΝΟΣ ΕΥΑΓΓΕΛΟΣ ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΣΤΑ ΟΡΘΟΓΩΝΙΑ ΤΡΙΓΩΝΑ Το τετράγωνο μιας κάθετης πλευράς είναι ίσο με την υποτείνουσα επί την προβολή της πλευράς στην υποτείνουσα. ΑΒ 2 = ΒΓ ΑΔ ή ΑΓ 2 = ΒΓ ΓΔ Σε κάθε
ΑΣΚΗΣΕΙΣ ΓΕΩΜΕΤΡΙΑΣ Β ΛΥΚΕΙΟΥ
 ΑΣΚΗΣΕΙΣ ΓΕΩΜΕΤΡΙΑΣ Β ΛΥΚΕΙΟΥ (Τελευταία ενηµέρωση: Νοέµβριος 2016) Ανέστης Τσοµίδης Κατερίνη Περιεχόµενα 1 Αναλογίες 2 1.1 Το ϑεώρηµα του Θαλή.......................... 2 1.2 Τα ϑεωρήµατα των διχοτόµων......................
ΑΣΚΗΣΕΙΣ ΓΕΩΜΕΤΡΙΑΣ Β ΛΥΚΕΙΟΥ (Τελευταία ενηµέρωση: Νοέµβριος 2016) Ανέστης Τσοµίδης Κατερίνη Περιεχόµενα 1 Αναλογίες 2 1.1 Το ϑεώρηµα του Θαλή.......................... 2 1.2 Τα ϑεωρήµατα των διχοτόµων......................
ΓΕΩΜΕΤΡΙΚΕΣ ΚΑΤΑΣΚΕΥΕΣ ΣΤΟΧΟΙ: Με τη συμπλήρωση του στόχου αυτού θα μπορείτε να: Σχεδιάζετε τρίγωνα, τετράπλευρα και πολύγωνα.
 ΓΕΩΜΕΤΡΙΚΕΣ ΚΑΤΑΣΚΕΥΕΣ ΣΤΟΧΟΙ: Με τη συμπλήρωση του στόχου αυτού θα μπορείτε να: Σχεδιάζετε τρίγωνα, τετράπλευρα και πολύγωνα. ΓΕΝΙΚΑ: Οι γεωμετρικές κατασκευές εφαρμόζονται στην επίλυση σχεδιαστικών προβλημάτων
ΓΕΩΜΕΤΡΙΚΕΣ ΚΑΤΑΣΚΕΥΕΣ ΣΤΟΧΟΙ: Με τη συμπλήρωση του στόχου αυτού θα μπορείτε να: Σχεδιάζετε τρίγωνα, τετράπλευρα και πολύγωνα. ΓΕΝΙΚΑ: Οι γεωμετρικές κατασκευές εφαρμόζονται στην επίλυση σχεδιαστικών προβλημάτων
2. Αν ΑΒΓΔ είναι ένα τετράπλευρο περιγεγραμμένο σε κύκλο ακτίνας ρ, να δείξετε ότι ισχύει: ΑΒ + ΓΔ 4ρ.
 Θαλής Β' Λυκείου 1995-1996 1. Έστω κύκλος ακτίνας 1, στον οποίο ορίζουμε ένα συγκεκριμένο σημείο Α 0. Στη συνέχεια ορίζουμε τα σημεία Α ν ως εξής: Το μήκος του τόξου Α 0 Α ν (όπου αυτό μπορεί να είναι
Θαλής Β' Λυκείου 1995-1996 1. Έστω κύκλος ακτίνας 1, στον οποίο ορίζουμε ένα συγκεκριμένο σημείο Α 0. Στη συνέχεια ορίζουμε τα σημεία Α ν ως εξής: Το μήκος του τόξου Α 0 Α ν (όπου αυτό μπορεί να είναι
ΓΕΩΜΕΤΡΙΑ ΤΗΣ Α ΛΥΚΕΙΟΥ. ΚΕΦΑΚΑΙΟ 3 ο -ΤΡΙΓΩΝΑ
 ΓΕΩΜΕΤΡΙΑ ΤΗΣ Α ΛΥΚΕΙΟΥ ΟΙ ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΑΠΟΤΕΛΟΥΝ ΜΕΡΟΣ ΤΟΥ ΘΕΜΑΤΟΣ Α ΤΩΝ ΕΞΕΤΑΣΕΩΝ (ΘΕΜΑ ΘΕΩΡΙΑΣ) Α. ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ - ΛΑΘΟΥΣ ΚΕΦΑΚΑΙΟ 3 ο -ΤΡΙΓΩΝΑ 1. Ένα τρίγωνο είναι οξυγώνιο όταν έχει
ΓΕΩΜΕΤΡΙΑ ΤΗΣ Α ΛΥΚΕΙΟΥ ΟΙ ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΑΠΟΤΕΛΟΥΝ ΜΕΡΟΣ ΤΟΥ ΘΕΜΑΤΟΣ Α ΤΩΝ ΕΞΕΤΑΣΕΩΝ (ΘΕΜΑ ΘΕΩΡΙΑΣ) Α. ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ - ΛΑΘΟΥΣ ΚΕΦΑΚΑΙΟ 3 ο -ΤΡΙΓΩΝΑ 1. Ένα τρίγωνο είναι οξυγώνιο όταν έχει
ΘΕΩΡΙA 5. Μονάδες 5x2=10 A2. Πότε ένα τετράπλευρο ονομάζεται τραπέζιο;
 1 ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΓΕΩΜΕΤΡΙΑΣ Α ΛΥΚΕΙΟΥ ΜΕ ΝΕΟ ΣΥΣΤΗΜΑ 14 ΘΕΩΡΙA 5 ΘΕΜΑ A 1. A1. Να μεταφέρετε στην κόλλα απαντήσεων το γράμμα που αντιστοιχεί σε κάθε πρόταση και δίπλα να σημειώσετε το γράμμα Σ αν
1 ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΓΕΩΜΕΤΡΙΑΣ Α ΛΥΚΕΙΟΥ ΜΕ ΝΕΟ ΣΥΣΤΗΜΑ 14 ΘΕΩΡΙA 5 ΘΕΜΑ A 1. A1. Να μεταφέρετε στην κόλλα απαντήσεων το γράμμα που αντιστοιχεί σε κάθε πρόταση και δίπλα να σημειώσετε το γράμμα Σ αν
2ο ΘΕΜΑ. μ Σε ισοσκελές τρίγωνο ΑΒΓ AB
 2ο ΘΕΜΑ 2845. Σε ισοσκελές τρίγωνο ΑΒΓ AB A φέρουμε τη ΑΔ και μια ευθεία (ε) παράλληλη προς τη ΒΓ, που τέμνει τις πλευρές ΑΒ και ΑΓ στα σημεία Ε και Ζ αντίστοιχα. Να αποδείξετε ότι: α) Το τρίγωνο ΑΕΖ είναι
2ο ΘΕΜΑ 2845. Σε ισοσκελές τρίγωνο ΑΒΓ AB A φέρουμε τη ΑΔ και μια ευθεία (ε) παράλληλη προς τη ΒΓ, που τέμνει τις πλευρές ΑΒ και ΑΓ στα σημεία Ε και Ζ αντίστοιχα. Να αποδείξετε ότι: α) Το τρίγωνο ΑΕΖ είναι
Β.1.8. Παραπληρωματικές και Συμπληρωματικές γωνίες Κατά κορυφήν γωνίες
 Β.1.6. Είδη γωνιών Κάθετες ευθείες 1. Ορθή γωνία λέγεται η γωνία της οποίας το μέτρο είναι ίσο με 90 ο. 2. Οξεία γωνία λέγεται κάθε γωνία με μέτρο μικρότερο των 90 ο. 3. Αμβλεία γωνία λέγεται κάθε γωνία
Β.1.6. Είδη γωνιών Κάθετες ευθείες 1. Ορθή γωνία λέγεται η γωνία της οποίας το μέτρο είναι ίσο με 90 ο. 2. Οξεία γωνία λέγεται κάθε γωνία με μέτρο μικρότερο των 90 ο. 3. Αμβλεία γωνία λέγεται κάθε γωνία
ΚΕΦΑΛΑΙΟ λ + λ = + = + = = = λ.
 ΚΦΑΛΑΙΟ 11. Παραθέτουμε για εύκολη αναφορά το πινακάκι με την αντιστοιχία χορδών-αποστημάτων-τόξων που χρειάζεται σε όλες σχεδόν τις παρακάτω ασκήσεις Κανονικό εξάγωνο Πλευρά λν Χορδή λ = Απόστημα α =
ΚΦΑΛΑΙΟ 11. Παραθέτουμε για εύκολη αναφορά το πινακάκι με την αντιστοιχία χορδών-αποστημάτων-τόξων που χρειάζεται σε όλες σχεδόν τις παρακάτω ασκήσεις Κανονικό εξάγωνο Πλευρά λν Χορδή λ = Απόστημα α =
ΓΕΩΜΕΤΡΙΑ Γ γυμνασίου από Σχολικό Βιβλίο + Ασκήσεις Εξάσκησης
 ΓΕΩΜΕΤΡΙΑ Γ γυμνασίου από Σχολικό Βιβλίο + Ασκήσεις Εξάσκησης ΙΣΟΤΗΤΑ ΤΡΙΓΩΝΩΝ Γρήγορη Επανάληψη Θεωρίας Ένα τρίγωνο ανάλογα με το είδος των γωνιών του ονομάζεται: Σε κάθε ορθογώνιο τρίγωνο η πλευρά που
ΓΕΩΜΕΤΡΙΑ Γ γυμνασίου από Σχολικό Βιβλίο + Ασκήσεις Εξάσκησης ΙΣΟΤΗΤΑ ΤΡΙΓΩΝΩΝ Γρήγορη Επανάληψη Θεωρίας Ένα τρίγωνο ανάλογα με το είδος των γωνιών του ονομάζεται: Σε κάθε ορθογώνιο τρίγωνο η πλευρά που
α <β +γ τότε είναι οξυγώνιο.
 ΘΕΜΑΤΑ ΠΡΟΑΓΩΓΙΚΩΝ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ ΜΑΪΟΣ ΙΟΥΝΙΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: ΓΕΩΜΕΤΡΙΑ ΘΕΜΑ Α A1. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν γράφοντας στην κόλλα σας τη λέξη Σωστό ή Λάθος δίπλα στο γράμμα που
ΘΕΜΑΤΑ ΠΡΟΑΓΩΓΙΚΩΝ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ ΜΑΪΟΣ ΙΟΥΝΙΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: ΓΕΩΜΕΤΡΙΑ ΘΕΜΑ Α A1. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν γράφοντας στην κόλλα σας τη λέξη Σωστό ή Λάθος δίπλα στο γράμμα που
24 ΔΙΑΓΩΝΙΣΜΑΤΑ ΓΕΩΜΕΤΡΙΑΣ Α ΛΥΚΕΙΟΥ
 1ο Α. Nα αποδείξετε ότι το άθροισμα των γωνιών κάθε τριγώνου είναι 2 ορθές. Β. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν γράφοντας στο τετράδιό σας τη λέξη Σωστό ή Λάθος δίπλα στο γράμμα που αντιστοιχεί
1ο Α. Nα αποδείξετε ότι το άθροισμα των γωνιών κάθε τριγώνου είναι 2 ορθές. Β. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν γράφοντας στο τετράδιό σας τη λέξη Σωστό ή Λάθος δίπλα στο γράμμα που αντιστοιχεί
= π 3 και a = 2, β =2 2. a, β
 1 of 68 Δίνονται τα διανύσματα a και β με a, β = π 3 και a =, β =. α) Να βρείτε το εσωτερικό γινόμενο a β. (Μονάδες 8) β) Αν τα διανύσματα a + β και κ a + β είναι κάθετα να βρείτε την τιμή του κ. γ) Να
1 of 68 Δίνονται τα διανύσματα a και β με a, β = π 3 και a =, β =. α) Να βρείτε το εσωτερικό γινόμενο a β. (Μονάδες 8) β) Αν τα διανύσματα a + β και κ a + β είναι κάθετα να βρείτε την τιμή του κ. γ) Να
Γεωμετρία. Κεφ 1 ο : Γεωμετρια.
 Μαθηματικά Γ Γυμνασίου Γεωμετρία. Κεφ 1 ο : Γεωμετρια. Μέρος Α Θεωρία. 1. Με τι είναι ίσο το άθροισμα των γωνιών ενός τριγώνου; 2. Ποιο τρίγωνο λέγετε οξυγώνιο αμβλυγώνιο ορθογώνιο. 3. Ποιο τρίγωνο λέγετε
Μαθηματικά Γ Γυμνασίου Γεωμετρία. Κεφ 1 ο : Γεωμετρια. Μέρος Α Θεωρία. 1. Με τι είναι ίσο το άθροισμα των γωνιών ενός τριγώνου; 2. Ποιο τρίγωνο λέγετε οξυγώνιο αμβλυγώνιο ορθογώνιο. 3. Ποιο τρίγωνο λέγετε
β) Να αποδείξετε ότι τα τρίγωνα ΑΒΓ και ΚΛΓ είναι όμοια και στη συνέχεια να συμπληρώσετε
 ΘΕΜΑ 4 Στο διπλανό τραπέζιο ΑΒΓΔ η ευθεία ΜΛ είναι παράλληλη στις βάσεις ΑΒ και ΔΓ του τραπεζίου και ισχύει ότι = α) Να αποδείξετε ότι = και = (Μονάδες 8) β) Να αποδείξετε ότι τα τρίγωνα ΑΒΓ και ΚΛΓ είναι
ΘΕΜΑ 4 Στο διπλανό τραπέζιο ΑΒΓΔ η ευθεία ΜΛ είναι παράλληλη στις βάσεις ΑΒ και ΔΓ του τραπεζίου και ισχύει ότι = α) Να αποδείξετε ότι = και = (Μονάδες 8) β) Να αποδείξετε ότι τα τρίγωνα ΑΒΓ και ΚΛΓ είναι
Διαίρεση ευθυγράμμου τμήματος σε ν ίσα τμήματα
 ΜΕΡΟΣ Β. ΛΟΓΟΣ ΕΥΘΥΓΡΑΜΜΩΝ ΤΜΗΜΑΤΩΝ 7. ΛΟΓΟΣ ΕΥΘΥΓΡΑΜΜΩΝ ΤΜΗΜΑΤΩΝ Ίσα τμήματα μεταξύ παραλλήλων ευθειών Αν παράλληλες ευθείες ορίζουν ίσα τμήματα σε μια ευθεία, τότε θα ορίζουν ίσα τμήματα και σε οποιαδήποτε
ΜΕΡΟΣ Β. ΛΟΓΟΣ ΕΥΘΥΓΡΑΜΜΩΝ ΤΜΗΜΑΤΩΝ 7. ΛΟΓΟΣ ΕΥΘΥΓΡΑΜΜΩΝ ΤΜΗΜΑΤΩΝ Ίσα τμήματα μεταξύ παραλλήλων ευθειών Αν παράλληλες ευθείες ορίζουν ίσα τμήματα σε μια ευθεία, τότε θα ορίζουν ίσα τμήματα και σε οποιαδήποτε
ΚΥΚΛΟΣ. Ερωτήσεις του τύπου «Σωστό-Λάθος»
 ΚΥΚΛΟΣ Ερωτήσεις του τύπου «Σωστό-Λάθος» Σωστό Λάθος 1. Αν α είναι η απόσταση ευθείας ε από το κέντρο του κύκλου (Ο, ρ) τότε: αν α > ρ η ε λέγεται εξωτερική του κύκλου αν α = ρ η ε λέγεται τέμνουσα του
ΚΥΚΛΟΣ Ερωτήσεις του τύπου «Σωστό-Λάθος» Σωστό Λάθος 1. Αν α είναι η απόσταση ευθείας ε από το κέντρο του κύκλου (Ο, ρ) τότε: αν α > ρ η ε λέγεται εξωτερική του κύκλου αν α = ρ η ε λέγεται τέμνουσα του
24 ΔΙΑΓΩΝΙΣΜΑΤΑ ΓΕΩΜΕΤΡΙΑΣ Α ΛΥΚΕΙΟΥ
 4 ΔΙΑΓΩΝΙΣΜΑΤΑ ΓΕΩΜΕΤΡΙΑΣ Α ΛΥΚΕΙΟΥ Δίνεται παραλληλόγραμμο ΑΒΓΔ με ΑΒ=ΒΓ. Φέρνουμε το ΑΕ ΒΓ και έστω Ζ,Η τα μέσα των ΔΓ και ΑΒ αντίστοιχα. Ν.δ.ο. α) το ΖΓΒΗ είναι ρόμβος ( 9 μον.) β) ΗΖ=ΗΕ ( 8 μον.) γ)
4 ΔΙΑΓΩΝΙΣΜΑΤΑ ΓΕΩΜΕΤΡΙΑΣ Α ΛΥΚΕΙΟΥ Δίνεται παραλληλόγραμμο ΑΒΓΔ με ΑΒ=ΒΓ. Φέρνουμε το ΑΕ ΒΓ και έστω Ζ,Η τα μέσα των ΔΓ και ΑΒ αντίστοιχα. Ν.δ.ο. α) το ΖΓΒΗ είναι ρόμβος ( 9 μον.) β) ΗΖ=ΗΕ ( 8 μον.) γ)
Ασκήσεις Επανάληψης Τάξη Δ Εν. 1: Διανύσματα
 Ασκήσεις Επανάληψης Τάξη Δ 016-017 Εν. 1: Διανύσματα 1. Να ονομάσετε τα στοιχεία ενός διανύσματος.. Δίνεται το παραλληλόγραμμο ΑΒΓΔ, όπως φαίνεται στο σχήμα. Να χαρακτηρίσετε ΣΩΣΤΟ ή ΛΑΘΟΣ τις πιο κάτω
Ασκήσεις Επανάληψης Τάξη Δ 016-017 Εν. 1: Διανύσματα 1. Να ονομάσετε τα στοιχεία ενός διανύσματος.. Δίνεται το παραλληλόγραμμο ΑΒΓΔ, όπως φαίνεται στο σχήμα. Να χαρακτηρίσετε ΣΩΣΤΟ ή ΛΑΘΟΣ τις πιο κάτω
Μεθοδική Επανάληψη Γεωμετρίας Β Λυκείου
 Μεθοδική Επανάληψη Γεωμετρίας Β Λυκείου Στέλιος Μιχαήλογλου www.askisopolis.gr 8ο Κεφάλαιο: Ομοιότητα. Πότε δύο ευθύγραμμα σχήματα λέγονται όμοια; Τι ονομάζεται λόγος ομοιότητας αυτών; Με τι ισούται ο
Μεθοδική Επανάληψη Γεωμετρίας Β Λυκείου Στέλιος Μιχαήλογλου www.askisopolis.gr 8ο Κεφάλαιο: Ομοιότητα. Πότε δύο ευθύγραμμα σχήματα λέγονται όμοια; Τι ονομάζεται λόγος ομοιότητας αυτών; Με τι ισούται ο
ΘΕΜΑΤΑ ΣΤΗΝ ΓΕΩΜΕΤΡΙΑ Β ΛΥΚΕΙΟΥ
 Επιμέλεια: ιώργος Ράπτης ΘΕΤ ΣΤΗΝ ΕΩΕΤΡΙ ΛΥΚΕΙΟΥ ΘΕ 1 ο. Να αποδείξετε ότι το εμβαδό τραπεζίου με βάσεις 1, και ύψος υ δίνεται από τον τύπο: ( 1+ ) υ Ε= ονάδες 1 B. ν φν, λν και αν είναι: η γωνία, η πλευρά
Επιμέλεια: ιώργος Ράπτης ΘΕΤ ΣΤΗΝ ΕΩΕΤΡΙ ΛΥΚΕΙΟΥ ΘΕ 1 ο. Να αποδείξετε ότι το εμβαδό τραπεζίου με βάσεις 1, και ύψος υ δίνεται από τον τύπο: ( 1+ ) υ Ε= ονάδες 1 B. ν φν, λν και αν είναι: η γωνία, η πλευρά
 Κεφάλαιο 9 Ο κύκλος Ορισμός. Ο κύκλος (Κ, r) με κέντρο Κ και ακτίνα r είναι το σχήμα που αποτελείται από όλα τα σημεία του επιπέδου που απέχουν απόσταση r από το σημείο Κ. Σχήμα 9.1: Στοιχεία ενός κύκλου.
Κεφάλαιο 9 Ο κύκλος Ορισμός. Ο κύκλος (Κ, r) με κέντρο Κ και ακτίνα r είναι το σχήμα που αποτελείται από όλα τα σημεία του επιπέδου που απέχουν απόσταση r από το σημείο Κ. Σχήμα 9.1: Στοιχεία ενός κύκλου.
ΦΡΟΝΤΙΣΤΗΡΙΑ «άµιλλα»
 1 ΜΕΤΡΙΚΕ ΧΕΕΙ ΘΕΩΡΙΑ Μετρικές σχέσεις στο ορθογώνιο τρίγωνο το ορθογώνιο τρίγωνο το τετράγωνο κάθε κάθετης πλευράς είναι ίσο µε το γινόµενο της υποτείνουσας επί την προβολή της κάθετης στην υποτείνουσα.
1 ΜΕΤΡΙΚΕ ΧΕΕΙ ΘΕΩΡΙΑ Μετρικές σχέσεις στο ορθογώνιο τρίγωνο το ορθογώνιο τρίγωνο το τετράγωνο κάθε κάθετης πλευράς είναι ίσο µε το γινόµενο της υποτείνουσας επί την προβολή της κάθετης στην υποτείνουσα.
Εισαγωγή 1. Εξωτερικά του παραλληλογράμμου ΑΒΓΔ κατασκευάζουμε τα τετράγωνα ΑΒΕΖ και ΔΓΘΗ. Να αποδείξετε ότι : α. ZH E, H
 Εισαγωγή 1. Εξωτερικά του παραλληλογράμμου ΑΒΓΔ κατασκευάζουμε τα τετράγωνα ΑΒΕΖ και ΔΓΘΗ. Να αποδείξετε ότι : α. ZH E, H, Z,. Τα τμήματα ΑΓ και ΗΕ έχουν κοινό μέσο γ. Το κέντρο του παραλληλογράμμου είναι
Εισαγωγή 1. Εξωτερικά του παραλληλογράμμου ΑΒΓΔ κατασκευάζουμε τα τετράγωνα ΑΒΕΖ και ΔΓΘΗ. Να αποδείξετε ότι : α. ZH E, H, Z,. Τα τμήματα ΑΓ και ΗΕ έχουν κοινό μέσο γ. Το κέντρο του παραλληλογράμμου είναι
ΜΑΘΗΜΑΤΙΚΑ ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ 1 ΚΕΦΑΛΑΙΟ 3 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ B ΓΥΝΜΑΣΙΟΥ. 1. Να λυθούν οι εξισώσεις και οι ανισώσεις :
 ΜΑΘΗΜΑΤΙΚΑ ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ. Να λυθούν οι εξισώσεις και οι ανισώσεις : α) γ) x x 3x 7x 9 4 5 0 x x x 3 6 3 4 β) δ) 3x x 3 x 4 3 5 x x. 4 4 3 5 x 4x 3 x 6x 7. Να λυθεί στο Q, η ανίσωση :. 5 8 8 3. Να λυθούν
ΜΑΘΗΜΑΤΙΚΑ ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ. Να λυθούν οι εξισώσεις και οι ανισώσεις : α) γ) x x 3x 7x 9 4 5 0 x x x 3 6 3 4 β) δ) 3x x 3 x 4 3 5 x x. 4 4 3 5 x 4x 3 x 6x 7. Να λυθεί στο Q, η ανίσωση :. 5 8 8 3. Να λυθούν
ΙΣΟΤΗΤΑ ΚΑΙ ΟΜΟΙΟΤΗΤΑ ΣΧΗΜΑΤΩΝ
 ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ Ερώτηση 1 η Ποια καλούνται κύρια και ποια δευτερεύοντα στοιχεία ενός τριγώνου; Τι ονομάζεται τριγωνική ανισότητα; Κύρια στοιχεία ενός τριγώνου είναι οι πλευρές και οι γωνίες του. Οι
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ Ερώτηση 1 η Ποια καλούνται κύρια και ποια δευτερεύοντα στοιχεία ενός τριγώνου; Τι ονομάζεται τριγωνική ανισότητα; Κύρια στοιχεία ενός τριγώνου είναι οι πλευρές και οι γωνίες του. Οι
ΘΕΩΡΙΑ ΣΤΗ ΓΕΩΜΕΤΡΙΑ ΓΙΑ ΤΗΝ Α ΓΥΜΝΑΣΙΟΥ Α. ΓΩΝΙΕΣ - ΚΥΚΛΟΣ
 ΘΕΩΡΙΑ ΣΤΗ ΓΕΩΜΕΤΡΙΑ ΓΙΑ ΤΗΝ Α ΓΥΜΝΑΣΙΟΥ Α. ΓΩΝΙΕΣ - ΚΥΚΛΟΣ 1. Απόσταση δύο σηµείων Α και Β είναι το µήκος του ευθύγραµµου τµήµατος που τα ενώνει. 2. Γωνία είναι το µέρος του επιπέδου που βρίσκεται µεταξύ
ΘΕΩΡΙΑ ΣΤΗ ΓΕΩΜΕΤΡΙΑ ΓΙΑ ΤΗΝ Α ΓΥΜΝΑΣΙΟΥ Α. ΓΩΝΙΕΣ - ΚΥΚΛΟΣ 1. Απόσταση δύο σηµείων Α και Β είναι το µήκος του ευθύγραµµου τµήµατος που τα ενώνει. 2. Γωνία είναι το µέρος του επιπέδου που βρίσκεται µεταξύ
ΚΕΦΑΛΑΙΟ 1 Ο ΓΕΩΜΕΤΡΙΑ
 ΜΕΡΟΣ ΚΕΦΛΙΟ 1 Ο ΕΩΜΕΤΡΙ 1.1 ΙΣΟΤΗΤ ΤΡΙΩΝΩΝ 1. Ποια ονομάζονται κύρια και ποια δευτερεύοντα στοιχεία τριγώνων; Κύρια στοιχεία ενός τριγώνου ονομάζουμε τις πλευρές και τις γωνίες του. Δευτερεύοντα στοιχεία
ΜΕΡΟΣ ΚΕΦΛΙΟ 1 Ο ΕΩΜΕΤΡΙ 1.1 ΙΣΟΤΗΤ ΤΡΙΩΝΩΝ 1. Ποια ονομάζονται κύρια και ποια δευτερεύοντα στοιχεία τριγώνων; Κύρια στοιχεία ενός τριγώνου ονομάζουμε τις πλευρές και τις γωνίες του. Δευτερεύοντα στοιχεία
2 Β Βάσεις παραλληλογράµµου Βαρύκεντρο Γ Γεωµετρική κατασκευή Γεωµετρικός τόπος (ς) Γωνία Οι απέναντι πλευρές του. Κέντρο βάρους τριγώνου, δηλ. το σηµ
 1 ΛΕΞΙΚΟ ΓΕΩΜΕΤΡΙΚΩΝ ΟΡΩΝ Α Ακτίνιο Ακτίνα κύκλου Ακτίνα σφαίρας Άκρα ευθύγραµµου τµήµατος Αµβλεία γωνία Αµβλυγώνιο Ανάλογα ευθύγραµµα τµήµατα Αντιδιαµετρικό σηµείο Αντικείµενες ηµιευθείες Άξονας συµµετρίας
1 ΛΕΞΙΚΟ ΓΕΩΜΕΤΡΙΚΩΝ ΟΡΩΝ Α Ακτίνιο Ακτίνα κύκλου Ακτίνα σφαίρας Άκρα ευθύγραµµου τµήµατος Αµβλεία γωνία Αµβλυγώνιο Ανάλογα ευθύγραµµα τµήµατα Αντιδιαµετρικό σηµείο Αντικείµενες ηµιευθείες Άξονας συµµετρίας
ΓΕΩΜΕΤΡΙΑ Β ΓΕΛ. ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ. ΚΕΦΑΛΑΙΟ:9 ο
 14 1 ΓΕΩΜΕΤΡΙΑ Β ΓΕΛ. ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΚΕΦΑΛΑΙΟ:9 ο _18997 ΘΕΜΑ Β Ένας άνθρωπος σπρώχνει ένα κουτί προς τα πάνω στη ράµπα του παρακάτω σχήµατος. α) Να αποδείξετε ότι για το ύψος y, που απέχει το κουτί από
14 1 ΓΕΩΜΕΤΡΙΑ Β ΓΕΛ. ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΚΕΦΑΛΑΙΟ:9 ο _18997 ΘΕΜΑ Β Ένας άνθρωπος σπρώχνει ένα κουτί προς τα πάνω στη ράµπα του παρακάτω σχήµατος. α) Να αποδείξετε ότι για το ύψος y, που απέχει το κουτί από
ΘΕΜΑΤΑ. Μονάδες 8. Δίνεται κύκλος (Ο, R) και σημείο Ρ εκτός αυτού. Φέρουμε την εφαπτομένη ΡΑ ώστε
 ΕΛ ΕΩΜΕΤΡΙΑ Β 1 ΕΛ ΕΩΜΕΤΡΙΑ Β 93 Α. Να αποδείξετε ότι: Σε κάθε ορθογώνιο τρίγωνο, το τετράγωνο μιας κάθετης πλευράς του είναι ίσο με το γινόμενο της υποτείνουσας επί την προβολή της πλευράς αυτής στην
ΕΛ ΕΩΜΕΤΡΙΑ Β 1 ΕΛ ΕΩΜΕΤΡΙΑ Β 93 Α. Να αποδείξετε ότι: Σε κάθε ορθογώνιο τρίγωνο, το τετράγωνο μιας κάθετης πλευράς του είναι ίσο με το γινόμενο της υποτείνουσας επί την προβολή της πλευράς αυτής στην
