5. Partial Autocorrelation Function of MA(1) Process:
|
|
|
- ĒΔανιήλ Βλαστός
- 5 χρόνια πριν
- Προβολές:
Transcript
1 54 5. Partial Autocorrelation Function of MA() Process: φ, = ρ() = θ + θ 2 0 ( ρ() ) ( φ2, ) ( φ() ) = ρ() φ 2,2 φ(2) ρ() ρ() ρ(2) = φ 2,2 = ρ() = ρ() ρ() ρ() 0 ρ() ρ() = ρ()2 ρ() 2 = θ 2 + θ 2 + θ4 0
2 55 ρ() ρ(2) φ 3, ρ() ρ() φ 3,2 = φ(2) ρ(2) ρ() φ 3,3 φ(3) ρ() ρ() ρ() ρ(2) ρ(2) ρ() ρ(3) = φ 3,3 = ρ() ρ(2) = ρ() ρ() ρ(2) ρ() φ() ρ() ρ() ρ() 0 0 ρ() 0 ρ() 0 ρ() ρ() 0 ρ() = ρ() 3 2ρ() 2 0
3 56 ρ() ρ(2) ρ(3) φ 4, ρ() ρ() ρ(2) φ 4,2 φ(2) = ρ(2) ρ() ρ() φ 4,3 φ(3) ρ(3) ρ(2) ρ() φ 4,4 φ(4) ρ() ρ(2) ρ() ρ() ρ() ρ(2) ρ(2) ρ() ρ(3) ρ(3) ρ(2) ρ() ρ(4) = φ 4,4 = ρ() ρ(2) ρ(3) = ρ() ρ() ρ(2) ρ(2) ρ() ρ() ρ(3) ρ(2) ρ() As a result, φ k,k 0 for all k =, 2, φ() ρ() 0 ρ() ρ() ρ() 0 0 ρ() ρ() 0 ρ() 0 0 ρ() ρ() 0 0 ρ() ρ() 0 0 ρ() 0
4 57 6. Likelihood Function of MA() Process: The autocovariance functions are: γ(0) = (+θ 2 )σ2 ɛ, γ() = θ σ 2 ɛ, and γ(τ) = 0 for τ = 2, 3,. The joint distribution of y, y 2,, y T is: ( f (y, y 2,, y T ) = (2π) T/2 V /2 exp ) 2 Y V Y where Y = y y 2. y T, V = σ 2 ɛ + θ 2 θ 0 0 θ + θ 2 θ θ θ 2 θ 0 0 θ + θ 2.
5 58 7. MA() +drift: y t = µ + ɛ t + θ ɛ t Mean of MA() Process: y t = µ + θ(l)ɛ t, where θ(l) = + θ L. Taking the expectation, E(y t ) = µ + θ(l)e(ɛ t ) = µ.
6 59 Example: MA(2) Model: y t = ɛ t + θ ɛ t + θ 2 ɛ t 2. Autocovariance Function of MA(2) Process: ( + θ 2 + θ2 2 )σ2 ɛ, for τ = 0, (θ + θ θ 2 )σ 2 ɛ, for τ =, γ(τ) = θ 2 σ 2 ɛ, for τ = 2, 0, otherwise. 2. let /β and /β 2 be two solutions of x from θ(x) = 0. For invertibility condition, both β and β 2 should be less than one in absolute value. Then, the MA(2) model is represented as: y t = ɛ t + θ ɛ t + θ 2 ɛ t 2
7 60 = ( + θ L + θ 2 L 2 )ɛ t = ( + β L)( + β 2 L)ɛ t AR( ) representation of the MA(2) model is given by: ɛ t = ( + β L)( + β 2 L) y t ( β /(β β 2 ) = + β L + β 2/(β β 2 ) + β 2 L ) y t
8 6 Y = 3. Likelihood Function: y y 2. y T where, V = σ 2 ɛ f (y, y 2,, y T ) = ( (2π) T/2 V /2 exp ) 2 Y V Y + θ 2 + θ2 2 θ + θ θ 2 θ 2 0 θ + θ θ 2 + θ 2 + θ2 2 θ + θ θ 2... θ 2 θ + θ θ θ θ 2 + θ2 2 θ + θ θ 2 0 θ 2 θ + θ θ 2 + θ 2 + θ2 2
9 62 4. MA(2) +drift: y t = µ + ɛ t + θ ɛ t + θ 2 ɛ t 2 Mean: y t = µ + θ(l)ɛ t, where θ(l) = + θ L + θ 2 L 2. Therefore, E(y t ) = µ + θ(l)e(ɛ t ) = µ
10 63 Example: MA(q) Model: y t = ɛ t + θ ɛ t + θ 2 ɛ t θ q ɛ t q. Mean of MA(q) Process: E(y t ) = E(ɛ t + θ ɛ t + θ 2 ɛ t θ q ɛ t q ) = 0 2. Autocovariance Function of MA(q) Process: q τ σ 2 ɛ(θ 0 θ τ + θ θ τ+ + + θ q τ θ q ) = σ 2 ɛ θ i θ τ+i, τ =, 2,, q, γ(τ) = i=0 0, τ = q +, q + 2,, where θ 0 =. 3. MA( q) process is stationary. 4. MA(q) +drift: y t = µ + ɛ t + θ ɛ t + θ 2 ɛ t θ q ɛ t q
11 64 Mean: y t = µ + θ(l)ɛ t, where θ(l) = + θ L + θ 2 L θ q L q. Therefore, we have: E(y t ) = µ + θ(l)e(ɛ t ) = µ.
12 ARMA Model ARMA (Autoregressive Moving Average ) Process. ARMA(p, q) y t = φ y t + φ 2 y t φ p y t p + ɛ t + θ ɛ t + θ 2 ɛ t θ q ɛ t q, which is rewritten as: φ(l)y t = θ(l)ɛ t, where φ(l) = φ L φ 2 L 2 φ p L p and θ(l) = +θ L+θ 2 L 2 + +θ q L q. 2. Likelihood Function: The variance-covariance matrix of Y, denoted by V, has to be computed.
13 66 Example: ARMA(,) Process: y t = φ y t + ɛ t + θ ɛ t Obtain the autocorrelation coefficient. The mean of y t is to take the expectation on both sides. E(y t ) = φ E(y t ) + E(ɛ t ) + θ E(ɛ t ), where the second and third terms are zeros. Therefore, we obtain: E(y t ) = 0. The autocovariance of y t is to take the expectation, multiplying y t τ on both sides. E(y t y t τ ) = φ E(y t y t τ ) + E(ɛ t y t τ ) + θ E(ɛ t y t τ ). Each term is given by: E(y t y t τ ) = γ(τ), E(y t y t τ ) = γ(τ ),
14 67 σ 2 ɛ, τ = 0, E(ɛ t y t τ ) = 0, τ =, 2,, Therefore, we obtain; (φ + θ )σ 2 ɛ, τ = 0, E(ɛ t y t τ ) = σ 2 ɛ, τ =, 0, τ = 2, 3,. γ(0) = φ γ() + ( + φ θ + θ 2 )σ2 ɛ, γ() = φ γ(0) + θ σ 2 ɛ, γ(τ) = φ γ(τ ), τ = 2, 3,. From the first two equations, γ(0) and γ() are computed by: ( φ ) ( γ(0) ) ( + φ θ + θ 2 ) φ γ() = σ 2 ɛ θ ( γ(0) ) ( ) φ ( + φ θ + θ 2 ) γ() = σ 2 ɛ φ θ
15 68 = σ2 ɛ φ 2 ( φ ) ( + φ θ + θ 2 ) φ θ ( = σ2 ɛ φ 2 + 2φ θ + θ 2 ( + φ θ )(φ + θ ) ). Thus, the initial value of the autocorrelation coefficient is given by: ρ() = ( + φ θ )(φ + θ ). + 2φ θ + θ 2 We have: ρ(τ) = φ ρ(τ ).
16 69 ARMA(p, q) +drift: y t = µ + φ y t + φ 2 y t 2 + φ p y t p + ɛ t + θ ɛ t + θ 2 ɛ t θ q ɛ t q. Mean of ARMA(p, q) Process: φ(l)y t = µ + θ(l)ɛ t, where φ(l) = φ L φ 2 L 2 φ p L p and θ(l) = + θ L + θ 2 L θ q L q. y t = φ(l) µ + φ(l) θ(l)ɛ t. Therefore, E(y t ) = φ(l) µ + φ(l) θ(l)e(ɛ t ) = φ() µ = µ φ φ 2 φ p.
17 ARIMA Model Autoregressive Integrated Moving Average (ARIMA ) Model ARIMA(p, d, q) Process φ(l) d y t = θ(l)ɛ t, where d y t = d ( L)y t = d y t d y t = ( L) d y t for d =, 2,, and 0 y t = y t.
18 7 5.6 SARIMA Model Seasonal ARIMA (SARIMA) Process:. SARIMA(p, d, q) φ(l) d s y t = θ(l)ɛ t, where s y t = ( L s )y t = y t y t s. s = 4 when y t denotes quarterly date and s = 2 when y t represents monthly data. 5.7 Optimal Prediction. AR(p) Process: y t = φ y t + + φ p y t p + ɛ t
19 72 (a) Define: E(y t+k Y t ) = y t+k t, where Y t denotes all the information available at time t. Taking the conditional expectation of y t+k = φ y t+k + +φ p y t+k p +ɛ t+k on both sides, y t+k t = φ y t+k t + + φ p y t+k p t, where y s t = y s for s t. (b) Optimal prediction is given by solving the above differential equation. 2. MA(q) Process: y t = ɛ t + θ ɛ t + + θ q ɛ t q (a) Let ˆɛ T, ˆɛ T,, ˆɛ be the estimated errors. (b) y t+k = ɛ t+k + θ ɛ t+k + + θ q ɛ t+k q
20 73 (c) Therefore, y t+k t = ɛ t+k t + θ ɛ t+k t + + θ q ɛ t+k q t, where ɛ s t = 0 for s > t and ɛ s t = ˆɛ s for s t. 3. ARMA(p, q) Process: y t = φ y t + + φ p y t p + ɛ t + θ ɛ t + + θ q ɛ t q (a) y t+k = φ y t+k + + φ p y t+k p + ɛ t+k + θ ɛ t+k + + θ q ɛ t+k q (b) Optimal prediction is: y t+k t = φ y t+k t + + φ p y t+k p t + ɛ t+k t + θ ɛ t+k t + + θ q ɛ t+k q t, where y s t = y s and ɛ s t = ˆɛ s for s t, and ɛ s t = 0 for s > t.
21 Identification. Based on AIC or SBIC given d, s, we obtain p, q. We choose p and q, where AIC or SBIC is minimized. (a) AIC (Akaike s Information Criterion) AIC = 2 log(likelihood) + 2k, where k = p + q, which is the number of parameters estimated. (b) SBIC (Shwarz s Bayesian Information Criterion) SBIC = 2 log(likelihood) + k log T, where T denotes the number of observations. 2. From the sample autocorrelation coefficient function ˆρ(k) and the partial autocorrelation coefficient function ˆφ k,k for k =, 2,, we obtain p, d, q, s.
22 75 AR(p) Process MA(q) Process Autocorrelation Function Gradually decreasing ρ(k) = 0, k = q +, q + 2, Partial Autocorrelation Function φ(k, k) = 0, Gradually decreasing k = p +, p + 2, (a) Compute s y t to remove seasonality. Compute the autocovariance functions of s y t. If the autocovariance functions have period s, we take ( L s ), again. (b) Determine the order of difference. Compute the partial autocovariance functions every time. If the autocovariance functions decrease as τ is large, go to the next step. (c) Determine the order of AR terms (i.e., p).
23 76 Compute the partial autocovariance functions every time. The partial autocovariance functions are close to zero after some τ, go to the next step. (d) Determine the order of MA terms (i.e., q). Compute the autocovariance functions every time. If the autocovariance functions are randomly around zero, end of the procedure.
24 Example of SARIMA using Consumption Data Construct SARIMA model using monthly and seasonally unadjusted consumption expenditure data and STATA2. Estimation Period: Jan., 970 Dec., 202 (T = 56). gen time=_n. tsset time time variable: time, to 56 delta: unit. corrgram expend LAG AC PAC Q Prob>Q [Autocorrelation] [Partial Autocor]
25 gen dexp=expend-l.expend ( missing value generated). corrgram dexp LAG AC PAC Q Prob>Q [Autocorrelation] [Partial Autocor]
26 79. gen sdex=dexp-l2.dexp (3 missing values generated). corrgram sdex LAG AC PAC Q Prob>Q [Autocorrelation] [Partial Autocor] arima sdex, ar(,2) ma() (setting optimization to BHHH) Iteration 0: log likelihood = Iteration : log likelihood =
27 80 Iteration 2: log likelihood = Iteration 3: log likelihood = Iteration 4: log likelihood = (switching optimization to BFGS) Iteration 5: log likelihood = Iteration 6: log likelihood = Iteration 7: log likelihood = Iteration 8: log likelihood = ARIMA regression Sample: 4-56 Number of obs = 503 Wald chi2(3) = Log likelihood = Prob > chi2 = OPG sdex Coef. Std. Err. z P> z [95% Conf. Interval] sdex _cons ARMA ar L L ma L /sigma
28 8 Note: The test of the variance against zero is one sided, and the two-sided confidence interval is truncated at zero.. estat ic Model Obs ll(null) ll(model) df AIC BIC Note: N=Obs used in calculating BIC; see [R] BIC note
29 82 6 Unit Root ( ) and Cointegration ( ) 6. Unit Root ( ) Test (Dickey-Fuller (DF) Test). Why is a unit root problem important? (a) Economic variables increase over time in general. One of the assumptions of OLS is stationarity on y t and x t. This assumption implies that T X X converges to a fixed matrix as T is large. That is, asymptotic normality of OLS estimator does not hold. (b) In nonstationary time series, the unit root is the most important. In the case of unit root, OLSE of the first-order autoregressive coefficient is consistent.
30 83 OLSE is T-consistent in the case of stationary AR() process, but OLSE is T-consistent in the case of nonstationay AR() process. (c) A lot of economic variables increase over time. It is important to check an economic variable is trend stationary (i.e., y t = a 0 + a t + ɛ t ) or difference stationary (i.e., y t = b 0 + y t + ɛ t ). Consider k-step ahead prediction for both cases. (Trend Stationarity) y t+k t = a 0 + a (t + k) (Difference Stationarity) y t+k t = b 0 k + y t 2. The Case of φ < : y t = φ y t + ɛ t, ɛ t i.i.d. N(0, σ 2 ɛ), y 0 = 0, t =,, T
31 84 Then, OLSE of φ is: ˆφ = y t y t. y 2 t In the case of φ <, ˆφ = φ + T T y t ɛ t y 2 t φ + E(y t ɛ t ) E(y 2 t ) = φ. Note as follows: T y t ɛ t E(y t ɛ t ) = 0.
32 85 By the central limit theorem, yɛ E(yɛ) V(yɛ) N(0, ) where yɛ = T y t ɛ t.
33 86 Therefore, E(yɛ) = 0, V(yɛ) = V( T y t ɛ t ) = E ( ( T = T 2 E( T y t ɛ t ) 2) ) T y t y s ɛ t ɛ s = T E( 2 s= y 2 t ɛ2 t ) = T σ2 ɛγ(0). yɛ σ 2 ɛ γ(0)/t = T σ ɛ γ(0) y t ɛ t N(0, ), which is rewritten as: T y t ɛ t N(0, σ 2 ɛγ(0)).
34 87 E(y2 t ) = γ(0), we have the following asymptotic distri- Using T bution: y 2 t T( ˆφ φ ) = T T y t ɛ t y 2 t N ( ) σ 2 ɛ 0, = N ( 0, φ 2 γ(0) ). Note that γ(0) = σ2 ɛ. φ 2 3. In the case of φ =, as expected, we have: T( ˆφ ) 0. That is, ˆφ has the distribution which converges in probability to φ = (i.e., degenerated distribution).
35 88 Is this true? 4. The Case of φ = : = Random Walk Process y t = y t + ɛ t with y 0 = 0 is written as: y t = ɛ t + ɛ t + ɛ t ɛ. Therefore, we can obtain: y t N(0, σ 2 ɛt). The variance of y t depends on time t. = y t is nonstationary. yt ɛ t 5. Remember that ˆφ = φ +. y 2 t (a) First, consider the numerator y t ɛ t. We have y 2 t = (y t + ɛ t ) 2 = y 2 t + 2y t ɛ t + ɛ 2 t.
36 89 Therefore, we obtain: y t ɛ t = 2 (y2 t y 2 t ɛ2 t ). Taking into account y 0 = 0, we have: y t ɛ t = 2 y2 T 2 ɛt 2. Divided by σ 2 ɛt on both sides, we have the following: σ 2 ɛt y t ɛ t = ( ) 2 y T 2 σ ɛ T 2σ 2 ɛ From y t N(0, σ 2 ɛt), we obtain the following result: ( y T σ ɛ T ) 2 χ 2 (). T ɛt 2.
37 90 Moreover, the second term is derived from: T ɛt 2 E(ɛt 2 ) = σ 2 ɛ. Therefore, σ 2 ɛt y t ɛ t = ( ) 2 y T 2 σ ɛ T 2σ 2 ɛ T ɛt 2 2 (χ2 () ). (b) Next, consider y 2 t. E y 2 t = E(y 2 t ) = σ 2 ɛ(t ) = σ 2 ɛ Thus, we obtain the following result: T E 2 y 2 t a fixed value, i.e., σ2 ɛ 2. T(T ). 2
38 9 Therefore, T 2 y 2 t a distribution. 6. Summarizing the results up to now, T( ˆφ φ ), not T( ˆφ φ ), has limiting distribution in the case of φ =. T( ˆφ φ ) = (/T) y t ɛ t (/T 2 ) y 2 t a distribution. 7. Basic Concepts of Random Walk Process: (a) Model: y t = y t + ɛ t, y 0 = 0, ɛ t N(0, ). Then, y t = ɛ t + ɛ t + + ɛ. Therefore, y t N(0, t).
39 92 = Nonstationary Process (i.e., variance depends on time t.) Difference between y s and y t (s > t) is: y s y t = ɛ s + ɛ s + + ɛ t+2 + ɛ t+. The distribution of y s y t is: y s y t N(0, s t). (b) Rewrite as follows: y t = y t + ɛ t = y t + e,t + e 2,t + + e N,t, where ɛ t = e,t + e 2,t + + e N,t. e,t, e 2,t,, e N,t are iid with e i,t N(0, /N). That is, suppose that there are N subperiods between time t and time t+.
HW 3 Solutions 1. a) I use the auto.arima R function to search over models using AIC and decide on an ARMA(3,1)
 HW 3 Solutions a) I use the autoarima R function to search over models using AIC and decide on an ARMA3,) b) I compare the ARMA3,) to ARMA,0) ARMA3,) does better in all three criteria c) The plot of the
HW 3 Solutions a) I use the autoarima R function to search over models using AIC and decide on an ARMA3,) b) I compare the ARMA3,) to ARMA,0) ARMA3,) does better in all three criteria c) The plot of the
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Introduction to the ML Estimation of ARMA processes
 Introduction to the ML Estimation of ARMA processes Eduardo Rossi University of Pavia October 2013 Rossi ARMA Estimation Financial Econometrics - 2013 1 / 1 We consider the AR(p) model: Y t = c + φ 1 Y
Introduction to the ML Estimation of ARMA processes Eduardo Rossi University of Pavia October 2013 Rossi ARMA Estimation Financial Econometrics - 2013 1 / 1 We consider the AR(p) model: Y t = c + φ 1 Y
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Stationary ARMA Processes
 Stationary ARMA Processes Eduardo Rossi University of Pavia October 2013 Rossi Stationary ARMA Financial Econometrics - 2013 1 / 45 Moving Average of order 1 (MA(1)) Y t = µ + ɛ t + θɛ t 1 t = 1,..., T
Stationary ARMA Processes Eduardo Rossi University of Pavia October 2013 Rossi Stationary ARMA Financial Econometrics - 2013 1 / 45 Moving Average of order 1 (MA(1)) Y t = µ + ɛ t + θɛ t 1 t = 1,..., T
2. ARMA 1. 1 This part is based on H and BD.
 2. ARMA 1 1 This part is based on H and BD. 1 1 MA 1.1 MA(1) Let ε t be WN with variance σ 2 and consider the zero mean 2 process Y t = ε t + θε t 1 (1) where θ is a constant. MA(1). This time series is
2. ARMA 1 1 This part is based on H and BD. 1 1 MA 1.1 MA(1) Let ε t be WN with variance σ 2 and consider the zero mean 2 process Y t = ε t + θε t 1 (1) where θ is a constant. MA(1). This time series is
Module 5. February 14, h 0min
 Module 5 Stationary Time Series Models Part 2 AR and ARMA Models and Their Properties Class notes for Statistics 451: Applied Time Series Iowa State University Copyright 2015 W. Q. Meeker. February 14,
Module 5 Stationary Time Series Models Part 2 AR and ARMA Models and Their Properties Class notes for Statistics 451: Applied Time Series Iowa State University Copyright 2015 W. Q. Meeker. February 14,
6.3 Forecasting ARMA processes
 122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
Stationary ARMA Processes
 University of Pavia 2007 Stationary ARMA Processes Eduardo Rossi University of Pavia Moving Average of order 1 (MA(1)) Y t = µ + ǫ t + θǫ t 1 t = 1,...,T ǫ t WN(0, σ 2 ) E(ǫ t ) = 0 E(ǫ 2 t) = σ 2 E(ǫ
University of Pavia 2007 Stationary ARMA Processes Eduardo Rossi University of Pavia Moving Average of order 1 (MA(1)) Y t = µ + ǫ t + θǫ t 1 t = 1,...,T ǫ t WN(0, σ 2 ) E(ǫ t ) = 0 E(ǫ 2 t) = σ 2 E(ǫ
Solutions to Exercise Sheet 5
 Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
Statistics 104: Quantitative Methods for Economics Formula and Theorem Review
 Harvard College Statistics 104: Quantitative Methods for Economics Formula and Theorem Review Tommy MacWilliam, 13 tmacwilliam@college.harvard.edu March 10, 2011 Contents 1 Introduction to Data 5 1.1 Sample
Harvard College Statistics 104: Quantitative Methods for Economics Formula and Theorem Review Tommy MacWilliam, 13 tmacwilliam@college.harvard.edu March 10, 2011 Contents 1 Introduction to Data 5 1.1 Sample
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Srednicki Chapter 55
 Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Απόκριση σε Μοναδιαία Ωστική Δύναμη (Unit Impulse) Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο. Απόστολος Σ.
 Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Queensland University of Technology Transport Data Analysis and Modeling Methodologies
 Queensland University of Technology Transport Data Analysis and Modeling Methodologies Lab Session #7 Example 5.2 (with 3SLS Extensions) Seemingly Unrelated Regression Estimation and 3SLS A survey of 206
Queensland University of Technology Transport Data Analysis and Modeling Methodologies Lab Session #7 Example 5.2 (with 3SLS Extensions) Seemingly Unrelated Regression Estimation and 3SLS A survey of 206
Math221: HW# 1 solutions
 Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
D Alembert s Solution to the Wave Equation
 D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
6. MAXIMUM LIKELIHOOD ESTIMATION
 6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
Estimation for ARMA Processes with Stable Noise. Matt Calder & Richard A. Davis Colorado State University
 Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
derivation of the Laplacian from rectangular to spherical coordinates
 derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Exercises 10. Find a fundamental matrix of the given system of equations. Also find the fundamental matrix Φ(t) satisfying Φ(0) = I. 1.
 Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
Solution Series 9. i=1 x i and i=1 x i.
 Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
Probability and Random Processes (Part II)
 Probability and Random Processes (Part II) 1. If the variance σ x of d(n) = x(n) x(n 1) is one-tenth the variance σ x of a stationary zero-mean discrete-time signal x(n), then the normalized autocorrelation
Probability and Random Processes (Part II) 1. If the variance σ x of d(n) = x(n) x(n 1) is one-tenth the variance σ x of a stationary zero-mean discrete-time signal x(n), then the normalized autocorrelation
Bayesian statistics. DS GA 1002 Probability and Statistics for Data Science.
 Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
DESIGN OF MACHINERY SOLUTION MANUAL h in h 4 0.
 DESIGN OF MACHINERY SOLUTION MANUAL -7-1! PROBLEM -7 Statement: Design a double-dwell cam to move a follower from to 25 6, dwell for 12, fall 25 and dwell for the remader The total cycle must take 4 sec
DESIGN OF MACHINERY SOLUTION MANUAL -7-1! PROBLEM -7 Statement: Design a double-dwell cam to move a follower from to 25 6, dwell for 12, fall 25 and dwell for the remader The total cycle must take 4 sec
The Simply Typed Lambda Calculus
 Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Fourier Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
 Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
1 String with massive end-points
 1 String with massive end-points Πρόβλημα 5.11:Θεωρείστε μια χορδή μήκους, τάσης T, με δύο σημειακά σωματίδια στα άκρα της, το ένα μάζας m, και το άλλο μάζας m. α) Μελετώντας την κίνηση των άκρων βρείτε
1 String with massive end-points Πρόβλημα 5.11:Θεωρείστε μια χορδή μήκους, τάσης T, με δύο σημειακά σωματίδια στα άκρα της, το ένα μάζας m, και το άλλο μάζας m. α) Μελετώντας την κίνηση των άκρων βρείτε
Second Order RLC Filters
 ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
5.4 The Poisson Distribution.
 The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Asymptotic distribution of MLE
 Asymptotic distribution of MLE Theorem Let {X t } be a causal and invertible ARMA(p,q) process satisfying Φ(B)X = Θ(B)Z, {Z t } IID(0, σ 2 ). Let ( ˆφ, ˆϑ) the values that minimize LL n (φ, ϑ) among those
Asymptotic distribution of MLE Theorem Let {X t } be a causal and invertible ARMA(p,q) process satisfying Φ(B)X = Θ(B)Z, {Z t } IID(0, σ 2 ). Let ( ˆφ, ˆϑ) the values that minimize LL n (φ, ϑ) among those
k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +
[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R + k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +](/thumbs/73/69566903.jpg) Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Durbin-Levinson recursive method
 Durbin-Levinson recursive method A recursive method for computing ϕ n is useful because it avoids inverting large matrices; when new data are acquired, one can update predictions, instead of starting again
Durbin-Levinson recursive method A recursive method for computing ϕ n is useful because it avoids inverting large matrices; when new data are acquired, one can update predictions, instead of starting again
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
 Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Μηχανική Μάθηση Hypothesis Testing
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
Second Order Partial Differential Equations
 Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Practice Exam 2. Conceptual Questions. 1. State a Basic identity and then verify it. (a) Identity: Solution: One identity is csc(θ) = 1
 Conceptual Questions. State a Basic identity and then verify it. a) Identity: Solution: One identity is cscθ) = sinθ) Practice Exam b) Verification: Solution: Given the point of intersection x, y) of the
Conceptual Questions. State a Basic identity and then verify it. a) Identity: Solution: One identity is cscθ) = sinθ) Practice Exam b) Verification: Solution: Given the point of intersection x, y) of the
forms This gives Remark 1. How to remember the above formulas: Substituting these into the equation we obtain with
 Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Homework 8 Model Solution Section
 MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
SCITECH Volume 13, Issue 2 RESEARCH ORGANISATION Published online: March 29, 2018
 Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
 Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Figure A.2: MPC and MPCP Age Profiles (estimating ρ, ρ = 2, φ = 0.03)..
 Supplemental Material (not for publication) Persistent vs. Permanent Income Shocks in the Buffer-Stock Model Jeppe Druedahl Thomas H. Jørgensen May, A Additional Figures and Tables Figure A.: Wealth and
Supplemental Material (not for publication) Persistent vs. Permanent Income Shocks in the Buffer-Stock Model Jeppe Druedahl Thomas H. Jørgensen May, A Additional Figures and Tables Figure A.: Wealth and
Concrete Mathematics Exercises from 30 September 2016
 Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Approximation of distance between locations on earth given by latitude and longitude
 Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Lecture 21: Properties and robustness of LSE
 Lecture 21: Properties and robustness of LSE BLUE: Robustness of LSE against normality We now study properties of l τ β and σ 2 under assumption A2, i.e., without the normality assumption on ε. From Theorem
Lecture 21: Properties and robustness of LSE BLUE: Robustness of LSE against normality We now study properties of l τ β and σ 2 under assumption A2, i.e., without the normality assumption on ε. From Theorem
Partial Differential Equations in Biology The boundary element method. March 26, 2013
 The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
Lecture 34 Bootstrap confidence intervals
 Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Pg The perimeter is P = 3x The area of a triangle is. where b is the base, h is the height. In our case b = x, then the area is
 Pg. 9. The perimeter is P = The area of a triangle is A = bh where b is the base, h is the height 0 h= btan 60 = b = b In our case b =, then the area is A = = 0. By Pythagorean theorem a + a = d a a =
Pg. 9. The perimeter is P = The area of a triangle is A = bh where b is the base, h is the height 0 h= btan 60 = b = b In our case b =, then the area is A = = 0. By Pythagorean theorem a + a = d a a =
Lecture 12: Pseudo likelihood approach
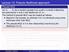 Lecture 12: Pseudo likelihood approach Pseudo MLE Let X 1,...,X n be a random sample from a pdf in a family indexed by two parameters θ and π with likelihood l(θ,π). The method of pseudo MLE may be viewed
Lecture 12: Pseudo likelihood approach Pseudo MLE Let X 1,...,X n be a random sample from a pdf in a family indexed by two parameters θ and π with likelihood l(θ,π). The method of pseudo MLE may be viewed
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3
 Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Homework for 1/27 Due 2/5
 Name: ID: Homework for /7 Due /5. [ 8-3] I Example D of Sectio 8.4, the pdf of the populatio distributio is + αx x f(x α) =, α, otherwise ad the method of momets estimate was foud to be ˆα = 3X (where
Name: ID: Homework for /7 Due /5. [ 8-3] I Example D of Sectio 8.4, the pdf of the populatio distributio is + αx x f(x α) =, α, otherwise ad the method of momets estimate was foud to be ˆα = 3X (where
( y) Partial Differential Equations
 Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate
Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate
b. Use the parametrization from (a) to compute the area of S a as S a ds. Be sure to substitute for ds!
 MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
Econ Spring 2004 Instructor: Prof. Kiefer Solution to Problem set # 5. γ (0)
 Cornell University Department of Economics Econ 60 - Spring 004 Instructor: Prof. Kiefer Solution to Problem set # 5. Autocorrelation function is defined as ρ h = γ h γ 0 where γ h =Cov X t,x t h =E[X
Cornell University Department of Economics Econ 60 - Spring 004 Instructor: Prof. Kiefer Solution to Problem set # 5. Autocorrelation function is defined as ρ h = γ h γ 0 where γ h =Cov X t,x t h =E[X
Notes on the Open Economy
 Notes on the Open Econom Ben J. Heijdra Universit of Groningen April 24 Introduction In this note we stud the two-countr model of Table.4 in more detail. restated here for convenience. The model is Table.4.
Notes on the Open Econom Ben J. Heijdra Universit of Groningen April 24 Introduction In this note we stud the two-countr model of Table.4 in more detail. restated here for convenience. The model is Table.4.
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 19/5/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
PARTIAL NOTES for 6.1 Trigonometric Identities
 PARTIAL NOTES for 6.1 Trigonometric Identities tanθ = sinθ cosθ cotθ = cosθ sinθ BASIC IDENTITIES cscθ = 1 sinθ secθ = 1 cosθ cotθ = 1 tanθ PYTHAGOREAN IDENTITIES sin θ + cos θ =1 tan θ +1= sec θ 1 + cot
PARTIAL NOTES for 6.1 Trigonometric Identities tanθ = sinθ cosθ cotθ = cosθ sinθ BASIC IDENTITIES cscθ = 1 sinθ secθ = 1 cosθ cotθ = 1 tanθ PYTHAGOREAN IDENTITIES sin θ + cos θ =1 tan θ +1= sec θ 1 + cot
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
An Introduction to Signal Detection and Estimation - Second Edition Chapter II: Selected Solutions
 An Introduction to Signal Detection Estimation - Second Edition Chapter II: Selected Solutions H V Poor Princeton University March 16, 5 Exercise : The likelihood ratio is given by L(y) (y +1), y 1 a With
An Introduction to Signal Detection Estimation - Second Edition Chapter II: Selected Solutions H V Poor Princeton University March 16, 5 Exercise : The likelihood ratio is given by L(y) (y +1), y 1 a With
ω ω ω ω ω ω+2 ω ω+2 + ω ω ω ω+2 + ω ω+1 ω ω+2 2 ω ω ω ω ω ω ω ω+1 ω ω2 ω ω2 + ω ω ω2 + ω ω ω ω2 + ω ω+1 ω ω2 + ω ω+1 + ω ω ω ω2 + ω
 0 1 2 3 4 5 6 ω ω + 1 ω + 2 ω + 3 ω + 4 ω2 ω2 + 1 ω2 + 2 ω2 + 3 ω3 ω3 + 1 ω3 + 2 ω4 ω4 + 1 ω5 ω 2 ω 2 + 1 ω 2 + 2 ω 2 + ω ω 2 + ω + 1 ω 2 + ω2 ω 2 2 ω 2 2 + 1 ω 2 2 + ω ω 2 3 ω 3 ω 3 + 1 ω 3 + ω ω 3 +
0 1 2 3 4 5 6 ω ω + 1 ω + 2 ω + 3 ω + 4 ω2 ω2 + 1 ω2 + 2 ω2 + 3 ω3 ω3 + 1 ω3 + 2 ω4 ω4 + 1 ω5 ω 2 ω 2 + 1 ω 2 + 2 ω 2 + ω ω 2 + ω + 1 ω 2 + ω2 ω 2 2 ω 2 2 + 1 ω 2 2 + ω ω 2 3 ω 3 ω 3 + 1 ω 3 + ω ω 3 +
10.7 Performance of Second-Order System (Unit Step Response)
 Lecture Notes on Control Systems/D. Ghose/0 57 0.7 Performance of Second-Order System (Unit Step Response) Consider the second order system a ÿ + a ẏ + a 0 y = b 0 r So, Y (s) R(s) = b 0 a s + a s + a
Lecture Notes on Control Systems/D. Ghose/0 57 0.7 Performance of Second-Order System (Unit Step Response) Consider the second order system a ÿ + a ẏ + a 0 y = b 0 r So, Y (s) R(s) = b 0 a s + a s + a
Lecture 2. Soundness and completeness of propositional logic
 Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
Appendix to On the stability of a compressible axisymmetric rotating flow in a pipe. By Z. Rusak & J. H. Lee
 Appendi to On the stability of a compressible aisymmetric rotating flow in a pipe By Z. Rusak & J. H. Lee Journal of Fluid Mechanics, vol. 5 4, pp. 5 4 This material has not been copy-edited or typeset
Appendi to On the stability of a compressible aisymmetric rotating flow in a pipe By Z. Rusak & J. H. Lee Journal of Fluid Mechanics, vol. 5 4, pp. 5 4 This material has not been copy-edited or typeset
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ
 ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ ΕΛΕΝΑ ΦΛΟΚΑ Επίκουρος Καθηγήτρια Τµήµα Φυσικής, Τοµέας Φυσικής Περιβάλλοντος- Μετεωρολογίας ΓΕΝΙΚΟΙ ΟΡΙΣΜΟΙ Πληθυσµός Σύνολο ατόµων ή αντικειµένων στα οποία αναφέρονται
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ ΕΛΕΝΑ ΦΛΟΚΑ Επίκουρος Καθηγήτρια Τµήµα Φυσικής, Τοµέας Φυσικής Περιβάλλοντος- Μετεωρολογίας ΓΕΝΙΚΟΙ ΟΡΙΣΜΟΙ Πληθυσµός Σύνολο ατόµων ή αντικειµένων στα οποία αναφέρονται
Section 7.6 Double and Half Angle Formulas
 09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
Lecture 2: ARMA Models
 Leture 2: ARMA Models Bus 41910, Autumn Quarter 2008, Mr Ruey S Tsay Autoregressive Moving-Average (ARMA) models form a lass of linear time series models whih are widely appliable and parsimonious in parameterization
Leture 2: ARMA Models Bus 41910, Autumn Quarter 2008, Mr Ruey S Tsay Autoregressive Moving-Average (ARMA) models form a lass of linear time series models whih are widely appliable and parsimonious in parameterization
Higher Derivative Gravity Theories
 Higher Derivative Gravity Theories Black Holes in AdS space-times James Mashiyane Supervisor: Prof Kevin Goldstein University of the Witwatersrand Second Mandelstam, 20 January 2018 James Mashiyane WITS)
Higher Derivative Gravity Theories Black Holes in AdS space-times James Mashiyane Supervisor: Prof Kevin Goldstein University of the Witwatersrand Second Mandelstam, 20 January 2018 James Mashiyane WITS)
Uniform Convergence of Fourier Series Michael Taylor
 Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
Math 446 Homework 3 Solutions. (1). (i): Reverse triangle inequality for metrics: Let (X, d) be a metric space and let x, y, z X.
 Math 446 Homework 3 Solutions. (1). (i): Reverse triangle inequalit for metrics: Let (X, d) be a metric space and let x,, z X. Prove that d(x, z) d(, z) d(x, ). (ii): Reverse triangle inequalit for norms:
Math 446 Homework 3 Solutions. (1). (i): Reverse triangle inequalit for metrics: Let (X, d) be a metric space and let x,, z X. Prove that d(x, z) d(, z) d(x, ). (ii): Reverse triangle inequalit for norms:
A Bonus-Malus System as a Markov Set-Chain. Małgorzata Niemiec Warsaw School of Economics Institute of Econometrics
 A Bonus-Malus System as a Markov Set-Chain Małgorzata Niemiec Warsaw School of Economics Institute of Econometrics Contents 1. Markov set-chain 2. Model of bonus-malus system 3. Example 4. Conclusions
A Bonus-Malus System as a Markov Set-Chain Małgorzata Niemiec Warsaw School of Economics Institute of Econometrics Contents 1. Markov set-chain 2. Model of bonus-malus system 3. Example 4. Conclusions
Jesse Maassen and Mark Lundstrom Purdue University November 25, 2013
 Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Numerical Analysis FMN011
 Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
5. Choice under Uncertainty
 5. Choice under Uncertainty Daisuke Oyama Microeconomics I May 23, 2018 Formulations von Neumann-Morgenstern (1944/1947) X: Set of prizes Π: Set of probability distributions on X : Preference relation
5. Choice under Uncertainty Daisuke Oyama Microeconomics I May 23, 2018 Formulations von Neumann-Morgenstern (1944/1947) X: Set of prizes Π: Set of probability distributions on X : Preference relation
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Every set of first-order formulas is equivalent to an independent set
 Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
CHAPTER 101 FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD
 CHAPTER FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD EXERCISE 36 Page 66. Determine the Fourier series for the periodic function: f(x), when x +, when x which is periodic outside this rge of period.
CHAPTER FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD EXERCISE 36 Page 66. Determine the Fourier series for the periodic function: f(x), when x +, when x which is periodic outside this rge of period.
Bayesian modeling of inseparable space-time variation in disease risk
 Bayesian modeling of inseparable space-time variation in disease risk Leonhard Knorr-Held Laina Mercer Department of Statistics UW May, 013 Motivation Ohio Lung Cancer Example Lung Cancer Mortality Rates
Bayesian modeling of inseparable space-time variation in disease risk Leonhard Knorr-Held Laina Mercer Department of Statistics UW May, 013 Motivation Ohio Lung Cancer Example Lung Cancer Mortality Rates
Problem Set 3: Solutions
 CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
MATHACHij = γ00 + u0j + rij
 Stata output for Hierarchical Linear Models. ***************************************. * Unconditional Random Intercept Model. *************************************** MATHACHij = γ00 + u0j + rij. mixed
Stata output for Hierarchical Linear Models. ***************************************. * Unconditional Random Intercept Model. *************************************** MATHACHij = γ00 + u0j + rij. mixed
Ηλεκτρονικοί Υπολογιστές IV
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ηλεκτρονικοί Υπολογιστές IV Μοντέλα χρονολογικών σειρών Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ηλεκτρονικοί Υπολογιστές IV Μοντέλα χρονολογικών σειρών Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Problem Set 9 Solutions. θ + 1. θ 2 + cotθ ( ) sinθ e iφ is an eigenfunction of the ˆ L 2 operator. / θ 2. φ 2. sin 2 θ φ 2. ( ) = e iφ. = e iφ cosθ.
 Chemistry 362 Dr Jean M Standard Problem Set 9 Solutions The ˆ L 2 operator is defined as Verify that the angular wavefunction Y θ,φ) Also verify that the eigenvalue is given by 2! 2 & L ˆ 2! 2 2 θ 2 +
Chemistry 362 Dr Jean M Standard Problem Set 9 Solutions The ˆ L 2 operator is defined as Verify that the angular wavefunction Y θ,φ) Also verify that the eigenvalue is given by 2! 2 & L ˆ 2! 2 2 θ 2 +
ΧΡΟΝΟΣΕΙΡΕΣ & ΠΡΟΒΛΕΨΕΙΣ-ΜΕΡΟΣ 7 ΕΛΕΓΧΟΙ. (TEST: Unit Root-Cointegration )
 ΧΡΟΝΟΣΕΙΡΕΣ & ΠΡΟΒΛΕΨΕΙΣ-ΜΕΡΟΣ 7 ΕΛΕΓΧΟΙ (TEST: Unit Root-Cointegration ) ΦΑΙΝΟΜΕΝΙΚΗ ΠΑΛΙΝΔΡΟΜΗΣΗ Η στασιμότητα των δεδομένων (χρονοσειρών) είναι θεωρητική προϋπόθεση για την παλινδρόμηση, δηλ. την εκτίμηση
ΧΡΟΝΟΣΕΙΡΕΣ & ΠΡΟΒΛΕΨΕΙΣ-ΜΕΡΟΣ 7 ΕΛΕΓΧΟΙ (TEST: Unit Root-Cointegration ) ΦΑΙΝΟΜΕΝΙΚΗ ΠΑΛΙΝΔΡΟΜΗΣΗ Η στασιμότητα των δεδομένων (χρονοσειρών) είναι θεωρητική προϋπόθεση για την παλινδρόμηση, δηλ. την εκτίμηση
