Asymptotic distribution of MLE
|
|
|
- Ἰοκάστη Τρικούπης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Asymptotic distribution of MLE Theorem Let {X t } be a causal and invertible ARMA(p,q) process satisfying Φ(B)X = Θ(B)Z, {Z t } IID(0, σ 2 ). Let ( ˆφ, ˆϑ) the values that minimize LL n (φ, ϑ) among those yielding a causal and invertible ARMA process 19 novembre / 15
2 Asymptotic distribution of MLE Theorem Let {X t } be a causal and invertible ARMA(p,q) process satisfying Φ(B)X = Θ(B)Z, {Z t } IID(0, σ 2 ). Let ( ˆφ, ˆϑ) the values that minimize LL n (φ, ϑ) among those yielding a causal and invertible ARMA process, and let ˆσ 2 = S( ˆφ, ˆϑ). Then n n 1/2 (( ˆφ, ˆϑ) (φ, ϑ)) = N(0, W ) and ˆσ 2 a.s. σ 2 19 novembre / 15
3 Asymptotic distribution of MLE Theorem Let {X t } be a causal and invertible ARMA(p,q) process satisfying Φ(B)X = Θ(B)Z, {Z t } IID(0, σ 2 ). Let ( ˆφ, ˆϑ) the values that minimize LL n (φ, ϑ) among those yielding a causal and invertible ARMA process, and let ˆσ 2 = S( ˆφ, ˆϑ). Then n n 1/2 (( ˆφ, ˆϑ) (φ, ϑ)) = N(0, W ) and ˆσ 2 a.s. σ 2 ( W = σ 2 E(Ut U t t) E(U t V t ) 1 U t t) E(V t U t t) E(V t V t with U t =. V t =. t) U t p+1 (Φ(B)U) t = Z t (Θ(B)V ) t = Z t. V t V t q+1 19 novembre / 15
4 Asymptotic distribution of MLE: examples {X t } AR(p) Then W = σ 2 (E(U t U t t)) 1 = σ 2 Γ 1 p. 19 novembre / 15
5 Asymptotic distribution of MLE: examples {X t } AR(p) Then W = σ 2 (E(U t U t t)) 1 = σ 2 Γ 1 p. Hence ˆφ N(φ, σ2 n Γ 1 p ) for n large. For p = 1, ˆϕ N(ϕ, 1 n (1 ϕ2 )). 19 novembre / 15
6 Asymptotic distribution of MLE: examples {X t } AR(p) Then W = σ 2 (E(U t U t t)) 1 = σ 2 Γ 1 p. Hence ˆφ N(φ, σ2 n Γ 1 p ) for n large. For p = 1, ˆϕ N(ϕ, 1 n (1 ϕ2 )). {X t } MA(q) Then W = σ 2 (E(V t V t t)) 1 = σ 2 (Γ q) 1 where Γ q is the covariance of the AR(q) process (Θ(B)V ) t = Z t. 19 novembre / 15
7 Asymptotic distribution of MLE: examples {X t } AR(p) Then W = σ 2 (E(U t U t t)) 1 = σ 2 Γ 1 p. Hence ˆφ N(φ, σ2 n Γ 1 p ) for n large. For p = 1, ˆϕ N(ϕ, 1 n (1 ϕ2 )). {X t } MA(q) Then W = σ 2 (E(V t V t t)) 1 = σ 2 (Γ q) 1 where Γ q is the covariance of the AR(q) process (Θ(B)V ) t = Z t. For q = 1, ˆϑ N(ϑ, 1 n (1 ϑ2 )). 19 novembre / 15
8 Asymptotic distribution of MLE: examples {X t } AR(p) Then W = σ 2 (E(U t U t t)) 1 = σ 2 Γ 1 p. Hence ˆφ N(φ, σ2 n Γ 1 p ) for n large. For p = 1, ˆϕ N(ϕ, 1 n (1 ϕ2 )). {X t } MA(q) Then W = σ 2 (E(V t V t t)) 1 = σ 2 (Γ q) 1 where Γ q is the covariance of the AR(q) process (Θ(B)V ) t = Z t. For q = 1, ˆϑ N(ϑ, 1 n (1 ϑ2 )). ( ) E(U {X t } ARMA(1, 1) W = σ t ) E(U t V t ) E(U t V t E(Vt 2 = ) ( (1 ϕ 2 ) 1 (1 + ϕϑ) 1 ) 1 (1 + ϕϑ) 1 (1 ϑ 2 ) novembre / 15
9 Asymptotic distribution of MLE: examples {X t } AR(p) Then W = σ 2 (E(U t U t t)) 1 = σ 2 Γ 1 p. Hence ˆφ N(φ, σ2 n Γ 1 p ) for n large. For p = 1, ˆϕ N(ϕ, 1 n (1 ϕ2 )). {X t } MA(q) Then W = σ 2 (E(V t V t t)) 1 = σ 2 (Γ q) 1 where Γ q is the covariance of the AR(q) process (Θ(B)V ) t = Z t. For q = 1, ˆϑ N(ϑ, 1 n (1 ϑ2 )). ( ) E(U {X t } ARMA(1, 1) W = σ t ) E(U t V t ) E(U t V t E(Vt 2 = ) ( (1 ϕ 2 ) 1 (1 + ϕϑ) 1 ) 1 (1 + ϕϑ) 1 (1 ϑ 2 ) 1. One easily obtains the asymptotic variance of ( ˆφ, ˆϑ). 19 novembre / 15
10 Comparison of estimators Estimator Method of Fitted Parameter moments innovations MLE AR(1) ϕ ˆρ(1) ˆϑ m,1 MA(1) ϑ 1 1 4(ˆρ(1)) 2 2ˆρ(1) ˆϑ m,1 ARMA(1,1) ϕ ˆρ(2)/ˆρ(1) ˆϑ m,2 / ˆϑ m,1 ϑ ugly expression ˆϑ m,1 ˆϑ m,2 / ˆϑ m,1 if ˆρ(1) novembre / 15
11 Comparison of estimators Asymptotic variance Method of Fitted Par. moments innovations MLE (1) (2) (3) 1 AR(1) ϕ n (1 ϕ2 1 1 ) n n (1 ϕ2 ) 1 1+ϑ MA(1) ϑ +4ϑ 4 +ϑ 6 +ϑ n (1 ϑ 2 ) 2 n n (1 ϑ2 ) 1 ARMA(1,1) ϕ n ϑ 1 n (1+ϕϑ) 2 (1 ϕ 2 ) (ϕ+ϑ) 2 (1+ϕϑ) 2 (1 ϑ 2 ) (ϕ+ϑ) 2 19 novembre / 15
12 Comparison of estimators Asymptotic variance Method of Fitted Par. moments innovations MLE (1) (2) (3) 1 AR(1) ϕ n (1 ϕ2 1 1 ) n n (1 ϕ2 ) 1 1+ϑ MA(1) ϑ +4ϑ 4 +ϑ 6 +ϑ n (1 ϑ 2 ) 2 n n (1 ϑ2 ) 1 ARMA(1,1) ϕ n ϑ 1 n (1+ϕϑ) 2 (1 ϕ 2 ) (ϕ+ϑ) 2 (1+ϕϑ) 2 (1 ϑ 2 ) (ϕ+ϑ) 2 Relative asymptotic efficiency e(ϑ) of (asymptotically unbiased) estimators of the parameter ϑ: ratio of asymptotic variances ϑ = ϑ = 0.25 e(ϑ; 1, 2) = 0.37 ϑ = 0.5 e(ϑ; 2, 3) = 0.75 ϑ = ϑ = ϑ = novembre / 15
13 A tool to compute asymptotic variances Theorem Let σ 2 n 0 and X n µ σ n = N(0, 1). Then g(x n ) g(µ) σ n = N(0, (g (µ) 2 ) i.e. g(x n ) N(g(µ), (g (µ)) 2 σ 2 n). Let X n k-dim., g : R k R m and X n µ σ n = N(0, V ). Let (DVD) ii > 0 where D ij = g i x j (µ). Then g(x n ) g(µ) σ n = N(0, DVD t ) i.e. g(x n ) N(g(µ), DVD t σ 2 n). 19 novembre / 15
14 Model choice: introduction MLE provides estimates for any given model, e.g. ARMA(p,q). How do we choose? The residuals should resemble a white noise. Residuals can be defined as Ŵ t = (X t ˆX t ( ˆφ, ˆϑ))((r t 1 ( ˆφ, ˆϑ)) 1/2. (X t ˆX t (φ, ϑ))((r t 1 (φ, ϑ)) 1/2 is a white-noise sequence, and Ŵ t should be close. This can be tested, e.g. by computing the ACF of {Ŵt}. To avoid overfitting, the order can be selected through a criterion. 19 novembre / 15
15 Model choice: FPE criterion FPE (Final Prediction Error) is an estimate of the one-step prediction error (in L 2 norm) for an independent realization of the observed process. Assume (X 1,..., X n ) a realization of a causal AR(p) process with coefficients ϕ 1,..., ϕ n and (Y 1,..., Y n ) an independent realization of the same. 19 novembre / 15
16 Model choice: FPE criterion FPE (Final Prediction Error) is an estimate of the one-step prediction error (in L 2 norm) for an independent realization of the observed process. Assume (X 1,..., X n ) a realization of a causal AR(p) process with coefficients ϕ 1,..., ϕ n and (Y 1,..., Y n ) an independent realization of the same. The mean-square prediction error is FPE = E(Y n+1 ˆϕ 1 Y n ˆϕ n Y n+1 p ) 2 19 novembre / 15
17 Model choice: FPE criterion FPE (Final Prediction Error) is an estimate of the one-step prediction error (in L 2 norm) for an independent realization of the observed process. Assume (X 1,..., X n ) a realization of a causal AR(p) process with coefficients ϕ 1,..., ϕ n and (Y 1,..., Y n ) an independent realization of the same. The mean-square prediction error is FPE = E(Y n+1 ˆϕ 1 Y n ˆϕ n Y n+1 p ) 2 p p = E Y n+1 ϕ j Y n+1 j ( ˆϕ j ϕ j )Y n+1 j j=1 j= novembre / 15
18 Model choice: FPE criterion FPE (Final Prediction Error) is an estimate of the one-step prediction error (in L 2 norm) for an independent realization of the observed process. Assume (X 1,..., X n ) a realization of a causal AR(p) process with coefficients ϕ 1,..., ϕ n and (Y 1,..., Y n ) an independent realization of the same. The mean-square prediction error is FPE = E(Y n+1 ˆϕ 1 Y n ˆϕ n Y n+1 p ) 2 p p = E Y n+1 ϕ j Y n+1 j ( ˆϕ j ϕ j )Y n+1 j j=1 Y n+1 p j=1 ϕ jy n+1 j = Z n+1 is independent of other terms, and has variance σ 2. Furthermore, ˆφ φ is independent of {Y t }. j= novembre / 15
19 Model choice: FPE criterion FPE (Final Prediction Error) is an estimate of the one-step prediction error (in L 2 norm) for an independent realization of the observed process. Assume (X 1,..., X n ) a realization of a causal AR(p) process with coefficients ϕ 1,..., ϕ n and (Y 1,..., Y n ) an independent realization of the same. The mean-square prediction error is FPE = E(Y n+1 ˆϕ 1 Y n ˆϕ n Y n+1 p ) 2 p p = E Y n+1 ϕ j Y n+1 j ( ˆϕ j ϕ j )Y n+1 j j=1 Y n+1 p j=1 ϕ jy n+1 j = Z n+1 is independent of other terms, and has variance σ 2. Furthermore, ˆφ φ is independent of {Y t }. Hence p FPE = σ 2 + E(( ˆϕ j ϕ j )( ˆϕ i ϕ i ))E(Y n+1 j Y n+1 i ) i,j=1 j=1 = σ 2 + E( Γ p ( ˆφ φ), ˆφ φ ) novembre / 15
20 FPE criterion: estimation FPE = σ 2 + E( Γ p ( ˆφ φ), ˆφ φ ). 19 novembre / 15
21 FPE criterion: estimation FPE = σ 2 + E( Γ p ( ˆφ φ), ˆφ φ ). Fact: if X is an n-dimensional random vector with V(X ) = S and A is an n n matrix, then E( AX, X ) = tr(as). 19 novembre / 15
22 FPE criterion: estimation FPE = σ 2 + E( Γ p ( ˆφ φ), ˆφ φ ). Fact: if X is an n-dimensional random vector with V(X ) = S and A is an n n matrix, then E( AX, X ) = tr(as). Furthermore, it was stated V( ˆφ φ) σ2 n Γ 1 p ) for n large. 19 novembre / 15
23 FPE criterion: estimation FPE = σ 2 + E( Γ p ( ˆφ φ), ˆφ φ ). Fact: if X is an n-dimensional random vector with V(X ) = S and A is an n n matrix, then E( AX, X ) = tr(as). Furthermore, it was stated V( ˆφ φ) σ2 tr(γ p Γ 1 p ) = p, FPE σ 2 (1 + p n ). n Γ 1 p ) for n large. As 19 novembre / 15
24 FPE criterion: estimation FPE = σ 2 + E( Γ p ( ˆφ φ), ˆφ φ ). Fact: if X is an n-dimensional random vector with V(X ) = S and A is an n n matrix, then E( AX, X ) = tr(as). Furthermore, it was stated V( ˆφ φ) σ2 n Γ 1 p ) for n large. As tr(γ p Γ 1 p ) = p, FPE σ 2 (1 + p n ). Replacing σ 2 n by the estimator ˆσ n p 2, one finally obtains the quantity that should be minimized. ( ) n + p ˆσ 2 n p 19 novembre / 15
25 FPE criterion: estimation FPE = σ 2 + E( Γ p ( ˆφ φ), ˆφ φ ). Fact: if X is an n-dimensional random vector with V(X ) = S and A is an n n matrix, then E( AX, X ) = tr(as). Furthermore, it was stated V( ˆφ φ) σ2 n Γ 1 p ) for n large. As tr(γ p Γ 1 p ) = p, FPE σ 2 (1 + p n ). Replacing σ 2 n by the estimator ˆσ n p 2, one finally obtains the quantity ( ) n + p ˆσ 2 n p that should be minimized. Increasing p will generally decrease ˆσ 2, but will be penalized by the other factor. 19 novembre / 15
26 Use of FPE on lake data for (ord in 1:4) Model ˆσ2 FPE { armle = AR(1) ar.mle(huron2, AR(2) order=ord,aic=f) AR(3) print(armle) AR(4) #coefficients and sigma Model ϕ 1 ϕ 2 ϕ 3 ϕ 4 print(armle$var.pred AR(1) *(n+ord)/(n-ord)) AR(2) # FPE } AR(3) AR(4) novembre / 15
27 Diagnostics of selected model Residuals vs. time ACF Residuals Residuals ACF Time Lag It seems ok. 19 novembre / 15
28 Diagnostics of AR(1) For comparison, residuals of AR(1) Residuals vs. time ACF Residuals Residuals ACF Time Lag 19 novembre / 15
29 Akaike criterion: Kullback-Leibler discrepancy Given a family of probability densities {f ( ; ψ), ψ Ψ}, Kullback-Leibler s index of f ( ; ψ) relative to f ( ; ϑ) is (ψ ϑ) = E ϑ ( 2 log(f (X ; ψ))) = 2 log(f (x; ψ))f (x; ϑ) dx. R n 19 novembre / 15
30 Akaike criterion: Kullback-Leibler discrepancy Given a family of probability densities {f ( ; ψ), ψ Ψ}, Kullback-Leibler s index of f ( ; ψ) relative to f ( ; ϑ) is (ψ ϑ) = E ϑ ( 2 log(f (X ; ψ))) = 2 log(f (x; ψ))f (x; ϑ) dx. R n Kullback-Leibler s discrepancy between f ( ; ψ) and f ( ; ϑ) is ( ) f (x; ψ) d(ψ ϑ) = (ψ ϑ) (ϑ ϑ) = 2 log f (x; ϑ) dx. R n f (x; ϑ) 19 novembre / 15
31 Akaike criterion: Kullback-Leibler discrepancy Given a family of probability densities {f ( ; ψ), ψ Ψ}, Kullback-Leibler s index of f ( ; ψ) relative to f ( ; ϑ) is (ψ ϑ) = E ϑ ( 2 log(f (X ; ψ))) = 2 log(f (x; ψ))f (x; ϑ) dx. R n Kullback-Leibler s discrepancy between f ( ; ψ) and f ( ; ϑ) is ( ) f (x; ψ) d(ψ ϑ) = (ψ ϑ) (ϑ ϑ) = 2 log f (x; ϑ) dx. R n f (x; ϑ) Jensen s inequality implies E(log(Y )) log(e(y )) for any random variable. 19 novembre / 15
32 Akaike criterion: Kullback-Leibler discrepancy Given a family of probability densities {f ( ; ψ), ψ Ψ}, Kullback-Leibler s index of f ( ; ψ) relative to f ( ; ϑ) is (ψ ϑ) = E ϑ ( 2 log(f (X ; ψ))) = 2 log(f (x; ψ))f (x; ϑ) dx. R n Kullback-Leibler s discrepancy between f ( ; ψ) and f ( ; ϑ) is ( ) f (x; ψ) d(ψ ϑ) = (ψ ϑ) (ϑ ϑ) = 2 log f (x; ϑ) dx. R n f (x; ϑ) Jensen s inequality implies E(log(Y )) log(e(y )) for any random variable. Hence ( ) f (x; ψ) d(ψ ϑ) 2 log f (x; ϑ) dx = 0 R n f (x; ϑ) with equality only if f (x; ψ) = f (x; ϑ) a.e. [f ( ; ϑ)]. 19 novembre / 15
33 Approximating Kullback-Leibler discrepancy Given observations X 1,..., X n, we would like to minimize d(ψ ϑ) among all candidate models ψ, given the true model ϑ. 19 novembre / 15
34 Approximating Kullback-Leibler discrepancy Given observations X 1,..., X n, we would like to minimize d(ψ ϑ) among all candidate models ψ, given the true model ϑ. As the true model is unknown, we estimate d(ψ ϑ). 19 novembre / 15
35 Approximating Kullback-Leibler discrepancy Given observations X 1,..., X n, we would like to minimize d(ψ ϑ) among all candidate models ψ, given the true model ϑ. As the true model is unknown, we estimate d(ψ ϑ). Let ψ = (φ, ϑ, σ 2 ) the parameters of an ARMA(p,q) model and ˆψ the MLE based on X 1,..., X n. Let Y an independent realization of the same process. Then 2 log L Y ( ˆφ, ˆϑ, ˆσ 2 ) = n log(2π) + n log( ˆσ 2 ) + log(r 0... r n 1 ) + S Y ( ˆφ, ˆϑ) ˆσ 2 19 novembre / 15
36 Approximating Kullback-Leibler discrepancy Given observations X 1,..., X n, we would like to minimize d(ψ ϑ) among all candidate models ψ, given the true model ϑ. As the true model is unknown, we estimate d(ψ ϑ). Let ψ = (φ, ϑ, σ 2 ) the parameters of an ARMA(p,q) model and ˆψ the MLE based on X 1,..., X n. Let Y an independent realization of the same process. Then 2 log L Y ( ˆφ, ˆϑ, ˆσ 2 ) = n log(2π) + n log( ˆσ 2 ) + log(r 0... r n 1 ) + S Y ( ˆφ, ˆϑ) ˆσ 2 = 2 log L X ( ˆφ, ˆϑ, ˆσ 2 ) + S Y ( ˆφ, ˆϑ) ˆσ 2 S X ( ˆφ, ˆϑ) ˆσ 2 19 novembre / 15
37 Approximating Kullback-Leibler discrepancy Given observations X 1,..., X n, we would like to minimize d(ψ ϑ) among all candidate models ψ, given the true model ϑ. As the true model is unknown, we estimate d(ψ ϑ). Let ψ = (φ, ϑ, σ 2 ) the parameters of an ARMA(p,q) model and ˆψ the MLE based on X 1,..., X n. Let Y an independent realization of the same process. Then 2 log L Y ( ˆφ, ˆϑ, ˆσ 2 ) = n log(2π) + n log( ˆσ 2 ) + log(r 0... r n 1 ) + S Y ( ˆφ, ˆϑ) ˆσ 2 = 2 log L X ( ˆφ, ˆϑ, ˆσ 2 ) + S Y ( ˆφ, ˆϑ) ˆσ 2 S X ( ˆφ, ˆϑ) ˆσ 2 = 2 log L X ( ˆφ, ˆϑ, ˆσ 2 ) + S Y ( ˆφ, ˆϑ) ˆσ 2 n = 19 novembre / 15
38 Approximating Kullback-Leibler discrepancy Given observations X 1,..., X n, we would like to minimize d(ψ ϑ) among all candidate models ψ, given the true model ϑ. As the true model is unknown, we estimate d(ψ ϑ). Let ψ = (φ, ϑ, σ 2 ) the parameters of an ARMA(p,q) model and ˆψ the MLE based on X 1,..., X n. Let Y an independent realization of the same process. Then 2 log L Y ( ˆφ, ˆϑ, ˆσ 2 ) = n log(2π) + n log( ˆσ 2 ) + log(r 0... r n 1 ) + S Y ( ˆφ, ˆϑ) ˆσ 2 = 2 log L X ( ˆφ, ˆϑ, ˆσ 2 ) + S Y ( ˆφ, ˆϑ) ˆσ 2 S X ( ˆφ, ˆϑ) ˆσ 2 = 2 log L X ( ˆφ, ˆϑ, ˆσ 2 ) + S Y ( ˆφ, ˆϑ) n = ˆσ 2 ( ) E ϑ ( ( ˆψ ϑ)) = E (φ,ϑ,σ 2 )( 2 log L X ( ˆφ, ˆϑ, ˆσ 2 S Y ( ˆφ, ˆϑ) )) + E (φ,ϑ,σ 2 ) n. ˆσ 2 19 novembre / 15
39 Kullback-Leibler discrepancy and AICC Using linear approximations, and asymptotic distributions of estimators, one arrives at ( ) S Y ( ˆφ, ˆϑ) σ 2 (n + p + q). E (φ,ϑ,σ 2 ) Similarly n ˆσ 2 = S X ( ˆφ, ˆϑ) for large n is distributed as σ 2 χ 2 (n p q 2) and is asymptotically independent of ( ˆφ, ˆϑ). 19 novembre / 15
40 Kullback-Leibler discrepancy and AICC Using linear approximations, and asymptotic distributions of estimators, one arrives at ( ) S Y ( ˆφ, ˆϑ) σ 2 (n + p + q). E (φ,ϑ,σ 2 ) Similarly n ˆσ 2 = S X ( ˆφ, ˆϑ) for large n is distributed as σ 2 χ 2 (n p q 2) and is asymptotically independent of ( ˆφ, ˆϑ). Hence ( ) S Y ( ˆφ, ˆϑ) σ 2 (n + p + q) E (φ,ϑ,σ 2 ) σ 2 σ 2 (n p q 2)/n 19 novembre / 15
41 Kullback-Leibler discrepancy and AICC Using linear approximations, and asymptotic distributions of estimators, one arrives at ( ) S Y ( ˆφ, ˆϑ) σ 2 (n + p + q). E (φ,ϑ,σ 2 ) Similarly n ˆσ 2 = S X ( ˆφ, ˆϑ) for large n is distributed as σ 2 χ 2 (n p q 2) and is asymptotically independent of ( ˆφ, ˆϑ). Hence ( ) S Y ( ˆφ, ˆϑ) σ 2 (n + p + q) E (φ,ϑ,σ 2 ) σ 2 σ 2 (n p q 2)/n From E ϑ ( ( ˆψ ϑ)) = E (φ,ϑ,σ 2 )( 2 log L X ( ˆφ, ˆϑ, ˆσ ( ) 2 )) + E SY ( ˆφ, ˆϑ) (φ,ϑ,σ 2 ) n σ 2 AICC = 2 log L X ( ˆφ, ˆϑ, ˆσ 2 2(p + q + 1)n ) + n p q is an approximate unbiased estimate of ( ˆϑ ϑ). 19 novembre / 15
42 Criteria for model choice The order is chosen by minimizing the value of AICC (Corrected Akaike s Information Criterion): 2 log L X ( ˆφ, ˆϑ, ˆσ 2 ) + 2(p+q+1)n n p q. The second term can be considered a penalty for models with a large number of parameters. 19 novembre / 15
43 Criteria for model choice The order is chosen by minimizing the value of AICC (Corrected Akaike s Information Criterion): 2 log L X ( ˆφ, ˆϑ, ˆσ 2 ) + 2(p+q+1)n n p q. The second term can be considered a penalty for models with a large number of parameters. For n large it is approximately the same as Akaike s information Criterion (AIC): 2 log L X ( ˆφ, ˆϑ, ˆσ 2 ) + 2(p + q + 1), but carries a higher penalty for finite n, and thus is somewhat less likely to overfit. 19 novembre / 15
44 Criteria for model choice The order is chosen by minimizing the value of AICC (Corrected Akaike s Information Criterion): 2 log L X ( ˆφ, ˆϑ, ˆσ 2 ) + 2(p+q+1)n n p q. The second term can be considered a penalty for models with a large number of parameters. For n large it is approximately the same as Akaike s information Criterion (AIC): 2 log L X ( ˆφ, ˆϑ, ˆσ 2 ) + 2(p + q + 1), but carries a higher penalty for finite n, and thus is somewhat less likely to overfit. A rule of thumb is the fits of model 1 and model 2 are not significantly different if AICC 1 AICC 2 < 2 (only the difference matters, not the absolute value of AICC). Hence, we may decide to choose model 1 if it simpler than 2 (or its residuals are closer to white-noise) even if AICC 1 > AICC 2 as long as AICC 1 < AICC novembre / 15
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Introduction to the ML Estimation of ARMA processes
 Introduction to the ML Estimation of ARMA processes Eduardo Rossi University of Pavia October 2013 Rossi ARMA Estimation Financial Econometrics - 2013 1 / 1 We consider the AR(p) model: Y t = c + φ 1 Y
Introduction to the ML Estimation of ARMA processes Eduardo Rossi University of Pavia October 2013 Rossi ARMA Estimation Financial Econometrics - 2013 1 / 1 We consider the AR(p) model: Y t = c + φ 1 Y
Estimation for ARMA Processes with Stable Noise. Matt Calder & Richard A. Davis Colorado State University
 Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
6.3 Forecasting ARMA processes
 122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
HW 3 Solutions 1. a) I use the auto.arima R function to search over models using AIC and decide on an ARMA(3,1)
 HW 3 Solutions a) I use the autoarima R function to search over models using AIC and decide on an ARMA3,) b) I compare the ARMA3,) to ARMA,0) ARMA3,) does better in all three criteria c) The plot of the
HW 3 Solutions a) I use the autoarima R function to search over models using AIC and decide on an ARMA3,) b) I compare the ARMA3,) to ARMA,0) ARMA3,) does better in all three criteria c) The plot of the
Solution Series 9. i=1 x i and i=1 x i.
 Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
Bayesian statistics. DS GA 1002 Probability and Statistics for Data Science.
 Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
Module 5. February 14, h 0min
 Module 5 Stationary Time Series Models Part 2 AR and ARMA Models and Their Properties Class notes for Statistics 451: Applied Time Series Iowa State University Copyright 2015 W. Q. Meeker. February 14,
Module 5 Stationary Time Series Models Part 2 AR and ARMA Models and Their Properties Class notes for Statistics 451: Applied Time Series Iowa State University Copyright 2015 W. Q. Meeker. February 14,
Durbin-Levinson recursive method
 Durbin-Levinson recursive method A recursive method for computing ϕ n is useful because it avoids inverting large matrices; when new data are acquired, one can update predictions, instead of starting again
Durbin-Levinson recursive method A recursive method for computing ϕ n is useful because it avoids inverting large matrices; when new data are acquired, one can update predictions, instead of starting again
Homework for 1/27 Due 2/5
 Name: ID: Homework for /7 Due /5. [ 8-3] I Example D of Sectio 8.4, the pdf of the populatio distributio is + αx x f(x α) =, α, otherwise ad the method of momets estimate was foud to be ˆα = 3X (where
Name: ID: Homework for /7 Due /5. [ 8-3] I Example D of Sectio 8.4, the pdf of the populatio distributio is + αx x f(x α) =, α, otherwise ad the method of momets estimate was foud to be ˆα = 3X (where
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
Approximation of distance between locations on earth given by latitude and longitude
 Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Statistics 104: Quantitative Methods for Economics Formula and Theorem Review
 Harvard College Statistics 104: Quantitative Methods for Economics Formula and Theorem Review Tommy MacWilliam, 13 tmacwilliam@college.harvard.edu March 10, 2011 Contents 1 Introduction to Data 5 1.1 Sample
Harvard College Statistics 104: Quantitative Methods for Economics Formula and Theorem Review Tommy MacWilliam, 13 tmacwilliam@college.harvard.edu March 10, 2011 Contents 1 Introduction to Data 5 1.1 Sample
Lecture 34 Bootstrap confidence intervals
 Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ
 ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ ΕΛΕΝΑ ΦΛΟΚΑ Επίκουρος Καθηγήτρια Τµήµα Φυσικής, Τοµέας Φυσικής Περιβάλλοντος- Μετεωρολογίας ΓΕΝΙΚΟΙ ΟΡΙΣΜΟΙ Πληθυσµός Σύνολο ατόµων ή αντικειµένων στα οποία αναφέρονται
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ ΕΛΕΝΑ ΦΛΟΚΑ Επίκουρος Καθηγήτρια Τµήµα Φυσικής, Τοµέας Φυσικής Περιβάλλοντος- Μετεωρολογίας ΓΕΝΙΚΟΙ ΟΡΙΣΜΟΙ Πληθυσµός Σύνολο ατόµων ή αντικειµένων στα οποία αναφέρονται
Finite Field Problems: Solutions
 Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Numerical Analysis FMN011
 Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Concrete Mathematics Exercises from 30 September 2016
 Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
 Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
Every set of first-order formulas is equivalent to an independent set
 Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
6. MAXIMUM LIKELIHOOD ESTIMATION
 6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
Figure A.2: MPC and MPCP Age Profiles (estimating ρ, ρ = 2, φ = 0.03)..
 Supplemental Material (not for publication) Persistent vs. Permanent Income Shocks in the Buffer-Stock Model Jeppe Druedahl Thomas H. Jørgensen May, A Additional Figures and Tables Figure A.: Wealth and
Supplemental Material (not for publication) Persistent vs. Permanent Income Shocks in the Buffer-Stock Model Jeppe Druedahl Thomas H. Jørgensen May, A Additional Figures and Tables Figure A.: Wealth and
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
Second Order Partial Differential Equations
 Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
LAD Estimation for Time Series Models With Finite and Infinite Variance
 LAD Estimatio for Time Series Moels With Fiite a Ifiite Variace Richar A. Davis Colorao State Uiversity William Dusmuir Uiversity of New South Wales 1 LAD Estimatio for ARMA Moels fiite variace ifiite
LAD Estimatio for Time Series Moels With Fiite a Ifiite Variace Richar A. Davis Colorao State Uiversity William Dusmuir Uiversity of New South Wales 1 LAD Estimatio for ARMA Moels fiite variace ifiite
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
derivation of the Laplacian from rectangular to spherical coordinates
 derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
Μηχανική Μάθηση Hypothesis Testing
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
Partial Differential Equations in Biology The boundary element method. March 26, 2013
 The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
Lecture 21: Properties and robustness of LSE
 Lecture 21: Properties and robustness of LSE BLUE: Robustness of LSE against normality We now study properties of l τ β and σ 2 under assumption A2, i.e., without the normality assumption on ε. From Theorem
Lecture 21: Properties and robustness of LSE BLUE: Robustness of LSE against normality We now study properties of l τ β and σ 2 under assumption A2, i.e., without the normality assumption on ε. From Theorem
5.4 The Poisson Distribution.
 The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
Lecture 12: Pseudo likelihood approach
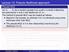 Lecture 12: Pseudo likelihood approach Pseudo MLE Let X 1,...,X n be a random sample from a pdf in a family indexed by two parameters θ and π with likelihood l(θ,π). The method of pseudo MLE may be viewed
Lecture 12: Pseudo likelihood approach Pseudo MLE Let X 1,...,X n be a random sample from a pdf in a family indexed by two parameters θ and π with likelihood l(θ,π). The method of pseudo MLE may be viewed
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
Theorem 8 Let φ be the most powerful size α test of H
 Testing composite hypotheses Θ = Θ 0 Θ c 0 H 0 : θ Θ 0 H 1 : θ Θ c 0 Definition 16 A test φ is a uniformly most powerful (UMP) level α test for H 0 vs. H 1 if φ has level α and for any other level α test
Testing composite hypotheses Θ = Θ 0 Θ c 0 H 0 : θ Θ 0 H 1 : θ Θ c 0 Definition 16 A test φ is a uniformly most powerful (UMP) level α test for H 0 vs. H 1 if φ has level α and for any other level α test
w o = R 1 p. (1) R = p =. = 1
 Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 205 ιδάσκων : Α. Μουχτάρης Τριτη Σειρά Ασκήσεων Λύσεις Ασκηση 3. 5.2 (a) From the Wiener-Hopf equation we have:
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 205 ιδάσκων : Α. Μουχτάρης Τριτη Σειρά Ασκήσεων Λύσεις Ασκηση 3. 5.2 (a) From the Wiener-Hopf equation we have:
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
 Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Απόκριση σε Μοναδιαία Ωστική Δύναμη (Unit Impulse) Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο. Απόστολος Σ.
 Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
 Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Math221: HW# 1 solutions
 Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3
 Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
SCHOOL OF MATHEMATICAL SCIENCES G11LMA Linear Mathematics Examination Solutions
 SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
Probability and Random Processes (Part II)
 Probability and Random Processes (Part II) 1. If the variance σ x of d(n) = x(n) x(n 1) is one-tenth the variance σ x of a stationary zero-mean discrete-time signal x(n), then the normalized autocorrelation
Probability and Random Processes (Part II) 1. If the variance σ x of d(n) = x(n) x(n 1) is one-tenth the variance σ x of a stationary zero-mean discrete-time signal x(n), then the normalized autocorrelation
2. ARMA 1. 1 This part is based on H and BD.
 2. ARMA 1 1 This part is based on H and BD. 1 1 MA 1.1 MA(1) Let ε t be WN with variance σ 2 and consider the zero mean 2 process Y t = ε t + θε t 1 (1) where θ is a constant. MA(1). This time series is
2. ARMA 1 1 This part is based on H and BD. 1 1 MA 1.1 MA(1) Let ε t be WN with variance σ 2 and consider the zero mean 2 process Y t = ε t + θε t 1 (1) where θ is a constant. MA(1). This time series is
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
An Inventory of Continuous Distributions
 Appendi A An Inventory of Continuous Distributions A.1 Introduction The incomplete gamma function is given by Also, define Γ(α; ) = 1 with = G(α; ) = Z 0 Z 0 Z t α 1 e t dt, α > 0, >0 t α 1 e t dt, α >
Appendi A An Inventory of Continuous Distributions A.1 Introduction The incomplete gamma function is given by Also, define Γ(α; ) = 1 with = G(α; ) = Z 0 Z 0 Z t α 1 e t dt, α > 0, >0 t α 1 e t dt, α >
Solutions to Exercise Sheet 5
 Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
MAT Winter 2016 Introduction to Time Series Analysis Study Guide for Midterm
 MAT 3379 - Winter 2016 Introduction to Time Series Analysis Study Guide for Midterm You will be allowed to have one A4 sheet (one-sided) of notes date: Monday, Febraury 29, Midterm 1 Topics 1 Evaluate
MAT 3379 - Winter 2016 Introduction to Time Series Analysis Study Guide for Midterm You will be allowed to have one A4 sheet (one-sided) of notes date: Monday, Febraury 29, Midterm 1 Topics 1 Evaluate
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
Reminders: linear functions
 Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
Queensland University of Technology Transport Data Analysis and Modeling Methodologies
 Queensland University of Technology Transport Data Analysis and Modeling Methodologies Lab Session #7 Example 5.2 (with 3SLS Extensions) Seemingly Unrelated Regression Estimation and 3SLS A survey of 206
Queensland University of Technology Transport Data Analysis and Modeling Methodologies Lab Session #7 Example 5.2 (with 3SLS Extensions) Seemingly Unrelated Regression Estimation and 3SLS A survey of 206
Finite difference method for 2-D heat equation
 Finite difference method for 2-D heat equation Praveen. C praveen@math.tifrbng.res.in Tata Institute of Fundamental Research Center for Applicable Mathematics Bangalore 560065 http://math.tifrbng.res.in/~praveen
Finite difference method for 2-D heat equation Praveen. C praveen@math.tifrbng.res.in Tata Institute of Fundamental Research Center for Applicable Mathematics Bangalore 560065 http://math.tifrbng.res.in/~praveen
Exercises to Statistics of Material Fatigue No. 5
 Prof. Dr. Christine Müller Dipl.-Math. Christoph Kustosz Eercises to Statistics of Material Fatigue No. 5 E. 9 (5 a Show, that a Fisher information matri for a two dimensional parameter θ (θ,θ 2 R 2, can
Prof. Dr. Christine Müller Dipl.-Math. Christoph Kustosz Eercises to Statistics of Material Fatigue No. 5 E. 9 (5 a Show, that a Fisher information matri for a two dimensional parameter θ (θ,θ 2 R 2, can
Partial Trace and Partial Transpose
 Partial Trace and Partial Transpose by José Luis Gómez-Muñoz http://homepage.cem.itesm.mx/lgomez/quantum/ jose.luis.gomez@itesm.mx This document is based on suggestions by Anirban Das Introduction This
Partial Trace and Partial Transpose by José Luis Gómez-Muñoz http://homepage.cem.itesm.mx/lgomez/quantum/ jose.luis.gomez@itesm.mx This document is based on suggestions by Anirban Das Introduction This
CHAPTER 48 APPLICATIONS OF MATRICES AND DETERMINANTS
 CHAPTER 48 APPLICATIONS OF MATRICES AND DETERMINANTS EXERCISE 01 Page 545 1. Use matrices to solve: 3x + 4y x + 5y + 7 3x + 4y x + 5y 7 Hence, 3 4 x 0 5 y 7 The inverse of 3 4 5 is: 1 5 4 1 5 4 15 8 3
CHAPTER 48 APPLICATIONS OF MATRICES AND DETERMINANTS EXERCISE 01 Page 545 1. Use matrices to solve: 3x + 4y x + 5y + 7 3x + 4y x + 5y 7 Hence, 3 4 x 0 5 y 7 The inverse of 3 4 5 is: 1 5 4 1 5 4 15 8 3
Math 6 SL Probability Distributions Practice Test Mark Scheme
 Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1
 Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1 A Brief History of Sampling Research 1915 - Edmund Taylor Whittaker (1873-1956) devised a
Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1 A Brief History of Sampling Research 1915 - Edmund Taylor Whittaker (1873-1956) devised a
Congruence Classes of Invertible Matrices of Order 3 over F 2
 International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
Aquinas College. Edexcel Mathematical formulae and statistics tables DO NOT WRITE ON THIS BOOKLET
 Aquinas College Edexcel Mathematical formulae and statistics tables DO NOT WRITE ON THIS BOOKLET Pearson Edexcel Level 3 Advanced Subsidiary and Advanced GCE in Mathematics and Further Mathematics Mathematical
Aquinas College Edexcel Mathematical formulae and statistics tables DO NOT WRITE ON THIS BOOKLET Pearson Edexcel Level 3 Advanced Subsidiary and Advanced GCE in Mathematics and Further Mathematics Mathematical
Exercises 10. Find a fundamental matrix of the given system of equations. Also find the fundamental matrix Φ(t) satisfying Φ(0) = I. 1.
 Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
Fourier Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
CRASH COURSE IN PRECALCULUS
 CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
Jesse Maassen and Mark Lundstrom Purdue University November 25, 2013
 Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Lecture 2. Soundness and completeness of propositional logic
 Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
Practice Exam 2. Conceptual Questions. 1. State a Basic identity and then verify it. (a) Identity: Solution: One identity is csc(θ) = 1
 Conceptual Questions. State a Basic identity and then verify it. a) Identity: Solution: One identity is cscθ) = sinθ) Practice Exam b) Verification: Solution: Given the point of intersection x, y) of the
Conceptual Questions. State a Basic identity and then verify it. a) Identity: Solution: One identity is cscθ) = sinθ) Practice Exam b) Verification: Solution: Given the point of intersection x, y) of the
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 19/5/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Stationary ARMA Processes
 Stationary ARMA Processes Eduardo Rossi University of Pavia October 2013 Rossi Stationary ARMA Financial Econometrics - 2013 1 / 45 Moving Average of order 1 (MA(1)) Y t = µ + ɛ t + θɛ t 1 t = 1,..., T
Stationary ARMA Processes Eduardo Rossi University of Pavia October 2013 Rossi Stationary ARMA Financial Econometrics - 2013 1 / 45 Moving Average of order 1 (MA(1)) Y t = µ + ɛ t + θɛ t 1 t = 1,..., T
5. Choice under Uncertainty
 5. Choice under Uncertainty Daisuke Oyama Microeconomics I May 23, 2018 Formulations von Neumann-Morgenstern (1944/1947) X: Set of prizes Π: Set of probability distributions on X : Preference relation
5. Choice under Uncertainty Daisuke Oyama Microeconomics I May 23, 2018 Formulations von Neumann-Morgenstern (1944/1947) X: Set of prizes Π: Set of probability distributions on X : Preference relation
Generalized additive models in R
 www.nr.no Generalized additive models in R Magne Aldrin, Norwegian Computing Center and the University of Oslo Sharp workshop, Copenhagen, October 2012 Generalized Linear Models - GLM y Distributed with
www.nr.no Generalized additive models in R Magne Aldrin, Norwegian Computing Center and the University of Oslo Sharp workshop, Copenhagen, October 2012 Generalized Linear Models - GLM y Distributed with
5. Partial Autocorrelation Function of MA(1) Process:
 54 5. Partial Autocorrelation Function of MA() Process: φ, = ρ() = θ + θ 2 0 ( ρ() ) ( φ2, ) ( φ() ) = ρ() φ 2,2 φ(2) ρ() ρ() ρ(2) = φ 2,2 = ρ() = ρ() ρ() ρ() 0 ρ() ρ() = ρ()2 ρ() 2 = θ 2 + θ 2 + θ4 0
54 5. Partial Autocorrelation Function of MA() Process: φ, = ρ() = θ + θ 2 0 ( ρ() ) ( φ2, ) ( φ() ) = ρ() φ 2,2 φ(2) ρ() ρ() ρ(2) = φ 2,2 = ρ() = ρ() ρ() ρ() 0 ρ() ρ() = ρ()2 ρ() 2 = θ 2 + θ 2 + θ4 0
 1 1 1 2 1 2 2 1 43 123 5 122 3 1 312 1 1 122 1 1 1 1 6 1 7 1 6 1 7 1 3 4 2 312 43 4 3 3 1 1 4 1 1 52 122 54 124 8 1 3 1 1 1 1 1 152 1 1 1 1 1 1 152 1 5 1 152 152 1 1 3 9 1 159 9 13 4 5 1 122 1 4 122 5
1 1 1 2 1 2 2 1 43 123 5 122 3 1 312 1 1 122 1 1 1 1 6 1 7 1 6 1 7 1 3 4 2 312 43 4 3 3 1 1 4 1 1 52 122 54 124 8 1 3 1 1 1 1 1 152 1 1 1 1 1 1 152 1 5 1 152 152 1 1 3 9 1 159 9 13 4 5 1 122 1 4 122 5
ESTIMATION OF SYSTEM RELIABILITY IN A TWO COMPONENT STRESS-STRENGTH MODELS DAVID D. HANAGAL
 ESTIMATION OF SYSTEM RELIABILITY IN A TWO COMPONENT STRESS-STRENGTH MODELS DAVID D. HANAGAL Department of Statistics, University of Poona, Pune-411007, India. Abstract In this paper, we estimate the reliability
ESTIMATION OF SYSTEM RELIABILITY IN A TWO COMPONENT STRESS-STRENGTH MODELS DAVID D. HANAGAL Department of Statistics, University of Poona, Pune-411007, India. Abstract In this paper, we estimate the reliability
Optimal Parameter in Hermitian and Skew-Hermitian Splitting Method for Certain Two-by-Two Block Matrices
 Optimal Parameter in Hermitian and Skew-Hermitian Splitting Method for Certain Two-by-Two Block Matrices Chi-Kwong Li Department of Mathematics The College of William and Mary Williamsburg, Virginia 23187-8795
Optimal Parameter in Hermitian and Skew-Hermitian Splitting Method for Certain Two-by-Two Block Matrices Chi-Kwong Li Department of Mathematics The College of William and Mary Williamsburg, Virginia 23187-8795
Lecture 7: Overdispersion in Poisson regression
 Lecture 7: Overdispersion in Poisson regression Claudia Czado TU München c (Claudia Czado, TU Munich) ZFS/IMS Göttingen 2004 0 Overview Introduction Modeling overdispersion through mixing Score test for
Lecture 7: Overdispersion in Poisson regression Claudia Czado TU München c (Claudia Czado, TU Munich) ZFS/IMS Göttingen 2004 0 Overview Introduction Modeling overdispersion through mixing Score test for
Divergence for log concave functions
 Divergence or log concave unctions Umut Caglar The Euler International Mathematical Institute June 22nd, 2013 Joint work with C. Schütt and E. Werner Outline 1 Introduction 2 Main Theorem 3 -divergence
Divergence or log concave unctions Umut Caglar The Euler International Mathematical Institute June 22nd, 2013 Joint work with C. Schütt and E. Werner Outline 1 Introduction 2 Main Theorem 3 -divergence
2. Let H 1 and H 2 be Hilbert spaces and let T : H 1 H 2 be a bounded linear operator. Prove that [T (H 1 )] = N (T ). (6p)
![2. Let H 1 and H 2 be Hilbert spaces and let T : H 1 H 2 be a bounded linear operator. Prove that [T (H 1 )] = N (T ). (6p) 2. Let H 1 and H 2 be Hilbert spaces and let T : H 1 H 2 be a bounded linear operator. Prove that [T (H 1 )] = N (T ). (6p)](/thumbs/40/21364883.jpg) Uppsala Universitet Matematiska Institutionen Andreas Strömbergsson Prov i matematik Funktionalanalys Kurs: F3B, F4Sy, NVP 2005-03-08 Skrivtid: 9 14 Tillåtna hjälpmedel: Manuella skrivdon, Kreyszigs bok
Uppsala Universitet Matematiska Institutionen Andreas Strömbergsson Prov i matematik Funktionalanalys Kurs: F3B, F4Sy, NVP 2005-03-08 Skrivtid: 9 14 Tillåtna hjälpmedel: Manuella skrivdon, Kreyszigs bok
Overview. Transition Semantics. Configurations and the transition relation. Executions and computation
 Overview Transition Semantics Configurations and the transition relation Executions and computation Inference rules for small-step structural operational semantics for the simple imperative language Transition
Overview Transition Semantics Configurations and the transition relation Executions and computation Inference rules for small-step structural operational semantics for the simple imperative language Transition
Calculating the propagation delay of coaxial cable
 Your source for quality GNSS Networking Solutions and Design Services! Page 1 of 5 Calculating the propagation delay of coaxial cable The delay of a cable or velocity factor is determined by the dielectric
Your source for quality GNSS Networking Solutions and Design Services! Page 1 of 5 Calculating the propagation delay of coaxial cable The delay of a cable or velocity factor is determined by the dielectric
10.7 Performance of Second-Order System (Unit Step Response)
 Lecture Notes on Control Systems/D. Ghose/0 57 0.7 Performance of Second-Order System (Unit Step Response) Consider the second order system a ÿ + a ẏ + a 0 y = b 0 r So, Y (s) R(s) = b 0 a s + a s + a
Lecture Notes on Control Systems/D. Ghose/0 57 0.7 Performance of Second-Order System (Unit Step Response) Consider the second order system a ÿ + a ẏ + a 0 y = b 0 r So, Y (s) R(s) = b 0 a s + a s + a
ES440/ES911: CFD. Chapter 5. Solution of Linear Equation Systems
 ES440/ES911: CFD Chapter 5. Solution of Linear Equation Systems Dr Yongmann M. Chung http://www.eng.warwick.ac.uk/staff/ymc/es440.html Y.M.Chung@warwick.ac.uk School of Engineering & Centre for Scientific
ES440/ES911: CFD Chapter 5. Solution of Linear Equation Systems Dr Yongmann M. Chung http://www.eng.warwick.ac.uk/staff/ymc/es440.html Y.M.Chung@warwick.ac.uk School of Engineering & Centre for Scientific
Econ Spring 2004 Instructor: Prof. Kiefer Solution to Problem set # 5. γ (0)
 Cornell University Department of Economics Econ 60 - Spring 004 Instructor: Prof. Kiefer Solution to Problem set # 5. Autocorrelation function is defined as ρ h = γ h γ 0 where γ h =Cov X t,x t h =E[X
Cornell University Department of Economics Econ 60 - Spring 004 Instructor: Prof. Kiefer Solution to Problem set # 5. Autocorrelation function is defined as ρ h = γ h γ 0 where γ h =Cov X t,x t h =E[X
Tridiagonal matrices. Gérard MEURANT. October, 2008
 Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in
 Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
Tutorial on Multinomial Logistic Regression
 Tutorial on Multinomial Logistic Regression Javier R Movellan June 19, 2013 1 1 General Model The inputs are n-dimensional vectors the outputs are c-dimensional vectors The training sample consist of m
Tutorial on Multinomial Logistic Regression Javier R Movellan June 19, 2013 1 1 General Model The inputs are n-dimensional vectors the outputs are c-dimensional vectors The training sample consist of m
CHAPTER 101 FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD
 CHAPTER FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD EXERCISE 36 Page 66. Determine the Fourier series for the periodic function: f(x), when x +, when x which is periodic outside this rge of period.
CHAPTER FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD EXERCISE 36 Page 66. Determine the Fourier series for the periodic function: f(x), when x +, when x which is periodic outside this rge of period.
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 24/3/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Όλοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα μικρότεροι του 10000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Αν κάπου κάνετε κάποιες υποθέσεις
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Όλοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα μικρότεροι του 10000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Αν κάπου κάνετε κάποιες υποθέσεις
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Supplementary Appendix
 Supplementary Appendix Measuring crisis risk using conditional copulas: An empirical analysis of the 2008 shipping crisis Sebastian Opitz, Henry Seidel and Alexander Szimayer Model specification Table
Supplementary Appendix Measuring crisis risk using conditional copulas: An empirical analysis of the 2008 shipping crisis Sebastian Opitz, Henry Seidel and Alexander Szimayer Model specification Table
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 6/5/2006
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Ολοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα είναι μικρότεροι το 1000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Διάρκεια: 3,5 ώρες Καλή
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Ολοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα είναι μικρότεροι το 1000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Διάρκεια: 3,5 ώρες Καλή
Uniform Convergence of Fourier Series Michael Taylor
 Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
