3. Μαγνετοστατικά πεδία (Μagnetostatic fields)
|
|
|
- Πηνελόπεια Βασιλόπουλος
- 9 χρόνια πριν
- Προβολές:
Transcript
1 3. Μαγνετοστατικά πεδία (Μagnetostatic fields) Στο προηγούμενο κεφάλαιο μιλήσαμε για τα στατικά ηλεκτρικά πεδία που χαρακτηρίζονται από το Ε και το D. Σε αυτό το κεφάλαιο θα επικεντρωθούμε στα στατικά μαγνητικά πεδία, τα οποία χαρακτηρίζονται από το H (Ένταση Μαγνητικού Πεδίου (A/m)) και το B (Μαγνητική Πυκνότητα Ροής (Wb/m ή Tesla (T)). Αναλογίες μεταξύ ηλεκτρικών και μαγνητικών πεδίων φαίνονται στον πιο κάτω πίνακα: Παράγοντας (Term) Ηλεκτρικό πεδίο Μαγνητικό πεδίο Βασικοί νόμοι Q Q μ F a 0 Idl a r db 4πε r 4π R D. d s Q enc H. d l I enc Νόμοι δυνάμεων FQ.E FQu x B Στοιχεία πηγής (source dq QuIdl elements) Ένταση πεδίου I V E ( V / m ) H ( A / m ) l l Ψ Ψ D ( C / m ) B ( Wb / m ) S S Πυκνότητα ροής(flux density) Σχέσεις μεταξύ πεδίων DεE BμΗ Δυναμικά (potentials) E V H V m ( J 0 ) V ρ L dl μ Idl A 4 πε r 4πR Ροή(flux) Ψ D. ds Ψ B. ds Πυκνότητα ενέργειας(energy density) Εξίσωση Πουασόν(Poisson s equation) του Ψ Q CV dv I C dt Ψ LI V di L dt w E D.E w m B. H ρ J ν Α μ V ε R
2 Υπάρχουν δύο πολύ σημαντικοί νόμοι στα μαγνητικά πεδία () ο νόμος του Μπιότ-Σαβάρτ (Biot-Savart s law) και () ο νόμος του Αμπέρ για τα κυκλώματα (Ampere s law). Νόμος του Μπιότ-Σαβάρτ (Biot-Savart s law) O νόμος λέει ότι η ένταση του μαγνητικού πεδίου dh που παράγεται σε ένα σημείο Ρ, όπως φαίνεται στο πιο κάτω σχήμα, από ένα διαφορικό στοιχείο ρεύματος (differential current element) Idl είναι ανάλογη με το γινόμενο Idl και το ημίτονο (sine) της γωνίας α και είναι αντιστρόφως ανάλογο με το τετράγωνο της απόστασης R μεταξύ του Ρ και του στοιχείου. dh Idl sin 4π R a d H Idl R 4π R ή σε διανυσματική μορφή 3 O νόμος του Μπιότ-Σαβάρτ, σε σχέση με το διανεμημένο ρεύμα, γίνεται dh Idl a R ή 4π R L Idl 4π R a R H για επικαμπύλιο ρεύμα
3 dh K ds a R ή H 4π R S K ds 4π R a R για ρεύμα επιφάνειας dh J dv a R ή H 4π R v J dv 4π R a R για ρεύμα όγκου. Τα Idl (I σε Amperes), KdS (K σε A/m) και Jdv (J σε A/m ). Για παράδειγμα, ας εφαρμόσουμε τις πιο πάνω εξισώσεις για να υπολογίσουμε το πεδίο που παράγεται λόγω ενός μεταφορέα ρεύματος ευθείας γραμμής (straight) μήκους ΑΒ όπως φαίνεται στο πιο κάτω σχήμα. 3
4 Αν υποθέσουμε τη συμβολή του dh στο σημείο Ρ λόγω του στοιχείου dl στο σημείο (0,0,z) τότε dh Idl R 3 και αφού 4π R dl dz a z και Rρa ρ za z dl x Rρdz a φ και έχοντας το zρcot α, dz -ρcosec α dα I καταλήγουμε στο H 4π α α Ι 4πρ ρ cos ec ada 3 3 ρ cos ec a α φ a a sin( a φ a ) da ή I H (cos a cos a )a φ 4πρ 4
5 Παράδειγμα 3. Ένας κυκλικός βρόγχος βρίσκεται στο x + y 9, z0 και τον διαπερνά σταθερό ρεύμα 0Α στη κατεύθυνση του a φ όπως φαίνεται στο πιο κάτω σχήμα. Να υπολογίσετε το Η στα σημεία (0,0,4) και (0,0,-4). (sd 7.3 p98) dh Idl R 4π R 3 όπου dl ρdϕaϕ a dl R ρ a ρ ϕ z 0 ρd ϕ 0 ρhdϕaρ + ρ dϕa z 0 a h R ( 0,0, h ) ( x, y,0) ρ aρ + haz ( ρhdϕ aρ + ρ dϕa z) dhρaρ + dhzaz I dh 3 4π ( ρ + h ) Λόγω συμμετρίας η συνιστώσα στην κατεύθυνση aρ είναι 0. H ρ π 0 H dh zaz 0 π z 0 4π Iρ dϕa Αντικαθιστούμε I 0A, ρ3, h4 ( ) 0( 3) az ( ) ( ) 3 9 ( + 6) (αφού dl R είναι το ίδιο για h και h) Iρ πa H 0, 0, 4 H 0, 0, a A/m Iρ a 3 3 ( ρ + h ) 4π ( ρ + h ) 3 ( ρ + h ) z ( ) a ( + ) 0 3 z H 0, 0, a 3 z A/m 9 6 z z 5
6 Νόμος του Αμπέρ για τα κυκλώματα Εξίσωση του Μάξουελ (Ampere s circuit law-maxwell s equation) Ο νόμος του Αμπέρ για τα κυκλώματα λέει ότι το επικαμπύλιο ολοκλήρωμα (line integral) της εφαπτόμενης συνιστώσας του Η γύρω από μια κλειστή πορεία, είναι το ίδιο με το συνολικό ρεύμα που εσωκλείεται από αυτή τη πορεία ή αλλιώς H. dl I enc Από το νόμο του Αμπέρ βγαίνει και η τρίτη εξίσωση του Μάξγουελ (Maxwell s third equation) που είναι H J όπου Ienc J ds S και J είναι η πυκνότητα ρεύματος (A/m ) Εφαρμογές του νόμου του Αμπέρ (Applications of Ampere s law) Θα χρησιμοποιήσουμε το νόμο του Αμπέρ για να υπολογίσουμε το Η για κάποιες συμμετρικές διανομές ρεύματος όπως ένα άπειρο επικαμπύλιο ρεύμα (infinite line current), άπειρη επιφάνεια ρεύματος (infinite current sheet) και άπειρη ομοαξονική γραμμή μετάδοσης (infinite coaxial transmission line). 6
7 Άπειρο επικαμπύλιο ρεύμα (infinite line current) Έχουμε το ρεύμα Ι στη κατεύθυνση του άξονα z όπως φαίνεται στο πιο κάτω σχήμα. Για να υπολογίσουμε το Η στο σημείο Ρ, θα επιτρέψουμε μια κλειστή πορεία που θα περνά από το σημείο Ρ όπου ονομάζεται Αμπερική πορεία (Amperian path). Δεδομένου ότι το ρ είναι σταθερό I H a φ. ρ d φa φ Η φ ρ d φ Η πρ φ φ ή Η Ι πρ α φ 7
8 Άπειρή επιφάνεια ρεύματος (infinite current sheet) Ας υποθέσουμε ότι έχουμε μια άπειρη επιφάνεια ρεύματος στο επίπεδο z0 όπως φαίνεται στο πιο κάτω σχήμα. Aν η πυκνότητα του ρεύματος είναι ομοιόμορφη ΚΚ y α y A/m, με την εφαρμογή του νόμου του Αμπέρ στη κλειστή τετραγωνική πορεία μας δίνει H. dl I enc K y b Γενικά, για μια άπειρη επιφάνεια ρεύματος με πυκνότητα ρεύματος Κ A/m H K a n όπου α n είναι ένα κάθετο διάνυσμα που κατευθύνεται απó το επίπεδο του ρεύματος επιφάνειας στο σημείο που μας ενδιαφέρει. 8
9 Άπειρη ομοαξονική γραμμή μετάδοσης (Infinite coaxial transmission line) Ας θεωρήσουμε ότι έχουμε μία άπειρη ομοαξονική γραμμή μετάδοσης που περιέχει δύο ομόκεντρους κυλίνδρους που έχουν τον άξονά τους στην κατεύθυνση του άξονα z. Η τομή (cross section) των γραμμών φαίνεται στο πιο κάτω σχήμα όπου ο άξονας z είναι έξω από τη σελίδα. Ο εσωτερικός αγωγός έχει ακτίνα α και έχει ρεύμα Ι, ο εξωτερικός έχει ακτίνα b, πάχος t και έχει ρεύμα Ι. Θέλουμε να υπολογίσουμε το Η παντού, δεδομένου ότι το ρεύμα είναι ομοιόμορφα διανεμημένο και στους δυο αγωγούς. Θα εφαρμόσουμε το νόμο του Αμπέρ για κάθε μια από τις 4 περιοχές 0 ρ α, α ρ b, b ρ b + t, ρ b + t. Για τη περιοχή καταλήγουμε στο 0 ρ α χρησιμοποιώντας το νόμο του Αμπέρ H φ Iρ πα 9
10 Για τη περιοχή καταλήγουμε στο α ρ b χρησιμοποιώντας το νόμο του Αμπέρ H φ I πρ Για τη περιοχή b ρ b + t χρησιμοποιώντας το νόμο του Αμπέρ καταλήγουμε στο 0
11 H φ Ι πρ ρ t b + bt Για τη περιοχή καταλήγουμε στο ρ b + t χρησιμοποιώντας το νόμο του Αμπέρ H φ 0
12 Παράδειγμα 3. Ένα πηνίο σχήματος δακτυλίου του οποίου οι διαστάσεις φαίνονται στο πιο κάτω σχήμα έχει N στροφές και ρεύμα Ι. Να υπολογίσετε το H μέσα και έξω από το πηνίο. (sd 7.6 p309)
13 Πυκνότητα μαγνητικής ροής-εξίσωση του Μάξγουελ (Magnetic flux density-maxwell s equation) H πυκνότητα μαγνητικής ροής Β είναι παρόμοια με την πυκνότητα ηλεκτρικής ροής D. Όπως το Dε ο Ε σε ελεύθερο χώρο, έτσι και το Bμ ο Η όπου μ ο είναι μια σταθερά που ονομάζεται διαπερατότητα του ελεύθερου χώρου (permeability of free space) σε Henry/meter (H/m) και έχει τη τιμή μ ο 4π x 0-7 Η/m. Η μαγνητική ροή μέσα σε από μια επιφάνεια S είναι Ψ S B. ds και μετριέται σε Webers (Wb) και η πυκνότητα μαγνητικής ροής μετριέται σε (Wb/m ) ή Teslas (T). Η γραμμή της μαγνητικής ροής Β είναι η γραμμή όπου η βελόνα της πυξίδας θα ευθυγραμμιστεί αν τοποθετηθεί σε μαγνητικό πεδίο. Για παράδειγμα, οι μαγνητικές γραμμές ροής λόγω ενός ευθύγραμμου σύρματος φαίνονται στο πιο κάτω σχήμα. 3
14 Σε ένα ηλεκτροστατικό πεδίο η ροή που περνά μέσα από μια κλειστή επιφάνεια είναι η ίδια με το εσωκλειόμενο φορτίο δηλαδή Ψ D. ds Q Για αυτό το λόγο μπορούμε να έχουμε ένα απομονωμένο ηλεκτρικό φορτίο όπως φαίνεται στο πιο κάτω σχήμα. Aντίθετα οι μαγνητικές γραμμές ροής είναι πάντοτε κλειστές όπως φαίνονται στο πιο κάτω σχήμα. Αυτό γίνεται για το λόγο ότι δεν είναι δυνατό να έχουμε απομονωμένους μαγνητικούς πόλους (ή μαγνητικά φορτία). Για παράδειγμα, αν προσπαθήσουμε να απομονώσουμε ένα μαγνητικό πόλο με το να κόψουμε ένα μαγνήτη σε δύο, θα καταλήξουμε με δύο κομμάτια με το κάθε ένα να έχει βόρειο και νότιο πόλο όπως φαίνεται στο πιο κάτω σχήμα. Έτσι η συνολική ροή μέσα από μια κλειστή επιφάνεια σε ένα μαγνητικό πεδίο πρέπει να είναι ίση με μηδέν. B.dS 0 Η εξίσωση αυτή ονομάζεται ο νόμος της διατήρησης της μαγνητικής ροής (law of conservation of magnetic flux). Από αυτή την εξίσωση μπορούμε να καταλήξουμε στη τέταρτη εξίσωση του Μάξγουελ (fourth Maxwell s equation) που είναι 4
15 . B 0 Η πιο πάνω εξίσωση δείχνει ότι τα μαγνετοστατικά πεδία δεν έχουν ούτε πηγή ούτε αρνητική πηγή (sink). 5
16 Εξισώσεις του Μάξγουελ για στατικά ηλεκτρομαγνητικά πεδία (Maxwell s equations for static EM fields) O πιο κάτω πίνακας περιλαμβάνει συγκεντρωμένες τις 4 εξισώσεις του Μάξγουελ. Διαφορική μορφή D Μορφή ολοκληρώματος D. ds ρ ν dv. ρ ν S v. Β 0 B.dS 0 Ε 0 E.dl 0 Η J H. dl J. ds S L L S Σημειώσεις Νόμος του Γκάους Μη ύπαρξη μαγνητικού μονοπόλου Διατήρηση του ηλεκτροστατικού πεδίου Νόμος του Αμπέρ 6
17 Μαγνητικά βαθμωτά και διανυσματικά δυναμικά (Magnetic scalars and vector potentials) Aς θυμηθούμε ότι πολλά από τα προβλήματα των ηλεκτροστατικών πεδίων απλοποιήθηκαν με το συσχετισμό που κάναμε για το δυναμικό V και την ένταση του ηλεκτρικού πεδίου Ε ( E V ). Τον ίδιο συσχετισμό μπορούμε να κάνουμε με το δυναμικό και το μαγνετοστατικό πεδίο Β. Το μαγνητικό δυναμικό μπορεί να είναι βαθμωτό V m αλλά και διανυσματικό Α. Το βαθμωτό μαγνητικό δυναμικό συσχετίζεται με το H με τη πιο κάτω εξίσωση: H V m όταν J0 Το διανυσματικό μαγνητικό δυναμικό συσχετίζεται με το Β με τη πιο κάτω εξίσωση: B A Το Α ορίζεται ως το μαγνετοστατικό διανυσματικό δυναμικό (magnetic vector potential) και έχει μονάδα μέτρησης Tm, ή Wb/m. Ακόμα μπορούμε να ορίσουμε τα πιο κάτω: A L μ ο Ιdl 4πR για επικαμπύλιο ρεύμα (line current) A S μ ο K ds 4πR για ρεύμα επιφάνειας (surface current) 7
18 A V μ ο J dv 4πR για ρεύμα όγκου(volume current) Επίσης με την αντικατάσταση της εξίσωσης B A μέσα στην εξίσωση Ψ B ds και χρησιμοποιώντας το θεώρημα του Στόουκ S (Stoke s theorem) καταλήγουμε στο Ψ L A.dl Τότε η μαγνητική και ηλεκτρική ροή μέσα σε ένα δεδομένο εμβαδό μπορεί να βρεθεί από τις εξισώσεις Ψ S B ds Ψ και L A. dl Η χρησιμοποίηση του μαγνητικού διανυσματικού δυναμικού προσφέρει μίαν ισχυρή προσέγγιση στη λύση ηλεκτρομαγνητικών προβλημάτων, ειδικά αυτών που σχετίζονται με αντένες. 8
19 Παράδειγμα 3.3 Δίνεται το μαγνητικό διανυσματικό δυναμικό (magnetic vector potential) Α -ρ /4 a z Wb/m, να υπολογίσετε την ολική μαγνητική ροή που διασχίζει την επιφάνεια φ π/, ρ m, 0 z 5 m. (sd 7.7 p37) Μέθοδος 5 z 0 ρ A ρ B A a a S a ρ z ϕ ϕ d dρdz ϕ 5 Ψ B ds ρdρdz ρ ( 5) 3.75 Wb 4 4 S Μέθοδος 3 z B Α 4 x y Ψ d Ψ +Ψ +Ψ +Ψ L A l όπου L είναι η καμπύλη που περικλείει την 3 4 επιφάνεια S. Το Α έχει μόνο συνιστώσα στο a z. ΨΨ Ψ 3 0 ΨΨ +Ψ 4 () dz + () 4 5 ( 4)( 5) 3.75 Wb dz 9
20 Εξαγωγή των νόμων του Μπιότ-Σαβάρτ Αμπέρ (Derivation of Biot-Savart s law and Ampere s law) Αφού ο νόμος του Μπιότ-Σαβάρτ είναι βασικά σε επικαμπύλιο ρεύμα (line current) θα ξεκινήσουμε τη εξαγωγή με το B ' μ Ιdl μ Ι 4π R 4π ο ο L L R dl ' αν χρησιμοποιήσουμε την πιο κάτω ιδιότητα ( f F ) f F + ( f ) F και στη θέση του F έχουμε το dl και του f το /R τότε καταλήγουμε στο B μ ο I ' dl + 4π L R R dl ' Αφού το λειτουργά σε συνάρτηση του (x,y,z) και το di είναι συνάρτηση του (x,y,z ' ), τότε dl 0 ' Ακόμα ( x x ) / ' ' [ + ( y y ) + ( z ) ] R z R ( x x ' ) a + ( y y ' ) a ( z x y z R / ' ' ' [( x x ) + ( y y ) + ( z z ) ] 3 R + z ' ) a a όπου το α R είναι το μοναδιαίο διάνυσμα από το σημείο πηγής (source point) στο σημείο πεδίου (field point). Με τα πιο πάνω καταλήγουμε στο μ I B ο dl a R 4π R L 0
21 όπου είναι ο νόμος του Μπιότ-Σαβάρτ. Μπορούμε ακόμα να δείξουμε ότι για ένα στατικό μαγνητικό πεδίο. A 0 και A μ J όπου ονομάζεται η διανυσματική εξίσωση τoυ Πουασόν (vector Poisson s equation). Επίσης μπορούμε να δείξουμε και πως εξάγεται ο νόμος του Αμπέρ. Από το θεώρημα του Στόουκ (Stoke s theorem) και την εξίσωση B A καταλήγουμε H. ds ο ( A). dl H ds μ L S ο S και χρησιμοποιώντας τις πιο κάτω ιδιότητες (. A) A A,. 0 καταλήγουμε στο A, A μ J ο A A μ J ο και αντικαθιστώντας στην εξίσωση H. ds ( A). dl HdS μ L S ο S καταλήγουμε στο νόμο του Αμπέρ που είναι H. dl J. ds L S I
22 Μαγνητικό δίπολο (A magnetic dipole) Ένα κομμάτι μαγνήτης ή ένα μικρός βρόγχος ρεύματος (filamentary current loop) συνήθως ονομάζονται μαγνητικά δίπολα. Ας υπολογίσουμε το μαγνητικό πεδίο Β σε ένα σημείο Ρ(r,θ,φ) που δημιουργείται λόγω ενός κυκλικού βρόγχου με ρεύμα I (circular loop currying current I) όπως φαίνεται στο πιο κάτω σχήμα. Το μαγνητικό διανυσματικό δυναμικό στο σημείο Ρ είναι A μ ο Ι 4π dl r Μπορεί να αποδειχτεί ότι σε ένα μακρινό σημείο r>>α, το Α έχει μόνο συνιστώσα του φ και δίνεται από μ A ο Iπα θ μ a φ ή A ο 4πr sin m a 4πr όπου miπα a z, και a z x a r sin θ a φ. Υπολογίζουμε τη πυκνότητα της μαγνητικής ροής Β από το r
23 B A και είναι B μ m ο ( cosθa + sin ) 3 r θa θ 4π r Στον πιο κάτω πίνακα συγκρίνονται τα ηλεκτρικά και μαγνητικά μονόπολα και δίπολα. 3
24 Μαγνητισμός στα υλικά (Magnetization in materials) B μ ο μ H r όπου το Β είναι η πυκνότητα μαγνητικής ροής (magnetic flux density) και μετριέται σε Τέσλα (Τ), το Η είναι η ένταση μαγνητικής ροής (magnetic field strength) και μετριέται σε Α/m και το μμ ο μ r ονομάζεται η διαπερατότητα του υλικού που μετριέται σε Henrys per meter (Η/m). Επίσης ορίζουμε το Μ (magnetization) ως τη μαγνητική δίπολη ροπή ανά μονάδα όγκου (magnetic dipole moment per unit volume) και μετριέται σε Α/m. Η σχέση του Μ με το Η φαίνεται στη παρά κάτω σχέση M χ mh όπου χ m είναι μια ποσότητα χωρίς διαστάσεις και ονομάζεται μαγνητική ευαισθησία (magnetic susceptibility) του υλικού. Σημείωση: Τα πιο πάνω ισχύουν μόνο σε γραμμικά και ισοτροπικά υλικά (linear and isotropic). 4
25 Μαγνητικές Οριακές συνθήκες (Magnetic boundary conditions) Oρίζουμε μαγνητικές οριακές συνθήκες τις συνθήκες που πρέπει το μαγνητικό πεδίο να ικανοποιεί στη διεπαφή (interface) δύο μέσων. Ας υποθέσουμε τη διεπαφή (interface) μεταξύ δυο μαγνητικών μέσων και, που χαρακτηρίζονται από το μ και το μ αντίστοιχα όπως φαίνεται στο πιο κάτω σχήμα. Mε εφαρμογή των εξισώσεων καταλήγουμε στο B.dS 0 Δh 0 και H dl I B n Bn Ακόμα μπορούμε να δείξουμε ότι μ H μ H ή n n ( H H) an K όπου τα a n είναι ένα μοναδιαίο διάνυσμα που κατευθύνεται από το μέσο στο. 5
26 Εάν η διεπαφή δεν έχει ρεύμα ή εάν τα μέσα δεν είναι αγωγοί, μπορούμε να γράψουμε H t H t ή B t μ Bt μ Απόδειξη 6
27 Παράδειγμα 3.4 Δίνεται το Η -a x + 6a y + 4a z A/m στη περιοχή y x 0, όπως φαίνεται στο πιο κάτω σχήμα, όπου μ 5μ ο. Να υπολογίσετε (α) το Μ και το Β εάν το χ μ (μ r ) (β) το Η και το Β στη περιοχή y x 0, όπου μ μ ο. (sd 8.8 p 366) Το y-x είναι επίπεδο και το y-x είναι η περιοχή (βάζοντας το σημείο (0,0) μπορούμε να το δούμε καθαρά). Ένα κάθετο μοναδιαίο διάνυσμα στο f ax + ay επίπεδο f ( x,y) y-x- δίδεται από a n f (α) χμ ( μ ) ( )( ) 7 B μh μoμrh 4π 0 ( 5)( ax + 6ay + 4az) M H H 5 a + 6a + 4a 8a + 4a + 6 a A/m x y z x y z.57a a a μwb/m x y z ax + ay ax + ay (β) H ( H a ) a ( a + 6a + 4a ) 4a + 4a Όμως H H + H n t n n n x y z x y ( ) ( ) H H H a + 6a + 4a 4a + 4a a + a + 4a Χρησιμοποιώντας τις οριακές συνθήκες παίρνουμε t n x y z x y x y z 7
28 H H a + a + 4a t t x y z B B μ H μ H n n n n μ 5 H H 4a + 4a 0a + 0a ( ) n n x y x y μ Έτσι H Hn + Ht ax + ay + a z 8 4 A/m -7 και B μh μoμrh( 4π 0 )( )( 8ax + ay + 4a z) 0.a a a μwb/m x y z 8
29 Παράδειγμα 3.5 Το επίπεδο xy είναι η διεπαφή (interface) μεταξύ δύο διαφορετικών μέσων. Το μέσο ( z 0) το γεμίσαμε με ένα υλικό που έχει μ r 6, και το μέσο ( z 0) το γεμίσαμε με άλλο υλικό που έχει μ r 4. Αν στη διεπαφή υπάρχει ρεύμα (/μ ο )a y ma/m, και Β 5a x + 8a z mwb/m, να υπολογίσετε το Η και το Β. (sd 8.9 p 368) Σε αυτή την περίπτωση k 0 ( B x,b y,bz ) B B 8 a B 8 n n z z B Όμως H ( a + a ) 5 8 ma/m x z μ 4μo B H B a + B a +B a ma/m ( ) x x y y z z μ 6μo B σε mwb/m Έχοντας την κάθετη συνιστώσα μπορούμε να βρούμε την εφαπτομένη από ( H H) a n k H an H a n + k ( Bxax + B yay+bzaz) az ( 5ax + 8az) az + a y 6μo 4μo μo Εξισώνοντας τις συνιστώσες παίρνουμε 9
30 Bx 5 6 B y 0 + ή Bx B.5ax + 8 a z mwb/m B H ( 0.5ax +.33 a z) ma/m μ μo και H (.5ax + a z) ma/m μ o 30
31 Επαγωγέας και επαγωγή (Inductors and inductance) Ένα κύκλωμα (κλειστό μονοπάτι) που έχει ρεύμα Ι, παράγει ένα μαγνητικό πεδίο Β το οποίο προκαλεί ροή Ψ B. ds που περνά μέσα από κάθε στροφή, όπως φαίνεται στο πιο κάτω σχήμα. Αν το κύκλωμα έχει Ν όμοιες στροφές, ορίζουμε το λ ως τη σύζευξη ροής (flux linkage) λ ΝΨ Ακόμα αν το μέσο που περιτριγυρίζει το κύκλωμα είναι γραμμικό, το λ είναι ανάλογο με το ρεύμα Ι λ LI όπου L είναι μια σταθερά που ονομάζεται η επαγωγή (inductance) του κυκλώματος. Κύκλωμα ή μέρος κυκλώματος που έχει επαγωγή ονομάζεται επαγωγέας (inductor). Από τις πιο πάνω εξισώσεις μπορούμε να ορίσουμε την επαγωγή L ως 3
32 L λ I NΨ I Η μονάδα μέτρησης της επαγωγής είναι Henry (H), το οποίο είναι το ίδιο με Webers/ampere. H επαγωγή που ορίσαμε πιο πάνω συνήθως αναφέρεται ως αυτεπαγωγή (self-inductance). Μαγνητική ενέργεια (Magnetic Energy) Όπως η δυναμική ενέργεια στα ηλεκτροστατικά πεδία είναι D. Edv εe dv W E έτσι και στα μαγνητικά πεδία μπορούμε να ορίσουμε ένα παρόμοιο τύπο για τη μαγνητική ενέργεια. Ο τύπος αυτός είναι W m LI και έτσι W m wm dv B. Hdv μh dv Υπολογισμός Αυτεπαγωγής Για να υπολογίσουμε την αυτεπαγωγή ακολουθούμε τα πιο κάτω βήματα:. Διαλέγουμε τις κατάλληλες συντεταγμένες. Υποθέτουμε ότι ο επαγωγέας έχει ρεύμα Ι 3. Υπολογίζουμε το Β από το νόμο του Μπιότ-Σαβάρτ (ή του Αμπέρ αν υπάρχει συμμετρία) και μετά υπολογίζουμε το Ψ από το Ψ 4. Τέλος υπολογίζουμε το L από το B. ds NΨ L λ. I I 3
33 33
34 Παράδειγμα 3.6 Να υπολογίσετε την αυτεπαγωγή (self-inductance) ανά μονάδα μήκους για έναν άπειρα μεγάλο σωληνοειδές πηνίο. (sd 8.0 p376) 34
35 Παράδειγμα 3.7 Να υπολογίσετε την αυτεπαγωγή ενός ομοαξονικού καλωδίου με εσωτερική ακτίνα α και εξωτερική b. (sd 8. p377) z axis x I I I x dρ dρ ρ ρ a a b b Μέθοδος : Από το προηγούμενο παράδειγμα με την εφαρμογή του νόμου μiρ μi του Αμπέρ για 0 ρ a B a ϕ και για a ρ b B a ϕ πa πρ L in (εσωτερική επαγωγή) για dρ I enc πρ d λ dψ dψ αφού το Ι είναι ομοιόμορφα κατανεμημένο I πa μiρdρdz ρ d λ πa a Για μήκος l του καλωδίου a l 3 μiρ dρdz μil λin μl λ L 4 in Επαγωγή ανά μονάδα μήκους πa 8π I 8π ρ 0 z 0 Lin μ L l 8π L ext (εξωτερική επαγωγή) για dρ μi dψ B dρdz dρdz πρ Το συνολικό ρεύμα Ι είναι μέσα στο μονοπάτι που εσωκλείει την ροή 35
36 λ b l μ dρdz μ λ μ Ψ ln Lext ln πρ π π ρ az0 μl b LL in +Lext ln π + 4 a L μ b L ln H/m l π + 4 a I Il b l b a I a Μέθοδος : Χρησιμοποιώντας Wm L I ή L I B Wm B Hdv dv μ V V a π l B I in 4 I dv μ I μ 4π a V ρ 0ϕ 0 z 0 a π l μ 3 μl ρ dρ dϕ dz 4 4π a 8π ρ 0 ϕ 0 z 0 L L a π l B μ I ext I dv μ I μ 4π ρ V ρ 0ϕ 0 z 0 a π l μ dρ μl b dϕ dz ln 4π ρ π a ρ 0 ϕ 0 z 0 LL +L in ext μl b ln π + 4 a μ ρ ρ d ρ d ϕ dz ρdρdϕdz W m όπου όπως προηγουμένως 36
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ 1 .1 ΤΟ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΚΙΝΟΥΜΕΝΟΥ ΦΟΡΤΙΟΥ Ας θεωρούμε το μαγνητικό πεδίο ενός κινούμενου σημειακού φορτίου q. Ονομάζουμε τη θέση του φορτίου σημείο πηγής
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ 1 .1 ΤΟ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΚΙΝΟΥΜΕΝΟΥ ΦΟΡΤΙΟΥ Ας θεωρούμε το μαγνητικό πεδίο ενός κινούμενου σημειακού φορτίου q. Ονομάζουμε τη θέση του φορτίου σημείο πηγής
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ Ο ΝΟΜΟΣ ΤΟΥ GAUSS
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ Ο ΝΟΜΟΣ ΤΟΥ GAUSS 1 1. ΗΛΕΚΤΡΙΚΗ ΡΟΗ O νόμος του Gauss και o νόμος του Coulomb είναι δύο εναλλακτικές διατυπώσεις της ίδιας βασικής σχέσης μεταξύ μιας κατανομής φορτίου και του
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ Ο ΝΟΜΟΣ ΤΟΥ GAUSS 1 1. ΗΛΕΚΤΡΙΚΗ ΡΟΗ O νόμος του Gauss και o νόμος του Coulomb είναι δύο εναλλακτικές διατυπώσεις της ίδιας βασικής σχέσης μεταξύ μιας κατανομής φορτίου και του
ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ. Παράδειγµα: Κίνηση φορτισµένου σωµατιδίου µέσα σε µαγνητικό πεδίο. z B. m υ MAΓΝΗTIKΟ ΠΕ ΙΟ
 1 ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ.. Αν δοκιµαστικό φορτίο q βρεθεί κοντά σε αγωγό που διαρρέεται από ρεύµα, υφίσταται δύναµη κάθετη προς την διεύθυνση της ταχύτητάς του και µε µέτρο ανάλογο της ταχύτητάς του, F qυ Β (νόµος
1 ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ.. Αν δοκιµαστικό φορτίο q βρεθεί κοντά σε αγωγό που διαρρέεται από ρεύµα, υφίσταται δύναµη κάθετη προς την διεύθυνση της ταχύτητάς του και µε µέτρο ανάλογο της ταχύτητάς του, F qυ Β (νόµος
Η αρνητική φορά του άξονα z είναι προς τη σελίδα. Για να βρούμε το μέτρο του Β χρησιμοποιούμε την Εξ. (2.3). Στο σημείο Ρ 1 ισχύει
 ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα.. Σταθερό ρεύμα 5 Α μέσω χάλκινου σύρματος ρέει προς δεξαμενή ανοδείωσης. Υπολογίστε το μαγνητικό πεδίο που δημιουργείται από το τμήμα του σύρματος μήκους, cm, σε ένα σημείο που
ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα.. Σταθερό ρεύμα 5 Α μέσω χάλκινου σύρματος ρέει προς δεξαμενή ανοδείωσης. Υπολογίστε το μαγνητικό πεδίο που δημιουργείται από το τμήμα του σύρματος μήκους, cm, σε ένα σημείο που
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΜΑΓΝΗΤΙΚΑ ΠΕΔΙΑ ΚΑΙ ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΜΑΓΝΗΤΙΚΑ ΠΕΔΙΑ ΚΑΙ ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ 1 1. ΜΑΓΝΗΤΙΣΜΟΣ Μαγνητικά φαινόμενα παρατηρήθηκαν για πρώτη φορά πριν από τουλάχιστον 2500 χρόνια σε κομμάτια μαγνητισμένου σιδηρομεταλλεύματος,
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΜΑΓΝΗΤΙΚΑ ΠΕΔΙΑ ΚΑΙ ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ 1 1. ΜΑΓΝΗΤΙΣΜΟΣ Μαγνητικά φαινόμενα παρατηρήθηκαν για πρώτη φορά πριν από τουλάχιστον 2500 χρόνια σε κομμάτια μαγνητισμένου σιδηρομεταλλεύματος,
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΕΠΑΓΩΓΗ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΕΠΑΓΩΓΗ 1 3.1 ΠΕΙΡΑΜΑΤΑ ΕΠΑΓΩΓΗΣ Το Σχ. 3.1 δείχνει μερικά από τα πειράματα που πραγματοποίησε o Michael Faraday. Στο Σχ. 3.1(α, β, γ) ένα πηνίο συνδέεται με γαλβανόμετρο.
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΕΠΑΓΩΓΗ 1 3.1 ΠΕΙΡΑΜΑΤΑ ΕΠΑΓΩΓΗΣ Το Σχ. 3.1 δείχνει μερικά από τα πειράματα που πραγματοποίησε o Michael Faraday. Στο Σχ. 3.1(α, β, γ) ένα πηνίο συνδέεται με γαλβανόμετρο.
ΝΟΜΟΣ ΤΟΥ GAUSS ΚΕΦ.. 23
 ΝΟΜΟΣ ΤΟΥ GAUSS ΚΕΦ.. 23 Ροή (γενικά): Ηλεκτρική Ροή Η ποσότητα ενός μεγέθους που διέρχεται από μία επιφάνεια. Ε Ε dα dα θ Ε Ε θ Ηλεκτρική ροή dφ Ε μέσω στοιχειώδους επιφάνειας da (αφού da στοιχειώδης
ΝΟΜΟΣ ΤΟΥ GAUSS ΚΕΦ.. 23 Ροή (γενικά): Ηλεκτρική Ροή Η ποσότητα ενός μεγέθους που διέρχεται από μία επιφάνεια. Ε Ε dα dα θ Ε Ε θ Ηλεκτρική ροή dφ Ε μέσω στοιχειώδους επιφάνειας da (αφού da στοιχειώδης
ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ (ΚΕΦ 28)
 ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ (ΚΕΦ 8) B που παράγεται από κινούμενο φορτίο Το Ηλ. Πεδίο στο P (δεν φαίνεται) είναι E = 1 4πε 0 q r rˆ Για το Μαγνητικό Πεδίο στο P προκύπτει πειραματικά ότι: µ 0 qv rˆ B = 4π
ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ (ΚΕΦ 8) B που παράγεται από κινούμενο φορτίο Το Ηλ. Πεδίο στο P (δεν φαίνεται) είναι E = 1 4πε 0 q r rˆ Για το Μαγνητικό Πεδίο στο P προκύπτει πειραματικά ότι: µ 0 qv rˆ B = 4π
ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ
 ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ B που παράγεται από κινούμενο φορτίο Το Ηλ. Πεδίο στο P (δεν φαίνεται) είναι E 1 4 0 q r 2 rˆ Για το Μαγνητικό Πεδίο στο P προκύπτει πειραματικά ότι: 0 qv rˆ Έχουμε εισάγει την
ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ B που παράγεται από κινούμενο φορτίο Το Ηλ. Πεδίο στο P (δεν φαίνεται) είναι E 1 4 0 q r 2 rˆ Για το Μαγνητικό Πεδίο στο P προκύπτει πειραματικά ότι: 0 qv rˆ Έχουμε εισάγει την
Εφαρμογές Νόμος Gauss, Ηλεκτρικά πεδία. Ιωάννης Γκιάλας 7 Μαρτίου 2014
 Εφαρμογές Νόμος Gauss, Ηλεκτρικά πεδία Ιωάννης Γκιάλας 7 Μαρτίου 14 Άσκηση: Ηλεκτρικό πεδίο διακριτών φορτίων Δύο ίσα θετικά φορτία q βρίσκονται σε απόσταση α μεταξύ τους. Να βρεθεί η ακτίνα του κύκλου,
Εφαρμογές Νόμος Gauss, Ηλεκτρικά πεδία Ιωάννης Γκιάλας 7 Μαρτίου 14 Άσκηση: Ηλεκτρικό πεδίο διακριτών φορτίων Δύο ίσα θετικά φορτία q βρίσκονται σε απόσταση α μεταξύ τους. Να βρεθεί η ακτίνα του κύκλου,
Δυναμική Ενέργεια σε Ηλεκτρικό πεδίο, Διαφορά ηλεκτρικού δυναμικού. Ιωάννης Γκιάλας 14 Μαρτίου 2014
 Δυναμική Ενέργεια σε Ηλεκτρικό πεδίο, Διαφορά ηλεκτρικού δυναμικού Ιωάννης Γκιάλας 14 Μαρτίου 2014 Έργο ηλεκτροστατικής δύναμης W F Δl W N i i1 F Δl i Η μετατόπιση Δl περιγράφεται από ένα διάνυσμα που
Δυναμική Ενέργεια σε Ηλεκτρικό πεδίο, Διαφορά ηλεκτρικού δυναμικού Ιωάννης Γκιάλας 14 Μαρτίου 2014 Έργο ηλεκτροστατικής δύναμης W F Δl W N i i1 F Δl i Η μετατόπιση Δl περιγράφεται από ένα διάνυσμα που
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Το Σέλας συμβαίνει όταν υψηλής ενέργειας, φορτισμένα σωματίδια από τον Ήλιο ταξιδεύουν στην άνω ατμόσφαιρα της Γης λόγω της ύπαρξης του μαγνητικού της πεδίου. Μαγνητισμός
Φυσική για Μηχανικούς Εικόνα: Το Σέλας συμβαίνει όταν υψηλής ενέργειας, φορτισμένα σωματίδια από τον Ήλιο ταξιδεύουν στην άνω ατμόσφαιρα της Γης λόγω της ύπαρξης του μαγνητικού της πεδίου. Μαγνητισμός
ΤΥΠΟΛΟΓΙΟ-ΒΑΣΙΚΟΙ ΟΡΙΣΜΟΙ
 ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ 3.3 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ ΤΥΠΟΛΟΓΙΟ-ΒΑΣΙΚΟΙ ΟΡΙΣΜΟΙ Οι μαγνητικοί πόλοι υπάρχουν πάντοτε σε ζευγάρια. ΔΕΝ ΥΠΑΡΧΟΥΝ ΜΑΓΝΗΤΙΚΑ ΜΟΝΟΠΟΛΑ. Οι ομώνυμοι πόλοι απωθούνται, ενώ οι
ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ 3.3 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ ΤΥΠΟΛΟΓΙΟ-ΒΑΣΙΚΟΙ ΟΡΙΣΜΟΙ Οι μαγνητικοί πόλοι υπάρχουν πάντοτε σε ζευγάρια. ΔΕΝ ΥΠΑΡΧΟΥΝ ΜΑΓΝΗΤΙΚΑ ΜΟΝΟΠΟΛΑ. Οι ομώνυμοι πόλοι απωθούνται, ενώ οι
ΦΥΕ 14 6η ΕΡΓΑΣΙΑ Παράδοση ( Οι ασκήσεις είναι ϐαθµολογικά ισοδύναµες)
 ΑΣΚΗΣΗ 1 ΦΥΕ 14 6η ΕΡΓΑΣΙΑ Παράδοση 30-06-08 ( Οι ασκήσεις είναι ϐαθµολογικά ισοδύναµες) Α) Τρία σηµειακά ϕορτία τοποθετούνται στις κορυφές ενός τετραγώνου πλευράς α, όπως ϕαίνεται στο σχήµα 1. Υπολογίστε
ΑΣΚΗΣΗ 1 ΦΥΕ 14 6η ΕΡΓΑΣΙΑ Παράδοση 30-06-08 ( Οι ασκήσεις είναι ϐαθµολογικά ισοδύναµες) Α) Τρία σηµειακά ϕορτία τοποθετούνται στις κορυφές ενός τετραγώνου πλευράς α, όπως ϕαίνεται στο σχήµα 1. Υπολογίστε
ΠΕΡΙΕΧΟΜΕΝΑ ΤΟΜΟΣ Ι ΕΙΣΑΓΩΓΗ 1
 ΤΟΜΟΣ Ι ΕΙΣΑΓΩΓΗ 1 1 ΟΙ ΒΑΣΙΚΟΙ ΝΟΜΟΙ ΤΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟΥ ΠΕΔΙΟΥ 7 1.1 Μονάδες και σύμβολα φυσικών μεγεθών..................... 7 1.2 Προθέματα φυσικών μεγεθών.............................. 13 1.3 Αγωγοί,
ΤΟΜΟΣ Ι ΕΙΣΑΓΩΓΗ 1 1 ΟΙ ΒΑΣΙΚΟΙ ΝΟΜΟΙ ΤΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟΥ ΠΕΔΙΟΥ 7 1.1 Μονάδες και σύμβολα φυσικών μεγεθών..................... 7 1.2 Προθέματα φυσικών μεγεθών.............................. 13 1.3 Αγωγοί,
Κλασική Ηλεκτροδυναμική Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΜΑΓΝΗΤΟΣΤΑΤΙΚΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΜΑΓΝΗΤΟΣΤΑΤΙΚΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
1.Η δύναμη μεταξύ δύο φορτίων έχει μέτρο 120 N. Αν η απόσταση των φορτίων διπλασιαστεί, το μέτρο της δύναμης θα γίνει:
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΩΝ ΕΠΙΛΟΓΩΝ Ηλεκτρικό φορτίο Ηλεκτρικό πεδίο 1.Η δύναμη μεταξύ δύο φορτίων έχει μέτρο 10 N. Αν η απόσταση των φορτίων διπλασιαστεί, το μέτρο της δύναμης θα γίνει: (α)
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΩΝ ΕΠΙΛΟΓΩΝ Ηλεκτρικό φορτίο Ηλεκτρικό πεδίο 1.Η δύναμη μεταξύ δύο φορτίων έχει μέτρο 10 N. Αν η απόσταση των φορτίων διπλασιαστεί, το μέτρο της δύναμης θα γίνει: (α)
Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Πολυτεχνική Σχολή Πανεπιστήμιο Κύπρου
 Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Πολυτεχνική Σχολή Πανεπιστήμιο Κύπρου ΗΜΥ 331 Ηλεκτρομαγνητικά Πεδία Ενδιάμεση Εξέταση 7 Νοεμβρίου 2011 10.30-11.45 π.μ. ΗΜΥ 331: Ηλεκτρομαγνητικά
Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Πολυτεχνική Σχολή Πανεπιστήμιο Κύπρου ΗΜΥ 331 Ηλεκτρομαγνητικά Πεδία Ενδιάμεση Εξέταση 7 Νοεμβρίου 2011 10.30-11.45 π.μ. ΗΜΥ 331: Ηλεκτρομαγνητικά
Μαγνητικό Πεδίο. Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ
 Μαγνητικό Πεδίο Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ Προτεινόμενη βιβλιογραφία: SERWAY, Physics fo scientists and enginees YOUNG H.D., Univesity
Μαγνητικό Πεδίο Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ Προτεινόμενη βιβλιογραφία: SERWAY, Physics fo scientists and enginees YOUNG H.D., Univesity
8. ΜΑΓΝΗΤΙΣΜΟΣ. Φυσική ΙΙ Δ. Κουζούδης. Πρόβλημα 8.6.
 1 8. ΜΑΓΝΗΤΙΣΜΟΣ Πρόβλημα 8.6. Το σύρμα του παρακάτω σχήματος έχει άπειρο μήκος και διαρρέεται από ρεύμα I. Υπολογίστε με τη βοήθεια του νόμου του Biot-Savart με ολοκλήρωση το μέτρο και την κατεύθυνση
1 8. ΜΑΓΝΗΤΙΣΜΟΣ Πρόβλημα 8.6. Το σύρμα του παρακάτω σχήματος έχει άπειρο μήκος και διαρρέεται από ρεύμα I. Υπολογίστε με τη βοήθεια του νόμου του Biot-Savart με ολοκλήρωση το μέτρο και την κατεύθυνση
1. Νόμος του Faraday Ορισμός της μαγνητικής ροής στην γενική περίπτωση τυχαίου μαγνητικού πεδίου και επιφάνειας:
 1. Νόμος του Faaday Ορισμός της μαγνητικής ροής στην γενική περίπτωση τυχαίου μαγνητικού πεδίου και επιφάνειας: dφ d A Φ d A Αν το μαγνητικό πεδίο είναι ομογενές και η επιφάνεια επίπεδη: Φ A Ο νόμος του
1. Νόμος του Faaday Ορισμός της μαγνητικής ροής στην γενική περίπτωση τυχαίου μαγνητικού πεδίου και επιφάνειας: dφ d A Φ d A Αν το μαγνητικό πεδίο είναι ομογενές και η επιφάνεια επίπεδη: Φ A Ο νόμος του
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
ΤΥΠΟΛΟΓΙΟ. q e = C Φορτίο Ηλεκτρονίου 1.1. Ηλεκτρικό Πεδίο 2.1. Ηλεκτρικό Πεδίο Σημειακού Φορτίου Q Ηλεκτρικό Πεδίο Σημειακού
 ΤΥΠΟΛΟΓΙΟ q e = 1.6 10 19 C Φορτίο Ηλεκτρονίου 1.1 F = k Q 1 Q 2 r 2 = 9 10 9 Q 1 Q 2 r 2 Νόμος Coulomb 1.2 E = F q E = k Q r 2 E = k Q r 2 e r E = 2kλ ρ E = 2kλ ρ e ρ ε 0 = 1/4πk = 8.85 10 12 S. I. Ε
ΤΥΠΟΛΟΓΙΟ q e = 1.6 10 19 C Φορτίο Ηλεκτρονίου 1.1 F = k Q 1 Q 2 r 2 = 9 10 9 Q 1 Q 2 r 2 Νόμος Coulomb 1.2 E = F q E = k Q r 2 E = k Q r 2 e r E = 2kλ ρ E = 2kλ ρ e ρ ε 0 = 1/4πk = 8.85 10 12 S. I. Ε
ΠΑΡΑΡΤΗΜΑ Γ. Επικαμπύλια και Επιφανειακά Ολοκληρώματα. Γ.1 Επικαμπύλιο Ολοκλήρωμα
 ΠΑΡΑΡΤΗΜΑ Γ Επικαμπύλια και Επιφανειακά Ολοκληρώματα Η αναγκαιότητα για τον ορισμό και την περιγραφή των ολοκληρωμάτων που θα περιγράψουμε στο Παράρτημα αυτό προκύπτει από το γεγονός ότι τα μεγέθη που
ΠΑΡΑΡΤΗΜΑ Γ Επικαμπύλια και Επιφανειακά Ολοκληρώματα Η αναγκαιότητα για τον ορισμό και την περιγραφή των ολοκληρωμάτων που θα περιγράψουμε στο Παράρτημα αυτό προκύπτει από το γεγονός ότι τα μεγέθη που
πάχος 0 πλάτος 2a μήκος
 B1) Δεδομένου του τύπου E = 2kλ/ρ που έχει αποδειχθεί στο μάθημα και περιγράφει το ηλεκτρικό πεδίο Ε μιας άπειρης γραμμής φορτίου με γραμμική πυκνότητα φορτίου λ σε σημείο Α που βρίσκεται σε απόσταση ρ
B1) Δεδομένου του τύπου E = 2kλ/ρ που έχει αποδειχθεί στο μάθημα και περιγράφει το ηλεκτρικό πεδίο Ε μιας άπειρης γραμμής φορτίου με γραμμική πυκνότητα φορτίου λ σε σημείο Α που βρίσκεται σε απόσταση ρ
Μαγνητικό Πεδίο. Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ
 Μαγνητικό Πεδίο Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ Προτεινόμενη βιβλιογραφία: SERWAY, Physics for scientists and engineers YOUNG H.D., University
Μαγνητικό Πεδίο Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ Προτεινόμενη βιβλιογραφία: SERWAY, Physics for scientists and engineers YOUNG H.D., University
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Πηγές μαγνητικού πεδίου Νόμος Ampere. Ιωάννης Γκιάλας 21 Μαίου 2014
 Πηγές μαγνητικού πεδίου Νόμος Ampere Ιωάννης Γκιάλας 21 Μαίου 214 Στόχοι διάλεξης Να κατανοηθεί πως προκαλείται το μαγνητικό πεδίο Νόμος Biot-Savart Μαγνητικό πεδίο ευθύγραμμου ρευματοφόρου αγωγού Μαγνητική
Πηγές μαγνητικού πεδίου Νόμος Ampere Ιωάννης Γκιάλας 21 Μαίου 214 Στόχοι διάλεξης Να κατανοηθεί πως προκαλείται το μαγνητικό πεδίο Νόμος Biot-Savart Μαγνητικό πεδίο ευθύγραμμου ρευματοφόρου αγωγού Μαγνητική
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΕ Γ.Ο.Ι. ΧΩΡΟΥΣ
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΕ Γ.Ο.Ι. ΧΩΡΟΥΣ
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ
 ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ 1. Οι δυναμικές γραμμές ηλεκτροστατικού πεδίου α Είναι κλειστές β Είναι δυνατόν να τέμνονται γ Είναι πυκνότερες σε περιοχές όπου η ένταση του πεδίου είναι μεγαλύτερη δ Ξεκινούν
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ 1. Οι δυναμικές γραμμές ηλεκτροστατικού πεδίου α Είναι κλειστές β Είναι δυνατόν να τέμνονται γ Είναι πυκνότερες σε περιοχές όπου η ένταση του πεδίου είναι μεγαλύτερη δ Ξεκινούν
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Το Σέλας συμβαίνει όταν υψηλής ενέργειας, φορτισμένα σωματίδια από τον Ήλιο ταξιδεύουν στην άνω ατμόσφαιρα της Γης λόγω της ύπαρξης του μαγνητικού της πεδίου. Μαγνητισμός
Φυσική για Μηχανικούς Εικόνα: Το Σέλας συμβαίνει όταν υψηλής ενέργειας, φορτισμένα σωματίδια από τον Ήλιο ταξιδεύουν στην άνω ατμόσφαιρα της Γης λόγω της ύπαρξης του μαγνητικού της πεδίου. Μαγνητισμός
ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ
 ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν μια
ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν μια
Ηλεκτρομαγνητισμός. Ηλεκτρικό πεδίο νόμος Gauss. Νίκος Ν. Αρπατζάνης
 Ηλεκτρομαγνητισμός Ηλεκτρικό πεδίο νόμος Gauss Νίκος Ν. Αρπατζάνης Νόμος Gauss Ο νόµος του Gauss εκφράζει τη σχέση μεταξύ της συνολικής ηλεκτρικής ροής που διέρχεται από μια κλειστή επιφάνεια και του φορτίου
Ηλεκτρομαγνητισμός Ηλεκτρικό πεδίο νόμος Gauss Νίκος Ν. Αρπατζάνης Νόμος Gauss Ο νόµος του Gauss εκφράζει τη σχέση μεταξύ της συνολικής ηλεκτρικής ροής που διέρχεται από μια κλειστή επιφάνεια και του φορτίου
ΔΥΝΑΜΙΚΟ ΔΙΑΦΟΡΑ ΔΥΝΑΜΙΚΟΥ
 ΔΥΝΑΜΙΚΟ ΔΙΑΦΟΡΑ ΔΥΝΑΜΙΚΟΥ Υποθέστε ότι έχουμε μερικά ακίνητα φορτισμένα σώματα (σχ.). Τα σώματα αυτά δημιουργούν γύρω τους ηλεκτρικό πεδίο. Αν σε κάποιο σημείο Α του ηλεκτρικού πεδίου τοποθετήσουμε ένα
ΔΥΝΑΜΙΚΟ ΔΙΑΦΟΡΑ ΔΥΝΑΜΙΚΟΥ Υποθέστε ότι έχουμε μερικά ακίνητα φορτισμένα σώματα (σχ.). Τα σώματα αυτά δημιουργούν γύρω τους ηλεκτρικό πεδίο. Αν σε κάποιο σημείο Α του ηλεκτρικού πεδίου τοποθετήσουμε ένα
Λύση: Η δύναμη σε ρευματοφόρο αγωγό δίνεται από την
 1) Στο παρακάτω σχήμα το τμήμα της καμπύλης ΚΛ μεταξύ x = 1 και x = 3.5 αντιστοιχεί σε ένα αγωγό που διαρρέεται από ρεύμα Ι = 1.5 Α με τη φορά που δείχνεται. Η καμπύλη είναι δευτεροβάθμια ως προς x με
1) Στο παρακάτω σχήμα το τμήμα της καμπύλης ΚΛ μεταξύ x = 1 και x = 3.5 αντιστοιχεί σε ένα αγωγό που διαρρέεται από ρεύμα Ι = 1.5 Α με τη φορά που δείχνεται. Η καμπύλη είναι δευτεροβάθμια ως προς x με
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
HMY331 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΠΕΔΙΑ
 HMY331 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΠΕΔΙΑ Διδάσκων Δρ Γ. Η. Γεωργίου Μαθήματα Δευτέρα και Πέμπτη 10.30-12.00 π.μ. Σύστημα Αξιολόγησης 1. Τελική Εξέταση 60% 2. Ενδιάμεση Εξέταση 40% Κατοίκον εργασία 5 κατοίκον εργασίες
HMY331 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΠΕΔΙΑ Διδάσκων Δρ Γ. Η. Γεωργίου Μαθήματα Δευτέρα και Πέμπτη 10.30-12.00 π.μ. Σύστημα Αξιολόγησης 1. Τελική Εξέταση 60% 2. Ενδιάμεση Εξέταση 40% Κατοίκον εργασία 5 κατοίκον εργασίες
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν
ΘΕΜΑ 1. Ονοματεπώνυμο. Τμήμα
 Εισαγωγή στις Φυσικές Επιστήμες (9-7-007) Ηλεκτρομαγνητισμός Ονοματεπώνυμο Τμήμα ΘΕΜΑ 1 Α. Μια μονωτική ράβδος μήκους l φέρει ομογενώς κατανεμημένο θετικό φορτίο Q και είναι διατεταγμένη κατά μήκος του
Εισαγωγή στις Φυσικές Επιστήμες (9-7-007) Ηλεκτρομαγνητισμός Ονοματεπώνυμο Τμήμα ΘΕΜΑ 1 Α. Μια μονωτική ράβδος μήκους l φέρει ομογενώς κατανεμημένο θετικό φορτίο Q και είναι διατεταγμένη κατά μήκος του
ΕΝΟΤΗΤΑ ΙΙΙ ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ
 ΕΝΟΤΗΤΑ ΙΙΙ ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ 19 Μαγνητικό πεδίο Μαγνητικό πεδίο ονοµάζεται ο χώρος στον οποίο ασκούνται δυνάµεις σε οποιοδήποτε κινούµενο φορτίο εισάγεται σε αυτόν. Επειδή το ηλεκτρικό ρεύµα είναι διατεταγµένη
ΕΝΟΤΗΤΑ ΙΙΙ ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ 19 Μαγνητικό πεδίο Μαγνητικό πεδίο ονοµάζεται ο χώρος στον οποίο ασκούνται δυνάµεις σε οποιοδήποτε κινούµενο φορτίο εισάγεται σε αυτόν. Επειδή το ηλεκτρικό ρεύµα είναι διατεταγµένη
Πρόβλημα 7.1. την πρώτη, ένα R όταν συγκλίνει στην δεύτερη). Επομένως
 Πρόβλημα 7.1 (a) Αν Q είναι το φορτίο του εσωτερικού κελύφους, τότε στο χώρο ανάμεσα στα δύο κελύφη, και (c) Για πολύ μεγάλο b (b>>a), ο δεύτερος όρος είναι αμελητέος, και Ουσιαστικά όλη η αντίσταση είναι
Πρόβλημα 7.1 (a) Αν Q είναι το φορτίο του εσωτερικού κελύφους, τότε στο χώρο ανάμεσα στα δύο κελύφη, και (c) Για πολύ μεγάλο b (b>>a), ο δεύτερος όρος είναι αμελητέος, και Ουσιαστικά όλη η αντίσταση είναι
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Στοιχεία Ηλεκτρικών Κυκλωμάτων
 Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Στοιχεία Ηλεκτρικών Κυκλωμάτων Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Νόμος Ampere Το ολοκλήρωμα του μαγνητικού
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Στοιχεία Ηλεκτρικών Κυκλωμάτων Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Νόμος Ampere Το ολοκλήρωμα του μαγνητικού
Νόμος Ampere- Διανυσματικό Δυναμικό
 Νόμος Ampere- Διανυσματικό Δυναμικό Δομή Διάλεξης Μαγνητικό πεδίο ευθύγραμμων αγωγών Ο στροβιλισμός και η κλίση μαγνητικού πεδίου: ο νόμος του Ampere Εφαρμογές του Νόμου του Ampere To διανυσματικό δυναμικό
Νόμος Ampere- Διανυσματικό Δυναμικό Δομή Διάλεξης Μαγνητικό πεδίο ευθύγραμμων αγωγών Ο στροβιλισμός και η κλίση μαγνητικού πεδίου: ο νόμος του Ampere Εφαρμογές του Νόμου του Ampere To διανυσματικό δυναμικό
1. Ηλεκτρικό Φορτίο. Ηλεκτρικό Φορτίο και Πεδίο 1
 . Ηλεκτρικό Φορτίο Το ηλεκτρικό φορτίο είναι ένα από τα βασικά χαρακτηριστικά των σωματιδίων από τα οποία οικοδομείται η ύλη. Υπάρχουν δύο είδη φορτίου (θετικό αρνητικό). Κατά την φόρτιση το φορτίο δεν
. Ηλεκτρικό Φορτίο Το ηλεκτρικό φορτίο είναι ένα από τα βασικά χαρακτηριστικά των σωματιδίων από τα οποία οικοδομείται η ύλη. Υπάρχουν δύο είδη φορτίου (θετικό αρνητικό). Κατά την φόρτιση το φορτίο δεν
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΕ ΤΕΛΕΙΟΥΣ ΑΓΩΓΟΥΣ
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΕ ΤΕΛΕΙΟΥΣ ΑΓΩΓΟΥΣ
ΕΦΑΡΜΟΣΜΕΝΟΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ ΜΙΚΡΟΚΥΜΑΤΑ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΣΤΕΡΕΑΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. ΕΦΑΡΜΟΣΜΕΝΟΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ ΜΙΚΡΟΚΥΜΑΤΑ.. Α.Μ.. ΛΑΜΙΑ 2015 Παράδοση και προφορική εξέταση της εργασίας Για να ληφθεί
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΣΤΕΡΕΑΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. ΕΦΑΡΜΟΣΜΕΝΟΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ ΜΙΚΡΟΚΥΜΑΤΑ.. Α.Μ.. ΛΑΜΙΑ 2015 Παράδοση και προφορική εξέταση της εργασίας Για να ληφθεί
ΣΤΟΧΟΙ : Ο μαθητής να μπορεί να :
 ΠΗΝΙΟ ΣΤΟΧΟΙ : Ο μαθητής να μπορεί να : Αναφέρει τι είναι το πηνίο Αναφέρει από τι αποτελείται το πηνίο Αναφέρει τις ιδιότητες του πηνίου Αναφέρει το βασικό χαρακτηριστικό του πηνίου Αναφέρει τη σχέση
ΠΗΝΙΟ ΣΤΟΧΟΙ : Ο μαθητής να μπορεί να : Αναφέρει τι είναι το πηνίο Αναφέρει από τι αποτελείται το πηνίο Αναφέρει τις ιδιότητες του πηνίου Αναφέρει το βασικό χαρακτηριστικό του πηνίου Αναφέρει τη σχέση
Μεταβαλλόμενα μαγνητικά πεδία
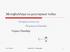 Μεταβαλλόμενα μαγνητικά πεδία Ιστορική εισαγωγή Νόμος Faraday Πειράματα Faraday V e = dφ dt 12/11/2018 Φυσική ΙΙΙ Γ. Βούλγαρης 1 Νόμος του Lentz (1834) Πειράματα Lentz Παράδειγμα Διατήρηση Ενέργειας Helmhotz
Μεταβαλλόμενα μαγνητικά πεδία Ιστορική εισαγωγή Νόμος Faraday Πειράματα Faraday V e = dφ dt 12/11/2018 Φυσική ΙΙΙ Γ. Βούλγαρης 1 Νόμος του Lentz (1834) Πειράματα Lentz Παράδειγμα Διατήρηση Ενέργειας Helmhotz
ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ & ΠΕΔΙΑ
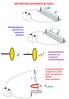 ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ & ΠΕΔΙΑ =0 Αλληλεπιδράσεις μαγνητών με ηλεκτρικά ρεύματα Αλληλεπιδράσεις μαγνητών με κινούμενα ηλεκτρικά φορτία Οι αλληλεπιδράσεις συμβαίνουν μόνον όταν τα ηλεκτρικά φορτία είναι κινούμενα
ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ & ΠΕΔΙΑ =0 Αλληλεπιδράσεις μαγνητών με ηλεκτρικά ρεύματα Αλληλεπιδράσεις μαγνητών με κινούμενα ηλεκτρικά φορτία Οι αλληλεπιδράσεις συμβαίνουν μόνον όταν τα ηλεκτρικά φορτία είναι κινούμενα
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Το Σέλας συμβαίνει όταν υψηλής ενέργειας, φορτισμένα σωματίδια από τον Ήλιο ταξιδεύουν στην άνω ατμόσφαιρα της Γης λόγω της ύπαρξης του μαγνητικού της πεδίου. Μαγνητισμός
Φυσική για Μηχανικούς Εικόνα: Το Σέλας συμβαίνει όταν υψηλής ενέργειας, φορτισμένα σωματίδια από τον Ήλιο ταξιδεύουν στην άνω ατμόσφαιρα της Γης λόγω της ύπαρξης του μαγνητικού της πεδίου. Μαγνητισμός
ΕΡΓΑΣΙΑ 6. Ημερομηνία Παράδοσης: 29/6/09
 ΕΡΓΑΣΙΑ 6 Ημερομηνία Παράδοσης: 9/6/9 1. Ένας ομογενώς φορτισμένος μονωτικός κυκλικός δίσκος ακτίνας με συνολικό φορτίο τοποθετείται στο επίπεδο xy. Να βρείτε το ηλεκτρικό πεδίο σε σημείο P που βρίσκεται
ΕΡΓΑΣΙΑ 6 Ημερομηνία Παράδοσης: 9/6/9 1. Ένας ομογενώς φορτισμένος μονωτικός κυκλικός δίσκος ακτίνας με συνολικό φορτίο τοποθετείται στο επίπεδο xy. Να βρείτε το ηλεκτρικό πεδίο σε σημείο P που βρίσκεται
Ορίζοντας την δυναμική ενέργεια σαν: Για μετακίνηση του φορτίου ανάμεσα στις πλάκες: Ηλεκτρικό Δυναμικό 1
 Ηλεκτρική Δυναμική Ενέργεια Ένα ζεύγος παράλληλων φορτισμένων μεταλλικών πλακών παράγει ομογενές ηλεκτρικό πεδίο Ε. Το έργο που παράγεται πάνω σε θετικό δοκιμαστικό φορτίο είναι: W W Fl q y q l q y Ορίζοντας
Ηλεκτρική Δυναμική Ενέργεια Ένα ζεύγος παράλληλων φορτισμένων μεταλλικών πλακών παράγει ομογενές ηλεκτρικό πεδίο Ε. Το έργο που παράγεται πάνω σε θετικό δοκιμαστικό φορτίο είναι: W W Fl q y q l q y Ορίζοντας
8η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ1 Ασκήσεις 8 ου Κεφαλαίου
 8η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ1 Ασκήσεις 8 ου Κεφαλαίου 1. Ένα σύρμα μεγάλου μήκους φέρει ρεύμα 30 Α, με φορά προς τα αριστερά κατά μήκος του άξονα x. Ένα άλλο σύρμα μεγάλου μήκους φέρει
8η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ1 Ασκήσεις 8 ου Κεφαλαίου 1. Ένα σύρμα μεγάλου μήκους φέρει ρεύμα 30 Α, με φορά προς τα αριστερά κατά μήκος του άξονα x. Ένα άλλο σύρμα μεγάλου μήκους φέρει
Πυκνότητα φορτίου. dq dv. Μικρή Περιοχή. φορτίου. Χωρική ρ Q V. Επιφανειακή σ. dq da Γραµµική λ Q A. σ = dq dl. Q l. Γ.
 Πυκνότητα φορτίου Πυκνότητα φορτίου Οµοιόµορφη Μικρή Περιοχή Χωρική ρ Q V ρ= dq dv Επιφανειακή σ Q A σ = dq da Γραµµική λ Q l λ= dq dl Γ. Βούλγαρης 1 Παράσταση της έντασης Ηλεκτρικού Πεδίου. Η Εφαπτόµενη
Πυκνότητα φορτίου Πυκνότητα φορτίου Οµοιόµορφη Μικρή Περιοχή Χωρική ρ Q V ρ= dq dv Επιφανειακή σ Q A σ = dq da Γραµµική λ Q l λ= dq dl Γ. Βούλγαρης 1 Παράσταση της έντασης Ηλεκτρικού Πεδίου. Η Εφαπτόµενη
Νόμος Faraday Κανόνας Lenz Αυτεπαγωγή - Ιωάννης Γκιάλας 27 Μαίου 2014
 Νόμος Faraday Κανόνας Lenz Αυτεπαγωγή - Ιωάννης Γκιάλας 7 Μαίου 014 Στόχοι διάλεξης Πώς να: υπολογίζει την μεταβολή της μαγνητικής ροής. εφαρμόζει το νόμο του Faraday για τον υπολογισμό της επαγόμενης
Νόμος Faraday Κανόνας Lenz Αυτεπαγωγή - Ιωάννης Γκιάλας 7 Μαίου 014 Στόχοι διάλεξης Πώς να: υπολογίζει την μεταβολή της μαγνητικής ροής. εφαρμόζει το νόμο του Faraday για τον υπολογισμό της επαγόμενης
Μαθηματικά για μηχανικούς ΙΙ ΑΣΚΗΣΕΙΣ
 Μαθηματικά για μηχανικούς ΙΙ ΑΣΚΗΣΕΙΣ Κεφάλαιο 1 1 Να βρείτε (και να σχεδιάσετε) το πεδίο ορισμού των πιο κάτω συναρτήσεων f (, ) 9 4 (γ) f (, ) f (, ) 16 4 1 Να υπολογίσετε το κάθε όριο αν υπάρχει ή να
Μαθηματικά για μηχανικούς ΙΙ ΑΣΚΗΣΕΙΣ Κεφάλαιο 1 1 Να βρείτε (και να σχεδιάσετε) το πεδίο ορισμού των πιο κάτω συναρτήσεων f (, ) 9 4 (γ) f (, ) f (, ) 16 4 1 Να υπολογίσετε το κάθε όριο αν υπάρχει ή να
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ και ΕΦΑΡΜΟΓΕΣ ΕΡΩΤΗΜΑΤΟΛΟΓΙΟ ΜΑΘΗΜΑΤΟΣ
 1 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ και ΕΦΑΡΜΟΓΕΣ ΕΡΩΤΗΜΑΤΟΛΟΓΙΟ ΜΑΘΗΜΑΤΟΣ 1) Να αναφέρετε τις 4 παραδοχές που ισχύουν για το ηλεκτρικό φορτίο 2) Εξηγήστε πόσα είδη κατανοµών ηλεκτρικού φορτίου υπάρχουν. ιατυπώστε τους
1 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ και ΕΦΑΡΜΟΓΕΣ ΕΡΩΤΗΜΑΤΟΛΟΓΙΟ ΜΑΘΗΜΑΤΟΣ 1) Να αναφέρετε τις 4 παραδοχές που ισχύουν για το ηλεκτρικό φορτίο 2) Εξηγήστε πόσα είδη κατανοµών ηλεκτρικού φορτίου υπάρχουν. ιατυπώστε τους
ΣΗΜΕΙΩΣΕΙΣ ΣΤΟΙΧΕΙΑ ΔΙΑΝΥΣΜΑΤΙΚΗΣ ΑΝΑΛΥΣΗΣ
 ΣΗΜΕΙΩΣΕΙΣ ΣΤΟΙΧΕΙΑ ΙΑΝΥΣΜΑΤΙΚΗΣ ΑΝΑΛΥΣΗΣ Σκοπός Σκοπός του κεφαλαίου είναι η ανασκόπηση βασικών μαθηματικών εργαλείων που αφορούν τη μελέτη διανυσματικών συναρτήσεων [π.χ. E(, t) ]. Τα εργαλεία αυτά είναι
ΣΗΜΕΙΩΣΕΙΣ ΣΤΟΙΧΕΙΑ ΙΑΝΥΣΜΑΤΙΚΗΣ ΑΝΑΛΥΣΗΣ Σκοπός Σκοπός του κεφαλαίου είναι η ανασκόπηση βασικών μαθηματικών εργαλείων που αφορούν τη μελέτη διανυσματικών συναρτήσεων [π.χ. E(, t) ]. Τα εργαλεία αυτά είναι
ΧΡΟΝΟΕΞΑΡΤΩΜΕΝΑ ΗΜΜ ΠΕΔΙΑ
 Kεφ. 17 (part I, pages 1-10) ΧΡΟΝΟΕΞΑΡΤΩΜΕΝΑ ΗΜΜ ΠΕΔΙΑ Νόμος του Faraday Η επαγόμενη ΗΕΔ στο κύκλωμα C ισούται με τη χρονική μεταβολή της μαγνητικής ροής που διαπερνά το κύκλωμα, dφβ ΕΗΕΔ =!! όπου ΦΒ =
Kεφ. 17 (part I, pages 1-10) ΧΡΟΝΟΕΞΑΡΤΩΜΕΝΑ ΗΜΜ ΠΕΔΙΑ Νόμος του Faraday Η επαγόμενη ΗΕΔ στο κύκλωμα C ισούται με τη χρονική μεταβολή της μαγνητικής ροής που διαπερνά το κύκλωμα, dφβ ΕΗΕΔ =!! όπου ΦΒ =
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
ΜΑΓΝΗΤΙΣΜΟΣ ΚΑΙ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ
 ΜΑΓΗΤΙΣΜΟΣ ΚΑΙ ΗΛΕΚΤΡΟΜΑΓΗΤΙΣΜΟΣ 1. α εξηγήσετε τι είναι ο μαγνήτης. 2. α αναφέρετε τρεις βασικές ιδιότητες των μαγνητών. 3. Πόσους πόλους έχει ένας μαγνήτης και πώς ονομάζονται; 4. Τι θα συμβεί αν κόψουμε
ΜΑΓΗΤΙΣΜΟΣ ΚΑΙ ΗΛΕΚΤΡΟΜΑΓΗΤΙΣΜΟΣ 1. α εξηγήσετε τι είναι ο μαγνήτης. 2. α αναφέρετε τρεις βασικές ιδιότητες των μαγνητών. 3. Πόσους πόλους έχει ένας μαγνήτης και πώς ονομάζονται; 4. Τι θα συμβεί αν κόψουμε
ΛΥΣΕΙΣ 6 ης ΕΡΓΑΣΙΑΣ (Ημερομηνία παράδοσης 3 Ιουλίου 2005)
 Άσκηση 1. (1 μονάδες) ΛΥΣΕΙΣ 6 ης ΕΡΓΑΣΙΑΣ (Ημερομηνία παράδοσης Ιουλίου 5) Α) Δοκιμαστικό φορτίο q αφήνεται σε κάποιο σημείο μέσα σε ομογενές ηλεκτρικό πεδίο εντάσεως Ε. Να εξετάσετε πώς θα κινηθεί το
Άσκηση 1. (1 μονάδες) ΛΥΣΕΙΣ 6 ης ΕΡΓΑΣΙΑΣ (Ημερομηνία παράδοσης Ιουλίου 5) Α) Δοκιμαστικό φορτίο q αφήνεται σε κάποιο σημείο μέσα σε ομογενές ηλεκτρικό πεδίο εντάσεως Ε. Να εξετάσετε πώς θα κινηθεί το
ΑΝΩΤΑΤΟ ΣΥΜΒΟΥΛΙΟ ΕΠΙΛΟΓΗΣ ΠΡΟΣΩΠΙΚΟΥ ΕΡΩΤΗΜΑΤΟΛΟΓΙΟ
 ΑΝΩΤΑΤΟ ΣΥΜΒΟΥΛΙΟ ΕΠΙΛΟΓΗΣ ΠΡΟΣΩΠΙΚΟΥ ΔΙΑΓΩΝΙΣΜΟΣ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΕΤΟΥΣ 008 ( ΠΡΟΚΗΡΥΞΗ 5Π /008) ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΔΙΑΓΩΝΙΣΜΟΥ Κλάδος-Ειδικότητα: ΠΕ 1.05 ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΞΕΤΑΣΗ ΣΤΗΝ ΠΡΩΤΗ ΘΕΜΑΤΙΚΗ
ΑΝΩΤΑΤΟ ΣΥΜΒΟΥΛΙΟ ΕΠΙΛΟΓΗΣ ΠΡΟΣΩΠΙΚΟΥ ΔΙΑΓΩΝΙΣΜΟΣ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΕΤΟΥΣ 008 ( ΠΡΟΚΗΡΥΞΗ 5Π /008) ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΔΙΑΓΩΝΙΣΜΟΥ Κλάδος-Ειδικότητα: ΠΕ 1.05 ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΞΕΤΑΣΗ ΣΤΗΝ ΠΡΩΤΗ ΘΕΜΑΤΙΚΗ
Ηλεκτρομαγνητισμός. Μαγνητικό πεδίο. Νίκος Ν. Αρπατζάνης
 Ηλεκτρομαγνητισμός Μαγνητικό πεδίο Νίκος Ν. Αρπατζάνης Μαγνητικοί πόλοι Κάθε μαγνήτης, ανεξάρτητα από το σχήμα του, έχει δύο πόλους. Τον βόρειο πόλο (Β) και τον νότιο πόλο (Ν). Μεταξύ των πόλων αναπτύσσονται
Ηλεκτρομαγνητισμός Μαγνητικό πεδίο Νίκος Ν. Αρπατζάνης Μαγνητικοί πόλοι Κάθε μαγνήτης, ανεξάρτητα από το σχήμα του, έχει δύο πόλους. Τον βόρειο πόλο (Β) και τον νότιο πόλο (Ν). Μεταξύ των πόλων αναπτύσσονται
ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΥ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΥ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΥ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778
k ) 2 P = a2 x 2 P = 2a 2 x y 2 Q = b2 y 2 Q = 2b 2 y z 2 R = c2 z 2 R = 2c 2 z P x = 2a 2 Q y = 2b 2 R z = 2c 2 3 (a2 +b 2 +c 2 ) I = 64π
 Γενικά Μαθηματικά ΙΙΙ Πέμπτο σετ ασκήσεων, Λύσεις Άσκηση 1 Το θεώρημα Gauss γενικά διατυπώνεται ως: F dv = ( F η)dσ (1) V Για την άσκηση όπου μας δίνεται η σφαίρα x + y + z 4 = Φ, το κάθετο διάνυσμα η,
Γενικά Μαθηματικά ΙΙΙ Πέμπτο σετ ασκήσεων, Λύσεις Άσκηση 1 Το θεώρημα Gauss γενικά διατυπώνεται ως: F dv = ( F η)dσ (1) V Για την άσκηση όπου μας δίνεται η σφαίρα x + y + z 4 = Φ, το κάθετο διάνυσμα η,
Κεφάλαιο Η2. Ο νόµος του Gauss
 Κεφάλαιο Η2 Ο νόµος του Gauss Ο νόµος του Gauss Ο νόµος του Gauss µπορεί να χρησιµοποιηθεί ως ένας εναλλακτικός τρόπος υπολογισµού του ηλεκτρικού πεδίου. Ο νόµος του Gauss βασίζεται στο γεγονός ότι η ηλεκτρική
Κεφάλαιο Η2 Ο νόµος του Gauss Ο νόµος του Gauss Ο νόµος του Gauss µπορεί να χρησιµοποιηθεί ως ένας εναλλακτικός τρόπος υπολογισµού του ηλεκτρικού πεδίου. Ο νόµος του Gauss βασίζεται στο γεγονός ότι η ηλεκτρική
Διανύσματα 1. Διανύσματα Πρόσθεση Διανυσμάτων Φυσική ποσότητα που περιγράφεται μόνο από ένα αριθμό ονομάζεται βαθμωτή.
 Διανύσματα 1. Διανύσματα Πρόσθεση Διανυσμάτων Φυσική ποσότητα που περιγράφεται μόνο από ένα αριθμό ονομάζεται βαθμωτή. Η διανυσματική ποσότητα έχει διεύθυνση, φορά και μέτρο. Δύο διανυσματικές ποσότητες
Διανύσματα 1. Διανύσματα Πρόσθεση Διανυσμάτων Φυσική ποσότητα που περιγράφεται μόνο από ένα αριθμό ονομάζεται βαθμωτή. Η διανυσματική ποσότητα έχει διεύθυνση, φορά και μέτρο. Δύο διανυσματικές ποσότητες
1η ΠΑΡΟΥΣΙΑΣΗ. Ηλεκτρικά πεδία
 1η ΠΑΡΟΥΣΙΑΣΗ Ηλεκτρικά πεδία Ηλεκτρισμός και μαγνητισμός Κλάδος της Φυσικής που μελετάει τα ηλεκτρικά και τα μαγνητικά φαινόμενα. (Σχεδόν) όλα τα φαινομενα που αντιλαμβανόμαστε με τις αισθήσεις μας οφείλονται
1η ΠΑΡΟΥΣΙΑΣΗ Ηλεκτρικά πεδία Ηλεκτρισμός και μαγνητισμός Κλάδος της Φυσικής που μελετάει τα ηλεκτρικά και τα μαγνητικά φαινόμενα. (Σχεδόν) όλα τα φαινομενα που αντιλαμβανόμαστε με τις αισθήσεις μας οφείλονται
Δυναμική Ηλεκτρικών Μηχανών
 Δυναμική Ηλεκτρικών Μηχανών Ενότητα 1: Εισαγωγή Βασικές Αρχές Επ. Καθηγήτρια Τζόγια Χ. Καππάτου Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Δυναμική Ηλεκτρικών Μηχανών Ενότητα 1: Εισαγωγή Βασικές Αρχές Επ. Καθηγήτρια Τζόγια Χ. Καππάτου Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
b proj a b είναι κάθετο στο
 ΦΥΛΛΑ ΙΟ ΑΣΚΗΣΕΩΝ. Βρείτε όλα τα σηµεία P τέτοια ώστε η απόσταση του P από το A(, 5, 3) είναι διπλάσια από την απόσταση του P από το B(6, 2, 2). είξτε ότι το σύνολο όλων αυτών των σηµείων είναι σφαίρα.
ΦΥΛΛΑ ΙΟ ΑΣΚΗΣΕΩΝ. Βρείτε όλα τα σηµεία P τέτοια ώστε η απόσταση του P από το A(, 5, 3) είναι διπλάσια από την απόσταση του P από το B(6, 2, 2). είξτε ότι το σύνολο όλων αυτών των σηµείων είναι σφαίρα.
( ) ( ) ( )z. HMY Φωτονική. Διάλεξη 08 Οι εξισώσεις του Maxwell. r = A r. B r. ˆ det = Βαθμωτά και διανυσματικά μεγέθη
 HMY - Φωτονική Διάλεξη 8 Οι εξισώσεις του Mawell Βαθμωτά και διανυσματικά μεγέθη Πολλαπλασιασμός Πρόσθεση διανυσμάτων Βαθμωτό: το μέγεθος που για τον προσδιορισμό του χρειάζεται μόνο το μέτρο του και η
HMY - Φωτονική Διάλεξη 8 Οι εξισώσεις του Mawell Βαθμωτά και διανυσματικά μεγέθη Πολλαπλασιασμός Πρόσθεση διανυσμάτων Βαθμωτό: το μέγεθος που για τον προσδιορισμό του χρειάζεται μόνο το μέτρο του και η
1η ΠΑΡΟΥΣΙΑΣΗ. Ηλεκτρικά φορτία, ηλεκτρικές δυνάμεις και πεδία
 1η ΠΑΡΟΥΣΙΑΣΗ Ηλεκτρικά φορτία, ηλεκτρικές δυνάμεις και πεδία Ηλεκτρισμός και μαγνητισμός Κλάδος της Φυσικής που μελετάει τα ηλεκτρικά και τα μαγνητικά φαινόμενα. (Σχεδόν) όλα τα φαινομενα που αντιλαμβανόμαστε
1η ΠΑΡΟΥΣΙΑΣΗ Ηλεκτρικά φορτία, ηλεκτρικές δυνάμεις και πεδία Ηλεκτρισμός και μαγνητισμός Κλάδος της Φυσικής που μελετάει τα ηλεκτρικά και τα μαγνητικά φαινόμενα. (Σχεδόν) όλα τα φαινομενα που αντιλαμβανόμαστε
ΠΕΡΙΕΧΟΜΕΝΑ 1. ΙΑΝΥΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ. 1.3.1 Μετατροπή από καρτεσιανό σε κυλινδρικό σύστηµα... 6 1.3.2 Απειροστές ποσότητες... 7
 ΠΕΡΙΕΧΟΜΕΝΑ 1. ΙΑΝΥΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ 1.1 Φυσικά µεγέθη... 1 1.2 ιανυσµατική άλγεβρα... 2 1.3 Μετατροπές συντεταγµένων... 6 1.3.1 Μετατροπή από καρτεσιανό σε κυλινδρικό σύστηµα... 6 1.3.2 Απειροστές ποσότητες...
ΠΕΡΙΕΧΟΜΕΝΑ 1. ΙΑΝΥΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ 1.1 Φυσικά µεγέθη... 1 1.2 ιανυσµατική άλγεβρα... 2 1.3 Μετατροπές συντεταγµένων... 6 1.3.1 Μετατροπή από καρτεσιανό σε κυλινδρικό σύστηµα... 6 1.3.2 Απειροστές ποσότητες...
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Το Σέλας συμβαίνει όταν υψηλής ενέργειας, φορτισμένα σωματίδια από τον Ήλιο ταξιδεύουν στην άνω ατμόσφαιρα της Γης λόγω της ύπαρξης του μαγνητικού της πεδίου. Μαγνητισμός
Φυσική για Μηχανικούς Εικόνα: Το Σέλας συμβαίνει όταν υψηλής ενέργειας, φορτισμένα σωματίδια από τον Ήλιο ταξιδεύουν στην άνω ατμόσφαιρα της Γης λόγω της ύπαρξης του μαγνητικού της πεδίου. Μαγνητισμός
Μαθηματικά για μηχανικούς ΙΙ ΛΥΣΕΙΣ/ΑΠΑΝΤΗΣΕΙΣ ΑΣΚΗΣΕΩΝ
 Μαθηματικά για μηχανικούς ΙΙ ΛΥΣΕΙΣ/ΑΠΑΝΤΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Κεφάλαιο 1 1 Να βρείτε (και να σχεδιάσετε) το πεδίο ορισμού των πιο κάτω συναρτήσεων f (, ) 9 4 (γ) f (, ) f (, ) 16 4 1 D (, ) :9 0, 4 0 (, ) :
Μαθηματικά για μηχανικούς ΙΙ ΛΥΣΕΙΣ/ΑΠΑΝΤΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Κεφάλαιο 1 1 Να βρείτε (και να σχεδιάσετε) το πεδίο ορισμού των πιο κάτω συναρτήσεων f (, ) 9 4 (γ) f (, ) f (, ) 16 4 1 D (, ) :9 0, 4 0 (, ) :
ΤΟ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ
 VΙ TO ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ V ΤΟ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ ΒΑΣΙΚΕΣ ΕΝΕΡΓΕΙΑΚΕΣ ΣΧΕΣΕΙΣ ΤΟΥ ΠΕ ΙΟΥ VΙ. Πυκνότητα ενέργειας του ηλεκτρικού πεδίου σε γραικό και ισότροπο έσο we εe VΙ. Πυκνότητα ενέργειας του
VΙ TO ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ V ΤΟ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ ΒΑΣΙΚΕΣ ΕΝΕΡΓΕΙΑΚΕΣ ΣΧΕΣΕΙΣ ΤΟΥ ΠΕ ΙΟΥ VΙ. Πυκνότητα ενέργειας του ηλεκτρικού πεδίου σε γραικό και ισότροπο έσο we εe VΙ. Πυκνότητα ενέργειας του
Ασκήσεις 6 ου Κεφαλαίου
 Ασκήσεις 6 ου Κεφαλαίου 1. Μία ράβδος ΟΑ έχει μήκος l και περιστρέφεται γύρω από τον κατακόρυφο άξονα Οz, που είναι κάθετος στο άκρο της Ο με σταθερή γωνιακή ταχύτητα ω. Να βρεθεί r η επαγώμενη ΗΕΔ στη
Ασκήσεις 6 ου Κεφαλαίου 1. Μία ράβδος ΟΑ έχει μήκος l και περιστρέφεται γύρω από τον κατακόρυφο άξονα Οz, που είναι κάθετος στο άκρο της Ο με σταθερή γωνιακή ταχύτητα ω. Να βρεθεί r η επαγώμενη ΗΕΔ στη
Experiments are the only means of knowledge. Anyother is poetry and imagination. M.Plank 2 ΟΙ ΕΞΙΣΩΣΕΙΣ ΤΟΥ MAXWELL
 ΚΥΜΑΤΙΚΗ-ΟΠΤΙΚΗ 7 xpeiments ae the only means o knowledge. Anyothe is poety and imagination. M.Plank 2 ΟΙ ΕΞΙΣΩΣΕΙΣ ΤΟΥ MAXWLL Σε µια πρώτη παρουσίαση του θέµατος δίνονται οι εξισώσεις του Maxwell στο
ΚΥΜΑΤΙΚΗ-ΟΠΤΙΚΗ 7 xpeiments ae the only means o knowledge. Anyothe is poety and imagination. M.Plank 2 ΟΙ ΕΞΙΣΩΣΕΙΣ ΤΟΥ MAXWLL Σε µια πρώτη παρουσίαση του θέµατος δίνονται οι εξισώσεις του Maxwell στο
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
W f. P V f εμβαδό βρόχου υστέρησης. P f εμβαδό βρόχου υστέρησης. Ενέργεια του μαγνητικού πεδίου. Ενέργεια του μαγνητικού πεδίου
 Ενέργεια του μαγνητικού πεδίου Ενέργεια του μαγνητικού πεδίου (magnei field energy) : W f λ() λ(0) idλ Συνενέργεια (oenergy) : W i () i(0) λdi Αν θεωρήσουμε γραμμική (ακόρεστη) καμπύλη μαγνήτισης λ() Li()
Ενέργεια του μαγνητικού πεδίου Ενέργεια του μαγνητικού πεδίου (magnei field energy) : W f λ() λ(0) idλ Συνενέργεια (oenergy) : W i () i(0) λdi Αν θεωρήσουμε γραμμική (ακόρεστη) καμπύλη μαγνήτισης λ() Li()
ΗΛΕΚΤΡΟΝΙΚΑ ΣΤΟΙΧΕΙΑ & ΚΥΚΛΩΜΑΤΑ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΗΛΕΚΤΡΟΤΕΧΝΙΑ
 ΗΛΕΚΤΡΟΝΙΚΑ ΣΤΟΙΧΕΙΑ & ΚΥΚΛΩΜΑΤΑ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΗΛΕΚΤΡΟΤΕΧΝΙΑ 1 ΝΟΜΟΣ ΤΟΥ OHM (ΩΜ) Για πολλά υλικά ο λόγος της πυκνότητας του ρεύματος προς το ηλεκτρικό πεδίο είναι σταθερός και ανεξάρτητος από το ηλεκτρικό
ΗΛΕΚΤΡΟΝΙΚΑ ΣΤΟΙΧΕΙΑ & ΚΥΚΛΩΜΑΤΑ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΗΛΕΚΤΡΟΤΕΧΝΙΑ 1 ΝΟΜΟΣ ΤΟΥ OHM (ΩΜ) Για πολλά υλικά ο λόγος της πυκνότητας του ρεύματος προς το ηλεκτρικό πεδίο είναι σταθερός και ανεξάρτητος από το ηλεκτρικό
Ηλεκτρομαγνητισμός. Αυτεπαγωγή. Νίκος Ν. Αρπατζάνης
 Ηλεκτρομαγνητισμός Αυτεπαγωγή Νίκος Ν. Αρπατζάνης Εξισώσεις Maxwell Στα τέλη του 19 ου αιώνα, οι γνώσεις γύρω απ τα ηλεκτρικά και μαγνητικά πεδία συνοψίζονταν στις εξισώσεις Maxwell: Νόμος Gauss: τα ηλεκτρικά
Ηλεκτρομαγνητισμός Αυτεπαγωγή Νίκος Ν. Αρπατζάνης Εξισώσεις Maxwell Στα τέλη του 19 ου αιώνα, οι γνώσεις γύρω απ τα ηλεκτρικά και μαγνητικά πεδία συνοψίζονταν στις εξισώσεις Maxwell: Νόμος Gauss: τα ηλεκτρικά
8 η Διάλεξη Ηλεκτρομαγνητική ακτινοβολία, φαινόμενα συμβολής, περίθλαση
 11//17 8 η Διάλεξη Ηλεκτρομαγνητική ακτινοβολία, φαινόμενα συμβολής, περίθλαση Φίλιππος Φαρμάκης Επ. Καθηγητής 1 Ηλεκτρομαγνητισμός Πως συνδέονται ο ηλεκτρισμός με τον μαγνητισμό; Πως παράγονται τα κύματα;
11//17 8 η Διάλεξη Ηλεκτρομαγνητική ακτινοβολία, φαινόμενα συμβολής, περίθλαση Φίλιππος Φαρμάκης Επ. Καθηγητής 1 Ηλεκτρομαγνητισμός Πως συνδέονται ο ηλεκτρισμός με τον μαγνητισμό; Πως παράγονται τα κύματα;
Ασκήσεις 2 ου Κεφαλαίου, Νόμος του Gauss
 Ασκήσεις 2 ου Κεφαλαίου, Νόμος του Guss 22.36.Μία αγώγιμη σφαίρα με φορτίο q έχει ακτίνα α. Η σφαίρα βρίσκεται στο εσωτερικό μίας κοίλης ομόκεντρης αγώγιμης σφαίρας με εσωτερική ακτίνα και εξωτερική ακτίνα.
Ασκήσεις 2 ου Κεφαλαίου, Νόμος του Guss 22.36.Μία αγώγιμη σφαίρα με φορτίο q έχει ακτίνα α. Η σφαίρα βρίσκεται στο εσωτερικό μίας κοίλης ομόκεντρης αγώγιμης σφαίρας με εσωτερική ακτίνα και εξωτερική ακτίνα.
ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ. Κ. Γ. Ευθυμιάδης Αικ. Σιακαβάρα Ε. Παπαδημητράκη-Χλίχλια Ι. Α. Τσουκαλάς
 ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ Κ. Γ. Ευθυμιάδης Αικ. Σιακαβάρα Ε. Παπαδημητράκη-Χλίχλια Ι. Α. Τσουκαλάς ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ Α Έκδοση Συγγραφείς Κ. Γ. Ευθυμιάδης Αικ. Σιακαβάρα Ε. Παπαδημητράκη-Χλίχλια
ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ Κ. Γ. Ευθυμιάδης Αικ. Σιακαβάρα Ε. Παπαδημητράκη-Χλίχλια Ι. Α. Τσουκαλάς ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ Α Έκδοση Συγγραφείς Κ. Γ. Ευθυμιάδης Αικ. Σιακαβάρα Ε. Παπαδημητράκη-Χλίχλια
E = E 0 + E = E 0 P ϵ 0. = 1 + χ r. = Q E 0 l
 Πυκνωτής με διηλεκτρικό Πυκνωτής με ορθογώνιους οπλισμούς εμβαδού A και απόσταση μεταξύ των οπλισμών l έχει ϕορτίο Q. Η επιϕανειακή πυκνότητα ϕορτίου σε κάθε οπλισμό θα είνα σ = ±Q/A. Το ηλεκτρικό πεδίο
Πυκνωτής με διηλεκτρικό Πυκνωτής με ορθογώνιους οπλισμούς εμβαδού A και απόσταση μεταξύ των οπλισμών l έχει ϕορτίο Q. Η επιϕανειακή πυκνότητα ϕορτίου σε κάθε οπλισμό θα είνα σ = ±Q/A. Το ηλεκτρικό πεδίο
ΔΙΑΛΕΞΗ 2 Νόμος Gauss, κίνηση σε ηλεκτρικό πεδίο. Ι. Γκιάλας Χίος, 28 Φεβρουαρίου 2014
 ΔΙΑΛΕΞΗ 2 Νόμος Gauss, κίνηση σε ηλεκτρικό πεδίο Ι. Γκιάλας Χίος, 28 Φεβρουαρίου 214 Ασκηση συνολικό φορτίο λεκτρικό φορτίο Q είναι κατανεμημένο σε σφαιρικό όγκο ακτίνας R με πυκνότητα ορτίου ανάλογη του
ΔΙΑΛΕΞΗ 2 Νόμος Gauss, κίνηση σε ηλεκτρικό πεδίο Ι. Γκιάλας Χίος, 28 Φεβρουαρίου 214 Ασκηση συνολικό φορτίο λεκτρικό φορτίο Q είναι κατανεμημένο σε σφαιρικό όγκο ακτίνας R με πυκνότητα ορτίου ανάλογη του
Ενημέρωση. Η διδασκαλία του μαθήματος, όλες οι ασκήσεις προέρχονται από το βιβλίο: «Πανεπιστημιακή
 Ενημέρωση Η διδασκαλία του μαθήματος, πολλά από τα σχήματα και όλες οι ασκήσεις προέρχονται από το βιβλίο: «Πανεπιστημιακή Φυσική» του Hugh Young των Εκδόσεων Παπαζήση, οι οποίες μας επέτρεψαν τη χρήση
Ενημέρωση Η διδασκαλία του μαθήματος, πολλά από τα σχήματα και όλες οι ασκήσεις προέρχονται από το βιβλίο: «Πανεπιστημιακή Φυσική» του Hugh Young των Εκδόσεων Παπαζήση, οι οποίες μας επέτρεψαν τη χρήση
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Στοιχεία Ηλεκτρικών Κυκλωμάτων
 Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Στοιχεία Ηλεκτρικών Κυκλωμάτων Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Νόμος Faraday Η μεταβαλλόμενη μαγνητική
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Στοιχεία Ηλεκτρικών Κυκλωμάτων Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Νόμος Faraday Η μεταβαλλόμενη μαγνητική
(ΚΕΦ 32) f( x x f( x) x z y
 (ΚΕΦ 3) f( x x f( x) x z y ΣΥΝΟΨΗ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΥ J. C. Maxwell (~1860) συνόψισε τη δουλειά ως τότε για το ηλεκτρικό και μαγνητικό πεδίο σε 4 εξισώσεις. Όμως, κατανόησε ότι οι εξισώσεις αυτές (όπως
(ΚΕΦ 3) f( x x f( x) x z y ΣΥΝΟΨΗ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΥ J. C. Maxwell (~1860) συνόψισε τη δουλειά ως τότε για το ηλεκτρικό και μαγνητικό πεδίο σε 4 εξισώσεις. Όμως, κατανόησε ότι οι εξισώσεις αυτές (όπως
Κλασική Hλεκτροδυναμική
 Κλασική Hλεκτροδυναμική Ενότητα 1: Εισαγωγή Ανδρέας Τερζής Σχολή Θετικών επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι μια σύντομη επανάληψη στις βασικές έννοιες της ηλεκτροστατικής.
Κλασική Hλεκτροδυναμική Ενότητα 1: Εισαγωγή Ανδρέας Τερζής Σχολή Θετικών επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι μια σύντομη επανάληψη στις βασικές έννοιες της ηλεκτροστατικής.
Andre-Marie Ampère Γάλλος φυσικός Ανακάλυψε τον ηλεκτροµαγνητισµό. Ασχολήθηκε και µε τα µαθηµατικά.
 Μαγνητικά πεδία Τα µαγνητικά πεδία δηµιουργούνται από κινούµενα ηλεκτρικά φορτία. Μπορούµε να υπολογίσουµε το µαγνητικό πεδίο που δηµιουργούν διάφορες κατανοµές ρευµάτων. Ο νόµος του Ampère χρησιµεύει
Μαγνητικά πεδία Τα µαγνητικά πεδία δηµιουργούνται από κινούµενα ηλεκτρικά φορτία. Μπορούµε να υπολογίσουµε το µαγνητικό πεδίο που δηµιουργούν διάφορες κατανοµές ρευµάτων. Ο νόµος του Ampère χρησιµεύει
0 Φυσική Γενικής Παιδείας Β Λυκείου Ηλεκτρομαγνητισμός Ηλεκτρομαγνητισμός. Κώστας Παρασύρης - Φυσικός
 0 Φυσική Γενικής Παιδείας Β Λυκείου Ηλεκτρομαγνητισμός - 3.3 Ηλεκτρομαγνητισμός 1 Φυσική Γενικής Παιδείας Β Λυκείου Ηλεκτρομαγνητισμός - 1. Μαγνητικό πεδίο Βασικές έννοιες Μαγνητικά φαινόμενα παρατηρήθηκαν
0 Φυσική Γενικής Παιδείας Β Λυκείου Ηλεκτρομαγνητισμός - 3.3 Ηλεκτρομαγνητισμός 1 Φυσική Γενικής Παιδείας Β Λυκείου Ηλεκτρομαγνητισμός - 1. Μαγνητικό πεδίο Βασικές έννοιες Μαγνητικά φαινόμενα παρατηρήθηκαν
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ & ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Η. Ν. Γλύτσης, Tηλ.: 210-7722479 - e-mail:
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ & ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Η. Ν. Γλύτσης, Tηλ.: 210-7722479 - e-mail:
Μαγνητισμός. Ενότητα 2. Ηλεκτρισμός & Μαγνητισμός
 Σημειώσεις Γενικής Φυσικής - ΒΕΤ Μ. Μπενής / 2016 Ηλεκτρισμός & Μαγνητισμός Ενότητα 2. Ηλεκτρισμός & Μαγνητισμός Μαγνητισμός Το φαινόμενο της μαγνήτισης είναι γνωστό από την αρχαιότητα. Παρατηρήθηκε πως
Σημειώσεις Γενικής Φυσικής - ΒΕΤ Μ. Μπενής / 2016 Ηλεκτρισμός & Μαγνητισμός Ενότητα 2. Ηλεκτρισμός & Μαγνητισμός Μαγνητισμός Το φαινόμενο της μαγνήτισης είναι γνωστό από την αρχαιότητα. Παρατηρήθηκε πως
ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ Γ
 ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ Γ ΜΑΘΗΜΑ 2 Ισοδύναμο Ηλεκτρικό Κύκλωμα Σύγχρονων Μηχανών Ουρεϊλίδης Κωνσταντίνος, Υποψ. Διδακτωρ Υπολογισμός Αυτεπαγωγής και αμοιβαίας επαγωγής Πεπλεγμένη μαγνητική ροή συναρτήσει των
ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ Γ ΜΑΘΗΜΑ 2 Ισοδύναμο Ηλεκτρικό Κύκλωμα Σύγχρονων Μηχανών Ουρεϊλίδης Κωνσταντίνος, Υποψ. Διδακτωρ Υπολογισμός Αυτεπαγωγής και αμοιβαίας επαγωγής Πεπλεγμένη μαγνητική ροή συναρτήσει των
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ-ΟΠΤΙΚΗ, ΑΠΑΝΤΗΣΕΙΣ-ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΤΗΝ ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ ΠΕΡΙΟ ΟΥ ΙΟΥΝΙΟΥ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ-ΟΠΤΙΚΗ, ΑΠΑΝΤΗΣΕΙΣ-ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΤΗΝ ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ ΠΕΡΙΟ ΟΥ ΙΟΥΝΙΟΥ Ανδρέας Ζούπας 2 Αυγούστου 212 Οι λύσεις απλώς προτείνονται και σαφώς οποιαδήποτε σωστή λύση είναι αποδεκτή! Θέµα-1
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ-ΟΠΤΙΚΗ, ΑΠΑΝΤΗΣΕΙΣ-ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΤΗΝ ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ ΠΕΡΙΟ ΟΥ ΙΟΥΝΙΟΥ Ανδρέας Ζούπας 2 Αυγούστου 212 Οι λύσεις απλώς προτείνονται και σαφώς οποιαδήποτε σωστή λύση είναι αποδεκτή! Θέµα-1
