Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο Λύσεις ενδέκατου φυλλαδίου ασκήσεων.
|
|
|
- Αμύντα Βυζάντιος
- 6 χρόνια πριν
- Προβολές:
Transcript
1 Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 8-9. Λύσεις ενδέκατου φυλλαδίου ασκήσεων.. (i) Βρείτε μία παράγουσα της + στο (, + ). Ποιές είναι όλες οι παράγουσες της + στο (, + ); (ii) Βρείτε μία παράγουσα της + στο (, + ) ώστε η τιμή της στο = να είναι 3. Πόσες τέτοιες παράγουσες υπάρχουν; Λύση: (i) Η συνάρτηση + log είναι παράγουσα της + στο (, + ). Επειδή το (, + ) είναι διάστημα, συνεπάγεται ότι οι συναρτήσεις + log + c, όπου c είναι αυθαίρετη σταθερή συνάρτηση, είναι όλες οι παράγουσες της + στο (, + ). (ii) Για να βρούμε μία παράγουσα με τίμη 3 στο =, γράφουμε + log + c = 3 και βρίσκουμε c = 4. Άρα υπάρχει μόνο μία παράγουσα της + στο (, + ) με τιμή 3 στο = και αυτή είναι η συνάρτηση + log 4. {, αν <. Αποδείξτε ότι η f() = δεν έχει παράγουσα στο (, + )., αν Λύση: Έστω F παράγουσα της f στο (, + ). Δηλαδή, έστω F () = f() για κάθε (, + ). Επειδή ισχύει F () = = ( ) για (, ) και η F είναι συνεχής (ως παραγωγίσιμη) στο (, ], συνεπάγεται ότι υπάρχει c ώστε να ισχύει F () = + c για (, ]. Ομοίως, επειδή ισχύει F () = = για (, + ) και η F είναι συνεχής (ως παραγωγίσιμη) στο [, + ), συνεπάγεται ότι υπάρχει c ώστε να ισχύει F () = + c για [, + ). Βλέπουμε ότι c = F () = c και, συμβολίζοντας c = c = c, συμπεραίνουμε ότι ισχύει { + c, αν F () = + c, αν Τώρα, όμως, είναι F () = (γιατί;) και F +() = (γιατί;), οπότε η F δεν έχει παράγωγο στο. Αυτό είναι άτοπο διότι πρέπει να ισχύει F () = f() =. 3. (i) Βρείτε ένα αόριστο ολοκλήρωμα της sin στο (, + ). Ποιά είναι όλα τα αόριστα ολοκληρώματα της sin στο (, + ); Με άλλα λόγια, ποιό είναι το ( sin ) d; (ii) Βρείτε ένα αόριστο ολοκλήρωμα της sin στο (, + ) ώστε η τιμή του στο = π να είναι. Πόσα τέτοια αόριστα ολοκληρώματα υπάρχουν; Λύση: (i) Η συνάρτηση ( sin t) dt = + cos cos = + cos είναι ένα αόριστο ολοκλήρωμα της sin στο (, + ). Επειδή το (, + ) είναι διάστημα, συνεπάγεται ότι οι συναρτήσεις +cos +c, όπου c είναι αυθαίρετη σταθερή συνάρτηση στο (, + ), είναι όλα τα αόριστα ολοκληρώματα της sin στο (, + ). Δηλαδή ( sin ) d = + cos + c. (ii) Για να βρούμε ένα αόριστο ολοκλήρωμα με τίμη στο = π, γράφουμε π+cos π+c = και βρίσκουμε c = π. Άρα υπάρχει μόνο ένα αόριστο ολοκλήρωμα της sin στο (, + ) με τιμή στο = π και αυτό είναι η συνάρτηση + cos π.
2 4. Έστω f() d = g() d sin. Με τί είναι ίση η παράσταση f() d g() d; Λύση: Η παράσταση f() d g() d είναι όλες οι συναρτήσεις sin + c = + sin + c, όπου c είναι αυθαίρετη σταθερή συνάρτηση στο (, + ). 5. Βρείτε συνεχή συνάρτηση f στο (, + ) και αριθμό ώστε να ισχύει f(t) dt = 3 για κάθε. Πόσες λύσεις υπάρχουν; Λύση: Αν υπάρχει f συνεχής στο (, + ) ώστε να ισχύει f(t) dt = 3 για κάθε, τότε παραγωγίζοντας αυτήν τη σχέση, βρίσκουμε ότι ισχύει f() = 6 για κάθε. Με την συνάρτηση f() = 6 έχουμε f(t) dt = 6t dt = 3 3, οπότε ισχύει f(t) dt = 3 για κάθε αν και μόνο αν 3 =. Άρα υπάρχουν ακριβώς μία συνάρτηση, η f() = 6, και ακριβώς δύο, το = και το =. 6. Υπάρχει συνεχής συνάρτηση f στο (, + ) ώστε να ισχύει f(t) dt = cos για κάθε ; Ίδια ερώτηση για την f(t) dt = cos. Λύση: Δεν είναι δυνατό να ισχύει f(t) dt = cos για κάθε, αφού δεν ισχύει για =. Αντιθέτως, η f(t) dt = cos ισχύει για =. Τώρα, αν υπάρχει f συνεχής στο (, + ) ώστε να ισχύει f(t) dt = cos για κάθε, τότε παραγωγίζοντας αυτήν τη σχέση, βρίσκουμε ότι ισχύει f() = sin για κάθε. Με την f() = sin έχουμε, πράγματι, ότι ισχύει f(t) dt = sin t dt = cos για κάθε. 7. Έστω f ορισμένη στο διάστημα I και ολοκληρώσιμη σε κάθε κλειστό και φραγμένο υποδιάστημα του I. Επίσης, έστω g, h ορισμένες στο σύνολο A με τιμές στο I και η συνάρτηση F με τύπο F () = g() h() f(t) dt για A. (i) Αν οι g, h είναι παραγωγίσιμες στο A και η f είναι συνεχής στα g( ) και h( ), αποδείξτε ότι η F είναι παραγωγίσιμη στο και F ( ) = g ( )f(g( )) h ( )f(h( )). (ii) Βρείτε τα πεδία ορισμού των συναρτήσεων και τις παραγώγους τους. t t e t +t dt, e t t dt Λύση: Το πρώτο πράγμα που σκεφτόμαστε για την παράσταση F () = g() h() f(t) dt είναι αν η συνάρτηση f είναι ολοκληρώσιμη στο κλειστό διάστημα με άκρα g() και h() (ώστε να έχει νόημα το ολοκλήρωμα). Στην συγκεκριμένη περίπτωση αυτό εξασφαλίζεται από τις υποθέσεις μας: οι τιμές των συναρτήσεων g, h είναι στο I, οπότε για κάθε A τα g(), h() ανήκουν στο I και, επειδή το I είναι διάστημα και η f είναι ολοκληρώσιμη σε κάθε κλειστό και φραγμένο υποδιάστημα του I, η f είναι ολοκληρώσιμη στο κλειστό διάστημα με άκρα g() και h(). (i) Θεωρούμε οποιοδήποτε I και γράφουμε F () = g() h() f(t) dt = g() f(t) dt h() f(t) dt για A. Η συνάρτηση G() = g() f(t) dt είναι σύνθεση του αόριστου ολοκληρώματος K() = f(t) dt και της g(): G() = K(g()) για A. Επειδή η g είναι παραγωγίσιμη στο και η K είναι παραγωγίσμη στο g( ) (αφού η f είναι συνεχής στο g( )), συνεπάγεται ότι η G είναι παραγωγίσμη στο και G ( ) = K (g( ))g ( ) = f(g( ))g ( ).
3 Ακριβώς όμοια, η συνάρτηση H() = h() f(t) dt είναι σύνθεση του αόριστου ολοκληρώματος K() = f(t) dt και της h(): H() = K(h()) για A. Επειδή η h είναι παραγωγίσιμη στο και η K είναι παραγωγίσμη στο h( ) (αφού η f είναι συνεχής στο h( )), συνεπάγεται ότι η H είναι παραγωγίσμη στο και Συμπεραίνουμε ότι H ( ) = K (h( ))h ( ) = f(h( ))h ( ). F ( ) = G ( ) H ( ) = f(g( ))g ( ) f(h( ))h ( ). (ii) Η συνάρτηση f(t) = ορίζεται σε ολόκληρο το (, + ) και, ως συνεχής, e t +t είναι ολοκληρώσιμη σε κάθε κλειστό και φραγμένο υποδιάστημα του (, + ). Άρα η F () = t t dt ορίζεται σε ολόκληρο το (, + ) και ισχύει e t +t t t F () = ( ) ( ) ( ) e +( ) για κάθε. Η συνάρτηση f(t) = et t ορίζεται και είναι συνεχής στο (, ) και στο (, + ) και μάλιστα απειρίζεται όταν το t πλησιάζει το είτε από τα δεξιά του είτε από τα αριστερά του. Άρα για να είναι η f ολοκληρώσιμη στο κλειστό διάστημα με άκρα και πρέπει αυτά να ανήκουν είτε και τα δύο στο (, ) είτε και τα δύο στο (, + ) και άρα πρέπει να ανήκουν και τα δύο στο (, + ) (αφού > ). Άρα το πεδίο ορισμού της F () = e t t dt είναι το (, + ) και ισχύει F () = e e για >. 8. Αποδείξτε ότι lim + e et dt =. Λύση: Επειδή lim + e = +, εφαρμόζουμε τον δεύτερο κανόνα του l Hopitâl και βρίσκουμε lim + e et dt = lim + e e = lim + =. 9. Βρείτε > και b ώστε lim + e b c d t +t dt =. Λύση: Είναι lim + (e b c d t ) = b και lim + +t dt =. Άρα, αν b, τότε lim + e b c d t +t dt = και, επομένως, b =. Τώρα, από τον κανόνα του l Hopitâl συνεπάγεται lim + e c d t +t dt = lim + e c d + = lim + e c d. Για να εφαρμόσουμε τον κανόνα του l Hopitâl πρέπει να υπάρχει το τελευταίο όριο. Και, πράγματι, το όριο αυτό υπάρχει και είναι ίσο με αν c, οπότε σ αυτήν την περίπτωση καταλήγουμε σε άτοπο, ή, αν c =, είναι ίσο με lim + e d = lim + e d. Και πάλι, για να εφαρμόσουμε τον κανόνα του l Hopitâl πρέπει να υπάρχει το τελευταίο όριο. Το όριο αυτό υπάρχει και είναι ίσο με αν d, οπότε σ αυτήν την περίπτωση καταλήγουμε σε άτοπο, ή, αν d =, είναι ίσο με lim + e = lim + 3 e =.
4 Άρα πρέπει να είναι b = c = και d = και τότε = lim + = e (/) lim + και, επομένως, = 4. e = t +t dt = lim + e = lim + e. Αποδείξτε τις παρακάτω ιδιότητες με κατάλληλη αλλαγή μεταβλητής. (i) b+c +c f( c) d = b f() d. (ii) λb λ f( b λ) d = λ f() d για κάθε λ >. Μελετήστε το γεωμετρικό περιεχόμενο αυτών των ιδιοτήτων, θεωρώντας επιπλέον ότι ισχύει f() για κάθε [, b]. Λύση: (i) Στο b+c +c f( c) d κάνουμε την αλλαγή μεταβλητής = ϕ() = c, για την οποία ισχύει ϕ () = και ϕ( + c) =, ϕ(b + c) = b, και βρίσκουμε b+c +c f( c) d = b+c +c f(ϕ())ϕ () d = ϕ(b+c) ϕ(+c) f() d = b f() d. Το γεωμετρικό περιεχόμενο αυτής της ιδιότητας φαίνεται στο σχήμα. Η συνάρτηση f( c) είναι η f() μεταφερμένη οριζόντια κατά c. Το b+c +c f( c) d είναι το εμβαδόν κάτω από το γράφημα της f( c) στο διάστημα [ + c, b + c] και είναι ίσο με το εμβαδό κάτω από το γράφημα της f() στο διάστημα [, b] το οποίο με τη σειρά του είναι το b f() d. (ii) Στο λb λ f( ) λ d κάνουμε την αλλαγή μεταβλητής = ϕ() = λ, για την οποία ισχύει ϕ () = λ και ϕ(λ) =, ϕ(λb) = b, και βρίσκουμε λb λ f( ) λb λ d = λ λ f(ϕ())ϕ () d = λ ϕ(λb) ϕ(λ) f() d = λ b f() d. 4
5 Το γεωμετρικό περιεχόμενο αυτής της ιδιότητας φαίνεται στο σχήμα. Το γράφημα της συνάρτησης f( λ ) προκύπτει όταν πολλαπλασιάσουμε τις -συντεταγμένες των σημείων του γραφήματος της f() με τον ίδιο αριθμό λ. Το λb λ f( λ) d είναι το εμβαδόν κάτω από το γράφημα της f( λ ) στο διάστημα [λ, λb] και προκύπτει από το εμβαδό κάτω από το γράφημα της f() στο διάστημα [, b], δηλαδή από το b f() d, όταν το πολλαπλασιάσουμε με τον αριθμό λ.. (i) Αν η f : [ b, ] [, b] R είναι άρτια αποδείξτε ότι b f() d = b f() d. (ii) Αν η f : [ b, ] [, b] R είναι περιττή αποδείξτε ότι b f() d = b f() d. (iii) Αν η f : [ b, b] R είναι άρτια αποδείξτε ότι b b f() d = b f() d. (iv) Αν η f : [ b, b] R είναι περιττή αποδείξτε ότι b b f() d =. Ποιό είναι το γεωμετρικό περιεχόμενο αυτών των ιδιοτήτων; Λύση: (i) Στο b f() d γράφουμε f() = f( ) (αφού η f είναι άρτια) και κάνουμε την αλλαγή μεταβλητής = ϕ() =, για την οποία ισχύει ϕ () = και ϕ( ) =, ϕ( b) = b, και βρίσκουμε b f() d = b f( ) d = b f(ϕ())ϕ () d = ϕ( ) = b f() d = b f() d. ϕ( b) f() d (ii) Στο b f() d γράφουμε f() = f( ) (αφού η f είναι περιττή) και κάνουμε την ίδια αλλαγή μεταβλητής = ϕ() = που κάναμε στο (i) και βρίσκουμε b f() d = b f( ) d = b f(ϕ())ϕ () d = ϕ( ) = b f() d = b f() d. ϕ( b) f() d Το γεωμετρικό περιεχόμενο των (i) και (ii) φαίνονται καθαρά στο παραπάνω σχήμα: τα εμβαδά δεξιά του -άξονα είναι ίδια με τα εμβαδά αριστερά του -άξονα λόγω συμμετρίας είτε ως προς τον -άξονα είτε ως προς το σημείο (, ). (iii) Το (i) με = λέει ότι b f() d = b f() d και άρα b b f() d = b f() d + b f() d = b f() d. (iv) Το (ii) με = λέει ότι b f() d = b f() d και άρα b b f() d = b f() d + b f() d =. 5
6 . Αν η f : R R είναι περιοδική με περίοδο T > αποδείξτε ότι: (i) b+t +T f() d = b f() d. (ii) +T f() d = b+t b f() d. Ποιό είναι το γεωμετρικό περιεχόμενο αυτών των ιδιοτήτων; Λύση: (i) Στο b+t +T f() d γράφουμε f() = f( T ) (αφού η f έχει περίοδο T ) και κάνουμε την αλλαγή μεταβλητής = ϕ() = T, για την οποία ισχύει ϕ () = και ϕ( + T ) =, ϕ(b + T ) = b, και βρίσκουμε b+t +T f() d = b+t +T f( T ) d = b+t +T f(ϕ())ϕ () d = ϕ(b+t ) = b f() d. (ii) Χρησιμοποιώντας το (i) έχουμε +T ϕ(+t ) f() d f() d = b f() d + b+t b f() d + +T b+t f() d = b+t +T f() d + b+t b f() d + +T b+t f() d = b+t b f() d. Το γεωμετρικό περιεχόμενο της (i) φαίνεται στο σχήμα. Λόγω περιοδικότητας, η συνάρτηση στο διάστημα [ + T, b + T ] είναι ίδια με την συνάρτηση στο διάστημα [, b]. Άρα το εμβαδό κάτω από το γράφημά της στο διάστημα [ + T, b + T ] είναι ίσο με το εμβαδό κάτω από το γράφημά της στο διάστημα [, b]. Αν προσθέσουμε στα δύο αυτά ίσα εμβαδά το εμβαδό κάτω από το γράφημα στο διάστημα [b, + T ], τότε προκύπτει ότι τα εμβαδά κάτω από το γράφημα στα διαστήματα [, +T ] και [b, b+t ] είναι ίσα. Αυτό είναι το γεωμετρικό περιεχόμενο της (ii). 3. Με αλλαγές μεταβλητής βρείτε τα: 3 cos( 4 ) d, cos sin d, sin d, + d, + d, + d, + ( ++5) d, sin +cos (sin cos ) 3 d, 5 d, 6 4 sin cos d, + d, sin d, sin 4 d, 4 d, e 3 d, + 3 cos sin() d, d, sin + d, d, 3 d, cos 3 sin d, d, (+cos ) 3 e 3 sin cos d, tn d, ( 4 +) d, log d, +log 4+ d, 6 d, sin 3 d, +e d, rctn (+) d, + d,
7 e +e d, rcsin d, +cos d +cos d. Λύση: Θα δούμε πλήρως πώς υπολογίζονται επτά από τα ολοκληρώματα και για τα υπόλοιπα θα αναφέρω απλώς την αλλαγή μεταβλητής που πρέπει να γίνει. Σε αρκετές περιπτώσεις μπορεί κανείς να βρει διαφορετικό δρόμο υπολογισμού με άλλες αλλαγές μεταβλητής και άλλες αλγεβρικές πράξεις. (i) Για το tn d γράφουμε tn = sin cos και χρησιμοποιούμε αλλαγή μεταβλητής = cos. Έτσι tn d = sin cos d = d =cos = (log + c) =cos = log cos + c. (ii) Για το +e d κάνουμε αλλαγή μεταβλητής = e και τότε +e d = (+) d =e. Κατόπιν, έχουμε (+) = + και άρα (+) d = d + d = log log + + c = log Επομένως, +e d = ( log + ) + c =e = log e +e + c. + + c. Παρατηρήστε ότι στο ολοκλήρωμα (+) d, το οποίο χρησιμοποιήσαμε, η μεταβλητή ανήκει στο (, + ) αφού είναι = e. Επομένως, στον υπολογισμό του θα μπορούσαμε να γράψουμε (+) d = d + χωρίς να χρησιμοποιήσουμε απόλυτες τιμές. (iii) Για το sin 3 d γράφουμε sin 3 = sin sin = ( cos ) sin και κάνουμε αλλαγή μεταβλητής = cos. Τότε sin 3 d = ( ) d =cos = ( c ) =cos = 3 cos3 cos + c. d = log log( + ) + c = log + + c (iv) Για το sin 4 d χρησιμοποιούμε την ταυτότητα sin = cos() και την αλλαγή μεταβλητής = και βρίσκουμε sin 4 d = 4 ( cos()) d = 8 ( cos ) d =. Τώρα ( cos ) d = d cos d + cos d = sin + cos d. Τώρα χρησιμοποιούμε την ταυτότητα cos = +cos() και την αλλαγή μεταβλητής u = και τότε cos d = ( + cos()) d = 4 ( + cos u) du u= = 4 (u + sin u + c) u= = + 4 sin() + c. Άρα ( cos ) d = sin sin() + c = 3 sin + 4 sin() + c και, τέλος, sin 4 d = ( 3 8 sin + 4 sin() + c) = = sin() + 3 sin(4) + c. 7
8 (v) Για το d κάνουμε την αλλαγή μεταβλητής = 4 και έχουμε d = d 4 =/ = (rcsin + c) =/ = rcsin + c. (vi) Για το d κάνουμε την αλλαγή μεταβλητής = 4+ και έχουμε 4+ d = + d =/ = (rctn + c) =/ = rctn + c. (vii) Για το +cos d χρησιμοποιούμε μία από τις προηγούμενες ταυτότητες στη μορφή + cos = cos και την αλλαγή μεταβλητής = και βρίσκουμε +cos d = cos (/) d = cos d =/ = (tn + c) =/ = tn + c. Για το 3 cos( 4 ) d κάνουμε αλλαγή μεταβλητής = 4. Για το cos sin d κάνουμε αλλαγή μεταβλητής = cos. Για το sin d κάνουμε αλλαγή μεταβλητής =. Για το d κάνουμε αλλαγή μεταβλητής = + +. Για το + d κάνουμε αλλαγή μεταβλητής = +. Για το + d κάνουμε αλλαγή μεταβλητής = +. Για το + d κάνουμε αλλαγή μεταβλητής = +. Για το d κάνουμε αλλαγή μεταβλητής =. Για το + d κάνουμε αλλαγή μεταβλητής = ( ++5) Για το sin +cos d κάνουμε αλλαγή μεταβλητής = sin cos. (sin cos ) 3 Για το d κάνουμε αλλαγή μεταβλητής =. Για το 3 d κάνουμε αλλαγή μεταβλητής =. Για το 5 6 d κάνουμε αλλαγή μεταβλητής = 6. Για το 4 sin cos d κάνουμε αλλαγή μεταβλητής = 4 sin. Για το sin d κάνουμε αλλαγή μεταβλητής = + cos. (+cos ) 3 Για το cos 3 sin d γράφουμε cos3 sin sin. Για το + d κάνουμε αλλαγή μεταβλητής = +. = ( sin ) cos sin και κάνουμε αλλαγή μεταβλητής = Για το e 3 d κάνουμε αλλαγή μεταβλητής = 3. Για το e 3 sin cos d κάνουμε αλλαγή μεταβλητής = 3 sin. Για το sin d κάνουμε αλλαγή μεταβλητής =. Για το + 3 cos sin() d κάνουμε αλλαγή μεταβλητής = + 3 cos (και θυμόμαστε ότι sin cos = sin()). Για το ( 4 +) d γράφουμε ( 4 +) = 3 4 ( 4 +) και κάνουμε αλλαγή μεταβλητής = 4. Για το log d κάνουμε αλλαγή μεταβλητής = + log. +log Για το rctn (+) d κάνουμε αλλαγή μεταβλητής = και κατόπιν u = rctn. Για το d γράφουμε = 5 4 (+ ) και κάνουμε αλλαγή μεταβλητής = 5 ( + ). Για το + d γράφουμε + = ( ) και κάνουμε αλλαγή μεταβλητής = 7 ( ). 8
9 Για το e d κάνουμε αλλαγή μεταβλητής = e. +e Για το rcsin d κάνουμε αλλαγή μεταβλητής = rcsin. Για το +cos d κάνουμε αλλαγή μεταβλητής = tn (και θυμόμαστε ότι cos = tn + ) και κατόπιν u = /3. 4. Με ολοκληρώσεις κατά μέρη και αλλαγές μεταβλητής βρείτε τα: e sin(3) d, 3 e d, 3 e d, e d, sin d, log d, log 4 d, rcsin d, rctn d, rcsin d, rctn d, rctn d, cos d, rctn(e ) e d, sin 4 d, e rctn ( +) 3/ d, cos d, d, ( +) log( + + ) d. Λύση: Θα δούμε πλήρως πώς υπολογίζονται πέντε από τα ολοκληρώματα και για τα υπόλοιπα αναφέρω σχετικά πλήρεις υποδείξεις για το τί πρέπει να γίνει. Όπως και στην προηγούμενη άσκηση, σε αρκετές περιπτώσεις μπορεί κανείς να βρει διαφορετικό δρόμο υπολογισμού. (i) Στο 3 e d κάνουμε αλλαγή μεταβλητής = και έχουμε 3 e d = e d =. Κατόπιν, e d = (e ) d = e e d = e e d = e e + c και άρα 3 e d = (e e + c) = = e e + c. (ii) Για το rcsin d έχουμε rcsin d = rcsin d = rcsin (rcsin ) d = rcsin d. Τώρα, με αλλαγή μεταβλητής = βρίσκουμε d = d = = ( + c) = = + c και, επομένως, (iii) Για το d γράφουμε cos rcsin d = rcsin + + c. cos d = (tn ) d = tn tn d = tn tn d = tn + log cos + c, αφού βάσει της προηγούμενης άσκησης έχουμε ότι tn d = log cos + c. (iv) Για το ( +) d έχουμε d = ( +) ( + ) d = = ( +) + + d = 9 ( +) + ( +) + + d rctn + c.
10 (v) Για το rctn(e ) e d κάνουμε αλλαγή μεταβλητής = e και γράφουμε Τώρα rctn rctn(e ) e και, με αλλαγή μεταβλητής u =, ( +) d = Επίσης, d = rctn d =e. d = ( ) rctn d = rctn + (rctn ) d = rctn + ( +) d ( +) d = u(u+) du u=. u(u+) du = ( u ) u+ du = log u log u + + c = log u u+ + c. Άρα και και, τέλος, ( +) d = ( log u rctn u+ ) + c = u= log d = rctn + log + + c + + c rctn(e ) e d = ( rctn + log + + c) =e = rctn(e ) e + e log e + + c. Παρατηρήστε ότι στο ολοκλήρωμα u(u+) du, το οποίο χρησιμοποιήσαμε, η μεταβλητή u ανήκει στο (, + ) αφού είναι u = = e. Άρα στον υπολογισμό του θα μπορούσαμε να γράψουμε u(u+) du = ( u ) u+ du = log u log(u + ) + c = log u u+ + c χωρίς να χρησιμοποιήσουμε απόλυτες τιμές. Στο e sin(3) d κάντε αλλαγή μεταβλητής = και στο e sin( 3 ) d που θα προκύψει κάντε δύο φορές ολοκλήρωση κατά μέρη με e = (e ). Στο 3 e d κάντε αλλαγή μεταβλητής = και στο 3 e d που θα προκύψει κάντε τρεις φορές ολοκλήρωση κατά μέρη με e = (e ). Στο e d κάντε αλλαγή μεταβλητής = και στο e d που θα προκύψει κάντε ολοκλήρωση κατά μέρη με e = (e ). Στο sin d κάντε ολοκλήρωση κατά μέρη με sin = (cos ) και ξανά ολοκλήρωση κατά μέρη με cos = (sin ). Στο log d κάντε ολοκλήρωση κατά μέρη με = ( ). Στο log 4 d κάντε τέσσερις διαδοχικές ολοκληρώσεις κατά μέρη με = ( 3 3 ). Στο rctn d κάντε ολοκλήρωση κατά μέρη με = και μετά αλλαγή μεταβλητής = +. Στο rcsin d κάντε ολοκλήρωση κατά μέρη με = ( 3 3 ) και μετά αλλαγή μεταβλητής =. Στο rctn d κάντε ολοκλήρωση κατά μέρη με = ( ). Στο rctn d + που θα προκύψει γράψτε = και χωρίστε το ολοκλήρωμα σε δύο ολοκληρώματα. Το ένα είναι το rctn d που είδαμε προηγουμένως και στο άλλο κάντε αλλαγή + + μεταβλητής = rctn. Στο rctn d κάντε αλλαγή μεταβλητής =, στο rctn d που θα προκύψει κάντε ολοκλήρωση κατά μέρη με = ( ) και στο d που θα προκύψει γράψτε +
11 =. + + Στο cos d κάντε ολοκλήρωση κατά μέρη με cos = cos (sin ) και στο sin d που θα προκύψει γράψτε sin = cos. Στο sin 4 d κάντε ολοκλήρωση κατά μέρη με sin = (cos ) και στο sin cos d που θα προκύψει γράψτε cos = sin. Στο e rctn ( +) 3/ d κάντε αλλαγή μεταβλητής = rctn και στο e sin d που θα προκύψει κάντε δύο ολοκληρώσεις κατά μέρη με e = (e ). Στο log( + + ) d κάντε ολοκλήρωση κατά μέρη με = και στο που θα προκύψει κάντε αλλαγή μεταβλητής = Υπολογίστε τα ολοκληρώματα ρητών συναρτήσεων: d, d, d, + ( ) 3 d, ( 4+4)( 4+5) d, ( ++) d, 4 + d, d, 4 d, d, 5 + d, d, d, 4 + d, 6 + d. + d Λύση: (i) Το + 3 έχει τις ρίζες 3 και, οπότε + 3 = ( + 3)( ). Τώρα βρίσκουμε αριθμούς A, B ώστε να ισχύει = 5+3 (+3)( ) = A +3 + B για κάθε 3,. Η τελευταία ισότητα γράφεται ισοδύναμα = A( ) + B( + 3) = (A + B) + ( A + 3b) για κάθε 3,. Προφανώς, αυτή η ισότητα ισχύει αν A + B = 5 A + 3B = 3 Λύνουμε το σύστημα και βρίσκουμε A = 3 και B =. Άρα = 5+3 (+3)( ) = για κάθε 3,. Επομένως d = 3 +3 d + d = 3 log log + c. (ii) Όπως στο (i) παραγοντοποιούμε: = ( ). Τώρα βρίσκουμε αριθμούς A, B ώστε να ισχύει = + = A ( ) + B ( ) για κάθε. Η τελευταία ισότητα γράφεται ισοδύναμα για κάθε. Η ισότητα ισχύει αν + = A( ) + B = A + ( A + B) A = A + B =
12 Λύνουμε το σύστημα και βρίσκουμε A = και B = 4. Άρα = + = ( ) + 4 ( ) για κάθε. Επομένως d = d + 4 d = log 4 ( ) + c. (iii) Παραγοντοποιούμε: 3 + = ( )( + ). Βρίσκουμε αριθμούς A, B, C ώστε να ισχύει +5 ( )(+) = A + B + C = για κάθε,,. Η τελευταία ισότητα γράφεται ισοδύναμα + 5 = A( )( + ) + B( + ) + C( ) για κάθε,,. Η ισότητα ισχύει αν = (A + B + C) + (A + B C) + ( A) A + B + C = A + B C = 5 A = Λύνουμε το σύστημα και βρίσκουμε A =, B = και C =. Άρα = για κάθε,,. Επομένως +5 ( )(+) = + (+) = d + d + d = log + log log + + c. Η διαδικασία είναι παρόμοια για όλα τα ολοκληρώματα που απομένουν, οπότε θα είμαι πιο σύντομος, τονίζοντας μόνο τις διαφορές ανάλογα με την περίπτωση. (iv) Παραγοντοποιούμε: 3 + = ( )( + ). Αφού βρούμε A, B, C ώστε καταλήγουμε στο = A + B + + C, (+) d = A d + B + d + C d (+) = A log + B log + C + + c. (v) Παραγοντοποιούμε: 3 = ( )( ++) = ( )((+ ) ). Το ++ δεν παραγοντοποιείται. Βρίσκουμε A, B, C ώστε και τότε έχουμε = A + B(+ )+C (+ ) d = A 3 d + B + d + C d (+ ) + 3 (+ 4 ) = A log + B log (( + ) ) C rctn ( ( 3 + )) + c.
13 (vi) Βρίσκουμε A, B, C ώστε και τότε + d = A ( ) 3 + = A ( ) 3 + d + B 4 = A log B ( ) + C ( ) 3 d + C ( ) 8 B 4( ) C 6( ) + c. d ( )3 (vii) Παραγοντοποιούμε: 4 = ( )( + )( + ). Βρίσκουμε A, B, C, D ώστε 4 = A + B + + C+D + και τότε 4 d = A d + B + d + C + d + D + d = A log + B log + + C log( + ) + D rctn + c. (viii) Το 4 είναι το μοναδικό κλάσμα στην άσκηση αυτή στο οποίο ο αριθμητής δεν έχει μικρότερο βαθμό από τον παρονομαστή. Γράφουμε οπότε = , d = d. Παραγοντοποιούμε: = ( + )( + 4). Βρίσκουμε A, B, C, D ώστε και έχουμε d = A = A+B + + C+D +4 + d + B +4 d + D +4 d = A log( + ) + B rctn + C log( + 4) + D rctn + c. + d + C (i) Παραγοντοποιούμε: ( 4 + 4)( 4 + 5) = ( ) (( ) + ). Βρίσκουμε A, B, C, D ώστε και έχουμε ( 4+4)( 4+5) = A + B + C( )+D ( ) ( ) + ( 4+4)( 4+5) d = A d + B ( ) d + C + D ( ) + d ( ) + d = A log B + C log(( ) + ) + D rctn( ) + c. () Παραγοντοποιούμε: = ( )( + ) 3. Βρίσκουμε A, B, C, D ώστε = A + B + + C + (+) D (+) 3 και έχουμε d = A d + B + d + C d + D (+) d (+) 3 = A log + B log + C + D (+) + c. 3
14 (i) Παραγοντοποιούμε: 4 + = ( ) ( + ). Βρίσκουμε A, B, C, D ώστε 4 + = A + B + C ( ) + + D (+) και έχουμε 4 + d = A d + B d + C ( ) + d + D d (+) = A log B D + C log c. (ii) Είναι: + + = ( + ) +. Βρίσκουμε A, B, C, D ώστε = A(+)+B ( ++) (+) + + C(+)+D ((+) +) και έχουμε d = A ( ++) + (+) + d + B (+) + d + C + d ((+) +) + D ((+) +) d = A log(( + ) + ) + B rctn( + ) C ((+) +) + D ((+) +) d. Μένει να βρούμε το τελευταίο ολοκλήρωμα. Αρκεί να βρούμε το ( +) d. Γράφουμε d = + d = ( +) ( +) + d ( +) d = rctn d = rctn + ( +) = rctn + ( +) + d = rctn + = ( +) ( +) + rctn + c. + d ( +) d Επομένως d = ((+) +) d ( +) =+ = + ((+) +) + rctn( + ) + c και, επιτέλους (!!!!!!!!!!!!), d = A ( ++) log(( + ) C + ) + B rctn( + ) ((+) +) (iii) Το 4 + είναι πονηρό : + D(+) ((+) +) + D rctn( + ) + c. 4 + = = ( + ) = ( + + )( + ) = (( + ) )(( + ) + ). Κατά τα άλλα, προχωράμε όπως στο (viii). Για τα τελευταία δύο ολοκληρώματα, αναφέρω μόνο την παραγοντοποίηση των 5 + και 6 + : 5 + = ( + ) ( 5+ + )( ), 6 + = ( + )( )( 3 + ). Αποδείξτε, ξεκινώντας από την αριστερή μεριά των δύο ταυτοτήτων, τις παραγοντοποιήσεις και μετά υπολογίστε τα δύο ολοκληρώματα. 4
15 6. Βρείτε τα ολοκληρώματα ρητών συναρτήσεων των sin και cos : d, (+cos ) + sin d, 5+3 cos d, sin +sin d, sin +sin +cos d. Λύση: Σε όλα τα ολοκληρώματα κάνουμε αλλαγή μεταβλητής u = tn και χρησιμοποιούμε τις σχέσεις sin = Για παράδειγμα, με το Χωρίζουμε σε απλά κλάσματα: Επομένως, και άρα sin u +u, cos = u +u, d = +u du. sin +sin +cos d βρίσκουμε sin +sin +cos d = u (+u)(+u ) du u=tn(/). u (+u)(+u ) = + u +u +u +u. u (+u)(+u ) du = rctn u + log( + u ) log + u + c +sin +cos d = ( rctn u + log( + u ) log + u + c ) u=tn(/) = rctn(tn ) log cos log + tn + c = rctn(tn ) log sin + cos + c. 7. Βρείτε τα ολοκληρώματα: d, + d, d, d, + d, + d, + + d. Λύση: (i) Σε ολοκληρώματα στα οποία εμφανίζεται η παράσταση κάνουμε την αλλαγή μεταβλητής = u + u. Αν το βρίσκεται στο [, + ) θεωρούμε ότι και το u βρίσκεται στο [, + ) και τότε το u δίνεται από τον τύπο u = + και έχουμε και τις σχέσεις και = u u και d = u du. u Αν το βρίσκεται στο (, ] θεωρούμε ότι και το u βρίσκεται στο (, ] και τότε το u δίνεται από τον τύπο u = και έχουμε και τις σχέσεις και = u u και d = u du. u Άρα για το συγκεκριμένο d μετά από απλοποιήσεις έχουμε δύο περιπτώσεις. Αν το βρίσκεται στο [, + ), τότε d = ( u 4 u + ) 4u du u=+ 3 = ( 8 u log u 8u + c ) u=+ = 8 ( + ) log + 8(+ ) + c. Αν το βρίσκεται στο (, ], τότε d = ( u 4 u + ) 4u du u= 3 = ( 8 u + log u + + c ) 8u u= = 8 ( ) + log + 8( + c. ) 5
16 Παρατηρήστε ότι ( + )( ) = και άρα τα δύο αποτελέσματα που προέκυψαν είναι ταυτόσημα (απλώς διαφέρουν τα πεδία ορισμού τους: το [, + ) για το ένα και το (, ] για το άλλο). Με άλλα λόγια: d = 8 ( + ) log + 8(+ ) + c για (, ] [, + ). (ii) Για το d η αλλαγή μεταβλητής στο (i), δηλαδή η = u +, δίνει d = u du u=+ = log + + c d = u du u= = log + c u για [, + ), για (, ]. Όπως στο (i), οι δύο λύσεις είναι ταυτόσημες, οπότε d = log + + c για (, ] [, + ). (iii) Σε ολοκληρώματα στα οποία εμφανίζεται η παράσταση κάνουμε την αλλαγή μεταβλητής = u. Το βρίσκεται στο διάστημα [, ] και θεωρούμε ότι και το u u + βρίσκεται στο [, ], οπότε το u δίνεται από τον τύπο u = +. Έχουμε και τις σχέσεις = u +u και d = ( u ) (+u ) du. Άρα για το + d μετά από απλοποιήσεις έχουμε + d = u du +u u=/(+ ) = ( + ) +u du u=/(+ ) = ( u + rctn u + c) u=/(+ ) = + + rctn + + c για [, ]. (iv) Σε ολοκληρώματα στα οποία εμφανίζεται η παράσταση + κάνουμε την αλλαγή μεταβλητής = u u με u >. Με αυτήν την αλλαγή μεταβλητής προκύπτει u = + + και + = u + u και d = u + du. u Άρα για το + d μετά από απλοποιήσεις έχουμε + d = ( u 4 + u + ) 4u du u=+ 3 + = ( 8 u + log u + c ) 8u u=+ + = 8 ( + + ) + log( + + ) 8(+ + c. +) (v) Για το d η αλλαγή μεταβλητής στο (iv) δίνει + d = + u du u=+ + = log( + + ) + c. (vi) Για το d γράφουμε = ( ) 9 4 και κάνουμε την αλλαγή μεταβλητής t = 3 ( ). Μετά από απλοποιήσεις βρίσκουμε d = dt t t= 3 ( ). Στο (ii) βρήκαμε το t dt και καταλήγουμε στο d = ( log(t + t ) + c ) t= 3 ( ) = log ( + ) + c. 6
17 (vii) Για το + + d κάνουμε την αλλαγή μεταβλητής t = και βρίσκουμε + + d = Κατόπιν, κάνουμε αλλαγή μεταβλητής s = t t+ t + dt t=. t και έχουμε t t+ t + dt = s s+ s + ds s=t/. Τέλος, κάνουμε την αλλαγή μεταβλητής του (iv), δηλαδή s = u u s s+ ds = ( s + 4 ) 4u du u=s+ 4 s + = ( 4 u + u 3 + c ) u=s+ s + = 4 (s + s + ) + (s+ s +) 3 + c. με u >, και βρίσκουμε Άρα + + d = ( + + c. +) 3 7
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο Λύσεις έκτου φυλλαδίου ασκήσεων.
 Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 208-9. Λύσεις έκτου φυλλαδίου ασκήσεων.. Παρατηρήστε ότι ο πρώτος κανόνας αλλαγής μεταβλητής εφαρμόζεται μόνο στα εφτά πρώτα όρια ενώ ο δεύτερος κανόνας εφαρμόζεται
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 208-9. Λύσεις έκτου φυλλαδίου ασκήσεων.. Παρατηρήστε ότι ο πρώτος κανόνας αλλαγής μεταβλητής εφαρμόζεται μόνο στα εφτά πρώτα όρια ενώ ο δεύτερος κανόνας εφαρμόζεται
ΑΝΑΛΥΣΗ 2. Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ 2 Μ. Παπαδημητράκης. 1 ΔΩΔΕΚΑΤΟ ΜΑΘΗΜΑ Έστω συνάρτηση f ορισμένη σε διάστημα I. Λέμε ότι η F είναι αντιπαράγωγος της f στο I αν ισχύει F = f στο I. ΠΡΟΤΑΣΗ. Αν η F είναι αντιπαράγωγος της f στο
ΑΝΑΛΥΣΗ 2 Μ. Παπαδημητράκης. 1 ΔΩΔΕΚΑΤΟ ΜΑΘΗΜΑ Έστω συνάρτηση f ορισμένη σε διάστημα I. Λέμε ότι η F είναι αντιπαράγωγος της f στο I αν ισχύει F = f στο I. ΠΡΟΤΑΣΗ. Αν η F είναι αντιπαράγωγος της f στο
ΑΝΑΛΥΣΗ 2. Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ Μ. Παπαδημητράκης. 1 ΔΕΚΑΤΟ ΤΡΙΤΟ ΜΑΘΗΜΑ Χρησιμοποιούμε τα σύμβολα f και f() d για να συμβολίσουμε όλα μαζί τα αόριστα ολοκληρώματα της f σε ένα διάστημα I. Δηλαδή, γράφουμε f = f + c ή f() d =
ΑΝΑΛΥΣΗ Μ. Παπαδημητράκης. 1 ΔΕΚΑΤΟ ΤΡΙΤΟ ΜΑΘΗΜΑ Χρησιμοποιούμε τα σύμβολα f και f() d για να συμβολίσουμε όλα μαζί τα αόριστα ολοκληρώματα της f σε ένα διάστημα I. Δηλαδή, γράφουμε f = f + c ή f() d =
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο Λύσεις πρώτου φυλλαδίου ασκήσεων.
 Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 208-9.. Για καθεμία από τις ανισότητες Λύσεις πρώτου φυλλαδίου ασκήσεων. x + > 2, x x +, x x+2 > x+3 3x+, (x )(x 3) (x 2) 2 0 γράψτε ως διάστημα ή ως ένωση διαστημάτων
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 208-9.. Για καθεμία από τις ανισότητες Λύσεις πρώτου φυλλαδίου ασκήσεων. x + > 2, x x +, x x+2 > x+3 3x+, (x )(x 3) (x 2) 2 0 γράψτε ως διάστημα ή ως ένωση διαστημάτων
Απειροστικός Λογισμός Ι Ασκήσεις
 Απειροστικός Λογισμός Ι Ασκήσεις Μ. Παπαδημητράκης . Για καθεμία από τις ανισότητες ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΚΑΙ ΣΥΝΑΡΤΗΣΕΙΣ + >, +, + > +3 3+, ( )( 3) ( ) 0 γράψτε ως διάστημα ή ως ένωση διαστημάτων το σύνολο
Απειροστικός Λογισμός Ι Ασκήσεις Μ. Παπαδημητράκης . Για καθεμία από τις ανισότητες ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΚΑΙ ΣΥΝΑΡΤΗΣΕΙΣ + >, +, + > +3 3+, ( )( 3) ( ) 0 γράψτε ως διάστημα ή ως ένωση διαστημάτων το σύνολο
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο Λύσεις τέταρτου φυλλαδίου ασκήσεων. ( n(n+1) e 1 (
 . Αποδείξτε ότι: Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 08-9. Λύσεις τέταρτου φυλλαδίου ασκήσεων. +) 7 +) +), 5 +7 5 5, +log ) 7 log 4, +, ++ + + ) +4+4 + +4, + si +, +) +), + [ ], + + 0, + +, ) +,,
. Αποδείξτε ότι: Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 08-9. Λύσεις τέταρτου φυλλαδίου ασκήσεων. +) 7 +) +), 5 +7 5 5, +log ) 7 log 4, +, ++ + + ) +4+4 + +4, + si +, +) +), + [ ], + + 0, + +, ) +,,
Παντελής Μπουμπούλης, M.Sc., Ph.D. σελ. 2 math-gr.blogspot.com, bouboulis.mysch.gr
 VI Ολοκληρώματα Παντελής Μπουμπούλης, MSc, PhD σελ mth-grlogspotcom, ououlismyschgr ΜΕΡΟΣ Αρχική Συνάρτηση Ορισμός Έστω f μια συνάρτηση ορισμένη σε ένα διάστημα Δ Αρχική συνάρτηση ή παράγουσα της στο Δ
VI Ολοκληρώματα Παντελής Μπουμπούλης, MSc, PhD σελ mth-grlogspotcom, ououlismyschgr ΜΕΡΟΣ Αρχική Συνάρτηση Ορισμός Έστω f μια συνάρτηση ορισμένη σε ένα διάστημα Δ Αρχική συνάρτηση ή παράγουσα της στο Δ
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 Έντυπο Υποβολής Αξιολόγησης Γ.Ε. O φοιτητής συμπληρώνει την ενότητα «Υποβολή Εργασίας» και αποστέλλει το έντυπο σε δύο μη συρραμμένα αντίγραφα (ή ηλεκτρονικά) στον Καθηγητή-Σύμβουλο. Ο Καθηγητής-Σύμβουλος
Έντυπο Υποβολής Αξιολόγησης Γ.Ε. O φοιτητής συμπληρώνει την ενότητα «Υποβολή Εργασίας» και αποστέλλει το έντυπο σε δύο μη συρραμμένα αντίγραφα (ή ηλεκτρονικά) στον Καθηγητή-Σύμβουλο. Ο Καθηγητής-Σύμβουλος
ΑΝΑΛΥΣΗ 2. Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ 2 Μ. Παπαδημητράκης. ΔΕΚΑΤΟ ΤΕΤΑΡΤΟ ΜΑΘΗΜΑ Άσκηση. Έστω f συνεχής στο διάστημα I και έστω ότι ισχύει f() για κάθε I. Αν η f 2 είναι παραγωγίσιμη στο I, αποδείξτε ότι η f είναι παραγωγίσιμη στο
ΑΝΑΛΥΣΗ 2 Μ. Παπαδημητράκης. ΔΕΚΑΤΟ ΤΕΤΑΡΤΟ ΜΑΘΗΜΑ Άσκηση. Έστω f συνεχής στο διάστημα I και έστω ότι ισχύει f() για κάθε I. Αν η f 2 είναι παραγωγίσιμη στο I, αποδείξτε ότι η f είναι παραγωγίσιμη στο
Η Θεωρία στα Μαθηματικά κατεύθυνσης της Γ Λυκείου
 Η Θεωρία στα Μαθηματικά κατεύθυνσης της Γ Λυκείου wwwaskisopolisgr έκδοση 5-6 wwwaskisopolisgr ΣΥΝΑΡΤΗΣΕΙΣ 5 Τι ονομάζουμε πραγματική συνάρτηση; Έστω Α ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση
Η Θεωρία στα Μαθηματικά κατεύθυνσης της Γ Λυκείου wwwaskisopolisgr έκδοση 5-6 wwwaskisopolisgr ΣΥΝΑΡΤΗΣΕΙΣ 5 Τι ονομάζουμε πραγματική συνάρτηση; Έστω Α ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση
2.1 ΜΟΝΟΤΟΝΙΑ ΑΚΡΟΤΑΤΑ ΣΥΜΜΕΤΡΙΕΣ ΣΥΝΑΡΤΗΣΗ
 ΚΕΦΑΛΑΙΟ Ο : ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ. ΜΟΝΟΤΟΝΙΑ ΑΚΡΟΤΑΤΑ ΣΥΜΜΕΤΡΙΕΣ ΣΥΝΑΡΤΗΣΗΣ ΟΡΙΣΜΟΣ ΣΥΝΑΡΤΗΣΗΣ Συνάρτηση από ένα σύνολο Α σε ένα σύνολο Β λέγεται μια διαδικασία (κανόνας), με την οποία κάθε στοιχείο του
ΚΕΦΑΛΑΙΟ Ο : ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ. ΜΟΝΟΤΟΝΙΑ ΑΚΡΟΤΑΤΑ ΣΥΜΜΕΤΡΙΕΣ ΣΥΝΑΡΤΗΣΗΣ ΟΡΙΣΜΟΣ ΣΥΝΑΡΤΗΣΗΣ Συνάρτηση από ένα σύνολο Α σε ένα σύνολο Β λέγεται μια διαδικασία (κανόνας), με την οποία κάθε στοιχείο του
APEIROSTIKOS LOGISMOS I
 APEIROSTIKOS LOGISOS I ΟΛΟΗΜΕΡΟ ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΒΛΗΜΑΤΩΝ Λύσεις ασκήσεων φυλλαδίου. Άσκηση : Αποδείξτε με τον ορισμό ότι:. lim ( ) = +,. lim =,. lim ln( + ) = ln, + 4. lim + =. Λύση:. Θεωρούμε αυθαίρετο
APEIROSTIKOS LOGISOS I ΟΛΟΗΜΕΡΟ ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΒΛΗΜΑΤΩΝ Λύσεις ασκήσεων φυλλαδίου. Άσκηση : Αποδείξτε με τον ορισμό ότι:. lim ( ) = +,. lim =,. lim ln( + ) = ln, + 4. lim + =. Λύση:. Θεωρούμε αυθαίρετο
APEIROSTIKOS LOGISMOS I
 APEIROSTIKOS LOGISMOS I ΟΛΟΗΜΕΡΟ ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΒΛΗΜΑΤΩΝ Λύσεις ασκήσεων φυλλαδίου 4. Άσκηση : Υπολογίστε, αν υπάρχουν, τα παρακάτω όρια. Αν χρειάζεται, υπολογίστε τα αντίστοιχα πλευρικά όρια. + 4 3 + +,
APEIROSTIKOS LOGISMOS I ΟΛΟΗΜΕΡΟ ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΒΛΗΜΑΤΩΝ Λύσεις ασκήσεων φυλλαδίου 4. Άσκηση : Υπολογίστε, αν υπάρχουν, τα παρακάτω όρια. Αν χρειάζεται, υπολογίστε τα αντίστοιχα πλευρικά όρια. + 4 3 + +,
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο Λύσεις ένατου φυλλαδίου ασκήσεων.
 Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 018-19. Λύσεις ένατου φυλλαδίου ασκήσεων. 1. Έστω a < b. Αποδείξτε ότι υπάρχει ξ ώστε (i) a < ξ < b και e b e a = (b a)e ξ. (ii) a < ξ < b και cos b cos a = (e
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 018-19. Λύσεις ένατου φυλλαδίου ασκήσεων. 1. Έστω a < b. Αποδείξτε ότι υπάρχει ξ ώστε (i) a < ξ < b και e b e a = (b a)e ξ. (ii) a < ξ < b και cos b cos a = (e
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΓΕΝΙΚΑ ΘΕΜΑ Α. , έχει κατακόρυφη ασύμπτωτη την x 0.
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΓΕΝΙΚΑ ΘΕΜΑ Α Άσκηση Θεωρούμε τον παρακάτω ισχυρισμό: «Αν η συνάρτηση την» ορίζεται στο τότε δεν μπορεί να έχει κατακόρυφη ασύμπτωτη ) Να χαρακτηρίσετε τον παραπάνω ισχυρισμό γράφοντας
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΓΕΝΙΚΑ ΘΕΜΑ Α Άσκηση Θεωρούμε τον παρακάτω ισχυρισμό: «Αν η συνάρτηση την» ορίζεται στο τότε δεν μπορεί να έχει κατακόρυφη ασύμπτωτη ) Να χαρακτηρίσετε τον παραπάνω ισχυρισμό γράφοντας
Διαφορικές Εξισώσεις.
 Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 05-6. Λύσεις πρώτου φυλλαδίου ασκήσεων.. Για κάθε μία από τις παρακάτω διαφορικές εξισώσεις πείτε αν είναι γραμμική ή όχι και προσδιορίστε την τάξη της. α. y + y +
Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 05-6. Λύσεις πρώτου φυλλαδίου ασκήσεων.. Για κάθε μία από τις παρακάτω διαφορικές εξισώσεις πείτε αν είναι γραμμική ή όχι και προσδιορίστε την τάξη της. α. y + y +
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο Λύσεις δέκατου φυλλαδίου ασκήσεων. 2 x dx = 02 ( 2) 2
 Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 08-9. Λύσεις δέκατου φυλλαδίου ασκήσεων.. Υπολογίστε το x αν x < 0 4 fx) dx όταν fx) = αν 0 x 3/x αν < x 4 Λύση: Η f ταυτίζεται στο [, 0] με την συνεχή συνάρτηση
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 08-9. Λύσεις δέκατου φυλλαδίου ασκήσεων.. Υπολογίστε το x αν x < 0 4 fx) dx όταν fx) = αν 0 x 3/x αν < x 4 Λύση: Η f ταυτίζεται στο [, 0] με την συνεχή συνάρτηση
Για να εκφράσουμε τη διαδικασία αυτή, γράφουμε: :
 Η θεωρία στα μαθηματικά προσανατολισμού Γ υκείου Τι λέμε συνάρτηση με πεδίο ορισμού το σύνολο ; Έστω ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το μία διαδικασία (κανόνα), με την
Η θεωρία στα μαθηματικά προσανατολισμού Γ υκείου Τι λέμε συνάρτηση με πεδίο ορισμού το σύνολο ; Έστω ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το μία διαδικασία (κανόνα), με την
Λύσεις Εξετάσεων Φεβρουαρίου Ακ. Έτους
 ΜΑΘΗΜΑΤΙΚΑ, 6-7 ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΕΠΙΚ. ΚΑΘ. ΣΤΑΥΡΟΣ ΤΟΥΜΠΗΣ Λύσεις Εξετάσεων Φεβρουαρίου Ακ. Έτους 6-7. Περιοδικές Συναρτήσεις) Έστω συνεχής συνάρτηση f : R R περιοδική
ΜΑΘΗΜΑΤΙΚΑ, 6-7 ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΕΠΙΚ. ΚΑΘ. ΣΤΑΥΡΟΣ ΤΟΥΜΠΗΣ Λύσεις Εξετάσεων Φεβρουαρίου Ακ. Έτους 6-7. Περιοδικές Συναρτήσεις) Έστω συνεχής συνάρτηση f : R R περιοδική
ΚΕΦΑΛΑΙΟ 2 Ο «ΟΡΙΟ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ»
 ΜΕΘΟΔΟΛΟΓΙΑ & ΑΣΚΗΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ Γ ΕΠΑΛ ΚΕΦΑΛΑΙΟ Ο «ΟΡΙΟ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ» Επιμέλεια : Παλαιολόγου Παύλος Μαθηματικός ΚΕΦΑΛΑΙΟ ο : ΟΡΙΟ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ Α ΣΥΝΑΡΤΗΣΕΙΣ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ Πεδίο
ΜΕΘΟΔΟΛΟΓΙΑ & ΑΣΚΗΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ Γ ΕΠΑΛ ΚΕΦΑΛΑΙΟ Ο «ΟΡΙΟ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ» Επιμέλεια : Παλαιολόγου Παύλος Μαθηματικός ΚΕΦΑΛΑΙΟ ο : ΟΡΙΟ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ Α ΣΥΝΑΡΤΗΣΕΙΣ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ Πεδίο
ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΤΕΛΕΥΤΑΙΑ ΕΠΑΝΑΛΗΨΗ ΑΝΑΛΥΣΗ ΟΛΟΚΛΗΡΩΜΑΤΑ ΜΙΧΑΛΗΣ ΜΑΓΚΟΣ
 ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΤΕΛΕΥΤΑΙΑ ΕΠΑΝΑΛΗΨΗ ΑΝΑΛΥΣΗ ΟΛΟΚΛΗΡΩΜΑΤΑ ΜΙΧΑΛΗΣ ΜΑΓΚΟΣ . ΔΙΑΒΑΖΩ ΤΗ ΘΕΩΡΙΑ ΑΠΟ ΤΟ ΣΧΟΛΙΚΟ ΒΙΒΛΙΟ Σελ.303: Ορισμός (Αρχική συνάρτηση ή παράγουσα) Σελ.304: Απόδειξη του
ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΤΕΛΕΥΤΑΙΑ ΕΠΑΝΑΛΗΨΗ ΑΝΑΛΥΣΗ ΟΛΟΚΛΗΡΩΜΑΤΑ ΜΙΧΑΛΗΣ ΜΑΓΚΟΣ . ΔΙΑΒΑΖΩ ΤΗ ΘΕΩΡΙΑ ΑΠΟ ΤΟ ΣΧΟΛΙΚΟ ΒΙΒΛΙΟ Σελ.303: Ορισμός (Αρχική συνάρτηση ή παράγουσα) Σελ.304: Απόδειξη του
Ο ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE
 ΚΕΦΑΛΑΙΟ Ο ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ APACE ΚΑΙ ΟΙ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΣΤΗΝ ΕΠΙΛΥΣΗ ΓΡΑΜΜΙΚΩΝ ΔΙΑΦΟΡΙΚΩΝ KAI ΟΛΟΚΛΗΡΩΤΙΚΟ-ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΜΕ ΣΤΑΘΕΡΟΥΣ ΣΥΝΤΕΛΕΣΤΕΣ O μετασχηματισμός lc-ο αντίστροφος μετασχηματισμός
ΚΕΦΑΛΑΙΟ Ο ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ APACE ΚΑΙ ΟΙ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΣΤΗΝ ΕΠΙΛΥΣΗ ΓΡΑΜΜΙΚΩΝ ΔΙΑΦΟΡΙΚΩΝ KAI ΟΛΟΚΛΗΡΩΤΙΚΟ-ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΜΕ ΣΤΑΘΕΡΟΥΣ ΣΥΝΤΕΛΕΣΤΕΣ O μετασχηματισμός lc-ο αντίστροφος μετασχηματισμός
6. Ορισμένο Ολοκλήρωμα
 6. Ορισμένο Ολοκλήρωμα 6. Γενικά Ορισμοί Έστω ότι η f() είναι συνεχής συνάρτηση ορισμένη σε ένα διάστημα [,]. Χωρίζουμε το διάστημα [,] σε n υποδιαστήματα επιλέγοντας n+ σημεία τέτοια ώστε = < < < n-
6. Ορισμένο Ολοκλήρωμα 6. Γενικά Ορισμοί Έστω ότι η f() είναι συνεχής συνάρτηση ορισμένη σε ένα διάστημα [,]. Χωρίζουμε το διάστημα [,] σε n υποδιαστήματα επιλέγοντας n+ σημεία τέτοια ώστε = < < < n-
ΕΠΑΝΑΛΗΨΗ ΒΑΣΙΚΩΝ ΕΝΝΟΙΩΝ
 ΕΠΑΝΑΛΗΨΗ ΒΑΣΙΚΩΝ ΕΝΝΟΙΩΝ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ Το σύνολο των πραγματικών αριθμών Υπενθυμίζουμε ότι το σύνολο των πραγματικών αριθμών αποτελείται από τους ρητούς και τους άρρητους αριθμούς και παριστάνεται
ΕΠΑΝΑΛΗΨΗ ΒΑΣΙΚΩΝ ΕΝΝΟΙΩΝ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ Το σύνολο των πραγματικών αριθμών Υπενθυμίζουμε ότι το σύνολο των πραγματικών αριθμών αποτελείται από τους ρητούς και τους άρρητους αριθμούς και παριστάνεται
Περιεχόμενα. Κεφάλαιο 1 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΜΙΑ ΕΥΘΕΙΑ... 13 1.1 Οι συντεταγμένες ενός σημείου...13 1.2 Απόλυτη τιμή...14
 Περιεχόμενα Κεφάλαιο 1 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΜΙΑ ΕΥΘΕΙΑ... 13 1.1 Οι συντεταγμένες ενός σημείου...13 1.2 Απόλυτη τιμή...14 Κεφάλαιο 2 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΕΝΑ ΕΠΙΠΕΔΟ 20 2.1 Οι συντεταγμένες
Περιεχόμενα Κεφάλαιο 1 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΜΙΑ ΕΥΘΕΙΑ... 13 1.1 Οι συντεταγμένες ενός σημείου...13 1.2 Απόλυτη τιμή...14 Κεφάλαιο 2 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΕΝΑ ΕΠΙΠΕΔΟ 20 2.1 Οι συντεταγμένες
Διαφορικές Εξισώσεις.
 Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 2015-16. Λύσεις του τρίτου φυλλαδίου ασκήσεων. 1. Λύστε τις παρακάτω διαφορικές εξισώσεις. Αν προκύψει αλγεβρική σχέση ανάμεσα στις μεταβλητές x, y η οποία δεν λύνεται
Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 2015-16. Λύσεις του τρίτου φυλλαδίου ασκήσεων. 1. Λύστε τις παρακάτω διαφορικές εξισώσεις. Αν προκύψει αλγεβρική σχέση ανάμεσα στις μεταβλητές x, y η οποία δεν λύνεται
Μαθηματικά Γ Γυμνασίου
 Α λ γ ε β ρ ι κ έ ς π α ρ α σ τ ά σ ε ι ς 1.1 Πράξεις με πραγματικούς αριθμούς (επαναλήψεις συμπληρώσεις) A. Οι πραγματικοί αριθμοί και οι πράξεις τους Διδακτικοί στόχοι Θυμάμαι ποιοι αριθμοί λέγονται
Α λ γ ε β ρ ι κ έ ς π α ρ α σ τ ά σ ε ι ς 1.1 Πράξεις με πραγματικούς αριθμούς (επαναλήψεις συμπληρώσεις) A. Οι πραγματικοί αριθμοί και οι πράξεις τους Διδακτικοί στόχοι Θυμάμαι ποιοι αριθμοί λέγονται
sin(5x 2 ) sin(4x) e 5t 2 1 (ii) lim x 0 10x 3 (iii) lim (iv) lim. 10t sin(ax) = 1. = 1 1 a lim = sin(5x2 ) = 2. f (x) = sin x. = e5t 1 = 1 0 = 0.
 ΑΣΚΗΣΕΙΣ ΑΠΕΙΡΟΣΤΙΚΟΥ ΛΟΓΙΣΜΟΥ Ι, Φυλλάδιο 3 Λύσεις Ασκήσεων. Να υπολογίσετε τα παρακάτω όρια. sia) i) ποιες συνθήκες πρέπει να ισχύουν για τα a, β ώστε να έχει νόημα το όριο;) 0 siβ) si5 ) si4) cos cos
ΑΣΚΗΣΕΙΣ ΑΠΕΙΡΟΣΤΙΚΟΥ ΛΟΓΙΣΜΟΥ Ι, Φυλλάδιο 3 Λύσεις Ασκήσεων. Να υπολογίσετε τα παρακάτω όρια. sia) i) ποιες συνθήκες πρέπει να ισχύουν για τα a, β ώστε να έχει νόημα το όριο;) 0 siβ) si5 ) si4) cos cos
12 Το αόριστο ολοκλήρωµα
 Το αόριστο ολοκλήρωµα. Αντιπαράγωγοι Εστω ότι η y = f ( ορίζεται στο διάστηµα I, οποιουδήποτε τύπου. Αν µια δεύτερη συνάρτηση y = F(, που ορίζεται στο ίδιο διάστηµα I, έχει την ιδιότητα F ( = f (, για
Το αόριστο ολοκλήρωµα. Αντιπαράγωγοι Εστω ότι η y = f ( ορίζεται στο διάστηµα I, οποιουδήποτε τύπου. Αν µια δεύτερη συνάρτηση y = F(, που ορίζεται στο ίδιο διάστηµα I, έχει την ιδιότητα F ( = f (, για
ΚΕΦΑΛΑΙΟ 4 Ο ΣΤΟΙΧΕΙΑ ΟΛΟΚΛΗΡΩΤΙΚΟΥ ΛΟΓΙΣΜΟΥ
 ΜΕΘΟΔΟΛΟΓΙΑ & ΑΣΚΗΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ Γ ΕΠΑΛ ΚΕΦΑΛΑΙΟ Ο ΣΤΟΙΧΕΙΑ ΟΛΟΚΛΗΡΩΤΙΚΟΥ ΛΟΓΙΣΜΟΥ Επιμέλεια : Παλαιολόγου Παύλος Μαθηματικός ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ : ΠΑΡΑΓΟΥΣΕΣ ΟΡΙΣΜΟΣ Έστω συνάρτηση : R, όπου Δ διάστημα
ΜΕΘΟΔΟΛΟΓΙΑ & ΑΣΚΗΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ Γ ΕΠΑΛ ΚΕΦΑΛΑΙΟ Ο ΣΤΟΙΧΕΙΑ ΟΛΟΚΛΗΡΩΤΙΚΟΥ ΛΟΓΙΣΜΟΥ Επιμέλεια : Παλαιολόγου Παύλος Μαθηματικός ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ : ΠΑΡΑΓΟΥΣΕΣ ΟΡΙΣΜΟΣ Έστω συνάρτηση : R, όπου Δ διάστημα
Αόριστο ολοκλήρωμα. επαληθεύει την παραπάνω ισότητα.
 Αόριστο ολοκλήρωμα Αντιπαράγωγος μίας συνάρτησης f() ορισμένης σε ένα διάστημα [α,β] λέγεται κάθε συνάρτηση F() που επαληθεύει την ισότητα F( ) f ( ) F( ) c επαληθεύει την παραπάνω ισότητα. Αόριστο ολοκλήρωμα
Αόριστο ολοκλήρωμα Αντιπαράγωγος μίας συνάρτησης f() ορισμένης σε ένα διάστημα [α,β] λέγεται κάθε συνάρτηση F() που επαληθεύει την ισότητα F( ) f ( ) F( ) c επαληθεύει την παραπάνω ισότητα. Αόριστο ολοκλήρωμα
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο Λύσεις έβδομου φυλλαδίου ασκήσεων.
 Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 2018-19. Λύσεις έβδομου φυλλαδίου ασκήσεων. 1. Έχουν οι παρακάτω συναρτήσεις μέγιστη ή ελάχιστη τιμή στο διάστημα (0, 1); Στο διάστημα (, + ); Στο διάστημα [0,
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 2018-19. Λύσεις έβδομου φυλλαδίου ασκήσεων. 1. Έχουν οι παρακάτω συναρτήσεις μέγιστη ή ελάχιστη τιμή στο διάστημα (0, 1); Στο διάστημα (, + ); Στο διάστημα [0,
ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ
 Ο ΚΕΦΑΛΑΙΟ : ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΑΡΧΙΚΗ ΣΥΝΑΡΤΗΣΗ 6 Τι ονομάζουμε αρχική μιας συνάρτησης σε ένα διάστημα Δ ; Απάντηση : Αρχική συνάρτηση ή παράγουσα της στο Δ ονομάζουμε κάθε
Ο ΚΕΦΑΛΑΙΟ : ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΑΡΧΙΚΗ ΣΥΝΑΡΤΗΣΗ 6 Τι ονομάζουμε αρχική μιας συνάρτησης σε ένα διάστημα Δ ; Απάντηση : Αρχική συνάρτηση ή παράγουσα της στο Δ ονομάζουμε κάθε
Περιεχόμενα μεθόδευση του μαθήματος
 Περιεχόμενα μεθόδευση του μαθήματος. Πως ορίζεται η έννοια. Το όριο. To f() f() ; f() εφόσον υπάρχει είναι μονοσήμαντα ορισμένο; εξαρτιέται από τα άκρα α, β των ( α, ) και (, β ) ;. Πως ορίζονται τα πλευρικά
Περιεχόμενα μεθόδευση του μαθήματος. Πως ορίζεται η έννοια. Το όριο. To f() f() ; f() εφόσον υπάρχει είναι μονοσήμαντα ορισμένο; εξαρτιέται από τα άκρα α, β των ( α, ) και (, β ) ;. Πως ορίζονται τα πλευρικά
Διαφορικές Εξισώσεις.
 Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 05-6. Λύσεις δεύτερου φυλλαδίου ασκήσεων.. Βρείτε όλες τις λύσεις της εξίσωσης Bernoulli x y = xy + y 3 καθορίζοντας προσεκτικά το διάστημα στο οποίο ορίζεται καθεμιά
Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 05-6. Λύσεις δεύτερου φυλλαδίου ασκήσεων.. Βρείτε όλες τις λύσεις της εξίσωσης Bernoulli x y = xy + y 3 καθορίζοντας προσεκτικά το διάστημα στο οποίο ορίζεται καθεμιά
Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ
 Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ 1 Συναρτήσεις Όταν αναφερόμαστε σε μια συνάρτηση, ουσιαστικά αναφερόμαστε σε μια σχέση ή εξάρτηση. Στα μαθηματικά που θα μας απασχολήσουν, με απλά λόγια, η σχέση
Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ 1 Συναρτήσεις Όταν αναφερόμαστε σε μια συνάρτηση, ουσιαστικά αναφερόμαστε σε μια σχέση ή εξάρτηση. Στα μαθηματικά που θα μας απασχολήσουν, με απλά λόγια, η σχέση
Ονοματεπώνυμο Τμήμα. 1. Τι ονομάζουμε εμβαδόν ενός επιπέδου σχήματος (χωρίου) και πως υπολογίζεται αυτό; Απάντηση
 ΓΕΛ. ΚΑΣΤΡΙΤΣΙΟΥ ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 202- Ονοματεπώνυμο Τμήμα ΘΕΜΑ: ΕΜΒΑΔΟΝ ΠΑΡΑΒΟΛΙΚΟΥ ΧΩΡΙΟΥ. Τι ονομάζουμε εμβαδόν ενός επιπέδου σχήματος (χωρίου) και πως υπολογίζεται αυτό; Απάντηση Το πρόβλημα μελετήθηκε
ΓΕΛ. ΚΑΣΤΡΙΤΣΙΟΥ ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 202- Ονοματεπώνυμο Τμήμα ΘΕΜΑ: ΕΜΒΑΔΟΝ ΠΑΡΑΒΟΛΙΚΟΥ ΧΩΡΙΟΥ. Τι ονομάζουμε εμβαδόν ενός επιπέδου σχήματος (χωρίου) και πως υπολογίζεται αυτό; Απάντηση Το πρόβλημα μελετήθηκε
Ολοκληρώματα. Κώστας Γλυκός ΜΑΘΗΜΑΤΙΚΟΣ. Ασκήσεις για ΑΕΙ και ΤΕΙ. Kglykos.gr. σε Ολοκληρώματα. τεχνικές. 108 ασκήσεις. εκδόσεις.
 Ολοκληρώματα Κώστας Γλυκός Ασκήσεις για ΑΕΙ και ΤΕΙ σε Ολοκληρώματα τεχνικές 08 ασκήσεις Ι δ ι α ί τ ε ρ α μ α θ ή μ α τ α 6 9 7. 0 0. 8 8. 8 8 Kglkos.gr / / 0 7 εκδόσεις Καλό πήξιμο τηλ. Οικίας : 0-60.78
Ολοκληρώματα Κώστας Γλυκός Ασκήσεις για ΑΕΙ και ΤΕΙ σε Ολοκληρώματα τεχνικές 08 ασκήσεις Ι δ ι α ί τ ε ρ α μ α θ ή μ α τ α 6 9 7. 0 0. 8 8. 8 8 Kglkos.gr / / 0 7 εκδόσεις Καλό πήξιμο τηλ. Οικίας : 0-60.78
Εισαγωγή στις Φυσικές Επιστήμες ( ) Ονοματεπώνυμο Τμήμα ΘΕΜΑ 1. x x. x x x ( ) + ( 20) + ( + 4) = ( + ) + ( 10 + ) + ( )
 Ονοματεπώνυμο Τμήμα ο Ερώτημα Να υπολογιστούν τα αόριστα ολοκληρώματα α) ( + + ) e d β) + ( + 4)( 5) 5 89 ΘΕΜΑ d Απάντηση α) θέτω u = + +και υ = e, επομένως dυ = e και du = ( + ) d. ( + + ) e d= u dυ =
Ονοματεπώνυμο Τμήμα ο Ερώτημα Να υπολογιστούν τα αόριστα ολοκληρώματα α) ( + + ) e d β) + ( + 4)( 5) 5 89 ΘΕΜΑ d Απάντηση α) θέτω u = + +και υ = e, επομένως dυ = e και du = ( + ) d. ( + + ) e d= u dυ =
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο Λύσεις δεύτερου φυλλαδίου ασκήσεων.
 Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 08-9. Λύσεις δεύτερου φυλλαδίου ασκήσεων.. Βρείτε τα arccos και arcsin των 0, ±, ±, ±, ±. Λύση: Στο διάστημα [ π, π ] είναι (κατά αύξουσα διάταξη των γωνιών και
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 08-9. Λύσεις δεύτερου φυλλαδίου ασκήσεων.. Βρείτε τα arccos και arcsin των 0, ±, ±, ±, ±. Λύση: Στο διάστημα [ π, π ] είναι (κατά αύξουσα διάταξη των γωνιών και
ΕΡΩΤΗΣΕΙΣ ΜΑΘΗΤΩΝ. α) Το ορισμένο ολοκλήρωμα μιας συνεχούς συνάρτησης f σε ένα διάστημα [a, b] είναι όριο?
![ΕΡΩΤΗΣΕΙΣ ΜΑΘΗΤΩΝ. α) Το ορισμένο ολοκλήρωμα μιας συνεχούς συνάρτησης f σε ένα διάστημα [a, b] είναι όριο? ΕΡΩΤΗΣΕΙΣ ΜΑΘΗΤΩΝ. α) Το ορισμένο ολοκλήρωμα μιας συνεχούς συνάρτησης f σε ένα διάστημα [a, b] είναι όριο?](/thumbs/27/11825610.jpg) ΕΡΩΤΗΣΕΙΣ ΜΑΘΗΤΩΝ Ερώτηση α) Το ορισμένο ολοκλήρωμα μιας συνεχούς συνάρτησης f σε ένα διάστημα [, ] είναι όριο? β) Για να βρούμε το ορισμένο ολοκλήρωμα μιας συνεχούς συνάρτησης f σε ένα διάστημα [, ] πρέπει
ΕΡΩΤΗΣΕΙΣ ΜΑΘΗΤΩΝ Ερώτηση α) Το ορισμένο ολοκλήρωμα μιας συνεχούς συνάρτησης f σε ένα διάστημα [, ] είναι όριο? β) Για να βρούμε το ορισμένο ολοκλήρωμα μιας συνεχούς συνάρτησης f σε ένα διάστημα [, ] πρέπει
4.1 Το αόριστο ολοκλήρωµα - Βασικά ολοκληρώ-
 Κεφάλαιο 4 ΟΛΟΚΛΗΡΩΜΑ 4.1 Το αόριστο ολοκλήρωµα - Βασικά ολοκληρώ- µατα Ορισµός 4.1.1. Αρχική ή παράγουσα συνάρτηση ή αντιπαράγωγος µιας συνάρτησης f(x), x [, b], λέγεται κάθε συνάρτηση F (x) που επαληθεύει
Κεφάλαιο 4 ΟΛΟΚΛΗΡΩΜΑ 4.1 Το αόριστο ολοκλήρωµα - Βασικά ολοκληρώ- µατα Ορισµός 4.1.1. Αρχική ή παράγουσα συνάρτηση ή αντιπαράγωγος µιας συνάρτησης f(x), x [, b], λέγεται κάθε συνάρτηση F (x) που επαληθεύει
Ολοκληρώματα. Κώστας Γλυκός ΜΑΘΗΜΑΤΙΚΟΣ. Ασκήσεις για ΑΕΙ και ΤΕΙ. Kglykos.gr. σε Ολοκληρώματα. τεχνικές. 108 ασκήσεις. εκδόσεις.
 Ολοκληρώματα Κώστας Γλυκός Ασκήσεις για ΑΕΙ και ΤΕΙ σε Ολοκληρώματα τεχνικές 08 ασκήσεις Ι δ ι α ί τ ε ρ α μ α θ ή μ α τ α 6 9 7. 0 0. 8 8. 8 8 Kglkos.gr / / 0 9 εκδόσεις Καλό πήξιμο Τα πάντα για τα Ολοκληρώματα
Ολοκληρώματα Κώστας Γλυκός Ασκήσεις για ΑΕΙ και ΤΕΙ σε Ολοκληρώματα τεχνικές 08 ασκήσεις Ι δ ι α ί τ ε ρ α μ α θ ή μ α τ α 6 9 7. 0 0. 8 8. 8 8 Kglkos.gr / / 0 9 εκδόσεις Καλό πήξιμο Τα πάντα για τα Ολοκληρώματα
ΠΕΡΙΕΧΟΜΕΝΑ ΣΥΣΤΗΜΑΤΑ ΟΡΘΟΓΩΝΙΩΝ ΣΥΝΤΕΤΑΓΜΕΝΩΝ...23 ΑΠΟΛΥΤΗ ΤΙΜΗ. ΑΝΙΣΟΤΗΤΕΣ...15 ΚΕΦΑΛΑΙΟ 3 ΕΥΘΕΙΕΣ...32 ΚΕΦΑΛΑΙΟ 4 ΚΥΚΛΟΙ...43
 ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟ ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΩΝ ΣΥΝΤΕΤΑΓΜΕΝΩΝ. ΑΠΟΛΥΤΗ ΤΙΜΗ. ΑΝΙΣΟΤΗΤΕΣ...5 ΚΕΦΑΛΑΙΟ ΣΥΣΤΗΜΑΤΑ ΟΡΘΟΓΩΝΙΩΝ ΣΥΝΤΕΤΑΓΜΕΝΩΝ... ΚΕΦΑΛΑΙΟ ΕΥΘΕΙΕΣ... ΚΕΦΑΛΑΙΟ 4 ΚΥΚΛΟΙ...4 ΚΕΦΑΛΑΙΟ 5 ΕΞΙΣΩΣΕΙΣ ΚΑΙ ΟΙ
ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟ ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΩΝ ΣΥΝΤΕΤΑΓΜΕΝΩΝ. ΑΠΟΛΥΤΗ ΤΙΜΗ. ΑΝΙΣΟΤΗΤΕΣ...5 ΚΕΦΑΛΑΙΟ ΣΥΣΤΗΜΑΤΑ ΟΡΘΟΓΩΝΙΩΝ ΣΥΝΤΕΤΑΓΜΕΝΩΝ... ΚΕΦΑΛΑΙΟ ΕΥΘΕΙΕΣ... ΚΕΦΑΛΑΙΟ 4 ΚΥΚΛΟΙ...4 ΚΕΦΑΛΑΙΟ 5 ΕΞΙΣΩΣΕΙΣ ΚΑΙ ΟΙ
ΑΝΑΛΥΣΗ 2. Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ 2 Μ. Παπαδημητράκης. ΔΕΚΑΤΟ ΕΚΤΟ ΜΑΘΗΜΑ Τώρα θα μας απασχολήσουν τρία ερωτήματα σε σχέση με την κατά σημείο σύγκλιση ακολουθίας συναρτήσεων. Και για τα τρία ερωτήματα θα υποθέσουμε ότι f f στο
ΑΝΑΛΥΣΗ 2 Μ. Παπαδημητράκης. ΔΕΚΑΤΟ ΕΚΤΟ ΜΑΘΗΜΑ Τώρα θα μας απασχολήσουν τρία ερωτήματα σε σχέση με την κατά σημείο σύγκλιση ακολουθίας συναρτήσεων. Και για τα τρία ερωτήματα θα υποθέσουμε ότι f f στο
Έντυπο Yποβολής Αξιολόγησης ΓΕ
 Έντυπο Yποβολής Αξιολόγησης ΓΕ O φοιτητής συμπληρώνει την ενότητα «Υποβολή Εργασίας» και αποστέλλει το έντυπο σε δύο μη συρραμμένα αντίγραφα (ή ηλεκτρονικά) στον Καθηγητή-Σύμβουλο. Ο Καθηγητής-Σύμβουλος
Έντυπο Yποβολής Αξιολόγησης ΓΕ O φοιτητής συμπληρώνει την ενότητα «Υποβολή Εργασίας» και αποστέλλει το έντυπο σε δύο μη συρραμμένα αντίγραφα (ή ηλεκτρονικά) στον Καθηγητή-Σύμβουλο. Ο Καθηγητής-Σύμβουλος
ProapaitoÔmenec gn seic.
 ProapaitoÔmeec g seic. Α. Το σύνολο των πραγματικών αριθμών R και οι αλγεβρικές ιδιότητες των τεσσάρων πράξεων στο R. Το σύνολο των φυσικών αριθμών N = {1,, 3,... }. Προσέξτε: μερικά βιβλία (τα βιβλία
ProapaitoÔmeec g seic. Α. Το σύνολο των πραγματικών αριθμών R και οι αλγεβρικές ιδιότητες των τεσσάρων πράξεων στο R. Το σύνολο των φυσικών αριθμών N = {1,, 3,... }. Προσέξτε: μερικά βιβλία (τα βιβλία
OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ
 Ο ΚΕΦΑΛΑΙΟ : ΟΡΙΟ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΣΥΝΑΡΤΗΣΕΙΣ Έστω Α ένα υποσύνολο του Τι ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α ; Απάντηση : ΕΣΠ Β Έστω
Ο ΚΕΦΑΛΑΙΟ : ΟΡΙΟ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΣΥΝΑΡΤΗΣΕΙΣ Έστω Α ένα υποσύνολο του Τι ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α ; Απάντηση : ΕΣΠ Β Έστω
ΜΑΘΗΜΑΤΙΚΑ Ι Β ΜΕΡΟΣ
 ΤΕΙ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΡΟΦΙΜΩΝ ΜΑΘΗΜΑΤΙΚΑ Ι Περιληπτικές Σημειώσεις-Ασκήσεις Β ΜΕΡΟΣ ΦΩΤΟΥΛΑ ΑΡΓΥΡΟΠΟΥΛΟΥ KAΘ. ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑΤΟΣ ΔΕΟ Msc. Θεωρητικά Μαθηματικά ΚΑΛΑΜΑΤΑ 2016 0 ΠΕΡΙΕΧΟΜΕΝΑ
ΤΕΙ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΡΟΦΙΜΩΝ ΜΑΘΗΜΑΤΙΚΑ Ι Περιληπτικές Σημειώσεις-Ασκήσεις Β ΜΕΡΟΣ ΦΩΤΟΥΛΑ ΑΡΓΥΡΟΠΟΥΛΟΥ KAΘ. ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑΤΟΣ ΔΕΟ Msc. Θεωρητικά Μαθηματικά ΚΑΛΑΜΑΤΑ 2016 0 ΠΕΡΙΕΧΟΜΕΝΑ
2.1 ΠΡΑΞΕΙΣ ΚΑΙ ΟΙ ΙΔΙΟΤΗΤΕΣ ΤΟΥΣ
 ΚΕΦΑΛΑΙΟ : ΟΙ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ. ΠΡΑΞΕΙΣ ΚΑΙ ΟΙ ΙΔΙΟΤΗΤΕΣ ΤΟΥΣ Ρητός ονομάζεται κάθε αριθμός που έχει ή μπορεί να πάρει τη μορφή κλάσματος, όπου, είναι ακέραιοι με 0. Ρητοί αριθμοί : Q /, 0. Έτσι π.χ.
ΚΕΦΑΛΑΙΟ : ΟΙ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ. ΠΡΑΞΕΙΣ ΚΑΙ ΟΙ ΙΔΙΟΤΗΤΕΣ ΤΟΥΣ Ρητός ονομάζεται κάθε αριθμός που έχει ή μπορεί να πάρει τη μορφή κλάσματος, όπου, είναι ακέραιοι με 0. Ρητοί αριθμοί : Q /, 0. Έτσι π.χ.
Ολοκλήρωμα πραγματικής συνάρτησης
 ΚΕΦΑΛΑΙΟ 7 Ολοκλήρωμα πραγματικής συνάρτησης Σύνοψη Το κεφάλαιο αυτό αποτελεί το «πέρασμα» από το Διαφορικό στον Ολοκληρωτικό Λογισμό Η θεμελιώδης έννοια, για το σκοπό αυτό, είναι η αντιπαράγωγος ή αόριστο
ΚΕΦΑΛΑΙΟ 7 Ολοκλήρωμα πραγματικής συνάρτησης Σύνοψη Το κεφάλαιο αυτό αποτελεί το «πέρασμα» από το Διαφορικό στον Ολοκληρωτικό Λογισμό Η θεμελιώδης έννοια, για το σκοπό αυτό, είναι η αντιπαράγωγος ή αόριστο
ΑΝΑΛΥΣΗ 2. Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ 2 Μ. Παπαδημητράκης. ΕΙΚΟΣΤΟ ΔΕΥΤΕΡΟ ΜΑΘΗΜΑ Άσκηση 0... Θεωρήστε τη σειρά συναρτήσεων sin( ). Αποδείξτε ότι η σειρά συγκλίνει σε κάποια συνάρτηση s κατά σημείο στο R και ομοιόμορφα στο [ a, a]
ΑΝΑΛΥΣΗ 2 Μ. Παπαδημητράκης. ΕΙΚΟΣΤΟ ΔΕΥΤΕΡΟ ΜΑΘΗΜΑ Άσκηση 0... Θεωρήστε τη σειρά συναρτήσεων sin( ). Αποδείξτε ότι η σειρά συγκλίνει σε κάποια συνάρτηση s κατά σημείο στο R και ομοιόμορφα στο [ a, a]
Βιομαθηματικά BIO-156. Ολοκλήρωση. Ντίνα Λύκα. Εαρινό Εξάμηνο, 2017
 Βιομαθηματικά BIO-56 Ολοκλήρωση Ντίνα Λύκα Εαρινό Εξάμηνο, 07 lik@biology.uo.gr Ορισμός αντιπαραγώγου ή παράγουσας ή αρχικής συνάρτησης Μια συνάρτηση F ονομάζεται αντιπαράγωγος της σε ένα διάστημα Ι, αν
Βιομαθηματικά BIO-56 Ολοκλήρωση Ντίνα Λύκα Εαρινό Εξάμηνο, 07 lik@biology.uo.gr Ορισμός αντιπαραγώγου ή παράγουσας ή αρχικής συνάρτησης Μια συνάρτηση F ονομάζεται αντιπαράγωγος της σε ένα διάστημα Ι, αν
Μαθηματική Ανάλυση Ι
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Μαθηματική Ανάλυση Ι Ενότητα 8: Ολοκληρώματα Επίκουρος Καθηγητής Θ. Ζυγκιρίδης e-mil: tzygiridis@uowm.gr Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Μαθηματική Ανάλυση Ι Ενότητα 8: Ολοκληρώματα Επίκουρος Καθηγητής Θ. Ζυγκιρίδης e-mil: tzygiridis@uowm.gr Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών
ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ. Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ. Καρτάλη 28 (με Δημητριάδος) Βόλος τηλ.
 ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ. Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ. Καρτάλη 8 (με Δημητριάδος) Βόλος τηλ. 4598 Κεφάλαιο ο Ολοκληρωτικός Λογισμός Ολοκληρωτικός Λογισμός Μεθοδολογία Λυμένα
ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ. Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ. Καρτάλη 8 (με Δημητριάδος) Βόλος τηλ. 4598 Κεφάλαιο ο Ολοκληρωτικός Λογισμός Ολοκληρωτικός Λογισμός Μεθοδολογία Λυμένα
0x2 = 2. = = δηλαδή η f δεν. = 2. Άρα η συνάρτηση f δεν είναι συνεχής στο [0,3]. Συνεπώς δεν. x 2. lim f (x) = lim (2x 1) = 3 και x 2 x 2
![0x2 = 2. = = δηλαδή η f δεν. = 2. Άρα η συνάρτηση f δεν είναι συνεχής στο [0,3]. Συνεπώς δεν. x 2. lim f (x) = lim (2x 1) = 3 και x 2 x 2 0x2 = 2. = = δηλαδή η f δεν. = 2. Άρα η συνάρτηση f δεν είναι συνεχής στο [0,3]. Συνεπώς δεν. x 2. lim f (x) = lim (2x 1) = 3 και x 2 x 2](/thumbs/59/43483993.jpg) ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 8: ΘΕΩΡΗΜΑ BOLZANO - ΠΡΟΣΗΜΟ ΣΥΝΑΡΤΗΣΗΣ - ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ - ΘΕΩΡΗΜΑ ΜΕΓΙΣΤΗΣ ΚΑΙ ΕΛΑΧΙΣΤΗΣ ΤΙΜΗΣ - ΣΥΝΟΛΟ ΤΙΜΩΝ ΣΥΝΕΧΟΥΣ ΣΥΝΑΡΤΗΣΗΣ
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 8: ΘΕΩΡΗΜΑ BOLZANO - ΠΡΟΣΗΜΟ ΣΥΝΑΡΤΗΣΗΣ - ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ - ΘΕΩΡΗΜΑ ΜΕΓΙΣΤΗΣ ΚΑΙ ΕΛΑΧΙΣΤΗΣ ΤΙΜΗΣ - ΣΥΝΟΛΟ ΤΙΜΩΝ ΣΥΝΕΧΟΥΣ ΣΥΝΑΡΤΗΣΗΣ
ΑΝΑΛΥΣΗ 1 ΤΡΙΑΚΟΣΤΟ ΕΚΤΟ ΜΑΘΗΜΑ, Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ 1 ΤΡΙΑΚΟΣΤΟ ΕΚΤΟ ΜΑΘΗΜΑ, 14-1-14 Μ. Παπαδημητράκης. 1 Τις διάφορες απλές ιδιότητες των παραγώγων θα τις θεωρήσω γνωστές από πιο στοιχειώδη μαθήματα απειροστικού λογισμού και από το λύκειο. Τώρα
ΑΝΑΛΥΣΗ 1 ΤΡΙΑΚΟΣΤΟ ΕΚΤΟ ΜΑΘΗΜΑ, 14-1-14 Μ. Παπαδημητράκης. 1 Τις διάφορες απλές ιδιότητες των παραγώγων θα τις θεωρήσω γνωστές από πιο στοιχειώδη μαθήματα απειροστικού λογισμού και από το λύκειο. Τώρα
( x ), x είναι ίσες. x,x είναι ίσες. x 5, x δεν είναι ίσες
 (1). ΣΥΝΑΡΤΗΣΕΙΣ (Απαντήστε με σωστό ή λάθος) Να διευκρινίσουμε το εξής σημείο. Αν η ερώτηση είναι πχ, η συνάρτηση φ ικανοποιεί το τάδε, εννοείται η λέξη ΠΑΝΤΑ, οπότε αν υπάρχει έστω και μία φ που δεν
(1). ΣΥΝΑΡΤΗΣΕΙΣ (Απαντήστε με σωστό ή λάθος) Να διευκρινίσουμε το εξής σημείο. Αν η ερώτηση είναι πχ, η συνάρτηση φ ικανοποιεί το τάδε, εννοείται η λέξη ΠΑΝΤΑ, οπότε αν υπάρχει έστω και μία φ που δεν
ΑΝΑΛΥΣΗ 2. Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ 2 Μ. Παπαδημητράκης. ΕΙΚΟΣΤΟ ΠΕΜΠΤΟ ΜΑΘΗΜΑ Έστω μια δυναμοσειρά a (x ξ) = a 0 + a (x ξ) + a 2 (x ξ) 2 + με ακτίνα σύγκλισης R και με ρ = lim a. Αν x = ξ, η δυναμοσειρά συγκλίνει και έχει άθροισμα
ΑΝΑΛΥΣΗ 2 Μ. Παπαδημητράκης. ΕΙΚΟΣΤΟ ΠΕΜΠΤΟ ΜΑΘΗΜΑ Έστω μια δυναμοσειρά a (x ξ) = a 0 + a (x ξ) + a 2 (x ξ) 2 + με ακτίνα σύγκλισης R και με ρ = lim a. Αν x = ξ, η δυναμοσειρά συγκλίνει και έχει άθροισμα
κυρτές συναρτήσεις. Αν η g είναι γνησίως αύξουσα τότε η gof : είναι κυρτή. . Θα δείξουμε ότι η h είναι γνησίως αύξουσα.
 Άσκηση Έστω f, g: κυρτές συναρτήσεις Αν η g είναι γνησίως αύξουσα τότε η gof : είναι κυρτή Λύση Θα δείξουμε ότι η h ( ) Θέτουμε h( ) gof ( ) g f ( ) είναι γνησίως αύξουσα h( ) g f ( ) f ( ) Έχουμε ότι
Άσκηση Έστω f, g: κυρτές συναρτήσεις Αν η g είναι γνησίως αύξουσα τότε η gof : είναι κυρτή Λύση Θα δείξουμε ότι η h ( ) Θέτουμε h( ) gof ( ) g f ( ) είναι γνησίως αύξουσα h( ) g f ( ) f ( ) Έχουμε ότι
ΑΝΑΛΥΣΗ 2. Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ 2 Μ. Παπαδημητράκης. 1 ΕΝΑΤΟ ΜΑΘΗΜΑ Άσκηση 6.2.4. Έστω f φραγμένη στο [, b] και δυο ακολουθίες διαμερίσεων του [, b], η ( ) και η ( ), έτσι ώστε Σ(f;, b; ) Σ(f;, b; ) 0. Αποδείξτε ότι η f είναι
ΑΝΑΛΥΣΗ 2 Μ. Παπαδημητράκης. 1 ΕΝΑΤΟ ΜΑΘΗΜΑ Άσκηση 6.2.4. Έστω f φραγμένη στο [, b] και δυο ακολουθίες διαμερίσεων του [, b], η ( ) και η ( ), έτσι ώστε Σ(f;, b; ) Σ(f;, b; ) 0. Αποδείξτε ότι η f είναι
f(x) = και στην συνέχεια
 ΕΡΩΤΗΣΕΙΣ ΜΑΘΗΤΩΝ Ερώτηση. Στις συναρτήσεις μπορούμε να μετασχηματίσουμε πρώτα τον τύπο τους και μετά να βρίσκουμε το πεδίο ορισμού τους; Όχι. Το πεδίο ορισμού της συνάρτησης το βρίσκουμε πριν μετασχηματίσουμε
ΕΡΩΤΗΣΕΙΣ ΜΑΘΗΤΩΝ Ερώτηση. Στις συναρτήσεις μπορούμε να μετασχηματίσουμε πρώτα τον τύπο τους και μετά να βρίσκουμε το πεδίο ορισμού τους; Όχι. Το πεδίο ορισμού της συνάρτησης το βρίσκουμε πριν μετασχηματίσουμε
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ 4 η Ημερομηνία Αποστολής στον Φοιτητή: 5 Φεβρουαρίου 008 Ημερομηνία παράδοσης της Εργασίας: 4 Μαρτίου 008
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ 4 η Ημερομηνία Αποστολής στον Φοιτητή: 5 Φεβρουαρίου 008 Ημερομηνία παράδοσης της Εργασίας: 4 Μαρτίου 008
x + ax x x 4 να είναι παραγωγίσιμη στο x Υπόδειξη: Μπορείτε να εφαρμόσετε κανόνα L Hospital ή μπορεί σας χρειαστεί η sin sin = 2sin cos
 http://lar.maths.gr/, maths@maths.gr, Τηλ: 69795 Ενδεικτικές απαντήσεις ης Γραπτής Εργασίας ΠΛΗ -: Άσκηση. (5 μονάδες) i) ( μονάδες) Υπολογίστε την παράγωγο για κάθε μία από τις επόμενες συναρτήσεις: a)
http://lar.maths.gr/, maths@maths.gr, Τηλ: 69795 Ενδεικτικές απαντήσεις ης Γραπτής Εργασίας ΠΛΗ -: Άσκηση. (5 μονάδες) i) ( μονάδες) Υπολογίστε την παράγωγο για κάθε μία από τις επόμενες συναρτήσεις: a)
40 Ασκήσεις στον ΟΛΟΚΛΗΡΩΤΙΚΟ ΛΟΓΙΣΜΟ ( Επεξεργασία του ΜΑΝΩΛΗ ΨΑΡΡΑ)
 Άσκηση η 4 Ασκήσεις στον ΟΛΟΚΛΗΡΩΤΙΚΟ ΛΟΓΙΣΜΟ ( Επεξεργασία του ΜΑΝΩΛΗ ΨΑΡΡΑ) Έστω f, g είναι συνεχείς συναρτήσεις στο διάστημα, να δείξετε: Α. (Ανισότητα των Cauchy-Schwarz) Β.( Ανισότητα του Minkowski)
Άσκηση η 4 Ασκήσεις στον ΟΛΟΚΛΗΡΩΤΙΚΟ ΛΟΓΙΣΜΟ ( Επεξεργασία του ΜΑΝΩΛΗ ΨΑΡΡΑ) Έστω f, g είναι συνεχείς συναρτήσεις στο διάστημα, να δείξετε: Α. (Ανισότητα των Cauchy-Schwarz) Β.( Ανισότητα του Minkowski)
ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β. lim( x 3 1) 0. = δηλαδή το όριο είναι της. . Θα προσπαθήσουμε να βγάλουμε κοινό παράγοντα από αριθμητή και ( ) ( )( )
 ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 4: ΕΝΝΟΙΑ ΟΡΙΟΥ ΣΤΟ R - ΠΛΕΥΡΙΚΑ ΟΡΙΑ ΣΤΟ R - ΣΥΝΕΠΕΙΕΣ ΤΟΥ ΟΡΙΣΜΟΥ ΟΡΙΟΥ ΣΤΟ R - ΟΡΙΟ ΚΑΙ ΔΙΑΤΑΞΗ - ΟΡΙΑ ΚΑΙ ΠΡΑΞΕΙΣ [Κεφ 4: Όριο Συνάρτησης
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 4: ΕΝΝΟΙΑ ΟΡΙΟΥ ΣΤΟ R - ΠΛΕΥΡΙΚΑ ΟΡΙΑ ΣΤΟ R - ΣΥΝΕΠΕΙΕΣ ΤΟΥ ΟΡΙΣΜΟΥ ΟΡΙΟΥ ΣΤΟ R - ΟΡΙΟ ΚΑΙ ΔΙΑΤΑΞΗ - ΟΡΙΑ ΚΑΙ ΠΡΑΞΕΙΣ [Κεφ 4: Όριο Συνάρτησης
f(x) = lim f n (t) = d(t, x n ) d(t, x) = f(t)
 Κεφάλαιο 7 Ακολουθίες και σειρές συναρτήσεων 7.1 Ακολουθίες συναρτήσεων: κατά σημείο σύγκλιση Ορισμός 7.1.1. Εστω X σύνολο, (Y, ρ) μετρικός χώρος και f n, f : X Y (n = 1, 2,...). Λέμε ότι η ακολουθία συναρτήσεων
Κεφάλαιο 7 Ακολουθίες και σειρές συναρτήσεων 7.1 Ακολουθίες συναρτήσεων: κατά σημείο σύγκλιση Ορισμός 7.1.1. Εστω X σύνολο, (Y, ρ) μετρικός χώρος και f n, f : X Y (n = 1, 2,...). Λέμε ότι η ακολουθία συναρτήσεων
Μεθοδική Επανα λήψή. Επιμέλεια Κων/νος Παπασταματίου. Θεωρία - Λεξιλόγιο Βασικές Μεθοδολογίες. Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ.
 Μεθοδική Επανα λήψή Θεωρία - Λεξιλόγιο Βασικές Μεθοδολογίες Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ. Καρτάλη 8 Βόλος Τηλ. 4 598 Επιμέλεια Κων/νος Παπασταματίου Περιεχόμενα Συνοπτική Θεωρία με Ερωτήσεις Απαντήσεις...
Μεθοδική Επανα λήψή Θεωρία - Λεξιλόγιο Βασικές Μεθοδολογίες Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ. Καρτάλη 8 Βόλος Τηλ. 4 598 Επιμέλεια Κων/νος Παπασταματίου Περιεχόμενα Συνοπτική Θεωρία με Ερωτήσεις Απαντήσεις...
ΑΡΧΙΚΗ ΣΥΝΑΡΤΗΣΗ ΠΑΡΑΓΟΥΣΑ ΣΥΝΑΡΤΗΣΗΣ
 ΑΡΧΙΚΗ ΣΥΝΑΡΤΗΣΗ ΠΑΡΑΓΟΥΣΑ ΣΥΝΑΡΤΗΣΗΣ ΟΡΙΣΜΟΣ Έστω f μια συνάρτηση ορισμένη σε ένα διάστημα Δ Αρχική συνάρτηση ή παράγουσα της f στο Δ ονομάζεται κάθε συνάρτηση F που είναι παραγωγίσιμη στο Δ και ισχύει
ΑΡΧΙΚΗ ΣΥΝΑΡΤΗΣΗ ΠΑΡΑΓΟΥΣΑ ΣΥΝΑΡΤΗΣΗΣ ΟΡΙΣΜΟΣ Έστω f μια συνάρτηση ορισμένη σε ένα διάστημα Δ Αρχική συνάρτηση ή παράγουσα της f στο Δ ονομάζεται κάθε συνάρτηση F που είναι παραγωγίσιμη στο Δ και ισχύει
APEIROSTIKOS LOGISMOS I
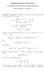 APEIROSTIKOS LOGISMOS I ΟΛΟΗΜΕΡΟ ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΒΛΗΜΑΤΩΝ Λύσεις ασκήσεων φυλλαδίου 3. Άσκηση : Προσδιορίστε, αν υπάρχουν, τις τιμές τού a για τις οποίες οι παρακάτω συναρτήσεις είναι συνεχείς. + +, αν >
APEIROSTIKOS LOGISMOS I ΟΛΟΗΜΕΡΟ ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΒΛΗΜΑΤΩΝ Λύσεις ασκήσεων φυλλαδίου 3. Άσκηση : Προσδιορίστε, αν υπάρχουν, τις τιμές τού a για τις οποίες οι παρακάτω συναρτήσεις είναι συνεχείς. + +, αν >
Α. Οι πραγματικοί αριθμοί και οι πράξεις τους
 ΜΑΘΗΜΑΤΙΚΑ Γ ΓΥΜΝΑΣΙΟΥ - -. Πράξεις με πραγματικούς αριθμούς Α. Οι πραγματικοί αριθμοί και οι πράξεις τους. Αν + y = -, να βρείτε τις τιμές των παραστάσεων: α A = + y + ( + y β B = ( - y -( y γ Γ = -(
ΜΑΘΗΜΑΤΙΚΑ Γ ΓΥΜΝΑΣΙΟΥ - -. Πράξεις με πραγματικούς αριθμούς Α. Οι πραγματικοί αριθμοί και οι πράξεις τους. Αν + y = -, να βρείτε τις τιμές των παραστάσεων: α A = + y + ( + y β B = ( - y -( y γ Γ = -(
Εισαγωγή Το σύνολο αναφοράς και οι περιορισμοί
 ΕΞΙΣΩΣΕΙΣ ΚΑΙ ΑΝΙΣΩΣΕΙΣ ΠΟΥ ΑΝΑΓΟΝΤΑΙ ΣΕ ΠΟΛΥΟΝΥΜΙΚΕΣ Εισαγωγή Το σύνολο αναφοράς και οι περιορισμοί Όταν έχουμε μία εξίσωση που περιέχει παρονομαστές ή ρίζες, πρέπει να βάζουμε περιορισμούς. Το νόημα
ΕΞΙΣΩΣΕΙΣ ΚΑΙ ΑΝΙΣΩΣΕΙΣ ΠΟΥ ΑΝΑΓΟΝΤΑΙ ΣΕ ΠΟΛΥΟΝΥΜΙΚΕΣ Εισαγωγή Το σύνολο αναφοράς και οι περιορισμοί Όταν έχουμε μία εξίσωση που περιέχει παρονομαστές ή ρίζες, πρέπει να βάζουμε περιορισμούς. Το νόημα
2x 2 + x + 1 (x + 3)(x 1) 2 dx, 2x (x + 1) dx. b x 1 + x dx x x 2 1, 6u 5 u 3 + u 2 du = 6u 3 u + 1 du. = u du.
 Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο 8: Τεχνικές ολοκλήρωσης Α Οµάδα. Υπολογίστε τα ακόλουθα ολοκληρώµατα : + + d, + + ( + 3)( ) d, 3 + 3 + 3 + + + d. Υπόδειξη. (α) Γράφουµε + + d
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο 8: Τεχνικές ολοκλήρωσης Α Οµάδα. Υπολογίστε τα ακόλουθα ολοκληρώµατα : + + d, + + ( + 3)( ) d, 3 + 3 + 3 + + + d. Υπόδειξη. (α) Γράφουµε + + d
4 ΟΛΟΚΛΗΡΩΜΑΤΑ 4.2 ΒΑΣΙΚΕΣ ΙΔΙΟΤΗΤΕΣ
 4 ΟΛΟΚΛΗΡΩΜΑΤΑ 4. ΠΑΡΑΓΟΥΣΑ Ή ΑΝΤΙΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΗΣ ΟΡΙΣΜΟΣ: Παράγουσα ή αντιπαράγωγος μιας συνάρτησης f() ορισμένη στο D(f) λέγεται η συνάρτηση F() για την οποία ισχύει F ()=f(). ΣΥΜΒΟΛΙΣΜΟΣ: F()=
4 ΟΛΟΚΛΗΡΩΜΑΤΑ 4. ΠΑΡΑΓΟΥΣΑ Ή ΑΝΤΙΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΗΣ ΟΡΙΣΜΟΣ: Παράγουσα ή αντιπαράγωγος μιας συνάρτησης f() ορισμένη στο D(f) λέγεται η συνάρτηση F() για την οποία ισχύει F ()=f(). ΣΥΜΒΟΛΙΣΜΟΣ: F()=
Συναρτήσεις Θεωρία Ορισμοί - Παρατηρήσεις
 Συναρτήσεις Θεωρία Ορισμοί - Παρατηρήσεις Ορισμός: Έστω Α, Β R. Πραγματική συνάρτηση πραγματικής μεταβλητής από το σύνολο Α στο σύνολο Β ονομάζουμε την διαδικασία κατά την οποία κάθε στοιχείο του συνόλου
Συναρτήσεις Θεωρία Ορισμοί - Παρατηρήσεις Ορισμός: Έστω Α, Β R. Πραγματική συνάρτηση πραγματικής μεταβλητής από το σύνολο Α στο σύνολο Β ονομάζουμε την διαδικασία κατά την οποία κάθε στοιχείο του συνόλου
Άλγεβρα Α Λυκείου Κεφάλαιο 2ο. οι πράξεις και οι ιδιότητές τους
 οι πράξεις και οι ιδιότητές τους Μερικές ακόμη ταυτότητες (επιπλέον από τις αξιοσημείωτες που βρίσκονται στο σχολικό βιβλίο) ) Διαφορά δυνάμεων με ίδιο εκθέτη: ειδικά αν ο εκθέτης ν είναι άρτιος υπάρχει
οι πράξεις και οι ιδιότητές τους Μερικές ακόμη ταυτότητες (επιπλέον από τις αξιοσημείωτες που βρίσκονται στο σχολικό βιβλίο) ) Διαφορά δυνάμεων με ίδιο εκθέτη: ειδικά αν ο εκθέτης ν είναι άρτιος υπάρχει
 = 1 A A = A A. A A + A2 y. A = (A x, A y ) = A x î + A y ĵ. z A. 2 A + A2 z
 Οκτώβριος 2017 Ν. Τράκας ΜΑΘΗΜΑΤΙΚΟ ΒΟΗΘΗΜΑ ΔΙΑΝΥΣΜΑΤΑ Διάνυσμα: κατεύθυνση (διεύθυνση και ϕορά) και μέτρο. Συμβολισμός: A ή A. Αναπαράσταση μέσω των συνιστωσών του: A = (A x, A y ) σε 2-διαστάσεις και
Οκτώβριος 2017 Ν. Τράκας ΜΑΘΗΜΑΤΙΚΟ ΒΟΗΘΗΜΑ ΔΙΑΝΥΣΜΑΤΑ Διάνυσμα: κατεύθυνση (διεύθυνση και ϕορά) και μέτρο. Συμβολισμός: A ή A. Αναπαράσταση μέσω των συνιστωσών του: A = (A x, A y ) σε 2-διαστάσεις και
Απειροστικός Λογισμός ΙΙΙ Υποδείξεις - Συχνά Λάθη
 Απειροστικός Λογισμός ΙΙΙ Υποδείξεις - Συχνά Λάθη Διδάσκοντες: Δάλλα - Αλικάκος 6 Ιουλίου 204 Θέμα (α) Από την γνωστή ανισότητα a 2 + b 2 2 ab, όταν (x, y) (0, 0), τότε ισχύει: f(x, y) f(0, 0) x 2 y 2x
Απειροστικός Λογισμός ΙΙΙ Υποδείξεις - Συχνά Λάθη Διδάσκοντες: Δάλλα - Αλικάκος 6 Ιουλίου 204 Θέμα (α) Από την γνωστή ανισότητα a 2 + b 2 2 ab, όταν (x, y) (0, 0), τότε ισχύει: f(x, y) f(0, 0) x 2 y 2x
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ - ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΩΡΙΑ & ΑΠΟΔΕΙΞΕΙΣ
 ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ - ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΩΡΙΑ & ΑΠΟΔΕΙΞΕΙΣ Επιμέλεια: Βασίλης Κράνιας wwwe-mathsgr ΑΝΑΛΥΣΗ Τι ονομάζουμε πραγματική συνάρτηση Έστω Α ένα υποσύνολο
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ - ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΩΡΙΑ & ΑΠΟΔΕΙΞΕΙΣ Επιμέλεια: Βασίλης Κράνιας wwwe-mathsgr ΑΝΑΛΥΣΗ Τι ονομάζουμε πραγματική συνάρτηση Έστω Α ένα υποσύνολο
ΑΥΤΟΜΑΤΙΣΤΕΣ ΦΥΣΙΚΗ ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ 2013-2014 ΔΕΥΤΕΡΑ 12-15 ΑΙΘ.ΖΑ115-116
 ΑΥΤΟΜΑΤΙΣΤΕΣ ΦΥΣΙΚΗ ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ 2013-2014 ΔΕΥΤΕΡΑ 12-15 ΑΙΘ.ΖΑ115-116 1 ΕΙΣΑΓΩΓΙΚΟ-ΠΑΡΑΓΩΓΟΙ Ορισμός παραγώγου συνάρτησης σε σημείο Μια συνάρτηση f (X) λέμε ότι είναι παραγωγίσιμη σ ένα σημείο του
ΑΥΤΟΜΑΤΙΣΤΕΣ ΦΥΣΙΚΗ ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ 2013-2014 ΔΕΥΤΕΡΑ 12-15 ΑΙΘ.ΖΑ115-116 1 ΕΙΣΑΓΩΓΙΚΟ-ΠΑΡΑΓΩΓΟΙ Ορισμός παραγώγου συνάρτησης σε σημείο Μια συνάρτηση f (X) λέμε ότι είναι παραγωγίσιμη σ ένα σημείο του
ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 10: ΕΥΡΕΣΗ ΤΟΠΙΚΩΝ ΑΚΡΟΤΑΤΩΝ
 ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ : ΕΥΡΕΣΗ ΤΟΠΙΚΩΝ ΑΚΡΟΤΑΤΩΝ [Ενότητα Προσδιορισμός των Τοπικών Ακροτάτων - Θεώρημα Εύρεση Τοπικών Ακροτάτων του κεφ..7 Μέρος Β του σχολικού βιβλίου]. ΑΣΚΗΣΕΙΣ Άσκηση.
ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ : ΕΥΡΕΣΗ ΤΟΠΙΚΩΝ ΑΚΡΟΤΑΤΩΝ [Ενότητα Προσδιορισμός των Τοπικών Ακροτάτων - Θεώρημα Εύρεση Τοπικών Ακροτάτων του κεφ..7 Μέρος Β του σχολικού βιβλίου]. ΑΣΚΗΣΕΙΣ Άσκηση.
Για την κατανόηση της ύλης αυτής θα συμβουλευθείτε επίσης το: βοηθητικό υλικό που υπάρχει στη
 ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ 4 η Ημερομηνία Αποστολής στον Φοιτητή: Φεβρουαρίου Ημερομηνία παράδοσης της Εργασίας: 6 Μαρτίου Πριν από την λύση κάθε άσκησης καλό είναι να
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ 4 η Ημερομηνία Αποστολής στον Φοιτητή: Φεβρουαρίου Ημερομηνία παράδοσης της Εργασίας: 6 Μαρτίου Πριν από την λύση κάθε άσκησης καλό είναι να
ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΟΜΑΔΕΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ : ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΡΟΛΟΓΟΣ Σε κάθε ενότητα αυτού του βιβλίου θα βρείτε : Βασική θεωρία με τη μορφή ερωτήσεων Μεθοδολογίες και σχόλια
ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΟΜΑΔΕΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ : ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΡΟΛΟΓΟΣ Σε κάθε ενότητα αυτού του βιβλίου θα βρείτε : Βασική θεωρία με τη μορφή ερωτήσεων Μεθοδολογίες και σχόλια
Θεώρημα Βolzano. Κατηγορία 1 η. 11.1 Δίνεται η συνάρτηση:
 Κατηγορία η Θεώρημα Βolzano Τρόπος αντιμετώπισης:. Όταν μας ζητούν να εξετάσουμε αν ισχύει το θεώρημα Bolzano για μια συνάρτηση f σε ένα διάστημα [, ] τότε: Εξετάζουμε την συνέχεια της f στο [, ] (αν η
Κατηγορία η Θεώρημα Βolzano Τρόπος αντιμετώπισης:. Όταν μας ζητούν να εξετάσουμε αν ισχύει το θεώρημα Bolzano για μια συνάρτηση f σε ένα διάστημα [, ] τότε: Εξετάζουμε την συνέχεια της f στο [, ] (αν η
d dx ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΗΣ
 ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΗΣ α) Η παράγωγος μιας συνάρτησης = f() σε ένα σημείο 0 εκφράζει το ρυθμό μεταβολής της συνάρτησης (ή τον παράγωγο αριθμό) στο σημείο 0. β) Γραφικά, η παράγωγος της συνάρτησης στο σημείο
ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΗΣ α) Η παράγωγος μιας συνάρτησης = f() σε ένα σημείο 0 εκφράζει το ρυθμό μεταβολής της συνάρτησης (ή τον παράγωγο αριθμό) στο σημείο 0. β) Γραφικά, η παράγωγος της συνάρτησης στο σημείο
Εργασία 2. Παράδοση 20/1/08 Οι ασκήσεις είναι βαθμολογικά ισοδύναμες
 Εργασία Παράδοση 0/1/08 Οι ασκήσεις είναι βαθμολογικά ισοδύναμες 1. Υπολογίστε τα παρακάτω όρια: Α. Β. Γ. όπου x> 0, y > 0 Δ. όπου Κάνετε απευθείας τις πράξεις χωρίς να χρησιμοποιήσετε παραγώγους. Επιβεβαιώστε
Εργασία Παράδοση 0/1/08 Οι ασκήσεις είναι βαθμολογικά ισοδύναμες 1. Υπολογίστε τα παρακάτω όρια: Α. Β. Γ. όπου x> 0, y > 0 Δ. όπου Κάνετε απευθείας τις πράξεις χωρίς να χρησιμοποιήσετε παραγώγους. Επιβεβαιώστε
Γ Ε Ν Ι Κ Ο Δ Ι Α Γ Ω Ν Ι Σ Μ Α Ο Ι Κ Ο Ν Ο Μ Ι Α Σ - Θ Ε Τ Ι Κ Η Σ Γ Τ Α Ξ Η Β. Ρ.
 Γ Ε Ν Ι Κ Ο Δ Ι Α Γ Ω Ν Ι Σ Μ Α Ο Ι Κ Ο Ν Ο Μ Ι Α Σ - Θ Ε Τ Ι Κ Η Σ 6 Γ Τ Α Ξ Η Β. Ρ. Θ Ε Μ Α ο Α. Έστω μια συνάρτηση f ορισμένη στο Δ. Αν η f είναι συνεχής στο Δ και f (χ)= για κάθε εσωτερικό σημείο του
Γ Ε Ν Ι Κ Ο Δ Ι Α Γ Ω Ν Ι Σ Μ Α Ο Ι Κ Ο Ν Ο Μ Ι Α Σ - Θ Ε Τ Ι Κ Η Σ 6 Γ Τ Α Ξ Η Β. Ρ. Θ Ε Μ Α ο Α. Έστω μια συνάρτηση f ορισμένη στο Δ. Αν η f είναι συνεχής στο Δ και f (χ)= για κάθε εσωτερικό σημείο του
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ Ι (ΘΕ ΠΛΗ ) ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ ΤΕΛΙΚΗΣ ΕΞΕΤΑΣΗΣ 9 Ιουνίου (διάρκεια ώρες και λ) Διαβάστε προσεκτικά και απαντήστε
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ Ι (ΘΕ ΠΛΗ ) ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ ΤΕΛΙΚΗΣ ΕΞΕΤΑΣΗΣ 9 Ιουνίου (διάρκεια ώρες και λ) Διαβάστε προσεκτικά και απαντήστε
Κεφάλαιο 2 ο ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ
 Κεφάλαιο ο ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ Σε προηγούμενες τάξεις γνωρίσαμε την έννοια της συνάρτησης και μελετήσαμε ορισμένες βασικές συναρτήσεις. Στο κεφάλαιο αυτό θα μελετήσουμε στη γενική τους μορφή ιδιότητες
Κεφάλαιο ο ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ Σε προηγούμενες τάξεις γνωρίσαμε την έννοια της συνάρτησης και μελετήσαμε ορισμένες βασικές συναρτήσεις. Στο κεφάλαιο αυτό θα μελετήσουμε στη γενική τους μορφή ιδιότητες
ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟ ΛΑΘΟΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ., τότε η f είναι πάντοτε συνεχής στο x., τότε η f είναι συνεχής στο x.
 ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟ ΛΑΘΟΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στο τετράδιό σας την ένδειξη σωστό ή λάθος δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση
ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟ ΛΑΘΟΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στο τετράδιό σας την ένδειξη σωστό ή λάθος δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση
ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Γ ΛΥΚΕΙΟΥ 2008
 ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Γ ΛΥΚΕΙΟΥ 8 ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Γ ΛΥΚΕΙΟΥ 8 ΕΠΙΚΑΙΡΟΠΟΙΗΜΕΝΗ ΣΤΟ ΠΛΑΙΣΙΟ ΤΗΣ ΝΕΑΣ ΥΛΗΣ ΜΑΘΗΜΑΤΙΚΑ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ
ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Γ ΛΥΚΕΙΟΥ 8 ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Γ ΛΥΚΕΙΟΥ 8 ΕΠΙΚΑΙΡΟΠΟΙΗΜΕΝΗ ΣΤΟ ΠΛΑΙΣΙΟ ΤΗΣ ΝΕΑΣ ΥΛΗΣ ΜΑΘΗΜΑΤΙΚΑ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ
ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ-ΛΑΘΟΥΣ
 ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ-ΛΑΘΟΥΣ 1. Αν f συνεχής στο [α, β] είναι f ( ) d 0 f ( ) 0 2. Αν f συνεχής και γν. αύξουσα στο [α, β] ισχύει ότι: f ( ) d 0. 3. Αν f ( ) d g( ) d, ό f ( ) g( ) ά [, ]. 4. Το σύνολο τιμών
ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ-ΛΑΘΟΥΣ 1. Αν f συνεχής στο [α, β] είναι f ( ) d 0 f ( ) 0 2. Αν f συνεχής και γν. αύξουσα στο [α, β] ισχύει ότι: f ( ) d 0. 3. Αν f ( ) d g( ) d, ό f ( ) g( ) ά [, ]. 4. Το σύνολο τιμών
ΜΕΘΟΔΟΛΟΓΙΕΣ & ΑΣΚΗΣΕΙΣ ΓΙΑ ΤΗΝ ΑΛΓΕΒΡΑ ΤΗΣ Α ΛΥΚΕΙΟΥ
 ΜΕΘΟΔΟΛΟΓΙΕΣ & ΑΣΚΗΣΕΙΣ ΓΙΑ ΤΗΝ ΑΛΓΕΒΡΑ ΤΗΣ Α ΛΥΚΕΙΟΥ Επιμέλεια : Παλαιολόγου Παύλος Μαθηματικός Αγαπητοί μαθητές. αυτό το βιβλίο αποτελεί ένα βοήθημα στην ύλη της Άλγεβρας Α Λυκείου, που είναι ένα από
ΜΕΘΟΔΟΛΟΓΙΕΣ & ΑΣΚΗΣΕΙΣ ΓΙΑ ΤΗΝ ΑΛΓΕΒΡΑ ΤΗΣ Α ΛΥΚΕΙΟΥ Επιμέλεια : Παλαιολόγου Παύλος Μαθηματικός Αγαπητοί μαθητές. αυτό το βιβλίο αποτελεί ένα βοήθημα στην ύλη της Άλγεβρας Α Λυκείου, που είναι ένα από
ΜΑΘΗΜΑΤΙΚΑ Θετικής & Τεχνολογικής Κατεύθυνσης Β ΜΕΡΟΣ (ΑΝΑΛΥΣΗ) ΚΕΦ 1 ο : Όριο Συνέχεια Συνάρτησης
 ΜΑΘΗΜΑΤΙΚΑ Θετικής & Τεχνολογικής Κατεύθυνσης Β ΜΕΡΟΣ (ΑΝΑΛΥΣΗ) ΚΕΦ ο : Όριο Συνέχεια Συνάρτησης Φυλλάδιο Φυλλάδι555 4 ο ο.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ
ΜΑΘΗΜΑΤΙΚΑ Θετικής & Τεχνολογικής Κατεύθυνσης Β ΜΕΡΟΣ (ΑΝΑΛΥΣΗ) ΚΕΦ ο : Όριο Συνέχεια Συνάρτησης Φυλλάδιο Φυλλάδι555 4 ο ο.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ
1ο Κεφάλαιο: Συστήματα
 ο Κεφάλαιο: Συστήματα Γραμμικά συστήματα i. Ποια εξίσωση λέγεται γραμμική; ii. Πως μεταβάλλεται η ευθεία y, 0 ή 0 για τις διάφορες τιμές των α,β,γ; iii. Τι ονομάζεται λύση μιας γραμμικής εξίσωσης; iv.
ο Κεφάλαιο: Συστήματα Γραμμικά συστήματα i. Ποια εξίσωση λέγεται γραμμική; ii. Πως μεταβάλλεται η ευθεία y, 0 ή 0 για τις διάφορες τιμές των α,β,γ; iii. Τι ονομάζεται λύση μιας γραμμικής εξίσωσης; iv.
ΑΝΑΛΥΣΗ 2 ΣΕ 37 ΜΑΘΗΜΑΤΑ
 ΑΝΑΛΥΣΗ 2 ΣΕ 37 ΜΑΘΗΜΑΤΑ Μ. Παπαδημητράκης. ΠΡΩΤΟ ΜΑΘΗΜΑ Έστω [, b] ένα κλειστό διάστημα με < b. Διαμέριση του [, b] είναι ένα οποιοδήποτε πεπερασμένο υποσύνολο του [, b] το οποίο περιέχει τουλάχιστον
ΑΝΑΛΥΣΗ 2 ΣΕ 37 ΜΑΘΗΜΑΤΑ Μ. Παπαδημητράκης. ΠΡΩΤΟ ΜΑΘΗΜΑ Έστω [, b] ένα κλειστό διάστημα με < b. Διαμέριση του [, b] είναι ένα οποιοδήποτε πεπερασμένο υποσύνολο του [, b] το οποίο περιέχει τουλάχιστον
ΒΑΣΙΚΗ ΜΕΘΟΔΟΛΟΓΙΑ ΣΤΑ ΟΛΟΚΛΗΡΩΜΑΤΑ. Α.Προσπαθείστε και απομνημονεύστε τον παρακάτω πίνακα βασικών ολοκληρωμάτων: v x
 ΒΑΣΙΚΗ ΜΕΘΟΔΟΛΟΓΙΑ ΣΤΑ ΟΛΟΚΛΗΡΩΜΑΤΑ Α.Προσπαθείστε και απομνημονεύστε τον παρακάτω πίνακα βασικών ολοκληρωμάτων:. c d c c. d c. d c. d c. e d e c 6. d c 7. d c 8. d ln c 9. d c. d c,. Β. Οι παρακάτω τύποι
ΒΑΣΙΚΗ ΜΕΘΟΔΟΛΟΓΙΑ ΣΤΑ ΟΛΟΚΛΗΡΩΜΑΤΑ Α.Προσπαθείστε και απομνημονεύστε τον παρακάτω πίνακα βασικών ολοκληρωμάτων:. c d c c. d c. d c. d c. e d e c 6. d c 7. d c 8. d ln c 9. d c. d c,. Β. Οι παρακάτω τύποι
Η ΜΕΘΟΔΕΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ
 Σελίδα 1 από 34 Η ΜΕΘΟΔΕΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ Μπάμπης Στεργίου 017 Εισαγωγή Οι εξισώσεις, η λύση τους, η εύρεση του πλήθους ριζών τους ή τα ερωτήματα που αφορούν στην ύπαρξη ριζών, αποτελούν ένα σημαντικό
Σελίδα 1 από 34 Η ΜΕΘΟΔΕΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ Μπάμπης Στεργίου 017 Εισαγωγή Οι εξισώσεις, η λύση τους, η εύρεση του πλήθους ριζών τους ή τα ερωτήματα που αφορούν στην ύπαρξη ριζών, αποτελούν ένα σημαντικό
Μαθηματικά. Ενότητα 2: Διαφορικός Λογισμός. Σαριαννίδης Νικόλαος Τμήμα Διοίκησης Επιχειρήσεων (Κοζάνη)
 Μαθηματικά Ενότητα 2: Διαφορικός Λογισμός Σαριαννίδης Νικόλαος Τμήμα Διοίκησης Επιχειρήσεων (Κοζάνη) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Μαθηματικά Ενότητα 2: Διαφορικός Λογισμός Σαριαννίδης Νικόλαος Τμήμα Διοίκησης Επιχειρήσεων (Κοζάνη) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Όριο και συνέχεια πραγματικής συνάρτησης
 ΚΕΦΑΛΑΙΟ 4 Όριο και συνέχεια πραγματικής συνάρτησης Αγνοώ το πώς με βλέπει ο κόσμος αλλά στον εαυτό μου, φαίνομαι σαν να μην ήμουν τίποτα άλλο από ένα αγοράκι που παίζει στην ακρογιαλιά και κατά καιρούς
ΚΕΦΑΛΑΙΟ 4 Όριο και συνέχεια πραγματικής συνάρτησης Αγνοώ το πώς με βλέπει ο κόσμος αλλά στον εαυτό μου, φαίνομαι σαν να μην ήμουν τίποτα άλλο από ένα αγοράκι που παίζει στην ακρογιαλιά και κατά καιρούς
