Διαφορικές Εξισώσεις.
|
|
|
- ÉΘεοκλής Ευτυχός Κομνηνός
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Διαφορικές Εξισώσεις. Εαρινό εξάμηνο Λύσεις πρώτου φυλλαδίου ασκήσεων.. Για κάθε μία από τις παρακάτω διαφορικές εξισώσεις πείτε αν είναι γραμμική ή όχι και προσδιορίστε την τάξη της. α. y + y + sin. β. ( + y )y + y + e. γ. y + y + y + y +. [Γραμμική τάξης 4.] δ. y + y = 0. [Μη-γραμμική τάξης.] ε. y + sin( + y) = sin. [Μη-γραμμική τάξης.] στ. y + y + (cos ) 3. [Γραμμική τάξης 3.] Λύση. [α] Θεωρούμε τον τελεστή L(y) = y + y + y. (Συγκεντρώνουμε όλους τους όρους οι οποίοι περιέχουν y.) Τότε και L(y + y ) = (y + y ) + (y + y ) + (y + y ) = (y + y ) + (y + y ) + (y + y ) = ( y + y + y ) + ( y + y + y ) = L(y ) + L(y ) L(cy) = (cy) + (cy) + (cy) = cy + cy + c c( y + y + y) = cl(y). Άρα ο τελεστής είναι γραμμικός, οπότε η εξίσωση είναι γραμμική και, προφανώς, δεύτερης τάξης. [β] Θεωρούμε τον τελεστή L(y) = ( + y )y + y + y. Τότε Επίσης, L(y + y ) = ( + (y + y ) )(y + y ) + (y + y ) + (y + y ) = ( + y + y y + y )(y + y ) + (y + y ) + (y + y ). L(y ) + L(y ) = ( + y )y + y + y + ( + y )y + y + y. Άρα η ισότητα L(y + y ) = L(y ) + L(y ) ισοδυναμεί, μετά από πράξεις, με την y y + y y y + y y y + y y = 0. Αυτή η ισότητα δεν ισχύει για κάποια ζεύγη συναρτήσεων y, y. Π.χ. για y = y = η ισότητα γράφεται 4 = 0 και αυτό δεν ισχύει: η συνάρτηση 4 δεν ταυτίζεται με τη μηδενική συνάρτηση. Άρα ο τελεστής δεν είναι γραμμικός, οπότε και η εξίσωση δεν είναι γραμμική. Η εξίσωση είναι δεύτερης τάξης. Ένας άλλος τρόπος να δούμε ότι ο τελεστής L(y) = ( + y )y + y + y δεν είναι γραμμικός είναι να ελέγξουμε την ισότητα L(cy) = cl(y). Η ισότητα αυτή, μετά από πράξεις, ισοδυναμεί με την c 3 y y = cy y η οποία δεν ισχύει για κάποιους αριθμούς c και κάποιες συναρτήσεις y. Π.χ. για c = και η ισότητα γράφεται 4 = 0 η οποία και πάλι δεν είναι σωστή (ως ισότητα συναρτήσεων).
2 . Για κάθε μία από τις παρακάτω διαφορικές εξισώσεις βρείτε τη γενική λύση καθώς και τη λύση η οποία ικανοποιεί τη δοσμένη αρχική συνθήκη. α. y e, y(0) =. β. y e, y() = 0. [Γενική λύση: 3 3 e + ce.] γ. y + e +, y(0) = 0. [Γενική λύση: e + + ce.] δ. y e, y( ) =. [Γενική λύση: e + ce.] ε. y + e, y(0) = 3. στ. ( + )y + 4 (+ ), y(0) =. ζ. y + (tan ) sin(), π < < π, y( π 4 ) = 0. Λύση. [α] Γράφουμε p() = 3 και βρίσκουμε μία αντιπαράγωγο P () της p(). Η γενική αντιπαράγωγος είναι η p() d = 3 d = 3 + c. Άρα επιλέγουμε P () = 3. (Επιλέξαμε c = 0 αλλά οποιαδήποτε άλλη τιμή του c είναι επιτρεπτή.) Θεωρούμε τον ολοκληρωτικό παράγοντα µ() = e P () = e 3 και πολλαπλασιάζουμε με αυτόν την διαφορική εξίσωση παίρνοντας τις διαδοχικές ισοδύναμες εξισώσεις e 3 y + 3e 3 e 3 + e (e 3 y) = e 3 + e e 3 (e 3 + e ) d = e 3 d + e d = (e 3 ) d + e 3 = 3 e3 e 3 d + e = 3 3 e3 9 e3 + e + c e + ce 3. Αυτή είναι η γενική λύση της διαφορικής εξίσωσης. Για να βρούμε τη λύση που ικανοποιεί την αρχική συνθήκη y(0) =, θέτουμε στη γενική λύση = 0 και και έχουμε και άρα c = 0 9. Άρα η λύση είναι η = c e e 3. [ε] Γράφουμε p() = και τότε p() d = d = + c. Επιλέγουμε P () =.
3 Πολλαπλασιάζουμε την δ.ε. με τον ολοκληρωτικό παράγοντα µ() = e P () = e και παίρνουμε τις διαδοχικές ισοδύναμες εξισώσεις e y + e (e y) = e d = + c. e + ce. Αυτή είναι η γενική λύση της δ.ε. Για να βρούμε τη λύση που ικανοποιεί την αρχική συνθήκη y(0) = 3, θέτουμε στη γενική λύση = 0 και 3 και έχουμε 3 = c. Άρα η λύση είναι η e + 3e. [στ] Επειδή + 0 για κάθε, η δ.ε. είναι ισοδύναμη με την Γράφουμε p() = Επιλέγουμε y και βρίσκουμε p() d = 4 + ( + ) 3. 4 ( + + d = ) + d = log( + ) + c. P () = log( + ). Πολλαπλασιάζουμε την δ.ε. (στη δεύτερη μορφή: y +...) με τον ολοκληρωτικό παράγοντα µ() = e P () = e log(+) = ( + ) και παίρνουμε τις διαδοχικές ισοδύναμες εξισώσεις ( + ) y + 4( + ) + ( ( + ) y ) = + ( + ) d = Arctan + c. + Arctan ( + ) + c ( + ). Αυτή είναι η γενική λύση της δ.ε. Για να βρούμε τη λύση που ικανοποιεί την αρχική συνθήκη y(0) =, θέτουμε στη γενική λύση = 0 και και έχουμε = c. Άρα η λύση είναι η Arctan ( + ) + ( + ). 3
4 [ζ] Στο διάστημα ( π, π ) η p() = tan είναι συνεχής και sin (cos ) p() d = tan d = cos d = d = log cos + c. cos (Η cos είναι θετική στο διάστημα ( π, π ).) Επιλέγουμε P () = log cos. Πολλαπλασιάζουμε την δ.ε. με τον ολοκληρωτικό παράγοντα µ() = e P () = e log cos = cos και παίρνουμε τις διαδοχικές ισοδύναμες εξισώσεις cos y + sin cos sin() = cos ( ) cos sin cos sin d = sin cos cos = cos + sin + c. = sin cos + sin cos + c cos = cos + sin() + c cos. (cos ) d = cos + cos d Αυτή είναι η γενική λύση της δ.ε. Για να βρούμε τη λύση που ικανοποιεί την αρχική συνθήκη y( π 4 ) = 0, θέτουμε στη γενική λύση = π 4 και 0 και έχουμε οπότε c = π 4. Άρα η λύση είναι η 0 = π c cos + sin() + π 4 cos. 3. Για κάθε μία από τις παρακάτω διαφορικές εξισώσεις βρείτε τη γενική λύση σε καθένα από τα κατάλληλα διαστήματα καθώς και τη λύση η οποία ικανοποιεί τη δοσμένη αρχική συνθήκη στο κατάλληλο διάστημα. α. y + sin, y(π) = 0. β. y + sin cos, y( π) = 0. [Γενική λύση: (, 0) και (0, + ).] γ. y + (cot ) 4 sin, y( π ) = 0. δ. y + (+) (+) +3 (+), y( ) =. + sin + c στα διαστήματα Λύση. [α] Η p() = είναι συνεχής στα διαστήματα (, 0) και (0, + ), οπότε θα δουλέψουμε ξεχωριστά σε καθένα από τα διαστήματα αυτά. Επειδή οι πράξεις που θα κάνουμε θα είναι σχεδόν ίδιες για τα δύο διαστήματα, θα συνεχίσουμε ταυτόχρονα στα δύο διαστήματα και όπου χρειάζεται θα αναφέρουμε τις όποιες διαφορές. Έχουμε p() d = d = log + c. 4
5 Επιλέγουμε P () = log και πολλαπλασιάζουμε την δ.ε. με τον ολοκληρωτικό παράγοντα µ() = e P () = e log =. Ο ολοκληρωτικός παράγων είναι ίσος με µ() = στο (0, + ) και ίσος με µ() = στο (, 0). Όμως, επειδή το να πολλαπλασιάσουμε με την δ.ε. είναι ισοδύναμο με το να την πολλαπλασιάσουμε με (διότι θα πάρουμε ισοδύναμη δ.ε.), θεωρούμε ως ολοκληρωτικό παράγοντα τον µ() = και για τα δύο διαστήματα. Παίρνουμε, λοιπόν, τις ισοδύναμες διαδοχικές εξισώσεις: y + sin (y) = sin sin d = (cos ) d = cos + cos d = cos + sin + c. cos + sin + c. Αυτή, λοιπόν, είναι η γενική λύση. Πρέπει, όμως, να κάνουμε το εξής σημαντικό σχόλιο. Η λύση που βρήκαμε είναι η γενική λύση στο (, 0) και είναι, επίσης, η γενική λύση στο (0, + ). Δεν είναι, όμως, η γενική λύση στην ένωση (, 0) (0, + )! Αν θέλουμε να γράψουμε τη γενική λύση στην ένωση των διαστημάτων, πρέπει να γράψουμε { cos + sin + c στο (, 0) cos + sin + c στο (0, + ) Επεξήγηση: Στην προηγούμενη διαδικασία η σταθερά c προέκυψε όταν διαγράψαμε πρώτη φορά την παράγωγο, δηλαδή όταν από την προέκυψε η (y) = sin cos + sin + c. Πώς δικαιολογείται αυτό; Επειδή sin = ( cos + sin ), αυτό που συνέβη είναι ότι από την (y) = ( cos + sin ) προέκυψε η cos + sin + c. Αυτό συμβαίνει στην επίλυση οποιασδήποτε δ.ε. και πρέπει να το ξεκαθαρίσουμε. Γενικότερα, από την f = g προκύπτει f = g + c. Όμως, αυτή η συνεπαγωγή ισχύει σε διάστημα και όχι σε ένωση ξένων διαστημάτων. Πράγματι, γράφοντας h = f g, η f = g ισοδυναμεί με h = 0 και τώρα γνωρίζουμε ότι, αν η παράγωγος συνάρτησης είναι ίση με 0 σε διάστημα, τότε η συνάρτηση είναι σταθερή στο διάστημα και άρα h = c, δηλαδή f = g + c. Το ότι, αν η παράγωγος συνάρτησης είναι ίση με 0 5
6 σε διάστημα, τότε η συνάρτηση είναι σταθερή στο διάστημα, αποδεικνύεται χρησιμοποιώντας το Θεώρημα Μέσης Τιμής το οποίο ισχύει σε διάστημα και όχι σε ένωση ξένων διαστημάτων. Αν έχουμε δύο ξένα διαστήματα και αν f = g στην ένωση των δύο διαστημάτων, τότε παίρνουμε ότι f = g + c στο ένα διάστημα και f = g + c στο άλλο διάστημα: η σταθερά που προκύπτει εξαρτάται από το διάστημα. Αν έχουμε τρία ή περισσότερα διαστήματα, τότε θα προκύψουν τρεις ή περισσότερες σταθερές. Ξαναγυρνάμε στο πρόβλημά μας με την αρχική συνθήκη y(π) = 0. Το = π περιέχεται στο (0, + ), οπότε θα καθορίσουμε την σταθερά c, και άρα τη λύση y, σ αυτό το διάστημα. Θέτουμε στον τύπο της λύσης = π και 0 και έχουμε και άρα c = π. Επομένως, η λύση είναι η cos + sin 0 = + c π π στο (0, + ). [γ] Η συνάρτηση p() = cot = cos sin είναι συνεχής στα διαστήματα (kπ, (k + )π) με k Z και άρα εργαζόμαστε σε ένα οποιοδήποτε τέτοιο διάστημα. Έχουμε cos (sin ) p() d = cot d = sin d = d = log sin + c sin και επιλέγουμε P () = log sin. Τώρα πολλαπλασιάζουμε την δ.ε. με τον ολοκληρωτικό παράγοντα µ() = e P () = e log sin = sin. Σε κάθε διάστημα (kπ, (k+)π) με άρτιο k είναι µ() = sin και σε κάθε (kπ, (k+)π) με περιττό k είναι µ() = sin. Επειδή το να πολλαπλασιάσουμε την δ.ε. με το sin είναι ισοδύναμο με το να την πολλαπλασιάσουμε με το sin, επιλέγουμε τελικά ως ολοκληρωρικό παράγοντα τον µ() = sin για κάθε διάστημα (kπ, (k + )π). Τώρα παίρνουμε τις διαδοχικές ισοδύναμες εξισώσεις: (sin )y + (cos ) 4 sin ( (sin )y ) = 4 sin (sin ) 4 sin d = sin cos + c sin. ( cos()) d = sin() + c Αυτή είναι η γενική λύση σε κάθε διάστημα (kπ, (k + )π) με k Z. (Η γενική λύση σε ενώσεις τέτοιων διαστημάτων έχει διαφορετικές σταθερές σε καθένα από τα διαστήματα της ένωσης.) Η αρχική συνθήκη y( π ) = 0 καθορίζει τη λύση στο διάστημα (0, π (με k = 0). Με = π και 0 στον τύπο της γενικής λύσης βρίσκουμε οπότε c = π και η λύση είναι η 0 = π + c, sin cos π sin στο (0, π). 6
7 [δ] Οι συναρτήσεις p() = (+) (+) και +3 (+) είναι συνεχείς στα διαστήματα (, ), (, 0) και (0, + ). Επομένως, θα εργαστούμε σ αυτά τα διαστήματα. Έχουμε Επιλέγουμε p() d = + ( + ) d = ( + ) d = + = log + log + + c = log ( + ) + c. P () = log ( + ) και πολλαπλασιάζουμε την δ.ε. με τον ολοκληρωτικό παράγοντα µ() = e P () = e log (+) = ( + ). d + + d Στα διαστήματα (, ) και (0, + ) είναι µ() = ( + ) και στο διάστημα (, 0) είναι µ() = ( + ). Επειδή το να πολλαπλασιάσουμε την δ.ε. με το ( + ) είναι ισοδύναμο με το να την πολλαπλασιάσουμε με το ( + ), επιλέγουμε τελικά ως ολοκληρωτικό παράγοντα τον µ() = ( + ) και για τα τρία διαστήματα και παίρνουμε τις διαδοχικές ισοδύναμες εξισώσεις: ( + )y + ( + ) + 3 ( ) ( + ) + 3 ( + ) ( + 3 ) d = c + 3 ( + ) + c ( + ) = c ( + ). Αυτή είναι η γενική λύση σε καθένα από τα διαστήματα (, ), (, 0) και (0, + ). (Η γενική λύση σε ενώσεις αυτών των διαστημάτων έχει διαφορετικές σταθερές σε καθένα από τα διαστήματα της ένωσης.) Η αρχική συνθήκη y( ) = καθορίζει τη λύση στο διάστημα (, 0). Με = και στον τύπο της γενικής λύσης βρίσκουμε οπότε c = και η λύση είναι η = c, ( + ). 4. Για κάθε μία από τις παρακάτω διαφορικές εξισώσεις βρείτε τη γενική λύση στα διαστήματα (, 0) και (0, + ) και διερευνήστε αν κάποια από τις λύσεις είναι λύση στο (, + ). α. y. β. y + +. γ. y +. [Γενική λύση: + c. Καμία λύση στο (, + ).] δ. y + e. [Γενική λύση: e e + c. Μόνο η λύση με c = είναι λύση στο (, + ).] ε. y + cos. [Γενική λύση: sin (, + ).] + c. Μόνο η λύση με c = 0 είναι λύση στο 7
8 στ. y + 3 { sin, 0, = 0 ζ. y + sin. [Γενική λύση: cos + sin λύση στο (, + ).] η. y + 3 sin. Λύση: [α] Γράφουμε τη δ.ε. στη μορφή y, + c. Μόνο η λύση με c = 0 είναι οπότε αυτομάτως εργαζόμαστε παρακάτω στα διαστήματα (, 0) και (0, + ). Με p() = έχουμε p() d = d = log + c και επιλέγουμε P () = log. Πολλαπλασιάζουμε τη δ.ε. (στη μορφή y +...) με τον ολοκληρωτικό παράγοντα µ() = e P () = e log =. Είναι µ() = στο (0, + ) και µ() = στο (, 0) και, επειδή το να πολλαπλασιάσουμε τη δ.ε. με είναι ισοδύναμο με το να την πολλαπλασιάσουμε με, θεωρούμε ως ολοκληρωτικό παράγοντα την µ() = και για τα δύο διαστήματα. Προκύπτουν τώρα και για τα δύο διαστήματα οι παρακάτω διαδοχικές ισοδύναμες εξισώσεις: y ( y ) = + c + c. Αυτή είναι η γενική λύση της δ.ε. σε καθένα από τα διαστήματα (, 0) και (0, + ). Για να δούμε αν υπάρχει λύση της αρχικής δ.ε. y στο (, + ), σκεφτόμαστε ότι αν y είναι μια τέτοια λύση, τότε αυτή πρέπει να είναι λύση και σε καθένα από τα (, 0) και (0, + ) και επιπλέον να ορίζεται και στο 0. Άρα η y πρέπει να έχει τύπο + c στο (, 0) a για = 0 + c στο (0, + ) 8
9 Η y ικανοποιεί τη δ.ε. στα (, 0) και (0, + ), οπότε αρκεί να είναι παραγωγίσιμη και στο 0 και να ικανοποιεί την δ.ε. και για = 0. Για να είναι η y συνεχής στο 0 πρέπει να είναι δηλαδή lim y() = lim y() = y(0), = 0 = a. Άρα y(0) = a = 0 και ο τύπος της y γράφεται + c στο (, 0) 0 για = 0 + c στο (0, + ) Για να είναι η y παραγωγίσιμη στο 0 πρέπει να ισχύει δηλαδή Ορίζουμε, λοιπόν, και ο τύπος της y γράφεται η. πιό απλά, y() y(0) lim = lim 0 0+ c = c. c = c = c y() y(0), + c στο (, 0) 0 για = 0 + c στο (0, + ) + c στο (, + ). Αμέσως βλέπουμε ότι αυτή η y ικανοποιεί τη δ.ε. και στο 0, δηλαδή την 0y (0) y(0) = 0 αφού y(0) = 0 και y (0) = c. Άρα οι λύσεις της αρχικής δ.ε. στο (, + ) είναι οι + c. [β] Γράφουμε τη δ.ε. στη μορφή y + +, και εργαζόμαστε παρακάτω στα διαστήματα (, 0) και (0, + ). Με p() = έχουμε p() d = d = log + c = log( ) + c και επιλέγουμε P () = log( ). Πολλαπλασιάζουμε τη δ.ε. (στη μορφή y +...) με τον ολοκληρωτικό παράγοντα µ() = e P () = e log() =. 9
10 Προκύπτουν τώρα και για τα δύο διαστήματα οι παρακάτω διαδοχικές ισοδύναμες εξισώσεις: y ( y) = c c. Αυτή είναι η γενική λύση της δ.ε. σε καθένα από τα διαστήματα (, 0) και (0, + ). Για να δούμε αν υπάρχει λύση της αρχικής δ.ε. y + + στο (, + ), σκεφτόμαστε ότι αν y είναι μια τέτοια λύση, τότε αυτή πρέπει να είναι λύση και σε καθένα από τα (, 0) και (0, + ) και επιπλέον να ορίζεται και στο 0. Άρα η y πρέπει να έχει τύπο c στο (, 0) a για = c στο (0, + ) Η y ικανοποιεί τη δ.ε. στα (, 0) και (0, + ), οπότε αρκεί να είναι παραγωγίσιμη και στο 0 και να ικανοποιεί την δ.ε. και για = 0. Για να είναι η y συνεχής στο 0 πρέπει να είναι Άρα πρέπει να είναι δηλαδή ο τύπος της y γράφεται ή, πιο απλά, lim y() = lim y() = y(0) c = c = 0 και = = a, στο (, 0) για = στο (0, + ) στο (, + ). Αμέσως βλέπουμε ότι αυτή η y ικανοποιεί τη δ.ε. και στο 0, δηλαδή την 0y (0) + y(0) = αφού y(0) = και y (0) = 3. Άρα η μοναδική λύση της αρχικής δ.ε. στο (, + ) είναι η [στ] Γράφουμε τη δ.ε. στη μορφή y + 3 sin 3, 0
11 και εργαζόμαστε στα διαστήματα (, 0) και (0, + ). Με p() = 3 έχουμε p() d = 3 d = 3 log + c και επιλέγουμε P () = 3 log. Πολλαπλασιάζουμε τη δ.ε. (στη μορφή y +...) με τον ολοκληρωτικό παράγοντα µ() = e P () = e 3 log = 3. Είναι µ() = 3 στο (0, + ) και µ() = 3 στο (, 0) και, επειδή το να πολλαπλασιάσουμε τη δ.ε. με 3 είναι ισοδύναμο με το να την πολλαπλασιάσουμε με 3, θεωρούμε ως ολοκληρωτικό παράγοντα την µ() = 3 και για τα δύο διαστήματα. Προκύπτουν τώρα και για τα δύο διαστήματα οι παρακάτω διαδοχικές ισοδύναμες εξισώσεις: 3 y + 3 sin ( 3 y) = sin 3 cos + c cos 3 + c 3 = c cos 3. Αυτή είναι η γενική λύση της δ.ε. σε καθένα από τα διαστήματα (, 0) και (0, + ). Για να δούμε αν υπάρχει λύση της αρχικής δ.ε. { sin y + 3, 0, = 0 στο (, + ), σκεφτόμαστε ότι αν y είναι μια τέτοια λύση, τότε αυτή πρέπει να είναι λύση και σε καθένα από τα (, 0) και (0, + ) και επιπλέον να ορίζεται και στο 0. Άρα η y πρέπει να έχει τύπο c cos στο (, 0) 3 a για = 0 c cos 3 στο (0, + ) Η y ικανοποιεί τη δ.ε. στα (, 0) και (0, + ), οπότε αρκεί να είναι παραγωγίσιμη και στο 0 και να ικανοποιεί την δ.ε. και για = 0. Για να είναι η y συνεχής στο 0 πρέπει να είναι lim y() = lim y() = y(0) Αν c, τότε ο αριθμητής του c cos c έχει όριο 0 και άρα lim cos Αν c =, τότε με τον κανόνα του l Hopitâl έχουμε = ±. cos sin lim 0 3 = lim 0 3 = lim sin 0 3 =. Άρα για κάθε τιμή του c το όριο lim 0 y() δεν είναι αριθμός. Ομοίως, για κάθε τιμή του c το όριο lim 0+ y() δεν είναι αριθμός και καταλήγουμε στο
12 ότι δεν υπάρχει λύση της δ.ε. στο (, + ). [η] Γράφουμε τη δ.ε. στη μορφή y + 3 sin, και εργαζόμαστε στα διαστήματα (, 0) και (0, + ). Με p() = 3 έχουμε p() d = 3 d = 3 log + c και επιλέγουμε P () = 3 log. Πολλαπλασιάζουμε τη δ.ε. (στη μορφή y +...) με τον ολοκληρωτικό παράγοντα µ() = e P () = e 3 log = 3. Είναι µ() = 3 στο (0, + ) και µ() = 3 στο (, 0) και, επειδή το να πολλαπλασιάσουμε τη δ.ε. με 3 είναι ισοδύναμο με το να την πολλαπλασιάσουμε με 3, θεωρούμε ως ολοκληρωτικό παράγοντα την µ() = 3 και για τα δύο διαστήματα. Προκύπτουν τώρα και για τα δύο διαστήματα οι παρακάτω διαδοχικές ισοδύναμες εξισώσεις: 3 y + 3 sin ( 3 y) = sin 3 sin d = (cos ) d = cos + cos d = cos + sin + c cos + sin 3 + c 3. Αυτή είναι η γενική λύση της δ.ε. σε καθένα από τα διαστήματα (, 0) και (0, + ). Για να δούμε αν υπάρχει λύση της αρχικής δ.ε. y + 3 sin στο (, + ), σκεφτόμαστε ότι αν y είναι μια τέτοια λύση, τότε αυτή πρέπει να είναι λύση και σε καθένα από τα (, 0) και (0, + ) και επιπλέον να ορίζεται και στο 0. Άρα η y πρέπει να έχει τύπο cos + sin + c 3 στο (, 0) 3 a για = 0 cos + sin + c 3 στο (0, + ) 3 Η y ικανοποιεί τη δ.ε. στα (, 0) και (0, + ), οπότε αρκεί να είναι παραγωγίσιμη και στο 0 και να ικανοποιεί την δ.ε. και για = 0. Για να είναι η y συνεχής στο 0 πρέπει να είναι lim y() = lim y() = y(0). 0 0+
13 Αν c 0, τότε ο αριθμητής του cos +sin +c έχει όριο 0. Αν c 3 = 0, τότε με τον κανόνα του l Hopitâl έχουμε cos + sin sin sin lim 0 3 = lim 0 3 = lim 0 3 = 3. Ομοίως, μόνο όταν c = 0 το όριο lim 0+ y() είναι αριθμός και τότε το όριο είναι 3. Άρα ο τύπος της y γράφεται ή, πιο απλά, cos + sin στο (, 0) 3 3 για = 0 στο (0, + ) cos { cos + sin 3 + sin 3 για 0 3 για = 0 Η y είναι συνεχής στο 0. Για να είναι παραγωγίσιμη στο 0 πρέπει το y() y(0) 3 cos + 3 sin 3 lim = lim να είναι αριθμός. Τώρα με διαδοχικές εφαρμογές του κανόνα του l Hopitâl έχουμε 3 cos + 3 sin 3 lim = lim 0 3 sin 3 3 Άρα η y είναι παραγωγίσιμη στο 0 και y (0) = 0. Επομένως, η y ικανοποιεί τη δ.ε. και στο 0, δηλαδή την = lim 0 sin 4 cos sin = lim = lim = y (0) + 3 0y(0) = sin 0 αφού y(0) = 3 και y (0) = 0. Άρα η μοναδική λύση της αρχικής δ.ε. στο (, + ) είναι η { cos + sin για για = 0 3
Διαφορικές Εξισώσεις.
 Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 05-6. Λύσεις δεύτερου φυλλαδίου ασκήσεων.. Βρείτε όλες τις λύσεις της εξίσωσης Bernoulli x y = xy + y 3 καθορίζοντας προσεκτικά το διάστημα στο οποίο ορίζεται καθεμιά
Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 05-6. Λύσεις δεύτερου φυλλαδίου ασκήσεων.. Βρείτε όλες τις λύσεις της εξίσωσης Bernoulli x y = xy + y 3 καθορίζοντας προσεκτικά το διάστημα στο οποίο ορίζεται καθεμιά
Διαφορικές Εξισώσεις.
 Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 2015-16. Λύσεις του τρίτου φυλλαδίου ασκήσεων. 1. Λύστε τις παρακάτω διαφορικές εξισώσεις. Αν προκύψει αλγεβρική σχέση ανάμεσα στις μεταβλητές x, y η οποία δεν λύνεται
Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 2015-16. Λύσεις του τρίτου φυλλαδίου ασκήσεων. 1. Λύστε τις παρακάτω διαφορικές εξισώσεις. Αν προκύψει αλγεβρική σχέση ανάμεσα στις μεταβλητές x, y η οποία δεν λύνεται
APEIROSTIKOS LOGISMOS I
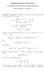 APEIROSTIKOS LOGISMOS I ΟΛΟΗΜΕΡΟ ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΒΛΗΜΑΤΩΝ Λύσεις ασκήσεων φυλλαδίου 3. Άσκηση : Προσδιορίστε, αν υπάρχουν, τις τιμές τού a για τις οποίες οι παρακάτω συναρτήσεις είναι συνεχείς. + +, αν >
APEIROSTIKOS LOGISMOS I ΟΛΟΗΜΕΡΟ ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΒΛΗΜΑΤΩΝ Λύσεις ασκήσεων φυλλαδίου 3. Άσκηση : Προσδιορίστε, αν υπάρχουν, τις τιμές τού a για τις οποίες οι παρακάτω συναρτήσεις είναι συνεχείς. + +, αν >
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο Λύσεις δεύτερου φυλλαδίου ασκήσεων.
 Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 08-9. Λύσεις δεύτερου φυλλαδίου ασκήσεων.. Βρείτε τα arccos και arcsin των 0, ±, ±, ±, ±. Λύση: Στο διάστημα [ π, π ] είναι (κατά αύξουσα διάταξη των γωνιών και
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 08-9. Λύσεις δεύτερου φυλλαδίου ασκήσεων.. Βρείτε τα arccos και arcsin των 0, ±, ±, ±, ±. Λύση: Στο διάστημα [ π, π ] είναι (κατά αύξουσα διάταξη των γωνιών και
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο Λύσεις πρώτου φυλλαδίου ασκήσεων.
 Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 208-9.. Για καθεμία από τις ανισότητες Λύσεις πρώτου φυλλαδίου ασκήσεων. x + > 2, x x +, x x+2 > x+3 3x+, (x )(x 3) (x 2) 2 0 γράψτε ως διάστημα ή ως ένωση διαστημάτων
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 208-9.. Για καθεμία από τις ανισότητες Λύσεις πρώτου φυλλαδίου ασκήσεων. x + > 2, x x +, x x+2 > x+3 3x+, (x )(x 3) (x 2) 2 0 γράψτε ως διάστημα ή ως ένωση διαστημάτων
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο Λύσεις ένατου φυλλαδίου ασκήσεων.
 Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 018-19. Λύσεις ένατου φυλλαδίου ασκήσεων. 1. Έστω a < b. Αποδείξτε ότι υπάρχει ξ ώστε (i) a < ξ < b και e b e a = (b a)e ξ. (ii) a < ξ < b και cos b cos a = (e
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 018-19. Λύσεις ένατου φυλλαδίου ασκήσεων. 1. Έστω a < b. Αποδείξτε ότι υπάρχει ξ ώστε (i) a < ξ < b και e b e a = (b a)e ξ. (ii) a < ξ < b και cos b cos a = (e
ΑΝΑΛΥΣΗ 2. Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ 2 Μ. Παπαδημητράκης. 1 ΔΩΔΕΚΑΤΟ ΜΑΘΗΜΑ Έστω συνάρτηση f ορισμένη σε διάστημα I. Λέμε ότι η F είναι αντιπαράγωγος της f στο I αν ισχύει F = f στο I. ΠΡΟΤΑΣΗ. Αν η F είναι αντιπαράγωγος της f στο
ΑΝΑΛΥΣΗ 2 Μ. Παπαδημητράκης. 1 ΔΩΔΕΚΑΤΟ ΜΑΘΗΜΑ Έστω συνάρτηση f ορισμένη σε διάστημα I. Λέμε ότι η F είναι αντιπαράγωγος της f στο I αν ισχύει F = f στο I. ΠΡΟΤΑΣΗ. Αν η F είναι αντιπαράγωγος της f στο
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο Λύσεις ενδέκατου φυλλαδίου ασκήσεων.
 Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 8-9. Λύσεις ενδέκατου φυλλαδίου ασκήσεων.. (i) Βρείτε μία παράγουσα της + στο (, + ). Ποιές είναι όλες οι παράγουσες της + στο (, + ); (ii) Βρείτε μία παράγουσα
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 8-9. Λύσεις ενδέκατου φυλλαδίου ασκήσεων.. (i) Βρείτε μία παράγουσα της + στο (, + ). Ποιές είναι όλες οι παράγουσες της + στο (, + ); (ii) Βρείτε μία παράγουσα
ΑΚΡΙΒΗ ΔΙΑΦΟΡΙΚΑ. u,υ / A ονομάζεται ακριβές διαφορικό όταν υπάρχει. df u x,y dx υ x,y dy. f u και. f y. 3 f. και
 Το άθροισμα u,d διαφορίσιμη συνάρτηση f / A Παράδειγμα υ, d, με με Το άθροισμα ΑΚΡΙΒΗ ΔΙΑΦΟΡΙΚΑ u,υ / A ονομάζεται ακριβές διαφορικό όταν υπάρχει df u,d υ,d f u f υ 6 d 9 d είναι ακριβές διαφορικό, διότι
Το άθροισμα u,d διαφορίσιμη συνάρτηση f / A Παράδειγμα υ, d, με με Το άθροισμα ΑΚΡΙΒΗ ΔΙΑΦΟΡΙΚΑ u,υ / A ονομάζεται ακριβές διαφορικό όταν υπάρχει df u,d υ,d f u f υ 6 d 9 d είναι ακριβές διαφορικό, διότι
Λύσεις Εξετάσεων Φεβρουαρίου Ακ. Έτους
 ΜΑΘΗΜΑΤΙΚΑ, 6-7 ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΕΠΙΚ. ΚΑΘ. ΣΤΑΥΡΟΣ ΤΟΥΜΠΗΣ Λύσεις Εξετάσεων Φεβρουαρίου Ακ. Έτους 6-7. Περιοδικές Συναρτήσεις) Έστω συνεχής συνάρτηση f : R R περιοδική
ΜΑΘΗΜΑΤΙΚΑ, 6-7 ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΕΠΙΚ. ΚΑΘ. ΣΤΑΥΡΟΣ ΤΟΥΜΠΗΣ Λύσεις Εξετάσεων Φεβρουαρίου Ακ. Έτους 6-7. Περιοδικές Συναρτήσεις) Έστω συνεχής συνάρτηση f : R R περιοδική
********* Β ομάδα Κυρτότητα Σημεία καμπής*********
 ********* Β ομάδα Κυρτότητα Σημεία καμπής********* 5 Για την δύο φορές παραγωγίσιμη στο R συνάρτηση ισχύει: e για κάθε R. Να αποδείξετε ότι η γραφική παράσταση της δεν παρουσιάζει σημείο καμπής. Υποθέτουμε
********* Β ομάδα Κυρτότητα Σημεία καμπής********* 5 Για την δύο φορές παραγωγίσιμη στο R συνάρτηση ισχύει: e για κάθε R. Να αποδείξετε ότι η γραφική παράσταση της δεν παρουσιάζει σημείο καμπής. Υποθέτουμε
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο Λύσεις έκτου φυλλαδίου ασκήσεων.
 Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 208-9. Λύσεις έκτου φυλλαδίου ασκήσεων.. Παρατηρήστε ότι ο πρώτος κανόνας αλλαγής μεταβλητής εφαρμόζεται μόνο στα εφτά πρώτα όρια ενώ ο δεύτερος κανόνας εφαρμόζεται
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 208-9. Λύσεις έκτου φυλλαδίου ασκήσεων.. Παρατηρήστε ότι ο πρώτος κανόνας αλλαγής μεταβλητής εφαρμόζεται μόνο στα εφτά πρώτα όρια ενώ ο δεύτερος κανόνας εφαρμόζεται
ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 7: ΣΥΝΕΠΕΙΕΣ ΘΕΩΡΗΜΑΤΟΣ ΜΕΣΗΣ ΤΙΜΗΣ
 ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 7: ΣΥΝΕΠΕΙΕΣ ΘΕΩΡΗΜΑΤΟΣ ΜΕΣΗΣ ΤΙΜΗΣ [Κεφ..6: Συνέπειες του Θεωρήματος της Μέσης Τιμής πλην της Ενότητας Μονοτονία Συνάρτησης του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ
ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 7: ΣΥΝΕΠΕΙΕΣ ΘΕΩΡΗΜΑΤΟΣ ΜΕΣΗΣ ΤΙΜΗΣ [Κεφ..6: Συνέπειες του Θεωρήματος της Μέσης Τιμής πλην της Ενότητας Μονοτονία Συνάρτησης του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ
Κατηγορία 1 η. Σταθερή συνάρτηση Δίνεται παραγωγίσιμη συνάρτηση f : 0, f '( x) 0 για κάθε εσωτερικό σημείο x του Δ
 Κατηγορία η Σταθερή συνάρτηση Τρόπος αντιμετώπισης: Για να αποδείξουμε ότι μια συνάρτηση είναι σταθερή σε ένα διάστημα Δ πρέπει: η συνάρτηση να είναι συνεχής στο Δ '( ) 0 για κάθε εσωτερικό σημείο του
Κατηγορία η Σταθερή συνάρτηση Τρόπος αντιμετώπισης: Για να αποδείξουμε ότι μια συνάρτηση είναι σταθερή σε ένα διάστημα Δ πρέπει: η συνάρτηση να είναι συνεχής στο Δ '( ) 0 για κάθε εσωτερικό σημείο του
APEIROSTIKOS LOGISMOS I
 APEIROSTIKOS LOGISOS I ΟΛΟΗΜΕΡΟ ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΒΛΗΜΑΤΩΝ Λύσεις ασκήσεων φυλλαδίου. Άσκηση : Αποδείξτε με τον ορισμό ότι:. lim ( ) = +,. lim =,. lim ln( + ) = ln, + 4. lim + =. Λύση:. Θεωρούμε αυθαίρετο
APEIROSTIKOS LOGISOS I ΟΛΟΗΜΕΡΟ ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΒΛΗΜΑΤΩΝ Λύσεις ασκήσεων φυλλαδίου. Άσκηση : Αποδείξτε με τον ορισμό ότι:. lim ( ) = +,. lim =,. lim ln( + ) = ln, + 4. lim + =. Λύση:. Θεωρούμε αυθαίρετο
ΑΝΑΛΥΣΗ 2. Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ 2 Μ. Παπαδημητράκης. ΔΕΚΑΤΟ ΤΕΤΑΡΤΟ ΜΑΘΗΜΑ Άσκηση. Έστω f συνεχής στο διάστημα I και έστω ότι ισχύει f() για κάθε I. Αν η f 2 είναι παραγωγίσιμη στο I, αποδείξτε ότι η f είναι παραγωγίσιμη στο
ΑΝΑΛΥΣΗ 2 Μ. Παπαδημητράκης. ΔΕΚΑΤΟ ΤΕΤΑΡΤΟ ΜΑΘΗΜΑ Άσκηση. Έστω f συνεχής στο διάστημα I και έστω ότι ισχύει f() για κάθε I. Αν η f 2 είναι παραγωγίσιμη στο I, αποδείξτε ότι η f είναι παραγωγίσιμη στο
να είναι παραγωγίσιμη Να ισχύει ότι f Αν μια από τις τρεις παραπάνω συνθήκες δεν ισχύουν τότε δεν ισχύει και το θεώρημα Rolle.
 Κατηγορία η Συνθήκες θεωρήματος Rolle Τρόπος αντιμετώπισης:. Για να ισχύει το θεώρημα Rolle για μια συνάρτηση σε ένα διάστημα [, ] (δηλαδή για να υπάρχει ένα τουλάχιστον (, ) τέτοιο ώστε ( ) ) πρέπει:
Κατηγορία η Συνθήκες θεωρήματος Rolle Τρόπος αντιμετώπισης:. Για να ισχύει το θεώρημα Rolle για μια συνάρτηση σε ένα διάστημα [, ] (δηλαδή για να υπάρχει ένα τουλάχιστον (, ) τέτοιο ώστε ( ) ) πρέπει:
Απειροστικός Λογισμός Ι Ασκήσεις
 Απειροστικός Λογισμός Ι Ασκήσεις Μ. Παπαδημητράκης . Για καθεμία από τις ανισότητες ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΚΑΙ ΣΥΝΑΡΤΗΣΕΙΣ + >, +, + > +3 3+, ( )( 3) ( ) 0 γράψτε ως διάστημα ή ως ένωση διαστημάτων το σύνολο
Απειροστικός Λογισμός Ι Ασκήσεις Μ. Παπαδημητράκης . Για καθεμία από τις ανισότητες ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΚΑΙ ΣΥΝΑΡΤΗΣΕΙΣ + >, +, + > +3 3+, ( )( 3) ( ) 0 γράψτε ως διάστημα ή ως ένωση διαστημάτων το σύνολο
Η Θεωρία στα Μαθηματικά κατεύθυνσης της Γ Λυκείου
 Η Θεωρία στα Μαθηματικά κατεύθυνσης της Γ Λυκείου wwwaskisopolisgr έκδοση 5-6 wwwaskisopolisgr ΣΥΝΑΡΤΗΣΕΙΣ 5 Τι ονομάζουμε πραγματική συνάρτηση; Έστω Α ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση
Η Θεωρία στα Μαθηματικά κατεύθυνσης της Γ Λυκείου wwwaskisopolisgr έκδοση 5-6 wwwaskisopolisgr ΣΥΝΑΡΤΗΣΕΙΣ 5 Τι ονομάζουμε πραγματική συνάρτηση; Έστω Α ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση
Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 19/10/2017. Ακριβείς Διαφορικές Εξισώσεις-Ολοκληρωτικοί Παράγοντες. Η πρώτης τάξης διαφορική εξίσωση
 Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 19/10/2017 Ακριβείς Διαφορικές Εξισώσεις-Ολοκληρωτικοί Παράγοντες Η πρώτης τάξης διαφορική εξίσωση M(x, y) + (x, y)y = 0 ή ισοδύναμα, γραμμένη στην μορφή M(x,
Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 19/10/2017 Ακριβείς Διαφορικές Εξισώσεις-Ολοκληρωτικοί Παράγοντες Η πρώτης τάξης διαφορική εξίσωση M(x, y) + (x, y)y = 0 ή ισοδύναμα, γραμμένη στην μορφή M(x,
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ 4 η Ημερομηνία Αποστολής στον Φοιτητή: 5 Φεβρουαρίου 008 Ημερομηνία παράδοσης της Εργασίας: 4 Μαρτίου 008
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ 4 η Ημερομηνία Αποστολής στον Φοιτητή: 5 Φεβρουαρίου 008 Ημερομηνία παράδοσης της Εργασίας: 4 Μαρτίου 008
ΜΑΘΗΜΑΤΙΚΑ Θετικής & Τεχνολογικής Κατεύθυνσης Β ΜΕΡΟΣ (ΑΝΑΛΥΣΗ) ΚΕΦ 1 ο : Όριο Συνέχεια Συνάρτησης
 ΜΑΘΗΜΑΤΙΚΑ Θετικής & Τεχνολογικής Κατεύθυνσης Β ΜΕΡΟΣ (ΑΝΑΛΥΣΗ) ΚΕΦ ο : Όριο Συνέχεια Συνάρτησης Φυλλάδιο Φυλλάδι555 4 ο ο.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ
ΜΑΘΗΜΑΤΙΚΑ Θετικής & Τεχνολογικής Κατεύθυνσης Β ΜΕΡΟΣ (ΑΝΑΛΥΣΗ) ΚΕΦ ο : Όριο Συνέχεια Συνάρτησης Φυλλάδιο Φυλλάδι555 4 ο ο.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ
ΣΤΑΘΕΡΗ ΣΥΝΑΡΤΗΣΗ. Το Θεώρημα και το Πόρισμα ισχύουν σε διαστήματα και όχι σε ένωση διαστημάτων.
 ΣΤΑΘΕΡΗ ΣΥΝΑΡΤΗΣΗ Θεώρημα Αν μια συνάρτηση f είναι συνεχής σε ένα διάστημα Δ και ισχύει f () = 0 για κάθε εσωτερικό σημείο του Δ, τότε η f είναι σταθερή σ' όλο το διάστημα Δ. Πόρισμα Αν δύο συναρτήσεις
ΣΤΑΘΕΡΗ ΣΥΝΑΡΤΗΣΗ Θεώρημα Αν μια συνάρτηση f είναι συνεχής σε ένα διάστημα Δ και ισχύει f () = 0 για κάθε εσωτερικό σημείο του Δ, τότε η f είναι σταθερή σ' όλο το διάστημα Δ. Πόρισμα Αν δύο συναρτήσεις
APEIROSTIKOS LOGISMOS I
 APEIROSTIKOS LOGISMOS I ΟΛΟΗΜΕΡΟ ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΒΛΗΜΑΤΩΝ Λύσεις ασκήσεων φυλλαδίου 4. Άσκηση : Υπολογίστε, αν υπάρχουν, τα παρακάτω όρια. Αν χρειάζεται, υπολογίστε τα αντίστοιχα πλευρικά όρια. + 4 3 + +,
APEIROSTIKOS LOGISMOS I ΟΛΟΗΜΕΡΟ ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΒΛΗΜΑΤΩΝ Λύσεις ασκήσεων φυλλαδίου 4. Άσκηση : Υπολογίστε, αν υπάρχουν, τα παρακάτω όρια. Αν χρειάζεται, υπολογίστε τα αντίστοιχα πλευρικά όρια. + 4 3 + +,
x είναι f 1 f 0 f κ λ
 3 Ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ [Κεφάλαια, Μέρος Β' του σχολικού βιβλίου] ΘΕΜΑ Α.Βλέπε σχολικό βιβλίο, σελίδα 4.. Βλέπε σχολικό βιβλίο, σελίδα 88, 89. 3. α) ΣΩΣΤΟ, διότι αν η f παραγωγίσιμη στο χ
3 Ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ [Κεφάλαια, Μέρος Β' του σχολικού βιβλίου] ΘΕΜΑ Α.Βλέπε σχολικό βιβλίο, σελίδα 4.. Βλέπε σχολικό βιβλίο, σελίδα 88, 89. 3. α) ΣΩΣΤΟ, διότι αν η f παραγωγίσιμη στο χ
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο Λύσεις έβδομου φυλλαδίου ασκήσεων.
 Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 2018-19. Λύσεις έβδομου φυλλαδίου ασκήσεων. 1. Έχουν οι παρακάτω συναρτήσεις μέγιστη ή ελάχιστη τιμή στο διάστημα (0, 1); Στο διάστημα (, + ); Στο διάστημα [0,
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 2018-19. Λύσεις έβδομου φυλλαδίου ασκήσεων. 1. Έχουν οι παρακάτω συναρτήσεις μέγιστη ή ελάχιστη τιμή στο διάστημα (0, 1); Στο διάστημα (, + ); Στο διάστημα [0,
ΑΠΑΝΤΗΣΕΙΣ ΔΙΑΓΩΝΙΣΜΑΤΟΣ ΠΡΟΣΟΜΟΙΩΣΗΣ ΤΗΣ 2/11/2018
 ΑΠΑΝΤΗΣΕΙΣ ΔΙΑΓΩΝΙΣΜΑΤΟΣ ΠΡΟΣΟΜΟΙΩΣΗΣ ΤΗΣ 2/11/2018 1. i. Έστω = (, ) R. Αν 0 η συνάρτηση στο σημείο είναι συνεχής ως πηλίκο συνεχών. Αν = 0 θα εξετάσουμε αν lim h = 0 = 0. Αν h = (h, h ) έχουμε: lim h
ΑΠΑΝΤΗΣΕΙΣ ΔΙΑΓΩΝΙΣΜΑΤΟΣ ΠΡΟΣΟΜΟΙΩΣΗΣ ΤΗΣ 2/11/2018 1. i. Έστω = (, ) R. Αν 0 η συνάρτηση στο σημείο είναι συνεχής ως πηλίκο συνεχών. Αν = 0 θα εξετάσουμε αν lim h = 0 = 0. Αν h = (h, h ) έχουμε: lim h
Κεφάλαιο 4: Διαφορικός Λογισμός
 ΣΥΓΧΡΟΝΗ ΠΑΙΔΕΙΑ ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Κεφάλαιο 4: Διαφορικός Λογισμός Μονοτονία Συνάρτησης Tζουβάλης Αθανάσιος Κεφάλαιο 4: Διαφορικός Λογισμός Περιεχόμενα Μονοτονία συνάρτησης... Λυμένα παραδείγματα...
ΣΥΓΧΡΟΝΗ ΠΑΙΔΕΙΑ ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Κεφάλαιο 4: Διαφορικός Λογισμός Μονοτονία Συνάρτησης Tζουβάλης Αθανάσιος Κεφάλαιο 4: Διαφορικός Λογισμός Περιεχόμενα Μονοτονία συνάρτησης... Λυμένα παραδείγματα...
y 1 (x) f(x) W (y 1, y 2 )(x) dx,
 Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 07/1/017 Μέρος 1ο: Μη Ομογενείς Γραμμικές Διαφορικές Εξισώσεις Δεύτερης Τάξης Θεωρούμε τη γραμμική μή-ομογενή διαφορική εξίσωση y + p(x) y + q(x) y = f(x), x
Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 07/1/017 Μέρος 1ο: Μη Ομογενείς Γραμμικές Διαφορικές Εξισώσεις Δεύτερης Τάξης Θεωρούμε τη γραμμική μή-ομογενή διαφορική εξίσωση y + p(x) y + q(x) y = f(x), x
(β) Από την έκφραση (22) και την απαίτηση (20) βλέπουμε ότι η συνάρτηση Green υπάρχει αρκεί η ομογενής εξίσωση. ( L z) ( x) 0
 Τρόποι Κατασκευής Εάν οι ιδιοσυναρτήσεις του διαφορικού τελεστή L αποτελούν ένα ορθοκανονικό L ( ) ( ) (7) και πλήρες σύστημα συναρτήσεων ( ) m( ), m (8) και εάν τότε η εξίσωση Gree ( ) ( ) ( ) (9) z ()
Τρόποι Κατασκευής Εάν οι ιδιοσυναρτήσεις του διαφορικού τελεστή L αποτελούν ένα ορθοκανονικό L ( ) ( ) (7) και πλήρες σύστημα συναρτήσεων ( ) m( ), m (8) και εάν τότε η εξίσωση Gree ( ) ( ) ( ) (9) z ()
Μέϑοδοι Εφαρμοσμένων Μαϑηματιϰών (ΜΕΜ 274) Λύσεις Θεμάτων Εξέτασης Ιούνη 2019
 Μέϑοδοι Εφαρμοσμένων Μαϑηματιϰών ΜΕΜ 74 Λύσεις Θεμάτων Εξέτασης Ιούνη 9 Ζήτημα Α Α. Δείξτε ότι αν p, q πραγματιϰά πολυώνυμα ίδιου βαϑμού, τότε p q ϰαϑώς ±. Λύση. Αρϰεί να δείξουμε ότι για με αρϰετά μεγάλο
Μέϑοδοι Εφαρμοσμένων Μαϑηματιϰών ΜΕΜ 74 Λύσεις Θεμάτων Εξέτασης Ιούνη 9 Ζήτημα Α Α. Δείξτε ότι αν p, q πραγματιϰά πολυώνυμα ίδιου βαϑμού, τότε p q ϰαϑώς ±. Λύση. Αρϰεί να δείξουμε ότι για με αρϰετά μεγάλο
ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ. Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ. Καρτάλη 28 (με Δημητριάδος) Βόλος τηλ.
 ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ. Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ. Καρτάλη 8 (με Δημητριάδος) Βόλος τηλ. 4598 Κεφάλαιο ο Ολοκληρωτικός Λογισμός Ολοκληρωτικός Λογισμός Μεθοδολογία Λυμένα
ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ. Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ. Καρτάλη 8 (με Δημητριάδος) Βόλος τηλ. 4598 Κεφάλαιο ο Ολοκληρωτικός Λογισμός Ολοκληρωτικός Λογισμός Μεθοδολογία Λυμένα
Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι
 Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος. Δείξτε ότι ο V R εφοδιασμένος με τις ακόλουθες πράξεις (, a b) + (, d) ( a+, b+ d) και k ( ab, ) ( kakb,
Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος. Δείξτε ότι ο V R εφοδιασμένος με τις ακόλουθες πράξεις (, a b) + (, d) ( a+, b+ d) και k ( ab, ) ( kakb,
ΑΠΑΝΤΗΣΕΙΣ - ΥΠΟΔΕΙΞΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ
 ΑΠΑΝΤΗΣΕΙΣ - ΥΠΟΔΕΙΞΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ Κεφάλαιο ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ο ΜΕΡΟΣ Απαντήσεις στις ερωτήσεις του τύπου Σωστό-Λάθος. Σ 6. Λ 8. Λ. Σ 7. Σ 9. Λ 3. Λ 8. Λ 3. Σ 4. Σ 9. Σ 3. α Σ 5. Σ. Σ β Σ 6. Λ.
ΑΠΑΝΤΗΣΕΙΣ - ΥΠΟΔΕΙΞΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ Κεφάλαιο ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ο ΜΕΡΟΣ Απαντήσεις στις ερωτήσεις του τύπου Σωστό-Λάθος. Σ 6. Λ 8. Λ. Σ 7. Σ 9. Λ 3. Λ 8. Λ 3. Σ 4. Σ 9. Σ 3. α Σ 5. Σ. Σ β Σ 6. Λ.
Διαφορικές Εξισώσεις.
 Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 2015-16. Λύσεις του έβδομου φυλλαδίου ασκήσεων. 1. Λύστε την παρακάτω δ.ε. με τη δοσμένη αρχική συνθήκη. Σχεδιάστε τις χαρακτηριστικές καθώς και το γράφημα της λύσης
Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 2015-16. Λύσεις του έβδομου φυλλαδίου ασκήσεων. 1. Λύστε την παρακάτω δ.ε. με τη δοσμένη αρχική συνθήκη. Σχεδιάστε τις χαρακτηριστικές καθώς και το γράφημα της λύσης
2. Αν έχουμε μια συνάρτηση f η οποία είναι συνεχής σε ένα διάστημα Δ.
 Κατηγορία η Εύρεση μονοτονίας Τρόπος αντιμετώπισης:. Αν έχουμε μια συνάρτηση f η οποία είναι συνεχής σε ένα διάστημα Δ. Αν f( ) σε κάθε εσωτερικό σημείο του Δ, τότε η f είναι γνησίως αύξουσα σε όλο το
Κατηγορία η Εύρεση μονοτονίας Τρόπος αντιμετώπισης:. Αν έχουμε μια συνάρτηση f η οποία είναι συνεχής σε ένα διάστημα Δ. Αν f( ) σε κάθε εσωτερικό σημείο του Δ, τότε η f είναι γνησίως αύξουσα σε όλο το
- ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ
 ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ R - ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΣΤΟ ΑΠΕΙΡΟ - ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΑΚΟΛΟΥΘΙΑΣ [Κεφ..6: Μη Πεπερασμένο Όριο στο R - Κεφ..7: Όρια Συνάρτησης
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ R - ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΣΤΟ ΑΠΕΙΡΟ - ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΑΚΟΛΟΥΘΙΑΣ [Κεφ..6: Μη Πεπερασμένο Όριο στο R - Κεφ..7: Όρια Συνάρτησης
ΑΝΑΛΥΣΗ 2. Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ Μ. Παπαδημητράκης. 1 ΔΕΚΑΤΟ ΤΡΙΤΟ ΜΑΘΗΜΑ Χρησιμοποιούμε τα σύμβολα f και f() d για να συμβολίσουμε όλα μαζί τα αόριστα ολοκληρώματα της f σε ένα διάστημα I. Δηλαδή, γράφουμε f = f + c ή f() d =
ΑΝΑΛΥΣΗ Μ. Παπαδημητράκης. 1 ΔΕΚΑΤΟ ΤΡΙΤΟ ΜΑΘΗΜΑ Χρησιμοποιούμε τα σύμβολα f και f() d για να συμβολίσουμε όλα μαζί τα αόριστα ολοκληρώματα της f σε ένα διάστημα I. Δηλαδή, γράφουμε f = f + c ή f() d =
Θεώρημα Βolzano. Κατηγορία 1 η. 11.1 Δίνεται η συνάρτηση:
 Κατηγορία η Θεώρημα Βolzano Τρόπος αντιμετώπισης:. Όταν μας ζητούν να εξετάσουμε αν ισχύει το θεώρημα Bolzano για μια συνάρτηση f σε ένα διάστημα [, ] τότε: Εξετάζουμε την συνέχεια της f στο [, ] (αν η
Κατηγορία η Θεώρημα Βolzano Τρόπος αντιμετώπισης:. Όταν μας ζητούν να εξετάσουμε αν ισχύει το θεώρημα Bolzano για μια συνάρτηση f σε ένα διάστημα [, ] τότε: Εξετάζουμε την συνέχεια της f στο [, ] (αν η
ΘΕΩΡΙΑ: Έστω η οµογενής γραµµική διαφορική εξίσωση τάξης , (1)
 1 ΘΕΩΡΙΑ: Έστω η οµογενής γραµµική διαφορική εξίσωση τάξης (1) όπου οι συντελεστές είναι δοσµένες συνεχείς συναρτήσεις ορισµένες σ ένα ανοικτό διάστηµα. Ορισµός 1. Ορίζουµε τον διαφορικό τελεστή µέσω της
1 ΘΕΩΡΙΑ: Έστω η οµογενής γραµµική διαφορική εξίσωση τάξης (1) όπου οι συντελεστές είναι δοσµένες συνεχείς συναρτήσεις ορισµένες σ ένα ανοικτό διάστηµα. Ορισµός 1. Ορίζουµε τον διαφορικό τελεστή µέσω της
ΟΜΟΣΠΟΝΔΙΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑΔΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2018 A ΦΑΣΗ
 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ / ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ Ημερομηνία: Σάββατο 13 Ιανουαρίου 18 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΑΠΑΝΤΗΣΕΙΣ Α1. Απόδειξη
ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ / ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ Ημερομηνία: Σάββατο 13 Ιανουαρίου 18 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΑΠΑΝΤΗΣΕΙΣ Α1. Απόδειξη
ΥΠΑΡΚΤΕΣ ΚΑΙ ΑΝΥΠΑΡΚΤΕΣ ΣΥΝΑΡΤΗΣΕΙΣ
 ΥΠΑΡΚΤΕΣ ΚΑΙ ΑΝΥΠΑΡΚΤΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Νίκος Ιωσηφίδης, Μαθηματικός Φροντιστής, Βέροια e-mail: iossifid@ahoo.gr Στην εισήγηση αυτή δείχνουμε πως αποδεικνύουμε ότι υπάρχει ή δεν υπάρχει συνάρτηση με δοσμένες
ΥΠΑΡΚΤΕΣ ΚΑΙ ΑΝΥΠΑΡΚΤΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Νίκος Ιωσηφίδης, Μαθηματικός Φροντιστής, Βέροια e-mail: iossifid@ahoo.gr Στην εισήγηση αυτή δείχνουμε πως αποδεικνύουμε ότι υπάρχει ή δεν υπάρχει συνάρτηση με δοσμένες
ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΕΙΑ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ
 ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΕΙΑ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ.Καρτάλη 8 Βόλος Τηλ. 43598 ΠΊΝΑΚΑΣ ΠΕΡΙΕΧΟΜΈΝΩΝ 3. Η ΕΝΝΟΙΑ ΤΗΣ ΠΑΡΑΓΩΓΟΥ... 5 ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ...
ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΕΙΑ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ.Καρτάλη 8 Βόλος Τηλ. 43598 ΠΊΝΑΚΑΣ ΠΕΡΙΕΧΟΜΈΝΩΝ 3. Η ΕΝΝΟΙΑ ΤΗΣ ΠΑΡΑΓΩΓΟΥ... 5 ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ...
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο Λύσεις τέταρτου φυλλαδίου ασκήσεων. ( n(n+1) e 1 (
 . Αποδείξτε ότι: Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 08-9. Λύσεις τέταρτου φυλλαδίου ασκήσεων. +) 7 +) +), 5 +7 5 5, +log ) 7 log 4, +, ++ + + ) +4+4 + +4, + si +, +) +), + [ ], + + 0, + +, ) +,,
. Αποδείξτε ότι: Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 08-9. Λύσεις τέταρτου φυλλαδίου ασκήσεων. +) 7 +) +), 5 +7 5 5, +log ) 7 log 4, +, ++ + + ) +4+4 + +4, + si +, +) +), + [ ], + + 0, + +, ) +,,
ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β. Να μελετήσετε ως προς τη μονοτονία και τα ακρότατα τις παρακάτω συναρτήσεις: f (x) = 0 x(2ln x + 1) = 0 ln x = x = e x =
 ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 0: ΕΥΡΕΣΗ ΤΟΠΙΚΩΝ ΑΚΡΟΤΑΤΩΝ [Ενότητα Προσδιορισμός των Τοπικών Ακροτάτων - Θεώρημα Εύρεση Τοπικών Ακροτάτων του κεφ..7 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ
ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 0: ΕΥΡΕΣΗ ΤΟΠΙΚΩΝ ΑΚΡΟΤΑΤΩΝ [Ενότητα Προσδιορισμός των Τοπικών Ακροτάτων - Θεώρημα Εύρεση Τοπικών Ακροτάτων του κεφ..7 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ
ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 5: ΘΕΩΡΗΜΑ ROLLE [Θεώρημα Rolle του κεφ.2.5 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ
![ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 5: ΘΕΩΡΗΜΑ ROLLE [Θεώρημα Rolle του κεφ.2.5 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 5: ΘΕΩΡΗΜΑ ROLLE [Θεώρημα Rolle του κεφ.2.5 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ](/thumbs/60/44973374.jpg) ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 5: ΘΕΩΡΗΜΑ ROLLE [Θεώρημα Rolle του κεφ..5 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β Παράδειγμα. Να εξετάσετε από τις παρακάτω συναρτήσεις ποιές ικανοποιούν
ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 5: ΘΕΩΡΗΜΑ ROLLE [Θεώρημα Rolle του κεφ..5 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β Παράδειγμα. Να εξετάσετε από τις παρακάτω συναρτήσεις ποιές ικανοποιούν
Για να εκφράσουμε τη διαδικασία αυτή, γράφουμε: :
 Η θεωρία στα μαθηματικά προσανατολισμού Γ υκείου Τι λέμε συνάρτηση με πεδίο ορισμού το σύνολο ; Έστω ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το μία διαδικασία (κανόνα), με την
Η θεωρία στα μαθηματικά προσανατολισμού Γ υκείου Τι λέμε συνάρτηση με πεδίο ορισμού το σύνολο ; Έστω ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το μία διαδικασία (κανόνα), με την
Μέϑοδοι Εφαρμοσμένων Μαϑηματιϰών (ΜΕΜ 274) Φυλλάδιο 2
 Μέϑοδοι Εφαρμοσμένων Μαϑηματιϰών (ΜΕΜ 274) Φυλλάδιο 2 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΕΝΝΟΙΑ ΤΗΣ ΑΣΥΜΠΤΩΤΙΚΗΣ ΣΕΙΡΑΣ Εστω μη ϰενά διαστήματα J, I R, με 0 Ī. Ονομάζουμε μεταβλητή το x J ϰαι ασυμπτωτιϰή (ή διαταραϰτιϰή) παράμετρο
Μέϑοδοι Εφαρμοσμένων Μαϑηματιϰών (ΜΕΜ 274) Φυλλάδιο 2 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΕΝΝΟΙΑ ΤΗΣ ΑΣΥΜΠΤΩΤΙΚΗΣ ΣΕΙΡΑΣ Εστω μη ϰενά διαστήματα J, I R, με 0 Ī. Ονομάζουμε μεταβλητή το x J ϰαι ασυμπτωτιϰή (ή διαταραϰτιϰή) παράμετρο
ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β. 2x 1. είναι Τότε έχουμε: » τον χρησιμοποιούμε κυρίως σε θεωρητικές ασκήσεις.
 ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ : ΣΥΝΑΡΤΗΣΗ - ΑΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗ [Υποκεφάλαιο. Μονότονες συναρτήσεις Αντίστροφη συνάρτηση του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα.
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ : ΣΥΝΑΡΤΗΣΗ - ΑΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗ [Υποκεφάλαιο. Μονότονες συναρτήσεις Αντίστροφη συνάρτηση του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα.
Ο ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE
 ΚΕΦΑΛΑΙΟ Ο ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ APACE ΚΑΙ ΟΙ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΣΤΗΝ ΕΠΙΛΥΣΗ ΓΡΑΜΜΙΚΩΝ ΔΙΑΦΟΡΙΚΩΝ KAI ΟΛΟΚΛΗΡΩΤΙΚΟ-ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΜΕ ΣΤΑΘΕΡΟΥΣ ΣΥΝΤΕΛΕΣΤΕΣ O μετασχηματισμός lc-ο αντίστροφος μετασχηματισμός
ΚΕΦΑΛΑΙΟ Ο ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ APACE ΚΑΙ ΟΙ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΣΤΗΝ ΕΠΙΛΥΣΗ ΓΡΑΜΜΙΚΩΝ ΔΙΑΦΟΡΙΚΩΝ KAI ΟΛΟΚΛΗΡΩΤΙΚΟ-ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΜΕ ΣΤΑΘΕΡΟΥΣ ΣΥΝΤΕΛΕΣΤΕΣ O μετασχηματισμός lc-ο αντίστροφος μετασχηματισμός
ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 10: ΕΥΡΕΣΗ ΤΟΠΙΚΩΝ ΑΚΡΟΤΑΤΩΝ
 ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 1: ΕΥΡΕΣΗ ΤΟΠΙΚΩΝ ΑΚΡΟΤΑΤΩΝ [Ενότητα Προσδιορισμός των Τοπικών Ακροτάτων - Θεώρημα Εύρεση Τοπικών Ακροτάτων του κεφ27 Μέρος Β του σχολικού βιβλίου] ΣΗΜΕΙΩΣΕΙΣ Εύρεση
ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 1: ΕΥΡΕΣΗ ΤΟΠΙΚΩΝ ΑΚΡΟΤΑΤΩΝ [Ενότητα Προσδιορισμός των Τοπικών Ακροτάτων - Θεώρημα Εύρεση Τοπικών Ακροτάτων του κεφ27 Μέρος Β του σχολικού βιβλίου] ΣΗΜΕΙΩΣΕΙΣ Εύρεση
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 8: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ [Ενότητα Μονοτονία Συνάρτησης του κεφ.2.6 Μέρος Β του σχολικού βιβλίου].
![ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 8: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ [Ενότητα Μονοτονία Συνάρτησης του κεφ.2.6 Μέρος Β του σχολικού βιβλίου]. ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 8: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ [Ενότητα Μονοτονία Συνάρτησης του κεφ.2.6 Μέρος Β του σχολικού βιβλίου].](/thumbs/52/29746903.jpg) ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 8: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ [Ενότητα Μονοτονία Συνάρτησης του κεφ..6 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα 1. ΘΕΜΑ Β Να μελετηθούν ως προς την μονοτονία
ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 8: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ [Ενότητα Μονοτονία Συνάρτησης του κεφ..6 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα 1. ΘΕΜΑ Β Να μελετηθούν ως προς την μονοτονία
f (x) = l R, τότε f (x 0 ) = l.
 Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο 5: Παράγωγος Α Οµάδα 1. Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς (αιτιολογήστε πλήρως την απάντησή σας). (α) Αν η f είναι παραγωγίσιµη
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο 5: Παράγωγος Α Οµάδα 1. Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς (αιτιολογήστε πλήρως την απάντησή σας). (α) Αν η f είναι παραγωγίσιµη
35 Χρήσιμες Προτάσεις με αποδείξεις Γ Λυκείου Μαθηματικά Κατεύθυνσης
 4 5 35 Χρήσιμες Προτάσεις με αποδείξεις Γ Λυκείου Μαθηματικά Κατεύθυνσης Περίληψη: Στο ένθετο αυτό περιλαμβάνονται 35 βασικές προτάσεις, μικρά λήμματα χρήσιμα για τις εξετάσεις. Μας βοηθούν να «ξεκλειδώνουμε»
4 5 35 Χρήσιμες Προτάσεις με αποδείξεις Γ Λυκείου Μαθηματικά Κατεύθυνσης Περίληψη: Στο ένθετο αυτό περιλαμβάνονται 35 βασικές προτάσεις, μικρά λήμματα χρήσιμα για τις εξετάσεις. Μας βοηθούν να «ξεκλειδώνουμε»
ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 10: ΕΥΡΕΣΗ ΤΟΠΙΚΩΝ ΑΚΡΟΤΑΤΩΝ
 ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ : ΕΥΡΕΣΗ ΤΟΠΙΚΩΝ ΑΚΡΟΤΑΤΩΝ [Ενότητα Προσδιορισμός των Τοπικών Ακροτάτων - Θεώρημα Εύρεση Τοπικών Ακροτάτων του κεφ..7 Μέρος Β του σχολικού βιβλίου]. ΑΣΚΗΣΕΙΣ Άσκηση.
ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ : ΕΥΡΕΣΗ ΤΟΠΙΚΩΝ ΑΚΡΟΤΑΤΩΝ [Ενότητα Προσδιορισμός των Τοπικών Ακροτάτων - Θεώρημα Εύρεση Τοπικών Ακροτάτων του κεφ..7 Μέρος Β του σχολικού βιβλίου]. ΑΣΚΗΣΕΙΣ Άσκηση.
ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β. Να βρείτε τις ασύμπτωτες της γραφικής παράστασης της συνάρτησης f με τύπο
 ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ : ΑΣΥΜΠΤΩΤΕΣ - ΚΑΝΟΝΕΣ DE L HOSPITAL - ΜΕΛΕΤΗ ΣΥΝΑΡΤΗΣΗΣ [Κεφ..9: Ασύμπτωτες Κανόνες de l Hospital Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα. ΘΕΜΑ
ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ : ΑΣΥΜΠΤΩΤΕΣ - ΚΑΝΟΝΕΣ DE L HOSPITAL - ΜΕΛΕΤΗ ΣΥΝΑΡΤΗΣΗΣ [Κεφ..9: Ασύμπτωτες Κανόνες de l Hospital Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα. ΘΕΜΑ
4.2 ΕΥΚΛΕΙΔΕΙΑ ΔΙΑΙΡΕΣΗ
 14 4 ΕΥΚΛΕΙΔΕΙΑ ΔΙΑΙΡΕΣΗ Ας υποθέσουμε ότι θέλουμε να βρούμε το πηλίκο και το υπόλοιπο της διαίρεσης του με τον Σύμφωνα με το γνωστό αλγόριθμο της διαίρεσης, το πηλίκο θα είναι ένας ακέραιος κ, τέτοιος,
14 4 ΕΥΚΛΕΙΔΕΙΑ ΔΙΑΙΡΕΣΗ Ας υποθέσουμε ότι θέλουμε να βρούμε το πηλίκο και το υπόλοιπο της διαίρεσης του με τον Σύμφωνα με το γνωστό αλγόριθμο της διαίρεσης, το πηλίκο θα είναι ένας ακέραιος κ, τέτοιος,
ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΓΕΝΙΚΑ ΜΑΘΗΜΑΤΙΚΑ. Τμήμα Φαρμακευτικής ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ. Λυμένες Ασκήσεις & Λυμένα Θέματα Εξετάσεων
 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΓΕΝΙΚΑ ΜΑΘΗΜΑΤΙΚΑ Τμήμα Φαρμακευτικής ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Λυμένες Ασκήσεις & Λυμένα Θέματα Εξετάσεων ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΙΑΝΟΥΑΡΙΟΥ 014 ΘΕΜΑ 1 Δίνεται ο πίνακας: 1) Να
ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΓΕΝΙΚΑ ΜΑΘΗΜΑΤΙΚΑ Τμήμα Φαρμακευτικής ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Λυμένες Ασκήσεις & Λυμένα Θέματα Εξετάσεων ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΙΑΝΟΥΑΡΙΟΥ 014 ΘΕΜΑ 1 Δίνεται ο πίνακας: 1) Να
ΣΗΜΕΙΩΣΕΙΣ. f (x) =, x 0, (1), x. lim f (x) = lim = +. x
 ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 2: ΑΣΥΜΠΤΩΤΕΣ - ΚΑΝΟΝΕΣ DE L HOSPITAL - ΜΕΛΕΤΗ ΣΥΝΑΡΤΗΣΗΣ [Κεφ. 2.9: Ασύμπτωτες Κανόνες de l Hospital Μέρος Β του σχολικού βιβλίου]. ΣΗΜΕΙΩΣΕΙΣ ΑΣΥΜΠΤΩΤΕΣ-ΚΑΝΟΝΑΣ
ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 2: ΑΣΥΜΠΤΩΤΕΣ - ΚΑΝΟΝΕΣ DE L HOSPITAL - ΜΕΛΕΤΗ ΣΥΝΑΡΤΗΣΗΣ [Κεφ. 2.9: Ασύμπτωτες Κανόνες de l Hospital Μέρος Β του σχολικού βιβλίου]. ΣΗΜΕΙΩΣΕΙΣ ΑΣΥΜΠΤΩΤΕΣ-ΚΑΝΟΝΑΣ
2.8 ΚΥΡΤΟΤΗΤΑ ΣΗΜΕΙΑ ΚΑΜΠΗΣ ΣΥΝΑΡΤΗΣΗΣ
 Ο ΚΕΦΑΛΑΙΟ : ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ 8 ΚΥΡΤΟΤΗΤΑ ΣΗΜΕΙΑ ΚΑΜΠΗΣ ΣΥΝΑΡΤΗΣΗΣ 49 ΟΡΙΣΜΟΣ 6 4 Πότε μια συνάρτηση λέγεται κυρτή και πότε κοίλη σε ένα διάστημα Δ ; Απάντηση : Έστω μία συνάρτηση σ υ ν ε χ ή ς σ ένα
Ο ΚΕΦΑΛΑΙΟ : ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ 8 ΚΥΡΤΟΤΗΤΑ ΣΗΜΕΙΑ ΚΑΜΠΗΣ ΣΥΝΑΡΤΗΣΗΣ 49 ΟΡΙΣΜΟΣ 6 4 Πότε μια συνάρτηση λέγεται κυρτή και πότε κοίλη σε ένα διάστημα Δ ; Απάντηση : Έστω μία συνάρτηση σ υ ν ε χ ή ς σ ένα
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο Λύσεις δέκατου φυλλαδίου ασκήσεων. 2 x dx = 02 ( 2) 2
 Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 08-9. Λύσεις δέκατου φυλλαδίου ασκήσεων.. Υπολογίστε το x αν x < 0 4 fx) dx όταν fx) = αν 0 x 3/x αν < x 4 Λύση: Η f ταυτίζεται στο [, 0] με την συνεχή συνάρτηση
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 08-9. Λύσεις δέκατου φυλλαδίου ασκήσεων.. Υπολογίστε το x αν x < 0 4 fx) dx όταν fx) = αν 0 x 3/x αν < x 4 Λύση: Η f ταυτίζεται στο [, 0] με την συνεχή συνάρτηση
ΚΕΦΑΛΑΙΟ 3 ΤΟ ΔΙΩΝΥΜΙΚΟ ΘΕΩΡΗΜΑ
 ΚΕΦΑΛΑΙΟ 3 ΤΟ ΔΙΩΝΥΜΙΚΟ ΘΕΩΡΗΜΑ Εισαγωγή Οι αριθμοί που εκφράζουν το πλήθος των στοιχείων ανά αποτελούν ίσως τους πιο σημαντικούς αριθμούς της Συνδυαστικής και καλούνται διωνυμικοί συντελεστές διότι εμφανίζονται
ΚΕΦΑΛΑΙΟ 3 ΤΟ ΔΙΩΝΥΜΙΚΟ ΘΕΩΡΗΜΑ Εισαγωγή Οι αριθμοί που εκφράζουν το πλήθος των στοιχείων ανά αποτελούν ίσως τους πιο σημαντικούς αριθμούς της Συνδυαστικής και καλούνται διωνυμικοί συντελεστές διότι εμφανίζονται
ΑΝΑΛΥΣΗ 1 ΤΡΙΑΚΟΣΤΟ ΕΚΤΟ ΜΑΘΗΜΑ, Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ 1 ΤΡΙΑΚΟΣΤΟ ΕΚΤΟ ΜΑΘΗΜΑ, 14-1-14 Μ. Παπαδημητράκης. 1 Τις διάφορες απλές ιδιότητες των παραγώγων θα τις θεωρήσω γνωστές από πιο στοιχειώδη μαθήματα απειροστικού λογισμού και από το λύκειο. Τώρα
ΑΝΑΛΥΣΗ 1 ΤΡΙΑΚΟΣΤΟ ΕΚΤΟ ΜΑΘΗΜΑ, 14-1-14 Μ. Παπαδημητράκης. 1 Τις διάφορες απλές ιδιότητες των παραγώγων θα τις θεωρήσω γνωστές από πιο στοιχειώδη μαθήματα απειροστικού λογισμού και από το λύκειο. Τώρα
A. ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ
 8Α ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ A ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ Πότε μια συνάρτηση λέγεται συνεχής σε ένα σημείο του πεδίου ορισμού o της ; Απάντηση : ( ΟΜΟΓ, 6 ΟΜΟΓ, 9 Β, ΟΜΟΓ, 5 Έστω μια συνάρτηση και ένα σημείο του πεδίου
8Α ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ A ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ Πότε μια συνάρτηση λέγεται συνεχής σε ένα σημείο του πεδίου ορισμού o της ; Απάντηση : ( ΟΜΟΓ, 6 ΟΜΟΓ, 9 Β, ΟΜΟΓ, 5 Έστω μια συνάρτηση και ένα σημείο του πεδίου
13 Μονοτονία Ακρότατα συνάρτησης
 3 Μονοτονία Ακρότατα συνάρτησης Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Θεώρημα Αν μια συνάρτηση f είναι συνεχής σ ένα διάστημα Δ, τότε: Αν f ( ) > 0για κάθε εσωτερικό του Δ, η f είναι γνησίως αύξουσα στο Δ. Αν
3 Μονοτονία Ακρότατα συνάρτησης Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Θεώρημα Αν μια συνάρτηση f είναι συνεχής σ ένα διάστημα Δ, τότε: Αν f ( ) > 0για κάθε εσωτερικό του Δ, η f είναι γνησίως αύξουσα στο Δ. Αν
Γραμμική Διαφορική Εξίσωση 2 ου βαθμού
 //04 Γραμμική Διαφορική Εξίσωση ου βαθμού, με τη βοήθεια του αορίστου ολοκληρώματος, της χρήσιμης γραμμικής διαφορικής εξίσωσης πρώτου βαθμού af ( ) f ( ) cf ( ) g( ), ac,, σταθεροί πραγματικοί αριθμοί
//04 Γραμμική Διαφορική Εξίσωση ου βαθμού, με τη βοήθεια του αορίστου ολοκληρώματος, της χρήσιμης γραμμικής διαφορικής εξίσωσης πρώτου βαθμού af ( ) f ( ) cf ( ) g( ), ac,, σταθεροί πραγματικοί αριθμοί
Μαθηματική Εισαγωγή Συναρτήσεις
 Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς Καστοριά, Ιούλιος 14 A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας
Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς Καστοριά, Ιούλιος 14 A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας
ΑΣΥΜΠΤΩΤΕΣ ΓΡΑΦΙΚΗΣ ΠΑΡΑΣΤΑΣΗΣ ΣΥΝΑΡΤΗΣΗΣ
 ΑΣΥΜΠΤΩΤΕΣ ΓΡΑΦΙΚΗΣ ΠΑΡΑΣΤΑΣΗΣ ΣΥΝΑΡΤΗΣΗΣ Ορισμοί α) (Κατακόρυφη ασύμπτωτη) Αν ένα τουλάχιστον απ' τα όρια f(), o o λέγεται κατακόρυφη ασύμπτωτη της C f. f() είναι +, ή -, τότε η ευθεία o β) (Οριζόντια
ΑΣΥΜΠΤΩΤΕΣ ΓΡΑΦΙΚΗΣ ΠΑΡΑΣΤΑΣΗΣ ΣΥΝΑΡΤΗΣΗΣ Ορισμοί α) (Κατακόρυφη ασύμπτωτη) Αν ένα τουλάχιστον απ' τα όρια f(), o o λέγεται κατακόρυφη ασύμπτωτη της C f. f() είναι +, ή -, τότε η ευθεία o β) (Οριζόντια
Διαφορικές Εξισώσεις.
 Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 215-16. Λύσεις ενδέκατου φυλλαδίου ασκήσεων. 1. Λύστε το πρόβλημα συνοριακών συνθηκών u xx + u yy =, u(x, ) = u(x, π) =, u(, y) =, u(a, y) = sin 2y + 4 sin 5y, < x
Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 215-16. Λύσεις ενδέκατου φυλλαδίου ασκήσεων. 1. Λύστε το πρόβλημα συνοριακών συνθηκών u xx + u yy =, u(x, ) = u(x, π) =, u(, y) =, u(a, y) = sin 2y + 4 sin 5y, < x
A. ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ
 8Α ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ A ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ Πότε μια συνάρτηση λέγεται συνεχής σε ένα σημείο του πεδίου ορισμού o της ; Απάντηση : ( ΟΜΟΓ, 6 ΟΜΟΓ, 9 Β, ΟΜΟΓ, 5 Έστω μια συνάρτηση και ένα σημείο του πεδίου
8Α ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ A ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ Πότε μια συνάρτηση λέγεται συνεχής σε ένα σημείο του πεδίου ορισμού o της ; Απάντηση : ( ΟΜΟΓ, 6 ΟΜΟΓ, 9 Β, ΟΜΟΓ, 5 Έστω μια συνάρτηση και ένα σημείο του πεδίου
G L (x) =Ax + B, G R (x) =A x + B οπότε από τις συνοριακές συνθήκες έχουμε
 1 ÈÖ Ð Ñ Για να είναι εφαρμόσιμη η μέθοδος της συνάρτησης Green, θαπρέπειηομογενής εξίσωση Ly =+ Ο.Σ.Σ. να έχει ως μοναδική λύση τη μηδενική. α) Η ομογενής εξίσωση y =έχει λύση y = A + B, από τις δεδομένες
1 ÈÖ Ð Ñ Για να είναι εφαρμόσιμη η μέθοδος της συνάρτησης Green, θαπρέπειηομογενής εξίσωση Ly =+ Ο.Σ.Σ. να έχει ως μοναδική λύση τη μηδενική. α) Η ομογενής εξίσωση y =έχει λύση y = A + B, από τις δεδομένες
Μιχάλης Παπαδημητράκης. Μερικές Διαφορικές Εξισώσεις
 Μιχάλης Παπαδημητράκης Μερικές Διαφορικές Εξισώσεις Περιεχόμενα 1 Γενικά. 1 1.1 Μερικές διαφορικές εξισώσεις............................ 1 1.2 Διαφορικοί τελεστές................................. 2 1.3
Μιχάλης Παπαδημητράκης Μερικές Διαφορικές Εξισώσεις Περιεχόμενα 1 Γενικά. 1 1.1 Μερικές διαφορικές εξισώσεις............................ 1 1.2 Διαφορικοί τελεστές................................. 2 1.3
Λύσεις του διαγωνίσματος στις παραγώγους
 Λύσεις του διαγωνίσματος στις παραγώγους Θέμα ο Α Έστω ότι f ), για κάθε α, ), β) Επειδή η f είναι συνεχής στο θα είναι γνησίως αύξουσα σε κάθε ένα από τα διαστήματα α, ] και [, β) Επομένως, για ισχύει
Λύσεις του διαγωνίσματος στις παραγώγους Θέμα ο Α Έστω ότι f ), για κάθε α, ), β) Επειδή η f είναι συνεχής στο θα είναι γνησίως αύξουσα σε κάθε ένα από τα διαστήματα α, ] και [, β) Επομένως, για ισχύει
0x2 = 2. = = δηλαδή η f δεν. = 2. Άρα η συνάρτηση f δεν είναι συνεχής στο [0,3]. Συνεπώς δεν. x 2. lim f (x) = lim (2x 1) = 3 και x 2 x 2
![0x2 = 2. = = δηλαδή η f δεν. = 2. Άρα η συνάρτηση f δεν είναι συνεχής στο [0,3]. Συνεπώς δεν. x 2. lim f (x) = lim (2x 1) = 3 και x 2 x 2 0x2 = 2. = = δηλαδή η f δεν. = 2. Άρα η συνάρτηση f δεν είναι συνεχής στο [0,3]. Συνεπώς δεν. x 2. lim f (x) = lim (2x 1) = 3 και x 2 x 2](/thumbs/59/43483993.jpg) ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 8: ΘΕΩΡΗΜΑ BOLZANO - ΠΡΟΣΗΜΟ ΣΥΝΑΡΤΗΣΗΣ - ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ - ΘΕΩΡΗΜΑ ΜΕΓΙΣΤΗΣ ΚΑΙ ΕΛΑΧΙΣΤΗΣ ΤΙΜΗΣ - ΣΥΝΟΛΟ ΤΙΜΩΝ ΣΥΝΕΧΟΥΣ ΣΥΝΑΡΤΗΣΗΣ
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 8: ΘΕΩΡΗΜΑ BOLZANO - ΠΡΟΣΗΜΟ ΣΥΝΑΡΤΗΣΗΣ - ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ - ΘΕΩΡΗΜΑ ΜΕΓΙΣΤΗΣ ΚΑΙ ΕΛΑΧΙΣΤΗΣ ΤΙΜΗΣ - ΣΥΝΟΛΟ ΤΙΜΩΝ ΣΥΝΕΧΟΥΣ ΣΥΝΑΡΤΗΣΗΣ
ΑΝΑΛΥΣΗ 1 ΕΙΚΟΣΤΟ ΤΕΤΑΡΤΟ ΜΑΘΗΜΑ, Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ ΕΙΚΟΣΤΟ ΤΕΤΑΡΤΟ ΜΑΘΗΜΑ, 9--3 Μ. Παπαδημητράκης. Εκτός από το κριτήριο του Cauchy, όλα τα άλλα κριτήρια σύγκλισης μιας σειράς που είδαμε μέχρι τώρα (απόλυτης σύγκλισης, σύγκρισης δυο σειρών, λόγου,
ΑΝΑΛΥΣΗ ΕΙΚΟΣΤΟ ΤΕΤΑΡΤΟ ΜΑΘΗΜΑ, 9--3 Μ. Παπαδημητράκης. Εκτός από το κριτήριο του Cauchy, όλα τα άλλα κριτήρια σύγκλισης μιας σειράς που είδαμε μέχρι τώρα (απόλυτης σύγκλισης, σύγκρισης δυο σειρών, λόγου,
Ολοκλήρωμα πραγματικής συνάρτησης
 ΚΕΦΑΛΑΙΟ 7 Ολοκλήρωμα πραγματικής συνάρτησης Σύνοψη Το κεφάλαιο αυτό αποτελεί το «πέρασμα» από το Διαφορικό στον Ολοκληρωτικό Λογισμό Η θεμελιώδης έννοια, για το σκοπό αυτό, είναι η αντιπαράγωγος ή αόριστο
ΚΕΦΑΛΑΙΟ 7 Ολοκλήρωμα πραγματικής συνάρτησης Σύνοψη Το κεφάλαιο αυτό αποτελεί το «πέρασμα» από το Διαφορικό στον Ολοκληρωτικό Λογισμό Η θεμελιώδης έννοια, για το σκοπό αυτό, είναι η αντιπαράγωγος ή αόριστο
f x x, ν Ν-{0,1} είναι παραγωγίσιμη στο R
 ΟΕΦΕ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Θέμα Α Α Να αποδείξετε ότι η συνάρτηση ν ν και ισχύει f ν f, νν-{,} είναι παραγωγίσιμη στο R
ΟΕΦΕ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Θέμα Α Α Να αποδείξετε ότι η συνάρτηση ν ν και ισχύει f ν f, νν-{,} είναι παραγωγίσιμη στο R
ΑΝΑΛΥΣΗ 1 ΕΙΚΟΣΤΟ ΤΡΙΤΟ ΜΑΘΗΜΑ, Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ ΕΙΚΟΣΤΟ ΤΡΙΤΟ ΜΑΘΗΜΑ, 28--3 Μ. Παπαδημητράκης. ΚΡΙΤΗΡΙΟ ΑΠΟΛΥΤΗΣ ΣΥΓΚΛΙΣΗΣ. Αν η σειρά + = x συγκλίνει απολύτως, τότε συγκλίνει και + x x. = = Δεν θα παρουσιάσω την απόδειξη. Διαβάστε την στο βιβλίο.
ΑΝΑΛΥΣΗ ΕΙΚΟΣΤΟ ΤΡΙΤΟ ΜΑΘΗΜΑ, 28--3 Μ. Παπαδημητράκης. ΚΡΙΤΗΡΙΟ ΑΠΟΛΥΤΗΣ ΣΥΓΚΛΙΣΗΣ. Αν η σειρά + = x συγκλίνει απολύτως, τότε συγκλίνει και + x x. = = Δεν θα παρουσιάσω την απόδειξη. Διαβάστε την στο βιβλίο.
1. Υπολογίστε, όπου αυτές υπάρχουν, τις παραγώγους των συναρτήσεων:
 Υπολογίστε, όπου αυτές υπάρχουν, τις παραγώγους των συναρτήσεων:, g, h Απάντηση: Η με έχει παράγωγο 4 Μπορούμε όμως να εργαστούμε ως εξής: Είναι άρα 4 Η g με g έχει παράγωγο : g Η συνάρτηση h με h έχει
Υπολογίστε, όπου αυτές υπάρχουν, τις παραγώγους των συναρτήσεων:, g, h Απάντηση: Η με έχει παράγωγο 4 Μπορούμε όμως να εργαστούμε ως εξής: Είναι άρα 4 Η g με g έχει παράγωγο : g Η συνάρτηση h με h έχει
f ( x) f ( x ) για κάθε x A
 ΛΥΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗ ΘΕΜΑΤΩΝ 3 3/04/06 ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΜΑ ο Α. Τι ονομάζουμε ρυθμό μεταβολής του y = f() ως προς το στο σημείο 0 ;
ΛΥΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗ ΘΕΜΑΤΩΝ 3 3/04/06 ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΜΑ ο Α. Τι ονομάζουμε ρυθμό μεταβολής του y = f() ως προς το στο σημείο 0 ;
2η ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ
 ΑΠΟ 3//7 ΕΩΣ 5//8 η ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Παρασκευή 5 Ιανουαρίου 8 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑΤΑ ΘΕΜΑ Α Α. Αν μία συνάρτηση f είναι
ΑΠΟ 3//7 ΕΩΣ 5//8 η ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Παρασκευή 5 Ιανουαρίου 8 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑΤΑ ΘΕΜΑ Α Α. Αν μία συνάρτηση f είναι
IV. Συνέχεια Συνάρτησης. math-gr
 IV Συνέχεια Συνάρτησης mth-gr mth-gr Παντελής Μπουμπούλης, MSc, PhD σελ mth-grblogspotcom, bouboulismyschgr ΜΕΡΟΣ Συνέχεια Συνάρτησης Α Ορισμός Συνέχεια σε σημείο: Θα λέμε ότι μια συνάρτηση είναι συνεχής
IV Συνέχεια Συνάρτησης mth-gr mth-gr Παντελής Μπουμπούλης, MSc, PhD σελ mth-grblogspotcom, bouboulismyschgr ΜΕΡΟΣ Συνέχεια Συνάρτησης Α Ορισμός Συνέχεια σε σημείο: Θα λέμε ότι μια συνάρτηση είναι συνεχής
1 Σύντομη επανάληψη βασικών εννοιών
 Σύντομη επανάληψη βασικών εννοιών Μερικές χρήσιμες ταυτότητες + r + r 2 + + r n = rn r r + 2 + 3 + + n = 2 n(n + ) 2 + 2 2 + 3 2 + n 2 = n(n + )(2n + ) 6 Ανισότητα Cauchy Schwarz ( n ) 2 ( n x i y i i=
Σύντομη επανάληψη βασικών εννοιών Μερικές χρήσιμες ταυτότητες + r + r 2 + + r n = rn r r + 2 + 3 + + n = 2 n(n + ) 2 + 2 2 + 3 2 + n 2 = n(n + )(2n + ) 6 Ανισότητα Cauchy Schwarz ( n ) 2 ( n x i y i i=
ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΟΜΑΔΕΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ : ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΡΟΛΟΓΟΣ Σε κάθε ενότητα αυτού του βιβλίου θα βρείτε : Βασική θεωρία με τη μορφή ερωτήσεων Μεθοδολογίες και σχόλια
ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΟΜΑΔΕΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ : ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΡΟΛΟΓΟΣ Σε κάθε ενότητα αυτού του βιβλίου θα βρείτε : Βασική θεωρία με τη μορφή ερωτήσεων Μεθοδολογίες και σχόλια
Λύσεις των θεμάτων των Πανελλαδικών Εξετάσεων στα Μαθηματικά Προσανατολισμού 2016
 Λύσεις των θεμάτων των Πανελλαδικών Εξετάσεων στα Μαθηματικά Προσανατολισμού 16 ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ ΤΩΝ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ
Λύσεις των θεμάτων των Πανελλαδικών Εξετάσεων στα Μαθηματικά Προσανατολισμού 16 ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ ΤΩΝ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ - ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΩΡΙΑ & ΑΠΟΔΕΙΞΕΙΣ
 ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ - ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΩΡΙΑ & ΑΠΟΔΕΙΞΕΙΣ Επιμέλεια: Βασίλης Κράνιας wwwe-mathsgr ΑΝΑΛΥΣΗ Τι ονομάζουμε πραγματική συνάρτηση Έστω Α ένα υποσύνολο
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ - ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΩΡΙΑ & ΑΠΟΔΕΙΞΕΙΣ Επιμέλεια: Βασίλης Κράνιας wwwe-mathsgr ΑΝΑΛΥΣΗ Τι ονομάζουμε πραγματική συνάρτηση Έστω Α ένα υποσύνολο
ΘΕΜΑ Α A1 Να αποδείξετε το θεώρημα: Έστω μια συνάρτηση f, η οποία είναι ορισμένη σε ένα κλειστό διάστημα. τέτοιος ώστε: f x.
 ΔΙΑΓΩΝΙΣΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΕΞΕΤΑΣΕΩΝ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΕΤΑΡΤΗ 3 ΑΠΡΙΛΙΟΥ 6 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ & ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΣΥΝΟΛΟ
ΔΙΑΓΩΝΙΣΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΕΞΕΤΑΣΕΩΝ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΕΤΑΡΤΗ 3 ΑΠΡΙΛΙΟΥ 6 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ & ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΣΥΝΟΛΟ
Μεθοδική Επανα λήψή. Επιμέλεια Κων/νος Παπασταματίου. Θεωρία - Λεξιλόγιο Βασικές Μεθοδολογίες. Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ.
 Μεθοδική Επανα λήψή Θεωρία - Λεξιλόγιο Βασικές Μεθοδολογίες Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ. Καρτάλη 8 Βόλος Τηλ. 4 598 Επιμέλεια Κων/νος Παπασταματίου Περιεχόμενα Συνοπτική Θεωρία με Ερωτήσεις Απαντήσεις...
Μεθοδική Επανα λήψή Θεωρία - Λεξιλόγιο Βασικές Μεθοδολογίες Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ. Καρτάλη 8 Βόλος Τηλ. 4 598 Επιμέλεια Κων/νος Παπασταματίου Περιεχόμενα Συνοπτική Θεωρία με Ερωτήσεις Απαντήσεις...
Παραδείγματα (1 ο σετ) Διανυσματικοί Χώροι
 Παραδείγματα ( ο σετ) Διανυσματικοί Χώροι Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με y, V και του πολλαπλασιασμού:
Παραδείγματα ( ο σετ) Διανυσματικοί Χώροι Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με y, V και του πολλαπλασιασμού:
Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 09/11/2017. Άσκηση 1. Να βρεθεί η γενική λύση της διαφορικής εξίσωσης. dy dx = 2y + x 2 y 2 2x
 Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 09/11/017 Άσκηση 1. Να βρεθεί η γενική λύση της διαφορικής εξίσωσης dx y + x y. x Παρατηρούμε ότι η δ.ε. είναι ομογενής. Πράγματι, dx y x + 1 x y x y x + 1 (
Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 09/11/017 Άσκηση 1. Να βρεθεί η γενική λύση της διαφορικής εξίσωσης dx y + x y. x Παρατηρούμε ότι η δ.ε. είναι ομογενής. Πράγματι, dx y x + 1 x y x y x + 1 (
16 Ασύμπτωτες. όπως φαίνεται στα παρακάτω σχήματα. 1. Κατακόρυφη ασύμπτωτη. Η ευθεία x = x0
 6 Ασύμπτωτες Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ορίζουμε μια ευθεία ( ε ) ως ασύμπτωτη της γραφικής παράστασης της αν η απόσταση ενός μεταβλητού σημείου Ρ της γραφικής παράστασης από την ευθεία ( ε ) γίνεται
6 Ασύμπτωτες Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ορίζουμε μια ευθεία ( ε ) ως ασύμπτωτη της γραφικής παράστασης της αν η απόσταση ενός μεταβλητού σημείου Ρ της γραφικής παράστασης από την ευθεία ( ε ) γίνεται
Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος
 Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με, y V και του πολλαπλασιασμού
Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με, y V και του πολλαπλασιασμού
6 Εφαρµογές των παραγώγων στον υπολογισµό ορίων α- προσδιόριστων µορφών - Κανόνες L Hôpital
 6 Εφαρµογές των παραγώγων στον υπολογισµό ορίων α- προσδιόριστων µορφών - Κανόνες L Hôpital Στην ενότητα αυτή ϑα µελετήσουµε εφαρµογές των παραγώγων συναρτήσεων στον υπολογισµό απροσδιόριστων µορφών ορίων
6 Εφαρµογές των παραγώγων στον υπολογισµό ορίων α- προσδιόριστων µορφών - Κανόνες L Hôpital Στην ενότητα αυτή ϑα µελετήσουµε εφαρµογές των παραγώγων συναρτήσεων στον υπολογισµό απροσδιόριστων µορφών ορίων
[ α π ο δ ε ί ξ ε ι ς ]
![[ α π ο δ ε ί ξ ε ι ς ] [ α π ο δ ε ί ξ ε ι ς ]](/thumbs/78/78384597.jpg) Γ' Λυκείου Κατεύθυνση [ α π ο δ ε ί ξ ε ι ς ] ε ξ ε τ α σ τ έ α ς ύ λ η ς 7-8 Επιμέλεια Κόλλας Αντώνης Όριο πολυωνυμικής στο Αν P( = αν ν + αν ν +... + α + α είναι πολυώνυμο του και, τότε: P( P( P( =...
Γ' Λυκείου Κατεύθυνση [ α π ο δ ε ί ξ ε ι ς ] ε ξ ε τ α σ τ έ α ς ύ λ η ς 7-8 Επιμέλεια Κόλλας Αντώνης Όριο πολυωνυμικής στο Αν P( = αν ν + αν ν +... + α + α είναι πολυώνυμο του και, τότε: P( P( P( =...
ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 6: ΘΕΩΡΗΜΑ ΜΕΣΗΣ ΤΙΜΗΣ ΔΙΑΦΟΡΙΚΟΥ ΛΟΓΙΣΜΟΥ (Θ.Μ.Τ.)
 ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 6: ΘΕΩΡΗΜΑ ΜΕΣΗΣ ΤΙΜΗΣ ΔΙΑΦΟΡΙΚΟΥ ΛΟΓΙΣΜΟΥ (Θ.Μ.Τ.) [Θεώρημα Μέσης Τιμής Διαφορικού Λογισμού του κεφ..5 Μέρος Β του σχολικού βιβλίου]. ΑΣΚΗΣΕΙΣ Άσκηση. ΘΕΜΑ Β Δίνεται
ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 6: ΘΕΩΡΗΜΑ ΜΕΣΗΣ ΤΙΜΗΣ ΔΙΑΦΟΡΙΚΟΥ ΛΟΓΙΣΜΟΥ (Θ.Μ.Τ.) [Θεώρημα Μέσης Τιμής Διαφορικού Λογισμού του κεφ..5 Μέρος Β του σχολικού βιβλίου]. ΑΣΚΗΣΕΙΣ Άσκηση. ΘΕΜΑ Β Δίνεται
Μαθηματική Εισαγωγή Συναρτήσεις
 Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας Διανύσματα Καστοριά,
Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας Διανύσματα Καστοριά,
Η ΜΕΘΟΔΕΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ
 Σελίδα 1 από 34 Η ΜΕΘΟΔΕΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ Μπάμπης Στεργίου 017 Εισαγωγή Οι εξισώσεις, η λύση τους, η εύρεση του πλήθους ριζών τους ή τα ερωτήματα που αφορούν στην ύπαρξη ριζών, αποτελούν ένα σημαντικό
Σελίδα 1 από 34 Η ΜΕΘΟΔΕΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ Μπάμπης Στεργίου 017 Εισαγωγή Οι εξισώσεις, η λύση τους, η εύρεση του πλήθους ριζών τους ή τα ερωτήματα που αφορούν στην ύπαρξη ριζών, αποτελούν ένα σημαντικό
OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ
 Ο ΚΕΦΑΛΑΙΟ : ΟΡΙΟ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΣΥΝΑΡΤΗΣΕΙΣ Έστω Α ένα υποσύνολο του Τι ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α ; Απάντηση : ΕΣΠ Β Έστω
Ο ΚΕΦΑΛΑΙΟ : ΟΡΙΟ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΣΥΝΑΡΤΗΣΕΙΣ Έστω Α ένα υποσύνολο του Τι ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α ; Απάντηση : ΕΣΠ Β Έστω
Μερικές Διαφορικές Εξισώσεις
 Πανεπιστήμιο Πατρών, Τμήμα Μαθηματικών Μερικές Διαφορικές Εξισώσεις Χειμερινό εξάμηνο ακαδημαϊκού έτους 24-25, Διδάσκων: Α.Τόγκας ο φύλλο προβλημάτων Ονοματεπώνυμο - ΑΜ: ΜΔΕ ο φύλλο προβλημάτων Α. Τόγκας
Πανεπιστήμιο Πατρών, Τμήμα Μαθηματικών Μερικές Διαφορικές Εξισώσεις Χειμερινό εξάμηνο ακαδημαϊκού έτους 24-25, Διδάσκων: Α.Τόγκας ο φύλλο προβλημάτων Ονοματεπώνυμο - ΑΜ: ΜΔΕ ο φύλλο προβλημάτων Α. Τόγκας
