2.1 Περιοδικές συναρτήσεις και τριγωνομετρικά αναπτύγματα
|
|
|
- Νέμεσις Αβραμίδης
- 4 χρόνια πριν
- Προβολές:
Transcript
1 Σειρές Fourier. Σειρές Fourier. Περιοδικές συναρτήσεις και τριγωνομετρικά αναπτύγματα Μία συνάρτηση f() είναι περιοδική με περίοδο όταν ισχύει f(+)=f(). Η ελάχιστη δυνατή περίοδος λέγεται και θεμελιώδης περίοδος. Εμείς όταν λέμε περίοδο θα αναφερόμαστε σε αυτήν. Μία συνηθισμένη περιοδική συνάρτηση είναι η y=a si(ω) όπου το ω ονομάζεται (γωνιακή ή κυκλική) συχνότητα και το Α είναι το πλάτος. Στο παρακάτω σχήμα παρατηρούμε ότι για την συνάρτηση si(ω) όσο το ω μεγαλώνει τόσο μικραίνει η περίοδος της συνάρτησης η οποία ισούται με Τ=π/ω. f ( ) si( ), g( ) si( ), h( ) si(3 ).5 si( ) si( ) si(3 ) Επίσης για την συνάρτηση y=a si() η οποία έχει πεδίο τιμών [Α,-Α] όσο το Α (θετικό) μεγαλώνει τόσο το πλάτος της ταλάντωσης μεγαλώνει.
2 si( ) si( ) Η γραφική παράσταση της συνάρτησης si( ) είναι η γραφική παράσταση της si( ) μετατοπισμένη κατά θ (αριστερά εάν το θ είναι αρνητικό, δεξιά σε αντίθετη περίπτωση). Το θ ονομάζεται φάση..5 3 si( ) si( ) Ανάλογη είναι και η συμπεριφορά της συνάρτησης συνημίτονο. Ο Je Bptiste Fourier (768-83) απόδειξε ότι κάθε περιοδική y=f(χ) συνάρτηση μπορεί να γραφεί ως ένα άπειρο άθροισμα ημιτονοειδών συναρτήσεων της μορφής: f ( ) A A si( ) A si( )... A si( )... A A si( ) και τελικά να προσεγγιστεί από ένα πεπερασμένο f ( ) A A si( ) A si( )... A si( ) Αυτή είναι η βάση των σειρών Fourier. Ο όρος A si( ) ονομάζεται πρώτη αρμονική, ο A si( ) δεύτερη αρμονική κ.λ.π. Παράδειγμα: Έστω για [, ] y si( ) si(3 ) si(5 ) 3 5
3 Σειρές Fourier Οι τρεις αρμονικές ξεχωριστά είναι Αν πάρω τους δύο πρώτους όρους του αθροίσματος έχω το γράφημα: Αν πάρω και τους τρεις όρους του αθροίσματος έχω το γράφημα: Είναι φανερό ότι προσθέτοντας και άλλους παρόμοιους όρους το γράφημα μοιάζει όλο και περισσότερο με ένα σήμα. Επίσης όταν y si( ) si(3 ).3 si( ) το γράφημα στο διάστημα [,π] είναι το ακόλουθο: 3
4 Αποκόπτοντας το τελευταίο όρο δηλαδή όταν y si( ) si(3 ) παίρνουμε Όπου μοιάζει η αποκοπή αυτού του όρου να λειτούργησε ως φίλτρο. Τέτοια αναπτύγματα συναρτήσεων σε τριγωνομετρικά αθροίσματα βρίσκουν πολλές εφαρμογές. Για παράδειγμα, μπορούν να χρησιμοποιηθούν για το φιλτράρισμα θορύβου στην ανάλυση σημάτων. Επίσης στις τηλεπικοινωνίες βρίσκουν εφαρμογή στη μεταφορά του συνεχούς σήματος της φωνής μέσω δορυφόρου από ένα σημείο του πλανήτη σε ένα άλλο. Η μεταφορά του συνεχούς σήματος της φωνής, αφού ψηφιοποιηθεί, και η αποστολή του bit προς bit απαιτεί την επεξεργασία και μεταφορά μεγάλου όγκου δεδομένων. Εάν το σήμα αναπτυχθεί σε ένα τριγωνομετρικό άθροισμα, αρκεί να μεταφερθούν μόνο οι συντελεστές (φάσεις, συχνότητες και πλάτη) και στον προορισμό να εφαρμοστεί ο κατάλληλος τύπος ώστε να αναπαραχθεί το σήμα. Μία τέτοια διαδικασία είναι πολύ πιο οικονομική. Από τη σχέση f( ) A A si( ) χρησιμοποιώντας την τριγωνομετρική ταυτότητα si( b) si( )cos( b) cos( )si( b ) έχουμε ότι f( ) A A si( )cos( ) cos( )si( )
5 Θέτοντας A και Σειρές Fourier f ( ) [ cos( ) b si( )] A si( ), b A cos( ) και ω =π/ Τ φθάνουμε στον τύπο f ( ) [ cos( ) b si( )] Μπορεί να αποδειχθεί ότι ισχύει : ή όπου b. f ( ) f ( )cos( ) b f ( )si( ) και οι σχέσεις που συνδέουν τους συντελεστές είναι A b, rct b. Παρατήρηση Ανάλογα κάθε περιοδική συνάρτηση μπορεί να γραφεί ως ένα άπειρο άθροισμα συνημιτονοειδών συναρτήσεων. Από τη σχέση f ( ) A A cos( ) A cos( )... A cos( )... A A cos( ) χρησιμοποιώντας την τριγωνομετρική ταυτότητα cos( b) cos( )cos( b) si( )si( b) Έχουμε ότι f( ) A A cos( )cos( ) si( )si( ) Θέτοντας A και cos( ), si( ) Φθάνουμε στον τύπο A b A και ω =π/ Τ f ( ) [ cos( ) b si( )] και οι σχέσεις που συνδέουν τους συντελεστές είναι b A b, rct. 5
6 Θα πρέπει να σημειώσουμε ότι οι γωνίες φάσεων μεταξύ του ημιτονοειδούς αναπτύγματος και του συνημιτονοειδούς αναπτύγματος διαφέρουν κατά π/. Δηλαδή.. Σύγκλιση σειράς Fourier Η σύγκλιση της σειράς Fourier επιτυγχάνεται στα σημεία που είναι συνεχής μία περιοδική συνάρτηση f() εάν ισχύουν οι συνθήκες Dirichlet :. Η f() είναι απόλυτα ολοκληρώσιμη σε μία περίοδο, δηλαδή ισχύει f ( ). Ο αριθμός των μεγίστων και ελαχίστων του f() είναι πεπερασμένος στο διάστημα της περιόδου. 3. Η f() είναι τμηματικά συνεχής με πεπερασμένο αριθμό ασυνέχειας στο διάστημα της περιόδου. Τέλος, στα σημεία ασυνέχειας η σειρά Fourier συγκλίνει στο ημιάθροισμα των πλευρικών ορίων f ( ) f ( ). Παρατήρηση Εάν μας ζητείται στην εκφώνηση να αναπτύξουμε σε σειρά Fourier τη συνάρτηση και όχι απλά να βρούμε τη σειρά Fourier της συνάρτησης θα πρέπει να βρούμε στα σημεία ασυνέχειας το που συγκλίνει η σειρά. Αναπτύσσοντας τη σειρά Fourier σε όλα τα σημεία που είναι η σειρά συνεχής και βρίσκοντας που συγκλίνει στα σημεία ασυνέχειας, μπορούμε να πούμε ότι η σειρά Fourier παριστάνει τη συνάρτηση στο διάστημα της περιοδικότητας της. Εξαιτίας της περιοδικότητας της συνάρτησης η σειρά την παριστάνει σε όλο το..3 Χρήσιμοι τύποι στον υπολογισμό των σειρών Fourier Οι άρτιοι αριθμοί περιγράφονται από τη σχέση: =k όταν κ=,,3,... οι περιττοί από τη σχέση =k+ όταν k=,,,3,... ή =k- όταν κ=,,3,,... 6
7 Σειρές Fourier k ( ) k όταν κ=,,,3,... ή k ( ) k όταν κ=,,3,... Χρήσιμοι τύποι: cos( ) ( ), si( ). Αν, k k τότε si( ) si( k ). Αν k, k τότε k si( ) si( k ) ( ) ( ) οπότε si( ) ( ),, Επίσης cos( ) = k + = k + = k + 3 = k + Από την τριγωνομετρία γνωρίζουμε ότι Επίσης ισχύουν: si( ) si( ) και cos( ) cos( ). si( ) ' cos( ), cos( ) ' si( ) και e ' e. Ο τύπος της παραγοντικής ολοκλήρωσης είναι ' ' f g f g f g. Με χρήση των παραπάνω τύπων μπορούμε να υπολογίσουμε τα ολοκληρώματα: si( ) cos c cos( ) si c si ' si cos si si si cos c cos ' si cos 7
8 cos cos si cos c e e c ' ' ' e e e e e e e e e e ' c. Λυμένα παραδείγματα Παράδειγμα Αναπτύξτε σε σειρά Fourier στο διάστημα [, ) την περιοδική συνάρτηση με γραφική παράσταση: Από το σχήμα γίνεται φανερό ότι η υπό μελέτη συνάρτηση στο διάστημα [,) είναι σταθερά ίση με μηδέν, ενώ στο [, ) ο τύπος της είναι f()=, ώστε η γραφική της παράσταση να είναι το ευθύγραμμο τμήμα με αρχή το σημείο (,) και πέρας το σημείο (π,π). Άρα ο γενικός τύπος της θα είναι:, - f ( ), f ( ) f ( ), Χρησιμοποιώντας τους τύπους Τ=π και διάστημα ολοκλήρωσης αυτό της περιόδου [, ), έχουμε το ανάπτυγμα Fourier της f() ως εξής: όπου: ( cos( ) si( )), f ( ) ( ) ( ). 8
9 Σειρές Fourier f ( ) cos( ) ( cos( ) cos( ) ) si( ) si( ) si( ) ( ( ) ) ( ) si( ) cos( ) ( si( ) ) ( (cos( ) cos()) (( ) ) Η τελευταία σχέση μπορεί να αναλυθεί περαιτέρω αν λάβουμε υπόψη μας ότι ) ( ), αν =k, αν =k-, ως εξής:, αν =k, αν =k- (k ), k=,,3,. Ανάλογα υπολογίζουμε ότι: b f ( ) si( ) ( si( ) si( ) ) cos( ) cos( ) cos( ) ( ( ) ) ( ) cos( ) ( ) si( ) ( cos( ) ) ( ) ( ) ( ) ( ). Οι πρώτοι όροι των συντελεστών δίνονται στο παρακάτω πίνακα: b Το ζητούμενο ανάπτυγμα Fourier της f( ) είναι: ( ) ( cos((k ) )) ( si( )) k (k ) cos( ) cos(3 ) cos(5 ) si( ) si( ) si(3 ) si( ) si(5 ) si(6 )
10 Για το σημείο ασυνέχειας της συνάρτησης ισχύει ότι f ( ) ( f( ) f( )) ( ) οπότε η σειρά που υπολογίσαμε παριστάνει την f ( ),, στο διάστημα περιοδικότητας της. Οπότε λόγω της περιοδικότητας η σειρά παριστάνει την f σε όλο το. Δηλαδή, f ( ) cos( ) cos(3 ) cos(5 ) si( ) si( ) si(3 ) si( ) si(5 ) si(6 ) Παράδειγμα Αναπτύξτε τη σειρά Fourier της συνάρτησης, - f ( ), f( ) f( ), Η γραφική παράσταση της συνάρτησης είναι: Γνωρίζουμε ότι το ανάπτυγμα Fourier της f( ) είναι: ( cos( ) b si( )) Στην περίπτωση μας Τ=π και διάστημα ολοκλήρωσης αυτό της περιόδου [, ), οπότε f ( ) και
11 Σειρές Fourier f ( )cos( ) cos( ) cos( ) = si( ) d(si( )) [ si( )] si( ) = cos( ) [ si( ) si( )] [cos( )] ( ) [cos( ) ] ' Δηλαδή Επίσης αν =k, k=,,3,.. αν =k- (k ) b f ( )si( ) si( ) si( ) cos( ) si( ) cos( ) cos( ) ' cos( ) cos( ) ' cos( ) cos( ) ' cos( ) cos( ) cos( ) cos( ) cos( ) cos( ) si( ) ( ) ( ) cos( ) cos( ) Δηλαδή b k k, k=,,3,.. k (k )
12 Συνοψίζοντας έχουμε ότι και οι πρώτοι έξι συντελεστές, b δίνονται στον παρακάτω πίνακα: b Για το σημείο ασυνέχειας της συνάρτησης ισχύει ότι f ( ) ( f( ) f ( )) ( ) και για το σημείο ασυνέχειας της συνάρτησης ισχύει ότι f () ( f( ) f ( )) ( ) οπότε η σειρά που υπολογίσαμε παριστάνει την f ( ), στο, διάστημα περιοδικότητας της. Οπότε λόγω της περιοδικότητας η σειρά παριστάνει την f σε όλο το. Δηλαδή f ( ) cos( ) cos(3 ) cos(5 ) si( ) si( ) si(3 ) si( ) si(5 ) si(6 ) Παράδειγμα Αναπτύξτε σε σειρά Fourier την συνάρτηση f : με f ( ) f ( ) για κάθε, και f ( ), -π,,,. Υπολογίζουμε αναλυτικά τους συντελεστές του αναπτύγματος Fourier ( cos( ) b si( )) για Τ=π και διάστημα ολοκλήρωσης αυτό της περιόδου [, ), οπότε έχουμε
13 f ( ) ( ) Σειρές Fourier Στα παρακάτω χρησιμοποιούμε παραγοντική ολοκλήρωση και έχουμε: f( ) cos( ) cos( ) cos( ) si( ) ' si( ) ' si( ) ( )' si( ) si( ) ( )' si( ) si( ) si( ) cos( ) cos( ) ( cos() cos( )) ( cos( ) cos()) ( ) ( ) ( ( ) ) ( ( ) ) Δηλαδή και k ( ), k=,,3,.. k (k ) b f ( ) si( ) si( ) si( ) cos( ) ' cos( ) ' cos( ) ( )' cos( ) cos( ) ( )' cos( ) cos() cos( ) cos( ) cos( ) cos() cos( ) 3
14 si( ) si( ) ( ) ( ) ( ) ( ) ( ) Έτσι, το ανάπτυγμα Fourier της συνάρτησης f( ) είναι: ( ) ( ) ( ) ( ) cos( ) si( ). Στην περίπτωση όπου b η συνάρτηση είναι παντού συνεχής. Όταν bυπάρχει σημείο ασυνέχειας της συνάρτηση στο σημείο και τα k, k. Για το σημείο ασυνέχειας της συνάρτησης στο ισχύει ότι: ( ) f ( ) ( f ( ) f ( )) ( ) οπότε η σειρά που υπολογίσαμε παριστάνει την ( ) f ( ), στο διάστημα περιοδικότητας της. Οπότε λόγω της περιοδικότητας η σειρά παριστάνει την f σε όλο το. Παράδειγμα Βρείτε τη σειρά Fourier της συνάρτησης f ( ),. Ποιες είναι οι τιμές για και για της σειράς Fourier; Λύση Έχουμε Τ=π και διάστημα ολοκλήρωσης αυτό της περιόδου [, ). Το σχήμα της συνάρτησης είναι: f( ) f( ) y f( ) f( ) y
15 Σειρές Fourier Η σειρά Fourier δίνεται από την παράσταση ( cos( ) b si( )) όπου οι συντελεστές υπολογίζονται ως εξής: f f cos( ) cos( ) (κάνοντας δύο φορές παραγοντική ολοκλήρωση) si cos si si cos si b f si si (κάνοντας δύο φορές παραγοντική ολοκλήρωση) cos si cos 3 ( ) cos si cos cos 3 3 Άρα η σειρά Fourier της f έχει ως εξής: si cos b 3 cos( ) si( ) Η σειρά Fourier της f για και συγκλίνει στην τιμή f = f f f( ) ( ) / Παράδειγμα ( ) ( ) / =. Βρείτε τη σειρά Fourier της συνάρτησης ημιανορθωμένο ημίτονο. Λύση Η συνάρτηση αυτή είναι περιοδική f ( ) f ( ) και ορισμένη στη βασική της περίοδο έχει τύπο f ( ) m(,si( )) si( ) γραφική της παράσταση είναι η ακόλουθη:. Η 5
16 Η σειρά Fourier δίνεται από την παράσταση ( cos( ) b si( )) όπου οι συντελεστές υπολογίζονται ως εξής: cos( ) cos() ( ) f si( ) cos( ) f cos( ) si( )cos( ) Εδώ θεωρούμε δύο περιπτώσεις. Αρχικά για υπολογίζουμε cos( ) si( )cos( ) si( ) cos( ) cos( ) cos() = Για, χρησιμοποιώντας την τριγωνομετρική ταυτότητα ' υπολογίζουμε si( )cos( b) (si( b) si( b)) si( )cos( ) si( ) si( ) ' cos( ) cos( ) cos( ) cos( ) cos( ) cos() cos( ) cos() cos( ) cos( ) ( ) ( ) ( ) 6
17 Σειρές Fourier Εδώ χρησιμοποιήσαμε την τριγωνομετρική ταυτότητα cos( b) cos( b ). Τελικά έχουμε ότι: αν =k-, k=,,3,.. αν =k ( k ) b f Επίσης si si( )si Εδώ θεωρούμε δύο περιπτώσεις. Αρχικά για, χρησιμοποιώντας την τριγωνομετρική ταυτότητα cos si ( ) υπολογίζουμε cos cos b si( )si si si( ) Επίσης, για, χρησιμοποιώντας τις τριγωνομετρικές ταυτότητες υπολογίζουμε si( )si( b) (cos( b) cos( b)) και si( b) si( b) b si( )si cos( ) cos( ) ' si( ) si( ) si( ) si( ) si( ) si() si( ) si() si( ) si( ) Συνοψίζοντας έχουμε ότι και οι πρώτοι έξι συντελεστές, b δίνονται στον παρακάτω πίνακα: b και τελικά cos( ) cos( ) cos(6 ) f ( ) m(,si( ))
18 .5 Αναπτύγματα Fourier σε άρτιες συναρτήσεις και περιττές συναρτήσεις Μία συνάρτηση ορισμένη σε ένα διάστημα [, ] είναι άρτια εφόσον ισχύει η σχέση f ( ) f ( ) [, ]. Οι άρτιες συναρτήσεις είναι συμμετρικές ως προς τον άξονα yy '. Παράδειγμα η y cos( ) Μία συνάρτηση ορισμένη σε ένα διάστημα [, ] είναι περιττή εφόσον ισχύει η σχέση f ( ) f ( ) [, ]. Οι περιττές συναρτήσεις είναι συμμετρικές ως προς την αρχή των αξόνων. Παράδειγμα η y si( ) Το άθροισμα δύο άρτιων συναρτήσεων είναι πάντα άρτια συνάρτηση, το άθροισμα δύο περιττών συναρτήσεων είναι πάντα περιττή. Το άθροισμα άρτιας και περιττής συνάρτησης δεν μπορούμε να το χαρακτηρίσουμε ως άρτια ή περιττή. Επίσης το γινόμενο δύο άρτιων συναρτήσεων είναι πάντα άρτια συνάρτηση, το γινόμενο δύο περιττών συναρτήσεων είναι πάντα άρτια. Το γινόμενο άρτιας και περιττής συνάρτησης είναι πάντα περιττή συνάρτηση. Μπορεί εύκολα να αποδειχθεί ότι για f συνεχής συνάρτηση στο διάστημα [, ]( ) και [, ] αν η f είναι άρτια f ( ) f ( ) και αν η f είναι περιττή f ( ) - 8
19 Σειρές Fourier Σύμφωνα με το παραπάνω όταν το διάστημα [, ] είναι της συμμετρικής μορφής [ /, / ] οπότε: Εάν η συνάρτηση f() είναι άρτια το / b f ( )si( ) / αφού είναι ολοκλήρωμα άρτιας επί περιττής δηλαδή περιττής σε συμμετρικής μορφής διάστημα. Εάν η συνάρτηση f() είναι περιττή τόσο / / f ( ) αφού είναι ολοκλήρωμα περιττής συνάρτησης όσο και / f ( )cos( ) / αφού είναι ολοκλήρωμα περιττής επί άρτιας δηλαδή περιττής σε συμμετρικής μορφής διάστημα. Κάθε περιοδική συνάρτηση μπορεί να γραφεί ως ένα άθροισμα δύο συναρτήσεων μίας άρτιας και μίας περιττής. Όταν αναπτύσσουμε μια περιοδική συνάρτηση σε σειρά Fourier ( cos( ) b si( )) τότε αυτή γράφεται ως άθροισμα δύο μερών, ενός άρτιου και ενός περιττού. Το cos( ) αποτελεί το άρτιο μέρος και το b si( ) αποτελεί το περιττό μέρος του αναπτύγματος της συνάρτησης. Είναι αυτονόητο ότι όταν η περιοδική συνάρτηση είναι άρτια το περιττό μέρος της δεν θα πρέπει να υπάρχει (οπότεb ) ενώ όταν είναι περιττή το άρτιο μέρος της δεν θα πρέπει να υπάρχει (οπότε ). Λυμένα παραδείγματα. Παράδειγμα Να βρείτε τη σειρά Fourier της περιοδικής συνάρτησης f : με f ( ) f ( ) για κάθε, αν f ( ),,, 9
20 και στη συνέχεια να επαναπροσδιοριστεί στα σημεία, ώστε η σειρά Fourier να παριστάνει την f σε όλο το. Η γραφική παράσταση της συνάρτησης είναι: Η συνάρτηση f είναι περιττή, οπότε και b f ( )si( ) si( ) si( ) u si( ) si( ) d( ) si( ) si( ) d( ) si( ) si( u) du cos( ) cos( ) si( ), cos( ) ( ), ' Εναλλακτικά εάν παρατηρήσω ότι η προς ολοκλήρωση ποσότητα είναι άρτια συνάρτηση ως γινόμενο της περιττής f( ) με την περιττή si( ) έχω b f ( )si( ) f ( )si( ) si( ) si( ) ' cos( ) cos( ) cos( ) ( ),, Oπότε, ο αντίστοιχος πίνακάς είναι:
21 Σειρές Fourier b Συνεπώς η σειρά είναι η si(3 ) si(5 ) si(7 ) si( ) Για το σημείο έχουμε f ( ) ( f( ) f( )) ( ( )) Για το σημείο έχουμε f () f ( ) f ( ) ( ) οπότε εάν θεωρήσουμε την f ( ),,,, η σειρά που υπολογίσαμε την παριστάνει σε το διάστημα της περιοδικότητας της και εξαιτίας της περιοδικότητας της συνάρτησης η σειρά την παριστάνει σε παριστάνει την f σε όλο το. Παράδειγμα Να βρείτε τη σειρά Fourier της περιοδικής συνάρτησης f : με f ( ) f ( ) για κάθε, αν, f ( ),, Η γραφική παράσταση της συνάρτησης είναι:
22 Η συνάρτηση f είναι άρτια, οπότε b και / / f ( ) f ( ) / Παρατηρώ ότι στο, η προς ολοκλήρωση ποσότητα είναι άρτια συνάρτηση ως γινόμενο της άρτιας f( ) με την άρτια cos( ), οπότε έχω f ( )cos( ) f ( )cos( ) cos( ) / si( ) si( ) / Αν, k k N τότε si( ) si( k ). Αν k, k,,... τότε k si( ) si( k ) ( ) ( ) Επομένως αν =k si( ), k=,,3,.. ( ) αν =k- Οι πρώτοι επτά συντελεστές συνοψίζονται στον ακόλουθο πίνακα: Και η σειρά Fourier είναι η cos(3 ) cos(5 ) cos(7 ) cos( ) Παρατηρούμε ότι για τα σημεία ασυνέχειας, ο παραπάνω τύπος αποτυγχάνει να υπολογίσει με ακρίβεια την τιμή της συνάρτησης. Για παράδειγμα για η σειρά έχει τιμή cos cos cos cos
23 Σειρές Fourier η οποία δεν ισούται με το f. Για αυτό θα πρέπει να ορίσουμε στα σημεία αυτά τις τιμές που θα πρέπει να έχει η συνάρτηση. Για το σημείο ασυνέχειας έχουμε: f ( ) f ( ) f ( ) Για το σημείο ασυνέχειας έχουμε: οπότε εάν θεωρήσουμε την f ( ) f ( ) f ( ),, f ( ),,, η σειρά που υπολογίσαμε την παριστάνει σε το διάστημα της περιοδικότητας της και εξαιτίας της περιοδικότητας της συνάρτησης η σειρά την παριστάνει σε όλο το. Παράδειγμα Αναπτύξτε τη σειρά Fourier της συνάρτησης f : με f ( ) f ( ) για κάθε, αν f ( ) όταν. Η συνάρτηση είναι παντού συνεχής με γραφική παράσταση: 3
24 Επειδή f ( ) f ( ) η συνάρτηση είναι άρτια και επομένως αναπτύσσεται μόνο μέσω των συνημιτονικών αρμονικών f ( ) cos. ( ) Για έχουμε, το ακόλουθο ολοκλήρωμα άρτιας συνάρτησης ως γινόμενο της άρτιας f( ) με την άρτια cos( ), οπότε έχω : si f ( )cos( ) cos( ) cos( ) si si cos si si (cos ), v k (cos ), v k (k ) k,,3,... ' Οι πρώτοι συντελεστές συνοψίζονται στον ακόλουθο πίνακα: Συνεπώς το ανάπτυγμα της f σε σειρά Fourier είναι cos (k ) cos(3 ) cos(5 ) cos(7 ) f ( ) cos( )... Παράδειγμα k (k ) Αναπτύξτε τη σειρά Fourier της συνάρτησης f : με f ( ) f ( ) για κάθε, αν f ( ) όταν. Η συνάρτηση έχει γραφική παράσταση:
25 Σειρές Fourier Επειδή φανερά f ( ) f ( ) η συνάρτηση είναι περιττή και επομένως και η συνάρτηση αναπτύσσεται μόνο μέσω των ημιτονικών αρμονικών f ( ) b si όπου, εάν παρατηρήσω ότι η προς ολοκλήρωση ποσότητα είναι άρτια συνάρτηση ως γινόμενο της περιττής f( ) με την περιττή si( ), έχω b f ( )si( ) f ( )si( ) si( ) cos( ) si( ) cos( ) ( ) Oπότε, ο αντίστοιχος πίνακάς είναι: b Συνεπώς η σειρά είναι η si( ) si( ) si(3 ) si( ) si(5 ) si(6 ) si(7 ) Για το σημείο ασυνέχειας έχουμε οπότε εάν θεωρήσουμε την f ( ) ( f( ) f( )) ( ( )) f ( ), η σειρά που υπολογίσαμε την παριστάνει σε το διάστημα της περιοδικότητας της και εξαιτίας της περιοδικότητας της συνάρτησης η σειρά την παριστάνει σε παριστάνει την f σε όλο το. Παράδειγμα Γενικεύοντας μπορούμε να θεωρήσουμε τη συνάρτηση f : f ( ) f ( ) για κάθε, και f ( ) -,,. με και μπορούμε (όπως είδαμε σε προηγούμενο παράδειγμα) να υπολογίσουμε: 5
26 ( ) ( ) ( ) ( ) b ( ) Στην περίπτωση όπου, (τριγωνικό σήμα) η συνάρτηση άρτια οπότε ισχύει ότι b και, ( ( ) ). Στην περίπτωση όπου, (πριονωτό σήμα, swtooth) η συνάρτηση είναι περιττή οπότε ισχύει, και Παράδειγμα b ( ) Υπολογίστε τη σειρά Fourier της συνάρτησης f : με f ( ) f ( ) για κάθε, αν f ( ) si( / ) όταν.. 6
27 Δεδομένου ότι ισχύει si si f ( ) si( / ), - είναι περιττή. Η συνάρτηση f είναι περιττή, άρα και η Σειρές Fourier συνάρτηση b f ( )si( ). Για να διευκολυνθούμε στον υπολογισμό των b θα υπολογίσουμε το I si( / )si( ) χρησιμοποιώντας την τριγωνομετρική ταυτότητα: Έχουμε si( )si( b) cos b cos b. I si( / )si( ) cos cos si si C. / / Άρα, εάν παρατηρήσω ότι η προς ολοκλήρωση ποσότητα είναι άρτια συνάρτηση ως γινόμενο της περιττής f( ) με την περιττή si( ) έχω b f ( )si( ) f ( )si( ) f ( )si( ) si ( ) si ( ) / / si si cos( ) cos( ) cos( ) cos( ) 8 ( ) 8 cos( ) cos( ) Oπότε, το ο αντίστοιχος πίνακας είναι: b H συνάρτηση f ( ) si( / ), - δεν είναι συνεχής στο σημείο όπου θεωρούμε 7
28 f ( ) f ( ) f ( ) ( ), και η σειρά είναι: f ( ) 8 ( ) b si( ) si( ) 8 si( ) si( ) 3 si(3 ) si( ) για την συνάρτηση f ( ) si( / ),... Παράδειγμα Βρείτε τη σειρά Fourier της συνάρτησης πλήρως ανορθωμένο ημίτονο. Λύση Η συνάρτηση αυτή είναι περιοδική f ( ) f ( ) και ορισμένη στη βασική της περίοδο έχει τύπο f ( ) si( ) si( ) si( ). Δεδομένου ότι ισχύει si( ) si( ) η συνάρτηση είναι άρτια. Η γραφική της παράσταση είναι η ακόλουθη: Εφόσον συνάρτηση f( ) είναι άρτια έχουμε ότι b και η σειρά Fourier δίνεται από την παράσταση όπου οι συντελεστές υπολογίζονται ως εξής: cos( ) cos( ) cos() ( ) f si( ) cos( ) f cos( ) = si( )cos( ) 8
29 Σειρές Fourier Στο παραπάνω, χρησιμοποιήσαμε το γεγονός ότι η συνάρτηση f ( )cos( ) είναι άρτια, ως γινόμενο δύο αρτίων συναρτήσεων. Για τον υπολογισμό του ολοκληρώματος πρέπει να θεωρήσουμε δύο περιπτώσεις. Αρχικά για υπολογίζουμε cos( ) si( )cos( ) si( ) cos( ) cos( ) cos() = Για, χρησιμοποιώντας την τριγωνομετρική ταυτότητα υπολογίζουμε si( )cos( b) (si( b) si( b)) si( )cos( ) si( ) si( ) ' cos( ) cos( ) cos( ) cos( ) cos( ) cos() cos( ) cos() cos( ) cos( ) ( ) ( ) ( ) Εδώ χρησιμοποιήσαμε την τριγωνομετρική ταυτότητα cos( b) cos( b ). ' Τελικά έχουμε ότι: αν =k-, k=,,3,.. αν =k ( k ) Συνοψίζοντας έχουμε ότι και οι πρώτοι έξι συντελεστές, b δίνονται στον παρακάτω πίνακα: και τελικά cos( ) cos( ) cos(6 ) f ( ) si( )
30 .6 Η εκθετική μορφή του αναπτύγματος Fourier Εάν i είναι η μιγαδική μονάδα (φανταστική μονάδα i τύπος του Euler: i e cos( ) isi( ) Από αυτόν έχουμε επίσης i e cos( ) isi( ) Από την πρόσθεση των δύο αυτών ταυτοτήτων έχουμε ότι cos( ) ), τότε ισχύει ο e i e i και αφαιρώντας si( ) e i e i i Οπότε f ( ) [ cos( ) b si( )] i i i i e e e e [ b )] i i i i i e e e e [ b b )] i i i i i i e e e e [ ib ib )] i i i i i i [ e e e e b i b i )] ib i ib i [ e e ] c [ c e c e ] i i όπου c, c ib και ib c ο συζυγής του. Οπότε, ib b c i f ( )cos( ) i f ( )si( ) i f ( ) cos( ) i si( ) f ( ) e Όμοια αποδεικνύεται και ο τύπος για το c. Στην περίπτωση που το διάστημα περιοδικότητας είναι της συμμετρικής μορφής [ /, / ] οι τύποι αυτοί γίνονται: / i c f ( ) e / και / i c f ( ) e, / 3
31 Σειρές Fourier Οπότε συνολικά / i c f ( ) e,,,,... και / Οι συντελεστές c i f ( ) c e. είναι μιγαδικοί αριθμοί για τους οποίους ισχύει Re( c ) και b Im( c ), c c και c c, όπου Re( c ), Im( c ), c και c είναι αντίστοιχα το πραγματικό μέρος, το μιγαδικό μέρος, το μέτρο και το όρισμα του μιγαδικού c. Σύμφωνα με το θεώρημα του Prsevl η μέση ισχύς σε ένα συνεχές σήμα f( ) και οι συντελεστές c συνδέονται με τη σχέση: / / f ( ) c. Παράδειγμα Να βρείτε την εκθετική μορφή του αναπτύγματος Fourier της περιοδικής πριονωτής (swtooth) συνάρτησης f ( ) για [, ) και f ( ) f ( ). Οπότε Τ=π και το διάστημα ολοκλήρωσης είναι αυτό της περιόδου [, ), οπότε από τους τύπους έχουμε: c f ( ) Στη συνέχεια θα χρησιμοποιήσουμε το ακόλουθο ολοκλήρωμα: i i i i i e e ie e i i e c c e c i ( i) i 3
32 από όπου έχουμε / i i i i c f ( ) e e e / i i i i e e i i i i i e e i e e i i i διότι si si i e cos i i e cos i i i e e i si i i e e cos Οι συντελεστές για =-,-3,-,-,,,,3, συνοψίζονται στον ακόλουθο πίνακα: 3 3 c i i 3 i i -i i i 3 i Για το σημείο ασυνέχειας έχουμε f ( ) f ( ) f ( ) ( ) οπότε εάν θεωρήσουμε την f ( ),, Και τελικά η σειρά που υπολογίσαμε i i i f ( ) c e e i i i i 3 i i i i i i 3 i i 3 i i... e e e ie ie e e e παριστάνει την ( ) f στο διάστημα της περιοδικότητας της και εξαιτίας της περιοδικότητας της συνάρτησης η σειρά την παριστάνει σε όλο το. 3
33 Σειρές Fourier Παράδειγμα Να βρείτε την εκθετική μορφή του αναπτύγματος Fourier της περιοδικής τριγωνικής συνάρτησης f ( ) για [, ) και f ( ) f ( ). Η συνάρτηση είναι παντού συνεχής με γραφική παράσταση: Οπότε Τ=π και =- π περιόδου [, ), οπότε από τους τύπους έχουμε: και το διάστημα ολοκλήρωσης είναι αυτό της c f () Στη συνέχεια θα χρησιμοποιήσουμε το ακόλουθο ολοκλήρωμα: i i i i i e e ie e i i e c c e c i ( i) i από όπου έχουμε i i i i e e e i i e i και i i i i i i e i e e e και τελικά / i i i i c f ( ) e e ( ) e e / i i e i i i i e ( ) e e i i i i ( e e ) i ( e e ) ( ) περιττό άρτιο διότι si si i e cos i i e cos i i i e e i si i i e e cos 33
34 Οι συντελεστές για =-,, συνοψίζονται στον ακόλουθο πίνακα: 3 3 c 9 9 Και τελικά η σειρά που υπολογίσαμε f c e 5 e 9 e ie e 9 e 5 e i i5 i3 i i i 3 i5 ( ) Παράδειγμα Να βρείτε την εκθετική μορφή του αναπτύγματος συνάρτησης f : με f ( ) f ( ) για κάθε, αν Fourier της περιοδικής, f ( ),, Οπότε Τ= και και το διάστημα ολοκλήρωσης είναι αυτό της περιόδου [,), οπότε από τους τύπους έχουμε:.5.5 i i i i c f ( ) e ( e e e ) i i i e e e i i.5 i.5 3
35 i / i i / i / i i / e e e e e e i i/ i/ e e si si c i διότι i i / e cos i si e cos / isi / si i e cos i i i e e i si και Εδώ εισάγουμε τον συμβολισμό si( ) si c ( ). Επίσης υπολογίζουμε i / e i cos / si / i/ i/ e e i si / Σειρές Fourier.5.5 c f ( ) ( ) Οπότε αφού ισχύει si( ) ( ),, Οι συντελεστές για =-5,-,-3,-,-,,,,3,,5 συνοψίζονται στον ακόλουθο πίνακα: c Και τελικά η σειρά Fourier είναι η si i e i5 i3 i i i 3 i5... e e e e e e Για το σημείο ασυνέχειας έχουμε f ( ) f ( ) f ( ) ( ) Για το σημείο ασυνέχειας έχουμε 35
36 οπότε εάν θεωρήσουμε την f ( ) f ( ) f ( ) ( ) f ( ) Και τελικά η σειρά που υπολογίσαμε παριστάνει την f( ) στο διάστημα της περιοδικότητας της και εξαιτίας της περιοδικότητας της συνάρτησης η σειρά την παριστάνει σε όλο το..7 Το φάσμα συχνοτήτων Όταν ένα κύμα αναλύεται μέσω μιας σειράς Fourier σε άθροισμα ημιτονοειδών (ή συνημιτονοειδών) αρμονικών το γράφημα των πλατών Α και Α λέγεται διακριτό φάσμα πλατών και το γράφημα των φάσεων φ (ή των θ ) λέγεται διακριτό διακριτό φάσμα συχνοτήτων. φάσμα φάσεων. Τα δύο μαζί αποτελούν το Είχαμε δει ότι για την τριγωνομετρική μορφή των σειρών Fourier το πλάτος των αρμονικών και η φάση τους συνδέεται με τους συντελεστές της σειράς με βάση τους τύπους A A b, rct b εάν b αναπτύσσεται σε ημίτονα και rct όταν έχουμε συνημιτονικές αρμονικές. Υπενθυμίζουμε ότι οι γωνίες φάσεων μεταξύ του ημιτονοειδούς αναπτύγματος και του συνημιτονοειδούς αναπτύγματος διαφέρουν κατά π/. Δηλαδή. Στην ανάλυση που ακολουθεί θα εργαστούμε με τις γωνίες φάσματος από όπου μπορούμε με τη χρήση του τύπου έχουμε τις γωνίες φάσματος. Παράδειγμα 36
37 Σειρές Fourier Η σειρά Fourier της άρτιας περιοδικής συνάρτησης f : με f ( ) f ( ) για κάθε, αν, f ( ),, βρήκαμε ότι έχει συντελεστές b και, οπότε si( ) si c ( ) A b b, rct rct. Οι συντελεστές Α για =.. συνοψίζονται στον ακόλουθο πίνακα: A και το διακριτό φάσμα πλατών είναι το ακόλουθο: A Στην περίπτωση της εκθετικής μορφής έχουμε ib b c c A c, και παρόμοια A c. 37
38 Άξονας μιγαδικών b A c Άξονας πραγματικών Παρατήρηση Το τεταρτημόριο στο οποίο βρίσκεται η και si( ) cos( ) Αν δηλαδή των και b και b, η γωνία εξαρτάται από τα πρόσημα των. Πιο συγκεκριμένα: βρίσκεται στο πρώτο τεταρτημόριο b (οπότε δεν προσθέτουμε τίποτα στο rct ). Αν και b, η γωνία βρίσκεται στο δεύτερο τεταρτημόριο b (οπότε προσθέτουμε στο rct ). Αν και b, η γωνία βρίσκεται στο τρίτο τεταρτημόριο (οπότε b αφαιρούμε στο rct ). Αν και b, η γωνία b (οπότε δεν προσθέτουμε τίποτα στο rct ). Από το μέτρο των συντελεστών βρίσκεται στο τέταρτο τεταρτημόριο c μπορώ να βρω το πλάτος A c για κάθε μία από τις αρμονικές συνιστώσες του αναπτύγματος σε εκθετική μορφή. Επίσης, από τη σχέση rct b b ή την rct και μπορώ να βρω τις αντίστοιχες φάσεις. Επίσης ισχύει A c. Έτσι μπορούμε να σχεδιάσουμε και το φάσμα των συχνοτήτων για την περίπτωση των όρων της εκθετικής μορφής του αναπτύγματος Fourier. Παράδειγμα Εάν π.χ. c 3iμπορώ να πω ότι η συνιστώσα αυτή έχει πλάτος 3 5 οπότε A c Επίσης, η γωνία φάσης rct(3 / ) 36.8 (για συνημιτονικά αναπτύγματα) αφού και 38
39 Σειρές Fourier 3 οπότε η γωνία βρίσκεται στο πρώτο τεταρτημόριο και b για ημιτονικά αναπτύγματα. Παράδειγμα Να βρείτε την εκθετική μορφή του αναπτύγματος Fourier ενός παλμού με πλάτος 5 και διάρκεια /5 που επαναλαμβάνεται με περίοδο Τ. Βρείτε τη συνάρτηση που τον περιγράφει και σχεδιάστε τον. Σχεδιάστε το διακριτό φάσμα πλατών και το διακριτό φάσμα των φάσεων. Η συνάρτηση έχει τύπο, / / f ( ) 5, / /, / / και γράφημα : y 5 / / / / Από τον τύπο / / i i c f ( ) e 5e / / i / i i 5 i e e e si si c i 5 5 Αφού e e i 5 i 5 cos cos / isi 5 5 isi 5 5 Επίσης υπολογίζουμε / / / / / i 5 5 e e i si 5 5 / c f ( ) 5. Οι συντελεστές για =-5,-,-3,-,-,,,,3,,5 συνοψίζονται στον ακόλουθο πίνακα: 39
40 c si 5si 3 5 5si 5 3 5si 5si 5 5 5si 5 5si 5 3 5si 5 3 5si 5 si Παρατηρούμε ότι τα c είναι πραγματικοί αριθμοί οπότε τα πλάτη ισούται με το μέτρο ενός πραγματικού αριθμού που είναι ο ίδιος ο αριθμός..8 c Αν δούμε πιο αναλυτικά το φάσμα πλατών παρατηρούμε ότι η πέμπτη, η δέκατη, η δέκατη πέμπτη κ.λ.π αρμονική είναι. Οπότε όπως και η σταθερή c δεν έχουν φάση. Το φάσμα πλατών A c είναι το ακόλουθο:.8.6. A. A Επίσης, παρατηρούμε ότι οι συντελεστές έχουν μόνο πραγματικό μέρος ib Δηλαδή ισχύει c si c b, si c 5 5.
41 Σειρές Fourier b Οπότε οι γωνίες φάσης rct έχουν τόξο εφαπτομένης (για συνημιτονικά αναπτύγματα). Άρα η γωνία φάσης μπορεί να πάρει τιμές [,, ]. Όπως φαίνεται από το παραπάνω σχήμα για =-,-3,-,-,,,3, έχουμε συντελεστή c θετικό, οπότε και το α θετικό. Δηλαδή έχουμε ένα σχήμα της μορφής: Άξονας μιγαδικών Άξονας πραγματικών και συμπεραίνομε ότι η φάση θα είναι, για =-,-3,-,-,,,3,. Όταν το c όπως φαίνεται από το σχήμα είναι αρνητικό (=-9,-8,-7,-6, 6,7,8,9) τότε και το α θα πρέπει να είναι αρνητικό. Άξονας μιγαδικών Άξονας πραγματικών Συμπεραίνουμε ότι η φάση θα είναι -π ή π. Επιλέγουμε να είναι π για =-9, -8,-7,-6 και π για =6,7,8,9 εφόσον ισχύει c c και c c. Συνοψίζοντας τα παραπάνω έχουμε ότι το φάσμα των φάσεων είναι: Φυσικά, τα παραπάνω αφορούν τις γωνίες φάσματος (αθροίσματος σε συνημίτονα). Όπως έχουμε πει με τη χρήση του τύπου έχουμε τις γωνίες φάσματος (αθροίσματος σε ημίτονα).
42 .8 Συμπληρωματικές Ασκήσεις. Να υπολογιστεί η σειρά Fourier, η οποία αντιπροσωπεύει την παράσταση στο διάστημα. Λύση: Θεωρώ την συνάρτηση f ( ). Η ζητούμενη σειρά Fourier δίνεται από την παράσταση ( cos( ) b si( )), όπου οι συντελεστές υπολογίζονται ως εξής: f ( ) ( ) Με παραγοντική ολοκλήρωση μπορούμε εύκολα να δείξουμε ότι: cos( ) ( )si( ) cos( ) c και 3 cos( ) si( ) cos( ) c. Παρατηρούμε ότι η συνάρτηση f ( ) cos( ) είναι άρτια ενώ η συνάρτηση f ( ) cos( ) είναι περιττή και ότι το διάστημα ολοκλήρωση είναι συμμετρικό ως προς την αρχή των αξόνων. Οπότε μπορούμε εύκολα να υπολογίσουμε τους συντελεστές ως εξής: ( )cos( ) cos( ) cos( ) cos( ) cos ( )si 3 cos ( ). Όμοια, υπολογίζουμε και τους συντελεστές b : b ( )si( ) si( ) si( ) si( ) si cos cos cos ( ). Τελικά, αντικαθιστώντας τους συντελεστές και b 3 έχουμε: f ( ) ( ) cos ( ) si 3 cos si cos si...
43 Σειρές Fourier. Να βρεθεί η σειρά Fourier της συνάρτησης, f ( ), όπου. Λύση: Στη περίπτωση μας και επομένως f ( ) f ( )cos( ) cos( ) cos( ) = si( ) d(si( )) [ si( ) si( ) ] = ( ) [cos( )] [cos( ) ] b f ( )si( ) si( ) si( ) cos( ) si( ) cos( ) cos( ) ' cos( ) cos( ) ' cos( ) cos( ) ' cos( ) cos( ) cos( ) cos( ) cos( ) cos( ) si( ) cos( ) cos( ) ( ) ( ) Οπότε η σειρά είναι η [ cos( ) b si( )] 3
44 3. Να βρείτε τη σειρά Fourier της περιοδικής συνάρτησης f : με f ( ) f ( ) για κάθε, αν όπου., f ( ), Η συνάρτηση f είναι άρτια διότι f ( ) f ( ), άρα b και / f ( ) f ( ) /, / Ξέρουμε ότι για f συνεχής συνάρτηση στο διάστημα [, ]( ) και [, ] αν η f είναι άρτια άρτιας επί άρτια. f ( ) f ( ). Η f ( )cos( ) είναι άρτια ως γινόμενο f ( )cos( ) f ( )cos( ) cos( ) / si( ) si( ) / Αν, k k τότε si( ) si( k ). Αν k, k τότε k si( ) si( k ) ( ) ( ) Επομένως ( ), si( ), Και η σειρά Fourier είναι η cos(3 ) cos(5 ) cos(7 ) cos Για παράδειγμα για η σειρά έχει τιμή
45 Σειρές Fourier cos cos cos cos... η οποία δεν ισούται με το f. Για αυτό θα πρέπει να ορίσουμε στα σημεία αυτά τις τιμές που θα πρέπει να έχει η συνάρτηση Για το σημείο έχουμε f ( ) f ( ) f ( ) Για το σημείο έχουμε f ( ) f ( ) f ( ) οπότε εάν θεωρήσουμε την,, f ( ),,, η σειρά που υπολογίσαμε την παριστάνει σε το διάστημα της περιοδικότητας της και εξαιτίας της περιοδικότητας της συνάρτησης η σειρά την παριστάνει σε όλο το.. Να βρείτε τη σειρά Fourier της περιοδικής συνάρτησης f : με f ( ) f ( ) για κάθε, αν f ( ),, και στη συνέχεια να επαναπροσδιοριστεί η συνάρτηση στο σημείο Fourier να παριστάνει την f σε όλο το. ώστε η σειρά Λύση Η συνάρτηση γράφεται f ( ),, Εφόσον Τ=π και =-π η σειρά Fourier είναι της μορφής: f( ) [ cos( ) b si( )] Υπολογίζουμε τους συντελεστές της σειράς: 5
46 ( ) f si( ) / f ( )cos( ) cos( ) [ ] si( ) si( ) si( ) cos( ) Δηλαδή cos( ) ( ),, cos( ) / b f ( )si( ) si( ) [ ] cos( ) cos( ) cos( ) si( ) cos( ) ( ) = Δηλαδή b,, Επομένως η σειρά Fourier είναι η ( ) cos[(k ) ] si( ) k (k ) cos cos(3 ) cos(5 ) si si( ) si(3 ) si( )... 3 Για το σημείο εάν θεωρήσουμε την ισχύει f ( ) f ( ) f ( ) οπότε 6
47 Σειρές Fourier f ( ),, η σειρά που υπολογίσαμε την παριστάνει στο διάστημα της περιοδικότητας της και εξαιτίας της περιοδικότητας της συνάρτησης η σειρά την παριστάνει σε όλο το. 5. Να βρείτε τη σειρά Fourier της περιοδικής συνάρτησης f : με f ( ) f ( ) για κάθε, αν f ( ),,, όπου. Λύση Η συνάρτηση f είναι περιττή διότι f ( ) f ( ), άρα και Ξέρουμε ότι για f συνεχής συνάρτηση στο διάστημα [, ]( ) και [, ] αν η f είναι άρτια περιττής επί περιττή. f ( ) f ( ). Η f ( )si( ) είναι άρτια ως γινόμενο cos( ) b f ( )si( ) si( ), cos( ) ( ), Συνεπώς η σειρά είναι η si(3 ) si(5 ) si(7 ) si Χρησιμοποιώντας παραγοντική ολοκλήρωση υπολογίστε τα ολοκληρώματα ( )si, ( )cos Να βρεθεί η τριγωνομετρική σειρά Fourier της f() = +π, -π<<π. Χρησιμοποιώντας το προηγούμενο ανάπτυγμα δείξτε ότι Χρησιμοποιώντας Mtlb σχεδιάστε την f() = +π στο διάστημα (-π,π) καθώς και τα μερικά αθροίσματα του αναπτύγματός της σε σειρά Fourier για, 3 και 5 όρους. Λύση 7
48 ( )si si si cos ( )' cos C cos cos ( )' cos C cos cos cos C cos si cos C ( )cos( ) cos( ) cos( ) si( ) si( ) ( )' C si( ) si( ) si( ) ( )' C si( ) si( ) cos( ) C si( ) cos( ) si( ) C Εφόσον Τ=π και =-π η σειρά Fourier είναι της μορφής: [ cos( ) b si( )] Υπολογίζουμε τους συντελεστές της σειράς: f ( ) ( ) f ( )cos( ) ( )cos( ) si( ) cos( ) si( ) b f ( )si( ) ( )si( ) cos si cos = cos cos cos cos cos ( ) όπου χρησιμοποιήσαμε ότι cos( ) cos( ), si( ) si( ), si( ), cos( ) ( ). Δηλαδή 8
49 Σειρές Fourier b,, Επομένως η σειρά Fourier είναι η [ cos( ) b si( )] ( ) si( ) si si( ) si(3 ) si( ) si(5 ) Έχουμε από τα παραπάνω si si( ) si(3 ) si( ) si(5 ) Θέτοντας στην παραπάνω έχουμε 3 5 si si( ) si( ) si( ) si( ) si(3 ) Ο κώδικας σε Mtlb: >> cler ll >> =lispce(-pi,pi); >> f=+pi; >> f=pi+*si(); >> f3=pi+*(si()-/*si(*)+/3*si(3*)); >> f5=pi+*(si()-/*si(*)+/3*si(3*)-/*si(*)+/5*si(5*)); >>f7=pi+*(si()-/*si(*)+/3*si(3*)-/*si(*)+/5*si(5*)- /6*si(6*)+/7*si(7*)); >> plot(,f,,f,,f3,,f5,,f7) Το αποτέλεσμα f f f3 f5 f
50 μας δείχνει ότι όσο περισσότερους όρους θεωρήσουμε τόσο καλύτερη προσέγγιση της συνάρτησης επιτυγχάνουμε. 7. Μία περιοδική συνάρτηση περιγράφεται από τον ακόλουθο τύπο σε μία περίοδό της. f ( ), / 5,, / 5 Κάντε το γράφημά της σε τρεις περιόδους, πείτε ποια είναι η περίοδός της και βρείτε την εκθετική μορφή του αναπτύγματός της Fourier. Γράψτε τους όρους του αναπτύγματος από =- έως. Λύση Το γράφημα: Η περίοδος της είναι π/5. Αρχικά / /5 5 /5 c f ( ) /5. / /5 Αυτό βγαίνει και άμεσα από την παρατήρηση ότι η συνάρτηση είναι περιττή. Από τον τύπο / /5 i 5 i i c f ( ) e e e / /5 /5 i5 ' /5 i5 ' i5 i5 e e e e i5 i5 /5 /5 i5 i5 /5 e e i i e e i5 i5 i5 /5 i i e e i Αφού 5
51 si si Σειρές Fourier i e cos i i i e e cos i και cos( ) ( ) έχουμε e cos i ά c cos( ) cos( ) ( ) 8 i i i ό i 8 i 3 3 i5 i5 i5 i5 i5 i5 i5 i5 i5 c e c 3e c e ce c3e e e e e 8. Μία περιοδική συνάρτηση περιγράφεται από τον ακόλουθο τύπο σε μία περίοδό της.. f ( ) /, /, / / Κάντε το γράφημά της σε μία περίοδο και αφού την χαρακτηρίσετε ως άρτια ή περιττή βρείτε το ανάπτυγμα της σε τριγωνομετρική σειρά Fourier. Γράψτε τους οκτώ πρώτους όρους της σειράς. Λύση Το γράφημα: Η συνάρτηση f είναι περιττή, άρα και 5
52 / b f ( )si( ) si( ) si( ) / / / / si( ) si( ) d( ) si( ) si( ) d( ) / u / / / si( ) si( u) du si( ) / cos( ) si( ) cos( ) / Αφού cos( ) = k + = k + = k + 3 = k + ισχύει cos( ) = k + = k + = k + 3 = k + Συνεπώς η σειρά είναι η si( ) si(3 ) si( ) si(5 ) si( ) 3 5 si(6 ) si(7 ) si(8 ) Παρατήρηση το ότι / / si( ) si( ) si( ) / μπορεί να εξαχθεί και από το ότι η si( ) είναι περιττή οπότε το / / si( ) si( ) si( ) / / 9. Έχετε έναν παλμό πλάτους 5 με διάρκεια π που επαναλαμβάνεται με περίοδο π. Με βάση την γραφική της παράσταση που σας δίνεται, γράψτε τον τύπο της συνάρτησης στο διάστημα [ π,π] που είναι μία περίοδος. Χαρακτηρίστε τη συνάρτηση ως άρτια ή περιττή. Αναπτύξτε την εκθετική σειρά Fourier της συνάρτησης και εξηγήστε ποιες τιμές θα εμφανίζει σε γράφημα το διακριτό φάσμα πλατών για τις τέσσερις πρώτες αρμονικές. y 5 / / 3 / 5 / 5
53 Σειρές Fourier Λύση Η συνάρτηση είναι άρτια διότι το γράφημά της είναι συμμετρικό ως προς τον άξονα yy και έχει τύπο:, / f ( ) 5, / /, / Από τον τύπο i i c f ( ) e 5e / / / / 5 5 i i i 5 5 e e e si sic i i Αφού e e i cos isi i e e i si cos isi 5 / 5 Επίσης c f ( ) 5. / / / Για τα πλάτη ισχύει A c άρα το γράφημα θα παρουσιάζει τα Α,Α,Α,Α3.. Σχεδιάστε τον παλμό ο οποίος, σε μία περίοδό του, περιγράφεται από την συνάρτηση που ακολουθεί. Στη συνέχεια χαρακτηρίστε τη συνάρτηση αυτή ως άρτια ή περιττή και βρείτε τους πέντε πρώτους όρους της τριγωνομετρικής σειράς Fourier του παλμού., f ( ),, Λύση Το γράφημα είναι: 53
54 y / / 3 / 5 / Η συνάρτηση f είναι άρτια διότι f ( ) f ( ), άρα b και / / f ( ) f ( ) 8 / Ξέρουμε ότι για f συνεχής συνάρτηση στο διάστημα [, ]( ) και [, ] αν η f είναι άρτια ως γινόμενο άρτιας επί άρτια. f ( ) f ( ). Η f ( )cos( ) είναι άρτια f ( )cos( ) f ( )cos( ) cos( ) / si( ) si( ) si c( ) / Αν, k k τότε si( ) si( k ). Αν k, k τότε k si( ) si( k ) ( ) ( ) Επομένως ( ), si( ), Και η σειρά Fourier είναι η cos(3 ) cos(5 ) cos(7 ) cos ΠΑΡΑΤΗΡΗΣΗ: Το παρόν υλικό δεν αποτελεί αυτόνομο διδακτικό υλικό, βασίζεται στο σύγγραμμα που διανέμεται και στην προτεινόμενη βιβλιογραφία του μαθήματος. Το περιεχόμενο του αρχείου απλά αποτελεί περίγραμμα των παραδόσεων του μαθήματος. Αποτελούν τις διαφάνειες της διδασκαλίας μαθήματος από το διδάσκοντα για δική του χρήση και παρακαλώ να μη χρησιμοποιηθεί και να μην αναπαραχθεί και διανεμηθεί για άλλο σκοπό. Ιδιαίτερα παραδείγματα και σχήματα έχουν αντληθεί από τα συγγράμματα :. Fourier Series, W. Bolto. Σήματα και συστήματα, Καραμπόγιας, Θεοδωρίδης ΕΑΠ 5
Αόριστο ολοκλήρωμα. επαληθεύει την παραπάνω ισότητα.
 Αόριστο ολοκλήρωμα Αντιπαράγωγος μίας συνάρτησης f() ορισμένης σε ένα διάστημα [α,β] λέγεται κάθε συνάρτηση F() που επαληθεύει την ισότητα F( ) f ( ) F( ) c επαληθεύει την παραπάνω ισότητα. Αόριστο ολοκλήρωμα
Αόριστο ολοκλήρωμα Αντιπαράγωγος μίας συνάρτησης f() ορισμένης σε ένα διάστημα [α,β] λέγεται κάθε συνάρτηση F() που επαληθεύει την ισότητα F( ) f ( ) F( ) c επαληθεύει την παραπάνω ισότητα. Αόριστο ολοκλήρωμα
3. Κεφάλαιο Μετασχηματισμός Fourier
 3 Κεφάλαιο 3 Ορισμοί Ο μετασχηματισμός Fourir αποτελεί την επέκταση των σειρών Fourir στη γενική κατηγορία των συναρτήσεων (περιοδικών και μη) Όπως και στις σειρές οι συναρτήσεις θα εκφράζονται με τη βοήθεια
3 Κεφάλαιο 3 Ορισμοί Ο μετασχηματισμός Fourir αποτελεί την επέκταση των σειρών Fourir στη γενική κατηγορία των συναρτήσεων (περιοδικών και μη) Όπως και στις σειρές οι συναρτήσεις θα εκφράζονται με τη βοήθεια
2 ο κεφάλαιο: Ανάλυση και Σύνθεση κυματομορφών με τον Μετασχηματισμό Fourier
 2 ο κεφάλαιο: Ανάλυση και Σύνθεση κυματομορφών με τον Μετασχηματισμό Fourier Η βασική ιδέα στην ανάλυση των κυματομορφών με την βοήθεια του μετασχηματισμού Fourier συνίσταται στο ότι μία κυματομορφή
2 ο κεφάλαιο: Ανάλυση και Σύνθεση κυματομορφών με τον Μετασχηματισμό Fourier Η βασική ιδέα στην ανάλυση των κυματομορφών με την βοήθεια του μετασχηματισμού Fourier συνίσταται στο ότι μία κυματομορφή
2. Ανάλυση και Σύνθεση κυματομορφών με την μέθοδο Fourier
 2.1 2. Ανάλυση και Σύνθεση κυματομορφών με την μέθοδο Fourier 2.1 Εισαγωγή Η βασική ιδέα στην ανάλυση των κυματομορφών με την βοήθεια της μεθόδου Fourier συνίσταται στο ότι μία κυματομορφή μιας οποιασδήποτε
2.1 2. Ανάλυση και Σύνθεση κυματομορφών με την μέθοδο Fourier 2.1 Εισαγωγή Η βασική ιδέα στην ανάλυση των κυματομορφών με την βοήθεια της μεθόδου Fourier συνίσταται στο ότι μία κυματομορφή μιας οποιασδήποτε
Σήματα και Συστήματα. Διάλεξη 6: Ανάλυση Σημάτων σε Ανάπτυγμα Σειράς Fourier. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 6: Ανάλυση Σημάτων σε Ανάπτυγμα Σειράς Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ανάλυση Σημάτων σε Ανάπτυγμα Σειράς Fourier 1. Ανάπτυγμα σήματος σε Σειρά Fourier
Σήματα και Συστήματα Διάλεξη 6: Ανάλυση Σημάτων σε Ανάπτυγμα Σειράς Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ανάλυση Σημάτων σε Ανάπτυγμα Σειράς Fourier 1. Ανάπτυγμα σήματος σε Σειρά Fourier
Κεφάλαιο 0 Μιγαδικοί Αριθμοί
 Κεφάλαιο 0 Μιγαδικοί Αριθμοί 0 Βασικοί ορισμοί και πράξεις Είναι γνωστό ότι δεν υπάρχει πραγματικός αριθμός που επαληθεύει την εξίσωση x Η ανάγκη επίλυσης τέτοιων εξισώσεων οδηγεί στο σύνολο των μιγαδικών
Κεφάλαιο 0 Μιγαδικοί Αριθμοί 0 Βασικοί ορισμοί και πράξεις Είναι γνωστό ότι δεν υπάρχει πραγματικός αριθμός που επαληθεύει την εξίσωση x Η ανάγκη επίλυσης τέτοιων εξισώσεων οδηγεί στο σύνολο των μιγαδικών
Περιεχόμενα. Κεφάλαιο 1 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΜΙΑ ΕΥΘΕΙΑ... 13 1.1 Οι συντεταγμένες ενός σημείου...13 1.2 Απόλυτη τιμή...14
 Περιεχόμενα Κεφάλαιο 1 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΜΙΑ ΕΥΘΕΙΑ... 13 1.1 Οι συντεταγμένες ενός σημείου...13 1.2 Απόλυτη τιμή...14 Κεφάλαιο 2 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΕΝΑ ΕΠΙΠΕΔΟ 20 2.1 Οι συντεταγμένες
Περιεχόμενα Κεφάλαιο 1 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΜΙΑ ΕΥΘΕΙΑ... 13 1.1 Οι συντεταγμένες ενός σημείου...13 1.2 Απόλυτη τιμή...14 Κεφάλαιο 2 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΕΝΑ ΕΠΙΠΕΔΟ 20 2.1 Οι συντεταγμένες
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής Σειρά Fourier Ορθοκανονικές Συναρτήσεις Στοεδάφιοαυτόθαδιερευνήσουμεεάνκαικάτωαπό
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής Σειρά Fourier Ορθοκανονικές Συναρτήσεις Στοεδάφιοαυτόθαδιερευνήσουμεεάνκαικάτωαπό
Εισαγωγή στις Τηλεπικοινωνίες. Δομή της παρουσίασης
 6 Nv 6 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Ανάπτυξη σε Σειρές Furier Αθανάσιος
6 Nv 6 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Ανάπτυξη σε Σειρές Furier Αθανάσιος
Τηλεπικοινωνίες. Ενότητα 2.1: Ανάλυση Fourier. Μιχάλας Άγγελος Τμήμα Μηχανικών Πληροφορικής ΤΕ
 Τηλεπικοινωνίες Ενότητα 2.1: Ανάλυση Fourier Μιχάλας Άγγελος Τμήμα Μηχανικών Πληροφορικής ΤΕ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό,
Τηλεπικοινωνίες Ενότητα 2.1: Ανάλυση Fourier Μιχάλας Άγγελος Τμήμα Μηχανικών Πληροφορικής ΤΕ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό,
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Ι
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Ι Εκθετική Ορισμοί & Ιδιότητες Επιμέλεια: Αθανάσιος Ν. Σκόδρας, Καθηγητής Γεώργιος Α. Βασκαντήρας, Υπ. Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών & Τεχνολογίας Υπολογιστών Άδειες Χρήσης
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Ι Εκθετική Ορισμοί & Ιδιότητες Επιμέλεια: Αθανάσιος Ν. Σκόδρας, Καθηγητής Γεώργιος Α. Βασκαντήρας, Υπ. Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών & Τεχνολογίας Υπολογιστών Άδειες Χρήσης
Ο ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE
 ΚΕΦΑΛΑΙΟ Ο ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ APACE ΚΑΙ ΟΙ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΣΤΗΝ ΕΠΙΛΥΣΗ ΓΡΑΜΜΙΚΩΝ ΔΙΑΦΟΡΙΚΩΝ KAI ΟΛΟΚΛΗΡΩΤΙΚΟ-ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΜΕ ΣΤΑΘΕΡΟΥΣ ΣΥΝΤΕΛΕΣΤΕΣ O μετασχηματισμός lc-ο αντίστροφος μετασχηματισμός
ΚΕΦΑΛΑΙΟ Ο ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ APACE ΚΑΙ ΟΙ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΣΤΗΝ ΕΠΙΛΥΣΗ ΓΡΑΜΜΙΚΩΝ ΔΙΑΦΟΡΙΚΩΝ KAI ΟΛΟΚΛΗΡΩΤΙΚΟ-ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΜΕ ΣΤΑΘΕΡΟΥΣ ΣΥΝΤΕΛΕΣΤΕΣ O μετασχηματισμός lc-ο αντίστροφος μετασχηματισμός
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΗΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΗΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ Ενότητα : ΑΝΑΛΥΣΗ FOURIER (H ΣΕΙΡΑ FOURIER ΚΑΙ Ο ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER) Aναστασία Βελώνη Τμήμα Η.Υ.Σ 1 Άδειες
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΗΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ Ενότητα : ΑΝΑΛΥΣΗ FOURIER (H ΣΕΙΡΑ FOURIER ΚΑΙ Ο ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER) Aναστασία Βελώνη Τμήμα Η.Υ.Σ 1 Άδειες
Σήματα και Συστήματα. Διάλεξη 1: Σήματα Συνεχούς Χρόνου. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 1: Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Εισαγωγή στα Σήματα 1. Σκοποί της Θεωρίας Σημάτων 2. Κατηγορίες Σημάτων 3. Χαρακτηριστικές Παράμετροι
Σήματα και Συστήματα Διάλεξη 1: Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Εισαγωγή στα Σήματα 1. Σκοποί της Θεωρίας Σημάτων 2. Κατηγορίες Σημάτων 3. Χαρακτηριστικές Παράμετροι
Σήματα και Συστήματα. Διάλεξη 2: Στοιχειώδη Σήματα Συνεχούς Χρόνου. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 2: Στοιχειώδη Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Στοιχειώδη Σήματα Συνεχούς Χρόνου 1. Μοναδιαία Βηματική Συνάρτηση 2. Κρουστική Συνάρτηση ή
Σήματα και Συστήματα Διάλεξη 2: Στοιχειώδη Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Στοιχειώδη Σήματα Συνεχούς Χρόνου 1. Μοναδιαία Βηματική Συνάρτηση 2. Κρουστική Συνάρτηση ή
Σήματα και Συστήματα. Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier 1. Μετασχηματισμός Fourier
Σήματα και Συστήματα Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier 1. Μετασχηματισμός Fourier
Προφανώς, μια συνάρτηση μπορεί να μην είναι ούτε άρτια ούτε περιττή. Όμως, μπορεί να γραφεί σαν άθροισμα μιας άρτιας fe
 Άρτιο και Περιττό μέρος Συνάρτησης Προφανώς, μια συνάρτηση μπορεί να μην είναι ούτε άρτια ούτε περιττή. Όμως, μπορεί να γραφεί σαν άθροισμα μιας άρτιας e και μιας περιττής συνάρτησης, ως εξής: Αν e και,
Άρτιο και Περιττό μέρος Συνάρτησης Προφανώς, μια συνάρτηση μπορεί να μην είναι ούτε άρτια ούτε περιττή. Όμως, μπορεί να γραφεί σαν άθροισμα μιας άρτιας e και μιας περιττής συνάρτησης, ως εξής: Αν e και,
1. ΚΕΦΑΛΑΙΟ ΕΙΣΑΓΩΓΗ ΣΤΑ ΣΗΜΑΤΑ
 . ΚΕΦΑΛΑΙΟ ΕΙΣΑΓΩΓΗ ΣΤΑ ΣΗΜΑΤΑ Σκοπός του κεφαλαίου αυτού είναι να δώσει μια γενική εικόνα του τι είναι σήμα και να κατατάξει τα διάφορα σήματα σε κατηγορίες ανάλογα με τις βασικές ιδιότητες τους. Επίσης,
. ΚΕΦΑΛΑΙΟ ΕΙΣΑΓΩΓΗ ΣΤΑ ΣΗΜΑΤΑ Σκοπός του κεφαλαίου αυτού είναι να δώσει μια γενική εικόνα του τι είναι σήμα και να κατατάξει τα διάφορα σήματα σε κατηγορίες ανάλογα με τις βασικές ιδιότητες τους. Επίσης,
HMY 220: Σήματα και Συστήματα Ι
 Σύγκλιση Σειρών Fourier Ιδιότητες Σειρών Fourier Παραδείγματα HMY 220: Σήματα και Συστήματα Ι ΔΙΑΛΕΞΗ #10 Τρεις ισοδύναμες μορφές: () = = = = Σειρές Fourier j( 2π ) t Τ.. x () t FS a jω0t xt () = ae =
Σύγκλιση Σειρών Fourier Ιδιότητες Σειρών Fourier Παραδείγματα HMY 220: Σήματα και Συστήματα Ι ΔΙΑΛΕΞΗ #10 Τρεις ισοδύναμες μορφές: () = = = = Σειρές Fourier j( 2π ) t Τ.. x () t FS a jω0t xt () = ae =
6. Ορισμένο Ολοκλήρωμα
 6. Ορισμένο Ολοκλήρωμα 6. Γενικά Ορισμοί Έστω ότι η f() είναι συνεχής συνάρτηση ορισμένη σε ένα διάστημα [,]. Χωρίζουμε το διάστημα [,] σε n υποδιαστήματα επιλέγοντας n+ σημεία τέτοια ώστε = < < < n-
6. Ορισμένο Ολοκλήρωμα 6. Γενικά Ορισμοί Έστω ότι η f() είναι συνεχής συνάρτηση ορισμένη σε ένα διάστημα [,]. Χωρίζουμε το διάστημα [,] σε n υποδιαστήματα επιλέγοντας n+ σημεία τέτοια ώστε = < < < n-
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 Έντυπο Υποβολής Αξιολόγησης Γ.Ε. O φοιτητής συμπληρώνει την ενότητα «Υποβολή Εργασίας» και αποστέλλει το έντυπο σε δύο μη συρραμμένα αντίγραφα (ή ηλεκτρονικά) στον Καθηγητή-Σύμβουλο. Ο Καθηγητής-Σύμβουλος
Έντυπο Υποβολής Αξιολόγησης Γ.Ε. O φοιτητής συμπληρώνει την ενότητα «Υποβολή Εργασίας» και αποστέλλει το έντυπο σε δύο μη συρραμμένα αντίγραφα (ή ηλεκτρονικά) στον Καθηγητή-Σύμβουλο. Ο Καθηγητής-Σύμβουλος
Μαθηματική Εισαγωγή Συναρτήσεις
 Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας Διανύσματα Καστοριά,
Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας Διανύσματα Καστοριά,
HMY 220: Σήματα και Συστήματα Ι
 Σύγκλιση Σειρών Fourier Ιδιότητες Σειρών Fourier Παραδείγματα HMY 0: Σήματα και Συστήματα Ι ΔΙΑΛΕΞΗ #10 Σειρές Fourier: Προσέγγιση Οι Σειρές Fourier μπορούν να αναπαραστήσουν μια πολύ μεγάλη κλάση περιοδικών
Σύγκλιση Σειρών Fourier Ιδιότητες Σειρών Fourier Παραδείγματα HMY 0: Σήματα και Συστήματα Ι ΔΙΑΛΕΞΗ #10 Σειρές Fourier: Προσέγγιση Οι Σειρές Fourier μπορούν να αναπαραστήσουν μια πολύ μεγάλη κλάση περιοδικών
Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας. Εισηγητής Αναστάσιος Κεσίδης
 Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας Εισηγητής Αναστάσιος Κεσίδης Επεξεργασία στο πεδίο της συχνότητας Φασματικές τεχνικές Γενικά Τεχνικές αναπαράστασης και ανάλυσης
Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας Εισηγητής Αναστάσιος Κεσίδης Επεξεργασία στο πεδίο της συχνότητας Φασματικές τεχνικές Γενικά Τεχνικές αναπαράστασης και ανάλυσης
Μαθηματική Εισαγωγή Συναρτήσεις
 Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς Καστοριά, Ιούλιος 14 A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας
Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς Καστοριά, Ιούλιος 14 A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας
Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο
 Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο Σύνοψη Στο κεφάλαιο αυτό παρουσιάζεται η ιδέα του συμπτωτικού πολυωνύμου, του πολυωνύμου, δηλαδή, που είναι του μικρότερου δυνατού βαθμού και που, για συγκεκριμένες,
Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο Σύνοψη Στο κεφάλαιο αυτό παρουσιάζεται η ιδέα του συμπτωτικού πολυωνύμου, του πολυωνύμου, δηλαδή, που είναι του μικρότερου δυνατού βαθμού και που, για συγκεκριμένες,
Ανάλυση Ηλεκτρικών Κυκλωμάτων
 Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 11: Η ημιτονοειδής διέγερση Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 978-960-93-7110-0 κωδ. ΕΥΔΟΞΟΣ: 50657177
Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 11: Η ημιτονοειδής διέγερση Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 978-960-93-7110-0 κωδ. ΕΥΔΟΞΟΣ: 50657177
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ Θ.Ε. ΠΛΗ22 ( ) ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ #1 ΑΠΑΝΤΗΣΕΙΣ
 Θ.Ε. ΠΛΗ (0-3) ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ # ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Στόχος της άσκησης είναι η εξοικείωση με γραφικές παραστάσεις βασικών σημάτων και πράξεις, καθώς και τον υπολογισμό ΜΣ Fourier βασικών σημάτων με τη χρήση
Θ.Ε. ΠΛΗ (0-3) ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ # ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Στόχος της άσκησης είναι η εξοικείωση με γραφικές παραστάσεις βασικών σημάτων και πράξεις, καθώς και τον υπολογισμό ΜΣ Fourier βασικών σημάτων με τη χρήση
Βασικές Γνώσεις Μαθηματικών Α - Β Λυκείου
 Βασικές Γνώσεις Μαθηματικών Α - Β Λυκείου Αριθμοί 1. ΑΡΙΘΜΟΙ Σύνολο Φυσικών αριθμών: Σύνολο Ακέραιων αριθμών: Σύνολο Ρητών αριθμών: ακέραιοι με Άρρητοι αριθμοί: είναι οι μη ρητοί π.χ. Το σύνολο Πραγματικών
Βασικές Γνώσεις Μαθηματικών Α - Β Λυκείου Αριθμοί 1. ΑΡΙΘΜΟΙ Σύνολο Φυσικών αριθμών: Σύνολο Ακέραιων αριθμών: Σύνολο Ρητών αριθμών: ακέραιοι με Άρρητοι αριθμοί: είναι οι μη ρητοί π.χ. Το σύνολο Πραγματικών
Εισαγωγή στις Τηλεπικοινωνίες
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Ανάπτυξη σε Σειρές Furier Αθανάσιος Κανάτας
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Ανάπτυξη σε Σειρές Furier Αθανάσιος Κανάτας
Σήματα και Συστήματα. Διάλεξη 8: Ιδιότητες του Μετασχηματισμού Fourier. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 8: Ιδιότητες του Μετασχηματισμού ourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ιδιότητες του Μετασχηματισμού ourier 1. Ιδιότητες του Μετασχηματισμού ourier 2. Θεώρημα
Σήματα και Συστήματα Διάλεξη 8: Ιδιότητες του Μετασχηματισμού ourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ιδιότητες του Μετασχηματισμού ourier 1. Ιδιότητες του Μετασχηματισμού ourier 2. Θεώρημα
[1] είναι ταυτοτικά ίση με το μηδέν. Στην περίπτωση που το στήριγμα μιας συνάρτησης ελέγχου φ ( x)
![[1] είναι ταυτοτικά ίση με το μηδέν. Στην περίπτωση που το στήριγμα μιας συνάρτησης ελέγχου φ ( x) [1] είναι ταυτοτικά ίση με το μηδέν. Στην περίπτωση που το στήριγμα μιας συνάρτησης ελέγχου φ ( x)](/thumbs/52/30132893.jpg) [] 9 ΣΥΝΑΡΤΗΣΙΑΚΟΙ ΧΩΡΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER Η «συνάρτηση» δέλτα του irac Η «συνάρτηση» δέλτα ορίζεται μέσω της σχέσης φ (0) αν 0 δ[ φ ] = φ δ dx = (9) 0 αν 0 όπου η φ είναι μια συνάρτηση που ανήκει
[] 9 ΣΥΝΑΡΤΗΣΙΑΚΟΙ ΧΩΡΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER Η «συνάρτηση» δέλτα του irac Η «συνάρτηση» δέλτα ορίζεται μέσω της σχέσης φ (0) αν 0 δ[ φ ] = φ δ dx = (9) 0 αν 0 όπου η φ είναι μια συνάρτηση που ανήκει
Ο μετασχηματισμός Fourier
 Ο μετασχηματισμός Fourier είναι από τα διαδεδομένα εργαλεία μετατροπής δεδομένων και συναρτήσεων (μιας ή περισσοτέρων διαστάσεων) από αυτό που ονομάζεται περιοχή χρόνου (time domain) στην περιοχή συχνότητας
Ο μετασχηματισμός Fourier είναι από τα διαδεδομένα εργαλεία μετατροπής δεδομένων και συναρτήσεων (μιας ή περισσοτέρων διαστάσεων) από αυτό που ονομάζεται περιοχή χρόνου (time domain) στην περιοχή συχνότητας
Μέτρηση του όγκου και του εμβαδού ορθών πρισμάτων Κανονική Πυραμίδα 1 Βάσης) (Απόστημα) 2 1 ό Βάσης) (Ύψος) 3
 Βασικά σύνολα αριθμών -Σύνολο φυσικών: Ν = {0,., } ΤΥΠΟΛΟΓΙΟ ΜΑΘΗΜΑΤΙΚΩΝ -Σύνολο ακεραίων: Ζ= { -.-.0.,, } Συμβολίζουμε με ν=κ και τους άρτιους και τους περιττούς αντίστοιχα. * -Σύνολο ρητών: Q =, Z &
Βασικά σύνολα αριθμών -Σύνολο φυσικών: Ν = {0,., } ΤΥΠΟΛΟΓΙΟ ΜΑΘΗΜΑΤΙΚΩΝ -Σύνολο ακεραίων: Ζ= { -.-.0.,, } Συμβολίζουμε με ν=κ και τους άρτιους και τους περιττούς αντίστοιχα. * -Σύνολο ρητών: Q =, Z &
Σήματα και Συστήματα. Διάλεξη 7: Μετασχηματισμός Fourier. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 7: Μετασχηματισμός Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μετασχηματισμός Fourier 1. Ορισμός του Μετασχηματισμού Fourier 2. Φυσική Σημασία του Μετασχηματισμού
Σήματα και Συστήματα Διάλεξη 7: Μετασχηματισμός Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μετασχηματισμός Fourier 1. Ορισμός του Μετασχηματισμού Fourier 2. Φυσική Σημασία του Μετασχηματισμού
ΣΕΙΡΕΣ ΚΑΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ FOURIER. e ω. Το βασικό πρόβλημα στις σειρές Fourier είναι ο υπολογισμός των συντελεστών c
 ΣΕΙΡΕΣ ΚΑΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ FOURIER x(t+kτ) = x(t) = π/ω f = / x(t) = = 8 c j t e ω c = (a-jb ) Το βασικό πρόβλημα στις σειρές Fourier είναι ο υπολογισμός των συντελεστών c. Αυτός γίνεται κατορθωτός αν
ΣΕΙΡΕΣ ΚΑΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ FOURIER x(t+kτ) = x(t) = π/ω f = / x(t) = = 8 c j t e ω c = (a-jb ) Το βασικό πρόβλημα στις σειρές Fourier είναι ο υπολογισμός των συντελεστών c. Αυτός γίνεται κατορθωτός αν
x[n] = e u[n 1] 4 x[n] = u[n 1] 4 X(z) = z 1 H(z) = (1 0.5z 1 )(1 + 4z 2 ) z 2 (βʹ) H(z) = H min (z)h lin (z) 4 z 1 1 z 1 (z 1 4 )(z 1) (1)
![x[n] = e u[n 1] 4 x[n] = u[n 1] 4 X(z) = z 1 H(z) = (1 0.5z 1 )(1 + 4z 2 ) z 2 (βʹ) H(z) = H min (z)h lin (z) 4 z 1 1 z 1 (z 1 4 )(z 1) (1) x[n] = e u[n 1] 4 x[n] = u[n 1] 4 X(z) = z 1 H(z) = (1 0.5z 1 )(1 + 4z 2 ) z 2 (βʹ) H(z) = H min (z)h lin (z) 4 z 1 1 z 1 (z 1 4 )(z 1) (1)](/thumbs/61/45634776.jpg) Ασκήσεις με Συστήματα στο Χώρο του Ζ Επιμέλεια: Γιώργος Π. Καφεντζης Δρ. Επιστήμης Η/Υ Πανεπιστημίου Κρήτης Δρ. Επεξεργασίας Σήματος Πανεπιστημίου Rennes 1 7 Νοεμβρίου 015 1. Υπολόγισε τον μετ. Ζ και την
Ασκήσεις με Συστήματα στο Χώρο του Ζ Επιμέλεια: Γιώργος Π. Καφεντζης Δρ. Επιστήμης Η/Υ Πανεπιστημίου Κρήτης Δρ. Επεξεργασίας Σήματος Πανεπιστημίου Rennes 1 7 Νοεμβρίου 015 1. Υπολόγισε τον μετ. Ζ και την
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής Μετασχηματισμός Fourier Στο κεφάλαιο αυτό θα εισάγουμε και θα μελετήσουμε
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής Μετασχηματισμός Fourier Στο κεφάλαιο αυτό θα εισάγουμε και θα μελετήσουμε
Μιγαδική ανάλυση Μέρος Α Πρόχειρες σημειώσεις 1. Μιγαδικοί αριθμοί. ΤΕΤΥ Εφαρμοσμένα Μαθηματικά Μιγαδική Ανάλυση Α 1
 ΤΕΤΥ Εφαρμοσμένα Μαθηματικά Μιγαδική Ανάλυση Α 1 Μιγαδική ανάλυση Μέρος Α Πρόχειρες σημειώσεις 1 Μιγαδικοί αριθμοί Τι είναι και πώς τους αναπαριστούμε Οι μιγαδικοί αριθμοί είναι μια επέκταση του συνόλου
ΤΕΤΥ Εφαρμοσμένα Μαθηματικά Μιγαδική Ανάλυση Α 1 Μιγαδική ανάλυση Μέρος Α Πρόχειρες σημειώσεις 1 Μιγαδικοί αριθμοί Τι είναι και πώς τους αναπαριστούμε Οι μιγαδικοί αριθμοί είναι μια επέκταση του συνόλου
1ο Κεφάλαιο: Συστήματα
 ο Κεφάλαιο: Συστήματα Γραμμικά συστήματα i. Ποια εξίσωση λέγεται γραμμική; ii. Πως μεταβάλλεται η ευθεία y, 0 ή 0 για τις διάφορες τιμές των α,β,γ; iii. Τι ονομάζεται λύση μιας γραμμικής εξίσωσης; iv.
ο Κεφάλαιο: Συστήματα Γραμμικά συστήματα i. Ποια εξίσωση λέγεται γραμμική; ii. Πως μεταβάλλεται η ευθεία y, 0 ή 0 για τις διάφορες τιμές των α,β,γ; iii. Τι ονομάζεται λύση μιας γραμμικής εξίσωσης; iv.
. Σήματα και Συστήματα
 Σήματα και Συστήματα Βασίλειος Δαλάκας & Παναγιώτης Ριζομυλιώτης Τμήμα Πληροφορικής & Τηλεματικής Χαροκόπειο Πανεπιστήμιο Σήματα και Συστήματα 1/17 Πρόβλημα 1 (βιβλίο σελίδα 93) Να αποδειχθεί ότι: α) Κάθε
Σήματα και Συστήματα Βασίλειος Δαλάκας & Παναγιώτης Ριζομυλιώτης Τμήμα Πληροφορικής & Τηλεματικής Χαροκόπειο Πανεπιστήμιο Σήματα και Συστήματα 1/17 Πρόβλημα 1 (βιβλίο σελίδα 93) Να αποδειχθεί ότι: α) Κάθε
ΑΝΑΠΤΥΓΜA - ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ. Περιγράψουµε τον τρόπο ανάπτυξης σε σειρά Fourier ενός περιοδικού αναλογικού σήµατος.
 3. ΚΕΦΑΛΑΙΟ ΑΝΑΠΤΥΓΜA - ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ Περιγράψουµε τον τρόπο ανάπτυξης σε σειρά Fourier ενός περιοδικού αναλογικού σήµατος. Ορίσουµε το µετασχηµατισµό Fourier ενός µη περιοδικού
3. ΚΕΦΑΛΑΙΟ ΑΝΑΠΤΥΓΜA - ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ Περιγράψουµε τον τρόπο ανάπτυξης σε σειρά Fourier ενός περιοδικού αναλογικού σήµατος. Ορίσουµε το µετασχηµατισµό Fourier ενός µη περιοδικού
ΠΕΡΙΕΧΟΜΕΝΑ ΣΥΣΤΗΜΑΤΑ ΟΡΘΟΓΩΝΙΩΝ ΣΥΝΤΕΤΑΓΜΕΝΩΝ...23 ΑΠΟΛΥΤΗ ΤΙΜΗ. ΑΝΙΣΟΤΗΤΕΣ...15 ΚΕΦΑΛΑΙΟ 3 ΕΥΘΕΙΕΣ...32 ΚΕΦΑΛΑΙΟ 4 ΚΥΚΛΟΙ...43
 ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟ ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΩΝ ΣΥΝΤΕΤΑΓΜΕΝΩΝ. ΑΠΟΛΥΤΗ ΤΙΜΗ. ΑΝΙΣΟΤΗΤΕΣ...5 ΚΕΦΑΛΑΙΟ ΣΥΣΤΗΜΑΤΑ ΟΡΘΟΓΩΝΙΩΝ ΣΥΝΤΕΤΑΓΜΕΝΩΝ... ΚΕΦΑΛΑΙΟ ΕΥΘΕΙΕΣ... ΚΕΦΑΛΑΙΟ 4 ΚΥΚΛΟΙ...4 ΚΕΦΑΛΑΙΟ 5 ΕΞΙΣΩΣΕΙΣ ΚΑΙ ΟΙ
ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟ ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΩΝ ΣΥΝΤΕΤΑΓΜΕΝΩΝ. ΑΠΟΛΥΤΗ ΤΙΜΗ. ΑΝΙΣΟΤΗΤΕΣ...5 ΚΕΦΑΛΑΙΟ ΣΥΣΤΗΜΑΤΑ ΟΡΘΟΓΩΝΙΩΝ ΣΥΝΤΕΤΑΓΜΕΝΩΝ... ΚΕΦΑΛΑΙΟ ΕΥΘΕΙΕΣ... ΚΕΦΑΛΑΙΟ 4 ΚΥΚΛΟΙ...4 ΚΕΦΑΛΑΙΟ 5 ΕΞΙΣΩΣΕΙΣ ΚΑΙ ΟΙ
7. ΑΝΩΜΑΛΑ ΣΗΜΕΙΑ, ΠΟΛΟΙ ΚΑΙ ΤΟ ΘΕΩΡΗΜΑ ΤΩΝ ΟΛΟΚΛΗΡΩΤΙΚΩΝ ΥΠΟΛΟΙΠΩΝ. και σε κάθε γειτονιά του z
 7. ΑΝΩΜΑΛΑ ΣΗΜΕΙΑ, ΠΟΛΟΙ ΚΑΙ ΤΟ ΘΕΩΡΗΜΑ ΤΩΝ ΟΛΟΚΛΗΡΩΤΙΚΩΝ ΥΠΟΛΟΙΠΩΝ Ένα σημείο λέγεται ανώμαλο σημείο της συνάρτησης f( ) αν η f( ) δεν είναι αναλυτική στο και σε κάθε γειτονιά του υπάρχει ένα τουλάχιστον
7. ΑΝΩΜΑΛΑ ΣΗΜΕΙΑ, ΠΟΛΟΙ ΚΑΙ ΤΟ ΘΕΩΡΗΜΑ ΤΩΝ ΟΛΟΚΛΗΡΩΤΙΚΩΝ ΥΠΟΛΟΙΠΩΝ Ένα σημείο λέγεται ανώμαλο σημείο της συνάρτησης f( ) αν η f( ) δεν είναι αναλυτική στο και σε κάθε γειτονιά του υπάρχει ένα τουλάχιστον
ΘΕΜΑΤΑ ΚΑΙ ΑΣΚΗΣΕΙΣ ΓΙΑ «ΜΑΘΗΜΑΤΙΚΑ ΙΙ» ΑΚΟΛΟΥΘΙΕΣ ΚΑΙ ΟΡΙΑ ΑΚΟΛΟΥΘΙΩΝ. lim. (β) n +
 ΘΕΜΑΤΑ ΚΑΙ ΑΣΚΗΣΕΙΣ ΓΙΑ «ΜΑΘΗΜΑΤΙΚΑ ΙΙ» ΑΚΟΛΟΥΘΙΕΣ ΚΑΙ ΟΡΙΑ ΑΚΟΛΟΥΘΙΩΝ ) Να υπολογιστούν τα όρια των κάτωθι ακολουθιών με : (α) + 5 + 7 + + (β) + 5 + + (γ) + + + (δ) ( 5 ) + + 4 + ( ) + 5 ) Να βρεθούν
ΘΕΜΑΤΑ ΚΑΙ ΑΣΚΗΣΕΙΣ ΓΙΑ «ΜΑΘΗΜΑΤΙΚΑ ΙΙ» ΑΚΟΛΟΥΘΙΕΣ ΚΑΙ ΟΡΙΑ ΑΚΟΛΟΥΘΙΩΝ ) Να υπολογιστούν τα όρια των κάτωθι ακολουθιών με : (α) + 5 + 7 + + (β) + 5 + + (γ) + + + (δ) ( 5 ) + + 4 + ( ) + 5 ) Να βρεθούν
3.4 ΟΙ ΤΡΙΓΩΝΟΜΕΤΡΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ
 3.4 ΟΙ ΤΡΙΓΩΝΟΜΕΤΡΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Μια συνάρτηση με πεδίο ορισμού το σύνολο Α, λέγεται περιοδική, όταν υπάρχει πραγματικός αριθμός Τ>0 τέτοιος, ώστε για κάθε να ισχύει ότι και ( ) και ( ). Ο αριθμός Τ
3.4 ΟΙ ΤΡΙΓΩΝΟΜΕΤΡΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Μια συνάρτηση με πεδίο ορισμού το σύνολο Α, λέγεται περιοδική, όταν υπάρχει πραγματικός αριθμός Τ>0 τέτοιος, ώστε για κάθε να ισχύει ότι και ( ) και ( ). Ο αριθμός Τ
HMY 220: Σήματα και Συστήματα Ι
 HMY 22: Σήματα και Συστήματα Ι ΔΙΑΛΕΞΗ # Αναπαράσταση περιοδικών σημάτων με μιγαδικά εκθετικά σήματα: Οι σειρές Fourier Υπολογισμός συντελεστών Fourier Ανάλυση σημάτων σε μιγαδικά εκθετικά σήματα Είδαμε
HMY 22: Σήματα και Συστήματα Ι ΔΙΑΛΕΞΗ # Αναπαράσταση περιοδικών σημάτων με μιγαδικά εκθετικά σήματα: Οι σειρές Fourier Υπολογισμός συντελεστών Fourier Ανάλυση σημάτων σε μιγαδικά εκθετικά σήματα Είδαμε
. Όλες οι συναρτήσεις δεν μπορούν να παρασταθούν στο καρτεσιανό επίπεδο όπως για παράδειγμα η συνάρτηση του Dirichlet:
 Κεφάλαιο: Συναρτήσεις Γραφική παράσταση συνάρτησης Γράφημα μιας συνάρτησης ( ) ονομάζουμε το σύνολο των σημείων G( ) (, ( ) ) / A που είναι υποσύνολο του. Το γράφημα αυτό { } συνήθως παριστάνεται πάνω
Κεφάλαιο: Συναρτήσεις Γραφική παράσταση συνάρτησης Γράφημα μιας συνάρτησης ( ) ονομάζουμε το σύνολο των σημείων G( ) (, ( ) ) / A που είναι υποσύνολο του. Το γράφημα αυτό { } συνήθως παριστάνεται πάνω
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Αντίστροφος Μετασχηματισμός Laplace Στην
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Αντίστροφος Μετασχηματισμός Laplace Στην
Τριγωνομετρικά πολυώνυμα
 Κεφάλαιο Τριγωνομετρικά πολυώνυμα Κύριες βιβλιογραφικές αναφορές για αυτό το Κεφάλαιο είναι οι Zygmund, Katznelson 4 και Stein and Shakarchi.. Μερικά βασικά περί μιγαδικών αριθμών Υποθέτουμε ως γνωστές
Κεφάλαιο Τριγωνομετρικά πολυώνυμα Κύριες βιβλιογραφικές αναφορές για αυτό το Κεφάλαιο είναι οι Zygmund, Katznelson 4 και Stein and Shakarchi.. Μερικά βασικά περί μιγαδικών αριθμών Υποθέτουμε ως γνωστές
Κεφάλαιο 6 : Φασματική Ανάλυση Σημάτων Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 6 : Φασματική Ανάλυση Σημάτων Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Φασματική Αάλ Ανάλυση Περιοδικών Σημάτων (Μιγαδικέςδ έ Σειρές
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 6 : Φασματική Ανάλυση Σημάτων Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Φασματική Αάλ Ανάλυση Περιοδικών Σημάτων (Μιγαδικέςδ έ Σειρές
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής Φυσική Σημασία του Μετασχηματισμού Fourier Ο μετασχηματισμός Fourier
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής Φυσική Σημασία του Μετασχηματισμού Fourier Ο μετασχηματισμός Fourier
ΚΕΦΑΛΑΙΟ 3 ο ΣΥΝΑΡΤΗΣΕΙΣ, ΤΡΙΓΩΝΟΜΕΤΡΙΑ( FUNCTIONS,TRIGONOMETRY)
 ΚΕΦΑΛΑΙΟ 3 ο ΣΥΝΑΡΤΗΣΕΙΣ, ΤΡΙΓΩΝΟΜΕΤΡΙΑ( FUNCTIONS,TRIGONOMETRY) 3.1 ΘΕΩΡΙΑ-ΤΥΠΟΛΟΓΙΟ-ΠΑΡΑΔΕΙΓΜΑΤΑ ΣΥΝΑΡΤΗΣΕΙΣ Συνάρτηση, ή απεικόνιση όπως ονομάζεται διαφορετικά, είναι μια αντιστοίχιση μεταξύ δύο συνόλων,
ΚΕΦΑΛΑΙΟ 3 ο ΣΥΝΑΡΤΗΣΕΙΣ, ΤΡΙΓΩΝΟΜΕΤΡΙΑ( FUNCTIONS,TRIGONOMETRY) 3.1 ΘΕΩΡΙΑ-ΤΥΠΟΛΟΓΙΟ-ΠΑΡΑΔΕΙΓΜΑΤΑ ΣΥΝΑΡΤΗΣΕΙΣ Συνάρτηση, ή απεικόνιση όπως ονομάζεται διαφορετικά, είναι μια αντιστοίχιση μεταξύ δύο συνόλων,
ΑΡΧΕΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΑΡΧΕΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Ενότητα #1: Περιοδικά σήματα, τριγωνομετρικές σειρές περιοδικών σημάτων Χ. ΚΑΡΑΪΣΚΟΣ Τμήμα Μηχανικών Αυτοματισμού
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΑΡΧΕΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Ενότητα #1: Περιοδικά σήματα, τριγωνομετρικές σειρές περιοδικών σημάτων Χ. ΚΑΡΑΪΣΚΟΣ Τμήμα Μηχανικών Αυτοματισμού
Ψηφιακή Επεξεργασία Σημάτων
 Ψηφιακή Επεξεργασία Σημάτων Ενότητα 1: Σήματα Διακριτού Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Σήματα Διακριτού Χρόνου Εισαγωγή Διαφορές Αναλογικής Ψηφιακής Επεξεργασίας Παραγωγή Ψηφιακών
Ψηφιακή Επεξεργασία Σημάτων Ενότητα 1: Σήματα Διακριτού Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Σήματα Διακριτού Χρόνου Εισαγωγή Διαφορές Αναλογικής Ψηφιακής Επεξεργασίας Παραγωγή Ψηφιακών
x + ax x x 4 να είναι παραγωγίσιμη στο x Υπόδειξη: Μπορείτε να εφαρμόσετε κανόνα L Hospital ή μπορεί σας χρειαστεί η sin sin = 2sin cos
 http://lar.maths.gr/, maths@maths.gr, Τηλ: 69795 Ενδεικτικές απαντήσεις ης Γραπτής Εργασίας ΠΛΗ -: Άσκηση. (5 μονάδες) i) ( μονάδες) Υπολογίστε την παράγωγο για κάθε μία από τις επόμενες συναρτήσεις: a)
http://lar.maths.gr/, maths@maths.gr, Τηλ: 69795 Ενδεικτικές απαντήσεις ης Γραπτής Εργασίας ΠΛΗ -: Άσκηση. (5 μονάδες) i) ( μονάδες) Υπολογίστε την παράγωγο για κάθε μία από τις επόμενες συναρτήσεις: a)
ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ 2014
 ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ 4 ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ Α Α Έστω μία συνάρτηση f η οποία είναι συνεχής σε ένα διάστημα Δ. Αν f σε κάθε εσωτερικό σημείο
ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ 4 ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ Α Α Έστω μία συνάρτηση f η οποία είναι συνεχής σε ένα διάστημα Δ. Αν f σε κάθε εσωτερικό σημείο
Παράδειγμα 14.2 Να βρεθεί ο μετασχηματισμός Laplace των συναρτήσεων
 Κεφάλαιο 4 Μετασχηματισμός aplace 4. Μετασχηματισμός aplace της εκθετικής συνάρτησης e Είναι Άρα a a a u( a ( a ( a ( aj F( e e d e d [ e ] [ e ] ( a e (c ji, με a (4.9 a a a [ e u( ] a, με a (4.3 Η σχέση
Κεφάλαιο 4 Μετασχηματισμός aplace 4. Μετασχηματισμός aplace της εκθετικής συνάρτησης e Είναι Άρα a a a u( a ( a ( a ( aj F( e e d e d [ e ] [ e ] ( a e (c ji, με a (4.9 a a a [ e u( ] a, με a (4.3 Η σχέση
Εναλλασσόμενο και μιγαδικοί
 (olts) Εναλλασσόμενο και μιγαδικοί Γενικά Σε κυκλώματα DC, οι ηλεκτρικές μεγέθη εξαρτώνται αποκλειστικά από τις ωμικές αντιστάσεις, φυσικά μετά την ολοκλήρωση πιθανών μεταβατικών φαινομένων λόγω παρουσίας
(olts) Εναλλασσόμενο και μιγαδικοί Γενικά Σε κυκλώματα DC, οι ηλεκτρικές μεγέθη εξαρτώνται αποκλειστικά από τις ωμικές αντιστάσεις, φυσικά μετά την ολοκλήρωση πιθανών μεταβατικών φαινομένων λόγω παρουσίας
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΗΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΗΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ Ενότητα 1, Μέρος 2ο: ΠΕΡΙ ΣΗΜΑΤΩΝ Aναστασία Βελώνη Τμήμα Η.Υ.Σ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΗΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ Ενότητα 1, Μέρος 2ο: ΠΕΡΙ ΣΗΜΑΤΩΝ Aναστασία Βελώνη Τμήμα Η.Υ.Σ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Οι σειρές Fourier. Eισαγωγικές Επισημάνσεις
 παραρτημα Α Οι σειρές Fourier Μέρος (Ι) Eισαγωγικές Επισημάνσεις Ο Γάλλος μαθηματικός Jean Baptist Fourier μελετώντας την διάδοση της θερμότητας στα στερεά σώματα και στην προσπάθειά του να δώσει σε κλειστή
παραρτημα Α Οι σειρές Fourier Μέρος (Ι) Eισαγωγικές Επισημάνσεις Ο Γάλλος μαθηματικός Jean Baptist Fourier μελετώντας την διάδοση της θερμότητας στα στερεά σώματα και στην προσπάθειά του να δώσει σε κλειστή
ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ
 Ο ΚΕΦΑΛΑΙΟ : ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΑΡΧΙΚΗ ΣΥΝΑΡΤΗΣΗ 6 Τι ονομάζουμε αρχική μιας συνάρτησης σε ένα διάστημα Δ ; Απάντηση : Αρχική συνάρτηση ή παράγουσα της στο Δ ονομάζουμε κάθε
Ο ΚΕΦΑΛΑΙΟ : ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΑΡΧΙΚΗ ΣΥΝΑΡΤΗΣΗ 6 Τι ονομάζουμε αρχική μιας συνάρτησης σε ένα διάστημα Δ ; Απάντηση : Αρχική συνάρτηση ή παράγουσα της στο Δ ονομάζουμε κάθε
Ο μετασχηματισμός Fourier
 Ο μετασχηματισμός Fourier είναι από τα διαδεδομένα εργαλεία μετατροπής δεδομένων και συναρτήσεων (μιας ή περισσοτέρων διαστάσεων) από αυτό που ονομάζεται περιοχή χρόνου (time domain) στην περιοχή συχνότητας
Ο μετασχηματισμός Fourier είναι από τα διαδεδομένα εργαλεία μετατροπής δεδομένων και συναρτήσεων (μιας ή περισσοτέρων διαστάσεων) από αυτό που ονομάζεται περιοχή χρόνου (time domain) στην περιοχή συχνότητας
ΣΗΜΕΙΩΣΕΙΣ. Από προηγούμενες τάξεις γνωρίζουμε ότι το τετράγωνο οποιουδήποτε πραγματικού αριθμού
 ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i ΙΔΙΟΤΗΤΕΣ
ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i ΙΔΙΟΤΗΤΕΣ
ΑΝΑΠΤΥΓΜA - ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ. Περιγράψουμε τον τρόπο ανάπτυξης σε σειρά Fourier ενός περιοδικού αναλογικού σήματος.
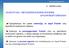 3. ΚΕΦΑΛΑΙΟ ΑΝΑΠΤΥΓΜA - ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ OURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ Περιγράψουμε τον τρόπο ανάπτυξης σε σειρά ourir ενός περιοδικού αναλογικού σήματος. Ορίσουμε το μετασχηματισμό ourir ενός μη περιοδικού
3. ΚΕΦΑΛΑΙΟ ΑΝΑΠΤΥΓΜA - ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ OURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ Περιγράψουμε τον τρόπο ανάπτυξης σε σειρά ourir ενός περιοδικού αναλογικού σήματος. Ορίσουμε το μετασχηματισμό ourir ενός μη περιοδικού
0 0 30 π/6 45 π/4 60 π/3 90 π/2
 Βασικός Πίνακας Μοίρες (Degrees) Ακτίνια (Radians) ΓΩΝΙΕΣ 0 0 30 π/6 45 π/4 60 π/3 90 π/2 Έστω ότι θέλω να μετατρέψω μοίρες σε ακτίνια : Έχω μία γωνία σε φ μοίρες. Για να την κάνω σε ακτίνια, πολλαπλασιάζω
Βασικός Πίνακας Μοίρες (Degrees) Ακτίνια (Radians) ΓΩΝΙΕΣ 0 0 30 π/6 45 π/4 60 π/3 90 π/2 Έστω ότι θέλω να μετατρέψω μοίρες σε ακτίνια : Έχω μία γωνία σε φ μοίρες. Για να την κάνω σε ακτίνια, πολλαπλασιάζω
Στοχαστικές Μέθοδοι στους Υδατικούς Πόρους Φασματική ανάλυση χρονοσειρών
 Στοχαστικές Μέθοδοι στους Υδατικούς Πόρους Φασματική ανάλυση χρονοσειρών Δημήτρης Κουτσογιάννης Τομέας Υδατικών Πόρων και Περιβάλλοντος, Σχολή Πολιτικών Μηχανικών, Εθνικό Μετσόβιο Πολυτεχνείο Αθήνα Επανέκδοση
Στοχαστικές Μέθοδοι στους Υδατικούς Πόρους Φασματική ανάλυση χρονοσειρών Δημήτρης Κουτσογιάννης Τομέας Υδατικών Πόρων και Περιβάλλοντος, Σχολή Πολιτικών Μηχανικών, Εθνικό Μετσόβιο Πολυτεχνείο Αθήνα Επανέκδοση
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Αντίστροφος Μετασχηματισμός Laplace Στην
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Αντίστροφος Μετασχηματισμός Laplace Στην
Κλασική Ηλεκτροδυναμική Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΤΕΧΝΙΚΕΣ ΥΠΟΛΟΓΙΣΜΟΥ ΗΛΕΚΤΡΙΚΟΥ ΔΥΝΑΜΙΚΟΥ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΤΕΧΝΙΚΕΣ ΥΠΟΛΟΓΙΣΜΟΥ ΗΛΕΚΤΡΙΚΟΥ ΔΥΝΑΜΙΚΟΥ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Ι
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Ι Σήματα και Συστήματα στο Πεδίο της Επιμέλεια: Αθανάσιος N. Σκόδρας, Καθηγητής Γεώργιος Α. Βασκαντήρας, Υπ. Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών & Τεχνολογίας Υπολογιστών Άδειες
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Ι Σήματα και Συστήματα στο Πεδίο της Επιμέλεια: Αθανάσιος N. Σκόδρας, Καθηγητής Γεώργιος Α. Βασκαντήρας, Υπ. Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών & Τεχνολογίας Υπολογιστών Άδειες
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (Θ.Ε. ΠΛΗ ) 5 η ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ Ημερομηνία Ανάρτησης Μαρτίου 4 Ημερομηνία Παράδοσης της εργασίας από τον Φοιτητή Απριλίου 4 Πριν
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (Θ.Ε. ΠΛΗ ) 5 η ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ Ημερομηνία Ανάρτησης Μαρτίου 4 Ημερομηνία Παράδοσης της εργασίας από τον Φοιτητή Απριλίου 4 Πριν
Σήματα και Συστήματα
 Σήματα και Συστήματα Διάλεξη 12: Ιδιότητες του Μετασχηματισμού aplace Ο αντίστροφος Μετασχηματισμός aplace Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ιδιότητες του Μετασχηματισμού aplace 1. Ιδιότητες
Σήματα και Συστήματα Διάλεξη 12: Ιδιότητες του Μετασχηματισμού aplace Ο αντίστροφος Μετασχηματισμός aplace Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ιδιότητες του Μετασχηματισμού aplace 1. Ιδιότητες
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ. Θ.Ε. ΠΛΗ22 ( ) 1η Γραπτή Εργασία
 Θ.Ε. ΠΛΗ22 (2012-13) 1η Γραπτή Εργασία ΕΚΦΩΝΗΣΕΙΣ (έκδοση v2 με διόρθωση του ερωτήματος 4δ) Στόχος: Βασικό στόχο της 1 ης εργασίας αποτελεί η εξοικείωση με τις διαφορετικές κατηγορίες σημάτων, η περιγραφή
Θ.Ε. ΠΛΗ22 (2012-13) 1η Γραπτή Εργασία ΕΚΦΩΝΗΣΕΙΣ (έκδοση v2 με διόρθωση του ερωτήματος 4δ) Στόχος: Βασικό στόχο της 1 ης εργασίας αποτελεί η εξοικείωση με τις διαφορετικές κατηγορίες σημάτων, η περιγραφή
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΓΕΝΙΚΟ ΤΜΗΜΑ
 ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΓΕΝΙΚΟ ΤΜΗΜΑ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΕΦΑΡΜΟΣΜΕΝΕΣ ΕΠΙΣΤΗΜΕΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑ ΔΙΠΛΩΜΑΤΙΚΗ ΔΙΑΤΡΙΒΗ ΜΕΤΑΠΤΥΧΙΑΚΟΥ ΔΙΠΛΩΜΑΤΟΣ ΕΙΔΙΚΕΥΣΗΣ ΚΑΤΕΥΘΥΝΣΗ : «ΕΦΑΡΜΟΣΜΕΝΑ ΚΑΙ ΥΠΟΛΟΓΙΣΤΙΚΑ
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΓΕΝΙΚΟ ΤΜΗΜΑ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΕΦΑΡΜΟΣΜΕΝΕΣ ΕΠΙΣΤΗΜΕΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑ ΔΙΠΛΩΜΑΤΙΚΗ ΔΙΑΤΡΙΒΗ ΜΕΤΑΠΤΥΧΙΑΚΟΥ ΔΙΠΛΩΜΑΤΟΣ ΕΙΔΙΚΕΥΣΗΣ ΚΑΤΕΥΘΥΝΣΗ : «ΕΦΑΡΜΟΣΜΕΝΑ ΚΑΙ ΥΠΟΛΟΓΙΣΤΙΚΑ
Κεφάλαιο 5 Γραμμικοί Μετασχηματισμοί
 Κεφάλαιο 5 Γραμμικοί Μετασχηματισμοί 5 Γενικά Γραμμικοί Μετασχηματισμοί Μία σχέση μεταξύ των στοιχείων δύο συνόλων Α,Β αντιστοιχίζει στοιχεία του Α με στοιχεία του Β άλλου μέσω ενός κανόνα που μπορεί να
Κεφάλαιο 5 Γραμμικοί Μετασχηματισμοί 5 Γενικά Γραμμικοί Μετασχηματισμοί Μία σχέση μεταξύ των στοιχείων δύο συνόλων Α,Β αντιστοιχίζει στοιχεία του Α με στοιχεία του Β άλλου μέσω ενός κανόνα που μπορεί να
α. Σύνδεση δύο απλών αρμονικών ταλαντώσεων ίδιας συχνότητας και ίδιας διεύθυνσης, οι οποίες
 ΣΥΝΘΕΣΗ ΤΑΛΑΝΤΩΣΕΩΝ α. Σύνδεση δύο απλών αρμονικών ταλαντώσεων ίδιας συχνότητας και ίδιας διεύθυνσης, οι οποίες εξελίσσονται γύρω από την ίδια δέση ισορροπίας Έστω ότι ένα σώμα εκτελεί ταυτόχρονα δύο απλές
ΣΥΝΘΕΣΗ ΤΑΛΑΝΤΩΣΕΩΝ α. Σύνδεση δύο απλών αρμονικών ταλαντώσεων ίδιας συχνότητας και ίδιας διεύθυνσης, οι οποίες εξελίσσονται γύρω από την ίδια δέση ισορροπίας Έστω ότι ένα σώμα εκτελεί ταυτόχρονα δύο απλές
Ανάλυση Ηλεκτρικών Κυκλωμάτων
 Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 13: Ισχύς σε κυκλώματα ημιτονοειδούς διέγερσης Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 9789609371100 κωδ.
Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 13: Ισχύς σε κυκλώματα ημιτονοειδούς διέγερσης Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 9789609371100 κωδ.
Ημερομηνία: Παρασκευή 28 Οκτωβρίου 2016 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ
 ΤΑΞΗ: ΜΑΘΗΜΑ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ Ημερομηνία: Παρασκευή 8 Οκτωβρίου 016 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α Α1. Να δώσετε τους ορισμούς των: α) Γνησίως φθίνουσα συνάρτηση β) Ολικό ελάχιστο
ΤΑΞΗ: ΜΑΘΗΜΑ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ Ημερομηνία: Παρασκευή 8 Οκτωβρίου 016 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α Α1. Να δώσετε τους ορισμούς των: α) Γνησίως φθίνουσα συνάρτηση β) Ολικό ελάχιστο
Μιγαδικοί Αριθμοί. Μαθηματικά Γ! Λυκείου Θετική και Τεχνολογική Κατεύθυνση. Υποδειγματικά λυμένες ασκήσεις Ασκήσεις προς λύση
 Μιγαδικοί Αριθμοί Μαθηματικά Γ! Λυκείου Θετική και Τεχνολογική Κατεύθυνση Υποδειγματικά λυμένες ασκήσεις Ασκήσεις προς λύση ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Υποδειγματικά Λυμένες Ασκήσεις Άλυτες Ασκήσεις ΛΑ Να βρείτε
Μιγαδικοί Αριθμοί Μαθηματικά Γ! Λυκείου Θετική και Τεχνολογική Κατεύθυνση Υποδειγματικά λυμένες ασκήσεις Ασκήσεις προς λύση ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Υποδειγματικά Λυμένες Ασκήσεις Άλυτες Ασκήσεις ΛΑ Να βρείτε
Η ΣΕΙΡΑ FOURIER ΚΑΙ Ο ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΥΣΗ ΣΗΜΑΤΩΝ ΩΣ ΠΡΟΣ ΗΜΙΤΟΝΙΚΕΣ ΣΥΝΙΣΤΩΣΕΣ. xt A t A t A t t
 Η ΣΕΙΡΑ FOURIER ΚΑΙ Ο ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΥΣΗ ΣΗΜΑΤΩΝ ΩΣ ΠΡΟΣ ΗΜΙΤΟΝΙΚΕΣ ΣΥΝΙΣΤΩΣΕΣ Θεωρήστε ένα σήµα συνεχούς χρόνου το οποίο είναι άθροισµα συνηµιτονικών όρων της µορφής () = cos( ω + ϕ ) + cos
Η ΣΕΙΡΑ FOURIER ΚΑΙ Ο ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΥΣΗ ΣΗΜΑΤΩΝ ΩΣ ΠΡΟΣ ΗΜΙΤΟΝΙΚΕΣ ΣΥΝΙΣΤΩΣΕΣ Θεωρήστε ένα σήµα συνεχούς χρόνου το οποίο είναι άθροισµα συνηµιτονικών όρων της µορφής () = cos( ω + ϕ ) + cos
Μιγαδικός λογισμός και ολοκληρωτικοί Μετασχηματισμοί
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μιγαδικός λογισμός και ολοκληρωτικοί Μετασχηματισμοί ΣΥΝΑΡΤΗΣΙΑΚΟΙ ΧΩΡΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER Διδάσκων : Επίκ Καθ Κολάσης Χαράλαμπος Άδειες Χρήσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μιγαδικός λογισμός και ολοκληρωτικοί Μετασχηματισμοί ΣΥΝΑΡΤΗΣΙΑΚΟΙ ΧΩΡΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER Διδάσκων : Επίκ Καθ Κολάσης Χαράλαμπος Άδειες Χρήσης
x(t) = sin 2 (5πt) cos(22πt) = x 2 (t)dt
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 6-7 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λυµένες Ασκήσεις - Σειρές Fourier. Εστω το σήµα xt
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 6-7 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λυµένες Ασκήσεις - Σειρές Fourier. Εστω το σήµα xt
X = συνεχης. Είναι εμφανές ότι αναγκαία προϋπόθεση για την ύπαρξη της ροπογεννήτριας
 Ροπογεννήτριες (mome geerig fucios), πιθανογεννήτριες (robbiliy geerig fucios) και χαρακτηριστικές συναρτήσεις (chrcerisic fucios) Η ροπογεννήτρια συνάρτηση της τμ είναι η πραγματική συνάρτηση πραγματικής
Ροπογεννήτριες (mome geerig fucios), πιθανογεννήτριες (robbiliy geerig fucios) και χαρακτηριστικές συναρτήσεις (chrcerisic fucios) Η ροπογεννήτρια συνάρτηση της τμ είναι η πραγματική συνάρτηση πραγματικής
ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΟΜΑΔΕΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ : ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΡΟΛΟΓΟΣ Σε κάθε ενότητα αυτού του βιβλίου θα βρείτε : Βασική θεωρία με τη μορφή ερωτήσεων Μεθοδολογίες και σχόλια
ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΟΜΑΔΕΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ : ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΡΟΛΟΓΟΣ Σε κάθε ενότητα αυτού του βιβλίου θα βρείτε : Βασική θεωρία με τη μορφή ερωτήσεων Μεθοδολογίες και σχόλια
Για να εκφράσουμε τη διαδικασία αυτή, γράφουμε: :
 Η θεωρία στα μαθηματικά προσανατολισμού Γ υκείου Τι λέμε συνάρτηση με πεδίο ορισμού το σύνολο ; Έστω ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το μία διαδικασία (κανόνα), με την
Η θεωρία στα μαθηματικά προσανατολισμού Γ υκείου Τι λέμε συνάρτηση με πεδίο ορισμού το σύνολο ; Έστω ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το μία διαδικασία (κανόνα), με την
Μ Α Θ Η Μ Α Τ Α Γ Λ Υ Κ Ε Ι Ο Υ
 Μ Α Θ Η Μ Α Τ Α Γ Λ Υ Κ Ε Ι Ο Υ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ (Α ΜΕΡΟΣ: ΣΥΝΑΡΤΗΣΕΙΣ) Επιμέλεια: Καραγιάννης Ιωάννης, Σχολικός Σύμβουλος Μαθηματικών
Μ Α Θ Η Μ Α Τ Α Γ Λ Υ Κ Ε Ι Ο Υ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ (Α ΜΕΡΟΣ: ΣΥΝΑΡΤΗΣΕΙΣ) Επιμέλεια: Καραγιάννης Ιωάννης, Σχολικός Σύμβουλος Μαθηματικών
Ιατρικά Ηλεκτρονικά. Χρήσιμοι Σύνδεσμοι. ΙΑΤΡΙΚΑ ΗΛΕΚΤΡΟΝΙΚΑ - ΔΙΑΛΕΞΗ 5α. Σημειώσεις μαθήματος: E mail:
 Ιατρικά Ηλεκτρονικά Δρ. Π. Ασβεστάς Τμήμα Μηχανικών Βιοϊατρικής Τεχνολογίας Τ.Ε Χρήσιμοι Σύνδεσμοι Σημειώσεις μαθήματος: http://medisp.bme.teiath.gr/eclass/courses/tio127/ E mail: pasv@teiath.gr 2 1 Περιοδικά
Ιατρικά Ηλεκτρονικά Δρ. Π. Ασβεστάς Τμήμα Μηχανικών Βιοϊατρικής Τεχνολογίας Τ.Ε Χρήσιμοι Σύνδεσμοι Σημειώσεις μαθήματος: http://medisp.bme.teiath.gr/eclass/courses/tio127/ E mail: pasv@teiath.gr 2 1 Περιοδικά
Συστήµατα τα οποία χαρακτηρίζονται από γραµµικές εξισώσεις διαφορών µε σταθερούς συντελεστές
 Συστήµατα τα οποία χαρακτηρίζονται από γραµµικές εξισώσεις διαφορών µε σταθερούς συντελεστές x h γραµµική εξίσωση διαφορών µε σταθερούς συντελεστές της µορφής x µπορεί να θεωρηθεί ως ένας αλγόριθµος υπολογισµού
Συστήµατα τα οποία χαρακτηρίζονται από γραµµικές εξισώσεις διαφορών µε σταθερούς συντελεστές x h γραµµική εξίσωση διαφορών µε σταθερούς συντελεστές της µορφής x µπορεί να θεωρηθεί ως ένας αλγόριθµος υπολογισµού
Να υπολογίζουμε τους τριγωνομετρικούς αριθμούς οξείας γωνίας. Τη γωνία σε κανονική θέση και τους τριγωνομετρικούς αριθμούς γωνίας σε κανονική θέση.
 Ενότητα 4 Τριγωνομετρία Στην ενότητα αυτή θα μάθουμε: Να υπολογίζουμε τους τριγωνομετρικούς αριθμούς οξείας γωνίας. Τη γωνία σε κανονική θέση και τους τριγωνομετρικούς αριθμούς γωνίας σε κανονική θέση.
Ενότητα 4 Τριγωνομετρία Στην ενότητα αυτή θα μάθουμε: Να υπολογίζουμε τους τριγωνομετρικούς αριθμούς οξείας γωνίας. Τη γωνία σε κανονική θέση και τους τριγωνομετρικούς αριθμούς γωνίας σε κανονική θέση.
Κεφάλαιο 6 Ιδιοτιμές και Ιδιοδιανύσματα
 Κεφάλαιο 6 Ορισμοί Έστω Α ένας πίνακας με πραγματικά στοιχεία Ο πραγματικός ή μιγαδικός αριθμός λ καλείται ιδιοτιμή του πίνακα Α εάν υπάρχει μη μηδενικό διάνυσμα v με πραγματικά ή μιγαδικά στοιχεία τέτοιο
Κεφάλαιο 6 Ορισμοί Έστω Α ένας πίνακας με πραγματικά στοιχεία Ο πραγματικός ή μιγαδικός αριθμός λ καλείται ιδιοτιμή του πίνακα Α εάν υπάρχει μη μηδενικό διάνυσμα v με πραγματικά ή μιγαδικά στοιχεία τέτοιο
Οι Μιγαδικοί Αριθμοί
 Οι Μιγαδικοί Αριθμοί Οι μιγαδικοί αριθμοί αρχικά βοήθησαν στην επίλυση δευτεροβάθμιων εξισώσεων των οποίων η διακρίνουσα είναι αρνητική Το γενικότερο πρόβλημα βέβαια είναι ότι δεν υπάρχει πραγματικός αριθμός
Οι Μιγαδικοί Αριθμοί Οι μιγαδικοί αριθμοί αρχικά βοήθησαν στην επίλυση δευτεροβάθμιων εξισώσεων των οποίων η διακρίνουσα είναι αρνητική Το γενικότερο πρόβλημα βέβαια είναι ότι δεν υπάρχει πραγματικός αριθμός
Συναρτήσεις Θεωρία Ορισμοί - Παρατηρήσεις
 Συναρτήσεις Θεωρία Ορισμοί - Παρατηρήσεις Ορισμός: Έστω Α, Β R. Πραγματική συνάρτηση πραγματικής μεταβλητής από το σύνολο Α στο σύνολο Β ονομάζουμε την διαδικασία κατά την οποία κάθε στοιχείο του συνόλου
Συναρτήσεις Θεωρία Ορισμοί - Παρατηρήσεις Ορισμός: Έστω Α, Β R. Πραγματική συνάρτηση πραγματικής μεταβλητής από το σύνολο Α στο σύνολο Β ονομάζουμε την διαδικασία κατά την οποία κάθε στοιχείο του συνόλου
2.3 ΜΕΤΡΟ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ
 ΕΠΙΜΕΛΕΙΑ : ΠΑΛΑΙΟΛΟΓΟΥ ΠΑΥΛΟΣ.ptetragono.gr Σελίδα. ΜΕΤΡΟ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ Να βρεθεί το μέτρο των μιγαδικών :..... 0 0. 5 5 6.. 0 0. 5. 5 5 0 0 0 0 0 0 0 0 ΜΕΘΟΔΟΛΟΓΙΑ : ΜΕΤΡΟ ΜΙΓΑΔΙΚΟΥ Αν τότε. Αν χρειαστεί
ΕΠΙΜΕΛΕΙΑ : ΠΑΛΑΙΟΛΟΓΟΥ ΠΑΥΛΟΣ.ptetragono.gr Σελίδα. ΜΕΤΡΟ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ Να βρεθεί το μέτρο των μιγαδικών :..... 0 0. 5 5 6.. 0 0. 5. 5 5 0 0 0 0 0 0 0 0 ΜΕΘΟΔΟΛΟΓΙΑ : ΜΕΤΡΟ ΜΙΓΑΔΙΚΟΥ Αν τότε. Αν χρειαστεί
κι επιβάλλοντας τις συνοριακές συνθήκες παίρνουμε ότι θα πρέπει
 Πρόβλημα 22. Θεωρούμε το ακόλουθο πρόβλημα συνοριακών τιμών για τη εξίσωση του Laplace u + u = 0, 1 < < 1, 1 < < 1, u(, 1) = f(), u(, 1) = 0, u( 1, ) = 0, u(1, ) = 0. α) Σωστό ή λάθος; Αν f( ) = f() είναι
Πρόβλημα 22. Θεωρούμε το ακόλουθο πρόβλημα συνοριακών τιμών για τη εξίσωση του Laplace u + u = 0, 1 < < 1, 1 < < 1, u(, 1) = f(), u(, 1) = 0, u( 1, ) = 0, u(1, ) = 0. α) Σωστό ή λάθος; Αν f( ) = f() είναι
Σφαίρα σε ράγες: Η συνάρτηση Lagrange. Ν. Παναγιωτίδης
 Η Εξίσωση Euler-Lagrange Σφαίρα σε ράγες: Η συνάρτηση Lagrange Ν. Παναγιωτίδης Έστω σύστημα δυο συγκλινόντων ραγών σε σχήμα Χ που πάνω τους κυλίεται σφαίρα ακτίνας. Θεωρούμε σύστημα συντεταγμένων με οριζόντιους
Η Εξίσωση Euler-Lagrange Σφαίρα σε ράγες: Η συνάρτηση Lagrange Ν. Παναγιωτίδης Έστω σύστημα δυο συγκλινόντων ραγών σε σχήμα Χ που πάνω τους κυλίεται σφαίρα ακτίνας. Θεωρούμε σύστημα συντεταγμένων με οριζόντιους
Συστήµατα τα οποία χαρακτηρίζονται από γραµµικές εξισώσεις διαφορών µε σταθερούς συντελεστές
 Συστήµατα τα οποία χαρακτηρίζονται από γραµµικές εξισώσεις διαφορών µε σταθερούς συντελεστές x h γραµµική εξίσωση διαφορών µε σταθερούς συντελεστές της µορφής x µπορεί να θεωρηθεί ως ένας αλγόριθµος υπολογισµού
Συστήµατα τα οποία χαρακτηρίζονται από γραµµικές εξισώσεις διαφορών µε σταθερούς συντελεστές x h γραµµική εξίσωση διαφορών µε σταθερούς συντελεστές της µορφής x µπορεί να θεωρηθεί ως ένας αλγόριθµος υπολογισµού
ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΟΠΤΙΚΗΣ - ΟΠΤΟΗΛΕΚΤΡΟΝΙΚΗΣ & LASER ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ & Τ/Υ ΑΣΚΗΣΗ ΝΟ7 ΟΠΤΙΚΗ FOURIER. Γ. Μήτσου
 ΕΡΓΑΣΗΡΙΟ ΦΥΣΙΚΗΣ ΟΠΙΚΗΣ - ΟΠΟΗΛΕΚΡΟΝΙΚΗΣ & LASER ΜΗΜΑ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ & /Υ ΑΣΚΗΣΗ ΝΟ7 ΟΠΙΚΗ FOURIER Γ. Μήτσου Μάρτιος 8 Α. Θεωρία. Εισαγωγή Η επεξεργασία οπτικών δεδοµένων, το φιλτράρισµα χωρικών συχνοτήτων
ΕΡΓΑΣΗΡΙΟ ΦΥΣΙΚΗΣ ΟΠΙΚΗΣ - ΟΠΟΗΛΕΚΡΟΝΙΚΗΣ & LASER ΜΗΜΑ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ & /Υ ΑΣΚΗΣΗ ΝΟ7 ΟΠΙΚΗ FOURIER Γ. Μήτσου Μάρτιος 8 Α. Θεωρία. Εισαγωγή Η επεξεργασία οπτικών δεδοµένων, το φιλτράρισµα χωρικών συχνοτήτων
OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ
 Ο ΚΕΦΑΛΑΙΟ : ΟΡΙΟ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΣΥΝΑΡΤΗΣΕΙΣ Έστω Α ένα υποσύνολο του Τι ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α ; Απάντηση : ΕΣΠ Β Έστω
Ο ΚΕΦΑΛΑΙΟ : ΟΡΙΟ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΣΥΝΑΡΤΗΣΕΙΣ Έστω Α ένα υποσύνολο του Τι ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α ; Απάντηση : ΕΣΠ Β Έστω
f(x) = και στην συνέχεια
 ΕΡΩΤΗΣΕΙΣ ΜΑΘΗΤΩΝ Ερώτηση. Στις συναρτήσεις μπορούμε να μετασχηματίσουμε πρώτα τον τύπο τους και μετά να βρίσκουμε το πεδίο ορισμού τους; Όχι. Το πεδίο ορισμού της συνάρτησης το βρίσκουμε πριν μετασχηματίσουμε
ΕΡΩΤΗΣΕΙΣ ΜΑΘΗΤΩΝ Ερώτηση. Στις συναρτήσεις μπορούμε να μετασχηματίσουμε πρώτα τον τύπο τους και μετά να βρίσκουμε το πεδίο ορισμού τους; Όχι. Το πεδίο ορισμού της συνάρτησης το βρίσκουμε πριν μετασχηματίσουμε
Λύσεις Εξετάσεων Φεβρουαρίου Ακ. Έτους
 ΜΑΘΗΜΑΤΙΚΑ, 6-7 ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΕΠΙΚ. ΚΑΘ. ΣΤΑΥΡΟΣ ΤΟΥΜΠΗΣ Λύσεις Εξετάσεων Φεβρουαρίου Ακ. Έτους 6-7. Περιοδικές Συναρτήσεις) Έστω συνεχής συνάρτηση f : R R περιοδική
ΜΑΘΗΜΑΤΙΚΑ, 6-7 ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΕΠΙΚ. ΚΑΘ. ΣΤΑΥΡΟΣ ΤΟΥΜΠΗΣ Λύσεις Εξετάσεων Φεβρουαρίου Ακ. Έτους 6-7. Περιοδικές Συναρτήσεις) Έστω συνεχής συνάρτηση f : R R περιοδική
