hm 2,, , hm 2, A CTA GEO GRA PH ICA S IN ICA
|
|
|
- Άδωνις Αποστόλου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 A CTA GEO GRA PH ICA S IN ICA V o l. 53, N o. Jan., 998 (, 000) 9,,,,,,,,,,,,,,,,,,,,,, hm 2,,,,,,,, km 2, t, 74%, t, 872%,,,,, hm 2, 0 4 t 08 hm hm 2, : 99720; : China Academic Journal Electronic Publishing House. All rights reserved.
2 : hm 2, hm 2 (994 ) Ξ Tab Technology indices of coal-m in ing collapse in Yan teng- L ianghua i (994) ( ) ( 0 8 t) (km 2 ) ( 0 4 t) t (hm 2 ) ( 0 4 hm 2 ) (m ) (m ) (hm 2 ga) ( 0 4 hm 2 ) Ξ :, 200,,,,,,,, : (),,,, 3 mm gm 6 mm gm,,,,,,, 70% 2 m 20 m ; hm 2, 779%, 25 m 4 m, hm 2, (2),, 400 hm 2,, 85% 989, hm 2, hm % ; hm 2 ; China Academic Journal Electronic Publishing House. All rights reserved.
3 , hm 2, 000 hm 2, 0 000, hm 2, hm hm 2, 00,,,? (3),,,,, ;,,,, 4675%, 734%, 45% 0%, 204% 0%, 40% 70%,, (4), ; ( ) 77 km 2 27 m,,, 6 m 5 m 5 m, , 4 9,, , 994 7,,,,,,,, 2,,,,, 2, 045H 0 055H 0 (H 0 ) 300 m m 2,, ,, ; 4 8, ; 70% 90%,,,, 60% 70%, 2, 30% 50%, 3 ;,, China Academic Journal Electronic Publishing House. All rights reserved.
4 : 27 P (x, y ) T H (x ) x P, T S (x ), : T H = T H (x ) T S = T S (x ) (22) T H T S P f (x ) Υ (x ) k (x ), : f (x ) = d T H (x ) Υ(x ) = d2 dx P x T H : T H (x ) = T H o 2 Υ(x ) = - + Π 0 f (x ) = T H o 2ΠT H o x r dx 2 T H (x ) k (x ) = (x ) : e - t2 dt - + Π 0 e - Π( x ) 2 r - r x e - Π( x ) 2 r - T S (x ) = bt H o e - Π( x ) 2 r - e - Π(x - L ) 2 + H otan - Η Π k (x ) = - 2ΠbT H o y : x e - Π( x ) 2 r - T H o 2 x - T H (y ) = ( + Π 0 : k (y ) = - 2ΠbT H o Υ(y ) = - 2 f (y ) = T H o y e - Π( y ) 2 r - L 2ΠT H o y - d T S (x ) (222) dx,,, 08 09, b China Academic Journal Electronic Publishing House. All rights reserved. r2 x - x - L e - t2 dt (223) e - Π(x - L ) 2 (224) L 2 e - Π(x - L ) 2 (225) e - t2 dt - - Π x r e - Π(x - L ) 2 + T H otan - Η r e - Π( x r ) 2 - y r e - t2 dt) - ( + Π 0 e - Π( y ) 2 r - r y e - Π( y ) 2 r - T S (y ) = bt H o e - Π( y ) 2 r - e - Π(y - L ) 2 + T H otan- Η Π, P (x, y ) : 2 T H p (x, y ) = L r2 y - y - L - Π x - L e - 2 t dt r2 (226) e - Π(x - L ) 2 (227) e - t2 dt) (228) e - Π(y - L ) 2 (229) 2 L e - Π(y - L ) 2 (220) e - Π(y - L ) 2 + T H otan - Η r e - Π( y r ) 2 - r2 e - t2 dt - - Π y r - Π y - L e - Π(y - L ) 2 e - 2 t dt (22) (222) T H (x ) g T H (y ) (223) T H o (22) (223), T H o, b, r, L, Η h, Α, Q,, : = T H ogq co sα
5 , Η Α Α 22 T S (x, y, o) TV (x, y, o) T H (x, y, o) P (x, y, o),, P (x, y, o) T P (x, y, o) : T P (x, y, o) ) = T S (x, y, o) + TV (x, y, o) + T H (x, y, o) (224) T S (x, y, o) = - 4 hgπ 2 h ishθh i (Θh i+ chθh i+ + shθh i+ sinνl sinγl 2sinΝx co sγy dνdγ o (shθh ichθh i + Θh i) (shθh i+ chθh i+ + Θh i+ ) + G ( i - Χi+ ) G i+ ( - Χi) (sh2 Θh i - Θ 2 Γ 2 ) sh 2 Θh i+ Γ TV (x, y, o) = - 4 hgπ 2 h ishθh i (shθh i+ + Θh i+ chθh i+ ) sinνl sinγl 2co sνx sinγy dνdy o (shθh ichθh i + Θh i) (shθh i+ chθh i+ + Θh i+ ) + G ( i - Χi+ ) G i+ ( - Χi) (sh2 Θh i - Θ 2 h 2 i ) sh 2 Θh i+ Ν (225) (226) T H (x, y, o) = - 4 hgπ 2 (shθh i + Θh ichθh i) (shθh i+ chθh i+ + shθh i+ ) sinνl sinγl 2co sνx co sγyd ΝdΓ 0 (shθh ichθh i + Θh i) (shθh i+ chθh i+ + Θh i+ ) + G ( i - Χi+ ) G i+ ( - Χi) (sh2 Θh i - Θ 2 h 2 i ) sh 2 Θh i+ ΝΓ (227) (225) (227), h i, h i+ i i ; h, L, L 2 ; G i, Χi i ; G i+, Χi+ i ; Ν, Γ, Θ= Ν 2 + Γ 2 ; x, y,,,,,,,,,, (223) (224),, d = 5nco sαgkm Χ (n, Α, k, m, Χ,,, ) d 02 hm 2 g0 4 t 030 hm 2 g0 4 t China Academic Journal Electronic Publishing House. All rights reserved.
6 : 29 3,,,,,,,, 3,,, 70,,,,,,,,,,,,,, 0 8 t t ; ;, t t,,, 32,, 96%,,,,, ( ) ; 400 m, ;,, ;,,,, ;, ,,,,, China Academic Journal Electronic Publishing House. All rights reserved.
7 30 53,,,,,,,,,,, ( ), ;,,,, 34,,,,,,, ;,,,, 35,,, t 67, 8,,,,, ;, ; ; ;,,,,,,,.., , , , 995 (5). 5,.., 994 (). 6.., 993 (2). 7,.., 995 (3) China Academic Journal Electronic Publishing House. All rights reserved.
8 : 3 8.., 997 (2). 9,,.., 996 (). THE NEGAT IVE EFFECTS, EVOL UT IO NARY PATTERNS AND COM PREHENSIVE M ANAGEM ENT OF COAL -M IN ING AREAS IN YANTENG-L IANGHUA I REGION Fang Chuanglin M ao H anying (Institu te of Geog rap hy, Ch inese A cad emy of S ciences, B eij ing 000) Key words coal2m ining co llap se, resources overlapp ing, negative effect, evo lutionary pattern comp rehensive m anagem ent Abstract Coal2m ining and co llap se are a pair of contradictions w hich are usually objective realities in resou rces overlapp ing areas. Yanzhou2T engzhou2l ianghuai ( H uainan2h uaibei) region is the mo st impo rtant energy base of the region of East China, the long period overloaded coal m ining here has contributed indeliblely to the relaxation of energy supp ly tension in East China. N ow it is one of the 9 m ajo r territo rial comp rehensive developm ent regions in China. But the land co l2 lap se due to the coal2m ining has given rise to a series of eco logical p roblem s and deep ly social contradictions. To sovlve these p roblem s, it is effectively to begin w ith the app roach to the ba2 sic law s of dynam ic evo lution in coal2m ining areas using the m ining co llap se theo ry and the theo2 ry of fluid m ichanics. O nly after this should w e adjust the coal2m ining po licy, imp rove the m in2 ing m ethod, adop t the restrictive m in ing strategy, and m u ltifo rm coo rdinate exp lo it pattern, take fo rth the exp lo it m anagem ent pattern coo rdinated by governm ent, enterp rise and peasants, renovate separately in line w ith ocal conditions, and determ ine the tim e series and intensities of the region developm ent of overlapp ing resources acco rding to the law of m arket p rice, w e should also m ake favourable po licies, take mo re fund from m ultip le channels, so as to ensure the coo r2 dinate exp lo itation of various resources at the sam e areas and the sustainable developm ent of the region.,, 966 9,, 3, 5, China Academic Journal Electronic Publishing House. All rights reserved.
GPS, 0. 5 kg ( In tegrated Fertility Index, IF I) 1. 1 SPSS 10. IF I =
 34 11 () V o l. 34 N o. 11 2006 11 Jour. of N o rthw est Sci2T ech U niv. of A gri. and Fo r. (N aṫ Sci. Ed. ) N ov. 2006 α 1, 1, 2, 1 (1, 450002; 2, 410007) [ ]12 () 1 612,, ( IF I ) : (1), ( ) ( ), ph
34 11 () V o l. 34 N o. 11 2006 11 Jour. of N o rthw est Sci2T ech U niv. of A gri. and Fo r. (N aṫ Sci. Ed. ) N ov. 2006 α 1, 1, 2, 1 (1, 450002; 2, 410007) [ ]12 () 1 612,, ( IF I ) : (1), ( ) ( ), ph
Jou rnal of M athem atical Study
 38 4 2005 12 Jou rnal of M athem atical Study V ol 38 o 4 D ec 2005 α (, 361005),, (SVV ), SVV, SVV, SVV - H elm holtz, (SEM ); (SVV ); O 174 52 A 1,, 1g, ( ),, 80,, ( [ 4 ]),,,, (e g [ 1 ]),, Gibbs,,,,,,
38 4 2005 12 Jou rnal of M athem atical Study V ol 38 o 4 D ec 2005 α (, 361005),, (SVV ), SVV, SVV, SVV - H elm holtz, (SEM ); (SVV ); O 174 52 A 1,, 1g, ( ),, 80,, ( [ 4 ]),,,, (e g [ 1 ]),, Gibbs,,,,,,
Error ana lysis of P2wave non2hyperbolic m oveout veloc ity in layered media
 28 1 2009 3 Vol128 No11 GLOBAL GEOLOGY Mar1 2009 : 1004 5589 (2009) 01 0098 05 P 1, 1, 2, 1 1., 130026; 2., 100027 :,,,, 1%,,, 12187%,, : ; ; ; : P63114 : A Abstract: Error ana lysis of P2wave non2hyperbolic
28 1 2009 3 Vol128 No11 GLOBAL GEOLOGY Mar1 2009 : 1004 5589 (2009) 01 0098 05 P 1, 1, 2, 1 1., 130026; 2., 100027 :,,,, 1%,,, 12187%,, : ; ; ; : P63114 : A Abstract: Error ana lysis of P2wave non2hyperbolic
China Academic Journal Electronic Publishing House. All rights reserved. O ct., 2005
 23 10( 142) V ol. 23, N o. 10 200510 System s Engineering O ct., 2005 100124098 (2005) 1020081205 Ξ 1, 2, 1 2, (1., 710049; 21, 266033),,,,,,,, ; ; F224. 32 A 20 6070 [1, 2 ], 1, 1. 1, (1) T = {1, 2},
23 10( 142) V ol. 23, N o. 10 200510 System s Engineering O ct., 2005 100124098 (2005) 1020081205 Ξ 1, 2, 1 2, (1., 710049; 21, 266033),,,,,,,, ; ; F224. 32 A 20 6070 [1, 2 ], 1, 1. 1, (1) T = {1, 2},
T he Op tim al L PM Po rtfo lio M odel of H arlow s and Its So lving M ethod
 2003 6 6 00026788 (2003) 0620042206 H arlow, 2 3, (., 70049; 2., 7006; 3., 200433) H arlow,,,,, ;, ; ; F832. 5; F830. 9 A T he Op tim al L PM Po rtfo lio M odel of H arlow s ad Its So lvig M ethod W AN
2003 6 6 00026788 (2003) 0620042206 H arlow, 2 3, (., 70049; 2., 7006; 3., 200433) H arlow,,,,, ;, ; ; F832. 5; F830. 9 A T he Op tim al L PM Po rtfo lio M odel of H arlow s ad Its So lvig M ethod W AN
(T rip tery g ium w ilf ord ii Hook) ,Beroza [6 ] 4 W ilfo rine W ilfo rdine W ilfo rgine W il2. Euon ine 1. 0% 1980, 1. 1 ; 1. 0%, ; 0.
![(T rip tery g ium w ilf ord ii Hook) ,Beroza [6 ] 4 W ilfo rine W ilfo rdine W ilfo rgine W il2. Euon ine 1. 0% 1980, 1. 1 ; 1. 0%, ; 0. (T rip tery g ium w ilf ord ii Hook) ,Beroza [6 ] 4 W ilfo rine W ilfo rdine W ilfo rgine W il2. Euon ine 1. 0% 1980, 1. 1 ; 1. 0%, ; 0.](/thumbs/92/108790990.jpg) 34 12 ( ) V o l. 34 N o. 12 2006 12 Jour. of N o rthw est Sci2T ech U niv. of A gri. and Fo r. (N aṫ Sci. Ed. ) D ec. 2006 Ξ 1, 3, 1, 2, 1, 2, 1, 1, 2 (1, 712100; 2, 712100; 3, 450008) [ ], 0. 1%, 3 48
34 12 ( ) V o l. 34 N o. 12 2006 12 Jour. of N o rthw est Sci2T ech U niv. of A gri. and Fo r. (N aṫ Sci. Ed. ) D ec. 2006 Ξ 1, 3, 1, 2, 1, 2, 1, 1, 2 (1, 712100; 2, 712100; 3, 450008) [ ], 0. 1%, 3 48
, 2166 m, 4162 m,,, 29 10 3 m 3 gs, 924 10 8 m 3,, 5 10, 7117%, 11 4, 2813%,, 266 10 3 m 3 gs, ;, ;,,,,,,,,
 55 2 2000 3 A CTA GEO GRA PH ICA S IN ICA V o l. 55, N o. 2 M ar., 2000 : 037525444 (2000) 0220243208 1, 1, 2 (11,, 200062; 21, 200002) :, 4,, 3,,,, : ; ; ; ; : P34315; P967 : A,, 80, 1, 2166 m, 4162 m,,,
55 2 2000 3 A CTA GEO GRA PH ICA S IN ICA V o l. 55, N o. 2 M ar., 2000 : 037525444 (2000) 0220243208 1, 1, 2 (11,, 200062; 21, 200002) :, 4,, 3,,,, : ; ; ; ; : P34315; P967 : A,, 80, 1, 2166 m, 4162 m,,,
G IS N N E E, , km 2, 92% A CTA GEO GRA PH ICA S IN ICA
 55 4 2000 7 A CTA GEO GRA PH ICA S IN ICA V o l. 55, N o. 4 July, 2000 : 037525444 (2000) 0420407210 G IS,, (, 100101) : G IS, 1982 1997 ;, : ; ; ; G IS; : F301124; F29312; N 94511 : A 20 80 90, [1, 2
55 4 2000 7 A CTA GEO GRA PH ICA S IN ICA V o l. 55, N o. 4 July, 2000 : 037525444 (2000) 0420407210 G IS,, (, 100101) : G IS, 1982 1997 ;, : ; ; ; G IS; : F301124; F29312; N 94511 : A 20 80 90, [1, 2
V o l. 53, N o. 3 M ay, 1998 A CTA GEO GRA PH ICA S IN ICA ) m 3 gs,
 53 3 1998 5 A CTA GEO GRA PH ICA S IN ICA V o l. 53, N o. 3 M ay, 1998 (, 11201), 1,,,, [1, 2 ] 60 00 m 3 gs, 266 300 m 3 gs, 01226 8 [2 ],,, 2 A B ( 1a),,, 1a E F, E F, CN F ( 1b), 1a A CN F 1b A Cf,
53 3 1998 5 A CTA GEO GRA PH ICA S IN ICA V o l. 53, N o. 3 M ay, 1998 (, 11201), 1,,,, [1, 2 ] 60 00 m 3 gs, 266 300 m 3 gs, 01226 8 [2 ],,, 2 A B ( 1a),,, 1a E F, E F, CN F ( 1b), 1a A CN F 1b A Cf,
6 cm, 1. 2 IAA, NAA, 2. 1
 30 6 ( ) V o l. 30 N o. 6 2002 12 Jour. of N o rthw est Sci2T ech U niv. of A gri. and Fo r. (N aṫ Sci. Ed. ) D ec. 2002 Ξ 1, 2, 2, 3, 1, 4, 1 (1 ; 2 ; 3, 712100; 4, 733200) [],,,,,, ; 1g2 M S, 1g3M S
30 6 ( ) V o l. 30 N o. 6 2002 12 Jour. of N o rthw est Sci2T ech U niv. of A gri. and Fo r. (N aṫ Sci. Ed. ) D ec. 2002 Ξ 1, 2, 2, 3, 1, 4, 1 (1 ; 2 ; 3, 712100; 4, 733200) [],,,,,, ; 1g2 M S, 1g3M S
26 3 V o l. 26 N o A cta Eco logiae A n im alis Dom astici M ay ,
 26 3 V o l. 26 N o. 3 2005 5 A cta Eco logiae A n im alis Dom astici M ay 2005,,,,, (, 524088) [ ] 1 200, 3,, 28 31, 83 87%, 1 2 0. 1% 0. 3% : 1 38 47 (P < 0. 05), 48 57 1 (P < 0. 05),,, 1 (P > 0. 05)
26 3 V o l. 26 N o. 3 2005 5 A cta Eco logiae A n im alis Dom astici M ay 2005,,,,, (, 524088) [ ] 1 200, 3,, 28 31, 83 87%, 1 2 0. 1% 0. 3% : 1 38 47 (P < 0. 05), 48 57 1 (P < 0. 05),,, 1 (P > 0. 05)
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
Fo recasting Stock M arket Q uo tation s via Fuzzy N eu ral N etw o rk Based on T 2S M odel
 2001 2 2 : 100026788 (2001) 0220066207 T 2S,, (, 400044) : T 2S,,, ( ),,. : ; ; α Fo recasting Stock M arket Q uo tation s via Fuzzy N eu ral N etw o rk Based on T 2S M odel CH EN X ing, M EN G W ei2dong,
2001 2 2 : 100026788 (2001) 0220066207 T 2S,, (, 400044) : T 2S,,, ( ),,. : ; ; α Fo recasting Stock M arket Q uo tation s via Fuzzy N eu ral N etw o rk Based on T 2S M odel CH EN X ing, M EN G W ei2dong,
, Litrrow. Maxwell. Helmholtz Fredholm, . 40 Maystre [4 ], Goray [5 ], Kleemann [6 ] PACC: 4210, 4110H
![, Litrrow. Maxwell. Helmholtz Fredholm, . 40 Maystre [4 ], Goray [5 ], Kleemann [6 ] PACC: 4210, 4110H , Litrrow. Maxwell. Helmholtz Fredholm, . 40 Maystre [4 ], Goray [5 ], Kleemann [6 ] PACC: 4210, 4110H](/thumbs/88/115525025.jpg) 57 6 2008 6 100023290Π2008Π57 (06) Π3486208 ACTA PHYSICA SINICA Vol. 57,No. 6,June,2008 ν 2008 Chin. Phys. Soc. 3 1) 2) 1) g 1) (, 130033) 2) (, 100049) (2007 9 11 ;2007 11 14 ),Littrow,,.,., Litrrow.
57 6 2008 6 100023290Π2008Π57 (06) Π3486208 ACTA PHYSICA SINICA Vol. 57,No. 6,June,2008 ν 2008 Chin. Phys. Soc. 3 1) 2) 1) g 1) (, 130033) 2) (, 100049) (2007 9 11 ;2007 11 14 ),Littrow,,.,., Litrrow.
V o l122, N o13 M ay, 2003 PRO GR ESS IN GEO GRA PH Y : (2003) , : TU 984. , (Eco logy fo r evil) [1 ] (R ich Boyer), 2.
![V o l122, N o13 M ay, 2003 PRO GR ESS IN GEO GRA PH Y : (2003) , : TU 984. , (Eco logy fo r evil) [1 ] (R ich Boyer), 2. V o l122, N o13 M ay, 2003 PRO GR ESS IN GEO GRA PH Y : (2003) , : TU 984. , (Eco logy fo r evil) [1 ] (R ich Boyer), 2.](/thumbs/93/114354980.jpg) 22 3 2003 5 PRO GR ESS IN GEO GRA PH Y V o l122, N o13 M ay, 2003 : 100726301 (2003) 03203162010, (, 710061) :, (R ich Boyer), 2001,, : ; ; ; ; : TU 984 1,,, (Eco logy fo r evil) [1 ], ( ), (D avid1 Sm
22 3 2003 5 PRO GR ESS IN GEO GRA PH Y V o l122, N o13 M ay, 2003 : 100726301 (2003) 03203162010, (, 710061) :, (R ich Boyer), 2001,, : ; ; ; ; : TU 984 1,,, (Eco logy fo r evil) [1 ], ( ), (D avid1 Sm
Galatia SIL Keyboard Information
 Galatia SIL Keyboard Information Keyboard ssignments The main purpose of the keyboards is to provide a wide range of keying options, so many characters can be entered in multiple ways. If you are typing
Galatia SIL Keyboard Information Keyboard ssignments The main purpose of the keyboards is to provide a wide range of keying options, so many characters can be entered in multiple ways. If you are typing
G IS A CTA GEO GRA PH ICA S IN ICA. V o l. 55, N o. 1 Jan., 2000 : (2000) E2m ail: lreis1ac1cn
 55 1 2000 1 A CTA GEO GRA PH ICA S IN ICA V o l. 55, N o. 1 Jan., 2000 : 037525444 (2000) 01200015210 G IS,,, (, 100101) :,,,,, : ; ; : X91515 : A 1 111,, 3,,,, 112,,,,,,,,,, [1 ] ; ( ) : 1999210207; :
55 1 2000 1 A CTA GEO GRA PH ICA S IN ICA V o l. 55, N o. 1 Jan., 2000 : 037525444 (2000) 01200015210 G IS,,, (, 100101) :,,,,, : ; ; : X91515 : A 1 111,, 3,,,, 112,,,,,,,,,, [1 ] ; ( ) : 1999210207; :
V ladim irov A CTA GEO GRA PH ICA S IN ICA China Academic Journal Electronic Publishing House. All rights reserved.
 55 3 2000 5 A CTA GEO GRA PH ICA S IN ICA V o l. 55, N o. 3 M ay, 2000 : 037525444 (2000) 0320257209 1, 2, 1 (11, 100101; 21, 100875) :, 40, 4,, 39, : ; ; ; : P33112; P333; P34311 : A 20 70, 1972 1998
55 3 2000 5 A CTA GEO GRA PH ICA S IN ICA V o l. 55, N o. 3 M ay, 2000 : 037525444 (2000) 0320257209 1, 2, 1 (11, 100101; 21, 100875) :, 40, 4,, 39, : ; ; ; : P33112; P333; P34311 : A 20 70, 1972 1998
Im pact of capac ity a lloca tion on bullwh ip effect in supply cha in
 7 4 00 8 JOU RNAL O F SYST EM S EN G IN EER IN G V o l 7 N o 4 A ug 00 ( 30007) : - - - : ; ; ; ; : F5 : A : 000578 (00) 04034009 Im pact of capac ity a lloca tio o bullwh ip effect i supply cha i W AN
7 4 00 8 JOU RNAL O F SYST EM S EN G IN EER IN G V o l 7 N o 4 A ug 00 ( 30007) : - - - : ; ; ; ; : F5 : A : 000578 (00) 04034009 Im pact of capac ity a lloca tio o bullwh ip effect i supply cha i W AN
ED SS (Environm en tal D ecision Suppo rt
 55 6 2000 11 A CTA GEO GRA PH ICA S IN ICA V o l. 55, N o. 6 N ov., 2000 : 037525444 (2000) 0620652209 1, 1, 1, 2, 3 (11, 510655; 21, 510000; 31, 511400) : ED SS (Environm ental D ecision Suppo rt System
55 6 2000 11 A CTA GEO GRA PH ICA S IN ICA V o l. 55, N o. 6 N ov., 2000 : 037525444 (2000) 0620652209 1, 1, 1, 2, 3 (11, 510655; 21, 510000; 31, 511400) : ED SS (Environm ental D ecision Suppo rt System
Bank A ssetgl iab ility Sheet w ith Em bedded Op tion s
 00 8 8 : 10006788 (00) 08005506, (, 710049) :,, ;, ; : ; ; ; ; ; : F830 : A α Con tro l O ver In terest R ate R isk of Bank A ssetgl iab ility Sheet w ith Em bedded Op tion s LU O D aw ei, W AN D ifang
00 8 8 : 10006788 (00) 08005506, (, 710049) :,, ;, ; : ; ; ; ; ; : F830 : A α Con tro l O ver In terest R ate R isk of Bank A ssetgl iab ility Sheet w ith Em bedded Op tion s LU O D aw ei, W AN D ifang
A CTA GEO GRA PH ICA S IN ICA
 55 6 2000 11 A CTA GEO GRA PH ICA S IN ICA V o l. 55, N o. 6 N ov., 2000 : 037525444 (2000) 0620744207, (, 510070) :, 6 87, 3 ( ), 1485 1897, 3 1485 1527 1606 1767 1835 1897, 2 3 016, - 1 : ; ; : P53416;
55 6 2000 11 A CTA GEO GRA PH ICA S IN ICA V o l. 55, N o. 6 N ov., 2000 : 037525444 (2000) 0620744207, (, 510070) :, 6 87, 3 ( ), 1485 1897, 3 1485 1527 1606 1767 1835 1897, 2 3 016, - 1 : ; ; : P53416;
CHAPTER 101 FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD
 CHAPTER FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD EXERCISE 36 Page 66. Determine the Fourier series for the periodic function: f(x), when x +, when x which is periodic outside this rge of period.
CHAPTER FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD EXERCISE 36 Page 66. Determine the Fourier series for the periodic function: f(x), when x +, when x which is periodic outside this rge of period.
A Knowledge M odel for D esign of Population Nutr ien t Index D ynam ics in W heat
 2005, 25 (3): 47 52 Journal of T riticeae C rop s Ξ,,,, ( g,, 210095) :,,,,, ( ) 2,, RM S E 8. 13 kgghm 2, RM S E 0. 20%, : ; ; ; ; : S 512. 1; S 311 : A : 100921041 (2005) 0320047206 A Knowledge M odel
2005, 25 (3): 47 52 Journal of T riticeae C rop s Ξ,,,, ( g,, 210095) :,,,,, ( ) 2,, RM S E 8. 13 kgghm 2, RM S E 0. 20%, : ; ; ; ; : S 512. 1; S 311 : A : 100921041 (2005) 0320047206 A Knowledge M odel
) V o l. 40 N o. 6 : A : Q ,, W ard [ 1 ] (A v icenn ia m a rina) (K and elia cand el)
![) V o l. 40 N o. 6 : A : Q ,, W ard [ 1 ] (A v icenn ia m a rina) (K and elia cand el) ) V o l. 40 N o. 6 : A : Q ,, W ard [ 1 ] (A v icenn ia m a rina) (K and elia cand el)](/thumbs/93/114276195.jpg) 40 6 ( ) V o l 40 N o 6 2001 11 Jou rnal of X iam en U n iversity (N atu ral Science) N ov 2001 : 043820479 (2001) 0621350205,,,, (, 361005) :, (N R ), N R N R, N ac l ; N R : ( 0 30 ; 0 20 )N R, 30, 89
40 6 ( ) V o l 40 N o 6 2001 11 Jou rnal of X iam en U n iversity (N atu ral Science) N ov 2001 : 043820479 (2001) 0621350205,,,, (, 361005) :, (N R ), N R N R, N ac l ; N R : ( 0 30 ; 0 20 )N R, 30, 89
A CTA GEO GRA PH ICA S IN ICA
 56 2 2001 3 A CTA GEO GRA PH ICA S IN ICA V o l. 56, N o. 2 M ar., 2001 : 037525444 (2001) 0220232207 (, 100871) :,,,,,, : ; ; ; ; : P149 : A 1, (DBS) [1 ] (CAD ) [2, 3 ] ( G IS ) [4 6 ] ( ES ) [7 ] (MM
56 2 2001 3 A CTA GEO GRA PH ICA S IN ICA V o l. 56, N o. 2 M ar., 2001 : 037525444 (2001) 0220232207 (, 100871) :,,,,,, : ; ; ; ; : P149 : A 1, (DBS) [1 ] (CAD ) [2, 3 ] ( G IS ) [4 6 ] ( ES ) [7 ] (MM
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ. Πτυχιακή Εργασία
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ Πτυχιακή Εργασία ΣΥΜΠΛΗΡΩΜΑΤΙΚΕΣ ΚΑΙ ΕΝΑΛΛΑΚΤΙΚΕΣ ΘΕΡΑΠΕΙΕΣ ΩΣ ΠΡΟΣ ΤΗ ΔΙΑΧΕΙΡΙΣΗ ΤΟΥ ΠΟΝΟΥ ΣΕ ΑΣΘΕΝΕΙΣ ΜΕ ΚΑΡΚΙΝΟ. Ονοματεπώνυμο:
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ Πτυχιακή Εργασία ΣΥΜΠΛΗΡΩΜΑΤΙΚΕΣ ΚΑΙ ΕΝΑΛΛΑΚΤΙΚΕΣ ΘΕΡΑΠΕΙΕΣ ΩΣ ΠΡΟΣ ΤΗ ΔΙΑΧΕΙΡΙΣΗ ΤΟΥ ΠΟΝΟΥ ΣΕ ΑΣΘΕΝΕΙΣ ΜΕ ΚΑΡΚΙΝΟ. Ονοματεπώνυμο:
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
(2006) , ; (M OD S) (VA P) ,
 (2006) 65 Practical guidelines for m echan ical ven tilation (2006) S ociety of C ritical Care M ed icine Ch inese M ed ical A ssociation Corresp ond ing au thors: Q IN Y ing 2z h i (D ep artm ent of Intensive
(2006) 65 Practical guidelines for m echan ical ven tilation (2006) S ociety of C ritical Care M ed icine Ch inese M ed ical A ssociation Corresp ond ing au thors: Q IN Y ing 2z h i (D ep artm ent of Intensive
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
, , ; ,,, ,,, ; > cm , 62. 5% 66. 5%, 0. 2 g g,, 67% , , ;, , : V o l. 24, N o. 4 A ug.
 24 4 2 0 0 5 8 Sichuan W ater Pow er V o l. 24 N o. 4 A ug. 2 0 0 5 ( 611731) : : : TU 435 TU 441 : B : 100122184 (2005) 0420024205 1 3. 1 3. 1. 1 : 1 1 2 : > 0. 25 cm 3. 1. 2 : 62. 5% 66. 5% 0. 2 g 0.
24 4 2 0 0 5 8 Sichuan W ater Pow er V o l. 24 N o. 4 A ug. 2 0 0 5 ( 611731) : : : TU 435 TU 441 : B : 100122184 (2005) 0420024205 1 3. 1 3. 1. 1 : 1 1 2 : > 0. 25 cm 3. 1. 2 : 62. 5% 66. 5% 0. 2 g 0.
, E, PRO GR ESS IN GEO GRA PH Y. V o l122, N o15 Sep t1, 2003 : (2003) , 263, (0 1m ) P93511; P42616
 22 5 2003 9 PRO GR ESS IN GEO GRA PH Y V o l122, N o15 Sep t1, 2003 : 100726301 (2003) 0520454209 1, 1, 2, 3 (11 100875; 21, 100877; 31 100875) : 1982 1998 AV HRR pathfinder, 29 263, (0 1m ), 1982 1998
22 5 2003 9 PRO GR ESS IN GEO GRA PH Y V o l122, N o15 Sep t1, 2003 : 100726301 (2003) 0520454209 1, 1, 2, 3 (11 100875; 21, 100877; 31 100875) : 1982 1998 AV HRR pathfinder, 29 263, (0 1m ), 1982 1998
Depth versus Rigidity in the Design of International Trade Agreements. Leslie Johns
 Depth versus Rigidity in the Design of International Trade Agreements Leslie Johns Supplemental Appendix September 3, 202 Alternative Punishment Mechanisms The one-period utility functions of the home
Depth versus Rigidity in the Design of International Trade Agreements Leslie Johns Supplemental Appendix September 3, 202 Alternative Punishment Mechanisms The one-period utility functions of the home
ZrO 2, ZrO 2. (M ) W O 3g ( 100% ) SO 4 2- W O 3 M oo 3, SO ( Zr (OH ) 4 ) ( ( 0. 1 mo l. L - 1 A gno 3 ), Zr (OH ) 4 SO (0.
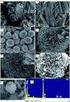 14 2 V o l. 14,N o. 2 2000 4 JOU RNAL O F M OL ECULA R CA TAL YS IS (CH INA ) A p r. 2000 : 100123555 (2000) 0220111208 WO 3gZrO 2 - g. ZrO 2,,, 1) (, 130022) : ZrO 2 WO 3gZrO 2 SO 4 2- gzro 2 M oo 3gZrO
14 2 V o l. 14,N o. 2 2000 4 JOU RNAL O F M OL ECULA R CA TAL YS IS (CH INA ) A p r. 2000 : 100123555 (2000) 0220111208 WO 3gZrO 2 - g. ZrO 2,,, 1) (, 130022) : ZrO 2 WO 3gZrO 2 SO 4 2- gzro 2 M oo 3gZrO
(H ipp op hae rham noid es L. ) , ; SHB 2g , 1. 0, 2. 0, 3. 0, 4. 0, 5. 0 ml mm. : Y = X - 0.
 34 10 () V o l. 34 N o. 10 2006 10 Jour. of N o rthw est Sci2T ech U niv. of gri. and Fo r. (N aṫ Sci. Ed. ) O cṫ 2006 Ξ 1, 2, 1, 2, 3, 2, 2 (1, 712081; 2, 712100; 3, 123000) [ ],,, : V ( ) V ( 95% ) =
34 10 () V o l. 34 N o. 10 2006 10 Jour. of N o rthw est Sci2T ech U niv. of gri. and Fo r. (N aṫ Sci. Ed. ) O cṫ 2006 Ξ 1, 2, 1, 2, 3, 2, 2 (1, 712081; 2, 712100; 3, 123000) [ ],,, : V ( ) V ( 95% ) =
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
A CTA GEO GRA PH ICA S IN ICA
 54 4 1999 7 A CTA GEO GRA PH ICA S IN ICA V o l. 54, N o. 4 July, 1999 : 037525444 (1999) 0420299210 2, (, 510275) :,,, 2,, : ; 2; : F2992127: A,, :,,, [1 ] ; 1995, GD P 52129% 51136%, [2 ] ;, [3 ] 2,
54 4 1999 7 A CTA GEO GRA PH ICA S IN ICA V o l. 54, N o. 4 July, 1999 : 037525444 (1999) 0420299210 2, (, 510275) :,,, 2,, : ; 2; : F2992127: A,, :,,, [1 ] ; 1995, GD P 52129% 51136%, [2 ] ;, [3 ] 2,
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Mean bond enthalpy Standard enthalpy of formation Bond N H N N N N H O O O
 Q1. (a) Explain the meaning of the terms mean bond enthalpy and standard enthalpy of formation. Mean bond enthalpy... Standard enthalpy of formation... (5) (b) Some mean bond enthalpies are given below.
Q1. (a) Explain the meaning of the terms mean bond enthalpy and standard enthalpy of formation. Mean bond enthalpy... Standard enthalpy of formation... (5) (b) Some mean bond enthalpies are given below.
( , ,
 33 9 ( ) V o l. 33 N o. 9 2005 9 Jour. of N o rthw est Sci2T ech U niv. of A gri. and Fo r. (N aṫ Sci. Ed. ) Sep. 2005 Ξ 1, 2, 1, 1, 1, 1, 1, 2 (1 010018; 2 512005) [],, 8 8 9, () (),,,,,, ;, ;,, ;,,,
33 9 ( ) V o l. 33 N o. 9 2005 9 Jour. of N o rthw est Sci2T ech U niv. of A gri. and Fo r. (N aṫ Sci. Ed. ) Sep. 2005 Ξ 1, 2, 1, 1, 1, 1, 1, 2 (1 010018; 2 512005) [],, 8 8 9, () (),,,,,, ;, ;,, ;,,,
(Biomass utilization for electric energy production)
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ T.Ε.I. ΠΕΙΡΑΙΑ ΣΧΟΛΗ: ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ: ΗΛΕΚΤΡΟΛΟΓΙΑΣ Επιβλέπων: ΠΕΤΡΟΣ Γ. ΒΕΡΝΑΔΟΣ, Ομότιμος Καθηγητής Συνεπιβλέπουσα: ΕΡΙΕΤΤΑ Ι. ΖΟΥΝΤΟΥΡΙΔΟΥ, Παν. Υπότροφος
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ T.Ε.I. ΠΕΙΡΑΙΑ ΣΧΟΛΗ: ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ: ΗΛΕΚΤΡΟΛΟΓΙΑΣ Επιβλέπων: ΠΕΤΡΟΣ Γ. ΒΕΡΝΑΔΟΣ, Ομότιμος Καθηγητής Συνεπιβλέπουσα: ΕΡΙΕΤΤΑ Ι. ΖΟΥΝΤΟΥΡΙΔΟΥ, Παν. Υπότροφος
A Study of the O rigin of Comp lex ity in the Science of Comp lex ity
 2002 10 10 : 100026788 (2002) 1020066206 1 2, (1., 510090; 2., 519070) : Λ, Λ,, Λ :, Λ, 20 90 (CA S), Λ CA S Λ,, Λ, Λ : ; ; : N 94 : A A Study of the O rigin of Comp lex ity in the Science of Comp lex
2002 10 10 : 100026788 (2002) 1020066206 1 2, (1., 510090; 2., 519070) : Λ, Λ,, Λ :, Λ, 20 90 (CA S), Λ CA S Λ,, Λ, Λ : ; ; : N 94 : A A Study of the O rigin of Comp lex ity in the Science of Comp lex
1998, 18 (1): 1 7. A cta T heriolog ica S inica (,, ) (Grow th layer group s, GL Gs) 168, 42,
 1998, 18 (1): 17 A cta T heriolog ica S inica Ξ (,, 210097), 3,, 3 C (O dum, 1983), 0 2, 24 11 3 R 0 Κ1, rm 0,, ; ; ; ;, (Sh i2 rak ihara, 1993; Gao, 1993)Gao (1993) 3 56,, (, 1995),, 3,, 1974 229, 86,
1998, 18 (1): 17 A cta T heriolog ica S inica Ξ (,, 210097), 3,, 3 C (O dum, 1983), 0 2, 24 11 3 R 0 Κ1, rm 0,, ; ; ; ;, (Sh i2 rak ihara, 1993; Gao, 1993)Gao (1993) 3 56,, (, 1995),, 3,, 1974 229, 86,
Appendix to On the stability of a compressible axisymmetric rotating flow in a pipe. By Z. Rusak & J. H. Lee
 Appendi to On the stability of a compressible aisymmetric rotating flow in a pipe By Z. Rusak & J. H. Lee Journal of Fluid Mechanics, vol. 5 4, pp. 5 4 This material has not been copy-edited or typeset
Appendi to On the stability of a compressible aisymmetric rotating flow in a pipe By Z. Rusak & J. H. Lee Journal of Fluid Mechanics, vol. 5 4, pp. 5 4 This material has not been copy-edited or typeset
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
 Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
ΜΕΛΕΤΗ ΣΥΜΠΕΡΙΦΟΡΑΣ ΦΛΟΓΩΝ ΠΡΟΠΑΝΙΟΥ ΣΤΑΘΕΡΟΠΟΙΗΜΕΝΩΝ ΣΕ ΕΠΙΠΕΔΟ ΣΩΜΑ ΜΕ ΔΙΑΣΤΡΩΜΑΤΩΜΕΝΗ ΕΙΣΑΓΩΓΗ ΜΙΓΜΑΤΟΣ
 ΜΕΛΕΤΗ ΣΥΜΠΕΡΙΦΟΡΑΣ ΦΛΟΓΩΝ ΠΡΟΠΑΝΙΟΥ ΣΤΑΘΕΡΟΠΟΙΗΜΕΝΩΝ ΣΕ ΕΠΙΠΕΔΟ ΣΩΜΑ ΜΕ ΔΙΑΣΤΡΩΜΑΤΩΜΕΝΗ ΕΙΣΑΓΩΓΗ ΜΙΓΜΑΤΟΣ Ειδική Ερευνητική Εργασία Υποβληθείσα στο Τμήμα Φυσικής του Πανεπιστημίου Πατρών Υπό ΤΣΙΡΩΝΗ ΓΕΩΡΓΙΟ
ΜΕΛΕΤΗ ΣΥΜΠΕΡΙΦΟΡΑΣ ΦΛΟΓΩΝ ΠΡΟΠΑΝΙΟΥ ΣΤΑΘΕΡΟΠΟΙΗΜΕΝΩΝ ΣΕ ΕΠΙΠΕΔΟ ΣΩΜΑ ΜΕ ΔΙΑΣΤΡΩΜΑΤΩΜΕΝΗ ΕΙΣΑΓΩΓΗ ΜΙΓΜΑΤΟΣ Ειδική Ερευνητική Εργασία Υποβληθείσα στο Τμήμα Φυσικής του Πανεπιστημίου Πατρών Υπό ΤΣΙΡΩΝΗ ΓΕΩΡΓΙΟ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΗΛΕΚΤΡΟΚΙΝΗΣΗ ΚΑΙ ΑΝΑΛΥΣΗ ΤΗΣ VEHICLE TO GRID (V2G) ΛΕΙΤΟΥΡΓΙΑΣ Μεταπτυχιακή
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΗΛΕΚΤΡΟΚΙΝΗΣΗ ΚΑΙ ΑΝΑΛΥΣΗ ΤΗΣ VEHICLE TO GRID (V2G) ΛΕΙΤΟΥΡΓΙΑΣ Μεταπτυχιακή
SPECIAL FUNCTIONS and POLYNOMIALS
 SPECIAL FUNCTIONS and POLYNOMIALS Gerard t Hooft Stefan Nobbenhuis Institute for Theoretical Physics Utrecht University, Leuvenlaan 4 3584 CC Utrecht, the Netherlands and Spinoza Institute Postbox 8.195
SPECIAL FUNCTIONS and POLYNOMIALS Gerard t Hooft Stefan Nobbenhuis Institute for Theoretical Physics Utrecht University, Leuvenlaan 4 3584 CC Utrecht, the Netherlands and Spinoza Institute Postbox 8.195
ΥΒΡΙΔΙΚΟ ΣΥΣΤΗΜΑ ΠΑΡΑΓΩΓΗΣ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΣΕ ΙΣΤΙΟΠΛΟΪΚΑ ΣΚΑΦΗ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΩΝ ΒΙΟΜΗΧΑΝΙΚΩΝ ΔΙΑΤΑΞΕΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΑΠΟΦΑΣΕΩΝ ΥΒΡΙΔΙΚΟ ΣΥΣΤΗΜΑ ΠΑΡΑΓΩΓΗΣ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΣΕ ΙΣΤΙΟΠΛΟΪΚΑ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΩΝ ΒΙΟΜΗΧΑΝΙΚΩΝ ΔΙΑΤΑΞΕΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΑΠΟΦΑΣΕΩΝ ΥΒΡΙΔΙΚΟ ΣΥΣΤΗΜΑ ΠΑΡΑΓΩΓΗΣ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΣΕ ΙΣΤΙΟΠΛΟΪΚΑ
Lifting Entry (continued)
 ifting Entry (continued) Basic planar dynamics of motion, again Yet another equilibrium glide Hypersonic phugoid motion Planar state equations MARYAN 1 01 avid. Akin - All rights reserved http://spacecraft.ssl.umd.edu
ifting Entry (continued) Basic planar dynamics of motion, again Yet another equilibrium glide Hypersonic phugoid motion Planar state equations MARYAN 1 01 avid. Akin - All rights reserved http://spacecraft.ssl.umd.edu
E stab lish ing Syn thesis Evaluation Index
 2004 10 10 100026788 (2004) 1020080209 PL S, (, 100083) PL S (partial least square),, ;,,,, PL S,, PL S ; ; O 212 A T he A pp lication R esearch of Partial L east Square Path M odeling on E stab lish ing
2004 10 10 100026788 (2004) 1020080209 PL S, (, 100083) PL S (partial least square),, ;,,,, PL S,, PL S ; ; O 212 A T he A pp lication R esearch of Partial L east Square Path M odeling on E stab lish ing
? 9 Ξ : Α : 4 < ; : ; 4 ϑ Α Λ Χ< : Χ 9 : Α Α Χ : ;: Ψ 8< ;: 9 : > Α ϑ < > = 8 Α;< 4 <9 Ξ : 9 : > Α 4 Α < >
 # % & ( ) ) +,. / 0, 1 / )., / 2 (& 3 5 % 6 6 7 8 : ; < : / : ; = 5 >
# % & ( ) ) +,. / 0, 1 / )., / 2 (& 3 5 % 6 6 7 8 : ; < : / : ; = 5 >
M in ing Recursive Function s Ba sed on Gene Expression Programm ing
 39 5 ( ) Vol. 39 No. 5 2007 9 JOURNAL OF SICHUAN UN IVERSITY ( ENGINEER ING SC IENCE ED ITION) Sep t. 2007 : 100923087 (2007) 0520127206 1, 2, 1, η 1, 3, 1, 1, 1, 2 (1., 610065; 2., 610074; 3., 610041)
39 5 ( ) Vol. 39 No. 5 2007 9 JOURNAL OF SICHUAN UN IVERSITY ( ENGINEER ING SC IENCE ED ITION) Sep t. 2007 : 100923087 (2007) 0520127206 1, 2, 1, η 1, 3, 1, 1, 1, 2 (1., 610065; 2., 610074; 3., 610041)
Policy Coherence. JEL Classification : J12, J13, J21 Key words :
 ** 80%1.89 2005 7 35 Policy Coherence JEL Classification : J12, J13, J21 Key words : ** Family Life and Family Policy in France and Germany: Implications for Japan By Tomoko Hayashi and Rieko Tamefuji
** 80%1.89 2005 7 35 Policy Coherence JEL Classification : J12, J13, J21 Key words : ** Family Life and Family Policy in France and Germany: Implications for Japan By Tomoko Hayashi and Rieko Tamefuji
( ) , ) , ; kg 1) 80 % kg. Vol. 28,No. 1 Jan.,2006 RESOURCES SCIENCE : (2006) ,2 ,,,, ; ;
 28 1 2006 1 RESOURCES SCIENCE Vol. 28 No. 1 Jan. 2006 :1007-7588(2006) 01-0002 - 07 20 1 1 2 (11 100101 ; 21 101149) : 1978 1978 2001 ; 2010 ; ; ; : ; ; 24718kg 1) 1990 26211kg 260kg 1995 2001 238kg( 1)
28 1 2006 1 RESOURCES SCIENCE Vol. 28 No. 1 Jan. 2006 :1007-7588(2006) 01-0002 - 07 20 1 1 2 (11 100101 ; 21 101149) : 1978 1978 2001 ; 2010 ; ; ; : ; ; 24718kg 1) 1990 26211kg 260kg 1995 2001 238kg( 1)
b. Use the parametrization from (a) to compute the area of S a as S a ds. Be sure to substitute for ds!
 MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
THE CALOR IC VAL UE OF M A IN PLANT SPEC IES AT D INGHUSHAN, GUANGDO NG, CH INA
 1999, 23 (2) 148 154 A cta Phytoecolog ica S in ica Ξ (, 510650) 4 37 : : 1724217 2453313J g - 1 1818815 2587910 J g - 1 ; 1492711 1928718 J g - 1 1562017 2034518J g - 1, 1615811 2181519J g - 1 1690819
1999, 23 (2) 148 154 A cta Phytoecolog ica S in ica Ξ (, 510650) 4 37 : : 1724217 2453313J g - 1 1818815 2587910 J g - 1 ; 1492711 1928718 J g - 1 1562017 2034518J g - 1, 1615811 2181519J g - 1 1690819
U (x, y ) = : K (x i- x k) K (x i- x k, y j- y l), 2. 1
 22 5 V o l 22, N o 5 2002 9 TR IBOLO GY Sep, 2002,, (, 100084) :, (FFT )., 2 (Green ),,, 3,. ; ; FFT; ; TH 117. 2 A 100420595 (2002) 0520390205,.,,,. L ub rech t [1 ]. (FFT ) [2 5 ]., [4, 5 ].,L iu [6
22 5 V o l 22, N o 5 2002 9 TR IBOLO GY Sep, 2002,, (, 100084) :, (FFT )., 2 (Green ),,, 3,. ; ; FFT; ; TH 117. 2 A 100420595 (2002) 0520390205,.,,,. L ub rech t [1 ]. (FFT ) [2 5 ]., [4, 5 ].,L iu [6
CE 530 Molecular Simulation
 C 53 olecular Siulation Lecture Histogra Reweighting ethods David. Kofke Departent of Cheical ngineering SUNY uffalo kofke@eng.buffalo.edu Histogra Reweighting ethod to cobine results taken at different
C 53 olecular Siulation Lecture Histogra Reweighting ethods David. Kofke Departent of Cheical ngineering SUNY uffalo kofke@eng.buffalo.edu Histogra Reweighting ethod to cobine results taken at different
Μηχανισμοί πρόβλεψης προσήμων σε προσημασμένα μοντέλα κοινωνικών δικτύων ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΕΠΙΚΟΙΝΩΝΙΩΝ, ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ Μηχανισμοί πρόβλεψης προσήμων σε προσημασμένα μοντέλα κοινωνικών
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΕΠΙΚΟΙΝΩΝΙΩΝ, ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ Μηχανισμοί πρόβλεψης προσήμων σε προσημασμένα μοντέλα κοινωνικών
AREAS AND LENGTHS IN POLAR COORDINATES. 25. Find the area inside the larger loop and outside the smaller loop
 SECTIN 9. AREAS AND LENGTHS IN PLAR CRDINATES 9. AREAS AND LENGTHS IN PLAR CRDINATES A Click here for answers. S Click here for solutions. 8 Find the area of the region that is bounded by the given curve
SECTIN 9. AREAS AND LENGTHS IN PLAR CRDINATES 9. AREAS AND LENGTHS IN PLAR CRDINATES A Click here for answers. S Click here for solutions. 8 Find the area of the region that is bounded by the given curve
Application of a novel immune network learn ing algorithm to fault diagnosis
 3 5 Vol. 3. 5 2008 10 CAA I Transactions on Intelligent System s Oct. 2008 1, 2, 1, 2 (1., 525000; 2., 030024) :,.,.,.,., 5. : ; ; ; : TP18 : A : 167324785 (2008) 0520449206 Application of a novel immune
3 5 Vol. 3. 5 2008 10 CAA I Transactions on Intelligent System s Oct. 2008 1, 2, 1, 2 (1., 525000; 2., 030024) :,.,.,.,., 5. : ; ; ; : TP18 : A : 167324785 (2008) 0520449206 Application of a novel immune
R &D on Key T echno logies Based on W eb Info rm ation Pub lish ing System
 2000 11 11 : 100026788 (2000) 1120051206 W eb,, (, 100083) : W eb ( ), : W eb ; ; : T P391 α R &D on Key T echno logies Based on W eb Info rm ation Pub lish ing System SHAN Si2qing, L I Zong2jian, X IA
2000 11 11 : 100026788 (2000) 1120051206 W eb,, (, 100083) : W eb ( ), : W eb ; ; : T P391 α R &D on Key T echno logies Based on W eb Info rm ation Pub lish ing System SHAN Si2qing, L I Zong2jian, X IA
P rogresses in H azardou s M aterials L ogistics R esearch
 2000 7 7 : 10002788 (2000) 072011220 ( 710049) : : 1) 2) 3) ( ) 4) 5) D SS G IS : ; ; : X32 α P rogresses n H azardou s M aterals L ogstcs R esearch W AN G Kan2lang (T he Schoo l of M anagem ent X an J
2000 7 7 : 10002788 (2000) 072011220 ( 710049) : : 1) 2) 3) ( ) 4) 5) D SS G IS : ; ; : X32 α P rogresses n H azardou s M aterals L ogstcs R esearch W AN G Kan2lang (T he Schoo l of M anagem ent X an J
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ. Πτυχιακή Εργασία. Κόπωση και ποιότητα ζωής ασθενών με καρκίνο.
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ Πτυχιακή Εργασία Κόπωση και ποιότητα ζωής ασθενών με καρκίνο Μαργαρίτα Μάου Λευκωσία 2012 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ ΤΜΗΜΑ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ Πτυχιακή Εργασία Κόπωση και ποιότητα ζωής ασθενών με καρκίνο Μαργαρίτα Μάου Λευκωσία 2012 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ ΤΜΗΜΑ
A summation formula ramified with hypergeometric function and involving recurrence relation
 South Asian Journal of Mathematics 017, Vol. 7 ( 1): 1 4 www.sajm-online.com ISSN 51-151 RESEARCH ARTICLE A summation formula ramified with hypergeometric function and involving recurrence relation Salahuddin
South Asian Journal of Mathematics 017, Vol. 7 ( 1): 1 4 www.sajm-online.com ISSN 51-151 RESEARCH ARTICLE A summation formula ramified with hypergeometric function and involving recurrence relation Salahuddin
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΑΓΡΟΝΟΜΩΝ & ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΓΕΩΓΡΑΦΙΑΣ ΚΑΙ ΠΕΡΙΦΕΡΕΙΑΚΟΥ ΣΧΕΔΙΑΣΜΟΥ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ «Η ΕΞΕΛΙΞΗ ΤΗΣ ΠΟΛΗΣ ΤΗΣ ΚΑΛΑΜΑΤΑΣ ΜΕ ΕΠΙΚΕΝΤΡΟ ΤΟ ΙΣΤΟΡΙΚΟ ΤΗΣ ΚΕΝΤΡΟ»
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΑΓΡΟΝΟΜΩΝ & ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΓΕΩΓΡΑΦΙΑΣ ΚΑΙ ΠΕΡΙΦΕΡΕΙΑΚΟΥ ΣΧΕΔΙΑΣΜΟΥ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ «Η ΕΞΕΛΙΞΗ ΤΗΣ ΠΟΛΗΣ ΤΗΣ ΚΑΛΑΜΑΤΑΣ ΜΕ ΕΠΙΚΕΝΤΡΟ ΤΟ ΙΣΤΟΡΙΚΟ ΤΗΣ ΚΕΝΤΡΟ»
MOTROL. COMMISSION OF MOTORIZATION AND ENERGETICS IN AGRICULTURE 2014, Vol. 16, No. 5,
 MOTROL. COMMISSION OF MOTORIZATION AND ENERGETICS IN AGRICULTURE 2014, Vol. 16, No. 5, 3 14 -, :., 83, 66404 e-mail: chupinvr@istu.irk.ru...,,., -,.,. :,,,,,, -, - [1].,.., [2, 3].,.,,,.,,, [4, 5].,..1.
MOTROL. COMMISSION OF MOTORIZATION AND ENERGETICS IN AGRICULTURE 2014, Vol. 16, No. 5, 3 14 -, :., 83, 66404 e-mail: chupinvr@istu.irk.ru...,,., -,.,. :,,,,,, -, - [1].,.., [2, 3].,.,,,.,,, [4, 5].,..1.
ΣΧΕΔΙΑΣΜΟΣ ΚΑΙ ΕΝΙΣΧΥΣΗ ΤΩΝ ΚΟΜΒΩΝ ΟΠΛΙΣΜΕΝΟΥ ΣΚΥΡΟΔΕΜΑΤΟΣ ΜΕ ΒΑΣΗ ΤΟΥΣ ΕΥΡΩΚΩΔΙΚΕΣ
 Σχολή Μηχανικής και Τεχνολογίας Πτυχιακή εργασία ΣΧΕΔΙΑΣΜΟΣ ΚΑΙ ΕΝΙΣΧΥΣΗ ΤΩΝ ΚΟΜΒΩΝ ΟΠΛΙΣΜΕΝΟΥ ΣΚΥΡΟΔΕΜΑΤΟΣ ΜΕ ΒΑΣΗ ΤΟΥΣ ΕΥΡΩΚΩΔΙΚΕΣ Σωτήρης Παύλου Λεμεσός, Μάιος 2018 i ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ
Σχολή Μηχανικής και Τεχνολογίας Πτυχιακή εργασία ΣΧΕΔΙΑΣΜΟΣ ΚΑΙ ΕΝΙΣΧΥΣΗ ΤΩΝ ΚΟΜΒΩΝ ΟΠΛΙΣΜΕΝΟΥ ΣΚΥΡΟΔΕΜΑΤΟΣ ΜΕ ΒΑΣΗ ΤΟΥΣ ΕΥΡΩΚΩΔΙΚΕΣ Σωτήρης Παύλου Λεμεσός, Μάιος 2018 i ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ
Η ΜΑΛΑΞΗ ΚΑΙ ΤΑ ΕΙ Η ΤΗΣ ΣΤΟ ΙΝΣΤΙΤΟΥΤΟ ΑΙΣΘΗΤΙΚΗΣ
 ΤΕΙ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΕΠΑΓΓΕΛΜΑΤΩΝ ΥΓΕΙΑΣ ΚΑΙ ΠΡΟΝΟΙΑΣ ΤΜΗΜΑ ΑΙΣΘΗΤΙΚΗΣ ΚΑΙ ΚΟΣΜΕΤΟΛΟΓΙΑΣ Η ΜΑΛΑΞΗ ΚΑΙ ΤΑ ΕΙ Η ΤΗΣ ΣΤΟ ΙΝΣΤΙΤΟΥΤΟ ΑΙΣΘΗΤΙΚΗΣ Σταµάτη Κωνσταντίνα Φεβρουάριος 2012 ΕΠΙΒΛΕΠΟΥΣΑ ΚΑΘΗΓΗΤΡΙΑ
ΤΕΙ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΕΠΑΓΓΕΛΜΑΤΩΝ ΥΓΕΙΑΣ ΚΑΙ ΠΡΟΝΟΙΑΣ ΤΜΗΜΑ ΑΙΣΘΗΤΙΚΗΣ ΚΑΙ ΚΟΣΜΕΤΟΛΟΓΙΑΣ Η ΜΑΛΑΞΗ ΚΑΙ ΤΑ ΕΙ Η ΤΗΣ ΣΤΟ ΙΝΣΤΙΤΟΥΤΟ ΑΙΣΘΗΤΙΚΗΣ Σταµάτη Κωνσταντίνα Φεβρουάριος 2012 ΕΠΙΒΛΕΠΟΥΣΑ ΚΑΘΗΓΗΤΡΙΑ
«ΑΝΑΠΣΤΞΖ ΓΠ ΚΑΗ ΥΩΡΗΚΖ ΑΝΑΛΤΖ ΜΔΣΔΩΡΟΛΟΓΗΚΩΝ ΓΔΓΟΜΔΝΩΝ ΣΟΝ ΔΛΛΑΓΗΚΟ ΥΩΡΟ»
 ΓΔΩΠΟΝΗΚΟ ΠΑΝΔΠΗΣΖΜΗΟ ΑΘΖΝΩΝ ΣΜΗΜΑ ΑΞΙΟΠΟΙΗΗ ΦΤΙΚΩΝ ΠΟΡΩΝ & ΓΕΩΡΓΙΚΗ ΜΗΥΑΝΙΚΗ ΣΟΜΕΑ ΕΔΑΦΟΛΟΓΙΑ ΚΑΙ ΓΕΩΡΓΙΚΗ ΥΗΜΕΙΑ ΕΙΔΙΚΕΤΗ: ΕΦΑΡΜΟΓΕ ΣΗ ΓΕΩΠΛΗΡΟΦΟΡΙΚΗ ΣΟΤ ΦΤΙΚΟΤ ΠΟΡΟΤ «ΑΝΑΠΣΤΞΖ ΓΠ ΚΑΗ ΥΩΡΗΚΖ ΑΝΑΛΤΖ ΜΔΣΔΩΡΟΛΟΓΗΚΩΝ
ΓΔΩΠΟΝΗΚΟ ΠΑΝΔΠΗΣΖΜΗΟ ΑΘΖΝΩΝ ΣΜΗΜΑ ΑΞΙΟΠΟΙΗΗ ΦΤΙΚΩΝ ΠΟΡΩΝ & ΓΕΩΡΓΙΚΗ ΜΗΥΑΝΙΚΗ ΣΟΜΕΑ ΕΔΑΦΟΛΟΓΙΑ ΚΑΙ ΓΕΩΡΓΙΚΗ ΥΗΜΕΙΑ ΕΙΔΙΚΕΤΗ: ΕΦΑΡΜΟΓΕ ΣΗ ΓΕΩΠΛΗΡΟΦΟΡΙΚΗ ΣΟΤ ΦΤΙΚΟΤ ΠΟΡΟΤ «ΑΝΑΠΣΤΞΖ ΓΠ ΚΑΗ ΥΩΡΗΚΖ ΑΝΑΛΤΖ ΜΔΣΔΩΡΟΛΟΓΗΚΩΝ
Srednicki Chapter 55
 Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Επιβλέπουσα Καθηγήτρια: ΣΟΦΙΑ ΑΡΑΒΟΥ ΠΑΠΑΔΑΤΟΥ
 EΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΕΚΠΑΙΔΕΥΤΙΚΟ ΤΕΧΝΟΛΟΓΙΚΟ ΙΔΡΥΜΑ ΤΕΙ ΙΟΝΙΩΝ ΝΗΣΩΝ ΤΜΗΜΑ ΔΗΜΟΣΙΩΝ ΣΧΕΣΕΩΝ & ΕΠΙΚΟΙΝΩΝΙΑΣ Ταχ. Δ/νση : Λεωφ. Αντ.Τρίτση, Αργοστόλι Κεφαλληνίας Τ.Κ. 28 100 τηλ. : 26710-27311 fax : 26710-27312
EΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΕΚΠΑΙΔΕΥΤΙΚΟ ΤΕΧΝΟΛΟΓΙΚΟ ΙΔΡΥΜΑ ΤΕΙ ΙΟΝΙΩΝ ΝΗΣΩΝ ΤΜΗΜΑ ΔΗΜΟΣΙΩΝ ΣΧΕΣΕΩΝ & ΕΠΙΚΟΙΝΩΝΙΑΣ Ταχ. Δ/νση : Λεωφ. Αντ.Τρίτση, Αργοστόλι Κεφαλληνίας Τ.Κ. 28 100 τηλ. : 26710-27311 fax : 26710-27312
Εξοικονόμηση Ενέργειας σε Εγκαταστάσεις Δρόμων, με Ρύθμιση (Dimming) ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΗΣ ΙΣΧΥΟΣ Εξοικονόμηση Ενέργειας σε Εγκαταστάσεις Δρόμων, με Ρύθμιση (Dimming) ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ Νικηφόρος
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΗΣ ΙΣΧΥΟΣ Εξοικονόμηση Ενέργειας σε Εγκαταστάσεις Δρόμων, με Ρύθμιση (Dimming) ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ Νικηφόρος
Assalamu `alaikum wr. wb.
 LUMP SUM Assalamu `alaikum wr. wb. LUMP SUM Wassalamu alaikum wr. wb. Assalamu `alaikum wr. wb. LUMP SUM Wassalamu alaikum wr. wb. LUMP SUM Lump sum lump sum lump sum. lump sum fixed price lump sum lump
LUMP SUM Assalamu `alaikum wr. wb. LUMP SUM Wassalamu alaikum wr. wb. Assalamu `alaikum wr. wb. LUMP SUM Wassalamu alaikum wr. wb. LUMP SUM Lump sum lump sum lump sum. lump sum fixed price lump sum lump
A CTA GEO GRA PH ICA S IN ICA
 55 2 2000 3 A CTA GEO GRA PH ICA S IN ICA V o l. 55, N o. 2 M ar., 2000 : 037525444 (2000) 0220129210 1, 1, Guen ther F ischer 2, Sylvia P rieler 2 (11, 100101; 21, ) : 1958 1997 310,, 3, H adcm 2 CGCM
55 2 2000 3 A CTA GEO GRA PH ICA S IN ICA V o l. 55, N o. 2 M ar., 2000 : 037525444 (2000) 0220129210 1, 1, Guen ther F ischer 2, Sylvia P rieler 2 (11, 100101; 21, ) : 1958 1997 310,, 3, H adcm 2 CGCM
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΨΥΧΟΛΟΓΙΚΕΣ ΕΠΙΠΤΩΣΕΙΣ ΣΕ ΓΥΝΑΙΚΕΣ ΜΕΤΑ ΑΠΟ ΜΑΣΤΕΚΤΟΜΗ ΓΕΩΡΓΙΑ ΤΡΙΣΟΚΚΑ Λευκωσία 2012 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΨΥΧΟΛΟΓΙΚΕΣ ΕΠΙΠΤΩΣΕΙΣ ΣΕ ΓΥΝΑΙΚΕΣ ΜΕΤΑ ΑΠΟ ΜΑΣΤΕΚΤΟΜΗ ΓΕΩΡΓΙΑ ΤΡΙΣΟΚΚΑ Λευκωσία 2012 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
A CTA GEO GRA PH ICA S IN ICA
 55 5 2000 9 A CTA GEO GRA PH ICA S IN ICA V o l. 55, N o. 5 Sep., 2000 : 037525444 (2000) 0520607210 1998 1, 1, 2, 1 (11, 730000; 21, 730000) : M. W ackernagel 1996, ( ), ( ),,, 1998, 1998 01564 hm 2 :
55 5 2000 9 A CTA GEO GRA PH ICA S IN ICA V o l. 55, N o. 5 Sep., 2000 : 037525444 (2000) 0520607210 1998 1, 1, 2, 1 (11, 730000; 21, 730000) : M. W ackernagel 1996, ( ), ( ),,, 1998, 1998 01564 hm 2 :
CYPRUS UNIVERSITY OF TECHNOLOGY. Faculty of Engineering and Technology. Department of Civil Engineering and Geomatics. Dissertation Thesis
 CYPRUS UNIVERSITY OF TECHNOLOGY Faculty of Engineering and Technology Department of Civil Engineering and Geomatics Dissertation Thesis GEOSPATIAL TECHNOLOGIES FOR REAL ESTATE AND LAND VALUATION IN CYPRUS
CYPRUS UNIVERSITY OF TECHNOLOGY Faculty of Engineering and Technology Department of Civil Engineering and Geomatics Dissertation Thesis GEOSPATIAL TECHNOLOGIES FOR REAL ESTATE AND LAND VALUATION IN CYPRUS
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ. Πτυχιακή εργασία
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ Πτυχιακή εργασία ΕΠΙΠΤΩΣΕΙΣ ΤΗΣ ΚΑΚΗΣ ΔΙΑΤΡΟΦΗΣ ΣΤΗ ΠΡΟΣΧΟΛΙΚΗ ΗΛΙΚΙΑ ΜΕ ΑΠΟΤΕΛΕΣΜΑ ΤΗ ΠΑΧΥΣΑΡΚΙΑ Έλλη Φωτίου 2010364426 Επιβλέπουσα
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ Πτυχιακή εργασία ΕΠΙΠΤΩΣΕΙΣ ΤΗΣ ΚΑΚΗΣ ΔΙΑΤΡΟΦΗΣ ΣΤΗ ΠΡΟΣΧΟΛΙΚΗ ΗΛΙΚΙΑ ΜΕ ΑΠΟΤΕΛΕΣΜΑ ΤΗ ΠΑΧΥΣΑΡΚΙΑ Έλλη Φωτίου 2010364426 Επιβλέπουσα
ΑΓΓΛΙΚΑ IV. Ενότητα 6: Analysis of Greece: Your Strategic Partner in Southeast Europe. Ιφιγένεια Μαχίλη Τμήμα Οικονομικών Επιστημών
 Ενότητα 6: Analysis of Greece: Your Strategic Partner in Southeast Europe Ιφιγένεια Μαχίλη Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό,
Ενότητα 6: Analysis of Greece: Your Strategic Partner in Southeast Europe Ιφιγένεια Μαχίλη Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό,
F ig. 1 Flow chart of comprehen sive design in the research of com patibil ity. E2m ail: ac. cn
 V o l. 25 N o. 9 2 0 0 4 9 CH EM ICAL JOU RNAL O F CH IN ESE UN IV ERS IT IES 1632 1636,,,, (, 116011) H PL C2PAD 2M S,,.,. H PL C2PAD 2M S.,.,,. 2 ; ; O 652. 7 A 025120790 (2004) 0921632205,,., [1 5 ]
V o l. 25 N o. 9 2 0 0 4 9 CH EM ICAL JOU RNAL O F CH IN ESE UN IV ERS IT IES 1632 1636,,,, (, 116011) H PL C2PAD 2M S,,.,. H PL C2PAD 2M S.,.,,. 2 ; ; O 652. 7 A 025120790 (2004) 0921632205,,., [1 5 ]
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΚΡΗΤΗΣ ΣΧΟΛΗ ΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ ΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΚΡΗΤΗΣ ΣΧΟΛΗ ΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ ΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ Το franchising ( δικαιόχρηση ) ως µέθοδος ανάπτυξης των επιχειρήσεων λιανικού εµπορίου
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΚΡΗΤΗΣ ΣΧΟΛΗ ΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ ΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ Το franchising ( δικαιόχρηση ) ως µέθοδος ανάπτυξης των επιχειρήσεων λιανικού εµπορίου
ΠΩΣ ΕΠΗΡΕΑΖΕΙ Η ΜΕΡΑ ΤΗΣ ΕΒΔΟΜΑΔΑΣ ΤΙΣ ΑΠΟΔΟΣΕΙΣ ΤΩΝ ΜΕΤΟΧΩΝ ΠΡΙΝ ΚΑΙ ΜΕΤΑ ΤΗΝ ΟΙΚΟΝΟΜΙΚΗ ΚΡΙΣΗ
 Σχολή Διοίκησης και Οικονομίας Κρίστια Κυριάκου ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ ΕΜΠΟΡΙΟΥ,ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΝΑΥΤΙΛΙΑΣ Της Κρίστιας Κυριάκου ii Έντυπο έγκρισης Παρουσιάστηκε
Σχολή Διοίκησης και Οικονομίας Κρίστια Κυριάκου ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ ΕΜΠΟΡΙΟΥ,ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΝΑΥΤΙΛΙΑΣ Της Κρίστιας Κυριάκου ii Έντυπο έγκρισης Παρουσιάστηκε
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Επιβλέπων καθηγητής: Δρ Βασίλειος Ραφτόπουλος ΠΟΙΟΤΗΤΑ ΖΩΗΣ ΣΕ ΜΕΤΕΜΜΗΝΟΠΑΥΣΙΑΚΕΣ ΓΥΝΑΙΚΕΣ ΜΕΤΑ ΑΠΟ ΟΣΤΕΟΠΟΡΩΤΙΚΑ ΚΑΤΑΓΜΑΤΑ ΣΠΟΝΔΥΛΙΚΗΣ ΣΤΗΛΗΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ Επιβλέπων καθηγητής: Δρ Βασίλειος Ραφτόπουλος ΠΟΙΟΤΗΤΑ ΖΩΗΣ ΣΕ ΜΕΤΕΜΜΗΝΟΠΑΥΣΙΑΚΕΣ ΓΥΝΑΙΚΕΣ ΜΕΤΑ ΑΠΟ ΟΣΤΕΟΠΟΡΩΤΙΚΑ ΚΑΤΑΓΜΑΤΑ ΣΠΟΝΔΥΛΙΚΗΣ ΣΤΗΛΗΣ Από τη
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ Επιβλέπων καθηγητής: Δρ Βασίλειος Ραφτόπουλος ΠΟΙΟΤΗΤΑ ΖΩΗΣ ΣΕ ΜΕΤΕΜΜΗΝΟΠΑΥΣΙΑΚΕΣ ΓΥΝΑΙΚΕΣ ΜΕΤΑ ΑΠΟ ΟΣΤΕΟΠΟΡΩΤΙΚΑ ΚΑΤΑΓΜΑΤΑ ΣΠΟΝΔΥΛΙΚΗΣ ΣΤΗΛΗΣ Από τη
ΔΕΛΤΙΟ ΔΕΔΟΜΕΝΩN ΑΣΦΑΛΕΙΑΣ ΥΛΙΚΟΥ BOSTIK OPF GREY
 ΔΕΛΤΙΟ ΔΕΔΟΜΕΝΩN ΑΣΦΑΛΕΙΑΣ ΥΛΙΚΟΥ According to Regulation (EC) No 1907/2006 1 ΣΤΟΙΧΕΙΑ ΟΥΣΙΑΣ/ΠΑΡΑΣΚΕΥΑΣΜΑΤΟΣ ΚΑΙ ΕΤΑΙΡΕΙΑΣ/ΕΠΙΧΕΙΡΗΣΗΣ ΟΝΟΜΑΣIΑ ΠΡΟIOΝΤΟΣ ΑΡ. ΠΡΟIOΝΤΟΣ 068865 ΕΦΑΡΜΟΓH ΠΡΟΜΗΘΕΥΤHΣ 2 ΠPOΣΔIOPIΣMOΣ
ΔΕΛΤΙΟ ΔΕΔΟΜΕΝΩN ΑΣΦΑΛΕΙΑΣ ΥΛΙΚΟΥ According to Regulation (EC) No 1907/2006 1 ΣΤΟΙΧΕΙΑ ΟΥΣΙΑΣ/ΠΑΡΑΣΚΕΥΑΣΜΑΤΟΣ ΚΑΙ ΕΤΑΙΡΕΙΑΣ/ΕΠΙΧΕΙΡΗΣΗΣ ΟΝΟΜΑΣIΑ ΠΡΟIOΝΤΟΣ ΑΡ. ΠΡΟIOΝΤΟΣ 068865 ΕΦΑΡΜΟΓH ΠΡΟΜΗΘΕΥΤHΣ 2 ΠPOΣΔIOPIΣMOΣ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΑΧΕΙΡΗΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ. Πτυχιακή εργασία ΑΝΑΠΤΥΞΗ ΔΕΙΚΤΩΝ ΠΟΙΟΤΗΤΑΣ ΕΔΑΦΟΥΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΑΧΕΙΡΗΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Πτυχιακή εργασία ΑΝΑΠΤΥΞΗ ΔΕΙΚΤΩΝ ΠΟΙΟΤΗΤΑΣ ΕΔΑΦΟΥΣ [Μαρία Μαρκουλλή] Λεμεσός 2015 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΑΧΕΙΡΗΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Πτυχιακή εργασία ΑΝΑΠΤΥΞΗ ΔΕΙΚΤΩΝ ΠΟΙΟΤΗΤΑΣ ΕΔΑΦΟΥΣ [Μαρία Μαρκουλλή] Λεμεσός 2015 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ
ΜΑΡΙΟΛΑΚΟΣ Η., ΦΟΥΝΤΟΥΛΗΣ Ι., ΣΠΥΡΙΔΩΝΟΣ Ε., ΑΝΔΡΕΑΔΑΚΗΣ Ε., ΚΑΠΟΥΡΑΝΗ, Ε.
 ΔΗΜΟΣΙΕΥΣΗ Νο 95 ΜΑΡΙΟΛΑΚΟΣ Η., ΦΟΥΝΤΟΥΛΗΣ Ι., ΣΠΥΡΙΔΩΝΟΣ Ε., ΑΝΔΡΕΑΔΑΚΗΣ Ε., ΚΑΠΟΥΡΑΝΗ, Ε. (2003). Το πρόβλημα του νερού στη Θεσσαλία και προτάσεις για την αντιμετώπισή του στα πλαίσια της αειφόρου ανάπτυξης.
ΔΗΜΟΣΙΕΥΣΗ Νο 95 ΜΑΡΙΟΛΑΚΟΣ Η., ΦΟΥΝΤΟΥΛΗΣ Ι., ΣΠΥΡΙΔΩΝΟΣ Ε., ΑΝΔΡΕΑΔΑΚΗΣ Ε., ΚΑΠΟΥΡΑΝΗ, Ε. (2003). Το πρόβλημα του νερού στη Θεσσαλία και προτάσεις για την αντιμετώπισή του στα πλαίσια της αειφόρου ανάπτυξης.
Finite Field Problems: Solutions
 Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Fourier Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Jesse Maassen and Mark Lundstrom Purdue University November 25, 2013
 Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Πτυχιακή Εργασία Η ΠΟΙΟΤΗΤΑ ΖΩΗΣ ΤΩΝ ΑΣΘΕΝΩΝ ΜΕ ΣΤΗΘΑΓΧΗ
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ Πτυχιακή Εργασία Η ΠΟΙΟΤΗΤΑ ΖΩΗΣ ΤΩΝ ΑΣΘΕΝΩΝ ΜΕ ΣΤΗΘΑΓΧΗ Νικόλας Χριστοδούλου Λευκωσία, 2012 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ Πτυχιακή Εργασία Η ΠΟΙΟΤΗΤΑ ΖΩΗΣ ΤΩΝ ΑΣΘΕΝΩΝ ΜΕ ΣΤΗΘΑΓΧΗ Νικόλας Χριστοδούλου Λευκωσία, 2012 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ
(2006) ,A RD S. AL Ig A RD S. AL IgA RD S A RD S A RD S A RD S , A RD S 25% 50%, 11% 25%, 9% 26% 1 AL IgARD S , A RD S 50% 6815%
 706 g (2006) Guidel ines for managem en t of acute lung in jurygacute resp ira tory d istress syndrom e: an ev idence- ba sed update by the Ch inese Soc iety of Cr itical Care M edic ine (2006) Ch inese
706 g (2006) Guidel ines for managem en t of acute lung in jurygacute resp ira tory d istress syndrom e: an ev idence- ba sed update by the Ch inese Soc iety of Cr itical Care M edic ine (2006) Ch inese
1 String with massive end-points
 1 String with massive end-points Πρόβλημα 5.11:Θεωρείστε μια χορδή μήκους, τάσης T, με δύο σημειακά σωματίδια στα άκρα της, το ένα μάζας m, και το άλλο μάζας m. α) Μελετώντας την κίνηση των άκρων βρείτε
1 String with massive end-points Πρόβλημα 5.11:Θεωρείστε μια χορδή μήκους, τάσης T, με δύο σημειακά σωματίδια στα άκρα της, το ένα μάζας m, και το άλλο μάζας m. α) Μελετώντας την κίνηση των άκρων βρείτε
: (2003)
 21 2 2003 6 A CTA SED IM EN TOLO G ICA S IN ICA V o l. 21 N o. 2 Jun. 2003 : 100020550 (2003) 0220345205 1 2 1 3 1 ( 730000) 2 ( 730000) 3 ( 730020),, 1969 T E122. 1 A,,,,, 200,,,, (,, ) 1, 2,, ;,,,, (
21 2 2003 6 A CTA SED IM EN TOLO G ICA S IN ICA V o l. 21 N o. 2 Jun. 2003 : 100020550 (2003) 0220345205 1 2 1 3 1 ( 730000) 2 ( 730000) 3 ( 730020),, 1969 T E122. 1 A,,,,, 200,,,, (,, ) 1, 2,, ;,,,, (
Supporting information. An unusual bifunctional Tb-MOF for highly sensing of Ba 2+ ions and remarkable selectivities of CO 2 /N 2 and CO 2 /CH 4
 Electronic Supplementary Material (ESI) for Journal of Materials Chemistry A. This journal is The Royal Society of Chemistry 2015 Supporting information An unusual bifunctional Tb-MOF for highly sensing
Electronic Supplementary Material (ESI) for Journal of Materials Chemistry A. This journal is The Royal Society of Chemistry 2015 Supporting information An unusual bifunctional Tb-MOF for highly sensing
D esign and Imp lem en tation of Parallel Genetic A lgo rithm
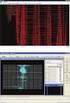 2004 6 6 : 100026788 (2004) 0620061206 1, 2, 1 2, (1., 230027; 2., 230039) : PGA, : ; ; : T P301. 6 : A D esign and Imp lem en tation of Parallel Genetic A lgo rithm fo r F inding Roo ts Comp lex Functional
2004 6 6 : 100026788 (2004) 0620061206 1, 2, 1 2, (1., 230027; 2., 230039) : PGA, : ; ; : T P301. 6 : A D esign and Imp lem en tation of Parallel Genetic A lgo rithm fo r F inding Roo ts Comp lex Functional
