Διαφορικές Εξισώσεις.
|
|
|
- Ê Παπαγεωργίου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Διαφορικές Εξισώσεις. Εαρινό εξάμηνο Λύσεις του έβδομου φυλλαδίου ασκήσεων. 1. Λύστε την παρακάτω δ.ε. με τη δοσμένη αρχική συνθήκη. Σχεδιάστε τις χαρακτηριστικές καθώς και το γράφημα της λύσης τις χρονικές στιγμές t = 0, 1, 2. u t + 3u x = 0, u(x, 0) = 1/(1 + x 2 ). Λύση. Βρίσκουμε τη χαρακτηριστική καμπύλη (x(t), t) η οποία τέμνει τον x-άξονα σε τυχόν σημείο (x 0, 0). Αυτή ικανοποιεί το x (t) = 3 για t σε κάποιο διάστημα I Από την x (t) = 3 παίρνουμε x(t) = 3t + c και από την βρίσκουμε (3t + x 0, t). Η καρτεσιανή εξίσωση της χαρακτηριστικής είναι x = 3t + x 0, οπότε η χαρακτηριστική είναι ευθεία με κλίση 3 ως προς τον t-άξονα. t u(3t + x 0, t) = 3u x (3t + x 0, t) + u t (3t + x 0, t) = 0 οπότε η u(3t + x 0, t) είναι σταθερή συνάρτηση του t στο R. Η σταθερή τιμή εξαρτάται από το x 0, οπότε u(3t + x 0, t) = f(x 0 ) Γράφουμε 3t + x 0 = x, οπότε x 0 = x 3t, και έχουμε u(x, t) = f(x 3t) για x, t R. Συνδυάζουμε με την αρχική συνθήκη u(x, 0) = 1/(1 + x 2 ) για t = 0 και έχουμε f(x) = u(x, 0) = x 2. u(x, t) = (x 3t) 2 για x, t R. 2. Λύστε την παρακάτω δ.ε. με τη δοσμένη αρχική συνθήκη και σχεδιάστε τις χαρακτηριστικές. u t + xu x = xu, x (t) = x(t) για t σε κάποιο διάστημα I 1
2 Από την x (t) = x(t) παίρνουμε x(t) = ce t και από την βρίσκουμε (x 0 e t, t). Η καρτεσιανή εξίσωση της χαρακτηριστικής είναι x = x 0 e t και αποτελεί το γράφημα της συνάρτησης x(t) = x 0 e t. t u(x 0e t, t) = x 0 e t u x (x 0 e t, t) + u t (x 0 e t, t) = x 0 e t u(x 0 e t, t). Για απλούστευση του συμβολισμού γράφουμε, προσωρινά, v(t) = u(x 0 e t, t) οπότε v (t) = x 0 e t v(t). Λύνουμε αυτήν την διαφορική εξίσωση και βρίσκουμε v(t) = ce x 0e t. Η σταθερά c εξαρτάται από το x 0, οπότε u(x 0 e t, t) = v(t) = f(x 0 )e x 0e t Γράφουμε x 0 e t = x, οπότε x 0 = xe t, και έχουμε u(x, t) = f(xe t )e x για x, t R. f(x) = ϕ(x)e x και f(x)e x = u(x, t) = ϕ(xe t )e xe t e x για x, t R. 3. Λύστε την παρακάτω δ.ε. με τη δοσμένη αρχική συνθήκη και σχεδιάστε τις χαρακτηριστικές. u t + (t/x)u x = 0, x (t) = t x(t) για t σε κάποιο διάστημα I Επειδή πρέπει να είναι x(t) 0, λόγω συνέχειας θα ισχύει είτε x(t) > 0 για κάθε t I είτε x(t) < 0 για κάθε t I. 2
3 Από την x = t x παίρνουμε τις διαδοχικές ισοδύναμες ισότητες xx = t x x t t = x x = t t t t x 2 = t 2 + c x = ± t 2 + c. Από την βρίσκουμε c = x 2 0. Επειδή πρέπει να είναι x(0) 0, έχουμε x 0 0 και άρα c > 0. είτε x(t) = t 2 + x 2 0 για κάθε t R είτε x(t) = t 2 + x 2 0 για κάθε t R. Στην πρώτη περίπτωση η χαρακτηριστική καμπύλη είναι υπερβολή στο δεξιό xt-ημιεπίπεδο με ασύμπτωτες την ευθεία x = t για t + και την ευθεία x = t για t. Στη δεύτερη περίπτωση η χαρακτηριστική καμπύλη είναι υπερβολή στο αριστερό xt-ημιεπίπεδο με ασύμπτωτες την ευθεία x = t για t + και την ευθεία x = t για t. Και στις δύο περιπτώσεις έχουμε t u(x(t), t) = x (t)u x (x(t), t)+u t (x(t), t) = t x(t) u x(x(t), t)+u t (x(t), t) = 0. u(x(t), t) = c, όπου η σταθερά c εξαρτάται από το x 0 που βρίσκεται στον τύπο του x(t). Δηλαδή c = f(x 0 ) για κάποια συνάρτηση f στο (, 0) (0, + ) (επειδή x 0 0). Στην περίπτωση όπου x(t) = t 2 + x 2 0 για κάθε t έχουμε x 0 = x(0) > 0 και u( t 2 + x 2 0, t) = f(x 0) και, γράφοντας t 2 + x 2 0 = x, οπότε x > t και x 0 = x 2 t 2, έχουμε u(x, t) = f( x 2 t 2 ) για x, t R με x > t. f(x) = u(x, 0) = ϕ(x) u(x, t) = ϕ( x 2 t 2 ) για x > t. για x, t R με x > t. Στην περίπτωση όπου x(t) = t 2 + x 2 0 για κάθε t έχουμε x 0 = x(0) < 0 και u( t 2 + x 2 0, t) = f(x 0). Γράφοντας t 2 + x 2 0 = x, οπότε x < t και x 0 = x 2 t 2, έχουμε u(x, t) = f( x 2 t 2 ) για x, t R με x < t. f(x) = u(x, 0) = ϕ(x) u(x, t) = ϕ( x 2 t 2 ) για x < t. για x, t R με x < t. Το χωρίο του xt-επιπέδου στο οποίο προσδιορίζεται μονοσήμαντα η λύση είναι το σύνολο των σημείων (x, t) που ικανοποιούν την x > t ή την x < t, δηλαδή η ένωση του δεξιού και του αριστερού τεταρτημορίου που ορίζονται από τις ευθείες x = ±t. Αυτό είναι το χωρίο το οποίο καλύπτεται από τις χαρακτηριστικές οι οποίες τέμνουν τον x-άξονα (εκτός του σημείου x = 0). 3
4 4. Λύστε την παρακάτω δ.ε. με τη δοσμένη αρχική συνθήκη και σχεδιάστε τις χαρακτηριστικές. u t + u x = 4, u(x, 0) = sin x για 0 < x < π. [u(x, t) = sin(x t) + 4t για 0 < x t < π.] 5. Λύστε την παρακάτω δ.ε. με τη δοσμένη αρχική συνθήκη και σχεδιάστε τις χαρακτηριστικές. u t + xu x = (x + t)u, u(x, 0) = ϕ(x) για 1 < x < 1. x (t) = x(t) για t σε κάποιο διάστημα I Από την x (t) = x(t) παίρνουμε x(t) = ce t και από την βρίσκουμε (x 0 e t, t). Η καρτεσιανή εξίσωση της χαρακτηριστικής είναι x = x 0 e t και αποτελεί το γράφημα της συνάρτησης x(t) = x 0 e t. t u(x 0e t, t) = x 0 e t u x (x 0 e t, t) + u t (x 0 e t, t) = (x 0 e t + t)u(x 0 e t, t). Για απλούστευση του συμβολισμού γράφουμε, προσωρινά, v(t) = u(x 0 e t, t) οπότε v (t) = (x 0 e t + t)v(t). Λύνουμε αυτήν την διαφορική εξίσωση και βρίσκουμε v(t) = ce x 0e t + t2 2. Η σταθερά c εξαρτάται από το x 0, οπότε u(x 0 e t, t) = v(t) = f(x 0 )e x 0e t + t2 2 Γράφουμε x 0 e t = x, οπότε x 0 = xe t, και έχουμε u(x, t) = f(xe t )e x+ t2 2 για x, t R. f(x)e x = u(x, 0) = ϕ(x) για 1 < x < 1. 4
5 f(x) = ϕ(x)e x για 1 < x < 1 και u(x, t) = ϕ(xe t )e xe t e x+ t2 2 για x, t R με 1 < xe t < 1. Το χωρίο του xt-επιπέδου στο οποίο καθορίζεται μονοσήμαντα η λύση από την αρχική συνθήκη είναι το σύνολο των (x, t) που ικανοποιούν τις e t < x < e t. Αυτό είναι και το σύνολο που καλύπτεται από τις χαρακτηριστικές οι οποίες τέμνουν τον x-άξονα στο διάστημα ( 1, 1). 6. Λύστε την παρακάτω δ.ε. με τη δοσμένη αρχική συνθήκη και σχεδιάστε τις χαρακτηριστικές. [u(x, t) = 1 + sin(x t)e xt t2 2.] u t + u x = x(u + 1), u(x, 0) = sin x. 7. Λύστε την παρακάτω δ.ε. με τη δοσμένη αρχική συνθήκη. u t (x + t)u x = (x + t 1)e t, [u(x, t) = t(x + t 1) + ϕ(x + t).] 5
Διαφορικές Εξισώσεις.
 Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 2015-16. Λύσεις του τρίτου φυλλαδίου ασκήσεων. 1. Λύστε τις παρακάτω διαφορικές εξισώσεις. Αν προκύψει αλγεβρική σχέση ανάμεσα στις μεταβλητές x, y η οποία δεν λύνεται
Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 2015-16. Λύσεις του τρίτου φυλλαδίου ασκήσεων. 1. Λύστε τις παρακάτω διαφορικές εξισώσεις. Αν προκύψει αλγεβρική σχέση ανάμεσα στις μεταβλητές x, y η οποία δεν λύνεται
Διαφορικές Εξισώσεις.
 Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 05-6. Λύσεις δεύτερου φυλλαδίου ασκήσεων.. Βρείτε όλες τις λύσεις της εξίσωσης Bernoulli x y = xy + y 3 καθορίζοντας προσεκτικά το διάστημα στο οποίο ορίζεται καθεμιά
Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 05-6. Λύσεις δεύτερου φυλλαδίου ασκήσεων.. Βρείτε όλες τις λύσεις της εξίσωσης Bernoulli x y = xy + y 3 καθορίζοντας προσεκτικά το διάστημα στο οποίο ορίζεται καθεμιά
Μιχάλης Παπαδημητράκης. Μερικές Διαφορικές Εξισώσεις
 Μιχάλης Παπαδημητράκης Μερικές Διαφορικές Εξισώσεις Περιεχόμενα 1 Γενικά. 1 1.1 Μερικές διαφορικές εξισώσεις............................ 1 1.2 Διαφορικοί τελεστές................................. 2 1.3
Μιχάλης Παπαδημητράκης Μερικές Διαφορικές Εξισώσεις Περιεχόμενα 1 Γενικά. 1 1.1 Μερικές διαφορικές εξισώσεις............................ 1 1.2 Διαφορικοί τελεστές................................. 2 1.3
Διαφορικές Εξισώσεις.
 Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 215-16. Λύσεις ενδέκατου φυλλαδίου ασκήσεων. 1. Λύστε το πρόβλημα συνοριακών συνθηκών u xx + u yy =, u(x, ) = u(x, π) =, u(, y) =, u(a, y) = sin 2y + 4 sin 5y, < x
Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 215-16. Λύσεις ενδέκατου φυλλαδίου ασκήσεων. 1. Λύστε το πρόβλημα συνοριακών συνθηκών u xx + u yy =, u(x, ) = u(x, π) =, u(, y) =, u(a, y) = sin 2y + 4 sin 5y, < x
Μερικές Διαφορικές Εξισώσεις
 Πανεπιστήμιο Πατρών, Τμήμα Μαθηματικών Μερικές Διαφορικές Εξισώσεις Χειμερινό εξάμηνο ακαδημαϊκού έτους 24-25, Διδάσκων: Α.Τόγκας ο φύλλο προβλημάτων Ονοματεπώνυμο - ΑΜ: ΜΔΕ ο φύλλο προβλημάτων Α. Τόγκας
Πανεπιστήμιο Πατρών, Τμήμα Μαθηματικών Μερικές Διαφορικές Εξισώσεις Χειμερινό εξάμηνο ακαδημαϊκού έτους 24-25, Διδάσκων: Α.Τόγκας ο φύλλο προβλημάτων Ονοματεπώνυμο - ΑΜ: ΜΔΕ ο φύλλο προβλημάτων Α. Τόγκας
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο Λύσεις πρώτου φυλλαδίου ασκήσεων.
 Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 208-9.. Για καθεμία από τις ανισότητες Λύσεις πρώτου φυλλαδίου ασκήσεων. x + > 2, x x +, x x+2 > x+3 3x+, (x )(x 3) (x 2) 2 0 γράψτε ως διάστημα ή ως ένωση διαστημάτων
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 208-9.. Για καθεμία από τις ανισότητες Λύσεις πρώτου φυλλαδίου ασκήσεων. x + > 2, x x +, x x+2 > x+3 3x+, (x )(x 3) (x 2) 2 0 γράψτε ως διάστημα ή ως ένωση διαστημάτων
Μερικές Διαφορικές Εξισώσεις
 Πανεπιστήμιο Πατρών, Τμήμα Μαθηματικών Μερικές Διαφορικές Εξισώσεις Χειμερινό εξάμηνο ακαδημαϊκού έτους 14-15, Διδάσκων: Α.Τόγκας ο φύλλο προβλημάτων Ονοματεπώνυμο - ΑΜ: Πρόβλημα 1. Για κάθε μια από τις
Πανεπιστήμιο Πατρών, Τμήμα Μαθηματικών Μερικές Διαφορικές Εξισώσεις Χειμερινό εξάμηνο ακαδημαϊκού έτους 14-15, Διδάσκων: Α.Τόγκας ο φύλλο προβλημάτων Ονοματεπώνυμο - ΑΜ: Πρόβλημα 1. Για κάθε μια από τις
Ο Λ Ο Κ Λ Η Ρ Ω Μ Α Τ Α
 Ο Λ Ο Κ Λ Η Ρ Ω Μ Α Τ Α Α Σ Κ Η Σ Ε Ι Σ 1. Να υπολογιστεί το ολοκλήρωμα: Ι ΑΠ. 36 2. Να δείξετε ότι: i) Για κάθε x (0, + ), 2x e x + e x -1 > 0 ii) Θεωρώ την συνάρτηση f(x) = 2x e x + e x - 1 iii. Αρκεί
Ο Λ Ο Κ Λ Η Ρ Ω Μ Α Τ Α Α Σ Κ Η Σ Ε Ι Σ 1. Να υπολογιστεί το ολοκλήρωμα: Ι ΑΠ. 36 2. Να δείξετε ότι: i) Για κάθε x (0, + ), 2x e x + e x -1 > 0 ii) Θεωρώ την συνάρτηση f(x) = 2x e x + e x - 1 iii. Αρκεί
Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 19/10/2017. Ακριβείς Διαφορικές Εξισώσεις-Ολοκληρωτικοί Παράγοντες. Η πρώτης τάξης διαφορική εξίσωση
 Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 19/10/2017 Ακριβείς Διαφορικές Εξισώσεις-Ολοκληρωτικοί Παράγοντες Η πρώτης τάξης διαφορική εξίσωση M(x, y) + (x, y)y = 0 ή ισοδύναμα, γραμμένη στην μορφή M(x,
Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 19/10/2017 Ακριβείς Διαφορικές Εξισώσεις-Ολοκληρωτικοί Παράγοντες Η πρώτης τάξης διαφορική εξίσωση M(x, y) + (x, y)y = 0 ή ισοδύναμα, γραμμένη στην μορφή M(x,
Διαφορικές Εξισώσεις.
 Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 05-6. Λύσεις πρώτου φυλλαδίου ασκήσεων.. Για κάθε μία από τις παρακάτω διαφορικές εξισώσεις πείτε αν είναι γραμμική ή όχι και προσδιορίστε την τάξη της. α. y + y +
Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 05-6. Λύσεις πρώτου φυλλαδίου ασκήσεων.. Για κάθε μία από τις παρακάτω διαφορικές εξισώσεις πείτε αν είναι γραμμική ή όχι και προσδιορίστε την τάξη της. α. y + y +
(a) = lim. f y (a, b) = lim. (b) = lim. f y (x, y) = lim. g g(a + h) g(a) h g(b + h) g(b)
 1 ΑΝΑΛΥΣΗ ΙΙ Μερική Παράγωγος Μερικές Παράγωγοι Ορισμός 1: a) Εστω f(x y) : U R R μία συνάρτηση δύο μεταβλητών και (a b) ένα σημείο του U. Θεωρούμε ότι μεταβάλλεται μόνο το x ένω το y παραμένει σταθερό
1 ΑΝΑΛΥΣΗ ΙΙ Μερική Παράγωγος Μερικές Παράγωγοι Ορισμός 1: a) Εστω f(x y) : U R R μία συνάρτηση δύο μεταβλητών και (a b) ένα σημείο του U. Θεωρούμε ότι μεταβάλλεται μόνο το x ένω το y παραμένει σταθερό
ΕΦΑΠΤΟΜΕΝΗ ΤΗΣ ΓΡΑΦΙΚΗΣ ΠΑΡΑΣΤΑΣΗΣ ΜΙΑΣ ΣΥΝΑΡΤΗΣΗΣ
 ΕΝΟΤΗΤΑ 1.4. 5 ο ΜΑΘΗΜΑ ΕΦΑΠΤΟΜΕΝΗ ΤΗΣ ΓΡΑΦΙΚΗΣ ΠΑΡΑΣΤΑΣΗΣ ΜΙΑΣ ΣΥΝΑΡΤΗΣΗΣ Σκοπός της ενότητας Σκοπός της ενότητας είναι ο ορισμός εφαπτομένης της γραφικής παράστασης μιας συνάρτησης σε κάποιο σημείο της,
ΕΝΟΤΗΤΑ 1.4. 5 ο ΜΑΘΗΜΑ ΕΦΑΠΤΟΜΕΝΗ ΤΗΣ ΓΡΑΦΙΚΗΣ ΠΑΡΑΣΤΑΣΗΣ ΜΙΑΣ ΣΥΝΑΡΤΗΣΗΣ Σκοπός της ενότητας Σκοπός της ενότητας είναι ο ορισμός εφαπτομένης της γραφικής παράστασης μιας συνάρτησης σε κάποιο σημείο της,
ΜΑΘΗΜΑΤΙΚΑ ΙΙ ιδάσκων : Ε. Στεφανόπουλος 12 ιουνιου 2017
 Πανεπιστηµιο Πατρων Πολυτεχνικη Σχολη Τµηµα Μηχανικων Η/Υ & Πληροφορικης ΜΑΘΗΜΑΤΙΚΑ ΙΙ ιδάσκων : Ε. Στεφανόπουλος 12 ιουνιου 217 Θ1. Θεωρούµε την συνάρτηση f(x, y, z) = 1 + x 2 + 2y 2 z. (αʹ) Να ϐρεθεί
Πανεπιστηµιο Πατρων Πολυτεχνικη Σχολη Τµηµα Μηχανικων Η/Υ & Πληροφορικης ΜΑΘΗΜΑΤΙΚΑ ΙΙ ιδάσκων : Ε. Στεφανόπουλος 12 ιουνιου 217 Θ1. Θεωρούµε την συνάρτηση f(x, y, z) = 1 + x 2 + 2y 2 z. (αʹ) Να ϐρεθεί
Απειροστικός Λογισμός ΙΙ, εαρινό εξάμηνο Φυλλάδιο ασκήσεων επανάληψης.
 Απειροστικός Λογισμός ΙΙ, εαρινό εξάμηνο 2016-17. Φυλλάδιο ασκήσεων επανάληψης. 1. Για καθεμία από τις παρακάτω συναρτήσεις ελέγξτε βάσει του ορισμού της παραγωγισιμότητας αν είναι παραγωγίσιμη στο αντίστοιχο
Απειροστικός Λογισμός ΙΙ, εαρινό εξάμηνο 2016-17. Φυλλάδιο ασκήσεων επανάληψης. 1. Για καθεμία από τις παρακάτω συναρτήσεις ελέγξτε βάσει του ορισμού της παραγωγισιμότητας αν είναι παραγωγίσιμη στο αντίστοιχο
1. Τα σημεία ακροτάτου της συνάρτησης x + 2y + 2z υπό την συνθήκη x 2 + y 2 + z 2 = 1 είναι τα
 1. Τα σημεία ακροτάτου της συνάρτησης x + 2y + 2z υπό την συνθήκη x 2 + y 2 + z 2 = 1 είναι τα ±(1/3, 2/3, 2/3). [±(0, 0, 1), ±(0, 1/ 2, 1/ 2), ±(0, 1/ 2, 1/ 2).] 1. Τα σημεία ακροτάτου της συνάρτησης
1. Τα σημεία ακροτάτου της συνάρτησης x + 2y + 2z υπό την συνθήκη x 2 + y 2 + z 2 = 1 είναι τα ±(1/3, 2/3, 2/3). [±(0, 0, 1), ±(0, 1/ 2, 1/ 2), ±(0, 1/ 2, 1/ 2).] 1. Τα σημεία ακροτάτου της συνάρτησης
Καρτεσιανές συντεταγμένες Γραφική παράσταση συνάρτησης
 Καρτεσιανές συντεταγμένες Γραφική παράσταση συνάρτησης Ορθοκανονικό σύστημα αξόνων ονομάζεται ένα σύστημα από δύο κάθετους άξονες με κοινή αρχή στους οποίους οι μονάδες έχουν το ίδιο μήκος. Υπάρχουν περιπτώσεις
Καρτεσιανές συντεταγμένες Γραφική παράσταση συνάρτησης Ορθοκανονικό σύστημα αξόνων ονομάζεται ένα σύστημα από δύο κάθετους άξονες με κοινή αρχή στους οποίους οι μονάδες έχουν το ίδιο μήκος. Υπάρχουν περιπτώσεις
Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 09/11/2017. Άσκηση 1. Να βρεθεί η γενική λύση της διαφορικής εξίσωσης. dy dx = 2y + x 2 y 2 2x
 Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 09/11/017 Άσκηση 1. Να βρεθεί η γενική λύση της διαφορικής εξίσωσης dx y + x y. x Παρατηρούμε ότι η δ.ε. είναι ομογενής. Πράγματι, dx y x + 1 x y x y x + 1 (
Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 09/11/017 Άσκηση 1. Να βρεθεί η γενική λύση της διαφορικής εξίσωσης dx y + x y. x Παρατηρούμε ότι η δ.ε. είναι ομογενής. Πράγματι, dx y x + 1 x y x y x + 1 (
ΚΕΦΑΛΑΙΟ 3 ο ΣΥΝΑΡΤΗΣΕΙΣ, ΤΡΙΓΩΝΟΜΕΤΡΙΑ( FUNCTIONS,TRIGONOMETRY)
 ΚΕΦΑΛΑΙΟ 3 ο ΣΥΝΑΡΤΗΣΕΙΣ, ΤΡΙΓΩΝΟΜΕΤΡΙΑ( FUNCTIONS,TRIGONOMETRY) 3.1 ΘΕΩΡΙΑ-ΤΥΠΟΛΟΓΙΟ-ΠΑΡΑΔΕΙΓΜΑΤΑ ΣΥΝΑΡΤΗΣΕΙΣ Συνάρτηση, ή απεικόνιση όπως ονομάζεται διαφορετικά, είναι μια αντιστοίχιση μεταξύ δύο συνόλων,
ΚΕΦΑΛΑΙΟ 3 ο ΣΥΝΑΡΤΗΣΕΙΣ, ΤΡΙΓΩΝΟΜΕΤΡΙΑ( FUNCTIONS,TRIGONOMETRY) 3.1 ΘΕΩΡΙΑ-ΤΥΠΟΛΟΓΙΟ-ΠΑΡΑΔΕΙΓΜΑΤΑ ΣΥΝΑΡΤΗΣΕΙΣ Συνάρτηση, ή απεικόνιση όπως ονομάζεται διαφορετικά, είναι μια αντιστοίχιση μεταξύ δύο συνόλων,
α) γνησίως αύξουσα σε ένα διάστημα Δ του πεδίου ορισμού της (Σχ.α), όταν β) γνησίως φθίνουσα σε ένα διάστημα Δ του πεδίου ορισμού της (Σχ.
 ΜΟΝΟΤΟΝΙΑ. ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ. ΜΟΝΟΤΟΝΙΑ - ΑΚΡΟΤΑΤΑ - ΣΥΜΜΕΤΡΙΕΣ Μια συνάρτηση f λέγεται: α) γνησίως αύξουσα σε ένα διάστημα Δ του πεδίου ορισμού της (Σχ.α), όταν για οποιαδήποτε χ,χ Δ με χ
ΜΟΝΟΤΟΝΙΑ. ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ. ΜΟΝΟΤΟΝΙΑ - ΑΚΡΟΤΑΤΑ - ΣΥΜΜΕΤΡΙΕΣ Μια συνάρτηση f λέγεται: α) γνησίως αύξουσα σε ένα διάστημα Δ του πεδίου ορισμού της (Σχ.α), όταν για οποιαδήποτε χ,χ Δ με χ
Διαφορικός Λογισμός πολλών μεταβλητών
 Διαφορικός Λογισμός πολλών μεταβλητών Πρόχειρες σημειώσεις Μιχάλης Παπαδημητράκης Τμήμα Μαθηματικών Πανεπιστήμιο Κρήτης 1η εβδομάδα. Τα στοιχεία του R n είναι όλα τα n-διάστατα διανύσματα ή, ισοδύναμα,
Διαφορικός Λογισμός πολλών μεταβλητών Πρόχειρες σημειώσεις Μιχάλης Παπαδημητράκης Τμήμα Μαθηματικών Πανεπιστήμιο Κρήτης 1η εβδομάδα. Τα στοιχεία του R n είναι όλα τα n-διάστατα διανύσματα ή, ισοδύναμα,
lim f ( x) x + f ( x) x a x a x a 2x 1
 Ασύµπτωτες γραφικής παραστάσεως συναρτήσεως Ασύµπτωτες της γραφικής παραστάσεως συναρτήσεως y f ( ) ονοµάζονται οι ευθείες που για πολύ µικρές ή µεγάλες τιµές των, y προσεγγίζουν ικανοποιητικά την γραφική
Ασύµπτωτες γραφικής παραστάσεως συναρτήσεως Ασύµπτωτες της γραφικής παραστάσεως συναρτήσεως y f ( ) ονοµάζονται οι ευθείες που για πολύ µικρές ή µεγάλες τιµές των, y προσεγγίζουν ικανοποιητικά την γραφική
Λύσεις στο Επαναληπτικό Διαγώνισμα 2
 Τμήμα Μηχανικών Οικονομίας και Διοίκησης Απειροστικός Λογισμός ΙΙ Γ. Καραγιώργος ykarag@aegean.gr Λύσεις στο Επαναληπτικό Διαγώνισμα 2 Για τυχόν παρατηρήσεις, απορίες ή λάθη που θα βρείτε, στείλτε μου
Τμήμα Μηχανικών Οικονομίας και Διοίκησης Απειροστικός Λογισμός ΙΙ Γ. Καραγιώργος ykarag@aegean.gr Λύσεις στο Επαναληπτικό Διαγώνισμα 2 Για τυχόν παρατηρήσεις, απορίες ή λάθη που θα βρείτε, στείλτε μου
Λ. Ζαχείλας. Επίκουρος Καθηγητής Εφαρμοσμένων Μαθηματικών Τμήμα Οικονομικών Επιστημών Πανεπιστήμιο Θεσσαλίας. Οικονομική Δυναμική 29/6/14
 1 Λ. Ζαχείλας Επίκουρος Καθηγητής Εφαρμοσμένων Μαθηματικών Τμήμα Οικονομικών Επιστημών Πανεπιστήμιο Θεσσαλίας Οικονομική Δυναμική 9 Συνεχή δυναμικά συστήματα Μέρος 1 ο Λουκάς Ζαχείλας Ορισμός Διαφορικής
1 Λ. Ζαχείλας Επίκουρος Καθηγητής Εφαρμοσμένων Μαθηματικών Τμήμα Οικονομικών Επιστημών Πανεπιστήμιο Θεσσαλίας Οικονομική Δυναμική 9 Συνεχή δυναμικά συστήματα Μέρος 1 ο Λουκάς Ζαχείλας Ορισμός Διαφορικής
ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β. 2x 1. είναι Τότε έχουμε: » τον χρησιμοποιούμε κυρίως σε θεωρητικές ασκήσεις.
 ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ : ΣΥΝΑΡΤΗΣΗ - ΑΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗ [Υποκεφάλαιο. Μονότονες συναρτήσεις Αντίστροφη συνάρτηση του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα.
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ : ΣΥΝΑΡΤΗΣΗ - ΑΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗ [Υποκεφάλαιο. Μονότονες συναρτήσεις Αντίστροφη συνάρτηση του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα.
Συναρτήσεις Θεωρία Ορισμοί - Παρατηρήσεις
 Συναρτήσεις Θεωρία Ορισμοί - Παρατηρήσεις Ορισμός: Έστω Α, Β R. Πραγματική συνάρτηση πραγματικής μεταβλητής από το σύνολο Α στο σύνολο Β ονομάζουμε την διαδικασία κατά την οποία κάθε στοιχείο του συνόλου
Συναρτήσεις Θεωρία Ορισμοί - Παρατηρήσεις Ορισμός: Έστω Α, Β R. Πραγματική συνάρτηση πραγματικής μεταβλητής από το σύνολο Α στο σύνολο Β ονομάζουμε την διαδικασία κατά την οποία κάθε στοιχείο του συνόλου
7.2 ΜΕΛΕΤΗ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ f(x) = x
 7. ΜΕΛΕΤΗ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ () = α ΘΕΩΡΙΑ. Μορφή της συνάρτησης (Ισοσκελής υπερβολή) Ιδιότητες Πεδίο ορισµού g() = R = (, 0) (0, + ) Είναι περιττή, άρα συµµετρική ως προς την αρχή των αξόνων Είναι γν.φθίνουσα
7. ΜΕΛΕΤΗ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ () = α ΘΕΩΡΙΑ. Μορφή της συνάρτησης (Ισοσκελής υπερβολή) Ιδιότητες Πεδίο ορισµού g() = R = (, 0) (0, + ) Είναι περιττή, άρα συµµετρική ως προς την αρχή των αξόνων Είναι γν.φθίνουσα
Κατηγορία 1 η. Σταθερή συνάρτηση Δίνεται παραγωγίσιμη συνάρτηση f : 0, f '( x) 0 για κάθε εσωτερικό σημείο x του Δ
 Κατηγορία η Σταθερή συνάρτηση Τρόπος αντιμετώπισης: Για να αποδείξουμε ότι μια συνάρτηση είναι σταθερή σε ένα διάστημα Δ πρέπει: η συνάρτηση να είναι συνεχής στο Δ '( ) 0 για κάθε εσωτερικό σημείο του
Κατηγορία η Σταθερή συνάρτηση Τρόπος αντιμετώπισης: Για να αποδείξουμε ότι μια συνάρτηση είναι σταθερή σε ένα διάστημα Δ πρέπει: η συνάρτηση να είναι συνεχής στο Δ '( ) 0 για κάθε εσωτερικό σημείο του
ΑΠΑΝΤΗΣΕΙΣ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΠΑΝΤΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Α Α1. Απόδειξη σχολικού βιβλίου σελίδα 135.
 ΑΠΑΝΤΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Α Α1. Απόδειξη σχολικού βιβλίου σελίδα 135. Α2. α) Η πρόταση είναι ψευδής. β) Αιτιολόγηση: Σελίδα 99 σχολικού βιβλίου (η f(x)= x είναι συνεχής στο x=0
ΑΠΑΝΤΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Α Α1. Απόδειξη σχολικού βιβλίου σελίδα 135. Α2. α) Η πρόταση είναι ψευδής. β) Αιτιολόγηση: Σελίδα 99 σχολικού βιβλίου (η f(x)= x είναι συνεχής στο x=0
Καρτεσιανές συντεταγμένες Γραφική παράσταση συνάρτησης
 Καρτεσιανές συντεταγμένες Γραφική παράσταση συνάρτησης Ορθοκανονικό σύστημα αξόνων ονομάζεται ένα σύστημα από δύο κάθετους άξονες με κοινή αρχή στους οποίους οι μονάδες έχουν το ίδιο μήκος. Υπάρχουν περιπτώσεις
Καρτεσιανές συντεταγμένες Γραφική παράσταση συνάρτησης Ορθοκανονικό σύστημα αξόνων ονομάζεται ένα σύστημα από δύο κάθετους άξονες με κοινή αρχή στους οποίους οι μονάδες έχουν το ίδιο μήκος. Υπάρχουν περιπτώσεις
Πεπερασμένες Διαφορές.
 Κεφάλαιο 1 Πεπερασμένες Διαφορές. 1.1 Προσέγγιση παραγώγων. 1.1.1 Πρώτη παράγωγος. Από τον ορισμό της παραγώγου για συναρτήσεις μιας μεταβλητής γνωρίζουμε ότι η παράγωγος μιας συνάρτησης f στο σημείο x
Κεφάλαιο 1 Πεπερασμένες Διαφορές. 1.1 Προσέγγιση παραγώγων. 1.1.1 Πρώτη παράγωγος. Από τον ορισμό της παραγώγου για συναρτήσεις μιας μεταβλητής γνωρίζουμε ότι η παράγωγος μιας συνάρτησης f στο σημείο x
2. Μια παραγωγίσιμη συνάρτηση f(x, y, z) έχει f(x 0, y 0, z 0 ) (0, 0, 0) και μηδενικό στιγμιαίο
 1. Έστω E το εφαπτόμενο επίπεδο στο γράφημα της f(x, y) = x 2 + 3xy στο σημείο (1, 1, 4). Σε ποιά σημεία της η επιφάνεια με καρτεσιανή εξίσωση 5x 2 + 3y 2 + z 2 = 9 έχει μοναδιαίο κάθετο διάνυσμα το οποίο
1. Έστω E το εφαπτόμενο επίπεδο στο γράφημα της f(x, y) = x 2 + 3xy στο σημείο (1, 1, 4). Σε ποιά σημεία της η επιφάνεια με καρτεσιανή εξίσωση 5x 2 + 3y 2 + z 2 = 9 έχει μοναδιαίο κάθετο διάνυσμα το οποίο
Κατακόρυφη - Οριζόντια μετατόπιση καμπύλης
 1 Κατακόρυφη - Οριζόντια μετατόπιση καμπύλης Έστω ότι έχουμε την συνάρτηση: f(x) = x + 3x 1 H γραφική της παράσταση είναι: Και την συνάρτηση f(x) = x + 3x + η οποία έχει προκύψει από την προηγούμενη αφού
1 Κατακόρυφη - Οριζόντια μετατόπιση καμπύλης Έστω ότι έχουμε την συνάρτηση: f(x) = x + 3x 1 H γραφική της παράσταση είναι: Και την συνάρτηση f(x) = x + 3x + η οποία έχει προκύψει από την προηγούμενη αφού
ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ
 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ Άσκηση 1. Έστω ότι η συνάρτηση f: R R είναι γνησίως αύξουσα στο R και η γραφική της παράσταση τέµνει τον άξονα y y στο. Να λύσετε την ανίσωση: f(x 9)
ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ Άσκηση 1. Έστω ότι η συνάρτηση f: R R είναι γνησίως αύξουσα στο R και η γραφική της παράσταση τέµνει τον άξονα y y στο. Να λύσετε την ανίσωση: f(x 9)
ΑΣΚΗΣΕΙΣ: ΟΡΙΑ ΚΑΙ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΕΩΝ
 ΑΣΚΗΣΕΙΣ: ΟΡΙΑ ΚΑΙ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΕΩΝ Όρια συναρτήσεων. Άσκηση. Ποιό είναι το σύνολο στο οποίο έχει νόημα και ποιό το σύνολο στο οποίο ισχύει καθεμιά από τις ανισότητες: x+2 > 00, > 000, < < ; x 2 x
ΑΣΚΗΣΕΙΣ: ΟΡΙΑ ΚΑΙ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΕΩΝ Όρια συναρτήσεων. Άσκηση. Ποιό είναι το σύνολο στο οποίο έχει νόημα και ποιό το σύνολο στο οποίο ισχύει καθεμιά από τις ανισότητες: x+2 > 00, > 000, < < ; x 2 x
9 εύτερη παράγωγος κι εφαρµογές
 9 εύτερη παράγωγος κι εφαρµογές Εστω ότι η y = f x είναι παραγωγίσιµη σε κάποιο διάστηµα το οποίο περιέχει τον x 0 και ότι η f x η οποία ορίζεται στο διάστηµα αυτό έχει µε την σειρά της παράγωγο στο x
9 εύτερη παράγωγος κι εφαρµογές Εστω ότι η y = f x είναι παραγωγίσιµη σε κάποιο διάστηµα το οποίο περιέχει τον x 0 και ότι η f x η οποία ορίζεται στο διάστηµα αυτό έχει µε την σειρά της παράγωγο στο x
7.1 ΜΕΛΕΤΗ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ
 7.1 ΜΕΛΕΤΗ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ f ( ) 1. Μορφή της συνάρτησης f ( ) Ιδιότητες Έχει πεδίο ορισµού ολο το R Είναι άρτια, άρα συµµετρική ως προς τον άξονα y y Είναι γνησίως φθίνουσα στο διάστηµα (,0] Είναι γνησίως
7.1 ΜΕΛΕΤΗ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ f ( ) 1. Μορφή της συνάρτησης f ( ) Ιδιότητες Έχει πεδίο ορισµού ολο το R Είναι άρτια, άρα συµµετρική ως προς τον άξονα y y Είναι γνησίως φθίνουσα στο διάστηµα (,0] Είναι γνησίως
ΑΠΑΝΤΗΣΕΙΣ ΣΤΙΣ ΑΣΚΗΣΕΙΣ ΠΡΟΕΤΟΙΜΑΣΙΑΣ ΓΙΑ ΤΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ
 ΑΠΑΝΤΗΣΕΙΣ ΣΤΙΣ ΑΣΚΗΣΕΙΣ ΠΡΟΕΤΟΙΜΑΣΙΑΣ ΓΙΑ ΤΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ 1. Τι ονομάζουμε συνάρτηση; Συνάρτηση ονομάζεται η αλληλεξάρτηση (ή η σχέση) δυο μεταβλητών εις τρόπον ώστε για κάθε τιμή της μιας
ΑΠΑΝΤΗΣΕΙΣ ΣΤΙΣ ΑΣΚΗΣΕΙΣ ΠΡΟΕΤΟΙΜΑΣΙΑΣ ΓΙΑ ΤΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ 1. Τι ονομάζουμε συνάρτηση; Συνάρτηση ονομάζεται η αλληλεξάρτηση (ή η σχέση) δυο μεταβλητών εις τρόπον ώστε για κάθε τιμή της μιας
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο Λύσεις έκτου φυλλαδίου ασκήσεων.
 Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 208-9. Λύσεις έκτου φυλλαδίου ασκήσεων.. Παρατηρήστε ότι ο πρώτος κανόνας αλλαγής μεταβλητής εφαρμόζεται μόνο στα εφτά πρώτα όρια ενώ ο δεύτερος κανόνας εφαρμόζεται
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 208-9. Λύσεις έκτου φυλλαδίου ασκήσεων.. Παρατηρήστε ότι ο πρώτος κανόνας αλλαγής μεταβλητής εφαρμόζεται μόνο στα εφτά πρώτα όρια ενώ ο δεύτερος κανόνας εφαρμόζεται
1.1 Βασικές Έννοιες των Διαφορικών Εξισώσεων
 Κεφάλαιο 1 Εισαγωγικά Στο κεφάλαιο αυτό θα παρουσιάσουμε τις βασικές έννοιες και ορισμούς των Διαφορικών Εξισώσεων. Στο εδάφιο 1.1 παρουσιάζονται οι βασικές έννοιες και ορισμοί των διαφορικών εξισώσεων
Κεφάλαιο 1 Εισαγωγικά Στο κεφάλαιο αυτό θα παρουσιάσουμε τις βασικές έννοιες και ορισμούς των Διαφορικών Εξισώσεων. Στο εδάφιο 1.1 παρουσιάζονται οι βασικές έννοιες και ορισμοί των διαφορικών εξισώσεων
α) f(x(t), y(t)) = 0,
 Ρητές καμπύλες Μια επίπεδη αλγεβρική καμπύλη V (f) είναι το σύνολο όλων των σημείων του επιπέδου K 2 που μηδενίζουν κάποιο συγκεκριμένο ανάγωγο πολυώνυμο f K[x, y], δηλαδή V (f) = {(x 0, y 0 ) K 2 f(x
Ρητές καμπύλες Μια επίπεδη αλγεβρική καμπύλη V (f) είναι το σύνολο όλων των σημείων του επιπέδου K 2 που μηδενίζουν κάποιο συγκεκριμένο ανάγωγο πολυώνυμο f K[x, y], δηλαδή V (f) = {(x 0, y 0 ) K 2 f(x
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΓΕΝΙΚΑ ΘΕΜΑ Α. , έχει κατακόρυφη ασύμπτωτη την x 0.
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΓΕΝΙΚΑ ΘΕΜΑ Α Άσκηση Θεωρούμε τον παρακάτω ισχυρισμό: «Αν η συνάρτηση την» ορίζεται στο τότε δεν μπορεί να έχει κατακόρυφη ασύμπτωτη ) Να χαρακτηρίσετε τον παραπάνω ισχυρισμό γράφοντας
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΓΕΝΙΚΑ ΘΕΜΑ Α Άσκηση Θεωρούμε τον παρακάτω ισχυρισμό: «Αν η συνάρτηση την» ορίζεται στο τότε δεν μπορεί να έχει κατακόρυφη ασύμπτωτη ) Να χαρακτηρίσετε τον παραπάνω ισχυρισμό γράφοντας
ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2015 ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ
 ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ Στασίνου 36, Γραφ. 102, Στρόβολος 2003, Λευκωσία Τηλ. 357 22378101 Φαξ: 357 22379122 cms@cms.org.cy, www.cms.org.cy ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2015 ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Ημερομηνία:
ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ Στασίνου 36, Γραφ. 102, Στρόβολος 2003, Λευκωσία Τηλ. 357 22378101 Φαξ: 357 22379122 cms@cms.org.cy, www.cms.org.cy ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2015 ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Ημερομηνία:
2x 2 y. f(y) = f(x, y) = (xy, x + y)
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ 1. Εστω f : R R η συνάρτηση με τύπο y + x sin 1, για y 0, f(x, y) = y 0, για y = 0. (α) Να αποδειχθεί οτι lim f(x, y) = 0. (x,y) (0,0) (β) Να αποδειχθεί οτι το lim(lim f(x, y)) δεν
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ 1. Εστω f : R R η συνάρτηση με τύπο y + x sin 1, για y 0, f(x, y) = y 0, για y = 0. (α) Να αποδειχθεί οτι lim f(x, y) = 0. (x,y) (0,0) (β) Να αποδειχθεί οτι το lim(lim f(x, y)) δεν
Εφαρμοσμένα Μαθηματικά
 Εφαρμοσμένα Μαθηματικά ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ενότητα 6: Διπλά Ολοκληρώματα Δρ. Περικλής Παπαδόπουλος Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε Κάντε κλικ για
Εφαρμοσμένα Μαθηματικά ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ενότητα 6: Διπλά Ολοκληρώματα Δρ. Περικλής Παπαδόπουλος Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε Κάντε κλικ για
Πανελλαδικές εξετάσεις Μαθηµατικά Προσανατολισµού Γ Λυκείου. Ενδεικτικές Απαντήσεις ϑεµάτων. Θέµα Β. (α) ϑεωρία. (ϐ) i, ii) ϑεωρία.
 Πανελλαδικές εξετάσεις 09 Μαθηµατικά Προσανατολισµού Γ Λυκείου Ενδεικτικές Απαντήσεις ϑεµάτων Θέµα Α Α α) ϑεωρία ϐ) i, ii) ϑεωρία Α ϑεωρία Α3 ϑεωρία Α4 α) Λάθος {, x < 0 διότι για τη συνάρτηση fx) = ισχύει
Πανελλαδικές εξετάσεις 09 Μαθηµατικά Προσανατολισµού Γ Λυκείου Ενδεικτικές Απαντήσεις ϑεµάτων Θέµα Α Α α) ϑεωρία ϐ) i, ii) ϑεωρία Α ϑεωρία Α3 ϑεωρία Α4 α) Λάθος {, x < 0 διότι για τη συνάρτηση fx) = ισχύει
Εργασία 2. Παράδοση 20/1/08 Οι ασκήσεις είναι βαθμολογικά ισοδύναμες
 Εργασία Παράδοση 0/1/08 Οι ασκήσεις είναι βαθμολογικά ισοδύναμες 1. Υπολογίστε τα παρακάτω όρια: Α. Β. Γ. όπου x> 0, y > 0 Δ. όπου Κάνετε απευθείας τις πράξεις χωρίς να χρησιμοποιήσετε παραγώγους. Επιβεβαιώστε
Εργασία Παράδοση 0/1/08 Οι ασκήσεις είναι βαθμολογικά ισοδύναμες 1. Υπολογίστε τα παρακάτω όρια: Α. Β. Γ. όπου x> 0, y > 0 Δ. όπου Κάνετε απευθείας τις πράξεις χωρίς να χρησιμοποιήσετε παραγώγους. Επιβεβαιώστε
Συνήθεις Διαφορικές Εξισώσεις Ι ΣΔΕ Bernoulli, Riccati, Ομογενείς. Διαφορικές Εξισώσεις Bernoulli, Riccati και Ομογενείς
 Συνήθεις Διαφορικές Εξισώσεις Ι ΣΔΕ Bernoulli, Riccati, Ομογενείς Διαφορικές Εξισώσεις Bernoulli, Riccati και Ομογενείς Οι εξισώσεις Bernoulli αποτελούν την κλάση των μη γραμμικών διαφορικών εξισώσεων
Συνήθεις Διαφορικές Εξισώσεις Ι ΣΔΕ Bernoulli, Riccati, Ομογενείς Διαφορικές Εξισώσεις Bernoulli, Riccati και Ομογενείς Οι εξισώσεις Bernoulli αποτελούν την κλάση των μη γραμμικών διαφορικών εξισώσεων
ΔΕΙΓΜΑ ΠΡΙΝ ΤΙΣ ΔΙΟΡΘΩΣΕΙΣ - ΕΚΔΟΣΕΙΣ ΚΡΙΤΙΚΗ
 Συναρτήσεις Προεπισκόπηση Κεφαλαίου Τα μαθηματικά είναι μια γλώσσα με ένα συγκεκριμένο λεξιλόγιο και πολλούς κανόνες. Πριν ξεκινήσετε το ταξίδι σας στον Απειροστικό Λογισμό, θα πρέπει να έχετε εξοικειωθεί
Συναρτήσεις Προεπισκόπηση Κεφαλαίου Τα μαθηματικά είναι μια γλώσσα με ένα συγκεκριμένο λεξιλόγιο και πολλούς κανόνες. Πριν ξεκινήσετε το ταξίδι σας στον Απειροστικό Λογισμό, θα πρέπει να έχετε εξοικειωθεί
Σήματα και Συστήματα. Διάλεξη 13: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Laplace. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 13: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Laplace Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Laplace 1. Επίλυση Γραμμικών
Σήματα και Συστήματα Διάλεξη 13: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Laplace Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Laplace 1. Επίλυση Γραμμικών
ΜΕΜ251 Αριθμητική Ανάλυση
 ΜΕΜ251 Αριθμητική Ανάλυση Διάλεξη 10, 12 Μαρτίου 2018 Μιχάλης Πλεξουσάκης Τμήμα Μαθηματικών και Εφαρμοσμένων Μαθηματικών Περιεχόμενα 1. Παρεμβολή 2. Παράσταση και υπολογισμός του πολυωνύμου παρεμβολής
ΜΕΜ251 Αριθμητική Ανάλυση Διάλεξη 10, 12 Μαρτίου 2018 Μιχάλης Πλεξουσάκης Τμήμα Μαθηματικών και Εφαρμοσμένων Μαθηματικών Περιεχόμενα 1. Παρεμβολή 2. Παράσταση και υπολογισμός του πολυωνύμου παρεμβολής
ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ
 ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Ξεφυλλίζοντας τα σχολικά βιβλία της Α και Β Λυκείου θα συναντήσουμε τις παρακάτω 10 "βασικές" συναρτήσεις των οποίων τη γραφική παράσταση πρέπει να γνωρίζουμε:
ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Ξεφυλλίζοντας τα σχολικά βιβλία της Α και Β Λυκείου θα συναντήσουμε τις παρακάτω 10 "βασικές" συναρτήσεις των οποίων τη γραφική παράσταση πρέπει να γνωρίζουμε:
ΣΥΝΑΡΤΗΣΕΙΣ ΔΥΟ ΜΕΤΑΒΛΗΤΩΝ
 ΣΥΝΑΡΤΗΣΕΙΣ ΔΥΟ ΜΕΤΑΒΛΗΤΩΝ Έννοια συνάρτησης Παραγώγιση Ακρότατα Ασκήσεις Βασικές έννοιες Στην Οικονομία, τα περισσότερα από τα μετρούμενα μεγέθη, εξαρτώνται από άλλα μεγέθη. Π.χ η ζήτηση από την τιμή,
ΣΥΝΑΡΤΗΣΕΙΣ ΔΥΟ ΜΕΤΑΒΛΗΤΩΝ Έννοια συνάρτησης Παραγώγιση Ακρότατα Ασκήσεις Βασικές έννοιες Στην Οικονομία, τα περισσότερα από τα μετρούμενα μεγέθη, εξαρτώνται από άλλα μεγέθη. Π.χ η ζήτηση από την τιμή,
Ιόνιο Πανεπιστήμιο - Τμήμα Πληροφορικής
 Ιόνιο Πανεπιστήμιο - Τμήμα Πληροφορικής Μαθηματικός Λογισμός Ενότητα: ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ- ΠΟΛΛΑΠΛΗ ΟΛΟΚΛΗΡΩΣΗ- ΠΑΡΑΔΕΙΓΜΑΤΑ Παναγιώτης Βλάμος Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Ιόνιο Πανεπιστήμιο - Τμήμα Πληροφορικής Μαθηματικός Λογισμός Ενότητα: ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ- ΠΟΛΛΑΠΛΗ ΟΛΟΚΛΗΡΩΣΗ- ΠΑΡΑΔΕΙΓΜΑΤΑ Παναγιώτης Βλάμος Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΛΥΣΕΙΣ ΤΟΥ ΔΙΑΓΩΝΙΣΜΑΤΟΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ (Α)
 ΛΥΣΕΙΣ ΤΟΥ ΔΙΑΓΩΝΙΣΜΑΤΟΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ (Α) 1. Τι ξέρετε για τη γραφική παράσταση της οικογένειας συναρτήσεων με εξίσωση ; H γραφική παράσταση της για κάθε πραγματική τιμή του είναι ευθεία γραμμή η οποία
ΛΥΣΕΙΣ ΤΟΥ ΔΙΑΓΩΝΙΣΜΑΤΟΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ (Α) 1. Τι ξέρετε για τη γραφική παράσταση της οικογένειας συναρτήσεων με εξίσωση ; H γραφική παράσταση της για κάθε πραγματική τιμή του είναι ευθεία γραμμή η οποία
ΤΡΟΧΙΕΣ ΣΤΟ ΧΩΡΟ ΤΩΝ ΘΕΣΕΩΝ ΚΑΙ ΤΑΧΥΤΗΤΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 0 ΜΕΤΑΠΤΥΧΙΑΚΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΗ ΦΥΣΙΚΗ Ι Καθηγητής: Σ Πνευματικός Μάθημα ο ΤΡΟΧΙΕΣ ΣΤΟ ΧΩΡΟ ΤΩΝ ΘΕΣΕΩΝ ΚΑΙ ΤΑΧΥΤΗΤΩΝ Η Κλασική Μηχανική, ως ορθολογική
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 0 ΜΕΤΑΠΤΥΧΙΑΚΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΗ ΦΥΣΙΚΗ Ι Καθηγητής: Σ Πνευματικός Μάθημα ο ΤΡΟΧΙΕΣ ΣΤΟ ΧΩΡΟ ΤΩΝ ΘΕΣΕΩΝ ΚΑΙ ΤΑΧΥΤΗΤΩΝ Η Κλασική Μηχανική, ως ορθολογική
ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ Σεπτέµβριος 2006
 ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ Σεπτέµβριος 006 Θέµα ο. Για την διαφορική εξίσωση + ' =, > 0 α) Να δειχτεί ότι όλες οι λύσεις τέµνουν κάθετα την ευθεία =. β) Να βρεθεί η γενική λύση. γ) Να βρεθεί και να σχεδιαστεί
ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ Σεπτέµβριος 006 Θέµα ο. Για την διαφορική εξίσωση + ' =, > 0 α) Να δειχτεί ότι όλες οι λύσεις τέµνουν κάθετα την ευθεία =. β) Να βρεθεί η γενική λύση. γ) Να βρεθεί και να σχεδιαστεί
II. Συναρτήσεις. math-gr
 II Συναρτήσεις Παντελής Μπουμπούλης, MSc, PhD σελ blogspotcom, bouboulismyschgr ΜΕΡΟΣ 1 ΣΥΝΑΡΤΗΣΕΙΣ Α Βασικές Έννοιες Ορισμός: Έστω Α ένα υποσύνολο του συνόλου των πραγματικών αριθμών R Ονομάζουμε πραγματική
II Συναρτήσεις Παντελής Μπουμπούλης, MSc, PhD σελ blogspotcom, bouboulismyschgr ΜΕΡΟΣ 1 ΣΥΝΑΡΤΗΣΕΙΣ Α Βασικές Έννοιες Ορισμός: Έστω Α ένα υποσύνολο του συνόλου των πραγματικών αριθμών R Ονομάζουμε πραγματική
ΘΕΩΡΗΜΑ BOLZANO..Αν μια συνάρτηση f είναι συνεχής σε ένα κλειστό διάστημα [α,β].και f(α).f(β)<0 Τότε υπάρχει ένα τουλάχιστον χ 0
![ΘΕΩΡΗΜΑ BOLZANO..Αν μια συνάρτηση f είναι συνεχής σε ένα κλειστό διάστημα [α,β].και f(α).f(β)<0 Τότε υπάρχει ένα τουλάχιστον χ 0 ΘΕΩΡΗΜΑ BOLZANO..Αν μια συνάρτηση f είναι συνεχής σε ένα κλειστό διάστημα [α,β].και f(α).f(β)<0 Τότε υπάρχει ένα τουλάχιστον χ 0](/thumbs/20/426791.jpg) ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ-ΘΕΩΡΗΜΑ BOLZANO ΘΕΩΡΗΜΑ BOLZANO..Αν μια συνάρτηση f είναι συνεχής σε ένα κλειστό διάστημα [α,β].και f(α).f(β)
ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ-ΘΕΩΡΗΜΑ BOLZANO ΘΕΩΡΗΜΑ BOLZANO..Αν μια συνάρτηση f είναι συνεχής σε ένα κλειστό διάστημα [α,β].και f(α).f(β)
δίου ορισμού, μέσου του τύπου εξαρτημένης μεταβλητής του πεδίου τιμών που λέγεται εικόνα της f για x α f α.
 3.1 Η έννοια της συνάρτησης Ορισμοί Συνάρτηση f από ένα συνόλου Α σε ένα σύνολο Β είναι μια αντιστοιχία των στοιχείων του Α στα στοιχεία του Β, κατά την οποία κάθε στοιχείο του Α αντιστοιχεί σε ένα μόνο
3.1 Η έννοια της συνάρτησης Ορισμοί Συνάρτηση f από ένα συνόλου Α σε ένα σύνολο Β είναι μια αντιστοιχία των στοιχείων του Α στα στοιχεία του Β, κατά την οποία κάθε στοιχείο του Α αντιστοιχεί σε ένα μόνο
1 GRAMMIKES DIAFORIKES EXISWSEIS DEUTERAS TAXHS
 1 GRAMMIKES DIAFORIKES EXISWSEIS DEUTERAS TAXHS Γραμμικές μη ομογενείς διαφορικές εξισώσεις δευτέρας τάξης λέγονται οι εξισώσεις τύπου y + p(x)y + g(x)y = f(x) (1.1) Οταν f(x) = 0 η εξίσωση y + p(x)y +
1 GRAMMIKES DIAFORIKES EXISWSEIS DEUTERAS TAXHS Γραμμικές μη ομογενείς διαφορικές εξισώσεις δευτέρας τάξης λέγονται οι εξισώσεις τύπου y + p(x)y + g(x)y = f(x) (1.1) Οταν f(x) = 0 η εξίσωση y + p(x)y +
ΜΕΡΟΣ 1 ΣΥΝΑΡΤΗΣΕΙΣ. f : A R και στη συνέχεια δίνουμε τον τύπο της συνάρτησης, π.χ.
 Συναρτήσεις σελ ΜΕΡΟΣ 1 ΣΥΝΑΡΤΗΣΕΙΣ Α Βασικές Έννοιες Ορισμός: Έστω Α ένα υποσύνολο του συνόλου των πραγματικών αριθμών R Ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α μια διαδικασία (κανόνα),
Συναρτήσεις σελ ΜΕΡΟΣ 1 ΣΥΝΑΡΤΗΣΕΙΣ Α Βασικές Έννοιες Ορισμός: Έστω Α ένα υποσύνολο του συνόλου των πραγματικών αριθμών R Ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α μια διαδικασία (κανόνα),
u x = 2uu y u y = 0 ϕ x = x t h (t), ϕ xx = x2 t 3 h (t) και ϕ y = y t h (t), ϕ yy = y2 t 3 h (t). t 2 h (t) + x2
 ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ & ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΟΜΕΑΣ ΜΑΘΗΜΑΤΙΚΩΝ Εξετάσεις στη Μιγαδική Ανάλυση ΟΜΑΔΑ: Β 9 Ιουνίου, 07 Θ. αʹ) Αν το G είναι ένας τόπος, δηλαδή ένα ανοικτό και συνεκτικό σύνολο στο
ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ & ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΟΜΕΑΣ ΜΑΘΗΜΑΤΙΚΩΝ Εξετάσεις στη Μιγαδική Ανάλυση ΟΜΑΔΑ: Β 9 Ιουνίου, 07 Θ. αʹ) Αν το G είναι ένας τόπος, δηλαδή ένα ανοικτό και συνεκτικό σύνολο στο
Συνήθεις Διαφορικές Εξισώσεις Ι Το πρόβλημα αρχικών τιμών. Προκαταρκτικά. Το πρόβλημα αρχικών τιμών μιας σδε πρώτης τάξης
 Συνήθεις Διαφορικές Εξισώσεις Ι Το πρόβλημα αρχικών τιμών Προκαταρκτικά Το πρόβλημα αρχικών τιμών μιας σδε πρώτης τάξης y = F (, y), y( ) = y, (, y) D R 2 συνίσταται στο να βρούμε την συνάρτηση y = f(),
Συνήθεις Διαφορικές Εξισώσεις Ι Το πρόβλημα αρχικών τιμών Προκαταρκτικά Το πρόβλημα αρχικών τιμών μιας σδε πρώτης τάξης y = F (, y), y( ) = y, (, y) D R 2 συνίσταται στο να βρούμε την συνάρτηση y = f(),
= 1. z n 1 = z z n = 1. f(z) = x 0. (0, 0) = lim
 ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ & ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΟΜΕΑΣ ΜΑΘΗΜΑΤΙΚΩΝ 1η Σειρά Ασκήσεων στη Μιγαδική Ανάλυση 1. Να λυθεί η εξίσωση: 4 1 + 3i. Λύση. Επειδή 1 + 3i e πi/3, οι λύσεις της εξίσωσης 4 1 + 3i
ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ & ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΟΜΕΑΣ ΜΑΘΗΜΑΤΙΚΩΝ 1η Σειρά Ασκήσεων στη Μιγαδική Ανάλυση 1. Να λυθεί η εξίσωση: 4 1 + 3i. Λύση. Επειδή 1 + 3i e πi/3, οι λύσεις της εξίσωσης 4 1 + 3i
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο Λύσεις ένατου φυλλαδίου ασκήσεων.
 Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 018-19. Λύσεις ένατου φυλλαδίου ασκήσεων. 1. Έστω a < b. Αποδείξτε ότι υπάρχει ξ ώστε (i) a < ξ < b και e b e a = (b a)e ξ. (ii) a < ξ < b και cos b cos a = (e
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 018-19. Λύσεις ένατου φυλλαδίου ασκήσεων. 1. Έστω a < b. Αποδείξτε ότι υπάρχει ξ ώστε (i) a < ξ < b και e b e a = (b a)e ξ. (ii) a < ξ < b και cos b cos a = (e
Η συνάρτηση y = αχ 2. Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd
 Η συνάρτηση y = αχ Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd 1 Η συνάρτηση y = αχ με α 0 Μια συνάρτηση της μορφής y = α + β + γ με α 0 ονομάζεται τετραγωνική συνάρτηση.
Η συνάρτηση y = αχ Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd 1 Η συνάρτηση y = αχ με α 0 Μια συνάρτηση της μορφής y = α + β + γ με α 0 ονομάζεται τετραγωνική συνάρτηση.
ΕΝΟΤΗΤΑ 1: ΟΡΙΣΜΟΣ ΠΕΔΙΟ ΟΡΙΣΜΟΥ ΠΡΑΞΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Α
 ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 1: ΟΡΙΣΜΟΣ ΠΕΔΙΟ ΟΡΙΣΜΟΥ ΠΡΑΞΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΛΥΜΕΝΑ ΘΕΜΑΤΑ Ερώτηση θεωρίας 1 ΘΕΜΑ Α Τι ονομάζουμε πραγματική συνάρτηση
ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 1: ΟΡΙΣΜΟΣ ΠΕΔΙΟ ΟΡΙΣΜΟΥ ΠΡΑΞΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΛΥΜΕΝΑ ΘΕΜΑΤΑ Ερώτηση θεωρίας 1 ΘΕΜΑ Α Τι ονομάζουμε πραγματική συνάρτηση
cos t dt = 0. t cos t 2 dt = 1 8 f(x, y, z) = (2xyz, x 2 z, x 2 y) (2xyz) = (x2 z) (x 2 z) = (x2 y) 1 u du =
 ΛΥΣΕΙΣ. Οι ασκήσεις από το βιβλίο των Marsden - Tromba. 1. 7.1.()(b) σ (t) (cos t sin t 1) οπότε σ (t) και σ f(x y z) ds π (c) σ (t) i + tj οπότε σ (t) 1 + 4t και σ f(x y z) ds 1 t cos 1 + 4t dt 1 8 cos
ΛΥΣΕΙΣ. Οι ασκήσεις από το βιβλίο των Marsden - Tromba. 1. 7.1.()(b) σ (t) (cos t sin t 1) οπότε σ (t) και σ f(x y z) ds π (c) σ (t) i + tj οπότε σ (t) 1 + 4t και σ f(x y z) ds 1 t cos 1 + 4t dt 1 8 cos
Παραδείγματα τριπλών oλοκληρωμάτων Επιμέλεια: Ι. Λυχναρόπουλος
 Παραδείγματα τριπλών oλοκληρωμάτων Επιμέλεια: Ι. Λυχναρόπουλος Παράδειγμα Να υπολογισθεί το ολοκλήρωμα I = x e + z dv όπου = [, ] [,] [,] Η ολοκλήρωση, όπως φαίνεται από τα άκρα ολοκλήρωσης, γίνεται πάνω
Παραδείγματα τριπλών oλοκληρωμάτων Επιμέλεια: Ι. Λυχναρόπουλος Παράδειγμα Να υπολογισθεί το ολοκλήρωμα I = x e + z dv όπου = [, ] [,] [,] Η ολοκλήρωση, όπως φαίνεται από τα άκρα ολοκλήρωσης, γίνεται πάνω
- ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 3: ΣΥΝΑΡΤΗΣΗ 1-1 ΑΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗ
 ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ : ΣΥΝΑΡΤΗΣΗ - ΑΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗ [Υποκεφάλαιο. Μονότονες συναρτήσεις Αντίστροφη συνάρτηση του σχολικού βιβλίου]. ΑΣΚΗΣΕΙΣ Άσκηση. ΘΕΜΑ Β Να
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ : ΣΥΝΑΡΤΗΣΗ - ΑΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗ [Υποκεφάλαιο. Μονότονες συναρτήσεις Αντίστροφη συνάρτηση του σχολικού βιβλίου]. ΑΣΚΗΣΕΙΣ Άσκηση. ΘΕΜΑ Β Να
5.1 Συναρτήσεις δύο ή περισσοτέρων µεταβλητών
 Κεφάλαιο 5 ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ 5.1 Συναρτήσεις δύο ή περισσοτέρων µεταβλητών Οταν ένα µεταβλητό µέγεθος εξαρτάται αποκλειστικά από τις µεταβολές ενός άλλου µεγέθους, τότε η σχέση που συνδέει
Κεφάλαιο 5 ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ 5.1 Συναρτήσεις δύο ή περισσοτέρων µεταβλητών Οταν ένα µεταβλητό µέγεθος εξαρτάται αποκλειστικά από τις µεταβολές ενός άλλου µεγέθους, τότε η σχέση που συνδέει
Εισαγωγή στις Φυσικές Επιστήμες ( ) Ονοματεπώνυμο Τμήμα ΘΕΜΑ 1. x x. x x x ( ) + ( 20) + ( + 4) = ( + ) + ( 10 + ) + ( )
 Ονοματεπώνυμο Τμήμα ο Ερώτημα Να υπολογιστούν τα αόριστα ολοκληρώματα α) ( + + ) e d β) + ( + 4)( 5) 5 89 ΘΕΜΑ d Απάντηση α) θέτω u = + +και υ = e, επομένως dυ = e και du = ( + ) d. ( + + ) e d= u dυ =
Ονοματεπώνυμο Τμήμα ο Ερώτημα Να υπολογιστούν τα αόριστα ολοκληρώματα α) ( + + ) e d β) + ( + 4)( 5) 5 89 ΘΕΜΑ d Απάντηση α) θέτω u = + +και υ = e, επομένως dυ = e και du = ( + ) d. ( + + ) e d= u dυ =
Λύσεις θεμάτων Α εξεταστικής περιόδου εαρινού εξαμήνου (Ιούνιος 2015)
 Λύσεις θεμάτων Α εξεταστικής περιόδου εαρινού εξαμήνου 204 5 (Ιούνιος 205) ΘΕΜΑ Ο (4,0 μονάδες) Στο παρακάτω σχήμα δίνεται το δομικό (λειτουργικό) διάγραμμα ενός συστήματος. α. Να προσδιοριστούν οι τιμές
Λύσεις θεμάτων Α εξεταστικής περιόδου εαρινού εξαμήνου 204 5 (Ιούνιος 205) ΘΕΜΑ Ο (4,0 μονάδες) Στο παρακάτω σχήμα δίνεται το δομικό (λειτουργικό) διάγραμμα ενός συστήματος. α. Να προσδιοριστούν οι τιμές
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ
 ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ Ε.1 I. 1. α 2 = 9 α = 3 ψ p: α 2 = 9, q: α = 3 Σύνολο αλήθειας της p: Α = {-3,3}, Σύνολο αλήθειας της q: B = {3} A B 2. α 2 = α α = 1 ψ p: α 2 = α, q: α = 1 Σύνολο
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ Ε.1 I. 1. α 2 = 9 α = 3 ψ p: α 2 = 9, q: α = 3 Σύνολο αλήθειας της p: Α = {-3,3}, Σύνολο αλήθειας της q: B = {3} A B 2. α 2 = α α = 1 ψ p: α 2 = α, q: α = 1 Σύνολο
ΓΕΝΙΚΑ ΜΑΘΗΜΑΤΙΚΑ Ι ΝΙΚΟΛΑΟΣ ΣΤΕΡΓΙΟΥΛΑΣ. Μέρος 2ο ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
 ΓΕΝΙΚΑ ΜΑΘΗΜΑΤΙΚΑ Ι ΝΙΚΟΛΑΟΣ ΣΤΕΡΓΙΟΥΛΑΣ Μέρος 2ο ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Παραμετρικές Εξισώσεις Παραμετρικές Εξισώσεις Άσκηση 1 Άσκηση 1 Λύση: (αριστερόστροφη) Άσκηση 1 Άσκηση
ΓΕΝΙΚΑ ΜΑΘΗΜΑΤΙΚΑ Ι ΝΙΚΟΛΑΟΣ ΣΤΕΡΓΙΟΥΛΑΣ Μέρος 2ο ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Παραμετρικές Εξισώσεις Παραμετρικές Εξισώσεις Άσκηση 1 Άσκηση 1 Λύση: (αριστερόστροφη) Άσκηση 1 Άσκηση
ΑΣΚΗΣΕΙΣ Β ΛΥΚΕΙΟΥ -- ΑΛΓΕΒΡΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ
 ΑΣΚΗΣΕΙΣ Β ΛΥΚΕΙΟΥ -- ΑΛΓΕΒΡΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Άσκηση η Γραμμικά συστήματα Δίνονται οι ευθείες : y3 και :y 5. Να βρεθεί το R, ώστε οι ευθείες να τέμνονται. Οι ευθείες και θα τέμνονται όταν το μεταξύ
ΑΣΚΗΣΕΙΣ Β ΛΥΚΕΙΟΥ -- ΑΛΓΕΒΡΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Άσκηση η Γραμμικά συστήματα Δίνονται οι ευθείες : y3 και :y 5. Να βρεθεί το R, ώστε οι ευθείες να τέμνονται. Οι ευθείες και θα τέμνονται όταν το μεταξύ
ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 10 ΙΟΥΝΙΟΥ 2019 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΑΠΑΝΤΗΣΕΙΣ
 ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 10 ΙΟΥΝΙΟΥ 2019 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΜΑ Α ΑΠΑΝΤΗΣΕΙΣ Α1. α. Ορισμός στο σχολικό βιβλίο σελίδα 15. β. i) Μια συνάρτηση
ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 10 ΙΟΥΝΙΟΥ 2019 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΜΑ Α ΑΠΑΝΤΗΣΕΙΣ Α1. α. Ορισμός στο σχολικό βιβλίο σελίδα 15. β. i) Μια συνάρτηση
1ο τεταρτημόριο x>0,y>0 Ν Β
 ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ ΣΥΝΑΡΤΗΣΗΣ( 6.2 ) Καρτεσιανό σύστημα συντεταγμένων ονομάζεται ένα επίπεδο εφοδιασμένο με δύο κάθετους άξονες οι οποίοι έχουν κοινή αρχή Ο και είναι αριθμημένοι με τις ίδιες μονάδες μήκους.
ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ ΣΥΝΑΡΤΗΣΗΣ( 6.2 ) Καρτεσιανό σύστημα συντεταγμένων ονομάζεται ένα επίπεδο εφοδιασμένο με δύο κάθετους άξονες οι οποίοι έχουν κοινή αρχή Ο και είναι αριθμημένοι με τις ίδιες μονάδες μήκους.
ΕΦΑΠΤΟΜΕΝΗ ΓΡΑΦΙΚΗΣ ΠΑΡΑΣΤΑΣΗΣ ΣΥΝΑΡΤΗΣΗΣ
 ΕΦΑΠΤΟΜΕΝΗ ΓΡΑΦΙΚΗΣ ΠΑΡΑΣΤΑΣΗΣ ΣΥΝΑΡΤΗΣΗΣ Ορισμός εφαπτομένης καμπύλης Αν μία συνάρτηση f είναι παραγωγίσιμη στο x, τότε ορίζουμε ως εφαπτομένη της γραφικής παράστασης της f στο σημείο Α(x, f(x )) την
ΕΦΑΠΤΟΜΕΝΗ ΓΡΑΦΙΚΗΣ ΠΑΡΑΣΤΑΣΗΣ ΣΥΝΑΡΤΗΣΗΣ Ορισμός εφαπτομένης καμπύλης Αν μία συνάρτηση f είναι παραγωγίσιμη στο x, τότε ορίζουμε ως εφαπτομένη της γραφικής παράστασης της f στο σημείο Α(x, f(x )) την
ΑΠΑΝΤΗΣΕΙΣ - ΥΠΟΔΕΙΞΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ
 ΑΠΑΝΤΗΣΕΙΣ - ΥΠΟΔΕΙΞΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ Κεφάλαιο ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ο ΜΕΡΟΣ Απαντήσεις στις ερωτήσεις του τύπου Σωστό-Λάθος. Σ 6. Λ 8. Λ. Σ 7. Σ 9. Λ 3. Λ 8. Λ 3. Σ 4. Σ 9. Σ 3. α Σ 5. Σ. Σ β Σ 6. Λ.
ΑΠΑΝΤΗΣΕΙΣ - ΥΠΟΔΕΙΞΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ Κεφάλαιο ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ο ΜΕΡΟΣ Απαντήσεις στις ερωτήσεις του τύπου Σωστό-Λάθος. Σ 6. Λ 8. Λ. Σ 7. Σ 9. Λ 3. Λ 8. Λ 3. Σ 4. Σ 9. Σ 3. α Σ 5. Σ. Σ β Σ 6. Λ.
4. Να βρείτε την εξίσωση της ευθείας που διέρχεται από την αρχή των αξόνων και το σημείο Α(,.
 1. Τι ξέρετε για τη γραφική παράσταση των συναρτήσεων της μορφής ; Πώς ονομάζεται το ; Η γραφική παράσταση των συναρτήσεων της μορφής, είναι ευθεία γραμμή που διέρχεται από την αρχή των αξόνων. Το ονομάζεται
1. Τι ξέρετε για τη γραφική παράσταση των συναρτήσεων της μορφής ; Πώς ονομάζεται το ; Η γραφική παράσταση των συναρτήσεων της μορφής, είναι ευθεία γραμμή που διέρχεται από την αρχή των αξόνων. Το ονομάζεται
Παραρτήματα. Παράρτημα 1 ο : Μιγαδικοί Αριθμοί
 Παράρτημα ο : Μιγαδικοί Αριθμοί Παράρτημα ο : Μετασχηματισμός Lplce Παράρτημα 3 ο : Αντίστροφος μετασχηματισμός Lplce Παράρτημα 4 ο : Μετασχηματισμοί δομικών διαγραμμάτων Παράρτημα 5 ο : Τυποποιημένα σήματα
Παράρτημα ο : Μιγαδικοί Αριθμοί Παράρτημα ο : Μετασχηματισμός Lplce Παράρτημα 3 ο : Αντίστροφος μετασχηματισμός Lplce Παράρτημα 4 ο : Μετασχηματισμοί δομικών διαγραμμάτων Παράρτημα 5 ο : Τυποποιημένα σήματα
ΑΚΡΙΒΗ ΔΙΑΦΟΡΙΚΑ. u,υ / A ονομάζεται ακριβές διαφορικό όταν υπάρχει. df u x,y dx υ x,y dy. f u και. f y. 3 f. και
 Το άθροισμα u,d διαφορίσιμη συνάρτηση f / A Παράδειγμα υ, d, με με Το άθροισμα ΑΚΡΙΒΗ ΔΙΑΦΟΡΙΚΑ u,υ / A ονομάζεται ακριβές διαφορικό όταν υπάρχει df u,d υ,d f u f υ 6 d 9 d είναι ακριβές διαφορικό, διότι
Το άθροισμα u,d διαφορίσιμη συνάρτηση f / A Παράδειγμα υ, d, με με Το άθροισμα ΑΚΡΙΒΗ ΔΙΑΦΟΡΙΚΑ u,υ / A ονομάζεται ακριβές διαφορικό όταν υπάρχει df u,d υ,d f u f υ 6 d 9 d είναι ακριβές διαφορικό, διότι
ΑΛΓΕΒΡΑ B ΛΥΚΕΙΟΥ. Γενικής Παιδείας ΑΠΑΝΤΗΣΕΙΣ ΛΥΣΕΙΣ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ
 ΑΛΓΕΒΡΑ B ΛΥΚΕΙΥ Γενικής Παιδείας ΑΠΑΝΤΗΣΕΙΣ ΛΥΣΕΙΣ ΣΧΛΙΚΥ ΒΙΒΛΙΥ Σχολικό βιβλίο: Απαντήσεις Λύσεις Κεφάλαιο ο: Συστήματα Γραμμικά συστήματα Α ΜΑΔΑΣ Έχουμε: = 4 i = 6 = + = + = = Άρα, η λύση του συστήματος
ΑΛΓΕΒΡΑ B ΛΥΚΕΙΥ Γενικής Παιδείας ΑΠΑΝΤΗΣΕΙΣ ΛΥΣΕΙΣ ΣΧΛΙΚΥ ΒΙΒΛΙΥ Σχολικό βιβλίο: Απαντήσεις Λύσεις Κεφάλαιο ο: Συστήματα Γραμμικά συστήματα Α ΜΑΔΑΣ Έχουμε: = 4 i = 6 = + = + = = Άρα, η λύση του συστήματος
b proj a b είναι κάθετο στο
 ΦΥΛΛΑ ΙΟ ΑΣΚΗΣΕΩΝ. Βρείτε όλα τα σηµεία P τέτοια ώστε η απόσταση του P από το A(, 5, 3) είναι διπλάσια από την απόσταση του P από το B(6, 2, 2). είξτε ότι το σύνολο όλων αυτών των σηµείων είναι σφαίρα.
ΦΥΛΛΑ ΙΟ ΑΣΚΗΣΕΩΝ. Βρείτε όλα τα σηµεία P τέτοια ώστε η απόσταση του P από το A(, 5, 3) είναι διπλάσια από την απόσταση του P από το B(6, 2, 2). είξτε ότι το σύνολο όλων αυτών των σηµείων είναι σφαίρα.
ΜΙΓΑ ΙΚΟΣ ΛΟΓΙΣΜΟΣ ΚΑΙ ΟΛΟΚΛ. ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΓΡΑΠΤΕΣ ΕΞΕΤΑΣΕΙΣ ΣΕΠΤΕΜΒΡΙΟΥ 2010 ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ
 ΜΙΓΑ ΙΚΟΣ ΛΟΓΙΣΜΟΣ ΚΑΙ ΟΛΟΚΛ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΘΕΜΑ ΓΡΑΠΤΕΣ ΕΞΕΤΑΣΕΙΣ ΣΕΠΤΕΜΒΡΙΟΥ ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ α) Η f ( ) έχει πραγµατικό µέρος φανταστικό µέρος u( x, y) x y = και v( x, y) = ( x + y xy), όπου = x+
ΜΙΓΑ ΙΚΟΣ ΛΟΓΙΣΜΟΣ ΚΑΙ ΟΛΟΚΛ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΘΕΜΑ ΓΡΑΠΤΕΣ ΕΞΕΤΑΣΕΙΣ ΣΕΠΤΕΜΒΡΙΟΥ ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ α) Η f ( ) έχει πραγµατικό µέρος φανταστικό µέρος u( x, y) x y = και v( x, y) = ( x + y xy), όπου = x+
ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΓΕΝΙΚΩΝ ΛΥΚΕΙΩΝ. f ( x) 0 0 2x 0 x 0
 ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΓΕΝΙΚΩΝ ΛΥΚΕΙΩΝ ΑΠΑΝΤΗΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΚΑΙ ΟΙΚΟΝΟΜΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) 8 ΜΑΪΟΥ 6 ΘΕΜΑ Α Α. Θεωρία, βλ. σχολικό βιβλίο
ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΓΕΝΙΚΩΝ ΛΥΚΕΙΩΝ ΑΠΑΝΤΗΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΚΑΙ ΟΙΚΟΝΟΜΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) 8 ΜΑΪΟΥ 6 ΘΕΜΑ Α Α. Θεωρία, βλ. σχολικό βιβλίο
Homework#13 Trigonometry Honors Study Guide for Final Test#3
 Homework#13 Trigonometry Honors Study Guide for Final Test#3 1. Στο παρακάτω σχήμα δίνεται ο μοναδιαίος κύκλος: Να γράψετε τις συντεταγμένες του σημείου ή το όνομα του άξονα: 1. (ε 1) είναι ο άξονας 11.
Homework#13 Trigonometry Honors Study Guide for Final Test#3 1. Στο παρακάτω σχήμα δίνεται ο μοναδιαίος κύκλος: Να γράψετε τις συντεταγμένες του σημείου ή το όνομα του άξονα: 1. (ε 1) είναι ο άξονας 11.
ΚΕΦΑΛΑΙΟ 1ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 2: ΜΟΝΟΤΟΝΙΑ - ΑΚΡΟΤΑΤΑ
 ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ : ΜΟΝΟΤΟΝΙΑ - ΑΚΡΟΤΑΤΑ Μονοτονία Συνάρτησης Έστω οι συναρτήσεις f, g, h, των οποίων οι γραφικές παραστάσεις φαίνονται στα επόμενα σχήματα («Σχήμα», «Σχήμα», «Σχήμα
ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ : ΜΟΝΟΤΟΝΙΑ - ΑΚΡΟΤΑΤΑ Μονοτονία Συνάρτησης Έστω οι συναρτήσεις f, g, h, των οποίων οι γραφικές παραστάσεις φαίνονται στα επόμενα σχήματα («Σχήμα», «Σχήμα», «Σχήμα
ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 3: ΕΦΑΠΤΟΜΕΝΗ [Κεφάλαιο 2.1: Πρόβλημα εφαπτομένης του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β
![ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 3: ΕΦΑΠΤΟΜΕΝΗ [Κεφάλαιο 2.1: Πρόβλημα εφαπτομένης του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 3: ΕΦΑΠΤΟΜΕΝΗ [Κεφάλαιο 2.1: Πρόβλημα εφαπτομένης του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β](/thumbs/63/49303177.jpg) ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ : ΕΦΑΠΤΟΜΕΝΗ [Κεφάλαιο.: Πρόβλημα εφαπτομένης του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα. ΘΕΜΑ Β Έστω μια παραγωγίσιμη στο συνάρτηση, τέτοια ώστε για κάθε x
ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ : ΕΦΑΠΤΟΜΕΝΗ [Κεφάλαιο.: Πρόβλημα εφαπτομένης του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα. ΘΕΜΑ Β Έστω μια παραγωγίσιμη στο συνάρτηση, τέτοια ώστε για κάθε x
Εισαγωγή. Κεφάλαιο Διαφορικές εξισώσεις
 Κεφάλαιο Εισαγωγή Θα παρουσιάσουμε τις διαφορικές εξισώσεις και τα αντίστοιχα προβλήματα αρχικών και συνοριακών τιμών που θα συναντήσουμε στα επόμενα κεφάλαια. Επίσης, θα δούμε ορισμένες ιδιότητες και
Κεφάλαιο Εισαγωγή Θα παρουσιάσουμε τις διαφορικές εξισώσεις και τα αντίστοιχα προβλήματα αρχικών και συνοριακών τιμών που θα συναντήσουμε στα επόμενα κεφάλαια. Επίσης, θα δούμε ορισμένες ιδιότητες και
APEIROSTIKOS LOGISMOS I
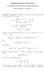 APEIROSTIKOS LOGISMOS I ΟΛΟΗΜΕΡΟ ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΒΛΗΜΑΤΩΝ Λύσεις ασκήσεων φυλλαδίου 3. Άσκηση : Προσδιορίστε, αν υπάρχουν, τις τιμές τού a για τις οποίες οι παρακάτω συναρτήσεις είναι συνεχείς. + +, αν >
APEIROSTIKOS LOGISMOS I ΟΛΟΗΜΕΡΟ ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΒΛΗΜΑΤΩΝ Λύσεις ασκήσεων φυλλαδίου 3. Άσκηση : Προσδιορίστε, αν υπάρχουν, τις τιμές τού a για τις οποίες οι παρακάτω συναρτήσεις είναι συνεχείς. + +, αν >
A = x x 1 + 2x 2 + 4
 Επιχειρησιακή Ερευνα η Σειρά Ασκήσεων Ενδεικτικές Λύσεις 1. (α ) Η συνάρτηση f(x 1, x ) = x 1 + x x 1 x + x μπορεί να γραφεί ως f( x) = x A x + b x όπου x = x 1 A = 1 1 1 x b = 0 Θα χρειαστούμε το διάνυσμα
Επιχειρησιακή Ερευνα η Σειρά Ασκήσεων Ενδεικτικές Λύσεις 1. (α ) Η συνάρτηση f(x 1, x ) = x 1 + x x 1 x + x μπορεί να γραφεί ως f( x) = x A x + b x όπου x = x 1 A = 1 1 1 x b = 0 Θα χρειαστούμε το διάνυσμα
ΕΙΔΙΚΗ ΘΕΩΡΙΑ ΤΗΣ ΣΧΕΤΙΚΟΤΗΤΑΣ
 ΕΙΔΙΚΗ ΘΕΩΡΙΑ ΤΗΣ ΣΧΕΤΙΚΟΤΗΤΑΣ Διδάσκων: Θεόδωρος Ν. Τομαράς 1. Μετασχηματισμοί συντεταγμένων και συμμετρίες. 1α. Στροφές στο επίπεδο. Θεωρείστε δύο καρτεσιανά συστήματα συντεταγμένων στο επίπεδο, στραμμένα
ΕΙΔΙΚΗ ΘΕΩΡΙΑ ΤΗΣ ΣΧΕΤΙΚΟΤΗΤΑΣ Διδάσκων: Θεόδωρος Ν. Τομαράς 1. Μετασχηματισμοί συντεταγμένων και συμμετρίες. 1α. Στροφές στο επίπεδο. Θεωρείστε δύο καρτεσιανά συστήματα συντεταγμένων στο επίπεδο, στραμμένα
Διαφορικές εξισώσεις 302.
 Διαφορικές εξισώσεις 32. Μαθηματικό Αθήνας Συλλογή ασκήσεων 1 Λύτες: Βουλγαρίδου Εύα Ορμάνογλου Στράβων Παπαμικρούλη Ελένη Παπανίκου Μυρτώ Καθηγητές: Αθανασιάδου - Μπαρμπάτης Επιμέλεια L A TEX: Βώβος Μάριος
Διαφορικές εξισώσεις 32. Μαθηματικό Αθήνας Συλλογή ασκήσεων 1 Λύτες: Βουλγαρίδου Εύα Ορμάνογλου Στράβων Παπαμικρούλη Ελένη Παπανίκου Μυρτώ Καθηγητές: Αθανασιάδου - Μπαρμπάτης Επιμέλεια L A TEX: Βώβος Μάριος
< και δεδομένου ότι η f είναι γνησίως μονότονη, συμπεραίνουμε ότι
 _1696 α) f ( 5) = f ( 4) = 9 Αφού
_1696 α) f ( 5) = f ( 4) = 9 Αφού
Τίτλος Μαθήματος: Διαφορική Γεωμετρία
 71 Τίτλος Μαθήματος: Διαφορική Γεωμετρία Ενότητα: Λσμένα Παραδείγματα Όνομα Καθηγητή: Ανδρέας Αρβανιτογεώργος Τμήμα: Μαθηματικών 71 72 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
71 Τίτλος Μαθήματος: Διαφορική Γεωμετρία Ενότητα: Λσμένα Παραδείγματα Όνομα Καθηγητή: Ανδρέας Αρβανιτογεώργος Τμήμα: Μαθηματικών 71 72 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ÖÑÏÍÔÉÓÔÇÑÉÏ ÊÏÑÕÖÇ ÓÅÑÑÅÓ ΜΑΘΗΜΑΤΙΚΑ ΘΕΜΑ Α ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ & ΕΠΑ.Λ. Β 19 ΜΑΪΟΥ 2010 ΕΚΦΩΝΗΣΕΙΣ
 ΘΕΜΑ Α ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ & ΕΠΑ.Λ. Β 9 ΜΑΪΟΥ 00 ΕΚΦΩΝΗΣΕΙΣ A. Έστω f µια συνάρτηση ορισµένη σε ένα διάστηµα. Αν F είναι µια παράγουσα της f στο, τότε να αποδείξετε ότι: όλες οι συναρτήσεις
ΘΕΜΑ Α ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ & ΕΠΑ.Λ. Β 9 ΜΑΪΟΥ 00 ΕΚΦΩΝΗΣΕΙΣ A. Έστω f µια συνάρτηση ορισµένη σε ένα διάστηµα. Αν F είναι µια παράγουσα της f στο, τότε να αποδείξετε ότι: όλες οι συναρτήσεις
Διαφορικόσ Λογιςμόσ. Παράγωγοσ. Εξίςωςη εφαπτομένησ όταν γνωρίζουμε το ςημείο επαφήσ
 Διαφορικόσ Λογιςμόσ Παράγωγοσ Εξίςωςη εφαπτομένησ όταν γνωρίζουμε το ςημείο επαφήσ 1 ε καθεμία από τισ επόμενεσ περιπτώςεισ να βρείτε την εξίςωςη τησ εφαπτομένησ τησ γραφικήσ παράςταςησ τησ ςτο ςημείο
Διαφορικόσ Λογιςμόσ Παράγωγοσ Εξίςωςη εφαπτομένησ όταν γνωρίζουμε το ςημείο επαφήσ 1 ε καθεμία από τισ επόμενεσ περιπτώςεισ να βρείτε την εξίςωςη τησ εφαπτομένησ τησ γραφικήσ παράςταςησ τησ ςτο ςημείο
ΜΔΕ Άσκηση 6 Α. Τόγκας
 Πρόβλημα 15. Για κάθε μια αό τις ακόλουθες αρχικές τιμές θερμοκρασίας i) να βρεθεί η λύση στην μορφή μια σειράς Fourier της εξίσωσης της θερμότητας με εριοδικές συνοριακές συνθήκες u t = u x x < x
Πρόβλημα 15. Για κάθε μια αό τις ακόλουθες αρχικές τιμές θερμοκρασίας i) να βρεθεί η λύση στην μορφή μια σειράς Fourier της εξίσωσης της θερμότητας με εριοδικές συνοριακές συνθήκες u t = u x x < x
