Ανάλυση Συζευκτών Γραμμοσειρών με Μεθόδους Ολοκληρωτικών Εξισώσεων ΔΙΔΑΚΤΟΡΙΚΗ ΔΙΑΤΡΙΒΗ
|
|
|
- Ζωή Βαμβακάς
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΥΣΤΗΜΑΤΩΝ ΜΕΤΑΔΟΣΗΣ ΠΛΗΡΟΦΟΡΙΑΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ Ανάλυση Συζευκτών Γραμμοσειρών με Μεθόδους Ολοκληρωτικών Εξισώσεων ΔΙΔΑΚΤΟΡΙΚΗ ΔΙΑΤΡΙΒΗ Νικόλαος Λ. Τσίτσας Αθήνα, Σεπτέμβριος 006
2
3 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΥΣΤΗΜΑΤΩΝ ΜΕΤΑΔΟΣΗΣ ΠΛΗΡΟΦΟΡΙΑΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ Ανάλυση Συζευκτών Γραμμοσειρών με Μεθόδους Ολοκληρωτικών Εξισώσεων ΔΙΔΑΚΤΟΡΙΚΗ ΔΙΑΤΡΙΒΗ Νικόλαος Λ. Τσίτσας Συμβουλευτική Επιτροπή : Δήμητρα Ι. Κακλαμάνη Νικόλαος Κ. Ουζούνογλου Ιάκωβος Σ. Βενιέρης Εγκρίθηκε από την επταμελή εξεταστική επιτροπή την 8 η Σεπτεμβρίου Δήμητρα Κακλαμάνη Αναπ. Καθηγήτρια Ε.Μ.Π.... Ηλίας Γλύτσης Καθηγητής Ε.Μ.Π.... Νικόλαος Ουζούνογλου Καθηγητής Ε.Μ.Π.... Γεώργιος Φικιώρης Λέκτορας Ε.Μ.Π.... Ιάκωβος Βενιέρης Καθηγητής Ε.Μ.Π.... Δημήτριος Φραντζεσκάκης Αναπ. Καθηγητής Ε.Κ.Π.Α.... Ηρακλής Αβραμόπουλος Αναπ. Καθηγητής Ε.Μ.Π. Αθήνα, Σεπτέμβριος 006 3
4 ... Νικόλαος Λ. Τσίτσας Διδάκτωρ Ηλεκτρολόγος Μηχανικός και Μηχανικός Υπολογιστών Ε.Μ.Π. Copyright Νικόλαος Λ. Τσίτσας, 006. Με επιφύλαξη παντός δικαιώματος. All rights reserved. Απαγορεύεται η αντιγραφή, αποθήκευση και διανομή της παρούσας εργασίας, εξ ολοκλήρου ή τμήματος αυτής, για εμπορικό σκοπό. Επιτρέπεται η ανατύπωση, αποθήκευση και διανομή για σκοπό μη κερδοσκοπικό, εκπαιδευτικής ή ερευνητικής φύσης, υπό την προϋπόθεση να αναφέρεται η πηγή προέλευσης και να διατηρείται το παρόν μήνυμα. Ερωτήματα που αφορούν τη χρήση της εργασίας για κερδοσκοπικό σκοπό πρέπει να απευθύνονται προς τον συγγραφέα. Οι απόψεις και τα συμπεράσματα που περιέχονται σε αυτό το έγγραφο εκφράζουν τον συγγραφέα και δεν πρέπει να ερμηνευθεί ότι αντιπροσωπεύουν τις επίσημες θέσεις του Εθνικού Μετσόβιου Πολυτεχνείου.
5 Περίληψη Οι συζεύκτες γραμμοσειρών αποτελούν βασικά δομικά στοιχεία σημαντικών οπτικών διατάξεων, οι οποίες χρησιμοποιούνται ευρέως στα σύγχρονα οπτικά δίκτυα. Μεταξύ των οπτικών διατάξεων συγκαταλέγονται τα οπτικά φίλτρα επιλογής συχνοτήτων, οι πολυπλέκτες και αποπολυπλέκτες, τα συντονιζόμενα lasers και τα lasers κατανεμημένης ανάδρασης καθώς επίσης και οι οπτικοί διακόπτες. Τα ηλεκτρομαγνητικά φαινόμενα, που εμφανίζονται στις διατάξεις των συζευκτών γραμμοσειρών, έχουν ήδη μελετηθεί με προσεγγιστικές μεθόδους, όπως οι μέθοδοι διαταραχών, η θεωρία των συζευγμένων ρυθμών και η θεωρία Floquet-Bloch. Σε αυτές τις μεθόδους η ακρίβεια των λύσεων προϋποθέτει αρκετούς περιορισμούς, όπως μικρό πάχος γραμμοσειρών, μεγάλη απόσταση διαχωρισμού των δύο κυματοδηγών και μικρές διαφορές των δεικτών διάθλασης των εμπλεκομένων μέσων. Αντικείμενο της Διδακτορικής Διατριβής αποτελεί η μελέτη των φαινομένων σύζευξης σε κυματοδηγούς γραμμοσειρών με μεθοδολογία ολοκληρωτικών εξισώσεων. Η αναπτυσσόμενη μεθοδολογία, η οποία συνδυάζει ημιαναλυτικές τεχνικές ολοκληρωτικών εξισώσεων, βασίζεται ουσιαστικά στη Μέθοδο των Ροπών με συναρτήσεις βάσης συνολικού χώρου. Ειδικότερα, με εφαρμογή της μεθόδου Sommerfeld επιτυγχάνεται Fourier ολοκληρωτική αναπαράσταση της συνάρτησης Green του ομογενούς (χωρίς γραμμοσειρές) προβλήματος. Περαιτέρω, διατυπώνεται ολοκληρωτική εξίσωση ως προς το ηλεκτρικό πεδίο κυμάτων, τα οποία διαδίδονται κατά μήκος του άξονα του συζεύκτη. Για τη λύση της εν λόγω ολοκληρωτικής εξίσωσης εφαρμόζονται τεχνικές Galerkin συνολικού χώρου, οι οποίες οδηγούν σε συγκεκριμένο ομογενές γραμμικό σύστημα. Οι σταθερές διάδοσης των κυματοδηγούμενων ρυθμών είναι οι τιμές εκείνες, για τις οποίες το εν λόγω σύστημα έχει μη τετριμμένη λύση. Η κύρια πρωτοτυπία της Διδακτορικής Διατριβής συνίσταται στην εισαγωγή μεθοδολογίας ολοκληρωτικών εξισώσεων, η οποία αναπτύσσεται και εφαρμόζεται για τη μελέτη των φαινομένων κυματοδήγησης σε συζεύκτες γραμμοσειρών. Εξάλλου, η αριθμητική υλοποίηση της αναπτυχθείσας μεθοδολογίας παράγει αρκετά πρωτότυπα και ενδιαφέροντα αριθμητικά αποτελέσματα, αναφερόμενα στη βέλτιστη σχεδίαση των χαρακτηριστικών των γραμμοσειρών, τα οποία προσφέρουν το ελάχιστο δυνατό μήκος σύζευξης και τη μέγιστη δυνατή αποδοτικότητα σύζευξης. Τα συγκριτικά πλεονεκτήματα της αναπτυσσόμενης μεθοδολογίας έναντι των μεθόδων: διαταραχών, θεωρίας των συζευγμένων ρυθμών και θεωρίας Floquet-Bloch εντοπίζονται στην ακρίβεια, την απλότητα καθώς επίσης και την αριθμητική αποδοτικότητα. Εξάλλου, η 5
6 χρησιμοποιούμενη μεθοδολογία δίνει ακριβή αποτελέσματα για γραμμοσειρές μεγάλου πάχους και για ισχυρά συζευγμένους κυματοδηγούς σε αντίθεση με τις προαναφερόμενες μεθόδους. Ιδιαιτέρως, εκφράζεται αναλυτικά η συνάρτηση Green και υπολογίζονται αναλυτικά όλα τα εμφανιζόμενα ολοκληρώματα με συνέπειες τη σημαντική μείωση του υπολογιστικού κόστους, την αύξηση της ακρίβειας των αποτελεσμάτων και την επίτευξη λύσεως χωρίς άλλες προσεγγίσεις εκτός εκείνης της τελικής κολόβωσης του γραμμικού συστήματος. Τα αριθμητικά αποτελέσματα της Διατριβής υπερτερούν σημαντικά σε αξιοπιστία και ακρίβεια των αντιστοίχων αποτελεσμάτων, τα οποία επιτυγχάνονται με τις προγενέστερες μεθόδους. Η αξιολόγηση των αποτελεσμάτων αυτών διαμορφώνει συγκεκριμένες τεχνικέςσχεδιαστικές προδιαγραφές της υπό μελέτη διάταξης, οι οποίες μπορεί να αξιοποιηθούν κατάλληλα σε πολλές εφαρμογές της ολοκληρωμένης οπτικοηλεκτρονικής. Λέξεις Κλειδιά Κατευθυντικοί συζεύκτες, γραμμοσειρές, οπτικοί κυματοδηγοί, κυματοδηγοί διηλεκτρικών πλακών, κυματοδηγούμενα κύματα, ολοκληρωμένη οπτική, οπτικά φίλτρα, ολοκληρωτικές εξισώσεις, μέθοδος των ροπών, τεχνικές Galerkin. 6
7 Abstract Grating-assisted couplers constitute fundamental guided-wave components of important optical devices, used widely in synchronous optical networks. Among these optical devices are included optical wavelength filters, multiplexers and demultiplexers, tunable lasers and distributed feedback lasers as well as optical switches. The electromagnetic phenomena, associated with the operation of grating couplers, have already been investigated by means of approximate methods, such as perturbation methods, coupled-mode theory and Floquet-Bloch theory. In these methods the accuracy of the solutions is subject to various limitations and constraints, such as small grating width, large separation distance between the slab waveguides and small differences of the refractive indices of the media involved. The subject of this Doctoral Thesis is the investigation of the coupling phenomena in grating waveguides by applying an integral equation methodology. The developed methodology, which combines semianalytical integral equation techniques, is essentially based on the Method of Moments with entire domain basis functions. In particular, by applying Sommerfeld s method, a Fourier integral representation of the Green s function of the homogeneous (non-grating) problem is derived. Furthermore, an integral equation is established with respect to the electric field of waves guided along the coupler s axis. This integral equation is solved by applying entire domain Galerkin techniques, leading to a homogeneous linear system. The propagation constants of the wave guided modes correspond to the non-trivial solution of this linear system. The main originality of the Doctoral Thesis lies in the introduction of an integral equation methodology, which is developed and applied for the investigation of the wave guiding phenomena in grating-assisted couplers. Besides, the numerical implementation of the developed methodology derives several original and interesting numerical results, referring to the optimal design of the grating characteristics, combining the minimal coupling length with the maximal coupling efficiency. The relative benefits of the developed methodology with respect to the perturbation methods, the coupled-mode theory and the Floquet-Bloch theory lie on its accuracy, simplicity as well as its numerical efficiency. On the other hand, the developed methodology provides accurate results for gratings with large widths and strongly coupled waveguides, in contrast to the aforementioned methods. In addition, the Green s function is analytically expressed and all the integrals involved are analytically computed resulting to the significant reduction of the 7
8 computational cost, the high increase of the results accuracy and a solution with no other approximation than that of the final truncation of the linear system. The numerical results obtained exhibit superior validity and accuracy with respect to those derived by applying the methods mentioned above. These results serve certain design specifications of the structure under investigation, which may be exploited appropriately in various applications of integrated optoelectronics. KeyWords Directional couplers, grating, optical waveguides, slab waveguides, guided waves, integrated optics, optical filters, integral equations, method of moments, Galerkin techniques. 8
9 Στους γονείς μου που μου χάραξαν τους δρόμους της γνώσης 9
10 Θεωρώ καθήκον μου να εκφράσω τις θερμές και ειλικρινείς ευχαριστίες μου προς την επιβλέπουσα καθηγήτρια κ. Δήμητρα Κακλαμάνη και τον καθηγητή κ. Νικόλαο Ουζούνογλου για την υπόδειξη του θέματος, την πολύτιμη επιστημονική καθοδήγηση και βοήθειά τους, καθώς επίσης και την εν γένει ηθική ενίσχυση και συμπαράσταση κατά τη διάρκεια της εκπόνησης της παρούσας Διδακτορικής Διατριβής. 0
11 ΠΕΡΙΕΧΟΜΕΝΑ ΕΙΣΑΓΩΓΗ...5 ΚΕΦΑΛΑΙΟ. ΒΑΣΙΚΑ ΣΤΟΙΧΕΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗΣ ΘΕΩΡΙΑΣ Εξισώσεις Maxwell Διαφορική μορφή εξισώσεων Maxwell Ολοκληρωτική μορφή εξισώσεων Maxwell..... Καταστατικές σχέσεις-συνοριακές συνθήκες Εξισώσεις Maxwell σε ανομοιογενή ισοτροπικό χώρο Διανυσματικές κυματικές εξισώσεις Τμηματικά σταθερή κατανομή του δείκτη διάθλασης Αποσύζευξη εξισώσεων Maxwell...8 ΚΕΦΑΛΑΙΟ. ΚΑΤΕΥΘΥΝΤΙΚΟΙ ΣΥΖΕΥΚΤΕΣ ΣΕ ΟΠΤΙΚΕΣ ΔΙΑΤΑΞΕΙΣ Αρχή λειτουργίας κατευθυντικών συζευκτών Κυματοδήγηση σε ασυμμετρικούς κατευθυντικούς συζεύκτες Αντιπροσωπευτικά παραδείγματα κατευθυντικών συζευκτών Εισαγωγή γραμμοσειρών σε κατευθυντικούς συζεύκτες Μέθοδοι ανάλυσης της κυματοδήγησης σε συζεύκτες γραμμοσειρών Θεωρία Συζευγμένων Ρυθμών Θεωρία Floquet-Bloch Μέθοδοι Ολοκληρωτικών Εξισώσεων Άλλες μέθοδοι ανάλυσης της κυματοδήγησης Εφαρμογές των κυματοδηγών γραμμοσειρών στις οπτικές επικοινωνίες...5 ΚΕΦΑΛΑΙΟ 3. ΑΝΑΛΥΣΗ ΣΥΖΕΥΓΜΕΝΩΝ ΣΥΜΜΕΤΡΙΚΩΝ ΚΥΜΑΤΟΔΗΓΩΝ ΜΕ ΓΡΑΜΜΟΣΕΙΡΕΣ Συμμετρικός Συζεύκτης Γραμμοσειρών Θεώρημα Floquet και χωρικές αρμονικές περιοδικών δομών Αναλυτική έκφραση της συνάρτησης Green Ολοκληρωτική αναπαράσταση ηλεκτρικού πεδίου Επίλυση της ολοκληρωτικής εξίσωσης με τη μέθοδο Galerkin Ειδικές περιπτώσεις συζευκτών γραμμοσειρών Κυματοδήγηση σε έναν απομονωμένο κυματοδηγό παρουσία γραμμοσειρών Κυματοδήγηση σε συζεύκτη δύο παραλλήλων πλακών παρουσία γραμμοσειρών στην κάτω πλάκα Κυματοδήγηση σε συζεύκτη δύο παραλλήλων πλακών παρουσία γραμμοσειρών στην άνω πλάκα Αριθμητική υλοποίηση της μεθόδου Έλεγχος σύγκλισης, αποδοτικότητα και εγκυρότητα της μεθόδου...09 ΚΕΦΑΛΑΙΟ 4. ΑΝΑΛΥΣΗ ΑΣΥΜΜΕΤΡΙΚΩΝ ΚΥΜΑΤΟΔΗΓΩΝ ΜΕ ΓΡΑΜΜΟΣΕΙΡΕΣ Ασυμμετρικός συζεύκτης γραμμοσειρών Συνάρτηση Green της ομογενούς διάταξης Επίλυση της ολοκληρωτικής εξίσωσης με τη μέθοδο Galerkin Έλεγχος σύγκλισης, αποδοτικότητα και εγκυρότητα της μεθόδου...30 ΚΕΦΑΛΑΙΟ 5. ΑΡΙΘΜΗΤΙΚΑ ΑΠΟΤΕΛΕΣΜΑΤΑ-ΣΧΕΔΙΑΣΤΙΚΕΣ ΠΡΟΔΙΑΓΡΑΦΕΣ Συμμετρικοί Συζεύκτες Συζεύκτης με γραμμοσειρές στον κυματοδηγό...35
12 5... Συζεύκτης με γραμμοσειρές και στους δύο κυματοδηγούς Ασυμμετρικοί Συζεύκτες Μήκος κύματος συντονισμού Επίδραση του πάχους των γραμμοσειρών Επίδραση του δείκτη διάθλασης των γραμμοσειρών Φυσική σύζευξη μεταξύ των κυματοδηγών Βέλτιστη περίοδος και duty cycle γραμμοσειρών Συζεύκτης με δύο γραμμοσειρές...6 ΚΕΦΑΛΑΙΟ 6. ΕΠΙΣΚΟΠΗΣΗ, ΣΥΓΚΡΙΤΙΚΗ ΑΞΙΟΛΟΓΗΣΗ ΚΑΙ ΠΡΟΟΠΤΙΚΕΣ...63 ΠΑΡΑΡΤΗΜΑ Α...67 ΠΑΡΑΡΤΗΜΑ Β...7 ΠΑΡΑΡΤΗΜΑ Γ...75 ΔΗΜΟΣΙΕΥΣΕΙΣ...85 ΒΙΒΛΙΟΓΡΑΦΙΑ...86 Πίνακας σχημάτων Σχήμα. Γεωμετρία εφαρμογής συνοριακών συνθηκών...4 Σχήμα. Γεωμετρία ασυμμετρικού κατευθυντικού συζεύκτη...3 Σχήμα. Πεδιακές κατανομές των ΤΕ z ρυθμών συμμετρικού συζεύκτη...34 Σχήμα.3 Σήμα διέγερσης στο z= Σχήμα.4 Πεδιακή κατανομή στην απόσταση σύζευξης ισχύος z=l...35 Σχήμα.5 Πεδιακές κατανομές των ΤΕ z ρυθμών σύγχρονου ασυμμετρικού συζεύκτη...36 Σχήμα.6 Σήμα διέγερσης στο z= Σχήμα.7 Πεδιακή κατανομή στην απόσταση σύζευξης ισχύος z=l...37 Σχήμα.8 Πεδιακές κατανομές των TE z ρυθμών ασύγχρονου ασυμμετρικού συζεύκτη...38 Σχήμα.9 Σήμα διέγερσης στο z= Σχήμα.0 Πεδιακή κατανομή στην απόσταση σύζευξης ισχύος z=l...39 Σχήμα. Γεωμετρία ασυμμετρικού κατευθυντικού συζεύκτη γραμμοσειρών...40 Σχήμα. Βέλτιστες περίοδοι γραμμοσειρών συναρτήσει της απόστασης των κυματοδηγών...44 Σχήμα.3 Γεωμετρία του πολυστρωματικού κατευθυντικού συζεύκτη γραμμοσειρών...45 Σχήμα.4 Γεωμετρία του κατευθυντικού συζεύκτη γραμμοσειρών...48 Σχήμα.5 Κατάτμηση της γεωμετρίας σε συνοριακά στοιχεία...48 Σχήμα.6 Σχηματικό διάγραμμα οπτικού φίλτρου συχνοτήτων, σχηματισμένου σε GaAs....5 Σχήμα.7 Καμπύλες διασποράς του άρτιου και περιττού ρυθμού στο συζεύκτη γραμμοσειρών. Οι (a) και (b) αντιστοιχούν σε Κ+ΔΚ και Κ-ΔΚ, όπου ΔΚ μία μικρή μεταβολή, οφειλόμενη στη μεταβολή ΔΛ της περιόδου....5 Σχήμα.8 Σχηματικό διάγραμμα του πολυπλέκτη παρεμβολής δύο ρυθμών με χρήση κυματοδηγού γραμμοσειρών Σχήμα.9 (a) Διάταξη συζεύκτη γραμμοσειρών με ενεργούς κυματοδηγούς InP (b) Σχηματικό διάγραμμα του ευρυζωνικού πολυπλέκτη πρόσθεσης...53 Σχήμα.0 Σχηματικό διάγραμμα αποπολυπλέκτη με φίλτρα συζευκτών γραμμοσειρών. Λ, Λ και Λ 3 είναι διαφορετικές περίοδοι των γραμμοσειρών....54
13 Σχήμα. Σχηματικό διάγραμμα ασυμμετρικού συζεύκτη γραμμοσειρών, χρησιμοποιούμενου σε αποπολυπλέκτες Σχήμα. Φάσμα του -- παλμού Σχήμα.3 Διατάξεις ορθογωνικών γραμμοσειρών, που χρησιμοποιούνται για μετατροπή ρυθμών...56 Σχήμα.4 Φάσματα των εξαγομένων ρυθμών: (α) και (β) Σχήμα.5 Σχηματικό διάγραμμα του συντονιζομένου laser ημιαγωγών με ενσωματωμένο φίλτρο κατευθυντικού συζεύκτη γραμμοσειρών...58 Σχήμα.6 Σχηματικό διάγραμμα τετράθυρου συζεύκτη γραμμοσειρών Σχήμα.7 Σχηματικό διάγραμμα διδιάστατου δαχτυλιδιού συντονισμού γραμμοσειρών Σχήμα.8 Ανακλαστήρας-ταλαντωτής Bragg...60 Σχήμα.9 Σχηματικό διάγραμμα συζεύκτη γραμμοσειρών γραμμικής εστίασης...6 Σχήμα.30 Διάταξη κεραίας γραμμοσειρών χιλιοστομετρικών κυμάτων...6 Σχήμα 3. Γεωμετρία του συμμετρικού συζεύκτη γραμμοσειρών...64 Σχήμα 3. Γεωμετρία του χωρίς γραμμοσειρές προβλήματος...69 Σχήμα 3.3 Διαχωρισμός της διάταξης του συζεύκτη γραμμοσειρών από ορθογώνια 8 Σχήμα 3.4 Απομονωμένος κυματοδηγός παρουσία γραμμοσειρών...04 Σχήμα 3.5 Συζεύκτης δύο παραλλήλων πλακών παρουσία γραμμοσειρών στην κάτω πλάκα...05 Σχήμα 3.6 Συζεύκτης δύο παραλλήλων πλακών παρουσία γραμμοσειρών στην άνω πλάκα...07 Σχήμα 3.7 Τυπική καμπύλη του μέτρου της ορίζουσας ως προς το κανονικοποιημένο φανταστικό μέρος β/k Σχήμα 4. Γεωμετρία του ασυμμετρικού συζεύκτη γραμμοσειρών...4 Σχήμα 4. Γεωμετρία του ομογενούς (χωρίς γραμμοσειρές) προβλήματος...5 Σχήμα 4.3 Γεωμετρία του χωρίς γραμμοσειρές προβλήματος της απομονωμένης διηλεκτρικής πλάκας...0 Σχήμα 4.4 (α) Φανταστικά μέρη β /k 0, β /k 0 και (β) πραγματικά μέρη α /k 0, α /k 0 των σταθερών διάδοσης των ρυθμών γραμμοσειρών συναρτήσει του Λ/λ...3 Σχήμα 5. (α) Φανταστικά μέρη β e /k 0, β o /k 0 και (β) πραγματικά μέρη α e /k 0, α o /k 0 των σταθερών διάδοσης των ρυθμών γραμμοσειρών συναρτήσει του πάχους w των γραμμοσειρών, για n =3., h=μm, λ=.5μm και d =l =Λ/ Σχήμα 5. (α) β e /k 0, β ο /k 0 (συνεχείς γραμμές) και Ν e /k 0, Ν ο /k 0 (διακεκομμένες γραμμές) και (b) α e /k 0, α ο /k 0 συναρτήσει του κανονικοποιημένου μήκους κύματος Λ/λ για n =3., h=μm, w=0.μm και d =l =Λ/...38 Σχήμα 5.3 Καμπύλες διασποράς β e /k 0, β ο /k 0 (συνεχείς γραμμές) του περιοδικού συζεύκτη με d =l =Λ/ και κ e /k 0, κ ο /k 0 (διακεκομμένες γραμμές) του μη περιοδικού συζεύκτη με d =0 και l =Λ συναρτήσει του μήκους κύματος Λ/λ, για n =3., h=μm, w=0.μm Σχήμα 5.4 (α) β e /k 0, β ο /k 0 και (β) α e /k 0, α ο /k 0 συναρτήσει του κανονικοποιημένου δείκτη διάθλασης n /n των γραμμοσειρών για w=0.μm, h=μm, λ=.5μm and d =l =Λ/....4 Σχήμα 5.5 (α) β e s /k 0, β ο s /k 0 (συνεχείς) και β e w /k 0, β ο w /k 0 (διακεκομμένες) και (β) α e s /k 0, α ο s /k 0 (συνεχείς) και α e w /k 0, α ο w /k 0 (διακεκομμένες) συναρτήσει του Λ/λ, για n =3. (w: ασθενής διαταραχή) και n =3.4 (s: ισχυρή διαταραχή), h=μm, w=0.μm και d =l =Λ/....4 Σχήμα 5.6 (α) β e /k 0, β ο /k 0 (συνεχείς γραμμές) και Ν e /k 0, Ν ο /k 0 (διακεκομμένες γραμμές) και (β) α e /k 0, α ο /k 0 συναρτήσει της απόστασης διαχωρισμού h για w=0.μm, n =3., λ=.5μm και d =l =Λ/
14 Σχήμα 5.7 (α) β e /k 0, β ο /k 0 και (β) α e /k 0, α ο /k 0 συναρτήσει του n /n για τον συζεύκτη με γραμμοσειρές και στους δύο κυματοδηγούς με q=, d =l =Λ/ και λ=.5μm...46 Σχήμα 5.8 (α) Φανταστικά μέρη β /k 0, β /k 0 (συνεχείς γραμμές) και Ν /k 0 +λ/λ, Ν /k 0 (διακεκομμένες γραμμές) των σταθερών διάδοσης των ρυθμών γραμμοσειρών και των σύνθετων ρυθμών και (β) πραγματικά μέρη α /k 0, α /k 0 των σταθερών διάδοσης των ρυθμών γραμμοσειρών συναρτήσει (και στις δύο περιπτώσεις (α) και (β)) του Λ/λ, για d 3 =0.55 μm, w =0.05 μm, n 6 =3, n h, = Σχήμα 5.9 (α) β /k 0, β /k 0 και (β) α /k 0, α /k 0 συναρτήσει του πάχους w των γραμμοσειρών, για λ=.47 μm (διακεκομμένες) και λ=.53 μm (συνεχείς γραμμές) με d 3 =0.55 μm, n 6 = Σχήμα 5.0 (α) β /k 0, β /k 0 και (β) α /k 0, α /k 0 συναρτήσει του δείκτη διάθλασης n 6 των γραμμοσειρών, για λ=.5 μm (διακεκομμένες) και λ=.53 μm (συνεχείς γραμμές) με d 3 =0.55 μm, w =0.05 μm Σχήμα 5. (α) β /k 0, β /k 0 (συνεχείς) και Ν ng /k 0, Ν ng /k 0 (διακεκομμένες γραμμές) και (β) α /k 0, α /k 0 συναρτήσει της απόστασης διαχωρισμού d 3, για w =0.05 μm, λ=.5μm, n 6 = Σχήμα 5. β /k 0, β /k 0 (συνεχείς) και Ν /k 0 λ/λ, N /k 0 (διακεκομμένες γραμμές) συναρτήσει της περιόδου Λ των γραμμοσειρών, για λ=.5μm, t=, b =l =Λ/, n h, = Σχήμα 5.3 Απόσταση Δβ/k 0 = β β /k 0 συναρτήσει της περιόδου Λ των γραμμοσειρών, για μεταβλητά duty cycles dc και πλήθη t των ορθογωνίων...6 Σχήμα 5.4 β /k 0 και β /k 0 συναρτήσει της περιόδου Λ των γραμμοσειρών, για τον ασυμμετρικό συζεύκτη με γραμμοσειρές και στους δύο κυματοδηγούς του εδαφίου Σχήμα 6. Διαχωρισμός κατάλληλου τμήματος της διάταξης δύο απείρων συμμετρικών διηλεκτρικών πλακών από ένα ορθογώνιο Πίνακας πινάκων Πίνακας 3. Πρότυπο σύγκλισης της κανονικοποιημένης σταθεράς διάδοσης του απομονωμένου κυματοδηγού γραμμοσειρών.... Πίνακας 4. Πρότυπο σύγκλισης των κανονικοποιημένων φανταστικών μερών των σταθερών διάδοσης του συζεύκτη γραμμοσειρών του Σχήματος 4. με n =, n =3., n 3 =n 5 =n 6 =n 7 =3, n 4 =3.5, d =0.5 μm, d 3 =0.55 μm, d 4 =0. μm, w =0. μm, w =0.05 μm, Λ=0.748 μm, λ=.5 μm, t=, a =s =b =l =Λ/ Πίνακας 5. Απόσταση των σταθερών διάδοσης των ρυθμών γραμμοσειρών...45 Πίνακας 5. β e /k 0 ως προς λ για τις περιπτώσεις (n =3.): (i) q=0 (συζεύκτης χωρίς γραμμοσειρές), (ii) q=, d =Λ/4, l =Λ/4, (iii) q=, d =Λ/0, d =Λ/0, d =Λ/, l =Λ/0, l =3Λ/0, (iv) q=8, d i =i Λ/0, l i =Λ/0,i=,,8, (v) q=, d =0, l =Λ (μη περιοδικός συζεύκτης) Πίνακας 5.3 β o /k 0 ως προς λ για τις πέντε περιπτώσεις του Πίνακας Πίνακας 5.4 Βέλτιστες περίοδοι και βέλτιστα μήκη σύζευξης για μεταβλητό duty cycle και πλήθος ορθογωνίων ανά επανάληψη των γραμμοσειρών, όπως δείχνει το Σχήμα
15 ΕΙΣΑΓΩΓΗ Διατάξεις κυματοδήγησης οπτικών σημάτων, οι οποίες περιέχουν περιοδικά μεταβαλλόμενο δείκτη διάθλασης και επιφανειακά χαραγμένες γραμμοσειρές (surface grating), αποτελούν βασικά δομικά στοιχεία των ολοκληρωμένων οπτικοηλεκτρονικών συστημάτων. Ειδικότερα, διατάξεις κυματοδηγών επιπέδων διηλεκτρικών πλακών (slab waveguides) με περιοδικά χαραγμένες γραμμοσειρές εξυπηρετούν στη μεταφορά ενέργειας από μία διηλεκτρική πλάκα σε άλλη και χρησιμοποιούνται αποτελεσματικά σε κατευθυντικούς συζεύκτες, οπτικά φίλτρα επιλογής συχνοτήτων, lasers κατανεμημένης ανάδρασης, οπτικούς διακόπτες, πολυπλέκτες, αποπολυπλέκτες και αρκετές άλλες διατάξεις ολοκληρωμένης οπτικής (βλ. π.χ. [] και []). Προγενέστερες μεθοδολογίες-συνοπτική επισκόπηση της Βιβλιογραφίας Η ηλεκτρομαγνητική ανάλυση των προαναφερομένων διατάξεων σύζευξης και κυματοδήγησης έχει ήδη αναπτυχθεί με αρκετές μεθόδους. Οι αρχικές μέθοδοι συνδυάζουν τα αναπτύγματα διαταραχών των ρυθμών του συζεύκτη με τεχνικές συζευγμένων κυμάτων για τη μελέτη της επίδρασης των γραμμοσειρών στην όλη διάταξη (βλ. π.χ. [3]-[6]). Οι εν λόγω τεχνικές αποσαφηνίζουν οπωσδήποτε την εικόνα της φυσικής διαδικασίας της σύζευξης, αλλά οδηγούν μόνο σε προσεγγιστικά αποτελέσματα. Εξάλλου, την κύρια μεθοδολογία ανάλυσης των φαινομένων κυματοδήγησης σε διατάξεις συζευκτών γραμμοσειρών συνιστά η θεωρία των συζευγμένων ρυθμών (βλ. ενδεικτικά [7]-[]). Όμως, η ακρίβεια των λύσεων, οι οποίες επιτυγχάνονται με εφαρμογή της μεθοδολογίας αυτής, προϋποθέτει αρκετούς περιορισμούς, όπως μικρό πάχος γραμμοσειρών, μεγάλη απόσταση διαχωρισμού των δύο κυματοδηγών και μικρές διαφορές των δεικτών διάθλασης των εμπλεκομένων μέσων. Επίσης, έχουν προταθεί μέθοδοι πινάκων μεταφοράς, οι οποίες χρησιμοποιούν τεχνικές προσαρμογής ρυθμών, αλλά τα αποτελέσματά τους υπόκεινται στους περιορισμούς της θεωρίας συζευγμένων ρυθμών. Σε συγκεκριμένες πρακτικές εφαρμογές απαιτούνται υπολογιστικές τεχνικές ακριβέστερες της θεωρίας των συζευγμένων ρυθμών για τον υπολογισμό σημαντικών μεγεθών, όπως οι σταθερές διάδοσης των κυματοδηγούμενων ρυθμών, ο διαχωρισμός της ενέργειας ανάμεσα στους κυματοδηγούς και οι απώλειες ακτινοβολίας. Για το σκοπό αυτό έχουν αναπτυχθεί αρκετά ακριβείς τεχνικές, οι οποίες στηρίζονται στη θεωρία Floquet-Bloch (βλ. ενδεικτικά []-[9]). Οι εν λόγω τεχνικές χρησιμοποιούν αυστηρές (ακριβείς) εκφράσεις των ρυθμών των κυματοδηγών, οι οποίες οδηγούν σε ακριβή αποτελέσματα, αναφερόμενα στην επίδοση των συζευκτών γραμμοσειρών. Όμως, η ακρίβεια των αποτελεσμάτων εξαρτάται από τον αριθμητικό 5
16 υπολογισμό των ολοκληρωμάτων ή την αριθμητική επίλυση συστημάτων γραμμικών διαφορικών εξισώσεων πρώτης τάξεως. Εξάλλου, σημειώνουμε ότι η διάδοση στους συζεύκτες γραμμοσειρών έχει επίσης διερευνηθεί με εφαρμογή της θεωρίας γραμμών μεταφοράς [30]-[3] και τεχνικών στο πεδίο του χρόνου [3]-[34]. Αντικείμενο και μεθοδολογία της Διδακτορικής Διατριβής Στην ανά χείρας διατριβή μελετώνται τα φαινόμενα κυματοδήγησης σε άπειρο περιοδικό οπτικό συζεύκτη γραμμοσειρών με τη βοήθεια ημιαναλυτικών τεχνικών ολοκληρωτικών εξισώσεων, εφαρμόζοντας τη Μέθοδο των Ροπών με συναρτήσεις βάσης συνολικού χώρου (entire domain basis functions). Ειδικότερα, τα στρώματα των γραμμοσειρών μοντελοποιούνται ως άπειρα στρώματα με περιοδικά χαραγμένες ορθογώνιες ασυνέχειες. Ως εφαρμογή της μεθόδου Sommerfeld επιτυγχάνεται αναλυτική έκφραση της συνάρτησης Green του ομογενούς (χωρίς γραμμοσειρές) προβλήματος μέσω ολοκληρώματος Fourier. Περαιτέρω, διατυπώνεται ολοκληρωτική αναπαράσταση του ηλεκτρικού πεδίου των TE πολωμένων ηλεκτρομαγνητικών κυμάτων, τα οποία διαδίδονται κατά μήκος του άξονα του συζεύκτη. Εξάλλου, περιορίζοντας το διάνυσμα παρατήρησης στις ορθογώνιες ασυνέχειες, διαπιστώνουμε ότι η εν λόγω ολοκληρωτική αναπαράσταση μετατρέπεται σε ολοκληρωτική εξίσωση του ηλεκτρικού πεδίου στις ασυνέχειες. Για τη λύση της εν λόγω ολοκληρωτικής εξίσωσης εφαρμόζονται τεχνικές Galerkin συνολικού χώρου (entire domain Galerkin techniques), οι οποίες οδηγούν σε συγκεκριμένο ομογενές γραμμικό σύστημα. Οι σταθερές διάδοσης των κυματοδηγούμενων ρυθμών είναι οι τιμές εκείνες, για τις οποίες το εν λόγω σύστημα έχει μη τετριμμένη λύση, και υπολογίζονται ως ρίζες της ορίζουσας του πίνακα του συστήματος. Η ανάλυση αφορά διάδοση εγκάρσια ηλεκτρικών (ΤΕ) κυμάτων. Όμως, η μέθοδος μπορεί να επεκταθεί για τη μελέτη της διάδοσης εγκάρσια μαγνητικών (ΤΜ) κυμάτων, θεωρώντας ως άγνωστη συνάρτηση το μαγνητικό πεδίο στο χωρίο των γραμμοσειρών. Η προτεινόμενη μεθοδολογία αναφέρεται αρχικά στη μελέτη των φαινομένων κυματοδήγησης στη διάταξη του συμμετρικού συζεύκτη γραμμοσειρών, αποτελούμενου από όμοιους κυματοδηγούς ευρισκόμενους εντός του ελευθέρου χώρου, και αναλύεται διεξοδικά στο Κεφάλαιο 3. Η συμμετρία της διάταξης διευκολύνει την αποσαφήνιση των βασικών ιδεών και των τεχνικών χαρακτηριστικών της μεθόδου. Η διεύρυνση της μεθοδολογίας για τις περιπτώσεις ασυμμετρικών συζευκτών γραμμοσειρών προϋποθέτει ορισμένες επεκτάσεις, προσαρμογές, και βελτιώσεις της αρχικής μεθόδου, οι οποίες συνοψίζονται στο Κεφάλαιο 4. Στην προκειμένη περίπτωση η ασυμμετρία του συζεύκτη επιβάλλει σημαντική πολυπλοκότητα στην ανάλυση και 6
17 τους υπολογισμούς των αναλυτικών εκφράσεων της συνάρτησης Green και των blocks του πίνακα του γραμμικού συστήματος καθώς επίσης και σε αρκετά σημεία της αριθμητικής υλοποίησης. Κύρια πλεονεκτήματα της αναπτυσσόμενης μεθοδολογίας είναι η ακρίβεια και η απλότητα καθώς επίσης και η αριθμητική αποδοτικότητα, η οποία συνίσταται στη μεγάλη ακρίβεια των αποτελεσμάτων με χρήση μικρού αριθμού όρων των αναπτυγμάτων (βλ. [35] και [36]). Επιπλέον, εκφράζεται αναλυτικά η συνάρτηση Green και υπολογίζονται αναλυτικά όλα τα εμφανιζόμενα ολοκληρώματα. Έτσι, μειώνεται σημαντικά το υπολογιστικό κόστος, αυξάνεται η ακρίβεια των αποτελεσμάτων και επιτυγχάνεται μία λύση χωρίς άλλες προσεγγίσεις εκτός εκείνης της τελικής κολόβωσης (truncation) των συνόλων των συναρτήσεων ανάπτυξης και δοκιμής. Εξάλλου, αξίζει να σημειώσουμε ότι η χρησιμοποιούμενη μέθοδος δίνει ακριβή αποτελέσματα για γραμμοσειρές μεγάλου πάχους και για ισχυρά συζευγμένους κυματοδηγούς, ενώ οι προγενέστερες μέθοδοι προϋποθέτουν σημαντικούς περιορισμούς των φυσικών και γεωμετρικών παραμέτρων των γραμμοσειρών (για περισσότερες λεπτομέρειες παραπέμπουμε στη σχετική συζήτηση στο [8]). Τα φαινόμενα διάδοσης σε συζεύκτες γραμμοσειρών έχουν επίσης μελετηθεί με εφαρμογή τεχνικών ολοκληρωτικών εξισώσεων [37]-[39], οι οποίες είναι διαφορετικές από τις χρησιμοποιούμενες στην παρούσα διατριβή. Ειδικότερα, στις Εργασίες [37]-[39] χρησιμοποιείται η συνάρτηση Green ελευθέρου χώρου και εφαρμόζεται η μέθοδος συνοριακών στοιχείων για την επίλυση της ολοκληρωτικής εξίσωσης στο επίπεδο χωρίο των γραμμοσειρών. Επίσης, ο ακριβής υπολογισμός των σταθερών διάδοσης εξαρτάται από τη διακριτοποίηση σε συνοριακά στοιχεία, η οποία σε ορισμένες περιπτώσεις συμβάλλει σε μεγάλη αύξηση του υπολογιστικού κόστους. Εξάλλου, η μεθοδολογία της παρούσας διατριβής επιτρέπει την αναλυτική εκτέλεση όλων των υπολογισμών και δεν απαιτεί διακριτοποίηση της εμφανιζομένης ολοκληρωτικής εξίσωσης, σε αντίθεση με την περίπτωση της μεθόδου των συνοριακών στοιχείων. Επιπροσθέτως, η συνάρτηση Green της διάταξης των συζευγμένων κυματοδηγών, η οποία χρησιμοποιείται εδώ, παρέχει μία πλέον συμπαγή διατύπωση, η οποία ικανοποιεί συμφυώς τις συνοριακές συνθήκες. Η αριθμητική υλοποίηση της αναπτυχθείσας μεθόδου παράγει αρκετά ενδιαφέροντα αριθμητικά αποτελέσματα. Πιο συγκεκριμένα παρουσιάζονται αριθμητικά αποτελέσματα αναφερόμενα στη βέλτιστη σχεδίαση των χαρακτηριστικών των γραμμοσειρών, τα οποία προσφέρουν το ελάχιστο δυνατό μήκος σύζευξης και τη μέγιστη δυνατή αποδοτικότητα σύζευξης (διατηρώντας μικρή απόσταση μεταξύ των σταθερών διάδοσης). Επίσης, ερμηνεύεται ο τρόπος επίδρασης του πάχους, του δείκτη διάθλασης και του κύκλου καθήκοντος των 7
18 γραμμοσειρών ως επιπρόσθετων μηχανισμών ελέγχου της βέλτιστης συμπεριφοράς του συζεύκτη αναφορικά με τα επιθυμητά λειτουργικά χαρακτηριστικά. Αναλύονται εκτενώς τα βέλτιστα χαρακτηριστικά του ασυμμετρικού συζεύκτη γραμμοσειρών για την αποδοτική λειτουργία του ως ζωνοπερατού φίλτρου οπτικών συχνοτήτων. Η αξιολόγηση αυτών των αποτελεσμάτων διαμορφώνει συγκεκριμένες τεχνικές-σχεδιαστικές προδιαγραφές της υπό μελέτη διάταξης. Δομή της Διδακτορικής Διατριβής Η δομή της ανά χείρας διατριβής συνοψίζεται ως εξής: Στο Κεφάλαιο παρουσιάζονται συνοπτικά οι αρχές και η μεθοδολογία του Ηλεκτρομαγνητισμού, που απαιτούνται για τη μελέτη προβλημάτων οπτικών συζευκτών. Στο Κεφάλαιο αναλύεται εκτενώς η αρχή λειτουργίας των κατευθυντικών συζευκτών και περιγράφονται συστηματικά οι γνωστές μέθοδοι ανάλυσης της κυματοδήγησης σε κατευθυντικούς συζεύκτες γραμμοσειρών. Στο Κεφάλαιο 3 καταχωρείται αναλυτική μελέτη των φαινομένων κυματοδήγησης σε συζευγμένους δισδιάστατους συμμετρικούς κυματοδηγούς με περιοδικά χαραγμένες γραμμοσειρές με χρήση των τεχνικών της Μεθόδου των Ροπών. Η εν λόγω μελέτη αφορά κυρίως στον ακριβή προσδιορισμό των μιγαδικών σταθερών διάδοσης των κυματοδηγούμενων κυμάτων. Στο Κεφάλαιο 4 εντοπίζονται και συνοψίζονται οι προαπαιτούμενες επεκτάσεις, προσαρμογές, και βελτιώσεις της αρχικής μεθόδου για τη διερεύνηση της κυματοδήγησης σε ασυμμετρικούς συζεύκτες γραμμοσειρών. Στο Κεφάλαιο 5 παρουσιάζονται αρκετά αριθμητικά αποτελέσματα, αναφερόμενα στην εξέλιξη των μιγαδικών σταθερών διάδοσης συναρτήσει των γεωμετρικών και φυσικών χαρακτηριστικών των γραμμοσειρών, τα οποία αξιοποιούνται αποτελεσματικά στη σχεδίαση συζευκτών γραμμοσειρών. Τέλος, στο Κεφάλαιο 6 καταγράφονται τα συμπεράσματα της διατριβής και προτείνονται κατευθύνσεις για μελλοντική εργασία. 8
19 ΚΕΦΑΛΑΙΟ ΚΕΦΑΛΑΙΟ. ΒΑΣΙΚΑ ΣΤΟΙΧΕΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗΣ ΘΕΩΡΙΑΣ Στο Κεφάλαιο αυτό παρουσιάζονται συνοπτικά με τις απαραίτητες προσαρμογές και βελτιώσεις (επεκτάσεις) οι αρχές και η μεθοδολογία του Ηλεκτρομαγνητισμού που απαιτούνται για τη μελέτη προβλημάτων οπτικών συζευκτών. Ακριβέστερα, στην παράγραφο. καταγράφονται και αναλύονται η διαφορική και ολοκληρωτική μορφή των εξισώσεων Maxwell στο πεδίο του χρόνου. Επιπλέον, διατυπώνονται οι χρονοανεξάρτητες εξισώσεις Maxwell στην περίπτωση αρμονικής χρονικής εξάρτησης των πεδιακών μεγεθών. Οι εξισώσεις Maxwell συμπληρώνονται από κατάλληλες συντακτικές σχέσεις και συνοριακές συνθήκες, οι οποίες καταχωρούνται στην παράγραφο.. Εξάλλου, στην παράγραφο.3 εξάγονται οι χρονοανεξάρτητες εξισώσεις Maxwell σε ανομοιογενή ισοτροπικό χώρο και μελετώνται οι αντίστοιχες διανυσματικές κυματικές εξισώσεις για το ηλεκτρικό και το μαγνητικό πεδίο. Στην ειδική περίπτωση τμηματικά σταθερής κατανομής του δείκτη διάθλασης οι προαναφερόμενες διανυσματικές κυματικές εξισώσεις ανάγονται στις γνωστές μη ομογενείς διανυσματικές εξισώσεις Helmholtz. Η αποσύζευξη των εξισώσεων Maxwell στην περίπτωση ανεξαρτησίας των πεδιακών μεγεθών από την εγκάρσια μεταβλητή περιγράφεται στην παράγραφο.4. Η εν λόγω αποσύζευξη οδηγεί στη μελέτη των δύο ξεχωριστών ηλεκτρομαγνητικών προβλημάτων, του εγκάρσια ηλεκτρικού (ΤΕ-transverse electric) και του εγκάρσια μαγνητικού (ΤΜ-transverse magnetic). 9
20 .. Εξισώσεις Maxwell Οι εξισώσεις Maxwell διατυπώθηκαν από τον James Clerk Maxwell το 873. Μέχρι τότε, ορισμένες ατελείς μορφές αυτών των εξισώσεων προϋπήρχαν σε εργασίες των Faraday, Ampere, Gauss και Poisson. Η βασική συνεισφορά του Maxwell συνίσταται στη θεώρηση ως προσθετέου του όρου του ρεύματος μετατόπισης (displacement current) στις προαναφερθείσες εξισώσεις [40]-[4]. Αυτό συνέβαλε σημαντικά και στην απόδειξη της αρχής ότι το ηλεκτρομαγνητικό πεδίο μπορεί να υπάρξει ως κύματα. Πειραματικά, η κυματική φύση των εξισώσεων Maxwell επιβεβαιώθηκε από τον Heinrich Hertz το 888. Εξάλλου, αν και η επιφάνεια της γης είναι καμπύλη, ο Guglielmo Marconi επέτυχε το 90 μέσω της ανάκλασης των ραδιοκυμάτων στην ιονόσφαιρα, τη μετάδοση ραδιοκυμάτων κατά μήκος του Ατλαντικού Ωκεανού. Έκτοτε η σημασία των εξισώσεων Maxwell έχει αναδειχθεί σε πολυάριθμες φυσικές και τεχνολογικές εφαρμογές της θεωρίας μικροκυμάτων και κεραιών, των ασυρμάτων και οπτικών τηλεπικοινωνιών, radar καθώς επίσης και σε πολλές εφαρμογές ευθέων και αντιστρόφων προβλημάτων σκέδασης. Οι εξισώσεις (νόμοι) Maxwell διατυπώνονται σε διαφορική και σε ολοκληρωτική μορφή, οι οποίες αναλύονται στα ακόλουθα δύο εδάφια.... Διαφορική μορφή εξισώσεων Maxwell Οι εξισώσεις Maxwell σε διαφορική μορφή είναι οι εξής E(,) r t = B(,) r t t (.) H(,) r t = D(,) r t + J(,) r t t (.) D(,) r t = ρ(,) r t (.3) B(,) r t = 0 (.4) Οι χωροχρονικές διανυσματικές συναρτήσεις Ε, Η, D, B, J: Ω και η χωροχρονική μιγαδική συνάρτηση ρ: Ω εκφράζουν
21 E(r,t): ένταση ηλεκτρικού πεδίου (Volts/m) H(r,t): ένταση μαγνητικού πεδίου (Amperes/m) D(r,t): ηλεκτρική μετατόπιση (ροή) (Coulombs/m ) Β(r,t): πυκνότητα μαγνητικής ροής (Webers/m ) J(r,t): πυκνότητα ηλεκτρικού ρεύματος (Amperes/m ) ρ(r,t): πυκνότητα ηλεκτρικού φορτίου (Coulombs/m 3 ) Η εξίσωση (.) είναι γνωστή ως νόμος Faraday. Η εξίσωση (.) χωρίς τον όρο D του t ρεύματος μετατόπισης είναι γνωστή ως νόμος Ampere. Ο όρος του ρεύματος μετατόπισης εισήχθη ως προσθετέος στο νόμο του Ampere από τον Maxwell. Ο εν λόγω όρος συζευγνύει το μαγνητικό πεδίο με τη χρονικά μεταβαλλόμενη ηλεκτρική ροή και επιτρέπει τη δυνατότητα ύπαρξης των ηλεκτρομαγνητικών πεδίων ως κυμάτων, τα οποία, ως αποδείχτηκε κατόπιν, ταυτίζονται με τα οπτικά κύματα (για λεπτομέρειες βλ. [40] και [4]). Εξάλλου, οι εξισώσεις (.3) και (.4) είναι συνέπειες του νόμου Gauss, ο οποίος εκφράζει τη διατήρηση της ροής, και είναι γνωστές ως νόμοι Gauss για το ηλεκτρικό και το μαγνητικό πεδίο αντιστοίχως. Οι εξισώσεις Maxwell συμπληρώνονται από την εξίσωση συνεχείας J(,) r t + (,) t 0 t ρ r = (.5) η οποία εκφράζει την ιδιότητα ότι η απόκλιση της πυκνότητας ρεύματος J από έναν απειροστό όγκο, ο οποίος περιβάλλει το σημείο r, είναι ίση με το ρυθμό μείωσης της πυκνότητας ηλεκτρικού φορτίου ρ ως προς το χρόνο t. Εξάλλου, αξίζει να σημειώσουμε ότι οι εξισώσεις (.)-(.5) δεν είναι ανεξάρτητες, αφού οι (.4) και (.3) προκύπτουν από τις (.) και (.). Ακριβέστερα, η απόκλιση της (.) οδηγεί στην (.4), ενώ η απόκλιση της (.) μέσω της εξίσωσης συνεχείας (.5) οδηγεί στην (.3). Στα επόμενα υποθέτουμε ότι οι προαναφερθείσες πεδιακές και ρευματικές χωροχρονικές συναρτήσεις μεταβάλλονται αρμονικά ως προς χρόνο με βάση τον παράγοντα exp(jωt) (ω είναι η κυκλική συχνότητα), δηλαδή ισχύει Η διανυσματική συνάρτηση A(r): V [ ω ] A( r, t) = Re A( r )exp( j t) (.6) αναφέρεται ως παραστατικός μιγάς ή φάσορας 3 3 (phasor). Υπό την προϋπόθεση (.6) οι (.)-(.4) ανάγονται στις χρονοανεξάρτητες εξισώσεις Maxwell
22 Er () = jωbr () (.7) Hr () = jωdr () + Jr () (.8) Dr () = ρ() r (.9) Br () = 0 (.0) Εναλλακτικά οι (.7)-(.0) προκύπτουν επίσης και με τη βοήθεια του μετασχηματισμού Fourier ως προς το χρόνο των (.)-(.4) και συνεπώς οι φάσορες είναι ουσιαστικά οι μετασχηματισμοί Fourier των χωροχρονικών πεδιακών συναρτήσεων. Για αυτό το λόγο, οι φάσορες, που επαληθεύουν τις (.7)-(.0), αναφέρονται επίσης και ως λύσεις στο πεδίο συχνοτήτων (frequency domain solutions) των εξισώσεων Maxwell, ενώ οι χωροχρονικές συναρτήσεις που επαληθεύουν τις (.)-(.4) αναφέρονται ως λύσεις στο πεδίο του χρόνου (time domain solutions) των εξισώσεων Maxwell. Τα πλεονεκτήματα της χρήσης των (.7)-(.0) εντοπίζονται ουσιαστικά στην απουσία χρονικής εξάρτησης και χρονικών παραγώγων.... Ολοκληρωτική μορφή εξισώσεων Maxwell Οι εξισώσεις Maxwell (.)-(.4) αναδιατυπώνονται επίσης σε ολοκληρωτική μορφή, η οποία αναδεικνύει μία διαφορετική ενόραση των προβλημάτων (βλ. [43] και [44]). Η ολοκληρωτική μορφή των εξισώσεων Maxwell είναι η εξής E(,) r t dl = B(,) t d t r S (.) C S H(,) r t dl = D(,) t d + J(,) t d t r S r S (.) C S S V D(,) r t ds= ρ(,) r t dv (.3) V B(,) r t ds = 0 (.4) V όπου S είναι μία απλή, λεία και C 3 παραμετρική επιφάνεια του με γεωμετρικό σύνορο C θετικά προσανατολισμένο ως προς ένα συνεχές διανυσματικό πεδίο μοναδιαίων καθέτων 3 διανυσμάτων της S και V ένα κανονικό υποσύνολο του με τμηματικά C σύνορο V. Οι εξισώσεις (.) και (.) προκύπτουν αντιστοίχως μετά από ολοκλήρωση των μελών των (.) και (.) στην επιφάνεια S και εφαρμογή του θεωρήματος Stokes. Οι εξισώσεις (.3) και (.4) προκύπτουν μετά από ολοκλήρωση των μελών των (.3) και (.4) στο σύνολο V και εφαρμογή του θεωρήματος Gauss.
23 Σύμφωνα με την (.) η ηλεκτρεγερτική δύναμη κατά μήκος του γεωμετρικού συνόρου C της επιφάνειας S ισούται με το ρυθμό μείωσης της μαγνητικής ροής, η οποία διαπερνά την επιφάνεια αυτή. Εξάλλου, η εξίσωση (.) συνεπάγεται ότι η μαγνητεγερτική δύναμη κατά μήκος του συνόρου C ισούται με το άθροισμα του ρυθμού αύξησης της ηλεκτρικής ροής δια μέσου της επιφάνειας S και του ρεύματος που διαπερνά την S. Δηλαδή, μία χρονικά μεταβαλλόμενη ηλεκτρική ροή (ρεύμα μετατόπισης) ή ένα ηλεκτρικό ρεύμα παράγουν μία μαγνητεγερτική δύναμη, ή απλούστερα ένα μαγνητικό πεδίο, το οποίο περιβάλλει τα ρεύματα. Επιπροσθέτως, η εξίσωση (.3) εκφράζει την ιδιότητα ότι η ηλεκτρική ροή η οποία εξέρχεται 3 από υποσύνολο V του δια μέσου της επιφάνειας V ισούται με το συνολικό ηλεκτρικό φορτίο που εμπερικλείεται στο V. Η εξίσωση (.4) εκφράζει την ιδιότητα ότι η μαγνητική ροή η οποία εξέρχεται από το V δια μέσου του V ισούται με μηδέν. Οι εξισώσεις (.3) και (.4) αποτελούν ουσιαστικά διατυπώσεις της διατήρησης της ηλεκτρικής και μαγνητικής ροής αντιστοίχως. Τα θέματα της παρούσας διατριβής μελετώνται με χρήση των χρονοανεξάρτητων εξισώσεων Maxwell στη διαφορική μορφή (.7)-(.0)... Καταστατικές σχέσεις-συνοριακές συνθήκες Επειδή από τις τέσσερις εξισώσεις Maxwell μόνο οι δύο είναι ανεξάρτητες, στην πράξη εργαζόμαστε με τις (.7) και (.8). Όμως, στις δύο αυτές διανυσματικές εξισώσεις υπάρχουν τέσσερις διανυσματικοί άγνωστοι E, H, D, B. Έτσι, για να έχουμε επαρκή αριθμό εξισώσεων, χρειαζόμαστε άλλες δύο εξισώσεις που να συνδέουν τα E, H, D, B. Αυτές είναι οι καταστατικές σχέσεις (constitutive relations), οι οποίες εξαρτώνται από και χαρακτηρίζουν το φυσικό μέσο στο οποίο διατυπώνονται οι εξισώσεις Maxwell. Οι καταστατικές σχέσεις στη γενική περίπτωση ενός ανισοτροπικού μέσου Dr () = ε() r E() r (.5) Br () = μ() r H() r (.6) συνδέουν τα E και D και τα H και B μέσω των 3 3 τανυστών ε και μ. Επειδή οι ε και μ είναι χωρικές συναρτήσεις, το μέσο αναφέρεται ως ανομοιογενές. Στις ειδικές περιπτώσεις των ισοτροπικών μέσων οι σχέσεις (.5) και (.6) είναι ανεξάρτητες από την πόλωση των πεδίων και ανάγονται στις 3
24 όπου ε και μ μιγαδικές χωρικές βαθμωτές συναρτήσεις. Dr () = ε () rer () (.7) Br () = μ() rhr () (.8) Οι εξισώσεις Maxwell και οι καταστατικές σχέσεις συμπληρώνονται από κατάλληλες συνοριακές συνθήκες (boundary conditions), τις οποίες πρέπει να πληρούν το ηλεκτρικό και μαγνητικό πεδίο στις διαχωριστικές επιφάνειες μεταβολής των φυσικών παραμέτρων του μέσου. Συγκεκριμένα, στη διαχωριστική επιφάνεια S δύο μέσων με αντίστοιχες φυσικές παραμέτρους (ε,μ ) και (ε,μ ), η οποία δεν περιέχει επιφανειακές κατανομές φορτίων ή ρευμάτων Σχήμα. Γεωμετρία εφαρμογής συνοριακών συνθηκών ισχύουν για το ηλεκτρικό και μαγνητικό πεδίο οι συνοριακές συνθήκες μετάδοσης (transmission boundary conditions) [45] nˆ E () r = nˆ E () r (.9) ε ne ˆ () r= ε ne ˆ () r (.0) nˆ H () r = nˆ H () r (.) μ nˆ H () r = μ nˆ H () r (.) Οι (.9) και (.) εκφράζουν ότι οι εφαπτομενικές συνιστώσες του ηλεκτρικού και του μαγνητικού πεδίου είναι συνεχείς στην S. Επιπλέον, οι (.0) και (.) εκφράζουν ότι οι κάθετες συνιστώσες της ηλεκτρικής μετατόπισης και της μαγνητικής επαγωγής είναι συνεχείς στην S. 4
25 .3. Εξισώσεις Maxwell σε ανομοιογενή ισοτροπικό χώρο.3.. Διανυσματικές κυματικές εξισώσεις Οι χρονοανεξάρτητες εξισώσεις Maxwell (.7)-(.0) σε ισοτροπικό ανομοιογενές μέσο με μαγνητική διαπερατότητα μ(r) και ηλεκτρική επιτρεπτότητα ε(r) ανάγονται στις Er () = jωμ() rhr () (.3) Hr () = jωε () rer () + Jr () (.4) ( ε ) () rer () = ρ() r (.5) ( ) μ( rhr ) () = 0 (.6) Λαμβάνοντας το στροβιλισμό της μ (.3) μέσω της (.4) ευρίσκουμε ωε = ω μ() r Er rer Jr () () () j () (.7) Με παρόμοιο τρόπο, λαμβάνοντας το στροβιλισμό της ε (.4) μέσω της (.3) ευρίσκουμε () ωμ() () () ε() Hr rhr = ε() Jr (.8) r r Οι εξισώσεις (.7) και (.8), οι οποίες εμπλέκουν μόνον το ηλεκτρικό και το μαγνητικό πεδίο αντιστοίχως, αναφέρονται ως διανυσματικές κυματικές εξισώσεις [40]. Περαιτέρω, σε μέσο με σταθερή μαγνητική διαπερατότητα μ=μ 0 και ηλεκτρική επιτρεπτότητα ε(r)=ε 0 n (r), όπου n(r) ο δείκτης διάθλασης, οι εξισώσεις (.3)-(.6) εξειδικεύονται ως εξής E( r) = jωμ0h( r) (.9) H ( r) = jωε n ( r) E( r) + J( ) (.30) ( ) 0 r n () rer () = ρ()/ r ε (.3) 0 Hr () = 0 (.3) Υπολογίζοντας το στροβιλισμό των πεδίων της (.9) και λαμβάνοντας υπόψη την (.30), ευρίσκουμε 5
26 E r) k n ( r) E( r) = jωμ J( ) (.33) ( 0 0 r όπου k 0 = ω ε 0μ0 ο κυματικός αριθμός του ελευθέρου χώρου. Εφαρμόζοντας τώρα τη γνωστή διανυσματική ταυτότητα ([46], (4.6)) για το πεδίο E, από την (.33) λαμβάνουμε ( kn ) ( ) + () r E() r = E() r + jωμ J() r (.34) 0 0 Τώρα εφαρμόζοντας στην (.3) τον κανόνα υπολογισμού της απόκλισης γινομένου βαθμωτής επί διανυσματική συνάρτηση ([46], (4.5)) και χρησιμοποιώντας τη σχέση n ( r) = n( r) n( r) (.35) λαμβάνουμε ρ( r) Er () = ( n() r) Er () + n() r ε n () r Ο συνδυασμός των (.34) και (.36) οδηγεί στην εξίσωση ( kn ) ( n r ) () ρ() r + 0 () r E() r + E() r = + jωμ 0J() r n() r ε 0n () r 0 (.36) (.37) Περαιτέρω υπολογίζοντας το στροβιλισμό των πεδίων της (.30) και χρησιμοποιώντας τον κανόνα υπολογισμού του στροβιλισμού γινομένου βαθμωτής επί διανυσματική συνάρτηση ([46], (4.7)) ευρίσκουμε ( ) Hr () = jωε 0 n () () + n () () r Er r Er + Jr () (.38) Συνδυάζοντας τις (.9), (.30), (.3), (.35), (.38) και λαμβάνοντας υπόψη τη γνωστή διανυσματική ταυτότητα ([46], (4.6)), έχουμε n() r n() r + () r H() r + H() r = J() r J() r n() r n() r ( k0 n ) ( ) (.39) Οι (.37) και (.39) αποτελούν ουσιαστικά τις εξειδικεύσεις των διανυσματικών κυματικών εξισώσεων (.7) και (.8) σε μέσα με ε(r)=ε 0 n (r) και μ=μ Τμηματικά σταθερή κατανομή του δείκτη διάθλασης Θεωρούμε τις ειδικές περιπτώσεις μέσων Μ, στα οποία ο δείκτης διάθλασης n(r) είναι τμηματικά σταθερός, δηλαδή το Μ εκφράζεται ως ένωση N M = = i M i υποσυνόλων του Μ i με Int M Int M = i j, όπου n(r)=n i (σταθερό) για κάθε r Int M i. Υπενθυμίζουμε ότι i j 6
27 Int M = M \ M. Υπό αυτές τις προϋποθέσεις και επειδή ισχύει n ( r ) = 0 για i i i διανυσματικές κυματικές εξισώσεις (.7) και (.8) ανάγονται στις r N i = Int M i, οι Er () kner () = jωμ Jr (), 0 i 0 N i = r Int M (.40) i Hr () kn 0 i Hr () = Jr (), N i = r Int M (.4) Επιπλέον, με τη βοήθεια της εξίσωσης συνεχείας (.5) διαπιστώνουμε ότι οι (.37) και (.39) ανάγονται στις γνωστές μη ομογενείς διανυσματικές εξισώσεις Helmholtz ( kni ) ( Jr ()) + () r E() r = jωμ J() r, Στις συνοριακές επιφάνειες 0 0 jωε 0ni ( + n ( r )) H( r) = J( r) k, 0 i N i = i r Int M (.4) N i = i r Int M (.43) M i (μεταβολής του δείκτη διάθλασης) απαιτούνται οι κατάλληλες συνοριακές συνθήκες συνέχειας (.9) και (.) των εφαπτομενικών συνιστωσών του ηλεκτρικού και του μαγνητικού πεδίου, οι οποίες υπαγορεύονται από τις εξισώσεις Maxwell. Στο καρτεσιανό σύστημα συντεταγμένων Οxyz με xˆ, ŷ και ẑ συμβολίζουμε τα μοναδιαία i διανύσματα (κατευθύνσεις) των αξόνων του συστήματος. Έτσι, το τυχόν διάνυσμα v του εκφράζεται ως εξής v = v xˆ + v yˆ + v x y z zˆ 3 όπου v =< vx, ˆ >, v =< vy, ˆ >, v =< vz, ˆ > x y z οι συνιστώσες του v ως προς το Οxyz. Ειδικότερα οι καρτεσιανές συνιστώσες των (.4) και (.43) εκφράζονται ως εξής (για u=x, y, z) ( ) ( ( Jr ())) u + kn() r E() r = jωμ J() r (.44) 0 i u 0 u jωε 0ni ( + kn 0 ()) H() = ( ()) r r J r (.45) i u u Στην περίπτωσή του συζεύκτη γραμμοσειρών που θα μελετήσουμε το θεωρούμενο μέσο Μ είναι ο χώρος εκφρασμένος ως πεπερασμένη ένωση λωρίδων, με πλευρές παράλληλες προς τον ίδιο άξονα. Στο εσωτερικό κάθε λωρίδας ο δείκτης διάθλασης προϋποτίθεται σταθερός. 7
28 .4. Αποσύζευξη εξισώσεων Maxwell Οι εξισώσεις Maxwell (.9) και (.30) στο καρτεσιανό σύστημα συντεταγμένων εκφράζονται ως εξής E z y E y z = jωμ 0 H x (.46) E x z E z x = jωμ 0 H y (.47) E y x E x y = jωμ 0 H z (.48) H y z H y z = jω ε n ( x, y, z) E + J (.49) 0 x x H z x H x z = jω ε n ( x, y, z) E + J (.50) 0 y y H y x H y x = jω ε n ( x, y, z) E + J (.5) 0 z z Οι (.46)-(.5) αποτελούν ένα 6 6 σύστημα μερικών διαφορικών εξισώσεων πρώτης τάξης. Υποθέτοντας ότι τα πεδιακά μεγέθη και οι ρευματικές κατανομές του προβλήματος είναι ανεξάρτητα της μεταβλητής y (οπότε = 0 ), παρατηρούμε ότι οι (.46)-(.5) απλουστεύονται y ως εξής Ey ( x, z) = z jωμ H ( x, z) 0 Ex ( x, z) Ez ( x, z) = jωμ0hy ( x, z) z x Ey ( x, z) = jωμ0hz ( x, z) x x Hy ( x, z) = jω ε0n ( x, z) Ex( x, z) + Jx( x, z) z Hx ( x, z) Hz ( x, z) = jω ε0n ( x, z) Ey( x, z) + Jy( x, z) z x Hy ( x, z) = jω ε0n ( x, z) Ez( x, z) + Jz( x, z) x (.5) (.53) (.54) (.55) (.56) (.57) 8
29 Οι (.5), (.54) και (.56) αποτελούν ένα ανεξάρτητο σύστημα εξισώσεων ως προς τις συνιστώσες Ε y, H x, H z, ενώ οι (.53), (.55) και (.57) ως προς τις συνιστώσες Ε x, Ε z, H y και επομένως το πρόβλημα αποσυμπλέκεται σε δύο 3 3 συστήματα. Από τις (.5), (.54) και (.56) συνάγεται ότι το πεδίο που κυματοδηγείται παράλληλα στον άξονα z είναι εγκάρσια ηλεκτρικό (ΤΕ z -transverse electric), ενώ από τις (.53), (.55) και (.57) το πεδίο είναι εγκάρσια μαγνητικό (ΤΜ z -transverse magnetic). Στην περίπτωση ΤΕ z κατανομής πεδίου η λύση του προβλήματος ανάγεται στον προσδιορισμό της βαθμωτής συνάρτησης E y, η οποία ικανοποιεί την (.44) σε κάθε περιοχή σταθερού δείκτη διάθλασης, καθώς επίσης και τις συνθήκες συνέχειας (.9) στις συνοριακές επιφάνειες. Οι συναρτήσεις H x και H z προσδιορίζονται στη συνέχεια από τις (.5) και (.54). Αντιστοίχως, στην περίπτωση ΤΜ z κατανομής πεδίου η λύση του προβλήματος ανάγεται στον προσδιορισμό της Η y, η οποία ικανοποιεί την (.45) σε κάθε περιοχή σταθερού δείκτη διάθλασης και τις συνοριακές συνθήκες συνέχειας (.). Οι Ε x και Ε z προσδιορίζονται από τις (.55) και (.57). 9
30 ΚΕΦΑΛΑΙΟ ΚΕΦΑΛΑΙΟ. ΚΑΤΕΥΘΥΝΤΙΚΟΙ ΣΥΖΕΥΚΤΕΣ ΣΕ ΟΠΤΙΚΕΣ ΔΙΑΤΑΞΕΙΣ Στο Κεφάλαιο αυτό αναλύεται η αρχή λειτουργίας των κατευθυντικών συζευκτών και δικαιολογείται η σκοπιμότητα εισαγωγής γραμμοσειρών σε κατευθυντικούς συζεύκτες. Επίσης, καταχωρείται συστηματική περιγραφή των γνωστών μεθόδων ανάλυσης της κυματοδήγησης σε κατευθυντικούς συζεύκτες γραμμοσειρών. Περαιτέρω, καταγράφονται λεπτομερώς οι εφαρμογές των συζευκτών γραμμοσειρών στους διάφορους κλάδους των οπτικών επικοινωνιών. Ακριβέστερα, στην παράγραφο. διατυπώνεται και αναλύεται η αρχή λειτουργίας των κατευθυντικών συζευκτών. Ειδικότερα, τα ηλεκτρομαγνητικά πεδία εκφράζονται σε κάθε περιοχή σταθερού δείκτη διάθλασης ως γραμμικοί συνδυασμοί των λύσεων της αντίστοιχης ομογενούς εξίσωσης Helmholtz. Η εφαρμογή των συνοριακών συνθηκών οδηγεί σε ένα ομογενές γραμμικό σύστημα με άγνωστους τους συντελεστές των γραμμικών συνδυασμών. Τα ιδιάζοντα σημεία του εν λόγω συστήματος αποτελούν τις σταθερές διάδοσης των κυματοδηγούμενων κυμάτων. Η αρχή λειτουργίας των κατευθυντικών συζευκτών αποσαφηνίζεται με τη μελέτη του συμμετρικού συζεύκτη, του σύγχρονου ασύμμετρου συζεύκτη και του ασύγχρονου ασύμμετρου συζεύκτη. Η γεωμετρία του κατευθυντικού συζεύκτη γραμμοσειρών περιγράφεται στην παράγραφο., όπου αποσαφηνίζεται επίσης και η σκοπιμότητα εισαγωγής γραμμοσειρών σε κατευθυντικούς συζεύκτες. Πιο συγκεκριμένα, η εισαγωγή γραμμοσειρών με κατάλληλα χαρακτηριστικά στη διάταξη οδηγεί στη σύζευξη των δύο (αρχικά ασύζευκτων) ρυθμών της ομογενούς διάταξης και στην αποδοτική ανταλλαγή του φωτός μεταξύ των δύο κυματοδηγών. Στην παράγραφο.3 αναλύονται εκτενώς διάφορες γνωστές μέθοδοι αναφερόμενες στη μελέτη των φαινομένων κυματοδήγησης σε συζεύκτες γραμμοσειρών. Ιδιαίτερη έμφαση δίνεται στην περιγραφή της Μεθόδου των Συζευγμένων Ρυθμών, η οποία είναι η κλασικότερη τεχνική ανάλυσης συζευκτών γραμμοσειρών. Αντιπροσωπευτικές εφαρμογές των συζευκτών γραμμοσειρών στις οπτικές επικοινωνίες καταχωρούνται στην παράγραφο.4. Μεταξύ αυτών συγκαταλέγονται εκείνες σε οπτικά φίλτρα, συντονιζόμενα lasers, διατάξεις πολυπλεξίας και αποπολυπλεξίας, μετατροπείς ρυθμών οπτικών παλμών πολύ μεγάλου εύρους ζώνης, οπτικούς διακόπτες και lasers κατανεμημένης ανάδρασης. 30
31 .. Αρχή λειτουργίας κατευθυντικών συζευκτών Οι κατευθυντικοί συζεύκτες χρησιμοποιούνται αποτελεσματικά σε πολλές περιοχές της ολοκληρωμένης οπτικής, συνήθως ως διαχωριστές δέσμης (beam splitters), οπτικά φίλτρα (optical filters) και οπτικοί διακόπτες (optical switches) (βλ. [], [], [47] και [48]). Στο Σχήμα. φαίνεται η γεωμετρία ενός ασύμμετρου κατευθυντικού συζεύκτη, ο οποίος αποτελείται από δύο μη συμμετρικές παράλληλες διηλεκτρικές πλάκες (slabs), τοποθετημένες σε κατάλληλα μικρή απόσταση, ώστε να θεωρούνται συζευγμένες. Σχήμα. Γεωμετρία ασυμμετρικού κατευθυντικού συζεύκτη Οι δύο κυματοδηγοί έχουν πάχη d και d 4 και δείκτες διάθλασης n και n 4. Ο χώρος μεταξύ των δύο κυματοδηγών έχει πάχος d 3 και δείκτη διάθλασης n 3. Οι «ημιάπειροι χώροι» πάνω από τον κυματοδηγό και κάτω από τον κυματοδηγό έχουν δείκτες διάθλασης n και n 5 αντίστοιχα. H διάταξη θεωρείται ομοιόμορφη κατά μήκος του y-άξονα. Σημειώνουμε ότι η κυματοδήγηση στην εν λόγω διάταξη γίνεται κατά μήκος του z-άξονα. Η γενική αρχή λειτουργίας του κατευθυντικού συζεύκτη είναι η εξής: Ένας από τους δύο κυματοδηγούς ορίζεται ως θύρα εισόδου (στην περίπτωσή μας ο ) και ο άλλος (ο ) ως θύρα εξόδου του οπτικού σήματος. Θεωρούμε ότι ισχύς εισόδου P in εισέρχεται από τη θύρα εισόδου και μετά από ένα ορισμένο μήκος L, το οποίο καλείται μήκος σύζευξης (coupling length), ένα 3
32 πολύ μεγάλο ποσοστό α της P in εξέρχεται ως ισχύς εξόδου P out από τη θύρα εξόδου. Σχετικά αναζητούμε τις βέλτιστες τιμές των φυσικών και γεωμετρικών παραμέτρων της διάταξης, έτσι ώστε το ποσοστό α να προσεγγίζει το 00%, δηλαδή όλη η ισχύς εισόδου να μεταβιβάζεται στη θύρα εξόδου.... Κυματοδήγηση σε ασυμμετρικούς κατευθυντικούς συζεύκτες Τα φαινόμενα κυματοδήγησης σε ασύμμετρους κατευθυντικούς συζεύκτες έχουν διερευνηθεί συστηματικά στη βιβλιογραφία (βλ. ενδεικτικά [7]). Όπως εξηγήθηκε στην παράγραφο.4, οι κυματοδηγούμενοι ΤΕ z και ΤM z ρυθμοί στην κατεύθυνση ẑ προσδιορίζονται από το ηλεκτρικό πεδίο E y (x,z) και το μαγνητικό πεδίο H y (x,z). Αναζητούμε λύσεις των εξισώσεων (.44) και (.45) της μορφής E= E ( x, z) yˆ = e( x)exp[ j( ωt β z)] y ˆ y H = H ( x, z) yˆ = h( x)exp[ j( ωt β z)] y ˆ y όπου β η σταθερά διάδοσης. Για την ενιαία αντιμετώπιση των ΤΕ z και ΤM z ρυθμών, εισάγουμε κατάλληλη συνάρτηση Ψ(x), η οποία αντιπροσωπεύει την e(x) για τους ΤΕ z ρυθμούς και την h(x) για τους ΤM z ρυθμούς. Επειδή οι συναρτήσεις E y (x,z) και H y (x,z) αποτελούν λύσεις της ομογενούς βαθμωτής εξίσωσης Helmholtz (.44) σε κάθε επίπεδο χωρίο σταθερού δείκτη διάθλασης και στους ημιάπειρους χώρους x>d 3 +d και x< d 3 d 4 πρέπει να πληρούν τη συνθήκη ακτινοβολίας, η Ψ(x) εκφράζεται ως εξής όπου με [ ] Aexp g( x d3 d), x d3+ d d d Acosh g( x d3 ) + A3sinh g( x d3 ), d3 x d3+ d Ψ( x) = A4exp( g3x) + A5exp( g3x), d3 x d3 d d A cosh g ( x+ d + ) + A sinh g ( x+ d + ), d d x d A8exp [ g5( x+ d3 + d4) ], x d3 d g ( β) = β k n ( i =,...,5) i 0 i Re{ g ( β )} 0, Re{ g ( β)} 0, Im{ g ( β)} 0, Im{ g ( β)} Οι άγνωστοι συντελεστές Α -Α 8 προσδιορίζονται με εφαρμογή των οριακών συνθηκών των εφαπτομενικών πεδιακών συνιστωσών στα διαχωριστικά επίπεδα αλλαγής του δείκτη 3
33 διάθλασης. Συγκεκριμένα για τους ΤΕ z ρυθμούς απαιτείται η συνέχεια των E y και H z ενώ για τους ΤM z ρυθμούς η συνέχεια των H y και E z. Συνδυάζοντας τώρα τις (.9) και (.30), συμπεραίνουμε ότι οι συναρτήσεις Ψ και Ψ x πρέπει να είναι συνεχείς για τους ΤΕ z ρυθμούς και Ψ οι Ψ και συνεχείς για τους ΤM z ρυθμούς στα επίπεδα x=d 3 +d, x=d 3, x= d 3 και x= d 3 d 4. n x Η εφαρμογή των εν λόγω οριακών συνθηκών οδηγεί σε ένα 8 8 ομογενές γραμμικό σύστημα CA=0 (.) 8 όπου το διάνυσμα Α του περιέχει τους άγνωστους συντελεστές Α -Α 8 και ο 8 8 πίνακας C, του οποίου τα στοιχεία είναι συναρτήσεις της παραμέτρου β, είναι ο εξής d d cosh( g ) sinh( g ) g g d g d sinh( g ) cosh( g ) m m m d d 0 cosh( g ) sinh( g ) exp( gd 3 3) exp( gd 3 3) g d g d g3 g3 0 sinh( g ) cosh( g ) exp( g3d3) exp( g3d3) m m m3 m 3 C = d4 d exp( gd 3 3) exp( gd 3 3) cosh( g4 ) sinh( g4 ) 0 g3 g3 g4 d4 g4 d exp( gd 3 3) exp( gd 3 3) sinh( g4 ) cosh( g4 ) 0 m3 m3 m4 m4 d4 d cosh( g4 ) sinh( g4 ) g4 d4 g4 d4 g sinh( g4 ) cosh( g4 ) m4 m4 m5 όπου z, TE modes mi = ( i =,...,5) z ni, TM modes Το ομογενές σύστημα (.) έχει μη τετριμμένες λύσεις μόνο όταν η ορίζουσά του είναι ίση με το μηδέν. Η διάταξη του ασύμμετρου κατευθυντικού συζεύκτη υποστηρίζει κυματοδηγούμενα κύματα για τις τιμές της παραμέτρου β, οι οποίες αποτελούν λύσεις της εξίσωσης det(c)=0 Μετά τον προσδιορισμό των εν λόγω τιμών της παραμέτρου β, θέτοντας κάποιον από τους συντελεστές Α i ίσο με τη μονάδα και παραλείποντας μία από τις 8 εξισώσεις του (.) αναγόμαστε σε ένα 7 7 μη ομογενές σύστημα, το οποίο επιλύεται με αριθμητικές μεθόδους. 33
34 ... Αντιπροσωπευτικά παραδείγματα κατευθυντικών συζευκτών Για την αποσαφήνιση και την κατανόηση της αρχής λειτουργίας των κατευθυντικών συζευκτών περιγράφονται ορισμένα αντιπροσωπευτικά παραδείγματα συζευκτών και οπτικοποιούνται οι πεδιακές κατανομές των συζευγμένων ρυθμών τους. ) Συμμετρικός συζεύκτης με n =n 3 =n 5 =3., n =n 4 =3.3, d =d 4 =μm, d 3 =0.5μm και λ=.5μm. Το πεδίο στη διάταξη του συμμετρικού συζεύκτη θεωρείται ως υπέρθεση των πεδίων των άρτιων (even) και των περιττών (odd) ρυθμών, δηλαδή ισχύει η ανάλυση Ψ ( x, z) = A Ψ ( x)exp( jβ z) + A Ψ ( x)exp( jβ z) e e Οι κανονικοποιημένες σταθερές διάδοσης των άρτιων και περιττών ΤΕ z ρυθμών υπολογίζονται β e /k 0 =3.689 και β ο /k 0 = Οι αντίστοιχες πεδιακές κατανομές E y (x,z) στο επίπεδο z=0 απεικονίζονται στο Σχήμα.. e o o o Σχήμα. Πεδιακές κατανομές των ΤΕ z ρυθμών συμμετρικού συζεύκτη Όπως φαίνεται στο Σχήμα., μπορούμε να υπερθέσουμε τους δύο ρυθμούς κατά τέτοιο τρόπο, ώστε να συμβάλλουν στον κυματοδηγό και να αναιρούνται στον κυματοδηγό. Συγκεκριμένα, στο Σχήμα.3 απεικονίζονται οι πεδιακές κατανομές στο επίπεδο z=0 για την επιλογή Α e = και Α ο =. 34
35 Σχήμα.3 Σήμα διέγερσης στο z=0 Για την εν λόγω επιλογή η αρχική διέγερση στο επίπεδο z=0 εφαρμόζεται στον κυματοδηγό, ενώ στον κυματοδηγό εμφανίζεται μόνον ένα ελάχιστο ποσοστό υπολειπόμενης ενέργειας. Το μέτρο της πεδιακής κατανομής E y (x,z) μετά από απόσταση είναι ίσο με και απεικονίζεται στο Σχήμα.4. L = π /( β β ) (.) e Ψ ( x, L) = Ψ ( x) + Ψ ( x) e o o Σχήμα.4 Πεδιακή κατανομή στην απόσταση σύζευξης ισχύος z=l 35
36 Συγκρίνοντας τα Σχήματα.3 και.4, συμπεραίνουμε ότι μετά από απόσταση L έχει επιτευχθεί σχεδόν πλήρης ανταλλαγή ισχύος, δηλαδή το μεγαλύτερο ποσοστό της αρχικής ισχύος στην τομή του επιπέδου z=0 με τον κυματοδηγό οδηγήθηκε στην τομή του επιπέδου z=l με τον κυματοδηγό. Για το λόγο αυτό το μήκος L ονομάζεται μήκος σύζευξης (coupling length) [7]. ) Σύγχρονος ασύμμετρος συζεύκτης με n =n 3 =n 5 =3., n =3.3, n 4 =3.35, d = μm, d 3 =0.5 μm d 4 = μm και λ=.5 μm. Με τις αναφερόμενες τιμές των παραμέτρων οι κανονικοποιημένες σταθερές διάδοσης των ΤΕ z ρυθμών β /k 0 =3.695 και β /k 0 =3.659 έχουν αρκετά μικρή διαφορά και συνεπώς ο συζεύκτης θεωρείται σύγχρονος. Οι αντίστοιχες πεδιακές κατανομές στο επίπεδο z=0 απεικονίζονται στο Σχήμα.5. Σχήμα.5 Πεδιακές κατανομές των ΤΕ z ρυθμών σύγχρονου ασυμμετρικού συζεύκτη Όπως παρατηρούμε στο Σχήμα.5, δεν εμφανίζεται πλέον η συμμετρία των πεδιακών κατανομών του συμμετρικού συζεύκτη του Σχήματος.. Όμως οι δύο ρυθμοί μπορούν να θεωρηθούν ως συμμετρικοί (symmetric) και αντισυμμετρικοί (antisymmetric) ως προς το επίπεδο x=0. Εξάλλου, με κατάλληλη υπέρθεση των συμμετρικών και αντισυμμετρικών ρυθμών μπορούμε να πετύχουμε σήμα εισόδου στο επίπεδο z=0, στο οποίο σήμα το μεγαλύτερο ποσοστό της ενέργειας ευρίσκεται στον κυματοδηγό (βλ. Σχήμα.6). 36
37 Σχήμα.6 Σήμα διέγερσης στο z=0 Από τη σύγκριση των Σχημάτων.3 και.6 προκύπτει ότι το ποσοστό της υπολειπόμενης ενέργειας στον κυματοδηγό είναι μεγαλύτερο στην περίπτωση του ασύμμετρου συζεύκτη. Εν τούτοις και στην περίπτωση αυτή, όπως φαίνεται στο Σχήμα.7, μετά από απόσταση ίση με το μήκος σύζευξης L, που δίνεται από την (.), επιτυγχάνεται σχεδόν πλήρης ανταλλαγή ισχύος. Σχήμα.7 Πεδιακή κατανομή στην απόσταση σύζευξης ισχύος z=l 37
38 3) Ασύγχρονος ασύμμετρος συζεύκτης με n =, n =3.3, n 3 =n 5 =3., n 4 =3.5, d = μm, d 3 =0.5 μm, d 4 = 0.3 μm και λ=.5 μm. Στην προκειμένη περίπτωση ο συζεύκτης θεωρείται ασύγχρονος, διότι οι κανονικοποιημένες τιμές των σταθερών διάδοσης β /k 0 =3.343 και β /k 0 =3.559 των ΤΕ z ρυθμών, απέχουν σημαντικά μεταξύ τους. Στο Σχήμα.8 απεικονίζονται οι πεδιακές κατανομές στο επίπεδο z=0. Σχήμα.8 Πεδιακές κατανομές των TE z ρυθμών ασύγχρονου ασυμμετρικού συζεύκτη Όπως φαίνεται στο Σχήμα.8, το μεγαλύτερο μέρος της ισχύος καθενός από τους δύο ρυθμούς ευρίσκεται εντός διαφορετικών κυματοδηγών. Οι εν λόγω ρυθμοί έχουν μεγάλη ομοιότητα με τους ρυθμούς του καθενός κυματοδηγού, όταν αυτός θεωρείται απομονωμένος. Επιπλέον ένα μικρό μέρος της ισχύος του ρυθμού, ο οποίος παρίσταται από τη διακεκομμένη γραμμή, υπάρχει στον κυματοδηγό, ενώ αντιθέτως η ισχύς του ρυθμού, ο οποίος παρίσταται από τη συνεχή γραμμή, στον κυματοδηγό είναι σχεδόν μηδενική. Το φαινόμενο αυτό οφείλεται στην ανισότητα β k n 0, η οποία οδηγεί σε πραγματικό g, με συνέπεια ο αντίστοιχος 0 > ρυθμός να είναι αποσβεννύμενος (evanescent) εντός του κυματοδηγού. Όμως, και στην περίπτωση αυτή, επιλέγοντας κατάλληλη υπέρθεση των ρυθμών επιτυγχάνουμε στο επίπεδο z=0 το σήμα εισόδου του Σχήματος.9, στο οποίο σήμα η αρχική ενεργειακή διέγερση βρίσκεται στον κυματοδηγό. 38
39 Σχήμα.9 Σήμα διέγερσης στο z=0 Περαιτέρω, όπως φαίνεται στο Σχήμα.0, σε απόσταση ίση με το μήκος σύζευξης L, που δίνεται από την (.), το μεγαλύτερο ποσοστό της ενέργειας παραμένει στον κυματοδηγό. Σχήμα.0 Πεδιακή κατανομή στην απόσταση σύζευξης ισχύος z=l Εξάλλου όπως προκύπτει από τα Σχήματα.9 και.0, στην περίπτωση ασύγχρονου συζεύκτη, δεν είναι δυνατόν να επιτευχθεί ανταλλαγή της ενέργειας του φωτός από τον κυματοδηγό εισόδου στον κυματοδηγό εξόδου. 39
40 Συνοψίζοντας τις περιπτώσεις, και 3, συμπεραίνουμε ότι στους ασυμμετρικούς συζεύκτες είναι δυνατή η ανταλλαγή ενέργειας μεταξύ των κυματοδηγών, μόνο σε εκείνα τα μήκη κύματος, όπου οι τιμές των σταθερών διάδοσης των δύο ρυθμών διαφέρουν ελάχιστα μεταξύ τους. Το συμπέρασμα αυτό υπαγορεύει τη χρήση των ασύμμετρων κατευθυντικών συζευκτών ως ζωνοπερατά φίλτρα (bandpass filters)... Εισαγωγή γραμμοσειρών σε κατευθυντικούς συζεύκτες Η σύζευξη της φωτεινής ισχύος σε ασύγχρονους ασύμμετρους συζεύκτες, η οποία οδηγεί σε ανταλλαγή της ενέργειας μεταξύ των δύο κυματοδηγών, επιτυγχάνεται με τη χρήση γραμμοσειρών περίθλασης (diffraction grating). Πιο συγκεκριμένα, στον ένα από τους δύο κυματοδηγούς της διάταξης του κατευθυντικού συζεύκτη του Σχήματος. χαράσσονται περιοδικά γραμμοσειρές. Η προκύπτουσα διάταξη αναφέρεται συνήθως ως ασυμμετρικός κατευθυντικός συζεύκτης γραμμοσειρών (asymmetric grating assisted directional optical coupler). Στο Σχήμα. οπτικοποιείται η γεωμετρία ενός ασυμμετρικού κατευθυντικού συζεύκτη γραμμοσειρών. Σχήμα. Γεωμετρία ασυμμετρικού κατευθυντικού συζεύκτη γραμμοσειρών 40
41 Οι γραμμοσειρές με περίοδο Λ, πάχος w και δείκτη διάθλασης n 6 ευρίσκονται στο άνω μέρος του κυματοδηγού, αλλά η διάταξη λειτουργεί εξίσου ή περισσότερο αποδοτικά, όταν οι γραμμοσειρές τοποθετηθούν στο κάτω μέρος του κυματοδηγού ή και ακόμα όταν ο συζεύκτης φέρει δύο γραμμοσειρές μία στον κυματοδηγό και μία στον κυματοδηγό. Σε κάθε περίπτωση η διάταξη αποτελεί μία περιοδική δομή, διότι οι γραμμοσειρές δημιουργούν ένα άπειρο στρώμα, του οποίου η διηλεκτρική σταθερά είναι Λ-περιοδική συνάρτηση ως προς z. Οι περιοδικές γραμμοσειρές συνταιριάζουν τα διαφορετικά γεωμετρικά και φυσικά χαρακτηριστικά των δύο κυματοδηγών και έτσι συμβάλλουν ουσιαστικά στην ενίσχυση της διαδικασία σύζευξης. Ακριβέστερα, σύμφωνα με τα αναφερόμενα στην παράγραφο., η σύζευξη της φωτεινής ενέργειας στους κατευθυντικούς συζεύκτες επιτυγχάνεται μόνο όταν οι ρυθμοί των δύο κυματοδηγών έχουν την ίδια ή σχεδόν την ίδια σταθερά διάδοσης. Αυτό πρακτικά σημαίνει ότι οι δύο κυματοδηγοί πρέπει να έχουν παρόμοια, αν όχι τα ίδια, χαρακτηριστικά [7]. Επιπλέον, οι ασύζευκτοι ρυθμοί της ομογενούς διάταξης των δύο ασύγχρονων κυματοδηγών προσομοιάζουν τους ρυθμούς των δύο κυματοδηγών, όταν αυτοί θεωρούνται σε απομόνωση, ενώ συγχρόνως οι σταθερές διάδοσης των δύο ρυθμών απέχουν σημαντικά μεταξύ τους. Έτσι, η εισαγωγή γραμμοσειρών με κατάλληλα χαρακτηριστικά στη διάταξη οδηγεί στη σύζευξη των δύο (αρχικά ασύζευκτων) ρυθμών της ομογενούς διάταξης και στην αποδοτική ανταλλαγή του φωτός μεταξύ των δύο κυματοδηγών..3. Μέθοδοι ανάλυσης της κυματοδήγησης σε συζεύκτες γραμμοσειρών Εκτενείς μελέτες των κατευθυντικών συζευκτών γραμμοσειρών έχουν εμφανιστεί στη βιβλιογραφία. Αντικείμενο των μελετών αυτών αποτελεί ο καθορισμός των μεταβολών, που επιφέρει στις σταθερές διάδοσης των κυματοδηγούμενων ηλεκτρομαγνητικών κυμάτων η παρουσία των γραμμοσειρών, και ο προσδιορισμός των τιμών των χαρακτηριστικών των γραμμοσειρών (πάχος w, περίοδος Λ, δείκτης διάθλασης n 6 ) για τις οποίες επιτυγχάνεται η βέλτιστη ανταλλαγή φωτεινής ισχύος μεταξύ των δύο κυματοδηγών. Οι κυριότερες μέθοδοι ανάλυσης των φαινομένων κυματοδήγησης σε συζεύκτες γραμμοσειρών είναι οι εξής: 4
42 .3.. Θεωρία Συζευγμένων Ρυθμών H Θεωρία των Συζευγμένων Ρυθμών (ΘΣΡ) (Coupled Mode Theory-CMT) αποτελεί την κύρια μεθοδολογία ανάλυσης των φαινομένων κυματοδήγησης σε διατάξεις συζευκτών γραμμοσειρών (βλ. ενδεικτικά [7]-[]). Η αρχική μορφή της θεωρίας αναφέρεται ως Συμβατική Θεωρία Συζευγμένων Ρυθμών (Conventional Coupled Mode Theory) και η μετέπειτα αυστηρότερη θεμελίωσή της ως Μη-Ορθογωνική Θεωρία Συζευγμένων Ρυθμών (Non- Orthogonal Coupled Mode Theory). Λεπτομερής επισκόπηση των δύο αυτών μεθόδων περιέχεται στην Εργασία [8]. α) Συμβατική Θεωρία Συζευγμένων Ρυθμών Η σύζευξη της ηλεκτρομαγνητικής ισχύος στη διάταξη του συζεύκτη γραμμοσειρών υπαγορεύεται ουσιαστικά από τη φυσική σύζευξη μεταξύ των δύο κυματοδηγών, όπως στην περίπτωση του συζεύκτη χωρίς γραμμοσειρές, και την περιοδική σύζευξη, η οποία οφείλεται στις γραμμοσειρές. Η Συμβατική ΘΣΡ μελετά μόνο τη σύζευξη, η οποία οφείλεται στις γραμμοσειρές, και έτσι ερευνά ορθογώνιους ρυθμούς των κυματοδηγών. Υπό την προϋπόθεση απουσίας των γραμμοσειρών, τα πλάτη α και α των ρυθμών των δύο κυματοδηγών (βλ. Σχήμα.), τα οποία ευρίσκονται σε αρκετά μεγάλη απόσταση μεταξύ τους (ασύζευκτα) αποτελούν λύσεις των διαφορικών εξισώσεων da da = jβa, = jβ a dz dz όπου β και β είναι οι σταθερές διάδοσης των ρυθμών. Όταν η απόσταση των κυματοδηγών είναι μικρή, οι ρυθμοί του ενός συζευγνύονται με τους ρυθμούς του άλλου, ως αποτέλεσμα της αλληλεπίδρασης των αποσβεννύμενων (evanescent) πεδίων. Ειδικότερα στην τελευταία περίπτωση, υπό συνθήκες ασθενούς σύζευξης (η απόσταση d 3 δεν είναι πολύ μικρή), τα κανονικοποιημένα πλάτη â και â των ρυθμών αποτελούν λύση του συστήματος συζευγμένων διαφορικών εξισώσεων πρώτης τάξης. daˆ daˆ = jδ aˆ ˆ jκ a, dz dz όπου β + δ = β K K = jδ aˆ jκ aˆ (.3) 4
43 είναι ο παράγοντας ασυμφωνίας φάσης (phase mismatch factor) και Κ, Κ και κ είναι οι σταθεροί συντελεστές (ανεξάρτητοι της μεταβλητής z) ιδίας και αμοιβαίας σύζευξης. Στην περίπτωση του συζεύκτη γραμμοσειρών (βλ. Σχήμα.) υπό συνθήκες ασθενούς σύζευξης τα κανονικοποιημένα πλάτη â και â των ρυθμών αποτελούν λύση του συστήματος (.3), όπου όμως ο παράγοντας ασυμφωνίας φάσης δ και ο συντελεστής αμοιβαίας σύζευξης κ δίδονται από τους τύπους Οι β + C δ = 0 β C 0 mπ Λ, κ (.4) + m m = C = C m C ij είναι οι συντελεστές της σειράς Fourier των συντελεστών σύζευξης Κ ij = + m mπ K ij Cij exp j z m= Λ Σημειώνουμε ότι στην περίπτωση συζευκτών γραμμοσειρών οι συντελεστές σύζευξης K ij δεν είναι πλέον ανεξάρτητοι της μεταβλητής z, αλλά είναι περιοδικές συναρτήσεις του z. Η πλήρης μεταφορά ισχύος στη διάταξη του Σχήματος. επιτυγχάνεται για την τιμή της περιόδου Λ η οποία αντιστοιχεί μέσω της (.4) στον παράγοντα ασυμφωνίας φάσης δ=0 (βλ. [8]). Στην περίπτωση κυματοδηγών με πολύ διαφορετικά χαρακτηριστικά, οπότε η φυσική σύζευξη μεταξύ τους μπορεί να αγνοηθεί, η βέλτιστη περίοδος υπολογίζεται π Λ A = (.5) β β Η Συμβατική ΘΣΡ δεν δίνει ακριβή αποτελέσματα, όταν οι δύο κυματοδηγοί ευρίσκονται σε πολύ μικρή απόσταση (ισχυρά συζευγμένοι) και κοντά στον συγχρονισμό, γεγονός που αποτελεί σημαντικό περιορισμό της θεωρίας. β) Μη Ορθογωνική Θεωρία Συζευγμένων Ρυθμών Η Συμβατική ΘΣΡ αγνοεί τη φυσική σύζευξη μεταξύ των κυματοδηγών, επειδή ερευνά ορθογώνιους ρυθμούς των κυματοδηγών. Σύμφωνα με τη Μη Ορθογωνική ΘΣΡ το πεδίο (Ε, Η) που αναπτύσσεται στο συζεύκτη γραμμοσειρών εκφράζεται ως εξής E = c e + ce, H c h + ch = (.6) όπου e, e και h, h είναι τα ηλεκτρικά και μαγνητικά πεδία των κυρίαρχων ρυθμών στους κυματοδηγούς και. Υπό τις προϋποθέσεις ότι οι ρυθμοί δεν έχουν ισχυρή σύζευξη και οι γραμμοσειρές δεν προκαλούν μεγάλες ανακλάσεις, η (.6) αποτελεί ικανοποιητική προσέγγιση του πραγματικού πεδίου του συζεύκτη. Στην προκειμένη περίπτωση, υπό την προϋπόθεση ότι οι 43
44 γραμμοσειρές έχουν μικρό πάχος h, το σύστημα των εξισώσεων των συζευγμένων ρυθμών έχει τη μορφή dw j j dz = BW LW (.7) όπου ο πίνακας Β έχει στοιχεία τις σταθερές διάδοσης και ο W τα πλάτη των ρυθμών, ενώ ο L είναι ο πίνακας σύζευξης των ρυθμών εξαιτίας των γραμμοσειρών. Η λύση του συστήματος (.7) οδηγεί στον παράγοντα ασυμφωνίας φάσης β s β a δ w = π Λ όπου β s και β a είναι οι σταθερές διάδοσης των συμμετρικών και αντισυμμετρικών ρυθμών. Εφαρμόζοντας τη συνθήκη προσαρμογής της φάσης δ w =0, ευρίσκουμε τη βέλτιστη περίοδο των γραμμοσειρών π Λ W = (.8) β β s a Για τη σύγκριση των βέλτιστων περιόδων Λ Α και Λ W, που καθορίζονται στις δύο θεωρίες, θεωρούμε συζεύκτη γραμμοσειρών με n =, n =3.3, n 3 = 3., n 4 =3.5, n 5 =3, d = μm, d 4 = 0.3 μm και λ=.5 μm. Στο Σχήμα. απεικονίζονται οι βέλτιστες περίοδοι Λ Α και Λ W συναρτήσει της απόστασης d 3 των δύο κυματοδηγών. Σχήμα. Βέλτιστες περίοδοι γραμμοσειρών συναρτήσει της απόστασης των κυματοδηγών Η περίοδος Λ Α είναι ανεξάρτητη της απόστασης d 3, ενώ η περίοδος Λ W αυξάνεται με τη d 3. Η απόσταση των γραφημάτων των Λ Α και Λ W μεγαλώνει αρκετά καθώς μικραίνει η d 3. Για 44
45 μικρές αποστάσεις d 3 η Λ W αποτελεί καλύτερη προσέγγιση της ακριβούς τιμής της βέλτιστης περιόδου Λ από την Λ Α. Η ακρίβεια των λύσεων, οι οποίες επιτυγχάνονται με τη ΘΣΡ, προϋποθέτει τους εξής περιορισμούς ) Η απόσταση d 3 των δύο κυματοδηγών δεν είναι πολύ μικρή. ) Το πάχος w των γραμμοσειρών, συγκρινόμενο με το πάχος του κυματοδηγού, είναι μικρό. 3) Οι διαφορές των δεικτών διάθλασης των διαφορετικών μέσων δεν είναι πολύ μεγάλες. 4) Τα φαινόμενα ακτινοβολίας από τις γραμμοσειρές θεωρούνται αμελητέα. Ορισμένες βελτιωμένες παραλλαγές της ΘΣΡ, οι οποίες λαμβάνουν υπόψη τις απώλειες λόγω ακτινοβολίας και προσεγγίζουν με μεγαλύτερη ακρίβεια τους ρυθμούς για περιπτώσεις ισχυρής σύζευξης, έχουν επίσης εμφανιστεί στην πρόσφατη βιβλιογραφία (βλ. π.χ. [9] και [0])..3.. Θεωρία Floquet-Bloch H Θεωρία Floquet-Bloch συνιστά μία αυστηρή μεθοδολογία μελέτης των φαινομένων κυματοδήγησης σε διατάξεις συζευκτών γραμμοσειρών (βλ. ενδεικτικά []-[9]). Με βάση τη Θεωρία Floquet Bloch αναλύονται τα φαινόμενα κυματοδήγησης στον πολυστρωματικό συζεύκτη γραμμοσειρών του Σχήματος.3. Σχήμα.3 Γεωμετρία του πολυστρωματικού κατευθυντικού συζεύκτη γραμμοσειρών 45
46 Το βαθμωτό πεδίο F i (F i =Ε yi για ΤΕ z ρυθμούς και F i =H yi για ΤΜ z ρυθμούς) ενός ρυθμού με σταθερά διάδοσης β και σταθερά εξασθένησης α στο i-οστό στρώμα του συζεύκτη γραμμοσειρών αναπτύσσεται σε σειρά Fourier ως εξής (βλ. π.χ. [6]) F ( x, z) = i + n= f ( i) n ( x) exp ( jk z) ( ) όπου f i n ( x) είναι κατάλληλες χωρικές αρμονικές συναρτήσεις και k zn π = β + ja + n Λ zn Στα ομοιόμορφα στρώματα s Σ i άνω και κάτω από το στρώμα των γραμμοσειρών, οι i= i k ( ) συναρτήσεις f i n ( x) είναι λύσεις της διαφορικής εξίσωσης δεύτερης τάξης ( i ( k k ) f ( x) = 0 i k ( i) d f n ( x) ) + ε i 0 zn n, (.9) dx ( ) Κάθε προσδιοριστέα συνάρτηση f i n ( x) εκφράζεται ως γραμμικός συνδυασμός των γνωστών γραμμικά ανεξάρτητων λύσεων της (.9), οι δε άγνωστοι συντελεστές των γραμμικών συνδυασμών προσδιορίζονται από τις συνοριακές συνθήκες στις διαχωριστικές επιφάνειες x i (i=,,s ). Έτσι διαμορφώνεται το γραμμικό σύστημα όπου T C = M C (.0) ( i) ( i) ( i+ ) ( i+ ) n n n n (i) C n είναι το διάνυσμα των άγνωστων συντελεστών στο στρώμα i και T, M είναι οι πίνακες μετάβασης από το στρώμα i στο στρώμα i+. Στο στρώμα k των γραμμοσειρών οι συνιστώσες των χωρικών αρμονικών συναρτήσεων ( ) ( ) n ( x) και g k n ( x) των πεδίων F και G (F=Ε y, G=H z για ΤΕ z ρυθμούς και F=H y, G=E z για ΤΜ z f k ρυθμούς) αποτελούν λύσεις του συστήματος των συζευγμένων διαφορικών εξισώσεων d f ( x) 0 Q( k z0 ) = f ( x) ( x) ( k ) (.) dx g P z0 0 g( x) όπου P και Q είναι κατάλληλοι πίνακες, οι οποίοι προσδιορίζονται από τις εξισώσεις Maxwell. Το εν λόγω σύστημα επιλύεται αριθμητικά (βλ. [] και [6]) και οι λύσεις του είναι οι τιμές του πεδίου στο στρώμα των γραμμοσειρών ως συναρτήσεις των αντιστοίχων τιμών στα σύνορα του στρώματος. Το γραμμικό σύστημα της μεθόδου είναι ( i) n ( i+ ) n D k ) f ( x ) = 0 (.) ( z0 k 46
47 και προκύπτει με συνδυασμό των (.0) και (.) και χρήση των συνοριακών συνθηκών στα επίπεδα x=x k και x=x k. Συνεπώς οι σταθερές διάδοσης των κυματοδηγούμενων στη διάταξη ρυθμών είναι οι λύσεις της εξίσωσης [ D ( )] 0 det 0 = k z και οι πεδιακές κατανομές σε κάθε στρώμα εκφράζονται με τη βοήθεια των λύσεων του ομογενούς συστήματος (.). Τέλος, το μήκος σύζευξης L, το οποίο προκύπτει από τη Θεωρία Floquet-Bloch είναι π L = (.3) π β s β a Λ όπου β s και β α οι σταθερές διάδοσης των κυματοδηγούμενων ρυθμών. Οι μέθοδοι της Θεωρίας Floquet-Bloch υπολογίζουν τις σταθερές διάδοσης με μεγαλύτερη ακρίβεια από εκείνες της Θεωρίας των Συζευγμένων Ρυθμών, διότι δεν λαμβάνουν υπόψη προσεγγίσεις για τη σύζευξη των ρυθμών και τα φυσικά και γεωμετρικά χαρακτηριστικά των γραμμοσειρών. Όμως, η ακρίβεια των αποτελεσμάτων της Θεωρίας Floquet-Bloch εξαρτάται από την αριθμητική επίλυση συστημάτων γραμμικών διαφορικών εξισώσεων πρώτης τάξεως και από την τάξη κολόβωσης των γραμμικών συστημάτων Μέθοδοι Ολοκληρωτικών Εξισώσεων Για τη μελέτη των φαινομένων κυματοδήγησης σε συζεύκτες γραμμοσειρών χρησιμοποιούνται επίσης και διάφορες Μέθοδοι Ολοκληρωτικών Εξισώσεων, οι οποίες βασίζονται στο μετασχηματισμό του προβλήματος συνοριακών τιμών σε μία ολοκληρωτική εξίσωση, η οποία επιλύεται με χρήση αριθμητικών ή ημιαναλυτικών τεχνικών (βλ. π.χ. [37]- [39]). Το βαθμωτό πεδίο Ψ σε κάθε στρώμα της διάταξης του συζεύκτη γραμμοσειρών του Σχήματος.4 ικανοποιεί τη διαφορική εξίσωση x + z Ψ ( x, z) + k όπου k η σχετική διηλεκτρική σταθερά του στρώματος. 0 kψ( x, z) = 0 (.4) 47
48 Σχήμα.4 Γεωμετρία του κατευθυντικού συζεύκτη γραμμοσειρών Η συνάρτηση Green G(r,r,k) του ελευθέρου χώρου με σχετική διηλεκτρική σταθερά k είναι λύση της διαφορικής εξίσωσης ( r, r, ) + 0 ( r, r, ) = ( r r t G k k kg k δ ) (.5) Συνδυάζοντας τις διαφορικές εξισώσεις (.4) και (.5) με τη δεύτερη ταυτότητα του Green (βλ. [50], (5.39)) για τις συναρτήσεις G και Ψ [ G( r, r, k) Ψ Ψ t ( r) ( r) t G( r, r, k) ] ds = R k C k Ψ( r) G( r,, k) G( r, r, k) Ψ( r) dl n n r ευρίσκουμε την ολοκληρωτική αναπαράσταση της Ψ(r) Ψ( r ) G( r, r, k) Ψ( r) = G(, r r, k) Ψ( r ) dl, Rk n n r (.6) Ck Το χωρίο R k παριστά την εγκάρσια διατομή του στρώματος με σχετική διηλεκτρική σταθερά k και η καμπύλη C k είναι το σύνορο του R k (βλ. Σχήμα.5). Σχήμα.5 Κατάτμηση της γεωμετρίας σε συνοριακά στοιχεία Περιορίζοντας το διάνυσμα παρατήρησης r στο σύνορο C k, από την (.6) λαμβάνουμε την ολοκληρωτική εξίσωση Ψ( r ) G( r, r, k) Ψ( r ) = G( r, r, k) Ψ( r ) dl C n n, r Ck k (.7) 48
49 όπου το ολοκλήρωμα θεωρείται υπό την έννοια της principal value. Η ολοκληρωτική εξίσωση (.7) λύνεται με τη Μέθοδο των Συνοριακών Στοιχείων (Boundary Element Method). Συγκεκριμένα η (.7) διακριτοποιείται και μετατρέπεται στην εξίσωση πινάκων (ως προς τις άγνωστες μεταβλητές u i και q i ) ui = N j= q G j ij N j= u j D ij (.8) όπου G( ri, rj, k) G ij = G( ri, rj, k) dl, Dij = dl n C j C j (.9) Τα u i και q i εκφράζουν το πεδίο και την κάθετη παράγωγο του πεδίου στο i-οστό συνοριακό στοιχείο, και υποτίθενται σταθερά. Τα ολοκληρώματα τα οποία εμφανίζονται στους τύπους (.9) υπολογίζονται με αριθμητικές μεθόδους (βλ. π.χ. [38] και [39]) και η εξίσωση (.8) μετατρέπεται στο ομογενές σύστημα F ( γ u 0 ) q = 0 (.0) όπου γ 0 =α+jβ η μιγαδική σταθερά διάδοσης των κυματοδηγούμενων κυμάτων, η οποία είναι λύση της εξίσωσης [ F ( γ )] 0 det 0 = Οι τεχνικές των ολοκληρωτικών εξισώσεων με χρήση της μεθόδου των συνοριακών στοιχείων πλεονεκτούν έναντι της Θεωρίας Συζευγμένων Ρυθμών, επειδή δεν προϋποθέτουν προσεγγίσεις για τα φυσικά και γεωμετρικά χαρακτηριστικά των γραμμοσειρών. Όμως, ο ακριβής υπολογισμός των σταθερών διάδοσης εξαρτάται από τη διακριτοποίηση σε συνοριακά στοιχεία, γεγονός που μπορεί σε ορισμένες περιπτώσεις να οδηγήσει σε μεγάλη αύξηση του απαιτούμενου υπολογιστικού κόστους Άλλες μέθοδοι ανάλυσης της κυματοδήγησης Εκτός των ευρέως χρησιμοποιουμένων μεθόδων, τις οποίες αναλύσαμε προηγουμένως, εμφανίζονται επίσης στη βιβλιογραφία και οι ακόλουθες ειδικές μέθοδοι, τις οποίες περιγράφουμε συνοπτικά. 49
50 α) Θεωρία Γραμμών Μεταφοράς (Transmission Line Theory) Η μέθοδος αναφέρεται στη μελέτη του πολυστρωματικού συζεύκτη γραμμοσειρών του Σχήματος.3 και παρουσιάζεται στις [30]-[3]. Τα κυματοδηγούμενα πεδία προκύπτουν ως λύσεις ισοδυνάμων προβλημάτων ηλεκτρικών δικτύων. Εξάγονται σχέσεις, ανάλογες εκείνων οι οποίες προκύπτουν σε προβλήματα διάδοσης σε γραμμές μεταφοράς, οι οποίες εξυπηρετούν την ενοποιημένη μελέτη φαινομένων σκέδασης και κυματοδήγησης σε συζεύκτες γραμμοσειρών. β) Τεχνικές Αντίστροφης Σκέδασης (Inverse Scattering Algorithms) Οι μέθοδοι αυτές χρησιμοποιούνται για τον υπολογισμό των συντελεστών σύζευξης των κυματοδηγούμενων ρυθμών με εφαρμογή αλγορίθμων αντίστροφης σκέδασης (βλ. [5]-[54]). Εξυπηρετούν κυρίως σχεδιαστικές εφαρμογές, όπου η διάταξη του συζεύκτη γραμμοσειρών απαιτείται να εμφανίζει συγκεκριμένα λειτουργικά χαρακτηριστικά, όπως παραδείγματος χάριν να λειτουργεί ως ζωνοπερατό φίλτρο συγκεκριμένης τάξης. γ) Μέθοδοι Διαταραχών (Perturbation Methods) Οι μέθοδοι των διαταραχών μοντελοποιούν την επίδραση των γραμμοσειρών χρησιμοποιώντας τα αναπτύγματα διαταραχών των ρυθμών του συζεύκτη (βλ. [3]-[6]). Οι τεχνικές αυτές δίνουν μία σαφή εικόνα της φυσικής διαδικασίας της σύζευξης, αλλά δεν δίνουν ακριβή αποτελέσματα για περιπτώσεις γραμμοσειρών με σχετικά μεγάλες γεωμετρικές διαστάσεις ή με δείκτη διάθλασης πολύ διαφορετικό από τους δείκτες των υπολοίπων περιοχών. δ) Μέθοδοι στο Πεδίο του Χρόνου (Time-Domain Methods) Οι μέθοδοι αυτές χρησιμοποιούν κυρίως τη μέθοδο των πεπερασμένων διαφορών στο πεδίο του χρόνου (finite-difference time-domain method) [3]-[34] για την αριθμητική επίλυση των χρονοεξαρτώμενων εξισώσεων του Maxwell (.)-(.4) στα διάφορα στρώματα ενός κυματοδηγού γραμμοσειρών. Τα μειονεκτήματά τους εστιάζονται στο ότι δεν παρέχουν φυσική διαίσθηση της διαδικασίας σύζευξης του φωτός καθώς και ότι οι λύσεις υπόκεινται σε περιορισμούς εξαιτίας της αριθμητικής επίλυσης των διαφορικών εξισώσεων και της ενδεχόμενης μεγάλης αύξησης του απαιτούμενου υπολογιστικού κόστους. 50
51 .4. Εφαρμογές των κυματοδηγών γραμμοσειρών στις οπτικές επικοινωνίες Οι κυματοδηγοί, που εμφανίζουν περιοδική μεταβολή του δείκτη διάθλασης κατά μήκος της διεύθυνσης κυματοδήγησης, συνιστούν μία σημαντική κατηγορία διατάξεων, οι οποίες αποτελούν βασικά δομικά στοιχεία των οπτικών δικτύων. Στη συνέχεια συνοψίζουμε τις βασικές εφαρμογές συζευκτών γραμμοσειρών στις οπτικές επικοινωνίες. Οπτικά φίλτρα συχνοτήτων (optical wavelength filters) Μία χαρακτηριστική διάταξη φίλτρου επιλογής συχνοτήτων, η οποία αναλύεται στις [47] και [48], φαίνεται στο Σχήμα.6. Αποτελείται από δύο στρωματικούς κυματοδηγούς, σχηματισμένους επάνω σε υπόστρωμα AlGaAs/GaAs. Οι γραμμοσειρές χαράσσονται στον άνω κυματοδηγό με περίοδο Λ (=π/k), η οποία εκλέγεται κατάλληλα ως προς ένα κεντρικό μήκος κύματος λειτουργίας λ c (operating center wavelength). Σχήμα.6 Σχηματικό διάγραμμα οπτικού φίλτρου συχνοτήτων, σχηματισμένου σε GaAs. Οι δύο κυματοδηγοί υποστηρίζουν διαδιδομένους ρυθμούς με διαφορετική συμμετρία, οπότε η κατευθυντική σύζευξη μεταξύ των δύο ρυθμών λαμβάνει χώρα όταν ικανοποιείται η συνθήκη Bragg πρώτης τάξης [9]: β ( λ ) β ( λ ) =, e c o c K όπου β e και β o είναι οι σταθερές διάδοσης των αρτίων και περιττών ρυθμών. Φωτεινό σήμα εισόδου εισάγεται στον κάτω κυματοδηγό και διαδίδεται ως ο περιττός ρυθμός του κυματοδηγού. Το σήμα αυτό συζευγνύεται αποδοτικά στον άνω κυματοδηγό ως άρτιος ρυθμός, 5
52 μόνον όταν λ=λ c. Αντιθέτως, φωτεινά σήματα με μήκη κύματος διαφορετικά του λ c παραμένουν ασύζευκτα και συνεχίζουν να διαδίδονται ως περιττοί ρυθμοί στον κάτω κυματοδηγό. Στο Σχήμα.7 απεικονίζονται οι ενεργοί δείκτες διάθλασης των δύο κυματοδηγούμενων ρυθμών συναρτήσει του μήκους κύματος. Το κεντρικό μήκος κύματος λ c του φίλτρου εμφανίζεται στο σημείο τομής της καμπύλης διασποράς του περιττού ρυθμού με εκείνη του άρτιου ως αποτέλεσμα της περίθλασης των γραμμοσειρών. Μία μεταβολή ΔΛ της περιόδου γραμμοσειρών οδηγεί σε μία μετατόπιση του σημείου τομής, σύμφωνα με την προαναφερόμενη συνθήκη Bragg, και σε μία μεταβολή Δλ c του κεντρικού μήκους κύματος. Σχήμα.7 Καμπύλες διασποράς του άρτιου και περιττού ρυθμού στο συζεύκτη γραμμοσειρών. Οι (a) και (b) αντιστοιχούν σε Κ+ΔΚ και Κ-ΔΚ, όπου ΔΚ μία μικρή μεταβολή, οφειλόμενη στη μεταβολή ΔΛ της περιόδου. Πολυπλέκτες-αποπολυπλέκτες (multiplexers- demultiplexers) Το Σχήμα.8 απεικονίζει έναν πολυπλέκτη μηκών κύματος, ο οποίος βασίζεται σε παρεμβολή δύο ρυθμών με χρήση κυματοδηγών γραμμοσειρών (wavelength division multiplexer with grating-assisted two-mode intereference) [57]. Χρησιμοποιείται ένας περιοδικός κυματοδηγός γραμμοσειρών με ισχυρή διασπορά, ο οποίος υποστηρίζει δύο κυματοδηγούμενους ρυθμούς. Δύο μήκη κύματος λ και λ, τα οποία εισέρχονται στη διάταξη, πολυπλέκονται και διαχωρίζονται στην έξοδο από μία πολύ μικρή (ultrashort) φασματική απόσταση. 5
53 Σχήμα.8 Σχηματικό διάγραμμα του πολυπλέκτη παρεμβολής δύο ρυθμών με χρήση κυματοδηγού γραμμοσειρών. Η διάταξη αποτελείται από έναν κυματοδηγό με δείκτη διάθλασης n r, ο οποίος ευρίσκεται εντός υλικού με δείκτη διάθλασης n c. Στον κυματοδηγό χαράσσονται m επαναλήψεις γραμμοσειρών με πάχος W g, ενώ το πάχος σύζευξης είναι W m. Οι παράμετροι αυτές πρέπει να επιλέγονται προσεκτικά, προκειμένου ο κυματοδηγός να υποστηρίζει μόνο δύο διαδιδόμενους ρυθμούς σε ένα φασματικό εύρος, στο οποίο να περιέχονται τα μήκη κύματος λ και λ, που πρόκειται να πολυπλεχθούν. Εξάλλου, το σχηματικό διάγραμμα ενός πολυπλέκτη πρόσθεσης (add multiplexer) με χρήση συζεύκτη γραμμοσειρών απεικονίζεται στο Σχήμα.9 (βλ. [58]). Σχήμα.9 (a) Διάταξη συζεύκτη γραμμοσειρών με ενεργούς κυματοδηγούς InP (b) Σχηματικό διάγραμμα του ευρυζωνικού πολυπλέκτη πρόσθεσης. Η κλασική υλοποίηση ενός πολυπλέκτη πρόσθεσης βασίζεται στο γεγονός ότι η μεταφορά ισχύος στο συζεύκτη γραμμοσειρών εξαρτάται από το μήκος κύματος, εξαιτίας του απαιτούμενου ταιριάσματος μεταξύ της περιόδου των γραμμοσειρών και της διαφοράς των 53
54 σταθερών διάδοσης των ρυθμών. Σήματα άλλων συχνοτήτων θα διέλθουν εκ του κυματοδηγού χωρίς να επηρεαστούν από τις γραμμοσειρές, ενώ το επιθυμητό μήκος κύματος λ add στην είσοδο πρόσθεσης θα συζευχθεί με τα μήκη κύματος λ, λ, λ 3 στον άλλο κυματοδηγό. Ο εν λόγω πολυπλέκτης αποτελείται από δύο παράλληλους κυματοδηγούς καναλιού InGaAs με δείκτη διάθλασης 3.6, μήκος.5μm και πάχη 0.4 μm και 0.5μm, ευρισκομένους σε υλικό InP με δείκτη διάθλασης 3.4. Η περιοδική διάταξη γραμμοσειρών εισάγεται στον κυματοδηγό πρόσθεσης πάχους 0.5μm. Περαιτέρω, στο Σχήμα.0 απεικονίζεται μία χαρακτηριστική διάταξη αποπολυπλέκτη, η οποία υλοποιείται με χρήση ασυμμετρικού κατευθυντικού συζεύκτη γραμμοσειρών [59]. Σχήμα.0 Σχηματικό διάγραμμα αποπολυπλέκτη με φίλτρα συζευκτών γραμμοσειρών. Λ, Λ και Λ 3 είναι διαφορετικές περίοδοι των γραμμοσειρών. Ο αποπολυπλέκτης αποτελείται από μία σειρά φίλτρων επιλογής συχνοτήτων ασυμμετρικών συζευκτών γραμμοσειρών. Δύο οπτικοί κυματοδηγοί τοποθετούνται παράλληλα μεταξύ τους. Οπτικά σήματα διαφορετικών μηκών κύματος διαδιδόμενα στον κυματοδηγό συζευγνύονται σε διαφορετικά τμήματα με τη χρήση διαφορετικών γραμμοσειρών. Οι χρησιμοποιούμενοι συζεύκτες γραμμοσειρών αποτελούνται από δύο μονορυθμικούς κυματοδηγούς, οι οποίοι έχουν σταθερές διάδοσης αρκετά διαφορετικές και τοποθετούνται σε πολύ κοντινή απόσταση. Εξαιτίας της ισχυρής ασυμμετρίας, η φυσική σύζευξη μεταξύ των δύο κυματοδηγών είναι τόσο ασθενής, ώστε το φωτεινό σήμα, το οποίο διαδίδεται στον ένα κυματοδηγό, να παραμένει σε αυτόν. Για αυτό το λόγο εισάγεται περιοδική διαταραχή στο σύστημα των δύο κυματοδηγών, προκειμένου να ενισχυθεί η σύζευξη του φωτός μεταξύ των κυματοδηγών. Ένα σχηματικό διάγραμμα ασυμμετρικού συζεύκτη γραμμοσειρών, ο οποίος χρησιμοποιείται σε αποπολυπλέκτες, απεικονίζεται στο Σχήμα.. Οι παράμετροι του συζεύκτη δείκτες διάθλασης των υλικών, πάχη των κυματοδηγών, πάχος και περίοδος των γραμμοσειρών, επιλέγονται κατάλληλα για να ικανοποιούνται τα απαιτούμενα κριτήρια σύζευξης. 54
55 Σχήμα. Σχηματικό διάγραμμα ασυμμετρικού συζεύκτη γραμμοσειρών, χρησιμοποιούμενου σε αποπολυπλέκτες. Επισκόπηση της αρχής λειτουργίας πολυπλεκτών και αποπολυπλεκτών με χρήση συζευκτών γραμμοσειρών περιέχεται στην [60]. Μετατροπείς ρυθμών (mode converters) οπτικών παλμών πολύ μεγάλου εύρους ζώνης (ultrawide-band pulses) Χρησιμοποιείται ένας βασικός τριστρωματικός κυματοδηγός, ο οποίος για συχνότητα φέροντος Hz μπορεί να υποστηρίξει εφτά διαδιδόμενους ρυθμούς [6]. Στην είσοδο του κυματοδηγού εισέρχεται ένας παλμός έξι κύκλων, αναφερόμενος ως -- παλμός. Το φάσμα αυτού του παλμού απεικονίζεται στο Σχήμα. και έχει το μεγαλύτερο μέρος του συχνοτικού του περιεχομένου επάνω από τα κατώφλια των εφτά διαδιδομένων ρυθμών. Σχήμα. Φάσμα του -- παλμού. Η μετατροπή ρυθμών υλοποιείται με τη βοήθεια μιας διάταξης γραμμοσειρών, η οποία κατασκευάζεται, παραμορφώνοντας (deforming) τα σύνορα μεταξύ των στρωμάτων του βασικού 55
56 κυματοδηγού, ώστε να δημιουργηθεί ένα ορθογωνικό ή ημιτονοειδές προφίλ γραμμοσειρών (βλ. Σχήμα.3). Η μετατροπή από τον i-οστό ρυθμό κυματοδηγού με σταθερά διάδοσης β i στον j- οστό ρυθμό με σταθερά διάδοσης β j προϋποθέτει η περίοδος Λ να ικανοποιεί τη συνθήκη προσαρμογής φάσης Λ = π / β β. i j Θεωρούμε ως σήμα εισόδου κατάλληλο συνδυασμό των ρυθμών και 5 με περιβάλλουσα εκείνη του -- παλμού του (βλ. Σχήμα.). Σε κάποια αρκετά μεγάλη απόσταση από το σημείο εισόδου του παλμού εξάγονται με κατάλληλες τεχνικές τα φασματικά περιεχόμενα των δύο ρυθμών [6] (βλ. Σχήμα.4). Το φάσμα του κάθε ενός εξαγόμενου ρυθμού ευρίσκεται σε πολύ καλή συμφωνία με εκείνο του αρχικού -- διεγειρόμενου σήματος. Σχήμα.3 Διατάξεις ορθογωνικών γραμμοσειρών, που χρησιμοποιούνται για μετατροπή ρυθμών. 56
57 (α) (β) Σχήμα.4 Φάσματα των εξαγομένων ρυθμών: (α) και (β) 5. Συντονιζόμενα (tunable) lasers Σχηματικό διάγραμμα ενός συντονιζόμενου laser με ενσωματωμένο κατευθυντικό φίλτρο συζεύκτη γραμμοσειρών απεικονίζεται στο Σχήμα.5 (βλ. [55]). Η διάταξη αποτελείται από τρία τμήματα. Ένας απλός κυματοδηγός μήκους L στο άνω κυματοδηγικό στρώμα παρέχει κέρδος ή ενίσχυση στον κυματοδηγούμενο ρυθμό, ο οποίος διέρχεται μέσω αυτού. Ο αριστερός τερματισμός του κυματοδηγού αυτού χαρακτηρίζεται από συντελεστή ανάκλασης r. Ένας άλλος απλός κυματοδηγός μήκους L στο κάτω κυματοδηγικό στρώμα εξυπηρετεί ως «παράθυρο» στο αριστερό τμήμα με συντελεστή ανάκλασης r. Τέλος, ένας κατευθυντικός συζεύκτης γραμμοσειρών μήκους L εισάγεται μεταξύ των τμημάτων κέρδους και παραθύρου. Ο συζεύκτης χρησιμοποιείται ως φίλτρο συχνοτήτων για να συνταιριάσει τα φασματικά χαρακτηριστικά της διάταξης ως προς την επιλεκτικότητα των διαμήκων ρυθμών (longitudinal mode selectivity). 57
58 Σχήμα.5 Σχηματικό διάγραμμα του συντονιζομένου laser ημιαγωγών με ενσωματωμένο φίλτρο κατευθυντικού συζεύκτη γραμμοσειρών. Επίσης, αξίζει να σημειώσουμε ότι οι συζεύκτες γραμμοσειρών χρησιμοποιούνται ακόμη σε laser κατανεμημένης ανάδρασης (distributed feedback lasers) [56] και οπτικές πηγές ακτινοβολίας [64]. Οπτικός διακόπτης (optical switch) Για την υλοποίηση ενός οπτικού διακόπτη χρησιμοποιείται ο τετράθυρος συζεύκτης γραμμοσειρών, ο οποίος απεικονίζεται στο Σχήμα.6 (βλ. [6]). Σχήμα.6 Σχηματικό διάγραμμα τετράθυρου συζεύκτη γραμμοσειρών. Ο συζεύκτης αποτελείται από δύο όμοιους κυματοδηγούς με σταθερά διάδοσης β 0. Κάθε κυματοδηγός υποστηρίζει ένα μοναδικό ρυθμό, ο οποίος οδεύει και προς τις δύο κατευθύνσεις. Οι κυματοδηγοί ευρίσκονται σε αρκετά μεγάλη απόσταση στις εισόδους και τις εξόδους και σε 58
59 αρκετά μικρή απόσταση κοντά στην περιοχή σύζευξης, προκειμένου οι ρυθμοί τους να αλληλεπιδρούν και να λαμβάνει χώρα ανταλλαγή ενέργειας. Οι γραμμοσειρές τοποθετούνται και στους δύο κυματοδηγούς στην περιοχή σύζευξης. Η περίοδος Λ= π/ β0 των γραμμοσειρών εκλέγεται ώστε να ταιριάζει τις φάσεις των κυμάτων, που διαδίδονται προς τις ίδιες και προς αντίθετες κατευθύνσεις. Επίσης, λαμβάνουν χώρα δύο επιπρόσθετοι μηχανισμοί ανταλλαγής ενέργειας: ) Ευθεία σύζευξη Bragg: Ένας ρυθμός, π.χ. ο Α, ανακλάται προς τον ίδιο κυματοδηγό και ανταλλάσσει ενέργεια με το ρυθμό Α 3, ο οποίος οδεύει στην αντίθετη κατεύθυνση. ) Σύζευξη Bragg ανταλλαγής: Ένας ρυθμός, π.χ. ο Α, ανακλάται προς τον απέναντι κυματοδηγό και ανταλλάσσει ενέργεια με το ρυθμό Α 4, ο οποίος οδεύει στην αντίθετη κατεύθυνση στον απέναντι κυματοδηγό. Τα προαναφερόμενα φυσικά φαινόμενα αναλύονται με τη Θεωρία Συζευγμένων Ρυθμών [6] και προσδιορίζονται οι τιμές των παραμέτρων των γραμμοσειρών για την επίτευξη της επιθυμητής λειτουργίας του τετράθυρου συζεύκτη ως οπτικού διακόπτη, δηλαδή για την εξαγωγή του οπτικού σήματος σε μία επιλεγμένη πόρτα, όταν η είσοδος τοποθετείται σε μία συγκεκριμένη πόρτα. Εξάλλου, οι διατάξεις των γραμμοσειρών χρησιμοποιούνται επίσης και σε Δαχτυλίδια συντονισμού (ring resonators) Τα δαχτυλίδια συντονισμού γραμμοσειρών (βλ. Σχήμα.7) λειτουργούν σύμφωνα με το φαινόμενο γαλαρίας (whispering gallery) [65]. Η επισύναψη γραμμοσειρών στην εξωτερική επιφάνεια των δαχτυλιδιών εξασφαλίζει στη διάταξη συνθήκες μονορυθμικής λειτουργίας. 59
60 Σχήμα.7 Σχηματικό διάγραμμα διδιάστατου δαχτυλιδιού συντονισμού γραμμοσειρών. Ανακλαστήρες μιας συχνότητας (single frequency reflecting mirrors) Οι ανακλαστήρες κατασκευάζονται με συντονιστές Bragg (μεταλλικοί σωλήνες με αυλακωμένα τοιχώματα, βλ. Σχήμα.8) και χρησιμοποιούνται σε ενισχυτές υψηλής ισχύος και σε ταλαντωτές χιλιοστομετρικών και υποχιλιοστομετρικών κυμάτων [66]. Σχήμα.8 Ανακλαστήρας-ταλαντωτής Bragg. Παράλληλη εξαγωγή δεδομένων σε συστήματα οπτικών καρτών Η παράλληλη εξαγωγή δεδομένων επιτυγχάνεται με το συζεύκτη γραμμοσειρών γραμμικής εστίασης (linearly focusing grating coupler), ο οποίος απεικονίζεται στο Σχήμα.9. Ο συζεύκτης χρησιμοποιείται για το σχηματισμό μιας γραμμής εστίασης, η οποία είναι απαραίτητη για παράλληλη παραλαβή (parallel pickup) των οπτικών δεδομένων [67]. 60
61 Σχήμα.9 Σχηματικό διάγραμμα συζεύκτη γραμμοσειρών γραμμικής εστίασης. Κεραίες χιλιοστομετρικών κυμάτων Διάταξη μίας κεραίας γραμμοσειρών χιλιοστομετρικών κυμάτων απεικονίζεται στο Σχήμα.30. Η ακτινοβολία από τις διηλεκτρικές κεραίες γραμμοσειρών επηρεάζεται από την περιοδική διαταραχή των κυμάτων, που οδηγούνται στο ομοιόμορφο τμήμα της διάταξης του (μη περιοδικού) κυματοδηγού. Αυτή η ακτινοβολία εμφανίζεται μόνο σε συγκεκριμένες κατευθύνσεις του χώρου, οι οποίες καθορίζονται κυρίως από τη σταθερά φάσης της αδιατάρακτης διάταξης και την περίοδο των διαταραχών [63]. Σχήμα.30 Διάταξη κεραίας γραμμοσειρών χιλιοστομετρικών κυμάτων. 6
62 ΚΕΦΑΛΑΙΟ 3 ΚΕΦΑΛΑΙΟ 3. ΑΝΑΛΥΣΗ ΣΥΖΕΥΓΜΕΝΩΝ ΣΥΜΜΕΤΡΙΚΩΝ ΚΥΜΑΤΟΔΗΓΩΝ ΜΕ ΓΡΑΜΜΟΣΕΙΡΕΣ Στο Κεφάλαιο αυτό παρουσιάζεται εκτενής μελέτη των φαινομένων κυματοδήγησης σε συζευγμένους δισδιάστατους συμμετρικούς κυματοδηγούς με περιοδικά χαραγμένες γραμμοσειρές ως εφαρμογή των τεχνικών της Μεθόδου των Ροπών (Method of Moments). Η μελέτη αφορά κυρίως στον ακριβή προσδιορισμό των μιγαδικών σταθερών διάδοσης των κυματοδηγούμενων κυμάτων. Για την επίλυση των ολοκληρωτικών εξισώσεων, οι οποίες εμφανίζονται, χρησιμοποιούνται τεχνικές Galerkin συνολικού χώρου (entire domain Galerkin techniques). Ακριβέστερα, στην παράγραφο 3. περιγράφεται η γεωμετρία της διάταξης των συζευγμένων δισδιάστατων συμμετρικών κυματοδηγών με περιοδικά χαραγμένες γραμμοσειρές. Στην παράγραφο 3. διατυπώνεται το θεώρημα του Floquet και αναλύεται ο ρόλος των χωρικών αρμονικών, που υπαγορεύουν την κυματική διάδοση σε περιοδικές δομές. Ως εφαρμογή της μεθόδου Sommerfeld επιτυγχάνεται στην παράγραφο 3.3 αναλυτική έκφραση μέσω ολοκληρώματος Fourier της συνάρτησης Green του ομογενούς (χωρίς γραμμοσειρές) προβλήματος. Στην παράγραφο 3.4 ευρίσκεται ολοκληρωτική αναπαράσταση του ηλεκτρικού πεδίου των TE z πολωμένων ηλεκτρομαγνητικών κυμάτων, που διαδίδονται παράλληλα προς τον z-άξονα στη διάταξη του συζεύκτη. Εφαρμόζοντας την τεχνική Galerkin συνολικού χώρου (entire domain Galerkin technique), περιγράφουμε στην παράγραφο 3.5 μία αυστηρή μέθοδο για τον ακριβή προσδιορισμό των μιγαδικών σταθερών διάδοσης των κυματοδηγούμενων στη διάταξη κυμάτων. Στην παράγραφο 3.6 μελετώνται ενοποιημένα ως ειδικές περιπτώσεις της γενικής μεθόδου, η οποία αναπτύσσεται στις παραγράφους , οι διατάξεις του ενός απομονωμένου κυματοδηγού παρουσία γραμμοσειρών, συζεύκτη παρουσία γραμμοσειρών στον άνω κυματοδηγό και συζεύκτη παρουσία γραμμοσειρών στον κάτω κυματοδηγό. Ορισμένα στοιχεία αριθμητικής υλοποίησης της προτεινομένης μεθόδου παρουσιάζονται στην παράγραφο 3.7. Εξάλλου, στην παράγραφο 3.8 γίνεται έλεγχος σύγκλισης της μεθόδου, διαπιστώνεται η υψηλή αποδοτικότητά της και επιβεβαιώνεται η εγκυρότητά της. 6
63 3.. Συμμετρικός Συζεύκτης Γραμμοσειρών Η διάταξη του συμμετρικού συζεύκτη γραμμοσειρών (symmetric grating assisted optical coupler), η οποία απεικονίζεται στο Σχήμα 3., αποτελείται από δύο άπειρες επίπεδες και παράλληλες διηλεκτρικές πλάκες (slab waveguides) με δείκτη διάθλασης n, πάχος d, και απόσταση μεταξύ τους h. Ο χώρος θεωρείται μαγνητικά ομοιόμορφος με σταθερή μαγνητική διαπερατότητα μ=μ 0 και εκτός των πλακών θεωρείται ομογενής με δείκτη διάθλασης n 0 και κυματικό αριθμό k 0. Κατά μήκος των πλακών έχουν χαραχθεί περιοδικά ορθογώνιες γραμμοσειρές με δείκτη διάθλασης n και πάχος w. Οι γραμμοσειρές διαμορφώνουν δύο στρώματα με Λ-περιοδική κατανομή του δείκτη διάθλασης στον άξονα κυματοδήγησης z, ένα ευρισκόμενο στο άνω μέρος της πλάκας και το άλλο στο κάτω μέρος της πλάκας. Η κάθε επανάληψη των γραμμοσειρών αποτελείται από q ορθογώνια (rectangles) με διαμήκη χαρακτηριστικά d i και l i (i=,,q). Αξίζει να σημειώσουμε ότι στην παρούσα διατύπωση ο αριθμός και οι διαμήκεις διαστάσεις των ορθογωνίων των γραμμοσειρών μπορούν να μεταβάλλονται εντός κάθε επανάληψης σύμφωνα με τα χαρακτηριστικά μεγέθη d i, l i, q. Όμως, στις εργασίες [7]-[] που βασίζονται στη Θεωρία Συζευγμένων Ρυθμών και στις []-[9] στη Θεωρία Floquet-Bloch, εξετάζονται μόνο δυαδικές (binary) γραμμοσειρές, οι οποίες περιέχουν ένα ορθογώνιο ανά επανάληψη. Η όλη διάταξη υποτίθεται ομοιόμορφη κατά μήκος του άξονα y. Έτσι, η περιοδική επέκταση ως προς z [0,Λ] της τμηματικά σταθερής συνάρτησης n0, x> h+ d, 0 z Λ n, h d < x< h+ d, z ( di, di + li) i=,..., q n, h d < x< h d + w, z ( di, di + li) i=,..., q nxz (, ) = n0, d< x< h d, 0 z Λ n, d w< x< d, z ( di, di + li) i=,..., q n, d < x< d, z ( di, di + li) i=,..., q n0 x< d, 0 z Λ (3.) καθορίζει την κατανομή του δείκτη διάθλασης της διάταξης του Σχήματος
64 Σχήμα 3. Γεωμετρία του συμμετρικού συζεύκτη γραμμοσειρών 64
65 3.. Θεώρημα Floquet και χωρικές αρμονικές περιοδικών δομών Η θεμελιώδης αρχή της Φυσικής, η οποία διέπει την κυματική διάδοση σε περιοδικές δομές, εκφράζεται από το θεώρημα του Floquet ([43], Ch. 9). Θεώρημα Floquet Tο κυματοδηγούμενο πεδίο Ψ(x,y,z) κατά τις κατευθύνσεις μήκος του άξονα z δομή εκφράζεται ως εξής ± ẑ σε μία Λ-περιοδική κατά γ z Ψ ( x, yz, ) = e uxyz (,, ) (3.) όπου γ η μιγαδική σταθερά διάδοσης του κυματοδηγούμενου πεδίου και u(x,y,z) κατάλληλη Λ- περιοδική ως προς z συνάρτηση, δηλαδή ισχύει uxyz (,, + rλ) = uxyz (,, ), r (3.3) Απόδειξη Το κυματοδηγούμενο πεδίο Ψ(x,y,z) κατά τις κατευθύνσεις σχέση γ rλ Ψ(,, Λ) Ψ(,, ), xyz+ r = e xyz r ± ẑ ικανοποιεί τη Εξάλλου, για τη συνάρτηση ±γ z uxyz (,, ) = e Ψ ( xyz,, ), παρατηρούμε ότι ισχύει uxyz r e xyz r γ ( z r ) (,, + Λ ) = ± + Λ Ψ (,, + Λ ) Τώρα από τις τρεις παραπάνω σχέσεις, προκύπτει άμεσα η (3.3). Θεωρούμε μία περιοδική δομή κατά μήκος του άξονα z, της οποίας η σχετική διηλεκτρική σταθερά ε r είναι Λ-περιοδική συνάρτηση ως προς z, δηλαδή ισχύει ε ( z+ Λ) = ε ( z) (3.4) r r Εφαρμόζοντας το θεώρημα του Floquet για το βαθμωτό παράγοντα Ψ(x,z) του ηλεκτρικού πεδίου E( x, z) = Ψ( x, z)ˆ y, ενός κυματοδηγούμενου κατά την κατεύθυνση γ, λαμβάνουμε + ẑ TE z ρυθμού με μιγαδική σταθερά διάδοσης γ z Ψ ( x, z) = e u( x, z), (3.5) 65
66 όπου u(x,z) είναι μία Λ-περιοδική συνάρτηση ως προς z. Σύμφωνα με τα αναφερόμενα στο εδάφιο.3., για μία τμηματικά σταθερή κατανομή του δείκτη διάθλασης, ο παράγοντας Ψ του ηλεκτρικού πεδίου ικανοποιεί τη βαθμωτή εξίσωση Helmholtz x z + + k 0ε r ( z) Ψ ( x, z) = 0, (3.6) και οι συνιστώσες H x και H z υπολογίζονται από την Ε y μέσω των σχέσεων (.5) και (.54). Υπό την προϋπόθεση ότι ο παράγοντας Ψ(x,z) εκφράζεται ως Ψ ( x, z) = ϕ( x) v( z), προκύπτει η συνήθης διαφορική εξίσωση d dz + k0ε r ( z) + λ v( z) = 0, (3.7) όπου ϕ ( x) λ = ϕ( x) Έστω v (z) και v (z) οι δύο γραμμικά ανεξάρτητες λύσεις της διαφορικής εξίσωσης δευτέρου βαθμού (3.7). Επειδή μία διαφορική εξίσωση δευτέρου βαθμού έχει μόνο δύο γραμμικά ανεξάρτητες λύσεις, η γενική λύση V(z) εκφράζεται ως γραμμικός συνδυασμός V z) = Av ( z) + Bv ( ) (3.8) ( z με μιγαδικούς συντελεστές Α και Β. Εξάλλου, αν v(z) είναι λύση της (3.7), τότε από την (3.4) έπεται ότι και η v(z+λ) είναι επίσης λύση της (3.7). Έτσι εφαρμόζοντας την (3.8), έχουμε v z + Λ) = a v ( z) + a v ( ), v z + Λ) = a v ( z) + a v ( ) (3.9) ( z ( z όπου α ij κατάλληλοι μιγαδικοί συντελεστές, για τους οποίους ισχύει η συνθήκη ([43], (9) Ch. 9) a a a a (3.0) = Τώρα συνδυάζοντας τις (3.8) και (3.9), ευρίσκουμε V z + Λ) = ( Aa + Ba ) v ( z) + ( Aa + Ba ) v ( ) (3.) ( z Η V(z) παριστάνει κύμα που οδεύει παράλληλα προς το θετικό άξονα z υπό την προϋπόθεση γ Λ V ( z + Λ) = e V ( z) (3.) 66
67 Συνδυασμός των (3.8), (3.) και (3.) οδηγεί στη διαμόρφωση ενός ομογενούς γραμμικού συστήματος με αγνώστους τα Α και Β. Το εν λόγω σύστημα έχει μη τετριμμένη λύση όταν ισχύει η συνθήκη e γλ e γλ ( a + a) + = 0, (3.3) η οποία προκύπτει μηδενίζοντας την ορίζουσα του συστήματος και χρησιμοποιώντας την (3.0). Η εξίσωση (3.3) έχει τις λύσεις γ Λ ±θ e = e, όπου a + a θ = cosh Παρατηρούμε ότι αν γ επαληθεύει την εξίσωση (3.3), τότε την επαληθεύουν επίσης και τα γ, π n και τα γ + j ( n ), που σημαίνει ότι οι κυματοδηγούμενοι ρυθμοί στην περιοδική δομή Λ έχουν μιγαδικές σταθερές διάδοσης π n γn = γ + j, n (3.4) Λ Τώρα, υπό τις προϋποθέσεις, οι οποίες αναλύονται στο Παράρτημα Β, η συνάρτηση u(x,z) αναπτύσσεται ως προς z στη σειρά Fourier + n n= Συνδυάζοντας τις (3.5) και (3.5) λαμβάνουμε πn j z Λ u( x, z) = ϕ ( x) e (3.5) + π n γ + j z Λ ϕn xe n= Ψ ( xz, ) = ( ) (3.6) Επομένως το πεδίο ενός ρυθμού εκφράζεται ως άθροισμα σειράς συναρτήσεων με σταθερές διάδοσης γ n ( n ), οι οποίες δίνονται από τη σχέση (3.4). Ο γενικός όρος ϕ γ n z n( x) e της σειράς (3.6), ο οποίος συνυπάρχει στο πεδίο του ρυθμού, ονομάζεται χωρική (Floquet) αρμονική του θεμελιώδους ρυθμού με σταθερά διάδοσης γ 0 =γ. Επειδή ο παράγοντας Ψ(x,z) του ηλεκτρικού πεδίου, ο οποίος εκφράζεται από την (3.6), πρέπει να αποτελεί λύση της διαφορικής εξίσωσης (3.6) σε κάθε περιοχή σταθερού δείκτη διάθλασης n i, θα έχουμε όπου ϕ ( x) g ϕ ( x) = 0 (3.7) n i, n n 67
68 π n in, γ 0 i g = + j k n, i= 0,, Λ (3.8) Οι συναρτήσεις φ n (x) εκφράζονται ως γραμμικοί συνδυασμοί των θεμελιωδών λύσεων της διαφορικής εξίσωσης (3.7). Οι συντελεστές των εν λόγω γραμμικών συνδυασμών συνιστούν το διάνυσμα των αγνώστων του γραμμικού συστήματος της μεθόδου επίλυσης. Εξάλλου, όταν στη διάταξη υπάρχει και προσπίπτον πεδίο, τότε το γραμμικό σύστημα είναι ένα μη ομογενές επιλύσιμο σύστημα και η λύση του δίνει τους συντελεστές των γραμμικών συνδυασμών. Όταν στη διάταξη δεν υπάρχει προσπίπτον πεδίο, τότε το γραμμικό σύστημα είναι ομογενές και οι σταθερές διάδοσης των ρυθμών κυματοδήγησης είναι οι ρίζες της ορίζουσας του συστήματος Αναλυτική έκφραση της συνάρτησης Green Για την μελέτη της κυματοδήγησης στη διάταξη του συζεύκτη του Σχήματος 3. με τη Μέθοδο των Ροπών προαπαιτείται κατάλληλη αναλυτική έκφραση της συνάρτησης Green του ομογενούς (χωρίς γραμμοσειρές) προβλήματος. Αρχικά μελετάμε την περίπτωση ΤΕ z πολωμένων ηλεκτρομαγνητικών κυμάτων. Συγκεκριμένα θεωρούμε ότι η διάταξη των δύο κυματοδηγών του Σχήματος 3. διεγείρεται από μία διδιάστατη, άπειρη κατά μήκος του άξονα y γραμμική ηλεκτρική ρευματική πηγή με κανονικοποιημένη πυκνότητα ρεύματος J( xz, ) = δ( x x ) δ( z z ) yˆ, d x d, z (3.9) jωμ 0 όπου δ( ) η συνάρτηση Dirac και (x,z ) η θέση, στην οποία εφαρμόζεται η διέγερση, και η οποία στην προκειμένη περίπτωση ευρίσκεται εντός του κυματοδηγού. 68
69 Σχήμα 3. Γεωμετρία του χωρίς γραμμοσειρές προβλήματος Ως συνάρτηση Green G (x,z;x',z') ορίζεται το ηλεκτρικό πεδίο E y (x,z) (απόκριση), το οποίο παράγεται στη διάταξη από τη ρευματική πηγή J(x,z) (διέγερση) της (3.9). Επειδή το ηλεκτρικό πεδίο E y (x,z) πληρεί την εξίσωση (.4), με τη βοήθεια της (3.9) προκύπτει ότι η συνάρτηση Green του προβλήματος των δύο συμμετρικών απείρων διηλεκτρικών πλακών είναι λύση της εξίσωσης όπου ( ) + k n ( x) G ( rr ; ) = δ ( r r ) (3.0) 0 = + x z εφόσον τα πεδιακά μεγέθη είναι ανεξάρτητα από τη μεταβλητή y, και r = x xˆ + z zˆ, r = x xˆ + z zˆ είναι τα διανύσματα παρατήρησης και της πηγής αντίστοιχα. Για το συγκεκριμένο πρόβλημα, η τμηματικά σταθερή συνάρτηση 69
70 n0, x> h+ d n, h d < x< h+ d nx ( ) = n0, d< x< h d n, d < x< d n0, x< d εκφράζει την κατανομή του δείκτη διάθλασης. Επιπλέον οι G (; rr ) και G (; ) rr, ως x εφαπτομενικές συνιστώσες του ηλεκτρικού και του μαγνητικού πεδίου πρέπει να ικανοποιούν τις κατάλληλες συνοριακές συνθήκες συνέχειας στις διαχωριστικές επιφάνειες x=±d και x=h±d μεταβολής του δείκτη διάθλασης. Ως εφαρμογή του θεωρήματος Green αποδεικνύεται στο Παράρτημα Α ότι η συνάρτηση Green είναι συμμετρική ως προς τη διέγερση και την απόκριση. Ο υπολογισμός της συνάρτησης Green επιτυγχάνεται με χρήση της μεθόδου Sommerfeld, η οποία συνοψίζεται ως εξής (για λεπτομερή περιγραφή της μεθόδου βλ. π.χ. [68] Section 6.3 και [69] Section 9.8): ) Tο ηλεκτρικό πεδίο, το οποίο προκαλεί η ρευματική κατανομή J(x,z) της (3.9), θεωρουμένη στον ελεύθερο χώρο με δείκτη διάθλασης n, εκφράζεται ως ολοκλήρωμα Fourier κατάλληλης γνωστής συναρτήσεως. Το εν λόγω πεδίο αναφέρεται ως πρωτογενές (primary) ή ως συνάρτηση Green ελευθέρου χώρου και αποτελεί το ανώμαλο μέρος της προσδιοριστέας συνάρτησης Green. ) Οι διαχωριστικές επιφάνειες x=±d, x=h±d δημιουργούν ανακλώμενα και διαθλώμενα πεδία εντός και εκτός των κυματοδηγών. Τα πεδία αυτά αναφέρονται ως δευτερογενή (secondary). Επειδή τα εν λόγω πεδία ικανοποιούν τις αντίστοιχες κυματικές εξισώσεις και τη συνθήκη ακτινοβολίας, αυτά εκφράζονται ως κατάλληλοι γραμμικοί συνδυασμοί ολοκληρωμάτων Fourier. 3) Οι άγνωστοι συντελεστές των δευτερογενών πεδίων προσδιορίζονται με τη βοήθεια των οριακών συνθηκών για τα επίπεδα x=±d, x=h±d. 4) Το ζητούμενο ηλεκτρικό πεδίο για το χώρο εντός του κυματοδηγού θα είναι η υπέρθεση πρωτογενούς και δευτερογενούς πεδίου ενώ για τους χώρους εκτός του κυματοδηγού μόνο το δευτερογενές. 70
71 όπου Το πρωτογενές πεδίο G pr εκφράζεται ως ολοκλήρωμα Fourier (βλ. [70], (.60)) + g x x jλ ( z z ) e Gpr ( x, z; x, z ) = dλ e, ( x, z) 4π (3.) g g ( λ) = ( λ k n ) / 0 Η συνάρτηση g (λ) είναι πλειότιμη μιγαδική συνάρτηση. Επιλέγουμε το πρόσημο της ρίζας έτσι ώστε Re{ g ( λ)} > 0, ώστε το πεδίο G pr να παριστά κύμα, το οποίο οδεύει αποσβεννύμενο καθώς x +, και Im{ g ( λ)} > 0 για να παριστάνει η (3.), με βάση τη χρονική αρμονική εξάρτηση exp(jωt), κύματα που απομακρύνονται από το επίπεδο x=x και οδεύουν προς το ±. H έκφραση (3.) χρησιμοποιείται παρακάτω στην εφαρμογή των οριακών συνθηκών στα επίπεδα x=±d. Εξάλλου, αξίζει να σημειώσουμε ότι το πρωτογενές πεδίο προκύπτει επίσης και ως η θεμελιώδης λύση του διδιάστατου τελεστή Helmholtz στον ελεύθερο χώρο. Συγκεκριμένα το πρωτογενές πεδίο G (; rr ) ικανοποιεί, ως γνωστόν, τη διαφορική εξίσωση pr ( kn) G pr δ ( ) + 0 (; rr) = r r, r (3.) Η (3.) έχει δύο γραμμικά ανεξάρτητες λύσεις ψ (r, r ) και ψ (r, r ) με j () j ψ (, rr ) = H 0 ( k 0 n r r ), ψ () (, rr ) = H 0 ( k 0 n r r ) 4 4 ( ) (βλ. [7], (5.3), (5.50)), όπου ( ) (i=,) η κυλινδρική συνάρτηση Hankel πρώτου και H i 0 z δευτέρου είδους και μηδενικής τάξης. Οι συναρτήσεις ψ (r,r ) και ψ (r,r ) με βάση και τη χρονική εξάρτηση exp(jωt) παριστάνουν κύματα τα οποία απομακρύνονται από την πηγή και πλησιάζουν προς την πηγή αντιστοίχως. Συνεπώς η φυσικά αποδεκτή λύση της (3.) είναι η ψ (r,r ), οπότε έχουμε Βάσει του τύπου j () Gpr ( x, z; x, z ) = H 0 k0n x x + z z 4 ( ) ( ) + g x x jλ ( z z ) e () dλe jπh = 0 k0n ( x x ) + ( z z ) g (βλ. [73]), οι εκφράσεις (3.) και (3.3) ταυτίζονται. (3.3) Το δευτερογενές πεδίο G ( x, z; x, z ), το οποίο οφείλεται στην ασυνέχεια της κατανομής sec του δείκτη διάθλασης στα επίπεδα x=±d, x=h±d, εκφράζεται στις πέντε περιοχές του επιπέδου ως ολοκλήρωμα Fourier 7
72 + jλ ( z z ) λ γ λ ( ) (3.4) Gsec ( x, z; x, z ) = d e (, x, x ), x, z 4π Εξάλλου, η προσδιοριστέα φασματική συνάρτηση γ, η οποία αποτελεί λύση σε κάθε περιοχή σταθερού δείκτη διάθλασης της διαφορικής εξίσωσης γ( λ, xx, ) ( λ kn 0 ( x) ) γ( λ, xx, ) = 0 x εκφράζεται ως γραμμικός συνδυασμός A8( λ)exp[ g0( λ)( x h d)], x> h+ d A6( λ)cosh[ g( λ)( x h)] A7( λ)sinh[ g( λ)( x h)], h d < x< h+ d h h γ( λ, xx, ) = A4( λ)cosh[ g0( λ)( x )] + A5( λ)sinh[ g0( λ)( x )], d < x< h d A( λ)cosh( g( λ) x) A3( λ)sinh( g( λ) x), d < x< d A( λ)exp[ g0( λ)( x+ d)], x< d των θεμελιωδών λύσεων της εν λόγω εξίσωσης, όπου 0 λ ) ( ) / g ( = λ k n 0 0 (3.5) (3.6) Το πρόσημο αυτής της τετραγωνικής ρίζας επιλέγεται έτσι ώστε Re{ g 0 ( λ)} > 0 και Im{ g 0 ( λ)} > 0, για να έχουμε φυσικά αποδεκτή λύση και στα δύο μη φραγμένα χωρία (, d) και ( h+ d, + ). Οι άγνωστοι φασματικοί συντελεστές Α (λ)-α 8 (λ) προσδιορίζονται παρακάτω με εφαρμογή των οριακών συνθηκών στις διαχωριστικές επιφάνειες x=±d, x=h±d. Τώρα εφαρμόζοντας τη μέθοδο Sommerfeld, συμπεραίνουμε ότι το συνολικό πεδίο εντός του κυματοδηγού είναι η υπέρθεση του πρωτογενούς και του δευτερογενούς πεδίου, και επιπλέον το συνολικό πεδίο εκτός του κυματοδηγού είναι το δευτερογενές πεδίο. Δηλαδή το συνολικό πεδίο G (x,z;x',z'), το οποίο επάγεται στη διάταξη από τη διέγερση J(x,z) της (3.9), δίνεται από Gsec( x, z; x, z ) + Gpr ( x, z; x, z ), x [ d, d] G ( x, z; x, z ) = (3.7) Gsec ( x, z; x, z ), x [ d, d] Οι εφαπτομενικές συνιστώσες Ε y και H z του ηλεκτρικού και του μαγνητικού πεδίου στα επίπεδα x=±d, x=h±d πρέπει να είναι συνεχείς. Βάσει της σχέσης (.54) για να είναι συνεχής η H z αρκεί E να είναι συνεχής η y, οπότε στην προκειμένη περίπτωση οι οριακές συνθήκες εκφράζονται x ως εξής 7
73 G ( xzx, ;, z ) = G ( xzx, ;, z ) + G ( dzx, ;, z ) sec x d sec ± x d pr G (, ;, ) (, ;, ) Gpr ( d, z; x, z ) sec x z x z Gsec x z x z = + x x ± x x d x d G ( x, z ; x, z ) G ( x, z ; x, z = ) ± sec x h d sec x h d Gsec ( x, z; x, z ) Gsec ( x, z; x, z ) = x x ± x h d x h d (3.8) Αντικαθιστώντας τις εκφράσεις (3.), (3.4) και (3.6) στις οριακές συνθήκες (3.8), λαμβάνουμε ένα 8 8 γραμμικό σύστημα ως προς τους αγνώστους συντελεστές Α (λ)-α 8 (λ). Για τη λύση του εν λόγω συστήματος θεωρούμε τις βοηθητικές συναρτήσεις P = P( g, g, d) = g cosh( g d) + g sinh( g d) e e o o 0 0 P = P( g, g, d) = g sinh( g d) + g cosh( g d) e e 0 0 Q = Q ( g, g, d) = g cosh( g d) g sinh( g d) o o 0 0 Q = Q ( g, g, d) = g cosh( g d) g sinh( g d) 0 0 K = ( QePo QoPe)/, ε = exp[ g0( h d)] όπου οι συναρτήσεις με δείκτες e και o είναι άρτιες (even) και περιττές (odd) συναρτήσεις του g. Παρατηρούμε ότι ισχύει ε 0, καθώς h (με g 0 και d σταθεροποιημένα), αφού Re{ g 0 } > 0. Οι συντελεστές Α -Α 8 προκύπτουν ως λύσεις του γραμμικού συστήματος (3.8) και είναι οι εξής: cosh( gx ) sinh( gx ) A( λ) = P 0 Pe PP o e Kε Pe Po cosh( gx ) sinh( gx ) ε + KQoQe + Qe Qo cosh( gx ) A( λ) = P0 Pe ( Po Pe) g( Po Pe K ε ) Pe ε cosh( gx ) + K Qe( QoPo + K) + g0gsinh( gx) Qe 73
74 sinh( gx ) A3( λ) = P0 Pe ( Po Pe) g( Po Pe K ε ) Po sinh( gx ) + Kε Qo( QePe K) + g0gcosh( gx ) Qo PP o e cosh( gx ) sinh( gx ) A4 ( λ) = ε + PP o e Kε Pe Po PP o e cosh( gx ) sinh( gx ) A5 ( λ) = ε + PP o e + Kε Pe Po A A cosh( ) sinh( ) PP o e g0 gx gx 6( λ) = ε + PP o e Kε Pe Po cosh( ) sinh( ) PP o e g0 gx gx 7( λ) = ε + PP o e Kε Pe Po PP o e g0g cosh( gx ) sinh( gx ) A8 ( λ) = ε + PP o e Kε Pe Po (3.9) Αντικαθιστώντας τους υπολογισθέντες συντελεστές (3.9) στην έκφραση (3.6) του δευτερογενούς πεδίου και χρησιμοποιώντας τις (3.) και (3.7), ευρίσκουμε το ηλεκτρικό πεδίο σε όλες τις περιοχές του χώρου + jλ ( z z ) λ 4π G ( x, z; x, z ) = d e δ ( λ, x, x ) (3.30) όπου 74
75 δ ( λ, xx, ) = PP o e Kε cosh( gx ) sinh( gx ) PP o e g0gε + exp[ g0 ( x h d )], x h+ d Pe Po cosh( gx ) sinh( gx ) cosh[ g( x h)] sinh[ g( x h)] Po Pg e 0ε +, h d x h+ d Pe Po Pe Po cosh( gx ) sinh( gx ) PP o e + [ PoPeexp[ g0( x d)] + Kε exp[ g0( x h+ d)] ], d x h d Pe P o 3 3 cosh( gx ) sinh( gx ) PP o e cosh( gx ) sinh( gx ) + Pe Po g Pe Po d x x d KQoQeP ope cosh( gx ) sinh( gx ) + ε +, g Qe Qo 3 3 PP o e cosh( gx ) sinh( gx ) g Pe Po d x x d KQoQeP ope cosh( gx ) sinh( gx ) cosh( gx ) sinh( gx ) + ε + +, g Qe Qo Pe Po cosh( gx ) sinh( gx ) PP o e Pe Po x d cosh( gx ) sinh( gx ) + KQoQeε + exp[ g0( x+ d)], Qe Qo (3.3) Παρατηρήσεις ) Η έκφραση (3.30) σε συνδυασμό με την (3.3) αναδεικνύει τη συμμετρία της συνάρτησης Green και εξυπηρετεί τη διατύπωση αναλυτικών εκφράσεων των στοιχείων του πίνακα της Μεθόδου των Ροπών, όπως αναλύεται στις επόμενες παραγράφους. Οι όροι cosh(g x) και cosh(g x ) αντιπροσωπεύουν άρτια κύματα και οι όροι sinh(g x) και sinh(g x ) περιττά κύματα ως προς τις μεταβλητές x και x. Εξάλλου, ιδιαίτερο ενδιαφέρον παρουσιάζουν οι πόλοι λ=β i της ολοκληρωτέας συνάρτησης στην (3.30), οι οποίοι είναι λύσεις της αλγεβρικής εξίσωσης ( P P Kε )( P P + Kε ) = 0 o e o e (3.3) Οι πόλοι λ=β i αντιστοιχούν στις σταθερές διάδοσης των κυματοδηγούμενων στη διάταξη των συζευγμένων κυματοδηγών επιφανειακών κυμάτων (surface waves) και αποτελούν ένα πεπερασμένο σύνολο πραγματικών αριθμών με n β / k n 0 i 0 75
76 Πιο συγκεκριμένα οι πόλοι λ=β e για τους οποίους ισχύει P o P e Kε=0 είναι οι σταθερές διάδοσης των κυματοδηγούμενων ΤΕ z άρτιων κυμάτων, ενώ οι πόλοι λ=β ο για τους οποίους ισχύει P o P e +Kε=0 είναι οι σταθερές διάδοσης των κυματοδηγούμενων ΤΕ z περιττών κυμάτων. ) Στην (3.3) δεν εμφανίζεται αυτοτελώς ο ανώμαλος όρος της συνάρτησης Green, ο οποίος αντιστοιχεί στο πρωτογενές πεδίο, που δίνεται από την (3.) (ή ισοδύναμα από την (3.3)). Η έκφραση της συνάρτησης Green ( ( ) ( ) ) j () G( x, z; x, z ) = H0 k0n x x + z z 4 για το χώρο εντός του κυματοδηγού, όπου + 4π + jλ ( z z ) dλe δ ( λ, x, x ), x d δ PP cosh( gx)cosh( gx ) sinh( gx)sinh( gx ) (3.33) Kε ( QP 0 o + K)cosh( gx )cosh( gx ) ( QP e e K)sinh( gx )sinh( gx ) + g + gg 0 cosh( gx )sinh( gx ) gg 0 sinh( gx )cosh( gx ) o e ( λ, xx, ) = ( Po Pe) PP o e Kε g Pe Po αποσαφηνίζει την επίδραση του πρωτογενούς πεδίου. Για το χώρο εκτός του κυματοδηγού (με x >d), όπου δεν υπάρχει πρωτογενές πεδίο, η συνάρτηση Green εξακολουθεί να δίνεται από τις (3.30) και (3.3). 3) Όπως αποδεικνύεται στο Παράρτημα Α, η συνάρτηση Green είναι συμμετρική ως προς τη διέγερση και την απόκριση. Η εν λόγω ιδιότητα προκύπτει και ως συνέπεια της (3.3), αφού εναλλάσσοντας το διάνυσμα παρατήρησης (x,z) με το διάνυσμα διέγερσης (x,z ) στο χώρο εντός του κυματοδηγού, από την (3.3) έπεται G ( x, z; x, z ) = G ( x, z ; x, z), d x, x d, z, z 4) Η (3.3) για h, οπότε ε 0, ανάγεται στην 76
77 cosh( gx ) sinh( gx ) + exp[ g0 ( x d )], x d Pe Po PP o e cosh( gx ) sinh( gx ) cosh( gx ) sinh( gx ) +, d x x d g Pe Po Pe Po δ( λ, xx, ) = PP o e cosh( gx ) sinh( gx ) cosh( gx ) sinh( gx ) +, d x x d g Pe Po Pe Po cosh( gx ) sinh( gx ) exp[ g0 ( x+ d )], x d Pe Po (3.34) Οι (3.30) και (3.34) εκφράζουν τη συνάρτηση Green του προβλήματος της μίας απομονωμένης διηλεκτρικής πλάκας (βλ. [70], (.65) και (.66)). 5) Το επαγόμενο ηλεκτρικό πεδίο διέγερσης με πυκνότητα ρεύματος J( xz, ) = δ( x x ) δ( z z ) yˆ, h d x h+ d, z jωμ 0 η οποία ευρίσκεται εντός του κυματοδηγού, υπολογίζεται από το αντίστοιχο πεδίο όπου η πηγή ευρίσκεται εντός του κυματοδηγού, αξιοποιώντας τη συμμετρία της διάταξης. Στην προκειμένη περίπτωση το πρωτογενές πεδίο εκφράζεται από τον τύπο (3.), ενώ το δευτερογενές πεδίο εκφράζεται ως ολοκλήρωμα Fourier + jλ ( z z ) = 4π G ( x, z; x, z ) dλe γ ( λ, x, x ) όπου A 8( λ)exp[ g0( λ)( x h d)], x> h+ d A 6( λ)cosh[ g( λ)( x h)] A 7( λ)sinh[ g( λ)( x h)], h d < x< h+ d h h γ( λ, xx, ) = A 4( λ)cosh[ g0( λ)( x )] + A 5( λ)sinh[ g0( λ)( x )], d < x< h d A ( λ)cosh( g( λ) x) A 3( λ)sinh( g( λ) x), d < x< d A ( λ)exp[ g0( λ)( x+ d)], x< d (3.35) Οι άγνωστοι φασματικοί συντελεστές A - A 8 στην (3.35) προσδιορίζονται από τους υπολογισθέντες συντελεστές A -A 8 του αρχικού προβλήματος μέσω των σχέσεων A ( x ) = A ( h x ), A ( x ) = A ( h x ), A ( x ) = A ( h x ), A ( x ) = A ( h x ) A ( x ) = A ( h x ), A ( x ) = A ( h x ), A ( x ) = A ( h x ), A ( x ) = A( h x ) (3.36)
78 Έτσι συνδυάζοντας τις (3.9) και (3.36) ευρίσκουμε PP o e g0g cosh( g( h x )) sinh( g( h x )) A ( λ) = ε + PP o e Kε Pe Po A A cosh( ( )) sinh( ( )) PP o e g0 g h x g h x ( λ) = ε + PP o e Kε Pe Po cosh( ( )) sinh( ( )) PP o e g0 g h x g h x 3( λ) = ε + PP o e Kε Pe Po PP o e cosh( g( h x )) sinh( g( h x )) A 4( λ) = ε + PP o e Kε Pe Po PP o e cosh( g( h x )) sinh( g( h x )) A 5( λ) = ε + PP o e + Kε Pe Po cosh( g( h x )) A 6( λ) = P0 Pe ( Po Pe) g( Po Pe K ε ) Pe cosh( g( h x )) + Kε Qe( QoPo + K) + g0gsinh( g( h x )) Qe sinh( g( h x )) A 7( λ) = P0 Pe ( Po Pe) g( Po Pe K ε ) Po sinh( g ( h x )) + Kε Qo( QePe K) + g0gcosh( g( h x)) Qo cosh( g( h x )) sinh( g( h x )) A 8( λ) = P 0 Pe PP o e Kε Pe Po cosh( g ( h x )) sinh( g ( h x )) + KQoQeε + Qe Qo (3.37) Αντικαθιστώντας τους υπολογισθέντες συντελεστές (3.37) στην έκφραση (3.35) του δευτερογενούς πεδίου και λαμβάνοντας υπόψη την έκφραση (3.) του πρωτογενούς πεδίου στο χώρο εντός του κυματοδηγού, ευρίσκουμε το ηλεκτρικό πεδίο σε όλες τις περιοχές του επιπέδου, όπου + jλ ( z z ) 4π G ( x, z; x, z ) = dλe δ ( λ, x, x ) (3.38) 78
79 δ ( λ, xx, ) = PP o e Kε cosh( g( h x )) sinh( g( h x )) PP 0 e + Pe Po x h+ d cosh( g( h x )) sinh( g( h x )) KQoQeε + exp[ g0( x h d)], Qe Qo 3 3 PP o e cosh( g( h x )) sinh( g( h x )) g Pe Po h d x x h+ d KPPQQ o e o e cosh( g( h x )) sinh( g( h x )) cosh( g( x h)) sinh( g( x h)) + ε +, g Qe Qo Pe P o 3 3 cosh( g( h x )) sinh( g( h x )) PP o e cosh( g( x h)) sinh( g( x h)) + + Pe Po g Pe Po h d x x h+ d KPo PeQQ o e cosh( g( x h)) sinh( g( x h)) + ε, g Qe Q o cosh( g( h x )) sinh( g( h x )) PP o e + [ PP o eexp( g0( x h+ d)) + Kε exp( g0( x d)) ], d x h d Pe Po cosh( g( h x )) sinh( g( h x )) cosh( gx ) sinh( gx ) PP o e g0ε + +, d x d Pe Po Pe Po cosh( g( h x )) sinh( g( h x )) PP o e g0gε + exp[ g0 ( x+ d )], x d Pe Po (3.39) 3.4. Ολοκληρωτική αναπαράσταση ηλεκτρικού πεδίου Θεωρούμε TE z πολωμένα ηλεκτρομαγνητικά κύματα, τα οποία διαδίδονται παράλληλα προς τον άξονα z στη διάταξη του Σχήματος 3. υπό την παρουσία του γνωστού προσπίπτοντος ηλεκτρικού πεδίου E 0 = Ψ 0 ( x, z) yˆ Αφού, όπως αναφέρθηκε στην παράγραφο.4, το άγνωστο κυματοδηγούμενο ηλεκτρικό πεδίο E = Ψ( x, z) yˆ έχει μόνο y συνιστώσα, η λύση του προβλήματος ανάγεται στον προσδιορισμό του άγνωστου βαθμωτού παράγοντα ηλεκτρικού πεδίου Ψ(x,z). Ο άγνωστος βαθμωτός παράγοντας Ψ του ηλεκτρικού πεδίου προσδιορίζεται υπό τις ακόλουθες προϋποθέσεις, οι οποίες υπαγορεύονται από τη φυσική και τη γεωμετρία του προβλήματος 79
80 Ψ είναι τμηματικά C συνάρτηση: C στα επίπεδα χωρία σταθερού δείκτη διάθλασης και C στα σύνορα των χωρίων αυτών. (και άρα η Ψ είναι τοπικά Riemann ολοκληρώσιμη συνάρτηση) Ψ L( ) L ( ) (απόλυτα και τετραγωνικά Lebesque ολοκληρώσιμη συνάρτηση του, βλ. Παράρτημα Β). Η Ψ αποτελεί λύση της εξισώσεως Helmholtz (B.0) στα χωρία σταθερού δείκτη διάθλασης. Σε όλα τα επόμενα υποθέτουμε (χωρίς ιδιαίτερη αναφορά) ότι η συνάρτηση Ψ ικανοποιεί τις προαναφερόμενες συνθήκες. Θεώρημα Ο βαθμωτός παράγοντας Ψ(x,z) του ηλεκτρικού πεδίου έχει την ολοκληρωτική αναπαράσταση Ψ ( xz, ) =Ψ ( xz, ) + k( n n) Ψ( x, z ) Gxzx (, ;, z ) ds, ( xz, ) (3.40) 0 0 S d όπου G είναι η συνάρτηση Green του ομογενούς (χωρίς γραμμοσειρές) προβλήματος και S d είναι η συνολική επιφάνεια των γραμμοσειρών. Απόδειξη Σύμφωνα με τα αναφερόμενα στο εδάφιο.3. η συνάρτηση Ψ(x,z) ικανοποιεί τη βαθμωτή εξίσωση Helmholtz ( ) + kn xz Ψ xz = xz (3.4) 0 (, ) (, ) 0, (, ) όπου n(x,z) η κατανομή του δείκτη διάθλασης, η οποία εκφράζεται από τον τύπο (3.). Επίσης η Ψ( x, z) Ψ(x,z) και η πληρούν τις κατάλληλες συνοριακές συνθήκες συνέχειας στις x διαχωριστικές επιφάνειες μεταβολής του δείκτη διάθλασης. Εξάλλου ο παράγοντας Ψ 0 (x,z) του προσπίπτοντος ηλεκτρικού πεδίου είναι λύση της βαθμωτής εξίσωσης Helmholtz όπου ( h ) + kn( x) Ψ ( xz, ) = 0, (3.4) 0 0 n0, x> h+ d n, h d < x< h+ d nh ( x) = n0, d < x< h d n, d < x< d n0, x< d 80
81 η κατανομή του δείκτη διάθλασης της ομογενούς (χωρίς γραμμοσειρές) διάταξης. Επίσης, η συνάρτηση Green G της διάταξης των δύο κυματοδηγών αποτελεί λύση της διαφορικής εξίσωσης (3.0). Στο Σχήμα 3.3 εμφανίζεται κατάλληλος διαχωρισμός της διάταξης του συζεύκτη γραμμοσειρών του Σχήματος 3., ο οποίος εξυπηρετεί την εφαρμογή των τύπων του Green. Ακριβέστερα θεωρούμε την ορθογώνια διαμέριση του επιπέδου L = [ x, x ] ( iλ,( i+)λ], i i, η οποία περιέχει την i-οστή επανάληψη των γραμμοσειρών στον άξονα κυματοδήγησης z της διάταξης. Επιπλέον k d i (k=,,5) και j a i, j b i (j=,,q) είναι τα επίπεδα χωρία της τομής του ορθογωνίου L i με την υπό μελέτη διάταξη του συζεύκτη. Ειδικότερα j a i και j b i, (j=,,q) είναι οι επιφάνειες των q ορθογωνίων της i-οστής επανάληψης των γραμμοσειρών στους κυματοδηγούς και αντίστοιχα. Σχήμα 3.3 Διαχωρισμός της διάταξης του συζεύκτη γραμμοσειρών από ορθογώνια 8
82 Εφαρμόζοντας τώρα το δεύτερο τύπο του Green (βλ. [50], (5.39)) για τις συναρτήσεις k j j Ψ Ψ 0 και G επάνω σε κάθε ένα από τα χωρία σταθερού δείκτη διάθλασης d 0 και a 0, b 0, τα οποία περιέχονται στο εσωτερικό του ορθογωνίου L 0, λαμβάνουμε M0 M 0 ( ( r) ( r) ) ( rr ; ) ( rr ; ) ( ( r) ( r) ) Ψ Ψ 0 G G Ψ Ψ 0 ds = r r ( ( ) ( )) ( ; ) ( ; ) ( ( ) ( )) Ψ r Ψ ˆ 0 r G G Ψ Ψ 0 dl r rr rr r r r ni (3.43) k j j όπου Μ = d 0 ή a 0 ή b 0. Αθροίζοντας τις (3.43) και λαμβάνοντας υπόψη ότι τα επικαμπύλια ολοκληρώματα αλληλοεξουδετερώνονται στα κοινά σύνορα των χωρίων, σύμφωνα με τα αναφερόμενα στο Παράρτημα Α, ευρίσκουμε d0 s0 L0 ( ( r ) ( r )) ( r; r ) ( r; r ) ( ( r ) ( r )) Ψ Ψ 0 G G Ψ Ψ 0 ds = r r ( ( ) ( )) ( ; ) ( ; ) ( ( ) ( )) Ψ r Ψ ˆ 0 r G G Ψ Ψ 0 dl r r r r r r r r ni I L0 (3.44) q q j j όπου s0 = a0 b0 j= j= είναι η συνολική επιφάνεια της βασικής επανάληψης των γραμμοσειρών των δύο κυματοδηγών και 5 j d0 d0 j = =. Όμως οι συναρτήσεις G, Ψ και Ψ 0 είναι λύσεις των διαφορικών εξισώσεων Helmholtz (3.0), (3.4) και (3.4) αντιστοίχως, οπότε από την (3.44) έχουμε 3 5 d0 d0 d0 ( Ψ( r) Ψ 0( r) )( 0 0 ( rr ; ) δ ( r r) ) ( rr ; )( 0 0Ψ( r) 0 0Ψ 0( r) ) kng G kn + kn ds + ( Ψ( r) Ψ 0( r) )( 0 ( rr ; ) δ ( r r) ) ( rr ; )( 0 Ψ( r) 0 Ψ 0( r) ) kng G kn + kn ds + 4 d0 d0 ( Ψ( r ) Ψ 0( r )) kng 0 ( r; r ) δ r r r r 0 r 0 0 r s0 ( ( )) G( ; )( k n Ψ( ) + k n Ψ ( )) ds = IL 0 (3.45) Μετά την εκτέλεση των πράξεων στις προς ολοκλήρωση συναρτήσεις παρατηρούμε ότι η (3.45) γράφεται 0 0 s0 d0 s0 ( ) δ 0 k ( n n ) Ψ( r ) G( r; r ) ds Ψ( r ) Ψ ( r ) ( r r ) ds = IL (3.46) Στη συνέχεια εφαρμόζοντας την ίδια διαδικασία στα ορθογώνια L i, (i=±, ±, ±3,...) ευρίσκουμε ( ) k ( n n ) Ψ( r ) G( r; r ) ds Ψ( r ) Ψ ( r ) δ ( r r ) ds = I (3.47) 0 0 si di si Li 8
83 όπου q q j j si = ai bi j= j= η συνολική επιφάνεια της i-οστής επανάληψης των γραμμοσειρών και 5 d i = d. Τώρα από τις (3.46) και (3.47), λαμβάνουμε j = j i ( ) Ψ( ) ( ; ) ( Ψ( ) Ψ0( )) δ ( ) = i= s i= i i di s = i k n n r G r r ds r r r r ds I (3.48) Για τον υπολογισμό των διπλών ολοκληρωμάτων επάνω στα εσωτερικά i Li d s των L i σκεφτόμαστε ως εξής. Το διάνυσμα παρατήρησης r θα ανήκει σε κάποιο ορθογώνιο L k, οπότε με βάση την ιδιότητα-ορισμό της συνάρτησης δέλτα, το διπλό ολοκλήρωμα πάνω σε αυτό θα είναι ίσο με Ψ(r) Ψ 0 (r), ενώ για κάθε άλλο ορθογώνιο L i, i k θα είναι ίσο με μηδέν. Επομένως η (3.48) ανάγεται στην Ψ( r) = Ψ () r + k ( n n ) Ψ( r ) G( r; r ) ds I (3.49) i= si Τέλος, επειδή τα επικαμπύλια ολοκληρώματα I L αθροιζόμενα, αλληλοεξουδετερώνονται i επάνω στην κοινή πλευρά των διαδοχικών ορθογωνίων L i, θα έχουμε + L i i= x= x x= x i= ( ( ) ( )) ( ; ) ( ; ) ( ( ) ( )) I = Ψ r Ψ ˆ 0 r G G Ψ Ψ 0 dl r rr rr r r r ni + ( ( ) ( )) ( ; ) ( ; ) ( ( ) ( )) Ψ r Ψ ˆ 0 r G G Ψ Ψ 0 dl r r r r r r r r n i I( x ) + I( x ) Όμως επαναλαμβάνοντας τη διαδικασία απόδειξης της συμμετρίας της συνάρτησης Green, η οποία περιγράφεται στο Παράρτημα Α, συμπεραίνουμε ότι lim I( x ) = 0, x x + Έτσι από τις (3.49) και (3.50) προκύπτει η ολοκληρωτική αναπαράσταση + 0 k0 n n G ds i= s i Ψ () r =Ψ () r + ( ) Ψ( r ) (; r r ), r Li lim I( x ) = 0 (3.50) της λύσης Ψ(r) του προβλήματος, η οποία οδηγεί στην (3.40) με βάση το ότι Sd = si είναι η συνολική επιφάνεια των άπειρων γραμμοσειρών. Σύμφωνα με την (3.40) ο παράγοντας Ψ(r) του ηλεκτρικού πεδίου στο τυχόν σημείο παρατήρησης r εκφράζεται ως άθροισμα του παράγοντα Ψ 0 (r) του προσπίπτοντος ηλεκτρικού πεδίου και του παράγοντα + i= i 83
84 Ψ () = ( ) Ψ( )G( ; ) ε r k0 n n r r r ds S d του επαγόμενου πεδίου λόγω της παρουσίας των γραμμοσειρών. Η φυσική ερμηνεία του παράγοντα Ψ ε (r) περιγράφεται ως εξής: Σύμφωνα με την ([70], (.)) η διαφορά του δείκτη διάθλασης n n στην περιοχή των γραμμοσειρών προκαλεί ένα ρεύμα μετατόπισης jωε ˆ 0( n n)ψ( ry ), r Sd Jε () r = 0, r Sd Όμως, επειδή η κρουστική ρευματική διέγερση (3.9) προκαλεί ηλεκτρικό πεδίο ίσο με G (; rr ), το ρεύμα μετατόπισης J ε (r), σύμφωνα με την αρχή της υπέρθεσης, προκαλεί τον παράγοντα ηλεκτρικού πεδίου Ψ ε (r) Επίλυση της ολοκληρωτικής εξίσωσης με τη μέθοδο Galerkin Για τη μελέτη των φαινομένων κυματοδήγησης στη διάταξη του συζεύκτη γραμμοσειρών υποθέτουμε ότι δεν υπάρχει προσπίπτον πεδίο ή οποιαδήποτε άλλη επιβαλλόμενη εξωτερικά διέγερση και αναζητούμε χρονικά αρμονικές λύσεις των εξισώσεων Maxwell, θεωρώντας τα ηλεκτρικά πεδία στην επιφάνεια των γραμμοσειρών σαν ισοδύναμα ρεύματα πόλωσης [74]. Θεωρώντας τη διαμέριση S = S S, όπου d d d S d και S d είναι οι συνολικές εγκάρσιες διατομές των γραμμοσειρών των κυματοδηγών και αντίστοιχα, παρατηρούμε ότι η ολοκληρωτική αναπαράσταση (3.40) ισοδύναμα γράφεται Ψ ( xz, ) = k0( n n) G( xzx, ;, z ) Ψ( x, z ) dxdz Sd + G( x, z; x, z ) Ψ( x, z ) dxdz, ( x, z) Sd (3.5) όπου G και G είναι οι συναρτήσεις Green, οι οποίες δίνονται από τις σχέσεις (3.30) και (3.38), και αντιστοιχούν σε διεγέρσεις που ευρίσκονται εντός των κυματοδηγών και και Ψ και Ψ είναι οι παράγοντες του ηλεκτρικού πεδίου στους κυματοδηγούς και. Σύμφωνα με τα αναφερόμενα στην παράγραφο 3., το ηλεκτρικό πεδίο ενός ρυθμού κυματοδήγησης με μιγαδική σταθερά διάδοσης γ καθορίζεται από τους τύπους (3.) και (3.3) του θεωρήματος Floquet και επομένως η ολοκληρωτική αναπαράσταση (3.5) αναδιατυπώνεται ως εξής 84
85 u( x, z) = k0( n n) G( x, z; x, z ) u( x, z )exp( γ ( z z )) dx dz Sd + G( x, z; x, z ) u( x, z )exp( γ ( z z )) dx dz Sd (3.5) όπου u(x,z), u (x,z) και u (x,z) είναι Λ-περιοδικές συναρτήσεις ως προς z. Σε όλα τα επόμενα για τη συνάρτηση u υποθέτουμε ότι ισχύουν οι προϋποθέσεις της Ψ (βλ. σελ. 79) και επιπλέον οι (Β.8) και (Β.9). Περιορίζοντας το διάνυσμα παρατήρησης (x,z) στην (3.5) σε κάθε ένα από τα επίπεδα χωρία ολοκλήρωσης, η ολοκληρωτική αναπαράσταση (3.5) οδηγεί σε δύο ολοκληρωτικές εξισώσεις για τους άγνωστους παράγοντες u (x,z) και u (x,z) στην επιφάνεια των γραμμοσειρών. Η τεχνική Galerkin συνολικού χώρου θα εφαρμοστεί στα επόμενα για τη λύση της (3.5). Η συνολική εγκάρσια διατομή S d των γραμμοσειρών εκφράζεται ως αριθμήσιμη ένωση + ( ) S = S S των διατομών d r r r= q r i i i i= S = [ d w, d] [ d + rλ, d + l + rλ] (3.53) q r i i i i= S = [ h d, h d + w] [ d + rλ, d + l + rλ] της r-οστής επανάληψης των γραμμοσειρών των κυματοδηγών και. Τώρα εκφράζοντας τις προαναφερόμενες συναρτήσεις Green G και G ως ολοκληρώματα Fourier μέσω των τύπων (3.30) και (3.38), διαπιστώνουμε ότι η ολοκληρωτική αναπαράσταση (3.5) εκφράζεται και ως εξής k0( n n) uxz (, ) = 4π + + dλexp[ jλ( z z )] δ( λ, x, x ) u( x, z )exp[ γ( z z)] dxdz r= Sr + + dλexp[ jλ( z z )] δ( λ, x, x ) u( x, z )exp[ γ( z z)] dxdz Sr (3.54) Εφαρμόζοντας τώρα το μετασχηματισμό ζ = z rλ, διαπιστώνουμε ότι τα διπλά ολοκληρώματα επάνω στις S r και ολοκληρώματα επάνω στις πρότυπες επαναλήψεις S r, τα οποία εμφανίζονται στον τύπο (3.54), ανάγονται σε S 0 και S 0, οι οποίες παριστούν την εγκάρσια 85
86 διατομή των γραμμοσειρών του κάθε κυματοδηγού στο διάστημα από z=0 έως z=λ και επομένως ο τύπος (3.54) ισοδύναμα γράφεται k0( n n) uxz (, ) = exp( γ z) 4π + + dλ exp( jλ( z ζ rλ )) δ( λ, x, x ) u( x, ζ + rλ)exp( γ( ζ + rλ)) dxd ζ r= S0 + + dλ exp( jλ( z ζ rλ )) δ( λ, x, x ) u( x, ζ + rλ)exp( γ( ζ + rλ)) dxd ζ S0 Λαμβάνοντας υπόψη την περιοδικότητα των συναρτήσεων u (x,z) και u (x,z) ως προς τη μεταβλητή z και εφαρμόζοντας τον κανόνα ολοκλήρωσης σειράς κατά όρους, διαπιστώνουμε ότι ισχύει k0( n n) uxz (, ) = exp( γ z) 4π + + u( x, ζ )exp( γζ ) exp( jλ( z ζ )) δ( λ, x, x ) exp( jrλ( λ + jγ )) dλ dxd ζ S r= u( x, ζ )exp( γζ ) exp( jλ( z ζ )) δ( λ, x, x ) exp( jrλ( λ+ jγ)) dλdx dζ S r= 0 (3.55) Στη συνέχεια εφαρμόζουμε τον τύπο του Poisson + + r j T f ( t pt) = F e p= T r= T όπου οι συναρτήσεις f και F αποτελούν ζεύγος μετασχηματισμού Fourier (βλ. [73], (4.8.8)), επιλέγοντας f(t)=δ(t) (οπότε F(t)=), t=λ+jγ και T = π. Έτσι ευρίσκουμε Λ + jrλ( j ) p e π γ λ + ( j π + = δ λ+ γ ) Λ Λ r= p= πrt (3.56) Συνδυάζοντας τώρα τις (3.55) και (3.56), λαμβάνουμε 86
87 k0( n n) uxz (, ) = exp( γ z) Λ + + π p u( x, ζ )exp( γζ ) exp( jλ( z ζ )) δ( λ, x, x ) δ ( λ + jγ ) dλdxd ζ p Λ S = π p + u( x, ζ )exp( γζ ) exp( jλ( z ζ )) δ ( λ, x, x ) δ ( λ + jγ ) dλdxd ζ S p= Λ 0 (3.57) Λαμβάνοντας υπόψη τη βασική ιδιότητα-ορισμό της γενικευμένης συνάρτησης Dirac δ + παρατηρούμε ότι η (3.57) ανάγεται g( λ) δ( λ λ ) dλ = g( λ ) 0 0 k0( n n) uxz (, ) = exp( γ z) Λ + π p π p u( x, ζ )exp( γζ ) exp[ ( γ + j )( z ζ )] δ( jγ +, x, x ) dxd ζ (3.58) p Λ Λ S = 0 π p π p + + u( x, ζ )exp( γζ ) exp[ ( γ + j )( z ζ )] δ ( jγ +, x, x ) dxd ζ p Λ Λ S = 0 Η τελευταία μετά την εκτέλεση των πράξεων στις προς ολοκλήρωση συναρτήσεις, αναδιατυπώνεται ως εξής k0( n n) uxz (, ) = Λ + π p π p π p exp( j z) u( x, )exp( j ) ( j, x, x) dxd p Λ ζ ζ δ γ + ζ = Λ Λ S0 π p π p ζ ζ δ γ ζ + u( x, )exp( j ) ( j +, x, x) dxd Λ Λ S0 (3.59) Περαιτέρω, οι συναρτήσεις u (x,ζ) και u (x,ζ), οι οποίες ορίζονται στις πρότυπες επαναλήψεις Fourier S 0 και, n n= S 0, υπό τις προϋποθέσεις της (Β.6), αναπτύσσονται ως προς ζ στις σειρές + + π n π n u ( x, ζ ) = ϕ ( x)exp( j ζ), u( x, ζ ) = ϕ, n( x)exp( j ζ) (3.60) Λ Λ όπου οι συντελεστές ϕ, ( x ) και ϕ, ( x ) είναι οι εγκάρσιες συνιστώσες των χωρικών n n n= αρμονικών. Υπό την ορολογία της Μεθόδου των Ροπών οι συναρτήσεις 87
88 [ Λ ] και ϕ [ π ζ ] ϕ, ( x )exp j n ( πn / ) ζ, ( x n )exp j ( n / Λ ) αναφέρονται ως συναρτήσεις ανάπτυξης (expansion functions). Εξάλλου, υπό τις φυσικές προϋποθέσεις (Β.9)-(Β.), λαμβάνοντας υπόψη την (3.7) οδηγούμαστε στις διαφορικές εξισώσεις όπου ϕ ( x) g ϕ ( x) = 0, d w x d, n, n, n ϕ ( x) g ϕ ( x) = 0, h d x h d + w, n, n, n πn πn gin, = gi jγ + = jγ + k0ni ( i= 0,,) Λ Λ / (3.6) (3.6) Ο προσδιορισμός των συναρτήσεων ϕ,n και ϕ,n επιτυγχάνεται με την ακόλουθη διαδικασία. Οι συναρτήσεις ϕ,n και ϕ,n εκφράζονται ως γραμμικοί συνδυασμοί των θεμελιωδών λύσεων των διαφορικών εξισώσεων (3.6) + w w ϕ, n( x) = cn exp g, n( x d + ) + cn exp g, n( x d+ ) + w w ϕ, n( x) = cn exp g, n( x h+ d ) + cn exp g, n( x h+ d ) (3.63) όπου c, c ± ± n n είναι προσδιοριστέοι συντελεστές. Στους γραμμικούς συνδυασμούς (3.63) οι θεμελιώδεις λύσεις εκφράζονται ως προς τους άξονες συμμετρίας των γραμμοσειρών x= d ( w/) του κυματοδηγού και x= h d + ( w/) του κυματοδηγού, διότι οι εκφράσεις αυτές οδηγούν σε μικρότερα ορίσματα των εκθετικών συναρτήσεων, και έτσι εξασφαλίζεται μεγαλύτερη ευστάθεια των αριθμητικών αποτελεσμάτων. Τώρα από τις (3.60) και (3.63) προκύπτει αμέσως ότι + + w w π n u( x, ζ ) = cn exp( g, n( x d + )) + cn exp( g, n( x d + )) exp( j ζ ) n= Λ + + w w π n u( x, ζ ) = cn exp( g, n( x h+ d )) + cn exp( g, n( x h+ d )) exp( j ζ ) n= Λ (3.64) 88
89 Συνδυάζοντας τώρα τις (3.59) και (3.64), εκφράζοντας τα διπλά ολοκληρώματα επάνω στις πρότυπες επαναλήψεις S 0 και S 0 ως αθροίσματα διπλών ολοκληρωμάτων επάνω στα ορθογώνια, τα οποία καθορίζονται από τις (3.53), και εφαρμόζοντας ολοκλήρωση σειράς κατά όρους, ευρίσκουμε + k0( n n) π p uxz (, ) = exp( j z) Λ p= Λ q di+ li d + + w w dζ dx cn exp( g, n( x d + )) + cn exp( g, n( x d + )) i n = di d w = π( p n) π p exp( j ζ ) δ( jγ +, x, x ) Λ Λ q di+ li h d+ w + + w + dζ dx w cn exp( g, n( x h+ d )) + cn exp( g, n( x h+ d )) i= di h d n= π( p n) π p exp( j ζ ) δ( jγ +, x, x ) Λ Λ + k0( n n) π p = exp( j z) Λ p= Λ q + di+ li d + w w dζ dx cn exp( g, n( x d + )) + cn exp( g, n( x d + )) n= i= di d w π( p n) π p exp( j ζ ) δ( jγ +, x, x ) Λ Λ q + di+ li h d+ w + w w + dζ dx cn exp( g, n( x h+ d )) + cn exp( g, n( x h+ d )) i= n= di h d π( p n) π p exp( j ζ ) δ( jγ +, x, x ) Λ Λ Περαιτέρω, παρατηρούμε ότι τα διπλά ολοκληρώματα, τα οποία εμφανίζονται στο δεύτερο μέλος της τελευταίας ισότητας, εκφράζονται ως γινόμενα απλών ολοκληρωμάτων (συναρτήσεων μιας μεταβλητής), και έτσι λαμβάνουμε 89
90 + k0( n n) π p uxz (, ) = exp( j z) p= Λ + q di+ l i π ( p n) exp( j ζ ) dζ n= Λ i= di Λ d + w π p cn exp( g, n( x d + )) δ( jγ +, x, x ) dx Λ d w d w π p + cn exp( g, n( x d + )) δ( jγ +, x, x ) dx d w Λ h d+ w + w π p + cn exp( g, n( x h+ d )) δ( jγ +, x, x ) dx h d Λ h d+ w w π p + cn exp( g, n( x h+ d )) δ( jγ +, x, x ) dx Λ h d (3.65) Όπως προκύπτει από τη μορφή του τελευταίου τύπου, ο παράγοντας u(x,z) σε κάθε περιοχή του επιπέδου εκφράζεται ως άθροισμα διπλής σειράς γινομένων δύο συναρτήσεων των γεωμετρικών χαρακτηριστικών των γραμμοσειρών. Περαιτέρω θεωρούμε την αδιάστατη συνάρτηση J :, q i i J exp [ j( π / ) ζ ] dζ = Λ ( ) (3.66) i= d + l Λ di η οποία εμπεριέχει τις πληροφορίες για τα γεωμετρικά χαρακτηριστικά των γραμμοσειρών στο διαμήκη άξονα z. Υπολογίζοντας το ολοκλήρωμα, ευρίσκουμε J q { exp[ j π ( di / Λ)] ( exp[ j π ( li / Λ)] )}, 0 jπ i= = q li, = 0 Λ i= (3.67) Όπως φαίνεται από την (3.67), οι τιμές J της συνάρτησης J εξαρτώνται μόνο από τις ανηγμένες (κανονικοποιημένες) τιμές di / Λ και li / Λ των d i και l i ως προς την περίοδο Λ της διάταξης. Επίσης, θεωρούμε τις συναρτήσεις d ± w π p Qnp ( x) = exp ± g, n( x d + ) δ( jγ +, x, x ) dx, x Λ d w (3.68) h d+ w ± w π p Qnp ( x) = exp ± g, n( x h+ d ) δ( jγ +, x, x ) dx, x Λ h d 90
91 οι οποίες εμπεριέχουν τις πληροφορίες για τα γεωμετρικά χαρακτηριστικά των γραμμοσειρών ± στον εγκάρσιο άξονα x. Ο αναλυτικός υπολογισμός των Q np ( x) βοήθεια των συναρτήσεων ± και Q np ( x) επιτυγχάνεται με τη d w p ε ( g, x) = exp[ g ( x d + )] δ ( jγ + π, x, x ) dx, x Λ d w (3.69) h d+ w w π p ε ( g, x) = exp[ g ( x h+ d )] δ ( jγ +, x, x ) dx, x Λ μέσω των οποίων οι συναρτήσεις h d Q ± np και Q ± np εκφράζονται ως εξής Q ( x) = ε ( ± g, x), ± np, n Q ( x) = ε ( ± g, x) (3.70) ± np, n Επειδή οι δ και δ εξαρτώνται από τη σχετική θέση διέγερσης και απόκρισης, τα ολοκληρώματα των συναρτήσεων που εμφανίζονται στα δεύτερα μέλη των (3.69) διασπώνται ως αθροίσματα d x = dx + dx d w x d, d w d x h d+ w x h d+ w dx = dx + dx h d h d x όπου σε καθένα προσθετέο χρησιμοποιούνται οι κατάλληλοι κλάδοι των δ και δ. Από τους δύο αυτούς τύπους με τη βοήθεια των εκφράσεων (3.3) και (3.39) των δ και δ υπολογίζουμε τα ολοκληρώματα της (3.69) και ευρίσκουμε 9
92 ε( g, x) = ( g g, p) ( Po Pe K ε ) w Pe( g, g, p, d) Po( g, g, p, d) PP o e g0, pg, pε exp( g ) + Pe( g0, p, g, p, d) Po( g0, p, g, p, d) w Pe( g, g, p, d w) Po( g, g, p, d w) exp( g ) + exp[ g0, p ( x h d)], Pe( g0, p, g, p, d) Po( g0, p, g, p, d) ( w Pe g, g, p, d) Po( g, g, p, d) PP o e g0, pε exp( g ) + Pe( g0, p, g, p, d) Po( g0, p, g, p, d) w Pe( g, g, p, d w) Po( g, g, p, d w) cosh[ g, p( x h)] sinh[ g, p( x h)] exp( g ) + +, Pe( g0, p, g, p, d) Po( g0, p, g, p, d) Pe Po w Pe( g, g, p, d) Po( g, g, p, d) PP o e exp( g ) + Pe( g0, p, g, p, d) Po( g0, p, g, p, d) w Pe( g, g, p, d w) Po( g, g, p, d w) exp( g ) + Pe( g0, p, g, p, d) Po( g0, p, g, p, d) { PP o eexp[ g0, p( x d)] + Kε exp[ g0, p( x h+ d)] }, w ( PP o e Kε )exp[ g( x d+ )] PP Pe( g, g, p, d) Po( g, g, p, d) o e w cosh( g, px) sinh( g, px) exp( g ) + g, p Pe( g0, p, g, p, d) Po( g0, p, g, p, d) Pe Po w Pe( g, g, p, d w) Po( g, g, p, d w) cosh( g, px) sinh( g, px) exp( g ) + Pe( g0, p, g, p, d) Po( g0, p, g, p, d) Pe P o KP P( e g, g, p, d opq e oq e w ) Po( g, g, p, d) cosh( g, px) sinh( g, px) + ε exp( g ) + + g, p Qe( g0, g, p, d) Qo( g0, p, g, p, d) Pe Po w Pe( g, g, p, d w) Po( g, g, p, d w) cosh( g, px) sinh( g, px) exp( g ) + +, Pe( g0, p, g, p, d) Po( g0, p, g, p, d) Qe Qo 3 3 PP e(,, p, ) o(,, p, ) o e w P g g d P g g d exp( g ) g, p Pe( g0, p, g, p, d) Po( g0, p, g, p, d) 3 3 PP Pe( g, g, p, d w) Po( g, g, p, d w) o e w exp( g ) g, p Pe( g0, p, g, p, d) Po( g0, p, g, p, d) KP ( e,, p, ) o(,, p, ) opq e oqe w P g g d P g g d + ε exp( g ) + g, p Qe( g0, p, g, p, d) Qo( g0, p, g, p, d) KP P( e g, g, p, d w) Po( g, g, p, d w) cosh( opq e oqe w g, px) sinh( g, px) ε exp( g ) + +, g, p Qe( g0, p, g, p, d) Qo( g0, p, g, p, d) Pe Po ( w Pe g, g, p, d) Po( g, g, p, d) PP 0 e exp( g ) Pe( g0, p, g, p, d) Po( g0, p, g, p, d) P( w e g, g, p, d w) Po( g, g, p, d w) PP 0 e exp( g ) Pe( g0, p, g, p, d) Po( g0, p, g, p, d) ( w Pe g, g, p, d) Po( g, g, p, d) + KQoQeε exp( g ) + Qe( g0, p, g, p, d) Qo( g0, p, g, p, d) P( w e g, g, p, d w) Po( g, g, p, d w) KQoQeε exp( g ) + exp[ g0, p ( x + d)], Qe( g0, p, g, p, d) Qo( g0, p, g, p, d) x h+ d h d x h+ d d x h d d w x d d x d w x d 9
93 ε ( g, x) = ( g g, p) ( Po Pe K ε ) w Pe( g, g, p, d) Po( g, g, p, d) PP 0 e exp( g ) Pe( g0, p, g, p, d) Po( g0, p, g, p, d) ( w Pe g, g, p, d w) Po( g, g, p, d w) PP 0 e exp( g ) Pe( g0, p, g, p, d) Po( g0, p, g, p, d) x h+ d ( w Pe g, g, p, d) Po( g, g, p, d) + KQoQeε exp( g ) + Qe( g0, p, g, p, d) Qo( g0, p, g, p, d) ( w Pe g, g, p, d w) Po( g, g, p, d w) KQoQeε exp( g ) + exp[ g0, p ( x h d)], Qe( g0, p, g, p, d) Qo( g0, p, g, p, d) 3 3 PP (,,, ) (,,, ) o e w Pe g g p d Po g g p d exp( g ) g, p Pe( g0, p, g, p, d) Po( g0, p, g, p, d) 3 3 PP Pe( g, g, p, d w) Po( g, g, p, d w) o e w exp( g ) g, p Pe( g0, p, g, p, d) Po( g0, p, g, p, d) h d + w x h+ d KPoPQ e oq ( e w Pe g, g, p, d) Po( g, g, p, d) + ε exp( g ) + g, p Qe( g0, p, g, p, d) Qo( g0, p, g, p, d) KP P( e g, g, p, d w) Po( g, g, p, d w) cosh( g, p( x h)) sinh( g opq e oqe w, p( x h)) ε exp( g ) +, g, p Qe( g0, p, g, p, d) Qo( g0, p, g, p, d) Pe Po w ( PP o e Kε )exp[ g( h x d+ )] 3 3 PP Pe( g, g, p, d) Po( g, g, p, d) cosh( g, p( x h)) sinh( g, p( x h)) o e w + exp( g ) g, p Pe( g0, p, g, p, d) Po( g0, p, g, p, d) Pe Po w Pe( g, g, p, d w) Po( g, g, p, d w) cosh( g, p( x h)) sinh( g, p( x h)) exp( g ) + + h d x h d + w Pe( g0, p, g, p, d) Po( g0, p, g, p, d) Pe Po KP P( e g, g, p, d) Po( g, g, p, d) opq e oq e w cosh( g, p( x h)) sinh( g, p( x h)) + ε exp( g ) + g, p Qe( g0, p, g, p, d) Qo( g0, p, g, p, d) Pe Po w Pe( g, g, p, d w) Po( g, g, p, d w) cosh( g, p( x h)) sinh( g, p( x h)) exp( g ) +, Pe( g0, p, g, p, d) Po( g0, p, g, p, d) Qe Qo w Pe( g, g, p, d) Po( g, g, p, d) PP o e exp( g ) + Pe( g0, p, g, p, d) Po( g0, p, g, p, d) w Pe( g, g, p, d w) Po( g, g, p, d w) exp( g ) + d x h d Pe( g0, p, g, p, d) Po( g0, p, g, p, d) { PP o eexp[ g0, p( x h+ d)] + Kε exp[ g0, p( x d)] }, ( w Pe g, g, p, d) Po( g, g, p, d) PPg o e 0, pε exp( g ) + Pe( g0, p, g, p, d) Po( g0, p, g, p, d) d x d w Pe( g, g, p, d w) Po( g, g, p, d w) cosh( g, px) sinh( g, px) exp( g ) + +, Pe( g0, p, g, p, d) Po( g0, p, g, p, d) Pe Po w Pe( g, g, p, d) Po( g, g, p, d) PPg o e 0, pg, pε exp( g ) + Pe( g0, p, g, p, d) Po( g0, p, g, p, d) x d w Pe( g, g, p, d w) Po( g, g, p, d w) exp( g ) + exp[ g0, p ( x+ d)], Pe( g0, p, g, p, d) Po( g0, p, g, p, d) 93
94 Λαμβάνοντας υπόψη τους ορισμούς (3.66) και (3.70) των συναρτήσεων J και παρατηρούμε ότι η (3.65) γράφεται ως εξής Q ± np, Q ± np, k0( n n) uxz (, ) = (3.7) + + π p Jp n exp( j z) cn Qnp ( x) + cn Qnp ( x) + cn Qnp ( x) + cn Qnp ( x), ( x, z) p= n= Λ Το διάνυσμα παρατήρησης (x,z) στην (3.7) ανήκει στον χώρο των αγνώστων συντελεστών n n. Όμως για τον προσδιορισμό ± c, c ± της (3.7) με τη μέθοδο Galerkin απαιτείται το διάνυσμα παρατήρησης να ευρίσκεται στην επιφάνεια των γραμμοσειρών. Υπό αυτή την προϋπόθεση διακρίνουμε τις ακόλουθες δύο περιπτώσεις Περίπτωση. Το διάνυσμα παρατήρησης (x,z) ανήκει στην επιφάνεια των γραμμοσειρών του κυματοδηγού, δηλαδή ( x, z) Sd. Στην περίπτωση αυτή σύμφωνα με την (3.60) η συνάρτηση u(x,z) αναπτύσσεται στη σειρά Fourier + π n uxz (, ) = ϕ, n( x)exp( j z), ( xz, ) S Λ n= όπου οι χωρικές αρμονικές συναρτήσεις ϕ, ( x ) προσδιορίζονται από την (3.63). Συνδυάζοντας τώρα το προηγούμενο ανάπτυγμα με την (3.7), λαμβάνουμε + n= π n k0( n n) ϕ, n( x)exp( j z) = Λ + + p= n= n π p J j z c Q x c Q x c Q x c Q x Λ p n exp( ) n np ( ) + n np ( ) + n np ( ) + n np ( ) d (3.7) Στη συνέχεια λαμβάνοντας τα εσωτερικά γινόμενα των δύο μελών της (3.7) με τις δοκιμαστικές συναρτήσεις (test functions) ευρίσκουμε w π m ± g x d + + j z x z S m Λ exp, m( ) exp, (, ) d, 94
95 + q + d rλ+ di+ li πn w πm ϕ ( x)exp( j z)exp ± g ( x d + ) exp( j z) dzdx =, n, m r= i= n= Λ d w rλ+ d Λ i + q + + d rλ+ di+ li k0( n n) p n n np n np n np n np r= i= n= p= d w rλ+ di J c Q ( x) c Q ( x) c Q ( x) c Q ( x) π p w πm exp( j z)exp ± g, m( x d + ) exp( j z) dzdx Λ Λ Επειδή οι προς ολοκλήρωση συναρτήσεις δύο μεταβλητών εκφράζονται ως γινόμενα συναρτήσεων μιας μεταβλητής, τα εμφανιζόμενα διπλά ολοκληρώματα εκφράζονται ως γινόμενα δύο απλών ολοκληρωμάτων και έτσι η τελευταία ισοδύναμα γράφεται + q + rλ+ di+ l i d π ( m n) w exp j z dz ϕ ( x)exp ± g ( x d + ) dx =, n, m r= i= n= rλ+ d Λ i d w + q + + rλ+ di+ li k0( n n) π ( m p) Jp n exp j z dz r= i= n= p= Λ rλ+ d i d d w w cn Qnp ( x) + cn Qnp ( x) + cn Qnp ( x) + cn Qnp ( x) exp ± g, m( x d + ) dx Για την μετατροπή των προηγουμένων διπλών ολοκληρωμάτων σε διπλά ολοκληρώματα επάνω στην πρότυπη επανάληψη + + S 0, εφαρμόζουμε το μετασχηματισμό ζ=z rλ και ευρίσκουμε q di+ li d π ( m n) w exp[ j πrm ( n)] exp j ζ dζ ϕ ( x)exp ± g ( x d+ ) dx =, n, m r= n= i= d Λ i d w q di+ li k0( n n) π ( m p) Jp nexp[ j πr( m p)] exp j ζ dζ r= p= n= i= Λ d i d w cn Qnp ( x) + cn Qnp ( x) + cn Qnp ( x) + cn Qnp ( x) exp ± g, m( x d + ) dx d w (3.73) Λαμβάνοντας υπόψη τον ορισμό (3.66) της συνάρτησης J και ότι exp[ j π r( m n)] =, παρατηρούμε ότι η (3.73) αναδιατυπώνεται ως εξής + + d w J ϕ ( x)exp ± g ( x d + ) dx = m n, n, m r= n= d w k0( n n) Jm pjp n r= p= n= d n np n np n np n np, m d w w c Q ( x) + c Q ( x) + c Q ( x) + c Q ( x) exp ± g ( x d + ) dx η δε τελευταία ισοδύναμα γράφεται 95
96 d w J ϕ ( x)exp ± g ( x d + ) dx + + m n, n, m r= n= d w k0( n n) + + p= n= J J m p p n d w cn Qnp ( x) + cn Qnp ( x) + cn Qnp ( x) + cn Qnp ( x) exp ± g, m( x d + ) dx = 0 d w Επειδή η ποσότητα εντός της αγκύλης είναι ανεξάρτητη του r, αυτή θα πρέπει να ισούται με το μηδέν, και άρα ισχύει η σχέση + d + + w k0( n n) Jm n ϕ, n( x)exp ± g, m( x d + ) dx Jm pj p n n= = d w p= n= d d w η οποία ισοδύναμα γράφεται w cn Qnp ( x) + cn Qnp ( x) + cn Qnp ( x) + cn Qnp ( x) exp ± g, m( x d + ) dx w J c exp g ( x d + ) exp ± g ( x d + ) dx + d + w m n n, n, m n= d w d w w + cn exp g, n( x d + ) exp ± g, m( x d + ) dx = d w + + d k0( n n) + + w Jm pjp n cn Qnp( x)exp ± g, m( x d + ) dx p= n= d w d d w + + n np, m n np, m d w d w w + c Q ( x)exp ± g ( x d + ) dx+ c Q ( x)exp ± g ( x d + ) dx d w + cn Qnp ( x)exp ± g, m( x d + ) dx d w (3.74) Περαιτέρω για τον υπολογισμό των ολοκληρωμάτων, τα οποία εμφανίζονται στην προηγουμένη σχέση, θεωρούμε τις μιγαδικές συναρτήσεις K ±±, τύπους Q ±± d ±± w mn, m, n d w και Q ±±, οι οποίες ορίζονται από τους w K = exp ± g ( x d + ) exp ± g ( x d + ) dx ( m, n ) (3.75) d i±± w i± mnp, m np d w Q = exp ± g ( x d + ) Q ( x) dx ( i =, ) ( m, n, p ) (3.76) 96
97 Ο πρώτος εκθέτης ± στα στοιχεία ±± K mn και i Q ±± mnp αντιστοιχεί στους όρους, w και ο δεύτερος εκθέτης στους όρους exp[ ± g, n( x d + )] και (3.68) με τις (3.75) και (3.76) λαμβάνουμε w exp[ ± g m( x d + )] i Q ± np. Τώρα συνδυάζοντας τις K ±± mn w g g ± ± = w, ± g, m ± g, n = 0 sinh ( ±, m ±, n), g, m g, n 0 w ( ± g, m ± g, n) Q = K + R + H Q ( ) ±± ±± ±± ±± mnp mn mnp mnp ( g, n g, p) ( g, n g, p) = ±± ±± mnp mnp ( g, n g, p) H (3.77) (3.78) (3.79) όπου R ±± mnp w ( gm± gn) 3 3 Po ( g0p, gp, d) Pe ( g0p, gp, d) = g p Po ( g0p, gp, d) Pe ( g0p, gp, d) K ( g0p, gp, d) ε ( gm gp) w ( ± gm± g ) n P e( gm, gp, d) Po( gm, gp, d) Pe( gn, gp, d) Po( gn, gp, d) e + Pe( g0p, gp, d) Po( g0p, gp, d) Pe( g0p, gp, d) Po( g0p, gp, d) w ( ± gm g ) n P( e gm, gp, d) Po( gm, gp, d) Pe( gn, gp, d w) Po( gn, gp, d w) e + Pe( g0p, gp, d) Po( g0p, gp, d) Pe( g0p, gp, d) Po( g0p, gp, d) e Pe( gm, gp, d w) Po( gm, gp, d w) Pe( gn, gp, d) Po( gn, gp, d) + Pe( g0p, gp, d) Po( g0p, gp, d) Pe( g0p, gp, d) Po( g0p, gp, d) w ( gm g ) n P( e gm, gp, d w) Po( gm, gp, d w) Pe( gn, gp, d w) Po( gn, gp, d w) + e + Pe( g0p, gp, d) Po( g0p, gp, d) Pe( g0p, gp, d) Po( g0p, gp, d) (3.80) 97
98 H w ( gm gn) K( g =, g, d) P( g, g, d) P( g, g, d) Q ( g, g, d) Q ( g, g, d) ±± 0p p o 0p p e 0p p o 0p p e 0p p mnp ε g p Po ( g0p, gp, d) Pe ( g0p, gp, d) K ( g0p, gp, d) ε ( gm gp) w ( ± gm± g ) n P( e gm, gp, d) Po( gm, gp, d) Pe( gn, gp, d) Po( gn, gp, d) e + + Pe( g0p, gp, d) Po( g0p, gp, d) Qe( g0p, gp, d) Qo( g0p, gp, d) w ( ± gm gn) P( e gm, gp, d) Po( gm, gp, d) Pe( gn, gp, d w) Po( gn, gp, d w) e + + Qe( g0p, gp, d) Qo( g0p, gp, d) Pe( g0p, gp, d) Po( g0p, gp, d) w ( gm± g ) n P( e gm, gp, d w) Po( gm, gp, d w) Pe( gn, gp, d) Po( gn, gp, d) e + + Pe( g0p, gp, d) Po( g0p, gp, d) Qe( g0p, gp, d) Qo( g0p, gp, d) + e H ±± mnp w ( gm ± gn ) Pe( gm, gp, d w) Po( gm, gp, d w) Pe( gn, gp, d w) Po( gn, gp, d w) + + Qe( g0p, gp, d) Qo( g0p, gp, d) Pe( g0p, gp, d) Po( g0p, gp, d) g0ppo ( g0p, gp, d) Pe ( g0p, gp, d) = ε Po ( g0p, gp, d) Pe ( g0p, gp, d) K ( g0p, gp, d) ε ( gm gp) w ( ± gm± g ) n P( e gm, gp, d) Po( gm, gp, d) Pe( ± gn, gp, d w) Po( ± gn, gp, d w) e + + Pe( g0p, gp, d) Po( g0p, gp, d) Pe( g0p, gp, d) Po( g0p, gp, d) w ( ± gm g ) n P( e gm, gp, d) Po( gm, gp, d) Pe( ± gn, gp, d) Po( ± gn, gp, d) e + + Pe( g0p, gp, d) Po( g0p, gp, d) Pe( g0p, gp, d) Po( g0p, gp, d) e (3.8) Pe( gm, gp, d w) Po( gm, gp, d w) Pe( ± gn, gp, d w) Po( ± gn, gp, d w) + + Pe( g0p, gp, d) Po( g0p, gp, d) Pe( g0p, gp, d) Po( g0p, gp, d) w ( gm g ) n P( e gm, gp, d w) Po( gm, gp, d w) Pe( ± gn, gp, d) Po( ± gn, gp, d) + e + + Pe( g0p, gp, d) Po( g0p, gp, d) Pe( g0p, gp, d) Po( g0p, gp, d) (3.8) Τέλος, συνδυάζοντας την (3.74) με τους ορισμούς (3.75) και (3.76), ευρίσκουμε + n= ±+ + ± ( ) J K c + K c = k ( n n ) + + p= n= m n mn n mn n 0 + ±+ ± + ±+ ± ( ) J J c Q + c Q + c Q + c Q ( m ) m p p n n mnp n mnp n mnp n mnp (3.83) Περίπτωση. Το διάνυσμα παρατήρησης (x,z) ανήκει στην επιφάνεια των γραμμοσειρών του κυματοδηγού, δηλαδή ( x, z) Sd. Στην προκειμένη περίπτωση, σύμφωνα με την (3.60), η συνάρτηση u(x,z) αναπτύσσεται ως προς z στη σειρά Fourier + π n uxz (, ) = ϕ, n( x)exp( j z), ( xz, ) S Λ n= όπου οι χωρικές αρμονικές συναρτήσεις ϕ, ( x ) προσδιορίζονται μέσω της (3.63). n d Συνδυάζοντας τώρα το εν λόγω ανάπτυγμα Fourier της u(x,z) με την (3.7), λαμβάνουμε 98
99 + π n k0( n n) ϕ ( x)exp( j z) = Λ π p J p n exp( j z) cn Qnp ( x) + cn Qnp ( x) + cn Qnp ( x) + cn Qnp ( x) Λ, n n= + + p= n= (3.84) Περαιτέρω, θεωρώντας τα εσωτερικά γινόμενα των δύο μελών της (3.84) με τις δοκιμαστικές συναρτήσεις ευρίσκουμε + q + w π m ± g x h+ d + j z x z S m Λ exp, m( ) exp, (, ) d, h d+ w rλ+ di+ li πn w πm ϕ ( x)exp( j z)exp ± g ( x h+ d ) exp( j z) dzdx=, n, m r= i= n= Λ h d rλ+ d Λ i + q + + h d+ w rλ+ di+ li k0( n n) p n n np n np n np n np r= i= n= p= h d rλ+ di J c Q ( x) c Q ( x) c Q ( x) c Q ( x) π p w πm exp( j z)exp ± g, m ( x h+ d ) exp( j z) dzdx Λ Λ Επαναλαμβάνοντας τη διαδικασία, την οποία περιγράψαμε για τη μελέτη της περίπτωσης, για τη μετατροπή των διπλών ολοκληρωμάτων σε ολοκληρώματα επάνω στην πρότυπη επανάληψη S 0, και εφαρμόζοντας το μετασχηματισμό ζ=z rλ, καταλήγουμε στη σχέση + h d+ w + w w Jm n cn exp g, n( x h+ d ) exp, m( ) ± g x h+ d dx = h d h d+ w w w + cn exp g, n( x h+ d ) exp g, m( x h d ) dx ± + = h d k n n x h d dx n + + h d+ w 0( ) + + w Jm pjp n cn Qnp( x)exp ± g, m ( + ) p= n= h d h d+ w h d+ w w + + n np, m n np, m h d h d h d+ w w cn Qnp ( x)exp g, m( x h d ) dx h d w + c Q ( x)exp ± g ( x h+ d ) dx+ c Q ( x)exp ± g ( x h+ d ) dx + ± + (3.85) Για τον υπολογισμό των ολοκληρωμάτων, τα οποία εμφανίζονται στην (3.85), θεωρούμε τις μιγαδικές συναρτήσεις K ±±, Q ±± και h d+ w ±± w mn, m, n h d Q ±±, οι οποίες ορίζονται από τους τύπους w K = exp ± g ( x h+ d ) exp ± g ( x h+ d ) dx ( m, n ) (3.86) 99
100 h d+ w i±± w i± mnp, m np h d Q = exp ± g ( x h+ d ) Q ( x) dx ( i=, ) ( m, n, p ) (3.87) όπου ο πρώτος εκθέτης ± στα στοιχεία ±± K mn και i Q ±± mnp αντιστοιχεί στους όρους w exp[ ( )] ± g, m x h+ d και ο δεύτερος εκθέτης στους όρους, n i Q ± np. Με τη βοήθεια των (3.77) και (3.86) επαληθεύεται εύκολα ότι ισχύει w exp[ ± g ( x h+ d )] και K = K ±± ±± mn mn Εξάλλου, συνδυάζοντας τις (3.68) με τις (3.87), ευρίσκουμε Q = ±± ±± mnp mnp ( g, n g, p) H Q = K + R + H ( ) ±± ±± ±± ±± mnp mn mnp mnp ( g, n g, p) ( g, n g, p) (3.88) (3.89) όπου R ±± mnp w ( g m g n) 3 3 Po ( g0p, gp, d) Pe ( g0p, gp, d) = g p Po ( g0p, gp, d) Pe ( g0p, gp, d) K ( g0p, gp, d) ε ( gm gp) w ( ± gm± g ) n P( e ± gm, gp, d w) Po( ± gm, gp, d w) Pe( ± gn, gp, d w) Po( ± gn, gp, d w) e + Pe( g0p, gp, d) Po( g0p, gp, d) Pe( g0p, gp, d) Po( g0p, gp, d) w ( ± gm g ) n P( e ± gm, gp, d w) Po( ± gm, gp, d w) Pe( ± gn, gp, d) Po( ± gn, gp, d) e + Pe( g0p, gp, d) Po( g0p, gp, d) Pe( g0p, gp, d) Po( g0p, gp, d) e ± Pe( ± gm, gp, d) Po( ± gm, gp, d) Pe( ± gn, gp, d w) Po( ± gn, gp, d w) + Pe( g0p, gp, d) Po( g0p, gp, d) Pe( g0p, gp, d) Po( g0p, gp, d) w ( gm g ) n P( e ± gm, gp, d) Po( ± gm, gp, d) Pe( ± gn, gp, d) Po( ± gn, gp, d) + e + Pe( g0p, gp, d) Po( g0p, gp, d) Pe( g0p, gp, d) Po( g0p, gp, d) (3.90) 00
101 H ±± mnp g0ppo ( g0p, gp, d) Pe ( g0p, gp, d) = ε Po ( g0p, gp, d) Pe ( g0p, gp, d) K ( g0p, gp, d) ε ( gm gp) w ( ± gm± g ) n P( e ± gm, gp, d w) Po( ± gm, gp, d w) Pe( gn, gp, d) Po( gn, gp, d) e + + Pe( g0p, gp, d) Po( g0p, gp, d) Pe( g0p, gp, d) Po( g0p, gp, d) w ( ± gm g ) n P ( e ± gm, gp, d w) Po( ± gm, gp, d w) Pe( gn, gp, d w) Po( gn, gp, d w) e + + Pe( g0p, gp, d) Po( g0p, gp, d) Pe( g0p, gp, d) Po( g0p, gp, d) e ± Pe( ± gm, gp, d) Po( ± gm, gp, d) Pe( gn, gp, d) Po( gn, gp, d) + + Pe( g0p, gp, d) Po( g0p, gp, d) Pe( g0p, gp, d) Po( g0p, gp, d) w ( gm gn) w ( gm g ) n P( e ± gm, gp, d) Po( ± gm, gp, d) Pe( gn, gp, d w) Po( gn, gp, d w) + e + + Pe( g0p, gp, d) Po( g0p, gp, d) Pe( g0p, gp, d) Po( g0p, gp, d) (3.9) H w ( gm gn) K( g =, g, d) P( g, g, d) P( g, g, d) Q ( g, g, d) Q ( g, g, d) ±± 0p p o 0p p e 0p p o 0p p e 0p p mnp ε g p Po ( g0p, gp, d) Pe ( g0p, gp, d) K ( g0p, gp, d) ε ( gm gp) w ( ± gm± g ) n P( e ± gm, gp, d w) Po( ± gm, gp, d w) Pe( ± gn, gp, d w) Po( ± gn, gp, d w) e + + Qe( g0p, gp, d) Qo( g0p, gp, d) Pe( g0p, gp, d) Po( g0p, gp, d) w ( ± gm gn) P( e ± gm, gp, d w) Po( ± gm, gp, d w) Pe( ± gn, gp, d) Po( ± gn, gp, d) e + + Pe( g0p, gp, d) Po( g0p, gp, d) Qe( g0p, gp, d) Qo( g0p, gp, d) w ( gm± g ) n P( e ± gm, gp, d) Po( ± gm, gp, d) Pe( ± gn, gp, d w) Po( ± gn, gp, d w) e + + Qe( g0p, gp, d) Qo( g0p, gp, d) Pe( g0p, gp, d) Po( g0p, gp, d) + e Pe( ± gm, gp, d) Po( ± gm, gp, d) Pe( ± gn, gp, d) Po( ± gn, gp, d) + + Pe( g0p, gp, d) Po( g0p, gp, d) Qe( g0p, gp, d) Qo( g0p, gp, d) (3.9) Τέλος, συνδυάζοντας την (3.85) με τους ορισμούς (3.86) και (3.87), ευρίσκουμε + n= ±+ + ± ( ) J K c + K c = k ( n n ) + + p= n= m n mn n mn n 0 + ±+ ± + ±+ ± ( ) J J c Q + c Q + c Q + c Q, m m p p n n mnp n mnp n mnp n mnp (3.93) Διαμόρφωση και επίλυση του γραμμικού συστήματος της μεθόδου Οι (3.83) και (3.93) αποτελούν ένα άπειρο τετραγωνικό ομογενές σύστημα συζευγμένων αλγεβρικών εξισώσεων ως προς τους αγνώστους συντελεστές c, c ( n ). Για την ± ± n n αριθμητική επίλυση του απείρου συστήματος θεωρούμε το truncated ομογενές γραμμικό σύστημα 8 N + 4 εξισώσεων ως προς τους 8 N + 4 αγνώστους c, c ( n= N,..., N), το οποίο ± ± n n προκύπτει λαμβάνοντας υπόψη τις χωρικές αρμονικές συναρτήσεις στα αναπτύγματα (3.60) και 0
102 τις δοκιμαστικές συναρτήσεις στα εσωτερικά γινόμενα με μέγιστη απόλυτη τάξη Ν. Το εν λόγω truncated σύστημα γράφεται υπό μορφή block πινάκων ως εξής A A A A A A A A + + A A A A A A A A + + c c c c + + = 0 ±± όπου A (, i j =,) είναι τετραγωνικοί (N + ) (N + ) πίνακες με στοιχεία ij k ( n n ) + ±± 0 ±± mn = Jm n + J m pjp n Kmn p= g, n g, p ( A ) + k0( n n) + J J R H + p= g, n g, p ±± ±± ( ) m p p n mnp mnp (3.94) + ±± k0( n n) ±± ( A ) mn = J m p J p n H mnp p= g, n g, p + ±± k0( n n) ±± ( A ) mn = J m p J p n H mnp p= g, n g, p (3.95) και k ( n n ) + ±± 0 ±± mn = Jm n + J m pjp n Kmn p= g, n g, p ( A ) ± ± c, c είναι τα (N + ) + k0( n n) + J J R H + p= g, n g, p ±± ±± ( ) m p p n mnp mnp διανύσματα των συντελεστών ± c, c ±. Σημειώνουμε ότι τα n n στοιχεία ij H ±± mnp αντιπροσωπεύουν τη σύζευξη μεταξύ των δύο κυματοδηγών και προσεγγίζουν το 0 καθώς h (ε 0), οδηγώντας σε αποσύζευξη (decoupling) του γραμμικού συστήματος (3.94). Όπως διαπιστώνεται εύκολα με τη βοήθεια των τύπων (3.80)-(3.8) και (3.90)-(3.9), υφίστανται οι εξής συμμετρίες K ±± = K, mn mn R ±± mnp = Rmnp, H ±± mnp = H mnp, Εξάλλου, συνδυάζοντας τις (3.95) και (3.96), προκύπτουν επίσης οι συμμετρίες A ±± = A, ±± = βάσει των οποίων το γραμμικό σύστημα (3.94) ισοδύναμα γράφεται H ±± mnp = Hmnp (3.96) A A (3.97) 0
103 A A A A A A A A A A A A A A A A c c c c + + = 0 (3.98) Οι συμμετρίες (3.97) απλουστεύουν ουσιαστικά την υπολογιστική πολυπλοκότητα του προβλήματος, καθώς απαιτείται πλέον μόνον ο υπολογισμός των 8 από τους 6 υποπίνακες, οι οποίοι απαρτίζουν τον πίνακα του γραμμικού συστήματος (3.94). Η απλούστευση αυτή είναι πολύ σημαντική, αφού το τυχόν στοιχείο του κάθε υποπίνακα εκφράζεται ως άθροισμα σειράς ως προς τη μεταβλητή p, και άρα ο αριθμός των αθροισμάτων των σειρών, που χρειάζεται να υπολογίσουμε αριθμητικά, είναι 8 (N+) αντί 6 (N+). Οι ρυθμοί, που είναι δυνατόν να κυματοδηγηθούν, αντιστοιχούν στις μη τετριμμένες λύσεις της (3.98), δηλαδή στις τιμές της παραμέτρου γ για τις οποίες ο αντίστοιχος πίνακας του γραμμικού συστήματος είναι ιδιάζων. Οι μη τετριμμένες λύσεις της (3.98) μπορούν στη συνέχεια να χρησιμοποιηθούν για τον υπολογισμό της κατανομής του ηλεκτρικού πεδίου των κυματοδηγούμενων ρυθμών μέσω της βασικής ολοκληρωτικής αναπαράστασης (3.5) Ειδικές περιπτώσεις συζευκτών γραμμοσειρών Μελέτες της κυματοδήγησης στις περιπτώσεις ) ενός απομονωμένου κυματοδηγού παρουσία γραμμοσειρών ) συζεύκτη παρουσία γραμμοσειρών στον άνω κυματοδηγό 3) συζεύκτη παρουσία γραμμοσειρών στον κάτω κυματοδηγό εμφανίζονται αυτοτελώς στη βιβλιογραφία σε κάθε περίπτωση (βλ. [75] και [76]). Στην εργασία αυτή οι τρεις παραπάνω περιπτώσεις μελετώνται ενοποιημένα ως ειδικές περιπτώσεις της γενικής μεθόδου, η οποία αναπτύσσεται στις παραγράφους
104 3.6.. Κυματοδήγηση σε έναν απομονωμένο κυματοδηγό παρουσία γραμμοσειρών Η διάταξη της περιπτώσεως αυτής απεικονίζεται στο παρακάτω σχήμα Σχήμα 3.4 Απομονωμένος κυματοδηγός παρουσία γραμμοσειρών Από τη γενική ολοκληρωτική αναπαράσταση (3.5) προκύπτει στην προκειμένη περίπτωση η ολοκληρωτική αναπαράσταση Ψ ( xz, ) = k( n n) Gxzx (, ;, z ) Ψ( x, z ) dxdz, ( xz, ) 0 S d του παράγοντα ηλεκτρικού πεδίου Ψ, όπου G είναι η συνάρτηση Green της μίας απομονωμένης διηλεκτρικής πλάκας, η οποία δίνεται από την (3.34), και S d είναι η συνολική επιφάνεια των γραμμοσειρών. Εξάλλου, το αντίστοιχο truncated γραμμικό σύστημα είναι το (4N + ) (4N + ) ομογενές γραμμικό σύστημα A A c + = A A c 0 (3.99) όπου ± ± c είναι τα (N + ) διανύσματα με συνιστώσες τους αγνώστους c ( n= N,..., N), οι n οποίοι εμφανίζονται στα αναπτύγματα Fourier (3.60), και ±± A οι (N ) (N ) + + πίνακες με στοιχεία k ( n n ) + ±± 0 ±± mn = Jm n + J m pjp n Kmn p= ( g, n g, p) ( A ) + k0( n n) ±± + J m pjp nrmnp p= ( g, n g, p) 04
105 όπου R ±± mnp w ( ± gm gn ) P( g, g, d) P( g, g, d) = o 0p p e 0p p g ( g g ) p m p w ( ± gm± g ) n P e( gm, gp, d) Po( gm, gp, d) Pe( gn, gp, d) Po( gn, gp, d) e + Pe( g0p, gp, d) Po( g0p, gp, d) Pe( g0p, gp, d) Po( g0p, gp, d) e Pe( gm, gp, d) Po( gm, gp, d) Pe( gn, gp, d w) Po( gn, gp, d w) + Pe( g0p, gp, d) Po( g0p, gp, d) Pe( g0p, gp, d) Po( g0p, gp, d) w ( gm± g ) n P( e gm, gp, d w) Po( gm, gp, d w) Pe( gn, gp, d) Po( gn, gp, d) e + Pe( g0p, gp, d) Po( g0p, gp, d) Pe( g0p, gp, d) Po( g0p, gp, d) w ( gm gn) P( e gm, gp, d w) Po( gm, gp, d w) Pe( gn, gp, d w) Po( gn, g p, d w) + e + Pe( g0p, gp, d) Po( g0p, gp, d) Pe( g0p, gp, d) Po( g0p, gp, d) Δηλαδή, τα blocks blocks ±± A του πίνακα του γραμμικού συστήματος (3.99) προκύπτουν από τα ±± A του πίνακα του γραμμικού συστήματος (3.98) για ε= Κυματοδήγηση σε συζεύκτη δύο παραλλήλων πλακών παρουσία γραμμοσειρών στην κάτω πλάκα Η διάταξη του εν λόγω συζεύκτη απεικονίζεται στο παρακάτω σχήμα Σχήμα 3.5 Συζεύκτης δύο παραλλήλων πλακών παρουσία γραμμοσειρών στην κάτω πλάκα 05
106 Στην προκειμένη περίπτωση η γενική ολοκληρωτική αναπαράσταση (3.5) εξειδικεύεται στην ολοκληρωτική αναπαράσταση Ψ ( x, z) = k ( n n ) G ( x, z; x, z ) Ψ( x, z ) dxdz, ( x, z) 0 S d του παράγοντα ηλεκτρικού πεδίου Ψ, όπου G είναι η συνάρτηση Green των δύο συζευγμένων πλακών, η οποία δίνεται από την (3.30) και αντιστοιχεί σε διέγερση εντός της πλάκας, και είναι η συνολική επιφάνεια των γραμμοσειρών. Εξάλλου, το αντίστοιχο truncated γραμμικό σύστημα είναι το (4N + ) (4N + ) ομογενές γραμμικό σύστημα S d A A c + = A A c 0 (3.00) όπου c ± ± είναι τα (N+) διανύσματα με συνιστώσες τους αγνώστους c ( n= N,..., N), οι οποίοι εμφανίζονται στα αναπτύγματα Fourier (3.60), και στοιχεία Δηλαδή, τα blocks + ±± 0 ±± mn = Jm n + J m pjp n Kmn p= ( g, n g, p) ( A ) k ( n n ) + k0( n n) + J m pjp n Rmnp+ Hmnp p= ( g, n g, p) ±± ±± ( ) n ±± A οι (N+) (N+) πίνακες με ±± A του πίνακα του γραμμικού συστήματος (3.00) είναι τα blocks πίνακα του γραμμικού συστήματος (3.95). ±± A του Κυματοδήγηση σε συζεύκτη δύο παραλλήλων πλακών παρουσία γραμμοσειρών στην άνω πλάκα Η διάταξη του εν λόγω συζεύκτη απεικονίζεται στο παρακάτω σχήμα 06
107 Σχήμα 3.6 Συζεύκτης δύο παραλλήλων πλακών παρουσία γραμμοσειρών στην άνω πλάκα Στην προκειμένη περίπτωση η γενική ολοκληρωτική αναπαράσταση (3.5) ανάγεται στην ολοκληρωτική αναπαράσταση Ψ ( x, z) = k ( n n ) G ( x, z; x, z ) Ψ( x, z ) dx dz, ( x, z) 0 S d όπου G είναι η συνάρτηση Green των δύο συζευγμένων πλακών, η οποία αντιστοιχεί σε διέγερση εντός της πλάκας και δίνεται από την (3.38). Εξάλλου, το αντίστοιχο truncated γραμμικό σύστημα είναι το όπου Δηλαδή, τα blocks A A c + = A A c + ±± 0 ±± mn = Jm n + J m pjp n Kmn p= ( g, n g, p) ( A ) k ( n n ) + k0( n n) + J m pjp n Rmnp+ Hmnp p= ( g, n g, p) 0 ±± ±± ( ) ±± A του πίνακα του γραμμικού συστήματος (3.0) είναι τα blocks πίνακα του γραμμικού συστήματος (3.98). (3.0) ±± A του 07
108 3.7. Αριθμητική υλοποίηση της μεθόδου Το ουσιαστικό τμήμα της αριθμητικής υλοποίησης μιας μεθόδου Galerkin συνολικού χώρου συνίσταται στον ακριβή και αποδοτικό προσδιορισμό των ριζών της ορίζουσας του πίνακα (3.98) μέσω μίας ρουτίνας εύρεσης ριζών μη γραμμικών εξισώσεων. Στην προτεινόμενη μέθοδο εφαρμόζεται η επαναληπτική μιγαδική μέθοδος Müller. Ο προσδιορισμός κατάλληλων αρχικών σημείων αυτής της μεθόδου επιτυγχάνεται με τη γραφική διαδικασία, η οποία αναλύεται παρακάτω. Όπως εξηγήσαμε στο εδάφιο.., οι κυματοδηγούμενοι βασικοί ρυθμοί του συμμετρικού συζεύκτη χωρίς γραμμοσειρές, ο οποίος απεικονίζεται στο Σχήμα 3., έχουν σχεδόν ίσες καθαρά φανταστικές σταθερές διάδοσης jn e και jn o. Υπό την παρουσία των γραμμοσειρών οι δύο βασικοί ρυθμοί εξελίσσονται σε δύο διαφορετικούς ρυθμούς γραμμοσειρών με μιγαδικές σταθερές διάδοσης γ e = αe + jβe, γ o = αo + jβo Εξάλλου, στην πράξη χρησιμοποιούνται συνήθως γραμμοσειρές, των οποίων οι σταθερές β e και β ο προσεγγίζουν τις N e και N o, ενώ οι τιμές των α e /k 0 και α ο /k 0 είναι της τάξης του 0-3 [5]. Οι κανονικοποιημένες σταθερές διάδοσης των ρυθμών γραμμοσειρών του συμμετρικού συζεύκτη είναι οι ρίζες της ορίζουσας του γραμμικού συστήματος (3.98) και υπολογίζονται εδώ με εφαρμογή της επαναληπτικής μιγαδικής μεθόδου Müller. Ο προσδιορισμός κατάλληλων αρχικών σημείων (initial points) επιτυγχάνεται με την ακόλουθη γραφική διαδικασία: Αρχικά, θεωρούμε καθαρά φανταστικές σταθερές διάδοσης γ=jβ με n β / k n 0 0 και σχεδιάζουμε τη γραφική παράσταση του μέτρου της ορίζουσας ως προς το κανονικοποιημένο φανταστικό μέρος β/k 0. Ένα τυπικό (ποιοτικό) διάγραμμα για μία ποικιλία δεικτών διάθλασης και γεωμετρικών χαρακτηριστικών των γραμμοσειρών δίνεται στο Σχήμα
109 Σχήμα 3.7 Τυπική καμπύλη του μέτρου της ορίζουσας ως προς το κανονικοποιημένο φανταστικό μέρος β/k 0 Το διάγραμμα έχει δύο τοπικά μέγιστα (συντονισμούς) στα φανταστικά μέρη N e /k 0 και N o /k 0 των σταθερών διάδοσης των ρυθμών στην ομογενή διάταξη των συζευγμένων κυματοδηγών και δύο τοπικά ελάχιστα στα φανταστικά μέρη β e /k 0 και β o /k 0 των σταθερών διάδοσης των κυματοδηγούμενων ρυθμών γραμμοσειρών. Οι δύο θέσεις συντονισμού jn e /k 0 και jn o /k 0 είναι οι ρίζες της συνάρτησης PP Kε, που εμφανίζεται ως παρανομαστής στην (3.3). Στη o e συνέχεια, ως αρχικά σημεία της μιγαδικής μεθόδου Müller μπορούμε να θεωρήσουμε τις ήδη γραφικά προσδιορισμένες τιμές των β e /k 0 και β o /k 0. Έτσι, εφαρμόζοντας τη μέθοδο Müller προσδιορίζουμε με ακρίβεια τις μιγαδικές σταθερές διάδοσης γ e /k 0 και γ o /k 0 των ρυθμών γραμμοσειρών. Στην περίπτωση που ο συζεύκτης γραμμοσειρών δεν διαφέρει σημαντικά από την ομογενή διάταξη των συζευγμένων κυματοδηγών, οι αποστάσεις (β e N e )/k 0 και (β o N o )/k 0 είναι πολύ μικρές. Συνεπώς, για να προσδιορίσουμε σωστά τα αρχικά σημεία β e /k 0 και β o /k 0, πρέπει να θεωρήσουμε μία πυκνή διαμέριση κοντά στις γνωστές τιμές N e /k 0 και N o /k Έλεγχος σύγκλισης, αποδοτικότητα και εγκυρότητα της μεθόδου Ο έλεγχος σύγκλισης συνίσταται στην καταγραφή των σχετικών διαφορών μεταξύ των διαδοχικών προσεγγίσεων των σταθερών διάδοσης, οι οποίες προκύπτουν από την εφαρμογή της 09
110 προτεινομένης μεθόδου, η οποία αναπτύχθηκε στις παραγράφους Υψηλή αποδοτικότητα της μεθόδου προκύπτει από την αξιολόγηση των αποτελεσμάτων του ελέγχου σύγκλισης, της επιτυγχανομένης ακρίβειας και του απαιτούμενου υπολογιστικού χρόνου και τη συσχέτισή τους με αντίστοιχα που έχουν εμφανιστεί στη βιβλιογραφία. Εξάλλου, η εγκυρότητα της μεθόδου επιβεβαιώνεται μετά από σύγκριση ορισμένων αριθμητικών αποτελεσμάτων της με αντίστοιχα γνωστά αποτελέσματα άλλων ερευνητών. Ακριβέστερα, θεωρούμε έναν απομονωμένο κυματοδηγό γραμμοσειρών (isolated grating slab) (βλ. Σχήμα 3. υπό την απουσία του κυματοδηγού ) με τις σταθερές τιμές του [75]: n 0 =, n =.36, k 0 d=, k 0 w=, k 0 Λ=4, q=, d =l =Λ/. Εφαρμόζοντας τις τεχνικές των παραγράφων , παρατηρούμε ότι η κανονικοποιημένη σταθερά διάδοσης του απομονωμένου κυματοδηγού γραμμοσειρών είναι η ρίζα της ορίζουσας του πίνακα του γραμμικού συστήματος (3.99). Σύμφωνα με τα αναφερόμενα στην παράγραφο 3.7 ο ακριβής υπολογισμός των ριζών της ορίζουσας επιτυγχάνεται με εφαρμογή της μιγαδικής μεθόδου Müller. Τα πρότυπα σύγκλισης της σταθεράς διάδοσης, τα οποία προκύπτουν με εφαρμογή της παρούσας μεθόδου και εκείνης της εργασίας [75] (χρησιμοποιώντας ανάλυσης γραμμών μεταφοράς) παρουσιάζονται στον Πίνακας 3.. Η σχετική διαφορά ανάμεσα στα τελικά πρότυπα, η οποία επιτυγχάνεται με τις δύο μεθόδους είναι μικρότερη από % και συνεπώς η συμφωνία μεταξύ των μεθόδων θεωρείται ικανοποιητική. Επιπροσθέτως, υψηλή ακρίβεια (της τάξης 0 6 ) της παρούσας μεθόδου επιτυγχάνεται θεωρώντας μόνο N=3 συντελεστές ανάπτυξης στην (3.60). Εξάλλου, οι μέθοδοι που βασίζονται στη θεωρία Floquet-Bloch [5] απαιτούν για επαρκή σύγκλιση χωρικές αρμονικές. Όμως, ο αριθμός όρων N=3 είναι πολύ μικρότερος από τον αντίστοιχο που απαιτείται στις τεχνικές ολοκληρωτικών εξισώσεων (βλ. [38] και [39]), οι οποίες χρησιμοποιούν συναρτήσεις βάσεις μερικού χώρου (sub domain basis functions) και την μέθοδο συνοριακών στοιχείων (boundary element method), όπου 500 συνοριακά στοιχεία απαιτούνται για σύγκλιση της σταθεράς διάδοσης σε τάξη 0 4. Αυτή η αποδοτικότητα της παρούσας τεχνικής οφείλεται στο ότι ο άγνωστος παράγοντας ηλεκτρικού πεδίου και οι όροι ανάπτυξης συνολικού χώρου πληρούν τους ίδιους φυσικούς νόμους. Επίσης, αφού η παρούσα μέθοδος επιτρέπει όλοι οι υπολογισμοί να γίνουν αναλυτικά, είναι πολύ αποδοτική σε όρους υπολογιστικού χρόνου (CPU time). Ακριβέστερα, 0.5 seconds (Pentium IV,.80 GHz με GByte RAM) επαρκούν για τον υπολογισμό της ορίζουσας του πίνακα του γραμμικού συστήματος. 0
111 Εργασία [75] Παρούσα μέθοδος N β/k 0 (β Ν β Ν )/β Ν a β/k 0 (β Ν β Ν )/β Ν a a Σχετική διαφορά μεταξύ των λύσεων για διαδοχικές τιμές του N. Πίνακας 3. Πρότυπο σύγκλισης της κανονικοποιημένης σταθεράς διάδοσης του απομονωμένου κυματοδηγού γραμμοσειρών.
112 ΚΕΦΑΛΑΙΟ 4 ΚΕΦΑΛΑΙΟ 4. ΑΝΑΛΥΣΗ ΑΣΥΜΜΕΤΡΙΚΩΝ ΚΥΜΑΤΟΔΗΓΩΝ ΜΕ ΓΡΑΜΜΟΣΕΙΡΕΣ Στο Κεφάλαιο 3 η διάταξη του συζεύκτη γραμμοσειρών αποτελείται από δύο παράλληλες διηλεκτρικές πλάκες (slab waveguides) με τα ίδια φυσικά και γεωμετρικά χαρακτηριστικά και ο χώρος εκτός των πλακών έχει σταθερό δείκτη διάθλασης (συμμετρικός συζεύκτης). Στο παρόν Κεφάλαιο μελετώνται τα φαινόμενα κυματοδήγησης σε ασυμμετρικό συζεύκτη γραμμοσειρών, ο οποίος αποτελείται από δύο κυματοδηγούς με διαφορετικά φυσικά και γεωμετρικά χαρακτηριστικά, ενώ τα στρώματα εκτός των κυματοδηγών έχουν διαφορετικούς δείκτες διάθλασης. Η χρησιμοποιούμενη γενική μεθοδολογία συνίσταται στη εφαρμογή της Μεθόδου των Ροπών, η οποία οδηγεί σε ολοκληρωτική εξίσωση που επιλύεται με τη βοήθεια τεχνικών Galerkin συνολικού χώρου. Ακριβέστερα, στην παράγραφο 4. περιγράφεται η γεωμετρία της διάταξης δύο συζευγμένων δισδιάστατων ασυμμετρικών πλακών με περιοδικά χαραγμένες γραμμοσειρές. Στην παράγραφο 4. επιτυγχάνεται αναλυτική έκφραση μέσω ολοκληρώματος Fourier της συνάρτησης Green του ομογενούς (χωρίς γραμμοσειρές) προβλήματος. Στην παράγραφο 4.3 αναπτύσσεται η γενική μεθοδολογία και στην παράγραφο 4.4 διερευνώνται ο έλεγχος σύγκλισης, η υψηλή αποδοτικότητα και η εγκυρότητα της μεθόδου.
113 4.. Ασυμμετρικός συζεύκτης γραμμοσειρών Η γεωμετρική διάταξη του ασυμμετρικού κατευθυντικού συζεύκτη γραμμοσειρών, η οποία απεικονίζεται στο Σχήμα 4., αποτελείται από δύο ανόμοιες άπειρες επίπεδες και παράλληλες διηλεκτρικές πλάκες με δείκτες διάθλασης n και n 4, πάχη d και d 4 και απόσταση μεταξύ τους d 3. Εξάλλου, τα επίπεδα χωρία υπεράνω, μεταξύ και κάτω από τις πλάκες υποτίθενται ομογενή με δείκτες διάθλασης n, n 3 και n 5 αντιστοίχως. Επιπλέον, κατά μήκος των πλακών έχουν χαραχθεί περιοδικά ορθογώνιες γραμμοσειρές με δείκτες διάθλασης n 6 και n 7, πάχη w και w, μήκη l i και s i και αποστάσεις από τον x-άξονα b i και a i (i=,,t), οι οποίες αποτελούν μία Λ- περιοδική δομή κατά μήκος του άξονα κυματοδήγησης z. Η όλη διάταξη έχει σταθερή μαγνητική διαπερατότητα μ=μ 0 και υποτίθεται ομοιόμορφη κατά μήκος του y-άξονα. Έτσι, η κατανομή του δείκτη διάθλασης της διάταξης του Σχήματος 4. προσδιορίζεται από την περιοδική επέκταση ως προς το z της κλιμακωτής συνάρτησης n(x,z), η οποία ορίζεται στο (, + ) [0, Λ ] ως εξής n, x > d3 + d, z [0, Λ] n, d3 < x < d3 + d, z [ bi, bi + li] n6, d3 < x < d3 + w, z [ bi, bi + li] nxz (, ) = n3, d3 < x< d3, z [0, Λ] n7, d3 w < x< d3, z [ ai, ai + si] n4, d3 d4 < x< d3, z [ ai, ai + si] n5, x < d3 d4, z [0, Λ] (4.) Αξίζει να σημειώσουμε ότι στη βιβλιογραφία έχουν θεωρηθεί έως τώρα μόνο δυαδικές γραμμοσειρές (με ένα ορθογώνιο ανά επανάληψη) [8]-[9]. Στην παρούσα διατριβή το πλήθος t και οι γεωμετρικές διαστάσεις l i, s i των ορθογωνίων εντός κάθε επανάληψης των γραμμοσειρών μπορούν να επιλεχθούν αυθαίρετα. Σε όλα τα επόμενα προϋποτίθεται και καταπιέζεται η χρονική αρμονική εξάρτηση exp(jωt) των πεδιακών μεγεθών. 3
114 Σχήμα 4. Γεωμετρία του ασυμμετρικού συζεύκτη γραμμοσειρών 4
115 4.. Συνάρτηση Green της ομογενούς διάταξης Η διερεύνηση των φαινομένων κυματοδήγησης ΤΕ z πολωμένων ηλεκτρομαγνητικών κυμάτων στη διάταξη του συζεύκτη του Σχήματος 4. με εφαρμογή της Μεθόδου των Ροπών προϋποθέτει κατάλληλη αναλυτική έκφραση της συνάρτησης Green του ομογενούς (χωρίς γραμμοσειρές) προβλήματος. Για το σκοπό αυτό, θεωρούμε την περίπτωση όπου η ομογενής διάταξη των δύο συζευγμένων κυματοδηγών του Σχήματος 4. διεγείρεται από μία διδιάστατη, άπειρη κατά μήκος του y-άξονα, γραμμική ηλεκτρική ρευματική πηγή με κανονικοποιημένη πυκνότητα ρεύματος J( xz, ) = δ( x x ) δ( z z ) yˆ, d3 d4 x d3, z (4.) jωμ 0 όπου (x,z ) η θέση, στην οποία εφαρμόζεται η διέγερση, και η οποία ευρίσκεται εντός του κυματοδηγού. Σχήμα 4. Γεωμετρία του ομογενούς (χωρίς γραμμοσειρές) προβλήματος Σύμφωνα με τα αναφερόμενα στην παράγραφο 3.3, ως συνάρτηση Green G ( x, z; x, z ) ορίζεται το ηλεκτρικό πεδίο E y (x,z), το οποίο παράγεται στη διάταξη από τη ρευματική πηγή J(x,z) της (4.) και αποτελεί λύση της διαφορικής εξίσωσης Helmholtz ( h ) + k n ( x) G ( rr ; ) = δ ( r r ) 0 5
116 όπου η τμηματικά σταθερή συνάρτηση n, x> d3+ d n, d3 < x< d3+ d nh ( x) = n3, d3 < x< d3 n, d d < x< d n5, x< d3 d εκφράζει την κατανομή του δείκτη διάθλασης της διάταξης των συζευγμένων κυματοδηγών. Επιπλέον, οι συναρτήσεις G (; rr ) και G( rr ; ) x απαιτείται να ικανοποιούν τις κατάλληλες συνοριακές συνθήκες συνέχειας (.9) και (.) στις διαχωριστικές επιφάνειες x=d 3 +d, x=±d 3 και x= d 3 d 4 μεταβολής του δείκτη διάθλασης. Η συνάρτηση Green εκφράζεται αναλυτικά ως κατάλληλο Fourier ολοκλήρωμα με εφαρμογή της μεθόδου Sommerfeld, την οποία συνοψίσαμε στην παράγραφο 3.3. Το πρωτογενές πεδίο G pr, το οποίο παράγεται από τη ρευματική πηγή (4.) υπό την απουσία των δύο κυματοδηγών και την προϋπόθεση ότι ο είναι γεμάτος με το υλικό του κυματοδηγού, εκφράζεται ως το ολοκλήρωμα Fourier (βλ. [70], (.60)) όπου + g4 ( λ ) x x jλ ( z z ) e Gpr ( x, z; x, z ) = dλ e, ( x, z) 4 π (4.3) g ( λ) ( λ ) / 0 i g ( λ) = k n ( i =,...,5) (4.4) i το δε πρόσημο της συνάρτησης g 4 (λ) επιλέγεται έτσι, ώστε Re{ g4( λ )} > 0 και Im{ g4( λ )} > 0 (βλ. και παράγραφο 3.3). Το δευτερογενές πεδίο G sec, το επαγόμενο στην διάταξη των συζευγμένων κυματοδηγών, το οποίο οφείλεται στις ασυνέχειες της κατανομής του δείκτη διάθλασης στα επίπεδα x=d 3 +d, x=±d 3 και x= d 3 d 4, εκφράζεται σε κάθε μία από τις πέντε περιοχές του επιπέδου ως ολοκλήρωμα Fourier + jλ ( z z ) (, ;, sec ) λ γ( λ,, ) 4π G x z x z = d e x x (4.5) Η προσδιοριστέα φασματική συνάρτηση γ, η οποία αποτελεί λύση της διαφορικής εξίσωσης γ( λ, xx, ) [ λ kn 0 h ( x)] γ( λ, xx, ) = 0 x εκφράζεται ως γραμμικός συνδυασμός των θεμελιωδών λύσεων αυτής 4 (4.6) 6
117 A( λ)exp[ g( x d3 d)], x d3+ d d d A( λ)cosh g( x d3 ) 3( )sinh ( 3 ), A λ g x d d x d + d γ( λ, xx, ) = A4( λ)exp( gx 3 ) + A5( λ)exp( gx 3 ), d3 x d3 d4 d4 A6( λ)cosh g4( x+ d3+ ) + A7( λ)sinh g4( x+ d3+ ), d d x d A8( λ)exp[ g5( x+ d3 + d4)], x d3 d Για να προκύπτει φυσικά αποδεκτή λύση στα μη φραγμένα χωρία (, d3 d4) και ( d + d, + ), επιλέγεται το πρόσημο των συναρτήσεων g και g 5 έτσι ώστε 3 Re{ g( λ )} > 0, Im{ g( λ )} > 0, Re{ g5( λ )} > 0 και Im{ g5( λ )} > 0 Οι άγνωστοι φασματικοί συντελεστές Α (λ)-α 8 (λ) προσδιορίζονται παρακάτω με εφαρμογή των οριακών συνθηκών στις διαχωριστικές επιφάνειες. Εφαρμόζοντας τώρα τη μέθοδο Sommerfeld, ευρίσκουμε το συνολικό πεδίο Gsec ( x, z; x, z ), x d3 G ( x, z; x, z ) = Gpr ( x, z; x, z ) + Gsec ( x, z; x, z ), d3 d4 x d3 (4.8) Gsec ( x, z; x, z ), x d4 το επαγόμενο στη διάταξη από τη διέγερση J της (4.). (4.7) Εφαρμόζοντας τις συνοριακές συνθήκες συνέχειας στα επίπεδα x = d3 + d, x =± d3 και x = d3 d4, λαμβάνουμε ένα 8 8 γραμμικό σύστημα με αγνώστους τους συντελεστές Α -Α 8. Για τη λύση του εν λόγω συστήματος θεωρούμε τις βοηθητικές συναρτήσεις d d Pe ( f, g, d) = f cosh g + gsinh g d d, Po ( f, g, d) = gcosh g + f sinh g d d d d Qe ( f, g, d) = f cosh g gsinh g, Qo ( f, g, d) = gcosh g f sinh g Qe( e, g, dp ) o( f, g, d) Qo( e, g, dp ) e( f, g, d) Kef (,, gd, ) =, Pe( egdp,, ) o( f, gd, ) + Po( egdp,, ) e( f, gd, ) Λ ( e, f, g, d) =, ε = exp ( g d ) 3 3 όπου οι δείκτες e και o δηλώνουν άρτιες (even) και περιττές (odd) συναρτήσεις του g. Εξάλλου, επιλέγοντας Re{ g 3} > 0, παρατηρούμε ότι ισχύει lim ε = 0. Περαιτέρω, υπολογίζοντας αναλυτικά τις λύσεις Α -Α 8 του γραμμικού συστήματος και αντικαθιστώντας τις εκφράσεις τους στην ολοκληρωτική παράσταση (4.5) του δευτερογενούς πεδίου, με τη βοήθεια των (4.3) και (4.8) ευρίσκουμε το ηλεκτρικό πεδίο σε όλες τις περιοχές του χώρου d3,, 7
118 όπου + jλ ( z z ) λ 4π G ( x, z; x, z ) = d e δ ( λ, x, x ) (4.9) δ( λ, x, x ) = [ Λ( g3, g5, g4, d4) Λ( g, g3, g, d) K( g3, g5, g4, d4) K( g3, g, g, d) ε ] d4 d4 cosh g4( x + d3+ ) sinh g4( x + d3 + ) ε g3gpo( g5, g4, d4) Pe( g5, g4, d4) + exp [ g( x d3 d), ] x d3+ d Pe( g5, g4, d4) Po( g5, g4, d4) Po( g, g, d) Pe( g, g, d) Po( g5, g4, d4) Pe( g5, g4, d4) g3ε d4 d4 d d cosh g4( x d3 ) sinh g4( x d3 + ) cosh g( x d3 ) sinh g( x d3 ) +, Pe( g5, g4, d4) Po( g5, g4, d4) Pe( g, g, d) Po ( g, g, d) d x d + d { Λ + + ε } 3 3 ( g3, g, g, d)exp[ g3( x d3)] K( g3, g, g, d)exp[ g3( x d3)] Po( g5, g4, d4) Pe( g5, g4, d4) d4 d4 cosh g4( x + d3+ ) sinh g4( x + d3 + ) d3 x d3 +, Pe( g5, g4, d4) Po( g5, g4, d4) ( g4) K( g3, g, g, d) Qe( g3, g4, d4) Pe( g5, g4, d4) Qo( g3, g4, d4) Po( g5, g4, d4) ε d4 d4 d4 cosh g4( x d3 ) sinh g4( x d d3+ ) cosh g4( x+ d3+ ) sinh g4( x+ d3 + ) + + Pe( g5, g4, d4) Po( g5, g4, d4) Qe( g3, g4, d4) Qo ( g3, g4, d4) + ( g4) Λ( g, g3, g, d) Pe( g3, g4, d4) Pe( g5, g4, d4) Po( g5, g4, d4) Po( g3, g4, d4) d d x x d d4 d4 cosh g4( x d3 ) sinh g4( x d4 d d3+ ) cosh g4( x+ d3+ ) sinh g4( x+ d3 + ) +, Pe( g5, g4, d4) Po( g5, g4, d4) Pe( g3, g4, d4) Po( g3, g4, d4) ( g4) K( g3, g, g, d) Qe( g3, g4, d4) Pe( g5, g4, d4) Qo( g3, g4, d4) Po( g5, g4, d4) ε d cosh g4( x d d d + d3+ ) sinh g ( x + d + ) cosh ( ) sinh ( ) g x+ d + g x+ d Qe( g3, g4, d4) Qo( g3, g4, d4) Pe( g5, g4, d4) Po( g5, g4, d4) + ( g4) Λ( g, g3, g, d) Pe( g3, g4, d4) Pe( g5, g4, d4) Po( g5, g4, d4) Po ( g3, g4, d4) d4 d4 d4 d4 cosh g4( x + d3+ ) sinh 4( 3 ) cosh 4( 3 ) sinh 4( 3 ) g x + d + g x d g x d , Pe( g3, g4, d4) Po( g3, g4, d4) Pe( g5, g4, d4) Po( g5, g4, d4) d4 d4 cosh g4( x + d3+ ) sinh g4( x + d3 + ) K( g3, g, g, d) Qo( g3, g4, d4) Qe( g3, g4, d4) ε + exp[ g5( x+ d3+ d4)] Qe( g3, g4, d4) Qo( g3, g4, d4) d4 cosh g4( x d4 + d3+ ) sinh g4( x d3 ) + + +Λ( g, g3, g, d) Po( g3, g4, d4) Pe( g3, g4, d4) exp[ g5( x+ d3+ d4)], Pe( g3, g4, d4) Po( g3, g4, d4) d d x x d x d d 3 4 (4.0) 8
119 Παρατηρήσεις ) Η έκφραση (4.9) της συνάρτησης Green σε συνδυασμό με την (4.0) εξυπηρετεί τις διατυπώσεις αναλυτικών εκφράσεων των στοιχείων του πίνακα της Μεθόδου των Ροπών. Εξάλλου, ιδιαίτερο ενδιαφέρον παρουσιάζουν οι πόλοι λ=±β i της ολοκληρωτέας συνάρτησης στην (4.9), οι οποίοι είναι λύσεις της αλγεβρικής εξίσωσης Λ g g g d Λ g g g d K g g g d K g g g d ε = (4.) ( 3, 5, 4, 4) (, 3,, ) ( 3, 5, 4, 4) ( 3,,, ) 0 Οι πόλοι λ=±β i αντιστοιχούν στις σταθερές διάδοσης των κυματοδηγούμενων στην διάταξη επιφανειακών κυμάτων και αποτελούν ένα πεπερασμένο σύνολο πραγματικών αριθμών όπου min{ n } β / k max{ n } j i 0 j j 5 j 5 ) Η διάταξη του ασυμμετρικού συζεύκτη γραμμοσειρών του Σχήματος 4., μέσω των επιλογών n = n3 = n5 = n0, n = n4 = n, d = d4 = d, d3 = h d, συμπίπτει με τη διάταξη του συμμετρικού συζεύκτη γραμμοσειρών του Σχήματος 3.. Για τις εν λόγω επιλογές των φυσικών και γεωμετρικών χαρακτηριστικών της διάταξης παρατηρούμε ότι η έκφραση (4.9) της συνάρτησης Green του ασύμμετρου ομογενούς προβλήματος ανάγεται στην έκφραση (3.30) της συνάρτησης Green του αντιστοίχου συμμετρικού ομογενούς προβλήματος, το οποίο μελετήθηκε στο Κεφάλαιο 3. 3) Οι (4.9) και (4.0) για d 3 (ε 0) ανάγονται αντιστοίχως στις + jλ ( z z ) δ( λ, xx, ) Gxzx (, ;, z ) = dλe 4 π (4.) Λ( g, g, g, d )
120 ( ) ( ) cosh gx 4 sinh gx 4 ) d4 Po( g5, g4, d4) Pe( g5, g4, d4) + exp g3( x ), d4 Pe( g5, g4, d4) Po( g5, g4, d4) x Pe( g3, g4, d4) Pe( g5, g4, d4) Po( g5, g4, d4) Po( g3, g4, d4) g 4 cosh ( gx 4 ) sinh ( gx 4 ) cosh ( gx 4 ) sinh ( gx 4 ) d4 d4 +, x x Pe( g5, g4, d4) Po( g5, g4, d4) Pe( g3, g4, d4) Po( g3, g4, d4) δ( λ, xx, ) = P( g, g, d ) P( g, g, d ) P( g, g, d ) P( g, g, d ) e e o o g4 cosh ( gx 4 ) sinh ( gx 4 ) cosh ( gx 4 ) sinh ( gx 4 ) d4 d4 +, x x Pe( g3, g4, d4) Po( g3, g4, d4) Pe( g5, g4, d4) Po( g5, g4, d4) cosh ( gx ) sinh ( gx ) d d Po( g, g, d ) P( g, g, d ) exp g ( x+ ), x e Pe( g3, g4, d4) Po( g3, g4, d4) Η G είναι η συνάρτηση Green του προβλήματος της απομονωμένης διηλεκτρικής πλάκας του Σχήματος 4.3. Σχήμα 4.3 Γεωμετρία του χωρίς γραμμοσειρές προβλήματος της απομονωμένης διηλεκτρικής πλάκας Εξάλλου οι πόλοι λ=±α i της ολοκληρωτέας συνάρτησης της (4.) είναι λύσεις της αλγεβρικής εξίσωσης Λ ( g, g, g, d ) = και αντιστοιχούν στις σταθερές διάδοσης των κυματοδηγούμενων επιφανειακών κυμάτων στη διηλεκτρική πλάκα. 0
121 4) Στην περίπτωση όπου η ρευματική πηγή ευρίσκεται εντός του κυματοδηγού, κατά παρόμοιο τρόπο διαπιστώνουμε ότι το ολικό πεδίο G εκφράζεται ως ολοκλήρωμα Fourier όπου + jλ ( z z ) 4π G ( x, z; x, z ) = dλe δ ( λ, x, x ) (4.3) δ( λ, x, x ) = [ Λ( g3, g, g, d) Λ( g5, g3, g4, d4) K( g3, g, g, d) K( g3, g5, g4, d4) ε ] d d K( g3, g5, g4, d4) ε Qo( g3, g, d)cosh g( x d3 ) Qe( g3, g, d)sinh g( x d3 ) exp[ g( x d3 d)] d d +Λ( g5, g3, g4, d4) Po( g3, g, d)cosh g( x d3 ) ( 3,, )sinh ( 3 ) exp[ ( 3 )], 3 + Pe g g d g x d g x d d x d + d ( g) K( g3, g5, g4, d4) Pe( g, g, d) Po( g, g, d) Qe( g3, g, d) Qo( g3, g, d) ε d cosh g( x d d d d3 ) sinh g( x d3 ) cosh g( x d3 ) sinh g( x d3 ) Qe ( g3, g, d) Qo( g3, g, d) Pe( g, g, d) Po( g, g, d) d 3 x x d3 + d + ( g) Λ( g5, g3, g4, d4) Pe( g, g, d) Po( g, g, d) Pe( g3, g, d) Po( g3, g, d) d d d d cosh g( x d3 ) sinh ( 3 ) cosh ( 3 ) sinh ( 3 ) g x d g x d g x d +, Pe( g3, g, d) Po( g3, g, d) Pe( g, g, d) Po( g, g, d) ( g) K( g3, g5, g4, d4) Pe( g, g, d) Po( g, g, d) Qe( g3, g, d) Qo( g3, g, d) ε d d d d cosh g( x d3 ) sinh g( x d3 ) cosh g( x d3 ) sinh g( x d3 ) Pe( g, g, d) Po( g, g, d) Qe( g3, g, d) Qo ( g3, g, d) d 3 x x d3 + d + ( g) Λ( g5, g3, g4, d4) Pe( g, g, d) Po( g, g, d) Pe( g3, g, d) Po( g3, g, d) d d d cosh g( x d3 ) sinh g( x d d3 ) cosh g( x d3 ) 3 sinh g ( x d ) +, Pe( g, g, d) Po( g, g, d) Pe( g3, g, d) Po( g3, g, d) { Λ( g3, g5, g4, d4)exp[ g3( x d3)] + ε K( g3, g5, g4, d4)exp[ g3( x+ d3)] } Po( g, g, d) Pe( g, g, d) d d cosh g( x d3 ) sinh g( x d3 ), d3 x d3 Pe ( g, g, d) Po ( g, g, d) ε g3pe( g, g, d) Po( g, g, d) Pe( g5, g4, d4) Po( g5, g4, d4) d d cosh g( x d3 ) sinh g( x d4 d4 d3 ) cosh g4( x+ d ) sinh ( ) g x+ d d d x d +, Pe( g, g, d) Po( g, g, d) Pe( g5, g4, d4) Po( g5, g4, d4) d d cosh g( x d3 ) sinh g( x d3 ) ε ggp 3 4 e( g, g, d) Po( g, g, d) exp[ g5( x+ d3+ d4)], x d3 d4 Pe( g, g, d) Po( g, g, d)
122 4.3. Επίλυση της ολοκληρωτικής εξίσωσης με τη μέθοδο Galerkin Θεωρούμε TE z πολωμένα ηλεκτρομαγνητικά κύματα, τα οποία διαδίδονται παράλληλα προς τον άξονα z στη διάταξη του Σχήματος 4.. Το άγνωστο κυματοδηγούμενο ηλεκτρικό πεδίο E = Ψ( x, z) yˆ (4.4) έχει μόνο y συνιστώσα και επομένως η λύση του προβλήματος ανάγεται στον προσδιορισμό του άγνωστου βαθμωτού παράγοντα ηλεκτρικού πεδίου Ψ(x,z). Απουσία εξωτερικής διέγερσης, ο ασυμμετρικός συζεύκτης γραμμοσειρών υποστηρίζει κυματοδηγούμενους ρυθμούς υπό την προϋπόθεση ότι ο παράγοντας Ψ του ηλεκτρικού πεδίου της διάταξης έχει την ολοκληρωτική αναπαράσταση Ψ ( xz, ) = k( n n) G( xzx, ;, z ) Ψ ( x, z ) dxdz Sd + k( n n) G( xzx, ;, z ) Ψ ( x, z ) dxdz, ( xz, ) 0 6 Sd (4.5) όπου G και G είναι οι συναρτήσεις Green, οι οποίες αντιστοιχούν σε διεγέρσεις εντός των κυματοδηγών και, S d και S d οι ολικές εγκάρσιες διατομές των γραμμοσειρών των κυματοδηγών και και Ψ και Ψ είναι οι παράγοντες ηλεκτρικού πεδίου στις ορθογώνιες γραμμοσειρές των κυματοδηγών και (δηλαδή οι περιορισμοί του Ψ στα S d και αντιστοίχως). Η (4.5) ουσιαστικά αποτελεί μία ομογενή ολοκληρωτική εξίσωση Fredholm δευτέρου είδους. Η ολοκληρωτική αναπαράσταση (4.5) δικαιολογείται (αποδεικνύεται) επεκτείνοντας τις τεχνικές που οδηγούν στην αντίστοιχη αναπαράσταση (3.40). Σύμφωνα με τα αναφερόμενα στην παράγραφο 3., ο παράγοντας Ψ του ηλεκτρικού πεδίου ενός ρυθμού κυματοδήγησης, διαδιδόμενου παράλληλα με την κατεύθυνση ẑ, καθορίζεται από το θεώρημα Floquet Ψ ( x, z) = u( x, z)exp( γ z) (4.6) όπου γ η προσδιοριστέα μιγαδική σταθερά διάδοσης του ρυθμού και u(x,z) μία Λ-περιοδική συνάρτηση του z. Επομένως, θεωρώντας τους περιορισμούς u και u της u στα S d και S d S d και συνδυάζοντας τις (4.5) και (4.6), διαπιστώνουμε ότι η ολοκληρωτική αναπαράσταση (4.5) αναδιατυπώνεται ως εξής u( x, z) = k ( n n ) G ( x, z; x, z ) u ( x, z )exp[ γ ( z z )] dx dz Sd + k ( n n ) G ( x, z; x, z ) u ( x, z )exp[ γ ( z z )] dxdz, ( x, z) 0 6 Sd (4.7)
123 Περαιτέρω, εκφράζοντας με τη βοήθεια των τύπων (4.9) και (4.3) τις προαναφερόμενες συναρτήσεις Green G και G ως ολοκληρώματα Fourier, λαμβάνουμε + + k0( n7 n4) u( x, z) = dλexp[ jλ( z z )] δ( λ, x, x ) u( x, z )exp[ γ( z z)] dx dz 4π r= S r + + k0( n6 n) + dλexp[ jλ( z z )] δ( λ, x, x ) u( x, z )exp[ γ( z z)] dxdz 4π r= Sr όπου οι εγκάρσιες διατομές S r και κυματοδηγούς και ορίζονται από (4.8) S r της r-οστής επανάληψης των γραμμοσειρών στους t r 3 3 i i i i= S = [ d w, d ] [ a + rλ, a + s + rλ] (4.9) t r 3 3 i i i i= S = [ d, d + w ] [ b + rλ, b + l + rλ] Ο μετασχηματισμός ζ =z rλ ανάγει τα διπλά ολοκληρώματα επάνω στις S d και S d, τα οποία εμφανίζονται στον τύπο (4.8), σε ολοκληρώματα επάνω στις βασικές επαναλήψεις S 0 και S 0, οι οποίες παριστούν την εγκάρσια διατομή των γραμμοσειρών του κάθε κυματοδηγού στο διάστημα από z=0 έως z=λ. Έτσι, με τη βοήθεια του αθροιστικού τύπου του Poisson για τη συνάρτηση Dirac (3.56) και ακολουθώντας τη διαδικασία της παραγράφου 3.5, η (4.8) ανάγεται στην + k0( n7 n4) π p π p π p uxz (, ) = exp( j z) u( x, ζ )exp( j ζ ) δ( jγ +, xx, ) dxd ζ Λ p= Λ Λ Λ S 0 + k0( n6 n) π p π p π p + exp( j z) u( x, ζ )exp( j ζ ) δ( jγ +, x, x ) dxd ζ Λ p= Λ Λ Λ S 0 (4.0) Η λύση της εξίσωσης (4.0) επιτυγχάνεται με εφαρμογή μίας τεχνικής Galerkin συνολικού χώρου, η οποία συνοψίζεται στα επόμενα βήματα. 3
124 . Οι παράγοντες ηλεκτρικού πεδίου u =u (x,z) και u =u (x,z), οι οποίοι εμφανίζονται στα αντίστοιχα ολοκληρώματα επάνω στις βασικές επαναλήψεις αναπτύσσονται στις σειρές Fourier ως προς z + (, ) = ϕ, n ( )exp( ) (, ) 0 n= Λ S 0 και S 0 των γραμμοσειρών, π n u x z x j z x z S (4.) π n u x z x j z x z S (4.) + (, ) = ϕ, n ( )exp( ) (, ) 0 n= Λ Εξάλλου, επειδή οι u και u αποτελούν λύσεις της αντίστοιχης ομογενούς εξίσωσης Helmholtz στον επίπεδο χωρίο των γραμμοσειρών, οι εγκάρσιες συνιστώσες φ,n και φ,n των χωρικών αρμονικών (συντελεστές Fourier) ικανοποιούν τις διαφορικές εξισώσεις ϕ ( x) g ϕ ( x) = 0, d w x d, n 7, n, n 3 3 ϕ ( x) g ϕ ( x) = 0, d x d + w, n 6, n, n 3 3 Συνεπώς, οι συναρτήσεις φ,n και φ,n εκφράζονται ως γραμμικοί συνδυασμοί + w w ϕ, n( x) = cn exp g7, n( x+ d3 + ) + cn exp g7, n( x+ d3 + ) (4.3) (4.4) + w w ϕ, n( x) = cn exp g6, n( x d3 ) + cn exp g6, n( x d3 ) ± των θεμελιωδών λύσεων των διαφορικών εξισώσεων (4.3), όπου c, c ± είναι προσδιοριστέοι συντελεστές και πn πn gin, = gi( jγ + ) = ( jγ + ) k0ni ( i =,...,7) (4.5) Λ Λ Τώρα, ακολουθώντας τη διαδικασία της παραγράφου 3.5, συνδυάζουμε τις (4.0) έως (4.5) και ευρίσκουμε k ( n n ) π p uxz J j z c Q x c Q x (, ) = p nexp( ) ( ) ( ) n np + n np p= n= Λ + + k0( n6 n) π p Jp nexp( j z) cnqnp( x) cnqnp( x), ( x, z) + p= n= Λ όπου οι συναρτήσεις J p n και Q ± np ορίζονται ως εξής / n n (4.6) 4
125 a + s t i i π q J q = exp j ζ d ζ Λ i= Λ, ai b + l t i i π q J q = exp j ζ d ζ Λ i= Λ bi d3 ± w np 7, n 3 δ d3 w π p Q ( x) = exp ± g ( x + d + ) ( jγ +, x, x ) dx Λ d3+ w ± w np 6, n 3 δ d 3 π p Q ( x) = exp ± g ( x d ) ( jγ +, x, x ) dx Λ Η εξίσωση (4.6) δηλώνει ότι ο παράγοντας ηλεκτρικού πεδίου u εκφράζεται ως διπλή σειρά γινομένων δύο συναρτήσεων μιας μεταβλητής, όπου η πρώτη J p n εξαρτάται από τα γεωμετρικά χαρακτηριστικά των γραμμοσειρών κατά μήκος του z-άξονα και η δεύτερη τα γεωμετρικά χαρακτηριστικά των γραμμοσειρών κατά μήκος του x-άξονα. Q ± np από. Για τον προσδιορισμό των αγνώστων συντελεστών c, c ± ± n n της (4.6) με τη μέθοδο Galerkin, θεωρούμε ότι το διάνυσμα παρατήρησης (x,z) στην (4.6) περιορίζεται στο επίπεδο χωρίο των γραμμοσειρών, διακρίνοντας τις ακόλουθες δύο περιπτώσεις Περίπτωση. Το διάνυσμα παρατήρησης (x,z) ανήκει στην επιφάνεια S d των γραμμοσειρών του κυματοδηγού. Στην περίπτωση αυτή η συνάρτηση u=u (x,z) στην (4.6) αρχικά αναπτύσσεται σε σειρά Fourier ως προς z της μορφής (4.). Στη συνέχεια θεωρώντας τα εσωτερικά γινόμενα των δύο μελών της (4.6) με τις δοκιμαστικές συναρτήσεις w π m exp ± g7, m( x+ d3 + ) exp + j z, ( x, z) Sd ( m ) Λ εκτελώντας τις ολοκληρώσεις που προκύπτουν και ακολουθώντας ανάλογη διαδικασία εκείνης της παραγράφου 3.5, ευρίσκουμε την αλγεβρική εξίσωση ±+ + ± + ±+ ± ( + ) = 0( 7 4) ( + ) Jm n Kmn cn Kmn cn k n n J p njm p cn Qmnp cn Qmnp n= n= p= k0( n6 n) J p njm p cn Qmnp + cn Qmnp n= p= + ±+ ± ( ) (4.7) όπου οι άπειροι πίνακες [ K ±± mn ] και [ Q i±± ] (i=,) ορίζονται ως εξής mnp d3 ±± w w mn = ± 7, m ± 7, n d3 w K exp g ( x d ) exp g ( x d ) dx (4.8) d3 i±± w i± mnp 7, m 3 np d3 w Q = exp ± g ( x+ d + ) Q ( x) dx ( i =, ) (4.9) 5
126 Περίπτωση. Το διάνυσμα παρατήρησης (x,z) ανήκει στην επιφάνεια S d των γραμμοσειρών του κυματοδηγού. Στην προκειμένη περίπτωση η συνάρτηση u=u (x,z) στην (4.6) αρχικά αναπτύσσεται σε σειρά Fourier ως προς z της μορφής (4.). Στη συνέχεια θεωρώντας τα εσωτερικά γινόμενα των δύο μελών της (4.6) με τις δοκιμαστικές συναρτήσεις w π m Λ ευρίσκουμε την αλγεβρική εξίσωση exp ± g6, m( x d3 ) exp + j z, ( x, z) Sd ( m ) ±+ + ± + ±+ ± ( + ) = 0( 7 4) ( + ) Jm n Kmn cn Kmn cn k n n Jp njm p cn Qmnp cn Qmnp n= n= p= k0( n6 n) J p njm p cn Qmnp + cn Qmnp n= p= + ±+ ± ( ) (4.30) όπου οι άπειροι πίνακες [ K ±± mn ] και [ Q i±± ] mnp (i=,) ορίζονται ως εξής d3+ w w w mn = ± 6, m 3 ± 6, n 3 d3 ±± K exp g ( x d ) exp g ( x d ) dx (4.3) d3+ w i±± w i± mnp 6, m 3 np d 3 Q = exp ± g ( x d ) Q ( x) dx ( i=, ) (4.3) 3. Οι εξισώσεις (4.7) και (4.30) των περιπτώσεων και αποτελούν ένα άπειρο τετραγωνικό ομογενές γραμμικό σύστημα συζευγμένων αλγεβρικών εξισώσεων ως προς τους αγνώστους συντελεστές c, c ( n ). Για την αριθμητική επίλυση αυτού του απείρου ± ± n n συστήματος θεωρούμε το αντίστοιχο truncated ομογενές γραμμικό σύστημα 8 N + 4 εξισώσεων ως προς τους 8 N + 4 αγνώστους c, c ( n= N,..., N), το οποίο προκύπτει λαμβάνοντας ± ± n n υπόψη τις χωρικές αρμονικές συναρτήσεις στα αναπτύγματα (4.), (4.) και τις δοκιμαστικές συναρτήσεις στα εσωτερικά γινόμενα με μέγιστη απόλυτη τάξη Ν. Το εν λόγω truncated σύστημα γράφεται υπό μορφή block πινάκων ως εξής A A A A A A A A + + A A A A A A A A + + c c c c + + = 0 ±± ±± Τα στοιχεία ( A ij ) mn των (N+) (N+) πινάκων A ij (i,j=,) δίνονται από (4.33) 6
127 + ±± ±± mn = Jm n + J p njm p Kmn p= g7, n g4, p ( A ) p= g7, n g4, p k ( n n ) k ( n n ) + J J ( R + H ) ±± ±± p n m p mnp mnp k ( n n ) ( A ) mn p n m p mnp + ±± 0 6 ±± = J J H p= g6, n g, p k ( n n ) ( A ) mn p n m p mnp + ±± ±± = J J H p= g7, n g4, p + ±± 0 6 ±± mn = Jm n + J p njm p Kmn p= g6, n g, p ( A ) p= g6, n g, p k ( n n ) k ( n n ) + J J ( R + H ) ±± ±± p n m p mnp mnp (4.34) και c ±, c ± είναι τα (N+) διανύσματα των συντελεστών ± c, c ±. Τα στοιχεία n n i R ±± mnp και ij H ±± mnp ορίζονται από R Λ( g, p, g3, p, g, p, d) Pe( g3, p, g4, p, d4) Pe( g5, p, g4, p, d4) Po( g5, p, g4, p, d4) Po( g3, p, g4, p, d4) ±± mnp = ( g7, m g4, p) g4, p Λ( g3, p, g5, p, g4, p, d4) Λ( g, p, g3, p, g, p, d) K( g3, p, g5, p, g4, p, d4) K( g3, p, g, p, g, p, d) ε w Pe( g7, m, g4, p, d4) Po( g7, m, g4, p, d4) Pe( g7, n, g4, p, d4) Po( g7, n, g4, p, d4) exp ( ± g7, m ± g7, n) + Pe ( g5, p, g4, p, d4 ) Po ( g5, p, g4, p, d 4 ) Pe ( g3, p, g4, p, d4 ) Po ( g3, p, g4, p, d 4 ) ± g g exp ( 7, m 7, n) ± + exp ( g7, m g7, n) w Pe( g7, m, g4, p, d4) Po( g7, m, g4, p, d4) Pe( g7, n, g4, p, d4 w ) Po( g7, n, g4, p, d4 w ) Pe( g3, p, g4, p, d4) Po( g3, p, g4, p, d4) + Pe( g5, p, g4, p, d4) Po( g5, p, g4, p, d4) w Pe( g7, m, g4, p, d4 w) Po( g7, m, g4, p, d4 w) Pe( g7, n, g4, p, d4) Po( g7, n, g4, p, d4) + Pe( g5, p, g4, p, d4) Po( g5, p, g4, p, d4) Pe( g3, p, g4, p, d4) Po( g3, p, g4, p, d4) w P( g, g, d w) P( g, g, d w) P( g, g, d w) P( g, g, d w) e 7, m 4, p 4 o 7, m 4, p 4 e 7, n 4, p 4 o 7, n 4, p 4 exp ( g7, m g7, n) + Pe ( g3, p, g4, p, d4) Po( g3, p, g4, p, d4) Pe( g5, p, g4, p, d4) Po( g5, p, g4, p, d4) (4.35) 7
128 R Λ( g5, p, g3, p, g4, p, d4) Pe( g, p, g, p, d) Po( g, p, g, p, d) Pe( g3, p, g, p, d) Po( g3, p, g, p, d) ±± mnp = ( g6, m g ) g,, ( 3,, 5,, 4,, 4) (,, 3,,,, ) ( 3,, 5,, 4,, 4) ( 3,,,,,, ) p p Λ g p g p g p d Λ g p g p g p d K g p g p g p d K g p g p g p d ε w Pe( ± g6, m, g, p, d w ) Po( ± g6, m, g, p, d w ) Pe( ± g6, n, g, p, d w ) Po( ± g6, n, g, p, d w ) exp ( ± g6, m ± g6, n) + Pe ( g3, p, g, p, d ) Po ( g3, p, g, p, d ) Pe ( g, p, g, p, d ) Po ( g, p, g, p, d ) w Pe( ± g6, m, g, p, d w ) Po( ± g6, m, g, p, d w) Pe( ± g6, n, g, p, d) Po( ± g6, n, g, p, d) exp ( ± g6, m g6, n) + Pe ( g, p, g, p, d ) Po ( g, p, g, p, d ) Pe ( g3, p, g, p, d ) Po ( g3, p, g, p, d ) ± + H exp ( g6, m g6, n) g g exp ( 6, m 6, n) ±± mnp = w Pe( ± g6, m, g, p, d) Po( ± g6, m, g, p, d) Pe( ± g6, n, g, p, d w ) Po( ± g6, n, g, p, d w ) + Pe( g3, p, g, p, d) Po( g3, p, g, p, d) Pe( g, p, g, p, d) Po( g, p, g, p, d) w Pe( ± g6, m, g, p, d) Po( ± g6, m, g, p, d) Pe( ± g6, n, g, p, d) Po( ± g6, n, g, p, d) + Pe( g, p, g, p, d) Po( g, p, g, p, d) Pe( g3, p, g, p, d) Po( g3, p, g, p, d) K( g, g, g, d ) Q ( g, g, d ) P( g, g, d ) Q ( g, g, d ) P ( g, g, d ) ε 3, p, p, p e 3, p 4, p 4 e 5, p 4, p 4 o 3, p 4, p 4 o 5, p 4, p 4 7, m 4, p 4, p Λ 3, p 5, p 4, p 4 Λ, p 3, p, p 3, p 5, p 4, p 4 3, p, p, p ε ( g g ) g ( g, g, g, d ) ( g, g, g, d ) K( g, g, g, d ) K( g, g, g, d ) w Pe( g7, m, g4, p, d4) Po( g7, m, g4, p, d4) Po( g7, n, g4, p, d4) Pe( g7, n, g4, p, d4) exp ( ± g7, m ± g7, n) + Pe ( g5, p, g4, p, d4 ) Po ( g5, p, g4, p, d + 4 ) Qo ( g3, p, g4, p, d4 ) Qe ( g3, p, g4, p, d 4 ) w Pe( g7, m, g4, p, d4 w ) Po( g7, m, g4, p, d4 w ) Po( g7, n, g4, p, d4) Pe( g7, n, g4, p, d4) exp ( g7, m ± g7, n) + Pe( g5, p, g4, p, d4) Po( g5, p, g4, p, d4) + Qo( g3, p, g4, p, d4) Qe( g3, p, g4, p, d4) ± g + H g exp ( 7, m 7, n) w Pe( g7, m, g4, p, d4) Po( g7, m, g4, p, d4) Pe( g7, n, g4, p, d4 w ) Po( g7, n, g4, p, d4 w ) + + Qe( g3, p, g4, p, d4) Qo( g3, p, g4, p, d4) Pe( g5, p, g4, p, d4) Po( g5, p, g4, p, d4) e 7, m 4, p 4 o 7, m 4, p 4 e 7, n 4, p 4 o 7, n 4, p 4 exp ( g7, m g7, n) + + Qe ( g3, p, g4, p, d4) Qo( g3, p, g4, p, d4) Pe( g5, p, g4, p, d4) Po( g5, p, g4, p, d4) ±± mnp = (4.36) w P( g, g, d w) P ( g, g, d w) P( g, g, d w) P ( g, g, d w) ε g3, ppe( g, p, g, p, d) Po( g, p, g, p, d) Pe( g5, p, g4, p, d4) Po( g5, p, g4, p, d4) ( g7, m g4, p) Λ( g3, p, g5, p, g4, p, d4) Λ( g, p, g3, p, g, p, d) K( g3, p, g5, p, g4, p, d4) K( g3, p, g, p, g, p, d) ε w w Pe( g7, m, g4, p, d4) Po( g7, m, g4, p, d4) Pe( ± g6, n, g, p, d w ) Po( ± g6, n, g, p, d w ) exp ± g7, m ± g6, n + + Pe( g5, p, g4, p, d4) Po( g5, p, g4, p, d4) Pe( g, p, g, p, d) Po( g, p, g, p, d) w w Pe( g7, m, g4, p, d4) Po( g7, m, g4, p, d4) Pe( ± g6, n, g, p, d) Po( ± g6, n, g, p, d) g6, n + + Pe( g5, p, g4, p, d4) Po( g5, p, g4, p, d4) Pe( g, p, g, p, d) Po( g, p, g, p, d) exp ± g7, m (4.37) w w Pe( g7, m, g4, p, d4 w ) Po( g7, m, g4, p, d4 w ) Pe( ± g6, n, g, p, d w ) Po( ± g6, n, g, p, d w ) exp g7, m ± g6, n + + Pe( g5, p, g4, p, d4) Po( g5, p, g4, p, d4) Pe( g, p, g, p, d) Po( g, p, g, p, d) w w Pe( g7, m, g4, p, d4 w ) Po( g7, m, g4, p, d4 w ) Pe( ± g6, n, g, p, d) Po( ± g6, n, g, p, d) + exp g7, m g6, n + + Pe( g5, p, g4, p, d4) Po( g5, p, g4, p, d4) Pe( g, p, g, p, d) Po( g, p, g, p, d) H ±± mnp = Po( g, p, g, p, d) Pe( g, p, g, p, d) Po( g5, p, g4, p, d4) Pe( g5, p, g4, p, d4) g3, pε ( g6, m g, p) Λ( g3, p, g5, p, g4, p, d4) Λ( g, p, g3, p, g, p, d) K( g3, p, g5, p, g4, p, d4) K( g3, p, g, p, g, p, d) ε w w Pe( ± g6, m, g, p, d w ) Po( ± g6, m, g, p, d w ) Pe( g7, n, g4, p, d4) Po( g7, n, g4, p, d4) exp ± g6, m ± g7, n + + Pe( g, p, g, p, d) Po( g, p, g, p, d) Pe( g5, p, g4, p, d4) Po( g5, p, g4, p, d4) ± 6, m (4.38) w w Pe( ± g6, m, g, p, d w ) Po( ± g6, m, g, p, d w ) Pe( g7, n, g4, p, d4 w ) Po( g7, n, g4, p, d4 w ) exp g g7, n + + Pe( g, p, g, p, d) Po( g, p, g, p, d) Pe( g5, p, g4, p, d4) Po( g5, p, g4, p, d4) w w Pe( ± g6, m, g, p, d) Po( ± g6, m, g, p, d) Pe( g7, n, g4, p, d4) Po( g7, n, g4, p, d4) exp g6, m ± g7, n + + Pe( g, p, g, p, d) Po( g, p, g, p, d) Pe( g5, p, g4, p, d4) Po( g5, p, g4, p, d4) w w Pe( ± g6, m, g, p, d) Po( ± g6, m, g, p, d) Pe( g7, n, g4, p, d4 w ) Po( g7, n, g4, p, d4 w ) + exp g6, m g7, n + + Pe( g, p, g, p, d) Po( g, p, g, p, d) Pe( g5, p, g4, p, d4) Po( g5, p, g4, p, d4) (4.39) 8
129 H ±± mnp = K( g, g, g, d ) P( g, g, d ) P( g, g, d ) Q ( g, g, d ) Q ( g, g, d ) ε 3, p 5, p 4, p 4 e, p, p o, p, p e 3, p, p o 3, p, p 6, m, p, p Λ 3, p 5, p 4, p 4 Λ, p 3, p, p 3, p 5, p 4, p 4 3, p, p, p ε ( g g ) g ( g, g, g, d ) ( g, g, g, d ) K( g, g, g, d ) K( g, g, g, d ) w Pe( ± g6, m, g, p, d w ) Po( ± g6, m, g, p, d w ) Pe( ± g6, n, g, p, d w ) Po( ± g6, n, g, p, d w ) exp ( ± g6, m ± g6, n) + + Qe ( g3, p, g, p, d ) Qo ( g3, p, g, p, d ) Pe ( g, p, g, p, d ) Po ( g, p, g, p, d ) w Pe( ± g6, m, g, p, d w ) Po( ± g6, m, g, p, d w) Pe( ± g6, n, g, p, d) Po( ± g6, n, g, p, d) exp ( ± g6, m g6, n) + + Pe ( g, p, g, p, d ) Po ( g, p, g, p, d ) Qe ( g3, p, g, p, d ) Qo ( g3, p, g, p, d ) w Pe( ± g6, m, g, p, d) Po( ± g6, m, g, p, d) Pe( ± g6, n, g, p, d w) Po( ± g6, n, g, p, d w) exp ( g6, m ± g6, n) + + Qe( g3, p, g, p, d) Qo( g3, p, g, p, d) Pe( g, p, g, p, d) Po( g, p, g, p, d) + g g exp ( 6, m 6, n) w Pe( ± g6, m, g, p, d) Po( ± g6, m, g, p, d) Pe( ± g6, n, g, p, d) Po( ± g6, n, g, p, d) + + Pe( g, p, g, p, d) Po( g, p, g, p, d) Qe( g3, p, g, p, d) Qo( g3, p, g, p, d) (4.40) Οι μιγαδικές σταθερές διάδοσης των ρυθμών, που είναι δυνατόν να κυματοδηγούμενων στη διάταξη, είναι εκείνες οι τιμές της παραμέτρου γ για τις οποίες το truncated σύστημα (4.33) έχει μη τετριμμένη λύση ή ισοδύναμα ο αντίστοιχος πίνακας του truncated συστήματος είναι ιδιάζων. Στη συνέχεια, οι μη τετριμμένες λύσεις της (4.33) μπορούν να χρησιμοποιηθούν για τον υπολογισμό της κατανομής του ηλεκτρικού πεδίου των κυματοδηγούμενων ρυθμών μέσω της βασικής ολοκληρωτικής αναπαράστασης (4.7). Τέλος, αναφερόμενοι στο truncated γραμμικό σύστημα (4.33) σημειώνουμε ότι (i) Στις λύσεις πρέπει να εφαρμοστεί ένας έλεγχος σύγκλισης (convergence control) για αυξανόμενο αριθμό Ν των συναρτήσεων ανάπτυξης. Ένα από τα βασικά πλεονεκτήματα της μεθόδου μας είναι ότι μικρές τιμές του N (N 5) παρέχουν ικανοποιητική σύγκλιση ανεξάρτητα από τις τιμές των φυσικών και γεωμετρικών παραμέτρων της διάταξης του συζεύκτη (για λεπτομέρειες βλ. [35]). (ii) Οι πίνακες [ H ij±± ], οι οποίοι αντιπροσωπεύουν τη σύζευξη μεταξύ των δύο mnp κυματοδηγών, προσεγγίζουν τον πίνακα 0 καθώς d 3 (ε 0), οδηγώντας σε αποσύζευξη (decoupling) του γραμμικού συστήματος (4.33). (iii) Στην ειδική περίπτωση ενός συμμετρικού συζεύκτη γραμμοσειρών (όπου n =n 3 =n 5, n =n 4 και d =d 4 ) το γραμμικό σύστημα (4.33) ανάγεται στο σύστημα (3.98) της παραγράφου 3.5. (iv) Οι ειδικές περιπτώσεις: (α) ενός απομονωμένου κυματοδηγού γραμμοσειρών (βλ. Σχήμα 4. υπό την απουσία του κυματοδηγού ) και (β) ενός συζεύκτη με γραμμοσειρές στον ένα κυματοδηγό (βλ. Σχήμα 4. υπό την απουσία των γραμμοσειρών του κυματοδηγού ), οι οποίες έχουν αναλυθεί αυτοτελώς στη βιβλιογραφία (βλ. [75] και [76] για (α) και [9], [5] και [38] για (β)), ενοποιούνται εδώ ως ειδικές περιπτώσεις της μεθόδου μας. Ακριβέστερα, 9
130 εφαρμογές τεχνικών Galerkin συνολικού χώρου οδηγούν και στις δύο περιπτώσεις στο truncated (4N+) (4N+) ομογενές γραμμικό σύστημα A A c + = A A c Στην περίπτωση (α) A ±± είναι τα blocks είναι τα blocks ±± A του συστήματος (4.33). 0 (4.4) ±± A του συστήματος (4.33) για ε=0 και στην (β) A ±± 4.4. Έλεγχος σύγκλισης, αποδοτικότητα και εγκυρότητα της μεθόδου Σύμφωνα με τα αναφερόμενα στις παραγράφους , οι πραγματικοί δείκτες των ρυθμών του ασυμμετρικού συζεύκτη γραμμοσειρών είναι οι ρίζες της ορίζουσας του γραμμικού συστήματος (4.33), οι οποίες υπολογίζονται με ακρίβεια, εφαρμόζοντας την επαναληπτική μιγαδική μέθοδο Müller. Το ουσιαστικό τμήμα αυτής της μεθόδου αφορά τον προσδιορισμό καταλλήλων αρχικών σημείων, ο οποίος επιτυγχάνεται με τη γραφική διαδικασία της παραγράφου 3.7. Για κάθε σύνολο παραμέτρων του συζεύκτη γραμμοσειρών ο απαιτούμενος αριθμός χωρικών αρμονικών συναρτήσεων στα αναπτύγματα Fourier (4.) και (4.) καθορίζεται με εφαρμογή ελέγχου σύγκλισης στις υπολογισθείσες σταθερές διάδοσης. Ένα αντιπροσωπευτικό πρότυπο σύγκλισης απεικονίζεται στον Πίνακας 4.. N β /k 0 (β,ν β,ν )/β,ν a β /k 0 (β,ν β,ν )/β,ν a a Σχετική διαφορά των λύσεων για τις διαδοχικές τιμές του N. Πίνακας 4. Πρότυπο σύγκλισης των κανονικοποιημένων φανταστικών μερών των σταθερών διάδοσης του συζεύκτη γραμμοσειρών του Σχήματος 4. με n =, n =3., n 3 =n 5 =n 6 =n 7 =3, n 4 =3.5, d =0.5 μm, d 3 =0.55 μm, d 4 =0. μm, w =0. μm, w =0.05 μm, Λ=0.748 μm, λ=.5 μm, t=, a =s =b =l =Λ/. 30
131 Όπως παρατηρούμε στον Πίνακας 4., με την παρούσα μέθοδο επιτυγχάνεται υψηλή ακρίβεια (της τάξης 0 7 ) θεωρώντας μόνο N+= συντελεστές ανάπτυξης στις (4.) και (4.). Η τάξη 8N+4=8 5+4=44 είναι πάρα πολύ μικρότερη από εκείνη του αντιστοίχου συστήματος των τεχνικών ολοκληρωτικών εξισώσεων συνδυασμένων με τη μέθοδο των συνοριακών στοιχείων (βλ. [38] και [39]), οι οποίες απαιτούν 500 συνοριακά στοιχεία για σύγκλιση τάξεως 0 4 των σταθερών διάδοσης. Αυτή η αποδοτικότητα της παρούσας μεθόδου οφείλεται στο ότι ο άγνωστος παράγοντας ηλεκτρικού πεδίου και οι όροι ανάπτυξης συνολικού χώρου (entire domain expansion terms) ικανοποιούν τους ίδιους φυσικούς νόμους. Επίσης, επειδή η παρούσα μέθοδος εμφανίζει ολοκληρώματα, τα οποία υπολογίζονται αναλυτικά, είναι πολύ αποδοτική σε όρους υπολογιστικού χρόνου (CPU time). Για τον υπολογισμό της ορίζουσας του πίνακα του γραμμικού συστήματος 0.5 δευτερόλεπτα (Pentium IV,.80 GHz with GByte of RAM) είναι επαρκή. Για τον έλεγχο της εγκυρότητας της μεθόδου θεωρούμε συζεύκτη με σταθερές παραμέτρους n =, n =3., n 3 =n 5 =3, n 4 =3.5, n 6 =3, d =0.5 μm, d 3 =0.55 μm, d 4 =0. μm, w =0.05 μm, Λ=0.748 μm, t=, b =l =Λ/ και τις γραμμοσειρές ευρισκόμενες στον κυματοδηγό (βλ. Σχήμα 4. υπό την απουσία των γραμμοσειρών του κυματοδηγού ). Οι καμπύλες διασποράς β /k 0 και β /k 0 των ρυθμών γραμμοσειρών ως προς το κανονικοποιημένο μήκος κύματος Λ/λ απεικονίζονται στο Σχήμα 4.4(α) και οι καμπύλες εξασθένησης α /k 0 και α /k 0 των ρυθμών γραμμοσειρών στο Σχήμα 4.4(β). Οι καμπύλες των Σχημάτων 4.4(α) και 4.4(β) είναι σε πλήρη συμφωνία με εκείνες των Σχημάτων 4a και 4b της [5], οι οποίες έχουν σχεδιαστεί για τις ίδιες τιμές των παραμέτρων, και έτσι επιβεβαιώνεται η εγκυρότητα της προτεινομένης μεθόδου. 3
132 (α) (β) Σχήμα 4.4 (α) Φανταστικά μέρη β /k 0, β /k 0 και (β) πραγματικά μέρη α /k 0, α /k 0 των σταθερών διάδοσης των ρυθμών γραμμοσειρών συναρτήσει του Λ/λ 3
133 ΚΕΦΑΛΑΙΟ 5 ΚΕΦΑΛΑΙΟ 5. ΑΡΙΘΜΗΤΙΚΑ ΑΠΟΤΕΛΕΣΜΑΤΑ-ΣΧΕΔΙΑΣΤΙΚΕΣ ΠΡΟΔΙΑΓΡΑΦΕΣ Στο Κεφάλαιο αυτό καταγράφονται διάφορα σημαντικά αριθμητικά αποτελέσματα, αναφερόμενα κυρίως στη μεταβολή των σταθερών διάδοσης ως προς τις διάφορες παραμέτρους του συζεύκτη γραμμοσειρών, και σχολιάζεται διεξοδικά ο ρόλος των γραμμοσειρών στην κυματοδήγηση των ηλεκτρομαγνητικών κυμάτων. Τα συμπεράσματα, τα οποία εξάγονται από την επεξεργασία των εν λόγω αριθμητικών αποτελεσμάτων, αξιοποιούνται για τον εντοπισμό τεχνικών χαρακτηριστικών και σχεδιαστικών προδιαγραφών κατάλληλων διατάξεων συζευκτών γραμμοσειρών, οι οποίες εξυπηρετούν συγκεκριμένες τεχνολογικές εφαρμογές. Τα αριθμητικά αποτελέσματα, τα οποία παρουσιάζονται στην παράγραφο 5., αναφέρονται σε συμμετρικούς συζεύκτες γραμμοσειρών και επιτυγχάνονται με αριθμητική υλοποίηση της ημιαναλυτικής μεθόδου Galerkin, που αναλύθηκε στο Κεφάλαιο 3. Ειδικότερα, καταγράφονται οι μεταβολές των σταθερών διάδοσης ως συναρτήσεις του πάχους w, των γεωμετρικών χαρακτηριστικών d i, l i, Λ, του δείκτη διάθλασης n και του πλήθους q των ορθογωνίων των γραμμοσειρών. Επίσης, σχεδιάζονται διαγράμματα μεταβολών των σταθερών διάδοσης συναρτήσει της απόστασης διαχωρισμού h των δύο κυματοδηγών, τα οποία ερμηνεύουν τη φυσική σύζευξη των κυματοδηγών του συζεύκτη γραμμοσειρών. Στην παράγραφο 5. παρουσιάζονται αντίστοιχα αριθμητικά αποτελέσματα, αναφερόμενα σε ασυμμετρικούς συζεύκτες γραμμοσειρών, τα οποία προκύπτουν με εφαρμογή της ημιαναλυτικής μεθόδου που αναλύθηκε στο Κεφάλαιο 4. Επιπροσθέτως, εντοπίζονται και καταγράφονται τα φυσικά και γεωμετρικά χαρακτηριστικά των γραμμοσειρών, τα οποία οδηγούν στο ελάχιστο δυνατό μήκος σύζευξης και στη μέγιστη δυνατή αποδοτικότητα σύζευξης. Παράλληλα, αναλύεται διεξοδικά η αποδοτική λειτουργία του συζεύκτη γραμμοσειρών ως ζωνοπερατό φίλτρο οπτικών συχνοτήτων. Επίσης, μελετάται ο συζεύκτης με γραμμοσειρές και στους δύο κυματοδηγούς και διαπιστώνεται ότι η παρουσία των δύο γραμμοσειρών παρέχει ευελιξία στη σχεδίαση των συζευκτών γραμμοσειρών και επιφέρει σημαντική βελτίωση της αποδοτικότητας του μηχανισμού μεταφοράς ενέργειας. Τέλος, αξίζει να σημειώσουμε ότι τα αριθμητικά αποτελέσματα της παραγράφου αυτής βελτιώνουν εκείνα των μεθόδων συζευγμένων ρυθμών για τις περιπτώσεις γραμμοσειρών, οι οποίες επιφέρουν μεγάλες διαταραχές στην ομογενή διάταξη, και πολύ διαφορετικών κυματοδηγών. 33
134 5.. Συμμετρικοί Συζεύκτες Σύμφωνα με τα αναφερόμενα στο εδάφιο.., οι κυματοδηγούμενοι βασικοί ρυθμοί (basic modes) του συμμετρικού συζεύκτη χωρίς γραμμοσειρές, ο οποίος απεικονίζεται στο Σχήμα., εμφανίζονται κατά ζεύγη και έχουν σχεδόν ίσες κανονικοποιημένες μιγαδικές σταθερές διάδοσης. Εξάλλου, όταν οι δείκτες διάθλασης όλων των περιοχών είναι πραγματικοί αριθμοί (μέσα χωρίς απώλειες), τότε οι κανονικοποιημένες σταθερές διάδοσης (effective indices) N e /k 0 και N o /k 0 των δύο κυματοδηγούμενων ρυθμών είναι φανταστικοί αριθμοί και τα αντίστοιχα ηλεκτρικά πεδία e E y και o E y εμφανίζουν άρτια και περιττή συμμετρία ως προς τον άξονα συμμετρίας (x=h/) της διάταξης (βλ. Σχήμα.). Περαιτέρω, οι δύο βασικοί ρυθμοί συμμετρικού συζεύκτη υπό την παρουσία γραμμοσειρών μετατρέπονται (εξελίσσονται) σε δύο διαφορετικούς ρυθμούς γραμμοσειρών (grating modes) με μιγαδικές σταθερές διάδοσης γ e = αe + jβe, γ o = αo + jβo (5.) Για αρκετά μεγάλες τιμές του λόγου Λ/λ, τα πραγματικά μέρη α e και α ο των γ e και γ ο είναι εν γένει διάφορα του μηδενός, ακόμα και για μέσα χωρίς απώλειες. Αυτό οφείλεται στις απώλειες ακτινοβολίας της διάταξης λόγω της παρουσίας των γραμμοσειρών, και για αυτό οι ρυθμοί αυτοί χαρακτηρίζονται ως ρυθμοί διαρροής (leaky modes) []. Εξάλλου, για τις συνήθεις γραμμοσειρές, οι οποίες χρησιμοποιούνται στην πράξη, οι τιμές των β e /k 0 και β ο /k 0 προσεγγίζουν τις τιμές των N e /k 0 και N o /k 0 των βασικών ρυθμών, ενώ οι τιμές των α e /k 0 και α ο /k 0 είναι της τάξης του 0-3 [5]. Σύμφωνα με τη σχετική ανάλυση της παραγράφου 3.5, οι μιγαδικές σταθερές διάδοσης των κυματοδηγούμενων ρυθμών στη διάταξη του συμμετρικού συζεύκτη γραμμοσειρών είναι εκείνες οι τιμές του γ, για τις οποίες το σύστημα (3.98) έχει μη τετριμμένη λύση, δηλαδή ο πίνακας του συστήματος είναι ιδιάζων. Επομένως, οι κανονικοποιημένες σταθερές διάδοσης είναι οι ρίζες γ/k 0 της ορίζουσας του πίνακα του συστήματος (3.98). Η μέθοδος που αναλύθηκε στις παραγράφους έχει εφαρμοστεί σε δύο διαφορετικές διατάξεις, οι οποίες αποτελούνται από κυματοδηγούς γραμμοσειρών: (i) ένα συζεύκτη γραμμοσειρών με τις γραμμοσειρές στην κάτω πλάκα, και (ii) ένα συζεύκτη γραμμοσειρών με γραμμοσειρές και στις δύο πλάκες. Τα συμπεράσματα, τα οποία εξάγονται παρακάτω από την επεξεργασία των αριθμητικών αποτελεσμάτων, μπορεί να αξιοποιηθούν για εντοπισμό τεχνικών χαρακτηριστικών και προδιαγραφών κατάλληλων διατάξεων συζευκτών γραμμοσειρών, οι οποίες εξυπηρετούν συγκεκριμένες τεχνολογικές εφαρμογές. 34
135 5... Συζεύκτης με γραμμοσειρές στον κυματοδηγό Τα επόμενα αριθμητικά αποτελέσματα αναφέρονται στη διάταξη συμμετρικού συζεύκτη δύο παραλλήλων πλακών παρουσία γραμμοσειρών στην κάτω πλάκα (βλ. Σχήμα 3. υπό την απουσία των γραμμοσειρών του κυματοδηγού ) με τις σταθερές τιμές n 0 =3., n =3.3, d=0.5μm, Λ=0.75μm και q= των παραμέτρων. Οι ρυθμοί αυτού του συζεύκτη δεν είναι πλέον άρτιοι και περιττοί (όπως του αντιστοίχου χωρίς γραμμοσειρές). Παρόλα αυτά, συνεχίζουμε να συμβολίζουμε με α e +jβ e and α o +jβ o τις σταθερές διάδοσης των ρυθμών του συζεύκτη για να δηλώσουμε την εξέλιξη των αντιστοίχων ρυθμών του χωρίς γραμμοσειρές συζεύκτη. Οι μεταβολές των σταθερών διάδοσης των ρυθμών γραμμοσειρών εξαρτώνται κατά ουσιαστικό τρόπο από τα γεωμετρικά χαρακτηριστικά των γραμμοσειρών w, d i, l i, Λ, το δείκτη διάθλασής της n και την απόσταση διαχωρισμού h των δύο συζευγμένων κυματοδηγών. Έτσι, διακρίνουμε τις περιπτώσεις. Μεταβολή των σταθερών διάδοσης ως προς το πάχος w των γραμμοσειρών Στην περίπτωση αυτή θεωρούμε συζεύκτη γραμμοσειρών με τις σταθερές τιμές n =3., h=μm, λ=.5μm και d =l =Λ/ των παραμέτρων. Το Σχήμα 5.(α) απεικονίζει τα φανταστικά μέρη β e /k 0 και β o /k 0 των σταθερών διάδοσης των ρυθμών γραμμοσειρών και το Σχήμα 5.(β) τα αντίστοιχα πραγματικά μέρη α e /k 0 και α o /k 0 σαν συνάρτηση του πάχους w των γραμμοσειρών. Τα φανταστικά μέρη β e /k 0 και β o /k 0 προσεγγίζουν τις τιμές Ν e /k 0 =3.689 και Ν ο /k 0 =3.666 των άρτιων και περιττών βασικών ρυθμών (του αντίστοιχου χωρίς γραμμοσειρές συζεύκτη) καθώς το w προσεγγίζει το 0. Περαιτέρω, όπως φαίνεται στο Σχήμα 5.(α), οι αποστάσεις β e Ν e /k 0 και β o Ν o /k 0 μεταξύ των σταθερών διάδοσης των ρυθμών γραμμοσειρών από τις σταθερές διάδοσης των βασικών ρυθμών αυξάνονται με το w, δηλαδή η επίδραση των γραμμοσειρών γίνεται ισχυρότερη καθώς αυξάνεται το w. Επίσης, η απόσταση Δβ= β e β o /k 0 των κανονικοποιημένων φανταστικών μερών των σταθερών διάδοσης των ρυθμών γραμμοσειρών αυξάνεται με το w (ενώ η ελάχιστη απόσταση β e β o /k 0 =0.003 αντιστοιχεί σε πάχος w=0, δηλαδή στη διάταξη του συμμετρικού συζεύκτη χωρίς γραμμοσειρές). 35
136 (α) (β) Σχήμα 5. (α) Φανταστικά μέρη β e /k 0, β o /k 0 και (β) πραγματικά μέρη α e /k 0, α o /k 0 των σταθερών διάδοσης των ρυθμών γραμμοσειρών συναρτήσει του πάχους w των γραμμοσειρών, για n =3., h=μm, λ=.5μm και d =l =Λ/. 36
137 Επιπροσθέτως, αναφορικά με τις καμπύλες του Σχήματος 5.(β), ο παράγοντας εξασθένησης α o /k 0 έχει δύο τοπικά ελάχιστα στα πάχη γραμμοσειρών 0.04 και 0.75 μm, ενώ ο α e /k 0 είναι σχετικά αμετάβλητος (insensitive) με το πάχος των γραμμοσειρών. Είναι γνωστό ότι [7], τα πάχη των γραμμοσειρών, που δίνουν την πιο αποδοτική σύζευξη (best coupling efficiency), βρίσκονται σε εκείνα τα διαστήματα του w, όπου η διαφορά Δα= α e α o /k 0 έχει ελάχιστη τιμή. Εξάλλου, σε κάθε ένα από αυτά τα διαστήματα η εξασθένιση λαμβάνει τις μικρότερες τιμές της. Στη συγκεκριμένη περίπτωση, αυτά τα καλύτερα διαστήματα εμφανίζονται κοντά στα w=0.04 και w=0.75 μm (Δα=0 για w=0.04, 0.5, 0.5 μm). Όμως, το Δβ ελαχιστοποιείται κοντά στο w=0, οδηγώντας σε μικρή αποδοτικότητα σύζευξης, εξαιτίας των σχετικά μεγάλων μηκών σύζευξης. Έτσι, η καλύτερη αποδοτικότητα σύζευξης αναμένεται να λάβει χώρα κοντά στο w=0.75 μm. Τελικά, για w>0.5 μm, η απόσταση Δα αυξάνεται και η αποδοτικότητα σύζευξης μειώνεται με το w. Μεταβολή των σταθερών διάδοσης ως προς τα γεωμετρικά χαρακτηριστικά d i, l i, Λ Στην προκειμένη περίπτωση, θεωρούμε συζεύκτη γραμμοσειρών με τις σταθερές τιμές h=μm και w=0.μm των παραμέτρων. Οι καμπύλες διασποράς β e /k 0 και β ο /k 0 των ρυθμών γραμμοσειρών και Ν e /k 0 και Ν ο /k 0 των βασικών ρυθμών ως προς το κανονικοποιημένο μήκος κύματος Λ/λ για d =l =Λ/ και n =3. απεικονίζονται στο Σχήμα 5.(α). Οι αντίστοιχες καμπύλες εξασθένησης α e /k 0 και α ο /k 0 των ρυθμών γραμμοσειρών απεικονίζονται στο Σχήμα 5.(β). Οι καμπύλες διασποράς Ν e /k 0 και Ν ο /k 0 υπό την παρουσία των γραμμοσειρών μετατοπίζονται αριστερά (εξελίσσονται) στις καμπύλες β e /k 0 και β ο /k 0. Επίσης, για κάθε τιμή του Λ/λ, η απόσταση β e β o /k 0 είναι αρκετά μεγαλύτερη από την αντίστοιχη απόσταση N e N o /k 0. Επιπρόσθετα, οι τιμές των σταθερών εξασθένησης είναι της τάξης 0 4, ενώ οι καμπύλες των α e /k 0 και α o /k 0 δεν τέμνονται. 37
138 (α) (β) Σχήμα 5. (α) β e /k 0, β ο /k 0 (συνεχείς γραμμές) και Ν e /k 0, Ν ο /k 0 (διακεκομμένες γραμμές) και (b) α e /k 0, α ο /k 0 συναρτήσει του κανονικοποιημένου μήκους κύματος Λ/λ για n =3., h=μm, w=0.μm και d =l =Λ/. 38
139 Το Σχήμα 5.3 απεικονίζει τις καμπύλες διασποράς κ e /k 0 και κ ο /k 0 ενός μη περιοδικού συζεύκτη με d =0 και l =Λ (δηλαδή, όπου το στρώμα των γραμμοσειρών είναι ομογενές με δείκτη διάθλασης n ), καθώς επίσης και τις καμπύλες διασποράς β e /k 0 και β ο /k 0 ενός περιοδικού συζεύκτη γραμμοσειρών με d =l =Λ/ συναρτήσει του κανονικοποιημένου μήκους κύματος Λ/λ για n =3.. Οι καμπύλες διασποράς κ e /k 0 και κ ο /k 0 του μη περιοδικού συζεύκτη χωρίς γραμμοσειρές, υπό την παρουσία των γραμμοσειρών, μετατοπίζονται δεξιά στις καμπύλες β e /k 0 και β ο /k 0 του περιοδικού συζεύκτη. Επίσης, για κάθε σταθεροποιημένο μήκος κύματος Λ/λ, οι αρχικές αποστάσεις κ e κ o /k 0 των ρυθμών του μη περιοδικού συζεύκτη είναι αρκετά μεγαλύτερες από τις αποστάσεις β e β o /k 0 των ρυθμών γραμμοσειρών του περιοδικού συζεύκτη (μετά την εισαγωγή περιοδικότητας στη διάταξη). Σχήμα 5.3 Καμπύλες διασποράς β e /k 0, β ο /k 0 (συνεχείς γραμμές) του περιοδικού συζεύκτη με d =l =Λ/ και κ e /k 0, κ ο /k 0 (διακεκομμένες γραμμές) του μη περιοδικού συζεύκτη με d =0 και l =Λ συναρτήσει του μήκους κύματος Λ/λ, για n =3., h=μm, w=0.μm. 39
140 Μεταβολή των σταθερών διάδοσης ως προς το δείκτη διάθλασης n των γραμμοσειρών Στο εδάφιο αυτό εξετάζεται η επίδραση του δείκτη διάθλασης n των γραμμοσειρών στις μεταβολές των σταθερών διάδοσης των κυματοδηγούμενων ρυθμών συζεύκτη γραμμοσειρών με h=μm, λ=.5μm, w=0.μm και d =l =Λ/. Στο Σχήμα 5.4(α) απεικονίζονται τα φανταστικά μέρη β e /k 0 και β o /k 0 των σταθερών διάδοσης των ρυθμών γραμμοσειρών και στο Σχήμα 5.4(β) τα αντίστοιχα πραγματικά μέρη α e /k 0 και α o /k 0 συναρτήσει του κανονικοποιημένου δείκτη διάθλασης n /n των γραμμοσειρών. H ελαχιστοποίηση της απόστασης Δβ των δύο ρυθμών, η οποία καθορίζει τον πλήρη συγχρονισμό του συζεύκτη, επιτυγχάνεται για n /n =, οπότε η διάταξη εκφυλίζεται σε συζεύκτη χωρίς γραμμοσειρές. Εξάλλου, η απόσταση Δβ των δύο ρυθμών αυξάνει με το λόγο n n /n, δηλαδή ο συζεύκτης γίνεται όλο και περισσότερο ασύγχρονος. Επίσης, το Σχήμα 5.4(β) δείχνει ότι για n /n <, η εξασθένηση α ο /k 0 λαμβάνει μεγάλες τιμές και η α e /k 0 δεν παρουσιάζει μεγάλες μεταβολές, ενώ για n /n > ισχύουν οι αντίστροφοι ισχυρισμοί. Αφού το n /n = αντιστοιχεί στον χωρίς γραμμοσειρές συζεύκτη, αποτελούμενο από μέσα χωρίς απώλειες, στην περιοχή του n /n =, οι α e /k 0 και α ο /k 0 προσεγγίζουν το μηδέν. Στη συνέχεια, στο Σχήμα 5.5(α) απεικονίζονται οι καμπύλες διασποράς β e /k 0 and β ο /k 0 των ρυθμών γραμμοσειρών συναρτήσει του κανονικοποιημένου μήκους κύματος Λ/λ για ισχυρή (strong) διαταραχή (n =3.4) και ασθενή (weak) διαταραχή (n =3.) με d =l =Λ/. Επίσης, στο Σχήμα 5.5(β) απεικονίζονται οι αντίστοιχες καμπύλες εξασθένησης α e /k 0 και α ο /k 0. Οι καμπύλες διασποράς β e /k 0 and β ο /k 0 μετατοπίζονται προς τα δεξιά καθώς αυξάνεται ο δείκτης διάθλασης n (δηλαδή όσο οι γραμμοσειρές επιφέρουν ισχυρότερη διαταραχή στο ομογενές πρόβλημα). Επιπλέον, οι αποστάσεις β e β o /k 0 των ρυθμών γραμμοσειρών αυξάνονται αισθητά με το δείκτη διάθλασης n των γραμμοσειρών. Οι σταθερές εξασθένησης α s ο /k 0 και α w ο /k 0 είναι πολύ κοντά σε τιμή, ενώ η α s e /k 0 είναι πολύ μεγαλύτερη από την α w e /k 0, εξαιτίας του ότι οι απώλειες ακτινοβολίας που προκαλούνται από την περίθλαση των γραμμοσειρών αυξάνονται με το n. 40
141 (α) (β) Σχήμα 5.4 (α) β e /k 0, β ο /k 0 και (β) α e /k 0, α ο /k 0 συναρτήσει του κανονικοποιημένου δείκτη διάθλασης n /n των γραμμοσειρών για w=0.μm, h=μm, λ=.5μm and d =l =Λ/. 4
142 (α) (β) Σχήμα 5.5 (α) β e s /k 0, β ο s /k 0 (συνεχείς) και β e w /k 0, β ο w /k 0 (διακεκομμένες) και (β) α e s /k 0, α ο s /k 0 (συνεχείς) και α e w /k 0, α ο w /k 0 (διακεκομμένες) συναρτήσει του Λ/λ, για n =3. (w: ασθενής διαταραχή) και n =3.4 (s: ισχυρή διαταραχή), h=μm, w=0.μm και d =l =Λ/. 4
143 Μελέτη της φυσικής σύζευξης των κυματοδηγών Σύμφωνα με τα αναφερόμενα στην παράγραφο.3, η σύζευξη της ηλεκτρομαγνητικής ισχύος στη διάταξη του συζεύκτη γραμμοσειρών υπαγορεύεται ουσιαστικά από δύο διακριτές φυσικές διαδικασίες: (i) τη φυσική σύζευξη μεταξύ των δύο κυματοδηγών (όπως και στην περίπτωση του συζεύκτη χωρίς γραμμοσειρές) και (ii) την περιοδική σύζευξη, η οποία οφείλεται στις διαταραχές που επιφέρουν οι γραμμοσειρές και απεικονίζεται στα Σχήματα 5. έως 5.5. Για τη μελέτη της φυσικής σύζευξης θεωρούμε συζεύκτη γραμμοσειρών με n =3., λ=.5μm, w=0.μm, και d =l =Λ/, του οποίου οι καμπύλες διασποράς β e /k 0 και β ο /k 0 των ρυθμών γραμμοσειρών και Ν e /k 0 και Ν ο /k 0 των βασικών ρυθμών ως προς την απόσταση διαχωρισμού h των δύο κυματοδηγών απεικονίζονται στο Σχήμα 5.6(α). Επίσης στο Σχήμα 5.6(β) απεικονίζονται οι αντίστοιχοι παράγοντες εξασθένησης α e /k 0 και α ο /k 0. Όπως φαίνεται στο Σχήμα 5.6(α), οι αποστάσεις β e β o /k 0 και N e N o /k 0 των ρυθμών γραμμοσειρών και των βασικών ρυθμών είναι περίπου ίσες για αρκετά μικρές τιμές της απόστασης h. Επιπλέον, η απόσταση N e N o /k 0 είναι περίπου μηδέν για αρκετά μεγάλες τιμές της απόστασης h, διότι καθώς η απόσταση h αυξάνεται, οι σταθερές διάδοσης των δύο ρυθμών προσεγγίζουν την κοινή σταθερά διάδοσης των δύο κυματοδηγών, όταν αυτά βρίσκονται σε απομόνωση. Εξάλλου, για αρκετά μεγάλες τιμές της h η απόσταση β e β o /k 0 σταθεροποιείται κοντά στην απόλυτη τιμή της διαφοράς των σταθερών διάδοσης των δύο κυματοδηγών, όταν αυτοί βρεθούν σε απομόνωση. Αυτή η απόλυτη τιμή αναμένεται να είναι διάφορη του μηδενός διότι ο κυματοδηγός περιέχει τις γραμμοσειρές ενώ ο κυματοδηγός όχι. Ειδικότερα, για μεγάλες τιμές της h η σταθερά διάδοσης β e /k 0 προσεγγίζει τη άρτια σταθερά διάδοσης του απομονωμένου κυματοδηγού, ενώ η σταθερά διάδοσης β o /k 0 προσεγγίζει τη σταθερά διάδοσης του απομονωμένου κυματοδηγού με περιοδικά χαραγμένες γραμμοσειρές του (βλ. Σχήμα 3.4). Περαιτέρω, το Σχήμα 5.6(β) δείχνει ότι η απόσταση Δα είναι πολύ μικρή για h κοντά στα.4μm. Εξάλλου, για h>.4μm, η Δα αυξάνεται με την απόσταση h. Επίσης, η σταθερά α o /k 0 προσεγγίζει την κανονικοποιημένη σταθερά εξασθένησης του απομονωμένου κυματοδηγού γραμμοσειρών για αρκετά μεγάλα h, ενώ η α e /k 0 προσεγγίζει το μηδέν, δηλαδή τη σταθερά εξασθένησης του απομονωμένου (χωρίς γραμμοσειρές) κυματοδηγού. 43
144 (α) (β) Σχήμα 5.6 (α) β e /k 0, β ο /k 0 (συνεχείς γραμμές) και Ν e /k 0, Ν ο /k 0 (διακεκομμένες γραμμές) και (β) α e /k 0, α ο /k 0 συναρτήσει της απόστασης διαχωρισμού h για w=0.μm, n =3., λ=.5μm και d =l =Λ/. 44
145 5... Συζεύκτης με γραμμοσειρές και στους δύο κυματοδηγούς Θεωρούμε συμμετρικό συζεύκτη γραμμοσειρών με γραμμοσειρές χαραγμένες και στους δύο κυματοδηγούς (βλ. Σχήμα 3.) και n 0 =3., n =3.3, d=0.5μm, Λ=0.75μm, h=μm, w=0.μm. Οι κανονικοποιημένες σταθερές διάδοσης των ρυθμών γραμμοσειρών είναι οι ρίζες της ορίζουσας του γραμμικού συστήματος (3.98). Τα φανταστικά μέρη β e /k 0, β o /k 0 και τα πραγματικά μέρη α e /k 0, α ο /k 0 των σταθερών διάδοσης των ρυθμών γραμμοσειρών συναρτήσει του κανονικοποιημένου δείκτη διάθλασης των γραμμοσειρών n /n απεικονίζονται στα Σχήματα 5.7(α) και 5.7(β). Ο Πίνακας 5. απεικονίζει την αντίστοιχη μεταβολή της απόστασης Δβ= β e β o /k 0. Μία συγκριτική εξέταση των Σχημάτων 5.4(α) και 5.7(α) δείχνει ότι η απόσταση Δβ για το συζεύκτη του εδαφίου 5.. αυξάνεται με την n n /n, ενώ η Δβ για το συζεύκτη του εδαφίου 5.. δεν παρουσιάζει μεγάλες μεταβολές με την n n /n. Επίσης, ο Πίνακας 5. δείχνει ότι η απόσταση Δβ των ρυθμών γραμμοσειρών είναι μικρότερη από την N e N o /k 0 των βασικών ρυθμών για n <n και μεγαλύτερη από την N e N o /k 0 για n >n. Αυτό σημαίνει ότι ο δείκτη διάθλασης των γραμμοσειρών μπορεί να δράσει σαν ένας μηχανισμός ελέγχου, κάνοντας τον συζεύκτη περισσότερο ή λιγότερο σύγχρονο από εκείνον που αντιστοιχεί στην αδιατάρακτη (χωρίς γραμμοσειρές) διάταξη. Επιπλέον, οι α e /k 0 και α ο /k 0 προσεγγίζουν το μηδέν κοντά στο n /n = (το ίδιο φαινόμενο είχε παρατηρηθεί στο Σχήμα 5.4(β)) και η απόσταση Δα δεν παρουσιάζει μεγάλες μεταβολές με το λόγο n /n. n /n β e β o /k Πίνακας 5. Απόσταση των σταθερών διάδοσης των ρυθμών γραμμοσειρών συναρτήσει του n /n για λ=.5μm. 45
146 (α) (β) Σχήμα 5.7 (α) β e /k 0, β ο /k 0 και (β) α e /k 0, α ο /k 0 συναρτήσει του n /n για τον συζεύκτη με γραμμοσειρές και στους δύο κυματοδηγούς με q=, d =l =Λ/ και λ=.5μm. 46
147 Οι Πίνακες 5. και 5.3 δείχνουν την εξάρτηση των σταθερών διάδοσης από τα γεωμετρικά χαρακτηριστικά (d i, l i, i=,,q) των γραμμοσειρών κατά μήκος του z-άξονα. Η συνολική επιφάνεια της εγκάρσιας διατομής των γραμμοσειρών, που αντιστοιχεί στο διάστημα [0,Λ], αποτελεί το βασικό παράγοντα, ο οποίος καθορίζει τις τιμές των σταθερών διάδοσης. Εξάλλου, οι σταθερές διάδοσης είναι πρακτικά ανεξάρτητες από το συνολικό αριθμό q των ορθογωνίων, που αποτελούν την βασική επανάληψη των γραμμοσειρών. λ (μm) β e /k 0 (i) (ii) (iii) (iv) (v) Πίνακας 5. β e /k 0 ως προς λ για τις περιπτώσεις (n =3.): (i) q=0 (συζεύκτης χωρίς γραμμοσειρές), (ii) q=, d =Λ/4, l =Λ/4, (iii) q=, d =Λ/0, d =Λ/0, d =Λ/, l =Λ/0, l =3Λ/0, (iv) q=8, d i =i Λ/0, l i =Λ/0,i=,,8, (v) q=, d =0, l =Λ (μη περιοδικός συζεύκτης). λ (μm) β o /k 0 (i) (ii) (iii) (iv) (v) Πίνακας 5.3 β o /k 0 ως προς λ για τις πέντε περιπτώσεις του Πίνακας
148 5.. Ασυμμετρικοί Συζεύκτες Η ανάλυση των φαινομένων διάδοσης και σύζευξης στη διάταξη του ασυμμετρικού συζεύκτη γραμμοσειρών και η σύγκριση της αναπτυχθείσας μεθόδου με εκείνη της Θεωρίας Συζευγμένων Ρυθμών προϋποθέτουν αρχικά την εισαγωγή των ασύζευκτων (uncoupled) ρυθμών, οι οποίοι διαδίδονται στον αντίστοιχο χωρίς γραμμοσειρές συζεύκτη και στη συνέχεια τη θεώρηση της παρουσίας των γραμμοσειρών με σκοπό τη μελέτη της εξέλιξης των ασύζευκτων ρυθμών στους συζευγμένους. Οι τεχνικές που βασίζονται στη Θεωρία Συζευγμένων Ρυθμών παρέχουν προσεγγιστικές εκφράσεις των σταθερών διάδοσης του συζεύκτη γραμμοσειρών μέσω των σταθερών του συζεύκτη χωρίς γραμμοσειρές. Αυτές οι εκφράσεις ισχύουν υπό ορισμένους περιορισμούς ως προς τη γεωμετρία και τα υλικά του συζεύκτη (βλ. επίσης τη σχετική συζήτηση της [8], Section 4). Εξάλλου, η παρούσα ημιαναλυτική μέθοδος εφαρμόζεται για τον υπολογισμό των συζευγμένων ρυθμών στο συζεύκτη γραμμοσειρών χωρίς να εμπλέκει τους ασύζευκτους ρυθμούς του συζεύκτη χωρίς γραμμοσειρές. Έτσι, αυτή η μέθοδος εφαρμόζεται χωρίς τους προαναφερόμενους περιορισμούς και είναι πολύ πιο ακριβής από τη Θεωρία Συζευγμένων Ρυθμών. Προς αυτή την κατεύθυνση, αρχικά θεωρούμε τους ρυθμούς του μη περιοδικού συζεύκτη, ο οποίος προκύπτει από το συζεύκτη γραμμοσειρών του Σχήματος 4. με αντικατάσταση των στρωμάτων των γραμμοσειρών από δύο ομογενή στρώματα με πάχη w, w και μέσους δείκτες διάθλασης t t n7 s i + n i 4 a = i= i n h, =, Λ t t n6 l i + n i b = i= i n h, = Οι ρυθμοί της διάταξης του μη περιοδικού συζεύκτη υπολογίζονται με ακρίβεια λύνοντας το αντίστοιχο ομογενές πρόβλημα συνοριακών τιμών και οι υπολογισμοί δηλώνουν ότι εμφανίζονται σε ζεύγη ονομαζόμενα σύνθετοι ρυθμοί (compound modes) [9]. Στην περίπτωση ενός συζεύκτη, αποτελούμενου από στρώματα χωρίς απώλειες, οι αντίστοιχοι πραγματικοί δείκτες (effective indices) των δύο σύνθετων ρυθμών γίνονται καθαρά φανταστικοί με τιμές jν /k 0 και jν /k 0. Αξιοσημείωτη ανταλλαγή φωτεινής ενέργειας λαμβάνει χώρα μόνο όταν οι δύο κυματοδηγοί είναι σε συγχρονισμό (δηλαδή τα Ν /k 0 και Ν /k 0 είναι σχεδόν ίσα). Όμως, οι ρυθμοί ενός συζεύκτη αποτελούμενου από μη σύγχρονους κυματοδηγούς προσομοιάζουν με εκείνους των απομονωμένων κυματοδηγών, όπου το μεγαλύτερο ποσό ισχύος συγκεντρώνεται σε κάθε κυματοδηγό. Έτσι, δεν λαμβάνει χώρα ουσιαστική ανταλλαγή φωτός, όταν στους δύο κυματοδηγούς δεν υπάρχει συμφωνία φάσης (βλ. [7] και [9]). Λ 48
149 Περαιτέρω, η παρουσία των γραμμοσειρών συνεπάγεται ότι οι σύνθετοι ρυθμοί εξελίσσονται προοδευτικά σε ένα ζεύγος ρυθμών γραμμοσειρών (grating modes) με μιγαδικές σταθερές διάδοσης γ = α + jβ ( i =,) (5.) i i i Οι παράγοντες εξασθένησης α i είναι μη μηδενικοί για μεγάλες τιμές του λόγου Λ/λ, ακόμα και όταν όλα τα στρώματα είναι χωρίς απώλειες. Αυτό οφείλεται στις απώλειες ακτινοβολίας οι οποίες προκαλούνται από την περίθλαση στις γραμμοσειρές, έτσι ώστε οι ρυθμοί να χαρακτηρίζονται ως ρυθμοί διαρροής (leaky modes) []. Για τους χρησιμοποιούμενους στην πράξη συζεύκτες γραμμοσειρών οι πραγματικοί δείκτες β /k 0 και β /k 0 είναι κοντά σε τιμή με τους Ν /k 0 και Ν /k 0, ενώ οι α /k 0 και α /k 0 είναι το πολύ της τάξης του 0 3 (βλ. επίσης [5]). Τώρα, σύμφωνα με τις (4.6), (4.) και (4.) κάθε γ i αντιστοιχεί σε έναν παράγοντα ηλεκτρικού πεδίου Ψ(x,z) ο οποίος συμπεριφέρεται με βάση τον όρο exp { [ γ + ( π / Λ )] } i j n z κατά μήκος της διαμήκους κατεύθυνσης z των γραμμοσειρών. Οι διακριτές τιμές γ in, = αi+ j[ βi+ ( πn/ Λ )] ( i=,) ( n ) (5.3) είναι οι σταθερές διάδοσης των απείρου αριθμησίμου πλήθους διαφορετικών Floquet αρμονικών, τις οποίες επιβάλλει σε μία άπειρη περιοδική διάταξη το θεώρημα Floquet. Στα επόμενα αριθμητικά αποτελέσματα, θεωρούμε μόνο τις πρώτης τάξης (n=±) Floquet αρμονικές για σύγκριση με τα αποτελέσματα της Θεωρίας Συζευγμένων Ρυθμών και της Θεωρίας Floquet- Bloch. Η Θεωρία Συζευγμένων Ρυθμών προβλέπει τη συνθήκη προσαρμογής φάσης (phasematching condition) Λ / λ = k /( N N ) (5.4) 0 Η φυσική σημασία αυτής της συνθήκης είναι ότι οι καμπύλες Ν /k 0 και Ν /k 0 ως προς Λ/λ τέμνουν τις Ν /k 0 +λ/λ και Ν /k 0 λ/λ αντιστοίχως [5]. Έτσι, οι πρώτης τάξης Floquet αρμονικές «συνταιριάζονται» υπό την έννοια ότι οι + ( ) Floquet αρμονική του Ν /k 0 (Ν /k 0 ) έχει την ίδια φάση με την Ν /k 0 (Ν /k 0 ). Σημειώνουμε ότι οι πρώτης τάξης Floquet αρμονικές του μη περιοδικού συζεύκτη θεωρούνται στις οριακές καταστάσεις όπου η περιοδική διάταξη συμπίπτει με τη μη περιοδική [5]. Η συνθήκη (5.4) μπορεί να ερμηνευθεί με τους ακόλουθους δύο τρόπους: (i) Για ένα σταθεροποιημένο μήκος κύματος λειτουργίας λ η λύση Λ=Λ w της εξίσωσης (5.4) προσδιορίζει τη βέλτιστη περίοδο των γραμμοσειρών (optimal grating period), η οποία αντιστοιχεί στο συνταίριασμα των πρώτης τάξης Floquet αρμονικής. 49
150 (ii) Για μία σταθεροποιημένη περίοδο γραμμοσειρών Λ η λύση λ=λ w της εξίσωσης (5.4) προσδιορίζει το αντίστοιχο βέλτιστο μήκος κύματος λειτουργίας (optimal operating wavelength). Τα ακόλουθα αριθμητικά αποτελέσματα δηλώνουν ότι το βέλτιστο μήκος κύματος λειτουργίας και η βέλτιστη περίοδος των γραμμοσειρών είναι αρκετά διαφορετικά από εκείνα που προβλέπει η Θεωρία Συζευγμένων Ρυθμών και επιπλέον είναι πολύ κοντά σε τιμή σε εκείνα που προβλέπει η Θεωρία Floquet-Bloch. Περαιτέρω, το μήκος σύζευξης (coupling length) L c, δηλαδή το απαιτούμενο μήκος για πλήρη ανταλλαγή του φωτός μεταξύ των δύο κυματοδηγών, μπορεί να εκτιμηθεί από [6], [7] L c π = min β β (5.5) Το μήκος σύζευξης συνιστά μία επιπρόσθετη σημαντική παράμετρο, η οποία πρέπει να ληφθεί υπόψη στη διαδικασία σχεδίασης ενός ασυμμετρικού συζεύκτη γραμμοσειρών. Αυτό οφείλεται στο ότι, παρόλο που οι σταθερές εξασθένησης α/k 0 είναι επαρκώς μικρές, οι συνολικές απώλειες ακτινοβολίας (εκφραζόμενες από το αl c ) μπορεί να γίνουν τόσο μεγάλες ώστε να καταστούν απαγορευτικές για την αποδοτική λειτουργία του συζεύκτη. Εφαρμόζοντας τις τεχνικές των παραγράφων 4. και 4.3, συμπεραίνουμε ότι οι πραγματικοί δείκτες των ρυθμών του ασυμμετρικού συζεύκτη γραμμοσειρών είναι οι ρίζες της ορίζουσας του γραμμικού συστήματος (4.33) (για συζεύκτη με τις γραμμοσειρές ευρισκόμενες σε ένα μόνο κυματοδηγό αντί για το (4.33) θεωρούμε το σύστημα (4.4)). Τα ακόλουθα αριθμητικά αποτελέσματα αναδεικνύουν την επίδραση των γραμμοσειρών στη διαδικασία σύζευξης μέσω της σχεδίασης των σταθερών διάδοσης ως προς τα φυσικά και γεωμετρικά χαρακτηριστικά των γραμμοσειρών. Για κάθε σύνολο παραμέτρων του συζεύκτη ο απαιτούμενος αριθμός χωρικών αρμονικών συναρτήσεων στα αναπτύγματα Fourier (4.) και (4.) προσδιορίζεται με εφαρμογή ελέγχου σύγκλισης στις υπολογισθείσες σταθερές διάδοσης (ο οποίος καθορίζεται στην παράγραφο 4.4). Στα επόμενα εδάφια θεωρούμε συζεύκτη με σταθερές παραμέτρους n =, n =3., n 3 =n 5 =3, n 4 =3.5, d =0.5 μm, d 4 =0. μm, Λ=0.748 μm, t=, b =l =Λ/ και τις γραμμοσειρές ευρισκόμενες στον κυματοδηγό (βλ. Σχήμα 4. υπό την απουσία των γραμμοσειρών του κυματοδηγού ). 50
151 5... Μήκος κύματος συντονισμού Οι καμπύλες διασποράς των ρυθμών γραμμοσειρών και των συνθέτων ρυθμών ως προς το κανονικοποιημένο μήκος κύματος Λ/λ απεικονίζονται στο Σχήμα 5.8(α) και οι καμπύλες εξασθένησης των ρυθμών γραμμοσειρών στο Σχήμα 5.8(β). Οι καμπύλες των Σχημάτων 5.8(α) και 5.8(β) είναι σε πλήρη συμφωνία με εκείνες των Σχημάτων 4a και 4b της [5]. Το μήκος κύματος συντονισμού (resonant wavelength), το οποίο αντιστοιχεί στην ελαχιστοποίηση της απόστασης Δβ= β β, λαμβάνει χώρα στη θέση λ opt =.4983 μm. Αυτή η τιμή του λ opt είναι πολύ κοντά στην.4978 μm, που έχει υπολογισθεί στην [5] με εφαρμογή της Θεωρίας Floquet- Bloch. Το αντίστοιχο του μήκους κύματος συντονισμού, όπως προβλέπεται από τη Θεωρία Συζευγμένων Ρυθμών, (δηλαδή το σημείο τομής των καμπυλών Ν /k 0 +λ/λ και Ν /k 0 ) είναι λ cm =.5 μm. Αυτή η μικρή διαφορά οφείλεται στο ότι η Θεωρία Συζευγμένων Ρυθμών παρέχει προσεγγιστικές εκφράσεις των σταθερών διάδοσης του συζεύκτη γραμμοσειρών με όρους των σταθερών του συζεύκτη χωρίς γραμμοσειρές, ενώ η παρούσα μέθοδος ουσιαστικά δίνει ακριβή αποτελέσματα για την πραγματική περιοδική διάταξη. Όμως, υπάρχουν συγκεκριμένες περιπτώσεις, όπως παραδείγματος χάριν όταν οι γραμμοσειρές ευρίσκονται στο άνω μέρος του κυματοδηγού, όπου η διαφορά μεταξύ της ακριβούς τιμής λ opt και της προσεγγιστικής τιμής λ cm μπορεί να γίνει πολύ μεγάλη (βλ. επίσης τη συζήτηση στην [5]). Το Σχήμα 5.8(α) δείχνει την ασυμπτωτική συμπεριφορά των καμπυλών διασποράς β /k 0, β /k 0 ως προς τις ευθείες Ν /k 0 +λ/λ, N /k 0. Ακριβέστερα, η καμπύλη β /k 0 (β /k 0 ) έχει ως ασύμπτωτες τις ευθείες Ν /k 0 +λ/λ (N /k 0 ) για μεγάλα Λ/λ και τις N /k 0 (Ν /k 0 +λ/λ) για μικρά Λ/λ. Εξάλλου, η συγκριτική εξέταση των καμπυλών διασποράς ενός συμμετρικού συζεύκτη γραμμοσειρών (Σχήματα 5.(α) και 5.3) με εκείνες ενός ασυμμετρικού συζεύκτη (Σχήμα 5.8(α)) αναδεικνύει ότι παρόλο που οι καμπύλες διασποράς β e, β o του συμμετρικού συζεύκτη είναι σχεδόν παράλληλες μεταξύ τους (με μεγάλες αποστάσεις β e β o ), οι καμπύλες β, β του ασυμμετρικού συζεύκτη προσεγγίζουν η μία την άλλη κοντά στο μήκος κύματος συντονισμού λ opt (με ελάχιστη απόσταση β β στη θέση λ opt ) και αποκλίνουν μακριά από το λ opt (οσφυϊκή (waist) συμπεριφορά). Έτσι, αφού αποδοτική ανταλλαγή του φωτός λαμβάνει χώρα μόνο σε εκείνα τα μήκη κύματος πολύ κοντά στο λ opt, όπου οι σταθερές διάδοσης των ρυθμών γραμμοσειρών γίνονται σχεδόν ίσες (βλ. [9] και [5]), ο ασυμμετρικός συζεύκτης γραμμοσειρών μπορεί να λειτουργήσει αποδοτικά σαν οπτικό ζωνοπερατό φίλτρο συχνοτήτων. Επιπλέον, οι σταθερές εξασθένησης α, α, που εμφανίζονται στο Σχήμα 5.8(β), είναι αρκετά μικρής τάξης για κάθε λ και τέμνονται στη θέση λ=.49 μm. Αντιθέτως, οι σταθερές εξασθένησης ενός συμμετρικού συζεύκτη γραμμοσειρών δεν τέμνονται (βλ. Σχήμα 5.(α)). 5
152 (α) (β) Σχήμα 5.8 (α) Φανταστικά μέρη β /k 0, β /k 0 (συνεχείς γραμμές) και Ν /k 0 +λ/λ, Ν /k 0 (διακεκομμένες γραμμές) των σταθερών διάδοσης των ρυθμών γραμμοσειρών και των σύνθετων ρυθμών και (β) πραγματικά μέρη α /k 0, α /k 0 των σταθερών διάδοσης των ρυθμών γραμμοσειρών συναρτήσει (και στις δύο περιπτώσεις (α) και (β)) του Λ/λ, για d 3 =0.55 μm, w =0.05 μm, n 6 =3, n h, =3.. 5
153 5... Επίδραση του πάχους των γραμμοσειρών Τα Σχήματα 5.9(α) και 5.9(β) δείχνουν τα φανταστικά μέρη β /k 0, β /k 0 και τα πραγματικά μέρη α /k 0, α /k 0 των σταθερών διάδοσης των ρυθμών γραμμοσειρών συναρτήσει του πάχους w των γραμμοσειρών για μήκη κύματος λ=.47 μm και λ=.53 μm. Η απόσταση Δβ/k 0 λαμβάνει την ελάχιστη τιμή της στη θέση w,opt =0.03 μm για λ=.47 μm και στη θέση w,opt =0.073 μm για λ=.53 μm (σύμφωνα με το εδάφιο 5.., w,opt =0.05 μm για λ=.4983 μm). Έτσι το πάχος των γραμμοσειρών μπορεί να δράσει σαν ένας επιπρόσθετος μηχανισμός ελέγχου (additional control mechanism) της συνθήκης συντονισμού του συζεύκτη. Ακριβέστερα, η βέλτιστη τιμή w,opt αυξάνεται με το μήκος κύματος λειτουργίας λ. Επίσης, η απόσταση Δβ/k 0 αυξάνεται και η αποδοτικότητα σύζευξης μειώνεται καθώς το w >w,opt αυξάνεται. Η τελευταία ιδιότητα έχει επίσης αναφερθεί στις [7] και [9], χωρίς όμως να έχει γίνει μία περαιτέρω έρευνα για την εξάρτηση του w,opt από το λ. Εξάλλου, για αρκετά μικρά w <w,opt και αρκετά μεγάλα w >w,opt τα αντίστοιχα τμήματα των καμπυλών για λ=.47 μm και λ=.53 μm είναι παράλληλες ευθείες. Στη συμμετρική περίπτωση, παρατηρήθηκε ότι w opt =0 μm (δηλαδή πρόκειται για συζεύκτη χωρίς γραμμοσειρές) για όλα τα μήκη κύματος λ. Περαιτέρω, ως γνωστόν [7] τα πάχη των γραμμοσειρών, τα οποία παράγουν τις βέλτιστες αποδοτικότητες σύζευξης, αντιστοιχούν σε εύρη του w, όπου το Δα/k 0 = α α /k 0 έχει ένα ελάχιστο. Σε κάθε ένα από αυτά τα εύρη η εξασθένηση λαμβάνει τις μικρότερες τιμές της. Οι καμπύλες του Σχήματος 5.9(β) δείχνουν ότι οι σταθερές εξασθένησης α /k 0 και α /k 0 τέμνονται στο w,opt =0.03 μm για λ=.47 μm και στο w,opt = μm για λ=.53 μm. Οι τιμές αυτές του w,opt είναι πολύ κοντά σε εκείνες, οι οποίες αντιστοιχούν στην ελαχιστοποίηση της Δβ/k 0 και εμφανίζονται στο Σχήμα 5.9(α). Παρόλο ότι οι καμπύλες α /k 0 και α /k 0 για λ=.47 μm τέμνονται επίσης στο w =0.05 μm, ο συζεύκτης δεν πρέπει να σχεδιαστεί με αυτό το πάχος των γραμμοσειρών, αφού για w =0.05 μm η απόσταση Δβ/k 0 είναι πολύ μεγάλη και συνεπώς η αποδοτικότητα της σύζευξης πολύ μικρή. Επιπλέον, η α /k 0 λαμβάνει ελάχιστο και η α /k 0 μέγιστο κοντά στο w,opt =0.03 μm, ενώ η αντίστροφη κατάσταση εμφανίζεται κοντά w,opt = μm. Αυτή η συμπεριφορά είναι τυπική για ένα συντονιζόμενο σύστημα (resonant system) και ερμηνεύει το γεγονός ότι κοντά στο πάχος συντονισμού w,opt εμφανίζεται μία ζώνη αποκοπής (stop band) για τον ένα διαδιδόμενο ρυθμό και μία ζώνη διέλευσης (pass band) για τον άλλον [7]. 53
154 (α) (β) Σχήμα 5.9 (α) β /k 0, β /k 0 και (β) α /k 0, α /k 0 συναρτήσει του πάχους w των γραμμοσειρών, για λ=.47 μm (διακεκομμένες) και λ=.53 μm (συνεχείς γραμμές) με d 3 =0.55 μm, n 6 =3. 54
155 5..3. Επίδραση του δείκτη διάθλασης των γραμμοσειρών Στα Σχήματα 5.0(α) και 5.0(β) απεικονίζονται οι μεταβολές των φανταστικών και των πραγματικών μερών των σταθερών διάδοσης συναρτήσει του δείκτη διάθλασης n 6 των γραμμοσειρών για λ=.5 μm και λ=.53 μm. Και για τα δύο μήκη κύματος η απόσταση Δβ/k 0 λαμβάνει ελάχιστο στη θέση n 6 =3 (=n 3 ). Η ελάχιστη απόσταση για λ=.5 μm είναι μίας τάξης μεγέθους μικρότερη από την για λ=.53 μm. Έτσι, οι γραμμοσειρές παρέχουν πιο αποδοτική σύζευξη για λ=.5 μm. Εξάλλου, η β /k 0 παραμένει σχεδόν σταθερή ως προς το n 6, ενώ η β /k 0 αυξάνεται γνησίως με το n 6. Συνεπώς, ο συζεύκτης γίνεται περισσότερο ασύγχρονος καθώς το n 6 αυξάνεται. Στην περίπτωση του συμμετρικού συζεύκτη ο δείκτης διάθλασης συντονισμού των γραμμοσειρών συμπίπτει με εκείνον του συζεύκτη χωρίς γραμμοσειρές. Επιπλέον, το Σχήμα 5.0(β) δείχνει ότι η απόσταση Δα/k 0 λαμβάνει κοντά στο n 6 =3 τοπικά ελάχιστα με τιμές 0 5 και 0 4 για λ=.5 μm και λ=.53 μm αντιστοίχως. Επίσης, αφού για n 6 =n ο συζεύκτης γραμμοσειρών συμπίπτει με το συζεύκτη χωρίς γραμμοσειρές αποτελούμενο από μέσα χωρίς απώλειες, στην περιοχή του n 6 =n, οι α /k 0 και α /k 0 προσεγγίζουν το μηδέν. 55
156 (α) (β) Σχήμα 5.0 (α) β /k 0, β /k 0 και (β) α /k 0, α /k 0 συναρτήσει του δείκτη διάθλασης n 6 των γραμμοσειρών, για λ=.5 μm (διακεκομμένες) και λ=.53 μm (συνεχείς γραμμές) με d 3 =0.55 μm, w =0.05 μm. 56
157 5..4. Φυσική σύζευξη μεταξύ των κυματοδηγών Οι δύο διαφορετικές διαδικασίες: (i) η φυσική σύζευξη μεταξύ των δύο κυματοδηγών (όπως και στην περίπτωση του μη περιοδικού ή του χωρίς γραμμοσειρές συζεύκτη) και (ii) η περιοδική σύζευξη εξαιτίας των διαταραχών που επιφέρουν οι γραμμοσειρές (και η οποία απεικονίζεται στα Σχήματα ), υπαγορεύουν τη σύζευξη της ηλεκτρομαγνητικής ισχύος στο συζεύκτη γραμμοσειρών [8]. Για τη μελέτη της φυσικής σύζευξης σχεδιάζουμε στο Σχήμα 5.(α) τις μεταβολές των φανταστικών μερών β /k 0, β /k 0 και N ng /k 0, N ng /k 0 των σταθερών διάδοσης των ρυθμών γραμμοσειρών και των βασικών ρυθμών (b =0, l =Λ, n 6 =n ) συναρτήσει της απόστασης διαχωρισμού d 3. Επίσης, το Σχήμα 5.(β) δείχνει τα αντίστοιχα πραγματικά μέρη α /k 0, α /k 0 των σταθερών διάδοσης των ρυθμών γραμμοσειρών. Οι αποστάσεις β β /k 0 και α α /k 0 λαμβάνουν την ελάχιστη τιμή τους στη βέλτιστη απόσταση διαχωρισμού (optimal separation distance) (d 3 ) opt =0.537 μm. Εξάλλου, στους συμμετρικούς συζεύκτες η απόσταση β β /k 0 δεν ελαχιστοποιείται για καμία απόσταση διαχωρισμού d 3 (βλ. Σχήμα 5.6(α)). Αναφερόμενοι τώρα στο Σχήμα 5.(α), παρατηρούμε ότι για αρκετά μικρό d 3, οι β β /k 0 και N ng N ng /k 0 είναι πολύ κοντά (όπως και στη συμμετρική περίπτωση). Για αρκετά μεγάλο d 3, η N ng N ng /k 0 σταθεροποιείται κοντά στην απόλυτη τιμή 0.03 της διαφοράς των σταθερών διάδοσης των δύο (χωρίς γραμμοσειρές) κυματοδηγών, όταν αυτά θεωρούνται σε απομόνωση. Όμως, η β β /k 0 σταθεροποιείται κοντά στην απόλυτη τιμή της διαφοράς των σταθερών διάδοσης του απομονωμένου κυματοδηγού (με χαρακτηριστικά n 4, d 4 ) και του απομονωμένου κυματοδηγού γραμμοσειρών (με χαρακτηριστικά n, d, βλ. Σχήμα 4. υπό την απουσία του κυματοδηγού ). Ακριβέστερα, οι β /k 0 και N ng /k 0 προσεγγίζουν τη σταθερά διάδοσης 3.96 του απομονωμένου κυματοδηγού (με n 4, d 4 ), ενώ οι β /k 0 και N ng /k 0 προσεγγίζουν αντιστοίχως τις σταθερές διάδοσης 3.0 του απομονωμένου κυματοδηγού γραμμοσειρών και 3.09 του απομονωμένου κυματοδηγού (με n, d ). Επιπλέον, το Σχήμα 5.(β) δείχνει ότι οι α /k 0 και α /k 0 προσεγγίζουν για αρκετά μεγάλο d 3 τις σταθερές εξασθένησης 0 του απομονωμένου κυματοδηγού, αποτελούμενο από υλικά χωρίς απώλειες, και του απομονωμένου κυματοδηγού γραμμοσειρών αντιστοίχως. 57
158 (α) (β) Σχήμα 5. (α) β /k 0, β /k 0 (συνεχείς) και Ν ng /k 0, Ν ng /k 0 (διακεκομμένες γραμμές) και (β) α /k 0, α /k 0 συναρτήσει της απόστασης διαχωρισμού d 3, για w =0.05 μm, λ=.5μm, n 6 =3. 58
159 5..5. Βέλτιστη περίοδος και duty cycle γραμμοσειρών Στο εδάφιο αυτό θεωρούμε τον ασυμμετρικό συζεύκτη γραμμοσειρών με n =, n =3.3, n 3 =n 6 =3., n 4 =3.5, n 5 =3, d =.05 μm, d 3 =0.55 μm, d 4 =0.3 μm, w =0. μm, λ=.5 μm. Στο Σχήμα 5. εμφανίζονται οι μεταβολές των φανταστικών μερών β /k 0, β /k 0 και Ν /k 0 λ/λ, N /k 0 των σταθερών διάδοσης των ρυθμών γραμμοσειρών και των συνθέτων ρυθμών συναρτήσει της περιόδου Λ των γραμμοσειρών. Σχήμα 5. β /k 0, β /k 0 (συνεχείς) και Ν /k 0 λ/λ, N /k 0 (διακεκομμένες γραμμές) συναρτήσει της περιόδου Λ των γραμμοσειρών, για λ=.5μm, t=, b =l =Λ/, n h, =3.5. Αξίζει να σημειώσουμε ότι οι καμπύλες του Σχήματος 5. συμφωνούν πλήρως με εκείνες του Σχήματος της [4]. Η απόσταση Δβ/k 0 = β β /k 0 λαμβάνει την ελάχιστη τιμή της 0.00 στη θέση Λ opt =3.87 μm (πολύ κοντά στο 3.68 μm, το οποίο έχει υπολογιστεί στην [4] με εφαρμογή της Θεωρίας Floquet-Bloch). Εξάλλου, η βέλτιστη περίοδος των γραμμοσειρών, η προβλεπόμενη από τη Θεωρία Συζευγμένων Ρυθμών, εμφανίζεται στο σημείο τομής Λ cm =3.463 μm των ευθειών Ν /k 0 και Ν /k 0 λ/λ. Όπως εξηγήσαμε στο εδάφιο 5.., η μικρή διαφορά μεταξύ των Λ opt και Λ cm οφείλεται στις προσεγγίσεις, που επιβάλλονται από τη Θεωρία Συζευγμένων Ρυθμών. 59
160 Περαιτέρω, για να μελετήσουμε την εξάρτηση των σταθερών διάδοσης από τα γεωμετρικά χαρακτηριστικά (b i, l i, t) των γραμμοσειρών κατά μήκος του z-άξονα, εισάγουμε το duty cycle των γραμμοσειρών t l i= i dc = 00% Λ Το Σχήμα 5.3 εμφανίζει την απόσταση Δβ/k 0 = β β /k 0 συναρτήσει της περιόδου Λ των γραμμοσειρών για μεταβλητό duty cycles dc και πλήθος t των ορθογωνίων. Εξάλλου, ο Πίνακας 5.4 παριστάνει τις βέλτιστες περιόδους Λ opt και τα βέλτιστα μήκη σύζευξης L c, που προσδιορίζονται από την ελάχιστη τιμή του Δβ/k 0, όπως δείχνει το Σχήμα 5.3. Η ελάχιστη τιμή 0 4 του min(δβ/k 0 ) αντιστοιχεί σε dc=5%, t= και το ελάχιστο μήκος σύζευξης 0.68 mm σε dc=50%, t= (δυαδικές γραμμοσειρές). Επειδή αποδοτική μεταφορά της φωτεινής ισχύος εξασφαλίζεται μόνο όταν οι δύο ρυθμοί έχουν σχεδόν ίδιες σταθερές διάδοσης, είναι λογικό να επιλέξουμε dc=5% και t=. Όμως, το μεγάλο μήκος σύζευξης L c =3.75 mm, το οποίο αντιστοιχεί σε dc=5% και t=, θα μπορούσε να καταστεί απαγορευτικό (εξαιτίας των περιορισμών οι οποίοι επιβάλλονται από την εξασθένηση των ρυθμών) για τη σύζευξη μιας επαρκούς ποσότητας οπτικής ισχύος μεταξύ των κυματοδηγών. Για αυτό, οι επιλογές dc=75% και t= ή φαίνεται σε ορισμένες περιπτώσεις να είναι καταλληλότερες, επειδή συνδυάζουν μία σχετικά μικρή απόσταση Δβ/k 0 =8 0 4 με ένα όχι υπερβολικά μεγάλο μήκος σύζευξης L c =0.938 mm. dc % t min( Δβ /k 0 ) Λ opt (μm) L c (mm) ( 6 Λ opt ) ( 7 Λ opt ) ( Λ opt ) ( 79 Λ opt ) ( 3 Λ opt ) ( 3 Λ opt ) Πίνακας 5.4 Βέλτιστες περίοδοι και βέλτιστα μήκη σύζευξης για μεταβλητό duty cycle και πλήθος ορθογωνίων ανά επανάληψη των γραμμοσειρών, όπως δείχνει το Σχήμα
161 Σχήμα 5.3 Απόσταση Δβ/k 0 = β β /k 0 συναρτήσει της περιόδου Λ των γραμμοσειρών, για μεταβλητά duty cycles dc και πλήθη t των ορθογωνίων Συζεύκτης με δύο γραμμοσειρές Στο εδάφιο αυτό, διερευνούμε συζεύκτη με γραμμοσειρές και στους δύο κυματοδηγούς με παραμέτρους n =, n =3.3, n 3 =n 5 =3., n 4 =3.5, n 6 =n 7 =3., d =μm, d 3 =μm, d 4 =0.3μm, w =w =0.μm, t=, b =l =a =s =Λ/, λ=.5μm. Ο Marcuse [7] έχει ήδη μελετήσει τον αντίστοιχο συζεύκτη χωρίς γραμμοσειρές και σημειώσει ότι οι θεμελιώδεις ρυθμοί των δύο απομονωμένων κυματοδηγών χωρίς γραμμοσειρές έχουν σημαντικά διαφορετικές σταθερές διάδοσης (N ng /k 0 =3.559, N ng /k 0 =3.343), και συνεπώς αρκετά λίγη ισχύς μπορεί να ανταλλαγεί μεταξύ των δύο κυματοδηγών. Στο Σχήμα 5.4 εμφανίζονται οι μεταβολές των φανταστικών μερών β /k 0 και β /k 0 των σταθερών διάδοσης των ρυθμών γραμμοσειρών συναρτήσει της περιόδου Λ των γραμμοσειρών. Η απόσταση Δβ/k 0 λαμβάνει την ελάχιστη τιμή της 0.00 στη θέση Λ opt =3.84 μm, όπου το αντίστοιχο μήκος σύζευξης είναι L c =0.683mm. Εξάλλου, αξίζει να σημειώσουμε ότι ο ασυμμετρικός συζεύκτης γραμμοσειρών, που έχει προταθεί από τον Marcuse [9], παρουσιάζει κατά προσέγγιση μήκος σύζευξης L c =5mm (βλ. Σχήμα 3a της [9]). Οπωσδήποτε, φαίνεται ότι αυτό το μεγάλο μήκος σύζευξης δεν θα οδηγούσε σε αποδοτική σύζευξη της οπτικής ισχύος μεταξύ των δύο κυματοδηγών, ακόμα και στις περιπτώσεις συζευκτών με μέτριες σταθερές 6
162 εξασθένησης. Όμως, οι απώλειες εξασθένησης του συζεύκτη γραμμοσειρών με L c =0.683mm, ο οποίος προτείνεται εδώ, δεν επηρεάζουν σημαντικά την ποσότητα της μεταφερόμενης ενέργειας. Συνεπώς, η παρουσία των δύο γραμμοσειρών παρέχει ευελιξία στη σχεδίαση των συζευκτών γραμμοσειρών, επιφέροντας σημαντική βελτίωση της αποδοτικότητας του μηχανισμού μεταφοράς ενέργειας. Σχήμα 5.4 β /k 0 και β /k 0 συναρτήσει της περιόδου Λ των γραμμοσειρών, για τον ασυμμετρικό συζεύκτη με γραμμοσειρές και στους δύο κυματοδηγούς του εδαφίου
163 ΚΕΦΑΛΑΙΟ 6 ΚΕΦΑΛΑΙΟ 6. ΕΠΙΣΚΟΠΗΣΗ, ΣΥΓΚΡΙΤΙΚΗ ΑΞΙΟΛΟΓΗΣΗ ΚΑΙ ΠΡΟΟΠΤΙΚΕΣ Στο Κεφάλαιο αυτό συνοψίζονται η χρησιμότητα και η σημασία των συζευκτών γραμμοσειρών και επισκοπούνται οι προγενέστερες μέθοδοι μελέτης των ηλεκτρομαγνητικών φαινομένων, τα οποία εμφανίζονται στις διατάξεις αυτές. Επίσης, επισημαίνονται η πρωτοτυπία της μεθοδολογίας και των αριθμητικών αποτελεσμάτων και αξιολογούνται συγκριτικά με αντίστοιχα προυπάρχοντα αποτελέσματα. Τέλος, ενδεικνύονται οι γενικές κατευθύνσεις της μελλοντικής εργασίας. Χρηστικότητα και αρχή λειτουργίας των συζευκτών γραμμοσειρών Οι συζεύκτες γραμμοσειρών αποτελούν βασικά δομικά στοιχεία σημαντικών οπτικών διατάξεων, οι οποίες χρησιμοποιούνται ευρέως στα σύγχρονα οπτικά δίκτυα. Μεταξύ των οπτικών διατάξεων συγκαταλέγονται τα οπτικά φίλτρα επιλογής συχνοτήτων, οι πολυπλέκτες και αποπολυπλέκτες, τα συντονιζόμενα lasers και τα lasers κατανεμημένης ανάδρασης καθώς επίσης και οι οπτικοί διακόπτες. Η γενική αρχή λειτουργίας ενός κατευθυντικού συζεύκτη συνοψίζεται ως εξής: Ένας από τους δύο κυματοδηγούς ορίζεται ως θύρα εισόδου και ο άλλος ως θύρα εξόδου του οπτικού σήματος. Ισχύς εισόδου εισέρχεται στη θύρα εισόδου και μετά από ένα ορισμένο μήκος ένα ποσοστό της ισχύος εισόδου συζευγνύεται στον άλλο κυματοδηγό και εξέρχεται ως ισχύς εξόδου από τη θύρα εξόδου. Αναζητούμε τις βέλτιστες τιμές των φυσικών και γεωμετρικών παραμέτρων της διάταξης, οι οποίες μεγιστοποιούν το ποσοστό της ισχύος εισόδου που μεταβιβάζεται στη θύρα εξόδου. Η κύρια συνεισφορά των γραμμοσειρών συνίσταται στην ουσιαστική ενίσχυση της διαδικασία σύζευξης του φωτός από τον ένα κυματοδηγό στον άλλο, συνταιριάζοντας τα διαφορετικά γεωμετρικά και φυσικά χαρακτηριστικά των δύο κυματοδηγών. Προγενέστερες μεθοδολογίες Τα ηλεκτρομαγνητικά φαινόμενα, που εμφανίζονται στις διατάξεις των συζευκτών γραμμοσειρών, έχουν ήδη μελετηθεί με αρκετές μεθόδους. Αντικείμενα των μελετών αυτών αποτελούν ο καθορισμός των μεταβολών, που επιφέρει στις σταθερές διάδοσης των κυματοδηγούμενων ηλεκτρομαγνητικών κυμάτων η παρουσία των γραμμοσειρών, και ο 63
164 προσδιορισμός των τιμών των φυσικών και γεωμετρικών χαρακτηριστικών των γραμμοσειρών (πάχος, περίοδος, δείκτης διάθλασης) για τις οποίες επιτυγχάνεται η βέλτιστη ανταλλαγή φωτεινής ισχύος μεταξύ των δύο κυματοδηγών. Οι κύριες μέθοδοι μελέτης του προβλήματος, που έχουν εμφανιστεί στη βιβλιογραφία, είναι οι μέθοδοι διαταραχών, η θεωρία των συζευγμένων ρυθμών και η θεωρία Floquet-Bloch. Οι μέθοδοι διαταραχών αποσαφηνίζουν οπωσδήποτε την εικόνα της φυσικής διαδικασίας της σύζευξης, αλλά οδηγούν μόνο σε προσεγγιστικά αποτελέσματα. Η ακρίβεια των λύσεων, οι οποίες επιτυγχάνονται με εφαρμογή της θεωρίας των συζευγμένων ρυθμών, προϋποθέτει αρκετούς περιορισμούς, όπως μικρό πάχος γραμμοσειρών, μεγάλη απόσταση διαχωρισμού των δύο κυματοδηγών και μικρές διαφορές των δεικτών διάθλασης των εμπλεκομένων μέσων. Οι τεχνικές, οι οποίες στηρίζονται στη θεωρία Floquet-Bloch, οδηγούν σε ακριβή αποτελέσματα, αναφερόμενα στην επίδοση των συζευκτών γραμμοσειρών, των οποίων όμως η ακρίβεια εξαρτάται από την αριθμητική επίλυση συστημάτων γραμμικών διαφορικών εξισώσεων πρώτης τάξεως. Μεθοδολογία της διατριβής Για τη μελέτη των φαινομένων κυματοδήγησης σε συζεύκτες γραμμοσειρών αναπτύσσεται και εφαρμόζεται μεθοδολογία ολοκληρωτικών εξισώσεων, η οποία συνδυάζει ημιαναλυτικές τεχνικές ολοκληρωτικών εξισώσεων, που επιλύονται με εφαρμογή της Μεθόδου των Ροπών με συναρτήσεις βάσης συνολικού χώρου. Ειδικότερα, με εφαρμογή της μεθόδου Sommerfeld επιτυγχάνεται Fourier ολοκληρωτική αναπαράσταση της συνάρτησης Green του ομογενούς (χωρίς γραμμοσειρές) προβλήματος. Περαιτέρω, διατυπώνεται ολοκληρωτική εξίσωση ως προς το ηλεκτρικό πεδίο κυμάτων, τα οποία διαδίδονται κατά μήκος του άξονα του συζεύκτη. Για τη λύση της εν λόγω ολοκληρωτικής εξίσωσης εφαρμόζονται τεχνικές Galerkin συνολικού χώρου, οι οποίες οδηγούν σε συγκεκριμένο ομογενές γραμμικό σύστημα. Οι σταθερές διάδοσης των κυματοδηγούμενων ρυθμών είναι οι τιμές εκείνες για τις οποίες το εν λόγω σύστημα έχει μη τετριμμένη λύση. Πρωτοτυπία της μεθοδολογίας και των αποτελεσμάτων Η κύρια πρωτοτυπία της Διδακτορικής Διατριβής συνίσταται στην εισαγωγή μεθοδολογίας ολοκληρωτικών εξισώσεων, η οποία αναπτύσσεται και εφαρμόζεται στη μελέτη των φαινομένων κυματοδήγησης σε συζεύκτες γραμμοσειρών. Εξάλλου, η αριθμητική υλοποίηση της 64
165 μεθοδολογίας παράγει αρκετά πρωτότυπα και ενδιαφέροντα αριθμητικά κυρίως αποτελέσματα, αναφερόμενα στη βέλτιστη σχεδίαση των χαρακτηριστικών των γραμμοσειρών, τα οποία προσφέρουν το ελάχιστο δυνατό μήκος σύζευξης και τη μέγιστη δυνατή αποδοτικότητα σύζευξης. Συγκριτική αξιολόγηση της μεθοδολογίας και των αποτελεσμάτων Τα συγκριτικά πλεονεκτήματα της αναπτυσσόμενης μεθοδολογίας έναντι των μεθόδων διαταραχών, θεωρίας των συζευγμένων ρυθμών και θεωρίας Floquet-Bloch εντοπίζονται στην ακρίβεια, την απλότητα καθώς επίσης και την αριθμητική αποδοτικότητα (μεγάλη ακρίβεια των αποτελεσμάτων με χρήση μικρού αριθμού όρων των αναπτυγμάτων). Εξάλλου, η χρησιμοποιούμενη μεθοδολογία δίνει ακριβή αποτελέσματα για γραμμοσειρές μεγάλου πάχους και για ισχυρά συζευγμένους κυματοδηγούς, ενώ οι προγενέστερες μέθοδοι προϋποθέτουν σημαντικούς περιορισμούς των φυσικών και γεωμετρικών παραμέτρων των γραμμοσειρών. Ιδιαιτέρως, αξίζει να σημειώσουμε ότι εκφράζεται αναλυτικά η συνάρτηση Green και υπολογίζονται αναλυτικά όλα τα εμφανιζόμενα ολοκληρώματα με συνέπειες τη σημαντική μείωση του υπολογιστικού κόστους, την αύξηση της ακρίβειας των αποτελεσμάτων και την επίτευξη λύσεως χωρίς άλλες προσεγγίσεις εκτός εκείνης της τελικής κολόβωσης του γραμμικού συστήματος. Τα αριθμητικά αποτελέσματα της Διατριβής υπερτερούν σημαντικά σε αξιοπιστία και ακρίβεια των αντιστοίχων αποτελεσμάτων, τα οποία επιτυγχάνονται με τις προγενέστερες μεθόδους. Επίσης, ερμηνεύονται και αξιολογούνται για πρώτη φορά οι επιδράσεις του πάχους, του δείκτη διάθλασης και του κύκλου καθήκοντος των γραμμοσειρών ως επιπροσθέτων μηχανισμών ελέγχου της βέλτιστης συμπεριφοράς του συζεύκτη. Η αξιολόγηση των αποτελεσμάτων αυτών διαμορφώνει συγκεκριμένες τεχνικές-σχεδιαστικές προδιαγραφές της υπό μελέτη διάταξης, οι οποίες μπορεί να αξιοποιηθούν κατάλληλα σε πολλές εφαρμογές της ολοκληρωμένης οπτικοηλεκτρονικής. Μελλοντική εργασία Η αναπτυχθείσα μεθοδολογία εφαρμόζεται για τη μελέτη των φαινομένων σύζευξης και κυματοδήγησης σε συζεύκτη γραμμοσειρών με περιοδικές γραμμοσειρές απείρου πλήθους. Σε αρκετές εφαρμογές η συνθήκη της άπειρης περιοδικότητας μπορεί να είναι αποδεκτή. Όμως, σε ορισμένες περιπτώσεις είναι επίσης χρήσιμο να μοντελοποιηθούν γραμμοσειρές με πεπερασμένο 65
166 μήκος. Οι πεπερασμένες γραμμοσειρές έχουν διαφορετικά χαρακτηριστικά περίθλασης από τις άπειρες εξαιτίας των φαινομένων άκρων, τα οποία προκαλούνται από τους τερματισμούς των πεπερασμένων γραμμοσειρών. Η παρούσα μελέτη των φαινομένων κυματοδήγησης σε συζεύκτη με άπειρες περιοδικές γραμμοσειρές χρησιμοποιεί κατά ουσιαστικό τρόπο το Θεώρημα Floquet, το οποίο ισχύει όμως μόνο για μέσα με περιοδική μεταβολή του δείκτη διάθλασης. Προκειμένου να μελετήσουμε συζεύκτες με πεπερασμένες γραμμοσειρές απαιτούνται κατάλληλες προσαρμογές και βελτιώσεις της αναπτυχθείσας μεθοδολογίας, τις οποίες θα προσπαθήσουμε να διατυπώσουμε και να αξιοποιήσουμε στη μελλοντική εργασία. Το εν λόγω πρόβλημα δεν αντιμετωπίζεται πλέον ως πρόβλημα αναζήτησης των μη τετριμμένων λύσεων ενός ομογενούς γραμμικού συστήματος, αλλά πρέπει να αντιμετωπιστεί ως ένα πρόβλημα σκέδασηςπερίθλασης, το οποίο οδηγεί σε ένα μη ομογενές γραμμικό σύστημα. Στη Διδακτορική Διατριβή εξετάζεται το πρόβλημα κυματοδήγησης σε συζεύκτη γραμμοσειρών. Όμως, παρουσιάζει επίσης ιδιαίτερο ενδιαφέρον και η μελέτη του προβλήματος σκέδασης επιπέδου κύματος από διάταξη κυματοδηγού γραμμοσειρών. Η αναπτυχθείσα μεθοδολογία μπορεί να εφαρμοστεί με ορισμένες απαραίτητες τροποποιήσεις και επεκτάσεις και για τη μελέτη του εν λόγω προβλήματος σκέδασης. Συγκεκριμένα, με εφαρμογή της Μεθόδου των Ροπών με τεχνικές Galerkin συνολικού χώρου διαμορφώνεται ένα επιλύσιμο μη ομογενές γραμμικό αλγεβρικό σύστημα, του οποίου οι λύσεις χρησιμοποιούνται για τον προσδιορισμό του σκεδαζόμενου σε όλες τις περιοχές του χώρου και μεταδιδόμενου στον κυματοδηγό ηλεκτρικού πεδίου. Η σχεδίαση ενός συζεύκτη γραμμοσειρών συνίσταται στην κατάλληλη επιλογή των βέλτιστων φυσικών και γεωμετρικών χαρακτηριστικών των κυματοδηγών και των γραμμοσειρών, τα οποία προσφέρουν το ελάχιστο δυνατό μήκος σύζευξης και τη μέγιστη δυνατή αποδοτικότητα σύζευξης. Η εν λόγω βελτιστοποίηση στη Διδακτορική Διατριβή επιτυγχάνεται χωριστά για κάθε χαρακτηριστικό μέγεθος της διάταξης (θεωρώντας τα υπόλοιπα μεγέθη σταθεροποιημένα). Όμως, η εφαρμογή προχωρημένων τεχνικών βελτιστοποίησης, όπως είναι π.χ. οι Γενετικοί Αλγόριθμοι, οι οποίοι εκτελούν μία τυχαία αναζήτηση για το ολικό βέλτιστο στον πολυδιάστατο χώρο των παραμέτρων βελτιστοποίησης, θα μπορούσε να προσδιορίσει μία πιο αποδοτική βελτιστοποίηση χωρίς τους προηγούμενους περιορισμούς (δηλαδή με την ταυτόχρονη μεταβολή όλων των χαρακτηριστικών μεγεθών της διάταξης). 66
167 ΠΑΡΑΡΤΗΜΑ Α ΣΥΜΜΕΤΡΙΑ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ GREEN Στο Παράρτημα αυτό επιβεβαιώνεται η αρχή ότι η εναλλαγή των θέσεων παρατήρησης και διέγερσης στη διάταξη δύο απείρων συμμετρικών διηλεκτρικών πλακών διατηρεί το ηλεκτρικό πεδίο. Για το σκοπό αυτό υπενθυμίζουμε καταρχήν από την παράγραφο 3.3 ότι ως συνάρτηση Green G(r;r ) στη συγκεκριμένη διάταξη ορίζεται το ηλεκτρικό πεδίο E y (x,z) (απόκριση), το οποίο παράγεται στη διάταξη από τη ρευματική πηγή (διέγερση) της (3.9). Η ισχύς της προαναφερομένης αρχής εξασφαλίζεται από το ακόλουθο θεώρημα. Η εν λόγω αρχή, εκτός από τη θεωρητική της σημασία, μπορεί να χρησιμοποιηθεί ουσιαστικά και για την απλούστευση (συντόμευση) των υπολογισμών προς εύρεση της συνάρτησης Green σε πολυστρωματικά μέσα (layered media). Θεώρημα Η συνάρτηση Green G (; ),, rr rr της διάταξης δύο απείρων συμμετρικών διηλεκτρικών πλακών είναι συμμετρική, δηλαδή ισχύει G(; rr ) = G( r ;), r rr, Απόδειξη Στο παρακάτω Σχήμα σχεδιάζεται κατάλληλος διαχωρισμός σε ορθογώνια D i (i=,,5) του τμήματος της διάταξης δύο απείρων συμμετρικών διηλεκτρικών πλακών, το οποίο ευρίσκεται εντός ορθογωνίου L, και ο οποίος διαχωρισμός εξυπηρετεί την εφαρμογή των τύπων του Green. Τα ορθογώνια D i (i=,,5) προκύπτουν ως τομές του ορθογωνίου L με τη διάταξη των δύο πλακών. 67
168 Σχήμα 6. Διαχωρισμός κατάλληλου τμήματος της διάταξης δύο απείρων συμμετρικών διηλεκτρικών πλακών από ένα ορθογώνιο. Εφαρμόζοντας το δεύτερο τύπο του Green για τις συναρτήσεις Green G(r;r ) και G(r;r ),, r r σε κάθε ορθογώνιο D i, λαμβάνουμε Di G(; rr) G(; rr) G(; rr) G(; rr) dxdz [ (; ) (; ) (; ) (; ) ] = G rr G rr G rr G rr nˆ dl Di i (Α.) όπου nˆ i είναι το μοναδιαίο εξωτερικό κάθετο διάνυσμα του D i. Αθροίζοντας κατά μέλη τις (Α.) και λαμβάνοντας υπόψη ότι nˆ i G G =, ευρίσκουμε n i D 5 Di i= G(; rr) G(; rr) G(; rr) G(; rr) dxdz = G(; rr) G(; rr) G(; rr) G(; rr) dl ni ni (Α.) όπου D 5 D G(; rr), G(; rr ) = i. Επειδή, όπως αναφέραμε στην παράγραφο 3.3, οι συναρτήσεις i= G( rr ; ) x G( rr ; ) και x προϋποτίθενται συνεχείς στο ορθογώνιο D και τα μοναδιαία 68
11 ΧΡΟΝΙΚΑ ΜΕΤΑΒΑΛΛΟΜΕΝΑ ΠΕΔΙΑ
 xx ΤΟΜΟΣ ΙI 11 ΧΡΟΝΙΚΑ ΜΕΤΑΒΑΛΛΟΜΕΝΑ ΠΕΔΙΑ 741 11.1 Διαφορική και ολοκληρωτική μορφή των εξισώσεων Maxwell Ρεύμα μετατόπισης...................................... 741 11.2 Οι εξισώσεις Maxwell σε μιγαδική
xx ΤΟΜΟΣ ΙI 11 ΧΡΟΝΙΚΑ ΜΕΤΑΒΑΛΛΟΜΕΝΑ ΠΕΔΙΑ 741 11.1 Διαφορική και ολοκληρωτική μορφή των εξισώσεων Maxwell Ρεύμα μετατόπισης...................................... 741 11.2 Οι εξισώσεις Maxwell σε μιγαδική
ΠΕΡΙΕΧΟΜΕΝΑ ΤΟΜΟΣ Ι ΕΙΣΑΓΩΓΗ 1
 ΤΟΜΟΣ Ι ΕΙΣΑΓΩΓΗ 1 1 ΟΙ ΒΑΣΙΚΟΙ ΝΟΜΟΙ ΤΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟΥ ΠΕΔΙΟΥ 7 1.1 Μονάδες και σύμβολα φυσικών μεγεθών..................... 7 1.2 Προθέματα φυσικών μεγεθών.............................. 13 1.3 Αγωγοί,
ΤΟΜΟΣ Ι ΕΙΣΑΓΩΓΗ 1 1 ΟΙ ΒΑΣΙΚΟΙ ΝΟΜΟΙ ΤΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟΥ ΠΕΔΙΟΥ 7 1.1 Μονάδες και σύμβολα φυσικών μεγεθών..................... 7 1.2 Προθέματα φυσικών μεγεθών.............................. 13 1.3 Αγωγοί,
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ & ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Η. Ν. Γλύτσης, Tηλ.: 21-7722479 - e-mail:
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ & ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Η. Ν. Γλύτσης, Tηλ.: 21-7722479 - e-mail:
Περιεχόμενα διάλεξης
 4η Διάλεξη Οπτικές ίνες Γ. Έλληνας, Διάλεξη 4, σελ. 1 Περιεχόμενα διάλεξης Ηλεκτρομαγνητικά κύματα Κυματική Εξίσωση Ακριβής Λύση Οπτικών Ινών Ταξινόμηση Τρόπων Αριθμός Τρόπων Γ. Έλληνας, Διάλεξη 4, σελ.
4η Διάλεξη Οπτικές ίνες Γ. Έλληνας, Διάλεξη 4, σελ. 1 Περιεχόμενα διάλεξης Ηλεκτρομαγνητικά κύματα Κυματική Εξίσωση Ακριβής Λύση Οπτικών Ινών Ταξινόμηση Τρόπων Αριθμός Τρόπων Γ. Έλληνας, Διάλεξη 4, σελ.
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Ηλίας Γλύτσης, Τηλ. 21-7722479, e-mail:
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Ηλίας Γλύτσης, Τηλ. 21-7722479, e-mail:
ΠΕΡΙΕΧΟΜΕΝΑ 1. ΙΑΝΥΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ. 1.3.1 Μετατροπή από καρτεσιανό σε κυλινδρικό σύστηµα... 6 1.3.2 Απειροστές ποσότητες... 7
 ΠΕΡΙΕΧΟΜΕΝΑ 1. ΙΑΝΥΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ 1.1 Φυσικά µεγέθη... 1 1.2 ιανυσµατική άλγεβρα... 2 1.3 Μετατροπές συντεταγµένων... 6 1.3.1 Μετατροπή από καρτεσιανό σε κυλινδρικό σύστηµα... 6 1.3.2 Απειροστές ποσότητες...
ΠΕΡΙΕΧΟΜΕΝΑ 1. ΙΑΝΥΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ 1.1 Φυσικά µεγέθη... 1 1.2 ιανυσµατική άλγεβρα... 2 1.3 Μετατροπές συντεταγµένων... 6 1.3.1 Μετατροπή από καρτεσιανό σε κυλινδρικό σύστηµα... 6 1.3.2 Απειροστές ποσότητες...
Μικροκυματικές Επικοινωνίες & Τεχνολογίες Χιλιοστομετρικών Κυμάτων
 Μικροκυματικές Επικοινωνίες & Τεχνολογίες Χιλιοστομετρικών Κυμάτων ΕΙΣΑΓΩΓΗ - Το μάθημα αυτό πραγματεύεται θεμελιώδεις έννοιες των γραμμών μεταφοράς στην επιστημονική περιοχή των ηλεκτρονικών συστημάτων
Μικροκυματικές Επικοινωνίες & Τεχνολογίες Χιλιοστομετρικών Κυμάτων ΕΙΣΑΓΩΓΗ - Το μάθημα αυτό πραγματεύεται θεμελιώδεις έννοιες των γραμμών μεταφοράς στην επιστημονική περιοχή των ηλεκτρονικών συστημάτων
AΠΟΦΑΣΗ της από 3/4/2012 Συνεδρίασης του Δ.Σ. του Τμήματος Φυσικής. ΕΞΕΤΑΣΤΕΑ ΥΛΗ ΦΥΣΙΚΗΣ ΙΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ) Για το 5ο εξάμηνο
 ΕΞΕΤΑΣΤΕΑ ΥΛΗ ΦΥΣΙΚΗΣ ΙΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ) Ι. Ηλεκτρικό φορτίο-διατήρηση φορτίου-κβάντωση φορτίου-νόμος Coulomb-Ενέργεια συστήματος φορτίων-ηλεκτρικό πεδίο-κατανομές φορτίου-ροή, Νόμος Gauss. ΙΙ. Ηλεκτρικό
ΕΞΕΤΑΣΤΕΑ ΥΛΗ ΦΥΣΙΚΗΣ ΙΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ) Ι. Ηλεκτρικό φορτίο-διατήρηση φορτίου-κβάντωση φορτίου-νόμος Coulomb-Ενέργεια συστήματος φορτίων-ηλεκτρικό πεδίο-κατανομές φορτίου-ροή, Νόμος Gauss. ΙΙ. Ηλεκτρικό
Κλασική Ηλεκτροδυναμική Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΗΛΕΚΤΡΟΣΤΑΤΙΚΑ ΠΕΔΙΑ ΣΤΗΝ ΥΛΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΗΛΕΚΤΡΟΣΤΑΤΙΚΑ ΠΕΔΙΑ ΣΤΗΝ ΥΛΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΛΥΣΕΙΣ ΕΞΙΣΩΣΗΣ ΚΥΜΑΤΟΣ ΣΤΟΥΣ ΚΥΜΑΤΟΔΗΓΟΥΣ ΔΙΑΦΟΡΩΝ ΔΙΑΤΟΜΩΝ
 ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ : Φυσικής και Εφαρμοσμένων Μαθηματικών Μάθημα : Εφαρμοσμένα Μαθηματικά Διδάσκων: Αν. καθηγητής Χρ. Σχοινάς Προαιρετική
ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ : Φυσικής και Εφαρμοσμένων Μαθηματικών Μάθημα : Εφαρμοσμένα Μαθηματικά Διδάσκων: Αν. καθηγητής Χρ. Σχοινάς Προαιρετική
Κλασική Ηλεκτροδυναμική Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΕΙΣΑΓΩΓΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΕΙΣΑΓΩΓΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Κλασική Ηλεκτροδυναμική Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΜΑΓΝΗΤΟΣΤΑΤΙΚΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΜΑΓΝΗΤΟΣΤΑΤΙΚΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΚΥΜΑΤΟ ΗΓΗΣΗ. «Μικροοπτικές διατάξεις-ολοκληρωµένα οπτικά»
 ΚΥΜΑΤΟ ΗΓΗΣΗ Επίπεδοι κυµατοδηγοί Προσέγγιση γεωµετρικής οπτικής Προσέγγιση κυµατικής οπτικής και συνοριακών συνθηκών Οπτικές ίνες ιασπορά Μέθοδοι ανάπτυξης κυµατοδηγών Ηχρήση των κυµάτων στις επικοινωνίες
ΚΥΜΑΤΟ ΗΓΗΣΗ Επίπεδοι κυµατοδηγοί Προσέγγιση γεωµετρικής οπτικής Προσέγγιση κυµατικής οπτικής και συνοριακών συνθηκών Οπτικές ίνες ιασπορά Μέθοδοι ανάπτυξης κυµατοδηγών Ηχρήση των κυµάτων στις επικοινωνίες
ΚΕΦΑΛΑΙΟ 4ο : Θεωρητική προσέγγιση της FDTD
 ΚΦΑΛΑΙΟ 4ο : Θεωρητική προσέγγιση της DTD 4.. ισαγωγή Από τις τρεις µεθόδους πρόβλεψης των επενεργειών της ηλεκτροµαγνητικής ακτινοβολίας πειραµατική αναλυτική υπολογιστική- η υπολογιστική είναι η νεότερη
ΚΦΑΛΑΙΟ 4ο : Θεωρητική προσέγγιση της DTD 4.. ισαγωγή Από τις τρεις µεθόδους πρόβλεψης των επενεργειών της ηλεκτροµαγνητικής ακτινοβολίας πειραµατική αναλυτική υπολογιστική- η υπολογιστική είναι η νεότερη
ΠΑΡΑΡΤΗΜΑ Γ. Επικαμπύλια και Επιφανειακά Ολοκληρώματα. Γ.1 Επικαμπύλιο Ολοκλήρωμα
 ΠΑΡΑΡΤΗΜΑ Γ Επικαμπύλια και Επιφανειακά Ολοκληρώματα Η αναγκαιότητα για τον ορισμό και την περιγραφή των ολοκληρωμάτων που θα περιγράψουμε στο Παράρτημα αυτό προκύπτει από το γεγονός ότι τα μεγέθη που
ΠΑΡΑΡΤΗΜΑ Γ Επικαμπύλια και Επιφανειακά Ολοκληρώματα Η αναγκαιότητα για τον ορισμό και την περιγραφή των ολοκληρωμάτων που θα περιγράψουμε στο Παράρτημα αυτό προκύπτει από το γεγονός ότι τα μεγέθη που
ΥΠΟΛΟΓΙΣΤΙΚΕΣ ΤΕΧΝΙΚΕΣ ΓΙΑ ΣΥΣΤΗΜΑΤΑ ΜΕΤΑΔΟΣΗΣ ΠΛΗΡΟΦΟΡΙΑΣ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΥΠΟΛΟΓΙΣΤΙΚΕΣ ΤΕΧΝΙΚΕΣ ΓΙΑ ΣΥΣΤΗΜΑΤΑ ΜΕΤΑΔΟΣΗΣ ΠΛΗΡΟΦΟΡΙΑΣ Δ.-Θ. Κακλαμάνη, Καθηγήτρια ΕΜΠ Δρ. Σ. Καπελλάκη,
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΥΠΟΛΟΓΙΣΤΙΚΕΣ ΤΕΧΝΙΚΕΣ ΓΙΑ ΣΥΣΤΗΜΑΤΑ ΜΕΤΑΔΟΣΗΣ ΠΛΗΡΟΦΟΡΙΑΣ Δ.-Θ. Κακλαμάνη, Καθηγήτρια ΕΜΠ Δρ. Σ. Καπελλάκη,
Experiments are the only means of knowledge. Anyother is poetry and imagination. M.Plank 2 ΟΙ ΕΞΙΣΩΣΕΙΣ ΤΟΥ MAXWELL
 ΚΥΜΑΤΙΚΗ-ΟΠΤΙΚΗ 7 xpeiments ae the only means o knowledge. Anyothe is poety and imagination. M.Plank 2 ΟΙ ΕΞΙΣΩΣΕΙΣ ΤΟΥ MAXWLL Σε µια πρώτη παρουσίαση του θέµατος δίνονται οι εξισώσεις του Maxwell στο
ΚΥΜΑΤΙΚΗ-ΟΠΤΙΚΗ 7 xpeiments ae the only means o knowledge. Anyothe is poety and imagination. M.Plank 2 ΟΙ ΕΞΙΣΩΣΕΙΣ ΤΟΥ MAXWLL Σε µια πρώτη παρουσίαση του θέµατος δίνονται οι εξισώσεις του Maxwell στο
ΗΜ & Διάδοση ΗΜ Κυμάτων
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΗΜ & Διάδοση ΗΜ Κυμάτων Ενότητα : Κυματική Εξίσωση & Επίπεδο ΗΜ Κύμα Σαββαΐδης Στυλιανός Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε. Άδειες
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΗΜ & Διάδοση ΗΜ Κυμάτων Ενότητα : Κυματική Εξίσωση & Επίπεδο ΗΜ Κύμα Σαββαΐδης Στυλιανός Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε. Άδειες
«ΜΕΛΕΤΗ ΙΑΤΑΞΕΩΝ ΦΩΤΟΝΙΚΩΝ ΚΡΥΣΤΑΛΛΩΝ ΓΙΑ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΕΣ ΕΦΑΡΜΟΓΕΣ»
 ΠΡΟΣΚΛΗΣΗ ΕΝ ΙΑΦΕΡΟΝΤΟΣ ΓΙΑ ΕΚΠΟΝΗΣΗ Ι ΑΚΤΟΡΙΚΗΣ ΙΑΤΡΙΒΗΣ «ΜΕΛΕΤΗ ΙΑΤΑΞΕΩΝ ΦΩΤΟΝΙΚΩΝ ΚΡΥΣΤΑΛΛΩΝ ΓΙΑ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΕΣ ΕΦΑΡΜΟΓΕΣ» Υπεύθυνος Καθηγητής: κ. Θωµάς Σφηκόπουλος Υπεύθυνος Επιστηµονικός Συνεργάτες:
ΠΡΟΣΚΛΗΣΗ ΕΝ ΙΑΦΕΡΟΝΤΟΣ ΓΙΑ ΕΚΠΟΝΗΣΗ Ι ΑΚΤΟΡΙΚΗΣ ΙΑΤΡΙΒΗΣ «ΜΕΛΕΤΗ ΙΑΤΑΞΕΩΝ ΦΩΤΟΝΙΚΩΝ ΚΡΥΣΤΑΛΛΩΝ ΓΙΑ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΕΣ ΕΦΑΡΜΟΓΕΣ» Υπεύθυνος Καθηγητής: κ. Θωµάς Σφηκόπουλος Υπεύθυνος Επιστηµονικός Συνεργάτες:
ΥΠΟΛΟΓΙΣΤΙΚΕΣ ΤΕΧΝΙΚΕΣ ΓΙΑ ΣΥΣΤΗΜΑΤΑ ΜΕΤΑΔΟΣΗΣ ΠΛΗΡΟΦΟΡΙΑΣ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΥΠΟΛΟΓΙΣΤΙΚΕΣ ΤΕΧΝΙΚΕΣ ΓΙΑ ΣΥΣΤΗΜΑΤΑ ΜΕΤΑΔΟΣΗΣ ΠΛΗΡΟΦΟΡΙΑΣ Διδάσκουσα: Δ.-Θ. Κακλαμάνη Web Sites: http://olympos.esd.ece.ntua.gr
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΥΠΟΛΟΓΙΣΤΙΚΕΣ ΤΕΧΝΙΚΕΣ ΓΙΑ ΣΥΣΤΗΜΑΤΑ ΜΕΤΑΔΟΣΗΣ ΠΛΗΡΟΦΟΡΙΑΣ Διδάσκουσα: Δ.-Θ. Κακλαμάνη Web Sites: http://olympos.esd.ece.ntua.gr
Νόμος Ampere- Διανυσματικό Δυναμικό
 Νόμος Ampere- Διανυσματικό Δυναμικό Δομή Διάλεξης Μαγνητικό πεδίο ευθύγραμμων αγωγών Ο στροβιλισμός και η κλίση μαγνητικού πεδίου: ο νόμος του Ampere Εφαρμογές του Νόμου του Ampere To διανυσματικό δυναμικό
Νόμος Ampere- Διανυσματικό Δυναμικό Δομή Διάλεξης Μαγνητικό πεδίο ευθύγραμμων αγωγών Ο στροβιλισμός και η κλίση μαγνητικού πεδίου: ο νόμος του Ampere Εφαρμογές του Νόμου του Ampere To διανυσματικό δυναμικό
Κλασική Ηλεκτροδυναμική Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΤΕΧΝΙΚΕΣ ΥΠΟΛΟΓΙΣΜΟΥ ΗΛΕΚΤΡΙΚΟΥ ΔΥΝΑΜΙΚΟΥ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΤΕΧΝΙΚΕΣ ΥΠΟΛΟΓΙΣΜΟΥ ΗΛΕΚΤΡΙΚΟΥ ΔΥΝΑΜΙΚΟΥ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
Κλασική Ηλεκτροδυναμική
 Κλασική Ηλεκτροδυναμική Ενότητα 22: Κυματοπακέτα-Κυματοδηγοί Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι να παρουσιάσει την έννοια του κυματοπακέτου,
Κλασική Ηλεκτροδυναμική Ενότητα 22: Κυματοπακέτα-Κυματοδηγοί Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι να παρουσιάσει την έννοια του κυματοπακέτου,
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ & ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Η. Ν. Γλύτσης, Tηλ.: 210-7722479 - e-mail:
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ & ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Η. Ν. Γλύτσης, Tηλ.: 210-7722479 - e-mail:
ΣΗΜΕΙΩΣΕΙΣ ΣΤΟΙΧΕΙΑ ΔΙΑΝΥΣΜΑΤΙΚΗΣ ΑΝΑΛΥΣΗΣ
 ΣΗΜΕΙΩΣΕΙΣ ΣΤΟΙΧΕΙΑ ΙΑΝΥΣΜΑΤΙΚΗΣ ΑΝΑΛΥΣΗΣ Σκοπός Σκοπός του κεφαλαίου είναι η ανασκόπηση βασικών μαθηματικών εργαλείων που αφορούν τη μελέτη διανυσματικών συναρτήσεων [π.χ. E(, t) ]. Τα εργαλεία αυτά είναι
ΣΗΜΕΙΩΣΕΙΣ ΣΤΟΙΧΕΙΑ ΙΑΝΥΣΜΑΤΙΚΗΣ ΑΝΑΛΥΣΗΣ Σκοπός Σκοπός του κεφαλαίου είναι η ανασκόπηση βασικών μαθηματικών εργαλείων που αφορούν τη μελέτη διανυσματικών συναρτήσεων [π.χ. E(, t) ]. Τα εργαλεία αυτά είναι
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ και ΕΦΑΡΜΟΓΕΣ ΕΡΩΤΗΜΑΤΟΛΟΓΙΟ ΜΑΘΗΜΑΤΟΣ
 1 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ και ΕΦΑΡΜΟΓΕΣ ΕΡΩΤΗΜΑΤΟΛΟΓΙΟ ΜΑΘΗΜΑΤΟΣ 1) Να αναφέρετε τις 4 παραδοχές που ισχύουν για το ηλεκτρικό φορτίο 2) Εξηγήστε πόσα είδη κατανοµών ηλεκτρικού φορτίου υπάρχουν. ιατυπώστε τους
1 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ και ΕΦΑΡΜΟΓΕΣ ΕΡΩΤΗΜΑΤΟΛΟΓΙΟ ΜΑΘΗΜΑΤΟΣ 1) Να αναφέρετε τις 4 παραδοχές που ισχύουν για το ηλεκτρικό φορτίο 2) Εξηγήστε πόσα είδη κατανοµών ηλεκτρικού φορτίου υπάρχουν. ιατυπώστε τους
Κλασική Ηλεκτροδυναμική
 Κλασική Ηλεκτροδυναμική Ενότητα 18: Νόμοι Maxwell Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι να παρουσίασει τις εξισώσεις Maxwell. 2 Περιεχόμενα ενότητας
Κλασική Ηλεκτροδυναμική Ενότητα 18: Νόμοι Maxwell Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι να παρουσίασει τις εξισώσεις Maxwell. 2 Περιεχόμενα ενότητας
Δυναμική Ηλεκτρικών Μηχανών
 Δυναμική Ηλεκτρικών Μηχανών Ενότητα 4: Μέθοδος Μικρών Μεταβολών Επ. Καθηγήτρια Τζόγια Χ. Καππάτου Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Δυναμική Ηλεκτρικών Μηχανών Ενότητα 4: Μέθοδος Μικρών Μεταβολών Επ. Καθηγήτρια Τζόγια Χ. Καππάτου Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΠΡΟΣΟΧΗ : Nέα Ύλη για τις Κατατακτήριες από 2012 και μετά στην Φυσική Ι. Για το 3ο εξάμηνο. ΕΞΕΤΑΣΤΕΑ ΥΛΗ στο μάθημα ΦΥΣΙΚΗ Ι - ΜΗΧΑΝΙΚΗ
 ΠΡΟΣΟΧΗ : Nέα Ύλη για τις Κατατακτήριες από 2012 και μετά στην Φυσική Ι ΕΞΕΤΑΣΤΕΑ ΥΛΗ στο μάθημα ΦΥΣΙΚΗ Ι - ΜΗΧΑΝΙΚΗ 1. Κινηματική (ευθύγραμμη και καμπυλόγραμμη κίνηση) 2. Σχετική κίνηση-μετασχηματισμοί
ΠΡΟΣΟΧΗ : Nέα Ύλη για τις Κατατακτήριες από 2012 και μετά στην Φυσική Ι ΕΞΕΤΑΣΤΕΑ ΥΛΗ στο μάθημα ΦΥΣΙΚΗ Ι - ΜΗΧΑΝΙΚΗ 1. Κινηματική (ευθύγραμμη και καμπυλόγραμμη κίνηση) 2. Σχετική κίνηση-μετασχηματισμοί
Ανάλυση της κυματοδήγησης στις οπτικές ίνες με την ηλεκτρομαγνητική θεωρία
 Ανάλυση της κυματοδήγησης στις οπτικές ίνες με την ηλεκτρομαγνητική θεωρία Τρόποι διάδοσης ηλεκτρομαγνητικών κυμάτων Στο κενό, τα ηλεκτρομαγνητικά κύματα διαδίδονται έχοντας το ηλεκτρικό πεδίο Ε και το
Ανάλυση της κυματοδήγησης στις οπτικές ίνες με την ηλεκτρομαγνητική θεωρία Τρόποι διάδοσης ηλεκτρομαγνητικών κυμάτων Στο κενό, τα ηλεκτρομαγνητικά κύματα διαδίδονται έχοντας το ηλεκτρικό πεδίο Ε και το
ΠΕΡΙΕΧΟΜΕΝΑ 1. ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ 2. ΣΤΟΙΧΕΙΑ ΗΛΕΚΤΡΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ
 ΠΕΡΙΕΧΟΜΕΝΑ 1. ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ 1.1 Εισαγωγή 1.1 1.2 Συμβολισμοί και μονάδες 1.3 1.3 Φορτίο, τάση και ενέργεια 1.5 Φορτίο και ρεύμα 1.5 Τάση 1.6 Ισχύς και Ενέργεια 1.6 1.4 Γραμμικότητα 1.7 Πρόσθεση
ΠΕΡΙΕΧΟΜΕΝΑ 1. ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ 1.1 Εισαγωγή 1.1 1.2 Συμβολισμοί και μονάδες 1.3 1.3 Φορτίο, τάση και ενέργεια 1.5 Φορτίο και ρεύμα 1.5 Τάση 1.6 Ισχύς και Ενέργεια 1.6 1.4 Γραμμικότητα 1.7 Πρόσθεση
website:
 Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 31 Μαρτίου 2019 1 Δυνάμεις μάζας και επαφής Δυνάμεις μάζας ή δυνάμεις όγκου ονομάζονται οι δυνάμεις που είναι
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 31 Μαρτίου 2019 1 Δυνάμεις μάζας και επαφής Δυνάμεις μάζας ή δυνάμεις όγκου ονομάζονται οι δυνάμεις που είναι
Παραδείγματα Λυμένες ασκήσεις Κεφαλαίου 5
 Παραδείγματα Λυμένες ασκήσεις Κεφαλαίου 5 Παράδειγμα : Υπενθυμίζεται η γενική μορφή της σχέσεως διασποράς για την περίπτωση αλληλεπίδρασης κύματος-ρεύματος, παρουσία και των επιδράσεων της επιφανειακής
Παραδείγματα Λυμένες ασκήσεις Κεφαλαίου 5 Παράδειγμα : Υπενθυμίζεται η γενική μορφή της σχέσεως διασποράς για την περίπτωση αλληλεπίδρασης κύματος-ρεύματος, παρουσία και των επιδράσεων της επιφανειακής
Πρόλογος. Κατάλογος Σχημάτων
 Περιεχόμενα Πρόλογος Κατάλογος Σχημάτων v xv 1 ΜΔΕ πρώτης τάξης 21 1.1 Γενικότητες........................... 21 1.2 Εισαγωγή............................ 24 1.2.1 Γεωμετρικές θεωρήσεις στο πρόβλημα της
Περιεχόμενα Πρόλογος Κατάλογος Σχημάτων v xv 1 ΜΔΕ πρώτης τάξης 21 1.1 Γενικότητες........................... 21 1.2 Εισαγωγή............................ 24 1.2.1 Γεωμετρικές θεωρήσεις στο πρόβλημα της
Hλεκτρομηχανικά Συστήματα Mετατροπής Ενέργειας
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Μηχανολόγων Μηχανικών Τομέας Μηχανολογικών Κατασκευών και Αυτομάτου Ελέγχου 2.3.26.3 Hλεκτρομηχανικά Συστήματα Mετατροπής Ενέργειας Εξέταση 3 ου Eξαμήνου (20 Φεβρουαρίου
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Μηχανολόγων Μηχανικών Τομέας Μηχανολογικών Κατασκευών και Αυτομάτου Ελέγχου 2.3.26.3 Hλεκτρομηχανικά Συστήματα Mετατροπής Ενέργειας Εξέταση 3 ου Eξαμήνου (20 Φεβρουαρίου
ΜΕΤΡΗΣΗ ΚΑΙ ΦΑΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ ΜΗ ΙΟΝΙΖΟΥΣΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗΣ ΑΚΤΙΝΟΒΟΛΙΑΣ
 ΜΕΤΡΗΣΗ ΚΑΙ ΦΑΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ ΜΗ ΙΟΝΙΖΟΥΣΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗΣ ΑΚΤΙΝΟΒΟΛΙΑΣ Οποτε ακούτε ραδιόφωνο, βλέπετε τηλεόραση, στέλνετε SMS χρησιµοποιείτε ηλεκτροµαγνητική ακτινοβολία (ΗΜΑ). Η ΗΜΑ ταξιδεύει µε
ΜΕΤΡΗΣΗ ΚΑΙ ΦΑΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ ΜΗ ΙΟΝΙΖΟΥΣΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗΣ ΑΚΤΙΝΟΒΟΛΙΑΣ Οποτε ακούτε ραδιόφωνο, βλέπετε τηλεόραση, στέλνετε SMS χρησιµοποιείτε ηλεκτροµαγνητική ακτινοβολία (ΗΜΑ). Η ΗΜΑ ταξιδεύει µε
ΚΥΜΑΤΙΚΗ-ΟΠΤΙΚΗ 1. Σχήµα 1 Σχήµα 2
 ΚΥΜΑΤΙΚΗ-ΟΠΤΙΚΗ The law of natue ae witten in the language of mathematic G.Galileo God ued beautiful mathematic in ceating the wold P.Diac ΣΥΝΤΟΜΗ ΜΑΘΗΜΑΤΙΚΗ ΕΙΣΑΓΩΓΗ Α. ΣΤΟΙΧΕΙΑ ΙΑΝΥΣΜΑΤΙΚΗΣ ΑΝΑΛΥΣΗΣ.Ροή
ΚΥΜΑΤΙΚΗ-ΟΠΤΙΚΗ The law of natue ae witten in the language of mathematic G.Galileo God ued beautiful mathematic in ceating the wold P.Diac ΣΥΝΤΟΜΗ ΜΑΘΗΜΑΤΙΚΗ ΕΙΣΑΓΩΓΗ Α. ΣΤΟΙΧΕΙΑ ΙΑΝΥΣΜΑΤΙΚΗΣ ΑΝΑΛΥΣΗΣ.Ροή
Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών
 Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών Οι παρούσες σημειώσεις αποτελούν βοήθημα στο μάθημα Αριθμητικές Μέθοδοι του 5 ου εξαμήνου του ΤΜΜ ημήτρης Βαλουγεώργης Καθηγητής Εργαστήριο Φυσικών
Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών Οι παρούσες σημειώσεις αποτελούν βοήθημα στο μάθημα Αριθμητικές Μέθοδοι του 5 ου εξαμήνου του ΤΜΜ ημήτρης Βαλουγεώργης Καθηγητής Εργαστήριο Φυσικών
& Εφαρμογές. (εργαστήριο) Μικροκύματα
 Μικροκύματα & Εφαρμογές (εργαστήριο) ΜΙΚΡΟΚΥΜΑΤΙΚΑ ΣΤΟΙΧΕΙΑ Στο κεφάλαιο αυτό γίνεται παρουσίαση των κυριότερων μικροκυματικών στοιχείων, που συνήθως χρησιμοποιούνται σε μικροκυματικές εφαρμογές στην περιοχή
Μικροκύματα & Εφαρμογές (εργαστήριο) ΜΙΚΡΟΚΥΜΑΤΙΚΑ ΣΤΟΙΧΕΙΑ Στο κεφάλαιο αυτό γίνεται παρουσίαση των κυριότερων μικροκυματικών στοιχείων, που συνήθως χρησιμοποιούνται σε μικροκυματικές εφαρμογές στην περιοχή
6 Εισαγωγή στα Συστήματα Ηλεκτρικής Ενέργειας
 Πρόλογος Σ το βιβλίο αυτό περιλαμβάνεται η ύλη του μαθήματος «Εισαγωγή στα Συστήματα Ηλεκτρικής Ενέργειας» που διδάσκεται στους φοιτητές του Γ έτους σπουδών του Τμήματος Ηλεκτρολόγων Μηχανικών και Τεχνολογίας
Πρόλογος Σ το βιβλίο αυτό περιλαμβάνεται η ύλη του μαθήματος «Εισαγωγή στα Συστήματα Ηλεκτρικής Ενέργειας» που διδάσκεται στους φοιτητές του Γ έτους σπουδών του Τμήματος Ηλεκτρολόγων Μηχανικών και Τεχνολογίας
Το μαθηματικό μοντέλο της FDTD (1)
 (Fe Dfferece - Tme Doma) Το μαθηματικό μοντέλο της FDTD () Η FDTD αποτελεί μια από τις πιο δημοφιλείς μεθόδους για την αριθμητική επίλυση των εξισώσεων του Mawell. Το μαθηματικό της μοντέλο βασίζεται στη
(Fe Dfferece - Tme Doma) Το μαθηματικό μοντέλο της FDTD () Η FDTD αποτελεί μια από τις πιο δημοφιλείς μεθόδους για την αριθμητική επίλυση των εξισώσεων του Mawell. Το μαθηματικό της μοντέλο βασίζεται στη
3.1 Η Αρχή της υπέρθεσης (ή της επαλληλίας)
 ΚΕΦ. 3 Γενικές αρχές της κυματικής 3.1-1 3.1 Η Αρχή της υπέρθεσης (ή της επαλληλίας) 3.1.1 Γενική διατύπωση 3.1. Εύρος ισχύος της αρχής της υπέρθεσης 3.1.3 Μαθηματικές συνέπειες της αρχής της υπέρθεσης
ΚΕΦ. 3 Γενικές αρχές της κυματικής 3.1-1 3.1 Η Αρχή της υπέρθεσης (ή της επαλληλίας) 3.1.1 Γενική διατύπωση 3.1. Εύρος ισχύος της αρχής της υπέρθεσης 3.1.3 Μαθηματικές συνέπειες της αρχής της υπέρθεσης
HMY331 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΠΕΔΙΑ
 HMY331 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΠΕΔΙΑ Διδάσκων Δρ Γ. Η. Γεωργίου Μαθήματα Δευτέρα και Πέμπτη 10.30-12.00 π.μ. Σύστημα Αξιολόγησης 1. Τελική Εξέταση 60% 2. Ενδιάμεση Εξέταση 40% Κατοίκον εργασία 5 κατοίκον εργασίες
HMY331 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΠΕΔΙΑ Διδάσκων Δρ Γ. Η. Γεωργίου Μαθήματα Δευτέρα και Πέμπτη 10.30-12.00 π.μ. Σύστημα Αξιολόγησης 1. Τελική Εξέταση 60% 2. Ενδιάμεση Εξέταση 40% Κατοίκον εργασία 5 κατοίκον εργασίες
ΧΡΟΝΙΚΑ ΜΕΤΑΒΑΛΛΟΜΕΝΑ ΠΕΔΙΑ
 ΚΕΦΑΛΑΙΟ 11 ΧΡΟΝΙΚΑ ΜΕΤΑΒΑΛΛΟΜΕΝΑ ΠΕΔΙΑ Στα προηγούμενα κεφάλαια ασχοληθήκαμε, ως επί το πλείστον, με τη μελέτη πεδίων που τα μεγέθη τους δεν μεταβάλλονταν με τον χρόνο. Στο κεφάλαιο αυτό, θα επεκτείνουμε
ΚΕΦΑΛΑΙΟ 11 ΧΡΟΝΙΚΑ ΜΕΤΑΒΑΛΛΟΜΕΝΑ ΠΕΔΙΑ Στα προηγούμενα κεφάλαια ασχοληθήκαμε, ως επί το πλείστον, με τη μελέτη πεδίων που τα μεγέθη τους δεν μεταβάλλονταν με τον χρόνο. Στο κεφάλαιο αυτό, θα επεκτείνουμε
ΜΕΤΡΗΣΕΙΣ ΚΑΙ ΕΦΑΡΜΟΓΕΣ ΥΨΗΛΩΝ ΤΑΣΕΩΝ
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Τομέας Ηλεκτρικής Ισχύος Εργαστήριο Υψηλών Τάσεων ΜΕΤΡΗΣΕΙΣ ΚΑΙ ΕΦΑΡΜΟΓΕΣ ΥΨΗΛΩΝ ΤΑΣΕΩΝ (Αριθμητικές μέθοδοι υπολογισμού
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Τομέας Ηλεκτρικής Ισχύος Εργαστήριο Υψηλών Τάσεων ΜΕΤΡΗΣΕΙΣ ΚΑΙ ΕΦΑΡΜΟΓΕΣ ΥΨΗΛΩΝ ΤΑΣΕΩΝ (Αριθμητικές μέθοδοι υπολογισμού
Εισαγωγή στις Τηλεπικοινωνίες. Δομή της παρουσίασης
 6 Nv 6 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Ανάπτυξη σε Σειρές Furier Αθανάσιος
6 Nv 6 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Ανάπτυξη σε Σειρές Furier Αθανάσιος
Ηλεκτρική Μετατόπιση- Γραμμικά Διηλεκτρικά
 Ηλεκτρική Μετατόπιση- Γραμμικά Διηλεκτρικά Δομή Διάλεξης Ηλεκτρική Μετατόπιση: Ορισμός-Χρησιμότητα-Οριακές συνθήκες Γραμμικά Διηλεκτρικά: Ορισμός - Εφαρμογές Ενέργεια σε Διηλεκτρικά Δυνάμεις σε Διηλεκτρικά
Ηλεκτρική Μετατόπιση- Γραμμικά Διηλεκτρικά Δομή Διάλεξης Ηλεκτρική Μετατόπιση: Ορισμός-Χρησιμότητα-Οριακές συνθήκες Γραμμικά Διηλεκτρικά: Ορισμός - Εφαρμογές Ενέργεια σε Διηλεκτρικά Δυνάμεις σε Διηλεκτρικά
Kεφάλαιο 4. Συστήματα διαφορικών εξισώσεων. F : : F = F r, όπου r xy
 4 Εισαγωγή Kεφάλαιο 4 Συστήματα διαφορικών εξισώσεων Εστω διανυσματικό πεδίο F : : F = Fr, όπου r x, και είναι η ταχύτητα στο σημείο πχ ενός ρευστού στο επίπεδο Εστω ότι ψάχνουμε τις τροχιές κίνησης των
4 Εισαγωγή Kεφάλαιο 4 Συστήματα διαφορικών εξισώσεων Εστω διανυσματικό πεδίο F : : F = Fr, όπου r x, και είναι η ταχύτητα στο σημείο πχ ενός ρευστού στο επίπεδο Εστω ότι ψάχνουμε τις τροχιές κίνησης των
y T - yy z x T + yy T + yz T + yx T + xy T + zy T - xz T - zx T - zz T - xx T + xx T + zx T + xz T + zz T - zy T - xy T - yx T - yz
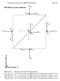 Συµπληρωµατικές Σηµειώσεις στα ΗΜ Πεδία (Κ. Χιτζανίδης Μάιος 2017 ΗΜ τάσεις σε υλικές επιφάνειες T + yy T + yz T + yx T + zy T + xy T - xx T - xz T - zx T - zz T + zz T + zx T + xz T + xx T - xy T - zy
Συµπληρωµατικές Σηµειώσεις στα ΗΜ Πεδία (Κ. Χιτζανίδης Μάιος 2017 ΗΜ τάσεις σε υλικές επιφάνειες T + yy T + yz T + yx T + zy T + xy T - xx T - xz T - zx T - zz T + zz T + zx T + xz T + xx T - xy T - zy
HMY 333 Φωτονική Διάλεξη 12 Οπτικοί κυματοδηγοί
 4 Hsiu. Ha Ανάκλαση και μετάδοση του φωτός σε μια διηλεκτρική επαφή HMY 333 Φωτονική Διάλεξη Οπτικοί κυματοδηγοί i i i r i si c si v c hp://www.e.readig.ac.u/clouds/awell/ c 3 Γωνία πρόσπτωσης < κρίσιμη
4 Hsiu. Ha Ανάκλαση και μετάδοση του φωτός σε μια διηλεκτρική επαφή HMY 333 Φωτονική Διάλεξη Οπτικοί κυματοδηγοί i i i r i si c si v c hp://www.e.readig.ac.u/clouds/awell/ c 3 Γωνία πρόσπτωσης < κρίσιμη
( ) ( ) ( )z. HMY Φωτονική. Διάλεξη 08 Οι εξισώσεις του Maxwell. r = A r. B r. ˆ det = Βαθμωτά και διανυσματικά μεγέθη
 HMY - Φωτονική Διάλεξη 8 Οι εξισώσεις του Mawell Βαθμωτά και διανυσματικά μεγέθη Πολλαπλασιασμός Πρόσθεση διανυσμάτων Βαθμωτό: το μέγεθος που για τον προσδιορισμό του χρειάζεται μόνο το μέτρο του και η
HMY - Φωτονική Διάλεξη 8 Οι εξισώσεις του Mawell Βαθμωτά και διανυσματικά μεγέθη Πολλαπλασιασμός Πρόσθεση διανυσμάτων Βαθμωτό: το μέγεθος που για τον προσδιορισμό του χρειάζεται μόνο το μέτρο του και η
ΚΕΦΑΛΑΙΟ 3: ιατύπωση σκεδαζόµενου πεδίου στο FDTD
 ΚΕΦΑΛΑΙΟ 3: ιατύπωση σκεδαζόµενου πεδίου στο FDTD H µέθοδος πεπερασµένων διαφορών στο πεδίο του χρόνου (Finite Difference Time Domain method είναι µια από τις πιο γνωστές και εύχρηστες αριθµητικές µεθόδους
ΚΕΦΑΛΑΙΟ 3: ιατύπωση σκεδαζόµενου πεδίου στο FDTD H µέθοδος πεπερασµένων διαφορών στο πεδίο του χρόνου (Finite Difference Time Domain method είναι µια από τις πιο γνωστές και εύχρηστες αριθµητικές µεθόδους
max 0 Eκφράστε την διαφορά των δύο θετικών λύσεων ώς πολλαπλάσιο του ω 0, B . Αναλύοντας το Β σε σειρά άπειρων όρων ώς προς γ/ω 0 ( σειρά
 . Να αποδείξετε ότι σε ένα ταλαντούμενο σύστημα ενός βαθμού ελευθερίας, μάζας και σταθεράς ελατηρίου s με πολύ ασθενή απόσβεση (γω, όπου γ r/, r η σταθερά αντίστασης και s/ ) το πλήρες εύρος στο μισό του
. Να αποδείξετε ότι σε ένα ταλαντούμενο σύστημα ενός βαθμού ελευθερίας, μάζας και σταθεράς ελατηρίου s με πολύ ασθενή απόσβεση (γω, όπου γ r/, r η σταθερά αντίστασης και s/ ) το πλήρες εύρος στο μισό του
Ηλεκτρομαγνητισμός. Ηλεκτρικό πεδίο νόμος Gauss. Νίκος Ν. Αρπατζάνης
 Ηλεκτρομαγνητισμός Ηλεκτρικό πεδίο νόμος Gauss Νίκος Ν. Αρπατζάνης Εισαγωγή Ο νόµος του Gauss: Μπορεί να χρησιµοποιηθεί ως ένας εναλλακτικός τρόπος υπολογισµού της έντασης του ηλεκτρικού πεδίου. Βασίζεται
Ηλεκτρομαγνητισμός Ηλεκτρικό πεδίο νόμος Gauss Νίκος Ν. Αρπατζάνης Εισαγωγή Ο νόµος του Gauss: Μπορεί να χρησιµοποιηθεί ως ένας εναλλακτικός τρόπος υπολογισµού της έντασης του ηλεκτρικού πεδίου. Βασίζεται
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ & ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Η. Ν. Γλύτσης, Tηλ.: 210-7722479 - e-mil:
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ & ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Η. Ν. Γλύτσης, Tηλ.: 210-7722479 - e-mil:
Q2-1. Η Φυσική του Φούρνου Μικροκυμάτων. Theory. Μέρος Α: Δομή και λειτουργία του μάγνητρον (6.6 points) Greek (Greece)
 Η Φυσική του Φούρνου Μικροκυμάτων Q2-1 Αυτό το πρόβλημα πραγματεύεται την παραγωγή ακτινοβολίας μικροκυμάτων σε ένα φούρνο μικροκυμάτων, και τη χρήση της στη θέρμανση του φαγητού. Η ακτινοβολία μικροκυμάτων
Η Φυσική του Φούρνου Μικροκυμάτων Q2-1 Αυτό το πρόβλημα πραγματεύεται την παραγωγή ακτινοβολίας μικροκυμάτων σε ένα φούρνο μικροκυμάτων, και τη χρήση της στη θέρμανση του φαγητού. Η ακτινοβολία μικροκυμάτων
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ Ο ΝΟΜΟΣ ΤΟΥ GAUSS
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ Ο ΝΟΜΟΣ ΤΟΥ GAUSS 1 1. ΗΛΕΚΤΡΙΚΗ ΡΟΗ O νόμος του Gauss και o νόμος του Coulomb είναι δύο εναλλακτικές διατυπώσεις της ίδιας βασικής σχέσης μεταξύ μιας κατανομής φορτίου και του
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ Ο ΝΟΜΟΣ ΤΟΥ GAUSS 1 1. ΗΛΕΚΤΡΙΚΗ ΡΟΗ O νόμος του Gauss και o νόμος του Coulomb είναι δύο εναλλακτικές διατυπώσεις της ίδιας βασικής σχέσης μεταξύ μιας κατανομής φορτίου και του
Περιοχές Ακτινοβολίας Κεραιών
 Κεραίες ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ Δημοσθένης Βουγιούκας Αναπληρωτής Καθηγητής Τμήμα Μηχανικών Πληροφοριακών & Επικοινωνιακών Συστημάτων Περιοχές Ακτινοβολίας Κεραιών 2 1 Σημειακή Πηγή 3 Κατακόρυφα Πολωμένο
Κεραίες ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ Δημοσθένης Βουγιούκας Αναπληρωτής Καθηγητής Τμήμα Μηχανικών Πληροφοριακών & Επικοινωνιακών Συστημάτων Περιοχές Ακτινοβολίας Κεραιών 2 1 Σημειακή Πηγή 3 Κατακόρυφα Πολωμένο
Δυναμική Μηχανών I. Διάλεξη 20. Χειμερινό Εξάμηνο 2013 Τμήμα Μηχανολόγων Μηχ., ΕΜΠ
 Δυναμική Μηχανών I Διάλεξη 2 Χειμερινό Εξάμηνο 213 Τμήμα Μηχανολόγων Μηχ., ΕΜΠ 1 Ανακοινώσεις Εξέταση Μαθήματος: 1/4/214, 12. Απαιτείται αποδεικτικό ταυτότητας Απαγορεύεται η παρουσία & χρήση κινητού!
Δυναμική Μηχανών I Διάλεξη 2 Χειμερινό Εξάμηνο 213 Τμήμα Μηχανολόγων Μηχ., ΕΜΠ 1 Ανακοινώσεις Εξέταση Μαθήματος: 1/4/214, 12. Απαιτείται αποδεικτικό ταυτότητας Απαγορεύεται η παρουσία & χρήση κινητού!
Εξισώσεις του Maxwell
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΑΣΥΡΜΑΤΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Εισαγωγή στα Η/Μ Κύματα Αθανάσιος Κανάτας Καθηγητής Παν/μίου Πειραιώς Εξισώσεις του Maxwell
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΑΣΥΡΜΑΤΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Εισαγωγή στα Η/Μ Κύματα Αθανάσιος Κανάτας Καθηγητής Παν/μίου Πειραιώς Εξισώσεις του Maxwell
Μηχανισµοί & Εισαγωγή στο Σχεδιασµό Μηχανών Ακαδηµαϊκό έτος: Ε.Μ.Π. Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο υναµικής και Κατασκευών - 3.
 ΜΗΧΑΝΙΣΜΟΙ & ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕ ΙΑΣΜΟ ΜΗΧΑΝΩΝ - 3.1 - Cpright ΕΜΠ - Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο υναµικής και Κατασκευών - 2012. Με επιφύλαξη παντός δικαιώµατος. All rights reserved. Απαγορεύεται
ΜΗΧΑΝΙΣΜΟΙ & ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕ ΙΑΣΜΟ ΜΗΧΑΝΩΝ - 3.1 - Cpright ΕΜΠ - Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο υναµικής και Κατασκευών - 2012. Με επιφύλαξη παντός δικαιώµατος. All rights reserved. Απαγορεύεται
Αξιοποίηση της Τεχνολογίας των Μεταϋλικών για Αποδοτικότερη Ασύρματη Μεταφορά Ενέργειας
 3 o Technology Forum Αξιοποίηση της Τεχνολογίας των Μεταϋλικών για Αποδοτικότερη Ασύρματη Μεταφορά Ενέργειας Αντώνιος Λάλας 1, 2, Νικόλαος Κανταρτζής 2, Δημήτριος Τζοβάρας 1 και Θεόδωρος Τσιμπούκης 2 1
3 o Technology Forum Αξιοποίηση της Τεχνολογίας των Μεταϋλικών για Αποδοτικότερη Ασύρματη Μεταφορά Ενέργειας Αντώνιος Λάλας 1, 2, Νικόλαος Κανταρτζής 2, Δημήτριος Τζοβάρας 1 και Θεόδωρος Τσιμπούκης 2 1
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΕ Γ.Ο.Ι. ΧΩΡΟΥΣ
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΕ Γ.Ο.Ι. ΧΩΡΟΥΣ
Δομή Διάλεξης. Ορισμός Ηλεκτρικού Δυναμικού και συσχέτιση με το Ηλεκτρικό Πεδίο
 Ηλεκτρικό Δυναμικό Δομή Διάλεξης Ορισμός Ηλεκτρικού Δυναμικού και συσχέτιση με το Ηλεκτρικό Πεδίο Ιδιότητες ηλεκτρικού δυναμικού (χρησιμότητα σε υπολογισμούς, σημείο αναφοράς, αρχή υπέρθεσης) Διαφορικές
Ηλεκτρικό Δυναμικό Δομή Διάλεξης Ορισμός Ηλεκτρικού Δυναμικού και συσχέτιση με το Ηλεκτρικό Πεδίο Ιδιότητες ηλεκτρικού δυναμικού (χρησιμότητα σε υπολογισμούς, σημείο αναφοράς, αρχή υπέρθεσης) Διαφορικές
ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ, Αγωγοί Διηλεκτρικά. Ν. Τράκας, Ι. Ράπτης Ζωγράφου 27.3.
 ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) 8-9 η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ Αγωγοί Διηλεκτρικά Ν. Τράκας Ι. Ράπτης Ζωγράφου 7.3.9 Να επιστραφούν λυμένες μέχρι.4.9 οι ασκήσεις 3 4 5 [ΠΡΟΣΟΧΗ: Οι λύσεις
ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) 8-9 η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ Αγωγοί Διηλεκτρικά Ν. Τράκας Ι. Ράπτης Ζωγράφου 7.3.9 Να επιστραφούν λυμένες μέχρι.4.9 οι ασκήσεις 3 4 5 [ΠΡΟΣΟΧΗ: Οι λύσεις
1η ΠΑΡΟΥΣΙΑΣΗ. Ηλεκτρικά πεδία
 1η ΠΑΡΟΥΣΙΑΣΗ Ηλεκτρικά πεδία Ηλεκτρισμός και μαγνητισμός Κλάδος της Φυσικής που μελετάει τα ηλεκτρικά και τα μαγνητικά φαινόμενα. (Σχεδόν) όλα τα φαινομενα που αντιλαμβανόμαστε με τις αισθήσεις μας οφείλονται
1η ΠΑΡΟΥΣΙΑΣΗ Ηλεκτρικά πεδία Ηλεκτρισμός και μαγνητισμός Κλάδος της Φυσικής που μελετάει τα ηλεκτρικά και τα μαγνητικά φαινόμενα. (Σχεδόν) όλα τα φαινομενα που αντιλαμβανόμαστε με τις αισθήσεις μας οφείλονται
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΕ ΤΕΛΕΙΟΥΣ ΑΓΩΓΟΥΣ
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΕ ΤΕΛΕΙΟΥΣ ΑΓΩΓΟΥΣ
ΑΡΧΕΣ ΛΕΙΤΟΥΡΓΙΑΣ ΗΛΕΚΤΡΙΚΩΝ ΜΗΧΑΝΩΝ ΕΝΑΛΛΑΣΣΟΜΕΝΟΥ ΡΕΥΜΑΤΟΣ
 ΑΡΧΕΣ ΛΕΙΤΟΥΡΓΙΑΣ ΗΛΕΚΤΡΙΚΩΝ ΜΗΧΑΝΩΝ ΕΝΑΛΛΑΣΣΟΜΕΝΟΥ ΡΕΥΜΑΤΟΣ Οι ηλεκτρικές μηχανές εναλλασσομένου ρεύματος (ΕΡ) χωρίζονται σε δύο κατηγορίες: στις σύγχρονες (που χρησιμοποιούνται συνήθως ως γεννήτριες)
ΑΡΧΕΣ ΛΕΙΤΟΥΡΓΙΑΣ ΗΛΕΚΤΡΙΚΩΝ ΜΗΧΑΝΩΝ ΕΝΑΛΛΑΣΣΟΜΕΝΟΥ ΡΕΥΜΑΤΟΣ Οι ηλεκτρικές μηχανές εναλλασσομένου ρεύματος (ΕΡ) χωρίζονται σε δύο κατηγορίες: στις σύγχρονες (που χρησιμοποιούνται συνήθως ως γεννήτριες)
8 η Διάλεξη Ηλεκτρομαγνητική ακτινοβολία, φαινόμενα συμβολής, περίθλαση
 11//17 8 η Διάλεξη Ηλεκτρομαγνητική ακτινοβολία, φαινόμενα συμβολής, περίθλαση Φίλιππος Φαρμάκης Επ. Καθηγητής 1 Ηλεκτρομαγνητισμός Πως συνδέονται ο ηλεκτρισμός με τον μαγνητισμό; Πως παράγονται τα κύματα;
11//17 8 η Διάλεξη Ηλεκτρομαγνητική ακτινοβολία, φαινόμενα συμβολής, περίθλαση Φίλιππος Φαρμάκης Επ. Καθηγητής 1 Ηλεκτρομαγνητισμός Πως συνδέονται ο ηλεκτρισμός με τον μαγνητισμό; Πως παράγονται τα κύματα;
Ασύρματη Μεταφορά Ενέργειας Αξιοποιώντας την Τεχνολογία των Μεταϋλικών
 1 st Energy Tech Forum Ανοικτή Συζήτηση για την Ενεργειακή Τεχνολογία και την Καινοτομία Ασύρματη Μεταφορά Ενέργειας Αξιοποιώντας την Τεχνολογία των Μεταϋλικών Αντώνιος Λάλας 1, 2, Νικόλαος Κανταρτζής
1 st Energy Tech Forum Ανοικτή Συζήτηση για την Ενεργειακή Τεχνολογία και την Καινοτομία Ασύρματη Μεταφορά Ενέργειας Αξιοποιώντας την Τεχνολογία των Μεταϋλικών Αντώνιος Λάλας 1, 2, Νικόλαος Κανταρτζής
Κεφάλαιο31 Εξισώσεις Maxwellκαι ΗλεκτροµαγνητικάΚύµατα. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο31 Εξισώσεις Maxwellκαι ΗλεκτροµαγνητικάΚύµατα ΠεριεχόµεναΚεφαλαίου 31 Τα µεταβαλλόµενα ηλεκτρικά πεδία παράγουν µαγνητικά πεδία. Ο Νόµος του Ampère-Ρεύµα µετατόπισης Νόµος του Gauss s στο µαγνητισµό
Κεφάλαιο31 Εξισώσεις Maxwellκαι ΗλεκτροµαγνητικάΚύµατα ΠεριεχόµεναΚεφαλαίου 31 Τα µεταβαλλόµενα ηλεκτρικά πεδία παράγουν µαγνητικά πεδία. Ο Νόµος του Ampère-Ρεύµα µετατόπισης Νόµος του Gauss s στο µαγνητισµό
Σήματα και Συστήματα. Διάλεξη 7: Μετασχηματισμός Fourier. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 7: Μετασχηματισμός Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μετασχηματισμός Fourier 1. Ορισμός του Μετασχηματισμού Fourier 2. Φυσική Σημασία του Μετασχηματισμού
Σήματα και Συστήματα Διάλεξη 7: Μετασχηματισμός Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μετασχηματισμός Fourier 1. Ορισμός του Μετασχηματισμού Fourier 2. Φυσική Σημασία του Μετασχηματισμού
Κλασική Ηλεκτροδυναμική Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΗΛΕΚΤΡΟΣΤΑΤΙΚΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΗΛΕΚΤΡΟΣΤΑΤΙΚΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ. Κ. Γ. Ευθυμιάδης Αικ. Σιακαβάρα Ε. Παπαδημητράκη-Χλίχλια Ι. Α. Τσουκαλάς
 ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ Κ. Γ. Ευθυμιάδης Αικ. Σιακαβάρα Ε. Παπαδημητράκη-Χλίχλια Ι. Α. Τσουκαλάς ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ Α Έκδοση Συγγραφείς Κ. Γ. Ευθυμιάδης Αικ. Σιακαβάρα Ε. Παπαδημητράκη-Χλίχλια
ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ Κ. Γ. Ευθυμιάδης Αικ. Σιακαβάρα Ε. Παπαδημητράκη-Χλίχλια Ι. Α. Τσουκαλάς ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ Α Έκδοση Συγγραφείς Κ. Γ. Ευθυμιάδης Αικ. Σιακαβάρα Ε. Παπαδημητράκη-Χλίχλια
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΦΥΣΙΚΗ, Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΝΟΤΗΤΑ 1: ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ*
 ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΦΥΣΙΚΗ, Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΝΟΤΗΤΑ 1: ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ* διατυπώνουν τον ορισμό του μαγνητικού πεδίου διατυπώνουν και να εφαρμόζουν τον ορισμό της έντασης του μαγνητικού πεδίου διατυπώνουν
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΦΥΣΙΚΗ, Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΝΟΤΗΤΑ 1: ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ* διατυπώνουν τον ορισμό του μαγνητικού πεδίου διατυπώνουν και να εφαρμόζουν τον ορισμό της έντασης του μαγνητικού πεδίου διατυπώνουν
ΕΞΙΣΩΣΕΙΣ MAXWELL ΣΕ ΜΕΣΟ
 ΕΞΙΣΩΣΕΙΣ MAXWELL ΣΕ ΜΕΣΟ ΤΙ ΕΞΕΤΑΖΟΥΜΕ? ΤΟ ΦΩΣ ΙΑ Ι ΕΤΑΙ ΣΕ ΕΝΑ ΜΕΣΟ (ΓΥΑΛΙ, κα) ΑΠΑΙΤΕΙΤΑΙ ΜΕΛΕΤΗ ΤΗΣ ΙΑ ΟΣΗΣ ΣΤΟ ΜΕΣΟ ΕΦΑΡΜΟΓΗ ΣΥΝΟΡΙΑΚΩΝ ΣΥΝΘΗΚΩΝ ευθύγραµµη διάδοσητου φωτός Πυθαγόρας, ηµόκριτος, Εµπεδοκλής,
ΕΞΙΣΩΣΕΙΣ MAXWELL ΣΕ ΜΕΣΟ ΤΙ ΕΞΕΤΑΖΟΥΜΕ? ΤΟ ΦΩΣ ΙΑ Ι ΕΤΑΙ ΣΕ ΕΝΑ ΜΕΣΟ (ΓΥΑΛΙ, κα) ΑΠΑΙΤΕΙΤΑΙ ΜΕΛΕΤΗ ΤΗΣ ΙΑ ΟΣΗΣ ΣΤΟ ΜΕΣΟ ΕΦΑΡΜΟΓΗ ΣΥΝΟΡΙΑΚΩΝ ΣΥΝΘΗΚΩΝ ευθύγραµµη διάδοσητου φωτός Πυθαγόρας, ηµόκριτος, Εµπεδοκλής,
(ΚΕΦ 32) f( x x f( x) x z y
 (ΚΕΦ 3) f( x x f( x) x z y ΣΥΝΟΨΗ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΥ J. C. Maxwell (~1860) συνόψισε τη δουλειά ως τότε για το ηλεκτρικό και μαγνητικό πεδίο σε 4 εξισώσεις. Όμως, κατανόησε ότι οι εξισώσεις αυτές (όπως
(ΚΕΦ 3) f( x x f( x) x z y ΣΥΝΟΨΗ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΥ J. C. Maxwell (~1860) συνόψισε τη δουλειά ως τότε για το ηλεκτρικό και μαγνητικό πεδίο σε 4 εξισώσεις. Όμως, κατανόησε ότι οι εξισώσεις αυτές (όπως
ΠΕΡΙΕΧΟΜΕΝΑ KΕΦΑΛΑΙΟ 1 ΣΤΟΙΧΕΙΑ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ 1
 ΠΕΡΙΕΧΟΜΕΝΑ KΕΦΑΛΑΙΟ 1 ΣΤΟΙΧΕΙΑ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ 1 1.1 Εισαγωγή... 1 1.2 Λύση ΔΕ, αντίστροφο πρόβλημα αυτής... 3 Ασκήσεις... 10 1.3 ΔΕ πρώτης τάξης χωριζομένων μεταβλητών... 12 Ασκήσεις... 15 1.4 Ομογενείς
ΠΕΡΙΕΧΟΜΕΝΑ KΕΦΑΛΑΙΟ 1 ΣΤΟΙΧΕΙΑ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ 1 1.1 Εισαγωγή... 1 1.2 Λύση ΔΕ, αντίστροφο πρόβλημα αυτής... 3 Ασκήσεις... 10 1.3 ΔΕ πρώτης τάξης χωριζομένων μεταβλητών... 12 Ασκήσεις... 15 1.4 Ομογενείς
ΟΛΟΚΛΗΡΩΜΕΝΗ ΟΠΤΙΚΗ. Χειμερινό Εξάμηνο Γενικές Πληροφορίες. Αιθ. 008(Ν. Κτίρια, ΗΜΜΥ) Ηλίας Ν. Γλύτσης (Παλαιά Κτίρια ΗΜΜΥ)
 04/10/2017 ΟΛΟΚΛΗΡΩΜΕΝΗ ΟΠΤΙΚΗ Χειμερινό Εξάμηνο 2017-2018 Γενικές Πληροφορίες Ώρα: Τετάρτη 08:45-11:30 Αίθουσα: Αιθ. 008(Ν. Κτίρια, ΗΜΜΥ) Καθηγητής: Ηλίας Ν. Γλύτσης Γραφείο: 2.2.22 (Παλαιά Κτίρια ΗΜΜΥ)
04/10/2017 ΟΛΟΚΛΗΡΩΜΕΝΗ ΟΠΤΙΚΗ Χειμερινό Εξάμηνο 2017-2018 Γενικές Πληροφορίες Ώρα: Τετάρτη 08:45-11:30 Αίθουσα: Αιθ. 008(Ν. Κτίρια, ΗΜΜΥ) Καθηγητής: Ηλίας Ν. Γλύτσης Γραφείο: 2.2.22 (Παλαιά Κτίρια ΗΜΜΥ)
1η ΠΑΡΟΥΣΙΑΣΗ. Ηλεκτρικά φορτία, ηλεκτρικές δυνάμεις και πεδία
 1η ΠΑΡΟΥΣΙΑΣΗ Ηλεκτρικά φορτία, ηλεκτρικές δυνάμεις και πεδία Ηλεκτρισμός και μαγνητισμός Κλάδος της Φυσικής που μελετάει τα ηλεκτρικά και τα μαγνητικά φαινόμενα. (Σχεδόν) όλα τα φαινομενα που αντιλαμβανόμαστε
1η ΠΑΡΟΥΣΙΑΣΗ Ηλεκτρικά φορτία, ηλεκτρικές δυνάμεις και πεδία Ηλεκτρισμός και μαγνητισμός Κλάδος της Φυσικής που μελετάει τα ηλεκτρικά και τα μαγνητικά φαινόμενα. (Σχεδόν) όλα τα φαινομενα που αντιλαμβανόμαστε
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ ΗΡΩΩΝ ΠΟΛΥΤΕΧΝΕΙΟΥ 9 - ΖΩΓΡΑΦΟΥ, 157 73 ΑΘΗΝΑ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ ΗΡΩΩΝ ΠΟΛΥΤΕΧΝΕΙΟΥ 9 - ΖΩΓΡΑΦΟΥ, 157 73 ΑΘΗΝΑ
ΠΡΟΒΛΗΜΑΤΑ ΔΥΟ ΔΙΑΣΤΑΣΕΩΝ
 ΠΡΟΒΛΗΜΑΤΑ ΔΥΟ ΔΙΑΣΤΑΣΕΩΝ Η ανάλυση προβλημάτων δύο διαστάσεων με τη μέθοδο των Πεπερασμένων Στοιχείων περιλαμβάνει τα ίδια βήματα όπως και στα προβλήματα μιας διάστασης. Η ανάλυση γίνεται λίγο πιο πολύπλοκη
ΠΡΟΒΛΗΜΑΤΑ ΔΥΟ ΔΙΑΣΤΑΣΕΩΝ Η ανάλυση προβλημάτων δύο διαστάσεων με τη μέθοδο των Πεπερασμένων Στοιχείων περιλαμβάνει τα ίδια βήματα όπως και στα προβλήματα μιας διάστασης. Η ανάλυση γίνεται λίγο πιο πολύπλοκη
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Ανάλυση ακτινοβολίας φασικής στοιχειοκεραίας
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Ανάλυση ακτινοβολίας φασικής στοιχειοκεραίας
ΔΥΝΑΜΙΚΗ ΜΗΧΑΝΩΝ Ι
 Δυναμική Μηχανών Ι Ακαδημαϊκό έτος: 015-016 ΔΥΝΑΜΙΚΗ ΜΗΧΑΝΩΝ Ι - 1.1- Δυναμική Μηχανών Ι Ακαδημαϊκό έτος: 015-016 Copyright ΕΜΠ - Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο Δυναμικής και Κατασκευών - 015.
Δυναμική Μηχανών Ι Ακαδημαϊκό έτος: 015-016 ΔΥΝΑΜΙΚΗ ΜΗΧΑΝΩΝ Ι - 1.1- Δυναμική Μηχανών Ι Ακαδημαϊκό έτος: 015-016 Copyright ΕΜΠ - Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο Δυναμικής και Κατασκευών - 015.
Κεφάλαιο Η2. Ο νόµος του Gauss
 Κεφάλαιο Η2 Ο νόµος του Gauss Ο νόµος του Gauss Ο νόµος του Gauss µπορεί να χρησιµοποιηθεί ως ένας εναλλακτικός τρόπος υπολογισµού του ηλεκτρικού πεδίου. Ο νόµος του Gauss βασίζεται στο γεγονός ότι η ηλεκτρική
Κεφάλαιο Η2 Ο νόµος του Gauss Ο νόµος του Gauss Ο νόµος του Gauss µπορεί να χρησιµοποιηθεί ως ένας εναλλακτικός τρόπος υπολογισµού του ηλεκτρικού πεδίου. Ο νόµος του Gauss βασίζεται στο γεγονός ότι η ηλεκτρική
Κλασική Ηλεκτροδυναμική Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΜΑΓΝΗΤΟΣΤΑΤΙΚΑ ΠΕΔΙΑ ΣΤΗΝ ΥΛΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΜΑΓΝΗΤΟΣΤΑΤΙΚΑ ΠΕΔΙΑ ΣΤΗΝ ΥΛΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Παράδειγμα 14.2 Να βρεθεί ο μετασχηματισμός Laplace των συναρτήσεων
 Κεφάλαιο 4 Μετασχηματισμός aplace 4. Μετασχηματισμός aplace της εκθετικής συνάρτησης e Είναι Άρα a a a u( a ( a ( a ( aj F( e e d e d [ e ] [ e ] ( a e (c ji, με a (4.9 a a a [ e u( ] a, με a (4.3 Η σχέση
Κεφάλαιο 4 Μετασχηματισμός aplace 4. Μετασχηματισμός aplace της εκθετικής συνάρτησης e Είναι Άρα a a a u( a ( a ( a ( aj F( e e d e d [ e ] [ e ] ( a e (c ji, με a (4.9 a a a [ e u( ] a, με a (4.3 Η σχέση
ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ Γ
 ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ Γ ΜΑΘΗΜΑ 2 Ισοδύναμο Ηλεκτρικό Κύκλωμα Σύγχρονων Μηχανών Ουρεϊλίδης Κωνσταντίνος, Υποψ. Διδακτωρ Υπολογισμός Αυτεπαγωγής και αμοιβαίας επαγωγής Πεπλεγμένη μαγνητική ροή συναρτήσει των
ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ Γ ΜΑΘΗΜΑ 2 Ισοδύναμο Ηλεκτρικό Κύκλωμα Σύγχρονων Μηχανών Ουρεϊλίδης Κωνσταντίνος, Υποψ. Διδακτωρ Υπολογισμός Αυτεπαγωγής και αμοιβαίας επαγωγής Πεπλεγμένη μαγνητική ροή συναρτήσει των
ΜΗΧΑΝΙΣΜΟΙ ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕΔΙΑΣΜΟ ΜΗΧΑΝΩΝ
 Μηχανισμοί & Εισαγωγή στο Σχεδιασμό Μηχανών Ακαδημαϊκό έτος: 214-215 ΜΗΧΑΝΙΣΜΟΙ & ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕΔΙΑΣΜΟ ΜΗΧΑΝΩΝ -A.1 - Μηχανισμοί & Εισαγωγή στο Σχεδιασμό Μηχανών Ακαδημαϊκό έτος: 214-215 Copyright ΕΜΠ
Μηχανισμοί & Εισαγωγή στο Σχεδιασμό Μηχανών Ακαδημαϊκό έτος: 214-215 ΜΗΧΑΝΙΣΜΟΙ & ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕΔΙΑΣΜΟ ΜΗΧΑΝΩΝ -A.1 - Μηχανισμοί & Εισαγωγή στο Σχεδιασμό Μηχανών Ακαδημαϊκό έτος: 214-215 Copyright ΕΜΠ
υναµική Μηχανών Ι Ακαδηµαϊκό έτος : Ε. Μ. Π. Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο υναµικής και Κατασκευών ΥΝΑΜΙΚΗ ΜΗΧΑΝΩΝ Ι - 22.
 υναµική Μηχανών Ι Ακαδηµαϊκό έτος: 0-0 ΥΝΑΜΙΚΗ ΜΗΧΑΝΩΝ Ι -. - υναµική Μηχανών Ι Ακαδηµαϊκό έτος: 0-0 Cprigh ΕΜΠ - Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο υναµικής και Κατασκευών - 0. Με επιφύλαξη παντός
υναµική Μηχανών Ι Ακαδηµαϊκό έτος: 0-0 ΥΝΑΜΙΚΗ ΜΗΧΑΝΩΝ Ι -. - υναµική Μηχανών Ι Ακαδηµαϊκό έτος: 0-0 Cprigh ΕΜΠ - Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο υναµικής και Κατασκευών - 0. Με επιφύλαξη παντός
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Ο Μετασχηματισμός Ζ. Ανάλυση συστημάτων με το μετασχηματισμό Ζ
 Ο Μετασχηματισμός Ζ Ανάλυση συστημάτων με το μετασχηματισμό Ζ Ο μετασχηματισμός Z (Ζ-Τransform: ZT) χρήσιμο μαθηματικό εργαλείο για την ανάλυση των διακριτών σημάτων και συστημάτων αποτελεί ό,τι ο μετασχηματισμός
Ο Μετασχηματισμός Ζ Ανάλυση συστημάτων με το μετασχηματισμό Ζ Ο μετασχηματισμός Z (Ζ-Τransform: ZT) χρήσιμο μαθηματικό εργαλείο για την ανάλυση των διακριτών σημάτων και συστημάτων αποτελεί ό,τι ο μετασχηματισμός
Μοριακή Φασματοσκοπία I. Παραδόσεις μαθήματος Θ. Λαζαρίδης
 Μοριακή Φασματοσκοπία I Παραδόσεις μαθήματος Θ. Λαζαρίδης 2 Τι μελετά η μοριακή φασματοσκοπία; Η μοριακή φασματοσκοπία μελετά την αλληλεπίδραση των μορίων με την ηλεκτρομαγνητική ακτινοβολία Από τη μελέτη
Μοριακή Φασματοσκοπία I Παραδόσεις μαθήματος Θ. Λαζαρίδης 2 Τι μελετά η μοριακή φασματοσκοπία; Η μοριακή φασματοσκοπία μελετά την αλληλεπίδραση των μορίων με την ηλεκτρομαγνητική ακτινοβολία Από τη μελέτη
ΣΕΜΦΕ ΕΜΠ Φυσική ΙΙΙ (Κυματική) Διαγώνισμα επί πτυχίω εξέτασης 02/06/2017 1
 ΣΕΜΦΕ ΕΜΠ Φυσική ΙΙΙ (Κυματική) Διαγώνισμα επί πτυχίω εξέτασης /6/7 Διάρκεια ώρες. Θέμα. Θεωρηστε ενα συστημα δυο σωματων ισων μαζων (μαζας Μ το καθενα) και δυο ελατηριων (χωρις μαζα) με σταθερες ελατηριων
ΣΕΜΦΕ ΕΜΠ Φυσική ΙΙΙ (Κυματική) Διαγώνισμα επί πτυχίω εξέτασης /6/7 Διάρκεια ώρες. Θέμα. Θεωρηστε ενα συστημα δυο σωματων ισων μαζων (μαζας Μ το καθενα) και δυο ελατηριων (χωρις μαζα) με σταθερες ελατηριων
ΟΡΙΑΚΟ ΣΤΡΩΜΑ: ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΘΕΩΡΗΤΙΚΗ ΑΝΑΛΥΣΗ. Σημειώσεις. Επιμέλεια: Άγγελος Θ. Παπαϊωάννου, Ομοτ. Καθηγητής ΕΜΠ
 ΟΡΙΑΚΟ ΣΤΡΩΜΑ: ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΘΕΩΡΗΤΙΚΗ ΑΝΑΛΥΣΗ Σημειώσεις Επιμέλεια: Άγγελος Θ. Παπαϊωάννου, Ομοτ. Καθηγητής ΕΜΠ Αθήνα, Απρίλιος 13 1. Η Έννοια του Οριακού Στρώματος Το οριακό στρώμα επινοήθηκε για
ΟΡΙΑΚΟ ΣΤΡΩΜΑ: ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΘΕΩΡΗΤΙΚΗ ΑΝΑΛΥΣΗ Σημειώσεις Επιμέλεια: Άγγελος Θ. Παπαϊωάννου, Ομοτ. Καθηγητής ΕΜΠ Αθήνα, Απρίλιος 13 1. Η Έννοια του Οριακού Στρώματος Το οριακό στρώμα επινοήθηκε για
Περιεχόμενα. Λίγα λόγια για τους συγγραφείς
 Περιεχόμενα Λίγα λόγια για τους συγγραφείς xii Εισαγωγή xiii 1 Συναρτήσεις 1 1.1 Ανασκόπηση των συναρτήσεων 1 1.2 Παράσταση συναρτήσεων 12 1.3 Τριγωνομετρικές συναρτήσεις 26 Ασκήσεις επανάληψης 34 2 Όρια
Περιεχόμενα Λίγα λόγια για τους συγγραφείς xii Εισαγωγή xiii 1 Συναρτήσεις 1 1.1 Ανασκόπηση των συναρτήσεων 1 1.2 Παράσταση συναρτήσεων 12 1.3 Τριγωνομετρικές συναρτήσεις 26 Ασκήσεις επανάληψης 34 2 Όρια
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER
 4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Σκοπός του κεφαλαίου είναι να παρουσιάσει μερικές εφαρμογές του Μετασχηματισμού Fourier (ΜF). Ειδικότερα στο κεφάλαιο αυτό θα περιγραφούν έμμεσοι τρόποι
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Σκοπός του κεφαλαίου είναι να παρουσιάσει μερικές εφαρμογές του Μετασχηματισμού Fourier (ΜF). Ειδικότερα στο κεφάλαιο αυτό θα περιγραφούν έμμεσοι τρόποι
Περιεχόμενα. Λίγα λόγια για τους συγγραφείς
 Περιεχόμενα Λίγα λόγια για τους συγγραφείς xii Εισαγωγή xiii 1 Συναρτήσεις 1 1.1 Ανασκόπηση των συναρτήσεων 1 1.2 Παράσταση συναρτήσεων 12 1.3 Τριγωνομετρικές συναρτήσεις 26 Ασκήσεις επανάληψης 34 2 Όρια
Περιεχόμενα Λίγα λόγια για τους συγγραφείς xii Εισαγωγή xiii 1 Συναρτήσεις 1 1.1 Ανασκόπηση των συναρτήσεων 1 1.2 Παράσταση συναρτήσεων 12 1.3 Τριγωνομετρικές συναρτήσεις 26 Ασκήσεις επανάληψης 34 2 Όρια
Γράφημα της συνάρτησης = (δηλ. της περιττής περιοδικής επέκτασης της f = f( x), 0 x p στο R )
 Γράφημα της συνάρτησης f( x), αν p x< 0 F( x) = f( x), αν 0 x p και F( x+ 2 p) = F( x), x R (δηλ. της περιττής περιοδικής επέκτασης της f = f( x), 0 x p στο R ) ΠΡΟΛΟΓΟΣ Το Βιβλίο αυτό απευθύνεται στους
Γράφημα της συνάρτησης f( x), αν p x< 0 F( x) = f( x), αν 0 x p και F( x+ 2 p) = F( x), x R (δηλ. της περιττής περιοδικής επέκτασης της f = f( x), 0 x p στο R ) ΠΡΟΛΟΓΟΣ Το Βιβλίο αυτό απευθύνεται στους
Κυματοδηγοί Waveguides
 Κυματοδηγοί Waveguides ρυθμός-τρόπος-mode Κυματοδηγοί (a)ορθογώνιοι (b)κυκλικοί (c) Ορθογώνιοι κυκλικής εξωτερικής διατομής Αντανάκλαση σε αγώγιμη επιφάνεια Modes USA
Κυματοδηγοί Waveguides ρυθμός-τρόπος-mode Κυματοδηγοί (a)ορθογώνιοι (b)κυκλικοί (c) Ορθογώνιοι κυκλικής εξωτερικής διατομής Αντανάκλαση σε αγώγιμη επιφάνεια Modes USA
