ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ
|
|
|
- Κάρμη Αθανασιάδης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 + ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΣΤΑΤΙΣΤΙΚΗΣ ΕΠΙΔΡΑΣΗ ΤΩΝ ΚΑΙΡΙΚΩΝ ΣΥΝΘΗΚΩΝ ΣΤΑ ΟΔΙΚΑ ΑΤΥΧΗΜΑΤΑ Μαρία-Χριστίνα Νικολάου Πολυκρέτη ΕΡΓΑΣΙΑ Που υποβλήθηκε στο Τμήμα Στατιστικής του Οικονομικού Πανεπιστημίου Αθηνών ως μέρος των απαιτήσεων για την απόκτηση Μεταπτυχιακού Διπλώματος Συμπληρωματικής Ειδίκευσης στη Στατιστική Μερικής Παρακολούθησης (Part-time) Αθήνα Ιούνιος 2012
2
3 ΑΦΙΕΡΩΣΗ Στην Αλήθεια και στην ανακάλυψή της από όλους όσους που την αναζητούν..
4
5 ΕΥΧΑΡΙΣΤΙΕΣ Στους γονείς μου, στους φίλους μου (ιδιαιτέρως στον Χρήστο Ροδόπουλο και στην Ευαγγελία Αγγελοπούλου) και σε λοιπούς συνανθρώπους μου που με ενίσχυσαν με διαφόρους τρόπους. Ευχαριστώ θερμά και τον επιβλέποντα καθηγητή μου κ. Δημήτριο Καρλή για την πολύτιμη βοήθειά του και ανοχή του. Ι
6 ΙΙ
7 ΒΙΟΓΡΑΦΙΚΟ ΣΗΜΕΙΩΜΑ Γεννηθείσα στην Αθήνα, σχολικά χρόνια στην Κόρινθο. Προπτυχιακές σπουδές στη Στατιστική στο Οικονομικό Πανεπιστήμιο Αθηνών. Παράλληλα με το μεταπτυχιακό της έκανε σπουδές στη Βυζαντινή μουσική. Ερευνητικά ενδιαφέροντα της είναι η μελέτη κοινωνικών φαινομένων, η έρευνα σε θέματα υγείας, η επίδραση της μουσικής και της θρησκευτικότητας σε διάφορους τομείς της ζωής του ανθρώπου. Άλλα ενδιαφέροντά της είναι η μελέτη της αρχαίας ελληνικής μουσικής, η ανάγνωση ποιητικών και πεζών λογοτεχνικών έργων, η μελέτη αρχαίας ελληνικής γραμματείας και πατερικών κειμένων, οι ενασχόληση με οικιακές τέχνες (χειροτεχνία, υφαντική κλπ), η ποδηλασία. III
8 IV
9 ABSTRACT Maria-Christina Polykreti THE EFFECT OF THE CLIMATE IN ROAD ACCIDENTS April 2012 The effect of various factors in road accidents is investigated in order to prevent them. This study investigates the influence of weather on road accidents. The data are taken from the Netherlands. Some statistical models are fitted, such as the Negative Binomial model, the Poisson model, and some Zero-Inflated models, in order to find the most appropriate one to describe the relationship between weather and number of accidents taking place at the specific period. As more suitable was chosen a zero-inflated negative binomial model. According to this, it seems that in this country, the presence of rainfall and the increased duration of a rainfall, increases the number of accidents. Similarly, positive effect on the rate of accidents has the presence of the phenomenon of the storm (storm with rain and lightning). In contrast, as expected, the increasing of the horizontal visibility has a negative impact to road accidents. Moreover, increasing of accidents frequency expected in conditions where traffic on roads increase, eg during the everyday afternoon-evening hours, compared with the traffic at weekend or at early morning and evening hours or when weather is good (sunshine with long duration etc). V
10 VI
11 ΠΕΡΙΛΗΨΗ Μαρία-Χριστίνα Πολυκρέτη ΕΠΙΔΡΑΣΗ ΤΩΝ ΚΑΙΡΙΚΩΝ ΣΥΝΘΗΚΩΝ ΣΤΑ ΟΔΙΚΑ ΑΤΥΧΗΜΑΤΑ Απρίλιος 2012 Η επίδραση διαφόρων παραγόντων στα οδικά ατυχήματα αποτελεί αντικείμενο έρευνας προκειμένου για την πρόληψή τους. Η παρούσα μελέτη ερευνά την επίδραση των καιρικών συνθηκών στα οδικά ατυχήματα. Τα δεδομένα που αφορούν στις καιρικές συνθήκες και στον αριθμό των ατυχημάτων προέρχονται από την Ολλανδία. Σε αυτά έγινε προσαρμογή κάποιων κατάλληλων στατιστικών μοντέλων, όπως το Αρνητικό Διωνυμικό, το μοντέλο Poisson, καθώς και Ζero-Ιnflated μοντέλων προκειμένου να βρεθεί το καταλληλότερο που περιγράφει τη σχέση μεταξύ των καιρικών συνθηκών και του αριθμού ατυχημάτων που πραγματοποιούνται σε συγκεκριμένο χρονικό διάστημα. Ως καταλληλότερο επιλέχθηκε ένα Ζero-Ιnflated Αρνητικό Διωνυμικό μοντέλο. Σύμφωνα με αυτό, φαίνεται ότι στην συγκεκριμένη χώρα, η παρουσία βροχόπτωσης και η αυξανόμενη διάρκειά της, αυξάνει τον αριθμό των ατυχημάτων. Ομοίως, θετική επίδραση στη συχνότητα των ατυχημάτων έχει η παρουσία του φαινομένου της καταιγίδας (θύελλα με βροχόπτωση και κεραυνούς). Αντίθετα, όπως είναι αναμενόμενο, η αύξηση της οριζόντιας ορατότητας επιδρά αρνητικά στην παρουσία ατυχημάτων. Επιπλέον, αύξηση της συχνότητας ατυχημάτων αναμένεται σε συνθήκες κατά τις οποίες αυξάνεται η κυκλοφορία στους δρόμους, π.χ. κατά τις μεταμεσημβρινές -απογευματινές ώρες, σε σύγκριση με τις πρώτες πρωινές και νυχτερινές ώρες και όταν υπάρχει καλοκαιρία (ηλιοφάνεια μεγάλης διάρκειας κ.λπ). VII
12 VIIΙ
13 ΚΑΤΑΛΟΓΟΣ ΠΕΡΙΕΧΟΜΕΝΩΝ 1. ΕΙΣΑΓΩΓΗ 2. TΑ ΜΟΝΤΕΛΑ-ΘΕΩΡΗΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 3. ΑΝΑΛΥΣΗ ΤΩΝ ΔΕΔΟΜΕΝΩΝ ΑΤΥΧΗΜΑΤΩΝ 3.1. Περιγραφικά στατιστικά και συσχετίσεις μεταξύ του αριθμού ατυχημάτων και των μεταβλητών κλίματος 3.2. Έλεγχοι σχετικά με τη μορφή του κατάλληλου μοντέλου 4. ΤΟ ΒΕΛΤΙΣΤΟ ΜΟΝΤΈΛΟ ΚΑΙ Η ΕΡΜΗΝΕΊΑ ΤΟΥ 5. ΣΥΜΠΕΡΑΣΜΑΤΑ ΠΑΡΑΡΤΗΜΑ Α ΠΑΡΑΡΤΗΜΑ Β ΒΙΒΛΙΟΓΡΑΦΙΑ Σελίδα IX
14 X
15 ΚΑΤΑΛΟΓΟΣ ΠΙΝΑΚΩΝ Πίνακας Πίνακας 1. Πίνακας περιγραφικών στατιστικών για τον αριθμό ατυχημάτων (ωριαίες μετρήσεις) Πίνακας 2. Κατανομή Συχνότητας, Κατανομή Πυκνότητας Πιθανότητας και Κατανομή Πιθανότητας (Αθροιστική) του αριθμού ατυχημάτων (ωριαίες μετρήσεις) Σελίδα Πίνακας 3α. Περιγραφικά στοιχεία των συνεχών επεξηγηματικών μεταβλητών Πίνακας 3β. Περιγραφικά στοιχεία των κατηγορικών επεξηγηματικών μεταβλητών Πίνακας 4. Το μοντέλο ΖΙΝΒ που περιλαμβάνει ως εξαρτημένη μεταβλητή τον αριθμό των ατυχημάτων και όλες τις υπόλοιπες μεταβλητές (κλίματος και χρόνου) ως επεξηγηματικές Πίνακας 5. Μοντέλα ΖΙΝΒ με τα αντίστοιχα loglikelihood ratio test και τα AIC σε φθίνουσα σειρά Πίνακας 6. Οι συντελεστές και οι μεταβλητές του μοντέλου X1z Πίνακας 7. Οι αναμενόμενες, σύμφωνα με το Χ1z20 ΖΙΝΒ μοντέλο, και οι παρατηρούμενες συχνότητες του αριθμού ατυχημάτων Πίνακας 8. Αναμενόμενες συχνότητες των προσαρμοσμένων μοντέλων Χ1z20 και bglmnb και η παρατηρούμενη συχνότητα. Π1. Πίνακες αποτελεσμάτων ελέγχου καλής προσαρμογής χ 2 της Αρνητικής Διωνυμικής κατανομής και της κατανομής Poisson στα δεδομένα οδικών ατυχημάτων Π2. Πίνακες αποτελεσμάτων του Kolmogorov-Smirnov ελέγχου καλής προσαρμογής της Αρνητικής Διωνυμικής κατανομής και της Poisson στα οδικά ατυχήματα XI
16 XII
17 ΚΑΤΑΛΟΓΟΣ ΓΡΑΦΗΜΑΤΩΝ Γράφημα Σελίδα Διάγραμμα 1. Αθροιστική πιθανότητα του αριθμού ατυχημάτων 17 Ραβδόγραμμα 1. Συγκριτικό ραβδόγραμμα της παρατηρούμενης από τα δεδομένα και της αναμενόμενης από το μοντέλο συχνότητας του αριθμού των ατυχημάτων Δ1. Διάγραμμα σημείων του αριθμού ατυχημάτων ανά ημερομηνία 33 Δ2. Ιστογράμματα συχνότητας του αριθμού ατυχημάτων ανά ημέρα 33 Δ3. Διάγραμμα σημείων του αριθμού ατυχημάτων ανά ώρα 35 Δ4. Διάγραμμα σημείων του αριθμού ατυχημάτων ανά διεύθυνση του ανέμου 35 Δ5. Διάγραμμα σημείων του αριθμού ατυχημάτων ανά μέση ταχύτητα του ανέμου 35 Δ6. Διάγραμμα σημείων του αριθμού ατυχημάτων ανά μέση ωριαία ταχύτητα του ανέμου 36 Δ7. Διάγραμμα σημείων του αριθμού ατυχημάτων ανά μέγιστη ριπή του ανέμου 36 Δ8. Διάγραμμα σημείων του αριθμού ατυχημάτων ανά ωριαία ηλιακή ακτινοβολία 36 Δ9. Διάγραμμα σημείων του αριθμού ατυχημάτων ανά διάρκεια βροχόπτωσης 37 Δ10. Διάγραμμα σημείων του αριθμού ατυχημάτων ανά ποσότητα βροχόπτωσης 37 Δ11. Διάγραμμα σημείων του αριθμού ατυχημάτων ανά διάρκεια ηλιοφάνειας 37 Δ12. Διάγραμμα σημείων του αριθμού ατυχημάτων ανά ποσοστό σχετικής υγρασίας 38 Δ13. Διάγραμμα σημείων του αριθμού ατυχημάτων ανά ορατότητα 38 Δ14. Διάγραμμα σημείων του αριθμού ατυχημάτων ανά συνολική κατάσταση καιρού (codec weather) 38 Δ15. Ιστογράμματα συχνότητας του αριθμού ατυχημάτων ανά απουσία και παρουσία χαλαζιού 39 Δ16. Ιστογράμματα συχνότητας του αριθμού ατυχημάτων ανά απουσία και παρουσία θύελλας με καταιγίδα 39 Δ17. Ιστογράμματα συχνότητας του αριθμού ατυχημάτων ανά απουσία και παρουσία βροχόπτωσης 39 Δ18. Ιστογράμματα συχνότητας του αριθμού ατυχημάτων ανά απουσία και παρουσία χιονιού 40 Δ19. Ιστογράμματα συχνότητας του αριθμού ατυχημάτων ανά απουσία και παρουσία πάγου 40 Δ20. Ιστογράμματα συχνότητας του αριθμού ατυχημάτων ανά απουσία και παρουσία ομίχλης 40 Δ21. Διάγραμμα σημείων του αριθμού ατυχημάτων ανά κάλυψη της συνολικής επιφάνειας του ουρανού 41 Δ22. Διάγραμμα σημείων του αριθμού ατυχημάτων ανά 27 XIIΙ
18 θερμοκρασία 41 Δ23. Ιστογράμματα συχνότητας του αριθμού ατυχημάτων ανά απουσία και παρουσία χαλαζιού 41 Δ24. Ιστογράμματα συχνότητας του αριθμού ατυχημάτων ανά απουσία και παρουσία χαλαζιού 42 Δ25. Ραβδόγραμμα παρατηρούμενης και εκτιμώμενης συχνότητας μηδέν ατυχημάτων, στα δύο επικρατέστερα μοντέλα 42 Δ26. Ραβδόγραμμα παρατηρούμενης και εκτιμώμενης συχνότητας ενός ατυχήματος στα δύο επικρατέστερα μοντέλα 42 Δ27. Ραβδόγραμμα παρατηρούμενης και εκτιμώμενης συχνότητας δύο ατυχημάτων στα δύο επικρατέστερα μοντέλα 43 Δ28. Ραβδόγραμμα παρατηρούμενης και εκτιμώμενης συχνότητας τριών, τεσσάρων, πέντε και έξι ατυχημάτων στα δύο 44 επικρατέστερα μοντέλα XIV
19 1. ΕΙΣΑΓΩΓΗ Η μείωση των οδικών ατυχημάτων και η αύξηση της οδικής ασφάλειας αποτελεί τις τελευταίες δεκαετίες προτεραιότητα για τις εθνικές πολιτικές των περισσότερων ευρωπαϊκών κρατών. Ειδικότερα στην Ελλάδα, τα στατιστικά στοιχεία που σχετίζονται με τα οδικά ατυχήματα είναι ιδιαίτερα απογοητευτικά. Αναφέρεται χαρακτηριστικά ότι, μόνο κατά τον μήνα Αύγουστο του 2009, τα οδικά ατυχήματα που πραγματοποιήθηκαν στην ελληνική επικράτεια και προκάλεσαν τον τραυματισμό ή το θάνατο ατόμων ανήλθαν στα (ΕΣΥΕ, Αύγουστος 2009). Οι σημαντικές κοινωνικές και οικονομικές επιπτώσεις που επισύρει η παρουσία του φαινομένου καθιστά αναγκαία την επισταμένη διερεύνηση των παραγόντων που επιδρούν σε αυτό. Πολλοί είναι παράγοντες που είναι γνωστό ότι επιδρούν στην πραγματοποίηση ενός ατυχήματος, κυριότεροι από τους οποίους είναι ο άνθρωπος (οδηγός, πεζός κλπ), το όχημα και οι οδικές υποδομές (οδόστρωμα, σήμανση κλπ). Η συγκεκριμένη εργασία έχει ως σκοπό τη διερεύνηση της επίδρασης των καιρικών φαινομένων στην εμφάνιση οδικών ατυχημάτων. Η επίδραση των καιρικών συνθηκών στα οδικά ατυχήματα είναι ευρέως αντιληπτή. Ωστόσο, η μελέτη και η ποσοτική εκτίμηση της σχέσης μεταξύ των δύο φαινομένων δεν είναι αρκετά εκτεταμένη. Έτσι η παρούσα έρευνα έχει ως επιμέρους στόχους, αφενός μεν, την εύρεση εκείνων των καιρικών συνθηκών που επιδρούν θετικά, σε αντιπαράθεση με εκείνες που επιδρούν ανασχετικά στην εμφάνιση οδικών ατυχημάτων, αφετέρου στην ποσοτικοποίηση της σχέσης και στην πρόβλεψη εμφάνισης ατυχημάτων, δοθέντος των καιρικών συνθηκών, μέσω ενός προβλεπτικού στατιστικού μοντέλου. Η παρούσα μελέτη φιλοδοξεί να συμβάλλει στον εμπλουτισμό της γνώσης σχετικά με οδικά ατυχήματα και να ενισχύσει την προσπάθεια για μείωση των οδικών ατυχημάτων, ιδιαίτερα στην Ελλάδα. Ωστόσο, η εν λόγω έρευνα υπόκειται σε περιορισμούς για τους παρακάτω λόγους: 1. Τα δεδομένα δεν προέρχονται από την Ελλάδα, αλλά από την Ολλανδία και έτσι τα συμπεράσματα πιθανώς να μην μπορούν να αναχθούν στην συγκεκριμένη χώρα, καθώς η επίδραση των διαφόρων παραγόντων που επιδρούν στο φαινόμενο, καθώς και των καιρικών συνθηκών, διαφέρουν από χώρα σε χώρα. 2. Τα δεδομένα αποτελούν μια συλλογή καιρικών συνθηκών και τροχαίων ατυχημάτων κατά τη διάρκεια ενός συγκεκριμένου έτους (2002). Η έλλειψη διαχρονικών στοιχείων, 1
20 ενδεχομένως να μειώνει την αξιοπιστία των συμπερασμάτων, καθώς ειδικές συνθήκες (θεσμικό πλαίσιο, νομοθεσία, κατασκευή οδοστρωμάτων κ.α.) που πραγματοποιήθηκαν το συγκεκριμένο έτος ενδεχομένως να επηρέασαν την έρευνα. 3. Ένα ολοκληρωμένο προβλεπτικό μοντέλο που εκτιμά των αριθμό των ατυχημάτων μέσω της μεταβολής των καιρικών συνθηκών, ενδεχομένως να πρέπει να λάβει υπόψη και άλλους παράγοντες που επιδρούν στην εμφάνιση του φαινομένου (ψυχολογική κατάσταση οδηγού, οδήγηση υπό την επήρεια ουσιών, οδική συμπεριφορά του οδηγού, ταχύτητα οδήγησης κ.λπ.), προκειμένου να εξαλειφθεί η επίδρασή τους. 4. Είναι ευρέως γνωστό ότι σημαντικό ρόλο στα τροχαία ατυχήματα παίζει η κίνηση ή με άλλα λόγια πόσα οχήματα μοιράζονται το δρόμο. Είναι επίσης γνωστό ότι οι καιρικές συνθήκες επιδρούν σε αυτήν την παράμετρο και συνεπώς μία μείωση των ατυχημάτων μπορεί να οφείλεται απλώς στην μειωμένη κίνηση οχημάτων στο δρόμο. Επομένως, χρειάζεται προσοχή στην ερμηνεία των αποτελεσμάτων. Στη συνέχεια γίνεται αναφορά στα θεωρητικά μοντέλα που περιγράφουν το φαινόμενο των οδικών ατυχημάτων. Ακολούθως, παρουσιάζονται τα περιγραφικά στατιστικά στοιχεία και γραφήματα της συλλογής των δεδομένων μας και ελέγχουμε κάποιες υποθέσεις προκειμένου να βρούμε το καταλληλότερο μοντέλο που προσαρμόζεται σε αυτά. Στη συνέχεια επιλέγεται το καταλληλότερο μοντέλο, όπως αυτό προκύπτει έπειτα από σύγκριση διαφόρων βέλτιστων μοντέλων, εφαρμόζεται στα δεδομένα και ελέγχεται η καλή προσαρμογή του. Τέλος, παρουσιάζονται τα συμπεράσματα της έρευνας. 2
21 2. ΤΑ ΜΟΝΤΕΛΑ - ΘΕΩΡΗΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Υπάρχει ένα πλήθος από δημοσιευμένες ερευνητικές εργασίες που αναφέρονται στην μελέτη των οδικών ατυχημάτων και της σχέσης τους με διάφορους παράγοντες, οι οποίες χρησιμοποιούν διάφορες μεθοδολογικές προσεγγίσεις και στατιστικά μοντέλα. Ερευνητικά και πανεπιστημιακά ιδρύματα όπως το Bureau of Transportation Statistics, το Swedish National Road and Transportation Research Institute κ.α., έχουν εκπονήσει εργασίες σχετικά με τη μελέτη ατυχημάτων. Διάφορες μελέτες έχουν δημοσιευτεί σε πολλά επιστημονικά περιοδικά όπως, το περιοδικό Accident Analysis & Prevention, Traffic Injury Prevention, Health and Place, Safety Science κ.α, στις οποίες έχουν προταθεί διάφορες μεθοδολογικές προσεγγίσεις και ποικίλα στατιστικά μοντέλα. Αναφέρεται ότι στην εργασία των D. Lord κ.α (D. Lord et al (2004)) διερευνώνται τα μοντέλα που μπορούν να εφαρμοστούν σε δεδομένα οδικών ατυχημάτων, και ειδικότερα του διωνυμικού μοντέλου, του μοντέλου Poisson, του Αρνητικού Διωνυμικού, των Zero Inflated μοντέλων κ.α. Το γραμμικό μοντέλο: Το κλασικό γραμμικό μοντέλο είναι της μορφής y = Xb + e και περιγράφεται με τη βοήθεια πινάκων ως εξής y y 1 2 y n x x p b 11 x e1 = x x p b 21 x e2 x x n xn np b 1 2 p en όπου y = [y 1, y 2,, y n ] T είναι η στήλη της εξαρτημένης μεταβλητής, ο πίνακας Χ διάστασης n p είναι ο πίνακας των τιμών των ανεξάρτητων-επεξηγηματικών μεταβλητών, ενώ κάθε γραμμή αναφέρεται σε μια διαφορετική παρατήρηση και κάθε στήλη σε διαφορετική ανεξάρτητη μεταβλητή. Η στήλη των παραμέτρων b = [b 1, b 2,..,b p ] T περιλαμβάνει τους συντελεστές των ανεξάρτητων μεταβλητών, ενώ η στήλη e = [e 1, e 2,,e n ] είναι τα κατάλοιπα ή αλλιώς τα τυχαία σφάλματα. Στο κλασσικό γραμμικό μοντέλο υποθέτουμε ότι τα κατάλοιπα είναι ανεξάρτητα, ακολουθούν την κανονική κατανομή και ότι Ε(e i ) = 0 και Var(e i ) = σ 2. Επίσης τα y i (στήλη y) ακολουθούν την κανονική κατανομή με Ε(y i ) = μ i και 3
22 Var(y i ) = σ 2 σταθερή. Η αναμενόμενη τιμή των y δοθέντως των X εκτιμάται από την σχέση, που αποτελεί και το μοντέλο απλής γραμμικής παλινδρόμισης: μ = Ε(y X ) = α+ Xb όπου α=[α 1, α 2,...α n ] T η στήλη με τους σταθερούς όρους της εκτιμώμενης γραμμικής παλινδρόμησης και μ = [μ 1, μ 2,...μ n ] η στήλη με τις αναμενόμενες τιμές των y i. Για δεδομένες τιμές του διανύσματος b, μπορεί να οριστεί το διάνυσμα των τυχαίων σφαλμάτων ως e( b) = y E( y). Ο Gauss, έδειξε ότι οι εκτιμητές του διανύσματος b που προκύπτουν από την ελαχιστοποίηση των ελαχίστων τετραγώνων των καταλοίπων έχουν τη μικρότερη διακύμανση συγκριτικά με τους υπόλοιπους αμερόληπτους εκτιμητές. Το Γενικευμένο Γραμικό Μοντέλο (Γ.Γ.Μ.): Αποτελεί γενίκευση του μοντέλου γραμμικής παλινδρόμησης, με την έννοια ότι δεν περιορίζεται από την υπόθεση της κανονικότητας των y i,όπως αναφέρεται παρακάτω. Διαρθρώνεται από 3 μέρη: α) τη τυχαία συνιστώσα (random component): αναφέρεται στην κατανομή πιθανότητας του διανύσματος y. Εδώ, δεν αποτελεί προϋπόθεση η κανονικότητα των y i, αλλά το να κατανέμονται σύμφωνα με κάποια κατανομή που ανήκει στην εκθετική οικογένεια κατανομών (Κανονική, Bernoulli, Poisson κλπ) β) τη συστηματική συνιστώσα (systematic component): περιλαμβάνει τις επεξηγηματικές μεταβλητές Χ j ως γραμμικό συνδυασμό που εκτιμά τα y i και γ) τη συνάρτηση σύνδεσης (link function): είναι η συνάρτηση που συνδέει τη συστηματική συνιστώσα του μοντέλου με την τυχαία συνιστώσα. Εκφράζει τον τρόπο με τον οποίο η Ε(y) = μ σχετίζεται με τις επεξηγηματικές μεταβλητές στο γραμμικό μοντέλο, μέσω μιας συγκεκριμένης συνάρτησης g(μ). Στην περίπτωση του κλασσικού μοντέλου παλινδρόμησης, όπου ισχύει η υπόθεση της κανονικότητας της τυχαίας συνιστώσας, η συνάρτηση σύνδεσης είναι η g(μ) = μ. Στη περίπτωση που η εξαρτημένη μεταβλητή εκφράζει αριθμό γεγονότων (π.χ. ατυχημάτων) στη μονάδα χρόνου, ακολουθεί δηλαδή κατανομή Poisson, κατάλληλη συνάρτηση σύνδεσης είναι η g(μ) = lnμ και τότε έχουμε το μοντέλο Poisson. Στην περίπτωση όπου το διάνυσμα της εξαρτημένης μεταβλητής ακολουθεί τη Διωνυμική κατανομή τότε η συνάρτηση σύνδεσης είναι η λεγόμενη logit link: g(μ) = ln[μ/(1-μ)] και το μοντέλο ονομάζεται μοντέλο λογιστικής παλινδρόμησης. Άλλη συνάρτηση σύνδεσης στην περίπτωση της Διωνυμικής κατανομής είναι η g(μ) = Φ -1 (μ), όπου Φ(x) είναι η συνάρτηση της αθροιστικής κανονικής κατανομής και το μοντέλο λέγεται probit. 4
23 Τέλος, το Γ.Γ.Μ. είναι κατάλληλο όταν η σχέση μεταξύ εξαρτημένων και των συντελεστών των ανεξάρτητων μεταβλητών δεν είναι γραμμική. Αναλυτικότερα τα διάφορα μοντέλα παρουσιάζονται παρακάτω. Μοντέλο Poisson: Παραδοσιακά, η κατανομή Poisson είναι κατάλληλη για να περιγράψει δεδομένα που αναφέρονται σε αριθμό γεγονότων, όπως είναι ο αριθμός ατυχημάτων (Zhuo Li et al (2007)), εφόσον θεωρηθεί ότι τα ατυχήματα είναι αποτέλεσμα αποκλειστικά τυχαίων παραγόντων. Η συνάρτηση κατανομής της Poisson είναι: P(Y=y) = y λ λ e y!, λ 0 όπου y = 0,1,2,3...ο αριθμός των ατυχημάτων και λ = E(Y) = Var(Y) (η αναμενόμενη τιμή της κατανομής Poisson συμπίπτει με την διακύμανση). Καθώς η μέση τιμή ισούται με τη διακύμανση, κάθε παράγοντας που επηρεάζει το μέσο, θα επηρεάσει και τη διακύμανση. Έτσι, η υπόθεση της ομοσκεδαστικότητας δεν είναι κατάλληλη για δεδομένα Poisson (G. Rodrigues (2009)). Η κατανομή Poisson μπορεί να χρησιμοποιηθεί και ως μια οριακή μορφή της Διωνυμικής κατανομής αν θεωρήσουμε την κατανομή του αριθμού των επιτυχιών ενός μεγάλου αριθμού δοκιμών (n) Bernoulli με μικρή πιθανότητα επιτυχίας (π) σε κάθε δοκιμή. Ειδικότερα, αν Υ~ Β(n,π) τότε η κατανομή του Υ όταν n και π 0, με λ = nπ προσεγγίζει την κατανομή Poisson με μέση τιμή λ. Έτσι η κατανομή Poisson αποτελεί μια προσέγγιση της Διωνυμικής για ανάλυση σπάνιων γεγονότων, όπου η πιθανότητα επιτυχίας (π) είναι μικρή και ο αριθμός των δοκιμών (n) πολύ μεγάλος. Εναλλακτικά, άλλος τρόπος που περιγράφει την κατανομή Poisson είναι μια στοχαστική διαδικασία που περιγράφεται ως εξής: Υποθέτουμε γεγονότα που πραγματοποιούνται τυχαία στο χρόνο με τρόπο ώστε α) η πιθανότητα να συμβεί τουλάχιστον ένα γεγονός σε δεδομένο χρονικό διάστημα είναι ανάλογη του μήκους του διαστήματος, β) η πιθανότητα να συμβούν 2 ή περισσότερα γεγονότα σε ένα πολύ μικρό χρονικό διάστημα είναι αμελητέα και γ) ο αριθμός των γεγονότων που πραγματοποιούνται σε μη συνεχή χρονικά διαστήματα είναι αμοιβαία ανεξάρτητος. Σε αυτήν την περίπτωση η κατανομή πιθανότητας του αριθμού των γεγονότων σε σταθερό χρονικό διάστημα είναι η Poisson με μέση τιμή λ = νt, όπου ν = ο αριθμός των πραγματοποιούμενων γεγονότων στη μονάδα του χρόνου και t = το μήκος του χρονικού διαστήματος. Η διαδικασία ονομάζεται διαδικασία Poisson (G. Rodrigues (2009)). 5
24 Προκειμένου για την κατασκευή του μοντέλου Poisson, υποθέτουμε ένα δείγμα με n παρατηρήσεις y 1, y 2, y 3 y n που μπορούν να θεωρηθούν ως πραγματοποιήσεις ανεξάρτητων τυχαίων μεταβλητών Poisson, με αναμενόμενη τιμή λ i (και διακύμανση), που εξαρτάται από ένα διάνυσμα επεξηγηματικών μεταβλητών X i. Το απλό γραμμικό μοντέλο λ i = Χ iτ β έχει το μειονέκτημα ότι ενώ το δεξί μέρος της ισότητας παίρνει τιμές σε όλο το R, το + αριστερό όπου βρίσκεται η μέση τιμή της Poisson παίρνει μόνο θετικές τιμές, δηλ. στο R. Μια λύση είναι ο μετασχηματισμός της τυχαίας συνιστώσας, χρησιμοποιώντας τον φυσικό λογάριθμο ως συνάρτηση σύνδεσης. Έτσι το μοντέλο παίρνει τη μορφή: ln(λ i ) = X iτ β (λογαριθμικό γραμμικό μοντέλο). Συνεπώς, από το λογαριθμικό μοντέλο συνεπάγεται ότι λ i = exp{x iτ β}. Έτσι, η κατανομή των Υ δοθέντος των Χ παίρνει την εξής μορφή: T y (exp{ X β}) T exp{ X β} P(Y=y Χ) = e i (μοντέλο παλινδρόμησης Poisson) y! Οι συντελεστές παλινδρόμησης β j του διανύσματος β αναπαριστούν το ποσό μεταβολής στο λογάριθμο του μέσου της εξαρτημένης μεταβλητής, αν η ανεξάρτητη x j αυξηθεί κατά μία μονάδα, όταν οι υπόλοιπες ανεξάρτητες μεταβλητές παραμείνουν αμετάβλητες. Δηλαδή ότι αν αυξηθεί η x j κατά μία μονάδα, ο μέσος των y αναμένεται να αυξηθεί κατά exp(β j ). Επίσης σύμφωνα με το μοντέλο ισχύει ότι: Ε(Υ Χ) = Var(Υ Χ) = exp{x T β) Προκειμένου να εκτιμηθούν οι παράμετροι β του μοντέλου, χρησιμοποιείται ο λογάριθμος της συνάρτησης μέγιστης πιθανοφάνειας. Η συνάρτηση, για το μοντέλο είναι: n T T T lnl = [ λi + yi X i β ln yi!] = [ exp{ X i β} + yi X i β ln yi!] i= 1 i= 1 n Οι παράμετροι του μοντέλου (διάνυσμα β) μπορούν να εκτιμηθούν, παραγωγίζοντας τη συνάρτηση ως προς το διάνυσμα β. Έτσι ο λογάριθμος μέγιστης πιθανοφάνειας παίρνει τη μορφή: L = n lnl β = X i [exp (X T i β ) y i ]=0 i 1 6
25 Αρνητικό Διωνυμικό Μοντέλο: Αν όμως υποτεθεί ότι κάθε υποκείμενο έχει μια συγκεκριμένη προδιάθεση να πάθει ατύχημα εξ αιτίας συγκεκριμένων και σταθερών παραγόντων που επιδρούν, οι οποίοι διαφέρουν μεταξύ των διαφορετικών υποκειμένων, και ότι το συμβάν δεν εξαρτάται μόνο από τυχαίους, αλλά και από σταθερούς παράγοντες, τότε ο αριθμός των ατυχημάτων ακολουθεί Αρνητική Διωνυμική κατανομή (M. Zografi and E. Xekalaki (2001)). Συνώνυμο αυτού είναι ότι οι σταθεροί και διαφορετικοί παράγοντες που επιδρούν έχουν ως αποτέλεσμα η κατανομή του παρατηρούμενου αριθμού ατυχημάτων να έχει διακύμανση μεγαλύτερη από τη μέση τιμή της. Στην περίπτωση αυτή η κατανομή του αριθμού των ατυχημάτων δεν προσεγγίζεται ικανοποιητικά από την Poisson, ενώ καταλληλότερη είναι η Αρνητική Διωνυμική. Η συνάρτηση κατανομής της Αρνητικής Διωνυμικής κατανομής είναι: P(Y = y) = Γ( ν + y) Γ( ν ) Γ( y + 1) ν ν µ + ν ν 1 μ,ν>0 µ + ν y όπου x =0,1,..ο αριθμός των ατυχημάτων, μ = Ε(y) η αναμενόμενη τιμή, 1 ν = η παράμετρος διασποράς της κατανομής και Γ(α) = (α-1)!, δοθέντος ότι το α είναι θετικός ακέραιος αριθμός. Η διακύμανση δίνεται από τον τύπο: Var(y) = µ + µ 2 ν Από αυτό προκύπτει ότι όσο αυξάνεται η παράμετρος διασποράς τόσο αυξάνεται και η διακύμανση. Επιπλέον, αν η παράμετρος διασποράς γίνει 0 ( v ), τότε η διακύμανση var(y) = Ε(y) = μ, και η κατανομή συγκλίνει στην Poisson. Συνεπώς, το Αρνητικό διωνυμικό μοντέλο είναι περισσότερο γενικό από το αντίστοιχο Poisson και μπορεί να ιδωθεί ως μια μίξη κατανομών Poisson. Το αρνητικό διωνυμικό μοντέλο δημιουργείται χρησιμοποιώντας ως συνάρτηση σύνδεσης την η i = ln p µ i = µ i +ν j= 1 x ij β j Ωστόσο, εναλλακτική επιλογή είναι ο λογαριθμικός μετασχηματισμός του μέσου, η ίδια συνάρτηση δηλαδή που χρησιμοποιείται στην κατανομή Poisson (ln(μ i )). Χρησιμοποιώντας ως συνάρτηση σύνδεσης την η i = ln(μ i ) = p x ij j= 1 β, η κατανομή των Υ δοθέντος των Χ, παίρνει τη μορφή (αρνητικό διωνυμικό μοντέλο παλινδρόμησης): j 7
26 P(Y = y Χ) = 1) ( ) ( ) ( + Γ Γ + Γ y y ν ν ν ν β ν } + exp{ T X y T X + ν β ν } exp{ 1 Σύμφωνα με το μοντέλο, ισχύουν τα εξής: Ε(Υ Χ) = exp{x T β) και Var(Υ Χ) = exp{x T β) + ν T β}) 2 (exp{x Η συνάρτηση μέγιστης πιθανοφάνειας του μοντέλου είναι: lnl = ( ) ( ) ( ) = Γ Γ + Γ n i i i i i i i y y y 1 ln ln 1 ln ν µ µ µ ν ν ν ν ν = = = + = n i y k y j y y k j ) ) ln( ( ln ln ln ln ν µ ν µ ν ν ν ν = = = = = + = n i p j j ij p j j ij y k y j x y x y k j exp )ln ( ln ln ln ν β ν β ν ν ν ν Οι εκτιμητές μέγιστης πιθανοφάνειας των παραμέτρων του μοντέλου προκύπτουν από τη λύση της εξίσωσης: L = lnl β =0 Zero-inflated Μοντέλο: Στις περιπτώσεις όπου ο παρατηρούμενος αριθμός των γεγονότων εμφανίζει πολύ υψηλή συχνότητα στο μηδέν (0), τότε καταλληλότερη κατανομή περιγραφής των γεγονότων είναι μια κατανομή «διογκωμένη στο μηδέν» (zero-inflated distribution) και τα αντίστοιχα μοντέλα που εφαρμόζονται είναι τα μοντέλα «διογκωμένα» στο μηδέν (Ζero- Ιnflated models- ZI). Η βασική παραδοχή στα zero-inflated μοντέλα είναι ότι τα μηδενικά γεγονότα προέρχονται από δύο διαφορετικές πηγές: από τη μία πηγή προέρχονται τα μηδενικά γεγονότα τα οποία, κατά μία έννοια, ήταν αναπόφευκτο να εμφανιστούν, (π.χ. λόγω της φύσης της συλλογής των δεδομένων κ.τ.λ.) και το άλλο μέρος περιλαμβάνει τα μηδενικά γεγονότα που παρατηρήθηκαν και ακολουθούν κάποια κατανομή (Poisson ή Αρνητική Διωνυμική). Άλλη περίπτωση κατά την οποία είναι δυνατόν να εμφανιστεί πολύ υψηλή συχνότητα μηδενικών γεγονότων είναι το διάστημα μέσα στο οποίο συλλέγονται τα δεδομένα (μικρά διαστήματα όπως π.χ. ωριαίες μετρήσεις) με αποτέλεσμα στο δείγμα να εμφανίζονται πολύ περισσότερα μηδενικά ατυχήματα από εκείνα που αναμένονται από την συνάρτηση κατανομής. 8
27
28 Ε(y) = (1-q)μ και Var(y) = (1-q)(1+ ν µ +qμ)μ Λόγω του ότι η κατανομή που υποθέτουμε έχει δύο σκέλη (ένα για τα μηδενικά γεγονότα και ένα όταν πραγματοποιηθεί τουλάχιστον ένα γεγονός), το ZI μοντέλο έχει επίσης 2 συναρτήσεις σύνδεσης: η μία αφορά στην σύνδεση των επεξηγηματικών μεταβλητών Χ j με την πραγματοποίηση μηδενικών γεγονότων. Χρησιμοποιεί τη συνάρτηση logit: p q η = ln( ) = 1 q c ij j= 1 β, όταν y=0 και c ij υποσύνολο των x ij j μοντελοποιώντας έτσι την πιθανότητα να παρατηρηθούν επιπλέον μηδενικά ατυχήματα σε σχέση με την πιθανότητα να συμβούν μηδενικά ατυχήματα που ακολουθούν κάποια κατανομή, ενώ το σκέλος που αφορά στην εμφάνιση τουλάχιστον ενός γεγονότος η συνάρτηση σύνδεσης είναι ο φυσικός λογάριθμος του αναμενόμενου αριθμού γεγονότων (δηλαδή την η i = ln(μ i ), όπως ισχύει στο μοντέλο Poisson και στο αρνητικό διωνυμικό μοντέλο). Σε αυτήν την περίπτωση η συνάρτηση σύνδεσης παίρνει τη μορφή: η i = ln(μ i ) = p j= 1 ω ξ ij j, όταν y=0 και ω ij υποσύνολο των x ij Πρέπει να σημειωθεί ότι οι επεξηγηματικές μεταβλητές που σχετίζονται με την πιθανότητα εμφάνισης των επιπλέον μηδενικών γεγονότων, σε σχέση με τα μηδενικά γεγονότα που κατανέμονται βάσει κάποιας κατανομής, δεν είναι απαραίτητο να συμπίπτουν με εκείνες που σχετίζονται με την εμφάνιση τουλάχιστον ενός γεγονότος. Η συνάρτηση πιθανοφάνειας του μοντέλου είναι: p ν exp{ ωijξ j} + ν n p p j= 1 lnl= 1 + exp{ c ij β j} + ln exp{ cij β j} + + i= 1 j= 1 i: y= 0 j= 1 ν p exp{ ω ξ } + ν ν ω ijξ j} ν + ij j p j= 1 ln + y i ln 1+ exp{ i: y> 0 ν j= 1 ( ln Γ( ν ) + ln Γ(1 + yi ) ln Γ( ν + y i )) i: y> 0 10
29 Πρέπει να σημειωθεί ότι η χρήση των zero-inflated μοντέλων έχει αποτελέσει αιτία έντονης συζήτησης αναφορικά με την καταλληλότητά τους. Έχει δειχθεί ότι η αρκετά συνηθισμένη παρατήρηση πλεοναζόντων μηδενικών γεγονότων οφείλεται μάλλον στην επιλογή μιας μη κατάλληλης χρονικής κλίμακας για την ανάλυση, παρά στην υπόθεση ότι τα γεγονότα (ατυχήματα) προέρχονται από μια διπλή διαδικασία (που προέρχονται από δύο διαφορετικές πηγές D. Lord et al (2005)).. Ωστόσο, οι εργασίες και οι μελέτες που αφορούν σε μοντέλα οδικών και άλλων ατυχημάτων (Kumara and Chin (2003), Li et al. (2008), J. Carson, F.Mannering (2001), S.P. Miaou (1994) κ.α.) χρησιμοποιούν πολύ συχνά τα zero inflated μοντέλα, καθώς αυτά προσαρμόζονται πολύ ικανοποιητικά στις παρατηρούμενες μετρήσεις. Επιπλέον τα μοντέλα αυτά μπορούν να χρησιμοποιηθούν για προβλέψεις (D. Lord et al (2005)). Άλλα μοντέλα: Επίσης, ο M. Ridout (M. Ridout et al (1998)) αναφέρει και άλλα μοντέλα που μπορούν να εφαρμοστούν σε διακριτά δεδομένα με πλεονάζουσα συχνότητα μηδενικών (0) γεγονότων όπως τα hurdle μοντέλα, τα ημιπαραμετρικά hurdle μοντέλα και τα μοντέλα διαδικασιών γεννήσεως. Ακολούθως παρουσιάζονται συνοπτικά κάποια από αυτά. Hurdle (φραγμένα) μοντέλα: Βασίζονται στην υπόθεση ότι οι μηχανισμοί που παράγουν τις μηδενικές παρατηρήσεις πιθανότατα διαφέρουν από τους μηχανισμούς που παράγουν τον αριθμό εμφάνισης γεγονότων. Για να την ανάπτυξη ενός τέτοιου μοντέλου απαιτείται ο καθορισμός α) της πιθανότητας π 0, να μην εμφανιστεί κανένα γεγονός και β) της κατανομής (διακριτής με τιμές >0) του αριθμού των γεγονότων. Όπως αναφέρει ο Ridout (M. Ridout et al (1998)) στην βιβλιογραφία της οικονομικής επιστήμης, αυτός ο τύπος μοντέλου ονομάζεται hurdle (φράγμα), όπου π + = 1-π 0 είναι η πιθανότητα υπερπήδησης του «φράχτη» και παραγωγής μη μηδενικών γεγονότων. Άλλο όνομα αυτού του μοντέλου είναι two part model (διμερές μοντέλο). Τυπικά, η κατανομή στο β) μέρος του μοντέλου είναι περικομμένη στο 0 (zero-truncated distribution). Στην περίπτωση που εφαρμόζεται περικομμένη στο 0 κατανομή Poisson, τότε η κατανομή των Y δίνεται από τον τύπο: π 0 y Pr(Y=y) = (1 π 0 ) exp{ λ} λ (1 exp{ λ}) y! y = 0 y > 0 11
30 Στην ουσία, πρόκειται για μια αναπαραμετροποίηση της κατανομής zero-inflated Poisson, με π 0 = q + ( 1 q)exp{ λ}. Ωστόσο, στο μοντέλο παλινδρόμησης οι παράμετροι που μοντελοποιούνται διαφέρουν και έτσι τα μοντέλα δεν είναι ίδια. Οι συναρτήσεις σύνδεσης που χρησιμοποιούνται είναι η log-log για το π + και η log για το λ. Δηλ. log(λ)=χβ και log[-log(1-π + )]=Χγ Ημιπαραμετρικά hurdle μοντέλα: Τα ημιπαραμετρικά hurdle μοντέλα βασίζονται στη λογική ότι αν εφαρμοστεί ένα σύνηθες μοντέλο Poisson σε δεδομένα που εμφανίζουν μεγαλύτερη διακύμανση από εκείνη που αναμένεται σύμφωνα με την κατανομή Poisson τότε, υπό αμερόληπτες συνθήκες, οι εκτιμήσεις των παραμέτρων είναι συνεπείς και αποτελεσματικοί. Ωστόσο, τα τυπικά σφάλματά τους θα υποεκτιμούνται, αλλά η χρήση μιας απλής διευθέτησης της ετερογένειας μπορεί να τα διορθώσει. Αυτή η προσέγγιση είναι ανθεκτική, η οποία σε αντίθεση με την μέθοδο εκτίμησης μέγιστης πιθανοφάνειας, δεν απαιτεί ισχυρές υποθέσεις για την κατανομή αριθμού των γεγονότων. Δυστυχώς, στην περίπτωση των hurdle ή των zero-truncated μοντέλων, ο ανεπιτυχής προσδιορισμός της κατανομής που ακολουθούν τα δεδομένα οδηγεί σε ασυνεπείς εκτιμήσεις των παραμέτρων του μοντέλου. Για παράδειγμα οι Grogger & Carson (1991) που εφάρμοσαν μερικά zero-truncated Poisson μοντέλα σε προσομοιωμένα δεδομένα από zero-truncated αρνητικές διωνυμικές κατανομές, βρήκαν μεροληψία στους εκτιμητές μέχρι 30%. Η πηγή της ασυνέπειας είναι το γεγονός ότι η αναμενόμενη τιμή μιας zero-truncated κατανομής εξαρτάται από τη μορφή της πιθανότητας να πραγματοποιηθούν μηδενικά γεγονότα. Αν δηλαδή μια κατανομή Poisson και μια Αρνητική Διωνυμική κατανομή με ίδια αναμενόμενη τιμή περικοπούν στο μηδέν, τότε οι αναμενόμενες τιμές των περικομμένων στο 0 κατανομών θα διαφέρουν. Αυτό δεν οφείλεται στο ότι απλώς διαφέρουν οι διακυμάνσεις τους, καθώς το ίδιο ισχύει και μεταξύ μιας αρνητικής διωνυμικής κατανομής και μιας κατανομής Neyman τύπου Α, που έχουν ίδια αναμενόμενη τιμή και διακύμανση. Μια περισσότερο ισχυρή αξιόπιστη (robust) προσέγγιση αναπτύχθηκε από τον Gurmu (1997), δημιουργώντας ένα ημιπαραμετρικό hurdle μοντέλο. Υποθέτει ένα μικτό Poisson μοντέλο, όπου η κατανομή του Υ, δεσμευμένη ως προς V, είναι η Poisson(Vμ) και το V έχει συνάρτηση πυκνότητας πιθανότητας h(u) και E(V) = 1. Υπό τον όρο ότι η κατανομή του V ικανοποιεί κάποιες συνθήκες εξομάλυνσης, η κατανομή h(u) έχει μια άπειρη επέκταση σειρών Laguerre. Αν η επέκταση περικοπεί μετά από κάποιο ορισμένο αριθμό όρων και κανονικοποιηθεί προκειμένου να δίνει μια κατάλληλη κατανομή πιθανότητας, τότε είναι πιθανό να παραχθεί μια περίπλοκη, αλλά ρητή, έκφραση για την κατανομή του Υ, επιτρέποντας κατά συνέπεια την εκτίμηση 12
31 παραμέτρων μέγιστης πιθανοφάνειας. Η μέθοδος είναι ημιπαραμετρική στο μέτρο που η επιλογή του αριθμού των όρων στον οποίο γίνεται η περικοπή οδηγείται από τα δεδομένα, π.χ. με τη χρήση του κριτηρίου πληροφορίας Akaike. Χρησιμοποιώντας ένα μόνο όρο για την επέκταση, είναι ίσο με την υπόθεση της μιας Γάμμα κατανομής για το V και μιας Αρνητικής Διωνυμικής κατανομής για τα Υ. Μοντέλα διαδικασιών γεννήσεως: Μια διαφορετική προσέγγιση είναι η υπόθεση ότι ο αριθμός εμφάνισης γεγονότων σε μια ορισμένη περίοδο ακολουθεί μια «καθαρή» διαδικασία γέννησης με: Pr{Y(t + δt) = y + 1 Y(t) = y} = λ y δt + o(δt). Αν λ y = λ είναι ανεξάρτητο από το y τότε η κατανομή του αριθμού των γεγονότων κατά το τέλος της περιόδου (χρόνος t = 1) είναι Poisson(λ). Εναλλακτικά, αν η σειρά λ y αυξάνεται γραμμικά σε σχέση με το y τότε η κατανομή είναι η Αρνητική Διωνυμική. Γενικότερα, κάθε διακριτή κατανομή μπορεί να ληφθεί από μια κατάλληλη επιλογή της ακολουθίας λ y. Πρακτικά, η ακολουθία: λ y = λ0 λ1 y = 0 y > 0 με λ 1 > λ 0, μπορεί να είναι χρήσιμη για δεδομένα με πλεονάζοντα μηδενικά. Αυτό θα υπονοούσε ότι ο ρυθμός με τον οποίο τα γεγονότα πραγματοποιούνται αυξάνεται μετά την πραγματοποίηση του πρώτου γεγονότος. Για τα μοντέλα παλινδρόμησης, τα λ 1 και λ 0 μπορούν να αφορούν τις συνεχείς μεταβλητές λογαριθμικών μοντέλων. 13
32 14
33 3. ΑΝΑΛΥΣΗ ΤΩΝ ΔΕΔΟΜΕΝΩΝ ΑΤΥΧΗΜΑΤΩΝ 3.1. Περιγραφικά στατιστικά και συσχετίσεις μεταξύ του αριθμού ατυχημάτων και των μεταβλητών κλίματος Η μεταβλητή που μελατάμε είναι ο αριθμός των ατυχημάτων που πραγματοποιήθηκαν στην Ολλανδία κατά το έτος 2002 ανά ώρα, οπότε και παρατηρήθηκαν κάποιες συγκεκριμένες καιρικές συνθήκες (υγρασία, θερμοκρασία, χιονόπτωση, ταχύτητα αέρα, ορατότητα κ.α.). Σύμφωνα με τα στοιχεία, κατά τη διάρκεια του έτους πραγματοποιήθηκαν συνολικά 1113 ατυχήματα. Προκειμένου να μελετηθεί η μορφή της μεταβλητής που αφορά στον αριθμό ατυχημάτων, υπολογίστηκαν μέτρα κεντρικής τάσης και διασποράς των δεδομένων και άλλα χαρακτηριστικά όπως π.χ. η κυρτότητα και η ασυμμετρία. Επιπλέον δημιουργήθηκε το ιστόγραμμα συχνότητας και το διάγραμμα αθροιστικής πιθανότητας του αριθμού ατυχημάτων. Τέλος εφαρμόστηκαν έλεγχοι καλής προσαρμογής συγκεκριμένων και γνωστών κατανομών για προσέγγιση της κατανομής των ατυχημάτων του προβλήματός μας από αυτές. Στον ακόλουθο πίνακα (Πίνακας 1) παρουσιάζονται κάποια μέτρα κεντρικής τάσης και διασποράς της υπό μελέτη μεταβλητής, στον Πίνακα 2 παρουσιάζεται η κατανομή των δεδομένων του αριθμού των ατυχημάτων, ενώ στους Πίνακες 3α και 3β παρουσιάζονται κάποια περιγραφικά στοιχεία των μεταβλητών του κλίματος. Πίνακας 1. Πίνακας περιγραφικών στατιστικών για τον αριθμό ατυχημάτων (ωριαίες μετρήσεις) Αριθμός ατυχημάτων N 8760 Μέσος 0,127 Τυπικό σφάλμα Μέσου 0,004 Διάμεσος 0 Επικρατούσα τιμή 0 Τυπική Απόκλιση 0,411 Διακύμανση 0,169 Ασυμμετρία 4,294 Τυπικό σφάλμα Ασυμμετρίας 0,026 Κύρτωση 27,034 Τυπικό σφάλμα Κύρτωσης 0,052 Εύρος 6 Ελάχιστο 0 Μέγιστο 6 Ποσοστιαία σημεία
34 Πίνακας 2. Κατανομή Συχνότητας, Κατανομή Πυκνότητας Πιθανότητας και Κατανομή Πιθανότητας (Αθροιστική) του αριθμού ατυχημάτων (ωριαίες μετρήσεις) Κατανομή αριθμού ατυχημάτων Συχνότητα % Πιθανότητα % Αθροιστική Πιθανότητα ,5 89, ,8 98, ,3 99, ,3 99, Σύνολο Πίνακας 3α. Περιγραφικά στοιχεία των συνεχών επεξηγηματικών μεταβλητών 1 DD FF FX FH T U Q SQ RD RH VV WW N Παρατηρήσεις Μέσος 213,9 48,5 80,7 48,4 109,7 82,6 42,9 2,0 0,7 0,9 58,8 25,9 5,1 Τυπ. Απόκλιση 163,8 30,0 46,4 29,6 59,6 12,3 70,7 3,5 2,3 5,2 13,7 23,2 2,7 Ελάχιστη τιμή ο τεταρτημόριο Διάμεσος ο τεταρτημόριο Μέγιστη τιμή Πίνακας 3β. Περιγραφικά στοιχεία των κατηγορικών επεξηγηματικών μεταβλητών 2 WW_M WW_R WW_S WW_H WW_O WW_Y Απουσία παράγοντα Παρουσία παράγοντα Από τους Πίνακες 1 και 2 διαπιστώνεται ότι η κατανομή του αριθμού ατυχημάτων είναι έντονα ασύμμετρη προς τα δεξιά το οποίο φαίνεται τόσο από τη σχετική θέση της μέσης τιμής σε σχέση με τη διάμεσο ( X >M), όσο και από την τιμή του δείκτη ασυμμετρίας (4,29). Φαίνεται δηλαδή να υπάρχει μια μακριά δεξιά ουρά στην κατανομή των δεδομένων μας δεδομένου ότι η πλειονότητα των δεδομένων εμφανίζει 0 ατυχήματα και ότι η συχνότητες των πραγματοποιήσιμων ατυχημάτων είναι μικρές συγκριτικά με το μέγεθος του δείγματος. Συγκεκριμένα, στο 89,5% των περιπτώσεων σημειώθηκαν 0 ατυχήματα. Το γεγονός αυτό οφείλεται στο ότι, καθώς οι μετρήσεις είναι ωριαίες, ενδεχομένως να υπήρξαν ώρες κατά τις 1 DD=Κατεύθυνση του ανέμου (βαθμοί), FF=Μέση ταχύτητα του ανέμου (0,1m/sec), FH= Μέση ωριαία ταχύτητα του ανέμου (0,1m/sec), FX= Μέγιστη ριπή ανέμου, T= Θερμοκρασία (0,1 βαθμούς Κελσίου), Q= Ολική ωριαία ακτινοβολία (Joule/cm 2 ), SQ= Διάρκεια ηλιοφάνειας (0,1 ώρες), RD= Διάρκεια βροχόπτωσης (0,1 ώρες), RH= Ποσότητα βροχόπτωσης (0,1mm), U= Ποσοστό σχετικής υγρασίας, VV= Οριζόντια ορατότητα, N= Συνολική κάλυψη της επιφάνειας του ουρανού, WW= Κωδικοποίηση του καιρού 2 WW_H= Χαλάζι (παρουσία/ απουσία), WW_O= Θύελλα με καταιγίδα(παρουσία/ απουσία), WW_M= Ομίχλη (παρουσία/ απουσία), WW_R=Βροχόπτωση (παρουσία/ απουσία), WW_S= Χιόνι (παρουσία/ απουσία), WW_Y= Παγετός (παρουσία/ απουσία) 16
35 οποίες δεν συνέβη κανένα ατύχημα εξαιτίας της μη κυκλοφορίας οχημάτων κατά την ώρα αυτή (πχ πρώτες πρωινές ώρες, μετά τα μεσάνυχτα). Το Διάγραμμα Πιθανότητας που ακολουθεί επιβεβαιώνει τη μορφή αυτή των δεδομένων και παρουσιάζει γραφικά την πιθανότητα να συμβούν ατυχήματα το πολύ μέχρι κάποιον συγκεκριμένο αριθμό. Διάγραμμα 1. Αθροιστική πιθανότητα του αριθμού ατυχημάτων Διάγραμμα αθροιστικής πιθανότητας του αριθμού ατυχημάτων Πιθανότητα Αριθμός ατυχημάτων Εκτός από την διερεύνηση της υπό μελέτη μεταβλητής μεμονωμένα, το ενδιαφέρον εστιάζεται στην εύρεση πιθανών σχέσεων μεταξύ του αριθμού των ατυχημάτων και των λοιπών μεταβλητών χρόνου και κλίματος. Προκειμένου να ειδωθούν πιθανές σχέσεις του αριθμού των ατυχημάτων με τις υπόλοιπες μεταβλητές δημιουργήθηκαν τα ακόλουθα Διαγράμματα σημείων (Scatter plots) και Ιστογράμματα (Παράρτημα Β). Μελετώντας τα διαγράμματα παρατηρούμε, όπως είναι αναμενόμενο, ότι ανεξαρτήτως καιρικών συνθηκών, ημέρας και ώρας, η εμφάνιση ατυχήματος αποτελεί σπάνιο γεγονός, δοθέντος ότι η μέτρηση γίνεται ανά ώρα. Αναφορικά με τον εντοπισμό της σχέσης μεταξύ αριθμού ατυχημάτων και καιρικών συνθηκών και άλλων παραγόντων, δεν είναι εύκολο να εντοπιστούν με αυτόν τον τρόπο οι όποιες συσχετίσεις υφίστανται οι μεταβλητές του κλίματος με την υπο μελέτη μεταβλητή. Επίσης, η χρήση των γνωστών δεικτών γραμμικής συσχέτισης δεν ενδείκνυνται, εφόσον εντοπίζουν μόνο γραμμικές σχέσεις. Επιπλέον, προκειμένου να εντοπιστεί η πραγματική επίδραση μιας μεταβλητής στον αριθμό των ατυχημάτων πρέπει να ληφθούν υπόψη και οι υπόλοιπες μεταβλητές, ώστε να απομακρυνθεί η επίδραση που αυτές ασκούν στον αριθμό των ατυχημάτων. Έτσι, προκειμένου να εξηγηθεί 17
36 ο αριθμός των ατυχημάτων μέσω των καιρικών συνθηκών, απαιτείται η εύρεση ενός μοντέλου το οποίο θα εξηγεί την επίδραση μιας μεταβλητής κλίματος στον αριθμό ατυχημάτων, λαμβάνοντας ταυτόχρονα υπόψη και την επίδραση των υπολοίπων μεταβλητών σε αυτήν Έλεγχοι σχετικά με τη μορφή του κατάλληλου μοντέλου Προκειμένου να βρεθεί η κατάλληλη μορφή του μοντέλου είναι αναγκαία η εύρεση της κατανομής που μοιάζει/πλησιάζει την δειγματοληπτική κατανομή του αριθμού των ατυχημάτων. Εφαρμόζοντας ελέγχους καλής προσαρμογής (Kolmogorov- Smirnov και X 2 ) για τον έλεγχο της προσαρμογής των κατανομών της Αρνητικής Διωνυμικής και της Poisson στα δεδομένα, προέκυψε το συμπέρασμα ότι η Αρνητική Διωνυμική κατανομή κάνει καλύτερη προσαρμογή στα δεδομένα μας από ότι η κατανομή Poisson. Για τον υπολογισμό των συγκεκριμένων κατανομών Poisson και Αρνητικής Διωνυμικής έγινε εκτίμηση των παραμέτρων τους από το δείγμα (λ της Poisson: λ = μέση τιμή = 0,1268, και για την Αρνητική Διωνυμική: p = πιθανότητα να έχουμε τουλάχιστον ν = 1 επιτυχία). Στο πλαίσιο Π1 του Παραρτήματος Β, εμφανίζονται οι πίνακες με τα αποτελέσματα των ελέγχων, όπως αυτά προέκυψαν από το στατιστικό πακέtο R. Ο έλεγχος δείχνει ότι δεν απορρίπτεται η υπόθεση ότι τα δεδομένα προέρχονται από την Αρνητική Διωνυμική κατανομή, ενώ η μηδενική υπόθεση απορρίπτεται για την κατανομή Poisson. Ωστόσο, τα προειδοποιητικά μηνύματα αναφέρουν ότι ο έλεγχος μπορεί να μην είναι αρκετά αξιόπιστος. Έτσι, χρησιμοποιούμε εναλλακτικά τον έλεγχο καλής προσαρμογής των Kolmogorov Smirnov, ο οποίος δίνει τα αποτελέσματα που παρουσιάζονται στο πλαίσιο Π2. του Παραρτήματος Β. Σύμφωνα με τα αποτελέσματα του ελέγχου Kolmogorov-Smirnov, η Αρνητική Διωνυμική φαίνεται να εξηγεί καλύτερα τα δεδομένα από την Poisson, (η Η ο ότι τα δεδομένα προέρχονται από την Αρνητική Διωνυμική κατανομή έχει p-value = 1, ενώ για την Η ο ότι τα δεδομένα προέρχονται από την κατανομή Poisson, το p-value = 0,1037). Ωστόσο, αφενός και ο εν λόγω έλεγχος εμφανίζει προειδοποιητικά μηνύματα αδυναμίας υπολογισμού της ακριβούς τιμής p-value στην ουρά της κατανομής, λόγω του ότι η συχνότητα στην ουρά της κατανομής των δεδομένων μας είναι πολύ μικρή (P(x>4) 0) και αφετέρου η υπόθεση ότι τα δεδομένα προέρχονται από την κατανομή Poisson δεν απορρίπτεται με πιθανότητα 10,4%. Από τα παραπάνω συμπεραίνουμε ότι, ενώ οι έλεγχοι συγκλίνουν στο ότι η Αρνητική Διωνυμική κατανομή φαίνεται να περιγράφει καλύτερα τα δεδομένα απ ότι η 18
37 Poisson, δεν είναι απολύτως αξιόπιστα. Για αυτόν τον λόγο εφαρμόστηκε και ένας τρίτος έλεγχος, ο έλεγχος λόγου πιθανοφανειών για «υπερδιακύμανση» σε δεδομένα μέτρησης (likelihood ratio test for over-dispersion in count data A. Colin Cameron and P. Trivrndi (1998)). Ο εν λόγω έλεγχος συγκρίνει την πιθανοφάνεια ενός μοντέλου αρνητικής διωνυμικής παλινδρόμησης με την πιθανοφάνεια ενός μοντέλου Poisson, ελέγχοντας τη μηδενική υπόθεση: Η 0 : Η διακύμανση του μοντέλου δε διαφέρει σημαντικά από τη μέση τιμή (εναλλακτικά ότι το μοντέλο που προσαρμόζεται καλύτερα είναι το Poisson) Εφαρμόζοντας τον έλεγχο στο στατιστικό πακέτο R, προέκυψε το αποτέλεσμα ότι τα δεδομένα παρέχουν ισχυρές ενδείξεις προκειμένου να μην δεχθούμε την μηδενική υπόθεση (κριτική τιμή της συνάρτησης ελέγχου Τ c =2,7055<T o =128,5237 => p-value<0,001). Συνεπώς, μπορούμε να δεχθούμε ότι ο αριθμός ατυχημάτων ακολουθεί την Αρνητική Διωνυμική κατανομή. Ωστόσο, από τους πίνακες συχνοτήτων διαπιστώνεται ότι η υπό μελέτη μεταβλητή εμφανίζει πολύ υψηλή συχνότητα στην τιμή μηδέν (0). Έτσι, θα πρέπει να ελεγχθεί αν ένα μοντέλο Poisson που περιλαμβάνει μεγάλο αριθμό μηδενικών γεγονότων (Zero-inflated Poisson model, ΖΙΡ) είναι καταλληλότερο από ένα από μοντέλο παλινδρόμησης που βασίζεται στην απλή Αρνητική Διωνυμική κατανομή (GLMNB). Ομοίως, θα πρέπει να ελεγχθεί, δοθέντος ότι τα 0 ατυχήματα αποτελούν το 89,5% των δεδομένων, αν καταλληλότερο μοντέλο είναι ένα αρνητικό διωνυμικό μοντέλο «διογκωμένο» στο 0 (zero-inflated negative binomial model, ΖΙΝΒ), συγκριτικά με το απλό Διωνυμικό μοντέλο και το μοντέλο ΖΙΡ. Έτσι, εφαρμόζεται ο έλεγχος Vuong 3 μεταξύ των μοντέλων: Α) ΖΙΝΒ και γενικευμένου γραμμικού μοντέλου Αρνητικής Διωνυμικής κατανομής (GLMNB) Β) GLMNB και ZIP και Γ) ΖΙΝΒ και ΖΙΡ Είναι σημαντικό να ειπωθεί εδώ ότι οι έλεγχοι έγιναν για μοντέλα στα οποία περιλαμβάνονται όλες οι μεταβλητές. Η συγκεκριμένη επιλογή έγινε προκειμένου να 3 Ο έλεγχος Vuong συγκρίνει την προσαρμογή 2 μοντέλων σε μια συλλογή δεδομένων. Προυπόθεση για την εφαρμογή του ελέγχου είναι ότι τα 2 μοντέλα δεν πρέπει να είναι φωλιασμένα. Πρόκειται για έναν έλεγχο λόγου πιθανοφανειών (likelihood ratio test) 2 μοντέλων προς σύγκριση και χρησιμοποιεί το κριτήριο πληροφορίας Kullback Leibler. 19
38 εντοπιστούν οι διαφορές στα μοντέλα που έχουν τις ίδιες μεταβλητές αλλά υποθέτουν διαφορετική κατανομή και άρα έχουν διαφορετική μορφή. Σε αυτήν την περίπτωση, οι έλεγχοι έδειξαν ότι το μοντέλο ΖΙΝΒ φαίνεται να είναι καλύτερο από τα υπόλοιπα δύο μοντέλα για τα συγκεκριμένα δεδομένα. Η υπόθεση, ότι τα δεδομένα ακολουθούν μία Αρνητική Διωνυμική κατανομή με πλεονάζοντα στο μηδέν (0) στοιχεία και ότι συνεπώς ένα Αρνητικό Διωνυμικό μοντέλο διογκωμένο στο μηδέν (0) περιγράφει καλύτερα τα δεδομένα μας, είναι εύλογη, δοθέντος ότι οι πλεονάζουσες μηδενικές παρατηρήσεις ενδεχομένως να προέρχονται από 2 πηγές: α) λόγω του ότι δεν παρατηρήθηκε ατύχημα και β) λόγω του ότι κάποιες ώρες και υπό κάποιες καιρικές συνθήκες δεν κυκλοφορούσαν οχήματα και πεζοί στους δρόμους, οπότε και δεν παρατηρήθηκαν ατυχήματα (D. Lord et al (2005)). Ωστόσο, η επιλογή του κατάλληλου μοντέλου θα εξαρτηθεί από την σύγκριση εκείνων των ZIP, ZINB και GLMNB μοντέλων που ικανοποιούν κάποια κριτήρια βέλτιστης προσαρμογής (μέγιστο λογάριθμο πιθανοφάνειας, ελάχιστη τιμή κριτηρίου πληροφορίας Akaike, καλύτερη προβλεπτικότητα σε συνδυασμό με το ελάχιστο δυνατό αριθμό μεταβλητών στο μοντέλο). Σχετικά με την επιλογή του καταλληλότερου μοντέλου, γίνεται εκτενής αναφορά στο επόμενο κεφάλαιο. 20
39 4. ΤΟ ΒΕΛΤΙΣΤΟ ΜΟΝΤΈΛΟ ΚΑΙ Η ΕΡΜΗΝΕΙΑ ΤΟΥ Σύμφωνα με την ανάλυση του προηγούμενου κεφαλαίου, φαίνεται ότι στα δεδομένα μας προσαρμόζεται καλύτερα ένα μοντέλο ZINB, συγκριτικά με τα λοιπά μοντέλα που ελέγχθηκαν (Poisson, ΖΙΡ, GLMNB). Προκειμένου για την εύρεση του βέλτιστου ΖΙΝΒ μοντέλου, αρχικά δημιουργήθηκε ένα ΖΙΝΒ μοντέλο το οποίο περιλάμβανε όλες τις μεταβλητές της συλλογής των δεδομένων μας. (Πίνακας 4). Σε αυτόν παρατηρούμε ότι: 1. η παράμετρος θ της Αρνητικής Διωνυμικής κατανομής είναι στατιστικά σημαντική και 2. στο Διωνυμικό μέρος του μοντέλου, όπου εκτιμάται η πιθανότητα να υπάρχουν πλεονάζοντα μηδενικά ατυχήματα παρουσία κάποιας μεταβλητής, υπάρχουν κάποιες μεταβλητές που είναι στατιστικά σημαντικές. Σύμφωνα με το αρχικό ΖΙΝΒ μοντέλο που εμφανίζεται στον Πίνακα 4, φαίνεται ότι η έντονη παρουσία ηλιοφάνειας και βροχόπτωσης έχουν στατιστικά σημαντική επίδραση στην εμφάνιση ατυχημάτων. Επίσης, υπάρχουν ενδείξεις ότι ο βαθμός κάλυψης του ουρανού και η παρουσία θύελλας με καταιγίδα επιδρούν σημαντικά και θετικά στον αριθμό οδικών ατυχημάτων. Τέλος, φαίνεται ότι περισσότερα ατυχήματα πραγματοποιούνται τις καθημερινές (Δευτέρα έως Παρασκευή), συγκριτικά με το Σαββατοκύριακο. Επιπλέον, όπως ήταν αναμενόμενο, η σχέση μεταξύ οριζόντιας ορατότητας και αριθμού οδικών ατυχημάτων είναι αντίστροφη, η αύξηση δηλαδή της οριζόντιας ορατότητας συμβάλλει στη μείωση των ατυχημάτων. Ωστόσο, η επίδραση αυτή δεν είναι στατιστικά σημαντική, όταν ληφθούν όλες οι μεταβλητές υπόψη. Επιπλέον, η παρουσία χαλαζιού επιδρά επίσης θετικά στην εμφάνιση οδικών ατυχημάτων, η οποία επίδραση όμως δεν είναι στατιστικά σημαντική. Όσον αφορά στα μηδενικά ατυχήματα που παρατηρήθηκαν, σύμφωνα με τον Πίνακα 4. η αύξηση της ποσοστιαίας υγρασίας επιδρά αρνητικά στην εμφάνιση 0 ατυχημάτων. Επίσης, φαίνεται ότι καθώς οι ώρες της ημέρας περνούν και καθώς η επιφάνεια του ουρανού καλύπτεται (πιθανώς από συννεφιά), αυξάνεται η πιθανότητα να παρατηρηθούν μηδενικά ατυχήματα. Επιπλέον, αξίζει να σημειωθεί ότι η παρουσία σπάνιων και ακραίων φυσικών φαινομένων, όπως η παρουσία χαλαζόπτωσης και η παρουσία παγετού, μειώνουν την πιθανότητα εμφάνισης μηδενικών ατυχημάτων, αν και η επίδρασή τους δεν είναι στατιστικά σημαντική. 21
40 Πίνακας 4. Το μοντέλο ΖΙΝΒ που περιλαμβάνει ως εξαρτημένη μεταβλητή τον αριθμό των ατυχημάτων και όλες τις υπόλοιπες μεταβλητές (κλίματος και χρόνου) ως επεξηγηματικές Count model coefficients (negbin with log link): Variable Variable s description Estimate Std. Error z-value Pr(> z ) (Intercept) Σταθερά e-08 *** DD Κατεύθυνση ανέμου FF Μέση ταχύτητα ανέμου FX Μέγιστη ριπή ανέμου U % σχετικής υγρασίας Q Ολική ηλιακή ακτινοβολία SQ Ωριαία διάρκεια ηλιοφάνειας e-05 *** RD Ωριαία διάρκεια βροχόπτωσης *** RH Ωριαία ποσότητα βροχόπτωσης VV Οριζόντια ορατότητα WW_MΝαί Παρουσία ομίχλης WW_RΝαί Παρουσία βροχόπτωσης *** WW_SΝαί Παρουσία χιονόπτωσης WW_HΝαί Παρουσία χαλαζόπτωσης WW_OΝαί Παρουσία θύελλας με καταιγίδα WW_YΝαί Παρουσία παγετού N Συνολική κάλυψη του ουρανού ACC_UTHOUR Ώρα <2e-16 *** ACC_Day2_Δευτέρα Ημέρα Δευτέρα e-06 *** ACC_Day3_Τρίτη Ημέρα Τρίτη ** ACC_Day4_Τετάρτη Ημέρα Τετάρτη *** ACC_Day5_Πέμπτη Ημέρα Πέμπτη e-07 *** ACC_Day6_Παρ/ευή Ημέρα Παρασκευή e-05 *** ACC_Day7_Σάββατο Ημέρα Σάββατο Month Μήνας T_fac32 Θερμοκρασία (0 C έως 10 C) T_fac33 Θερμοκρασία (10,1 C και άνω) Log(theta) Zero-inflation model coefficients (binomial with logit link): Variable Variable s description Estimate Std. Error z-value Pr(> z ) (Intercept) Σταθερά DD Κατεύθυνση ανέμου FF Μέση ταχύτητα ανέμου FX Μέγιστη ριπή ανέμου U % σχετικής υγρασίας ** Q Ωριαία ηλιακή ακτινοβολία SQ Ωριαία διάρκεια ηλιοφάνειας RD Ωριαία διάρκεια βροχόπτωσης RH Ωριαία ποσότητα βροχόπτωσης VV Οριζόντια ορατότητα WW_MΝαί Παρουσία ομίχλης WW_RΝαί Παρουσία βροχόπτωσης WW_SΝαί Παρουσία χιονόπτωσης WW_HΝαί Παρουσία χαλαζόπτωσης WW_OΝαί Παρουσία θύελλας με καταιγίδα WW_YΝαί Παρουσία παγετού N Συνολική κάλυψη του ουρανού * ACC_UTHOUR Ώρα <2e-16 *** ACC_Day2_Δευτέρα Ημέρα Δευτέρα ACC_Day3_Τρίτη Ημέρα Τρίτη ACC_Day4_Τετάρτη Ημέρα Τετάρτη ACC_Day5_Πέμπτη Ημέρα Πέμπτη ACC_Day6_Παρ/ευή Ημέρα Παρασκευή ACC_Day7_Σάββατο Ημέρα Σάββατο Month Μήνας T_fac32 Θερμοκρασία (0 ºC έως 10 ºC) T_fac33 Θερμοκρασία (10,1 ºC και άνω) Signif. codes: 0 '***' '**' 0.01 '*' 0.05 '.' Theta = Number of Iterations in BFGS optimization: 86 Log-likelihood: on 55 Df 22 22
41 Αντίθετα, η παρουσία ομίχλης και χιονόπτωσης φαίνεται ότι αυξάνουν την πιθανότητα εμφάνισης μηδενικών ατυχημάτων (επίδραση που δεν είναι ωστόσο στατιστικά σημαντική), σε σύγκριση με την απουσία τους, γεγονός που μπορεί να οφείλεται στο ότι η παρουσία των εν λόγω καιρικών φαινομένων αποτρέπει τα άτομα να κυκλοφορούν στο δρόμο. Ωστόσο, δεν είναι όλες οι μεταβλητές στατιστικά σημαντικές, άρα δεν επιδρούν όλες σημαντικά στην εμφάνιση ατυχημάτων. Επιπλέον, πιθανώς να υπάρχει έντονη συσχέτιση και αλληλοεξάρτηση μεταξύ κάποιων μεταβλητών, γεγονός που επηρεάζει την στατιστική σημαντικότητα κάποιων μεταβλητών. Για την εύρεση του βέλτιστου και προβλεπτικού μοντέλου χρησιμοποιήθηκε η μέθοδος προοδευτικής προσθήκης μεταβλητών (forward regression), προσθέτοντας σταδιακά τις στατιστικά σημαντικές μεταβλητές από το αρχικό μοντέλο, ενώ για την τη σύγκριση μεταξύ των ZINB-μοντέλων, χρησιμοποιήθηκαν το κριτήριο πληροφορίας Akaike (Akaike Information Criteria, AIC) και ο έλεγχος του λογαρίθμου του λόγου πιθανοφανειών (loglikelihood ratio test). Στον Πίνακα 5. εμφανίζονται τα μοντέλα και τα κριτήρια AIC και loglikelihood ratio, όπως αυτά προέκυψαν με την μέθοδο προοδευτικής προσθήκης μεταβλητών. Η μορφή του μοντέλου y~x1+x2 z1+z2 έχει την εξής ερμηνεία: y είναι η εξαρτημένη μεταβλητή, x1+x2 είναι οι ανεξάρτητες μεταβλητές που ερμηνεύουν την εμφάνιση ατυχημάτων όταν y>0 και z1+z2 είναι οι ανεξάρτητες μεταβλητές που ερμηνεύουν την εμφάνιση των μηδενικών ατυχημάτων. Επίσης, πρέπει να σημειωθεί ότι στα στοιχεία υπήρχαν και κενές εγγραφές, οι οποίες έπρεπε, είτε να απομακρυνθούν, είτε να συμπληρωθούν με μία κατάλληλη μέθοδο. Κρίθηκε ότι εφόσον το πλήθος των εγγραφών είναι μεγάλο (8760 εγγραφές), η απομάκρυνση κάποιου μικρού ποσοστού από αυτά δεν θα επηρεάσει σημαντικά τα αποτελέσματα. Το μεγαλύτερο ποσοστό κενών εγγραφών βρίσκεται στη μεταβλητή WW (codec weather) (5175 κενές εγγραφές από το σύνολο των 8760 τιμών, ήτοι το 59,08% των τιμών της). Έτσι, απομακρύνθηκε από τη συλλογή των δεδομένων. Στη συνέχεια διαγράφηκαν όλες οι εγγραφές οι οποίες περιείχαν έστω και μία κενή τιμή. Ο αριθμός των εγγραφών που διαγράφηκαν από το σύνολο των δεδομένων είναι 529, ήτοι το 6,04% του συνόλου των εγγραφών. Με βάσει τα κριτήρια AIC και loglikelihood ratio test, επιλέχθηκε ως βέλτιστο μοντέλο το Χ1z22, το οποίο έχει ελάχιστη τιμή AIC (μαρκαρισμένο με έντονους χαρακτήρες στον Πίνακα 5). Το μοντέλο είναι σχεδόν πανομοιότυπο με το Χ1z16, με τη διαφορά ότι η μεταβλητή που αναφέρεται στην ώρα που έγινε η μέτρηση (ACC_UTHOUR), στο μέρος που εκτιμά τον παρατηρούμενο αριθμό ατυχημάτων, έχει αντικατασταθεί από τον παράγοντα με τέσσερα επίπεδα, κάθε ένα από τα οποία αποτελούν και ένα 6ωρο (Hour_fac4: 1 ο επίπεδο: από τα μεσάνυχτα. έως τις 6π.μ., 2 ο επίπεδο: από τις 6π.μ. έως τις 12 το μεσημέρι, 3 ο επίπεδο: από τις 12μ.μ. έως τις 6μ.μ. και 4 ο επίπεδο: από τις 6μ.μ. έως τα 23
42 μεσάνυχτα). Επίσης, είναι όμοιο με τα μοντέλα Χ1z20 και X1z21, με τη διαφορά ότι σε αυτά ο παράγοντας «Ώρα» (μεταβλητή ACC_UTHOUR) έχει 3 και 2 επίπεδα αντίστοιχα. Το μοντέλο X1z22 βρέθηκε ότι είναι καλύτερο από όλα τα μοντέλα, βάσει των δύο κριτηρίων ΑΙC & loglikelihood (το μοντέλο X1z22 έχει το μικρότερο κριτήριο AIC και το μεγαλύτερο κριτήριο loglikelihood σε σχέση με όλα τα υπόλοιπα μοντέλα του Πίνακα 5). Πίνακας 5. Μοντέλα ΖΙΝΒ με τα αντίστοιχα loglikelihood ratio test και τα AIC σε φθίνουσα σειρά Log No Μοντέλο likelihood AIC X1z1 acc_count ~ FF , ,87 X1z2 acc_count ~ FX FX -3217, ,35 X1z3 acc_count ~ FX + FH FH -3214, ,35 X1z4 acc_count ~ FX + FH + U FH -3209, ,71 X1z5 acc_count ~ FX + FH + U + Q FH -3178, ,72 X1z6 acc_count ~ FX + FH + U + Q + SQ FH -3169, ,31 X1z7 acc_count ~ FX + FH + U + Q + SQ + RD FH -3110, ,04 X1z8 acc_count ~ U + Q + SQ + RD + RH FH -3110, ,80 X1z9 acc_count ~ U + Q + SQ + RD + RH + VV FH -3107, ,64 X1z10 acc_count ~ U + Q + SQ + RD + RH + VV + WW_R FH -3090, ,55 X1z11 acc_count ~ U + Q + SQ + RD + RH + VV + WW_R + WW_H FH -3088, ,46 X1z12 acc_count ~ U + Q + SQ + RD + VV + WW_R + WW_O FH -3088, ,49 X1z13 acc_count ~ U + Q + SQ + RD + VV + WW_R + WW_O + WW_Y FH -3086, ,59 X1z14 acc_count ~ U + Q + SQ + RD + VV + WW_R + WW_O + WW_Y + N FH -3083, ,28 X1z15 acc_count ~ SQ + RD + VV + WW_R + WW_O + ACC_UTHOUR ACC_UTHOUR -3011, ,46 X1z21 acc_count ~ SQ + RD + VV + WW_R + WW_O + Hour_fac2 + ACC_Day ACC_UTHOUR -2992, ,59 X1z17 acc_count ~ SQ + RD + VV + WW_R + WW_O + ACC_UTHOUR + ACC_Day + Month_fac ACC_UTHOUR -2980, ,24 X1z18 acc_count ~ SQ + RD + VV + WW_R + WW_O + ACC_UTHOUR + ACC_Day + T_fac3 ACC_UTHOUR + T_fac3-2986, ,53 X1z19 acc_count ~ SQ + RD + U + WW_R + WW_O + ACC_UTHOUR + ACC_Day ACC_UTHOUR -2990, ,36 X1z16 acc_count ~ SQ + RD + VV + WW_R + WW_O + ACC_UTHOUR + ACC_Day ACC_UTHOUR -2989, ,49 X1z20 acc_count ~ SQ + RD + VV + WW_R + WW_O + Hour_fac3 + ACC_Day ACC_UTHOUR -2980, ,47 X1z22 acc_count ~ SQ + RD + VV + WW_R + WW_O + Hour_fac4 + ACC_Day ACC_UTHOUR -2954, ,23 Στον Πίνακα 6. παρουσιάζονται οι μεταβλητές και συντελεστές του μοντέλου Χ1z22. Όλες οι μεταβλητές είναι στατιστικά σημαντικές και στα δύο μέρη του μοντέλου (count & zero inflation). Σύμφωνα με το μοντέλο Χ1z22, ο αριθμός των ατυχημάτων σχετίζεται θετικά με τη διάρκεια ηλιοφάνειας, με τη διάρκεια βροχόπτωσης, με την παρουσία βροχόπτωσης και καταιγίδας και με την ημέρα, εφόσον αυτή είναι καθημερινή, ενώ σχετίζεται αρνητικά με την οριζόντια ορατότητα και την ώρα. Επίσης, φαίνεται ότι περισσότερα ατυχήματα γίνονται το διάστημα από τις 12μ.μ. έως και τις 6μ.μ συγκριτικά με τις πρώτες πρωινές ώρες (από τα μεσάνυχτα έως τις 6π.μ.), ενώ από τις 6μ.μ έως τα μεσάνυχτα ο αριθμός των ατυχημάτων μειώνεται στατιστικά σημαντικά σε σχέση με τις πρωινές ώρες. Επιπλέον, η εμφάνιση μηδενικών ατυχημάτων σχετίζεται αρνητικά με την ώρα, δηλαδή όσο περνάει η ώρα τόσο μειώνεται η πιθανότητα εμφάνισης μηδενικών ατυχημάτων. Αναλυτικότερα, δοθέντος ότι οι υπόλοιποι παράγοντες παραμένουν σταθεροί, αν η διάρκεια ηλιοφάνειας αυξηθεί κατά μία μονάδα (κατά το 1/10 της ώρας, ήτοι κατά 6 λεπτά) τότε ο αριθμός ατυχημάτων αναμένεται να αυξηθεί κατά περίπου 3%, ενώ άμα αυξηθεί κατά 1 ώρα 24
43 (δεκαπλασιαστεί η διάρκεια) τότε ο αριθμός των ατυχημάτων αναμένεται να αυξηθεί κατά exp(10x3%)-1=34,3%. Τούτο πιθανώς να οφείλεται στο γεγονός ότι, το φαινόμενο της ηλιοφάνειας μεγάλης διάρκειας συνοδεύεται από αύξηση στην κυκλοφοριακή κίνηση, οπότε αυξάνεται και ο κίνδυνος να συμβεί ατύχημα. Η παρουσία βροχόπτωσης αυξάνει τον αριθμό των ατυχημάτων κατά περίπου 65% συγκριτικά με τον αριθμό των ατυχημάτων, όταν δεν υπάρχει βροχόπτωση. Επίσης, αν η διάρκεια της βροχόπτωσης αυξηθεί κατά μία ώρα, ο αριθμός των ατυχημάτων αναμένεται να υπερδιπλασιαστεί και να αυξηθεί κατά 136%. Η βροχόπτωση μεγάλης διάρκειας πιθανώς μειώνει την ορατότητα του οδηγού, ενώ η παρουσία του φαινομένου της βροχής αυξάνει την ολισθηρότητα στους δρόμους, με αποτέλεσμα να αυξάνεται ο κίνδυνος ατυχήματος. Πίνακας 6. Οι συντελεστές και οι μεταβλητές του μοντέλου X1z22 Count model coefficients (negbin with log link): Estimate Std.Error z-value Pr(> z ) (Intercept) <2e-16 *** SQ ** RD e-08 *** VV ** WW_RΝαί e-06 *** WW_OΝαί ** Hour_fac Hour_fac * Hour_fac e-05 *** ACC_Day2_Δευτέρα e-05 *** ACC_Day3_Τρίτη ** ACC_Day4_Τετάρτη *** ACC_Day5_Πέμπτη e-07 *** ACC_Day6_Παρασκευή e-05 *** ACC_Day7_Σάββατο Log(theta) Zero-inflation model coefficients (binomial with logit link): Estimate Std.Error z-value Pr(> z ) (Intercept) 3, e-11 *** ACC_UTHOUR e-14 *** Signif. codes: 0 '***' '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Theta = 1,117 Number of iterations in BFGS optimization: 35 Log-likelihood: on 17 Df Αν η οριζόντια ορατότητα αυξηθεί κατά 1 μονάδα τότε αναμένεται ότι ο αριθμός των ατυχημάτων θα μειωθεί κατά 1% περίπου. Επίσης, η παρουσία θύελλας με καταιγίδα και κεραυνούς αυξάνει τον αριθμό των ατυχημάτων κατά 113% σε σχέση με τον αριθμό των ατυχημάτων που πραγματοποιούνται εν απουσία αυτού του καιρικού φαινομένου, δοθέντος ότι όλες οι υπόλοιπες συνθήκες παραμένουν σταθερές. 25
44 Το διάστημα της ημέρας μεταξύ των ωρών 12μ.μ 6μ.μ αυξάνεται ο αριθμός των ατυχημάτων κατά 51% περίπου σε σχέση με τον αριθμό ατυχημάτων που πραγματοποιείται το διάστημα από τα μεσάνυχτα έως τις 6π.μ., ενώ κατά τις βραδινές ώρες (από τις 6μ.μ έως τις 12 τα μεσάνυχτα) ο αριθμός αυτός μειώνεται κατά 56% σε σχέση με τα ατυχήματα που συμβαίνουν κατά τις πρώτες πρωινές ώρες. Τη Δευτέρα και την Πέμπτη τα ατυχήματα που πραγματοποιούνται είναι κατά 81% και 98% αντίστοιχα περισσότερα από εκείνα που συμβαίνουν την Κυριακή, ενώ ο αριθμός των ατυχημάτων το Σάββατο δε διαφέρει σημαντικά από εκείνον της Κυριακής. Αυτό μπορεί να οφείλεται στο ότι κατά τις συγκεκριμένες ώρες και ημέρες η κυκλοφοριακή κίνηση στους δρόμους είναι μεγαλύτερη, γεγονός που αυξάνει τον κίνδυνο εμφάνισης ατυχήματος. Ακόμα, μετρώντας από τα μεσάνυχτα, αν αυξηθεί ο χρόνος κατά μία ώρα, αναμένεται ότι η πιθανότητα να μην συμβεί κανένα ατύχημα μειώνεται κατά 45,5% περίπου σε σχέση με την πιθανότητα να συμβεί τουλάχιστον ένα ατύχημα. Πιο απλά, καθώς η νέα ημέρα ξημερώνει, η πιθανότητα να μην συμβεί κανένα ατύχημα μειώνεται σε σχέση με την πιθανότητα να συμβεί. Αυτό είναι πολύ λογικό διότι καθώς ξημερώνει, αυξάνεται η κυκλοφορία στους δρόμους και έτσι μειώνεται η πιθανότητα να μην συμβεί ατύχημα. Πρέπει επίσης να παρατηρηθεί ότι τo log(theta) του αρνητικού διωνυμικού μέρους του μοντέλου που εκτιμά τον αριθμό των ατυχημάτων, δεν είναι στατιστικά σημαντικό. Τούτο σημαίνει πως καταλληλότερο μοντέλο ενδεχομένως να είναι το αντίστοιχο ZIP (Zero- Inflated Poisson) μοντέλο. Το γεγονός αυτό πιθανώς να υποδηλώνει ότι σύμφωνα με το μοντέλο ΖΙΝΒ, τα δεδομένα έχουν υπερδιακύμανση, η οποία όμως οφείλεται κυρίως στην παρουσία του μεγάλου πλήθους μηδενικών παρατηρήσεων. Εννοεί δηλαδή ότι, αν κοιτάξουμε την κατανομή των δεδομένων, μεμονωμένα για αριθμό ατυχημάτων ίσο ή μεγαλύτερο του ενός (# ατυχημάτων 1), τότε μάλλον δεν υφίσταται η υπερδιακύμανση, ενώ αυτή υφίσταται όταν προστεθούν στην κατανομή και τα μηδενικά ατυχήματα. Ωστόσο, εφαρμόζοντας τον έλεγχο του Vuong για μη φωλιασμένα μοντέλα, απορρίπτεται η υπόθεση ότι το ZIP μοντέλο, που περιλαμβάνει τις ίδιες επεξηγηματικές μεταβλητές, αυτές του ΖΙΝΒ μοντέλου Χ1z22, είναι καλύτερο από το ΖΙΝΒ (Έλεγχος Vuong: Test-Statistic= , model2 > model1, p-value ). Προκειμένου να θεωρηθεί ότι το επιλεγμένο μοντέλο είναι πράγματι κατάλληλο, χρειάζεται να διερευνηθεί και το κατά πόσο αυτό περιγράφει καλά τα δεδομένα. Η καλή προσαρμογή του, συγκριτικά με το μοντέλο που διαθέτει μόνο μια σταθερά (null model), μπορεί να διαγνωστεί εφαρμόζοντας τον έλεγχο του λόγου των πιθανοφανειών (Likelihood ratio test). 26
45 Σύμφωνα με τον έλεγχο, το μοντέλο Χ1z22 κάνει καλύτερη προσαρμογή από το null (η τιμή του χ 2 είναι 560,83 με 15 βαθμούς ελευθερίας). Ένας άλλος τρόπος διερεύνησης της καλής προσαρμογής του μοντέλου στα δεδομένα είναι η σύγκριση των αναμενόμενων συχνοτήτων του αριθμού ατυχημάτων σε σχέση με τις παρατηρούμενες συχνότητες. Στον Πίνακα 7 παρουσιάζονται οι παρατηρούμενες από τη συλλογή δεδομένων και οι αναμενόμενες από το μοντέλο συχνότητες του αριθμού ατυχημάτων (ωριαίες μετρήσεις), ενώ το διάγραμμα που ακολουθεί εμφανίζει τα αντίστοιχα ραβδογράμματα. Πίνακας 7. Οι αναμενόμενες, σύμφωνα με το Χ1z22 ΖΙΝΒ μοντέλο, και οι παρατηρούμενες συχνότητες του αριθμού ατυχημάτων Αναμενόμενη συχνότητα X1z ,26 718,74 110,01 21,80 5,49 1,69 0,60 Παρατηρούμενη συχνότητα Ραβδόγραμμα 1. Συγκριτικό ραβδόγραμμα της παρατηρούμενης από τα δεδομένα και της αναμενόμενης από το μοντέλο συχνότητας του αριθμού των ατυχημάτων ,26 Παρατηρούμενη συχνότητα ατυχημάτων Α ναμενόμενη συχνότητα ατυχημάτων Συχνότητα , , ,80 1 5,49 2 1,69 2 0, Α ριθμός ατυχημάτων Όπως παρατηρείται από το διάγραμμα, το μοντέλο κάνει πολύ καλή προσαρμογή στα δεδομένα, καθώς οι εκτιμώμενες συχνότητες είναι πολύ κοντά στις παρατηρούμενες. Κάποιες μικρές διαφορές εντοπίζονται στην ουρά των κατανομών (φορές που αναμένεται να συμβούν 4 ατυχήματα μέσα σε μία ώρα = 5,5 ενώ οι φορές που παρατηρήθηκαν 4 ατυχήματα μέσα σε μία ώρα = 1). 27
46 Έχει ενδιαφέρον και η σύγκριση της προσαρμοστικότητας του μοντέλου Χ1z22 (δηλαδή του βέλτιστου ΖΙΝΒ μοντέλου) και με τα λοιπά βέλτιστα μοντέλα, ZIP και GLMNB. Προκειμένου για την εύρεση των βέλτιστων σε προσαρμογή μοντέλων ZIP & GLMNB (στο εξής τα ονομάζουμε bzip & bglmnb αντίστοιχα) χρησιμοποιήθηκε η ίδια μέθοδος όπως για το μοντέλο Χ1z22 (ZINB μοντέλο). Εφαρμόζοντας τον έλεγχο Vuong ανά δύο μοντέλα προκύπτει ότι: 1. Τα μοντέλα που υποθέτουν την Αρνητική Διωνυμική κατανομή (bglmnb & Χ1z22) είναι καλύτερα από το μοντέλο που υποθέτει την κατανομή Poisson (bzip). 2. Συγκρίνοντας το bglmnb με το X1z22 προκύπτει ότι το Διογκωμένο στο Μηδέν μοντέλο Χ1zz22 φαίνεται να κάνει καλύτερη προσαρμογή στα δεδομένα από ότι κάνει το Γενικευμένο Γραμμικό μοντέλο σε επίπεδο στατ. σημαντικότητας 1% (Χ1z22>bGLMNB, test-statistics = -2,439 p-value = ). Αυτό σημαίνει ότι υπάρχουν ενδείξεις ότι καταλληλότερο μοντέλο φαίνεται να είναι το Διογκωμένο στο μηδέν μοντέλο της Αρνητικής Διωνυμικής κατανομής. 3. Συγκρίνοντας τις εκτιμώμενες συχνότητες από τα δύο τελευταία μοντέλα με τις παρατηρούμενες, φαίνεται ότι οι διαφορές δεν είναι σημαντικές. Ο Πίνακας 8 και τα γραφήματα Δ22 έως Δ25 που βρίσκονται στο Παράρτημα Β, καταδεικνύουν γραφικά την παρατήρηση αυτή. Πίνακας 8. Αναμενόμενες συχνότητες των προσαρμοσμένων μοντέλων Χ1z22 και bglmnb και η παρατηρούμενη συχνότητα. Αναμενόμενη συχνότητα_χ1z20 Αναμενόμενη συχνότητα_bglmnb Παρατηρούμενη συχνότητα , , ,74 721, ,01 107, ,80 21, ,49 5, ,69 1, ,60 0,59 2 Πιο συγκεκριμένα, παρατηρούμε ότι το διογκωμένο στο μηδέν μοντέλο (Χ1z22) εκτιμά κάπως καλύτερα τις αναμενόμενες συχνότητες για 0 και 1 ατυχήματα, δηλαδή για τον μεγαλύτερο όγκο της πληροφορίας μας, ενώ το απλό μοντέλο αρνητικής διωνυμικής κατανομής φαίνεται να εκτιμά καλύτερα τη συχνότητα των 2 ατυχημάτων. Στην ουρά της κατανομής δεν προκύπτουν εμφανείς διαφορές μεταξύ των δύο μοντέλων. 28
47 Από τα παραπάνω επιβεβαιώνεται η αρχική υπόθεση ότι τα δεδομένα οδικών ατυχημάτων έχουν ως θεωρητική κατανομή την Αρνητική Διωνυμική κατανομή και συνεπώς μπορούν να περιγραφούν από κάποιο μοντέλο αρνητικής διωνυμικής κατανομής. Ωστόσο, λόγω της παρουσίας πολλών μηδενικών στα δεδομένα ατυχήματος, ένα μοντέλο Αρνητικής Διωνυμικής κατανομής διογκωμένο στο μηδέν είναι καταλληλότερο α) ως προβλεπτικό μοντέλo (D. Lord et al.(2005)) και β) επειδή μπορεί να δώσει εξήγηση σχετικά με τον/τους παράγοντα/ες που αποτελούν τις αιτίες παρουσίας πλεοναζόντων μηδενικών γεγονότων. 29
48 5. ΣΥΜΠΕΡΑΣΜΑΤΑ Προκειμένου για την πρόληψη των οδικών ατυχημάτων, στην παρούσα μελέτη διερευνήθηκε η επίδραση των καιρικών συνθηκών στην συχνότητα των ατυχημάτων. Τα δεδομένα προήλθαν από ωριαίες μετρήσεις του αριθμού ατυχημάτων, για ένα χρόνο. Καθώς παρατηρήθηκε υψηλή συχνότητα μηδενικών ατυχημάτων, το μοντέλο που επιλέχθηκε, ως καταλληλότερο για εκτιμήσεις και προβλέψεις αναφορικά με τη συχνότητα εμφάνισης ατυχημάτων, μέσω μεταβλητών κλίματος, είναι ένα διογκωμένο στο 0 μοντέλο Αρνητικής Διωνυμικής κατανομής. Σύμφωνα με τη βιβλιογραφία, το συγκεκριμένο μοντέλο εφαρμόζεται συχνά σε μελέτες οδικών ατυχημάτων. Ωστόσο, παρά το γεγονός ότι συνήθως κάνει πολύ καλή προσαρμογή στα δεδομένα, είναι αντικείμενο συζήτησης η καταλληλότητά του, από θεωρητική άποψη. Θεωρητικά, η κατανομή που περιγράφει το φαινόμενο είναι η Αρνητική Διωνυμική κατανομή, ενώ το διογκωμένο στο μηδέν μοντέλο επιλέχθηκε ως καταλληλότερο μοντέλο για προβλέψεις. Προσαρμόζοντάς το διογκωμένο στο μηδέν μοντέλο της Αρνητικής Διωνυμικής κατανομής, προκύπτει ότι, συγκεκριμένες καιρικές συνθήκες φαίνεται να ευνοούν την εμφάνιση ατυχημάτων, ενώ άλλες να την δυσχεραίνουν. Γενικότερα, θα μπορούσαμε να κατηγοριοποιήσουμε τις καιρικές συνθήκες σε 2 κατηγορίες: α) οι καιρικές συνθήκες που δυσχεραίνουν ή διευκολύνουν την ικανότητα του οδηγού να οδηγήσει ορθά (έλλειψη ορατότητας κ.λπ) και β) άλλες συνθήκες εξαιτίας των οποίων αυξάνεται ή μειώνεται ο κίνδυνος ατυχήματος (π.χ. αύξηση της κυκλοφορίας στους δρόμους κ.λπ.). Συγκεκριμένα, φαίνεται ότι η αύξηση της οριζόντιας ορατότητας συμβάλει στη μείωση του αριθμού των ατυχημάτων, ενώ αντίθετα, η βροχόπτωση και η μεγάλη διάρκειά της και η καταιγίδα φαίνεται ότι αυξάνουν τη συχνότητα των οδικών ατυχημάτων (καιρικές συνθήκες που εντάσσονται στην κατηγορία α). Ομοίως, η μεγάλης διάρκειας ηλιοφάνεια, συμβάλλει στην αύξηση της κυκλοφορίας στους δρόμους, γεγονός που επιδρά θετικά στην εμφάνιση οδικών ατυχημάτων. Επίσης, τις καθημερινές ημέρες εν ώρα αιχμής, από τις 6 π.μ. έως τις 6 μ.μ., η κυκλοφορία αυξάνεται συγκριτικά με το Σαββατοκύριακο και τις λοιπές ώρες, γεγονός που ευνοεί την παρουσία οδικών ατυχημάτων (κατηγορία β). 30
49 ΠΑΡΑΡΤΗΜΑ Α' Μερικές βασικές εντολές που χρησιμοποιήθηκαν στην επεξεργασία των δεδομένων στο στατιστικό πακέτο R. Χ<-read.table(file, header =TRUE, sep = "",..) # διαβάζονται τα δεδομένα από το αρχείο file, τα οποία είσε σε μορφή πίνακα και αποθηκεύονται στο αρχείο Χ. Η πρώτη γραμμή είναι τα ονόματα των στηλών-μεταβλητών. summary(x$acc_count) # δίνονται κάποια περιγραφικά της μεταβλητής acc_count που βρίσκεται στο αρχείο Χ table(x$acc_count) # πινακοποιούνται τα επίπεδα της μεταβλητής acc_count που βρίσκεται στο αρχείο Χ hist(x$acc_count) # κατασκευάζεται το ιστόγραμμα της μεταβλητής acc_count που βρίσκεται στο αρχείο Χ plot.ecdf(x$acc_count) #κατασκευάζεται το διάγραμμα αθροιστικής πιθανότητας της μεταβλητής acc_count που βρίσκεται στο αρχείο Χ plot(x$acc_count, X$WW) #κατασκευάζεται το διάγραμμα σημείων μεταξύ των μεταβλητών acc_count και WW που βρίσκονται στο αρχείο Χ cor.test(.test(x$acc_count, X$WW) #υπολογίζεται ο συντελεστής συσχέτισης μεταξύ των μεταβλητών acc_count και WW που βρίσκονται στο αρχείο Χ par(mfrow=c(1,2)) # ορίζεται παράμετρος διαίρεσης της οθόνης κάθετα σε 2 ίσα μέρη hist(x$acc_count[x$ww_h== Όχι ], labels=true) # κατασκευάζεται ιστόγραμμα της μεταβλητής acc_count, στο επίπεδο «Όχι» της binary μεταβλητής WW_H που ανήκουν στο αρχείο Χ neg_binom<- rnbinom(n, size, prob) #δημιουργείται το αντικείμενο neg_binom που περιέχει n τυχαίους αριθμούς αρνητικής διωνυμικής κατανομής με παράμετρο διασπορά size και πιθανότητα επιτυχίας ίση με prob. chisq.test(x$acc_count, neg_binom) # x 2 έλεγχος καλής προσαρμογής της αρνητικής διωνυμικής κατανομής (neg_binom) στη μεταβλητή acc_count που βρίσκεται στο αρχείο Χ chisq.test(x$acc_count, random_poisson) # x 2 έλεγχος καλής προσαρμογής της κατανομής Poisson (random_poisson) στη μεταβλητή acc_count που βρίσκεται στο αρχείο Χ ks.test(x$acc_count, neg_binom) # έλεγχος καλής προσαρμογής Kolmogorov-Smirnov της αρνητικής διωνυμικής κατανομής (neg_binom) στη μεταβλητή acc_count που βρίσκεται στο αρχείο Χ ks.test(x$acc_count, random_poisson) # έλεγχος καλής προσαρμογής Kolmogorov- Smirnov της κατανομής Poisson (random_poisson) στη μεταβλητή acc_count που βρίσκεται στο αρχείο Χ model_glm <- glm.nb(acc_count~., data=x) # δημιουργία γενικευμένου γραμμικού μοντέλου αρνητικής διωνυμικής κατανομής, με εξαρτημένη μεταβλητή την acc_count, επεξηγηματικές όλες τις υπόλοιπες μεταβλητές που βρίσκονται στο αρχείο Χ odtest(glm.nb(acc_count~., data=x)) # έλεγχος για υπεριδιακύμανση του αριθμού γεγονότων 31
50 model_zeroinfl<- zeroinfl(acc_count~., data=x, dist= negbin, link= logit ) # δημιουργία μοντέλου με πλεονάζοντα μηδενικά. Εξαρτημένη μεταβλητή=acc_count, κατανομή=αρνητική διωνυμική, link function για την παρουσία των μηδενικών γεγονότων = logit vuong(model_glm, model_zeroinfl) # έλεγχος σύγκρισης 2 μη φωλιασμένων μοντέλων, του γενικευμένου γραμμικού μοντέλου και του zeroinflated. loglik(model) # υπολογίζει τον λογάριθμο πιθανοφάνειας του μοντέλου model AIC(model) # υπολογίζει τo κριτήριο πληροφορίας Akaike του μοντέλου model coef(model) # υπολογίζει τους συντελεστές του μοντέλου model Υπολογισμός των αναμενόμενων συχνοτήτων του αριθμού των ατυχημάτων από το zeroinflated μοντέλο z15_x1: z15_x1<-zeroinfl(formula = acc_count ~ SQ ACC_UTHOUR, data = X, dist ="negbin", link="logit") # κατασκευάζεται το μοντέλο z15_x1 fitted.lambda<- exp( z15_x1$coef$count[1] + z15_x1$coef$count[2]* X$SQ) # υπολογίζονται τα λ prob<- z15_x1$coef$zero[1] + z15_x1$coef$zero[2]* X$ACC_UTHOUR prob<- exp(prob)/(1+exp(prob)) # υπολογίζονται οι πιθανότητες για τη συνάρτηση των μηδενικών γεγονότων theta<- z15_x1$theta # υπολογίζεται η παράμετρος θήτα dzeroinflnegbinom<- function(x, prob, mu, size) { (x==0)*prob + (1-prob)*dnbinom(x,mu=mu,size=size) } test<- dzeroinflnegbinom(x$acc_count, prob, fitted.lambda, theta) # υπολογίζεται η κατανομή sum(log(test)) n<-length(x$acc_count) #υπολογίζεται το μέγεθος του δείγματος m<-max(x$acc_count) #υπολογίζεται το μέγιστο αριθμό της Υ (αριθμός > ατυχημάτων) temp<- matrix(na,n,m+1) #δημιουργείται ο πίνακας temp που περιέχει ΝΑ s for (i in 1:n) { temp[i,] <- dzeroinflnegbinom(0:m, prob[i], fitted.lambda[i], theta) } #δημιουργείται ο πίνακας temp που περιέχει τις αναμενόμενες τιμές a1<-apply(temp,2,sum) # αναμενόμενες συχνότητες ανά αριθμό ατυχημάτων a2<- table(x$acc_count) # παρατηρούμενες συχνότητες ανά αρ. ατυχημάτων cbind(a1,a2) # δημιουργείται πίνακας με τις παρατηρούμενες συχνότητες (a1) και τις αναμενόμενες από το μοντέλο συχνότητες (a2) 32
51
52
53 Αριθμός ατυχημάτων 6 Δ3. Διάγραμμα σημείων του αριθμού ατυχημάτων ανά ώρα (ACC_UTHOUR) Ώρα της ημέρας Αριθμός ατυχημάτων 6 Δ4. Διάγραμμα σημείων του αριθμού ατυχημάτων ανά κατεύθυνση του ανέμου (DD) Διεύθυνση ανέμου Αριθμός ατυχημάτων 6 Δ5. Διάγραμμα σημείων του αριθμού ατυχημάτων ανά μέση ταχύτητα του ανέμου (FF) Μέση ταχύτητα ανέμου σε 0,1 m/s
54 Αριθμός ατυχημάτων 6 Δ6. Διάγραμμα σημείων του αριθμού ατυχημάτων ανά μέση ωριαία ταχύτητα του ανέμου (FH) Μέση ωριαία ταχύτητα ανέμου Αριθμός ατυχημάτων 6 Δ7. Διάγραμμα σημείων του αριθμού ατυχημάτων ανά μέγιστη ριπή του ανέμου (FX) Μέγιστη ριπή ανέμου Αριθμός ατυχημάτων 6 Δ8. Διάγραμμα σημείων του αριθμού ατυχημάτων ανά ωριαία ηλιακή ακτινοβολία (Q) Συνολική ωριαία ακτινοβολία σε Joule/cm^
55 Αριθμός ατυχημάτων 5 6 Δ9. Διάγραμμα σημείων του αριθμού ατυχημάτων ανά διάρκεια βροχόπτωσης (RD) Διάρκεια βροχόπτωσης σε 0,1 ώρες Αριθμός ατυχημάτων 6 Δ10. Διάγραμμα σημείων του αριθμού ατυχημάτων ανά ποσότητα βροχόπτωσης (RH) Ποσότητα βροχόπτωσης σε 0,1 mm Αριθμός ατυχημάτων 6 Δ11. Διάγραμμα σημείων του αριθμού ατυχημάτων ανά διάρκεια ηλιοφάνειας (SQ) Διάρκεια ηλιοφάνειας σε 0,1 ώρες
56 Αριθμός ατυχημάτων 5 6 Δ12. Διάγραμμα σημείων του αριθμού ατυχημάτων ανά ποσοστό σχετικής υγρασίας (U) Σχετική ποσοστιαία υγρασία Αριθμός ατυχημάτων 6 Δ13. Διάγραμμα σημείων του αριθμού ατυχημάτων ανά ορατότητα (VV) Οριζόντια ορατότητα Αριθμός ατυχημάτων 6 Δ14. Διάγραμμα σημείων του αριθμού ατυχημάτων ανά codec weather (WW) Codec weather κατά τη διάρκεια της τελευταίας ώρας
57
58
59
60
61
ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ ΠΡΩΤΟ: ΠΙΘΑΝΟΤΗΤΕΣ 11 ΚΕΦΑΛΑΙΟ 1 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΙΘΑΝΟΤΗΤΑΣ 13
 ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ ΠΡΩΤΟ: ΠΙΘΑΝΟΤΗΤΕΣ 11 ΚΕΦΑΛΑΙΟ 1 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΙΘΑΝΟΤΗΤΑΣ 13 ΚΕΦΑΛΑΙΟ 2 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΙΘΑΝΟΤΗΤΑΣ 20 2.1 Αβεβαιότητα, Τυχαία Διαδικασία, και Συναφείς Έννοιες 20 2.1.1 Αβεβαιότητα
ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ ΠΡΩΤΟ: ΠΙΘΑΝΟΤΗΤΕΣ 11 ΚΕΦΑΛΑΙΟ 1 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΙΘΑΝΟΤΗΤΑΣ 13 ΚΕΦΑΛΑΙΟ 2 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΙΘΑΝΟΤΗΤΑΣ 20 2.1 Αβεβαιότητα, Τυχαία Διαδικασία, και Συναφείς Έννοιες 20 2.1.1 Αβεβαιότητα
ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟ 3 ΔΕΣΜΕΥΜΕΝΗ ΠΙΘΑΝΟΤΗΤΑ, ΟΛΙΚΗ ΠΙΘΑΝΟΤΗΤΑ ΘΕΩΡΗΜΑ BAYES, ΑΝΕΞΑΡΤΗΣΙΑ ΚΑΙ ΣΥΝΑΦΕΙΣ ΕΝΝΟΙΕΣ 71
 ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ ΠΡΩΤΟ ΠΙΘΑΝΟΤΗΤΕΣ 11 ΚΕΦΑΛΑΙΟ 1 ΕΙΣΑΓΩΓΗ 13 ΚΕΦΑΛΑΙΟ 2 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΙΘΑΝΟΤΗΤΑΣ 19 2.1 Αβεβαιότητα, Τυχαία Διαδικασία, και Συναφείς Έννοιες 21 2.1.1 Αβεβαιότητα και Τυχαίο Πείραμα
ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ ΠΡΩΤΟ ΠΙΘΑΝΟΤΗΤΕΣ 11 ΚΕΦΑΛΑΙΟ 1 ΕΙΣΑΓΩΓΗ 13 ΚΕΦΑΛΑΙΟ 2 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΙΘΑΝΟΤΗΤΑΣ 19 2.1 Αβεβαιότητα, Τυχαία Διαδικασία, και Συναφείς Έννοιες 21 2.1.1 Αβεβαιότητα και Τυχαίο Πείραμα
Εισόδημα Κατανάλωση 1500 500 1600 600 1300 450 1100 400 600 250 700 275 900 300 800 352 850 400 1100 500
 Εισόδημα Κατανάλωση 1500 500 1600 600 1300 450 1100 400 600 250 700 275 900 300 800 352 850 400 1100 500 Πληθυσμός Δείγμα Δείγμα Δείγμα Ο ρόλος της Οικονομετρίας Οικονομική Θεωρία Διατύπωση της
Εισόδημα Κατανάλωση 1500 500 1600 600 1300 450 1100 400 600 250 700 275 900 300 800 352 850 400 1100 500 Πληθυσμός Δείγμα Δείγμα Δείγμα Ο ρόλος της Οικονομετρίας Οικονομική Θεωρία Διατύπωση της
ΜΗ ΓΡΑΜΜΙΚΗ ΠΑΛΙΝΔΡΟΜΙΣΗ
 ΜΗ ΓΡΑΜΜΙΚΗ ΠΑΛΙΝΔΡΟΜΙΣΗ Τα μη γραμμικά μοντέλα έχουν την πιο κάτω μορφή: η μορφή αυτή μοιάζει με τη μορφή που έχουμε για τα γραμμικά μοντέλα ( δηλαδή η παρατήρηση Y i είναι το άθροισμα της αναμενόμενης
ΜΗ ΓΡΑΜΜΙΚΗ ΠΑΛΙΝΔΡΟΜΙΣΗ Τα μη γραμμικά μοντέλα έχουν την πιο κάτω μορφή: η μορφή αυτή μοιάζει με τη μορφή που έχουμε για τα γραμμικά μοντέλα ( δηλαδή η παρατήρηση Y i είναι το άθροισμα της αναμενόμενης
ΚΑΤΑΝΟΜΈΣ. 8.1 Εισαγωγή. 8.2 Κατανομές Συχνοτήτων (Frequency Distributions) ΚΕΦΑΛΑΙΟ
 ΚΑΤΑΝΟΜΈΣ ΚΕΦΑΛΑΙΟ 8 81 Εισαγωγή Οι κατανομές διακρίνονται σε κατανομές συχνοτήτων, κατανομές πιθανοτήτων και σε δειγματοληπτικές κατανομές Στη συνέχεια θα γίνει αναλυτική περιγραφή αυτών 82 Κατανομές
ΚΑΤΑΝΟΜΈΣ ΚΕΦΑΛΑΙΟ 8 81 Εισαγωγή Οι κατανομές διακρίνονται σε κατανομές συχνοτήτων, κατανομές πιθανοτήτων και σε δειγματοληπτικές κατανομές Στη συνέχεια θα γίνει αναλυτική περιγραφή αυτών 82 Κατανομές
Α Ν Ω Τ Α Τ Ο Σ Υ Μ Β Ο Υ Λ Ι Ο Ε Π Ι Λ Ο Γ Η Σ Π Ρ Ο Σ Ω Π Ι Κ Ο Υ Ε Ρ Ω Τ Η Μ Α Τ Ο Λ Ο Γ Ι Ο
 Α Ν Ω Τ Α Τ Ο Σ Υ Μ Β Ο Υ Λ Ι Ο Ε Π Ι Λ Ο Γ Η Σ Π Ρ Ο Σ Ω Π Ι Κ Ο Υ Ε Ρ Ω Τ Η Μ Α Τ Ο Λ Ο Γ Ι Ο «Περιγραφική & Επαγωγική Στατιστική» 1. Πάνω από το 3 ο τεταρτημόριο ενός δείγματος βρίσκεται το: α) 15%
Α Ν Ω Τ Α Τ Ο Σ Υ Μ Β Ο Υ Λ Ι Ο Ε Π Ι Λ Ο Γ Η Σ Π Ρ Ο Σ Ω Π Ι Κ Ο Υ Ε Ρ Ω Τ Η Μ Α Τ Ο Λ Ο Γ Ι Ο «Περιγραφική & Επαγωγική Στατιστική» 1. Πάνω από το 3 ο τεταρτημόριο ενός δείγματος βρίσκεται το: α) 15%
3. Κατανομές πιθανότητας
 3. Κατανομές πιθανότητας Τυχαία Μεταβλητή Τυχαία μεταβλητή (τ.μ.) (X) είναι μια συνάρτηση που σε κάθε σημείο (ω) ενός δειγματικού χώρου (Ω) αντιστοιχεί έναν πραγματικό αριθμό. Ω ω X (ω ) R Διακριτή τ.μ.
3. Κατανομές πιθανότητας Τυχαία Μεταβλητή Τυχαία μεταβλητή (τ.μ.) (X) είναι μια συνάρτηση που σε κάθε σημείο (ω) ενός δειγματικού χώρου (Ω) αντιστοιχεί έναν πραγματικό αριθμό. Ω ω X (ω ) R Διακριτή τ.μ.
ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ ΠΡΩΤΟ ΠΙΘΑΝΟΤΗΤΕΣ 13 ΚΕΦΑΛΑΙΟ 1 ΕΙΣΑΓΩΓΗ 15 ΚΕΦΑΛΑΙΟ 2 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΙΘΑΝΟΤΗΤΑΣ 19
 ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ ΠΡΩΤΟ ΠΙΘΑΝΟΤΗΤΕΣ 13 ΚΕΦΑΛΑΙΟ 1 ΕΙΣΑΓΩΓΗ 15 ΚΕΦΑΛΑΙΟ 2 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΙΘΑΝΟΤΗΤΑΣ 19 2.1 Αβεβαιότητα, Τυχαία Διαδικασία, και Συναφείς Έννοιες 21 2.1.1 Αβεβαιότητα και Τυχαίο Πείραμα
ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ ΠΡΩΤΟ ΠΙΘΑΝΟΤΗΤΕΣ 13 ΚΕΦΑΛΑΙΟ 1 ΕΙΣΑΓΩΓΗ 15 ΚΕΦΑΛΑΙΟ 2 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΙΘΑΝΟΤΗΤΑΣ 19 2.1 Αβεβαιότητα, Τυχαία Διαδικασία, και Συναφείς Έννοιες 21 2.1.1 Αβεβαιότητα και Τυχαίο Πείραμα
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΣΤΑΤΙΣΤΙΚΗ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ. Κεφάλαιο 8. Συνεχείς Κατανομές Πιθανοτήτων Η Κανονική Κατανομή
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΑΤΡΑΣ Εργαστήριο Λήψης Αποφάσεων & Επιχειρησιακού Προγραμματισμού Καθηγητής Ι. Μητρόπουλος ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΣΤΑΤΙΣΤΙΚΗ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΑΤΡΑΣ Εργαστήριο Λήψης Αποφάσεων & Επιχειρησιακού Προγραμματισμού Καθηγητής Ι. Μητρόπουλος ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΣΤΑΤΙΣΤΙΚΗ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ
iii ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος
 iii ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος xi 1 Αντικείμενα των Πιθανοτήτων και της Στατιστικής 1 1.1 Πιθανοτικά Πρότυπα και Αντικείμενο των Πιθανοτήτων, 1 1.2 Αντικείμενο της Στατιστικής, 3 1.3 Ο Ρόλος των Πιθανοτήτων
iii ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος xi 1 Αντικείμενα των Πιθανοτήτων και της Στατιστικής 1 1.1 Πιθανοτικά Πρότυπα και Αντικείμενο των Πιθανοτήτων, 1 1.2 Αντικείμενο της Στατιστικής, 3 1.3 Ο Ρόλος των Πιθανοτήτων
Στατιστική. Εκτιμητική
 Στατιστική Εκτιμητική Χατζόπουλος Σταύρος 28/2/2018 και 01 /03/2018 Εισαγωγή Το αντικείμενο της Στατιστικής είναι η εξαγωγή συμπερασμάτων που αφορούν τον πληθυσμό ή το φαινόμενο που μελετάμε, με τη βοήθεια
Στατιστική Εκτιμητική Χατζόπουλος Σταύρος 28/2/2018 και 01 /03/2018 Εισαγωγή Το αντικείμενο της Στατιστικής είναι η εξαγωγή συμπερασμάτων που αφορούν τον πληθυσμό ή το φαινόμενο που μελετάμε, με τη βοήθεια
Λογιστική Παλινδρόµηση
 Κεφάλαιο 10 Λογιστική Παλινδρόµηση Στο κεφάλαιο αυτό ϑα δούµε την µέθοδο της λογιστικής παλινδρόµησης η οποία χρησιµεύει στο να αναπτύξουµε σχέση µίας δίτιµης ανεξάρτητης τυχαίας µετα- ϐλητής και συνεχών
Κεφάλαιο 10 Λογιστική Παλινδρόµηση Στο κεφάλαιο αυτό ϑα δούµε την µέθοδο της λογιστικής παλινδρόµησης η οποία χρησιµεύει στο να αναπτύξουµε σχέση µίας δίτιµης ανεξάρτητης τυχαίας µετα- ϐλητής και συνεχών
ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΤΜΗΜΑ ΟΡΓΑΝΩΣΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΔΙΔΑΣΚΩΝ: ΘΑΝΑΣΗΣ ΚΑΖΑΝΑΣ. Οικονομετρία
 ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΤΜΗΜΑ ΟΡΓΑΝΩΣΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΔΙΔΑΣΚΩΝ: ΘΑΝΑΣΗΣ ΚΑΖΑΝΑΣ Οικονομετρία 4.1 Πολλαπλό Γραμμικό Υπόδειγμα Παλινδρόμησης Γενικεύοντας τη διμεταβλητή (Y, X) συνάρτηση
ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΤΜΗΜΑ ΟΡΓΑΝΩΣΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΔΙΔΑΣΚΩΝ: ΘΑΝΑΣΗΣ ΚΑΖΑΝΑΣ Οικονομετρία 4.1 Πολλαπλό Γραμμικό Υπόδειγμα Παλινδρόμησης Γενικεύοντας τη διμεταβλητή (Y, X) συνάρτηση
Θεωρητικές Κατανομές Πιθανότητας
 Θεωρητικές Κατανομές Πιθανότητας Θεωρητικές Κατανομές Πιθανότητας Α. ΔΙΑΚΡΙΤΕΣ ΚΑΤΑΝΟΜΕΣ α) Διακριτή Ομοιόμορφη κατανομή β) Διωνυμική κατανομή γ) Υπεργεωμετρική κατανομή δ) κατανομή Poisson Β. ΣΥΝΕΧΕΙΣ
Θεωρητικές Κατανομές Πιθανότητας Θεωρητικές Κατανομές Πιθανότητας Α. ΔΙΑΚΡΙΤΕΣ ΚΑΤΑΝΟΜΕΣ α) Διακριτή Ομοιόμορφη κατανομή β) Διωνυμική κατανομή γ) Υπεργεωμετρική κατανομή δ) κατανομή Poisson Β. ΣΥΝΕΧΕΙΣ
ΕΦΑΡΜΟΣΜΕΝΗ ΣΤΑΤΙΣΤΙΚΗ Ι Συμπληρωματικές Σημειώσεις Δημήτριος Παντελής
 ΕΦΑΡΜΟΣΜΕΝΗ ΣΤΑΤΙΣΤΙΚΗ Ι Συμπληρωματικές Σημειώσεις Δημήτριος Παντελής ΣΤΑΤΙΣΤΙΚΕΣ ΕΚΤΙΜΗΣΕΙΣ Οι συναρτήσεις πιθανότητας ή πυκνότητας πιθανότητας των διαφόρων τυχαίων μεταβλητών χαρακτηρίζονται από κάποιες
ΕΦΑΡΜΟΣΜΕΝΗ ΣΤΑΤΙΣΤΙΚΗ Ι Συμπληρωματικές Σημειώσεις Δημήτριος Παντελής ΣΤΑΤΙΣΤΙΚΕΣ ΕΚΤΙΜΗΣΕΙΣ Οι συναρτήσεις πιθανότητας ή πυκνότητας πιθανότητας των διαφόρων τυχαίων μεταβλητών χαρακτηρίζονται από κάποιες
Πρόλογος... xv. Κεφάλαιο 1. Εισαγωγικές Έννοιες... 1
 Πρόλογος... xv Κεφάλαιο 1. Εισαγωγικές Έννοιες... 1 1.1.Ιστορική Αναδρομή... 1 1.2.Βασικές Έννοιες... 5 1.3.Πλαίσιο ειγματοληψίας (Sampling Frame)... 9 1.4.Κατηγορίες Ιατρικών Μελετών.... 11 1.4.1.Πειραµατικές
Πρόλογος... xv Κεφάλαιο 1. Εισαγωγικές Έννοιες... 1 1.1.Ιστορική Αναδρομή... 1 1.2.Βασικές Έννοιες... 5 1.3.Πλαίσιο ειγματοληψίας (Sampling Frame)... 9 1.4.Κατηγορίες Ιατρικών Μελετών.... 11 1.4.1.Πειραµατικές
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 07-08 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Επικ. Καθηγητής v.koutras@fme.aegea.gr Τηλ: 7035468 Θα μελετήσουμε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 07-08 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Επικ. Καθηγητής v.koutras@fme.aegea.gr Τηλ: 7035468 Θα μελετήσουμε
ΠΑΝΕΠΙΣΤΗΜΙΑΚΑ ΦΡΟΝΤΙΣΤΗΡΙΑ ΚΟΛΛΙΝΤΖΑ. Ερωτήσεις πολλαπλής επιλογής. Συντάκτης: Δημήτριος Κρέτσης
 ΠΑΝΕΠΙΣΤΗΜΙΑΚΑ ΦΡΟΝΤΙΣΤΗΡΙΑ ΚΟΛΛΙΝΤΖΑ Ερωτήσεις πολλαπλής επιλογής Συντάκτης: Δημήτριος Κρέτσης 1. Ο κλάδος της περιγραφικής Στατιστικής: α. Ασχολείται με την επεξεργασία των δεδομένων και την ανάλυση
ΠΑΝΕΠΙΣΤΗΜΙΑΚΑ ΦΡΟΝΤΙΣΤΗΡΙΑ ΚΟΛΛΙΝΤΖΑ Ερωτήσεις πολλαπλής επιλογής Συντάκτης: Δημήτριος Κρέτσης 1. Ο κλάδος της περιγραφικής Στατιστικής: α. Ασχολείται με την επεξεργασία των δεδομένων και την ανάλυση
Τμήμα Διοίκησης Επιχειρήσεων (Γρεβενά) Μάθημα: Στατιστική II Διάλεξη 1 η : Εισαγωγή-Επανάληψη βασικών εννοιών Εβδομάδα 1 η : ,
 Τμήμα Διοίκησης Επιχειρήσεων (Γρεβενά) Μάθημα: Στατιστική II Διάλεξη 1 η : Εισαγωγή-Επανάληψη βασικών εννοιών Εβδομάδα 1 η :1-0-017, 3-0-017 Διδάσκουσα: Κοντογιάννη Αριστούλα Σκοπός του μαθήματος Η παρουσίαση
Τμήμα Διοίκησης Επιχειρήσεων (Γρεβενά) Μάθημα: Στατιστική II Διάλεξη 1 η : Εισαγωγή-Επανάληψη βασικών εννοιών Εβδομάδα 1 η :1-0-017, 3-0-017 Διδάσκουσα: Κοντογιάννη Αριστούλα Σκοπός του μαθήματος Η παρουσίαση
Στατιστική Συμπερασματολογία
 Στατιστική Συμπερασματολογία Διαφάνειες 1 ου κεφαλαίου Βιβλίο: Κολυβά Μαχαίρα, Φ. & Χατζόπουλος Στ. Α. (2016). Μαθηματική Στατιστική, Έλεγχοι Υποθέσεων. [ηλεκτρ. βιβλ.] Αθήνα: Σύνδεσμος Ελληνικών Ακαδημαϊκών
Στατιστική Συμπερασματολογία Διαφάνειες 1 ου κεφαλαίου Βιβλίο: Κολυβά Μαχαίρα, Φ. & Χατζόπουλος Στ. Α. (2016). Μαθηματική Στατιστική, Έλεγχοι Υποθέσεων. [ηλεκτρ. βιβλ.] Αθήνα: Σύνδεσμος Ελληνικών Ακαδημαϊκών
Στατιστική Συμπερασματολογία
 Στατιστική Συμπερασματολογία Διαφάνειες 4 ου κεφαλαίου Ελεγχοσυναρτήσεις Γενικευμένου Λόγου Πιθανοφανειών Σταύρος Χατζόπουλος 27/03/2017, 03/04/2017, 24/04/2017 1 Εισαγωγή Έστω το τ.δ. X,,, από την κατανομή
Στατιστική Συμπερασματολογία Διαφάνειες 4 ου κεφαλαίου Ελεγχοσυναρτήσεις Γενικευμένου Λόγου Πιθανοφανειών Σταύρος Χατζόπουλος 27/03/2017, 03/04/2017, 24/04/2017 1 Εισαγωγή Έστω το τ.δ. X,,, από την κατανομή
Εφαρμοσμένη Στατιστική Δημήτριος Μπάγκαβος Τμήμα Μαθηματικών και Εφαρμοσμένων Μαθηματικών Πανεπισ τήμιο Κρήτης 2 Μαΐου /23
 Εφαρμοσμένη Στατιστική Δημήτριος Μπάγκαβος Τμήμα Μαθηματικών και Εφαρμοσμένων Μαθηματικών Πανεπιστήμιο Κρήτης 2 Μαΐου 2017 1/23 Ανάλυση Διακύμανσης. Η ανάλυση παλινδρόμησης μελετά τη στατιστική σχέση ανάμεσα
Εφαρμοσμένη Στατιστική Δημήτριος Μπάγκαβος Τμήμα Μαθηματικών και Εφαρμοσμένων Μαθηματικών Πανεπιστήμιο Κρήτης 2 Μαΐου 2017 1/23 Ανάλυση Διακύμανσης. Η ανάλυση παλινδρόμησης μελετά τη στατιστική σχέση ανάμεσα
Αναλυτική Στατιστική
 Αναλυτική Στατιστική Συμπερασματολογία Στόχος: εξαγωγή συμπερασμάτων για το σύνολο ενός πληθυσμού, αντλώντας πληροφορίες από ένα μικρό υποσύνολο αυτού Ορισμοί Πληθυσμός: σύνολο όλων των υπό εξέταση μονάδων
Αναλυτική Στατιστική Συμπερασματολογία Στόχος: εξαγωγή συμπερασμάτων για το σύνολο ενός πληθυσμού, αντλώντας πληροφορίες από ένα μικρό υποσύνολο αυτού Ορισμοί Πληθυσμός: σύνολο όλων των υπό εξέταση μονάδων
ΣΧ0ΛΗ ΤΕΧΝ0Λ0ΓΙΑΣ ΤΡΟΦΙΜΩΝ & ΔΙΑΤΡΟΦΗΣ ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΡΟΦΙΜΩΝ ΕΡΓΑΣΤΗΡΙΟ: ΟΡΓΑΝΟΛΗΠΤΙΚΟΥ ΕΛΕΓΧΟΥ ΓΙΑΝΝΑΚΟΥΡΟΥ ΜΑΡΙΑ ΤΑΛΕΛΛΗ ΑΙΚΑΤΕΡΙΝΗ
 ΣΧ0ΛΗ ΤΕΧΝ0Λ0ΓΙΑΣ ΤΡΟΦΙΜΩΝ & ΔΙΑΤΡΟΦΗΣ ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΡΟΦΙΜΩΝ ΕΡΓΑΣΤΗΡΙΟ: ΟΡΓΑΝΟΛΗΠΤΙΚΟΥ ΕΛΕΓΧΟΥ ΓΙΑΝΝΑΚΟΥΡΟΥ ΜΑΡΙΑ ΤΑΛΕΛΛΗ ΑΙΚΑΤΕΡΙΝΗ ΕΙΣΑΓΩΓΗ Ο όρος «ποιότητα», είναι μια απλή έννοια που εκφράζεται
ΣΧ0ΛΗ ΤΕΧΝ0Λ0ΓΙΑΣ ΤΡΟΦΙΜΩΝ & ΔΙΑΤΡΟΦΗΣ ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΡΟΦΙΜΩΝ ΕΡΓΑΣΤΗΡΙΟ: ΟΡΓΑΝΟΛΗΠΤΙΚΟΥ ΕΛΕΓΧΟΥ ΓΙΑΝΝΑΚΟΥΡΟΥ ΜΑΡΙΑ ΤΑΛΕΛΛΗ ΑΙΚΑΤΕΡΙΝΗ ΕΙΣΑΓΩΓΗ Ο όρος «ποιότητα», είναι μια απλή έννοια που εκφράζεται
Χ. Εμμανουηλίδης, 1
 Εφαρμοσμένη Στατιστική Έρευνα Απλό Γραμμικό Υπόδειγμα AΠΛΟ ΓΡΑΜΜΙΚΟ ΥΠΟ ΕΙΓΜΑ Δρ. Χρήστος Εμμανουηλίδης Αν. Καθηγητής Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Εφαρμοσμένη Στατιστική, Τμήμα Ο.Ε. ΑΠΘ Χ. Εμμανουηλίδης,
Εφαρμοσμένη Στατιστική Έρευνα Απλό Γραμμικό Υπόδειγμα AΠΛΟ ΓΡΑΜΜΙΚΟ ΥΠΟ ΕΙΓΜΑ Δρ. Χρήστος Εμμανουηλίδης Αν. Καθηγητής Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Εφαρμοσμένη Στατιστική, Τμήμα Ο.Ε. ΑΠΘ Χ. Εμμανουηλίδης,
ΟΙΚΟΝΟΜΕΤΡΙΑ. Παπάνα Αγγελική
 ΟΙΚΟΝΟΜΕΤΡΙΑ Ενότητα 2: Ανασκόπηση βασικών εννοιών Στατιστικής και Πιθανοτήτων Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ E-mail: angeliki.papana@gmail.com, agpapana@auth.gr Webpage: http://users.auth.gr/agpapana
ΟΙΚΟΝΟΜΕΤΡΙΑ Ενότητα 2: Ανασκόπηση βασικών εννοιών Στατιστικής και Πιθανοτήτων Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ E-mail: angeliki.papana@gmail.com, agpapana@auth.gr Webpage: http://users.auth.gr/agpapana
Απλή Παλινδρόμηση και Συσχέτιση
 Απλή Παλινδρόμηση και Συσχέτιση Πωλήσεις, Δαπάνες Διαφήμισης και Αριθμός Πωλητών Έτος Πωλήσεις (χιλ ) Διαφήμιση (χιλ ) Πωλητές (Άτομα) Έτος Πωλήσεις (χιλ ) Διαφήμιση (χιλ ) Πωλητές (Άτομα) 98 050 6 3 989
Απλή Παλινδρόμηση και Συσχέτιση Πωλήσεις, Δαπάνες Διαφήμισης και Αριθμός Πωλητών Έτος Πωλήσεις (χιλ ) Διαφήμιση (χιλ ) Πωλητές (Άτομα) Έτος Πωλήσεις (χιλ ) Διαφήμιση (χιλ ) Πωλητές (Άτομα) 98 050 6 3 989
Κεφάλαιο 10 Εισαγωγή στην Εκτίμηση
 Κεφάλαιο 10 Εισαγωγή στην Εκτίμηση Εκεί που είμαστε Κεφάλαια 7 και 8: Οι διωνυμικές,κανονικές, εκθετικές κατανομές και κατανομές Poisson μας επιτρέπουν να κάνουμε διατυπώσεις πιθανοτήτων γύρω από το Χ
Κεφάλαιο 10 Εισαγωγή στην Εκτίμηση Εκεί που είμαστε Κεφάλαια 7 και 8: Οι διωνυμικές,κανονικές, εκθετικές κατανομές και κατανομές Poisson μας επιτρέπουν να κάνουμε διατυπώσεις πιθανοτήτων γύρω από το Χ
ΘΕΩΡΙΑ ΟΙΚΟΝΟΜΕΤΡΙΑΣ ΣΥΝΟΠΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ
 ΘΕΩΡΙΑ ΟΙΚΟΝΟΜΕΤΡΙΑΣ ΣΥΝΟΠΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΑΠΛΟ ΓΡΑΜΜΙΚΟ ΥΠΟΔΕΙΓΜΑ Συντελεστής συσχέτισης (εκτιμητής Person: r, Y ( ( Y Y xy ( ( Y Y x y, όπου r, Y (ισχυρή θετική γραμμική συσχέτιση όταν, ισχυρή αρνητική
ΘΕΩΡΙΑ ΟΙΚΟΝΟΜΕΤΡΙΑΣ ΣΥΝΟΠΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΑΠΛΟ ΓΡΑΜΜΙΚΟ ΥΠΟΔΕΙΓΜΑ Συντελεστής συσχέτισης (εκτιμητής Person: r, Y ( ( Y Y xy ( ( Y Y x y, όπου r, Y (ισχυρή θετική γραμμική συσχέτιση όταν, ισχυρή αρνητική
ΠΕΡΙΕΧΟΜΕΝΑ. ΠΡΟΛΟΓΟΣ... vii ΠΕΡΙΕΧΟΜΕΝΑ... ix ΓΕΝΙΚΗ ΒΙΒΛΙΟΓΡΑΦΙΑ... xv. Κεφάλαιο 1 ΓΕΝΙΚΕΣ ΕΝΝΟΙΕΣ ΑΠΟ ΤΗ ΣΤΑΤΙΣΤΙΚΗ
 ΠΡΟΛΟΓΟΣ... vii ΠΕΡΙΕΧΟΜΕΝΑ... ix ΓΕΝΙΚΗ ΒΙΒΛΙΟΓΡΑΦΙΑ... xv Κεφάλαιο 1 ΓΕΝΙΚΕΣ ΕΝΝΟΙΕΣ ΑΠΟ ΤΗ ΣΤΑΤΙΣΤΙΚΗ 1.1 Πίνακες, κατανομές, ιστογράμματα... 1 1.2 Πυκνότητα πιθανότητας, καμπύλη συχνοτήτων... 5 1.3
ΠΡΟΛΟΓΟΣ... vii ΠΕΡΙΕΧΟΜΕΝΑ... ix ΓΕΝΙΚΗ ΒΙΒΛΙΟΓΡΑΦΙΑ... xv Κεφάλαιο 1 ΓΕΝΙΚΕΣ ΕΝΝΟΙΕΣ ΑΠΟ ΤΗ ΣΤΑΤΙΣΤΙΚΗ 1.1 Πίνακες, κατανομές, ιστογράμματα... 1 1.2 Πυκνότητα πιθανότητας, καμπύλη συχνοτήτων... 5 1.3
Βιοστατιστική ΒΙΟ-309
 Βιοστατιστική ΒΙΟ-309 Χειμερινό Εξάμηνο Ακαδ. Έτος 2015-2016 Ντίνα Λύκα lika@biology.uoc.gr 1. Εισαγωγή Εισαγωγικές έννοιες Μεταβλητότητα : ύπαρξη διαφορών μεταξύ ομοειδών μετρήσεων Μεταβλητή: ένα χαρακτηριστικό
Βιοστατιστική ΒΙΟ-309 Χειμερινό Εξάμηνο Ακαδ. Έτος 2015-2016 Ντίνα Λύκα lika@biology.uoc.gr 1. Εισαγωγή Εισαγωγικές έννοιες Μεταβλητότητα : ύπαρξη διαφορών μεταξύ ομοειδών μετρήσεων Μεταβλητή: ένα χαρακτηριστικό
5. ΤΟ ΓΕΝΙΚΟ ΓΡΑΜΜΙΚΟ ΜΟΝΤΕΛΟ (GENERAL LINEAR MODEL) 5.1 Εναλλακτικά μοντέλα του απλού γραμμικού μοντέλου: Το εκθετικό μοντέλο
 5. ΤΟ ΓΕΝΙΚΟ ΓΡΑΜΜΙΚΟ ΜΟΝΤΕΛΟ (GENERAL LINEAR MODEL) 5.1 Εναλλακτικά μοντέλα του απλού γραμμικού μοντέλου: Το εκθετικό μοντέλο Ένα εναλλακτικό μοντέλο της απλής γραμμικής παλινδρόμησης (που χρησιμοποιήθηκε
5. ΤΟ ΓΕΝΙΚΟ ΓΡΑΜΜΙΚΟ ΜΟΝΤΕΛΟ (GENERAL LINEAR MODEL) 5.1 Εναλλακτικά μοντέλα του απλού γραμμικού μοντέλου: Το εκθετικό μοντέλο Ένα εναλλακτικό μοντέλο της απλής γραμμικής παλινδρόμησης (που χρησιμοποιήθηκε
ΠΕΡΙΕΧΟΜΕΝΑ. Πρόλογος... 13
 ΠΕΡΙΕΧΟΜΕΝΑ / 7 ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος... 13 Κεφάλαιο 1: Περιγραφική Στατιστική... 15 1.1 Περιγραφική και Συμπερασματική Στατιστική... 15 1.2 Μεταβλητές - Τιμές - Παρατηρήσεις... 19 1.3 Είδη μεταβλητών...
ΠΕΡΙΕΧΟΜΕΝΑ / 7 ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος... 13 Κεφάλαιο 1: Περιγραφική Στατιστική... 15 1.1 Περιγραφική και Συμπερασματική Στατιστική... 15 1.2 Μεταβλητές - Τιμές - Παρατηρήσεις... 19 1.3 Είδη μεταβλητών...
Αντικείμενο του κεφαλαίου είναι: Ανάλυση συσχέτισης μεταξύ δύο μεταβλητών. Εξίσωση παλινδρόμησης. Πρόβλεψη εξέλιξης
 Γραμμική Παλινδρόμηση και Συσχέτιση Αντικείμενο του κεφαλαίου είναι: Ανάλυση συσχέτισης μεταξύ δύο μεταβλητών Εξίσωση παλινδρόμησης Πρόβλεψη εξέλιξης Διμεταβλητές συσχετίσεις Πολλές φορές χρειάζεται να
Γραμμική Παλινδρόμηση και Συσχέτιση Αντικείμενο του κεφαλαίου είναι: Ανάλυση συσχέτισης μεταξύ δύο μεταβλητών Εξίσωση παλινδρόμησης Πρόβλεψη εξέλιξης Διμεταβλητές συσχετίσεις Πολλές φορές χρειάζεται να
ΠΕΡΙΓΡΑΦΗ ΚΑΙ ΑΝΑΛΥΣΗ ΔΕΔΟΜΕΝΩΝ
 ΠΕΡΙΓΡΑΦΗ ΚΑΙ ΑΝΑΛΥΣΗ ΔΕΔΟΜΕΝΩΝ Είδη μεταβλητών Ποσοτικά δεδομένα (π.χ. ηλικία, ύψος, αιμοσφαιρίνη) Ποιοτικά δεδομένα (π.χ. άνδρας/γυναίκα, ναι/όχι) Διατεταγμένα (π.χ. καλό/μέτριο/κακό) 2 Περιγραφή ποσοτικών
ΠΕΡΙΓΡΑΦΗ ΚΑΙ ΑΝΑΛΥΣΗ ΔΕΔΟΜΕΝΩΝ Είδη μεταβλητών Ποσοτικά δεδομένα (π.χ. ηλικία, ύψος, αιμοσφαιρίνη) Ποιοτικά δεδομένα (π.χ. άνδρας/γυναίκα, ναι/όχι) Διατεταγμένα (π.χ. καλό/μέτριο/κακό) 2 Περιγραφή ποσοτικών
Διερεύνηση της επιρροής των καιρικών συνθηκών στη συμπεριφορά και την ασφάλεια νέων οδηγών σε αστικές οδούς με τη χρήση προσομοιωτή οδήγησης
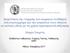 Διερεύνηση της επιρροής των καιρικών συνθηκών στη συμπεριφορά και την ασφάλεια νέων οδηγών σε αστικές οδούς με τη χρήση προσομοιωτή οδήγησης Μαρία Χαιρέτη Επιβλέπων καθηγητής: Γιώργος Γιαννής, Καθηγητής
Διερεύνηση της επιρροής των καιρικών συνθηκών στη συμπεριφορά και την ασφάλεια νέων οδηγών σε αστικές οδούς με τη χρήση προσομοιωτή οδήγησης Μαρία Χαιρέτη Επιβλέπων καθηγητής: Γιώργος Γιαννής, Καθηγητής
Βιοστατιστική ΒΙΟ-309
 Βιοστατιστική ΒΙΟ-309 Χειμερινό Εξάμηνο Ακαδ. Έτος 2017-2018 Ντίνα Λύκα lika@biology.uoc.gr 1. Εισαγωγή Εισαγωγικές έννοιες Μεταβλητότητα : ύπαρξη διαφορών μεταξύ ομοειδών μετρήσεων Μεταβλητή: ένα χαρακτηριστικό
Βιοστατιστική ΒΙΟ-309 Χειμερινό Εξάμηνο Ακαδ. Έτος 2017-2018 Ντίνα Λύκα lika@biology.uoc.gr 1. Εισαγωγή Εισαγωγικές έννοιες Μεταβλητότητα : ύπαρξη διαφορών μεταξύ ομοειδών μετρήσεων Μεταβλητή: ένα χαρακτηριστικό
ΣΤΑΤΙΣΤΙΚΟΙ ΠΙΝΑΚΕΣ. ΓΕΝΙΚΟΙ (περιέχουν όλες τις πληροφορίες που προκύπτουν από μια στατιστική έρευνα) ΕΙΔΙΚΟΙ ( είναι συνοπτικοί και σαφείς )
 Πληθυσμός (populaton) ονομάζεται ένα σύνολο, τα στοιχεία του οποίου εξετάζουμε ως προς τα χαρακτηριστικά τους. Μεταβλητές (varables ) ονομάζονται τα χαρακτηριστικά ως προς τα οποία εξετάζουμε έναν πληθυσμό.
Πληθυσμός (populaton) ονομάζεται ένα σύνολο, τα στοιχεία του οποίου εξετάζουμε ως προς τα χαρακτηριστικά τους. Μεταβλητές (varables ) ονομάζονται τα χαρακτηριστικά ως προς τα οποία εξετάζουμε έναν πληθυσμό.
ΠΟΣΟΤΙΚΕΣ ΜΕΘΟΔΟΙ ΙI (ΣΤΑΤΙΣΤΙΚΗ ΓΙΑ ΤΗ ΔΙΟΙΚΗΣΗ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ) (ΟΔΕ 2116)
 Σελίδα 1 ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΟΡΓΑΝΩΣΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΜΑΘΗΜΑ: ΠΟΣΟΤΙΚΕΣ ΜΕΘΟΔΟΙ ΙΙ (ΣΤΑΤΙΣΤΙΚΗ ΓΙΑ ΤΗ ΔΙΟΙΚΗΣΗ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ) (ΟΔΕ 2116) ΠΑΝΕΠΙΣΤΗΜΙΑΚΟΣ ΥΠΟΤΡΟΦΟΣ ΠΑΝΑΓΙΩΤΗΣ
Σελίδα 1 ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΟΡΓΑΝΩΣΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΜΑΘΗΜΑ: ΠΟΣΟΤΙΚΕΣ ΜΕΘΟΔΟΙ ΙΙ (ΣΤΑΤΙΣΤΙΚΗ ΓΙΑ ΤΗ ΔΙΟΙΚΗΣΗ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ) (ΟΔΕ 2116) ΠΑΝΕΠΙΣΤΗΜΙΑΚΟΣ ΥΠΟΤΡΟΦΟΣ ΠΑΝΑΓΙΩΤΗΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΔΙΟΙΚΗΣΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΔΙΟΙΚΗΣΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 06-07 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Επικ. Καθηγητής v.koutra@fme.aegea.gr Τηλ: 7035468 Θα μελετήσουμε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΔΙΟΙΚΗΣΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 06-07 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Επικ. Καθηγητής v.koutra@fme.aegea.gr Τηλ: 7035468 Θα μελετήσουμε
Περιεχόμενα. Πρόλογος... 15
 Περιεχόμενα Πρόλογος... 15 Κεφάλαιο 1 ΘΕΩΡΗΤΙΚΑ ΚΑΙ ΦΙΛΟΣΟΦΙΚΑ ΟΝΤΟΛΟΓΙΚΑ ΚΑΙ ΕΠΙΣΤΗΜΟΛΟΓΙΚΑ ΖΗΤΗΜΑΤΑ ΤΗΣ ΜΕΘΟΔΟΛΟΓΙΑΣ ΕΡΕΥΝΑΣ ΤΟΥ ΠΡΑΓΜΑΤΙΚΟΥ ΚΟΣΜΟΥ... 17 Το θεμελιώδες πρόβλημα των κοινωνικών επιστημών...
Περιεχόμενα Πρόλογος... 15 Κεφάλαιο 1 ΘΕΩΡΗΤΙΚΑ ΚΑΙ ΦΙΛΟΣΟΦΙΚΑ ΟΝΤΟΛΟΓΙΚΑ ΚΑΙ ΕΠΙΣΤΗΜΟΛΟΓΙΚΑ ΖΗΤΗΜΑΤΑ ΤΗΣ ΜΕΘΟΔΟΛΟΓΙΑΣ ΕΡΕΥΝΑΣ ΤΟΥ ΠΡΑΓΜΑΤΙΚΟΥ ΚΟΣΜΟΥ... 17 Το θεμελιώδες πρόβλημα των κοινωνικών επιστημών...
Υ: Νόσος. Χ: Παράγοντας Κινδύνου 1 (Ασθενής) 2 (Υγιής) Σύνολο. 1 (Παρόν) n 11 n 12 n 1. 2 (Απών) n 21 n 22 n 2. Σύνολο n.1 n.2 n..
 Μέτρα Κινδύνου για Δίτιμα Κατηγορικά Δεδομένα Σε αυτή την ενότητα θα ορίσουμε δείκτες μέτρησης του κινδύνου εμφάνισης μίας νόσου όταν έχουμε δίτιμες κατηγορικές μεταβλητές. Στην πιο απλή περίπτωση μας
Μέτρα Κινδύνου για Δίτιμα Κατηγορικά Δεδομένα Σε αυτή την ενότητα θα ορίσουμε δείκτες μέτρησης του κινδύνου εμφάνισης μίας νόσου όταν έχουμε δίτιμες κατηγορικές μεταβλητές. Στην πιο απλή περίπτωση μας
ΔΙΕΡΕΥΝΗΣΗ ΤΗΣ ΕΠΙΡΡΟΗΣ ΤΟΥ ΤΟΥΡΙΣΜΟΥ ΣΤΑ ΟΔΙΚΑ ΑΤΥΧΗΜΑΤΑ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΜΕΤΑΦΟΡΩΝ ΚΑΙ ΣΥΓΚΟΙΝΩΝΙΑΚΗΣ ΥΠΟΔΟΜΗΣ ΔΙΕΡΕΥΝΗΣΗ ΤΗΣ ΕΠΙΡΡΟΗΣ ΤΟΥ ΤΟΥΡΙΣΜΟΥ ΣΤΑ ΟΔΙΚΑ ΑΤΥΧΗΜΑΤΑ Βασίλειος Μπέλλος Επιβλέπων: Γιώργος Γιαννής,
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΜΕΤΑΦΟΡΩΝ ΚΑΙ ΣΥΓΚΟΙΝΩΝΙΑΚΗΣ ΥΠΟΔΟΜΗΣ ΔΙΕΡΕΥΝΗΣΗ ΤΗΣ ΕΠΙΡΡΟΗΣ ΤΟΥ ΤΟΥΡΙΣΜΟΥ ΣΤΑ ΟΔΙΚΑ ΑΤΥΧΗΜΑΤΑ Βασίλειος Μπέλλος Επιβλέπων: Γιώργος Γιαννής,
Γ. Πειραματισμός - Βιομετρία
 Γ. Πειραματισμός - Βιομετρία Πληθυσμοί και δείγματα Πληθυσμός Περιλαμβάνει όλες τις πιθανές τιμές μιας μεταβλητής, δηλαδή αναφέρεται σε μια παρατήρηση σε όλα τα άτομα του πληθυσμού Ο πληθυσμός προσδιορίζεται
Γ. Πειραματισμός - Βιομετρία Πληθυσμοί και δείγματα Πληθυσμός Περιλαμβάνει όλες τις πιθανές τιμές μιας μεταβλητής, δηλαδή αναφέρεται σε μια παρατήρηση σε όλα τα άτομα του πληθυσμού Ο πληθυσμός προσδιορίζεται
Στατιστική Ι. Ενότητα 7: Κανονική Κατανομή. Δρ. Γεώργιος Κοντέος Τμήμα Διοίκησης Επιχειρήσεων Γρεβενών
 Στατιστική Ι Ενότητα 7: Κανονική Κατανομή Δρ. Γεώργιος Κοντέος Τμήμα Διοίκησης Επιχειρήσεων Γρεβενών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Στατιστική Ι Ενότητα 7: Κανονική Κατανομή Δρ. Γεώργιος Κοντέος Τμήμα Διοίκησης Επιχειρήσεων Γρεβενών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
ΣΥΣΧΕΤΙΣΗ ΚΥΚΛΟΦΟΡΙΑΚΩΝ ΜΕΓΕΘΩΝ ΜΕ ΤΗ ΣΟΒΑΡΟΤΗΤΑ ΚΑΙ ΤΗΝ ΠΙΘΑΝΟΤΗΤΑ ΟΔΙΚΩΝ ΑΤΥΧΗΜΑΤΩΝ. Απόστολος Ζιακόπουλος
 1 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΜΕΤΑΦΟΡΩΝ ΚΑΙ ΣΥΓΚΟΙΝΩΝΙΑΚΗΣ ΥΠΟΔΟΜΗΣ ΣΥΣΧΕΤΙΣΗ ΚΥΚΛΟΦΟΡΙΑΚΩΝ ΜΕΓΕΘΩΝ ΜΕ ΤΗ ΣΟΒΑΡΟΤΗΤΑ ΚΑΙ ΤΗΝ ΠΙΘΑΝΟΤΗΤΑ ΟΔΙΚΩΝ ΑΤΥΧΗΜΑΤΩΝ Απόστολος Ζιακόπουλος
1 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΜΕΤΑΦΟΡΩΝ ΚΑΙ ΣΥΓΚΟΙΝΩΝΙΑΚΗΣ ΥΠΟΔΟΜΗΣ ΣΥΣΧΕΤΙΣΗ ΚΥΚΛΟΦΟΡΙΑΚΩΝ ΜΕΓΕΘΩΝ ΜΕ ΤΗ ΣΟΒΑΡΟΤΗΤΑ ΚΑΙ ΤΗΝ ΠΙΘΑΝΟΤΗΤΑ ΟΔΙΚΩΝ ΑΤΥΧΗΜΑΤΩΝ Απόστολος Ζιακόπουλος
Στατιστικές συναρτήσεις Γραφική και πινακοποιημένη αναπαράσταση δεδομένων (ιστόγραμμα) Διαχειριστής Σεναρίων Κινητός Μέσος σε Χρονοσειρές o o o
 ΙΩΑΝΝΗΣ Κ. ΔΗΜΗΤΡΙΟΥ Εφαρμογές Ποσοτικές Ανάλυσης με το Excel 141 ΑΝΑΛΥΣΗ ΔΕΔΟΜΕΝΩΝ Ανάλυση Δεδομένων Στατιστικές συναρτήσεις Γραφική και πινακοποιημένη αναπαράσταση δεδομένων (ιστόγραμμα) Διαχειριστής
ΙΩΑΝΝΗΣ Κ. ΔΗΜΗΤΡΙΟΥ Εφαρμογές Ποσοτικές Ανάλυσης με το Excel 141 ΑΝΑΛΥΣΗ ΔΕΔΟΜΕΝΩΝ Ανάλυση Δεδομένων Στατιστικές συναρτήσεις Γραφική και πινακοποιημένη αναπαράσταση δεδομένων (ιστόγραμμα) Διαχειριστής
ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΤΜΗΜΑ ΟΡΓΑΝΩΣΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΔΙΔΑΣΚΩΝ: ΘΑΝΑΣΗΣ ΚΑΖΑΝΑΣ. Οικονομετρία
 ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΤΜΗΜΑ ΟΡΓΑΝΩΣΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΔΙΔΑΣΚΩΝ: ΘΑΝΑΣΗΣ ΚΑΖΑΝΑΣ Οικονομετρία 6.1 Ετεροσκεδαστικότητα: Εισαγωγή Συχνά, η υπόθεση της σταθερής διακύμανσης των όρων σφάλματος,
ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΤΜΗΜΑ ΟΡΓΑΝΩΣΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΔΙΔΑΣΚΩΝ: ΘΑΝΑΣΗΣ ΚΑΖΑΝΑΣ Οικονομετρία 6.1 Ετεροσκεδαστικότητα: Εισαγωγή Συχνά, η υπόθεση της σταθερής διακύμανσης των όρων σφάλματος,
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΔΙΟΙΚΗΣΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΔΙΟΙΚΗΣΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 6-7 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Λέκτορας v.koutras@fme.aegea.gr Τηλ: 735468 Σε αρκετές εφαρμογές
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΔΙΟΙΚΗΣΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 6-7 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Λέκτορας v.koutras@fme.aegea.gr Τηλ: 735468 Σε αρκετές εφαρμογές
ΕΝΤΥΠΟ ΘΕΜΑΤΩΝ ΕΞΕΤΑΣΕΩΝ
 Όνομα: Επίθετο: Ημερομηνία: 7/07/207 Πρωί: Απόγευμα: Θεματική ενότητα: Αρχές Αναλογιστικής Προτυποποίησης, Κατασκευή και Αξιολόγηση Αναλογιστικών Προτύπων. Οι αναλογιστές μιας εταιρείας μοντελοποιούν την
Όνομα: Επίθετο: Ημερομηνία: 7/07/207 Πρωί: Απόγευμα: Θεματική ενότητα: Αρχές Αναλογιστικής Προτυποποίησης, Κατασκευή και Αξιολόγηση Αναλογιστικών Προτύπων. Οι αναλογιστές μιας εταιρείας μοντελοποιούν την
Τ Ε Ι Ιονίων Νήσων Τμήμα Εφαρμογών Πληροφορικής στη Διοίκηση και την Οικονομία. Υπεύθυνος: Δρ. Κολιός Σταύρος
 Τ Ε Ι Ιονίων Νήσων Τμήμα Εφαρμογών Πληροφορικής στη Διοίκηση και την Οικονομία Υπεύθυνος: Δρ. Κολιός Σταύρος Κατανομές Πιθανότητας Ως τυχαία μεταβλητή ορίζεται το σύνολο των τιμών ενός χαρακτηριστικού
Τ Ε Ι Ιονίων Νήσων Τμήμα Εφαρμογών Πληροφορικής στη Διοίκηση και την Οικονομία Υπεύθυνος: Δρ. Κολιός Σταύρος Κατανομές Πιθανότητας Ως τυχαία μεταβλητή ορίζεται το σύνολο των τιμών ενός χαρακτηριστικού
ΤΕΙ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ Μεταπτυχιακό Τραπεζικής & Χρηματοοικονομικής
 ΤΕΙ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ Μεταπτυχιακό Τραπεζικής & Χρηματοοικονομικής Υποθέσεις του Απλού γραμμικού υποδείγματος της Παλινδρόμησης Η μεταβλητή ε t (διαταρακτικός όρος) είναι τυχαία μεταβλητή με μέσο όρο
ΤΕΙ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ Μεταπτυχιακό Τραπεζικής & Χρηματοοικονομικής Υποθέσεις του Απλού γραμμικού υποδείγματος της Παλινδρόμησης Η μεταβλητή ε t (διαταρακτικός όρος) είναι τυχαία μεταβλητή με μέσο όρο
Βιοστατιστική ΒΙΟ-309
 Βιοστατιστική ΒΙΟ-309 Χειμερινό Εξάμηνο Ακαδ. Έτος 2013-2014 Ντίνα Λύκα lika@biology.uoc.gr 1. Εισαγωγή Εισαγωγικές έννοιες Μεταβλητή: ένα χαρακτηριστικό ή ιδιότητα που μπορεί να πάρει διαφορετικές τιμές
Βιοστατιστική ΒΙΟ-309 Χειμερινό Εξάμηνο Ακαδ. Έτος 2013-2014 Ντίνα Λύκα lika@biology.uoc.gr 1. Εισαγωγή Εισαγωγικές έννοιες Μεταβλητή: ένα χαρακτηριστικό ή ιδιότητα που μπορεί να πάρει διαφορετικές τιμές
Στατιστική. Ενότητα 3 η : Χαρακτηριστικά Τυχαίων Μεταβλητών Θεωρητικές Κατανομές Πιθανότητας για Διακριτή Τυχαία Μεταβλητή
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 3 η : Χαρακτηριστικά Τυχαίων Μεταβλητών Θεωρητικές Κατανομές Πιθανότητας για Διακριτή Τυχαία Μεταβλητή Γεώργιος Ζιούτας Άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 3 η : Χαρακτηριστικά Τυχαίων Μεταβλητών Θεωρητικές Κατανομές Πιθανότητας για Διακριτή Τυχαία Μεταβλητή Γεώργιος Ζιούτας Άδειες
ΠΕΡΙΓΡΑΦΙΚΗ ΣΤΑΤΙΣΤΙΚΗ Ι Κ. Μ. 436
 ΠΕΡΙΓΡΑΦΙΚΗ ΣΤΑΤΙΣΤΙΚΗ Ι Κ. Μ. 436 A εξάμηνο 2009-2010 Περιγραφική Στατιστική Ι users.att.sch.gr/abouras abouras@sch.gr sch.gr abouras@uth.gr Μέτρα θέσης Η θέση αντιπροσωπεύει τη θέση της κατανομής κατά
ΠΕΡΙΓΡΑΦΙΚΗ ΣΤΑΤΙΣΤΙΚΗ Ι Κ. Μ. 436 A εξάμηνο 2009-2010 Περιγραφική Στατιστική Ι users.att.sch.gr/abouras abouras@sch.gr sch.gr abouras@uth.gr Μέτρα θέσης Η θέση αντιπροσωπεύει τη θέση της κατανομής κατά
Συνολοκλήρωση και μηχανισμός διόρθωσης σφάλματος
 ΜΑΘΗΜΑ 10 ο Συνολοκλήρωση και μηχανισμός διόρθωσης σφάλματος Η μέθοδος της συνολοκλήρωσης είναι ένας τρόπος με τον οποίο μπορούμε να εκτιμήσουμε τη μακροχρόνια σχέση ισορροπίας που υπάρχει μεταξύ δύο ή
ΜΑΘΗΜΑ 10 ο Συνολοκλήρωση και μηχανισμός διόρθωσης σφάλματος Η μέθοδος της συνολοκλήρωσης είναι ένας τρόπος με τον οποίο μπορούμε να εκτιμήσουμε τη μακροχρόνια σχέση ισορροπίας που υπάρχει μεταξύ δύο ή
Τυχαία μεταβλητή (τ.μ.)
 Τυχαία μεταβλητή (τ.μ.) Τυχαία μεταβλητή (τ.μ.) είναι μια συνάρτηση X ( ) με πεδίο ορισμού το δειγματικό χώρο Ω του πειράματος και πεδίο τιμών ένα υποσύνολο πραγματικών αριθμών που συμβολίζουμε συνήθως
Τυχαία μεταβλητή (τ.μ.) Τυχαία μεταβλητή (τ.μ.) είναι μια συνάρτηση X ( ) με πεδίο ορισμού το δειγματικό χώρο Ω του πειράματος και πεδίο τιμών ένα υποσύνολο πραγματικών αριθμών που συμβολίζουμε συνήθως
Μέθοδος μέγιστης πιθανοφάνειας
 Μέθοδος μέγιστης πιθανοφάνειας Αν x =,,, παρατηρήσεις των Χ =,,,, τότε έχουμε διαθέσιμο ένα δείγμα Χ={Χ, =,,,} της κατανομής F μεγέθους με από κοινού σ.κ. της Χ f x f x Ορισμός : Θεωρούμε ένα τυχαίο δείγμα
Μέθοδος μέγιστης πιθανοφάνειας Αν x =,,, παρατηρήσεις των Χ =,,,, τότε έχουμε διαθέσιμο ένα δείγμα Χ={Χ, =,,,} της κατανομής F μεγέθους με από κοινού σ.κ. της Χ f x f x Ορισμός : Θεωρούμε ένα τυχαίο δείγμα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΔΙΟΙΚΗΣΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΔΙΟΙΚΗΣΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 5-6 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Λέκτορας v.koutras@fme.aegea.gr Τηλ: 735468 Σε αρκετές εφαρμογές
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΔΙΟΙΚΗΣΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 5-6 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Λέκτορας v.koutras@fme.aegea.gr Τηλ: 735468 Σε αρκετές εφαρμογές
ΔΙΕΡΕΥΝΗΣΗ ΚΛΙΜΑΤΙΚΩΝ ΑΛΛΑΓΩΝ ΓΙΑ ΤΟ ΝΗΣΙ ΤΗΣ ΝΑΞΟΥ
 ΔΙΕΡΕΥΝΗΣΗ ΚΛΙΜΑΤΙΚΩΝ ΑΛΛΑΓΩΝ ΓΙΑ ΤΟ ΝΗΣΙ ΤΗΣ ΝΑΞΟΥ ΜΑΜΜΑΣ ΚΩΝ/ΝΟΣ ΑΜ:331/2003032 ΝΟΕΜΒΡΙΟΣ 2010 Ευχαριστίες Σε αυτό το σημείο θα ήθελα να ευχαριστήσω όλους όσους με βοήθησαν να δημιουργήσω την παρούσα
ΔΙΕΡΕΥΝΗΣΗ ΚΛΙΜΑΤΙΚΩΝ ΑΛΛΑΓΩΝ ΓΙΑ ΤΟ ΝΗΣΙ ΤΗΣ ΝΑΞΟΥ ΜΑΜΜΑΣ ΚΩΝ/ΝΟΣ ΑΜ:331/2003032 ΝΟΕΜΒΡΙΟΣ 2010 Ευχαριστίες Σε αυτό το σημείο θα ήθελα να ευχαριστήσω όλους όσους με βοήθησαν να δημιουργήσω την παρούσα
ΟΙΚΟΝΟΜΕΤΡΙΑ. Παπάνα Αγγελική
 ΟΙΚΟΝΟΜΕΤΡΙΑ Ενότητα 6: Ανάλυση γραμμικού υποδείγματος Πολυμεταβλητή παλινδρόμηση (2 ο μέρος) Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ E-mail: angeliki.papana@gmail.com, agpapana@auth.gr Webpage:
ΟΙΚΟΝΟΜΕΤΡΙΑ Ενότητα 6: Ανάλυση γραμμικού υποδείγματος Πολυμεταβλητή παλινδρόμηση (2 ο μέρος) Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ E-mail: angeliki.papana@gmail.com, agpapana@auth.gr Webpage:
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ
 ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ Μ.Ν. Ντυκέν, Πανεπιστήμιο Θεσσαλίας Τ.Μ.Χ.Π.Π.Α. Ε. Αναστασίου, Πανεπιστήμιο Θεσσαλίας Τ.Μ.Χ.Π.Π.Α. ΔΙΑΛΕΞΗ 07 & ΔΙΑΛΕΞΗ 08 ΣΗΜΠΕΡΑΣΜΑΤΙΚΗ ΣΤΑΤΙΣΤΙΚΗ Βόλος, 016-017 ΕΙΣΑΓΩΓΗ ΣΤΗΝ
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ Μ.Ν. Ντυκέν, Πανεπιστήμιο Θεσσαλίας Τ.Μ.Χ.Π.Π.Α. Ε. Αναστασίου, Πανεπιστήμιο Θεσσαλίας Τ.Μ.Χ.Π.Π.Α. ΔΙΑΛΕΞΗ 07 & ΔΙΑΛΕΞΗ 08 ΣΗΜΠΕΡΑΣΜΑΤΙΚΗ ΣΤΑΤΙΣΤΙΚΗ Βόλος, 016-017 ΕΙΣΑΓΩΓΗ ΣΤΗΝ
ΟΙΚΟΝΟΜΕΤΡΙΑ. Β μέρος: Ετεροσκεδαστικότητα. Παπάνα Αγγελική
 ΟΙΚΟΝΟΜΕΤΡΙΑ Ενότητα 10: Οικονομετρικά προβλήματα: Παραβίαση των υποθέσεων Β μέρος: Ετεροσκεδαστικότητα Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ E-mail: angeliki.papana@gmail.com, agpapana@auth.gr
ΟΙΚΟΝΟΜΕΤΡΙΑ Ενότητα 10: Οικονομετρικά προβλήματα: Παραβίαση των υποθέσεων Β μέρος: Ετεροσκεδαστικότητα Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ E-mail: angeliki.papana@gmail.com, agpapana@auth.gr
Διάστημα εμπιστοσύνης της μέσης τιμής
 Διάστημα εμπιστοσύνης της μέσης τιμής Συντελεστής εμπιστοσύνης Όταν : x z c s < μ < x +z s c Ν>30 Στον πίνακα δίνονται κρίσιμες τιμές z c και η αντιστοίχισή τους σε διάφορους συντελεστές εμπιστοσύνης:
Διάστημα εμπιστοσύνης της μέσης τιμής Συντελεστής εμπιστοσύνης Όταν : x z c s < μ < x +z s c Ν>30 Στον πίνακα δίνονται κρίσιμες τιμές z c και η αντιστοίχισή τους σε διάφορους συντελεστές εμπιστοσύνης:
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 7-8 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Επικ. Καθηγητής v.koutras@fme.aegea.gr Τηλ: 735468 Σε αρκετές εφαρμογές
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 7-8 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Επικ. Καθηγητής v.koutras@fme.aegea.gr Τηλ: 735468 Σε αρκετές εφαρμογές
ΑΞΙΟΠΙΣΤΙΑ ΚΑΙ ΣΥΝΤΗΡΗΣΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Συμπληρωματικές Σημειώσεις Δημήτριος Παντελής. Pr T T0
 ΑΞΙΟΠΙΣΤΙΑ ΚΑΙ ΣΥΝΤΗΡΗΣΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Συμπληρωματικές Σημειώσεις Δημήτριος Παντελής Δεσμευμένη αξιοπιστία Η δεσμευμένη αξιοπιστία R t είναι η πιθανότητα το σύστημα να λειτουργήσει για χρονικό
ΑΞΙΟΠΙΣΤΙΑ ΚΑΙ ΣΥΝΤΗΡΗΣΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Συμπληρωματικές Σημειώσεις Δημήτριος Παντελής Δεσμευμένη αξιοπιστία Η δεσμευμένη αξιοπιστία R t είναι η πιθανότητα το σύστημα να λειτουργήσει για χρονικό
Απλή Γραμμική Παλινδρόμηση και Συσχέτιση 19/5/2017
 Απλή Γραμμική Παλινδρόμηση και Συσχέτιση 2 Εισαγωγή Η ανάλυση παλινδρόμησης περιλαμβάνει το σύνολο των μεθόδων της στατιστικής που αναφέρονται σε ποσοτικές σχέσεις μεταξύ μεταβλητών Πρότυπα παλινδρόμησης
Απλή Γραμμική Παλινδρόμηση και Συσχέτιση 2 Εισαγωγή Η ανάλυση παλινδρόμησης περιλαμβάνει το σύνολο των μεθόδων της στατιστικής που αναφέρονται σε ποσοτικές σχέσεις μεταξύ μεταβλητών Πρότυπα παλινδρόμησης
ΧΡΟΝΙΚΕΣ ΣΕΙΡΕΣ. Παπάνα Αγγελική
 ΧΡΟΝΙΚΕΣ ΣΕΙΡΕΣ 7ο μάθημα: Πολυμεταβλητή παλινδρόμηση (ΕΠΑΝΑΛΗΨΗ) Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ & ΠΑΜΑΚ E-mail: angeliki.papana@gmail.com, agpapana@auth.gr Webpage: http://users.auth.gr/agpapana
ΧΡΟΝΙΚΕΣ ΣΕΙΡΕΣ 7ο μάθημα: Πολυμεταβλητή παλινδρόμηση (ΕΠΑΝΑΛΗΨΗ) Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ & ΠΑΜΑΚ E-mail: angeliki.papana@gmail.com, agpapana@auth.gr Webpage: http://users.auth.gr/agpapana
ΣΤΑΤΙΣΤΙΚΗ ΕΠΙΧΕΙΡΗΣΕΩΝ ΕΙΔΙΚΑ ΘΕΜΑΤΑ. Κεφάλαιο 10. Εισαγωγή στην εκτιμητική
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΑΤΡΑΣ Εργαστήριο Λήψης Αποφάσεων & Επιχειρησιακού Προγραμματισμού Καθηγητής Ι. Μητρόπουλος ΣΤΑΤΙΣΤΙΚΗ ΕΠΙΧΕΙΡΗΣΕΩΝ ΕΙΔΙΚΑ ΘΕΜΑΤΑ
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΑΤΡΑΣ Εργαστήριο Λήψης Αποφάσεων & Επιχειρησιακού Προγραμματισμού Καθηγητής Ι. Μητρόπουλος ΣΤΑΤΙΣΤΙΚΗ ΕΠΙΧΕΙΡΗΣΕΩΝ ΕΙΔΙΚΑ ΘΕΜΑΤΑ
ΠΟΣΟΤΙΚΗ ΓΕΝΕΤΙΚΗ 03. ΜΕΣΗ ΤΙΜΗ & ΔΙΑΚΥΜΑΝΣΗ
 ΠΟΣΟΤΙΚΗ ΓΕΝΕΤΙΚΗ 03. ΜΕΣΗ ΤΙΜΗ & ΔΙΑΚΥΜΑΝΣΗ 1 ΠΟΣΟΤΙΚΟ ΓΝΩΡΙΣΜΑ ΑΑββΓΓδδεεΖΖ αριθμός φυτών 50 00 150 100 50 0 10 5 184 119 17 87 40 1 5 0-10 10-0 0-30 30-40 40-50 50-60 60-70 70-80 80-90 απόδοση/φ υτό
ΠΟΣΟΤΙΚΗ ΓΕΝΕΤΙΚΗ 03. ΜΕΣΗ ΤΙΜΗ & ΔΙΑΚΥΜΑΝΣΗ 1 ΠΟΣΟΤΙΚΟ ΓΝΩΡΙΣΜΑ ΑΑββΓΓδδεεΖΖ αριθμός φυτών 50 00 150 100 50 0 10 5 184 119 17 87 40 1 5 0-10 10-0 0-30 30-40 40-50 50-60 60-70 70-80 80-90 απόδοση/φ υτό
ΕΡΓΑΣΤΗΡΙΟ ΣΤΑΤΙΣΤΙΚΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΤΟΜΕΑΣ ΣΤΑΤΙΣΤΙΚΗΣ ΚΑΙ ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ ΕΡΓΑΣΤΗΡΙΟ ΣΤΑΤΙΣΤΙΚΗΣ Χ 2 test ανεξαρτησίας: σχέση 2 ποιοτικών μεταβλητών
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΤΟΜΕΑΣ ΣΤΑΤΙΣΤΙΚΗΣ ΚΑΙ ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ ΕΡΓΑΣΤΗΡΙΟ ΣΤΑΤΙΣΤΙΚΗΣ Χ 2 test ανεξαρτησίας: σχέση 2 ποιοτικών μεταβλητών
ΑΝΑΛΥΣΗ ΔΙΑΚΥΜΑΝΣΗΣ. Επικ. Καθ. Στέλιος Ζήμερας. Τμήμα Μαθηματικών Κατεύθυνση Στατιστικής και Αναλογιστικά Χρηματοοικονομικά Μαθηματικά
 ΑΝΑΛΥΣΗ ΔΙΑΚΥΜΑΝΣΗΣ Επικ Καθ Στέλιος Ζήμερας Τμήμα Μαθηματικών Κατεύθυνση Στατιστικής και Αναλογιστικά Χρηματοοικονομικά Μαθηματικά 5 Έστω για την σύγκριση δειγμάτων συλλέγουμε παρατηρήσεις Υ =,,, από
ΑΝΑΛΥΣΗ ΔΙΑΚΥΜΑΝΣΗΣ Επικ Καθ Στέλιος Ζήμερας Τμήμα Μαθηματικών Κατεύθυνση Στατιστικής και Αναλογιστικά Χρηματοοικονομικά Μαθηματικά 5 Έστω για την σύγκριση δειγμάτων συλλέγουμε παρατηρήσεις Υ =,,, από
Διερευνητική Ανάλυση Δεδομένων Exploratory Data Analysis
 Διερευνητική Ανάλυση Δεδομένων Exploratory Data Analysis Περιλαμβάνει ένα σύνολο αριθμητικών και γραφικών μεθόδων, που μας επιτρέπουν να αποκτήσουμε μια πρώτη εικόνα για την κατανομή των τιμών της μεταβλητής
Διερευνητική Ανάλυση Δεδομένων Exploratory Data Analysis Περιλαμβάνει ένα σύνολο αριθμητικών και γραφικών μεθόδων, που μας επιτρέπουν να αποκτήσουμε μια πρώτη εικόνα για την κατανομή των τιμών της μεταβλητής
Δρ. Χάϊδω Δριτσάκη. MSc Τραπεζική & Χρηματοοικονομική
 Ποσοτικές Μέθοδοι Δρ. Χάϊδω Δριτσάκη MSc Τραπεζική & Χρηματοοικονομική Τεχνολογικό Εκπαιδευτικό Ίδρυμα Δυτικής Μακεδονίας Western Macedonia University of Applied Sciences Κοίλα Κοζάνης 50100 Kozani GR
Ποσοτικές Μέθοδοι Δρ. Χάϊδω Δριτσάκη MSc Τραπεζική & Χρηματοοικονομική Τεχνολογικό Εκπαιδευτικό Ίδρυμα Δυτικής Μακεδονίας Western Macedonia University of Applied Sciences Κοίλα Κοζάνης 50100 Kozani GR
Λίγα λόγια για τους συγγραφείς 16 Πρόλογος 17
 Περιεχόμενα Λίγα λόγια για τους συγγραφείς 16 Πρόλογος 17 1 Εισαγωγή 21 1.1 Γιατί χρησιμοποιούμε τη στατιστική; 21 1.2 Τι είναι η στατιστική; 22 1.3 Περισσότερα για την επαγωγική στατιστική 23 1.4 Τρεις
Περιεχόμενα Λίγα λόγια για τους συγγραφείς 16 Πρόλογος 17 1 Εισαγωγή 21 1.1 Γιατί χρησιμοποιούμε τη στατιστική; 21 1.2 Τι είναι η στατιστική; 22 1.3 Περισσότερα για την επαγωγική στατιστική 23 1.4 Τρεις
ΑΝΑΛΥΣΗ ΣΥΧΝΟΤΗΤΑΣ ΥΔΡΟΛΟΓΙΚΩΝ ΦΑΙΝΟΜΕΝΩΝ
 ΑΝΑΛΥΣΗ ΣΥΧΝΟΤΗΤΑΣ ΥΔΡΟΛΟΓΙΚΩΝ ΦΑΙΝΟΜΕΝΩΝ Ανάλυση συχνότητας ενός υδρολογικού μεγέθους: Είναι η εύρεση της σχέσεως μεταξύ του υδρολογικού φαινομένου και της πιθανότητας εμφανίσεως του μεγέθους αυτού. Μεταβλητή:
ΑΝΑΛΥΣΗ ΣΥΧΝΟΤΗΤΑΣ ΥΔΡΟΛΟΓΙΚΩΝ ΦΑΙΝΟΜΕΝΩΝ Ανάλυση συχνότητας ενός υδρολογικού μεγέθους: Είναι η εύρεση της σχέσεως μεταξύ του υδρολογικού φαινομένου και της πιθανότητας εμφανίσεως του μεγέθους αυτού. Μεταβλητή:
Κεφ. Ιο ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΘΕΩΡΙΑΣ ΠΙΘΑΝΟΤΗΤΩΝ
 ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος 75 Κεφ. Ιο ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΘΕΩΡΙΑΣ ΠΙΘΑΝΟΤΗΤΩΝ 1.1. Τυχαία γεγονότα ή ενδεχόμενα 17 1.2. Πειράματα τύχης - Δειγματικός χώρος 18 1.3. Πράξεις με ενδεχόμενα 20 1.3.1. Ενδεχόμενα ασυμβίβαστα
ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος 75 Κεφ. Ιο ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΘΕΩΡΙΑΣ ΠΙΘΑΝΟΤΗΤΩΝ 1.1. Τυχαία γεγονότα ή ενδεχόμενα 17 1.2. Πειράματα τύχης - Δειγματικός χώρος 18 1.3. Πράξεις με ενδεχόμενα 20 1.3.1. Ενδεχόμενα ασυμβίβαστα
ΟΙΚΟΝΟΜΕΤΡΙΑ. Παπάνα Αγγελική
 ΟΙΚΟΝΟΜΕΤΡΙΑ Ενότητα 5: Ανάλυση γραμμικού υποδείγματος Πολυμεταβλητή παλινδρόμηση (1 ο μέρος) Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ E-mail: ageliki.papaa@gmail.com, agpapaa@auth.gr Webpage: http://users.auth.gr/agpapaa
ΟΙΚΟΝΟΜΕΤΡΙΑ Ενότητα 5: Ανάλυση γραμμικού υποδείγματος Πολυμεταβλητή παλινδρόμηση (1 ο μέρος) Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ E-mail: ageliki.papaa@gmail.com, agpapaa@auth.gr Webpage: http://users.auth.gr/agpapaa
Εργασία. στα. Γενικευμένα Γραμμικά Μοντέλα
 Εργασία στα Γενικευμένα Γραμμικά Μοντέλα Μ. Παρζακώνης ΜΕΣ/ 06015 Ο παρακάτω πίνακας δίνει τα αποτελέσματα 800 αιτήσεων για δάνειο σε μία τράπεζα. Ο πίνακας παρουσιάζει τον αριθμό των δανείων που εγκρίθηκαν,
Εργασία στα Γενικευμένα Γραμμικά Μοντέλα Μ. Παρζακώνης ΜΕΣ/ 06015 Ο παρακάτω πίνακας δίνει τα αποτελέσματα 800 αιτήσεων για δάνειο σε μία τράπεζα. Ο πίνακας παρουσιάζει τον αριθμό των δανείων που εγκρίθηκαν,
Αναπλ. Καθηγήτρια, Ελένη Κανδηλώρου. Αθήνα Σημειώσεις. Εκτίμηση των Παραμέτρων β 0 & β 1. Απλό γραμμικό υπόδειγμα: (1)
 Σημειώσεις Αναπλ. Καθηγήτρια, Ελένη Κανδηλώρου Αθήνα -3-7 Εκτίμηση των Παραμέτρων β & β Απλό γραμμικό υπόδειγμα: Y X () Η αναμενόμενη τιμή του Υ, δηλαδή, μέση τιμή του Υ, δίνεται παρακάτω: EY ( ) X EY
Σημειώσεις Αναπλ. Καθηγήτρια, Ελένη Κανδηλώρου Αθήνα -3-7 Εκτίμηση των Παραμέτρων β & β Απλό γραμμικό υπόδειγμα: Y X () Η αναμενόμενη τιμή του Υ, δηλαδή, μέση τιμή του Υ, δίνεται παρακάτω: EY ( ) X EY
Στοχαστική ανάλυση και προσοµοίωση υδροµετεωρολογικών διεργασιών σχετικών µε την αιολική και ηλιακή ενέργεια
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Στοχαστική ανάλυση και προσοµοίωση υδροµετεωρολογικών διεργασιών σχετικών µε την αιολική και ηλιακή ενέργεια
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Στοχαστική ανάλυση και προσοµοίωση υδροµετεωρολογικών διεργασιών σχετικών µε την αιολική και ηλιακή ενέργεια
ΟΙΚΟΝΟΜΕΤΡΙΑ. Παπάνα Αγγελική
 ΟΙΚΟΝΟΜΕΤΡΙΑ Ενότητα 13: Επανάληψη Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ E-mail: angeliki.papana@gmail.com, agpapana@auth.gr Webpage: http://users.auth.gr/agpapana 1 Γιατί μελετούμε την Οικονομετρία;
ΟΙΚΟΝΟΜΕΤΡΙΑ Ενότητα 13: Επανάληψη Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ E-mail: angeliki.papana@gmail.com, agpapana@auth.gr Webpage: http://users.auth.gr/agpapana 1 Γιατί μελετούμε την Οικονομετρία;
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ Συσχέτιση επιδόσεων οδικής ασφάλειας με δείκτες υγείας και οικονομίας στην Ευρωπαϊκή Ένωση της Μυρτώς Δαμιανού Αθήνα,
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ Συσχέτιση επιδόσεων οδικής ασφάλειας με δείκτες υγείας και οικονομίας στην Ευρωπαϊκή Ένωση της Μυρτώς Δαμιανού Αθήνα,
Διάλεξη 1 Βασικές έννοιες
 Εργαστήριο SPSS Ψ-4201 (ΕΡΓ) Λεωνίδας Α. Ζαμπετάκης Β.Sc., M.Env.Eng., M.Ind.Eng., D.Eng. Εmail: statisticsuoc@gmail.com Διαλέξεις αναρτημένες στο: Διαλέξεις: ftp://ftp.soc.uoc.gr/psycho/zampetakis/ Διάλεξη
Εργαστήριο SPSS Ψ-4201 (ΕΡΓ) Λεωνίδας Α. Ζαμπετάκης Β.Sc., M.Env.Eng., M.Ind.Eng., D.Eng. Εmail: statisticsuoc@gmail.com Διαλέξεις αναρτημένες στο: Διαλέξεις: ftp://ftp.soc.uoc.gr/psycho/zampetakis/ Διάλεξη
ΛΥΣΕΙΣ ΘΕΜΑΤΩΝ ΣΤΑΤΙΣΤΙΚΗ Ι ΜΕΡΟΣ Α (Σ. ΧΑΤΖΗΣΠΥΡΟΣ) . Δείξτε ότι η στατιστική συνάρτηση T = X( n)
 ΛΥΣΕΙΣ ΘΕΜΑΤΩΝ ΣΤΑΤΙΣΤΙΚΗ Ι ΜΕΡΟΣ Α (Σ. ΧΑΤΖΗΣΠΥΡΟΣ) Θέμα ο (Παρ..3.4, Παρ..4.3, Παρ..4.8.) Εάν = ( ) τυχαίο δείγμα από την ομοιόμορφη ( 0, ) X X,, X. Δείξτε ότι η στατιστική συνάρτηση T = X = το δειγματικό
ΛΥΣΕΙΣ ΘΕΜΑΤΩΝ ΣΤΑΤΙΣΤΙΚΗ Ι ΜΕΡΟΣ Α (Σ. ΧΑΤΖΗΣΠΥΡΟΣ) Θέμα ο (Παρ..3.4, Παρ..4.3, Παρ..4.8.) Εάν = ( ) τυχαίο δείγμα από την ομοιόμορφη ( 0, ) X X,, X. Δείξτε ότι η στατιστική συνάρτηση T = X = το δειγματικό
Στατιστική είναι το σύνολο των μεθόδων και θεωριών που εφαρμόζονται σε αριθμητικά δεδομένα προκειμένου να ληφθεί κάποια απόφαση σε συνθήκες
 Ορισμός Στατιστική είναι το σύνολο των μεθόδων και θεωριών που εφαρμόζονται σε αριθμητικά δεδομένα προκειμένου να ληφθεί κάποια απόφαση σε συνθήκες αβεβαιότητας. Βασικές έννοιες Η μελέτη ενός πληθυσμού
Ορισμός Στατιστική είναι το σύνολο των μεθόδων και θεωριών που εφαρμόζονται σε αριθμητικά δεδομένα προκειμένου να ληφθεί κάποια απόφαση σε συνθήκες αβεβαιότητας. Βασικές έννοιες Η μελέτη ενός πληθυσμού
ΧΡΟΝΙΚΕΣ ΣΕΙΡΕΣ. Παπάνα Αγγελική
 ΧΡΟΝΙΚΕΣ ΣΕΙΡΕΣ 7o Μάθημα: Απλή παλινδρόμηση (ΕΠΑΝΑΛΗΨΗ) Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ & ΠΑΜΑΚ E-mail: angeliki.papana@gmail.com, agpapana@auth.gr Webpage: http://users.auth.gr/agpapana
ΧΡΟΝΙΚΕΣ ΣΕΙΡΕΣ 7o Μάθημα: Απλή παλινδρόμηση (ΕΠΑΝΑΛΗΨΗ) Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ & ΠΑΜΑΚ E-mail: angeliki.papana@gmail.com, agpapana@auth.gr Webpage: http://users.auth.gr/agpapana
ΠΕΡΙΓΡΑΦΙΚΗ ΣΤΑΤΙΣΤΙΚΗ
 Π E Ρ IEXOMENA Πρόλογος... xiii ΜΕΡΟΣ ΠΡΩΤΟ ΠΕΡΙΓΡΑΦΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΚΕΦΑΛΑΙΟ 1 ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ ΠΑΡΟΥΣΙΑΣΗ ΤΩΝ ΣΤΑΤΙΣΤΙΚΩΝ Ε ΟΜΕΝΩΝ 1.1 Εισαγωγή... 3 1.2 Ορισµός και αντικείµενο της στατιστικής... 3
Π E Ρ IEXOMENA Πρόλογος... xiii ΜΕΡΟΣ ΠΡΩΤΟ ΠΕΡΙΓΡΑΦΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΚΕΦΑΛΑΙΟ 1 ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ ΠΑΡΟΥΣΙΑΣΗ ΤΩΝ ΣΤΑΤΙΣΤΙΚΩΝ Ε ΟΜΕΝΩΝ 1.1 Εισαγωγή... 3 1.2 Ορισµός και αντικείµενο της στατιστικής... 3
Το υπουργείο μας. Ατυχήματα - πρώτες βοήθειες στο σχολείο
 Αθήνα 29 Το υπουργείο μας Ατυχήματα - πρώτες βοήθειες στο σχολείο Χρήστος Τριπόδης Αναστάσιος Χριστάκης Παναγιώτα Γ. Ψυχογιού Νικόλαος Τριπόδης Αθήνα 29 Ατυχήματα - πρώτες βοήθειες στο σχολείο Συγγραφείς:
Αθήνα 29 Το υπουργείο μας Ατυχήματα - πρώτες βοήθειες στο σχολείο Χρήστος Τριπόδης Αναστάσιος Χριστάκης Παναγιώτα Γ. Ψυχογιού Νικόλαος Τριπόδης Αθήνα 29 Ατυχήματα - πρώτες βοήθειες στο σχολείο Συγγραφείς:
Πολλαπλή παλινδρόμηση (Multivariate regression)
 ΜΑΘΗΜΑ 3 ο 1 Πολλαπλή παλινδρόμηση (Multivariate regression) Η συμπεριφορά των περισσότερων οικονομικών μεταβλητών είναι συνάρτηση όχι μιας αλλά πολλών μεταβλητών Υ = f ( X 1, X 2,... X n ) δηλαδή η Υ
ΜΑΘΗΜΑ 3 ο 1 Πολλαπλή παλινδρόμηση (Multivariate regression) Η συμπεριφορά των περισσότερων οικονομικών μεταβλητών είναι συνάρτηση όχι μιας αλλά πολλών μεταβλητών Υ = f ( X 1, X 2,... X n ) δηλαδή η Υ
2.5 ΕΛΕΓΧΟΣ ΠΟΣΟΣΤΙΑΙΩΝ ΣΗΜΕΙΩΝ ΜΙΑΣ ΚΑΤΑΝΟΜΗΣ (The Quantile Test)
 .5 ΕΛΕΓΧΟΣ ΠΟΣΟΣΤΙΑΙΩΝ ΣΗΜΕΙΩΝ ΜΙΑΣ ΚΑΤΑΝΟΜΗΣ (The Quantile Test) Ο διωνυμικός έλεγχος μπορεί να χρησιμοποιηθεί για τον έλεγχο υποθέσεων αναφερομένων στα ποσοστιαία σημεία μίας τυχαίας μεταβλητής. Στην
.5 ΕΛΕΓΧΟΣ ΠΟΣΟΣΤΙΑΙΩΝ ΣΗΜΕΙΩΝ ΜΙΑΣ ΚΑΤΑΝΟΜΗΣ (The Quantile Test) Ο διωνυμικός έλεγχος μπορεί να χρησιμοποιηθεί για τον έλεγχο υποθέσεων αναφερομένων στα ποσοστιαία σημεία μίας τυχαίας μεταβλητής. Στην
Περιγραφική Ανάλυση ποσοτικών μεταβλητών
 Περιγραφική Ανάλυση ποσοτικών μεταβλητών Στο data file Worldsales.sav (αρχείο υποθετικών πωλήσεων ανά ήπειρο και προϊόν) Analyze Descriptive Statistics Frequencies Επιλογή μεταβλητής Revenue Πατάμε στο
Περιγραφική Ανάλυση ποσοτικών μεταβλητών Στο data file Worldsales.sav (αρχείο υποθετικών πωλήσεων ανά ήπειρο και προϊόν) Analyze Descriptive Statistics Frequencies Επιλογή μεταβλητής Revenue Πατάμε στο
Υ: Νόσος. Χ: Παράγοντας Κινδύνου 1 (Ασθενής) 2 (Υγιής) Σύνολο. 1 (Παρόν) n 11 n 12 n 1. 2 (Απών) n 21 n 22 n 2. Σύνολο n.1 n.2 n..
 Μέτρα Κινδύνου για Δίτιμα Κατηγορικά Δεδομένα Σε αυτή την ενότητα θα ορίσουμε δείκτες μέτρησης του κινδύνου εμφάνισης μίας νόσου όταν έχουμε δίτιμες κατηγορικές μεταβλητές. Στην πιο απλή περίπτωση μας
Μέτρα Κινδύνου για Δίτιμα Κατηγορικά Δεδομένα Σε αυτή την ενότητα θα ορίσουμε δείκτες μέτρησης του κινδύνου εμφάνισης μίας νόσου όταν έχουμε δίτιμες κατηγορικές μεταβλητές. Στην πιο απλή περίπτωση μας
9. Παλινδρόμηση και Συσχέτιση
 9. Παλινδρόμηση και Συσχέτιση Παλινδρόμηση και Συσχέτιση Υπάρχει σχέση ανάμεσα σε δύο ή περισσότερες μεταβλητές; Αν ναι, ποια είναι αυτή η σχέση; Πως μπορεί αυτή η σχέση να χρησιμοποιηθεί για να προβλέψουμε
9. Παλινδρόμηση και Συσχέτιση Παλινδρόμηση και Συσχέτιση Υπάρχει σχέση ανάμεσα σε δύο ή περισσότερες μεταβλητές; Αν ναι, ποια είναι αυτή η σχέση; Πως μπορεί αυτή η σχέση να χρησιμοποιηθεί για να προβλέψουμε
ΚΟΙΝΩΝΙΟΒΙΟΛΟΓΙΑ, ΝΕΥΡΟΕΠΙΣΤΗΜΕΣ ΚΑΙ ΕΚΠΑΙΔΕΥΣΗ
 A εξάμηνο 2009-2010 ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΚΟΙΝΩΝΙΟΒΙΟΛΟΓΙΑ, ΝΕΥΡΟΕΠΙΣΤΗΜΕΣ ΚΑΙ ΕΚΠΑΙΔΕΥΣΗ Μεθοδολογία Έρευνας και Στατιστική ΑΝΤΩΝΙΟΣ ΧΡ. ΜΠΟΥΡΑΣ Χειμερινό Εξάμηνο 2009-2010 Ποιοτικές και Ποσοτικές
A εξάμηνο 2009-2010 ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΚΟΙΝΩΝΙΟΒΙΟΛΟΓΙΑ, ΝΕΥΡΟΕΠΙΣΤΗΜΕΣ ΚΑΙ ΕΚΠΑΙΔΕΥΣΗ Μεθοδολογία Έρευνας και Στατιστική ΑΝΤΩΝΙΟΣ ΧΡ. ΜΠΟΥΡΑΣ Χειμερινό Εξάμηνο 2009-2010 Ποιοτικές και Ποσοτικές
ΚΕΦΑΛΑΙΟ 0. Απλή Γραμμική Παλινδρόμηση. Ένα Πρόβλημα. Η επιδιωκόμενη ιδιότητα. Ένα χρήσιμο γράφημα. Οι υπολογισμοί. Η μέθοδος ελαχίστων τετραγώνων ...
 ΚΕΦΑΛΑΙΟ 0 Ένα Πρόβλημα Δεδομένα.6 3. 3.8 4. 4.4 5.8 6.0 6.7 7. 7.8 5.6 7.9 8.0 8. 8. 9. 9.5 9.4 9.6 9.9 Απλή Γραμμική Παλινδρόμηση Μωυσιάδης Χρόνης 6 o Εξάμηνο Μαθηματικών Έχει σχέση το με το ; Ειδικότερα
ΚΕΦΑΛΑΙΟ 0 Ένα Πρόβλημα Δεδομένα.6 3. 3.8 4. 4.4 5.8 6.0 6.7 7. 7.8 5.6 7.9 8.0 8. 8. 9. 9.5 9.4 9.6 9.9 Απλή Γραμμική Παλινδρόμηση Μωυσιάδης Χρόνης 6 o Εξάμηνο Μαθηματικών Έχει σχέση το με το ; Ειδικότερα
ΤΥΠΟΛΟΓΙΟ ΣΤΑΤΙΣΤΙΚΗΣ
 - - ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ Πρόγραμμα Σπουδών: ΔΙΟΙΚΗΣΗ ΕΠΙΧΕΙΡΗΣΕΩΝ και ΟΡΓΑΝΙΣΜΩΝ Θεματική Ενότητα: ΔΕΟ3 Ποσοτικές Μέθοδοι Ακαδημαϊκό Έτος: 009-0 ΤΥΠΟΛΟΓΙΟ ΣΤΑΤΙΣΤΙΚΗΣ - - ΑΡΙΘΜΗΤΙΚΕΣ ΜΕΘΟΔΟΙ ΣΥΝΟΨΗΣ
- - ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ Πρόγραμμα Σπουδών: ΔΙΟΙΚΗΣΗ ΕΠΙΧΕΙΡΗΣΕΩΝ και ΟΡΓΑΝΙΣΜΩΝ Θεματική Ενότητα: ΔΕΟ3 Ποσοτικές Μέθοδοι Ακαδημαϊκό Έτος: 009-0 ΤΥΠΟΛΟΓΙΟ ΣΤΑΤΙΣΤΙΚΗΣ - - ΑΡΙΘΜΗΤΙΚΕΣ ΜΕΘΟΔΟΙ ΣΥΝΟΨΗΣ
Εφαρμοσμένη Στατιστική Δημήτριος Μπάγκαβος Τμήμα Μαθηματικών και Εφαρμοσμένων Μαθηματικών Πανεπισ τήμιο Κρήτης 22 Μαΐου /32
 Εφαρμοσμένη Στατιστική Δημήτριος Μπάγκαβος Τμήμα Μαθηματικών και Εφαρμοσμένων Μαθηματικών Πανεπιστήμιο Κρήτης 22 Μαΐου 2017 1/32 Εισαγωγή: Τυπικό παράδειγμα στατιστικού ελέγχου υποθέσεων. Ενας νέος τύπος
Εφαρμοσμένη Στατιστική Δημήτριος Μπάγκαβος Τμήμα Μαθηματικών και Εφαρμοσμένων Μαθηματικών Πανεπιστήμιο Κρήτης 22 Μαΐου 2017 1/32 Εισαγωγή: Τυπικό παράδειγμα στατιστικού ελέγχου υποθέσεων. Ενας νέος τύπος
ΟΙΚΟΝΟΜΕΤΡΙΑ. Παπάνα Αγγελική
 ΟΙΚΟΝΟΜΕΤΡΙΑ Ενότητα 3: Ανάλυση γραμμικού υποδείγματος Απλή παλινδρόμηση (2 ο μέρος) Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ E-mail: angeliki.papana@gmail.com, agpapana@auth.gr Webpage: http://users.auth.gr/agpapana
ΟΙΚΟΝΟΜΕΤΡΙΑ Ενότητα 3: Ανάλυση γραμμικού υποδείγματος Απλή παλινδρόμηση (2 ο μέρος) Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ E-mail: angeliki.papana@gmail.com, agpapana@auth.gr Webpage: http://users.auth.gr/agpapana
Συσχέτιση μεταξύ δύο συνόλων δεδομένων
 Διαγράμματα διασποράς (scattergrams) Συσχέτιση μεταξύ δύο συνόλων δεδομένων Η οπτική απεικόνιση δύο συνόλων δεδομένων μπορεί να αποκαλύψει με παραστατικό τρόπο πιθανές τάσεις και μεταξύ τους συσχετίσεις,
Διαγράμματα διασποράς (scattergrams) Συσχέτιση μεταξύ δύο συνόλων δεδομένων Η οπτική απεικόνιση δύο συνόλων δεδομένων μπορεί να αποκαλύψει με παραστατικό τρόπο πιθανές τάσεις και μεταξύ τους συσχετίσεις,
