ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΑΓΩΓΗΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΜΑΘΗΜΑ: ΔΙΔΑΚΤΙΚΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΔΙΔΑΣΚΩΝ: ΚΟΛΕΖΑ ΕΥΓΕΝΙΑ
|
|
|
- Ἀγλαΐα Ζέρβας
- 9 χρόνια πριν
- Προβολές:
Transcript
1 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΑΓΩΓΗΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΜΑΘΗΜΑ: ΔΙΔΑΚΤΙΚΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΔΙΔΑΣΚΩΝ: ΚΟΛΕΖΑ ΕΥΓΕΝΙΑ ΘΕΜΑ: Σχέδιο Διδασκαλίας Οικονόμου Άννα ΙΩΑΝΝΙΝΑ, Ιανουάριος 2008 ΜΑΘΗΜΑΤΙΚΑ Ε ΤΑΞΗΣ «Σμίκρυνση- Μεγέθυνση» 1
2 Βιβλίο μαθητή: κεφάλαιο 50, «Σμίκρυνση- μεγέθυνση», «Γεωγραφία και Μαθηματικά» (σελ ) Τετράδιο εργασιών: τεύχος δ (σελ ) ΠΕΡΙΕΧΟΜΕΝΑ Σελίδες Α μέρος Εισαγωγή.4 Τρόπος παρουσίασης του κεφαλαίου «Σμίκρυνση- Μεγέθυνση» στο βιβλίο του μαθητή 5 Β μέρος Εναλλακτική παρουσίαση του κεφαλαίου «Σμίκρυνση- Μεγέθυνση» 8 Πώς κάνουμε σμίκρυνση και μεγέθυνση σχήματος; 17 2
3 Διερευνητική δραστηριότητα (τανγκάμ) 18 Προβλήματα- Αξιολόγηση 20 Αυτοαξιολόγηση.25 Γ μέρος Επεκτάσεις- Συνδέσεις (σύνδεση με άλλες ενότητες του βιβλίου της Ε τάξης, διαθεματική σύνδεση) 26 Δ μέρος Λεξικό 29 Για το δάσκαλο (απαραίτητες διδακτικές οδηγίες)..30 3
4 Εναλλακτική παρουσίαση του κεφαλαίου «Σμίκρυνση- μεγέθυνση». Κάθε ενότητα ανοίγει με μια σειρά από ενδιαφέρουσες ερωτήσεις ή πληροφορίες, που σχετίζονται άμεσα με το μαθηματικό περιεχόμενο της ενότητας. Αυτές οι ερωτήσεις και πληροφορίες έχουν σαν στόχο να εισάγουν τους μαθητές στην προβληματική της ενότητας, να κεντρίσουν την περιέργειά τους, να στρέψουν το ενδιαφέρον στα σημαντικότερα σημεία που διαπραγματεύεται η ενότητα και να συνδέσουν την ενότητα με θέματα που ήδη γνωρίζουν. Ειδικότερα, για το κεφάλαιο «Σμίκρυνση- μεγέθυνση» μια πιθανή εισαγωγή θα μπορούσε να είναι η παρακάτω: Στη καθημερινή ζωή συναντάμε συχνά τις έννοιες της σμίκρυνσης και της μεγέθυνσης. Παρατήρησε προσεκτικά τις παρακάτω εικόνες και συζήτησε στην τάξη σου τι βλέπεις στις εικόνες. Μεγενθυτικός φακός 4
5 μικροσκόπιο φωτοτυπικό μηχάνημα 5
6 κιάλια φωτογραφική μηχανή 6
7 τηλεσκόπιο μηχανή; Έχεις σκεφτεί ποτέ, πώς λειτουργεί η φωτογραφική Το φως που αντανακλάται από το αντικείμενο μπαίνει στη μηχανή διαμέσου του φακού ο οποίος αναγκάζει τις ακτίνες να περάσουν μέσα από τον ανοιχτό φωτοφράκτη και το διάφραγμα που καθορίζει τη φωτεινότητα και να σχηματίσουν ένα ανάποδο και αντίστροφο είδωλο πάνω στο φιλμ. Τα φωτοευαίσθητα χημικά του φιλμ ανταποκρίνονται σε διαφορετικά χρώματα και εντάσεις του φωτός σχηματίζοντας μια εικόνα σε λανθάνουσα κατάσταση η οποία μπορεί να εμφανιστεί και να δώσει την τελική έγχρωμη φωτογραφία. Η μηχανή επίσης έχει, ένα σύστημα σκόπευσης που σας επιτρέπει να καδράρετε το θέμα σας. 7
8 Όταν τραβάτε μια φωτογραφία, αναγκάζετε το φως που αντανακλάται από το αντικείμενό σας, να σχηματίσει ένα είδωλο που επιδρά πάνω στα ευαίσθητα χημικά του φιλμ. Η μηχανή ελέγχει αυτή τη διαδικασία με πολλούς τρόπους. Λειτουργία του φακού Τα φωτεινά κύματα που αντανακλώνται από το αντικείμενό σας, περνάνε μέσα στη μηχανή διαμέσου του φακού και του διαφράγματος. Οι σύγχρονοι έγχρωμοι φακοί είναι συνήθως κατασκευασμένοι από έναν αριθμό γυάλινων στοιχείων τα οποία μαζί αναγκάζουν τα φωτεινά κύματα να παρεκκλίνουν και να συναντηθούν σε ένα συγκεκριμένο σημείο πίσω από το φακό, σχηματίζοντας μια καθαρή εικόνα. Το επίπεδο στο οποίο η εικόνα είναι εστιασμένη καθαρή ονομάζεται εστιακό επίπεδο. Μέσα στη μηχανή το επίπεδο αυτό είναι σταθερό και ακριβώς εκεί είναι τοποθετημένο το φιλμ έτσι ώστε να καταγράψει την εικόνα. Η απόσταση ανάμεσα από το κέντρο του φακού και την κύρια εστία, σε χιλιοστά, προσδιορίζει την εστιακή απόσταση του φακού. Εστίαση Τα φωτεινά κύματα από τα κοντινά αντικείμενα συγκλίνουν πιο πίσω από το φακό, στο επίπεδο του ειδώλου. Για μια καθαρή φωτογραφία, αυτό το επίπεδο πρέπει να συμπέσει με το εστιακό επίπεδο, όπου βρίσκεται και το φιλμ αυτό ακριβώς είναι η εστίαση. Κατά την εστίαση ο ίδιος ο φακός μετακινείται για να φέρει το επίπεδο του ειδώλου σε σύμπτωση με το εστιακό επίπεδο. Μπορείτε εύκολα να παρατηρήσετε την κίνηση αυτή του φακού, αν γυρίσετε το δαχτυλίδι της εστίασης της μηχανής σας - ο φακός κινείται προς τα έξω για τα πιο κοντινά αντικείμενα. Ένας φακός εστιασμένος στο άπειρο φέρνει το φως από τα απομακρυσμένα αντικείμενα (παράλληλες ακτίνες κάτω) και το συγκεντρώνει στο εστιακό επίπεδο. Το φως από τα κοντινά αντικείμενα φτάνει στο φακό υπό γωνία και συγκεντρώνεται αρκετά πίσω του στο επίπεδο του ειδώλου Για να εστιαστούν τα κοντινά αντικείμενα, ο φακός έρχεται μπροστά μέχρι που το επίπεδο του ειδώλου να συμπέσει με το εστιακό επίπεδο όπου βρίσκεται το φιλμ. 8
9 Ήξερες ότι. Η εστιακή απόσταση ενός φακού καθορίζει το οπτικό του πεδίο και το μέγεθος στο οποίο μπορεί να δείξει μια εικόνα πάνω στο φιλμ σας. Ένας νορμάλ φακός δίνει ένα μέγεθος εικόνας και ένα οπτικό πεδίο παρόμοιο μ' αυτό που βλέπετε. Ένας φακός με μικρότερη εστιακή απόσταση καλύπτει ένα πιο πλατύ οπτικό πεδίο είναι ένας ευρυγώνιος φακός αλλά ελαττώνει το μέγεθος της εικόνας. Ένας φακός μεγάλης εστιακής απόστασης ή τηλεφακός μεγεθύνει τα μακρινά αντικείμενα δίνοντας ένα πιο μικρό οπτικό πεδίο. Ο χαρακτηρισμός όμως ενός φακού δεν εξαρτάται μόνο από την εστιακή του απόσταση αλλά και από το φορμά της μηχανής. Σε μια μηχανή 35 mm ο νορμάλ φακός είναι 50/55 mm, ένας ευρυγώνιος από 18 μέχρι 35 mm και ένας τηλεφακός από 75 μέχρι 1000 και περισσότερο. Σε μια μηχανή 110 ο νορμάλ φακός έχει εστιακή απόσταση περίπου 24 mm και σε μηχανή 6 χ 6 περίπου 80 mm. Έχεις σκεφτεί ποτέ, πώς λειτουργεί το τηλεσκόπιο; Ο βασικός σκοπός του τηλεσκοπίου είναι να συγκεντρώσει περισσότερο φως από ότι μπορεί να συγκεντρώσει το ανθρώπινο μάτι και στη συνέχεια να μεγενθύνει τα είδωλα έτσι ώστε να μπορέσουμε να διακρίνουμε αντικείμενα που δεν είναι δυνατό να διακρίνουμε δια γυμνού οφθαλμού. Το πιο σπουδαίο μέρος ενός τηλεσκοπίου είναι το κύριο οπτικό του σύστημα που αποτελείται από κάτοπτρα ή φακούς. Το σύστημα αυτό βρίσκεται προστατευμένο μέσα στον οπτικό σωλήνα και είναι το σύστημα εκείνο που συγκεντρώνει το φως. 9
10 Η καρδιά του οπτικού συστήματος είναι ένα κύριο κάτοπτρο ή ένας κύριος φακός. Η διάμετρός του ονομάζεται άνοιγμα του τηλεσκοπίου και καθορίζει κατά μεγάλο βαθμό τις δυνατότητες του τηλεσκοπίου μας. Ο τύπος του οπτικού συστήματος και ο τρόπος που συγκεντρώνει το φως καθορίζει τον τύπο του τηλεσκοπίου. Ένα άλλο σημαντικό χαρακτηριστικό που καθορίζει την οπτική συμπεριφορά του τηλεσκοπίου είναι ο εστιακός λόγος του που σχετίζεται με την απόσταση και τον τρόπο που είναι τοποθετημένα τα οπτικά του μέσα στον οπτικό σωλήνα. Το τηλεσκόπιο δεν αρκεί μόνο να μαζέψει περισσότερο φως, πρέπει και να μεγεθύνει την εικόνα που βλέπουμε. Αυτό το πετυχαίνει με τους προσοφθάλμιους φακούς που είναι οι φακοί μέσα από τους οποίους και κοιτάμε. Οι προσοφθάλμιοι είναι το δεύτερο σημαντικότερο στοιχείο των οπτικών του τηλεσκοπίου και σημαντικός παράγοντας για την οπτική απόδοση του τηλεσκοπίου. Επίσης οι προσοφθάλμιοι φακοί καθορίζουν και την μεγέθυνση που δίνει το τηλεσκόπιό μας. Η άλλη σημαντική πλευρά ενός τηλεσκοπίου είναι τα μηχανικά χαρακτηριστικά. 10
11 Ήξερες ότι. Όσο μεγαλύτερη είναι η φωτοσυλλεκτική επιφάνεια ενός τηλεσκοπίου, τόσο αμυδρότερα αντικείμενα είναι ικανό να ανιχνεύσει. Μεγέθυνση τηλεσκοπίου ονομάζεται η δυνατότητα που έχει ένα τηλεσκόπιο να παρουσιάζει ένα παρατηρούμενο αντικείμενο μεγαλύτερο απ όσο φαίνεται αυτό με γυμνό μάτι. Την μεγέθυνση ενός τηλεσκοπίου την υπολογίζουμε διαιρώντας την εστιακή απόσταση του αντικειμενικού φακού ή κατόπτρου διά αυτής του προσοφθάλμιου φακού. Το όριο ωφέλιμης μεγέθυνσης ενός τηλεσκοπίου εξαρτάται από τη διάμετρο του αντικειμενικού φακού: το όριο είναι σχεδόν το διπλάσιο της διαμέτρου σε χιλιοστά. Για παράδειγμα: Τηλεσκόπιο που φέρει αντικειμενικό φακό διαμέτρου 100 χιλιοστών έχει όριο ωφέλιμης μεγέθυνσης περίπου 200. Η μεγέθυνση τηλεσκοπίου διακρίνεται σε γραμμική και σε επιφανειακή. Γραμμική μεγέθυνση ονομάζεται ο αριθμός που φανερώνει πόσες φορές η φαινόμενη διάμετρος του αντικειμένου καθίσταται μεγαλύτερη. Επιφανειακή μεγέθυνση ονομάζεται ο αριθμός που φανερώνει πόσες φορές η φαινόμενη επιφάνεια του αντικειμένου καθίσταται μεγαλύτερη. Η επιφανειακή μεγέθυνση ισούται προς το τετράγωνο της γραμμικής, π.χ. αν ένα προσοφθάλμιο μεγεθύνει γραμμικά 10 φορές, η επιφανειακή μεγέθυνση είναι 100πλάσια Πώς κάνουμε σμίκρυνση και μεγέθυνση ενός σχήματος; Αφού κατανοήσαμε πώς λειτουργεί η φωτογραφική μηχανή και το τηλεσκόπιο, μπορούμε να μάθουμε ποια βήματα ακολουθούμε για να κάνουμε σμίκρυνση ή μεγέθυνση ενός σχήματος. Για να κάνουμε σμίκρυνση ή μεγέθυνση ενός σχήματος εργαζόμαστε ως εξής: Α. Χωρίζουμε το αρχικό σχήμα σε τετράγωνα. Β. Σχηματίζουμε ένα νέο πλέγμα με ίσο αριθμό από τετράγωνα. Αυτό που αλλάζει είναι το μήκος της πλευράς του κάθε τετραγώνου. Αν κάνουμε σμίκρυνση, τότε το μήκος της πλευράς του κάθε τετραγώνου θα είναι μικρότερο από το αρχικό. Αν κάνουμε μεγέθυνση θα είναι μεγαλύτερο. 11
12 Παρατήρηση: Όταν σχεδιάζουμε με σμίκρυνση ή μεγέθυνση πρέπει πάνω στο σχέδιο να γράφουμε την κλίμακα με τη μορφή διαίρεσης ή κλάσματος. Αναπαραγωγή: Στο νέο πλέγμα το μήκος της πλευράς του κάθε τετραγώνου δεν αλλάζει. Σμίκρυνση: Στο νέο πλέγμα το μήκος της πλευράς κάθε τετραγώνου είναι ίσο με το μισό της πλευράς του τετραγώνου στο αρχικό πλέγμα. Η κλίμακα είναι 1/2 ή 1:2 δηλαδή το σχήμα είναι 2 φορές μικρότερο από το πραγματικό. Μεγέθυνση: Στο νέο πλέγμα το μήκος της πλευράς κάθε τετραγώνου είναι διπλάσιο από την πλευρά του τετραγώνου στο αρχικό πλέγμα. Η κλίμακα είναι 2/1 ή 2:1 δηλαδή το σχήμα είναι 2 φορές μεγαλύτερο από το πραγματικό. Διερευνητική δραστηριότητα. Ακολουθεί μια διερευνητική δραστηριότητα. Δουλεύοντας με αυτή οι μαθητές αναπτύσσουν εννοιολογική κατανόηση, παραγωγικό συλλογισμό, και διαδικαστική ικανότητα. Η δραστηριότητα έχει χτιστεί σε σχέση με τους μαθηματικούς στόχους, και είναι με τέτοιο τρόπο διατυπωμένη ώστε να ευνοεί το μαθηματικό συλλογισμό και την επικοινωνία μεταξύ των μαθητών. 12
13 Οι μαθητές μπορούν να εργαστούν ατομικά, κατά ομάδες, ή συνολικά στην τάξη. Το Τανγκράμ είναι ένα Κινέζικο παιγνίδι που παίζεται ως εξής. Παίρνουμε ένα τετράγωνο και το χωρίζουμε όπως στο διπλανό σχήμα. Στη συνέχεια συνδυάζοντας τις 7 επιφάνειες προσπαθούμε να σχηματίσουμε διάφορες μορφές, ανθρώπων, ζώων ή πραγμάτων. Εδώ θα ασχοληθούμε με ένα τανγκράμ που αποτελείται από επτά σχήματα: πέντε τρίγωνα, ένα τετράγωνο και ένα παραλληλόγραμμο. Αυτά τα σχήματα προκύπτουν από το χωρισμό ενός τετραγώνου σύμφωνα με την παρακάτω εικόνα: Μπορείτε να τακτοποιήσετε κατάλληλα τα επτά κομμάτια και να σχηματίσετε την παρακάτω εικόνα, χρησιμοποιώντας ένα τετράγωνο χαρτί; 13
14 Ένας Κινέζος που τρέχει. Προσπάθησε να ξαναφτιάξεις την παραπάνω εικόνα, αλλά αυτή τη φορά χρησιμοποίησε το παρακάτω τανγκράμ. 14
15 Τι παρατηρείς; Προβλήματα- Αξιολόγηση 1. Σε καθεμία από τις επόμενες προτάσεις να βάλεις Σ αν η πρόταση είναι σωστή και Λ αν είναι λανθασμένη: α) Αν μεταφέρουμε ένα σχήμα στο χαρτί διατηρώντας τις πραγματικές του διαστάσεις, κάνουμε αναπαραγωγή. β) Κλίμακα 1:4 σημαίνει πως το σχέδιο μας είναι ¼ φορές μικρότερο από το πραγματικό. γ) Σμίκρυνση κάνουμε όταν το σχήμα που σχεδιάζουμε έχει διαστάσεις μεγαλύτερες από το πραγματικό. δ) Κλίμακα είναι το πηλίκο της απόστασης στο σχέδιο προς την πραγματική απόσταση. ε) Κλίμακα 10:1 σημαίνει πως το σχέδιο μας είναι 10 φορές μεγαλύτερο από το πραγματικό. στ) Κλίμακα 1/2 σημαίνει ότι το σχήμα μας είναι δύο φορές μικρότερο από το πραγματικό. 2. Να σχεδιάσεις με κλίμακα 1:2 τα ορθογώνια παραλληλόγραμμα με διαστάσεις: α) μήκος 6 εκ., πλάτος 2 εκ. β) μήκος 8 εκ., πλάτος 4 εκ. γ) μήκος 7 εκ., πλάτος 5 εκ. δ) μήκος 7 εκ., πλάτος 2,5 εκ. 3. Να σχεδιάσεις με κλίμακα 2:1 τα ορθογώνια παραλληλόγραμμα με διαστάσεις: α) μήκος 2,4 εκ., πλάτος 1,7 εκ. β) μήκος 1 εκ., πλάτος 0,5 εκ. γ) μήκος 0,9 εκ., πλάτος 0,6 εκ. δ) μήκος 3 εκ., πλάτος 2 εκ. 4. Η Άννα θέλει να σχεδιάσει το δωμάτιο της με κλίμακα 1:100. Το δωμάτιο της έχει σχήμα ορθογωνίου με μήκος 5 μ. και πλάτος 4 μ. Ποιες πρέπει να είναι οι διαστάσεις του ορθογωνίου που θα σχεδιάσει η Άννα; 5. Ένα οικόπεδο έχει σχήμα ορθογωνίου, με μήκος 95 μέτρα και πλάτος 80 μέτρα. Ο Γιάννης το σχεδίασε με κλίμακα 1:500. Ποιες είναι οι διαστάσεις του σχεδίου στο χαρτί; 15
16 6. Ένας βιολόγος παρατηρεί αμοιβάδες στο μικροσκόπιο, με μεγέθυνση 2.500:1. Το πραγματικό μήκος της αμοιβάδας είναι 0,048 χιλ. Ποιο είναι το μήκος της αμοιβάδας όπως φαίνεται στο μικροσκόπιο: α) σε χιλιοστά; β) σε εκατοστά; Ήξερες ότι Αμοιβάδες λέγεται μία ομοταξία πρωτοζώων, που έχουν μικρά ημικυκλικά πόδια με τα οποία μπορούν να κινηθούν. Υπάρχουν δυο είδη αμοιβάδων: Αυτές που έχουν κέλυφος και λέγονται θηκαμοιβάδες και εκείνες που δεν έχουν, οι γυμναμοιβάδες. Ζουν ελεύθερες μέσα στους ποταμούς και στις λίμνες. Μπορούν ακόμη να συναντηθούν και στις εκβολές των ποταμών εκεί που η θάλασσα δεν είναι τόσο αλμυρή, λόγω των νερών του ποταμού. Πολλά είδη απ' αυτές ζουν παρασιτικά μέσα στους διάφορους οργανισμούς ακόμα και στον οργανισμό του ανθρώπου. Οι αμοιβάδες που ζουν παρασιτικά λέγονται "συλλήβδην αμοιβάδες" (αμοιβαδόζωα 7. Ένας αρχιτέκτονας σχεδίασε ένα οικόπεδο σχήματος ορθογωνίου, με κλίμακα 1:650. Το οικόπεδο στο σχέδιο έχει μήκος 0,18 μ. και πλάτος 0,10 μ. Πόσα μέτρα είναι οι πραγματικές διαστάσεις του οικοπέδου; 16
17 8. Η Εύα είδε σε ένα χάρτη της Ελλάδας, με κλίμακα 1: , ότι η απόσταση Τρίπολη- Φλώρινα είναι 19,7 εκ. Πόσα χιλιόμετρα είναι η πραγματική απόσταση των δύο πόλεων; Ήξερες ότι.. Ο όρος χάρτης, παρ ότι προέρχεται από το λατινικό charta (επίσημο έγγραφο), καθιερώθηκε διεθνώς μόλις το 15 ο αιώνα. Μέχρι τότε επικρατούσε ο όρος mappa, ο οποίος στις αγγλόφωνες χώρες διατηρήθηκε ως map μέχρι σήμερα. 9. Η αυλή από το σπίτι του Γιώργου έχει τις διαστάσεις που φαίνονται στο παρακάτω σχήμα. Τι διαστάσεις είχε στην πραγματικότητα αυτή η αυλή; α) σε εκ.; β) σε μ.; 17
18 10. Ο Νίκος είδε σε ένα χάρτη της Ελλάδας, με κλίμακα 1; , ότι η απόσταση Αθήνα- Θεσσαλονίκη είναι 5,13 εκ. Πόσα χιλιόμετρα είναι η πραγματική απόσταση των δύο πόλεων; Ήξερες ότι.. Ανάλογα με τη κλίμακα τους οι χάρτες μπορούν να διαιρεθούν ως εξής: α) Χάρτες μεγάλης κλίμακας, από 1: και μεγαλύτερη. β) Χάρτες μεσαίας κλίμακας, από 1: μέχρι 1: γ) Χάρτες μικρής κλίμακας, από 1: και μικρότερη. 11. Ένα οικόπεδο έχει σχήμα τετραγώνου με πλευρά 210 μ. Ο Παύλος το σχεδίασε με πλευρά 21 εκ. 18
19 α) Να μετατρέψεις την πλευρά του τετραγώνου από μ. σε εκ. β) Να υπολογίσεις την κλίμακα του σχεδίου. 12. Ο Θοδωρής σχεδίασε ένα τετράγωνο με μήκος πλευράς 5 εκ. α) Να βρεις την περίμετρο και το εμβαδόν του τετραγώνου. β) Αν μεγεθύνει την πλευρά του τετραγώνου κατά 20 %, ποια θα είναι η περίμετρος και ποιο το εμβαδόν του νέου τετραγώνου που σχηματίζεται; γ) Αν σμικρύνει την πλευρά του τετραγώνου κατά 20%, ποια θα είναι η περίμετρος και το εμβαδόν του νέου τετραγώνου που σχηματίζεται; 13. Μια τριγωνική πλατεία είναι σχεδιασμένη με κλίμακα 1:500. Οι τρεις πλευρές της στο σχέδιο έχουν μήκη 2,6 εκ., 1,5 εκ. και 3,2 εκ. α) Ποιες είναι οι πραγματικές διαστάσεις της πλατείας σε μέτρα; β) Ποια είναι η περίμετρος της πλατείας; ΑΥΤΟΑΞΙΟΛΟΓΗΣΗ Απαντώ με ναι ή όχι τις παρακάτω ερωτήσεις. Ø Έμαθα πώς να κάνω σμίκρυνση; Ø Έμαθα πώς να κάνω μεγέθυνση; Ø Έμαθα τι ονομάζουμε αναπαραγωγή; Ø Έμαθα τι είναι κλίμακα; Ø Συνεργάστηκα με τους συμμαθητές μου; Επεκτάσεις Συνδέσεις (σύνδεση με άλλες ενότητες του βιβλίου της Ε τάξης, διαθεματική σύνδεση) Υπάρχουν διάφορα μαθηματικά πλαίσια όπου αναπτύσσεται ο κύριος διδακτικός στόχος του κεφαλαίου αυτού. Μερικά από αυτά είναι: αριθμοί και πράξεις, γεωμετρία, μετρήσεις, μοτίβο, προβλήματα. Επιπλέον, υπάρχουν μαθηματικές έννοιες που εμφανίζονται στο κεφάλαιο και δε θα αναπτυχθούν αναλυτικά, όπως: λόγοι, αναλογίες, υπολογισμός κλίμακας, κλάσματα με πολύ μεγάλο παρανομαστή (π.χ. διαβάζουμε 1 προς 1εκατομμύριο και όχι ένα εκατομμυριοστό). 19
20 Ωστόσο, o εκπαιδευτικός έχει την ευκαιρία να περάσει διαθεματικά από το μάθημα των Μαθηματικών στο μάθημα της Γεωγραφίας. Ειδικότερα: Διαθεματική σύνδεση με το μάθημα της Γεωγραφίας. Τα Μαθηματικά μπορούν να λειτουργήσουν ως έναυσμα για να μιλήσει ο δάσκαλος στους μαθητές του για την έννοια της κλίμακας των χαρτών. Για παράδειγμα, ο δάσκαλος μπορεί να χρησιμοποιήσει τα Μαθηματικά για να βοηθήσει τους μαθητές να κατανοήσουν τις παρακάτω γεωγραφικές έννοιες: Κλασματική κλίμακα Εκφράζεται ως κλάσμα με αριθμητή τη μονάδα και παρονομαστή έναν αριθμό που δείχνει πόσες φορές μία γραμμή στο χάρτη είναι μικρότερη από την αντίστοιχη της στο έδαφος. Κλίμακα, π.χ. 1: σημαίνει ότι 1 cm στο χάρτη αντιστοιχεί με cm στην επιφάνεια της Γης. Η σχέση μεταξύ της κλίμακας, της απόστασης στο χάρτη και της απόστασης στο έδαφος δίνεται από τον τύπο: Κ = Κλίμακα του χάρτη μ = Απόσταση στο χάρτη ή γραφικό μήκος. Μ = Πραγματική απόσταση ή φυσικό μήκος. Ανάλογα με την προβολή που χρησιμοποιήθηκε για την κατασκευή του χάρτη η κλίμακα μπορεί να ισχύει, είτε για όλη την έκταση του, είτε για ορισμένες διευθύνσεις, π.χ. για τον ισημερινό ή κεντρικό μεσημβρινό. Μία κλίμακα χαρακτηρίζεται μικρή, εφ' όσον η τιμή του παρονομαστή του κλάσματος είναι μεγάλη, και μεγάλη, εφ' όσον η τιμή αυτή είναι μικρή. Η κλίμακα χάρτη, π.χ., 1: είναι μικρότερη από την κλίμακα 1: ενός άλλου χάρτη με τις ίδιες εξωτερικές διαστάσεις. Γραφική κλίμακα Επειδή, με φωτομεγέθυνση ή φωτοσμίκρυνση του χάρτη, η κλασματική κλίμακα του δεν μπορεί να χρησιμοποιηθεί για τη μέτρηση αποστάσεων, στο περιθώριο όλων σχεδόν των επίσημων χαρτών σχεδιάζεται η γραφική τους κλίμακα. 20
21 Η γραφική κλίμακα είναι μια ευθεία γραμμή με υποδιαιρέσεις σε τμήματα που αντιστοιχούν σε Km ή m. (σχ. 15). Με απλή εφαρμογή της γραφικής κλίμακας μεταξύ δοθέντων σημείων του χάρτη, υπολογίζεται η πραγματική τους απόσταση. Για το λόγο αυτό, αλλά και επιπλέον επειδή, με φωτοσμίκρυνση ή φωτομεγέθυνση του χάρτη, η γραφική κλίμακα υφίσταται ανάλογη σμίκρυνση ή μεγέθυνση, αυτή χρησιμοποιείται συχνότερα από την κλασματική. Σχ. 15. Γραφική κλίμακα που χρησιμοποιείται στους τοπογραφικούς χάρτες της Ελληνικής Γεωγραφικής Υπηρεσίας Στρατού (Γ. Υ.Σ.). Σχέση μεταξύ κλίμακας και εμβαδού των χαρτών Το εμβαδά που καλύπτει ένας χάρτης ορισμένων εξωτερικών διαστάσεων καθορίζεται από την κλίμακα του. Όσο μικρότερη είναι η κλίμακα, τόσο μεγαλύτερο είναι το εμβαδό του χάρτη. Έχει αποδειχθεί ότι σε κάθε μεταβολή της κλίμακας ενός χάρτη, μεταβάλλεται και το εμβαδόν του. Αυτή η μεταβολή μάλιστα δεν είναι τυχαία, αλλά υπακούει σε ορισμένη μαθηματική σχέση. Το εμβαδόν π.χ. ενός τοπογραφικού χάρτη κλίμακας 1: που είναι ίσο με 250 km2, θα γίνει ίσο με Κm2, εφ όσον η κλίμακα γίνει 1: Δηλαδή, η μεταβολή του εμβαδού ενός χάρτη ορισμένων εξωτερικών διαστάσεων είναι αντιστρόφως ανάλογη του τετραγώνου της μεταβολής της κλίμακας. Στο παράδειγμα μας, η κλίμακα του χάρτη υποδιπλασιάστηκε και το εμβαδόν του τετραπλασιάστηκε. Προσδιορισμός της κλίμακας των Χαρτών Ο καθορισμός της κλίμακας σε χάρτη, που δεν υπάρχει η αντίστοιχη ένδειξη της, μπορεί να γίνει με την παρακάτω διαδικασία: Εκλέγονται δύο σημεία τα οποία υπάρχουν στο χάρτη αυτό και σ' έναν άλλο χάρτη γνωστής κλίμακας. Καθορίζονται οι αποστάσεις των δύο σημείων στους δύο χάρτες και στη συνέχεια υπολογίζεται η ζητούμενη κλίμακα με τη βοήθεια της πραγματικής απόστασης των σημείων, που υπολογίζεται από τον χάρτη με την γνωστή κλίμακα. Παράδειγμα: Η απόσταση δύο πόλεων σε χάρτη χωρίς κλίμακα είναι 5 cm. Σε χάρτη με κλίμακα 1: , η αντίστοιχη απόσταση των δύο πόλε- ων είναι 4 cm=4 km. Τα 5 cm, λοιπόν στο χάρτη χωρίς κλίμακα αντιστοι- χουν με φυσικό μήκος 4 Km. 21
22 Εκφράζουμε τα δύο μήκη στην ίδια μονάδα. Τα 5 cm αντιστοιχούν με cm, άρα το 1 cm με cm και η κλίμακα του χάρτη είναι ίση με 1: Διαθεματική σύνδεση με το μάθημα της Φυσικής. Πέρα από το μάθημα της Γεωγραφίας, o εκπαιδευτικός έχει την ευκαιρία να περάσει διαθεματικά από το μάθημα των Μαθηματικών στη Φυσική. Πιο συγκεκριμένα, μπορεί να τους αναφέρει ότι μπορούν να υπάρξουν περιπτώσεις μεγέθυνσης ή σμίκρυνσης όπου δεν υπάρχει κάποια αναλογία (με τη μορφή κλίμακας) σε σχέση με την αρχική κατάσταση. Για παράδειγμα, καθώς ο ανθρώπινος οργανισμός αναπτύσσεται (μεγεθύνεται), το κεφάλι του αναπτύσσεται (μεγεθύνεται) με διαφορετικό τρόπο. Αναλυτικότερα, ο εκπαιδευτικός μπορεί να ξεκινήσει ρωτώντας τους μαθητές αν ο άνθρωπος όπως το ηλιοτρόπιο και τα κοχύλια. Αυτό που αρχικά πρέπει να κάνει ο δάσκαλος είναι να δώσει μια φωτογραφία ενός ηλιοτροπίου (δες Εικόνα 1) στους μαθητές, έτσι ώστε και αυτοί που δεν το γνωρίζουν να το μάθουνε. Στη συνέχεια, οι μαθητές θα κάνουν παρατηρήσεις πάνω στη φωτογραφία, όπως για παράδειγμα το ότι υπάρχει μια κανονικότητα στον τρόπο με τον οποίο έχουν αναπτυχθεί τα σποράκια του. Εικόνα 1 Στη συνέχεια ο εκπαιδευτικός μπορεί να ψάξει μαζί με τους μαθητές στο internet πληροφορίες για το όστρακο nautilus pompilius (δες Εικόνα 2) και να συζητήσουν τον τρόπο με τον οποίο αναπτύσσεται. Εικόνα 2 22
23 Το όστρακο αυτό αναπτύσσεται πάντα με τέτοιο τρόπο ώστε το σχήμα του να διατηρείται. Κάθε καινούριος θάλαμος που προστίθεται στο κέλυφος του κοχυλιού είναι το ίδιο σχήμα με το προηγούμενο και το σχήμα του κελύφους σαν σύνολο παραμένει το ίδιο. Στο σημείο αυτό ο εκπαιδευτικός και οι μαθητές μπορούν να περάσουν και στον άνθρωπο συζητώντας το γεγονός πως αν και οι περισσότεροι ζωντανοί οργανισμοί αναπτύσσονται με συντελεστή μεγαλύτερο από 2 κατά τη διάρκεια της ζωής τους, με τον άνθρωπο δεν συμβαίνει το ίδιο. Σχετικά με το μέγεθος το σώματος, το κεφάλι ενός βρέφους είναι πολύ μεγαλύτερο από αυτό του ενήλικα. Αλλά και η άκρη της μύτης του βρέφους βρίσκεται ακριβώς στη μέση του προσώπου του, ενώ σε έναν ενήλικα στα 2/3 του μεγέθους του προσώπου από πάνω προς τα κάτω (δες Εικόνα 3). Εικόνα 3 Τα παιδιά μπορούν στο σημείο αυτό να κοιτάξουν τις μύτες τους σε ένα καθρέφτη, να εμπεδώσουν την έννοια του κλάσματος καθώς και να μετρήσουν την περίμετρο του κεφαλιού τους, το ύψος τους ή την απόσταση της μύτης τους από την κορυφή του κεφαλιού τους με μια μεζούρα. Σε όλα αυτά πρέπει να προστεθεί πως ο εκπαιδευτικός μετά από τα παραπάνω μπορεί να μιλήσει και για το πώς μπορούν οι ειδικοί της αστυνομίας να προβλέπουν πως τυχόν θα είναι κάποιος εξαφανισμένος εδώ και χρόνια (δες Εικόνες 4 και 5). Αφού γνωρίζουν το πώς αναπτύσσεται το ανθρώπινο κρανίο και τις αλλαγές που συμβαίνουν στα διάφορα σημεία του 23
24 καταφέρνουν με τη βοήθεια του ηλεκτρονικού υπολογιστή να δημιουργήσουν μια κατά προσέγγιση εικόνα του εξαφανισθέντος. Εικόνα 4 Εικόνα 5 Αφού τα παιδιά δούνε και τις αλλαγές στο σχήμα ενός ανθρώπινου κρανίου από τη βρεφική ηλικία μέχρι την ενηλικίωση συνειδητοποιούν πως η ανάπτυξη του ηλιοτρόπιου και των κοχυλιών δεν έχουν καμία σχέση με την ανάπτυξη του ανθρώπινου σώματος. Στη συνέχεια οι μαθητές μπορούν να προχωρήσουν είτε κάνοντας και άλλες μαθηματικές δραστηριότητες με τη χρήση διαφόρων εργαλείων πάνω στο ίδιο τους το σώμα ή περνάνε διαθεματικά σε άλλο μάθημα. Μπορούν δηλαδή να περάσουν στα Καλλιτεχνικά ζωγραφίζοντας κάτι που τους έκανε εντύπωση από όσα συζήτησαν ή φτιάχνοντας με πηλό κεφάλια ή και ολόκληρα μωρά και ενήλικες ή και τους ίδιους τους τους εαυτούς. Ακόμη, με αφορμή τα Μαθηματικά, ο δάσκαλος μπορεί να κάνει σύνδεση με το μάθημα της Γεωγραφίας 24
25 ΛΕΞΙΚΟ Όταν μεταφέρουμε ένα σχήμα στο χαρτί μπορούμε: α) να διατηρήσουμε τις πραγματικές του διαστάσεις, να κάνουμε δηλαδή αναπαραγωγή του σχήματος, β) να το σχεδιάσουμε μικρότερο από ότι είναι στην πραγματικά, να κάνουμε δηλαδή σμίκρυνση του σχήματος, γ) να το σχεδιάσουμε μεγαλύτερο από ότι είναι πραγματικά, να κάνουμε δηλαδή μεγέθυνση του σχήματος. Ακόμη, στο κεφάλαιο αυτό έγινε λόγος για τη κλίμακα. Κλίμακα ονομάζουμε το πηλίκο της απόστασης δύο σημείων στο σχέδιο, προς την πραγματική τους απόσταση: Η κλίμακα μας δείχνει πόσες φορές μικρότερο ή μεγαλύτερο είναι το μέγεθος ενός σχήματος από το πραγματικό. Για το δάσκαλο (Απαραίτητες διδακτικές οδηγίες) Για τη διδασκαλία του κεφαλαίου «Σμίκρυνση- Μεγέθυνση», θα μπορούσε να γίνει ένας συνδυασμός ανάμεσα στο τρόπο που παρουσιάζεται στο βιβλίο του δασκάλου και το τρόπο που προτείνουμε παραπάνω. 25
26 Ειδικότερα, πριν ξεκινήσει ο δάσκαλος τη διδασκαλία του, κρίνεται σκόπιμο να κάνει μια επανάληψη στις έννοιες περίμετρο, εμβαδόν και στις μονάδες μέτρησης τους. Ο δάσκαλος μπορεί να το πετύχει με μια σειρά από ερωτήσεις όπως: Τι ονομάζουμε περίμετρο ενός γεωμετρικού σχήματος; Πώς την υπολογίζουμε; Σε ένα γεωμετρικό σχήμα, ονομάζουμε περίμετρο, το μήκος του περιγράμματος του. Την περίμετρο ενός γεωμετρικού σχήματος μπορούμε να τη βρούμε εύκολα, αν αθροίσουμε τα μήκη όλων των πλευρών του. Παράδειγμα 1 ο Η περίμετρος του διπλανού τετραγώνου είναι: = 8 εκ. ή 4 2 = 8 τ.εκ. Παράδειγμα 2 ο Η περίμετρος του παραπάνω ορθογωνίου παραλληλογράμμου είναι: = 14 εκ. ή (2 4) + (2 3)= 8 + 6= 14 εκ. Ποια σχήματα ονομάζουμε ισοπεριμετρικά; Ισοπεριμετρικά ονομάζουμε τα διαφορετικά μεταξύ τους σχήματα που έχουν ίδια περίμετρο. 26
27 Παράδειγμα Ένα τετράγωνο με πλευρά 3 εκ. και ένα ισόπλευρο τρίγωνο με πλευρά 4 εκ. έχουν την ίδια περίμετρο, δηλαδή είναι ισοπεριμετρικά. Τι ονομάζουμε εμβαδόν ενός γεωμετρικού σχήματος; 27
28 Εμβαδόν ονομάζουμε το αποτέλεσμα που προκύπτει από τη μέτρηση της επιφάνειας ενός γεωμετρικού σχήματος. Παρατήρηση ü Η περίμετρος και το εμβαδόν είναι δύο διαφορετικά μεγέθη. ü Η περίμετρος είναι η μέτρηση του περιγράμματος μιας επιφάνειας, ενώ το εμβαδόν είναι η μέτρηση ολόκληρης της επιφάνειας. Παράδειγμα Στο παρακάτω σχήμα το εμβαδόν είναι ζωγραφισμένο με κόκκινο χρώμα, ενώ η περίμετρος με μαύρο. Τι είναι το τετραγωνικό εκατοστό (τ. εκ.) και που το χρησιμοποιούμε; Το τετραγωνικό εκατοστό (τ. εκ.) είναι η επιφάνεια που καλύπτει ένα τετράγωνο με μήκος πλευράς 1 εκατοστόμετρο: Το χρησιμοποιούμε για να υπολογίσουμε το εμβαδόν γεωμετρικών σχημάτων. Παρατηρήσεις ü Το εμβαδόν, εκτός από τ. εκ., το μετράμε και σε τετραγωνικά μέτρα (τ. μ.), τετραγωνικά χιλιοστόμετρα (τ. χιλ.) κ.τ.λ. 28
29 ü Η μονάδα μέτρησης της περιμέτρου είναι διαφορετική από τη μονάδα μέτρησης του εμβαδού. Την περίμετρο την μετράμε σε μέτρα (μ.), εκατοστόμετρα (εκ.) κ.λ.π. Παράδειγμα Το πρώτο σχήμα καλύπτει επιφάνεια 5 τετραγωνικών εκατοστών (τ. εκ.), άρα έχει εμβαδόν 5 τ.εκ. Το δεύτερο σχήμα καλύπτει επιφάνεια 6 τετραγωνικών εκατοστών (τ. εκ.), άρα έχει εμβαδόν 6 τ. εκ. Ποια σχήματα ονομάζουμε ισοεμβαδικά; Ισοεμβαδικά ονομάζουμε τα διαφορετικά μεταξύ τους σχήματα που έχουν το ίδιο εμβαδόν. Παράδειγμα 29
30 Υπολογίζουμε το εμβαδόν και την περίμετρο των παρακάτω σχημάτων, αν 1 = 1 τ.εκ. o Εμβαδόν τετραγώνου =4 τ.εκ. Περίμετρος τετραγώνου =8 εκ. o Εμβαδόν ορθογωνίου =4 τ.εκ. Περίμετρος ορθογωνίου =10 εκ. Τα σχήματα είναι ισοεμβαδικά, αλλά όχι ισοπεριμετρικά. Αφού οι μαθητές ξαναθυμηθούν τις παραπάνω έννοιες, μπορούν να ασχοληθούν με την ερώτηση ελέγχου που προτείνεται στο βιβλίο του δασκάλου. Μόλις επιλύσουν σωστά την ερώτηση ελέγχου, οι μαθητές μπορούν να ανοίξουν το βιβλίο τους και να διαβάσουν την ερώτηση αφόρμησης αναφορικά για το πώς διαβάζουμε το χάρτη της Ελλάδας. Παρατηρούν το χάρτη της Ελλάδας και σχολιάζουν την ύπαρξη υπομνήματος. Στη συνέχεια, ασχολούνται με τη δραστηριότητα- ανακάλυψη του βιβλίου τους και ακολουθεί διάλογος για ποιο λόγο χρησιμοποιούμε τη σμίκρυνση στους χάρτες. Στο σημείο αυτό, ο δάσκαλος μπορεί να παρουσιάσει στους μαθητές του τις εικόνες που δίνουμε στην εναλλακτική παρουσίαση του συγκεκριμένου κεφαλαίου. Αφού οι μαθητές παρατηρήσουν προσεκτικά τις εικόνες, θα συζητήσουν στη τάξη για το τι βλέπουν στις εν λόγω εικόνες. Έτσι μέσα από παραδείγματα της καθημερινής ζωής, ο δάσκαλος μπορεί να εισάγει τους μαθητές του στις έννοιες της σμίκρυνσης και της μεγέθυνσης. Ύστερα από αυτό, οι μαθητές θα επιστρέψουν στο 30
31 βιβλίο τους για να διαβάσουν τους ορισμούς που δίνει για τις έννοιες της αναπαραγωγής, της σμίκρυνσης και της μεγέθυνσης. Στη συνέχεια, ο δάσκαλος μπορεί να διαβάσει στους μαθητές του το πληροφοριακό υλικό για τη λειτουργία της φωτογραφικής μηχανής και του τηλεσκοπίου που δίνεται στην εναλλακτική παρουσίαση. Μετά την ανάγνωση του πληροφοριακού υλικού, ο δάσκαλος θα δείξει στους μαθητές του τα βήματα που ακολουθούμε για να κάνουμε σμίκρυνση ή μεγέθυνση ενός σχήματος όπως προτείνεται στην εναλλακτική παρουσίαση. Αφού οι μαθητές κατανοήσουν τη διαδικασία, είναι έτοιμοι να ασχοληθούν με τη διερευνητική δραστηριότητα (τανγράμ) όπως προτείνεται στην εναλλακτική παρουσίαση του κεφαλαίου. Πέρα από τη διερευνητική δραστηριότητα, οι μαθητές μπορούν να ασχοληθούν με τη πρώτη δραστηριότητα του βιβλίου τους. Θα ακολουθήσει μια σύνοψη της νέας γνώσης και θα γίνει ανάγνωση και ερμηνεία του συμπεράσματος στο βιβλίο του μαθητή. Στη συνέχεια, οι μαθητές θα ασχοληθούν με τις εργασίες του τετραδίου του μαθητή με τη σειρά που προτείνονται στο βιβλίο του δασκάλου. Θα ακολουθήσει η αξιολόγηση των μαθητών με την επίλυση των προβλημάτων που προτείνονται στην εναλλακτική παρουσίαση του κεφαλαίου. Αφού ολοκληρωθεί η αξιολόγηση, οι μαθητές θα κάνουν την αυτοαξιολογησή τους απαντώντας στις ερωτήσεις που δίνονται στην εναλλακτική παρουσίαση. Η διδασκαλία του συγκεκριμένου κεφαλαίου θα κλείσει με μια σύνοψη των εννοιών που διαπραγματεύτηκαν σε αυτό το κεφάλαιο, καθώς και την ανάγνωση του λεξιλογίου. Τέλος, μπορεί να γίνει διαθεματική σύνδεση των Μαθηματικών με άλλα μαθήματα, όπως προτείνεται στην εναλλακτική παρουσίαση του κεφαλαίου. 31
ΕΡΓΑΣΤΗΡΙΟ ΤΕΧΝΟΛΟΓΙΑΣ ΟΠΤΙΚΩΝ ΟΡΓΑΝΩΝ
 ΕΡΓΑΣΤΗΡΙΟ ΤΕΧΝΟΛΟΓΙΑΣ ΟΠΤΙΚΩΝ ΟΡΓΑΝΩΝ Άσκηση 4. Διαφράγματα. Θεωρία Στο σχεδιασμό οπτικών οργάνων πρέπει να λάβει κανείς υπόψη και άλλες παραμέτρους πέρα από το πού και πώς σχηματίζεται το είδωλο ενός
ΕΡΓΑΣΤΗΡΙΟ ΤΕΧΝΟΛΟΓΙΑΣ ΟΠΤΙΚΩΝ ΟΡΓΑΝΩΝ Άσκηση 4. Διαφράγματα. Θεωρία Στο σχεδιασμό οπτικών οργάνων πρέπει να λάβει κανείς υπόψη και άλλες παραμέτρους πέρα από το πού και πώς σχηματίζεται το είδωλο ενός
ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ ΦΩΤΟΓΡΑΦΙΑΣ Εν Αθήναις e-book 2012
 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ ΦΩΤΟΓΡΑΦΙΑΣ Εν Αθήναις e-book 2012 Συγγραφέας: dimdom 2 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ ΦΩΤΟΓΡΑΦΙΑΣ Εν Αθήναις e-book 2012 ΦΑΚΟΙ Τό φῶς ἀπό τά κοντινά ἀντικείμενα συγκλίνει πίσω ἀπό τό φακό, στό ἐπίπεδό
ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ ΦΩΤΟΓΡΑΦΙΑΣ Εν Αθήναις e-book 2012 Συγγραφέας: dimdom 2 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ ΦΩΤΟΓΡΑΦΙΑΣ Εν Αθήναις e-book 2012 ΦΑΚΟΙ Τό φῶς ἀπό τά κοντινά ἀντικείμενα συγκλίνει πίσω ἀπό τό φακό, στό ἐπίπεδό
Φωτογραφική μηχανή - Αρχή λειτουργίας.
 Ο25 Φωτογραφική μηχανή - Αρχή λειτουργίας. 1 Σκοπός Στην άσκηση αυτή γίνεται μία παρουσίαση των βασικών στοιχείων της φωτογραφικής μηχανής (φακός φωτοφράκτης - διάφραγμα αισθητήρας) καθώς και μία σύντομη
Ο25 Φωτογραφική μηχανή - Αρχή λειτουργίας. 1 Σκοπός Στην άσκηση αυτή γίνεται μία παρουσίαση των βασικών στοιχείων της φωτογραφικής μηχανής (φακός φωτοφράκτης - διάφραγμα αισθητήρας) καθώς και μία σύντομη
ΓΥΜΝΑΣΙΟ ΚΑΣΤΕΛΛΑΝΩΝ ΜΕΣΗΣ ΑΛΓΕΒΡΑ
 ΑΛΓΕΒΡΑ ΠΡΟΑΠΑΙΤΟΥΜΕΝΑ ΑΠΟ Α ΓΥΜΝΑΣΙΟΥ Ομόσημοι Ετερόσημοι αριθμοί Αντίθετοι Αντίστροφοι αριθμοί Πρόσθεση ομόσημων και ετερόσημων ρητών αριθμών Απαλοιφή παρενθέσεων Πολλαπλασιασμός και Διαίρεση ρητών αριθμών
ΑΛΓΕΒΡΑ ΠΡΟΑΠΑΙΤΟΥΜΕΝΑ ΑΠΟ Α ΓΥΜΝΑΣΙΟΥ Ομόσημοι Ετερόσημοι αριθμοί Αντίθετοι Αντίστροφοι αριθμοί Πρόσθεση ομόσημων και ετερόσημων ρητών αριθμών Απαλοιφή παρενθέσεων Πολλαπλασιασμός και Διαίρεση ρητών αριθμών
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ ΜΑΘΗΜΑΤΙΚΩΝ-Β ΦΑΣΗ ΘΕΜΑ ΔΙΔΑΣΚΑΛΙΑΣ: ΣΤΡΑΤΗΓΙΚΕΣ ΔΙΑΧΕΙΡΙΣΗΣ ΑΡΙΘΜΩΝ-19 ο ΚΕΦΑΛΑΙΟ ΣΧΟΛΕΙΟ: 2 ο ΠΕΙΡΑΜΑΤΙΚΟ ΦΛΩΡΙΝΑΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ ΜΑΘΗΜΑΤΙΚΩΝ-Β ΦΑΣΗ ΘΕΜΑ ΔΙΔΑΣΚΑΛΙΑΣ: ΣΤΡΑΤΗΓΙΚΕΣ ΔΙΑΧΕΙΡΙΣΗΣ ΑΡΙΘΜΩΝ-19 ο ΚΕΦΑΛΑΙΟ ΣΧΟΛΕΙΟ: 2 ο ΠΕΙΡΑΜΑΤΙΚΟ ΦΛΩΡΙΝΑΣ
Περιεχόμενο διδασκαλίας Στόχοι Παρατηρήσεις. υπολογίζουν το λόγο δύο λόγο δύο τμημάτων
 Νίκος Γ. Τόμπρος ΣΧΕΔΙΟ ΜΑΘΗΜΑΤΩΝ Ενότητα : ΟΜΟΙΟΤΗΤΑ (ΛΟΓΟΣ ΑΝΑΛΟΓΙΑ) Σκοποί: Η ανάπτυξη ενδιαφέροντος για το θέμα, η εξοικείωση με τη χρήση τεχνολογίας, η παρότρυνση για αναζήτηση πληροφοριών (εδώ σε
Νίκος Γ. Τόμπρος ΣΧΕΔΙΟ ΜΑΘΗΜΑΤΩΝ Ενότητα : ΟΜΟΙΟΤΗΤΑ (ΛΟΓΟΣ ΑΝΑΛΟΓΙΑ) Σκοποί: Η ανάπτυξη ενδιαφέροντος για το θέμα, η εξοικείωση με τη χρήση τεχνολογίας, η παρότρυνση για αναζήτηση πληροφοριών (εδώ σε
Κεφάλαιο 1 Εισαγωγή. Φυσική Β Γυμνασίου
 Κεφάλαιο 1 Εισαγωγή Φυσική Β Γυμνασίου Απαντήσεις ερωτήσεων σχολικού βιβλίου σχ. βιβλίο (σ.σ. 18-19) Γυμνάσιο: 9.000 μαθήματα με βίντεο-διδασκαλία για όλο το σχολικό έτος μόνο με 150 ευρώ! Μελέτη όπου,
Κεφάλαιο 1 Εισαγωγή Φυσική Β Γυμνασίου Απαντήσεις ερωτήσεων σχολικού βιβλίου σχ. βιβλίο (σ.σ. 18-19) Γυμνάσιο: 9.000 μαθήματα με βίντεο-διδασκαλία για όλο το σχολικό έτος μόνο με 150 ευρώ! Μελέτη όπου,
5ο Μάθημα ΜΕΤΡΗΣΗ ΕΠΙΦΑΝΕΙΑΣ ΚΑΙ ΟΓΚΟΥ
 5ο Μάθημα ΜΕΤΡΗΣΗ ΕΠΙΦΑΝΕΙΑΣ ΚΑΙ ΟΓΚΟΥ Μετρούμε αλλά και υπολογίζουμε Στο προηγούμενο μάθημα χρησιμοποιήσαμε το μέτρο, αλλά και άλλα όργανα με τα οποία μετρούμε το μήκος. Το σχήμα που μετρούμε με το μέτρο
5ο Μάθημα ΜΕΤΡΗΣΗ ΕΠΙΦΑΝΕΙΑΣ ΚΑΙ ΟΓΚΟΥ Μετρούμε αλλά και υπολογίζουμε Στο προηγούμενο μάθημα χρησιμοποιήσαμε το μέτρο, αλλά και άλλα όργανα με τα οποία μετρούμε το μήκος. Το σχήμα που μετρούμε με το μέτρο
Στόχοι ΑΠΣ για τα μαθηματικά της Ε τάξης
 Στόχοι ΑΠΣ για τα μαθηματικά της Ε τάξης ΘΕΜΑΤΙΚΕΣ ΕΝΟΤΗΤΕΣ ΚΕΦΑΛΑΙΑ ΣΤΟΧΟΙ ΧΡΟΝΟΣ Αριθμοί και πράξειςακέραιοι 2, 3, 4, 5 2. να μπορούν να εκφράζουν αριθμούς μέχρι και το 1.000.000 με διάφορους τρόπους
Στόχοι ΑΠΣ για τα μαθηματικά της Ε τάξης ΘΕΜΑΤΙΚΕΣ ΕΝΟΤΗΤΕΣ ΚΕΦΑΛΑΙΑ ΣΤΟΧΟΙ ΧΡΟΝΟΣ Αριθμοί και πράξειςακέραιοι 2, 3, 4, 5 2. να μπορούν να εκφράζουν αριθμούς μέχρι και το 1.000.000 με διάφορους τρόπους
Τεχνικό Τοπογραφικό Σχέδιο
 Τεχνικό Τοπογραφικό Σχέδιο Γ. Καριώτου ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ & ΜΗΧΑΝΙΚΩΝ ΤΟΠΟΓΡΑΦΙΑΣ ΚΑΙ ΓΕΩΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕ 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Τεχνικό Τοπογραφικό Σχέδιο Γ. Καριώτου ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ & ΜΗΧΑΝΙΚΩΝ ΤΟΠΟΓΡΑΦΙΑΣ ΚΑΙ ΓΕΩΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕ 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα. Αντώνης Πουλιάσης Φυσικός M.Sc. 12 ο ΓΥΜΝΑΣΙΟ ΠΕΡΙΣΤΕΡΙΟΥ
 Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Αντώνης Πουλιάσης Φυσικός M.Sc. 12 ο ΓΥΜΝΑΣΙΟ ΠΕΡΙΣΤΕΡΙΟΥ Πουλιάσης Αντώνης Φυσικός M.Sc. 2 Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Γεωμετρική
Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Αντώνης Πουλιάσης Φυσικός M.Sc. 12 ο ΓΥΜΝΑΣΙΟ ΠΕΡΙΣΤΕΡΙΟΥ Πουλιάσης Αντώνης Φυσικός M.Sc. 2 Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Γεωμετρική
ΜΑΘΗΣΗΣ Αλεξάνδρα Κούκιου
 Η ΜΕΤΑΤΡΟΠΉ ΜΙΑΣ ΑΣΚΗΣΗΣ ΜΑΘΗΣΗΣ Αλεξάνδρα Κούκιου ΤΟΥ ΣΧΟΛΙΚΟΥ ΒΙΒΛΊΟΥ ΣΕ ΕΡΓΑΛΕΙΟ ΔΙΕΡΕΥΝΗΤΙΚΉΣ Στο σχολικό βιβλίο της Β τάξης γυμνασίου υπάρχει η διπλανή άσκηση. Στόχος της άσκησης είναι να εφαρμόζουν
Η ΜΕΤΑΤΡΟΠΉ ΜΙΑΣ ΑΣΚΗΣΗΣ ΜΑΘΗΣΗΣ Αλεξάνδρα Κούκιου ΤΟΥ ΣΧΟΛΙΚΟΥ ΒΙΒΛΊΟΥ ΣΕ ΕΡΓΑΛΕΙΟ ΔΙΕΡΕΥΝΗΤΙΚΉΣ Στο σχολικό βιβλίο της Β τάξης γυμνασίου υπάρχει η διπλανή άσκηση. Στόχος της άσκησης είναι να εφαρμόζουν
Μαθηματικά: Αριθμητική και Άλγεβρα. Μάθημα 11 ο, Τμήμα Α. Γεωμετρία
 Μαθηματικά: ριθμητική και Άλγεβρα Μάθημα 11 ο, Τμήμα Γεωμετρία Η γεωμετρία σε σχέση με την άλγεβρα ή την αριθμητική έχει την εξής ιδιαιτερότητα: πρέπει να είμαστε πολύ ακριβείς στην περιγραφή μας (σκέψη
Μαθηματικά: ριθμητική και Άλγεβρα Μάθημα 11 ο, Τμήμα Γεωμετρία Η γεωμετρία σε σχέση με την άλγεβρα ή την αριθμητική έχει την εξής ιδιαιτερότητα: πρέπει να είμαστε πολύ ακριβείς στην περιγραφή μας (σκέψη
Μεγεθυντικός φακός. 1. Σκοπός. 2. Θεωρία. θ 1
 Μεγεθυντικός φακός 1. Σκοπός Οι μεγεθυντικοί φακοί ή απλά μικροσκόπια (magnifiers) χρησιμοποιούνται για την παρατήρηση μικροσκοπικών αντικειμένων ώστε να γίνουν καθαρά παρατηρήσιμες οι λεπτομέρειες τους.
Μεγεθυντικός φακός 1. Σκοπός Οι μεγεθυντικοί φακοί ή απλά μικροσκόπια (magnifiers) χρησιμοποιούνται για την παρατήρηση μικροσκοπικών αντικειμένων ώστε να γίνουν καθαρά παρατηρήσιμες οι λεπτομέρειες τους.
ΓΕΩΛΟΓΙΑ - ΓΕΩΓΡΑΦΙΑ Α ΓΥΜΝΑΣΙΟΥ
 ΓΕΩΛΟΓΙΑ - ΓΕΩΓΡΑΦΙΑ Α ΓΥΜΝΑΣΙΟΥ ΣΧΟΛΙΚΟ ΕΤΟΣ 2018 2019 ΤΟ ΣΧΟΛΙΚΟ ΒΙΒΛΙΟ ΜΕ ΕΡΩΤΗΣΕΙΣ- ΑΠΑΝΤΗΣΕΙΣ 1 Περιεχόμενα ΕΝΟΤΗΤΑ Α : ΧΑΡΤΕΣ Α1.4 Ποιον χάρτη να διαλέξω;. 3 Α1.3 Η χρήση των χαρτών στην καθημερινή
ΓΕΩΛΟΓΙΑ - ΓΕΩΓΡΑΦΙΑ Α ΓΥΜΝΑΣΙΟΥ ΣΧΟΛΙΚΟ ΕΤΟΣ 2018 2019 ΤΟ ΣΧΟΛΙΚΟ ΒΙΒΛΙΟ ΜΕ ΕΡΩΤΗΣΕΙΣ- ΑΠΑΝΤΗΣΕΙΣ 1 Περιεχόμενα ΕΝΟΤΗΤΑ Α : ΧΑΡΤΕΣ Α1.4 Ποιον χάρτη να διαλέξω;. 3 Α1.3 Η χρήση των χαρτών στην καθημερινή
ΤΙΤΛΟΣ ΑΝΟΙΧΤΗΣ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΠΡΑΚΤΙΚΗΣ
 ΤΙΤΛΟΣ ΑΝΟΙΧΤΗΣ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΠΡΑΚΤΙΚΗΣ ΔΗΜΟΤΙΚΟ ΣΧΟΛΕΙΟ ΣΚΥΔΡΑΣ Ομάδα ανάπτυξης Μαρία Τσικαλοπούλου, Μαθηματικός Σ Κ Υ Δ Ρ Α / 2 0 1 5 Το αντικείμενο με το οποίο θα ασχοληθούμε είναι τα μαθηματικά της
ΤΙΤΛΟΣ ΑΝΟΙΧΤΗΣ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΠΡΑΚΤΙΚΗΣ ΔΗΜΟΤΙΚΟ ΣΧΟΛΕΙΟ ΣΚΥΔΡΑΣ Ομάδα ανάπτυξης Μαρία Τσικαλοπούλου, Μαθηματικός Σ Κ Υ Δ Ρ Α / 2 0 1 5 Το αντικείμενο με το οποίο θα ασχοληθούμε είναι τα μαθηματικά της
Η κλίμακα σε ευρεία κλίμακα
 Η κλίμακα σε ευρεία κλίμακα ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ «Κανένα μάθημα δεν έχει τόσο μεγάλη παιδευτική δύναμη όσο η ενασχόληση με τους αριθμούς. Το κυριότερο που κάνει
Η κλίμακα σε ευρεία κλίμακα ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ «Κανένα μάθημα δεν έχει τόσο μεγάλη παιδευτική δύναμη όσο η ενασχόληση με τους αριθμούς. Το κυριότερο που κάνει
8. Σύνθεση και ανάλυση δυνάμεων
 8. Σύνθεση και ανάλυση δυνάμεων Βασική θεωρία Σύνθεση δυνάμεων Συνισταμένη Σύνθεση δυνάμεων είναι η διαδικασία με την οποία προσπαθούμε να προσδιορίσουμε τη δύναμη εκείνη που προκαλεί τα ίδια αποτελέσματα
8. Σύνθεση και ανάλυση δυνάμεων Βασική θεωρία Σύνθεση δυνάμεων Συνισταμένη Σύνθεση δυνάμεων είναι η διαδικασία με την οποία προσπαθούμε να προσδιορίσουμε τη δύναμη εκείνη που προκαλεί τα ίδια αποτελέσματα
ΕΝΔΕΙΚΤΙΚΕΣ ΔΟΚΙΜΑΣΙΕΣ ΜΑΘΗΜΑΤΙΚΩΝ ΓΙΑ ΤΗΝ ΕΙΣΑΓΩΓΗ ΜΑΘΗΤΩΝ ΣΤΑ ΠΡΟΤΥΠΑ-ΠΕΙΡΑΜΑΤΙΚΑ ΓΥΜΝΑΣΙΑ
 ΕΝΔΕΙΚΤΙΚΕΣ ΔΟΚΙΜΑΣΙΕΣ ΜΑΘΗΜΑΤΙΚΩΝ ΓΙΑ ΤΗΝ ΕΙΣΑΓΩΓΗ ΜΑΘΗΤΩΝ ΣΤΑ ΠΡΟΤΥΠΑ-ΠΕΙΡΑΜΑΤΙΚΑ ΓΥΜΝΑΣΙΑ ΔΟΚΙΜΑΣΙΑ 6 1) Να εκφράσετε τον αριθμό 48 σε γινόμενο πρώτων παραγόντων με δενδροδιάγραμμα. 2) Να συγκρίνετε
ΕΝΔΕΙΚΤΙΚΕΣ ΔΟΚΙΜΑΣΙΕΣ ΜΑΘΗΜΑΤΙΚΩΝ ΓΙΑ ΤΗΝ ΕΙΣΑΓΩΓΗ ΜΑΘΗΤΩΝ ΣΤΑ ΠΡΟΤΥΠΑ-ΠΕΙΡΑΜΑΤΙΚΑ ΓΥΜΝΑΣΙΑ ΔΟΚΙΜΑΣΙΑ 6 1) Να εκφράσετε τον αριθμό 48 σε γινόμενο πρώτων παραγόντων με δενδροδιάγραμμα. 2) Να συγκρίνετε
ΒΡΙΣΚΩ ΤΟ ΜΙΣΟ ΚΑΙ ΤΟ ΟΛΟΚΛΗΡΟ
 ΒΡΙΣΚΩ ΤΟ ΜΙΣΟ ΚΑΙ ΤΟ ΟΛΟΚΛΗΡΟ ΟΜΑΔΑ ΑΝΑΠΤΥΞΗΣ ΜΑΡΙΑ ΤΣΙΚΑΛΟΠΟΥΛΟΥ,ΜΑΘΗΜΑΤΙΚΟΣ ΣΧΟΛΕΙΟ Δημοτικό σχολείο Σκύδρας ΣΚΥΔΡΑ,2015 1. Συνοπτική περιγραφή της ανοιχτής εκπαιδευτικής Το αντικείμενο με το οποίο
ΒΡΙΣΚΩ ΤΟ ΜΙΣΟ ΚΑΙ ΤΟ ΟΛΟΚΛΗΡΟ ΟΜΑΔΑ ΑΝΑΠΤΥΞΗΣ ΜΑΡΙΑ ΤΣΙΚΑΛΟΠΟΥΛΟΥ,ΜΑΘΗΜΑΤΙΚΟΣ ΣΧΟΛΕΙΟ Δημοτικό σχολείο Σκύδρας ΣΚΥΔΡΑ,2015 1. Συνοπτική περιγραφή της ανοιχτής εκπαιδευτικής Το αντικείμενο με το οποίο
Μαθηματικά Α' Γυμ. - Ερωτήσεις Θεωρίας 1 ΕΡΩΤΗΣΕΙΣ. (1) Ποιοι είναι οι φυσικοί αριθμοί; Γράψε τέσσερα παραδείγματα.
 Μαθηματικά Α' Γυμ. - Ερωτήσεις Θεωρίας 1 ΕΡΩΤΗΣΕΙΣ (1) Ποιοι είναι οι φυσικοί αριθμοί; Γράψε τέσσερα παραδείγματα. (2) Ποιοι είναι οι άρτιοι και ποιοι οι περιττοί αριθμοί; Γράψε από τρία παραδείγματα.
Μαθηματικά Α' Γυμ. - Ερωτήσεις Θεωρίας 1 ΕΡΩΤΗΣΕΙΣ (1) Ποιοι είναι οι φυσικοί αριθμοί; Γράψε τέσσερα παραδείγματα. (2) Ποιοι είναι οι άρτιοι και ποιοι οι περιττοί αριθμοί; Γράψε από τρία παραδείγματα.
6 Γεωμετρικές κατασκευές
 6 Γεωμετρικές κατασκευές 6.1 Γενικά Στα σχέδια εφαρμόζουμε γεωμετρικές κατασκευές, προκειμένου να επιλύσουμε προβλήματα που απαιτούν μεγάλη σχεδιαστική και κατασκευαστική ακρίβεια. Τα γεωμετρικά - σχεδιαστικά
6 Γεωμετρικές κατασκευές 6.1 Γενικά Στα σχέδια εφαρμόζουμε γεωμετρικές κατασκευές, προκειμένου να επιλύσουμε προβλήματα που απαιτούν μεγάλη σχεδιαστική και κατασκευαστική ακρίβεια. Τα γεωμετρικά - σχεδιαστικά
2. Πόσοι ακέραιοι αριθμοί μεταξύ του 10 και του 100 αυξάνονται κατά 9 μονάδες, όταν αντιστραφούν τα ψηφία τους; Γ. Αν, Δ. Αν, τότε. τότε.
 11η Κυπριακή Μαθηματική Ολυμπιάδα πρίλιος 010 Χρόνος: 60 λεπτά ΛΥΚΕΙΟΥ 1. Το τελευταίο ψηφίο του αριθμού 1 3 5 Ε 9 7. Πόσοι ακέραιοι αριθμοί μεταξύ του 10 του 100 αυξάνονται κατά 9 μονάδες όταν αντιστραφούν
11η Κυπριακή Μαθηματική Ολυμπιάδα πρίλιος 010 Χρόνος: 60 λεπτά ΛΥΚΕΙΟΥ 1. Το τελευταίο ψηφίο του αριθμού 1 3 5 Ε 9 7. Πόσοι ακέραιοι αριθμοί μεταξύ του 10 του 100 αυξάνονται κατά 9 μονάδες όταν αντιστραφούν
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 ΜΕΤΡΗΣΗ ΕΜΒΑΔΟΥ
 Ονομ/μο:.... Τμήμα: ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 ΜΕΤΡΗΣΗ ΕΜΒΑΔΟΥ Πώς θα μετρήσουμε την επιφάνεια ενός θρανίου, ενός φύλλου, ή του πουκάμισου που φοράμε; Την έννοια της «επιφάνειας» τη συναντάμε στα αντικείμενα
Ονομ/μο:.... Τμήμα: ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 ΜΕΤΡΗΣΗ ΕΜΒΑΔΟΥ Πώς θα μετρήσουμε την επιφάνεια ενός θρανίου, ενός φύλλου, ή του πουκάμισου που φοράμε; Την έννοια της «επιφάνειας» τη συναντάμε στα αντικείμενα
ΣΧΟΛΗ ΑΝΘΡΩΠΙΣΤΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ
 ΣΧΟΛΗ ΑΝΘΡΩΠΙΣΤΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΠΜΣ «ΑΝΑΛΥΤΙΚΑ ΠΡΟΓΡΑΜΜΑΤΑ ΚΑΙ ΔΙΔΑΚΤΙΚΗ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ» Παραδείγματα Variation Μεταπτυχιακός Φοιτητής:
ΣΧΟΛΗ ΑΝΘΡΩΠΙΣΤΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΠΜΣ «ΑΝΑΛΥΤΙΚΑ ΠΡΟΓΡΑΜΜΑΤΑ ΚΑΙ ΔΙΔΑΚΤΙΚΗ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ» Παραδείγματα Variation Μεταπτυχιακός Φοιτητής:
ΤΕΤΡΑΔΙΟ ΕΡΓΑΣΙΩΝ ΜΑΘΗΜΑΤΙΚΑ Ε ΔΗΜΟΤΙΚΟΥ. Γεωμετρικά σχήματα - Η περίμετρος. Ενότητα 8. β τεύχος
 ΜΑΘΗΜΑΤΙΚΑ Ε ΔΗΜΟΤΙΚΟΥ ΤΕΤΡΑΔΙΟ ΕΡΓΑΣΙΩΝ 46 Γεωμετρικά σχήματα - Η περίμετρος Ενότητα 8 β τεύχος Γεωμετρικά σχήματα-η περίμετρος 46 1η Άσκηση Να κυκλώσεις όλα τα κανονικά πολύγωνα: 60 ο 108 ο 108 ο 120
ΜΑΘΗΜΑΤΙΚΑ Ε ΔΗΜΟΤΙΚΟΥ ΤΕΤΡΑΔΙΟ ΕΡΓΑΣΙΩΝ 46 Γεωμετρικά σχήματα - Η περίμετρος Ενότητα 8 β τεύχος Γεωμετρικά σχήματα-η περίμετρος 46 1η Άσκηση Να κυκλώσεις όλα τα κανονικά πολύγωνα: 60 ο 108 ο 108 ο 120
Μαθηματικά Α Γυμνασίου. Επαναληπτικές ερωτήσεις θεωρίας
 Μαθηματικά Α Γυμνασίου Επαναληπτικές ερωτήσεις θεωρίας Επαναληπτικές Ερωτήσεις Θεωρίας 1. Τι ονομάζεται Ελάχιστο Κοινό Πολλαπλάσιο (ΕΚΠ) δύο ή περισσότερων αριθμών; Ελάχιστο Κοινό Πολλαπλάσιο (ΕΚΠ) δύο
Μαθηματικά Α Γυμνασίου Επαναληπτικές ερωτήσεις θεωρίας Επαναληπτικές Ερωτήσεις Θεωρίας 1. Τι ονομάζεται Ελάχιστο Κοινό Πολλαπλάσιο (ΕΚΠ) δύο ή περισσότερων αριθμών; Ελάχιστο Κοινό Πολλαπλάσιο (ΕΚΠ) δύο
Ιωάννης Σ. Μιχέλης Μαθηματικός
 1 Άλγεβρα 1 ο Κεφάλαιο Ερώτηση 1 : Τι ονομάζεται αριθμητική και τι αλγεβρική παράσταση; Μία παράσταση, που περιέχει πράξεις με αριθμούς ονομάζεται αριθμητική παράσταση. Μία παράσταση, που περιέχει πράξεις
1 Άλγεβρα 1 ο Κεφάλαιο Ερώτηση 1 : Τι ονομάζεται αριθμητική και τι αλγεβρική παράσταση; Μία παράσταση, που περιέχει πράξεις με αριθμούς ονομάζεται αριθμητική παράσταση. Μία παράσταση, που περιέχει πράξεις
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ. Μια παράσταση που περιέχει πράξεις με μεταβλητές (γράμματα) και αριθμούς καλείται αλγεβρική, όπως για παράδειγμα η : 2x+3y-8
 ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
ΜΑΘΗΜΑΤΙΚΑ Α ΓΥΜΝΑΣΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ Α ΓΥΜΝΑΣΙΟΥ Πίνακας περιεχομένων Κεφάλαιο 1 - ΟΙ ΦΥΣΙΚΟΙ ΑΡΙΘΜΟΙ... 2 Κεφάλαιο 2 ο - ΤΑ ΚΛΑΣΜΑΤΑ... 6 Κεφάλαιο 3 ο - ΔΕΚΑΔΙΚΟΙ ΑΡΙΘΜΟΙ... 10 ΣΩΤΗΡΟΠΟΥΛΟΣ ΝΙΚΟΣ 1 Κεφάλαιο 1 - ΟΙ ΦΥΣΙΚΟΙ ΑΡΙΘΜΟΙ
ΜΑΘΗΜΑΤΙΚΑ Α ΓΥΜΝΑΣΙΟΥ Πίνακας περιεχομένων Κεφάλαιο 1 - ΟΙ ΦΥΣΙΚΟΙ ΑΡΙΘΜΟΙ... 2 Κεφάλαιο 2 ο - ΤΑ ΚΛΑΣΜΑΤΑ... 6 Κεφάλαιο 3 ο - ΔΕΚΑΔΙΚΟΙ ΑΡΙΘΜΟΙ... 10 ΣΩΤΗΡΟΠΟΥΛΟΣ ΝΙΚΟΣ 1 Κεφάλαιο 1 - ΟΙ ΦΥΣΙΚΟΙ ΑΡΙΘΜΟΙ
ΒΡΙΣΚΩ ΤΟ ΜΙΣΟ ΚΑΙ ΤΟ ΟΛΟΚΛΗΡΟ
 ΒΡΙΣΚΩ ΤΟ ΜΙΣΟ ΚΑΙ ΤΟ ΟΛΟΚΛΗΡΟ ΟΜΑΔΑ ΑΝΑΠΤΥΞΗΣ ΜΑΡΙΑ ΤΣΙΚΑΛΟΠΟΥΛΟΥ,ΜΑΘΗΜΑΤΙΚΟΣ ΣΧΟΛΕΙΟ - ΣΚΥΔΡΑ,2015 1. Συνοπτική περιγραφή της ανοιχτής εκπαιδευτικής Το αντικείμενο με το οποίο θα ασχοληθούμε είναι τα
ΒΡΙΣΚΩ ΤΟ ΜΙΣΟ ΚΑΙ ΤΟ ΟΛΟΚΛΗΡΟ ΟΜΑΔΑ ΑΝΑΠΤΥΞΗΣ ΜΑΡΙΑ ΤΣΙΚΑΛΟΠΟΥΛΟΥ,ΜΑΘΗΜΑΤΙΚΟΣ ΣΧΟΛΕΙΟ - ΣΚΥΔΡΑ,2015 1. Συνοπτική περιγραφή της ανοιχτής εκπαιδευτικής Το αντικείμενο με το οποίο θα ασχοληθούμε είναι τα
ΤΙΤΛΟΣ ΑΝΟΙΧΤΗΣ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΠΡΑΚΤΙΚΗς
 ΤΙΤΛΟΣ ΑΝΟΙΧΤΗΣ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΠΡΑΚΤΙΚΗς ΔΗΜΟΤΙΚΟ ΣΧΟΛΕΙΟ ΣΚΥΔΡΑΣ Ομάδα ανάπτυξης Μαρία Τσικαλοπούλου, Μαθηματικός Σ Κ Υ Δ Ρ Α / 2 0 1 5 Το αντικείμενο με το οποίο θα ασχοληθούμε είναι τα μαθηματικά της
ΤΙΤΛΟΣ ΑΝΟΙΧΤΗΣ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΠΡΑΚΤΙΚΗς ΔΗΜΟΤΙΚΟ ΣΧΟΛΕΙΟ ΣΚΥΔΡΑΣ Ομάδα ανάπτυξης Μαρία Τσικαλοπούλου, Μαθηματικός Σ Κ Υ Δ Ρ Α / 2 0 1 5 Το αντικείμενο με το οποίο θα ασχοληθούμε είναι τα μαθηματικά της
ΜΑΘΗΜΑΤΙΚΑ Γ Γυμνασίου
 ΜΑΘΗΜΑΤΙΚΑ Γ Γυμνασίου Κεφάλαιο ο Αλγεβρικές Παραστάσεις ΛΕΜΟΝΙΑ ΜΠΟΥΤΣΚΟΥ Γυμνάσιο Αμυνταίου ΜΑΘΗΜΑ Α. Πράξεις με πραγματικούς αριθμούς ΑΣΚΗΣΕΙΣ ) ) Να συμπληρώσετε τα κενά ώστε στην κατακόρυφη στήλη
ΜΑΘΗΜΑΤΙΚΑ Γ Γυμνασίου Κεφάλαιο ο Αλγεβρικές Παραστάσεις ΛΕΜΟΝΙΑ ΜΠΟΥΤΣΚΟΥ Γυμνάσιο Αμυνταίου ΜΑΘΗΜΑ Α. Πράξεις με πραγματικούς αριθμούς ΑΣΚΗΣΕΙΣ ) ) Να συμπληρώσετε τα κενά ώστε στην κατακόρυφη στήλη
ΤΑΞΗ: ΣΤ. Προτείνεται να μην αξιοποιηθούν διδακτικά από το Βιβλίο Μαθητή τα παρακάτω: 1 ο σελ. 7, 4 η άσκηση, σελ. 8, 2 ο πρόβλημα
 ΕΚΠΑΙΔΕΥΤΙΚΟ ΥΛΙΚΟ: Βιβλίο μαθητή, Μαθηματικά ΣΤ Δημοτικού, 2015, ένα τεύχος Τετράδιο εργασιών, Μαθηματικά ΣΤ Δημοτικού, 2015, α τεύχος Τετράδιο εργασιών, Μαθηματικά ΣΤ Δημοτικού, 2015, β τεύχος Τετράδιο
ΕΚΠΑΙΔΕΥΤΙΚΟ ΥΛΙΚΟ: Βιβλίο μαθητή, Μαθηματικά ΣΤ Δημοτικού, 2015, ένα τεύχος Τετράδιο εργασιών, Μαθηματικά ΣΤ Δημοτικού, 2015, α τεύχος Τετράδιο εργασιών, Μαθηματικά ΣΤ Δημοτικού, 2015, β τεύχος Τετράδιο
ΚΑΤΑΣΚΕΥΗ ΠΑΡΑΛΛΗΛΟΓΡΑΜΜΩΝ ΜΕ ΧΡΗΣΗ LOGO
 1 ΚΑΤΑΣΚΕΥΗ ΠΑΡΑΛΛΗΛΟΓΡΑΜΜΩΝ ΜΕ ΧΡΗΣΗ LOGO ΦΥΛΛΑ ΕΡΓΑΣΙΑΣ ΜΑΘΗΤΗ ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 1 1. Τοποθέτησε μια χελώνα στην επιφάνεια εργασίας. 2. Με ποια εντολή γράφει η χελώνα μας;.. 3. Γράψε την εντολή για να πάει
1 ΚΑΤΑΣΚΕΥΗ ΠΑΡΑΛΛΗΛΟΓΡΑΜΜΩΝ ΜΕ ΧΡΗΣΗ LOGO ΦΥΛΛΑ ΕΡΓΑΣΙΑΣ ΜΑΘΗΤΗ ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 1 1. Τοποθέτησε μια χελώνα στην επιφάνεια εργασίας. 2. Με ποια εντολή γράφει η χελώνα μας;.. 3. Γράψε την εντολή για να πάει
Εκπαιδευτικό Σενάριο: Αναλογίες. Βασίλης Παπαγεωργίου
 Εκπαιδευτικό Σενάριο: Αναλογίες Ιανουάριος 2011 1. Τίτλος Αναλογίες 2. Ταυτότητα Συγγραφέας: Γνωστική περιοχή των μαθηματικών: Άλγεβρα, Γεωμετρία Θέμα: Αναλογίες Συντεταγμένες στο επίπεδο 3. Σκεπτικό 2
Εκπαιδευτικό Σενάριο: Αναλογίες Ιανουάριος 2011 1. Τίτλος Αναλογίες 2. Ταυτότητα Συγγραφέας: Γνωστική περιοχή των μαθηματικών: Άλγεβρα, Γεωμετρία Θέμα: Αναλογίες Συντεταγμένες στο επίπεδο 3. Σκεπτικό 2
I. ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. math-gr
 I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
Οι γωνίες και που ονομάζονται «εντός εναλλάξ γωνίες» και είναι ίσες. «εντός-εκτός και επί τα αυτά μέρη γωνίες» και είναι ίσες.
 ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΑΝΑΒΡΥΤΩΝ ΜΑΘΗΜΑΤΑ ΓΙΑ ΤΟΝ ΔΙΑΓΩΝΙΣΜΟ «ΘΑΛΗΣ» ΤΑΞΗ Α ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΓΕΩΜΕΤΡΙΑ ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ 1. Μεσοκάθετος ενός ευθύγραμμου τμήματος ΑΒ ονομάζεται η ευθεία που είναι κάθετη
ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΑΝΑΒΡΥΤΩΝ ΜΑΘΗΜΑΤΑ ΓΙΑ ΤΟΝ ΔΙΑΓΩΝΙΣΜΟ «ΘΑΛΗΣ» ΤΑΞΗ Α ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΓΕΩΜΕΤΡΙΑ ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ 1. Μεσοκάθετος ενός ευθύγραμμου τμήματος ΑΒ ονομάζεται η ευθεία που είναι κάθετη
ΤΕΤΡΑΔΙΟ ΕΡΓΑΣΙΩΝ ΜΑΘΗΜΑΤΙΚΑ Ε ΔΗΜΟΤΙΚΟΥ. Εμβαδό τετραγώνου, ορθογωνίου και ορθογώνιου τριγώνου. Ενότητα 8. β τεύχος
 ΜΑΘΗΜΑΤΙΚΑ Ε ΔΗΜΟΤΙΚΟΥ ΤΕΤΡΑΔΙΟ ΕΡΓΑΣΙΩΝ 48 Ενότητα 8 Εμβαδό τετραγώνου, ορθογωνίου και ορθογώνιου τριγώνου β τεύχος Εμβαδό τετραγώνου, ορθογωνίου και ορθογώνιου τριγώνου 48 1η Άσκηση Να συμπληρώσεις τον
ΜΑΘΗΜΑΤΙΚΑ Ε ΔΗΜΟΤΙΚΟΥ ΤΕΤΡΑΔΙΟ ΕΡΓΑΣΙΩΝ 48 Ενότητα 8 Εμβαδό τετραγώνου, ορθογωνίου και ορθογώνιου τριγώνου β τεύχος Εμβαδό τετραγώνου, ορθογωνίου και ορθογώνιου τριγώνου 48 1η Άσκηση Να συμπληρώσεις τον
Ο15. Κοίλα κάτοπτρα. 2. Θεωρία. 2.1 Γεωμετρική Οπτική
 Ο15 Κοίλα κάτοπτρα 1. Σκοπός Σκοπός της άσκησης είναι η εύρεση της εστιακής απόστασης κοίλου κατόπτρου σχετικά μεγάλου ανοίγματος και την μέτρηση του σφάλματος της σφαιρικής εκτροπής... Θεωρία.1 Γεωμετρική
Ο15 Κοίλα κάτοπτρα 1. Σκοπός Σκοπός της άσκησης είναι η εύρεση της εστιακής απόστασης κοίλου κατόπτρου σχετικά μεγάλου ανοίγματος και την μέτρηση του σφάλματος της σφαιρικής εκτροπής... Θεωρία.1 Γεωμετρική
1 ΘΕΩΡΙΑΣ...με απάντηση
 1 ΘΕΩΡΙΑΣ.....με απάντηση ΑΛΓΕΒΡΑ Κεφάλαιο 1 0 Εξισώσεις Ανισώσεις 1. Τι ονομάζεται Αριθμητική και τι Αλγεβρική παράσταση; Ονομάζεται Αριθμητική παράσταση μια παράσταση που περιέχει πράξεις μεταξύ αριθμών.
1 ΘΕΩΡΙΑΣ.....με απάντηση ΑΛΓΕΒΡΑ Κεφάλαιο 1 0 Εξισώσεις Ανισώσεις 1. Τι ονομάζεται Αριθμητική και τι Αλγεβρική παράσταση; Ονομάζεται Αριθμητική παράσταση μια παράσταση που περιέχει πράξεις μεταξύ αριθμών.
1.3 Τα φυσικά μεγέθη και οι μονάδες τους
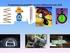 ΚΕΦΑΛΑΙΟ ο ΕΙΣΑΓΩΓΗ. Τα φυσικά μεγέθη και οι μονάδες τους. Τι είναι μέγεθος; Μέγεθος είναι κάθε ποσότητα που μπορεί να μετρηθεί.. Τι είναι μέτρηση; Είναι η διαδικασία σύγκρισης ίδιων μεγεθών.. Τι είναι
ΚΕΦΑΛΑΙΟ ο ΕΙΣΑΓΩΓΗ. Τα φυσικά μεγέθη και οι μονάδες τους. Τι είναι μέγεθος; Μέγεθος είναι κάθε ποσότητα που μπορεί να μετρηθεί.. Τι είναι μέτρηση; Είναι η διαδικασία σύγκρισης ίδιων μεγεθών.. Τι είναι
ΦΥΣΙΚΗ Γ ΓΥΜΝΑΣΙΟΥ 2.1 ΤΟ ΗΛΕΚΤΡΙΚΟ ΡΕΥΜΑ
 ΦΥΣΙΚΗ Γ ΓΥΜΝΑΣΙΟΥ 2Η ΕΝΟΤΗΤΑ ΗΛΕΚΤΡΙΚΟ ΡΕΥΜΑ 2.1 ΤΟ ΗΛΕΚΤΡΙΚΟ ΡΕΥΜΑ Τι είναι ; Ηλεκτρικό ρεύμα ονομάζεται η προσανατολισμένη κίνηση των ηλεκτρονίων ή γενικότερα των φορτισμένων σωματιδίων Που μπορεί να
ΦΥΣΙΚΗ Γ ΓΥΜΝΑΣΙΟΥ 2Η ΕΝΟΤΗΤΑ ΗΛΕΚΤΡΙΚΟ ΡΕΥΜΑ 2.1 ΤΟ ΗΛΕΚΤΡΙΚΟ ΡΕΥΜΑ Τι είναι ; Ηλεκτρικό ρεύμα ονομάζεται η προσανατολισμένη κίνηση των ηλεκτρονίων ή γενικότερα των φορτισμένων σωματιδίων Που μπορεί να
Στ Τάξη. Α/Α Μαθηματικό περιεχόμενο Δείκτες Επιτυχίας Ώρες Διδ. 1 ENOTHTA 1
 Ενδεικτική Οργάνωση Ενοτήτων Στ Τάξη Α/Α Μαθηματικό περιεχόμενο Δείκτες Επιτυχίας Ώρες Διδ. 1 ENOTHTA 1 15 Αρ3.1 Απαγγέλουν, διαβάζουν, γράφουν και αναγνωρίζουν ποσότητες αριθμών Επανάληψη μέχρι το 1 000
Ενδεικτική Οργάνωση Ενοτήτων Στ Τάξη Α/Α Μαθηματικό περιεχόμενο Δείκτες Επιτυχίας Ώρες Διδ. 1 ENOTHTA 1 15 Αρ3.1 Απαγγέλουν, διαβάζουν, γράφουν και αναγνωρίζουν ποσότητες αριθμών Επανάληψη μέχρι το 1 000
Πρόγραμμα Σπουδών Εκπαίδευσης Παιδιών-Προφύγων Τάξεις Ε+ΣΤ Δημοτικού
 Πρόγραμμα Σπουδών Εκπαίδευσης Παιδιών-Προφύγων 2016-2017 Τάξεις Ε+ΣΤ Δημοτικού Περιεχόμενα Στόχοι Πηγή Υλικού 3.1 Αριθμοί Οι μαθητές πρέπει: Σχολικά βιβλία Ε και ΣΤ Φυσικοί, Δεκαδικοί, μετρήσεις Να μπορούν
Πρόγραμμα Σπουδών Εκπαίδευσης Παιδιών-Προφύγων 2016-2017 Τάξεις Ε+ΣΤ Δημοτικού Περιεχόμενα Στόχοι Πηγή Υλικού 3.1 Αριθμοί Οι μαθητές πρέπει: Σχολικά βιβλία Ε και ΣΤ Φυσικοί, Δεκαδικοί, μετρήσεις Να μπορούν
ΠΟΥ ΔΙΑΔΙΔΕΤΑΙ ΤΟ ΦΩΣ
 1 ΦΩΣ Στο μικρόκοσμο θεωρούμε ότι το φως έχει δυο μορφές. Άλλοτε το αντιμετωπίζουμε με τη μορφή σωματιδίων που ονομάζουμε φωτόνια. Τα φωτόνια δεν έχουν μάζα αλλά μόνον ενέργεια. Άλλοτε πάλι αντιμετωπίζουμε
1 ΦΩΣ Στο μικρόκοσμο θεωρούμε ότι το φως έχει δυο μορφές. Άλλοτε το αντιμετωπίζουμε με τη μορφή σωματιδίων που ονομάζουμε φωτόνια. Τα φωτόνια δεν έχουν μάζα αλλά μόνον ενέργεια. Άλλοτε πάλι αντιμετωπίζουμε
ΚΕΦΑΛΑΙΟ 1 Ο ΓΕΩΜΕΤΡΙΑ
 ΜΕΡΟΣ ΚΕΦΛΙΟ 1 Ο ΕΩΜΕΤΡΙ 1.1 ΙΣΟΤΗΤ ΤΡΙΩΝΩΝ 1. Ποια ονομάζονται κύρια και ποια δευτερεύοντα στοιχεία τριγώνων; Κύρια στοιχεία ενός τριγώνου ονομάζουμε τις πλευρές και τις γωνίες του. Δευτερεύοντα στοιχεία
ΜΕΡΟΣ ΚΕΦΛΙΟ 1 Ο ΕΩΜΕΤΡΙ 1.1 ΙΣΟΤΗΤ ΤΡΙΩΝΩΝ 1. Ποια ονομάζονται κύρια και ποια δευτερεύοντα στοιχεία τριγώνων; Κύρια στοιχεία ενός τριγώνου ονομάζουμε τις πλευρές και τις γωνίες του. Δευτερεύοντα στοιχεία
ΜΕΡΟΣ Β ΕΓΧΕΙΡΙΔΙΟ ΚΑΘΗΓΗΤΗ
 941205 ΜΕΡΟΣ Β ΕΓΧΕΙΡΙΔΙΟ ΚΑΘΗΓΗΤΗ 2 Εισαγωγή Ευχαριστούμε που χρησιμοποιείτε την ενότητα για την έρευνα της μέτρησης. Ελπίζουμε πως το πακέτο και τα βιβλία εργασίας θα σας ικανοποιήσουν. Αν έχετε οποιεσδήποτε
941205 ΜΕΡΟΣ Β ΕΓΧΕΙΡΙΔΙΟ ΚΑΘΗΓΗΤΗ 2 Εισαγωγή Ευχαριστούμε που χρησιμοποιείτε την ενότητα για την έρευνα της μέτρησης. Ελπίζουμε πως το πακέτο και τα βιβλία εργασίας θα σας ικανοποιήσουν. Αν έχετε οποιεσδήποτε
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΤΗΣ ΟΠΤΙΚΗΣ
 ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΤΗΣ ΟΠΤΙΚΗΣ Μάθημα προς τους ειδικευόμενους γιατρούς στην Οφθαλμολογία, Στο Κ.Οφ.Κ.Α. την 18/11/2003. Υπό: Δρος Κων. Ρούγγα, Οφθαλμιάτρου. 1. ΑΝΑΚΛΑΣΗ ΤΟΥ ΦΩΤΟΣ Όταν μια φωτεινή ακτίνα ή
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΤΗΣ ΟΠΤΙΚΗΣ Μάθημα προς τους ειδικευόμενους γιατρούς στην Οφθαλμολογία, Στο Κ.Οφ.Κ.Α. την 18/11/2003. Υπό: Δρος Κων. Ρούγγα, Οφθαλμιάτρου. 1. ΑΝΑΚΛΑΣΗ ΤΟΥ ΦΩΤΟΣ Όταν μια φωτεινή ακτίνα ή
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ ΜΑΘΗΜΑΤΙΚΩΝ Β ΦΑΣΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ ΜΑΘΗΜΑΤΙΚΩΝ Β ΦΑΣΗΣ Θέμα Διδασκαλίας Προβλήματα με πρόσθεση και αφαίρεση κλασμάτων (Κεφάλαιο 23 ο ) Σχολείο: 2 ο
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ ΜΑΘΗΜΑΤΙΚΩΝ Β ΦΑΣΗΣ Θέμα Διδασκαλίας Προβλήματα με πρόσθεση και αφαίρεση κλασμάτων (Κεφάλαιο 23 ο ) Σχολείο: 2 ο
Μαθηματικά Β Γυμνασίου. Επανάληψη στη Θεωρία
 Μαθηματικά Β Γυμνασίου Επανάληψη στη Θεωρία Α.1.1: Η έννοια της μεταβλητής - Αλγεβρικές παραστάσεις Α.1.2: Εξισώσεις α βαθμού Α.1.4: Επίλυση προβλημάτων με τη χρήση εξισώσεων Α.1.5: Ανισώσεις α βαθμού
Μαθηματικά Β Γυμνασίου Επανάληψη στη Θεωρία Α.1.1: Η έννοια της μεταβλητής - Αλγεβρικές παραστάσεις Α.1.2: Εξισώσεις α βαθμού Α.1.4: Επίλυση προβλημάτων με τη χρήση εξισώσεων Α.1.5: Ανισώσεις α βαθμού
ΑΣΚΗΣΗ 1 Ποιο από τα δύο σχήματα Α, Β έχει το μεγαλύτερο εμβαδόν;
 ΜΕΡΟΣ Β. ΕΜΒΑΔΑ ΕΠΙΠΕΔΩΝ ΣΧΗΜΑΤΩΝ-ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ 05. ΕΜΒΑΔΟΝ ΕΠΙΠΕΔΗΣ ΕΠΙΦΑΝΕΙΑΣ Ορισμός Το εμβαδόν μιας επίπεδης επιφάνειας είναι ένας θετικός αριθμός, που εκφράζει την έκταση που καταλαμβάνει η επιφάνεια
ΜΕΡΟΣ Β. ΕΜΒΑΔΑ ΕΠΙΠΕΔΩΝ ΣΧΗΜΑΤΩΝ-ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ 05. ΕΜΒΑΔΟΝ ΕΠΙΠΕΔΗΣ ΕΠΙΦΑΝΕΙΑΣ Ορισμός Το εμβαδόν μιας επίπεδης επιφάνειας είναι ένας θετικός αριθμός, που εκφράζει την έκταση που καταλαμβάνει η επιφάνεια
Σχηματισμός ειδώλων. Εισαγωγή
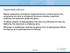 Σχηματισμός ειδώλων Είδωλα πραγματικών αντικειμένων σχηματίζονται όταν οι ακτίνες φωτός (που εκπέμπονται από αυτά τα αντικέιμενα) συναντούν επίπεδες ή καμπύλες επιφάνειες που βρίσκονται μεταξύ δύο μέσων.
Σχηματισμός ειδώλων Είδωλα πραγματικών αντικειμένων σχηματίζονται όταν οι ακτίνες φωτός (που εκπέμπονται από αυτά τα αντικέιμενα) συναντούν επίπεδες ή καμπύλες επιφάνειες που βρίσκονται μεταξύ δύο μέσων.
ΤΑ ΔΕΚΑΔΙΚΑ ΚΛΑΣΜΑΤΑ ΚΑΙ ΟΙ ΔΕΚΑΔΙΚΟΙ ΑΡΙΘΜΟΙ
 ΜΑΘΗΜΑΤΙΚΑ (Γ ΤΑΞΗ) ΟΝΟΜΑ:. (ΕΙΣΑΓΩΓΗ ΣΤΑ ΔΕΚΑΔΙΚΑ ΚΛΑΣΜΑΤΑ ΚΑΙ ΣΤΟΥΣ ΔΕΚΑΔΙΚΟΥΣ ΑΡΙΘΜΟΥΣ) ΤΑ ΔΕΚΑΔΙΚΑ ΚΛΑΣΜΑΤΑ ΚΑΙ ΟΙ ΔΕΚΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΛΑΤΕ ΝΑ ΣΚΕΦΤΟΥΜΕ ΜΑΖΙ: Υπάρχουν άραγε αριθμοί ανάμεσα στο 0 και
ΜΑΘΗΜΑΤΙΚΑ (Γ ΤΑΞΗ) ΟΝΟΜΑ:. (ΕΙΣΑΓΩΓΗ ΣΤΑ ΔΕΚΑΔΙΚΑ ΚΛΑΣΜΑΤΑ ΚΑΙ ΣΤΟΥΣ ΔΕΚΑΔΙΚΟΥΣ ΑΡΙΘΜΟΥΣ) ΤΑ ΔΕΚΑΔΙΚΑ ΚΛΑΣΜΑΤΑ ΚΑΙ ΟΙ ΔΕΚΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΛΑΤΕ ΝΑ ΣΚΕΦΤΟΥΜΕ ΜΑΖΙ: Υπάρχουν άραγε αριθμοί ανάμεσα στο 0 και
ΜΕΤΡΩΝΤΑΣ ΤΟΝ ΠΛΑΝΗΤΗ ΓΗ
 του Υποπυραγού Αλέξανδρου Μαλούνη* Μέρος 2 ο - Χαρτογραφικοί μετασχηματισμοί Εισαγωγή Είδαμε λοιπόν ως τώρα, ότι η γη θα μπορούσε να χαρακτηρισθεί και σφαιρική και αυτό μπορεί να γίνει εμφανές όταν την
του Υποπυραγού Αλέξανδρου Μαλούνη* Μέρος 2 ο - Χαρτογραφικοί μετασχηματισμοί Εισαγωγή Είδαμε λοιπόν ως τώρα, ότι η γη θα μπορούσε να χαρακτηρισθεί και σφαιρική και αυτό μπορεί να γίνει εμφανές όταν την
ΣΧΗΜΑΤΑ-ΓΡΑΜΜΕΣ-ΜΕΤΡΗΣΗ Μιχάλης Χριστοφορίδης Ανδρέας Σάββα Σύμβουλοι Μαθηματικών
 ΕΦΑΡΜΟΓΙΔΙΟ: Σχήματα-Γραμμές-Μέτρηση Είναι ένα εργαλείο που μας βοηθά στην κατασκευή και μέτρηση σχημάτων, γωνιών και γραμμών. Μας παρέχει ένα χάρακα, μοιρογνωμόνιο και υπολογιστική μηχανή για να μας βοηθάει
ΕΦΑΡΜΟΓΙΔΙΟ: Σχήματα-Γραμμές-Μέτρηση Είναι ένα εργαλείο που μας βοηθά στην κατασκευή και μέτρηση σχημάτων, γωνιών και γραμμών. Μας παρέχει ένα χάρακα, μοιρογνωμόνιο και υπολογιστική μηχανή για να μας βοηθάει
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΗ ΣΧΟΛΗ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ ΜΑΘΗΜΑΤΙΚΩΝ Β ΦΑΣΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΗ ΣΧΟΛΗ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Υπεύθυνος καθηγητής Χαράλαμπος Λεμονίδης Μέντορας Γεώργιος Γεωργιόπουλος ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ ΜΑΘΗΜΑΤΙΚΩΝ Β ΦΑΣΗΣ Θέμα Διδασκαλίας Πρόσθεση
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΗ ΣΧΟΛΗ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Υπεύθυνος καθηγητής Χαράλαμπος Λεμονίδης Μέντορας Γεώργιος Γεωργιόπουλος ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ ΜΑΘΗΜΑΤΙΚΩΝ Β ΦΑΣΗΣ Θέμα Διδασκαλίας Πρόσθεση
«ΕΦΑΡΜΟΣΜΕΝΗ ΔΙΔΑΚΤΙΚΗ ΜΑΘΗΜΑΤΙΚΩΝ» ΠΡΑΚΤΙΚΕΣ Β ΦΑΣΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΑΝΘΡΩΠΙΣΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΠΡΟΣΧΟΛΙΚΗΣ ΑΓΩΓΗΣ ΚΑΙ ΤΟΥ ΕΚΠΑΙΔΕΥΤΙΚΟΥ ΣΧΕΔΙΑΣΜΟΥ «ΕΦΑΡΜΟΣΜΕΝΗ ΔΙΔΑΚΤΙΚΗ ΜΑΘΗΜΑΤΙΚΩΝ» ΠΡΑΚΤΙΚΕΣ Β ΦΑΣΗΣ ΣΥΝΟΠΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ Διδάσκουσες:
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΑΝΘΡΩΠΙΣΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΠΡΟΣΧΟΛΙΚΗΣ ΑΓΩΓΗΣ ΚΑΙ ΤΟΥ ΕΚΠΑΙΔΕΥΤΙΚΟΥ ΣΧΕΔΙΑΣΜΟΥ «ΕΦΑΡΜΟΣΜΕΝΗ ΔΙΔΑΚΤΙΚΗ ΜΑΘΗΜΑΤΙΚΩΝ» ΠΡΑΚΤΙΚΕΣ Β ΦΑΣΗΣ ΣΥΝΟΠΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ Διδάσκουσες:
ΜΑΘΗΜΑΤΙΚΑ - Γ ΓΥΜΝΑΣΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ - Γ ΓΥΜΝΑΣΙΟΥ ΜΕΡΟΣ Α': ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ ο: Αλγεβρικές παραστάσεις Παράγραφος A..: Πράξεις με πραγματικούς αριθμούς (επαναλήψεις συμπληρώσεις) Β: Πράξεις με μονώνυμα Τα σημαντικότερα σημεία
ΜΑΘΗΜΑΤΙΚΑ - Γ ΓΥΜΝΑΣΙΟΥ ΜΕΡΟΣ Α': ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ ο: Αλγεβρικές παραστάσεις Παράγραφος A..: Πράξεις με πραγματικούς αριθμούς (επαναλήψεις συμπληρώσεις) Β: Πράξεις με μονώνυμα Τα σημαντικότερα σημεία
1 8 και ο δεύτερος παίρνει το υπόλοιπο. Παρακάτω, ο πρώτος παραπόταμος χωρίζεται στα 3 και το ένα τμήμα του παίρνει το του νερού του 8 ) 1 2
 Kangourou Sans Frontières Θέματα Καγκουρό 00 LEVELS: - (για μαθητές της Β' και ' τάξης Λυκείου) Ερωτήσεις βαθμών: ) Οι αριθμοί και και δύο άγνωστοι αριθμοί γράφονται μέσα στα τετραγωνάκια του διπλανού
Kangourou Sans Frontières Θέματα Καγκουρό 00 LEVELS: - (για μαθητές της Β' και ' τάξης Λυκείου) Ερωτήσεις βαθμών: ) Οι αριθμοί και και δύο άγνωστοι αριθμοί γράφονται μέσα στα τετραγωνάκια του διπλανού
ΑΛΓΕΒΡΑ Α ΓΥΜΝΑΣΙΟΥ ΑΝΑΛΟΓΑ ΚΑΙ ΑΝΤΙΣΤΡΟΦΩΣ ΑΝΑΛΟΓΑ ΠΟΣΑ ΕΠΙΜΕΛΕΙΑ : ΧΑΛΑΤΖΙΑΝ ΠΑΥΛΟΣ
 ΑΛΓΕΒΡΑ Α ΓΥΜΝΑΣΙΟΥ ΑΝΑΛΟΓΑ ΚΑΙ ΑΝΤΙΣΤΡΟΦΩΣ ΑΝΑΛΟΓΑ ΠΟΣΑ ΕΠΙΜΕΛΕΙΑ : ΧΑΛΑΤΖΙΑΝ ΠΑΥΛΟΣ ΚΕΦΑΛΑΙΟ 6 Ο ΑΝΑΛΟΓΑ ΠΟΣΑ ΚΑΙ ΑΝΤΙΣΤΡΟΦΩΣ ΑΝΑΛΟΓΑ ΠΟΣΑ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ 1. Προκειμένου να προσδιορίσουμε τη θέση ενός
ΑΛΓΕΒΡΑ Α ΓΥΜΝΑΣΙΟΥ ΑΝΑΛΟΓΑ ΚΑΙ ΑΝΤΙΣΤΡΟΦΩΣ ΑΝΑΛΟΓΑ ΠΟΣΑ ΕΠΙΜΕΛΕΙΑ : ΧΑΛΑΤΖΙΑΝ ΠΑΥΛΟΣ ΚΕΦΑΛΑΙΟ 6 Ο ΑΝΑΛΟΓΑ ΠΟΣΑ ΚΑΙ ΑΝΤΙΣΤΡΟΦΩΣ ΑΝΑΛΟΓΑ ΠΟΣΑ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ 1. Προκειμένου να προσδιορίσουμε τη θέση ενός
Η ΣΥΜΜΕΤΡΙΑ ΣΤΟ ΦΥΣΙΚΟ ΚΟΣΜΟ ΦΥΣΗ ΚΑΙ ΜΑΘΗΜΑΤΙΚΑ Η ΣΥΜΜΕΤΡΙΑ ΣΤΟ ΦΥΣΙΚΟ ΚΟΣΜΟ
 Η ΣΥΜΜΕΤΡΙΑ ΣΤΟ ΦΥΣΙΚΟ ΚΟΣΜΟ ΦΥΣΗ ΚΑΙ ΜΑΘΗΜΑΤΙΚΑ Η ΣΥΜΜΕΤΡΙΑ ΣΤΟ ΦΥΣΙΚΟ ΚΟΣΜΟ Επιμέλεια: Μιχαηλίσιν Άννα- Μαρία, Τζιώτης Δημήτρης, Τσάτσα Κωνσταντίνα Η συμμετρία στο φυσικό κόσμο Η συμμετρία που κατεξοχήν
Η ΣΥΜΜΕΤΡΙΑ ΣΤΟ ΦΥΣΙΚΟ ΚΟΣΜΟ ΦΥΣΗ ΚΑΙ ΜΑΘΗΜΑΤΙΚΑ Η ΣΥΜΜΕΤΡΙΑ ΣΤΟ ΦΥΣΙΚΟ ΚΟΣΜΟ Επιμέλεια: Μιχαηλίσιν Άννα- Μαρία, Τζιώτης Δημήτρης, Τσάτσα Κωνσταντίνα Η συμμετρία στο φυσικό κόσμο Η συμμετρία που κατεξοχήν
Γράφοντας ένα σχολικό βιβλίο για τα Μαθηματικά. Μαριάννα Τζεκάκη Αν. Καθηγήτρια Α.Π.Θ. Μ. Καλδρυμίδου Αν. Καθηγήτρια Πανεπιστημίου Ιωαννίνων
 Γράφοντας ένα σχολικό βιβλίο για τα Μαθηματικά Μαριάννα Τζεκάκη Αν. Καθηγήτρια Α.Π.Θ. Μ. Καλδρυμίδου Αν. Καθηγήτρια Πανεπιστημίου Ιωαννίνων Εισαγωγή Η χώρα μας απέκτησε Νέα Προγράμματα Σπουδών και Νέα
Γράφοντας ένα σχολικό βιβλίο για τα Μαθηματικά Μαριάννα Τζεκάκη Αν. Καθηγήτρια Α.Π.Θ. Μ. Καλδρυμίδου Αν. Καθηγήτρια Πανεπιστημίου Ιωαννίνων Εισαγωγή Η χώρα μας απέκτησε Νέα Προγράμματα Σπουδών και Νέα
ΕΡΩΤΗΣΕΙΣ ΘΕΜΑΤΑ ΘΕΩΡΙΑΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ Α ΓΥΜΝΑΣΙΟΥ ΑΛΓΕΒΡΑ
 1 ο ΚΕΦΑΛΑΙΟ ΕΡΩΤΗΣΕΙΣ ΘΕΜΑΤΑ ΘΕΩΡΙΑΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ Α ΓΥΜΝΑΣΙΟΥ ΑΛΓΕΒΡΑ 1. α. Τι γνωρίζετε για την Ευκλείδεια διαίρεση; Πότε λέγεται τέλεια; β. Αν σε μια διαίρεση είναι Δ=δ, πόσο είναι το πηλίκο και
1 ο ΚΕΦΑΛΑΙΟ ΕΡΩΤΗΣΕΙΣ ΘΕΜΑΤΑ ΘΕΩΡΙΑΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ Α ΓΥΜΝΑΣΙΟΥ ΑΛΓΕΒΡΑ 1. α. Τι γνωρίζετε για την Ευκλείδεια διαίρεση; Πότε λέγεται τέλεια; β. Αν σε μια διαίρεση είναι Δ=δ, πόσο είναι το πηλίκο και
ΜΙΚΡΟΙ ΑΡΧΙΤΕΚΤΟΝΕΣ. Το πρόβλημα. Δίνεται στους μαθητές το παρακάτω πρόβλημα:
 Περιγραφή ΜΙΚΡΟΙ ΑΡΧΙΤΕΚΤΟΝΕΣ Περίληψη Η κάτοψη μιας κατοικίας είναι ένα σύνθετο θέμα. Οι αρχιτέκτονες πρέπει να σχεδιάσουν μια σειρά παραμέτρων όπως ο τρόπος διανομής του χώρου η θέση των δωματίων του
Περιγραφή ΜΙΚΡΟΙ ΑΡΧΙΤΕΚΤΟΝΕΣ Περίληψη Η κάτοψη μιας κατοικίας είναι ένα σύνθετο θέμα. Οι αρχιτέκτονες πρέπει να σχεδιάσουν μια σειρά παραμέτρων όπως ο τρόπος διανομής του χώρου η θέση των δωματίων του
εξισώσεις-ανισώσεις Μαθηματικά α λυκείου Φροντιστήρια Μ.Ε. ΠΑΙΔΕΙΑ σύνολο) στα Μαθηματικά, τη Φυσική αλλά και σε πολλές επιστήμες
 Με τον διεθνή όρο φράκταλ (fractal, ελλ. μορφόκλασμα ή μορφοκλασματικό σύνολο) στα Μαθηματικά, τη Φυσική αλλά και σε πολλές επιστήμες ονομάζεται ένα γεωμετρικό σχήμα που επαναλαμβάνεται αυτούσιο σε άπειρο
Με τον διεθνή όρο φράκταλ (fractal, ελλ. μορφόκλασμα ή μορφοκλασματικό σύνολο) στα Μαθηματικά, τη Φυσική αλλά και σε πολλές επιστήμες ονομάζεται ένα γεωμετρικό σχήμα που επαναλαμβάνεται αυτούσιο σε άπειρο
Φύλλο Εργασίας 1 Μετρήσεις Μήκους Η Μέση Τιμή
 Φύλλο Εργασίας 1 Μετρήσεις Μήκους Η Μέση Τιμή α. Παρατηρώ, Πληροφορούμαι, Ενδιαφέρομαι Όπως θα μάθεις αναλυτικότερα στη Β και Γ γυμνασίου: Η μέτρηση είναι πρωταρχική και σημαντική διαδικασία για τη φυσική
Φύλλο Εργασίας 1 Μετρήσεις Μήκους Η Μέση Τιμή α. Παρατηρώ, Πληροφορούμαι, Ενδιαφέρομαι Όπως θα μάθεις αναλυτικότερα στη Β και Γ γυμνασίου: Η μέτρηση είναι πρωταρχική και σημαντική διαδικασία για τη φυσική
ΜΑΘΗΜΑΤΙΚΑ MATHEMATICS
 ΜΑΘΗΜΑΤΙΚΑ MATHEMATICS LEVEL: 11 12 (B - Γ Λυκείου) 10:00 11:00, 20 March 2010 THALES FOUNDATION 1 3 βαθμοί 1. Από την εικόνα μπορούμε να δούμε ότι: 1 + 3 + 5 + 7 = 4 4. Ποια είναι η τιμή του: 1 + 3 +
ΜΑΘΗΜΑΤΙΚΑ MATHEMATICS LEVEL: 11 12 (B - Γ Λυκείου) 10:00 11:00, 20 March 2010 THALES FOUNDATION 1 3 βαθμοί 1. Από την εικόνα μπορούμε να δούμε ότι: 1 + 3 + 5 + 7 = 4 4. Ποια είναι η τιμή του: 1 + 3 +
ΑΓΓΛΙΚΗ ΣΧΟΛΗ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2012. Χρόνος: 1 ώρα και 30 λεπτά
 ΑΓΓΛΙΚΗ ΣΧΟΛΗ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2012 ΜΑΘΗΜΑΤΙΚΑ ΠΡΩΤΗ ΤΑΞΗ Χρόνος: 1 ώρα και 30 λεπτά Να απαντήσετε σε ΟΛΕΣ τις ερωτήσεις. Όπου χρειάζεται να γίνουν πράξεις για να βρεθεί η απάντηση, να τις κάνετε
ΑΓΓΛΙΚΗ ΣΧΟΛΗ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2012 ΜΑΘΗΜΑΤΙΚΑ ΠΡΩΤΗ ΤΑΞΗ Χρόνος: 1 ώρα και 30 λεπτά Να απαντήσετε σε ΟΛΕΣ τις ερωτήσεις. Όπου χρειάζεται να γίνουν πράξεις για να βρεθεί η απάντηση, να τις κάνετε
Είδη τριγώνων ως προς τις πλευρές
 ΜΑΘΗΜΑΤΙΚΑ Ε ΔΗΜΟΤΙΚΟΥ ΤΕΤΡΑΔΙΟ ΕΡΓΑΣΙΩΝ 41 Είδη τριγώνων ως προς τις πλευρές Ενότητα 5 β τεύχος Είδη τριγώνων ως προς τις πλευρές 41 1η Άσκηση Να αντιστοιχίσεις: Το σκαληνό τρίγωνο έχει Το ισοσκελές τρίγωνο
ΜΑΘΗΜΑΤΙΚΑ Ε ΔΗΜΟΤΙΚΟΥ ΤΕΤΡΑΔΙΟ ΕΡΓΑΣΙΩΝ 41 Είδη τριγώνων ως προς τις πλευρές Ενότητα 5 β τεύχος Είδη τριγώνων ως προς τις πλευρές 41 1η Άσκηση Να αντιστοιχίσεις: Το σκαληνό τρίγωνο έχει Το ισοσκελές τρίγωνο
Ε Ρ Ω Τ Η Σ Ε Ι Σ Θ Ε Ω Ρ Ι Α Σ.
 Μ Ν Σ Υ Κ Σ Ε Ρ Ω Τ Η Σ Ε Ι Σ Θ Ε Ω Ρ Ι Σ. 1. Να γράψετε τους τύπους του εμβαδού των : (α) τετραγώνου (β) ορθογωνίου παραλληλογράμμου (γ) παραλληλογράμμου (δ) τριγώνου (ε) ορθογωνίου τριγώνου (στ) τραπεζίου.
Μ Ν Σ Υ Κ Σ Ε Ρ Ω Τ Η Σ Ε Ι Σ Θ Ε Ω Ρ Ι Σ. 1. Να γράψετε τους τύπους του εμβαδού των : (α) τετραγώνου (β) ορθογωνίου παραλληλογράμμου (γ) παραλληλογράμμου (δ) τριγώνου (ε) ορθογωνίου τριγώνου (στ) τραπεζίου.
Παράδειγμα 1 Γράψε ένα δεκαδικό αριθμό μεταξύ του 2 και του 3 που δεν περιέχει το 5 που περιέχει το 7 και που βρίσκεται όσο πιο κοντά γίνεται με το
 Παράδειγμα 1 Γράψε ένα δεκαδικό αριθμό μεταξύ του 2 και του 3 που δεν περιέχει το 5 που περιέχει το 7 και που βρίσκεται όσο πιο κοντά γίνεται με το 5/2 1 Παράδειγμα 2: Γράψε ένα κλάσμα που χρησιμοποιεί
Παράδειγμα 1 Γράψε ένα δεκαδικό αριθμό μεταξύ του 2 και του 3 που δεν περιέχει το 5 που περιέχει το 7 και που βρίσκεται όσο πιο κοντά γίνεται με το 5/2 1 Παράδειγμα 2: Γράψε ένα κλάσμα που χρησιμοποιεί
Βασικές Γεωμετρικές έννοιες
 Βασικές Γεωμετρικές έννοιες Σημείο Με την άκρη του μολυβιού μου ακουμπώντας την σε ένα κομμάτι χαρτί αφήνω ένα σημάδι το οποίο το λέω σημείο. Το σημείο το δίνω όνομα γράφοντας πάνω απ αυτό ένα κεφαλαίο
Βασικές Γεωμετρικές έννοιες Σημείο Με την άκρη του μολυβιού μου ακουμπώντας την σε ένα κομμάτι χαρτί αφήνω ένα σημάδι το οποίο το λέω σημείο. Το σημείο το δίνω όνομα γράφοντας πάνω απ αυτό ένα κεφαλαίο
Τι ονομάζουμε εμβαδόν μιας επίπεδης επιφάνειας; Αναφέρετε ονομαστικά τις μονάδες μέτρησης επιφανειών.
 1 Ονοματεπώνυμο μαθητή : Ημερομηνία :.../.../20... Μαθηματικές έννοιες: Εμβαδόν, Τετραγωνικό Μέτρο, Τετραγωνικό Δεκάμετρο, Τετραγωνικό Εκατοστόμετρο, Τετραγωνικό Χιλιοστόμετρο, Στρέμμα. Θυμόμαστε- Μαθαίνουμε:
1 Ονοματεπώνυμο μαθητή : Ημερομηνία :.../.../20... Μαθηματικές έννοιες: Εμβαδόν, Τετραγωνικό Μέτρο, Τετραγωνικό Δεκάμετρο, Τετραγωνικό Εκατοστόμετρο, Τετραγωνικό Χιλιοστόμετρο, Στρέμμα. Θυμόμαστε- Μαθαίνουμε:
Η θέση λοιπόν μπορεί να έχει θετική ή αρνητική τιμή, εξαρτάται από το αν είναι δεξιά ή αριστερά από το μηδέν.
 Βασικά σημεία θεωρίας για την Κίνηση (Έχει αφαιρεθεί πολύ ύλη από το κεφάλαιο. Για όποιον ενδιαφέρεται, η ύλη του κεφαλαίου υπάρχει στο τέλος αυτών των σημειώσεων. Με άλλα συμφωνώ και με άλλα όχι... Τα
Βασικά σημεία θεωρίας για την Κίνηση (Έχει αφαιρεθεί πολύ ύλη από το κεφάλαιο. Για όποιον ενδιαφέρεται, η ύλη του κεφαλαίου υπάρχει στο τέλος αυτών των σημειώσεων. Με άλλα συμφωνώ και με άλλα όχι... Τα
ΑΓΓΛΙΚΗ ΣΧΟΛΗ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Χρόνος: 1 ώρα και 30 λεπτά
 ΑΓΓΛΙΚΗ ΣΧΟΛΗ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2016 ΜΑΘΗΜΑΤΙΚΑ ΠΡΩΤΗ ΤΑΞΗ Χρόνος: 1 ώρα και 30 λεπτά Να απαντήσετε σε ΟΛΕΣ τις ερωτήσεις. Όπου χρειάζεται να γίνουν πράξεις για να βρεθεί η απάντηση, να τις κάνετε
ΑΓΓΛΙΚΗ ΣΧΟΛΗ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2016 ΜΑΘΗΜΑΤΙΚΑ ΠΡΩΤΗ ΤΑΞΗ Χρόνος: 1 ώρα και 30 λεπτά Να απαντήσετε σε ΟΛΕΣ τις ερωτήσεις. Όπου χρειάζεται να γίνουν πράξεις για να βρεθεί η απάντηση, να τις κάνετε
) = Απόσταση σημείου από ευθεία. Υπολογισμός Εμβαδού Τριγώνου. και A
 [Επιλογή Ιαν.. Εμβαδόν Τριγώνου ΣΤΟΧΟΙ: Ο µαθητής ϖρέϖει: να είναι ικανός να υϖολογίζει την αϖόσταση σηµείου αϖό ευθεία να είναι ικανός να υϖολογίζει το εµβαδό ενός τριγώνου αϖό τις συντεταγµένες των κορυφών
[Επιλογή Ιαν.. Εμβαδόν Τριγώνου ΣΤΟΧΟΙ: Ο µαθητής ϖρέϖει: να είναι ικανός να υϖολογίζει την αϖόσταση σηµείου αϖό ευθεία να είναι ικανός να υϖολογίζει το εµβαδό ενός τριγώνου αϖό τις συντεταγµένες των κορυφών
Άσκηση 1 Υπολογισμός της κλίμακας και μέτρηση οριζόντιων αποστάσεων
 Άσκηση 1 Υπολογισμός της κλίμακας και μέτρηση οριζόντιων αποστάσεων ΘΕΩΡΗΤΙΚΟ ΥΠΟΒΑΘΡΟ 1.1 Τρόποι έκφρασης της κλίμακας αεροφωτογραφιών Μια από τις σημαντικότερες παραμέτρους της αεροφωτογραφίας η οποία
Άσκηση 1 Υπολογισμός της κλίμακας και μέτρηση οριζόντιων αποστάσεων ΘΕΩΡΗΤΙΚΟ ΥΠΟΒΑΘΡΟ 1.1 Τρόποι έκφρασης της κλίμακας αεροφωτογραφιών Μια από τις σημαντικότερες παραμέτρους της αεροφωτογραφίας η οποία
ΜΑΘΗΜΑΤΙΚΑ Β ΓΥΜΝΑΣΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ Β ΓΥΜΝΑΣΙΟΥ Μέρος Β Κεφάλαιο 4ο Γεωμετρικά Στερεά Χρύσα Παπαγεωργίου Μαθηματικός - Πληροφορικός Το ορθό πρίσμα και τα στοιχεία του Κάθε ορθό πρίσμα έχει: Δύο έδρες παράλληλες, που είναι ίσα
ΜΑΘΗΜΑΤΙΚΑ Β ΓΥΜΝΑΣΙΟΥ Μέρος Β Κεφάλαιο 4ο Γεωμετρικά Στερεά Χρύσα Παπαγεωργίου Μαθηματικός - Πληροφορικός Το ορθό πρίσμα και τα στοιχεία του Κάθε ορθό πρίσμα έχει: Δύο έδρες παράλληλες, που είναι ίσα
ΕΠΑΝΑΛΗΨΗ ΓΕΩΜΕΤΡΙΑΣ Β ΛΥΚΕΙΟΥ ( α μέρος )
 ΕΠΑΝΑΛΗΨΗ ΓΕΩΜΕΤΡΙΑΣ Β ΛΥΚΕΙΟΥ ( α μέρος ) Ερωτήσεις Θεωρίας Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε στο τετράδιό
ΕΠΑΝΑΛΗΨΗ ΓΕΩΜΕΤΡΙΑΣ Β ΛΥΚΕΙΟΥ ( α μέρος ) Ερωτήσεις Θεωρίας Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε στο τετράδιό
Προτεινόμενη δομή σχεδίου μαθήματος για τα Μαθηματικά
 Καργιωτάκης Γιώργος, Μπελίτσου Νατάσσα Προτεινόμενη δομή σχεδίου μαθήματος για τα Μαθηματικά στις τάξεις Β, Δ και Ε (μιας διδακτικής ώρας). ΣΤΟΧΟΣ ΒΗΜΑΤΑ ΥΛΙΚΟ- ΧΡΟΝΟΣ ΕΝΕΡΓΕΙΕΣ Αρχική αξιολόγηση επιπέδου
Καργιωτάκης Γιώργος, Μπελίτσου Νατάσσα Προτεινόμενη δομή σχεδίου μαθήματος για τα Μαθηματικά στις τάξεις Β, Δ και Ε (μιας διδακτικής ώρας). ΣΤΟΧΟΣ ΒΗΜΑΤΑ ΥΛΙΚΟ- ΧΡΟΝΟΣ ΕΝΕΡΓΕΙΕΣ Αρχική αξιολόγηση επιπέδου
Κεφάλαιο 1: Κίνηση και γεωμετρικά σχήματα
 Ασκήσεις της Ενότητας 2 : Ζωγραφίζοντας με το ΒΥΟΒ -1- α. Η χρήση της πένας Κεφάλαιο 1: Κίνηση και γεωμετρικά σχήματα Υπάρχουν εντολές που μας επιτρέπουν να επιλέξουμε το χρώμα της πένας, καθώς και το
Ασκήσεις της Ενότητας 2 : Ζωγραφίζοντας με το ΒΥΟΒ -1- α. Η χρήση της πένας Κεφάλαιο 1: Κίνηση και γεωμετρικά σχήματα Υπάρχουν εντολές που μας επιτρέπουν να επιλέξουμε το χρώμα της πένας, καθώς και το
B Γυμνασίου. Ενότητα 9
 B Γυμνασίου Ενότητα 9 Γραμμικές εξισώσεις με μία μεταβλητή Διερεύνηση (1) Να λύσετε τις πιο κάτω εξισώσεις και ακολούθως να σχολιάσετε το πλήθος των λύσεων που βρήκατε σε καθεμιά. α) ( ) ( ) ( ) Διερεύνηση
B Γυμνασίου Ενότητα 9 Γραμμικές εξισώσεις με μία μεταβλητή Διερεύνηση (1) Να λύσετε τις πιο κάτω εξισώσεις και ακολούθως να σχολιάσετε το πλήθος των λύσεων που βρήκατε σε καθεμιά. α) ( ) ( ) ( ) Διερεύνηση
Μαθηματικά: Αριθμητική και Άλγεβρα. Μάθημα 10 ο, Τμήμα Α
 Μαθηματικά: Αριθμητική και Άλγεβρα Μάθημα 10 ο, Τμήμα Α Ορθογώνιο παραλληλόγραμμο 3 cm 5 cm Ο τύπος όπως είναι γραμμένος δείχνει ότι μπορούμε να πολλαπλασιάσουμε δύο μήκη. Ε=3cm x 5cm=15cm 2. Πώς καταλαβαίνετε
Μαθηματικά: Αριθμητική και Άλγεβρα Μάθημα 10 ο, Τμήμα Α Ορθογώνιο παραλληλόγραμμο 3 cm 5 cm Ο τύπος όπως είναι γραμμένος δείχνει ότι μπορούμε να πολλαπλασιάσουμε δύο μήκη. Ε=3cm x 5cm=15cm 2. Πώς καταλαβαίνετε
ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ Β ΓΥΜΝΑΣΙΟΥ. 1. 2( x 1) 3(2 x) 5( x 3) 2. 4x 2( x 3) 6 2x 3. 2x 3(4 x) x 5( x 1)
 ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ Β ΓΥΜΝΑΣΙΟΥ Α. Να λυθούν οι παρακάτω εξισώσεις: 1. ( x 1) ( x) 5( x ). x ( x ) 6 x. x ( x) x 5( x 1) x 1 (1 x) x ( x) x x. 1 x 5. x 6 1 1 ( ) 1 1 6. x 1 x 7. 1 x
ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ Β ΓΥΜΝΑΣΙΟΥ Α. Να λυθούν οι παρακάτω εξισώσεις: 1. ( x 1) ( x) 5( x ). x ( x ) 6 x. x ( x) x 5( x 1) x 1 (1 x) x ( x) x x. 1 x 5. x 6 1 1 ( ) 1 1 6. x 1 x 7. 1 x
ΕΝΟΤΗΤΑ 13 ΜΕΤΡΗΣΗ ΜΗΚΟΥΣ ΜΕ ΣΥΜΒΑΤΙΚΕΣ ΜΟΝΑΔΕΣ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΠΕΡΙΜΕΤΡΟ ΚΑΙ ΕΜΒΑΔΟΝ
 ΕΝΟΤΗΤΑ 13 ΜΕΤΡΗΣΗ ΜΗΚΟΥΣ ΜΕ ΣΥΜΒΑΤΙΚΕΣ ΜΟΝΑΔΕΣ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΠΕΡΙΜΕΤΡΟ ΚΑΙ ΕΜΒΑΔΟΝ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ ΜΕΤΡΗΣΗ Εκτίμηση και μέτρηση Μ1.1 Συγκρίνουν και σειροθετούν αντικείμενα με βάση το ύψος, το μήκος,
ΕΝΟΤΗΤΑ 13 ΜΕΤΡΗΣΗ ΜΗΚΟΥΣ ΜΕ ΣΥΜΒΑΤΙΚΕΣ ΜΟΝΑΔΕΣ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΠΕΡΙΜΕΤΡΟ ΚΑΙ ΕΜΒΑΔΟΝ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ ΜΕΤΡΗΣΗ Εκτίμηση και μέτρηση Μ1.1 Συγκρίνουν και σειροθετούν αντικείμενα με βάση το ύψος, το μήκος,
ΛΑΝΙΤΕΙΟ ΓΥΜΝΑΣΙΟ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ: ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΙΟΥΝΙΟΥ 2015
 ΛΑΝΙΤΕΙΟ ΓΥΜΝΑΣΙΟ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ: 014-015 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΙΟΥΝΙΟΥ 015 ΤΑΞΗ : Α ΜΑΘΗΜΑ : ΜΑΘΗΜΑΤΙΚΑ ΒΑΘΜΟΣ: ΗΜΕΡΟΜΗΝΙΑ : 05/06/015 ΔΙΑΡΚΕΙΑ : ώρες ΒΑΘΜΟΣ ΟΛΟΓΡΑΦΩΣ:. ΩΡΑ : 07:45 09:45 ΥΠΟΓΡΑΦΗ
ΛΑΝΙΤΕΙΟ ΓΥΜΝΑΣΙΟ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ: 014-015 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΙΟΥΝΙΟΥ 015 ΤΑΞΗ : Α ΜΑΘΗΜΑ : ΜΑΘΗΜΑΤΙΚΑ ΒΑΘΜΟΣ: ΗΜΕΡΟΜΗΝΙΑ : 05/06/015 ΔΙΑΡΚΕΙΑ : ώρες ΒΑΘΜΟΣ ΟΛΟΓΡΑΦΩΣ:. ΩΡΑ : 07:45 09:45 ΥΠΟΓΡΑΦΗ
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΙΝΣΤΙΤΟΥΤΟ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΠΟΛΙΤΙΚΗΣ. Μαθηματικά. Β μέρος. Λύσεις των ασκήσεων
 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΙΝΣΤΙΤΟΥΤΟ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΠΟΛΙΤΙΚΗΣ Μαθηματικά Β μέρος Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών και Σπουδών Οικονομίας & Πληροφορικής Λύσεις
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΙΝΣΤΙΤΟΥΤΟ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΠΟΛΙΤΙΚΗΣ Μαθηματικά Β μέρος Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών και Σπουδών Οικονομίας & Πληροφορικής Λύσεις
Από τι αποτελούνται; 4 όροι. Θεωρία. Κλάσμα ονομάζω τον αριθμό που φανερώνει. Κλάσματα ομώνυμα και ετερώνυμα. Μαθηματικά. Όνομα:
 Μαθηματικά Κεφάλαιο Όνομα: Ημερομηνία: / / Θεωρία Κλάσμα ονομάζω τον αριθμό που φανερώνει ένα μέρος ενός συνόλου. Παράδειγμα Τα κλάσματα τα χρησιμοποιούμε για να δηλώσουμε το μέρος ενός πράγματος, δηλαδή
Μαθηματικά Κεφάλαιο Όνομα: Ημερομηνία: / / Θεωρία Κλάσμα ονομάζω τον αριθμό που φανερώνει ένα μέρος ενός συνόλου. Παράδειγμα Τα κλάσματα τα χρησιμοποιούμε για να δηλώσουμε το μέρος ενός πράγματος, δηλαδή
ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1 ΜΑΘΗΜΑ 1 ο +2 ο ΕΝΝΟΙΑ ΔΙΑΝΥΣΜΑΤΟΣ Διάνυσμα ορίζεται ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ένα ευθύγραμμο τμήμα
ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1 ΜΑΘΗΜΑ 1 ο +2 ο ΕΝΝΟΙΑ ΔΙΑΝΥΣΜΑΤΟΣ Διάνυσμα ορίζεται ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ένα ευθύγραμμο τμήμα
Μαθηματικά Γ Γυμνασίου
 Α λ γ ε β ρ ι κ έ ς π α ρ α σ τ ά σ ε ι ς 1.1 Πράξεις με πραγματικούς αριθμούς (επαναλήψεις συμπληρώσεις) A. Οι πραγματικοί αριθμοί και οι πράξεις τους Διδακτικοί στόχοι Θυμάμαι ποιοι αριθμοί λέγονται
Α λ γ ε β ρ ι κ έ ς π α ρ α σ τ ά σ ε ι ς 1.1 Πράξεις με πραγματικούς αριθμούς (επαναλήψεις συμπληρώσεις) A. Οι πραγματικοί αριθμοί και οι πράξεις τους Διδακτικοί στόχοι Θυμάμαι ποιοι αριθμοί λέγονται
5.4. ΑΠΟΤΕΛΕΣΜΑΤΑ ΕΡΕΥΝΩΝ ΜΕ ΡΗΤΟΥΣ ΑΡΙΘΜΟΥΣ ΤΗΣ ΣΧΟΛΗΣ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΤΗΣ ΦΥΣΗΣ ΚΑΙ ΤΗΣ ΖΩΗΣ
 5.4. ΑΠΟΤΕΛΕΣΜΑΤΑ ΕΡΕΥΝΩΝ ΜΕ ΡΗΤΟΥΣ ΑΡΙΘΜΟΥΣ ΤΗΣ ΣΧΟΛΗΣ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΤΗΣ ΦΥΣΗΣ ΚΑΙ ΤΗΣ ΖΩΗΣ 5.4.1. Αποτελέσματα από το πρόγραμμα εξ αποστάσεως επιμόρφωσης δασκάλων και πειραματικής εφαρμογής των νοερών
5.4. ΑΠΟΤΕΛΕΣΜΑΤΑ ΕΡΕΥΝΩΝ ΜΕ ΡΗΤΟΥΣ ΑΡΙΘΜΟΥΣ ΤΗΣ ΣΧΟΛΗΣ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΤΗΣ ΦΥΣΗΣ ΚΑΙ ΤΗΣ ΖΩΗΣ 5.4.1. Αποτελέσματα από το πρόγραμμα εξ αποστάσεως επιμόρφωσης δασκάλων και πειραματικής εφαρμογής των νοερών
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΑΓΩΓΗΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΕΡΓΑΣΙΑ ΓΙΑ ΤΟ ΜΑΘΗΜΑ: ΘΕΜΑ: «Αριθμοί στην καθημερινή ζωή»
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΑΓΩΓΗΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΕΡΓΑΣΙΑ ΓΙΑ ΤΟ ΜΑΘΗΜΑ: ΔΙΔΑΚΤΙΚΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΙΙ ΘΕΜΑ: «Αριθμοί στην καθημερινή ζωή» Βόκα Δέσποινα & Δούρου
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΑΓΩΓΗΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΕΡΓΑΣΙΑ ΓΙΑ ΤΟ ΜΑΘΗΜΑ: ΔΙΔΑΚΤΙΚΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΙΙ ΘΕΜΑ: «Αριθμοί στην καθημερινή ζωή» Βόκα Δέσποινα & Δούρου
Διδακτική των Μαθηματικών
 Διδακτική των Μαθηματικών Ονοματεπώνυμο : Μαμτζέλλη Χρυσούλα Τάξη : Γ Δημοτικού Κεφάλαιο 43 : Η συμμετρία Πρόκειται για ένα εισαγωγικό μάθημα στην αξονική συμμετρία. Οι μαθητές θα μάθουν πότε δύο σχήματα
Διδακτική των Μαθηματικών Ονοματεπώνυμο : Μαμτζέλλη Χρυσούλα Τάξη : Γ Δημοτικού Κεφάλαιο 43 : Η συμμετρία Πρόκειται για ένα εισαγωγικό μάθημα στην αξονική συμμετρία. Οι μαθητές θα μάθουν πότε δύο σχήματα
ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ
 ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ ΑΣΚΗΣΗ 1: Ένα οπτικό φράγμα με δυο σχισμές που απέχουν μεταξύ τους απόσταση =0.0 mm είναι τοποθετημένο σε απόσταση =1,0 m από μια οθόνη. Το οπτικό φράγμα με τις δυο σχισμές φωτίζεται
ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ ΑΣΚΗΣΗ 1: Ένα οπτικό φράγμα με δυο σχισμές που απέχουν μεταξύ τους απόσταση =0.0 mm είναι τοποθετημένο σε απόσταση =1,0 m από μια οθόνη. Το οπτικό φράγμα με τις δυο σχισμές φωτίζεται
ΜΕΤΡΗΣΗ ΕΜΒΑΔΟΥ. Σχεδιασμός - Περιγραφή
 ΕΚΦΕ Α Αν. Αττικής - Υπεύθυνος Κ. Παπαμιχάλης Εργαστηριακές ασκήσεις Φυσικής Β ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 ΜΕΤΡΗΣΗ ΕΜΒΑΔΟΥ Η εικόνα έχει ληφθεί από τον ιστότοπο: http://www.vbhelper.co/vbgptoc.ht Πώς θα μετρήσουμε
ΕΚΦΕ Α Αν. Αττικής - Υπεύθυνος Κ. Παπαμιχάλης Εργαστηριακές ασκήσεις Φυσικής Β ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 ΜΕΤΡΗΣΗ ΕΜΒΑΔΟΥ Η εικόνα έχει ληφθεί από τον ιστότοπο: http://www.vbhelper.co/vbgptoc.ht Πώς θα μετρήσουμε
Οδηγίες για το SKETCHPAD Μωυσιάδης Πολυχρόνης - Δόρτσιος Κώστας. Με την εκτέλεση του Sketchpad παίρνουμε το παρακάτω παράθυρο σχεδίασης:
 Οδηγίες για το SKETCHPAD Μωυσιάδης Πολυχρόνης - Δόρτσιος Κώστας Με την εκτέλεση του Sketchpad παίρνουμε το παρακάτω παράθυρο σχεδίασης: παρόμοιο με του Cabri με αρκετές όμως διαφορές στην αρχιτεκτονική
Οδηγίες για το SKETCHPAD Μωυσιάδης Πολυχρόνης - Δόρτσιος Κώστας Με την εκτέλεση του Sketchpad παίρνουμε το παρακάτω παράθυρο σχεδίασης: παρόμοιο με του Cabri με αρκετές όμως διαφορές στην αρχιτεκτονική
+ = x 8x = x 8x 12 0 = 2 + = + = x 1 2x. x 2x 1 0 ( 1)
 ΠΡΟΒΛΗΜΑΤΑ ΣΤΙΣ ΚΛΑΣΜΑΤΙΚΕΣ ΕΞΙΣΩΣΕΙΣ Β ΒΑΘΜΟΥ ΜΕΘΟ ΟΛΟΓΙΑ Τα προβλήµατα των Μαθηµατικών χωρίζονται στις παρακάτω βασικές κατηγορίες : Κατηγορία 1η : Αναζητούν έναν άγνωστο Ονοµάζουµε χ αυτόν που αναζητούµε
ΠΡΟΒΛΗΜΑΤΑ ΣΤΙΣ ΚΛΑΣΜΑΤΙΚΕΣ ΕΞΙΣΩΣΕΙΣ Β ΒΑΘΜΟΥ ΜΕΘΟ ΟΛΟΓΙΑ Τα προβλήµατα των Μαθηµατικών χωρίζονται στις παρακάτω βασικές κατηγορίες : Κατηγορία 1η : Αναζητούν έναν άγνωστο Ονοµάζουµε χ αυτόν που αναζητούµε
(ΤΑ ΑΓΑΘΑ ΚΟΠΟΙΣ ΚΤΩΝΤΑΙ)
 (ΤΑ ΑΓΑΘΑ ΚΟΠΟΙΣ ΚΤΩΝΤΑΙ) 1. Να σχεδιάσετε ένα σκαληνό τρίγωνο με περίμετρο 10 cm. Περίμετρος ενός τριγώνου λέγεται το άθροισμα των μηκών των πλευρών του). Μια περίπτωση είναι οι πλευρές του να έχουν μήκος
(ΤΑ ΑΓΑΘΑ ΚΟΠΟΙΣ ΚΤΩΝΤΑΙ) 1. Να σχεδιάσετε ένα σκαληνό τρίγωνο με περίμετρο 10 cm. Περίμετρος ενός τριγώνου λέγεται το άθροισμα των μηκών των πλευρών του). Μια περίπτωση είναι οι πλευρές του να έχουν μήκος
