OSNOVE MINERALOGIJE I PETROLOGIJE OPĆA MINERALOGIJA SISTEMATSKA MINERALOGIJA PETROLOGIJA. Bazalt Ca-plagioklas, pirokseni.
|
|
|
- Ευγένεια Γούσιος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 OSNOVE MINERALOGIJE I PETROLOGIJE Metamorfne stijene nastaju metamorfozom iz starijih magmatskih, metamorfnih ili sedimentnih stijena, bez otapanja ili taljenja. KRISTALOGRAFIJA OPĆA MINERALOGIJA KEMIJSKA I FIZIKALNA SVOJSTVA MINERALA GENEZA MINERALA SISTEMATSKA MINERALOGIJA NESILIKATI SILIKATI PETROLOGIJA MAGMATSKIH STIJENA PETROLOGIJA PETROLOGIJA METAMORFNIH STIJENA PETROLOGIJA SEDIMENTNIH STIJENA Starije magmatske, metamorfne ili sedimentne stijene PROTOLIT Promjena p,t,c METAMORFOZA Geotermalni gradijent Difuzija iona pomoću fluida voda, karbonatni fluidi Pritisak naliježećih naslaga Preraspodjela mineralne tvari u skladu s novim p,t Vapnenac, CaCO 3 Bazalt Ca-plagioklas, pirokseni Promjena p,t,c Promjena p,t,c Mramor, CaCO 3 Amfibolit Na-plagioklas, amfibol, epidot 1
2 Čimbenici metamorfizma Temperatura Utiskivanje magme Trenje duž rasjednih linija Dubina zalijeganja (geotermalni gradijent) Udar meteorita Radioaktivni raspad Toplina ulaza = toplini izlaza = const. t Toplina ulaza > toplini izlaza = > t, endotermne reakcije (dehidratacija), progradna metamorfoza Toplina ulaza < toplini izlaza = < t, retrogradna metamorfoza Temperatura Pritisak Fluidi Sastav protolita Vrijeme Prijenos topline Kondukcija Konvekcija Radioaktivno zračenje Pritisak Promjena visine ili gustoće naliježećih naslaga Pliće (stijene krute) usmjereni tlak = stres Dublje (stijene plastične) neusmjereni tlak = litostatski Dvostruka debljina kontinentalne kore Normalna debljina kontinentalne kore Litostatski pritisak Duboki sedimentacijski bazen Metamorfoza tonjenja Statički stjenska masa miruje Dinamički stijenska masa se kreće Postanak usmjerenog stresa 2
3 Protolit Metamorfna stijena Fluidi Sastav protolita Dehidratacijom minerala pri progradnom metamorfizmu H 2 O, CO 2, CH 4, H 2 S δ vode > δ vodene pare pri T < T kritične (<373ºC i 217 bara) δ vode = δ vodene pare pri T > T kritične = fluidna faza ili fluid Porna voda iz sedimentnih stijena, meteorska ili magmatska voda Reaktanti Produkti Ovise o p, T, t, volatilima, i mogu biti različiti 1. Bez volatila polimorfne reakcije, izmjene kationa, izdvajanja 2. S volatilima dehidratacija, dekarbonizacija, oksidacija, redukcija Vrijeme Metamorfni procesi su izuzetno spori: ovise o brzini prijenosa topline, volumenu stijena podvrgnutih metamorfizmu, vrsti stijene, sadržaju fluida mineralne parageneze dostupne za istraživanje su često u metastabilnom stanju. UVJETI METAMORFIZMA T min ~ 150ºC (silikatne stijene) pojava prvog metamorfnog minerala (klorit, glaukofan) T max = T taljenja stijene ovisi o p, sastavu stijene i količini vode ( ºC u kori, i do 1500 ºC u plaštu) STUPNJEVI METAMORFOZE p, t, dubina, indeks minerali, mineralne zone, metamorfni facijesi, metamorfne izograde T vrlo-niski, niski, srednji, visoki P visoko i niskotlačna Dubina epizona, mezozona, katazona ~ dijagenetski uvjeti PRIMJER 1 GRANIT p = 5 kbar p = 5 kbar + H2O - H2O T taljenja = 660ºC T taljenja = 1000ºC PRIMJER 2 BAZALT p = 5 kbar p = 5 kbar + H2O - H2O T taljenja = 800ºC T taljenja = 1120ºC P min ~ P površinski P max = 40 kbar 3
4 Epizona < 300ºC Niski p Minerali s konstitucijskom vodom: kalcit, dolomit, glaukofan, talk, sericit, klorit, albit Mezozona ºC Stres litostatski p Rekristalizacija štapićasti i iglićasti minerali: granati, disten, Hbl, Bt, Ms, Na-Pl Katazona ºC litostatski p Bezvodni minerali >ρ Stijene homogene, slične magmatskim; granati, andaluzit, silimanit, diopsid, Hbl, alkalijski feldspati, Ca-Pl Indeks minerali: klorit biotit granat staurolit disten silimanit Mineralne zone zone čija je donja granica definirana prvom pojavom indeks minerala po kojemu je zona dobila naziv, a gornja granica prvom pojavom indeks minerala slijedeće zone: kloritna biotitna granatna staurolitna distenska silimanitna Problem: indeks minerali se u stijenama različitog sastava mogu pojaviti pri različitim p-t uvjetima Ispravnije Odrediti stupanj metamorfoze prema reakcijama u kojima su reaktanti i produkti 1 ili više minerala, uz odreñen p,t, utjecaj fluida i sastav protolita eksperimentalno ili iz termodinamičkih podataka Metamorfni facijesi skupina metamorfnih stijena nastalih pri odreñenim p,t uvjetima (zanemaren utjecaj fluida), a definira se mineralnom paragenezom stabilnom samo u tom facijesu Metamorfne izograde linije na karti koje spajaju mjesta istih indeks minerala na zemljinoj površini Pirometamorfoza 1. Prema prevladavajućem faktoru temperatura VRSTE METAMORFIZMA pritisak Lokalni metamorfizam Kontaktni - termalni Na kontaktu magme i okolnih stijena pri čemu se stijene parcijalno tale prijelaz prema magmatskim procesima. Termalni metamorfizam Dinamotermalni metamorfizam Dinamo ili kinematički metamorfizam 2. Prema veličini prostora Lokalni metamorfizam Regionalni metamorfizam 1. Kontaktni 2. Kataklastični 3. Hidrotermalni 4. Impaktni 1. Orogeni 2. Plutonski 3. Metamorfoza oceanskog dna 4. Metamorfoza tonjenja 4
5 Lokalni metamorfizam Kataklastični - kinematički Lokalni metamorfizam Hidrotermalni pneumatolitski - fluidi Metasomatoza migracija iona Autometasomatoza plinovi i pari zaostali nakon kristalizacije magme djeluju prije nastale stijene Alteracijske zone - izmjene primarnih stijena pod utjecajem pneuma ili hidrotermi Kontaktni met. Magmatska intruzija Kontaktni met. Lokalni metamorfizam Impaktna - >p, t, vrijeme kratko, taljenje Regionalni metamorfizam Orogeni - dinamotermalni Konvergentne granice ploča, t ºC Halls creek, Australija 5
6 Regionalni metamorfizam Plutonski Dublji dijelovi litosfere, >t, litostatski p (neusmjeren) granoblstične stijene, bezvodni minerali velike gustoće, nema ošre granice izmeñu plutonske metamorfoze i magmatizma. Regionalni metamorfizam Metamorfizam tonjenja <t (do 450º), sačuvane strukture i relikti protolita, slabija škriljavost, nepotpuna izmjena mineralnog sastava postanak se odreñuje mikroskopski Regionalni metamorfizam Metamorfizam oceanskog dna Ocean Tisuće kilometara ºC, p < 3kbar Hidrotermalne žile Metasomatoza 3. Prema stabilnosti mineralnih parageneza Progradna metamorfoza - dinamotermalna Endotermni proces primanja topline i mehaničke energije, procesi dehidratacije, dekarbonizacije (oslobañanje CO2, H2O). Nastaju novi minerali koji su stabilni uvjetima povišenja p, t. Retrogradna metamorfoza često pneumatolitna ii hidrotermalna, metamorfoza oceanskog dna, pri brzim ekshumacijama Snižavanjem p,t nastaju novi minerali, primarno iz visokotemperaturnih parageneza 4. Prema kemijskom sastavu Izokemijska metamorfoza Nema promjene kemijskog sastava u odnosu na protolit (vapnenac mramor) KOLOKVIJ 1. KOJIM PROCESOM nastaju magmatske stijene? 2. KOJIM PROCESOM nastaju metamorfne stijene? 3. Nabroji FAKTORE koji utječu na metamorfizam. 4. Nabroji TIPOVE metamorfizma prema prevladavajućem faktoru. 5. Nabroji TIPOVE metamorfizma prema veličini prostora. Alokemijska metamorfoza - metsomatoza Dolazi do promjene kemijskog sastava u odnosu na protolit (izmjene kationa) 6
7 Minerali Kako prepoznati metamorfnu stijenu? 1) Minerali zastupljeni u svim stijenama kvarc, kalcit, dolomit, piroksen, amfibol, tinjci, feldspati 2) Minerali tipični za metamorfne uvjete granat, disten, andaluzit, silimanit, jadeit, tremolit, aktinolit, glaukofan, serpentin, talk Mineralne zajednice Asocijacije karakterističnih minerala Struktura Blastične i kataklastične Tekstura Škriljava i homogena STRUKTURE METAMORFNIH STIJENA - BLASTIČNA Grč. blastos= klica Blastoza = rekristalizacija Blastična struktura = nastaje rekristalizacijom i rastom minerala u metamorfnim uvjetima (u čvrstom stanju!) Reliktne blastične strukture odražavaju strukturu protolita (npr. blastoporfirna) HOMEOBLASTIČNA vs. HETEROBLASTIČNA HOMEOBLASTIČNA MINERALNI SASTOJCI OJEDNAKIH VELIČINA Granoblastična minerali ojednakih dimenzija Lepidoblastična listićavi minerali Nematoblastična štapičasti ili igličasti minerali HETEROBLASTIČNA MINERALNI SASTOJCI RAZLIČITIH VELIČINA PORFIROBLASTIČNA - PORFIROBLASTI Foliacija Lineacija Homogena tekstura Lepidoblastična Nematoblastična Granoblastična 3 cm velik almandinski granat porfiroblast u gnajsu, Paraiba,Brazil 7
8 STRUKTURE METAMORFNIH STIJENA - KATAKLASTIČNA Deformirani minerali s anomalnim optičkim svojstvima, sekundarnim lamelama sraštanja i pukotinama. MILONITNA minerali zdrobljeni u prah, ponekad pretaljeni u staklo BREČASTA ILI MORTAL rubovi minerala zdrobljeni, jezgre očuvane PROFIROKLASTIČNA veći nezdrobljeni minerali (porfiroklasti) u sitnozdrobljenom matriksu OKCASTA stijena sadrži lećaste porfiroklaste (feldspati,kvarc), okružene stitnijim, listićavim mineralima PORFIROKLASTIČNA OKASTA STRUKTURE METAMORFNIH STIJENA TEKSTURE METAMORFNIH STIJENA ŠIVANA - nazubljena, zupčasto prodiranje jednog minerala u drugi pri visokoj temperaturi i tlaku. MOZAIČNA neorijentirana, poligonalna zrna, dodiruju se u jedno točci pod kutem od ~120º. ŠKRILJAVA stres Ploha škriljavosti stres Škriljavost ili folijacija Šivana Mozaična 8
9 PARALELNO - PRUGASTA Zrnasti minerali Listićavi minerali NAZIVI METAMORFNIH STIJENA HOMOGENA Kotaktna metamorfoza pri <p, >t ili metamorfoza pri >litostatskom p Korijen -Teksturno svojstvo (škriljavac) -Dominantni metamorfni mineral (amfibolit) 1. Prema strukturno-teksturnim svojstvima Slejt, filit, škriljavac, gnajs Kataklazit, milonit, ultramilonit ± Prefiks -Strukturno svojstvo (trakasti amfibolit) -Dodatna informacija o mineralnom sastavu (trakasti epidotni amfibolit) Boja Zeleni škriljavac Plavi škriljavac MRAMOR 2 Prema mineralnom sastavu Glavni minerali >5 vol% (muskovitni gnajs) Sporedni minerali <5 vol% (gnajs koji sadrži muskovit) Kataklastična metamorfoza s očuvanim mineralnim sastavom protolita (kataklazirani vapnenac) Ako stijena nema reliktnu ni metamorfnu strukturu naziv prema mineralnom sastavu (kvarc-klorit-epidotna stijena) 3. Prema protolitu Meta protolit metamorfna stijena, prefiks nazivu protolita (metagabro) Orto protolit magmatska stijena, prefiks nazivu metamorfne stijene (ortognajs) Para protolit sedimentna stijena, prefiks nazivu metamorfne stijene (paragnajs) 9
10 KLASIFIKACIJA METAMORFNIH STIJENA 1. Prema dubini postanka (p,t uvjeti) Epizona Mezozona Katazona 2. Prema strukturno-teksturnim obilježjima (stupanj folijacije i lineacije) Izražena (slejt, filit, škriljavac) Slabo izražena (gnajs, milonit, migmatit) Nema ili vrlo slabo izražena (mramor, kvarcit, skarn, hornfels) 3. Prema protolitu (ukoliko se može utvrditi) Meta-, orto-, para- 4. Prema mineralnoj paragenezi (metamorfnom facijesu) 5. Prema vrsti metamorfizma Dinamometamorfne, termalnometamorfne, dinamotermalne Lokalno i regionalno metamorfne Facijes plavih škriljavaca: glaukofan+px+ aragonit Granulitni facijes: bezvodni Opx+Cpx Amfibolitni facijes: Aktinolit+klorit +epidot+albit Facijes zelenih škriljavaca: plagioklas+hor nblenda Podfacijes zelenih škriljavaca Prema mineralnoj paragenezi (metamorfnom facijesu) Eklogitni facijes: omfacit+granat Tip metamorfizma Stijene Podfacijes zelenih škriljavaca Facijes zelenih škriljavaca plagioklas+hornblenda Amfibolitni facijes: Aktinolit+klorit+epidot+albit 1. Kontaktni (termalni) 2. Kataklastični (kinematički) Mramor, kvarcit, skarn, kornit Kataklazit, milonit, ultramilonit 3. Regionalni (dinamotermalni) Slejt, filit, škriljavac, gnajs, serpentinit, amfibolit, mramor, kvarcit, granulit, eklogit Facijes plavih škriljavaca: glaukofan+px+aragonit Granulitni facijes: bezvodni Opx+Cpx Eklogitni facijes: omfacit+granat 10
11 1. Kontaktni (termalni) metamorfizam MRAMOR -Metamorfozom (rekristalizacijom) VAPNENACA ILI DOLOMITA (kalcitni i dolomitni mramor) -Sastav KALCIT (DOLOMIT), tremolit, diopsid, granat, epidot, olivin -Tekstura - HOMOGENA, ako sadrži tinjac slabo škriljava -Struktura - GRANOBLASTIČNA -Boja - BIJEL, zelen, siv, crven, blijedo žut, nejednoliko ili jednoliko obojen od primjesa KVARCIT -Metamorfozom (rekristalizacijom) PJEŠČENJAKA ILI ROŽNJAKA -Sastav KVARC -Tekstura HOMOGENA -Struktura - GRANOBLASTIČNA -Boja - SVIJETLA ρ= 2,65 2,72 g/cm 3 ρ 0 = 2,65 2,71 g/cm 3 p = 0,4 2 % w = 0,1 0,3 % β p = MPa Lako se polira Sivocrni mramor kod Požege ρ= 2,64 2,70 g/cm 3 ρ 0 = 2,60 2,65 g/cm 3 p = 0,4 2 % w = 0,2 0,5 % β p = MPa Masivan, tvrd, otporan na atmosferilije 2. Kataklastični (kinematički) metamorfizam SKARN - Na kontaktu VAPNENCA i GRANITNE MAGME. Vapnenac metasomatski obogaćen Si, Al, Fe, Mg -Sastav silikati Ca, Mg, Fe (hedembergit, diopsid, tremolit, aktinolit, granati, forsterit, titanit) + magnetit, pirhotin, sulfidi Cu KORNIT ILI HORNFELS - Izmjenom PELITA, TUFA, SLEJTA u visokometamorfnim uvjetima, na kontaktu s kiselim intruzivima -Sastav kvarc, feldspati, biotit, granati, kalcit, biotit, piroksen, andaluzit -Tekstura HOMOGENA KATAKLAZIT -Oštri fragmenti nastali drobljenjem stijena usljed tektonskih zdrobljenih sastojaka iste stijene sličan breči, ali se osnovna masa sastoji od zdrobljenih čestica iste stijene. MILONIT -Stijena nastala gotovo potpunim drobljenjem ishodišne stijene u prah (i do 90 vol % matriksa). ULTRAMILONIT -Sadrži vrlo malo fragmenata (<10 vol%) u finozrnatoj osnovi tamne boje. Često dolazi do djelomičnog taljenja i postanka stakla 11
12 Kataklastična stijena 3. Regionalni (dinamotermalni) metamorfizam KRISTALASTI ŠKRILJAVCI Usmjereni pritisak + fluidi otapanje i ponovna rekristalizacja na mjestu manjeg pritiska, škriljave i paralelno-prugaste teksture ºC PROGRADNA (PROGRESIVNA) METAMORFOZA SLEJT FILIT TINJČEV ŠKRILJAVAC GNAJS Milonit Crveni, zeleni, crni PROGRADNA (PROGRESIVNA) METAMORFOZA SLEJT FILIT TINJČEV ŠKRILJAVAC GNAJS šejl slejt škriljavac gnajs Tekstura škriljasta Struktura - lepidoblastična filit migmatit šejl Crveni, zeleni, crni slejt škriljavac gnajs filit migmatit Plummer, Mcgeary & Carlson(2001): Physical Geology 12
13 ŠKRILJAVCI Prikaz približno prvih 30 km zemljine kore s metamorfnim mineralima nastalim iz šejla KLORITNI Klorit, albit, kvarc ZELENI Klorit, aktinolit, epidot, albit AMFIBOLSKI Aktinolit, hornblenda GLAUKOFANSKI Glaukofan, granat, muskovit, biotit, kalcit, albit Plummer, Mcgeary & Carlson(2001): Physical Geology SERPENTINIT Stijena nastala hidrotermalnom metamorfozom bazičnih i ultrabazičnih stijena Boja crna zelena Tekstura škriljava Struktura granoblastična lepidoblastična Minerali serpentin, olivin, piroksen, amfibol, magnetit, klorit, magnezit AMFIBOLIT Boja crna tamnozelena Tekstura homogena Struktura granoblastična nematoblastična Minerali >50 vol % hornblenda, >20 vol% neutralni bazični plagioklas + Bt, titanit, Q PARA progradnom metamorfozom lapora dobro izražena folijaija ORTO retrogradnom metamorfozom bazičnih stijena, slabo izražena folijacija. Odličan tehnički-grañevinski kamen 13
14 GRANULIT (plutonska metamorfoza) Nastaje iz sedimentnih (siltit, šej, arkoza) ili magmatskih kiselih, neutralnih i bazičnih stijena Tekstura masivna - gnajsoidna Struktura granoblastična Minerali kvarc, feldspati, pirokseni, granati, disten, silimanit (bezvodni minerali) EKLOGIT (plutonska metamorfoza) Nastaje iz gabroidnih stijena (bez feldspata) Minerali zeleni Px omfacit + granat MIGMATIT (plutonska metamorfoza) Silikatne stijene s tamnijim i svijetlijim dijelovima parcijalno taljenje (svijetliji dijelovi se lako take, tamniji teže) 14
REGIONALNO-METAMORFNE STENE ( ºC; 2-10 kbar)
 REGIONALNO-METAMORFNE STENE (200-800ºC; 2-10 kbar) PODELA PREMA TEKSTURI 1. ŠKRILJAVE I 2. MASIVNE METAMORFNE STENE PODELA PREMA STEPENU KRISTALINITETA (NE ZAVISI OD STEPENA METAMORFIZMA) 1. STENE VISOKOG
REGIONALNO-METAMORFNE STENE (200-800ºC; 2-10 kbar) PODELA PREMA TEKSTURI 1. ŠKRILJAVE I 2. MASIVNE METAMORFNE STENE PODELA PREMA STEPENU KRISTALINITETA (NE ZAVISI OD STEPENA METAMORFIZMA) 1. STENE VISOKOG
METAMORFNE STENE. Charles Luell - definisao pojam metamorfizma na osnovu promena u sedimentnim stenama sa promenom dubine.
 METAMORFNE STENE Charles Luell - definisao pojam metamorfizma na osnovu promena u sedimentnim stenama sa promenom dubine. Metamorfizam - skup fizičko-hemijskih procesa u steni u uslovima koji se razlikuju
METAMORFNE STENE Charles Luell - definisao pojam metamorfizma na osnovu promena u sedimentnim stenama sa promenom dubine. Metamorfizam - skup fizičko-hemijskih procesa u steni u uslovima koji se razlikuju
Anorganski nemetalni materijali Sij Stijene
 Anorganski nemetalni materijali Sij Stijene Stijene Stijene su prirodni mineralni agregati, ulaze u sastav zemljine kore kao samostalne i jasno ograničene mase Minerali izgrađuju stijene Stijene izgrađuju
Anorganski nemetalni materijali Sij Stijene Stijene Stijene su prirodni mineralni agregati, ulaze u sastav zemljine kore kao samostalne i jasno ograničene mase Minerali izgrađuju stijene Stijene izgrađuju
MINERAL? nema jedinstvenih kriterijuma za odgovor
 Predavanje 1. MINERALI, MINERALOGIJA NAUKA O MINERALIMA minerals (lat.) rudni logos (grč.) nauka Izučava prirodu supstanci koje su vezane za rudnike, rudne žile i Zemljinu koru. MINERAL? nema jedinstvenih
Predavanje 1. MINERALI, MINERALOGIJA NAUKA O MINERALIMA minerals (lat.) rudni logos (grč.) nauka Izučava prirodu supstanci koje su vezane za rudnike, rudne žile i Zemljinu koru. MINERAL? nema jedinstvenih
IZVORI, SASTAV I DINAMIKA MINERALNE SASTAVNICE TLA MINERALI - MINERALI I STIJENE - petrogeni minerali
 1 IZVORI, SASTAV I DINAMIKA MINERALNE SASTAVNICE TLA - MINERALI I STIJENE - petrogeni minerali MINERALI 2 primarni minerali sekundarni minerali pedogeni minerali postojanost minerala 3 minerali prema prozirnosti:
1 IZVORI, SASTAV I DINAMIKA MINERALNE SASTAVNICE TLA - MINERALI I STIJENE - petrogeni minerali MINERALI 2 primarni minerali sekundarni minerali pedogeni minerali postojanost minerala 3 minerali prema prozirnosti:
Treće predavanje. Hemija životne sredine I (T. Anđelković)
 Treće predavanje 1 CILJEVI PREDAVANJA Građa litosfere. Sastav Zemljine kore. Hemijski sastav i tipovi magme. Diferencijacija magme. Bovenova serija. Tipovi stena. Ciklus transformacije stena. ISHODI PREDAVANJA
Treće predavanje 1 CILJEVI PREDAVANJA Građa litosfere. Sastav Zemljine kore. Hemijski sastav i tipovi magme. Diferencijacija magme. Bovenova serija. Tipovi stena. Ciklus transformacije stena. ISHODI PREDAVANJA
Konstruisanje. Dobro došli na... SREDNJA MAŠINSKA ŠKOLA NOVI SAD DEPARTMAN ZA PROJEKTOVANJE I KONSTRUISANJE
 Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
Opća bilanca tvari - = akumulacija u dif. vremenu u dif. volumenu promatranog sustava. masa unijeta u dif. vremenu u dif. volumen promatranog sustava
 Opća bilana tvari masa unijeta u dif. vremenu u dif. volumen promatranog sustava masa iznijeta u dif. vremenu iz dif. volumena promatranog sustava - akumulaija u dif. vremenu u dif. volumenu promatranog
Opća bilana tvari masa unijeta u dif. vremenu u dif. volumen promatranog sustava masa iznijeta u dif. vremenu iz dif. volumena promatranog sustava - akumulaija u dif. vremenu u dif. volumenu promatranog
MINERALOGIJA KRISTAL MINERAL. Definicija: - kristalna vrsta, nastala v naravi (tudi umetno)
 MINERALOGIJA KRISTAL Definicija: - trdno telo - periodična prostorska razvrstitev kemičnih sestavin - ravne ploskve - stalni koti - nastanek: naravni, umetni procesi - anorganske, organske spojine MINERAL
MINERALOGIJA KRISTAL Definicija: - trdno telo - periodična prostorska razvrstitev kemičnih sestavin - ravne ploskve - stalni koti - nastanek: naravni, umetni procesi - anorganske, organske spojine MINERAL
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
INTELIGENTNO UPRAVLJANJE
 INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
DIMENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE
 TEORIJA ETONSKIH KONSTRUKCIJA T- DIENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE 3.5 f "2" η y 2 D G N z d y A "" 0 Z a a G - tačka presek koja određje položaj sistemne
TEORIJA ETONSKIH KONSTRUKCIJA T- DIENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE 3.5 f "2" η y 2 D G N z d y A "" 0 Z a a G - tačka presek koja određje položaj sistemne
6 SREDNJEZRNATI KLASTITI (PJEŠČENJACI)
 62 6 SREDNJEZRNATI KLASTITI (PJEŠČENJACI) veličina čestica: 2mm - 63μm 6.1 UVOD vrlo krupni pijesak krupni pijesak srednji pijesak sitni pijesak vrlo sitni pijesak litifikacija pijesak pješčenjak klastična
62 6 SREDNJEZRNATI KLASTITI (PJEŠČENJACI) veličina čestica: 2mm - 63μm 6.1 UVOD vrlo krupni pijesak krupni pijesak srednji pijesak sitni pijesak vrlo sitni pijesak litifikacija pijesak pješčenjak klastična
Što je sediment? Što je sedimentna stijena? OSNOVE MINERALOGIJE I PETROLOGIJE OPĆA MINERALOGIJA SISTEMATSKA PETROLOGIJA PETROLOGIJA
 Što je sediment? OSNOVE MINERALOGIJE I PETROLOGIJE OPĆA MINERALOGIJA SISTEMATSKA MINERALOGIJA PETROLOGIJA KRISTALOGRAFIJA KEMIJSKA I FIZIKALNA SVOJSTVA MINERALA GENEZA MINERALA NESILIKATI SILIKATI PETROLOGIJA
Što je sediment? OSNOVE MINERALOGIJE I PETROLOGIJE OPĆA MINERALOGIJA SISTEMATSKA MINERALOGIJA PETROLOGIJA KRISTALOGRAFIJA KEMIJSKA I FIZIKALNA SVOJSTVA MINERALA GENEZA MINERALA NESILIKATI SILIKATI PETROLOGIJA
PREDNAPETI BETON Primjer nadvožnjaka preko autoceste
 PREDNAPETI BETON Primjer nadvožnjaka preko autoceste 7. VJEŽBE PLAN ARMATURE PREDNAPETOG Dominik Skokandić, mag.ing.aedif. PLAN ARMATURE PREDNAPETOG 1. Rekapitulacija odabrane armature 2. Određivanje duljina
PREDNAPETI BETON Primjer nadvožnjaka preko autoceste 7. VJEŽBE PLAN ARMATURE PREDNAPETOG Dominik Skokandić, mag.ing.aedif. PLAN ARMATURE PREDNAPETOG 1. Rekapitulacija odabrane armature 2. Određivanje duljina
PT ISPITIVANJE PENETRANTIMA
 FSB Sveučilišta u Zagrebu Zavod za kvalitetu Katedra za nerazorna ispitivanja PT ISPITIVANJE PENETRANTIMA Josip Stepanić SADRŽAJ kapilarni učinak metoda ispitivanja penetrantima uvjeti promatranja SADRŽAJ
FSB Sveučilišta u Zagrebu Zavod za kvalitetu Katedra za nerazorna ispitivanja PT ISPITIVANJE PENETRANTIMA Josip Stepanić SADRŽAJ kapilarni učinak metoda ispitivanja penetrantima uvjeti promatranja SADRŽAJ
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE GODINE 8. RAZRED TOČNI ODGOVORI
 21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE)
 (Enegane) List: PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE) Na mjestima gdje se istovremeno troši električna i toplinska energija, ekonomičan način opskrbe energijom
(Enegane) List: PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE) Na mjestima gdje se istovremeno troši električna i toplinska energija, ekonomičan način opskrbe energijom
Funkcije dviju varjabli (zadaci za vježbu)
 Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
Opšte KROVNI POKRIVAČI I
 1 KROVNI POKRIVAČI I FASADNE OBLOGE 2 Opšte Podela prema zaštitnim svojstvima: Hladne obloge - zaštita hale od atmosferskih padavina, Tople obloge - zaštita hale od atmosferskih padavina i prodora hladnoće
1 KROVNI POKRIVAČI I FASADNE OBLOGE 2 Opšte Podela prema zaštitnim svojstvima: Hladne obloge - zaštita hale od atmosferskih padavina, Tople obloge - zaštita hale od atmosferskih padavina i prodora hladnoće
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
Postupak rješavanja bilanci energije
 Postupak rješavanja bilanci energije 1. Postaviti procesnu shemu 2. Riješiti bilancu tvari 3. Napisati potreban oblik jednadžbe za bilancu energije (zatvoreni otvoreni sustav) 4. Odabrati referentno stanje
Postupak rješavanja bilanci energije 1. Postaviti procesnu shemu 2. Riješiti bilancu tvari 3. Napisati potreban oblik jednadžbe za bilancu energije (zatvoreni otvoreni sustav) 4. Odabrati referentno stanje
Linearna algebra 2 prvi kolokvij,
 1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
Riješeni zadaci: Nizovi realnih brojeva
 Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
S t r a n a 1. 1.Povezati jonsku jačinu rastvora: a) MgCl 2 b) Al 2 (SO 4 ) 3 sa njihovim molalitetima, m. za so tipa: M p X q. pa je jonska jačina:
 S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
(P.I.) PRETPOSTAVKA INDUKCIJE - pretpostavimo da tvrdnja vrijedi za n = k.
 1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
RIJEŠENI ZADACI I TEORIJA IZ
 RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
PRILOG. Tab. 1.a. Dozvoljena trajna opterećenja bakarnih pravougaonih profila u(a) za θ at =35 C i θ=30 C, (θ tdt =65 C)
 PRILOG Tab. 1.a. Dozvoljena trajna opterećenja bakarnih pravougaonih profila u(a) za θ at =35 C i θ=30 C, (θ tdt =65 C) Tab 3. Vrednosti sačinilaca α i β za tipične konstrukcije SN-sabirnica Tab 4. Minimalni
PRILOG Tab. 1.a. Dozvoljena trajna opterećenja bakarnih pravougaonih profila u(a) za θ at =35 C i θ=30 C, (θ tdt =65 C) Tab 3. Vrednosti sačinilaca α i β za tipične konstrukcije SN-sabirnica Tab 4. Minimalni
OSNOVI GEOFIZIČKOG KAROTAŽA
 OSNOVI GEOFIZIČKOG KAROTAŽA Prvo predavanje Uvod Nastavnik dr Ivana Vasiljević docent Saradnik dipl. inž. Dragana Petrović student doktorslih studija Osnovi geofizičkog karotaža - statistika Školska godina
OSNOVI GEOFIZIČKOG KAROTAŽA Prvo predavanje Uvod Nastavnik dr Ivana Vasiljević docent Saradnik dipl. inž. Dragana Petrović student doktorslih studija Osnovi geofizičkog karotaža - statistika Školska godina
Upotreba tablica s termodinamičkim podacima
 Upotreba tablica s termodinamičkim podacima Nije moguće znati apsolutnu vrijednost specifične unutarnje energije u procesnog materijala, ali je moguće odrediti promjenu ove veličine, koja odgovara promjenama
Upotreba tablica s termodinamičkim podacima Nije moguće znati apsolutnu vrijednost specifične unutarnje energije u procesnog materijala, ali je moguće odrediti promjenu ove veličine, koja odgovara promjenama
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
 Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f
 IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
Pripremila i uredila: Doc. dr. sc. Blaženka Foretić OSNOVE KEMIJSKOG RAČUNANJA
 Pripremila i uredila: Doc. dr. sc. Blaženka Foretić OSNOVE KEMIJSKOG RAČUNANJA Relativna skala masa elemenata: atomska jedinica mase 1/12 mase atoma ugljika C-12. Unificirana jedinica atomske mase (u)
Pripremila i uredila: Doc. dr. sc. Blaženka Foretić OSNOVE KEMIJSKOG RAČUNANJA Relativna skala masa elemenata: atomska jedinica mase 1/12 mase atoma ugljika C-12. Unificirana jedinica atomske mase (u)
Program testirati pomoću podataka iz sledeće tabele:
 Deo 2: Rešeni zadaci 135 Vrednost integrala je I = 2.40407 42. Napisati program za izračunavanje koeficijenta proste linearne korelacije (Pearsonovog koeficijenta) slučajnih veličina X = (x 1,..., x n
Deo 2: Rešeni zadaci 135 Vrednost integrala je I = 2.40407 42. Napisati program za izračunavanje koeficijenta proste linearne korelacije (Pearsonovog koeficijenta) slučajnih veličina X = (x 1,..., x n
SEKUNDARNE VEZE međumolekulske veze
 PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
( , treći kolokvij) 3. Na dite lokalne ekstreme funkcije z = x 4 + y 4 2x 2 + 2y 2 3. (20 bodova)
 A MATEMATIKA (.6.., treći kolokvij. Zadana je funkcija z = e + + sin(. Izračunajte a z (,, b z (,, c z.. Za funkciju z = 3 + na dite a diferencijal dz, b dz u točki T(, za priraste d =. i d =.. c Za koliko
A MATEMATIKA (.6.., treći kolokvij. Zadana je funkcija z = e + + sin(. Izračunajte a z (,, b z (,, c z.. Za funkciju z = 3 + na dite a diferencijal dz, b dz u točki T(, za priraste d =. i d =.. c Za koliko
3. razred gimnazije- opšti i prirodno-matematički smer ALKENI. Aciklični nezasićeni ugljovodonici koji imaju jednu dvostruku vezu.
 ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Grafičko prikazivanje atributivnih i geografskih nizova
 Grafičko prikazivanje atributivnih i geografskih nizova Biserka Draščić Ban Pomorski fakultet u Rijeci 17. veljače 2011. Grafičko prikazivanje atributivnih nizova Atributivni nizovi prikazuju se grafički
Grafičko prikazivanje atributivnih i geografskih nizova Biserka Draščić Ban Pomorski fakultet u Rijeci 17. veljače 2011. Grafičko prikazivanje atributivnih nizova Atributivni nizovi prikazuju se grafički
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
 TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
( , 2. kolokvij)
 A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
Dijagonalizacija operatora
 Dijagonalizacija operatora Problem: Može li se odrediti baza u kojoj zadani operator ima dijagonalnu matricu? Ova problem je povezan sa sljedećim pojmovima: 1 Karakteristični polinom operatora f 2 Vlastite
Dijagonalizacija operatora Problem: Može li se odrediti baza u kojoj zadani operator ima dijagonalnu matricu? Ova problem je povezan sa sljedećim pojmovima: 1 Karakteristični polinom operatora f 2 Vlastite
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
( ) ( ) 2 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET. Zadaci za pripremu polaganja kvalifikacionog ispita iz Matematike. 1. Riješiti jednačine: 4
 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
K-Ar metoda datiranja
 K-Ar metoda datiranja K-Ar datiranje Najranija istraživanja vezana uz datiranje paleomagnetizma i magnetskog reverzibiliteta u bazaltima srednjo-oceanskih grebena. Kalij - I. grupa alkalnih elemenata (Li,
K-Ar metoda datiranja K-Ar datiranje Najranija istraživanja vezana uz datiranje paleomagnetizma i magnetskog reverzibiliteta u bazaltima srednjo-oceanskih grebena. Kalij - I. grupa alkalnih elemenata (Li,
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
zastori sunset curtain Kućište od željeza zaštićeno epoksidnim prahom, opruge od željeza. Lako i brzo se montiraju.
 zastori zastori sunset curtain Kućište od željeza zaštićeno epoksidnim prahom, opruge od željeza. Lako i brzo se montiraju. (mm) (mm) za PROZOR im (mm) tv25 40360 360 400 330x330 tv25 50450 450 500 410x410
zastori zastori sunset curtain Kućište od željeza zaštićeno epoksidnim prahom, opruge od željeza. Lako i brzo se montiraju. (mm) (mm) za PROZOR im (mm) tv25 40360 360 400 330x330 tv25 50450 450 500 410x410
2. Ako je funkcija f(x) parna onda se Fourierov red funkcije f(x) reducira na Fourierov kosinusni red. f(x) cos
 . KOLOKVIJ PRIMIJENJENA MATEMATIKA FOURIEROVE TRANSFORMACIJE 1. Za periodičnu funkciju f(x) s periodom p=l Fourierov red je gdje su a,a n, b n Fourierovi koeficijenti od f(x) gdje su a =, a n =, b n =..
. KOLOKVIJ PRIMIJENJENA MATEMATIKA FOURIEROVE TRANSFORMACIJE 1. Za periodičnu funkciju f(x) s periodom p=l Fourierov red je gdje su a,a n, b n Fourierovi koeficijenti od f(x) gdje su a =, a n =, b n =..
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika. Monotonost i ekstremi. Katica Jurasić. Rijeka, 2011.
 Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
1.4 Tangenta i normala
 28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
OBRTNA TELA. Vladimir Marinkov OBRTNA TELA VALJAK
 OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
radni nerecenzirani materijal za predavanja R(f) = {f(x) x D}
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Cenovnik spiro kanala i opreme - FON Inžinjering D.O.O.
 Cenovnik spiro kanala i opreme - *Cenovnik ažuriran 09.02.2018. Spiro kolena: Prečnik - Φ (mm) Spiro kanal ( /m) 90 45 30 Muf/nipli: Cevna obujmica: Brza diht spojnica: Elastična konekcija: /kom: Ø100
Cenovnik spiro kanala i opreme - *Cenovnik ažuriran 09.02.2018. Spiro kolena: Prečnik - Φ (mm) Spiro kanal ( /m) 90 45 30 Muf/nipli: Cevna obujmica: Brza diht spojnica: Elastična konekcija: /kom: Ø100
AGREGAT. Asistent: Josip Crnojevac, mag.ing.aedif. SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU
 AGREGAT Asistent: Josip Crnojevac, mag.ing.aeif. jcrnojevac@gmail.com SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU JOSIP JURAJ STROSSMAYER UNIVERSITY OF OSIJEK 1 Pojela agregata PODJELA AGREGATA - PREMA
AGREGAT Asistent: Josip Crnojevac, mag.ing.aeif. jcrnojevac@gmail.com SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU JOSIP JURAJ STROSSMAYER UNIVERSITY OF OSIJEK 1 Pojela agregata PODJELA AGREGATA - PREMA
Sveučilište u Zagrebu Rudarsko geološko naftni fakultet
 Sveučilište u Zagrebu Rudarsko geološko naftni fakultet SEMINAR: TOPLJIVE STIJENE : VAPNENCI, DOLOMITI I EVAPORITI Zlatko Topić R 6 Zagreb, 2009 SADRŽAJ: 1. UVOD....2 2. VAPNENCI..3 2.1 SASTAV I KLASIFIKACIJA
Sveučilište u Zagrebu Rudarsko geološko naftni fakultet SEMINAR: TOPLJIVE STIJENE : VAPNENCI, DOLOMITI I EVAPORITI Zlatko Topić R 6 Zagreb, 2009 SADRŽAJ: 1. UVOD....2 2. VAPNENCI..3 2.1 SASTAV I KLASIFIKACIJA
Vapno. Vapnenac/glinoviti vapnenac/dolomit. Kalcinacija. Kalcitno živo vapno + silikati. Hidratizacija (atmosferski tlak) Hidraulično.
 Vapno Vapno je naziv koji se koristi za čitav niz proizvoda dobivenih preradom (kalcinacijom i/ili hidratacijom) vapnenca ili dolomita. Proizvodi se razlikuju prema kemijskom sastavu i svojstvima te fizikalnom
Vapno Vapno je naziv koji se koristi za čitav niz proizvoda dobivenih preradom (kalcinacijom i/ili hidratacijom) vapnenca ili dolomita. Proizvodi se razlikuju prema kemijskom sastavu i svojstvima te fizikalnom
Klasifikacija blizu Kelerovih mnogostrukosti. konstantne holomorfne sekcione krivine. Kelerove. mnogostrukosti. blizu Kelerove.
 Klasifikacija blizu Teorema Neka je M Kelerova mnogostrukost. Operator krivine R ima sledeća svojstva: R(X, Y, Z, W ) = R(Y, X, Z, W ) = R(X, Y, W, Z) R(X, Y, Z, W ) + R(Y, Z, X, W ) + R(Z, X, Y, W ) =
Klasifikacija blizu Teorema Neka je M Kelerova mnogostrukost. Operator krivine R ima sledeća svojstva: R(X, Y, Z, W ) = R(Y, X, Z, W ) = R(X, Y, W, Z) R(X, Y, Z, W ) + R(Y, Z, X, W ) + R(Z, X, Y, W ) =
Elementarne čestice Elementarne ili osnovne ili fundamentalne čestice = Najmanji dijelovi od kojih je sastavljena tvar. Do 1950: Elektron, proton,
 Elementarne čestice Elementarne ili osnovne ili fundamentalne čestice = Najmanji dijelovi od kojih je sastavljena tvar. Do 1950: Elektron, proton, neutron Građa atoma Pozitron, neutrino, antineutrino Beta
Elementarne čestice Elementarne ili osnovne ili fundamentalne čestice = Najmanji dijelovi od kojih je sastavljena tvar. Do 1950: Elektron, proton, neutron Građa atoma Pozitron, neutrino, antineutrino Beta
Novi Sad god Broj 1 / 06 Veljko Milković Bulevar cara Lazara 56 Novi Sad. Izveštaj o merenju
 Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
2 PROCESI POSTANKA SEDIMENATA I SEDIMENTNIH STIJENA
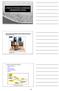 2 PROCESI POSTANKA SEDIMENATA I SEDIMENTNIH STIJENA sedimentne stijene nastaju djelovanjem fizičkih, kemijskih i bioloških procesa na površini ili plitko ispod površine Zemlje pri niskim temperaturama
2 PROCESI POSTANKA SEDIMENATA I SEDIMENTNIH STIJENA sedimentne stijene nastaju djelovanjem fizičkih, kemijskih i bioloških procesa na površini ili plitko ispod površine Zemlje pri niskim temperaturama
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
Srednjenaponski izolatori
 Srednjenaponski izolatori Linijski potporni izolatori tip R-ET Komercijalni naziv LPI 24 N ET 1) LPI 24 L ET/5 1)2) LPI 24 L ET/6 1)2) LPI 38 L ET 1) Oznaka prema IEC 720 R 12,5 ET 125 N R 12,5 ET 125
Srednjenaponski izolatori Linijski potporni izolatori tip R-ET Komercijalni naziv LPI 24 N ET 1) LPI 24 L ET/5 1)2) LPI 24 L ET/6 1)2) LPI 38 L ET 1) Oznaka prema IEC 720 R 12,5 ET 125 N R 12,5 ET 125
Akvizicija tereta. 5660t. Y= masa drva, X=masa cementa. Na brod će se ukrcati 1733 tona drva i 3927 tona cementa.
 Akvizicija tereta. Korisna nosivost broda je 6 t, a na brodu ia 8 cu. ft. prostora raspoloživog za sještaj tereta pod palubu. Navedeni brod treba krcati drvo i ceent, a na palubu ože aksialno ukrcati 34
Akvizicija tereta. Korisna nosivost broda je 6 t, a na brodu ia 8 cu. ft. prostora raspoloživog za sještaj tereta pod palubu. Navedeni brod treba krcati drvo i ceent, a na palubu ože aksialno ukrcati 34
KERAMIKA, BETON I DRVO
 VJEŽBE: četvrtak, 12:15-14:00 KERAMIKA, BETON I DRVO Vježba 1. Ionske i kovalentne strukture Prof.dr.sc. Lidija Ćurković STRUKTURA ČVRSTIH (krutih) TVARI ovisi o: 1. VRSTI VEZA IZMEĐU STRUKTURNIH JEDINICA
VJEŽBE: četvrtak, 12:15-14:00 KERAMIKA, BETON I DRVO Vježba 1. Ionske i kovalentne strukture Prof.dr.sc. Lidija Ćurković STRUKTURA ČVRSTIH (krutih) TVARI ovisi o: 1. VRSTI VEZA IZMEĐU STRUKTURNIH JEDINICA
Vježba: Uklanjanje organskih bojila iz otpadne vode koagulacijom/flokulacijom
 Kolegij: Obrada industrijskih otpadnih voda Vježba: Uklanjanje organskih bojila iz otpadne vode koagulacijom/flokulacijom Zadatak: Ispitati učinkovitost procesa koagulacije/flokulacije na obezbojavanje
Kolegij: Obrada industrijskih otpadnih voda Vježba: Uklanjanje organskih bojila iz otpadne vode koagulacijom/flokulacijom Zadatak: Ispitati učinkovitost procesa koagulacije/flokulacije na obezbojavanje
Periodičke izmjenične veličine
 EHNČK FAKULE SVEUČLŠA U RJEC Zavod za elekroenergeiku Sudij: Preddiploski sručni sudij elekroehnike Kolegij: Osnove elekroehnike Nosielj kolegija: Branka Dobraš Periodičke izjenične veličine Osnove elekroehnike
EHNČK FAKULE SVEUČLŠA U RJEC Zavod za elekroenergeiku Sudij: Preddiploski sručni sudij elekroehnike Kolegij: Osnove elekroehnike Nosielj kolegija: Branka Dobraš Periodičke izjenične veličine Osnove elekroehnike
Dimenzioniranje nosaa. 1. Uvjeti vrstoe
 Dimenzioniranje nosaa 1. Uvjeti vrstoe 1 Otpornost materijala prouava probleme 1. vrstoe,. krutosti i 3. elastine stabilnosti konstrukcija i dijelova konstrukcija od vrstog deformabilnog materijala. Moraju
Dimenzioniranje nosaa 1. Uvjeti vrstoe 1 Otpornost materijala prouava probleme 1. vrstoe,. krutosti i 3. elastine stabilnosti konstrukcija i dijelova konstrukcija od vrstog deformabilnog materijala. Moraju
KEMIJSKA KALASIFIKACIJA I UPORABA MINERALA
 KEMIJSKA KALASIFIKACIJA I UPORABA MINERALA Grupiranje minerala abecednim redom prema zajedničkom kemijskom elementu. Metalurgija Uporaba minerala Crna (dobijanje željeza i čelika Obojena (dobijanje svih
KEMIJSKA KALASIFIKACIJA I UPORABA MINERALA Grupiranje minerala abecednim redom prema zajedničkom kemijskom elementu. Metalurgija Uporaba minerala Crna (dobijanje željeza i čelika Obojena (dobijanje svih
a M a A. Može se pokazati da je supremum (ako postoji) jedinstven pa uvodimo oznaku sup A.
 3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
Prof. dr. sc. Z. Prelec ENERGETSKA POSTROJENJA Poglavlje: 7 (Regenerativni zagrijači napojne vode) List: 1
 (Regenerativni zagrijači napojne vode) List: 1 REGENERATIVNI ZAGRIJAČI NAPOJNE VODE Regenerativni zagrijači napojne vode imaju zadatak da pomoću pare iz oduzimanja turbine vrše predgrijavanje napojne vode
(Regenerativni zagrijači napojne vode) List: 1 REGENERATIVNI ZAGRIJAČI NAPOJNE VODE Regenerativni zagrijači napojne vode imaju zadatak da pomoću pare iz oduzimanja turbine vrše predgrijavanje napojne vode
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Heterogene ravnoteže taloženje i otapanje. u vodi u prisustvu zajedničkog iona u prisustvu kompleksirajućegreagensa pri različitim ph vrijednostima
 Heterogene ravnoteže taloženje i otapanje u vodi u prisustvu zajedničkog iona u prisustvu kompleksirajućegreagensa pri različitim ph vrijednostima Ako je BA teško topljiva sol (npr. AgCl) dodatkom
Heterogene ravnoteže taloženje i otapanje u vodi u prisustvu zajedničkog iona u prisustvu kompleksirajućegreagensa pri različitim ph vrijednostima Ako je BA teško topljiva sol (npr. AgCl) dodatkom
PRIMJER 3. MATLAB filtdemo
 PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
1 - KROVNA KONSTRUKCIJA : * krovni pokrivač, daska, letva: = 0,60 kn/m 2 * sneg, vetar : = 1,00 kn/m 2
 OPTEREĆENJE KROVNE KONSTRUKCIJE : * krovni pokrivač, daska, letva: = 0,60 kn/m 2 * sneg, vetar : = 1,00 kn/m 2 1.1. ROGOVI : * nagib krovne ravni : α = 35 º * razmak rogova : λ = 80 cm 1.1.1. STATIČKI
OPTEREĆENJE KROVNE KONSTRUKCIJE : * krovni pokrivač, daska, letva: = 0,60 kn/m 2 * sneg, vetar : = 1,00 kn/m 2 1.1. ROGOVI : * nagib krovne ravni : α = 35 º * razmak rogova : λ = 80 cm 1.1.1. STATIČKI
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
radni nerecenzirani materijal za predavanja
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Kažemo da je funkcija f : a, b R u točki x 0 a, b postiže lokalni minimum ako postoji okolina O(x 0 ) broja x 0 takva da je
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Kažemo da je funkcija f : a, b R u točki x 0 a, b postiže lokalni minimum ako postoji okolina O(x 0 ) broja x 0 takva da je
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri
 Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Στρωματογραφία-Ιστορική γεωλογία. Κρυπτοζωικός Μεγααιώνας Δρ. Ηλιόπουλος Γεώργιος Σχολή Θετικών Επιστημών Τμήμα Γεωλογίας
 Στρωματογραφία-Ιστορική γεωλογία Κρυπτοζωικός Μεγααιώνας Δρ. Ηλιόπουλος Γεώργιος Σχολή Θετικών Επιστημών Τμήμα Γεωλογίας Σκοποί ενότητας Σκοπός της ενότητας είναι η μελέτη του Κρυπτοζωικού Μεγααιώνα, κατά
Στρωματογραφία-Ιστορική γεωλογία Κρυπτοζωικός Μεγααιώνας Δρ. Ηλιόπουλος Γεώργιος Σχολή Θετικών Επιστημών Τμήμα Γεωλογίας Σκοποί ενότητας Σκοπός της ενότητας είναι η μελέτη του Κρυπτοζωικού Μεγααιώνα, κατά
Monday, May 30, Temperatura i toplina
 Temperatura i toplina Temperatura i termička ravnoteža - koncept temperature ukorijenjen je u kvalitativnim predodžbama o toplom i hladnom - tijelo koje je po osjetu toplo obično ima višu temperaturu nego
Temperatura i toplina Temperatura i termička ravnoteža - koncept temperature ukorijenjen je u kvalitativnim predodžbama o toplom i hladnom - tijelo koje je po osjetu toplo obično ima višu temperaturu nego
POVRŠINA TANGENCIJALNO-TETIVNOG ČETVEROKUTA
 POVRŠIN TNGENIJLNO-TETIVNOG ČETVEROKUT MLEN HLP, JELOVR U mnoštvu mnogokuta zanimljiva je formula za površinu četverokuta kojemu se istoobno može upisati i opisati kružnica: gje su a, b, c, uljine stranica
POVRŠIN TNGENIJLNO-TETIVNOG ČETVEROKUT MLEN HLP, JELOVR U mnoštvu mnogokuta zanimljiva je formula za površinu četverokuta kojemu se istoobno može upisati i opisati kružnica: gje su a, b, c, uljine stranica
Značenje indeksa. Konvencija o predznaku napona
 * Opšte stanje napona Tenzor napona Značenje indeksa Normalni napon: indeksi pokazuju površinu na koju djeluje. Tangencijalni napon: prvi indeks pokazuje površinu na koju napon djeluje, a drugi pravac
* Opšte stanje napona Tenzor napona Značenje indeksa Normalni napon: indeksi pokazuju površinu na koju djeluje. Tangencijalni napon: prvi indeks pokazuje površinu na koju napon djeluje, a drugi pravac
EMISIJA ŠTETNIH SASTOJAKA U ATMOSFERU IZ PROCESA IZGARANJA IZGARANJE - IZVOR EMISIJE
 Prof. dr. sc. Z. Prelec INŽENJERSTO ZAŠTITE OKOLIŠA Poglavlje: (Emisija u atmosferu) List: 1 EMISIJA ŠTETNIH SASTOJAKA U ATMOSFERU IZ PROCESA IZGARANJA IZGARANJE - IZOR EMISIJE Izgaranje - najveći uzrok
Prof. dr. sc. Z. Prelec INŽENJERSTO ZAŠTITE OKOLIŠA Poglavlje: (Emisija u atmosferu) List: 1 EMISIJA ŠTETNIH SASTOJAKA U ATMOSFERU IZ PROCESA IZGARANJA IZGARANJE - IZOR EMISIJE Izgaranje - najveći uzrok
TROŠENJE MINERALA I STIJENA
 Mramor Granit monomineralne kalcit Zbog čega je značajno? polimineralne ortoklas, kvarc, plagioklas, biotit, hornblenda ukupna anorganska tvar tla potječe iz susjednih sfera (litosfere, atmosfere i hidrosfere)
Mramor Granit monomineralne kalcit Zbog čega je značajno? polimineralne ortoklas, kvarc, plagioklas, biotit, hornblenda ukupna anorganska tvar tla potječe iz susjednih sfera (litosfere, atmosfere i hidrosfere)
konst. Električni otpor
 Sveučilište J. J. Strossmayera u sijeku Elektrotehnički fakultet sijek Stručni studij Električni otpor hmov zakon Pri protjecanju struje kroz vodič pojavljuje se otpor. Georg Simon hm je ustanovio ovisnost
Sveučilište J. J. Strossmayera u sijeku Elektrotehnički fakultet sijek Stručni studij Električni otpor hmov zakon Pri protjecanju struje kroz vodič pojavljuje se otpor. Georg Simon hm je ustanovio ovisnost
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
