6 SREDNJEZRNATI KLASTITI (PJEŠČENJACI)
|
|
|
- Ἄννα Λούπης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 62 6 SREDNJEZRNATI KLASTITI (PJEŠČENJACI) veličina čestica: 2mm - 63μm 6.1 UVOD vrlo krupni pijesak krupni pijesak srednji pijesak sitni pijesak vrlo sitni pijesak litifikacija pijesak pješčenjak klastična struktura klasti matriks autigeni minerali i cement pore Klastična struktura. tipovi zrna odlomci stijena kvarc feldspati tinjci i minerali glina teški minerali druge detritične komponente 6.2 DETRITIČNE KOMPONENTE faktori zastupljenost u izvorišnom području kemijska i mehanička stabilnost u sedimentnim okolišima Kemijska stabilnost minerala od najstabilnijih prema manje stabilnima.
2 63 sastav sastav izvornih stijena stabilnost tijekom transporta litične čestice porijeklo različite magmatske, metamorfne i starije sedimentne stijene planinski masivi i vulkanska područja Litične čestice sedimentnog porijekla. Vidno polje 3x2 mm. upotreba rekonstrukcija provenijencije Litične čestice magmatskog porijekla. Vidno polje 3x2 mm. kvarc najstabilniji mineral u sedimentnim uvjetima najzastupljeniji mineral u pješčenjacima (prosječno oko 65%, a doseže i gotovo 100%) porijeklo plutonske granitne stijene kiseli gnajsevi škriljavaca tipovi kvarcnih zrna: monokristalni kvarc (Qm) polikristalni kvarc (Qp) način potamnjenja jednoliko nejednoliko (undulozno) Monokristalni i polikristalni kvarc jednolikog i nejednolikog potamnjenja u mikroskopskom izbrusku. Vidno polje 3x2 mm. inkluzije fluidne mineralne (rutil, turmalin, magnetit, tinjci, klorit) značajke kvarcnih zrna iz pojedinih skupina stijena: vulkanske magmatske stijene monokristalan, jednolikog potamnjenja, bez inkluzija hidrotermalne žile monokristalan ili krupnokristalast polikristalni, sadrži brojne fluidne inkluzije metamorfne stijene polikristalni kvarc izduženih kristala preferirane orijentacije kvarc nejednolikog potamnjenja najvjerojatnije iz metamorfnih stijena, ali može biti i iz plutonskih magmatskih stijena
3 64 indeks zrelosti odnos Q m /Q p vedi indeks veda zrelost sedimenta Q jed. pot. /Q nejed. pot. A) B) Kvarcna zrna s regeneracijskim rubom (mikroskopski izbrusak; A) A-; B) A+. Primarni rub zrna markiran je crvenom hematitnom prevlakom. Vidno polje 1,2x0,8 mm. udio u pješčenjacima prosječno %, doseže 50 % (arkoze) feldspati mehanički i kemijski manje stabilni od kvarca zastupljenost u sedimentima ovisi o sastav izvorišnih stijena uglavnom potječu iz istih kristalinskih stijena kao i kvarc (granit, gnajs) klima humidna klima kemijsko trošenje feldspati nestaju aridna klima mehaničko trošenje feldspati preživljavaju brzina erozije alk. feldspati (ortoklas, mikroklin) su češdi u pješčenjacima od plagioklasa Mikroskopski izbrusak pješčenjaka bogatog alkalijskim feldspatima. Vidno polje 1,2x0,8 mm. tinjci i minerali glina listidavi minerali (filosilikati) česti u matriksu pješčenjaka i krupnijih klastita muskovit i biotit porijeklo magmatske stijene škriljavci filit biotit češdi u izvorišnim stijenama kemijski nestabilniji od muskovita rjeđi u sedimentnim stijenama A B Mikroskopski izbrusak pješčenjaka bogatog muskovitom i kaolinitom (A) odnosno biotitom (B). Vidno polje 1,2x0,8 mm.
4 65 minerali glina porijeklo detritični dobar pokazatelj građe izvorišnog područja, klime i procesa trošenja autigeni dijagenetskim procesima mogu prijedi u druge minerale glina specifična težina > 2,86 gcm -3 uglavnom silikati i oksidi udio u pijecima najčešde oko 1% teški minerali od ostatka sedimenta (laka mineralna frakcija) najčešde se odvajaju pomodu teških tekudina (prim. bromoform) značenje daju korisne informacije o provenijenciji i događanjima u izvorišnim područjima najčešdi neopaki teški minerali su apatit, epidot, granat, rutil, staurolit, turmalin i cirkon, a od opakih ilmenit i magnetit Karakteristični teški minerali različitih izvorišnih stijena. Teška mineralna frakcija pijesaka. druge detritične komponente karbonatna zrna fosili ili fragmenti fosila neskeletne karbonatne čestice (ooidi, peloidi, intraklasti) detritična zrna vapnenaca i dolomita (rijetka) skeletni fosfati glaukonit Mikroskopski izbrusak pješčenjaka bogatog glaukonitom. Vidno polje 3x2 mm.
5 MINERALOŠNA ZRELOST odraz procesa trošenja u izvorišnom području i stupnja prerade i transporta nezreli pješčenjaci bogati nestabilnim zrnima (čestice nestabilnih stijena, nestabilni teški minerali, feldspati) blizu izvorišnog područja ili su transportirani i istaloženi bez puno prerade zreli pješčenjaci sadrže čestice stabilnih stijena, puno kvarca i malo feldspata superzreli pješčenjaci sastavljeni gotovo isključivo od kvarca krajnji produkt intenzivnog trošenja nestabilne čestice odstranjene intenzivnom abrazijom ili preradom sedimenta indeks mineraloške zrelosti = kvarc + rožnjak/feldspati + čestice stijena 6.4 PODJELA PJEŠČENJAKA zasniva se mikroskopskim istraživanjima i zahtijeva procjenu postotnog udjela pojedinih tipova čestica potrebno je odrediti nekoliko stotina zrna (oko 400) poin-counting metodom u mikroskopskom izbrusku Tipovi pješčanih zrna. procjena modalnog sastava u mikroskopu usporedbom vidnog polja s dijagramima koji pokazuju izgled vidnog polja za pojedine postotne udjele neke od čestica Komparativne slike za približnu procjenu modalnog sastava pješčenjaka u mikroskopskom izbrusku. na terenu pažljivim promatranjem uzorka pod lupom
6 67 osnovna podjela pješčenjaka zasniva se na sadržaju matriksa tipovi areniti < 15% matriksa grauvake > 15% matriksa Klasifikacija pješčenjaka prema Pettijohn i ost., areniti čisti pješčenjaci podjela kvarcni areniti arkozni (feldspatski) areniti litoareniti (litični areniti) subarkoze sublitoareniti Podjela arenitnih pješčenjaka prema međusobnom udjelu kvarca, feldspata i čestica stijena; prema Pettijohn et al., nečisti pješčenjaci grauvake podjela kvarcne grauvake feldspatske grauvake litične grauvake Podjela grauvaka prema međusobnom udjelu kvarca, feldspata i čestica stijena, prema Pettijohn et al., 1987.
7 68 hibridni pješčenjaci uz klastične sastojke sadrže i neklastične sastojke derivirane unutar sedimentacijskog bazena najpoznatiji i najčešdi su: kalkarenacejski pješčenjaci sadrže preko 50% CaCO 3 u obliku karbonatnih zrna (ooidi, bioklasti) nastaju u područjima s karbonatnom produkcijom gdje postoji snažan donos terigenih klasta glaukonitni pješčenjaci fosfatni pješčenjaci Kalkarenacejski pješčenjak, okolica Vodina. Vidno polje 3x2 mm. sastav 6.5 NAJČEŠĆI TIPOVI PJEŠČENJAKA kvarcni areniti > 95% kvarca (uglavnom Q m i Q jed ) mineraloški najzreliji tip pješčenjaka strukturno zreli dobro zaobljena i dobro sortirana zrna vezivo je cement uvjeti postanka dugotrajna prerada sedimenta topla vlažna klima zaravnjen reljef i spora sedimentacija često sadrže kvarcna zrna drugog ili višeg ciklusa (višestruko pretaložena) 1 cm 1 mm Makroskopski izgled. Mikroskopski izgled (A-). 1 mm Mikroskopski izgled (A+). arkoze sastav > 25% feldspata (ortoklas, mikroklin) svježi kaolinitizirani/sericitizirani dosta kvarca (polikristalinični) čestice stijena (kvarc-feldspatske); detritični tinjci i nešto matriksa najčešde nastaju iz granita i gnajseva strukturno umjereno zreli klasti uglati do poluuglati sortiranost varira od loše do vrlo dobre vezivo: kvarcni ili kalcitni cement/ matriks uvjeti postanka semiaridna i glacijalna klima snažna erozija u visoko uzdignutom izvorišnom području Mikroskopski izgled (A-). 1 mm 2 cm Makroskopski izgled. Mikroskopski izgled (A+). 1 mm
8 69 čine oko 25% svih pješčenjaka litični areniti (litoareniti) sastav jako varijabilan (modalni, kemijski) više čestica stijena (litičnih čestica) nego feldspata sastav litičnih čestica peliti niskometamorfne stijene vulkanske stijene 2 cm 1 mm 1 mm Makroskopski izgled. Mikroskopski izgled (A+). Mikroskopski izgled (A+). struktura malo primarnog matriksa cement kalcitni ili kvarcni nezreli modalni sastav brza produkcija sedimenta kratak ili umjeren transport Dodatna podjela litičnih arenita obzirom na sastav litičnih čestica. (A-) grauvake matriks > 15% sitnozrnati sediment taložen istovremeno s pješčanom frakcijom pseudomatriks - nastaje dijagenetskim alteracijama nestabilnih litičnih fragmenata sastav matriksa: sericit i klorita + čestice kvarca i feldspata veličine silta klasti kvarc - dominira litične čestice (prim. peliti, metasedimenti) feldspati (A+) 2 m Izdanak grauvake. Vidi se karakteristična siva boja. Mikroskopski izgled. 1 mm Makroskopski izgled. 2 cm
9 DIJAGENEZA PJEŠČENJAKA sve mehaničke i kemijske promjene koje se događaju u pješčanom sedimentu od njegova taloženja do početka metamorfnih procesa faktori inicijalni taložni okoliš klima sastav i struktura sedimenta smjer dijageneze: migracija pornih fluida povijest zalijeganja faze dijageneze rana faza - trajanje tisude-milijuni god. - dubina zalijeganja 1-100m - vode su povezane s taložnim okolišem -brza modifikacija pornih voda otapanjem organske materije i mikrobiološkom aktivnošdu (oksidativni uvjeti reduktivni uvjeti) kasna faza - trajanje više desetaka milijuna godina - dubina zalijeganja do m - temperaturni raspon oko C - porne vode su modificirane reakcijama s mineralima glina, otapanjem nestabilnih čestica, precipitacijom autigenih minerala i miješanjem s vodama iz drugih izvora dijagenetski procesi mehanički proces kompakcija istiskivanje vode gušde pakiranje smanjenje poroznosti savijanje i drobljenje savijanja slabijih zrna (pseudomatriks) vede dubine prekrivanja otapanje pod pritiskom odvija se na kontaktima među zrnima suturirani kontakti (zrnima podjednake topivosti/čvrstode ) ili konkavno-konveksni kontakti (zrna različite topivosti) najvažniji dijagenetski proces: rasuti pijesak cementacija čvrsto vezana stijena - pješčenjak vrijeme cement tijekom rane dijageneze malim dubinama prekrivanja (bez zbijanja) tijekom kasne dijageneze vede dubine prekrivanja (zbijanje i tlačno otapanje) autigeni mineral izlučen u međuzrnskom prostoru, a koji je uzrokovao smanjenje međuzrnske poroznosti najčešdi su kalcitni cement i silika (SiO 2 ) cement
10 71 karbonatna cementacija najzastupljeniji cement u pješčenjacima je kalcit, (dolomit i siderit vrlo rijetki) precipitacija CaCO 3 započinje kad se prekorači produkt njegove topivosti izvor CaCO 3 može biti porna voda sama po sebi ili otapanje karbonatnih skeletnih zrna glavni tipovi poikilotopni cement veliki pojedinačni kristali veličine do nekoliko cm koji obavijaju više pješčanih zrna (A) (B) Poikilotopni kalcitni cement u kvarcnom arenitu (A) koji ispunjava i pukotine kalavosti u alk. feldspatu (B). Vidno polje 3x2mm (A) odnosno 1,2x0,8mm (B). mozaični ili druzni popunjava pore između pješčanih zrna veličina kristala raste od stjenke prema sredini pore cement Shematski prikaz mozaičnog ili druznog kalcitnog cementa. silika cementacija podrijetlo silike otapanje silikatnih minerala (feldspati, amfiboli, pirokseni) i silicijskih organizama (dijatomeje, radiolarije, silicispongije) otapanje pod pritiskom obogadivanje porne vode na siliku reprecipitacija iz podzemnih voda) tipovi overgrowth (regeneracijski rub) kvarca silika cement precipitira oko kvarcnog zrna u istoj optičkoj orijentaciji kao i zrno (A-) (A+) Overgrovth na kvarcnim zrnima u kvarcnom arenitu. Veličina vidnog polja 1,2x0,8 mm. mikrokvarc, megakvarc, kalcedon ili opal
11 72 autigeneza procesi postanak novih minerali povedanje ved postojedih minerala u sedimentu najčešdi autigeni minerali kvarc, kalcit, opal, kalcedon, dolomit, anhidrit, gips, muskovit, siderit, klorit, kaolinit, daje crvenu boju sedimentima presvlačenje i impregnacija hematitom najčešde se nalazi kao vrlo tanka prevlaka oko zrna ili boji u crveno autigene minerale glina i feldspate osnovni dijagenetski okoliši eogenetski (pripovršinski) mezogenetski (dubinski) telogenetski dijagenetski okoliši eogenetski (pripovršinski) okoliši podjela obzirom na kemizam pornih voda i asocirane procese: marinski okoliši nemarinski vrudi i vlažni okoliši nemarinski semiaridni i aridni okoliši marinski okoliši vedina pješčanih zrna je stabilna dijagenetski procesi počinju reakcijom modificirane morske porne vode i manje stabilnih minerala tipični redoslijed procesa: autigeneza min. glina zajedno s overgrowth kvarca i felspata karbonatna cementacija nemarinski vrudi i vlažni okoliši porne vode kisele zbog bakteriološke razgradnje organske materije slatka voda siromašna s K +, Mg 2+ i SO 4 2- kvarcni pijesci dijagenetski precipitati su kvarc overgrowth i kaolinit pijesci s mafitnim zrnima precipitacija siderita i klorita nemarinski semiaridni i aridni okoliši porne vode su generalno oksidirajude kemijsko ispiranje je manje izraženo glavni procesi formiranje crvenih slojeva (red beds) tipično za semiaridna područja otpuštanje Fe iz mafitnih minerala tijekom ranog prekrivanja precipitacija Fe oko pješčanih zrna u obliku Fe oksida koji postupno prelaze u hematit formiranje kalkreta formiranje vapnenačkog tla
12 73 mezogenetski (dubinski) okoliši pješčenjaci su podvrgnuti povišenim tlakovima i temperaturama, a porne vode su slanije mnoga pješčana zrna su nestabilna i počinju se otapati promjena sastava minerala glina (smektiti iliti) otapanje pod pritiskom oslobađa ione za cementaciju i autigenezu telogenetski okoliši ponovno izdizanje pješčenjaka na površinu klima je ponovno važan faktor aridna oksidacija Fe-sulfida i Fe-karbonata hematit humidna ispiranje feldspata, karbonata i teških minerala porast poroznosti
REGIONALNO-METAMORFNE STENE ( ºC; 2-10 kbar)
 REGIONALNO-METAMORFNE STENE (200-800ºC; 2-10 kbar) PODELA PREMA TEKSTURI 1. ŠKRILJAVE I 2. MASIVNE METAMORFNE STENE PODELA PREMA STEPENU KRISTALINITETA (NE ZAVISI OD STEPENA METAMORFIZMA) 1. STENE VISOKOG
REGIONALNO-METAMORFNE STENE (200-800ºC; 2-10 kbar) PODELA PREMA TEKSTURI 1. ŠKRILJAVE I 2. MASIVNE METAMORFNE STENE PODELA PREMA STEPENU KRISTALINITETA (NE ZAVISI OD STEPENA METAMORFIZMA) 1. STENE VISOKOG
2 PROCESI POSTANKA SEDIMENATA I SEDIMENTNIH STIJENA
 2 PROCESI POSTANKA SEDIMENATA I SEDIMENTNIH STIJENA sedimentne stijene nastaju djelovanjem fizičkih, kemijskih i bioloških procesa na površini ili plitko ispod površine Zemlje pri niskim temperaturama
2 PROCESI POSTANKA SEDIMENATA I SEDIMENTNIH STIJENA sedimentne stijene nastaju djelovanjem fizičkih, kemijskih i bioloških procesa na površini ili plitko ispod površine Zemlje pri niskim temperaturama
3 SEDIMENTNE STRUKTURE
 3 SEDIMENTNE STRUKTURE 3.1 UVOD fizičke osobine sedimenata koje su uglavnom odraz taložnih procesa, ali mogu biti i posttaložnog odnosno dijagenetskog podrijetla najčešće obuhvaćaju veličinu zrna morfologiju
3 SEDIMENTNE STRUKTURE 3.1 UVOD fizičke osobine sedimenata koje su uglavnom odraz taložnih procesa, ali mogu biti i posttaložnog odnosno dijagenetskog podrijetla najčešće obuhvaćaju veličinu zrna morfologiju
Anorganski nemetalni materijali Sij Stijene
 Anorganski nemetalni materijali Sij Stijene Stijene Stijene su prirodni mineralni agregati, ulaze u sastav zemljine kore kao samostalne i jasno ograničene mase Minerali izgrađuju stijene Stijene izgrađuju
Anorganski nemetalni materijali Sij Stijene Stijene Stijene su prirodni mineralni agregati, ulaze u sastav zemljine kore kao samostalne i jasno ograničene mase Minerali izgrađuju stijene Stijene izgrađuju
Što je sediment? Što je sedimentna stijena? OSNOVE MINERALOGIJE I PETROLOGIJE OPĆA MINERALOGIJA SISTEMATSKA PETROLOGIJA PETROLOGIJA
 Što je sediment? OSNOVE MINERALOGIJE I PETROLOGIJE OPĆA MINERALOGIJA SISTEMATSKA MINERALOGIJA PETROLOGIJA KRISTALOGRAFIJA KEMIJSKA I FIZIKALNA SVOJSTVA MINERALA GENEZA MINERALA NESILIKATI SILIKATI PETROLOGIJA
Što je sediment? OSNOVE MINERALOGIJE I PETROLOGIJE OPĆA MINERALOGIJA SISTEMATSKA MINERALOGIJA PETROLOGIJA KRISTALOGRAFIJA KEMIJSKA I FIZIKALNA SVOJSTVA MINERALA GENEZA MINERALA NESILIKATI SILIKATI PETROLOGIJA
TROŠENJE MINERALA I STIJENA
 Mramor Granit monomineralne kalcit Zbog čega je značajno? polimineralne ortoklas, kvarc, plagioklas, biotit, hornblenda ukupna anorganska tvar tla potječe iz susjednih sfera (litosfere, atmosfere i hidrosfere)
Mramor Granit monomineralne kalcit Zbog čega je značajno? polimineralne ortoklas, kvarc, plagioklas, biotit, hornblenda ukupna anorganska tvar tla potječe iz susjednih sfera (litosfere, atmosfere i hidrosfere)
PRERADA GROŽðA. Sveučilište u Splitu Kemijsko-tehnološki fakultet. Zavod za prehrambenu tehnologiju i biotehnologiju. Referati za vježbe iz kolegija
 Sveučilište u Splitu Kemijsko-tehnološki fakultet Zavod za prehrambenu tehnologiju i biotehnologiju Referati za vježbe iz kolegija PRERADA GROŽðA Stručni studij kemijske tehnologije Smjer: Prehrambena
Sveučilište u Splitu Kemijsko-tehnološki fakultet Zavod za prehrambenu tehnologiju i biotehnologiju Referati za vježbe iz kolegija PRERADA GROŽðA Stručni studij kemijske tehnologije Smjer: Prehrambena
METAMORFNE STENE. Charles Luell - definisao pojam metamorfizma na osnovu promena u sedimentnim stenama sa promenom dubine.
 METAMORFNE STENE Charles Luell - definisao pojam metamorfizma na osnovu promena u sedimentnim stenama sa promenom dubine. Metamorfizam - skup fizičko-hemijskih procesa u steni u uslovima koji se razlikuju
METAMORFNE STENE Charles Luell - definisao pojam metamorfizma na osnovu promena u sedimentnim stenama sa promenom dubine. Metamorfizam - skup fizičko-hemijskih procesa u steni u uslovima koji se razlikuju
Konstruisanje. Dobro došli na... SREDNJA MAŠINSKA ŠKOLA NOVI SAD DEPARTMAN ZA PROJEKTOVANJE I KONSTRUISANJE
 Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
OSNOVE MINERALOGIJE I PETROLOGIJE OPĆA MINERALOGIJA SISTEMATSKA MINERALOGIJA PETROLOGIJA. Bazalt Ca-plagioklas, pirokseni.
 OSNOVE MINERALOGIJE I PETROLOGIJE Metamorfne stijene nastaju metamorfozom iz starijih magmatskih, metamorfnih ili sedimentnih stijena, bez otapanja ili taljenja. KRISTALOGRAFIJA OPĆA MINERALOGIJA KEMIJSKA
OSNOVE MINERALOGIJE I PETROLOGIJE Metamorfne stijene nastaju metamorfozom iz starijih magmatskih, metamorfnih ili sedimentnih stijena, bez otapanja ili taljenja. KRISTALOGRAFIJA OPĆA MINERALOGIJA KEMIJSKA
PT ISPITIVANJE PENETRANTIMA
 FSB Sveučilišta u Zagrebu Zavod za kvalitetu Katedra za nerazorna ispitivanja PT ISPITIVANJE PENETRANTIMA Josip Stepanić SADRŽAJ kapilarni učinak metoda ispitivanja penetrantima uvjeti promatranja SADRŽAJ
FSB Sveučilišta u Zagrebu Zavod za kvalitetu Katedra za nerazorna ispitivanja PT ISPITIVANJE PENETRANTIMA Josip Stepanić SADRŽAJ kapilarni učinak metoda ispitivanja penetrantima uvjeti promatranja SADRŽAJ
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
Dimenzioniranje nosaa. 1. Uvjeti vrstoe
 Dimenzioniranje nosaa 1. Uvjeti vrstoe 1 Otpornost materijala prouava probleme 1. vrstoe,. krutosti i 3. elastine stabilnosti konstrukcija i dijelova konstrukcija od vrstog deformabilnog materijala. Moraju
Dimenzioniranje nosaa 1. Uvjeti vrstoe 1 Otpornost materijala prouava probleme 1. vrstoe,. krutosti i 3. elastine stabilnosti konstrukcija i dijelova konstrukcija od vrstog deformabilnog materijala. Moraju
IZVORI, SASTAV I DINAMIKA MINERALNE SASTAVNICE TLA MINERALI - MINERALI I STIJENE - petrogeni minerali
 1 IZVORI, SASTAV I DINAMIKA MINERALNE SASTAVNICE TLA - MINERALI I STIJENE - petrogeni minerali MINERALI 2 primarni minerali sekundarni minerali pedogeni minerali postojanost minerala 3 minerali prema prozirnosti:
1 IZVORI, SASTAV I DINAMIKA MINERALNE SASTAVNICE TLA - MINERALI I STIJENE - petrogeni minerali MINERALI 2 primarni minerali sekundarni minerali pedogeni minerali postojanost minerala 3 minerali prema prozirnosti:
AGREGAT. Asistent: Josip Crnojevac, mag.ing.aedif. SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU
 AGREGAT Asistent: Josip Crnojevac, mag.ing.aeif. jcrnojevac@gmail.com SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU JOSIP JURAJ STROSSMAYER UNIVERSITY OF OSIJEK 1 Pojela agregata PODJELA AGREGATA - PREMA
AGREGAT Asistent: Josip Crnojevac, mag.ing.aeif. jcrnojevac@gmail.com SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU JOSIP JURAJ STROSSMAYER UNIVERSITY OF OSIJEK 1 Pojela agregata PODJELA AGREGATA - PREMA
SEKUNDARNE VEZE međumolekulske veze
 PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
3. OSNOVNI POKAZATELJI TLA
 MEHANIKA TLA: Onovni paraetri tla 4. OSNONI POKAZATELJI TLA Tlo e atoji od tri faze: od čvrtih zrna, vode i vazduha i njihovo relativno učešće e opiuje odgovarajući pokazateljia.. Specifična težina (G)
MEHANIKA TLA: Onovni paraetri tla 4. OSNONI POKAZATELJI TLA Tlo e atoji od tri faze: od čvrtih zrna, vode i vazduha i njihovo relativno učešće e opiuje odgovarajući pokazateljia.. Specifična težina (G)
PREDNAPETI BETON Primjer nadvožnjaka preko autoceste
 PREDNAPETI BETON Primjer nadvožnjaka preko autoceste 7. VJEŽBE PLAN ARMATURE PREDNAPETOG Dominik Skokandić, mag.ing.aedif. PLAN ARMATURE PREDNAPETOG 1. Rekapitulacija odabrane armature 2. Određivanje duljina
PREDNAPETI BETON Primjer nadvožnjaka preko autoceste 7. VJEŽBE PLAN ARMATURE PREDNAPETOG Dominik Skokandić, mag.ing.aedif. PLAN ARMATURE PREDNAPETOG 1. Rekapitulacija odabrane armature 2. Određivanje duljina
Sveučilište u Zagrebu Rudarsko geološko naftni fakultet
 Sveučilište u Zagrebu Rudarsko geološko naftni fakultet SEMINAR: TOPLJIVE STIJENE : VAPNENCI, DOLOMITI I EVAPORITI Zlatko Topić R 6 Zagreb, 2009 SADRŽAJ: 1. UVOD....2 2. VAPNENCI..3 2.1 SASTAV I KLASIFIKACIJA
Sveučilište u Zagrebu Rudarsko geološko naftni fakultet SEMINAR: TOPLJIVE STIJENE : VAPNENCI, DOLOMITI I EVAPORITI Zlatko Topić R 6 Zagreb, 2009 SADRŽAJ: 1. UVOD....2 2. VAPNENCI..3 2.1 SASTAV I KLASIFIKACIJA
OSNOVI GEOFIZIČKOG KAROTAŽA
 OSNOVI GEOFIZIČKOG KAROTAŽA Prvo predavanje Uvod Nastavnik dr Ivana Vasiljević docent Saradnik dipl. inž. Dragana Petrović student doktorslih studija Osnovi geofizičkog karotaža - statistika Školska godina
OSNOVI GEOFIZIČKOG KAROTAŽA Prvo predavanje Uvod Nastavnik dr Ivana Vasiljević docent Saradnik dipl. inž. Dragana Petrović student doktorslih studija Osnovi geofizičkog karotaža - statistika Školska godina
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Vježba: Uklanjanje organskih bojila iz otpadne vode koagulacijom/flokulacijom
 Kolegij: Obrada industrijskih otpadnih voda Vježba: Uklanjanje organskih bojila iz otpadne vode koagulacijom/flokulacijom Zadatak: Ispitati učinkovitost procesa koagulacije/flokulacije na obezbojavanje
Kolegij: Obrada industrijskih otpadnih voda Vježba: Uklanjanje organskih bojila iz otpadne vode koagulacijom/flokulacijom Zadatak: Ispitati učinkovitost procesa koagulacije/flokulacije na obezbojavanje
Elementarne čestice Elementarne ili osnovne ili fundamentalne čestice = Najmanji dijelovi od kojih je sastavljena tvar. Do 1950: Elektron, proton,
 Elementarne čestice Elementarne ili osnovne ili fundamentalne čestice = Najmanji dijelovi od kojih je sastavljena tvar. Do 1950: Elektron, proton, neutron Građa atoma Pozitron, neutrino, antineutrino Beta
Elementarne čestice Elementarne ili osnovne ili fundamentalne čestice = Najmanji dijelovi od kojih je sastavljena tvar. Do 1950: Elektron, proton, neutron Građa atoma Pozitron, neutrino, antineutrino Beta
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
PRILOG. Tab. 1.a. Dozvoljena trajna opterećenja bakarnih pravougaonih profila u(a) za θ at =35 C i θ=30 C, (θ tdt =65 C)
 PRILOG Tab. 1.a. Dozvoljena trajna opterećenja bakarnih pravougaonih profila u(a) za θ at =35 C i θ=30 C, (θ tdt =65 C) Tab 3. Vrednosti sačinilaca α i β za tipične konstrukcije SN-sabirnica Tab 4. Minimalni
PRILOG Tab. 1.a. Dozvoljena trajna opterećenja bakarnih pravougaonih profila u(a) za θ at =35 C i θ=30 C, (θ tdt =65 C) Tab 3. Vrednosti sačinilaca α i β za tipične konstrukcije SN-sabirnica Tab 4. Minimalni
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
MINERAL? nema jedinstvenih kriterijuma za odgovor
 Predavanje 1. MINERALI, MINERALOGIJA NAUKA O MINERALIMA minerals (lat.) rudni logos (grč.) nauka Izučava prirodu supstanci koje su vezane za rudnike, rudne žile i Zemljinu koru. MINERAL? nema jedinstvenih
Predavanje 1. MINERALI, MINERALOGIJA NAUKA O MINERALIMA minerals (lat.) rudni logos (grč.) nauka Izučava prirodu supstanci koje su vezane za rudnike, rudne žile i Zemljinu koru. MINERAL? nema jedinstvenih
EMISIJA ŠTETNIH SASTOJAKA U ATMOSFERU IZ PROCESA IZGARANJA IZGARANJE - IZVOR EMISIJE
 Prof. dr. sc. Z. Prelec INŽENJERSTO ZAŠTITE OKOLIŠA Poglavlje: (Emisija u atmosferu) List: 1 EMISIJA ŠTETNIH SASTOJAKA U ATMOSFERU IZ PROCESA IZGARANJA IZGARANJE - IZOR EMISIJE Izgaranje - najveći uzrok
Prof. dr. sc. Z. Prelec INŽENJERSTO ZAŠTITE OKOLIŠA Poglavlje: (Emisija u atmosferu) List: 1 EMISIJA ŠTETNIH SASTOJAKA U ATMOSFERU IZ PROCESA IZGARANJA IZGARANJE - IZOR EMISIJE Izgaranje - najveći uzrok
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
(P.I.) PRETPOSTAVKA INDUKCIJE - pretpostavimo da tvrdnja vrijedi za n = k.
 1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri
 Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
KEMIJSKA KALASIFIKACIJA I UPORABA MINERALA
 KEMIJSKA KALASIFIKACIJA I UPORABA MINERALA Grupiranje minerala abecednim redom prema zajedničkom kemijskom elementu. Metalurgija Uporaba minerala Crna (dobijanje željeza i čelika Obojena (dobijanje svih
KEMIJSKA KALASIFIKACIJA I UPORABA MINERALA Grupiranje minerala abecednim redom prema zajedničkom kemijskom elementu. Metalurgija Uporaba minerala Crna (dobijanje željeza i čelika Obojena (dobijanje svih
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Srednjenaponski izolatori
 Srednjenaponski izolatori Linijski potporni izolatori tip R-ET Komercijalni naziv LPI 24 N ET 1) LPI 24 L ET/5 1)2) LPI 24 L ET/6 1)2) LPI 38 L ET 1) Oznaka prema IEC 720 R 12,5 ET 125 N R 12,5 ET 125
Srednjenaponski izolatori Linijski potporni izolatori tip R-ET Komercijalni naziv LPI 24 N ET 1) LPI 24 L ET/5 1)2) LPI 24 L ET/6 1)2) LPI 38 L ET 1) Oznaka prema IEC 720 R 12,5 ET 125 N R 12,5 ET 125
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE GODINE 8. RAZRED TOČNI ODGOVORI
 21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
Osnovni elementi mehanike tla
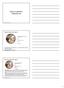 Osnovni elementi mehanike tla Tekstura sedimentnih stijena Cement naknadno izlučen u dijelu pornih prostora Pora Pora ispunjena vodom Matriks Zrno (klast) Shematski prikaz načina pakiranja zrna i načina
Osnovni elementi mehanike tla Tekstura sedimentnih stijena Cement naknadno izlučen u dijelu pornih prostora Pora Pora ispunjena vodom Matriks Zrno (klast) Shematski prikaz načina pakiranja zrna i načina
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Vapno. Vapnenac/glinoviti vapnenac/dolomit. Kalcinacija. Kalcitno živo vapno + silikati. Hidratizacija (atmosferski tlak) Hidraulično.
 Vapno Vapno je naziv koji se koristi za čitav niz proizvoda dobivenih preradom (kalcinacijom i/ili hidratacijom) vapnenca ili dolomita. Proizvodi se razlikuju prema kemijskom sastavu i svojstvima te fizikalnom
Vapno Vapno je naziv koji se koristi za čitav niz proizvoda dobivenih preradom (kalcinacijom i/ili hidratacijom) vapnenca ili dolomita. Proizvodi se razlikuju prema kemijskom sastavu i svojstvima te fizikalnom
10. STABILNOST KOSINA
 MEHANIKA TLA: Stabilnot koina 101 10. STABILNOST KOSINA 10.1 Metode proračuna koina Problem analize tabilnoti zemljanih maa vodi e na određivanje odnoa između rapoložive mičuće čvrtoće i proečnog mičućeg
MEHANIKA TLA: Stabilnot koina 101 10. STABILNOST KOSINA 10.1 Metode proračuna koina Problem analize tabilnoti zemljanih maa vodi e na određivanje odnoa između rapoložive mičuće čvrtoće i proečnog mičućeg
PRORAČUN GLAVNOG KROVNOG NOSAČA
 PRORAČUN GLAVNOG KROVNOG NOSAČA STATIČKI SUSTAV, GEOMETRIJSKE KARAKTERISTIKE I MATERIJAL Statički sustav glavnog krovnog nosača je slobodno oslonjena greda raspona l11,0 m. 45 0 65 ZAŠTITNI SLOJ BETONA
PRORAČUN GLAVNOG KROVNOG NOSAČA STATIČKI SUSTAV, GEOMETRIJSKE KARAKTERISTIKE I MATERIJAL Statički sustav glavnog krovnog nosača je slobodno oslonjena greda raspona l11,0 m. 45 0 65 ZAŠTITNI SLOJ BETONA
Pismeni ispit iz matematike GRUPA A 1. Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj, zatim naći 4 z.
 Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
MINERALOGIJA KRISTAL MINERAL. Definicija: - kristalna vrsta, nastala v naravi (tudi umetno)
 MINERALOGIJA KRISTAL Definicija: - trdno telo - periodična prostorska razvrstitev kemičnih sestavin - ravne ploskve - stalni koti - nastanek: naravni, umetni procesi - anorganske, organske spojine MINERAL
MINERALOGIJA KRISTAL Definicija: - trdno telo - periodična prostorska razvrstitev kemičnih sestavin - ravne ploskve - stalni koti - nastanek: naravni, umetni procesi - anorganske, organske spojine MINERAL
OBRTNA TELA. Vladimir Marinkov OBRTNA TELA VALJAK
 OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
PRETHODNI PRORACUN VRATILA (dimenzionisanje vratila)
 Predet: Mašinski eleenti Proračun vratila strana Dienzionisati vratilo elektrootora sledecih karakteristika: oinalna snaga P = 3kW roj obrtaja n = 400 in Shea opterecenja: Faktor neravnoernosti K =. F
Predet: Mašinski eleenti Proračun vratila strana Dienzionisati vratilo elektrootora sledecih karakteristika: oinalna snaga P = 3kW roj obrtaja n = 400 in Shea opterecenja: Faktor neravnoernosti K =. F
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
KONVEKSNI SKUPOVI. Definicije: potprostor, afin skup, konveksan skup, konveksan konus. 1/5. Back FullScr
 KONVEKSNI SKUPOVI Definicije: potprostor, afin skup, konveksan skup, konveksan konus. 1/5 KONVEKSNI SKUPOVI Definicije: potprostor, afin skup, konveksan skup, konveksan konus. 1/5 1. Neka su x, y R n,
KONVEKSNI SKUPOVI Definicije: potprostor, afin skup, konveksan skup, konveksan konus. 1/5 KONVEKSNI SKUPOVI Definicije: potprostor, afin skup, konveksan skup, konveksan konus. 1/5 1. Neka su x, y R n,
PRIMJER 3. MATLAB filtdemo
 PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
( , treći kolokvij) 3. Na dite lokalne ekstreme funkcije z = x 4 + y 4 2x 2 + 2y 2 3. (20 bodova)
 A MATEMATIKA (.6.., treći kolokvij. Zadana je funkcija z = e + + sin(. Izračunajte a z (,, b z (,, c z.. Za funkciju z = 3 + na dite a diferencijal dz, b dz u točki T(, za priraste d =. i d =.. c Za koliko
A MATEMATIKA (.6.., treći kolokvij. Zadana je funkcija z = e + + sin(. Izračunajte a z (,, b z (,, c z.. Za funkciju z = 3 + na dite a diferencijal dz, b dz u točki T(, za priraste d =. i d =.. c Za koliko
POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE
 **** MLADEN SRAGA **** 011. UNIVERZALNA ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE SKUP REALNIH BROJEVA α Autor: MLADEN SRAGA Grafički urednik: BESPLATNA - WEB-VARIJANTA Tisak: M.I.M.-SRAGA
**** MLADEN SRAGA **** 011. UNIVERZALNA ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE SKUP REALNIH BROJEVA α Autor: MLADEN SRAGA Grafički urednik: BESPLATNA - WEB-VARIJANTA Tisak: M.I.M.-SRAGA
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
Osnove elektrotehnike I popravni parcijalni ispit VARIJANTA A
 Osnove elektrotehnike I popravni parcijalni ispit 1..014. VARIJANTA A Prezime i ime: Broj indeksa: Profesorov prvi postulat: Što se ne može pročitati, ne može se ni ocijeniti. A C 1.1. Tri naelektrisanja
Osnove elektrotehnike I popravni parcijalni ispit 1..014. VARIJANTA A Prezime i ime: Broj indeksa: Profesorov prvi postulat: Što se ne može pročitati, ne može se ni ocijeniti. A C 1.1. Tri naelektrisanja
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
Numerička matematika 2. kolokvij (1. srpnja 2009.)
 Numerička matematika 2. kolokvij (1. srpnja 29.) Zadatak 1 (1 bodova.) Teorijsko pitanje. (A) Neka je G R m n, uz m n, pravokutna matrica koja ima puni rang po stupcima, tj. rang(g) = n. (a) Napišite puni
Numerička matematika 2. kolokvij (1. srpnja 29.) Zadatak 1 (1 bodova.) Teorijsko pitanje. (A) Neka je G R m n, uz m n, pravokutna matrica koja ima puni rang po stupcima, tj. rang(g) = n. (a) Napišite puni
Cenovnik spiro kanala i opreme - FON Inžinjering D.O.O.
 Cenovnik spiro kanala i opreme - *Cenovnik ažuriran 09.02.2018. Spiro kolena: Prečnik - Φ (mm) Spiro kanal ( /m) 90 45 30 Muf/nipli: Cevna obujmica: Brza diht spojnica: Elastična konekcija: /kom: Ø100
Cenovnik spiro kanala i opreme - *Cenovnik ažuriran 09.02.2018. Spiro kolena: Prečnik - Φ (mm) Spiro kanal ( /m) 90 45 30 Muf/nipli: Cevna obujmica: Brza diht spojnica: Elastična konekcija: /kom: Ø100
Polarizacija. Procesi nastajanja polarizirane svjetlosti: a) refleksija b) raspršenje c) dvolom d) dikroizam
 Polarzacja Proces asajaja polarzrae svjelos: a refleksja b raspršeje c dvolom d dkrozam Freselove jedadžbe Svjelos prelaz z opčkog sredsva deksa loma 1 u sredsvo deksa loma, dolaz do: refleksje (prema
Polarzacja Proces asajaja polarzrae svjelos: a refleksja b raspršeje c dvolom d dkrozam Freselove jedadžbe Svjelos prelaz z opčkog sredsva deksa loma 1 u sredsvo deksa loma, dolaz do: refleksje (prema
PROSTA GREDA (PROSTO OSLONJENA GREDA)
 ROS GRED (ROSO OSONJEN GRED) oprečna sila i moment savijanja u gredi y a b c d e a) Zadana greda s opterećenjem l b) Sile opterećenja na gredu c) Određivanje sila presjeka grede u presjeku a) Unutrašnje
ROS GRED (ROSO OSONJEN GRED) oprečna sila i moment savijanja u gredi y a b c d e a) Zadana greda s opterećenjem l b) Sile opterećenja na gredu c) Određivanje sila presjeka grede u presjeku a) Unutrašnje
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
( , 2. kolokvij)
 A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
Dijagonalizacija operatora
 Dijagonalizacija operatora Problem: Može li se odrediti baza u kojoj zadani operator ima dijagonalnu matricu? Ova problem je povezan sa sljedećim pojmovima: 1 Karakteristični polinom operatora f 2 Vlastite
Dijagonalizacija operatora Problem: Može li se odrediti baza u kojoj zadani operator ima dijagonalnu matricu? Ova problem je povezan sa sljedećim pojmovima: 1 Karakteristični polinom operatora f 2 Vlastite
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
 Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE)
 (Enegane) List: PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE) Na mjestima gdje se istovremeno troši električna i toplinska energija, ekonomičan način opskrbe energijom
(Enegane) List: PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE) Na mjestima gdje se istovremeno troši električna i toplinska energija, ekonomičan način opskrbe energijom
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
INTELIGENTNO UPRAVLJANJE
 INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
Linearna algebra 2 prvi kolokvij,
 1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
DIMENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE
 TEORIJA ETONSKIH KONSTRUKCIJA T- DIENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE 3.5 f "2" η y 2 D G N z d y A "" 0 Z a a G - tačka presek koja određje položaj sistemne
TEORIJA ETONSKIH KONSTRUKCIJA T- DIENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE 3.5 f "2" η y 2 D G N z d y A "" 0 Z a a G - tačka presek koja određje položaj sistemne
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Zadatak 4b- Dimenzionisanje rožnjače
 Zadatak 4b- Dimenzionisanje rožnjače Rožnjača je statičkog sistema kontinualnog nosača raspona L= 5x6,0m. Usvaja se hladnooblikovani šuplji profil pravougaonog poprečnog preseka. Raster rožnjača: λ r 2.5m
Zadatak 4b- Dimenzionisanje rožnjače Rožnjača je statičkog sistema kontinualnog nosača raspona L= 5x6,0m. Usvaja se hladnooblikovani šuplji profil pravougaonog poprečnog preseka. Raster rožnjača: λ r 2.5m
Mate Vijuga: Rijeseni zadaci iz matematike za srednju skolu 2. ARITMETICKI I GEOMETRIJSKI NIZ, RED, BINOMNI POUCAK. a n ti clan aritmetickog niza
 Mte Vijug: Rijesei zdci iz mtemtike z sredju skolu. ARITMETICKI I GEOMETRIJKI NIZ, RED, BINOMNI POUCAK. Aritmeticki iz Opci oblik ritmetickog iz: + - d Gdje je: prvi cl ritmetickog iz ti cl ritmetickog
Mte Vijug: Rijesei zdci iz mtemtike z sredju skolu. ARITMETICKI I GEOMETRIJKI NIZ, RED, BINOMNI POUCAK. Aritmeticki iz Opci oblik ritmetickog iz: + - d Gdje je: prvi cl ritmetickog iz ti cl ritmetickog
3. razred gimnazije- opšti i prirodno-matematički smer ALKENI. Aciklični nezasićeni ugljovodonici koji imaju jednu dvostruku vezu.
 ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
GLAZBENA UMJETNOST. Rezultati državne mature 2010.
 GLAZBENA UJETNOST Rezultati državne mature 2010. Deskriptivna statistika ukupnog rezultata PARAETAR VRIJEDNOST N 112 k 61 72,5 St. pogreška mjerenja 5,06 edijan 76,0 od 86 St. devijacija 15,99 Raspon 66
GLAZBENA UJETNOST Rezultati državne mature 2010. Deskriptivna statistika ukupnog rezultata PARAETAR VRIJEDNOST N 112 k 61 72,5 St. pogreška mjerenja 5,06 edijan 76,0 od 86 St. devijacija 15,99 Raspon 66
Periodičke izmjenične veličine
 EHNČK FAKULE SVEUČLŠA U RJEC Zavod za elekroenergeiku Sudij: Preddiploski sručni sudij elekroehnike Kolegij: Osnove elekroehnike Nosielj kolegija: Branka Dobraš Periodičke izjenične veličine Osnove elekroehnike
EHNČK FAKULE SVEUČLŠA U RJEC Zavod za elekroenergeiku Sudij: Preddiploski sručni sudij elekroehnike Kolegij: Osnove elekroehnike Nosielj kolegija: Branka Dobraš Periodičke izjenične veličine Osnove elekroehnike
Sveučilište u Zagrebu Građevinski fakultet Zavod za hidrotehniku Katedra za zdravstvenu hidrotehniku i okolišno inženjerstvo
 Napomena: Ovaj Izvještaj direktno se nastavlja na Izvještaj br. 3 Fizikalne i kemijske karakteristike pepela iz kolovoza 2015. godine. Sve metode korištene prilikom fizikalnih i kemijskih analiza provedenih
Napomena: Ovaj Izvještaj direktno se nastavlja na Izvještaj br. 3 Fizikalne i kemijske karakteristike pepela iz kolovoza 2015. godine. Sve metode korištene prilikom fizikalnih i kemijskih analiza provedenih
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Grafičko prikazivanje atributivnih i geografskih nizova
 Grafičko prikazivanje atributivnih i geografskih nizova Biserka Draščić Ban Pomorski fakultet u Rijeci 17. veljače 2011. Grafičko prikazivanje atributivnih nizova Atributivni nizovi prikazuju se grafički
Grafičko prikazivanje atributivnih i geografskih nizova Biserka Draščić Ban Pomorski fakultet u Rijeci 17. veljače 2011. Grafičko prikazivanje atributivnih nizova Atributivni nizovi prikazuju se grafički
Matematika 1 - vježbe. 11. prosinca 2015.
 Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
BIPOLARNI TRANZISTOR Auditorne vježbe
 BPOLARN TRANZSTOR Auditorne vježbe Struje normalno polariziranog bipolarnog pnp tranzistora: p n p p - p n B0 struja emitera + n B + - + - U B B U B struja kolektora p + B0 struja baze B n + R - B0 gdje
BPOLARN TRANZSTOR Auditorne vježbe Struje normalno polariziranog bipolarnog pnp tranzistora: p n p p - p n B0 struja emitera + n B + - + - U B B U B struja kolektora p + B0 struja baze B n + R - B0 gdje
K-Ar metoda datiranja
 K-Ar metoda datiranja K-Ar datiranje Najranija istraživanja vezana uz datiranje paleomagnetizma i magnetskog reverzibiliteta u bazaltima srednjo-oceanskih grebena. Kalij - I. grupa alkalnih elemenata (Li,
K-Ar metoda datiranja K-Ar datiranje Najranija istraživanja vezana uz datiranje paleomagnetizma i magnetskog reverzibiliteta u bazaltima srednjo-oceanskih grebena. Kalij - I. grupa alkalnih elemenata (Li,
Cauchyjev teorem. Postoji više dokaza ovog teorema, a najjednostvniji je uz pomoć Greenove formule: dxdy. int C i Cauchy Riemannovih uvjeta.
 auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
Zavrxni ispit iz Matematiqke analize 1
 Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
SJAJ MINERALA JE OSOBINA KOJA ZAVISI OD KOLIĈINE REFLEKTOVANE SVETLOSTI SA POVRŠINE MINERALA
 SJAJ MINERALA JE OSOBINA KOJA ZAVISI OD KOLIĈINE REFLEKTOVANE SVETLOSTI SA POVRŠINE MINERALA GLATKE POVRŠINE REFLEKTUJU VEĆU KOLIĈINU SVETLOSTI PA IMAJU I VEĆU SJAJNOST MINERALA RAVNE POVRŠINE - REFLEKTUJU
SJAJ MINERALA JE OSOBINA KOJA ZAVISI OD KOLIĈINE REFLEKTOVANE SVETLOSTI SA POVRŠINE MINERALA GLATKE POVRŠINE REFLEKTUJU VEĆU KOLIĈINU SVETLOSTI PA IMAJU I VEĆU SJAJNOST MINERALA RAVNE POVRŠINE - REFLEKTUJU
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
Opšte KROVNI POKRIVAČI I
 1 KROVNI POKRIVAČI I FASADNE OBLOGE 2 Opšte Podela prema zaštitnim svojstvima: Hladne obloge - zaštita hale od atmosferskih padavina, Tople obloge - zaštita hale od atmosferskih padavina i prodora hladnoće
1 KROVNI POKRIVAČI I FASADNE OBLOGE 2 Opšte Podela prema zaštitnim svojstvima: Hladne obloge - zaštita hale od atmosferskih padavina, Tople obloge - zaštita hale od atmosferskih padavina i prodora hladnoće
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
3 Klasifikacija tla i indeksni pokazatelji.
 3 Klasifikacija tla i indeksni pokazatelji. 3.1 Osnovne grupe tla Postoji niz različitih klasifikacija tla. Svakako, klasifikacija treba omogućiti da se pomoću jednostavnih pokusa svrstaju tla u grupe
3 Klasifikacija tla i indeksni pokazatelji. 3.1 Osnovne grupe tla Postoji niz različitih klasifikacija tla. Svakako, klasifikacija treba omogućiti da se pomoću jednostavnih pokusa svrstaju tla u grupe
1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II
 1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II Zadatak: Klipni mehanizam se sastoji iz krivaje (ekscentarske poluge) OA dužine R, klipne poluge AB dužine =3R i klipa kompresora B (ukrsne glave). Krivaja
1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II Zadatak: Klipni mehanizam se sastoji iz krivaje (ekscentarske poluge) OA dužine R, klipne poluge AB dužine =3R i klipa kompresora B (ukrsne glave). Krivaja
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
Više dokaza jedne poznate trigonometrijske nejednakosti u trokutu
 Osječki matematički list 000), 5 9 5 Više dokaza jedne poznate trigonometrijske nejednakosti u trokutu Šefket Arslanagić Alija Muminagić Sažetak. U radu se navodi nekoliko različitih dokaza jedne poznate
Osječki matematički list 000), 5 9 5 Više dokaza jedne poznate trigonometrijske nejednakosti u trokutu Šefket Arslanagić Alija Muminagić Sažetak. U radu se navodi nekoliko različitih dokaza jedne poznate
Program testirati pomoću podataka iz sledeće tabele:
 Deo 2: Rešeni zadaci 135 Vrednost integrala je I = 2.40407 42. Napisati program za izračunavanje koeficijenta proste linearne korelacije (Pearsonovog koeficijenta) slučajnih veličina X = (x 1,..., x n
Deo 2: Rešeni zadaci 135 Vrednost integrala je I = 2.40407 42. Napisati program za izračunavanje koeficijenta proste linearne korelacije (Pearsonovog koeficijenta) slučajnih veličina X = (x 1,..., x n
Dvanaesti praktikum iz Analize 1
 Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
5. Karakteristične funkcije
 5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
a) Kosi hitac Krivolinijsko gibanje materijalne toke Sastavljeno gibanje Specijalni sluajevi kosog hica: b) Horizontalni hitac c) Vertikalni hitac
 ) Kosi hic Kriolinijsko ibnje merijlne oke Ssljeno ibnje 5. dio 3 4 Specijlni slujei koso hic: b) orizonlni hic c) Veriklni hic b) orizonlni hic c) Veriklni hic 5 6 7 ) Kosi hic 8 Kosi hic (bez opor zrk)
) Kosi hic Kriolinijsko ibnje merijlne oke Ssljeno ibnje 5. dio 3 4 Specijlni slujei koso hic: b) orizonlni hic c) Veriklni hic b) orizonlni hic c) Veriklni hic 5 6 7 ) Kosi hic 8 Kosi hic (bez opor zrk)
Alarmni sustavi 07/08 predavanja 12. i 13. Detekcija metala, izvori napajanja u sustavima TZ
 Alarmni sustavi 07/08 predavanja 12. i 13. Detekcija metala, izvori napajanja u sustavima TZ pred.mr.sc Ivica Kuric Detekcija metala instrument koji detektira promjene u magnetskom polju generirane prisutnošću
Alarmni sustavi 07/08 predavanja 12. i 13. Detekcija metala, izvori napajanja u sustavima TZ pred.mr.sc Ivica Kuric Detekcija metala instrument koji detektira promjene u magnetskom polju generirane prisutnošću
