ABSTRACT. stratum variable C is always observed but the column variable B and row variable A might be
|
|
|
- Νίκη Ταμτάκος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 ABSTRACT Title of dissertation: stimating Common Odds Ratio with Missing Data Te-Ching Chen, Doctor of Philosophy, 005 Dissertation directed by: Professor Paul J. Smith Statistics Program, Department of Mathematics We derive estimates of expected cell counts for I J K contingency tables where the stratum variable C is always observed but the column variable B and row variable A might be missing. In particular, we investigate cases where only row variable A might be missing, either randomly or informatively. For K tables, we use Taylor expansion to study the biases and variances of the Mantel-Haenszel estimator and modified Mantel-Haenszel estimators of the common odds ratio using one pair of pseudotables for data without missing values and for data with missing values, based either on the completely observed subsample or on estimated cell means when both stratum and column variables are always observed. We examine both large table and sparse table asymptotics. Analytic studies and simulation results show that the Mantel-Haenszel estimators overestimate the common odds ratio but adding one pair of pseudotables reduces bias and variance. Mantel-Haenszel estimators with jacnifing also reduces the biases and variances. stimates using only the complete subsample seem to have larger bias than those based on full data, but when the total number of observations gets large, the bias is reduced. stimators based on estimated cell means seem to have larger biases and variances than those based only on complete subsample with randomly missing data. With informative missingness, estimators based on the estimated cell means do not converge to the correct common odds ratio under sparse asymptotics, and converge slowly for the large table asymptotics.
2 The Mantel-Haenszel estimators based on incorrectly estimated cell means when the variable A is informatively missing behave similarly to those based on the only complete subsamples. The asymptotic variance formula of the ratio estimators had smaller biases and variances than those based on jacnifing or bootstrapping. Bootstrapping may produce zero divisors and unstable estimates, but adding one pair of pseudotables eliminates these problems and reduces the variability.
3 stimating Common Odds Ratio With Missing Data by Te-Ching Chen Dissertation submitted to the Faculty of the Graduate School of the University of Maryland, College Par in partial fulfillment of the requirements for the degree of Doctor of Philosophy 005 Advisory Committee: Dr. Paul J. Smith, Chair/Advisor Dr. Benjamin Kedem Dr. Ryszard Sysi Dr. Grace L. Yang Dr. Chan Mitchell Dayton
4 c Copyright by Te-Ching Chen 005
5 To my families.
6 ACKNOWLDGMNTS With sincere gratitude, I wish to acnowledge the many individuals who have guided me in the process of completing my doctoral program, especially that of my advisor Dr. Paul J. Smith, whose guidance, encouragement, and extraordinary patience throughout my graduate study have contributed to my professional growth. I cannot than him enough for the support and help he provided in the process of writing this dissertation. I would also lie to express my appreciation and gratitude to professors Ryszard Sysi, Grace L. Yang, Chan Mitchell Dayton, and Benjamin Kedem, for their helpful suggestions for reviewing this study and serving on my committee. I would lie to express my sincere appreciation to Dr. Hwai-Chiuan Wang whose encouragement of studying in the United States opens both of my academic and life views, and to Dr. Anne Chao who introduced me to the joy of statistics and Ms. Mei-Gui Wang who inspired my interest in mathematics. I would lie to extend my thans to Ms. Juei-Hsien Luan, Ms. Shu-Yuan Chuang, Dr. Ronald Zeigler, Jeol smith, and Carolina Rojas-Bahr for their valuable suggestions and encouragement during difficult times. Special thans to Dr. Yan Xin, Yan Xin life science and technologyyxlst, and friends in the YXLST. Acnowledgment also goes to Dr. Cordell Blac and the Office of Multi-thnic Student ducation for their support of my dissertation studies. Lastly, than you all who have ever helped me. iii
7 TABL OF CONTNTS List of Tables vi List of Figures xi Introduction Literature Review 3. Missing Data Closed Form stimates Common Odds Ratio stimators Mantel-Haenszel stimator Mantel-Haenszel with Pseudotable Methods Jacnifing Mantel-Haenszel Method Variance stimation Formula Closed-Form stimators for I J K Tables 9 3. Variable C always observed Variables B and C always observed Negative ˆα i boundary problems Common Odds Ratio stimation 0 4. Methods Mantel-Haenszel stimator Mantel-Haenszel stimator with pseudo-data Missing Data Complete Data Only MAR Model Complete Data Only Informative Missingness Closed Form stimated Data for MAR Model iv
8 4..4 Closed Form stimated Data for Informative Missingness Model Independent binomial rows Simulation Results Simulation stimating the common odds ratio when A is MARB, C stimating the common odds ratio when A is missing informativea, C Variance stimation When A is MARB, C stimating Variance When A is Missing InformativeA, C Multinomial Data Summary and Future Research 9 6. Summary Simulation Findings Conclusions Future Research A Simulation Result Tables MAR Model 3 B Simulation Result Tables Informative Model 34 C Simulation Result Tables Variance stimation for MARB, C Model 43 D Simulation Result Tables Variance stimation for Informative Model 59 Simulation Result Tables MAR Model Multinomial 7 F Simulation Result Tables Informative Model Multinomial 74 G Simulation Result Tables Variance stimation for MAR Model Multinomial 86 H Simulation Result Tables Variance stimation for Informative Model Multinomial 88 Bibliography v
9 LIST OF TABLS. Two-way contingency table with missing data One Pair of Pseudotables the th table Closed Form stimates for I J K Tables Closed Form stimates for I J K Tables Continued Closed Form stimates for I J K Tables Continued Closed Form stimator B and C are Always Observed Boundary Solution for InformativeA, C when both B and C are always observed 9 4. closed form estimated cell means for InformativeA, C A. Mean of stimated Common Odds Ratio MAR Model for θ = A. Variance of stimated Common Odds Ratio MAR Model for θ = A.3 T value for stimated Common Odds Ratio MAR Model for θ = A.4 Mean of stimated Common Odds Ratio MAR Model for θ = A.5 Variance of stimated Common Odds Ratio MAR Model for θ = A.6 T value for stimated Common Odds Ratio MAR Model for θ = B. Mean of stimated Common Odds Ratio Informative A, C for θ = B. Variance of stimated Common Odds Ratio Informative A, C for θ = B.3 T value for stimated Common Odds Ratio Informative A, C for θ = B.4 Simulation Results Informative A, C: stimated Common Odds Ratio for θ = 3 44 B.5 Variance of stimated Common Odds Ratio Informative A, C for θ = B.6 T value for stimated Common Odds Ratio Informative A, C for θ = C. Variance stimation MAR Model for θ = Full Data vs. Complete Only C. Variance stimation MAR Model for θ = Full Data vs. stimated Data vi
10 C.3 Variance stimation MAR Model for θ = Full Data vs. Complete Only With Pseudo-Tables C.4 Variance stimation MAR Model for θ = Full Data vs. stimated Data With Pseudo-Tables C.5 Variance of Variance stimation MAR Model for θ = C.6 Variance of Variance stimation MAR Model for θ = With Pseudo-Tables... 5 C.7 Variance stimation MAR Model for θ = 3 Full Data vs. Complete Only C.8 Variance stimation MAR Model for θ = 3 Full Data vs. stimated Data C.9 Variance stimation MAR Model for θ = 3 Full Data vs. Complete Data Only with Pseduo-Tables C.0 Variance stimation MAR Model for θ = 3 Full Data vs. stimated Data with Pseduo-Tables C. Variance of Variance stimation MAR Model for θ = C. Variance of Variance stimation MAR Model for θ = 3 With Pseudo-Tables D. Variance stimation Informative A, C for θ = Full Data vs. Complete Only. 60 D. Variance stimation Informative A, C for θ = Full Data vs. stimated Data. 6 D.3 Variance stimation Informative A, C for θ = Full Data vs. Complete Only With Pseudo-Tables D.4 Variance stimation Informative A, C for θ = Full Data vs. stimated Data With Pseudo-Tables D.5 Variance of Variance stimation Informative A, C for θ = D.6 Variance of Variance stimation Informative A, C for θ = With Pseudo-Tables 65 D.7 Variance stimation Informative A, C for θ = 3 Full Data vs. Complete Only. 66 D.8 Variance stimation Informative A, C for θ = 3 Full Data vs. stimated Data. 67 D.9 Variance stimation Informative A, C for θ = 3 Full Data vs. Complete Only With Pseudo-Tables vii
11 D.0 Variance stimation Informative A, C for θ = 3 Full Data vs. stimated Data With Pseudo-Tables D. Variance of Variance stimation Informative A, C for θ = D. Variance of Variance stimation Informative A, C for θ = 3 With Pseudo-Tables 7. Mean of Mean of stimated Common Odds Ratio Multinomial MAR Model : for θ = Variance of stimated Common Odds Ratio Multinomial MAR Model for θ = T value for stimated Common Odds Ratio Multinomial MAR Model for θ = Mean of stimated Common Odds Ratio Multinomial MAR Model : for θ = Variance of stimated Common Odds Ratio Multinomial MAR Model for θ = T value for stimated Common Odds Ratio Multinomial MAR Model for θ = F. Mean of stimated Common Odds Ratio Multinomial Informative A, C for θ =.80 F. Variance of stimated Common Odds Ratio Multinomial Informative A, C Model for θ = F.3 T value for stimated Common Odds Ratio Multinomial Informative A, C Model for θ = F.4 Mean of stimated Common Odds Ratio Multinomial Informative A, C for θ = 3 83 F.5 Variance of stimated Common Odds Ratio Multinomial Informative A, C Model for θ = F.6 T value for stimated Common Odds Ratio Multinomial Informative A, C Model for θ = G. Variance stimation Multinomial MAR Model for θ = Full Data vs. Complete Only G. Variance stimation Multinomial MAR Model for θ = Full Data vs. stimated Data viii
12 G.3 Variance stimation Multinomial MAR Model for θ = Full Data vs. Complete Only With Pseudo-Tables G.4 Variance stimation Multinomial MAR Model for θ = Full Data vs. stimated Data With Pseudo-Tables G.5 Variance of Variance stimation Multinomial MAR Model for θ = G.6 Variance of Variance stimation Multinomial MAR Model stimate for θ = With Pseudo-Tables G.7 Variance stimation Multinomial MAR Model for θ = 3 Full Data vs. Complete Only G.8 Variance stimation Multinomial MAR Model for θ = 3 Full Data vs. stimated Data G.9 Variance stimation Multinomial MAR Model for θ = 3 Full Data vs. Complete Only With Pseudo-Tables G.0 Variance stimation Multinomial MAR Model for θ = 3 Full Data vs. stimated Data With Pseudo-Tables G. Variance of Variance stimation Multinomial MAR Model for θ = G. Variance of Variance stimation Multinomial MAR Model stimate for θ = 3 With Pseudo-Tables H. Variance stimation Multinomial Informative A, C Model: for θ = Full Data vs. Complete Only H. Variance stimation Multinomial Informative A, C Model:for θ = Full Data vs. stimated Data H.3 Variance stimation Multinomial Informative A, C Model:for θ = Full Data vs. Complete Only With Pseudo-Tables H.4 Variance stimation Multinomial Informative A, C Model:for θ = Full Data vs. stimated Data With Pseudo-Tables H.5 Variance of Variance stimation Multinomial Informative A, C Model for θ = 04 ix
13 H.6 Variance of Variance stimation Multinomial Informative A, C Model for θ = With Pseudo-Tables H.7 Variance stimation Multinomial Informative A, C Model:for θ = 3 Full Data vs. Complete Only H.8 Variance stimation Multinomial Informative A, C Model:for θ = 3 Full Data vs. stimated Data H.9 Variance stimation Multinomial Informative A, C Model:for θ = 3 Full Data vs. Complete Only With Pseudo-Tables H.0 Variance stimation Multinomial Informative A, C Model:for θ = 3 Full Data vs. stimated Data With Pseudo-Tables H. Variance of Variance stimation Multinomial Informative A, C Model for θ = 3 0 H. Variance stimation Informative A, C Model Multinomial: Variance of Variance stimate for θ = 3 With Pseudo-Tables x
14 LIST OF FIGURS 5. Mean: θ =, MAR, P missing = 0.5, P missing = 0.4 for K/, P missing = 0.4, P missing = 0.5 for > K/ Variance: θ =, MAR, P missing = 0.5, P missing = 0.4 for K/, P missing = 0.4, P missing = 0.5 for > K/ t: θ =, MAR, P missing = 0.5, P missing = 0.4 for K/, and P missing = 0.4, P missing = 0.5 for > K/ Mean: θ = 3, MAR, P missing = 0.5, P missing = 0.4 for K/, P missing = 0.4, P missing = 0.5 for > K/ Variance: θ = 3, MAR, P missing = 0.5, P missing = 0.4 for K/, P missing = 0.4, P missing = 0.5 for > K/ t: θ = 3, MAR, P missing = 0.5, P missing = 0.4 for K/, and P missing = 0.4, P missing = 0.5 for > K/ Mean: θ =, Missing Informative, P missing = 0.5, P missing = 0.4 for K/, P missing = 0.4, P missing = 0.5 for > K/ Variance: θ =, Missing Informative, P missing = 0.5, P missing = 0.4 for K/, P missing = 0.4, P missing = 0.5 for > K/ t: θ =, Missing Informative, P missing = 0.5, P missing = 0.4 for K/, P missing = 0.4, P missing = 0.5 for > K/ Mean: θ = 3, Missing Informative, P missing = 0.5, P missing = 0.4 for K/, P missing = 0.4, P missing = 0.5 for > K/ Variance: θ = 3, Missing Informative, P missing = 0.5, P missing = 0.4 for K/, P missing = 0.4, P missing = 0.5 for > K/ t: θ = 3, Missing Informative, P missing = 0.5, P missing = 0.4 for K/, P missing = 0.4, P missing = 0.5 for > K/ stimating Variance: θ =, MAR, P missing = 0.5, P missing = 0.4 for K/, P missing = 0.4, P missing = 0.5 for > K/ xi
15 5.4 stimating Variance: θ =, MAR, P missing = 0.5, P missing = 0.4 for K/, P missing = 0.4, P missing = 0.5 for > K/, With Pseudo- Tables Variance of stimating Variance: θ =, MAR, P missing = 0.5, P missing = 0.4 for K/, P missing = 0.4, P missing = 0.5 for > K/ Variance of stimating Variance: θ =, MAR, P missing = 0.5, P missing = 0.4 for K/, P missing = 0.4, P missing = 0.5 for > K/ With Pseudo-Table stimating Variance: θ = 3, MAR, P missing = 0.5, P missing = 0.4 for K/, P missing = 0.4, P missing = 0.5 for > K/ stimating Variance: θ = 3, MAR, P missing = 0.5, P missing = 0.4 for K/, P missing = 0.4, P missing = 0.5 for > K/, With Pseudo- Tables Variance of stimating Variance: θ = 3, MAR, P missing = 0.5, P missing = 0.4 for K/, P missing = 0.4, P missing = 0.5 for > K/ Variance of stimating Variance: θ = 3, MAR, P missing = 0.5, P missing = 0.4 for K/, P missing = 0.4, P missing = 0.5 for > K/ With Pseudo-Table xii
16 Chapter Introduction In real world studies where sequences of contingency table data are collected, frequently some tables are incomplete. Often investigators simply analyze the subsample of complete observations, ignoring possible effects of missing data. While this may be reasonable when only a small proportion of observations are incomplete, it could possibly cause incorrect estimates and variability when large amounts of data are missing. Another approach, imputation, is not always valid. When a large proportion of data is missing, incorrect estimation of variability is possible even if the imputation scheme does not produce bias. Statistical studies of the effects of missing data are summarized by Little and Rubin [30. They show that, in multivariate data with missing observations, estimates using only complete observations do lead to biased estimates of means and variances. They formulate mathematical models for missing data and suggest better techniques for dealing with missing data. In this dissertation, we study the effects of estimating the common odds ratio when the row variable is missing at random with missingness probability depending on the stratum and the column variables or when it is missing informatively with missingness probability depending on the variable itself and the stratum variable. We assume the column variable and the stratum variable are always observed, as in case control studies. We investigate estimators based on only the complete observations and in the closed-form imputation introduced by Baer, Rosenberger and Dersimonian [5. We use both mathematical proofs and simulations to study the effect of ignoring missing data, imputing missing data, and misspecifying the missing data mechanism.
17 The dissertation is organized as follows. In Chapter, we review the literature about missing data analysis, particular using the closed-form imputation of the cell counts for contingency tables and the common odds ratio estimation. In Chapter 3, we will show the three-way contingency tables closed-from. In Chapter 4, we study the biases for Mantel-Haenszel estimator of the common odds ratio and its adjustments, both in complete and incomplete contingency tables. for incomplete contingency tables. The results of the simulation are in Chapter 5. Chapter 6 states our conclusions and discusses some possible directions of further research.
18 Chapter Literature Review. Missing Data Let V be a matrix of random variables with n independent rows and p columns. ach row represents a different observation and each column represents a different categorical variable Y = Y, Y,..., Y p. One could rearrange V as a p-dimensional contingency table with W cells defined by the joint levels of the variables. The entries in the table are counts {z ij...t }, where z ij...t is the number of sampled cases in the cell with Y = i, Y = j,..., Y p = t. If the data matrix V has missing items, that is one or more column variables are not identifiable in some rows, we will convert the data matrix to a contingency table with p extra variables of R,..., R p = R which indicate whether Y,...Y p were observed. We write R r = when the rth variable is observed and R r = 0 otherwise. If the event that Y i is missing does not depend on Y i itself or any other Y, then we say Y i is Missing Completely at Random MCAR. That is, P R i Y, φ = P R i φ = π where φ denotes unnown parameters. If the event that Y i is missing does not depend on Y i itself but does depend on some other observed variables Y, i, then we say Y i is Missing at Random MAR. That is, P R i Y, φ = P R i {Y, R = }, φ Little and Rubin [30. In this situation, we will use the notation Y i is MARY, R =, or more simply MARY. Nonignorable missingness or informative missingness means that the missingness of Y i depends on either Y i itself or some unobserved Y. That is Y i is not MAR. Standard statistical methods were not designed to analyze missing data, so when some data 3
19 are missing, we should use other methods. Four groups of methods to analyze a data set with missing values were presented by Little and Rubin [30. a Procedures based on complete recorded units: When some variables are missing for some observations, a simple method is to analyze only the units with complete data. In general, this method can lead to serious biases and it may not be very efficient. However, under MCAR, the complete observations are a random sample of the full data set, so no bias occurs. b Imputation-based procedures: One fills in values for the missing data so that the data set become a completed data set, and then one simply uses standard methods to analyze the data. There are several imputation methods including hot dec imputation, mean imputation and regression imputation. The idea is somehow to find Ẑi,j, an estimate of the expected value of a missing Z i,j given the observed data, and substitute Ẑi,j in the sample. c Weighting procedures: In a complex survey, observations are given weights π i which are inversely proportional to the probability of selection. For instance, let x i be the ith value of a variable X. Then the population mean of X is often estimated by i π i x i / i π i,. where π i is the probability of that unit i is observed and π i is the design weight for observation i. Weighting procedures modify the weights in an attempt to adjust for nonresponse. The estimator. is replaced by π i ˆp i x i / π i ˆp i, where the sums are over data units where X is observed, and ˆp i is an estimate of the probability that X is observed for unit i. If the design weights are constant in subclasses of the sample, then the mean imputation and weighting lead to the same estimates of population means, although not the same estimates of sampling variances unless we mae adjustments to the data with mean imputation. d Model-based procedures: The analyst defines a model for the missing data mechanism 4
20 Table.: Two-way contingency table with missing data B = B = R b = R b = 0 R b = R b = 0 A = R a = R a = 0 z z 0 z 0 z 00 z z 0 z 0 z 00 A = R a = R a = 0 z z 0 z 0 z 00 z z 0 z 0 z 00 and bases inferences on the lielihood under that model. The advantages of this procedure are flexibility. However, there is a possibility of introducing bias if the model for missingness is misspecified. Methods b, v, and d all involve the use of a model, whether implicit or explicit. They are therefore potentially subject to biases.. Closed Form stimates Let A and B are two categorical variables with levels each and let R a and R b be the indicator variables we discussed in section.. The contingency table with missing data is as Table. Let µ ijl denote the expected cell counts of the i, j cells in a contingency table with R a = and R b = l. The log-linear model for two partially observed categorical variables with no three- or four-way interactions is log µ ijl = µ + α A i + α B j + α AB ij + β Ra + β R b l + β RaR b l + γ ARa i + γ AR b il + γ BRa j + γ BR b jl Baer, Rosenberger and Dersimonian[5 introduced the following parameterization of the model and led to closed-form ML estimates: 5
21 m ij = NP ra = i, B = j, R a =, R b = = exp{µ + α A i + α B j + α AB ij a ij = P rr a = 0, R b = A = i, B = j P rr a =, R b = A = i, B = j = exp{ [β Ra + β RaR b + γ ARa i + γ BRa j } b ij = P rr a =, R b = 0 A = i, B = j P rr a =, R b = A = i, B = j, = exp{ [β R b + β RaR b + γ AR b i + γ BR b j } + β Ra + β R b + β RaR b + γ ARa i + γ AR b i + γ BRa j + γ BR b J }, g = P rr a =, R b = A = i, B = jp rr a = 0, R b = 0 A = i, B = j P rr a =, R b = 0 A = i, B = jp rr a = 0, R b = A = i, B = j. = exp{4β RaR b }, so that µ ij = m ij, µ ij0 = m ij b ij, µ ij0 = m ij a ij, µ ij00 = m ij a ij b ij g, m ij 0, a ij 0, b ij 0, g 0, i j m ij + a ij + b ij + a ij b ij g = N. The cell probabilities are π ij.. = P ra = i, B = j = m ij + a ij + b ij + a ij b ij g, and the log-lielihood is L = {z ij logµ ij + z i+0 logµ i+0 0 i= j= =0 l=0 + z +j0 logµ +j0 0 + z ++00 logµ } µ ++++ where cd =, if = c and l = d, and 0, otherwise. To compute maximum lielihood estimator, one solves the system of equations L/ θ ijl = 0, where θ ijl includes all of µ, α s, β s and γ s. Closed-form solutions might be available, and boundary conditions might need to be used if any of the solutions to the lielihood equations falls outside the parameter space. 6
22 Table.: One Pair of Pseudotables Common Odds Ratio stimators.3. Mantel-Haenszel stimator Suppose there are K tables, let a, b, c and d be the data of the th table and let n be the sum of the data. The Mantel-Haenszel estimator [7 for the common odds ratio is ˆθ MH = K a d /n K b c /n.. Agresti [ and Santner and Duffy [4 discussed Mantel-Haenszel estimator. The Mantel-Haenszel estimator tends to overestimate the common odds ratio Breslow [7 studied for the sparse data and Hauc, Anderson and Leahy [ studied for the large strata cases. They modified the Mantel-Haenszel estimator by adding pseudocounts to each cells to reduce the bias and the common odds ratio estimator for adding s observations to each table is ˆθ P MHO = K a + s/4d s + s/4 K b + s/4c + s/4. In their study, the best choice of s is Mantel-Haenszel with Pseudotable Methods To reduce the bias of the Mantel-Haenszel estimator, Wypij and Santner [48 introduced the Pseudodata methods by adding one or more pairs of pseudotables as in Table.. They justified the pseudotable method using a Bayesian argument. The common odds ratio estimator for adding r pair of the pseudotables is K ˆθ P MH = a d /n + r/ K b c /n + r/ 7
23 .3.3 Jacnifing Mantel-Haenszel Method Pigeot and Strugholtz [35 used the idea of Quenouille [39 of using pseudo-values by calculating the same type of the estimators based on a reduced sample and investigated two jacnife techniques applied to the Mantel-Haenszel estimator by dropping one table every time or one observation at a time. When dropping table technique is in use, they calculated the ith pseudo-value J I i be determined as which can J I i = K ˆθ MH K ˆθ MH,i ˆθ MH = K K a d /n b c /n ˆθ MH,i = ˆθ JMH = K =, i a d /n K =, i b c /n K θ MH,i /K =.4 Variance stimation Formula The Mantel-Haenszel estimator is a ratio of sums of random terms which are not identically distributed. Using Taylor expansions on expressions of the form K ˆθ MH = y i K x i centered at θ = K [y i/ K [x i, one can write ˆθ MH θ. = K K [x i [ y i θ K x i. This suggests that approximate variance formula [ Varˆθ MH =. [ˆθ MH θ =. K K [x Vary i θx i. i This approach is detailed in Cochran [ for ratio estimator and was applied to the Mantel- Haenszel estimator by Breslow [7. 8
24 Chapter 3 Closed-Form stimators for I J K Tables Consider a three-way contingency table in which some cells are only partially observed. The th table is arranged as in Table 3., where z ijlmn denotes the data in the th table with the level of variable A = i and variable B = j. Here l = indicates that variable A is observed i is nown and l = 0 indicates that the level of variable A is unobserved i =. denotes unnown. The meaning of m and n are similar. The goal is to estimate the cell means µ ij from a fully observed I J K table. Let R a = indicate that variable A is observed and 0 if not. The meanings of R b and R c are similar. Assume there are no four-way or higher interactions for the categorical variables A, B, C, R a, R b and R c. The log-linear model is logµ ijlmn = µ + α A i + α B j + α C + α AB ij + β Ra l +γ ARa il +γ ABRa ijl +γ BCRc jn +γ CRaR b lm + β R b m + γ AR b im + γ ABR b ijm + γ ARaR b ilm + β Rc n + γarc in + γ CRaRc ln + γabrc ijn + α AC i + β RaR b lm + γ BRa jl + γ ARaRc iln + γ CR br c mn. + α BC j + βrar b ln + γ BR b jm + γ ACRa il + γ AR br c imn + α ABC ij + β R br c mn + γbrc jn + γ ACR b im + γ BRaR b jlm + β RaR br c lmn, + γ CRa l + γacrc in + γ CR b m + γ BRaRc jln + γ BCRa jl + +γcrc n + γ BCR b jm + γ BR br c jmn We extend Baer, Rosenberger and Dersimonian s [5 method to reparameterize as m ij = NP A = i, B = j, C =, R a =, R b =, R c = = expµ + α A i + α B j + α C + α AB ij + α AC i + α BC j + α ABC ij +β Ra + β R b + β Rc + β RaR b + β RaRc + β R br c + β RaR br c 9
25 Table 3.: the th table B = B =... B = J B =. A = z z... z J z +0 A = z z... z J z A = I z I z I... z IJ z I+0 A =. z +0 z z +JK0 z ++00 a ij = P R a = 0, R b =, R c = A = i, B = j, C = P R a =, R b =, R c = A = i, B = j, C = = expµ + α A i + α B j + α C + α AB ij + α AC i + α BC j + α ABC ij +β Ra 0 + β R b + β Rc + β RaR b 0 + β RaRc 0 + β R brc + β RaR br c 0 +γ ARa i0 +γ ABRa ij0 +γ BCRc j γ CRaR b 0 + γ AR b i + γ ABR b ji + γ ARaR b i0 + γ CRaRc 0 + γ ARc i + γ ABRc ji + γ BRa j0 + γ ARaRc i0 + γ CR br c / expµ + α A i + α B j + α c + α AB ij + γ BR b j + γ ACRa i0 + γ AR br c i + α AC i + γ BRc j + γ ACR b i + γ BRaR b j0 + α BC j + γ CRa 0 + γ ACRc i + γ CR b + γ BRaRc j0 + α ABC ij +β Ra + β R b + β Rc + β RaR b + β RaRc + β R brc + β RaR br c + γ BCRa j0 + γ CRc + γ BCR b j + γ BR br c j +γ ARa i +γ ABRa ij +γ BCRc j γ CRaR b + γ AR b i + γ ABR b ji + γ ARaR b i + γ CRaRc + γ ARc i + γ ABRc ji + γ BRa j + γ ARaRc i + γ CR br c + γ BR b j + γ ACRa i + γ AR br c i + γ BRc j + γ ACR b i + γ BRaR b j + γ CRa + γ ACRc i + γ CR b + γ BRaRc j + γ BCRa j + γ CRc + γ BCR b j + γ BR br c j 0
26 = expβ Ra 0 + β RaR b 0 + β RaRc 0 + β RaR br c 0 + γ ARa i0 + γ BRa j0 + γ CRa 0 + γ ABRa ij0 +γ ACRa i0 + γ BCRa j0 + γ ARaR b i0 + γ ARaRc i0 + γ BRaR b j0 + γ BRaRc j0 + γ CRaR b 0 + γ CRaRc 0 β Ra β RaR b β RaRc β RaR br c γ ARa i γ BRa j γ CRa γ ABRa ij γ ACRa i γ BCRa j γ ARaR b i γ ARaRc i γ BRaR b j γ BRaRc j γ CRaR b γ CRaRc = exp[ β Ra + β RaR b + β RaRc + β RaR br c + γ ARa i + γ BRa j + γ CRa + γ ABRa ij + γ ACRa i +γ BCRa j + γ ARaR b i + γ BRaR b j + γ CRaR b b ij = P R a =, R b = 0, R c = A = i, B = j, C = P R a =, R b =, R c = A = i, B = j, C = = exp[ β R b + β RaR b + β R br c + β RaR br c + γ AR b i + γ BR b j + γ CR b + γ ABR b ij + γ ACR b i +γ BCR b j + γ ARaRc i + γ BRaRc j + γ CRaRc c ij = P R a =, R b =, R c = 0 A = i, B = j, C = P R a =, R b =, R c = A = i, B = j, C = = exp[ β Rc + β RaRc + β R br c + β RaR br c + γ AR C i + γ BRc j + γ CRc + γ ABRc ij + γ ACRc i +γ BCRc j + γ AR br c i + γ BR BR c j + γ CR br c d ij = P R a = 0, R b = 0, R c = A = i, B = j, C = P R a = 0, R b =, R c = A = i, B = j, C = P R a =, R b =, R c = A = i, B = j, C = P R a =, R b = 0, R c = A = i, B = j, C = = exp[ β R b + β RaR b 0 + β R br c + β RaR br c 0 + γ AR b i + γ BR b j + γ CR b + γ ABR b ij +γ ACR b i + γ BCR b j + γ ARaR b i0 + γ AR br c i + γ BRaR b j0 + γ BR br c j + γ CRaR b 0 + γ CR br c exp[β R b + β RaR b + β R br c + β RaR br c + γ AR b i + γ BR b j + γ CR b + γ ABR b ij +γ ACR b i + γ BCR b j + γ ARaR b i + γ AR br c i + γ BRaR b j + γ BR br c j = exp[4β RaR b + β RaR br c + γ ARaR b i + γ BRaR b j + γ CRaR b e ij = P R a = 0, R b =, R c = 0 A = i, B = j, C = P R a = 0, R b =, R c = A = i, B = j, C = P R a =, R b =, R c = A = i, B = j, C = P R a =, R b =, R c = 0 A = i, B = j, C = = exp[4β RaRc + β RaR br c + γ ARaRc i + γ BRaRc j + γ CRaRc f ij = P R a =, R b = 0, R c = 0 A = i, B = j, C = P R a =, R b = 0, R c = A = i, B = j, C = P R a =, R b =, R c = A = i, B = j, C = P R a =, R b =, R c = 0 A = i, B = j, C = + γ CRaR b + γ CR br c
27 = exp[4β R br c + β RaR br c + γ AR br c i + γ BR br c j + γ CR br c g ij = P R a = 0, R b = 0, R c = 0 A = i, B = j, C = P R a = 0, R b = 0, R c = A = i, B = j, C = P R a = 0, R b =, R c = A = i, B = j, C = P R a = 0, R b =, R c = 0 A = i, B = j, C = P R a =, R b = 0, R c = A = i, B = j, C = P R a =, R b = 0, R c = 0 A = i, B = j, C = P R a =, R b =, R c = 0 A = i, B = j, C = P R a =, R b =, R c = A = i, B = j, C = = exp[ β Rc + β RaRc 0 + β R br c 0 + β RaR br c 00 + γ ARc i0 + γ BRc j0 + γ CRc 0 + γ ABRc ij0 +γ ACRc i0 + γ BCRc j0 + γ ARaRc i0 + γ AR br c i0 + γ BRaRc j0 + γ BR br c j0 + γ CRaRc 0 + γ CR br c 0 exp[β Rc + β RaRc 0 + β R br c + β RaR br c 0 + γ ARc i + γ BRc j + γ CRc + γ ABRc ij + γ ACRc i + γ BCRc j + γ ARaRc i0 + γ AR br c i + γ BRaRc j0 + γ BR br c j + γ CRaRc 0 + γ CR brc exp[β Rc + β RaRc + β R br c 0 + β RaR br c 0 + γ ARc i + γ BRc j + γ CRc + γ ABRc ij + γ ACRc i + γ BCRc j + γ ARaRc i + γ AR br c i0 + γ BRaRc j + γ BR br c j0 + γ CRaRc + γ CR br c j0 exp[ β Rc + β RaRc + β R br c + β RaR br c + γ ARc i + γ BRc j + γ CRc + γ ABRc ij + γ ACRc i + γ BCRc j + γ ARaRc i = exp[ 8β RaR br c = g independent of i, j,. + γ AR br c i + γ BRaRc j + γ BR br c j + γ CRaRc + γ CR br c Therefore, µ ij = m ij, µ ij0 = m ij a ij, µ ij0 = m ij b ij, µ ij0 = m ij c ij, µ ij00 = m ij a ij b ij d ij, µ ij00 = m ij a ij c ij e ij, µ ij00 = m ij b ij c ij f ij, µ ij000 = m ij a ij b ij c ij d ij e ij f ij g, m ij 0, a ij 0, b ij 0, d ij 0, e ij 0, f ij 0, g 0 3. Variable C always observed We examine the simpler case where the stratum variable C is always observed, but the row variable A and column variable B may be missing. As we assumed before, there are no four-way or higher
28 interactions, so that, after simplifying the subscript notation logµ ijlm = µ + α A i + α B j + α C + α AB ij +β Ra l + β R b m + β RaR b lm + α AC i + α BC j + α ABC ij +γ ARa il +γ ACRa il + γ AR b im + γ ACR b im + γbra jl + γ BR b jm + γarar b ilm + γcra l + γ BCRa jl + γ CR b m + γ BCR b jm + γabra ijl + γbrar b jlm + γ ABR b ijm + γ CRaR b lm. Hence m ij = NP A = i, B = j, C =, R a =, R b =, a ij = P R a = 0, R b =, R c = A = i, B = j, C = P R a =, R b =, R c = A = i, B = j, C =, b ij = P R a =, R b = 0, R c = A = i, B = j, C = P R a =, R b =, R c = A = i, B = j, C =, d ij = P R a = 0, R b = 0, R c = A = i, B = j, C = P R a = 0, R b =, R c = A = i, B = j, C =, P R a =, R b =, R c = A = i, B = j, C = P R a =, R b = 0, R c = A = i, B = j, C =, µ ij = m ij, µ ij0 = m ij a ij, µ ij0 = m ij b ij, µ ij00 = m ij a ij b ij d ij, m ij 0, a ij 0, b ij 0, d ij 0. Since R c always is in this case, we drop the sixth subscript to simplify the notation. Also note that e ij = f ij = g ij = 0. In this case one computes separate estimates for the K subtables of order I J. Tables 3., 3.3 and 3.4 list the closed form solutions for various missingness models. Under the common odds ratio assumption, the log-linear model is logµ ijlm = µ + α A i + α B j + α C + α AB ij +β Ra l +γ ARa il +γ ABRa ijl +γ BCRc jn +γ CRaR b lm + β R b m + γ AR b im + β Rc n + γ ABR b ijm + γ ARaR b ilm + γarc in + γ CRaRc ln + β RaR b lm + γabrc ijn + α AC i + γ BRa jl + γ ARaRc iln + γ CR br c mn. + βrar b ln + α BC j + γ BR b jm + γ ACRa il + γ AR br c imn + β R br c mn + γbrc jn + γ ACR b im + γ BRaR b jlm + β RaR br c lmn + γ CRa l + γacrc in + γ CR b m + γ BRaRc jln + γ BCRa jl + +γcrc n + γ BCR b jm + γ BR br c jmn 3
29 Table 3.: Closed Form stimates for I J K Tables a Missingness of both A, B depends on C ˆm 0 ij = z ij ˆm t+ ij = [z ij + z +j0 ˆm t ij / ˆmt /z ++ + z z ++0 +j + z i+0 ˆm t ij / ˆmt i+ â = z ++0 /z ++ ˆb = z ++0 /z ++ ˆd = z ++ z ++00 /z ++0 z ++0 b Missingness of A depends on C, Missingness of B depends on A, C ˆm ij = z ij z ++ z +j+ /z +++ z +j+ â = z ++0 /z ++ ˆbi = z i+0 / ˆm i+ ˆd = z ++ z ++00 /z ++0 z ++0 b Missingness of A depends on B, C Missingness of B depends on C ˆm ij = z ij z ++ z i++ /z +++ z i++ â j = z +j0 / ˆm +j ˆb = z ++0 /z ++ ˆd = z ++ z ++00 /z ++0 z ++0 4
30 Table 3.3: Closed Form stimates for I J K Tables Continued c Missingness of A depends on C Missingness of B depends on B, C ˆm ij = z ij z +j+ z ++ /z +++ z +j â = z ++0 /z ++ ˆbj such that j ˆm ijˆb j = z i+0 ˆd = z ++ z ++00 /z ++0 z ++0 c Missingness of A depends on A, C Missingness of B depends on C ˆm ij = z ij z i++ z ++ /z i+ z +++ â i such that i ˆm ijâ i = z +j0 ˆb = z ++0 /z ++ ˆd = z ++ z ++00 /z ++0 z ++0 d Missingness of A, B depends on A, C ˆm ij = z ij â i such that i z ijâ i = z +j0 ˆbi = z i+0 /z i+ ˆd = z ++00 / i z i+â iˆbi d Missingness of A, B depends on B, C ˆm ij = z ij â j = z +j0 /z +j ˆbj such that j z ijˆb j = z i+0 ˆd = z ++00 / j z +jâ jˆbj 5
31 Table 3.4: Closed Form stimates for I J K Tables Continued e Missingness of A depends on A, C Missingness of B depends on B, C ˆm ij = z ij â i such that i ˆm ijâ i = z +j0 ˆbj such that j z ijˆb j = z i+0 ˆd = z ++00 / i j z ijâ iˆbj f Missingness of A depends on B, C Missingness of B depends on A, C ˆm ij = z ij â j = z +j0 /z +j ˆbi = z i+0 /z i+ ˆd = z ++00 / i j z ijâ jˆbi 6
32 As αij ABC = 0 in the common odds ratio models, the closed form for ˆm ij will be the solutions of the system of equations m ij + a ij + b ij = z +j + i i m ij + a ij + b ij = z i+ + j j m ij + a ij + b ij = z ij+ + z +j0 m ij a ij m +j a ij + i z +j0 m ij a ij m +j a ij + j z +j0 m ij a ij m +j a ij + z i+0 z i+0 z i+0 m ij b ij m i+ b ij m i+0 b ij m ij b ij m i+ b ij m i+0 b ij m ij b ij m i+ b ij. m i+0 b ij But the â ij, ˆb ij, ˆd ij are still the same as in Tables 3., 3.3 and Variables B and C always observed In the special cases that both variables B and C are always observed, we consider the models in which missingness of variable A depends on C and either A or B but not both. In these models there are no four-way or higher interactions. After simplifying the subscript notation, we use µ ijl denote the expected cell counts and z ijl are the observations, and the log-linear model for the partially observed categorical variables is logµ ijl = µ + α A i + α B j + α C + α AB ij +β Ra l + γ ARa il + γ BRa jl + γ CRa l + α AC i + α BC j + γ ACRa il + α ABC ij 3. + γ BCRa jl. When missingness of A depends on A, C informative missingness, only γ ARa il, γ CRa l, γ ACRa il will be in the model, and when missingness of A depends on B, C Missing at Random or MARB, C, only γ BRa jl, γ CRa l, γ BCRa jl will be in the model. Moreover, as both B and C are always observed, b ij = 0 and g = 0 in both models, so only m ij and a ij need to be estimated. Table 3.5 shows the closed forms for these two models. 7
33 Table 3.5: Closed Form stimator B and C are Always Observed ModelM ARB, C Missing InformativeA, C ˆm ij z ij z ij â ij â.j = z +j0 z +j â i., such that i ˆm ijâ i. = z +j0 Closed-form solution requires I=J and non-negative estimates. 3.3 Negative ˆα i boundary problems In models c, c, d and d in Table 3.3, model e in Table 3.4 and the informative missingness model in Table 3.5, the closed-form solution might exist when I = J and the solutions of â i. or ˆb.j are nonnegative. If any solution of â i. is negative, the ML estimate lies on the boundary of the parameter space and boundary solutions need to be investigated. In the case that I = J =, we can obtain closed-form ML boundary estimates by setting one of the â i. = 0 in the lielihood equations. According to Baer, Rosenberger and Dersimonian [5, we must evaluate both boundaries â. and â. and calculate G in 3.3 to figure out which parameter is falling on the boundary of the parameter space. G = i + j j [ ˆmij z ij log + z ij i [ z +j0 log i ˆm ijâ ij z +j0 z i+0 log [ j ˆm ijˆb ij z i+0 [ i + z ++00 log j ˆm ijâ ijˆbij ˆd z If G = G, then both â. and â. are set to be zero. Also, if there are not enough independent equations to solve for â i., then the boundary solution will be used. In the informative missingness case, G = z ij log [ ˆm ij /z ij + i j j [ i z +j0 log ˆm ijâ ij z +j0 8
34 Table 3.6: Boundary Solution for InformativeA, C when both B and C are always observed â. = 0 â. = 0 ˆm j z j z + z j +z +j0 z + +z ++0 z mˆ + z j +z +j0 j z + +z ++0 â. 0 z j z ++0 z + â. z ++0 z + 0 The boundary estimates for K tables when both the stratum variable C and column variable B are always observed are presented in Table 3.6 9
35 Chapter 4 Common Odds Ratio stimation Consider K contingency tables where each table has n observations and K n = N. When the stratum variable C =, and no data are missing, we observe the table B = B = Total A = z z n A = z z n n for =,, K. We assume that the odds ratio π π /π π = θ independent of common odds ratio. We consider the cases where the stratum variable C and the column variable B are always observed but the row variable A might be missing for some of the n observations. Variable A is either missing at random depending on variables B and C MARB, C or informatively missing depending on variables A and C InformativeA, C. We study estimation of the common odds ratio based on the hypothetical fully observed data set, only the completely observed subset and closed-form estimated data set of Chapter Methods 4.. Mantel-Haenszel stimator The Mantel-Haenszel estimator for the common odds ratio is ˆθ MH = K = z z /n K = z z /n so that ˆθ MH θ = K = z z /n θz z /n K = z z /n 0
36 The quantities z, z, z have a multinomial distribution with parameters n, π, π, and π, where n z z z = z and π π π = π. Under the common odds ratio assumption, θ = π π π π, θπ π = π π, θπ π = π π π π, θπ π = π π π π π π, π + π θπ = π π π, π = π π π, π + π θ π = π π π Using properties of the multinomial distribution = π π π π π. π + π θ [ z z [z z /n = n = n [z z = n n n π π = n π π, and [z z /n = n π π. Therefore [ z z /n = = K n π π = K n π π /θ = = µ x.
37 When K and θ are fixed, µ x is ON and when n, and θ are fixed and the π ij are bounded away from 0, µ x is OK. When K and n are fixed, µ x is O/θ. Writing ˆθ MH = y/x and using a Taylor expansion, ˆθ MH θ can be written as y θx x = y θx µ x = y θx µ x [ x µ x + µ x y θx x µx µ x µ x + The expected value of the first term of 4. is [ K z z /n θz z /n /µ x = = µ x n [z z θz z y θx x µx 4. = µ x n n n π π θn n π π = µ x n π π θπ π = 0. µ x µ x We have The expected value of the second term of 4. is [ K z K z /n θz z /n z z /n µ x µ x [ [ z z θz z z z z z = µ x n n n + [ z z θz z z z z z µ x n n n = K µ A + B. x = [ [ z z θz z z z z z A = n n n [ z z θz z z z = n [ [ z z z z θz z n n [ [ = n z z z z θ n zz µ x
38 because [z z θz z = 0. As [ n z z z z = n [z z z n z z z = n [n z z z zz z z zz z z z = n [n z z z z z z z z z z z n [z z z z 3z z z = n n n n n π π π n n n n 3ππ π n n n n n 3π π π n n n n n 3π π π and Then n 3n n n π π π = n n n n π π π n n 3π + π + π 3 = n n n 3 π π π π n [ n zz = n [z z z z + z z z + n [z z z + z z = n n n n n 3π π + n n n π π + n n n n π π + n n π π = n n n 3 π π π π /θ n + n n π π π + π + n π π. n n [ [ n z z z z θ n zz 3
39 = n n n 3 π π π π n θ n n n 3 π π π π /θ n θ n n π π π + π + n π π n = θ n n π π [n π + π + = n n π π [n π π +. n This implies A = n π π n π π + n B = [ z z θz z z z z z µ x n n n = µ [z z θz z [z z [z z x n n = 0. Therefore, the leading term of the bias for the Mantel-Haenszel estimator is µ x K = A = µ x = µ x 0. K = n π π n π π + n n n π π [n π π + Because µ x = O/N and the sum is O n, µ x K A = O/N. The expected value of the third term of 4. is K z K z /n θz z /n z z /n [z z /n = µ 3 x µ x K [ z z θz z z z [z z. 4. n n n As the observations from different strata are independent, all of the expectations of cross-product terms are zeros. µ x 4
40 The th term of the summation in 4. is We have [ z z θz z n [ z z = z z n 3 z z [z z n n [ z 3 θ z 3 n 3 [ z z z z [z z n 3 + θ [ [ z z θz z z z +. [ z z z z n 3 n = n 3 [z z z z n [ z z [z z = n 3 [z z z z z z + z z z z z + n 3 [z z z z z + z z z z n 3 = n 3 n n n n 3n 4n 5π π π π + n 3 n n n n 3n 4π π π π π + π + n 3 n n n n 3π π π π = n n n n 3n 4n 5π π π π + n n n n 3n 4π π π π π + π + n n n n 3π π π π. Note that z 3 z 3 = z z z z z z + 3z 3 z + 3z z 3 z 3 z 9z z z z 3 + 6z z + 6z z 4z z z 3 z = z z z z z + z 3 z + 3z z 3z z z z + z z z z 3 = z z z z z + 3z z + z z 3 z z 3z z + z z 5
41 z 3 z = z z z z + 3z z z z z z = z z z z + z z + z z z z z z 3 = z z z z + 3z z z z z z = z z z + z z z z = z z z + z z. So zz 3 3 = z z z z z z + 3z z z z z + 3z z z z z + zz 3 + 9zz + z z 3 9zz 9z z + 8z z, = z z z z z z + 3z z z z z + 3z z z z z + z z z z + 9z z z z + z z z z + z z z + z z + z z z + z z 3z z, = z z z z z z + 3z z z z z + 3z z z z z + z z z z + 9z z z z + z z z z + z z z + z z z + z z. We have [z z z z z z n 6
42 = n n n n 3n 4n 5π 3 π 3 [z z z z z n = n n n n 3n 4π 3 π [z z z z z n = n n n n 3n 4π π 3 [z z z z = n n n n 3π 3 π [z z z z = n n n n 3π π [z z z z = n n n n 3π π 3 [z z z = n n n π π [z z z = n n n π π [z z = n n π π Hence [z 3 z 3 = n n n n 3n 4n 5π 3 π 3 + 3n n n n 3n 4π 3 π + 3n n n n 3n 4π π 3 + n n n n 3π 3 π + 9n n n n 3π π + n n n n 3π π 3 + n n n π π + n n n π π + n n π π. Therefore, [ z 3 z 3 n 3 = n n n n 3n 4n 5π 3 π 3 /θ 3 7
43 + 3 n n n n 3n 4π π /θ π + π + n n n n 3π π π /θ + 9 n n n n 3π π /θ + n n n n 3π π π /θ + n n n π π π /θ + n n n π π π /θ + n n π π /θ. Therefore, [ z z z z [ z 3 n 3 θ z 3 n 3 = n n n n 3n 4n 5ππ 3 /θ 3 + n n n n 3n 4π π /θ π π + n n n n 3π π /θ θ n n n n 3n 4n 5π 3 π 3 /θ 3 3θ n n n n 3n 4ππ /θ π π θ n n n n 3π + π π π /θ 9θ n n n n 3ππ /θ θ n n n π + π π π /θ θ n n π π /θ = n n n n 3n 4π π /θ π π 8 n n n n 3π π /θ θ n n n n 3π + π π π /θ θ n n n π + π π π /θ θ n n π π /θ = n n n n 3n 4π π π π /θ 6 n n n n 3π π /θ 8
44 n n n 3 n π π π + π n n n π π π π n n π π and [ [ z z z z [z z z n 3 + θ z [z z n 3 [ = n 3 z z z z θzz [z z [ = n n π π n [ [ n z z z z θ n zz = n π π θ n n π π [n π + π + = n π n π [n π π + /θ [ [ z z θz z z z = 0. n n So [ z z θz z z z [z z n n n = n n n n 3n 4π π π π /θ 6 n n n n 3π π /θ n n n 3 n π π π π n n n π π π π n n π π + n n π n π π π /θ + n π n π /θ. We also have n n n n 3n 4 + n n n 9
45 = n n n n 3n 4 + n n = n n n n + 7n + n n = n n n 6n = n n n. Writing N = K n, for fixed K and θ, µ x = O n and the third term of 4. is K z K z /n θz z /n z z /n [z z /n µ x µ x = µ 3 x K n n n ππ π π = O/N 3 = O/N 6 n n n n 3π π /θ n n n n 3π π π π n n n π π π π n n π π + n π n π/θ K On. Therefore, Bias MH = µ x = µ x K = K A + Remainder = O/N, n n π π [n π π + + O/N 4.3 as N, and the dominant term is positive. When n and K are fixed, we have µ x = O/θ and A = O, then the second term of 4. is µ x K A = Oθ O = Oθ, 30
46 and the third term of 4. is Oθ 3 O = Oθ 3. Therefore, for fixed K and N, when θ, the bias. For a fixed θ, bounded n and the π ij are bounded, away from 0, µ x = = K n π π K n c K max n c = OK. Then Leading term of the Bias = µ x K A = O/K OK = O/K and the third term of 4. is O/K 3 OK = O/K. So if n is fixed, K and K π π, the leading term of the bias also converges to 0. We have Next we investigate the variance. We have Var ˆθ MH θ. = Var = µ x = µ x = µ x K z z /n θz z /n = µ x [ K z z θz z 0 K K n [zz θz z z z + θ zz n [zz + [zz θ[z z z z. n [z z = [z z z z + z z z 3
47 + [z z z + z z = n n n n 3π π + n n n π π π + π + n n π π and [z z z z = n n n n 3π π π π [z z = n n n n 3π π + n n n π π π + π + n n π π. Under the common odds ratio assumption, π π = θπ π. Therefore the unconditional expected value of the th term of the summation in the variance formula is [z z θz z = n n n n 3π π + n n n π π π + π + n n π π θn n n n 3π π π π + θ n n n n 3π π + θ n n n π π π + π + θ n n π π = n n n n 3θπ π π π + n n n π π π + π + n n π π θn n n n 3π π π π + θn n n n 3π π π π + θn n n π π π + π + θn n π π = n n n π π π + π + θπ + π + n n π π + θ. So the variance is Var ˆθ MH θ. = µ x K n n n π π π + π + θ π π 3
48 + n π π + θ. n As µ x is ON when K and θ are fixed and OK when N and θ are fixed and the π ij are bounded away from 0, Var ˆθ MH θ is O/N for fixed K and θ and O/K for fixed N and θ with all cell probabilities bounded away from 0. For fixed N and K, µ x is O/θ that implies Var ˆθ MH θ is Oθ 3. Therefore, the Mantel-Haenszel method overestimates the common odds ratio, but when either the minimum table size or the number of strata goes to infinity bounded away from 0 cell probabilities, the estimator converges to the true common odds ratio. Hauc [9 and Breslow [7 derived similar results. 4.. Mantel-Haenszel stimator with pseudo-data To reduce the bias of the Mantel-Haenszel estimator, Wypij and Santner [48 introduced the pseudotable methods by adding to the original K table one or more pairs of the following pseudotables: Here we focus on the case where only one pair of pseudotables are added. Then ˆθ P MH = K = z z /n + / K = z z /n + / K = z z /n + θ K = z z /n + ˆθ P MH θ = z z /n + [ z z [ Denominator = + n = [ z z + n = n π π + 33
49 = µ x + = µ x,p MH. As in section 4.., writing ˆθ P MH = y P MH /x P MH and using Taylor expansion, ˆθ P MH θ can be written as y P MH θx P MH = y [ P MH θx P MH x P MH µ x,p MH +... x P MH µ x,p MH µ x,p MH = y P MH θx P MH yp MH θx P MH xp MH µ x,p MH µ x,p MH µ x,p MH µ x,p MH yp MH θx P MH xp MH µ x,p MH µ x,p MH The expected value of the first term of 4.4 is [ yp MH θx P MH = = = = = µ x,p MH [ µ x,p MH µ x,p MH µ x,p MH µ x,p MH θ µ x,p MH. [ K z z + K θ = n µ x,p MH = z z n K [ z z z z θ + θ n n = [ n n + π π θ n n π π + θ n n [ n π π θπ π + θ n In the cases of θ > the expected value of the first term is negative. The expected value of the second term of 4.4 is [ z z /n + / θ z z /n + / µ x,p MH [ z z [ z z z z = θ = µ + x,p MH n n n + [ θ z z µ + x,p MH n µ x,p MH [ z z θ z z z z µ x,p MH + µ x,p MH n n [ z z θ n n z z /n + / µ x,p MH µ x,p MH µ x,p MH 34
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
5.4 The Poisson Distribution.
 The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
Lecture 2. Soundness and completeness of propositional logic
 Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
Jesse Maassen and Mark Lundstrom Purdue University November 25, 2013
 Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Concrete Mathematics Exercises from 30 September 2016
 Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
6.3 Forecasting ARMA processes
 122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
Partial Differential Equations in Biology The boundary element method. March 26, 2013
 The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
Bayesian statistics. DS GA 1002 Probability and Statistics for Data Science.
 Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
Μηχανική Μάθηση Hypothesis Testing
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
Lecture 34 Bootstrap confidence intervals
 Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
CRASH COURSE IN PRECALCULUS
 CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Every set of first-order formulas is equivalent to an independent set
 Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
The Simply Typed Lambda Calculus
 Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Math221: HW# 1 solutions
 Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Approximation of distance between locations on earth given by latitude and longitude
 Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
SCHOOL OF MATHEMATICAL SCIENCES G11LMA Linear Mathematics Examination Solutions
 SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
Problem Set 3: Solutions
 CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
 Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
derivation of the Laplacian from rectangular to spherical coordinates
 derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
Estimation for ARMA Processes with Stable Noise. Matt Calder & Richard A. Davis Colorado State University
 Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
Numerical Analysis FMN011
 Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Solution Series 9. i=1 x i and i=1 x i.
 Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +
[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R + k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +](/thumbs/73/69566903.jpg) Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3
 Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 19/5/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Math 6 SL Probability Distributions Practice Test Mark Scheme
 Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
 Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Finite Field Problems: Solutions
 Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Tridiagonal matrices. Gérard MEURANT. October, 2008
 Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Congruence Classes of Invertible Matrices of Order 3 over F 2
 International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
Second Order RLC Filters
 ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
Exercises 10. Find a fundamental matrix of the given system of equations. Also find the fundamental matrix Φ(t) satisfying Φ(0) = I. 1.
 Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
Lecture 21: Properties and robustness of LSE
 Lecture 21: Properties and robustness of LSE BLUE: Robustness of LSE against normality We now study properties of l τ β and σ 2 under assumption A2, i.e., without the normality assumption on ε. From Theorem
Lecture 21: Properties and robustness of LSE BLUE: Robustness of LSE against normality We now study properties of l τ β and σ 2 under assumption A2, i.e., without the normality assumption on ε. From Theorem
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
Notes on the Open Economy
 Notes on the Open Econom Ben J. Heijdra Universit of Groningen April 24 Introduction In this note we stud the two-countr model of Table.4 in more detail. restated here for convenience. The model is Table.4.
Notes on the Open Econom Ben J. Heijdra Universit of Groningen April 24 Introduction In this note we stud the two-countr model of Table.4 in more detail. restated here for convenience. The model is Table.4.
Section 7.6 Double and Half Angle Formulas
 09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
Homework 8 Model Solution Section
 MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
SCITECH Volume 13, Issue 2 RESEARCH ORGANISATION Published online: March 29, 2018
 Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
CE 530 Molecular Simulation
 C 53 olecular Siulation Lecture Histogra Reweighting ethods David. Kofke Departent of Cheical ngineering SUNY uffalo kofke@eng.buffalo.edu Histogra Reweighting ethod to cobine results taken at different
C 53 olecular Siulation Lecture Histogra Reweighting ethods David. Kofke Departent of Cheical ngineering SUNY uffalo kofke@eng.buffalo.edu Histogra Reweighting ethod to cobine results taken at different
PARTIAL NOTES for 6.1 Trigonometric Identities
 PARTIAL NOTES for 6.1 Trigonometric Identities tanθ = sinθ cosθ cotθ = cosθ sinθ BASIC IDENTITIES cscθ = 1 sinθ secθ = 1 cosθ cotθ = 1 tanθ PYTHAGOREAN IDENTITIES sin θ + cos θ =1 tan θ +1= sec θ 1 + cot
PARTIAL NOTES for 6.1 Trigonometric Identities tanθ = sinθ cosθ cotθ = cosθ sinθ BASIC IDENTITIES cscθ = 1 sinθ secθ = 1 cosθ cotθ = 1 tanθ PYTHAGOREAN IDENTITIES sin θ + cos θ =1 tan θ +1= sec θ 1 + cot
TMA4115 Matematikk 3
 TMA4115 Matematikk 3 Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet Trondheim Spring 2010 Lecture 12: Mathematics Marvellous Matrices Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet
TMA4115 Matematikk 3 Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet Trondheim Spring 2010 Lecture 12: Mathematics Marvellous Matrices Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
Second Order Partial Differential Equations
 Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Lecture 12: Pseudo likelihood approach
 Lecture 12: Pseudo likelihood approach Pseudo MLE Let X 1,...,X n be a random sample from a pdf in a family indexed by two parameters θ and π with likelihood l(θ,π). The method of pseudo MLE may be viewed
Lecture 12: Pseudo likelihood approach Pseudo MLE Let X 1,...,X n be a random sample from a pdf in a family indexed by two parameters θ and π with likelihood l(θ,π). The method of pseudo MLE may be viewed
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
The challenges of non-stable predicates
 The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
FORMULAS FOR STATISTICS 1
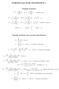 FORMULAS FOR STATISTICS 1 X = 1 n Sample statistics X i or x = 1 n x i (sample mean) S 2 = 1 n 1 s 2 = 1 n 1 (X i X) 2 = 1 n 1 (x i x) 2 = 1 n 1 Xi 2 n n 1 X 2 x 2 i n n 1 x 2 or (sample variance) E(X)
FORMULAS FOR STATISTICS 1 X = 1 n Sample statistics X i or x = 1 n x i (sample mean) S 2 = 1 n 1 s 2 = 1 n 1 (X i X) 2 = 1 n 1 (x i x) 2 = 1 n 1 Xi 2 n n 1 X 2 x 2 i n n 1 x 2 or (sample variance) E(X)
Homework for 1/27 Due 2/5
 Name: ID: Homework for /7 Due /5. [ 8-3] I Example D of Sectio 8.4, the pdf of the populatio distributio is + αx x f(x α) =, α, otherwise ad the method of momets estimate was foud to be ˆα = 3X (where
Name: ID: Homework for /7 Due /5. [ 8-3] I Example D of Sectio 8.4, the pdf of the populatio distributio is + αx x f(x α) =, α, otherwise ad the method of momets estimate was foud to be ˆα = 3X (where
DERIVATION OF MILES EQUATION FOR AN APPLIED FORCE Revision C
 DERIVATION OF MILES EQUATION FOR AN APPLIED FORCE Revision C By Tom Irvine Email: tomirvine@aol.com August 6, 8 Introduction The obective is to derive a Miles equation which gives the overall response
DERIVATION OF MILES EQUATION FOR AN APPLIED FORCE Revision C By Tom Irvine Email: tomirvine@aol.com August 6, 8 Introduction The obective is to derive a Miles equation which gives the overall response
Srednicki Chapter 55
 Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
 Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
6. MAXIMUM LIKELIHOOD ESTIMATION
 6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
Exercises to Statistics of Material Fatigue No. 5
 Prof. Dr. Christine Müller Dipl.-Math. Christoph Kustosz Eercises to Statistics of Material Fatigue No. 5 E. 9 (5 a Show, that a Fisher information matri for a two dimensional parameter θ (θ,θ 2 R 2, can
Prof. Dr. Christine Müller Dipl.-Math. Christoph Kustosz Eercises to Statistics of Material Fatigue No. 5 E. 9 (5 a Show, that a Fisher information matri for a two dimensional parameter θ (θ,θ 2 R 2, can
HISTOGRAMS AND PERCENTILES What is the 25 th percentile of a histogram? What is the 50 th percentile for the cigarette histogram?
 HISTOGRAMS AND PERCENTILES What is the 25 th percentile of a histogram? The point on the horizontal axis such that of the area under the histogram lies to the left of that point (and to the right) What
HISTOGRAMS AND PERCENTILES What is the 25 th percentile of a histogram? The point on the horizontal axis such that of the area under the histogram lies to the left of that point (and to the right) What
ω ω ω ω ω ω+2 ω ω+2 + ω ω ω ω+2 + ω ω+1 ω ω+2 2 ω ω ω ω ω ω ω ω+1 ω ω2 ω ω2 + ω ω ω2 + ω ω ω ω2 + ω ω+1 ω ω2 + ω ω+1 + ω ω ω ω2 + ω
 0 1 2 3 4 5 6 ω ω + 1 ω + 2 ω + 3 ω + 4 ω2 ω2 + 1 ω2 + 2 ω2 + 3 ω3 ω3 + 1 ω3 + 2 ω4 ω4 + 1 ω5 ω 2 ω 2 + 1 ω 2 + 2 ω 2 + ω ω 2 + ω + 1 ω 2 + ω2 ω 2 2 ω 2 2 + 1 ω 2 2 + ω ω 2 3 ω 3 ω 3 + 1 ω 3 + ω ω 3 +
0 1 2 3 4 5 6 ω ω + 1 ω + 2 ω + 3 ω + 4 ω2 ω2 + 1 ω2 + 2 ω2 + 3 ω3 ω3 + 1 ω3 + 2 ω4 ω4 + 1 ω5 ω 2 ω 2 + 1 ω 2 + 2 ω 2 + ω ω 2 + ω + 1 ω 2 + ω2 ω 2 2 ω 2 2 + 1 ω 2 2 + ω ω 2 3 ω 3 ω 3 + 1 ω 3 + ω ω 3 +
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΨΥΧΟΛΟΓΙΚΕΣ ΕΠΙΠΤΩΣΕΙΣ ΣΕ ΓΥΝΑΙΚΕΣ ΜΕΤΑ ΑΠΟ ΜΑΣΤΕΚΤΟΜΗ ΓΕΩΡΓΙΑ ΤΡΙΣΟΚΚΑ Λευκωσία 2012 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΨΥΧΟΛΟΓΙΚΕΣ ΕΠΙΠΤΩΣΕΙΣ ΣΕ ΓΥΝΑΙΚΕΣ ΜΕΤΑ ΑΠΟ ΜΑΣΤΕΚΤΟΜΗ ΓΕΩΡΓΙΑ ΤΡΙΣΟΚΚΑ Λευκωσία 2012 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ
CHAPTER 48 APPLICATIONS OF MATRICES AND DETERMINANTS
 CHAPTER 48 APPLICATIONS OF MATRICES AND DETERMINANTS EXERCISE 01 Page 545 1. Use matrices to solve: 3x + 4y x + 5y + 7 3x + 4y x + 5y 7 Hence, 3 4 x 0 5 y 7 The inverse of 3 4 5 is: 1 5 4 1 5 4 15 8 3
CHAPTER 48 APPLICATIONS OF MATRICES AND DETERMINANTS EXERCISE 01 Page 545 1. Use matrices to solve: 3x + 4y x + 5y + 7 3x + 4y x + 5y 7 Hence, 3 4 x 0 5 y 7 The inverse of 3 4 5 is: 1 5 4 1 5 4 15 8 3
Quadratic Expressions
 Quadratic Expressions. The standard form of a quadratic equation is ax + bx + c = 0 where a, b, c R and a 0. The roots of ax + bx + c = 0 are b ± b a 4ac. 3. For the equation ax +bx+c = 0, sum of the roots
Quadratic Expressions. The standard form of a quadratic equation is ax + bx + c = 0 where a, b, c R and a 0. The roots of ax + bx + c = 0 are b ± b a 4ac. 3. For the equation ax +bx+c = 0, sum of the roots
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 6/5/2006
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Ολοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα είναι μικρότεροι το 1000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Διάρκεια: 3,5 ώρες Καλή
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Ολοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα είναι μικρότεροι το 1000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Διάρκεια: 3,5 ώρες Καλή
Fourier Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Practice Exam 2. Conceptual Questions. 1. State a Basic identity and then verify it. (a) Identity: Solution: One identity is csc(θ) = 1
 Conceptual Questions. State a Basic identity and then verify it. a) Identity: Solution: One identity is cscθ) = sinθ) Practice Exam b) Verification: Solution: Given the point of intersection x, y) of the
Conceptual Questions. State a Basic identity and then verify it. a) Identity: Solution: One identity is cscθ) = sinθ) Practice Exam b) Verification: Solution: Given the point of intersection x, y) of the
Instruction Execution Times
 1 C Execution Times InThisAppendix... Introduction DL330 Execution Times DL330P Execution Times DL340 Execution Times C-2 Execution Times Introduction Data Registers This appendix contains several tables
1 C Execution Times InThisAppendix... Introduction DL330 Execution Times DL330P Execution Times DL340 Execution Times C-2 Execution Times Introduction Data Registers This appendix contains several tables
Statistics 104: Quantitative Methods for Economics Formula and Theorem Review
 Harvard College Statistics 104: Quantitative Methods for Economics Formula and Theorem Review Tommy MacWilliam, 13 tmacwilliam@college.harvard.edu March 10, 2011 Contents 1 Introduction to Data 5 1.1 Sample
Harvard College Statistics 104: Quantitative Methods for Economics Formula and Theorem Review Tommy MacWilliam, 13 tmacwilliam@college.harvard.edu March 10, 2011 Contents 1 Introduction to Data 5 1.1 Sample
Chapter 1 Introduction to Observational Studies Part 2 Cross-Sectional Selection Bias Adjustment
 Contents Preface ix Part 1 Introduction Chapter 1 Introduction to Observational Studies... 3 1.1 Observational vs. Experimental Studies... 3 1.2 Issues in Observational Studies... 5 1.3 Study Design...
Contents Preface ix Part 1 Introduction Chapter 1 Introduction to Observational Studies... 3 1.1 Observational vs. Experimental Studies... 3 1.2 Issues in Observational Studies... 5 1.3 Study Design...
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Strain gauge and rosettes
 Strain gauge and rosettes Introduction A strain gauge is a device which is used to measure strain (deformation) on an object subjected to forces. Strain can be measured using various types of devices classified
Strain gauge and rosettes Introduction A strain gauge is a device which is used to measure strain (deformation) on an object subjected to forces. Strain can be measured using various types of devices classified
New bounds for spherical two-distance sets and equiangular lines
 New bounds for spherical two-distance sets and equiangular lines Michigan State University Oct 8-31, 016 Anhui University Definition If X = {x 1, x,, x N } S n 1 (unit sphere in R n ) and x i, x j = a
New bounds for spherical two-distance sets and equiangular lines Michigan State University Oct 8-31, 016 Anhui University Definition If X = {x 1, x,, x N } S n 1 (unit sphere in R n ) and x i, x j = a
( y) Partial Differential Equations
 Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate
Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate
Introduction to the ML Estimation of ARMA processes
 Introduction to the ML Estimation of ARMA processes Eduardo Rossi University of Pavia October 2013 Rossi ARMA Estimation Financial Econometrics - 2013 1 / 1 We consider the AR(p) model: Y t = c + φ 1 Y
Introduction to the ML Estimation of ARMA processes Eduardo Rossi University of Pavia October 2013 Rossi ARMA Estimation Financial Econometrics - 2013 1 / 1 We consider the AR(p) model: Y t = c + φ 1 Y
Reminders: linear functions
 Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
Συστήματα Διαχείρισης Βάσεων Δεδομένων
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Συστήματα Διαχείρισης Βάσεων Δεδομένων Φροντιστήριο 9: Transactions - part 1 Δημήτρης Πλεξουσάκης Τμήμα Επιστήμης Υπολογιστών Tutorial on Undo, Redo and Undo/Redo
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Συστήματα Διαχείρισης Βάσεων Δεδομένων Φροντιστήριο 9: Transactions - part 1 Δημήτρης Πλεξουσάκης Τμήμα Επιστήμης Υπολογιστών Tutorial on Undo, Redo and Undo/Redo
Queensland University of Technology Transport Data Analysis and Modeling Methodologies
 Queensland University of Technology Transport Data Analysis and Modeling Methodologies Lab Session #7 Example 5.2 (with 3SLS Extensions) Seemingly Unrelated Regression Estimation and 3SLS A survey of 206
Queensland University of Technology Transport Data Analysis and Modeling Methodologies Lab Session #7 Example 5.2 (with 3SLS Extensions) Seemingly Unrelated Regression Estimation and 3SLS A survey of 206
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Fractional Colorings and Zykov Products of graphs
 Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Η ΠΡΟΣΩΠΙΚΗ ΟΡΙΟΘΕΤΗΣΗ ΤΟΥ ΧΩΡΟΥ Η ΠΕΡΙΠΤΩΣΗ ΤΩΝ CHAT ROOMS
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ Ι Ο Ν Ι Ω Ν Ν Η Σ Ω Ν ΤΜΗΜΑ ΔΗΜΟΣΙΩΝ ΣΧΕΣΕΩΝ & ΕΠΙΚΟΙΝΩΝΙΑΣ Ταχ. Δ/νση : ΑΤΕΙ Ιονίων Νήσων- Λεωφόρος Αντώνη Τρίτση Αργοστόλι Κεφαλληνίας, Ελλάδα 28100,+30
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ Ι Ο Ν Ι Ω Ν Ν Η Σ Ω Ν ΤΜΗΜΑ ΔΗΜΟΣΙΩΝ ΣΧΕΣΕΩΝ & ΕΠΙΚΟΙΝΩΝΙΑΣ Ταχ. Δ/νση : ΑΤΕΙ Ιονίων Νήσων- Λεωφόρος Αντώνη Τρίτση Αργοστόλι Κεφαλληνίας, Ελλάδα 28100,+30
Matrices and vectors. Matrix and vector. a 11 a 12 a 1n a 21 a 22 a 2n A = b 1 b 2. b m. R m n, b = = ( a ij. a m1 a m2 a mn. def
 Matrices and vectors Matrix and vector a 11 a 12 a 1n a 21 a 22 a 2n A = a m1 a m2 a mn def = ( a ij ) R m n, b = b 1 b 2 b m Rm Matrix and vectors in linear equations: example E 1 : x 1 + x 2 + 3x 4 =
Matrices and vectors Matrix and vector a 11 a 12 a 1n a 21 a 22 a 2n A = a m1 a m2 a mn def = ( a ij ) R m n, b = b 1 b 2 b m Rm Matrix and vectors in linear equations: example E 1 : x 1 + x 2 + 3x 4 =
HW 3 Solutions 1. a) I use the auto.arima R function to search over models using AIC and decide on an ARMA(3,1)
 HW 3 Solutions a) I use the autoarima R function to search over models using AIC and decide on an ARMA3,) b) I compare the ARMA3,) to ARMA,0) ARMA3,) does better in all three criteria c) The plot of the
HW 3 Solutions a) I use the autoarima R function to search over models using AIC and decide on an ARMA3,) b) I compare the ARMA3,) to ARMA,0) ARMA3,) does better in all three criteria c) The plot of the
About these lecture notes. Simply Typed λ-calculus. Types
 About these lecture notes Simply Typed λ-calculus Akim Demaille akim@lrde.epita.fr EPITA École Pour l Informatique et les Techniques Avancées Many of these slides are largely inspired from Andrew D. Ker
About these lecture notes Simply Typed λ-calculus Akim Demaille akim@lrde.epita.fr EPITA École Pour l Informatique et les Techniques Avancées Many of these slides are largely inspired from Andrew D. Ker
forms This gives Remark 1. How to remember the above formulas: Substituting these into the equation we obtain with
 Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
Figure A.2: MPC and MPCP Age Profiles (estimating ρ, ρ = 2, φ = 0.03)..
 Supplemental Material (not for publication) Persistent vs. Permanent Income Shocks in the Buffer-Stock Model Jeppe Druedahl Thomas H. Jørgensen May, A Additional Figures and Tables Figure A.: Wealth and
Supplemental Material (not for publication) Persistent vs. Permanent Income Shocks in the Buffer-Stock Model Jeppe Druedahl Thomas H. Jørgensen May, A Additional Figures and Tables Figure A.: Wealth and
Forced Pendulum Numerical approach
 Numerical approach UiO April 8, 2014 Physical problem and equation We have a pendulum of length l, with mass m. The pendulum is subject to gravitation as well as both a forcing and linear resistance force.
Numerical approach UiO April 8, 2014 Physical problem and equation We have a pendulum of length l, with mass m. The pendulum is subject to gravitation as well as both a forcing and linear resistance force.
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 24/3/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Όλοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα μικρότεροι του 10000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Αν κάπου κάνετε κάποιες υποθέσεις
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Όλοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα μικρότεροι του 10000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Αν κάπου κάνετε κάποιες υποθέσεις
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Οικονομία. Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Τέλος Ενότητας Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Τέλος Ενότητας Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί
