4. Izrek o kinetični in potencialni energiji
|
|
|
- Ἡρακλείδης Αβραμίδης
- 5 χρόνια πριν
- Προβολές:
Transcript
1 4. Izrek o kineični in poencialni energiji Točkaso elo Izračunajo delo (A) rezulane zunanjih sil ( F ), ki deluje na očkaso elo z aso : A= F ds= F dr, () kjer je ds vekor preika ds = dr r r ( + d) ir Uporabio II. Newonov zakon za gibanje očkasega elesa: dv F= a=. () d Enačbo () vsavio v enačbo () in dobio: dv dv A= F dr = a dr = dr = vd= dv v= dv v d d, (3) kjer so uporabili definiciji dr zapišio skalarni produk v dv : dv = vd, dv = ad. V nadaljevanju najprej alo drugače dv ϕ v v ( + d) v v dv v= v= ( vv ) dv d( v ) = dv v dv= v dv cosϕ = vdv ali: dv (4a) 57
2 d v v = dv v + v dv = v dv, od koder sledi: v dv= d( vv ) = d( v ) = vv d (4b) Ob upoševanju enačbe (4a), oziroa (4b) iz enačbe (3) sledi: v A = v dv = vd v = v = v v. (5) v v v Definirao kineično energijo očkasega elesa: Wk = v, (6) orej: A= F ds = W k. (7) Relacijo (7) ienujeo izrek o kineični energiji za očkaso elo. V nadaljevanju rezulano vseh zunanji sil razdelio na rezulano vseh osalih zunanjih sil razen sile eže ( F os ) M z Fg = G r r in silo eže (graviacijsko silo) F g : r, (8) ir Zelja R h r r h R = poler Zelje h = nadorska višina 58
3 kjer je G graviacijska konsana, očkasega elesa z aso. Torej: M z asa Zelje in r razdalja od središča Zelje do F= F + F, (9) os g oziroa: A= F + F ds = F + F dr = W os g os g k. () Iz enačbe () sledi: A = F dr = W F dr. () os os k g Zadnji člen v enačbi () predsavlja negaivno delo sile eže. V nadaljevanju negaivno delo sile eže ob upoševanju enačbe (8) izrazio alce drugače: Mz r Fg dr= G dr= GM d z r r 3 r r = r r = GM rd r= GM = GM = r r dr z 3 z z r r r r r M z M z M z = G = G G. r r r r Če definirao graviacijsko poencialno energijo očkase ase ko: () M W G r z p =, (3) lahko zapišeo enačbo () v obliki: F dr = W W = W g p, p, p enačbo () pa ko:, (4) Aos = Wk + Wp. (5) Enačbo (5) ienujeo izrek o kineični in poencialni energiji za očkaso elo. 59
4 Pri izpeljavi enačbe () so upoševali: dr dr ϕ r r ( + d) r r dr d r r = dr r + r dr = r dr, od koder sledi: r dr = d( r r) = d( r ) = rdr. (6) Narišio odvisnos graviacijske poencialne energije očkasega elesa od razdalje od središča Zelje r = R + h, (7) kjer je R poler Zelje, h pa nadorska višina. W p R r li W = p r Graviacijsko poencialno energijo lahko za ajhne nadorske višine h razvijao v vrso: Mz Mz Mz M z h h Wp = G = G = G = G r ( R h) h + + R R R R + R. (8) 6
5 h Iz enačbe (8) vidio, da za zelo ajhne nadorske višine velja približno zveza: R Mz h Mz Mz Wp G = G + G h. (9) R R R R Pri konsanni vrednosi ase in upoševanju definicije graviacijskega pospeška pri orski gladini M z =, g G 9.8s R lahko zapišeo enačbo (9) v obliki: Wp = g h. () GMz Konsanni člen v enačbi (9) so izpusili, saj v enačbi (5) nasopa le razlika R poencialnih energij, asa elesa pa se ne spreinja. Togo elo Dienzije ogih eles, ki jih obravnavao, so veliko anjše od polera Zelje, zao je graviacijski pospešek znoraj elesa prakično konsanen v vseh delih elesa. Zao sa izraza za graviacijsko poencialno energijo (3) in (), ki so ju izpeljali za očkaso elo, dobra udi za oga elesa končnih razsežnosi. Drugače pa je s kineično energijo ogega elesa, ki je v splošne ne oreo opisai z izrazo v (razen, če se ogo elo giblje po preici). Narišio sheasko ogo elo v karezične koordinane siseu (, y, z). V ežišče ogega elesa (T) posavio izhodišče lokalnega koordinanega sisea (', y', z'), kjer predposavio, da so koordinane osi laboraorijskega inercialnega koordinanega sisea (, y, z) paroa vzporedne z osi lokalnega ežiščnega sisea (', y', z'). 6
6 y y' d r r T z' T r * ' r rt r * krajevni vekor do ajhnega dela ogega elesa z aso d erjeno v laboraorijske siseu (, y, z) krajevni vekor do ežišča ogega elesa erjeno v laboraorijske siseu (, y, z) krajevni vekor do ajhnega dela ogega elesa z aso d erjeno v lokalne (ežiščne) koordinane siseu (', y', z') T ežišče ogega elesa Iz zgornje slike vidio, da velja zveza z * r = r T + r. () Če enačbo () odvajao po času na obeh sraneh enačaja dobio: * v = v T + v, () kjer je v * T hiros ežišča ogega elesa, v pa hiros ase d v ežiščne siseu. Izračunajo sedaj kineično energijo ogega elesa, za kaero vzaeo, da je vsoa kineičnih energij vseh as d, ki sesavljajo ogo elo z aso : Wk = v d= v vd Izraz () vsavio v enačbo (3a):. (3a) * * * * Wk = ( vt + v ) ( vt + v ) d= vtd+ vt v d+ v d. (3b) Drugi člen v gornje izrazu je enak nič. Koordinae ežišča v ežiščne siseu so nareč enake nič: 6
7 * * rt = r d=, zao je udi d * * r d = v d =. d (4) Iz enačb (3b) in (4) sledi: * Wk = vt + v d. (5) V splošne v vsake renuku obsaja neka os okoli kaere se s kono hirosjo ω vri obravnavano elo, ki je v izbrane renuku enaka za vse očkase ase d, ki sesavljajo ogo elo, zao velja (gleje sliko): v = R ω. (6) * * Ob upoševanju enačbe (6) lahko enačbo (5) zapišeo v obliki: * Wk = vt + J ω, (7) kjer so upoševali * * *, (8a) v d = ω R d = J ω * J = R * d. (8b) 63
8 Kineično energijo WT = vt ienujeo ranslacijska kineična energija ogega elesa, * Wr = J ω pa je roacijska kineična energija ogega elesa. Za izbrani ežiščni sise lahko v splošne zapišeo roacijsko kineično energijo ko: Wr = J αβ ω α ω β, (9) * * * * * * α=, y, z, β =, y, z, kjer so J * *, J * * in J * * vzrajnosni oeni okrog reh pravokonih osi *, y * in z *, yy zz J αβ ( α β) pa so deviacijski oeni (gleje še sr.47). Če so osi ežiščnega sisea hkrai udi glavne osi dobi izraz (9) obliko: Wr = J * ω + J * ω + J * ω y z 3. (3) Če pa se renuna os vrenja vedno ujea z eno ized glavnih osi, n.pr. z J *, je Wr = J * ω. (3) Nazorna ilusracija zadnjega priera je koaljenje hoogenega valja s polero R in aso po klancu navzdol brez podrsavanja. Če se valj koali brez podrsavanja sa hiros ežišča valja v T in kona hiros vrenja valja povezana z enačbo vt = Rω. (3) Trenuna os vrenja valja pri koaljenju brez podrsavanja se ujea z geoerijsko osjo valja, ki je hkrai udi ena ized glavnih osi. Vzrajnosni oen hoogenega valja okrog e osi je J= R, orej velja: 64
9 v 3 W v J v R v R 4 T k = T + ω = T + = T, (33) kjer so upoševali veljavnos enačbe (3). Če se valj po klancu ne bi koalil, apak bi sao drsel s hirosjo v T, bi bila usrezna kineična energija valja sao v T. Zgled: popolnoa prožen cenralni rk dveh vozičkov na zračni blazini Prožen rk dveh eles definirao ko rk pri kaere se ohranja skupna kineična energija. Ker * je rk cenralen, ne upoševao roacijske kineične energije vozičkov J ω (enačba (7)). Predposavio pa udi, da se pri rku graviacijska poencialna energija ne spreeni ( W p = ) in pa, da je delo vseh zunanjih sil enako nič (gleje še enačbo (5)). Velja orej ohraniev skupne kineične energije: ' ' v + v = v + v, (34) kjer sa in asi vozičkov, vozičkov po rku. ' v in ' v hirosi vozičkov pred rko er v in v hirosi pred rko: v ' v ' po rku: v v Ob predposavki, da je skupni sunek sil na oba vozička nič, se ohranja udi skupna gibalna količina obeh vozičkov: v + v = v + v. (35) ' ' 65
10 Iz enačb (34) in (35) lahko pri poznavanju,, vozičkov v in rko iruje, o je za ' v in v. Rešio enačbi (34) in (35) za poseben prier, ko drugi voziček pred ' v =. Tako preidea enačbi (34) in (35) v: ' v izračunao končni hirosi v= v+ v, (36) ' ' v = v + v, (37) od koder sledi: ' v = v+ v ' v = v + v (38) (39) Rešivi enačb (39) in (38) sa: v ' v =, (4) + ' v v = +. (4) Za poseben prier, ko sa asi obeh vozičkov enaki, sledi iz enačb (4) in (4): v =. ' v = v. 66
11 5. Haronično nedušeno nihanje Splošno: Poencialna energija ( D): Pogoj za iniu poencialne energije: dw d p = =, d W d = r r p > Izhodišče koordinanega sisea preakneo v iniu poencialne energije: W p parabola, ki se najbolje prilega krivulji v okolici iniua W p Za << razvijeo W p v Taylorjevo vrso: dw d W d W Wp = Wp( = ) , d d d p p p r = r = r = kjer so upoševali dw Wp = = in p = d = r (gleje sliko). Torej: W p k, () kjer je: 67
12 d W k = d p r = >. () dwp Sila F = = k. (3) d Zapišio II. Newonov zakon za gibanje ase : a = k, (4) d Pospešek a =, orej: d d = k, od koder sledi: d d d = k. (5) Rešiev diferencialne enačbe (5) iščeo z nasavko: π = sin + δ. (6) Iz enačbe (6) sledi: d π π v = = cos + δ d (7) kjer je: v π (8) apliuda hirosi. Velja udi: dv d π sin d d π a= = = + δ. (9) Enačbi (6) in (9) vsavio v diferencialno enačbo (5) in dobio: π k sin π π δ sin + = + δ, () 68
13 od koder sledi: π k = oziroa, () = π. () k π Vidio orej, da nasavek = sin + δ reši diferencialno enačbo (5), kjer je nihajni čas določen z enačbo (), δ pa je fazni zaik. Gibanje, določeno z enačbo (6), ienujeo haronično ali sinusno nedušeno nihanje. π = sin + δ δ Na zgornji sliki vidio, da velja zveza ω = π ω = lasna krožna frekvenca Lasna frekvenca ν = ω = π ν π ω = 69
14 7 Energija haroničnega nihanja o Kineična energija ase (gleje še enačbo (7)):. cos + = = δ π π v W k (3) o Poencialna energija (gleje enačbi () in (6)):. sin + = = δ π k k W p (4) o Celona energija:. sin cos = + = δ π δ π π k W W W p k (5) Ob upoševanju enačbe () preide enačba (5) v:. sin cos k k W = = δ π δ π (6) Ob upoševanju enačbe (8) in () velja:. v k v k = = π (7) Torej:. v k W = = (8)
15 Prieri nihal, ki nihajo sinusno. Nihalo na vijačno vze A: HORIZONTALNO gibanje ase k k konsana vzei Newonov zakon za gibanje ase : d d = k, (9) kjer je k sila vzei. Rešiev enačbe (9) že poznao (gleje enačbe (5) ()): π = sin + δ, () kjer je = π nihajni čas. () k B: VERTIKALNO gibanje ase celoen razezek vzei r ravnovesni razezek odsopanje od ravnovesnega razezka 7
16 Velja: = r +. () V ravnovesju napišeo pogoj za saično ravnovesje ase v obliki: k r = g. (3) Newonov zakon za gibanje ase pa ko: a = g k, (4) kjer je d pospešek ase. Torej: d d = g k ( r + ), (5) d kjer so upoševali enačbo (). Ob upoševanju enačbe (3) iz enačbe (5) sledi: d d = k. (6) Rešiev enačbe (6) pa že poznao od prej.. Nihalo na polžaso vze (sučno sinusno nihanje) Navor polžase vzei: M = Dϕ (7) kjer jeϕ zasuk vzei in D konsana vzei. 7
17 Zapišeo enačbo za vrenje ogega elesa okrog fiksne osi: d ϕ M = J, (8) d J vzrajnosni oen nihala, d ϕ α = koni pospešek, (9) d dϕ ω = kona hiros. (3) d Vsavio enačbo (7) v enačbo (8) in dobio: d ϕ J = Dϕ, (3) d oziroa: d ϕ D = ϕ. (3) d J Rešiev diferencialne enačbe (3) iščeo z nasavko: π ϕ = ϕ sin + δ. (33) dφ π π Kona hiros ω = = φ cos + δ, d kjer je (34) π ω = ϕ, (35) apliuda kone hirosi. Koni pospešek d ϕ π π α = = ϕ sin, + d δ (36) oziroa 73
18 d ϕ π = d ϕ. (37) Vidio, da nasavek (33) reši enačbo (3). Iz prierjave enačb (37) in (3) sledi: π = D J, (38) oziroa J = π. (39) D 3. Maeaično nihalo Zaporedne foografije odklona nike (odela) aeaičnega nihala (foo: U. Anzeljc). Obravnavao nihanje očkase ase, ki visi na zelo lahki niki dolžine l. l ϕ ϕ = odik g Navor sile eže g je: 74
19 M = gl sinϕ (4) Ob predposavki, da so odiki ajhni (ϕ << ) velja sin ϕ ϕ, orej M glϕ (4) Opis vrenja ogega elesa okrog fiksne osi: M d ϕ d = J, (4) kjer je J = l vzrajnosni oen očkase ase. Če vsavio enačbo (4) v enačbo (4) dobio: d ϕ d glϕ = l, oziroa: d ϕ g = ϕ d l. (43) Rešiev diferencialne enačbe (43) iščeo z nasavko: π ϕ = ϕ sin + δ. (44) Če enačbo (44) dvakra odvajao dobio: d ϕ π π sin + d = ϕ δ oziroa, (45) d φ π = φ d. (46) Vidio orej da nasavek (44) reši enačbo (43). Iz prierjave enačb (43) in (46) dobio: π g =, l od koder sledi izraz za nihajni čas: 75
20 l = π (47) g 4. Fizično nihalo r T ϕ os vrenja T ežišče r ročica rezulane sile eže T T g Navor rezulane sile eže g je: M = gr T sinϕ. (48) Ob predposavki ( sin ϕ ϕ) za (ϕ << ) velja: M gr T ϕ (49) Opis vrenja ogega elesa okrog fiksne osi: M d ϕ d = J (5) kjer je J vzrajnosni oen ogega elesa okrog izbrane osi. Če vsavio enačbo (49) v enačbo (5) dobio: d ϕ g r T ϕ = J, (5) d Enačbo (5) zapišeo v obliki: d ϕ d = g r J T ϕ. (5) Rešiev enačbe (5) iščeo z nasavko: 76
21 77 + = δ π ϕ ϕ sin. (53) Enačbo (53) dvakra odvajao po času in dobio:, sin d d + = δ π π ϕ ϕ (54) oziroa ϕ π ϕ d d =. (55) Iz prierjave ed enačbaa (5) in (55) sledi:, J g r T = π (56) oziroa: g r T J π =. (57) V posebne prieru r T J = in l r T = preide enačba (57) v enačbo (47): g l π =, ki velja za aeaično nihalo.
22 6. Dušeno nihanje Obravnavao prier nihala na vijačno vze. asa k konsana vzei V dosedanji obravnavi nihala na vijačno vze so predposavili, da je sila vzei k edina sila. Zanearili pa so silo renja, ki je sorazerna asi elesa. Pa udi silo upora, ki je pri ajhnih hirosih sorazerna hirosi v. V nadaljevanju zao poleg sile vzei upoševao udi silo dušenja Fd, ki jo zapišeo v približne zapisu ko: F = β v, (58) d kjer je asa in β koeficien dušenja. Zapišio II. Newonov zakon za gibanje ežišča ase : = k β, (59) kjer so definirali: d d,. (6) d d Enačbo (59) na obeh sraneh enačaja delio z aso in dobio: + β + ω =, (6) kjer je π k ω = =, (6) lasna krožna frekvenca nedušenega nihanja, pa lasni nihajni čas nedušenega nihanja (gleje enačbo ()). Rešiev enačbe (6) iščeo z nasavko: ye β = (63) kjer je y( ) neznana funkcija časa. Funkcijo (63) dvakra odvajao: 78
23 = β, (63a) β β ye ye β β β, (63b) = ye βye + β ye in dobljena izraza za in vsavio v diferencialno enačbo (6). Tako dobio: ( ω β ) + =. (64) β e y y Ker e β ( ω β ) v splošne ni enak nič, ora bii y+ =. (65) y Rešiev enačbe (65) je sinusno nihanje: ( ω δ) y= cos +, (66) kjer je: ω = ω β (67) lasna krožna frekvenca dušenega nihanja. Na osnovi enačb (63) in (66) zapišeo rešiev enačbe (6) v obliki: β ( ω δ) = e cos + e β δ = π (68) Funkcija (68) reši enačbo (6) le v prieru, ko je β< ω (gleje enačbo (67)). Če je β > ω se enačba (65) lahko zapiše v obliki: ( β ω ) y = y, (69) kjer je β ω >. Zao je v e prieru rešiev enačbe (69) eksponenna funkcija, pa udi celona rešiev (gleje še enačbo (63)) je eksponenna funkcija: = e α, α >. (7) 79
24 7. Vsiljeno nihanje asa k konsana vzei F apliuda vsiljene sile ω vsiljena krožna frekvenca Sila, ki vsiljuje nihanje: sin Enačba gibanja: = k β + F sinω, oziroa F = F ω (7) F + β + ω = sinω, (7) kjer je ω = k (73) lasna krožna frekvenca nedušenega nihanja in β koeficien dušenja. Če je ω << ω :,, orej: F ω sinω, oziroa: F = sinω. (74) ω Splošno rešiev diferencialne enačbe (7) iščeo z nasavko: = +, (75) h p kjer je p parikularna rešiev nehoogene diferencialne enačbe, h hoogene diferencialne enačbe + β + ω = (gleje enačbo (68)): pa je rešiev = e sin ω, h β ω = ω β. Lasno nihanje z lasno krožno frekvenco. h ' ω se po zadosi velike času zaduši, ker 8
25 Parikularno rešiev nehoogene diferencialne enačbe (7) iščeo z nasavko: ( ω δ) sin p = +, (76) kjer je ω krožna frekvenca vsiljene sile. V nadaljevanju iščeo in δ. Izraz (76) predelao v: = sin ω+ δ = sinωcosδ + cosωsinδ, oziroa (77) p sinω = A + A cosω, (78) p kjer so vpeljali nove oznake: cosδ = A er sin δ = A, (79) Odvode: = A ω cosω Aω sin ω, p = A ω sinω Aω cos ω, p vsavio v diferencialno enačbo (7): A ω sinω Aω cosω+ β Aωcosω β A ωsinω+ F + ω Asinω+ ω Acos ω= sinω Enačba (8) ora veljai posebej za člene s sin ( ω ) in posebej za člene z cos ω : (8) F Aω β Aω+ ω A=, A ω + β A ω+ ω A =, oziroa: F ω ω A βωa=, (8) ω ω A + βωa =. (8) ( ) Iz enačbe (8) ob upoševanju enačbe (79) sledi: A A sinδ βω g δ, orej: (83) = = = cosδ ω ω 8
26 βω g δ =. ω ω Enačbi (8) in (8) kvadrirao er sešejeo: ( ω ω ) ( A A ) 4 β ω ( A A ) F =. (84) Velja pa udi (gleje enačbo (79): A + A = cos δ + sin δ =. (85) Iz enačb (84) in (85) sledi: F ω ω + 4 βω =, od od pa: = F + 4 ω ω βω (86) Odvisnos apliude od vsiljene krožne frekvence ω: ( F ω ) β ω = ( F ) + 4 ω ω βω 4 3 β. ω = β.5 ω = β ω =.5.5 ω ω 8
27 Torej: β splošna rešiev enačbe (7) je: = e sin ( ω ) + sin ( ω+ δ) ( sin ) za zadosi velike čase niha nihalo sinusno ( ω δ ) h = se zaduši ( ω = ω β ) β lasno nihanje e sin ( ω ) F ω << ω : ω d : = je pri dω ω ω za β : ωa ω in ω ω >> : ω = ω = ω β a Odvisnos faznega zaika δ od vsiljene krožne frekvence ω: = + s frekvenco vsiljene sile δ π 3π 4 π π 4 β ω = β β. ω =.5 ω = β ω = βω g δ = ω ω.5.5 ω ω Torej: ω<< ω : δ F π ω ω: δ ( ) ω>> ω : δ π ω 83
28 Moč vsiljene sile sinω ωcos( ω δ) P = F v = F +. (87). Upoševali so: = sin ( ω+ δ) v= = ωcos ( ω+ δ) Ker cos( ω+ δ) = cos( ω) cosδ sin ( ω) sinδ : P = Fω ( ω) ( ω) δ ( ω) δ sin cos cos sin sin P= P d je: Povprečna oč cosδ P= Fω sin ( ω) d sinδ sin ( ω) d, orej: = = P F = ω δ. (88) sin V enačbo (88) vsavio: βω kjer je g δ =, ω ω in dobio: = ( F ) + 4 ω ω βω in sinδ = g δ, + g δ F F βω ω ω ω P = ( ω ω) + 4 βω 4βω + orej: ( ω ω ), P = F βω + 4 ω ω βω. (89) 84
29 dp Maksialna vrednos P je pri ωm ω dω = =. Sklep: za vse β je P največja pri ω P ωm = ω β. ω = β.5 ω = β ω =.5.5 ω ω 85
30 8. Sklopljeno nihanje I. odel: dve enaki fizični nihali sa sklopljeni z vzejo s konsano k b k ϕ ϕ bsin ϕ b k bsinϕ g g g g Enačbi gibanja (vrenje ogega elesa okoli fiksne osi): M = Jϕ, α= ϕ, zapišeo v obliki: J ϕ = g sinϕ + k b cos ϕ, (9a) J ϕ = g sinϕ k b cos ϕ, (9b) kjer so upoševali sin ( 9 ϕ) Ob upoševanju: 3 5 ϕ ϕ sin ϕ = ϕ +..., 3! 5! 4 ϕ ϕ cosϕ = +..., 3! 5! er ϕ << in ϕ << velja: (gleje še sliko): ± = cosϕ in = b sinϕ b sinϕ. sin ϕ ϕ, sin ϕ ϕ, cosϕ, cosϕ, in bsinϕ bsinϕ b( ϕ ϕ ) =. Enačbi (9a) in (9b) ako zapišeo v obliki: J ϕ g ϕ + k b ϕ ϕ, (9a) J ϕ g ϕ k b ϕ ϕ. (9a) 86
31 Definirao: ω = g J (lasna frekvenca fizičnega nihala) in kb D =. J Ob upoševanju gornjih definicij za ω in D prepišeo enačbi (9a) in (9a) v obliko: ϕ = ω ϕ + D ϕ ϕ, (9) ϕ = ω ϕ D ϕ ϕ. (9) Sešejeo enačbi (9) in (9): d d ( ϕ ϕ) ω ( ϕ ϕ) + = +. (93) Odšejeo enačbi (9) in (9): d d ( ϕ ϕ) ( ω D) ( ϕ ϕ) = +. (94) Rešivi enačb (93), (94) sa: ϕ + ϕ = ϕ cos ω, (93') ϕ ϕ = ϕ cosω, (94') kjer sa ω= ω in ω= ω + D dve lasni krožni frekvenci. Pri zapisu rešiev (93') in (94') so upoševali začena pogoja: ϕ =, ϕ ϕ = ob =, (95) oziroa (ob času = ): ϕ + ϕ = ϕ, ϕ ϕ = ϕ. (96) Torej: ϕ ϕ = ( cosω+ cos ω), (97') ϕ ϕ= ( cosω cosω). (98') Upoševao: 87
32 α β α+ β cosα+ cos β = cos cos, α β α+ β cosα cos β = sin sin. Dobio: ω ω ω + ω ϕ = ϕcos cos, (97) ω ω ω + ω ϕ = ϕ sin sin Definirao apliudo:. (98) ϕ ω ω ω + ω = ϕcos cos, apliuda ϕ ω ω ω + ω = ϕsin sin. Zaključek: apliuda ω+ ω nihali nihaa s frekvenco ω ω apliuda se spreinja s frekvenco ω = ω ω = + (99) ω D 88
33 Uripanje: u čas uripanja: ω ω u = π π u = ω ω Šibka sklopiev (D << ω ): D D D D ω= ( ω + D) = ω+ ω + ω = +, kjer ω ω ω ω <<. Uporabili so razvoj: + = ; če << : ω+ ω D Torej: ω +. ω Nihali nihaa s frekvenco, ki je le alo večja od lasne frekvence ω. ω ω D Izračunajo še. ω 89
34 II. odel: nihanje dveh sklopljenih nihal na vijačno vze k k' k Zapišeo II. Newonov zakon za asi : = k k', () = k k'. () Sešejeo enačbi () in (): ( + ) = ( + ) k (). Odšejeo enačbi () in (): ( ) = ( ) '( ) = ( + ')( ) k k k k. (3) Izbereo začena pogoja: = in = (ob času = ) Ob času = ako velja: + =, (4) = (5). Ob upoševanju enačb (4) in (5) napišeo rešivi enačb () in (3) v obliki: + = cos ω, = cos ω, k k+ k' kjer sa lasni krožni frekvenci: ω = in ω =. Iz enačb (6) in (7) sledi: (6) (7) ω ω ω + ω = cosω+ cosω = cos cos, (8) 9
35 ω ω ω + ω = cosω cosω = sin sin. (9) Upoševali so: α β α+ β cosα+ cos β = cos cos, α β α+ β cosα cos β = sin sin. Dobili so uripanje: cos ω ω cos ω + ω =, () sin ω ω sin ω + ω =, () kjer sa dve lasni krožni frekvenci: k ω= ω=, () ω ' = ω + k k Šibka sklopiev: k' << k Če uporabio. (3) + + za << iz enačb () in (3) sledi: ω+ ω k ' ω + k, (4) ω k ' ω. (5) ω k 9
36 Sesavljanje dveh pravokonih nihanj ( ω ) sin ( ω δ) = sin y= y (9) y ω = ω : δ = π δ = 4 π δ = 3π δ = δ = π 4 ω ω = : π δ = δ = 4 ω ω = 3 : δ = π δ = 4 9
37 9. Deforacija rdnih snovi Mrežne očke (vozlišča) v krisalni reži rdne snovi definirajo sao povprečno lego posaeznih aoov, ki sesavljajo krisal rdne snovi. Tako ko v plinu, udi v krisalu aoi ne irujejo, apak se erično gibljejo okrog svoje ravnovesne lege. Apliude odika so večje pri večji absoluni eperauri T. Sila ed sosednjia aooa rdne snovi v krisalni reži je odvisna od razdalje ed njia. Spodnja slika sheasko prikazuje poencialno energijo ed dvea aooa in usrezno silo Wp Fa =. Celona sila je sesavljena iz privlačnega in odbojnega dela. Privlačna sila ed r aooa je lahko na prier Coulobska privlačna sila ed poziivni in negaivni aoo, ako ko je o v krisalu NaCl. Odbojna sila pa je posledica Pauli-jevega izključivenega načela. Ko se dva aoa približaa, gredo elekroni z enakii kvannii ševili na višje energijske nivoje. Posledično se ed približevanje dveh aoov njuna energija veča, sila pa posane odbojna (gleje sliko ). W p r r r odbojna sila r privlačna sila slika 93
38 Pri ajhnih odikih od ravnovesne lege ( r r ora bii zadosi ajhen) lahko poencialno energijo ed aooa v krisalni reži v okolici ravnovesne razdalje r aproksiirao s parabolo (gleje še sr. 67) : W p = k r r C, () kjer je r razdalja ed dvea sosednjia aooa v krisalni reži (gleje sliko ). Usrezna sila ed aooa v bližini ravnovesne razdalje je poe: W = = r p Fa k r r () Vidio, da je v okolici ravnovesne razdalje ed sosednjii aoi sila ed sosednjia aooa linearno odvisna od razdalje ed njia, zao lahko aoske sile ed sosednjii aoi krisalne reže rdne snovi ponazorio z vijačnii vzei, ki povezujejo aoe ed seboj (slika). slika Poencialno energijo ed dvea sosednjia aooa v krisalni reži pa vzporedio s prožnosno energijo vzei. Model vijačnih vzei ed aoi krisala pojasni udi Hook-ov zakon. Ko nareč na akroskopsko elo deluje zunanja sila, se elo deforira, ravnovesna (poprečna) razdalja ed sosednjii aoi v krisalni reži (r) pa se zao spreeni na vrednos r. V nove ravnovesju se zao sile ed aoi krisala spreenijo. Linearna spreeba sile ed aoi (enačba ()) a F = k r r () na ikroskopske nivoju se odraža udi na akroskopske nivoju v linearni zvezi ed naezno (kopresijsko) silo F in podaljško (skrčko) elesa : F σ = = E, (3) S 94
39 F kjer je ε = relaivni podaljšek (skrček), σ = naezna ali kopresijska napeos in S S površina preseka na kaerega v pravokoni seri deluje sila F. Sorazernosni koeficien E (Youngov odul) je sorazeren ikroskopski konsani k v enačbi (). Enačbo (3) po Newonove sodobniku Roberu Hooku ienujeo Hookov zakon. F S F slika 3 Obočje veljavnosi Hookovega zakona F S obočje prožnosi obočje plasičnosi obočje sorazernosi (Hookov zakon) eja prožnosi eja naezne rdnosi eja sorazernosi slika 4 V nadaljevanju, poleg zgoraj opisane naezne (kopresijske) vzdolžne deforacije, našejeo še nekaere druge karakerisične deforacije za kaere velja linearna zveza ed napeosjo in deforacijo. 95
40 Srižna deforacija ϑ S F F slika 5a V prieru srižne deforacije deluje sila F na zgornjo in spodnjo ploskev vzdolž ploskve, o je v seri pravokono na noralo ploskve: F τ = = G ϑ, (4) S kjer je τ srižna napeos, G srižni odul, poen deforacijskega koa ϑ in površine S pa je razviden iz zgornje slike. Vsesransko siskanje (razpenjanje) F F F F S S S F F slika 5b V F = χ, (5) V S F V kjer je p = spreeba laka, ki deluje na površino elesa, relaivna spreeba S V voluna in χ sisljivos. Obrano vrednos sisljivosi ienujeo sisljivosni odul. χ 96
41 Torzija r rϕ= aϑ ϑ= ϕ a r ϕ dr ds = π rdr r df ϑ a R slika 6 Torzija je poseben prier srižne deforacije (gleje sliko): df ds = G ϑ, (6) r kjer je ds= π rdr, ϑ= ϕ in G srižni odul, od koder sledi: a df r = Gϕ, (7) π rdr a oziroa: d πgϕ = a F r dr. (8) Izračunajo navor dm s kaeri deluje sila df na cevasi izrez palice s polero r: πg ϕ M = r F= r r a 3 d d d (9) Celoen navor je poe: R 3 M dm r dr a πgϕ πgϕ R = = = a 4 4. () Vidio orej, da je navor, ki je poreben za orzijski zasuk palice za ko ϕ, sorazeren kou zasuka: M = Dϕ, () 97
42 kjer je 4 π GR D =. () a Vrednosi elasičnih konsan za nekaere rdne snovi in kapljevine * : SNOV N N E(Young-ov odul) G (srižni odul) χ N aluinij jeklo voda - -. seklo živo srebro * kapljevine se razlikujejo od rdne snovi po e, da ne prenašajo srižnih napeosi Upogib nosilca Poznavanje deforacij in napeosi pri upogibu nosilcev je zelo poebno pri konsrukciji srojev in zgradb. Ravni nosilci (preklade) na vhodih, vraih in oknih so izposavljeni veliki upogibni napeosi, zao so že v aničnih časih preklado nadoesili z loko (oboko): preklada v Mikenah (sara Grčija) saro riski lok goski lok udorski lok slika 7 Pri čise upogibu nosilca obsaja ako ienovana nevralna ravnina, ki pri upogibni deforaciji ohrani svojo površino. Nad nevralno ravnino se nosilec razeguje, pod nevralno ravnino pa je izposavljen siskanju. Pojav lahko opazujeo udi pri upognjeni leskovi palici, kjer se na noranji srani loka lubje naguba, na zunanji srani pa napne. slika 8: Upogib palice. 98
43 Ko prier v nadaljevanju analizirao napeosi in deforacije v zelo lahke nosilcu s krožni preseko s polero a, ki je na leve koncu vpe v seno, na desne koncu nosilca pa je z lahko žico prirjena sveilka z aso (slika 9). slika 9 Izhodišče koordinanega sisea posavio v središče. Sila eže sveilke F s = g upogiba nosilec. Vpliv lasne eže nosilca na njegov upogib zaneario. Zaradi sile F s se nosilec upogne v ravnini, y izbranega koordinanega sisea. Slika Zao se različni deli nosilca vzdolž osi y različno razegujejo. Znoraj nosilca obsaja na os y pravokona plas, ki se ne razegne ali skrči. Ko so že oenili jo ienujeo nevralna plas (ravnina). Vzdolž e ravnine (plasi) erio od koordinae odvisno ukrivljenos (gleje sliko ): C =, (3) R kjer je R krivinski radij nevralne ravnine na esu. Nad nevralno plasjo se eleeni vzdolžne plasi zaradi navora sile F s razegnejo (ali skrčijo), pod o plasjo pa se skrčijo (ali razegnejo), odvisno pač od predznaka ukrivljenosi C( ) (gleje še sliko ): 99
44 ( R ) ϑ R dϑ ds ds + d d dϑ r ε = =, (4) ds R R r orej: ε = d = C d, (5) kjer je d razdalja obravnavanega eleena nosilca od nevralne ravnine, ds r in ds dolžini ega eleena pred oziroa po upogibu nosilca, poen koovϑ in dϑ pa je razviden iz slike. Vrednos d na sliki je poziivna, če se ravnina nahaja pod nevralno ravnino in negaivna, če se obravnavana ravnina nahaja nad nevralno ravnino. Pri upogibu nosilca pod vplivo sile F so od nič različne udi nekaere srižne deforacije, ki pa jih boo v ej fazi napeosne analize nosilca zanearili. V nadaljnji analizi napeosi v nosilcu boo predposavili, da Hookov zakon v obliki enačbe (3) velja udi za posaezne zelo anke eleene vzdolžnih plasi v nosilcu na izbrani razdalji d od referenčne plasi. Torej, če vsavio ε iz enačbe (5) v Hookov zakon σ = E ε dobio: σ = Eε = EC d, (6) kjer je d poziiven za plasi, ki se pri upogibu razegnejo in negaiven za plasi, ki se pri upogibu skrčijo. ϑ R dϑ R R > poziivna ukrivljenos d < d > ϑ d ds d sr d dδ nevralna ravnina dsr = R dϑ dδ gϑ = d ( ds ) = ( d) + ( dδ ) r R R < negaivna ukrivljenos slika : Zaradi upogiba nosilca se eleen nosilca z dolžino ds r na razdalji d od nevralne ravnine razegne na dolžino ds. Sibol R označuje krivinski radij nevralne ravnine v izbrani očki, δ pa je verikalni odik izbrane očke v nevralni ravnini od sanja v kaere nosilec ni upognjen.
45 V ravnovesju se orajo sile zaradi noranjih napeosi uravnovesii z zunanjii silai v vsake delu nosilca. Ker v seri -osi na nosilec ne deluje nobena sila, ora bii vsoa vseh sil zaradi noranjih napeosi po prerezu nosilca enaka nič: σ d S =, (7) kjer je ds infiniezialni eleen površine preseka nosilca v ravnini y, z (gleje sliko ): a dy z z y ds zdy z = a y = slika Če vsavio izraz za σ iz enačbe (6) v enačbo (7) dobio: d EC d S =, (8) s kjer inegrirao po površini preseka nosilca v ravnini yz., Iz enačbe (8) pri izbrani vrednosi -a sledi: dds =. (9) S Ob upoševanju definicije d-ja in definicije predznaka krivinskega radija R (gleje sliko ), ako iz enačbe (9) sledi: d = y, () saj zaradi sierije velja (gleje sliki in ) yds =, () S pri čeer se nevralna ravnina ujea z,z ravnino (gleje sliko ), orej poeka po sredini nosilca, kjer je y =.
46 Elasične sile v prečne prerezu nosilca s površino S povzročajo navor, ki ia od nič različno koponeno sao v seri z-osi. Navor elasičnih sil nareč nasprouje zakrivljanju nosilca zaradi navora sile F S, ki ia udi sao z-koponeno različno od nič. Navor elasičnih sil M skuša nosilec izravnai, zao ga ienujejo udi upogibni navor elasičnih sil. S poočjo enačb (6) in () dobio: ds () σ d M = y S = y EC y = EC I S S kjer so upoševali enačbo (), C = kons. pri izbrane -u er I y ds S = (3) definirali ko upogibni vzrajnosni oen prereza nosilca s konsani preseko. Ker se ukrivljenos nosilca vzdolž osi spreinja, je udi elasični upogibni navor funkcija koordinae. Prečni presek nosilca ia obliko kroga z radije a, kaerega središče pravokono prebada -os izbranega koordinanega sisea (gleje še sliki in ). Torej: + a + a a I= y S = y z y= y a y y= π 4 4 d d d. (4) S a a Če iz enačbe () izraženo ukrivljenos M C =, (5) EI vsavio v enačbo (6), er upoševao idenieo () dobio: M σ = y. (6) I Poiščio še eksplicini izraz za ukrivljenos C( ). S slike je razvidno, da je ds = R dϑ, (7') r od koder sledi: dϑ C = =. (7) R s d r Ker je d δ = gϑ in ( ds ) r = d + dδ, iz enačbe (7) sledi d
47 d δ C = d. (8) 3 dδ + d Dokaz relacije (8) (gleje še sliko ): ( δ ) dδ dsr = d + d = d + d dδ dδ = = d d d gϑ d( g δ) (9a) V izraz d δ dϑ = d cos ϑ d d δ d dϑ = cos ϑ d d δ d δ d d d d dϑ = = + g ϑ dδ + d (9b) dϑ C = s d r vsavio enačbi (9a) in (9b) in dobio enačbo (8): d δ dϑ d C = = d sr dδ + d 3 (8) Ker je ukrivljenos nosilca zaradi navora sile F s pri vseh zelo ajhna približno velja d δ C = (9) d Če kobinirao enačbi (5) in (9) dobio: 3
48 d δ M =. (3) d EI Iz enačbe (3) izražen M z vsavio v enačbo (6). Tako dobio: d δ σ = Ey. (3) d Ker je elasični upogibni navor M funkcija koordinae, se v prerezu nosilca poleg naezne sile pojavi udi rezulanna srižna sila V, saj ora bii v ravnovesju vsoa navorov, ki delujejo na izbran eleen nosilca dolžine d, enak nič: M M + d + V d=, (3') d M M M + d+ V d=, (3) d dm M + = M + d. d kjer so upoševali ( d ) ( d ) V = V + = V = kons. slika 3 Tudi vsoa vseh sil v seri y osi ora bii enaka nič, orej V = kons. (33) Iz enačbe (3) dobio zvezo ed V in M, dm V = (34) d S poočjo enačb (3), (33) in (34) pa dobio 3 d δ V= EI (35) 3 d in 4 d EI δ =, (36) 4 d 4
49 kjer so upoševali d V d =, ker je V konsana. Diferencialno enačbo (36) rešujeo za prier predsavljen na slikah 9 in. Enačbo (36) širikra inegrirao na obeh sraneh enačaja: EI δ = α + α + α + α, (37) kjer so α, α, α3 in α4 konsane, ki jih določio iz robnih pogojev. Iz robnih pogojev pri = : δ ( = ) =, dδ ( = ) =, d (38) sledi: α = = (39) 3 α4 Iz robnega pogoja pri =, V = + F s =, (4) sledi: F α s =. (4) 6 d δ Levi prirjeni del nosilca prek prereza deluje na desni del z navoro M= EI (gleje enačbo (3)) in ga skuša zavrei navzgor. Sila navoro ( ) Fs : F s d pa ga želi zavrei navzdol z + ( ) = M F s. (4) V enačbo (4) vsavio M slika 4 d δ = EI (gleje enačbo (3)) in dobio: d 5
50 d δ EI + ( ) F s = (43) d Vsavio δ iz enačbe (37) v enačbo (43): 6α α+ F s =, (44) F za α vsavio izraz α s = (enačba (4)) in dobio: 6 α + =, F s oziroa: α = F s (45) Sedaj ko poznao konsane α, α, α3 in α4 lahko zapišeo celono rešiev (enačba (37): δ Fs + F 6 = EI 3 s Od od lahko izračunao s poočjo enačbe (3): s. (46) M = F (47) in s poočjo enačbe (3): σ Fy s = I ( ), (48) kjer je 4 π a I =. 4 Slika 5: Naezne in kopresijske napeosi v pee nosilcu. 6
Diferencialna enačba, v kateri nastopata neznana funkcija in njen odvod v prvi potenci
 Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Najprej zapišemo 2. Newtonov zakon za cel sistem v vektorski obliki:
 NALOGA: Po cesi vozi ovornjak z hirosjo 8 km/h. Tovornjak je dolg 8 m, širok 2 m in visok 4 m in ima maso 4 on. S srani začne pihai veer z hirosjo 5 km/h. Ob nekem času voznik zaspi in ne upravlja več
NALOGA: Po cesi vozi ovornjak z hirosjo 8 km/h. Tovornjak je dolg 8 m, širok 2 m in visok 4 m in ima maso 4 on. S srani začne pihai veer z hirosjo 5 km/h. Ob nekem času voznik zaspi in ne upravlja več
Tretja vaja iz matematike 1
 Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Odvode odvisnih spremenljivk po neodvisni spremenljivki bomo označevali s piko: Sistem navadnih diferencialnih enačb prvega reda ima obliko:
 4 Sisemi diferencialnih enačb V prakičnih primerih večkra naleimo na več diferencialnih enačb, ki opisujejo določen pojav in so medsebojno povezane edaj govorimo o sisemih diferencialnih enačb V eh enačbah
4 Sisemi diferencialnih enačb V prakičnih primerih večkra naleimo na več diferencialnih enačb, ki opisujejo določen pojav in so medsebojno povezane edaj govorimo o sisemih diferencialnih enačb V eh enačbah
Matematika 2. Diferencialne enačbe drugega reda
 Matematika 2 Diferencialne enačbe drugega reda (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) y 6y + 8y = 0, (b) y 2y + y = 0, (c) y + y = 0, (d) y + 2y + 2y = 0. Rešitev:
Matematika 2 Diferencialne enačbe drugega reda (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) y 6y + 8y = 0, (b) y 2y + y = 0, (c) y + y = 0, (d) y + 2y + 2y = 0. Rešitev:
SEMINARSKA NALOGA IZ FIZIKE NIHANJE VZMETNO, MATEMATIČNO IN FIZIČNO NIHALO
 SEMINARSKA NALOGA IZ FIZIKE NIHANJE VZMETNO, MATEMATIČNO IN FIZIČNO NIHALO Katjuša Reja Mozetič Politehnia Nova Gorica Šola za znanost o oolju, študjsi progra Oolje 1 Nihanje je v naravi zelo pogost pojav.
SEMINARSKA NALOGA IZ FIZIKE NIHANJE VZMETNO, MATEMATIČNO IN FIZIČNO NIHALO Katjuša Reja Mozetič Politehnia Nova Gorica Šola za znanost o oolju, študjsi progra Oolje 1 Nihanje je v naravi zelo pogost pojav.
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 5. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
PROCESIRANJE SIGNALOV
 Rešive pisega izpia PROCESIRANJE SIGNALOV Daum: 7... aloga Kolikša je ampliuda reje harmoske kompoee arisaega periodičega sigala? f() - -3 - - 3 Rešiev: Časova fukcija a iervalu ( /,/) je lieara fukcija:
Rešive pisega izpia PROCESIRANJE SIGNALOV Daum: 7... aloga Kolikša je ampliuda reje harmoske kompoee arisaega periodičega sigala? f() - -3 - - 3 Rešiev: Časova fukcija a iervalu ( /,/) je lieara fukcija:
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 22. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Statično in kinetično trenje
 Sila enja Sila enja: povzoči paske na koži, vpliva na speminjanje oblike elesa,... Po dugi sani pa nam omogoči, da hodimo po povšini, vozimo avomobile, plezamo po vveh,... Lasnosi sile enja: Sila enja
Sila enja Sila enja: povzoči paske na koži, vpliva na speminjanje oblike elesa,... Po dugi sani pa nam omogoči, da hodimo po povšini, vozimo avomobile, plezamo po vveh,... Lasnosi sile enja: Sila enja
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 21. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
PONOVITEV SNOVI ZA 4. TEST
 PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
Funkcijske vrste. Matematika 2. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 2. april Gregor Dolinar Matematika 2
 Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
p 1 ENTROPIJSKI ZAKON
 ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
1. Definicijsko območje, zaloga vrednosti. 2. Naraščanje in padanje, ekstremi. 3. Ukrivljenost. 4. Trend na robu definicijskega območja
 ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK
 1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
VAJE IZ NIHANJA. 3. Pospešek nihala na vijačno vzmet je: a. stalen, b. največji v skrajni legi, c. največji v ravnovesni legi, d. nič.
 VAJE IZ NIHANJA Izberi pravilen odgovor in fizikalno smiselno utemelji svojo odločitev. I. OPIS NIHANJA 1. Slika kaže nitno nihalo v ravnovesni legi in skrajnih legah. Amplituda je razdalja: a. Od 1 do
VAJE IZ NIHANJA Izberi pravilen odgovor in fizikalno smiselno utemelji svojo odločitev. I. OPIS NIHANJA 1. Slika kaže nitno nihalo v ravnovesni legi in skrajnih legah. Amplituda je razdalja: a. Od 1 do
Integralni račun. Nedoločeni integral in integracijske metrode. 1. Izračunaj naslednje nedoločene integrale: (a) dx. (b) x 3 +3+x 2 dx, (c) (d)
 Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
DUŠENO NIHANJE IN RESONANCA
 Politehnika Nova Gorica Šola za znanosti o okolju Univerzitetni študijski program OKOLJE Seminarska naloga DUŠENO NIHANJE IN RESONANCA Mentor: Doc.dr. Iztok Arčon Avtor: Nastja Tomšič Razred: 1.letnik
Politehnika Nova Gorica Šola za znanosti o okolju Univerzitetni študijski program OKOLJE Seminarska naloga DUŠENO NIHANJE IN RESONANCA Mentor: Doc.dr. Iztok Arčon Avtor: Nastja Tomšič Razred: 1.letnik
DELO SILE,KINETIČNA IN POTENCIALNA ENERGIJA ZAKON O OHRANITVI ENERGIJE
 Seinarska naloga iz fizike DELO SILE,KINETIČNA IN POTENCIALNA ENERGIJA ZAKON O OHRANITVI ENERGIJE Maja Kretič VSEBINA SEMINARJA: - Delo sile - Kinetična energija - Potencialna energija - Zakon o ohraniti
Seinarska naloga iz fizike DELO SILE,KINETIČNA IN POTENCIALNA ENERGIJA ZAKON O OHRANITVI ENERGIJE Maja Kretič VSEBINA SEMINARJA: - Delo sile - Kinetična energija - Potencialna energija - Zakon o ohraniti
Naloge iz vaj: Sistem togih teles C 2 C 1 F A 1 B 1. Slika 1: Sile na levi in desni lok.
 1 Rešene naloge Naloge iz vaj: Sistem togih teles 1. Tročleni lok s polmerom R sestavljen iz lokov in je obremenjen tako kot kaže skica. Določi sile podpor. Rešitev: Lok razdelimo na dva loka, glej skico.
1 Rešene naloge Naloge iz vaj: Sistem togih teles 1. Tročleni lok s polmerom R sestavljen iz lokov in je obremenjen tako kot kaže skica. Določi sile podpor. Rešitev: Lok razdelimo na dva loka, glej skico.
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 14. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Numerično reševanje. diferencialnih enačb II
 Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
diferencialne enačbe - nadaljevanje
 12. vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 diferencialne enačbe - nadaljevanje Ortogonalne trajektorije Dana je 1-parametrična družina krivulj F(x, y, C) = 0. Ortogonalne
12. vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 diferencialne enačbe - nadaljevanje Ortogonalne trajektorije Dana je 1-parametrična družina krivulj F(x, y, C) = 0. Ortogonalne
matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):
![matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij): matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):](/thumbs/87/96579490.jpg) 4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
Izmenični signali kompleksni račun
 zenicni_signali-kopleksni_racun(8).doc /7.6.6 zenični signali kopleksni račun Kopleksni račun e poebno orode za analizo vezi z izeničnii haroničnii signali. V osnovi diferencialne enačbe lahko z uporabo
zenicni_signali-kopleksni_racun(8).doc /7.6.6 zenični signali kopleksni račun Kopleksni račun e poebno orode za analizo vezi z izeničnii haroničnii signali. V osnovi diferencialne enačbe lahko z uporabo
POLA 1: 35 vprašanj izbirnega tipa. 1. Kolikšna je povprečna masa štirih uteži, kjer imajo tri maso po 1, 06 kg, ena pa 1, 02 kg?
 POL : 35 vprašanj izbirnega ipa. Kolikšna je povprečna masa širih ueži, kjer imajo ri maso po, 6 kg, ena pa, kg?, 6 kg, 5 kg, 4 kg, kg. Telo, ki sprva miruje, se v prvih dveh sekundah enakomerno pospešenega
POL : 35 vprašanj izbirnega ipa. Kolikšna je povprečna masa širih ueži, kjer imajo ri maso po, 6 kg, ena pa, kg?, 6 kg, 5 kg, 4 kg, kg. Telo, ki sprva miruje, se v prvih dveh sekundah enakomerno pospešenega
IZPIT IZ ANALIZE II Maribor,
 Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
Gimnazija Krˇsko. vektorji - naloge
 Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 10. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Kolokvij iz Klasične mehanike
 Kolokvij iz Klasične ehanike 16.4. 2010 1. Hokejist na ledeni ploskvi v Tivoliju sune pak s hitrostjo 30 /s natančno v seri proti severu. Za koliko bo zaradi vrtenja Zelje na poti 50 pak skrenil z začetne
Kolokvij iz Klasične ehanike 16.4. 2010 1. Hokejist na ledeni ploskvi v Tivoliju sune pak s hitrostjo 30 /s natančno v seri proti severu. Za koliko bo zaradi vrtenja Zelje na poti 50 pak skrenil z začetne
Če se telo giblje, definiramo še vektorja hitrosti v in pospeška a:
 FIZIKA 1. poglavje: Mehanika - B. Borštnik 1 MEHANIKA(prvi del) Kinematika Obravnavamo gibanje točkastega telesa. Izberemo si pravokotni desni koordinatni sistem (sl. 1), to je takšen, katerega os z kaže
FIZIKA 1. poglavje: Mehanika - B. Borštnik 1 MEHANIKA(prvi del) Kinematika Obravnavamo gibanje točkastega telesa. Izberemo si pravokotni desni koordinatni sistem (sl. 1), to je takšen, katerega os z kaže
SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK
 SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
Kotne in krožne funkcije
 Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba.
 1. Osnovni pojmi Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba. Primer 1.1: Diferencialne enačbe so izrazi: y
1. Osnovni pojmi Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba. Primer 1.1: Diferencialne enačbe so izrazi: y
*M * Osnovna in višja raven MATEMATIKA NAVODILA ZA OCENJEVANJE. Sobota, 4. junij 2011 SPOMLADANSKI IZPITNI ROK. Državni izpitni center
 Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Univerza v Ljubljani FS & FKKT. Varnost v strojništvu
 Univerza v Ljubljani FS & FKKT Varnost v strojništvu doc.dr. Boris Jerman, univ.dipl.inž.str. Govorilne ure: pisarna: FS - 414 telefon: 01/4771-414 boris.jerman@fs.uni-lj.si, (Tema/Subject: VDPN -...)
Univerza v Ljubljani FS & FKKT Varnost v strojništvu doc.dr. Boris Jerman, univ.dipl.inž.str. Govorilne ure: pisarna: FS - 414 telefon: 01/4771-414 boris.jerman@fs.uni-lj.si, (Tema/Subject: VDPN -...)
Funkcije več spremenljivk
 DODATEK C Funkcije več spremenljivk C.1. Osnovni pojmi Funkcija n spremenljivk je predpis: f : D f R, (x 1, x 2,..., x n ) u = f (x 1, x 2,..., x n ) kjer D f R n imenujemo definicijsko območje funkcije
DODATEK C Funkcije več spremenljivk C.1. Osnovni pojmi Funkcija n spremenljivk je predpis: f : D f R, (x 1, x 2,..., x n ) u = f (x 1, x 2,..., x n ) kjer D f R n imenujemo definicijsko območje funkcije
predavatelj: doc. Andreja Drobni Vidic
 1 RE ITVE 5. DOMAƒE NALOGE - TOTP - modul MATEMATIKA predavaelj: doc. Andreja Drobni Vidic UPORABA ODVODOV IN INTEGRALI Diferencialni ra un je omogo il re²evanje nalog, za kaere je pred em kazalo, da presegajo
1 RE ITVE 5. DOMAƒE NALOGE - TOTP - modul MATEMATIKA predavaelj: doc. Andreja Drobni Vidic UPORABA ODVODOV IN INTEGRALI Diferencialni ra un je omogo il re²evanje nalog, za kaere je pred em kazalo, da presegajo
MEHANIKA: sinopsis predavanj v šolskem letu 2003/2004
 MEHANIKA: sinopsis predavanj v šolskem letu 2003/2004 NTF, Visokošolski strokovni program KINEMATIKA 18. 2. 2004 Osnovne kinematične količine.: položaj r, hitrost, brzina, pospešek. Definicija vektorja
MEHANIKA: sinopsis predavanj v šolskem letu 2003/2004 NTF, Visokošolski strokovni program KINEMATIKA 18. 2. 2004 Osnovne kinematične količine.: položaj r, hitrost, brzina, pospešek. Definicija vektorja
Kotni funkciji sinus in kosinus
 Kotni funkciji sinus in kosinus Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z oznako cos x, DEFINICIJA V PRAVOKOTNEM TRIKOTNIKU: Kotna funkcija sinus je definirana kot razmerje
Kotni funkciji sinus in kosinus Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z oznako cos x, DEFINICIJA V PRAVOKOTNEM TRIKOTNIKU: Kotna funkcija sinus je definirana kot razmerje
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 15. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
SATCITANANDA. F = e E sila na naboj. = ΔW e. Rudolf Kladnik: Fizika za srednješolce 3. Svet elektronov in atomov
 Ruolf Klnik: Fizik z srenješolce Set elektrono in too Električno olje (11), gibnje elce električne olju Strn 55, nlog 1 Kolikšno netost or releteti elektron, se njego kinetičn energij oeč z 1 kev? Δ W
Ruolf Klnik: Fizik z srenješolce Set elektrono in too Električno olje (11), gibnje elce električne olju Strn 55, nlog 1 Kolikšno netost or releteti elektron, se njego kinetičn energij oeč z 1 kev? Δ W
TOPNOST, HITROST RAZTAPLJANJA
 OPNOS, HIOS AZAPLJANJA Denja: onos (oz. nasčena razona) redsavlja sanje, ko je oljene (rdn, ekoč, lnas) v ravnoežju z razono (oljenem, razoljenm v olu). - kvanavn zraz - r določen - homogena molekularna
OPNOS, HIOS AZAPLJANJA Denja: onos (oz. nasčena razona) redsavlja sanje, ko je oljene (rdn, ekoč, lnas) v ravnoežju z razono (oljenem, razoljenm v olu). - kvanavn zraz - r določen - homogena molekularna
Tema 1 Osnove navadnih diferencialnih enačb (NDE)
 Matematične metode v fiziki II 2013/14 Tema 1 Osnove navadnih diferencialnih enačb (NDE Diferencialne enačbe v fiziki Večina osnovnih enačb v fiziki je zapisana v obliki diferencialne enačbe. Za primer
Matematične metode v fiziki II 2013/14 Tema 1 Osnove navadnih diferencialnih enačb (NDE Diferencialne enačbe v fiziki Večina osnovnih enačb v fiziki je zapisana v obliki diferencialne enačbe. Za primer
IZRAČUN MEHANSKIH LASTNOSTI IN DEFORMACIJ ENOSTRANSKO IN DVOSTRANSKO VPETEGA NOSILCA
 Univerza v Ljubljani Fakulteta za elektrotehniko IZRAČUN MEHANSKIH LASTNOSTI IN DEFORMACIJ ENOSTRANSKO IN DVOSTRANSKO VPETEGA NOSILCA Seminarska naloga pri predmetu Razdelilna in industrijska omrežja Maks
Univerza v Ljubljani Fakulteta za elektrotehniko IZRAČUN MEHANSKIH LASTNOSTI IN DEFORMACIJ ENOSTRANSKO IN DVOSTRANSKO VPETEGA NOSILCA Seminarska naloga pri predmetu Razdelilna in industrijska omrežja Maks
vezani ekstremi funkcij
 11. vaja iz Matematike 2 (UNI) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 ekstremi funkcij več spremenljivk nadaljevanje vezani ekstremi funkcij Dana je funkcija f(x, y). Zanimajo nas ekstremi nad
11. vaja iz Matematike 2 (UNI) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 ekstremi funkcij več spremenljivk nadaljevanje vezani ekstremi funkcij Dana je funkcija f(x, y). Zanimajo nas ekstremi nad
Osnovni pojmi pri obravnavi periodičnih signalov
 Periodični signali, osnovni poji 7. Osnovni poji pri obravnavi periodičnih signalov Vsebina: Opis periodičnih signalov z periodo, frekvenco, krožno frekvenco. Razlaga pojov aplituda, faza, haronični signal.
Periodični signali, osnovni poji 7. Osnovni poji pri obravnavi periodičnih signalov Vsebina: Opis periodičnih signalov z periodo, frekvenco, krožno frekvenco. Razlaga pojov aplituda, faza, haronični signal.
TEHNIŠKA FIZIKA VS Strojništvo, 1. stopnja povzetek
 TEHNIŠKA FIZIKA VS Srojnišo,. sopnja pozeek. KINEMATIKA Premo gibanje To je gibanje po premici. Na premici izberemo koordinano izhodišče (o je očko, ki ji pripišemo koordinao nič) in označimo poziino in
TEHNIŠKA FIZIKA VS Srojnišo,. sopnja pozeek. KINEMATIKA Premo gibanje To je gibanje po premici. Na premici izberemo koordinano izhodišče (o je očko, ki ji pripišemo koordinao nič) in označimo poziino in
Delovna točka in napajalna vezja bipolarnih tranzistorjev
 KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
Frekvenčna analiza neperiodičnih signalov. Analiza signalov prof. France Mihelič
 Frekvenčna analiza neperiodičnih signalov Analiza signalov prof. France Mihelič Vpliv postopka daljšanja periode na spekter periodičnega signala Opazujmo družino sodih periodičnih pravokotnih impulzov
Frekvenčna analiza neperiodičnih signalov Analiza signalov prof. France Mihelič Vpliv postopka daljšanja periode na spekter periodičnega signala Opazujmo družino sodih periodičnih pravokotnih impulzov
Analiza 2 Rešitve 14. sklopa nalog
 Analiza Rešitve 1 sklopa nalog Navadne diferencialne enačbe višjih redov in sistemi diferencialnih enačb (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) 6 + 8 0, (b)
Analiza Rešitve 1 sklopa nalog Navadne diferencialne enačbe višjih redov in sistemi diferencialnih enačb (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) 6 + 8 0, (b)
Slika 5: Sile na svetilko, ki je obešena na žici.
 4. poglavje: Sile 5. Cestna svetilka visi na sredi 10 m dolge žice, ki je napeta čez cesto. Zaradi teže svetilke (30 N) se žica za toliko povesi, da pride sredina za 30 cm niže kot oba konca. Kako močno
4. poglavje: Sile 5. Cestna svetilka visi na sredi 10 m dolge žice, ki je napeta čez cesto. Zaradi teže svetilke (30 N) se žica za toliko povesi, da pride sredina za 30 cm niže kot oba konca. Kako močno
Domače naloge za 2. kolokvij iz ANALIZE 2b VEKTORSKA ANALIZA
 Domače naloge za 2. kolokvij iz ANALIZE 2b VEKTORSKA ANALIZA. Naj bo vektorsko polje R : R 3 R 3 dano s predpisom R(x, y, z) = (2x 2 + z 2, xy + 2yz, z). Izračunaj pretok polja R skozi površino torusa
Domače naloge za 2. kolokvij iz ANALIZE 2b VEKTORSKA ANALIZA. Naj bo vektorsko polje R : R 3 R 3 dano s predpisom R(x, y, z) = (2x 2 + z 2, xy + 2yz, z). Izračunaj pretok polja R skozi površino torusa
1. Trikotniki hitrosti
 . Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
. Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
Booleova algebra. Izjave in Booleove spremenljivke
 Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
Na pregledni skici napišite/označite ustrezne točke in paraboli. A) 12 B) 8 C) 4 D) 4 E) 8 F) 12
 Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
*M * MEHANIKA NAVODILA ZA OCENJEVANJE SPOMLADANSKI IZPITNI ROK. Četrtek, 1. junij Državni izpitni center SPLOŠNA MATURA
 Držani izpini cener *M7743* SPOMLDSKI IZPITI ROK MEHIK VODIL Z OCEJEVJE Čerek,. junij 07 SPLOŠ MTUR Držani izpini cener Ve praice pridržane. M7-74--3 IZPIT POL. naloga...3.4 3 F 7000 7000 0 k 7 k Izražena
Držani izpini cener *M7743* SPOMLDSKI IZPITI ROK MEHIK VODIL Z OCEJEVJE Čerek,. junij 07 SPLOŠ MTUR Držani izpini cener Ve praice pridržane. M7-74--3 IZPIT POL. naloga...3.4 3 F 7000 7000 0 k 7 k Izražena
386 4 Virtualni pomiki in virtualne sile. A 2 x E 2 = 0. (4.99)
 386 4 Virtualni pomiki in virtualne sile oziroma Ker je virtualna sila δf L poljubna, je enačba 4.99) izpolnjena le, če je δf L u L F ) L A x E =. 4.99) u L = F L A x E. Iz prikazanega primera sledi, da
386 4 Virtualni pomiki in virtualne sile oziroma Ker je virtualna sila δf L poljubna, je enačba 4.99) izpolnjena le, če je δf L u L F ) L A x E =. 4.99) u L = F L A x E. Iz prikazanega primera sledi, da
Zakonitosti hitrosti reakcije in konstante hitrosti (Rate laws)
 Zakonioi hiroi reakcije in konane hiroi (Rae law) Merjena hiro reakcije je odvina od koncenracije reakanov na neko poenco. v k [A] [B] k konana hiroi reakcije (neodvina od koncenracije) (odvina od T) Ekperimenalno
Zakonioi hiroi reakcije in konane hiroi (Rae law) Merjena hiro reakcije je odvina od koncenracije reakanov na neko poenco. v k [A] [B] k konana hiroi reakcije (neodvina od koncenracije) (odvina od T) Ekperimenalno
6.1.2 Togostna matrika linijskega elementa z ravno osjo po teoriji II. reda
 596 6 Geometrijska nelinearnost nosilcev varnost V E pa z enačbo V E = F E F dej 6.92) Z A x je označena ploščina prečnega prereza nosilca, količina i min je najmanjši vztrajnostni polmer, F dej pa je
596 6 Geometrijska nelinearnost nosilcev varnost V E pa z enačbo V E = F E F dej 6.92) Z A x je označena ploščina prečnega prereza nosilca, količina i min je najmanjši vztrajnostni polmer, F dej pa je
Akvizicija tereta. 5660t. Y= masa drva, X=masa cementa. Na brod će se ukrcati 1733 tona drva i 3927 tona cementa.
 Akvizicija tereta. Korisna nosivost broda je 6 t, a na brodu ia 8 cu. ft. prostora raspoloživog za sještaj tereta pod palubu. Navedeni brod treba krcati drvo i ceent, a na palubu ože aksialno ukrcati 34
Akvizicija tereta. Korisna nosivost broda je 6 t, a na brodu ia 8 cu. ft. prostora raspoloživog za sještaj tereta pod palubu. Navedeni brod treba krcati drvo i ceent, a na palubu ože aksialno ukrcati 34
!"#$ % &# &%#'()(! $ * +
 ,!"#$ % &# &%#'()(! $ * + ,!"#$ % &# &%#'()(! $ * + 6 7 57 : - - / :!", # $ % & :'!(), 5 ( -, * + :! ",, # $ %, ) #, '(#,!# $$,',#-, 4 "- /,#-," -$ '# &",,#- "-&)'#45)')6 5! 6 5 4 "- /,#-7 ",',8##! -#9,!"))
,!"#$ % &# &%#'()(! $ * + ,!"#$ % &# &%#'()(! $ * + 6 7 57 : - - / :!", # $ % & :'!(), 5 ( -, * + :! ",, # $ %, ) #, '(#,!# $$,',#-, 4 "- /,#-," -$ '# &",,#- "-&)'#45)')6 5! 6 5 4 "- /,#-7 ",',8##! -#9,!"))
SILA VZGONA. ma = F V F g = m v g m g = ρ v V v g ρ V g ma = V g (ρ v ρ), kjer smo upoštevali, da je telo v celoti potopljeno, sicer V <> V v.
 8 SILA VZGONA Sila vzgona F V = sili teže izpodrinjene tekočine: a F V = m v g = ρ v V v g, ρ kjer je ρ v gostota okolne (izpodrinjene) tekočine, V v ρ v pa njen volumen. Ko je telo v celoti potopljeno,
8 SILA VZGONA Sila vzgona F V = sili teže izpodrinjene tekočine: a F V = m v g = ρ v V v g, ρ kjer je ρ v gostota okolne (izpodrinjene) tekočine, V v ρ v pa njen volumen. Ko je telo v celoti potopljeno,
4. Zapiši Eulerjeve dinamične enačbe za prosto osnosimetrično vrtavko. ω 2
 Mehanikateoretičnavprašanjainodgovori 1/12 Newtonovamehanika 1. Določiravninogibanjatočkevpoljucentralnesile. Ravninagibanjagreskozicentersileinimanormalovsmerivrtilne količine 2. Zapišiperiodogibanjapremočrtnegagibanjapodvplivompotenciala
Mehanikateoretičnavprašanjainodgovori 1/12 Newtonovamehanika 1. Določiravninogibanjatočkevpoljucentralnesile. Ravninagibanjagreskozicentersileinimanormalovsmerivrtilne količine 2. Zapišiperiodogibanjapremočrtnegagibanjapodvplivompotenciala
1.4 Glavne normalne napetosti v nosilcu 145. Vzdolž nevtralne osi oklepajo normale ravnin glavnih napetosti s smerjo x naslednje kote
 1.4 Glavne normalne napetosti v nosilcu 145 Smeri glavnih normalnih napetosti vzdolž osi nosilca Vzdolž nevtralne osi oklepajo normale ravnin glavnih napetosti s smerjo x naslednje kote σ xx = M y z =
1.4 Glavne normalne napetosti v nosilcu 145 Smeri glavnih normalnih napetosti vzdolž osi nosilca Vzdolž nevtralne osi oklepajo normale ravnin glavnih napetosti s smerjo x naslednje kote σ xx = M y z =
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * FIZIKA NAVODILA ZA OCENJEVANJE. Petek, 10. junij 2016 SPLOŠNA MATURA
 Državni izpitni center *M16141113* SPOMLADANSKI IZPITNI ROK FIZIKA NAVODILA ZA OCENJEVANJE Petek, 1. junij 16 SPLOŠNA MATURA RIC 16 M161-411-3 M161-411-3 3 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor
Državni izpitni center *M16141113* SPOMLADANSKI IZPITNI ROK FIZIKA NAVODILA ZA OCENJEVANJE Petek, 1. junij 16 SPLOŠNA MATURA RIC 16 M161-411-3 M161-411-3 3 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor
LADISK Laboratorij za dinamiko strojev in konstrukcij. Višja dinamika. Rešene naloge iz analitične mehanike. Dr. Janko Slavič. 22.
 Univerza v Ljubljani Fakulteta za strojništvo LADISK Laboratorij za dinamiko strojev in konstrukcij Višja dinamika Rešene naloge iz analitične mehanike Dr. Janko Slavič 22. avgust 2012 Zadnja različica
Univerza v Ljubljani Fakulteta za strojništvo LADISK Laboratorij za dinamiko strojev in konstrukcij Višja dinamika Rešene naloge iz analitične mehanike Dr. Janko Slavič 22. avgust 2012 Zadnja različica
Kvantni delec na potencialnem skoku
 Kvantni delec na potencialnem skoku Delec, ki se giblje premo enakomerno, pride na mejo, kjer potencial naraste s potenciala 0 na potencial. Takšno potencialno funkcijo zapišemo kot 0, 0 0,0. Slika 1:
Kvantni delec na potencialnem skoku Delec, ki se giblje premo enakomerno, pride na mejo, kjer potencial naraste s potenciala 0 na potencial. Takšno potencialno funkcijo zapišemo kot 0, 0 0,0. Slika 1:
Poglavja: Navor (5. poglavje), Tlak (6. poglavje), Vrtilna količina (10. poglavje), Gibanje tekočin (12. poglavje)
 Poglavja: Navor (5. poglavje), Tlak (6. poglavje), Vrtilna količina (10. poglavje), Gibanje tekočin (12. poglavje) V./4. Deska, ki je dolga 4 m, je podprta na sredi. Na koncu deske stoji mož s težo 700
Poglavja: Navor (5. poglavje), Tlak (6. poglavje), Vrtilna količina (10. poglavje), Gibanje tekočin (12. poglavje) V./4. Deska, ki je dolga 4 m, je podprta na sredi. Na koncu deske stoji mož s težo 700
Energija magnetnega polja
 Energija magnenega polja. Energija magnenega polja Vsebina: moč in energija, energija sisema uljav, nadomesna indukivnos, energija v nelinearnih magnenih srukurah, gosoa energije, izračun indukivnosi iz
Energija magnenega polja. Energija magnenega polja Vsebina: moč in energija, energija sisema uljav, nadomesna indukivnos, energija v nelinearnih magnenih srukurah, gosoa energije, izračun indukivnosi iz
Iterativno reševanje sistemov linearnih enačb. Numerične metode, sistemi linearnih enačb. Numerične metode FE, 2. december 2013
 Numerične metode, sistemi linearnih enačb B. Jurčič Zlobec Numerične metode FE, 2. december 2013 1 Vsebina 1 z n neznankami. a i1 x 1 + a i2 x 2 + + a in = b i i = 1,..., n V matrični obliki zapišemo:
Numerične metode, sistemi linearnih enačb B. Jurčič Zlobec Numerične metode FE, 2. december 2013 1 Vsebina 1 z n neznankami. a i1 x 1 + a i2 x 2 + + a in = b i i = 1,..., n V matrični obliki zapišemo:
Periodičke izmjenične veličine
 EHNČK FAKULE SVEUČLŠA U RJEC Zavod za elekroenergeiku Sudij: Preddiploski sručni sudij elekroehnike Kolegij: Osnove elekroehnike Nosielj kolegija: Branka Dobraš Periodičke izjenične veličine Osnove elekroehnike
EHNČK FAKULE SVEUČLŠA U RJEC Zavod za elekroenergeiku Sudij: Preddiploski sručni sudij elekroehnike Kolegij: Osnove elekroehnike Nosielj kolegija: Branka Dobraš Periodičke izjenične veličine Osnove elekroehnike
1. Newtonovi zakoni in aksiomi o silah:
 1. Newtonovi zakoni in aksiomi o silah: A) Telo miruje ali se giblje enakomerno, če je vsota vseh zunanjih sil, ki delujejo na telo enaka nič. B) Če rezultanta vseh zunanjih sil, ki delujejo na telo ni
1. Newtonovi zakoni in aksiomi o silah: A) Telo miruje ali se giblje enakomerno, če je vsota vseh zunanjih sil, ki delujejo na telo enaka nič. B) Če rezultanta vseh zunanjih sil, ki delujejo na telo ni
Matematične metode v fiziki II. B. Golli, PeF
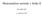 Matematične metode v fiziki II B. Golli, PeF 8. september 2014 2 Kazalo 1 Navadne diferencialne enačbe (NDE) 5 1.1 Uvod.............................................. 5 1.1.1 Diferencialne enačbe v fiziki.............................
Matematične metode v fiziki II B. Golli, PeF 8. september 2014 2 Kazalo 1 Navadne diferencialne enačbe (NDE) 5 1.1 Uvod.............................................. 5 1.1.1 Diferencialne enačbe v fiziki.............................
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 12. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
Navadne diferencialne enačbe
 Navadne diferencialne enačbe Navadne diferencialne enačbe prvega reda V celotnem poglavju bo y = dy dx. Diferencialne enačbe z ločljivima spremeljivkama Diferencialna enačba z ločljivima spremeljivkama
Navadne diferencialne enačbe Navadne diferencialne enačbe prvega reda V celotnem poglavju bo y = dy dx. Diferencialne enačbe z ločljivima spremeljivkama Diferencialna enačba z ločljivima spremeljivkama
Telo samo po sebi ne spremeni svoje lege ali oblike. To je lahko le posledica drugega telesa, ki nanj učinkuje.
 2. Dinamika 2.1 Sila III. PREDNJE 2. Dinamika (sila) Grška beseda (dynamos) - sila Gibanje teles pod vplivom zunanjih sil 2.1 Sila Telo samo po sebi ne spremeni svoje lege ali oblike. To je lahko le posledica
2. Dinamika 2.1 Sila III. PREDNJE 2. Dinamika (sila) Grška beseda (dynamos) - sila Gibanje teles pod vplivom zunanjih sil 2.1 Sila Telo samo po sebi ne spremeni svoje lege ali oblike. To je lahko le posledica
8. Diskretni LTI sistemi
 8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
7. VAJA IZ MEHANIKE TRDNIH TELES. (tenzor deformacij II) (tenzor majhnih deformacij in rotacij, kompatibilitetni pogoji)
 7. VAJA IZ MEHANIKE TRDNIH TELES (tenzor deformacij II) (tenzor majhnih deformacij in rotacij, kompatibilitetni pogoji) NALOGA 1: Pomik deformabilnega telesa je glede na kartezijski koordinatni sistem
7. VAJA IZ MEHANIKE TRDNIH TELES (tenzor deformacij II) (tenzor majhnih deformacij in rotacij, kompatibilitetni pogoji) NALOGA 1: Pomik deformabilnega telesa je glede na kartezijski koordinatni sistem
Matematka 1 Zadaci za drugi kolokvijum
 Matematka Zadaci za drugi kolokvijum 8 Limesi funkcija i neprekidnost 8.. Dokazati po definiciji + + = + = ( ) = + ln( ) = + 8.. Odrediti levi i desni es funkcije u datoj tački f() = sgn, = g() =, = h()
Matematka Zadaci za drugi kolokvijum 8 Limesi funkcija i neprekidnost 8.. Dokazati po definiciji + + = + = ( ) = + ln( ) = + 8.. Odrediti levi i desni es funkcije u datoj tački f() = sgn, = g() =, = h()
Izmenični signali. Dejan Križaj
 Izenični signali Dejan Križaj . . KAZALO 6. PREHODNI POJAVI... 4 PREHODNI POJAVI... 5 ZVEZE MED TOKOM IN NAPETOSTJO NA ELEMENTIH VEZJA... 6 ZAČETNI POGOJI... 6 POLNJENJE KONDENZATORJA... 7 PRAZNENJE KONDENZATORJA...
Izenični signali Dejan Križaj . . KAZALO 6. PREHODNI POJAVI... 4 PREHODNI POJAVI... 5 ZVEZE MED TOKOM IN NAPETOSTJO NA ELEMENTIH VEZJA... 6 ZAČETNI POGOJI... 6 POLNJENJE KONDENZATORJA... 7 PRAZNENJE KONDENZATORJA...
Energija magnetnega polja, prvič
 ENERGIJA POLJA_1(13).doc 1/11.6.6 Energija magnenega polja, prvič Izhajamo iz moči na uljavi, ki je enaka produku oka in napeosi na uljavi p = ul il. To so sedaj časovno spreminjajoče veličine, lahko bi
ENERGIJA POLJA_1(13).doc 1/11.6.6 Energija magnenega polja, prvič Izhajamo iz moči na uljavi, ki je enaka produku oka in napeosi na uljavi p = ul il. To so sedaj časovno spreminjajoče veličine, lahko bi
Matematika 1 - vježbe. 11. prosinca 2015.
 Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Kontrolne karte uporabljamo za sprotno spremljanje kakovosti izdelka, ki ga izdelujemo v proizvodnem procesu.
 Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * NAVODILA ZA OCENJEVANJE. Petek, 12. junij 2015 SPLOŠNA MATURA
 Državni izpitni center *M543* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Petek,. junij 05 SPLOŠNA MATURA RIC 05 M543 M543 3 IZPITNA POLA Naloga Odgovor Naloga Odgovor Naloga Odgovor Naloga Odgovor
Državni izpitni center *M543* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Petek,. junij 05 SPLOŠNA MATURA RIC 05 M543 M543 3 IZPITNA POLA Naloga Odgovor Naloga Odgovor Naloga Odgovor Naloga Odgovor
Errata (Includes critical corrections only for the 1 st & 2 nd reprint)
 Wedesday, May 5, 3 Erraa (Icludes criical correcios oly for he s & d repri) Advaced Egieerig Mahemaics, 7e Peer V O eil ISB: 978474 Page # Descripio 38 ie 4: chage "w v a v " "w v a v " 46 ie : chage "y
Wedesday, May 5, 3 Erraa (Icludes criical correcios oly for he s & d repri) Advaced Egieerig Mahemaics, 7e Peer V O eil ISB: 978474 Page # Descripio 38 ie 4: chage "w v a v " "w v a v " 46 ie : chage "y
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
KLASIČNA MEHANIKA. Peter Prelovšek
 KLASIČNA MEHANIKA Peter Prelovšek 2. junij 2013 2 Kazalo 1 Newtonova mehanika 7 1.1 Izhodišča, meje in osnove klasične mehanike.......... 7 1.1.1 Osnovni pojmi...................... 7 1.1.2 Newtonovi zakoni.....................
KLASIČNA MEHANIKA Peter Prelovšek 2. junij 2013 2 Kazalo 1 Newtonova mehanika 7 1.1 Izhodišča, meje in osnove klasične mehanike.......... 7 1.1.1 Osnovni pojmi...................... 7 1.1.2 Newtonovi zakoni.....................
GILBERT PRVI ZNANSTVEN PRISTOP
 Zgodovina in sila (1).doc 1/9 26/3/27 ZGODOVINA MAGNETIKE Iena za naravni agnet: FR: aiant (ljubeč) KIT: tzhu shih (ljubezenski kaen) GB: lodestone (leading, guiding stone) PPT PREZENTACIJA ZGODOVINE KITAJSKA
Zgodovina in sila (1).doc 1/9 26/3/27 ZGODOVINA MAGNETIKE Iena za naravni agnet: FR: aiant (ljubeč) KIT: tzhu shih (ljubezenski kaen) GB: lodestone (leading, guiding stone) PPT PREZENTACIJA ZGODOVINE KITAJSKA
3525$&8158&1(',=$/,&(6$1$92-1,095(7(120
 Srednja masinska skola OSOVE KOSTRUISAJA List1/8 355$&8158&1(',=$/,&(6$1$9-1,095(7(10 3ROD]QLSRGDFL maksimalno opterecenje Fa := 36000 visina dizanja h := 440 mm Rucna sila Fr := 350 1DYRMQRYUHWHQR optereceno
Srednja masinska skola OSOVE KOSTRUISAJA List1/8 355$&8158&1(',=$/,&(6$1$9-1,095(7(10 3ROD]QLSRGDFL maksimalno opterecenje Fa := 36000 visina dizanja h := 440 mm Rucna sila Fr := 350 1DYRMQRYUHWHQR optereceno
TRDNOST (VSŠ) - 1. KOLOKVIJ ( )
 TRDNOST (VSŠ) - 1. KOLOKVIJ (17. 12. 03) Pazljivo preberite besedilo vsake naloge! Naloge so točkovane enakovredno (vsaka 25%)! Pišite čitljivo! Uspešno reševanje! 1. Deformiranje telesa je podano s poljem
TRDNOST (VSŠ) - 1. KOLOKVIJ (17. 12. 03) Pazljivo preberite besedilo vsake naloge! Naloge so točkovane enakovredno (vsaka 25%)! Pišite čitljivo! Uspešno reševanje! 1. Deformiranje telesa je podano s poljem
*M * FIZIKA. Izpitna pola 2. Ponedeljek, 8. junij 2009 / 105 minut SPOMLADANSKI IZPITNI ROK
 Š i f r a k a n d i d a a : Državni izpini cener *M914111* SPOMLADANSKI IZPITNI ROK FIZIKA Izpina pola Ponedeljek, 8. junij 9 / 15 minu Dovoljeno gradivo in pripomočki: Kandida prinese nalivno pero ali
Š i f r a k a n d i d a a : Državni izpini cener *M914111* SPOMLADANSKI IZPITNI ROK FIZIKA Izpina pola Ponedeljek, 8. junij 9 / 15 minu Dovoljeno gradivo in pripomočki: Kandida prinese nalivno pero ali
MATEMATIKA I 1.kolokvij zadaci za vježbu I dio
 MATEMATIKA I kolokvij zadaci za vježbu I dio Odredie c 0 i kosinuse kueva koje s koordinanim osima čini vekor c = a b ako je a = i + j, b = i + k Odredie koliki je volumen paralelepipeda, čiji se bridovi
MATEMATIKA I kolokvij zadaci za vježbu I dio Odredie c 0 i kosinuse kueva koje s koordinanim osima čini vekor c = a b ako je a = i + j, b = i + k Odredie koliki je volumen paralelepipeda, čiji se bridovi
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
Poglavje 7. Poglavje 7. Poglavje 7. Regulacijski sistemi. Regulacijski sistemi. Slika 7. 1: Normirana blokovna shema regulacije EM
 Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
Poglavje 5. Poglavje 5. Poglavje 5. c = 1! SPOMNIMO SE!!! Regulacijski sistemi. Regulacijski sistemi
 Reglacjsk ssem lka 5. : Vekorja saorskega n roorskega oka v prosor Faklea za elekroehnko Reglacjsk ssem POMNIMO E!!! lka. 5: Kompleksn vekor saorskega oka γ jγ ( e ) j0 j ( ) c ( ) e ( ) e ( ) c! Faklea
Reglacjsk ssem lka 5. : Vekorja saorskega n roorskega oka v prosor Faklea za elekroehnko Reglacjsk ssem POMNIMO E!!! lka. 5: Kompleksn vekor saorskega oka γ jγ ( e ) j0 j ( ) c ( ) e ( ) e ( ) c! Faklea
UPOR NA PADANJE SONDE V ZRAKU
 UPOR NA PADANJE SONDE V ZRAKU 1. Hitrost in opravljena pot sonde pri padanju v zraku Za padanje v zraku je odgovorna sila teže. Poleg sile teže na padajoče telo deluje tudi sila vzgona, ki je enaka teži
UPOR NA PADANJE SONDE V ZRAKU 1. Hitrost in opravljena pot sonde pri padanju v zraku Za padanje v zraku je odgovorna sila teže. Poleg sile teže na padajoče telo deluje tudi sila vzgona, ki je enaka teži
