Γεννήτριες Συναρτήσεις
|
|
|
- Ναζωραῖος Λύκος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 3 Γεννήτριες Συναρτήσεις Περιεχόμενα Κεφαλαίου 3. Κανονικές Γεννήτριες Συναρτήσεις Πράξεις σε Γεννήτριες Συναρτήσεις Ακολουθία Fibonacci Γεννήτριες Συναρτήσεις για Απαρίθμηση Γεννήτριες Συναρτήσεις και Αναδρομικές Εξισώσεις Βιβλιογραφική Συζήτηση Ασκήσεις
2 80 Κεφάλαιο 3. Γεννήτριες Συναρτήσεις Έχει λεχθεί ότι οι γεννήτριες συναρτήσεις (generating functions) είναι «ένα νήμα όπου κρεμούμε μία ακολουθία αριθμών για επίδειξη». Επί της ουσίας, οι γεννήτριες συναρτήσεις είναι ένας κομψός και συνοπτικός συμβολισμός σειρών δυνάμεων, με τη βοήθεια των οποίων προβλήματα σειρών μετατρέπονται σε προβλήματα συναρτήσεων. Αυτό είναι σημαντικό, καθώς η διαχείριση συναρτήσεων είναι γενικώς ευκολότερη υπόθεση. Το αντικείμενο των συναρτήσεων αυτών είναι τεράστιο και έχουν γραφεί πολλά βιβλία μαθηματικών για αυτό. Στη συνέχεια του κεφαλαίου αυτού θα παρουσιασθούν μερικές πτυχές του αντικειμένου αυτού, ώστε εν τέλει με τη βοήθεια των γεννητριών συναρτήσεων: (α) να απαριθμούμε δυνατούς τρόπους εμφάνισης διαφορετικών καταστάσεων και (β) να επιλύουμε αναδρομικές εξισώσεις. 3. Κανονικές Γεννήτριες Συναρτήσεις Δεδομένης μίας ακολουθίας απείρων όρων a 0, a, a,..., η αντίστοιχη γεννήτρια συνάρτηση είναι μία σειρά δυνάμεων: f(x) = a 0 + a x + a x +... = a n x n που είναι τυπική (formal) με την έννοια ότι ορίζεται αλγεβρικά και όχι αναλυτικά. Η ανωτέρω συνάρτηση ονομάζεται κανονική (ordinary) γεννήτρια συνάρτηση και είναι η απλούστερη μορφή γεννήτριας συνάρτησης, καθώς στη βιβλιογραφία αναφέρεται ένα πλήθος άλλων συνθετότερων γεννητριών συναρτήσεων, οι οποίες όμως δεν θα μας απασχολήσουν στα πλαίσια του βιβλίου αυτού. Στη συνέχεια, με τον επόμενο συμβολισμό ισοδυναμούμε την αρχική ακολουθία αριθμών με την αντίστοιχη γεννήτρια συνάρτηση: < a 0, a, a, a 3,... > a 0 + a x + a x + a 3 x 3... Για παράδειγμα, έστω ότι δίνεται η απλή ακολουθία <,,,,... >, δηλαδή ισχύει a n = για κάθε n 0. Η αντίστοιχη γεννήτρια συνάρτηση είναι: f(x) = + x + x + x = x n
3 3.. Πράξεις σε Γεννήτριες Συναρτήσεις 8 Εύκολα προκύπτει ότι: f(x) = + x + x + x = + x ( + x + x + x ) = + x f(x) f(x) = x Επομένως, δοθείσης της ακολουθίας a n = για κάθε n 0, η αντίστοιχη γεννήτρια συνάρτηση είναι f(x) = /( x). Βέβαια, γνωρίζουμε από τις φθίνουσες γεωμετρικές προόδους, ότι η σχέση αυτή ισχύει μόνο αν x <, αλλά προς το παρόν δεν μας απασχολούν ζητήματα σύγκλισης. Ωστόσο, σημειώνεται το συμπέρασμα ότι με τη βοήθεια ιδιοτήτων της f(x) μπορούμε να εξάγουμε πληροφορία για την αντίστοιχη ακολουθία αριθμών. Ας εξετάσουμε ένα άλλο απλό παράδειγμα. Δίνεται η ακολουθία αριθμών <,,,,... >. Η αντίστοιχη γεννήτρια συνάρτηση είναι: f(x) = x + x x = ( ) n x n Με την ίδια τεχνική, όπως προηγουμένως, προκύπτει ότι η αντίστοιχη γεννήτρια συνάρτηση είναι f(x) = /( + x), δηλαδή ισχύει: <,,,,... > + x Διαισθητικά, λοιπόν, καταλαβαίνουμε ότι οι γεννήτριες συναρτήσεις ονομάζονται έτσι γιατί βοηθούν να γεννήσουμε τους συντελεστές της σειράς δυνάμεων. 3. Πράξεις σε Γεννήτριες Συναρτήσεις Στη συνέχεια εξετάζεται μία σειρά ιδιοτήτων. Οι ιδιότητες αυτές είναι εύκολο να αποδειχθούν από τον αναγνώστη. Πολλαπλασιασμός Αν πολλαπλασιάσουμε μία γεννήτρια συνάρτηση επί μία σταθερά, τότε κάθε
4 8 Κεφάλαιο 3. Γεννήτριες Συναρτήσεις όρος της αντίστοιχης ακολουθίας πολλαπλασιάζεται επί την αντίστοιχη σταθερά. Με βάση, λοιπόν, τον ανωτέρω κανόνα, εφόσον ισχύει: <,,,,... > x έπεται ότι ισχύει: <,,,,... > x Πρόσθεση Πρόσθεση δύο γεννητριών συναρτήσεων σημαίνει ότι πρέπει να προστεθούν οι αντίστοιχοι όροι των δύο ακολουθιών. Για παράδειγμα, λοιπόν, με βάση αυτόν τον κανόνα, εφόσον ισχύει ότι: και έπεται ότι ισχύει: <,,,,... > x <,,,,... > + x <, 0,, 0,... > x + + x = x Δεξιά Ολίσθηση Αν ισχύει ότι: < a 0, a, a, a 3,... > f(x) τότε αν προστεθούν στην αρχή της ακολουθίας k μηδενικά, έπεται ότι θα ισχύει: < 0, 0,..., 0, 0, a 0, a, a, a 3,... > x k f(x) Για παράδειγμα, αν προστεθούν k μηδενικά εμπρός από τη γνωστή ακολουθία <,,,,... >, τότε η αντίστοιχη γεννήτρια συνάρτηση είναι x k /( x). Παραγώγιση Αν παραγωγισθεί το ένα σκέλος, τότε πρέπει να παραγωγισθεί και το άλλο.
5 3.3. Ακολουθία Fibonacci 83 Για παράδειγμα, από τη γνωστή ακολουθία προκύπτει: d dx x = d dx ( + x + x + x ) ( x) = + x + 3x + 4x ( x) = (n + )x n Από την τελευταία σχέση προκύπτει ότι η γεννήτρια συνάρτηση f(x) = /( x) αντιστοιχεί στην ακολουθία <,, 3, 4,... >, ή αλλιώς ότι ισχύει γενικώς a n = n για κάθε n 0. Γενικότερα, μπορεί να αποδειχθεί ότι δεδομένης της αντιστοιχίας: ισχύει επίσης: < a 0, a, a, a 3,... > f(x) < a, a, 3a 3, 4a 4,... > f (x) Δηλαδή, παρατηρούμε ότι με τον κανόνα αυτό εκτελείται ταυτόχρονα: (α) μία αριστερή ολίσθηση και (β) ένας πολλαπλασιασμός κάθε όρου με το δείκτη του. Αν σε κάποια περίπτωση χρειαζόταν μόνο ο πολλαπλασιασμός, τότε θα μπορούσε να ακυρωθεί η αριστερή ολίσθηση εφαρμόζοντας και μία δεξιά ολίσθηση. Έστω, λοιπόν, ότι πρέπει να βρεθεί η γεννήτρια συνάρτηση της ακολουθίας < 0,, 4, 9,... >. Ισχύει κατά σειρά: <,,,,... > x <,, 3, 4,... > d dx x = ( x) x < 0,,, 3,... > ( x) <, 4, 9, 6,... > d x dx ( x) = + x ( x) 3 x( + x) < 0,, 4, 9,... > ( x) Ακολουθία Fibonacci Στο προηγούμενο κεφάλαιο δόθηκε ορισμός της ακολουθίας Fibonacci δεύτερης τάξης. Στο σημείο αυτό θα συνδεθεί η έννοια αυτή με τις γεννήτριες συ-
6 84 Κεφάλαιο 3. Γεννήτριες Συναρτήσεις ναρτήσεις. Συγκεκριμένα, θα αποδειχθεί ότι: < 0,,,, 3, 5, 8, 3,,... > x x x Με τη βοήθεια αυτής της σχέσης, στη συνέχεια θα βρεθεί ο κλειστός τύπος του n-οστού αριθμού Fibonacci, ενώ επίσης οι τεχνικές για την εύρεση αυτού του κλειστού τύπου θα εφαρμοσθούν και σε άλλες περιπτώσεις. Ορίζουμε, λοιπόν, τη συνάρτηση: f(x) = f 0 + f x + f x + f 3 x 3 + f 4 x Είναι ευνόητο ότι ισχύουν οι σχέσεις: < 0,, 0, 0, 0,... > x < 0, f 0, f, f, f 3,... > xf(x) < 0, 0, f 0, f, f,... > x f(x) Αθροίζοντας τις σχέσεις αυτές κατά μέλη, προκύπτει: < 0, + f 0, f + f 0, f + f, f 3 + f,... > x + xf(x) + x f(x) Το αριστερό σκέλος της σχέσης αυτής ταυτίζεται με το αριστερό σκέλος της αποδεικτέας σχέσης. Συνεπώς, πρέπει να αποδειχθεί και η ισότητα των δύο δεξιών σκελών. Όμως, το δεξιό σκέλος της τελευταίας σχέσης ισούται με f(x), δηλαδή ισχύει: f(x) = x + x f(x) + x f(x) f(x) = x x x Δεδομένης, λοιπόν, της γεννήτριας συνάρτησης για την ακολουθία Fibonacci, θα προσπαθήσουμε να εξάγουμε ένα κλειστό τύπο για το n-οστό αριθμό Fibonacci. Αρχικά, εκτελούμε μία παραγοντοποίηση του παρονομαστή της γεννήτριας συνάρτησης: x x = ( c x)( c x) όπου οι σταθερές c, c ισούνται με: c = + 5 c = 5
7 3.4. Γεννήτριες Συναρτήσεις για Απαρίθμηση 85 Στη συνέχεια, για τη διάσπαση του κλάσματος της γεννήτριας συνάρτησης γράφουμε τη σχέση ως εξής: x x x = c 3 c x + c 4 c x Αν δώσουμε δύο τυχαίες τιμές στη μεταβλητή x, λαμβάνουμε δύο γραμμικές εξισώσεις με αγνώστους τα c 3, c 4. Λύνοντας το παραγόμενο γραμμικό σύστημα με δύο αγνώστους και δύο εξισώσεις προκύπτει: c 3 = 5 c 4 = 5 Συνεπώς, ισχύει: x x x = ( ) 5 c x c x Όμως, για κάθε όρο της ανωτέρω παρένθεσης ισχύει: c x = + c x + c x +... c x = + c x + c x +... Αντικαθιστώντας τις τιμές αυτές προκύπτει: f(x) = ( ) 5 c x c x = ( + c x + c x +...) ( + c x + c x +...) 5 (( ) n ( f n = cn cn = ) n ) Γεννήτριες Συναρτήσεις για Απαρίθμηση Είναι γνωστά τα κλασικά αναπτύγματα των (a+b) και (a+b) 3. Γενικεύοντας ισχύει: ( ) ( ) ( ) n n n (a + b) n = a n + a n b + a n b ab n + b n n
8 86 Κεφάλαιο 3. Γεννήτριες Συναρτήσεις Αντικαθιστώντας a = και b = x προκύπτει: ( ) ( ) ( ) n n n ( + x) n = + x + x x n + x n = n n i=0 ( ) n x i i Προκύπτει, λοιπόν, ότι η γεννήτρια συνάρτηση (+x) n μπορεί να χρησιμεύσει για την εύρεση του πλήθους των συνδυασμών των n αντικειμένων λαμβανόμενων ανά k, για 0 k n. Δηλαδή, ο συντελεστής του όρου x k είναι το πλήθος των συνδυασμών που μπορούμε να επιλέξουμε k αντικείμενα από ένα σύνολο n αντικειμένων. Για το λόγο αυτό, μία γεννήτρια συνάρτηση που υπολογίζει το πλήθος συνδυασμών ή διατάξεων ονομάζεται απαριθμήτρια (enumerator). Ότι η γεννήτρια συνάρτηση (+x) n πράγματι εκτελεί την απαρίθμηση των συνδυασμών μπορεί να εξηγηθεί ως εξής: Έστω ένα μονομελές σύνολο {a }. Υπάρχει τρόπος να επιλεγούν 0 αντικείμενα, τρόπος να επιλεγεί αντικείμενο και 0 τρόποι να επιλεγούν περισσότερα αντικείμενα από το σύνολο αυτό. Άρα, για την περίπτωση αυτή, η γεννήτρια συνάρτηση είναι ( + x). Δοθέντος ενός άλλου μονομελούς συνόλου {a }, ισχύει το ίδιο σκεπτικό ως προς τη γεννήτρια συνάρτηση. Είναι ευνόητο ότι η γεννήτρια συνάρτηση για την επιλογή από την ένωση ανεξαρτήτων συνόλων είναι το γινόμενο των αντίστοιχων γεννητριών συναρτήσεων. Επομένως, η γεννήτρια συνάρτηση για την επιλογή αντικειμένων από το διμελές σύνολο {a, a } είναι ( + x). Προφανώς, υπάρχει τρόπος να επιλεγούν 0 αντικείμενα, τρόποι να επιλεγεί αντικείμενο, τρόπος να επιλεγούν αντικείμενα και 0 τρόποι να επιλεγούν περισσότερα αντικείμενα από το σύνολο αυτό. Αυτό το σκεπτικό μπορεί να γενικευθεί. Συνέλιξη Έστω A(x) η γεννήτρια συνάρτηση για την απαρίθμηση επιλογών από ένα σύνολο A και B(x) η γεννήτρια συνάρτηση για την απαρίθμηση επιλογών από ένα σύνολο B. Αν τα σύνολα A και B είναι ανεξάρτητα μεταξύ τους, τότε η γεννήτρια συνάρτηση για την απαρίθμηση επιλογών από το σύνολο A B είναι A(x) B(x). Πιο συγκεκριμένα, αν A(x) = a n x n και B(x) = b n x n τότε: όπου: C(x) = A(x) B(x) = c n x n c n = a 0 b n + a b n + a b n a n b 0
9 3.4. Γεννήτριες Συναρτήσεις για Απαρίθμηση 87 ενώ η ακολουθία c 0, c, c,... είναι η συνέλιξη (convolution) των ακολουθιών a 0, a, a,... και b 0, b, b,.... Πράγματι, το c n δίνει το πλήθος των επιλογών n αντικειμένων από το σύνολο A B. Γενικώς, μπορούμε να επιλέξουμε n αντικείμενα από την ένωση των συνόλων, επιλέγοντας j αντικείμενα από το σύνολο A και n j από το B. Αυτό μπορεί να γίνει κατά a j b n j τρόπους. Προσθέτοντας για όλες τις δυνατές τιμές του j, προκύπτει το ζητούμενο. Μέχρι στιγμής θεωρήθηκε ότι η επιλογή ενός συγκεκριμένου αντικειμένου από ένα σύνολο μπορεί να γίνει μόνο μία φορά, δηλαδή πρόκειται για επιλογή χωρίς αντικατάσταση. Ας θεωρήσουμε την περίπτωση της επιλογής με αντικατάσταση. Έστω, λοιπόν, ένα μονομελές σύνολο. Από το σύνολο αυτό μπορούμε να επιλέξουμε 0 αντικείμενα κατά τρόπο, αντικείμενο κατά τρόπο, αντικείμενα κατά τρόπο κοκ. Συνεπώς, η γεννήτρια συνάρτηση για την επιλογή n αντικειμένων με αντικατάσταση από ένα μονομελές σύνολο είναι: <,,,,... > + x + x + x = x Με βάση τον κανόνα της συνέλιξης, η γεννήτρια συνάρτηση για την επιλογή n αντικειμένων από την ένωση ανεξαρτήτων συνόλων δίνεται από γινόμενο των αντίστοιχων γεννητριών συναρτήσεων. Επομένως, προκύπτει ότι η ζητούμενη γεννήτρια συνάρτηση είναι f(x) = /( x) n. Το ερώτημα είναι ποιά είναι η τιμή κάποιου συντελεστή της σειράς των δυνάμεων. Για την εύρεση αυτού του κλειστού τύπου θα χρησιμοποιηθεί το Θεώρημα του Taylor. Ισχύει, λοιπόν, ότι: f(x) = f(0) + f (0)x + f (0)! x + f (0) 3! x f (k) (0) x k +... k! Το θεώρημα λέει ότι η τιμή του k-οστού συντελεστή της γεννήτριας συνάρτησης /( x) n δίνεται από την τιμή της k-οστής παραγώγου στο 0, διαιρεμένη δια k!. Επομένως, κατά σειρά έχουμε: f (x) = n( x) n f (x) = n(n + )( x) n f (x) = n(n + )(n + )( x) n 3 f (k) (x) = n(n + )(n + ) (n + k )( x) n k Επομένως, η τιμή του ζητούμενου k-οστού συντελεστή της γεννήτριας συνάρ-
10 88 Κεφάλαιο 3. Γεννήτριες Συναρτήσεις τησης είναι: f (k) (0)/k! = = n(n + ) (n + k ) k! ( ) (n + k )! n + k = (n )! k! k Στο σημείο αυτό συνοψίζουμε για ευκολία μερικά σημαντικά μέχρι στιγμής ευρεθέντα στον Πίνακα 3.. Γεννήτρια συνάρτηση Ακολουθία <,,,,... > x <,,,,... > +x <,,,,... > x <, 0,, 0,... > ( x) <,, 3, 4,... > ( x) < 0,,, 3,... > x ( x) <, 4, 9, 6,... > +x ( x) 3 x(+x) ( x) 3 < 0,, 4, 9,... > x < 0,,,, 3, 5, 8,... > x x Πίνακας 3.: Γεννήτριες συναρτήσεις ευρείας χρήσης 3.5 Γεννήτριες Συναρτήσεις και Αναδρομικές Εξισώσεις Στην επίλυση αναδρομικών εξισώσεων έχει εξ ολοκλήρου αφιερωθεί το Κεφάλαιο. Στο σημείο αυτό θα παρουσιασθεί ένας ακόμη τρόπος επίλυσης αναδρομικών εξισώσεων, ο οποίος στηρίζεται στην προηγούμενη θεωρία των γεννητριών συναρτήσεων. Αρχικά, ας εξετάσουμε μία απλή περίπτωση. Δίνεται, λοιπόν, η αναδρομική εξίσωση: t k = 3t k. Έστω ότι f(x) είναι η ζητούμενη γεννήτρια συνάρ-
11 3.5. Γεννήτριες Συναρτήσεις και Αναδρομικές Εξισώσεις 89 τηση. Διαδοχικά έχουμε: f(x) = a 0 + a x + a x + a 3 x 3 + a 4 x x f(x) = 3a 0 x + 3a x + 3a x f(x) 3xf(x) = a 0 + (a 3a 0 )x + (a 3a )x +... Όμως, οι παρενθέσεις της τελευταίας σχέσης ισούνται με 0. Επομένως, ισχύει: f(x) 3xf(x) = a 0 a 0 f(x) = 3x = a 0( + 3x + 3 x x ) Συνεπώς, ισχύει t k = 3 k a 0, όπου βέβαια a 0 είναι η αρχική συνθήκη. Ας εξετάσουμε τώρα μία πιο σύνθετη αναδρομική εξίσωση: t k = t k + 3t k όπου k, ενώ επίσης ισχύει t 0 = t =. Η προκύπτουσα ακολουθία είναι:,, 5, 3, 4,, 365,.... Για την εύρεση κλειστού τύπου για το t k θεωρούμε τη γεννήτρια συνάρτηση f(x) όπου: f(x) = + x + 5x + 3x 3 + 4x 4 + x x Και πάλι με μία σειρά αλγεβρικών χειρισμών μπορούμε να βρούμε τον κλειστό τύπο της γεννήτριας συνάρτησης και, επομένως, τον τύπο κάθε συντελεστή: f(x) = a 0 + a x + a x + a 3 x 3 + a 4 x x f(x) = a 0 x + a x + a x x f(x) = 3a 0 x + 3a x Αφαιρώντας κατά μέλη έχουμε: f(x) xf(x) 3x f(x) = a 0 +(a a 0 )x+(a a 3a 0 )x +(a 3 a 3a )x Όμως, εξ ορισμού είναι γνωστό ότι a n a n 3a n = 0 και, επομένως, ισχύει: f(x) x f(x) 3x f(x) = a 0 + (a a 0 )x f(x) = x x 3x = x ( 3x)( + x) = 3x + + x
12 90 Κεφάλαιο 3. Γεννήτριες Συναρτήσεις Στην τελευταία σχέση διαπιστώνουμε γνωστούς κλειστούς τύπους. Έτσι, καταλήγουμε ότι: t n = 3n + ( )n Ας εξετάσουμε ένα τελευταίο αλλά συνθετότερο παράδειγμα. Δίνονται οι αναδρομικές εξισώσεις: a n = a n + b n b n = a n + b n όπου a 0 = και b 0 = 0. Παρατηρούμε, όμως, ότι οι δύο εξισώσεις αυτές είναι «διαπλεκόμενες», γεγονός που καθιστά την επίλυσή τους δυσκολότερη. Αρχικά, λοιπόν, δεχόμαστε ότι ισχύει: A(x) = a n x n και B(x) = b n x n Πολλαπλασιάζουμε τις αρχικές αναδρομικές εξισώσεις επί x n, οπότε προκύπτει: a n x n = a n x n + b n x n b n x n = a n x n + b n x n Λόγω της ύπαρξης του δείκτη n, στις επόμενες σχέσεις το άθροισμα αρχίζει από και όχι από 0. Έχουμε λοιπόν: a n x n = n= b n x n = n= a n x n + b n x n n= a n x n + n= n= n= b n x n Συνεπώς, ισχύει: A(x) a 0 x 0 = x a n x n + x b n x n n= n= B(x) b 0 x 0 = x a n x n + x b n x n n= n=
13 3.6. Βιβλιογραφική Συζήτηση 9 ή ισοδύναμα: και A(x) = x a n x n + x b n x n B(x) 0 = x a n x n + x b n x n A(x) = xa(x) + xb(x) B(x) 0 = xa(x) + xb(x) Φθάσαμε σε ένα γραμμικό σύστημα εξισώσεων με αγνώστους, το οποίο επιλύεται και δίνει: A(x) = B(x) = x 4x + 3x = x 4x + 3x = x + x + 3x 3x Επομένως, από αυτές τις γεννήτριες συναρτήσεις προκύπτει ότι οι σειρές δυνάμεων είναι: + 3 n A(x) = x n και B(x) = 3 n x n 3.6 Βιβλιογραφική Συζήτηση Το αντικείμενο των γεννητριών συναρτήσεων είναι τεράστιο. Οι απαρχές του πηγαίνουν πίσω στον De Moivre. Στο κεφάλαιο αυτό εξετάσθηκαν οι κανονικές γεννήτριες συναρτήσεις. Στη βιβλιογραφία αναφέρεται ένα πλήθος άλλων τύπων γεννητριών συναρτήσεων, όπως οι εκθετικές, οι πιθανοτικές, οι σειρές Lambert, οι σειρές Bell, οι σειρές Dirichlet και άλλες. Το βιβλίο του Wilf διαπραγματεύεται αποκλειστικά το αντικείμενο αυτό [8]. Μάλιστα το βιβλίο είναι διαθέσιμο στο Διαδίκτυο και περιέχει λυμένες και άλυτες ασκήσεις. Στα βιβλία των Govinda Rao [4], Liu [7], Bryant [], Graham-Knuth-Patashnik [5] και Hofri [6] υπάρχουν εκτενή αντίστοιχα κεφάλαια (η σειρά των βιβλίων αντιστοιχεί σε αυξανόμενο βαθμό δυσκολίας). Η Άσκηση 6 προέρχεται από το άρθρο [], ενώ οι Ασκήσεις 9-0 από το άρθρο [3].
14 9 Κεφάλαιο 3. Γεννήτριες Συναρτήσεις 3.7 Ασκήσεις. Να βρεθούν οι γεννήτριες συναρτήσεις των ακολουθιών: <,, 4, 8,... >, και <, 8, 7, 64,... >.. Δίνεται η ακολουθία: <, 4, 6, 8,... >. Θα ανέμενονταν οι επόμενες τιμές της ακολουθίας να είναι: 0, κοκ. Ποιά είναι η γεννήτρια συνάρτηση που παράγει αυτή την ακολουθία; Να βρεθούν άλλες γεννήτριες συναρτήσεις που να δίνουν ακολουθίες με τους ίδιους 4 πρώτους όρους, αλλά η συνέχεια να είναι διαφορετική. 3. Να βρεθεί η συνάρτηση για τους συντελεστές του x n των γεννητριών συναρτήσεων: f(x) = x3, και x f(x) = x +3x Ποιοί είναι οι συντελεστές των δυνάμεων του x που αντιστοιχούν στη γεννήτρια συνάρτηση: f(x) = x 3, και f(x) = x. 5. Κατά πόσους τρόπους μπορεί: να τοποθετηθούν n πράσινα αντικείμενα σε ένα δοχείο; να επιλεγεί ένα αντικείμενο από ένα δοχείο με n διαφορετικά χρωματιστά αντικείμενα; 6. Δύο παίκτες Π και Π παίζουν τάβλι και το τελικό αποτέλεσμα είναι Σ:Σ. Να υπολογισθεί ο αριθμός των διαφορετικών τρόπων που μπορούμε να φθάσουμε στο αποτέλεσμα αυτό. Για παράδειγμα, αν το τελικό αποτέλεσμα είναι :, τότε υπάρχουν 3 διαφορετικοί τρόποι: (α) 0:, :, :, (β) :0, :, : και (γ) :0, :0, :. 7. Χρησιμοποιώντας τον κανόνα της συνέλιξης να βρεθεί με πόσους τρόπους μπορούν να τοποθετηθούν n φρούτα σε ένα δοχείο υπό τους εξής περιορισμούς: το πλήθος των μήλων να είναι άρτιο,
15 3.7. Ασκήσεις 93 το πλήθος των μπανανών να είναι πολλαπλάσιο του 3, το πλήθος των πορτοκαλιών να είναι τουλάχιστον 4 και το πλήθος των αχλαδιών να είναι το μέγιστο. 8. Κατά πόσους τρόπους μπορούμε να δώσουμε n 3 ευρώ σε 3 άτομα: με τον περιορισμό ότι κάθε άτομο θα πάρει τουλάχιστον ευρώ; χωρίς κάποιον περιορισμό; Πόσες λύσεις έχει η εξίσωση x + y + z = n; 9. Με πόσους τρόπους μπορεί να καλυφθεί ένα ορθογώνιο xn με κομμάτια ντόμινο x; Η άσκηση να επιλυθεί δοκιμάζοντας διαδοχικά για τιμές n = 0,,,.... Τι παρατηρείτε; 0. Με πόσους τρόπους μπορεί να καλυφθεί ένα ορθογώνιο 3xn με κομμάτια ντόμινο x; Επίσης, με πόσους τρόπους μπορεί να καλυφθεί ένα παραλληλεπίπεδο xxn με τούβλα xx;. Να βρεθεί η γεννήτρια συνάρτηση που παράγει την ίδια ακολουθία με την έξοδο των επομένων ψευδικωδικών: x <-- 3; i <--; while i<=5 do print(x); x <-- x-; i <-- +; x <-- ; i <--; while i<=5 do print(x); x <-- 5x-6; i <-- +; x <-- 6; i <--; while i<=5 do print(x); x <-- trunc(x/3)+6; i <-- +;
16 94 Κεφάλαιο 3. Γεννήτριες Συναρτήσεις. Δίνεται η αναδρομική εξίσωση: t k = t k + t k t k 3 όπου k 3, ενώ επίσης ισχύει t 0 = t = t =. Με τη βοήθεια γεννήτριας συνάρτησης να βρεθεί κλειστός τύπος για το t k. 3. Δίνεται η αναδρομική εξίσωση: t k = t k όπου k, ενώ επίσης ισχύει t 0 =. Με τη βοήθεια γεννήτριας συνάρτησης να βρεθεί κλειστός τύπος για το t k. 4. Δίνεται η αναδρομική εξίσωση: 3t k = 4t k + t k όπου k, ενώ επίσης ισχύει t 0 = t =. Με τη βοήθεια γεννήτριας συνάρτησης να βρεθεί κλειστός τύπος για το t k.
17 Βιβλιογραφία [] V. Bryant. Aspects of Combinatorics. Cambridge University Press, 993. [] D. Ginat. Starting top-down, refining bottom-up, sharpening by zoom-in. ACM SIGCSE Bulletin Inroads, 33(4):8 3, 00. [3] D. Ginat. Domino arrangments. ACM SIGCSE Bulletin Inroads, 39():4 5, 007. Also, 39(4):8-9. [4] H.S. Govinda Rao. Graph Theory and Combinatorics. Galgotia Publications, 006. [5] R. Graham, D.E. Knuth, and O. Patashnik. Concrete Mathematics. Addison- Wesley, 989. [6] M. Hofri. Analysis of Algorithms. Oxford University Press, 995. [7] C.L. Liu. Introduction to Combinatorial Mathematics. McGraw-Hill, 968. [8] H. Wilf. Generatingfunctionology. Academic Press,
Γεννήτριες Συναρτήσεις
 Γεννήτριες Συναρτήσεις ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αναπαράσταση Ακολουθιών Ακολουθία:
Γεννήτριες Συναρτήσεις ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αναπαράσταση Ακολουθιών Ακολουθία:
α n z n = 1 + 2z 2 + 5z 3 n=0
 Η ύλη συνοπτικά... Στοιχειώδης συνδυαστική Γεννήτριες συναρτήσεις Σχέσεις αναδρομής Θεωρία Μέτρησης Polyá Αρχή Εγκλεισμού - Αποκλεισμού Η ύλη συνοπτικά... Γεννήτριες συναρτήσεις Τι είναι η γεννήτρια Στην
Η ύλη συνοπτικά... Στοιχειώδης συνδυαστική Γεννήτριες συναρτήσεις Σχέσεις αναδρομής Θεωρία Μέτρησης Polyá Αρχή Εγκλεισμού - Αποκλεισμού Η ύλη συνοπτικά... Γεννήτριες συναρτήσεις Τι είναι η γεννήτρια Στην
P(n, r) = n! P(n, r) = n r. (n r)! n r. n+r 1 r n!
 Διακριτά Μαθηματικά Σύνοψη Θεωρίας Τυπολόγιο Αναστασία Κόλλια 20/11/2016 1 / 55 Κανόνες γινομένου και αθροίσματος Κανόνας αθροίσματος: Αν ένα γεγονός μπορεί να συμβεί κατά m τρόπους και ένα άλλο γεγονός
Διακριτά Μαθηματικά Σύνοψη Θεωρίας Τυπολόγιο Αναστασία Κόλλια 20/11/2016 1 / 55 Κανόνες γινομένου και αθροίσματος Κανόνας αθροίσματος: Αν ένα γεγονός μπορεί να συμβεί κατά m τρόπους και ένα άλλο γεγονός
Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύ
 Διακριτά Μαθηματικά Ι Ενότητα 2: Γεννήτριες Συναρτήσεις Μέρος 3 Διδάσκων: Χ. Μπούρας (bouras@cti.gr) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Διακριτά Μαθηματικά Ι Ενότητα 2: Γεννήτριες Συναρτήσεις Μέρος 3 Διδάσκων: Χ. Μπούρας (bouras@cti.gr) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
(Γραμμικές) Αναδρομικές Σχέσεις
 (Γραμμικές) Αναδρομικές Σχέσεις ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αναδρομικές Σχέσεις Αναπαράσταση
(Γραμμικές) Αναδρομικές Σχέσεις ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αναδρομικές Σχέσεις Αναπαράσταση
Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύ
 Διακριτά Μαθηματικά Ι Ενότητα 2: Γεννήτριες Συναρτήσεις Μέρος 1 Διδάσκων: Χ. Μπούρας (bouras@cti.gr) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Διακριτά Μαθηματικά Ι Ενότητα 2: Γεννήτριες Συναρτήσεις Μέρος 1 Διδάσκων: Χ. Μπούρας (bouras@cti.gr) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Γεννήτριες Συναρτήσεις
 Ακολουθίες Γεννήτριες Συναρτήσεις Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Ακολουθία: αριθμητική
Ακολουθίες Γεννήτριες Συναρτήσεις Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Ακολουθία: αριθμητική
Γεννήτριες Συναρτήσεις
 Γεννήτριες Συναρτήσεις ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αναπαράσταση Ακολουθιών Ακολουθία:
Γεννήτριες Συναρτήσεις ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αναπαράσταση Ακολουθιών Ακολουθία:
ΚΕΦΑΛΑΙΟ 5 ΑΚΟΛΟΥΘΙΕΣ ΑΡΙΘΜΗΤΙΚΗ ΓΕΩΜΕΤΡΙΚΗ ΠΡΟΟΔΟΣ
 ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 5 ΑΚΟΛΟΥΘΙΕΣ ΑΡΙΘΜΗΤΙΚΗ ΓΕΩΜΕΤΡΙΚΗ ΠΡΟΟΔΟΣ ΓΙΑΝΝΗΣ ΠΑΤΕΡΑΣ ΜΑΘΗΜΑΤΙΚΟΣ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ ΑΚΟΛΟΥΘΙΕΣ ΚΕΦΑΛΑΙΟ 5 ΑΡΙΘΜΗΤΙΚΗ ΠΡΟΟΔΟΣ ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ακολουθία ονομάζουμε
ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 5 ΑΚΟΛΟΥΘΙΕΣ ΑΡΙΘΜΗΤΙΚΗ ΓΕΩΜΕΤΡΙΚΗ ΠΡΟΟΔΟΣ ΓΙΑΝΝΗΣ ΠΑΤΕΡΑΣ ΜΑΘΗΜΑΤΙΚΟΣ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ ΑΚΟΛΟΥΘΙΕΣ ΚΕΦΑΛΑΙΟ 5 ΑΡΙΘΜΗΤΙΚΗ ΠΡΟΟΔΟΣ ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ακολουθία ονομάζουμε
(Γραμμικές) Αναδρομικές Σχέσεις
 (Γραμμικές) Αναδρομικές Σχέσεις Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αναδρομικές Σχέσεις
(Γραμμικές) Αναδρομικές Σχέσεις Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αναδρομικές Σχέσεις
(Γραμμικές) Αναδρομικές Σχέσεις
 (Γραμμικές) Αναδρομικές Σχέσεις ιδάσκοντες:. Φωτάκης. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αναδρομικές Σχέσεις Αναπαράσταση
(Γραμμικές) Αναδρομικές Σχέσεις ιδάσκοντες:. Φωτάκης. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αναδρομικές Σχέσεις Αναπαράσταση
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
Δηλαδή η ρητή συνάρτηση είναι πηλίκο δύο ακέραιων πολυωνύμων. Επομένως, το ζητούμενο ολοκλήρωμα είναι της μορφής
 D ολοκλήρωση ρητών συναρτήσεων Το θέμα μας στην ενότητα αυτή είναι η ολοκλήρωση ρητών συναρτήσεων. Ας θυμηθούμε πρώτα ποιες συναρτήσεις ονομάζονται ρητές. Ορισμός: Μία συνάρτηση ονομάζεται ρητή όταν μπορεί
D ολοκλήρωση ρητών συναρτήσεων Το θέμα μας στην ενότητα αυτή είναι η ολοκλήρωση ρητών συναρτήσεων. Ας θυμηθούμε πρώτα ποιες συναρτήσεις ονομάζονται ρητές. Ορισμός: Μία συνάρτηση ονομάζεται ρητή όταν μπορεί
ΚΕΦΑΛΑΙΟ 5 ΓΕΝΝΗΤΡΙΕΣ ΣΥΝΑΡΤΗΣΕΙΣ
 ΚΕΦΑΛΑΙΟ 5 ΓΕΝΝΗΤΡΙΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Εισαγωγή Οι γεννήτριες συναρτήσεις είναι ένα από τα ισχυρά εργαλεία για μια ενοποιημένη αντιμετώπιση πολλών κατηγοριών προβλημάτων απαρίθμησης Ο Lplce έθεσε πρώτος τις
ΚΕΦΑΛΑΙΟ 5 ΓΕΝΝΗΤΡΙΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Εισαγωγή Οι γεννήτριες συναρτήσεις είναι ένα από τα ισχυρά εργαλεία για μια ενοποιημένη αντιμετώπιση πολλών κατηγοριών προβλημάτων απαρίθμησης Ο Lplce έθεσε πρώτος τις
O n+2 = O n+1 + N n+1 = α n+1 N n+2 = O n+1. α n+2 = O n+2 + N n+2 = (O n+1 + N n+1 ) + (O n + N n ) = α n+1 + α n
 Η ύλη συνοπτικά... Στοιχειώδης συνδυαστική Γεννήτριες συναρτήσεις Σχέσεις αναδρομής Θεωρία Μέτρησης Polyá Αρχή Εγκλεισμού - Αποκλεισμού Σχέσεις Αναδρομής Γραμμικές Σχέσεις Αναδρομής με σταθερούς συντελεστές
Η ύλη συνοπτικά... Στοιχειώδης συνδυαστική Γεννήτριες συναρτήσεις Σχέσεις αναδρομής Θεωρία Μέτρησης Polyá Αρχή Εγκλεισμού - Αποκλεισμού Σχέσεις Αναδρομής Γραμμικές Σχέσεις Αναδρομής με σταθερούς συντελεστές
Σήματα και Συστήματα. Διάλεξη 13: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Laplace. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 13: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Laplace Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Laplace 1. Επίλυση Γραμμικών
Σήματα και Συστήματα Διάλεξη 13: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Laplace Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Laplace 1. Επίλυση Γραμμικών
n ίδια n διαφορετικά n n 0 n n n 1 n n n n 0 4
 Διακριτά Μαθηματικά Ι Επαναληπτικό Μάθημα 1 Συνδυαστική 2 Μεταξύ 2n αντικειμένων, τα n είναι ίδια. Βρείτε τον αριθμό των επιλογών n αντικειμένων από αυτά τα 2n αντικείμενα. Μεταξύ 3n + 1 αντικειμένων τα
Διακριτά Μαθηματικά Ι Επαναληπτικό Μάθημα 1 Συνδυαστική 2 Μεταξύ 2n αντικειμένων, τα n είναι ίδια. Βρείτε τον αριθμό των επιλογών n αντικειμένων από αυτά τα 2n αντικείμενα. Μεταξύ 3n + 1 αντικειμένων τα
a n + 6a n a n 2 + 8a n 3 = 0, a 0 = 1, a 1 = 2, a 2 = 8
 Διακριτά Μαθηματικά Σχέσεις Αναδρομής Ι 1 / 17 a n + 6a n 1 + 12a n 2 + 8a n 3 = 0, a 0 = 1, a 1 = 2, a 2 = 8 2 / 17 a n + 6a n 1 + 12a n 2 + 8a n 3 = 0, a 0 = 1, a 1 = 2, a 2 = 8 1ος τρόπος: Εχουμε τη
Διακριτά Μαθηματικά Σχέσεις Αναδρομής Ι 1 / 17 a n + 6a n 1 + 12a n 2 + 8a n 3 = 0, a 0 = 1, a 1 = 2, a 2 = 8 2 / 17 a n + 6a n 1 + 12a n 2 + 8a n 3 = 0, a 0 = 1, a 1 = 2, a 2 = 8 1ος τρόπος: Εχουμε τη
Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος
 Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με, y V και του πολλαπλασιασμού
Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με, y V και του πολλαπλασιασμού
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 2017-2018 Παρεμβολή και Παρεκβολή Εισαγωγή Ορισμός 6.1 Αν έχουμε στη διάθεσή μας τιμές μιας συνάρτησης
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 2017-2018 Παρεμβολή και Παρεκβολή Εισαγωγή Ορισμός 6.1 Αν έχουμε στη διάθεσή μας τιμές μιας συνάρτησης
2.1 Διαιρετότητα, ισοϋπόλοιποι αριθμοί. q Z, a = b q + r.
 Κεφάλαιο 2 Θεωρία Αριθμών Κύριες βιβλιογραφικές αναφορές για αυτό το Κεφάλαιο είναι οι Hardy and Wright 1979 και Graham, Knuth, and Patashnik 1994. 2.1 Διαιρετότητα, ισοϋπόλοιποι αριθμοί Θεώρημα 2.1 Αν
Κεφάλαιο 2 Θεωρία Αριθμών Κύριες βιβλιογραφικές αναφορές για αυτό το Κεφάλαιο είναι οι Hardy and Wright 1979 και Graham, Knuth, and Patashnik 1994. 2.1 Διαιρετότητα, ισοϋπόλοιποι αριθμοί Θεώρημα 2.1 Αν
Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι
 Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος. Δείξτε ότι ο V R εφοδιασμένος με τις ακόλουθες πράξεις (, a b) + (, d) ( a+, b+ d) και k ( ab, ) ( kakb,
Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος. Δείξτε ότι ο V R εφοδιασμένος με τις ακόλουθες πράξεις (, a b) + (, d) ( a+, b+ d) και k ( ab, ) ( kakb,
Περιεχόμενα. Πρόλογος 3
 Πρόλογος Η χρησιμότητα της Γραμμικής Άλγεβρας είναι σχεδόν αυταπόδεικτη. Αρκεί μια ματιά στο πρόγραμμα σπουδών, σχεδόν κάθε πανεπιστημιακού τμήματος θετικών επιστημών, για να διαπιστώσει κανείς την παρουσία
Πρόλογος Η χρησιμότητα της Γραμμικής Άλγεβρας είναι σχεδόν αυταπόδεικτη. Αρκεί μια ματιά στο πρόγραμμα σπουδών, σχεδόν κάθε πανεπιστημιακού τμήματος θετικών επιστημών, για να διαπιστώσει κανείς την παρουσία
Περιεχόμενα. Κεφάλαιο 3 Οι ιδιότητες των αριθμών... 37 3.1 Αριθμητικά σύνολα... 37 3.2 Ιδιότητες... 37 3.3 Περισσότερες ιδιότητες...
 Περιεχόμενα Πρόλογος... 5 Κεφάλαιο Βασικές αριθμητικές πράξεις... 5. Τέσσερις πράξεις... 5. Σύστημα πραγματικών αριθμών... 5. Γραφική αναπαράσταση πραγματικών αριθμών... 6.4 Οι ιδιότητες της πρόσθεσης
Περιεχόμενα Πρόλογος... 5 Κεφάλαιο Βασικές αριθμητικές πράξεις... 5. Τέσσερις πράξεις... 5. Σύστημα πραγματικών αριθμών... 5. Γραφική αναπαράσταση πραγματικών αριθμών... 6.4 Οι ιδιότητες της πρόσθεσης
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 1 η Ημερομηνία Αποστολής στον Φοιτητή: 20 Οκτωβρίου 2008
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 0 Οκτωβρίου 008 Ημερομηνία παράδοσης της Εργασίας: Νοεμβρίου 008 Πριν
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 0 Οκτωβρίου 008 Ημερομηνία παράδοσης της Εργασίας: Νοεμβρίου 008 Πριν
Εφαρμοσμένα Μαθηματικά ΙΙ 7ο Σετ Ασκήσεων (Λύσεις) Ορίζουσες Επιμέλεια: Ι. Λυχναρόπουλος
 Εφαρμοσμένα Μαθηματικά ΙΙ 7ο Σετ Ασκήσεων (Λύσεις) Ορίζουσες Επιμέλεια: Ι. Λυχναρόπουλος. Υπολογίστε τις ακόλουθες ορίζουσες a) 4 b) c) a b + a) 4 4 Παρατήρηση: Προσέξτε ότι ο συμβολισμός της ορίζουσας
Εφαρμοσμένα Μαθηματικά ΙΙ 7ο Σετ Ασκήσεων (Λύσεις) Ορίζουσες Επιμέλεια: Ι. Λυχναρόπουλος. Υπολογίστε τις ακόλουθες ορίζουσες a) 4 b) c) a b + a) 4 4 Παρατήρηση: Προσέξτε ότι ο συμβολισμός της ορίζουσας
Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύ
 Διακριτά Μαθηματικά Ι Ενότητα 2: Γεννήτριες Συναρτήσεις Μέρος 2 Διδάσκων: Χ. Μπούρας (bouras@cti.gr) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Διακριτά Μαθηματικά Ι Ενότητα 2: Γεννήτριες Συναρτήσεις Μέρος 2 Διδάσκων: Χ. Μπούρας (bouras@cti.gr) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
ΚΕΦΑΛΑΙΟ 3 ΤΟ ΔΙΩΝΥΜΙΚΟ ΘΕΩΡΗΜΑ
 ΚΕΦΑΛΑΙΟ 3 ΤΟ ΔΙΩΝΥΜΙΚΟ ΘΕΩΡΗΜΑ Εισαγωγή Οι αριθμοί που εκφράζουν το πλήθος των στοιχείων ανά αποτελούν ίσως τους πιο σημαντικούς αριθμούς της Συνδυαστικής και καλούνται διωνυμικοί συντελεστές διότι εμφανίζονται
ΚΕΦΑΛΑΙΟ 3 ΤΟ ΔΙΩΝΥΜΙΚΟ ΘΕΩΡΗΜΑ Εισαγωγή Οι αριθμοί που εκφράζουν το πλήθος των στοιχείων ανά αποτελούν ίσως τους πιο σημαντικούς αριθμούς της Συνδυαστικής και καλούνται διωνυμικοί συντελεστές διότι εμφανίζονται
Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 19/10/2017. Ακριβείς Διαφορικές Εξισώσεις-Ολοκληρωτικοί Παράγοντες. Η πρώτης τάξης διαφορική εξίσωση
 Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 19/10/2017 Ακριβείς Διαφορικές Εξισώσεις-Ολοκληρωτικοί Παράγοντες Η πρώτης τάξης διαφορική εξίσωση M(x, y) + (x, y)y = 0 ή ισοδύναμα, γραμμένη στην μορφή M(x,
Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 19/10/2017 Ακριβείς Διαφορικές Εξισώσεις-Ολοκληρωτικοί Παράγοντες Η πρώτης τάξης διαφορική εξίσωση M(x, y) + (x, y)y = 0 ή ισοδύναμα, γραμμένη στην μορφή M(x,
a n = 3 n a n+1 = 3 a n, a 0 = 1
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Κεφάλαιο 1 Συστήματα γραμμικών εξισώσεων
 Κεφάλαιο Συστήματα γραμμικών εξισώσεων Παραδείγματα από εφαρμογές Γραμμική Άλγεβρα Παράδειγμα : Σε ένα δίκτυο (αγωγών ή σωλήνων ή δρόμων) ισχύει ο κανόνας των κόμβων όπου το άθροισμα των εισερχόμενων ροών
Κεφάλαιο Συστήματα γραμμικών εξισώσεων Παραδείγματα από εφαρμογές Γραμμική Άλγεβρα Παράδειγμα : Σε ένα δίκτυο (αγωγών ή σωλήνων ή δρόμων) ισχύει ο κανόνας των κόμβων όπου το άθροισμα των εισερχόμενων ροών
Αναδρομικές ακολουθίες και Θεωρία Αριθμών
 Αναδρομικές ακολουθίες και Θεωρία Αριθμών Εμμανουήλ Καπνόπουλος Επιβλέπων καθηγητής Ιωάννης Αντωνιάδης Μεταπτυχιακή Εργασία Τμήμα Μαθηματικών και Εφαρμοσμένων Μαθηματικών Πανεπιστήμιο Κρήτης Ηράκλειο Οκτώβριος
Αναδρομικές ακολουθίες και Θεωρία Αριθμών Εμμανουήλ Καπνόπουλος Επιβλέπων καθηγητής Ιωάννης Αντωνιάδης Μεταπτυχιακή Εργασία Τμήμα Μαθηματικών και Εφαρμοσμένων Μαθηματικών Πανεπιστήμιο Κρήτης Ηράκλειο Οκτώβριος
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Γραμμικά Συστήματα Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Γραμμικό Σύστημα a11x1 + a12x2 + + a1 nxn = b1 a x + a x + +
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Γραμμικά Συστήματα Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Γραμμικό Σύστημα a11x1 + a12x2 + + a1 nxn = b1 a x + a x + +
Ασκήσεις3 Διαγωνίσιμες Γραμμικές Απεικονίσεις
 Ασκήσεις 5 Βασικά σημεία Ιδιότητες ιδιόχωρων: Έστω,, Ισχύουν τα εξής Ασκήσεις Διαγωνίσιμες Γραμμικές Απεικονίσεις κάποιες διακεκριμένες ιδιοτιμές της γραμμικής απεικόνισης : V V, όπου o Αν v v 0, όπου
Ασκήσεις 5 Βασικά σημεία Ιδιότητες ιδιόχωρων: Έστω,, Ισχύουν τα εξής Ασκήσεις Διαγωνίσιμες Γραμμικές Απεικονίσεις κάποιες διακεκριμένες ιδιοτιμές της γραμμικής απεικόνισης : V V, όπου o Αν v v 0, όπου
6. ΚΕΦΑΛΑΙΟ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE
 6. ΚΕΦΑΛΑΙΟ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ APACE Σκοπός του κεφαλαίου είναι να ορίσει τον αμφίπλευρο μετασχηματισμό aplace ή απλώς μετασχηματισμό aplace (Μ) και το μονόπλευρο μετασχηματισμό aplace (ΜΜ), να περιγράψει
6. ΚΕΦΑΛΑΙΟ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ APACE Σκοπός του κεφαλαίου είναι να ορίσει τον αμφίπλευρο μετασχηματισμό aplace ή απλώς μετασχηματισμό aplace (Μ) και το μονόπλευρο μετασχηματισμό aplace (ΜΜ), να περιγράψει
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Παραγώγιση Εισαγωγή Ορισμός 7. Αν y f x είναι μια συνάρτηση ορισμένη σε ένα διάστημα
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Παραγώγιση Εισαγωγή Ορισμός 7. Αν y f x είναι μια συνάρτηση ορισμένη σε ένα διάστημα
Τμήμα Τεχνολόγων Γεωπόνων - Φλώρινα
 Τμήμα Τεχνολόγων Γεωπόνων - Φλώρινα Μάθημα: Μαθηματικά Διάλεξη 1 η : Εισαγωγή-Επανάληψη βασικών εννοιών (1 ο, 2 ο, 3 ο Κεφάλαιο) 11-10-2017, 18-10-2017 Διδάσκουσα: Αριστούλα Κοντογιάννη ΩΡΕΣ ΔΙΔΑΣΚΑΛΙΑΣ
Τμήμα Τεχνολόγων Γεωπόνων - Φλώρινα Μάθημα: Μαθηματικά Διάλεξη 1 η : Εισαγωγή-Επανάληψη βασικών εννοιών (1 ο, 2 ο, 3 ο Κεφάλαιο) 11-10-2017, 18-10-2017 Διδάσκουσα: Αριστούλα Κοντογιάννη ΩΡΕΣ ΔΙΔΑΣΚΑΛΙΑΣ
ΛΧ1004 Μαθηματικά για Οικονομολόγους
 ΛΧ1004 Μαθηματικά για Οικονομολόγους Μάθημα 1 ου Εξαμήνου 2Θ+2Φ(ΑΠ) Ι. Δημοτίκαλης, Επίκουρος Καθηγητής 1 ΤΕΙ ΚΡΗΤΗΣ-ΤΜΗΜΑ Λ&Χ: jdim@staff.teicrete.gr ΠΡΟΤΕΙΝΟΜΕΝΟ ΒΙΒΛΙΟ ΕΦΑΡΜΟΓΕΣ ΜΑΘΗΜΑΤΙΚΟΥ ΛΟΓΙΣΜΟΥ
ΛΧ1004 Μαθηματικά για Οικονομολόγους Μάθημα 1 ου Εξαμήνου 2Θ+2Φ(ΑΠ) Ι. Δημοτίκαλης, Επίκουρος Καθηγητής 1 ΤΕΙ ΚΡΗΤΗΣ-ΤΜΗΜΑ Λ&Χ: jdim@staff.teicrete.gr ΠΡΟΤΕΙΝΟΜΕΝΟ ΒΙΒΛΙΟ ΕΦΑΡΜΟΓΕΣ ΜΑΘΗΜΑΤΙΚΟΥ ΛΟΓΙΣΜΟΥ
ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων
 ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων Μελετάμε εδώ τη συνθήκη της αύξουσας αλυσίδας υποπροτύπων και τη συνθήκη της φθίνουσας αλυσίδας υποπροτύπων Αυτές συνδέονται μεταξύ τους με την έννοια της συνθετικής σειράς
ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων Μελετάμε εδώ τη συνθήκη της αύξουσας αλυσίδας υποπροτύπων και τη συνθήκη της φθίνουσας αλυσίδας υποπροτύπων Αυτές συνδέονται μεταξύ τους με την έννοια της συνθετικής σειράς
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 2 η Ημερομηνία Αποστολής στον Φοιτητή: 28 Νοεμβρίου 2011
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 8 Νοεμβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 6 Ιανουαρίου 0 Οι ασκήσεις
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 8 Νοεμβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 6 Ιανουαρίου 0 Οι ασκήσεις
Matrix Algorithms. Παρουσίαση στα πλαίσια του μαθήματος «Παράλληλοι. Αλγόριθμοι» Γ. Καούρη Β. Μήτσου
 Matrix Algorithms Παρουσίαση στα πλαίσια του μαθήματος «Παράλληλοι Αλγόριθμοι» Γ. Καούρη Β. Μήτσου Περιεχόμενα παρουσίασης Πολλαπλασιασμός πίνακα με διάνυσμα Πολλαπλασιασμός πινάκων Επίλυση τριγωνικού
Matrix Algorithms Παρουσίαση στα πλαίσια του μαθήματος «Παράλληλοι Αλγόριθμοι» Γ. Καούρη Β. Μήτσου Περιεχόμενα παρουσίασης Πολλαπλασιασμός πίνακα με διάνυσμα Πολλαπλασιασμός πινάκων Επίλυση τριγωνικού
Παραδείγματα (2 ο σετ) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος
 Παραδείγματα ( ο σετ) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος Παράδειγμα Έστω ο υποχώρος W του R 5 που παράγεται από τα διανύσματα v=(,,-,,), v=(,,-,6,8), v=(,,,,6), v=(,,5,,8), v5=(,7,,,9). a)
Παραδείγματα ( ο σετ) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος Παράδειγμα Έστω ο υποχώρος W του R 5 που παράγεται από τα διανύσματα v=(,,-,,), v=(,,-,6,8), v=(,,,,6), v=(,,5,,8), v5=(,7,,,9). a)
(a 1, b 1 ) (a 2, b 2 ) = (a 1 a 2, b 1 b 2 ).
 ΕΜ0 - Διακριτά Μαθηματικά Ιανουαρίου 006 Άσκηση - Λύσεις Πρόβλημα [0 μονάδες] Εστω L και L δύο κυκλώματα σε ένα γράφημα G. Εστω a μία ακμή που ανήκει και στο L και στο L και έστω b μία ακμή που ανήκει
ΕΜ0 - Διακριτά Μαθηματικά Ιανουαρίου 006 Άσκηση - Λύσεις Πρόβλημα [0 μονάδες] Εστω L και L δύο κυκλώματα σε ένα γράφημα G. Εστω a μία ακμή που ανήκει και στο L και στο L και έστω b μία ακμή που ανήκει
(a + b) + c = a + (b + c), (ab)c = a(bc) a + b = b + a, ab = ba. a(b + c) = ab + ac
 Σημειώσεις μαθήματος Μ1212 Γραμμική Άλγεβρα ΙΙ Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2014 Κεφάλαιο 1 Διανυσματικοί Χώροι Στο εισαγωγικό μάθημα Γραμμικής Άλγεβρας ξεκινήσαμε μελετώντας
Σημειώσεις μαθήματος Μ1212 Γραμμική Άλγεβρα ΙΙ Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2014 Κεφάλαιο 1 Διανυσματικοί Χώροι Στο εισαγωγικό μάθημα Γραμμικής Άλγεβρας ξεκινήσαμε μελετώντας
ΑΛΓΕΒΡΑ Τ Ν Ο Π Σ Ι Κ Η Τ Λ Η
 Τ Ν Ο Π Σ Ι Κ Η Τ Λ Η ΑΛΓΕΒΡΑ Τα ςημαντικότερα ςημεία τησ θεωρίασ Ερωτήςεισ εμπζδωςησ- απαντήςεισ Μεθοδολογία αςκήςεων Προτεινόμενεσ αςκήςεισ του βιβλίου - διεξοδική ανάλυςη των λφςεων (ςκζψη-βήματα-επεξήγηςη
Τ Ν Ο Π Σ Ι Κ Η Τ Λ Η ΑΛΓΕΒΡΑ Τα ςημαντικότερα ςημεία τησ θεωρίασ Ερωτήςεισ εμπζδωςησ- απαντήςεισ Μεθοδολογία αςκήςεων Προτεινόμενεσ αςκήςεισ του βιβλίου - διεξοδική ανάλυςη των λφςεων (ςκζψη-βήματα-επεξήγηςη
Περιεχόμενα. Κεφάλαιο 3 Οι ιδιότητες των αριθμών Αριθμητικά σύνολα Ιδιότητες Περισσότερες ιδιότητες...
 Περιεχόμενα Πρόλογος 5 Κεφάλαιο Βασικές αριθμητικές πράξεις 5 Τέσσερις πράξεις 5 Σύστημα πραγματικών αριθμών 5 Γραφική αναπαράσταση πραγματικών αριθμών 6 Οι ιδιότητες της πρόσθεσης και του πολλαπλασιασμού
Περιεχόμενα Πρόλογος 5 Κεφάλαιο Βασικές αριθμητικές πράξεις 5 Τέσσερις πράξεις 5 Σύστημα πραγματικών αριθμών 5 Γραφική αναπαράσταση πραγματικών αριθμών 6 Οι ιδιότητες της πρόσθεσης και του πολλαπλασιασμού
4. Παραγώγιση πεπερασμένων διαφορών Σειρά Taylor Πολυωνυμική παρεμβολή
 . Παραγώγιση Η διαδικασία της υπολογιστικής επίλυσης συνήθων και μερικών διαφορικών εξισώσεων προϋποθέτει την προσέγγιση της εξαρτημένης μεταβλητής και των παραγώγων της στους κόμβους του πλέγματος. Ειδικά,
. Παραγώγιση Η διαδικασία της υπολογιστικής επίλυσης συνήθων και μερικών διαφορικών εξισώσεων προϋποθέτει την προσέγγιση της εξαρτημένης μεταβλητής και των παραγώγων της στους κόμβους του πλέγματος. Ειδικά,
Παράδειγμα 14.2 Να βρεθεί ο μετασχηματισμός Laplace των συναρτήσεων
 Κεφάλαιο 4 Μετασχηματισμός aplace 4. Μετασχηματισμός aplace της εκθετικής συνάρτησης e Είναι Άρα a a a u( a ( a ( a ( aj F( e e d e d [ e ] [ e ] ( a e (c ji, με a (4.9 a a a [ e u( ] a, με a (4.3 Η σχέση
Κεφάλαιο 4 Μετασχηματισμός aplace 4. Μετασχηματισμός aplace της εκθετικής συνάρτησης e Είναι Άρα a a a u( a ( a ( a ( aj F( e e d e d [ e ] [ e ] ( a e (c ji, με a (4.9 a a a [ e u( ] a, με a (4.3 Η σχέση
Περιεχόμενα. Κεφάλαιο 1 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΜΙΑ ΕΥΘΕΙΑ... 13 1.1 Οι συντεταγμένες ενός σημείου...13 1.2 Απόλυτη τιμή...14
 Περιεχόμενα Κεφάλαιο 1 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΜΙΑ ΕΥΘΕΙΑ... 13 1.1 Οι συντεταγμένες ενός σημείου...13 1.2 Απόλυτη τιμή...14 Κεφάλαιο 2 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΕΝΑ ΕΠΙΠΕΔΟ 20 2.1 Οι συντεταγμένες
Περιεχόμενα Κεφάλαιο 1 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΜΙΑ ΕΥΘΕΙΑ... 13 1.1 Οι συντεταγμένες ενός σημείου...13 1.2 Απόλυτη τιμή...14 Κεφάλαιο 2 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΕΝΑ ΕΠΙΠΕΔΟ 20 2.1 Οι συντεταγμένες
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΠΕΡΙΤΤΟΙ) Λυσεις Ασκησεων - Φυλλαδιο 2
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΠΕΡΙΤΤΟΙ) Λυσεις Ασκησεων - Φυλλαδιο 2 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai2017/lai2017html Παρασκευή 20 Οκτωβρίου 2017
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΠΕΡΙΤΤΟΙ) Λυσεις Ασκησεων - Φυλλαδιο 2 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai2017/lai2017html Παρασκευή 20 Οκτωβρίου 2017
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ. Μαθηματικά 2. Σταύρος Παπαϊωάννου
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ Μαθηματικά Σταύρος Παπαϊωάννου Ιούνιος 015 Τίτλος Μαθήματος Περιεχόμενα Χρηματοδότηση... Error! Bookmark not deined. Σκοποί Μαθήματος (Επικεφαλίδα
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ Μαθηματικά Σταύρος Παπαϊωάννου Ιούνιος 015 Τίτλος Μαθήματος Περιεχόμενα Χρηματοδότηση... Error! Bookmark not deined. Σκοποί Μαθήματος (Επικεφαλίδα
4. Παραγώγιση πεπερασμένων διαφορών Σειρά Taylor Πολυωνυμική παρεμβολή
 4. Παραγώγιση Η διαδικασία της υπολογιστικής επίλυσης συνήθων και μερικών διαφορικών εξισώσεων προϋποθέτει την προσέγγιση της εξαρτημένης μεταβλητής και των παραγώγων της στους κόμβους του πλέγματος. Ειδικά,
4. Παραγώγιση Η διαδικασία της υπολογιστικής επίλυσης συνήθων και μερικών διαφορικών εξισώσεων προϋποθέτει την προσέγγιση της εξαρτημένης μεταβλητής και των παραγώγων της στους κόμβους του πλέγματος. Ειδικά,
M. J. Lighthill. g(y) = f(x) e 2πixy dx, (1) d N. g (p) (y) =
 Εισαγωγή στην ανάλυση Fourier και τις γενικευμένες συναρτήσεις * M. J. Lighthill μετάφραση: Γ. Ευθυβουλίδης ΚΕΦΑΛΑΙΟ 2 Η ΘΕΩΡΙΑ ΤΩΝ ΓΕΝΙΚΕΥΜΕΝΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΚΑΙ ΤΩΝ ΜΕΤΑΣΧΗΜΑΤΙΣΜΩΝ ΤΟΥΣ FOURIER 2.1. Καλές
Εισαγωγή στην ανάλυση Fourier και τις γενικευμένες συναρτήσεις * M. J. Lighthill μετάφραση: Γ. Ευθυβουλίδης ΚΕΦΑΛΑΙΟ 2 Η ΘΕΩΡΙΑ ΤΩΝ ΓΕΝΙΚΕΥΜΕΝΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΚΑΙ ΤΩΝ ΜΕΤΑΣΧΗΜΑΤΙΣΜΩΝ ΤΟΥΣ FOURIER 2.1. Καλές
Ασκήσεις3 Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα.
 Ασκήσεις 0 Ασκήσεις Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα o H -στήλη του P P είναι E αν και μόνο αν η -στήλη του P είναι ιδιοδιάνυσμα του που αντιστοιχεί στην ιδιοτιμή
Ασκήσεις 0 Ασκήσεις Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα o H -στήλη του P P είναι E αν και μόνο αν η -στήλη του P είναι ιδιοδιάνυσμα του που αντιστοιχεί στην ιδιοτιμή
Γραμμική Άλγεβρα Ι,
 Γραμμική Άλγεβρα Ι, 207-8 Ασκήσεις2 και Ασκήσεις3: Γραμμοϊσοδύναμοι Πίνακες και Επίλυση Γραμμικών Συστημάτων Βασικά σημεία Γραμμοϊσοδυναμία πινάκων o Στοιχειώδεις πράξεις γραμμών o Ανηγμένη κλιμακωτή μορφή
Γραμμική Άλγεβρα Ι, 207-8 Ασκήσεις2 και Ασκήσεις3: Γραμμοϊσοδύναμοι Πίνακες και Επίλυση Γραμμικών Συστημάτων Βασικά σημεία Γραμμοϊσοδυναμία πινάκων o Στοιχειώδεις πράξεις γραμμών o Ανηγμένη κλιμακωτή μορφή
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (Εξ. Ιουνίου - 02/07/08) ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ
 Ονοματεπώνυμο:......... Α.Μ....... Ετος... ΑΙΘΟΥΣΑ:....... I. (περί τις 55μ. = ++5++. Σωστό ή Λάθος: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (Εξ. Ιουνίου - //8 ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ (αʹ Αν AB = BA όπου A, B τετραγωνικά και
Ονοματεπώνυμο:......... Α.Μ....... Ετος... ΑΙΘΟΥΣΑ:....... I. (περί τις 55μ. = ++5++. Σωστό ή Λάθος: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (Εξ. Ιουνίου - //8 ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ (αʹ Αν AB = BA όπου A, B τετραγωνικά και
Matrix Algorithms. Παρουσίαση στα πλαίσια του μαθήματος «Παράλληλοι Αλγόριθμοι» Γ. Καούρη Β. Μήτσου
 Matrix Algorithms Παρουσίαση στα πλαίσια του μαθήματος «Παράλληλοι Αλγόριθμοι» Γ. Καούρη Β. Μήτσου Περιεχόμενα παρουσίασης Πολλαπλασιασμός πίνακα με διάνυσμα Πολλαπλασιασμός πινάκων Επίλυση τριγωνικού
Matrix Algorithms Παρουσίαση στα πλαίσια του μαθήματος «Παράλληλοι Αλγόριθμοι» Γ. Καούρη Β. Μήτσου Περιεχόμενα παρουσίασης Πολλαπλασιασμός πίνακα με διάνυσμα Πολλαπλασιασμός πινάκων Επίλυση τριγωνικού
ΚΕΦΑΛΑΙΟ 3 Ο 3.2 Η ΕΝΝΟΙΑ ΤΟΥ ΓΡΑΜΜΙΚΟΥ ΣΥΣΤΗΜΑΤΟΣ ΚΑΙ Η. (Σ) όπου α, β, α, β, είναι οι
 ΚΕΦΑΛΑΙΟ 3 Ο ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΩΝ ΕΞΙΣΩΣΕΩΝ 3. Η ΕΝΝΟΙΑ ΤΟΥ ΓΡΑΜΜΙΚΟΥ ΣΥΣΤΗΜΑΤΟΣ ΚΑΙ Η ΓΡΑΦΙΚΗ ΕΠΙΛΥΣΗ ΤΟΥ. Ποια είναι η μορφή ενός συστήματος δύο γραμμικών εξισώσεων, δύο αγνώστων; Να δοθεί παράδειγμα.
ΚΕΦΑΛΑΙΟ 3 Ο ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΩΝ ΕΞΙΣΩΣΕΩΝ 3. Η ΕΝΝΟΙΑ ΤΟΥ ΓΡΑΜΜΙΚΟΥ ΣΥΣΤΗΜΑΤΟΣ ΚΑΙ Η ΓΡΑΦΙΚΗ ΕΠΙΛΥΣΗ ΤΟΥ. Ποια είναι η μορφή ενός συστήματος δύο γραμμικών εξισώσεων, δύο αγνώστων; Να δοθεί παράδειγμα.
ΒΟΗΘΗΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΣΤΑ ΓΕΝΙΚΑ ΜΑΘΗΜΑΤΙΚΑ
 ΤΜΗΜΑ ΔΙΕΘΝΟΥΣ ΕΜΠΟΡΙΟΥ ΒΟΗΘΗΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΣΤΑ ΓΕΝΙΚΑ ΜΑΘΗΜΑΤΙΚΑ ΚΕΦΑΛΑΙΑ: ) ΠΙΝΑΚΕΣ ) ΟΡΙΖΟΥΣΕΣ ) ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ 4) ΠΑΡΑΓΩΓΟΙ ΜΑΡΙΑ ΡΟΥΣΟΥΛΗ ΚΕΦΑΛΑΙΟ ΠΙΝΑΚEΣ ΠΡΑΓΜΑΤΙΚΩΝ ΑΡΙΘΜΩΝ ΟΡΙΣΜΟΣ Πίνακας
ΤΜΗΜΑ ΔΙΕΘΝΟΥΣ ΕΜΠΟΡΙΟΥ ΒΟΗΘΗΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΣΤΑ ΓΕΝΙΚΑ ΜΑΘΗΜΑΤΙΚΑ ΚΕΦΑΛΑΙΑ: ) ΠΙΝΑΚΕΣ ) ΟΡΙΖΟΥΣΕΣ ) ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ 4) ΠΑΡΑΓΩΓΟΙ ΜΑΡΙΑ ΡΟΥΣΟΥΛΗ ΚΕΦΑΛΑΙΟ ΠΙΝΑΚEΣ ΠΡΑΓΜΑΤΙΚΩΝ ΑΡΙΘΜΩΝ ΟΡΙΣΜΟΣ Πίνακας
,, δηλαδή στο σημείο αυτό παρουσιάζει τη μέγιστη τιμή της αν α < 0 2α 4α και την ελάχιστη τιμή της αν α > 0. β Στο διάστημα,
 Γενικής Παιδείας 1.4 Εφαρμογές των παραγώγων Το κριτήριο της πρώτης παραγώγου Στην Άλγεβρα της Α Λυκείου μελετήσαμε τη συνάρτηση f(x) = αx + βx + γ, α 0 και είδαμε ότι η γραφική της παράσταση είναι μία
Γενικής Παιδείας 1.4 Εφαρμογές των παραγώγων Το κριτήριο της πρώτης παραγώγου Στην Άλγεβρα της Α Λυκείου μελετήσαμε τη συνάρτηση f(x) = αx + βx + γ, α 0 και είδαμε ότι η γραφική της παράσταση είναι μία
Μεθοδολογία Επίλυσης Προβλημάτων ============================================================================ Π. Κυράνας - Κ.
 Μεθοδολογία Επίλυσης Προβλημάτων ============================================================================ Π. Κυράνας - Κ. Σάλαρης Πολλές φορές μας δίνεται να λύσουμε ένα πρόβλημα που από την πρώτη
Μεθοδολογία Επίλυσης Προβλημάτων ============================================================================ Π. Κυράνας - Κ. Σάλαρης Πολλές φορές μας δίνεται να λύσουμε ένα πρόβλημα που από την πρώτη
Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ
 Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ 1 Συναρτήσεις Όταν αναφερόμαστε σε μια συνάρτηση, ουσιαστικά αναφερόμαστε σε μια σχέση ή εξάρτηση. Στα μαθηματικά που θα μας απασχολήσουν, με απλά λόγια, η σχέση
Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ 1 Συναρτήσεις Όταν αναφερόμαστε σε μια συνάρτηση, ουσιαστικά αναφερόμαστε σε μια σχέση ή εξάρτηση. Στα μαθηματικά που θα μας απασχολήσουν, με απλά λόγια, η σχέση
Παραδείγματα Απαλοιφή Gauss Απαλοιφή Gauss Jordan
 Παραδείγματα Απαλοιφή Gauss Απαλοιφή Gauss Jodan Παράδειγμα x y Να επιλυθεί το ακόλουθο σύστημα: x y 6 Σε μορφή πινάκων το σύστημα γράφεται ως: x y 6 με απαλοιφή Gauss. Ο επαυξημένος πίνακας του συστήματος
Παραδείγματα Απαλοιφή Gauss Απαλοιφή Gauss Jodan Παράδειγμα x y Να επιλυθεί το ακόλουθο σύστημα: x y 6 Σε μορφή πινάκων το σύστημα γράφεται ως: x y 6 με απαλοιφή Gauss. Ο επαυξημένος πίνακας του συστήματος
Προχωρημένη απαρίθμηση
 Κεφάλαιο 4 Προχωρημένη απαρίθμηση Κύριες βιβλιογραφικές αναφορές για αυτό το Κεφάλαιο είναι οι C L Liu ad C Liu 1985, Graham, Kuth, ad Patashi 1994, Camero 1994 και Staley 1986 41 Διαμερίσεις και συνδυασμοί
Κεφάλαιο 4 Προχωρημένη απαρίθμηση Κύριες βιβλιογραφικές αναφορές για αυτό το Κεφάλαιο είναι οι C L Liu ad C Liu 1985, Graham, Kuth, ad Patashi 1994, Camero 1994 και Staley 1986 41 Διαμερίσεις και συνδυασμοί
I. ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. math-gr
 I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Λυσεις Ασκησεων - Φυλλαδιο 1
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Λυσεις Ασκησεων - Φυλλαδιο ιδασκοντες: Α. Μπεληγιάννης - Σ. Παπαδάκης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt.html Τετάρτη 7 Φεβρουαρίου 03 Ασκηση. είξτε ότι
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Λυσεις Ασκησεων - Φυλλαδιο ιδασκοντες: Α. Μπεληγιάννης - Σ. Παπαδάκης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt.html Τετάρτη 7 Φεβρουαρίου 03 Ασκηση. είξτε ότι
Εφαρμοσμένα Μαθηματικά ΙΙ 5ο Σετ Ασκήσεων (Λύσεις) Πίνακες Επιμέλεια: I. Λυχναρόπουλος
 Εφαρμοσμένα Μαθηματικά ΙΙ 5ο Σετ Ασκήσεων (Λύσεις) Πίνακες Επιμέλεια: I. Λυχναρόπουλος 3. Αν A 5 4, B 4, C να υπολογίσετε τις ακόλουθες πράξεις 4 3 8 3 7 3 (αν έχουν νόημα): α) AB, b) BA, c) CB, d) C B,
Εφαρμοσμένα Μαθηματικά ΙΙ 5ο Σετ Ασκήσεων (Λύσεις) Πίνακες Επιμέλεια: I. Λυχναρόπουλος 3. Αν A 5 4, B 4, C να υπολογίσετε τις ακόλουθες πράξεις 4 3 8 3 7 3 (αν έχουν νόημα): α) AB, b) BA, c) CB, d) C B,
Fast Fourier Transform
 Fast Fourier Transform Παναγιώτης Πατσιλινάκος ΕΜΕ 19 Οκτωβρίου 2017 Παναγιώτης Πατσιλινάκος (ΕΜΕ) Fast Fourier Transform 19 Οκτωβρίου 2017 1 / 20 1 Εισαγωγή Στόχος Προαπαιτούμενα 2 Η ιδέα Αντιστροφή -
Fast Fourier Transform Παναγιώτης Πατσιλινάκος ΕΜΕ 19 Οκτωβρίου 2017 Παναγιώτης Πατσιλινάκος (ΕΜΕ) Fast Fourier Transform 19 Οκτωβρίου 2017 1 / 20 1 Εισαγωγή Στόχος Προαπαιτούμενα 2 Η ιδέα Αντιστροφή -
Γραμμικός Προγραμματισμός Μέθοδος Simplex
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Επιχειρησιακή Έρευνα Γραμμικός Προγραμματισμός Μέθοδος Simplex Η παρουσίαση προετοιμάστηκε από τον Ν.Α. Παναγιώτου Περιεχόμενα Παρουσίασης 1. Πρότυπη Μορφή ΓΠ 2. Πινακοποίηση
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Επιχειρησιακή Έρευνα Γραμμικός Προγραμματισμός Μέθοδος Simplex Η παρουσίαση προετοιμάστηκε από τον Ν.Α. Παναγιώτου Περιεχόμενα Παρουσίασης 1. Πρότυπη Μορφή ΓΠ 2. Πινακοποίηση
ΠΕΡΙΕΧΟΜΕΝΑ 1 ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΑΚΟΛΟΥΘΙΕΣ ΑΡΙΘΜΩΝ EΞΙΣΩΣΕΙΣ...47 ΠΡΟΛΟΓΟΣ... 9
 ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ... 9 1 ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ...11 1.1 Βασικές θεωρητικές γνώσεις... 11 1.. Λυμένα προβλήματα... 19 1. Προβλήματα προς λύση... 4 1.4 Απαντήσεις προβλημάτων Πραγματικοί αριθμοί... 0 ΑΚΟΛΟΥΘΙΕΣ
ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ... 9 1 ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ...11 1.1 Βασικές θεωρητικές γνώσεις... 11 1.. Λυμένα προβλήματα... 19 1. Προβλήματα προς λύση... 4 1.4 Απαντήσεις προβλημάτων Πραγματικοί αριθμοί... 0 ΑΚΟΛΟΥΘΙΕΣ
Συνεχή Κλάσματα. Εμμανουήλ Καπνόπουλος Α.Μ 282
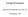 Συνεχή Κλάσματα Εμμανουήλ Καπνόπουλος Α.Μ 282 5 Νοεμβρίου 204 Ορισμός και ιδιότητες: Ορισμός: Έστω a 0, a, a 2,...a n ανεξάρτητες μεταβλητές, n N σχηματίζουν την ακολουθία {[a 0, a,..., a n ] : n N} όπου
Συνεχή Κλάσματα Εμμανουήλ Καπνόπουλος Α.Μ 282 5 Νοεμβρίου 204 Ορισμός και ιδιότητες: Ορισμός: Έστω a 0, a, a 2,...a n ανεξάρτητες μεταβλητές, n N σχηματίζουν την ακολουθία {[a 0, a,..., a n ] : n N} όπου
- ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ
 ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ R - ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΣΤΟ ΑΠΕΙΡΟ - ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΑΚΟΛΟΥΘΙΑΣ [Κεφ..6: Μη Πεπερασμένο Όριο στο R - Κεφ..7: Όρια Συνάρτησης
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ R - ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΣΤΟ ΑΠΕΙΡΟ - ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΑΚΟΛΟΥΘΙΑΣ [Κεφ..6: Μη Πεπερασμένο Όριο στο R - Κεφ..7: Όρια Συνάρτησης
Δίνεται το σύστημα μιας εισόδου και μιας εξόδου, το οποίο περιγράφεται από τις κάτωθι εξισώσεις:,, πίνακας,
 Παράδειγμα 3.2(Επίλυση συστήματος Jordan) Δίνεται το σύστημα μιας εισόδου και μιας εξόδου, το οποίο περιγράφεται από τις κάτωθι εξισώσεις: Όπου,, πίνακας, Να λυθεί το σύστημα με είσοδο τη συνάρτηση Επίλυση
Παράδειγμα 3.2(Επίλυση συστήματος Jordan) Δίνεται το σύστημα μιας εισόδου και μιας εξόδου, το οποίο περιγράφεται από τις κάτωθι εξισώσεις: Όπου,, πίνακας, Να λυθεί το σύστημα με είσοδο τη συνάρτηση Επίλυση
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α. ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 5: ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΥΠΟΧΩΡΟΙ ΓΡΑΜΜΙΚΗ ΑΝΕΞΑΡΤΗΣΙΑ ΒΑΣΕΙΣ & ΔΙΑΣΤΑΣΗ Δ.Χ. ΣΗΜΕΙΩΣΕΙΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α. ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 5: ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΥΠΟΧΩΡΟΙ ΓΡΑΜΜΙΚΗ ΑΝΕΞΑΡΤΗΣΙΑ ΒΑΣΕΙΣ & ΔΙΑΣΤΑΣΗ Δ.Χ. ΣΗΜΕΙΩΣΕΙΣ
Πολυωνυμικές εξισώσεις και ανισώσεις Εξισώσεις και ανισώσεις που ανάγονται σε πολυωνυμικές
 0 Πολυωνυμικές εξισώσεις και ανισώσεις Εξισώσεις και ανισώσεις που ανάγονται σε πολυωνυμικές Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Για να λύσουμε μια πολυωνυμική εξίσωση P(x) 0 (ή μια πολυωνυμική ανίσωση P(x)
0 Πολυωνυμικές εξισώσεις και ανισώσεις Εξισώσεις και ανισώσεις που ανάγονται σε πολυωνυμικές Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Για να λύσουμε μια πολυωνυμική εξίσωση P(x) 0 (ή μια πολυωνυμική ανίσωση P(x)
ΘΕΩΡΙΑ: Έστω η οµογενής γραµµική διαφορική εξίσωση τάξης , (1)
 1 ΘΕΩΡΙΑ: Έστω η οµογενής γραµµική διαφορική εξίσωση τάξης (1) όπου οι συντελεστές είναι δοσµένες συνεχείς συναρτήσεις ορισµένες σ ένα ανοικτό διάστηµα. Ορισµός 1. Ορίζουµε τον διαφορικό τελεστή µέσω της
1 ΘΕΩΡΙΑ: Έστω η οµογενής γραµµική διαφορική εξίσωση τάξης (1) όπου οι συντελεστές είναι δοσµένες συνεχείς συναρτήσεις ορισµένες σ ένα ανοικτό διάστηµα. Ορισµός 1. Ορίζουµε τον διαφορικό τελεστή µέσω της
Ιγνάτιος Ιωαννίδης Χρήσιμες Γνώσεις 5
 Ιγνάτιος Ιωαννίδης Χρήσιμες Γνώσεις 5 Α Σύνολα αριθμών Για τα σύνολα των αριθμών γνωρίζουμε ότι N Z Q R. ) Το N= { 0,,,,... } είναι το σύνολο των φυσικών αριθμών. ) Το Z = { 0, ±, ±, ±,... } είναι το σύνολο
Ιγνάτιος Ιωαννίδης Χρήσιμες Γνώσεις 5 Α Σύνολα αριθμών Για τα σύνολα των αριθμών γνωρίζουμε ότι N Z Q R. ) Το N= { 0,,,,... } είναι το σύνολο των φυσικών αριθμών. ) Το Z = { 0, ±, ±, ±,... } είναι το σύνολο
Η Έννοια της εξίσωσης:
 Η Έννοια της εξίσωσης: Θεωρία και λυμένα παραδείγματα Εξίσωση με έναν άγνωστο λέμε μια ισότητα η οποία περιέχει αριθμούς και έναν άγνωστο γράμμα ( μεταβλητή). Εξισώσεις είναι οι: χ+=8, χ-21=4,χ+1, 8χ=26.
Η Έννοια της εξίσωσης: Θεωρία και λυμένα παραδείγματα Εξίσωση με έναν άγνωστο λέμε μια ισότητα η οποία περιέχει αριθμούς και έναν άγνωστο γράμμα ( μεταβλητή). Εξισώσεις είναι οι: χ+=8, χ-21=4,χ+1, 8χ=26.
ΚΕΦΑΛΑΙΟ 2: ΟΡΙΖΟΥΣΕΣ
 ΚΕΦΑΛΑΙΟ ΚΕΦΑΛΑΙΟ :. ΕΙΣΑΓΩΓΗ Σε κάθε τετραγωνικό πίνακα ) τάξης n θα αντιστοιχίσουμε έναν πραγματικό ( ij αριθμό, τον οποίο θα ονομάσουμε ορίζουσα του πίνακα. Η ορίζουσα θα συμβολίζεται det ή Α ή n n
ΚΕΦΑΛΑΙΟ ΚΕΦΑΛΑΙΟ :. ΕΙΣΑΓΩΓΗ Σε κάθε τετραγωνικό πίνακα ) τάξης n θα αντιστοιχίσουμε έναν πραγματικό ( ij αριθμό, τον οποίο θα ονομάσουμε ορίζουσα του πίνακα. Η ορίζουσα θα συμβολίζεται det ή Α ή n n
Μαθηματικά. Ενότητα 2: Διαφορικός Λογισμός. Σαριαννίδης Νικόλαος Τμήμα Διοίκησης Επιχειρήσεων (Κοζάνη)
 Μαθηματικά Ενότητα 2: Διαφορικός Λογισμός Σαριαννίδης Νικόλαος Τμήμα Διοίκησης Επιχειρήσεων (Κοζάνη) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Μαθηματικά Ενότητα 2: Διαφορικός Λογισμός Σαριαννίδης Νικόλαος Τμήμα Διοίκησης Επιχειρήσεων (Κοζάνη) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΕΞΙΣΩΣΕΩΝ
 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΕΞΙΣΩΣΕΩΝ Θα ξεκινήσουµε την παρουσίαση των γραµµικών συστηµάτων µε ένα απλό παράδειγµα από τη Γεωµετρία, το οποίο ϑα µας ϐοηθήσει στην κατανόηση των συστηµάτων αυτών και των συνθηκών
ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΕΞΙΣΩΣΕΩΝ Θα ξεκινήσουµε την παρουσίαση των γραµµικών συστηµάτων µε ένα απλό παράδειγµα από τη Γεωµετρία, το οποίο ϑα µας ϐοηθήσει στην κατανόηση των συστηµάτων αυτών και των συνθηκών
τριώνυμο Η εξίσωση δευτέρου βαθμού στην πλήρη της μορφή ονομάζεται τριώνυμο, γιατί αποτελείται από τρία μονώνυμα. Η γενική μορφή της είναι:
 κεφάλαιο 4 Α τριώνυμο επίλυση της εξίσωσης δευτέρου βαθμού Η εξίσωση δευτέρου βαθμού στην πλήρη της μορφή ονομάζεται τριώνυμο, γιατί αποτελείται από τρία μονώνυμα. Η γενική μορφή της είναι: αx + βx + γ
κεφάλαιο 4 Α τριώνυμο επίλυση της εξίσωσης δευτέρου βαθμού Η εξίσωση δευτέρου βαθμού στην πλήρη της μορφή ονομάζεται τριώνυμο, γιατί αποτελείται από τρία μονώνυμα. Η γενική μορφή της είναι: αx + βx + γ
1 Αριθμητική κινητής υποδιαστολής και σφάλματα στρογγύλευσης
 1 Αριθμητική κινητής υποδιαστολής και σφάλματα στρογγύλευσης Στη συγκεκριμένη ενότητα εξετάζουμε θέματα σχετικά με την αριθμητική πεπερασμένης ακρίβειας που χρησιμοποιούν οι σημερινοί υπολογιστές και τα
1 Αριθμητική κινητής υποδιαστολής και σφάλματα στρογγύλευσης Στη συγκεκριμένη ενότητα εξετάζουμε θέματα σχετικά με την αριθμητική πεπερασμένης ακρίβειας που χρησιμοποιούν οι σημερινοί υπολογιστές και τα
Σήματα και Συστήματα. Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier 1. Μετασχηματισμός Fourier
Σήματα και Συστήματα Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier 1. Μετασχηματισμός Fourier
11. Ποιες είναι οι άμεσες συνέπειες της διαίρεσης;
 10. Τι ονομάζουμε Ευκλείδεια διαίρεση και τέλεια διαίρεση; Όταν δοθούν δύο φυσικοί αριθμοί Δ και δ, τότε υπάρχουν δύο άλλοι φυσικοί αριθμοί π και υ, έτσι ώστε να ισχύει: Δ = δ π + υ. Ο αριθμός Δ λέγεται
10. Τι ονομάζουμε Ευκλείδεια διαίρεση και τέλεια διαίρεση; Όταν δοθούν δύο φυσικοί αριθμοί Δ και δ, τότε υπάρχουν δύο άλλοι φυσικοί αριθμοί π και υ, έτσι ώστε να ισχύει: Δ = δ π + υ. Ο αριθμός Δ λέγεται
0x2 = 2. = = δηλαδή η f δεν. = 2. Άρα η συνάρτηση f δεν είναι συνεχής στο [0,3]. Συνεπώς δεν. x 2. lim f (x) = lim (2x 1) = 3 και x 2 x 2
![0x2 = 2. = = δηλαδή η f δεν. = 2. Άρα η συνάρτηση f δεν είναι συνεχής στο [0,3]. Συνεπώς δεν. x 2. lim f (x) = lim (2x 1) = 3 και x 2 x 2 0x2 = 2. = = δηλαδή η f δεν. = 2. Άρα η συνάρτηση f δεν είναι συνεχής στο [0,3]. Συνεπώς δεν. x 2. lim f (x) = lim (2x 1) = 3 και x 2 x 2](/thumbs/59/43483993.jpg) ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 8: ΘΕΩΡΗΜΑ BOLZANO - ΠΡΟΣΗΜΟ ΣΥΝΑΡΤΗΣΗΣ - ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ - ΘΕΩΡΗΜΑ ΜΕΓΙΣΤΗΣ ΚΑΙ ΕΛΑΧΙΣΤΗΣ ΤΙΜΗΣ - ΣΥΝΟΛΟ ΤΙΜΩΝ ΣΥΝΕΧΟΥΣ ΣΥΝΑΡΤΗΣΗΣ
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 8: ΘΕΩΡΗΜΑ BOLZANO - ΠΡΟΣΗΜΟ ΣΥΝΑΡΤΗΣΗΣ - ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ - ΘΕΩΡΗΜΑ ΜΕΓΙΣΤΗΣ ΚΑΙ ΕΛΑΧΙΣΤΗΣ ΤΙΜΗΣ - ΣΥΝΟΛΟ ΤΙΜΩΝ ΣΥΝΕΧΟΥΣ ΣΥΝΑΡΤΗΣΗΣ
2ογελ ΣΥΚΕΩΝ 2ογελ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β Λυκει(ου ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ
 ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β Λυκει(ου ο ΓΕΛ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β ΛΥΚΕΙΟΥ ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΣΧΟΛΙΚΟ ΕΤΟΣ -4 ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Επιμέλεια: ΧΑΛΑΤΖΙΑΝ ΠΑΥΛΟΣ
ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β Λυκει(ου ο ΓΕΛ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β ΛΥΚΕΙΟΥ ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΣΧΟΛΙΚΟ ΕΤΟΣ -4 ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Επιμέλεια: ΧΑΛΑΤΖΙΑΝ ΠΑΥΛΟΣ
Εισαγωγικά. 1 η Εβδομάδα. Κάθε Τρίτη (17:00-20:00) και Τετάρτη (13:00 15:00) στην αίθουσα Ι5. 4 ώρες Θεωρία (ΤΡ : 1η-2η ώρα, ΤΕ : 1η-2η ώρα)
 ΜΥΥ204 Διακριτά Μαθηματικά Μθ άι Εισαγωγικά 1 η Εβδομάδα Άνοιξη 2015 Τμήμα Μηχανικών Η/Υ & Πληροφορικής Παν. Ιωαννίνων Μερικά Οργανωτικά Θέματα ιδάσκων: ιαλέξεις: Κάθε Τρίτη (17:00-20:00) και Τετάρτη (13:00
ΜΥΥ204 Διακριτά Μαθηματικά Μθ άι Εισαγωγικά 1 η Εβδομάδα Άνοιξη 2015 Τμήμα Μηχανικών Η/Υ & Πληροφορικής Παν. Ιωαννίνων Μερικά Οργανωτικά Θέματα ιδάσκων: ιαλέξεις: Κάθε Τρίτη (17:00-20:00) και Τετάρτη (13:00
Για την κατανόηση της ύλης αυτής θα συμβουλευθείτε επίσης το: βοηθητικό υλικό που υπάρχει στη
 ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ 4 η Ημερομηνία Αποστολής στον Φοιτητή: Φεβρουαρίου Ημερομηνία παράδοσης της Εργασίας: 6 Μαρτίου Πριν από την λύση κάθε άσκησης καλό είναι να
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ 4 η Ημερομηνία Αποστολής στον Φοιτητή: Φεβρουαρίου Ημερομηνία παράδοσης της Εργασίας: 6 Μαρτίου Πριν από την λύση κάθε άσκησης καλό είναι να
Ψηφιακή Επεξεργασία Σημάτων
 Ψηφιακή Επεξεργασία Σημάτων Ενότητα 8: Μετασχηματισμός Ζ Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μετασχηματισμός Z Μετασχηματισμός Ζ (Ζ-Transform) Χρήσιμα Ζεύγη ΖT και Περιοχές Σύγκλισης (ROC) Ιδιότητες
Ψηφιακή Επεξεργασία Σημάτων Ενότητα 8: Μετασχηματισμός Ζ Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μετασχηματισμός Z Μετασχηματισμός Ζ (Ζ-Transform) Χρήσιμα Ζεύγη ΖT και Περιοχές Σύγκλισης (ROC) Ιδιότητες
Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών
 Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών Οι παρούσες σημειώσεις αποτελούν βοήθημα στο μάθημα Αριθμητικές Μέθοδοι του 5 ου εξαμήνου του ΤΜΜ ημήτρης Βαλουγεώργης Καθηγητής Εργαστήριο Φυσικών
Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών Οι παρούσες σημειώσεις αποτελούν βοήθημα στο μάθημα Αριθμητικές Μέθοδοι του 5 ου εξαμήνου του ΤΜΜ ημήτρης Βαλουγεώργης Καθηγητής Εργαστήριο Φυσικών
a = a a Z n. a = a mod n.
 Αλγεβρα Ι Χειμερινο Εξαμηνο 2017 18 Διάλεξη 1 Ενότητα 1. Πράξεις: Πράξεις στο σύνολο S, ο πίνακας της πράξης, αντιμεταθετικές πράξεις. Προσεταιριστικές πράξεις, το στοιχείο a 1 a 2 a n. Η πράξη «σύνθεση
Αλγεβρα Ι Χειμερινο Εξαμηνο 2017 18 Διάλεξη 1 Ενότητα 1. Πράξεις: Πράξεις στο σύνολο S, ο πίνακας της πράξης, αντιμεταθετικές πράξεις. Προσεταιριστικές πράξεις, το στοιχείο a 1 a 2 a n. Η πράξη «σύνθεση
ΜΑΘΗΜΑΤΙΚΑ - Γ ΓΥΜΝΑΣΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ - Γ ΓΥΜΝΑΣΙΟΥ ΜΕΡΟΣ Α': ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ ο: Αλγεβρικές παραστάσεις Παράγραφος A..: Πράξεις με πραγματικούς αριθμούς (επαναλήψεις συμπληρώσεις) Β: Πράξεις με μονώνυμα Τα σημαντικότερα σημεία
ΜΑΘΗΜΑΤΙΚΑ - Γ ΓΥΜΝΑΣΙΟΥ ΜΕΡΟΣ Α': ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ ο: Αλγεβρικές παραστάσεις Παράγραφος A..: Πράξεις με πραγματικούς αριθμούς (επαναλήψεις συμπληρώσεις) Β: Πράξεις με μονώνυμα Τα σημαντικότερα σημεία
Μαθηματικά Γ Γυμνασίου
 Α λ γ ε β ρ ι κ έ ς π α ρ α σ τ ά σ ε ι ς 1.1 Πράξεις με πραγματικούς αριθμούς (επαναλήψεις συμπληρώσεις) A. Οι πραγματικοί αριθμοί και οι πράξεις τους Διδακτικοί στόχοι Θυμάμαι ποιοι αριθμοί λέγονται
Α λ γ ε β ρ ι κ έ ς π α ρ α σ τ ά σ ε ι ς 1.1 Πράξεις με πραγματικούς αριθμούς (επαναλήψεις συμπληρώσεις) A. Οι πραγματικοί αριθμοί και οι πράξεις τους Διδακτικοί στόχοι Θυμάμαι ποιοι αριθμοί λέγονται
Γ. Ν. Π Α Π Α Δ Α Κ Η Σ Μ Α Θ Η Μ Α Τ Ι Κ Ο Σ ( M S C ) ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ. ΠΡΟΓΡΑΜΜΑ: Σπουδές στις Φυσικές Επιστήμες
 Γ. Ν. Π Α Π Α Δ Α Κ Η Σ Μ Α Θ Η Μ Α Τ Ι Κ Ο Σ ( M S C ) ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΠΡΟΓΡΑΜΜΑ: Σπουδές στις Φυσικές Επιστήμες ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΦΥΕ10 (Γενικά Μαθηματικά Ι) ΠΕΡΙΕΧΕΙ ΤΙΣ
Γ. Ν. Π Α Π Α Δ Α Κ Η Σ Μ Α Θ Η Μ Α Τ Ι Κ Ο Σ ( M S C ) ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΠΡΟΓΡΑΜΜΑ: Σπουδές στις Φυσικές Επιστήμες ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΦΥΕ10 (Γενικά Μαθηματικά Ι) ΠΕΡΙΕΧΕΙ ΤΙΣ
y 1 (x) f(x) W (y 1, y 2 )(x) dx,
 Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 07/1/017 Μέρος 1ο: Μη Ομογενείς Γραμμικές Διαφορικές Εξισώσεις Δεύτερης Τάξης Θεωρούμε τη γραμμική μή-ομογενή διαφορική εξίσωση y + p(x) y + q(x) y = f(x), x
Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 07/1/017 Μέρος 1ο: Μη Ομογενείς Γραμμικές Διαφορικές Εξισώσεις Δεύτερης Τάξης Θεωρούμε τη γραμμική μή-ομογενή διαφορική εξίσωση y + p(x) y + q(x) y = f(x), x
Κεφάλαιο 3.1 Εξισώσεις 1 ου Βαθμού Επιμέλεια Σημειώσεων: Ντάνος Γιώργος ΚΕΦΑΛΑΙΟ 3.1 ΕΞΙΣΩΣΕΙΣ 1 ΟΥ ΒΑΘΜΟΥ 1
 Κεφάλαιο 3.1 Εξισώσεις 1 ου Βαθμού Επιμέλεια Σημειώσεων: Ντάνος Γιώργος ΚΕΦΑΛΑΙΟ 3.1 ΕΞΙΣΩΣΕΙΣ 1 ΟΥ ΒΑΘΜΟΥ 1 Εξίσωση πρώτου βαθμού ή πρωτοβάθμια εξίσωση με άγνωστο x ονομάζεται κάθε εξίσωση της μορφής
Κεφάλαιο 3.1 Εξισώσεις 1 ου Βαθμού Επιμέλεια Σημειώσεων: Ντάνος Γιώργος ΚΕΦΑΛΑΙΟ 3.1 ΕΞΙΣΩΣΕΙΣ 1 ΟΥ ΒΑΘΜΟΥ 1 Εξίσωση πρώτου βαθμού ή πρωτοβάθμια εξίσωση με άγνωστο x ονομάζεται κάθε εξίσωση της μορφής
1.3 Συστήματα γραμμικών εξισώσεων με ιδιομορφίες
 Κεφάλαιο Συστήματα γραμμικών εξισώσεων Παραδείγματα από εφαρμογές Παράδειγμα : Σε ένα δίκτυο (αγωγών ή σωλήνων ή δρόμων) ισχύει ο κανόνας των κόμβων όπου το άθροισμα των εισερχόμενων ροών θα πρέπει να
Κεφάλαιο Συστήματα γραμμικών εξισώσεων Παραδείγματα από εφαρμογές Παράδειγμα : Σε ένα δίκτυο (αγωγών ή σωλήνων ή δρόμων) ισχύει ο κανόνας των κόμβων όπου το άθροισμα των εισερχόμενων ροών θα πρέπει να
Παραδείγματα Ιδιοτιμές Ιδιοδιανύσματα
 Παραδείγματα Ιδιοτιμές Ιδιοδιανύσματα Παράδειγμα Να βρείτε τις ιδιοτιμές και τα αντίστοιχα ιδιοδιανύσματα του πίνακα A 4. Επίσης να προσδιοριστούν οι ιδιοχώροι και οι γεωμετρικές πολλαπλότητες των ιδιοτιμών.
Παραδείγματα Ιδιοτιμές Ιδιοδιανύσματα Παράδειγμα Να βρείτε τις ιδιοτιμές και τα αντίστοιχα ιδιοδιανύσματα του πίνακα A 4. Επίσης να προσδιοριστούν οι ιδιοχώροι και οι γεωμετρικές πολλαπλότητες των ιδιοτιμών.
