METODE INTELIGENTE DE REZOLVARE A PROBLEMELOR REALE. Laura Dioşan Tema 2
|
|
|
- Καλλιστώ Καραμανλής
- 8 χρόνια πριν
- Προβολές:
Transcript
1 METODE INTELIGENTE DE REZOLVARE A PROBLEMELOR REALE Laura Dioşan Tema 2
2 Procesarea imaginilor De ce? Îmbunătăţirea calităţii imaginilor Reducerea zgomotolui şi a altor defecte Evidenţierea anumitor zone Determinarea contururilor Extragerea de informaţii Aplicaţii Recunoaşterea caracterelor Recunoaşterea amprentelor Prelucrarea imaginilor medicale Prelucrarea imaginilor din satelit
3 Procesarea imaginilor Captarea imaginilor şi reprezentarea lor Operaţii asupra imaginilor Operaţii geometrice Operaţii de îmbunătăţire Operaţii de comprimare Extragerea de informaţii relevante din imagini
4 Captarea imaginilor şi reprezentarea lor Captare Foto Video Reprezentare În domeniul spaţial (geometric) Imaginea = un ansamblu de valori plasate dupa o formă spaţială (regulată sau nu) de dimensiune supra-unitară (plan, spaţiu, dar nu dreaptă) Matrice de pixeli (picture elemnt) Reprezentare intuitivă dpdv al ochiului uman În domeniul frecvenţelor (spectral) Imaginea = un ansamblu de frecvenţe care compun imaginea (culoare frecvenţă lungime de undă (IP) amplitudine) Imaginea = semnal bidimensional Grafic, pe OX, OY se află distribuţia frecvenţelor pe cele 2 axe ale imaginii, iar culoarea pixelilor va reprezenta amplitudinea (mai deschis înseamnă amplitudine superioară) Reprezentare f. utilă în procesele de analiză, comprimare şi prelucrare a imaginilor
5 Captarea imaginilor şi reprezentarea lor domeniul spaţial Imaginea = ansamblu de pixeli Tipologia imaginilor în domeniul spaţial (geometric) După valoarea unui pixel Imagini scalare orice valoare este un scalar (intensitatea luminoasă, distanţa, temperatura) imagini monocrome (binare) 0/1 imagini alb-negru (cu nivele de gri) 8 biţi 0 negru 255 alb Imagini vectoriale orice valoare este un vector; imaginea vectorială = sandwich de imagini scalare Imagini color vectori de 3 componente Imagini satelitare vectori de componente Imagini termografice vectori de 2-5 componente în bandă de infraroşu
6 Captarea imaginilor şi reprezentarea lor domeniul spaţial Imagini color vectori de 3 componente Modelul RGB (Red-Green-Blue) (0,0,0) negru (255, 255, 255) alb Modelul HSI (Hue-Saturation-Intensity) Nuanţa unghiul culorii în cercul de culori (0-360 ) Saturaţia puritatea culorii (procentual) Intensitatea Modelul CMY (Cyan-Magenta-Yellow) (0,0,0) alb (255,255,255) negru Conversii între modele
7 Captarea imaginilor şi reprezentarea lor domeniul spaţial Tipologia imaginilor în domeniul spaţial (geometric) După semnificaţia valorilor Imagini de intensitate valori DP cu mărimea fizică măsurată în scenă Imagini indexate valorile sunt indici (adrese) într-un tabel asociat imaginii, în care se găseşte informaţia de intensitate
8 Captarea imaginilor şi reprezentarea lor domeniul spaţial Pp. o imagine de dimensiune MxN f ij valoarea pixelului de pe linia i şi coloana j P mulţimea tuturor pixelilor Vecinătăţi Pt. un pixel p situat la poziţia (i,j) Vecini ortogonali: p 1 (i-1,j), p 2 (i+1,j), p 3 (i,j-1), p 4 (i, j+1) Formează ansamblul N 4 (p) Vecini diagonali p 5 (i-1,j-1), p 6 (i-1,j+1), p 7 (i+1,j-1), p 8 (i+1,j+1) formează ansamblul N D (p) N 8 (p)=n 4 (p) U N D (p) Conectivităţi 2 pixeli p 1 (i 1,j 1 ) şi p 2 (i 2,j 2 ) se află în relaţie de k-conectivitate dacă p 1 єn k (p 2 ) sau p 2 єn k (p 1 ), k є {4,8} Drum de lungime n mulţimea de pixeli D n ={p 1,p 2,...,p n } a.î. p i se află în relaţie de conectivitate cu p i+1, i=1,2,...,n-1 Pixelii p şi q sunt conectaţi dacă există un drum între ei Regiune set de pixeli conectaţi
9 Captarea imaginilor şi reprezentarea lor domeniul spaţial Metrici între 2 pixeli p 1 (i 1,j 1 ) şi p 2 (i 2,j 2 ) Distanţa Euclideană d(p 1,p 2 )=[(i 1 -i 2 ) 2 +(j 1 -j 2 ) 2 ] 1/2 Distanţa Manhattan d 4 (p 1,p 2 )= i 1 -i 2 + j 1 -j 2 N 4 (p)={qєp a.î. d 4 (p,q) 1} Distanţa jocului de şah d 8 (p 1,p 2 )=max( i 1 -i 2, j 1 -j 2 ) N 8 (p)={qєp a.î. d 8 (p,q) 1}
10 Captarea imaginilor şi reprezentarea lor domeniul frecvenţelor Imaginea = ansamblu de frecvenţe Transformarea unei imagini din domeniul spaţial în domeniul spectral Serii Fourier Matrice de pixeli matrice de frecvenţe (lungimi de undă) Orice undă (sinusoidală) poate fi descompusă într-o sumă de mai multe sinusoidale
11 Captarea imaginilor şi reprezentarea lor Operaţii asupra imaginilor Operaţii geometrice Operaţii de îmbunătăţire Operaţii de comprimare Operaţii de segmentare Operaţii de restaurare Extragerea de informaţii relevante din imagini
12 Operaţii geometrice Pentru reprezentarea spaţială a imaginilor Nu modifică valorile pixelilor (compoziţia) Modifică aşezarea lor spaţială (structura) Translaţie Modificarea după o traiectorie dreaptă a coordonatelor unui pixel Rotaţie x =x+tx y =y+ty Modificarea după o traiectorie circulară a coordonatelor unui pixel Coordonate carteziene coordonate polare x=r cos(ө) y=r sin(ө) x = r cos(ө+φ) y = r sin(ө+φ) Oglindire Faţă de o axă de simetrie
13 Operaţii de îmbunătăţire Îmbunătăţirea calităţii imaginilor Originale sau nu Prin accentuarea unor caracteristici Muchii Contururi Contrast Nu modifică cantitatea de informaţie din imagine Modificarea valorii unor pixeli Reducerea degradărilor perceptuale sau aleatoare: Contrast scăzut Imagine supra- sau sub-expusă Zgomot suprapus peste semnalul util
14 Restaurare Reducerea degradărilor deterministe Mişcare Lipsa focalizării Defecte optice
15 Segmentare Descompunerea imaginii în elementele componente
16 Compresie Reducerea volumului de date necesare reprezentării informaţiei dintr-o imagine
17 Operaţii de îmbunătăţire Pentru reprezentarea spaţială În funcţie de numărul de pixeli din imaginea iniţială folosiţi pentru calculul valorii unui pixel în imaginea prelucrată Operaţii punctuale 1 1 Operaţii de vecinătate (locale) k 1 Operaţii integrale (unitare) nxm 1
18 Operaţii de îmbunătăţire Operaţii punctuale 1 1 g(x,y)=ø(f(x,y)) Negativarea imaginilor Modificarea contrastului Decuparea
19 Operaţii de îmbunătăţire Operaţii punctuale 1 1 Negativarea imaginilor Ø(x)=(L-1)-x, de obicei L = 256 Ø((R,G,B))=((L-1)-R,(L-1)-G,(L-1)-B)) Utilitate Imagini negative (de tip peliculă)
20 Operaţii de îmbunătăţire Operaţii punctuale 1 1 Modificarea contrastului Accentuarea contrastului Pantă subunitară apropierea nivelelor de gri Pantă supraunitară depărtarea nivelelor de gri Caz particular: întinderea maximă a contrastului Nivelele de gri din [a,b] vor fi distanţate Restul nivelelor de gri vor fi înlocuite cu alb, respectiv negru Caz particular: binarizarea (a = b)
21 Operaţii de îmbunătăţire Operaţii punctuale 1 1 Decuparea Cu păstrarea fundalului Fără păstrarea fundalului Utilitate decuparea regiunilor de temperatură joasă reprezentate de nori din imaginile obţinute de un satelit meteo
22 Operaţii de îmbunătăţire Operaţii de vecinătate (locale) k 1 În funcţie de scop: op. care vizează reducerea zgomotului sau a altor defecte (filtrare) filtre trece-jos op. care vizează accentuarea detaliilor (evidenţierea muchiilor, a contururilor, etc) filtre trece-sus În funcţie de tip op. liniare combinaţii liniare între pixeli vecini op. neliniare combinaţii complexe între pixeli
23 Operaţii de îmbunătăţire Operaţii de vecinătate (locale) k 1 operaţii de filtrare Tehnici de filtrare Filtrare prin tehnica ferestrei glisante convoluţie bidimensională Filtru = mască de filtrare (convoluţie) = formă + coeficienţi + origine = kernel Convoluţie = schimbarea intensităţii unui pixel a.î. să reflecte intensitatea pixelilor vecini Filtrare prin estimare statistică Filtrare prin clustering Filtre liniare noua valoare a pixelui = combinaţie liniară a mai multor pixeli din imaginea originală (principiul superpoziţiei) g(m,n) = (k,l)єw w kl *f(m-k,n-l), unde W o structură de puncte vecinătate w kl coeficienţii filtrului (tehnica ferestri glisante) Tipologie Filtre de netezire Suma coeficienţilor = 1 Filtru de mediere Toţi coeficienţii sunt egali (=1/k 2 ) Filtre de detectare a contururilor filtre trece-sus Suma coeficienţilor = 0 Filtre de accentuare a contrastelor Filtre derivative
24 Operaţii de îmbunătăţire Operaţii de vecinătate (locale) k 1 operaţii de filtrare Filtre neliniare Tehnica ferestrei glisante ordonarea pixelilor Tipologie Filtre de ordine Filtru median eliminarea zgomotului sare şi piper Filtru de minim Filtru de maxim Filtre adaptive modificarea formei şi a coeficienţilor ferestrei de filtrare Filtre bazate pe distanţă (relativă) coeficienţii se calculează în funcţie de distanţa dintre punctul respectiv şi un punct fix Filtre bazate pe orientare fereastra are formă liniară, orientată după o anumită direcţie Filtre distanţă-direcţie combinaţia celor 2 filtre precedente
25 Operaţii de îmbunătăţire Operaţii integrale (unitare) nxm 1 Egalizarea histogramei Scop: manipularea contrastului Transformarea Fourier discretă Transformarea cosinus discretă Transformarea sinus discretă Transformarea Walsh-Hadamard Transformarea Karhaunen-Loeve
26 Operaţii integrale (unitare) nxm 1 Egalizarea histogramei Histograma nivelurilor de gri O funcţie care asociază fiecărui nivel de gri prezent în imagine frecvenţa sa (relativă) de apariţie Estimarea densităţii de probabilitate Utilitate Îmbunătăţirea constrastului Îmbunătăţirea luminozităţii segmentarea imaginii Ne-ajunsuri Lipsa informaţiilor privind locaţia pixelilor poziţia relativă a pixelilor
27 Operaţii integrale (unitare) nxm 1 Egalizarea histogramei Egalizarea histogramei reprezintă o operaţie de accentuare a contrastului şi are ca scop obţinerea unei histograme uniforme Algoritm Se calculează histograma h(x) imaginii Se calculează histograma cumulativă h c (x) Se calculează noile nivele de gri x =(h c (x)-h cmin )/(h cmax -h cmin )*(L-1)+0.5
28 Extragerea atributelor Metodă de captare a conţinutului vizual al imaginilor în vederea indexării lor Atribute vizuale - tipologie În funcţie de domeniu: Generale Ex. Culoare, textură, formă Pot fi considerate la nivelul unui pixel unei regiuni de pixeli întregii imagini Specifice Amprente Feţe umane În funcţie de modul de extragere De nivel primar Extrase direct din imagine De nivel înalt Determinate pe baza atributelor de nivel primar Exemple de atribute Contururi (margini ale unor regiuni) Intersecţii (puncte de interes, colţuri) Regiuni de interes Creste
29 Extragerea atributelor Atribute vizuale Generale Culoare reprezentată prin diferite modele atribute Histograma culorii pixelilor Histograma gradienţilor orientaţi (Histogram of oriented gradients)
30 Extragerea atributelor Atribute vizuale Generale Culoare Histograma culorii pixelilor Procentul fiecărei culori care apare în imagine (h k, k=1,2,...,k, K nr. de culori) nu ţine cont de poziţia culorilor (se pierde informaţia regională) partiţionarea imaginii în regiuni şi determinarea histogramelor regionale
31 Extragerea atributelor Atribute vizuale Generale Culoare Histograma gradienţilor orientaţi (Histogram of oriented gradients HOG) Determinare Nivele de calcul Îmbunătăţiri Parametri Instrumente
32 Extragerea atributelor Atribute vizuale Generale Culoare HOG determinare Gradientul unei imagini O schimbare direcţională a intensităţii sau culorii întro imagine Este orientat în direcţia în care apare cea mai rapidă schimbare de culaore Magnitudinea gradientului
33 Extragerea atributelor Atribute vizuale Generale Culoare HOG determinare Gradientul unei imagini Se poate aproxima magnitudinea gradientului în cazul discret (domeniul spaţial al imaginii) De ordin I operatori Sobel algoritmul Cany Schar Roeberts Cross Prewitt Costella De ordin II: Operatori Laplacieni ai Gaussianului
34 Extragerea atributelor Atribute vizuale Generale Culoare HOG determinare Gradient = vectori orientaţi în direcţia celor mai semnificative schimbări de culoare Paşi Se calculează magnitudinea fiecărui piexel Se calculează gradientul orientat pentru fiecare pixel Se calculează histograma gradienţilor orientaţi
35 Extragerea atributelor Atribute vizuale Generale Culoare HOG determinare Pas1: se calculează magnitudinea gradientului fiecărui piexel De ce? Magnitudinea = cât de abruptă este schimbarea Cum? Pentru o imagine I de dimensiune nxm, se efectuează o convoluţie pe Ox cu un anumit filtru-mască Dx Ex. Dx = [-1,0,1], Ix = Dx*I o convoluţie pe Oy cu un anumit filtr-mască Dy Ex. Dy = [-1,0,1] T, Iy = Dy*I
36 Extragerea atributelor Atribute vizuale Generale Culoare HOG determinare Pas2: Se calculează orientarea gradientului pentru fiecare pixel De ce? Orientarea direcţia modificărilor Cum? =arctan(iy/ix) radians se transformă unghiul din radiani în grade =*180/ [-180,180] se determină gradientul: cu semn - se translatează unghiul din [-180,180] în [0,360] fără semn - se translatează unghiul din [-180,180] în [0,180] se obţine o matrice O cu nxm valori
37 Extragerea atributelor Atribute vizuale Generale Culoare HOG - determinare Pas3: se calculează histograma gradienţilor orientaţi folosind matricea O Se împarte domeniul unghiului orientării D în k sectoare egale D = [0.360] sau D = [0,180] Primul sector va cuprinde unghiuri între 0 şi D /k, Al doilea sector va cuprinde unghiuri între D /k şi 2* D /k ş.a.m.d. k=4,8,9,16,18,36,... Pentru fiecare sector se numără pixelii a căror orientare a gradientului cade în sectorul respectiv Numărul de pixeli din fiecare sector se poate pondera cu Voturi binare aparţine (1) sau nu (0) acelui sector Voturi bazate pe magnitudinea gradientului Voturi bazate pe pătratul magnitudinii Voturi bazate pe rădăcina pătrată a magnitudinii Se reprezintă grafic valorile obţinute Pe axa Ox se trec sectoarele domeniului Pe axa Oy se trece numărul de pixeli (ponderat) din fiecare sector
38 Extragerea atributelor Atribute vizuale Generale Culoare HOG Nivele de calcul La nivelul întregii imagini La nivelul unei celule a imaginii Câte imagini, atâtea histograme concatenarea histogramelor Îmbunătăţiri Considerarea unor blocuri de celule R-HOG C-HOG Normalizarea la nivel de bloc pentru a ţine cont de culorile vecine L2-norm L1-Norm
39 Extragerea atributelor Atribute vizuale Generale Culoare HOG Parametri Scara gradientului Dimensiunea unei celule/unui bloc Numărul de sectoare Procentul suprapunerii blocurilor Instrumente OpenCV PMT Altele
40 Extragerea atributelor Atribute vizuale Generale Textură Caracteristica tactilă sau vizuală a unei suprafeţe Elementele componente = texteli Forme geometrice care se repetă pe o suprafaţă Tipologie Texturi slabe interacţii slabe între texteli Texturi puternice > interacţii puternice între texteli Cuantifică Diferenţele între nivelurile de gri (contrastul) Mărimea regiunii unde apar modificări (fereastră) Direcţia sau lipsa ei
41 Extragerea atributelor Atribute vizuale Generale Textură Poate fi analizată prin metode Sintactice (structurale) relaţiile spaţiale din textură ~ gramatică (texteli simboluri terminale, relaţiile reguli de transformare) Statistice De ordin I calculate la nivel de pixel: Media µ= k=1,2,...,k k*p k Varianţa σ 2 = k=1,2,...,k (k-µ) 2 *p k Turtirea (skewness) γ 3 =1/ σ 3 k=1,2,...,k (k-µ) 3 *p k Excesul (kurtosis) γ 4 =1/ σ 4 k=1,2,...,k (k-µ) 4 *p k -3, unde p k =h k / k=1,2,...,k h k procentul fiecărei culori care apare în imagine (h k, k=1,2,...,k, K nr. de culori)
42 Extragerea atributelor Atribute vizuale Generale Textură Poate fi analizată prin metode Sintactice Statistice De ordin II calculate la nivelul unei vecinătăţi de 2 pixeli Matricea de co-ocurenţă a nivelurilor de gri C(i,j)=cardinal{((x 1,y 1 ), (x 2,y 2 )) pentru care f(x 1,y 1 )=i şi f(x 2,y 2 )=j, (x 2,y 2 ) = (x!,y 1 )+(d*cosө,d*sinө)}, i,j=1,2,...,k Energia i=1,2,...,k j=1,2,...,k C(i,j) 2 Inerţia i=1,2,...,k j=1,2,...,k (i-j) 2 C(i,j) Corelaţia i=1,2,...,k j=1,2,...,k (ij)c(i,j)-µ i µ j /σ i σ j Momentul diferenţei i=1,2,...,k j=1,2,...,k C(i,j)/(1+(i-j) 2 ) Entropia i=1,2,...,k j=1,2,...,k C(i,j)logC(i,j) Filtre Gabor Atribute de tip Markov unde: µ i = i=1,2,...,k i j=1,2,...,k C(i,j) µ j = j=1,2,...,k j i=1,2,...,k C(i,j) σ i = i=1,2,...,k (i-µ i ) 2 j=1,2,...,k C(i,j) σ j = i=1,2,...,k (j-µ J ) 2 j=1,2,...,k C(i,j)
43 Extragerea atributelor Atribute vizuale Generale Formă Metode bazate pe Regiuni Contur
44 Extragerea atributelor Atribute vizuale Generale Formă Metode bazate pe Regiuni Momentele geometrice Momentele centrale şi momentele centrale normalizate Invarianţii momentului Momentele Zernike şi Legendre Momentele complexe
45 Extragerea atributelor Atribute vizuale Generale Formă Metode bazate pe Contur Circularitatea cir=4pa/p 2 Rata aspectului ar=(p1+p2)/c Iregularitatea unghiului de discontinuitate ( Ө i - Ө i+1 /2π(n-2)) 1/2 Iregularitatea lungimii lir= L i -L i+1 /K, unde K=2P pt n>3 şi K=P pt n=3 Complexitatea com=10-3/n
46 Extragerea atributelor Detecţia contururilor Contururile sunt acolo unde apar schimbări de culoare Schimbările de direcţie ale unei funcţii pot fi detectate cu ajutorul derivatei I cele mai mari schimbări apar acolo unde derivata I are magnitudine (normă, mărime, dimensiune) maximă derivata II = 0
47 Extragerea atributelor Algoritmi pentru extragerea atributelor Scale-invariant feature transform (SIFT) Biblioteca OpenCV Speeded Up Robust Features (SURF) opencv Gradient Location and Orientation Histogram (GLOH) Local Energy based Shape Histogram (LESH)
48 Extragerea atributelor Trebuie ghidată cf. următoarelor principii Atributele trebuie să conţină suficientă informaţie despre imagine şi nu trebuie folosite informaţii specifice în procesul de extracţie Atributele trebuie să fie uşor calculabile imagini mari şi numeroase
49 Compresia imaginilor Compresie la nivel de pixel Compresie predictivă (bazată pe o vecinătate) Compresie cu transformate Compresie cu fractali, etc Segmentarea imaginilor
50 VC_Workshop/presentations/pdf/daniela_t utorial2.pdf
prin egalizarea histogramei
 Lucrarea 4 Îmbunătăţirea imaginilor prin egalizarea histogramei BREVIAR TEORETIC Tehnicile de îmbunătăţire a imaginilor bazate pe calculul histogramei modifică histograma astfel încât aceasta să aibă o
Lucrarea 4 Îmbunătăţirea imaginilor prin egalizarea histogramei BREVIAR TEORETIC Tehnicile de îmbunătăţire a imaginilor bazate pe calculul histogramei modifică histograma astfel încât aceasta să aibă o
prin operaţii punctuale
 Lucrarea 3 Îmbunătăţirea imaginilor prin operaţii punctuale BREVIAR TEORETIC Termenul general de îmbunătăţire a imaginilor se referă la o clasă largă de operaţii, ce au ca scop mărirea detectabilităţii
Lucrarea 3 Îmbunătăţirea imaginilor prin operaţii punctuale BREVIAR TEORETIC Termenul general de îmbunătăţire a imaginilor se referă la o clasă largă de operaţii, ce au ca scop mărirea detectabilităţii
Metode iterative pentru probleme neliniare - contractii
 Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Planul determinat de normală şi un punct Ecuaţia generală Plane paralele Unghi diedru Planul determinat de 3 puncte necoliniare
 1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
OPERATII DE PRELUCRARE A IMAGINILOR C. VERTAN
 OPERATII DE PRELUCRARE A IMAGINILOR Prelucrare = Black Box Image In, Image Out Analiza imaginilor este Image In, Description Out Tipuri de operatii de prelucrare Clasificare dupa numarul de pixeli din
OPERATII DE PRELUCRARE A IMAGINILOR Prelucrare = Black Box Image In, Image Out Analiza imaginilor este Image In, Description Out Tipuri de operatii de prelucrare Clasificare dupa numarul de pixeli din
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate.
 Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
MARCAREA REZISTOARELOR
 1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
Sisteme de Recunoastere a Formelor Laborator 3-4 Histograma Orientarilor Gradientilor
 Sisteme de Recunoastere a Formelor Laborator 3-4 Histograma Orientarilor Gradientilor 1. Obiectie Descriptorii de tip histograma a orientarii gratientilor, sau descriptori HOG, sunt descriptori de trasatori
Sisteme de Recunoastere a Formelor Laborator 3-4 Histograma Orientarilor Gradientilor 1. Obiectie Descriptorii de tip histograma a orientarii gratientilor, sau descriptori HOG, sunt descriptori de trasatori
Sisteme de Recunoastere a Formelor Laborator 5 Histograma Orientarilor Gradientilor
 Sisteme de Recunoastere a Formelor Laborator 5 Histograma Orientarilor Gradientilor 1. Obiectie Descriptorii de tip histograma a orientarii gratientilor, sau descriptori HOG, sunt descriptori de trasatori
Sisteme de Recunoastere a Formelor Laborator 5 Histograma Orientarilor Gradientilor 1. Obiectie Descriptorii de tip histograma a orientarii gratientilor, sau descriptori HOG, sunt descriptori de trasatori
Sisteme diferenţiale liniare de ordinul 1
 1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
Definiţia generală Cazul 1. Elipsa şi hiperbola Cercul Cazul 2. Parabola Reprezentari parametrice ale conicelor Tangente la conice
 1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
LIMITARILE FILTRARII LINIARE A IMAGINILOR
 La ce folosea filtrarea liniara de netezire? LIMITARILE FILTRARII LINIARE A IMAGINILOR Reducerea efectelor zgomotului aditiv, de tip Gaussian suprapus imaginii. ZAGA : f ( l, = f0( l, + z( l, z( l, N(
La ce folosea filtrarea liniara de netezire? LIMITARILE FILTRARII LINIARE A IMAGINILOR Reducerea efectelor zgomotului aditiv, de tip Gaussian suprapus imaginii. ZAGA : f ( l, = f0( l, + z( l, z( l, N(
Zgomotul se poate suprapune informaţiei utile în două moduri: g(x, y) = f(x, y) n(x, y) (6.2)
 Lucrarea 6 Zgomotul în imagini BREVIAR TEORETIC Zgomotul este un semnal aleator, care afectează informaţia utilă conţinută într-o imagine. El poate apare de-alungul unui lanţ de transmisiune, sau prin
Lucrarea 6 Zgomotul în imagini BREVIAR TEORETIC Zgomotul este un semnal aleator, care afectează informaţia utilă conţinută într-o imagine. El poate apare de-alungul unui lanţ de transmisiune, sau prin
(a) se numeşte derivata parţială a funcţiei f în raport cu variabila x i în punctul a.
 Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Captura imaginilor. este necesară o sursă de lumină (λ: lungimea de undă a sursei)
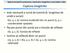 Captura imaginilor este necesară o sursă de lumină (λ: lungimea de undă a sursei) E(x, y, z, λ): lumina incidentă într-un punct (x, y, z coordonatele spațiale) fiecare punct din scenă are o funcție de
Captura imaginilor este necesară o sursă de lumină (λ: lungimea de undă a sursei) E(x, y, z, λ): lumina incidentă într-un punct (x, y, z coordonatele spațiale) fiecare punct din scenă are o funcție de
LIMITARILE FILTRARII LINIARE A IMAGINILOR C. VERTAN
 LIMITARILE FILTRARII LINIARE A IMAGINILOR La ce folosea filtrarea liniara de netezire? Reducerea efectelor zgomotului aditiv, de tip Gaussian suprapus imaginii. ZAGA : f ( l, c) = f0( l, c) + z( l, c)
LIMITARILE FILTRARII LINIARE A IMAGINILOR La ce folosea filtrarea liniara de netezire? Reducerea efectelor zgomotului aditiv, de tip Gaussian suprapus imaginii. ZAGA : f ( l, c) = f0( l, c) + z( l, c)
Metode de interpolare bazate pe diferenţe divizate
 Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
Tehnici de imbunatatire si restaurare a imaginilor
 Tehnici de imbunatatire si restaurare a imaginilor Tehnici de imbunatatire si restaurare a imaginilor... 1 I. Tehnici de imbunatatire si restaurare in domeniul spatial... 3 1. Conversia nivelelor de gri...
Tehnici de imbunatatire si restaurare a imaginilor Tehnici de imbunatatire si restaurare a imaginilor... 1 I. Tehnici de imbunatatire si restaurare in domeniul spatial... 3 1. Conversia nivelelor de gri...
Procesarea Imaginilor
 Procesarea Imaginilor SEGMENTAREA IMAGINILOR Mihai Ivanovici Universitatea Transilvania din Braşov Page 1 of 29 1 Segmentarea reprezintă împărţirea imaginii în zone de interes, după anumite criterii Fiecărui
Procesarea Imaginilor SEGMENTAREA IMAGINILOR Mihai Ivanovici Universitatea Transilvania din Braşov Page 1 of 29 1 Segmentarea reprezintă împărţirea imaginii în zone de interes, după anumite criterii Fiecărui
a n (ζ z 0 ) n. n=1 se numeste partea principala iar seria a n (z z 0 ) n se numeste partea
 Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Integrala nedefinită (primitive)
 nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
Transformate pentru semnale multidimensionale
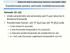 Transformate pentru semnale multidimensionale Semnale 1D: s(t) Unele caracteristici ale semnalului pot fi ușor descrise în domeniul frecvență Transformata Fourier: s(t) S(ω) (sau s(t) S(f t )) unde t este
Transformate pentru semnale multidimensionale Semnale 1D: s(t) Unele caracteristici ale semnalului pot fi ușor descrise în domeniul frecvență Transformata Fourier: s(t) S(ω) (sau s(t) S(f t )) unde t este
Laborator 11. Mulţimi Julia. Temă
 Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Conice. Lect. dr. Constantin-Cosmin Todea. U.T. Cluj-Napoca
 Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
5. FUNCŢII IMPLICITE. EXTREME CONDIŢIONATE.
 5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
Analiza și Prelucrarea Digitală a Semnalelor Video
 Analiza și Prelucrarea Digitală a Semnalelor Video Conf. dr. ing. Radu Ovidiu Preda radu@comm.pub.ro Ș.l. dr. ing. Ionuţ Pirnog ionut@comm.pub.ro Site disciplină: www.comm.pub.ro/preda/apdsv Analiza și
Analiza și Prelucrarea Digitală a Semnalelor Video Conf. dr. ing. Radu Ovidiu Preda radu@comm.pub.ro Ș.l. dr. ing. Ionuţ Pirnog ionut@comm.pub.ro Site disciplină: www.comm.pub.ro/preda/apdsv Analiza și
RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii transversale, scrisă faţă de una dintre axele de inerţie principale:,
 REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
Segmentarea imaginilor
 Lucrarea 0 Segmentarea imaginilor BREVIAR TEORETIC Segmentarea reprezintă împărţirea imaginii în zone de interes, după anumite criterii. Fiecărui pixel i se va atribui o valoare, 0 sau, reprezentând apartenenţa
Lucrarea 0 Segmentarea imaginilor BREVIAR TEORETIC Segmentarea reprezintă împărţirea imaginii în zone de interes, după anumite criterii. Fiecărui pixel i se va atribui o valoare, 0 sau, reprezentând apartenenţa
Esalonul Redus pe Linii (ERL). Subspatii.
 Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
Ecuaţia generală Probleme de tangenţă Sfera prin 4 puncte necoplanare. Elipsoidul Hiperboloizi Paraboloizi Conul Cilindrul. 1 Sfera.
 pe ecuaţii generale 1 Sfera Ecuaţia generală Probleme de tangenţă 2 pe ecuaţii generale Sfera pe ecuaţii generale Ecuaţia generală Probleme de tangenţă Numim sferă locul geometric al punctelor din spaţiu
pe ecuaţii generale 1 Sfera Ecuaţia generală Probleme de tangenţă 2 pe ecuaţii generale Sfera pe ecuaţii generale Ecuaţia generală Probleme de tangenţă Numim sferă locul geometric al punctelor din spaţiu
Curs 14 Funcţii implicite. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi"
 Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Seminar 5 Analiza stabilității sistemelor liniare
 Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].
![Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].](/thumbs/72/67648751.jpg) Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
Curs 2 DIODE. CIRCUITE DR
 Curs 2 OE. CRCUTE R E CUPRN tructură. imbol Relația curent-tensiune Regimuri de funcționare Punct static de funcționare Parametrii diodei Modelul cu cădere de tensiune constantă Analiza circuitelor cu
Curs 2 OE. CRCUTE R E CUPRN tructură. imbol Relația curent-tensiune Regimuri de funcționare Punct static de funcționare Parametrii diodei Modelul cu cădere de tensiune constantă Analiza circuitelor cu
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM 1 electronica.geniu.ro
 Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Componente şi Circuite Electronice Pasive. Laborator 3. Divizorul de tensiune. Divizorul de curent
 Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
Seminariile Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reziduurilor
 Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Lab06: Extragerea trăsăturilor şi selecţia trăsăturilor. Aplicaţie pentru recunoaşterea obiectelor bazată pe formă.
 Lab06: Extragerea trăsăturilor şi selecţia trăsăturilor Aplicaţie pentru recunoaşterea obiectelor bazată pe formă. Aplicație practică a extragerii şi selecţiei trăsăturilor Recunoaşterea celor 4 forme
Lab06: Extragerea trăsăturilor şi selecţia trăsăturilor Aplicaţie pentru recunoaşterea obiectelor bazată pe formă. Aplicație practică a extragerii şi selecţiei trăsăturilor Recunoaşterea celor 4 forme
2.1 Sfera. (EGS) ecuaţie care poartă denumirea de ecuaţia generală asferei. (EGS) reprezintă osferă cu centrul în punctul. 2 + p 2
 .1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
.1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE
 DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
III. Serii absolut convergente. Serii semiconvergente. ii) semiconvergentă dacă este convergentă iar seria modulelor divergentă.
 III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile
 Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Curs 1 Şiruri de numere reale
 Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
5.5. REZOLVAREA CIRCUITELOR CU TRANZISTOARE BIPOLARE
 5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
Aplicaţii ale principiului I al termodinamicii la gazul ideal
 Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Subiecte Clasa a VIII-a
 Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Geometrie computationala 2. Preliminarii geometrice
 Platformă de e-learning și curriculă e-content pentru învățământul superior tehnic Geometrie computationala 2. Preliminarii geometrice Preliminarii geometrice Spatiu Euclidean: E d Spatiu de d-tupluri,
Platformă de e-learning și curriculă e-content pentru învățământul superior tehnic Geometrie computationala 2. Preliminarii geometrice Preliminarii geometrice Spatiu Euclidean: E d Spatiu de d-tupluri,
R R, f ( x) = x 7x+ 6. Determinați distanța dintre punctele de. B=, unde x și y sunt numere reale.
 5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
Algebra si Geometrie Seminar 9
 Algebra si Geometrie Seminar 9 Decembrie 017 ii Equations are just the boring part of mathematics. I attempt to see things in terms of geometry. Stephen Hawking 9 Dreapta si planul in spatiu 1 Notiuni
Algebra si Geometrie Seminar 9 Decembrie 017 ii Equations are just the boring part of mathematics. I attempt to see things in terms of geometry. Stephen Hawking 9 Dreapta si planul in spatiu 1 Notiuni
Examen AG. Student:... Grupa:... ianuarie 2011
 Problema 1. Pentru ce valori ale lui n,m N (n,m 1) graful K n,m este eulerian? Problema 2. Să se construiască o funcţie care să recunoască un graf P 3 -free. La intrare aceasta va primi un graf G = ({1,...,n},E)
Problema 1. Pentru ce valori ale lui n,m N (n,m 1) graful K n,m este eulerian? Problema 2. Să se construiască o funcţie care să recunoască un graf P 3 -free. La intrare aceasta va primi un graf G = ({1,...,n},E)
2. Sisteme de forţe concurente...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...3
 SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
Criptosisteme cu cheie publică III
 Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...4
 SEMINAR 3 MMENTUL FRŢEI ÎN RAPRT CU UN PUNCT CUPRINS 3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere...1 3.1. Aspecte teoretice...2 3.2. Aplicaţii rezolvate...4 3. Momentul forţei
SEMINAR 3 MMENTUL FRŢEI ÎN RAPRT CU UN PUNCT CUPRINS 3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere...1 3.1. Aspecte teoretice...2 3.2. Aplicaţii rezolvate...4 3. Momentul forţei
Erori si incertitudini de măsurare. Modele matematice Instrument: proiectare, fabricaţie, Interacţiune măsurand instrument:
 Erori i incertitudini de măurare Sure: Modele matematice Intrument: proiectare, fabricaţie, Interacţiune măurandintrument: (tranfer informaţie tranfer energie) Influente externe: temperatura, preiune,
Erori i incertitudini de măurare Sure: Modele matematice Intrument: proiectare, fabricaţie, Interacţiune măurandintrument: (tranfer informaţie tranfer energie) Influente externe: temperatura, preiune,
5.1. Noţiuni introductive
 ursul 13 aitolul 5. Soluţii 5.1. oţiuni introductive Soluţiile = aestecuri oogene de două sau ai ulte substanţe / coonente, ale căror articule nu se ot seara rin filtrare sau centrifugare. oonente: - Mediul
ursul 13 aitolul 5. Soluţii 5.1. oţiuni introductive Soluţiile = aestecuri oogene de două sau ai ulte substanţe / coonente, ale căror articule nu se ot seara rin filtrare sau centrifugare. oonente: - Mediul
Proiectarea filtrelor prin metoda pierderilor de inserţie
 FITRE DE MIROUNDE Proiectarea filtrelor prin metoda pierderilor de inserţie P R Puterea disponibila de la sursa Puterea livrata sarcinii P inc P Γ ( ) Γ I lo P R ( ) ( ) M ( ) ( ) M N P R M N ( ) ( ) Tipuri
FITRE DE MIROUNDE Proiectarea filtrelor prin metoda pierderilor de inserţie P R Puterea disponibila de la sursa Puterea livrata sarcinii P inc P Γ ( ) Γ I lo P R ( ) ( ) M ( ) ( ) M N P R M N ( ) ( ) Tipuri
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor X) functia f 1
 Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Profesor Blaga Mirela-Gabriela DREAPTA
 DREAPTA Fie punctele A ( xa, ya ), B ( xb, yb ), C ( xc, yc ) şi D ( xd, yd ) în planul xoy. 1)Distanţa AB = (x x ) + (y y ) Ex. Fie punctele A( 1, -3) şi B( -2, 5). Calculaţi distanţa AB. AB = ( 2 1)
DREAPTA Fie punctele A ( xa, ya ), B ( xb, yb ), C ( xc, yc ) şi D ( xd, yd ) în planul xoy. 1)Distanţa AB = (x x ) + (y y ) Ex. Fie punctele A( 1, -3) şi B( -2, 5). Calculaţi distanţa AB. AB = ( 2 1)
5.4. MULTIPLEXOARE A 0 A 1 A 2
 5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
Subiecte Clasa a VII-a
 lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
a. 11 % b. 12 % c. 13 % d. 14 %
 1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
Curs 4 Serii de numere reale
 Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
 4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
Spatii liniare. Exemple Subspaţiu liniar Acoperire (înfăşurătoare) liniară. Mulţime infinită liniar independentă
 Noţiunea de spaţiu liniar 1 Noţiunea de spaţiu liniar Exemple Subspaţiu liniar Acoperire (înfăşurătoare) liniară 2 Mulţime infinită liniar independentă 3 Schimbarea coordonatelor unui vector la o schimbare
Noţiunea de spaţiu liniar 1 Noţiunea de spaţiu liniar Exemple Subspaţiu liniar Acoperire (înfăşurătoare) liniară 2 Mulţime infinită liniar independentă 3 Schimbarea coordonatelor unui vector la o schimbare
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor
 Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
2 Transformări liniare între spaţii finit dimensionale
 Transformări 1 Noţiunea de transformare liniară Proprietăţi. Operaţii Nucleul şi imagine Rangul şi defectul unei transformări 2 Matricea unei transformări Relaţia dintre rang şi defect Schimbarea matricei
Transformări 1 Noţiunea de transformare liniară Proprietăţi. Operaţii Nucleul şi imagine Rangul şi defectul unei transformări 2 Matricea unei transformări Relaţia dintre rang şi defect Schimbarea matricei
Tratarea numerică a semnalelor
 LUCRAREA 5 Tratarea numerică a semnalelor Filtre numerice cu răspuns finit la impuls (filtre RFI) Filtrele numerice sunt sisteme discrete liniare invariante în timp care au rolul de a modifica spectrul
LUCRAREA 5 Tratarea numerică a semnalelor Filtre numerice cu răspuns finit la impuls (filtre RFI) Filtrele numerice sunt sisteme discrete liniare invariante în timp care au rolul de a modifica spectrul
ANALIZA IMAGINILOR C. VERTAN
 ANALIZA IMAGINILOR ANALIZA IMAGINILOR Titular curs : Prof. Dr. Ing. Constantin VERTAN cvertan@alpha.imag.pub.ro B141 Laborator : As. Dr. Ing. Laura FLOREA lflorea@alpha.imag.pub.ro B141/ B135A Chestiuni
ANALIZA IMAGINILOR ANALIZA IMAGINILOR Titular curs : Prof. Dr. Ing. Constantin VERTAN cvertan@alpha.imag.pub.ro B141 Laborator : As. Dr. Ing. Laura FLOREA lflorea@alpha.imag.pub.ro B141/ B135A Chestiuni
Componente şi Circuite Electronice Pasive. Laborator 4. Măsurarea parametrilor mărimilor electrice
 Laborator 4 Măsurarea parametrilor mărimilor electrice Obiective: o Semnalul sinusoidal, o Semnalul dreptunghiular, o Semnalul triunghiular, o Generarea diferitelor semnale folosind placa multifuncţională
Laborator 4 Măsurarea parametrilor mărimilor electrice Obiective: o Semnalul sinusoidal, o Semnalul dreptunghiular, o Semnalul triunghiular, o Generarea diferitelor semnale folosind placa multifuncţională
Aparate de măsurat. Măsurări electronice Rezumatul cursului 2. MEE - prof. dr. ing. Ioan D. Oltean 1
 Aparate de măsurat Măsurări electronice Rezumatul cursului 2 MEE - prof. dr. ing. Ioan D. Oltean 1 1. Aparate cu instrument magnetoelectric 2. Ampermetre şi voltmetre 3. Ohmetre cu instrument magnetoelectric
Aparate de măsurat Măsurări electronice Rezumatul cursului 2 MEE - prof. dr. ing. Ioan D. Oltean 1 1. Aparate cu instrument magnetoelectric 2. Ampermetre şi voltmetre 3. Ohmetre cu instrument magnetoelectric
Toate subiectele sunt obligatorii. Timpul de lucru efectiv este de 3 ore. Se acordă din oficiu 10 puncte. SUBIECTUL I.
 Modelul 4 Se acordă din oficiu puncte.. Fie numărul complex z = i. Calculaţi (z ) 25. 2. Dacă x şi x 2 sunt rădăcinile ecuaţiei x 2 9x+8 =, atunci să se calculeze x2 +x2 2 x x 2. 3. Rezolvaţi în mulţimea
Modelul 4 Se acordă din oficiu puncte.. Fie numărul complex z = i. Calculaţi (z ) 25. 2. Dacă x şi x 2 sunt rădăcinile ecuaţiei x 2 9x+8 =, atunci să se calculeze x2 +x2 2 x x 2. 3. Rezolvaţi în mulţimea
Problema a II - a (10 puncte) Diferite circuite electrice
 Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
Seria Balmer. Determinarea constantei lui Rydberg
 Seria Balmer. Determinarea constantei lui Rydberg Obiectivele lucrarii analiza spectrului in vizibil emis de atomii de hidrogen si determinarea lungimii de unda a liniilor serie Balmer; determinarea constantei
Seria Balmer. Determinarea constantei lui Rydberg Obiectivele lucrarii analiza spectrului in vizibil emis de atomii de hidrogen si determinarea lungimii de unda a liniilor serie Balmer; determinarea constantei
Vectori liberi Produs scalar Produs vectorial Produsul mixt. 1 Vectori liberi. 2 Produs scalar. 3 Produs vectorial. 4 Produsul mixt.
 liberi 1 liberi 2 3 4 Segment orientat liberi Fie S spaţiul geometric tridimensional cu axiomele lui Euclid. Orice pereche de puncte din S, notată (A, B) se numeşte segment orientat. Dacă A B, atunci direcţia
liberi 1 liberi 2 3 4 Segment orientat liberi Fie S spaţiul geometric tridimensional cu axiomele lui Euclid. Orice pereche de puncte din S, notată (A, B) se numeşte segment orientat. Dacă A B, atunci direcţia
Să se arate că n este număr par. Dan Nedeianu
 Primul test de selecție pentru juniori I. Să se determine numerele prime p, q, r cu proprietatea că 1 p + 1 q + 1 r 1. Fie ABCD un patrulater convex cu m( BCD) = 10, m( CBA) = 45, m( CBD) = 15 și m( CAB)
Primul test de selecție pentru juniori I. Să se determine numerele prime p, q, r cu proprietatea că 1 p + 1 q + 1 r 1. Fie ABCD un patrulater convex cu m( BCD) = 10, m( CBA) = 45, m( CBD) = 15 și m( CAB)
V O. = v I v stabilizator
 Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Examen AG. Student:... Grupa: ianuarie 2016
 16-17 ianuarie 2016 Problema 1. Se consideră graful G = pk n (p, n N, p 2, n 3). Unul din vârfurile lui G se uneşte cu câte un vârf din fiecare graf complet care nu-l conţine, obţinându-se un graf conex
16-17 ianuarie 2016 Problema 1. Se consideră graful G = pk n (p, n N, p 2, n 3). Unul din vârfurile lui G se uneşte cu câte un vârf din fiecare graf complet care nu-l conţine, obţinându-se un graf conex
Scoruri standard Curba normală (Gauss) M. Popa
 Scoruri standard Curba normală (Gauss) M. Popa Scoruri standard cunoaştere evaluare, măsurare evaluare comparare (Gh. Zapan) comparare raportare la un sistem de referință Povestea Scufiței Roşii... 70
Scoruri standard Curba normală (Gauss) M. Popa Scoruri standard cunoaştere evaluare, măsurare evaluare comparare (Gh. Zapan) comparare raportare la un sistem de referință Povestea Scufiței Roşii... 70
Compresia de imagini. Standardul JPEG
 Tehnici de Compresie a Semnalelor Multimedia Lucrare de laborator Compresia de imagini. Standardul JPEG I. Obiectivul lucrării Lucrarea îşi propune familiarizarea cu metodele şi algoritmii utilizaţi în
Tehnici de Compresie a Semnalelor Multimedia Lucrare de laborator Compresia de imagini. Standardul JPEG I. Obiectivul lucrării Lucrarea îşi propune familiarizarea cu metodele şi algoritmii utilizaţi în
* K. toate K. circuitului. portile. Considerând această sumă pentru toate rezistoarele 2. = sl I K I K. toate rez. Pentru o bobină: U * toate I K K 1
 FNCȚ DE ENERGE Fie un n-port care conține numai elemente paive de circuit: rezitoare dipolare, condenatoare dipolare și bobine cuplate. Conform teoremei lui Tellegen n * = * toate toate laturile portile
FNCȚ DE ENERGE Fie un n-port care conține numai elemente paive de circuit: rezitoare dipolare, condenatoare dipolare și bobine cuplate. Conform teoremei lui Tellegen n * = * toate toate laturile portile
CURS MECANICA CONSTRUCŢIILOR
 CURS 10+11 MECANICA CONSTRUCŢIILOR Conf. Dr. Ing. Viorel Ungureanu CINEMATICA SOLIDULUI RIGID In cadrul cinematicii punctului material s-a arătat ca a studia mişcarea unui punct înseamnă a determina la
CURS 10+11 MECANICA CONSTRUCŢIILOR Conf. Dr. Ing. Viorel Ungureanu CINEMATICA SOLIDULUI RIGID In cadrul cinematicii punctului material s-a arătat ca a studia mişcarea unui punct înseamnă a determina la
SEMINAR 14. Funcţii de mai multe variabile (continuare) ( = 1 z(x,y) x = 0. x = f. x + f. y = f. = x. = 1 y. y = x ( y = = 0
 Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
SERII NUMERICE. Definiţia 3.1. Fie (a n ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0
 SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
ECO-STATISTICA-NOTITZZE DE LABORATOR
 ECO-STATISTICA: OBIECTIVE: A. EVALUAREA CELEI MAI PROBABILE VALORI A UNEI CARACTERISTICI A MEDIULUI IN ZONA INVESTIGATA si a ERORII DE ESTIMARE In zona investigata cu o probabilitate de 90% (riscul asumat
ECO-STATISTICA: OBIECTIVE: A. EVALUAREA CELEI MAI PROBABILE VALORI A UNEI CARACTERISTICI A MEDIULUI IN ZONA INVESTIGATA si a ERORII DE ESTIMARE In zona investigata cu o probabilitate de 90% (riscul asumat
Seminar 3. Problema 1. a) Reprezentaţi spectrul de amplitudini şi faze pentru semnalul din figură.
 Seminar 3 Problema 1. a) Reprezentaţi spectrul de amplitudini şi faze pentru semnalul din figură. b) Folosind X ( ω ), determinaţi coeficienţii dezvoltării SFE pentru semnalul () = ( ) xt t x t kt şi reprezentaţi
Seminar 3 Problema 1. a) Reprezentaţi spectrul de amplitudini şi faze pentru semnalul din figură. b) Folosind X ( ω ), determinaţi coeficienţii dezvoltării SFE pentru semnalul () = ( ) xt t x t kt şi reprezentaţi
Segmentarea imaginilor APIM8-1
 Segmentarea imaginilor APIM8-1 Ce este segmentarea? segmentarea = impartirea unei imagini in regiuni cu o anumita semnificatie regiuni cu o anumita semnificatie = obiecte sau zone de interes cel mai simplu
Segmentarea imaginilor APIM8-1 Ce este segmentarea? segmentarea = impartirea unei imagini in regiuni cu o anumita semnificatie regiuni cu o anumita semnificatie = obiecte sau zone de interes cel mai simplu
riptografie şi Securitate
 riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
Procesarea Imaginilor
 UNIVERSITATEA TRANSILVANIA DIN BRAŞOV Laurenţiu-Mihail IVANOVICI Procesarea Imaginilor Îndrumar de laborator 2006 c 2003 EDITURA UNIVERSITĂŢII TRANSILVANIA BRAŞOV Adresa: 500030 Brasov, B-dul Eroilor,
UNIVERSITATEA TRANSILVANIA DIN BRAŞOV Laurenţiu-Mihail IVANOVICI Procesarea Imaginilor Îndrumar de laborator 2006 c 2003 EDITURA UNIVERSITĂŢII TRANSILVANIA BRAŞOV Adresa: 500030 Brasov, B-dul Eroilor,
Transformări de frecvenţă
 Lucrarea 22 Tranformări de frecvenţă Scopul lucrării: prezentarea metodei de inteză bazate pe utilizarea tranformărilor de frecvenţă şi exemplificarea aceteia cu ajutorul unui filtru trece-jo de tip Sallen-Key.
Lucrarea 22 Tranformări de frecvenţă Scopul lucrării: prezentarea metodei de inteză bazate pe utilizarea tranformărilor de frecvenţă şi exemplificarea aceteia cu ajutorul unui filtru trece-jo de tip Sallen-Key.
Ce sunt imaginile digitale şi cum sunt ele memorate?
 Procesarea imaginilor medicale Ce sunt imaginile digitale şi cum sunt ele memorate? Ca fiinţe, analizăm curent orice imagine vedem, până la a recunoaşte obiecte sau fiinţe chiar dacă imaginea este incompletă.
Procesarea imaginilor medicale Ce sunt imaginile digitale şi cum sunt ele memorate? Ca fiinţe, analizăm curent orice imagine vedem, până la a recunoaşte obiecte sau fiinţe chiar dacă imaginea este incompletă.
TEMA 9: FUNCȚII DE MAI MULTE VARIABILE. Obiective:
 TEMA 9: FUNCȚII DE MAI MULTE VARIABILE 77 TEMA 9: FUNCȚII DE MAI MULTE VARIABILE Obiective: Deiirea pricipalelor proprietăţi matematice ale ucţiilor de mai multe variabile Aalia ucţiilor de utilitate şi
TEMA 9: FUNCȚII DE MAI MULTE VARIABILE 77 TEMA 9: FUNCȚII DE MAI MULTE VARIABILE Obiective: Deiirea pricipalelor proprietăţi matematice ale ucţiilor de mai multe variabile Aalia ucţiilor de utilitate şi
COLEGIUL NATIONAL CONSTANTIN CARABELLA TARGOVISTE. CONCURSUL JUDETEAN DE MATEMATICA CEZAR IVANESCU Editia a VI-a 26 februarie 2005.
 SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
Orice izometrie f : (X, d 1 ) (Y, d 2 ) este un homeomorfism. (Y = f(x)).
 Teoremă. (Y = f(x)). Orice izometrie f : (X, d 1 ) (Y, d 2 ) este un homeomorfism Demonstraţie. f este continuă pe X: x 0 X, S Y (f(x 0 ), ε), S X (x 0, ε) aşa ca f(s X (x 0, ε)) = S Y (f(x 0 ), ε) : y
Teoremă. (Y = f(x)). Orice izometrie f : (X, d 1 ) (Y, d 2 ) este un homeomorfism Demonstraţie. f este continuă pe X: x 0 X, S Y (f(x 0 ), ε), S X (x 0, ε) aşa ca f(s X (x 0, ε)) = S Y (f(x 0 ), ε) : y
Teme de implementare in Matlab pentru Laboratorul de Metode Numerice
 Teme de implementare in Matlab pentru Laboratorul de Metode Numerice As. Ruxandra Barbulescu Septembrie 2017 Orice nelamurire asupra enunturilor/implementarilor se rezolva in cadrul laboratorului de MN,
Teme de implementare in Matlab pentru Laboratorul de Metode Numerice As. Ruxandra Barbulescu Septembrie 2017 Orice nelamurire asupra enunturilor/implementarilor se rezolva in cadrul laboratorului de MN,
Capitolul COTAREA DESENELOR TEHNICE LECŢIA 21
 Capitolul COTAREA DESENELOR TEHNICE LECŢIA 21! 21.1. Generalităţi.! 21.2. Elementele cotării.! 21.3. Aplicaţii.! 21.1. Generalităţi! Dimensiunea este o caracteristică geometrică liniară sau unghiulară,care
Capitolul COTAREA DESENELOR TEHNICE LECŢIA 21! 21.1. Generalităţi.! 21.2. Elementele cotării.! 21.3. Aplicaţii.! 21.1. Generalităţi! Dimensiunea este o caracteristică geometrică liniară sau unghiulară,care
Sisteme liniare - metode directe
 Sisteme liniare - metode directe Radu T. Trîmbiţaş 27 martie 2016 1 Eliminare gaussiană Să considerăm sistemul liniar cu n ecuaţii şi n necunoscute Ax = b, (1) unde A K n n, b K n 1 sunt date, iar x K
Sisteme liniare - metode directe Radu T. Trîmbiţaş 27 martie 2016 1 Eliminare gaussiană Să considerăm sistemul liniar cu n ecuaţii şi n necunoscute Ax = b, (1) unde A K n n, b K n 1 sunt date, iar x K
1.7. AMPLIFICATOARE DE PUTERE ÎN CLASA A ŞI AB
 1.7. AMLFCATOARE DE UTERE ÎN CLASA A Ş AB 1.7.1 Amplificatoare în clasa A La amplificatoarele din clasa A, forma de undă a tensiunii de ieşire este aceeaşi ca a tensiunii de intrare, deci întreg semnalul
1.7. AMLFCATOARE DE UTERE ÎN CLASA A Ş AB 1.7.1 Amplificatoare în clasa A La amplificatoarele din clasa A, forma de undă a tensiunii de ieşire este aceeaşi ca a tensiunii de intrare, deci întreg semnalul
Lectia VI Structura de spatiu an E 3. Dreapta si planul ca subspatii ane
 Subspatii ane Lectia VI Structura de spatiu an E 3. Dreapta si planul ca subspatii ane Oana Constantinescu Oana Constantinescu Lectia VI Subspatii ane Table of Contents 1 Structura de spatiu an E 3 2 Subspatii
Subspatii ane Lectia VI Structura de spatiu an E 3. Dreapta si planul ca subspatii ane Oana Constantinescu Oana Constantinescu Lectia VI Subspatii ane Table of Contents 1 Structura de spatiu an E 3 2 Subspatii
Metode Runge-Kutta. 18 ianuarie Probleme scalare, pas constant. Dorim să aproximăm soluţia problemei Cauchy
 Metode Runge-Kutta Radu T. Trîmbiţaş 8 ianuarie 7 Probleme scalare, pas constant Dorim să aproximăm soluţia problemei Cauchy y (t) = f(t, y), a t b, y(a) = α. pe o grilă uniformă de (N + )-puncte din [a,
Metode Runge-Kutta Radu T. Trîmbiţaş 8 ianuarie 7 Probleme scalare, pas constant Dorim să aproximăm soluţia problemei Cauchy y (t) = f(t, y), a t b, y(a) = α. pe o grilă uniformă de (N + )-puncte din [a,
VII.2. PROBLEME REZOLVATE
 Teoria Circuitelor Electrice Aplicaţii V PROBEME REOVATE R7 În circuitul din fiura 7R se cunosc: R e t 0 sint [V] C C t 0 sint [A] Se cer: a rezolvarea circuitului cu metoda teoremelor Kirchhoff; rezolvarea
Teoria Circuitelor Electrice Aplicaţii V PROBEME REOVATE R7 În circuitul din fiura 7R se cunosc: R e t 0 sint [V] C C t 0 sint [A] Se cer: a rezolvarea circuitului cu metoda teoremelor Kirchhoff; rezolvarea
