Ce sunt imaginile digitale şi cum sunt ele memorate?
|
|
|
- Φώτιος Αγγελίδου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Procesarea imaginilor medicale Ce sunt imaginile digitale şi cum sunt ele memorate? Ca fiinţe, analizăm curent orice imagine vedem, până la a recunoaşte obiecte sau fiinţe chiar dacă imaginea este incompletă. Mintea omenească este însă incapabilă să facă măsurări pe o imagine, lucru posibil pentru maşină, dacă imaginea este corect achiziţionată şi memorată, mintea omenească şi maşina se completează reciproc. Imaginea digitală, replica numerică a imaginii optice, poate fi memorată în fişiere cu numeroase formate, fiecare dintre ele adaptate unei anumite utilizări: captură, prelucrare, arhivare, imprimare, publicare în presa scrisă sau pe Internet etc. Imaginile pot fi împărţite în două categorii: imaginile vectoriale (care sunt de fapt fişiere de coordonate din care, de exemplu pleacă şi se termină o linie, sau codul unei culori care umple o anumită suprafaţă) şi imaginile matriciale sau hărţi de biţi (bitmap) din care fac parte formatele BMP, JPEG, GIF etc. pe care le vom discuta pentru o mai bună înţelegere a necesităţii existenţei lor. Imaginile matriciale sunt alcătuite din pixeli (contracţie de la PICture ELement). Pixelii pot fi asemuiţi cu plăcile de faianţă de pe un perete. Ca şi acestea din urmă, pixelii sunt dispuşi în rânduri suprapuse pentru a "acoperi" forma imaginii. Cu cât aceeaşi imagine este reprezentată pe mai mulţi pixeli cu atât claritatea ei creşte. Monitoarele curente folosesc 72 pixeli/inch. Imaginile pot fi alb-negru sau color: pentru imaginile alb-negru şi în tonuri de gri, deoarece ochiul uman nu poate distinge mai mult de 200 nuanţe de gri, s-a considerat că 256 (2 la puterea 8) este cel mai apropiat număr care satisface aceasta situaţie, de aceea, imaginile alb-negru sunt codificate cu 8 biţi pentru fiecare pixel; există însă şi imagini 16-bit (cu un cod de 16 biţi pentru fiecare pixel) sau 32-bit (cu un cod de 16 biţi pentru fiecare pixel). pentru imaginile color s-a păstrat numărul de 256 de nuanţe pentru fiecare din cele 3 culori de bază: roşu, verde, albastru. Prin combinarea celor 3 rezultă o imagine numită RGB (abrevierea de la Red, Green, Blue), codificată pe 3 bytes (3 X 1 byte (8 biţi) = 24 biţi) care generează peste 16 milioane de culori (mult mai mult decât percepe ochiul uman). Vom detalia puţin câteva din cele mai uzuale formate:.bmp harta de biţi (Bitmap) reprezintă forma brută a unei imagini, adică fiecare pixel ce compune imaginea este memorat individual (format foarte bun pentru procesarea de imagini). Spre exemplu o poză de 800 X 600 pixeli va fi memorată pe 800 X 600 X 24 biţi = biţi (~11 Mb = ~1.37MB), indiferent de informaţia care se află în interiorul pozei. Pornind de la acest inconvenient (dimensiunea foarte mare pe disc) a apărut necesitatea dezvoltării formatelor ce comprimă memorarea imaginii (încercând în acelaşi timp să se păstreze cât mai multă informaţie din imaginea originală). Vom discuta acum 2 din cele mai uzuale formate de comprimare..gif (Graphic Interchange Format) este un format foarte puternic (calitate bună, comprimare foarte puternică), dar are dezavantajul de a memora o paletă de numai 256 culori (8 biţi). Cu alte cuvinte memorează o paletă la fel de mare ca imaginea alb-negru (ca să ne dăm seama de rata de compresie). Ca ordin de mărime aceeaşi imagine de 800 X 600 ar avea o dimensiune maximă de ordinul KB. Răspunsul la întrebarea Când ar trebui să folosesc.gif? va fi: atunci când imaginea color(rgb) foloseşte din paleta sa de peste 16 milioane de culori un număr cât mai mic (ţinta fiind 256). O altă utilizare ar putea fi la imaginile de mici dimensiuni (ţinta ar fi imaginile la care lungime X lătimea nu depăşeşte 256 pixeli)..jpeg (Joint Photographic Expert Group) este un algoritm de compresie care a fost destinat comprimării imaginilor alb-negru sau color luate din realitate. Algoritmul de comprimare se bazează pe sensibilitatea crescută a ochiului uman la variaţiile mici de luminanţă (mai mulţi biţi pentru luminanţă) si sensibilitatea mai redusă la variaţiile mici de culoare (mai puţini biţi pentru variaţiile mici de culoare). O proprietate foarte utilă a JPEG-ului este capacitatea acestuia de a avea un grad variabil de comprimare, ales de utilizator. Aceasta înseamnă că dacă dorim obţinerea unui fişier de imagine cât mai mic, se poate alege o rată mare de comprimare, în dauna calităţii; invers, pentru a menţine calitatea la o cota ridicată, alegem un grad redus de comprimare. Când ar trebui să folosesc 1
2 .JPG?. De cate ori avem de-a face cu o imagine din realitate sau de câte ori dorim să stabilim noi gradul de comprimare al imaginii. DICOM. Fişierele DICOM, folosite pentru memorarea imaginilor medicale, conţin pe lângă imagine în sine metadate care oferă informaţii despre imagine (mărime, dimensiuni, adâncime, modalitatea folosită, setări ale echipamentului, etc.). Pentru citirea acestor informaţii se foloseşte de exemplu funcţia dicominfo din MATLAB. De ce să modificăm o imagine? Procesul de achiziţie al imaginilor este laborios. Există sute, până la milioane de senzori optici care transformă lumina în curent electric şi apoi în biţi. Toate aceste procese, pe lângă caracteristicele senzorului (uneori precare) şi erori ce nu ţin de achiziţia propriu-zisă, cum ar fi optica aparatului, duc la deformarea imaginilor şi mai mult, la adăugarea de zgomot. Prin modificările pe care le facem asupra unei imagini acoperim, pe cât se poate, aceste neajunsuri, imaginea rezultată fiind gata pentru prelucrări ulterioare. Ce vom urmări în lucrarea noastră practică? În cursul acestei lucrări practice vom învăţa să procesăm imagini în programul ImageJ, să le transformăm din imagini colorate în imagini în tonuri de gri (pentru o reprezentare mai simplă şi o înţelegere mai bună a conceptelor), să ajustăm intensitatea unei imagini (pentru o vizualizare mai bună), să filtrăm o imagine (pentru a reduce, pe cât posibil, zgomotul) şi în final să realizăm câteva operaţii morfologice, care vor pregăti imaginea pentru eventuale măsurători şi/sau alte extrageri de informaţie. ImageJ este un program de procesare şi analiză de imagini. Este capabil să afişeze imagini de tip 8-bit, 16-bit, 32-bit, şi poate executa editări, analize, măsurători suplimentare, salvări, listări. Poate interpreta diverse formate de imagini: TIFF, GIF, JPEG, BMP, DICOM etc. O facilitate importantă este capacitatea de a crea stive de imagini care partajează o singură fereastră de afişare. Poate realiza diverse calcule statistice pentru anumite zone selectate de utilizator sau pentru întreaga imagine. Poate măsura distanţe şi unghiuri. Permite diverse procesări standard: netezire (smooth), detecţia contururilor, filtrare mediană etc. Permite totodată realizarea transformărilor geometrice - cum ar fi scalarea, rotirea, răsturnarea (flip). Imaginile pot fi mărite de până la 32 de ori. Fiecare imagine este deschisă într-o fereastră separată, iar numărul limită de ferestre este determinat doar de memoria disponibilă. ImageJ este un program cu o arhitectură deschisă fiind extins prin adăugarea plugin-urilor. Interfaţa utilizator Lansarea programului in executie se realizeaza prin comanda: Start -> Programs -> ImageJ -> ImageJ. 2
3 Apare urmatoarea fereastră de dialog: Spre deosebire de majoritatea programelor de procesare de imagini, ImageJ nu are propriu-zis o zonă de lucru principală. Fereastra principală conţine doar meniul cuprinzând totalitatea comenzilor şi câteva toolbar-uri. Toate imaginile deschise cu ImageJ sunt afişate in ferestre separate, la fel şi histogramele, meniurile adiţionale de tip pop-up sau ferestrele de configurare. Rezultatele măsurătorilor efectuate asupra unei imagini sunt afişate în Tabelul Rezultatelor. Majoritatea ferestrelor adiţionale pot fi redimensionate şi mutate în diverse locuri pe ecran. 1 Selecţie rectangulara (cu sau fără colturi rotunjite) (click dreapta pentru a defini tipul selecţiei) 2 Selecţie ovala, eliptica sau de tip brush (click dreapta pentru a defini tipul selecţiei) 3 Selecţie tip poligon 4 Selecţie liberă 5 Linie dreapta, segmentata, segment oarecare sau săgeţi (click dreapta pentru a defini tipul selecţiei) 6 Unghi 7 Selecţie tip punct sau multi-punct Tool 8 Bagheta magica 9 Text 10 Lupa (se pot folosi şi tastele + şi - ) 11 Scroll 12 Selecţie culoare A H Macro-uri (se încarcă din StartupMacros.txt, macros/tools/ or macros/toolsets/ 13 Alege alt macro sau adaugă un plugin Imaginile utilizate în cadrul acestui laborator se găsesc în folderul: C:\Kit\Studenti\Informatica Medicala\10.imagistica ImageJ\Imagini LP Tipuri de imagini în ImageJ Programul ImageJ poate afişa fie imagini individuale, fie multiple imagini interconectate spaţial sau temporal în cadrul aceleiaşi ferestre. Aceste seturi de imagini poartă numele de stive. Pentru exemplificare, se pot deschide imagini incluse în setul demo al programului sau din alte surse. 1. Comanda de deschidere a imaginilor incluse in setul demo al programului: File -> Open Samples. Se alege <<Bat Cochlea Renderings>>. 2. Se deschide setul corespunzător de imagini într-o noua fereastră. În partea de sus a acesteia se pot observa: numărul imaginii curente şi numărul total de imagini din set, rezoluția, tipul şi dimensiunea imaginii curente. Schimbarea imaginii curente se realizează folosind bara de derulare (scroll) din partea de jos a ferestrei. 3
4 3. Numărul imaginii curente este afişat în permanenţă în colţul din stânga sus al ferestrei. 4. Numărul imaginii curente este afişat în permanenţă în colţul din stânga sus al ferestrei. Deschiderea unei imagini alese de utilizator se realizează utilizând comanda: File -> Open. Ca rezultat, o nouă fereastră adiţională se va deschide şi va afişata imaginea dorită. 1. Comanda de deschidere a imaginilor alese de utilizator: File -> Open. 2. Apare o fereastră de dialog din care se poate selecta imaginea dorită. Ulterior, se apasă butonul Open. 3. Imaginea selectată apare într-o fereastră separată. Trecerea la o imagine în tonuri de gri Atunci când utilizatorul doreşte să aplice diverse tehnici de procesare pentru care culoarea reprezintă o informaţie prea puţin relevantă (de ex. determinarea contururilor unei imagini), se poate realiza în prealabil o trecere la o imagine în tonuri de gri (se realizează astfel simplificarea codificării imaginii, dar şi accesul la o paletă mai largă de tehnici de procesare). 4
5 Acest lucru se realizează astfel: Image -> Type -> 32-bit. 2. Imaginea rezultată în urma trecerii la tonuri de gri. 1. Comanda de convertire a unei imagini în tonuri de gri: Image -> Type -> 32-bit. Ajustarea intensităţii unei imagini Contrastul şi luminozitatea unei imagini se pot modifica astfel: Image -> Adjust -> Brightness/Contrast. Se va deschide o fereastră de dialog adiţională ce va permite modificarea parametrilor. Imaginea deschisă şi graficul din partea de sus a ferestrei de dialog vor reflecta în timp real modificările efectuate asupra parametrilor. La final, se apasă butonul Apply. 1. Comanda de modificare a contrastului şi luminozităţii unei imagini: Image -> Adjust -> Brightness/Contrast. 2. Apare o fereastră de dialog care reflectă valoarea celor doi parametri, precum şi raportul dintre aceştia. 5
6 3. Modificaţi valorile prin acţiunea asupra elementelor de derulare (scroll). Raportul dintre contrast şi luminozitate este reflectat mereu în graficul evidenţiat mai jos. La final, se apasă butonul Apply. 4. Observaţi diferenţele dintre imaginea obţinută în urma prelucrării şi imaginea originală. Filtrarea imaginilor Unele imagini sunt zgomotoase. Imaginile numerice sunt susceptibile la diverse tipuri de zgomot. Zgomotul este rezultatul erorilor în achiziţia iniţială a imaginii, al căror rezultat sunt valori ale pixelilor care nu reflectă intensitatea din imaginea adevărată. Zgomotul poate apărea în imagine în mai multe feluri depinzând de cum este creată imaginea. Dacă imaginea este scanată dintr-o fotografie, granulaţia filmului sau hârtiei fotografice este o sursă de zgomot. Dacă imaginea este achiziţionată direct, de exemplu cu un aparat foto digital, mecanismul de achiziţie (senzorul CCD) poate introduce zgomot în imagine. Transmisia electronică a imaginii poate ea însăşi să introducă zgomot. Reducerea zgomotului sau favorizarea unor anumite componente ale imaginii se fac prin operaţia de filtrare. Filtrarea este o tehnică de modificare sau îmbunătăţire a imaginii, pentru a favoriza anumite componente sau pentru a elimina alte componente. Zgomotul unei imagini este redus prin înlocuirea valorii fiecărui pixel cu mediana valorilor pixelilor învecinaţi (se consideră o vecinătate circulară, identificată prin rază). În cazul unui set de date, mediana reprezintă valoarea numerică ce separă întregul set în două jumătăţi: inferioară (valori < valoarea mediană) şi superioară (valori > valoarea mediană). Mediana unui set finit de date poate fi obţinută ordonând crescător elementele din set şi alegându-l pe cel de la mijloc. Dacă setul conţine un număr impar de elemente, atunci există o unică valoare de mijloc. Dacă setul conţine un număr par, atunci valoarea mediană reprezintă media aritmetică a celor două elemente de la mijloc. Ex > Valoarea mediană este > Valoarea mediană este 3.5 Filtrarea prin determinarea medianei este totodată o tehnică de netezire a imaginii (aşa cum este, de exemplu, filtrarea liniară Gaussiană). Toate tehnicile de netezire a imaginilor sunt eficiente în ceea ce priveşte eliminarea zgomotului, dar prezintă dezavantajul de a afecta contururile obiectelor incluse în acea imagine. Contururile sunt elemente critice în cadrul unei imagini, astfel că este foarte important să eliminăm zgomotul şi să le păstrăm pe cât posibil neafectate. Pentru un nivel moderat de zgomot, mediana reprezintă modalitatea ideală de a înlătura zgomotul, conservând contururile, de aceea este o tehnică des utilizată în procesarea imaginilor. Filtrarea unei imagini se realizează astfel: Process -> Filters -> Median. 6
7 1. Se deschide o imagine care prezintă zgomot (observaţi aspectul acesteia). 2. Comanda de filtrare a unei imagini: Process -> Filters -> Median. 3. Apare o fereastră de dialog în care se solicită introducerea razei vecinătăţii pixelilor care intră în calculul medianei. Dacă check-box-ul <<Preview>> este bifat, atunci orice modificare a razei este vizibilă în timp real în imaginea deschisă. La final, se apasă butonul OK. 4. Observaţi diferenţele dintre imaginea obţinută în urma prelucrării şi imaginea originală. Operaţii morfologice Procesarea morfologică a imaginii este o tehnică utilizată pentru extragerea sau modificarea informaţiei referitoare la forma şi structura obiectelor dintr-o imagine. Operatorii morfologici, cum ar fi dilatarea sau eroziunea, sunt utili în particular pentru analiza imaginilor binare, deşi utilizarea lor poate fi extinsă şi pentru analiza imaginilor în tonuri de gri sau color. În cadrul operaţiei de eroziune, fiecare pixel al obiectului care atinge un pixel al fundalului se schimbă într-un pixel din fundal. În cadrul operaţiei de dilatare, fiecare pixel din fundal care atinge un pixel dintr-un obiect este schimbat într-un pixel din obiect. Graniţa aceasta este stabilită cu ajutorul pixelilor învecinaţi (se consideră o vecinătate circulară, identificată prin rază). Aplicarea operatorului morfologic eroziune se realizează astfel: Process -> Filters -> Minimum. 7
8 1. Se deschide o imagine (observaţi aspectul acesteia). 2. Comanda de filtrare a unei imagini: Process -> Filters -> Minimum. 3. Apare o fereastră de dialog în care se solicită introducerea razei vecinătăţii pixelilor care intră în calculul operaţiei morfologice. Dacă check-box-ul <<Preview>> este bifat, atunci orice modificare a razei este vizibilă în timp real în imaginea deschisă. La final, se apasă butonul OK. 4. Observaţi diferenţele dintre imaginea obţinută în urma prelucrării şi imaginea originală. Acest filtru aplică operatorul morfologic de eroziune prin înlocuirea valorii fiecărui pixel din imagine cu cea mai mică valoare a pixelilor învecinaţi. Aplicarea operatorului morfologic dilatare se realizează astfel: Process -> Filters -> Maximum. 8
9 1. Se deschide o imagine (observaţi aspectul acesteia). 2. Comanda de filtrare a unei imagini: Process -> Filters -> Maximum. 3. Apare o fereastră de dialog în care se solicită introducerea razei vecinătăţii pixelilor care intră în calculul operaţiei morfologice. Dacă check-box-ul <<Preview>> este bifat, atunci orice modificare a razei este vizibilă în timp real în imaginea deschisă. La final, se apasă butonul OK. 4. Observaţi diferenţele dintre imaginea obţinută în urma prelucrării şi imaginea originală. Acest filtru aplică operatorul morfologic de dilatare prin înlocuirea valorii fiecărui pixel din imagine cu cea mai mare valoare a pixelilor învecinaţi. Cei doi operatori morfologici se pot combina în ordinea dilatare-erodare şi rezultă închiderea morfologică şi erodare-dilatare şi rezultă deschiderea morfologică. Pe baza deschiderii şi închiderii morfologice se definesc şi alte operaţii necesare în prelucrarea imaginilor. Operaţiile prezentate anterior pot fi aplicate direct şi din meniul Binary, dar se pot folosi numai în cazul imaginilor 8-bit: 9
10 1. Deschideţi o imagine în tonuri de gri, codificată 32- bit. Comanda de lansare directă a operaţiei de dilatare a acesteia este: Process -> Binary -> Dilate. 2. Deoarece comanda a fost lansată pentru o imagine în tonuri de gri 32-bit, apare o fereastră de dialog prin care utilizatorul este notificat de faptul că operaţia solicitată necesită o imagine codificată 8-bit, fie în tonuri de gri, fie color. Segmentarea unei imagini Studiul unui anumit obiect din cadrul unei imagini implică evidenţierea conturului său prin intermediul procedurii de segmentare a imaginii. Segmentarea şi extragerea conturului reprezintă etape importante în analiza de imagine. Imaginile segmentate se folosesc cu precădere în multe aplicaţii diferite cum ar fi diagnosticarea, planificarea terapiei, localizarea leziunilor patologice, studiul structurilor anatomice, chirurgia computer-integrată. Segmentarea imaginilor reprezintă o sarcină dificilă datorită variaţiilor de formă ale obiectelor, precum şi de calitatea imaginilor achiziţionate. În general majoritatea imaginilor biomedicale sunt preluate cu artefacte de eşantionare, zgomot care duce la apariţia de erori când sunt aplicate metode stricte de prelucrare a imaginii. Procesul de segmentare este considerat ca un proces de clasificare a obiectelor dintr-o imagine, iar într-o oarecare măsură este echivalent cu identificarea obiectului în sine, ca o consecinţă a segmentării diferitelor obiecte (realizarea fizică de clase sau modele abstracte) care sunt localizate perfect în cadrul imaginii digitale. Scopul segmentării este simplificarea reprezentării imaginilor în informaţie utilă prin partiţionarea în regiuni. Segmentarea imaginilor este o metodă folosită pentru a localiza anumite obiecte sau contururi într-o imagine. Pentru imaginile cu caracter medical au fost propuse mai multe metode de segmentare. Segmentarea obţinută cu ajutorul tehnicilor tradiţionale de procesare de bază a imaginii, cum ar fi valoarea de prag sau histograma, necesită intervenţia umană în vederea obţinerii de rezultate satisfăcătoare. Automatizarea acestor abordări este dificilă datorită complexităţii formei, umbrelor şi variabilităţii de la nivelul obiectelor individuale. Mai mult, zgomotul şi alte artefacte ale imaginii pot determina apariţia de regiuni şi contururi incorecte, sau discontinuităţi ale obiectelor obţinute prin intermediul aceste metode. Cu toate acestea, în pofida apariţiei unei suite de algoritmi de mare complexitate, segmentarea imaginii rămâne dependentă de aplicaţie, fără a putea fi identificată o soluţie unică pentru această provocare. Conturul (perimetrul) unui obiect este definit ca ansamblul pixelilor obiectului respectiv care au cel puţin un vecin in afara obiectului. Segmentarea imaginilor prin această metodă constă în localizarea pixelilor care corespund contururilor obiectelor prezente în acea imagine. Ulterior, se presupune că numărul obiectelor prezente este egal cu numărul contururilor dintr-o imagine, în condiţiile în care un contur al unei zone sau al unei imagini este automat un contur închis. Pentru precizia segmentării, în cazul determinării unui obiect, perimetrul conturului detectat trebuie să fie aproximativ egal cu cel al obiectului din imaginea iniţială. Dificultatea metodei apare însă odată cu necesitatea de a defini un contur într-o imagine. Un contur sau o caracteristică liniară reprezintă o schimbare bruscă sau o discontinuitate a pixelilor pe o anumită direcţie din imagine. Determinarea conturului în ImageJ se realizează astfel: Process -> Find Edges. 10
11 1. Comanda de determinare a contururilor unei imagini: Process -> Find Edges. 2. Observaţi diferenţele dintre imaginea obţinută în urma prelucrării şi imaginea originală. Toate contururile dintre obiectele prezente în imagine au fost evidenţiate. Detecţia contururilor oferă rezultate mai bune în cazul imaginilor alb negru. Pentru acest lucru, se realizează iniţial binarizarea imaginii (conversia într-o imagine alb-negru) şi ulterior detecţia contururilor. 1. Comanda de binarizare a unei imagini: Process -> Binary -> Make Binary. 2. Observaţi diferenţele dintre imaginea obţinută în urma prelucrării şi imaginea originală. Imaginea prezintă acum doar obiecte identificate cu negru. 3. Lansaţi comanda de determinare a contururilor: Process -> Find Edges. 4. Observaţi diferenţele dintre imaginea obţinută în urma prelucrării şi imaginea originală. Contururile obiectelor prezente în imagine au fost clar evidenţiate. 11
12 Măsurători ImageJ permite realizarea unui set de măsurători statistice ale unei imagini. În funcţie de selecţia efectuată, aplicaţia calculează şi afişează într-un tabel rezultate legate de calcule statistice ale ariei, ale lungimii liniilor şi unghiurilor, sau ale coordonatelor. Măsurătorile efectuate pot fi selectate din fereastra de dialog <<Set measurements>> (Analyze -> Set Measurements). 1. Pentru selectarea măsurătorilor ce vor fi efectuate, se lansează comanda: Analyze -> Set Measurements. 2. Apare o fereastră de dialog în care se pot bifa o serie de măsurători dorite. La final, se apasă butonul OK. Măsurătorile posibile sunt: Area aria selecţiei exprimată în pixeli 2 sau în unităţi de măsură 2 (mm 2, μm 2 etc.) Mean gray value valoarea medie a nivelurilor de gri din aria selectată. Aceasta reprezintă suma tuturor nivelurilor de gri din aria selectată, împărţită la numărul de pixeli. Pentru imagini RGB, media este calculată prin conversia fiecărui pixel în nivel de gri, folosind formula gri = (roşu + verde + albastru)/3. Standard deviation deviaţia standard a tonurilor de gri folosite pentru a calcula valoarea medie menţionată anterior. Modal gray value tonul de gri cel mai întâlnit în aria selectată. Corespunde vârfului histogramei. Min & max gray level nivelurile minim şi maxim ale tonurilor de gri din aria selectată. Centroid punctul central al ariei selectate. Este calculat ca fiind media coordonatelor x şi y ale tuturor pixelilor din aria selectată. Center of mass media luminozităţii tuturor pixelilor din aria selectată. Perimeter lungimea marginii exterioare a selecţiei. Perimetrul unei selecţii compuse este calculat prin descompunerea selecţiei în arii individuale. (Notă: perimetrul unei selecţii compuse poate să difere de suma perimetrelor individuale, datoritămetode de calcul diferite.) Bounding rectangle reprezintă cel mai mic dreptunghi care încadrează aria selectată. Fit ellipse reprezintă elipsa care încadrează aria selectată. Shape descriptors calculează şi afişează următorii descriptori de formă: Circularity: 4π * Arie / Perimetru 2 - valoarea 1.0 indică un cerc. Pe măsură ce valoarea se apropie de 0, indică o formă alungită. Aspect ratio: menţinerea proporţiilor elipsei care încadrează aria selectată. Roundness: inversul parametrului Aspect Ratio. Solidity: Arie / Arie convexă. Feret s diameter: cea mai mare distanţă dintre oricare două puncte de pe conturul ariei selectate. Integrated density Suma valorilor pixelilor din aria selectată. Este echivalentul produsului dintre Arie şi Valoarea medie a nivelurilor de gri. Median valoarea mediană a pixelilor din aria selectată. Skewness momentul de ordin trei al mediei. Kurtosis momentul de ordin patru al mediei. Area fraction pentru imaginile care au valori de prag definite, reprezintă procentul pixelilor din aria selectată care au fost marcaţi cu roşu; pentru celelalte imagini, reprezintă procentul pixelilor cu valori diferite de zero. Stack position reprezintă poziţia în cadrul stivei de imagini. Ulterior, pentru o anumită imagine, se pot determina valorile măsurătorilor selectate anterior. 12
13 1. Comanda de determinare a valorilor măsurătorilor pentru o imagine: Analyze -> Measure. 2. Apare ulterior o fereastră de dialog în care sunt afişate, sub formă tabelară, valorile măsurătorilor selectate. 3. La închiderea acestei ferestre, utilizatorul este întrebat dacă doreşte salvarea măsurătorilor. În cazul în care nu există o arie selectată, la comanda Analyse -> Measure se calculează valorile măsurătorilor selectate pentru întreaga imagine. Dacă înainte de lansarea comenzii se selectează o anumită arie, atunci măsurătorile se vor aplica doar acelei arii selectate. 1. Se selectează o anumită arie din imagine. 2. Se afişează valorile măsurate (prin comanda Analyze -> Measure). Acestea sunt valabile doar pentru porţiunea selectată. Exemple de utilizare 1. În cadrul patologiei ginecologice, screening-ul citologiei colului uterin este de mare importanţă pentru detectarea precoce a modificărilor potenţial maligne de la acest nivel. Celulele epiteliale se nasc din celulele bazale, apoi se maturează încet spre parbazale, intermediare şi în final devin celule superficiale (exfoliative). Diferenţierea între 13
14 aceste celule, pe lângă intensitatea culorii, se face în funcţie de raportul nucleu citoplasmă. În imaginea de mai jos sunt prezente câteva celule, în partea din stânga fiind celule superficiale cu nucleu mic picnotic, iar în partea din dreapta celule intermediare cu nucleul mare şi citoplasma mai redusă. Folosindu-ne de modificarea contrastului şi de setarea unui threshold oportun, se pot selecta iniţial nucleii, apoi nucleii şi citoplasma, astfel încât putem calcula raportul nucleu-citoplasma pentru cele 2 tipuri de celule. 1. Se deschide o imagine relevantă. 2. În fereastra de selecţie a măsurătorilor, se bifează doar aria. Se apasă OK şi fereastra dispare. 3. Se alege modul de selecţie Linie şi se trasează diametrul unui nucleu. În timpul desenării, apar în timp real unghiul şi lungimea liniei de selecţie. 4. Se afişează valoarea măsurătorii selectate (Arie) şi se obţine lungimea liniei trasate. 5. Se repetă aceeaşi operaţie pentru diametrul citoplasmei şi se afişează valoarea măsurată. Ulterior, se calculează raportul dintre cele două valori. 14
15 2. Atunci când nu este disponibilă unitatea de măsura pentru poze (nu avem calibrarea), se poate realiza o calibrare aproximativă a unei imagini, măsurând elemente cărora le ştim dimensiunea. Astfel, ştim deja ca diametrul mediu al unei hematii este de aproximativ 7 microni. Măsurând diametrul a hematii, putem astfel face o calibrare aproximativă. Împărţim 7 microni (dimensiunea normală a unei hematii) la media dimensiunii hematiilor măsurate. Aflam astfel câţi microni are un pixel din imagine. Totuşi, având în vedere că există modificări patologice ale dimensiunii hematiilor - ca în anemii - calibrarea poate avea mult de suferit. În unele cazuri, din păcate este tot ce avem. Analiza particulelor Comanda Analyze -> Analyze particles - numără şi măsoară obiectele din cadrul unei imagini binare (sau care are definite valori de prag Image -> Adjust -> Threshold). Analiza este realizată asupra ariei selectate sau asupra întregii imagini, în cazul lipsei selecţiei. Etapele sunt următoarele: se scanează selecţia (sau imaginea) până când se întâlneşte marginea unui obiect; se evidenţiază conturul acelui obiect folosind Bagheta Magică şi se efectuează măsurătorile selectate; se umple acel obiect pentru a nu îl mai scana a doua oară şi se continuă scanarea în căutarea unui nou obiect, până la atingerea marginii selecţiei (sau imaginii). Acestea se realizează intern, fiind transparente pentru utilizaror. Pentru a testa această opţiune a programului ImageJ, se parcurg paşii următori: - se binarizează imaginea - se aleg următoarele măsurători: Standard Deviation, Min & max gray value; Perimeter (vezi imaginea de mai sus) - se selectează o zonă restrânsă - se calculează măsurătorile 1. Comanda de binarizare a unei imagini: Process -> Binary -> Make Binary. 2. Se alege modul de selecţie rectangular. 3. Se selectează o porţiune din imagine. 4. Comanda de analiză a particulelor: Analyze -> Analyze particles. 15
16 5. Apare o fereastră de dialog care prezintă parametrii de analiză. Se aleg opţiunile dorite (nu uitaţi să bifaţi opţiunea <Display results> pentru afişarea rezultatelor) şi la final se apasă butonul OK. 6. După apăsarea butonului OK apare o fereastră de dialog care prezintă rezultatul analizei. Scheletizarea este reprezentată de reducerea obiectelor la linii, fără a schimba radical structura imaginii. Se aplică doar imaginilor binare astfel: Process -> Binary -> Scheletonize. 1. Iniţial se binarizează imaginea dorită (Process -> Binary -> Make Binary). 2. Se obţine o imagine alb-negru. 3. Comanda de scheletizare a unei imagini binare: Process -> Binary -> Scheletonize 4. Observaţi diferenţele dintre imaginea obţinută în urma prelucrării şi imaginea binară. 16
17 Afişarea histogramei unei imagini Histograma unei imagini reprezintă distribuţia nivelurilor de gri în cazul imaginilor în tonuri de gri, sau a nivelurilor celor trei canale în cazul imaginilor RGB, în cadrul imaginii. Pentru o imagine pe 8 biţi, histograma va afişa numărul de pixeli pentru fiecare valoare de culoare posibilă (256 valori). Utilitatea histogramei este evidentă în prelucrarea imaginilor capturate direct în format digital. Evaluarea unei imagini cu ajutorul histogramei permite o apreciere rapidă a paşilor necesari pentru a îmbunătăţi calitatea imaginii. Comanda Analyze -> Histogram determină afişarea histogramei unei imagini. 1. Comanda de afişare a histogramei unei imagini: Analyze -> Histogram. 2. Ulterior, apare o fereastră de dialog cu opţiuni referitoare la caracteristicile histogramei. După setările dorite, se apasă butonul OK. 3. Ulterior apăsării butonului OK, apare graficul asociat histogramei, într-o nouă fereastră de dialog O prelucrare clasică a imaginilor digitale o reprezintă îmbunătăţirea contrastului prin egalizarea histogramei. Acest lucru se realizează astfel: 17
18 1. Comanda pentru îmbunătăţirea contrastului: Process -> Enhance Contrast. 2. Apare o fereastră de dialog în care se bifează opţiunea <<Equalize histogram>>. La final, se apasă butonul OK. 3. După apăsarea butonului OK, contrastul imaginii originale este modificat. Observaţi diferenţele dintre imaginea obţinută în urma prelucrării şi imaginea originală. 4. Afişaţi din nou histograma imaginii (Analyze -> Histogram) şi observaţi diferenţele dintre aceasta şi histograma imaginii originale (afişată la punctul anterior). Comparaţi histograma curentă cu cea obţinută anterior. Alte operaţii interesante, ca exerciţii Alegeţi o imagine şi exersaţi prelucrările disponibile în ImageJ asupra variantei color, în tonuri de gri sau binare (alb-negru). Observaţi diferenţele. BIBLIOGRAFIE TĂRÂŢĂ MIHAI (2010), Informatică medicală, SITECH, Craiova ISBN , vol. I şi II, 568 pagini, Cap. Analiza si prelucrarea imaginilor medicale 18
MARCAREA REZISTOARELOR
 1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
Metode iterative pentru probleme neliniare - contractii
 Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
prin egalizarea histogramei
 Lucrarea 4 Îmbunătăţirea imaginilor prin egalizarea histogramei BREVIAR TEORETIC Tehnicile de îmbunătăţire a imaginilor bazate pe calculul histogramei modifică histograma astfel încât aceasta să aibă o
Lucrarea 4 Îmbunătăţirea imaginilor prin egalizarea histogramei BREVIAR TEORETIC Tehnicile de îmbunătăţire a imaginilor bazate pe calculul histogramei modifică histograma astfel încât aceasta să aibă o
Curs 1 Şiruri de numere reale
 Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate.
 Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE
 DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
III. Serii absolut convergente. Serii semiconvergente. ii) semiconvergentă dacă este convergentă iar seria modulelor divergentă.
 III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
Metode de interpolare bazate pe diferenţe divizate
 Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
(a) se numeşte derivata parţială a funcţiei f în raport cu variabila x i în punctul a.
 Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Curs 14 Funcţii implicite. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi"
 Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
a n (ζ z 0 ) n. n=1 se numeste partea principala iar seria a n (z z 0 ) n se numeste partea
 Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
prin operaţii punctuale
 Lucrarea 3 Îmbunătăţirea imaginilor prin operaţii punctuale BREVIAR TEORETIC Termenul general de îmbunătăţire a imaginilor se referă la o clasă largă de operaţii, ce au ca scop mărirea detectabilităţii
Lucrarea 3 Îmbunătăţirea imaginilor prin operaţii punctuale BREVIAR TEORETIC Termenul general de îmbunătăţire a imaginilor se referă la o clasă largă de operaţii, ce au ca scop mărirea detectabilităţii
Lab06: Extragerea trăsăturilor şi selecţia trăsăturilor. Aplicaţie pentru recunoaşterea obiectelor bazată pe formă.
 Lab06: Extragerea trăsăturilor şi selecţia trăsăturilor Aplicaţie pentru recunoaşterea obiectelor bazată pe formă. Aplicație practică a extragerii şi selecţiei trăsăturilor Recunoaşterea celor 4 forme
Lab06: Extragerea trăsăturilor şi selecţia trăsăturilor Aplicaţie pentru recunoaşterea obiectelor bazată pe formă. Aplicație practică a extragerii şi selecţiei trăsăturilor Recunoaşterea celor 4 forme
Esalonul Redus pe Linii (ERL). Subspatii.
 Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
5.4. MULTIPLEXOARE A 0 A 1 A 2
 5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
5. FUNCŢII IMPLICITE. EXTREME CONDIŢIONATE.
 5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
1.7. AMPLIFICATOARE DE PUTERE ÎN CLASA A ŞI AB
 1.7. AMLFCATOARE DE UTERE ÎN CLASA A Ş AB 1.7.1 Amplificatoare în clasa A La amplificatoarele din clasa A, forma de undă a tensiunii de ieşire este aceeaşi ca a tensiunii de intrare, deci întreg semnalul
1.7. AMLFCATOARE DE UTERE ÎN CLASA A Ş AB 1.7.1 Amplificatoare în clasa A La amplificatoarele din clasa A, forma de undă a tensiunii de ieşire este aceeaşi ca a tensiunii de intrare, deci întreg semnalul
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM 1 electronica.geniu.ro
 Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor X) functia f 1
 Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Curs 4 Serii de numere reale
 Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Zgomotul se poate suprapune informaţiei utile în două moduri: g(x, y) = f(x, y) n(x, y) (6.2)
 Lucrarea 6 Zgomotul în imagini BREVIAR TEORETIC Zgomotul este un semnal aleator, care afectează informaţia utilă conţinută într-o imagine. El poate apare de-alungul unui lanţ de transmisiune, sau prin
Lucrarea 6 Zgomotul în imagini BREVIAR TEORETIC Zgomotul este un semnal aleator, care afectează informaţia utilă conţinută într-o imagine. El poate apare de-alungul unui lanţ de transmisiune, sau prin
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor
 Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
 4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
5.5. REZOLVAREA CIRCUITELOR CU TRANZISTOARE BIPOLARE
 5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
Subiecte Clasa a VIII-a
 Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
 10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
SERII NUMERICE. Definiţia 3.1. Fie (a n ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0
 SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
riptografie şi Securitate
 riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
Laborator 11. Mulţimi Julia. Temă
 Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Planul determinat de normală şi un punct Ecuaţia generală Plane paralele Unghi diedru Planul determinat de 3 puncte necoliniare
 1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
Criptosisteme cu cheie publică III
 Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
Captura imaginilor. este necesară o sursă de lumină (λ: lungimea de undă a sursei)
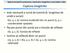 Captura imaginilor este necesară o sursă de lumină (λ: lungimea de undă a sursei) E(x, y, z, λ): lumina incidentă într-un punct (x, y, z coordonatele spațiale) fiecare punct din scenă are o funcție de
Captura imaginilor este necesară o sursă de lumină (λ: lungimea de undă a sursei) E(x, y, z, λ): lumina incidentă într-un punct (x, y, z coordonatele spațiale) fiecare punct din scenă are o funcție de
V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile
 Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Aplicaţii ale principiului I al termodinamicii la gazul ideal
 Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
V O. = v I v stabilizator
 Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Seminariile Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reziduurilor
 Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Integrala nedefinită (primitive)
 nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
Problema a II - a (10 puncte) Diferite circuite electrice
 Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
Definiţia generală Cazul 1. Elipsa şi hiperbola Cercul Cazul 2. Parabola Reprezentari parametrice ale conicelor Tangente la conice
 1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
Asupra unei inegalităţi date la barajul OBMJ 2006
 Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
Curs 2 DIODE. CIRCUITE DR
 Curs 2 OE. CRCUTE R E CUPRN tructură. imbol Relația curent-tensiune Regimuri de funcționare Punct static de funcționare Parametrii diodei Modelul cu cădere de tensiune constantă Analiza circuitelor cu
Curs 2 OE. CRCUTE R E CUPRN tructură. imbol Relația curent-tensiune Regimuri de funcționare Punct static de funcționare Parametrii diodei Modelul cu cădere de tensiune constantă Analiza circuitelor cu
2. Sisteme de forţe concurente...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...3
 SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
Laborator 1: INTRODUCERE ÎN ALGORITMI. Întocmit de: Claudia Pârloagă. Îndrumător: Asist. Drd. Gabriel Danciu
 INTRODUCERE Laborator 1: ÎN ALGORITMI Întocmit de: Claudia Pârloagă Îndrumător: Asist. Drd. Gabriel Danciu I. NOŢIUNI TEORETICE A. Sortarea prin selecţie Date de intrare: un şir A, de date Date de ieşire:
INTRODUCERE Laborator 1: ÎN ALGORITMI Întocmit de: Claudia Pârloagă Îndrumător: Asist. Drd. Gabriel Danciu I. NOŢIUNI TEORETICE A. Sortarea prin selecţie Date de intrare: un şir A, de date Date de ieşire:
Proiectarea filtrelor prin metoda pierderilor de inserţie
 FITRE DE MIROUNDE Proiectarea filtrelor prin metoda pierderilor de inserţie P R Puterea disponibila de la sursa Puterea livrata sarcinii P inc P Γ ( ) Γ I lo P R ( ) ( ) M ( ) ( ) M N P R M N ( ) ( ) Tipuri
FITRE DE MIROUNDE Proiectarea filtrelor prin metoda pierderilor de inserţie P R Puterea disponibila de la sursa Puterea livrata sarcinii P inc P Γ ( ) Γ I lo P R ( ) ( ) M ( ) ( ) M N P R M N ( ) ( ) Tipuri
Subiecte Clasa a VII-a
 lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
Componente şi Circuite Electronice Pasive. Laborator 4. Măsurarea parametrilor mărimilor electrice
 Laborator 4 Măsurarea parametrilor mărimilor electrice Obiective: o Semnalul sinusoidal, o Semnalul dreptunghiular, o Semnalul triunghiular, o Generarea diferitelor semnale folosind placa multifuncţională
Laborator 4 Măsurarea parametrilor mărimilor electrice Obiective: o Semnalul sinusoidal, o Semnalul dreptunghiular, o Semnalul triunghiular, o Generarea diferitelor semnale folosind placa multifuncţională
Conice. Lect. dr. Constantin-Cosmin Todea. U.T. Cluj-Napoca
 Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
Seminar 5 Analiza stabilității sistemelor liniare
 Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii transversale, scrisă faţă de una dintre axele de inerţie principale:,
 REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
Examen AG. Student:... Grupa:... ianuarie 2011
 Problema 1. Pentru ce valori ale lui n,m N (n,m 1) graful K n,m este eulerian? Problema 2. Să se construiască o funcţie care să recunoască un graf P 3 -free. La intrare aceasta va primi un graf G = ({1,...,n},E)
Problema 1. Pentru ce valori ale lui n,m N (n,m 1) graful K n,m este eulerian? Problema 2. Să se construiască o funcţie care să recunoască un graf P 3 -free. La intrare aceasta va primi un graf G = ({1,...,n},E)
Componente şi Circuite Electronice Pasive. Laborator 3. Divizorul de tensiune. Divizorul de curent
 Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
Valori limită privind SO2, NOx şi emisiile de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili
 Anexa 2.6.2-1 SO2, NOx şi de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili de bioxid de sulf combustibil solid (mg/nm 3 ), conţinut de O 2 de 6% în gazele de ardere, pentru
Anexa 2.6.2-1 SO2, NOx şi de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili de bioxid de sulf combustibil solid (mg/nm 3 ), conţinut de O 2 de 6% în gazele de ardere, pentru
Aparate de măsurat. Măsurări electronice Rezumatul cursului 2. MEE - prof. dr. ing. Ioan D. Oltean 1
 Aparate de măsurat Măsurări electronice Rezumatul cursului 2 MEE - prof. dr. ing. Ioan D. Oltean 1 1. Aparate cu instrument magnetoelectric 2. Ampermetre şi voltmetre 3. Ohmetre cu instrument magnetoelectric
Aparate de măsurat Măsurări electronice Rezumatul cursului 2 MEE - prof. dr. ing. Ioan D. Oltean 1 1. Aparate cu instrument magnetoelectric 2. Ampermetre şi voltmetre 3. Ohmetre cu instrument magnetoelectric
4. Măsurarea tensiunilor şi a curenţilor electrici. Voltmetre electronice analogice
 4. Măsurarea tensiunilor şi a curenţilor electrici oltmetre electronice analogice oltmetre de curent continuu Ampl.c.c. x FTJ Protectie Atenuator calibrat Atenuatorul calibrat divizor rezistiv R in const.
4. Măsurarea tensiunilor şi a curenţilor electrici oltmetre electronice analogice oltmetre de curent continuu Ampl.c.c. x FTJ Protectie Atenuator calibrat Atenuatorul calibrat divizor rezistiv R in const.
Geometrie computationala 2. Preliminarii geometrice
 Platformă de e-learning și curriculă e-content pentru învățământul superior tehnic Geometrie computationala 2. Preliminarii geometrice Preliminarii geometrice Spatiu Euclidean: E d Spatiu de d-tupluri,
Platformă de e-learning și curriculă e-content pentru învățământul superior tehnic Geometrie computationala 2. Preliminarii geometrice Preliminarii geometrice Spatiu Euclidean: E d Spatiu de d-tupluri,
Analiza și Prelucrarea Digitală a Semnalelor Video
 Analiza și Prelucrarea Digitală a Semnalelor Video Conf. dr. ing. Radu Ovidiu Preda radu@comm.pub.ro Ș.l. dr. ing. Ionuţ Pirnog ionut@comm.pub.ro Site disciplină: www.comm.pub.ro/preda/apdsv Analiza și
Analiza și Prelucrarea Digitală a Semnalelor Video Conf. dr. ing. Radu Ovidiu Preda radu@comm.pub.ro Ș.l. dr. ing. Ionuţ Pirnog ionut@comm.pub.ro Site disciplină: www.comm.pub.ro/preda/apdsv Analiza și
Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].
![Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].](/thumbs/72/67648751.jpg) Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
Teme de implementare in Matlab pentru Laboratorul de Metode Numerice
 Teme de implementare in Matlab pentru Laboratorul de Metode Numerice As. Ruxandra Barbulescu Septembrie 2017 Orice nelamurire asupra enunturilor/implementarilor se rezolva in cadrul laboratorului de MN,
Teme de implementare in Matlab pentru Laboratorul de Metode Numerice As. Ruxandra Barbulescu Septembrie 2017 Orice nelamurire asupra enunturilor/implementarilor se rezolva in cadrul laboratorului de MN,
SEMINAR 14. Funcţii de mai multe variabile (continuare) ( = 1 z(x,y) x = 0. x = f. x + f. y = f. = x. = 1 y. y = x ( y = = 0
 Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
Cum folosim cazuri particulare în rezolvarea unor probleme
 Cum folosim cazuri particulare în rezolvarea unor probleme GHEORGHE ECKSTEIN 1 Atunci când întâlnim o problemă pe care nu ştim s-o abordăm, adesea este bine să considerăm cazuri particulare ale acesteia.
Cum folosim cazuri particulare în rezolvarea unor probleme GHEORGHE ECKSTEIN 1 Atunci când întâlnim o problemă pe care nu ştim s-o abordăm, adesea este bine să considerăm cazuri particulare ale acesteia.
R R, f ( x) = x 7x+ 6. Determinați distanța dintre punctele de. B=, unde x și y sunt numere reale.
 5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
a. Caracteristicile mecanice a motorului de c.c. cu excitaţie independentă (sau derivaţie)
 Caracteristica mecanică defineşte dependenţa n=f(m) în condiţiile I e =ct., U=ct. Pentru determinarea ei vom defini, mai întâi caracteristicile: 1. de sarcină, numită şi caracteristica externă a motorului
Caracteristica mecanică defineşte dependenţa n=f(m) în condiţiile I e =ct., U=ct. Pentru determinarea ei vom defini, mai întâi caracteristicile: 1. de sarcină, numită şi caracteristica externă a motorului
COLEGIUL NATIONAL CONSTANTIN CARABELLA TARGOVISTE. CONCURSUL JUDETEAN DE MATEMATICA CEZAR IVANESCU Editia a VI-a 26 februarie 2005.
 SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
a. 11 % b. 12 % c. 13 % d. 14 %
 1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
Sisteme diferenţiale liniare de ordinul 1
 1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
Procesarea Imaginilor
 Procesarea Imaginilor SEGMENTAREA IMAGINILOR Mihai Ivanovici Universitatea Transilvania din Braşov Page 1 of 29 1 Segmentarea reprezintă împărţirea imaginii în zone de interes, după anumite criterii Fiecărui
Procesarea Imaginilor SEGMENTAREA IMAGINILOR Mihai Ivanovici Universitatea Transilvania din Braşov Page 1 of 29 1 Segmentarea reprezintă împărţirea imaginii în zone de interes, după anumite criterii Fiecărui
Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25
 Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25 LAGĂRELE CU ALUNECARE!" 25.1.Caracteristici.Părţi componente.materiale.!" 25.2.Funcţionarea lagărelor cu alunecare.! 25.1.Caracteristici.Părţi componente.materiale.
Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25 LAGĂRELE CU ALUNECARE!" 25.1.Caracteristici.Părţi componente.materiale.!" 25.2.Funcţionarea lagărelor cu alunecare.! 25.1.Caracteristici.Părţi componente.materiale.
Exemple de probleme rezolvate pentru cursurile DEEA Tranzistoare bipolare cu joncţiuni
 Problema 1. Se dă circuitul de mai jos pentru care se cunosc: VCC10[V], 470[kΩ], RC2,7[kΩ]. Tranzistorul bipolar cu joncţiuni (TBJ) este de tipul BC170 şi are parametrii β100 şi VBE0,6[V]. 1. să se determine
Problema 1. Se dă circuitul de mai jos pentru care se cunosc: VCC10[V], 470[kΩ], RC2,7[kΩ]. Tranzistorul bipolar cu joncţiuni (TBJ) este de tipul BC170 şi are parametrii β100 şi VBE0,6[V]. 1. să se determine
a. 0,1; 0,1; 0,1; b. 1, ; 5, ; 8, ; c. 4,87; 6,15; 8,04; d. 7; 7; 7; e. 9,74; 12,30;1 6,08.
 1. În argentometrie, metoda Mohr: a. foloseşte ca indicator cromatul de potasiu, care formeazǎ la punctul de echivalenţă un precipitat colorat roşu-cărămiziu; b. foloseşte ca indicator fluoresceina, care
1. În argentometrie, metoda Mohr: a. foloseşte ca indicator cromatul de potasiu, care formeazǎ la punctul de echivalenţă un precipitat colorat roşu-cărămiziu; b. foloseşte ca indicator fluoresceina, care
Reflexia şi refracţia luminii.
 Reflexia şi refracţia luminii. 1. Cu cat se deplaseaza o raza care cade sub unghiul i =30 pe o placa plan-paralela de grosime e = 8,0 mm si indicele de refractie n = 1,50, pe care o traverseaza? Caz particular
Reflexia şi refracţia luminii. 1. Cu cat se deplaseaza o raza care cade sub unghiul i =30 pe o placa plan-paralela de grosime e = 8,0 mm si indicele de refractie n = 1,50, pe care o traverseaza? Caz particular
8 Intervale de încredere
 8 Intervale de încredere În cursul anterior am determinat diverse estimări ˆ ale parametrului necunoscut al densităţii unei populaţii, folosind o selecţie 1 a acestei populaţii. În practică, valoarea calculată
8 Intervale de încredere În cursul anterior am determinat diverse estimări ˆ ale parametrului necunoscut al densităţii unei populaţii, folosind o selecţie 1 a acestei populaţii. În practică, valoarea calculată
REDRESOARE MONOFAZATE CU FILTRU CAPACITIV
 REDRESOARE MONOFAZATE CU FILTRU CAPACITIV I. OBIECTIVE a) Stabilirea dependenţei dintre tipul redresorului (monoalternanţă, bialternanţă) şi forma tensiunii redresate. b) Determinarea efectelor modificării
REDRESOARE MONOFAZATE CU FILTRU CAPACITIV I. OBIECTIVE a) Stabilirea dependenţei dintre tipul redresorului (monoalternanţă, bialternanţă) şi forma tensiunii redresate. b) Determinarea efectelor modificării
Stabilizator cu diodă Zener
 LABAT 3 Stabilizator cu diodă Zener Se studiază stabilizatorul parametric cu diodă Zener si apoi cel cu diodă Zener şi tranzistor. Se determină întâi tensiunea Zener a diodei şi se calculează apoi un stabilizator
LABAT 3 Stabilizator cu diodă Zener Se studiază stabilizatorul parametric cu diodă Zener si apoi cel cu diodă Zener şi tranzistor. Se determină întâi tensiunea Zener a diodei şi se calculează apoi un stabilizator
III. Reprezentarea informaţiei în sistemele de calcul
 Metode Numerice Curs 3 III. Reprezentarea informaţiei în sistemele de calcul III.1. Reprezentarea internă a numerelor întregi III. 1.1. Reprezentarea internă a numerelor întregi fără semn (pozitive) Reprezentarea
Metode Numerice Curs 3 III. Reprezentarea informaţiei în sistemele de calcul III.1. Reprezentarea internă a numerelor întregi III. 1.1. Reprezentarea internă a numerelor întregi fără semn (pozitive) Reprezentarea
Examen AG. Student:... Grupa: ianuarie 2016
 16-17 ianuarie 2016 Problema 1. Se consideră graful G = pk n (p, n N, p 2, n 3). Unul din vârfurile lui G se uneşte cu câte un vârf din fiecare graf complet care nu-l conţine, obţinându-se un graf conex
16-17 ianuarie 2016 Problema 1. Se consideră graful G = pk n (p, n N, p 2, n 3). Unul din vârfurile lui G se uneşte cu câte un vârf din fiecare graf complet care nu-l conţine, obţinându-se un graf conex
Transformări de frecvenţă
 Lucrarea 22 Tranformări de frecvenţă Scopul lucrării: prezentarea metodei de inteză bazate pe utilizarea tranformărilor de frecvenţă şi exemplificarea aceteia cu ajutorul unui filtru trece-jo de tip Sallen-Key.
Lucrarea 22 Tranformări de frecvenţă Scopul lucrării: prezentarea metodei de inteză bazate pe utilizarea tranformărilor de frecvenţă şi exemplificarea aceteia cu ajutorul unui filtru trece-jo de tip Sallen-Key.
2.1 Sfera. (EGS) ecuaţie care poartă denumirea de ecuaţia generală asferei. (EGS) reprezintă osferă cu centrul în punctul. 2 + p 2
 .1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
.1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R. 4.1 Proprietăţi topologice ale lui R Puncte de acumulare
 Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R În cele ce urmează, vom studia unele proprietăţi ale mulţimilor din R. Astfel, vom caracteriza locul" unui punct în cadrul unei mulţimi (în limba
Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R În cele ce urmează, vom studia unele proprietăţi ale mulţimilor din R. Astfel, vom caracteriza locul" unui punct în cadrul unei mulţimi (în limba
Erori si incertitudini de măsurare. Modele matematice Instrument: proiectare, fabricaţie, Interacţiune măsurand instrument:
 Erori i incertitudini de măurare Sure: Modele matematice Intrument: proiectare, fabricaţie, Interacţiune măurandintrument: (tranfer informaţie tranfer energie) Influente externe: temperatura, preiune,
Erori i incertitudini de măurare Sure: Modele matematice Intrument: proiectare, fabricaţie, Interacţiune măurandintrument: (tranfer informaţie tranfer energie) Influente externe: temperatura, preiune,
Scoruri standard Curba normală (Gauss) M. Popa
 Scoruri standard Curba normală (Gauss) M. Popa Scoruri standard cunoaştere evaluare, măsurare evaluare comparare (Gh. Zapan) comparare raportare la un sistem de referință Povestea Scufiței Roşii... 70
Scoruri standard Curba normală (Gauss) M. Popa Scoruri standard cunoaştere evaluare, măsurare evaluare comparare (Gh. Zapan) comparare raportare la un sistem de referință Povestea Scufiței Roşii... 70
Capitolul 14. Asamblari prin pene
 Capitolul 14 Asamblari prin pene T.14.1. Momentul de torsiune este transmis de la arbore la butuc prin intermediul unei pene paralele (figura 14.1). De care din cotele indicate depinde tensiunea superficiala
Capitolul 14 Asamblari prin pene T.14.1. Momentul de torsiune este transmis de la arbore la butuc prin intermediul unei pene paralele (figura 14.1). De care din cotele indicate depinde tensiunea superficiala
z a + c 0 + c 1 (z a)
 1 Serii Laurent (continuare) Teorema 1.1 Fie D C un domeniu, a D şi f : D \ {a} C o funcţie olomorfă. Punctul a este pol multiplu de ordin p al lui f dacă şi numai dacă dezvoltarea în serie Laurent a funcţiei
1 Serii Laurent (continuare) Teorema 1.1 Fie D C un domeniu, a D şi f : D \ {a} C o funcţie olomorfă. Punctul a este pol multiplu de ordin p al lui f dacă şi numai dacă dezvoltarea în serie Laurent a funcţiei
Εμπορική αλληλογραφία Ηλεκτρονική Αλληλογραφία
 - Εισαγωγή Stimate Domnule Preşedinte, Stimate Domnule Preşedinte, Εξαιρετικά επίσημη επιστολή, ο παραλήπτης έχει ένα ειδικό τίτλο ο οποίος πρέπει να χρησιμοποιηθεί αντί του ονόματος του Stimate Domnule,
- Εισαγωγή Stimate Domnule Preşedinte, Stimate Domnule Preşedinte, Εξαιρετικά επίσημη επιστολή, ο παραλήπτης έχει ένα ειδικό τίτλο ο οποίος πρέπει να χρησιμοποιηθεί αντί του ονόματος του Stimate Domnule,
Măsurări în Electronică şi Telecomunicaţii 4. Măsurarea impedanţelor
 4. Măsurarea impedanţelor 4.2. Măsurarea rezistenţelor în curent continuu Metoda comparaţiei ceastă metodă: se utilizează pentru măsurarea rezistenţelor ~ 0 montaj serie sau paralel. Montajul serie (metoda
4. Măsurarea impedanţelor 4.2. Măsurarea rezistenţelor în curent continuu Metoda comparaţiei ceastă metodă: se utilizează pentru măsurarea rezistenţelor ~ 0 montaj serie sau paralel. Montajul serie (metoda
Să se arate că n este număr par. Dan Nedeianu
 Primul test de selecție pentru juniori I. Să se determine numerele prime p, q, r cu proprietatea că 1 p + 1 q + 1 r 1. Fie ABCD un patrulater convex cu m( BCD) = 10, m( CBA) = 45, m( CBD) = 15 și m( CAB)
Primul test de selecție pentru juniori I. Să se determine numerele prime p, q, r cu proprietatea că 1 p + 1 q + 1 r 1. Fie ABCD un patrulater convex cu m( BCD) = 10, m( CBA) = 45, m( CBD) = 15 și m( CAB)
GEOMETRIE PLANĂ TEOREME IMPORTANTE ARII. bh lh 2. abc. abc. formula înălţimii
 GEOMETRIE PLNĂ TEOREME IMPORTNTE suma unghiurilor unui triunghi este 8º suma unghiurilor unui patrulater este 6º unghiurile de la baza unui triunghi isoscel sunt congruente într-un triunghi isoscel liniile
GEOMETRIE PLNĂ TEOREME IMPORTNTE suma unghiurilor unui triunghi este 8º suma unghiurilor unui patrulater este 6º unghiurile de la baza unui triunghi isoscel sunt congruente într-un triunghi isoscel liniile
Tipuri de celule sub microscopul optic
 Tipuri de celule sub microscopul optic Termenul de celulă a fost introdus de R. Hooke în cartea sa Micrographia publicată în 1665 în care descrie observaţii făcute cu microscopul şi telescopul. Microscopul
Tipuri de celule sub microscopul optic Termenul de celulă a fost introdus de R. Hooke în cartea sa Micrographia publicată în 1665 în care descrie observaţii făcute cu microscopul şi telescopul. Microscopul
2. Circuite logice 2.4. Decodoare. Multiplexoare. Copyright Paul GASNER
 2. Circuite logice 2.4. Decodoare. Multiplexoare Copyright Paul GASNER Definiţii Un decodor pe n bits are n intrări şi 2 n ieşiri; cele n intrări reprezintă un număr binar care determină în mod unic care
2. Circuite logice 2.4. Decodoare. Multiplexoare Copyright Paul GASNER Definiţii Un decodor pe n bits are n intrări şi 2 n ieşiri; cele n intrări reprezintă un număr binar care determină în mod unic care
CURS: METODE EXPERIMENTALE ÎN FCS
 Cunoaşterea în fizică se bazează pe experimente şi măsurători. Pentru verificarea oricărei teorii => experiment => măsurători. Toate măsurătorile sunt afectate de erori. Nu putem măsura ă ceva cu exactitate
Cunoaşterea în fizică se bazează pe experimente şi măsurători. Pentru verificarea oricărei teorii => experiment => măsurători. Toate măsurătorile sunt afectate de erori. Nu putem măsura ă ceva cu exactitate
Orice izometrie f : (X, d 1 ) (Y, d 2 ) este un homeomorfism. (Y = f(x)).
 Teoremă. (Y = f(x)). Orice izometrie f : (X, d 1 ) (Y, d 2 ) este un homeomorfism Demonstraţie. f este continuă pe X: x 0 X, S Y (f(x 0 ), ε), S X (x 0, ε) aşa ca f(s X (x 0, ε)) = S Y (f(x 0 ), ε) : y
Teoremă. (Y = f(x)). Orice izometrie f : (X, d 1 ) (Y, d 2 ) este un homeomorfism Demonstraţie. f este continuă pe X: x 0 X, S Y (f(x 0 ), ε), S X (x 0, ε) aşa ca f(s X (x 0, ε)) = S Y (f(x 0 ), ε) : y
LUCRAREA NR. 1 STUDIUL SURSELOR DE CURENT
 LUCAEA N STUDUL SUSELO DE CUENT Scopul lucrării În această lucrare se studiază prin simulare o serie de surse de curent utilizate în cadrul circuitelor integrate analogice: sursa de curent standard, sursa
LUCAEA N STUDUL SUSELO DE CUENT Scopul lucrării În această lucrare se studiază prin simulare o serie de surse de curent utilizate în cadrul circuitelor integrate analogice: sursa de curent standard, sursa
FLUXURI MAXIME ÎN REŢELE DE TRANSPORT. x 4
 FLUXURI MAXIME ÎN REŢELE DE TRANSPORT Se numeşte reţea de transport un graf în care fiecărui arc îi este asociat capacitatea arcului şi în care eistă un singur punct de intrare şi un singur punct de ieşire.
FLUXURI MAXIME ÎN REŢELE DE TRANSPORT Se numeşte reţea de transport un graf în care fiecărui arc îi este asociat capacitatea arcului şi în care eistă un singur punct de intrare şi un singur punct de ieşire.
5.1. Noţiuni introductive
 ursul 13 aitolul 5. Soluţii 5.1. oţiuni introductive Soluţiile = aestecuri oogene de două sau ai ulte substanţe / coonente, ale căror articule nu se ot seara rin filtrare sau centrifugare. oonente: - Mediul
ursul 13 aitolul 5. Soluţii 5.1. oţiuni introductive Soluţiile = aestecuri oogene de două sau ai ulte substanţe / coonente, ale căror articule nu se ot seara rin filtrare sau centrifugare. oonente: - Mediul
SIGURANŢE CILINDRICE
 SIGURANŢE CILINDRICE SIGURANŢE CILINDRICE CH Curent nominal Caracteristici de declanşare 1-100A gg, am Aplicaţie: Siguranţele cilindrice reprezintă cea mai sigură protecţie a circuitelor electrice de control
SIGURANŢE CILINDRICE SIGURANŢE CILINDRICE CH Curent nominal Caracteristici de declanşare 1-100A gg, am Aplicaţie: Siguranţele cilindrice reprezintă cea mai sigură protecţie a circuitelor electrice de control
Laborator 6. Integrarea ecuaţiilor diferenţiale
 Laborator 6 Integrarea ecuaţiilor diferenţiale Responsabili: 1. Surdu Cristina(anacristinasurdu@gmail.com) 2. Ştirbăţ Bogdan(bogdanstirbat@yahoo.com) Obiective În urma parcurgerii acestui laborator elevul
Laborator 6 Integrarea ecuaţiilor diferenţiale Responsabili: 1. Surdu Cristina(anacristinasurdu@gmail.com) 2. Ştirbăţ Bogdan(bogdanstirbat@yahoo.com) Obiective În urma parcurgerii acestui laborator elevul
Statisticǎ - curs 3. 1 Seria de distribuţie a statisticilor de eşantioane 2. 2 Teorema limitǎ centralǎ 5. 3 O aplicaţie a teoremei limitǎ centralǎ 7
 Statisticǎ - curs 3 Cuprins 1 Seria de distribuţie a statisticilor de eşantioane 2 2 Teorema limitǎ centralǎ 5 3 O aplicaţie a teoremei limitǎ centralǎ 7 4 Estimarea punctualǎ a unui parametru; intervalul
Statisticǎ - curs 3 Cuprins 1 Seria de distribuţie a statisticilor de eşantioane 2 2 Teorema limitǎ centralǎ 5 3 O aplicaţie a teoremei limitǎ centralǎ 7 4 Estimarea punctualǎ a unui parametru; intervalul
VII.2. PROBLEME REZOLVATE
 Teoria Circuitelor Electrice Aplicaţii V PROBEME REOVATE R7 În circuitul din fiura 7R se cunosc: R e t 0 sint [V] C C t 0 sint [A] Se cer: a rezolvarea circuitului cu metoda teoremelor Kirchhoff; rezolvarea
Teoria Circuitelor Electrice Aplicaţii V PROBEME REOVATE R7 În circuitul din fiura 7R se cunosc: R e t 0 sint [V] C C t 0 sint [A] Se cer: a rezolvarea circuitului cu metoda teoremelor Kirchhoff; rezolvarea
Seminar Algebra. det(a λi 3 ) = 0
 Rezolvari ale unor probleme propuse "Matematica const în a dovedi ceea ce este evident în cel mai puµin evident mod." George Polya P/Seminar Valori si vectori proprii : Solutie: ( ) a) A = Valorile proprii:
Rezolvari ale unor probleme propuse "Matematica const în a dovedi ceea ce este evident în cel mai puµin evident mod." George Polya P/Seminar Valori si vectori proprii : Solutie: ( ) a) A = Valorile proprii:
Tratarea numerică a semnalelor
 LUCRAREA 5 Tratarea numerică a semnalelor Filtre numerice cu răspuns finit la impuls (filtre RFI) Filtrele numerice sunt sisteme discrete liniare invariante în timp care au rolul de a modifica spectrul
LUCRAREA 5 Tratarea numerică a semnalelor Filtre numerice cu răspuns finit la impuls (filtre RFI) Filtrele numerice sunt sisteme discrete liniare invariante în timp care au rolul de a modifica spectrul
Morfologie matematică pentru imagini binare şi în tonuri de gri
 Morfologie matematică pentru imagini binare şi în tonuri de gri M. Ivanovici, A. Căliman, B. Budescu 19 decembrie 2011 BREVIAR TEORETIC Etimologia cuvântului morfologie are la bază cuvintele greceşti morphos
Morfologie matematică pentru imagini binare şi în tonuri de gri M. Ivanovici, A. Căliman, B. Budescu 19 decembrie 2011 BREVIAR TEORETIC Etimologia cuvântului morfologie are la bază cuvintele greceşti morphos
