Άριστες κατά Pareto Κατανομές και το Πρώτο Θεώρημα Ευημερίας
|
|
|
- Οινώνη Πολίτης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Άριστες κατά Pareto Κατανομές και το Πρώτο Θεώρημα Ευημερίας - Υποθέτουμε μια οικονομία που αποτελείται από: Δύο καταναλωτές 1,. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ και το καταναλωτικό αγαθό Α. - Οι προτιμήσεις των καταναλωτών παριστάνονται από τις συναρτήσεις χρησιμότητας: U1( X1, A1) : Συνάρτηση χρησιμότητας του καταναλωτή 1 U( X, A) : Συνάρτηση χρησιμότητας του καταναλωτή - Οι περιουσίες των καταναλωτών παριστάνονται από τα διανύσματα περιουσιών: e1 = ( ex1, ea 1) = ( T1,0) : Διάνυσμα περιουσίας του καταναλωτή 1 e = ( e, e ) = ( T,0) : Διάνυσμα περιουσίας του καταναλωτή X A -Hσυνάρτηση παραγωγής της επιχείρησης είναι: A = f( L). 1
2 - Ορισμός. Μια εφικτή κατανομή ( X1, A1),(( X, A),( L, A) ονομάζεται άριστη κατά Pareto αν δεν υπάρχει άλλη εφικτή κατανομή ( X, A ),(( X, A ),( L, A ) τέτοια ώστε: ( ) 1 1 U j( X j, A j) U j( X j, Aj) για κάθε καταναλωτή j = AB, και U ( X, A ) > U ( X, A ) για κάποιον καταναλωτή j. j j j j j j ( ) - Δηλαδή: Δεν υπάρχει άλλη κατανομή που ωφελεί κάποιον καταναλωτή χωρίς ταυτόχρονα να ζημιώνει κάποιον άλλον. - Δεν υπάρχει δυνατότητα μετακίνησης από μια άριστη κατά Pareto κατανομή κατά τρόπο ώστε να ωφελούνται όλα τα άτομα στην οικονομία (ή: κατά τρόπο ώστε να ωφελείται κάποιος καταναλωτής χωρίς ταυτόχρονα να ζημιώνεται κάποιος άλλος). - Οποιαδήποτε μετακίνηση η οποία ωφελεί κάποιον καταναλωτή πρέπει αναγκαστικά να ζημιώνει κάποιον άλλον.
3 - Δηλαδή: Δεν υπάρχει δυνατότητα να γίνουν αμοιβαία επωφελείς ανταλλαγές μεταξύ των καταναλωτών (όλαταοφέληαπότις συναλλαγές έχουν εξαντληθεί). Υπολογισμός Άριστων κατά Pareto Κατανομών - Για να υπολογίσουμε μια άριστη κατά Pareto κατανομή, μεγιστοποιούμε τη χρησιμότητα του καταναλωτή 1 υπό τον περιορισμό ότι η χρησιμότητα του καταναλωτή είναι (τουλάχιστον) ίση με κάποιο επίπεδο (στόχο) χρησιμότητας U, ενώ ταυτόχρονα λαμβάνουμε υπόψη τους τεχνολογικούς περιορισμούς και τους περιορισμούς των πόρων στην οικονομία. ( ) - Πρόταση. Μια κατανομή ( X είναι άριστη 1, A1),(( X, A),( L, A) κατά Pareto αν και μόνο αν αποτελεί λύση του παρακάτω προβλήματος βελτιστοποίησης: 3
4 max U ( X, A) { X, A, X, A, L, A} st.. U( X, A) U (1) A f( L) () X1+ X + L T1+ T (3) (PΟP) A1+ A A (4) (Pareto Optimality 0 X1 T1 (5) Problem) 0 X T (6) A1, A, L, A 0 Ο περιορισμός (1) απαιτεί να επιτυγχάνεται τουλάχιστον ο στόχος χρησιμότητας ( U ) για τον καταναλωτή. Ο περιορισμός () είναι ο τεχνολογικός περιορισμός της οικονομίας. Οι περιορισμοί (3) και (4) ονομάζονται περιορισμοί των πόρων (Resource Constraints) και εξασφαλίζουν ότι η λύση του POP είναι μια εφικτή κατανομή. 4
5 L = U ( X, A) + λ[ U ( X, A ) U ] + μ[ f( L) A] + ν ( T + T X X L) ν ( A A A ) + ρ ( T X ) + ρ ( T X ) FOCs : U 0, X 0 X X X 1 = ν1 ρ1 1 = U ν 0, A 0 A A A 1 = 1 = U = 0, = 0 X X X A λ ν1 ρ X U λ A = ν 0, A = 0 A = μ+ ν 0, A = 0 A A f = μ ν1 0, L = 0 5
6 = U( X, A) U 0, λ = 0 λ λ = f( L) A 0, μ = 0 μ μ ν ν = T + T X X L 0, ν = ν1 = A A A 0, ν = 0 1 ν = T X 0, ρ = 0 ρ ρ ρ1 = T X 0, ρ = 0 ρ Υπόθεση: 0 < X < T, 0 < X < T, A, A, L, A> 0. Τότε: X X < T ρ = < T ρ =
7 U U X > 0 = ν = 0 ν = > 0 X + X + L= T + T (7) X1 X1 X1 U U A > 0 = ν = 0 ν = > 0 A + A = A (8) A1 A1 A1 ν Επίσης: = ν U U / X / A = MRS 1 - Άρα: Για να είναι μια κατανομή άριστη κατά Pareto, οι περιορισμοί των πόρων πρέπει να ισχύουν με ισότητα (δηλαδή πρέπει να καταναλώνεται ολόκληρη η διαθέσιμη ποσότητα κάθε αγαθού). X U ν U / X > 0 = λ ν = 0 λ = = > X X U / X U / X U ( X, A ) = U (10) (10) ν U λ X 1 = 7 (9) (11)
8 - Άρα: Για να είναι μια κατανομή άριστη κατά Pareto, πρέπει να επιτυγχάνεται ακριβώς ο στόχος χρησιμότητας U. A U U > 0 = λ ν = 0 ν = λ (1) A A A ν U / X 1 (11),(1) = = MRS (13) ν U / A ν U / X U / X (9),(13) = = MRS = = MRS (14) ν U1/ A1 U/ A - Δηλαδή: Για να είναι μια κατανομή άριστη κατά Pareto, o οριακός λόγος υποκατάστασης πρέπει να είναι ο ίδιος για τους καταναλωτές 1 και. A > 0 = μ+ ν = 0 μ= ν > 0 A = f ( L) A - Δηλαδή: Για να είναι μια κατανομή άριστη κατά Pareto, πρέπει να παράγεται η μέγιστη δυνατή ποσότητα προϊόντος από κάθε δεδομένη 8 ποσότητα εργασίας.
9 f f f L > 0 = μ ν1 = 0 ν1 = μ = ν. Άρα: ν1 f = = MPL ν ν (15) 1 (14),(16) = MRS1 = MRS = MPL (16) ν - Δηλαδή: Για να είναι μια κατανομή άριστη κατά Pareto, o οριακός λόγος υποκατάστασης για τους καταναλωτές 1, πρέπει να είναι ίσος με το οριακό προϊόν της εργασίας. - Παρατήρηση: Στη λύση του POP, οι περιορισμοί (1) έως (4) θα ισχύουν με ισότητα. Συνθήκες ης Τάξης (Ικανές Συνθήκες Μεγιστοποίησης): Αν οι συναρτήσεις χρησιμότητας των καταναλωτών είναι οιονεί κοίλες και η συνάρτηση παραγωγής της επιχείρησης είναι κοίλη, τότε κάθε λύση 9 των FOCs αποτελεί ολικό μέγιστο του POP.
10 - Γνωρίζουμε ότι σε κάθε ανταγωνιστική ισορροπία πρέπει να ισχύει: w MRS 1 MRS MP L p = = = - Άρα: Κάθε ανταγωνιστική ισορροπία ικανοποιεί τη συνθήκη βελτιστοποίησης κατά Pareto (δηλαδή τη συνθήκη 16). 1 ο Θεμελιώδες Θεώρημα Ευημερίας (First Fundamental Theorem of Welfare Economics - FWT). Κάθε ανταγωνιστική ισορροπία είναι άριστη κατά Pareto. - Μια πιο επίσημη διατύπωση του FWT είναι η εξής: ( ) Αν ( w, p),( X 1, A1),(( X, A),( L, A) ισορροπία, τότεηκατανομήισορροπίας είναι άριστη κατά Pareto. είναι μια ανταγωνιστική (( X ) 1, A1),(( X, A),( L, A) 10
11 Παρατηρήσεις για το 1 ο Θεώρημα Ευημερίας (1) Το FWT είναι η επίσημη διατύπωση της θέσης του Adam Smith για το αόρατο χέρι της αγοράς. - Μολονότι όλα τα άτομα στην οικονομία επιδιώκουν να ικανοποιήσουν μόνο το προσωπικό τους συμφέρον, μοιάζουν σαν να κατευθύνονται από ένα αόρατο χέρι που τα οδηγεί σε επιλογές οι οποίες μεγιστοποιούν την κοινωνική ευημερία. () Το FWT υποδεικνύει τις ανταγωνιστικές αγορές ως ένα γενικό μηχανισμό κατανομής των πόρων που μπορεί να χρησιμοποιηθεί για την επίτευξη άριστων κατά Pareto αποτελεσμάτων στην οικονομία. Αφού κάθε ανταγωνιστική ισορροπία είναι άριστη κατά Pareto, η μόνη δικαιολογία που υπάρχει για παρέμβαση στην οικονομία είναι η επίτευξη αναδιανεμητικών σκοπών. (3) Η ανταγωνιστική ισορροπία είναι άριστη κατά Pareto αλλά δεν εξασφαλίζει κατ ανάγκη την ίση ( δίκαιη ) διανομή των οικονομικών οφελών μεταξύ των καταναλωτών. 11
12 - Αν η αρχική διανομή των περιουσιών ευνοεί τον έναν από τους δύο καταναλωτές, τότε και η τελική κατανομή της ανταγωνιστικής ισορροπίας θα ευνοεί επίσης τον ίδιο καταναλωτή. - Γενικά: Η ανταγωνιστική ισορροπία (η οποία προκύπτει από ηθελημένες συναλλαγές στις ανταγωνιστικές αγορές) τείνει να αναπαράγει τις ανισότητες που χαρακτηρίζουν την αρχική διανομή των περιουσιών μεταξύ των καταναλωτών. Η επίτευξη μιας λιγότερο άνισης διανομής των οικονομικών οφελών προϋποθέτει κάποιου είδους παρέμβαση στην αγορά (π.χ. με τη χρήση ενός συστήματος φόρων και επιδοτήσεων) για την εκπλήρωση των επιθυμητών αναδιανεμητικών σκοπών. (4) Το FWT ισχύει υπό τις εξής υποθέσεις: (i) Οι αγορές είναι πλήρεις (κάθε τωρινό ή μελλοντικό αγαθό που αντιστοιχεί σε κάθε πιθανή κατάσταση του κόσμου αποτελεί αντικείμενο συναλλαγής σε μια αγορά). 1
13 (ii) Όλες οι αγορές είναι τέλεια ανταγωνιστικές (οι καταναλωτές και οι επιχειρήσεις θεωρούν δεδομένες τις τιμές όλων των αγαθών). - Αν υπάρχει ατελής ανταγωνισμός (δηλαδή αν κάποιοι καταναλωτές ή κάποιες επιχειρήσεις κατέχουν δύναμη στην αγορά και οι αποφάσεις τους επηρεάζουν τις τιμές), τότε η ισορροπία δεν είναι άριστη κατά Pareto. (iii) Δενυπάρχουνεξωτερικότητες(externalities) και δημόσια αγαθά στην οικονομία. - Αν υπάρχουν εξωτερικότητες ή / και δημόσια αγαθά, τότε η ανταγωνιστική ισορροπία δεν είναι άριστη κατά Pareto. (iv) Οι καταναλωτές και οι επιχειρήσεις έχουν τέλεια πληροφόρηση για τις τιμές των αγαθών και οι επιχειρήσεις έχουν τέλεια πληροφόρηση για τις ενέργειες και τις δεξιότητες των παραγωγικών συντελεστών. - Αν υπάρχει ατελής ή ασυμμετρική πληροφόρηση στην αγορά, τότε η ανταγωνιστική ισορροπία δεν είναι άριστη κατά Pareto. 13
14 Το Όριο Pareto - Λύνουμε το POP και βρίσκουμε όλες τις άριστες κατά Pareto κατανομές ως συνάρτηση του στόχου χρησιμότητας U : ( X ( U ), A( U ), X ( U ), A ( U ), L( U ), AU ( )) 1 1 (Άριστες κατά Pareto Κατανομές) - Αντικαθιστούμε τις άριστες κατά Pareto ποσότητες X1( U), A1( U) στη συνάρτηση χρησιμότητας του καταναλωτή 1 και παίρνουμε το όριο Pareto ή σύνορο Pareto ή σύνορο δυνατοτήτων χρησιμότητας (Pareto Frontier ή Utility Possibilities Frontier UPF ): U ( U ) = U [ X ( U ), A( U )] Το όριο Pareto παριστάνει το σύνολο των συνδυασμών χρησιμοτήτων (U 1,U ) που αντιστοιχούν στις άριστες κατά Pareto κατανομές. ( ) - Πρόταση. Μια κατανομή X1, A1, X, A, L, A είναι άριστη κατά Pareto αν και μόνο αν ο συνδυασμός χρησιμοτήτων που αντιστοιχεί στη συγκεκριμένη κατανομή ανήκει στο όριο Pareto, δηλαδή: ( U ( X, A), U ( X, A ) UPF ) (UPF) 14
15 U 1 D E H UPF G F 0 U - Τα σημεία D, E, F είναι άριστα κατά Pareto (δηλαδή αντιστοιχούν σε άριστες κατά Pareto κατανομές), διότι βρίσκονται πάνω στο UPF. -To σημείο G δεν είναι άριστο κατά Pareto, διότι βρίσκεται κάτω από το UPF (οποιαδήποτε μετακίνηση από το σημείο G σε κάποιο σημείο εντός της γραμμοσκιασμένης περιοχής ωφελεί ταυτόχρονα και τους δύο καταναλωτές 1,). - Το σημείο H είναι ανέφικτο (δηλαδή αντιστοιχεί σε κάποια μη εφικτή κατανομή), διότι βρίσκεται πάνω από το UPF. 15
16 - Παράδειγμα 1 (Υπολογισμός Άριστων κατά Pareto Κατανομών). Έστω μια οικονομία που αποτελείται από: Δύο καταναλωτές: 1 και. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ και το καταναλωτικό αγαθό Α. - Οι προτιμήσεις των καταναλωτών παριστάνονται από τις συναρτήσεις χρησιμότητας: U1( X1, A1) = X1+ 3ln A1 U( X, A) = A - Οι περιουσίες των καταναλωτών παριστάνονται από τα διανύσματα: e1 = ( ex1, ea 1) = (4,0) e = ( ex, ea) = (0,0) - Η συνάρτηση παραγωγής της επιχείρησης είναι: A= f( L) = L 16
17 - Έχουμε ήδη υπολογίσει την ανταγωνιστική ισορροπία για τη συγκεκριμένη οικονομία, υποθέτοντας ότι ο καταναλωτής είναι ο μοναδικός ιδιοκτήτης της επιχείρησης [βλ. Week (1 of ), σελ. 7-14]: ( w, p) = (1, 1/) ( ( X ) 1, A1),( X, A),( L, A ) = ((1,6), (0,0), (3,6)) ( U ) 1 U, = (1+ 3ln6,0) (Τιμές Ισορροπίας) (Χρησιμότητες Ισορροπίας) (Κατανομή Ισορροπίας) - Υπολογίζουμε τις άριστες κατά Pareto κατανομές λύνοντας το POP: max U ( X, A) = X + 3ln A { X, A, A, L, A} st.. U( A) = A U (17) A L (18) X1 + L 4 (19) A1+ A A (0) X1 4 (1) X, A, A, L, A
18 - Παρατήρηση: Αν ισχύει ο περιορισμός (19), τότε ισχύει και ο (1). Μπορούμε να αγνοήσουμε τον περιορισμό (1). - Στη λύση του προβλήματος, οι περιορισμοί (18), (19) και (0) θα ισχύουν με ισότητα: A= L (18 ) X1+ L= 4 L= 4 X1 (19 ) A + A = A (0 ) 1 - Αντικαθιστούμε τις (19 ), (0 ) στην (18 ) και παίρνουμε: (19 ) (18 ) A + A = 8 X (18 ) (0 ) Άρα, το POP γράφεται: max U ( X, A) = X + 3ln A { X, A, A } st.. U ( A ) = A U A + A = 8 X X, A, A (POP) 18
19 - Βοηθητικό βήμα: Βρίσκουμε το διάστημα των τιμών που μπορεί να πάρει η παράμετρος Η ελάχιστη τιμή της U min U. U = 0 (για A = 0) Η μέγιστη τιμή της είναι: είναι: U (18 ) max 1 1 U = 8 (για X = A = 0 A = 8) U Λύνουμε το POP και βρίσκουμε τις άριστες κατά Pareto κατανομές. (i) Για 0 U U ( X, A ) = (0, U ) ( X1, A1) = (1,6) U ( LA, ) = (3 +,6 + U), οι άριστες κατά Pareto κατανομές είναι: 19
20 (ii) Για U 8 ( X, A) = (0,8 U ) 1 1 ( X, A) = (0, U) ( LA, ) = (4,8), οι άριστες κατά Pareto κατανομές είναι: - Αντικαθιστούμε τις άριστες κατά Pareto ποσότητες Χ 1,A 1 στη συνάρτηση χρησιμότητας του καταναλωτή 1 και παίρνουμε το όριο Pareto: U 1 = + U 1 3ln6 U, αν 0 3ln(8 U ), αν U 8 (UPF) 0
21 U 1 1+3ln6 Ε UPF 3ln U Αξιολόγηση Ανταγωνιστικής Ισορροπίας - Επαληθεύουμε ότι η ανταγωνιστική ισορροπία είναι άριστη κατά Pareto (δηλαδή ότι ισχύει το FWT). 1
22 1 ος τρόπος. Επαληθεύουμε ότι o συνδυασμός χρησιμοτήτων ισορροπίας( U1, U ) = (1+ 3ln6,0) ικανοποιεί την εξίσωση του ορίου Pareto (δηλαδή ότι η ανταγωνιστική ισορροπία ανήκει στο UPF). i Για U = U = 0, η άριστη κατά Pareto τιμή της U είναι : U 1 U = 1+ 3ln6 = 1+ 3ln6 = U, πράγματι Άρα, ο συνδυασμός χρησιμοτήτων ισορροπίας (σημείο Ε στο διάγραμμα της σελ. 1) ανήκει στο όριο Pareto. H ανταγωνιστική ισορροπία είναι άριστη κατά Pareto, δηλαδή ισχύει το FWT. ος τρόπος. Επαληθεύουμε ότι η κατανομή ισορροπίας είναι άριστη κατά Pareto. i Για U = U = 0, οι άριστες κατά Pareto ποσότητες είναι :
23 X A U = 1 = 1 = X, πράγματι. = 6 = A, πράγματι A = U = 0 = A, πράγματι. L= U + = = L A= + U = = A 3 3, πράγματι. 6 6, πράγματι. H ανταγωνιστική ισορροπία είναι άριστη κατά Pareto, δηλαδή ισχύει το FWT. 3
24 - Παράδειγμα. Έστω μια οικονομία που αποτελείται από: Δύο καταναλωτές: 1 και. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ και το καταναλωτικό αγαθό Α. - Οι προτιμήσεις των καταναλωτών παριστάνονται από τις συναρτήσεις χρησιμότητας: U1( X1, A1) = X1+ 3ln A1 U( X, A) = A - Οι περιουσίες των καταναλωτών παριστάνονται από τα διανύσματα: e1 = ( ex1, ea 1) = (,0) e = ( ex, ea) = (0,0) - Η συνάρτηση παραγωγής της επιχείρησης είναι: A= f( L) = 4 L 4
25 - Έχουμε ήδη υπολογίσει την ανταγωνιστική ισορροπία για τη συγκεκριμένη οικονομία, υποθέτοντας ότι οι καταναλωτές 1, μοιράζονται εξίσου τα κέρδη της επιχείρησης [βλ. Week (1 of ), σελ. 15-0]: ( w, p) = (1, 1/ ) ( ( X ) ( ) 1, A1),( X, A),( L, A ) = (0,3 ), (0, ), (,4 ) ( U ) 1 U, = (3ln(3 ), ) (Τιμές Ισορροπίας) (Χρησιμότητες Ισορροπίας) (Κατανομή Ισορροπίας) - Υπολογίζουμε τις άριστες κατά Pareto κατανομές λύνοντας το POP: max U ( X, A) = X + 3ln A { X, A, A, L, A} st.. U( A) = A U () A 4 L (3) X1 + L (4) A1+ A A (5) X1 (6) X, A, A, L, A
26 - Παρατήρηση: Αν ισχύει ο περιορισμός (4), τότε ισχύει και ο (6). Μπορούμε να αγνοήσουμε τον περιορισμό (6). - Στη λύση του προβλήματος, οι περιορισμοί (3), (4) και (5) θα ισχύουν με ισότητα: A= 4 L (3 ) X1+ L= L= X1 (4 ) A1+ A = A (5 ) - Αντικαθιστούμε τις (4 ), (5 ) στην (3 ) και παίρνουμε: (4 ) (3 ) A + A = 4 X (3 ) (5 ) Άρα, το POP γράφεται: max U ( X, A) = X + 3ln A { X, A, A } st.. U( A) = A U A + A = 4 X X, A, A (POP) 6
27 - Βοηθητικό βήμα: Βρίσκουμε το διάστημα των τιμών που μπορεί να πάρει η παράμετρος Η ελάχιστη τιμή της U. U min U = 0 (για A = 0) Η μέγιστη τιμή της είναι: είναι: U (18 ) max 1 1 U = 4 (για X = A = 0 A = 4 ) U Λύνουμε το POP και βρίσκουμε τις άριστες κατά Pareto κατανομές. (i) Για 0 U 144 ( X1, A1) =, ( U + 96 U) ( X, A ) = 0, U ( ), οι άριστες κατά Pareto κατανομές είναι: + 96 U ( LA, ) =, ( U 96 U) U 96 U + + U 7
28 (ii) Για U 4 ( X, A) = (0,4 U ) 1 1 ( X, A ) = (0, U ) ( LA, ) = (,4 ), οι άριστες κατά Pareto κατανομές είναι: - Αντικαθιστούμε τις άριστες κατά Pareto ποσότητες Χ 1,A 1 στη συνάρτηση χρησιμότητας του καταναλωτή 1 και παίρνουμε το όριο Pareto: U 1 = 144 U + 96 U + 3ln( ), αν 0 U ( U + 96 U ) 3ln(4 U ), αν U 4 (UPF) 8
29 U 1 5/+ 3ln( 6) 3ln(3 ) Ε UPF U Αξιολόγηση Ανταγωνιστικής Ισορροπίας - Επαληθεύουμε ότι η ανταγωνιστική ισορροπία είναι άριστη κατά Pareto (δηλαδή ότι ισχύει το FWT). 9
30 1 ος τρόπος. Επαληθεύουμε ότι o συνδυασμός χρησιμοτήτων ισορροπίας ( U ικανοποιεί την εξίσωση του 1, U ) = (3ln(3 ), ) ορίου Pareto (δηλαδή ότι η ανταγωνιστική ισορροπία ανήκει στο UPF). i Για U = U =, η άριστη κατά Pareto τιμή της U είναι : 1 U = 3ln(4 U ) = 3ln(3 ) = U, πράγματι Άρα, ο συνδυασμός χρησιμοτήτων ισορροπίας (σημείο Ε στο διάγραμμα της σελ. 9) ανήκει στο όριο Pareto. H ανταγωνιστική ισορροπία είναι άριστη κατά Pareto, δηλαδή ισχύει το FWT. ος τρόπος. Επαληθεύουμε ότι η κατανομή ισορροπίας είναι άριστη κατά Pareto. i Για U = U =, οι άριστες κατά Pareto ποσότητες είναι : 30
31 X = 0 = X, πράγματι. 1 1 A = 4 U = 3 = A, πράγματι. 1 1 A = U = = A, πράγματι. L= = A= = L, πράγματι. 4 A, πράγματι. H ανταγωνιστική ισορροπία είναι άριστη κατά Pareto, δηλαδή ισχύει το FWT. 31
32 - Παράδειγμα 3. Έστω μια οικονομία που αποτελείται από: Δύο καταναλωτές: 1 και. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ και το καταναλωτικό αγαθό Α. - Οι προτιμήσεις των καταναλωτών παριστάνονται από τις συναρτήσεις χρησιμότητας: U ( X, A) = X + A U( X, A) = X + A - Οι περιουσίες των καταναλωτών παριστάνονται από τα διανύσματα: e1 = ( ex1, ea 1) = (,0) e = ( e, e ) = (,0) X A - Η συνάρτηση παραγωγής της επιχείρησης είναι: A= f( L) = L 3
33 - Έχουμε ήδη υπολογίσει την ανταγωνιστική ισορροπία για τη συγκεκριμένη οικονομία, υποθέτοντας ότι οι καταναλωτές 1, μοιράζονται εξίσου τα κέρδη της επιχείρησης [βλ. Week (1 of ), σελ. 1-7]: ( w, p) = (1,1) ( ( X ) 1, A1),( X, A),( L, A ) = ((1,1), (1,1), (,)) ( U ) 1 U, = (3,3) (Τιμές Ισορροπίας) (Χρησιμότητες Ισορροπίας) (Κατανομή Ισορροπίας) - Υπολογίζουμε τις άριστες κατά Pareto κατανομέςλύνονταςτοpop: max U ( X, A) = X + A { X, X, A, A, L, A} st.. U( A) = X + A U (7) A L (8) X1+ X + L 4 (9) A1+ A A (30) X1 (31) X (3) X, A, X, A, L, A
34 - Στη λύση του προβλήματος, οι περιορισμοί (8), (9) και (30) θα ισχύουν με ισότητα: A= L (8 ) X1+ X + L= 4 L= 4 X1 X (9 ) A + A = A (30 ) 1 - Αντικαθιστούμε τις (9 ), (30 ) στην (8 ) και παίρνουμε: (9 ) (8 ) A + A = 4 X X (8 ) (30 ) Άρα, το POP γράφεται: max U ( X, A) = X + A { X, X, A, A } st.. U ( A ) = X + A U A1+ A = 4 X1 X X1 X X, A, X, A (POP) 34
35 - Βοηθητικό βήμα: Βρίσκουμε το διάστημα των τιμών που μπορεί να πάρει η παράμετρος Η ελάχιστη τιμή της U. U min U = 0 (για A = 0) Η μέγιστη τιμή της είναι: είναι: U (8 ) max 1 = 1 = = U : Για X A 0 A 4 X, οπότε λύνουμε το πρόβλημα: max U ( X, A ) = X + A { X, A } A = 4 X 0 X A 0 - Ηλύσητουπροβλήματοςείναι: οπότε: 0 U + max U ( X ) = X + 4 X { X } max st.. 0 X X = A = U = +, 35
36 - Λύνουμε το POP και βρίσκουμε τις άριστες κατά Pareto κατανομές. (i) Για 0 U ( ) ( ) ( X, A) =, U /4 1 1 ( X, A ) = 0, U /4 ( ) ( LA, ) =, (ii) Για U 4 ( X, A) = (4 U,1) 1 1 ( X, A ) = ( U,1) ( LA, ) = (,) (iii) Για 4 U +, οι άριστες κατά Pareto κατανομές είναι:, οι άριστες κατά Pareto κατανομές είναι: ( ) ( ) ( X, A) = 0, ( U ) /4 1 1 ( X, A ) =,( U ) /4 ( ) ( LA, ) =,, οι άριστες κατά Pareto κατανομές είναι: 36
37 - Αντικαθιστούμε τις άριστες κατά Pareto ποσότητες Χ 1,A 1 στη συνάρτηση χρησιμότητας του καταναλωτή 1 και παίρνουμε το όριο Pareto: + 8 U, αν 0 U U 1 = 6 U, αν U 4 8 ( U ), αν 4 U + (UPF) U Ε UPF U 37
38 Αξιολόγηση Ανταγωνιστικής Ισορροπίας - Επαληθεύουμε ότι η ανταγωνιστική ισορροπία είναι άριστη κατά Pareto (δηλαδή ότι ισχύει το FWT). 1 ος τρόπος. Επαληθεύουμε ότι o συνδυασμός χρησιμοτήτων ισορροπίας ( U1, U ) = (3,3) ικανοποιεί την εξίσωση του ορίου Pareto (δηλαδή ότι η ανταγωνιστική ισορροπία ανήκει στο UPF). i Για U = U = 3, η άριστη κατά Pareto τιμή της U είναι : 1 U = 6 U = 3 = U, πράγματι Άρα, ο συνδυασμός χρησιμοτήτων ισορροπίας (σημείο Ε στο διάγραμμα της σελ. 37) ανήκει στο όριο Pareto. H ανταγωνιστική ισορροπία είναι άριστη κατά Pareto, δηλαδή ισχύει το FWT. 38
39 ος τρόπος. Επαληθεύουμε ότι η κατανομή ισορροπίας είναι άριστη κατά Pareto. i Για U = U = 3, οι άριστες κατά Pareto ποσότητες είναι : X = 4 U = 1 = X, πράγματι. A 1 1 = 1 = A, πράγματι. 1 1 X = U = 1 = X, πράγματι. A L A = 1 = A, πράγματι., πράγματι. = = L, πράγματι. = = A H ανταγωνιστική ισορροπία είναι άριστη κατά Pareto, δηλαδή ισχύει το FWT. 39
Άριστες κατά Pareto Κατανομές και το Πρώτο Θεώρημα Ευημερίας
 Άριστες κατά Pareto Κατανομές και το Πρώτο Θεώρημα Ευημερίας - Υποθέτουμε μια οικονομία που αποτελείται από: Δύο καταναλωτές 1,. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ και το καταναλωτικό αγαθό
Άριστες κατά Pareto Κατανομές και το Πρώτο Θεώρημα Ευημερίας - Υποθέτουμε μια οικονομία που αποτελείται από: Δύο καταναλωτές 1,. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ και το καταναλωτικό αγαθό
Άριστες κατά Pareto Κατανομές
 Άριστες κατά Pareto Κατανομές - Ορισμός. Μια κατανομή x = (x, x ) = (( 1, )( 1, )) ονομάζεται άριστη κατά Pareto αν δεν υπάρχει άλλη κατανομή x = ( x, x ) τέτοια ώστε: U j( x j) U j( xj) για κάθε καταναλωτή
Άριστες κατά Pareto Κατανομές - Ορισμός. Μια κατανομή x = (x, x ) = (( 1, )( 1, )) ονομάζεται άριστη κατά Pareto αν δεν υπάρχει άλλη κατανομή x = ( x, x ) τέτοια ώστε: U j( x j) U j( xj) για κάθε καταναλωτή
Γενική Ανταγωνιστική Ισορροπία
 Γενική Ανταγωνιστική Ισορροπία - Υποθέτουμε μια οικονομία που αποτελείται από: Δύο καταναλωτές 1,. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ και το καταναλωτικό αγαθό Α. - Οι προτιμήσεις των καταναλωτών
Γενική Ανταγωνιστική Ισορροπία - Υποθέτουμε μια οικονομία που αποτελείται από: Δύο καταναλωτές 1,. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ και το καταναλωτικό αγαθό Α. - Οι προτιμήσεις των καταναλωτών
Εργοδοτικές Εισφορές και Φορολογία στους Εργάτες
 Εργοδοτικές Εισφορές και Φορολογία στους Εργάτες Έστω μια οικονομία που αποτελείται από: Δύο καταναλωτές: 1 και. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ (ή: την εργασία ) και το καταναλωτικό αγαθό
Εργοδοτικές Εισφορές και Φορολογία στους Εργάτες Έστω μια οικονομία που αποτελείται από: Δύο καταναλωτές: 1 και. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ (ή: την εργασία ) και το καταναλωτικό αγαθό
To 2 ο Θεμελιώδες Θεώρημα Ευημερίας
 o 2 ο Θεμελιώδες Θεώρημα Ευημερίας - Το 1 ο Θεώρημα Ευημερίας (FW) εξασφαλίζει ότι η ανταγωνιστική ισορροπία είναι άριστη κατά Pareto αλλά δεν εξασφαλίζει μια ίση διανομή των οικονομικών οφελών μεταξύ
o 2 ο Θεμελιώδες Θεώρημα Ευημερίας - Το 1 ο Θεώρημα Ευημερίας (FW) εξασφαλίζει ότι η ανταγωνιστική ισορροπία είναι άριστη κατά Pareto αλλά δεν εξασφαλίζει μια ίση διανομή των οικονομικών οφελών μεταξύ
Μονοψωνιακή Ισορροπία
 Μονοψωνιακή Ισορροπία - Αν η αγορά εργασίας είναι πλήρως ανταγωνιστική, τότε η ατομική επιχείρηση θεωρεί δεδομένο το μισθό και, επομένως, αντιμετωπίζει μια πλήρως ελαστική (οριζόντια) καμπύλη προσφοράς
Μονοψωνιακή Ισορροπία - Αν η αγορά εργασίας είναι πλήρως ανταγωνιστική, τότε η ατομική επιχείρηση θεωρεί δεδομένο το μισθό και, επομένως, αντιμετωπίζει μια πλήρως ελαστική (οριζόντια) καμπύλη προσφοράς
Γενική Ανταγωνιστική Ισορροπία και Αποτελεσματικές κατά Pareto Κατανομές σε Ανταλλακτική Οικονομία
 Γενική Ανταγωνιστική Ισορροπία και Αποτελεσματικές κατά Pareto Κατανομές σε Ανταλλακτική Οικονομία Βασικές Υποθέσεις (i) Οι αγορές όλων των αγαθών είναι τέλεια ανταγωνιστικές. Οι καταναλωτές και οι επιχειρήσεις
Γενική Ανταγωνιστική Ισορροπία και Αποτελεσματικές κατά Pareto Κατανομές σε Ανταλλακτική Οικονομία Βασικές Υποθέσεις (i) Οι αγορές όλων των αγαθών είναι τέλεια ανταγωνιστικές. Οι καταναλωτές και οι επιχειρήσεις
Μονοπωλιακή Ισορροπία - Αν η αγορά του αγαθού Α είναι πλήρως ανταγωνιστική, τότε η ατομική επιχείρηση θεωρεί δεδομένη την τιμή (p) και, επομένως,
 Μονοπωλιακή Ισορροπία - Αν η αγορά του αγαθού Α είναι πλήρως ανταγωνιστική, τότε η ατομική επιχείρηση θεωρεί δεδομένη την τιμή (p) και, επομένως, αντιμετωπίζει μια πλήρως ελαστική (οριζόντια) καμπύλη ζήτησης
Μονοπωλιακή Ισορροπία - Αν η αγορά του αγαθού Α είναι πλήρως ανταγωνιστική, τότε η ατομική επιχείρηση θεωρεί δεδομένη την τιμή (p) και, επομένως, αντιμετωπίζει μια πλήρως ελαστική (οριζόντια) καμπύλη ζήτησης
Διάλεξη 3. Οικονομικά της ευημερίας. Οικονομικά της ευημερίας 3/9/2017. Περίγραμμα. Εργαλεία δεοντολογικής ανάλυσης
 Περίγραμμα Διάλεξη Εργαλεία δεοντολογικής ανάλυσης Συνθήκες για αποτελεσματικότητα κατά areto Συνθήκες για ισορροπία σε ανταγωνιστικές αγορές Το πρώτο θεώρημα των οικονομικών της ευημερίας Το δεύτερο θεώρημα
Περίγραμμα Διάλεξη Εργαλεία δεοντολογικής ανάλυσης Συνθήκες για αποτελεσματικότητα κατά areto Συνθήκες για ισορροπία σε ανταγωνιστικές αγορές Το πρώτο θεώρημα των οικονομικών της ευημερίας Το δεύτερο θεώρημα
Γενική Ανταγωνιστική Ισορροπία σε Οικονομία με Έναν Καταναλωτή και Έναν Παραγωγό
 Γενική Ανταγωνιστική Ισορροπία σε Οικονομία με Έναν Καταναλωτή και Έναν Παραγωγό - Ορισμός. Μια ανταγωνιστική οικονομία που διέπεται από το θεσμό της ατομικής ιδιοκτησίας είναι μια οικονομία όπου: (i)
Γενική Ανταγωνιστική Ισορροπία σε Οικονομία με Έναν Καταναλωτή και Έναν Παραγωγό - Ορισμός. Μια ανταγωνιστική οικονομία που διέπεται από το θεσμό της ατομικής ιδιοκτησίας είναι μια οικονομία όπου: (i)
Διάκριση Τιμών 2 ου Βαθμού: Μη Γραμμική Τιμολόγηση (Nonlinear Pricing) - Η διάκριση τιμών 3 ου βαθμού προϋποθέτει ότι η μονοπωλιακή
 Διάκριση Τιμών ου Βαθμού: Μη Γραμμική Τιμολόγηση (Nonlinear Pricing) -H διάκριση τιμών 1 ου βαθμού προϋποθέτει ότι η μονοπωλιακή επιχείρηση γνωρίζει τις ατομικές συναρτήσεις ζήτησης όλων των καταναλωτών.
Διάκριση Τιμών ου Βαθμού: Μη Γραμμική Τιμολόγηση (Nonlinear Pricing) -H διάκριση τιμών 1 ου βαθμού προϋποθέτει ότι η μονοπωλιακή επιχείρηση γνωρίζει τις ατομικές συναρτήσεις ζήτησης όλων των καταναλωτών.
Διάλεξη 3. Οικονομικά της ευημερίας 2/26/2016. Περίγραμμα. Εργαλεία δεοντολογικής ανάλυσης. Αποτελεσματικότητα κατά Pareto: ορισμός. ορισμός.
 Περίγραμμα Διάλεξη Εργαλεία δεοντολογικής ανάλυσης υνθήκες για αποτελεσματικότητα κατά areto υνθήκες για ισορροπία σε ανταγωνιστικές αγορές Το πρώτο θεώρημα των οικονομικών της ευημερίας Το δεύτερο θεώρημα
Περίγραμμα Διάλεξη Εργαλεία δεοντολογικής ανάλυσης υνθήκες για αποτελεσματικότητα κατά areto υνθήκες για ισορροπία σε ανταγωνιστικές αγορές Το πρώτο θεώρημα των οικονομικών της ευημερίας Το δεύτερο θεώρημα
ΔΗΜΟΣΙΑ ΟΙΚΟΝΟΜΙΚΗ Ι
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΔΗΜΟΣΙΑ ΟΙΚΟΝΟΜΙΚΗ Ι Ενότητα 3: Εργαλεία Κανονιστικής Ανάλυσης Κουτεντάκης Φραγκίσκος Γαληνού Αργυρώ Τμήμα Οικονομικών Επιστημών Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΔΗΜΟΣΙΑ ΟΙΚΟΝΟΜΙΚΗ Ι Ενότητα 3: Εργαλεία Κανονιστικής Ανάλυσης Κουτεντάκης Φραγκίσκος Γαληνού Αργυρώ Τμήμα Οικονομικών Επιστημών Άδειες Χρήσης Το παρόν εκπαιδευτικό
Κατώτατος Μισθός. - Οι περιουσίες των καταναλωτών παριστάνονται από τα διανύσματα:
 Κατώτατος Μισθός Έστω μια οικονομία που αποτελείται από: Δύο καταναλωτές: και. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ και το καταναλωτικό αγαθό Α. - Οι προτιμήσεις των καταναλωτών παριστάνονται
Κατώτατος Μισθός Έστω μια οικονομία που αποτελείται από: Δύο καταναλωτές: και. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ και το καταναλωτικό αγαθό Α. - Οι προτιμήσεις των καταναλωτών παριστάνονται
Προσφορά Εργασίας Προτιμήσεις και Συνάρτηση Χρησιμότητας ( Χ,Α συνάρτηση χρησιμότητας U(X,A)
 Προσφορά Εργασίας - Έστω ότι υπάρχουν δύο αγαθά Α και Χ στην οικονομία. Το αγαθό Α παριστάνει τα διάφορα καταναλωτικά αγαθά. Το αγαθό Χ παριστάνει τον ελεύθερο χρόνο. Προτιμήσεις και Συνάρτηση Χρησιμότητας
Προσφορά Εργασίας - Έστω ότι υπάρχουν δύο αγαθά Α και Χ στην οικονομία. Το αγαθό Α παριστάνει τα διάφορα καταναλωτικά αγαθά. Το αγαθό Χ παριστάνει τον ελεύθερο χρόνο. Προτιμήσεις και Συνάρτηση Χρησιμότητας
Πλεόνασμα του Καταναλωτή, Πλεόνασμα του Παραγωγού και η Αποτελεσματικότητα της Ανταγωνιστικής Αγοράς - Η αλληλεπίδραση της συνολικής ζήτησης και της
 Πλεόνασμα του Καταναλωτή, Πλεόνασμα του Παραγωγού και η Αποτελεσματικότητα της Ανταγωνιστικής Αγοράς - Η αλληλεπίδραση της συνολικής ζήτησης και της προσφοράς προσδιορίζει την τιμή και την ποσότητα ισορροπίας
Πλεόνασμα του Καταναλωτή, Πλεόνασμα του Παραγωγού και η Αποτελεσματικότητα της Ανταγωνιστικής Αγοράς - Η αλληλεπίδραση της συνολικής ζήτησης και της προσφοράς προσδιορίζει την τιμή και την ποσότητα ισορροπίας
Γενίκευση: Πλήρως Μη Γραμμική Τιμολόγηση
 Γενίκευση: Πλήρως Μη Γραμμική Τιμολόγηση (Σχεδιασμός Συμβολαίων υπό Συνθήκες Ασυμμετρικής Πληροφόρησης) -H τιμολόγηση δύο μερών Τ(q)=α+pq αποτελείται από ένα σταθερό βασικό αντίτιμο (α) και ένα γραμμικό
Γενίκευση: Πλήρως Μη Γραμμική Τιμολόγηση (Σχεδιασμός Συμβολαίων υπό Συνθήκες Ασυμμετρικής Πληροφόρησης) -H τιμολόγηση δύο μερών Τ(q)=α+pq αποτελείται από ένα σταθερό βασικό αντίτιμο (α) και ένα γραμμικό
(1β) Μη Χωροθετικά Υποδείγματα Διαφοροποιημένου Προϊόντος με Ενδογενές Πλήθος Επιχειρήσεων
 (β) Μη Χωροθετικά Υποδείγματα Διαφοροποιημένου Προϊόντος με Ενδογενές Πλήθος Επιχειρήσεων Ελεύθερη Είσοδος και Ισορροπία Μηδενικών Κερδών - Η δυνατότητα νέων επιχειρήσεων να εισέρχονται ελεύθερα στην αγορά
(β) Μη Χωροθετικά Υποδείγματα Διαφοροποιημένου Προϊόντος με Ενδογενές Πλήθος Επιχειρήσεων Ελεύθερη Είσοδος και Ισορροπία Μηδενικών Κερδών - Η δυνατότητα νέων επιχειρήσεων να εισέρχονται ελεύθερα στην αγορά
ΑΝΤΑΛΛΑΓΗ. Οι συναρτήσεις χρησιμότητας των ατόμων Α και Β είναι αντίστοιχα. και. και το αρχικό απόθεμα και.
 ΑΝΤΑΛΛΑΓΗ Άσκηση 5 Οι συναρτήσεις χρησιμότητας των ατόμων Α και Β είναι αντίστοιχα u ( x, x ) = x + x 1 2 1 2 και u ( x, x ) = x + x 1 2 1 2 Ω = (2,0) Ω = (0,1) και το αρχικό απόθεμα και. Να προσδιοριστεί
ΑΝΤΑΛΛΑΓΗ Άσκηση 5 Οι συναρτήσεις χρησιμότητας των ατόμων Α και Β είναι αντίστοιχα u ( x, x ) = x + x 1 2 1 2 και u ( x, x ) = x + x 1 2 1 2 Ω = (2,0) Ω = (0,1) και το αρχικό απόθεμα και. Να προσδιοριστεί
Διάλεξη 11. Γενική Ισορροπία με Παραγωγή VA 31
 Διάλεξη 11 Γενική Ισορροπία με Παραγωγή VA 31 1 Οικονομίες ανταλλαγής (ξανά) Καθόλου παραγωγή, μόνο αρχικά αποθέματα, οπότε δεν υπάρχει περιγραφή του πώς οι πόροι μετατρέπονται σε αγαθά. Γενική ισορροπία:
Διάλεξη 11 Γενική Ισορροπία με Παραγωγή VA 31 1 Οικονομίες ανταλλαγής (ξανά) Καθόλου παραγωγή, μόνο αρχικά αποθέματα, οπότε δεν υπάρχει περιγραφή του πώς οι πόροι μετατρέπονται σε αγαθά. Γενική ισορροπία:
Ελαχιστοποίηση του Κόστους
 Ελαχιστοποίηση του Κόστους - H ανάλυση του προβλήματος ελαχιστοποίησης του κόστους παρουσιάζει τα εξής πλεονεκτήματα σε σχέση με το πρόβλημα μεγιστοποίησης του κέρδους: (1) Επιτρέπει τη διατύπωση μιας
Ελαχιστοποίηση του Κόστους - H ανάλυση του προβλήματος ελαχιστοποίησης του κόστους παρουσιάζει τα εξής πλεονεκτήματα σε σχέση με το πρόβλημα μεγιστοποίησης του κέρδους: (1) Επιτρέπει τη διατύπωση μιας
(2) Χωροθετικά Υποδείγματα Διαφοροποιημένου Προϊόντος
 () Χωροθετικά Υποδείγματα Διαφοροποιημένου Προϊόντος - Στα χωροθετικά υποδείγματα διαφοροποιημένου προϊόντος, οι καταναλωτές είναι ετερογενείς (δηλαδή έχουν διαφορετικές προτιμήσεις μεταξύ τους ή βρίσκονται
() Χωροθετικά Υποδείγματα Διαφοροποιημένου Προϊόντος - Στα χωροθετικά υποδείγματα διαφοροποιημένου προϊόντος, οι καταναλωτές είναι ετερογενείς (δηλαδή έχουν διαφορετικές προτιμήσεις μεταξύ τους ή βρίσκονται
ΠΑΡΑΡΤΗΜΑ: ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΑΡΙΣΤΟΥ ΠΕΡΙΒΑΛΛΟΝΤΙΚΟΥ ΦΟΡΟΥ
 ΠΑΡΑΡΤΗΜΑ: ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΑΡΙΣΤΟΥ ΠΕΡΙΒΑΛΛΟΝΤΙΚΟΥ ΦΟΡΟΥ Ας υποθέσουμε ότι έχουμε ένα αγαθό το οποίο δημιουργεί κατά την παραγωγή ή την κατανάλωσή του έναν ρύπο, και ας υποθέσουμε ότι για κάθε μία μονάδα
ΠΑΡΑΡΤΗΜΑ: ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΑΡΙΣΤΟΥ ΠΕΡΙΒΑΛΛΟΝΤΙΚΟΥ ΦΟΡΟΥ Ας υποθέσουμε ότι έχουμε ένα αγαθό το οποίο δημιουργεί κατά την παραγωγή ή την κατανάλωσή του έναν ρύπο, και ας υποθέσουμε ότι για κάθε μία μονάδα
ΔΥΝΑΜΗ ΣΤΗΝ ΑΓΟΡΑ (Παράδειγμα: ΜΟΝΟΠΩΛΙΟ)
 Θεωρήματα Οικονομικών της Ευημερίας (1) Οι ανταγωνιστικές αγορές συντονίζουν τις αποφάσεις των καταναλωτών και των παραγωγών εξασφαλίζοντας Pareto αποτελεσματικές κατανομές των παραγωγικών πόρων και των
Θεωρήματα Οικονομικών της Ευημερίας (1) Οι ανταγωνιστικές αγορές συντονίζουν τις αποφάσεις των καταναλωτών και των παραγωγών εξασφαλίζοντας Pareto αποτελεσματικές κατανομές των παραγωγικών πόρων και των
Ισορροπία σε Αγορές Διαφοροποιημένων Προϊόντων
 Ισορροπία σε Αγορές Διαφοροποιημένων Προϊόντων - Στο υπόδειγμα ertrand, οι επιχειρήσεις, παράγουν ένα ομοιογενές αγαθό, οπότε η τιμή είναι η μοναδική μεταβλητή που ενδιαφέρει τους καταναλωτές και οι καταναλωτές
Ισορροπία σε Αγορές Διαφοροποιημένων Προϊόντων - Στο υπόδειγμα ertrand, οι επιχειρήσεις, παράγουν ένα ομοιογενές αγαθό, οπότε η τιμή είναι η μοναδική μεταβλητή που ενδιαφέρει τους καταναλωτές και οι καταναλωτές
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΕΡΩΤΗΣΕΙΣ ΔΗΜΟΣΙΑ
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΕΡΩΤΗΣΕΙΣ ΔΗΜΟΣΙΑ 1. Στην περίπτωση των εξωτερικών επιβαρύνσεων στην παραγωγή, η επιβολή ενός φόρου ανά µονάδα προϊόντος ίσου µε το µέγεθος της οριακής εξωτερικής επιβάρυνσης µπορεί να οδηγήσει:
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΕΡΩΤΗΣΕΙΣ ΔΗΜΟΣΙΑ 1. Στην περίπτωση των εξωτερικών επιβαρύνσεων στην παραγωγή, η επιβολή ενός φόρου ανά µονάδα προϊόντος ίσου µε το µέγεθος της οριακής εξωτερικής επιβάρυνσης µπορεί να οδηγήσει:
Μεγιστοποίηση της Χρησιμότητας
 Μεγιστοποίηση της Χρησιμότητας - Πρόβλημα Καταναλωτή: Επιλογή καταναλωτικού συνδυασμού x=(x, x ) υπό ένα σύνολο φυσικών, θεσμικών και οικονομικών περιορισμών κατά τρόπο ώστε να μεγιστοποιεί τη χρησιμότητά
Μεγιστοποίηση της Χρησιμότητας - Πρόβλημα Καταναλωτή: Επιλογή καταναλωτικού συνδυασμού x=(x, x ) υπό ένα σύνολο φυσικών, θεσμικών και οικονομικών περιορισμών κατά τρόπο ώστε να μεγιστοποιεί τη χρησιμότητά
Κριτικές στο Υπόδειγμα Cournot
 Κριτικές στο Υπόδειγμα Cournot -To υπόδειγμα Cournot έχει υποστεί τρία είδη κριτικής: () Το υπόδειγμα Cournot υποθέτει ότι κάθε επιχείρηση μεγιστοποιεί μόνο τα δικά της κέρδη και, επομένως, δε λαμβάνει
Κριτικές στο Υπόδειγμα Cournot -To υπόδειγμα Cournot έχει υποστεί τρία είδη κριτικής: () Το υπόδειγμα Cournot υποθέτει ότι κάθε επιχείρηση μεγιστοποιεί μόνο τα δικά της κέρδη και, επομένως, δε λαμβάνει
Διάκριση Τιμών 3 ου Βαθμού: Κατάτμηση της Αγοράς
 Διάκριση Τιμών 3 ου Βαθμού: Κατάτμηση της Αγοράς (arket Segmentation ή ultimarket Price iscrimination) -H διάκριση τιμών 1 ου βαθμού προϋποθέτει ότι η μονοπωλιακή επιχείρηση γνωρίζει τις ατομικές συναρτήσεις
Διάκριση Τιμών 3 ου Βαθμού: Κατάτμηση της Αγοράς (arket Segmentation ή ultimarket Price iscrimination) -H διάκριση τιμών 1 ου βαθμού προϋποθέτει ότι η μονοπωλιακή επιχείρηση γνωρίζει τις ατομικές συναρτήσεις
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τµήµα Οικονοµικών Επιστηµών Ακαδηµαϊκό έτος (διαβάζουμε κεφ. 4 από Μ. Χλέτσο και σημειώσεις στο eclass)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τµήµα Οικονοµικών Επιστηµών Ακαδηµαϊκό έτος 2016-17 ΠΟΛΙΤΙΚΗ ΟΙΚΟΝΟΜΙΑ ΤΗΣ ΚΟΙΝΩΝΙΚΗΣ ΠΟΛΙΤΙΚΗΣ (διαβάζουμε κεφ. 4 από Μ. Χλέτσο και σημειώσεις στο eclass) 1 ιάλεξη2 Ανταγωνισμός, οικονομική
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τµήµα Οικονοµικών Επιστηµών Ακαδηµαϊκό έτος 2016-17 ΠΟΛΙΤΙΚΗ ΟΙΚΟΝΟΜΙΑ ΤΗΣ ΚΟΙΝΩΝΙΚΗΣ ΠΟΛΙΤΙΚΗΣ (διαβάζουμε κεφ. 4 από Μ. Χλέτσο και σημειώσεις στο eclass) 1 ιάλεξη2 Ανταγωνισμός, οικονομική
Κοινωνικοοικονομική Αξιολόγηση Επενδύσεων Διάλεξη 3 η. Αποτελεσματικότητα και Ευημερία
 Κοινωνικοοικονομική Αξιολόγηση Επενδύσεων Διάλεξη 3 η Αποτελεσματικότητα και Ευημερία Ζητήματα που θα εξεταστούν: Πότε και πως επιτυγχάνεται η οικονομική αποτελεσματικότητα Θεωρήματα των οικονομικών της
Κοινωνικοοικονομική Αξιολόγηση Επενδύσεων Διάλεξη 3 η Αποτελεσματικότητα και Ευημερία Ζητήματα που θα εξεταστούν: Πότε και πως επιτυγχάνεται η οικονομική αποτελεσματικότητα Θεωρήματα των οικονομικών της
Επιλογή Ποιότητας και Κάθετη Διαφοροποίηση Προϊόντος
 Επιλογή Ποιότητας και Κάθετη Διαφοροποίηση Προϊόντος - Τα προϊόντα που παράγουν οι επιχειρήσεις μπορούν να διαφοροποιούνται ως προς ένα πλήθος χαρακτηριστικών. Παράδειγμα: Τα αυτοκίνητα διαφοροποιούνται
Επιλογή Ποιότητας και Κάθετη Διαφοροποίηση Προϊόντος - Τα προϊόντα που παράγουν οι επιχειρήσεις μπορούν να διαφοροποιούνται ως προς ένα πλήθος χαρακτηριστικών. Παράδειγμα: Τα αυτοκίνητα διαφοροποιούνται
2. Διαφήμιση σε Αγορές όπου υπάρχουν πολλές Επιχειρήσεις
 . Διαφήμιση σε Αγορές όπου υπάρχουν πολλές Επιχειρήσεις Α. Ενημερωτική Διαφήμιση στη Μονοπωλιακά Ανταγωνιστική Αγορά (Butters, Gerard 977, Equilibrium Distribution of Prices and Advertising) -To υπόδειγμα
. Διαφήμιση σε Αγορές όπου υπάρχουν πολλές Επιχειρήσεις Α. Ενημερωτική Διαφήμιση στη Μονοπωλιακά Ανταγωνιστική Αγορά (Butters, Gerard 977, Equilibrium Distribution of Prices and Advertising) -To υπόδειγμα
Μεγιστοποίηση του Κέρδους
 Μεγιστοποίηση του Κέρδους - Έστω η συνάρτηση παραγωγής: q = f ( x,..., x ). - Η τιμή του παραγόμενου προϊόντος είναι και οι τιμές των εισροών είναι w= ( w,..., w ). - Υπόθεση: Η επιχείρηση είναι αποδέκτης
Μεγιστοποίηση του Κέρδους - Έστω η συνάρτηση παραγωγής: q = f ( x,..., x ). - Η τιμή του παραγόμενου προϊόντος είναι και οι τιμές των εισροών είναι w= ( w,..., w ). - Υπόθεση: Η επιχείρηση είναι αποδέκτης
Κεφάλαιο 33 Παραγωγή
 HAL R. VARIAN Μικροοικονομική Μια σύγχρονη προσέγγιση 3 η έκδοση Εκδόσεις Κριτική Κεφάλαιο 33 Παραγωγή Ύλη για τη Μίκρο ΙΙ: όλο το κεφάλαιο Οικονομίες ανταλλαγής (αναθεώρηση) Καμία παραγωγή, μόνο αποθέματα,
HAL R. VARIAN Μικροοικονομική Μια σύγχρονη προσέγγιση 3 η έκδοση Εκδόσεις Κριτική Κεφάλαιο 33 Παραγωγή Ύλη για τη Μίκρο ΙΙ: όλο το κεφάλαιο Οικονομίες ανταλλαγής (αναθεώρηση) Καμία παραγωγή, μόνο αποθέματα,
Οικονομικά Υποδείγματα: Εισαγωγικές Έννοιες - Τα οικονομικά υποδείγματα περιγράφουν τη συμπεριφορά επιχειρήσεων-καταναλωτών και την αλληλεπίδρασή
 Οικονομικά Υποδείγματα: Εισαγωγικές Έννοιες - Τα οικονομικά υποδείγματα περιγράφουν τη συμπεριφορά επιχειρήσεων-καταναλωτών και την αλληλεπίδρασή τους στις διάφορες αγορές. - Τα οικονομικά υποδείγματα:
Οικονομικά Υποδείγματα: Εισαγωγικές Έννοιες - Τα οικονομικά υποδείγματα περιγράφουν τη συμπεριφορά επιχειρήσεων-καταναλωτών και την αλληλεπίδρασή τους στις διάφορες αγορές. - Τα οικονομικά υποδείγματα:
ΜΙΚΡΟ-ΟΙΚΟΝΟΜΙΚΗ ΣΗΜΕΙΩΣΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ ΟΙΚΟΝΟΜΙΑ ΜΜΕ ΕΝΟΤΗΤΑ 5η: Οικονομίες & Νεοκλασική Πολιτική Οικονομία
 ΜΙΚΡΟ-ΟΙΚΟΝΟΜΙΚΗ ΣΗΜΕΙΩΣΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ ΟΙΚΟΝΟΜΙΑ ΜΜΕ ΕΝΟΤΗΤΑ 5η: Οικονομίες & Νεοκλασική Πολιτική Οικονομία ΑΤΕΙ ΙΟΝΙΩΝ ΝΗΣΩΝ Τμήμα Δημοσίων Σχέσεων & Επικοινωνίας Α. Κουμπαρέλης Καθηγητής Εφαρμογών
ΜΙΚΡΟ-ΟΙΚΟΝΟΜΙΚΗ ΣΗΜΕΙΩΣΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ ΟΙΚΟΝΟΜΙΑ ΜΜΕ ΕΝΟΤΗΤΑ 5η: Οικονομίες & Νεοκλασική Πολιτική Οικονομία ΑΤΕΙ ΙΟΝΙΩΝ ΝΗΣΩΝ Τμήμα Δημοσίων Σχέσεων & Επικοινωνίας Α. Κουμπαρέλης Καθηγητής Εφαρμογών
(2β) Το Υπόδειγμα της Κυκλικής Πόλης ή Υπόδειγμα του Salop
 (2β) Το Υπόδειγμα της Κυκλικής Πόλης ή Υπόδειγμα του alop (alop, teve 979, Moopolstc Competto wth Outsde Goods) - Υποθέτουμε μια πόλη που παριστάνεται από την περιφέρεια ενός κύκλου με περίμετρο L=. p
(2β) Το Υπόδειγμα της Κυκλικής Πόλης ή Υπόδειγμα του alop (alop, teve 979, Moopolstc Competto wth Outsde Goods) - Υποθέτουμε μια πόλη που παριστάνεται από την περιφέρεια ενός κύκλου με περίμετρο L=. p
 25. Μία τυπική επιχείρηση που λειτουργεί σε καθεστώς τέλειου ανταγωνισμού, στη μακροχρόνια θέση ισορροπίας της: α. πραγματοποιεί θετικά οικονομικά κέρδη. β. πραγματοποιεί μηδενικά οικονομικά κέρδη. γ.
25. Μία τυπική επιχείρηση που λειτουργεί σε καθεστώς τέλειου ανταγωνισμού, στη μακροχρόνια θέση ισορροπίας της: α. πραγματοποιεί θετικά οικονομικά κέρδη. β. πραγματοποιεί μηδενικά οικονομικά κέρδη. γ.
Κεφάλαιο 32 Ανταλλαγή
 HL R. VRIN Μικροοικονομική Μια σύγχρονη προσέγγιση 3 η έκδοση Εκδόσεις Κριτική Κεφάλαιο 32 Ανταλλαγή Ύλη για τη Μίκρο ΙΙ: όλο το κεφάλαιο Ανάλυση μερικής ισορροπίας/ανάλυση γενικής ισορροπίας Τέλειος ανταγωνισμός/ατελής
HL R. VRIN Μικροοικονομική Μια σύγχρονη προσέγγιση 3 η έκδοση Εκδόσεις Κριτική Κεφάλαιο 32 Ανταλλαγή Ύλη για τη Μίκρο ΙΙ: όλο το κεφάλαιο Ανάλυση μερικής ισορροπίας/ανάλυση γενικής ισορροπίας Τέλειος ανταγωνισμός/ατελής
Εισαγωγή. Αποτελεσματικότητα κατά Pareto. 1. ΑΝΤΑΓΩΝΙΣΜΟΣ ΚΑΙ ΟΙΚΟΝΟΜΙΚΗ ΑΠΟΤΕΛΕΣΜΑΤΙΚΟΤΗΤΑ (επεξεργασία σημειώσεων Β. Ράπανου)
 1. ΑΝΤΑΓΩΝΙΣΜΟΣ ΚΑΙ ΟΙΚΟΝΟΜΙΚΗ ΑΠΟΤΕΛΕΣΜΑΤΙΚΟΤΗΤΑ (επεξεργασία σημειώσεων Β. Ράπανου) Εισαγωγή Μια από τις πιο βασικές διακρίσεις στην οικονομική θεωρία είναι μεταξύ των εννοιών της οικονομικής αποτελεσματικότητας
1. ΑΝΤΑΓΩΝΙΣΜΟΣ ΚΑΙ ΟΙΚΟΝΟΜΙΚΗ ΑΠΟΤΕΛΕΣΜΑΤΙΚΟΤΗΤΑ (επεξεργασία σημειώσεων Β. Ράπανου) Εισαγωγή Μια από τις πιο βασικές διακρίσεις στην οικονομική θεωρία είναι μεταξύ των εννοιών της οικονομικής αποτελεσματικότητας
Διάλεξη 10. Γενική Ισορροπία VA 30
 Διάλεξη 10 Γενική Ισορροπία V 30 1 Μερική & Γενική Ισορροπία Μέχρι τώρα εξετάζαμε γενικά την αγορά ενός αγαθού μεμονωμένα. Το πώς δηλαδή η προσφορά και η ζήτηση επηρεάζονται από την τιμή του συγκεκριμένου
Διάλεξη 10 Γενική Ισορροπία V 30 1 Μερική & Γενική Ισορροπία Μέχρι τώρα εξετάζαμε γενικά την αγορά ενός αγαθού μεμονωμένα. Το πώς δηλαδή η προσφορά και η ζήτηση επηρεάζονται από την τιμή του συγκεκριμένου
ΑΓΟΡΕΣ ΚΑΙ ΑΠΟΤΕΛΕΣΜΑΤΙΚΟΤΗΤΑ
 ΑΓΟΡΕΣ ΚΑΙ ΑΠΟΤΕΛΕΣΜΑΤΙΚΟΤΗΤΑ Εισαγωγικά Στο μάθημα αυτό θα συζητήσουμε την σπουδαιότητα την οποία έχει ο πλήρης προσδιορισμός των δικαιωμάτων ιδιοκτησίας στην αποτελεσματική κατανομή των πόρων Θα εξετάσουμε
ΑΓΟΡΕΣ ΚΑΙ ΑΠΟΤΕΛΕΣΜΑΤΙΚΟΤΗΤΑ Εισαγωγικά Στο μάθημα αυτό θα συζητήσουμε την σπουδαιότητα την οποία έχει ο πλήρης προσδιορισμός των δικαιωμάτων ιδιοκτησίας στην αποτελεσματική κατανομή των πόρων Θα εξετάσουμε
- Παράδειγμα 2. Εκτέλεση Πέναλτι ή Κορώνα-Γράμματα (Heads or Tails) - Ένας ποδοσφαιριστής ετοιμάζεται να εκτελέσει ένα πέναλτι, το οποίο προσπαθεί να
 - Παράδειγμα. Εκτέλεση Πέναλτι ή Κορώνα-Γράμματα (Heads or Tails) - Ένας ποδοσφαιριστής ετοιμάζεται να εκτελέσει ένα πέναλτι, το οποίο προσπαθεί να αποκρούσει ένας τερματοφύλακας. - Αν οι δύο παίκτες επιλέξουν
- Παράδειγμα. Εκτέλεση Πέναλτι ή Κορώνα-Γράμματα (Heads or Tails) - Ένας ποδοσφαιριστής ετοιμάζεται να εκτελέσει ένα πέναλτι, το οποίο προσπαθεί να αποκρούσει ένας τερματοφύλακας. - Αν οι δύο παίκτες επιλέξουν
10/3/17. Κεφάλαιο 33 Παραγωγή. Μικροοικονομική. Οικονοµίες ανταλλαγής (αναθεώρηση) Τώρα, προσθέστε παραγωγή... Η οικονοµία του Ροβινσώνα Κρούσου
 1/3/17 HAL R. VARIAN Μικροοικονομική Μια σύγχρονη προσέγγιση 3 η έκδοση Κεφάλαιο 33 Παραγωγή Οικονοµίες ανταλλαγής (αναθεώρηση) Καμία παραγωγή, μόνο αποθέματα, άρα καμία περιγραφή για το πώς οι πόροι μετατρέπονται
1/3/17 HAL R. VARIAN Μικροοικονομική Μια σύγχρονη προσέγγιση 3 η έκδοση Κεφάλαιο 33 Παραγωγή Οικονοµίες ανταλλαγής (αναθεώρηση) Καμία παραγωγή, μόνο αποθέματα, άρα καμία περιγραφή για το πώς οι πόροι μετατρέπονται
Ελαχιστοποίηση του Κόστους
 Ελαχιστοποίηση του Κόστους - H ανάλυση του προβλήματος ελαχιστοποίησης του κόστους παρουσιάζει τα εξής πλεονεκτήματα σε σχέση με το πρόβλημα μεγιστοποίησης των κερδών: () Επιτρέπει τη διατύπωση μιας θεωρίας
Ελαχιστοποίηση του Κόστους - H ανάλυση του προβλήματος ελαχιστοποίησης του κόστους παρουσιάζει τα εξής πλεονεκτήματα σε σχέση με το πρόβλημα μεγιστοποίησης των κερδών: () Επιτρέπει τη διατύπωση μιας θεωρίας
ΟΙΚΟΝΟΜΙΚΗ ΤΩΝ ΔΙΚΤΥΩΝ ΚΑΙ ΤΗΣ ΠΛΗΡΟΦΟΡΗΣΗΣ (ECΟ465) ΤΗΛΕΠΙΚΟΙΝΩΝΙΕΣ ΜΕΡΟΣ Α
 ΟΙΚΟΝΟΜΙΚΗ ΤΩΝ ΔΙΚΤΥΩΝ ΚΑΙ ΤΗΣ ΠΛΗΡΟΦΟΡΗΣΗΣ (ECΟ465) ΤΗΛΕΠΙΚΟΙΝΩΝΙΕΣ ΜΕΡΟΣ Α 1 o Ο κλάδος των τηλεπικοινωνιών (τηλέφωνο, fax, e-mail, υπηρεσίες μηνυμάτων, κ.τ.λ) αποτελεί το πιο απλό και φυσικό παράδειγμα
ΟΙΚΟΝΟΜΙΚΗ ΤΩΝ ΔΙΚΤΥΩΝ ΚΑΙ ΤΗΣ ΠΛΗΡΟΦΟΡΗΣΗΣ (ECΟ465) ΤΗΛΕΠΙΚΟΙΝΩΝΙΕΣ ΜΕΡΟΣ Α 1 o Ο κλάδος των τηλεπικοινωνιών (τηλέφωνο, fax, e-mail, υπηρεσίες μηνυμάτων, κ.τ.λ) αποτελεί το πιο απλό και φυσικό παράδειγμα
Ολιγοπωλιακή Ισορροπία
 Ολιγοπωλιακή Ισορροπία - Χρησιμοποιούμε τις βασικές αρχές της θεωρίας παιγνίων για να εξετάσουμε τη στρατηγική αλληλεπίδραση των επιχειρήσεων σε ατελώς ανταγωνιστικές αγορές, εστιάζοντας την προσοχή μας
Ολιγοπωλιακή Ισορροπία - Χρησιμοποιούμε τις βασικές αρχές της θεωρίας παιγνίων για να εξετάσουμε τη στρατηγική αλληλεπίδραση των επιχειρήσεων σε ατελώς ανταγωνιστικές αγορές, εστιάζοντας την προσοχή μας
ΜΑΘΗΜΑΤΙΚΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ 2 5/9/2002 Απαντήστε σε μια από τις δυο ερωτήσεις. 3. Να υπολογιστεί η ανταγωνιστική ισορροπία και τα σημεία
 ΜΑΘΗΜΑΤΙΚΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ 5/9/00 Απαντήστε σε μια από τις δυο ερωτήσεις. 1.Θεωρουμε οικονομία αποτελούμενη από ένα καταναλωτή, με προτιμήσεις U log+ logx,και περιουσία μόνο μια μονάδα του αγαθού
ΜΑΘΗΜΑΤΙΚΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ 5/9/00 Απαντήστε σε μια από τις δυο ερωτήσεις. 1.Θεωρουμε οικονομία αποτελούμενη από ένα καταναλωτή, με προτιμήσεις U log+ logx,και περιουσία μόνο μια μονάδα του αγαθού
HAL R. VARIAN. Μικροοικονομική. Μια σύγχρονη προσέγγιση. 3 η έκδοση
 HAL R. VARIAN Μικροοικονομική Μια σύγχρονη προσέγγιση 3 η έκδοση Κεφάλαιο 33 Παραγωγή Οικονοµίες ανταλλαγής (αναθεώρηση) Καμία παραγωγή, μόνο αποθέματα, άρα καμία περιγραφή για το πώς οι πόροι μετατρέπονται
HAL R. VARIAN Μικροοικονομική Μια σύγχρονη προσέγγιση 3 η έκδοση Κεφάλαιο 33 Παραγωγή Οικονοµίες ανταλλαγής (αναθεώρηση) Καμία παραγωγή, μόνο αποθέματα, άρα καμία περιγραφή για το πώς οι πόροι μετατρέπονται
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος Τμήμα Οικονομικών Επιστημών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος 20-202 Τμήμα Οικονομικών Επιστημών Χειμώνας-Άνοιξη Μάθημα: Δημόσια Οικονομική Διδασκαλία: Βασίλης Θ. Ράπανος Γεωργία Καπλάνογλου Ημερομηνία παράδοσης: Απριλίου 202 Οι
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος 20-202 Τμήμα Οικονομικών Επιστημών Χειμώνας-Άνοιξη Μάθημα: Δημόσια Οικονομική Διδασκαλία: Βασίλης Θ. Ράπανος Γεωργία Καπλάνογλου Ημερομηνία παράδοσης: Απριλίου 202 Οι
ΚΟΙΝΩΝΙΚΗ ΠΟΛΙΤΙΚΗ ΣΤΗΝ ΕΥΡΩΠΑΪΚΗ ΕΝΩΣΗ Διάλεξη 2α. ΕΙΣΑΓΩΓΗ ΣΤΗ ΓΕΝΙΚΗ ΙΣΟΡΡΟΠΙΑ ΚΑΙ ΤΗΝ ΟΙΚΟΝΟΜΙΚΗ ΤΗΣ ΕΥΗΜΕΡΙΑΣ
 ΚΟΙΝΩΝΙΚΗ ΠΟΛΙΤΙΚΗ ΣΤΗΝ ΕΥΡΩΠΑΪΚΗ ΕΝΩΣΗ Διάλεξη 2α. ΕΙΣΑΓΩΓΗ ΣΤΗ ΓΕΝΙΚΗ ΙΣΟΡΡΟΠΙΑ ΚΑΙ ΤΗΝ ΟΙΚΟΝΟΜΙΚΗ ΤΗΣ ΕΥΗΜΕΡΙΑΣ ΟΙΚΟΝΟΜΙΚΗ ΤΗΣ ΕΥΗΜΕΡΙΑΣ (welfare economics): Ο κλάδος της οικονομικής επιστήμης που ασχολείται
ΚΟΙΝΩΝΙΚΗ ΠΟΛΙΤΙΚΗ ΣΤΗΝ ΕΥΡΩΠΑΪΚΗ ΕΝΩΣΗ Διάλεξη 2α. ΕΙΣΑΓΩΓΗ ΣΤΗ ΓΕΝΙΚΗ ΙΣΟΡΡΟΠΙΑ ΚΑΙ ΤΗΝ ΟΙΚΟΝΟΜΙΚΗ ΤΗΣ ΕΥΗΜΕΡΙΑΣ ΟΙΚΟΝΟΜΙΚΗ ΤΗΣ ΕΥΗΜΕΡΙΑΣ (welfare economics): Ο κλάδος της οικονομικής επιστήμης που ασχολείται
1. Επιλογή Διαφημιστικής Δαπάνης στη Μονοπωλιακή Αγορά
 1. Επιλογή Διαφημιστικής Δαπάνης στη Μονοπωλιακή Αγορά 1Α. Δελεαστική Διαφήμιση στη Μονοπωλιακή Αγορά - Έστω ότι η αγορά ενός αγαθού είναι μονοπωλιακή και η διαφήμιση του προϊόντος είναι δελεαστική δηλαδή
1. Επιλογή Διαφημιστικής Δαπάνης στη Μονοπωλιακή Αγορά 1Α. Δελεαστική Διαφήμιση στη Μονοπωλιακή Αγορά - Έστω ότι η αγορά ενός αγαθού είναι μονοπωλιακή και η διαφήμιση του προϊόντος είναι δελεαστική δηλαδή
1. Επιλογή Ποιότητας στην Ολιγοπωλιακή Αγορά: Κάθετη Διαφοροποίηση Προϊόντος
 . Επιλογή Ποιότητας στην Ολιγοπωλιακή Αγορά: Κάθετη Διαφοροποίηση Προϊόντος - Ορισμός. Αν η αύξηση του επιπέδου ενός χαρακτηριστικού που διαφοροποιεί τα προϊόντα των επιχειρήσεων ωφελεί κάποιους καταναλωτές
. Επιλογή Ποιότητας στην Ολιγοπωλιακή Αγορά: Κάθετη Διαφοροποίηση Προϊόντος - Ορισμός. Αν η αύξηση του επιπέδου ενός χαρακτηριστικού που διαφοροποιεί τα προϊόντα των επιχειρήσεων ωφελεί κάποιους καταναλωτές
Θεωρία: dq1 dq1 dq1 P1 E1. dq2 dq2 dq2 P2 E2 1 1 P E E. d π dp dc dq dq dq. dp dc dq dq
 Θεωρία: Θέµα ο Η συνάρτηση κέρδους του µονοπωλητή ο οποίος πραγµατοποιεί διάκριση τιµών τρίτου βαθµού µεταξύ δύο αγορών και είναι η π µε τύπο π (, ) = R ( ) + R ( ) C( + ) Συνθήκες α' τάξης = R ' C ' =
Θεωρία: Θέµα ο Η συνάρτηση κέρδους του µονοπωλητή ο οποίος πραγµατοποιεί διάκριση τιµών τρίτου βαθµού µεταξύ δύο αγορών και είναι η π µε τύπο π (, ) = R ( ) + R ( ) C( + ) Συνθήκες α' τάξης = R ' C ' =
1. ΣΤΑΤΙΚΗ ΑΡΙΣΤΟΠΟΙΗΣΗ
 . ΣΤΑΤΙΚΗ ΑΡΙΣΤΟΠΟΙΗΣΗ. Μέγιστα και Ελάχιστα Συναρτήσεων Χωρίς Περιορισμούς Συναρτήσεις μιας Μεταβλητής Εστω f ( x) είναι συνάρτηση μιας μόνο μεταβλητής. Εστω επίσης ότι x είναι ένα σημείο στο πεδίο ορισμού
. ΣΤΑΤΙΚΗ ΑΡΙΣΤΟΠΟΙΗΣΗ. Μέγιστα και Ελάχιστα Συναρτήσεων Χωρίς Περιορισμούς Συναρτήσεις μιας Μεταβλητής Εστω f ( x) είναι συνάρτηση μιας μόνο μεταβλητής. Εστω επίσης ότι x είναι ένα σημείο στο πεδίο ορισμού
2.10. Τιμή και ποσότητα ισορροπίας
 .. Τιμή και ποσότητα ισορροπίας ίδαμε ότι η βασική επιδίωξη των επιχειρήσεων είναι η επίτευξη του μέγιστου κέρδους με την πώληση όσο το δυνατόν μεγαλύτερων ποσοτήτων ενός αγαθού στη μεγαλύτερη δυνατή τιμή
.. Τιμή και ποσότητα ισορροπίας ίδαμε ότι η βασική επιδίωξη των επιχειρήσεων είναι η επίτευξη του μέγιστου κέρδους με την πώληση όσο το δυνατόν μεγαλύτερων ποσοτήτων ενός αγαθού στη μεγαλύτερη δυνατή τιμή
ΚΑΙ ΑΠΟΤΕΛΕΣΜΑΤΙΚΟΤΗΤΑ
 ΚΑΤΑΝΑΛΩΤΕΣ, ΠΑΡΑΓΩΓΟΙ ΚΑΙ ΑΠΟΤΕΛΕΣΜΑΤΙΚΟΤΗΤΑ ΑΓΟΡΩΝ Κεφάλαιο 7 Οικονοµικά της ευηµερίας! Τα οικονοµικά της ευηµερίας εξετάζουν τους τρόπους µε τους οποίους η κατανοµή των πόρων επηρεάζει την ευηµερία
ΚΑΤΑΝΑΛΩΤΕΣ, ΠΑΡΑΓΩΓΟΙ ΚΑΙ ΑΠΟΤΕΛΕΣΜΑΤΙΚΟΤΗΤΑ ΑΓΟΡΩΝ Κεφάλαιο 7 Οικονοµικά της ευηµερίας! Τα οικονοµικά της ευηµερίας εξετάζουν τους τρόπους µε τους οποίους η κατανοµή των πόρων επηρεάζει την ευηµερία
Μεγιστοποίηση του Κέρδους
 Μεγιστοποίηση του Κέρδους - Έστω η συνάρτηση παραγωγής: f( K, L). - Η τιμή του παραγόμενου προϊόντος είναι p, ητιμήτηςεργασίας είναι w και η τιμή του κεφαλαίου είναι r. - Υπόθεση: Η επιχείρηση είναι αποδέκτης
Μεγιστοποίηση του Κέρδους - Έστω η συνάρτηση παραγωγής: f( K, L). - Η τιμή του παραγόμενου προϊόντος είναι p, ητιμήτηςεργασίας είναι w και η τιμή του κεφαλαίου είναι r. - Υπόθεση: Η επιχείρηση είναι αποδέκτης
Βασικές Αρχές της Θεωρίας Παιγνίων
 Βασικές Αρχές της Θεωρίας Παιγνίων - Ορισμός. Αν οι επιλογές μιας επιχείρησης εξαρτώνται από την αναμενόμενη αντίδραση των υπόλοιπων επιχειρήσεων που συμμετέχουν στην αγορά, τότε υπάρχει στρατηγική αλληλεπίδραση
Βασικές Αρχές της Θεωρίας Παιγνίων - Ορισμός. Αν οι επιλογές μιας επιχείρησης εξαρτώνται από την αναμενόμενη αντίδραση των υπόλοιπων επιχειρήσεων που συμμετέχουν στην αγορά, τότε υπάρχει στρατηγική αλληλεπίδραση
www.onlineclassroom.gr
 ΜΕΡΟΣ Β Ερωτήσεις πολλαπλών επιλογών Στις παρακάτω 10 ερωτήσεις, να γράψετε τον αριθμό της κάθε ερώτησης στην εργασία σας και δίπλα του το γράμμα που αντιστοιχεί στη σωστή απάντηση. Η κάθε σωστή απάντηση
ΜΕΡΟΣ Β Ερωτήσεις πολλαπλών επιλογών Στις παρακάτω 10 ερωτήσεις, να γράψετε τον αριθμό της κάθε ερώτησης στην εργασία σας και δίπλα του το γράμμα που αντιστοιχεί στη σωστή απάντηση. Η κάθε σωστή απάντηση
Η Καμπύλη Προσφοράς της Επιχείρησης
 Η Καμπύλη Προσφοράς της Επιχείρησης - Μπορούμε να διατυπώσουμε το πρόβλημα μεγιστοποίησης των κερδών και να βρούμε τις συναρτήσεις ζήτησης εισροών, τη συνάρτηση προσφοράς και τη συνάρτηση κερδών της επιχείρησης
Η Καμπύλη Προσφοράς της Επιχείρησης - Μπορούμε να διατυπώσουμε το πρόβλημα μεγιστοποίησης των κερδών και να βρούμε τις συναρτήσεις ζήτησης εισροών, τη συνάρτηση προσφοράς και τη συνάρτηση κερδών της επιχείρησης
Διάλεξη 4. Οικονομικά της ευημερίας: Γενική ισορροπία 9/3/2017. Οικονομικά της ευημερίας: Γενική ισορροπία. Οικονομική της ευημερίας
 Διάλεξη 4 Οικονομική της Οικονομικά της : Γενική ισορροπία Οικονομικά της είναι ο κλάδος της οικονομικής θεωρίας που ασχολείται με το κατά πόσο είναι επιθυμητές από την κοινωνία κάποιες εναλλακτικές οικονομικές.
Διάλεξη 4 Οικονομική της Οικονομικά της : Γενική ισορροπία Οικονομικά της είναι ο κλάδος της οικονομικής θεωρίας που ασχολείται με το κατά πόσο είναι επιθυμητές από την κοινωνία κάποιες εναλλακτικές οικονομικές.
Θεωρία Καταναλωτή. Υποδειγματοποίηση της συμπεριφοράς του καταναλωτή. Βασική έννοια: Βελτιστοποίηση υπό περιορισμό.
 Θεωρία Καταναλωτή Υποδειγματοποίηση της συμπεριφοράς του καταναλωτή. Βασική έννοια: Βελτιστοποίηση υπό περιορισμό. Προτιμήσεις (preferences) Εισοδηματικός περιορισμός (budget constraint) Άριστη επιλογή
Θεωρία Καταναλωτή Υποδειγματοποίηση της συμπεριφοράς του καταναλωτή. Βασική έννοια: Βελτιστοποίηση υπό περιορισμό. Προτιμήσεις (preferences) Εισοδηματικός περιορισμός (budget constraint) Άριστη επιλογή
ΕΦΑΡΜΟΣΜΕΝΗ ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΑΣΚΗΣΕΙΣ ΕΙΣΑΓΩΓΗ Ο ΜΗΧΑΝΙΣΜΟΣ ΤΗΣ ΑΓΟΡΑΣ
 ΕΦΑΡΜΟΣΜΕΝΗ ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΑΣΚΗΣΕΙΣ ΕΙΣΑΓΩΓΗ Ο ΜΗΧΑΝΙΣΜΟΣ ΤΗΣ ΑΓΟΡΑΣ Άσκηση 1 Αν το επιτόκιο είναι 10%, ποια είναι η παρούσα αξία των κερδών της Monroe orporation στα επόμενα 5 χρόνια; Χρόνια στο μέλλον
ΕΦΑΡΜΟΣΜΕΝΗ ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΑΣΚΗΣΕΙΣ ΕΙΣΑΓΩΓΗ Ο ΜΗΧΑΝΙΣΜΟΣ ΤΗΣ ΑΓΟΡΑΣ Άσκηση 1 Αν το επιτόκιο είναι 10%, ποια είναι η παρούσα αξία των κερδών της Monroe orporation στα επόμενα 5 χρόνια; Χρόνια στο μέλλον
1. Με βάση τον κανόνα της ψηφοφορίας με απλή πλειοψηφία, η ποσότητα του δημόσιου αγαθού που θα παρασχεθεί είναι η κοινωνικά αποτελεσματική ποσότητα.
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος 2013-2014 Τμήμα Οικονομικών Επιστημών Εξεταστική περίοδος Ιουλίου Εξέταση στο μάθημα: Δημόσια Οικονομική Διδασκαλία: Γεωργία Καπλάνογλου Η εξέταση αποτελείται από δύο
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος 2013-2014 Τμήμα Οικονομικών Επιστημών Εξεταστική περίοδος Ιουλίου Εξέταση στο μάθημα: Δημόσια Οικονομική Διδασκαλία: Γεωργία Καπλάνογλου Η εξέταση αποτελείται από δύο
3. Ανταγωνισμός ως προς τις Τιμές: Το Υπόδειγμα Bertrand
 3. Ανταγωνισμός ως προς τις Τιμές: Το Υπόδειγμα ertrand - To υπόδειγμα Cournot υποθέτει ότι κάθε επιχείρηση επιλέγει την παραγόμενη ποσότητα προϊόντος, ενώ στην πραγματικότητα οι επιχειρήσεις ανταγωνίζονται
3. Ανταγωνισμός ως προς τις Τιμές: Το Υπόδειγμα ertrand - To υπόδειγμα Cournot υποθέτει ότι κάθε επιχείρηση επιλέγει την παραγόμενη ποσότητα προϊόντος, ενώ στην πραγματικότητα οι επιχειρήσεις ανταγωνίζονται
Το Υπόδειγμα του Αντιπροσωπευτικού Νοικοκυριού
 Το Υπόδειγμα του Αντιπροσωπευτικού Νοικοκυριού Ramsey-Cass-Koopmans 1 Το Υπόδειγμα του Ramsey To υπόδειγμα αντιπροσωπευτικού νοικοκυριού oφείλεται στον Ramsey (1928), ο οποίος είχε πρώτος αναλύσει τη βέλτιστη
Το Υπόδειγμα του Αντιπροσωπευτικού Νοικοκυριού Ramsey-Cass-Koopmans 1 Το Υπόδειγμα του Ramsey To υπόδειγμα αντιπροσωπευτικού νοικοκυριού oφείλεται στον Ramsey (1928), ο οποίος είχε πρώτος αναλύσει τη βέλτιστη
Διάλεξη 4. Οικονομική της ευημερίας. 1 Ράπανος-Καπλάνογλου 2016/7
 Διάλεξη 4 Οικονομική της ευημερίας 1 Οικονομικά της ευημερίας: Γενική ισορροπία Οικονομικά της ευημερίας είναι ο κλάδος της οικονομικής θεωρίας που ασχολείται με το κατά πόσο είναι επιθυμητές από την κοινωνία
Διάλεξη 4 Οικονομική της ευημερίας 1 Οικονομικά της ευημερίας: Γενική ισορροπία Οικονομικά της ευημερίας είναι ο κλάδος της οικονομικής θεωρίας που ασχολείται με το κατά πόσο είναι επιθυμητές από την κοινωνία
Notes. Notes. Notes. Notes. T A = ŵ A p 1 e A 1 p 2e A 2 T B = ŵ B p 1 e A 1 p 2e B 2. 1 x A. 2 x B
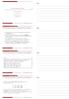 Γενική Ισορροπία-Ευημερία Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 3 Δεκεμβρίου 2012 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) Γενική Ισορροπία-Ευημερία 3 Δεκεμβρίου 2012 1 / 17 Το πρώτο Θ.Θ.Ο.Ε. μας λέει ότι κάθε
Γενική Ισορροπία-Ευημερία Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 3 Δεκεμβρίου 2012 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) Γενική Ισορροπία-Ευημερία 3 Δεκεμβρίου 2012 1 / 17 Το πρώτο Θ.Θ.Ο.Ε. μας λέει ότι κάθε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος Τμήμα Οικονομικών Επιστημών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος 206-207 Τμήμα Οικονομικών Επιστημών Χειμώνας-Άνοιξη Μάθημα: Δημόσια Οικονομική Διδασκαλία: Γεωργία Καπλάνογλου ο Πακέτο Ασκήσεων Ημερομηνία παράδοσης: Τρίτη Απριλίου
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος 206-207 Τμήμα Οικονομικών Επιστημών Χειμώνας-Άνοιξη Μάθημα: Δημόσια Οικονομική Διδασκαλία: Γεωργία Καπλάνογλου ο Πακέτο Ασκήσεων Ημερομηνία παράδοσης: Τρίτη Απριλίου
Ανεξαρτησία της διαδικασίας Ατομικισμός Μη-πατερναλισμός Φιλανθρωπία
 Pareto Αποτελεσματική Κατανομή «Μία κατανομή είναι κατά Pareto αποτελεσματική εάν δεν υπάρχει άλλη εφικτή κατανομή που να ωφελεί ένα άτομο χωρίς να ζημιώνει κάποιο άλλο» Υποθέσεις Ανεξαρτησία της διαδικασίας
Pareto Αποτελεσματική Κατανομή «Μία κατανομή είναι κατά Pareto αποτελεσματική εάν δεν υπάρχει άλλη εφικτή κατανομή που να ωφελεί ένα άτομο χωρίς να ζημιώνει κάποιο άλλο» Υποθέσεις Ανεξαρτησία της διαδικασίας
ΘΕΩΡΙΑ ΧΡΗΣΙΜΟΤΗΤΑΣ ΚΑΤΑΝΑΛΩΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ
 Ένθετο Κεφάλαιο ΘΕΩΡΙΑ ΧΡΗΣΙΜΟΤΗΤΑΣ ΚΑΤΑΝΑΛΩΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ Μικροοικονομική Ε. Σαρτζετάκης 1 Καταναλωτική συμπεριφορά Σκοπός αυτής της διάλεξης είναι να εξετάσουμε τον τρόπο με τον οποίο οι καταναλωτές
Ένθετο Κεφάλαιο ΘΕΩΡΙΑ ΧΡΗΣΙΜΟΤΗΤΑΣ ΚΑΤΑΝΑΛΩΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ Μικροοικονομική Ε. Σαρτζετάκης 1 Καταναλωτική συμπεριφορά Σκοπός αυτής της διάλεξης είναι να εξετάσουμε τον τρόπο με τον οποίο οι καταναλωτές
Το Υπόδειγμα της Οριακής Τιμολόγησης
 Το Υπόδειγμα της Οριακής Τιμολόγησης (ilgrom, Paul and John Roberts 98, imit Pricing and Entry under Incomplete Information) - Μια επιχείρηση ακολουθεί πολιτική οριακής τιμολόγησης (limit pricing) όταν
Το Υπόδειγμα της Οριακής Τιμολόγησης (ilgrom, Paul and John Roberts 98, imit Pricing and Entry under Incomplete Information) - Μια επιχείρηση ακολουθεί πολιτική οριακής τιμολόγησης (limit pricing) όταν
ΦΟΙΤΗΤΙΚΟ ΔΙΔΑΣΚΑΛΕΙΟ Facebook: Didaskaleio Foititiko
 Άσκηση. «Σε ορισμένες περιπτώσεις παρατηρείται στον κλάδο της γεωργίας της Ευρωπαϊκής Ένωσης το φαινομενικά παράδοξο να ευημερούν οι αγρότες περισσότερο όταν οι σοδειές τους δεν είναι καλές, και να πλήττονται
Άσκηση. «Σε ορισμένες περιπτώσεις παρατηρείται στον κλάδο της γεωργίας της Ευρωπαϊκής Ένωσης το φαινομενικά παράδοξο να ευημερούν οι αγρότες περισσότερο όταν οι σοδειές τους δεν είναι καλές, και να πλήττονται
Συναρτήσεις Κόστους και η Καμπύλη Προσφοράς της Ανταγωνιστικής Επιχείρησης
 Συναρτήσεις Κόστους και η Καμπύλη Προσφοράς της Ανταγωνιστικής Επιχείρησης - Στο εξής, συμβολίζουμε την ποσότητα του καταναλωτικού αγαθού με q. - Έστω ότι η συνάρτηση παραγωγής της επιχείρησης είναι: q=f(k,l),
Συναρτήσεις Κόστους και η Καμπύλη Προσφοράς της Ανταγωνιστικής Επιχείρησης - Στο εξής, συμβολίζουμε την ποσότητα του καταναλωτικού αγαθού με q. - Έστω ότι η συνάρτηση παραγωγής της επιχείρησης είναι: q=f(k,l),
ΔΥΝΑΜΙΚΗ ΑΠΟΤΕΛΕΣΜΑΤΙΚΟΤΗΤΑ ΚΑΙ ΑΠΟΤΥΧΙΕΣ ΤΗΣ ΑΓΟΡΑΣ. (Συνέχεια)
 ΔΥΝΑΜΙΚΗ ΑΠΟΤΕΛΕΣΜΑΤΙΚΟΤΗΤΑ ΚΑΙ ΑΠΟΤΥΧΙΕΣ ΤΗΣ ΑΓΟΡΑΣ (Συνέχεια) Πηγές αποτυχίας των αγορών Δημόσια αγαθά Είναι τα αγαθά των οποίων η χρήση δεν μπορεί να αποκλειστεί και ως εκ τούτου είναι ελευθέρα για
ΔΥΝΑΜΙΚΗ ΑΠΟΤΕΛΕΣΜΑΤΙΚΟΤΗΤΑ ΚΑΙ ΑΠΟΤΥΧΙΕΣ ΤΗΣ ΑΓΟΡΑΣ (Συνέχεια) Πηγές αποτυχίας των αγορών Δημόσια αγαθά Είναι τα αγαθά των οποίων η χρήση δεν μπορεί να αποκλειστεί και ως εκ τούτου είναι ελευθέρα για
Philip McCann Αστική και περιφερειακή οικονομική. 2 η έκδοση. Chapter 1
 Philip McCann Αστική και περιφερειακή οικονομική 2 η έκδοση Chapter 1 Κεφάλαιο 1 Χωροθέτηση δραστηριοτήτων Περιεχόμενα διάλεξης Υπόδειγμα για τη χωροθέτηση της παραγωγής Weber και Moses Ανάλυση της περιοχής
Philip McCann Αστική και περιφερειακή οικονομική 2 η έκδοση Chapter 1 Κεφάλαιο 1 Χωροθέτηση δραστηριοτήτων Περιεχόμενα διάλεξης Υπόδειγμα για τη χωροθέτηση της παραγωγής Weber και Moses Ανάλυση της περιοχής
Γενική Ισορροπία-Ευηµερία. 2ο Θεµελιώδες Θεώρηµα των Οικονοµικών της ευηµερίας. Notes. Notes. Notes. Notes. Κώστας Ρουµανιάς.
 Γενική Ισορροπία-Ευηµερία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 19 Απριλίου 2013 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία-Ευηµερία 19 Απριλίου 2013 1 / 20 Το πρώτο Θ.Θ.Ο.Ε. µας λέει ότι κάθε Βαλρασιανή
Γενική Ισορροπία-Ευηµερία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 19 Απριλίου 2013 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία-Ευηµερία 19 Απριλίου 2013 1 / 20 Το πρώτο Θ.Θ.Ο.Ε. µας λέει ότι κάθε Βαλρασιανή
Τόμος Γ - Δημόσια Οικονομική
 Τόμος Γ - Δημόσια Οικονομική 1. Η καμπύλη δυνατοτήτων χρησιμότητας δύο καταναλωτών, του Α και του Β, δίνεται από τη σχέση 2U A + U B = 250, όπου U A είναι η χρησιμότητα του καταναλωτή Α, και U B είναι
Τόμος Γ - Δημόσια Οικονομική 1. Η καμπύλη δυνατοτήτων χρησιμότητας δύο καταναλωτών, του Α και του Β, δίνεται από τη σχέση 2U A + U B = 250, όπου U A είναι η χρησιμότητα του καταναλωτή Α, και U B είναι
Notes. Notes. Notes. Notes
 Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 26 Μαΐου 2012 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) 26 Μαΐου 2012 1 / 19 Εως τώρα τα αγαθά που θεωρήσαμε ότι καταναλώνει ο καταναλωτής ήταν ιδιωτικά αγαθά. Με απλά λόγια
Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 26 Μαΐου 2012 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) 26 Μαΐου 2012 1 / 19 Εως τώρα τα αγαθά που θεωρήσαμε ότι καταναλώνει ο καταναλωτής ήταν ιδιωτικά αγαθά. Με απλά λόγια
Ερωτήσεις πολλαπλών επιλογών
 Ερωτήσεις πολλαπλών επιλογών Β1) Υποθέστε ότι στη θέση ισορροπίας της αγοράς ενός αγαθού η ζήτησή του ως προς την τιμή του είναι ελαστική. Μία μείωση της προσφοράς του αγαθού, με όλους τους άλλους παράγοντες
Ερωτήσεις πολλαπλών επιλογών Β1) Υποθέστε ότι στη θέση ισορροπίας της αγοράς ενός αγαθού η ζήτησή του ως προς την τιμή του είναι ελαστική. Μία μείωση της προσφοράς του αγαθού, με όλους τους άλλους παράγοντες
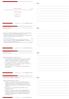
1 = = = x x = x. 4 u = = = MRS MRS. x x. MRS = MRS = = x = x x [1] x12 x x W W
![1 = = = x x = x. 4 u = = = MRS MRS. x x. MRS = MRS = = x = x x [1] x12 x x W W 1 = = = x x = x. 4 u = = = MRS MRS. x x. MRS = MRS = = x = x x [1] x12 x x W W](/thumbs/82/86418028.jpg) Θέµα ο (α) Μια κατανοµή στο εσωτερικό του κουτιού Edgeworth είναι άριστη κατά areto αν MRS MRS Έχουµε τα ακόλουθα MRS 3 3 4 4 4 3 3 4 4 4, MRS 3 3 3 3 3 3 Στην αρχική κατανοµή βρίσκουµε 00 MRS(50, 00)
Θέµα ο (α) Μια κατανοµή στο εσωτερικό του κουτιού Edgeworth είναι άριστη κατά areto αν MRS MRS Έχουµε τα ακόλουθα MRS 3 3 4 4 4 3 3 4 4 4, MRS 3 3 3 3 3 3 Στην αρχική κατανοµή βρίσκουµε 00 MRS(50, 00)
HAL R. VARIAN. Μικροοικονομική. Μια σύγχρονη προσέγγιση. 3 η έκδοση
 HL R. VRIN Μικροοικονομική Μια σύγχρονη προσέγγιση 3 η έκδοση Κεφάλαιο 32 Ανταλλαγή Ανταλλαγή Δύο καταναλωτές, και. Τα αποθέματα των αγαθών τους 1 και 2 είναι π.χ. 1 2 w = ( w1, w2 ) και w w w w = ( 6,
HL R. VRIN Μικροοικονομική Μια σύγχρονη προσέγγιση 3 η έκδοση Κεφάλαιο 32 Ανταλλαγή Ανταλλαγή Δύο καταναλωτές, και. Τα αποθέματα των αγαθών τους 1 και 2 είναι π.χ. 1 2 w = ( w1, w2 ) και w w w w = ( 6,
Ο ΠΡΟΣΔΙΟΡΙΣΜΟΣ TΩN ΤΙΜΩΝ
 ΚΕΦΑΛΑΙΟ ΠΕΜ Ο ΠΡΟΣΔΙΟΡΙΣΜΟΣ TΩN ΤΙΜΩΝ 1. Έννοια και λειτουργία της αγοράς Σε μια πρωτόγονη οικονομία, όπως του Ροβινσώνα Κρούσου, όπου δεν υπάρχει καταμερισμός της εργασίας ο άνθρωπος παράγει μόνος του
ΚΕΦΑΛΑΙΟ ΠΕΜ Ο ΠΡΟΣΔΙΟΡΙΣΜΟΣ TΩN ΤΙΜΩΝ 1. Έννοια και λειτουργία της αγοράς Σε μια πρωτόγονη οικονομία, όπως του Ροβινσώνα Κρούσου, όπου δεν υπάρχει καταμερισμός της εργασίας ο άνθρωπος παράγει μόνος του
Διάλεξη 8. Οικονομική Πολιτική και Αναδιανομή
 Διάλεξη 8 Οικονομική Πολιτική και Αναδιανομή 1 2 Εισαγωγικά Στο τμήμα αυτό θα μελετήσουμε το πλαίσιο που θα μας δώσει τη δυνατότητα να εξετάσουμε την αναδιανεμητική πολιτική της κυβέρνησης, τόσο από δεοντολογική
Διάλεξη 8 Οικονομική Πολιτική και Αναδιανομή 1 2 Εισαγωγικά Στο τμήμα αυτό θα μελετήσουμε το πλαίσιο που θα μας δώσει τη δυνατότητα να εξετάσουμε την αναδιανεμητική πολιτική της κυβέρνησης, τόσο από δεοντολογική
Εισαγωγικά. Εισαγωγικά. Διανομή εισοδήματος. Διάλεξη 8. Διανομή εισοδήματος Συντελεστής Gini
 Διάλεξη 8 Οικονομική Πολιτική και Αναδιανομή 2 Εισαγωγικά Στο τμήμα αυτό θα μελετήσουμε το πλαίσιο που θα μας δώσει τη δυνατότητα να εξετάσουμε την αναδιανεμητική πολιτική της κυβέρνησης, τόσο από δεοντολογική
Διάλεξη 8 Οικονομική Πολιτική και Αναδιανομή 2 Εισαγωγικά Στο τμήμα αυτό θα μελετήσουμε το πλαίσιο που θα μας δώσει τη δυνατότητα να εξετάσουμε την αναδιανεμητική πολιτική της κυβέρνησης, τόσο από δεοντολογική
max f( x,..., x ) st. : g ( x,..., x ) 0 g ( x,..., x ) 0
 Μαθηματικές Μέθοδοι Βελτιστοποίησης - Εστιάζουμε στο ακόλουθο πρόβλημα μεγιστοποίησης μιας αντικειμενικής συνάρτησης f υπό ένα σύνολο ανισοτικών περιορισμών: max f( x,..., x ) { x,..., x } 1 n 1 st. :
Μαθηματικές Μέθοδοι Βελτιστοποίησης - Εστιάζουμε στο ακόλουθο πρόβλημα μεγιστοποίησης μιας αντικειμενικής συνάρτησης f υπό ένα σύνολο ανισοτικών περιορισμών: max f( x,..., x ) { x,..., x } 1 n 1 st. :
Ζήτηση, Προσφορά και Ισορροπία στην Ανταγωνιστική Αγορά
 Ζήτηση, Προσφορά και Ισορροπία στην Ανταγωνιστική Αγορά - Ορισμός: Η αγορά ενός αγαθού είναι η διαδικασία (θεσμικό πλαίσιο) μέσω της οποίας έρχονται σε επικοινωνία οι αγοραστές και οι πωλητές του συγκεκριμένου
Ζήτηση, Προσφορά και Ισορροπία στην Ανταγωνιστική Αγορά - Ορισμός: Η αγορά ενός αγαθού είναι η διαδικασία (θεσμικό πλαίσιο) μέσω της οποίας έρχονται σε επικοινωνία οι αγοραστές και οι πωλητές του συγκεκριμένου
Μικροοικονοµική Θεωρία ΙΙΙ (1/4) Ενότητα # ΧΧΧ : Μικροοικονοµική
 ΕΛΛΗΝΙΚΗ ΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μικροοικονοµική Θεωρία ΙΙΙ (1/4) Ενότητα # ΧΧΧ : Μικροοικονοµική Βαγγέλης Τζουβελέκας Τµήµα Οικονοµικών Επιστηµών Β. Τζουβελέκας Μικροοικονοµική Θεωρία ΙΙΙ (1/4)
ΕΛΛΗΝΙΚΗ ΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μικροοικονοµική Θεωρία ΙΙΙ (1/4) Ενότητα # ΧΧΧ : Μικροοικονοµική Βαγγέλης Τζουβελέκας Τµήµα Οικονοµικών Επιστηµών Β. Τζουβελέκας Μικροοικονοµική Θεωρία ΙΙΙ (1/4)
Δημόσια Οικονομική. Κατ επιλογήν υποχρεωτικό, 3 ώρες εβδομαδιαίως, Θεωρία, Διδάσκον: Νικόλαος Τσούνης. Νικόλαος Τσούνης Δημόσια Οικονομική 1
 Κατ επιλογήν υποχρεωτικό, 3 ώρες εβδομαδιαίως, Θεωρία, Διδάσκον: 1 Κοινωνική Ευημερία και Ιδιωτικός Τομέας Συνθήκες μεγιστοποίησης κοινωνικής ευημερίας Άριστη κατανομή των παραγωγικών πόρων Πραγματοποίηση
Κατ επιλογήν υποχρεωτικό, 3 ώρες εβδομαδιαίως, Θεωρία, Διδάσκον: 1 Κοινωνική Ευημερία και Ιδιωτικός Τομέας Συνθήκες μεγιστοποίησης κοινωνικής ευημερίας Άριστη κατανομή των παραγωγικών πόρων Πραγματοποίηση
2. Έστω ότι η αγοραία συνάρτηση ζήτησης για κάποιο αγαθό είναι:
 ΟΙΚ 362 ΔΟΜΗ ΚΑΙ ΣΤΡΑΤΗΓΙΚΗ ΕΠΙΧΕΙΡΗΣΕΩΝ 2 η Σειρά Ασκήσεων 1 Έστω ότι η αγοραία συνάρτηση ζήτησης για κάποιο αγαθό είναι: q( p) = 1000 50 p Υποθέτουμε αρχικά ότι υπάρχει μία επιχείρηση στην αγορά και
ΟΙΚ 362 ΔΟΜΗ ΚΑΙ ΣΤΡΑΤΗΓΙΚΗ ΕΠΙΧΕΙΡΗΣΕΩΝ 2 η Σειρά Ασκήσεων 1 Έστω ότι η αγοραία συνάρτηση ζήτησης για κάποιο αγαθό είναι: q( p) = 1000 50 p Υποθέτουμε αρχικά ότι υπάρχει μία επιχείρηση στην αγορά και
Βασική θεωρία Ολιγοπωλιακού ανταγωνισµού
 Βασική θεωρία Ολιγοπωλιακού ανταγωνισµού Οµοιογενή Προϊόντα Ισορροπία Courot-Nash Έστω δυοπώλιο µε συνάρτηση ζήτησης: ( ) a b a, b > 0 () Βέβαια ισχύει ότι: + () Ακόµα υποθέτουµε ότι η τεχνολογία παραγωγής
Βασική θεωρία Ολιγοπωλιακού ανταγωνισµού Οµοιογενή Προϊόντα Ισορροπία Courot-Nash Έστω δυοπώλιο µε συνάρτηση ζήτησης: ( ) a b a, b > 0 () Βέβαια ισχύει ότι: + () Ακόµα υποθέτουµε ότι η τεχνολογία παραγωγής
Κεφάλαιο 6 Το πρότυπο υπόδειγμα του εμπορίου
 Κεφάλαιο 6 Το πρότυπο υπόδειγμα του εμπορίου 6-1 Περίγραμμα Σχετική προσφορά και σχετική ζήτηση Όροι εμπορίου και ευημερία Επιδράσεις της οικονομικής μεγέθυνσης, των δασμών επί των εισαγωγών και των εξαγωγικών
Κεφάλαιο 6 Το πρότυπο υπόδειγμα του εμπορίου 6-1 Περίγραμμα Σχετική προσφορά και σχετική ζήτηση Όροι εμπορίου και ευημερία Επιδράσεις της οικονομικής μεγέθυνσης, των δασμών επί των εισαγωγών και των εξαγωγικών
Η ΘΕΩΡΙΑ ΤΗΣ ΕΠΙΧΕΙΡΗΣΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΘΗΓΗΤΗΣ ΚΩΣΤΑΣ ΒΕΛΕΝΤΖΑΣ Η ΘΕΩΡΙΑ ΤΗΣ ΕΠΙΧΕΙΡΗΣΗΣ. Μερικές έννοιες Η συνάρτηση παραγωγής (, ), όπου είναι το συνολικό προϊόν και και οι συντελεστές
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΘΗΓΗΤΗΣ ΚΩΣΤΑΣ ΒΕΛΕΝΤΖΑΣ Η ΘΕΩΡΙΑ ΤΗΣ ΕΠΙΧΕΙΡΗΣΗΣ. Μερικές έννοιες Η συνάρτηση παραγωγής (, ), όπου είναι το συνολικό προϊόν και και οι συντελεστές
Ενότητα 2η Α ορέ ρ ς έ ς και ι ευ ε ηµ η ερ ε ί ρ α
 Ενότητα 2 η Αγορές και ευηµερία Περίγραµµα Εισαγωγή στην κανονιστική ανάλυση Πλεόνασµα καταναλωτή Πλεόνασµα παραγωγού Αποτελεσµατικότητα κατά Pareto Αποτελεσµατικότητα και ισότητα Συνθήκες για ισορροπία
Ενότητα 2 η Αγορές και ευηµερία Περίγραµµα Εισαγωγή στην κανονιστική ανάλυση Πλεόνασµα καταναλωτή Πλεόνασµα παραγωγού Αποτελεσµατικότητα κατά Pareto Αποτελεσµατικότητα και ισότητα Συνθήκες για ισορροπία
Bˆ min{ K, L } 2 L 2 K. 2.Stolper-Samuelson Να ευρεθει η επιδραςη μιασ μικρησ αυξηςησ τησ παραμετρου ςτον λογο. τιμη του αγαθου Κ τιμη του αγαθου L
 [2x2] January 31, 2011 ΟΙΚΟΝΟΜΙΑ ενασ καταναλωτησ αγαθα Α,Β,, Δυο επιχειρηςεισ Η ΕΠΙΧΕΙΡΗΗ 1 παραγει το αγαθο απο τα αγαθα, με ςυναρτηςη παραγωγησ ˆ min{,2 } (1 Η ΕΠΙΧΕΙΡΗΗ 2 παραγει το αγαθο απο τα αγαθα,
[2x2] January 31, 2011 ΟΙΚΟΝΟΜΙΑ ενασ καταναλωτησ αγαθα Α,Β,, Δυο επιχειρηςεισ Η ΕΠΙΧΕΙΡΗΗ 1 παραγει το αγαθο απο τα αγαθα, με ςυναρτηςη παραγωγησ ˆ min{,2 } (1 Η ΕΠΙΧΕΙΡΗΗ 2 παραγει το αγαθο απο τα αγαθα,
6. Το Υπόδειγμα των Επικαλυπτόμενων Γενεών: Ανταλλαγή I
 6. Το Υπόδειγμα τν Επικαλυπτόμενν Γενεών: Ανταλλαγή I 6.. Ερτήσεις Σχολιάστε την εγκυρότητα τν παρακάτ προτάσεν. Αν πιστεύετε ότι μια πρόταση είναι σστή κάτ από ορισμένες προϋποθέσεις τότε να αναφέρετε
6. Το Υπόδειγμα τν Επικαλυπτόμενν Γενεών: Ανταλλαγή I 6.. Ερτήσεις Σχολιάστε την εγκυρότητα τν παρακάτ προτάσεν. Αν πιστεύετε ότι μια πρόταση είναι σστή κάτ από ορισμένες προϋποθέσεις τότε να αναφέρετε
Θεωρία παραγωγού. Μικροοικονομική Θεωρία Ι / Διάλεξη 11 / Φ. Κουραντή 1
 Θεωρία παραγωγού Σκοπός: Μεγιστοποίηση κερδών (υπάρχουν κι άλλοι σκοποί, π.χ. ένας μάνατζερ επιδιώκει την μεγιστοποίηση εσόδων κτλ. Τελικά όμως σκοπεύει στην μεγιστοποίηση των κερδών για να μπορέσει να
Θεωρία παραγωγού Σκοπός: Μεγιστοποίηση κερδών (υπάρχουν κι άλλοι σκοποί, π.χ. ένας μάνατζερ επιδιώκει την μεγιστοποίηση εσόδων κτλ. Τελικά όμως σκοπεύει στην μεγιστοποίηση των κερδών για να μπορέσει να
Διάλεξη 13. Φορολογία και διανομή του εισοδήματος
 Διάλεξη 13 Φορολογία και διανομή του εισοδήματος 1 Γενικά Υπάρχουν δύο βασικές έννοιες για το πως επιμερίζεται το φορολογικό βάρος: Νομική επίπτωση Με βάση το νόμο το βάρος του φόρου το φέρει εκείνος που
Διάλεξη 13 Φορολογία και διανομή του εισοδήματος 1 Γενικά Υπάρχουν δύο βασικές έννοιες για το πως επιμερίζεται το φορολογικό βάρος: Νομική επίπτωση Με βάση το νόμο το βάρος του φόρου το φέρει εκείνος που
