Γενική Ανταγωνιστική Ισορροπία σε Οικονομία με Έναν Καταναλωτή και Έναν Παραγωγό
|
|
|
- Βοανηργες Παπανδρέου
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Γενική Ανταγωνιστική Ισορροπία σε Οικονομία με Έναν Καταναλωτή και Έναν Παραγωγό - Ορισμός. Μια ανταγωνιστική οικονομία που διέπεται από το θεσμό της ατομικής ιδιοκτησίας είναι μια οικονομία όπου: (i) Κάθε αγαθό αποτελεί αντικείμενο συναλλαγής σε μία αγορά (δηλαδή οι αγορές είναι πλήρεις). (ii) Οι καταναλωτές και οι επιχειρήσεις έχουν τέλεια πληροφόρηση για τις τιμές όλων των αγαθών. (iii) Οι καταναλωτές και οι επιχειρήσεις λαμβάνουν τις αποφάσεις τους θεωρώντας δεδομένες τις τιμές όλων των αγαθών (δηλαδή όλες οι αγορές είναι πλήρως ανταγωνιστικές). (iv) Οι καταναλωτές επιλέγουν την ποσότητα που θα καταναλώσουν από κάθε αγαθό και την προσφερόμενη ποσότητα εργασίας κατά τρόπο ώστε να μεγιστοποιούν τη χρησιμότητά τους υπό τον 1 εισοδηματικό τους περιορισμό.
2 (v) Οι επιχειρήσεις επιλέγουν τις χρησιμοποιούμενες ποσότητες εισροών και τις παραγόμενες ποσότητες των αγαθών κατά τρόπο ώστε να μεγιστοποιούν τα κέρδη τους υπό τον τεχνολογικό περιορισμό. (vi) To εισόδημα κάθε καταναλωτή αποτελείται από την αγοραία αξία της περιουσίας του και το μερίδιό του στα κέρδη των επιχειρήσεων. - Υποθέτουμε αρχικά μια οικονομία που αποτελείται από: Έναν καταναλωτή. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ (ή: την εργασία L) και το καταναλωτικό αγαθό Α. - Ο καταναλωτής περιγράφεται πλήρως από: (i) Τις προτιμήσεις του, οι οποίες παριστάνονται από τη συνάρτηση χρησιμότητας U(A,L), με U/ A > 0 και U/ L < 0. (όπου L είναι η προσφερόμενη ποσότητα εργασίας και Α είναι η ποσότητα του αγαθού A που καταναλώνει το άτομο). 2
3 (ii) Την περιουσία του, η οποία παριστάνεται από το διάνυσμα περιουσίας (endowment vector): e= ( ex, ea) = ( T,0), όπου e X (e A ) είναι η περιουσία που διαθέτει ο καταναλωτής απότοαγαθόx (A). - Ο καταναλωτής είναι ο μοναδικός ιδιοκτήτης της επιχείρησης. - Η επιχείρηση χρησιμοποιεί ως μοναδική εισροή την εργασία για να παράγει το καταναλωτικό αγαθό, σύμφωνα με τη συνάρτηση παραγωγής: Aˆ = f( Lˆ ), όπου ˆL είναι η χρησιμοποιούμενη ποσότητα εργασίας και Â είναι η παραγόμενη ποσότητα προϊόντος εκ μέρους της επιχείρησης. Ανταγωνιστική Ισορροπία - Έστω ότι η τιμή του αγαθού Χ (δηλαδή o μισθός της εργασίας) είναι w και η τιμή του αγαθού Α είναι p. 3
4 - Για κάθε διάνυσμα τιμών (w, p), το εισόδημα του καταναλωτή είναι η αγοραία αξία της περιουσίας του και τα κέρδη (π) που εισπράττει ως ιδιοκτήτης της επιχείρησης: M = w e + p e + π = wt + π X A - Ο εισοδηματικός περιορισμός του καταναλωτή είναι: wx + pa wt + π - Επειδή η συνάρτηση χρησιμότητας είναι εκφρασμένη σε όρους εργασίας (L), γράφουμε επίσης τον εισοδηματικό περιορισμό (1) σε όρους εργασίας χρησιμοποιώντας τον χρονικό περιορισμό του ατόμου: L = T X (2) (1) pa wl + π (3) (1) (2) - Ησχέση(3) είναι η μορφή του εισοδηματικού περιορισμού που χρησιμοποιούμε παρακάτω. 4
5 - Ορισμός. Μια ανταγωνιστική (ή Βαλρασιανή) ισορροπία στην υπό εξέταση οικονομία αποτελείται από ένα διάνυσμα τιμών ( w*, p*) και έναδιάνυσμαποσοτήτων(( L*, A*),( Lˆ *, Aˆ *)) τέτοια ώστε: (i) Ο καταναλωτής μεγιστοποιεί τη χρησιμότητά του υπό τον εισοδηματικό του περιορισμό: 2 * * U( L*, A*) U( L, A), ( L, A) R+ : p A wl + π (ii) Η επιχείρηση μεγιστοποιεί τα κέρδη της υπό τον τεχνολογικό περιορισμό: 2 π( Lˆ*, Aˆ*) π ( Lˆ, Aˆ ), ( Lˆ, Aˆ ) R : Aˆ ˆ + f ( L ) (iii) Όλες οι αγορές εκκαθαρίζονται, δηλαδήησυνολικήζήτηση(d) είναι ίση με τη συνολική προσφορά (S) για όλα τα αγαθά: DL = SL Lˆ( w *, p *) = L ( w *, p *) : Ισορροπία στην αγορά εργασίας DA = SA A( w*, p*) = Aˆ ( w*, p*) όπου Lwp (, ): H συνάρτηση προσφοράς εργασίας εκ μέρους του καταναλωτή. Lwp ˆ(, ) : 5 H συνάρτηση ζήτησης εργασίας εκ μέρους της επιχείρησης. : Ισορροπία στην αγορά του αγαθού Α
6 A( wp, ): Aˆ( wp, ): H συνάρτηση ζήτησης του αγαθού Α εκ μέρους του καταναλωτή. H συνάρτηση προσφοράς του αγαθού Α εκ μέρους της επιχείρησης. O Νόμος του Walras - Η υπερβάλλουσα ζήτηση εργασίας για κάθε διάνυσμα τιμών (w,p) είναι η διαφορά ανάμεσα στη συνολική ζήτηση και τη συνολική προσφορά εργασίας: ED ( wp, ) = D( wp, ) S( wp, ) = Lwp ˆ(, ) Lwp (, ) L L L - Η υπερβάλλουσα ζήτηση του αγαθού Α για κάθε διάνυσμα τιμών (w,p) είναι η διαφορά ανάμεσα στη συνολική ζήτηση και τη συνολική προσφορά του αγαθού Α: ED ( wp, ) = D( wp, ) S( wp, ) = Awp (, ) Awp ˆ(, ) A A A - Το διάνυσμα τιμών ισορροπίας (w*,p*) είναιεκείνοτοδιάνυσμα τιμών για το οποίο η συνολική ζήτηση είναι ίση με τη συνολική προσφορά (δηλαδή η υπερβάλλουσα ζήτηση είναι ίση με μηδέν) σε όλες τις αγορές: 6
7 DL( w*, p*) = SL( w*, p*) EDL( w*, p*) = 0 D ( w*, p*) = S ( w*, p*) ED ( w*, p*) = 0 A A A - Νόμος του Walras. Για οποιοδήποτε διάνυσμα τιμών (w, p), η συνολική αξία της υπερβάλλουσας ζήτησης για όλα τα αγαθά ισούται με μηδέν: w ED + p ED = L A 0 - Απόδειξη. Για να μεγιστοποιείται η χρησιμότητα του καταναλωτή, ο εισοδηματικός περιορισμός πρέπει να ισχύει με ισότητα για κάθε διάνυσμα τιμών: pawp (, ) = wlwp (, ) + π ( wp, ) = wlwp (, ) + pawp ˆ(, ) wlwp ˆ(, ) p [ Awp (, ) Awp ˆ(, )] + w [ Lwp ˆ(, ) Lwp (, )] = 0 ped + wed = 0 A L 7
8 - Γενίκευση Νόμου του Walras: Αν υπάρχουν n αγαθά στην οικονομία, τότε: n ped i i( p ) = 0 για κάθε διάνυσμα τιμών p=(p 1,,p n ), i=1 όπου p i είναι η τιμή του αγαθού i και ED i είναι η υπερβάλλουσα ζήτηση για το αγαθό i. - Πρόταση. Έστω ότι υπάρχουν n αγαθά στην οικονομία. Αν D i (p)=s i (p) για κάθε i k και p k > 0, τότε πρέπει επίσης να ισχύει: D k (p)=s k (p). - Δηλαδή: Αν όλες οι αγορές εκτός από την αγορά του αγαθού k βρίσκονται σε ισορροπία, τότε πρέπει και η αγορά του αγαθού k να βρίσκεται σε ισορροπία. - Απόδειξη: Έστω ότι για το διάνυσμα τιμών p = ( p1,..., p n ) όλες οι αγορές εκτός από την αγορά k βρίσκονται σε ισορροπία: D ( p) = S ED ( p) = 0, i k (4) i i i 8
9 - ΑπότονόμοτουWalras, ισχύει (για οποιοδήποτε διάνυσμα τιμών, άρα και για το διάνυσμα p): n i=1 ped( p) = 0 ped( p) + ped( p) = 0 i i i i k k i k p > 0 k ped( p) = 0 ED( p) = 0, δηλαδή η αγορά k βρίσκεται k k k επίσης σε ισορροπία. - Άρα, οι n συνθήκες ισορροπίας: D1( p) = S1( p) D ( p) = S ( p) n n δεν είναι ανεξάρτητες μεταξύ τους. - Έχουμε μόνο (n 1) ανεξάρτητες εξισώσεις με n αγνώστους (p 1,,p n ) => Μπορούμε να υπολογίσουμε μόνο τις (n 1) τιμές σε σχέση με την n-οστή τιμή, η οποία αποτελεί ελεύθερη μεταβλητή. (4) 9
10 - Δηλαδή: Μπορούμε να υπολογίσουμε μόνο τις (n 1) σχετικές τιμές (και όχι τις απόλυτες τιμές) ισορροπίας. - Για παράδειγμα, μπορούμε να υπολογίσουμε τις τιμές p 2,p 3,, p n σε σχέση με την τιμή p 1 : p2 p p n p p p 3,,..., : Σχετικές τιμές των αγαθών 2,...,n Εφόσον χρησιμοποιούμε την τιμή του αγαθού 1 ως ελεύθερη μεταβλητή, μπορούμε να θέσουμε την τιμή p 1 ίση με μια σταθερά. - Συχνά, είναι βολικό να χρησιμοποιούμε την τυποποίηση p 1 =1και * * να υπολογίζουμε τις υπόλοιπες τιμές ισορροπίας p,..., 2 pn (οι οποίες ερμηνεύονται σαν να μετρώνται σε σχέση με την τιμή του αγαθού 1). - Στην περίπτωση αυτή, το αγαθό 1 (σε σχέση με την τιμή του οποίου μετρώνται οι τιμές των υπόλοιπων αγαθών) ονομάζεται αγαθό αναφοράς ή αποτιμητής (numeraire good). 10
11 - Στην οικονομία που εξετάζουμε, υπάρχουν n=2 αγαθά: το αγαθό Χ (δηλαδή η εργασία L) και το αγαθό Α. Οι δύο συνθήκες ισορροπίας: DL( w, p) = SL( w, p) D ( w, p) = S ( w, p) A A δεν είναι ανεξάρτητες μεταξύ τους. - Έχουμε μόνο μία ανεξάρτητη εξίσωση με 2 αγνώστους (w,p). Μπορούμε να υπολογίσουμε μόνο τη σχετική τιμή ισορροπίας (και όχι τις απόλυτες τιμές w, p). - Για παράδειγμα, μπορούμε να υπολογίσουμε την τιμή (w) της εργασίας σε σχέση με την τιμή (p) του αγαθού Α δηλαδή, μπορούμε να υπολογίσουμε μόνο τον πραγματικό μισθό w / p. - Εφόσον χρησιμοποιούμε την τιμή (p) του αγαθού A ως ελεύθερη μεταβλητή, μπορούμε να θέσουμε την τιμή p ίση με μια σταθερά. 11
12 Χρησιμοποιούμε την τυποποίηση p=1 και υπολογίζουμε το μισθό ισορροπίας w* (δηλαδή χρησιμοποιούμε το αγαθό Α ως αποτιμητή). - Παράδειγμα 1 (Υπολογισμός Ανταγωνιστικής Ισορροπίας). Έστω μια οικονομία που αποτελείται από: Έναν καταναλωτή. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ (ή: την εργασία L) και το καταναλωτικό αγαθό Α. - Οι προτιμήσεις του καταναλωτή παριστάνονται από τη συνάρτηση χρησιμότητας: 1 2 U( L, A) = A L 2 - Η περιουσία του καταναλωτή παριστάνεται από το διάνυσμα: e= ( e, e ) = (1,0) : Ο καταναλωτής διαθέτει μία μονάδα του αγαθού Χ. X A 12
13 - Ο καταναλωτής είναι ο μοναδικός ιδιοκτήτης της επιχείρησης. - Η συνάρτηση παραγωγής της επιχείρησης είναι: 1 Aˆ = f( Lˆ) = Lˆ (Φθίνουσες Αποδόσεις Κλίμακας) 4 Μεθοδολογία Υπολογισμού Ανταγωνιστικής Ισορροπίας 1. Ορίζουμε μία τιμή για κάθε αγαθό και υπολογίζουμε το εισόδημα κάθε καταναλωτή. - Η τιμή του αγαθού Χ είναι w και η τιμή του αγαθού Α είναι p. Χρησιμοποιούμε το αγαθό Α ως αποτιμητή, δηλαδή θέτουμε p=1 και αναζητούμε το μισθό ισορροπίας w*. - To εισόδημα του καταναλωτή (εκφρασμένο σε όρους εργασίας) είναι το εισόδημα που προέρχεται από εργασία και τα κέρδη που εισπράττει ως ιδιοκτήτης της επιχείρησης: M = wl+ π 13
14 2. Λύνουμε το πρόβλημα μεγιστοποίησης της χρησιμότητας για κάθε καταναλωτή. (Δηλαδή, υπολογίζουμε τη συνάρτηση ζήτησης του αγαθού Α και τη συνάρτηση προσφοράς εργασίας για κάθε καταναλωτή). - Κάθε καταναλωτής μεγιστοποιεί τη χρησιμότητά του υπό τον εισοδηματικό του περιορισμό. 1 2 max U( L, A) = A L { LA, } 2 st.. pa M = wl+ π A wl+ π (UMP ) 0 L 1 A 0 - ΗλύσητουUMP είναι: w, αν w 1 Lw ( ) = 1, αν w 1 (5) (Συνάρτηση Προσφοράς Εργασίας) 14
15 A( w ) = w 2 + π, αν w 1 w+ π, αν w 1 (6) (Συνάρτηση Ζήτησης αγαθού Α) 3. Λύνουμε το πρόβλημα μεγιστοποίησης των κερδών για κάθε επιχείρηση. (Δηλαδή, υπολογίζουμε τις συναρτήσεις ζήτησης εισροών, τη συνάρτηση προσφοράς και τη συνάρτηση κερδών για κάθε επιχείρηση). - Κάθε επιχείρηση μεγιστοποιεί τα κέρδη της υπό τον τεχνολογικό περιορισμό (δηλαδή τη συνάρτηση παραγωγής). max Π = paˆ wlˆ = Aˆ wlˆ { LA ˆ, ˆ} 1 max Π = Lˆ wlˆ ˆ 1 { Lˆ } st.. A= Lˆ 4 4 st.. Lˆ 0 LA ˆ, ˆ 0 (PMP) 15
16 - ΗλύσητουPMP είναι: Lw 2 ˆ( ) = 1/64w (7) (Συνάρτηση Ζήτησης Εργασίας) Aˆ( w ) = 1/32 w (8) (Συνάρτηση Προσφοράς) π ( w) = 1/64w (9) (Συνάρτηση Κερδών) 4. Γράφουμε τις συνθήκες ισορροπίας για όλες τις αγορές και λύνουμε ως προς τις τιμές ισορροπίας. i i DL = SL Lw ˆ( ) = Lw ( ) (10) D = S A( w) = Aˆ ( w) (11) A A (Συνθήκη Ισορροπίας στην Αγορά Εργασίας) (Συνθήκη Ισορροπίας στην Αγορά του Αγαθού Α) - Γιαναυπολογίσουμετις (n 1) = 1 σχετικές τιμές ισορροπίας (δηλαδή το μισθό ισορροπίας w*), αρκεί να χρησιμοποιήσουμε τις (n 1) = 1 συνθήκες ισορροπίας. (Υπενθύμιση: Αν η μία από τις δύο αγορές βρίσκεται σε ισορροπία, τότε θα βρίσκεται επίσης σε ισορροπία και η άλλη αγορά.) 16
17 - Χρησιμοποιούμε τη συνθήκη ισορροπίας στην αγορά εργασίας και λύνουμε ως προς w. i Για w 1, είναι: (5) Lw ˆ( ) = Lw ( ) w= 1/4 i Για (7) w 1, είναι: (5) Lw ˆ( ) = Lw ( ) w= 1/8 απορρίπτεται (7) - Χρησιμοποιούμε το μισθό ισορροπίας (w*=1/4 ) για να υπολογίσουμε τα κέρδη, τις ποσότητες ισορροπίας και τη χρησιμότητα ισορροπίας: π * = 1/16, Lˆ * = L* = 1/4, Aˆ = A= 1/8 U* = 3/32 - Άρα, η ανταγωνιστική ισορροπία στην οικονομία είναι: ( w*, p*) = (1/4, 1) ( L*, A*) = ( Lˆ *, Aˆ *) = (1/ 8, 1/ 4) U* = 3/32 (Τιμές Ισορροπίας) (Ποσότητες Ισορροπίας) (Χρησιμότητα Ισορροπίας) 17
18 Γραφική Απεικόνιση Ανταγωνιστικής Ισορροπίας Â, A 2 U* = 3/32: A= 3/32 + L /2 * 1 1 BC. Π : A= + L 16 4 A ˆ* = A* = 1/8 Ε Π * = 1/16 A ˆ = L ˆ /4 Γενική Ανταγωνιστική Ισορροπία 0 L ˆ* = L* = 1/4 - Στο σημείο ισορροπίας Ε: (i) O καταναλωτής μεγιστοποιεί τη χρησιμότητά του υπό τον εισοδηματικό περιορισμό (δηλαδή, το σημείο Ε είναι το σημείο επαφής ανάμεσα στη γραμμή του εισοδηματικού περιορισμού και την καμπύλη αδιαφορίας του καταναλωτή). 18 ˆL,L
19 (ii) Η επιχείρηση μεγιστοποιεί τα κέρδη της υπό τον τεχνολογικό περιορισμό (δηλαδή, το σημείο Ε είναι το σημείο επαφής ανάμεσα στη γραμμή ίσου κέρδους και τη συνάρτηση παραγωγής της επιχείρησης). (iii) Όλες οι αγορές εκκαθαρίζονται (δηλαδή, στο σημείο Ε ισχύει: L ˆ = L και A= Aˆ ). - Η γραμμή ίσου κέρδους που διέρχεται από το σημείο ισορροπίας ταυτίζεται με τη γραμμή του εισοδηματικού περιορισμού. Το σημείο ισορροπίας (Ε) είναιτοσημείοεπαφήςανάμεσαστην καμπύλη αδιαφορίας του καταναλωτή και τη συνάρτηση παραγωγής της επιχείρησης. Lw ( ) w 1 Ισορροπία στην Αγορά Εργασίας w*=1/4 Ε Lw ˆ( ) 0 ˆL,L L ˆ* = L* = 1/4 1 19
20 - Παράδειγμα 2 (Υπολογισμός Ανταγωνιστικής Ισορροπίας). Έστω μια οικονομία που αποτελείται από: Έναν καταναλωτή. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ (ή: την εργασία L) και το καταναλωτικό αγαθό Α. - Οι προτιμήσεις του καταναλωτή παριστάνονται από τη συνάρτηση χρησιμότητας: 1 2 U( L, A) = A L 2 - Η περιουσία του καταναλωτή παριστάνεται από το διάνυσμα: e= ( e, e ) = (1,0) : Ο καταναλωτής διαθέτει μία μονάδα του αγαθού Χ. X A - Ο καταναλωτής είναι ο μοναδικός ιδιοκτήτης της επιχείρησης. - Η συνάρτηση παραγωγής της επιχείρησης είναι: Aˆ = f( Lˆ) = Lˆ (Σταθερές Αποδόσεις Κλίμακας) 20
21 - Ακολουθούμε τη μεθοδολογία που περιγράφτηκε παραπάνω για να υπολογίσουμε την ανταγωνιστική ισορροπία στην οικονομία. 1. Ορίζουμε μία τιμή για κάθε αγαθό και υπολογίζουμε το εισόδημα κάθε καταναλωτή. - Η τιμή του αγαθού Χ είναι w και η τιμή του αγαθού Α είναι p. Θέτουμε p=1 και αναζητούμε το μισθό ισορροπίας w*. - To εισόδημα του καταναλωτή είναι: M = wl+ π 2. Λύνουμε το πρόβλημα μεγιστοποίησης της χρησιμότητας (UMP) για κάθε καταναλωτή. - ΗλύσητουUMP είναι (βλ.σελ.14-15): Lw ( ) = w, αν w 1 1, αν w 1 (12) (Συνάρτηση Προσφοράς Εργασίας) 21
22 A( w ) = w 2 + π, αν w 1 w+ π, αν w 1 (13) (Συνάρτηση Ζήτησης αγαθού Α) 3. Λύνουμε το πρόβλημα μεγιστοποίησης των κερδών για κάθε επιχείρηση. max Π = paˆ wlˆ = Aˆ wlˆ { LA ˆ, ˆ} st.. Aˆ = Lˆ LA ˆ, ˆ 0 - ΗλύσητουPMP είναι:, αν w < 1 Lw ˆ( ) = 0, αν w = 1 0, αν w > 1 max Π = Lˆ wlˆ = (1 w) Lˆ { Lˆ } st.. Lˆ 0 (14) (Συνάρτηση Ζήτησης Εργασίας) (PMP) 22
23 , αν w < 1 ˆ( ) 0, αν w = 1 A w = 0, αν w > 1 (15) (Συνάρτηση Προσφοράς) π ( w) =, αν w < 1 (16) (Συνάρτηση Κερδών) 0, αν w 1 4. Γράφουμε τις συνθήκες ισορροπίας για όλες τις αγορές και λύνουμε ως προς το μισθό ισορροπίας. i i DL = SL Lw ˆ( ) = Lw ( ) (17) D = S A( w) = Aˆ ( w) (18) A A (Συνθήκη Ισορροπίας στην Αγορά Εργασίας) (Συνθήκη Ισορροπίας στην Αγορά του Αγαθού Α) - Χρησιμοποιούμε τη συνθήκη ισορροπίας στην αγορά εργασίας και λύνουμε ως προς w. 23
24 Για w<1, είναι: (12) Lw ˆ( ) = Lw ( ) = w : Αδύνατο (14) Για w> 1, είναι: (12) Lw ˆ( ) = Lw ( ) 0 = 1 : Αδύνατο (14) Για w= 1, είναι: (12) Lw ˆ( ) = Lw ( ) Lˆ = 1 (14) - Χρησιμοποιούμε το μισθό ισορροπίας (w*=1) για να υπολογίσουμε τα κέρδη, τις ποσότητες ισορροπίας και τη χρησιμότητα ισορροπίας: π * = 0, Lˆ * = L* = 1, Aˆ = A= 1 U* = 1/2 - Άρα, η ανταγωνιστική ισορροπία στην οικονομία είναι: ( w*, p*) = (1, 1) ( L*, A*) = ( Lˆ *, Aˆ *) = (1,1) U* = 1/2 (Τιμές Ισορροπίας) (Ποσότητες Ισορροπίας) (Χρησιμότητα Ισορροπίας) 24
25 Â, A Γραφική Απεικόνιση Ισορροπίας 2 U* = 1/2: A= 1/2 + L /2 Aˆ = Lˆ * BC. Π : A= L Ε A ˆ* = A* = 1 Γενική Ανταγωνιστική Ισορροπία π*=0 w L ˆ* = L* = 1 Lw ( ) ˆL,L w*=1 Ε Lw ˆ( ) Ισορροπία στην Αγορά Εργασίας 0 ˆL,L L ˆ* = L* = 1 25
26 - Παρατήρηση: Αν η συνάρτηση παραγωγής χαρακτηρίζεται από σταθερές αποδόσεις κλίμακας, τότε η ανταγωνιστική ισορροπία είναι συμβατή μόνο με μηδενικά κέρδη για την επιχείρηση. - Δηλαδή, στην περίπτωση αυτή ο μισθός ισορροπίας (w*) προσδιορίζεται από τη συνθήκη: p = AC(w*). - Άρα: Αν η συνάρτηση παραγωγής έχει σταθερές αποδόσεις κλίμακας, τότε ο μισθός ισορροπίας εξαρτάται μόνο από την τεχνολογία παραγωγής και είναι ανεξάρτητος από τις συνθήκες ζήτησης (δηλαδή είναι ανεξάρτητος από τις προτιμήσεις και τις περιουσίες των καταναλωτών). 26
27 - Παράδειγμα 3 (Υπολογισμός Ανταγωνιστικής Ισορροπίας). Έστω μια οικονομία που αποτελείται από: Έναν καταναλωτή. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ (ή: την εργασία L) και το καταναλωτικό αγαθό Α. - Οι προτιμήσεις του καταναλωτή παριστάνονται από τη συνάρτηση χρησιμότητας: 1 2 U( L, A) = A L 2 - Η περιουσία του καταναλωτή παριστάνεται από το διάνυσμα: e= ( e, e ) = (1,0) : Ο καταναλωτής διαθέτει μία μονάδα του αγαθού Χ. X A - Ο καταναλωτής είναι ο μοναδικός ιδιοκτήτης της επιχείρησης. - Η συνάρτηση παραγωγής της επιχείρησης είναι: Aˆ = f( Lˆ) = Lˆ2 (Αύξουσες Αποδόσεις Κλίμακας) 27
28 - Ακολουθούμε τη μεθοδολογία που περιγράφτηκε παραπάνω για να υπολογίσουμε την ανταγωνιστική ισορροπία στην οικονομία. 1. Ορίζουμε μία τιμή για κάθε αγαθό και υπολογίζουμε το εισόδημα κάθε καταναλωτή. - Η τιμή του αγαθού Χ είναι w και η τιμή του αγαθού Α είναι p. Θέτουμε p=1 και αναζητούμε το μισθό ισορροπίας w*. - To εισόδημα του καταναλωτή είναι: M = wl+ π 2. Λύνουμε το πρόβλημα μεγιστοποίησης της χρησιμότητας (UMP) για κάθε καταναλωτή. - ΗλύσητουUMP είναι (βλ.σελ.14-15): Lw ( ) = w, αν w 1 1, αν w 1 (19) (Συνάρτηση Προσφοράς Εργασίας) 28
29 A( w ) = w 2 + π, αν w 1 w+ π, αν w 1 (20) (Συνάρτηση Ζήτησης αγαθού Α) 3. Λύνουμε το πρόβλημα μεγιστοποίησης των κερδών για κάθε επιχείρηση. max Π = paˆ wlˆ = Aˆ wlˆ { LA ˆ, ˆ} st.. Aˆ = Lˆ 2 LA ˆ, ˆ 0 max Π { Lˆ } st.. Lˆ 0 ˆ 2 = L wlˆ (PMP) - Στην περίπτωση αυτή, το PMP δεν έχει λύση: Lw ˆ( ) =, Aw ˆ ( ) =, π ( w ) = (21) 4. Γράφουμε τις συνθήκες ισορροπίας για όλες τις αγορές και λύνουμε ως προς το μισθό ισορροπίας. 29
30 i i D = S Lw ˆ( ) = Lw ( ) (22) L L D = S A( w) = Aˆ ( w) (23) A A (Συνθήκη Ισορροπίας στην Αγορά Εργασίας) (Συνθήκη Ισορροπίας στην Αγορά του Αγαθού Α) - Χρησιμοποιούμε τη συνθήκη ισορροπίας στην αγορά εργασίας και λύνουμε ως προς w. i Για w 1, είναι: (19) Lw ˆ( ) = Lw ( ) = w Αδύνατο i Για (21) w 1, είναι: (19) Lw ˆ( ) = Lw ( ) = 1 Αδύνατο (21) - Συμπέρασμα: Αν η συνάρτηση παραγωγής έχει αύξουσες αποδόσεις κλίμακας, τότε δεν υπάρχει ανταγωνιστική ισορροπία στην οικονομία. 30
31 - Παράδειγμα 4 (Υπολογισμός Ανταγωνιστικής Ισορροπίας). Έστω μια οικονομία που αποτελείται από: Έναν καταναλωτή. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ και το καταναλωτικό αγαθό Α. - Οι προτιμήσεις του καταναλωτή παριστάνονται από τη συνάρτηση χρησιμότητας: U( X, A) = ln A+ 2ln X - Η περιουσία του καταναλωτή παριστάνεται από το διάνυσμα: e= ( e, e ) = (1,0) : Ο καταναλωτής διαθέτει μία μονάδα του αγαθού Χ. X A - Ο καταναλωτής είναι ο μοναδικός ιδιοκτήτης της επιχείρησης. - Η συνάρτηση παραγωγής της επιχείρησης είναι: Aˆ = f( Lˆ) = 4 Lˆ 31
32 - Ακολουθούμε τη μεθοδολογία που περιγράφτηκε παραπάνω για να υπολογίσουμε την ανταγωνιστική ισορροπία στην οικονομία. 1. Ορίζουμε μία τιμή για κάθε αγαθό και υπολογίζουμε το εισόδημα κάθε καταναλωτή. - Η τιμή του αγαθού Χ είναι w και η τιμή του αγαθού Α είναι p. Θέτουμε p=1 και αναζητούμε το μισθό ισορροπίας w*. - To εισόδημα του καταναλωτή είναι η αγοραία αξία της περιουσίας του και τα κέρδη που εισπράττει ως ιδιοκτήτης της επιχείρησης: M = w e + p e + π = w+ π X A 2. Λύνουμε το πρόβλημα μεγιστοποίησης της χρησιμότητας για κάθε καταναλωτή. max U( X, A) = ln A+ 2ln X { Χ, A} s.. t wx + pa M = w + π wx + A w + π 0 X 1, A 0 (UMP ) 32
33 - ΗλύσητουUMP είναι: ( 1, π ), αν w 2π (24) 2 w+ π w+ π,, αν w 2π 3 w 3 ( X( w), A( w )) = (Συναρτήσεις Ζήτησης των αγαθών Χ, Α) Lw ( ) = 0, αν w 2π w 2 π 3w, αν w 2π (25) (Συνάρτηση Προσφοράς Εργασίας) 3. Λύνουμε το πρόβλημα μεγιστοποίησης των κερδών για κάθε επιχείρηση. max Π = paˆ wlˆ = Aˆ wlˆ ˆ ˆ max Π = 4 Lˆ wlˆ { LA, } st.. Aˆ = 4 Lˆ LA ˆ, ˆ 0 { Lˆ } st.. Lˆ 0 (PMP) 33
34 - ΗλύσητουPMP είναι: Lw 2 ˆ( ) = 4/ w (26) (Συνάρτηση Ζήτησης Εργασίας) Aˆ( w ) = 8/ w (27) (Συνάρτηση Προσφοράς) π ( w) = 4/ w (28) (Συνάρτηση Κερδών) 4. Γράφουμε τις συνθήκες ισορροπίας για όλες τις αγορές και λύνουμε ως προς το μισθό ισορροπίας. i DL = SL Lw ˆ( ) = Lw ( ) (29) [ή, ισοδύναμα: D = S X( w) + Lˆ( w) = e X + Lˆ = 1 (29 ) i X X X D = S A( w) = Aˆ ( w) (30) A A (Συνθήκη Ισορροπίας στην Αγορά Εργασίας) (Συνθήκη Ισορροπίας στην Αγορά του αγαθού Χ) ] (Συνθήκη Ισορροπίας στην Αγορά του Αγαθού Α) - Χρησιμοποιούμε τη συνθήκη ισορροπίας στην αγορά εργασίας και λύνουμε ως προς w. 34
35 Για w 2π, είναι: (25) 4 Lw ˆ( ) = Lw ( ) = 0 : Αδύνατο (26) 2 w Για w 2π (28) w (28) w, είναι: - Χρησιμοποιούμε το μισθό ισορροπίας w = για να υπολογίσουμε τα κέρδη, τις ποσότητες ισορροπίας και τη χρησιμότητα ισορροπίας: π * = 2 5 / 5, Lˆ * = L* = 1/ 5, Aˆ * = A* = 4 5 / 5, X* = 4 / U* = ln = (25) = (26) ( * 2 5) Lw ˆ( ) Lw ( ) w Άρα, η ανταγωνιστική ισορροπία στην οικονομία είναι: 35
36 ( w*, p*) = (2 5, 1) ( L*, A*, X*) = (1/5, 4 5/5, 4/5) ( Lˆ *, Aˆ *) = (1/5, 4 5/5) 64 5 U* = ln 125 (Τιμές Ισορροπίας) (Ποσότητες Ισορροπίας) (Χρησιμότητα Ισορροπίας) Γραφική Απεικόνιση Ισορροπίας - Αντικαθιστούμε τη συνάρτηση κερδών στη συνάρτηση προσφοράς εργασίας (25) και γράφουμε τη συνάρτηση προσφοράς εργασίας ως εξής: Lw ( ) = 0, αν w w 2, αν w 2 2 (31) (Συνάρτηση Προσφοράς Εργασίας) 36
37 - Απεικονίζουμε τις συναρτήσεις ζήτησης και προσφοράς εργασίας [σχέσεις (26) και (31)] στο παρακάτω διάγραμμα, το οποίο παριστάνει την ισορροπία στην αγορά εργασίας: w Lw ( ) w * = 2 5 w R = 2 2 Ε L ˆ* = L* = 1/5 1/3 Ισορροπία στην Αγορά Εργασίας ˆ( 0 Lw) ˆL,L 37
Γενική Ανταγωνιστική Ισορροπία
 Γενική Ανταγωνιστική Ισορροπία - Υποθέτουμε μια οικονομία που αποτελείται από: Δύο καταναλωτές 1,. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ και το καταναλωτικό αγαθό Α. - Οι προτιμήσεις των καταναλωτών
Γενική Ανταγωνιστική Ισορροπία - Υποθέτουμε μια οικονομία που αποτελείται από: Δύο καταναλωτές 1,. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ και το καταναλωτικό αγαθό Α. - Οι προτιμήσεις των καταναλωτών
Γενική Ανταγωνιστική Ισορροπία και Αποτελεσματικές κατά Pareto Κατανομές σε Ανταλλακτική Οικονομία
 Γενική Ανταγωνιστική Ισορροπία και Αποτελεσματικές κατά Pareto Κατανομές σε Ανταλλακτική Οικονομία Βασικές Υποθέσεις (i) Οι αγορές όλων των αγαθών είναι τέλεια ανταγωνιστικές. Οι καταναλωτές και οι επιχειρήσεις
Γενική Ανταγωνιστική Ισορροπία και Αποτελεσματικές κατά Pareto Κατανομές σε Ανταλλακτική Οικονομία Βασικές Υποθέσεις (i) Οι αγορές όλων των αγαθών είναι τέλεια ανταγωνιστικές. Οι καταναλωτές και οι επιχειρήσεις
Κατώτατος Μισθός. - Οι περιουσίες των καταναλωτών παριστάνονται από τα διανύσματα:
 Κατώτατος Μισθός Έστω μια οικονομία που αποτελείται από: Δύο καταναλωτές: και. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ και το καταναλωτικό αγαθό Α. - Οι προτιμήσεις των καταναλωτών παριστάνονται
Κατώτατος Μισθός Έστω μια οικονομία που αποτελείται από: Δύο καταναλωτές: και. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ και το καταναλωτικό αγαθό Α. - Οι προτιμήσεις των καταναλωτών παριστάνονται
Μονοψωνιακή Ισορροπία
 Μονοψωνιακή Ισορροπία - Αν η αγορά εργασίας είναι πλήρως ανταγωνιστική, τότε η ατομική επιχείρηση θεωρεί δεδομένο το μισθό και, επομένως, αντιμετωπίζει μια πλήρως ελαστική (οριζόντια) καμπύλη προσφοράς
Μονοψωνιακή Ισορροπία - Αν η αγορά εργασίας είναι πλήρως ανταγωνιστική, τότε η ατομική επιχείρηση θεωρεί δεδομένο το μισθό και, επομένως, αντιμετωπίζει μια πλήρως ελαστική (οριζόντια) καμπύλη προσφοράς
Εργοδοτικές Εισφορές και Φορολογία στους Εργάτες
 Εργοδοτικές Εισφορές και Φορολογία στους Εργάτες Έστω μια οικονομία που αποτελείται από: Δύο καταναλωτές: 1 και. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ (ή: την εργασία ) και το καταναλωτικό αγαθό
Εργοδοτικές Εισφορές και Φορολογία στους Εργάτες Έστω μια οικονομία που αποτελείται από: Δύο καταναλωτές: 1 και. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ (ή: την εργασία ) και το καταναλωτικό αγαθό
Η αρχική γραμμή του εισοδηματικού περιορισμού είναι: Η νέα γραμμή του εισοδηματικού περιορισμού είναι: wt + V w
 Επιπτώσεις μιας Μεταβολής του Εισοδήματος (V) που δεν προέρχεται από Εργασία - Κανονικά και Κατώτερα Αγαθά (i) Αν η ζήτηση ενός αγαθού αυξάνεται καθώς αυξάνεται το εισόδημα του ατόμου, τότε το αγαθό ονομάζεται
Επιπτώσεις μιας Μεταβολής του Εισοδήματος (V) που δεν προέρχεται από Εργασία - Κανονικά και Κατώτερα Αγαθά (i) Αν η ζήτηση ενός αγαθού αυξάνεται καθώς αυξάνεται το εισόδημα του ατόμου, τότε το αγαθό ονομάζεται
Προσφορά Εργασίας Προτιμήσεις και Συνάρτηση Χρησιμότητας ( Χ,Α συνάρτηση χρησιμότητας U(X,A)
 Προσφορά Εργασίας - Έστω ότι υπάρχουν δύο αγαθά Α και Χ στην οικονομία. Το αγαθό Α παριστάνει τα διάφορα καταναλωτικά αγαθά. Το αγαθό Χ παριστάνει τον ελεύθερο χρόνο. Προτιμήσεις και Συνάρτηση Χρησιμότητας
Προσφορά Εργασίας - Έστω ότι υπάρχουν δύο αγαθά Α και Χ στην οικονομία. Το αγαθό Α παριστάνει τα διάφορα καταναλωτικά αγαθά. Το αγαθό Χ παριστάνει τον ελεύθερο χρόνο. Προτιμήσεις και Συνάρτηση Χρησιμότητας
To 2 ο Θεμελιώδες Θεώρημα Ευημερίας
 o 2 ο Θεμελιώδες Θεώρημα Ευημερίας - Το 1 ο Θεώρημα Ευημερίας (FW) εξασφαλίζει ότι η ανταγωνιστική ισορροπία είναι άριστη κατά Pareto αλλά δεν εξασφαλίζει μια ίση διανομή των οικονομικών οφελών μεταξύ
o 2 ο Θεμελιώδες Θεώρημα Ευημερίας - Το 1 ο Θεώρημα Ευημερίας (FW) εξασφαλίζει ότι η ανταγωνιστική ισορροπία είναι άριστη κατά Pareto αλλά δεν εξασφαλίζει μια ίση διανομή των οικονομικών οφελών μεταξύ
(1β) Μη Χωροθετικά Υποδείγματα Διαφοροποιημένου Προϊόντος με Ενδογενές Πλήθος Επιχειρήσεων
 (β) Μη Χωροθετικά Υποδείγματα Διαφοροποιημένου Προϊόντος με Ενδογενές Πλήθος Επιχειρήσεων Ελεύθερη Είσοδος και Ισορροπία Μηδενικών Κερδών - Η δυνατότητα νέων επιχειρήσεων να εισέρχονται ελεύθερα στην αγορά
(β) Μη Χωροθετικά Υποδείγματα Διαφοροποιημένου Προϊόντος με Ενδογενές Πλήθος Επιχειρήσεων Ελεύθερη Είσοδος και Ισορροπία Μηδενικών Κερδών - Η δυνατότητα νέων επιχειρήσεων να εισέρχονται ελεύθερα στην αγορά
Άριστες κατά Pareto Κατανομές και το Πρώτο Θεώρημα Ευημερίας
 Άριστες κατά Pareto Κατανομές και το Πρώτο Θεώρημα Ευημερίας - Υποθέτουμε μια οικονομία που αποτελείται από: Δύο καταναλωτές 1,. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ και το καταναλωτικό αγαθό
Άριστες κατά Pareto Κατανομές και το Πρώτο Θεώρημα Ευημερίας - Υποθέτουμε μια οικονομία που αποτελείται από: Δύο καταναλωτές 1,. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ και το καταναλωτικό αγαθό
ΜΑΘΗΜΑΤΙΚΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ 2 5/9/2002 Απαντήστε σε μια από τις δυο ερωτήσεις. 3. Να υπολογιστεί η ανταγωνιστική ισορροπία και τα σημεία
 ΜΑΘΗΜΑΤΙΚΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ 5/9/00 Απαντήστε σε μια από τις δυο ερωτήσεις. 1.Θεωρουμε οικονομία αποτελούμενη από ένα καταναλωτή, με προτιμήσεις U log+ logx,και περιουσία μόνο μια μονάδα του αγαθού
ΜΑΘΗΜΑΤΙΚΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ 5/9/00 Απαντήστε σε μια από τις δυο ερωτήσεις. 1.Θεωρουμε οικονομία αποτελούμενη από ένα καταναλωτή, με προτιμήσεις U log+ logx,και περιουσία μόνο μια μονάδα του αγαθού
Μονοπωλιακή Ισορροπία - Αν η αγορά του αγαθού Α είναι πλήρως ανταγωνιστική, τότε η ατομική επιχείρηση θεωρεί δεδομένη την τιμή (p) και, επομένως,
 Μονοπωλιακή Ισορροπία - Αν η αγορά του αγαθού Α είναι πλήρως ανταγωνιστική, τότε η ατομική επιχείρηση θεωρεί δεδομένη την τιμή (p) και, επομένως, αντιμετωπίζει μια πλήρως ελαστική (οριζόντια) καμπύλη ζήτησης
Μονοπωλιακή Ισορροπία - Αν η αγορά του αγαθού Α είναι πλήρως ανταγωνιστική, τότε η ατομική επιχείρηση θεωρεί δεδομένη την τιμή (p) και, επομένως, αντιμετωπίζει μια πλήρως ελαστική (οριζόντια) καμπύλη ζήτησης
Ελαχιστοποίηση του Κόστους
 Ελαχιστοποίηση του Κόστους - H ανάλυση του προβλήματος ελαχιστοποίησης του κόστους παρουσιάζει τα εξής πλεονεκτήματα σε σχέση με το πρόβλημα μεγιστοποίησης του κέρδους: (1) Επιτρέπει τη διατύπωση μιας
Ελαχιστοποίηση του Κόστους - H ανάλυση του προβλήματος ελαχιστοποίησης του κόστους παρουσιάζει τα εξής πλεονεκτήματα σε σχέση με το πρόβλημα μεγιστοποίησης του κέρδους: (1) Επιτρέπει τη διατύπωση μιας
Άριστες κατά Pareto Κατανομές και το Πρώτο Θεώρημα Ευημερίας
 Άριστες κατά Pareto Κατανομές και το Πρώτο Θεώρημα Ευημερίας - Υποθέτουμε μια οικονομία που αποτελείται από: Δύο καταναλωτές 1,. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ και το καταναλωτικό αγαθό
Άριστες κατά Pareto Κατανομές και το Πρώτο Θεώρημα Ευημερίας - Υποθέτουμε μια οικονομία που αποτελείται από: Δύο καταναλωτές 1,. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ και το καταναλωτικό αγαθό
Μεγιστοποίηση της Χρησιμότητας
 Μεγιστοποίηση της Χρησιμότητας - Πρόβλημα Καταναλωτή: Επιλογή καταναλωτικού συνδυασμού x=(x, x ) υπό ένα σύνολο φυσικών, θεσμικών και οικονομικών περιορισμών κατά τρόπο ώστε να μεγιστοποιεί τη χρησιμότητά
Μεγιστοποίηση της Χρησιμότητας - Πρόβλημα Καταναλωτή: Επιλογή καταναλωτικού συνδυασμού x=(x, x ) υπό ένα σύνολο φυσικών, θεσμικών και οικονομικών περιορισμών κατά τρόπο ώστε να μεγιστοποιεί τη χρησιμότητά
Ισορροπία σε Αγορές Διαφοροποιημένων Προϊόντων
 Ισορροπία σε Αγορές Διαφοροποιημένων Προϊόντων - Στο υπόδειγμα ertrand, οι επιχειρήσεις, παράγουν ένα ομοιογενές αγαθό, οπότε η τιμή είναι η μοναδική μεταβλητή που ενδιαφέρει τους καταναλωτές και οι καταναλωτές
Ισορροπία σε Αγορές Διαφοροποιημένων Προϊόντων - Στο υπόδειγμα ertrand, οι επιχειρήσεις, παράγουν ένα ομοιογενές αγαθό, οπότε η τιμή είναι η μοναδική μεταβλητή που ενδιαφέρει τους καταναλωτές και οι καταναλωτές
 25. Μία τυπική επιχείρηση που λειτουργεί σε καθεστώς τέλειου ανταγωνισμού, στη μακροχρόνια θέση ισορροπίας της: α. πραγματοποιεί θετικά οικονομικά κέρδη. β. πραγματοποιεί μηδενικά οικονομικά κέρδη. γ.
25. Μία τυπική επιχείρηση που λειτουργεί σε καθεστώς τέλειου ανταγωνισμού, στη μακροχρόνια θέση ισορροπίας της: α. πραγματοποιεί θετικά οικονομικά κέρδη. β. πραγματοποιεί μηδενικά οικονομικά κέρδη. γ.
Η Καμπύλη Προσφοράς της Επιχείρησης
 Η Καμπύλη Προσφοράς της Επιχείρησης - Μπορούμε να διατυπώσουμε το πρόβλημα μεγιστοποίησης των κερδών και να βρούμε τις συναρτήσεις ζήτησης εισροών, τη συνάρτηση προσφοράς και τη συνάρτηση κερδών της επιχείρησης
Η Καμπύλη Προσφοράς της Επιχείρησης - Μπορούμε να διατυπώσουμε το πρόβλημα μεγιστοποίησης των κερδών και να βρούμε τις συναρτήσεις ζήτησης εισροών, τη συνάρτηση προσφοράς και τη συνάρτηση κερδών της επιχείρησης
Άριστες κατά Pareto Κατανομές
 Άριστες κατά Pareto Κατανομές - Ορισμός. Μια κατανομή x = (x, x ) = (( 1, )( 1, )) ονομάζεται άριστη κατά Pareto αν δεν υπάρχει άλλη κατανομή x = ( x, x ) τέτοια ώστε: U j( x j) U j( xj) για κάθε καταναλωτή
Άριστες κατά Pareto Κατανομές - Ορισμός. Μια κατανομή x = (x, x ) = (( 1, )( 1, )) ονομάζεται άριστη κατά Pareto αν δεν υπάρχει άλλη κατανομή x = ( x, x ) τέτοια ώστε: U j( x j) U j( xj) για κάθε καταναλωτή
Διάκριση Τιμών 2 ου Βαθμού: Μη Γραμμική Τιμολόγηση (Nonlinear Pricing) - Η διάκριση τιμών 3 ου βαθμού προϋποθέτει ότι η μονοπωλιακή
 Διάκριση Τιμών ου Βαθμού: Μη Γραμμική Τιμολόγηση (Nonlinear Pricing) -H διάκριση τιμών 1 ου βαθμού προϋποθέτει ότι η μονοπωλιακή επιχείρηση γνωρίζει τις ατομικές συναρτήσεις ζήτησης όλων των καταναλωτών.
Διάκριση Τιμών ου Βαθμού: Μη Γραμμική Τιμολόγηση (Nonlinear Pricing) -H διάκριση τιμών 1 ου βαθμού προϋποθέτει ότι η μονοπωλιακή επιχείρηση γνωρίζει τις ατομικές συναρτήσεις ζήτησης όλων των καταναλωτών.
Ζήτηση, Προσφορά και Ισορροπία στην Ανταγωνιστική Αγορά
 Ζήτηση, Προσφορά και Ισορροπία στην Ανταγωνιστική Αγορά - Ορισμός: Η αγορά ενός αγαθού είναι η διαδικασία (θεσμικό πλαίσιο) μέσω της οποίας έρχονται σε επικοινωνία οι αγοραστές και οι πωλητές του συγκεκριμένου
Ζήτηση, Προσφορά και Ισορροπία στην Ανταγωνιστική Αγορά - Ορισμός: Η αγορά ενός αγαθού είναι η διαδικασία (θεσμικό πλαίσιο) μέσω της οποίας έρχονται σε επικοινωνία οι αγοραστές και οι πωλητές του συγκεκριμένου
2.10. Τιμή και ποσότητα ισορροπίας
 .. Τιμή και ποσότητα ισορροπίας ίδαμε ότι η βασική επιδίωξη των επιχειρήσεων είναι η επίτευξη του μέγιστου κέρδους με την πώληση όσο το δυνατόν μεγαλύτερων ποσοτήτων ενός αγαθού στη μεγαλύτερη δυνατή τιμή
.. Τιμή και ποσότητα ισορροπίας ίδαμε ότι η βασική επιδίωξη των επιχειρήσεων είναι η επίτευξη του μέγιστου κέρδους με την πώληση όσο το δυνατόν μεγαλύτερων ποσοτήτων ενός αγαθού στη μεγαλύτερη δυνατή τιμή
ΕΦΑΡΜΟΣΜΕΝΗ ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΑΣΚΗΣΕΙΣ ΕΙΣΑΓΩΓΗ Ο ΜΗΧΑΝΙΣΜΟΣ ΤΗΣ ΑΓΟΡΑΣ
 ΕΦΑΡΜΟΣΜΕΝΗ ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΑΣΚΗΣΕΙΣ ΕΙΣΑΓΩΓΗ Ο ΜΗΧΑΝΙΣΜΟΣ ΤΗΣ ΑΓΟΡΑΣ Άσκηση 1 Αν το επιτόκιο είναι 10%, ποια είναι η παρούσα αξία των κερδών της Monroe orporation στα επόμενα 5 χρόνια; Χρόνια στο μέλλον
ΕΦΑΡΜΟΣΜΕΝΗ ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΑΣΚΗΣΕΙΣ ΕΙΣΑΓΩΓΗ Ο ΜΗΧΑΝΙΣΜΟΣ ΤΗΣ ΑΓΟΡΑΣ Άσκηση 1 Αν το επιτόκιο είναι 10%, ποια είναι η παρούσα αξία των κερδών της Monroe orporation στα επόμενα 5 χρόνια; Χρόνια στο μέλλον
Επιλογή Ποιότητας και Κάθετη Διαφοροποίηση Προϊόντος
 Επιλογή Ποιότητας και Κάθετη Διαφοροποίηση Προϊόντος - Τα προϊόντα που παράγουν οι επιχειρήσεις μπορούν να διαφοροποιούνται ως προς ένα πλήθος χαρακτηριστικών. Παράδειγμα: Τα αυτοκίνητα διαφοροποιούνται
Επιλογή Ποιότητας και Κάθετη Διαφοροποίηση Προϊόντος - Τα προϊόντα που παράγουν οι επιχειρήσεις μπορούν να διαφοροποιούνται ως προς ένα πλήθος χαρακτηριστικών. Παράδειγμα: Τα αυτοκίνητα διαφοροποιούνται
Συναρτήσεις Κόστους και η Καμπύλη Προσφοράς της Ανταγωνιστικής Επιχείρησης
 Συναρτήσεις Κόστους και η Καμπύλη Προσφοράς της Ανταγωνιστικής Επιχείρησης - Στο εξής, συμβολίζουμε την ποσότητα του καταναλωτικού αγαθού με q. - Έστω ότι η συνάρτηση παραγωγής της επιχείρησης είναι: q=f(k,l),
Συναρτήσεις Κόστους και η Καμπύλη Προσφοράς της Ανταγωνιστικής Επιχείρησης - Στο εξής, συμβολίζουμε την ποσότητα του καταναλωτικού αγαθού με q. - Έστω ότι η συνάρτηση παραγωγής της επιχείρησης είναι: q=f(k,l),
ΑΝΤΑΛΛΑΓΗ. Οι συναρτήσεις χρησιμότητας των ατόμων Α και Β είναι αντίστοιχα. και. και το αρχικό απόθεμα και.
 ΑΝΤΑΛΛΑΓΗ Άσκηση 5 Οι συναρτήσεις χρησιμότητας των ατόμων Α και Β είναι αντίστοιχα u ( x, x ) = x + x 1 2 1 2 και u ( x, x ) = x + x 1 2 1 2 Ω = (2,0) Ω = (0,1) και το αρχικό απόθεμα και. Να προσδιοριστεί
ΑΝΤΑΛΛΑΓΗ Άσκηση 5 Οι συναρτήσεις χρησιμότητας των ατόμων Α και Β είναι αντίστοιχα u ( x, x ) = x + x 1 2 1 2 και u ( x, x ) = x + x 1 2 1 2 Ω = (2,0) Ω = (0,1) και το αρχικό απόθεμα και. Να προσδιοριστεί
Διάλεξη 10. Γενική Ισορροπία VA 30
 Διάλεξη 10 Γενική Ισορροπία V 30 1 Μερική & Γενική Ισορροπία Μέχρι τώρα εξετάζαμε γενικά την αγορά ενός αγαθού μεμονωμένα. Το πώς δηλαδή η προσφορά και η ζήτηση επηρεάζονται από την τιμή του συγκεκριμένου
Διάλεξη 10 Γενική Ισορροπία V 30 1 Μερική & Γενική Ισορροπία Μέχρι τώρα εξετάζαμε γενικά την αγορά ενός αγαθού μεμονωμένα. Το πώς δηλαδή η προσφορά και η ζήτηση επηρεάζονται από την τιμή του συγκεκριμένου
Ελαστικότητες Ζήτησης
 Ελαστικότητες Ζήτησης - Η ευαισθησία της ζητούμενης ποσότητας x σε μεταβολές της τιμής μπορεί να μετρηθεί άμεσα από το λόγο Δx / Δ (ήαπότην παράγωγο x / ). - Αυτό το μέτρο ευαισθησίας έχει το μειονέκτημα
Ελαστικότητες Ζήτησης - Η ευαισθησία της ζητούμενης ποσότητας x σε μεταβολές της τιμής μπορεί να μετρηθεί άμεσα από το λόγο Δx / Δ (ήαπότην παράγωγο x / ). - Αυτό το μέτρο ευαισθησίας έχει το μειονέκτημα
Θεωρία: dq1 dq1 dq1 P1 E1. dq2 dq2 dq2 P2 E2 1 1 P E E. d π dp dc dq dq dq. dp dc dq dq
 Θεωρία: Θέµα ο Η συνάρτηση κέρδους του µονοπωλητή ο οποίος πραγµατοποιεί διάκριση τιµών τρίτου βαθµού µεταξύ δύο αγορών και είναι η π µε τύπο π (, ) = R ( ) + R ( ) C( + ) Συνθήκες α' τάξης = R ' C ' =
Θεωρία: Θέµα ο Η συνάρτηση κέρδους του µονοπωλητή ο οποίος πραγµατοποιεί διάκριση τιµών τρίτου βαθµού µεταξύ δύο αγορών και είναι η π µε τύπο π (, ) = R ( ) + R ( ) C( + ) Συνθήκες α' τάξης = R ' C ' =
Μεγιστοποίηση του Κέρδους
 Μεγιστοποίηση του Κέρδους - Έστω η συνάρτηση παραγωγής: f( K, L). - Η τιμή του παραγόμενου προϊόντος είναι p, ητιμήτηςεργασίας είναι w και η τιμή του κεφαλαίου είναι r. - Υπόθεση: Η επιχείρηση είναι αποδέκτης
Μεγιστοποίηση του Κέρδους - Έστω η συνάρτηση παραγωγής: f( K, L). - Η τιμή του παραγόμενου προϊόντος είναι p, ητιμήτηςεργασίας είναι w και η τιμή του κεφαλαίου είναι r. - Υπόθεση: Η επιχείρηση είναι αποδέκτης
ΠΑΡΑΡΤΗΜΑ: ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΑΡΙΣΤΟΥ ΠΕΡΙΒΑΛΛΟΝΤΙΚΟΥ ΦΟΡΟΥ
 ΠΑΡΑΡΤΗΜΑ: ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΑΡΙΣΤΟΥ ΠΕΡΙΒΑΛΛΟΝΤΙΚΟΥ ΦΟΡΟΥ Ας υποθέσουμε ότι έχουμε ένα αγαθό το οποίο δημιουργεί κατά την παραγωγή ή την κατανάλωσή του έναν ρύπο, και ας υποθέσουμε ότι για κάθε μία μονάδα
ΠΑΡΑΡΤΗΜΑ: ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΑΡΙΣΤΟΥ ΠΕΡΙΒΑΛΛΟΝΤΙΚΟΥ ΦΟΡΟΥ Ας υποθέσουμε ότι έχουμε ένα αγαθό το οποίο δημιουργεί κατά την παραγωγή ή την κατανάλωσή του έναν ρύπο, και ας υποθέσουμε ότι για κάθε μία μονάδα
Ερωτήσεις πολλαπλών επιλογών
 Ερωτήσεις πολλαπλών επιλογών Β1) Υποθέστε ότι στη θέση ισορροπίας της αγοράς ενός αγαθού η ζήτησή του ως προς την τιμή του είναι ελαστική. Μία μείωση της προσφοράς του αγαθού, με όλους τους άλλους παράγοντες
Ερωτήσεις πολλαπλών επιλογών Β1) Υποθέστε ότι στη θέση ισορροπίας της αγοράς ενός αγαθού η ζήτησή του ως προς την τιμή του είναι ελαστική. Μία μείωση της προσφοράς του αγαθού, με όλους τους άλλους παράγοντες
1 = = = x x = x. 4 u = = = MRS MRS. x x. MRS = MRS = = x = x x [1] x12 x x W W
![1 = = = x x = x. 4 u = = = MRS MRS. x x. MRS = MRS = = x = x x [1] x12 x x W W 1 = = = x x = x. 4 u = = = MRS MRS. x x. MRS = MRS = = x = x x [1] x12 x x W W](/thumbs/82/86418028.jpg) Θέµα ο (α) Μια κατανοµή στο εσωτερικό του κουτιού Edgeworth είναι άριστη κατά areto αν MRS MRS Έχουµε τα ακόλουθα MRS 3 3 4 4 4 3 3 4 4 4, MRS 3 3 3 3 3 3 Στην αρχική κατανοµή βρίσκουµε 00 MRS(50, 00)
Θέµα ο (α) Μια κατανοµή στο εσωτερικό του κουτιού Edgeworth είναι άριστη κατά areto αν MRS MRS Έχουµε τα ακόλουθα MRS 3 3 4 4 4 3 3 4 4 4, MRS 3 3 3 3 3 3 Στην αρχική κατανοµή βρίσκουµε 00 MRS(50, 00)
Διάλεξη 3. Οικονομικά της ευημερίας. Οικονομικά της ευημερίας 3/9/2017. Περίγραμμα. Εργαλεία δεοντολογικής ανάλυσης
 Περίγραμμα Διάλεξη Εργαλεία δεοντολογικής ανάλυσης Συνθήκες για αποτελεσματικότητα κατά areto Συνθήκες για ισορροπία σε ανταγωνιστικές αγορές Το πρώτο θεώρημα των οικονομικών της ευημερίας Το δεύτερο θεώρημα
Περίγραμμα Διάλεξη Εργαλεία δεοντολογικής ανάλυσης Συνθήκες για αποτελεσματικότητα κατά areto Συνθήκες για ισορροπία σε ανταγωνιστικές αγορές Το πρώτο θεώρημα των οικονομικών της ευημερίας Το δεύτερο θεώρημα
Ασκήσεις 1. Με τα δεδομένα του παρακάτω πίνακα: Τιμή (Ρ) Ποσότητα (Q D )
 2 ο ΚΕΦΑΛΑΙΟ ΕΡΩΤΗΣΕΙΣ 1. Ποια είναι η επιδίωξη του καταναλωτή και ποιοι παράγοντες την περιορίζουν; 2. Ποιος καταναλωτής ονομάζεται ορθολογικός και πότε λέμε ότι βρίσκεται σε ισορροπία; 3. Να διατυπώσετε
2 ο ΚΕΦΑΛΑΙΟ ΕΡΩΤΗΣΕΙΣ 1. Ποια είναι η επιδίωξη του καταναλωτή και ποιοι παράγοντες την περιορίζουν; 2. Ποιος καταναλωτής ονομάζεται ορθολογικός και πότε λέμε ότι βρίσκεται σε ισορροπία; 3. Να διατυπώσετε
1. Επιλογή Διαφημιστικής Δαπάνης στη Μονοπωλιακή Αγορά
 1. Επιλογή Διαφημιστικής Δαπάνης στη Μονοπωλιακή Αγορά 1Α. Δελεαστική Διαφήμιση στη Μονοπωλιακή Αγορά - Έστω ότι η αγορά ενός αγαθού είναι μονοπωλιακή και η διαφήμιση του προϊόντος είναι δελεαστική δηλαδή
1. Επιλογή Διαφημιστικής Δαπάνης στη Μονοπωλιακή Αγορά 1Α. Δελεαστική Διαφήμιση στη Μονοπωλιακή Αγορά - Έστω ότι η αγορά ενός αγαθού είναι μονοπωλιακή και η διαφήμιση του προϊόντος είναι δελεαστική δηλαδή
Ολιγοπωλιακή Ισορροπία
 Ολιγοπωλιακή Ισορροπία - Χρησιμοποιούμε τις βασικές αρχές της θεωρίας παιγνίων για να εξετάσουμε τη στρατηγική αλληλεπίδραση των επιχειρήσεων σε ατελώς ανταγωνιστικές αγορές, εστιάζοντας την προσοχή μας
Ολιγοπωλιακή Ισορροπία - Χρησιμοποιούμε τις βασικές αρχές της θεωρίας παιγνίων για να εξετάσουμε τη στρατηγική αλληλεπίδραση των επιχειρήσεων σε ατελώς ανταγωνιστικές αγορές, εστιάζοντας την προσοχή μας
Διάλεξη 3. Οικονομικά της ευημερίας 2/26/2016. Περίγραμμα. Εργαλεία δεοντολογικής ανάλυσης. Αποτελεσματικότητα κατά Pareto: ορισμός. ορισμός.
 Περίγραμμα Διάλεξη Εργαλεία δεοντολογικής ανάλυσης υνθήκες για αποτελεσματικότητα κατά areto υνθήκες για ισορροπία σε ανταγωνιστικές αγορές Το πρώτο θεώρημα των οικονομικών της ευημερίας Το δεύτερο θεώρημα
Περίγραμμα Διάλεξη Εργαλεία δεοντολογικής ανάλυσης υνθήκες για αποτελεσματικότητα κατά areto υνθήκες για ισορροπία σε ανταγωνιστικές αγορές Το πρώτο θεώρημα των οικονομικών της ευημερίας Το δεύτερο θεώρημα
ΦΟΙΤΗΤΙΚΟ ΔΙΔΑΣΚΑΛΕΙΟ Facebook: Didaskaleio Foititiko
 Άσκηση. «Σε ορισμένες περιπτώσεις παρατηρείται στον κλάδο της γεωργίας της Ευρωπαϊκής Ένωσης το φαινομενικά παράδοξο να ευημερούν οι αγρότες περισσότερο όταν οι σοδειές τους δεν είναι καλές, και να πλήττονται
Άσκηση. «Σε ορισμένες περιπτώσεις παρατηρείται στον κλάδο της γεωργίας της Ευρωπαϊκής Ένωσης το φαινομενικά παράδοξο να ευημερούν οι αγρότες περισσότερο όταν οι σοδειές τους δεν είναι καλές, και να πλήττονται
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΑΠΑΝΤΗΣΕΙΣ ( )
 ΘΕΜΑ Α Α1. α. Σωστό ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΑΠΑΝΤΗΣΕΙΣ (14.06.2017) ΟΜΑΔΑ ΠΡΩΤΗ β. Λάθος γ. Λάθος δ. Λάθος ε. Σωστό Α2. Σωστή επιλογή (γ) Α3. Σωστή επιλογή (δ) ΘΕΜΑ Β Β1. Σχολικό Βιβλίο (σελ. 16-17)
ΘΕΜΑ Α Α1. α. Σωστό ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΑΠΑΝΤΗΣΕΙΣ (14.06.2017) ΟΜΑΔΑ ΠΡΩΤΗ β. Λάθος γ. Λάθος δ. Λάθος ε. Σωστό Α2. Σωστή επιλογή (γ) Α3. Σωστή επιλογή (δ) ΘΕΜΑ Β Β1. Σχολικό Βιβλίο (σελ. 16-17)
(2β) Το Υπόδειγμα της Κυκλικής Πόλης ή Υπόδειγμα του Salop
 (2β) Το Υπόδειγμα της Κυκλικής Πόλης ή Υπόδειγμα του alop (alop, teve 979, Moopolstc Competto wth Outsde Goods) - Υποθέτουμε μια πόλη που παριστάνεται από την περιφέρεια ενός κύκλου με περίμετρο L=. p
(2β) Το Υπόδειγμα της Κυκλικής Πόλης ή Υπόδειγμα του alop (alop, teve 979, Moopolstc Competto wth Outsde Goods) - Υποθέτουμε μια πόλη που παριστάνεται από την περιφέρεια ενός κύκλου με περίμετρο L=. p
ΑΣΚΗΣΕΙΣ ΣΤΟ ΥΠΟ ΕΙΓΜΑ ΖΗΤΗΣΗΣ ΚΑΙ ΠΡΟΣΦΟΡΑΣ
 ΑΣΚΗΣΕΙΣ ΣΤΟ ΥΠΟ ΕΙΓΜΑ ΖΗΤΗΣΗΣ ΚΑΙ ΠΡΟΣΦΟΡΑΣ Άσκηση 1: ίνεται ο πίνακας ζήτησης και προσφοράς ενός αγαθού Χ: Τιµή Ζητούµενη Προσφερόµενη ποσότητα ποσότητα 54 10 3 50 1 19 46 14 15 44 15 13 40 17 9 Ζητείται
ΑΣΚΗΣΕΙΣ ΣΤΟ ΥΠΟ ΕΙΓΜΑ ΖΗΤΗΣΗΣ ΚΑΙ ΠΡΟΣΦΟΡΑΣ Άσκηση 1: ίνεται ο πίνακας ζήτησης και προσφοράς ενός αγαθού Χ: Τιµή Ζητούµενη Προσφερόµενη ποσότητα ποσότητα 54 10 3 50 1 19 46 14 15 44 15 13 40 17 9 Ζητείται
Οικονομικό Πρόβλημα &
 Οικονομικό Πρόβλημα & Οικονομική Επιστήμη Ανεπάρκεια Σπανιότητα Οικονομική επιστήμη Πως κατανέμονται οι διαθέσιμοι πόροι για την ικανοποίηση των αναγκών Περιορισμένοι Εργασία Κεφάλαιο Απεριόριστες Πρώτες
Οικονομικό Πρόβλημα & Οικονομική Επιστήμη Ανεπάρκεια Σπανιότητα Οικονομική επιστήμη Πως κατανέμονται οι διαθέσιμοι πόροι για την ικανοποίηση των αναγκών Περιορισμένοι Εργασία Κεφάλαιο Απεριόριστες Πρώτες
Bˆ min{ K, L } 2 L 2 K. 2.Stolper-Samuelson Να ευρεθει η επιδραςη μιασ μικρησ αυξηςησ τησ παραμετρου ςτον λογο. τιμη του αγαθου Κ τιμη του αγαθου L
 [2x2] January 31, 2011 ΟΙΚΟΝΟΜΙΑ ενασ καταναλωτησ αγαθα Α,Β,, Δυο επιχειρηςεισ Η ΕΠΙΧΕΙΡΗΗ 1 παραγει το αγαθο απο τα αγαθα, με ςυναρτηςη παραγωγησ ˆ min{,2 } (1 Η ΕΠΙΧΕΙΡΗΗ 2 παραγει το αγαθο απο τα αγαθα,
[2x2] January 31, 2011 ΟΙΚΟΝΟΜΙΑ ενασ καταναλωτησ αγαθα Α,Β,, Δυο επιχειρηςεισ Η ΕΠΙΧΕΙΡΗΗ 1 παραγει το αγαθο απο τα αγαθα, με ςυναρτηςη παραγωγησ ˆ min{,2 } (1 Η ΕΠΙΧΕΙΡΗΗ 2 παραγει το αγαθο απο τα αγαθα,
3. Ανταγωνισμός ως προς τις Τιμές: Το Υπόδειγμα Bertrand
 3. Ανταγωνισμός ως προς τις Τιμές: Το Υπόδειγμα ertrand - To υπόδειγμα Cournot υποθέτει ότι κάθε επιχείρηση επιλέγει την παραγόμενη ποσότητα προϊόντος, ενώ στην πραγματικότητα οι επιχειρήσεις ανταγωνίζονται
3. Ανταγωνισμός ως προς τις Τιμές: Το Υπόδειγμα ertrand - To υπόδειγμα Cournot υποθέτει ότι κάθε επιχείρηση επιλέγει την παραγόμενη ποσότητα προϊόντος, ενώ στην πραγματικότητα οι επιχειρήσεις ανταγωνίζονται
Κριτικές στο Υπόδειγμα Cournot
 Κριτικές στο Υπόδειγμα Cournot -To υπόδειγμα Cournot έχει υποστεί τρία είδη κριτικής: () Το υπόδειγμα Cournot υποθέτει ότι κάθε επιχείρηση μεγιστοποιεί μόνο τα δικά της κέρδη και, επομένως, δε λαμβάνει
Κριτικές στο Υπόδειγμα Cournot -To υπόδειγμα Cournot έχει υποστεί τρία είδη κριτικής: () Το υπόδειγμα Cournot υποθέτει ότι κάθε επιχείρηση μεγιστοποιεί μόνο τα δικά της κέρδη και, επομένως, δε λαμβάνει
4.1 Ζήτηση εργασίας στο βραχυχρόνιο διάστημα - Ανταγωνιστικές αγορές
 4. ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΑΝΑΛΥΣΗ ΤΗΣ ΑΓΟΡΑΣ ΕΡΓΑΣΙΑΣ (ΝΕΟΚΛΑΣΙΚΟ ΥΠΟΔΕΙΓΜΑ). ΖΗΤΗΣΗ ΕΡΓΑΣΙΑΣ Η ζήτηση εργασίας στο σύνολο της οικονομίας ορίζεται ως ο αριθμός εργαζομένων που οι επιχειρήσεις επιθυμούν να απασχολούν
4. ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΑΝΑΛΥΣΗ ΤΗΣ ΑΓΟΡΑΣ ΕΡΓΑΣΙΑΣ (ΝΕΟΚΛΑΣΙΚΟ ΥΠΟΔΕΙΓΜΑ). ΖΗΤΗΣΗ ΕΡΓΑΣΙΑΣ Η ζήτηση εργασίας στο σύνολο της οικονομίας ορίζεται ως ο αριθμός εργαζομένων που οι επιχειρήσεις επιθυμούν να απασχολούν
ΕΡΓΑΣΙΕΣ 5 ου ΚΕΦΑΛΑΙΟΥ 1 η Ομάδα: Ερωτήσεις πολλαπλής επιλογής
 ΕΡΓΑΣΙΕΣ 5 ου ΚΕΦΑΛΑΙΟΥ 1 η Ομάδα: Ερωτήσεις πολλαπλής επιλογής 1. Η επιβολή στην αγορά ενός αγαθού μιας τιμής που είναι μικρότερη της τιμής ισορροπίας θα προκαλέσει: α) Πλεόνασμα β) Έλλειμμα γ) Νέα ισορροπία
ΕΡΓΑΣΙΕΣ 5 ου ΚΕΦΑΛΑΙΟΥ 1 η Ομάδα: Ερωτήσεις πολλαπλής επιλογής 1. Η επιβολή στην αγορά ενός αγαθού μιας τιμής που είναι μικρότερη της τιμής ισορροπίας θα προκαλέσει: α) Πλεόνασμα β) Έλλειμμα γ) Νέα ισορροπία
ΤΕΙ Κρήτης-ΣΔΟ-Τμήμα Λογιστικής Μάθημα: Δημόσια Οικονομική Γραπτή Εξέταση ΧΕ Διδάσκων: Αναστασάκης Ανδρέας
 Θέμα 1 ο : Ομάδα Α 1γ, 2β, 3β, 4β, 5α Θέμα 2 ο : Έστω δύο άτομα Α και Β, που καταναλώνουν δύο δημόσια αγαθά, Χ και Μ. Το άτομο Α έχει την συνάρτηση χρησιμότητας U Α = 2X 2 + 0,5Μ 2, το δε άτομο Β έχει
Θέμα 1 ο : Ομάδα Α 1γ, 2β, 3β, 4β, 5α Θέμα 2 ο : Έστω δύο άτομα Α και Β, που καταναλώνουν δύο δημόσια αγαθά, Χ και Μ. Το άτομο Α έχει την συνάρτηση χρησιμότητας U Α = 2X 2 + 0,5Μ 2, το δε άτομο Β έχει
Κεφάλαιο 32 Ανταλλαγή
 HL R. VRIN Μικροοικονομική Μια σύγχρονη προσέγγιση 3 η έκδοση Εκδόσεις Κριτική Κεφάλαιο 32 Ανταλλαγή Ύλη για τη Μίκρο ΙΙ: όλο το κεφάλαιο Ανάλυση μερικής ισορροπίας/ανάλυση γενικής ισορροπίας Τέλειος ανταγωνισμός/ατελής
HL R. VRIN Μικροοικονομική Μια σύγχρονη προσέγγιση 3 η έκδοση Εκδόσεις Κριτική Κεφάλαιο 32 Ανταλλαγή Ύλη για τη Μίκρο ΙΙ: όλο το κεφάλαιο Ανάλυση μερικής ισορροπίας/ανάλυση γενικής ισορροπίας Τέλειος ανταγωνισμός/ατελής
Επιχειρησιακά Μαθηματικά (1)
 Τηλ:10.93.4.450 ΠΟΣΟΤΙΚΕΣ ΜΕΘΟΔΟΙ ΔΕΟ 13 ΤΟΜΟΣ Α Επιχειρησιακά Μαθηματικά (1) ΑΘΗΝΑ ΟΚΤΩΒΡΙΟΣ 01 Τηλ:10.93.4.450 ΚΕΦΑΛΑΙΟ 1 Ο Συνάρτηση μιας πραγματικής μεταβλητής Ορισμός : Συνάρτηση f μιας πραγματικής
Τηλ:10.93.4.450 ΠΟΣΟΤΙΚΕΣ ΜΕΘΟΔΟΙ ΔΕΟ 13 ΤΟΜΟΣ Α Επιχειρησιακά Μαθηματικά (1) ΑΘΗΝΑ ΟΚΤΩΒΡΙΟΣ 01 Τηλ:10.93.4.450 ΚΕΦΑΛΑΙΟ 1 Ο Συνάρτηση μιας πραγματικής μεταβλητής Ορισμός : Συνάρτηση f μιας πραγματικής
ΘΕΩΡΙΑ ΧΡΗΣΙΜΟΤΗΤΑΣ ΚΑΤΑΝΑΛΩΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ
 Ένθετο Κεφάλαιο ΘΕΩΡΙΑ ΧΡΗΣΙΜΟΤΗΤΑΣ ΚΑΤΑΝΑΛΩΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ Μικροοικονομική Ε. Σαρτζετάκης 1 Καταναλωτική συμπεριφορά Σκοπός αυτής της διάλεξης είναι να εξετάσουμε τον τρόπο με τον οποίο οι καταναλωτές
Ένθετο Κεφάλαιο ΘΕΩΡΙΑ ΧΡΗΣΙΜΟΤΗΤΑΣ ΚΑΤΑΝΑΛΩΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ Μικροοικονομική Ε. Σαρτζετάκης 1 Καταναλωτική συμπεριφορά Σκοπός αυτής της διάλεξης είναι να εξετάσουμε τον τρόπο με τον οποίο οι καταναλωτές
2. Διαφήμιση σε Αγορές όπου υπάρχουν πολλές Επιχειρήσεις
 . Διαφήμιση σε Αγορές όπου υπάρχουν πολλές Επιχειρήσεις Α. Ενημερωτική Διαφήμιση στη Μονοπωλιακά Ανταγωνιστική Αγορά (Butters, Gerard 977, Equilibrium Distribution of Prices and Advertising) -To υπόδειγμα
. Διαφήμιση σε Αγορές όπου υπάρχουν πολλές Επιχειρήσεις Α. Ενημερωτική Διαφήμιση στη Μονοπωλιακά Ανταγωνιστική Αγορά (Butters, Gerard 977, Equilibrium Distribution of Prices and Advertising) -To υπόδειγμα
Θεωρία παραγωγού. Μικροοικονομική Θεωρία Ι / Διάλεξη 11 / Φ. Κουραντή 1
 Θεωρία παραγωγού Σκοπός: Μεγιστοποίηση κερδών (υπάρχουν κι άλλοι σκοποί, π.χ. ένας μάνατζερ επιδιώκει την μεγιστοποίηση εσόδων κτλ. Τελικά όμως σκοπεύει στην μεγιστοποίηση των κερδών για να μπορέσει να
Θεωρία παραγωγού Σκοπός: Μεγιστοποίηση κερδών (υπάρχουν κι άλλοι σκοποί, π.χ. ένας μάνατζερ επιδιώκει την μεγιστοποίηση εσόδων κτλ. Τελικά όμως σκοπεύει στην μεγιστοποίηση των κερδών για να μπορέσει να
Βασικές Έννοιες των Οικονομικών της Εργασίας οικονομικά της εργασίας αγορά αγορά εργασίας μισθός
 Βασικές Έννοιες των Οικονομικών της Εργασίας - Τα οικονομικά της εργασίας μελετούν τον τρόπο με τον οποίο λειτουργεί η αγορά εργασίας. - Ορισμός: Η αγορά ενός αγαθού είναι η διαδικασία (θεσμικό πλαίσιο)
Βασικές Έννοιες των Οικονομικών της Εργασίας - Τα οικονομικά της εργασίας μελετούν τον τρόπο με τον οποίο λειτουργεί η αγορά εργασίας. - Ορισμός: Η αγορά ενός αγαθού είναι η διαδικασία (θεσμικό πλαίσιο)
ΔΕΟ 34 ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΑΝΑΛΥΣΗΣ ΤΟΜΟΣ 1 ΜΙΚΡΟΟΙΚΟΝΟΜΙΑ
 ΥΠΟΣΤΗΡΙΚΤΙΚΑ ΜΑΘΗΜΑΤΑ ΕΑΠ ΔΕΟ 34 Ν. ΠΑΝΤΕΛΗ ΔΕΟ 34 ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΑΝΑΛΥΣΗΣ ΤΟΜΟΣ 1 ΜΙΚΡΟΟΙΚΟΝΟΜΙΑ ΤΥΠΟΛΟΓΙΟ & ΜΕΘΟΔΟΛΟΓΙΑ ΑΣΚΗΣΕΩΝ ΑΘΗΝΑ ΟΚΤΩΒΡΙΟΣ 2012 1 ΥΠΟΣΤΗΡΙΚΤΙΚΑ ΜΑΘΗΜΑΤΑ ΕΑΠ ΔΕΟ 34 ΚΟΣΤΗ Ν.
ΥΠΟΣΤΗΡΙΚΤΙΚΑ ΜΑΘΗΜΑΤΑ ΕΑΠ ΔΕΟ 34 Ν. ΠΑΝΤΕΛΗ ΔΕΟ 34 ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΑΝΑΛΥΣΗΣ ΤΟΜΟΣ 1 ΜΙΚΡΟΟΙΚΟΝΟΜΙΑ ΤΥΠΟΛΟΓΙΟ & ΜΕΘΟΔΟΛΟΓΙΑ ΑΣΚΗΣΕΩΝ ΑΘΗΝΑ ΟΚΤΩΒΡΙΟΣ 2012 1 ΥΠΟΣΤΗΡΙΚΤΙΚΑ ΜΑΘΗΜΑΤΑ ΕΑΠ ΔΕΟ 34 ΚΟΣΤΗ Ν.
3.1 Ανεξάρτητες αποφάσεις - Κατανομή χρόνου μεταξύ εργασίας και σχόλης
 3. ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΑΝΑΛΥΣΗ ΤΗΣ ΑΓΟΡΑΣ ΕΡΓΑΣΙΑΣ (ΝΕΟΚΛΑΣΙΚΟ ΥΠΟΔΕΙΓΜΑ). ΠΡΟΣΦΟΡΑ ΕΡΓΑΣΙΑΣ Ως προσφορά εργασίας ορίζεται το σύνολο των ωρών εργασίας που προσφέρονται προς εκμίσθωση μία δεδομένη χρονική στιγμή.
3. ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΑΝΑΛΥΣΗ ΤΗΣ ΑΓΟΡΑΣ ΕΡΓΑΣΙΑΣ (ΝΕΟΚΛΑΣΙΚΟ ΥΠΟΔΕΙΓΜΑ). ΠΡΟΣΦΟΡΑ ΕΡΓΑΣΙΑΣ Ως προσφορά εργασίας ορίζεται το σύνολο των ωρών εργασίας που προσφέρονται προς εκμίσθωση μία δεδομένη χρονική στιγμή.
ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ ΠΡΩΤΟΥ ΠΑΚΕΤΟΥ. max. ( ) (16 ) Q Q = +. [1]
![ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ ΠΡΩΤΟΥ ΠΑΚΕΤΟΥ. max. ( ) (16 ) Q Q = +. [1] ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ ΠΡΩΤΟΥ ΠΑΚΕΤΟΥ. max. ( ) (16 ) Q Q = +. [1]](/thumbs/64/51905132.jpg) ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ ΠΡΩΤΟΥ ΠΑΚΕΤΟΥ Θέµα ο. (α) Η µονοπωλιακή επιχείρηση µεγιστοποιεί το κέρδος της οποίο δίνεται από τη συνάρτηση π µε τύπο π ( ) = (6 ), δηλαδή λύνει το πρόβληµα max. π ( ) = (6 ) π '( ) =
ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ ΠΡΩΤΟΥ ΠΑΚΕΤΟΥ Θέµα ο. (α) Η µονοπωλιακή επιχείρηση µεγιστοποιεί το κέρδος της οποίο δίνεται από τη συνάρτηση π µε τύπο π ( ) = (6 ), δηλαδή λύνει το πρόβληµα max. π ( ) = (6 ) π '( ) =
Εξετάσεις Η επιβολή από το κράτος κατώτατης τιμής στα αγροτικά προϊόντα έχει ως σκοπό την προστασία του εισοδήματος των αγροτών.
 ΚΕΦΑΛΑΙΟ 5: Ο ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΤΩΝ ΤΙΜΩΝ Να σημειώσετε με Σ (σωστό) ή Λ (λάθος) στο τέλος των προτάσεων: 1. Η επιβολή από το κράτος ανώτατης τιμής σε ένα προϊόν δημιουργεί συνήθως «μαύρη αγορά». Εξετάσεις
ΚΕΦΑΛΑΙΟ 5: Ο ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΤΩΝ ΤΙΜΩΝ Να σημειώσετε με Σ (σωστό) ή Λ (λάθος) στο τέλος των προτάσεων: 1. Η επιβολή από το κράτος ανώτατης τιμής σε ένα προϊόν δημιουργεί συνήθως «μαύρη αγορά». Εξετάσεις
Μαρσαλιανή και Χικσιανή καμπύλη ζήτησης. Γραφική απεικόνιση. Μικροοικονομική Θεωρία Ι / Διάλεξη 7β / Φ. Κουραντή 1
 Μαρσαλιανή και Χικσιανή καμπύλη ζήτησης Γραφική απεικόνιση Μικροοικονομική Θεωρία Ι / Διάλεξη 7β / Φ. Κουραντή Ξεκινάμε με το εξής διάγραμμα Στο τμήμα αυτό απεικονίζουμε την επιλογή του καταναλωτή, μεταξύ
Μαρσαλιανή και Χικσιανή καμπύλη ζήτησης Γραφική απεικόνιση Μικροοικονομική Θεωρία Ι / Διάλεξη 7β / Φ. Κουραντή Ξεκινάμε με το εξής διάγραμμα Στο τμήμα αυτό απεικονίζουμε την επιλογή του καταναλωτή, μεταξύ
ΑΠΑΝΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ Αρ. Απάντηση Αρ. Απάντηση Ερώτησης 1. A 6. C 2. C 7. A 3. A 8. E 4. B 9. A 5. E 10. C
 Διάρκεια Εξέτασης: 10 Παρακαλώ να απαντήσετε σε όλα τα ερωτήματα. Απαντήστε με σαφήνεια και σε περίπτωση που χρησιμοποιήσετε διαγράμματα φροντίστε να είναι ευανάγνωστα και πλήρη. Κατανείμετε ανάλογα το
Διάρκεια Εξέτασης: 10 Παρακαλώ να απαντήσετε σε όλα τα ερωτήματα. Απαντήστε με σαφήνεια και σε περίπτωση που χρησιμοποιήσετε διαγράμματα φροντίστε να είναι ευανάγνωστα και πλήρη. Κατανείμετε ανάλογα το
Η προσδοκώµενη χρησιµότητα του κέρδους όταν η πιθανότητα η τιµή του προϊόντος Ρ1 είναι ψ, χ το επίπεδο παραγωγής και c(x) η συνάρτηση κόστους, είναι
 3. Θεωρία της Επιχείρησης 3. Η Ανταγωνιστική Επιχείρηση. Το τµήµα αυτό έχει δύο στόχους. Πρώτα να δείξει ότι αν υπάρχει ουδετερότητα απέναντι στον κίνδυνο, τότε η µέση αξία ενός αβέβαιου γεγονότος είναι
3. Θεωρία της Επιχείρησης 3. Η Ανταγωνιστική Επιχείρηση. Το τµήµα αυτό έχει δύο στόχους. Πρώτα να δείξει ότι αν υπάρχει ουδετερότητα απέναντι στον κίνδυνο, τότε η µέση αξία ενός αβέβαιου γεγονότος είναι
Το Νεοκλασσικό υπόδειγµα οικονοµικής µεγέθυνσης
 Το Νεοκλασσικό υπόδειγµα οικονοµικής µεγέθυνσης Α. Αποκεντρωµένη Οικονοµία Α. Νοικοκυριά Σε κάθε χρονική στιγµή υπάρχουν όµοια νοικοκυριά το καθ ένα εκ των οποίων συµβολίζεται µε τον δείκτη. Θα αναφερόµαστε
Το Νεοκλασσικό υπόδειγµα οικονοµικής µεγέθυνσης Α. Αποκεντρωµένη Οικονοµία Α. Νοικοκυριά Σε κάθε χρονική στιγµή υπάρχουν όµοια νοικοκυριά το καθ ένα εκ των οποίων συµβολίζεται µε τον δείκτη. Θα αναφερόµαστε
Q D1 = P και Q S = P.
 ΚΕΦΑΛΑΙΟ 5: Ο ΠΡΟΣ ΙΟΡΙΣΜΟΣ ΤΩΝ ΤΙΜΩΝ Να σηµειώσετε µε Σ (σωστό) ή Λ (λάθος) στο τέλος των προτάσεων: 1. Τιµή ισορροπίας είναι η τιµή στην οποία η ζητούµενη ποσότητα είναι ίση µε την προσφερόµενη ποσότητα.
ΚΕΦΑΛΑΙΟ 5: Ο ΠΡΟΣ ΙΟΡΙΣΜΟΣ ΤΩΝ ΤΙΜΩΝ Να σηµειώσετε µε Σ (σωστό) ή Λ (λάθος) στο τέλος των προτάσεων: 1. Τιµή ισορροπίας είναι η τιµή στην οποία η ζητούµενη ποσότητα είναι ίση µε την προσφερόµενη ποσότητα.
Γενική Ισορροπία. Γενική ισορροπία - Ανταλλαγή. Γενική ισορροπία - Ανταλλαγή. Notes. Notes. Notes. Notes. Κώστας Ρουµανιάς.
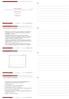 Γενική Ισορροπία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 19 Απριλίου 2013 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου 2013 1 / 23. Η οικονοµία των δύο καταναλωτών µε δύο αγαθά που παρουσιάσαµε
Γενική Ισορροπία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 19 Απριλίου 2013 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου 2013 1 / 23. Η οικονοµία των δύο καταναλωτών µε δύο αγαθά που παρουσιάσαµε
Δεύτερο πακέτο ασκήσεων και λύσεων
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος 04-05 Τμήμα Οικονομικών Επιστημών Μάθημα: Μικροοικονομική Ανάλυση της Κατανάλωσης και της Παραγωγής Δεύτερο πακέτο ασκήσεων και λύσεων Αντιστοιχούν τέσσερις μονάδες
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος 04-05 Τμήμα Οικονομικών Επιστημών Μάθημα: Μικροοικονομική Ανάλυση της Κατανάλωσης και της Παραγωγής Δεύτερο πακέτο ασκήσεων και λύσεων Αντιστοιχούν τέσσερις μονάδες
Σηµειώσεις. Μικροοικονοµικής Θεωρίας ΙΙΙ (ΜΙΚΟ 201)
 Σηµειώσεις Μικροοικονοµικής Θεωρίας ΙΙΙ (ΜΙΚΟ 201) «Γενική Ισορροπία του Πλήρους Ανταγωνισµού» Βαγγέλης Τζουβελέκας Ρέθυµνο, 2003 ΚΕΦΑΛΑΙΟ 2 ΓΕΝΙΚΗ ΙΣΟΡΡΟΠΙΑ ΤΟΥ ΠΛΗΡΟΥΣ ΑΝΤΑΓΩΝΙΣΜΟΥ 2.1 Γενική Ισορροπία
Σηµειώσεις Μικροοικονοµικής Θεωρίας ΙΙΙ (ΜΙΚΟ 201) «Γενική Ισορροπία του Πλήρους Ανταγωνισµού» Βαγγέλης Τζουβελέκας Ρέθυµνο, 2003 ΚΕΦΑΛΑΙΟ 2 ΓΕΝΙΚΗ ΙΣΟΡΡΟΠΙΑ ΤΟΥ ΠΛΗΡΟΥΣ ΑΝΤΑΓΩΝΙΣΜΟΥ 2.1 Γενική Ισορροπία
Πλεόνασμα του Καταναλωτή, Πλεόνασμα του Παραγωγού και η Αποτελεσματικότητα της Ανταγωνιστικής Αγοράς - Η αλληλεπίδραση της συνολικής ζήτησης και της
 Πλεόνασμα του Καταναλωτή, Πλεόνασμα του Παραγωγού και η Αποτελεσματικότητα της Ανταγωνιστικής Αγοράς - Η αλληλεπίδραση της συνολικής ζήτησης και της προσφοράς προσδιορίζει την τιμή και την ποσότητα ισορροπίας
Πλεόνασμα του Καταναλωτή, Πλεόνασμα του Παραγωγού και η Αποτελεσματικότητα της Ανταγωνιστικής Αγοράς - Η αλληλεπίδραση της συνολικής ζήτησης και της προσφοράς προσδιορίζει την τιμή και την ποσότητα ισορροπίας
ΖΗΤΗΣΗ, ΠΡΟΣΦΟΡΑ ΚΑΙ ΙΣΣΟΡΟΠΙΑ ΑΓΟΡΑΣ
 1 ΚΦΑΛΑΙΟ 6 ΖΗΤΗΣΗ, ΠΡΟΣΦΟΡΑ ΚΑΙ ΙΣΣΟΡΟΠΙΑ ΑΓΟΡΑΣ Οι καµπύλες ζήτησης και προσφοράς είναι αναγκαίες για να προσδιορίσουν την τιµή στην αγορά. Η εξοµοίωσή τους καθορίζει την τιµή και τη ποσότητα ισορροπίας,
1 ΚΦΑΛΑΙΟ 6 ΖΗΤΗΣΗ, ΠΡΟΣΦΟΡΑ ΚΑΙ ΙΣΣΟΡΟΠΙΑ ΑΓΟΡΑΣ Οι καµπύλες ζήτησης και προσφοράς είναι αναγκαίες για να προσδιορίσουν την τιµή στην αγορά. Η εξοµοίωσή τους καθορίζει την τιµή και τη ποσότητα ισορροπίας,
Οικονομικά για Νομικούς Μέρος 1ο Οι δυνάμεις της προσφοράς και της ζήτησης
 Πανεπιστήμιο Πειραιώς, Τμήμα Τραπεζικής και Χρηματοοικονομικής Διοικητικής Μεταπτυχιακό Πρόγραμμα «Χρηματοοικονομική Ανάλυση για Στελέχη» Οικονομικά για Νομικούς Μέρος 1ο Οι δυνάμεις της προσφοράς και
Πανεπιστήμιο Πειραιώς, Τμήμα Τραπεζικής και Χρηματοοικονομικής Διοικητικής Μεταπτυχιακό Πρόγραμμα «Χρηματοοικονομική Ανάλυση για Στελέχη» Οικονομικά για Νομικούς Μέρος 1ο Οι δυνάμεις της προσφοράς και
Μικροοικονοµική Θεωρία. Γενική ισορροπία - Ανταλλαγή. Γενική ισορροπία - Ανταλλαγή. Notes. Notes. Notes. Notes. Κώστας Ρουµανιάς. 23 Σεπτεµβρίου 2014
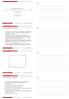 Μικροοικονοµική Θεωρία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 23 Σεπτεµβρίου 2014 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Μικροοικονοµική Θεωρία 23 Σεπτεµβρίου 2014 1 / 23. Η οικονοµία των δύο καταναλωτών µε δύο αγαθά
Μικροοικονοµική Θεωρία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 23 Σεπτεµβρίου 2014 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Μικροοικονοµική Θεωρία 23 Σεπτεµβρίου 2014 1 / 23. Η οικονοµία των δύο καταναλωτών µε δύο αγαθά
Μεγιστοποίηση του Κέρδους
 Μεγιστοποίηση του Κέρδους - Έστω η συνάρτηση παραγωγής: q = f ( x,..., x ). - Η τιμή του παραγόμενου προϊόντος είναι και οι τιμές των εισροών είναι w= ( w,..., w ). - Υπόθεση: Η επιχείρηση είναι αποδέκτης
Μεγιστοποίηση του Κέρδους - Έστω η συνάρτηση παραγωγής: q = f ( x,..., x ). - Η τιμή του παραγόμενου προϊόντος είναι και οι τιμές των εισροών είναι w= ( w,..., w ). - Υπόθεση: Η επιχείρηση είναι αποδέκτης
Ελαχιστοποίηση του Κόστους
 Ελαχιστοποίηση του Κόστους - H ανάλυση του προβλήματος ελαχιστοποίησης του κόστους παρουσιάζει τα εξής πλεονεκτήματα σε σχέση με το πρόβλημα μεγιστοποίησης των κερδών: () Επιτρέπει τη διατύπωση μιας θεωρίας
Ελαχιστοποίηση του Κόστους - H ανάλυση του προβλήματος ελαχιστοποίησης του κόστους παρουσιάζει τα εξής πλεονεκτήματα σε σχέση με το πρόβλημα μεγιστοποίησης των κερδών: () Επιτρέπει τη διατύπωση μιας θεωρίας
Αποτροπή Εισόδου: Το Υπόδειγμα των Spence-Dixit
 Αποτροπή Εισόδου: Το Υπόδειγμα των pence-dixit pence, Michael 977, Entry, apacity, Investment and Oligopolisting Pricing Dixit, Avinash 979, A Model of Duopoly uggesting a Theory of Entry Barriers - Στο
Αποτροπή Εισόδου: Το Υπόδειγμα των pence-dixit pence, Michael 977, Entry, apacity, Investment and Oligopolisting Pricing Dixit, Avinash 979, A Model of Duopoly uggesting a Theory of Entry Barriers - Στο
Θεωρία Καταναλωτή. Υποδειγματοποίηση της συμπεριφοράς του καταναλωτή. Βασική έννοια: Βελτιστοποίηση υπό περιορισμό.
 Θεωρία Καταναλωτή Υποδειγματοποίηση της συμπεριφοράς του καταναλωτή. Βασική έννοια: Βελτιστοποίηση υπό περιορισμό. Προτιμήσεις (preferences) Εισοδηματικός περιορισμός (budget constraint) Άριστη επιλογή
Θεωρία Καταναλωτή Υποδειγματοποίηση της συμπεριφοράς του καταναλωτή. Βασική έννοια: Βελτιστοποίηση υπό περιορισμό. Προτιμήσεις (preferences) Εισοδηματικός περιορισμός (budget constraint) Άριστη επιλογή
Εθνικό & Καποδιστριακό Πανεπιστήμιο Αθηνών Σχολή Οικονομικών & Πολιτικών Επιστημών Τμήμα Οικονομικών Επιστημών Τομέας Πολιτικής Οικονομίας
 Εθνικό & Καποδιστριακό Πανεπιστήμιο Αθηνών Σχολή Οικονομικών & Πολιτικών Επιστημών Τμήμα Οικονομικών Επιστημών Τομέας Πολιτικής Οικονομίας Άσκηση στο μάθημα «Εισαγωγή στην Οικονομική Ανάλυση» Νίκος Θεοχαράκης
Εθνικό & Καποδιστριακό Πανεπιστήμιο Αθηνών Σχολή Οικονομικών & Πολιτικών Επιστημών Τμήμα Οικονομικών Επιστημών Τομέας Πολιτικής Οικονομίας Άσκηση στο μάθημα «Εισαγωγή στην Οικονομική Ανάλυση» Νίκος Θεοχαράκης
ΛΥΜΕΝΕΣ ΕΦΑΡΜΟΓΕΣ ΣΤΟ 2 ο ΚΕΦΑΛΑΙΟ
 ΛΥΜΕΝΕΣ ΕΦΑΡΜΟΓΕΣ ΣΤΟ 2 ο ΚΕΦΑΛΑΙΟ 1. Έστω συνάρτηση ζήτησης με τύπο Q = 200 4P. Να βρείτε: α) Την ελαστικότητα ως προς την τιμή όταν η τιμή αυξάνεται από 10 σε 12. 1ος τρόπος Αν P 0 10 τότε Q 0 200 410
ΛΥΜΕΝΕΣ ΕΦΑΡΜΟΓΕΣ ΣΤΟ 2 ο ΚΕΦΑΛΑΙΟ 1. Έστω συνάρτηση ζήτησης με τύπο Q = 200 4P. Να βρείτε: α) Την ελαστικότητα ως προς την τιμή όταν η τιμή αυξάνεται από 10 σε 12. 1ος τρόπος Αν P 0 10 τότε Q 0 200 410
(γ) Τις μορφές στρατηγικής αλληλεπίδρασης που αναπτύσσονται
 Βασικές Έννοιες Οικονομικών των Επιχειρήσεων - Τα οικονομικά των επιχειρήσεων μελετούν: (α) Τον τρόπο με τον οποίο λαμβάνουν τις αποφάσεις τους οι επιχειρήσεις. (β) Τις μορφές στρατηγικής αλληλεπίδρασης
Βασικές Έννοιες Οικονομικών των Επιχειρήσεων - Τα οικονομικά των επιχειρήσεων μελετούν: (α) Τον τρόπο με τον οποίο λαμβάνουν τις αποφάσεις τους οι επιχειρήσεις. (β) Τις μορφές στρατηγικής αλληλεπίδρασης
ΟΜΑΔΑ Β Σχολικό βιβλίο σελ ως «μεταβλητούς συντελεστές μαζί με το αντίστοιχο διάγραμμα. TC Συνολικό κόστος. VC Μεταβλητό κόστος
 ΛΥΣΕΙΣ ΑΟΘ 1 ΓΙΑ ΑΡΙΣΤΑ ΔΙΑΒΑΣΜΕΝΟΥΣ ΟΜΑΔΑ Α Α1 γ Α2 β Α3 δ Α4 Σ Α5 Σ Α6 Σ Α7 Σ Α8 Λ ΟΜΑΔΑ Β Σχολικό βιβλίο σελ. 57-59 ως «μεταβλητούς συντελεστές μαζί με το αντίστοιχο διάγραμμα. ΟΜΑΔΑ Γ Γ1. Είναι γνωστό
ΛΥΣΕΙΣ ΑΟΘ 1 ΓΙΑ ΑΡΙΣΤΑ ΔΙΑΒΑΣΜΕΝΟΥΣ ΟΜΑΔΑ Α Α1 γ Α2 β Α3 δ Α4 Σ Α5 Σ Α6 Σ Α7 Σ Α8 Λ ΟΜΑΔΑ Β Σχολικό βιβλίο σελ. 57-59 ως «μεταβλητούς συντελεστές μαζί με το αντίστοιχο διάγραμμα. ΟΜΑΔΑ Γ Γ1. Είναι γνωστό
Η ακόλουθη συνάρτηση συνδέει συνολικό κόστος TC και παραγόμενη ποσότητα Q: TC = Q + 3Q 2
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΔΕΟ13 ΑΣΚΗΣΗ 1 [Μέρος Α] Η ακόλουθη συνάρτηση συνδέει συνολικό κόστος TC και παραγόμενη ποσότητα : TC = 000 +10 + 3 (A)Γράψτε τις συναρτήσεις του Οριακού Κόστους (Marginal Cost
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΔΕΟ13 ΑΣΚΗΣΗ 1 [Μέρος Α] Η ακόλουθη συνάρτηση συνδέει συνολικό κόστος TC και παραγόμενη ποσότητα : TC = 000 +10 + 3 (A)Γράψτε τις συναρτήσεις του Οριακού Κόστους (Marginal Cost
Ο ΠΡΟΣΔΙΟΡΙΣΜΟΣ TΩN ΤΙΜΩΝ
 ΚΕΦΑΛΑΙΟ ΠΕΜ Ο ΠΡΟΣΔΙΟΡΙΣΜΟΣ TΩN ΤΙΜΩΝ 1. Έννοια και λειτουργία της αγοράς Σε μια πρωτόγονη οικονομία, όπως του Ροβινσώνα Κρούσου, όπου δεν υπάρχει καταμερισμός της εργασίας ο άνθρωπος παράγει μόνος του
ΚΕΦΑΛΑΙΟ ΠΕΜ Ο ΠΡΟΣΔΙΟΡΙΣΜΟΣ TΩN ΤΙΜΩΝ 1. Έννοια και λειτουργία της αγοράς Σε μια πρωτόγονη οικονομία, όπως του Ροβινσώνα Κρούσου, όπου δεν υπάρχει καταμερισμός της εργασίας ο άνθρωπος παράγει μόνος του
Μικροοικονομική Ανάλυση Ι. Ανδρέας Δριχούτης, PhD Επίκουρος Καθηγητής Τμ. Αγροτικής Οικονομίας & Ανάπτυξης Γεωπονικό Πανεπιστήμιο Αθηνών
 Μικροοικονομική Ανάλυση Ι Ανδρέας Δριχούτης, h Επίκουρος Καθηγητής Τμ. Αγροτικής Οικονομίας & Ανάπτυξης Γεωπονικό Πανεπιστήμιο Αθηνών Οικονομικό Πρόβλημα & Οικονομική Επιστήμη Ανεπάρκεια Σπανιότητα Οικονομική
Μικροοικονομική Ανάλυση Ι Ανδρέας Δριχούτης, h Επίκουρος Καθηγητής Τμ. Αγροτικής Οικονομίας & Ανάπτυξης Γεωπονικό Πανεπιστήμιο Αθηνών Οικονομικό Πρόβλημα & Οικονομική Επιστήμη Ανεπάρκεια Σπανιότητα Οικονομική
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ
 ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ Κεφάλαιο 2 ο : Η Ζήτηση των Αγαθών ΕΠΙΜΕΛΕΙΑ: ΝΙΚΟΣ Χ. ΤΖΟΥΜΑΚΑΣ ΟΙΚΟΝΟΜΟΛΟΓΟΣ Ασκήσεις 1. Στην αγορά ενός αγαθού συμμετέχουν δύο καταναλωτές, των οποίων οι ατομικές συναρτήσεις
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ Κεφάλαιο 2 ο : Η Ζήτηση των Αγαθών ΕΠΙΜΕΛΕΙΑ: ΝΙΚΟΣ Χ. ΤΖΟΥΜΑΚΑΣ ΟΙΚΟΝΟΜΟΛΟΓΟΣ Ασκήσεις 1. Στην αγορά ενός αγαθού συμμετέχουν δύο καταναλωτές, των οποίων οι ατομικές συναρτήσεις
Μικροοικονομική Ανάλυση της Κατανάλωσης και της Παραγωγής
 Μικροοικονομική Ανάλυση της Κατανάλωσης και της Παραγωγής Διάλεξη 11: Μεγιστοποίηση κέρδους Ανδρέας Παπανδρέου Σχολή Οικονομικών και Πολιτικών Επιστημών Τμήμα Οικονομικών Επιστημών Οικονομικό κέρδος Μια
Μικροοικονομική Ανάλυση της Κατανάλωσης και της Παραγωγής Διάλεξη 11: Μεγιστοποίηση κέρδους Ανδρέας Παπανδρέου Σχολή Οικονομικών και Πολιτικών Επιστημών Τμήμα Οικονομικών Επιστημών Οικονομικό κέρδος Μια
Διάκριση Τιμών 3 ου Βαθμού: Κατάτμηση της Αγοράς
 Διάκριση Τιμών 3 ου Βαθμού: Κατάτμηση της Αγοράς (arket Segmentation ή ultimarket Price iscrimination) -H διάκριση τιμών 1 ου βαθμού προϋποθέτει ότι η μονοπωλιακή επιχείρηση γνωρίζει τις ατομικές συναρτήσεις
Διάκριση Τιμών 3 ου Βαθμού: Κατάτμηση της Αγοράς (arket Segmentation ή ultimarket Price iscrimination) -H διάκριση τιμών 1 ου βαθμού προϋποθέτει ότι η μονοπωλιακή επιχείρηση γνωρίζει τις ατομικές συναρτήσεις
ΠΡΟΣΦΟΡΑ ΚΑΙ ΖΗΤΗΣΗ. Οι αγοραίες δυνάµεις της προσφοράς και ζήτησης
 ΠΡΟΣΦΟΡΑ ΚΑΙ ΖΗΤΗΣΗ Κεφάλαιο 4 Οι αγοραίες δυνάµεις της προσφοράς και ζήτησης! Προσφορά και Ζήτηση είναι οι πιο γνωστοί οικονοµικοί όροι! Η λειτουργία των αγορών προσδιορίζεται από δύο βασικές δυνάµεις,
ΠΡΟΣΦΟΡΑ ΚΑΙ ΖΗΤΗΣΗ Κεφάλαιο 4 Οι αγοραίες δυνάµεις της προσφοράς και ζήτησης! Προσφορά και Ζήτηση είναι οι πιο γνωστοί οικονοµικοί όροι! Η λειτουργία των αγορών προσδιορίζεται από δύο βασικές δυνάµεις,
Ισορροπία σε Αγορές Ομοιογενών Προϊόντων
 Ισορροπία σε Αγορές Ομοιογενών Προϊόντων 1. Τέλειος Ανταγωνισμός και Μονοπώλιο 1Α. Επιλογή του Παραγόμενου Προϊόντος εκ μέρους της Ανταγωνιστικής Επιχείρησης - Υποθέτουμε ότι υπάρχει μια επιχείρηση στην
Ισορροπία σε Αγορές Ομοιογενών Προϊόντων 1. Τέλειος Ανταγωνισμός και Μονοπώλιο 1Α. Επιλογή του Παραγόμενου Προϊόντος εκ μέρους της Ανταγωνιστικής Επιχείρησης - Υποθέτουμε ότι υπάρχει μια επιχείρηση στην
ΔΕΟ43. Απάντηση 2ης ΓΕ Επιμέλεια: Γιάννης Σαραντής. ΘΕΡΜΟΠΥΛΩΝ 17 Περιστέρι ,
 ΔΕΟ43 Απάντηση 2ης ΓΕ 2016-2017 Επιμέλεια: Γιάννης Σαραντής 1 ΑΣΚΗΣΗ Νο 1 (20%) ΟΔΗΓΙΑ: Σε κάθε ερώτηση πολλαπλής επιλογής επιλέγετε μία απάντηση, και η επιλογή σας σημειώνεται με 1 στο αντίστοιχο πεδίο
ΔΕΟ43 Απάντηση 2ης ΓΕ 2016-2017 Επιμέλεια: Γιάννης Σαραντής 1 ΑΣΚΗΣΗ Νο 1 (20%) ΟΔΗΓΙΑ: Σε κάθε ερώτηση πολλαπλής επιλογής επιλέγετε μία απάντηση, και η επιλογή σας σημειώνεται με 1 στο αντίστοιχο πεδίο
ΟΙΚΟΝΟΜΙΚΗ ΤΩΝ ΔΙΚΤΥΩΝ ΚΑΙ ΤΗΣ ΠΛΗΡΟΦΟΡΗΣΗΣ (ECΟ465) ΤΗΛΕΠΙΚΟΙΝΩΝΙΕΣ ΜΕΡΟΣ Α
 ΟΙΚΟΝΟΜΙΚΗ ΤΩΝ ΔΙΚΤΥΩΝ ΚΑΙ ΤΗΣ ΠΛΗΡΟΦΟΡΗΣΗΣ (ECΟ465) ΤΗΛΕΠΙΚΟΙΝΩΝΙΕΣ ΜΕΡΟΣ Α 1 o Ο κλάδος των τηλεπικοινωνιών (τηλέφωνο, fax, e-mail, υπηρεσίες μηνυμάτων, κ.τ.λ) αποτελεί το πιο απλό και φυσικό παράδειγμα
ΟΙΚΟΝΟΜΙΚΗ ΤΩΝ ΔΙΚΤΥΩΝ ΚΑΙ ΤΗΣ ΠΛΗΡΟΦΟΡΗΣΗΣ (ECΟ465) ΤΗΛΕΠΙΚΟΙΝΩΝΙΕΣ ΜΕΡΟΣ Α 1 o Ο κλάδος των τηλεπικοινωνιών (τηλέφωνο, fax, e-mail, υπηρεσίες μηνυμάτων, κ.τ.λ) αποτελεί το πιο απλό και φυσικό παράδειγμα
Διάλεξη 11. Γενική Ισορροπία με Παραγωγή VA 31
 Διάλεξη 11 Γενική Ισορροπία με Παραγωγή VA 31 1 Οικονομίες ανταλλαγής (ξανά) Καθόλου παραγωγή, μόνο αρχικά αποθέματα, οπότε δεν υπάρχει περιγραφή του πώς οι πόροι μετατρέπονται σε αγαθά. Γενική ισορροπία:
Διάλεξη 11 Γενική Ισορροπία με Παραγωγή VA 31 1 Οικονομίες ανταλλαγής (ξανά) Καθόλου παραγωγή, μόνο αρχικά αποθέματα, οπότε δεν υπάρχει περιγραφή του πώς οι πόροι μετατρέπονται σε αγαθά. Γενική ισορροπία:
ΤΥΠΟΛΟΓΙΟ ΑΟΘ
 ΤΥΠΟΛΟΓΙΟ 1 ου ΚΕΦΑΛΑΙΟΥ Κόστος ευκαιρίας ή εναλλακτικό κόστος Για μια οικονομία που παράγει δύο αγαθά, Χ και Ψ, το κόστος ευκαιρίας των αγαθών Χ και Ψ δίνεται από τους ακόλουθους τύπους: Χ σε όρους ή
ΤΥΠΟΛΟΓΙΟ 1 ου ΚΕΦΑΛΑΙΟΥ Κόστος ευκαιρίας ή εναλλακτικό κόστος Για μια οικονομία που παράγει δύο αγαθά, Χ και Ψ, το κόστος ευκαιρίας των αγαθών Χ και Ψ δίνεται από τους ακόλουθους τύπους: Χ σε όρους ή
Δεύτερο πακέτο ασκήσεων
 ΕΚΠΑ Ακαδημαϊκό έτος 018-019 Τμήμα Οικονομικών Επιστημών Μάθημα: Μικροοικονομική Θεωρία Ι Δεύτερο πακέτο ασκήσεων Προθεσμία παράδοσης Παρασκευή 7 Δεκεμβρίου (στο μάθημα της κ. Κουραντή, του κ. Παπανδρέου
ΕΚΠΑ Ακαδημαϊκό έτος 018-019 Τμήμα Οικονομικών Επιστημών Μάθημα: Μικροοικονομική Θεωρία Ι Δεύτερο πακέτο ασκήσεων Προθεσμία παράδοσης Παρασκευή 7 Δεκεμβρίου (στο μάθημα της κ. Κουραντή, του κ. Παπανδρέου
Πλήρης ανταγωνισμός. Καθηγήτρια: Β. ΠΕΚΚΑ- ΟΙΚΟΝΟΜΟΥ. Υποψήφια Διδάκτωρ: Σ. ΤΑΚΑΟΓΛΟΥ
 Πλήρης ανταγωνισμός Καθηγήτρια: Β. ΠΕΚΚΑ- ΟΙΚΟΝΟΜΟΥ Υποψήφια Διδάκτωρ: Σ. ΤΑΚΑΟΓΛΟΥ Θα Εξετάσουμε: Τέλειο ανταγωνισμό Υποθέσεις λειτουργίας τέλειου ανταγωνισμού Συνολικό, Μέσο και Οριακό έσοδο Βραχυχρόνια
Πλήρης ανταγωνισμός Καθηγήτρια: Β. ΠΕΚΚΑ- ΟΙΚΟΝΟΜΟΥ Υποψήφια Διδάκτωρ: Σ. ΤΑΚΑΟΓΛΟΥ Θα Εξετάσουμε: Τέλειο ανταγωνισμό Υποθέσεις λειτουργίας τέλειου ανταγωνισμού Συνολικό, Μέσο και Οριακό έσοδο Βραχυχρόνια
Notes. Notes. Notes. Notes. C = p x x 1 + p y y 1. pxx + pyy = 160
 Ελαχιστοποίηση κόστους Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 9 Οκτωβρίου 2012 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) Ελαχιστοποίηση κόστους 9 Οκτωβρίου 2012 1 / 36 Κόστος Το πρόβλημα εύρεσης ενός άριστου καλαθιού
Ελαχιστοποίηση κόστους Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 9 Οκτωβρίου 2012 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) Ελαχιστοποίηση κόστους 9 Οκτωβρίου 2012 1 / 36 Κόστος Το πρόβλημα εύρεσης ενός άριστου καλαθιού
Πανελλήνιες Εξετάσεις Ημερήσιων Γενικών Λυκείων. Εξεταζόμενο Μάθημα: Αρχές Οικονομικής Θεωρίας. Ημ/νία: 31 Μαΐου Απαντήσεις Θεμάτων
 Πανελλήνιες Εξετάσεις Ημερήσιων Γενικών Λυκείων Εξεταζόμενο Μάθημα: Αρχές Οικονομικής Θεωρίας Ημ/νία: 31 Μαΐου 2013 Απαντήσεις Θεμάτων ΟΜΑΔΑ ΠΡΩΤΗ Α1. α. Σωστό β. Σωστό γ. Λάθος δ. Σωστό ε. Λάθος Α2. β.
Πανελλήνιες Εξετάσεις Ημερήσιων Γενικών Λυκείων Εξεταζόμενο Μάθημα: Αρχές Οικονομικής Θεωρίας Ημ/νία: 31 Μαΐου 2013 Απαντήσεις Θεμάτων ΟΜΑΔΑ ΠΡΩΤΗ Α1. α. Σωστό β. Σωστό γ. Λάθος δ. Σωστό ε. Λάθος Α2. β.
ΣΥΝΘΕΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ
 ΣΥΝΘΕΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Α. Με ολοκληρωμένη λύση ΘΕΜΑ 1 ο Επιχείρηση χρησιμοποιεί την εργασία ως μοναδικό μεταβλητό παραγωγικό συντελεστή. Τα στοιχεία κόστους της επιχείρησης δίνονται στον επόμενο πίνακα:
ΣΥΝΘΕΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Α. Με ολοκληρωμένη λύση ΘΕΜΑ 1 ο Επιχείρηση χρησιμοποιεί την εργασία ως μοναδικό μεταβλητό παραγωγικό συντελεστή. Τα στοιχεία κόστους της επιχείρησης δίνονται στον επόμενο πίνακα:
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τµήµα Οικονοµικών Επιστηµών Ακαδηµαϊκό έτος (διαβάζουμε κεφ. 4 από Μ. Χλέτσο και σημειώσεις στο eclass)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τµήµα Οικονοµικών Επιστηµών Ακαδηµαϊκό έτος 2016-17 ΠΟΛΙΤΙΚΗ ΟΙΚΟΝΟΜΙΑ ΤΗΣ ΚΟΙΝΩΝΙΚΗΣ ΠΟΛΙΤΙΚΗΣ (διαβάζουμε κεφ. 4 από Μ. Χλέτσο και σημειώσεις στο eclass) 1 ιάλεξη2 Ανταγωνισμός, οικονομική
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τµήµα Οικονοµικών Επιστηµών Ακαδηµαϊκό έτος 2016-17 ΠΟΛΙΤΙΚΗ ΟΙΚΟΝΟΜΙΑ ΤΗΣ ΚΟΙΝΩΝΙΚΗΣ ΠΟΛΙΤΙΚΗΣ (διαβάζουμε κεφ. 4 από Μ. Χλέτσο και σημειώσεις στο eclass) 1 ιάλεξη2 Ανταγωνισμός, οικονομική
ΔΕΟ34. Ενδεικτική Απάντηση 1ης γραπτής εργασίας Επιμέλεια: Γιάννης Σαραντής
 ΔΕΟ34 Ενδεικτική Απάντηση 1ης γραπτής εργασίας 2016-17 Επιμέλεια: Γιάννης Σαραντής 16/11/2016 2 Ερώτηση 1 α1) Αρχικό σημείο ισορροπίας της αγοράς είναι το σημείο Δ και η τιμή ισορροπίας του κλάδου είναι
ΔΕΟ34 Ενδεικτική Απάντηση 1ης γραπτής εργασίας 2016-17 Επιμέλεια: Γιάννης Σαραντής 16/11/2016 2 Ερώτηση 1 α1) Αρχικό σημείο ισορροπίας της αγοράς είναι το σημείο Δ και η τιμή ισορροπίας του κλάδου είναι
1. Κατανομή πόρων σε συνθήκες στατικής αποτελεσματικότητας
 Εφαρμογές Θεωρίας 1. Κατανομή πόρων σε συνθήκες στατικής αποτελεσματικότητας Έστω ότι η συνάρτηση ζήτησης για την κατανάλωση του νερού ενός φράγματος (εκφρασμένη σε ευρώ) είναι q = 12-P και το οριακό κόστος
Εφαρμογές Θεωρίας 1. Κατανομή πόρων σε συνθήκες στατικής αποτελεσματικότητας Έστω ότι η συνάρτηση ζήτησης για την κατανάλωση του νερού ενός φράγματος (εκφρασμένη σε ευρώ) είναι q = 12-P και το οριακό κόστος
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ
 ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ Κεφάλαιο 4 ο : Η Προσφορά των Αγαθών ΕΠΙΜΕΛΕΙΑ: ΝΙΚΟΣ Χ. ΤΖΟΥΜΑΚΑΣ ΟΙΚΟΝΟΜΟΛΟΓΟΣ Ασκήσεις 1. Δίνονται τα διπλανά δεδομένα μιας επιχείρησης στη βραχυχρόνια περίοδο. i. Να κάνετε
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ Κεφάλαιο 4 ο : Η Προσφορά των Αγαθών ΕΠΙΜΕΛΕΙΑ: ΝΙΚΟΣ Χ. ΤΖΟΥΜΑΚΑΣ ΟΙΚΟΝΟΜΟΛΟΓΟΣ Ασκήσεις 1. Δίνονται τα διπλανά δεδομένα μιας επιχείρησης στη βραχυχρόνια περίοδο. i. Να κάνετε
