Topology, Localization, and Quantum Information in Atomic, Molecular and Optical Systems
|
|
|
- Λαφιδὼθ Ἀβιούδ Δοξαράς
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Topology, Localization, and Quantum Information in Atomic, Molecular and Optical Systems The Harvard community has made this article openly available. Please share how this access benefits you. Your story matters. Citation Accessed Citable Link Terms of Use Yao, Norman Ying Topology, Localization, and Quantum Information in Atomic, Molecular and Optical Systems. Doctoral dissertation, Harvard University. May 1, :52:49 AM EDT This article was downloaded from Harvard University's DASH repository, and is made available under the terms and conditions applicable to Other Posted Material, as set forth at (Article begins on next page)
2
3
4
5
6 W
7
8 40 87 G σσ LL (z) Gσσ LR (z) Πσσ LL (z) Πσσ LR (z)
9 ν =1/2
10 W
11
12
13
14
15
16
17
18 ß
19
20
21 Energy Site H = ij t ij c i c j + h.c. + i µ i n i t ij {µ i } µ i W W =0 t =0 W t t i + j t µ i µ j j
22 e r/ξ ξ H = α c αc α + α,β,γ,δ V α,β,γ,δ c αc β c γc δ.
23 ν =1/2 ν =1/2
24 1/r 2 H sd = 1 2N k,k,α,β J(k k )c k,α σ αβc k,β J(k k ) σ 1 2 J RKKY S 1 S 2 J RKKY r ξ J RKKY
25 J RKKY (r) = 1 8πr 3 J 2 exρ f ν 2 0 cos(2k f r) J ex ρ f ν o k f r ξ J SC RKKY (r) = 1 8πrξ 2 J 2 exρ f ν 2 0 cos(2k f r)e r/ξ. ξ 2 r ξ (ξ/r) 2 r 1 J RKKY H 0 = k,α ɛ k c k,α c k,α + k [c k c k + c k c k ]. Ψ k =(c k,c k,c k,c k )T H 0
26 H 0 = k Ψ k (ɛ kτ 3 + k τ 2 σ 2 )Ψ k. τ 1,2,3 σ 1,2,3 τ {c k,c k } σ G 0 (k, ω) = 1 iω ɛ k τ 3 k τ 2 σ 2. G(k, k,ω)=g 0 (k, ω)δ(k k )+G 0 (k, ω)t (k, k,ω)g 0 (k,ω) J(k k )=J ex T (ω) = 1 N (SJ ex /2) 2 g 0 (ω) 1 (g 0 (ω)sj ex /2) 2 g 0 (ω) =1/N k G 0(k, ω) S k ω + τ 2 σ 2 g 0 (ω) = πρ f 2 ω. 2 E b < ω = E b
27 2 ( 1+π 2 (JS/2) 2 ρ 2 f ) (ω + ωπ2 (JS/2) 2 ρ f ) 2 =0 E b = 1 π2 (JS/2) 2 ρ 2 f. 1+π 2 (JS/2) 2 ρ 2 f J ex 0 E b J ex E b S =1 0 e 0 e 1 e I =1/
28 H e,n = 0 S 2 z + µ e BS z + µ n BI z + AS z I z, 0 =2.87 µ e = 2.8 µ n = 0.43 A =3.0 ẑ
29
30 (a) R 1 R 2 R R1 (b) 2R 2,,,,,! 1 "! 2 " = =,,, Pair 1 Pair 2 R2 R R <r<2r t 1/r α α d d d =1
31 α = β β<α β<α d<α d<α d<α d<β d<β d<β+2 d<β/2 d< αβ α+β d<β/2 d<β/2 d<(β +2)/2 d< α(β+2) α+β+4 1/2 S z H = i ɛ i S z i ij t ij r ij α (S+ i S j + h.c.)+ ij V ij r ij β Sz i S z j ɛ i W α β β α ɛ i ɛ j t ij / r ij α R 1 < r ij < 2R 1 N 1 (R 1 ) (ρr d 1) t/rα 1 W ρ N 1 (R 1 ) R 1 d>α d = α δ t/r1 α
32 Dynamic Polarization (D) ν =1/2 α = β =1 α = β =2 (a) (c) α = β =3/2 α = β =3 (b) (d) Disorder Width (W ) d =1 t =1,V =2 α = β =1 α = β =3/2 α = β =2 α = β =3 W c 10 V S z R 2 δ 1,δ 2 >V(R 2 ) δ 1 δ 2 R 2 2R 2 N 2 (R 1,R 2 ) (n 1 (R 1 )R d 2) V/Rβ 2 t/r α 1, n 1 = ρn 1 N 2 R 2 R 1 R 2 d<β R 1 R 2 V/Rβ 2 t/r α 1 [1, V/Rβ 2 ] R t/r1 α 1 R β/α 2 d< αβ α+β
33 N 3 (R 1,R 2,R 3 ) (n 2 (R 1,R 2 )R d 3) V/Rβ 3 V/R β 2 n 2 = n 1 N 2 R 3 R 1,R 2 R 1 R 2 R 3 d<β/2 R 1 R β/α 2 R 2 R 3 t ij,v ij R 1 <R 2 V/R β 2 VR 2 1/R β+2 2 N 2 α = β d<β/2 α<β+4 α>β+4 α d c =1.5 α = β =3 d c =1.5 α =6 β =3 d c 2.3
34 d =1 α = β =1, 3/2, 2, 3 L =14 ν =1/2 W V ij = V =2 t ij = t =1 D ˆF = j Sz j e i2πj/l η k Dη k =1 k ˆF k k ˆF k k ˆF ˆF. k D Dη k L D 1 D 0 D α =2, 3 α =1 α =3 α =3/2 d =1 1 <α c < 3 α c =2
35 (a) (b) (c) z y x E (d) 1, 1 (e) 1, 1 1, 1 1, 1 1, 1 2B 0, 0 i t ij 1 r 6 ij ŷ ẑ ˆx = 1, 1, = 0, 0 α = β =3 α =6 j ŷ ẑ t ˆx α E d V d 2 /R 3 β =3 B W
36 V d 2 E 0 V 0 ν =1/2, 1/3, 1/4 L =16, 18, 20 H m = BJ 2 d z E = J =0,m j =0 = J =1,m j =1 H dd = 1 d i (1 3ˆr ij ˆr ij )d j 2 i j d rij 3 H dd {, } ɛ i = j i d s d a α = β =3 d rij 3 s,a = 1 dz 1 ± 0 d z 0 2 ɛ i W d sd a a ν(1 ν) 3 a0 0 d =1 d c =3/2 α = β =3
37 Dynamic Polarization (D) (a) β =3 V/t = ν =1/ Disorder Width (W ) Disorder Width (W ) (b) V/t =1 V/t =2 V/t =4 MBL Ergodic /4 1/3 1/2 Filling Fraction (ν) α β =3 W W c 1.4t V/t =1, 2, 4 d c =3 d =2 B = J =1,m j = 1 = J =1,m j =1 J z H = t 2 [ ij r (d i ij 6 + ) 2 (d j ) 2 +(d i ) 2 (d j +) 2] α =6 β =3 d =2 d c 2.3 d c =2.5 H NV = D 0 S 2 z + µ e BS z D 0
38 e Dk2t D D =0 T 1 k T 2 D T2 a 2 0/T 2 T 2 T 1 D T2 D e a 2 0/T a0 T a0 l (l 2 + Dt) d/2 e t/t T a0 10µ T T 1 25
39 2 3 T a0 1µ T 1,T 2 10
40 π/2 τ z i ±1
41 Ĥ = i h i τ z i + ij J ij τ z i τ z j + ijk J ijk τ z i τ z j τ z k +... J ij, J ijk,... ξ τi z τ z i Ĥ... + =( + )/ 2 h ( ) = h + j J jτ z j + j,k J jkτ z j τ z k +... π t/2 h ( ) t/2 t/2 π h ( )
42 spin echo DEER F(t) D(t) W L J z = J F (t) d ξ t/2 π π/2 τ z
43 ψ(t) = R π/2 e iĥ t 2 R π R π/2 e iĥ t 2 R π/2 ψ(0), Rr π/2 = j r (ˆ1 iˆσ y j )/ 2 Rr π =(Rr π/2 ) 2 D(t) ψ(t) ˆτ z ψ(t) = ( 1+e 2iJ Ij τ j ) t 2 j II N τ j j D(t) J Ij j I N J Ij t 1 J Ij t 1 1 D(t) D(t) D osc (t) D(t) = D(t)+D osc (t), D(t) =1/2 N (t), 1/2
44 J Ij exp( j I /ξ) j I ξ log(t) t t 0 /J Ik k = I + d N fast =0 t 0 t t 0 e N/ξ N (t) ξ log(t/t 0 ) D(t) t ξ ln 2 t t 0 e N/ξ D( ) 2 N (1 + t D(t) 2 /t 2 0) α/2 t t 0 e N/ξ =, 2 N t t 0 e N/ξ α = ξ ln 2 D osc (t) D osc (t) D osc (t)
45 1 0.8 fit J z =0.1J J z = J W =6J =3 d =3 N =7 Ĥ = J 2 (Ŝ+ i ij Ŝ j + Ŝ+ j Ŝ i )+J z Ŝi z Ŝz j + i ij h i Ŝ z i Ŝa j a {x, y, z} ±1/2 Ŝ± j = Ŝx j ± iŝy j h i [ W ; W ] J z =0 Ĥ W>0 J z 0 W/J S τ
46 fit J z =0.1J J z = J d =3 d =7 W =8J N =3 α W d = 7 N = 3 α = c 1 / ln(c 2 W ) ξ 1/ ln(w ) D( ) N J z D( ) J z N c/1.8 N L =12 S z ψ(0) D(0) = ψ(0) ˆσ z ψ(0) > 0 D(t) π/2 t =0
47 D(t) =A/(1 + t 2 /t 2 0) α/2 A D osc (t) D(t) D(t) d t 0 [ exp(d/ξ)] d α α α = c 1 / ln(c 2 W ) α = ξ ln 2 ξ 1/ ln(w ) N f(k) =c/1.8 N 1/2 N
48 J,J z T 1 1 J ξ ln(j 1 ) 6ξ 10 J /J J (1 10) 5µ 1 100µ 1 /J 1 (0.5 5) 10 3 J /J
49
50 1/2 H = ij JS + i S j + ij J σ + i σ j + i J z S z i σ z i + h.c S σ XY J J J z J 0 σ S {σ i } ±J z
51 J!" J #" J! J J J J J J z S J σ J N =20 Stot z = σtot z =0 σ J =1.0 J z 10.0 J J S ent = ρ A log ρ A = ρ B log ρ B A B D
52 N =8 Sent J =1.0 J =0.01 J z = 10.0 J =1.0 J =0.001 J z = 10.0 J =1.0 J = J z = 10.0 Fractional Polarization k =1 k =2 Time (1/J) Time (1/J) Time (1/J) Time (1/J) N = 16 Fractional Polarization Sent k =1 J =1.0 J =0.01 J z = 10.0 S-chain!!-chain" J =1.0 J =0.001 J z = 10.0 J =1.0 J = J z = 10.0 Time (1/J) Time (1/J) Time (1/J) N = 8 S z tot = σ z tot =0 k =1 S σ k =2 t int t d N = 16 k =1
53 ˆF = j Sz j e i2πj/l Sj z σj z k D k =1 k ˆF k k ˆF k k ˆF ˆF, k D D k N =8 J =10 2, 10 3, 10 4 J S ent t 1/J t 1/J J t 1/J J t int t>t int t>t d t int t d J S ent
54 t int 1/J t int 1/J 2 J, J J z t int J z t int J J S t d J z /J 2 J 2 /J z S t d D k=1 k =2 t e L k =1/L e Dk2t t d L 2 /D D J 2 /J z N =16 e 8 J t int t d
55 Sent J int J SPL quasi MBL thermal t L 2 /D t e L Short chain thermal t L 2 /D J d J 2 /J z SPL t e L Long chain 1/J 1/J int t (1/J) 1/J d 1/J 1/J int 1/J d t (1/J) ρ N = 8 N = 12 N = 16 d ρ/dw W/J S ent 1/J t>t int =1/J int J t>t d =1/J d D J 2 /J z S ent e L L 2 N
56 2.0 Sent J independent J 2 Time (1/J) t int J J 2 J L 2 t d 1/Dk 2 L 2 J =10 2 t int t d J J =10 5 S ent t d σ σ J
57 H W = i b z i S z i + i b z i σ z i b, b W H W ρ ψ = 1 N N i ψ Si+1 z Si z ψ H W ( ) N d ρ dw c. W/J d ρ dw N H T = H + H W J =1.0 J =0.01 J z = <W < N =8, N =16 ρ ψ J/3 ρ H W
58 H h = ij JS i S j + ij J σ i σ j + i J z S z i σ z i. J 0 t int 1/J J S J 2 J S ent J S σ JJ /J z 1/t d J 2 /J z
59
60 ẑ Θ 0, Φ 0 {X, Y, Z} ij {X, Y } H dd = 1 κ 2 i j R 3 ij [ ] d i d j 3(d i ˆR ij )(d j ˆR ij ), κ 1/4πɛ 0 µ 0 /4π R ij d i d j 0 ±1 ẑ
61 ±1 0 Ω + Ω Ω +, Ω 0 B = α( 1 + β 1 ) D = α ( β ) α =Ω + / Ω αβ =Ω / Ω Ω = Ω 2 + Ω + 2 E 0 = Ω 2 / E B = + Ω 2 / E D = d R 0 κd 2 /R0 3 Ω 2 / D 0 B 0 D B 0 a i = B 0 i n i = a i a i H B = ij t ij a i a j + 1 V ij n i n j, 2 i j t ij = B i 0 j H dd 0 i B j t ii = j i ( 0 i0 j H dd 0 i 0 j B i 0 j H dd B i 0 j ) V ij = B i B j H dd B i B j + 0 i 0 j H dd 0 i 0 j B i 0 j H dd B i 0 j 0 i B j H dd 0 i B j N i = i a i a i κd 2 /R0 3 H dd H B
62 J =1 Ω (r) Ω + (r) Ω ± δ J = 1 l p l t l t l W (p l) β π/n κ =1,i j t ij = d2 01 R 3 [ χ i (q 0 + [q 2 ]σ x + [q 2 ]σ y )χ j ], t ii = j i 2 q 0 R 3 (d0 d B i (d 0 ) 2 ), V ij =2 q 0 R 3 [ d B i d B j d 0 d B i d 0 d B j +(d 0 ) 2], d 0 d B ẑ 0 B d χ i = α i (1,β i ) T i q 0 = 1(1 2 3cos2 (Φ Φ 0 )sin 2 (Θ 0 )) q 2 = 3[cos(Φ Φ 2 0)cosΘ 0 i sin(φ Φ 0 )] 2 σ (R, Φ) R ij ij R Φ q 0 q 2 d B i
63 π/n (Θ 0, Φ 0 )=(sin 1 ( 2/3),π/4) q 0 =0 ˆX Ŷ H dd d + i d+ j d i d j d ± = (d x ± id y )/ 2 t ˆX ij = d2 01 χ R0 3 i tŷij = d2 01 χ R0 3 i [ 1 2 σx [ 1 2 σx σy 3 2 σy ] ] χ j, χ j. β =Ω /Ω + β β B 1 1 β Φ=π/4 W (p) = p t ij l Ψ l =arg[w (p l )] = arg[t 2 l t 2 l ] t l t l θ l =arg(t l ) θ l =arg(t l )= θ l+1 Ψ l =2θ l 2θ l+1 π/n θ l+1 = η l π η 2N β θ l β l+1 β l = sin( π 3 η + l π 2N ) sin( π 3 + η l π 2N ),
64 4N β 1 π/n t ij H B β = β 1,β 2 β 1 β 2 β 1 β 2 d B i ±1
65 β = β 1,β 2 Ψ, Ψ g 1 g 2 /R 3 β 2 β 1 c = 1 4π dkx dk y ( kx ˆd ky ˆd) ˆd H(k) = d(k) σ + f(k) ẑ H m = BJ 2 d z E + H D, B J d z ẑ E H D J =1 J, M E M J 0 ±1 ±1
66 d 1 d B i = d 1 V ij = 2 q 0 R 3 (d0 d 1 ) 2. V ij /t ij (d 0 d 1 ) 2 /d Ω H B N ν
67 (Θ 0, Φ 0 )=(0.46, 0.42) β 1 =3.6e 2.69i β 2 =5.8e 5.63i 1/27R 0 > 10 S(R, 0) = n(r)n(0) ν = 1/2 (Θ 0, Φ 0 )=(0.66,π/4) β 1 = 2.82e iφ 1 β 2 = 4.84e iφ 2 (d 0 d 1 ) 2 /d ĝ 1 ĝ 2 N s = 24 2π θ 1 4π θ 2
68 c = 1 ν =1/2 (d 0 d 1 ) 2 /d S(R, 0) = n(r)n(0) N s =32 ĝ 1 ĝ 2 φ 1 = φ 2 =0.1 k 2 =0,k 1 =0, 2π/3, 4π/3 ĝ 2 N s =24 ĝ 2
69
70 E H m = BJ 2 d z E E 0, 0 J =1 1, 1 1, 0 1, 1 J ẑ J, m E
71 φ {X, Y } ẑ Θ 0 Φ 0 {x, y, z} {X, Y, Z} J =0, 1 0, 0 M J = N s = 24 Θ 0 E =0 J =1
72 J =1 e 1 e 2 M H r = [ e 1 (Ω 1 1, 1 +Ω 2 1, 0 )+ e 2 (Ω 3 1, 0 +Ω 4 1, 1 )+ ] Ω i = 1 Ω(Ω 2 Ω 4 1, 1 Ω 1 Ω 4 1, 0 +Ω 1 Ω 3 1, 1 ) Ω H dd = 1 κ 2 i j R 3 ij [ ] d i d j 3(d i ˆR ij )(d j ˆR ij ), κ =1/(4πɛ 0 ) R ij i j d i d j d R 0 d κd 2 /R0 3 Ω i {, } 2B a i = i j i t ij = i j H dd i j
73 V ij = i j H dd i j + i j H dd i j i j H dd i j i j H dd i j H B = ij t ij a i a j + 1 V ij n i n j, 2 i j N = i a i a i t ii {a, b, A, B} J =1 a i t ij V ij g 1 g 2 C = 1 f 11.5 J =1 ν ν =1/2 N s =44 Θ 0 =cos 1 (1/ 3) ν =1/2
74 a b A B J =1 φ g 1 g 2 f 11.5 C = 1 {Θ 0, Φ 0 } = {0.68, 5.83} σ xy = 1 2π F (θx,θ y )dθ x dθ y = 0.5 {θ x,θ y } F (θ x,θ y )= ( Ψ θ y Ψ θ x Ψ θ x Ψ θ y ) ν =1/2 Q torus = ( N uc +1 N b N uc+1 2N b ) ( Nuc 1 N b N uc+1 2N b ) Nuc = N s /2 N b ν =1/2 Θ 0
75 σ xy ν =1/2 ν =1/2
76 d µ e 1 e 2 J,m = 2, ±2 v =41 (3) 1 Σ +
77 ν = 1/2 ν =1/2 N s = 24 N b =6 1/(3R 0 ) 3 (k x,k y )=(0, 0) (k x,k y )=( π, 0) ν =1/2 k x,k y N s = 16 N s = 44 N b =5 36 Q torus µ = E Nb +1 E Nb E Nb N b ν =1/2 ν =1/2 de/dθ 0 Θ 0 de/dθ 0 E =0.4 8
78 H lattice H hf Ω i H lattice H hf H hf 1 =160 E = B/d 0.5 Ω i E 1,0 E 1,1 M H lattice H hf Ω i
79
80 (a) (b) E b " η η " BCS ψ BCS E b r < ξ η η r ξ r r<ξ
81 r ξ H 0 =,σ ɛ c,σ c,σ + [c c + c c ]. ψ BCS J E b = 1 (πjsn 0/2) 2 β2 = 1 1+(πJSN 0 /2) 2 1+β 2 N 0 tan(δ) β = πjsn 0 /2 E b = cos(2δ) E b δ
82 T K exp ( 1/JN 0 ) T K β 1/ ln( /T K ) 1 φ sh ( ) 1 e /ξ sin(2δ) r ξ r<ξ η η η η r L r R ẑ H int = J σ d σ[s L f( L )c σ( )c σ ( )+S R f( R )c σ( )c σ ( )], S L(R) f( ) H int = J σ d d σ[s L e i( )r L f, + S R e i( )r R f, ]c σ, c σ, f
83 Ψ =(c,,c, ) H 0 = d Ψ [ɛ τ z + τ x ]Ψ τ H int = J d d Ψ [S Le i( )r L f, + S R e i( )r R f, ]Ψ + E 0 E 0 = J d f, [S L + S R ] H T = H 0 + H int d n = d (u n, ψ, + v n, ψ, ) H T = ε n d nd n 1 ε n = 2 n n n E tot = 1 ε n = E V n ε n (d nd n 1 2 ). dɛ ɛ δρ(ɛ) E V δρ(ɛ) I(r) I(r) =E, tot E, tot = 1 2 dɛ ɛ [δρ, (ɛ) δρ, (ɛ)]. δρ(ɛ) = 1 { [G π, (z) G(0) (z)]} z = ɛ + i0 + G (0) (z) =[z (ɛ τ z + τ x )] 1 G, (z)
84 T G, (z) =G (0) (z)+g(0) (z)t, G(0) (z), T, T T δρ(ɛ) = 1 π { [G(0) (z)t, G(0) (z)]} = 1 π { [JSΠ(1 JSG) 1 ]} Π G S 4 4 Π ll (z) = G ll (z) = d G (0) (z)g(0) (z)ei ( l l ) d G (0) (z)ei ( l l ) S ll = S l δ ll τ 0. τ 0 l l {L, R} J 1 [JSΠ(1 JSG) 1 ] [J 2 SΠSG] I( ) = E fβ 2 π(k f r) cos(2k fr)e 2r 3 ξ F1 [ 2r ξ ] + β2 (k f r) 2 sin2 (k f r)e 2r ξ F2 [ 2r ξ ]. k f r = L R
85 Interaction (khz) 400! 0! -400! 100! 150! R (nm) J YSR! RKKY E b ! E f = 11.7 k f = N 0 = 35 3 ξ =1.6µ J YSR E b 10 2 J YSR r ξ F 1 [α] =α dxe α( x ) F 0 2 [α] = 2 π x ) dx e α( 0 (x 2 +1) 1/r 2 /E f r E f /( k f ) ξ I( ) e 2r ξ O(J 2 )
86 J E b 0 η ɛ ɛ 0 [G, (z)] E b F (E b ) [1 SG(E b )] = 0. k f r 1 η η/e b F (E b )+η F (E b )=0
87 1 β η = 1 cos 2 (k f r) 1 β 2(k f e 2r r) 2 ξ. F (E b )+η F (E b )+ 1 2 η2 F (E b )+ 1 6 η3 F (E b )=0 η = 2 cos(k f r) (k f r) 2 e 2r ξ β 1 I(r) J YSR = η η E b 0 β 1 J YSR η J YSR = 1 cos 2 (k f r) 2r 1 β 2(k f r) 2 e ξ, 1 1 β U(r)c L, c R, U(r) =cos(k fr)/(k f r) 2E b β E b J YSR J YSR k f r> 1 1 β > ξ r.
88 r ξ J YSR r λ f ξ ξ / k f ξ J YSR = η η 1 r 2 β J YSR J YSR J YSR >J RKKY r J YSR
89 2 T K I I T K
90 ɛ = E b E b E b
91 ( /T K ) c S =1/2 /T K > ( /T K ) c S G =1/2 /T K < ( /T K ) c S G =0 H BCS = dk [ ξ (2π) 3 k c kσ c kσ + ( c k c k + h.c.)] σ 1/2 S 1 S 2 H int = J 2 S 1ψ 1σ ψ 1 + J 2 S 2ψ 2σ ψ 2. ψ 1 ψ 2 H T = H BCS + H int T K
92 H T P S 2 =0 SU c (2) Q x =(Q + + Q )/2 Q y =(Q + Q )/2i Q z = 1 dk 2 σ (c (2π) 3 kσ c kσ 1) 2 Q+ = dk c (2π) 3 k c π k Q = ( Q +) 0 U c (1) Q P S Q S 0 S =0 P = Q =0 T 0 S =1 P =+ Q =0 D + D S =1/2 P = ± Q =1 S 2 Q =2 P = π
93 (S, Q, P ) S 0 (0, 0, ) T 0 (1, 0, +) D ± ( 1, 1, ±) 2 S 2 (0, 2, ) /T K /T K 1 S S = sin(k F R) k F R R = R 1 R 2 k F S D ± I I J I/T K
94 S = 0.1 I/T K /T K S =1 S =1/2 S =0 S 2 S 0 /T K T 0 I<0 S 0 I>0 I T K, =0 S 2 I, T K Q =0 Q =2 S 0 S 2 =0 =0
95 /T K I/T K = 0.58 S = 0.1 S 2 D + T 0 S 0 T 0 I eff = E S0 E T0 I T K T K ω T K S =0 S =1/2 T K I 0 D + T K S =0 S =0 D ± /T K D ± D + S =1 1/2 /T K
96 S 2 φ ( ) 1 e /ζ sin(2δ) E = 1 β2 1+β 2 ζ β tan(δ) =JSN 0 π/2 N 0 T k F R β E sh =0 I <0 I >0 F 1 S 1 σψ 1 T 0 D + D 4
97 (a) 1.0 Esh/ Esh/ (b) I<0 I>0 Molecular Doublet Mol. Triplet Molecular Doublet Triplet Kondo Mol. Singlet β k F R 4.1 Kondo Singlet k F R 2.6 k F R 4.1 β = JNSπ/2 β 0.86 β 1.3 k F R Pb =1.55 T 20 mk T 0 S 0 E = hν S 0 S 0 D ± E S 0 di/dv S 0 T 0
98 T 0 D + D T 0 S 0 hν = E (D +,S 2 ) (D +,T 0 ) S 2 S 0
99
100 g κ
101 1/2 H = H 0 + H H 0 = N 1 i=1 κ(s+ i S i+1 + S i S+ i+1 ) H = g(s 0 + S1 + S + N+1 S N + ) S ± = S x ± is y S = σ / 2 σ =1 g κ H c i = e iπ i 1 0 S + j S j S i H 0 H 0 = N 1 i=1 κ(c i c i+1 + c i c i+1 ) f k = 1 N jkπ A j=1 sin N+1 c j k =1,,N A =(N+1 2 )1/2 H 0 = N k=1 E kf k f k E k =2κ cos kπ N+1 t k = g A H = N t k (c 0f k +( 1) k 1 c N+1 f k + ), k=1 kπ sin N N+1 k = z (N +1)/2 H t z g/a
102 g κ κ a b k = z g κ/ N E z E z±1 κ/n ( 1) z 1 c N+1 H eff = t z (c 0f z + c N+1 f z + ) H eff τ = π 2tz U eff = e iτh eff =( 1) f z f z (1 (c 0 + c N+1 )(c 0 + c N+1 )) {(1,c 0,c N+1,c 0c N+1 ) 00 0,N+1} U fermi eff =( 1) n 0+n N+1 +n z ( 1) n 0n N+1 0,N+1, n θ = f θ f θ H eff
103 0,N+1 =( 1) n 0n N+1 Φ i =(α + β ) 0 (α + β ) N+1 Ψ M,nz Ψ M = N j=1 S+ j S j n z N Φ f =( 0,j N+1,j ) 0,N+1 0,N+1 Φ i j=1 a a = a a = a a a b a b b b b F = i=1,2,3 [σi E(σ i )]
104 E e ikτ K N N H = i,j K i,js + i S j ɛ =1 F g/κ g κ ɛ ( ) 2 5 t k k z 3 E k [1 + ( 1) k+z cos(e k τ)] z = N+1 2 ( ) 10 t 2 k k z 3 E k N κ ɛ 0 g τ τ N t z t z κ/n τ 1/t z N/κ N N N E =0 H = (S0 z + SN+1 z ) N
105 =E k t k E =0 g L g R g L g R τ N/g
106 N =7 g/κ ɛ 0 = 10 3 τ 1/κ
107 g
108 T 1
109 L =12 N 1 H = κσi x σi+1 x + i=1 N i=1 Bσ z i κ B σi x σ ± i =(σi x ± iσ y i )/2 c i = σ+ i e iπ i 1 j=1 σ+ j σ j N 1 H JW = κ(c i c i+1 + c i c i+1 c ic i+1 c ic i+1 ) i=1 N B(c i c i c i c i ) i=1
110 H JW φ A φ φ =(c 1,c 2,...,c N,c 1,c 2,...,c N )T A ɛ ɛ Λ= 0 0 ɛ ɛ 2 ψ ψaψ T =Λ ±ɛ k d k = ψ 2k 1,j φ j d k = ψ 2k,jφ j k =1,,N H JW = N ɛ k (d k d k d k d k ), k=1 d ɛ k κ 2 + B 2 2Bκcos q k q k = kπ/(n +1) 0 N +1 g B H = g(σ x 0σ x 1 + σ x Nσ x N+1)+B (σ z 0 + σ z N+1).
111 H JW = g(c 0c 1 + c 0c 1 + c 1c 0 c 0 c 1 ) g(c N c N+1 + c N c N+1 + c N+1 c N c N c N+1 ) + B (c 0c 0 c 0 c 0 + c N+1 c N+1 c N+1 c N+1 ). B = ɛ z d z c i = N k=1 (ψt ) i,2k 1 d k + N k=1 (ψt ) i,2k d k c 1 c N d gψ 2z 1,1 = gψ 2z 1,N B, ɛ z ɛ z±1 H eff ɛ z (d zd z d z d z)+ɛ z (c 0c 0 c 0 c 0)+ɛ z (c N+1 c N+1 c N+1 c N+1 ) gψ 2z 1,1 (c 0d z + d zc 0 ) gψ 2z 1,N (c N+1 d z + d zc N+1 ). B<κ
112 g t "E g t "E >> gt (1) (2) g τ = π 2gψ2z 1,1 U eff = e iτh eff =( 1) n z ( 1) (c 0 +c N+1 )(c 0+c N+1 )/2 = ( 1) nz (1 (c 0 + c N+1 )(c 0 + c N+1 )), n z = d zd z U eff Ψ={ Ω,c 0 Ω,c N+1 Ω,c 0c N+1 Ω } Ω c 0 c N U eff Ψ=( 1) n z Ψ e iπ i 1 j=1 σ+ j σ j 2 =
113 a b = a b = a b a b 0
114 0 (QR) 1 2 N-1 N N+1 (QR) 0 N +1 X F = [ σ i E(σ i ) ], i=x,y,z E H = g(σ + 0 σ 1 + σ + N σ N+1 + )+ N 1 i=1 κ(σ+ i σ i+1 + ) U H t =2τ ρ DS ch
115 F DS = = = i=x,y,z i=x,y,z i=x,y,z [ σ i 0U(σ i 0 ρ DS ch )U ] [ U σ i 0U(σ i 0 ρ DS ch ) ] [ σ i 0(t)(σ i 0 ρ DS ch ) ], σ i 0(t) M = e ikt K (N +2) (N +2) H = N+1 i,j=0 K ijc i c j c m = i n K mnc n c m (t) = n M mnc n σ + 0 (t) =U σ + 0 U = U c 0U = i M 0ic i = i M 0iσ + i e iπσ+ l σ l, l<i σ0(t) z = 2c 0(t)c 0 (t) 1= 1+2 M0iM 0j c i c j ij = 1+2 M0iM 0j σ + i σ j e iπσ+ l σ l, ij i<l<j c 0 F DS σ ± =(σ x ± iσ y )/2 [σ0(t)(σ x 0 x ρ ch )] = [ (σ 0 + (t)+σ0 (t))((σ σ0 ) ρ ch ) ] σ 0 + (t)(σ0 ρ ch ) σ0 (t)(σ 0 + ρ ch ) i =0
116 [ σ + 0 (t)(σ0 ρ ch ) ] [ = ( ] M0iσ + i e iπσ+ l σ l )(σ 0 ρ ch ) i l<i = [ ] M00σ 0 + σ0 ρ ch = M 00. [ σ 0 (t)(σ + 0 ρ ch ) ] = M 00 σ z [σ0(t)(σ z 0 z ρ ch )] = [ σ0 z ρ ch ] [ + (2 ] M0iM 0j σ + i σ j e iπσ+ l σ l )(σ z 0 ρ ch ) ij i<l<j = [ 2M 00M 00 σ + 0 σ 0 σ z 0 ρ ch ] =2 M00 2, i = j i = j =0 [σ z 0]=0 F DS = (M 00 + M 00 + M 00 2 ). N +1 0 F SS = i=x,y,z [ σ i 0(t)(ρ SS ch σ i N+1) ],
117 ρ SS ch {0,,N} F SS σ x 0(t) = c 0(t)+c 0 (t) = i M 0ic i + M 0ic i = i i 1 [{ (M 0i )σi x + (M 0i )σ y i } ( σl z )]. l=0 i N +1 [σ x 0(t)(ρ ch σ x N+1)] = 2 (M 0,N+1 ) [ρ SS ch N ( σl z )]. l=0 σ y σ z [σ z 0(t)(ρ SS ch σz N+1 )] = 2 M 0,N+1 2 F SS = [2 (M 0,N+1) [ρ SS ch N ( σl z )] + M 0,N+1 2 ). l=0 F SS =1 M 0,N+1 =1 [ρ SS N ch l=0 ( σz l )] =1 P = N l=0 ( σz l ) = a b = a b {0 a, 0 b, 1,,N,(N +1) b, (N +1) a } U b {0 b, 1,,N,(N +1) b } U a
118 {0 a, 1,,N,(N +1) a } U = U b U a F enc = i=x,y,z [ σ i N+1(t)(σ i 0 ρ PP ch ρ N+1 ) ]. ρ PP ch {1,,N} σi 0 0 ρ N+1 (N +1) 0a,N+1 a 0b,N+1 b = P 2 = H Ua U a H Ua H Ua = g(c 0 a e iπn 0 b c 1 + c N eiπn (N+1) b c (N+1)a + ) F enc = 1 6 (2 M 0,N+1 2 [ M 2 0,N+1 M 0,0 M N+1,N+1 ] + M 0,N i M N+1,i M i,0 2 ) M
119 1/r 3 H B = N ωa i a i + i=1 N 1 i=1 κ(a i a i+1 + a i+1 a i). b k = 1 A A = (N +1)/2 k =1,,N H = k (ω + ɛ k)b k b k j sin jkπ N+1 a j ɛ k =2κcos( kπ ) N+1 H B = g(a 0a 1 + a N a N+1 + )+ω (a 0a 0 + a N+1 a N+1) g ω a 1 a N b k H B + H B = N t k (a 0b k +( 1) k 1 a N+1 b k + ) k=1 + ω (a 0a 0 + a N+1 a N+1)+ N (ω + ɛ k )b k b k, t k =(g/a)sin[kπ/(n +1)] b z ω = ω + ɛ z t z ɛ z ɛ z±1 H B eff = 2t z (η 0b z + b zη 0 ) η 0 =1/ 2(a 0 + a N+1 ) k=1
120 ξ ± =1/ 2(η 0 ± b z ) H B eff = 2t z (ξ +ξ + + ξ ξ ). H B eff τ B = π/( 2t z ) U B eff = e ihb eff τ B =( 1) ξ + ξ + ( 1) ξ ξ (U B eff ) ξ ± (U B eff )= ξ ± a 0 a N+1 a 0 (τ) (U B eff) a 0 (U B eff) = a N+1, a N+1 (τ) (U B eff) a N+1 (U B eff) = a 0, 0 1 a N+1 (τ) =M N+1,0 a 0 + ɛa ɛ ɛ =1 M N+1,0 2 g 2 a ɛ a i i =1,...,N +1 N +1 n N+1 (τ) =(1 ɛ) n 0 + ɛ n ɛ n i = a i a i n ɛ kt/ω > 1 g g ω/(kt)
121 40 Number of States T1 NV (units of ms) T1 NV (units of s) Participation Ratio Number of States Participation Ratio Number of States Participation Ratio Number of States Participation Ratio N = 11 T 1 d = 10 κ = 50 σ d σ d g L g R N = 51 N = 51 κ = 50
122 g g T 1 ɛ = L k z(g 2 ψ k,l 2 + g 2 R 2 k ψ k,r 2 2 k )+N t T 1, g L(R) ψ k,l(r) k z k N t T 1 N
123 g L g R t z = g L ψ z,l = g R ψ z,r t = π/ 2t z ɛ = k z ( ψk,l 2 gl 2 2 k + ψ ) z,l 2 ψ k,r 2 Nπ + ψ z,r 2 2 k 2T1 g L ψ z,l, ( g L = Nπ 3 2 2T 1 ψ z,l k z ψ k,l 2 2 k ) + ψ 1 z,l 2 ψ k,r 2. ψ z,r 2 2 k 1/ T 1 10
124 {J i } J κ =1 g 0.7 T 1 N =11 N =51 1 ɛ 200 N =51 T 1
125 N PR = 1 N i=1 ψ i 4 N PR O(N) N PR N N PR σ κ σ κ 0.5κ < 2/3 T 1 5 gψ κ/n g = g M (N) κ N +2
126 g/κ N 1/6 N > 90% N = 100 J i = 1 2 (i +1)(N +1 i) H = N i=0 N+1 J i (σ + i σ i+1 + h.c.)+ i=0 h 2 σz i, h H = ij K ijc i c j K ij = J i δ j,i+1 + J j δ i,j+1 + hδ i,j H = N+1 k=0 ω kf k f k ω k = k + h N+1 2 c i (t) = j M ij(t)c i (0) h = N+1 t =2π M(2π) = 2 c i (2π) =c i (0) {J i } J i = J N i ψ H ψ ik =( 1) N+1+k ψ N+1 i,k
127 h = 3 (N +1) t = π 2 M ij = k ψ N+1 i,k ψ jk = δ N+1 i,j. {0, 1,...N} [ρ SS ch P ]=1 M 0,N+1 =1 F SS =1 h = 3(N +1) U 2 P = ( i) N+1 UP 2 = ( 1) N+1 F SS = [2 M 0,N+1 + M 0,N+1 2 ), F enc = [2 M 0,N+1 2 M 2 0,N+1 M 0,0 M N+1,N+1 + M 0,N i M N+1,i M i,0 2 ]. M 0,N+1 1 J i = 2 1 (i +1)(N +1 i) g κ J 0 = J N = g J 1 = J 2 =... = J N 1 = κ g/κ
128 1/T 1 M 0,N+1 1 N =2, 3 J i = 1 2 (i +1)(N +1 i) N>3 g = g M (N) ω k k N+1 2 h =0 F enc g M N 1/6 τ N 1/r 3 e iπ i 1 j=1 σ+ j σ j
129 XX N =12 90% N =10 98%
130 1/2 H N = γ e B S γn B I + A S z I z + A (S x I x + S y I y ), S 1/2 I A = A = N 1 H N = κ Si z Si+1 z + i=1 N (ω 0 + δ i )Si z, i=1 κ ω 0 δ i a 1 H eff = κsi z Si+1 z + JSNV z (Sa z + Sb z )+ i=1 N 1 i=b κs z i S z i+1, J a b
131 a)! 5-1%3-"617'01-"8234"53'. "!!!"#$%&'( "!!!!!!!!!!!! /&0010"(234 "!!!!)*"+,+-.( " b) J 9" 3 " % " * "!" c) - - N (1,N) (2,N 1) N +1 Q = H CP H CP Q M Q L Q M Q L
132 U eff = e ih eff T /2 S x NV e ih eff T /2 S x NV = e iκ S z i Sz i+1 T U local = e ih eff T e iκ S z i Sz i+1 T = e ijsz NV (Sz a+s z b )T κ(t + T )=2πm m U local N N th (N 1) st N +1 Q n+1 =( H i CP i ) n+1 U local Q M
133 Magnetic field gradient : Nitrogen impurity : Two-qubit NV Register Q L Q M Q L U directed = e ijsz NV Sz N T b H med = J(S z NV 1 + S z NV 2 )S z N b,
134 NV 1 NV 2 N b Q M ( H i CP i ) n+1
135 !"#$%&'()'*+#,-+%%&.'/-0",-1-2'!3/4'51,& '! "! "! "! #! "! $!!!! " "!!!! # #!!!! = %!! " 678'929%&: '! Q k m U p (k )! Q k #! 678'929%&: '! $ A B X U p = X 1 x π CP X 1 CP CP Q k =( H CP) k U (k) p = Q k U pq k n n +1 k = n 1 U swap = HU (k) p H XU (k) p Z HU (k) p H, X x Z z π
136
137 1/r 2 A B a R
138 %! $ " # A B a R λ Ω
139 1/r 6 1/2 H = 2 σi z + Ω 2 i σi x + i i<j C p r i r j p P i P j. Ω C p P i = =(1+σ z i )/2 m s =0 m s =1 H AB = i C p r A r i P p A P C p i + r B r i P p B P i. σa z σz B a R =[ζ(p)(p +1)C p / ] 1/p Ω=0
140 R max p r (r) p r (r) =n exp( nr) n R max = n 1 log N N = C p (a R R max ) p, L L A B E int = E E E + E, E αβ α A β B E int b 2 /L b
141 ε ε ε 1 + ε 2 ε 1 ε 2 ε 1 =exp[ 2 G t g/( λ)] G t g λ ε 1 =exp( c G t g / ) c G 1/L α = c G / = α 0 /L ε 2 = ε 2 (γt g ) γ t g ε 2 =1 exp[ (γt g ) δ ] (γt g ) δ δ
142 γ L γ = γ 0 L/L 0 γ 0 L 0 L 0 a R ε =exp( α 0 /Lt g )+(γ 0 L/L 0 t g ) δ. t opt α γ t opt = δl log[l 0 α 0 /(L 2 γ 0 )]/α 0 ε = ( δ L2 γ 0 log L ) δ 0α 0. L 0 α 0 L 2 γ 0 1/L 2 N a b ψ A,B =( A,B + A,B )/ 2
143 ψ SC = i i Ω(t) = ( ) Ω 0 sin 2 8t/t0 1+16t 2 /t 2 0 (t) = 0 [1 5exp( 4t/t 0 )], t 0 t = t 0 t π = π /E int π H H t g =2t 0 + t π F = ρ 2 AB ρ AB A B G t 0 F =1 cexp( d G t 0 ) c d ρ AB
144 F G t 0 G t 0 N = 34 t 0 Ω 0 p =3 C 3 = 100Ω 0 a 3 0 =2.3Ω 0 b =3a t 0 L/ a R F = 1 2 [1 c exp( d Gt 0 )] { 1+exp [ (γ 0 L/ a R t g ) 3]} δ =3 β t 0 G E int t 0 A B
145 S p =6 p =3 n =43 γ 0 = 10 KHz F =0.95 Ω 0 =2π 3.2 MHz 0 =2π 7 MHz C 3 n 3 =2π 320 MHz a =1µm γ 0 = 100 Hz Ω 0 =2π 80 KHz 0 =2π 170 KHz a =2nm T 2 m s =+1 m s = 1 T 1
146 γ 0
147 r a S =1 W
148 W 2.87 m s = 1 m s =1 m Ω m 0 1 H r = NΩ( 0 W +h.c.) 0 m s =0 W W = i.... N i NΩ/ H r = J W W J = NΩ 2 / m J J V dd W
149 m m>1 0 W Ω ext V dd J V dd Ω ext N =100 r =20nm m s =0, 1 σ α V ij = ( ) 1 3cos 2 µ 2 ϑ ij r i r j 3 { 1 4 [ 1+σ (i) z ][ 1+σ (j) z ] (i) σ + σ (j) } σ (i) σ (j) +, r i µ ϑ ij r i r j H = /2 i σ(i) z +Ω i σ(i) x + i<j V ij 0 m s =1 W H eff = N c µ 2 R 3 ( 1 q, 0 0 q,w +h.c.),
150 N c W 1 q, 0 m s =1 0 R =100nm m 2 m =3 φ ( N 2 N c = i...0 N φ ), i N c N Ω h 100 MHz N c 70 N Ω N c > 50 N c N c Ω NΩ/
151 N c Ω=0 Ω=h 110 MHz N c 70 = h 4 GHz) N c Ω 1 q, 0 m s =1 p q π t π R H eff R r V c t π 1/R 3
152 m s = 1 p q t π 600 µs V c 1/R 3 N N W N T 2 i W [ p W = p T2 1 W σ (i) z W 2] = 4 ( N p T ), N p T2 N
153 N T 2 W T eff 2 T 1 m s =1 m s =0 W m s =1 m s =0 p 1 0 T 1 p 0 1 T 1 p 1 0 T 1 0 m s =0 W 0 p W 0 = p T σ (i) 1 W 2 = p T1 1 0 N, N T W m s =1 T p 0 1 T 1 N p 0 1 T 1 T 1 T 2 T 1 /N T 2
154 R = 100 nm W T 2 T 1 1 T 1
155 t g t π T 1 /N T 2 ε =1 exp[ (4t π /T eff 2 ) 3 ] ε =10 2 T eff 2 =11ms 0 1 W W W 100 khz m s =1 A 2.14 MHz 14 N N N t π =70µs ε =10 2 T eff 2 =700µs ε =10 4 T eff 2 =3ms W
156
157
158
159 I =1/2 S =1 B Ω MW 0 e 1 e Ω RF 1 e t e n π 1 e n e τ π/2 n e e n n e S =1 0 e
160 0 e 1 e I =1/2 15 H e,n = 0 S 2 z + µ e BS z + µ n BI z + AS z I z, 0 =2.87 µ e = 2.8 µ n = 0.43 A =3.0 ẑ n e
161 0 e I z B z, µ 10µ
162 B z (y) = db z dy y + B z,0
163 6B;m`2 93, h?2 `+?Bi2+im`2 7Q` im`2 i2 [m MimK +QKTmi2`X U V irq@ /BK2MbBQM H?B2` `+?B+ H H iib+2 HHQrBM; 7Q` H2M;i?@b+ H2 # b2/ +QMi`QH- r?b+? 2M #H2b 7mHHv T ` H@ H2H QT2` ibqmbx i i?2 HQr2bi H2p2H- BM/BpB/m H TH [m2ii2b `2 QmiHBM2/ BM ;`2v M/ 2 +? +QMi BMb bbm;h2 +QKTmi ibqm H Lo `2;Bbi2`X i i?2 b2+qm/ H2p2H Q7?B2` `+?v- bmt2`@th [m2ii2- QmiHBM2/ BM r?bi2-2m+qkt bb2b H iib+2 Q7 TH [m2ii2bc 2 +? bmt2`@th [m2ii2 Bb b2t ` i2hv K MBTmH i2/ #v KB+`Q@bQH2MQB/ +QM}M2/ KB+`Qr p2 }2H/bX AM Q`/2` iq HHQr 7Q` [m MimK BM7Q`K ibqm i` Mb@ 72` +`Qbb #QmM/ `B2b Q7 bmt2`@th [m2ii2b- i?2`2 2tBbib /m H bmt2`@th [m2ii2 H iib+2 QmiHBM2/ BM `2/X U#V h?2 b+?2k ib+ Lo `2;Bbi2` BKTH Mi ibqm rbi?bm bmt2`@th [m2ii2x hrq `Qrb Q7 BM/B@ pb/m H TH [m2ii2b rbi?bm bmt2`@th [m2ii2 `2 b?qrmx Lo `2;Bbi2`b- +QMbBbiBM; Q7 M 2H2+i`QMB+ U;`22MV M/ Mm+H2 ` Uv2HHQrV btbm `2 /2TB+i2/ rbi?bm bi ;;2`2/ mt@bhqtbm; `` v r?b+? Bb `Qr@ `2T2iBiBp2X AM/BpB/m H `Qrb rbi?bm bbm;h2 TH [m2ii2 `2 bt2+b}2/ #v M BMi2;2` n rbi? n = 1 #2BM; i?2 #QiiQK `Qr M/ n = M #2BM; i?2 iqt `QrX hq +?B2p2 bi ;;2`2/ bi`m+im`2- r2 bt2+@ B7v mmb[m2 BKTH Mi ibqm `Qr rbi?bm 2 +? TH [m2ii2 r?2`2bm bbm;h2 BKTm`BiB2b `2 BKTH Mi2/ M/ bm#b2[m2mihv MM2 H2/X 6Q` ;Bp2M `Qr Q7 TH [m2ii2b- i?2 BKTH Mi ibqm `Qr +Q``2bTQM/BM; iq i?2 H27i@KQbi TH [m2ii2 Bb M 4 R- r?bh2 i?2 TH [m2ii2 iq i?2 BKK2/B i2 `B;?i? b BKTH Mi ibqm `Qr M 4 kc i?bb T ii2`m +QMiBMm2b mmibh i?2 }M H TH [m2ii2 BM ;Bp2M `Qr- r?b+? #v +QMbi`m+iBQM? b i?2?b;?2bi BKTH Mi ibqm `Qr MmK#2`X h?2 BKTH Mi ibqm T`Q+2bb Bb `2T2 i2/ 7Q` 2 +? `Qr Q7 TH [m2ii2b rbi?bm i?2 bmt2`@th [m2ii2 M/ +`2 i2b M `` v Q7 Lo `2;Bbi2`b- r?b+? 2 +? Q++mTv mmb[m2 `Qr BM i?2 bmt2`@th [m2ii2x abm+2 2 +? Lo `2;Bbi2` Q++mTB2b mmb[m2 `Qr rbi?bm i?2 bmt2`@th [m2ii2- i?2 K ;M2iB+ }2H/ ;` /B2Mi BM i?2 y /B`2+iBQM HHQrb 7Q` BM/BpB/m H bt2+i`qb+qtb+ //`2bbBM; Q7 bbm;h2 `2;Bbi2`bX *Q?2`2Mi +QmTHBM; Q7 bt ib HHv b2t ` i2/ Lo `2;Bbi2`b BM /D +2Mi TH [m2ii2b Bb K2/B i2/ #v / `F btbm +? BM / i #mb U.a*"V M/ Bb b+?2k ib+ HHv `2T`2b2Mi2/ #v i?2 +m`p2/ HBM2 +QMM2+iBM; BM/BpB/m H `2;Bbi2`bX h?2 b2+qm/ BKTH Mi ibqm bi2t +Q``2bTQM/b iq i?2 +`2 ibqm Q7 i?2b2?q`bxqmi H M/ p2`ib+ H / `F btbm +? BMbX R98
164 1/2 H int =4κSzS 1 z 2 + (ω 0 + δ i )Sz, i κ ω 0 δ i H drive = i=1,2 2Ω isx i cos[(ω 0 + δ i )t] (x, y, z) (z, y, x) i=1,2 H int = κ(s + 1 S 2 + S 1 S + 2 )+Ω 1 S 1 z +Ω 2 S 2 z. H int Ω 1 Ω 2 κ Ω 1 Ω 2 κ Ω 1 Ω 2 H int = i κ(s+ i S i+1 + S i S+ i+1 )+ i Ω isz i
165 κ 1/2 κ i,i+1 Ω i Ω i+1 H FFST = g(s + NV 1 S 1 N 1 + S + NV 2 S N + )+ i=1 κ(s + i S i+1 + S i S+ i+1 )
166 Ω i Ω j g κ g Ω
167 H FFST g B z (y)
168 N = T1 NV N = T1 NV T N 1 T N T NV 1
169 p SS err N(p SS off + p adia + p dip + p SS T 1 + p SS T 2). ( ) p SS off Ω 2 i g Ω i g p adia ( ) κ 2 p dip Ω i p SS T 1 T 1 p SS T 2 N N N p FFST err p FFST off + p fermi + p g + p FFST T 1 + p FFST T 2. p SS err p FFST err p fermi g/ N κ/n ( g/ N κ/n )2 p g g p SS err t FFST
170 T NV T 1 T 1 10 T 1 50 ɛ 1.4%
171
172 g H = ( ) Ω( ) Ω N S N x +4κS NV z S N z, Ω Ω N B = D = B + 2Ω 0 0 2Ω B Ω H = D D ( + 2Ω2 ) Ω2 1 2 Ω N( + N + N ) +2κ( B D + D B )( + N + N + ), ± N = N ± 2 N S N x 2κ { ( + D + D + ) 2Ω ( D + D ) } ( + N N + N + N ). { D, } g κ Ω
173 κ + κ 2 / 2 0 (α + β ) (α + β D ) π D D D Ω D
174
175
176 1/2
177 6B;m`2 8R, a+?2k ib+ `2T`2b2Mi ibqm Q7 iqtqhq;b+ HHv T`Qi2+i2/ bi i2 i` Mb72` h?2 ;`2v /`QTH2i `2T`2b2Mib k. `` v Q7 BMi2` +ibm; btbmb imm2/ BMiQ i?2 *ag" T? b2x Zm MimK btbm@`2;bbi2`b +QKTQb2/ Q7 i` Mb72` [m#bi U;`22MV M/ K2KQ`v [m#bi U;QH/V `2 `` M;2/ `QmM/ i?2 2/;2 Q7 i?2 k. /`QTH2i M/ +QmTHBM; #2ir22M i?2k Q++m`b i?`qm;? i?2 +?B` H 2/;2 KQ/2X URV "v K T@ TBM; i?2 [m MimK BM7Q`K ibqm QMiQ 72`KBQMB+ r p2@t +F2i U#Hm2V i` p2hbm; HQM; i?2 2/;2- i?2 [m MimK bi i2 + M #2 i` Mb72``2/ iq `2KQi2 `2;Bbi2`X h?2 r p2t +F2i i` p2hb QMHv BM i?2 /B`2+@ ibqm Q7 i?2 #Hm2 ``Qrc i?bb +?B` HBiv T`2p2Mib KQ/2 HQ+ HBx ibqm M/ /2bi`m+iBp2 # +Fb+ ii2`bm;x i bt2+b}2/ ibk2 i i?2 `2KQi2 `2;Bbi2` HQ+ ibqm- i?2 +QmTHBM; Bb im`m2/ QM M/ i?2 r p2t +F2i Bb + Tim`2/ UkVX :Bp2M M M+BHH `v K2KQ`v [m#bi M/ HQ+ H `2;Bbi2` K MBTmH ibqmb- irq@[m#bi ; i2 UjV + M #2 T2`7Q`K2/ #27Q`2 i?2 [m MimK bi i2 Bb i` Mb72``2/ # +F iq i?2 Q`B;BM H `2;Bbi2` M/ biq`2/ U9@8VX h?bb HHQrb 7Q` mmbp2`b H +QKTmi ibqm #2ir22M i?2 K2KQ`v [m#bib Q7 bt ib HHv b2t ` i2/ `2;Bbi2`bX?QM2v+QK# H iib+2 b /2TB+i2/ BM 6B;X 8k (jkd)x h?2 bbq+b i2/ > KBHiQMB M M im` HHv ;2M2` HBx2b i?2 EBi 2p KQ/2H (jrn) M/ 72 im`2b +?B` H btbm HB[mB/ ;`QmM/ bi i2 U*aG" T? b2vh0 = 1! x x 1! y y 1! z z κσi σj + κσi σj + κσi σj, 2 x,x! 2 y,y! 2 z,z! links links UdXRV links r?2`2 1σ `2 S mhb btbm QT2` iq`b U! = 1VX h?2 KQ/2H K v #2 bqhp2/ #v BMi`Q/m+BM; 7Qm` J DQ` M QT2` iq`b- {γ 0, γ 1, γ 2, γ 3 } 7Q` 2 +? btbm- b b?qrm b+?2k ib+ HHv BM 6B;X 8k M/ #v `2T`2b2MiBM; i?2 btbm H;2#` b, σ x = iγ 1 γ 0 - σ y = iγ 2 γ 0 - σ z = iγ 3 γ 0 (jk8- jkd)x h?2 J DQ` M QT2` iq`b `2 >2`KBiB M M/ b ibb7v i?2 bi M/ `/ MiB+QKKmi ibqm `2H ibqm {γ l, γ m } = 2δlm X h?2 >BH#2`i bt +2 bbq+b i2/ rbi? i?2 T?vbB+ H btbm Bb irq@/bk2mbbqm H bm#bt +2 Q7 i?2 2ti2M/2/ 7Qm`@/BK2MbBQM H J DQ` M >BH#2`i bt +2c i?mb- r2 Kmbi BKTQb2 i?2 ; m;2 T`QD2+iBQM- P = 1+D 2 r?2`2 D = γ 1 γ 2 γ 3 γ 0 (jk8)x R8N
178 H γ = i 4 κ i,j Û i,j γ 0 i γ 0 j, Ûi,j = iγ α i γ α j α ij ij Ûi,j Û i,j Ûl,m {U i,j = ±1} {U i,j } γ 0 U i,j 2 w(p) = ij p U i,j p p ij U i,j =+1 γ 0 π/2 w(p) =+1 π π/2 π/2 w(p) = 1 v Q κ i,j Q k,i(iu i,j )Q k,j = δ kk ɛ k H γ = 1 N/2 2 k= N/2 ɛ kc k c k c k = 1 2 j Q k,jγj 0 N k
179 ɛ k = ɛ k c k = c k k>0 H γ = k>0 ɛ k (c k c k 1 2 ), c k c k b U i,j H T = H 0 + H int H int L R H int = S 2 (σz L + σ z R)+g L σ β L σβ a + g R σ η R ση b. S β,η g L g R
180 Ûi,j γ 0 i π π/2 U ij w(p) = 1
181 a b H int = S 2 (iγl 3γ0 L + iγ3 R γ0 R )+g LγL 1γ1 aγl 0γ0 a + g R γr 1 γ1 b γ0 R γ0 b σ x σ x U i,j U L,a U R,b H T = H + H int = k>0 ɛ k (c k c k 1 2 ) + S (c L c L 1 2 )+ S(c R c R 1 2 ) g L U L,a (c L + c L ) i 2 ( k Q k,ac k + k Q k,a c k ) g R U R,b (c R + c R ) i 2 ( k Q k,bc k + k Q k,b c k ), c L,R =1/2(γL,R 0 iγ L,R 3 ) c L,R =1/2(γ L,R 0 + iγ L,R 3 ) σ z
182 L R S > 0 g L,g R < S c k S k ɛ k H eff = i g L Q k,a c L 2 c k i g R Q k,b c R 2 c k + h.c. τ ɛ κ/l l τ l/κ
183 61 40 y k y a = π b =0.46κ 0.14κ 0.17κ S g L (t) g L (t) = vf(t), dt t f(t ) 2 f(t) v g R (t) S l
184 T N v n p e v/t n p π N v π ξ a a π
185 v H p H T H p H e = v dp 2π pc pc p = v dx γ(x)(i )γ(x),
186 c p = c p {c k } p {γ(x),γ(y)} = δ(x y) c p H e = λ dx γ(x)(i )γ(x)(i ) 2 γ(x)(i ) 3 γ(x), λ Γ int p ɛ p k B T Γ int p Γ int p λ2 p 13 + λ2 p 11 T 2 + O(T 4 ). v v κ λ κ( κ κ )2 a 7 Γ int p κ2 S ( κ κ )4 (ap) 14 S = vp p<1/a Γ dec p σ α i Γ dec p S(ω)
187 e d/ξ d i S(ω 0 ) e ω 0/k B T ω 0 =2 v S l Γ dec p e S/k B T + le V /k B T. S(ω) 1 ω 2 +1/t 2 c t c Γ dec p 1/ 2 v v 1/t c
188 e S/k B T S l
189 L R R L
190
191
192 N ρ = i ρ i ρ i Q = { +,, + i, i, 0, 1 } ρ F tol ρ i M i
193 F i =1/ Q ρ i Tr[ρ i M i (ρ i )] p h = 1 Q Tr[P acc M(ρ)] 1 e ND(F exp F tol ), ρ Q Q = Q N P acc M = i M i F exp =1/N i F i D F tol F tol N F tol N F tol N (2F tol 1)N 2F tol 1 p d = 1 Q ρ Q Tr [ P 2 acct (ρ) ] e ND(2F tol 1 2/3), T 2F tol 1 > 2/3 5/6
194 a b original qticket:... cloned qticket:... F tol N " 1 " 2 " 3 minimum overlap " N #2 F tol N " 1 " 2 " 3 " N #1 " N 1" " N #2 " N #1 " N "# +" 0" " Z challenge questions " X F tol F tol N (2F tol 1)N Ftol cv = 1+1/ 2 2
195 X Z { 0, +, 0,, 1, +, 1,, +, 0,, 0, +, 1,, 1 }. n r n r 2 X Z Ftol cv r n F exp >Ftol cv n
196 r p cv h ( rd(fexp F cv 1 e )) n tol. F cv tol > 1+1/ / Ftol cv p cv d ( ) 2 v ( 2 1/2+e rd(f tol 1+1/ 2 2 )) n, v F dishonest <F tol <F exp
197 , 0 0, + 1, + 0, + 0, + +, 1, 0 1, + Z X 0, 0 0, 1 1, 1 0, 1, + +,, + +, n = 4 r =2 8 F tol =3/4 F tol =3/4 F tol > 1/2+1/ 8
198 c
199 c (c+1)(c+2) X 1,...,X n {0, 1} δ i S {1,...,n} Pr [ i S X ] i i S δ i Pr[ n X i γn] e nd(γ δ) i=1 δ := n 1 N i=1 δ i γ δ γ 1 D(p q) =p ln p q +(1 p)ln 1 p 1 q (X =1)=p (X =1)=q
200 P ρ acc N F tol ρ = N i=1 ρ i 0 F tol 1 P ρ acc = N ( bi ρ i + b i ρ i ). b: b 1 F tol N i=1 b {0, 1} N N b 1 = N i=1 b i b i =1 b i ρ i = ρ i b 1 F tol N 1 b M i F i F exp =1/N i F i F exp >F tol p v 1 e ND(F tol F exp). X =(X 1,...,X N ) Pr[ X = b]= 1 Q = N i=1 [ Tr M(ρ) ρ Q N ( bi ρ i + b ) ] i ρ i i=1 1 Tr [ M i (ρ i )(b i ρ i + 6 b i ρ i ) ] ρ i Q
201 X i Pr[X i ]=F i 1 Q ρ Q Tr[P accm(ρ)] ρ = Pr[ N i=1 X i F tol N] L 1 µ
202 (a) (c) (b) (d) ±1 { +1, 1 } S =1 m s =0, ±1 E B ( =1) H NV =(D 0 + d E z )S 2 z + µ B g s S B d [ Ex (S x S y + S y S x )+E y (S 2 x S 2 y) ],
203 D 0 /2π 2.88 g s 2 µ B d d ±1 B = g s µ B B z / E ±1 E = E 0 (a + a ) a ω m E 0 ±1 0 = B ω m D 0 ±1 0 H i = g ( σ + i a + a σ i ) σ ± i = ±1 i 1 i g J z = 1 2 i 1 i 1 1 i 1 J ± = J x ± ij y = i σ± i H = ω m a a + B J z + g ( a J + aj + ), g
204 L w, h ( ) 1/2 g 2π 180 L 3 w GHz, ρe ρ E (L, w, h) =(1, 0.1, 0.1) µ ω m /2π 1 g/2π 1 g e /2π 10 T 2 η = g2 T 2 γ n th γ = ω m /Q n th =(e ω m/k B T 1) 1 T Q =10 6 T 2 =10 T =4 η 0.8 g = B ω m H ( ) e R He R R = g a J aj + (g/ ) 2 H eff = ω m a a + ( B + λa a ) J z + λ 2 J +J, λ =2g 2 / J + J = J 2 J 2 z + J z J
205 J 2 z ψ 0 x J x ψ 0 = J ψ 0 J 2 y = J 2 z = J/2 J 2 z z J z J 2 min = 1 2 ( V + V 2 + V 2 yz ξ 2 = 2J J min 2 J x 2, ) V ± = J 2 y ± J 2 z Vyz = J y J z + J z J y /2 ξ 2 < 1 H eff [ ρ = i λ 2 J z 2 + ( B + λa a ) ] J z,ρ + 1 D[σ 2T z]ρ i 2 +Γ γ ( n th +1)D[J ]+Γ γ n th D[J + ], i D[c]ρ = cρc 1 2 ( c cρ + ρc c ) T 1 2 λ/2 B T 1
206 Γ γ = γg 2 / 2 n = a a n ψ 0 N =100 n th T 1 2 Γ γ ξ 2 Γ γ T 2 N J 1 n th 1 ξ 2 4Γ γ n th Jλ 2 t + t T 2. t ξ 2 opt 2 Jη, t opt = T 2 / Jη J ξopt 2 J 2/3 n = a a J z
207 1 0.5 ξ (a) 10 n th = J λt ξ 2 opt 0.1 (b) N N N N = 100 T 2 = 10 n th n th =1 T 2 =1 ω m /2π =1 g/2π =1 Q = 10 6 T 2 H int (t) =λj z f(t)δn(t). f(t) J z J z π δn(t) =n(t) n n
208 n S n (ω) = dte iωt δn(t)δn(0) J + (t) = e χ e iµ(jz 1/2) J + (0), J 2 +(t) J + (t)j z (t) χ µ dω χ = λ 2 F (ωτ) 2π µ = λ 2 dω 2π ω 2 Sn (ω), K(ωτ) A ω 2 n (ω), S n (ω) =(S n (ω)+s n ( ω)) /2 A n (ω) =(S n (ω) S n ( ω)) /2 F (ωτ) = ω2 dte iωt f(t) 2 τ 2 π K(ωτ) µ F K F M =4 S n (ω) =2γ n th ( n th +1)/(ω 2 + γ 2 ) ω =0 χ 0 (t) = 1λ2 n 2 2 th t2 n th 1 T2 2/λ n th t = t opt n th > J M π
209 t χ th λ 2 γ n 2 th t3 /M 2 Γ γ T 1 2 M n th γt2 ω dr = ω m + δ S n (ω) ω = ±δ n dr n th n dr ( n th +1) n dr t/m =2π/δ π χ dr ( λ δ ) 2 ndr n th γt µ λ2 δ n drt n dr n th χ th Γ γ n dr M =4 g J eff <J J 1 g i i g i/ i g2 i i g2 i / i g4 i g i
210 Sn(ω) f (t) t/τ F (ωτ) ξ (a) 0.1 (b) K (ωτ) δ 0 δ ω J λt ξ 2 min (c) F K M =4 f(t) M =4 n th = 10 n dr = 10 3, , 10 6 n th = 50, 10 M =4 g/2π =1 T 2 = 10 N = 100 ω m /2π =1 Q = 10 6 n dr (1, 0.1, 0.1) µ N N eff 100 η 1 H int = λ ( σ 1 + σ2 +h.c. )
211 4
212 σ y Q = ν/ ν ν ν ν
213 Excitation Laser Si Photodiode Diamond Film Bragg Mirror Microwave Line µ > 0 ±
214 H gs =(D gs + d σ z )S 2 z + gµ b S B + d σ x (S x S y + S y S x )+d σ y (S 2 x S 2 y) d, C 3v D gs µ b S k k = {x, y, z} σ D gs S z ω 0 ±1 ω D gs ω D gs B 1 =2b 1 cos(2πωt)ˆx H gs V = e 2πiωtS2 z H gs =(D gs + d σ z ω)s 2 z + gµ b B z S z + gµ b b 1 S x
215 ρ = 1 i [H gs,ρ]+ k L k ρl k 1 2 L k L kρ 1 2 ρl k L k ρ L k r k I Ω=gµ b b 1 =D gs ω F (I,Ω, ) = γρ ss 22 + γ2 κ+γ ρss 33 ρ ss 22 ρ ss 33 F σ y (τ) = πQ (S/N) τ τ S/N C 1
216 A V 3 E 3 A I D es γ orbital states electron spin sublevels D gs κ λ 1 E 1 A1 S B 9.5 x 105 I 0 9 F(!) (photons/sec) C ν Detuning from resonance,! (Hz) 3 E 3 A 1 E 1 A I γ κ λ S z 0 ±1 C 1 T2 =88 σ y (τ) = τ 1/2 Q S/N
217 D gs T δω δωt T 1 T T c T c T c T 2 m f =0 π T T 2 π ) 2 x ) τ π x τ π ) 2 x θ ) φ θ φ t p θ = gµ b b 1 t p Ω 1 gµ b b 1 (D gs Ω),gµ b B z
218 U echo = e i π 2 Sx e i(δωs2 z +bs z )τ e i π 2 Sx e i π 2 Sx e i π 2 Sx e i(δωs2 z +bs z )τ e i π 2 Sx = WW W W = e i π 2 Sx e i(δωs2 z +bs z)τ e i π 2 Sx = e i(δω ˆX bs y )τ, W W = e i π 2 S x e i(δωs2 z +bs z )τ e i π 2 S x = e i(δω ˆX+bS y)τ, ˆX ˆX = [ ˆX,S y ]=0 W W U echo = e 2i(D gs Ω)τ ˆX ˆX 0 π 4 ˆx U 45 = e i π 4 S y U 45 0 = 1 2 ( 0 i + + ±1 S z U echo U 45 0 = 1 ( ) ie iδωτ + + e iδωτ 0. 2 Sz 2 δν S z B A S z I z π/2 π/4 S z
219 Optical Pumping Z π π π 4 T T 4 TF } S 2 z X Y S z S z S 2 z S z S 2 z Sz 2 2T S z ψ 0 = m s =0 U echo ψ f = U echo U 45 ψ 0 = 1 2 sin(φ) cos(φ)( ) φ =(D gs ω)t = δωt ˆM ˆM = a b ( ) a b ˆM
220 ψ f δω ω 0 = 1 ω 0 ˆM ˆM / ω ˆM 2 = ˆM 2 ˆM 2 2a 3b ˆM M τ = M T δω ω 0 M = ξ D gs Tτ ξ 5 b 0 a λ/γ T = T 2 1 D gs =2870 δω/ω 0 = / τ 0.2% N 1/ N N µ 3 3 1/ N / τ / τ 100µ 1 2 σ pulsed y / τ
221 T 1/2 2T e (2T/T 2) n n 3 T 2 T e n =1 2 S/N T e D gs 1µ
222 T 2, 10 20µ D gs dd gs /dt = 74.2(7) dd gs /dt 100 dd gs /dt =100 D gs dd gs /dt 75 dd gs /dt
223 δ D gs V ij S i S j = κ 2 3ˆri ˆr j δ ij r 3 S i S j S i κ a r (1) = aŷ r (2) = 3a ˆx a 2 2ŷ r(3) = 3a a ˆx 2 2ŷ H = V ij S i S j = 3κ 4a 3 (S2 z 2/3). ɛ kl H = S i S j V ij = κ 2 ( ) 3ˆr i ˆr j δ ij ɛ r k r 3 kl ˆr l S i S j = 3κ 2a 3 [ 3 4 (ɛ xx + ɛ yy )(S 2 z 2/3) (ɛ xx ɛ yy )(S 2 x S 2 y) (ɛ xy + ɛ yx )(S x S y + S y S x ) 1 2 ɛ zx(s x S z + S z S x ) 1 2 ɛ zy(s y S z + S z S y )]. α = 3 4 (ɛ xx + ɛ yy ) 3κ 2a 3 3κ 4a 3 a =2.38 α = 4.32(ɛ xx + ɛ yy ) =2.88
224 (a) "(T) (b) area A!d, Ed Diamond 1 Diamond 2 "0 clock 1 clock 2 (c)!1, E1 clamp1 Diamond clamp2 z T0 T!2, E2 Pz=Fz/A=Y! #T dd gs /dt η 1,2 E 1,2 ɛ xx = ɛ yy = ɛ zz dd gs dt ( ) =( ) 15, 1K 5 δ 3 ddgs dt
225 E 1 η c1 E 2 η c2 <η c1 T ɛ 1,2 η d (1 + η c1,2 E c1,2 /E d ) T T T 0 ω 0 T T
226 ω 1 (T ) = ω 0 + β 1 T ω 2 (T ) = ω 0 + β 2 T β 1,2 = dɛ dd gs dt dɛ = η d (1 + η c1,2 E c1,2 /E d )(dd gs /dɛ) τ =0 T 0 T 0 t φ 1,2 (t) =ω 0 t + t 0 β 1,2 T (t )dt ± φ 0, φ 0 = ξ t/ T 2,N φ(t) =φ 2 (t) φ 1 (t) = t 0 β 1,2 T (t )dt ± 2 φ 0 β 1,2 β 2 β 1 φ 1 (t) φ 2 (t) t φ 1(t) = φ 1 (t) β 1 T (t )dt 0 ( t ) = φ 1 (t) β 1,2 T (t )dt 0 = φ 1 (t) β 1 β 1,2 ( φ(t) 2 φ 0 ). β 1 β 1,2 t t ω 1 ω 1 = = ( ξ β1 (1+2 T2 NtD gs β 1,2 ) 2 ) 1/2 ( ) ( ( ) ) 2 1/2 ω β ω T =T 0 β 1,2
227 D ZFS (khz) (a) (b) (c) Brass Tungsten khz, 6.92 mk Temperature (mk) D ZFS (khz) T=5 mk T=10 mk Position (mm) diamond d clamp D gs β 1,2 β 1 ν beat 10 Q 10 6 D gs β 1,2 η d (1 + η c1,2 E c1,2 /E d )/( 75 T 0.01 dd gs /dt
228 D gs σ ɛ F ijkl S i S j ɛ kl F Sz 2 (D gs + A 1 (ɛ xx + ɛ yy )+A 2 ɛ zz )(S 2 z 2/3) A 1 A 2 ɛ xx = ɛ yy = ɛ zz dd gs /dt =2A 1 + A 2 T T 0 L d L = L d η d T P = E d L d /L = E d ε d = E d Tη d L T 0.01K
229 Al + ion clock Ensemble NV Echo (0.01ppb x 1mm 3 ) TXCO Commercial Rb Single NV Echo Rb Chip Clock Ensemble NV CW SAW Oscillator Allan Deviation after 1s averaging Single NV CW / f N 2
230 σ y = τ 1/2 9 /
231 200 m s =0 m s = ±1 d /dt = (2π)77 / N
232 " #!!"#$%&'( )%*%&+( Temperatureaccuracy Kelvin CdSe QD SThM Nano Diamond Raman Liquid crystal Infrared Green FluorescentProtein Seebeck! "!! "!,-./0'( )%*%&+( #! " " ProjectedNano Diamond Bulk Diamond Sensor size um ±1 0 (T ) δ
233 ! 1.1 " !"#$!" "!" Normalized fluorescence population τ (us) T ( o C) 2τ 50 2π 2τ = 250 µ 2τ = 50 µ 2τ 2τ m s =0 m s = 1 η = C d /dt 1 T Nt, T t C T C /
234 ω 1 2 ( 0 + B ) B = 1 2 ( ) τ 2π +1 1 τ ± % τ η =(9± 1.8) / 2τ =250µ δt =1.8 ± 0.3 2τ (2d /dt 2τ) 1 2τ < 2τ 1 µ
235 N 500 = nm 2.5
236 " # Normalized fluorescence data max. slope meas. freq. y ( µm) ! $ " #!"#$ % & ω (GHz) x ( µm)! 4 $ off AU Fit on AU Fit " theory NV data T (K) T (K) 5! # $ % & laser power ( µw) distance ( µm) µ
237 0.8 ± 0.1 µ 0.8 µ δt =(44± 10) T (r) = Q 4πκr Q κ r 72 ± µ 1 T =( 20 ± 50)
238 12 µ 0.5 ± µ 3.9 ± µ /
239 y ( µm) " x ( µm) # $ +$'()*!"#$$$$$$$!"%$$$$$$$$!#$$$$$$$$%$$$$$$$$$#$$$$$$$$"%$$$$$$$"#!" &'()#$!"$ &'()#$ &'()#%!"%!"#$$$$$$$!"%$$$$$$$$!#$$$$$$$$%$$$$$$$$$#$$$$$$$$"%$$$$$$$"# & '()* T K Pos 1 Pos 2 y ( µm) &'()! T (K) !"#$ Au Fluorescence (kcps) *#+#$%-. /#+#,15#3,1%#4 y ( µm) !"% *#+#$%,-. /#+# 60 /#+#012#3,1$# x ( µm) x ( µm) /
240 50 µ 5 =2.87 f 1,2 f (ω )+ f ω ω f 3,4 f (ω + )+ f ω ω+ ( ) δω + δb + δt d dt ( ) δω δb + δt d dt δt = δω (f 1 + f 2 ) (f 3 + f 4 ) d /dt (f 1 f 2 )+(f 3 f 4 ), ω ± δω δb
241 C 0.03 δt σ δt = σ/(c d dt 2τ) c 2τ t<30 s t η = δt t m 1 δt = N 1 ΣN i=1 (T i mp i ) 2 T i P i σ (δt) =δt 1 2 Γ 2 (n/2) Γ( ) N 1 Γ 2 ((n 1)/2)
242 9 / 250 µ 13 T 1 / µ / n 200 µ B µ 50 µ
243 2
244 S 1,S 2 R H 12 = ɛ 1 S z 1 + ɛ 2 S z 2 + t 12 (S + 1 S 2 + S 1 S + 2 )+V 12 S z 1S z 2 ɛ i W t 12,V 12 R R t 12,V 12 ɛ i W t 12 = = S z =0 δ a = ɛ 1 ɛ 2 δ a t a = t 12 τ α a, S z =0
245 (a), (b) r 1 r =, =, t R 2 = (c) a δ a + δ b + V ab,,, δ b δ a V δ ab a δ b V ab, = 3 r 3 r 4 4 b, (δ a + δ b )+V ab R 1 S 1 S 2 a S 3 S 4 b t a,t b H ab H a = δ a τ z a + t a τ x a τ x a V 12 S z 1S z 2 S z =0 a =12 b =34 R 1 R 2 t(r 2 ) ɛ i W a b S z a =0 S z b =0 H ab = δ a τ z a + t a τ x a + δ b τ z b + t b τ x b + V ab τ z a τ z b V ab = V 13 V 14 V 23 + V 24 τa z = S1 z = S2 z H ab H ab
246 R 1,R 2 V ab 0 t a/b 0 τ z δ a/b t a/b t 2 a + δ 2 a, t 2 b + δ2 b V ab t a t b µ α µ z H ab τ µ O(1) τ x τ z H = H ab + H cd + H int = ab µ z ab + cd µ z cd + V αβ µ α abµ β cd, α,β {x,z} H int = V ac τ z a τ z c + V ad τ z a τ z d + V bcτ z b τ z c + V bd τ z b τ z d µ V (r) 1/r 1/r 3
247 V (r) 1/r β V ab = V 13 V 14 V 23 + V 24 ( 1 = 1 ) ( ) R β 13 R β 14 R β 24 R β 23 ( ) ( ) 1 = R 2 + r 4 r β R r 3 r 1 β R 2 + r 3 r 2 1 β R 2 + r 4 r 2 β 1 ( ) β 2r3 r 1 +2r 4 r 2 2r 4 r 1 2r 3 r 2 R2 1. R β 2 R R β+2 2 R 1 <R 2 /2 R 2 1 R ij V ab = V 13 V 14 V 23 + V 24 a b V ab R 2 1/R 5 2 V ab N 2 (R 1,R 2 ) V/R β 2 VR 2 1/R β+2 2
248 R 1 R 2 N 2 (R 1,R 2 ) (n 1 (R 1 )R2) d VR2 1/R β+2 2 t/r1 α R d (β+2) 2, n 1 = ρn 1 n 1 (R 1 )R d 2 R 2 2R 2 VR2 1 /Rβ+2 2 t/r1 α R 1 R 2 d>β+2 R 2 V (R 2 ) t(r 1 ) V (R 2 ) t(r 1 ) R2 1 /Rβ+2 2 1/R1 α 1/10 R 2 R α+2 β+2 1 N 2 (R 1,R 2 ) R1 d+2 (R α+2 β+2 1 ) d (β+2) α+2 d α+d β+2 = R1. d> α(β+2) α+β+4
249 N 3 (R 1,R 2,R 3 ) (n 2 (R 1,R 2 )R d 3) Ṽ/Rβ 3 Ṽ/R β 2 =(n 2 (R 1,R 2 )R3) d ṼR2 1/R β+2 3 ṼR1/R 2 β+2 2 = R 2d α+2 1 R d 2 R d β 2 3 n 2 = n 1 N 2 R 3 R 1,R 2 R 1 R 2 R 3 d>(β +2)/2 R 1 R (β+2)/(α+2) 2 R 2 R 3 N 3 V σ z α>β+4 R 1 R 2 R 3 α>β R 2 R 1 R β+2/α+2 2 R 1 R β/α 2 R <R 2 R 2 O(1) R 1 R <R 2
250 R N 2 (R 1, R) ρn 1 (R 1 ) R d R d α 1 R d. O(1) R R α/d 1 1 R 2 V (R 2 ) t(r 1 ) R >R 2 R = R 2 R 1 R = R 2 V R <R 2 R 2 R R 2 R α/d 1 1 R α β 1 d c = αβ α+β d< αβ α+β R 2 O(1) N 2 (R 2 ) 1 R 2
251 R 2 N 2 (R 1,R 2 ) R 2 α = β R 1 R 2 R 2 N 2 (R 2 ) 1 1 N 2 (R 2 )=ρ 2 R 2d β 2 V W = R2d β2 = 1 W ρ 2 V = 1 1 ρ 2 a β 0 W V/a β 0 D = W V/a β 0 ρ 1/a d 0 R 2 a 0 D 1/(2d β), d = β =3 R 2 a 0 3 D d =2 R 2 a 0 D α = β =3 d c =1.5 D>1 d c α = β =3 d z i d z j
252 i<j d z i d z j r 3 ij = i<j (d s i + d a i σ z i )(d s j + d a j σ z j ) r 3 ij = i<j (d s ) 2 r 3 ij + i<j d a d s (σ z rij 3 i + σj z )+ i<j (d a ) 2 σ z rij 3 i σj z, d z = d s + d a d z = d a d s ɛ i = i j d a d s i ɛ rij 3 i = j i d a d s Q rij 3 j = ν da d s a 3 0 l lat 1 ν l 3 Q j =1 0 δɛ 2 i = ɛ2 i ɛ i 2 ɛ 2 i = ( )( d a d s d j i k i Q a d s rij 3 j Q rik 3 k ) Q j Q k = νδ jk + ν 2 (1 δ jk ) ( ) 2 [ ɛ 2 i = (ν ν 2 ) 1 l lat + ( ν ) 1 2 l 6 l lat ] l 3 d a d s a 3 0 W = ɛ ɛ 2i = 2i ɛ i 2 = da d s (ν ν a 3 2 ) 1 0 l, 6 l lat ν 1 W ν da d s ρ ν/a 3 0 W = da d s (ν ν a 2 ) 1 3 l lat 0 l 6 a N 2 (R 2 )=ρ 2 R 2d β 2 V W = R2d 32 = 1 W ρ 2 V = 1 1 ρ 2 a 3 0 d a d s (ν ν a 2 ) 3 l lat 0 V/a l 6.
253 V (d a ) 2 ( d s 1 R 2 a 0 (ν ν d a ν 2 ) ) 1 2d l 6 l lat ν 1 ( ) 1/3 d d =3 R 2 s a0 d a / ν d =2 R 2 ds d a a 0 /ν 3/2
254 H B = ij t ija i a j i j V ijn i n j X Y (Θ 0, Φ 0 ) = s 1, 1 + v 1, 1 + w 1, 0 s =Ω 2 Ω 4 / Ω v =Ω 1 Ω 3 / Ω w = Ω 1 Ω 4 / Ω i j R =(R, θ, φ) {x, y, z} H = 1 6 4πɛ 0 R 3 2 ( 1) q C q(θ, 2 φ)tq 2 (d (i), d (j) ), q= 2 C k q (θ, φ) k z q T 2 2 ( ) T±2(d 2 (i), d (j) )=d (i) ± d (j) ± T±1(d 2 (i), d (j) )= d (i) z d (j) ± + d (i) ± d (j) z / 2
255 ( T0 2 (d (i), d (j) )= d (i) d (j) + +2d (i) z d (j) z ) + d (i) + d (j) / 6 d ± = (d x ± id y )/ 2 1, 0 1, ±1 T 2 ±1 t ij i j T 2 0 i j = 2 3 [d2 00w i w j 1 2 d2 01(v i v j + s i s j )], i j T 2 +2 i j = d 2 01(v i s j ), i j T 2 2 i j = d 2 01(s i v j ), d 00 = 1, 0 d z 0, 0 d 01 = 1, ±1 d ± 0, 0 t ij V ij V ij = i j H dd i j + i j H dd i j i j H dd i j i j H dd i j i d i = d 1 ( s i 2 + v i 2 )+µ 0 w i 2 d 1 = 1, ±1 d z 1, ±1 µ 0 = 1, 0 d z 1, 0 1, 0 V ij
256 ij d i j d z d z (d +d + d d + ) i j = d 2 0, i j d z d z (d +d + d d + ) i j = d i d 0, i j d z d z (d +d + d d + ) i j = d 0 d j, i j d z d z (d +d + d d + ) i j = d i d j 1 2 µ2 01(s i wi w j s j + w i vi v j wj + ) i j d + d + i j = µ 2 01(s i wi w j vj + w i vi s j wj ), i j d d i j = µ 2 01(w i s i v j wj + v i wi w j s j), d 0 = 0, 0 d z 0, 0 µ 01 = 1, ±1 d ± 1, 0 1, 0 1, ±1 H dd t ii = j i ( i j H dd i j i j H dd i j ) t ii 2B {a, b, A, B} a A b B t ij V ij g 1, g 2 w t ij V ij a A b B g 2 w a/b = w A/B w a/b = w A/B
257 I 1 =4 I 2 =3/2 H Q , ±1 T±2 2 H dd Ω M H hf {a, b, A, B} A H hf A = a H hf a = B H hf B = b H hf b 10 3
258 A B t ii E(R, t) =E(R)e iωt + ˆX H lattice = E(R) α(ω)e(r) E(R) = E(R) p β p(r)e p e p α(ω) H lattice = E 2 (R) [ 2α α 3 +(α α ) p C 2 pγ p ] α α γ 0 = β 0 2 1/3 γ ±1 =1/ 3(β0β ± β β 0 ) γ ±2 = 2/3β β ± [ ] H lattice = E 2 2α α (R) +(α α ) 0, 0 C0 2 0, 0 γ 0 3 H lattice = E 2 (R)[ 2α α 3 +(α α ){γ 0 ( s 2 1, 1 C 2 0 1, 1 + v 2 1, 1 C 2 0 1, 1 + w 2 1, 0 C 2 0 1, 0 )+γ 2 sv 1, 1 C 2 2 1, 1 + γ 2 s v 1, 1 C 2 2 1, 1 }]. δe = H lattice H lattice A B {s, v, w} t ii
259 σ + π σ γ ±2 γ ±1 =E 1,0 E 1,1 H lattice ˆx ŷ ẑ λ 0 {a, b, A, B} λ L = R 0 λ 0 λ L λ L k ˆX Ŷ λ L k ( ˆX ± Ŷ ) 2λ L ˆk ẑ Ω 2 Ω 3 Ω 1 =Ω 4 =0 Ω 1 =Ω 4 Ω 2 =Ω 3 =0 M Θ 0 =0.68, Φ 0 =5.83
260 k x k y Θ 0 =0.05 E 32 Θ 0 =1.05 E 28 Θ 0 =0.68 E 36 Θ 0 =0.25 E 40 {θ a,θ b,φ a,φ b,α a,α b,γ a,γ b } = {0.53, 0.97, 1.36, 3.49, 2.84, 2.03, 4.26, 3.84} s i =sin(α i )sin(θ i ) v i =sin(α i )cos(θ i )e iφ i w i =cos(α i )e iγ i ν =1/2 N s =24 {Θ 0, Φ 0,θ a,θ b,φ a,φ b,α a,α b,γ a,γ b } = {0.65, 3.68, 2.4, 2.97, 6.06, 4.1, 0.97, 2.74, 3.44, 1.74} f 7 A B a b γ A = π + γ a γ B = π + γ b w a/b = w A/B E 8 ν =1/2 Θ 0
261 40 87 Θ 0 A B d 00 = d 01 1, ±1 s i s i d 00 /d 01 v i v i d 00 /d 01 (0, 0) ( π, 0) E < 4 A B
262
263 I(r) = β2 4π 0 [G 0 (r; z)g 0 (r; z)]dx G 0 (r; z) = d 3 k z+ɛτ z+ τ x z 2 ɛ 2 2 G 0 (r; z = ix) = 2πρ 0 k f r e 2 +x 2 /v f r (cos(k f r) ) 2 + x 2 τ z +sin(k f r)[ix + τ x ]. 2 + x 2
264 [G 0 (r; z)g 0 (r; z)] I(r) = = k f r 0 x dx e 0 β 2 π(k f r 0 ) 2 E f β 2 [ 2 + x 2 cos(2k f r 0 )] π(k f r 0 ) 2 (x ) [ cos(2k f r 0 ) 0 dx e k f r 0 x E f ] +2 2 sin 2 (k f r) k f r 0 x dx e E f 0 (x ) x x I(r) = β 2 cos(2k π(k f r 0 ) 2 f r 0 ) 0 dx [ e k f r 0 x 2 +1 E f ] +2sin 2 (k f r) 0 k f r 0 x 2 +1 E f dx e (x 2 +1) dx [e k f r 0 ] x E f = E k f r 0 f 1 k f r 0 e E f 0 dx [ e k f r 0 x 2 +1 ] E f = E f k f r 0 e k f r 0 E f [ ] kf r 0 F 1 E f F 1 F 1 [α] =α 0 dxe α( x ). k f r 0 x 2 +1 dx e E f 0 (x 2 +1) = π k f r 0 [ ] 2 e E kf f r 0 F 2 E f
265 F 2 F 2 [α] = 2 π 0 x dx e α( ). (x 2 +1) I(r) = E fβ 2 π(k f r 0 ) cos(2k fr 3 0 )e k f r 0 [ ] E kf f r 0 F 1 + β2 = E [ fβ 2 π(k f r 0 ) cos(2k fr 3 0 )e 2r 0 2r0 ξ F1 ξ k f r 0 E f (k f r 0 ) 2 sin2 (k f r)e E f ] [ + β2 (k f r 0 ) 2 sin2 (k f r)e 2r 0 2r0 ξ F2 ξ [ ] kf r 0 F 2 E f ] F 1 F 2 F 1 [α] =α 0 dxe α( x ) 1.25(α +0.65) 1/2 F 2 [α] = 2 π 0 x dx e α( ) (x 2 +1) 0.8. (α +0.65) 1/2 [G, (z) G (0) (z)] = [SΠ+SΠSG + SΠSGSG +...]= [SΠ(z)(1 SG(0) (z)) 1 ]. S S
266 SC Interaction (khz) Interaction Strength Hz 6! ! Full SC Correction Perturbative SC Correction β =0.01 0! 3! 5! 7! Distance between spins nm R (nm) β =0.01 =0 S [SΠ(z)(1 SG (0) (z)) 1 ] [SΠ(z)SG (0) (z)]. Π(z) G(z) [SΠ(z)SG (0) (z)] = n,m Ψ n S Ψ m Ψ m S Ψ n. (z ε m ) 2 (z ε n ) E tot +iλ 0 iλ = = iλ iλ iλ dɛ 4π 2Re[ iɛ (iɛ ε m ) 2 (iɛ ε n ) ] ɛdɛ ɛ 4πi (iɛ ε m ) 2 (iɛ ε n ) dɛ 4π ɛ (ɛ + iε m ) 2 (ɛ + iε n ). ±i iε m,n iλ
267 iλ iε n iλ dɛ ɛ iλ 4π (ɛ + iε m ) 2 (ɛ + iε n ) = 1 ε n (ε n Λ). 2 (ε n ε m ) 2 m iλ dɛ ɛ iλ 4π (ɛ + iε m ) 2 (ɛ + iε n ) = 1 ε n (ε n Λ) + ε m (ε m Λ) 4 (ε n ε m ) 2 = 1 (ε n Λ) 4 (ε n ε m ) = 1 4 iλ iλ dɛ 1 2π (ɛ + iε m )(ɛ + iε n ). 4δE tot =2 +iλ 0 0 dɛ 4π 2 [i [SG(0) (iɛ)sg (0) (iɛ)]] dɛ 4π 2 [i [SG(0) (iɛ)sg (0) (iɛ)]] iλ 0 dɛ 4π 2 [i [SG(0) (iɛ)sg (0) (iɛ)]], G σσ LL (z) Gσσ LR (z) Πσσ LL (z) Πσσ LR (z) G σσ LL (z) Gσσ LR (z) Πσσ LL (z) Πσσ LR (z) L R G σσ LL (z) =Gσσ RR (z)
268 G σσ LR (z) =Gσσ RL (z) G σσ LL (z) = d 3 1 k z 2 2 ɛ 2 z ɛ k k z + ɛ k = ρ 0 2 z 2 z z G σσ LR (z) G σσ LR(z) = d 3 1 k z 2 2 ɛ 2 z ɛ k k z + ɛ k e ik r 0, r 0 = r L r R G σσ LR (z) = 2 z 2 r v 0 f ρ 0 e k f r 0 2 z 2 z sin(k fr 0 )+ 2 z 2 cos(k f r 0 ) sin(k f r 0 ) sin(k f r 0 ) z sin(k f r 0 ) 2 z 2 cos(k f r 0 ). Π σσ LL (z) Π σσ LL (z) = ρ 0 ( 2 z 2 ) 3/2 z z. k f r 1
REPORT DOCUMENTATION PAGE
 REPORT DOCUMENTATION PAGE Form Approved OMB NO. 0704-0188 The public reporting burden for this collection of information is estimated to average 1 hour per response, including the time for reviewing instructions,
REPORT DOCUMENTATION PAGE Form Approved OMB NO. 0704-0188 The public reporting burden for this collection of information is estimated to average 1 hour per response, including the time for reviewing instructions,
A Classical Perspective on Non-Diffractive Disorder
 A Classical Perspective on Non-Diffractive Disorder The Harvard community has made this article openly available. Please share how this access benefits you. Your story matters. Citation Accessed Citable
A Classical Perspective on Non-Diffractive Disorder The Harvard community has made this article openly available. Please share how this access benefits you. Your story matters. Citation Accessed Citable
Defects in Hard-Sphere Colloidal Crystals
 Defects in Hard-Sphere Colloidal Crystals The Harvard community has made this article openly available. Please share how this access benefits you. Your story matters. Citation Accessed Citable Link Terms
Defects in Hard-Sphere Colloidal Crystals The Harvard community has made this article openly available. Please share how this access benefits you. Your story matters. Citation Accessed Citable Link Terms
Gradient Descent for Optimization Problems With Sparse Solutions
 Gradient Descent for Optimization Problems With Sparse Solutions The Harvard community has made this article openly available. Please share how this access benefits you. Your story matters Citation Chen,
Gradient Descent for Optimization Problems With Sparse Solutions The Harvard community has made this article openly available. Please share how this access benefits you. Your story matters Citation Chen,
Diamond platforms for nanoscale photonics and metrology
 Diamond platforms for nanoscale photonics and metrology The Harvard community has made this article openly available. Please share how this access benefits you. Your story matters. Citation Accessed Citable
Diamond platforms for nanoscale photonics and metrology The Harvard community has made this article openly available. Please share how this access benefits you. Your story matters. Citation Accessed Citable
C 1 D 1. AB = a, AD = b, AA1 = c. a, b, c : (1) AC 1 ; : (1) AB + BC + CC1, AC 1 = BC = AD, CC1 = AA 1, AC 1 = a + b + c. (2) BD 1 = BD + DD 1,
 1 1., BD 1 B 1 1 D 1, E F B 1 D 1. B = a, D = b, 1 = c. a, b, c : (1) 1 ; () BD 1 ; () F; D 1 F 1 (4) EF. : (1) B = D, D c b 1 E a B 1 1 = 1, B1 1 = B + B + 1, 1 = a + b + c. () BD 1 = BD + DD 1, BD =
1 1., BD 1 B 1 1 D 1, E F B 1 D 1. B = a, D = b, 1 = c. a, b, c : (1) 1 ; () BD 1 ; () F; D 1 F 1 (4) EF. : (1) B = D, D c b 1 E a B 1 1 = 1, B1 1 = B + B + 1, 1 = a + b + c. () BD 1 = BD + DD 1, BD =
m i N 1 F i = j i F ij + F x
 N m i i = 1,..., N m i Fi x N 1 F ij, j = 1, 2,... i 1, i + 1,..., N m i F i = j i F ij + F x i mi Fi j Fj i mj O P i = F i = j i F ij + F x i, i = 1,..., N P = i F i = N F ij + i j i N i F x i, i = 1,...,
N m i i = 1,..., N m i Fi x N 1 F ij, j = 1, 2,... i 1, i + 1,..., N m i F i = j i F ij + F x i mi Fi j Fj i mj O P i = F i = j i F ij + F x i, i = 1,..., N P = i F i = N F ij + i j i N i F x i, i = 1,...,
Solutions - Chapter 4
 Solutions - Chapter Kevin S. Huang Problem.1 Unitary: Ût = 1 ī hĥt Û tût = 1 Neglect t term: 1 + hĥ ī t 1 īhĥt = 1 + hĥ ī t ī hĥt = 1 Ĥ = Ĥ Problem. Ût = lim 1 ī ] n hĥ1t 1 ī ] hĥt... 1 ī ] hĥnt 1 ī ]
Solutions - Chapter Kevin S. Huang Problem.1 Unitary: Ût = 1 ī hĥt Û tût = 1 Neglect t term: 1 + hĥ ī t 1 īhĥt = 1 + hĥ ī t ī hĥt = 1 Ĥ = Ĥ Problem. Ût = lim 1 ī ] n hĥ1t 1 ī ] hĥt... 1 ī ] hĥnt 1 ī ]
Ax = b. 7x = 21. x = 21 7 = 3.
 3 s st 3 r 3 t r 3 3 t s st t 3t s 3 3 r 3 3 st t t r 3 s t t r r r t st t rr 3t r t 3 3 rt3 3 t 3 3 r st 3 t 3 tr 3 r t3 t 3 s st t Ax = b. s t 3 t 3 3 r r t n r A tr 3 rr t 3 t n ts b 3 t t r r t x 3
3 s st 3 r 3 t r 3 3 t s st t 3t s 3 3 r 3 3 st t t r 3 s t t r r r t st t rr 3t r t 3 3 rt3 3 t 3 3 r st 3 t 3 tr 3 r t3 t 3 s st t Ax = b. s t 3 t 3 3 r r t n r A tr 3 rr t 3 t n ts b 3 t t r r t x 3
 k k ΚΕΦΑΛΑΙΟ 1 G = (V, E) V E V V V G E G e = {v, u} E v u e v u G G V (G) E(G) n(g) = V (G) m(g) = E(G) G S V (G) S G N G (S) = {u V (G)\S v S : {v, u} E(G)} G v S v V (G) N G (v) = N G ({v}) x V (G)
k k ΚΕΦΑΛΑΙΟ 1 G = (V, E) V E V V V G E G e = {v, u} E v u e v u G G V (G) E(G) n(g) = V (G) m(g) = E(G) G S V (G) S G N G (S) = {u V (G)\S v S : {v, u} E(G)} G v S v V (G) N G (v) = N G ({v}) x V (G)
 k k ΚΕΦΑΛΑΙΟ 1 G = (V, E) V E V V V G E G e = {v, u} E v u e v u G G V (G) E(G) n(g) = V (G) m(g) = E(G) G S V (G) S G N G (S) = {u V (G)\S v S : {v, u} E(G)} G v S v V (G) N G (v) = N G ({v}) x V (G)
k k ΚΕΦΑΛΑΙΟ 1 G = (V, E) V E V V V G E G e = {v, u} E v u e v u G G V (G) E(G) n(g) = V (G) m(g) = E(G) G S V (G) S G N G (S) = {u V (G)\S v S : {v, u} E(G)} G v S v V (G) N G (v) = N G ({v}) x V (G)
Parts Manual. Trio Mobile Surgery Platform. Model 1033
 Trio Mobile Surgery Platform Model 1033 Parts Manual For parts or technical assistance: Pour pièces de service ou assistance technique : Für Teile oder technische Unterstützung Anruf: Voor delen of technische
Trio Mobile Surgery Platform Model 1033 Parts Manual For parts or technical assistance: Pour pièces de service ou assistance technique : Für Teile oder technische Unterstützung Anruf: Voor delen of technische
Estimation of grain boundary segregation enthalpy and its role in stable nanocrystalline alloy design
 Supplemental Material for Estimation of grain boundary segregation enthalpy and its role in stable nanocrystalline alloy design By H. A. Murdoch and C.A. Schuh Miedema model RKM model ΔH mix ΔH seg ΔH
Supplemental Material for Estimation of grain boundary segregation enthalpy and its role in stable nanocrystalline alloy design By H. A. Murdoch and C.A. Schuh Miedema model RKM model ΔH mix ΔH seg ΔH
Το άτομο του Υδρογόνου
 Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες
Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες
(... )..!, ".. (! ) # - $ % % $ & % 2007
 (! ), "! ( ) # $ % & % $ % 007 500 ' 67905:5394!33 : (! ) $, -, * +,'; ), -, *! ' - " #!, $ & % $ ( % %): /!, " ; - : - +', 007 5 ISBN 978-5-7596-0766-3 % % - $, $ &- % $ % %, * $ % - % % # $ $,, % % #-
(! ), "! ( ) # $ % & % $ % 007 500 ' 67905:5394!33 : (! ) $, -, * +,'; ), -, *! ' - " #!, $ & % $ ( % %): /!, " ; - : - +', 007 5 ISBN 978-5-7596-0766-3 % % - $, $ &- % $ % %, * $ % - % % # $ $,, % % #-
Dissertation for the degree philosophiae doctor (PhD) at the University of Bergen
 Dissertation for the degree philosophiae doctor (PhD) at the University of Bergen Dissertation date: GF F GF F SLE GF F D Ĉ = C { } Ĉ \ D D D = {z : z < 1} f : D D D D = D D, D = D D f f : D D
Dissertation for the degree philosophiae doctor (PhD) at the University of Bergen Dissertation date: GF F GF F SLE GF F D Ĉ = C { } Ĉ \ D D D = {z : z < 1} f : D D D D = D D, D = D D f f : D D
u(x, y) =f(x, y) Ω=(0, 1) (0, 1)
 u(x, y) =f(x, y) Ω=(0, 1) (0, 1) u(x, y) =g(x, y) Γ=δΩ ={0, 1} {0, 1} Ω Ω Ω h Ω h h ˆ Ω ˆ u v = fv Ω u = f in Ω v V H 1 (Ω) V V h V h ψ 1,ψ 2,...,ψ N, ˆ ˆ u v = Ω Ω fv v V ˆ ˆ u v = Ω ˆ ˆ u ψ i = Ω Ω Ω
u(x, y) =f(x, y) Ω=(0, 1) (0, 1) u(x, y) =g(x, y) Γ=δΩ ={0, 1} {0, 1} Ω Ω Ω h Ω h h ˆ Ω ˆ u v = fv Ω u = f in Ω v V H 1 (Ω) V V h V h ψ 1,ψ 2,...,ψ N, ˆ ˆ u v = Ω Ω fv v V ˆ ˆ u v = Ω ˆ ˆ u ψ i = Ω Ω Ω
F (x) = kx. F (x )dx. F = kx. U(x) = U(0) kx2
 F (x) = kx x k F = F (x) U(0) U(x) = x F = kx 0 F (x )dx U(x) = U(0) + 1 2 kx2 x U(0) = 0 U(x) = 1 2 kx2 U(x) x 0 = 0 x 1 U(x) U(0) + U (0) x + 1 2 U (0) x 2 U (0) = 0 U(x) U(0) + 1 2 U (0) x 2 U(0) =
F (x) = kx x k F = F (x) U(0) U(x) = x F = kx 0 F (x )dx U(x) = U(0) + 1 2 kx2 x U(0) = 0 U(x) = 1 2 kx2 U(x) x 0 = 0 x 1 U(x) U(0) + U (0) x + 1 2 U (0) x 2 U (0) = 0 U(x) U(0) + 1 2 U (0) x 2 U(0) =
 W τ R W j N H = 2 F obj b q N F aug F obj b q Ψ F aug Ψ ( ) ϱ t + + p = 0 = 0 Ω f = Γ Γ b ϱ = (, t) = (, t) Ω f Γ b ( ) ϱ t + + p = V max 4 3 2 1 0-1 -2-3 -4-4 -3-2 -1 0 1 2 3 4 x 4 x 1 V mn V max
W τ R W j N H = 2 F obj b q N F aug F obj b q Ψ F aug Ψ ( ) ϱ t + + p = 0 = 0 Ω f = Γ Γ b ϱ = (, t) = (, t) Ω f Γ b ( ) ϱ t + + p = V max 4 3 2 1 0-1 -2-3 -4-4 -3-2 -1 0 1 2 3 4 x 4 x 1 V mn V max
 ϕ n n n n = 1,..., N n n {X I, Y I } {X r, Y r } (x c, y c ) q r = x a y a θ X r = [x r, y r, θ r ] X I = [x I, y I, θ I ] X I = R(θ)X r R(θ) R(θ) = cosθ sinθ 0 sinθ cosθ 0 0 0 1 Ẋ I = R(θ)Ẋr y r ẏa r
ϕ n n n n = 1,..., N n n {X I, Y I } {X r, Y r } (x c, y c ) q r = x a y a θ X r = [x r, y r, θ r ] X I = [x I, y I, θ I ] X I = R(θ)X r R(θ) R(θ) = cosθ sinθ 0 sinθ cosθ 0 0 0 1 Ẋ I = R(θ)Ẋr y r ẏa r
ΠΕΡΙΟΔΙΚΟΣ ΠΙΝΑΚΑΣ ΣΤΟΙΧΕΙΩΝ
 ΠΕΡΙΟΔΙΚΟΣ ΠΙΝΑΚΑΣ ΣΤΟΙΧΕΙΩΝ Περίοδοι περιοδικού πίνακα Ο περιοδικός πίνακας αποτελείται από 7 περιόδους. Ο αριθμός των στοιχείων που περιλαμβάνει κάθε περίοδος δεν είναι σταθερός, δηλ. η περιοδικότητα
ΠΕΡΙΟΔΙΚΟΣ ΠΙΝΑΚΑΣ ΣΤΟΙΧΕΙΩΝ Περίοδοι περιοδικού πίνακα Ο περιοδικός πίνακας αποτελείται από 7 περιόδους. Ο αριθμός των στοιχείων που περιλαμβάνει κάθε περίοδος δεν είναι σταθερός, δηλ. η περιοδικότητα
 φ(t) TE 0 φ(z) φ(z) φ(z) φ(z) η(λ) G(z,λ) λ φ(z) η(λ) η(λ) = t CIGS 0 G(z,λ)φ(z)dz t CIGS η(λ) φ(z) 0 z
φ(t) TE 0 φ(z) φ(z) φ(z) φ(z) η(λ) G(z,λ) λ φ(z) η(λ) η(λ) = t CIGS 0 G(z,λ)φ(z)dz t CIGS η(λ) φ(z) 0 z
Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού.
 Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού. Περιοδικός πίνακας: α. Είναι µια ταξινόµηση των στοιχείων κατά αύξοντα
Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού. Περιοδικός πίνακας: α. Είναι µια ταξινόµηση των στοιχείων κατά αύξοντα
!"#$ % &# &%#'()(! $ * +
 ,!"#$ % &# &%#'()(! $ * + ,!"#$ % &# &%#'()(! $ * + 6 7 57 : - - / :!", # $ % & :'!(), 5 ( -, * + :! ",, # $ %, ) #, '(#,!# $$,',#-, 4 "- /,#-," -$ '# &",,#- "-&)'#45)')6 5! 6 5 4 "- /,#-7 ",',8##! -#9,!"))
,!"#$ % &# &%#'()(! $ * + ,!"#$ % &# &%#'()(! $ * + 6 7 57 : - - / :!", # $ % & :'!(), 5 ( -, * + :! ",, # $ %, ) #, '(#,!# $$,',#-, 4 "- /,#-," -$ '# &",,#- "-&)'#45)')6 5! 6 5 4 "- /,#-7 ",',8##! -#9,!"))
!!" #7 $39 %" (07) ..,..,.. $ 39. ) :. :, «(», «%», «%», «%» «%». & ,. ). & :..,. '.. ( () #*. );..,..'. + (# ).
 1 00 3 !!" 344#7 $39 %" 6181001 63(07) & : ' ( () #* ); ' + (# ) $ 39 ) : : 00 %" 6181001 63(07)!!" 344#7 «(» «%» «%» «%» «%» & ) 4 )&-%/0 +- «)» * «1» «1» «)» ) «(» «%» «%» + ) 30 «%» «%» )1+ / + : +3
1 00 3 !!" 344#7 $39 %" 6181001 63(07) & : ' ( () #* ); ' + (# ) $ 39 ) : : 00 %" 6181001 63(07)!!" 344#7 «(» «%» «%» «%» «%» & ) 4 )&-%/0 +- «)» * «1» «1» «)» ) «(» «%» «%» + ) 30 «%» «%» )1+ / + : +3
ΓΗ ΚΑΙ ΣΥΜΠΑΝ. Εικόνα 1. Φωτογραφία του γαλαξία μας (από αρχείο της NASA)
 ΓΗ ΚΑΙ ΣΥΜΠΑΝ Φύση του σύμπαντος Η γη είναι μία μονάδα μέσα στο ηλιακό μας σύστημα, το οποίο αποτελείται από τον ήλιο, τους πλανήτες μαζί με τους δορυφόρους τους, τους κομήτες, τα αστεροειδή και τους μετεωρίτες.
ΓΗ ΚΑΙ ΣΥΜΠΑΝ Φύση του σύμπαντος Η γη είναι μία μονάδα μέσα στο ηλιακό μας σύστημα, το οποίο αποτελείται από τον ήλιο, τους πλανήτες μαζί με τους δορυφόρους τους, τους κομήτες, τα αστεροειδή και τους μετεωρίτες.
Ι ΙΟΤΗΤΕΣ ΤΩΝ ΑΤΟΜΩΝ. Παππάς Χρήστος Επίκουρος Καθηγητής
 ΗΛΕΚΤΡΟΝΙΚΗ ΟΜΗ ΚΑΙ Ι ΙΟΤΗΤΕΣ ΤΩΝ ΑΤΟΜΩΝ Παππάς Χρήστος Επίκουρος Καθηγητής ΤΟ ΜΕΓΕΘΟΣ ΤΩΝ ΑΤΟΜΩΝ Ατομική ακτίνα (r) : ½ της απόστασης μεταξύ δύο ομοιοπυρηνικών ατόμων, ενωμένων με απλό ομοιοπολικό δεσμό.
ΗΛΕΚΤΡΟΝΙΚΗ ΟΜΗ ΚΑΙ Ι ΙΟΤΗΤΕΣ ΤΩΝ ΑΤΟΜΩΝ Παππάς Χρήστος Επίκουρος Καθηγητής ΤΟ ΜΕΓΕΘΟΣ ΤΩΝ ΑΤΟΜΩΝ Ατομική ακτίνα (r) : ½ της απόστασης μεταξύ δύο ομοιοπυρηνικών ατόμων, ενωμένων με απλό ομοιοπολικό δεσμό.
ITU-R P (2012/02) &' (
 ITU-R P.530-4 (0/0) $ % " "#! &' ( P ITU-R P. 530-4 ii.. (IPR) (ITU-T/ITU-R/ISO/IEC).ITU-R http://www.itu.int/itu-r/go/patents/en. ITU-T/ITU-R/ISO/IEC (http://www.itu.int/publ/r-rec/en ) () ( ) BO BR BS
ITU-R P.530-4 (0/0) $ % " "#! &' ( P ITU-R P. 530-4 ii.. (IPR) (ITU-T/ITU-R/ISO/IEC).ITU-R http://www.itu.int/itu-r/go/patents/en. ITU-T/ITU-R/ISO/IEC (http://www.itu.int/publ/r-rec/en ) () ( ) BO BR BS
ΝΟΜΟΣ ΤΗΣ ΠΕΡΙΟ ΙΚΟΤΗΤΑΣ : Οι ιδιότητες των χηµικών στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού.
 1. Ο ΠΕΡΙΟ ΙΚΟΣ ΠΙΝΑΚΑΣ Οι άνθρωποι από την φύση τους θέλουν να πετυχαίνουν σπουδαία αποτελέσµατα καταναλώνοντας το λιγότερο δυνατό κόπο και χρόνο. Για το σκοπό αυτό προσπαθούν να οµαδοποιούν τα πράγµατα
1. Ο ΠΕΡΙΟ ΙΚΟΣ ΠΙΝΑΚΑΣ Οι άνθρωποι από την φύση τους θέλουν να πετυχαίνουν σπουδαία αποτελέσµατα καταναλώνοντας το λιγότερο δυνατό κόπο και χρόνο. Για το σκοπό αυτό προσπαθούν να οµαδοποιούν τα πράγµατα
τροχιακά Η στιβάδα καθορίζεται από τον κύριο κβαντικό αριθµό (n) Η υποστιβάδα καθορίζεται από τους δύο πρώτους κβαντικούς αριθµούς (n, l)
 ΑΤΟΜΙΚΑ ΤΡΟΧΙΑΚΑ Σχέση κβαντικών αριθµών µε στιβάδες υποστιβάδες - τροχιακά Η στιβάδα καθορίζεται από τον κύριο κβαντικό αριθµό (n) Η υποστιβάδα καθορίζεται από τους δύο πρώτους κβαντικούς αριθµούς (n,
ΑΤΟΜΙΚΑ ΤΡΟΧΙΑΚΑ Σχέση κβαντικών αριθµών µε στιβάδες υποστιβάδες - τροχιακά Η στιβάδα καθορίζεται από τον κύριο κβαντικό αριθµό (n) Η υποστιβάδα καθορίζεται από τους δύο πρώτους κβαντικούς αριθµούς (n,
... 5 A.. RS-232C ( ) RS-232C ( ) RS-232C-LK & RS-232C-MK RS-232C-JK & RS-232C-KK
 RS-3C WIWM050 014.1.9 P1 :8... 1... 014.0.1 1 A... 014.0. 1... RS-3C()...01.08.03 A.. RS-3C()...01.08.03 3... RS-3C()... 003.11.5 4... RS-3C ()... 00.10.01 5... RS-3C().008.07.16 5 A.. RS-3C().0 1.08.
RS-3C WIWM050 014.1.9 P1 :8... 1... 014.0.1 1 A... 014.0. 1... RS-3C()...01.08.03 A.. RS-3C()...01.08.03 3... RS-3C()... 003.11.5 4... RS-3C ()... 00.10.01 5... RS-3C().008.07.16 5 A.. RS-3C().0 1.08.
ITU-R P (2009/10)
 ITU-R.45-4 (9/) % # GHz,!"# $$ # ITU-R.45-4.. (IR) (ITU-T/ITU-R/ISO/IEC).ITU-R http://www.tu.t/itu-r/go/patets/e. (http://www.tu.t/publ/r-rec/e ) () ( ) BO BR BS BT F M RA S RS SA SF SM SNG TF V.ITU-R
ITU-R.45-4 (9/) % # GHz,!"# $$ # ITU-R.45-4.. (IR) (ITU-T/ITU-R/ISO/IEC).ITU-R http://www.tu.t/itu-r/go/patets/e. (http://www.tu.t/publ/r-rec/e ) () ( ) BO BR BS BT F M RA S RS SA SF SM SNG TF V.ITU-R
 a; b 2 R; a < b; f : [a; b] R! R y 2 R: y : [a; b]! R; ( y (t) = f t; y(t) ; a t b; y(a) = y : f (t; y) 2 [a; b]r: f 2 C ([a; b]r): y 2 C [a; b]; y(a) = y ; f y ỹ ỹ y ; jy ỹ j ky ỹk [a; b]; f y; ( y (t)
a; b 2 R; a < b; f : [a; b] R! R y 2 R: y : [a; b]! R; ( y (t) = f t; y(t) ; a t b; y(a) = y : f (t; y) 2 [a; b]r: f 2 C ([a; b]r): y 2 C [a; b]; y(a) = y ; f y ỹ ỹ y ; jy ỹ j ky ỹk [a; b]; f y; ( y (t)
 J J l 2 J T l 1 J T J T l 2 l 1 J J l 1 c 0 J J J J J l 2 l 2 J J J T J T l 1 J J T J T J T J {e n } n N {e n } n N x X {λ n } n N R x = λ n e n {e n } n N {e n : n N} e n 0 n N k 1, k 2,..., k n N λ
J J l 2 J T l 1 J T J T l 2 l 1 J J l 1 c 0 J J J J J l 2 l 2 J J J T J T l 1 J J T J T J T J {e n } n N {e n } n N x X {λ n } n N R x = λ n e n {e n } n N {e n : n N} e n 0 n N k 1, k 2,..., k n N λ
SUPPLEMENTAL INFORMATION. Fully Automated Total Metals and Chromium Speciation Single Platform Introduction System for ICP-MS
 Electronic Supplementary Material (ESI) for Journal of Analytical Atomic Spectrometry. This journal is The Royal Society of Chemistry 2018 SUPPLEMENTAL INFORMATION Fully Automated Total Metals and Chromium
Electronic Supplementary Material (ESI) for Journal of Analytical Atomic Spectrometry. This journal is The Royal Society of Chemistry 2018 SUPPLEMENTAL INFORMATION Fully Automated Total Metals and Chromium
Note: Please use the actual date you accessed this material in your citation.
 MIT OpenCourseWare http://ocw.mit.edu 6.03/ESD.03J Electromagnetics and Applications, Fall 005 Please use the following citation format: Markus Zahn, 6.03/ESD.03J Electromagnetics and Applications, Fall
MIT OpenCourseWare http://ocw.mit.edu 6.03/ESD.03J Electromagnetics and Applications, Fall 005 Please use the following citation format: Markus Zahn, 6.03/ESD.03J Electromagnetics and Applications, Fall
Q π (/) ^ ^ ^ Η φ. <f) c>o. ^ ο. ö ê ω Q. Ο. o 'c. _o _) o U 03. ,,, ω ^ ^ -g'^ ο 0) f ο. Ε. ιη ο Φ. ο 0) κ. ο 03.,Ο. g 2< οο"" ο φ.
 II 4»» «i p û»7'' s V -Ζ G -7 y 1 X s? ' (/) Ζ L. - =! i- Ζ ) Η f) " i L. Û - 1 1 Ι û ( - " - ' t - ' t/î " ι-8. Ι -. : wî ' j 1 Τ J en " il-' - - ö ê., t= ' -; '9 ',,, ) Τ '.,/,. - ϊζ L - (- - s.1 ai
II 4»» «i p û»7'' s V -Ζ G -7 y 1 X s? ' (/) Ζ L. - =! i- Ζ ) Η f) " i L. Û - 1 1 Ι û ( - " - ' t - ' t/î " ι-8. Ι -. : wî ' j 1 Τ J en " il-' - - ö ê., t= ' -; '9 ',,, ) Τ '.,/,. - ϊζ L - (- - s.1 ai
r r t r r t t r t P s r t r P s r s r r rs tr t r r t s ss r P s s t r t t tr r r t t r t r r t t s r t rr t Ü rs t 3 r r r 3 rträ 3 röÿ r t
 r t t r t ts r3 s r r t r r t t r t P s r t r P s r s r P s r 1 s r rs tr t r r t s ss r P s s t r t t tr r 2s s r t t r t r r t t s r t rr t Ü rs t 3 r t r 3 s3 Ü rs t 3 r r r 3 rträ 3 röÿ r t r r r rs
r t t r t ts r3 s r r t r r t t r t P s r t r P s r s r P s r 1 s r rs tr t r r t s ss r P s s t r t t tr r 2s s r t t r t r r t t s r t rr t Ü rs t 3 r t r 3 s3 Ü rs t 3 r r r 3 rträ 3 röÿ r t r r r rs
Microscopie photothermique et endommagement laser
 Microscopie photothermique et endommagement laser Annelise During To cite this version: Annelise During. Microscopie photothermique et endommagement laser. Physique Atomique [physics.atom-ph]. Université
Microscopie photothermique et endommagement laser Annelise During To cite this version: Annelise During. Microscopie photothermique et endommagement laser. Physique Atomique [physics.atom-ph]. Université
 a; b 2 R; a < b; f : [a; b] R! R y 2 R: y : [a; b]! R; ( y (t) = f t; y(t) ; a t b; y(a) = y : f (t; y) 2 [a; b]r: f 2 C ([a; b]r): y 2 C [a; b]; y(a) = y ; f y ỹ ỹ y ; jy ỹ j ky ỹk [a; b]; f y; ( y (t)
a; b 2 R; a < b; f : [a; b] R! R y 2 R: y : [a; b]! R; ( y (t) = f t; y(t) ; a t b; y(a) = y : f (t; y) 2 [a; b]r: f 2 C ([a; b]r): y 2 C [a; b]; y(a) = y ; f y ỹ ỹ y ; jy ỹ j ky ỹk [a; b]; f y; ( y (t)
 γ 1 6 M = 0.05 F M = 0.05 F M = 0.2 F M = 0.2 F M = 0.05 F M = 0.05 F M = 0.05 F M = 0.2 F M = 0.05 F 2 2 λ τ M = 6000 M = 10000 M = 15000 M = 6000 M = 10000 M = 15000 1 6 τ = 36 1 6 τ = 102 1 6 M = 5000
γ 1 6 M = 0.05 F M = 0.05 F M = 0.2 F M = 0.2 F M = 0.05 F M = 0.05 F M = 0.05 F M = 0.2 F M = 0.05 F 2 2 λ τ M = 6000 M = 10000 M = 15000 M = 6000 M = 10000 M = 15000 1 6 τ = 36 1 6 τ = 102 1 6 M = 5000
! "# $ % $&'& () *+ (,-. / 0 1(,21(,*) (3 4 5 "$ 6, ::: ;"<$& = = 7 + > + 5 $?"# 46(A *( / A 6 ( 1,*1 B"',CD77E *+ *),*,*) F? $G'& 0/ (,.
 ! " #$%&'()' *('+$,&'-. /0 1$23(/%/4. 1$)('%%'($( )/,)$5)/6%6 7$85,-9$(- /0 :/986-$, ;2'$(2$ 1'$-/-$)('')5( /&5&-/ 5(< =(4'($$,'(4 1$%$2/996('25-'/(& ;/0->5,$ 1'$-/%'')$(($/3?$%9'&-/?$( 5(< @6%-'9$
! " #$%&'()' *('+$,&'-. /0 1$23(/%/4. 1$)('%%'($( )/,)$5)/6%6 7$85,-9$(- /0 :/986-$, ;2'$(2$ 1'$-/-$)('')5( /&5&-/ 5(< =(4'($$,'(4 1$%$2/996('25-'/(& ;/0->5,$ 1'$-/%'')$(($/3?$%9'&-/?$( 5(< @6%-'9$
Errata (Includes critical corrections only for the 1 st & 2 nd reprint)
 Wedesday, May 5, 3 Erraa (Icludes criical correcios oly for he s & d repri) Advaced Egieerig Mahemaics, 7e Peer V O eil ISB: 978474 Page # Descripio 38 ie 4: chage "w v a v " "w v a v " 46 ie : chage "y
Wedesday, May 5, 3 Erraa (Icludes criical correcios oly for he s & d repri) Advaced Egieerig Mahemaics, 7e Peer V O eil ISB: 978474 Page # Descripio 38 ie 4: chage "w v a v " "w v a v " 46 ie : chage "y
Jeux d inondation dans les graphes
 Jeux d inondation dans les graphes Aurélie Lagoutte To cite this version: Aurélie Lagoutte. Jeux d inondation dans les graphes. 2010. HAL Id: hal-00509488 https://hal.archives-ouvertes.fr/hal-00509488
Jeux d inondation dans les graphes Aurélie Lagoutte To cite this version: Aurélie Lagoutte. Jeux d inondation dans les graphes. 2010. HAL Id: hal-00509488 https://hal.archives-ouvertes.fr/hal-00509488
!"! #!"!!$ #$! %!"&' & (%!' #!% #" *! *$' *.!! )#/'.0! )#/.*!$,)# * % $ %!!#!!%#'!)$! #,# #!%# ##& )$&# 11!!#2!
 # $ #$ % (% # )*%%# )# )$ % # * *$ * #,##%#)#% *-. )#/###%. )#/.0 )#/.* $,)# )#/ * % $ % # %# )$ #,# # %# ## )$# 11 #2 #**##%% $#%34 5 # %## * 6 7(%#)%%%, #, # ## # *% #$# 8# )####, 7 9%%# 0 * #,, :;
# $ #$ % (% # )*%%# )# )$ % # * *$ * #,##%#)#% *-. )#/###%. )#/.0 )#/.* $,)# )#/ * % $ % # %# )$ #,# # %# ## )$# 11 #2 #**##%% $#%34 5 # %## * 6 7(%#)%%%, #, # ## # *% #$# 8# )####, 7 9%%# 0 * #,, :;
ITU-R P (2012/02)
 ITU-R P.56- (0/0 P ITU-R P.56- ii.. (IPR (ITU-T/ITU-R/ISO/IEC.ITU-R ttp://www.itu.int/itu-r/go/patents/en. (ttp://www.itu.int/publ/r-rec/en ( ( BO BR BS BT F M P RA RS S SA SF SM SNG TF V 0.ITU-R ITU 0..(ITU
ITU-R P.56- (0/0 P ITU-R P.56- ii.. (IPR (ITU-T/ITU-R/ISO/IEC.ITU-R ttp://www.itu.int/itu-r/go/patents/en. (ttp://www.itu.int/publ/r-rec/en ( ( BO BR BS BT F M P RA RS S SA SF SM SNG TF V 0.ITU-R ITU 0..(ITU
m 1, m 2 F 12, F 21 F12 = F 21
 m 1, m 2 F 12, F 21 F12 = F 21 r 1, r 2 r = r 1 r 2 = r 1 r 2 ê r = rê r F 12 = f(r)ê r F 21 = f(r)ê r f(r) f(r) < 0 f(r) > 0 m 1 r1 = f(r)ê r m 2 r2 = f(r)ê r r = r 1 r 2 r 1 = 1 m 1 f(r)ê r r 2 = 1 m
m 1, m 2 F 12, F 21 F12 = F 21 r 1, r 2 r = r 1 r 2 = r 1 r 2 ê r = rê r F 12 = f(r)ê r F 21 = f(r)ê r f(r) f(r) < 0 f(r) > 0 m 1 r1 = f(r)ê r m 2 r2 = f(r)ê r r = r 1 r 2 r 1 = 1 m 1 f(r)ê r r 2 = 1 m
Łs t r t rs tø r P r s tø PrØ rø rs tø P r s r t t r s t Ø t q s P r s tr. 2stŁ s q t q s t rt r s t s t ss s Ø r s t r t. Łs t r t t Ø t q s
 Łs t r t rs tø r P r s tø PrØ rø rs tø P r s r t t r s t Ø t q s P r s tr st t t t Ø t q s ss P r s P 2stŁ s q t q s t rt r s t s t ss s Ø r s t r t P r røs r Łs t r t t Ø t q s r Ø r t t r t q t rs tø
Łs t r t rs tø r P r s tø PrØ rø rs tø P r s r t t r s t Ø t q s P r s tr st t t t Ø t q s ss P r s P 2stŁ s q t q s t rt r s t s t ss s Ø r s t r t P r røs r Łs t r t t Ø t q s r Ø r t t r t q t rs tø
HONDA. Έτος κατασκευής
 Accord + Coupe IV 2.0 16V (CB3) F20A2-A3 81 110 01/90-09/93 0800-0175 11,00 2.0 16V (CB3) F20A6 66 90 01/90-09/93 0800-0175 11,00 2.0i 16V (CB3-CC9) F20A8 98 133 01/90-09/93 0802-9205M 237,40 2.0i 16V
Accord + Coupe IV 2.0 16V (CB3) F20A2-A3 81 110 01/90-09/93 0800-0175 11,00 2.0 16V (CB3) F20A6 66 90 01/90-09/93 0800-0175 11,00 2.0i 16V (CB3-CC9) F20A8 98 133 01/90-09/93 0802-9205M 237,40 2.0i 16V
ITU-R P (2012/02) khz 150
 (0/0) khz 0 P ii (IPR) (ITU-T/ITU-R/ISO/IEC) ITU-R http://www.itu.int/itu-r/go/patents/en http://www.itu.int/publ/r-rec/en BO BR BS BT F M P RA RS S SA SF SM SNG TF V ITU-R 0 ITU 0 (ITU) khz 0 (0-009-00-003-00-994-990)
(0/0) khz 0 P ii (IPR) (ITU-T/ITU-R/ISO/IEC) ITU-R http://www.itu.int/itu-r/go/patents/en http://www.itu.int/publ/r-rec/en BO BR BS BT F M P RA RS S SA SF SM SNG TF V ITU-R 0 ITU 0 (ITU) khz 0 (0-009-00-003-00-994-990)
Between Square and Circle
 DOCTORAL T H E SIS Between Square and Circle A Study on the Behaviour of Polygonal Steel Profiles Under Compression Panagiotis Manoleas Steel Structures Printed by Luleå University of Technology, Graphic
DOCTORAL T H E SIS Between Square and Circle A Study on the Behaviour of Polygonal Steel Profiles Under Compression Panagiotis Manoleas Steel Structures Printed by Luleå University of Technology, Graphic
rs r r â t át r st tíst Ó P ã t r r r â
 rs r r â t át r st tíst P Ó P ã t r r r â ã t r r P Ó P r sã rs r s t à r çã rs r st tíst r q s t r r t çã r r st tíst r t r ú r s r ú r â rs r r â t át r çã rs r st tíst 1 r r 1 ss rt q çã st tr sã
rs r r â t át r st tíst P Ó P ã t r r r â ã t r r P Ó P r sã rs r s t à r çã rs r st tíst r q s t r r t çã r r st tíst r t r ú r s r ú r â rs r r â t át r çã rs r st tíst 1 r r 1 ss rt q çã st tr sã
! " #! $ %&! '( #)!' * +#, " -! %&! "!! ! " #$ % # " &' &'... ()* ( +, # ' -. + &', - + &' / # ' -. + &' (, % # , 2**.
 ! " #! $ %&! '( #)!' * +#, " -! %&! "!!! " #$ % # " &' &'... ()* ( +, # ' -. + &', - + &' / 0123 4 # ' -. + &' (, % #. -5 0126, 2**., 2, + &' %., 0, $!, 3,. 7 8 ', $$, 9, # / 3:*,*2;
! " #! $ %&! '( #)!' * +#, " -! %&! "!!! " #$ % # " &' &'... ()* ( +, # ' -. + &', - + &' / 0123 4 # ' -. + &' (, % #. -5 0126, 2**., 2, + &' %., 0, $!, 3,. 7 8 ', $$, 9, # / 3:*,*2;
A 1 A 2 A 3 B 1 B 2 B 3
 16 0 17 0 17 0 18 0 18 0 19 0 20 A A = A 1 î + A 2 ĵ + A 3ˆk A (x, y, z) r = xî + yĵ + zˆk A B A B B A = A 1 B 1 + A 2 B 2 + A 3 B 3 = A B θ θ A B = ˆn A B θ A B î ĵ ˆk = A 1 A 2 A 3 B 1 B 2 B 3 W = F
16 0 17 0 17 0 18 0 18 0 19 0 20 A A = A 1 î + A 2 ĵ + A 3ˆk A (x, y, z) r = xî + yĵ + zˆk A B A B B A = A 1 B 1 + A 2 B 2 + A 3 B 3 = A B θ θ A B = ˆn A B θ A B î ĵ ˆk = A 1 A 2 A 3 B 1 B 2 B 3 W = F
d dx x 2 = 2x d dx x 3 = 3x 2 d dx x n = nx n 1
 d dx x 2 = 2x d dx x 3 = 3x 2 d dx x n = nx n1 x dx = 1 2 b2 1 2 a2 a b b x 2 dx = 1 a 3 b3 1 3 a3 b x n dx = 1 a n +1 bn +1 1 n +1 an +1 d dx d dx f (x) = 0 f (ax) = a f (ax) lim d dx f (ax) = lim 0 =
d dx x 2 = 2x d dx x 3 = 3x 2 d dx x n = nx n1 x dx = 1 2 b2 1 2 a2 a b b x 2 dx = 1 a 3 b3 1 3 a3 b x n dx = 1 a n +1 bn +1 1 n +1 an +1 d dx d dx f (x) = 0 f (ax) = a f (ax) lim d dx f (ax) = lim 0 =
 μ μ dω I ν S da cos θ da λ λ Γ α/β MJ Capítulo 1 % βpic ɛ Eridani V ega β P ic F ormalhaut 10 9 15% 70 Virgem 47 Ursa Maior Debris Disk Debris Disk μ 90% L ac = GM M ac R L ac R M M ac L J T
μ μ dω I ν S da cos θ da λ λ Γ α/β MJ Capítulo 1 % βpic ɛ Eridani V ega β P ic F ormalhaut 10 9 15% 70 Virgem 47 Ursa Maior Debris Disk Debris Disk μ 90% L ac = GM M ac R L ac R M M ac L J T
Homework 8 Model Solution Section
 MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
 Molekulare Ebene (biochemische Messungen) Zelluläre Ebene (Elektrophysiologie, Imaging-Verfahren) Netzwerk Ebene (Multielektrodensysteme) Areale (MRT, EEG...) Gene Neuronen Synaptische Kopplung kleine
Molekulare Ebene (biochemische Messungen) Zelluläre Ebene (Elektrophysiologie, Imaging-Verfahren) Netzwerk Ebene (Multielektrodensysteme) Areale (MRT, EEG...) Gene Neuronen Synaptische Kopplung kleine
())*+,-./0-1+*)*2, *67()(,01-+4(-8 9 0:,*2./0 30 ;+-7 3* *),+*< 7+)0 3* (=24(-) 04(-() 18(4-3-) 3-2(>*+)(3-3*
 ! " # $ $ %&&' % $ $! " # ())*+,-./0-1+*)*2,-3-4050+*67()(,01-+4(-8 9 0:,*2./0 30 ;+-7 3* *),+*< 7+)0 3* *),+-30 *5 35(2(),+-./0 30 *,0+ 3* (=24(-) 04(-() 18(4-3-) 3-2(>*+)(3-3* *3*+-830-+-2?< +(*2,-30+
! " # $ $ %&&' % $ $! " # ())*+,-./0-1+*)*2,-3-4050+*67()(,01-+4(-8 9 0:,*2./0 30 ;+-7 3* *),+*< 7+)0 3* *),+-30 *5 35(2(),+-./0 30 *,0+ 3* (=24(-) 04(-() 18(4-3-) 3-2(>*+)(3-3* *3*+-830-+-2?< +(*2,-30+
!"!# ""$ %%"" %$" &" %" "!'! " #$!
 " "" %%"" %" &" %" " " " % ((((( ((( ((((( " %%%% & ) * ((( "* ( + ) (((( (, (() (((((* ( - )((((( )((((((& + )(((((((((( +. ) ) /(((( +( ),(, ((((((( +, 0 )/ (((((+ ++, ((((() & "( %%%%%%%%%%%%%%%%%%%(
" "" %%"" %" &" %" " " " % ((((( ((( ((((( " %%%% & ) * ((( "* ( + ) (((( (, (() (((((* ( - )((((( )((((((& + )(((((((((( +. ) ) /(((( +( ),(, ((((((( +, 0 )/ (((((+ ++, ((((() & "( %%%%%%%%%%%%%%%%%%%(
 V r,k j F k m N k+1 N k N k+1 H j n = 7 n = 16 Ṽ r ñ,ñ j Ṽ Ṽ j x / Ṽ W 2r V r D N T T 2r 2r N k F k N 2r Ω R 2 n Ω I n = { N: n} n N R 2 x R 2, I n Ω R 2 u R 2, I n x k+1 = x k + u k, u, x R 2,
V r,k j F k m N k+1 N k N k+1 H j n = 7 n = 16 Ṽ r ñ,ñ j Ṽ Ṽ j x / Ṽ W 2r V r D N T T 2r 2r N k F k N 2r Ω R 2 n Ω I n = { N: n} n N R 2 x R 2, I n Ω R 2 u R 2, I n x k+1 = x k + u k, u, x R 2,
Teor imov r. ta matem. statist. Vip. 94, 2016, stor
 eor imov r. ta matem. statist. Vip. 94, 6, stor. 93 5 Abstract. e article is devoted to models of financial markets wit stocastic volatility, wic is defined by a functional of Ornstein-Ulenbeck process
eor imov r. ta matem. statist. Vip. 94, 6, stor. 93 5 Abstract. e article is devoted to models of financial markets wit stocastic volatility, wic is defined by a functional of Ornstein-Ulenbeck process
 01 π π 4 1 2 I(t) C V C L V L C L Q(t) Φ(t) (L, C) Q(t) V C + V L =0 Q(t) C + Q(t) Ld2 =0 dt 2 d 2 Q(t) + Q(t) dt 2 LC =0 d 2 Q(t) + ω dt 0Q(t) 2 =0 2 Q(t) ω0 2 = 1 LC V L + V C =0 d 2 Φ(t)
01 π π 4 1 2 I(t) C V C L V L C L Q(t) Φ(t) (L, C) Q(t) V C + V L =0 Q(t) C + Q(t) Ld2 =0 dt 2 d 2 Q(t) + Q(t) dt 2 LC =0 d 2 Q(t) + ω dt 0Q(t) 2 =0 2 Q(t) ω0 2 = 1 LC V L + V C =0 d 2 Φ(t)
 l 1 p r i = ρ ij α j + w i j=1 ρ ij λ α j j p w i p α j = 1, α j 0, j = 1,..., p j=1 R B B B m j [ρ 1j, ρ 2j,..., ρ Bj ] T = }{{} α + [,,..., ] R B p p α [α 1,..., α p ] [w 1,..., w p ] M m 1 m 2,
l 1 p r i = ρ ij α j + w i j=1 ρ ij λ α j j p w i p α j = 1, α j 0, j = 1,..., p j=1 R B B B m j [ρ 1j, ρ 2j,..., ρ Bj ] T = }{{} α + [,,..., ] R B p p α [α 1,..., α p ] [w 1,..., w p ] M m 1 m 2,
Περιεχόμενα. A(x 1, x 2 )
 Περιεχόμενα A(x 1, x 2 7 Ολοκληρώματα της Μαγνητοϋδροδυναμικής και Μαγνητοϋδροδυναμικά Κύματα Σχήμα 7.1: Οι τριδιάστατες ελικοειδείς μαγνητικές γραμμές στις οποίες εφάπτεται το διάνυσμα του μαγνητικού
Περιεχόμενα A(x 1, x 2 7 Ολοκληρώματα της Μαγνητοϋδροδυναμικής και Μαγνητοϋδροδυναμικά Κύματα Σχήμα 7.1: Οι τριδιάστατες ελικοειδείς μαγνητικές γραμμές στις οποίες εφάπτεται το διάνυσμα του μαγνητικού
ECE Spring Prof. David R. Jackson ECE Dept. Notes 2
 ECE 634 Spring 6 Prof. David R. Jackson ECE Dept. Notes Fields in a Source-Free Region Example: Radiation from an aperture y PEC E t x Aperture Assume the following choice of vector potentials: A F = =
ECE 634 Spring 6 Prof. David R. Jackson ECE Dept. Notes Fields in a Source-Free Region Example: Radiation from an aperture y PEC E t x Aperture Assume the following choice of vector potentials: A F = =
ΠΕΡΙΟΔΙΚΟ ΣΥΣΤΗΜΑ ΤΩΝ ΣΤΟΙΧΕΙΩΝ (1) Ηλία Σκαλτσά ΠΕ ο Γυμνάσιο Αγ. Παρασκευής
 ΠΕΡΙΟΔΙΚΟ ΣΥΣΤΗΜΑ ΤΩΝ ΣΤΟΙΧΕΙΩΝ (1) Ηλία Σκαλτσά ΠΕ04.01 5 ο Γυμνάσιο Αγ. Παρασκευής Όπως συμβαίνει στη φύση έτσι και ο άνθρωπος θέλει να πετυχαίνει σπουδαία αποτελέσματα καταναλώνοντας το λιγότερο δυνατό
ΠΕΡΙΟΔΙΚΟ ΣΥΣΤΗΜΑ ΤΩΝ ΣΤΟΙΧΕΙΩΝ (1) Ηλία Σκαλτσά ΠΕ04.01 5 ο Γυμνάσιο Αγ. Παρασκευής Όπως συμβαίνει στη φύση έτσι και ο άνθρωπος θέλει να πετυχαίνει σπουδαία αποτελέσματα καταναλώνοντας το λιγότερο δυνατό
! "#" "" $ "%& ' %$(%& % &'(!!")!*!&+ ,! %$( - .$'!"
 ! "#" "" $ "%& ' %$(%&!"#$ % &'(!!")!*!&+,! %$( -.$'!" /01&$23& &4+ $$ /$ & & / ( #(&4&4!"#$ %40 &'(!"!!&+ 5,! %$( - &$ $$$".$'!" 4(02&$ 4 067 4 $$*&(089 - (0:;
! "#" "" $ "%& ' %$(%&!"#$ % &'(!!")!*!&+,! %$( -.$'!" /01&$23& &4+ $$ /$ & & / ( #(&4&4!"#$ %40 &'(!"!!&+ 5,! %$( - &$ $$$".$'!" 4(02&$ 4 067 4 $$*&(089 - (0:;
Ταλαντώσεις 6.1 Απλή Αρµονική Ταλάντωση σε µία ιάσταση Ελατήριο σε οριζόντιο επίπεδο Σχήµα 6.1
 6 Ταλαντώσεις 6.1 Απλή Αρµονική Ταλάντωση σε µία ιάσταση 6.1.1 Ελατήριο σε οριζόντιο επίπεδο Υποθέτουµε ότι το ελατήριο έχει αρχικό µήκος µηδέν, ιδανικό ελατήριο. F=-kx x K M x Σχήµα 6.1 ιαστάσεις µεγεθών
6 Ταλαντώσεις 6.1 Απλή Αρµονική Ταλάντωση σε µία ιάσταση 6.1.1 Ελατήριο σε οριζόντιο επίπεδο Υποθέτουµε ότι το ελατήριο έχει αρχικό µήκος µηδέν, ιδανικό ελατήριο. F=-kx x K M x Σχήµα 6.1 ιαστάσεις µεγεθών
m r = F m r = F ( r) m r = F ( v) F = F (x) m dv dt = F (x) vdv = F (x)dx d dt = dx dv dt dx = v dv dx
 m r = F m r = F ( r) m r = F ( v) x F = F (x) m dv dt = F (x) d dt = dx dv dt dx = v dv dx vdv = F (x)dx 2 mv2 x 2 mv2 0 = F (x )dx x 0 K = 2 mv2 W x0 x = x x 0 F (x)dx K K 0 = W x0 x x, x 2 x K 2 K =
m r = F m r = F ( r) m r = F ( v) x F = F (x) m dv dt = F (x) d dt = dx dv dt dx = v dv dx vdv = F (x)dx 2 mv2 x 2 mv2 0 = F (x )dx x 0 K = 2 mv2 W x0 x = x x 0 F (x)dx K K 0 = W x0 x x, x 2 x K 2 K =
 f RF f LO f RF ±f LO Ιδανικός μείκτης RF Είσοδος f RF f RF ± f LO IF Έξοδος f LO LO Είσοδος f RF f LO (ω RF t) (ω LO t) = 1 2 [(ω RF + ω LO )t + (ω RF ω LO )t] RF LO IF f RF ± f LO 0 180 +1 RF IF 1 LO
f RF f LO f RF ±f LO Ιδανικός μείκτης RF Είσοδος f RF f RF ± f LO IF Έξοδος f LO LO Είσοδος f RF f LO (ω RF t) (ω LO t) = 1 2 [(ω RF + ω LO )t + (ω RF ω LO )t] RF LO IF f RF ± f LO 0 180 +1 RF IF 1 LO
MICROMASTER Vector MIDIMASTER Vector
 s MICROMASTER Vector MIDIMASTER Vector... 2 1.... 4 2. -MICROMASTER VECTOR... 5 3. -MIDIMASTER VECTOR... 16 4.... 24 5.... 28 6.... 32 7.... 54 8.... 56 9.... 61 Siemens plc 1998 G85139-H1751-U553B 1.
s MICROMASTER Vector MIDIMASTER Vector... 2 1.... 4 2. -MICROMASTER VECTOR... 5 3. -MIDIMASTER VECTOR... 16 4.... 24 5.... 28 6.... 32 7.... 54 8.... 56 9.... 61 Siemens plc 1998 G85139-H1751-U553B 1.
 !"#!"!"# $ "# '()!* '+!*, -"*!" $ "#. /01 023 43 56789:3 4 ;8< = 7 >/? 44= 7 @ 90A 98BB8: ;4B0C BD :0 E D:84F3 B8: ;4BG H ;8
!"#!"!"# $ "# '()!* '+!*, -"*!" $ "#. /01 023 43 56789:3 4 ;8< = 7 >/? 44= 7 @ 90A 98BB8: ;4B0C BD :0 E D:84F3 B8: ;4BG H ;8
(x y) = (X = x Y = y) = (Y = y) (x y) = f X,Y (x, y) x f X
 X, Y f X,Y x, y X x, Y y f X Y x y X x Y y X x, Y y Y y f X,Y x, y f Y y f X Y x y x y X Y f X,Y x, y f X Y x y f X,Y x, y f Y y x y X : Ω R Y : Ω E X < y Y Y y 0 X Y y x R x f X Y x y gy X Y gy gy : Ω
X, Y f X,Y x, y X x, Y y f X Y x y X x Y y X x, Y y Y y f X,Y x, y f Y y f X Y x y x y X Y f X,Y x, y f X Y x y f X,Y x, y f Y y x y X : Ω R Y : Ω E X < y Y Y y 0 X Y y x R x f X Y x y gy X Y gy gy : Ω
Mesh Parameterization: Theory and Practice
 Mesh Parameterization: Theory and Practice Kai Hormann, Bruno Lévy, Alla Sheffer To cite this version: Kai Hormann, Bruno Lévy, Alla Sheffer. Mesh Parameterization: Theory and Practice. This document is
Mesh Parameterization: Theory and Practice Kai Hormann, Bruno Lévy, Alla Sheffer To cite this version: Kai Hormann, Bruno Lévy, Alla Sheffer. Mesh Parameterization: Theory and Practice. This document is
Déformation et quantification par groupoïde des variétés toriques
 Défomation et uantification pa goupoïde de vaiété toiue Fédéic Cadet To cite thi veion: Fédéic Cadet. Défomation et uantification pa goupoïde de vaiété toiue. Mathématiue [math]. Univeité d Oléan, 200.
Défomation et uantification pa goupoïde de vaiété toiue Fédéic Cadet To cite thi veion: Fédéic Cadet. Défomation et uantification pa goupoïde de vaiété toiue. Mathématiue [math]. Univeité d Oléan, 200.
Physique des réacteurs à eau lourde ou légère en cycle thorium : étude par simulation des performances de conversion et de sûreté
 Physique des réacteurs à eau lourde ou légère en cycle thorium : étude par simulation des performances de conversion et de sûreté Alexis Nuttin To cite this version: Alexis Nuttin. Physique des réacteurs
Physique des réacteurs à eau lourde ou légère en cycle thorium : étude par simulation des performances de conversion et de sûreté Alexis Nuttin To cite this version: Alexis Nuttin. Physique des réacteurs
AC 1 = AB + BC + CC 1, DD 1 = AA 1. D 1 C 1 = 1 D 1 F = 1. AF = 1 a + b + ( ( (((
 ? / / / o/ / / / o/ / / / 1 1 1., D 1 1 1 D 1, E F 1 D 1. = a, D = b, 1 = c. a, b, c : #$ #$ #$ 1) 1 ; : 1)!" ) D 1 ; ) F ; = D, )!" D 1 = D + DD 1, % ) F = D + DD 1 + D 1 F, % 4) EF. 1 = 1, 1 = a + b
? / / / o/ / / / o/ / / / 1 1 1., D 1 1 1 D 1, E F 1 D 1. = a, D = b, 1 = c. a, b, c : #$ #$ #$ 1) 1 ; : 1)!" ) D 1 ; ) F ; = D, )!" D 1 = D + DD 1, % ) F = D + DD 1 + D 1 F, % 4) EF. 1 = 1, 1 = a + b
Studies in Magnetism and Superconductivity under Extreme Pressure
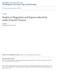 Washington University in St. Louis Washington University Open Scholarship All Theses and Dissertations (ETDs) 1-1-2011 Studies in Magnetism and Superconductivity under Extreme Pressure Wenli Bi Washington
Washington University in St. Louis Washington University Open Scholarship All Theses and Dissertations (ETDs) 1-1-2011 Studies in Magnetism and Superconductivity under Extreme Pressure Wenli Bi Washington
! " #$% & '()()*+.,/0.
 ! " #$% & '()()*+,),--+.,/0. 1!!" "!! 21 # " $%!%!! &'($ ) "! % " % *! 3 %,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,0 %%4,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,5
! " #$% & '()()*+,),--+.,/0. 1!!" "!! 21 # " $%!%!! &'($ ) "! % " % *! 3 %,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,0 %%4,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,5
(product-operator) I I cos ω ( t sin ω ( t x x ) + Iy )
 (product-operator) I I cos( t) + I sin( t) x x y z 2π (rad) y 1 y t x = 2πν x t (rad) sin t Iy# cos t t Ix# Ix# (t ) z Ix# Iy# Ix# (t ) z Ix cos (t ) + Iy sin (t ) -x -y t y I-y# I-y# (t ) z (t ) z x I-y#
(product-operator) I I cos( t) + I sin( t) x x y z 2π (rad) y 1 y t x = 2πν x t (rad) sin t Iy# cos t t Ix# Ix# (t ) z Ix# Iy# Ix# (t ) z Ix cos (t ) + Iy sin (t ) -x -y t y I-y# I-y# (t ) z (t ) z x I-y#
J! "#$ %"& ( ) ) ) " *+, -./0-, *- /! /!+12, ,. 6 /72-, 0,,3-8 / ',913-51:-*/;+ 5/<3/ +15;+ 5/<3=9 -!.1!-9 +17/> ) ) &
 J! "#$ %"& J ' ( ) ) ) " *+, -./0-, L *- /! /!+12,3-4 % +15,. 6 /72-, 0,,3-8 / ',913-51:-*/;+ 5/01 ',913-51:--
J! "#$ %"& J ' ( ) ) ) " *+, -./0-, L *- /! /!+12,3-4 % +15,. 6 /72-, 0,,3-8 / ',913-51:-*/;+ 5/01 ',913-51:--
 γ n ϑ n n ψ T 8 Q 6 j, k, m, n, p, r, r t, x, y f m (x) (f(x)) m / a/b (f g)(x) = f(g(x)) n f f n I J α β I = α + βj N, Z, Q ϕ Εὐκλείδης ὁ Ἀλεξανδρεύς Στοιχεῖα ἄκρος καὶ μέσος λόγος ὕδωρ αἰθήρ ϕ φ Φ τ
γ n ϑ n n ψ T 8 Q 6 j, k, m, n, p, r, r t, x, y f m (x) (f(x)) m / a/b (f g)(x) = f(g(x)) n f f n I J α β I = α + βj N, Z, Q ϕ Εὐκλείδης ὁ Ἀλεξανδρεύς Στοιχεῖα ἄκρος καὶ μέσος λόγος ὕδωρ αἰθήρ ϕ φ Φ τ
Κεφάλαιο 1 Πραγματικοί Αριθμοί 1.1 Σύνολα
 x + = 0 N = {,, 3....}, Z Q, b, b N c, d c, d N + b = c, b = d. N = =. < > P n P (n) P () n = P (n) P (n + ) n n + P (n) n P (n) n P n P (n) P (m) P (n) n m P (n + ) P (n) n m P n P (n) P () P (), P (),...,
x + = 0 N = {,, 3....}, Z Q, b, b N c, d c, d N + b = c, b = d. N = =. < > P n P (n) P () n = P (n) P (n + ) n n + P (n) n P (n) n P n P (n) P (m) P (n) n m P (n + ) P (n) n m P n P (n) P () P (), P (),...,
 1951 {0, 1} N = N \ {0} n m M n, m N F x i = (x i 1,..., xi m) x j = (x 1 j,..., xn j ) i j M M i j x i j m n M M M M T f : F m F f(m) f M (f(x 1 1,..., x1 m),..., f(x n 1,..., xn m)) T R F M R M R x
1951 {0, 1} N = N \ {0} n m M n, m N F x i = (x i 1,..., xi m) x j = (x 1 j,..., xn j ) i j M M i j x i j m n M M M M T f : F m F f(m) f M (f(x 1 1,..., x1 m),..., f(x n 1,..., xn m)) T R F M R M R x
ΜΕΤΑΠΤΥΧΙΑΚΗ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ. Ελευθερίου Β. Χρυσούλα. Επιβλέπων: Νικόλαος Καραμπετάκης Καθηγητής Α.Π.Θ.
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΘΕΩΡΗΤΙΚΗ ΠΛΗΡΟΦΟΡΙΚΗ ΚΑΙ ΘΕΩΡΙΑ ΣΥΣΤΗΜΑΤΩΝ ΚΑΙ ΕΛΕΓΧΟΥ Αναγνώριση συστημάτων με δεδομένη συνεχή και κρουστική συμπεριφορά
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΘΕΩΡΗΤΙΚΗ ΠΛΗΡΟΦΟΡΙΚΗ ΚΑΙ ΘΕΩΡΙΑ ΣΥΣΤΗΜΑΤΩΝ ΚΑΙ ΕΛΕΓΧΟΥ Αναγνώριση συστημάτων με δεδομένη συνεχή και κρουστική συμπεριφορά
Ó³ Ÿ , º 1(130).. 7Ä ±μ. Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê
 Ó³ Ÿ. 006.. 3, º 1(130).. 7Ä16 Š 530.145 ˆ ƒ ˆ ˆŒ ˆŸ Š ƒ.. ±μ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê É μ ² Ö Ó μ μ Ö μ μ²õ μ É μ ÌÉ ±ÊÎ É ² ³ É μ - Î ±μ μ ÊÌ ±μ Ëμ ³ μ- ±² μ ÒÌ ³μ ²ÖÌ Ê ±. ³ É ÔÉμ μ μ μ Ö, Ö ²ÖÖ Ó ±μ³
Ó³ Ÿ. 006.. 3, º 1(130).. 7Ä16 Š 530.145 ˆ ƒ ˆ ˆŒ ˆŸ Š ƒ.. ±μ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê É μ ² Ö Ó μ μ Ö μ μ²õ μ É μ ÌÉ ±ÊÎ É ² ³ É μ - Î ±μ μ ÊÌ ±μ Ëμ ³ μ- ±² μ ÒÌ ³μ ²ÖÌ Ê ±. ³ É ÔÉμ μ μ μ Ö, Ö ²ÖÖ Ó ±μ³
!"#!$% &' ( )*+*,% $ &$ -.&01#(2$#3 4-$ #35667
 !"#!$% & &' ( )*+*,% $ -*(-$ -.*/% $- &$ -.&01#(2$#3 4-$ #35667 5051 & 00000000000000000000000000000000000000000000000000000000000000000000000000000 9 508&:;&& 0000000000000000000000000000000000000000000000000
!"#!$% & &' ( )*+*,% $ -*(-$ -.*/% $- &$ -.&01#(2$#3 4-$ #35667 5051 & 00000000000000000000000000000000000000000000000000000000000000000000000000000 9 508&:;&& 0000000000000000000000000000000000000000000000000
 f H f H ψ n( x) α = 0.01 n( x) α = 1 n( x) α = 3 n( x) α = 10 n( x) α = 30 ū i ( x) α = 1 ū i ( x) α = 3 ū i ( x) α = 10 ū i ( x) α = 30 δū ij ( x) α = 1 δū ij ( x) α = 3 δū ij ( x) α = 10 δū ij ( x)
f H f H ψ n( x) α = 0.01 n( x) α = 1 n( x) α = 3 n( x) α = 10 n( x) α = 30 ū i ( x) α = 1 ū i ( x) α = 3 ū i ( x) α = 10 ū i ( x) α = 30 δū ij ( x) α = 1 δū ij ( x) α = 3 δū ij ( x) α = 10 δū ij ( x)
a(z) = k 0 1 z k = k 0 2 k z k = k 0 z k = (1 + z) n. k
 !" #$%% $&$'$ # %( $)%*&%' '+ &'&% ! " " # $ " " % " & ' # () *+ (, *,-.$ / " " " * $ 0 * " # " $ * $ 0 # % " & ', # ' * # " & #! " # %& *%& $ % & ' " ( z D log! ) * (% % (+, ) " " -. // 0 ', % 0 ', %
!" #$%% $&$'$ # %( $)%*&%' '+ &'&% ! " " # $ " " % " & ' # () *+ (, *,-.$ / " " " * $ 0 * " # " $ * $ 0 # % " & ', # ' * # " & #! " # %& *%& $ % & ' " ( z D log! ) * (% % (+, ) " " -. // 0 ', % 0 ', %
Multi-GPU numerical simulation of electromagnetic waves
 Multi-GPU numerical simulation of electromagnetic waves Philippe Helluy, Thomas Strub To cite this version: Philippe Helluy, Thomas Strub. Multi-GPU numerical simulation of electromagnetic waves. ESAIM:
Multi-GPU numerical simulation of electromagnetic waves Philippe Helluy, Thomas Strub To cite this version: Philippe Helluy, Thomas Strub. Multi-GPU numerical simulation of electromagnetic waves. ESAIM:
ITU-R P (2009/10)
 ITU-R.38-6 (009/0 $% #! " #( ' * & ' /0,-. # GHz 00 MHz 900 ITU-R.38-6 ii.. (IR (ITU-T/ITU-R/ISO/IEC.ITU-R http://www.itu.int/itu-r/go/patents/en. (http://www.itu.int/publ/r-rec/en ( ( BO BR BS BT F M
ITU-R.38-6 (009/0 $% #! " #( ' * & ' /0,-. # GHz 00 MHz 900 ITU-R.38-6 ii.. (IR (ITU-T/ITU-R/ISO/IEC.ITU-R http://www.itu.int/itu-r/go/patents/en. (http://www.itu.int/publ/r-rec/en ( ( BO BR BS BT F M
Formulas of Agrawal s Fiber-Optic Communication Systems NA n 2 ; n n. NA( )=n1 a
 Formula o grawal Fiber-Oti Communiation Sytem Chater (ntroution) 8 / max m M / E nh N h M m 4 6.66. J e 9.6 / m log /mw SN / / /, NZ SN log / Z max N E Chater (Otial Fiber) Setion - (Geometrial Oti erition)
Formula o grawal Fiber-Oti Communiation Sytem Chater (ntroution) 8 / max m M / E nh N h M m 4 6.66. J e 9.6 / m log /mw SN / / /, NZ SN log / Z max N E Chater (Otial Fiber) Setion - (Geometrial Oti erition)
Answers to practice exercises
 Answers to practice exercises Chapter Exercise (Page 5). 9 kg 2. 479 mm. 66 4. 565 5. 225 6. 26 7. 07,70 8. 4 9. 487 0. 70872. $5, Exercise 2 (Page 6). (a) 468 (b) 868 2. (a) 827 (b) 458. (a) 86 kg (b)
Answers to practice exercises Chapter Exercise (Page 5). 9 kg 2. 479 mm. 66 4. 565 5. 225 6. 26 7. 07,70 8. 4 9. 487 0. 70872. $5, Exercise 2 (Page 6). (a) 468 (b) 868 2. (a) 827 (b) 458. (a) 86 kg (b)
ITU-R P ITU-R P (ITU-R 204/3 ( )
 1 ITU-R P.530-1 ITU-R P.530-1 (ITU-R 04/3 ) (007-005-001-1999-1997-1995-1994-199-1990-1986-198-1978)... ( ( ( 1 1. 1 : - - ) - ( 1 ITU-R P.530-1..... 6.3. :. ITU-R P.45 -. ITU-R P.619 -. ) (ITU-R P.55
1 ITU-R P.530-1 ITU-R P.530-1 (ITU-R 04/3 ) (007-005-001-1999-1997-1995-1994-199-1990-1986-198-1978)... ( ( ( 1 1. 1 : - - ) - ( 1 ITU-R P.530-1..... 6.3. :. ITU-R P.45 -. ITU-R P.619 -. ) (ITU-R P.55
Answers - Worksheet A ALGEBRA PMT. 1 a = 7 b = 11 c = 1 3. e = 0.1 f = 0.3 g = 2 h = 10 i = 3 j = d = k = 3 1. = 1 or 0.5 l =
 C ALGEBRA Answers - Worksheet A a 7 b c d e 0. f 0. g h 0 i j k 6 8 or 0. l or 8 a 7 b 0 c 7 d 6 e f g 6 h 8 8 i 6 j k 6 l a 9 b c d 9 7 e 00 0 f 8 9 a b 7 7 c 6 d 9 e 6 6 f 6 8 g 9 h 0 0 i j 6 7 7 k 9
C ALGEBRA Answers - Worksheet A a 7 b c d e 0. f 0. g h 0 i j k 6 8 or 0. l or 8 a 7 b 0 c 7 d 6 e f g 6 h 8 8 i 6 j k 6 l a 9 b c d 9 7 e 00 0 f 8 9 a b 7 7 c 6 d 9 e 6 6 f 6 8 g 9 h 0 0 i j 6 7 7 k 9
Transfert sécurisé d Images par combinaison de techniques de compression, cryptage et de marquage
 Transfert sécurisé d Images par combinaison de techniques de compression, cryptage et de marquage José Marconi Rodrigues To cite this version: José Marconi Rodrigues. Transfert sécurisé d Images par combinaison
Transfert sécurisé d Images par combinaison de techniques de compression, cryptage et de marquage José Marconi Rodrigues To cite this version: José Marconi Rodrigues. Transfert sécurisé d Images par combinaison
 χ 2 1 N =0 1 1 2 3 npn 1 2 1 9 N =0 1 1 1 1 2 6 6 4 9 B V 70 100 10 1 2 2 2 2 a 1 a 2 δ 1, δ 2 δ 3. b 1 b 2 Γ, K, K M K K A B a 1 = ( ) ( ) 3a 2, a 3a, a 2 2 = 2, a, 2 a = a 1 = a 2 2.46 ( ) (
χ 2 1 N =0 1 1 2 3 npn 1 2 1 9 N =0 1 1 1 1 2 6 6 4 9 B V 70 100 10 1 2 2 2 2 a 1 a 2 δ 1, δ 2 δ 3. b 1 b 2 Γ, K, K M K K A B a 1 = ( ) ( ) 3a 2, a 3a, a 2 2 = 2, a, 2 a = a 1 = a 2 2.46 ( ) (
Inflation and Reheating in Spontaneously Generated Gravity
 Univesità di Bologna Inflation and Reheating in Spontaneously Geneated Gavity (A. Ceioni, F. Finelli, A. Tonconi, G. Ventui) Phys.Rev.D81:123505,2010 Motivations Inflation (FTV Phys.Lett.B681:383-386,2009)
Univesità di Bologna Inflation and Reheating in Spontaneously Geneated Gavity (A. Ceioni, F. Finelli, A. Tonconi, G. Ventui) Phys.Rev.D81:123505,2010 Motivations Inflation (FTV Phys.Lett.B681:383-386,2009)
L. F avart. CLAS12 Workshop Genova th of Feb CLAS12 workshop Feb L.Favart p.1/28
 L. F avart I.I.H.E. Université Libre de Bruxelles H Collaboration HERA at DESY CLAS Workshop Genova - 4-8 th of Feb. 9 CLAS workshop Feb. 9 - L.Favart p./8 e p Integrated luminosity 96- + 3-7 (high energy)
L. F avart I.I.H.E. Université Libre de Bruxelles H Collaboration HERA at DESY CLAS Workshop Genova - 4-8 th of Feb. 9 CLAS workshop Feb. 9 - L.Favart p./8 e p Integrated luminosity 96- + 3-7 (high energy)
