|
|
|
- ÊἙρμῆς Τρικούπης
- 6 χρόνια πριν
- Προβολές:
Transcript
1
2
3
4 χ 2
5 1 N =0
6 1
7
8
9 1 2 3
10 npn N =0 1 1
11 1 1 2
12 B V
13
14
15
16
17
18
19
20 1
21
22 a 1 a 2 δ 1, δ 2 δ 3. b 1 b 2 Γ, K, K M K K
23 A B a 1 = ( ) ( ) 3a 2, a 3a, a 2 2 = 2, a, 2 a = a 1 = a ( ) ( a δ 1 =, 0, δ 2 = 3 ) ( a 2 3, a, δ 2 3 = ) a 2 3, a, 2 a = δ 1 = δ 2 = δ
24 ( ) ( ) 2π b 1 =, 2π 2π, b 3a a 2 =, 2π. 3a a Γ M K K Γ ( ) ( ) 2π ΓK =, 2π, ΓK 2π =, 2π. 3a 3a 3a 3a H = t c n,a c m,b + n,m c n,α(c n,α ) p z n α = A, B t n, m H(k) = 3 n=1 t 0 e ik δ n, e ik δ n 0 {c A (k), c B (k)} c n,α K q = k K
25 K H(q) = v F σ q. σ v F c/300 ( / ) K K H(q )=H (q) q = k K K Ψ(q) = 1 2 e iθ q/2 ±e iθ q/2, p z A B ε(q) =± v F q, q = 0 0.6
26 ε k K K 2 Γ K K M K K Γ, K, K M
27 2 α = 1 4πϵ 0 e 2 c 1 137, e 2 /4πϵ 0 r pc = c/r ϵ 0
28 e 2 α = πϵ v F ϵ = ϵ 0 ϵ r ϵ r ϵ r 2 c/300 H(q) = v F σ q + V (r),
29 V (r) v l E = F V (r). V (r) a l E a. 2 V (r) a λ F l E λ F λ F =2π/q F ε F l E λ F l E >λ F
30 N =0 ε =0 ε =0 l B = eb = 26. B l B l m l m
31 q Π q + ea a = a = l B 2 (Π x iπ y ), l B 2 (Π x + iπ y ). K H(q) = 2 v F l B 0 a. a 0 ε = (N) v F l B 2N.
32 τ ee τ p, τ ee τ p
33 1 1
34 (0, 0)
35
36
37 2
38 q ϵ r φ(r) = 1 4πϵ 0 ϵ r q r.
39 n φ(r) = 1 4πϵ 0 ϵ r q r e k r. k k 3 = 4πe 2 ϵ n µ, k 2 = 2πe2 n ϵ µ, 3 2 ϵ = ϵ 0 ϵ r k 1 n/ µ = g(µ)
40 µ ε F T =0 eφ ε(k F )/ n = µ ε(n) ε(n 1) N N 1 µ ε(k F )=µ
41 µ E µ eφ Q = CV, Q C V C E C Q
42 C Q = dq dv = ed( en) = e 2 dn d(ev ) dµ. N e e V µ = ev V 1 V 2 = µ 1 µ 2, e V 2 µ 2 V 1 µ 1
43 C Q = e 2 dn dµ = e 2 d dµ e 2 d dµ µ dεg(ε)f(ε) dεg(ε)+ [O((T/µ) 2m )] m=1 e 2 g(µ), T 0, n T g(ε) f(ε) dn/dµ C = ( ) 1 = C QC E. C Q C E C Q + C E C Q C E C C E
44 Q ε = ϵ 2 dr 3 E 2 } {{ } ε E µ + µ dε εg (ε)+ dε εg (ε) 0 } {{ 0 } ε Q Q + dqv 0 } {{ } ε S ε E ε Q
45 2 V C 2 C V =0 V > 0 eφ C µ C e V = eφ + µ g ( ) ε S
46 C E, = ϵ 0 ϵ r A d = ϵa d, A d ϵ r E = Q ϵa = N e, ϵ N e ε E = (N e) 2 2C E,. ε Q ε S ε S = Q V = e N V.
47 ε =0= N e 2 + N C E, N ( µ 0 µ ) dε εg (ε)+ dε εg (ε) e V. 0 > N g (ε) = [ ] N, ε N + N =0, 3 3
48 e V = n e 2 C E, + µ, n = N /A C E, F/ 2 ev eφ µ eφ = n e 2 C E,. ev eφ V = 10 d = 300 ε r =4 2 µ = v F πn n = n µ V = n e/c E, n = µ
49 µ ( e V = n e ) C E, C Q,
50 [ ( C Q, = 2e2 k B T π( v F ) 2 ln 2 1+ µ )], k B T F/m 2 e k B v F µ µ k B T C Q, 2e2 v F π n, n
51 C Q, = 2e2 v F π ng + n, n G n V = ε F = C Q, µ 2 C E = 2πlϵ 0ϵ r 1 (d/r) d r 2πlϵ 0ϵ r (2d/r), F l ϵ 0 ϵ r d r
52 ϵ r =4 r =1 d =5 C E 100 µ 1 C M Q, = 8e2 hv F 310 µ 1,
53 C SC,n Q, = C SC,p Q, = 2 q=1 2 q=1 e 2 [ n e (q) 1 (2N 0e x n n(q))(α +2βx n +3γx 2 ] n) k B T 2N 0 e x, n e 2 [ n h (q) 1 (2N 0e x p n(q))(α +2βx p +3γx 2 ] p) k B T 2N 0 e x, p x = 2ε ε (q), 2k B T x = 2ε ε (q). 2k B T C SC,n Q, CSC,p Q, n e(h) (q) q N 0 ε g (q) q α, β, γ q
54 17, 20, 23, 26, 29, ε C k B T ε k B T ε C
55 ε = v F 2L 600 µ, k B T 200 µ, ε C = e2 C C 00 = CM Q,C E C M Q, + C E 50, C E 100 µ 1 20 eφ C E, µ C ev = eφ + µ
56 2 V C 2 C V =0 V > 0
57 4 100 V e(v V )= µ eφ. V (V V ) φ
58 2 V V C C 2 C C V > 0 V > 0 C C V C V V V C 2
59 N + N + N =0 e(v V )=e 2 (n + n ) C E, + µ (n ), V ev = µ µ eφ. ev = µ (n )+µ (n ) e 2 n C E,. V V
60 V V di/dv V V V V 1.6
61 0.1 1 V V n V V n ev = µ +,
62 V V n V = en C E, + V +, V
63 dv dv = e2 C E, dn dµ +1. g (V,V )= dn = C ( ) E, dv dµ e 2 1 C E, dv e 2 ( dv dv ), g (V,V ) V dv /dv 1 µ = ev, ( ) dv C Q, = C E,, dv n V V C ε F = µ
64 n = v F = / χ 2 V V =0 n x
65 n m s x x x χ 2 s x =1 V / V V /2 V V V y x x x s x y y y s y x V y V
66 n m {i, j} dv dv = s y V ij s x V. ij s x s y x y {i, j} χ 2 n m {i, j} z χ 2 ij = n {z ( V [i + n + s x ], V [j + s y ] ) z ( V [i + n], V [j] )} 2 n z( V [i + n], V [j] ), z ( V [i], V [j] ) V V {i, j} n x χ 2 s x s x χ 2
67 V V ν =1 4
68 9 3 0 V x C q ν =1 4
69 V V
70
71
72 3
73 0.3
74
75 µ 30 µ 150 µ µ
76 1 100 µ 3
77
78
79
80 1
81 0.01%
82 10 µ 10 µ 50 µ
83
84 % % σ(ω) = π ωd ϵ(ω) 1 2 d c c d ϵ(ω) ω 500 ϵ =6 ϵ ϵ > 100 σ = µ
85 100 µ 1 µ 100 µ /(hc/500 )
86 (33, 33), (16, 7), (6, 5), (22, 14)
87 H = (p qa)2 2m. A =0 H = H 0 + V (t) = p2 2m q m A p, A(r,t)=A 0 ne i(k r ωt) + n E = A/ t V (t) = q m (n p)e 0 ω ωt = V 0 ωt. V 0 Γ i f = 2π f V 0 i 2 δ(ε f ε i + ω), f V 0 i = qe 0 f n p i mω
88 : k =0, E : J =0( k = 0), E : J = ±1( k = ±2/d), E ( ) j J = j s =0 E =0 J =0 j σ(ω) ϵ(ω) χ e (ω) =ϵ(ω) 1 σ(ω) ϵ(ω)
89 (8, 0) (8, 8) ϵ(ω)
90 ϵ(ω) ϵ(ω) E 22 = M11 E 11 = M 11 +
91 E ii M ii E 11 E 22 E 11 E 22 E 11 E E 33 E E 33 E 44 E 11 E 22
92
93 t =2.9 a = ϵ(ω)
94 E ii 1/d d µ µ 150
95 % 25%
96 532
97
98
99
100 140 5
101 3/7/ µ
102 40 µ 1 µ 10 µ 2 25 µ
103 4 10
104 4
105 3 E = ρ ϵ 0 B =0 E = B t B = µ 0 J + µ 0 ϵ 0 E t c
106
107 r α =(ct, r), ( ) α 1 = c t,, ( ) p α ε = c, p, J α =(ρc, J), ( ) k α ω = c, k, ( ) A α φ = c, A, {t, x, y, z} = {0, 1, 2, 3} 0 1, 2,
108 E = A t φ, B = A, 0 E x c E y c E z c E x F αβ = α A β β A α c 0 B z B y =. E y c B z 0 B x E z c B y B x B x B y B z G αβ = 1 E 2 ε αβγδf γδ B x 0 z c E y c =, B y E z E c 0 x c E B y z c E x c 0
109 ε αβγδ +1 {αβγδ} {1, 2, 3, 4} ε αβγδ = 1 {αβγδ} {1, 2, 3, 4}, S αβ... = L α κl β λ... Sκλ..., S αβ... =(L 1 ) κ α(l 1 ) λ β... S κλ..., S S x γ v c γ 0 0 L α v c β = γ γ 0 0, (L 1 ) α β = v γ c γ 0 0 v c γ γ 0 0,
110 v γ = 1 ( 1 v2 c 2 ), γ i γ i β = v/c S αβ... = g αγ g βδ... S γδ..., g αβ = g αβ =
111 S S v E = E, B = B, E = γ(e + v B), B = γ (B 1c ) 2 v E. α F αβ = µ 0 J β, α G αβ =0, ) F αβ F αβ = =2 (B 2 E2, c 2 F αβ G αβ = = 4 c E B.
112 B < E/c B < E/c B = E/c E B E B =0 E =0 B =0 B 2 E 2 /c 2 < > 0 h
113 λ = h p, λ p h i [ ] t Ψ(r,t)= 2 2m 2 + V (r,t) Ψ(r,t), = h/2π m V (r,t) Ψ(r,t)
114 ε 2 = p 2 c 2 + m 2 c 4, ε m c p ε = i, p = i, t
115 2 2 Ψ(r,t) t 2 = ( 2 c m 2 c 4) Ψ(r,t). 4 4 i Ψ(r,t) t = ( i c α + βmc 2) Ψ(r,t).
116 I 2 0 β = 0 I 2 0 σ y α 2 = σ y 0, α 1 =, α 3 = 0 σ x σ x 0 0 σ z σ z 0,, I σ 0 1 σ x = 1 0, σ y = 0 i 1 0, σ z =. i (ic γ µ µ mc 2 )Ψ(r,t)=0. µ 0, 1, 2, 3 t, x, y, z µ =(c 1 / t, ) γ µ 4 4
117 γ 0 0 = I 2 I 2 0 γ 2 0 = σ y σ y 0, γ 1 =, γ 3 = 0 σ x σ x 0 0 σ z σ z 0,. {γ µ,γ ν } = γ µ γ ν + γ ν γ µ =2g µν I 4 g µν I Ψ +, (r,t) Ψ +, (r,t) Ψ(r,t)=, Ψ, (r,t) Ψ, (r,t)
118 (ic σ µ µ )ψ(r) =0, σ µ = σ µ µ = {0, 1, 2} {t, x, y} σ 0 = iσ z {σ µ,σ ν } = σ µ σ ν + σ ν σ µ =2I cσ pψ(r) =εψ(r),
119 v F c p = q = (q x,q y )= i ( x, y ) c/300 H = v F (σ q)+v (x), σ =(σ x,σ y ) q =(q x,q y ) x, y V (x) V (x)
120 v l E F V (r) a. l E V (r) a 1 4 l E 4 a cc 1.42
121
122 ε =0 ( ε, q, e, m, + v ) ε h = ε e, k h = k e, h e k q = k K q (+ ε, + q, + e, + m, + v )
123 1 K v dr dt = i [H, r] = i [ v F σ q, r] = v F σ, σ r q K σ q v = Ψ(q) v F σ Ψ(q) = ±v F q q,
124 v =(1/ ) ε/ k 1 V (x) x dv x dt = i [H,v x] = i [ v F σ q + V (x),v F σ x ] =2v 2 F σ z q y. q y y dq y dt = i [H,q y]=0, q y q y (t) =q y (0) q y =0
125 l E λ F T (θ) 2 = θθ t 2( ), θ+θ t 2 θ ( ) θ t = 1 ε V 0 ε θ + π. l E λ F T (θ) 2 = e π v F q 2 y/ee = e πq F w 2θ, ε = eew w
126 npn pnp T (θ) 2 = 2 θ 1 2 (q xd) 2 θ, q xd = 2πl 1 2(ε/V 0 )+(ε/v 0 ) 2 2 θ l = V 0 d/ 2π v F = V 0 d/2π npn x x
127 w =0 T 2 w V 0 = T 2 100
128 npn npn n = d = 100 V 0 =1
129 q xd = πn, N q d pn
130 [ (cα p + βmc 2 ) Ze ] ψ(r) =ε r H ψ(r). Z ] ε H = mc [1+ 2 (Zα) ( ( ) ). 2 n j j (Zα) 2 1s 2 n =1 j =1/2 1/α 137 α Z = 172
131 r 0 Z 1/r 2 1/r ε = 2 2mr 2 Ze 2 4πϵ 0 r. r 0 = 4πϵ 0 2 me 2.
132 ε = 2 c +(mc 2 ) 2 Ze2 r 4πϵ 0 r. Z 1/α α Z 1/α 137 Z = 172 Z 1s 2 Z 1.6 1s 2 Γ 2e
133 Z Z Z Z Z 1.6 Z Z Z
134 2e 2e 2e Z Z cr = 172 Zα > j ε H = ε 0 + iγ. ε 0 Γ
135 10 19 δε 0 (Z Z ). Γ (Z Z ) 2, Z = 118 α 1/137 α 1 Zα > 1 137
136 Z = 1e ( v F σ p + V ) ψ(x) =εψ(x).
137 V = Ne2 L 2πLϵ 0 ϵ r x, 2 + d 2 L N d ε r x = L V (x = L) =0
138 L L 1
139 1 1 y 1 x ψ(x) =Ce iq yy u A (x), u B (x) q y y u A(B) A(B) C x u A = x u B = ( ε ) + V v u B + q y u A, F ) u A q y u A. ( ε v F V x d/10 u A (x = 200 d) = u B (x = 200 d) = 1 ψ(x) 2
140 ψ(x) 2 2 ε q y v F π/l π/l N 1 1 1
141 1
142 5 2 2
143 E = v F B B > E/v F B < E/v F
144
145 v = E/B E B c v F B c = E/v F
146 H = v F σ Π, Π q + ea A =(A x,a y,a z ) B = A z ε (N) =(N) v F l B 2N, l B = /eb N H = v F σ Π + eex, E x v F iv F σ ( µ µ + i e ) A µ ψ(x µ )=0,
147 µ = {0, 1, 2} {t, x, y} σ µ σ 0 = iσ z A µ =(φ/v F,A 1,A 2 ) φ E B =0 B> E/v F E =0 S y E S v = E/B E =0 B = B 1 β 2 β = v/v F iv F σ ( µ µ + i e ) A µ ψ(x µ )=0. A 1 = Bx 2 x 2 = y ( ) iv F σ µ µ + iσ 1 e B x 2 ψ(x µ )=0. ε (N) =(N) v F l B 2N(1 β 2 ) 1 4, B = B 1 β 2 l B v F c 3 p µ =(ε/v F,p 1,p 2 ) 3
148 B β = 0, 0.6, 0.8 0, 0.2, , 6, 9
149 v F c 3 ε (N) =(N) v F l B 2N(1 β 2 ) 3 4 v F βq y, (p 1,p 2 )= (q 1,q 2 )= (q x,q y ) q ε =(N +1/2) ω c k y E B m 2 ( ) E 2. B (1 β 2 ) (3/4) 2
150 V V V φ V V
151 B V di/dv V V =0
152 E E B c
153 V B V V
154 q =4α q F =4α πn, α q F n d = d q 1, B c = E v F = n e C dv F = n e 1 (d /r) 2πlϵdv F, l 500 d 6 r 1 α 0.5 ϵ = ϵ 0 ϵ r ϵ r 4 n n =2
155 C = C (d ) d d d E = n e/c d C (d B c B c V =0 B c =0 B c V V B c
156 V =0 V B E =0 E = E =3 10 6
157 V 10 V =0 V =3 V =6 V V V Gr =2 V V =0 V =2 B c V B c B B B c
158 B V G = i 4e 2 h Γ i LΓ i R (Γ i L +Γ i R) 2 +(µ ε i ) 2, i ε i Γ i L(R) i µ µ µ Γ i ε i g (ε) g (ε) = N g γ N π γn 2 +(ε ε (N)) 2
159 g = 4eB 2π, ε = v F 2e BN, γ N N n = µ 0 dεg (ε). V B V B B = α(b B c ) α = 1 (B c /B) 2 B c = E/v F V n
160 n ε C V V n /ε C ε C ε C B c V B V B c V V C Q 9 C Q V V
161 V V V C Q C Q V V
162 9 V V N =0 V 150 µ 2
163 7 5 3 V 150 µ 2
164 V =1.5, 1, 0.5,
165 V E = V = ε/e V (x) V V N =0
166 pp p nn n pp p nn n npn pnp V V 1 5
167 N =0 N =0 V V 0.2 V N =0 N =0 N =0 V B =3, 5, 7, 9 f(x) = a 1+e b (x+c) + a d. b (x c) 1+e C q 0.5 µ 2
168 N = 0 N = 0 B =3, 5, 7, 9 V c 1 5 < 1 14 B c = E/v F 1 µ 2
169 3 B c = E/v F 9 V r h d V (x) = eφ 0 2 [ x 2 +(h d) 2 x 2 +(h + d) 2 ], φ 0 = φ 0 [ ], (2h r)/r φ 0 1 r 1 h d ϵ =2 1 5
170 B c = E/v F E c B c N =0 1 1 B c = E c /v F
171 6
172 1 2
173 pnp npn pnp npn pnp 1 y x q θ = q t θ t,
174 q θ θ t q ( ) θ c = 1 qt. q
175 πn = = qx 2 + qy 2 n = θ t θ. q θ c pn pnp
176 n n θ c n n θ c pnp M pnp pnp M =1 U 0
177 γ ak 2 a k =2π/λ
178 4 6 1 H(q) = v F σ q + V (x). V (x) 1 U 0 d 4 6
179 M
180 2 2 M d λ U0 d v F, M =0, 1, 2... v F
181 δµ = x = δµ =5 U 0 U 0
182
183 1 U 0, 45, 90, 180
184 1 V
185 V V V =0.5 V =5 V 5 V V = C q C q C q C q V =0 1.5 V =0.5 C q
186 0.5V 1V V
187 V =0, 0.5, 1 0, 50, 100 µ 2
188 C q V
189 V 0.6 V 0.2 V
190 U =0.45 C V =7.25 V 17 C C V C V
191 40 30 U V V =7.25 V 17 C C V =4.25, 6.25, 7.25 C V C
192 V C 4 1
193
194 7
195
196 k B T
197 2 2 1
198 1 D ν
199 I V R D = V I.
200 2
201
202 dp 1 dt dp 2 dt = q 1 (E 1 + v 1 B) p 1 τ 1 (p 1 p 2 ) τ D, = q 2 (E 2 + v 2 B) p 2 τ 2 (p 2 p 1 ) τ D, {1, 2} q i =+ n i e, n i e p i = m i v i B τ 1,2 τ D v 2 =0 ρ D = E 2 en 1 v 1 = m 1 n 1 n 2 e 2 τ D, 2 n =[ 2 ] ρ D (L/W )=R D τ D
203 1 2 dp 2 dt = = ( dq (2π) 2 q dq (2π) 2 q df (q) dt dk1 (2π) 2 ) { } dk2 (2π) 2 W k1,k 1 +q,k 2,k 2 q { f(k 1 ) [ 1 f(k 1 + q) ] f 0 (k 2 ) [ 1 f 0 (k 2 q) ] f(k 1 + q) [ 1 f(k 1 ) ] f 0 (k 2 q) [ 1 f 0 (k 2 ) ]}. f f 0 q 1, 2 W k1,k 1 +q,k 2,k 2 q = 2π V(q) 2 δ(ε k1 + ε k2 ε k1 +q ε k2 q). 2 V(q) = 2πe 2 q 2πe 2 q e qd 2πe 2 q e qd 2πe 2 q. e d
204 q 1 d q = mv/
205 dp 2 dt = v k B T dq (2π) 2 ( q)2 V (q) 2 dk1 (2π) 2 { f 0 (k 2 ) [ 1 f 0 (k 2 q) ]} δ(ε k1 + ε k2 ε k1 +q ε k2 q). dk2 {f (2π) 2 0 (k 1 ) [ 1 f 0 (k 1 + q) ]} dp 2 dt = v k B T dq (2π) 2 ( q)2 V (q) 2 dω [χ 1(q,ω)] [χ 2 (q,ω)] 2. ( ω/k B T ) χ i (q,ω)= dk i f 0 (k i ) f 0 (k i + q) (2π) 2 ω ε(k i )+ε(k i + q) iη. [χ i (q,ω)] = dk i (2π) 2 [ f0 (k i ) f 0 (k i + q) ] δ( ω ε(k i )+ε(k i + q)).
206 q 2 1 dp 2 dt = n 2 ee 2.
207 ρ D = 1 1 n 1 n 2 e 2 2k B T dq (2π) 2 ( q)2 V (q) 2 dω [χ 1(q,ω)] [χ 2 (q,ω)] 2. ( ω/k B T ) k B T ω ρ D = π 2 ζ(3) (k B T ) 2 1 e 2 16 ε F 1 ε F 2 q 1 q 2 k F 1 k F 2 d 4, ζ(3) q ε Fi k Fi T 2 2 T 2 T 2 (ε F /k B T ) T 2 T 2 1 1
208 q 1 1 k B T V (q) q d 1/n [χ(q,ω)]
209 dσ ρ D ρ 1 dσ 2 2 d(en 1 ) d(en 2 ) ρ 1, σ i n i ρ i i B B 2 B 2
210 (κ 1 δt 1 )+a(δt 1 δt 2 )+λδt 1 = j 1,q, (κ 2 δt 2 )+a(δt 2 δt 1 )+λδt 2 =0. δt(r) =T (r) T 0 T 0 T i (r) i j 1,q 1 κ i i λ a dε dt = 2π dq 2 (ε(k + q) ε(k)) V (q) 2 (2π) dk2 {f (2π) 2 0 (k 1 ) [ 1 f 0 (k 1 + q) ]} dk1 (2π) 2 { f 0 (k 2 ) [ 1 f 0 (k 2 q) ]} δ(ε k1 + ε k2 ε k1 +q ε k2 q).
211 dε dt = π dω(n 2 (ω) N 1 (ω))( ω) dq (2π) 2 V (q) 2 [χ 1 (q,ω)] [χ 2 (q,ω)], N i (ω) = 1 e ω/k BT i 1, i a d 2 ε/dtdt j el 11 /T el 12 µ =, j q L 21 /T L 22 1 T
212 L L 11 = T e 2 σ, L 12 = eql 11, L 22 T 2 κ, L S = 1 et L 12L 1 11, Q = 1 e L 12L 1 11 = st e = ST, j q = Qj.
213 Q S s S Q s σ κ 2 x, y j q j L 12 (B) =L 21 (B). j =0 E = µ e = T e L 1 11 L 12 1 T = 1 T L 1 11 QL 11 T = Q T T, [Q, L] =0
214 (κ 1 + κ 2 ) δt = DQ 1 j 1. D D = I 2 I δt 2 j 1,q ρ D = Q 2DQ 1 T (κ 1 + κ 2 ). Q j q = Qj Q Q R D,H 1 T (κ 1 + κ 2 ) Q 1,xyQ 2,xx, R D L WT(κ 1 + κ 2 ) Q 1,xyQ 2,xy, L W D = I 2
215 [Q 1, Q 2 ]=0 ρ D (1) (2) D I 2 ρ D [Q 1, DQ 2 ] 0 κ
216 δt(r)
217 δt (r) δt (r) ρ D = 1 Q 1 Q 2 δµ 2 ( q)δµ 1 (q) 2T (κ 1 + κ 2 ) µ 1 µ 2 q 1+lq 2, l q Q δµ 2 ( q)δµ 1 (q) Q = π2 3e (k BT ) 2 σ 1 σ µ. σ Q B 2
218 T 2 T 4
219
220 α δα i δt = j L ij γ j, δs δt = j γ j δα j δt, L ij (B) =L ji ( B). γ s γ δs/δt 0 L L ij i j γ j α j α, γ
221 j L 11 /T L 12 µ =, j q L 21 /T L 22 1 T L 12 (B) =L 21 ( B). V 1 R 11 R 12 = V 2 R 21 R 22 I 1 I 2, R 12 (B) =R 21 ( B) j 1 σ 11 σ 12 ( V + S T ) 1 =, j 2 σ 21 σ 22 ( V + S T ) 2
222 S σ 12 σ 21 α γ
223
224 V p C p V ac I p 5
225 10
226 >
227 1µ
228 V = 5
229 250, 230,
230 µ 2
231 200, 170, µ 2
232 0.14Ω/K µ 130, /V s V
233 V Ω
234 V V 10 Q D 1
235
236 8
237 2 2
238
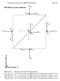
239
240
241 2 1
242
243
244 A
245 a 1 a 2 δ 1, δ 2 δ 3. b 1 b 2 Γ, K, K M K K a 1 = ( ) ( ) 3a 2, a 3a, a 2 2 = 2, a, 2
246 a = a 1 = a ( ) ( a δ 1 =, 0, δ 2 = 3 ) ( a 2 3, a, δ 2 3 = ) a 2 3, a, 2 a = δ 1 = δ 2 = δ k k k
247 ( ) ( ) 2π b 1 =, 2π 2π, b 3a a 2 =, 2π, 3a a Γ M K K Γ ( ) ( ) 2π ΓK =, 2π, ΓK 2π =, 2π. 3a 3a 3a 3a
248
249 H Ψ(k, r) = ε(k) Ψ(k, r), Ψ H H = 2 2m 2 + N [U(r R n )+U(r R n δ 1 )]. n=1 R n = {n 1,n 2 } n n 1a 1 + n 2 a 2 N n {n 1,n 2 } δ 1 B A A B Ψ(k, r) = C A (k) Φ A (k, r) + C B (k) Φ B (k, r). Φ A (k, r) Φ B (k, r) A B C A C B
250 k r N Φ A (k, r) = 1 N Φ B (k, r) = 1 N N n=1 N n=1 e ik R A n φ(r RAn ), e ik R B n φ(r R Bn ), φ(r R An ) φ(r R Bn ) R An R Bn A B R Bn = R An + δ 1 sp 2 2s 2p x 2p y sp 2 σ σ σ 2p z 2p z ε(k) Ψ(k, r) Ψ(k, r) H Ψ(k, r) = ε(k) Ψ(k, r) Ψ(k, r),
251 ε(k) k {Φ A (k, r), Φ B (k, r)} C A (k) Ψ(k) =, C B (k) Φ A (k, r) H Φ A (k, r) Φ A (k, r) H Φ B (k, r) H(k) = Φ B (k, r) H Φ A (k, r) Φ B (k, r) H Φ B (k, r) H AA = H AB = H AA H AB H BA H BB HAB H AA = H (k), Φ A (k, r) Φ A (k, r) Φ A (k, r) Φ B (k, r) S(k) = Φ B (k, r) Φ A (k, r) Φ B (k, r) Φ B (k, r) = S AA S BA S AB = S AA S AB S BB SAB S AA = S (k).
252 A B S lm = δ lm. H(k)Ψ(k) =ε(k)s(k)ψ(k), [H(k) ε(k)s(k)] = 0,
253 ε(k) = ε 0(k) ± ε 0 (k) 2 4(S AA (k) 2 S AB (k) 2 )(H AA (k) 2 H AB (k) 2 ) 2(S AA (k) 2 S AB (k) 2, ) ε 0 (k) =(2H AA (k)s AA (k) S AB (k)h AB(k) H AB (k)s AB(k). S AB S AB S AA =1 S AB =0 H AA = 1 N = 1 N N N e ik (R A R l Am ) φ(r R Am ) H φ(r R Al ), l=1 m=1 N l=1 m=1 N e ik (R A R l Am ) ε 2 δ lm = ε 2, H φ(r RAl ) = ε 2 φ(r RAl ) φ(r R Al ) 2p z R Al ε 2
254 H AB = 1 N 1 N N N e ik (R B R l Am ) φ(r R Am ) H φ(r RBl ), l=1 m=1 N l=1 n=1 3 e ik δ n t =(e ik δ 1 + e ik δ 2 + e ik δ 3 )t. φ(r R Am ) H φ(r R Bl ) δ n 1,2,3 A B t t t γ 0 ε(k) =±t 1+4 3a a 2 k x 2 k y +4 2 a 2 k y. ε 2 =0 K K
255 K π p z π p z K K K K K K 0 H(k) = H AB = H BA 0 3 n=1 t 0 e ik δ n. e ik δ n 0
256 ε k K K Γ K K M K K Γ, K, K M
257 q = k K, q = k K, K 3t a 0 e i5π/6 (q x iq y ) H(q) (1 + O(q/K) 2 ) 2 e i5π/6 (q x + iq y ) 0 3t a 0 q x iq y H(q) =. 2 q x + iq y 0 K {Φ A (k, r), Φ B (k, r)} {Φ A (q, r), Φ B (q, r)} {Φ A,K, Φ B,K } q K K {Φ A,K, Φ B,K } {Φ A,K, Φ B,K }
258 0 H(q) =± v F q x iq y, q x + iq y 0 H(q 0 )=± v F q x + iq y, q x iq y 0 v F = 3t a 2 c/300, c K H(q) = v F σ q, σ 0 1 σ x = 1 0, σ y = 0 i, i 0 σ z q 2 xy σ z
259 K K H(q )=H (q) K K {Φ A,K, Φ B,K, Φ A,K, Φ B,K } σ q 0 H(q) = v F, 0 σ q ε(q) =± v F q. q 2 c v F pc mc 2 ε = ω = ck = pc
260 K H(q) = v F σ q + m vf 2 σ z = m vf 2 v F (q x iq y ), v F (q x + iq y ) m vf 2 m ε(q) =± ( v F q ) 2 +(m vf 2 ) 2, σ z =2m v 2 F.
261 k k it it x x k k H(k) =H ( k), H(k) =H( k). k q
262 A B 0 H(q) = v F q e iθ q, e iθ q 0 H(q )= v F q 0 e iθ q, e iθ q 0 q 2 = q 2 x + q 2 y ( ) θ q = 1 qx, q y
263 Ψ(q) = 1 2 Ψ(q )= 1 2 e iθ q/2 ±e iθ q/2 e iθ q /2, ±e iθ q /2, {Φ A,K, Φ B,K } {Φ A,K, Φ B,K } k q q K K Ψ(q )=Ψ (q) Ψ(r) = r Ψ = kf 0 qf 0 = 1 2 ( qf dk r k k Ψ q F dq r q q Ψ + 0 dqe iq r 0 e iθ q/2 ±e iθ q/2 dq r q q Ψ + q F 0 dq e iq r e iθ q /2 ±e iθ q /2 ). k F
264 K K Ψ(q, r) = 1 2 Ψ(q, r) = 1 2 e iθ q/2 ±e iθ q/2 e iθ q /2 ±e iθ q /2 e iq r, e iq r. A B A B π 2π
265 q i q f V (r) Γ i f = 2π Ψ(q f, r) V (r) Ψ(q i, r) 2 δ(ε f ε i ). Ψ(q f, r) V (r) Ψ(q i, r) = V (q i q f ) (θ qi,q f /2), θ qi,q f θ qi,q f = π q K K K
266 K K K K K K q σ Ψ(q) =±Ψ(q), q q σ q Ψ(q )= Ψ(q ),
267 d g(ε) = g L d N i=0 δ(ε ε(k i )) L g g(ε) g k dk d =2 g 2 (ε) = g 4π 2 0 dk 2πk δ(ε ε(k)). g =2 2=4 ε = v F q k q g (ε) = 2ε π 2 vf 2, g 2 (ε) = m/(π 2 )
268 m =( 2 ε/ k 2 ) 1 ω c = eb m, B m τ c = 2 A(ε) eb ε, A(ε) ε m = 2 2π A(k) k k ε, ω c =2π/τ c A(k) =πk 2 m = k v F.
269 ε = pv F = kv F, p = m v F v F c m 1 1
270
271 B
272 (n, m) = (37, 1) (33, 9) 1 132, 000, 000 1
273 a 1 a 2 30 C T θ C = na 1 + ma 2, n m 0 m n (n, m) C T = t 1 a 1 + t 2 a 2, t 1 t 2 C T =0.
274 30 (0, 0) (n, m) C T θ m =0 θ =0 n = m θ = π/6 1 C a 1 (θ) = C a 1 C a 1 = 2n + m 2 n. 2 + nm + m 2 K
275 K K G G = 1 N H (mb 1 nb 2 ), G = 1 N H ( t 2 b 1 + t 1 b 2 ), G G N H N H = C T a 1 a e ik C =1,
276 (10, 0) (10, 5) (10, 10) k k = 2πj C, j =0, 1,...,N H 1, j
277 L = N uc T N uc e ik N uc T =1, k = 2πl N uc T, l =0, 1,...,N uc 1, l N uc 1 k = ( π ) T, π. T G G k = k G + k G G = k G + 2πj G C G, π/ T <k <π/ T j =0, 1,...,N H 1 G / G G / G k j j 2π/ T
278 1 (n, m) 1 k = ΓK (θ).
279 (n, m) =(8, 0) (12, 0)
280 (n, m) =(8, 8) (12, 12)
281 (n, m) =(8, 2) (12, 2)
282 n m =3l, l =0, 1, 2,... l 0 1/3 2/ (n m, 3) = 1 2 (n m, 3) = 2 0
283 1 g 1 (ε) = g k π ε, ε g g(ε) g g (ε F )=g = 8 = , 3aπγ0 hv F g γ a 2.46 v F (n, 0) (n, m)
284 g (ε, j) g γ 0 ε 2 ε, ε 2 ε 2 1 ε ( jπ ε 1 (j) =±γ n ( jπ ε 2 (j) =±γ n ),(m=0) ± γ ),(m=0) ± γ ( ) ja, d ( ) ja, d j a d d = C π = a n 2 + nm + m 2 π,(m=0) an π. j 0 Γ j = (2n/3) ε 1 (j) ε =0
285 n = dεf(ε)g (ε, j), f(ε) n M,e(h) = ±g (ε ε F ), n e n h 2 n e (q) = q=1 2 n h (q) = q=1 2 2N 0 e x j=1 1+Ae αx +βx 2 +γx 3 2 j=1 2N 0 e x 1+Ae αx +βx 2 +γx 3, x = 2ε ε 2k B T,, x = 2ε ε 2k B T. α, β, γ A α = 0.88,β = ,γ = ,A =0.66 q j j = (2n/3)
286 ε g N 0 (2ε N 0 = g γ 1 + k B T ) 2πk B T 0 4ε 2 ε 1 g πk 4 B Tε, ε 1 + k B T/2 ε /2 ε 2 2γ 0 µ <k B T n e(h) = n i e ±µ/k BT, 3 n i ε g m n i = 2g γ 0 (ε g + k B T ) πk B T e ε g/2k B T, ε g +4γ 0 ε g ( ) πj ε g =2ε (j) =2γ n m = 2a ccγ 0, d 4 2 3γ 0 a 2 ε 2γ 0 + ε g. a cc a j = (2n/3)
287 > > K K E ii 2ja ccγ 0, d
288 (8, 0) (8, 2) (8, 8)
289 t =2.9 a = j i γ 0 d j =1, 2, 4, 5... E 11,E 22,E 33,E j =3, 6... E11 M,E22 M...
290 (8, 0) (8, 8) E 11,E 22,E 33 π/2 π/2
291 π π π π
292 C λ F =2π/k f
293 1 1 1
294 k = π L, L L ε = v F k = v F π L. ε v F /2L 1
295 ε 1 ε C ε 1 dk x dk y dk z k x k y k z dk x dk y dk z k x k y dk z 1 1 L λ F L
296 {0, 1, 2, 3} 2 hγ <ε C, h Γ ε C ε C
297 e V 0 Q = Nq = CV, q =, e V < 0 Q N q e = e = C V U E = Q 0 = Q2 2C, dq V (q ) dq = e dn N
298 ε C du E dn = N e2 N=1 C = e2 N=1 C. τ = RC R C τ t t
299 ε t 2. ε t RC t = RC ε = 2RC. t RC RC RC
300 ε C = e2 C ε = 2RC. R h e 2 R Q. R Q R Q = (18) Ω π Γ 1/τ
301 k B T<ε C. ε i U E ε(n) = N ε i + U E (N). i=1 ε i ε i 1 = ε Q i = j C ij V j.
302 {i, j} = {0, } {0, 1, 2, 3} Q i i 3 Q 0 = C 00 V 0 + C 0j V j, j=1 V 0 V 0 = Q 0 3 j=1 C 0jV j C 00. C 00 C 00 = 3 j=1 C 0j U E = Q 0 dq 0 V 0 (Q 0 ) 3 = Q2 j=1 Q C 0jV j 2C 00 C 00 Q = Ne ε(n) = N i=1 ε i + e2 N 2 2C 00 en 3 j=1 C 0j C 00 V j
303 µ E (N) =ε(n) ε(n 1) ( = ε N + e2 N 1 ) + e C 00 2 ( = ε N + e2 N 1 ) e C j=1 C 0j C 00 V j 3 α j V j. j=1 µ E µ µ = ε N α i = C 0i C 00, C 00 i
304 10 12 N =0 N = 10 N = 11 N = 11 N = 12
305 ev e 2 /C 00 ε C kt e 2 /C 00 ε C ev = µ E, µ E, V µ E, µ E (N) µ E,
306 N 1 N +1 C 00 ) C C α ε c ε V > 0 µ E, µ E (N) µ E, V < 0
307
308 V ε C V > 0 µ E, µ E (N) µ E, µ E, =0 ev = µ E, ev µ E (N) 0 V α 1 α V + V α α V g + 1 eα 1 [ε e(1 α ) N + e2 C 00 ( [ε N + e2 N C 00 ( N + 1 )], 2 )]. i {i} = {0, } {0, 1, 2, 3} V < 0
309 V V + dv dv = α g 1 α s = dv = α g = C g, dv α s C s C g C 00 C s, µ E (N) µ E (N 1) = ε N ε }{{ N 1 + e2 } C 00 ε (N) = ε (N)+ε C. V =0 V = V =0 µ E (N) =0 V N V (N) = 1 ( [ε eα N + e2 N 1 )]. C 00 2
310 V (N) V (N 1) = 1 eα ( ε (N)+ε C )= ε (N) eα + e C 00. V N N 0 N
311 g 0 (ε) =g δ(ε ε N ), N=0 g g(ε) ε N ε N = v F πn. L ε ε k B T ε C T = g (ε) = gl v F π,
312 Γ,i Γ,i i i Γ i = Γ,i + Γ,i = τ, τ G = e2 h MT. M T
313 Γ k B T ε C. i G i = ( ge k B T Γ,i Γ,i ) 1 2 ( α (V V,i ) 2k B T ). k B T Γ ε C, ( G = ge ) 1 h 2 Γ h Γ Γ α (V 2,i V ) 2 +(hγ/2) 2.
314 i g 1 1
315
316
317 R<R Q hγ ε C
318 D 2 1
319 1 1 F = q(e + v B). 2 I x B z L W V H V xy = v x B z W. V = IR R xy = V H I x = v xb z W nev x W = B z ne
320 2 R xy = V H I x = E yw j x W = E y j x = ρ H ρ xy. R xx = ρ xx (L/W ) R H = E y j x B z = 1 ne, j x = I x /W = nev x 2 e = e n R H 2 /C R H h/e 2
321 C dr p(r) =h(n + γ), h N A γ 1/2 v d = 1 q F B B 2 = E B B 2,
322 1 K K q Π q Π q + ea 0 Π x iπ y 0 0 Π x + iπ y H(q) =v F, Π x + iπ y 0 0 Π x iπ y 0
323 {Φ A,K, Φ B,K, Φ A,K, Φ B,K } ψ A,K (q) ψ B,K (q) Ψ(q) =, ψ A,K (q) ψ B,K (q) ψ (A,B),(K,K ) (q) K v F (Π x + iπ y )ψ A,K = εψ B,K, v F (Π x iπ y )ψ B,K = εψ A,K. v 2 F (Π x iπ y )(Π x + iπ y )ψ A,K = ε 2 ψ A,K, v 2 F (Π x + iπ y )(Π x iπ y )ψ B,K = ε 2 ψ B,K. ψ B,K
324 A =( B z y, 0, 0) p i = q i ε 2 ψ B,K = v 2 F ( (px eb z y + ip y )(p x eb z y ip y ) ) ψ B,K = v 2 F ( (px eb z y) 2 + i[p y,p x eb z y]+p 2 y) ψb,k = vf 2 ( (px eb z y) 2 e B z + p 2 y) ψb,k ( 1 ( ε ) ) ( 2 p 2 y + e Bz ψ 2m v B,K = F 2m + (eb z) 2 ( y p ) ) 2 x ψ 2m eb B,K z [p x,p y ] = 0 [p y,y] = i y 0 ( p 2 y 2m + 1 ) ( 2 mω2 (y y 0 ) 2 ψ = ω N + 1 ) ψ, 2 N 0, 1, m ( (ε,k,b v F ) 2 + e Bz ( )ψ B,K = ω c N + 1 ) ψ 2 B,K, ε ε,k,b B z 2 B
325 ε,k,b ω c = eb z m, y 0 = q x eb z = l 2 Bq x, ε,k,b = (N)v F 2 ebz N = (N) v F l B 2 N = (N) ω D N, l B = = 26 eb z Bz [T ], ω D = v F 2eBz. ω c 2 y 0 ε,k,b B K N ω D l B N... 1, 0, N N N =0 ε =0
326 ψ A,K ε,k,a = (N)v F 2 ebz ( N + 1) = (N) ω D N +1, N =... 1, 0, 1... ε =0 ψ B,K ψ A,K ε =0 K A B
327 K (N)( i)φ N 1 (q x ) Ψ N,K (q x )= C N e iq xx φ N (q x ). W 0 0 K 0 Ψ N,K (q x )= C N e iq xx 0, W φ N (q x ) (N)( i)φ N 1 (q x ) φ N (y, q x )= 1 N =0 0 N =0 C N =, (N) =, 1 2 N 0 N N N 0 ( ) 1 ( N N! πlb 2 1 (y q x lb) 2 2 ) [ (y qx l 2 ] 2 lb 2 H B) N. l B H N φ N y 0 y 0 x 0 <y<l y q x 0 q x L y /lb 2 N 0 A B
328 N =0 N =0 K B K A L x = L L y = W y y x x q x =2π/L x 0 <y<l y q x 0 q x L y /lb 2
329 N = g L Ly /l 2 B x dq 2π x = g L xl y 0 2πlB 2 = g B za Φ 0. g g =4 Φ 0 l B A g N N Φ 0 = h e =2πl2 BB z, l B = 26, eb z Bz n = N A g = g 2πlB 2, ν = n e n. = g B z Φ 0, Φ 0 2πlB 2 l B Φ 0 n g g ν n e
330 ω C,D τ 1, ω C,D k B T, τ k B T ω C,D ω C 1 ω D 1500
331 a = a = l B 2 (Π x iπ y ), l B 2 (Π x + iπ y ), V (y) y x H(q) =v F σ Π + V (y)σ z = ξ 2 v F 0 a V (y) 0 +, l B a 0 0 V (y) σ =(σ x,σ y ) ξ =+1, 1 K, K K K {Φ A,K, Φ B,K } {Φ B,K, Φ A,K }
332 y 0 V (y) V (y 0 )+ V y +..., y0 y 0 = lbq 2 x V (y) =V (y 0 ) ( ) 2 ε,n 0 = ± V (y 0 ) 2 vf +2 N, l B ε,n=0 = ξv (y 0 ). y 0 x v x (q x )= 1 ε q x = l2 B V (y 0 ) y 0 = 1 eb z V (y 0 ) y 0,
333 I x = dq x λv x (q x ) = e L x L x 2π Ly /l 2 B 0 Ly dq x v x (q x ) = e 1 V (y 2πlB 2 dy 0 ) 0 0 eb z y 0 = e ( V (Ly ) V (0) ) 2π = e h µ. λ = e /L x V H = µ e, R xy = V H I x = h e 2 = R Q. R Q R Q = (18) Ω ( σ xy =4 N + 1 ) e 2 2 h, G Q = e2 h, ( ν =4 N + 1 ) = ±2, ±6, ±
334 g = g s g v =2 2=4 1/2 2π π p p + ea dr k + e C C dr A +Γ B =2π(N + γ). Γ B Γ B = π
335 R xx R xx R xx R xy k = e(v B), k = e(r B)+. A = B B dr r ds B = 2π C S e (N + γ γ B) 2Φ Φ=Φ 0 (N + γ γ B ) Φ=Φ 0 (N + γ γ B )
336 S Φ 0 = h/e γ B =Γ B /2π γ B =1/2 B πk 2 N =(N + γ γ B ) 2πeB = (N ) 2πeB N 2πeB, γ =1/2 γ B =1/2 γ B =0 k =0 k 0 N 1/2
337 ν =2
338
339 E
340 n = N/ = [ 3 ] ρ = mn = [ 3 ] p = mnv = ρv = [ 2 1 ] µ = η = [ 1 1 ] ν = µ/ρ = [ 2 1 ] φ = E = P = neφ = [J 3 ] J = nv = [ 1 2 ] = v L/ν = ρ v L/µ = γ p =1/τ p = [ 1 ] D ν = ντ p =
341 N e = ( ) m E v 2 3 ρ + (ρv) =0, t v t = (v )v 1 ρ P + ν 2 v + f, P, v ρ n r t (v )v P/ρ ν 2 v f = F/m
342 (v )v ν 2 v v L (106 1 ) (10 6 ) ν ( = , ) v F 10 3 (v )v =0 P = P (r) v = v(r) ρ = f = γ p v v(r) =0, 1 ρ P (r) =ν 2 v(r) γ p v(r).
343 n J(r) =0, σ e φ(r)+d2 ν 2 J(r) =J(r). J(r) σ = ne 2 τ p /m ej(r) =σe(r). 2 xy v x = ψ y, v y = ψ x, ζ = v x y v y x, ψ = ψ(x, y) ζ = ζ(x, y) 2
344 x, y v x x + v y y =0, ( 1 P 2 ρ x = ν v x x 2 + y 2 ( 1 P 2 ρ y = ν v y x v y y 2 2 v x ) γ p v x, ) γ p v y. y x 2 ζ = γ p ν ζ, 2 P =0. ψ, ζ, P 2 ψ = ζ. γ p ν
345 v v b = l v b n, n v v b l b l b =0 v = v b v b =0
346 : v b =0,v b =0 ψ b =0, ψ x = v y b =0, ψ b y = v x b =0. b ψ x,y+1 = ψ x,y + ψ y + 2 x,y ψ 2 y 2 x,y 2 ψ y x,y = 2 2 ζ. 1 ν τ =1/γ p D ν = ντ
347 ν τ ν τ D ν = ντ D ν 30
348 τ ee τ p τ ee τ p τ p τ e ph τ e
349 2 e ph e e 150
350 τ e = ev F µ πn, µ ( ) 100 ε τ ee =0.1 1, F, T k B T T 1 T 2 T 4 T 0.1T BG τ e ph, T 1 T 0.1T BG T BG T 100
351 µ = 10 µ = 50 µ = 100 τ e l e µ T = 10 T = 100 T = 200 τ ee l ee 1 µ τ e ph l e ph µ 1 µ 150 f(r, k,t) f t f = v r F 1 f k + f t, f = f(r, k,t) F = F(r) v = ε(k)/ ( k) f(r, k,t) t = f 0(r, k) f(r, k,t), τ(k)
352 f 0 f 0 (r, k) = 1 e (ε(k) µ(r))/k BT (r) +1. τ(r, k) F =0 f(r, k,t)=f(r, k,t= 0)e t/τ(r,k) + f 0 (r, k). f = ( ) m 3/2 4πv 2 e mv2 2k B T. 2πk B T k p = mv = k p
353 A(r, k) p = k ( d 3 ( k) A(r, k) t + v r + F 1 k ) f = d 3 ( k) A(r, k) f t, A n(r,t)= d 3 ( k) f(r, k,t), A(r,t) = 1 n(r,t) d 3 ( k) A(r, k)f(r, k,t), t na + r nva n v A n F 1 A = r k d 3 ( k) A f t, A = A(r,t) f/ t = 0 A =1
354 A = k = mv t (mn v )+ mn vv nf =0, r f t =0, vv v v vv δvδv = (v v )(v v ) = vv v v v v + v v = vv v v v v + v v = vv v v, t (ρ v )+ρ ( v v + δvδv ) nf =0, r f t =0.
355 σ = ρ δvδv σ xx τ xy τ xz = τ yx σ yy τ yz τ zx τ zy σzz P 0 0 σ xx + P τ xy τ xz = 0 P 0 + τ yx σ yy + P τ yz 0 0 P τ zx τ zy σ zz + P } {{ } } {{ } = P I 3 + τ {r} = {x, y, z} = {x 1, x 2, x 3 } σ ii τ ij P = 1 3 (σ xx + σ yy + σ zz ), σ ii = v i x i
356 ( vi τ ij = µ + v ) j + δ x j x ij λ v i λ (ρv)+ρ( v)v + ρ(v )v + P τ nf =0. t λ =0 v =0 τ = µ 2 v v t = (v )v 1 ρ P + ν 2 v + f, f t =0, ν = µ/ρ F/m
357 F
358
359 µ
360
361
362 µ µ µ µ µ µ :1 4
363 /3 15 5, 15, , 0.3,
364
365 2 3 2 ϵ 9 ϵ µ Ω % % 1 µ µ µ 3200 µ µ
366 Ω 500 µ µ
367 µ 150 µ (x, y) =( 4500, 4500), (4500, 4500) : µ
368
369 ( 2 )
370 , % > %
371
372 400 30
373
374
375 1.6
376
377 G
378 V V V =1 V =
379 6 6
380 4
381
382
383 9
384 70 100
385 10 10
386
387
388
389
390
391
392
393
394
395 n p
396
397
398
399 ϵ µ
400
401
402
403
404
405
406
407
408
409
410
411
412
... 5 A.. RS-232C ( ) RS-232C ( ) RS-232C-LK & RS-232C-MK RS-232C-JK & RS-232C-KK
RS-3C WIWM050 014.1.9 P1 :8... 1... 014.0.1 1 A... 014.0. 1... RS-3C()...01.08.03 A.. RS-3C()...01.08.03 3... RS-3C()... 003.11.5 4... RS-3C ()... 00.10.01 5... RS-3C().008.07.16 5 A.. RS-3C().0 1.08.
Parts Manual. Trio Mobile Surgery Platform. Model 1033
Trio Mobile Surgery Platform Model 1033 Parts Manual For parts or technical assistance: Pour pièces de service ou assistance technique : Für Teile oder technische Unterstützung Anruf: Voor delen of technische
! "#" "" $ "%& ' %$(%& % &'(!!")!*!&+ ,! %$( - .$'!"
! "#" "" $ "%& ' %$(%&!"#$ % &'(!!")!*!&+,! %$( -.$'!" /01&$23& &4+ $$ /$ & & / ( #(&4&4!"#$ %40 &'(!"!!&+ 5,! %$( - &$ $$$".$'!" 4(02&$ 4 067 4 $$*&(089 - (0:;
HONDA. Έτος κατασκευής
Accord + Coupe IV 2.0 16V (CB3) F20A2-A3 81 110 01/90-09/93 0800-0175 11,00 2.0 16V (CB3) F20A6 66 90 01/90-09/93 0800-0175 11,00 2.0i 16V (CB3-CC9) F20A8 98 133 01/90-09/93 0802-9205M 237,40 2.0i 16V
m i N 1 F i = j i F ij + F x
N m i i = 1,..., N m i Fi x N 1 F ij, j = 1, 2,... i 1, i + 1,..., N m i F i = j i F ij + F x i mi Fi j Fj i mj O P i = F i = j i F ij + F x i, i = 1,..., N P = i F i = N F ij + i j i N i F x i, i = 1,...,
u = 0 u = ϕ t + Π) = 0 t + Π = C(t) C(t) C(t) = K K C(t) ϕ = ϕ 1 + C(t) dt Kt 2 ϕ = 0
u = (u, v, w) ω ω = u = 0 ϕ u u = ϕ u = 0 ϕ 2 ϕ = 0 u t = u ω 1 ρ Π + ν 2 u Π = p + (1/2)ρ u 2 + ρgz ω = 0 ( ϕ t + Π) = 0 ϕ t + Π = C(t) C(t) C(t) = K K C(t) ϕ = ϕ 1 + C(t) dt Kt C(t) ϕ ϕ 1 ϕ = ϕ 1 p ρ
Κεφάλαιο 1 Πραγματικοί Αριθμοί 1.1 Σύνολα
x + = 0 N = {,, 3....}, Z Q, b, b N c, d c, d N + b = c, b = d. N = =. < > P n P (n) P () n = P (n) P (n + ) n n + P (n) n P (n) n P n P (n) P (m) P (n) n m P (n + ) P (n) n m P n P (n) P () P (), P (),...,
Sheet H d-2 3D Pythagoras - Answers
1. 1.4cm 1.6cm 5cm 1cm. 5cm 1cm IGCSE Higher Sheet H7-1 4-08d-1 D Pythagoras - Answers. (i) 10.8cm (ii) 9.85cm 11.5cm 4. 7.81m 19.6m 19.0m 1. 90m 40m. 10cm 11.cm. 70.7m 4. 8.6km 5. 1600m 6. 85m 7. 6cm
!!" #7 $39 %" (07) ..,..,.. $ 39. ) :. :, «(», «%», «%», «%» «%». & ,. ). & :..,. '.. ( () #*. );..,..'. + (# ).
1 00 3 !!" 344#7 $39 %" 6181001 63(07) & : ' ( () #* ); ' + (# ) $ 39 ) : : 00 %" 6181001 63(07)!!" 344#7 «(» «%» «%» «%» «%» & ) 4 )&-%/0 +- «)» * «1» «1» «)» ) «(» «%» «%» + ) 30 «%» «%» )1+ / + : +3
A 1 A 2 A 3 B 1 B 2 B 3
16 0 17 0 17 0 18 0 18 0 19 0 20 A A = A 1 î + A 2 ĵ + A 3ˆk A (x, y, z) r = xî + yĵ + zˆk A B A B B A = A 1 B 1 + A 2 B 2 + A 3 B 3 = A B θ θ A B = ˆn A B θ A B î ĵ ˆk = A 1 A 2 A 3 B 1 B 2 B 3 W = F
!"#$ % &# &%#'()(! $ * +
,!"#$ % &# &%#'()(! $ * + ,!"#$ % &# &%#'()(! $ * + 6 7 57 : - - / :!", # $ % & :'!(), 5 ( -, * + :! ",, # $ %, ) #, '(#,!# $$,',#-, 4 "- /,#-," -$ '# &",,#- "-&)'#45)')6 5! 6 5 4 "- /,#-7 ",',8##! -#9,!"))
!"!# ""$ %%"" %$" &" %" "!'! " #$!
" "" %%"" %" &" %" " " " % ((((( ((( ((((( " %%%% & ) * ((( "* ( + ) (((( (, (() (((((* ( - )((((( )((((((& + )(((((((((( +. ) ) /(((( +( ),(, ((((((( +, 0 )/ (((((+ ++, ((((() & "( %%%%%%%%%%%%%%%%%%%(
!"! #!"!!$ #$! %!"&' & (%!' #!% #" *! *$' *.!! )#/'.0! )#/.*!$,)# * % $ %!!#!!%#'!)$! #,# #!%# ##& )$&# 11!!#2!
# $ #$ % (% # )*%%# )# )$ % # * *$ * #,##%#)#% *-. )#/###%. )#/.0 )#/.* $,)# )#/ * % $ % # %# )$ #,# # %# ## )$# 11 #2 #**##%% $#%34 5 # %## * 6 7(%#)%%%, #, # ## # *% #$# 8# )####, 7 9%%# 0 * #,, :;
Ax = b. 7x = 21. x = 21 7 = 3.
3 s st 3 r 3 t r 3 3 t s st t 3t s 3 3 r 3 3 st t t r 3 s t t r r r t st t rr 3t r t 3 3 rt3 3 t 3 3 r st 3 t 3 tr 3 r t3 t 3 s st t Ax = b. s t 3 t 3 3 r r t n r A tr 3 rr t 3 t n ts b 3 t t r r t x 3
C 1 D 1. AB = a, AD = b, AA1 = c. a, b, c : (1) AC 1 ; : (1) AB + BC + CC1, AC 1 = BC = AD, CC1 = AA 1, AC 1 = a + b + c. (2) BD 1 = BD + DD 1,
1 1., BD 1 B 1 1 D 1, E F B 1 D 1. B = a, D = b, 1 = c. a, b, c : (1) 1 ; () BD 1 ; () F; D 1 F 1 (4) EF. : (1) B = D, D c b 1 E a B 1 1 = 1, B1 1 = B + B + 1, 1 = a + b + c. () BD 1 = BD + DD 1, BD =
Molekulare Ebene (biochemische Messungen) Zelluläre Ebene (Elektrophysiologie, Imaging-Verfahren) Netzwerk Ebene (Multielektrodensysteme) Areale (MRT, EEG...) Gene Neuronen Synaptische Kopplung kleine
!"#!"!"# $ "# '()!* '+!*, -"*!" $ "#. /01 023 43 56789:3 4 ;8< = 7 >/? 44= 7 @ 90A 98BB8: ;4B0C BD :0 E D:84F3 B8: ;4BG H ;8
!"#! $%&'$% %(' ') '#*#(& ( #'##+,-'!$%(' & ('##$%(' &#' & ('##$%('. )!#)! ##%' " (&! #!$"/001
!"#! $%&'$% %(' ') '#*#(& ( #'##+,-'!$%(' & ('##$%(' &#' & ('##$%('. ') '#*#(& )!#)! ##%' " (&! #!$"/001 ')!' &'# 2' '#)!( 3(&/004&' 5#(& /006 # '#)! 7!+8 8 8 #'%# ( #'## +,-'!$%(' & ('##$%('9&#' & ('##$%('9')
k k ΚΕΦΑΛΑΙΟ 1 G = (V, E) V E V V V G E G e = {v, u} E v u e v u G G V (G) E(G) n(g) = V (G) m(g) = E(G) G S V (G) S G N G (S) = {u V (G)\S v S : {v, u} E(G)} G v S v V (G) N G (v) = N G ({v}) x V (G)
γ n ϑ n n ψ T 8 Q 6 j, k, m, n, p, r, r t, x, y f m (x) (f(x)) m / a/b (f g)(x) = f(g(x)) n f f n I J α β I = α + βj N, Z, Q ϕ Εὐκλείδης ὁ Ἀλεξανδρεύς Στοιχεῖα ἄκρος καὶ μέσος λόγος ὕδωρ αἰθήρ ϕ φ Φ τ
a,b a f a = , , r = = r = T
!" #$%" &' &$%( % ) *+, -./01/ 234 5 0462. 4-7 8 74-9:;:; < =>?@ABC>D E E F GF F H I E JKI L H F I F HMN E O HPQH I RE F S TH FH I U Q E VF E WXY=Z M [ PQ \ TE K JMEPQ EEH I VF F E F GF ]EEI FHPQ HI E
TALAR ROSA -. / ',)45$%"67789
TALAR ROSA!"#"$"%$&'$%(" )*"+%(""%$," *$ -. / 0"$%%"$&'1)2$3!"$ ',)45$%"67789 ," %"(%:,;,"%,$"$)$*2
ITU-R P (2012/02)
ITU-R P.56- (0/0 P ITU-R P.56- ii.. (IPR (ITU-T/ITU-R/ISO/IEC.ITU-R ttp://www.itu.int/itu-r/go/patents/en. (ttp://www.itu.int/publ/r-rec/en ( ( BO BR BS BT F M P RA RS S SA SF SM SNG TF V 0.ITU-R ITU 0..(ITU
! " #! $ % & $ ' ( % & # ) * +, - ) % $!. /. $! $
[ ] # $ %&$'( %&#) *+,-) %$./.$ $ .$0)(0 1 $( $0 $2 3. 45 6# 27 ) $ # * (.8 %$35 %$'( 9)$- %0)-$) %& ( ),)-)) $)# *) ) ) * $ $ $ %$&) 9 ) )-) %&:: *;$ $$)-) $( $ 0,$# #)$.$0#$ $8 $8 $8 $8,:,:,:,: :: ::
f : G G G = 7 12 = 5 / N. x 2 +1 (x y) z = (x+y+xy) z = x+y+xy+z+(x+y+xy)z = x+y+z+xy+yz+xz+xyz.
Σ.Παπαδόπουλος 1 1 Βασικές έννοιες ομάδας Εστω G ένα σύνολο με G. Μία πράξη στο G είναι μία συνάρτηση f : G G G. Αντί f(x, y) γράφουμε x y και αν δεν υπάρχει περίπτωση σύγχυσης xy. Είναι φανερό ότι σε
Περιεχόμενα. A(x 1, x 2 )
Περιεχόμενα A(x 1, x 2 7 Ολοκληρώματα της Μαγνητοϋδροδυναμικής και Μαγνητοϋδροδυναμικά Κύματα Σχήμα 7.1: Οι τριδιάστατες ελικοειδείς μαγνητικές γραμμές στις οποίες εφάπτεται το διάνυσμα του μαγνητικού
k k ΚΕΦΑΛΑΙΟ 1 G = (V, E) V E V V V G E G e = {v, u} E v u e v u G G V (G) E(G) n(g) = V (G) m(g) = E(G) G S V (G) S G N G (S) = {u V (G)\S v S : {v, u} E(G)} G v S v V (G) N G (v) = N G ({v}) x V (G)
! " #$% & '()()*+.,/0.
! " #$% & '()()*+,),--+.,/0. 1!!" "!! 21 # " $%!%!! &'($ ) "! % " % *! 3 %,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,0 %%4,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,5
Łs t r t rs tø r P r s tø PrØ rø rs tø P r s r t t r s t Ø t q s P r s tr. 2stŁ s q t q s t rt r s t s t ss s Ø r s t r t. Łs t r t t Ø t q s
Łs t r t rs tø r P r s tø PrØ rø rs tø P r s r t t r s t Ø t q s P r s tr st t t t Ø t q s ss P r s P 2stŁ s q t q s t rt r s t s t ss s Ø r s t r t P r røs r Łs t r t t Ø t q s r Ø r t t r t q t rs tø
F (x) = kx. F (x )dx. F = kx. U(x) = U(0) kx2
F (x) = kx x k F = F (x) U(0) U(x) = x F = kx 0 F (x )dx U(x) = U(0) + 1 2 kx2 x U(0) = 0 U(x) = 1 2 kx2 U(x) x 0 = 0 x 1 U(x) U(0) + U (0) x + 1 2 U (0) x 2 U (0) = 0 U(x) U(0) + 1 2 U (0) x 2 U(0) =
#%" )*& ##+," $ -,!./" %#/%0! %,!
-!"#$% -&!'"$ & #("$$, #%" )*& ##+," $ -,!./" %#/%0! %,! %!$"#" %!#0&!/" /+#0& 0.00.04. - 3 3,43 5 -, 4 $ $.. 04 ... 3. 6... 6.. #3 7 8... 6.. %9: 3 3 7....3. % 44 8... 6.4. 37; 3,, 443 8... 8.5. $; 3
Déformation et quantification par groupoïde des variétés toriques
Défomation et uantification pa goupoïde de vaiété toiue Fédéic Cadet To cite thi veion: Fédéic Cadet. Défomation et uantification pa goupoïde de vaiété toiue. Mathématiue [math]. Univeité d Oléan, 200.
l 1 p r i = ρ ij α j + w i j=1 ρ ij λ α j j p w i p α j = 1, α j 0, j = 1,..., p j=1 R B B B m j [ρ 1j, ρ 2j,..., ρ Bj ] T = }{{} α + [,,..., ] R B p p α [α 1,..., α p ] [w 1,..., w p ] M m 1 m 2,
C M. V n: n =, (D): V 0,M : V M P = ρ ρ V V. = ρ
»»...» -300-0 () -300-03 () -3300 3.. 008 4 54. 4. 5 :.. ;.. «....... :. : 008. 37.. :....... 008.. :. :.... 54. 4. 5 5 6 ... : : 3 V mnu V mn AU 3 m () ; N (); N A 6030 3 ; ( ); V 3. : () 0 () 0 3 ()
m r = F m r = F ( r) m r = F ( v) F = F (x) m dv dt = F (x) vdv = F (x)dx d dt = dx dv dt dx = v dv dx
m r = F m r = F ( r) m r = F ( v) x F = F (x) m dv dt = F (x) d dt = dx dv dt dx = v dv dx vdv = F (x)dx 2 mv2 x 2 mv2 0 = F (x )dx x 0 K = 2 mv2 W x0 x = x x 0 F (x)dx K K 0 = W x0 x x, x 2 x K 2 K =
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ Ι
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ Ι ΣΤΑΤΙΚΕΣ ΧΑΡΑΚΤΗΡΙΣΤΙΚΕΣ ΚΑΜΠΥΛΕΣ ΑΜΦΙΠΟΛΙΚΩΝ ΤΡΑΝΖΙΣΤΟΡ ΕΠΑΦΩΝ Η άσκηση αποτελείται από δύο τμήματα: 1) μελέτη των χαρακτηριστικών καμπύλων εισόδου και εξόδου των τρανζίστορ για
())*+,-./0-1+*)*2, *67()(,01-+4(-8 9 0:,*2./0 30 ;+-7 3* *),+*< 7+)0 3* (=24(-) 04(-() 18(4-3-) 3-2(>*+)(3-3*
! " # $ $ %&&' % $ $! " # ())*+,-./0-1+*)*2,-3-4050+*67()(,01-+4(-8 9 0:,*2./0 30 ;+-7 3* *),+*< 7+)0 3* *),+-30 *5 35(2(),+-./0 30 *,0+ 3* (=24(-) 04(-() 18(4-3-) 3-2(>*+)(3-3* *3*+-830-+-2?< +(*2,-30+
4. Zapiši Eulerjeve dinamične enačbe za prosto osnosimetrično vrtavko. ω 2
Mehanikateoretičnavprašanjainodgovori 1/12 Newtonovamehanika 1. Določiravninogibanjatočkevpoljucentralnesile. Ravninagibanjagreskozicentersileinimanormalovsmerivrtilne količine 2. Zapišiperiodogibanjapremočrtnegagibanjapodvplivompotenciala
DC BOOKS. H-ml-c-n-s-b- -p-d-n- -v A-d-n-b-p-w-a-p-¼-v
BÀ. tdmj³ Xn-cp-h-\- -]p-cw kz-tz-in. 2004 ap-xâ [-\-Im-cy ]-{X-{]-hÀ- -\cw-k v. XpS- w Zo-]n-I- Zn-\- -{X- nâ. C-t mä am-xr-`q-an Zn-\- -{X- n-sâ {]-Xnhmc _n-kn\-kv t]pm-b "[-\-Im-cy-' n-sâbpw ssz-\w-zn-\
-! " #!$ %& ' %( #! )! ' 2003
-! "#!$ %&' %(#!)!' ! 7 #!$# 9 " # 6 $!% 6!!! 6! 6! 6 7 7 &! % 7 ' (&$ 8 9! 9!- "!!- ) % -! " 6 %!( 6 6 / 6 6 7 6!! 7 6! # 8 6!! 66! #! $ - (( 6 6 $ % 7 7 $ 9!" $& & " $! / % " 6!$ 6!!$#/ 6 #!!$! 9 /!
..., ISBN: :.!". # -. $, %, 1983 &"$ $ $. $, %, 1988 $ $. ## -. $, ', 1989 (( ). '. ') "!$!. $, %, 1991 $ 1. * $. $,.. +, 2001 $ 2. $. $,, 1992 # $!
!! " 007 : ISBN: # $! % :!" # - $ % 983 &"$ $ $ $ % 988 $ $ ## - $ ' 989 (( ) ' ') "!$! $ % 99 $ * $ $ + 00 $ $ $ 99!! " 007 -!" % $ 006 ---- $ 87 $ (( %( %(! $!$!" -!" $ $ %( * ( *!$ "!"!* "$!$ (!$! "
(... )..!, ".. (! ) # - $ % % $ & % 2007
(! ), "! ( ) # $ % & % $ % 007 500 ' 67905:5394!33 : (! ) $, -, * +,'; ), -, *! ' - " #!, $ & % $ ( % %): /!, " ; - : - +', 007 5 ISBN 978-5-7596-0766-3 % % - $, $ &- % $ % %, * $ % - % % # $ $,, % % #-
ψ (x) = e γ x A 3 x < a b / 2 A 2 cos(kx) B 2 b / 2 < x < b / 2 sin(kx) cosh(γ x) A 1 sin(kx) a b / 2 < x < b / 2 cos(kx) + B 2 e γ x x > a + b / 2
Σπουδές στις Φυσικές Επιστήµες ΦΥΕ 40 Κβαντική Φυσική 014-015 ΕΡΓΑΣΙΑ 3 η Υπόδειξη λύσεων ΑΣΚΗΣΗ 1 Η άρτια κυµατοσυνάρτηση θα δίνεται από (x) = A 3 e γ x x < a b / A cos(kx) B sin(kx) a b / < x < b / A
!" #$! '() -*,*( *(*)* *. 1#,2 (($3-*-/*/330%#& !" #$ -4*30*/335*
!" #$ %#&! '( (* + #*,*(**!',(+ *,*( *(** *. * #*,*(**( 0* #*,*(**(***&, 1#,2 (($3**330%#&!" #$ 4*30*335* ( 6777330"$% 8.9% '.* &(",*( *(** *. " ( : %$ *.#*,*(**." %#& 6 &;" * (.#*,*(**( #*,*(**(***&,
W τ R W j N H = 2 F obj b q N F aug F obj b q Ψ F aug Ψ ( ) ϱ t + + p = 0 = 0 Ω f = Γ Γ b ϱ = (, t) = (, t) Ω f Γ b ( ) ϱ t + + p = V max 4 3 2 1 0-1 -2-3 -4-4 -3-2 -1 0 1 2 3 4 x 4 x 1 V mn V max
Η κατανομή ορμής Από την στατιστική μηχανική, ο αριθμός των μικροσκοπικών καταστάσεων dn στο στοιχείο όγκου του χώρου των φάσεων d 3 p d 3 r είναι
ΤομοντέλοτουαερίουFermi ΤομοντέλοαυτόδιατυπώθηκεαπότονHansBethe.ΥποθέτουμεότιZπρωτόνια και N νετρόνια(φερμιόνια) καταλαμβάνουν ανεξάρτητα τον πυρηνικό όγκο Ω. Οιαλληλεπιδράσειςμεταξύτωνσωματίων(πυρηνικήκαιCoulomb)αγνοούνται.
Coupled Fluid Flow and Elastoplastic Damage Analysis of Acid. Stimulated Chalk Reservoirs
Nazanin Jahani Coupled Fluid Flow and Elastoplastic Damage Analysis of Acid Stimulated Chalk Reservoirs Thesis for the degree of Philosophiae Doctor Trondheim, October 2015 Norwegian University of Science
1. ίνονται τα διανύσµατα: x=(a+µ,1), y=(0,b), a,b>0. Για ποιες τιµές του µ τα διανύσµατα είναι: (α) γραµµικά εξαρτηµένα, (β) γραµµικά ανεξάρτητα.
. ίνονται τα διανύσµατα: x=(a+µ,), y=(0,b), a,b>0. Για ποιες τιµές του µ τα διανύσµατα είναι: (α) γραµµικά εξαρτηµένα, (β) γραµµικά ανεξάρτητα.. ίνονται τα διανύσµατα (x,0), (0,y), (z,0). Είναι γραµµικά
Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α
Α Ρ Χ Α Ι Α Ι Σ Τ Ο Ρ Ι Α Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α Σ η µ ε ί ω σ η : σ υ ν ά δ ε λ φ ο ι, ν α µ ο υ σ υ γ χ ω ρ ή σ ε τ ε τ ο γ ρ ή γ ο ρ ο κ α ι α τ η µ έ λ η τ ο ύ
Note: Please use the actual date you accessed this material in your citation.
MIT OpeCueWae hp://cw.m.eu 6.13/ESD.13J Elecmagec a pplca, Fall 5 Pleae ue he llwg ca ma: Maku Zah, Ech Ippe, a Dav Sael, 6.13/ESD.13J Elecmagec a pplca, Fall 5. (Maachue Iue Techlgy: MIT OpeCueWae). hp://cw.m.eu
Το άτομο του Υδρογόνου
Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες
Κινητική θεωρία ιδανικών αερίων
Κινητική θεωρία ιδανικών αερίων (γέφυρα μακροσκοπικών και μικροσκοπικών ποσοτήτων) Εμπειρικές σχέσεις Boyle, Gay-Lussac, Charles, υπόθεση Avogadro «όταν δυο ή περισσότερα αέρια έχουν τα ίδια V, P και Τ
ΗΛΙΑΣΚΟΣ ΦΡΟΝΤΙΣΤΗΡΙΑ. Γενικής Παιδείας Άλγεβρα Β Λυκείου ΥΠΗΡΕΣΙΕΣ ΠΑΙΔΕΙΑΣ ΥΨΗΛΟΥ ΕΠΙΠΕΔΟΥ. Επιμέλεια: Γ. ΦΩΤΟΠΟΥΛΟΣ Σ. ΗΛΙΑΣΚΟΣ
ΗΛΙΑΣΚΟΣ ΦΡΟΝΤΙΣΤΗΡΙΑ ΥΠΗΡΕΣΙΕΣ ΠΑΙΔΕΙΑΣ ΥΨΗΛΟΥ ΕΠΙΠΕΔΟΥ Γενικής Παιδείας Άλγεβρα Β Λυκείου Επιμέλεια: Γ. ΦΩΤΟΠΟΥΛΟΣ Σ. ΗΛΙΑΣΚΟΣ e-mail: info@iliaskos.gr www.iliaskos.gr ΗΛΙΑΣΚΟΣ ΦΡΟΝΤΙΣΤΗΡΙΑ. y y 4 y
Sur les articles de Henri Poincaré SUR LA DYNAMIQUE. Le texte fondateur de la Relativité en langage scientiþque moderne. par Anatoly A.
Sur les articles de Henri Poincaré SUR LA DYNAMIQUE DE L ÉLECTRON Le texte fondateur de la Relativité en langage scientiþque moderne par Anatoly A. LOGUNOV Directeur de l'institut de Physique des Hautes
ΑΝΑΛΥΣΗ ΙΙ- ΠΟΛΙΤΙΚΟΙ ΜΗΧΑΝΙΚΟΙ ΦΥΛΛΑΔΙΟ 2/2012
ΑΝΑΛΥΣΗ ΙΙ- ΠΟΛΙΤΙΚΟΙ ΜΗΧΑΝΙΚΟΙ ΦΥΛΛΑΔΙΟ /0 Έστω r rx, y, z, I a, b συνάρτηση C τάξης και r r r x y z Nα αποδείξετε ότι: d dr r (α) r r, I r r r d dr d r (β) r r, I dr (γ) Αν r 0, για κάθε I κάθε I d (δ)
J! "#$ %"& ( ) ) ) " *+, -./0-, *- /! /!+12, ,. 6 /72-, 0,,3-8 / ',913-51:-*/;+ 5/<3/ +15;+ 5/<3=9 -!.1!-9 +17/> ) ) &
J! "#$ %"& J ' ( ) ) ) " *+, -./0-, L *- /! /!+12,3-4 % +15,. 6 /72-, 0,,3-8 / ',913-51:-*/;+ 5/01 ',913-51:--
5 Ι ^ο 3 X X X. go > 'α. ο. o f Ο > = S 3. > 3 w»a. *= < ^> ^ o,2 l g f ^ 2-3 ο. χ χ. > ω. m > ο ο ο - * * ^r 2 =>^ 3^ =5 b Ο? UJ. > ο ο.
728!. -θ-cr " -;. '. UW -,2 =*- Os Os rsi Tf co co Os r4 Ι. C Ι m. Ι? U Ι. Ι os ν ) ϋ. Q- o,2 l g f 2-2 CT= ν**? 1? «δ - * * 5 Ι -ΐ j s a* " 'g cn" w *" " 1 cog 'S=o " 1= 2 5 ν s/ O / 0Q Ε!θ Ρ h o."o.
d dx x 2 = 2x d dx x 3 = 3x 2 d dx x n = nx n 1
d dx x 2 = 2x d dx x 3 = 3x 2 d dx x n = nx n1 x dx = 1 2 b2 1 2 a2 a b b x 2 dx = 1 a 3 b3 1 3 a3 b x n dx = 1 a n +1 bn +1 1 n +1 an +1 d dx d dx f (x) = 0 f (ax) = a f (ax) lim d dx f (ax) = lim 0 =
apj1 SSGA* hapla P6 _1G hao1 1Lh_PSu AL..AhAo1 *PJ"AL hp_a*a
n n 1/2 n (n 1) 0/1 l 2 E x X X x X E x X g(x) := 1 g(x). X f : X C L p f p := (E x X f(x) p ) 1/p f,g := E x X f(x)g(x) x X X X X := {f : X [0, ) : f 1 =1}. X µ A A X x X µ A (x) :=α 1 1 A (x) 1 A A α
m 1, m 2 F 12, F 21 F12 = F 21
m 1, m 2 F 12, F 21 F12 = F 21 r 1, r 2 r = r 1 r 2 = r 1 r 2 ê r = rê r F 12 = f(r)ê r F 21 = f(r)ê r f(r) f(r) < 0 f(r) > 0 m 1 r1 = f(r)ê r m 2 r2 = f(r)ê r r = r 1 r 2 r 1 = 1 m 1 f(r)ê r r 2 = 1 m
' ( )* * +,,, ) - ". &!: &/#&$&0& &!& $#/&! 1 2!#&, #/&2!#&3 &"&!3, #&- &2!#&, "#4 $!&$3% 2!% #!.1 & &!" //! &-!!
..!! "#$% #&" 535.34 ' ( )* *,,, ) - ". &!: 1.4.7 &/#&$&& &!&11 5.7.1 $#/&! 1!#&, #/&!#&3 &"&!3, #&- &!#&, "#4 $!&$3%!% #!.1 & &!" //! &-!!% 3 #&$&/!: /&!&# &-!!%, "#&&# 56$.., //! &-!!% ).. &$ 13 .
u(x, y) =f(x, y) Ω=(0, 1) (0, 1)
u(x, y) =f(x, y) Ω=(0, 1) (0, 1) u(x, y) =g(x, y) Γ=δΩ ={0, 1} {0, 1} Ω Ω Ω h Ω h h ˆ Ω ˆ u v = fv Ω u = f in Ω v V H 1 (Ω) V V h V h ψ 1,ψ 2,...,ψ N, ˆ ˆ u v = Ω Ω fv v V ˆ ˆ u v = Ω ˆ ˆ u ψ i = Ω Ω Ω
SWOT 1. Analysis and Planning for Cross-border Co-operation in Central European Countries. ISIGInstitute of. International Sociology Gorizia
SWOT 1 Analysis and Planning for Cross-border Co-operation in Central European Countries ISIGInstitute of International Sociology Gorizia ! " # $ % ' ( )!$*! " "! "+ +, $,,-,,.-./,, -.0",#,, 12$,,- %
Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού.
Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού. Περιοδικός πίνακας: α. Είναι µια ταξινόµηση των στοιχείων κατά αύξοντα
ΗΛΙΑΣΚΟΣ ΦΡΟΝΤΙΣΤΗΡΙΑ. Θετικής - Τεχνολογικής Κατεύθυνσης Φυσική Γ Λυκείου ΥΠΗΡΕΣΙΕΣ ΠΑΙΔΕΙΑΣ ΥΨΗΛΟΥ ΕΠΙΠΕΔΟΥ. Επιμέλεια: ΘΕΟΛΟΓΟΣ ΤΣΙΑΡΔΑΚΛΗΣ
ΗΛΙΑΣΚΟΣ ΦΡΟΝΤΙΣΤΗΡΙΑ ΥΠΗΡΕΣΙΕΣ ΠΑΙΔΕΙΑΣ ΥΨΗΛΟΥ ΕΠΙΠΕΔΟΥ Θετικής - Τεχνολογικής Κατεύθυνσης Φυσική Γ Λυκείου Επιμέλεια: ΘΕΟΛΟΓΟΣ ΤΣΙΑΡΔΑΚΛΗΣ e-mail: info@iliaskos.gr www.iliaskos.gr - f= f= f t+ 0 ) max
ϕ n n n n = 1,..., N n n {X I, Y I } {X r, Y r } (x c, y c ) q r = x a y a θ X r = [x r, y r, θ r ] X I = [x I, y I, θ I ] X I = R(θ)X r R(θ) R(θ) = cosθ sinθ 0 sinθ cosθ 0 0 0 1 Ẋ I = R(θ)Ẋr y r ẏa r
y T - yy z x T + yy T + yz T + yx T + xy T + zy T - xz T - zx T - zz T - xx T + xx T + zx T + xz T + zz T - zy T - xy T - yx T - yz
Συµπληρωµατικές Σηµειώσεις στα ΗΜ Πεδία (Κ. Χιτζανίδης Μάιος 2017 ΗΜ τάσεις σε υλικές επιφάνειες T + yy T + yz T + yx T + zy T + xy T - xx T - xz T - zx T - zz T + zz T + zx T + xz T + xx T - xy T - zy
ΗΛΕΚΤΡΟΝΙΚΗ Ι Ενότητα 7
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΗΛΕΚΤΡΟΝΙΚΗ Ι Ενότητα 7: Πόλωση των BJT - Ισοδύναμα κυκλώματα Χατζόπουλος Αλκιβιάδης Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχ. Υπολογιστών
Q π (/) ^ ^ ^ Η φ. <f) c>o. ^ ο. ö ê ω Q. Ο. o 'c. _o _) o U 03. ,,, ω ^ ^ -g'^ ο 0) f ο. Ε. ιη ο Φ. ο 0) κ. ο 03.,Ο. g 2< οο"" ο φ.
II 4»» «i p û»7'' s V -Ζ G -7 y 1 X s? ' (/) Ζ L. - =! i- Ζ ) Η f) " i L. Û - 1 1 Ι û ( - " - ' t - ' t/î " ι-8. Ι -. : wî ' j 1 Τ J en " il-' - - ö ê., t= ' -; '9 ',,, ) Τ '.,/,. - ϊζ L - (- - s.1 ai
Li % % % % % % % % % % 3d 4s V V V V d V V V n O V V V O V n O V n O % % X X % % % 10 10 cm Li Li Li LiMO 2 Li 1 x MO 2 + xl + 1 + xe C + xl + 1 + xe Li x C LiMO 2 +C Li x C + Li 1 x MO 2
Α Ρ Ι Θ Μ Ο Σ : 6.913
Α Ρ Ι Θ Μ Ο Σ : 6.913 ΠΡΑΞΗ ΚΑΤΑΘΕΣΗΣ ΟΡΩΝ ΔΙΑΓΩΝΙΣΜΟΥ Σ τ η ν Π ά τ ρ α σ ή μ ε ρ α σ τ ι ς δ ε κ α τ έ σ σ ε ρ ι ς ( 1 4 ) τ ο υ μ ή ν α Ο κ τ ω β ρ ί ο υ, η μ έ ρ α Τ ε τ ά ρ τ η, τ ο υ έ τ ο υ ς δ
Επιμέλεια:xr.tsif Σελίδα 1 ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΓΙΑ ΜΑΘΗΤΙΚΟΥΣ ΔΙΑΓΩΝΙΣΜΟΥΣ ΤΕΥΧΟΣ 9ο ΑΣΚΗΣΕΙΣ 801-900 Αφιερωμένο σε κάθε μαθητή που ασχολείται ή πρόκειται να ασχοληθεί με Μαθηματικούς διαγωνισμούς Τσιφάκης
ITU-R P (2009/10)
ITU-R.45-4 (9/) % # GHz,!"# $$ # ITU-R.45-4.. (IR) (ITU-T/ITU-R/ISO/IEC).ITU-R http://www.tu.t/itu-r/go/patets/e. (http://www.tu.t/publ/r-rec/e ) () ( ) BO BR BS BT F M RA S RS SA SF SM SNG TF V.ITU-R
(x y) = (X = x Y = y) = (Y = y) (x y) = f X,Y (x, y) x f X
X, Y f X,Y x, y X x, Y y f X Y x y X x Y y X x, Y y Y y f X,Y x, y f Y y f X Y x y x y X Y f X,Y x, y f X Y x y f X,Y x, y f Y y x y X : Ω R Y : Ω E X < y Y Y y 0 X Y y x R x f X Y x y gy X Y gy gy : Ω
!"#!$% &' ( )*+*,% $ &$ -.&01#(2$#3 4-$ #35667
!"#!$% & &' ( )*+*,% $ -*(-$ -.*/% $- &$ -.&01#(2$#3 4-$ #35667 5051 & 00000000000000000000000000000000000000000000000000000000000000000000000000000 9 508&:;&& 0000000000000000000000000000000000000000000000000
Επέκταση του μοντέλου DRUDE. - Θεωρία SOMMERFELD
Επέκταση του μοντέλου DRUDE - Θεωρία SOMMERFELD ΕΠΕΚΤΑΣΗ ΤΟΥ ΜΟΝΤΕΛΟΥ DRUDE-ΘΕΩΡΙΑ SOMMERFELD Drude: κατανομή ταχυτήτων e: f MB u = n m πkt 3/ e mu k BT u Sommerfeld: το e - είναι κύμα χρήση κυματοσυνάρτησης
x y z xy yz zx, να αποδείξετε ότι x=y=z.
ΑΣΚΗΣΕΙΣ ΣΤΗΝ ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ ΚΕΦ. ο A. Ταυτότητες, ιδιότητες δυνάμεων, διάταξη.1 Να παραγοντοποιήσετε τις παρακάτω παραστάσεις: 1. 15a x 15a y 5a x 5a y. a x a x a x a x 3 3 4 3 3 3 3. x 4xy 16 4 y
Η Ομάδα SL(2,C) και οι αναπαραστάσεις της
SL(2, C) SO(3, 1) D : Λ D(Λ) SO(3, 1) 2 1 D : ±A D(π(±A)) SL(2, C) SL(2, C) SO(3, 1) SL(2, C) SO(3, 1) ξ i (, ) K i x µ p µ J µν T µν A µ ψ α J i = J i, () K i = K i, ( ) K i M 0i = (iξ i K i ) A i = 1
a -80.6MPa, m =49.4MPa a =80.6MPa, m =-49.4MPa. a =49.4MPa, m =-80.6MPa a =-49.4MPa, m =-80.6MPa
1 2 1 2 3 4 5 0.24 0.24 4.17 4.17 6 a m a -80.6MPa, m =49.4MPa a =80.6MPa, m =-49.4MPa a =49.4MPa, m =-80.6MPa a =-49.4MPa, m =-80.6MPa 1 7 max min m a r 8 9 1 ] ] S [S] S [S] 2 ] ] S [S] S [S] 3 ] ] S
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ ˆ ˆ. Ô² ±É µ µ É µ, µ²ó ÊÖ µ ÊÕ µí Ê Ê ± ɵ Ö. ³Ò ² Ê ±
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 003.. 34.. 1 Š 539.165 ˆŒŒ ˆ Ÿ ˆŸ Š ˆ ˆ. Œ µ µ± µ ³µ µ ÉÓ µ É µ² ÊÕ Ëµ ³ ²Ó ÊÕ ³³ É Í Õ ± ɵ µ É µ Ô² ±É µ µ É µ, µ²ó ÊÖ µ ÊÕ µí Ê Ê ± ɵ Ö. ³Ò ² Ê ± ³ Ö É Ö, µ² É µ ̵ ³µ É µ µ ÉÓ µ µ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ. Θερμοδυναμική ΚΙΝΗΤΙΚΗ ΘΕΩΡΙΑ ΙΔΑΝΙΚΩΝ ΑΕΡΙΩΝ. Διδάσκων : Καθηγητής Γ. Φλούδας
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Θερμοδυναμική ΚΙΝΗΤΙΚΗ ΘΕΩΡΙΑ ΙΔΑΝΙΚΩΝ ΑΕΡΙΩΝ Διδάσκων : Καθηγητής Γ. Φλούδας Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
http://www.mathematica.gr/forum/viewtopic.php?f=109&t=15584
Επιμέλεια : xr.tsif Σελίδα 1 ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΓΙΑ ΜΑΘΗΤΙΚΟΥΣ ΔΙΑΓΩΝΙΣΜΟΥΣ ΕΚΦΩΝΗΣΕΙΣ ΤΕΥΧΟΣ ΑΣΚΗΣΕΙΣ 101-00 Αφιερωμέν σε κάθε μαθητή πυ ασχλείται ή πρόκειται να ασχληθεί με Μαθηματικύς διαγωνισμύς
,, #,#, %&'(($#(#)&*"& 3,,#!4!4! +&'(#,-$#,./$012 5 # # %, )
!! "#$%&'%( (%)###**#+!"#$ ',##-.#,,, #,#, /01('/01/'#!2#! %&'(($#(#)&*"& 3,,#!4!4! +&'(#,-$#,./$012 5 # # %, ) 6###+! 4! 4! 4,*!47! 4! (! 8!9%,,#!41! 4! (! 4!5),!(8! 4! (! :!;!(7! (! 4! 4!!8! (! 8! 4!!8(!44!
f H f H ψ n( x) α = 0.01 n( x) α = 1 n( x) α = 3 n( x) α = 10 n( x) α = 30 ū i ( x) α = 1 ū i ( x) α = 3 ū i ( x) α = 10 ū i ( x) α = 30 δū ij ( x) α = 1 δū ij ( x) α = 3 δū ij ( x) α = 10 δū ij ( x)
MÉTHODES ET EXERCICES
J.-M. MONIER I G. HABERER I C. LARDON MATHS PCSI PTSI MÉTHODES ET EXERCICES 4 e édition Création graphique de la couverture : Hokus Pokus Créations Dunod, 2018 11 rue Paul Bert, 92240 Malakoff www.dunod.com
ΚΕΦΑΛΑΙΟ 1 ο ΔΙΑΝΥΣΜΑΤΑ
taexeiolag ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ΑΣΚΗΣΗ 1 uuuu uuuu uuuu Αν OA OB 3O 0 και ΚΕΦΑΛΑΙΟ 1 ο ΔΙΑΝΥΣΜΑΤΑ uuuu uuuu uuuu OA OB 1, O α Να δείξετε ότι τα σημεία Α, Β, Γ είναι συνευθειακά
Επιμέλεια:xr.tsif Σελίδα 1 ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΓΙΑ ΜΑΘΗΤΙΚΟΥΣ ΔΙΑΓΩΝΙΣΜΟΥΣ ΤΕΥΧΟΣ 8ο ΑΣΚΗΣΕΙΣ 701-800 Αφιερωμένο σε κάθε μαθητή που ασχολείται ή πρόκειται να ασχοληθεί με Μαθηματικούς διαγωνισμούς Τσιφάκης
! " # $ % # "& #! $! !! % " # '! $ % !! # #!!! ) " ***
! " # $ % # # $ # # "& # $! $! #!! % " # '! $ % "!! $ "!!! # ( #!!! ) #! " *** # .....5.......9..........9.....4.3....... 9.4. -...3.......36....36......4.3....45.3......46.3......5.3.3....59.3.4.......65
ΗΛΕΚΤΡΟΝΙΚΗ Ι. 1. Ημιαγωγική γ δίοδος Ένωση pn 2. Τρανζίστορ FET
ΗΛΕΚΤΡΟΝΙΚΗ Ι 1. Ημιαγωγική γ δίοδος Ένωση pn 2. Τρανζίστορ FET 3. Πόλωση των FET - Ισοδύναμα κυκλώματα 4. Ενισχυτές με FET 5. Διπολικό τρανζίστορ (BJT) 6. Πόλωση των BJT - Ισοδύναμα κυκλώματα 7. Ενισχυτές
! "# $ % $&'& () *+ (,-. / 0 1(,21(,*) (3 4 5 "$ 6, ::: ;"<$& = = 7 + > + 5 $?"# 46(A *( / A 6 ( 1,*1 B"',CD77E *+ *),*,*) F? $G'& 0/ (,.
! " #$%&'()' *('+$,&'-. /0 1$23(/%/4. 1$)('%%'($( )/,)$5)/6%6 7$85,-9$(- /0 :/986-$, ;2'$(2$ 1'$-/-$)('')5( /&5&-/ 5(< =(4'($$,'(4 1$%$2/996('25-'/(& ;/0->5,$ 1'$-/%'')$(($/3?$%9'&-/?$( 5(< @6%-'9$
χ (1) χ (3) χ (1) χ (3) L x, L y, L z ( ) ħ2 2 2m x + 2 2 y + 2 ψ (x, y, z) = E 2 z 2 x,y,z ψ (x, y, z) E x,y,z E x E y E z ħ2 2m 2 x 2ψ (x) = E xψ (x) ħ2 2m 2 y 2ψ (y) = E yψ (y) ħ2 2m 2 z 2ψ (z)
Erkki Mäkinen ja Timo Poranen Algoritmit
rkki Mäkinen ja Timo Poranen Algoritmit TITOJNKÄSITTLYTITIDN LAITOS TAMPRN YLIOPISTO D 2008 6 TAMPR 2009 TAMPRN YLIOPISTO TITOJNKÄSITTLYTITIDN LAITOS JULKAISUSARJA D VRKKOJULKAISUT D 2008 6, TOUKOKUU 2009
3.1. Δυνάμεις μεταξύ ηλεκτρικών φορτίων
ΛΥΣΗ ΠΡΟΒΛΗΜΑΤΩΝ 3.1 3.1. Δυνάμεις μεταξύ ηλεκτρικών φορτίων 1. Έστω φορτίο Q περιέχει n ηλεκτρόνια - θα έχουμε Q = n-q e, επομέ- Q νως n =, αρα: (α) n = 0,625 10 19 e (β) n = 0,625 10 16 e (γ) n = 0,625
Α Δ Ι. Παρασκευή 13 Δεκεμβρίου 2013
Α Δ Ι Α - Φ 7 Δ : Ν. Μαρμαρίδης - Α. Μπεληγιάννης Ι Μ : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2013/asi2013.html, https://sites.google.com/site/maths4edu/home/algdom114 Παρασκευή 13 Δεκεμβρίου
J J l 2 J T l 1 J T J T l 2 l 1 J J l 1 c 0 J J J J J l 2 l 2 J J J T J T l 1 J J T J T J T J {e n } n N {e n } n N x X {λ n } n N R x = λ n e n {e n } n N {e n : n N} e n 0 n N k 1, k 2,..., k n N λ
Wb/ Μ. /Α Ua-, / / Βζ * / 3.3. Ηλεκτρομαγνητισμός Ι Μ. 1. Β = k. 3. α) Β = Κ μ Π 2. B-r, 2 10~ ~ 2 α => I = ~ } Α k M I = 20Α
ΛΥΣΗ ΠΡΟΒΛΗΜΑΤΩΝ 3.3 39 3.3. Ηλεκτρομαγνητισμός 1. Β = k 21 9 1Π 2 β = 10 " ίιτκ τ^β = 2 10 " τ 3. α) Β = Κ μ 21 B-r, 2 10~ 5 20 10~ 2 α => I = ~ } Α k M -2 2-10 I = 20Α ϊ)β 2 2Ι = Κ ψ- _ 10' 10^40 7 2
.1. 8,5. µ, (=,, ) . Ρ( )... Ρ( ).
ΡΧΗ 1Η Ε ε Γ Α Ο ΗΡ Ε Ε Ε Ε Η Ε Ο Ε Ο Ε Η 14 Ο Ο 2001 Ε Ε Ο Ε Ο Η Ε Η εε : Η Ο ΧΕ Η Ο Ο Ε εά : Ε (6) Ε Α 1ο Α.1. π µ µ ά : Ρ ( ) = Ρ ( ) Ρ ( ). 8,5 Α.2. µ π µπ µ π µ µ, (=,, ) : Ρ ( )... 1 Ρ( ) 2 Ρ( )...
μ μ dω I ν S da cos θ da λ λ Γ α/β MJ Capítulo 1 % βpic ɛ Eridani V ega β P ic F ormalhaut 10 9 15% 70 Virgem 47 Ursa Maior Debris Disk Debris Disk μ 90% L ac = GM M ac R L ac R M M ac L J T
ΑΣΚΗΣΕΙΣ ΣΤΗΝ ΠΑΡΑΒΟΛΗ
ΑΣΚΗΣΕΙΣ ΣΤΗΝ ΠΑΡΑΒΟΛΗ ΕΞΙΣΩΣΗ ΠΑΡΑΒΟΛΗΣ 8. Να βρεθεί η εξίσωση της παραβολής με κορυφή το (0, 0) στις παρακάτω περιπτώσεις: α) είναι συμμετρική ως προς το θετικό ημιάξονα Οx και έχει παράμετρο p = 5 β)
r r t r r t t r t P s r t r P s r s r r rs tr t r r t s ss r P s s t r t t tr r r t t r t r r t t s r t rr t Ü rs t 3 r r r 3 rträ 3 röÿ r t
r t t r t ts r3 s r r t r r t t r t P s r t r P s r s r P s r 1 s r rs tr t r r t s ss r P s s t r t t tr r 2s s r t t r t r r t t s r t rr t Ü rs t 3 r t r 3 s3 Ü rs t 3 r r r 3 rträ 3 röÿ r t r r r rs