OCHIUL UMAN CEL MAI REMARCABIL INSTRUMENT OPTIC
|
|
|
- Λαμία Μπουκουβαλαίοι
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Investeşte în oameni! Proiect cofinanţat din Fondul Social European prin Programul Operaţional Sectorial Dezvoltarea Resurselor Umane Axa prioritară: 1 Educaţia şi formarea profesională în sprijinul creşterii economice şi socieţătii bazate pe cunoaştere Domeniul major de intervenţie: 1.1 Acces la educaţie şi formare profesională iniţială de calitate Titlul proiectului: Şcoala viitorului! Împreună pentru o societate bazată pe cunoaştere Cod Contract: POSDRU/17/1.1/G/20765 Beneficiar: Inspectoratul Şcolar al Judeţului Vâlcea OCHIUL UMAN CEL MAI REMARCABIL INSTRUMENT OPTIC Profesor Cătălina STANCA Colegiul Naţional Alexandru Ioan Cuza, Galaţi Prezenta lucrare de laborator este o incursiune în lumea surprinzătoare a ochiului nostru. Activităţile propuse evidenţiază elementele componente ale acestuia şi rolul fiecăruia, stabilind o analogie între părţile componente şi anumite instrumente optice. Obiective urmărite Identificarea părţilor componente ale ochiului uman Identificarea defectelor de vedere şi a lentilelor care le pot corecta Analizarea asemănărilor şi deosebirilor care există între ochiul uman şi aparatul de fotografiat.
2 Noţiuni teoretice Ochiul este organul ce are ca principală funcție aceea de a detecta lumina. El se compune dintr-un sistem sensibil la schimbările de lumină, capabil să le transforme în impulsuri electrice. La om, ochiul are forma unei sfere și este localizat în orbita oculară. În ciuda dimensiunii reduse, ochiul nostru este un organ extrem de complex: el percepe formele, mișcările, reliefurile, culorile și diferențele de luminozitate. In activităţile ce vor urma vom afla mai multe despre componenţa ochiului şi rolul fiecărui element. Activitatea 1: Ce se afla in interiorul ochiului nostru Prima activitate îşi propune identificarea părţilor componente ale ochiului nostru şi analizarea rolului lor în formarea imaginii. Materiale necesare (pentru fiecare elev în parte): fişa de lucru Fişa de lucru numărul 1 Ce se află în interiorul ochiului nostru Văzul este cel mai complex dintre simţurile noastre. Creierul foloseşte pentru vedere o parte mult mai mare decât pentru celelalte simţuri. Ochii sunt globi de consistenţă tare, cu diametru de circa 2,5 cm plini cu lichid. Priviţi cu atenţie schema ochiului uman din imagine, încercând să identificaţi elementele componente descrise mai jos: Sclerotica este partea albă (numită şi albul ochiului). Ea este ca o manta dură care păstrează forma sferică a ochiului şi-l protejează. Cornea este o membrana transparentă, ce lasă lumina să intre în ochi şi ajută la focalizarea privirii. In spatele corneei se află o zonă lichidă numită umoarea apoasă. În spatele corneei se găsește irisul irisul, un disc colorat (diferit la fiecare persoană) în culori precum verde, albastru, căprui. Irisul se găseşte în faţa cristalinului, el comportându-se ca o diafragmă ce reglează cantitatea de lumină ce intră în interiorul ochiului.
3 Irisul este perforat în centru de un orificiu de culoare neagră, denumit pupilă. In lumină puternică irisul micşorează pupila, astfel încât în ochi să nu intre prea multă lumină, care ar putea dăuna celulelor - senzor din interior. In lumină slabă irisul măreşte pupila pentru a lăsa să intre mai multă lumină. Cristalinul este o lentilă biconvexă care va forma o imagine reală, răsturnată şi mai mică decât obiectul pe care îl privim. In spatele cristalinului, ochiul este umplut cu o substanţă transparentă, gelatinoasă, numită umoare sticloasă. Retina Retina este o membrană subţire ce acoperă doar partea din spate a globului ocular. Nervii ochiului răspândiţi în interiorul retinei, transformă retina într-un ecran sensibil la lumină care o ajută să formeze imagini. Pleoapele și genele protejează ochii. O membrană subțire transparentă, denumită conjunctivă, căptușește interiorul pleoapelor și o parte din sclerotică. Glande mici, localizate sub pleoape, produc în permanență lacrimile. Acestea sunt etalate într-un strat uniform, în urma mișcărilor de clipire a pleoapelor, ceea ce împiedică uscarea acestor suprafețe. Figura 1 Reprezentarea schematică a părţilor componente ale ochiului uman Uitaţi-vă la ochiul colegului vostru. Identificaţi acele părţi ale ochiului pe care le puteţi vedea. Pentru ca un obiect să fie văzut în mod clar, imaginea trebuie să se formeze exact pe retină. Pentru a vedea obiecte situate la distanţe diferite, ochiul se reglează singur schimbându-şi forma cristalinului. Dacă obiectul este aproape, distanţa la care se formează imaginea creşte, ceea ce obligă lentila cristalinului să devină rotundă şi mai groasă. Aceasta face ca distanţa focală a cristalinului să se micşoreze, iar distanţa la care se formează imaginea să se menţinută constantă, altfel spus ca imaginea să se formeaze tot pe retină.
4 Dacă obiectul este situat la depărtare, distanţa la care se formează imaginea scade, ceea ce obligă lentila cristalinului să devină mai subţire şi mai plată. Acest lucru duce la creşterea distanţei focale a cristalinului, ajutând imaginea să se formeaze pe retină. Capacitatea ochiului de a forma imagini ale unor obiecte situate la distanţe diferite se numeşte putere de acomodare. Figura 2 Reprezentare schematică a formării imaginii pe retină Care sunt distanţele între care putem observa clar imaginile obiectelor? Punctul proximum (P.P.) este cea mai mică distanţă la care putem aşeza un obiect pentru a obţine imagini clare pe retină. Pentru un ochi normal, punctul proximum se află la 25cm de ochi. Punctul remotum (P.R.) este cea mai îndepărtată distanţă la care putem aşeza un obiect pentru a obţine imagini clare pe retină, cu ochiul pe deplin relaxat. Pentru un ochi normal, punctul remotum se află la infinit (adică la distanţe de 20m). Activitatea 2:Defecte de vedere
5 Activitatea îşi propune prezentarea defectelor de vedere şi a modalităţilor de corectare. Partea experimentală urmăreşte investigarea miopiei şi a corectării cu lentilele divergente. Materiale necesare (pentru fiecare grupă de lucru): 2 surse de lumină, un banc optic; o lentilă convergentă (C 1 = 6δ); o lentilă convergentă (C 2 = 2,5δ); o lentilă convergentă (C 3 = 5,75δ); o lentilă divergentă un ecran; Fişa de lucru numărul 2 Defecte de vedere Aţi văzut că pentru un ochi normal obţinem imagini clare ale obiectelor situate la distanţe cuprinse între aproximativ 25 cm şi până la distanţe foarte mari, pe care noi le numim infinit. Multe persoane au însă defecte de vedere, care micşorează abilitatea lor de a vedea clar obiectele aflate în acest interval de distanţe. La acestea se adaugă şi avansarea în vârstă, fapt ce contribuie la reducerea capacităţii de a vedea clar. În cazul în care ochiul îşi pierde capacitatea de a modifica forma cristalinului, vederea devine neclară. De aceea trebuie aleşi ochelarii corespunzători pentru a corecta defectele ochilor. O persoană mioapă poate vedea obiectele apropiate foarte clar, dar are dificultate în focalizarea obiectelor îndepărtate. Acest lucru se întâmplă atunci când există un glob ocular alungit ceea ce face ca imaginea să se formeze în faţa retinei. Ochelari de vedere cu lentile divergente sunt folosiţi pentru a corecta miopia. (a) (b) Figura 3 Formarea imaginii la un ochi miop (a) şi corectarea acestui defect cu ochelari de vedere (b) O persoană cu hipermetropie poate vedea foarte clar obiectele îndepărtate, dar are dificultate în focalizarea obiectelor aflate la distanţă mică. Acest lucru se întâmplă atunci când există un glob ocular scurt făcând ca imaginea să se formeze dincolo de retină.
6 Ochelari de vedere cu lentile convergente sunt folosiţi pentru a corecta hipermetropia. (a) (b) Figura 4 Formarea imaginii la un ochi hipermetrop(a) şi corectarea acestui defect cu ochelari de vedere (b) Pentru o persoană mai în vârstă, puterea de acomodare a ochiului este redusă ca urmare a scăderii elasticităţii cristalinului şi a diminuării capacităţii muşchilor ochiului de a asigura modificarea cristalinului. Această incapacitate este numită prezbitism. Pentru a remedia această situaţie, sunt prescrise lentile bifocale. Dacă curbura cristalinului nu este bine definită spunem că ochiul nostru suferă de astigmatism. Astigmatismul se caracterizează printr-o vedere înceţoşată şi dureri de cap. O persoană cu acest defect nu va vedea liniile orizontale şi verticale la fel de distinct şi de clar. Acest defect este, de obicei, corectat cu lentile cilindrice. Figura 5 Ochiul cu astigmatism nu distinge liniile orizontale la fel de clar ca cele verticale Cel mai comun defect de vedere este miopia, care aţi văzut că presupune observarea clară a obiectelor apropiate, dar observarea difuză a obiectelor îndepărtate. Dacă ar fi să analizăm distanţe pentru P.P şi P.R, la un ochi cu miopie vom avea următoarea
7 situaţie: La un ochi cu hipermetropie, situaţia este următoarea: Activitatea îşi propune analizarea experimentală a miopiei şi a modalităţii de corectare. Sarcini de lucru: Realizaţi dispozitivul experimental din imagine şi identificaţi rolul fiecărui element în construcţia ochiului uman (pentru început nu puneţi lentila corectoare):
8 lentila C 1 reprezintă cornea lentila C 2 reprezintă cristalinul. Vom folosi lentila C 2 atunci când vom vizualiza obiectele îndepărtate şi lentila C 3 atunci când vom vizualiza obiectele apropiate ecranul reprezintă retina Mai întâi plasaţi o sursă de lumină foarte departe de sistemul de lentile; Pentru a încerca să focalizaţi imaginea sursei îndepărtate folosiţi lentila convergentă C 2 =2,5δ care corespunde situaţiei în care ochiul nostru se adaptează pentru a vedea obiecte foarte îndepărtate; Incercaţi să focalizaţi imaginea sursei pe ecran. Dacă aţi reuşit acest lucru măsuraţi distanţa d. Valoarea distanţei d este...şi corespunde distanţei dintre cristalin şi retină în cazul unui ochi normal adaptat pentru vedere la infinit. Fără a schimba distanţa d înlocuiţi lentila C 2 cu lentila C 3 ; Folosiţi acum cea de-a doua sursă de lumină aşezată la o distanţă mică de sistemul de lentile; Incercaţi să focalizaţi din nou fasciculul pe ecran. Măsuraţi distanţa dintre sursă şi sistemul de lentile. Corespunde această distanţă P.P. pentru un ochi normal?... Pentru a studia miopia măriţi distanţa d la 16-17cm. Având încă lentila C 3 şi sursa de lumină la distanţă mică determinaţi P.P. pentru un ochi miop. Ce distanţă aţi găsit?... Schimbaţi lentila C 3 cu lentila C 2 pentru a determina P.R. al ochiului miop. Folosiţi de această dată sursa de lumină îndepărtată de lentile. Ce distanţă aţi găsit?... Introduceţi lentila corectoare C 4. Se schimă caracteristicile imaginii obţinute pe acran prin introducerea acestei lentile?... Dacă aţi introdus lentila corectoare cât a devenit P.R... Schimbaţi din nou C 2 cu C 3 şi determinaţi P.P. cu lentila corectoare. Dacă aţi introdus lentila corectoare cât a devenit P.P... Activitatea 3: Ochiul uman si aparatul de fotografiat
9 Scopul acestei activităţi este acela de a analiza asemănările şi deosebirile dintre ochiul uman şi aparatul de fotografiat. Materiale necesare (pentru o grupă de lucru): o cutie de lapte (aproximativ 10cm lungime şi diametru de 10cm); o bucată de carton de culoare neagră (35cm 30cm); o rolă de bandă adezivă; o bucată de hârtie cerată. Fişa de lucru numărul 3 Ochiul uman şi aparatul de fotografiat Ochiul este cel care ne ajută să observăm lucrurile din jurul nostru, dar pentru a ni le aminti peste timp este bine să folosim un aparat de fotografiat. Ochiul nostru este foarte asemănător aparatului de fotografiat. Prin ce se aseamănă? Prin ce se deosebeşte? Vom vedea în cele ce urmează. Pentru început vom construi un aparat de fotografiat. Sarcinile de lucru sunt prezentate mai jos. Indepărtaţi capacul cutiei de lapte; Folosindu-vă de un cui şi de ajutorul unui adult, faceţi o gaură în fundul cutiei ca în imagine; Construiţi un tub îngust din bucata de carton de culoare neagră, având grijă ca tubul să poată intra în cutia de lapte; Acoperiţi o parte a tubului cu hârtia cerată. Pentru aceasta puteţi folosi rola de bandă adezivă; Introduceţi capătul acoperit al tubului de carton în cutie. Aţi construit în acest fel un aparat simplu de fotografiat; Indreptaţi aparatul vostru spre un obiect îndepărtat (o clădire, un copac). Uitaţi-vă la obiect prin capătul deschis al tubului. Mişcaţi tubul din carton în interiorul cutiei pentru a
10 obţine o imagine clară a obiectului. Ce se formează pe hârtia cerată? Comparaţi imaginea pe care o observaţi cu obiectul la care vă uitaţi; Un aparat de fotografiat adevărat are un obiectiv în loc de un orificiu şi foloseşte un film fotografic ca şi ecran, în loc de hârtia cerată. Elementele de bază ale aparatului de fotografiat sunt: o lentilă convergentă, un film sensibil la lumină pentru a înregistra imaginea şi un obturator care reglează cantitatea de lumină care cade pe film. Lentila aparatului formează o imagine răsturnată, reală şi mai mică decât obiectul. Un aparat de fotografiat este asemănător cu un ochi uman. Obturatorul aparatului controlează cantitatea de lumină care intră în aparat, la fel cum procedează pleoapele din ochiul nostru. Un aparat de fotografiat are o lentilă convergentă sau un sistem de lentile cu ajutorul
11 cărora se formează imaginile, la fel ca şi cristalinul ochiului uman. Filmul fotografic este asemănător cu retina sensibilă la lumină. Pe ambele elemente se formează imagini răsturnate, reale, mai mici decât obiectul. Citiţi cu atenţie sarcinile de mai jos: Incercuiţi răspunsul corect! 1) Ce parte a ochiului uman refractă lumina şi formează imaginea unui obiect? a. cornea b. irisul c. cristalinul d. retina 2) Un aparat de fotografiat formează imaginea pe un film fotografic în timp ce ochiul uman formează imaginea pe: a. cornee b. iris c. pupilă d. retină 3) Ce afirmaţie este falsă? a. Pleoapele închid sau deschid ochii. b. Irisul permite ochiului să observe obiectele din apropiere. c. Pupila controlează intensitatea luminii primite. d. Retina serveşte ca ecran pentru formarea imaginii. 4) Ce poate face un aparat de fotografiat şi nu poate face ochiul uman? a. Să formeze imagini ale unui obiect. b. Să se adapteze la lumina strălucitoare. c. Poate schimba focalizarea de la distanţe mici la distanţe mari. d. Poate oferi o înregistrare permanentă a scenei pe care o urmăreşte.
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate.
 Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Reflexia şi refracţia luminii.
 Reflexia şi refracţia luminii. 1. Cu cat se deplaseaza o raza care cade sub unghiul i =30 pe o placa plan-paralela de grosime e = 8,0 mm si indicele de refractie n = 1,50, pe care o traverseaza? Caz particular
Reflexia şi refracţia luminii. 1. Cu cat se deplaseaza o raza care cade sub unghiul i =30 pe o placa plan-paralela de grosime e = 8,0 mm si indicele de refractie n = 1,50, pe care o traverseaza? Caz particular
Metode iterative pentru probleme neliniare - contractii
 Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Curs 4 Serii de numere reale
 Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
MARCAREA REZISTOARELOR
 1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM 1 electronica.geniu.ro
 Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
riptografie şi Securitate
 riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
Planul determinat de normală şi un punct Ecuaţia generală Plane paralele Unghi diedru Planul determinat de 3 puncte necoliniare
 1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
Problema a II - a (10 puncte) Diferite circuite electrice
 Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
Laborator 11. Mulţimi Julia. Temă
 Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
5. FUNCŢII IMPLICITE. EXTREME CONDIŢIONATE.
 5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
(a) se numeşte derivata parţială a funcţiei f în raport cu variabila x i în punctul a.
 Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Aplicaţii ale principiului I al termodinamicii la gazul ideal
 Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Curs 14 Funcţii implicite. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi"
 Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE
 DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
III. Serii absolut convergente. Serii semiconvergente. ii) semiconvergentă dacă este convergentă iar seria modulelor divergentă.
 III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
Tipuri de celule sub microscopul optic
 Tipuri de celule sub microscopul optic Termenul de celulă a fost introdus de R. Hooke în cartea sa Micrographia publicată în 1665 în care descrie observaţii făcute cu microscopul şi telescopul. Microscopul
Tipuri de celule sub microscopul optic Termenul de celulă a fost introdus de R. Hooke în cartea sa Micrographia publicată în 1665 în care descrie observaţii făcute cu microscopul şi telescopul. Microscopul
Curs 1 Şiruri de numere reale
 Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Seminariile Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reziduurilor
 Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
a n (ζ z 0 ) n. n=1 se numeste partea principala iar seria a n (z z 0 ) n se numeste partea
 Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Subiecte Clasa a VII-a
 lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
Optica este o ramură a fizicii care studiază proprietăţile şi natura luminii, modul de producere a acesteia, şi legile propagării şi interacţiunii
 Optica este o ramură a fizicii care studiază proprietăţile şi natura luminii, modul de producere a acesteia, şi legile propagării şi interacţiunii luminii cu substanţa. Optica geometrica este acea parte
Optica este o ramură a fizicii care studiază proprietăţile şi natura luminii, modul de producere a acesteia, şi legile propagării şi interacţiunii luminii cu substanţa. Optica geometrica este acea parte
 10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
1.7. AMPLIFICATOARE DE PUTERE ÎN CLASA A ŞI AB
 1.7. AMLFCATOARE DE UTERE ÎN CLASA A Ş AB 1.7.1 Amplificatoare în clasa A La amplificatoarele din clasa A, forma de undă a tensiunii de ieşire este aceeaşi ca a tensiunii de intrare, deci întreg semnalul
1.7. AMLFCATOARE DE UTERE ÎN CLASA A Ş AB 1.7.1 Amplificatoare în clasa A La amplificatoarele din clasa A, forma de undă a tensiunii de ieşire este aceeaşi ca a tensiunii de intrare, deci întreg semnalul
Sisteme diferenţiale liniare de ordinul 1
 1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
Componente şi Circuite Electronice Pasive. Laborator 3. Divizorul de tensiune. Divizorul de curent
 Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor X) functia f 1
 Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
V O. = v I v stabilizator
 Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Definiţia generală Cazul 1. Elipsa şi hiperbola Cercul Cazul 2. Parabola Reprezentari parametrice ale conicelor Tangente la conice
 1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
 4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
5.5. REZOLVAREA CIRCUITELOR CU TRANZISTOARE BIPOLARE
 5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
a. 11 % b. 12 % c. 13 % d. 14 %
 1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
Integrala nedefinită (primitive)
 nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor
 Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
5.4. MULTIPLEXOARE A 0 A 1 A 2
 5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
Activitatea A5. Introducerea unor module specifice de pregătire a studenţilor în vederea asigurării de şanse egale
 POSDRU/156/1.2/G/138821 Investeşte în oameni! FONDUL SOCIAL EUROPEAN Programul Operaţional Sectorial pentru Dezvoltarea Resurselor Umane 2007 2013 Axa prioritară nr. 1 Educaţiaşiformareaprofesionalăînsprijinulcreşteriieconomiceşidezvoltăriisocietăţiibazatepecunoaştere
POSDRU/156/1.2/G/138821 Investeşte în oameni! FONDUL SOCIAL EUROPEAN Programul Operaţional Sectorial pentru Dezvoltarea Resurselor Umane 2007 2013 Axa prioritară nr. 1 Educaţiaşiformareaprofesionalăînsprijinulcreşteriieconomiceşidezvoltăriisocietăţiibazatepecunoaştere
COLEGIUL NATIONAL CONSTANTIN CARABELLA TARGOVISTE. CONCURSUL JUDETEAN DE MATEMATICA CEZAR IVANESCU Editia a VI-a 26 februarie 2005.
 SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
Subiecte Clasa a VIII-a
 Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Seminar 5 Analiza stabilității sistemelor liniare
 Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile
 Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Activitatea A5. Introducerea unor module specifice de pregătire a studenților în vederea asigurării de șanse egale
 Investește în oameni! FONDUL SOCIAL EUROPEAN Programul Operațional Sectorial pentru Dezvoltarea Resurselor Umane 2007 2013 Axa prioritară nr. 1 Educația și formarea profesională în sprijinul creșterii
Investește în oameni! FONDUL SOCIAL EUROPEAN Programul Operațional Sectorial pentru Dezvoltarea Resurselor Umane 2007 2013 Axa prioritară nr. 1 Educația și formarea profesională în sprijinul creșterii
Ecuaţia generală Probleme de tangenţă Sfera prin 4 puncte necoplanare. Elipsoidul Hiperboloizi Paraboloizi Conul Cilindrul. 1 Sfera.
 pe ecuaţii generale 1 Sfera Ecuaţia generală Probleme de tangenţă 2 pe ecuaţii generale Sfera pe ecuaţii generale Ecuaţia generală Probleme de tangenţă Numim sferă locul geometric al punctelor din spaţiu
pe ecuaţii generale 1 Sfera Ecuaţia generală Probleme de tangenţă 2 pe ecuaţii generale Sfera pe ecuaţii generale Ecuaţia generală Probleme de tangenţă Numim sferă locul geometric al punctelor din spaţiu
LUCRAREA NR. 3 DETERMINAREA DISTANŢEI FOCALE A OGLINZILOR SFERICE
 LUCRAREA NR. 3 DETERMINAREA DISTANŢEI FOCALE A OGLINZILOR SFERICE Tema lucrării: 1) Determinarea distanţei focale a unei oglinzi concave ) Determinarea distanţei focale a unei oglinzi convexe 3) Studiul
LUCRAREA NR. 3 DETERMINAREA DISTANŢEI FOCALE A OGLINZILOR SFERICE Tema lucrării: 1) Determinarea distanţei focale a unei oglinzi concave ) Determinarea distanţei focale a unei oglinzi convexe 3) Studiul
STUDIUL MICROSCOPULUI
 LUCRAREA NR. 6 STUDIUL MICROSCOPULUI Tema lucrării: 1) Etalonarea micrometrului ocular. 2) Măsurarea dimensiunilor unui obiect mic. 3) Determinarea aperturii numerice. 4) Determinarea grosismentului microscopului
LUCRAREA NR. 6 STUDIUL MICROSCOPULUI Tema lucrării: 1) Etalonarea micrometrului ocular. 2) Măsurarea dimensiunilor unui obiect mic. 3) Determinarea aperturii numerice. 4) Determinarea grosismentului microscopului
y ' n x n x Noţiuni fundamentale de optică geometrică. Elemente de biofizica analizorului vizual
 Noţiuni fundamentale de optică geometrică. Elemente de biofizica analizorului vizual Noţiuni fundamentale de optică geometrică. Elemente de biofizica analizorului vizual Noţiuni de optică geometrică Numim
Noţiuni fundamentale de optică geometrică. Elemente de biofizica analizorului vizual Noţiuni fundamentale de optică geometrică. Elemente de biofizica analizorului vizual Noţiuni de optică geometrică Numim
R R, f ( x) = x 7x+ 6. Determinați distanța dintre punctele de. B=, unde x și y sunt numere reale.
 5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
SERII NUMERICE. Definiţia 3.1. Fie (a n ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0
 SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].
![Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].](/thumbs/72/67648751.jpg) Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
BARAJ DE JUNIORI,,Euclid Cipru, 28 mai 2012 (barajul 3)
 BARAJ DE JUNIORI,,Euclid Cipru, 8 mi 0 (brjul ) Problem Arătţi că dcă, b, c sunt numere rele cre verifică + b + c =, tunci re loc ineglitte xy + yz + zx Problem Fie şi b numere nturle nenule Dcă numărul
BARAJ DE JUNIORI,,Euclid Cipru, 8 mi 0 (brjul ) Problem Arătţi că dcă, b, c sunt numere rele cre verifică + b + c =, tunci re loc ineglitte xy + yz + zx Problem Fie şi b numere nturle nenule Dcă numărul
Asupra unei inegalităţi date la barajul OBMJ 2006
 Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
Curs 2 Şiruri de numere reale
 Curs 2 Şiruri de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Convergenţă şi mărginire Teoremă Orice şir convergent este mărginit. Demonstraţie Fie (x n ) n 0 un
Curs 2 Şiruri de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Convergenţă şi mărginire Teoremă Orice şir convergent este mărginit. Demonstraţie Fie (x n ) n 0 un
Criptosisteme cu cheie publică III
 Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25
 Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25 LAGĂRELE CU ALUNECARE!" 25.1.Caracteristici.Părţi componente.materiale.!" 25.2.Funcţionarea lagărelor cu alunecare.! 25.1.Caracteristici.Părţi componente.materiale.
Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25 LAGĂRELE CU ALUNECARE!" 25.1.Caracteristici.Părţi componente.materiale.!" 25.2.Funcţionarea lagărelor cu alunecare.! 25.1.Caracteristici.Părţi componente.materiale.
Examen AG. Student:... Grupa:... ianuarie 2011
 Problema 1. Pentru ce valori ale lui n,m N (n,m 1) graful K n,m este eulerian? Problema 2. Să se construiască o funcţie care să recunoască un graf P 3 -free. La intrare aceasta va primi un graf G = ({1,...,n},E)
Problema 1. Pentru ce valori ale lui n,m N (n,m 1) graful K n,m este eulerian? Problema 2. Să se construiască o funcţie care să recunoască un graf P 3 -free. La intrare aceasta va primi un graf G = ({1,...,n},E)
Captura imaginilor. este necesară o sursă de lumină (λ: lungimea de undă a sursei)
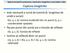 Captura imaginilor este necesară o sursă de lumină (λ: lungimea de undă a sursei) E(x, y, z, λ): lumina incidentă într-un punct (x, y, z coordonatele spațiale) fiecare punct din scenă are o funcție de
Captura imaginilor este necesară o sursă de lumină (λ: lungimea de undă a sursei) E(x, y, z, λ): lumina incidentă într-un punct (x, y, z coordonatele spațiale) fiecare punct din scenă are o funcție de
Conice. Lect. dr. Constantin-Cosmin Todea. U.T. Cluj-Napoca
 Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
Capitolul 4. Integrale improprii Integrale cu limite de integrare infinite
 Capitolul 4 Integrale improprii 7-8 În cadrul studiului integrabilităţii iemann a unei funcţii s-au evidenţiat douăcondiţii esenţiale:. funcţia :[ ] este definită peintervalînchis şi mărginit (interval
Capitolul 4 Integrale improprii 7-8 În cadrul studiului integrabilităţii iemann a unei funcţii s-au evidenţiat douăcondiţii esenţiale:. funcţia :[ ] este definită peintervalînchis şi mărginit (interval
Esalonul Redus pe Linii (ERL). Subspatii.
 Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
Microscopie optica. Masuratori cu microscopul optic
 . Masuratori cu microscopul optic Tehnici de microscopie de transmisie Microscopie de baleiaj utilizand lasere Microscopie confocala Microscopie in camp apropiat Microscopie electronica Microscopie Microscopie
. Masuratori cu microscopul optic Tehnici de microscopie de transmisie Microscopie de baleiaj utilizand lasere Microscopie confocala Microscopie in camp apropiat Microscopie electronica Microscopie Microscopie
SEMINAR 14. Funcţii de mai multe variabile (continuare) ( = 1 z(x,y) x = 0. x = f. x + f. y = f. = x. = 1 y. y = x ( y = = 0
 Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
Metode de interpolare bazate pe diferenţe divizate
 Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii transversale, scrisă faţă de una dintre axele de inerţie principale:,
 REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...4
 SEMINAR 3 MMENTUL FRŢEI ÎN RAPRT CU UN PUNCT CUPRINS 3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere...1 3.1. Aspecte teoretice...2 3.2. Aplicaţii rezolvate...4 3. Momentul forţei
SEMINAR 3 MMENTUL FRŢEI ÎN RAPRT CU UN PUNCT CUPRINS 3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere...1 3.1. Aspecte teoretice...2 3.2. Aplicaţii rezolvate...4 3. Momentul forţei
2.1 Sfera. (EGS) ecuaţie care poartă denumirea de ecuaţia generală asferei. (EGS) reprezintă osferă cu centrul în punctul. 2 + p 2
 .1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
.1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
1. PROPRIETĂȚILE FLUIDELOR
 1. PROPRIETĂȚILE FLUIDELOR a) Să se exprime densitatea apei ρ = 1000 kg/m 3 în g/cm 3. g/cm 3. b) tiind că densitatea glicerinei la 20 C este 1258 kg/m 3 să se exprime în c) Să se exprime în kg/m 3 densitatea
1. PROPRIETĂȚILE FLUIDELOR a) Să se exprime densitatea apei ρ = 1000 kg/m 3 în g/cm 3. g/cm 3. b) tiind că densitatea glicerinei la 20 C este 1258 kg/m 3 să se exprime în c) Să se exprime în kg/m 3 densitatea
5.1. Noţiuni introductive
 ursul 13 aitolul 5. Soluţii 5.1. oţiuni introductive Soluţiile = aestecuri oogene de două sau ai ulte substanţe / coonente, ale căror articule nu se ot seara rin filtrare sau centrifugare. oonente: - Mediul
ursul 13 aitolul 5. Soluţii 5.1. oţiuni introductive Soluţiile = aestecuri oogene de două sau ai ulte substanţe / coonente, ale căror articule nu se ot seara rin filtrare sau centrifugare. oonente: - Mediul
6 n=1. cos 2n. 6 n=1. n=1. este CONV (fiind seria armonică pentru α = 6 > 1), rezultă
 Semiar 5 Serii cu termei oarecare Probleme rezolvate Problema 5 Să se determie atura seriei cos 5 cos Soluţie 5 Şirul a 5 este cu termei oarecare Studiem absolut covergeţa seriei Petru că cos a 5 5 5 şi
Semiar 5 Serii cu termei oarecare Probleme rezolvate Problema 5 Să se determie atura seriei cos 5 cos Soluţie 5 Şirul a 5 este cu termei oarecare Studiem absolut covergeţa seriei Petru că cos a 5 5 5 şi
Difractia de electroni
 Difractia de electroni 1 Principiul lucrari Verificarea experimentala a difractiei electronilor rapizi pe straturi de grafit policristalin: observarea inelelor de interferenta ce apar pe ecranul fluorescent.
Difractia de electroni 1 Principiul lucrari Verificarea experimentala a difractiei electronilor rapizi pe straturi de grafit policristalin: observarea inelelor de interferenta ce apar pe ecranul fluorescent.
Analiza și Prelucrarea Digitală a Semnalelor Video
 Analiza și Prelucrarea Digitală a Semnalelor Video Conf. dr. ing. Radu Ovidiu Preda radu@comm.pub.ro Ș.l. dr. ing. Ionuţ Pirnog ionut@comm.pub.ro Site disciplină: www.comm.pub.ro/preda/apdsv Analiza și
Analiza și Prelucrarea Digitală a Semnalelor Video Conf. dr. ing. Radu Ovidiu Preda radu@comm.pub.ro Ș.l. dr. ing. Ionuţ Pirnog ionut@comm.pub.ro Site disciplină: www.comm.pub.ro/preda/apdsv Analiza și
Εμπορική αλληλογραφία Ηλεκτρονική Αλληλογραφία
 - Εισαγωγή Stimate Domnule Preşedinte, Stimate Domnule Preşedinte, Εξαιρετικά επίσημη επιστολή, ο παραλήπτης έχει ένα ειδικό τίτλο ο οποίος πρέπει να χρησιμοποιηθεί αντί του ονόματος του Stimate Domnule,
- Εισαγωγή Stimate Domnule Preşedinte, Stimate Domnule Preşedinte, Εξαιρετικά επίσημη επιστολή, ο παραλήπτης έχει ένα ειδικό τίτλο ο οποίος πρέπει να χρησιμοποιηθεί αντί του ονόματος του Stimate Domnule,
2. Sisteme de forţe concurente...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...3
 SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
z a + c 0 + c 1 (z a)
 1 Serii Laurent (continuare) Teorema 1.1 Fie D C un domeniu, a D şi f : D \ {a} C o funcţie olomorfă. Punctul a este pol multiplu de ordin p al lui f dacă şi numai dacă dezvoltarea în serie Laurent a funcţiei
1 Serii Laurent (continuare) Teorema 1.1 Fie D C un domeniu, a D şi f : D \ {a} C o funcţie olomorfă. Punctul a este pol multiplu de ordin p al lui f dacă şi numai dacă dezvoltarea în serie Laurent a funcţiei
Continue. Answer: a. 0,25 b. 0,15 c. 0,1 d. 0,2 e. 0,3. Answer: a. 0,1 b. 0,25 c. 0,17 d. 0,02 e. 0,3
 Concurs Phi: Setul 1 - Clasa a VII-a Logout e-desc» Concurs Phi» Quizzes» Setul 1 - Clasa a VII-a» Attempt 1 1 Pentru a deplasa uniform pe orizontala un corp de masa m = 18 kg se actioneaza asupra lui
Concurs Phi: Setul 1 - Clasa a VII-a Logout e-desc» Concurs Phi» Quizzes» Setul 1 - Clasa a VII-a» Attempt 1 1 Pentru a deplasa uniform pe orizontala un corp de masa m = 18 kg se actioneaza asupra lui
Examen AG. Student:... Grupa: ianuarie 2016
 16-17 ianuarie 2016 Problema 1. Se consideră graful G = pk n (p, n N, p 2, n 3). Unul din vârfurile lui G se uneşte cu câte un vârf din fiecare graf complet care nu-l conţine, obţinându-se un graf conex
16-17 ianuarie 2016 Problema 1. Se consideră graful G = pk n (p, n N, p 2, n 3). Unul din vârfurile lui G se uneşte cu câte un vârf din fiecare graf complet care nu-l conţine, obţinându-se un graf conex
a. 0,1; 0,1; 0,1; b. 1, ; 5, ; 8, ; c. 4,87; 6,15; 8,04; d. 7; 7; 7; e. 9,74; 12,30;1 6,08.
 1. În argentometrie, metoda Mohr: a. foloseşte ca indicator cromatul de potasiu, care formeazǎ la punctul de echivalenţă un precipitat colorat roşu-cărămiziu; b. foloseşte ca indicator fluoresceina, care
1. În argentometrie, metoda Mohr: a. foloseşte ca indicator cromatul de potasiu, care formeazǎ la punctul de echivalenţă un precipitat colorat roşu-cărămiziu; b. foloseşte ca indicator fluoresceina, care
Ακαδημαϊκός Λόγος Κύριο Μέρος
 - Επίδειξη Συμφωνίας În linii mari sunt de acord cu...deoarece... Επίδειξη γενικής συμφωνίας με άποψη άλλου Cineva este de acord cu...deoarece... Επίδειξη γενικής συμφωνίας με άποψη άλλου D'une façon générale,
- Επίδειξη Συμφωνίας În linii mari sunt de acord cu...deoarece... Επίδειξη γενικής συμφωνίας με άποψη άλλου Cineva este de acord cu...deoarece... Επίδειξη γενικής συμφωνίας με άποψη άλλου D'une façon générale,
Cum folosim cazuri particulare în rezolvarea unor probleme
 Cum folosim cazuri particulare în rezolvarea unor probleme GHEORGHE ECKSTEIN 1 Atunci când întâlnim o problemă pe care nu ştim s-o abordăm, adesea este bine să considerăm cazuri particulare ale acesteia.
Cum folosim cazuri particulare în rezolvarea unor probleme GHEORGHE ECKSTEIN 1 Atunci când întâlnim o problemă pe care nu ştim s-o abordăm, adesea este bine să considerăm cazuri particulare ale acesteia.
Aparate de măsurat. Măsurări electronice Rezumatul cursului 2. MEE - prof. dr. ing. Ioan D. Oltean 1
 Aparate de măsurat Măsurări electronice Rezumatul cursului 2 MEE - prof. dr. ing. Ioan D. Oltean 1 1. Aparate cu instrument magnetoelectric 2. Ampermetre şi voltmetre 3. Ohmetre cu instrument magnetoelectric
Aparate de măsurat Măsurări electronice Rezumatul cursului 2 MEE - prof. dr. ing. Ioan D. Oltean 1 1. Aparate cu instrument magnetoelectric 2. Ampermetre şi voltmetre 3. Ohmetre cu instrument magnetoelectric
Tema I FORMAREA IMAGINII
 Tema I FORMAREA IMAGINII Nevoia de imagini a omului modern creste de la zi la zi. In general, functiile imaginilor sunt urmatoarele : - functia documentara - prezinta concret, imaginea unor termeni si
Tema I FORMAREA IMAGINII Nevoia de imagini a omului modern creste de la zi la zi. In general, functiile imaginilor sunt urmatoarele : - functia documentara - prezinta concret, imaginea unor termeni si
Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R. 4.1 Proprietăţi topologice ale lui R Puncte de acumulare
 Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R În cele ce urmează, vom studia unele proprietăţi ale mulţimilor din R. Astfel, vom caracteriza locul" unui punct în cadrul unei mulţimi (în limba
Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R În cele ce urmează, vom studia unele proprietăţi ale mulţimilor din R. Astfel, vom caracteriza locul" unui punct în cadrul unei mulţimi (în limba
Transformări de frecvenţă
 Lucrarea 22 Tranformări de frecvenţă Scopul lucrării: prezentarea metodei de inteză bazate pe utilizarea tranformărilor de frecvenţă şi exemplificarea aceteia cu ajutorul unui filtru trece-jo de tip Sallen-Key.
Lucrarea 22 Tranformări de frecvenţă Scopul lucrării: prezentarea metodei de inteză bazate pe utilizarea tranformărilor de frecvenţă şi exemplificarea aceteia cu ajutorul unui filtru trece-jo de tip Sallen-Key.
2. CONDENSATOARE 2.1. GENERALITĂŢI PRIVIND CONDENSATOARELE DEFINIŢIE UNITĂŢI DE MĂSURĂ PARAMETRII ELECTRICI SPECIFICI CONDENSATOARELOR SIMBOLURILE
 2. CONDENSATOARE 2.1. GENERALITĂŢI PRIVIND CONDENSATOARELE DEFINIŢIE UNITĂŢI DE MĂSURĂ PARAMETRII ELECTRICI SPECIFICI CONDENSATOARELOR SIMBOLURILE CONDENSATOARELOR 2.2. MARCAREA CONDENSATOARELOR MARCARE
2. CONDENSATOARE 2.1. GENERALITĂŢI PRIVIND CONDENSATOARELE DEFINIŢIE UNITĂŢI DE MĂSURĂ PARAMETRII ELECTRICI SPECIFICI CONDENSATOARELOR SIMBOLURILE CONDENSATOARELOR 2.2. MARCAREA CONDENSATOARELOR MARCARE
* K. toate K. circuitului. portile. Considerând această sumă pentru toate rezistoarele 2. = sl I K I K. toate rez. Pentru o bobină: U * toate I K K 1
 FNCȚ DE ENERGE Fie un n-port care conține numai elemente paive de circuit: rezitoare dipolare, condenatoare dipolare și bobine cuplate. Conform teoremei lui Tellegen n * = * toate toate laturile portile
FNCȚ DE ENERGE Fie un n-port care conține numai elemente paive de circuit: rezitoare dipolare, condenatoare dipolare și bobine cuplate. Conform teoremei lui Tellegen n * = * toate toate laturile portile
4. Măsurarea tensiunilor şi a curenţilor electrici. Voltmetre electronice analogice
 4. Măsurarea tensiunilor şi a curenţilor electrici oltmetre electronice analogice oltmetre de curent continuu Ampl.c.c. x FTJ Protectie Atenuator calibrat Atenuatorul calibrat divizor rezistiv R in const.
4. Măsurarea tensiunilor şi a curenţilor electrici oltmetre electronice analogice oltmetre de curent continuu Ampl.c.c. x FTJ Protectie Atenuator calibrat Atenuatorul calibrat divizor rezistiv R in const.
Proiectarea filtrelor prin metoda pierderilor de inserţie
 FITRE DE MIROUNDE Proiectarea filtrelor prin metoda pierderilor de inserţie P R Puterea disponibila de la sursa Puterea livrata sarcinii P inc P Γ ( ) Γ I lo P R ( ) ( ) M ( ) ( ) M N P R M N ( ) ( ) Tipuri
FITRE DE MIROUNDE Proiectarea filtrelor prin metoda pierderilor de inserţie P R Puterea disponibila de la sursa Puterea livrata sarcinii P inc P Γ ( ) Γ I lo P R ( ) ( ) M ( ) ( ) M N P R M N ( ) ( ) Tipuri
Aplicaţii ale principiului I al termodinamicii în tehnică
 Aplicaţii ale principiului I al termodinamicii în tehnică Sisteme de încălzire a locuinţelor Scopul tuturor acestor sisteme, este de a compensa pierderile de căldură prin pereţii locuinţelor şi prin sistemul
Aplicaţii ale principiului I al termodinamicii în tehnică Sisteme de încălzire a locuinţelor Scopul tuturor acestor sisteme, este de a compensa pierderile de căldură prin pereţii locuinţelor şi prin sistemul
ActivitateaA5. Introducerea unor module specifice de pregătire a studenţilor în vederea asigurării de şanse egale
 Investeşte în oameni! FONDUL SOCIAL EUROPEAN Programul Operaţional Sectorial pentru Dezvoltarea Resurselor Umane 007 013 Axa prioritară nr. 1 Educaţia şi formarea profesională în sprijinul creşterii economice
Investeşte în oameni! FONDUL SOCIAL EUROPEAN Programul Operaţional Sectorial pentru Dezvoltarea Resurselor Umane 007 013 Axa prioritară nr. 1 Educaţia şi formarea profesională în sprijinul creşterii economice
Capitolul 14. Asamblari prin pene
 Capitolul 14 Asamblari prin pene T.14.1. Momentul de torsiune este transmis de la arbore la butuc prin intermediul unei pene paralele (figura 14.1). De care din cotele indicate depinde tensiunea superficiala
Capitolul 14 Asamblari prin pene T.14.1. Momentul de torsiune este transmis de la arbore la butuc prin intermediul unei pene paralele (figura 14.1). De care din cotele indicate depinde tensiunea superficiala
- Optica Ondulatorie
 - Optica Ondulatorie *Proiect coordonat de Dna. Prof. Domisoru Daniela *Elevii participanti: Simion Vlad, Codreanu Alexandru, Domnisoru Albert-Leonard *Colegiul National Vasile Alecsandri GALATI *Concursul
- Optica Ondulatorie *Proiect coordonat de Dna. Prof. Domisoru Daniela *Elevii participanti: Simion Vlad, Codreanu Alexandru, Domnisoru Albert-Leonard *Colegiul National Vasile Alecsandri GALATI *Concursul
VII.2. PROBLEME REZOLVATE
 Teoria Circuitelor Electrice Aplicaţii V PROBEME REOVATE R7 În circuitul din fiura 7R se cunosc: R e t 0 sint [V] C C t 0 sint [A] Se cer: a rezolvarea circuitului cu metoda teoremelor Kirchhoff; rezolvarea
Teoria Circuitelor Electrice Aplicaţii V PROBEME REOVATE R7 În circuitul din fiura 7R se cunosc: R e t 0 sint [V] C C t 0 sint [A] Se cer: a rezolvarea circuitului cu metoda teoremelor Kirchhoff; rezolvarea
Matrice. Determinanti. Sisteme liniare
 Matrice 1 Matrice Adunarea matricelor Înmulţirea cu scalar. Produsul 2 Proprietăţi ale determinanţilor Rangul unei matrice 3 neomogene omogene Metoda lui Gauss (Metoda eliminării) Notiunea de matrice Matrice
Matrice 1 Matrice Adunarea matricelor Înmulţirea cu scalar. Produsul 2 Proprietăţi ale determinanţilor Rangul unei matrice 3 neomogene omogene Metoda lui Gauss (Metoda eliminării) Notiunea de matrice Matrice
CURS 11: ALGEBRĂ Spaţii liniare euclidiene. Produs scalar real. Spaţiu euclidian. Produs scalar complex. Spaţiu unitar. Noţiunea de normă.
 Sala: 2103 Decembrie 2014 Conf. univ. dr.: Dragoş-Pătru Covei CURS 11: ALGEBRĂ Specializarea: C.E., I.E., S.P.E. Nota: Acest curs nu a fost supus unui proces riguros de recenzare pentru a fi oficial publicat.
Sala: 2103 Decembrie 2014 Conf. univ. dr.: Dragoş-Pătru Covei CURS 11: ALGEBRĂ Specializarea: C.E., I.E., S.P.E. Nota: Acest curs nu a fost supus unui proces riguros de recenzare pentru a fi oficial publicat.
Tranzistoare bipolare şi cu efect de câmp
 apitolul 3 apitolul 3 26. Pentru circuitul de polarizare din fig. 26 se cunosc: = 5, = 5, = 2KΩ, = 5KΩ, iar pentru tranzistor se cunosc următorii parametrii: β = 200, 0 = 0, μa, = 0,6. a) ă se determine
apitolul 3 apitolul 3 26. Pentru circuitul de polarizare din fig. 26 se cunosc: = 5, = 5, = 2KΩ, = 5KΩ, iar pentru tranzistor se cunosc următorii parametrii: β = 200, 0 = 0, μa, = 0,6. a) ă se determine
Integrale cu parametru
 1 Integrle proprii cu prmetru 2 3 Integrle proprii cu prmetru Definiţi 1.1 Dcă f : [, b ] E R, E R este o funcţie cu propriette că pentru orice y E, funcţi de vribilă x x f (x, y) este integrbilă pe intervlul
1 Integrle proprii cu prmetru 2 3 Integrle proprii cu prmetru Definiţi 1.1 Dcă f : [, b ] E R, E R este o funcţie cu propriette că pentru orice y E, funcţi de vribilă x x f (x, y) este integrbilă pe intervlul
Cursul Măsuri reale. D.Rusu, Teoria măsurii şi integrala Lebesgue 15
 MĂSURI RELE Cursul 13 15 Măsuri reale Fie (,, µ) un spaţiu cu măsură completă şi f : R o funcţie -măsurabilă. Cum am văzut în Teorema 11.29, dacă f are integrală pe, atunci funcţia de mulţime ν : R, ν()
MĂSURI RELE Cursul 13 15 Măsuri reale Fie (,, µ) un spaţiu cu măsură completă şi f : R o funcţie -măsurabilă. Cum am văzut în Teorema 11.29, dacă f are integrală pe, atunci funcţia de mulţime ν : R, ν()
Componente şi Circuite Electronice Pasive. Laborator 4. Măsurarea parametrilor mărimilor electrice
 Laborator 4 Măsurarea parametrilor mărimilor electrice Obiective: o Semnalul sinusoidal, o Semnalul dreptunghiular, o Semnalul triunghiular, o Generarea diferitelor semnale folosind placa multifuncţională
Laborator 4 Măsurarea parametrilor mărimilor electrice Obiective: o Semnalul sinusoidal, o Semnalul dreptunghiular, o Semnalul triunghiular, o Generarea diferitelor semnale folosind placa multifuncţională
Laborator 1: INTRODUCERE ÎN ALGORITMI. Întocmit de: Claudia Pârloagă. Îndrumător: Asist. Drd. Gabriel Danciu
 INTRODUCERE Laborator 1: ÎN ALGORITMI Întocmit de: Claudia Pârloagă Îndrumător: Asist. Drd. Gabriel Danciu I. NOŢIUNI TEORETICE A. Sortarea prin selecţie Date de intrare: un şir A, de date Date de ieşire:
INTRODUCERE Laborator 1: ÎN ALGORITMI Întocmit de: Claudia Pârloagă Îndrumător: Asist. Drd. Gabriel Danciu I. NOŢIUNI TEORETICE A. Sortarea prin selecţie Date de intrare: un şir A, de date Date de ieşire:
T R A I A N ( ) Trigonometrie. \ kπ; k. este periodică (perioada principală T * =π ), impară, nemărginită.
 Trignmetrie Funcţia sinus sin : [, ] este peridică (periada principală T * = ), impară, mărginită. Funcţia arcsinus arcsin : [, ], este impară, mărginită, bijectivă. Funcţia csinus cs : [, ] este peridică
Trignmetrie Funcţia sinus sin : [, ] este peridică (periada principală T * = ), impară, mărginită. Funcţia arcsinus arcsin : [, ], este impară, mărginită, bijectivă. Funcţia csinus cs : [, ] este peridică
c c. se anulează (5p) 3. Imaginea unui obiect real dată de o lentilă divergentă este întotdeauna:
 Varianta 1 - optica B. ELEMENTE DE TERMODINAMICĂ, C. PRODUCEREA ŞI UTILIZAREA CURENTULUI CONTINUU, elementară e = 1,6 10 19 C, masa electronului m e = 9,1 10 31 kg. SUBIECTUL I Varianta 001 1. O rază de
Varianta 1 - optica B. ELEMENTE DE TERMODINAMICĂ, C. PRODUCEREA ŞI UTILIZAREA CURENTULUI CONTINUU, elementară e = 1,6 10 19 C, masa electronului m e = 9,1 10 31 kg. SUBIECTUL I Varianta 001 1. O rază de
Capitolul 2 - HIDROCARBURI 2.3.ALCHINE
 Capitolul 2 - HIDROCARBURI 2.3.ALCHINE TEST 2.3.3 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. 1. Acetilena poate participa la reacţii de
Capitolul 2 - HIDROCARBURI 2.3.ALCHINE TEST 2.3.3 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. 1. Acetilena poate participa la reacţii de
