MAGNETNI MATERIALI, HISTEREZNA ZANKA IN RAČUNANJE MAGNETNIH STRUKTUR
|
|
|
- Ποδαργη Βουρδουμπάς
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Equation Section 9Vsebina Magnetni ateriali 9. MAGNETNI MATERIALI, HISTEREZNA ZANKA IN RAČUNANJE MAGNETNIH STRUKTUR poglavja: agnetni ateriali (diaagnetiki, paraagnetiki, antiferiagnetiki, feriagnetiki, superparaagnetiki, feroagnetiki), krivulja agnetenja, histerezna zanka, razagnetenje, računanje agnetnih struktur. Kot so že oenili, iajo vsi ateriali določene agnetne lastnosti, le da so očno izražene le pri zelo redkih. Glede na obnašanje snovi v agnetne polju jih delio na diaagnetike, paraagnetike, feroagnetike, antiferoagnetike, feriagnetike in superparaagnetike. Diaagnetiki izkazujejo izredno šibke agnetne lastnosti. Magnetni dipolni oenti kroženja elektronov in njihovega spina se v taki snovi kopenzirajo. Se pa pod vplivo zunanjega agnetnega polja nekoliko celo zanjša agnetno polje v notranjosti, ker je vpliv zunanjega polja na spin elektronov nekoliko očnejši kot na orbitalni oent. Te snovi iajo negativno agnetno susceptibilnost oziroa relativno pereabilnost, ki je alo anjša od 1. Prieri takih snovi so Cu (relativna pereabilnost,999983), Au, Ag, Hg, H 2 O (,999991), itd. Če diaagnetik postavio v bližino očnega trajnega agneta, bo ed njia odbojna sila (neodvisno od pola agneta). To je odkril že Michael Faraday leta 1846 na prieru bizuta (,99983). SLIKA: M kaže v nasprotni seri kot vzbujanje. Diaagnetik se odbija od trajnega agneta: sila je v seri anjše gostote polja. Paraagnetiki so snovi, v katerih ni ravnotežja ed agnetnii dipolnii oenti zaradi kroženja elektronov in spina. Vsak ato izkazuje rezultančni agnetni dipolni oent, ki pa se zaradi neurejenosti strukture kopenzirajo. Se pa s postavitvijo take snovi v agnetno 1/13
2 Magnetni ateriali 9. polje v določeni eri agnetno polje v notranjosti nekoliko poveča (userijo se agnetni dipoli) v seri zunanjega polja. Take snovi so npr. aluinij (1,2), platina, angan, kisik, zrak (1,4). V sislu upoštevanja agnetnih lastnosti dia- in paraagnetikov bi lahko zaključili, da je njihova susceptibilnost v praksi najpogostelje zanearljiva. SLIKA: Magnetizacija kaže v seri vzbujalnega polja. Sila na paraagnetik v polju je v seri večje gostote polja. SLIKA: B(H) agnetilna krivulja za vakuu, diaagnetike in paraagnetike. Antiferiagnetiki so snovi, v katerih se agnetni oenti sosednjih atoov userijo v nasprotni seri, zato je skupen agnetni oent teh snovi pri vzpostavitvi zunanjega polja enak nič. Feriagnetiki iajo tudi nasprotno userjene agnetne oente, vendar njihova vrednost ni enaka nič. Še vedno pa ni ta efekt tako izrazit kot pri feroagnetikih. So pa določeni feriagnetiki, ki jih ienujeo feriti izredno poebni v elektrotehniki, saj je v nasprotju z feroagnetiki 2/13
3 Magnetni ateriali 9. njihova električna prevodnost zelo ajhna, kar s prido izkoriščao ta, kjer bi sicer ieli velike izgube zaradi ohskih tokov (vrtinčni toki) pri višjih frekvencah. Srečao ga tudi v naravi, kot agnetit (železov oksid Fe 3 O 4 ). Superparaagnetiki so feroagnetiki, ki so vešani v dielektričen aterial. Uporabljajo se npr. za audio in video trakove. Feroagnetiki. V feroagnetikih ia vsak ato relativno velik agnetni dipolni oent. Le ta je posledica neuravnoteženih oentov spinov elektronov, kar se da prikazati z uporabo spoznanj kvantne fizike. Tipični predstavnik feroagnetikov so železo (5), nikel (6) in kobalt (25), ki so v periodične sisteu na estih 26, 27 in 28. Poleg izraženih dipolnih oentov na nivoju atoa, se ti atoi v kristalni strukturi grupirajo v obočja, ki ji pravio agnetne doene, znotraj katerih so oenti orientirani, navzven pa so doene neurejene in zato tudi agnetno polje ni izrazito. Lahko pa se pod vplivo zunanjega polja agnetni oenti v doenah userijo v ser zunanjega polja. Proces orientiranja se odvija po fazah, tako, da se najprej nekoliko povečajo doene, katerih stene tvorijo ajhen kot glede na zunanje polje. Pri taki reorientaciji je polje reverzibilno: če izklopio zunanje polje, se doene vrnejo v prvoten položaj. Če se zunanje polje še dodatno poveča, se začnejo obračati celotne doene. Če pote izklopio zunanje polje, se doene ne vrnejo več v začetno stanje, teveč ostanejo delno orientirane. Če pa zunanje polje še povečujeo, prihaja do nasičenja, ko so praktično že vsi dipolni oenti doen userjeni v ser polja. Povečevanje polja s strani feroagnetika ni več ogoče. Gostota agnetnega pretoka sicer še naprej narašča vendar le kot posledica povečevanja vzbujanja. Relativna pereabilnost se ob približevanju nasičenja zanjšuje in približuje vrednosti 1 (feroagnetik se obnaša kot zrak). SLIKA: Prier zgradbe feroagnetnega ateriala z doenai in agnetnii dipolnii oenti. Prikaz userjanja dipolov pred agnetizacijo in ob nasičenju. 3/13
4 Magnetni ateriali 9. Krivulja agnetenja. Zania nas, kako se agnetizacija spreinja z večanje vzbujalne gostote agnetnega pretoka. Naesto opazovanja M(B), je bolj običajno, da zunanje vzbujanje opišeo z jakostjo agnetnega polja H, rezultat agnetenja pa opazujeo z naraščanje gostote agnetnega pretoka B. Dobio torej B(H) krivuljo, ki pa pri feroagnetikih ni linearna. Na začetku je naklon anjši, pote največji in pri velikih vzbujanjih zopet anjši (nasičenje). Začetni krivulji agnetenja rečeo deviška krivulja, ker se ob izklopu zunanjega vzbujanja gostota pretoka ne vrne na nič, pač pa na neko vrednost, ki je različna od nič. SLIKA: Magnetilna krivulja s tipičnii izrazi: deviška krivulja, nasičenje. Meja reverzibilnega in ireverzibilnega procesa. Prikaz zveze B(H) v vakuuu. Relativne pereabilnost (statična, dinaična, inkreentalna) Z upoštevanje zveze ed Bje in Hje je relativna pereabilnost definirana kot B µ = r,s µ H. (9.1) To pereabilnost ienujeo tudi statična in je prierna za obravnavo v prierih, ko se agnetilni tok ne spreinja ali pa je take oblike, da jo lahko dobro aproksiirao s preico. Tej pereabilnosti rečeo tudi statična, saj ni definiran z naklono krivulje pač pa z razerje ed B in H. Zadnji odsek predstavlja nasičenje, kjer relativna pereabilnost 4/13
5 Magnetni ateriali 9. postane enaka 1. Pri feroagnetikih so vrednosti relativne pereabilnosti nekaj tisoč do nekaj sto tisoč. Vrednost statične relativne pereabilnosti je odvisna od točke računanja in bo zaradi nelinarne agnetilne krivulje tudi saa nelinearna. V sislu lažjega računanja jo pogosto poenostavio tako, da linearizirao agnetilno krivuljo. Tako postane statična relativna pereabilnost konstanta. V nasičenju pa ia relativna statična pereabilnost vrednost 1. V določenih prierih (npr. pri vzbujanju z ajhnii izeničnii signali) je bolj prierno upoštevati le del krivulje agnetenja pri čeer je bolj siselno upoštevati naklon na krivuljo v določeni (delovni) točki. Tako dobio dinaično relativno pereabilnost, ki je definirana kot µ r,d = 1 db µ dh. SLIKA: Prikaz statične relativne pereabilnosti kot razerje ed B in µ H v točki. Krivulja ia določen aksiu in pade v nasičenju na vrednost 1. Če iao opravka z izenični signalo, ki je superponiran na enosernega, je običajno bolj prierno uporabiti t.i. inkreentalno relativno pereabilnost, ki ni definirana z odvodo krivulje pač pa z diferencai v lokalni histerezni zanki dinaične pereabilnosti. B µ r,i =. Ta je anjša od µ H Histerezna zanka: Do določenega Bja je proces agnetenja še reverzibilen, ko pa je ta vrednost presežena, se pri zanjševanju vzbujanja B počasneje zanjšuje kot pri povečevanju. Dobio histrezno zanko. Ko je vzbujanje izklopljeno, ostane v aterialu določeno polje, ki ga ienujeo reanenčno in označio z Br. Če ser vzbujanja obrneo, se zanjšuje polje in pri določeni vrednosti vzbujanja pade na nič. Tej točki vzbujanja rečeo 5/13
6 Magnetni ateriali 9. koercitivna jakost polja in jo označio s Hc. Pri še povečane vzbujanju prideo do nasičenja v negativni seri. Vzbujanje zopet zanjšujeo do nič in nato do nasičenja, kjer se začetna in končna krivulja stakneta. SLIKA: Histerezna krivulja s prikazo reanenčne gostote agnetnega pretoka (B r ), ki ostane v aterialu po izklopu vzbujanja in koercitivne jakost polja (H c ), kjer je gostota pretoka enaka nič. Mehkoagnetni in trdoagnetni ateriali. Če želio aterial uporabiti kot trajni agnet, je prierno uporabiti aterial, ki ia veliko vrednost reanenčne gostote polja. Poleg tega je poebno tudi, da ga ni lahko razagnetiti, torej ora ieti veliko tudi koercitivno jakost polja. Najboljši ateriali za trajni agnet iajo veliko vrednost produkta H c in B r. Taki aterialo rečeo tudi trdoagnetni. Mehkoagnetni ateriali iajo ozko histerezno zanko in veliko pereabilnost. Tipičen ehkoagnetni aterial je čisto železo. Zelo ozke histerezne zanke iajo tudi feritni ateriali. SLIKA: Prierjava ed histerezno zanko ehkoagnetnega ateriala in trdoagnetnega ateriala. Razagnetenje. Običajni način razagnetenja je zanjševanje izeničnega polja, pri čeer pa orao začeti razagnetenje z aplitudo, pri kateri je aterial v nasičenju. Določeni 6/13
7 Magnetni ateriali 9. ateriali so zelo občutljivi na ehanske udarce (so krhki), ki tudi lahko delno spreenijo agnetne lastnosti. Poleg tega vsak aterial izgubi agnetne lastnosti pri dovolj visoki teperaturi, ki jo ienujeo Curiejeva teperatura. Pri tej teperaturi snov zaradi povečanega teričnega gibanja izgubi agnetne lastnosti. Pri železu je T c =77 C. SLIKA: Prier uporabe prečno agnetiziranega trajnega agneta NeFeB za aplikacijo dajalnika kota, ki se ga določa z odčitavanje agnetnega polja. Pod senzorje se nahaja čip z nožico Hallovih eleentov in eleenti za obdelavo signalov. Čip je bil razvit na Fakulteti za elektrotehniko v Ljubljani, celotni produkt pa trži slovensko podjetje RLS: 7/13
8 Magnetni ateriali 9. RAČUNANJE MAGNETNIH STRUKTUR Spoznali so obliko Aperovega zakona izraženo z jakostjo agnetnega polja H: H dl = NI. Ugotovili so, da je ta oblika zapisa posebno prierna za obravnavo polja v L snoveh z izraženii agnetnii lastnosti (npr. feroagnetiki). Zveza ed gostoto B = µ H + M = µ µ H = µ H, kjer je zveza lahko agnetnega pretoka in jakostjo polja je ( ) r podana v ateatični obliki (konstantna pereabilnost ali nelinearna funkcija H-ja) ali pa je podana grafično v obliki agnetilne krivulje. Za analizo agnetnih struktur na služi ravno Aperov zakon, ki pa ga orao nekoliko poenostaviti. Naesto v integralni obliki ga zapišeo kot vsoto posaeznih padcev agnetne napetosti. Tako dobio obliko N Hi li = Θ. (9.2) i= 1 Desna stran enačbe predstavlja tokovno vzbujanje (lahko je več takih vzbujanj), leva stran enačbe pa so padci agnetne napetosti na posaeznih odsekih po zaključeni agnetni poti. Pri te so orali narediti določeno poenostavitev in sicer, da je po preseku jedra polje hoogeno in da računao razdalje l i po srednji dolžini gostotnice (po sredini jedra). Poleg zgornjega zapisa, ki spoinja na Kirchofov zakon o vsoti napetosti po zaključeni poti, potrebujeo še povezavo ed gostotai pretoka v sosednjih odsekih poti. To zvezo dobio iz zakona o brezizvornosti agnetnega polja ( B d A = ), ki ga zopet zapišeo v diskretni A obliki N Φi =, (9.3) i= 1 kjer je N število odcepov. Poglejo si to na prieru E oblike jedra na sliki. SLIKA: Prikaz srednjih dolžin gostotnic ter vsote fluksov v jedru E oblike. Veljati ora: Φ1 + Φ2 + Φ3 =. 8/13
9 Magnetni ateriali 9. PRIMERI IZRAČUNOV: Prier 1: Navitje na feroagnetne jedru s konstantno pereabilnostjo brez zračne reže: Na feroagnetne jedru pravokotnega preseka 1 c 2 s sredno dolžino gostotnice 24 c je navitje s toko 1,2 A in 15 ovoji. Relativna pereabilnost feroagnetika je 647. Določite gostoto agnetnega pretoka, fluks v jedru in induktivnost navitja. (SLIKA) Izračun: NI = Hl H = 75 A/ B = µ rµ H =,6 T Φ = BA = Wb NΦ L = = 7,5 H. I Prier 2: Navitje na jedru iz feroagnetika s konstantno pereabilnostjo in z zračno režo: Vzeio enako jedro kot v prieru 1, pri čeer naj ia jedro še 1 široko zračno režo. Privzeio, da v zračni reži ni stresanja polja (enako hoogeno kot v jedru). Kolikšno polje dobio v zračni reži in feroagnetiku pri enake vzbujanju ter kolikšna je induktivnost navijta? (SLIKA) Izračun: Vsota vseh padcev agnetnih napetosti po zaključeni dolžini agnetne poti ora biti enaka agnetneu vzbujanju N i= 1 H l = Θ. Iao dva padca agnetnih napetosti: eno i i v feroagnetiku in drugo v zračni reži. Predpostavili boo, da je polje v feroagnetiku (index ) hoogeno po prerezu in da računao integral po srednji dolžini agnetne poti: H l + H zr lzr = NI. Sedaj Hje izrazio z Bji, pri čeer je potrebno upoštevati različne relativne pereabilnosti (v zraku le µ ): B B l + lzr = NI. (9.4) µ µ µ zr r Da dobio zvezo ed polje v feroagnetiku in zračni reži uporabio enačbo (9.3) iz katere sledi, da ora biti fluks skozi jedro enak fluksu skozi zračno režo: Φ = Φ zr torej zaradi predpostavljene hoogenosti polja B A Bzr Azr =. Če zaneario stresanje polja v zračni reži ( A = Azr ), je gostota polja v feroagnetiku enako velika gostoti polja v zračni reži: B = Bzr. Z upoštevanje tega v enačbi (9.4) dobio izraz za izračun 9/13
10 Magnetni ateriali 9. µ NI polja v feroagnetiku (in zračni reži) B = l + l µ r zr. Vidio, da se je polje znotraj feroagnetika zanjšalo glede na prejšnji prier (,9 T) in sedaj znaša,16 T. Prav tako se zanjša tudi lastna induktivnost, ki je sedaj 2 H. Vprašanje: Zakaj pote sploh uporabiti zračno režo, če pa tako očno zanjša polje? Ponavadi je zračno režo potrebno uporabiti zato, da se zanjšajo nelinearnosti, ki so posledica nelinearne zveze ed Bje in Hje, ki se odraža v nelinearni relativni pereabilnosti. Zračna reža deluje kot agnetni upor, ki je popolnoa linearen in zanjša končen vpliv nelinearnosti feroagnetika. Potrebno je najti ravno pravi koprois, ki daje dovolj velik odziv, nelinearnosti pa orajo biti znotraj določenih okvirov (eja). Prier 3: Navitje na feroagnetne jedru brez zračne reže. Upoštevao agnetilno krivulja feroagnetika. Vzeio feroagnetno jedro iz litega jekla pravokotne preseka 1 c 2. Na jedru je navitje s 15 ovoji, srednjo dolžino gostotnice 24 c in toko 1,2 A. Določio gostoto agnetnega pretoka, fluks v jedru in induktivnost navitja. Izračun: Zapišeo H l = NI od koder sledi H = 75 A/. B določio iz agnetilne krivulje, kot prikazuje slika. Dobio B =,95 T. Fluks bo torej = 95 µwb in induktivnost L=11,8 H. Ta induktivnost ni več linearna, teveč je odvisna od toka vzbujanja, edte ko je bila pri jedru s konstantno pereabilnostjo konstantna. SLIKA: Prier določitve gostote pretoka iz znane jakosti polja. 1/13
11 Magnetni ateriali 9. Prier 4: Navitje na jedru z zračno režo. Upoštevao agnetilno krivuljo feroagnetika. Podan je NI, iščeo fluks ali gostoto pretoka. Vzeio jedro iz prieru 3, ki pa u dodao 1 široko zračno režo. Zopet lahko pišeo H l + H zr lzr = NI. Jakost polja v zračni reži izrazio z gostoto pretoka v zračni reži, ki je ob zanearitvi stresanja polja enaka kot v jedru. Torej velja B H l l + l = NI. To je enačba z dvea neznankaa. Druga zveza ed B in H je ( ) zr zr µ podana z agnetilno krivuljo. Prier lahko rešio s preizkušanje ali pa grafično: Izračun s preizkušanje: enačbo napišeo z vstavljenii vrednosti (enostavneje kar brez enot) H, 24 + B 796 = 18. Pri pravilno izbrane B in H ora biti leva stran enačbe enaka 18. Izbereo si določen B in na agnetilni krivulji poiščeo ustrezen H. Preverio če rezultat ustreza in se s preizkušanje bližao rešitvi. B = 1 T, H = 8 A/, H,24 + B 796 = 988 ; nogo preveč B =,5 T, H = 32 A/, H,24 + B 796 = 475 ; nogo preveč B =,2 T, H = 2 A/, H,24 + B 796 = 27 ; blizu rešitve B =,15 T, H = 15 A/, H,24 + B 796 = 155,4 ; prealo Zaključio, da ora biti B ed,2 in,15 T. Izračun z grafični postopko: Gornja enačba predstavlja enačbo preice, ki v presečišču z agnetilno krivuljo določa delovno točko. Potrebujeo dve točki na preici. Najbolj enostavno kar B (H =) =,226 T in H (B =) = 75 A/. Skozi ti dve točki potegneo preico in odčitao delovno točko. SLIKA: Prier grafičnega določanja delovne točke in posledično agnetne napetosti. 11/13
12 Magnetni ateriali 9. Prier 5: Jedro z zračno režo. Podan fluks ali gostota toka, iščeo NI. Isto kot prier 3 in 4, le da iščeo agnetno napetost pri želeni gostoti pretoka v zračni reži. Na prier pri B =,5 T. Enačba je enaka kot v prejšnje prieru, postopek pa je direkten. Ker zaneario stresanje polja v zračni reži, je gostota pretoka v jedru enaka kot v zračni reži. Iz agnetilne krivulje odčitao H pri B =,5 T, ki je 32 A/ in vstavio v enačbo. Dobio 475 A. Prier 6: Izračun trajnega agneta. Poiščio velikost agnetizacije trajnega agneta z zračno režo dolžine 5, pri čeer je agnet oblike toroida okroglega preseka notranjega polera 2,5 c in zunanjega polera 3,5 c. V zračni reži so izerili polje 5 T (spreenjena vrednost!). 3,5 c+2,5c l = 2π = 6π c. 2 Izračun: Ker ni (zunanjega) vzbujanja, bo veljalo H l + H l =, od koder je H H l zr zr zr zr =.Vidio, da je ser jakosti polja v agnetu različna kot v zračni reži. In ker l je ser gostote pretoka v zračni reži enaka seri jakosti polja ( B = µ H ), lahko zaključio, da je ser B-ja v agnetu različna od seri H-ja (to so ugotovili tudi že v prejšnje poglavju). Ker zvezo ed B in H v zraku vedno poznao, lahko določio H v železu H Bzr l µ = = 1,84 ka/. Ker sta fluksa v zračni reži in agnetu enaka, sta tudi gostoti l pretoka enaki (če ne upoštevao stresanja polja) je polje v agnetu enako veliko kot polje v zračni reži,,5 T. Z upoštevanje stresanja bi orali upoštevati efektivno zanjšanje zračne reže za (Carterjev) faktor približno,7. Magnetizacijo dobio iz izraza B = µ H + µ M, od koder je M B 3 = H = 4,87 1 A/. µ SLIKA: Jakost polja in gostota pretoka ter agnetizacija v agnetu in zračni reži. 12/13
13 Magnetni ateriali 9. Delovna točka agneta. Ugotovili so, da sta B in H pri trajne agnetu nasprotnega B lzr predznaka, saj velja H =. Torej se delovna točka agneta nahaja na agnetilni l krivulji v druge kvadrantu. Teu delu histerezne zanke rečeo tudi krivulja deagnetizacije ali razagnetilna krivulja. Enačba predstavlja naklon preice in v presečišču s krivuljo agnetenja določa delovno točko. Za trajni agnet si večinoa želio, da ia či večji produkt B-ja in H-ja. Optialna delovna točka je ta, kjer je produkt Bja in Hja največji. Kot boo videli, določa produkt B-ja in H-ja gostoto agnetne energije v jedru. Desno od grafa B(-H) običajno narišeo še graf B(B H), kjer lahko identificirao točko z največji produkto BH. SLIKA: Delovna točka trajnega agneta. Prieri kolokvijev in izpitov: Magnetizacija, trajni agnet: kolokvij, 9. aj 25 izpit, 2. junij 26 izpit, 19. januar 26 izpit, 8. aprila 22 izpit, 24. junij 24 Feroagnetik podan z agnetilno krivuljo: kolokvij, 13. april 26 kolokvij, 3. aj 24 kolokvij, 15. april 24 kolokvij, 7. aja 22 Feroagnetik z ali brez zračne reže, konstantna pereabilnost: kolokvij, 4. aj 26 izpit 23. junija 26 13/13
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 5. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Diferencialna enačba, v kateri nastopata neznana funkcija in njen odvod v prvi potenci
 Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Tretja vaja iz matematike 1
 Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 21. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Funkcijske vrste. Matematika 2. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 2. april Gregor Dolinar Matematika 2
 Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Izmenični signali kompleksni račun
 zenicni_signali-kopleksni_racun(8).doc /7.6.6 zenični signali kopleksni račun Kopleksni račun e poebno orode za analizo vezi z izeničnii haroničnii signali. V osnovi diferencialne enačbe lahko z uporabo
zenicni_signali-kopleksni_racun(8).doc /7.6.6 zenični signali kopleksni račun Kopleksni račun e poebno orode za analizo vezi z izeničnii haroničnii signali. V osnovi diferencialne enačbe lahko z uporabo
Delovna točka in napajalna vezja bipolarnih tranzistorjev
 KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 22. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Osnovni pojmi pri obravnavi periodičnih signalov
 Periodični signali, osnovni poji 7. Osnovni poji pri obravnavi periodičnih signalov Vsebina: Opis periodičnih signalov z periodo, frekvenco, krožno frekvenco. Razlaga pojov aplituda, faza, haronični signal.
Periodični signali, osnovni poji 7. Osnovni poji pri obravnavi periodičnih signalov Vsebina: Opis periodičnih signalov z periodo, frekvenco, krožno frekvenco. Razlaga pojov aplituda, faza, haronični signal.
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 14. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
GILBERT PRVI ZNANSTVEN PRISTOP
 Zgodovina in sila (1).doc 1/9 26/3/27 ZGODOVINA MAGNETIKE Iena za naravni agnet: FR: aiant (ljubeč) KIT: tzhu shih (ljubezenski kaen) GB: lodestone (leading, guiding stone) PPT PREZENTACIJA ZGODOVINE KITAJSKA
Zgodovina in sila (1).doc 1/9 26/3/27 ZGODOVINA MAGNETIKE Iena za naravni agnet: FR: aiant (ljubeč) KIT: tzhu shih (ljubezenski kaen) GB: lodestone (leading, guiding stone) PPT PREZENTACIJA ZGODOVINE KITAJSKA
*M * Osnovna in višja raven MATEMATIKA NAVODILA ZA OCENJEVANJE. Sobota, 4. junij 2011 SPOMLADANSKI IZPITNI ROK. Državni izpitni center
 Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
NAVOR NA (TOKO)VODNIK V MAGNETNEM POLJU
 NAVOR NA (TOKO)VODNIK V MAGNETNEM POLJU Equatio n Section 6Vsebina poglavja: Navor kot vektorski produkt ročice in sile, magnetni moment, navor na magnetni moment, d'arsonvalov ampermeter/galvanometer.
NAVOR NA (TOKO)VODNIK V MAGNETNEM POLJU Equatio n Section 6Vsebina poglavja: Navor kot vektorski produkt ročice in sile, magnetni moment, navor na magnetni moment, d'arsonvalov ampermeter/galvanometer.
Gimnazija Krˇsko. vektorji - naloge
 Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 10. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Numerično reševanje. diferencialnih enačb II
 Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * NAVODILA ZA OCENJEVANJE. Petek, 12. junij 2015 SPLOŠNA MATURA
 Državni izpitni center *M543* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Petek,. junij 05 SPLOŠNA MATURA RIC 05 M543 M543 3 IZPITNA POLA Naloga Odgovor Naloga Odgovor Naloga Odgovor Naloga Odgovor
Državni izpitni center *M543* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Petek,. junij 05 SPLOŠNA MATURA RIC 05 M543 M543 3 IZPITNA POLA Naloga Odgovor Naloga Odgovor Naloga Odgovor Naloga Odgovor
Transformator. Delovanje transformatorja I. Delovanje transformatorja II
 Transformator Transformator je naprava, ki v osnovi pretvarja napetost iz enega nivoja v drugega. Poznamo vrsto različnih izvedb transformatorjev, glede na njihovo specifičnost uporabe:. Energetski transformator.
Transformator Transformator je naprava, ki v osnovi pretvarja napetost iz enega nivoja v drugega. Poznamo vrsto različnih izvedb transformatorjev, glede na njihovo specifičnost uporabe:. Energetski transformator.
Poglavje 7. Poglavje 7. Poglavje 7. Regulacijski sistemi. Regulacijski sistemi. Slika 7. 1: Normirana blokovna shema regulacije EM
 Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK
 SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
3. AMPEROV ZAKON. SLIKA: Zanka v magnetnem polju. Integral komponente magnetnega polja v smeri zanke je sorazmeren toku, ki ga zanka oklepa.
 3. AMPEROV ZAKON Equation Section 3 Vsebina poglavja: Integral polja po zaključeni zanki je sorazmeren toku, ki ga zanka objame. Izračuni polja s pomočjo Amperovega zakona za: tokovno premico, solenoid,
3. AMPEROV ZAKON Equation Section 3 Vsebina poglavja: Integral polja po zaključeni zanki je sorazmeren toku, ki ga zanka objame. Izračuni polja s pomočjo Amperovega zakona za: tokovno premico, solenoid,
KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK
 1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
PONOVITEV SNOVI ZA 4. TEST
 PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
Osnove elektrotehnike uvod
 Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
MAGNETNI PRETOK FLUKS
 MGNETNI PRETOK FLUKS Equation Section 4 Vsebina poglavja: Določitev magnetnega pretoka, brezizvornost magnetnega polja, upodobitev polja z gostotnicami, induktivnost, lastna induktivnost, magnetni sklep.
MGNETNI PRETOK FLUKS Equation Section 4 Vsebina poglavja: Določitev magnetnega pretoka, brezizvornost magnetnega polja, upodobitev polja z gostotnicami, induktivnost, lastna induktivnost, magnetni sklep.
IZPIT IZ ANALIZE II Maribor,
 Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
1. Definicijsko območje, zaloga vrednosti. 2. Naraščanje in padanje, ekstremi. 3. Ukrivljenost. 4. Trend na robu definicijskega območja
 ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
Trdomagnetni materiali
 Troagnetni ateriali Razagnetenje lahko opazujeo na va načina: s poočjo faktorja razagnetenja ke pa lahko osega le vrenosti k e < 1, H = M, kjer je M agnetenje agneta, k e s poočjo koeficienta pereance
Troagnetni ateriali Razagnetenje lahko opazujeo na va načina: s poočjo faktorja razagnetenja ke pa lahko osega le vrenosti k e < 1, H = M, kjer je M agnetenje agneta, k e s poočjo koeficienta pereance
1. Trikotniki hitrosti
 . Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
. Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
Kontrolne karte uporabljamo za sprotno spremljanje kakovosti izdelka, ki ga izdelujemo v proizvodnem procesu.
 Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
Na pregledni skici napišite/označite ustrezne točke in paraboli. A) 12 B) 8 C) 4 D) 4 E) 8 F) 12
 Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
Izmenični signali. Dejan Križaj
 Izenični signali Dejan Križaj . . KAZALO 6. PREHODNI POJAVI... 4 PREHODNI POJAVI... 5 ZVEZE MED TOKOM IN NAPETOSTJO NA ELEMENTIH VEZJA... 6 ZAČETNI POGOJI... 6 POLNJENJE KONDENZATORJA... 7 PRAZNENJE KONDENZATORJA...
Izenični signali Dejan Križaj . . KAZALO 6. PREHODNI POJAVI... 4 PREHODNI POJAVI... 5 ZVEZE MED TOKOM IN NAPETOSTJO NA ELEMENTIH VEZJA... 6 ZAČETNI POGOJI... 6 POLNJENJE KONDENZATORJA... 7 PRAZNENJE KONDENZATORJA...
Kotne in krožne funkcije
 Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
5.6 Ostale lastnosti feromagnetnih materialov
 5.6 Ostale lastnosti feromagnetnih materialov Pri izdelavi magnetnih materialov imajo pomembno vlogo tudi nepravilnosti v njihovi strukturi. Če je material izdelan brez nepravilnosti, premikanje Blochovih
5.6 Ostale lastnosti feromagnetnih materialov Pri izdelavi magnetnih materialov imajo pomembno vlogo tudi nepravilnosti v njihovi strukturi. Če je material izdelan brez nepravilnosti, premikanje Blochovih
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * NAVODILA ZA OCENJEVANJE. Sreda, 3. junij 2015 SPLOŠNA MATURA
 Državni izpitni center *M15143113* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sreda, 3. junij 2015 SPLOŠNA MATURA RIC 2015 M151-431-1-3 2 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor Naloga Odgovor
Državni izpitni center *M15143113* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sreda, 3. junij 2015 SPLOŠNA MATURA RIC 2015 M151-431-1-3 2 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor Naloga Odgovor
Booleova algebra. Izjave in Booleove spremenljivke
 Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
INDUCIRANA NAPETOST (11)
 INDUCIRANA NAPETOST_1(11d).doc 1/17 29.3.2007 INDUCIRANA NAPETOST (11) V tem poglavju bomo nadgradili spoznanja o magnetnih pojavih v stacionarnih razmerah (pri konstantnem toku) z analizo razmer pri časovno
INDUCIRANA NAPETOST_1(11d).doc 1/17 29.3.2007 INDUCIRANA NAPETOST (11) V tem poglavju bomo nadgradili spoznanja o magnetnih pojavih v stacionarnih razmerah (pri konstantnem toku) z analizo razmer pri časovno
matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):
![matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij): matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):](/thumbs/87/96579490.jpg) 4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
Funkcije več spremenljivk
 DODATEK C Funkcije več spremenljivk C.1. Osnovni pojmi Funkcija n spremenljivk je predpis: f : D f R, (x 1, x 2,..., x n ) u = f (x 1, x 2,..., x n ) kjer D f R n imenujemo definicijsko območje funkcije
DODATEK C Funkcije več spremenljivk C.1. Osnovni pojmi Funkcija n spremenljivk je predpis: f : D f R, (x 1, x 2,..., x n ) u = f (x 1, x 2,..., x n ) kjer D f R n imenujemo definicijsko območje funkcije
diferencialne enačbe - nadaljevanje
 12. vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 diferencialne enačbe - nadaljevanje Ortogonalne trajektorije Dana je 1-parametrična družina krivulj F(x, y, C) = 0. Ortogonalne
12. vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 diferencialne enačbe - nadaljevanje Ortogonalne trajektorije Dana je 1-parametrična družina krivulj F(x, y, C) = 0. Ortogonalne
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 15. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
1. Enosmerna vezja. = 0, kar zaključena
 1. Enosmerna vezja Vsebina polavja: Kirchoffova zakona, Ohmov zakon, električni viri (idealni realni, karakteristika vira, karakteristika bremena matematično in rafično, delovna točka). V enosmernih vezjih
1. Enosmerna vezja Vsebina polavja: Kirchoffova zakona, Ohmov zakon, električni viri (idealni realni, karakteristika vira, karakteristika bremena matematično in rafično, delovna točka). V enosmernih vezjih
8. Diskretni LTI sistemi
 8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
TEHNOLOGIJA MATERIALOV
 Naslov vaje: Nastavljanje delovne točke trajnega magneta Pri vaji boste podrobneje spoznali enega od možnih postopkov nastavljanja delovne točke trajnega magneta. Trajne magnete uporabljamo v različnih
Naslov vaje: Nastavljanje delovne točke trajnega magneta Pri vaji boste podrobneje spoznali enega od možnih postopkov nastavljanja delovne točke trajnega magneta. Trajne magnete uporabljamo v različnih
MERITVE LABORATORIJSKE VAJE. Študij. leto: 2011/2012 UNIVERZA V MARIBORU. Skupina: 9
 .cwww.grgor nik ol i c NVERZA V MARBOR FAKTETA ZA EEKTROTEHNKO, RAČNANŠTVO N NFORMATKO 2000 Maribor, Smtanova ul. 17 Študij. lto: 2011/2012 Skupina: 9 MERTVE ABORATORJSKE VAJE Vaja št.: 4.1 Določanj induktivnosti
.cwww.grgor nik ol i c NVERZA V MARBOR FAKTETA ZA EEKTROTEHNKO, RAČNANŠTVO N NFORMATKO 2000 Maribor, Smtanova ul. 17 Študij. lto: 2011/2012 Skupina: 9 MERTVE ABORATORJSKE VAJE Vaja št.: 4.1 Določanj induktivnosti
Osnove matematične analize 2016/17
 Osnove matematične analize 216/17 Neža Mramor Kosta Fakulteta za računalništvo in informatiko Univerza v Ljubljani Kaj je funkcija? Funkcija je predpis, ki vsakemu elementu x iz definicijskega območja
Osnove matematične analize 216/17 Neža Mramor Kosta Fakulteta za računalništvo in informatiko Univerza v Ljubljani Kaj je funkcija? Funkcija je predpis, ki vsakemu elementu x iz definicijskega območja
Integralni račun. Nedoločeni integral in integracijske metrode. 1. Izračunaj naslednje nedoločene integrale: (a) dx. (b) x 3 +3+x 2 dx, (c) (d)
 Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
3. Uporaba Biot-Savartovega zakona. Tokovna daljica: Premica: Tokovna zanka:
 1. Magnetostatika 1. Amperov zakon magnetne sile (med tokovnima elementoma) Pravilno predvideva, da če električni tok povzroča magnetno polje in s tem odklon magnetne igle, mora obstajati tudi sila med
1. Magnetostatika 1. Amperov zakon magnetne sile (med tokovnima elementoma) Pravilno predvideva, da če električni tok povzroča magnetno polje in s tem odklon magnetne igle, mora obstajati tudi sila med
vezani ekstremi funkcij
 11. vaja iz Matematike 2 (UNI) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 ekstremi funkcij več spremenljivk nadaljevanje vezani ekstremi funkcij Dana je funkcija f(x, y). Zanimajo nas ekstremi nad
11. vaja iz Matematike 2 (UNI) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 ekstremi funkcij več spremenljivk nadaljevanje vezani ekstremi funkcij Dana je funkcija f(x, y). Zanimajo nas ekstremi nad
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * FIZIKA NAVODILA ZA OCENJEVANJE. Petek, 10. junij 2016 SPLOŠNA MATURA
 Državni izpitni center *M16141113* SPOMLADANSKI IZPITNI ROK FIZIKA NAVODILA ZA OCENJEVANJE Petek, 1. junij 16 SPLOŠNA MATURA RIC 16 M161-411-3 M161-411-3 3 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor
Državni izpitni center *M16141113* SPOMLADANSKI IZPITNI ROK FIZIKA NAVODILA ZA OCENJEVANJE Petek, 1. junij 16 SPLOŠNA MATURA RIC 16 M161-411-3 M161-411-3 3 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor
Državni izpitni center *M * JESENSKI IZPITNI ROK ELEKTROTEHNIKA NAVODILA ZA OCENJEVANJE. Četrtek, 27. avgust 2009 SPLOŠNA MATURA
 Š i f r a k a n d i d a t a : Državni izpitni center *M097711* ELEKTROTEHNIKA JESENSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Četrtek, 7. avgust 009 SPLOŠNA MATURA RIC 009 M09-771-1- A01 Z galvanizacijskim
Š i f r a k a n d i d a t a : Državni izpitni center *M097711* ELEKTROTEHNIKA JESENSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Četrtek, 7. avgust 009 SPLOŠNA MATURA RIC 009 M09-771-1- A01 Z galvanizacijskim
Transformator. Izmenični signali, transformator 22.
 zmenični signali, transformator. Transformator Vsebina: Zapis enačb transformatorja kot dveh sklopljenih tuljav, napetostna prestava, povezava medd maksimalnim fluksom in napetostjo, neobremenjen transformator
zmenični signali, transformator. Transformator Vsebina: Zapis enačb transformatorja kot dveh sklopljenih tuljav, napetostna prestava, povezava medd maksimalnim fluksom in napetostjo, neobremenjen transformator
p 1 ENTROPIJSKI ZAKON
 ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 12. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
Fazni diagram binarne tekočine
 Fazni diagram binarne tekočine Žiga Kos 5. junij 203 Binarno tekočino predstavljajo delci A in B. Ti se med seboj lahko mešajo v različnih razmerjih. V nalogi želimo izračunati fazni diagram take tekočine,
Fazni diagram binarne tekočine Žiga Kos 5. junij 203 Binarno tekočino predstavljajo delci A in B. Ti se med seboj lahko mešajo v različnih razmerjih. V nalogi želimo izračunati fazni diagram take tekočine,
Zaporedna in vzporedna feroresonanca
 Visokonapetostna tehnika Zaporedna in vzporedna feroresonanca delovanje regulacijskega stikala T3 174 kv Vaja 9 1 Osnovni pogoji za nastanek feroresonance L C U U L () U C () U L = U L () U C = ωc V vezju
Visokonapetostna tehnika Zaporedna in vzporedna feroresonanca delovanje regulacijskega stikala T3 174 kv Vaja 9 1 Osnovni pogoji za nastanek feroresonance L C U U L () U C () U L = U L () U C = ωc V vezju
2. ATOM, MOLEKULA, MOL
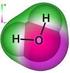 2. ATO, OLEKULA, OL ATO, OLEKULA, OL Iz Daltonove teorije sledi: eleenti so zgrajeni iz enakih atoov vsi atoi istega eleenta iajo enako aso in enake lastnosti atoi različnih eleentov iajo različne ase
2. ATO, OLEKULA, OL ATO, OLEKULA, OL Iz Daltonove teorije sledi: eleenti so zgrajeni iz enakih atoov vsi atoi istega eleenta iajo enako aso in enake lastnosti atoi različnih eleentov iajo različne ase
Kotni funkciji sinus in kosinus
 Kotni funkciji sinus in kosinus Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z oznako cos x, DEFINICIJA V PRAVOKOTNEM TRIKOTNIKU: Kotna funkcija sinus je definirana kot razmerje
Kotni funkciji sinus in kosinus Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z oznako cos x, DEFINICIJA V PRAVOKOTNEM TRIKOTNIKU: Kotna funkcija sinus je definirana kot razmerje
Frekvenčna analiza neperiodičnih signalov. Analiza signalov prof. France Mihelič
 Frekvenčna analiza neperiodičnih signalov Analiza signalov prof. France Mihelič Vpliv postopka daljšanja periode na spekter periodičnega signala Opazujmo družino sodih periodičnih pravokotnih impulzov
Frekvenčna analiza neperiodičnih signalov Analiza signalov prof. France Mihelič Vpliv postopka daljšanja periode na spekter periodičnega signala Opazujmo družino sodih periodičnih pravokotnih impulzov
9. Notranja energija in toplota
 9. Notranja energija in toplota - Toplota je tisti del notranje energije, ki se pretaka ed dvea telesoa, ko je ed njia teperaturna razlika! - Notranja energija telesa je sestavljena iz kinetične energije
9. Notranja energija in toplota - Toplota je tisti del notranje energije, ki se pretaka ed dvea telesoa, ko je ed njia teperaturna razlika! - Notranja energija telesa je sestavljena iz kinetične energije
Matematika. Funkcije in enačbe
 Matematika Funkcije in enačbe (1) Nariši grafe naslednjih funkcij: (a) f() = 1, (b) f() = 3, (c) f() = 3. Rešitev: (a) Linearna funkcija f() = 1 ima začetno vrednost f(0) = 1 in ničlo = 1/. Definirana
Matematika Funkcije in enačbe (1) Nariši grafe naslednjih funkcij: (a) f() = 1, (b) f() = 3, (c) f() = 3. Rešitev: (a) Linearna funkcija f() = 1 ima začetno vrednost f(0) = 1 in ničlo = 1/. Definirana
ATOM, MOLEKULA, MOL. vsi atomi istega elementa imajo enako maso in enake lastnosti
 2. AO, OLEKULA, OL Iz Daltonove teorije sledi: eleenti so zgrajeni iz enakih atoov vsi atoi istega eleenta iajo enako aso in enake lastnosti atoi različnih eleentov iajo različne ase atoi različnih eleentov
2. AO, OLEKULA, OL Iz Daltonove teorije sledi: eleenti so zgrajeni iz enakih atoov vsi atoi istega eleenta iajo enako aso in enake lastnosti atoi različnih eleentov iajo različne ase atoi različnih eleentov
Iterativno reševanje sistemov linearnih enačb. Numerične metode, sistemi linearnih enačb. Numerične metode FE, 2. december 2013
 Numerične metode, sistemi linearnih enačb B. Jurčič Zlobec Numerične metode FE, 2. december 2013 1 Vsebina 1 z n neznankami. a i1 x 1 + a i2 x 2 + + a in = b i i = 1,..., n V matrični obliki zapišemo:
Numerične metode, sistemi linearnih enačb B. Jurčič Zlobec Numerične metode FE, 2. december 2013 1 Vsebina 1 z n neznankami. a i1 x 1 + a i2 x 2 + + a in = b i i = 1,..., n V matrični obliki zapišemo:
Merilniki gostote magnetnega polja na osnovi Lorentzove sile
 Merilniki gostote magnetnega polja na osnovi Lorentzove sile Lorentzova sila je temelj tako allovega kot tudi magnetoupornostnega efekta v polprevodniških strukturah. Zgradba in osnovni princip delovanja
Merilniki gostote magnetnega polja na osnovi Lorentzove sile Lorentzova sila je temelj tako allovega kot tudi magnetoupornostnega efekta v polprevodniških strukturah. Zgradba in osnovni princip delovanja
PROCESIRANJE SIGNALOV
 Rešive pisega izpia PROCESIRANJE SIGNALOV Daum: 7... aloga Kolikša je ampliuda reje harmoske kompoee arisaega periodičega sigala? f() - -3 - - 3 Rešiev: Časova fukcija a iervalu ( /,/) je lieara fukcija:
Rešive pisega izpia PROCESIRANJE SIGNALOV Daum: 7... aloga Kolikša je ampliuda reje harmoske kompoee arisaega periodičega sigala? f() - -3 - - 3 Rešiev: Časova fukcija a iervalu ( /,/) je lieara fukcija:
NEPARAMETRIČNI TESTI. pregledovanje tabel hi-kvadrat test. as. dr. Nino RODE
 NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
Izpeljava Jensenove in Hölderjeve neenakosti ter neenakosti Minkowskega
 Izeljava Jensenove in Hölderjeve neenakosti ter neenakosti Minkowskega 1. Najosnovnejše o konveksnih funkcijah Definicija. Naj bo X vektorski rostor in D X konveksna množica. Funkcija ϕ: D R je konveksna,
Izeljava Jensenove in Hölderjeve neenakosti ter neenakosti Minkowskega 1. Najosnovnejše o konveksnih funkcijah Definicija. Naj bo X vektorski rostor in D X konveksna množica. Funkcija ϕ: D R je konveksna,
Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba.
 1. Osnovni pojmi Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba. Primer 1.1: Diferencialne enačbe so izrazi: y
1. Osnovni pojmi Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba. Primer 1.1: Diferencialne enačbe so izrazi: y
ΓΗ ΚΑΙ ΣΥΜΠΑΝ. Εικόνα 1. Φωτογραφία του γαλαξία μας (από αρχείο της NASA)
 ΓΗ ΚΑΙ ΣΥΜΠΑΝ Φύση του σύμπαντος Η γη είναι μία μονάδα μέσα στο ηλιακό μας σύστημα, το οποίο αποτελείται από τον ήλιο, τους πλανήτες μαζί με τους δορυφόρους τους, τους κομήτες, τα αστεροειδή και τους μετεωρίτες.
ΓΗ ΚΑΙ ΣΥΜΠΑΝ Φύση του σύμπαντος Η γη είναι μία μονάδα μέσα στο ηλιακό μας σύστημα, το οποίο αποτελείται από τον ήλιο, τους πλανήτες μαζί με τους δορυφόρους τους, τους κομήτες, τα αστεροειδή και τους μετεωρίτες.
13. Jacobijeva metoda za računanje singularnega razcepa
 13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
LASTNOSTI IN ZAKONITOSTI ELEKTRIČNIH KROGOV
 LASTNOST N ZAKONTOST ELEKTČNH KOGOV Enostavni električni krog Najenostavnejši je električni krog je krog, v katere je na izvor električne napetosti priključen en sa porabnik. Če tudi vtičnico orežne napetosti
LASTNOST N ZAKONTOST ELEKTČNH KOGOV Enostavni električni krog Najenostavnejši je električni krog je krog, v katere je na izvor električne napetosti priključen en sa porabnik. Če tudi vtičnico orežne napetosti
( , 2. kolokvij)
 A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
1 Lastna nihanja molekul CO in CO 2 : model na zračni
 1 Lastna nihanja molekul CO in CO 2 : model na zračni drči Pri vaji opazujemo lastna nihanja molekul CO in CO 2 na preprostem modelu na zračni drči. Pri molekuli CO 2 se omejimo na lastna nihanja, pri
1 Lastna nihanja molekul CO in CO 2 : model na zračni drči Pri vaji opazujemo lastna nihanja molekul CO in CO 2 na preprostem modelu na zračni drči. Pri molekuli CO 2 se omejimo na lastna nihanja, pri
Splošno o interpolaciji
 Splošno o interpolaciji J.Kozak Numerične metode II (FM) 2011-2012 1 / 18 O funkciji f poznamo ali hočemo uporabiti le posamezne podatke, na primer vrednosti r i = f (x i ) v danih točkah x i Izberemo
Splošno o interpolaciji J.Kozak Numerične metode II (FM) 2011-2012 1 / 18 O funkciji f poznamo ali hočemo uporabiti le posamezne podatke, na primer vrednosti r i = f (x i ) v danih točkah x i Izberemo
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
Univerza v Novi Gorici Fakulteta za znanosti o okolju Okolje (I. stopnja) Meteorologija 2013/2014. Energijska bilanca pregled
 Univerza v Novi Gorici Fakulteta za znanosti o okolu Okole (I. stopna) Meteorologia 013/014 Energiska bilanca pregled 1 Osnovni pomi energiski tok: P [W = J/s] gostota energiskega toka: [W/m ] toplota:q
Univerza v Novi Gorici Fakulteta za znanosti o okolu Okole (I. stopna) Meteorologia 013/014 Energiska bilanca pregled 1 Osnovni pomi energiski tok: P [W = J/s] gostota energiskega toka: [W/m ] toplota:q
Definicija. definiramo skalarni produkt. x i y i. in razdaljo. d(x, y) = x y = < x y, x y > = n (x i y i ) 2. i=1. i=1
 Funkcije več realnih spremenljivk Osnovne definicije Limita in zveznost funkcije več spremenljivk Parcialni odvodi funkcije več spremenljivk Gradient in odvod funkcije več spremenljivk v dani smeri Parcialni
Funkcije več realnih spremenljivk Osnovne definicije Limita in zveznost funkcije več spremenljivk Parcialni odvodi funkcije več spremenljivk Gradient in odvod funkcije več spremenljivk v dani smeri Parcialni
Vaje iz MATEMATIKE 2. Vektorji
 Študij AHITEKTURE IN URBANIZMA, šol. l. 06/7 Vaje iz MATEMATIKE. Vektorji Vektorji: Definicija: Vektor je usmerjena daljica. Oznake: AB, a,... Enakost vektorjev: AB = CD: če lahko vektor AB vzporedno premaknemo
Študij AHITEKTURE IN URBANIZMA, šol. l. 06/7 Vaje iz MATEMATIKE. Vektorji Vektorji: Definicija: Vektor je usmerjena daljica. Oznake: AB, a,... Enakost vektorjev: AB = CD: če lahko vektor AB vzporedno premaknemo
Matematika vaja. Matematika FE, Ljubljana, Slovenija Fakulteta za Elektrotehniko 1000 Ljubljana, Tržaška 25, Slovenija
 Matematika 1 3. vaja B. Jurčič Zlobec 1 1 Univerza v Ljubljani, Fakulteta za Elektrotehniko 1000 Ljubljana, Tržaška 25, Slovenija Matematika FE, Ljubljana, Slovenija 2011 Določi stekališča zaporedja a
Matematika 1 3. vaja B. Jurčič Zlobec 1 1 Univerza v Ljubljani, Fakulteta za Elektrotehniko 1000 Ljubljana, Tržaška 25, Slovenija Matematika FE, Ljubljana, Slovenija 2011 Določi stekališča zaporedja a
SATCITANANDA. F = e E sila na naboj. = ΔW e. Rudolf Kladnik: Fizika za srednješolce 3. Svet elektronov in atomov
 Ruolf Klnik: Fizik z srenješolce Set elektrono in too Električno olje (11), gibnje elce električne olju Strn 55, nlog 1 Kolikšno netost or releteti elektron, se njego kinetičn energij oeč z 1 kev? Δ W
Ruolf Klnik: Fizik z srenješolce Set elektrono in too Električno olje (11), gibnje elce električne olju Strn 55, nlog 1 Kolikšno netost or releteti elektron, se njego kinetičn energij oeč z 1 kev? Δ W
17. Električni dipol
 17 Električni dipol Vsebina poglavja: polarizacija prevodnika (snovi) v električnem polju, električni dipolni moment, polarne in nepolarne snovi, dipol v homogenem in nehomogenem polju, potencial in polje
17 Električni dipol Vsebina poglavja: polarizacija prevodnika (snovi) v električnem polju, električni dipolni moment, polarne in nepolarne snovi, dipol v homogenem in nehomogenem polju, potencial in polje
Analiza 2 Rešitve 14. sklopa nalog
 Analiza Rešitve 1 sklopa nalog Navadne diferencialne enačbe višjih redov in sistemi diferencialnih enačb (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) 6 + 8 0, (b)
Analiza Rešitve 1 sklopa nalog Navadne diferencialne enačbe višjih redov in sistemi diferencialnih enačb (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) 6 + 8 0, (b)
OSNOVE ELEKTROTEHNIKE II. Magnetostatika. Dejan Križaj
 OSNOVE ELEKTROTEHNIKE II Magnetostatika Dejan Križaj 11 Section 1 KRATKO KAZALO (GLAVNA POGLAVJA) UVOD - ZGODOVINA MAGNETIKE 1. SILA NA (TOKO)VODNIK V MAGNETNEM POLJU. BIOT-SAVARTOV ZAKON Magnetno polje
OSNOVE ELEKTROTEHNIKE II Magnetostatika Dejan Križaj 11 Section 1 KRATKO KAZALO (GLAVNA POGLAVJA) UVOD - ZGODOVINA MAGNETIKE 1. SILA NA (TOKO)VODNIK V MAGNETNEM POLJU. BIOT-SAVARTOV ZAKON Magnetno polje
Domače naloge za 2. kolokvij iz ANALIZE 2b VEKTORSKA ANALIZA
 Domače naloge za 2. kolokvij iz ANALIZE 2b VEKTORSKA ANALIZA. Naj bo vektorsko polje R : R 3 R 3 dano s predpisom R(x, y, z) = (2x 2 + z 2, xy + 2yz, z). Izračunaj pretok polja R skozi površino torusa
Domače naloge za 2. kolokvij iz ANALIZE 2b VEKTORSKA ANALIZA. Naj bo vektorsko polje R : R 3 R 3 dano s predpisom R(x, y, z) = (2x 2 + z 2, xy + 2yz, z). Izračunaj pretok polja R skozi površino torusa
Vaje: Električni tokovi
 Barbara Rovšek, Bojan Golli, Ana Gostinčar Blagotinšek Vaje: Električni tokovi 1 Merjenje toka in napetosti Naloga: Izmerite tok, ki teče skozi žarnico, ter napetost na žarnici Za izvedbo vaje potrebujete
Barbara Rovšek, Bojan Golli, Ana Gostinčar Blagotinšek Vaje: Električni tokovi 1 Merjenje toka in napetosti Naloga: Izmerite tok, ki teče skozi žarnico, ter napetost na žarnici Za izvedbo vaje potrebujete
UPOR NA PADANJE SONDE V ZRAKU
 UPOR NA PADANJE SONDE V ZRAKU 1. Hitrost in opravljena pot sonde pri padanju v zraku Za padanje v zraku je odgovorna sila teže. Poleg sile teže na padajoče telo deluje tudi sila vzgona, ki je enaka teži
UPOR NA PADANJE SONDE V ZRAKU 1. Hitrost in opravljena pot sonde pri padanju v zraku Za padanje v zraku je odgovorna sila teže. Poleg sile teže na padajoče telo deluje tudi sila vzgona, ki je enaka teži
Matematika 1. Gregor Dolinar. 2. januar Fakulteta za elektrotehniko Univerza v Ljubljani. Gregor Dolinar Matematika 1
 Mtemtik 1 Gregor Dolinr Fkultet z elektrotehniko Univerz v Ljubljni 2. jnur 2014 Gregor Dolinr Mtemtik 1 Izrek (Izrek o povprečni vrednosti) Nj bo m ntnčn spodnj mej in M ntnčn zgornj mej integrbilne funkcije
Mtemtik 1 Gregor Dolinr Fkultet z elektrotehniko Univerz v Ljubljni 2. jnur 2014 Gregor Dolinr Mtemtik 1 Izrek (Izrek o povprečni vrednosti) Nj bo m ntnčn spodnj mej in M ntnčn zgornj mej integrbilne funkcije
Tabele termodinamskih lastnosti vode in vodne pare
 Univerza v Ljubljani Fakulteta za strojništvo Laboratorij za termoenergetiko Tabele termodinamskih lastnosti vode in vodne pare po modelu IAPWS IF-97 izračunano z XSteam Excel v2.6 Magnus Holmgren, xsteam.sourceforge.net
Univerza v Ljubljani Fakulteta za strojništvo Laboratorij za termoenergetiko Tabele termodinamskih lastnosti vode in vodne pare po modelu IAPWS IF-97 izračunano z XSteam Excel v2.6 Magnus Holmgren, xsteam.sourceforge.net
Kvantni delec na potencialnem skoku
 Kvantni delec na potencialnem skoku Delec, ki se giblje premo enakomerno, pride na mejo, kjer potencial naraste s potenciala 0 na potencial. Takšno potencialno funkcijo zapišemo kot 0, 0 0,0. Slika 1:
Kvantni delec na potencialnem skoku Delec, ki se giblje premo enakomerno, pride na mejo, kjer potencial naraste s potenciala 0 na potencial. Takšno potencialno funkcijo zapišemo kot 0, 0 0,0. Slika 1:
Matematika 2. Diferencialne enačbe drugega reda
 Matematika 2 Diferencialne enačbe drugega reda (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) y 6y + 8y = 0, (b) y 2y + y = 0, (c) y + y = 0, (d) y + 2y + 2y = 0. Rešitev:
Matematika 2 Diferencialne enačbe drugega reda (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) y 6y + 8y = 0, (b) y 2y + y = 0, (c) y + y = 0, (d) y + 2y + 2y = 0. Rešitev:
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
Termodinamika vlažnega zraka. stanja in spremembe
 Termodinamika vlažnega zraka stanja in spremembe Termodinamika vlažnega zraka Najpogostejši medij v sušilnih procesih konvektivnega sušenja je VLAŽEN ZRAK Obravnavamo ga kot dvokomponentno zmes Suhi zrak
Termodinamika vlažnega zraka stanja in spremembe Termodinamika vlažnega zraka Najpogostejši medij v sušilnih procesih konvektivnega sušenja je VLAŽEN ZRAK Obravnavamo ga kot dvokomponentno zmes Suhi zrak
Električni potencial in električna napetost Ker deluje na električni naboj, ki se nahaja v električnem polju, sila, opravi električno
 FIZIKA 3. poglavje: Elektrika in magnetizem - B. Borštnik 1 ELEKTRIKA IN MAGNETIZEM Elektrostatika Snov je sestavljena iz atomov in molekul. Atome si lahko predstavljamo kot kroglice s premerom nekaj desetink
FIZIKA 3. poglavje: Elektrika in magnetizem - B. Borštnik 1 ELEKTRIKA IN MAGNETIZEM Elektrostatika Snov je sestavljena iz atomov in molekul. Atome si lahko predstavljamo kot kroglice s premerom nekaj desetink
Visokošolski strokovni študijski program»tehnologija polimerov«
 Visokošolski strokovni študijski program»tehnologija polimerov«predmet: ELEKTROTEHNIKA Predavatelj: dr. Konrad Steblovnik Asistent: Drago Šebez 1 Elektrostatika. Električna polja. Sile v električnem polju.
Visokošolski strokovni študijski program»tehnologija polimerov«predmet: ELEKTROTEHNIKA Predavatelj: dr. Konrad Steblovnik Asistent: Drago Šebez 1 Elektrostatika. Električna polja. Sile v električnem polju.
MATEMATIČNI IZRAZI V MAFIRA WIKIJU
 I FAKULTETA ZA MATEMATIKO IN FIZIKO Jadranska cesta 19 1000 Ljubljan Ljubljana, 25. marec 2011 MATEMATIČNI IZRAZI V MAFIRA WIKIJU KOMUNICIRANJE V MATEMATIKI Darja Celcer II KAZALO: 1 VSTAVLJANJE MATEMATIČNIH
I FAKULTETA ZA MATEMATIKO IN FIZIKO Jadranska cesta 19 1000 Ljubljan Ljubljana, 25. marec 2011 MATEMATIČNI IZRAZI V MAFIRA WIKIJU KOMUNICIRANJE V MATEMATIKI Darja Celcer II KAZALO: 1 VSTAVLJANJE MATEMATIČNIH
V tem poglavju bomo vpeljali pojem determinante matrike, spoznali bomo njene lastnosti in nekaj metod za računanje determinant.
 Poglavje IV Determinanta matrike V tem poglavju bomo vpeljali pojem determinante matrike, spoznali bomo njene lastnosti in nekaj metod za računanje determinant 1 Definicija Preden definiramo determinanto,
Poglavje IV Determinanta matrike V tem poglavju bomo vpeljali pojem determinante matrike, spoznali bomo njene lastnosti in nekaj metod za računanje determinant 1 Definicija Preden definiramo determinanto,
Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού.
 Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού. Περιοδικός πίνακας: α. Είναι µια ταξινόµηση των στοιχείων κατά αύξοντα
Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού. Περιοδικός πίνακας: α. Είναι µια ταξινόµηση των στοιχείων κατά αύξοντα
FAKULTETA ZA STROJNIŠTVO Matematika 4 Pisni izpit 22. junij Navodila
 FAKULTETA ZA STROJNIŠTVO Matematika 4 Pisni izpit 22 junij 212 Ime in priimek: Vpisna št: Navodila Pazljivo preberite besedilo naloge, preden se lotite reševanja Veljale bodo samo rešitve na papirju, kjer
FAKULTETA ZA STROJNIŠTVO Matematika 4 Pisni izpit 22 junij 212 Ime in priimek: Vpisna št: Navodila Pazljivo preberite besedilo naloge, preden se lotite reševanja Veljale bodo samo rešitve na papirju, kjer
3. VAJA IZ TRDNOSTI. Rešitev: Pomik v referenčnem opisu: u = e y 2 e Pomik v prostorskem opisu: u = ey e. e y,e z = e z.
 3. VAJA IZ TRDNOSTI (tenzor deformacij) (pomiki togega telesa, Lagrangev in Eulerjev opis, tenzor velikih deformacij, tenzor majhnih deformacij in rotacij, kompatibilitetni pogoji) NALOGA 1: Gumijasti
3. VAJA IZ TRDNOSTI (tenzor deformacij) (pomiki togega telesa, Lagrangev in Eulerjev opis, tenzor velikih deformacij, tenzor majhnih deformacij in rotacij, kompatibilitetni pogoji) NALOGA 1: Gumijasti
Estimation of grain boundary segregation enthalpy and its role in stable nanocrystalline alloy design
 Supplemental Material for Estimation of grain boundary segregation enthalpy and its role in stable nanocrystalline alloy design By H. A. Murdoch and C.A. Schuh Miedema model RKM model ΔH mix ΔH seg ΔH
Supplemental Material for Estimation of grain boundary segregation enthalpy and its role in stable nanocrystalline alloy design By H. A. Murdoch and C.A. Schuh Miedema model RKM model ΔH mix ΔH seg ΔH
